code
stringlengths 2.5k
150k
| kind
stringclasses 1
value |
|---|---|
# 5. Putting it all together
**Bring together all of the skills you acquired in the previous chapters to work on a real-life project. From connecting to a database and populating it, to reading and querying it.**
It's time to put all your effort so far to good use on a census case study.
### Census case study
The case study is broken down into three parts.
1. we are going to prepare SQLAlchemy and the database.
2. we will load the data into the database.
3. we solve a few data science type problems with our query knowledge.
### Part 1: preparing SQLAlchemy and the database
For part 1 we are going to focus on preparing SQLAlchemy and the database. You might remember this example from Chapter 1. We import `create_engine` and `Metadata`, then create the engine and initialize the metadata.
```python
from sqlalchemy import create_engine, MetaData
engine = create_engine('sqlite:///census_nyc.sqlite')
metadata = MetaData()
```
### Part 1: preparing SQLAlchemy and the database
Then we will build the census table to hold our data. You might remember the employees table we built in Chapter 4. We begin by importing the `Table` and `Column` objects along with all the types we are going to use in our table. Next we define our Table using the Table object by giving it a name, the metadata object, and then each of the columns we want in our table. Finally we create the table in the database by using the create all method on the metadata with the engine.
```python
from sqlalchemy import Table, Column, String, Integer, Numeric, Boolean
engine = create_engine('sqlite:///')
metadata = MetaData()
employees = Table('employees', metadata,
Column('id', Integer()),
Column('name', String(255)),
Column('salary', Numeric()),
Column('active', Boolean()))
metadata.create_all(engine)
```
## Setup the engine and metadata
In this exercise, your job is to create an engine to the database that will be used in this chapter. Then, you need to initialize its metadata.
Recall how you did this in Chapter 1 by leveraging `create_engine()` and `MetaData()`.
- Import `create_engine` and `MetaData` from `sqlalchemy`.
- Create an `engine` to the chapter 5 database by using `'sqlite:///chapter5.sqlite'` as the connection string.
- Create a MetaData object as `metadata`.
```
# Import create_engine, MetaData
from sqlalchemy import create_engine, MetaData
# Define an engine to connect to chapter5.sqlite: engine
engine = create_engine('sqlite:///chapter5.sqlite')
# Initialize MetaData: metadata
metadata = MetaData()
```
## Create the table to the database
Having setup the engine and initialized the metadata, you will now define the `census` table object and then create it in the database using the `metadata` and `engine` from the previous exercise. To create it in the database, you will have to use the `.create_all()` method on the `metadata` with `engine` as the argument.
- Import `Table`, `Column`, `String`, and `Integer` from `sqlalchemy`.
- Define a `census` table with the following columns:
- `'state'` - String - length of 30
- `'sex'` - String - length of 1
- `'age'` - Integer
- `'pop2000'` - Integer
- `'pop2008'` - Integer
- Create the table in the database using the `metadata` and `engine`.
```
# Import Table, Column, String, and Integer
from sqlalchemy import Table, Column, String, Integer
# Build a census table: census
census = Table('census', metadata,
Column('state', String(30)),
Column('sex', String(1)),
Column('age', Integer),
Column('pop2000', Integer),
Column('pop2008', Integer))
# Create the table in the database
metadata.create_all(engine)
```
---
## Populating the database
With our table in place, we can now load the data into it. The US Census Agency gave us a CSV file full of data that we need to load into the table.
### Part 2: populating the database
We'll start that by building a `values_list` like we did in chapter 4 with this exercise.
```python
values_list = []
for row in csv_reader:
data = {'state': row[0], 'sex': row[1], 'age': row[2],
'pop2000': row[3], 'pop2008': row[4]}
values_list.append(data)
```
We begin by defining an empty list then looping over the rows of the CSV. Then we build a dictionary for each CSV row that has the data for that row matched up with the column we want to store it in. Then we append the dictionary to the values list.
### Part 2: Populating the Database
Now we can insert that `values_list` as we did in Chapter 4 like this example. We we start by importing the `insert` statement. Then we build an insert statement for our table, finally we use the execute method on our connection with the statement and values list to insert the data into the table.
```python
from sqlalchemy import insert
stmt = insert(employees)
result_proxy = connection.execute(stmt, values_list)
print(result_proxy.rowcount)
```
```
2
```
To review how many rows were inserted, we use the `rowcount` method of the `ResultProxy`.
## Reading the data from the CSV
Leverage the Python CSV module from the standard library and load the data into a list of dictionaries.
- Create an empty list called `values_list`.
- Iterate over the rows of `csv_reader` with a for loop, creating a dictionary called `data` for each row and append it to `values_list`.
- Within the for loop, `row` will be a list whose entries are `'state'`, `'sex'`, `'age'`, `'pop2000'` and `'pop2008'` (in that order).
```
import csv
csv_reader = csv.reader(open('census.csv'))
# Create an empty list: values_list
values_list = []
# Iterate over the rows
for row in csv_reader:
# Create a dictionary with the values
data = {'state': row[0], 'sex': row[1], 'age': row[2],
'pop2000': row[3], 'pop2008': row[4]}
# Append the dictionary to the values list
values_list.append(data)
```
## Load data from a list into the Table
Using the multiple insert pattern, in this exercise, you will load the data from `values_list` into the table.
- Import `insert` from `sqlalchemy`.
- Build an insert statement for the `census` table.
- Execute the statement `stmt` along with `values_list`. You will need to pass them both as arguments to `connection.execute()`.
- Print the `rowcount` attribute of `results`.
```
# Import insert
from sqlalchemy import insert
# Build insert statement: stmt
stmt = insert(census)
# Use values_list to insert data: results
results = connection.execute(stmt, values_list)
# Print rowcount
print(results.rowcount)
```
---
## Querying the database
### Part 3: answering data science questions with queries
Here is an example of how we calculated an average in an exercise from Chapter 3. We began by importing the select statement. Next we built a select statement that creates a weighted average. We do this by summing the result of multiplying the age with the population and dividing that by the sum of the total population and labeling that average age. Next we grouped by the sex column to determine the average `age` for each `sex`. Finally, we executed the query and fetched all the results.
```python
from sqlalchemy import select
stmt = select([census.columns.sex,
(func.sum(census.columns.pop2008 *
census.columns.age) /
func.sum(census.columns.pop2008)
). label('avarage_age')])
stmt = stmt.group_by(census.columns.sex)
resutls = connection.execute(stmt).fetchall()
```
### Part 3: answering data science questions with queries
We learned how to calculate a percentage by using the case and cast clauses in Chapter 3. We begin by importing `case`, `cast`, and `Float`. Then we build a select statement that calculates the sum of the `pop2008` column in cases where the state is New York. Then we divided that by the sum of the total population which is cast to a Float so we would get Decimal values. Finally, we multiplied by 100 to get a percentage and labeled it `ny_percent`.
```python
from sqlalchemy import case, cast, Float
stmt = select([
(func.sum(
case([
(census.columns.state == 'New York',
census.columns.pop2008)
], else_=0)) /
cast(func.sum(census.columns.pop2008),
Float) * 100). label('ny_percent')])
```
Also from Chapter 3, we learned how calculate the difference between two columns grouped by another column. We start by building a `select` statement, that selects the column we want to determine the change by, which in this case is `age`. Then we calculate the difference between the population in 2008 and in 2000, and we label that `pop_change`. Remember to wrap the difference calculation in parentheses so you can label it. Next, we order by `pop_change` and finally we limit it to just 5 results.
```python
stmt = select([census.columns.age,
(census.columns.pop2008 -
census.columns.pop2000).label('pop_chage')
])
stmt = stmt.order_by('pop_change')
stmt = stmt.limit(5)
```
## Determine the average age by population
To calculate a weighted average, we first find the total sum of weights multiplied by the values we're averaging, then divide by the sum of all the weights.
For example, if we wanted to find a weighted average of `data = [10, 30, 50]` weighted by `weights = [2,4,6]`, we would compute *(2*10 + 4*30 + 6*50) / (2+4+6)*, or `sum(weights * data) / sum(weights)`.
In this exercise, however, you will make use of **`func.sum()`** together with select to `select` the weighted average of a column from a table. You will still work with the `census` data, and you will compute the average of age weighted by state population in the year 2000, and then group this weighted average by sex.
- Import `select` and `func` from `sqlalchemy`.
- Write a statement to `select` the average of age (`age`) weighted by population in **2000** (`pop2000`) from `census`.
```
# Import select and func
from sqlalchemy import select, func
# Select the average of age weighted by pop2000
stmt = select([func.sum(census.columns.pop2000 *
census.columns.age) /
func.sum(census.columns.pop2000)])
```
- Modify the select statement to alias the new column with weighted average as `'average_age'` using `.label()`.
```
# Import select and func
from sqlalchemy import select, func
# Relabel the new column as average_age
stmt = select([(func.sum(census.columns.pop2000 *
census.columns.age) /
func.sum(census.columns.pop2000)).label('average_age')
])
```
- Modify the select statement to select the `sex` column of `census` in addition to the weighted average, with the `sex` column coming first.
- Group by the `sex` column of `census`.
```
# Import select and func
from sqlalchemy import select, func
# Add the sex column to the select statement
stmt = select([census.columns.sex,
(func.sum(census.columns.pop2000 *
census.columns.age) /
func.sum(census.columns.pop2000)).label('average_age'),
])
# Group by sex
stmt = stmt.group_by(census.columns.sex)
```
- Execute the statement on the `connection` and fetch all the results.
- Loop over the results and print the values in the `sex` and `average_age` columns for each record in the results.
```
# Import select and func
from sqlalchemy import select, func
# Select sex and average age weighted by 2000 population
stmt = select([census.columns.sex,
(func.sum(census.columns.pop2000 *
census.columns.age) /
func.sum(census.columns.pop2000)).label('average_age')
])
# Group by sex
stmt = stmt.group_by(census.columns.sex)
# Execute the query and fetch all the results
connection = engine.connect()
results = connection.execute(stmt).fetchall()
# Print the sex and average age column for each result
for result in results:
print(result.sex, result.average_age)
```
## Determine the percentage of population by gender and state
In this exercise, you will write a query to determine the percentage of the population in 2000 that comprised of women. You will group this query by state.
- Import `case`, `cast` and `Float` from `sqlalchemy`.
- Define a statement to select `state` and the percentage of women in 2000.
- Inside `func.sum()`, use `case()` to select women (using the `sex` column) from `pop2000`. Remember to specify `else_=0` if the `sex` is not `'F'`.
- To get the percentage, divide the number of women in the year 2000 by the overall population in 2000. Cast the divisor - `census.columns.pop2000` - to `Float` before multiplying by 100.
- Group the query by `state`.
- Execute the query and store it as `results`.
- Print `state` and `percent_female` for each record.
```
# import case, cast and Float from sqlalchemy
from sqlalchemy import case, cast, Float, desc
# Build a query to calculate the percentage of women in 2000: stmt
stmt = select([census.columns.state,
(func.sum(
case([
(census.columns.sex == 'F',
census.columns.pop2000)
], else_=0)) /
cast(func.sum(census.columns.pop2000),
Float) * 100).label('percent_female')
])
# Group By state
stmt = stmt.group_by(census.columns.state)
stmt = stmt.order_by(desc('percent_female'))
# Execute the query and store the results: results
results = connection.execute(stmt).fetchall()
# Print the percentage
for result in results:
print(result.state, result.percent_female)
```
*Interestingly, the District of Columbia had the highest percentage of women in 2000, while Alaska had the highest percentage of males.*
## Determine the difference by state from the 2000 and 2008 censuses
In this final exercise, you will write a query to calculate the states that changed the most in population. You will limit your query to display only the top 10 states.
- Build a statement to:
- Select `state`.
- Calculate the difference in population between 2008 (`pop2008`) and 2000 (`pop2000`).
- Group the query by `census.columns.state` using the `.group_by()` method on `stmt`.
- Order by `'pop_change'` in descending order using the `.order_by()` method with the `desc()` function on `'pop_change'`.
- ~Limit the query to the top `10` states using the `.limit()` method.~
- Execute the query and store it as `results`.
- Print the state and the population change for each result.
```
# Build query to return state name and population difference from 2008 to 2000
stmt = select([census.columns.state,
(census.columns.pop2008-
census.columns.pop2000).label('pop_change')
])
# Group by State
stmt = stmt.group_by(census.columns.state)
# Order by Population Change
stmt = stmt.order_by(desc('pop_change'))
# Limit to top 10
##stmt = stmt.limit(10)
# Use connection to execute the statement and fetch all results
results = connection.execute(stmt).fetchall()
# Print the state and population change for each record
for result in results:
print('{}:{}'.format(result.state, result.pop_change))
```
| github_jupyter |
# Prepare environment
```
!pip install git+https://github.com/katarinagresova/ensembl_scraper.git@6d3bba8e6be7f5ead58a3bbaed6a4e8cd35e62fd
```
# Create config file
```
import yaml
config = {
"root_dir": "../../datasets/",
"organisms": {
"homo_sapiens": {
"regulatory_feature"
}
}
}
user_config = 'user_config.yaml'
with open(user_config, 'w') as handle:
yaml.dump(config, handle)
```
# Prepare directories
```
from pathlib import Path
BASE_FILE_PATH = Path("../../datasets/human_ensembl_regulatory/")
# copied from https://stackoverflow.com/a/57892171
def rm_tree(pth: Path):
for child in pth.iterdir():
if child.is_file():
child.unlink()
else:
rm_tree(child)
pth.rmdir()
if BASE_FILE_PATH.exists():
rm_tree(BASE_FILE_PATH)
```
# Run tool
```
!python -m scraper.ensembl_scraper -c user_config.yaml
```
# Reformating
```
!mkdir -p ../../datasets/human_ensembl_regulatory/train
!mkdir -p ../../datasets/human_ensembl_regulatory/test
!mv ../../datasets/homo_sapiens_regulatory_feature_open_chromatin_region/train/positive.csv ../../datasets/human_ensembl_regulatory/train/ocr.csv
!mv ../../datasets/homo_sapiens_regulatory_feature_open_chromatin_region/test/positive.csv ../../datasets/human_ensembl_regulatory/test/ocr.csv
!mv ../../datasets/homo_sapiens_regulatory_feature_promoter/train/positive.csv ../../datasets/human_ensembl_regulatory/train/promoter.csv
!mv ../../datasets/homo_sapiens_regulatory_feature_promoter/test/positive.csv ../../datasets/human_ensembl_regulatory/test/promoter.csv
!mv ../../datasets/homo_sapiens_regulatory_feature_enhancer/train/positive.csv ../../datasets/human_ensembl_regulatory/train/enhancer.csv
!mv ../../datasets/homo_sapiens_regulatory_feature_enhancer/test/positive.csv ../../datasets/human_ensembl_regulatory/test/enhancer.csv
def chop_sequnces(file_path, max_len):
df = pd.read_csv(file_path)
df_array = df.values
new_df_array = []
index = 0
for row in df_array:
splits = ((row[3] - row[2]) // max_len) + 1
if splits == 1:
new_df_array.append([index, row[1], row[2], row[3], row[4]])
index += 1
elif splits == 2:
length = (row[3] - row[2]) // 2
new_df_array.append([
index,
row[1],
row[2],
row[2] + length,
row[4]
])
index += 1
new_df_array.append([
index,
row[1],
row[2] + length + 1,
row[3],
row[4]
])
index += 1
else:
length = (row[3] - row[2]) // splits
new_df_array.append([
index,
row[1],
row[2],
row[2] + length,
row[4]
])
index += 1
for i in range(1, splits - 1):
new_df_array.append([
index,
row[1],
row[2] + i*length + 1,
row[2] + (i + 1)*length,
row[4]
])
index += 1
new_df_array.append([
index,
row[1],
row[2] + (splits - 1)*length + 1,
row[3],
row[4]
])
index += 1
new_df = pd.DataFrame(new_df_array, columns=df.columns)
new_df.to_csv(file_path, index=False)
chop_sequnces("../../datasets/human_ensembl_regulatory/train/promoter.csv", 700)
chop_sequnces("../../datasets/human_ensembl_regulatory/test/promoter.csv", 700)
!find ../../datasets/human_ensembl_regulatory/ -type f -name "*.csv" -exec gzip {} \;
!mv ../../datasets/homo_sapiens_regulatory_feature_enhancer/metadata.yaml ../../datasets/human_ensembl_regulatory/metadata.yaml
with open("../../datasets/human_ensembl_regulatory/metadata.yaml", "r") as stream:
try:
config = yaml.safe_load(stream)
except yaml.YAMLError as exc:
print(exc)
config
new_config = {
'classes' : {
'ocr': {
'type': config['classes']['positive']['type'],
'url': config['classes']['positive']['url'],
'extra_processing': 'ENSEMBL_HUMAN_GENOME'
},
'promoter': {
'type': config['classes']['positive']['type'],
'url': config['classes']['positive']['url'],
'extra_processing': 'ENSEMBL_HUMAN_GENOME'
},
'enhancer': {
'type': config['classes']['positive']['type'],
'url': config['classes']['positive']['url'],
'extra_processing': 'ENSEMBL_HUMAN_GENOME'
}
},
'version': config['version']
}
new_config
with open("../../datasets/human_ensembl_regulatory/metadata.yaml", 'w') as handle:
yaml.dump(new_config, handle)
```
# Cleaning
```
!rm user_config.yaml
!rm -rf ../../datasets/tmp/
!rm -rf ../../datasets/homo_sapiens_regulatory_feature_CTCF_binding_site
!rm -rf ../../datasets/homo_sapiens_regulatory_feature_enhancer
!rm -rf ../../datasets/homo_sapiens_regulatory_feature_promoter
!rm -rf ../../datasets/homo_sapiens_regulatory_feature_promoter_flanking_region
!rm -rf ../../datasets/homo_sapiens_regulatory_feature_TF_binding_site
!rm -rf ../../datasets/homo_sapiens_regulatory_feature_open_chromatin_region
```
# Testing
```
from genomic_benchmarks.loc2seq import download_dataset
download_dataset("human_ensembl_regulatory", local_repo=True)
from genomic_benchmarks.data_check import info
info("human_ensembl_regulatory", 0, local_repo=True)
```
| github_jupyter |
# Source detection with Gammapy
## Context
The first task in a source catalogue production is to identify significant excesses in the data that can be associated to unknown sources and provide a preliminary parametrization in term of position, extent, and flux. In this notebook we will use Fermi-LAT data to illustrate how to detect candidate sources in counts images with known background.
**Objective: build a list of significant excesses in a Fermi-LAT map**
## Proposed approach
This notebook show how to do source detection with Gammapy using the methods available in `~gammapy.detect`.
We will use images from a Fermi-LAT 3FHL high-energy Galactic center dataset to do this:
* perform adaptive smoothing on counts image
* produce 2-dimensional test-statistics (TS)
* run a peak finder to detect point-source candidates
* compute Li & Ma significance images
* estimate source candidates radius and excess counts
Note that what we do here is a quick-look analysis, the production of real source catalogs use more elaborate procedures.
We will work with the following functions and classes:
* `~gammapy.maps.WcsNDMap`
* `~gammapy.detect.ASmooth`
* `~gammapy.detect.TSMapEstimator`
* `~gammapy.detect.find_peaks`
* `~gammapy.detect.compute_lima_image`
## Setup
As always, let's get started with some setup ...
```
%matplotlib inline
import matplotlib.pyplot as plt
import matplotlib.cm as cm
from gammapy.maps import Map
from gammapy.detect import (
ASmooth,
TSMapEstimator,
find_peaks,
compute_lima_image,
)
from gammapy.catalog import SOURCE_CATALOGS
from gammapy.cube import PSFKernel
from gammapy.stats import significance
from astropy.coordinates import SkyCoord
from astropy.convolution import Tophat2DKernel
import astropy.units as u
import numpy as np
# defalut matplotlib colors without grey
colors = [
u"#1f77b4",
u"#ff7f0e",
u"#2ca02c",
u"#d62728",
u"#9467bd",
u"#8c564b",
u"#e377c2",
u"#bcbd22",
u"#17becf",
]
```
## Read in input images
We first read in the counts cube and sum over the energy axis:
```
counts = Map.read("$GAMMAPY_DATA/fermi-3fhl-gc/fermi-3fhl-gc-counts.fits.gz")
background = Map.read(
"$GAMMAPY_DATA/fermi-3fhl-gc/fermi-3fhl-gc-background.fits.gz"
)
exposure = Map.read(
"$GAMMAPY_DATA/fermi-3fhl-gc/fermi-3fhl-gc-exposure.fits.gz"
)
maps = {"counts": counts, "background": background, "exposure": exposure}
kernel = PSFKernel.read(
"$GAMMAPY_DATA/fermi-3fhl-gc/fermi-3fhl-gc-psf.fits.gz"
)
```
## Adaptive smoothing
For visualisation purpose it can be nice to look at a smoothed counts image. This can be performed using the adaptive smoothing algorithm from [Ebeling et al. (2006)](https://ui.adsabs.harvard.edu/abs/2006MNRAS.368...65E/abstract).
In the following example the `threshold` argument gives the minimum significance expected, values below are clipped.
```
%%time
scales = u.Quantity(np.arange(0.05, 1, 0.05), unit="deg")
smooth = ASmooth(threshold=3, scales=scales)
images = smooth.run(**maps)
plt.figure(figsize=(15, 5))
images["counts"].plot(add_cbar=True, vmax=10);
```
## TS map estimation
The Test Statistic, TS = 2 ∆ log L ([Mattox et al. 1996](https://ui.adsabs.harvard.edu/abs/1996ApJ...461..396M/abstract)), compares the likelihood function L optimized with and without a given source.
The TS map is computed by fitting by a single amplitude parameter on each pixel as described in Appendix A of [Stewart (2009)](https://ui.adsabs.harvard.edu/abs/2009A%26A...495..989S/abstract). The fit is simplified by finding roots of the derivative of the fit statistics (default settings use [Brent's method](https://en.wikipedia.org/wiki/Brent%27s_method)).
```
%%time
estimator = TSMapEstimator()
images = estimator.run(maps, kernel.data)
```
### Plot resulting images
```
plt.figure(figsize=(15, 5))
images["sqrt_ts"].plot(add_cbar=True);
plt.figure(figsize=(15, 5))
images["flux"].plot(add_cbar=True, stretch="sqrt", vmin=0);
plt.figure(figsize=(15, 5))
images["niter"].plot(add_cbar=True);
```
## Source candidates
Let's run a peak finder on the `sqrt_ts` image to get a list of point-sources candidates (positions and peak `sqrt_ts` values).
The `find_peaks` function performs a local maximun search in a sliding window, the argument `min_distance` is the minimum pixel distance between peaks (smallest possible value and default is 1 pixel).
```
sources = find_peaks(images["sqrt_ts"], threshold=8, min_distance=1)
nsou = len(sources)
sources
# Plot sources on top of significance sky image
plt.figure(figsize=(15, 5))
_, ax, _ = images["sqrt_ts"].plot(add_cbar=True)
ax.scatter(
sources["ra"],
sources["dec"],
transform=plt.gca().get_transform("icrs"),
color="none",
edgecolor="w",
marker="o",
s=600,
lw=1.5,
);
```
Note that we used the instrument point-spread-function (PSF) as kernel, so the hypothesis we test is the presence of a point source. In order to test for extended sources we would have to use as kernel an extended template convolved by the PSF. Alternatively, we can compute the significance of an extended excess using the Li & Ma formalism, which is faster as no fitting is involve.
## Li & Ma significance maps
We can compute significance for an observed number of counts and known background using an extension of equation (17) from the [Li & Ma (1983)](https://ui.adsabs.harvard.edu/abs/1983ApJ...272..317L/abstract) (see `gammapy.stats.significance` for details). We can perform this calculation intergating the counts within different radius. To do so we use an astropy Tophat kernel with the `compute_lima_image` function.
```
%%time
radius = np.array([0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.4, 0.5])
pixsize = counts.geom.pixel_scales[0].value
nr = len(radius)
signi = np.zeros((nsou, nr))
excess = np.zeros((nsou, nr))
for kr in range(nr):
npixel = radius[kr] / pixsize
kernel = Tophat2DKernel(npixel)
result = compute_lima_image(counts, background, kernel)
signi[:, kr] = result["significance"].data[sources["y"], sources["x"]]
excess[:, kr] = result["excess"].data[sources["y"], sources["x"]]
```
For simplicity we saved the significance and excess at the position of the candidates found previously on the TS map, but we could aslo have applied the peak finder on these significances maps for each scale, or alternatively implemented a 3D peak detection (in longitude, latitude, radius). Now let's look at the significance versus integration radius:
```
plt.figure()
for ks in range(nsou):
plt.plot(radius, signi[ks, :], color=colors[ks])
plt.xlabel("Radius")
plt.ylabel("Li & Ma Significance")
plt.title("Guessing optimal radius of each candidate");
```
We can add the optimal radius guessed and the corresdponding excess to the source candidate properties table.
```
# rename the value key to sqrt(TS)_PS
sources.rename_column("value", "sqrt(TS)_PS")
index = np.argmax(signi, axis=1)
sources["significance"] = signi[range(nsou), index]
sources["radius"] = radius[index]
sources["excess"] = excess[range(nsou), index]
sources
# Plot candidates sources on top of significance sky image with radius guess
plt.figure(figsize=(15, 5))
_, ax, _ = images["sqrt_ts"].plot(add_cbar=True, cmap=cm.Greys_r)
phi = np.arange(0, 2 * np.pi, 0.01)
for ks in range(nsou):
x = sources["x"][ks] + sources["radius"][ks] / pixsize * np.cos(phi)
y = sources["y"][ks] + sources["radius"][ks] / pixsize * np.sin(phi)
ax.plot(x, y, "-", color=colors[ks], lw=1.5);
```
Note that the optimal radius of nested sources is likely overestimated due to their neighbor. We limited this example to only the most significant source above ~8 sigma. When lowering the detection threshold the number of candidated increase together with the source confusion.
## What next?
In this notebook, we have seen how to work with images and compute TS and significance images from counts data, if a background estimate is already available.
Here's some suggestions what to do next:
- Look how background estimation is performed for IACTs with and without the high-level interface in [analysis_1](analysis_1.ipynb) and [analysis_2](analysis_2.ipynb) notebooks, respectively
- Learn about 2D model fitting in the [image_analysis](image_analysis.ipynb) notebook
- find more about Fermi-LAT data analysis in the [fermi_lat](fermi_lat.ipynb) notebook
- Use source candidates to build a model and perform a 3D fitting (see [analysis_3d](analysis_3d.ipynb), [analysis_mwl](analysis_mwl) notebooks for some hints)
| github_jupyter |
# Quasi-Laplace approximation for Poisson data
- toc: true
- badges: true
- comments: true
- categories: [jupyter]
### About
The [quasi-Laplace approximation]({% post_url 2020-06-22-intuition-for-quasi-Laplace %}) may be extended to approximate the posterior of a Poisson distribution with a Gaussian, as we will see here.
We approximate the regularized likelihood
$\mathscr{L}_{\mathrm{reg}}(\boldsymbol{\beta})$
defined as the product of the likelihood and a Gaussian *regularizer*,
\begin{equation*}
\mathscr{L}_{\mathrm{reg}}(\boldsymbol{\beta}) \triangleq p\left(\mathbf{y} \mid \mathbf{X}, \boldsymbol{\beta}\right)
\mathcal{N}\left( \boldsymbol{\beta} \mid \mathbf{0}, \mathbf{\Lambda}^{-1} \right) \propto
\mathcal{N}\left( \boldsymbol{\beta} \mid \mathbf{m}, \mathbf{S} \right)
\end{equation*}
such that the mode of the regularized likelihood is near the mode of the posterior.
The prior $p\left(\boldsymbol{\beta}\mid g \right)$ is a mixture of Gaussians with known variances but unknown mixture proportions.
The precision matrix $\mathbf{\Lambda}$ is defined as a diagonal matrix, $\mathbf{\Lambda} \triangleq \mathrm{diag}\left(\boldsymbol{\lambda}\right)$, whose elements $\lambda_j$ are roughly set to some expected value to ensure that the regularized likelihood is centered at the mode of the posterior.
```
#collapse_hide
import numpy as np
np.set_printoptions(precision = 4, suppress=True)
from scipy import optimize
from scipy.special import gammaln
import matplotlib.pyplot as plt
from matplotlib import cm
from matplotlib import ticker as plticker
from mpl_toolkits.axes_grid1 import make_axes_locatable
import sys
sys.path.append("../../utils/")
import mpl_stylesheet
mpl_stylesheet.banskt_presentation(fontfamily = 'latex-clearsans', fontsize = 18, colors = 'banskt', dpi = 72)
```
### Generate toy data
Let us consider a Poisson model with sparse coefficients, so that the number of causal variables `ncausal` is much less than the number of variables `nvar` in the model. This is ensured by sampling the betas from a Gaussian mixture prior of `nGcomp` components with variances given by $\sigma_k^2$ (`sigmak2`) and the mixture proportions given by `probk`. The sparsity is controlled by the variable `sparsity` that specifies the mixture proportion of the zero-th component $\mathcal{N}(0, 0)$ (or the delta function).
```
nsample = 20
nvar = 30
nGcomp = 3
sparsity = 0.8
prior_strength = 20
num_inf = 1e4 # a large number for 1/sigma_k^2 when sigma_k^2 = 0
probk = np.zeros(nGcomp)
probk[0] = sparsity
probk[1:(nGcomp - 1)] = (1 - sparsity) / (nGcomp - 1)
probk[nGcomp - 1] = 1 - np.sum(probk)
sigmak2 = np.array([prior_strength * np.square(np.power(2, (i)/nGcomp) - 1) for i in range(nGcomp)])
```
We use the exponential link function $\lambda_i = \exp\left(\mathbf{X}_i\boldsymbol{\beta}\right)$ to generate the response variable $y_i$ for $i = 1, \ldots, N$ samples using the Poisson probability distribution
\begin{equation*}
p\left(y_i \mid \mathbf{X}_i, \boldsymbol{\beta}\right) = \frac{\lambda_i^{y_i}e^{-\lambda_i}}{y_i!}
\end{equation*}
$\mathbf{X}$ is centered and scaled such that for each variable $j$, the variance is $\mathrm{var}(\mathbf{x}_j) = 1$.
```
# collapse-hide
def standardize(X):
Xnorm = (X - np.mean(X, axis = 0))
Xstd = Xnorm / np.std(Xnorm, axis = 0)
return Xstd
def poisson_data(X, beta):
Xbeta = np.dot(X, beta)
pred = np.exp(Xbeta)
Y = np.random.poisson(pred)
return Y
X = np.random.rand(nsample * nvar).reshape(nsample, nvar)
X = standardize(X)
gammajk = np.random.multinomial(1, probk, size = nvar)
beta = np.zeros(nvar)
for j in range(nvar):
if gammajk[j, 0] != 1:
kidx = np.where(gammajk[j, :] == 1)[0][0]
kstd = np.sqrt(sigmak2[kidx])
beta[j] = np.random.normal(loc = 0., scale = kstd)
ncausal = beta[beta != 0].shape[0]
betavar = np.var(beta[beta != 0])
Y = poisson_data(X, beta)
```
Let us have a look at the generated data.
```
# collapse-hide
print(f'There are {ncausal} non-zero coefficients with variance {betavar:.4f}')
fig = plt.figure(figsize = (12,6))
ax1 = fig.add_subplot(121)
ax2 = fig.add_subplot(122)
Xbeta = np.dot(X, beta)
ax1.scatter(Xbeta, np.log(Y+1), s = 10)
ax2.hist(Y)
ax1.set_xlabel(r'$\sum_i X_{ni} \beta_i$')
ax1.set_ylabel(r'$\log(Y_n + 1)$')
ax2.set_xlabel(r'$Y_n$')
ax2.set_ylabel('Number')
plt.tight_layout(pad = 2.0)
plt.show()
```
### True posterior vs quasi-Laplace posterior
We select two causal variables (with maximum effect size) and fix all the others to optimum values to understand how the likelihood and posterior depends on these two chosen variables. To avoid the sum over the indicator variables, we use the joint prior $p\left(\boldsymbol{\beta}, \boldsymbol{\gamma} \mid g\right)$.
Some useful function definitions:
```
# collapse-hide
def get_log_likelihood(Y, X, beta):
Xbeta = np.dot(X, beta)
logL = np.sum(Y * Xbeta - np.exp(Xbeta))# - gammaln(Y+1))
return logL
def get_log_prior(beta, gammajk, probk, sigmak2):
logprior = 0
for j, b in enumerate(beta):
k = np.where(gammajk[j, :] == 1)[0][0]
logprior += np.log(probk[k])
if k > 0:
logprior += - 0.5 * (np.log(2 * np.pi) + np.log(sigmak2[k]) + b * b / sigmak2[k])
return logprior
def plot_contours(ax, X, Y, Z, beta, norm, cstep = 10, zlabel = ""):
zmin = np.min(Z) - 1 * np.std(Z)
zmax = np.max(Z) + 1 * np.std(Z)
ind = np.unravel_index(np.argmax(Z, axis=None), Z.shape)
levels = np.linspace(zmin, zmax, 200)
clevels = np.linspace(zmin, zmax, 20)
cmap = cm.YlOrRd_r
if norm:
cset1 = ax.contourf(X, Y, Z, levels, norm = norm,
cmap=cm.get_cmap(cmap, len(levels) - 1))
else:
cset1 = ax.contourf(X, Y, Z, levels,
cmap=cm.get_cmap(cmap, len(levels) - 1))
cset2 = ax.contour(X, Y, Z, clevels, colors='k')
for c in cset2.collections:
c.set_linestyle('solid')
ax.set_aspect("equal")
ax.scatter(beta[0], beta[1], color = 'blue', s = 100)
ax.scatter(X[ind[1]], Y[ind[0]], color = 'k', s = 100)
divider = make_axes_locatable(ax)
cax = divider.append_axes("right", size="5%", pad=0.2)
cbar = plt.colorbar(cset1, cax=cax)
ytickpos = np.arange(int(zmin / cstep) * cstep, zmax, cstep)
cbar.set_ticks(ytickpos)
if zlabel:
cax.set_ylabel(zlabel)
#loc = plticker.AutoLocator()
#ax.xaxis.set_major_locator(loc)
#ax.yaxis.set_major_locator(loc)
def regularized_log_likelihood(beta, X, Y, L):
nvar = beta.shape[0]
Xbeta = np.dot(X, beta)
## Function
llb = np.sum(Y * Xbeta - np.exp(Xbeta))# - gammaln(Y+1))
#reg = 0.5 * np.sum(np.log(L)) - 0.5 * np.einsum('i,i->i', np.square(beta), L)
reg = - 0.5 * np.einsum('i,i->i', np.square(beta), L)
loglik = llb + reg
## Gradient
pred = 1 / (1 + np.exp(-Xbeta))
der = np.einsum('i,ij->j', Y, X) - np.einsum('ij, i->j', X, np.exp(Xbeta)) - np.multiply(beta, L)
return -loglik, -der
def precisionLL(X, beta, L):
nvar = X.shape[1]
Xbeta = np.dot(X, beta)
pred = np.exp(Xbeta)
hess = - np.einsum('i,ij,ik->jk', pred, X, X)
hess[np.diag_indices(nvar)] -= L
return -hess
def get_mS(X, Y, beta0, L):
nvar = X.shape[1]
args = X, Y, L
gmode = optimize.minimize(regularized_log_likelihood,
beta0,
args=args,
method='L-BFGS-B',
jac=True,
bounds=None,
options={'maxiter': 20000000,
'maxfun': 20000000,
'ftol': 1e-9,
'gtol': 1e-9
#'disp': True
})
M = gmode.x
Sinv = precisionLL(X, M, L)
return M, Sinv
def get_qL_log_posterior(beta, L, M, Sinv, logdetSinv, logprior):
blessM = beta - M
bMSbM = np.dot(blessM.T, np.dot(Sinv, blessM))
bLb = np.einsum('i, i', np.square(beta), L)
logdetLinv = - np.sum(np.log(L))
logposterior = 0.5 * (logdetSinv + logdetLinv - bMSbM + bLb)
logposterior += logprior
return logposterior
```
We calculate the likelihood, prior, *true* posterior and the quasi-Laplace posterior. Note that the posteriors are not normalized. We apply quasi-Laplace (QL) approximation with some $\mathbf{\Lambda}$ and show QL posterior distribution, which is given by
\begin{equation*}
p\left(\mathbf{y} \mid \mathbf{X}, \boldsymbol{\beta}\right) p\left(\boldsymbol{\beta}\mid g \right)
\propto
\frac{\mathcal{N}\left( \boldsymbol{\beta} \mid \mathbf{m}, \mathbf{S} \right)
p\left(\boldsymbol{\beta}\mid g \right)
}{
\mathcal{N}\left( \boldsymbol{\beta} \mid \mathbf{0}, \mathbf{\Lambda}^{-1} \right)
}
\end{equation*}
Here, we assume that we know $\mathbf{\Lambda}$. In reality, we will not know $\mathbf{\Lambda}$ but will have to learn it from the data or make some educated guess from the prior choice.
```
np.max(beta)
# collapse-hide
bchoose = np.argsort(abs(beta))[-2:]
nplotx = 20
nploty = 20
b1min = -0.5
b1max = 4
b2min = -4
b2max = 0.5
beta1 = np.linspace(b1min, b1max, nplotx)
beta2 = np.linspace(b2min, b2max, nploty)
logL = np.zeros((nploty, nplotx))
logPr = np.zeros((nploty, nplotx))
logPs = np.zeros((nploty, nplotx))
logQL = np.zeros((nploty, nplotx))
thisbeta = beta.copy()
mask = np.ones(nvar, bool)
mask[bchoose] = False
true_pi = np.sum(gammajk, axis = 0) / np.sum(gammajk)
#reg = 1 / np.einsum('i,i', true_pi, sigmak2)
#regL = np.repeat(reg, nvar)
regL = np.repeat(num_inf, nvar)
for j, b in enumerate(beta):
k = np.where(gammajk[j, :] == 1)[0][0]
if k > 0:
regL[j] = 1 / sigmak2[k]
M, Sinv = get_mS(X, Y, beta, regL)
sgndetSinv, logdetSinv = np.linalg.slogdet(Sinv)
for i, b1 in enumerate(beta1):
for j, b2 in enumerate(beta2):
thisbeta[bchoose] = np.array([b1, b2])
logL[j, i] = get_log_likelihood(Y, X, thisbeta)
logPr[j, i] = get_log_prior(thisbeta, gammajk, probk, sigmak2)
logQL[j, i] = get_qL_log_posterior(thisbeta, regL, M, Sinv, logdetSinv, logPr[j, i])
logPs = logL + logPr
```
Here, we plot the contour maps. The x and y-axis show the two coefficients $\beta_1$ and $\beta_2$, which we chose to vary. The blue dot shows the coordinates of the true values of $\{\beta_1, \beta_2\}$ and the black dot shows the maximum of the log probabilities. Note how the non-Gaussian *true* posterior is now approximated by a Gaussian QL posterior.
```
fig = plt.figure(figsize = (12, 8))
ax1 = fig.add_subplot(221)
ax2 = fig.add_subplot(222)
ax3 = fig.add_subplot(223)
ax4 = fig.add_subplot(224)
norm = cm.colors.Normalize(vmin=np.min(logPs), vmax=np.max(logPs))
plot_contours(ax1, beta1, beta2, logL, beta[bchoose], None, cstep = 5000, zlabel = "Log Likelihood")
plot_contours(ax2, beta1, beta2, logPr, beta[bchoose], None, cstep = 5, zlabel = "Log Prior")
plot_contours(ax3, beta1, beta2, logPs, beta[bchoose], None, cstep = 5000, zlabel = "Log Posterior")
plot_contours(ax4, beta1, beta2, logQL, beta[bchoose], None, cstep = 5000, zlabel = "Log QL Posterior")
plt.tight_layout()
plt.show()
```
### Effect of regularizer
Let us assume that we do not know $\mathbf{\Lambda}$ and all $\lambda_j$'s are equal. Here we look at how the QL posterior changes with varying $\beta_2$ for different values of $\lambda_j$.
Here we define a function for calculating the QL posterior and true posterior for changing the coefficients of a single variable:
```
# collapse-hide
def get_logQL_logPs_single_variable(X, Y, beta, regvar, betavar, bidx,
regL, gammajk, probk, sigmak2):
nvar = beta.shape[0]
nplotrv = regvar.shape[0]
nplotx = betavar.shape[0]
logL = np.zeros(nplotx)
logPr = np.zeros(nplotx)
logPs = np.zeros(nplotx)
logQL = np.zeros((nplotrv, nplotx))
thisbeta = beta.copy()
thisL = regL.copy()
for j, b2 in enumerate(betavar):
thisbeta[bidx] = b2
logL[j] = get_log_likelihood(Y, X, thisbeta)
logPr[j] = get_log_prior(thisbeta, gammajk, probk, sigmak2)
logPs = logL + logPr
for i, r1 in enumerate(regvar):
thisL = np.repeat(r1, nvar)
#thisL[bidx] = r1
M, Sinv = get_mS(X, Y, beta, thisL)
sgndetSinv, logdetSinv = np.linalg.slogdet(Sinv)
for j, b2 in enumerate(betavar):
thisbeta[bidx] = b2
logQL[i, j] = get_qL_log_posterior(thisbeta, thisL, M, Sinv, logdetSinv, logPr[j])
return logPs, logQL
```
And then look at the posteriors for $\beta_2$.
```
#collapse-hide
nplotx_rv = 200
nplotrv = 4
bmin = -4
bmax = 0
rvmin = 1
rvmax = 100
bidx = bchoose[1]
fig = plt.figure(figsize = (8, 8))
ax1 = fig.add_subplot(111)
betavals = np.linspace(bmin, bmax, nplotx_rv)
regvals = np.linspace(rvmin, rvmax, nplotrv)
logPs_rv, logQL_rv = get_logQL_logPs_single_variable(X, Y, beta, regvals, betavals, bidx,
regL, gammajk, probk, sigmak2)
ax1.plot(betavals, logPs_rv, lw = 3, zorder = 2, label = 'True Posterior')
ax1.scatter(betavals[np.argmax(logPs_rv)], logPs_rv[np.argmax(logPs_rv)], s = 40, zorder = 10, color = 'black')
for i, r1 in enumerate(regvals):
ax1.plot(betavals, logQL_rv[i, :], lw = 2, zorder = 5, label = f'$\lambda =${r1:.2f}')
ix = np.argmax(logQL_rv[i, :])
ax1.scatter(betavals[ix], logQL_rv[i, ix], s = 40, zorder = 10, color = 'black')
ax1.axvline(beta[bidx], ls = 'dotted', zorder = 1)
ax1.legend(handlelength = 1.5)
ax1.set_xlabel(r'$\beta$')
ax1.set_ylabel('Log Posterior')
plt.tight_layout()
plt.show()
```
What happens to the QL posterior for other variables? Let us look at every $\beta_j$ and their individual maximum posterior, while all others are kept fixed at optimum values. Here, we have arranged the $\beta_j$ in ascending order.
```
#collapse-hide
bmin = -5
bmax = 5
bidx_sorted = np.argsort(beta)
bidx_sorted_nz = bidx_sorted #bidx_sorted[beta[bidx_sorted]!=0]
betavals = np.linspace(bmin, bmax, nplotx_rv)
regvals = np.linspace(rvmin, rvmax, nplotrv)
maxQL = np.zeros((nplotrv, len(bidx_sorted_nz)))
maxPs = np.zeros(len(bidx_sorted_nz))
for i, bidx in enumerate(bidx_sorted_nz):
_logPs, _logQL = get_logQL_logPs_single_variable(X, Y, beta, regvals, betavals, bidx,
regL, gammajk, probk, sigmak2)
maxPs[i] = betavals[np.argmax(_logPs)]
for j in range(len(regvals)):
maxQL[j, i] = betavals[np.argmax(_logQL[j, :])]
fig = plt.figure(figsize = (16, 8))
ax1 = fig.add_subplot(111)
xvals = np.arange(len(bidx_sorted_nz))
ax1.plot(xvals, maxPs, lw = 2, zorder = 2, label = 'True Posterior')
for i, r1 in enumerate(regvals):
ax1.plot(xvals, maxQL[i, :], lw = 2, zorder = 5, label = f'$\lambda =${r1:.2f}')
ax1.scatter(xvals, maxPs, s = 20, zorder = 1)
for i, r1 in enumerate(regvals):
ax1.scatter(xvals, maxQL[i, :], s = 20, zorder = 1)
ax1.scatter(xvals, beta[bidx_sorted_nz], s = 80, zorder = 10, color = 'maroon', label = 'Input')
ax1.legend(handlelength = 1.5)
ax1.set_xlabel(r'Index of $\beta$')
ax1.set_ylabel(r'$\beta$ at maximum log posterior')
ax1.set_xticks(xvals)
ax1.set_xticklabels([f'{idx}' for idx in bidx_sorted_nz])
plt.tight_layout()
plt.show()
```
| github_jupyter |
```
import nltk
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from nltk.stem import WordNetLemmatizer
from nltk.corpus import wordnet
import re, collections
from collections import defaultdict
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.metrics import mean_squared_error, r2_score, cohen_kappa_score
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression, Ridge, Lasso
from sklearn.svm import SVR
from sklearn.ensemble import RandomForestRegressor
from sklearn.ensemble import AdaBoostRegressor
from spellchecker import SpellChecker
from nltk.tokenize import word_tokenize
import string
from sklearn.metrics import classification_report
from sklearn import svm
from sklearn.model_selection import cross_val_score
from sklearn.metrics import classification_report
from sklearn.preprocessing import MinMaxScaler
import seaborn as sns
import matplotlib.pyplot as plt
from matplotlib import rcParams
```
## Loading data
```
#dataframe = pd.read_csv('all_essaysets.csv', encoding = 'latin-1')
dataframe = pd.read_csv('training.tsv', encoding = 'latin-1', sep='\t')
dataframe.describe()
dataframe.head()
```
## Methods
```
# selecting which set to be used 1-8
# in order to combine them all assign set number to 9
def select_set(dataframe,setNumber):
if setNumber == 9:
dataframe2 = dataframe[dataframe.essay_set ==1]
texts = dataframe2['essay']
scores = dataframe2['domain1_score']
scores = scores.apply(lambda x: (x*3)/scores.max())
for i in range(1,9):
dataframe2 = dataframe[dataframe.essay_set == i]
texts = texts.append(dataframe2['essay'])
s = dataframe2['domain1_score']
s = s.apply(lambda x: (x*3)/s.max())
scores = scores.append(s)
else:
dataframe2 = dataframe[dataframe.essay_set ==setNumber]
texts = dataframe2['essay']
scores = dataframe2['domain1_score']
scores = scores.apply(lambda x: (x*3)/scores.max())
return texts, scores
# get histogram plot of scores and average score
def get_hist_avg(scores,bin_count):
print(sum(scores)/len(scores))
scores.hist(bins=bin_count)
#average word length for a text
def avg_word_len(text):
clean_essay = re.sub(r'\W', ' ', text)
words = nltk.word_tokenize(clean_essay)
total = 0
for word in words:
total = total + len(word)
average = total / len(words)
return average
# word count in a given text
def word_count(text):
clean_essay = re.sub(r'\W', ' ', text)
return len(nltk.word_tokenize(clean_essay))
# char count in a given text
def char_count(text):
return len(re.sub(r'\s', '', str(text).lower()))
# sentence count in a given text
def sent_count(text):
return len(nltk.sent_tokenize(text))
#tokenization of texts to sentences
def sent_tokenize(text):
stripped_essay = text.strip()
tokenizer = nltk.data.load('tokenizers/punkt/english.pickle')
raw_sentences = tokenizer.tokenize(stripped_essay)
tokenized_sentences = []
for raw_sentence in raw_sentences:
if len(raw_sentence) > 0:
clean_sentence = re.sub("[^a-zA-Z0-9]"," ", raw_sentence)
tokens = nltk.word_tokenize(clean_sentence)
tokenized_sentences.append(tokens)
return tokenized_sentences
# lemma, noun, adjective, verb, adverb count for a given text
def count_lemmas(text):
noun_count = 0
adj_count = 0
verb_count = 0
adv_count = 0
lemmas = []
lemmatizer = WordNetLemmatizer()
tokenized_sentences = sent_tokenize(text)
for sentence in tokenized_sentences:
tagged_tokens = nltk.pos_tag(sentence)
for token_tuple in tagged_tokens:
pos_tag = token_tuple[1]
if pos_tag.startswith('N'):
noun_count += 1
pos = wordnet.NOUN
lemmas.append(lemmatizer.lemmatize(token_tuple[0], pos))
elif pos_tag.startswith('J'):
adj_count += 1
pos = wordnet.ADJ
lemmas.append(lemmatizer.lemmatize(token_tuple[0], pos))
elif pos_tag.startswith('V'):
verb_count += 1
pos = wordnet.VERB
lemmas.append(lemmatizer.lemmatize(token_tuple[0], pos))
elif pos_tag.startswith('R'):
adv_count += 1
pos = wordnet.ADV
lemmas.append(lemmatizer.lemmatize(token_tuple[0], pos))
else:
pos = wordnet.NOUN
lemmas.append(lemmatizer.lemmatize(token_tuple[0], pos))
lemma_count = len(set(lemmas))
return noun_count, adj_count, verb_count, adv_count, lemma_count
def token_word(text):
text = "".join([ch.lower() for ch in text if ch not in string.punctuation])
tokens = nltk.word_tokenize(text)
return tokens
def misspell_count(text):
spell = SpellChecker()
# find those words that may be misspelled
misspelled = spell.unknown(token_word(text))
#print(misspelled)
return len(misspelled)
def create_features(texts):
data = pd.DataFrame(columns=('Average_Word_Length','Sentence_Count','Word_Count',
'Character_Count', 'Noun_Count','Adjective_Count',
'Verb_Count', 'Adverb_Count', 'Lemma_Count' , 'Misspell_Count'
))
data['Average_Word_Length'] = texts.apply(avg_word_len)
data['Sentence_Count'] = texts.apply(sent_count)
data['Word_Count'] = texts.apply(word_count)
data['Character_Count'] = texts.apply(char_count)
temp=texts.apply(count_lemmas)
noun_count,adj_count,verb_count,adverb_count,lemma_count = zip(*temp)
data['Noun_Count'] = noun_count
data['Adjective_Count'] = adj_count
data['Verb_Count'] = verb_count
data['Adverb_Count'] = adverb_count
data['Lemma_Count'] = lemma_count
data['Misspell_Count'] = texts.apply(misspell_count)
return data
def data_prepare(texts,scores):
#create features from the texts and clean non graded essays
data = create_features(texts)
data.describe()
t1=np.where(np.asanyarray(np.isnan(scores)))
scores=scores.drop(scores.index[t1])
data=data.drop(scores.index[t1])
#scaler = MinMaxScaler()
#data = scaler.fit_transform(data)
#train test split
X_train, X_test, y_train, y_test = train_test_split(data, scores, test_size = 0.3)
#checking is there any nan cells
print(np.any(np.isnan(scores)))
print(np.all(np.isfinite(scores)))
return X_train, X_test, y_train, y_test, data
def lin_regression(X_train,y_train,X_test,y_test):
regr = LinearRegression()
regr.fit(X_train, y_train)
y_pred = regr.predict(X_test)
# The mean squared error
mse=mean_squared_error(y_test, y_pred)
mse_per= 100*mse/3
print("Mean squared error: {}".format(mse))
print("Mean squared error in percentage: {}".format(mse_per))
#explained variance score
print('Variance score: {}'.format(regr.score(X_test, y_test)))
def adaBoost_reg(X_train,y_train,X_test,y_test):
#regr = RandomForestRegressor(max_depth=2, n_estimators=300)
#regr = SVR(gamma='scale', C=1, kernel='linear')
regr = AdaBoostRegressor()
regr.fit(X_train, y_train)
y_pred = regr.predict(X_test)
# The mean squared error
mse=mean_squared_error(y_test, y_pred)
mse_per= 100*mse/3
print("Mean squared error: {}".format(mse))
print("Mean squared error in percentage: {}".format(mse_per))
#explained variance score
print('Variance score: {}'.format(regr.score(X_test, y_test)))
feature_importance = regr.feature_importances_
# make importances relative to max importance
feature_importance = 100.0 * (feature_importance / feature_importance.max())
feature_names = list(('Average_Word_Length','Sentence_Count','Word_Count',
'Character_Count', 'Noun_Count','Adjective_Count',
'Verb_Count', 'Adverb_Count', 'Lemma_Count' ,'Misspell_Count'
))
feature_names = np.asarray(feature_names)
sorted_idx = np.argsort(feature_importance)
pos = np.arange(sorted_idx.shape[0]) + .5
plt.subplot(1, 2, 2)
plt.barh(pos, feature_importance[sorted_idx], align='center')
plt.yticks(pos, feature_names[sorted_idx])
plt.xlabel('Relative Importance')
plt.title('Variable Importance')
plt.show()
# convert numerical scores to labels
# (0-1.5) bad (1.5-2.3) average (2.3-3) good
# bad: '0'
# average '1'
# good '2'
def convert_scores(scores):
def mapping(x):
if x < np.percentile(scores,25):
return 0
elif x < np.percentile(scores,75):
return 1
else:
return 2
return scores.apply(mapping)
# selecting which set to be used 1-8
# in order to combine them all assign set number to 9
def select_set_classification(dataframe,setNumber):
if setNumber == 9:
dataframe2 = dataframe[dataframe.essay_set ==1]
texts = dataframe2['essay']
scores = dataframe2['domain1_score']
scores = scores.apply(lambda x: (x*3)/scores.max())
scores = convert_scores(scores)
for i in range(1,9):
dataframe2 = dataframe[dataframe.essay_set == i]
texts = texts.append(dataframe2['essay'])
s = dataframe2['domain1_score']
s = s.apply(lambda x: (x*3)/s.max())
s = convert_scores(s)
scores = scores.append(s)
else:
dataframe2 = dataframe[dataframe.essay_set ==setNumber]
texts = dataframe2['essay']
scores = dataframe2['domain1_score']
scores = scores.apply(lambda x: (x*3)/scores.max())
scores = convert_scores(scores)
return texts, scores
```
## Dataset selection
```
# 1-8
# 9:all sets combined
texts, scores = select_set(dataframe,1)
get_hist_avg(scores,5)
X_train, X_test, y_train, y_test, data = data_prepare(texts,scores)
```
## Regression Analysis
```
print('Testing for Linear Regression \n')
lin_regression(X_train,y_train,X_test,y_test)
print('Testing for Adaboost Regression \n')
adaBoost_reg(X_train,y_train,X_test,y_test)
```
## Dataset selection 2
```
# 1-8
# 9:all sets combined
texts, scores = select_set_classification(dataframe,1)
X_train, X_test, y_train, y_test, data = data_prepare(texts,scores)
```
## Classification analysis
```
a=[0.1,1,10,100,500,1000]
for b in a:
clf = svm.SVC(C=b, gamma=0.00001)
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
print (b)
print (clf.score(X_test,y_test))
print (np.mean(cross_val_score(clf, X_train, y_train, cv=3)))
clf = svm.SVC(C=100, gamma=0.00001)
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
print('Cohen’s kappa score: {}'.format(cohen_kappa_score(y_test,y_pred)))
print(classification_report(y_test, y_pred))
```
## Data Analysis
```
sns.countplot(scores)
zero = data[(data["Character_Count"] > 0) & (scores == 0)]
one = data[(data["Character_Count"] > 0) & (scores == 1)]
two = data[(data["Character_Count"] > 0) & (scores == 2)]
sns.distplot(zero["Character_Count"], bins=10, color='r')
sns.distplot(one["Character_Count"], bins=10, color='g')
sns.distplot(two["Character_Count"], bins=10, color='b')
plt.title("Score Distribution with respect to Character_Count",fontsize=20)
plt.xlabel("Character_Count",fontsize=15)
plt.ylabel("Distribuition of the scores",fontsize=15)
plt.show()
zero = data[(data["Lemma_Count"] > 0) & (scores == 0)]
one = data[(data["Lemma_Count"] > 0) & (scores == 1)]
two = data[(data["Lemma_Count"] > 0) & (scores == 2)]
sns.distplot(zero["Lemma_Count"], bins=10, color='r')
sns.distplot(one["Lemma_Count"], bins=10, color='g')
sns.distplot(two["Lemma_Count"], bins=10, color='b')
plt.title("Score Distribution with respect to lemma count",fontsize=20)
plt.xlabel("Lemma Count",fontsize=15)
plt.ylabel("Distribuition of the scores",fontsize=15)
plt.show()
zero = data[(data["Sentence_Count"] > 0) & (scores == 0)]
one = data[(data["Sentence_Count"] > 0) & (scores == 1)]
two = data[(data["Sentence_Count"] > 0) & (scores == 2)]
sns.distplot(zero["Sentence_Count"], bins=10, color='r')
sns.distplot(one["Sentence_Count"], bins=10, color='g')
sns.distplot(two["Sentence_Count"], bins=10, color='b')
plt.title("Score Distribution with respect to sentence count",fontsize=20)
plt.xlabel("Sentence Count",fontsize=15)
plt.ylabel("Distribuition of the scores",fontsize=15)
plt.show()
zero = data[(data["Word_Count"] > 0) & (scores == 0)]
one = data[(data["Word_Count"] > 0) & (scores == 1)]
two = data[(data["Word_Count"] > 0) & (scores == 2)]
sns.distplot(zero["Word_Count"], bins=10, color='r')
sns.distplot(one["Word_Count"], bins=10, color='g')
sns.distplot(two["Word_Count"], bins=10, color='b')
plt.title("Score Distribution with respect to word count",fontsize=20)
plt.xlabel("Word_Count",fontsize=15)
plt.ylabel("Distribuition of the scores",fontsize=15)
plt.show()
zero = data[(data["Average_Word_Length"] > 0) & (scores == 0)]
one = data[(data["Average_Word_Length"] > 0) & (scores == 1)]
two = data[(data["Average_Word_Length"] > 0) & (scores == 2)]
sns.distplot(zero["Average_Word_Length"], bins=10, color='r')
sns.distplot(one["Average_Word_Length"], bins=10, color='g')
sns.distplot(two["Average_Word_Length"], bins=10, color='b')
plt.title("Score Distribution with respect to Average_Word_Length",fontsize=20)
plt.xlabel("Average_Word_Length",fontsize=15)
plt.ylabel("Distribuition of the scores",fontsize=15)
plt.show()
```
### Kappa Score Reliability
According to Cohen's original article, values ≤ 0 as indicating no agreement and 0.01–0.20 as none to slight, 0.21–0.40 as fair, 0.41– 0.60 as moderate, 0.61–0.80 as substantial, and 0.81–1.00 as almost perfect agreement. McHugh says that many texts recommend 80% agreement as the minimum acceptable interrater agreement.
| github_jupyter |
# Hello Segmentation
A very basic introduction to using segmentation models with OpenVINO.
We use the pre-trained [road-segmentation-adas-0001](https://docs.openvinotoolkit.org/latest/omz_models_model_road_segmentation_adas_0001.html) model from the [Open Model Zoo](https://github.com/openvinotoolkit/open_model_zoo/). ADAS stands for Advanced Driver Assistance Services. The model recognizes four classes: background, road, curb and mark.
## Imports
```
import cv2
import matplotlib.pyplot as plt
import numpy as np
import sys
from openvino.inference_engine import IECore
sys.path.append("../utils")
from notebook_utils import segmentation_map_to_image
```
## Load the Model
```
ie = IECore()
net = ie.read_network(
model="model/road-segmentation-adas-0001.xml")
exec_net = ie.load_network(net, "CPU")
output_layer_ir = next(iter(exec_net.outputs))
input_layer_ir = next(iter(exec_net.input_info))
```
## Load an Image
A sample image from the [Mapillary Vistas](https://www.mapillary.com/dataset/vistas) dataset is provided.
```
# The segmentation network expects images in BGR format
image = cv2.imread("data/empty_road_mapillary.jpg")
rgb_image = cv2.cvtColor(image, cv2.COLOR_BGR2RGB)
image_h, image_w, _ = image.shape
# N,C,H,W = batch size, number of channels, height, width
N, C, H, W = net.input_info[input_layer_ir].tensor_desc.dims
# OpenCV resize expects the destination size as (width, height)
resized_image = cv2.resize(image, (W, H))
# reshape to network input shape
input_image = np.expand_dims(
resized_image.transpose(2, 0, 1), 0
)
plt.imshow(rgb_image)
```
## Do Inference
```
# Run the infernece
result = exec_net.infer(inputs={input_layer_ir: input_image})
result_ir = result[output_layer_ir]
# Prepare data for visualization
segmentation_mask = np.argmax(result_ir, axis=1)
plt.imshow(segmentation_mask[0])
```
## Prepare Data for Visualization
```
# Define colormap, each color represents a class
colormap = np.array([[68, 1, 84], [48, 103, 141], [53, 183, 120], [199, 216, 52]])
# Define the transparency of the segmentation mask on the photo
alpha = 0.3
# Use function from notebook_utils.py to transform mask to an RGB image
mask = segmentation_map_to_image(segmentation_mask, colormap)
resized_mask = cv2.resize(mask, (image_w, image_h))
# Create image with mask put on
image_with_mask = cv2.addWeighted(resized_mask, alpha, rgb_image, 1 - alpha, 0)
```
## Visualize data
```
# Define titles with images
data = {"Base Photo": rgb_image, "Segmentation": mask, "Masked Photo": image_with_mask}
# Create subplot to visualize images
f, axs = plt.subplots(1, len(data.items()), figsize=(15, 10))
# Fill subplot
for ax, (name, image) in zip(axs, data.items()):
ax.axis('off')
ax.set_title(name)
ax.imshow(image)
# Display image
plt.show(f)
```
| github_jupyter |
# TD - Implémentation des arbres en POO
On va dans ce TD créer une classe arbre binaire qui va nous permettre d'implémenter cette structure de données avec toutes ses caractéristiques.
On se souvient du cours sur les arbres https://pixees.fr/informatiquelycee/n_site/nsi_term_structDo_arbre.html dans lequel on définit le noeud racine, les sous-arbres gauche et droit.
```
class ArbreBinaire:
def __init__(self, valeur): #un arbre est un noeud contenant une valeur et deux enfants gauche et droit
self.valeur = valeur #le noeud contient la valeur passée en paramètre
self.enfant_gauche = None #l'enfant gauche est vide au départ
self.enfant_droit = None #l'enfant droit est vide au départ
def insert_gauche(self, valeur): #on insere valeur à la racine du sous-arbre de gauche
if self.enfant_gauche == None:
self.enfant_gauche = ArbreBinaire(valeur)
else:
new_node = ArbreBinaire(valeur)
new_node.enfant_gauche = self.enfant_gauche
self.enfant_gauche = new_node
def insert_droit(self, valeur): #on insere valeur à la racine du sous-arbre de droite
if self.enfant_droit == None:
self.enfant_droit = ArbreBinaire(valeur)
else:
new_node = ArbreBinaire(valeur)
new_node.enfant_droit = self.enfant_droit
self.enfant_droit = new_node
def get_valeur(self): #on renvoit la valeur du noeud racine
return self.valeur
def get_gauche(self): #on renvoit le sous arbre gauche
return self.enfant_gauche
def get_droit(self): #on renvoit le sous arbre droit
return self.enfant_droit
def __str__(self): #affichage d'un arbre avec print()
if self!= None: #on écrit (enfantgauche)valeur(enfantdroit)
return "("+self.enfant_gauche.__str__()+")"+str(self.valeur)+"("+self.enfant_droit.__str__()+")"
else:
return ""
```
Il est important de comprendre comment la structure de donnée est implémentée : un arbre est défini par une valeur et deux sous arbres gauches et droits qui sont tous les deux initialiés à <code>None</code> au démarrage.
Lors de l'insertion d'une valeur à gauche ou à droite, on crée un nouvel arbre que l'on insère à la racine du sous-arbre de gauche (dans le cas de <code>insert_gauche()</code>) ou droite (dans le cas de <code>insert_droit()</code>)
## Exercice 1
Sur papier, dessinez ce qui se passe étape par étape quand vous éxécutez le code suivant :
```
arbre=ArbreBinaire(3)
arbre.insert_gauche(1)
arbre.insert_gauche(2) #on insère 2 à gauche, la valeur 1 se décale à gauche du 2
print(arbre)
```
## Exercice 2
Écrire le code permettant de créer l'arbre suivant
<img src="nsi_term_algo_arbre_1.png">
Voila le début du code ci-dessous pour vous aider à démarrer...
```
arbre=ArbreBinaire("A")
arbre.insert_gauche("B")
arbreg=arbre.get_gauche()
arbreg.insert_gauche("C") #les deux lignes précédentes peuvent-être abbrégées en arbre.get_gauche().insert_gauche("C")
# à suivre...
print(arbre)
```
| github_jupyter |
```
from __future__ import print_function
import math
from IPython import display
from matplotlib import cm
from matplotlib import gridspec
from matplotlib import pyplot as plt
import numpy as np
import pandas as pd
from sklearn import metrics
import tensorflow as tf
from tensorflow.python.data import Dataset
tf.logging.set_verbosity(tf.logging.ERROR)
pd.options.display.max_rows = 10
pd.options.display.float_format = '{:.1f}'.format
ls
dataset_all = pd.read_csv('prices.csv')
dataset_all.head()
dataset_all
def my_input_fn(features, targets, batch_size=1, shuffle=True, num_epochs=None):
"""Trains a linear regression model of one feature.
Args:
features: pandas DataFrame of features
targets: pandas DataFrame of targets
batch_size: Size of batches to be passed to the model
shuffle: True or False. Whether to shuffle the data.
num_epochs: Number of epochs for which data should be repeated. None = repeat indefinitely
Returns:
Tuple of (features, labels) for next data batch
"""
# Convert pandas data into a dict of np arrays.
features = {key:np.array(value) for key,value in dict(features).items()}
# Construct a dataset, and configure batching/repeating.
ds = Dataset.from_tensor_slices((features,targets)) # warning: 2GB limit
ds = ds.batch(batch_size).repeat(num_epochs)
# Shuffle the data, if specified.
if shuffle:
ds = ds.shuffle(buffer_size=10000)
# Return the next batch of data.
features, labels = ds.make_one_shot_iterator().get_next()
return features, labels
def train_model(learning_rate, steps, batch_size, input_feature="close"):
"""Trains a linear regression model of one feature.
Args:
learning_rate: A `float`, the learning rate.
steps: A non-zero `int`, the total number of training steps. A training step
consists of a forward and backward pass using a single batch.
batch_size: A non-zero `int`, the batch size.
input_feature: A `string` specifying a column from `california_housing_dataframe`
to use as input feature.
"""
periods = 10
steps_per_period = steps / periods
my_feature = input_feature
my_feature_data = dataset_all[[my_feature]]
my_label = "open"
targets = dataset_all[my_label]
# Create feature columns.
feature_columns = [tf.feature_column.numeric_column(my_feature)]
# Create input functions.
training_input_fn = lambda:my_input_fn(my_feature_data, targets, batch_size=batch_size)
prediction_input_fn = lambda: my_input_fn(my_feature_data, targets, num_epochs=1, shuffle=False)
# Create a linear regressor object.
my_optimizer = tf.train.GradientDescentOptimizer(learning_rate=learning_rate)
my_optimizer = tf.contrib.estimator.clip_gradients_by_norm(my_optimizer, 5.0)
linear_regressor = tf.estimator.LinearRegressor(
feature_columns=feature_columns,
optimizer=my_optimizer
)
# Set up to plot the state of our model's line each period.
plt.figure(figsize=(15, 6))
plt.subplot(1, 2, 1)
plt.title("Learned Line by Period")
plt.ylabel(my_label)
plt.xlabel(my_feature)
sample = dataset_all.sample(n=300)
plt.scatter(sample[my_feature], sample[my_label])
colors = [cm.coolwarm(x) for x in np.linspace(-1, 1, periods)]
# Train the model, but do so inside a loop so that we can periodically assess
# loss metrics.
print("Training model...")
print("RMSE (on training data):")
root_mean_squared_errors = []
for period in range (0, periods):
# Train the model, starting from the prior state.
linear_regressor.train(
input_fn=training_input_fn,
steps=steps_per_period
)
# Take a break and compute predictions.
predictions = linear_regressor.predict(input_fn=prediction_input_fn)
predictions = np.array([item['predictions'][0] for item in predictions])
# Compute loss.
root_mean_squared_error = math.sqrt(
metrics.mean_squared_error(predictions, targets))
# Occasionally print the current loss.
print(" period %02d : %0.2f" % (period, root_mean_squared_error))
# Add the loss metrics from this period to our list.
root_mean_squared_errors.append(root_mean_squared_error)
# Finally, track the weights and biases over time.
# Apply some math to ensure that the data and line are plotted neatly.
y_extents = np.array([0, sample[my_label].max()])
weight = linear_regressor.get_variable_value('linear/linear_model/%s/weights' % input_feature)[0]
bias = linear_regressor.get_variable_value('linear/linear_model/bias_weights')
x_extents = (y_extents - bias) / weight
x_extents = np.maximum(np.minimum(x_extents,
sample[my_feature].max()),
sample[my_feature].min())
y_extents = weight * x_extents + bias
plt.plot(x_extents, y_extents, color=colors[period])
print("Model training finished.")
# Output a graph of loss metrics over periods.
plt.subplot(1, 2, 2)
plt.ylabel('RMSE')
plt.xlabel('Periods')
plt.title("Root Mean Squared Error vs. Periods")
plt.tight_layout()
plt.plot(root_mean_squared_errors)
# Output a table with calibration data.
calibration_data = pd.DataFrame()
calibration_data["predictions"] = pd.Series(predictions)
calibration_data["targets"] = pd.Series(targets)
display.display(calibration_data.describe())
print("Final RMSE (on training data): %0.2f" % root_mean_squared_error)
train_model(
learning_rate=0.002,
steps=100,
batch_size=10,
input_feature="close"
)
def train_model(learning_rate, steps, batch_size, input_feature="close"):
"""Trains a linear regression model of one feature.
Args:
learning_rate: A `float`, the learning rate.
steps: A non-zero `int`, the total number of training steps. A training step
consists of a forward and backward pass using a single batch.
batch_size: A non-zero `int`, the batch size.
input_feature: A `string` specifying a column from `california_housing_dataframe`
to use as input feature.
"""
periods = 10
steps_per_period = steps / periods
my_feature = input_feature
my_feature_data = dataset_all[[my_feature]]
my_label = "open"
targets = dataset_all[my_label]
# Create feature columns.
feature_columns = [tf.feature_column.numeric_column(my_feature)]
# Create input functions.
training_input_fn = lambda:my_input_fn(my_feature_data, targets, batch_size=batch_size)
prediction_input_fn = lambda: my_input_fn(my_feature_data, targets, num_epochs=1, shuffle=False)
# Create a linear regressor object.
my_optimizer = tf.train.GradientDescentOptimizer(learning_rate=learning_rate)
my_optimizer = tf.contrib.estimator.clip_gradients_by_norm(my_optimizer, 5.0)
linear_regressor = tf.estimator.LinearRegressor(
feature_columns=feature_columns,
optimizer=my_optimizer
)
# Set up to plot the state of our model's line each period.
plt.figure(figsize=(15, 6))
plt.subplot(1, 2, 1)
plt.title("Learned Line by Period")
plt.ylabel(my_label)
plt.xlabel(my_feature)
sample = dataset_all.sample(n=300)
plt.scatter(sample[my_feature], sample[my_label])
colors = [cm.coolwarm(x) for x in np.linspace(-1, 1, periods)]
# Train the model, but do so inside a loop so that we can periodically assess
# loss metrics.
print("Training model...")
print("RMSE (on training data):")
root_mean_squared_errors = []
for period in range (0, periods):
# Train the model, starting from the prior state.
linear_regressor.train(
input_fn=training_input_fn,
steps=steps_per_period
)
# Take a break and compute predictions.
predictions = linear_regressor.predict(input_fn=prediction_input_fn)
predictions = np.array([item['predictions'][0] for item in predictions])
# Compute loss.
root_mean_squared_error = math.sqrt(
metrics.mean_squared_error(predictions, targets))
# Occasionally print the current loss.
print(" period %02d : %0.2f" % (period, root_mean_squared_error))
# Add the loss metrics from this period to our list.
root_mean_squared_errors.append(root_mean_squared_error)
# Finally, track the weights and biases over time.
# Apply some math to ensure that the data and line are plotted neatly.
y_extents = np.array([0, sample[my_label].max()])
weight = linear_regressor.get_variable_value('linear/linear_model/%s/weights' % input_feature)[0]
bias = linear_regressor.get_variable_value('linear/linear_model/bias_weights')
x_extents = (y_extents - bias) / weight
x_extents = np.maximum(np.minimum(x_extents,
sample[my_feature].max()),
sample[my_feature].min())
y_extents = weight * x_extents + bias
plt.plot(x_extents, y_extents, color=colors[period])
print("Model training finished.")
# Output a graph of loss metrics over periods.
plt.subplot(1, 2, 2)
plt.ylabel('RMSE')
plt.xlabel('Periods')
plt.title("Root Mean Squared Error vs. Periods")
plt.tight_layout()
plt.plot(root_mean_squared_errors)
# Output a table with calibration data.
calibration_data = pd.DataFrame()
calibration_data["predictions"] = pd.Series(predictions)
calibration_data["targets"] = pd.Series(targets)
display.display(calibration_data.describe())
print("Final RMSE (on training data): %0.2f" % root_mean_squared_error)
train_model(
learning_rate=0.002,
steps=100,
batch_size=10,
input_feature="high"
)
```
| github_jupyter |
# Linear_Reg
Author ~ Saurabh Kumar
Date ~ 05-Dec-21
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import warnings
warnings.filterwarnings("ignore")
#simple_linera_regression
class Simple_linear_regression:
def __init__(self,learning_rate=1e-3,n_steps=1000):
self.learning_rate =learning_rate
self.n_steps =n_steps
def fit(self,X,y):
# adding the bias term
X_train = np.c_[np.ones(X.shape[0]),X]
# random initialization of the model weights
self.W =np.random.rand((X_train.shape[1]))
# random initialization of the model weights
for i in range(self.n_steps):
self.W =self.W -self.learning_rate*self.cal_gradiant_descent(X_train,y)
def cal_gradiant_descent(self,X,y):
#calculating gradiant descent
return 2/X.shape[0] * np.dot(X.T,np.dot(X,self.W)-y)
def predict(self,X):
#Predicting Y for the X
#adding bias term
X_pred =np.c_[np.ones(X.shape[0]),X]
return np.dot(X_pred,self.W)
#creating dataset
from sklearn.datasets import make_regression
X , y = make_regression (n_samples=1000,n_features = 1,n_targets=1,bias =2.5,noise=40,random_state = 44)
print("X_shape =",X.shape)
print("y_shape =",y.shape)
#train_test_split
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test =train_test_split(X,y,test_size=.33,random_state=12)
print("Shape X_train :",X_train.shape)
print("Shape y_train :",y_train.shape)
print("Shape X_test :",X_test.shape)
print("Shape y_test :",y_test.shape)
%matplotlib inline
import matplotlib.pyplot as plt
plt.xlabel('X_train')
plt.ylabel('Y_train')
plt.title('Relationship between X_train and Y_train variables')
plt.scatter(X_train, y_train)
plt.xlabel('X_train')
plt.ylabel('Y_train')
plt.title('Relationship between X_train and Y_train variables')
sns.regplot(X_train, y_train)
#model
model = Simple_linear_regression()
model.fit(X_train,y_train)
#prediction
y_pred =model.predict(X_test)
#error
print("Mean squared error: %.2f" % np.mean((model.predict(X_test) - y_test) ** 2))
plt.xlabel('X_test')
plt.ylabel('Y')
plt.title('Real vs Predicted values comparison')
plt.scatter(X_test, y_test)
plt.scatter(X_test, y_pred)
#Same with Sklearn lib
from sklearn.linear_model import LinearRegression
modelSk =LinearRegression()
modelSk.fit(X_train,y_train)
y_predict=modelSk.predict(X_test)
#error
print("Mean squared error: %.2f" % np.mean((modelSk.predict(X_test) - y_test) ** 2))
def accuracy(X_test,y_test, y_pred):
print('accuracy (R^2):\n', modelSk.score(X_test, y_test)*100, '%')
accuracy(X_test,y_test,y_predict)
plt.xlabel('X_test')
plt.ylabel('Y')
plt.title('Real vs Predicted values comparison')
plt.scatter(X_test, y_test)
plt.scatter(X_test, y_predict)
```
| github_jupyter |
# Collaboration and Competition
---
In this notebook, you will learn how to use the Unity ML-Agents environment for the third project of the [Deep Reinforcement Learning Nanodegree](https://www.udacity.com/course/deep-reinforcement-learning-nanodegree--nd893) program.
### 1. Start the Environment
We begin by importing the necessary packages. If the code cell below returns an error, please revisit the project instructions to double-check that you have installed [Unity ML-Agents](https://github.com/Unity-Technologies/ml-agents/blob/master/docs/Installation.md) and [NumPy](http://www.numpy.org/).
```
from unityagents import UnityEnvironment
import numpy as np
import random
import torch
from collections import deque
import matplotlib.pyplot as plt
%matplotlib inline
from ddpg_agent import Agent
plt.style.use('fivethirtyeight')
%load_ext autoreload
%autoreload 2
import warnings
warnings.filterwarnings('ignore')
```
Next, we will start the environment! **_Before running the code cell below_**, change the `file_name` parameter to match the location of the Unity environment that you downloaded.
- **Mac**: `"path/to/Tennis.app"`
- **Windows** (x86): `"path/to/Tennis_Windows_x86/Tennis.exe"`
- **Windows** (x86_64): `"path/to/Tennis_Windows_x86_64/Tennis.exe"`
- **Linux** (x86): `"path/to/Tennis_Linux/Tennis.x86"`
- **Linux** (x86_64): `"path/to/Tennis_Linux/Tennis.x86_64"`
- **Linux** (x86, headless): `"path/to/Tennis_Linux_NoVis/Tennis.x86"`
- **Linux** (x86_64, headless): `"path/to/Tennis_Linux_NoVis/Tennis.x86_64"`
For instance, if you are using a Mac, then you downloaded `Tennis.app`. If this file is in the same folder as the notebook, then the line below should appear as follows:
```
env = UnityEnvironment(file_name="Tennis.app")
```
```
# Under Linux
#env = UnityEnvironment(file_name='Tennis_Linux/Tennis.x86_64', seed=123)
# Under Mac
env = UnityEnvironment(file_name='Tennis.app', seed=123)
```
Environments contain **_brains_** which are responsible for deciding the actions of their associated agents. Here we check for the first brain available, and set it as the default brain we will be controlling from Python.
```
# get the default brain
brain_name = env.brain_names[0]
brain = env.brains[brain_name]
```
### 2. Examine the State and Action Spaces
In this environment, two agents control rackets to bounce a ball over a net. If an agent hits the ball over the net, it receives a reward of +0.1. If an agent lets a ball hit the ground or hits the ball out of bounds, it receives a reward of -0.01. Thus, the goal of each agent is to keep the ball in play.
The observation space consists of 8 variables corresponding to the position and velocity of the ball and racket. Two continuous actions are available, corresponding to movement toward (or away from) the net, and jumping.
Run the code cell below to print some information about the environment.
```
# reset the environment
env_info = env.reset(train_mode=True)[brain_name]
# number of agents
num_agents = len(env_info.agents)
print('Number of agents:', num_agents)
# size of each action
action_size = brain.vector_action_space_size
print('Size of each action:', action_size)
# examine the state space
states = env_info.vector_observations
state_size = states.shape[1]
print('There are {} agents. Each observes a state with length: {}'.format(states.shape[0], state_size))
print('The state for the first agent looks like:', states[0])
```
### 3. Take Random Actions in the Environment
In the next code cell, you will learn how to use the Python API to control the agents and receive feedback from the environment.
Once this cell is executed, you will watch the agents' performance, if they select actions at random with each time step. A window should pop up that allows you to observe the agents.
Of course, as part of the project, you'll have to change the code so that the agents are able to use their experiences to gradually choose better actions when interacting with the environment!
```
for i in range(1, 20): # play game for 5 episodes
env_info = env.reset(train_mode=False)[brain_name] # reset the environment
states = env_info.vector_observations # get the current state (for each agent)
scores = np.zeros(num_agents) # initialize the score (for each agent)
while True:
actions = np.random.randn(num_agents, action_size) # select an action (for each agent)
actions = np.clip(actions, -1, 1) # all actions between -1 and 1
env_info = env.step(actions)[brain_name] # send all actions to tne environment
next_states = env_info.vector_observations # get next state (for each agent)
rewards = env_info.rewards # get reward (for each agent)
dones = env_info.local_done # see if episode finished
scores += env_info.rewards # update the score (for each agent)
states = next_states # roll over states to next time step
if np.any(dones): # exit loop if episode finished
break
print('Score (max over agents) from episode {}: {}'.format(i, np.max(scores)))
```
When finished, you can close the environment.
env.close()
### 4. It's Your Turn!
Now it's your turn to train your own agent to solve the environment! When training the environment, set `train_mode=True`, so that the line for resetting the environment looks like the following:
```python
env_info = env.reset(train_mode=True)[brain_name]
```
### 5. Competing multi-agents as multiple non-competing agents
```
# Utilities functions
def unity_step_wrap(actions):
"""Unity Environment action wrapper
Params
======
action (int): action to take
Return
======
OpenAI-like action outcome (tuple): bundled (next_state, reward, done)
"""
env_info = env.step(actions)[brain_name] # send the action to the environment
next_states = env_info.vector_observations # get the next state
rewards = env_info.rewards # get the reward
dones = env_info.local_done # see if episode has finished
return (next_states, rewards, dones)
def moving_average(a, n=3) :
ret = np.cumsum(a, dtype=float)
ret[n:] = ret[n:] - ret[:-n]
return ret[n - 1:] / n
def plot_scores(scores, smooth_window=100):
scores_smoothed = moving_average(scores, smooth_window)
# plot the scores
fig = plt.figure(figsize=(8, 6))
ax = fig.add_subplot(111)
plt.plot(np.arange(len(scores)), scores, linewidth=1, alpha=0.4, color='steelblue')
plt.plot(np.arange(len(scores))[smooth_window-1:,], scores_smoothed, linewidth=1.5, alpha=1, color='firebrick')
plt.ylabel('Score')
plt.xlabel('Episode #')
plt.show()
return fig
def load_checkpoint(filepath):
checkpoint = torch.load(filepath)
return (checkpoint['actor'], checkpoint['critic'], checkpoint['scores'])
agent = Agent(state_size=state_size, action_size=action_size, random_seed=2)
def ddpg(n_episodes=1000, max_t=1000, print_every=100, learn_every=5, min_noise=0.02, solved_score = 0.5, name="default"):
scores_deque = deque(maxlen=print_every)
scores = []
noise = 1.0
min_noise = min_noise
noise_reduction = min_noise**(1/n_episodes) # Reaches min_noise after n_episodes with exponential decrease
for i_episode in range(1, n_episodes+1):
env_info = env.reset(train_mode=True)[brain_name]
states = env_info.vector_observations
agent.reset()
scores_episode = np.zeros(num_agents)
noise *= noise_reduction
for t in range(max_t):
actions = agent.act(states, noise=max(noise, min_noise))
next_states, rewards, dones = unity_step_wrap(actions)
for state, action, reward, next_state, done in zip(states, actions, rewards, next_states, dones):
agent.save_experience(state, action, reward, next_state, done)
scores_episode += rewards
states = next_states
if t % learn_every == 0:
agent.step()
if np.any(dones):
break
score = np.max(scores_episode)
scores_deque.append(score)
scores.append(score)
print('\rEpisode {}\tAverage Score: {:.2f}'.format(i_episode, np.mean(scores_deque)), end="")
# Save checkpoint
checkpoint = {
'actor': agent.actor_local.state_dict(),
'critic': agent.critic_local.state_dict(),
'scores': scores
}
torch.save(checkpoint, 'saved-checkpoints/checkpoint-' + name + '.pth')
if i_episode % print_every == 0:
print('\rEpisode {}\tAverage Score: {:.2f}'.format(i_episode, np.mean(scores_deque)))
if np.mean(scores_deque) > solved_score:
break
return scores
```
* **Solving the environment**
```
scores = ddpg(n_episodes=10000, min_noise=0.02, learn_every=5, name='solved')
_, _, scores_solved = load_checkpoint('saved-checkpoints/checkpoint-solved.pth')
figure = plot_scores(scores_solved)
```
* **Monitoring beyond solving scores in the long run**
```
scores = ddpg(n_episodes=10000, min_noise=0.01, learn_every=5, solved_score = 99, name='in-the-long-run')
_, _, scores_long_run = load_checkpoint('saved-checkpoints/checkpoint-in-the-long-run.pth')
figure = plot_scores(scores_long_run)
```
* **Watching solved environment agent in action**
```
# Reloading networks weights
actor_weights, critic_weights, scores_solved = load_checkpoint('saved-checkpoints/checkpoint-solved.pth')
# Instantiating the agent
agent = Agent(state_size=state_size, action_size=action_size, random_seed=2)
agent.actor_local.load_state_dict(actor_weights)
agent.critic_local.load_state_dict(critic_weights)
# Agent acting over 30 episodes
for i in range(1, 30): # play game for 30 episodes
env_info = env.reset(train_mode=False)[brain_name] # reset the environment
states = env_info.vector_observations # get the current state (for each agent)
scores = np.zeros(num_agents) # initialize the score (for each agent)
while True:
actions = agent.act(states)
env_info = env.step(actions)[brain_name] # send all actions to tne environment
next_states = env_info.vector_observations # get next state (for each agent)
rewards = env_info.rewards # get reward (for each agent)
dones = env_info.local_done # see if episode finished
scores += env_info.rewards # update the score (for each agent)
states = next_states # roll over states to next time step
if np.any(dones): # exit loop if episode finished
break
print('Score (max over agents) from episode {}: {}'.format(i, np.max(scores)))
```
| github_jupyter |
<i>Copyright (c) Microsoft Corporation. All rights reserved.</i>
<i>Licensed under the MIT License.</i>
# Testing different Hyperparameters and Benchmarking
In this notebook, we will cover how to test different hyperparameters for a particular dataset and how to benchmark different parameters across a group of datasets using AzureML. We assume familiarity with the basic concepts and parameters, which are discussed in the [01_training_introduction.ipynb](01_training_introduction.ipynb), [02_mask_rcnn.ipynb](02_mask_rcnn.ipynb) and [03_training_accuracy_vs_speed.ipynb](03_training_accuracy_vs_speed.ipynb) notebooks.
We will be using a Faster R-CNN model with ResNet-50 backbone to find all objects in an image belonging to 4 categories: 'can', 'carton', 'milk_bottle', 'water_bottle'. We will then conduct hyper-parameter tuning to find the best set of parameters for this model. For this, we present an overall process of utilizing AzureML, specifically [Hyperdrive](https://docs.microsoft.com/en-us/python/api/azureml-train-core/azureml.train.hyperdrive?view=azure-ml-py) which can train and evaluate many different parameter combinations in parallel. We demonstrate the following key steps:
* Configure AzureML Workspace
* Create Remote Compute Target (GPU cluster)
* Prepare Data
* Prepare Training Script
* Setup and Run Hyperdrive Experiment
* Model Import, Re-train and Test
This notebook is very similar to the [24_exploring_hyperparameters_on_azureml.ipynb](../../classification/notebooks/24_exploring_hyperparameters_on_azureml.ipynb) hyperdrive notebook used for image classification. For key concepts of AzureML see this [tutorial](https://docs.microsoft.com/en-us/azure/machine-learning/service/tutorial-train-models-with-aml?view=azure-ml-py&toc=https%3A%2F%2Fdocs.microsoft.com%2Fen-us%2Fpython%2Fapi%2Fazureml_py_toc%2Ftoc.json%3Fview%3Dazure-ml-py&bc=https%3A%2F%2Fdocs.microsoft.com%2Fen-us%2Fpython%2Fazureml_py_breadcrumb%2Ftoc.json%3Fview%3Dazure-ml-py) on model training and evaluation.
```
import os
import sys
from distutils.dir_util import copy_tree
import numpy as np
import scrapbook as sb
import uuid
import azureml.core
from azureml.core import Workspace, Experiment
from azureml.core.compute import ComputeTarget, AmlCompute
from azureml.core.compute_target import ComputeTargetException
import azureml.data
from azureml.train.estimator import Estimator
from azureml.train.hyperdrive import (
RandomParameterSampling, GridParameterSampling, BanditPolicy, HyperDriveConfig, PrimaryMetricGoal, choice, uniform
)
import azureml.widgets as widgets
sys.path.append("../../")
from utils_cv.common.azureml import get_or_create_workspace
from utils_cv.common.data import unzip_url
from utils_cv.detection.data import Urls
```
Ensure edits to libraries are loaded and plotting is shown in the notebook.
```
%reload_ext autoreload
%autoreload 2
%matplotlib inline
```
We now define some parameters which will be used in this notebook:
```
# Azure resources
subscription_id = "YOUR_SUBSCRIPTION_ID"
resource_group = "YOUR_RESOURCE_GROUP_NAME"
workspace_name = "YOUR_WORKSPACE_NAME"
workspace_region = "YOUR_WORKSPACE_REGION" #Possible values eastus, eastus2, etc.
# Choose a size for our cluster and the maximum number of nodes
VM_SIZE = "STANDARD_NC6" #STANDARD_NC6S_V3"
MAX_NODES = 8
# Hyperparameter grid search space
IM_MAX_SIZES = [600] #Default is 1333 pixels, defining small values here to speed up training
LEARNING_RATES = [1e-4, 3e-4, 1e-3, 3e-3, 1e-2]
# Image data
DATA_PATH = unzip_url(Urls.fridge_objects_path, exist_ok=True)
# Path to utils_cv library
UTILS_DIR = os.path.join('..', '..', 'utils_cv')
```
### 1. Config AzureML workspace
Below we setup (or load an existing) AzureML workspace, and get all its details as follows. Note that the resource group and workspace will get created if they do not yet exist. For more information regaring the AzureML workspace see also the [20_azure_workspace_setup.ipynb](../../classification/notebooks/20_azure_workspace_setup.ipynb) notebook in the image classification folder.
To simplify clean-up (see end of this notebook), we recommend creating a new resource group to run this notebook.
```
ws = get_or_create_workspace(
subscription_id, resource_group, workspace_name, workspace_region
)
# Print the workspace attributes
print(
"Workspace name: " + ws.name,
"Workspace region: " + ws.location,
"Subscription id: " + ws.subscription_id,
"Resource group: " + ws.resource_group,
sep="\n",
)
```
### 2. Create Remote Target
We create a GPU cluster as our remote compute target. If a cluster with the same name already exists in our workspace, the script will load it instead. This [link](https://docs.microsoft.com/en-us/azure/machine-learning/service/how-to-set-up-training-targets#compute-targets-for-training) provides more information about how to set up a compute target on different locations.
By default, the VM size is set to use STANDARD\_NC6 machines. However, if quota is available, our recommendation is to use STANDARD\_NC6S\_V3 machines which come with the much faster V100 GPU. We set the minimum number of nodes to zero so that the cluster won't incur additional compute charges when not in use.
```
CLUSTER_NAME = "gpu-cluster"
try:
# Retrieve if a compute target with the same cluster name already exists
compute_target = ComputeTarget(workspace=ws, name=CLUSTER_NAME)
print("Found existing compute target.")
except ComputeTargetException:
# If it doesn't already exist, we create a new one with the name provided
print("Creating a new compute target...")
compute_config = AmlCompute.provisioning_configuration(
vm_size=VM_SIZE, min_nodes=0, max_nodes=MAX_NODES
)
# create the cluster
compute_target = ComputeTarget.create(ws, CLUSTER_NAME, compute_config)
compute_target.wait_for_completion(show_output=True)
# we can use get_status() to get a detailed status for the current cluster.
print(compute_target.get_status().serialize())
```
The compute cluster and its status can be seen in the portal. For example in the screenshot below, its automatically resizing (eventually to 0 nodes) to adjust to the number of open runs:
<img src="media/hyperdrive_cluster.jpg" width="800" alt="Compute cluster status">
### 3. Prepare data
In this notebook, we'll use the Fridge Objects dataset, which is already stored in the correct format. We then upload our data to the AzureML workspace.
```
# Retrieving default datastore that got automatically created when we setup a workspace
ds = ws.get_default_datastore()
# We now upload the data to a unique sub-folder to avoid accidentially training/evaluating also including older images.
data_subfolder = str(uuid.uuid4())
ds.upload(
src_dir=DATA_PATH, target_path=data_subfolder, overwrite=False, show_progress=True
)
```
Here's where you can see the data in your portal:
<img src="media/datastore.jpg" width="800" alt="Datastore screenshot for Hyperdrive notebook run">
### 4. Prepare training script
Next step is to prepare scripts that AzureML Hyperdrive will use to train and evaluate models with selected hyperparameters.
```
# Create a folder for the training script and copy the utils_cv library into that folder
script_folder = os.path.join(os.getcwd(), "hyperdrive")
os.makedirs(script_folder, exist_ok=True)
_ = copy_tree(UTILS_DIR, os.path.join(script_folder, 'utils_cv'))
%%writefile $script_folder/train.py
# Use different matplotlib backend to avoid error during remote execution
import matplotlib
matplotlib.use("Agg")
import matplotlib.pyplot as plt
import os
import sys
import argparse
import numpy as np
from pathlib import Path
from azureml.core import Run
from utils_cv.detection.dataset import DetectionDataset
from utils_cv.detection.model import DetectionLearner, get_pretrained_fasterrcnn
from utils_cv.common.gpu import which_processor
which_processor()
# Parse arguments passed by Hyperdrive
parser = argparse.ArgumentParser()
parser.add_argument('--data-folder', type=str, dest='data_dir')
parser.add_argument('--data-subfolder', type=str, dest='data_subfolder')
parser.add_argument('--epochs', type=int, dest='epochs', default=20)
parser.add_argument('--batch_size', type=int, dest='batch_size', default=2)
parser.add_argument('--learning_rate', type=float, dest='learning_rate', default=1e-4)
parser.add_argument('--min_size', type=int, dest='min_size', default=800)
parser.add_argument('--max_size', type=int, dest='max_size', default=1333)
parser.add_argument('--rpn_pre_nms_top_n_train', type=int, dest='rpn_pre_nms_top_n_train', default=2000)
parser.add_argument('--rpn_pre_nms_top_n_test', type=int, dest='rpn_pre_nms_top_n_test', default=1000)
parser.add_argument('--rpn_post_nms_top_n_train', type=int, dest='rpn_post_nms_top_n_train', default=2000)
parser.add_argument('--rpn_post_nms_top_n_test', type=int, dest='rpn_post_nms_top_n_test', default=1000)
parser.add_argument('--rpn_nms_thresh', type=float, dest='rpn_nms_thresh', default=0.7)
parser.add_argument('--box_score_thresh', type=float, dest='box_score_thresh', default=0.05)
parser.add_argument('--box_nms_thresh', type=float, dest='box_nms_thresh', default=0.5)
parser.add_argument('--box_detections_per_img', type=int, dest='box_detections_per_img', default=100)
args = parser.parse_args()
params = vars(args)
print(f"params = {params}")
# Get training and validation data
data_path = os.path.join(params['data_dir'], params["data_subfolder"])
print(f"data_path={data_path}")
data = DetectionDataset(data_path, train_pct=0.5, batch_size = params["batch_size"])
print(
f"Training dataset: {len(data.train_ds)} | Training DataLoader: {data.train_dl} \n \
Testing dataset: {len(data.test_ds)} | Testing DataLoader: {data.test_dl}"
)
# Get model
model = get_pretrained_fasterrcnn(
num_classes = len(data.labels)+1,
min_size = params["min_size"],
max_size = params["max_size"],
rpn_pre_nms_top_n_train = params["rpn_pre_nms_top_n_train"],
rpn_pre_nms_top_n_test = params["rpn_pre_nms_top_n_test"],
rpn_post_nms_top_n_train = params["rpn_post_nms_top_n_train"],
rpn_post_nms_top_n_test = params["rpn_post_nms_top_n_test"],
rpn_nms_thresh = params["rpn_nms_thresh"],
box_score_thresh = params["box_score_thresh"],
box_nms_thresh = params["box_nms_thresh"],
box_detections_per_img = params["box_detections_per_img"]
)
detector = DetectionLearner(data, model)
# Run Training
detector.fit(params["epochs"], lr=params["learning_rate"], print_freq=30)
print(f"Average precision after each epoch: {detector.ap}")
# Get accuracy on test set at IOU=0.5:0.95
acc = float(detector.ap[-1])
# Add log entries
run = Run.get_context()
run.log("accuracy", float(acc)) # Logging our primary metric 'accuracy'
run.log("data_dir", params["data_dir"])
run.log("epochs", params["epochs"])
run.log("batch_size", params["batch_size"])
run.log("learning_rate", params["learning_rate"])
run.log("min_size", params["min_size"])
run.log("max_size", params["max_size"])
run.log("rpn_pre_nms_top_n_train", params["rpn_pre_nms_top_n_train"])
run.log("rpn_pre_nms_top_n_test", params["rpn_pre_nms_top_n_test"])
run.log("rpn_post_nms_top_n_train", params["rpn_post_nms_top_n_train"])
run.log("rpn_post_nms_top_n_test", params["rpn_post_nms_top_n_test"])
run.log("rpn_nms_thresh", params["rpn_nms_thresh"])
run.log("box_score_thresh", params["box_score_thresh"])
run.log("box_nms_thresh", params["box_nms_thresh"])
run.log("box_detections_per_img", params["box_detections_per_img"])
```
### 5. Setup and run Hyperdrive experiment
#### 5.1 Create Experiment
Experiment is the main entry point into experimenting with AzureML. To create new Experiment or get the existing one, we pass our experimentation name 'hyperparameter-tuning'.
```
exp = Experiment(workspace=ws, name="hyperparameter-tuning")
```
#### 5.2. Define search space
Now we define the search space of hyperparameters. To test discrete parameter values use 'choice()', and for uniform sampling use 'uniform()'. For more options, see [Hyperdrive parameter expressions](https://docs.microsoft.com/en-us/python/api/azureml-train-core/azureml.train.hyperdrive.parameter_expressions?view=azure-ml-py).
Hyperdrive provides three different parameter sampling methods: 'RandomParameterSampling', 'GridParameterSampling', and 'BayesianParameterSampling'. Details about each method can be found [here](https://docs.microsoft.com/en-us/azure/machine-learning/service/how-to-tune-hyperparameters). Here, we use the 'GridParameterSampling'.
```
# Grid-search
param_sampling = GridParameterSampling(
{"--learning_rate": choice(LEARNING_RATES), "--max_size": choice(IM_MAX_SIZES)}
)
```
<b>AzureML Estimator</b> is the building block for training. An Estimator encapsulates the training code and parameters, the compute resources and runtime environment for a particular training scenario.
We create one for our experimentation with the dependencies our model requires as follows:
```
script_params = {"--data-folder": ds.as_mount(), "--data-subfolder": data_subfolder}
est = Estimator(
source_directory=script_folder,
script_params=script_params,
compute_target=compute_target,
entry_script="train.py",
use_gpu=True,
pip_packages=["nvidia-ml-py3", "fastai"],
conda_packages=[
"scikit-learn",
"pycocotools>=2.0",
"torchvision==0.3",
"cudatoolkit==9.0",
],
)
```
We now create a HyperDriveConfig object which includes information about parameter space sampling, termination policy, primary metric, estimator and the compute target to execute the experiment runs on.
```
hyperdrive_run_config = HyperDriveConfig(
estimator=est,
hyperparameter_sampling=param_sampling,
policy=None, # Do not use any early termination
primary_metric_name="accuracy",
primary_metric_goal=PrimaryMetricGoal.MAXIMIZE,
max_total_runs=None, # Set to none to run all possible grid parameter combinations,
max_concurrent_runs=MAX_NODES,
)
```
#### 5.3 Run Experiment
We now run the parameter sweep and visualize the experiment progress using the `RunDetails` widget:
<img src="media/hyperdrive_widget_run.jpg" width="700px">
Once completed, the accuracy for the different runs can be analyzed via the widget, for example below is a plot of the accuracy versus learning rate below (for two different image sizes)
<img src="media/hyperdrive_widget_analysis.jpg" width="700px">
```
hyperdrive_run = exp.submit(config=hyperdrive_run_config)
print(f"Url to hyperdrive run on the Azure portal: {hyperdrive_run.get_portal_url()}")
widgets.RunDetails(hyperdrive_run).show()
hyperdrive_run.wait_for_completion()
```
To load an existing Hyperdrive Run instead of start new one, we can use
```python
hyperdrive_run = azureml.train.hyperdrive.HyperDriveRun(exp, <your-run-id>, hyperdrive_run_config=hyperdrive_run_config)
```
We also can cancel the Run with
```python
hyperdrive_run.cancel().
```
Once all the child-runs are finished, we can get the best run and the metrics.
```
# Get best run and print out metrics
best_run = hyperdrive_run.get_best_run_by_primary_metric()
best_run_metrics = best_run.get_metrics()
parameter_values = best_run.get_details()["runDefinition"]["arguments"]
best_parameters = dict(zip(parameter_values[::2], parameter_values[1::2]))
print(f"* Best Run Id:{best_run.id}")
print(best_run)
print("\n* Best hyperparameters:")
print(best_parameters)
print(f"Accuracy = {best_run_metrics['accuracy']}")
print("Learning Rate =", best_run_metrics["learning_rate"])
hyperdrive_run.get_children_sorted_by_primary_metric()
```
### 7. Clean up
To avoid unnecessary expenses, all resources which were created in this notebook need to get deleted once parameter search is concluded. To simplify this clean-up step, we recommended creating a new resource group to run this notebook. This resource group can then be deleted, e.g. using the Azure Portal, which will remove all created resources.
```
# Log some outputs using scrapbook which are used during testing to verify correct notebook execution
sb.glue("best_accuracy", best_run_metrics["accuracy"])
```
| github_jupyter |
```
import os
import torch
from torch.utils.data import DataLoader, Dataset
from torchvision.transforms import ToTensor, ToPILImage
from torchvision.models.detection import fasterrcnn_resnet50_fpn
from torchvision.models.detection.faster_rcnn import FastRCNNPredictor
from PIL import Image
class PlayerDataset(Dataset):
def __init__(self, root):
self.root = root
self.images = list(sorted(os.listdir(root + '/images')))
self.targets = [target for target in list(sorted(os.listdir(root + '/targets'))) if target != 'classes.txt']
def __len__(self):
return len(self.images)
def __getitem__(self, idx):
image_path = os.path.join(self.root, 'images', self.images[idx])
target_path = os.path.join(self.root, 'targets', self.targets[idx])
image = ToTensor()(Image.open(image_path).convert("RGB"))
f = open(target_path)
target = f.readline().strip().split()
w = 1280
h = 720
center_x = float(target[1]) * w
center_y = float(target[2]) * h
bbox_w = float(target[3]) * w
bbox_h = float(target[4]) * h
x0 = round(center_x - (bbox_w / 2))
x1 = round(center_x + (bbox_w / 2))
y0 = round(center_y - (bbox_h / 2))
y1 = round(center_y + (bbox_h / 2))
print(x1 - x0)
print(y1 - y0)
boxes = torch.as_tensor([x0, y0, x1, y1], dtype=torch.float32)
labels = torch.as_tensor(0, dtype=torch.int64)
target = [{'boxes': boxes, 'labels': labels}]
return image, target
def train_model(model, optimizer, lr_scheduler, data_loader, device, num_epochs):
model.train()
for epoch in range(num_epochs):
running_loss = 0.0
for images, targets in data_loader:
images = list(image.to(device) for image in images)
targets = [{k: v.to(device) for k, v in t.items()} for t in targets]
print(targets)
loss_dict = model(images, targets)
losses = sum(loss for loss in loss_dict.values())
optimizer.zero_grad()
losses.backward()
optimizer.step()
lr_scheduler.step()
running_loss += losses.item()
print('epoch:%d loss: %.3f' % (epoch + 1, running_loss))
def evaluate(model, data_loader, device):
model.eval()
cpu_device = torch.device("cpu")
with torch.no_grad():
for images, targets in data_loader:
images = list(image.to(device) for image in images)
targets = [{k: v.to(device) for k, v in t.items()} for t in targets]
outputs = [{k: v.to(cpu_device) for k, v in t.items()} for t in model(images)]
print(outputs)
model = fasterrcnn_resnet50_fpn(num_classes=1)
device = torch.device('cuda') if torch.cuda.is_available() else torch.device('cpu')
model.to(device)
train_dataset = PlayerDataset('data/train')
test_dataset = PlayerDataset('data/test')
train_data_loader = DataLoader(train_dataset, batch_size=1, shuffle=True, num_workers=4)
test_data_loader = DataLoader(test_dataset, batch_size=1, shuffle=False, num_workers=4)
params = [p for p in model.parameters() if p.requires_grad]
optimizer = torch.optim.SGD(params, lr=0.005, momentum=0.9, weight_decay=0.0005)
lr_scheduler = torch.optim.lr_scheduler.StepLR(optimizer, step_size=3, gamma=0.1)
train_model(model, optimizer, lr_scheduler, train_data_loader, device, 1)
evaluate(model, test_data_loader, device)
```
| github_jupyter |
```
!git clone https://github.com/GraphGrailAi/ruGPT3-ZhirV
cd ruGPT3-ZhirV
cd ..
!pip3 install -r requirements.txt
```
Обучение эссе
!python pretrain_transformers.py \
--output_dir=/home/jovyan/ruGPT3-ZhirV/ \
--overwrite_output_dir \
--model_type=gpt2 \
--model_name_or_path=sberbank-ai/rugpt3large_based_on_gpt2 \
--do_train \
--train_data_file=/home/jovyan/ruGPT3-ZhirV/data/all_essays.jsonl \
--do_eval \
--eval_data_file=/home/jovyan/ruGPT3-ZhirV/data/valid_essays.jsonl \
--num_train_epochs 10 \
--overwrite_cache \
--block_size=1024 \
--per_gpu_train_batch_size 1 \
--gradient_accumulation_steps 8
# Обучение Жириновский
```
!python pretrain_transformers.py \
--output_dir=/home/jovyan/ruGPT3-ZhirV/ \
--overwrite_output_dir \
--model_type=gpt2 \
--model_name_or_path=sberbank-ai/rugpt3large_based_on_gpt2 \
--do_train \
--train_data_file=/home/jovyan/ruGPT3-ZhirV/data/girik_all2.jsonl \
--do_eval \
--eval_data_file=/home/jovyan/ruGPT3-ZhirV/data/girik_valid.jsonl \
--num_train_epochs 20 \
--overwrite_cache \
--block_size=1024 \
--per_gpu_train_batch_size 1 \
--gradient_accumulation_steps 8
```
# Генерация Жириновский
```
from transformers import GPT2Tokenizer, GPT2LMHeadModel
tokenizer = GPT2Tokenizer.from_pretrained("checkpoint-1000")
model = GPT2LMHeadModel.from_pretrained("checkpoint-1000")
model.to("cuda")
import copy
bad_word_ids = [
[203], # \n
[225], # weird space 1
[28664], # weird space 2
[13298], # weird space 3
[206], # \r
[49120], # html
[25872], # http
[3886], # amp
[38512], # nbsp
[10], # &
[5436], # & (another)
[5861], # http
[372], # yet another line break
[421, 4395], # МСК
[64], # \
[33077], # https
[1572], # ru
[11101], # Источник
]
def gen_fragment(context, bad_word_ids=bad_word_ids, print_debug_output=False):
input_ids = tokenizer.encode(context, add_special_tokens=False, return_tensors="pt").to("cuda")
input_ids = input_ids[:, -1700:]
input_size = input_ids.size(1)
output_sequences = model.generate(
input_ids=input_ids,
max_length=175 + input_size,
min_length=40 + input_size,
top_p=0.95,
#top_k=0,
do_sample=True,
num_return_sequences=1,
temperature=1.0, # 0.9,
pad_token_id=0,
eos_token_id=2,
bad_words_ids=bad_word_ids,
no_repeat_ngram_size=6
)
if len(output_sequences.shape) > 3:
output_sequences.squeeze_()
generated_sequence = output_sequences[0].tolist()[input_size:]
if print_debug_output:
for idx in generated_sequence:
print(idx, tokenizer.decode([idx], clean_up_tokenization_spaces=True).strip())
text = tokenizer.decode(generated_sequence, clean_up_tokenization_spaces=True)
text = text[: text.find("</s>")]
text = text[: text.rfind(".") + 1]
return context + text
def gen_girik(context, sign, bad_word_ids, print_debug_output=False):
bad_word_ids_girik = copy.copy(bad_word_ids)
bad_word_ids_girik += [tokenizer.encode(bad_word, add_prefix_space=True) for bad_word in signs]
bad_word_ids_girik += [tokenizer.encode("." + bad_word, add_prefix_space=False) for bad_word in signs]
return gen_fragment(context + "\n\n" + sign + "\n", bad_word_ids_girik, print_debug_output=False)
signs = ["Лингвистическому мусору и иностранным словам в русском языке не место!",
"Будет ли Путин президентом после 2024 года?",
"Кто победил: Армения или Азербайджан?",
"И последнее. Когда в России настанет долгожданный мир во всём мире? И чтобы больше таких вопросов не было.",
"Почему Европа постоянно вводит санкции против России?",
"Не надо шутить с войной. Здесь другие ребята.",
"Ночью наши учёные чуть-чуть изменят гравитационное поле Земли, и твоя страна будет под водой.",
"Что было бы, если бы Жириновский стал президентом?",
"Когда Россия станет самой богатой и могущественной страной в мире?",
"Джордж, Джордж! Посмотри ковбойские фильмы!",
"От чего коровы с ума сходят? От британской демократии.",
]
beginning = "Жириновский говорит:."
current_text = beginning
for sign in signs:
current_text = gen_girik(current_text, sign, bad_word_ids)
print(current_text)
```
| github_jupyter |
```
# Copyright 2022 Google LLC.
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
```
# 4. Model Training
This notebook demonstrates how to train a Propensity Model using BigQuery ML.
### Requirements
* Input features used for training needs to be stored as a BigQuery table. This can be done using [2. ML Data Preparation Notebook](2.ml_data_preparation.ipynb).
### Install and import required modules
```
# Uncomment to install required python modules
# !sh ../utils/setup.sh
# Add custom utils module to Python environment
import os
import sys
sys.path.append(os.path.abspath(os.pardir))
from gps_building_blocks.cloud.utils import bigquery as bigquery_utils
from utils import model
from utils import helpers
```
### Set paramaters
```
configs = helpers.get_configs('config.yaml')
dest_configs = configs.destination
# GCP project ID
PROJECT_ID = dest_configs.project_id
# Name of the BigQuery dataset
DATASET_NAME = dest_configs.dataset_name
# To distinguish the separate runs of the training pipeline
RUN_ID = 'TRAIN_01'
# BigQuery table name containing model development dataset
FEATURES_DEV_TABLE = f'features_dev_table_{RUN_ID}'
# BigQuery table name containing model testing dataset
FEATURES_TEST_TABLE = f'features_test_table_{RUN_ID}'
# Output model name to save in BigQuery
MODEL_NAME = f'propensity_model_{RUN_ID}'
```
Next, let's configure modeling options.
### Model and features configuration
Model options can be configured in detail based on BigQuery ML specifications
listed in [The CREATE MODEL statement](https://cloud.google.com/bigquery-ml/docs/reference/standard-sql/bigqueryml-syntax-create).
**NOTE**: Propensity modeling supports only following four types of models available in BigQuery ML:
- LOGISTIC_REG
- [AUTOML_CLASSIFIER](https://cloud.google.com/bigquery-ml/docs/reference/standard-sql/bigqueryml-syntax-create-automl)
- [BOOSTED_TREE_CLASSIFIER](https://cloud.google.com/bigquery-ml/docs/reference/standard-sql/bigqueryml-syntax-create-boosted-tree)
- [DNN_CLASSIFIER](https://cloud.google.com/bigquery-ml/docs/reference/standard-sql/bigqueryml-syntax-create-dnn-models)
In order to use specific model options, you can add options to following configuration exactly same as listed in the [The CREATE MODEL statement](https://cloud.google.com/bigquery-ml/docs/reference/standard-sql/bigqueryml-syntax-create). For example, if you want to trian [AUTOML_CLASSIFIER](https://cloud.google.com/bigquery-ml/docs/reference/standard-sql/bigqueryml-syntax-create-automl) with `BUDGET_HOURS=1`, you can specify it as:
```python
params = {
'model_type': 'AUTOML_CLASSIFIER',
'budget_hours': 1
}
```
```
# Read in Features table schema to select feature names for model training
sql = ("SELECT column_name "
f"FROM `{PROJECT_ID}.{DATASET_NAME}`.INFORMATION_SCHEMA.COLUMNS "
f"WHERE table_name='{FEATURES_DEV_TABLE}';")
print(sql)
features_schema = bq_utils.run_query(sql).to_dataframe()
# Columns to remove from the feature list
to_remove = ['window_start_ts', 'window_end_ts', 'snapshot_ts', 'user_id',
'label', 'key', 'data_split']
# Selected features for model training
training_features = [v for v in features_schema['column_name']
if v not in to_remove]
print('Number of training features:', len(training_features))
print(training_features)
# Set parameters for AUTOML_CLASSIFIER model
FEATURE_COLUMNS = training_features
TARGET_COLUMN = 'label'
params = {
'model_path': f'{PROJECT_ID}.{DATASET_NAME}.{MODEL_NAME}',
'features_table_path': f'{PROJECT_ID}.{DATASET_NAME}.{FEATURES_DEV_TABLE}',
'feature_columns': FEATURE_COLUMNS,
'target_column': TARGET_COLUMN,
'MODEL_TYPE': 'AUTOML_CLASSIFIER',
'BUDGET_HOURS': 1.0,
# Enable data_split_col if you want to use custom data split.
# Details on AUTOML data split column:
# https://cloud.google.com/automl-tables/docs/prepare#split
# 'DATA_SPLIT_COL': 'data_split',
'OPTIMIZATION_OBJECTIVE': 'MAXIMIZE_AU_ROC'
}
```
## Train the model
First, we initialize `PropensityModel` with config parameters.
```
bq_utils = bigquery_utils.BigQueryUtils(project_id=PROJECT_ID)
propensity_model = model.PropensityModel(bq_utils=bq_utils,
params=params)
```
Next cell triggers model training job in BigQuery which takes some time to finish depending on dataset size and model complexity. Set `verbose=True`, if you want to verify training query details.
```
propensity_model.train(verbose=False)
```
Following cell allows you to see detailed information about the input features used to train a model. It provides following columns:
- input — The name of the column in the input training data.
- min — The sample minimum. This column is NULL for non-numeric inputs.
- max — The sample maximum. This column is NULL for non-numeric inputs.
- mean — The average. This column is NULL for non-numeric inputs.
- stddev — The standard deviation. This column is NULL for non-numeric inputs.
- category_count — The number of categories. This column is NULL for non-categorical columns.
- null_count — The number of NULLs.
For more details refer to [help page](https://cloud.google.com/bigquery-ml/docs/reference/standard-sql/bigqueryml-syntax-feature).
```
propensity_model.get_feature_info()
```
### Evaluate the model
This section helps to do quick model evaluation to get following model metrics:
* recall
* accuracy
* f1_score
* log_loss
* roc_auc
Two optional parameters can be specified for evaluation:
* eval_table: BigQuery table containing evaluation dataset
* threshold: Custom probability threshold to be used for evaluation (to binarize the predictions). Default value is 0.5.
If neither of these options are specified, the model is evaluated using evaluation dataset split during training with default threshold of 0.5.
**NOTE:** This evaluation provides basic model performance metrics. For thorough evaluation refer to [5. Model evaluation notebook](5.model_evaluation_and_diagnostics.ipynb) notebook.
TODO(): Add sql code to calculate the proportion of positive examples in the evaluation dataset to be used as the *threshold*.
```
# Model performance on the model development dataset on which the final
# model has been trained
EVAL_TABLE_NAME = FEATURES_DEV_TABLE
eval_params = {
'eval_table_path': f'{PROJECT_ID}.{DATASET_NAME}.{EVAL_TABLE_NAME}',
'threshold': 0.5
}
propensity_model.evaluate(eval_params, verbose=False)
# Model performance on the held out test dataset
EVAL_TABLE_NAME = FEATURES_TEST_TABLE
eval_params = {
'eval_table_path': f'{PROJECT_ID}.{DATASET_NAME}.{EVAL_TABLE_NAME}',
'threshold': 0.5
}
propensity_model.evaluate(eval_params, verbose=False)
```
## Next
Use [5. Model evaluation notebook](5.model_evaluation_and_diagnostics.ipynb) to get detailed performance metrics of the model and decide of model actually solves the business problem.
| github_jupyter |
```
import torch
import torch.nn as nn
import onmt
import onmt.inputters
import onmt.modules
import onmt.utils
```
We begin by loading in the vocabulary for the model of interest. This will let us check vocab size and to get the special ids for padding.
```
vocab = dict(torch.load("../../data/data.vocab.pt"))
src_padding = vocab["src"].stoi[onmt.inputters.PAD_WORD]
tgt_padding = vocab["tgt"].stoi[onmt.inputters.PAD_WORD]
```
Next we specify the core model itself. Here we will build a small model with an encoder and an attention based input feeding decoder. Both models will be RNNs and the encoder will be bidirectional
```
emb_size = 10
rnn_size = 6
# Specify the core model.
encoder_embeddings = onmt.modules.Embeddings(emb_size, len(vocab["src"]),
word_padding_idx=src_padding)
encoder = onmt.encoders.RNNEncoder(hidden_size=rnn_size, num_layers=1,
rnn_type="LSTM", bidirectional=True,
embeddings=encoder_embeddings)
decoder_embeddings = onmt.modules.Embeddings(emb_size, len(vocab["tgt"]),
word_padding_idx=tgt_padding)
decoder = onmt.decoders.decoder.InputFeedRNNDecoder(hidden_size=rnn_size, num_layers=1,
bidirectional_encoder=True,
rnn_type="LSTM", embeddings=decoder_embeddings)
model = onmt.models.model.NMTModel(encoder, decoder)
# Specify the tgt word generator and loss computation module
model.generator = nn.Sequential(
nn.Linear(rnn_size, len(vocab["tgt"])),
nn.LogSoftmax())
loss = onmt.utils.loss.NMTLossCompute(model.generator, vocab["tgt"])
```
Now we set up the optimizer. This could be a core torch optim class, or our wrapper which handles learning rate updates and gradient normalization automatically.
```
optim = onmt.utils.optimizers.Optimizer(method="sgd", lr=1, max_grad_norm=2)
optim.set_parameters(model.named_parameters())
```
Now we load the data from disk. Currently will need to call a function to load the fields into the data as well.
```
# Load some data
data = torch.load("../../data/data.train.1.pt")
valid_data = torch.load("../../data/data.valid.1.pt")
data.load_fields(vocab)
valid_data.load_fields(vocab)
data.examples = data.examples[:100]
```
To iterate through the data itself we use a torchtext iterator class. We specify one for both the training and test data.
```
train_iter = onmt.inputters.OrderedIterator(
dataset=data, batch_size=10,
device=-1,
repeat=False)
valid_iter = onmt.inputters.OrderedIterator(
dataset=valid_data, batch_size=10,
device=-1,
train=False)
```
Finally we train.
```
trainer = onmt.Trainer(model, loss, loss, optim)
def report_func(*args):
stats = args[-1]
stats.output(args[0], args[1], 10, 0)
return stats
for epoch in range(2):
trainer.train(epoch, report_func)
val_stats = trainer.validate()
print("Validation")
val_stats.output(epoch, 11, 10, 0)
trainer.epoch_step(val_stats.ppl(), epoch)
```
To use the model, we need to load up the translation functions
```
import onmt.translate
translator = onmt.translate.Translator(beam_size=10, fields=data.fields, model=model)
builder = onmt.translate.TranslationBuilder(data=valid_data, fields=data.fields)
valid_data.src_vocabs
for batch in valid_iter:
trans_batch = translator.translate_batch(batch=batch, data=valid_data)
translations = builder.from_batch(trans_batch)
for trans in translations:
print(trans.log(0))
break
```
| github_jupyter |
# 决策树
- 非参数学习算法
- 天然解决多分类问题
- 也可以解决回归问题
- 非常好的可解释性
```
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import cross_val_score
from sklearn import datasets
iris = datasets.load_iris()
print(iris.DESCR)
X = iris.data[:, 2:] # 取后两个特征
y = iris.target
plt.scatter(X[y==0, 0], X[y==0, 1])
plt.scatter(X[y==1, 0], X[y==1, 1])
plt.scatter(X[y==2, 0], X[y==2, 1])
```
### 1. scikit-learn 中的决策树
```
from sklearn.tree import DecisionTreeClassifier
# entropy : 熵
dt_clf = DecisionTreeClassifier(max_depth=3, criterion="entropy")
dt_clf.fit(X, y)
def plot_decision_boundary(model, axis):
x0, x1 = np.meshgrid(
np.linspace(axis[0], axis[1], int((axis[1] - axis[0])*100)).reshape(1, -1),
np.linspace(axis[2], axis[3], int((axis[3] - axis[2])*100)).reshape(-1, 1)
)
X_new = np.c_[x0.ravel(), x1.ravel()]
y_predic = model.predict(X_new)
zz = y_predic.reshape(x0.shape)
from matplotlib.colors import ListedColormap
custom_cmap = ListedColormap(['#EF9A9A', '#FFF590', '#90CAF9'])
plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)
plot_decision_boundary(dt_clf, axis=(0.5, 7.5, 0, 3))
plt.scatter(X[y==0, 0], X[y==0, 1])
plt.scatter(X[y==1, 0], X[y==1, 1])
plt.scatter(X[y==2, 0], X[y==2, 1])
```
### 2. 如何构建决策树
**问题**
- 每个节点在那个维度做划分?
- 某个维度在那个值上做划分?
- 划分的标准就是,**划分后使得信息熵降低**
**信息熵**
- 熵在信息论中代表随机变量不确定的度量
- 熵越大,数据的不确定性越高
- 熵越小,数据的不确定性越低
$$H = -\sum_{i=1}^kp_i\log{(p_i)}$$
- 其中 $p_i$ 表示每一类信息在所有信息类别中占的比例

- 对于二分类,香农公式为:
$$H=-x\log(x)-(1-x)\log(1-x)$$
**信息熵函数**
```
def entropy(p):
return -p * np.log(p) - (1-p) * np.log(1-p)
x = np.linspace(0.01, 0.99)
plt.plot(x, entropy(x))
```
- 可以看出,当 x 越接近0.5,熵越高
### 3. 模拟使用信息熵进行划分
```
# 基于维度 d 的 value 值进行划分
def split(X, y, d, value):
index_a = (X[:, d] <= value)
index_b = (X[:, d] > value)
return X[index_a], X[index_b], y[index_a], y[index_b]
from collections import Counter
from math import log
# 计算每一类样本点的熵的和
def entropy(y):
counter = Counter(y)
res = 0.0
for num in counter.values():
p = num / len(y)
res += -p * log(p)
return res
# 寻找要划分的 value 值,寻找最小信息熵及相应的点
def try_split(X, y):
best_entropy = float('inf') # 最小的熵的值
best_d, best_v = -1, -1 # 划分的维度,划分的位置
# 遍历每一个维度
for d in range(X.shape[1]):
# 每两个样本点在 d 这个维度中间的值. 首先把 d 维所有样本排序
sorted_index = np.argsort(X[:, d])
for i in range(1, len(X)):
if X[sorted_index[i-1], d] != X[sorted_index[i], d]:
v = (X[sorted_index[i-1], d] + X[sorted_index[i], d]) / 2
x_l, x_r, y_l, y_r = split(X, y, d, v)
# 计算当前划分后的两部分结果熵是多少
e = entropy(y_l) + entropy(y_r)
if e < best_entropy:
best_entropy, best_d, best_v = e, d, v
return best_entropy, best_d, best_v
best_entropy, best_d, best_v = try_split(X, y)
print("best_entropy = ", best_entropy)
print("best_d", best_d)
print("best_v", best_v)
```
**即在第 0 个维度的 2.45 位置进行划分,可以得到最低的熵,值为 0.693**
```
X1_l, X1_r, y1_l, y1_r = split(X, y, best_d, best_v)
entropy(y1_r)
entropy(y1_l) # 从上图可以看出,粉红色部分只有一类,故熵为 0
best_entropy2, best_d2, best_v2 = try_split(X1_r, y1_r)
print("best_entropy = ", best_entropy2)
print("best_d", best_d2)
print("best_v", best_v2)
X2_l, X2_r, y2_l, y2_r = split(X1_r, y1_r, best_d2, best_v2)
entropy(y2_r)
entropy(y2_l)
```
| github_jupyter |
```
import pandas as pd
import numpy as np
from PIL import Image
import os
import sys
!pip install ipython-autotime
%load_ext autotime
%matplotlib inline
```
1. Extract your dataset and split into train_x, train_y, test_x and test_y.
2. Execute the following cells
---
## Hybrid Social Group Optimization
---
```
N = 5 # Number of persons in population
D = len(train_x.columns) # Number of features in dataset
g = 10 # Number of generations
c = 0.6 # Self Introspection factor
r0 = 1
r1 = 0.4
r2 = 0.6
print(r1, r2)
```
**Population Initialization**
```
population = np.random.choice([0,1,2,3,4,5,6,7,8,9], (N,D), p=[0.16, 0.16, 0.16, 0.16, 0.16, 0.04, 0.04, 0.04, 0.04, 0.04]) #Determines no. of features selected by probablity
population = population.astype(float)
print(population.shape)
population
fitness = np.zeros(N)
test_x.shape
def fitter_trait(X_old, X_new):
if X_new > X_old:
return X_old
else:
return X_new
```
**Fitness Function**
```
global classifier
classifier = Svc #Change classifier here
select = train_x.columns
selectno = len(train_x.columns)
classifier.fit(train_x, train_y)
select_acc = classifier.score(test_x, test_y)
def fitness_function(pop): #Fitness Function
for i in range(N):
new_train_x = train_x
new_test_x = test_x
global select
global selectno
global select_acc
new_train_x = new_train_x.drop(train_x.columns[pop[i] < 4], axis = 1)
new_test_x = new_test_x.drop(test_x.columns[pop[i] < 4], axis = 1)
classifier.fit(new_train_x, train_y)
fitness[i] = classifier.score(new_test_x, test_y)
if (fitness[i] > select_acc):
select = new_train_x.columns
# print(select.shape)
selectno = new_train_x.shape[1]
select_acc = fitness[i]
elif fitness[i] == select_acc and new_train_x.shape[1] < selectno:
select = new_train_x.columns
selectno = new_train_x.shape[1]
print("\nPerson "+ str(i+1))
print("No. of Features Used = "+ str(new_train_x.shape[1])+ "/"+str(D)+"\nFitness = " + str(fitness[i]))
print("Feature Used = ", end = " ")
#print(new_train_x.columns)
print(new_train_x.shape[1])
# Initializing Fitness values of population
# fitness_function(population)
# selectno
```
**Gbest : Fittest person in population**
```
###Determining GBest
gbest = 0
gbest_i = 0
def find_gbest():
gbest = max(fitness)#This can be any function
gbest_i = fitness.argmax()
print("Best fitness value for the generation = "+str(gbest) + " Person " + str(gbest_i+1)+"\n")
find_gbest()
#we chose maximum fitness value to be better for simplicity
def cal_fitness(person):
new_train_x = train_x
new_test_x = test_x
new_train_x = new_train_x.drop(train_x.columns[person < 4], axis = 1)
new_test_x = new_test_x.drop(test_x.columns[person < 4], axis = 1)
classifier.fit(new_train_x, train_y)
return classifier.score(new_test_x, test_y)
cal_fitness(population[0])
# new_train_x = train_x
# new_test_x = test_x
# new_train_x = new_train_x.drop(train_x.columns[person < 4], axis = 1)
# new_test_x = new_test_x.drop(test_x.columns[person < 4], axis = 1)
per1 = np.zeros((1,10000))
print(per1.shape)
per1[0][5] = 8
per1[0][89] = 7
per1[0][45] = 6
cal_fitness(per1[0])
```
---
**Mutation Phase**
```
def mutate():
gworst_i = fitness.argmin()
gworst = min(fitness)
mut = np.random.randint(0,2,size=(1,D))[0]
print("Mutating the Generation's Worst....Person "+ str(gworst_i+1))
for i in range(D):
if mut[i] > 0:
mut[i] = population[gbest_i][i]
else:
mut[i] = population[gworst_i][i]
if cal_fitness(mut) > gworst:
population[gworst_i] = mut
print("Person "+str(gworst_i)+" mutated")
else:
print("No Mutations in this generation")
mut = np.random.randint(0,2,size=(1,D))[0]
mut
div = pd.DataFrame(np.random.randint(0,2,size=(1,D))[0])
# div.iloc[:,div > 0] = population[2][div>0]
# div
```
---
**Improving Phase**
```
## Improving Phase
# i = 1
def improve():
print("Improving.......")
for i in range(N):
Xnew = population[i]
print('Persona '+ str(i+1))
for j in range(D):
Xnew[j] = c * population[i][j] + r0 * (population[gbest_i][j] - population[i][j])
try:
if cal_fitness(Xnew) > fitness[i]:
population[i] = Xnew
except:
print("Oops!", sys.exc_info()[0], "occurred.")
print("Next entry.")
```
---
**Acquiring Phase**
```
## Acquiring Phase
def acquire():
random_person = np.random.randint(low=0, high=N)
for i in range(N):
if random_person == i:
random_person = np.random.randint(low=0, high=N)
i = i - 1
continue
X_new = population[i]
if fitness[random_person] > fitness[i]:
for j in range(D):
X_new[j] = population[i][j] + r1*(population[random_person][j]-population[i][j]) + r2*(population[gbest_i][j]-population[i][j])
if cal_fitness(X_new) > fitness[i]:
population[i] = X_new
else:
for j in range(D):
X_new[j] = population[i][j] + r1*(population[i][j]-population[random_person][j]) + r2*(population[gbest_i][j]-population[i][j])
if cal_fitness(X_new) > fitness[i]:
population[i] = X_new
#Run
try:
for k in range(g):
print("Generation "+ str(k+1) + "\n---------------")
fitness_function(population)
find_gbest()
mutate()
improve()
acquire()
except:
print()
print("........................")
print("Optimal Solution Reached")
print("........................")
select.shape
```
| github_jupyter |
# Final Project
For the final project, you will need to implement a "new" statistical algorithm in Python from the research literature and write a "paper" describing the algorithm.
Suggested papers can be found in Sakai:Resources:Final_Project_Papers
## Paper
The paper should have the following:
### Title
Should be concise and informative.
### Abstract
250 words or less. Identify 4-6 key phrases.
### Background
State the research paper you are using. Describe the concept of the algorithm and why it is interesting and/or useful. If appropriate, describe the mathematical basis of the algorithm. Some potential topics for the background include:
- What problem does it address?
- What are known and possible applications of the algorithm?
- What are its advantages and disadvantages relative to other algorithms?
- How will you use it in your research?
### Description of algorithm
First, explain in plain English what the algorithm does. Then describes the details of the algorithm, using mathematical equations or pseudocode as appropriate.
### Describe optimization for performance
First implement the algorithm using plain Python in a straightforward way from the description of the algorithm. Then profile and optimize it using one or more appropriate methods, such as:
1. Use of better algorithms or data structures
2. Use of vectorization
3. JIT or AOT compilation of critical functions
4. Re-writing critical functions in C++ and using pybind11 to wrap them
5. Making use of parallelism or concurrency
6. Making use of distributed compuitng
Document the improvement in performance with the optimizations performed.
### Applications to simulated data sets
Are there specific inputs that give known outputs (e.g. there might be closed form solutions for special input cases)? How does the algorithm perform on these?
If no such input cases are available (or in addition to such input cases), how does the algorithm perform on simulated data sets for which you know the "truth"?
### Applications to real data sets
Test the algorithm on the real-world examples in the original paper if possible. Try to find at least one other real-world data set not in the original paper and test it on that. Describe and interpret the results.
### Comparative analysis with competing algorithms
Find two other algorithm that address a similar problem. Perform a comparison - for example, of accuracy or speed. You can use native libraries of the other algorithms - you do not need to code them yourself. Comment on your observations.
### Discussion/conclusion
Your thoughts on the algorithm. Does it fulfill a particular need? How could it be generalized to other problem domains? What are its limitations and how could it be improved further?
### References/bibliography
Make sure you cite your sources.
## Code
The code should be in a public GitHub repository with:
1. A README file
2. An open source license
3. Source code
4. Test code
5. Examples
6. A reproducible report
The package should be downloadable and installable with `python setup.py install`, or even posted to PyPI adn installable with `pip install package`. See https://packaging.python.org/tutorials/packaging-projects/ for how to upload to a Python repository. Use the repository at https://test.pypi.org - this is for testing and will be wiped clean after a period.
## Rubric
Here are some considerations I use when grading. Note that the "difficulty factor" of the chosen algorithm will be factored into the grading.
1. Is the abstract, background and discussion readable and clear?
2. Is the algorithm description clear and accurate?
3. Has the algorithm been optimized?
4. Are the applications to simulated/real data clear and useful?
5. Was the comparative analysis done well?
6. Is there a well-maintained GitHub repository for the code?
7. Is the document show evidence of literate programming?
8. Is the analysis reproducible?
9. Is the code tested? Are examples provided?
10. Is the package easily installable?
| github_jupyter |
# ClusterFinder Reference genomes reconstruction
This notebook validates the 10 genomes we obtained from NCBI based on the ClusterFinder supplementary table.
We check that the gene locations from the supplementary table match locations in the GenBank files.
```
from Bio import SeqIO
from Bio.SeqFeature import FeatureLocation
import pandas as pd
from Bio import Entrez
import seaborn as sns
def get_features_of_type(sequence, feature_type):
return [feature for feature in sequence.features if feature.type == feature_type]
def get_reference_gene_location(gene_csv_row):
start = gene_csv_row['gene start'] - 1
end = gene_csv_row['gene stop']
strand = 1 if gene_csv_row['gene strand'] == '+' else (-1 if gene_csv_row['gene strand'] == '-' else None)
return FeatureLocation(start, end, strand)
def feature_locus_matches(feature, reference_locus):
return feature.qualifiers.get('locus_tag',[None])[0] == reference_locus
```
# Loading reference cluster gene locations
```
reference_genes = pd.read_csv('../data/clusterfinder/labelled/CF_labelled_genes_orig.csv', sep=';')
reference_genes.head()
```
# Genes with no sequence
```
no_sequence_genes = reference_genes[reference_genes['NCBI ID'] == '?']
no_sequence_counts = no_sequence_genes.groupby('Genome ID')['gene locus'].count()
print('{} genes don\'t have a sequence!'.format(len(no_sequence_genes)))
pd.DataFrame({'missing genes':no_sequence_counts})
reference_ids = reference_genes[reference_genes['NCBI ID'] != '?']['NCBI ID'].unique()
reference_ids
```
# Validating that reference genes are found in our sequences
```
def validate_genome(record, record_reference_genes):
print('Validating {}'.format(record.id))
record_genes = get_features_of_type(record, 'gene')
record_cds = get_features_of_type(record, 'CDS')
validation = []
record_length = len(record.seq)
min_location = record_length
max_location = -1
prev_gene_index = None
prev_cluster_start = None
for i, reference_gene in record_reference_genes.iterrows():
reference_gene_location = get_reference_gene_location(reference_gene)
reference_gene_locus = reference_gene['gene locus']
reference_cluster_start = reference_gene['NPL start']
gene_matches_locus = [f for f in record_genes if feature_locus_matches(f, reference_gene_locus)]
cds_matches_locus = [f for f in record_cds if feature_locus_matches(f, reference_gene_locus)]
gene_matches_location = [f for f in gene_matches_locus if reference_gene_location == f.location]
cds_matches_location = [f for f in cds_matches_locus if reference_gene_location == f.location]
validation.append({
'gene_locus_not_found':not gene_matches_locus,
'cds_locus_not_found':not cds_matches_locus,
'gene_location_correct': bool(gene_matches_location),
'cds_location_correct': bool(cds_matches_location)
})
if not cds_matches_locus:
print('No CDS found for gene locus {}'.format(reference_gene_locus))
if gene_matches_locus:
gene_match = gene_matches_locus[0]
if not cds_matches_locus:
print(' Gene: ', gene_match.qualifiers)
# Use gene index to check if we have a consecutive sequence of genes (except when going from one cluster to another)
gene_index = [gi for gi,f in enumerate(record_genes) if feature_locus_matches(f, reference_gene_locus)][0]
if reference_cluster_start == prev_cluster_start and gene_index != prev_gene_index + 1:
print('Additional unexpected genes found before {} (index {} -> {}) at cluster start {}'.format(reference_gene_locus, prev_gene_index, gene_index, reference_cluster_start))
# Calculate min and max cluster gene location to see how much of the sequence is covered by the reference genes
min_location = min(gene_match.location.start, min_location)
max_location = max(gene_match.location.end, max_location)
prev_gene_index = gene_index
prev_cluster_start = reference_cluster_start
result = pd.DataFrame(validation).sum().to_dict()
result['location correct'] = min(result['gene_location_correct'], result['cds_location_correct']) / len(validation)
result['ID'] = record.id
result['genome'] = record_reference_genes.iloc[0]['Genome ID']
result['sequence length'] = record_length
result['total genes'] = len(record_genes)
result['reference genes'] = len(record_reference_genes)
result['first location'] = min_location / record_length
result['last location'] = max_location / record_length
result['covered'] = (max_location - min_location) / record_length
return result
validations = []
reference_gene_groups = reference_genes.groupby('NCBI ID')
records = SeqIO.parse('../data/clusterfinder/labelled/CF_labelled_contigs.gbk', 'genbank')
for record in records:
ncbi_id = record.id
print(ncbi_id)
record_reference_genes = reference_gene_groups.get_group(ncbi_id)
validations.append(validate_genome(record, record_reference_genes))
validations = pd.DataFrame(validations)
validations.set_index('ID', inplace=True)
validations
validations['location correct'].mean()
1 - validations['location correct'].mean()
validations[['genome','first location','last location','covered','location correct','reference genes','total genes']]
```
# Cluster genes
```
genes = pd.read_csv('../data/clusterfinder/labelled/CF_labelled_genes.csv', sep=';')
genes.head()
cluster_counts = genes.groupby('contig_id')['cluster_id'].nunique()
cluster_counts.sort_values().plot.barh()
gene_counts = genes.groupby('cluster_id')['locus_tag'].count()
gene_counts.hist(bins=50)
```
| github_jupyter |
# Realization of Recursive Filters
*This jupyter notebook is part of a [collection of notebooks](../index.ipynb) on various topics of Digital Signal Processing. Please direct questions and suggestions to [[email protected]](mailto:[email protected]).*
## Cascaded Structures
The realization of recursive filters with a high order may be subject to numerical issues. For instance, when the coefficients span a wide amplitude range, their quantization may require a small quantization step or may impose a large relative error for small coefficients. The basic concept of cascaded structures is to decompose a high order filter into a cascade of lower order filters, typically first and second order recursive filters.
### Decomposition into Second-Order Sections
The rational transfer function $H(z)$ of a linear time-invariant (LTI) recursive system can be [expressed by its zeros and poles](introduction.ipynb#Transfer-Function) as
\begin{equation}
H(z) = \frac{b_M}{a_N} \cdot \frac{\prod_{\mu=1}^{P} (z - z_{0\mu})^{m_\mu}}{\prod_{\nu=1}^{Q} (z - z_{\infty\nu})^{n_\nu}}
\end{equation}
where $z_{0\mu}$ and $z_{\infty\nu}$ denote the $\mu$-th zero and $\nu$-th pole of degree $m_\mu$ and $n_\nu$ of $H(z)$, respectively. The total number of zeros and poles is denoted by $P$ and $Q$.
The poles and zeros of a real-valued filter $h[k] \in \mathbb{R}$ are either single real valued or conjugate complex pairs. This motivates to split the transfer function into
* first order filters constructed from a single pole and zero
* second order filters constructed from a pair of conjugated complex poles and zeros
Decomposing the transfer function into these two types by grouping the poles and zeros into single poles/zeros and conjugate complex pairs of poles/zeros results in
\begin{equation}
H(z) = K \cdot \prod_{\eta=1}^{S_1} \frac{(z - z_{0\eta})}{(z - z_{\infty\eta})}
\cdot \prod_{\eta=1}^{S_2} \frac{(z - z_{0\eta}) (z - z_{0\eta}^*)} {(z - z_{\infty\eta})(z - z_{\infty\eta}^*)}
\end{equation}
where $K$ denotes a constant and $S_1 + 2 S_2 = N$ with $N$ denoting the order of the system. The cascade of two systems results in a multiplication of their transfer functions. Above decomposition represents a cascade of first- and second-order recursive systems. The former can be treated as a special case of second-order recursive systems. The decomposition is therefore known as decomposition into second-order sections (SOSs) or [biquad filters](https://en.wikipedia.org/wiki/Digital_biquad_filter). Using a cascade of SOSs the transfer function of the recursive system can be rewritten as
\begin{equation}
H(z) = \prod_{\mu=1}^{S} \frac{b_{0, \mu} + b_{1, \mu} \, z^{-1} + b_{2, \mu} \, z^{-2}}{1 + a_{1, \mu} \, z^{-1} + a_{2, \mu} \, z^{-2}}
\end{equation}
where $S = \lceil \frac{N}{2} \rceil$ denotes the total number of SOSs. These results state that any real valued system of order $N > 2$ can be decomposed into SOSs. This has a number of benefits
* quantization effects can be reduced by sensible grouping of poles/zeros, e.g. such that the spanned amplitude range of the filter coefficients is limited
* A SOS may be extended by a gain factor to further reduce quantization effects by normalization of the coefficients
* efficient and numerically stable SOSs serve as generic building blocks for higher-order recursive filters
### Example - Cascaded second-order section realization of a lowpass
The following example illustrates the decomposition of a higher-order recursive Butterworth lowpass filter into a cascade of second-order sections.
```
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.markers import MarkerStyle
from matplotlib.patches import Circle
import scipy.signal as sig
N = 9 # order of recursive filter
def zplane(z, p, title='Poles and Zeros'):
"Plots zero and pole locations in the complex z-plane"
ax = plt.gca()
ax.plot(np.real(z), np.imag(z), 'bo', fillstyle='none', ms = 10)
ax.plot(np.real(p), np.imag(p), 'rx', fillstyle='none', ms = 10)
unit_circle = Circle((0,0), radius=1, fill=False,
color='black', ls='solid', alpha=0.9)
ax.add_patch(unit_circle)
ax.axvline(0, color='0.7')
ax.axhline(0, color='0.7')
plt.title(title)
plt.xlabel(r'Re{$z$}')
plt.ylabel(r'Im{$z$}')
plt.axis('equal')
plt.xlim((-2, 2))
plt.ylim((-2, 2))
plt.grid()
# design filter
b, a = sig.butter(N, 0.2)
# decomposition into SOS
sos = sig.tf2sos(b, a, pairing='nearest')
# print filter coefficients
print('Coefficients of the recursive part \n')
print(['%1.2f'%ai for ai in a])
print('\n')
print('Coefficients of the recursive part of the individual SOS \n')
print('Section \t a1 \t\t a2')
for n in range(sos.shape[0]):
print('%d \t\t %1.5f \t %1.5f'%(n, sos[n, 4], sos[n, 5]))
# plot pole and zero locations
plt.figure(figsize=(5,5))
zplane(np.roots(b), np.roots(a), 'Poles and Zeros - Overall')
plt.figure(figsize=(10, 7))
for n in range(sos.shape[0]):
plt.subplot(231+n)
zplane(np.roots(sos[n, 0:3]), np.roots(sos[n, 3:6]), title='Poles and Zeros - Section %d'%n)
plt.tight_layout()
# compute and plot frequency response of sections
plt.figure(figsize=(10,5))
for n in range(sos.shape[0]):
Om, H = sig.freqz(sos[n, 0:3], sos[n, 3:6])
plt.plot(Om, 20*np.log10(np.abs(H)), label=r'Section %d'%n)
plt.xlabel(r'$\Omega$')
plt.ylabel(r'$|H_n(e^{j \Omega})|$ in dB')
plt.legend()
plt.grid()
```
**Exercise**
* What amplitude range is spanned by the filter coefficients?
* What amplitude range is spanned by the SOS coefficients?
* Change the pole/zero grouping strategy from `pairing='nearest'` to `pairing='keep_odd'`. What changes?
* Increase the order `N` of the filter. What changes?
Solution: Inspecting both the coefficients of the recursive part of the original filter and of the individual SOS reveals that the spanned amplitude range is lower for the latter. The choice of the pole/zero grouping strategy influences the locations of the poles/zeros in the individual SOS, the spanned amplitude range of their coefficients and the transfer functions of the individual sections. The total number of SOS scales with the order of the original filter.
**Copyright**
This notebook is provided as [Open Educational Resource](https://en.wikipedia.org/wiki/Open_educational_resources). Feel free to use the notebook for your own purposes. The text is licensed under [Creative Commons Attribution 4.0](https://creativecommons.org/licenses/by/4.0/), the code of the IPython examples under the [MIT license](https://opensource.org/licenses/MIT). Please attribute the work as follows: *Sascha Spors, Digital Signal Processing - Lecture notes featuring computational examples, 2016-2018*.
| github_jupyter |
# Utilizing daal4py in Data Science Workflows
The notebook below has been made to demonstrate daal4py in a data science context. It utilizes a Cycling Dataset for pyworkout-toolkit, and attempts to create a linear regression model from the 5 features collected for telemetry to predict the user's Power output in the absence of a power meter.
```
import pandas as pd
import matplotlib.pyplot as plt
import glob
import sys
%matplotlib inline
sys.version
```
This example will be exploring workout data pulled from Strava, processed into a CSV for Pandas and daal4py usage. Below, we utilize pandas to read in the CSV file, and look at the head of dataframe with .head()
```
workout_data_dd= pd.read_csv('data/batch/cycling_dataset.csv', index_col=0)
workout_data_dd.head()
```
The data above has several key features that would be of great use here.
- Altitude can affect performance, so it might be a useful feature.
- Cadence is the revolutions per minute of the crank, and may have possible influence.
- Heart Rate is a measure of the body's workout strain, and would have a high possibly of influence.
- Distance may have a loose correlation as it is highly route dependent, but might be possible.
- Speed has possible correlations as it ties directly into power.
## Explore and visualize some of the data
In general, we are trying to predict on the 'power' in Watts to see if we can generate a model that can predict one's power output without the usage of a cycling power meter. Below are some basic scatterplots as we explore the data. Scatterplots are great for looking for patterns and correlation in the data itself. Below, we can see that cadence and speed are positively correlated.
```
workout_data_dd.plot.scatter('cadence','power')
plt.show()
workout_data_dd.plot.scatter('hr','power')
plt.show()
workout_data_dd.plot.scatter('cadence','speed')
plt.show()
workout_data_dd.plot.scatter('speed','power')
plt.show()
workout_data_dd.plot.scatter('altitude','power')
plt.show()
workout_data_dd.plot.scatter('distance','power')
plt.show()
```
## Using daal4py for Machine Learning tasks
In the sections below, we will be using daal4py directly. After importing the model, we will arrange it in a separate independent and dependent dataframes, then use the daal4py's training and prediction classes to generate a workable model.
```
import daal4py as d4p
```
It is now the time to split the dataset into train and test sets. This is demonstrated below.
```
print(workout_data_dd.shape)
train_set = workout_data_dd[0:3000]
test_set = workout_data_dd[3000:]
print(train_set.shape, test_set.shape)
# Reduce the dataset, create X. We drop the target, and other non-essential features.
reduced_dataset = train_set.drop(['time','power','latitude','longitude'], axis=1)
# Get the target, create Y
target = train_set.power.values.reshape((-1,1))
# This is essentially doing np.array(dataset.power.values, ndmin=2).T
# as it needs to force a 2 dimensional array as we only have 1 target
```
X is 5 features by 3k rows, Y is 3k rows by 1 column
```
print(reduced_dataset.values.shape, target.shape)
```
## Training the model
Create the Linear Regression Model, and train the model with the data. We utilize daal4py's linear_regression_training class to create the model, then call .compute() with the independent and dependent data as the parameters.
```
d4p_lm = d4p.linear_regression_training(interceptFlag=True)
lm_trained = d4p_lm.compute(reduced_dataset.values, target)
print("Model has this number of features: ", lm_trained.model.NumberOfFeatures)
```
## Prediction (inference) with the trained model
Now that the model is trained, we can test it with the test part of the dataset. We drop the same features to match that of the trained model, and put it into daal4py's linear_regression_prediction class.
```
subset = test_set.drop(['time','power','latitude','longitude'], axis=1)
```
Now we can create the Prediction object and use the reduced dataset for prediction. The class's arguments use the independent data and the trained model from above as the parameters.
```
lm_predictor_component = d4p.linear_regression_prediction()
result = lm_predictor_component.compute(subset.values, lm_trained.model)
plt.plot(result.prediction[0:300])
plt.plot(test_set.power.values[0:300])
plt.show()
```
The graph above shows the Orange (predicted) result over the Blue (original data). This data is notoriously sparse in features leading to a difficult to predict target!
## Model properties
Another aspect of the model is the trained model's properties, which are explored below.
```
print("Betas:",lm_trained.model.Beta)
print("Number of betas:", lm_trained.model.NumberOfBetas)
print("Number of Features:", lm_trained.model.NumberOfFeatures)
```
## Additional metrics
We can generate metrics on the independent data with daal4py's low_order_moments() class.
```
metrics_processor = d4p.low_order_moments()
data = metrics_processor.compute(reduced_dataset.values)
data.standardDeviation
```
## Migrating the trained model for inference on external systems
Occasionally one may need to migrate the trained model to another system for inference only--this use case allows the training on a much more powerful machine with a larger dataset, and placing the trained model for inference-only on a smaller machine.
```
import pickle
with open('trained_model2.pickle', 'wb') as model_pi:
pickle.dump(lm_trained.model, model_pi)
model_pi.close
```
The trained model file above can be moved to an inference-only or embedded system. This is useful if the training is extreamly heavy or computed-limited.
```
with open('trained_model2.pickle', 'rb') as model_import:
lm_import = pickle.load(model_import)
```
The imported model from file is now usable again. We can check the betas from the model to ensure that the trained model is present.
```
lm_import.Beta
```
| github_jupyter |
# **JIVE: Joint and Individual Variation Explained**
JIVE (Joint and Individual Variation Explained) is a dimensional reduction algorithm that can be used when there are multiple data matrices (data blocks). The multiple data block setting means there are $K$ different data matrices, with the same number of observations $n$ and (possibly) different numbers of variables ($d_1, \dots, d_k$). JIVE finds modes of variation which are common (joint) to all $K$ data blocks and modes of individual variation which are specific to each block. For a detailed discussion of JIVE see [Angle-Based Joint and Individual Variation Explained](https://arxiv.org/pdf/1704.02060.pdf).[^1]
For a concrete example, consider a two block example from a medical study. Suppose there are $n=500$ patients (observations). For each patient we have $d_1 = 100$ bio-medical variables (e.g. hit, weight, etc). Additionally we have $d_2 = 10,000$ gene expression measurements for each patient.
## **The JIVE decomposition**
Suppose we have $K$ data data matrices (blocks) with the same number of observations, but possibly different numbers of variables; in particular let $X^{(1)}, \dots, X^{(K)}$ where $X^{(k)} \in \mathbb{R}^{n \times d_k}$. JIVE will then decompose each matrix into three components: joint signal, individual signal and noise
\begin{equation}
X^{(k)} = J^{(k)} + I^{(k)} + E^{(k)}
\end{equation}
where $J^{(k)}$ is the joint signal estimate, $I^{(k)}$ is the individual signal estimate and $E^{(k)}$ is the noise estimate (each of these matrices must the same shape as the original data block: $\mathbb{R}^{n \times d_k}$). Note: **we assume each data matrix** $X^{(k)}$ **has been column mean centered**.
The matrices satisfy the following constraints:
1. The joint matrices have a common rank: $rk(J^{(k)}) = r_{joint}$ for $k=1, \dots, K$.
2. The individual matrices have block specific ranks $rk(I^{(k)}) = r_{individual}^{(k)}$.
3. The columns of the joint matrices share a common space called the joint score space (a subspace of $\mathbb{R}^n$); in particular the $\text{col-span}(J^{(1)}) = \dots = \text{col-span}(J^{(K)})$ (hence the name joint).
4. Each individual spaces score subspace (of $\mathbb{R}^n$) is orthogonal to the the joint space; in particular $\text{col-span}(J^{(k)}) \perp \text{col-span}(I^{(k)})$ for $k=1, \dots, K$.
Note that JIVE may be more natural if we think about data matrices subspaces of $\mathbb{R}^n$ (the score space perspective). Typically we think of a data matrix as $n$ points in $\mathbb{R}^d$. The score space perspective views a data matrix as $d$ vectors in $\mathbb{R}^n$ (or rather the span of these vectors). One important consequence of this perspective is that it makes sense to related the data blocks in score space (e.g. as subspaces of $\mathbb{R}^n$) since they share observtions.
## Quantities of interest
There are a number of potential quantities of interest depending on the application. For example the user may be interested in the full matrices $J^{(k)}$ and/or $I^{(k)}$. By construction these matrices are not full rank and we may also be interested in their singular value decomposition which we define as
\begin{align}
& U^{(k)}_{joint}, D^{(k)}_{joint}, V^{(k)}_{joint} = \text{rank } r_{joint} \text{ SVD of } J^{(k)} \\
& U^{(k)}_{individual}, D^{(k)}_{individual}, V^{(k)}_{individual} = \text{rank } r_{individual}^{{k}} \text{ SVD of } I^{(k)}
\end{align}
One additional quantity of interest is $U_{joint} \in \mathbb{R}^{n \times r_{joint}}$ which is an orthogonal basis of $\text{col-span}(J^{(k)})$. This matrix is produced from an intermediate JIVE computation.
## **PCA analogy**
We give a brief discussion of the PCA/SVD decomposition (assuming the reading is already familiar).
#### Basic decomposition
Suppose we have a data matrix $X \in \mathbb{n \times d}$. Assume that $X$ has been column mean centered and consider the SVD decomposition (this is PCA since we have mean centered the data):
\begin{equation}
X = U D V^T.
\end{equation}
where $U \in \mathbb{R}^{n \times m}$, $D \in \mathbb{R}^{m \times m}$ is diagonal, and $V \in \mathbb{R}^{d \times m}$ with $m = min(n, d)$. Note $U^TU = V^TV = I_{m \times m}$.
Suppose we have decided to use a rank $r$ approximation. We can then decompose $X$ into a signal matrix ($A$) and an noise matrix ($E$)
\begin{equation}
X = A + E,
\end{equation}
where $A$ is the rank $r$ SVD approximation of $X$ i.e.
\begin{align}
A := & U_{:, 1:r} D_{1:r, 1:r} V_{:, 1:r}^T \\
= & \widetilde{U}, \widetilde{D} \widetilde{V}^T
\end{align}
The notation $U_{:, 1:r} \in \mathbb{R}^{n \times r}$ means the first $r$ columns of $U$. Similarly we can see the error matrix is $E :=U_{:, r+1:n} D_{r+1:m, r_1:m} V_{:, r+1:d}^T$.
#### Quantities of interest
There are many ways to use a PCA/SVD decomposition. Some common quantities of interest include
- The normalized scores: $\widetilde{U} \in \mathbb{R}^{n \times r}$
- The unnormalized scores: $\widetilde{U}\widetilde{D} \in \mathbb{R}^{n \times r}$
- The loadings: $\widetilde{V} \in \mathbb{R}^{d \times r}$
- The full signal approximation: $A \in \mathbb{R}^{n \times d}$
#### Scores and loadings
For both PCA and JIVE we use the notation $U$ (scores) and $V$ (loadings). These show up in several places.
We refer to all $U \in \mathbb{R}^{n \times r}$ matrices as scores. We can view the $n$ rows of $U$ as representing the $n$ data points with $r$ derived variables (put differently, columns of $U$ are $r$ derived variables). The columns of $U$ are orthonormal: $U^TU = I_{r \times r}$.
Sometimes we may want $UD$ i.e scale the columns of $U$ by $D$ (the columns are still orthogonal). The can be useful when we want to represent the original data by $r$ variables. We refer to $UD$ as unnormalized scores.
We refer to all $V\in \mathbb{R}^{d \times r}$ matrices as loadings[^2]. The j$th$ column of $V$ gives the linear combination of the original $d$ variables which is equal to the j$th$ unnormalized scores (j$th$ column of $UD$). Equivalently, if we project the $n$ data points (rows of $X$) onto the j$th$ column of $V$ we get the j$th$ unnormalized scores.
The typical geometric perspective of PCA is that the scores represent $r$ new derived variables. For example, if $r = 2$ we can look at a scatter plot that gives a two dimensional approximation of the data. In other words, the rows of the scores matrix are $n$ data points living in $\mathbb{R}^r$.
An alternative geometric perspective is the $r$ columns of the scores matrix are vectors living in $\mathbb{R}^n$. The original $d$ variables span a subspace of $\mathbb{R}^n$ given by $\text{col-span}(X)$. The scores then span a lower dimensional subspace of $\mathbb{R}^n$ that approximates $\text{col-span}(X)$.
The first perspective says PCA finds a lower dimensional approximation to a subspace in $\mathbb{R}^d$ (spanned by the $n$ data points). The second perspective says PCA finds a lower dimensional approximation to a subspace in $\mathbb{R}^n$ (spanned by the $d$ data points).
## **JIVE operating in score space**
For a data matrix $X$ let's call the span of the variables (columns) the *score subpace*, $\text{col-span}(X) \subset \mathbb{R}^n$. Typically we think of a data matrix as $n$ points in $\mathbb{R}^d$. The score space perspective reverses this and says a data matrix is $d$ points in $\mathbb{R}^n$. When thinking in the score space it's common to consider about subspaces i.e. the span of the $d$ variables in $\mathbb{R}^n$. In other words, if two data matrices have the same column span then their score subspaces are the same[^3].
JIVE partitions the score space of each data matrix into three subspaces: joint, individual and noise. The joint score subspace for each data block is the same. The individual score subspace, however, is (possibly) different for each of the $K$ blocks. The k$th$ block's individual score subspace is orthogonal to the joint score subspace. Recall that the $K$ data matrices have the same number of observations ($n$) so it makes sense to think about how the data matrices relate to each other in score space.
PCA partitions the score space into two subspaces: signal and noise (see above). For JIVE we might combine the joint and individual score subspaces and call this the signal score subspace.
# Footnotes
[^1]: Note this paper calls the algorithm AJIVE (angle based JIVE) however, we simply use JIVE. Additionally, the paper uses columns as observations in data matrices where as we use rows as observations.
[^2]: For PCA we used tildes (e.g. $\widetilde{U}$) to denote the "partial" SVD approximation however for the final JIVE decomposition we do not use tildes. This is intentional since for JIVE the SVD comes from the $I$ and $J$ matrices which are exactly rank $r$. Therefore we view this SVD as the "full" SVD.
[^3]: This might remind the reader of TODO
| github_jupyter |
```
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import check_lab05 as p
plt.rcParams.update({'font.size': 14})
plt.rcParams['lines.linewidth'] = 3
pi=np.pi
```
ME 3264 - Applied Measurements Laboratory
===========================================
Lab #5 - Linear Variable Differential Transformer(LVDT)
=====================================================
## Objective
The objectives of this laboratory are :
1. Gain familiarity with the physical operating principle of Linear Variable Differential Transformer (LVDT) measurements
2. Calibrate the LVDT measurement using voltage measurements
3. Determine relationship between supplied voltage amplitude and linear motion
4. Investigate effects of changing input frequency and sampling rate on response frequency
## Background
### Working principle of LVDT
A linear variable differential transformer (LVDT) is a device that can measure the absolute linear position or changes in position of a separate device. LVDTs operate on the principle of a transformer. Because it is a transformer, the LVDT requires an ac drive signal. As shown in Fig.1 (and Fig.2A) , an LVDT consists of a coil assembly and a core. The coil assembly is typically mounted to a stationary form, while the core is secured to the object whose position is being measured. The coil assembly consists of three coils of wire wound on the hollow form. A core of permeable material can slide freely through the center of the form. The inner coil is the primary, which is excited by an AC source as shown. Magnetic flux produced by the primary is coupled to the two secondary coils, inducing an AC voltage in each coil [2].
<center><img src="https://upload.wikimedia.org/wikipedia/commons/5/57/LVDT.png" alt="Drawing" style="width: 300px;"/> </center>
<center>Figure 1: Cutaway view of an LVDT. Current is driven through the primary coil at A, causing an induction current to be generated through the secondary coils at B. [4] </center>
### LVDT Measurement
An LVDT measures displacement by associating a specific signal value for any given position of the core. This association of a signal value to a position occurs through electromagnetic coupling of an AC excitation signal on the primary winding to the core and back to the secondary windings as shown in Fig.2B. The position of the core determines how tightly the signal of the primary coil is coupled to each of the secondary coils. The two secondary coils are series-opposed, which means wound in series but in opposite directions. This results in the two signals on each secondary being 180 deg out of phase. Therefore phase of the output signal determines direction and its amplitude, distance [2].
Fig.2C shows the operational characteristics of LVDT with respect to the core displacement.
<center><img src="https://ars.els-cdn.com/content/image/3-s2.0-B9780081028841000042-f04-12-9780081028841.jpg" alt="Drawing" style="width: 200px;"/> </center>
<center>Figure 2: The operation of the LVDT (A) Internal arrangement (B) Electrical circuit, the dots signify the positive ending of the winding (C) Operational characteristics [5] </center>
### Advantages of LVDT
LVDTs have a number of advantages, including -
* The ability to measure absolute position, the ability to be completely sealed from the environment, nearly frictionless operation, and excellent repeatability of the measurement
* Because the device relies on the coupling of magnetic flux, an LVDT can have infinite resolution. Therefore the smallest fraction of movement can be detected by suitable signal conditioning hardware, and the resolution of the transducer is solely determined by the resolution of the data acquisition system
* Linearity of operation as output is a direct and linear function of the input
## Part 1 - LVDT calibaration
### Problem 1 - Relate voltage to displacement
Let's consider a LVDT with it's core attached to a micrometer. Following table consists of core displacment, and mean DC voltage, recorded by DAQ in an experiment. Obtain the caliberation curve of LVDT using linear regression.
|Displacement| Mean DC |
|--- | --- |
|5 mm | 4.829 V |
|6 mm | 6.690 V |
|7 mm | 8.333 V |
|4 mm | 3.868 V |
|3 mm | 2.024 V |
|2 mm | 0.145 V |
|1 mm | -1.738 V |
```
from scipy.optimize import curve_fit
def func(x,a,b):
'''fits the linear equation y = a + bx
This equation can be replaced by polynomial or exponential
as per the fitting goals of the problem'''
return (a + b*x)
x = [5,6,7,4,3,2,1] # mm
y = [4.829,6.690,8.333,3.686,2.024,0.145,-1.738] # Volt
k,pcov=curve_fit(func, x, y)
k_error=np.sqrt(np.diag(pcov)) # Co-variance matrix
a = np.asarray(k[0])
b = np.asarray(k[1])
print("Caliberation equation for LVDT is y = %1.3f +%1.3fx \n "%(a,b))
print("Caliberation coefficent a =%1.3f +/- %1.3f \n"%(k[0],k_error[0]))
print("Caliberation coefficent b = %1.3f +/- %1.3f \n"%(k[1],k_error[1]))
plt.plot(x,y,'o',label='experiment')
plt.plot(x,func(x,a,b),label='model')
plt.legend()
plt.xlabel(r'Displacement, mm')
plt.ylabel('Mean DC, Volts')
```
Note - In the curvefit,
`k,pcov=curve_fit(func, x, y)`
* `k` - Optimal values for the parameters so that the sum of the squared residuals of (f(x,k) - y) is minimized.
* `pcov` - The estimated covariance of k. The diagonals provide the variance of the parameter estimate. To compute one standard deviation errors on the parameters, we use k_error = np.sqrt(np.diag(pcov)).
### Problem 2 - Check your work
Calculate the linear regression coefficents a and b, and their standard variances for data in problem 1 using linear least square fitting method described in [Ref 3](https://mathworld.wolfram.com/LeastSquaresFitting.html). Does these values compare well with the coefficents and standard variance values obtained from covarianc matrix in the above example?
```
## # enter your work here - Uncomment the following lines of code and make necessary changes
# n = len(x)
# # sum of squares
# x_mean = np.mean(x)
# y_mean =
# ss_xx = np.sum((x-x_mean)**2)
# ss_yy =
# ss_xy = np.sum((y-y_mean)*(x-x_mean))
# # linear regression coefficients
# b = ss_xy/ss_xx
# a = y_mean - b*x_mean
# print("Equation for linear egression line is y = %1.3f +%1.3fx \n "%(a,b))
# # correlation coefficient,
# r2 = ss_xy**2/ss_xx/ss_yy
# print("Correlation coefficient, is y = %1.3f \n "%(r2))
# # The standard errors for a and b
# s = (ss_yy -ss_xy**2/ss_xx)/(n-2)
# sigma_a = np.sqrt(s)*np.sqrt(1/n + (x_mean**2/ss_xx))
# sigma_b = np.sqrt(s)/np.sqrt(ss_xx)
# print("Std (a)= %1.3f\n "%sigma_a)
# print("Std (b)= %1.3f\n "%sigma_b)
p.check_p02(a, b)
```
## Part 2 - Calibrate Piezoelectric with LVDT output
In part 2, you compare the amplitude of input voltage for the piezoelectric motion to the amplitude of LVDT voltage output. When the output voltage is larger, the piezoelectric is moving further.
```
from IPython.display import YouTubeVideo
YouTubeVideo('NwE8B9IHvyo')
```
### Problem 3 - Calibrate Piezoelectric
Following table consists of amplitude of input voltage for the piezoelectric motion, and LVDT voltage output, recorded by DAQ in an experiment. Obtain the caliberation curve using linear regression. You can use `curve_fit` as expalined in Part 1.
|Input, Vpp | Output Vpp |
|--- | --- |
|1 | 0.00101 |
|2 | 0.00380 |
|4 | 0.00698 |
|4 | 0.01048 |
|5 | 0.01420 |
|6 | 0.01832 |
|7 | 0.02273 |
```
## enter your work here
```
## Part 3 - Explore frequency-response between Piezoelectric and LVDT
In part 3, you vary the frequency input to the piezoelectric and measure the frequency output measured by the LVDT. You are constrained by the Nyquist frequency in these measurements. If you collect data at 500 Hz, then the largest frequency you can reliably measure is 250 Hz. The concept of Nyquist frequency if further explored with Problem 4.
### Problem 4 - Nyquist frequency
Consider a case where signal generator sends a signal of the form of cos-wave to a piezo motor. The signal has frequency of 1-Hz with amplitude of 2 Vpp (Volts peak-to-peak) . The Data Aquisition System (DAQ) takes N measurements over the given timeframe from 0-10 seconds to measure the corresponding LVDT output signal. Plot and compare the input and measured signals.
```
N=20
t_collect=10 # time to collect data
t=np.linspace(0,t_collect,1000)
y=np.cos(2*pi*t)
tsample=np.linspace(0,10,N+1)
ysample=np.cos(2*pi*tsample)
plt.figure(20)
plt.plot(t,y,label='signal')
plt.plot(tsample,ysample,'o-',label='measure')
plt.legend(bbox_to_anchor=(1.05, 1), loc=2, borderaxespad=0.)
plt.xlabel('time (s)')
plt.ylabel('a.u.')
```
For N=20, it would appear that DAQ can capture a minimal example of input signal (just the peaks occuring at 1 Hz). Collecting data for N=20 over 10 seconds is equivalent to sampling at 20 samples/10 seconds = 2 Hz. This is called the Nyquist rate which is given as such
$f_{Nyquist}=2f_{signal}$. (1)
In Equation 1, the Nyquist rate (also Shannon Sampling) [\[6\]](https://github.uconn.edu/rcc02007/ME3264-Lab_03)[\[7\]](./jerri_1977-shannon_sampling.pdf)[\[8\]](./nyquist.pdf), $f_{Nyquist}$, is the minimum sampling rate necessary to capture the signal at frequency, $f_{signal}$. Try changing N<20 and consider the apparent signal frequencies.
If you try N=11 in the Python code below, you will see a phenomenon called "aliasing" or the "wagon-wheel effect" [\[9\]](http://www.onmyphd.com/?p=aliasing). When you look at the measured signal, it appears to have a frequency of 1 cycle/10 seconds = 0.1 Hz. This phenomenon is called the wagon-wheel effect because it is noticeable when recording spinning objects like a wagon wheel [or turbine](https://www.youtube.com/watch?v=vIsS4TP73AU). The wheel spins at a given frequency and the camera records at another frequency. When the ratio of the wheel frequency to camera recording frequency reaches certain values the wheel appears to stop, spin slower, or even backwards. [\[6\]](https://github.uconn.edu/rcc02007/ME3264-Lab_03)
Experimentally, we avoid aliasing by sampling above the Nyquist rate from equation 1.
```
N=11
t_collect=10 # time to collect data
t=np.linspace(0,t_collect,1000)
y=np.cos(2*pi*t)
tsample=np.linspace(0,10,N+1)
ysample=np.cos(2*pi*tsample)
plt.figure(20)
plt.plot(t,y,label='signal')
plt.plot(tsample,ysample,'o-',label='measure')
plt.legend(bbox_to_anchor=(1.05, 1), loc=2, borderaxespad=0.)
plt.xlabel('time (s)')
plt.ylabel('a.u.')
```
## Procedure
The procedure and details of the experiment are included in a lab-handout [1].
[ME3264_Lab_5_LVDT.pdf](https://drive.google.com/file/d/1FbykzotAE50SRTujNUjvF9vek97TlJXL/view?usp=sharing)
```
YouTubeVideo('FRWgpFApITo')
```
## Notes on error propagation and uncertainties
## References
1. [ME3264_Lab_5_LVDT.pdf](https://drive.google.com/file/d/1FbykzotAE50SRTujNUjvF9vek97TlJXL/view?usp=sharing)
2. [Measuring Position and Displacement with LVDTs](https://www.ni.com/en-us/innovations/white-papers/06/measuring-position-and-displacement-with-lvdts.html)
3. [Least Squares Fitting](https://mathworld.wolfram.com/LeastSquaresFitting.html)
4. [Linear variable differential transformer, From Wikipedia](https://en.wikipedia.org/wiki/Linear_variable_differential_transformer)
5. [Velocity and position transducers, Richard Crowder, in Electric Drives and Electromechanical Systems (Second Edition), 2020](https://www.sciencedirect.com/science/article/pii/B9780081028841000042)
6. [ME3263-Lab_03, Prof. Ryan Cooper](https://github.uconn.edu/rcc02007/ME3264-Lab_03)
| github_jupyter |
```
import tensorflow as tf
from tensorflow.keras import layers, Model
from tensorflow.keras.activations import relu
from tensorflow.keras.models import Sequential, load_model
from tensorflow.keras.callbacks import ModelCheckpoint, EarlyStopping
from tensorflow.keras.losses import BinaryCrossentropy
from tensorflow.keras.optimizers import RMSprop, Adam
from tensorflow.keras.metrics import binary_accuracy
import tensorflow_datasets as tfds
from tensorflow_addons.layers import InstanceNormalization
import numpy as np
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings('ignore')
print("Tensorflow", tf.__version__)
from packaging.version import parse as parse_version
assert parse_version(tf.__version__) < parse_version("2.4.0"), \
f"Please install TensorFlow version 2.3.1 or older. Your current version is {tf.__version__}."
gpus = tf.config.experimental.list_physical_devices('GPU')
tf.config.experimental.set_visible_devices(gpus[0], 'GPU')
logical_gpus = tf.config.experimental.list_logical_devices('GPU')
print(len(gpus), "Physical GPUs,", len(logical_gpus), "Logical GPU")
ds_train, ds_info = tfds.load('mnist', split='train', shuffle_files=True, with_info=True)
fig = tfds.show_examples(ds_info, ds_train)
batch_size = 400
global_batch_size = batch_size * 1
image_shape = (32, 32, 1)
def preprocess(features):
image = tf.image.resize(features['image'], image_shape[:2])
image = tf.cast(image, tf.float32)
image = (image-127.5)/127.5
label = features['label']
return image, label
ds_train = ds_train.map(preprocess)
ds_train = ds_train.cache() # put dataset into memory
ds_train = ds_train.shuffle(ds_info.splits['train'].num_examples)
ds_train = ds_train.batch(global_batch_size).repeat()
train_num = ds_info.splits['train'].num_examples
train_steps_per_epoch = round(train_num/batch_size)
print(train_steps_per_epoch)
class cDCGAN():
def __init__(self, input_shape):
self.z_dim = 100
self.input_shape = input_shape
self.num_classes = 10
# discriminator
self.n_discriminator = 1
self.discriminator = self.build_discriminator()
self.discriminator.trainable = False
self.optimizer_discriminator = RMSprop(1e-4)
# build generator pipeline with frozen discriminator
self.generator = self.build_generator()
discriminator_output = self.discriminator([self.generator.output, self.generator.input[1]])
self.model = Model(self.generator.input, discriminator_output)
self.model.compile(loss = self.bce_loss,
optimizer = RMSprop(1e-4))
self.discriminator.trainable = True
self.bce = tf.keras.losses.BinaryCrossentropy()
def conv_block(self, channels, kernels, strides=1,
batchnorm=True, activation=True):
model = tf.keras.Sequential()
model.add(layers.Conv2D(channels, kernels, strides=strides, padding='same'))
if batchnorm:
model.add(layers.BatchNormalization())
if activation:
model.add(layers.LeakyReLU(0.2))
return model
def bce_loss(self, y_true, y_pred):
loss = self.bce(y_true, y_pred)
return loss
def build_generator(self):
DIM = 64
input_label = layers.Input(shape=1, dtype=tf.int32, name='ClassLabel')
one_hot_label = tf.one_hot(input_label, self.num_classes)
one_hot_label = layers.Reshape((self.num_classes,))(one_hot_label)
input_z = layers.Input(shape=self.z_dim, name='LatentVector')
x = layers.Concatenate()([input_z, one_hot_label])
x = layers.Dense(4*4*4*DIM, activation=None)(x)
x = layers.Reshape((4,4,4*DIM))(x)
#x = layers.Concatenate()([x, embedding])
x = layers.UpSampling2D((2,2), interpolation="bilinear")(x)
x = self.conv_block(2*DIM, 5)(x)
x = layers.UpSampling2D((2,2), interpolation="bilinear")(x)
x = self.conv_block(DIM, 5)(x)
x = layers.UpSampling2D((2,2), interpolation="bilinear")(x)
output = layers.Conv2D(image_shape[-1], 5, padding='same', activation='tanh')(x)
return Model([input_z, input_label], output)
def build_discriminator(self):
DIM = 64
# label
input_label = layers.Input(shape=[1], dtype =tf.int32, name='ClassLabel')
encoded_label = tf.one_hot(input_label, self.num_classes)
embedding = layers.Dense(32 * 32 * 1, activation=None)(encoded_label)
embedding = layers.Reshape((32, 32, 1))(embedding)
# discriminator
input_image = layers.Input(shape=self.input_shape, name='Image')
x = layers.Concatenate()([input_image, embedding])
x = self.conv_block(DIM, 5, 2, batchnorm=False)(x)
x = self.conv_block(2*DIM, 5, 2)(x)
x = self.conv_block(4*DIM, 5, 2)(x)
x = layers.Flatten()(x)
output = layers.Dense(1, activation='sigmoid')(x)
return Model([input_image, input_label], output)
def train_discriminator(self, real_images, class_labels, batch_size):
real_labels = tf.ones(batch_size)
fake_labels = tf.zeros(batch_size)
g_input = tf.random.normal((batch_size, self.z_dim))
fake_class_labels = tf.random.uniform((batch_size,1), minval=0, maxval=10, dtype=tf.dtypes.int32)
fake_images = self.generator.predict([g_input, fake_class_labels])
with tf.GradientTape() as gradient_tape:
# forward pass
pred_fake = self.discriminator([fake_images, fake_class_labels])
pred_real = self.discriminator([real_images, class_labels])
# calculate losses
loss_fake = self.bce_loss(fake_labels, pred_fake)
loss_real = self.bce_loss(real_labels, pred_real)
# total loss
total_loss = 0.5*(loss_fake + loss_real)
# apply gradients
gradients = gradient_tape.gradient(total_loss, self.discriminator.trainable_variables)
self.optimizer_discriminator.apply_gradients(zip(gradients, self.discriminator.trainable_variables))
return loss_fake, loss_real
def train(self, data_generator, batch_size, steps, interval=100):
val_g_input = tf.random.normal((self.num_classes, self.z_dim))
val_class_labels = np.arange(self.num_classes)
real_labels = tf.ones(batch_size)
for i in range(steps):
real_images, class_labels = next(data_generator)
loss_fake, loss_real = self.train_discriminator(real_images, class_labels, batch_size)
discriminator_loss = 0.5*(loss_fake + loss_real)
# train generator
g_input = tf.random.normal((batch_size, self.z_dim))
fake_class_labels = tf.random.uniform((batch_size, 1),
minval=0, maxval=self.num_classes, dtype=tf.dtypes.int32)
g_loss = self.model.train_on_batch([g_input, fake_class_labels], real_labels)
if i%interval == 0:
msg = "Step {}: discriminator_loss {:.4f} g_loss {:.4f}"\
.format(i, discriminator_loss, g_loss)
print(msg)
fake_images = self.generator.predict([val_g_input,val_class_labels])
self.plot_images(fake_images)
def plot_images(self, images):
grid_row = 1
grid_col = 10
f, axarr = plt.subplots(grid_row, grid_col, figsize=(grid_col*1.5, grid_row*1.5))
for col in range(grid_col):
axarr[col].imshow((images[col,:,:,0]+1)/2, cmap='gray')
axarr[col].axis('off')
plt.show()
def sample_images(self, class_labels):
z = tf.random.normal((len(class_labels), self.z_dim))
images = self.generator.predict([z,class_labels])
self.plot_images(images)
return images
cdcgan = cDCGAN(image_shape)
tf.keras.utils.plot_model(cdcgan.discriminator, show_shapes=True)
tf.keras.utils.plot_model(cdcgan.generator, show_shapes=True)
cdcgan.train(iter(ds_train), batch_size, 2000, 200)
for i in range(5):
images = cdcgan.sample_images(np.array([0,1,2,3,4,5,6,7,8,9]))
```
| github_jupyter |
# 网络参数的初始化
[](https://gitee.com/mindspore/docs/blob/master/docs/mindspore/programming_guide/source_zh_cn/initializer.ipynb) [](https://obs.dualstack.cn-north-4.myhuaweicloud.com/mindspore-website/notebook/master/programming_guide/zh_cn/mindspore_initializer.ipynb) [](https://authoring-modelarts-cnnorth4.huaweicloud.com/console/lab?share-url-b64=aHR0cHM6Ly9vYnMuZHVhbHN0YWNrLmNuLW5vcnRoLTQubXlodWF3ZWljbG91ZC5jb20vbWluZHNwb3JlLXdlYnNpdGUvbm90ZWJvb2svbW9kZWxhcnRzL3Byb2dyYW1taW5nX2d1aWRlL21pbmRzcG9yZV9pbml0aWFsaXplci5pcHluYg==&imageid=65f636a0-56cf-49df-b941-7d2a07ba8c8c)
## 概述
MindSpore提供了权重初始化模块,用户可以通过封装算子和initializer方法来调用字符串、Initializer子类或自定义Tensor等方式完成对网络参数进行初始化。Initializer类是MindSpore中用于进行初始化的基本数据结构,其子类包含了几种不同类型的数据分布(Zero,One,XavierUniform,HeUniform,HeNormal,Constant,Uniform,Normal,TruncatedNormal)。下面针对封装算子和initializer方法两种参数初始化模式进行详细介绍。
## 使用封装算子对参数初始化
MindSpore提供了多种参数初始化的方式,并在部分算子中封装了参数初始化的功能。本节将介绍带有参数初始化功能的算子对参数进行初始化的方法,以`Conv2d`算子为例,分别介绍以字符串,`Initializer`子类和自定义`Tensor`等方式对网络中的参数进行初始化,以下代码示例中均以`Initializer`的子类`Normal`为例,代码示例中`Normal`均可替换成`Initializer`子类中任何一个。
### 字符串
使用字符串对网络参数进行初始化,字符串的内容需要与`Initializer`子类的名称保持一致,使用字符串方式进行初始化将使用`Initializer`子类中的默认参数,例如使用字符串`Normal`等同于使用`Initializer`的子类`Normal()`,代码样例如下:
```
import numpy as np
import mindspore.nn as nn
from mindspore import Tensor
from mindspore.common import set_seed
set_seed(1)
input_data = Tensor(np.ones([1, 3, 16, 50], dtype=np.float32))
net = nn.Conv2d(3, 64, 3, weight_init='Normal')
output = net(input_data)
print(output)
```
### Initializer子类
使用`Initializer`子类对网络参数进行初始化,与使用字符串对参数进行初始化的效果类似,不同的是使用字符串进行参数初始化是使用`Initializer`子类的默认参数,如要使用`Initializer`子类中的参数,就必须使用`Initializer`子类的方式对参数进行初始化,以`Normal(0.2)`为例,代码样例如下:
```
import numpy as np
import mindspore.nn as nn
from mindspore import Tensor
from mindspore.common import set_seed
from mindspore.common.initializer import Normal
set_seed(1)
input_data = Tensor(np.ones([1, 3, 16, 50], dtype=np.float32))
net = nn.Conv2d(3, 64, 3, weight_init=Normal(0.2))
output = net(input_data)
print(output)
```
### 自定义的Tensor
除上述两种初始化方法外,当网络要使用MindSpore中没有的数据类型对参数进行初始化,用户可以通过自定义`Tensor`的方式来对参数进行初始化,代码样例如下:
```
import numpy as np
import mindspore.nn as nn
from mindspore import Tensor
from mindspore import dtype as mstype
weight = Tensor(np.ones([64, 3, 3, 3]), dtype=mstype.float32)
input_data = Tensor(np.ones([1, 3, 16, 50], dtype=np.float32))
net = nn.Conv2d(3, 64, 3, weight_init=weight)
output = net(input_data)
print(output)
```
## 使用initializer方法对参数初始化
在上述代码样例中,给出了如何在网络中进行参数初始化的方法,如在网络中使用nn层封装`Conv2d`算子,参数`weight_init`作为要初始化的数据类型传入`Conv2d`算子,算子会在初始化时通过调用`Parameter`类,进而调用封装在`Parameter`类中的`initializer`方法来完成对参数的初始化。然而有一些算子并没有像`Conv2d`那样在内部对参数初始化的功能进行封装,如`Conv3d`算子的权重就是作为参数传入`Conv3d`算子,此时就需要手动的定义权重的初始化。
当对参数进行初始化时,可以使用`initializer`方法调用`Initializer`子类中不同的数据类型来对参数进行初始化,进而产生不同类型的数据。
使用initializer进行参数初始化时,支持传入的参数有`init`、`shape`、`dtype`:
- `init`:支持传入`Tensor`、 `str`、 `Initializer的子类`。
- `shape`:支持传入`list`、 `tuple`、 `int`。
- `dtype`:支持传入`mindspore.dtype`。
### init参数为Tensor
代码样例如下:
```python
import numpy as np
from mindspore import Tensor
from mindspore import dtype as mstype
from mindspore.common import set_seed
from mindspore.common.initializer import initializer
from mindspore.ops.operations import nn_ops as nps
set_seed(1)
input_data = Tensor(np.ones([16, 3, 10, 32, 32]), dtype=mstype.float32)
weight_init = Tensor(np.ones([32, 3, 4, 3, 3]), dtype=mstype.float32)
weight = initializer(weight_init, shape=[32, 3, 4, 3, 3])
conv3d = nps.Conv3D(out_channel=32, kernel_size=(4, 3, 3))
output = conv3d(input_data, weight)
print(output)
```
输出如下:
```text
[[[[[108 108 108 ... 108 108 108]
[108 108 108 ... 108 108 108]
[108 108 108 ... 108 108 108]
...
[108 108 108 ... 108 108 108]
[108 108 108 ... 108 108 108]
[108 108 108 ... 108 108 108]]
...
[[108 108 108 ... 108 108 108]
[108 108 108 ... 108 108 108]
[108 108 108 ... 108 108 108]
...
[108 108 108 ... 108 108 108]
[108 108 108 ... 108 108 108]
[108 108 108 ... 108 108 108]]]]]
```
### init参数为str
代码样例如下:
```python
import numpy as np
from mindspore import Tensor
from mindspore import dtype as mstype
from mindspore.common import set_seed
from mindspore.common.initializer import initializer
from mindspore.ops.operations import nn_ops as nps
set_seed(1)
input_data = Tensor(np.ones([16, 3, 10, 32, 32]), dtype=mstype.float32)
weight = initializer('Normal', shape=[32, 3, 4, 3, 3], dtype=mstype.float32)
conv3d = nps.Conv3D(out_channel=32, kernel_size=(4, 3, 3))
output = conv3d(input_data, weight)
print(output)
```
输出如下:
```text
[[[[[0 0 0 ... 0 0 0]
[0 0 0 ... 0 0 0]
[0 0 0 ... 0 0 0]]
...
[0 0 0 ... 0 0 0]
[0 0 0 ... 0 0 0]
[0 0 0 ... 0 0 0]]
...
[[0 0 0 ... 0 0 0]
[0 0 0 ... 0 0 0]
[0 0 0 ... 0 0 0]]
...
[0 0 0 ... 0 0 0]
[0 0 0 ... 0 0 0]
[0 0 0 ... 0 0 0]]]]]
```
### init参数为Initializer子类
代码样例如下:
```python
import numpy as np
from mindspore import Tensor
from mindspore import dtype as mstype
from mindspore.common import set_seed
from mindspore.ops.operations import nn_ops as nps
from mindspore.common.initializer import Normal, initializer
set_seed(1)
input_data = Tensor(np.ones([16, 3, 10, 32, 32]), dtype=mstype.float32)
weight = initializer(Normal(0.2), shape=[32, 3, 4, 3, 3], dtype=mstype.float32)
conv3d = nps.Conv3D(out_channel=32, kernel_size=(4, 3, 3))
output = conv3d(input_data, weight)
print(output)
```
```text
[[[[[0 0 0 ... 0 0 0]
[0 0 0 ... 0 0 0]
[0 0 0 ... 0 0 0]]
...
[0 0 0 ... 0 0 0]
[0 0 0 ... 0 0 0]
[0 0 0 ... 0 0 0]]
...
[[0 0 0 ... 0 0 0]
[0 0 0 ... 0 0 0]
[0 0 0 ... 0 0 0]]
...
[0 0 0 ... 0 0 0]
[0 0 0 ... 0 0 0]
[0 0 0 ... 0 0 0]]]]]
```
### 在Parameter中的应用
代码样例如下:
```
import numpy as np
from mindspore import dtype as mstype
from mindspore.common import set_seed
from mindspore.ops import operations as ops
from mindspore import Tensor, Parameter, context
from mindspore.common.initializer import Normal, initializer
set_seed(1)
weight1 = Parameter(initializer('Normal', [5, 4], mstype.float32), name="w1")
weight2 = Parameter(initializer(Normal(0.2), [5, 4], mstype.float32), name="w2")
input_data = Tensor(np.arange(20).reshape(5, 4), dtype=mstype.float32)
net = ops.Add()
output = net(input_data, weight1)
output = net(output, weight2)
print(output)
```
| github_jupyter |
```
import numpy as np
import pandas as pd
# load the contents of a file into a pandas Dataframe
input_file = '/Users/aurelianosancho/Google Drive/Pre_Processing/train.csv'
df_titanic = pd.read_csv(input_file)
```
$\textbf{NOTE}$ Although it is not demonstrated in this section, you must ensure that any feature engineering or imputation that is carried out on the training data is also carried out on the test data.
```
df_titanic.shape
df_titanic.columns
df_titanic.info()
df_titanic.describe()
df_titanic.isnull().sum()
df_titanic.head()
print(df_titanic.index.name)
```
To make the PassengerId attribute the index of the df_titanic dataframe, use the following snippet:
```
df_titanic.set_index("PassengerId", inplace=True)
print(df_titanic.index.name)
df_titanic.head()
# extract the target attribute into its own dataframe
df_titanic_target = df_titanic.loc[:,['Survived']]
# create a dataframe that contains the 10 feature variables
df_titanic_features = df_titanic.drop(['Survived'], axis=1)
df_titanic_target['Survived'].value_counts()
df_titanic_features['Embarked'].value_counts(dropna=False)
# histogram of target variable
%matplotlib inline
import matplotlib.pyplot as plt
df_titanic_target.hist(figsize=(5,5))
df_titanic_features.hist(figsize=(10,10))
# histogram of categorical attribute 'Embarked'
# computed from the output of the value_counts() function
vc = df_titanic_features['Embarked'].value_counts(dropna=False)
vc.plot(kind='bar')
# create a box plot of numeric features.
df_titanic_features.boxplot(figsize=(10,6))
# what features show the strongest correlation with the target variable?
corr_matrix = df_titanic.corr()
corr_matrix['Survived'].sort_values(ascending=False)
# visualize relationship between features using a
# matrix of scatter plots.
from pandas.plotting import scatter_matrix
scatter_matrix(df_titanic, figsize=(12,12))
df_titanic_features.boxplot(column='Age', figsize=(7,7))
# fill missing values with the median
median_age = df_titanic_features['Age'].median()
print (median_age)
28.0
df_titanic_features["Age"].fillna(median_age, inplace=True)
# fill missing values of the Embarked attribute
# with the most common value in the column
embarked_value_counts = df_titanic_features['Embarked'].value_counts(dropna=True)
most_common_value = embarked_value_counts.index[0]
print (most_common_value)
df_titanic_features["Embarked"].fillna(most_common_value, inplace=True)
# create a boolean feature 'CabinIsKnown'
# which will have True if the Cabin column
# does not have missing data
df_titanic_features['CabinIsKnown'] = ~df_titanic_features.Cabin.isnull()
# drop the Cabin column from the dataframe
df_titanic_features.drop(['Cabin'], axis=1, inplace=True)
# display the columns of the dataframe.
print (df_titanic_features.columns.values)
# display number of missing values in the columns
df_titanic_features.isnull().sum()
# create a numeric feature called FamilySize that is
# the sum of the SibSp and Parch features.
df_titanic_features['FamilySize'] = df_titanic_features.SibSp + df_titanic_features.Parch
# generate new categorical feature AgeCategory
bins_age = [0,20,30,40,50,150]
labels_age = ['<20','20-30','30-40','40-50','>50']
df_titanic_features['AgeCategory'] = pd.cut(df_titanic_features.Age,
bins=bins_age,
labels=labels_age,
include_lowest=True)
df_titanic_features.head()
# generate new categorical feature FareCategory
df_titanic_features['FareCategory'] = pd.qcut(df_titanic_features.Fare,
q=4,
labels=['Q1', 'Q2', 'Q3', 'Q4'])
# use one-hot encoding to convert categorical attributes
# into binary numeric attributes
df_titanic_features = pd.get_dummies(df_titanic_features, columns=['Sex','Embarked','CabinIsKnown','AgeCategory','FareCategory'])
# display the columns of the dataframe.
print (df_titanic_features.columns.values)
df_titanic_features.head()
# strong negative correlation between Sex_male and Sex_female.
# one of these can be dropped.
corr_matrix = df_titanic_features[['Sex_male', 'Sex_female']].corr()
print(corr_matrix)
# drop the Name, Ticket, Sex_female, CabinIsKnown_False features
# to get a dataframe that can be used for linear or logistic regression
df_titanic_features_numeric = df_titanic_features.drop(['Name', 'Ticket', 'Sex_female', 'CabinIsKnown_False'], axis=1)
df_titanic_features_numeric.head()
df_titanic_features_numeric.shape
####################### pre-processing Test #######################
input_file = '/Users/aurelianosancho/Google Drive/Pre_Processing/train.csv'
df_titanic_test = pd.read_csv(input_file)
df_titanic_test.set_index("PassengerId", inplace=True)
df_titanic_test_target = df_titanic_test.loc[:,['Survived']]
df_titanic_test_features = df_titanic_test.drop(['Survived'], axis=1)
median_age = df_titanic_test_features['Age'].median()
df_titanic_test_features["Age"].fillna(median_age, inplace=True)
embarked_value_counts = df_titanic_test_features['Embarked'].value_counts(dropna=True)
most_common_value = embarked_value_counts.index[0]
df_titanic_test_features["Embarked"].fillna(most_common_value, inplace=True)
df_titanic_test_features['CabinIsKnown'] = ~df_titanic_test_features.Cabin.isnull()
df_titanic_test_features.drop(['Cabin'], axis=1, inplace=True)
df_titanic_test_features['FamilySize'] = df_titanic_test_features.SibSp + df_titanic_test_features.Parch
bins_age = [0,20,30,40,50,150]
labels_age = ['<20','20-30','30-40','40-50','>50']
df_titanic_test_features['AgeCategory'] = pd.cut(df_titanic_test_features.Age,
bins=bins_age,
labels=labels_age,
include_lowest=True)
df_titanic_test_features['FareCategory'] = pd.qcut(df_titanic_test_features.Fare,
q=4,
labels=['Q1', 'Q2', 'Q3', 'Q4'])
df_titanic_test_features = pd.get_dummies(df_titanic_test_features, columns=['Sex','Embarked','CabinIsKnown','AgeCategory','FareCategory'])
df_titanic_test_features_numeric = df_titanic_test_features.drop(['Name', 'Ticket', 'Sex_female', 'CabinIsKnown_False'], axis=1)
```
* titanic_features_train = df_titanic_features_numeric
* titanic_features_test = df_titanic_test_features_numeric
* titanic_target_train = df_titanic_test_target
* titanic_target_test = df_titanic_target
```
df_titanic_test_features_numeric.shape
titanic_features_train = df_titanic_features_numeric
titanic_features_test = df_titanic_test_features_numeric
titanic_target_train = df_titanic_target
titanic_target_test = df_titanic_test_target
from sklearn.svm import SVC
svc_model = SVC(kernel='rbf', C=1, gamma='auto', probability=True)
svc_model.fit(titanic_features_train, titanic_target_train.values.ravel())
# train a logistic regression model on the diabetes dataset
from sklearn.linear_model import LogisticRegression
logit_model = LogisticRegression(penalty='l2', fit_intercept=True, solver='liblinear')
logit_model.fit(titanic_features_train, titanic_target_train.values.ravel())
# train a decision tree based binary classifier.
from sklearn.tree import DecisionTreeClassifier
dtree_model = DecisionTreeClassifier(max_depth=4)
dtree_model.fit(titanic_features_train, titanic_target_train.values.ravel())
# use the models to create predictions on the diabetes test set
svc_predictions = svc_model.predict(titanic_features_test)
logit_predictions = logit_model.predict(titanic_features_test)
dtree_predictions = dtree_model.predict(titanic_features_test)
# simplistic metric - the percentage of correct predictions
svc_correct = svc_predictions == titanic_target_test.values.ravel()
svc_correct_percent = np.count_nonzero(svc_correct) / svc_predictions.size * 100
logit_correct = logit_predictions == titanic_target_test.values.ravel()
logit_correct_percent = np.count_nonzero(logit_correct) / logit_predictions.size * 100
dtree_correct = dtree_predictions == titanic_target_test.values.ravel()
dtree_correct_percent = np.count_nonzero(dtree_correct) / dtree_predictions.size * 100
print ('SVC', svc_correct_percent, 'Logistic Regression', logit_correct_percent, 'DecisionTree', dtree_correct_percent)
from sklearn.metrics import confusion_matrix
cm_svc = confusion_matrix(titanic_target_test.values.ravel(), svc_predictions)
cm_logit = confusion_matrix(titanic_target_test.values.ravel(), logit_predictions)
cm_dtree = confusion_matrix(titanic_target_test.values.ravel(), dtree_predictions)
cm_svc
cm_logit
cm_dtree
tn_svc, fp_svc, fn_svc, tp_svc = cm_svc.ravel()
tn_logit, fp_logit, fn_logit, tp_logit = cm_logit.ravel()
tn_dtree, fp_dtree, fn_dtree, tp_dtree = cm_dtree.ravel()
print (tn_svc, fp_svc, fn_svc, tp_svc)
print (tn_logit, fp_logit, fn_logit, tp_logit)
print (tn_dtree, fp_dtree, fn_dtree, tp_dtree)
accuracy_svc = (tp_svc + tn_svc) / (tn_svc + fp_svc + fn_svc + tp_svc)
accuracy_logit = (tp_logit + tn_logit) / (tn_logit + fp_logit + fn_logit + tp_logit)
accuracy_dtree = (tp_dtree + tn_dtree) / (tn_dtree + fp_dtree + fn_dtree + tp_dtree)
precision_svc = tp_svc / (tp_svc + fp_svc)
precision_logit = tp_logit / (tp_logit + fp_logit)
precision_dtree = tp_dtree / (tp_dtree + fp_dtree)
recall_svc = tp_svc / (tp_svc + fn_svc)
recall_logit = tp_logit / (tp_svc + fn_logit)
recall_dtree = tp_dtree / (tp_dtree + fn_dtree)
print('Accuracy SVC:',accuracy_svc, 'Accuracy REG:', accuracy_logit, 'Accuracy DTREE:', accuracy_dtree)
print('Precision SVC:',precision_svc, 'Precision REG:',precision_logit, 'Precision DTREE:',precision_dtree)
print('Recall SVC:', recall_svc, 'Recall REG:',recall_logit, 'Recall DTREE:',recall_dtree)
# plot ROC curves for the three classifiers.
# compute prediction probabilities
svc_probabilities = svc_model.predict_proba(titanic_features_test)
logit_probabilities = logit_model.predict_proba(titanic_features_test)
dtree_probabilities = dtree_model.predict_proba(titanic_features_test)
# calculate the FPR and TPR for all thresholds of the SVC model
import sklearn.metrics as metrics
svc_fpr, svc_tpr, svc_thresholds = metrics.roc_curve(titanic_target_test.values.ravel(),
svc_probabilities[:,1],
pos_label=1,
drop_intermediate=False)
logit_fpr, logit_tpr, logit_thresholds = metrics.roc_curve(titanic_target_test.values.ravel(),
logit_probabilities[:,1],pos_label=1,
drop_intermediate=False)
# calculate the FPR and TPR for all thresholds of the decision tree model
dtree_fpr, dtree_tpr, dtree_thresholds = metrics.roc_curve(titanic_target_test.values.ravel(),
dtree_probabilities[:,1],pos_label=1,
drop_intermediate=False)
fig, axes = plt.subplots(1, 3, figsize=(18,6))
axes[0].set_title('ROC curve: SVC model')
axes[0].set_xlabel("True Positive Rate")
axes[0].set_ylabel("False Positive Rate")
axes[0].plot(svc_fpr, svc_tpr)
axes[0].axhline(y=0, color='k')
axes[0].axvline(x=0, color='k')
axes[1].set_title('ROC curve: Logit model')
axes[1].set_xlabel("True Positive Rate")
axes[1].set_ylabel("False Positive Rate")
axes[1].plot(logit_fpr, logit_tpr)
axes[1].axhline(y=0, color='k')
axes[1].axvline(x=0, color='k')
axes[2].set_title('ROC curve: Tree model')
axes[2].set_xlabel("True Positive Rate")
axes[2].set_ylabel("False Positive Rate")
axes[2].plot(dtree_fpr, dtree_tpr)
axes[2].axhline(y=0, color='k')
axes[2].axvline(x=0, color='k')
svc_auc = metrics.auc(svc_fpr, svc_tpr)
logit_auc = metrics.auc(logit_fpr, logit_tpr)
dtree_auc = metrics.auc(dtree_fpr, dtree_tpr)
print (svc_auc, logit_auc, dtree_auc)
```
The following code snippet uses the GridSearchCV class to try different hyperparameter
combinations for a multi-class decision tree classifier on the Iris flowers dataset and returns the hyperparameters that result in the best precision score:
```
# use grid search to find the hyperparameters that result
# in the best accuracy score for a decision tree
# based classifier on the Iris Flowers dataset
from sklearn.model_selection import GridSearchCV
from sklearn.tree import DecisionTreeClassifier
grid_params = {
'criterion': ['gini', 'entropy'],
'splitter': ['best', 'random'],
'max_depth': [2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12],
'min_samples_split': [2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12],
'max_features': ['auto', 'sqrt', 'log2'],
'presort': [True, False]
}
grid_search = GridSearchCV(estimator=DecisionTreeClassifier(),
param_grid=grid_params, scoring='accuracy',
cv=5, n_jobs=-1)
grid_search.fit(titanic_features_train.values, titanic_target_train)
best_parameters = grid_search.best_params_
print(best_parameters)
best_accuracy = grid_search.best_score_
print(best_accuracy)
```
| github_jupyter |
# The BioBB REST API
The **[BioBB REST API](https://mmb.irbbarcelona.org/biobb-api)** allows the execution of the **[BioExcel Building Blocks](https://mmb.irbbarcelona.org/biobb/)** in a remote server.
## Documentation
For an extense documentation section, please go to the **[BioBB REST API website help](https://mmb.irbbarcelona.org/biobb-api/rest)**.
## Settings
### Auxiliar libraries used
* [requests](https://pypi.org/project/requests/): Requests allows you to send *organic, grass-fed* HTTP/1.1 requests, without the need for manual labor.
* [nb_conda_kernels](https://github.com/Anaconda-Platform/nb_conda_kernels): Enables a Jupyter Notebook or JupyterLab application in one conda environment to access kernels for Python, R, and other languages found in other environments.
* [nglview](http://nglviewer.org/#nglview): Jupyter/IPython widget to interactively view molecular structures and trajectories in notebooks.
* [ipywidgets](https://github.com/jupyter-widgets/ipywidgets): Interactive HTML widgets for Jupyter notebooks and the IPython kernel.
* [plotly](https://plot.ly/python/offline/): Python interactive graphing library integrated in Jupyter notebooks.
### Conda Installation and Launch
```console
git clone https://github.com/bioexcel/biobb_REST_API_documentation.git
cd biobb_REST_API_documentation
conda env create -f conda_env/environment.yml
conda activate biobb_REST_API_documentation
jupyter-nbextension enable --py --user widgetsnbextension
jupyter-nbextension enable --py --user nglview
jupyter-notebook biobb_REST_API_documentation/notebooks/biobb_REST_API_documentation.ipynb
```
***
## Index
* [Behaviour](#behaviour)
* [Tools information](#tools_info)
* [List of packages](#list_pckg)
* [List of tools](#list_tools)
* [Tool's properties](#tools_prop)
* [Launch tool](#launch_tool)
* [Retrieve status](#retrieve_status)
* [Retrieve data](#retrieve_data)
* [Sample files](#sample_files)
* [All sample files](#all_sample)
* [Package sample files](#pckg_sample)
* [Tool sample files](#tool_sample)
* [Single sample file](#sample)
* [Examples](#examples)
* [Tools information](#tools_info_ex)
* [List of packages](#list_pckg_ex)
* [List of tools from a specific package](#list_tools_ex)
* [Tool's properties](#tools_prop_ex)
* [Launch tool](#launch_tool_ex)
* [Launch job with a YAML file config](#tool_yml_ex)
* [Launch job with a JSON file config](#tool_json_ex)
* [Launch job with a piython dictionary config](#tool_dict_ex)
* [Retrieve status](#retrieve_status_ex)
* [Retrieve data](#retrieve_data_ex)
* [Practical cases](#practical_cases)
* [Example 1: download PDB file from RSCB database](#example1)
* [Example 2: extract heteroatom from a given structure](#example2)
* [Example 3: extract energy components from a given GROMACS energy file](#example3)
***
<img src="https://bioexcel.eu/wp-content/uploads/2019/04/Bioexcell_logo_1080px_transp.png" alt="Bioexcel2 logo"
title="Bioexcel2 logo" width="400" />
***
<a id="behaviour"></a>
## Behaviour
The **BioBB REST API** works as an asynchronous launcher of jobs, as these jobs can last from a few seconds to several minutes, there are some steps that must be performed for having the complete results of every tool.
**BioExcel Building Blocks** are structured in **[packages and tools](http://mmb.irbbarcelona.org/biobb/availability/source)**. Every call to the **BioBB REST API** executes one single tool and returns the output file(s) related to this specific tool.
<a id="tools_info"></a>
### Tools information
<a id="list_pckg"></a>
#### List of packages
In order to get a complete **list of available packages**, we must do a **GET** request to the following endpoint:
`https://mmb.irbbarcelona.org/biobb-api/rest/v1/launch`
This endpoint returns a **JSON HTTP response** with status `200`. More information in the [BioBB REST API Documentation section](https://mmb.irbbarcelona.org/biobb-api/rest/#/List%20of%20Services/getPckgList).
<a id="list_tools"></a>
#### List of tools
If there is need for a **list of tools for a single package**, we must do a **GET** request to the following endpoint:
`https://mmb.irbbarcelona.org/biobb-api/rest/v1/launch/{package}`
This endpoint returns a **JSON HTTP response** with status `200` or a `404` status if the package id is incorrect. More information in the [BioBB REST API Documentation section](https://mmb.irbbarcelona.org/biobb-api/rest/#/List%20of%20Services/getToolsList).
<a id="tools_prop"></a>
#### Tool's properties
If there is only need for the **information of a single tool**, we must do a **GET** request to the following endpoint:
`https://mmb.irbbarcelona.org/biobb-api/rest/v1/launch/{package}/{tool}`
This endpoint returns a **JSON HTTP response** with status `200` or a `404` status if the package id and / or the tool id are incorrect. The reason for failure should be detailed in the JSON response. More information in the [BioBB REST API Documentation section](https://mmb.irbbarcelona.org/biobb-api/rest/#/Launch%20Tool/getLaunchTool).
<a id="launch_tool"></a>
### Launch tool
For **launching a tool**, we must do a **POST** request to the following endpoint:
`https://mmb.irbbarcelona.org/biobb-api/rest/v1/launch/{package}/{tool}`
In the body of this POST request, **we must add the file(s) needed as input** (included the properties config file in **JSON** or **YAML** format) and the name for the output(s). The detailed list of inputs and outputs with its respectives properties can be found in the **GET** request of this same endpoint.
This endpoint returns a **JSON HTTP response** with the following possible status:
* `303`: **The job has been successfully launched** and the user must save the token provided and follow to the next endpoint (defined in the same JSON response)
* `404`: **There was some error launching the tool.** The reason for failure should be detailed in the JSON response.
* `500`: The job has been launched, but **some internal server error** has occurred during the execution.
More information for a generic call in the [BioBB REST API Documentation section](https://mmb.irbbarcelona.org/biobb-api/rest/#/Launch%20Tool/postLaunchTool). The documentation for all the tools is available in the [BioBB REST API Tools Documentation section](https://mmb.irbbarcelona.org/biobb-api/tools-documentation?docExpansion=none). Interactive examples for all the tools are available in the [BioBB REST API Tools Execution section](https://mmb.irbbarcelona.org/biobb-api/tools-execution).
<a id="retrieve_status"></a>
### Retrieve status
If the previous endpoint returned a `303` status, we must do a **GET** request to the following endpoint providing the given token in the path:
`https://mmb.irbbarcelona.org/biobb-api/rest/v1/retrieve/status/{token}`
This endpoint checks the state of the job and returns a **JSON HTTP response** with the following possible status:
* `200`: **The job has finished successfully** and in the JSON response we can found a list of output files generated by the job with its correspondent id for retrieving them on the next endpoint (defined in the same JSON message).
* `202`: The job is **still running**.
* `404`: **Token incorrect, job unexisting or expired.**
* `500`: Some **internal server error** has occurred during the execution.
More information in the [BioBB REST API Documentation section](https://mmb.irbbarcelona.org/biobb-api/rest/#/Retrieve/getRetrieveStatus).
<a id="retrieve_data"></a>
### Retrieve data
Once the previous endpoint returns a `200` status, the output file(s) are ready for its retrieval, so we must do a **GET** request to the following endpoint providing the given **file id** in the path:
`https://mmb.irbbarcelona.org/biobb-api/rest/v1/retrieve/data/{id}`
This endpoint returns the **requested file** with a `200` status or a `404` status if the provided id is incorrect, the file doesn't exist or it has expired. More information in the [BioBB REST API Documentation section](https://mmb.irbbarcelona.org/biobb-api/rest/#/Retrieve/getRetrieveData).
Note that if we have executed a job that returns multiple output files, a call to this endpoint must be done **for each of the output files** generated by the job.
<a id="sample_files"></a>
### Sample files
The **BioBB REST API** provides sample files for most of the inputs and outputs of each tool. Files can be accessed thought the whole **BioBB REST API** hierarchical range.
<a id="all_sample"></a>
#### All sample files
In order to download **all the sample files**, we must do a **GET** request to the following endpoint:
`https://mmb.irbbarcelona.org/biobb-api/rest/v1/sample`
This endpoint returns the **requested file** with a `200` status. More information in the [BioBB REST API Documentation section](https://mmb.irbbarcelona.org/biobb-api/rest#/Sample%20Files/getSample).
<a id="pckg_sample"></a>
#### Package sample files
In order to download **all the sample files of a package**, we must do a **GET** request to the following endpoint:
`https://mmb.irbbarcelona.org/biobb-api/rest/v1/sample/{package}`
This endpoint returns the **requested file** with a `200` status or a `404` status if the package id is incorrect. More information in the [BioBB REST API Documentation section](https://mmb.irbbarcelona.org/biobb-api/rest#/Sample%20Files/getPackageSample).
<a id="tool_sample"></a>
#### Tool sample files
In order to download **all the sample files of a tool**, we must do a **GET** request to the following endpoint:
`https://mmb.irbbarcelona.org/biobb-api/rest/v1/sample/{package}/{tool}`
This endpoint returns the **requested file** with a `200` status or a `404` status if the package id and / or the tool id are incorrect. The reason for failure should be detailed in the JSON response. More information in the [BioBB REST API Documentation section](https://mmb.irbbarcelona.org/biobb-api/rest#/Sample%20Files/getToolSample).
<a id="sample"></a>
#### Single sample file
In order to download **a single sample file**, we must do a **GET** request to the following endpoint:
`https://mmb.irbbarcelona.org/biobb-api/rest/v1/sample/{package}/{tool}/{id}`
This endpoint returns the **requested file** with a `200` status or a `404` status if the package id and / or the tool id and / or the file id are incorrect. The reason for failure should be detailed in the JSON response. More information in the [BioBB REST API Documentation section](https://mmb.irbbarcelona.org/biobb-api/rest#/Sample%20Files/getSingleSample).
<a id="examples"></a>
## Examples
Below we will do **calls to all the previously defined endpoints** and define some **functions** for make easier the connection to the **BioBB REST API** through **Jupyter Notebook**.
First off, we will import the Python requests and json library and set the root URI for the **BioBB REST API**.
```
import requests
import json
apiURL = "https://mmb.irbbarcelona.org/biobb-api/rest/v1/"
```
<a id="tools_info_ex"></a>
### Tools information
Definition of simple GET / POST request functions and a class Response:
```
# Class for returning response status and json content of a requested URL
class Response:
def __init__(self, status, json):
self.status = status
self.json = json
# Perform GET request
def get_data(url):
r = requests.get(url)
return Response(r.status_code, json.loads(r.text))
# Perform POST request
def post_data(url, d, f):
r = requests.post(url, data = d, files = f)
return Response(r.status_code, json.loads(r.text))
```
<a id="list_pckg_ex"></a>
#### List of packages
For more information about this endpoint, please visit the [BioBB REST API Documentation section](https://mmb.irbbarcelona.org/biobb-api/rest#/List%20of%20Services/getPckgList).
##### Endpoint
**GET** `https://mmb.irbbarcelona.org/biobb-api/rest/v1/launch`
##### Code
```
url = apiURL + 'launch'
response = get_data(url)
print(json.dumps(response.json, indent=2))
```
<a id="list_tools_ex"></a>
#### List of tools from a specific package
For more information about this endpoint, please visit the [BioBB REST API Documentation section](https://mmb.irbbarcelona.org/biobb-api/rest#/List%20of%20Services/getToolsList).
##### Endpoint
**GET** `https://mmb.irbbarcelona.org/biobb-api/rest/v1/launch/{package}`
##### Code
```
package = 'biobb_analysis'
url = apiURL + 'launch/' + package
response = get_data(url)
print(json.dumps(response.json, indent=2))
```
<a id="tools_prop_ex"></a>
#### Tool's properties
For more information about this endpoint, please visit the [BioBB REST API Documentation section](https://mmb.irbbarcelona.org/biobb-api/rest#/Launch%20Tool/getLaunchTool).
##### Endpoint
**GET** `https://mmb.irbbarcelona.org/biobb-api/rest/v1/launch/{package}/{tool}`
##### Code
```
package = 'biobb_analysis'
tool = 'cpptraj_average'
url = apiURL + 'launch/' + package + '/' + tool
response = get_data(url)
print(json.dumps(response.json, indent=2))
```
<a id="launch_tool_ex"></a>
### Launch tool
For more information about this endpoint, please visit the [BioBB REST API Documentation section](https://mmb.irbbarcelona.org/biobb-api/rest#/Launch%20Tool/postLaunchTool). The documentation for all the tools is available in the [BioBB REST API Tools Documentation section](https://mmb.irbbarcelona.org/biobb-api/tools-documentation?docExpansion=none). Interactive examples for all the tools are available in the [BioBB REST API Tools Execution section](https://mmb.irbbarcelona.org/biobb-api/tools-execution).
Definition of functions needed for launch a job:
```
from io import BytesIO
from pathlib import Path
# Function used for encode python dictionary to JSON file
def encode_config(data):
jsonData = json.dumps(data)
binaryData = jsonData.encode()
return BytesIO(binaryData)
# Launch job
def launch_job(url, **kwargs):
data = {}
files = {}
# Fill data (output paths) and files (input files) objects
for key, value in kwargs.items():
# Inputs / Outputs
if type(value) is str:
if key.startswith('input'):
files[key] = (value, open(value, 'rb'))
elif key.startswith('output'):
data[key] = value
elif Path(value).is_file():
files[key] = (value, open(value, 'rb'))
# Properties (in case properties are provided as a dictionary instead of a file)
if type(value) is dict:
files['config'] = ('prop.json', encode_config(value))
# Request URL with data and files
response = post_data(url, data, files)
# Print REST API response
print(json.dumps(response.json, indent=2))
# Save token if status == 303
if response.status == 303:
token = response.json['token']
return token
```
Hereafter we will launch a job on *biobb_analysis.cpptraj_average* tool with the provided *files/* in the files folder of this same repository. The response is a JSON with the status code, the state of the job, a message and a token for checking the job status.
<a id="tool_yml_ex"></a>
#### Launch job with a YAML file config
##### File config
```yaml
properties:
in_parameters:
start: 1
end: -1
step: 1
mask: c-alpha
out_parameters:
format: pdb
```
##### Endpoint
**POST** `https://mmb.irbbarcelona.org/biobb-api/rest/v1/launch/{package}/{tool}`
##### Code
The function below sends POST data and files to the *{package}/{tool}* endpoint. The config properties are sent as a YAML file.
The response is a JSON with the status code, the state of the job, a message and a token that will be used for checking the job status in the next step.
```
# Launch BioBB on REST API with YAML config file
token = launch_job(url = apiURL + 'launch/biobb_analysis/cpptraj_average',
config = 'files/config.yml',
input_top_path = 'files/cpptraj.parm.top',
input_traj_path = 'files/cpptraj.traj.dcd',
output_cpptraj_path = 'output.cpptraj.average.pdb')
```
<a id="tool_json_ex"></a>
#### Launch job with a JSON file config
File config:
```json
{
"in_parameters": {
"start": 1,
"end": -1,
"step": 1,
"mask": "c-alpha"
},
"out_parameters": {
"format": "pdb"
}
}
```
##### Endpoint
**POST** `https://mmb.irbbarcelona.org/biobb-api/rest/v1/launch/{package}/{tool}`
##### Code
The function below sends POST data and files to the *{package}/{tool}* endpoint. The config properties are sent as a JSON file.
The response is a JSON with the status code, the state of the job, a message and a token that will be used for checking the job status in the next step.
```
# Launch BioBB on REST API with JSON config file
token = launch_job(url = apiURL + 'launch/biobb_analysis/cpptraj_average',
config = 'files/config.json',
input_top_path = 'files/cpptraj.parm.top',
input_traj_path = 'files/cpptraj.traj.dcd',
output_cpptraj_path = 'output.cpptraj.average.pdb')
```
<a id="tool_dict_ex"></a>
#### Launch job with a python dictionary config
##### Endpoint
**POST** `https://mmb.irbbarcelona.org/biobb-api/rest/v1/launch/{package}/{tool}`
##### Code
The function below sends POST data and files to the *{package}/{tool}* endpoint. The config properties are sent as a python dictionary embedded in the code.
The response is a JSON with the status code, the state of the job, a message and a token that will be used for checking the job status in the next step.
```
# Launch BioBB on REST API with JSON config file
prop = {
"in_parameters" : {
"start": 1,
"end": -1,
"step": 1,
"mask": "c-alpha"
},
"out_parameters" : {
"format": "pdb"
}
}
token = launch_job(url = apiURL + 'launch/biobb_analysis/cpptraj_average',
config = prop,
input_top_path = 'files/cpptraj.parm.top',
input_traj_path = 'files/cpptraj.traj.dcd',
output_cpptraj_path = 'output.cpptraj.average.pdb')
```
<a id="retrieve_status_ex"></a>
### Retrieve status
For more information about this endpoint, please visit the [BioBB REST API Documentation section](https://mmb.irbbarcelona.org/biobb-api/rest#/Retrieve/getRetrieveStatus).
Definition of functions needed for retrieve the status of a job:
```
import datetime
from time import sleep
# Checks status until a provided "ok" status is returned by the response
def check_status(url, ok, error):
counter = 0
while True:
if counter < 10: slp = 1
if counter >= 10 and counter < 60: slp = 10
if counter >= 60: slp = 60
counter = counter + slp
sleep(slp)
r = requests.get(url)
if r.status_code == ok or r.status_code == error:
return counter
break
# Function that checks the status and parses the reponse JSON for saving the output files in a list
def check_job(token, apiURL):
# define retrieve status URL
url = apiURL + 'retrieve/status/' + token
# check status until job has finished
counter = check_status(url, 200, 500)
# Get content when status = 200
response = get_data(url)
# Save id for the generated output_files
if response.status == 200:
out_files = []
for outf in response.json['output_files']:
item = { 'id': outf['id'], 'name': outf['name'] }
out_files.append(item)
# Print REST API response
print("Total elapsed time: %s" % str(datetime.timedelta(seconds=counter)))
print("REST API JSON response:")
print(json.dumps(response.json, indent=4))
if response.status == 200:
return out_files
else: return None
```
##### Endpoint
**GET** `https://mmb.irbbarcelona.org/biobb-api/rest/v1/retrieve/status/{token}`
##### Code
The function below checks the status of a job and awaits until the response status is `200`. The response is a JSON with the status code, the state of the job, a message, a list with all the generated output files and the date of the expiration of these files. Additionally, the function also provides the elapsed time since the job has been launched until it has finished.
```
# Check job status
out_files = check_job(token, apiURL)
```
<a id="retrieve_data_ex"></a>
### Retrieve data
For more information about this endpoint, please visit the [BioBB REST API Documentation section](https://mmb.irbbarcelona.org/biobb-api/rest#/Retrieve/getRetrieveData).
Definition of functions needed for retrieve the output file(s) generated by a job:
```
# Downloads to disk a file from a given URL
def get_file(url, filename):
r = requests.get(url, allow_redirects=True)
file = open(filename,'wb')
file.write(r.content)
file.close()
# Retrieves all the files provided in the out_files list
def retrieve_data(out_files, apiURL):
if not out_files:
return "No files provided"
for outf in out_files:
get_file(apiURL + 'retrieve/data/' + outf['id'], outf['name'])
```
##### Endpoint
**GET** `https://mmb.irbbarcelona.org/biobb-api/rest/v1/retrieve/data/{id}`
##### Code
The function below makes a single call to the *retrieve/data* endpoint for each output file got in the *retrieve/status* endpoint and save the generated file(s) to disk.
```
# Save generated file(s) to disk
retrieve_data(out_files, apiURL)
```
<a id="practical_cases"></a>
## Practical cases
Now we will execute some Bioexcel Building Blocks through the BioBB REST API and with the results we will do some interactions with other python libraries such as [plotly](https://plot.ly/python/offline/) or [nglview](http://nglviewer.org/#nglview).
<a id="example1"></a>
### Example 1: download PDB file from RSCB database
Launch the *biobb_io.pdb* job that downloads a PDB file from the RSCB database:
```
# Downloading desired PDB file
# Create properties dict and inputs/outputs
downloaded_pdb = '3EBP.pdb'
prop = {
'pdb_code': '3EBP',
'filter': False
}
# Launch bb on REST API
token = launch_job(url = apiURL + 'launch/biobb_io/pdb',
config = prop,
output_pdb_path = downloaded_pdb)
# Check job status
out_files = check_job(token, apiURL)
# Save generated file to disk
retrieve_data(out_files, apiURL)
```
Visualize downloaded PDB in NGLView:
```
import nglview
# Show protein
view = nglview.show_structure_file(downloaded_pdb)
view.add_representation(repr_type='ball+stick', selection='het')
view._remote_call('setSize', target='Widget', args=['','600px'])
view
view.render_image()
view.download_image(filename='ngl1.png')
```
<img src='ngl1.png'></img>
<a id="example2"></a>
### Example 2: extract heteroatom from a given structure
Launch the *biobb_structure_utils.extract_heteroatoms* job that extracts a heteroatom from a PDB file.
```
# Extracting heteroatom from a given structure
# Create properties dict and inputs/outputs
heteroatom = 'CPB.pdb'
prop = {
'heteroatoms': [{
'name': 'CPB'
}]
}
# Launch bb on REST API
token = launch_job(url = apiURL + 'launch/biobb_structure_utils/extract_heteroatoms',
config = prop,
input_structure_path = downloaded_pdb,
output_heteroatom_path = heteroatom)
# Check job status
out_files = check_job(token, apiURL)
# Save generated file to disk
retrieve_data(out_files, apiURL)
```
Visualize generated extracted heteroatom in NGLView:
```
# Show protein
view = nglview.show_structure_file(heteroatom)
view.add_representation(repr_type='ball+stick', selection='het')
view._remote_call('setSize', target='Widget', args=['','600px'])
view
view.render_image()
view.download_image(filename='ngl2.png')
```
<img src='ngl2.png'></img>
<a id="example3"></a>
### Example 3: extract energy components from a given GROMACS energy file
```
# GMXEnergy: Getting system energy by time
# Create prop dict and inputs/outputs
output_min_ene_xvg ='file_min_ene.xvg'
output_min_edr = 'files/1AKI_min.edr'
prop = {
'terms': ["Potential"]
}
# Launch bb on REST API
token = launch_job(url = apiURL + 'launch/biobb_analysis/gmx_energy',
config = prop,
input_energy_path = output_min_edr,
output_xvg_path = output_min_ene_xvg)
# Check job status
out_files = check_job(token, apiURL)
# Save generated file to disk
retrieve_data(out_files, apiURL)
```
Visualize generated energy file in plotly:
```
import plotly
import plotly.graph_objs as go
#Read data from file and filter energy values higher than 1000 Kj/mol^-1
with open(output_min_ene_xvg,'r') as energy_file:
x,y = map(
list,
zip(*[
(float(line.split()[0]),float(line.split()[1]))
for line in energy_file
if not line.startswith(("#","@"))
if float(line.split()[1]) < 1000
])
)
plotly.offline.init_notebook_mode(connected=True)
fig = {
"data": [go.Scatter(x=x, y=y)],
"layout": go.Layout(title="Energy Minimization",
xaxis=dict(title = "Energy Minimization Step"),
yaxis=dict(title = "Potential Energy KJ/mol-1")
)
}
plotly.offline.iplot(fig)
```
| github_jupyter |
An illustration of the metric and non-metric MDS on generated noisy data.
The reconstructed points using the metric MDS and non metric MDS are slightly shifted to avoid overlapping.
#### New to Plotly?
Plotly's Python library is free and open source! [Get started](https://plot.ly/python/getting-started/) by downloading the client and [reading the primer](https://plot.ly/python/getting-started/).
<br>You can set up Plotly to work in [online](https://plot.ly/python/getting-started/#initialization-for-online-plotting) or [offline](https://plot.ly/python/getting-started/#initialization-for-offline-plotting) mode, or in [jupyter notebooks](https://plot.ly/python/getting-started/#start-plotting-online).
<br>We also have a quick-reference [cheatsheet](https://images.plot.ly/plotly-documentation/images/python_cheat_sheet.pdf) (new!) to help you get started!
### Version
```
import sklearn
sklearn.__version__
```
### Imports
```
print(__doc__)
import plotly.plotly as py
import plotly.graph_objs as go
import numpy as np
from sklearn import manifold
from sklearn.metrics import euclidean_distances
from sklearn.decomposition import PCA
```
### Calculations
```
n_samples = 20
seed = np.random.RandomState(seed=3)
X_true = seed.randint(0, 20, 2 * n_samples).astype(np.float)
X_true = X_true.reshape((n_samples, 2))
# Center the data
X_true -= X_true.mean()
similarities = euclidean_distances(X_true)
# Add noise to the similarities
noise = np.random.rand(n_samples, n_samples)
noise = noise + noise.T
noise[np.arange(noise.shape[0]), np.arange(noise.shape[0])] = 0
similarities += noise
mds = manifold.MDS(n_components=2, max_iter=3000, eps=1e-9, random_state=seed,
dissimilarity="precomputed", n_jobs=1)
pos = mds.fit(similarities).embedding_
nmds = manifold.MDS(n_components=2, metric=False, max_iter=3000, eps=1e-12,
dissimilarity="precomputed", random_state=seed, n_jobs=1,
n_init=1)
npos = nmds.fit_transform(similarities, init=pos)
# Rescale the data
pos *= np.sqrt((X_true ** 2).sum()) / np.sqrt((pos ** 2).sum())
npos *= np.sqrt((X_true ** 2).sum()) / np.sqrt((npos ** 2).sum())
# Rotate the data
clf = PCA(n_components=2)
X_true = clf.fit_transform(X_true)
pos = clf.fit_transform(pos)
npos = clf.fit_transform(npos)
```
### Plot Results
```
data = []
p1 = go.Scatter(x=X_true[:, 0], y=X_true[:, 1],
mode='markers+lines',
marker=dict(color='navy', size=10),
line=dict(width=1),
name='True Position')
data.append(p1)
p2 = go.Scatter(x=pos[:, 0], y=pos[:, 1],
mode='markers+lines',
marker=dict(color='turquoise', size=10),
line=dict(width=1),
name='MDS')
data.append(p2)
p3 = go.Scatter(x=npos[:, 0], y=npos[:, 1],
mode='markers+lines',
marker=dict(color='orange', size=10),
line=dict(width=1),
name='NMDS')
data.append(p3)
similarities = similarities.max() / similarities * 100
similarities[np.isinf(similarities)] = 0
# Plot the edges
start_idx, end_idx = np.where(pos)
# a sequence of (*line0*, *line1*, *line2*), where::
# linen = (x0, y0), (x1, y1), ... (xm, ym)
segments = [[X_true[i, :], X_true[j, :]]
for i in range(len(pos)) for j in range(len(pos))]
values = np.abs(similarities)
for i in range(len(segments)):
p4 = go.Scatter(x=[segments[i][0][0],segments[i][1][0]],
y=[segments[i][0][1],segments[i][1][1]],
mode = 'lines',
showlegend=False,
line = dict(
color = 'lightblue',
width = 0.5))
data.append(p4)
layout = go.Layout(xaxis=dict(zeroline=False, showgrid=False,
ticks='', showticklabels=False),
yaxis=dict(zeroline=False, showgrid=False,
ticks='', showticklabels=False),
height=900, hovermode='closest')
fig = go.Figure(data=data, layout=layout)
py.iplot(fig)
```
### License
Author:
Nelle Varoquaux <[email protected]>
License:
BSD
```
from IPython.display import display, HTML
display(HTML('<link href="//fonts.googleapis.com/css?family=Open+Sans:600,400,300,200|Inconsolata|Ubuntu+Mono:400,700" rel="stylesheet" type="text/css" />'))
display(HTML('<link rel="stylesheet" type="text/css" href="http://help.plot.ly/documentation/all_static/css/ipython-notebook-custom.css">'))
! pip install git+https://github.com/plotly/publisher.git --upgrade
import publisher
publisher.publish(
'Multi-Dimensional Scaling.ipynb', 'scikit-learn/plot-mds/', 'Multi-Dimensional Scaling | plotly',
'',
title = 'Multi-Dimensional Scaling | plotly',
name = 'Multi-Dimensional Scaling',
has_thumbnail='true', thumbnail='thumbnail/mds.jpg',
language='scikit-learn', page_type='example_index',
display_as='manifold_learning', order=2,
ipynb= '~Diksha_Gabha/3320')
```
| github_jupyter |
# Web Coverage Service (WCS) Download Example
## Introduction
We'll demonstrate how to download a GeoTIFF data file from a public WCS service using Python 3.
### WCS Data Service
For this demonstration we'll use Landfire (LF_1.4.0): https://www.landfire.gov/data_access.php
For Landfire LF_1.4.0 we see that the base URL is https://landfire.cr.usgs.gov/arcgis/services/Landfire/US_140/MapServer/WCSServer
## WCS Requests
There are three types of WCS requests:
- GetCapabilities
- DescribeCoverage
- GetCoverage
Generally, you first do a GetCapabilities request to obtain high-level information about what data you can ask for from the WCS server.
You then perform a DescribeCoverage request to get information specific to the coverage you want to get data from.
Finally, you perform a GetCoverage to obtain the data itself.
### GetCapabilities
Let's perform a GetCapabilities request on the Landfire WCS server to see what the service can do.
```
import requests
# base WCS server URL
wcs_base_url = "https://landfire.cr.usgs.gov/arcgis/services/Landfire/US_140/MapServer/WCSServer"
# add on to the base WCS server URL to define GetCapabilities URL
wcs_get_capabilities_url = wcs_base_url + "?REQUEST=GetCapabilities&SERVICE=WCS"
# perform an HTTP GET request with the GetCapabilities URL
wcs_get_capabilities_response = requests.get(wcs_get_capabilities_url)
# show the resulting body of the GetCapabilities request
print("GetCapabilities Response:")
print(wcs_get_capabilities_response.text)
```
#### GetCapabilities results
The GetCapabilities request returns a lot of information for us.
We can see that the WCS server supports WCS version `1.0.0`, `1.1.0`, `1.1.1`, and `1.1.2` .
For the purposes of this guide, we're going to stick to WCS 1.0.0.
Within the contents section, we can see all of the available coverages. A coverage is just another word for a data layer.
For this guide, let's pick an arbitrary data layer: `US_VDIST2014`
### DescribeCoverage
We'll use the results we got from GetCoverage to perform a DescribeCoverage request to get more specific information about how to ultimately perform the GetCoverage Operation. We'll use WCS version `1.0.0` with coverage `US_VDIST2014` to perform the request.
```
import requests
# base WCS server URL
wcs_base_url = "https://landfire.cr.usgs.gov/arcgis/services/Landfire/US_140/MapServer/WCSServer"
# add on to the base WCS server URL to define DescribeCoverage URL
wcs_describe_coverage_url = wcs_base_url + "?SERVICE=WCS&VERSION=1.0.0&REQUEST=DescribeCoverage&COVERAGE=US_VDIST2014"
# perform an HTTP GET request with the DescribeCoverage URL
wcs_describe_coverage_response = requests.get(wcs_describe_coverage_url)
# show the resulting body of the DescribeCoverage request
print("DescribeCoverage Response:")
print(wcs_describe_coverage_response.text)
```
#### DescribeCoverage results
From the DescribeCoverage response, we can see information about the available bounding box for the layer, the Coordinate Reference System (CRS), the download data types (e.g. GeoTiff), and more. We'll use this information to help formulate a successful WCS GetCoverage request to download some actual data.
### GetCoverage
With the results from DescribeCoverage, we now know everything we need to know in order to download some data using a GetCoverage request.
One unfortunate aspect of WCS version 1.0.0 is that you must provide the resolution or number of pixels of your downloaded output file; you cannot omit this and simply ask for the download file to be in the native resolution of the source data. This means that you may need to perform some additional math to calculate the native resolution on your own before downloading the file. For the purposes of this tutorial, we'll simply download a 500 by 100 pixel image of the continental United States.
```
import requests
# base WCS server URL
wcs_base_url = "https://landfire.cr.usgs.gov/arcgis/services/Landfire/US_140/MapServer/WCSServer"
# add on to the base WCS server URL to define GetCoverage URL
wcs_get_coverage_url = wcs_base_url + "?SERVICE=WCS&VERSION=1.0.0&REQUEST=GetCoverage&FORMAT=GeoTIFF&COVERAGE=US_VDIST2014&BBOX=-127.98775263969655,22.765446426860603,-65.254445466369276,51.649681015029245&CRS=EPSG:4326&WIDTH=500&HEIGHT=100"
# perform an HTTP GET request with the DescribeCoverage URL
wcs_get_coverage_response = requests.get(wcs_get_coverage_url)
# download the resulting response image to disk
if wcs_get_coverage_response.status_code == 200:
with open("wcs-example.tif", 'wb') as f:
f.write(wcs_get_coverage_response.content)
```
#### GetCoverage results
At this point you should have a downloaded GeoTiff file called `wcs-example.tif`. Once you use the GetCapabilities and DescribeCoverage requests to dial in the types of GetCoverage requests you want to perform, you can simply tweak your GetCoverage requests to perform these types of requests in an automated fashion on your code.
| github_jupyter |
# Python datetime module
We will look at an important standard library, the [datetime library][1] which contains many powerful functions to support date, time and datetime manipulation. Pandas does not rely on this object and instead creates its own, a `Timestamp`, discussed in other notebooks.
The datetime library is part of the standard library, so it comes shipped along with every Python installation. Let's get started by importing it into our namespace.
[1]: https://docs.python.org/3/library/datetime.html
```
import datetime
```
## Create a date, a time and a datetime
The datetime module provides three separate objects for dates, times, and datetimes. Let's use the `date` type to construct a date. It takes three integers, the year, month and day. Here we create the date April 11, 2016.
```
my_date = datetime.date(2016, 4, 11)
my_date
type(my_date)
```
Use the `time` type to construct a time. It takes 4 integers - hours, minutes, seconds, and microseconds (one millionth of a second). Here we create the time 10:54:32.034512
```
my_time = datetime.time(10, 54, 32, 34512)
my_time
type(my_time)
```
Only the hour component is mandatory. For instance, we can create the time 5:44 with this:
```
datetime.time(5, 44)
```
Or you can specify just a particular component of time.
```
datetime.time(second=34)
```
Finally, we can construct a datetime with the `datetime` type, which takes up to 7 parameters - three for the date, and four for the time.
```
my_datetime = datetime.datetime(2016, 4, 11, 10, 54, 32, 34512)
my_datetime
type(my_datetime)
```
### Format changes when printed to the screen
Printing the objects from above to the screen provides a more readable view.
```
print(my_date)
print(my_time)
print(my_datetime)
```
## Attributes of date, time, and datetimes
Each individual component of the date, time, and datetime is available as an attribute.
```
my_date.year
my_date.month
my_date.day
my_time.hour
my_time.minute
my_time.second
my_datetime.day
my_datetime.microsecond
my_date.weekday()
```
## Methods of date, time, and datetimes
Several methods exist for each of these objects. The methods that begin with ISO represent the [International Standards Organization][1] formatting rules for dates, times, and datetimes. The particular standard here is [ISO 8601][2]. Python will return according to this standard.
[1]: https://www.iso.org/home.html
[2]: https://en.wikipedia.org/wiki/ISO_8601
```
my_date.weekday()
my_date.isoformat()
my_date.isocalendar()
my_time.isoformat()
my_datetime.isoformat()
# get the date from a datetime
my_datetime.date()
# get the time from a datetime
my_datetime.time()
```
## Alternate Constructors
You can create dates and datetimes from a single integer which represents the number of seconds since the Unix epoch, January 1, 1970 UTC. UTC is the timezone, [Coordinated Universal Time][1] and is 0 degrees longitude or 5 hours ahead of Easter Standard Time.
Passing the integer 0 to the `fromtimestamp` datetime constructor will return a datetime at the Unix epoch adjusted to your local timezone. If you are located in EST, then you will get returned December 31, 1969 7 p.m.
[1]: https://en.wikipedia.org/wiki/Coordinated_Universal_Time
```
datetime.datetime.fromtimestamp(0)
# 1 billion seconds from the unix epoch
datetime.datetime.fromtimestamp(10 ** 9)
```
The date type also has this constructor, but not time.
```
# also works for date
datetime.date.fromtimestamp(10 ** 9)
```
Can get todays date or datetime:
```
datetime.date.today()
datetime.datetime.now()
```
### Constructing from strings
The `strptime` alternate datetime constructor has the ability to convert a string into a datetime. In addition to the string, you must pass it a specific **format** to alert the constructor which part of the string corresponds to which component of the datetime. There are special character codes called **directives** which must be used to form this correspondence.
## Directives
All the directives can be found in the official [Python documentation for the datetime module][1]. Below are some common ones.
* **%y** - two digit year
* **%Y** - four digit year
* **%m** - Month
* **%d** - Day of the month
* **%H** - Hour (24-hour clock)
* **%I** - Hour (12-hour clock)
* **%M** - Minute
[1]: https://docs.python.org/3/library/datetime.html#strftime-strptime-behavior
### Examples of string parsing to datetimes
The `strptime` alternate constructor stands for string parse time (though it only parses datetimes). You must create a string with the correct directives that represents the format of the date string you are trying to convert to a datetime. For instance, the string '2016-10-22' can use the format '%Y-%m-%d' to parse it correctly.
```
s = '2016-10-22'
fmt = '%Y-%m-%d'
datetime.datetime.strptime(s, fmt)
s = '2016/1/22 5:32:44'
fmt = '%Y/%m/%d %H:%M:%S'
datetime.datetime.strptime(s, fmt)
s = 'January 23, 2019 5:22 PM'
fmt = '%B %d, %Y %H:%M %p'
datetime.datetime.strptime(s, fmt)
s = 'On January the 23rd 2019 at 5:22 PM'
fmt = 'On %B the %drd %Y at %H:%M %p'
datetime.datetime.strptime(s, fmt)
```
### Converting datetimes to string
The **strftime** method converts a date, time, or datetime to a string. It stands for **string format time**. Begin with a date, time, or datetime and use a string with directives to make the conversion.
```
# Convert directly into a string of your choice. Lookup directives online
my_date.strftime("%Y-%m-%d")
# Another more involved directive
my_date.strftime("Remembering back to %A, %B %d, %Y.... What a fantastic day that was.")
```
## Date and Datetime addition
It's possible to add an amount of time to a date or datetime object using the timedelta function. timedelta simply produces some amount of time measured in days, seconds and microseconds. You can then use this object to add to date or datetime objects.
**`timedelta`** objects are constructed with the following definition:
**`timedelta(days=0, seconds=0, microseconds=0, milliseconds=0, minutes=0, hours=0, weeks=0)`**
```
my_timedelta = datetime.timedelta(seconds=5000)
my_timedelta
type(my_timedelta)
# add to datetime
my_datetime + my_timedelta
# original
my_datetime
# add to date
my_date + my_timedelta
# original date. Nothing changed since 5000 seconds wasn't long enough to make an extra day
my_date
# now there is a change
my_date + datetime.timedelta(days = 5)
# add weeks
a = my_datetime + datetime.timedelta(weeks=72, days=4, hours=44)
# the difference between the underlying string representation and the print function
print(a.__repr__())
print(a)
datetime.timedelta(weeks=72, days=4, hours=44)
```
## Third-Party library `dateutil`
For improved datetime handling, you can use [dateutil][1], a more advanced third-party library. Pandas actually uses this library to for its complex date handling. Two of it's most useful features are string parsing and datetime addition.
### Advanced string handling
The `parse` function handles a wide variety of strings. It returns the same datetime type from above. See [many more examples][2] in the documentation.
[1]: https://dateutil.readthedocs.io/en/stable/
[2]: https://dateutil.readthedocs.io/en/stable/examples.html#parse-examples
```
from dateutil.parser import parse
parse('Jan 3, 2003 and 5:22')
```
Pandas uses this under the hood.
```
import pandas as pd
pd.Timestamp('Jan 3, 2003 and 5:22')
```
### Advanced datetime addition
An upgrade to the **`timedelta`** class exists with the **`relativedelta`** class. Check [this stackoverflow][1] post for more detail or see the [documentation for examples][2].
[1]: http://stackoverflow.com/questions/12433233/what-is-the-difference-between-datetime-timedelta-and-dateutil-relativedelta
[2]: https://dateutil.readthedocs.io/en/stable/relativedelta.html#examples
```
from dateutil.relativedelta import relativedelta
```
There are two ways to use it. First, you can pass it two datetimes to find the difference between the two.
```
dt1 = datetime.datetime(2016, 1, 20, 5, 33)
dt2 = datetime.datetime(2018, 3, 20, 6, 22)
relativedelta(dt1, dt2)
```
Second, create an amount of time with the parameters years, months, weeks, days, etc... and then add that to a datetime.
```
rd = relativedelta(months=3)
dt1 + rd
```
| github_jupyter |
```
import numpy as np
import pandas as pd
import time
import os
from pyspark.ml.clustering import KMeans
from pyspark.ml.evaluation import ClusteringEvaluator
from pyspark.ml.linalg import Vectors
from matplotlib import pyplot as plt
from pyspark.sql import SparkSession
# from pyspark.ml.clustering import KMeans, KMeansModel
import networkx as nx # thư viện để tạo, thao tác, học cấu trúc.... của các mạng phức tạp
import seaborn as sns # thư viện để trực quan hóa dữ liệu
sns.set_style('darkgrid', {'axes.facecolor': '.9'})
sns.set_palette(palette='deep')
sns_c = sns.color_palette(palette='deep')
float_formatter = lambda x: "%.6f" % x
np.set_printoptions(formatter={'float_kind':float_formatter})
def draw_graph(G):
pos = nx.spring_layout(G)
nx.draw_networkx_nodes(G, pos, node_size=10)
# nx.draw_networkx_labels(G, pos)
nx.draw_networkx_edges(G, pos, width=0.1, alpha=0.5)
def draw_graph_cluster(G, labels):
pos = nx.spring_layout(G)
nx.draw(
G,
pos,
node_color=node_colors,
node_size=10,
width=0.1,
alpha=0.5,
with_labels=False,
)
def get_node_color(label):
switcher = {
0: 'red',
1: 'blue',
2: 'orange',
3: 'gray',
4: 'violet',
5: 'pink',
6: 'purple',
7: 'brown',
8: 'yellow',
9: 'lime',
10: 'cyan'
}
return switcher.get(label, 'Invalid label')
spark = SparkSession.builder \
.master("local") \
.appName("CLustering") \
.config("spark.some.config.option", "some-value") \
.getOrCreate()
spark
base_path = os.getcwd()
# file_input = base_path + "/facebook_combined.txt"
file_input = base_path + "/ChG-Miner_miner-chem-gene.tsv"
file_input
pdf = pd.read_table(file_input, sep='\t', names=['src', 'dst'])
pdf.head()
pdf = pdf.to_numpy()
G = nx.Graph()
G.add_edges_from(pdf)
len(G.nodes())
len(G.edges())
# adjacency matrix
W = nx.adjacency_matrix(G)
print(W.todense())
# degree matrix
D = np.diag(np.sum(np.array(W.todense()), axis=1))
print(D)
# Laplacian matrix
L = D - W
print(L)
# eigenvalues, eigenvector
eigenvals, eigenvcts = np.linalg.eigh(L)
eigenvcts
eigenvals
eigenvals_sorted_indices = np.argsort(eigenvals)
eigenvals_sorted = eigenvals[eigenvals_sorted_indices]
eigenvals_sorted_indices
eigenvals_sorted
fig, ax = plt.subplots(figsize=(10, 6))
sns.lineplot(x=range(1, eigenvals_sorted_indices.size + 1), y=eigenvals_sorted, ax=ax)
ax.set(title='Sorted Eigenvalues Graph Laplacian', xlabel='index', ylabel=r'$\lambda$')
index_lim = 250
fig, ax = plt.subplots(figsize=(10, 6))
sns.scatterplot(x=range(1, eigenvals_sorted_indices[: index_lim].size + 1), y=eigenvals_sorted[: index_lim], s=80, ax=ax)
sns.lineplot(x=range(1, eigenvals_sorted_indices[: index_lim].size + 1), y=eigenvals_sorted[: index_lim], alpha=0.5, ax=ax)
ax.axvline(x=1, color=sns_c[3], label='zero eigenvalues', linestyle='--')
ax.legend()
ax.set(title=f'Sorted Eigenvalues Graph Laplacian (First {index_lim})', xlabel='index', ylabel=r'$\lambda$')
zero_eigenvals_index = np.argwhere(abs(eigenvals) < 0.02)
zero_eigenvals_index.squeeze()
proj_df = pd.DataFrame(eigenvcts[:, zero_eigenvals_index.squeeze()[206]])
# proj_df = proj_df.transpose()
proj_df = proj_df.rename(columns={0: 'features'})
proj_df
U = []
for x in proj_df['features']:
U.append(Vectors.dense(x))
pdf_train = pd.DataFrame(U, columns=['features'])
df = spark.createDataFrame(pdf_train)
display(df)
# train k-means model
cost = np.zeros(15)
for i in range(2,15):
kmeans = KMeans(k=i, seed=1)
model = kmeans.fit(df)
cost[i] = model.computeCost(df) # requires Spark 2.0 or later
fig, ax = plt.subplots(1,1, figsize =(8,6))
ax.plot(range(2,15),cost[2:15])
ax.set_xlabel('k')
ax.set_ylabel('cost')
plt.show()
# train
kmeans = KMeans(k=9, seed=1)
model = kmeans.fit(df)
# Make predictions
predictions = model.transform(df)
rows = predictions.select("features","prediction").collect()
# Evaluate clustering by computing Silhouette score
evaluator = ClusteringEvaluator()
silhouette = evaluator.evaluate(predictions)
silhouette
rows
node_colors = []
for label in rows:
node_colors.append(get_node_color(label.prediction))
```
| github_jupyter |
# VacationPy
----
#### Note
* Keep an eye on your API usage. Use https://developers.google.com/maps/reporting/gmp-reporting as reference for how to monitor your usage and billing.
* Instructions have been included for each segment. You do not have to follow them exactly, but they are included to help you think through the steps.
```
# Dependencies and Setup
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import requests
import gmaps
import os
# Import API key
from api_keys import g_key
```
### Store Part I results into DataFrame
* Load the csv exported in Part I to a DataFrame
```
# Import World Happiness Report Data 2021
city_data = pd.read_csv("../WeatherPy/city_data.csv")
city_data
```
### Humidity Heatmap
* Configure gmaps.
* Use the Lat and Lng as locations and Humidity as the weight.
* Add Heatmap layer to map.
```
# Configure gmaps
gmaps.configure(api_key=g_key)
# Store 'Lat' and 'Lng' into locations
locations = city_data[["Lat", "Lng"]].astype(float)
humidity = city_data['Humidity']
# Create a Humidity Heatmap
fig = gmaps.figure(center=(0, 0), zoom_level=2)
humidity_heatmap = gmaps.heatmap_layer(locations, weights=humidity,
dissipating=False, max_intensity=100,
point_radius = 1)
fig.add_layer(humidity_heatmap)
fig
```
### Create new DataFrame fitting weather criteria
* Narrow down the cities to fit weather conditions.
* Drop any rows will null values.
```
# Dropna in city_data
city_data_narrowed = city_data.dropna()
# Narrow down the cities to fit weather conditions
city_data_narrowed = city_data_narrowed[(city_data_narrowed['Max Temp'] > 70) & (city_data_narrowed['Max Temp'] < 80)]
city_data_narrowed = city_data_narrowed[city_data_narrowed['Wind Speed'] <= 10]
city_data_narrowed = city_data_narrowed[city_data_narrowed['Cloudiness'] == 0]
city_data_narrowed
```
### Hotel Map
* Store into variable named `hotel_df`.
* Add a "Hotel Name" column to the DataFrame.
* Set parameters to search for hotels with 5000 meters.
* Hit the Google Places API for each city's coordinates.
* Store the first Hotel result into the DataFrame.
* Plot markers on top of the heatmap.
```
# Store into variable named hotel_df
hotel_df = city_data_narrowed
# Add "Hotel Name" column
hotel_df['Hotel Name'] = ""
hotel_df
# Set parameters to search for hotels with 5000 meters
base_url = "https://maps.googleapis.com/maps/api/place/nearbysearch/json?"
params = {"type" : "hotel",
"keyword" : "hotel",
"radius" : 5000,
"key" : g_key}
# Hit the Google Places API for each city's coordinates
# Import time function
import time
# Print header
print('Beginning Data Retrieval')
print('------------------------------------------------------------')
# Loop through the hotel_df Dataframe with the iterrows function
for index, row in hotel_df.iterrows():
lat = row['Lat']
lng = row['Lng']
city_name = row['City']
params['location'] = f'{lat},{lng}'
print('Processing Record for {} (Index {}):'.format(city_name, index))
response = requests.get(base_url, params=params).json()
results = response['results']
try:
hotel_df.loc[index, 'Hotel Name'] = results[0]['name']
print('The closest hotel in {} is {}'.format(city_name, results[0]['name']))
except (KeyError, IndexError):
print('City not found. Skipping...')
print("------------------------------------------------------------")
# Limit waiting time
time.sleep(1)
pass
print("------------------------------------------------------------")
# Print footer
print('------------------------------------------------------------')
print('Data Retrieval Complete ')
print('------------------------------------------------------------')
# NOTE: Do not change any of the code in this cell
# Using the template add the hotel marks to the heatmap
info_box_template = """
<dl>
<dt>Name</dt><dd>{Hotel Name}</dd>
<dt>City</dt><dd>{City}</dd>
<dt>Country</dt><dd>{Country}</dd>
</dl>
"""
# Store the DataFrame Row
# NOTE: be sure to update with your DataFrame name
hotel_info = [info_box_template.format(**row) for index, row in hotel_df.iterrows()]
locations = hotel_df[["Lat", "Lng"]]
# Add marker layer ontop of heat map
markers = gmaps.marker_layer(locations, info_box_content = hotel_info)
fig.add_layer(markers)
# Display figure
fig
```
| github_jupyter |
# Hybrid Recommendations with the Movie Lens Dataset
__Note:__ It is recommended that you complete the companion __als_bqml.ipynb__ notebook before continuing with this __als_bqml_hybrid.ipynb__ notebook. This is, however, not a requirement for this lab as you have the option to bring over the dataset + trained model. If you already have the movielens dataset and trained model you can skip the "Import the dataset and trained model" section.
## Learning Objectives
1. Know extract user and product factors from a BigQuery Matrix Factorizarion Model
2. Know how to format inputs for a BigQuery Hybrid Recommendation Model
```
import os
import tensorflow as tf
PROJECT = "qwiklabs-gcp-04-8722038efd75" # REPLACE WITH YOUR PROJECT ID
# Do not change these
os.environ["PROJECT"] = PROJECT
os.environ["TFVERSION"] = '2.1'
```
## Import the dataset and trained model
In the previous notebook, you imported 20 million movie recommendations and trained an ALS model with BigQuery ML
To save you the steps of having to do so again (if this is a new environment) you can run the below commands to copy over the clean data and trained model.
First create the BigQuery dataset and copy over the data
```
!bq mk movielens
%%bigquery
CREATE OR REPLACE TABLE movielens.ratings AS
SELECT * FROM `cloud-training-demos`.movielens.ratings;
CREATE OR REPLACE TABLE movielens.movies AS
SELECT * FROM `cloud-training-demos`.movielens.movies;
```
Next, copy over the trained recommendation model. Note that if you're project is in the EU you will need to change the location from US to EU below. Note that as of the time of writing you cannot copy models across regions with `bq cp`.
```
%%bash
bq --location=US cp \
cloud-training-demos:movielens.recommender_16 \
movielens.recommender_16
```
Next, ensure the model still works by invoking predictions for movie recommendations:
```
%%bigquery --project $PROJECT
SELECT * FROM
ML.PREDICT(MODEL `movielens.recommender_16`, (
SELECT
movieId, title, 903 AS userId
FROM movielens.movies, UNNEST(genres) g
WHERE g = 'Comedy'
))
ORDER BY predicted_rating DESC
LIMIT 5
```
### Incorporating user and movie information
The matrix factorization approach does not use any information about users or movies beyond what is available from the ratings matrix. However, we will often have user information (such as the city they live, their annual income, their annual expenditure, etc.) and we will almost always have more information about the products in our catalog. How do we incorporate this information in our recommendation model?
The answer lies in recognizing that the user factors and product factors that result from the matrix factorization approach end up being a concise representation of the information about users and products available from the ratings matrix. We can concatenate this information with other information we have available and train a regression model to predict the rating.
### Obtaining user and product factors
We can get the user factors or product factors from ML.WEIGHTS. For example to get the product factors for movieId=96481 and user factors for userId=54192, we would do:
```
%%bigquery --project $PROJECT
SELECT
processed_input,
feature,
TO_JSON_STRING(factor_weights),
intercept
FROM ML.WEIGHTS(MODEL movielens.recommender_16)
WHERE
(processed_input = 'movieId' AND feature = '96481')
OR (processed_input = 'userId' AND feature = '54192')
```
Multiplying these weights and adding the intercept is how we get the predicted rating for this combination of movieId and userId in the matrix factorization approach.
These weights also serve as a low-dimensional representation of the movie and user behavior. We can create a regression model to predict the rating given the user factors, product factors, and any other information we know about our users and products.
### Creating input features
The MovieLens dataset does not have any user information, and has very little information about the movies themselves. To illustrate the concept, therefore, let’s create some synthetic information about users:
```
%%bigquery --project $PROJECT
CREATE OR REPLACE TABLE movielens.users AS
SELECT
userId,
RAND() * COUNT(rating) AS loyalty,
CONCAT(SUBSTR(CAST(userId AS STRING), 0, 2)) AS postcode
FROM
movielens.ratings
GROUP BY userId
```
Input features about users can be obtained by joining the user table with the ML weights and selecting all the user information and the user factors from the weights array.
```
%%bigquery --project $PROJECT
WITH userFeatures AS (
SELECT
u.*,
(SELECT ARRAY_AGG(weight) FROM UNNEST(factor_weights)) AS user_factors
FROM movielens.users u
JOIN ML.WEIGHTS(MODEL movielens.recommender_16) w
ON processed_input = 'userId' AND feature = CAST(u.userId AS STRING)
)
SELECT * FROM userFeatures
LIMIT 5
```
Similarly, we can get product features for the movies data, except that we have to decide how to handle the genre since a movie could have more than one genre. If we decide to create a separate training row for each genre, then we can construct the product features using.
```
%%bigquery --project $PROJECT
WITH productFeatures AS (
SELECT
p.* EXCEPT(genres),
g, (SELECT ARRAY_AGG(weight) FROM UNNEST(factor_weights))
AS product_factors
FROM movielens.movies p, UNNEST(genres) g
JOIN ML.WEIGHTS(MODEL movielens.recommender_16) w
ON processed_input = 'movieId' AND feature = CAST(p.movieId AS STRING)
)
SELECT * FROM productFeatures
LIMIT 5
```
Combining these two WITH clauses and pulling in the rating corresponding the movieId-userId combination (if it exists in the ratings table), we can create the training dataset.
**TODO 1**: Combine the above two queries to get the user factors and product factor for each rating.
```
%%bigquery --project $PROJECT
CREATE OR REPLACE TABLE movielens.hybrid_dataset AS
WITH userFeatures AS (
SELECT
u.*,
(SELECT ARRAY_AGG(weight) FROM UNNEST(factor_weights)) AS user_factors
FROM movielens.users u
JOIN ML.WEIGHTS(MODEL movielens.recommender_16) w
ON processed_input = 'userId' AND feature = CAST(u.userId AS STRING)
# TODO: Place the user features query here
),
productFeatures AS (
SELECT
p.* EXCEPT(genres),
g, (SELECT ARRAY_AGG(weight) FROM UNNEST(factor_weights))
AS product_factors
FROM movielens.movies p, UNNEST(genres) g
JOIN ML.WEIGHTS(MODEL movielens.recommender_16) w
ON processed_input = 'movieId' AND feature = CAST(p.movieId AS STRING)
# TODO: Place the product features query here
)
SELECT
p.* EXCEPT(movieId),
u.* EXCEPT(userId),
rating
FROM productFeatures p, userFeatures u
JOIN movielens.ratings r
ON r.movieId = p.movieId AND r.userId = u.userId
```
One of the rows of this table looks like this:
```
%%bigquery --project $PROJECT
SELECT *
FROM movielens.hybrid_dataset
LIMIT 1
```
Essentially, we have a couple of attributes about the movie, the product factors array corresponding to the movie, a couple of attributes about the user, and the user factors array corresponding to the user. These form the inputs to our “hybrid” recommendations model that builds off the matrix factorization model and adds in metadata about users and movies.
### Training hybrid recommendation model
At the time of writing, BigQuery ML can not handle arrays as inputs to a regression model. Let’s, therefore, define a function to convert arrays to a struct where the array elements are its fields:
```
%%bigquery --project $PROJECT
CREATE OR REPLACE FUNCTION movielens.arr_to_input_16_users(u ARRAY<FLOAT64>)
RETURNS
STRUCT<
u1 FLOAT64,
u2 FLOAT64,
u3 FLOAT64,
u4 FLOAT64,
u5 FLOAT64,
u6 FLOAT64,
u7 FLOAT64,
u8 FLOAT64,
u9 FLOAT64,
u10 FLOAT64,
u11 FLOAT64,
u12 FLOAT64,
u13 FLOAT64,
u14 FLOAT64,
u15 FLOAT64,
u16 FLOAT64
> AS (STRUCT(
u[OFFSET(0)],
u[OFFSET(1)],
u[OFFSET(2)],
u[OFFSET(3)],
u[OFFSET(4)],
u[OFFSET(5)],
u[OFFSET(6)],
u[OFFSET(7)],
u[OFFSET(8)],
u[OFFSET(9)],
u[OFFSET(10)],
u[OFFSET(11)],
u[OFFSET(12)],
u[OFFSET(13)],
u[OFFSET(14)],
u[OFFSET(15)]
));
```
which gives:
```
%%bigquery --project $PROJECT
SELECT movielens.arr_to_input_16_users(u).*
FROM (SELECT
[0., 1., 2., 3., 4., 5., 6., 7., 8., 9., 10., 11., 12., 13., 14., 15.] AS u)
```
We can create a similar function named movielens.arr_to_input_16_products to convert the product factor array into named columns.
**TODO 2**: Create a function that returns named columns from a size 16 product factor array.
```
%%bigquery --project $PROJECT
CREATE OR REPLACE FUNCTION movielens.arr_to_input_16_products(p ARRAY<FLOAT64>)
RETURNS
STRUCT<
p1 FLOAT64,
p2 FLOAT64,
p3 FLOAT64,
p4 FLOAT64,
p5 FLOAT64,
p6 FLOAT64,
p7 FLOAT64,
p8 FLOAT64,
p9 FLOAT64,
p10 FLOAT64,
p11 FLOAT64,
p12 FLOAT64,
p13 FLOAT64,
p14 FLOAT64,
p15 FLOAT64,
p16 FLOAT64
# TODO: Finish building this struct
> AS (STRUCT(
p[OFFSET(0)],
p[OFFSET(1)],
p[OFFSET(2)],
p[OFFSET(3)],
p[OFFSET(4)],
p[OFFSET(5)],
p[OFFSET(6)],
p[OFFSET(7)],
p[OFFSET(8)],
p[OFFSET(9)],
p[OFFSET(10)],
p[OFFSET(11)],
p[OFFSET(12)],
p[OFFSET(13)],
p[OFFSET(14)],
p[OFFSET(15)]
# TODO: Finish building this struct
));
```
Then, we can tie together metadata about users and products with the user factors and product factors obtained from the matrix factorization approach to create a regression model to predict the rating:
```
%%bigquery --project $PROJECT
CREATE OR REPLACE MODEL movielens.recommender_hybrid
OPTIONS(model_type='linear_reg', input_label_cols=['rating'])
AS
SELECT
* EXCEPT(user_factors, product_factors),
movielens.arr_to_input_16_users(user_factors).*,
movielens.arr_to_input_16_products(product_factors).*
FROM
movielens.hybrid_dataset
```
There is no point looking at the evaluation metrics of this model because the user information we used to create the training dataset was fake (not the RAND() in the creation of the loyalty column) -- we did this exercise in order to demonstrate how it could be done. And of course, we could train a dnn_regressor model and optimize the hyperparameters if we want a more sophisticated model. But if we are going to go that far, it might be better to consider using Auto ML tables, covered in the next section.
Copyright 2019 Google Inc. Licensed under the Apache License, Version 2.0 (the "License"); you may not use this file except in compliance with the License. You may obtain a copy of the License at http://www.apache.org/licenses/LICENSE-2.0 Unless required by applicable law or agreed to in writing, software distributed under the License is distributed on an "AS IS" BASIS, WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied. See the License for the specific language governing permissions and limitations under the License.
| github_jupyter |
# Introduction to XGBoost-Spark Cross Validation with GPU
The goal of this notebook is to show you how to levarage GPU to accelerate XGBoost spark cross validatoin for hyperparameter tuning. The best model for the given hyperparameters will be returned.
Here takes the application 'Mortgage' as an example.
A few libraries are required for this notebook:
1. NumPy
2. cudf jar
2. xgboost4j jar
3. xgboost4j-spark jar
#### Import the Required Libraries
```
from ml.dmlc.xgboost4j.scala.spark import XGBoostClassificationModel, XGBoostClassifier
from ml.dmlc.xgboost4j.scala.spark.rapids import CrossValidator
from pyspark.ml.evaluation import MulticlassClassificationEvaluator
from pyspark.ml.tuning import ParamGridBuilder
from pyspark.sql import SparkSession
from pyspark.sql.types import FloatType, IntegerType, StructField, StructType
from time import time
import os
```
As shown above, here `CrossValidator` is imported from package `ml.dmlc.xgboost4j.scala.spark.rapids`, not the spark's `tuning.CrossValidator`.
#### Create a Spark Session
```
spark = SparkSession.builder.appName("mortgage-cv-gpu-python").getOrCreate()
```
#### Specify the Data Schema and Load the Data
```
label = 'delinquency_12'
schema = StructType([
StructField('orig_channel', FloatType()),
StructField('first_home_buyer', FloatType()),
StructField('loan_purpose', FloatType()),
StructField('property_type', FloatType()),
StructField('occupancy_status', FloatType()),
StructField('property_state', FloatType()),
StructField('product_type', FloatType()),
StructField('relocation_mortgage_indicator', FloatType()),
StructField('seller_name', FloatType()),
StructField('mod_flag', FloatType()),
StructField('orig_interest_rate', FloatType()),
StructField('orig_upb', IntegerType()),
StructField('orig_loan_term', IntegerType()),
StructField('orig_ltv', FloatType()),
StructField('orig_cltv', FloatType()),
StructField('num_borrowers', FloatType()),
StructField('dti', FloatType()),
StructField('borrower_credit_score', FloatType()),
StructField('num_units', IntegerType()),
StructField('zip', IntegerType()),
StructField('mortgage_insurance_percent', FloatType()),
StructField('current_loan_delinquency_status', IntegerType()),
StructField('current_actual_upb', FloatType()),
StructField('interest_rate', FloatType()),
StructField('loan_age', FloatType()),
StructField('msa', FloatType()),
StructField('non_interest_bearing_upb', FloatType()),
StructField(label, IntegerType()),
])
features = [ x.name for x in schema if x.name != label ]
# You need to update them to your real paths!
dataRoot = os.getenv("DATA_ROOT", "/data")
train_data = spark.read.parquet(dataRoot + '/mortgage/parquet/train')
trans_data = spark.read.parquet(dataRoot + '/mortgage/parquet/eval')
```
#### Build a XGBoost-Spark CrossValidator
```
# First build a classifier of GPU version using *setFeaturesCols* to set feature columns
params = {
'eta': 0.1,
'gamma': 0.1,
'missing': 0.0,
'treeMethod': 'gpu_hist',
'maxDepth': 10,
'maxLeaves': 256,
'growPolicy': 'depthwise',
'objective': 'binary:logistic',
'minChildWeight': 30.0,
'lambda_': 1.0,
'scalePosWeight': 2.0,
'subsample': 1.0,
'nthread': 1,
'numRound': 100,
'numWorkers': 1,
}
classifier = XGBoostClassifier(**params).setLabelCol(label).setFeaturesCols(features)
# Then build the evaluator and the hyperparameters
evaluator = (MulticlassClassificationEvaluator()
.setLabelCol(label))
param_grid = (ParamGridBuilder()
.addGrid(classifier.maxDepth, [3, 6])
.addGrid(classifier.numRound, [100, 200])
.build())
# Finally the corss validator
cross_validator = (CrossValidator()
.setEstimator(classifier)
.setEvaluator(evaluator)
.setEstimatorParamMaps(param_grid)
.setNumFolds(3))
```
#### Start Cross Validation by Fitting Data to CrossValidator
```
def with_benchmark(phrase, action):
start = time()
result = action()
end = time()
print('{} takes {} seconds'.format(phrase, round(end - start, 2)))
return result
model = with_benchmark('Cross-Validation', lambda: cross_validator.fit(train_data)).bestModel
```
#### Transform On the Best Model
```
def transform():
result = model.transform(trans_data).cache()
result.foreachPartition(lambda _: None)
return result
result = with_benchmark('Transforming', transform)
result.select(label, 'rawPrediction', 'probability', 'prediction').show(5)
```
#### Evaluation
```
accuracy = with_benchmark(
'Evaluation',
lambda: MulticlassClassificationEvaluator().setLabelCol(label).evaluate(result))
print('Accuracy is ' + str(accuracy))
spark.stop()
```
| github_jupyter |
<a href="https://colab.research.google.com/github/ryanlandvater/qIS/blob/main/QuantImmunoSubtraction.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Quantitative Immuno-Subtraction Project
---
```
# %matplotlib notebook
import sys as sys
import pandas as pd #import pandas for file reading
import matplotlib as mpl #import matplotlib for graphing
import matplotlib.pyplot as plt #import plot module
import numpy as np #import numpy for arithmetic fns
import IPython #import IPhython for settings
from IPython import display as dsp #import IPython desplay
# from dsp import clear_output #import clear output for dynamics
dsp.set_matplotlib_formats('svg') # Create vector plots
print("Using Pandas to import data version:\t" + pd.__version__);
# print("Plotting with MatPlotLib version:\t" + mpl.__version__);
print("Using numpy version:\t\t\t" + np.__version__);
```
## Ryan's Curve Fit Playground
---
Begin by defining the relevant functions for non-linear least-squared curve fitting using the Newton-Gauss Method.
### Defining the Partial Differential Equations
1. Normal / Gaussian distribution ($\rho$):
$$ \rho = \frac{\alpha e^{\frac{-(x-\mu)^2}{2\sigma^2}}}{\sqrt{2\pi}\sigma} \ \text{where} \
\begin{aligned}
& \alpha = \text{amplitude} \\
& \mu = \text{mean} \\
& \sigma = \text{standard deviation}
\end{aligned}$$
2. Residuals $r$ for $y$ discrete readings $\left[0\dots N\right]$ taken at locations $x$ ($y_x$)
$$ r_x = \frac{1}{2}\left( y_x - \frac{\alpha e^{\frac{-(x-\mu)^2}{2\sigma^2}}}{\sqrt{2\pi}\sigma}\right)^2\\
r_x = \left[r_0,r_1,r_2,\dots,r_N\right]$$
3. Differentials of residuals with respect to normal distribution parameters:
1. Partial with respect to the amplitude
$$
\frac{\partial r_x}{\partial \alpha} =
\frac{\partial r_x}{\partial \rho_x}\frac{\partial \rho_x}{\partial \alpha} =
-\frac{e^{\frac{-(x-\mu)^2}{2\sigma^2}}}{\sqrt{2\pi}\sigma}\cdot
\left(y_x-\frac{\alpha e^{\frac{-(x-\mu)^2}{2\sigma^2}}}{\sqrt{2\pi}\sigma}\right) \\
\frac{\partial r_x}{\partial \alpha} = \left[\frac{\partial r_0}{\partial \alpha},\frac{\partial r_1}{\partial \alpha},\frac{\partial r_2}{\partial \alpha},\dots,\frac{\partial r_N}{\partial \alpha}\right] $$
2. Partial with respect to the mean
$$
\frac{\partial r_x}{\partial \mu} = \frac{\partial r_x}{\partial \rho_x}\frac{\partial \rho_x}{\partial \mu} = -\frac{\alpha(x-\mu)e^{\frac{-(x-\mu)^2}{2\sigma^2}}}{\sqrt{2\pi}\sigma^3}\cdot
\left(y_x-\frac{\alpha e^{\frac{-(x-\mu)^2}{2\sigma^2}}}{\sqrt{2\pi}\sigma}\right) \\
\frac{\partial r_x}{\partial \mu} = \left[\frac{\partial r_0}{\partial \mu},\frac{\partial r_1}{\partial \mu},\frac{\partial r_2}{\partial \mu},\dots,\frac{\partial r_N}{\partial \mu}\right] $$
3. Partial with respect to the standard deviation
$$
\frac{\partial r_x}{\partial \sigma} = \frac{\partial r_x}{\partial \rho_x}\frac{\partial \rho_x}{\partial \sigma} =
\left(\frac{\alpha e^{\frac{-(x-\mu)^2}{2\sigma^2}}}{\sqrt{2\pi}\sigma^2}-\frac{a(x-m)^2 e^{\frac{-(x-\mu)^2}{2\sigma^2}}}{\sqrt{2\pi}\sigma^4}\right) \cdot
\left(y_x-\frac{\alpha e^{\frac{-(x-\mu)^2}{2\sigma^2}}}{\sqrt{2\pi}\sigma}\right) \\
\frac{\partial r_x}{\partial \sigma} = \left[\frac{\partial r_0}{\partial \sigma},\frac{\partial r_1}{\partial \sigma},\frac{\partial r_2}{\partial \sigma},\dots,\frac{\partial r_N}{\partial \sigma}\right] $$
```
# param[0] = AMPLITUDE
# param[1] = MEAN
# param[2] = STANDARD DEVIATION
def conv_norm_dist(x,p):
result = [0] * len(x)
for p_ in p:
result += p_[0]*np.exp(-pow((x-p_[1]),2)/(2*pow(p_[2],2))) / (np.sqrt(2*np.pi)*p_[2])
return result
def norm_dist(x, p):
result = []
for p_ in p:
result.append(p_[0]*np.exp(-pow((x-p_[1]),2)/(2*pow(p_[2],2))) / (np.sqrt(2*np.pi)*p_[2]))
return result
def d_norm_dist_d_amp(x, p):
result=[]
for p_ in p:
result.append(np.exp(-pow((x-p_[1]),2)/(2*pow(p_[2],2))) / (np.sqrt(2*np.pi)*p_[2]))
return result
def d_norm_dist_d_mean(x, p):
result=[]
for p_ in p:
result.append(p_[0]*(x-p_[1])*np.exp(-pow(x-p_[1],2)/(2*pow(p_[2],2)))/(np.sqrt(2*np.pi)*pow(p_[2],3)))
return result
def d_norm_dist_d_sd(x, p):
result=[]
for p_ in p:
result.append((p_[0]*pow(x-p_[1],2)*np.exp(-pow(x-p_[1],2)/(2*pow(p_[2],2)))/(np.sqrt(2*np.pi)*pow(p_[2],4)))
-(p_[0]*np.exp(-pow(x-p_[1],2)/(2*pow(p_[2],2))) / (np.sqrt(2*np.pi)*pow(p_[2],2))))
return result
# Residuals return two
def residuals(y, x, p):
return 1/2 * pow(y - conv_norm_dist(x,p),2)
# dR/dRho returns
def d_r_d_rho(y,x,params = [3]):
return y - norm_dist(x, params)
def d_r_d_amp(y,x, params = [3]):
return -1 * d_r_d_rho(y,x,params) * d_norm_dist_d_amp(x,params)
def d_r_d_mean(y,x, params = [3]):
return -1 * d_r_d_rho(y,x,params) * d_norm_dist_d_mean(x,params)
def d_r_d_sd(y,x,params = [3]):
return -1 * d_r_d_rho(y,x, params) * d_norm_dist_d_sd(x,params)
# NUMERICAL DERIVATIVES
def num_d_r_d_amp(y,x, params = [3]):
step = params
results = []
for i in range(len(step)):
step[i][0] += 1
results.append(residuals(y,x,[step[i]]) - residuals(y,x,[params[i]]))
return results
def num_d_r_d_mean(y,x, params = [3]):
return residuals(y,x,amp,mean+1,sd) - residuals(y,x,params)
def num_d_r_d_sd(y,x, params = [3]):
return residuals(y,x,amp,mean,sd+1) - residuals(y,x,params)
```
### Class Declarations
---
The following code incapsulates the above functions in an object-oriented manner to provide greater ease of use.
```
class curve:
amp = 1.0
mean = 1.0
sd = 1.0
def __init__(self, init_amp, init_mean, init_sd):
self.amp = init_amp
self.mean = init_mean
self.sd = init_sd
# Generate a normal distribution using the curves parameters
def normal_dist(self, x):
return self.amp*np.exp(-pow((x-self.mean),2)/(2*pow(self.sd,2))) / (np.sqrt(2*np.pi)*self.sd)
# Mathematical differentials
def dR_dRho (self, x, y):
return y - self.normal_dist(x)
def dNorm_dAmp (self, x):
return np.exp(-pow((x-self.mean),2)/(2*pow(self.sd,2))) / (np.sqrt(2*np.pi)*self.sd)
def dNorm_dMean (self, x):
return self.amp*(x-self.mean)*np.exp(-pow(x-self.mean,2)/(2*pow(self.sd,2)))/(np.sqrt(2*np.pi)*pow(self.sd,3))
def dNorm_dSD (self, x):
return (self.amp*pow(x-self.mean,2)*np.exp(-pow(x-self.mean,2)/(2*pow(self.sd,2)))/(np.sqrt(2*np.pi)*pow(self.sd,4)))
-(self.amp*np.exp(-pow(x-self.mean,2)/(2*pow(self.sd,2))) / (np.sqrt(2*np.pi)*pow(self.sd,2)))
def dR_dAmp (self, x, y):
return -1 * self.dR_dRho(x, y) * self.dNorm_dAmp(x)
def dR_dMean (self, x, y):
return -1 * self.dR_dRho(x, y) * self.dNorm_dMean(x)
def dR_dSD (self, x, y):
return -1 * self.dR_dRho(x,y) * self.dNorm_dSD(x)
#Numerical differentials
def ndAmp (self, step, x):
return (self.amp+step)*np.exp(-pow((x-self.mean),2)/(2*pow(self.sd,2))) / (np.sqrt(2*np.pi)*self.sd)
def ndMean (self, step, x):
return self.amp*np.exp(-pow((x-(self.mean+step)),2)/(2*pow(self.sd,2))) / (np.sqrt(2*np.pi)*self.sd)
def ndSD (self, step, x):
return self.amp*np.exp(-pow((x-self.mean),2)/(2*pow((self.sd+step),2))) / (np.sqrt(2*np.pi)*(self.sd+step))
def ndR_ndAmp (self, step, x, y):
return np.power(y - self.ndAmp(step,x),2)/2 - np.power(y - self.normal_dist(x),2)/2
def ndR_ndMean (self, step, x, y):
return np.power(y - self.ndMean(step,x),2)/2 - np.power(y - self.normal_dist(x),2)/2
def ndR_ndSD (self, step, x, y):
return np.power(y - self.ndSD(step,x),2)/2 - np.power(y - self.normal_dist(x),2)/2
class curve_list:
x = 0
y = 0
n_curves = 0 # Number of curves within the list
curves = [] # List of curves
def __init__(self):
n_curves = 0
self.curves = []
def __getitem__(self, _index_) :
return self.curves[_index_]
def set_x_array(self, x):
self.x = x.copy()
def set_y_array(self, y):
self.y = y.copy()
def add_blank_curve(self) :
self.curves.append(curve(1,1,1))
self.n_curves += 1;
def add_curve(self, _curve_) :
self.curves.append(_curve_);
self.n_curves += 1;
def front(self):
return self[0]
def back(self):
return self[self.n_curves-1]
def get_residuals (self):
result = y.copy()
for curve in self.curves:
result -= curve.normal_dist(self.x)
result = 1/2 * np.power(result,2)
return result
def get_jacobian (self):
jacobian = []
for C in self.curves:
y = self.y.copy()
for C_ in self.curves:
if (C_ != C):
y -= C_.normal_dist(self.x)
jacobian.append(C.dR_dAmp(self.x,y))
jacobian.append(C.dR_dMean(self.x,y))
jacobian.append(C.dR_dSD(self.x,y))
return np.array(jacobian)
def get_nJacobian (self, step):
jacobian = []
for C in self.curves:
y = self.y.copy()
for C_ in self.curves:
if (C_ != C):
y -= C_.normal_dist(self.x)
jacobian.append(C.ndR_ndAmp(step,self.x,y))
jacobian.append(C.ndR_ndMean(step,self.x,y))
jacobian.append(C.ndR_ndSD(step,self.x,y))
return np.array(jacobian)
def get_sub_jacobian (self, index):
jacobian = []
jacobian.append(self.curves[index].dR_dAmp(self.x,self.y))
jacobian.append(self.curves[index].dR_dMean(self.x,self.y))
jacobian.append(self.curves[index].dR_dSD(self.x,self.y))
return np.array(jacobian)
def update_curves(self, deltas):
if (len(deltas)%3 != 0):
raise "Error, attempting to update curve parameters with an inappropriate number of features"
c_r = self.get_residuals();
for index in range(0,len(deltas),3):
C = self.curves[int(index/3)]
C.amp -= deltas[index]
C.mean -= deltas[index+1]
C.sd -= deltas[index+2]
u_r = self.get_residuals();
if (np.sum(u_r) > np.sum(c_r)):
for index in range(0,len(deltas),3):
C = self.curves[int(index/3)]
C.amp += deltas[index]
C.mean += deltas[index+1]
C.sd += deltas[index+2]
return False
return True
def update_sub_curve(self, index, deltas):
if (len(deltas) != 3):
raise "Error, this is only for a single curve"
c_r = self.get_residuals();
C = self.curves[index]
C.amp -= deltas[0]
C.mean -= deltas[1]
C.sd -= deltas[2]
# u_r = self.get_residuals();
# if (np.sum(u_r) > np.sum(c_r)):
# C = self.curves[index]
# C.amp += deltas[0]
# C.mean += deltas[1]
# C.sd += deltas[2]
# return False
# return True
def iterator (self):
return range(self.n_curves)
x = np.linspace(0,20,300)
# param = [[5,10,4],[2,4,2]]
# param = [[5,10,2],[3,4,1]]
param = [[3,3,0.5],[2,11,1],[2,14,2],[3,6,1.5,]]
y = conv_norm_dist(x,param);
dy_da = d_norm_dist_d_amp(x,param);
dy_dm = d_norm_dist_d_mean(x,param);
dy_ds = d_norm_dist_d_sd(x,param);
```
Below, a QC test to ensure the proper functioning of the above defined partial differential equations
```
fig, ax = plt.subplots();
# styles = ['-','--','-.']
ax.plot(x, y, '-');
for d_amp in dy_da:
ax.plot(x,d_amp,'-', label='$\partial\ rho / \partial\ amp$', color = 'green');
for d_mean in dy_dm:
ax.plot(x,d_mean,'-', label='$\partial\ rho / \partial\ mean$', color = 'red');
for d_sd in dy_ds:
ax.plot(x,d_sd,'-', label='$\partial\ rho / \partial\ sd$', color = 'purple');
ax.set_xlabel("x")
ax.set_ylabel("y")
ax.set_title("Test functions")
ax.legend()
plt.show()
```
### Initial Estimates and Peak Finding
Root finding methods require initial estimates in most instances. The role of the **peakFinder** class described below is to identify inflection points using the second derivative of the trace.
```
class peakFinder:
class peak:
index = 0
estimate = 1.0
def __init__(self, _index_, _estimate_):
self.index = _index_
self.estimate = _estimate_
peaks = []
inflections = []
def find_peaks (self, x):
index = 0
d_x = x[1:len(x-1)]
d_x2 = d_x[1:len(x-1)]
d_x3 = d_x2[1:len(x-1)]
d_y = np.diff(y)
d_y2 = np.diff(d_y)
d_y3 = np.diff(d_y2)
while index != (len(d_y3)-1):
if d_y3[index] < 0 and d_y3[index+1] > 0:
self.peaks.append(self.peak(index,d_x3[index]))
index+=1
self.inflections = d_y2.copy();
def get_peaks (self):
return self.peaks
def get_inflections(self):
return self.inflections
PF = peakFinder()
PF.find_peaks(x)
d_x = x[1:len(x-1)]
d_x2 = d_x[1:len(x-1)]
d_x3 = d_x2[1:len(x-1)]
d_y = np.diff(y)
d_y2 = np.diff(d_y)
d_y3 = np.diff(d_y2)
mean_est = []
mean_inx = []
index = 0
# while index != len(d_y2):
# if d_y2[index] < 0:
# start = index
# while d_y2[index] < 0:
# index+=1
# min_index = start;
# for sub_i in range(start,index):
# if d_y2[sub_i] < d_y2[min_index]:
# min_index = sub_i;
# mean_inx.append(min_index)
# mean_est.append(d_x2[min_index]);
# else:
# index+=1
#ALTERNATIVE METHODS
while index != (len(d_y3)-1):
if d_y3[index] < 0 and d_y3[index+1] > 0:
mean_inx.append(index)
mean_est.append(d_x3[index])
index+=1
fig, ax = plt.subplots();
ax.plot(x, y, '-');
# ax.plot(d_x, d_y,'-', label = 'dy_dx');
ax2 = plt.twinx()
ax2.plot(d_x2, [0]*d_x2,'--', color = 'green')
ax2.plot(d_x2, d_y2, '-', color = 'red', label = 'inflections');
ax.plot(mean_est, y[mean_inx] , 'o', color = 'orange')
ax2.plot(mean_est, d_y3[mean_inx] , 'o', color = 'red')
ax.set_xlabel("x")
ax.set_ylabel("y")
ax.set_title("Curve Enumeration / Initial Guess")
ax2.legend()
plt.show()
y_rn = y.copy()#+np.random.normal(0,.02,300)
CL = curve_list()
CL.set_x_array(x)
CL.set_y_array(y_rn)
for index in range(0,len(mean_est)) :
CL.add_blank_curve()
C = CL.back()
C.mean = mean_est[index]
C.amp = y_rn[mean_inx[index]]/conv_norm_dist(x,[[1.0,mean_est[index],1.0]])[mean_inx[index]]
y_est = [0] * len(x)
residuals = y_rn.copy()
fig, ax = plt.subplots();
ax.plot(x, y, '-');
for C in CL:
ax.plot(x, C.normal_dist(x),'--', label = 'init estimate');
ax.plot(x, CL.get_residuals(), '-', label = 'residuals');
ax.set_xlabel("x")
ax.set_ylabel("y")
ax.set_title("Test Residuals")
ax.legend()
plt.show()
```
### Defining the Jacobian
The Jacobian matrix is defined as follows:
$$ J = \left[
\begin{aligned}
&\frac{\partial r_0}{\partial \alpha_1},\frac{\partial r_1}{\partial \alpha_1},\frac{\partial r_2}{\partial \alpha_1},\dots,&\frac{\partial r_N}{\partial \alpha_1} \\
&\frac{\partial r_0}{\partial \mu_1},\frac{\partial r_1}{\partial \mu_1},\frac{\partial r_2}{\partial \mu_1},\dots, &\frac{\partial r_N}{\partial \mu_1}\\
&\frac{\partial r_0}{\partial \sigma_1},\frac{\partial r_1}{\partial \sigma_1},\frac{\partial r_2}{\partial \sigma_1},\dots, &\frac{\partial r_N}{\partial \sigma_1}\\
&\vdots &\vdots\\
&\frac{\partial r_0}{\partial \sigma_M},\frac{\partial r_1}{\partial \sigma_M},\frac{\partial r_2}{\partial \sigma_M},\dots, &\frac{\partial r_N}{\partial \sigma_M}
\end{aligned}
\right]
$$
For $M$ curves and $M\cdot3$ vertical entries. The total dimensions of the Jacobian are $[N x 3M]$ where $M*3 \leq N$.
```
# residuals(y,x,(param_est[0][0],param_est[0][1],param_est[0][2]))
np.sum(CL.get_residuals())
fig, ax = plt.subplots(CL.n_curves);
ax[0].set_title("Numerical Jacobians for "+str(len(CL.curves))+" Curves");
ax[CL.n_curves-1].set_xlabel("x")
# J = CL.get_jacobian()
J = CL.get_nJacobian(1.0)
for index in range(0,CL.n_curves):
ax_ = ax[index]
ax_.plot(x, J[index*3], '-', label = 'var = amplitude', color = 'green');
ax_.plot(x, J[index*3+1], '-', label = 'var = mean', color = 'red');
ax_.plot(x, J[index*3+2], '-', label = 'var = standard dev', color = 'purple')
ax_.set_ylabel("$\partial$ error / $\partial var$")
ax[0].legend()
plt.show()
```
The Newton Gauss Method iteratively finds the root of the derivative of the error ($\ ^{dr}/_{d\rho} = 0$) by estimating the change needed in the gaussian ($\Delta\rho$), which in and of itself is a function of $\Delta\alpha$, $\Delta\mu$, and $\Delta\sigma$. The Jacobian is convolved with its transpose ($J^TJ$) to acount for the fact we have calculated partial derivatives, and the Jacobian, multiplied by the residuals (i.e. the gradient $\nabla = J^T\cdot r$), is divided by this matrix.
```
import time
r = CL.get_residuals()
error = [np.sum(r)];
mu = error[0]
step = 1.0
# Figure preparation
fig, ax = plt.subplots();
_disp = dsp.display("", display_id=True)
ax.plot(x, y, '-k');
comb = [0]*len(x)
for C in CL:
comb += C.normal_dist(x)
ax.plot(x, C.normal_dist(x),'--', label = 'Curve Fit');
ax.plot(x, CL.get_residuals(), '-', label = 'Residuals');
ax.plot(x, comb, '-.k')
ax.set_xlabel("x")
ax.set_ylabel("y")
ax.set_title("Curve Fit Solution")
ax.legend()
ax2 = plt.twinx()
ax2.plot(np.linspace(0,x.max(),len(error)),np.log(error), '-.', color = 'red', label = 'Error')
ax2.set_ylabel("Log Cumulative Error")
ax2.legend()
_disp.update(fig)
while True:
_e = error[len(error)-1]
error.append(np.sum(CL.get_residuals()));
J = CL.get_nJacobian(step)
# J = CL.get_jacobian()
JtJ = np.matmul(J,J.transpose())
JtJ_i = np.linalg.inv(JtJ+mu*np.identity(len(JtJ))) # Get psudo-Hessian inverse matrix
g_r = np.matmul(J,r) # Get the gradient
deltas = np.matmul(g_r,JtJ_i) # Multiply the inverse Hessian by gradient
# deltas
if (CL.update_curves(deltas)):
r = CL.get_residuals()
error.append(np.sum(r))
# mu = error[len(error)-1]*0.1
# mu = error[len(error)-2] - error[len(error)-1]
mu /= 3.0
if (step < 1):
step *= 2
total = [0]*len(x)
for CI in range (0,len(CL.curves)):
trace = CL[CI].normal_dist(x)
total += trace
ax.lines[CI+1].set_ydata(trace)
ax.lines[len(CL.curves)+1].set_ydata(CL.get_residuals())
ax.lines[len(CL.curves)+2].set_ydata(total)
ax2.lines[0].set_xdata(np.linspace(0,x.max(),len(error)))
ax2.lines[0].set_ydata(np.log(error))
ax2.set_ylim(np.log(error[len(error)-1])*1.1,np.log(error[0])*1.1)
_disp.update(fig)
else:
mu *= 2
step /= 2
if (step < 1E-15):
break
fig, ax = plt.subplots();
_disp = dsp.display("", display_id=True)
ax.plot(x, y, '-', color = 'black');
for C in CL:
ax.plot(x, C.normal_dist(x),'--', label = 'Curve Fit');
ax.fill_between(x, C.normal_dist(x), alpha = 0.4)
ax.plot(x, CL.get_residuals(), '-', label = 'residuals');
ax.set_xlabel("x")
ax.set_ylabel("y")
ax.set_ylim(0,y_rn.max())
ax.set_title("Fit Results")
ax.legend()
plt.show()
for index in range(0, len(CL.curves)):
C = CL[index]
print("Curve "+ str(index)+" Result:"+
"\n\tAmplitude:\t"+str(C.amp)+
"\n\tMean:\t\t"+str(C.mean)+
"\n\tStdDev:\t\t"+str(C.sd)+"\n\n")
```
| github_jupyter |
<div>
<h1 style="margin-top: 50px; font-size: 33px; text-align: center"> Homework 5 - Visit the Wikipedia hyperlinks graph! </h1>
<br>
<div style="font-weight:200; font-size: 20px; padding-bottom: 15px; width: 100%; text-align: center;">
<right>Maria Luisa Croci, Livia Lilli, Pavan Kumar Alikana</right>
<br>
</div>
<hr>
</div>
# RQ1
```
import pandas as pd
import json
import pickle
from tqdm import tqdm
from collections import defaultdict
from heapq import *
import numpy as np
import collections
import networkx as nx
```
For our first requests, we can use 2 different approaches:
* We can start from the file building a dictionary that describe our graph; we do it because we will need this dictionary for the request 2;
* Or, better, we can use an easy command <b>nx.info</b>, to get all the informations we need.
So let's see!
## Approach 1
Let's start downloading <a href="https://drive.google.com/file/d/1ghPJ4g6XMCUDFQ2JPqAVveLyytG8gBfL/view">Wikicat hyperlink graph</a> .
It is a reduced version of the one we can find on SNAP.
Every row is an <b>edge</b>. The two elements of each row are the <b>nodes</b>, in particular the first is the <b> source</b>, the second represents the <b>destination</b>.
So, our first goal is open and read the file with python, and split each line with the new line charachter.
Then we take all the <i>source nodes</i> for each row, and we put them as keys into our <b>graph</b> dictionary. The values will be all the correspondent destination nodes.
But we have not done! Infact our scope is to analyze the graph, in particular discovering the following informations:
* If it is direct or not;
* The number of nodes;
* The number of edges;
* The average node degree. Is the graph dense?
To do this we want that our dictionary has as keys <u>all the nodes</u>, sources and destinations, and for now we have just the first ones. So we add as new keys all the nodes that are just destinations, putting as values empty lists.
Now we have the dictionary with all the nodes of our graph as keys, and as values there are all the eventual destinations!
```
F = open('wiki-topcats-reduced.txt','r')
all_rows = F.read().split('\n')
graph = {}
for row in all_rows:
row = row.split("\t")
if row[0] not in graph:
try:
graph[row[0]] = [row[1]]
except:
pass
else:
graph[row[0]].append(row[1])
lista = []
for l in graph.values():
lista+= l
for node in lista:
if node not in graph:
graph[node] = []
else:
pass
```
So, what can we say?
* We are in a case of <b>page ranking</b>. So for definition we have nodes representing sources and destinations, with edges with a particular direction. In other words, our graph has a set of edges which are <i>ordered pairs</i> of nodes, and for the graph theory we have a <b>directed graph</b>.
* The number of nodes is <u>461193</u>. It's just the number of keys of our dictionary.
* The number of edges is <u>2645247</u> and it's computed looking at all the lenghts of the <b>adjacency list</b>.
* In graph theory, the <b>degree</b> (or <i>valency</i>) of a vertex of a graph is the number of edges incident to the vertex. We need the <b>average node degree</b>, so we compute the ratio between number of edges and number of nodes. It results <u>5.735661642739591</u>.
#### Number of nodes
```
V = list(graph.keys())
n_nodes = len(V)
n_nodes
```
#### Number of edges
```
n_edges = 0
for l in graph.values():
n_edges += len(l)
n_edges
```
#### Avarage node degree
```
avg_degree = n_edges/n_nodes
avg_degree
```
## Approach 2
Although, since we need the average in and out degree because our graph is directed, we could use an easy command nx.info as follow, in order to obtain the basic informations.
First import the graph from the reduced file of the list of edges indicating with nx.DiGraph that what we want is an oriented graph.
```
graph = nx.read_edgelist("wiki-topcats-reduced.txt", delimiter="\t", create_using=nx.DiGraph())
print(nx.info(graph))
```
**Is the graph dense?**
With the following formula $D=\frac{E}{N(N-1)}$ we obtain a value that could go from 0 up to 1. It measure the probability that any pairs of vertex is connected, so technically if the density is close to 1 the number of edges is close to the maximal number of edges, viceversa if the density is close to 0 we have a graph with only few edges (called sparse graph).
```
nx.density(graph)
```
As we could expect, according to the number of nodes and edges that we already know, the density is very low, so it means that our graph is sparse.
# RQ2
Let's start creating a dictionary called <b>categories</b> where for every category taken from <i>wiki-topcats-categories.txt</i> file, we have the list of all its articles. But attention! We must take into account all the categories that has a number of articles greater than <b>3500</b>. So we filter our dictionary considering the categories with more that 3500 articles. Another, we take just the articles that are the result of the intersection between the set of articles of the category and the articles of our <b>graph</b>; in other words, we don't consider those nodes that are in our graph but not in our categories!
We create also a dictionary called <b>inv_dic</b> that shows for every node (article), a set of all the categories associated.
```
C = open('wiki-topcats-categories.txt','r')
categories = {}
for line in C.readlines():
l = line.split(' ')
cat = l[0].replace("Category:","").replace(";", "")
art = l[1:]
art[-1] = art[-1].replace("\n","")
if len(art) >= 3500:
categories[cat]= set(art).intersection(set(V))
all_set = categories.values()
all_nodes = []
for s in all_set:
all_nodes += s
inv_dic = {}
for node in all_nodes:
for cat in categories:
if node in categories[cat] and node not in inv_dic:
inv_dic[node] = [cat]
elif node in categories[cat] and node in inv_dic and cat not in inv_dic[node]:
inv_dic[node].append(cat)
else:
pass
```
## Block Ranking
Our scope now is, to take in input a category $C_0 = \{article_1, article_2, \dots \}$. Then we want to rank all of the nodes according to the following criterion:
Obtain a <b>block-ranking</b>, where the blocks are represented by the categories.
The first category of the rank, $C_0$, always corresponds to the input category. The order of the remaining categories is given by: $$distance(C_0, C_1) = median(ShortestPath(C_0, C_i))$$
How we do that? At first we create the functions we need.
Our input category is 'Year_of_birth_unknown' for convention because the one with the smaller number of nodes.
* The first function we write is the <b> ShortestPath</b> which takes in input a node (of the input category) and our graph. It computes the distances, using the visit in amplitude of the graph. For this we apply the <b><i>BFS</i></b> algorithm, that consists in searching graph data structures. It starts at the <i>tree root</i> (or some arbitrary node of a graph called <i>search key</i>), and at first it explores all of the neighbor nodes at the present depth prior, moving on to the nodes at the next depth level. The gif below shows this concept.
So the SorthestPath function creates a dictionary where the keys are the nodes (including the input node) and their value are the distances from the node of the input category.
The distance from the node of the input category to itself is written as zero. The others are started as -1, and then eventually incremented.
* Now it's the turn of <b>createDistancesDict</b> function, which take 4 elements as input: the input category, the graph, the <i>categories</i> dictionary and finally the <i>inv_dic</i>. In easy words, it applies the ShortestPath function to every node of the input cateogory creating a dictionary where each key is one of these nodes, and the value is a dictionary where for every other node of the graph there is the distance from the starting node of C0.
* Now we create the <b>dictDistanceCi</b> dictionary, where we wanna show for each category a list of all the distances of the correspondent nodes from the nodes of the input category. Of course we don't need the distances among the nodes of the input cateogory, so we don't consider them.
* A the end of our process, we compute for each category (taken from the precedent dictionary) the <b>median</b> of the correspondent distances. Then we add in an Ordered Dictionary called <b>rank</b> each category with its value of median. So we obtain our <b>BLOCK RANKING</b>.
<img src="https://upload.wikimedia.org/wikipedia/commons/5/5d/Breadth-First-Search-Algorithm.gif">
```
input_category = input()
def ShortestPath(c0, graph):
queue = []
queue.append(c0)
distanceDict = dict()
for node in graph:
distanceDict[node] = -1
distanceDict[c0] = 0
while queue:
vertex = queue.pop(0)
for i in graph[vertex]:
if distanceDict[i] == -1:
queue.append(i)
distanceDict[i] = distanceDict[vertex] + 1
return distanceDict
def calculateMedian(lista):
lung = len(lista)
#ordinata = sorted(lista)
ordinata = lista
if(lung % 2 != 0):
return ordinata[lung/2]
else:
return (ordinata[lung/2]) + (ordinata[lung/2 + 1]) /2
from collections import OrderedDict
import pickle
def createDistancesDict(c0, graph, dizionarioCatNodi, listNode):
#listNode è un dizionario <articolo, [categorie]>
#Prendo come categoria 0 la lista di nodi della categoria 0
Category0 = dizionarioCatNodi[c0]
#Dizionario dove per ogni chiave(articolo in C0) c'è un dizionatio (nodo, distanza) con la distanza verso tutti gli altri nodi
dictDistances = dict()
for node in tqdm(Category0):
try:
dictDistances[node] = ShortestPath(node, graph)
except Exception as e: print(e)
with open("distance_dict.p", 'wb') as handle:
pickle.dump(dictDistances, handle, protocol=pickle.HIGHEST_PROTOCOL)
createDistancesDict(input_category, graph, categories, inv_dic)
with open("distance_dict.p", 'rb') as handle:
dist_dict = pickle.load(handle)
dictDistanceCi = dict()
#inizializzo le distanze da C0 per ogni categoria ad una lista vuota
for cat in categories:
dictDistanceCi[cat] = []
#for every cat the distances of its nodes from nodes of C0
for node in dist_dict:
for node2 in dist_dict[node]:
for cat in inv_dic[node2]:
if cat != inv_dic[node]:
dictDistanceCi[cat].append(dist_dict[node][node2])
with open("dictDistanceCi.p", 'ab') as handle:
pickle.dump(dictDistanceCi, handle, protocol=pickle.HIGHEST_PROTOCOL)
with open("dictDistanceCi.p", 'rb') as handle:
dictDistanceCi = pickle.load(handle)
rank = OrderedDict()
for cat in tqdm(dictDistanceCi):
distance = np.median(dictDistanceCi[cat])
rank[cat] = distance
rank['Year_of_birth_unknown'] = 0
block_rank = {}
for tupla in rank:
block_rank[tupla[0]] = tupla[1]
for el in block_rank:
if block_rank[el] == -1.0:
block_rank[el] = 10000.0
block_rank = sorted(block_rank.items(), key=lambda x: x[1])
block_rank
```
Obtained the Ordered Dictionary <b>rank</b> we notice that there are some categories with median equal to -1. This means that these categories are not reachable from the input category and so the values of distance among their nodes and the input category ones didn't change its initial values -1 associated during the inizialization in the BFS. For this reason we give to them a big value, for example 10000, so that in the block rank they will stay at the end.
## Sorting nodes of category
Once we obtain the <i>block ranking vector</i>, we want to sort the nodes in each category. The way we should sort them is the following...
We have to compute the subgraph induced by $C_0$. Then, for each node, we compute the sum of the weigths of the <b>in-edges</b>. The nodes will be ordered by this score.
The following image explains how to do it for each step.
In other words, we have to consider a category, and for that category we must compute for each node the number of in-edges, but considering just those that have the source of the same category! For example, in the first image, the B node of the category "0" has got 2 in-edges, but only one is from a node of the same category.
<img src="https://raw.githubusercontent.com/CriMenghini/ADM-2018/master/Homework_5/imgs/algorithm.PNG">
For this scope we have created a function called <b>in_edges</b> that implements our idea of sorting, given as input a category.
So we apply this function for each category saving the correspondent dictionary on a file <i>pickle</i>, naming it as <i>"cat_i.p"</i> where i is the index of the i-category. To control the correspondence index-category, we create a dictionary where for each category we have its index; we call it <b>indexing</b>.
What does our <i>in_edge()</i> function do exactly?
Well, we can see that for a node <i>n1</i> of the choosen category, it starts a contator and for every node <i>n2</i> of our graph checks two important things:
* if there is an edge from <i>n2</i> to <i>n1</i>;
* if <i>n2</i>, the source node, is in the same category of <i>n1</i>;
If these 2 points are respected, then it increments the contator of <i>n1</i>.
At the end, it saves in a dictionary each node n1 and its contator, or in other words, the number of its in-edges.
But it's not finished! We want to sort the nodes in the dictionary in base of their values, so we just do it. Now the output is ready!
We have reported as examples some of our dictionaries saved on pickle. In particular you can see that for "the category 7" (that in our block ranking correponds to the <b>Category0</b>).
```
all_cat = list(categories.keys())
def in_edges(cat, graph):
n_cat = categories[cat]
d = {}
for n1 in tqdm(n_cat):
count = 0
for n2 in graph:
if n1 in graph[n2] and n2 in n_cat:
count += 1
d[n1] = count
d = sorted(d.items(), key=lambda x: x[1])
return d
for i in range(len(all_cat)):
dd = in_edges(all_cat[i], graph)
#pickle.dump(dd, open( "cat"+str(i)+".p", "wb" ) )
with open("cat"+str(i)+".p", 'wb') as handle:
pickle.dump(dd, handle, protocol=pickle.HIGHEST_PROTOCOL)
indexing = {}
for i in range(len(all_cat)):
indexing[all_cat[i]] = i
indexing
```
Here there is the indexing dictionary, that occurs to us to find the in_edge dictionary of a particular category, starting from its index.
Here, as promised, we have the dictionary for the category 0 of our block ranking, or in other words, the category7 of our indexing.
For convention we print just a portion of it, in particular a part where we can see the moment where the score changes.
```
with open("cat"+str(7)+".p", 'rb') as handle:
dd7 = pickle.load(handle)
print(dd7[1600:1700])
```
<img src="http://scalar.usc.edu/works/querying-social-media-with-nodexl/media/Network_theoryarticlenetworkonWikipedia1point5deg.jpg" height="200" width="400">
| github_jupyter |
# Multi-wavelength maps
New in version `0.2.1` is the ability for users to instantiate wavelength-dependent maps. Nearly all of the computational overhead in `starry` comes from computing rotation matrices and integrals of the Green's basis functions, which makes it **really** fast to compute light curves at different wavelengths if we simply recycle the results of all of these operations.
By "wavelength-dependent map" we mean a map whose spherical harmonic coefficients are a function of wavelength. Specifically, instead of setting the coefficient at $l, m$ to a scalar value, we can set it to a vector, where each element corresponds to the coefficient in a particular wavelength bin. Let's look at some examples.
## Instantiating multi-wavelength maps
The key is to pass the `nwav` keyword when instantiating a `starry` object. For simplicity, let's do `nwav=3`, corresponding to three wavelength bins.
```
%matplotlib inline
from starry import Map
map = Map(lmax=2, nwav=3)
```
Recall that the map coefficients are now *vectors*. Here's what the coefficient *matrix* now looks like:
```
map.y
```
Each row corresponds to a given spherical harmonic, and each column to a given wavelength bin. Let's set the $Y_{1,0}$ coefficient:
```
map[1, 0] = [0.3, 0.4, 0.5]
```
Here's our new map vector:
```
map.y
```
To visualize the map, we can call `map.show()` as usual, but now we actually get an *animation* showing us what the map looks like at each wavelength.
```
map.show()
```
(*Caveat: the* `map.animate()` *routine is disabled for multi-wavelength maps.*)
Let's set a few more coefficients:
```
map[1, -1] = [0, 0.1, -0.1]
map[2, -1] = [-0.1, -0.2, -0.1]
map[2, 2] = [0.3, 0.2, 0.1]
map.show()
```
OK, our map now has some interesting wavelength-dependent features. Let's compute some light curves! First, a simple phase curve:
```
import numpy as np
theta = np.linspace(0, 360, 1000)
map.axis = [0, 1, 0]
phase_curve = map.flux(theta=theta)
```
Let's plot it. The blue line is the first wavelength bin, the orange line is the second bin, and the green line is the third:
```
import matplotlib.pyplot as pl
%matplotlib inline
fig, ax = pl.subplots(1, figsize=(14, 6))
ax.plot(theta, phase_curve);
ax.set_xlabel(r'$\theta$ (degrees)', fontsize=16)
ax.set_ylabel('Flux', fontsize=16);
```
We can also compute an occultation light curve:
```
xo = np.linspace(-1.5, 1.5, 1000)
light_curve = map.flux(xo=xo, yo=0.2, ro=0.1)
```
Let's plot it. This time we normalize the light curve by the baseline for better plotting, since the map has a different total flux at each wavelength:
```
fig, ax = pl.subplots(1, figsize=(14, 6))
ax.plot(theta, light_curve / light_curve[0]);
ax.set_xlabel('Occultor position', fontsize=16)
ax.set_ylabel('Flux', fontsize=16);
```
As we mentioned above, there's not that much overhead to computing light curves in many different wavelength bins. Check it out:
```
import time
np.random.seed(1234)
def runtime(nwav, N=10):
total_time = 0
xo = np.linspace(-1.5, 1.5, 1000)
for n in range(N):
map = Map(lmax=2, nwav=nwav)
map[:, :] = np.random.randn(9, nwav)
tstart = time.time()
map.flux(xo=xo, yo=0.2, ro=0.1)
total_time += time.time() - tstart
return total_time / N
nwav = np.arange(1, 50)
t = [runtime(n) for n in nwav]
fig, ax = pl.subplots(1, figsize=(14, 7))
ax.plot(nwav, t, '.')
ax.plot(nwav, t, '-', color='C0', lw=1, alpha=0.3)
ax.set_xlabel('nwav', fontsize=16)
ax.set_ylabel('time (s)', fontsize=16);
ax.set_ylim(0, 0.003);
```
| github_jupyter |
## Machine Learning- Exoplanet Exploration
#### Extensive Data Dictionary: https://exoplanetarchive.ipac.caltech.edu/docs/API_kepcandidate_columns.html
Highlightable columns of note are:
* kepoi_name: A KOI is a target identified by the Kepler Project that displays at least one transit-like sequence within Kepler time-series photometry that appears to be of astrophysical origin and initially consistent with a planetary transit hypothesis
* kepler_name: [These names] are intended to clearly indicate a class of objects that have been confirmed or validated as planets—a step up from the planet candidate designation.
* koi_disposition: The disposition in the literature towards this exoplanet candidate. One of CANDIDATE, FALSE POSITIVE, NOT DISPOSITIONED or CONFIRMED.
* koi_pdisposition: The disposition Kepler data analysis has towards this exoplanet candidate. One of FALSE POSITIVE, NOT DISPOSITIONED, and CANDIDATE.
* koi_score: A value between 0 and 1 that indicates the confidence in the KOI disposition. For CANDIDATEs, a higher value indicates more confidence in its disposition, while for FALSE POSITIVEs, a higher value indicates less confidence in that disposition.
```
# # Update sklearn to prevent version mismatches
# !pip install sklearn --upgrade
# # install joblib
# !pip install joblib
```
### Import Dependencies
```
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
# Hide warning messages in notebook
import warnings
warnings.filterwarnings('ignore')
```
# Read the CSV and Perform Basic Data Cleaning
```
# Read/Load CSV file
df = pd.read_csv("exoplanet_data.csv")
# Drop the null columns where all values are null
df = df.dropna(axis='columns', how='all')
# Drop the null rows
df = df.dropna()
df.head()
```
## Basic Statistic Details
```
df.describe()
```
# Select Features (columns)
* Feature Selection: Removing irrelevant feature results in better performing model that is easeir to understands & model runs faster
```
target_names = df["koi_disposition"].unique()
#target_names
print(df["koi_disposition"].unique())
# Assign X (Independant data) and y (Dependant target)
# Set X equal to the entire data set, except for the first column
X = df.iloc[:, 1:]
# X.head()
# Set y equal to the first column
y = df.iloc[:,0].values.reshape(-1, 1)
# y.head()
from sklearn.ensemble import ExtraTreesClassifier
# Search for top 10 features according to feature importances
model = ExtraTreesClassifier()
model.fit(X,y)
model.feature_importances_
# sorted(zip(model.feature_importances_, X), reverse=True)
# Store the top (20) features as a series, using the column headers as the index
top_feat = pd.Series(model.feature_importances_, index=X.columns).nlargest(10)
top_feat
# Set features based on feature importances
X = df[top_feat.index]
# Use `koi_disposition` for the y values
y = df['koi_disposition']
# y = df['koi_disposition'].values.reshape(-1, 1)
```
# Create a Train Test Split
```
from sklearn.model_selection import train_test_split
# Split the data into smaller buckets for training and testing
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=1)
X_train.head()
# X and y Train shape have 5243 rows (80% of data)
X_train.shape, y_train.shape
# X and y Test shape have 1748 rows (20% of data)
X_test.shape, y_test.shape
```
# Pre-processing
Scale the data using the MinMaxScaler
MinMaxScaler:
* A way to normalize the input features/variables
* Features will be transformed into the range
* Scales the range of fetures from 0 to 1
```
from sklearn.preprocessing import MinMaxScaler
# Create a MinMaxScaler model and fit it to the training data
X_scaler = MinMaxScaler().fit(X_train)
# Transform the training and testing data using the X_scaler
X_train_scaled = X_scaler.transform(X_train)
X_test_scaled = X_scaler.transform(X_test)
#print(np.matrix(X_test_scaled))
```
# Train the Model
* Used Random Forest Model
```
from sklearn.ensemble import RandomForestClassifier
# Create a Randome Forest Model
model = RandomForestClassifier(n_estimators=200)
# Train (Fit) the model to the data
model.fit(X_train_scaled, y_train)
# Score/Validate the model using the test data
print(f"Training Data Score: {'%.3f' % model.score (X_train_scaled, y_train)}")
print(f"Testing Data Score: {'%.3f' % model.score(X_test_scaled, y_test) }")
# Printed the r2 score for the test data, testing is lower than training which is good we are not over feeding
```
## Model Accuracy
```
# Predicting the Test set results
y_predic = model.predict(X_test)
# Making the confusion Matrix
from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_test, y_predic)
from sklearn.metrics import accuracy_score
accuracy = accuracy_score(y_test, y_predic)
print('Test Model Accurracy: %.3f' % (accuracy))
```
## Prediction
```
predictions = model.predict(X_test_scaled)
# print(f"first 10 Predictions{predictions[:10].tolist()}")
# print(f"first 10 Actual{y_test[:10].tolist()}")
# Printing into a Dataframe (y_test can't be reshap on top)
df_pred = pd.DataFrame({"Actual":y_test, "Predicted":predictions})
df_pred.head()
```
# Hyperparameter Tuning
Use `GridSearchCV` to tune the model's parameters
```
# Check Random Forest Model parameters that can be used for Tuning
model = RandomForestClassifier()
model
from sklearn.model_selection import GridSearchCV
param_grid = {'max_depth': [1, 5, 15, 25, 35],
'n_estimators': [100, 300, 500, 700, 1000]}
grid = GridSearchCV(model, param_grid, verbose=3)
# Train the model with GridSearch
grid.fit(X_train_scaled, y_train)
# List the best parameters for this dataset
print('Best Parameter: ',grid.best_params_)
# List the best score
print('Best Score: %.3f' % grid.best_score_)
# Score the model
print('Model Score: %.3f' % grid.score(X_test_scaled, y_test))
# Make predictions with the hypertuned model
predictions = grid.predict(X_test_scaled)
df_grid = pd.DataFrame({"Actual":y_test, "Predicted":predictions})
df_grid.head()
# Calculate classification report
# print(np.array(y_test))
from sklearn.metrics import classification_report
print(classification_report(y_test, predictions,
target_names=target_names))
```
# Save the Model
* Using joblib
```
import joblib
filename = 'RandomForestClassifier.sav'
joblib.dump(RandomForestClassifier, filename)
```
| github_jupyter |
```
path = "D:\\School\\Bank_uppg_mockdata.txt"
class DataSource:
def datasource_conn():
text_file = open(path)
if(text_file.readable):
text_file.close()
return [True, "Connection successful"]
text_file.close()
return[False, "Connection unsuccessful"]
def get_all(self):
text_file = open(path)
customer_list = text_file.readlines()
text_file.close()
return customer_list
def update_by_id(self, id, target, input):
flag = True
customer_list = self.get_all()
i = 0
out_customer = ""
for customer in customer_list:
if(customer[0:customer.index(":")] == str(id)):
start_index = customer.index(":")
if(target == "name"):
customer = customer[0:start_index + 1] + input + customer[customer.index(":", start_index + 1):] + "\n"
flag = False
out_customer = customer
elif(target == "pnr"):
start_index = customer.index(":", start_index + 1)
customer = customer[0:start_index + 1] + input + customer[customer.index(":", start_index + 1):] + "\n"
flag = False
out_customer = customer
elif(target == 0):
for x in range(4):
start_index = customer.index(":", start_index + 1)
customer = customer[0:start_index + 1] + input + "\n"
flag = False
out_customer = customer
else:
for x in range(0,target):
start_index = customer.index("#", start_index + 1)
start_index = customer.index(":", start_index + 1)
start_index = customer.index(":", start_index + 1)
customer = customer[0:start_index + 1] + input + customer[customer.index(":", start_index + 1):] + "\n"
flag = False
out_customer = customer
customer_list[i] = customer
i += 1
if(flag):
return -1
text_file = open(path, "w")
for customer in customer_list:
text_file.write(customer)
text_file.close()
return out_customer
def find_by_id(self, id):
customer_list = self.get_all()
for customer in customer_list:
if(customer[0:customer.index(":")] == str(id)):
return customer
return -1
def find_by_pnr(self, pnr):
customer_list = self.get_all()
start_index = 0
for customer in customer_list:
start_index = customer.index(":", start_index + 1)
start_index = customer.index(":", start_index + 1)
print(customer[start_index + 1:customer.index(":", start_index + 1) - 1])
if(customer[start_index:customer.index(":")] == str(pnr)):
return customer
start_index = 0
def remove_by_id(self, id):
text_file = open(path, "r")
customer_list = text_file.readlines()
text_file.close()
i = 0
for customer in customer_list:
if(customer[0:customer.index(":")] == str(id)):
del customer_list[i]
i += 1
text_file = open(path, "w")
for customer in customer_list:
text_file.write(customer)
text_file.close()
def add_customer(self, id, name, pnr, acc_id):
customer = str(id) + ":" + name + ":" + str(pnr) + ":" + str(acc_id) + ":debit account:0.0\n"
customer_list = self.get_all()
customer_list.append(customer)
text_file = open(path, "w")
for customer in customer_list:
text_file.write(customer)
text_file.close()
def add_account(self, id, acc_id):
customer = self.find_by_id(id)
temp_customer = customer
customer = customer[:len(customer) - 1] + "#" + str(acc_id) + ":debit account:0.0\n"
customer_list = self.get_all()
i = 0
for x in customer_list:
if(x == temp_customer):
customer_list[i] = customer
break
i += 1
text_file = open(path, "w")
for customer in customer_list:
text_file.write(customer)
text_file.close()
def remove_account(self, id, acc_id):
customer = self.find_by_id(id)
start_index = 0
for x in range(3):
start_index = customer.index(":", start_index + 1)
if(customer.find(str(acc_id), start_index, customer.index(":", start_index + 1)) != -1):
if("#" in customer):
customer = customer[:start_index] + ":" + customer[customer.index("#") + 1:]
else:
self.remove_by_id(id)
elif("#" in customer[customer.index("#" + str(acc_id), customer.index("#")) + len(str(acc_id)) + 1:]):
start_index = customer.index("#" + str(acc_id), customer.index("#"))
customer = customer[:start_index] + customer[customer.index("#", start_index + 1):]
elif(customer[customer.rindex("#") + 1: customer.index(":", customer.rindex("#"))] == str(acc_id)):
customer = customer[:customer.rindex("#")] + "\n"
else:
return -1
i = 0
customer_list = self.get_all()
for temp_customer in customer_list:
if(temp_customer[0:temp_customer.index(":")] == str(id)):
break
i += 1
customer_list[i] = customer
text_file = open(path, "w")
for customer in customer_list:
text_file.write(customer)
text_file.close()
c = DataSource()
print(c.find_by_pnr(20020218))
```
| github_jupyter |
# Fingerprint Generators
## Creating and using a fingerprint generator
Fingerprint generators can be created by using the functions that return the type of generator desired.
```
from rdkit import Chem
from rdkit.Chem import rdFingerprintGenerator
mol = Chem.MolFromSmiles('CC(O)C(O)(O)C')
generator = rdFingerprintGenerator.GetAtomPairGenerator()
fingerprint = generator.GetSparseCountFingerprint(mol)
non_zero = fingerprint.GetNonzeroElements()
print(non_zero)
```
We can set the parameters for the fingerprint while creating the generator for it.
```
generator = rdFingerprintGenerator.GetAtomPairGenerator(minDistance = 1, maxDistance = 2, includeChirality = False)
fingerprint = generator.GetSparseCountFingerprint(mol)
non_zero = fingerprint.GetNonzeroElements()
print(non_zero)
```
We can provide the molecule dependent arguments while creating the fingerprint.
```
fingerprint = generator.GetSparseCountFingerprint(mol, fromAtoms = [1])
non_zero = fingerprint.GetNonzeroElements()
print(non_zero)
fingerprint = generator.GetSparseCountFingerprint(mol, ignoreAtoms = [1, 5])
non_zero = fingerprint.GetNonzeroElements()
print(non_zero)
```
## Types of fingerprint generators
Currently 4 fingerprint types are supported by fingerprint generators
```
generator = rdFingerprintGenerator.GetAtomPairGenerator()
fingerprint = generator.GetSparseCountFingerprint(mol)
non_zero = fingerprint.GetNonzeroElements()
print("Atom pair", non_zero)
generator = rdFingerprintGenerator.GetMorganGenerator(radius = 3)
fingerprint = generator.GetSparseCountFingerprint(mol)
non_zero = fingerprint.GetNonzeroElements()
print("Morgan", non_zero)
generator = rdFingerprintGenerator.GetRDKitFPGenerator()
fingerprint = generator.GetSparseCountFingerprint(mol)
non_zero = fingerprint.GetNonzeroElements()
print("RDKitFingerprint", non_zero)
generator = rdFingerprintGenerator.GetTopologicalTorsionGenerator()
fingerprint = generator.GetSparseCountFingerprint(mol)
non_zero = fingerprint.GetNonzeroElements()
print("TopologicalTorsion", non_zero)
```
## Invariant generators
It is possible to use a custom invariant generators while creating fingerprints. Invariant generators provide values to be used as invariants for each atom or bond in the molecule and these values affect the generated fingerprint.
```
simpleMol = Chem.MolFromSmiles('CCC')
generator = rdFingerprintGenerator.GetRDKitFPGenerator()
fingerprint = generator.GetSparseCountFingerprint(simpleMol)
non_zero = fingerprint.GetNonzeroElements()
print("RDKitFingerprint", non_zero)
atomInvariantsGen = rdFingerprintGenerator.GetAtomPairAtomInvGen()
generator = rdFingerprintGenerator.GetRDKitFPGenerator(atomInvariantsGenerator = atomInvariantsGen)
fingerprint = generator.GetSparseCountFingerprint(simpleMol)
non_zero = fingerprint.GetNonzeroElements()
print("RDKitFingerprint", non_zero)
```
Currently avaliable invariants generators are:
```
atomInvariantsGen = rdFingerprintGenerator.GetAtomPairAtomInvGen()
generator = rdFingerprintGenerator.GetMorganGenerator(radius = 3, atomInvariantsGenerator = atomInvariantsGen)
fingerprint = generator.GetSparseCountFingerprint(mol)
non_zero = fingerprint.GetNonzeroElements()
print("Morgan with AtomPairAtomInvGen", non_zero)
atomInvariantsGen = rdFingerprintGenerator.GetMorganAtomInvGen()
generator = rdFingerprintGenerator.GetMorganGenerator(radius = 3, atomInvariantsGenerator = atomInvariantsGen)
fingerprint = generator.GetSparseCountFingerprint(mol)
non_zero = fingerprint.GetNonzeroElements()
# Default for Morgan FP
print("Morgan with MorganAtomInvGen", non_zero)
atomInvariantsGen = rdFingerprintGenerator.GetMorganFeatureAtomInvGen()
generator = rdFingerprintGenerator.GetMorganGenerator(radius = 3, atomInvariantsGenerator = atomInvariantsGen)
fingerprint = generator.GetSparseCountFingerprint(mol)
non_zero = fingerprint.GetNonzeroElements()
print("Morgan with MorganFeatureAtomInvGen", non_zero)
atomInvariantsGen = rdFingerprintGenerator.GetRDKitAtomInvGen()
generator = rdFingerprintGenerator.GetMorganGenerator(radius = 3, atomInvariantsGenerator = atomInvariantsGen)
fingerprint = generator.GetSparseCountFingerprint(mol)
non_zero = fingerprint.GetNonzeroElements()
print("Morgan with RDKitAtomInvGen", non_zero)
bondInvariantsGen = rdFingerprintGenerator.GetMorganBondInvGen()
generator = rdFingerprintGenerator.GetMorganGenerator(radius = 3, bondInvariantsGenerator = bondInvariantsGen)
fingerprint = generator.GetSparseCountFingerprint(mol)
non_zero = fingerprint.GetNonzeroElements()
# Default for Morgan FP
print("Morgan with MorganBondInvGen", non_zero)
```
## Custom Invariants
It is also possible to provide custom invariants instead of using a invariants generator
```
generator = rdFingerprintGenerator.GetAtomPairGenerator()
fingerprint = generator.GetSparseCountFingerprint(simpleMol)
non_zero = fingerprint.GetNonzeroElements()
print(non_zero)
customAtomInvariants = [1, 1, 1]
fingerprint = generator.GetSparseCountFingerprint(simpleMol, customAtomInvariants = customAtomInvariants)
non_zero = fingerprint.GetNonzeroElements()
print(non_zero)
```
## Convenience functions
## Bulk fingerprint
| github_jupyter |
# Part 3: Launch a Grid Network Locally
In this tutorial, you'll learn how to deploy a grid network into a local machine and then interact with it using PySyft.
_WARNING: Grid nodes publish datasets online and are for EXPERIMENTAL use only. Deploy nodes at your own risk. Do not use OpenGrid with any data/models you wish to keep private._
In order to run an grid network locally you will need to run two different apps: a grid gateway and one or more grid workers. In this tutorial we will use the websocket app available [here](https://github.com/OpenMined/PyGrid/tree/dev/app/websocket) to start the grid workers.
## Starting the Grid Gateway
### Step 1: Download the repository
```bash
git clone https://github.com/OpenMined/PyGrid/
```
### Step 2: Download dependencies
You'll need to have the app dependencies installed. We recommend setting up an independent [conda environment](https://docs.conda.io/projects/conda/en/latest/user-guide/concepts/environments.html) to avoid problems with library versions.
You can install the dependencies by running:
```bash
cd PyGrid/gateway/
pip install -r requirements.txt
```
### Step 3: Make grid importable
Install grid as a python package
```bash
cd PyGrid
python setup.py install (or python setup.py develop)
```
### Step 4: Start gateway app
Then to start the app just run the `gateway.py` script. The `--start_local_db` automatically starts a local database so you don't have to configure one yourself.
```bash
python gateway.py --start_local_db --port=<port_number>
```
This will start the app on address: `http://0.0.0.0/<port_number>`.
To check what other arguments you can use when running this app, run:
```bash
python gateway.py --help
```
Let's start a grid gateway on port `5000`
```bash
python gateway.py --port=5000
```
Great, so if your app started successfully the script should still be running.
## Starting the Grid Worker App
### Step 5: Starting the Grid Worker app
This is the same procedure already described at Part 1. But we add a new argument when starting the app called `--gateway_url` this should equal to the address used by the grid network here it's "http://localhost:5000"
Let's start two workers:
* bob on port `3000`
* alice on port `3001`
```bash
python websocket_app.py --db_url=redis:///redis:6379 --id=bob --port=3000 --gateway_url=http://localhost:5000
```
```bash
python websocket_app.py --db_url=redis:///redis:6379 --id=alice --port=3001 --gateway_url=http://localhost:5000
```
We should always start the workers after starting the grid gateway!!
Great, so if your app started successfully the script should still be running.
### Step 6: Start communication with the Grid Gateway and workers
Let's start communication with the Gateway and the workers.
```
# General dependencies
import torch as th
import syft as sy
import grid as gr
hook = sy.TorchHook(th)
gateway = gr.GridNetwork("http://localhost:5000")
# WARNING: We should use the same id and port as the one used to start the app!!!
bob = gr.WebsocketGridClient(hook, id="bob", address="http://localhost:3000")
# If you don't connect to the worker you can't send messages to it
bob.connect()
# WARNING: We should use the same id and port as the one used to start the app!!!
alice = gr.WebsocketGridClient(hook, id="alice", address="http://localhost:3001")
# If you don't connect to the worker you can't send messages to it
alice.connect()
```
### Step 7: Use PySyft Like Normal
Now you can simply use the worker you created like you would any other normal PySyft worker. For more on how PySyft works, please see the PySyft tutorials: https://github.com/OpenMined/PySyft/tree/dev/examples/tutorials
```
x = th.tensor([1,2,3,4]).send(bob)
x
y = x + x
y
y.get()
```
### Step 7: Perform operations on Grid Network
So far we haven't done anything different, but here is the magic: we can interact with the network to query general information about it.
```
x = th.tensor([1, 2, 3, 4, 5]).tag("#tensor").send(bob)
```
We can search for a tensor in the entire network, and get pointers to all tensors.
```
gateway.search("#tensor")
y = th.tensor([1, 2, 3, 4, 5]).tag("#tensor").send(alice)
gateway.search("#tensor")
```
| github_jupyter |
```
# import sys
# sys.path.append('https://github.com/alphaBenj/RoughCut/blob/master/files/data_iex.py')
%matplotlib inline
import matplotlib.pyplot as plt
from matplotlib import colors
import data_iex as IEX
dir(IEX)
# ?filter=symbol,volume,lastSalePrice
iex = IEX.API()
dir(iex)
iex.lastTrade(['AAPL', 'IBM', "FLR"])
iex.lastTradeQuote(['AAPL', 'IBM'])
# %%timeit
iex.lastTrade(['AAPL', 'MSFT'])
# %%timeit -n 1
symList = ['AAPL', 'CSCO',"OXY","NFLX", "SBUX", "VXX", "MO", "PM", "TSLA","GE" ]
# symList = ['GE' ]
bars = iex.tradeBars(symList, bucket='1m')
# print (bars.columns)
bars
# bars[[ 'symbol','date', 'minute','open','high', 'low', 'close','volume','marketOpen',
# 'marketHigh','marketLow', 'marketClose', 'marketVolume', 'average','marketAverage',
# 'numberOfTrades', 'marketNumberOfTrades',
# ]]
try: bar = bars[['symbol','date','minute','open','high', 'low', 'close', 'volume',]]
except: bar = bars[['symbol','date','open','high', 'low', 'close', 'volume',]]
bar[bar['symbol']=="AAPL"]
https://api.iextrading.com/1.0/tops/last/?symbols=SNAP,fb,AIG%2b&format=csv
# https://api.iextrading.com/1.0/tops/?symbols=SNAP,fb,AIG%2b&format=csv
import pandas as pd
from urllib.request import Request, urlopen
import json
from pandas.io.json import json_normalize
import requests, io
_IEX_URL_PREFIX = r'https://api.iextrading.com/1.0/'
def get_trade_bars_data2( securities, bucket='1m'):
"""
Get bucketed trade/volume data. Supported buckets are: 1m, 3m, 6m, 1y, ytd, 2y, 5y
:param securities: list of securities
:param bucket:
:return: dataframe
"""
# securities = self.return_valid_securities(securities)
#https://api.iextrading.com/1.0/stock/market/batch?&types=time-series&range=5y&symbols=qep,oxy,flr,mo,pm,nflx
syms = (',').join(securities)
df = pd.DataFrame()
# Get price data for each security and then append the results together
# if securities:
# for symbol in securities:
# suffix = r'stock/{symbol}/chart/{bucket}'.format(symbol=symbol,bucket=bucket)
# df = self._url_to_dataframe(self._IEX_URL_PREFIX + suffix)
# df['symbol'] = symbol
# final_df = final_df.append(df, ignore_index=True)
# return final_df
# else: print('These stock(s) are invalid!')
# if securities:
# for symbol in securities:
suffix = r"stock/market/batch?&types=time-series&range={bucket}&symbols={symbol}".format(bucket=bucket,symbol=syms)
filter = "&filter=symbol,date,open,high,low,close,volume,changePercent,vwap"
urlData = requests.get(_IEX_URL_PREFIX + suffix+filter).content
rawData = json.loads(urlData)
for sym in list(rawData.keys()):
_df = pd.DataFrame(list(rawData.get(sym).values())[0])
_df["symbol"] = sym
print (_df.head())
df = pd.concat([df,_df])
return df
# %%timeit -n 1
securities = ['AAPL', 'CSCO',"OXY","NFLX", "SBUX", "VXX", "MO", "PM" ]
bars = get_trade_bars_data2( securities, bucket='2y')
# list(rd.keys())[0]
# _df = pd.DataFrame()
# _df = pd.DataFrame()
# print (_df.head())
# # for sym in list(rd.keys()):
# df = pd.DataFrame(list(rd.get(sym).values())[0])
# df["symbol"] = sym
# _df = pd.concat([_df,df])
# print (_df.head())
bar[bar['symbol']=="OXY"]
final_df
securities = ['oxy', "QEP","VXX","HI"]
str(securities).replace('"', "").replace("'", "").replace('[', "").replace(']', "").replace(' ', "")
(',').join(securities)
dllist = list(range(821))
print (round((len(dllist)),-2)/100+1)
dll = [ dllist[ x*100: (x+1)*100] for x in range(int(round((len(dllist)),-2)/100+1)) ]
range(int(round((len(dllist)),-2)/100+1))
dll
from IPython.core.display import HTML
HTML("<style>.container { width:98% !important; white-space: none; no-wrap: true; }</style>")
```
| github_jupyter |
#### Reactions processing with AQME - substrates + TS
```
# cell with import, system name and PATHs
import os, glob, subprocess
import shutil
from pathlib import Path
from aqme.csearch import csearch
from aqme.qprep import qprep
from aqme.qcorr import qcorr
from rdkit import Chem
import pandas as pd
```
###### Step 1: Determining the constraints for SN2 TS
```
# Provide the TS smiles to detemine the numbering for constraints
smi = 'C(C)(F)C.[OH-]'
mol = Chem.MolFromSmiles(smi)
mol = Chem.AddHs(mol)
for i,atom in enumerate(mol.GetAtoms()):
atom.SetAtomMapNum(i)
smi_new = Chem.MolToSmiles(mol)
print(smi_new)
mol
# distance and angle to fix are
# constraits_dist = [[0,2,1.8],[0,4,1.8]]
# constraits_angle = [[2,0,4,180]]
```
###### Step 2: Create a CSV as follows
```
data = pd.read_csv('example2.csv')
data
```
###### Step 3: Running CSEARCH on the CSV
```
# run CSEARCH conformational sampling, specifying:
# choose program for conformer sampling
# 1) RDKit ('rdkit'): Fast sampling, only works for systems with one molecule
# 2) CREST ('crest'): Slower sampling, works for noncovalent complexes and
# transition structures (see example of TS in the CSEARCH_CREST_TS.ipynb notebook
# from the CSEARCH_CMIN_conformer_generation folder)
# 3) Program for conformer sampling (program=program)
# 4) SMILES string (smi=smi)
# 5) Name for the output SDF files (name=name)
# 6) Include CREGEN post-analysis for CREST sampling (cregen=True)
csearch(input='example2.csv', program='crest', cregen=True, cregen_keywords='--ethr 0.1 --rthr 0.2 --bthr 0.3 --ewin 1')
```
###### Step 4: Create input files using QPREP
###### a. for TS with TS keywords
###### b. for substrates with substrate keywords
```
# set SDF filenames and directory where the new com files will be created
sdf_rdkit_files = ['CSEARCH/crest/TS_SN2_crest.sdf']
# choose program for input file generation, with the corresponding keywords line, memory and processors:
# 1) Gaussian ('gaussian')
program = 'gaussian'
qm_input = 'B3LYP/6-31G(d) opt=(ts,calcfc,noeigen) freq'
mem='40GB'
nprocs=36
# run QPREP input files generator, with:
# 1) Working directory (w_dir_main=sdf_path)
# 2) PATH to create the new SDF files (destination=com_path)
# 3) Files to convert (files=sdf_rdkit_files)
# 4) QM program for the input (program=program)
# 5) Keyword line for the Gaussian inputs (qm_input=qm_input)
# 6) Memory to use in the calculations (mem='24GB')
# 7) Processors to use in the calcs (nprocs=8)
qprep(files=sdf_rdkit_files,program=program,
qm_input=qm_input,mem=mem,nprocs=nprocs)
# set SDF filenames and directory where the new com files will be created
sdf_rdkit_files = ['CSEARCH/crest/F_crest.sdf', 'CSEARCH/crest/O_anion_crest.sdf']
# choose program for input file generation, with the corresponding keywords line, memory and processors:
# 1) Gaussian ('gaussian')
program = 'gaussian'
qm_input = 'B3LYP/6-31G(d) opt freq'
mem='40GB'
nprocs=36
# run QPREP input files generator, with:
# 1) Working directory (w_dir_main=sdf_path)
# 2) PATH to create the new SDF files (destination=com_path)
# 3) Files to convert (files=sdf_rdkit_files)
# 4) QM program for the input (program=program)
# 5) Keyword line for the Gaussian inputs (qm_input=qm_input)
# 6) Memory to use in the calculations (mem='24GB')
# 7) Processors to use in the calcs (nprocs=8)
qprep(files=sdf_rdkit_files,program=program,
qm_input=qm_input,mem=mem,nprocs=nprocs)
```
###### Step 5: Checking with QPREP for corrections
```
w_dir_main=os.getcwd()+'/QCALC'
# run the QCORR analyzer, with:
# 1) Working directory (w_dir_main=com_path)
# 2) Names of the QM output files (files='*.log')
# 3) Detect and fix calcs that converged during geometry optimization but didn't converge during frequency calcs (freq_conv='opt=(calcfc,maxstep=5)')
# 4) Type of initial input files where the LOG files come from (isom_type='com')
# 5) Folder with the initial input files (isom_inputs=com_path)
qcorr(w_dir_main=w_dir_main,files='*.log',freq_conv='opt=(calcfc,maxstep=5)')
```
###### Step 6: creation of DLPNO input files for ORCA single-point energy calculations
```
# choose output files to get atoms and coordinates to generate inputs for single-point energy calculations
success_dir = os.getcwd()+'/QCALC/successful_QM_outputs'
qm_files = '*.log'
# choose program for input file generation with QPREP, with the corresponding keywords line, memory and processors:
# 1) ORCA ('orca')
program = 'orca'
# a DLPNO example keywords line for ORCA calculations
# qm_input = 'Extrapolate(2/3,cc) def2/J cc-pVTZ/C DLPNO-CCSD(T) NormalPNO TightSCF RIJCOSX\n'
qm_input ='DLPNO-CCSD(T) def2-tzvpp def2-tzvpp/C\n'
qm_input += '%scf maxiter 500\n'
qm_input += 'end\n'
qm_input += '% mdci\n'
qm_input += 'Density None\n'
qm_input += 'end\n'
qm_input += '% elprop\n'
qm_input += 'Dipole False\n'
qm_input += 'end'
mem='4GB'
nprocs=8
# run QPREP input files generator, with:
# 1) Working directory (w_dir_main=sdf_path)
# 2) PATH to create the new SDF files (destination=com_path)
# 3) Files to convert (files=sdf_rdkit_files)
# 4) QM program for the input (program=program)
# 5) Keyword line for the Gaussian inputs (qm_input=qm_input)
# 6) Memory to use in the calculations (mem='24GB')
# 7) Processors to use in the calcs (nprocs=8)
qprep(w_dir_main=success_dir,destination=success_dir,files=qm_files,program=program,
qm_input=qm_input,mem=mem,nprocs=nprocs, suffix='DLPNO')
```
###### Step 7: Analysis with goodvibes
```
# track all the output files from Gaussian and ORCA
opt_files = glob.glob(f'{success_dir}/*.log')
spc_files = glob.glob(f'{success_dir}/*.out')
all_files = opt_files + spc_files
# move all the output files together to a folder called "GoodVibes_analysis" for simplicity
w_dir_main = Path(os.getcwd())
GV_folder = w_dir_main.joinpath('GoodVibes_analysis')
GV_folder.mkdir(exist_ok=True, parents=True)
for file in all_files:
shutil.copy(file, GV_folder)
# this commands runs GoodVibes, including the population % of each conformer
# (final results in the GoodVibes.out file)
os.chdir(GV_folder)
subprocess.run(['python', '-m', 'goodvibes', '--xyz','--pes', '../pes.yaml','--graph','../pes.yaml', '--spc', 'DLPNO', '*.log',])
os.chdir(w_dir_main)
```
| github_jupyter |
# Import all the necessary libraries
```
import cv2, time, pandas
from datetime import datetime
```
# Initialize the variables
```
first = None # This variable holds the value of the first frame
status_list = [None,None] # This variable holds the list of statuses - if Python has come across a frame greater than 1000 pixels
times = [] # This variable holds the timestamps during which a motion that was detected started and ended
df = pandas.DataFrame(columns = ["Start","End"]) # The dataframe that will hold the timestamp for each detected motion
```
# Capture the video
```
vid = cv2.VideoCapture(0) # To capture the video from the first camera of the device
```
# Process the video
```
while True:
check, frame = vid.read() # To read frame by frame
status = 0
gray_frame = cv2.cvtColor(frame, cv2.COLOR_BGR2GRAY)# To convert the image to grayscale
gray_frame = cv2.GaussianBlur(gray_frame,(21,21),0) # To make the image blurry so that noise is reduced and accuracy is improved
if first is None:
first = gray_frame
continue
diff = cv2.absdiff(first, gray_frame) # To compute and store the absolute difference between the frames
thresh_diff = cv2.threshold(diff,30,255,cv2.THRESH_BINARY)[1] # To convert differences less than 30 as WHITE and more than 30 as BLACK
thresh_diff = cv2.dilate(thresh_diff,None,iterations = 2) # To increase the object area
(_,cnts,_) = cv2.findContours(thresh_diff.copy(),cv2.RETR_EXTERNAL,cv2.CHAIN_APPROX_SIMPLE) # To find the contours of the frame
for contour in cnts: # To iterate through the contours
if cv2.contourArea(contour) < 1000: # To check if the contour area is less than 1000 pixels
continue
status = 1 # To remember that Python has found a frame that is bigger than 1000px
(x,y,w,h)= cv2.boundingRect(contour) # To find the rectangle bounding the contours
cv2.rectangle(frame,(x,y),(x+w,y+h),(0,255,0),3) # To draw a rectangle around the object
status_list.append(status)
if status_list[-1] == 1 and status_list[-2] == 0: # To figure out the start time
times.append(datetime.now()) # To store the start time
if status_list[-1] == 0 and status_list[-2] == 1: # To figure out the end tome
times.append(datetime.now()) # To store the end time
cv2.imshow("Gray",gray_frame) # To display the frames that are captured in gray scale
cv2.imshow("Difference",diff) # To display the difference between the frames
cv2.imshow("Threshold",thresh_diff) # To display the difference after the threshold has been applied
cv2.imshow("Color",frame) # To display the original color frames
key = cv2.waitKey(1) # To wait till a key is pressed
if key == ord('q'): # To quit if the key pressed is q
if status == 1:
times.append(datetime.now())
break
```
# Write the timestamps to a csv file
```
for i in range(0,len(times),2):
df=df.append({"Start":times[i],"End":times[i+1]},ignore_index=True) # To store the start and end times of when each motion was detected
df.to_csv("Times.csv") # To write to the Times.csv file
```
# End the video processing
```
vid.release() # To stop the capturing device from capturing video
cv2.destroyAllWindows # To close the windows and deallocate associated memory usage
```
| github_jupyter |
```
import sys
sys.path.append('../../code/')
import os
import json
from datetime import datetime
import time
from math import *
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import scipy.stats as stats
import igraph as ig
import networkx as nx
from load_data import load_citation_network, case_info
%load_ext autoreload
%autoreload 2
%matplotlib inline
data_dir = '../../data/'
court_name = 'scotus'
case_metadata = pd.read_csv(data_dir + 'clean/case_metadata_master.csv')
edgelist = pd.read_csv(data_dir + 'clean/edgelist_master.csv')
# net_dir = data_dir + 'clean/' + court_name + '/'
# case_metadata = pd.read_csv(net_dir + 'case_metadata.csv')
# edgelist = pd.read_csv(net_dir + 'edgelist.csv')
# edgelist.drop('Unnamed: 0', inplace=True, axis=1)
```
# Compare iterrows vs itertuples
```
start = time.time()
# create graph and add metadata
G = nx.DiGraph()
G.add_nodes_from(case_metadata.index.tolist())
nx.set_node_attributes(G, 'date', case_metadata['date'].to_dict())
for index, edge in edgelist.iterrows():
ing = edge['citing']
ed = edge['cited']
G.add_edge(ing, ed)
end = time.time()
print 'pandas took %d seconds to go though %d edges using iterrows' % (end - start, edgelist.shape[0])
# go through edglist using itertuples
start = time.time()
# create graph and add metadata
G = nx.DiGraph()
G.add_nodes_from(case_metadata.index.tolist())
nx.set_node_attributes(G, 'date', case_metadata['date'].to_dict())
for row in edgelist.itertuples():
ing = row[1]
ed = row[2]
G.add_edge(ing, ed)
end = time.time()
print 'pandas took %d seconds to go though %d edges using itertuples' % (end - start, edgelist.shape[0])
```
# load into igraph
```
# create a dictonary that maps court listener ids to igraph ids
cl_to_ig_id = {}
cl_ids = case_metadata['id'].tolist()
for i in range(case_metadata['id'].size):
cl_to_ig_id[cl_ids[i]] = i
start = time.time()
V = case_metadata.shape[0]
g = ig.Graph(n=V, directed=True)
g.vs['date'] = case_metadata['date'].tolist()
g.vs['name'] = case_metadata['id'].tolist()
ig_edgelist = []
missing_cases = 0
start = time.time()
# i = 1
for row in edgelist.itertuples():
# if log(i, 2) == int(log(i, 2)):
# print 'edge %d' % i
# i += 1
cl_ing = row[1]
cl_ed = row[2]
if (cl_ing in cl_to_ig_id.keys()) and (cl_ed in cl_to_ig_id.keys()):
ing = cl_to_ig_id[cl_ing]
ed = cl_to_ig_id[cl_ed]
else:
missing_cases += 0
ig_edgelist.append((ing, ed))
intermediate = time.time()
g.add_edges(ig_edgelist)
end = time.time()
print 'itertuples took %d seconds to go through %d edges' % (intermediate - start, edgelist.shape[0])
print 'igraph took %d seconds to add %d edges' % (end - start, edgelist.shape[0])
```
# igraph find vs. select
```
start = time.time()
R = 1000
for i in range(R):
g.vs.find(name='92891')
end = time.time()
print 'g.vs.find took %E seconds per lookup' % ((end - start)/R)
start = time.time()
R = 1000
for i in range(R):
g.vs.select(name='92891')
end = time.time()
print 'g.vs.select took %E seconds per lookup' % ((end - start)/R)
start = time.time()
R = 1000
for i in range(R):
cl_to_ig_id[92891]
end = time.time()
print 'pandas df lookup took %E seconds per lookup' % ((end - start)/R)
```
| github_jupyter |
## Download and extract zip from web
- Specifies the source link, destination url and file name to download and extract data files
- Currently reading from external folder as github does not support large files
- To rerun function for testing before submission
- To add checks and conditions for the function
- Link to zip download here: "https://s3-ap-southeast-1.amazonaws.com/grab-aiforsea-dataset/safety.zip"
```
import zipfile
import urllib.request
import pandas as pd
import numpy as np
import pickle
from tqdm import tqdm
SOURCE = "https://s3-ap-southeast-1.amazonaws.com/grab-aiforsea-dataset/safety.zip"
OUTPUT_PATH = "../grab-ai-safety-data"
FILE_NAME = ""
class DownloadProgressBar(tqdm):
'''Class for tqdm progress bar.'''
def update_to(self, b=1, bsize=1, tsize=None):
if tsize is not None:
self.total = tsize
self.update(b * bsize - self.n)
def maybe_download(url, output_path, dest_file_name):
'''Function that checks the validity of a desired URL,
downloads and extracts a ZIP file for the purposes of
the Grab AI challenge.
Args:
url (str): Download path of the dataset in question
output_path(str): path of the desired download destination
dest_file_name(str): Desired file name.
To include .zip extension
Returns:
None.
Extracts all relevant data files into a desired folder for
download.
'''
full_path = output_path+'/'+dest_file_name
with DownloadProgressBar(
unit='B',
unit_scale=True,
miniters=1,
desc=url.split("/")[-1]
) as t:
urllib.request.urlretrieve(
url,
filename=full_path,
reporthook=t.update_to
)
with zipfile.ZipFile(full_path, "r") as zip_ref:
zip_ref.extractall(output_path)
# download_url(SOURCE, OUTPUT_PATH, FILE_NAME)
df0 = pd.read_csv("../grab-ai-safety-data/features/part-00000-e6120af0-10c2-4248-97c4-81baf4304e5c-c000.csv")
df1 = pd.read_csv("../grab-ai-safety-data/features/part-00001-e6120af0-10c2-4248-97c4-81baf4304e5c-c000.csv")
df2 = pd.read_csv("../grab-ai-safety-data/features/part-00002-e6120af0-10c2-4248-97c4-81baf4304e5c-c000.csv")
df3 = pd.read_csv("../grab-ai-safety-data/features/part-00003-e6120af0-10c2-4248-97c4-81baf4304e5c-c000.csv")
df4 = pd.read_csv("../grab-ai-safety-data/features/part-00004-e6120af0-10c2-4248-97c4-81baf4304e5c-c000.csv")
df5 = pd.read_csv("../grab-ai-safety-data/features/part-00005-e6120af0-10c2-4248-97c4-81baf4304e5c-c000.csv")
df6 = pd.read_csv("../grab-ai-safety-data/features/part-00006-e6120af0-10c2-4248-97c4-81baf4304e5c-c000.csv")
df7 = pd.read_csv("../grab-ai-safety-data/features/part-00007-e6120af0-10c2-4248-97c4-81baf4304e5c-c000.csv")
df8 = pd.read_csv("../grab-ai-safety-data/features/part-00008-e6120af0-10c2-4248-97c4-81baf4304e5c-c000.csv")
df9 = pd.read_csv("../grab-ai-safety-data/features/part-00009-e6120af0-10c2-4248-97c4-81baf4304e5c-c000.csv")
response = pd.read_csv("../grab-ai-safety-data/labels/part-00000-e9445087-aa0a-433b-a7f6-7f4c19d78ad6-c000.csv")
```
## Merge and drop duplicates
- Join the feautres together with the labels
- Get rid of any obvious duplicates in the features and response
- No data cleaning or formatting to minimize data leakage
```
df_features = pd.concat(
[df1, df2, df3, df4, df5, df6, df7, df8, df9],
axis=0
).drop_duplicates(
keep=False
)
response = response.drop_duplicates(
subset="bookingID",
keep=False
)
df = pd.merge(
df_features,
response,
how="inner",
on="bookingID"
).sort_values(
["bookingID", "second"],
ascending=True
)
with open('../grab-ai-safety-data/df_full.pickle', 'wb') as f:
pickle.dump(df, f)
```
| github_jupyter |
```
%matplotlib inline
```
# Linear classifier on sensor data with plot patterns and filters
Here decoding, a.k.a MVPA or supervised machine learning, is applied to M/EEG
data in sensor space. Fit a linear classifier with the LinearModel object
providing topographical patterns which are more neurophysiologically
interpretable [1]_ than the classifier filters (weight vectors).
The patterns explain how the MEG and EEG data were generated from the
discriminant neural sources which are extracted by the filters.
Note patterns/filters in MEG data are more similar than EEG data
because the noise is less spatially correlated in MEG than EEG.
References
----------
.. [1] Haufe, S., Meinecke, F., Görgen, K., Dähne, S., Haynes, J.-D.,
Blankertz, B., & Bießmann, F. (2014). On the interpretation of
weight vectors of linear models in multivariate neuroimaging.
NeuroImage, 87, 96–110. doi:10.1016/j.neuroimage.2013.10.067
```
# Authors: Alexandre Gramfort <[email protected]>
# Romain Trachel <[email protected]>
# Jean-Remi King <[email protected]>
#
# License: BSD (3-clause)
import mne
from mne import io, EvokedArray
from mne.datasets import sample
from mne.decoding import Vectorizer, get_coef
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
from sklearn.pipeline import make_pipeline
# import a linear classifier from mne.decoding
from mne.decoding import LinearModel
print(__doc__)
data_path = sample.data_path()
```
Set parameters
```
raw_fname = data_path + '/MEG/sample/sample_audvis_filt-0-40_raw.fif'
event_fname = data_path + '/MEG/sample/sample_audvis_filt-0-40_raw-eve.fif'
tmin, tmax = -0.1, 0.4
event_id = dict(aud_l=1, vis_l=3)
# Setup for reading the raw data
raw = io.read_raw_fif(raw_fname, preload=True)
raw.filter(.5, 25, fir_design='firwin')
events = mne.read_events(event_fname)
# Read epochs
epochs = mne.Epochs(raw, events, event_id, tmin, tmax, proj=True,
decim=2, baseline=None, preload=True)
labels = epochs.events[:, -1]
# get MEG and EEG data
meg_epochs = epochs.copy().pick_types(meg=True, eeg=False)
meg_data = meg_epochs.get_data().reshape(len(labels), -1)
```
Decoding in sensor space using a LogisticRegression classifier
```
clf = LogisticRegression(solver='lbfgs')
scaler = StandardScaler()
# create a linear model with LogisticRegression
model = LinearModel(clf)
# fit the classifier on MEG data
X = scaler.fit_transform(meg_data)
model.fit(X, labels)
# Extract and plot spatial filters and spatial patterns
for name, coef in (('patterns', model.patterns_), ('filters', model.filters_)):
# We fitted the linear model onto Z-scored data. To make the filters
# interpretable, we must reverse this normalization step
coef = scaler.inverse_transform([coef])[0]
# The data was vectorized to fit a single model across all time points and
# all channels. We thus reshape it:
coef = coef.reshape(len(meg_epochs.ch_names), -1)
# Plot
evoked = EvokedArray(coef, meg_epochs.info, tmin=epochs.tmin)
evoked.plot_topomap(title='MEG %s' % name, time_unit='s')
```
Let's do the same on EEG data using a scikit-learn pipeline
```
X = epochs.pick_types(meg=False, eeg=True)
y = epochs.events[:, 2]
# Define a unique pipeline to sequentially:
clf = make_pipeline(
Vectorizer(), # 1) vectorize across time and channels
StandardScaler(), # 2) normalize features across trials
LinearModel(
LogisticRegression(solver='lbfgs'))) # 3) fits a logistic regression
clf.fit(X, y)
# Extract and plot patterns and filters
for name in ('patterns_', 'filters_'):
# The `inverse_transform` parameter will call this method on any estimator
# contained in the pipeline, in reverse order.
coef = get_coef(clf, name, inverse_transform=True)
evoked = EvokedArray(coef, epochs.info, tmin=epochs.tmin)
evoked.plot_topomap(title='EEG %s' % name[:-1], time_unit='s')
```
| github_jupyter |
```
import numpy as np
from bokeh.plotting import figure, output_file, show
from bokeh.io import output_notebook
from nsopy import SGMDoubleSimpleAveraging as DSA
from nsopy.loggers import EnhancedDualMethodLogger
output_notebook()
%cd ..
from smpspy.oracles import TwoStage_SMPS_InnerProblem
```
# Solving dual model using DSA with Entropy Prox Term
Instantiating inner problem
### Solve battery of problems
```
# Setup
BENCHMARKS_PATH = './smpspy/benchmark_problems/2_caroe_schultz/'
n_S_exp = [10, 50, 100, 500]
N_STEPS = 200
GAMMA = 1.0
# First generate traditional DSA
inner_problems = {}
methods = {}
method_loggers = {}
for n_S in n_S_exp:
ip = TwoStage_SMPS_InnerProblem(BENCHMARKS_PATH+'caroe_schultz_{}'.format(n_S))
dsa = DSA(ip.oracle, ip.projection_function, dimension=ip.dimension, gamma=GAMMA)
logger_dsa = EnhancedDualMethodLogger(dsa)
inner_problems[n_S] = ip
methods[n_S] = dsa
method_loggers[n_S] = logger_dsa
for n_S, method in methods.items():
for step in range(N_STEPS):
if not step % 100:
print('[n_S={}] step: {} of method {}'.format(n_S, str(step), str(method.desc)))
method.dual_step()
inner_problems_entropy = {}
methods_entropy = {}
method_loggers_entropy = {}
for n_S in n_S_exp:
R_a_posteriori = np.linalg.norm(methods[n_S].lambda_k, ord=np.inf)
R_safe = R_a_posteriori*1.1
ip = TwoStage_SMPS_InnerProblem(BENCHMARKS_PATH+'caroe_schultz_{}'.format(n_S), R=R_safe)
dsa_entropy = DSA(ip.oracle, ip.softmax_projection, dimension=ip.dimension, gamma=GAMMA)
logger_dsa_entropy = EnhancedDualMethodLogger(dsa_entropy)
inner_problems_entropy[n_S] = ip
methods_entropy[n_S] = dsa_entropy
method_loggers_entropy[n_S] = logger_dsa_entropy
for n_S, method in methods_entropy.items():
for step in range(N_STEPS):
if not step % 100:
print('[n_S={}] step: {} of method {}'.format(n_S, str(step), str(method.desc)))
method.dual_step()
# find "d*"
d_stars = {}
EPS = 0.01
for n_S in n_S_exp:
d_star_dsa = max(method_loggers[n_S].d_k_iterates)
d_star_dsa_entropy = max(method_loggers_entropy[n_S].d_k_iterates)
d_stars[n_S] = max(d_star_dsa, d_star_dsa_entropy) + EPS
p = figure(title="comparison", x_axis_label='iteration', y_axis_label='d* - d_k', y_axis_type='log', toolbar_location='above')
plot_colors = {
10: 'blue',
50: 'green',
100: 'red',
500: 'orange',
1000: 'purple',
}
for n_S in n_S_exp:
logger = method_loggers[n_S]
p.line(range(len(logger.d_k_iterates)), d_stars[n_S] - np.array(logger.d_k_iterates), legend="DSA, n_scen={}, gamma={}".format(n_S, GAMMA, inner_problems[n_S].R),
color=plot_colors[n_S], line_dash='dashed')
for n_S in n_S_exp:
logger = method_loggers_entropy[n_S]
p.line(range(len(logger.d_k_iterates)), d_stars[n_S] - np.array(logger.d_k_iterates), legend="DSA Entropy, n_scen={}, gamma={}, R={}".format(n_S, GAMMA, inner_problems_entropy[n_S].R),
color=plot_colors[n_S])
p.legend.location = "top_right"
p.legend.visible = True
p.legend.background_fill_alpha = 0.5
show(p)
```
### Single run
```
ip = TwoStage_SMPS_InnerProblem('./smpspy/benchmark_problems/2_caroe_schultz/caroe_schultz_10')
```
First solving it with DSA
```
GAMMA = 1.0
dsa = DSA(ip.oracle, ip.projection_function, dimension=ip.dimension, gamma=GAMMA)
logger_dsa = EnhancedDualMethodLogger(dsa)
for iteration in range(1000):
if not iteration%50:
print('Iteration: {}, d_k={}'.format(iteration, dsa.d_k))
dsa.dual_step()
```
Then get the required parameters (R is derived a posteriori)
```
R_a_posteriori = np.linalg.norm(dsa.lambda_k, ord=np.inf)
R_safe = R_a_posteriori*1.1
ip = TwoStage_SMPS_InnerProblem('./smpspy/benchmark_problems/2_caroe_schultz/caroe_schultz_10', R=R_safe)
print('A-posteriori R={}'.format(R_a_posteriori))
```
Solve it using DSA with Entropy prox function. **Note that the only difference is that we pass in softmax projection function!**
```
dsa_entropy = DSA(ip.oracle, ip.softmax_projection, dimension=ip.dimension, gamma=GAMMA)
logger_dsa_entropy = EnhancedDualMethodLogger(dsa_entropy)
for iteration in range(1000):
if not iteration%50:
print('Iteration: {}, d_k={}'.format(iteration, dsa_entropy.d_k))
dsa_entropy.dual_step()
logger_dsa.lambda_k_iterates[-1]
logger_dsa_entropy.lambda_k_iterates[-1]
p = figure(title="comparison", x_axis_label='iteration', y_axis_label='d_k')
p.line(range(len(logger_dsa.d_k_iterates)), logger_dsa.d_k_iterates, legend="DSA, gamma={}".format(GAMMA, R_safe))
p.line(range(len(logger_dsa_entropy.d_k_iterates)), logger_dsa_entropy.d_k_iterates, legend="DSA Entropy, gamma={}, R={}".format(GAMMA, R_safe), color='red')
p.legend.location = "bottom_right"
show(p)
```
| github_jupyter |
# Энтропия и критерий Джини
$p_i$ - вероятность нахождения системы в i-ом состоянии.
Энтропия Шеннона определяется для системы с N возможными состояниями следующим образом
$S = - \sum_{i=1}^Np_ilog_2p_i$
Критерий Джини (Gini Impurity). Максимизацию этого критерия можно интерпретировать как максимизацию числа пар объектов одного класса, оказавшихся в одном поддереве.
В общем случае критерий Джини считается как
$G = 1 - \sum_k(p_k)^2$
Необходимо посчитать, значения Энтропии и критерия Джини
```
import numpy as np
import math
def get_possibilities(y):
count = len(y)
uniq_values = set(y)
possibilities = []
for value in uniq_values:
possibilities.append(len(y[y ==value]) / count)
return possibilities
def gini_impurity(y: np.ndarray) -> float:
possibilities = get_possibilities(y)
sum = 0
for p in possibilities:
sum += p * p
return round(1 - sum, 3)
def entropy(y: np.ndarray) -> float:
possibilities = get_possibilities(y)
sum = 0
for p in possibilities:
sum += p * math.log2(p)
return round(-sum, 3)
def calc_criteria(y: np.ndarray) -> (float, float):
assert y.ndim == 1
return entropy(y), gini_impurity(y)
y = np.array([1,1,1,1,1,1,0,0,0,0])
calc_criteria(y)
```
# Information gain
Вам надо реализовать функцию inform_gain, которая будет вычислять прирост информации для критерия (энтропия или критерий Джини) при разбиении выбрки по признаку (threshold).
Прирост информации при разбиении выборки по признаку Q (например x≤12) определяется как
$IG(Q)=S_0- \sum_{i=1}^q\frac{N_i}{N}S_i$
где q - число групп после разбиения. $N_i$ - число элементов выборки, у которых признак Q имеет i-ое значение.
И написать функцию get_best_threshold, которая будет находить наилучшее разбиение выборки.
На вход подается:
- X - одномерный массив - значения признака.
- y - значения бинарных классов.
- criteria_func - функция критерия, для которой вычислется наилучшее разбиение (Добавлять код из предыдущей задачи не нужно, мы сами передадим нужную функцию).
- thr - значение разбиения
```
import numpy as np
import math
def get_possibilities(y):
count = len(y)
y = list(y)
uniq_values = set(y)
possibilities = []
for value in uniq_values:
possibilities.append(len(list(filter(lambda x: x == value, y))) / count)
return possibilities
def gini_impurity(y: np.ndarray) -> float:
possibilities = get_possibilities(y)
sum = 0
for p in possibilities:
sum += p * p
return round(1 - sum, 3)
def entropy(y: np.ndarray) -> float:
possibilities = get_possibilities(y)
sum = 0
for p in possibilities:
sum += p * math.log2(p)
return round(-sum, 3)
def len_check_criteria_func(arr, criteria_func):
if len(arr) == 0:
return 0
else:
return criteria_func(arr)
def inform_gain(X: np.ndarray, y: np.ndarray, threshold: float, criteria_func) -> float:
s0 = criteria_func(y)
count = y.shape[0]
first = []
second = []
for i in range(count):
if X[i] <= threshold:
first.append(y[i])
else:
second.append(y[i])
s1 = len_check_criteria_func(first, criteria_func)
s2 = len_check_criteria_func(second, criteria_func)
return s0 - len(first) / count * s1 - len(second) / count * s2
def get_best_threshold(X: np.ndarray, y: np.ndarray, criteria_func) -> (float, float):
best_threshold = 0
best_score = 0
uniq_values = set(X)
for value in uniq_values:
score = inform_gain(X, y, value, criteria_func)
if score > best_score:
best_score = score
best_threshold = value
return best_threshold, best_score
X = np.array([3, 9, 0, 4, 7, 2, 1, 6, 8, 5])
y = np.array([0, 1, 0, 0, 1, 0, 0, 1, 1, 1])
threshold=3
criteria_func=entropy
print(inform_gain(X, y, threshold, criteria_func))
X = np.array([3, 9, 0, 4, 7, 2, 1, 6, 8, 5])
y = np.array([0, 1, 0, 0, 1, 0, 0, 1, 1, 1])
criteria_func=entropy
get_best_threshold(X, y, criteria_func)
import math
print(1 -(-(5/6) * math.log2(5/6) - (1/6)* math.log2(1/6))* 0.6)
```
# Best split
Реализуйте функцию find_best_split, которая находит наилучшее разбиение по всем признакам. На вход подется обучающая выборка и функция критерий. Необходимо вернуть: индекс фичи, значение границы (threshold) и результат разбиение (information gain).
```
import math
def get_possibilities(y):
count = len(y)
y = list(y)
uniq_values = set(y)
possibilities = []
for value in uniq_values:
possibilities.append(len(list(filter(lambda x: x == value, y))) / count)
return possibilities
def gini_impurity(y: np.ndarray) -> float:
possibilities = get_possibilities(y)
sum = 0
for p in possibilities:
sum += p * p
return round(1 - sum, 3)
def entropy(y: np.ndarray) -> float:
possibilities = get_possibilities(y)
sum = 0
for p in possibilities:
sum += p * math.log2(p)
return round(-sum, 3)
def inform_gain(X: np.ndarray, y: np.ndarray, threshold: float, criteria_func) -> float:
s0 = criteria_func(y)
count = y.shape[0]
first = []
second = []
for i in range(count):
if X[i] <= threshold:
first.append(y[i])
else:
second.append(y[i])
s1 = criteria_func(first)
s2 = criteria_func(second)
return s0 - len(first) / count * s1 - len(second) / count * s2
def get_best_threshold(X: np.ndarray, y: np.ndarray, criteria_func) -> (float, float):
assert X.ndim == 1
assert y.ndim == 1
best_threshold = 0
best_score = 0
uniq_values = set(X)
for value in uniq_values:
score = inform_gain(X, y, value, criteria_func)
if score > best_score:
best_score = score
best_threshold = value
return best_threshold, best_score
def find_best_split(X, y, criteria_func):
assert X.ndim == 2
assert y.ndim == 1
best_feature = 0
best_score = 0
best_threshold = 0
for i in range(X.shape[1]):
feature_column = X[:, i]
threshold, score = get_best_threshold(feature_column, y, criteria_func)
if score > best_score:
best_score = score
best_feature = i
best_threshold = threshold
return best_feature, best_threshold, best_score
X = np.array([[1, 1], [1, -1], [-1,-1], [-1, 1]])
y = np.array([1, 1, 0, 0])
criteria_func=entropy
find_best_split(X, y, criteria_func)
```
# Мое дерево решений
Ваша задача реализовать свой простой KNNClassifier для бинарных данных. Вам нужно реализовать 3 метода:
fit - обучение классификатора
predict - предсказание для новых объектов
predict_proba - предсказание вероятностей новых объектов
У нашего классификатора будет лишь два гиперпараметра - максимальная глубина дерева max_depth и критерий разбиения criterion. Энтропия или Джини.
Все функции из предыдущих заданий нужно добавить в этот код.
На вход будет подаваться выборка объектов X. y - результат бинарной классификации 0 или 1.
```
import math
import numpy as np
from sklearn.base import BaseEstimator, ClassifierMixin
class MyDecisionTreeClassifier(BaseEstimator, ClassifierMixin):
def __init__(self, max_depth=4, criterion='entropy'):
self.eps = 0.001
self.max_depth = max_depth
self.criterion = criterion # 'entropy' or 'gini'
self.tree = {}
self._criteria_func = {
'gini': self._gini_impurity,
'entropy': self._entropy
}
def _get_possibilities(self, y):
count = len(y)
y = list(y)
uniq_values = set(y)
possibilities = []
for value in uniq_values:
possibilities.append(len(list(filter(lambda x: x == value, y))) / count)
return possibilities
def _entropy(self, y: np.ndarray) -> float:
possibilities = self._get_possibilities(y)
sum = 0
for p in possibilities:
sum += p * math.log2(p)
return round(-sum, 3)
def _gini_impurity(self, y: np.ndarray) -> float:
possibilities = self._get_possibilities(y)
sum = 0
for p in possibilities:
sum += p * p
return round(1 - sum, 3)
def _inform_gain(self, X: np.ndarray, y: np.ndarray, threshold: float, criteria_func) -> float:
print('X ', X)
print('threshold ', threshold)
print('y ', y)
s0 = criteria_func(y)
count = y.shape[0]
first = []
second = []
for i in range(count):
if X[i] < threshold - self.eps:
first.append(y[i])
else:
second.append(y[i])
print('first ', first)
print('second ', second)
s1 = criteria_func(first)
s2 = criteria_func(second)
return s0 - len(first) / count * s1 - len(second) / count * s2
def _get_best_threshold(self, X: np.ndarray, y: np.ndarray, criteria_func) -> (float, float):
found_bigger_score = False
best_threshold = 0
best_score = 0
uniq_values = set(X)
for value in uniq_values:
score = self._inform_gain(X, y, value, criteria_func)
print('value ', value, ' score ', score)
if score > best_score:
found_bigger_score = True
best_score = score
best_threshold = value
if found_bigger_score:
return best_threshold, best_score
return None, None
def _find_best_split(self, X, y, criteria_func):
best_feature = 0
best_score = 0
best_threshold = 0
found_best = False
for i in range(X.shape[1]):
feature_column = X[:, i]
threshold, score = self._get_best_threshold(feature_column, y, criteria_func)
print('X ', feature_column)
print('y ', y)
print('column ', i, ' threshold ', threshold, ' score ', score)
if score is None:
continue
if score > best_score:
found_best = True
best_score = score
best_feature = i
best_threshold = threshold
if found_best:
return best_feature, best_threshold
return None, None
def _get_biggest_class(self, y):
y = list(y)
return max(set(y), key = y.count)
def _get_probs(self, y):
count = y.shape[0]
ones_count = np.count_nonzero(y == 1)
null_count = count - ones_count
return [null_count / count, ones_count / count]
def _build_tree(self, X, y, depth=0):
if depth == 0:
return
is_leaf = False
split_feature, split_value = self._find_best_split(X, y, self._criteria_func[self.criterion])
if split_feature is None and split_value is None:
val = self._get_biggest_class(y)
return {'cond': val, 'leaf': True}
left_inds = X[:, split_feature] < split_value - self.eps
right_inds = X[:, split_feature] >= split_value - self.eps
left_tree = self._build_tree(X[left_inds], y[left_inds], depth - 1)
right_tree = self._build_tree(X[right_inds], y[right_inds], depth - 1)
if left_tree is None and right_tree is None:
is_leaf = True
if is_leaf and split_feature is not None:
biggest_class = self._get_biggest_class(y)
proba = self._get_probs(y)
return {'cond': biggest_class, 'leaf': True, 'proba': proba}
return {'cond': (split_feature, split_value), 'leaf': is_leaf,
'left': left_tree, 'right': right_tree}
def fit(self, X: np.ndarray, y: np.ndarray):
self.tree = self._build_tree(X, y, depth=self.max_depth)
return self
def _predict(self, X):
predictions = []
proba = []
for elem in X:
current_tree = self.tree
while type(current_tree['cond']) is tuple:
feature = current_tree['cond'][0]
value = current_tree['cond'][1]
if elem[feature] < value - self.eps:
current_tree = current_tree['left']
else:
current_tree = current_tree['right']
value = current_tree['cond']
if 'proba' in current_tree:
proba.append(current_tree['proba'])
elif value == 0:
proba.append([1.0, 0.0])
else:
proba.append([0.0, 1.0])
predictions.append(value)
return predictions, proba
def predict_proba(self, X: np.ndarray):
_, proba = self._predict(X)
return proba
def predict(self, X: np.ndarray): # получаем
predictions, _ = self._predict(X)
return predictions
# X_clf = np.array([[-1, 1], [-1, -1], [2.5, 1], [1, 1], [2, 2], [1, -1]])
# y_clf = np.array([0, 0, 0, 1, 1, 1])
X_clf = np.array([[1, 1], [2, -1], [-1, -1], [-1, -4], [2, 3], [3, 1]])
y_clf = np.array([1, 1, 0, 0, 0, 0])
model = MyDecisionTreeClassifier(max_depth=3, criterion='entropy').fit(X_clf, y_clf)
print(model.tree)
y_pred = model.predict(np.array([[2, 1], [0.5, 1]]))
print(y_pred) # np.array([1, 0])
y_prob = model.predict_proba(np.array([[2, 1], [0.5, 1]]))
print(y_prob) #np.array([[0.0, 1.0], [1.0, 0.0]])
```
# Наивный Байес
Требуется написать свой классификтор, на основе наивного баеса. Необходимо реализовать аналог MultinomialNB.
$y_{test}=argmax_cln(P(y_{test}=c))+\sum_{j=1}^mln(P(f_j|y_{test}=c)+ \alpha)$, c∈{0,1}
На вход подаются численные категориальные признаки. Классы: 00 и 11. У классификатора будет единственный параметр - alpha.
```
from sklearn.base import BaseEstimator, ClassifierMixin
from collections import defaultdict
from math import log, inf
import numpy as np
class MyNaiveBayes(BaseEstimator, ClassifierMixin):
def __init__(self, alpha=1):
self.alpha = alpha
self.classes = [0, 1]
self.class_counts = {0: 0, 1: 0}
self.class_possibilities = {0: 0, 1: 0}
self.indicators = {0: {}, 1: {}}
def fit(self, X: np.ndarray, y: np.ndarray):
self.class_counts = {0: 0, 1: 0}
self.class_possibilities = {0: 0, 1: 0}
self.indicators = {0: {}, 1: {}}
n = y.shape[0]
features_len = len(X[0])
for cls in self.classes:
for j in range(features_len):
self.indicators[cls][j] = {}
for i in range(n):
cls = y[i]
self.class_counts[cls] += 1
for feature_num in range(features_len):
feature_value = X[i][feature_num]
if feature_value not in self.indicators[cls][feature_num].keys():
self.indicators[cls][feature_num][feature_value] = 0
self.indicators[cls][feature_num][feature_value] += 1
for cls in self.classes:
self.class_possibilities[cls] = self.class_counts[cls] / n
return self
def predict(self, X: np.ndarray):
features_len = len(X[0])
result = []
for obj in X:
max_value = -inf
result_cls = None
for cls in self.classes:
value = log(self.class_possibilities[cls])
for feature_num in range(features_len):
feature_value = obj[feature_num]
if feature_value not in self.indicators[cls][feature_num].keys():
value += log(self.alpha)
else:
value += log(self.indicators[cls][feature_num][feature_value] / self.class_counts[cls] + self.alpha)
if value > max_value:
max_value = value
result_cls = cls
result.append(result_cls)
return result
X_clf = np.array([[1, 1], [1, -1], [-1,-1], [-1, 1]])
y_clf = np.array([1, 1, 0, 0])
model = MyNaiveBayes(alpha=1).fit(X_clf, y_clf)
print(model.class_counts)
print(model.class_possibilities)
print(model.indicators)
y_pred = model.predict(np.array([[1, 2], [-1, -2]]))
print(y_pred) # [1, 0]
from nltk.tokenize import WordPunctTokenizer, TweetTokenizer
from sklearn.feature_extraction.text import CountVectorizer, TfidfVectorizer
from sklearn.naive_bayes import MultinomialNB
from nltk.corpus import stopwords
import pandas as pd
import numpy as np
import math
import re
common_words = ['was', 'were', 'and', 'you', 'the', 'did']
stops = set(stopwords.words("english"))
def preprocess(df: pd.DataFrame):
wp = WordPunctTokenizer()
size = df.shape[0]
preprocessed = []
for i in range(size):
sentence = df.iloc[i]['text']
# sentence_parts = sentence.split(' ')
# sentence_parts = list(filter(lambda x: '@' not in x and '#' not in x, sentence_parts))
# sentence = ' '.join(sentence_parts)
tokenized = wp.tokenize(sentence)
tokenized = list(filter(lambda x:
len(x) > 2 and
x not in common_words and
re.search('\d+', x) is None, tokenized))
new_sentence = ' '.join(tokenized)
preprocessed.append(new_sentence)
return preprocessed
def predict(df_train: pd.DataFrame, df_test: pd.DataFrame):
predictions = df_train[:]['airline_sentiment']
positive_train = df_train[df_train['airline_sentiment'] == 'positive']
negative_train = df_train[df_train['airline_sentiment'] == 'negative']
positive_indices = positive_train.index.tolist()
negative_indices = negative_train.index.tolist()
positive_len = len(positive_indices)
negative_len = len(negative_indices)
whole_len = positive_len + negative_len
preprocessed_train = preprocess(df_train)
vectorizer = CountVectorizer()
X = vectorizer.fit_transform(preprocessed_train)
frequencies = np.array(X.toarray())
# preprocessed_test = preprocess(df_test)
# X_test = vectorizer.fit_transform(preprocessed_test)
# test_frequencies = np.array(X_test.toarray())
# clf = MultinomialNB()
# clf.fit(frequencies, predictions)
# test_predict = clf.predict(test_frequencies)
# print(test_predict)
all_words = vectorizer.get_feature_names()
all_words_dict = dict((all_words[i], i) for i in range(len(all_words)))
positive_frequencies = frequencies[positive_indices]
negative_frequencies = frequencies[negative_indices]
word_counts = frequencies.sum(axis=0)
positive_word_counts = positive_frequencies.sum(axis=0)
negative_word_counts = negative_frequencies.sum(axis=0)
positive_word_frequencies = (positive_word_counts / word_counts) / positive_len * whole_len
negative_word_frequencies = (negative_word_counts / word_counts) / negative_len * whole_len
preprocessed_test = preprocess(df_test)
predictions = []
eps = 0.001
logged_eps = math.log(eps)
wp = WordPunctTokenizer()
for i in range(len(preprocessed_test)):
sentence = preprocessed_test[i]
sentence_words = wp.tokenize(sentence)
positive_sum = 0
negative_sum = 0
for word in sentence_words:
if word in all_words_dict.keys():
word_index = all_words_dict[word]
positive_sum += math.log(positive_word_frequencies[word_index] + eps)
negative_sum += math.log(negative_word_frequencies[word_index] + eps)
else:
positive_sum += logged_eps
negative_sum += logged_eps
if positive_sum >= negative_sum:
predictions.append('positive')
else:
predictions.append('negative')
return predictions
train = pd.read_csv('./tweets_train.csv')
test = pd.read_csv('./tweets_test.csv')
predictions = predict(train, test)
test_sentiments = test[:]['airline_sentiment'].tolist()
true = 0
i = 0
for x, y in zip(predictions, test_sentiments):
if x == y:
true += 1
# else:
# print(i)
# print('true ', y)
# print(test.loc[i]['text'])
i += 1
print(true / len(predictions))
# print(predictions)
```
| github_jupyter |
```
import numpy as np
import keras
from keras.datasets import imdb
from keras.models import Sequential
from keras.layers import Dense, Dropout, Activation
from keras.preprocessing.text import Tokenizer
import matplotlib.pyplot as plt
%matplotlib inline
np.random.seed(42)
```
## Loading the data
The dataset comes preloaded in Keras, which means I don't need to open or read any files manually and one simple command will get us training and testing data. The command to load the data will actually split the words into training and testing sets and labels. There is a parameter for how many words we want to look at. I am setting it at 1000.
```
# load the data(it's comes preloaded with Keras)
(x_train, y_train), (x_test, y_test) = imdb.load_data(num_words=1000)
print(x_train.shape)
print(x_test.shape)
```
## Examining the data
Notice that the data has been already pre-processed, where all the words have numbers, and the reviews come in as a vector with the words that the review contains. For example, if the word 'the' is the first one in our dictionary, and a review contains the word 'the', then there is a 1 in the corresponding vector.
The output comes as a vector of 1's and 0's, where 1 is a positive sentiment for the review, and 0 is negative.
```
print(x_train[0])
print(y_train[0])
```
## One-hot encoding the data
Now, let's turn the input vectors into (0,1)-vectors. For example, if the pre-processed vector contains the number 14, then in the processed vector, the 14th entry will be 1.
```
# one-hot encoding the input into vector mode, each of length 1000
tokenizer = Tokenizer(num_words=1000)
x_train = tokenizer.sequences_to_matrix(x_train, mode='binary')
x_test = tokenizer.sequences_to_matrix(x_test, mode='binary')
print(x_train[0])
```
And we'll also one-hot encode the output.
```
# one-hot encoding the output
num_classes = 2
y_train = keras.utils.to_categorical(y_train, num_classes)
y_test = keras.utils.to_categorical(y_test, num_classes)
print(y_train.shape)
print(y_test.shape)
```
## Building the model architecture
```
# build the model architecture with one layer of length 100
model = Sequential()
model.add(Dense(512, activation='relu', input_dim=1000))
model.add(Dropout(0.5))
model.add(Dense(num_classes, activation='softmax'))
model.summary()
# compile the model using categorical_crossentropy loss, and rmsprop optimizer.
model.compile(loss='categorical_crossentropy',
optimizer='rmsprop',
metrics=['accuracy'])
```
## Training the model
```
# train the model
hist = model.fit(x_train, y_train,
batch_size=32,
epochs=10,
validation_data=(x_test, y_test),
verbose=2)
```
## Evaluating the model
```
# evaluate the model
score = model.evaluate(x_test, y_test, verbose=0)
print("Accuracy: ", score[1])
```
The trained model has an accuracy of 85.53%. Let's make some changes in our model architecture to improve the accuracy. It might be possible by adding one more hidden layer and dropout to reduce overfitting. Let's explore now.
```
# build the model architecture with one layer of length 100
model = Sequential()
model.add(Dense(512, activation='relu', input_dim=1000))
model.add(Dropout(0.5))
model.add(Dense(256, activation='relu')) # newly added layer
model.add(Dropout(0.3)) # added dropout regularization of 0.3
model.add(Dense(num_classes, activation='softmax'))
model.summary()
# compile the model using categorical_crossentropy loss, and rmsprop optimizer.
model.compile(loss='categorical_crossentropy',
optimizer='rmsprop',
metrics=['accuracy'])
# train the model
hist = model.fit(x_train, y_train,
batch_size=32,
epochs=10,
validation_data=(x_test, y_test),
verbose=2)
# evaluate the model
score = model.evaluate(x_test, y_test, verbose=0)
print("Accuracy: ", score[1])
```
Although small, the new model with an extra hidden and a dropout layer shows the accuracy of 85.73% which is higher than the previous model.
Let's experiment with applying reduced dropout of 0.2 and 0.1 to the corresponding dropout layers.
```
# build the model architecture with one layer of length 100
model = Sequential()
model.add(Dense(512, activation='relu', input_dim=1000))
model.add(Dropout(0.2)) # changed dropout to 0.2 from 0.5
model.add(Dense(256, activation='relu')) # newly added layer
model.add(Dropout(0.1)) # changed dropout to 0.1 from 0.3
model.add(Dense(num_classes, activation='softmax'))
model.summary()
# compile the model using categorical_crossentropy loss, and rmsprop optimizer.
model.compile(loss='categorical_crossentropy',
optimizer='rmsprop',
metrics=['accuracy'])
# train the model
hist = model.fit(x_train, y_train,
batch_size=32,
epochs=10,
validation_data=(x_test, y_test),
verbose=2)
# evaluate the model
score = model.evaluate(x_test, y_test, verbose=0)
print("Accuracy: ", score[1])
```
It can be observed that the acuracy takes a hit, being reduced to 84.48% from 85.73%, when the dropout values are changed from 0.5 to 0.2 for the first dropout layer and from 0.3 to 0.1 for the second dropout layer. For the chosen network configuration, reducing the dropout rate in the hidden layers did not lift performance. In fact, accuracy was worse than the baseline. The model starts to overfit in this case.
Lets's experiment with restoring the dropout rates close to their previous values, 0.5 and 0.4
```
# build the model architecture with one layer of length 100
model = Sequential()
model.add(Dense(512, activation='relu', input_dim=1000))
model.add(Dropout(0.5)) # changed dropout rate from to 0.2 to 0.5 again
model.add(Dense(256, activation='relu'))
model.add(Dropout(0.4)) # changed dropout rate of to 0.4 from 0.3
model.add(Dense(num_classes, activation='softmax'))
model.summary()
# compile the model using categorical_crossentropy loss, and rmsprop optimizer.
model.compile(loss='categorical_crossentropy',
optimizer='rmsprop',
metrics=['accuracy'])
```
Lets's see what happens when model is trained with increased batch_size of 200 aand higher epochs 0f 50.
```
# train the model
hist = model.fit(x_train, y_train,
batch_size=200,
epochs=50,
validation_data=(x_test, y_test),
verbose=2)
```
From the results, it is obvious that the model is overfitting. We need to tweak the hyperparameters again in order to improve the network's performance.
Let's explore the effect of increase in nodes of the hidden layer on the model's performaance.
```
# build the model architecture with one layer of length 100
model = Sequential()
model.add(Dense(512, activation='relu', input_dim=1000))
model.add(Dropout(0.5))
model.add(Dense(384, activation='relu')) # increased no. of nodes in the hidden layer from 256 to 384
model.add(Dropout(0.3)) # changed dropout rate to 0.3
model.add(Dense(num_classes, activation='softmax'))
model.summary()
# compile the model using categorical_crossentropy loss, and rmsprop optimizer.
model.compile(loss='categorical_crossentropy',
optimizer='rmsprop',
metrics=['accuracy'])
# train the model
hist = model.fit(x_train, y_train,
batch_size=32,
epochs=10,
validation_data=(x_test, y_test),
verbose=2)
```
The network performance shows improvement as compared to the performance of the previous network architecture.
Lets change the optimizer 'rmsprop' used in the previous model to 'adam' and check network's performance.
```
# build the model architecture with one layer of length 100
model = Sequential()
model.add(Dense(512, activation='relu', input_dim=1000))
model.add(Dropout(0.5))
model.add(Dense(384, activation='relu'))
model.add(Dropout(0.3))
model.add(Dense(num_classes, activation='softmax'))
model.summary()
# compile the model using categorical_crossentropy loss, and adam optimizer.
model.compile(loss='categorical_crossentropy',
optimizer='adam', # optimizer changed from 'rmsprop' to 'adam'
metrics=['accuracy'])
# train the model
hist = model.fit(x_train, y_train,
batch_size=32,
epochs=10,
validation_data=(x_test, y_test),
verbose=2)
# evaluate the model
score = model.evaluate(x_test, y_test, verbose=0)
print("Accuracy: ", score[1])
```
Here, in this case the 'rmsprop' seems to be a better optimizer than 'adam' for the model in terms of its performance(test accuracy) which is 85.70% and 84.96% respectively.
Now, let us add an extra hidden layer before the output layer and apply dropout to it.
```
# build the model architecture with one layer of length 100
model = Sequential()
model.add(Dense(512, activation='relu', input_dim=1000))
model.add(Dropout(0.5))
model.add(Dense(256, activation='relu'))
model.add(Dropout(0.3))
model.add(Dense(256, activation='relu')) # newly added hidden layer
model.add(Dropout(0.3)) # added dropout rate of 0.3
model.add(Dense(num_classes, activation='softmax'))
model.summary()
# compile the model using categorical_crossentropy loss, and rmsprop optimizer.
model.compile(loss='categorical_crossentropy',
optimizer='rmsprop',
metrics=['accuracy'])
model.fit(x_train, y_train,
batch_size=32,
epochs=10,
validation_data=(x_test, y_test),
verbose=2)
# evaluate the model
score = model.evaluate(x_test, y_test, verbose=0)
print("Accuracy: ", score[1])
```
Let's increase the number of nodes in the first hidden layer to 384 and see what happens.
```
# build the model architecture with one layer of length 100
model = Sequential()
model.add(Dense(512, activation='relu', input_dim=1000))
model.add(Dropout(0.5))
model.add(Dense(384, activation='relu')) # changed number of nodes to 384
model.add(Dropout(0.3))
model.add(Dense(256, activation='relu'))
model.add(Dropout(0.2)) # added dropout rate of 0.2
model.add(Dense(num_classes, activation='softmax'))
model.summary()
# compile the model using categorical_crossentropy loss, and rmsprop optimizer.
model.compile(loss='categorical_crossentropy',
optimizer='rmsprop',
metrics=['accuracy'])
model.fit(x_train, y_train,
batch_size=32,
epochs=10,
validation_data=(x_test, y_test),
verbose=2)
# evaluate the model
score = model.evaluate(x_test, y_test, verbose=0)
print("Accuracy: ", score[1])
```
This is our the best performing network architecture so far, which is configured by increasing the number of nodes in the first hidden layer from 256 to 384, while second hidden layer has 256 nodes.
| github_jupyter |
# Interpolation
### [Gerard Gorman](http://www.imperial.ac.uk/people/g.gorman), [Matthew Piggott](http://www.imperial.ac.uk/people/m.d.piggott), [Christian Jacobs](http://www.christianjacobs.uk)
## Interpolation vs curve-fitting
Consider a discrete set of data points
$$ (x_i, y_i),\quad i=0,\ldots,N,$$
and that we wish to approximate this data in some sense. The data may be known to be exact (if we wished to approximate a complex function by a simpler expression say), or it may have errors from measurement or observational techniques with known or unknown error bars.
### Interpolation
Interpolation assumes that these data points are exact (e.g. no measurement errors) and at distinct $x$ locations. It aims to fit a function (or curve), $y=f(x)$, to this data which exactly passes through the $N$ discrete points. This means that we have the additional constraint on the $x_s$'s that
$$x_0 < x_1 < \ldots < x_N,$$
and that
$$y_i=f(x_i),\quad \forall i.$$
In this case the function $f$ is known as the *interpolating function*, or simply the *interpolant*.
### Curve-fitting
Alternatively, when we have data with noise, or multiple different measurement values ($y$) at a given $x$ then we cannot fit a function/curve that goes through all points exactly, and rather have to perform **curve-fitting** - finding a function that approximates the data in some sense by does not necessarily hit all points. In this case we no longer have the requirement that
$$x_0 < x_1 < \ldots < x_N$$
and can consider the data simply as a *cloud of points*. This is the most typical case for real world data which contains variability and noise giving rise to multiple different measurements (i.e. $y$ values) at the same $x$ location.
An example of interpolation would be to simply fit a line between every successive two data points - this is a piecewise-linear (an example of the more general piecewise-polynomial) interpolation.
If we were to construct a single straight line ($y=mx+c$ where we have only two free parameters $m$ and $c$) that, for example, minimised that sum of the squares of the differences to the data, this would be what is known as a *least squares approximation* to the data using a linear function. In real data this fitting of data to a function has the effect of *smoothing* complex or noisy data.
### Choice of interpolating function
We have a lot of choice for how we construct the interpolating or curve-fitting function. Considerations for how to do this include the smoothness of the resulting function (i.e. how many smooth derivatives it has - cf. the piecewise polynomial case - what does this approximation tell us about the rate of change of the data?), replicating known positivity or periodicity, the cost of evaluating it, etc.
Some choices include: polynomials, piecewise polynomials, trigonometric series (sums of sines and cosines leading to an approximation similar to Fourier series).
# Lagrange polynomial
[Lagrange polynomials](http://mathworld.wolfram.com/LagrangeInterpolatingPolynomial.html) are a particularly popular choice for constructing an interpolant for a given data set. The Lagrange polynomial is the polynomial of the least degree that passes through each data point in the set. **The interpolating polynomial of the least degree is unique.**
Given a set of points as defined above, the Lagrange polynomial is defined as the linear combination
$$L(x) = \sum_{i=0}^{N} y_i \ell_i(x).$$
The functions $\ell_i$ are known as the *Lagrange basis polynomials* defined by the product
$$\ell_i(x) := \prod_{\begin{smallmatrix}0\le m\le N\\ m\neq i\end{smallmatrix}} \frac{x-x_m}{x_i-x_m} = \frac{(x-x_0)}{(x_i-x_0)} \cdots \frac{(x-x_{i-1})}{(x_i-x_{i-1})} \frac{(x-x_{i+1})}{(x_i-x_{i+1})} \cdots \frac{(x-x_k)}{(x_i-x_k)},$$
where $0\le i\le N$.
Notice from the definition the requirement that no two $x_i$ are the same, $x_i - x_m \neq 0$, so this expression is always well-defined (i.e. we never get a divide by zero!) The reason pairs $x_i = x_j$ with $y_i\neq y_j$ are not allowed is that no interpolation function $L$ such that $y_i = L(x_i)$ would exist; a function can only get one value for each argument $x_i$. On the other hand, if also $y_i = y_j$, then those two points would actually be one single point.
For all $i\neq j$, $\ell_j(x)$ includes the term $(x-x_i)$ in the numerator, so the whole product will be zero at $x=x_i$:
$\ell_{j\ne i}(x_i) = \prod_{m\neq j} \frac{x_i-x_m}{x_j-x_m} = \frac{(x_i-x_0)}{(x_j-x_0)} \cdots \frac{(x_i-x_i)}{(x_j-x_i)} \cdots \frac{(x_i-x_k)}{(x_j-x_k)} = 0$.
On the other hand,
$\ell_i(x_i) := \prod_{m\neq i} \frac{x_i-x_m}{x_i-x_m} = 1$
In other words, all basis polynomials are zero at $x=x_i$, except $\ell_i(x)$, for which it holds that $\ell_i(x_i)=1$, because it lacks the $(x-x_i)$ term.
It follows that $y_i \ell_i(x_i)=y_i$, so at each point $x_i$, $L(x_i)=y_i+0+0+\dots +0=y_i$, showing that $L$ interpolates the function exactly.
To help illustrate our discussion lets first create some data in Python and take a look at it.
```
%pylab inline
# Invent some raw data
x=numpy.array([0.5,2.0,4.0,5.0,7.0,9.0])
y=numpy.array([0.5,0.4,0.3,0.1,0.9,0.8])
# For clarity we are going to add a small margin to all the plots.
pylab.margins(0.1)
# We want to overlay a plot the raw data a few times so lets make this a function.
def plot_raw_data(x,y):
# Plot the data as black stars
pylab.plot(x,y,'k*',label='raw data')
pylab.xlabel('x')
pylab.ylabel('y')
pylab.grid(True)
# The simple plot function you used in Introduction to Programming last term
# will show a piecewise-linear approximation:
pylab.plot(x,y,'r',label='p/w linear')
# Overlay raw data
plot_raw_data(x,y)
# Add a legend
pylab.legend(loc='best')
pylab.show()
```
We can use [scipy.interpolate.lagrange](http://docs.scipy.org/doc/scipy/reference/generated/scipy.interpolate.lagrange.html)
from [SciPy](http://www.scipy.org) to generate the **Lagrange polynomial** for a dataset as shown below.
<span style="color:red">(Note: SciPy provides a [wide range of interpolators](http://docs.scipy.org/doc/scipy/reference/interpolate.html) with many different properties which we do not have time to go into in this course. When you need to interpolate data for your specific application then you should look up the literature to ensure you are using the best one.)</span>
```
import scipy.interpolate
# Create the Lagrange polynomial for the given points.
lp=scipy.interpolate.lagrange(x, y)
# Evaluate this fuction at a high resolution so that we can get a smooth plot.
xx=numpy.linspace(0.4, 9.1, 100)
pylab.plot(xx, lp(xx), 'b', label='Lagrange')
# Overlay raw data
plot_raw_data(x, y)
# Add a legend
pylab.legend(loc='best')
pylab.show()
```
# Error in Lagrange interpolation
Note that it can be proven that in the case where we are interpolating a known function (e.g. a complex non-polynomial function by a simpler polynomial), the error is proportional to the distance from any of the data points (which makes sense as the error is obviously zero at these points) and to the $(n+1)$-st derivative of that function evaluated at some location within the bounds of the data. I.e. the more complex (sharply varying) the function is, the higher the error could be.
### <span style="color:blue">Exercise 1: Approximating a function </span>
Sample the function $y(x)=x^3$ at the points $x=(1,2,3)$.
Write your own Python function to construct the Lagrange polynomials $L_0$, $L_1+L_0$ and $L_2+L_1+L_0$. Plot the resulting polynomials along with the error compared to the original exact function. (<span style="color:green">Guru tip: Using the pylab function [fill_between](http://matplotlib.org/examples/pylab_examples/fill_between_demo.html) provides a nice way of illustrating the difference between graphs.</span>)
# Curve fitting
Curve-fitting in the [least squares](http://mathworld.wolfram.com/LeastSquaresFitting.html) sense is popular when the dataset contains noise (nearly always the case when dealing with real world data). This is straightforward to do for polynomials of different polynomial degree using [numpy.polyfit](http://docs.scipy.org/doc/numpy/reference/generated/numpy.polyfit.html), see below.
```
# Calculate coefficients of polynomial degree 0 - ie a constant value.
poly_coeffs=numpy.polyfit(x, y, 0)
# Construct a polynomial function which we can use to evaluate for arbitrary x values.
p0 = numpy.poly1d(poly_coeffs)
pylab.plot(xx, p0(xx), 'k', label='Constant')
# Fit a polynomial degree 1 - ie a straight line.
poly_coeffs=numpy.polyfit(x, y, 1)
p1 = numpy.poly1d(poly_coeffs)
pylab.plot(xx, p1(xx), 'b', label='Linear')
# Quadratic
poly_coeffs=numpy.polyfit(x, y, 2)
p2 = numpy.poly1d(poly_coeffs)
pylab.plot(xx, p2(xx), 'r', label='Quadratic')
# Cubic
poly_coeffs=numpy.polyfit(x, y, 3)
p3 = numpy.poly1d(poly_coeffs)
pylab.plot(xx, p3(xx), 'g', label='Cubic')
# Overlay raw data
plot_raw_data(x, y)
# Add a legend
pylab.legend(loc='best')
pylab.show()
```
### <span style="color:blue">Exercise 2: Squared error calculation</span>
As described in the docs ([numpy.polyfit](http://docs.scipy.org/doc/numpy/reference/generated/numpy.polyfit.html)), least squares fitting minimises the square of the difference between the data provided and the polynomial,
$$E = \sum_{i=0}^{k} (p(x_i) - y_i)^2,$$
where $p(x_i)$ is the value of the polynomial function that has been fit to the data evaluated at point $x_i$, and $y_i$ is the $i^th$ data value.
Write a Python fucntion that evaluates the squared error, $E$, and use this function to evaluate the error for each of the polynomials calculated above. <span style="color:green">Tip: Try to pass the function *p* in as an argument to your error calculation function. One of the great features of Python is that it is easy to pass in functions as arguments.</span>
Why is the square of the difference used?
### <span style="color:blue">Exercise 3: Degree of approximation </span>
Extend the example above by fitting and plotting polynomials of increasing degree past cubic. At what *degree* does the resulting polynomial approximation equate to the Lagrange interpolant?
Why does this make sense?
<span style="color:green">Hint: think about the number of free parameters in a polynomial, and the amount of data you have.</span>
# Extrapolation
Take to remember that *interpolation* by definition is used to estimate $y$ for values of $x$ within the bounds of the available data (here $[0.5,0]$) with some confidence. *Extrapolation* on the other hand is the process of estimating (e.g. using the interpolating function) $y$ *outside* the bounds of the available data. However, extrapolation requires a great deal of care as it will become increasingly inaccurate as you go further out of bounds.
### <span style="color:blue">Exercise 4: Extrapolation </span>
Recreate the plots in the example above for different degrees of polynomial, setting the x-range from -2.0 to 13.0. What do you notice about extrapolation when you use higher degree polynomials?
# Challenge of the day
### <span style="color:blue">Exercise 5: Submarine landslide size in the North Atlantic </span>
Open the data file [Length-Width.dat](https://raw.githubusercontent.com/ggorman/Numerical-methods-1/master/notebook/data/Length-Width.dat) giving the lengths and widths of submarine landslides in the North Atlantic basin [from [Huhnerbach & Masson, 2004](http://www.sciencedirect.com/science/article/pii/S0025322704002774), Fig. 7]. Fit a linear best fit line using polyfit and try to recreate the image below.
<span style="color:green">Hint: You will need to take the log of the data before fitting a line to it. </span>
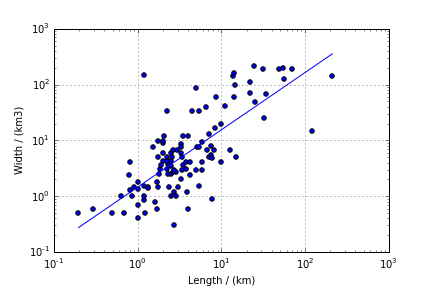
Reference: [V. Huhnerbach, D.G. Masson, Landslides in the North Atlantic and its adjacent seas:
an analysis of their morphology, setting and behaviour, Marine Geology 213 (2004) 343 – 362.](http://www.sciencedirect.com/science/article/pii/S0025322704002774)
| github_jupyter |
## Imperfect Tests and The Effects of False Positives
The US government has been widely criticized for its failure to test as many of its citizens for COVID-19 infections as other countries. But is mass testing really as easy as it seems? This analysis of the false positive and false negative rates of tests, using published sensitivities and specificities for COVID-19 rt-PCR and antigen tests, shows that even tests with slightly less than perfect results can produce very large numbers of false positives.
```
import sys
# Install required packages
#!{sys.executable} -mpip -q install matplotlib seaborn statsmodels pandas publicdata metapack
%matplotlib inline
import pandas as pd
import geopandas as gpd
import numpy as np
import metapack as mp
import rowgenerators as rg
import publicdata as pub
import matplotlib.pyplot as plt
import seaborn as sns
sns.set(color_codes=True)
```
As the world became more aware of the threat posed by COVID-19 in February 2020, US media began to draw attention to the disparity between the extent of testing being done in other countries versus the United States. The CDC released [fairly restrictive guidelines](https://www.cdc.gov/coronavirus/2019-ncov/hcp/clinical-criteria.html) for what conditions qualified a patient for a lab test for COVID-19 infections, and many media outlets criticized the US CDC for being unprepared to test for the virus.
Criticism intensified when the first version of tests created by the CDC [proved to be unreliable](https://www.forbes.com/sites/rachelsandler/2020/03/02/how-the-cdc-botched-its-initial-coronavirus-response-with-faulty-tests/#5bbf1d50670e). But there are important considerations that these reports have largely ignored, the most important of which is the false positive and false negative rates of the tests, which can produce results that are worse than useless when the prevalence of the condition — the percentage of people who are infected — is very low.
Every test — for nearly any sort of test — has an error rate: false positives and false negatives. False negatives are fairly easy to understand. If a 1,000 women who have breast cancer take a test that has a false positive rate of 1%, the test will report that 999 of them have cancer, and 1 who does not, even though she actually does.
The false positive rate is trickier, because it is multipled not by the number of women who have cancer, but by the number of women who take the test. If the situation is that a large number of women are tested, but few have cancer, the test can report many more false positives than women who actually have cancer.
There is evidence that the tests for the COVID-19 virus have a false positive rate large enough that if a large number of people are tested when the prevalence of COVID-19 infections are small, most of the reported positives are false positives.
# Primer on False Positives and Negatives
Research related to epidemiological tests typically does not report the false positive rate directly; instead it reports two parameters, the Selectivity and Specificity. [Wikipedia has an excellent article](https://en.wikipedia.org/wiki/Sensitivity_and_specificity) describing these parameters and how they related to false positive and false negative rates, and [Health News Review](https://www.healthnewsreview.org/) publishes this [very accessible overview of the most important concepts](https://www.healthnewsreview.org/toolkit/tips-for-understanding-studies/understanding-medical-tests-sensitivity-specificity-and-positive-predictive-value/). The most important part of the Wikipedia article to understand is the table in the [worked example](https://en.wikipedia.org/wiki/Sensitivity_and_specificity#Worked_example). When a test is administered, there are four possible outcomes. The test can return a positive result, which can be a true positive or a false positive, or it can return a negative result, which is a true negative or a false negative. If you organize those posibilities by what is the true condition ( does the patient have the vius or not ):
* Patient has virus
* True Positive ($\mathit{TP}$)
* False negative ($\mathit{FN}$)
* Patient does not have virus
* True Negative ($\mathit{TN}$)
* False Positive. ($\mathit{FP}$)
In the Wikipedia worked example table:
* The number of people who do have the virus is $\mathit{TP}+\mathit{FN}$, the true positives plus the false negatives, which are the cases that should have been reported positive, but were not.
* The number of people who do not have the virus is $\mathit{TN}+\mathit{FP}$, the true negatives and the false positives, which are the cases should have been reported positive, but were not.
The values of Sensitivity and Specificity are defined as:
$$\begin{array}{ll}
Sn = \frac{\mathit{TP}}{\mathit{TP} + \mathit{FN}} & \text{True positives outcomes divided by all positive conditions} \tag{1}\label{eq1}\\
Sp = \frac{\mathit{TN}}{\mathit{FP} + \mathit{TN}} & \text{True negatives outcomes divided by all negative conditions}\\
\end{array}$$
We want to know the number of false positives($\mathit{FP}$) given the number of positive conditions ($\mathit{TP}+\mathit{FN}$) and the total number of tests. To compute these, we need to have some more information about the number of people tested, and how common the disease is:
* Total test population $P$, the number of people being tested, which equals $\mathit{TP}+\mathit{FP}+\mathit{FN}+\mathit{TN}$
* The prevalence $p$, the population rate of positive condition.
We can do a little math to get:
$$\begin{array}{ll}
\mathit{TP} = Pp\mathit{Sn} & \text{}\\
\mathit{FP} = P(1-p)(1-\mathit{Sp}) \text{}\\
\mathit{TN} = P(1-p)\mathit{Sp} & \text{}\\
\mathit{FN} = Pp(1-\mathit{Sn})& \text{}\\
\end{array}$$
You can see examples of these equations worked out in the third line in the red and green cells of the [Worked Example](https://en.wikipedia.org/wiki/Sensitivity_and_specificity#Worked_example) on the Sensitivity and Specificity Wikipedia page.
It is important to note that when these four values are used to calculate $\mathit{Sp}$ and $\mathit{Sn}$, the population value $P$ cancels out, so $\mathit{Sp}$ and $\mathit{Sn}$ do not depend on the number of people tested.
One of the interesting questions when test results are reported is "What percentage of the positive results are true positives?" This is a particularly important question for the COVID-19 pandemic because there are a lot of reports that most people with the virus are asymptomatic. Are they really asymptomatic, or just false positives?
The metric we're interested here is the portion of positive results that are true positives, the positive predictive value, $\mathit{PPV}$:
$$\mathit{PPV} = \frac{\mathit{TP} }{ \mathit{TP} +\mathit{FP} } $$
Which expands to:
$$\mathit{PPV} = \frac{p\mathit{Sn} }{ p\mathit{Sn} + (1-p)(1-\mathit{Sp}) }\tag{2}\label{eq2} $$
It is important to note that $\mathit{PPV}$ is not dependent on $P$, the size of the population being tested. It depends only on the quality parameters of the test, $\mathit{Sn}$ and $\mathit{Sp}$, and the prevalence, $p$. For a given test, only the prevalence will change over time.
# Selctivity and Specificity Values
It has been dificult to find specificity and sensitivity values for COVID-19 tests, or any rt-PCR tests; research papers rarely publish the values. Howver, there are a few reports for the values for serology tests, and a few reports of values for rt-PRC tests for the MERS-CoV virus.
We can get values for an antibidy test for COVID-19 from a a recently published paper, _Development and Clinical Application of A Rapid IgM-IgG Combined Antibody Test for SARS-CoV-2 Infection Diagnosis_<sup><a href="#fnote2" rel="noopener" target="_self">2</a></sup>, which reports:
> The overall testing sensitivity was 88.66% and specificity was 90.63%
This test is significantly different from the most common early tests for COVID-19; this test looks for antibodies in the patient's blood, while most COVID-19 tests are rt-PCR assays that look for fragments of RNA from the virus.
The article _MERS-CoV diagnosis: An update._<sup><a href="#fnote4" rel="noopener" target="_self">4</a></sup> reports that for MERS-CoV:
> Song et al. developed a rapid immunochromatographic assay for the detection of MERS-CoV nucleocapsid protein from camel nasal swabs with 93.9% sensitivity and 100% specificity compared to RT-rtPCR
The article _Performance Evaluation of the PowerChek MERS (upE & ORF1a) Real-Time PCR Kit for the Detection of Middle East Respiratory Syndrome Coronavirus RNA_<sup><a href="#fnote5" rel="noopener" target="_self">5</a></sup> reports:
> The diagnostic sensitivity and specificity of the PowerChek MERS assay were both 100% (95% confidence interval, 91.1–100%).
The [Emergency Use Authorization for LabCorp's rt-PCR test](https://www.fda.gov/media/136151/download)<sup><a href="#fnote6" rel="noopener" target="_self">6</a></sup> reports:
~~~
Performance of the COVID-19 RT-PCR test against the expected results [ with NP swabs ] are:
Positive Percent Agreement 40/40 = 100% (95% CI: 91.24%-100%)
Negative Percent Agreement 50/50 = 100% (95% CI: 92.87% -100%)
~~~
Using the lower bound of the 95% CI, values convert to a specificity of .90 and sensitivity of .94.
A recent report characterizes Abbott Labs ID NOW system, used for influenza tests. [Abbott Labs recieved an EUA](https://www.fda.gov/media/136525/download), on 27 March 2020, for a version of the device for use with COVID-19. The study of the the influenza version states:
> The sensitivities of ID NOW 2 for influenza A were 95.9% and 95.7% in NPS and NPA, respectively, and for influenza B were 100% and 98.7% in NPS and NPA, respectively. The specificity was 100% for both influenza A and influenza B in NPS and NPA.
The results section of the paper provides these parameters, when compared to rRT-PCR:
<table>
<tr>
<th>Virus</th>
<th>Parameter</th>
<th>ID NOW 2</th>
<th> ID NOW 2 VTM</th>
</tr>
<tr>
<td>type A</td>
<td>Sensitivity (95% CI)</td>
<td>95.7 (89.2-98.8)</td>
<td>96.7 (90.8-99.3)</td>
</tr>
<tr>
<td></td>
<td>Specificity (95% CI)</td>
<td>100 (89.3-100) </td>
<td>100 (89.3-100)</td>
</tr>
<tr>
<td>Type B</td>
<td>Sensitivity (95% CI)</td>
<td>98.7 (93.0-100)</td>
<td>100 (96.2-100)</td>
</tr>
<tr>
<td></td>
<td>Specificity (95% CI)</td>
<td>100 (98.5-100)</td>
<td>100 (98.5-100)</td>
</tr>
</table>
A recent Medscape article<a href="#fnote7" rel="noopener" target="_self">7</a></sup> on the specificity and sensitivity of Influenza tests reports:
> In a study of the nucleic acid amplification tests ID Now (Abbott), Cobas Influenza A/B Assay (Roche Molecular Diagnostics), and Xpert Xpress Flu (Cepheid), Kanwar et al found the three products to have comparable sensitivities for influenza A (93.2%, 100%, 100%, respectively) and B (97.2%, 94.4%, 91.7%, respectively) detection. In addition, each product had greater than 97% specificity for influenza A and B detection.
> Rapid antigen tests generally have a sensitivity of 50-70% and a specificity of 90-95%. Limited studies have demonstrated very low sensitivity for detection of 2009 H1N1 with some commercial brands.
Based on these values, we'll explore the effects of sensitivity and specificities in the range of .9 to 1.
# PPV For Serology Test
First we'll look at the positive prediction value for the antibody test in reference (<a href="#fnote2" rel="noopener" target="_self">2</a>), which has the lowest published Sp and Sn values at .9063 and .8866. The plot below shows the portion of positive test results that are true positives s a function of the prevalence.
```
def p_vs_tpr(Sp, Sn):
for p in np.power(10,np.linspace(-7,np.log10(.5), num=100)): # range from 1 per 10m to 50%
ppv = (p*Sn) / ( (p*Sn)+(1-p)*(1-Sp))
yield (p, ppv)
def plot_ppv(Sp, Sn):
df = pd.DataFrame(list(p_vs_tpr(Sp, Sn)), columns='p ppv'.split())
df.head()
fig, ax = plt.subplots(figsize=(12,8))
df.plot(ax=ax, x='p',y='ppv', figsize=(10,10))
fig.suptitle(f'Portion of Positives that Are True Vs Prevalence\nFor test with Sp={Sp} and Sn={Sn}', fontsize=20)
ax.set_xlabel('Condition Prevalence in Portion of Tested Population', fontsize=18)
ax.set_ylabel('Portion of Positive Test Results that are True Positives', fontsize=18);
#ax.set_xscale('log')
#ax.set_yscale('log')
plot_ppv(Sp = .9063, Sn = .8866)
```
The important implication of this curve is that using a test with low Sp and Sn values in conditions of low prevalence will result in a very large portion of false positives.
# False Positives for LabCorp's test
Although the published results for the LabCorp test are 100% true positives and true negative rates, the 95% error margin is substantial, because the test was validatd with a relatively small number of samples. This analysis will use the published error margins to produce a distribution of positive prediction values. First, let's look at the distributions of the true positive and true negative rates, accounting for the published confidence intervals. These distributions are generated by converting the published true and false rates, and their CIs into gaussian distributions, and selecting only values that are 1 or lower from those distributions.
```
# Convert CI to standard error. The values are reported for a one-sided 95% CI,
# so we're multiplying by the conversion for a two-sided 90% ci
p_se = (1-.9124) * 1.645
n_se = (1-.9287) * 1.645
def select_v(se):
"""get a distribution value, which must be less than or equal to 1"""
while True:
v = np.random.normal(1, se)
if v <= 1:
return v
# These values are not TP and FP counts; they are normalized to
# prevalence
TP = np.array(list(select_v(p_se) for _ in range(100_000)))
TN = np.array(list(select_v(n_se) for _ in range(100_000)))
fig, ax = plt.subplots(1,2, figsize=(12,8))
sns.distplot( TP, ax=ax[0], kde=False);
ax[0].set_title('Distribution of Posibile True Positives Rates');
sns.distplot( TN, ax=ax[1], kde=False);
ax[1].set_title('Distribution of Posibile True Negative Rates');
fig.suptitle(f'Distribution of True Positive and Negative Rates'
'\nFor published confidence intervals and 4K random samples', fontsize=20);
```
It is important to note that these are not the distributions
From these distributions, we can calculate the distributions for the positive prediction value, the portion of all positive results that are true positives.
With these distributions, we can use ([Eq 2](#MathJax-Span-5239)) to compute the distributions of PPV for a variety of prevalences. In each chart, the 'mean' is the expectation value of the distribution, the weighted mean of the values. It is the most likely PPV valule for the given prevalence.
```
FP = 1-TN
FN = 1-TP
Sn = TP / (TP+FN)
Sp = TN / (TN+FP)
def ppv_dist_ufunc(p, Sp, Sn):
return (p*Sn) / ( (p*Sn)+(1-p)*(1-Sp))
def ppv_dist(p, Sp, Sn):
sp = np.random.choice(Sp, 1_000_000, replace=True)
sn = np.random.choice(Sn, 1_000_000, replace=True)
return ppv_dist_ufunc(p,sp, sn)
fig, axes = plt.subplots( 2,2, figsize=(15,15))
axes = axes.flat
def plot_axis(axn, prevalence):
ppvd = ppv_dist(prevalence, Sp, Sn)
wmean = (ppvd.sum()/len(ppvd)).round(4)
sns.distplot( ppvd, ax=axes[axn], kde=False);
axes[axn].set_title(f' prevalence = {prevalence}, mean={wmean}');
axes[axn].set_xlabel('Positive Prediction Value (PPV)')
axes[axn].set_ylabel('PPV Frequency')
plot_axis(0, .001)
plot_axis(1, .01)
plot_axis(2, .10)
plot_axis(3, .5)
fig.suptitle(f'Distribution of PPV Values for LabCorp Test\nBy condition prevalence', fontsize=20);
```
The implication of these charts is that, even for a test with published true positive and true negative rate of 100%, the uncertainties in the measurements can mean that there still a substantial problem of false positives for low prevalences.
Computing the mean PPV value or a range of prevalence values results in the following relationship.
```
def ppv_vs_p():
for p in np.power(10,np.linspace(-7,np.log10(1), num=100)): # range from 1 per 10m to 50%
ppvd = ppv_dist(p, Sp, Sn)
yield p, ppvd.sum()/len(ppvd)
ppv_v_p = pd.DataFrame(list(ppv_vs_p()), columns='p ppv'.split())
fig, ax = plt.subplots(figsize=(8,8))
sns.lineplot(x='p', y='ppv', data=ppv_v_p, ax=ax)
ax.set_xlabel('Prevalence')
ax.set_ylabel('Positive Predictive Value')
fig.suptitle("Positive Predictive Value vs Prevalence\nFor LabCorp Test", fontsize=18);
```
Compare this curve to the one presented earlier, for the antibody test with published sensitivity of 88.66% and specificity of 90.63%; The relationship between P and PPV for the rt-PCR test isn't much better.
But what if the tests are really, really good: .99 for both sensitivity and specificity? Here is the curve for that case:
```
def ppv_vs_p():
for p in np.power(10,np.linspace(-7,np.log10(1), num=100)): # range from 1 per 10m to 50%
ppvd = ppv_dist_ufunc(p, .99, .99)
yield p, ppvd
ppv_v_p = pd.DataFrame(list(ppv_vs_p()), columns='p ppv'.split())
fig, ax = plt.subplots(figsize=(8,8))
sns.lineplot(x='p', y='ppv', data=ppv_v_p, ax=ax)
ax.set_xlabel('Prevalence')
ax.set_ylabel('Positive Predictive Value')
fig.suptitle("Positive Predictive Value vs Prevalence\nFor Sp=.99, Sn=.99", fontsize=18);
```
This table shows the PPVs and false positive rate for a logrhythimic range of prevalences.
```
prevs = [1e-6, 1e-5, 1e-4, 1e-3, 1e-2, 1e-1]
names = ["1 per {}".format(round(1/p,0)) for p in prevs]
ppvs = [ppv_v_p.loc[(ppv_v_p.p-p).abs().idxmin()].ppv for p in prevs]
fp = [ str(round((1-ppv)*100,1))+"%" for ppv in ppvs]
df = pd.DataFrame({
'Rate': names,
'Prevalence': prevs,
'PPV': ppvs,
'False Positives Rate': fp
}).set_index('Prevalence')
df
```
This case is much better, across the range of prevalences, but for low prevalence, there are still a lot of false positives, and below 1 per 1000, it is nearly all false positives. Here is the same chart, but for Sp and Sn at 99.99%
```
def ppv_vs_p():
for p in np.power(10,np.linspace(-7,np.log10(1), num=100)): # range from 1 per 10m to 50%
ppvd = ppv_dist_ufunc(p, .9999, .9999)
yield p, ppvd
ppv_v_p = pd.DataFrame(list(ppv_vs_p()), columns='p ppv'.split())
ppvs = [ppv_v_p.loc[(ppv_v_p.p-p).abs().idxmin()].ppv for p in prevs]
fp = [ str(round((1-ppv)*100,1))+"%" for ppv in ppvs]
df = pd.DataFrame({
'Rate': names,
'Prevalence': prevs,
'PPV': ppvs,
'False Positives Rate': fp
}).set_index('Prevalence')
df
```
Even a very accurate test will not be able to distinguish healthy from sick better than a coin flip if the prevalence is less than 1 per 10,000.
# Conclusion
Tests with less than 100% specificity and selectivity, including those with published values of 100% but with a moderate confidence interval, are very sensitive to low condition prevalences. Considering the confidence intervals, to ensure that 50% of positive results are true positives requires a prevalence of about 10%, and 80% PPV requires about a 30% prevalence. This suggests that using rt-PCR tests to test a large population that has a low prevalence is likely to produce a large number of false positive results.
# References
* <a name="fnote1">1</a> Parikh, Rajul et al. “[Understanding and using sensitivity, specificity and predictive values.](https://www.ncbi.nlm.nih.gov/pmc/articles/PMC2636062/)” Indian journal of ophthalmology vol. 56,1 (2008): 45-50. doi:10.4103/0301-4738.37595
* <a name="fnote2">2</a> Li, Zhengtu et al. “[Development and Clinical Application of A Rapid IgM-IgG Combined Antibody Test for SARS-CoV-2 Infection Diagnosis.](https://pubmed.ncbi.nlm.nih.gov/32104917/)” Journal of medical virology, 10.1002/jmv.25727. 27 Feb. 2020, doi:10.1002/jmv.25727
* <a name="fnote3">3</a> Zhuang, G H et al. “[Potential False-Positive Rate Among the 'Asymptomatic Infected Individuals' in Close Contacts of COVID-19 Patients](https://pubmed.ncbi.nlm.nih.gov/32133832)” Zhonghua liuxingbingxue zazhi, vol. 41,4 485-488. 5 Mar. 2020, doi:10.3760/cma.j.cn112338-20200221-00144
* <a name="fnote4">4</a> Al Johani, Sameera, and Ali H Hajeer. “[MERS-CoV diagnosis: An update.](https://www.sciencedirect.com/science/article/pii/S1876034116300223)” Journal of infection and public health vol. 9,3 (2016): 216-9. doi:10.1016/j.jiph.2016.04.005
* <a name="fnote5">5</a> Huh, Hee Jae et al. “[Performance Evaluation of the PowerChek MERS (upE & ORF1a) Real-Time PCR Kit for the Detection of Middle East Respiratory Syndrome Coronavirus RNA.](http://www.annlabmed.org/journal/view.html?volume=37&number=6&spage=494)” Annals of laboratory medicine vol. 37,6 (2017): 494-498. doi:10.3343/alm.2017.37.6.494
* <a name="fnote7">7</a> [Emergency Use Authorization summary](https://www.fda.gov/media/136151/download) for LabCorp's COVID-19 rt-PCR test.
* Mitamura, Keiko et al. “[Clinical evaluation of ID NOW influenza A & B 2, a rapid influenza virus detection kit using isothermal nucleic acid amplification technology - A comparison with currently available tests.](https://pubmed.ncbi.nlm.nih.gov/31558351/?from_single_result=31558351)” Journal of infection and chemotherapy : official journal of the Japan Society of Chemotherapy vol. 26,2 (2020): 216-221. doi:10.1016/j.jiac.2019.08.015
* <a name="fnote7">8</a> Blanco, E. M. (2020, January 22). [What is the sensitivity and specificity of diagnostic influenza tests?](https://www.medscape.com/answers/2053517-197226/what-is-the-sensitivity-and-specificity-of-diagnostic-influenza-tests) Retrieved March 27, 2020, from https://www.medscape.com/answers/2053517-197226/what-is-the-sensitivity-and-specificity-of-diagnostic-influenza-tests
## Supporting Web Articles
The World Health Organization has a [web page with links to information the COVID-19 tests](https://www.who.int/emergencies/diseases/novel-coronavirus-2019/technical-guidance/laboratory-guidance) from many countries.
The CDC's page for [Rapid Diagnostic Testing for Influenza: Information for Clinical Laboratory Directors](https://www.cdc.gov/flu/professionals/diagnosis/rapidlab.htm) describes the minimum specificity and sensitivity for rapid influenza diagnostic tests, and shows some examples of PPV and flase positive rates.
Washington Post: [A ‘negative’ coronavirus test result doesn’t always mean you aren’t infected](https://www.washingtonpost.com/science/2020/03/26/negative-coronavirus-test-result-doesnt-always-mean-you-arent-infected/)
Prague Morning: [80% of Rapid COVID-19 Tests the Czech Republic Bought From China are Wrong](https://www.praguemorning.cz/80-of-rapid-covid-19-tests-the-czech-republic-bought-from-china-are-wrong/)
BusinessInsider: [Spain, Europe's worst-hit country after Italy, says coronavirus tests it bought from China are failing to detect positive cases](https://www.businessinsider.com/coronavirus-spain-says-rapid-tests-sent-from-china-missing-cases-2020-3?op=1)
Wikipedia has a good discussion of the false positives problem in the articl about the [Base Rate Falacy](https://en.wikipedia.org/wiki/Base_rate_fallacy#False_positive_paradox).
## Other References
The following references were referenced by Blanco <a href="#fnote6" rel="noopener" target="_self">6</a></sup>, but I haven't evaluated them yet.
Kanwar N, Michael J, Doran K, Montgomery E, Selvarangan R. Comparison of the ID NOWTM Influenza A & B 2, Cobas® Influenza A/B, and Xpert® Xpress Flu Point-of-Care Nucleic Acid Amplification Tests for Influenza A/B Detection in Children. J Clin Microbiol. 2020 Jan 15.
Blyth CC, Iredell JR, Dwyer DE. Rapid-test sensitivity for novel swine-origin influenza A (H1N1) virus in humans. N Engl J Med. 2009 Dec 17. 361(25):2493.
Evaluation of rapid influenza diagnostic tests for detection of novel influenza A (H1N1) Virus - United States, 2009. MMWR Morb Mortal Wkly Rep. 2009 Aug 7. 58(30):826-9.
Faix DJ, Sherman SS, Waterman SH. Rapid-test sensitivity for novel swine-origin influenza A (H1N1) virus in humans. N Engl J Med. 2009 Aug 13. 361(7):728-9.
Ginocchio CC, Zhang F, Manji R, Arora S, Bornfreund M, Falk L. Evaluation of multiple test methods for the detection of the novel 2009 influenza A (H1N1) during the New York City outbreak. J Clin Virol. 2009 Jul. 45(3):191-5.
Sambol AR, Abdalhamid B, Lyden ER, Aden TA, Noel RK, Hinrichs SH. Use of rapid influenza diagnostic tests under field conditions as a screening tool during an outbreak of the 2009 novel influenza virus: practical considerations. J Clin Virol. 2010 Mar. 47(3):229-33.
# Updates
* 2020-03-25: Changed conversion from CI to SE from 1.96 to 1.645; using the factor for a two sided 90% ci for the 95% one sided CI.
* 2020-03-27: Added parameters for Sp and Sn for the influenza version of Abbott Labs ID NOW device.
| github_jupyter |
<h1>Model Deployment</h1>
Once we have built and trained our models for feature engineering (using Amazon SageMaker Processing and SKLearn) and binary classification (using the XGBoost open-source container for Amazon SageMaker), we can choose to deploy them in a pipeline on Amazon SageMaker Hosting, by creating an Inference Pipeline.
https://docs.aws.amazon.com/sagemaker/latest/dg/inference-pipelines.html
This notebook demonstrates how to create a pipeline with the SKLearn model for feature engineering and the XGBoost model for binary classification.
Let's define the variables first.
```
import sagemaker
import sys
import IPython
# Let's make sure we have the required version of the SM PySDK.
required_version = '2.49.2'
def versiontuple(v):
return tuple(map(int, (v.split("."))))
if versiontuple(sagemaker.__version__) < versiontuple(required_version):
!{sys.executable} -m pip install -U sagemaker=={required_version}
IPython.Application.instance().kernel.do_shutdown(True)
import sagemaker
print(sagemaker.__version__)
import boto3
role = sagemaker.get_execution_role()
region = boto3.Session().region_name
sagemaker_session = sagemaker.Session()
bucket_name = sagemaker_session.default_bucket()
prefix = 'endtoendmlsm'
print(region)
print(role)
print(bucket_name)
```
## Retrieve model artifacts
First, we need to create two Amazon SageMaker **Model** objects, which associate the artifacts of training (serialized model artifacts in Amazon S3) to the Docker container used for inference. In order to do that, we need to get the paths to our serialized models in Amazon S3.
<ul>
<li>For the SKLearn model, in Step 02 (data exploration and feature engineering) we defined the path where the artifacts are saved</li>
<li>For the XGBoost model, we need to find the path based on Amazon SageMaker's naming convention. We are going to use a utility function to get the model artifacts of the last training job matching a specific base job name.</li>
</ul>
```
from notebook_utilities import get_latest_training_job_name, get_training_job_s3_model_artifacts
# SKLearn model artifacts path.
sklearn_model_path = 's3://{0}/{1}/output/sklearn/model.tar.gz'.format(bucket_name, prefix)
# XGBoost model artifacts path.
training_base_job_name = 'end-to-end-ml-sm-xgb'
latest_training_job_name = get_latest_training_job_name(training_base_job_name)
xgboost_model_path = get_training_job_s3_model_artifacts(latest_training_job_name)
print('SKLearn model path: ' + sklearn_model_path)
print('XGBoost model path: ' + xgboost_model_path)
```
## SKLearn Featurizer Model
Let's build the SKLearn model. For hosting this model we also provide a custom inference script, that is used to process the inputs and outputs and execute the transform.
The inference script is implemented in the `sklearn_source_dir/inference.py` file. The custom script defines:
- a custom `input_fn` for pre-processing inference requests. Our input function accepts only CSV input, loads the input in a Pandas dataframe and assigns feature column names to the dataframe
- a custom `predict_fn` for running the transform over the inputs
- a custom `output_fn` for returning either JSON or CSV
- a custom `model_fn` for deserializing the model
```
!pygmentize sklearn_source_dir/inference.py
```
Now, let's create the `SKLearnModel` object, by providing the custom script and S3 model artifacts as input.
```
import time
from sagemaker.sklearn import SKLearnModel
code_location = 's3://{0}/{1}/code'.format(bucket_name, prefix)
sklearn_model = SKLearnModel(name='end-to-end-ml-sm-skl-model-{0}'.format(str(int(time.time()))),
model_data=sklearn_model_path,
entry_point='inference.py',
source_dir='sklearn_source_dir/',
code_location=code_location,
role=role,
sagemaker_session=sagemaker_session,
framework_version='0.20.0',
py_version='py3')
```
## XGBoost Model
Similarly to the previous steps, we can create an `XGBoost` model object. Also here, we have to provide a custom inference script.
The inference script is implemented in the `xgboost_source_dir/inference.py` file. The custom script defines:
- a custom `input_fn` for pre-processing inference requests. This input function is able to handle JSON requests, plus all content types supported by the default XGBoost container. For additional information please visit: https://github.com/aws/sagemaker-xgboost-container/blob/master/src/sagemaker_xgboost_container/encoder.py. The reason for adding the JSON content type is that the container-to-container default request content type in an inference pipeline is JSON.
- a custom `model_fn` for deserializing the model
```
!pygmentize xgboost_source_dir/inference.py
```
Now, let's create the `XGBoostModel` object, by providing the custom script and S3 model artifacts as input.
```
import time
from sagemaker.xgboost import XGBoostModel
code_location = 's3://{0}/{1}/code'.format(bucket_name, prefix)
xgboost_model = XGBoostModel(name='end-to-end-ml-sm-xgb-model-{0}'.format(str(int(time.time()))),
model_data=xgboost_model_path,
entry_point='inference.py',
source_dir='xgboost_source_dir/',
code_location=code_location,
framework_version='0.90-2',
py_version='py3',
role=role,
sagemaker_session=sagemaker_session)
```
## Pipeline Model
Once we have models ready, we can deploy them in a pipeline, by building a `PipelineModel` object and calling the `deploy()` method.
```
import sagemaker
import time
from sagemaker.pipeline import PipelineModel
pipeline_model_name = 'end-to-end-ml-sm-xgb-skl-pipeline-{0}'.format(str(int(time.time())))
pipeline_model = PipelineModel(
name=pipeline_model_name,
role=role,
models=[
sklearn_model,
xgboost_model],
sagemaker_session=sagemaker_session)
endpoint_name = 'end-to-end-ml-sm-pipeline-endpoint-{0}'.format(str(int(time.time())))
print(endpoint_name)
pipeline_model.deploy(initial_instance_count=1,
instance_type='ml.m5.xlarge',
endpoint_name=endpoint_name)
```
<span style="color: red; font-weight:bold">Please take note of the endpoint name, since it will be used in the next workshop module.</span>
## Getting inferences
Finally we can try invoking our pipeline of models and get some inferences:
```
from sagemaker.serializers import CSVSerializer
from sagemaker.deserializers import JSONDeserializer
from sagemaker.predictor import Predictor
predictor = Predictor(
endpoint_name=endpoint_name,
sagemaker_session=sagemaker_session,
serializer=CSVSerializer(),
deserializer=JSONDeserializer())
#'Type', 'Air temperature [K]', 'Process temperature [K]', 'Rotational speed [rpm]', 'Torque [Nm]', 'Tool wear [min]'
payload = "L,298.4,308.2,1582,70.7,216"
print(predictor.predict(payload))
payload = "M,298.4,308.2,1582,30.2,214"
print(predictor.predict(payload))
payload = "L,298.4,308.2,30,70.7,216"
print(predictor.predict(payload))
#predictor.delete_endpoint()
```
Once we have tested the endpoint, we can move to the next workshop module. Please access the module <a href="https://github.com/aws-samples/amazon-sagemaker-build-train-deploy/tree/master/05_API_Gateway_and_Lambda" target="_blank">05_API_Gateway_and_Lambda</a> on GitHub to continue.
| github_jupyter |
## Preprocessing
```
# Import our dependencies
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
import pandas as pd
import tensorflow as tf
from keras.callbacks import ModelCheckpoint
# Import and read the charity_data.csv.
import pandas as pd
application_df = pd.read_csv("charity_data.csv")
application_df.head()
# Drop the non-beneficial ID columns, 'EIN' and 'NAME'.
application_df.drop(["EIN","NAME"],axis=1, inplace=True)
application_df.head()
# Determine the number of unique values in each column.
application_df.nunique()
# Look at APPLICATION_TYPE value counts for binning
application_df["APPLICATION_TYPE"].value_counts()
# Choose a cutoff value and create a list of application types to be replaced
# use the variable name `application_types_to_replace`
app_vc = application_df.APPLICATION_TYPE.value_counts()
application_types_to_replace = app_vc[app_vc < 500].index
# # Replace in dataframe
for app in application_types_to_replace:
application_df['APPLICATION_TYPE'] = application_df['APPLICATION_TYPE'].replace(app,"Other")
# # Check to make sure binning was successful
application_df['APPLICATION_TYPE'].value_counts()
# Look at CLASSIFICATION value counts for binning
application_df.CLASSIFICATION.value_counts()
# Choose a cutoff value and create a list of classifications to be replaced
# use the variable name `classifications_to_replace`
class_vc = application_df.CLASSIFICATION.value_counts()
classifications_to_replace = class_vc[class_vc < 1800].index
# Replace in dataframe
for cls in classifications_to_replace:
application_df['CLASSIFICATION'] = application_df['CLASSIFICATION'].replace(cls,"Other")
# Check to make sure binning was successful
application_df['CLASSIFICATION'].value_counts()
application_df.head()
# Convert categorical data to numeric with `pd.get_dummies`
application_dummies = pd.get_dummies(application_df)
application_dummies.head()
# Split our preprocessed data into our features and target arrays
y = application_dummies["IS_SUCCESSFUL"].values
X = application_dummies.drop(["IS_SUCCESSFUL"],1).values
# Split the preprocessed data into a training and testing dataset
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=78)
# Create a StandardScaler instances
scaler = StandardScaler()
# Fit the StandardScaler
X_scaler = scaler.fit(X_train)
# Scale the data
X_train_scaled = X_scaler.transform(X_train)
X_test_scaled = X_scaler.transform(X_test)
```
## Compile, Train and Evaluate the Model
```
# Define the model - deep neural net, i.e., the number of input features and hidden nodes for each layer.
number_input_features = len(X_train[0])
hidden_nodes_layer1 = 80
hidden_nodes_layer2 = 30
nn = tf.keras.models.Sequential()
# First hidden layer
nn.add(
tf.keras.layers.Dense(units=hidden_nodes_layer1, input_dim=number_input_features, activation="relu")
)
# Second hidden layer
nn.add(tf.keras.layers.Dense(units=hidden_nodes_layer2, activation="relu"))
# Output layer
nn.add(tf.keras.layers.Dense(units=1, activation="sigmoid"))
# Check the structure of the model
nn.summary()
# Compile the model
nn.compile(loss="binary_crossentropy", optimizer="adam", metrics=["accuracy"])
# Train the model
checkpoint = ModelCheckpoint("AlphabetSoupCharity.hdf5", monitor='loss', verbose=1, mode='auto', period=5)
fit_model = nn.fit(X_train_scaled,y_train,epochs=100,callbacks=[checkpoint])
# Evaluate the model using the test data
model_loss, model_accuracy = nn.evaluate(X_test_scaled,y_test,verbose=2)
print(f"Loss: {model_loss}, Accuracy: {model_accuracy}")
```
| github_jupyter |
Goal of this notebook to test several classifiers on the data set with different features
And beforehand i want to thank Jose Portilla for his magnificent "Python for Data Science and Machine Learning" course on Udemy , which helped me to dive into ML =)
### Let's begin
First of all neccesary imports
```
import numpy as np
import pandas as pd
import matplotlib as mpl
import matplotlib.pyplot as plt
import seaborn as sns
import string
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.model_selection import train_test_split
from nltk.stem import SnowballStemmer
from nltk.corpus import stopwords
%matplotlib inline
```
Let's read the data from csv file
```
sms = pd.read_csv('../input/spam.csv', encoding='latin-1')
sms.head()
```
Now drop "unnamed" columns and rename v1 and v2 to "label" and "message"
```
sms = sms.drop(['Unnamed: 2','Unnamed: 3','Unnamed: 4'],axis=1)
sms = sms.rename(columns = {'v1':'label','v2':'message'})
```
Let's look into our data
```
sms.groupby('label').describe()
```
Intresting that "Sorry, I'll call later" appears only 30 times here =)
Now let's create new feature "message length" and plot it to see if it's of any interest
```
sms['length'] = sms['message'].apply(len)
sms.head()
mpl.rcParams['patch.force_edgecolor'] = True
plt.style.use('seaborn-bright')
sms.hist(column='length', by='label', bins=50,figsize=(11,5))
```
Looks like the lengthy is the message, more likely it is a spam. Let's not forget this
### Text processing and vectorizing our meddages
Let's create new data frame. We'll need a copy later on
```
text_feat = sms['message'].copy()
```
Now define our tex precessing function. It will remove any punctuation and stopwords aswell.
```
def text_process(text):
text = text.translate(str.maketrans('', '', string.punctuation))
text = [word for word in text.split() if word.lower() not in stopwords.words('english')]
return " ".join(text)
text_feat = text_feat.apply(text_process)
vectorizer = TfidfVectorizer("english")
features = vectorizer.fit_transform(text_feat)
```
### Classifiers and predictions
First of all let's split our features to test and train set
```
features_train, features_test, labels_train, labels_test = train_test_split(features, sms['label'], test_size=0.3, random_state=111)
```
Now let's import bunch of classifiers, initialize them and make a dictionary to itereate through
```
from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC
from sklearn.naive_bayes import MultinomialNB
from sklearn.tree import DecisionTreeClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.ensemble import AdaBoostClassifier
from sklearn.ensemble import BaggingClassifier
from sklearn.ensemble import ExtraTreesClassifier
from sklearn.metrics import accuracy_score
svc = SVC(kernel='sigmoid', gamma=1.0)
knc = KNeighborsClassifier(n_neighbors=49)
mnb = MultinomialNB(alpha=0.2)
dtc = DecisionTreeClassifier(min_samples_split=7, random_state=111)
lrc = LogisticRegression(solver='liblinear', penalty='l1')
rfc = RandomForestClassifier(n_estimators=31, random_state=111)
abc = AdaBoostClassifier(n_estimators=62, random_state=111)
bc = BaggingClassifier(n_estimators=9, random_state=111)
etc = ExtraTreesClassifier(n_estimators=9, random_state=111)
```
Parametres are based on notebook:
[Spam detection Classifiers hyperparameter tuning][1]
[1]: https://www.kaggle.com/muzzzdy/d/uciml/sms-spam-collection-dataset/spam-detection-classifiers-hyperparameter-tuning/
```
clfs = {'SVC' : svc,'KN' : knc, 'NB': mnb, 'DT': dtc, 'LR': lrc, 'RF': rfc, 'AdaBoost': abc, 'BgC': bc, 'ETC': etc}
```
Let's make functions to fit our classifiers and make predictions
```
def train_classifier(clf, feature_train, labels_train):
clf.fit(feature_train, labels_train)
def predict_labels(clf, features):
return (clf.predict(features))
```
Now iterate through classifiers and save the results
```
pred_scores = []
for k,v in clfs.items():
train_classifier(v, features_train, labels_train)
pred = predict_labels(v,features_test)
pred_scores.append((k, [accuracy_score(labels_test,pred)]))
df = pd.DataFrame.from_items(pred_scores,orient='index', columns=['Score'])
df
df.plot(kind='bar', ylim=(0.9,1.0), figsize=(11,6), align='center', colormap="Accent")
plt.xticks(np.arange(9), df.index)
plt.ylabel('Accuracy Score')
plt.title('Distribution by Classifier')
plt.legend(bbox_to_anchor=(1.05, 1), loc=2, borderaxespad=0.)
```
Looks like ensemble classifiers are not doing as good as expected.
### Stemmer
It is said that stemming short messages does no goot or even harm predictions. Let's try this out.
Define our stemmer function
```
def stemmer (text):
text = text.split()
words = ""
for i in text:
stemmer = SnowballStemmer("english")
words += (stemmer.stem(i))+" "
return words
```
Stem, split, fit - repeat... Predict!
```
text_feat = text_feat.apply(stemmer)
features = vectorizer.fit_transform(text_feat)
features_train, features_test, labels_train, labels_test = train_test_split(features, sms['label'], test_size=0.3, random_state=111)
pred_scores = []
for k,v in clfs.items():
train_classifier(v, features_train, labels_train)
pred = predict_labels(v,features_test)
pred_scores.append((k, [accuracy_score(labels_test,pred)]))
df2 = pd.DataFrame.from_items(pred_scores,orient='index', columns=['Score2'])
df = pd.concat([df,df2],axis=1)
df
df.plot(kind='bar', ylim=(0.85,1.0), figsize=(11,6), align='center', colormap="Accent")
plt.xticks(np.arange(9), df.index)
plt.ylabel('Accuracy Score')
plt.title('Distribution by Classifier')
plt.legend(bbox_to_anchor=(1.05, 1), loc=2, borderaxespad=0.)
```
Looks like mostly the same . Ensemble classifiers doing a little bit better, NB still got the lead.
### What have we forgotten? Message length!
Let's append our message length feature to the matrix we fit into our classifiers
```
lf = sms['length'].as_matrix()
newfeat = np.hstack((features.todense(),lf[:, None]))
features_train, features_test, labels_train, labels_test = train_test_split(newfeat, sms['label'], test_size=0.3, random_state=111)
pred_scores = []
for k,v in clfs.items():
train_classifier(v, features_train, labels_train)
pred = predict_labels(v,features_test)
pred_scores.append((k, [accuracy_score(labels_test,pred)]))
df3 = pd.DataFrame.from_items(pred_scores,orient='index', columns=['Score3'])
df = pd.concat([df,df3],axis=1)
df
df.plot(kind='bar', ylim=(0.85,1.0), figsize=(11,6), align='center', colormap="Accent")
plt.xticks(np.arange(9), df.index)
plt.ylabel('Accuracy Score')
plt.title('Distribution by Classifier')
plt.legend(bbox_to_anchor=(1.05, 1), loc=2, borderaxespad=0.)
```
This time everyone are doing a little bit worse, except for LinearRegression and RandomForest. But the winner is still MultinominalNaiveBayes.
### Voting classifier
We are using ensemble algorithms here, but what about ensemble of ensembles? Will it beat NB?
```
from sklearn.ensemble import VotingClassifier
eclf = VotingClassifier(estimators=[('BgC', bc), ('ETC', etc), ('RF', rfc), ('Ada', abc)], voting='soft')
eclf.fit(features_train,labels_train)
pred = eclf.predict(features_test)
print(accuracy_score(labels_test,pred))
```
Better but nope.
### Final verdict - well tuned NaiveBayes is your friend in spam detection.
| github_jupyter |
# SimFin Test All Datasets
This Notebook performs automated testing of all the bulk datasets from SimFin. The datasets are first downloaded from the SimFin server and then various tests are performed on the data. An exception is raised if any problems are found.
This Notebook can be run as usual if you have `simfin` installed, by running the following command from the directory where this Notebook is located:
jupyter notebook
This Notebook can also be run using `pytest` which makes automated testing easier. You need to have the Python packages `simfin` and `nbval` installed. Then execute the following command from the directory where this Notebook is located:
pytest --nbval-lax -v test_bulk_data.ipynb
This runs the entire Notebook and outputs error messages for all the cells that raised an exception.
## IMPORTANT!
- When you make changes to this Notebook, remember to clear all cells before pushing it back to github, because that makes it easier to see the difference from the previous version. Select menu-item "Kernel / Restart & Clear Output".
- If you set `refresh_days=0` then it will force a new download of all the datasets.
```
# Set this to 0 to force a new download of all datasets.
refresh_days = 30
```
## Imports
```
import pandas as pd
import numpy as np
import warnings
import sys
import os
from IPython.display import display
import simfin as sf
from simfin.names import *
from simfin.datasets import *
```
## Are We Running Pytest?
```
# Boolean whether this is being run under pytest.
# This is useful when printing examples of errors
# if they take a long time to compute, because it
# is not necessary when running pytest.
running_pytest = ('PYTEST_CURRENT_TEST' in os.environ)
```
## Configure SimFin
```
sf.set_data_dir('~/simfin_data/')
sf.load_api_key(path='~/simfin_api_key.txt', default_key='free')
```
## Load All Datasets
```
%%time
data = AllDatasets(refresh_days=refresh_days)
# Example for annual Income Statements.
data.get(dataset='income', variant='annual', market='us').head()
```
## Lists of Datasets
These are in addition to the lists of datasets from `datasets.py`.
```
# Datasets that have a column named TICKER.
# Some tests are probably only necessary for 'companies'
# but we might as well test all datasets that use tickers.
datasets_tickers = ['companies'] + datasets_fundamental() + datasets_shareprices()
```
## Function for Testing Datasets
```
def test_datasets(test_name, datasets=None, variants=None,
markets=None,
test_func=None,
test_func_rows=None,
test_func_groups=None,
group_index=SIMFIN_ID,
process_df_none=False, raise_exception=True):
"""
Helper-function for running tests on many Pandas DataFrames.
:param test_name:
String with the name of the test.
:param datasets:
By default (datasets=None) all possible datasets
will be tested. Otherwise datasets is a list of
strings with dataset names to be tested.
:param variants:
By default (variants=None) all possible variants
for each dataset will be tested, as defined in
simfin.datasets.valid_variants. Otherwise variants
is a list of strings and only those variants
will be tested.
:param markets:
By default (markets=None) all possible markets
for each dataset will be tested, as defined in
simfin.datasets.valid_markets. Otherwise markets
is a list of strings and only those markets
will be tested.
:param test_func:
Function to be called on the Pandas DataFrame for
each dataset. If there are problems with the DataFrame
then return True, otherwise return False.
This is generally used for testing problems with the
entire DataFrame. For example, if the dataset is empty:
test_func = lambda df: len(df) == 0
If this returns True then there is a problem with df.
:param test_func_rows:
Similar to test_func but for testing individual rows
of a DataFrame. For example, test if SHARES_BASIC is
None, zero or negative:
test_func_rows = lambda df: (df[SHARES_BASIC] is None or
df[SHARES_BASIC] <= 0)
:param test_func_groups:
Similar to test_func but for testing groups of rows
in a DataFrame. For example, test on a per-stock basis
whether SHARES_BASIC is greater than twice its mean:
test_func_groups = lambda df: (df[SHARES_BASIC] >
df[SHARES_BASIC].mean() * 2).any()
:param group_index:
String with the column-name used to create groups when
using test_func_groups e.g. SIMFIN_ID for grouping by companies.
:param process_df_none:
Boolean whether to process (True) or skip (False)
DataFrames that are None, because they could not be loaded.
:param raise_exception:
Boolean. If True then raise an exception if there were
any problems, but wait until all datasets have been
tested, so we can print the list of datasets with problems.
If False then only show a warning if there were problems.
:return:
None
"""
# Convert to test_func.
if test_func_rows is not None:
# Convert test_func_rows to test_func.
test_func = lambda df: test_func_rows(df).any()
elif test_func_groups is not None:
# Convert test_func_groups to test_func.
# NOTE: We must use .any(axis=None) because if the DataFrame
# is empty then the groupby returns an empty DataFrame, and
# .any() then returns an empty Series, but we need a boolean.
# By using .any(axis=None) it is reduced to a boolean value.
test_func = lambda df: df.groupby(group_index, group_keys=False).apply(test_func_groups).any(axis=None)
# Number of problems found.
num_problems = 0
# For all datasets, variants and markets.
for dataset, variant, market, df in data.iter(datasets=datasets,
variants=variants,
markets=markets):
# Also process DataFrames that are None,
# because they could not be loaded?
if df is not None or process_df_none:
try:
# Perform the user-supplied test.
problem_found = test_func(df)
except:
# An exception occurred so we consider
# that to be a problem.
problem_found = True
if problem_found:
# Increase the number of problems found.
num_problems += 1
# Print the test's name. Only done once.
if num_problems==1:
print(test_name, file=sys.stderr)
# Print the dataset details.
msg = "dataset='{}', variant='{}', market='{}'"
msg = msg.format(dataset, variant, market)
print(msg, file=sys.stderr)
# Raise exception or generate warning?
if num_problems>0:
if raise_exception:
raise Exception(test_name)
else:
warnings.warn(test_name)
```
## Function for Getting Rows with Problems
When a test has found problems in a dataset, it does not show which specific rows have the problem. You can get all the problematic rows using this function:
```
def get_problem_rows(df, test_func_rows):
"""
Perform the given test on all rows of the given DataFrame
and return a DataFrame with only the problematic rows.
:param df:
Pandas DataFrame.
:param test_func_rows:
Function used for testing each row. This takes
a Pandas DataFrame as an argument and returns
a Pandas Series of booleans whether each row
in the original DataFrame has the error.
For example:
test_func_rows = lambda df: (df[SHARES_BASIC] is None or
df[SHARES_BASIC] <= 0)
:return:
Pandas DataFrame with only the problematic rows.
"""
# Index of the rows with problems.
idx = test_func_rows(df)
# Extract the rows with problems.
df2 = df[idx]
return df2
```
## Function for Getting Rows with Missing Data
```
def get_missing_data_rows(df, column):
"""
Return the rows of `df` where the data for the given
column is missing i.e. it is either NaN, None, or Null.
:param df:
Pandas DataFrame.
:param column:
Name of the column.
:return:
Pandas Series with the rows where the
column-data is missing.
"""
# Index for the rows where column-data is missing.
idx = df[column].isnull()
# Get those rows from the DataFrame.
df2 = df[idx]
return df2
```
## Function for Getting Problematic Groups
```
def get_problem_groups(df, test_func_groups, group_index):
"""
Perform the given test on the given DataFrame grouped by
the given index, and return a DataFrame with only the
problematic groups.
This is used to perform tests on a DataFrame on a per-group
basis, e.g. per-stock or per-company, and return a new
DataFrame with only the rows for the stocks that had problems.
:param df:
Pandas DataFrame.
:param test_func_groups:
Similar to test_func but for testing groups of rows
in a DataFrame. For example, test on a per-stock basis
whether SHARES_BASIC is greater than twice its mean:
test_func_groups = lambda df: (df[SHARES_BASIC] >
df[SHARES_BASIC].mean() * 2)
:param group_index:
String with the column-name used to create groups when
using test_func_groups e.g. SIMFIN_ID for grouping by companies.
:return:
Pandas DataFrame with only the problematic groups.
"""
return df.groupby(group_index).filter(test_func_groups)
```
## Function for Testing Equality with Tolerance
This function is useful when comparing floating point numbers, or when comparing accounting numbers that are supposed to have a strict relationship (e.g. Assets = Liabilities + Equity) but we might tolerate a small degree of error in the data e.g. 1%.
```
def isclose(x, y, tolerance=0.01):
"""
Compare whether x and y are approximately equal within
the given tolerance, which is a ratio so tolerance=0.01
means that we tolerate max 1% difference between x and y.
This is similar to numpy.isclose() but is a more efficient
implementation for Pandas which apparently does not have
this built-in already (v. 0.25.1)
:param x:
Pandas DataFrame or Series.
:param y:
Pandas DataFrame or Series.
:param tolerance:
Max allowed difference as a ratio e.g. 0.01 = 1%.
:return:
Pandas DataFrame or Series with booleans whether
x and y are approx. equal.
"""
return (x-y).abs() <= tolerance * y.abs()
```
# Tests
## Dataset could not be loaded
```
test_name = "Dataset could not be loaded"
test_func = lambda df: df is None
test_datasets(datasets=datasets_all(),
test_name=test_name, test_func=test_func,
process_df_none=True)
```
## Dataset is empty
```
test_name = "Dataset is empty"
test_func = lambda df: len(df) == 0
# Test for all markets. This only raises a warning,
# because some markets do have some of their datasets empty.
test_datasets(datasets=datasets_all(),
test_name=test_name, test_func=test_func,
raise_exception=False)
# Test only for the 'us' market. This raises an exception.
# It happened once that all the datasets were empty
# because of some bug on the server or whatever, so it
# is important to raise an exception in case this happens again.
test_datasets(datasets=datasets_all(), markets=['us'],
test_name=test_name, test_func=test_func,
raise_exception=True)
data.get(dataset='income-insurance', variant='quarterly', market='de')
```
## Shares Basic is None or <= 0
```
test_name = "SHARES_BASIC is None or <= 0"
test_func_rows = lambda df: (df[SHARES_BASIC] is None or
df[SHARES_BASIC] <= 0)
test_datasets(datasets=datasets_fundamental(),
test_name=test_name, test_func_rows=test_func_rows)
# Show the problematic rows for a dataset.
df = data.get(dataset='income', variant='annual', market='us')
get_problem_rows(df=df, test_func_rows=test_func_rows)
```
## Shares Diluted is None or <= 0
```
test_name = "SHARES_DILUTED is None or <= 0"
test_func_rows = lambda df: (df[SHARES_DILUTED] is None or
df[SHARES_DILUTED] <= 0)
test_datasets(datasets=datasets_fundamental(),
test_name=test_name, test_func_rows=test_func_rows)
# Show the problematic rows for a dataset.
df = data.get(dataset='income', variant='annual', market='us')
get_problem_rows(df=df, test_func_rows=test_func_rows)
```
## Shares Basic or Diluted looks strange
```
# List of SimFin-Id's to ignore in this test.
# Use this list when a company's share-counts look strange,
# but after manual inspection of the financial reports, the
# share-counts are actually correct.
ignore_simfin_ids = \
[ 53151, 61372, 82753, 99062, 148380, 166965, 258731, 378110,
498391, 520475, 543421, 543877, 546550, 592461, 620342, 652016,
652547, 658464, 658467, 659836, 667668, 689587, 698616, 704562,
768206, 778777, 794492, 798464, 826389, 867483, 890308, 896087,
899362, 951586]
# Ensure they are all unique.
ignore_simfin_ids = np.unique(ignore_simfin_ids)
ignore_simfin_ids
def test_func_groups(df_grp):
# Perform various tests on the share-counts.
# Assume `df_grp` only contains data for a single company,
# because this function should be called using:
# df.groupby(SIMFIN_ID).apply(test_func_groups)
# Ignore this company?
if df_grp[SIMFIN_ID].iloc[0] in ignore_simfin_ids:
return False
# Helper-function for calculating absolute ratio between
# a value and its average.
abs_ratio = lambda df: (df / df.mean() - 1).abs()
# Max absolute ratio allowed.
max_abs_ratio = 2
# Test whether Shares Basic is much different from its mean.
test1 = (abs_ratio(df_grp[SHARES_BASIC]) > max_abs_ratio).any()
# Test whether Shares Diluted is much different from its mean.
test2 = (abs_ratio(df_grp[SHARES_DILUTED]) > max_abs_ratio).any()
return (test1 | test2)
%%time
test_name = "Shares Basic or Shares Diluted looks strange"
test_datasets(datasets=datasets_fundamental(),
test_name=test_name,
test_func_groups=test_func_groups,
group_index=SIMFIN_ID)
# Show the problematic groups for a dataset.
if not running_pytest:
# Get the dataset.
df = data.get(dataset='income', variant='annual', market='us')
# Get the problematic groups.
df_problems = get_problem_groups(df=df,
test_func_groups=test_func_groups,
group_index=SIMFIN_ID)
# Print the problematic groups.
for _, df2 in df_problems.groupby(SIMFIN_ID):
display(df2[[SIMFIN_ID, REPORT_DATE, SHARES_BASIC, SHARES_DILUTED]])
```
## Share-Prices are Zero or Negative
```
test_name = "Share-prices are zero"
def test_func_rows(df):
return (df[OPEN] <= 0.0) & (df[LOW] <= 0.0) & \
(df[HIGH] <= 0.0) & (df[CLOSE] <= 0.0) & \
(df[VOLUME] <= 0.0)
test_datasets(datasets=['shareprices'],
test_name=test_name, test_func_rows=test_func_rows)
# Show the problematic rows for a dataset.
df = data.get(dataset='shareprices', variant='daily', market='us')
get_problem_rows(df=df, test_func_rows=test_func_rows)
```
## Revenue is negative
```
test_name = "REVENUE < 0"
test_func_rows = lambda df: (df[REVENUE] < 0)
# It is possible that Revenue is negative for banks and
# insurance companies, so we only test it for "normal" companies
# in the 'income' dataset.
test_datasets(datasets=['income'],
test_name=test_name, test_func_rows=test_func_rows)
# Show the problematic rows for a dataset.
df = data.get(dataset='income-insurance', variant='quarterly', market='us')
get_problem_rows(df=df, test_func_rows=test_func_rows)
```
## Assets != Liabilities + Equity (Exact Comparison)
This only generates a warning, because sometimes there are tiny rounding errors.
```
test_name = "Assets != Liabilities + Equity (Exact Comparison)"
test_func_rows = lambda df: (df[TOTAL_ASSETS] != df[TOTAL_LIABILITIES] + df[TOTAL_EQUITY])
test_datasets(datasets=datasets_balance(),
test_name=test_name, test_func_rows=test_func_rows,
raise_exception=False)
# Get the problematic rows for a dataset.
df = data.get(dataset='balance', variant='quarterly', market='us')
df2 = get_problem_rows(df=df, test_func_rows=test_func_rows)
# Only show the relevant columns.
df2[[TICKER, SIMFIN_ID, REPORT_DATE, TOTAL_ASSETS, TOTAL_LIABILITIES, TOTAL_EQUITY]]
```
## Assets != Liabilities + Equity (1% Tolerance)
The above test used exact comparison. We now allow for 1% error. This raises an exception.
```
def test_func_rows(df):
x = df[TOTAL_ASSETS]
y = df[TOTAL_LIABILITIES] + df[TOTAL_EQUITY]
# Compare x and y within 1% tolerance. Note the resulting
# boolean array is negated because we want to indicate
# which rows are problematic so x and y are not close.
return ~isclose(x=x, y=y, tolerance=0.01)
test_name = "Assets != Liabilities + Equity (1% Tolerance)"
test_datasets(datasets=datasets_balance(),
test_name=test_name, test_func_rows=test_func_rows)
# Get the problematic rows for a dataset.
df = data.get(dataset='balance', variant='annual', market='us')
df2 = get_problem_rows(df=df, test_func_rows=test_func_rows)
# Only show the relevant columns.
df2[[TICKER, SIMFIN_ID, REPORT_DATE, TOTAL_ASSETS, TOTAL_LIABILITIES, TOTAL_EQUITY]]
```
## Dates are invalid (Fundamentals)
```
# Lambda function for converting strings to dates. Format: YYYY-MM-DD
# This will raise an exception if invalid dates are encountered.
date_parser = lambda column: pd.to_datetime(column, yearfirst=True, dayfirst=False)
# Test function for the entire DataFrame.
# This cannot show which individual rows have problems.
def test_func(df):
result1 = date_parser(df[REPORT_DATE])
result2 = date_parser(df[PUBLISH_DATE])
# We only get to this point if date_parser() does not
# raise any exceptions, in which case we assume the
# data did not have any problems.
return False
test_name = "REPORT_DATE or PUBLISH_DATE is invalid"
test_datasets(datasets=datasets_fundamental(),
test_name=test_name, test_func=test_func)
```
## Dates are invalid (Share-Prices)
```
# Test function for the entire DataFrame.
# This cannot show which individual rows have problems.
def test_func(df):
result1 = date_parser(df[DATE])
# We only get to this point if date_parser() does not
# raise any exceptions, in which case we assume the
# data did not have any problems.
return False
test_name = "DATE is invalid"
test_datasets(datasets=datasets_shareprices(),
test_name=test_name, test_func=test_func)
```
## Duplicate Tickers
```
def get_duplicate_tickers(df):
"""
Return the rows of `df` where multiple SIMFIN_ID
have the same TICKER.
:param df: Pandas DataFrame with TICKER column.
:return: Pandas DataFrame.
"""
# Remove duplicate rows of [TICKER, SIMFIN_ID] pairs.
# For the 'companies' dataset this is not necessary,
# but for e.g. the 'income' dataset we have many rows
# for each [TICKER, SIMFIN_ID] pair because there are
# many financial reports for each of these ID pairs.
idx = df[[TICKER, SIMFIN_ID]].duplicated()
df2 = df[~idx]
# Now the DataFrame df2 only contains unique rows of
# [TICKER, SIMFIN_ID] so we need to check if there are
# any duplicate TICKER.
# Index for rows where TICKER is a duplicate.
idx1 = df2[TICKER].duplicated()
# Index for rows where TICKER is not NaN.
# These would otherwise show up as duplicates.
idx2 = df2[TICKER].notna()
# Index for rows where TICKER is a duplicate but not NaN.
idx = idx1 & idx2
# Get those rows from the DataFrame.
df2 = df2[idx]
return df2
# Test-function whether a DataFrame has duplicate tickers.
test_func = lambda df: (len(get_duplicate_tickers(df=df)) > 0)
test_name = "Duplicate Tickers"
test_datasets(datasets=datasets_tickers,
test_name=test_name, test_func=test_func)
# Show duplicate tickers in the 'companies' dataset.
df = data.get(dataset='companies', market='us')
get_duplicate_tickers(df=df)
# Show duplicate tickers in the 'income-annual' dataset.
df = data.get(dataset='income', variant='annual', market='us')
get_duplicate_tickers(df=df)
```
## Missing Tickers
```
# Test-function whether a DataFrame has missing tickers.
test_func = lambda df: (len(get_missing_data_rows(df=df, column=TICKER)) > 0)
test_name = "Missing Tickers"
test_datasets(datasets=datasets_tickers,
test_name=test_name, test_func=test_func)
# Show missing tickers in the 'companies' dataset.
df = data.get(dataset='companies', market='us')
get_missing_data_rows(df=df, column=TICKER)
# Show missing tickers in the 'income-annual' dataset.
df = data.get(dataset='income', variant='annual', market='us')
get_missing_data_rows(df=df, column=TICKER)
# Show missing tickers in the 'shareprices-daily' dataset.
df = data.get(dataset='shareprices', variant='daily', market='us')
get_missing_data_rows(df=df, column=TICKER)
```
## Missing Company Names
```
# Test-function whether a DataFrame has missing company names.
test_func = lambda df: (len(get_missing_data_rows(df=df, column=COMPANY_NAME)) > 0)
test_name = "Missing Company Name"
test_datasets(datasets=['companies'],
test_name=test_name, test_func=test_func)
# Show missing company names in the 'companies' dataset.
df = data.get(dataset='companies', market='us')
get_missing_data_rows(df=df, column=COMPANY_NAME)
```
## Missing Annual Reports
```
def missing_annual_reports(df):
"""
Return a list of the SIMFIN_ID's from the given DataFrame
that have missing annual reports.
:param df:
Pandas DataFrame with a dataset e.g. 'income-annual'.
It must have columns SIMFIN_ID and FISCAL_YEAR.
:return:
List of integers with SIMFIN_ID's that have missing reports.
"""
# The idea is to test for each SIMFIN_ID individually,
# whether the DataFrame has all the expected reports for
# consecutive Fiscal Years between the min/max years.
# Helper-function for processing a DataFrame for one SIMFIN_ID.
def _missing(df):
# Get the Fiscal Years from the DataFrame.
fiscal_years = df[FISCAL_YEAR]
# How many years between min and max fiscal years.
num_years = fiscal_years.max() - fiscal_years.min() + 1
# We expect the Series to have the same length, otherwise
# some reports must be missing between min and max years.
missing = (num_years != len(fiscal_years))
return missing
# Process all companies individually and get a Pandas
# DataFrame with a boolean for each SIMFIN_ID whether
# it has some missing Fiscal Years.
idx = df.groupby(SIMFIN_ID).apply(_missing)
# List of the SIMFIN_ID's that have missing reports.
simfin_ids = list(idx[idx].index.values)
return simfin_ids
test_name = "Missing annual reports"
test_func = lambda df: len(missing_annual_reports(df=df)) > 0
test_datasets(datasets=datasets_fundamental(),
variants=['annual'],
test_name=test_name, test_func=test_func)
# Get list of SIMFIN_ID's that have missing reports for a dataset.
if not running_pytest:
df = data.get(dataset='income', variant='annual', market='de')
display(missing_annual_reports(df=df))
def sort_annual_reports(df, simfin_id):
"""
Get the data for a given SIMFIN_ID and set the index to be
the sorted Fiscal Year so it is easier to see which are missing.
"""
return df.set_index([SIMFIN_ID, FISCAL_YEAR]).sort_index().loc[simfin_id]
# Show all the reports for a given SIMFIN_ID sorted by
# Fiscal Year so it is easier to see which are missing.
if not running_pytest:
display(sort_annual_reports(df=df, simfin_id=936426))
```
## Missing Quarterly Reports
```
def missing_quarterly_reports(df):
"""
Return a list of the SIMFIN_ID's from the given DataFrame
that have missing quarterly or ttm reports.
:param df:
Pandas DataFrame with a dataset e.g. 'income-annual'.
It must have columns SIMFIN_ID, FISCAL_YEAR, FISCAL_PERIOD.
:return:
List of integers with SIMFIN_ID's that have missing reports.
"""
# The idea is to test for each SIMFIN_ID individually,
# whether the DataFrame has all the expected reports for
# consecutive Fiscal Years and Periods between the min/max.
# Helper-function for processing a DataFrame for one SIMFIN_ID.
def _missing(df):
# Get the Fiscal Years and Periods from the DataFrame.
fiscal_years_periods = df[[FISCAL_YEAR, FISCAL_PERIOD]]
# The first Fiscal Year and Period.
min_year = fiscal_years_periods[FISCAL_YEAR].min()
min_idx = (fiscal_years_periods[FISCAL_YEAR] == min_year)
min_period = fiscal_years_periods[min_idx][FISCAL_PERIOD].min()
# The last Fiscal Year and Period.
max_year = fiscal_years_periods[FISCAL_YEAR].max()
max_idx = (fiscal_years_periods[FISCAL_YEAR] == max_year)
max_period = fiscal_years_periods[max_idx][FISCAL_PERIOD].max()
# How many years between min and max fiscal years.
num_years = max_year - min_year + 1
# Total number of Fiscal Periods between first and
# last Fiscal Years - if all Fiscal Periods were included.
num_periods = num_years * 4
# Used to map from Fiscal Period strings to ints.
# This is safer and easier to understand than
# e.g. def map_period(x): int(x[1])
map_period = \
{
'Q1': 1,
'Q2': 2,
'Q3': 3,
'Q4': 4
}
# Number of Fiscal Periods missing in the first year.
adj_min_period = map_period[min_period] - 1
# Number of Fiscal Periods missing in the last year.
adj_max_period = 4 - map_period[max_period]
# Adjust the number of Fiscal Periods between the min/max
# Fiscal Years and Periods by subtracting those periods
# missing in the first and last years.
expected_periods = num_periods - adj_min_period - adj_max_period
# If the expected number of Fiscal Periods between the
# min and max dates, is different from the actual number
# of Fiscal Periods in the DataFrame, then some are missing.
missing = (expected_periods != len(fiscal_years_periods))
return missing
# Process all companies individually and get a Pandas
# DataFrame with a boolean for each SIMFIN_ID whether
# it has some missing Fiscal Years.
idx = df.groupby(SIMFIN_ID).apply(_missing)
# List of the SIMFIN_ID's that have missing reports.
simfin_ids = list(idx[idx].index.values)
return simfin_ids
%%time
test_name = "Missing quarterly reports"
test_func = lambda df: len(missing_quarterly_reports(df=df)) > 0
test_datasets(datasets=datasets_fundamental(),
variants=['quarterly'],
test_name=test_name, test_func=test_func)
# Get list of SIMFIN_ID's that have missing reports for a dataset.
if not running_pytest:
df = data.get(dataset='income', variant='quarterly', market='us')
display(missing_quarterly_reports(df=df))
def sort_quarterly_reports(df, simfin_id):
"""
Get the data for a given SIMFIN_ID and set the index to be
the sorted Fiscal Year and Period so it is easier to see
which ones are missing.
"""
return df.set_index([SIMFIN_ID, FISCAL_YEAR, FISCAL_PERIOD]).sort_index().loc[simfin_id]
# Show all the reports for a given SIMFIN_ID sorted by
# Fiscal Year and Period so it is easier to see which are missing.
if not running_pytest:
display(sort_quarterly_reports(df=df, simfin_id=139560))
```
## Missing TTM Reports
Trailing-Twelve-Months (TTM) data is also quarterly so we can use the same helper-functions from above.
```
test_name = "Missing ttm reports"
test_func = lambda df: len(missing_quarterly_reports(df=df)) > 0
test_datasets(datasets=datasets_fundamental(),
variants=['ttm'],
test_name=test_name, test_func=test_func)
# Get list of SIMFIN_ID's that have missing reports for a dataset.
if not running_pytest:
df = data.get(dataset='income', variant='ttm', market='us')
display(missing_quarterly_reports(df=df))
# Show all the reports for a given SIMFIN_ID sorted by
# Fiscal Year and Period so it is easier to see which are missing.
if not running_pytest:
display(sort_quarterly_reports(df=df, simfin_id=89750))
```
| github_jupyter |
```
# coding=utf-8
from __future__ import absolute_import, division, print_function, unicode_literals
import argparse
import logging
import os
from pathlib import Path
import random
from io import open
import pickle
import math
import numpy as np
import requests
logging.basicConfig(format='%(asctime)s - %(levelname)s - %(name)s - %(message)s',
datefmt='%m/%d/%Y %H:%M:%S',
level=logging.INFO)
logger = logging.getLogger(__name__)
_CURPATH = Path.cwd()
_TMPDIR = _CURPATH / "squad_data"
_TRAINDIR = _TMPDIR / "squad_train"
_TESTFILE = "dev-v2.0.json"
_DATADIR = _CURPATH / "squad_data"
_TRAINFILE = "train-v2.0.json"
_URL = "https://rajpurkar.github.io/SQuAD-explorer/dataset/" + _TRAINFILE
_MODELS = _CURPATH / "models"
def maybe_download(directory, filename, uri):
filepath = os.path.join(directory, filename)
if not os.path.exists(directory):
logger.info(f"Creating new dir: {directory}")
os.makedirs(directory)
if not os.path.exists(filepath):
logger.info("Downloading und unpacking file, as file does not exist yet")
r = requests.get(uri, allow_redirects=True)
open(filepath, "wb").write(r.content)
return filepath
filename = maybe_download(_TMPDIR, _TRAINFILE, _URL)
import json
for files in os.listdir(_TMPDIR):
with open(_TMPDIR/files, "r", encoding="utf-8") as json_file:
data_dict = json.load(json_file)
data_dict = data_dict["data"]
number_articles = len(data_dict)
total = 0
hundreds = 0
twohundredf = 0
rest = 0
cont100 = 0
cont150 =0
contover = 0
for article in range(number_articles):
cur_number_context = len(data_dict[article]["paragraphs"])
print(f"This is article number {article}")
print(cur_number_context)
if cur_number_context < 70:
cont100 += 1
elif cur_number_context < 130:
cont150 += 1
else:
contover += cur_number_context
for context in range(cur_number_context -1, -1, -1 ):
num = len(data_dict[article]["paragraphs"][context]["context"].split())
#print(num)
if num < 50:
hundreds += 1
elif num < 100:
twohundredf += 1
else:
rest += 1
print(f"Hundreds is {hundreds}")
print(f"twohundreds is {twohundredf}")
print(f"Rest is {rest}")
print(f"cont 100 {cont100}")
print(f"cont 150 {cont150}")
print(f"cont over {contover}")
# data contains all the data
# title contains the title, paragrapsh contains qas, context (the paragraph)
# qas contains a list of dicts with the questions and the answers
# lets put all the stuff inside the get_item function, so that we get new data each epoch without rebuilding
# rebuild should just contain saving the json file or we dont even need rebuild
a = data_dict[0]
len(a)
a["paragraphs"][10]
a[0]["paragraphs"][0]["context"]
len(a[0]["paragraphs"])
for a in []:
print(a)
a = [-1] * 5
a
a.append(["CLS"])
a
["[MASK]"]* 5
```
| github_jupyter |
### Importing required stuff
```
import time
import math
import random
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
from datetime import timedelta
import scipy.misc
import glob
import sys
%matplotlib inline
```
### Helper files to load data
```
# Helper functions, DO NOT modify this
def get_img_array(path):
"""
Given path of image, returns it's numpy array
"""
return scipy.misc.imread(path)
def get_files(folder):
"""
Given path to folder, returns list of files in it
"""
filenames = [file for file in glob.glob(folder+'*/*')]
filenames.sort()
return filenames
def get_label(filepath, label2id):
"""
Files are assumed to be labeled as: /path/to/file/999_frog.png
Returns label for a filepath
"""
tokens = filepath.split('/')
label = tokens[-1].split('_')[1][:-4]
if label in label2id:
return label2id[label]
else:
sys.exit("Invalid label: " + label)
# Functions to load data, DO NOT change these
def get_labels(folder, label2id):
"""
Returns vector of labels extracted from filenames of all files in folder
:param folder: path to data folder
:param label2id: mapping of text labels to numeric ids. (Eg: automobile -> 0)
"""
files = get_files(folder)
y = []
for f in files:
y.append(get_label(f,label2id))
return np.array(y)
def one_hot(y, num_classes=10):
"""
Converts each label index in y to vector with one_hot encoding
"""
y_one_hot = np.zeros((num_classes, y.shape[0]))
y_one_hot[y, range(y.shape[0])] = 1
return y_one_hot
def get_label_mapping(label_file):
"""
Returns mappings of label to index and index to label
The input file has list of labels, each on a separate line.
"""
with open(label_file, 'r') as f:
id2label = f.readlines()
id2label = [l.strip() for l in id2label]
label2id = {}
count = 0
for label in id2label:
label2id[label] = count
count += 1
return id2label, label2id
def get_images(folder):
"""
returns numpy array of all samples in folder
each column is a sample resized to 30x30 and flattened
"""
files = get_files(folder)
images = []
count = 0
for f in files:
count += 1
if count % 10000 == 0:
print("Loaded {}/{}".format(count,len(files)))
img_arr = get_img_array(f)
img_arr = img_arr.flatten() / 255.0
images.append(img_arr)
X = np.column_stack(images)
return X
def get_train_data(data_root_path):
"""
Return X and y
"""
train_data_path = data_root_path + 'train'
id2label, label2id = get_label_mapping(data_root_path+'labels.txt')
print(label2id)
X = get_images(train_data_path)
y = get_labels(train_data_path, label2id)
return X, y
def save_predictions(filename, y):
"""
Dumps y into .npy file
"""
np.save(filename, y)
```
### Load test data from using the helper code from HW1
```
# Load the data
data_root_path = 'cifar10-hw2/'
X_train, Y_train = get_train_data(data_root_path) # this may take a few minutes
X_test_format = get_images(data_root_path + 'test')
X_test_format = X_test_format.T
#print('Data loading done')
X_train = X_train.T
Y_train = Y_train.T
```
### Load all the data
```
def unpickle(file):
import pickle
with open(file, 'rb') as fo:
data_dict = pickle.load(fo, encoding='bytes')
return data_dict
path = 'cifar-10-batches-py'
file = []
file.append('data_batch_1')
file.append('data_batch_2')
file.append('data_batch_3')
file.append('data_batch_4')
file.append('data_batch_5')
file.append('test_batch')
X_train = None
Y_train = None
X_test = None
Y_test = None
for i in range(6):
fname = path+'/'+file[i]
data_dict = unpickle(fname)
_X = np.array(data_dict[b'data'], dtype=float) / 255.0
_X = _X.reshape([-1, 3, 32, 32])
_X = _X.transpose([0, 2, 3, 1])
_X = _X.reshape(-1, 32*32*3)
_Y = data_dict[b'labels']
if X_train is None:
X_train = _X
Y_train = _Y
elif i != 5:
X_train = np.concatenate((X_train, _X), axis=0)
Y_train = np.concatenate((Y_train, _Y), axis=0)
else:
X_test = _X
Y_test = np.array(_Y)
print(data_dict[b'batch_label'])
# confirming the output
print(X_train.shape, Y_train.shape, X_test.shape, Y_test.shape)
```
### Defining Hyperparameters
```
# Convolutional Layer 1.
filter_size1 = 3
num_filters1 = 64
# Convolutional Layer 2.
filter_size2 = 3
num_filters2 = 64
# Fully-connected layer.
fc_1 = 256 # Number of neurons in fully-connected layer.
fc_2 = 128 # Number of neurons in fc layer
# Number of color channels for the images: 1 channel for gray-scale.
num_channels = 3
# image dimensions (only squares for now)
img_size = 32
# Size of image when flattened to a single dimension
img_size_flat = img_size * img_size * num_channels
# Tuple with height and width of images used to reshape arrays.
img_shape = (img_size, img_size)
# class info
classes = ['airplane','automobile','bird','cat','deer','dog','frog','horse','ship','truck']
num_classes = len(classes)
# batch size
batch_size = 64
# validation split
validation_size = .16
# learning rate
learning_rate = 0.001
# beta
beta = 0.01
# log directory
import os
log_dir = os.getcwd()
# how long to wait after validation loss stops improving before terminating training
early_stopping = None # use None if you don't want to implement early stoping
```
### Helper-function for plotting images
Function used to plot 9 images in a 3x3 grid (or fewer, depending on how many images are passed), and writing the true and predicted classes below each image.
```
def plot_images(images, cls_true, cls_pred=None):
if len(images) == 0:
print("no images to show")
return
else:
random_indices = random.sample(range(len(images)), min(len(images), 9))
print(images.shape)
images, cls_true = zip(*[(images[i], cls_true[i]) for i in random_indices])
# Create figure with 3x3 sub-plots.
fig, axes = plt.subplots(3, 3)
fig.subplots_adjust(hspace=0.3, wspace=0.3)
for i, ax in enumerate(axes.flat):
# Plot image.
ax.imshow(images[i].reshape(img_size, img_size, num_channels))
# Show true and predicted classes.
if cls_pred is None:
xlabel = "True: {0}".format(classes[cls_true[i]])
else:
xlabel = "True: {0}, Pred: {1}".format(cls_true[i], cls_pred[i])
# Show the classes as the label on the x-axis.
ax.set_xlabel(xlabel)
# Remove ticks from the plot.
ax.set_xticks([])
ax.set_yticks([])
# Ensure the plot is shown correctly with multiple plots
# in a single Notebook cell.
plt.show()
```
### Plot a few images to see if data is correct
```
# Plot the images and labels using our helper-function above.
plot_images(X_train, Y_train)
```
### Normalize
```
mean = np.mean(X_train, axis = 0)
stdDev = np.std(X_train, axis = 0)
X_train -= mean
X_train /= stdDev
X_test -= mean
X_test /= stdDev
X_test_format -= mean
X_test_format /= stdDev
```
### Tensorflow graph
### Regularizer
```
regularizer = tf.contrib.layers.l2_regularizer(scale=0.1)
```
### Weights and Bias
```
def new_weights(shape):
return tf.get_variable(name='weights',shape=shape,regularizer=regularizer)
def new_biases(length):
return tf.Variable(tf.constant(0.05, shape=[length]))
```
### Batch Norm
```
def batch_norm(x, n_out, phase_train):
"""
Batch normalization on convolutional maps.
Ref.: http://stackoverflow.com/questions/33949786/how-could-i-use-batch-normalization-in-tensorflow
Args:
x: Tensor, 4D BHWD input maps
n_out: integer, depth of input maps
phase_train: boolean tf.Varialbe, true indicates training phase
scope: string, variable scope
Return:
normed: batch-normalized maps
"""
with tf.variable_scope('batch_norm'):
beta = tf.Variable(tf.constant(0.0, shape=[n_out]),
name='beta', trainable=True)
gamma = tf.Variable(tf.constant(1.0, shape=[n_out]),
name='gamma', trainable=True)
batch_mean, batch_var = tf.nn.moments(x, [0,1,2], name='moments')
ema = tf.train.ExponentialMovingAverage(decay=0.5)
def mean_var_with_update():
ema_apply_op = ema.apply([batch_mean, batch_var])
with tf.control_dependencies([ema_apply_op]):
return tf.identity(batch_mean), tf.identity(batch_var)
mean, var = tf.cond(tf.equal(phase_train,1),
mean_var_with_update,
lambda: (ema.average(batch_mean), ema.average(batch_var)))
normed = tf.nn.batch_normalization(x, mean, var, beta, gamma, 1e-3)
return normed
```
### Helper function for summaries:
```
def variable_summaries(var):
"""Attach a lot of summaries to a Tensor (for TensorBoard visualization)."""
with tf.name_scope('summaries'):
mean = tf.reduce_mean(var)
tf.summary.scalar('mean', mean)
with tf.name_scope('stddev'):
stddev = tf.sqrt(tf.reduce_mean(tf.square(var - mean)))
tf.summary.scalar('stddev', stddev)
tf.summary.scalar('max', tf.reduce_max(var))
tf.summary.scalar('min', tf.reduce_min(var))
tf.summary.histogram('histogram', var)
```
### Convolutional Layer
```
def new_conv_layer(input, # The previous layer.
num_input_channels, # Num. channels in prev. layer.
filter_size, # Width and height of each filter.
num_filters, # Number of filters.
use_pooling=True, normalize=True, phase=1, batch_normalization =False): # Use 2x2 max-pooling.
# Shape of the filter-weights for the convolution.
# This format is determined by the TensorFlow API.
shape = [filter_size, filter_size, num_input_channels, num_filters]
# Create new weights aka. filters with the given shape.
with tf.variable_scope('weights'):
weights = new_weights(shape=shape)
#tf.add_to_collection(tf.GraphKeys.REGULARIZATION_LOSSES, weights)
variable_summaries(weights)
# Create new biases, one for each filter.
with tf.variable_scope('biases'):
biases = new_biases(length=num_filters)
variable_summaries(biases)
with tf.variable_scope('convolution_layer'):
layer = tf.nn.conv2d(input=input,
filter=weights,
strides=[1, 1, 1, 1],
padding='SAME')
# Add the biases to the results of the convolution.
# A bias-value is added to each filter-channel.
layer += biases
#layer = tf.layers.batch_normalization(layer,
# center=True, scale=True,
# training=phase)
#layer = tf.contrib.layers.batch_norm(layer,is_training=phase)
# Use pooling to down-sample the image resolution?
# Adding batch_norm
if batch_normalization == True:
layer = batch_norm(layer,num_filters, phase)
with tf.variable_scope('Max-Pooling'):
if use_pooling:
# This is 2x2 max-pooling, which means that we
# consider 2x2 windows and select the largest value
# in each window. Then we move 2 pixels to the next window.
layer = tf.nn.max_pool(value=layer,
ksize=[1, 2, 2, 1],
strides=[1, 2, 2, 1],
padding='SAME')
with tf.variable_scope('ReLU'):
# Rectified Linear Unit (ReLU).
# It calculates max(x, 0) for each input pixel x.
# This adds some non-linearity to the formula and allows us
# to learn more complicated functions.
layer = tf.nn.relu(layer)
tf.summary.histogram('activations', layer)
return layer, weights
```
### Flatten Layer
```
def flatten_layer(layer):
# Get the shape of the input layer.
layer_shape = layer.get_shape()
# The shape of the input layer is assumed to be:
# layer_shape == [num_images, img_height, img_width, num_channels]
# The number of features is: img_height * img_width * num_channels
# We can use a function from TensorFlow to calculate this.
num_features = layer_shape[1:4].num_elements()
# Reshape the layer to [num_images, num_features].
# Note that we just set the size of the second dimension
# to num_features and the size of the first dimension to -1
# which means the size in that dimension is calculated
# so the total size of the tensor is unchanged from the reshaping.
layer_flat = tf.reshape(layer, [-1, num_features])
# The shape of the flattened layer is now:
# [num_images, img_height * img_width * num_channels]
# Return both the flattened layer and the number of features.
return layer_flat, num_features
```
### FC Layer
```
def new_fc_layer(input, # The previous layer.
num_inputs, # Num. inputs from prev. layer.
num_outputs, # Num. outputs.
use_relu=True): # Use Rectified Linear Unit (ReLU)?
# Create new weights and biases.
with tf.variable_scope('weights'):
weights = new_weights(shape=[num_inputs, num_outputs])
with tf.variable_scope('biases'):
biases = new_biases(length=num_outputs)
# Calculate the layer as the matrix multiplication of
# the input and weights, and then add the bias-values.
with tf.variable_scope('matmul'):
layer = tf.matmul(input, weights) + biases
# Use ReLU?
if use_relu:
with tf.variable_scope('relu'):
layer = tf.nn.relu(layer)
return layer, weights
```
### Placeholder variables
```
x = tf.placeholder(tf.float32, shape=[None, img_size_flat], name='x')
x_image = tf.reshape(x, [-1, img_size, img_size, num_channels])
y_true = tf.placeholder(tf.float32, shape=[None, num_classes], name='y_true')
y_true_cls = tf.argmax(y_true, axis=1)
phase = tf.placeholder(tf.int32, name='phase')
keep_prob = tf.placeholder(tf.float32, name='keep_prob')
```
### Convolutional Layers
```
with tf.variable_scope('Layer-1'):
layer_conv1, weights_conv1 = \
new_conv_layer(input=x_image,
num_input_channels=num_channels,
filter_size=filter_size1,
num_filters=num_filters1,
use_pooling=True, phase=phase, batch_normalization=True)
with tf.variable_scope('Layer-2'):
layer_conv2, weights_conv2 = \
new_conv_layer(input=layer_conv1,
num_input_channels=num_filters1,
filter_size=filter_size2,
num_filters=num_filters2,
use_pooling=True, phase=phase)
```
### Flatten Layer
```
with tf.variable_scope('Flatten'):
layer_flat, num_features = flatten_layer(layer_conv2)
print(layer_flat,num_features)
```
### FC Layers
```
with tf.variable_scope('Fully-Connected-1'):
layer_fc1, weights_fc1 = new_fc_layer(input=layer_flat,
num_inputs=num_features,
num_outputs=fc_1,
use_relu=True)
with tf.variable_scope('Fully-Connected-2'):
layer_fc2, weights_fc2 = new_fc_layer(input=layer_fc1,
num_inputs=fc_1,
num_outputs=fc_2,
use_relu=True)
with tf.variable_scope('Fully-connected-3'):
layer_fc3, weights_fc3 = new_fc_layer(input=layer_fc2,
num_inputs=fc_2,
num_outputs=num_classes,
use_relu=False)
#with tf.variable_scope('dropout'):
# layer = tf.nn.dropout(layer_fc2,keep_prob)
```
### Softmax and argmax functions
```
with tf.variable_scope('Softmax'):
y_pred = tf.nn.softmax(layer_fc3)
y_pred_cls = tf.argmax(y_pred, axis=1)
```
### Cost-Function:
```
with tf.variable_scope('cross_entropy_loss'):
cross_entropy = tf.nn.softmax_cross_entropy_with_logits(logits=layer_fc3,
labels=y_true)
loss = tf.reduce_mean(cross_entropy)
tf.summary.scalar('cross_entropy', loss)
#with tf.variable_scope('Regularization'):
reg_variables = tf.get_collection(tf.GraphKeys.REGULARIZATION_LOSSES)
reg_term = tf.contrib.layers.apply_regularization(regularizer, reg_variables)
loss += reg_term
cost = loss
tf.summary.scalar('Total-Loss', cost)
```
### Using Adam Optimizer
```
#with tf.variable_scope('Optimize'):
optimizer = tf.train.GradientDescentOptimizer(learning_rate=1e-2).minimize(cost)
```
### Metrics
```
with tf.variable_scope('Metrics'):
correct_prediction = tf.equal(y_pred_cls, y_true_cls)
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
tf.summary.scalar('accuracy', accuracy)
```
### Tensorflow Session
```
session = tf.Session()
session.run(tf.global_variables_initializer())
```
### Summaries
```
merged = tf.summary.merge_all()
train_writer = tf.summary.FileWriter(log_dir + '/train', session.graph)
test_writer = tf.summary.FileWriter(log_dir + '/test')
print(X_train.shape)
def one_hot(y, num_classes=10):
"""
Converts each label index in y to vector with one_hot encoding
"""
y_one_hot = np.zeros((num_classes, y.shape[0]))
y_one_hot[y, range(y.shape[0])] = 1
return y_one_hot
Y_hot = one_hot(Y_train)
Y_hot = Y_hot.T
# split test and train:
x_dev_batch = X_train[0:5000,:]
y_dev_batch = Y_hot[0:5000,:]
X_train = X_train[5000:,:]
Y_hot = Y_hot[5000:,:]
```
### Training
```
train_batch_size = batch_size
def print_status(epoch, feed_dict_train, feed_dict_validate, train_loss, val_loss, step):
# Calculate the accuracy on the training-set.
summary, acc = session.run([merged,accuracy], feed_dict=feed_dict_train)
train_writer.add_summary(summary, step)
summary, val_acc = session.run([merged,accuracy], feed_dict=feed_dict_validate)
test_writer.add_summary(summary, step)
msg = "Epoch {0} --- Training Accuracy: {1:>6.1%}, Validation Accuracy: {2:>6.1%}, Training Loss: {3:.3f}, Validation Loss: {4:.3f}"
print(msg.format(epoch + 1, acc, val_acc, train_loss, val_loss))
# Counter for total number of iterations performed so far.
total_iterations = 0
batch_id = 1
def get_batch(X, Y, batch_size):
"""
Return minibatch of samples and labels
:param X, y: samples and corresponding labels
:parma batch_size: minibatch size
:returns: (tuple) X_batch, y_batch
"""
global batch_id
if batch_id*batch_size >= X.shape[0]:
batch_id = 1
if batch_id == 1:
permutation = np.random.permutation(X.shape[0])
X = X[permutation,:]
Y = Y[permutation,:]
lb = batch_size*(batch_id-1)
ub = batch_size*(batch_id)
X = X[lb:ub,:]
Y = Y[lb:ub,:]
batch_id += 1
return X,Y
def optimize(num_iterations):
# Ensure we update the global variable rather than a local copy.
global total_iterations
# Start-time used for printing time-usage below.
start_time = time.time()
best_val_loss = float("inf")
patience = 0
for i in range(total_iterations,
total_iterations + num_iterations):
# Get a batch of training examples.
# x_batch now holds a batch of images and
# y_true_batch are the true labels for those images
x_batch, y_true_batch = get_batch(X_train,Y_hot, train_batch_size)
# getting one hot form:
#y_true_batch = one_hot(y_true_batch)
#y_dev_batch = one_hot(y_dev_batch)
# Put the batch into a dict with the proper names
# for placeholder variables in the TensorFlow graph.
feed_dict_train = {x: x_batch,
y_true: y_true_batch, phase: 1, keep_prob:0.5}
feed_dict_validate = {x: x_dev_batch,
y_true: y_dev_batch, phase: 0, keep_prob:1.0}
# Run the optimizer using this batch of training data.
# TensorFlow assigns the variables in feed_dict_train
# to the placeholder variables and then runs the optimizer.
#print(x_batch.shape,y_true_batch.shape)
acc = session.run(optimizer, feed_dict=feed_dict_train)
# Print status at end of each epoch (defined as full pass through training dataset).
if i % int(X_train.shape[0]/batch_size) == 0 == 0:
train_loss = session.run(cost, feed_dict=feed_dict_train)
val_loss = session.run(cost, feed_dict=feed_dict_validate)
epoch = int(i / int(X_train.shape[0]/batch_size))
print('Iteration:',i)
print_status(epoch, feed_dict_train, feed_dict_validate, train_loss, val_loss, i)
if early_stopping:
if val_loss < best_val_loss:
best_val_loss = val_loss
patience = 0
else:
patience += 1
if patience == early_stopping:
break
# Update the total number of iterations performed.
total_iterations += num_iterations
# Ending time.
end_time = time.time()
# Difference between start and end-times.
time_dif = end_time - start_time
# close the writers
train_writer.close()
test_writer.close()
# Print the time-usage.
print("Time elapsed: " + str(timedelta(seconds=int(round(time_dif)))))
# Run the optimizer
optimize(num_iterations=16873)
Y_test_hot = one_hot(Y_test)
Y_test_hot = Y_test_hot.T
feed_dict_test= {x: X_test,y_true: Y_test_hot, phase: 0, keep_prob:1.0}
summary, acc = session.run([merged,accuracy], feed_dict=feed_dict_test)
print("Accuracy on test set is: %f%%"%(acc*100))
```
### Write out the results
```
feed_dict_test= {x: X_test_format,y_true: Y_test_hot, phase: 0, keep_prob:1.0}
y_pred = session.run(y_pred, feed_dict=feed_dict_test)
save_predictions('ans1-ck2840.npy', y_pred)
session.close()
```
| github_jupyter |
# Evaluation von Parsingtechniken
Das Parsing von Textdateien ist ein wichtiger Mechanismus, welcher wärend Informationsbearbeitung einen hohen Stellenwert innehält.
In order to be able to choose an adequate technique to be able to parse our custom DSL, we need to evaluate multiple of these techniques first.
*The following techniques are going to be evaluated and compared:*
- Parsing with an complete custom build Parser
- Parsing with help of the Pyparsing module
- Parsing an YAML config
- Parsing an XML config
```
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
RUNS = 20
```
## Measuring Technique
To measure the results we use an combination of the python performance timer functionality and an custom class. This custom class is going to measure the execution time of the different techniques. Thus the execution time is measured multiple times in a row to avoid false measurements due to system load or caching mechanisms.
## Performance Timer Class
```
import time
class PerformanceTimer:
timers = {}
def __init__(self, name: str = "", iterations: int = 20):
self.running = False
self.start = None
self.name = name
self.elapsed = 0.0
self.measurements = {}
self.successful_measurements = 0
self.iterations = iterations
PerformanceTimer.timers[self.name] = self
def measure_function(self, func, *args):
for i, arg in enumerate(args):
self.measurements[i] = []
for j in range(self.iterations):
self.start_timer()
func(arg)
self.stop_timer()
self.measurements[i].append(self.elapsed)
self.successful_measurements += 1
self.reset()
def start_timer(self):
if self.running is False:
self.start = time.perf_counter()
self.running = True
else:
raise Exception('Timer already started.')
def stop_timer(self):
if self.running is True:
# Elapsed time in ms
self.elapsed = (time.perf_counter() - self.start) * 1000
self.running = False
else:
raise Exception('Timer is not running.')
def reset(self):
self.start = None
self.elapsed = 0.0
self.running = False
def average_time(self):
result = []
for measurement_set in self.measurements.values():
result.append(sum(measurement_set) / self.iterations)
return result
def print(self):
print(('Timer: ' + self.name).center(50, '-'))
print('Finished: ' + str(not self.running))
print('Sample Sets: ' + str(len(self.measurements)))
print('Measurements: ' + str(self.successful_measurements))
if self.measurements:
print('Measured Times: ' + str(self.measurements))
else:
print('Elapsed Time: ' + str(self.elapsed))
print('\n')
```
## Manual Parsing
```
from parse_manual.parser import parse as parse_manual
manual_timer = PerformanceTimer('Manual Parsing', RUNS)
manual_timer.measure_function(parse_manual, './samples/sample.gen', './samples/sample-40.gen',
'./samples/sample-80.gen', './samples/sample-160.gen')
manual_timer.print()
```
### Function execution time development
```
plt.subplot(2, 2, 1)
plt.plot(manual_timer.measurements[0])
plt.title('20 Datapoints')
plt.xlim(1, RUNS)
plt.xlabel('runs')
plt.ylabel('time in ms')
plt.subplot(2, 2, 2)
plt.plot(manual_timer.measurements[1])
plt.title('40 Datapoints')
plt.xlim(1, RUNS)
plt.xlabel('runs')
plt.ylabel('time in ms')
plt.subplot(2, 2, 3)
plt.plot(manual_timer.measurements[2])
plt.title('80 Datapoints')
plt.xlim(1, RUNS)
plt.xlabel('runs')
plt.ylabel('time in ms')
plt.subplot(2, 2, 4)
plt.plot(manual_timer.measurements[3])
plt.title('160 Datapoints')
plt.xlim(1, RUNS)
plt.xlabel('runs')
plt.ylabel('time in ms')
plt.rcParams['figure.figsize'] = [30 / 2.54, 15 / 2.54]
plt.tight_layout()
plt.show()
```
### Individual function execution time results
```
df = pd.DataFrame(manual_timer.measurements)
df.columns = ['20 Datapoints', '40 Datapoints', '80 Datapoints', '160 Datapoints']
df
```
## Pyparsing
```
from parse_pyparsing.parser import parse as parse_pyparsing
# Pyparsing
pyparsing_timer = PerformanceTimer('Pyparsing', RUNS)
pyparsing_timer.measure_function(parse_pyparsing, './samples/sample.gen', './samples/sample-40.gen',
'./samples/sample-80.gen', './samples/sample-160.gen')
pyparsing_timer.print()
```
### Function execution time development
```
plt.subplot(2, 2, 1)
plt.plot(pyparsing_timer.measurements[0])
plt.title('20 Datapoints')
plt.xlim(1, RUNS)
plt.xlabel('runs')
plt.ylabel('time in ms')
plt.subplot(2, 2, 2)
plt.plot(pyparsing_timer.measurements[1])
plt.title('40 Datapoints')
plt.xlim(1, RUNS)
plt.xlabel('runs')
plt.ylabel('time in ms')
plt.subplot(2, 2, 3)
plt.plot(pyparsing_timer.measurements[2])
plt.title('80 Datapoints')
plt.xlim(1, RUNS)
plt.xlabel('runs')
plt.ylabel('time in ms')
plt.subplot(2, 2, 4)
plt.plot(pyparsing_timer.measurements[3])
plt.title('160 Datapoints')
plt.xlim(1, RUNS)
plt.xlabel('runs')
plt.ylabel('time in ms')
plt.rcParams['figure.figsize'] = [30 / 2.54, 15 / 2.54]
plt.tight_layout()
plt.show()
```
### Individual function execution time results
```
df = pd.DataFrame(pyparsing_timer.measurements)
df.columns = ['20 Datapoints', '40 Datapoints', '80 Datapoints', '160 Datapoints']
df
```
## YAML Parsing
```
from parse_yaml.parser import parse as parse_yaml
#YAML
yaml_timer = PerformanceTimer('YAML Parsing', RUNS)
yaml_timer.measure_function(parse_yaml, './samples/sample.yaml', './samples/sample-40.yaml', './samples/sample-80.yaml',
'./samples/sample-160.yaml')
yaml_timer.print()
```
### Function execution time development
```
plt.subplot(2, 2, 1)
plt.plot(yaml_timer.measurements[0])
plt.title('20 Datapoints')
plt.xlim(1, RUNS)
plt.xlabel('runs')
plt.ylabel('time in ms')
plt.subplot(2, 2, 2)
plt.plot(yaml_timer.measurements[1])
plt.title('40 Datapoints')
plt.xlim(1, RUNS)
plt.xlabel('runs')
plt.ylabel('time in ms')
plt.subplot(2, 2, 3)
plt.plot(yaml_timer.measurements[2])
plt.title('80 Datapoints')
plt.xlim(1, RUNS)
plt.xlabel('runs')
plt.ylabel('time in ms')
plt.subplot(2, 2, 4)
plt.plot(yaml_timer.measurements[3])
plt.title('160 Datapoints')
plt.xlim(1, RUNS)
plt.xlabel('runs')
plt.ylabel('time in ms')
plt.rcParams['figure.figsize'] = [30 / 2.54, 15 / 2.54]
plt.tight_layout()
plt.show()
```
### Individual function execution time results
```
df = pd.DataFrame(yaml_timer.measurements)
df.columns = ['20 Datapoints', '40 Datapoints', '80 Datapoints', '160 Datapoints']
df
```
## XML Parsing
```
from parse_xml.parser import parse as parse_xml
#XML
xml_timer = PerformanceTimer('XML Parsing', RUNS)
xml_timer.measure_function(parse_xml, './samples/sample.xml', './samples/sample-40.xml', './samples/sample-80.xml',
'./samples/sample-160.xml')
xml_timer.print()
```
### Function execution time development
```
plt.subplot(2, 2, 1)
plt.plot(xml_timer.measurements[0])
plt.title('20 Datapoints')
plt.xlim(1, RUNS)
plt.xlabel('runs')
plt.ylabel('time in ms')
plt.subplot(2, 2, 2)
plt.plot(xml_timer.measurements[1])
plt.title('40 Datapoints')
plt.xlim(1, RUNS)
plt.xlabel('runs')
plt.ylabel('time in ms')
plt.subplot(2, 2, 3)
plt.plot(xml_timer.measurements[2])
plt.title('80 Datapoints')
plt.xlim(1, RUNS)
plt.xlabel('runs')
plt.ylabel('time in ms')
plt.subplot(2, 2, 4)
plt.plot(xml_timer.measurements[3])
plt.title('160 Datapoints')
plt.xlim(1, RUNS)
plt.xlabel('runs')
plt.ylabel('time in ms')
plt.rcParams['figure.figsize'] = [30 / 2.54, 15 / 2.54]
plt.tight_layout()
plt.show()
```
### Individual function execution time results
```
df = pd.DataFrame(xml_timer.measurements)
df.columns = ['20 Datapoints', '40 Datapoints', '80 Datapoints', '160 Datapoints']
df
```
## Comparison
```
manual_avg = manual_timer.average_time()
pyparsing_avg = pyparsing_timer.average_time()
yaml_avg = yaml_timer.average_time()
xml_avg = xml_timer.average_time()
# Define y-axis labels
labels = ['Manual', 'Pyparsing', 'YAML', 'XML']
# Define y values
y = np.arange(len(labels))
# Define label helper function
def add_labels(bars):
for bar in bars:
width = bar.get_width()
label_y = bar.get_y() + bar.get_height() / 2
plt.text(width, label_y, s=f'{round(width, 4)}')
# Define plot helper function
def show_bar_plot(values, title):
# Create bar plot
bars = plt.barh(y, values, color=['#6CB1FF', '#FFE000', '#00FF7B', '#FF9800'])
# Axis labels and styling
plt.yticks(y, labels)
plt.xlabel('Time in ms')
add_labels(bars)
plt.title(title)
plt.show()
# Show Plots
## 20 Datapoints
x = [manual_avg[0], pyparsing_avg[0], yaml_avg[0], xml_avg[0]]
show_bar_plot(x, 'Time comparison 20 datapoints')
## 40 Datapoints
x = [manual_avg[1], pyparsing_avg[1], yaml_avg[1], xml_avg[1]]
show_bar_plot(x, 'Time comparison 40 datapoints')
## 80 Datapoints
x = [manual_avg[2], pyparsing_avg[2], yaml_avg[2], xml_avg[2]]
show_bar_plot(x, 'Time comparison 80 datapoints')
## 160 Datapoints
x = [manual_avg[3], pyparsing_avg[3], yaml_avg[3], xml_avg[3]]
show_bar_plot(x, 'Time comparison 160 datapoints')
```
| github_jupyter |
## Use the *Machine Learning Workflow* to process & transform Pima Indian data to create a prediction model.
### This model must predict which people are likely to develop diabetes with 70% accuracy!
##Import Libraries
```
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
#plot inline instead of seperate windows
%matplotlib inline
```
## Load and review data
```
df = pd.read_csv('./data/pima-data.csv')
df.shape
df.head()
df.isnull().values.any()
def plot_correlatedValues(df, size=11):
corr = df.corr()
fig, ax = plt.subplots(figsize=(size,size))
ax.matshow(corr)
plt.xticks(range(len(corr.columns)),corr.columns)
plt.yticks(range(len(corr.columns)),corr.columns)
plot_correlatedValues(df)
df.corr()
del df['skin']
df.head(5)
plot_correlatedValues(df)
```
change diabetes column values from True/False to 1/0
```
diabetes_map = {True:1, False:0}
diabetes_map
df['diabetes'] = df['diabetes'].map(diabetes_map)
df.head()
```
# check true/false ratio
```
num_true = len(df.loc[df['diabetes']==True])
num_false = len(df.loc[df['diabetes']==False] )
```
print("# of cases the diabetes is True:- {0}({1:2.2f}%)".format(num_true, (num_true /(num_true+num_false))*100 ))
print("# of cases the diabetes is False:- {0}({1:2.2f}%)".format(num_false, (num_false /(num_true+num_false))*100 ))
# Splitting the data
70% training : 30% testing
```
from sklearn.cross_validation import train_test_split
feature_col_names = ['num_preg','glucose_conc', 'diastolic_bp','thickness','insulin','bmi','diab_pred','age']
predicted_class_name = ['diabetes']
X = df[feature_col_names].values
y = df[predicted_class_name].values
split_test_size = 0.30
X_train, X_test , y_train, y_test = train_test_split(X,y,test_size= split_test_size, random_state=42)
print(' {0}({0:2.2f}%) in training set '.format((len(X_train)/len(df.index))*100))
print(' {0}({0:2.2f}%) in test set '.format((len(X_test)/len(df.index))*100))
```
Confirm the split of predict values was correctly done
```
print("Original True : {0} ({1:0.2f}%)".format(len(df.loc[df['diabetes'] == 1]), (len(df.loc[df['diabetes'] == 1])/len(df.index)) * 100.0))
print("Original False : {0} ({1:0.2f}%)".format(len(df.loc[df['diabetes'] == 0]), (len(df.loc[df['diabetes'] == 0])/len(df.index)) * 100.0))
print("")
print("Training True : {0} ({1:0.2f}%)".format(len(y_train[y_train[:] == 1]), (len(y_train[y_train[:] == 1])/len(y_train) * 100.0)))
print("Training False : {0} ({1:0.2f}%)".format(len(y_train[y_train[:] == 0]), (len(y_train[y_train[:] == 0])/len(y_train) * 100.0)))
print("")
print("Test True : {0} ({1:0.2f}%)".format(len(y_test[y_test[:] == 1]), (len(y_test[y_test[:] == 1])/len(y_test) * 100.0)))
print("Test False : {0} ({1:0.2f}%)".format(len(y_test[y_test[:] == 0]), (len(y_test[y_test[:] == 0])/len(y_test) * 100.0)))
```
rows have have unexpected 0 values?
```
print("# rows in dataframe {0}".format(len(df)))
print("# rows missing glucose_conc: {0}".format(len(df.loc[df['glucose_conc'] == 0])))
print("# rows missing diastolic_bp: {0}".format(len(df.loc[df['diastolic_bp'] == 0])))
print("# rows missing thickness: {0}".format(len(df.loc[df['thickness'] == 0])))
print("# rows missing insulin: {0}".format(len(df.loc[df['insulin'] == 0])))
print("# rows missing bmi: {0}".format(len(df.loc[df['bmi'] == 0])))
print("# rows missing diab_pred: {0}".format(len(df.loc[df['diab_pred'] == 0])))
print("# rows missing age: {0}".format(len(df.loc[df['age'] == 0])))
```
Impute missing values
```
from sklearn.preprocessing import Imputer
fill_0 = Imputer(missing_values=0, strategy='mean', axis=0)
X_train = fill_0.fit_transform(X_train)
X_test = fill_0.fit_transform(X_test)
```
Use Naive Bayes algorithm to train models
```
from sklearn.naive_bayes import GaussianNB
nb_model = GaussianNB()
nb_model.fit(X_train, y_train.ravel())
```
### Performance on Training Data
```
nb_predict_train = nb_model.predict(X_train)
from sklearn import metrics
print('Accuracy : {0:.4f}'.format(metrics.accuracy_score(y_train, nb_predict_train)))
print()
```
### Performance on Testing Data
```
nb_predict_test = nb_model.predict(X_test)
print('Accuracy : {0:.4f}'.format(metrics.accuracy_score(y_test, nb_predict_test)))
print()
```
#### Naive Bayes Metrics
```
print("Confusion Matrix")
print("{0}".format(metrics.confusion_matrix(y_test, nb_predict_test)))
print("")
print("Classification Report")
print(metrics.classification_report(y_test, nb_predict_test))
```
#### Random Forest
```
from sklearn.ensemble import RandomForestClassifier
rf_model = RandomForestClassifier(random_state=42)
rf_model.fit(X_train, y_train.ravel())
```
##### Prediction on Training Data
```
rf_predict_train = rf_model.predict(X_train)
print('Accuracy : {0:.4f}'.format(metrics.accuracy_score(y_train, rf_predict_train)))
print()
```
##### Prediction on Test Data
```
rf_predict_test = rf_model.predict(X_test)
print('Accuracy : {0:.4f}'.format(metrics.accuracy_score(y_test, rf_predict_test)))
print()
```
#### Random Forest Metrics
```
print("Confusion Matrix")
print("{0}".format(metrics.confusion_matrix(y_test, rf_predict_test)))
print("")
print("Classification Report")
print(metrics.classification_report(y_test, rf_predict_test))
```
#### Logistic Regression
```
from sklearn.linear_model import LogisticRegression
lr_model = LogisticRegression(C=0.7, random_state=42)
lr_model = lr_model.fit(X_train, y_train.ravel())
lr_predict_test = lr_model.predict(X_test)
print('Accuracy : {0:.4f}'.format(metrics.accuracy_score(y_test, lr_predict_test)))
print()
```
##### Logistic Regression Metrics
```
print("Confusion Matrix")
print("{0}".format(metrics.confusion_matrix(y_test, lr_predict_test)))
print("")
print("Classification Report")
print(metrics.classification_report(y_test, lr_predict_test))
```
###### Regularize
```
C_start = 0.1
C_end = 5
C_inc = 0.1
C_values, recall_scores = [], []
C_val = C_start
best_recall_score = 0
while (C_val < C_end):
C_values.append(C_val)
lr_model_loop = LogisticRegression(C=C_val, random_state=42, solver='liblinear')
lr_model_loop.fit(X_train, y_train.ravel())
lr_predict_loop_test = lr_model_loop.predict(X_test)
recall_score = metrics.recall_score(y_test, lr_predict_loop_test)
recall_scores.append(recall_score)
if (recall_score > best_recall_score):
best_recall_score = recall_score
best_lr_predict_test = lr_predict_loop_test
C_val = C_val + C_inc
best_score_C_val = C_values[recall_scores.index(best_recall_score)]
print("1st max value of {0:.3f} occured at C={1:.3f}".format(best_recall_score, best_score_C_val))
%matplotlib inline
plt.plot(C_values, recall_scores, "-")
plt.xlabel("C value")
plt.ylabel("recall score")
```
#### Logistic Regression with balanced weight class
```
C_start = 0.1
C_end = 5
C_inc = 0.1
C_values, recall_scores = [], []
C_val = C_start
best_recall_score = 0
while (C_val < C_end):
C_values.append(C_val)
lr_model_loop = LogisticRegression(C=C_val, class_weight="balanced", random_state=42, solver='liblinear', max_iter=10000)
lr_model_loop.fit(X_train, y_train.ravel())
lr_predict_loop_test = lr_model_loop.predict(X_test)
recall_score = metrics.recall_score(y_test, lr_predict_loop_test)
recall_scores.append(recall_score)
if (recall_score > best_recall_score):
best_recall_score = recall_score
best_lr_predict_test = lr_predict_loop_test
C_val = C_val + C_inc
best_score_C_val = C_values[recall_scores.index(best_recall_score)]
print("1st max value of {0:.3f} occured at C={1:.3f}".format(best_recall_score, best_score_C_val))
%matplotlib inline
plt.plot(C_values, recall_scores, "-")
plt.xlabel("C value")
plt.ylabel("recall score")
lr_model = LogisticRegression(class_weight='balanced',C=best_score_C_val, random_state=42)
lr_model.fit(X_train, y_train.ravel())
lr_predict_test = lr_model.predict(X_test)
print('Accuracy : {0:.4f}'.format(metrics.accuracy_score(y_test, lr_predict_test)))
print()
```
##### Metrics
```
print("Confusion Matrix")
print("{0}".format(metrics.confusion_matrix(y_test, lr_predict_test)))
print("")
print("Classification Report")
print(metrics.classification_report(y_test, lr_predict_test))
print(metrics.recall_score(y_test, lr_predict_test))
```
#### Logistic Regression with Cross-Validation
```
from sklearn.linear_model import LogisticRegressionCV
lr_model_cv = LogisticRegressionCV(n_jobs = -1 ,class_weight='balanced',Cs=3,cv=10,refit=False, random_state=42)
lr_model_cv.fit(X_train, y_train.ravel())
lr_cv_predict_test = lr_model_cv.predict(X_test)
print('Accuracy : {0:.4f}'.format(metrics.accuracy_score(y_test, lr_cv_predict_test)))
print()
```
##### Metrics
```
print("Confusion Matrix")
print("{0}".format(metrics.confusion_matrix(y_test, lr_cv_predict_test)))
print("")
print("Classification Report")
print(metrics.classification_report(y_test, lr_cv_predict_test))
```
| github_jupyter |

[](https://colab.research.google.com/github/JohnSnowLabs/spark-nlp-workshop/blob/master/tutorials/streamlit_notebooks/healthcare/NER_LEGAL_DE.ipynb)
# **Detect legal entities in German**
To run this yourself, you will need to upload your license keys to the notebook. Just Run The Cell Below in order to do that. Also You can open the file explorer on the left side of the screen and upload `license_keys.json` to the folder that opens.
Otherwise, you can look at the example outputs at the bottom of the notebook.
## 1. Colab Setup
Import license keys
```
import os
import json
from google.colab import files
license_keys = files.upload()
with open(list(license_keys.keys())[0]) as f:
license_keys = json.load(f)
sparknlp_version = license_keys["PUBLIC_VERSION"]
jsl_version = license_keys["JSL_VERSION"]
print ('SparkNLP Version:', sparknlp_version)
print ('SparkNLP-JSL Version:', jsl_version)
```
Install dependencies
```
%%capture
for k,v in license_keys.items():
%set_env $k=$v
!wget https://raw.githubusercontent.com/JohnSnowLabs/spark-nlp-workshop/master/jsl_colab_setup.sh
!bash jsl_colab_setup.sh
# Install Spark NLP Display for visualization
!pip install --ignore-installed spark-nlp-display
```
Import dependencies into Python and start the Spark session
```
import pandas as pd
from pyspark.ml import Pipeline
from pyspark.sql import SparkSession
import pyspark.sql.functions as F
import sparknlp
from sparknlp.annotator import *
from sparknlp_jsl.annotator import *
from sparknlp.base import *
import sparknlp_jsl
spark = sparknlp_jsl.start(license_keys['SECRET'])
# manually start session
# params = {"spark.driver.memory" : "16G",
# "spark.kryoserializer.buffer.max" : "2000M",
# "spark.driver.maxResultSize" : "2000M"}
# spark = sparknlp_jsl.start(license_keys['SECRET'],params=params)
```
## 2. Construct the pipeline
For more details: https://github.com/JohnSnowLabs/spark-nlp-models#pretrained-models---spark-nlp-for-healthcare
```
document_assembler = DocumentAssembler() \
.setInputCol('text')\
.setOutputCol('document')
sentence_detector = SentenceDetector() \
.setInputCols(['document'])\
.setOutputCol('sentence')
tokenizer = Tokenizer()\
.setInputCols(['sentence']) \
.setOutputCol('token')
# German word embeddings
word_embeddings = WordEmbeddingsModel.pretrained('w2v_cc_300d','de', 'clinical/models') \
.setInputCols(["sentence", 'token'])\
.setOutputCol("embeddings")
# German NER model
clinical_ner = MedicalNerModel.pretrained('ner_legal','de', 'clinical/models') \
.setInputCols(["sentence", "token", "embeddings"]) \
.setOutputCol("ner")
ner_converter = NerConverter()\
.setInputCols(['sentence', 'token', 'ner']) \
.setOutputCol('ner_chunk')
nlp_pipeline = Pipeline(stages=[
document_assembler,
sentence_detector,
tokenizer,
word_embeddings,
clinical_ner,
ner_converter])
```
## 3. Create example inputs
```
# Enter examples as strings in this array
input_list = [
"""Dementsprechend hat der Bundesgerichtshof mit Beschluss vom 24 August 2017 ( - III ZA 15/17 - ) das bei ihm von der Antragstellerin anhängig gemachte „ Prozesskostenhilfeprüfungsverfahre“ an das Bundesarbeitsgericht abgegeben. 2 Die Antragstellerin hat mit Schriftsatz vom 21 März 2016 und damit mehr als sechs Monate vor der Anbringung des Antrags auf Gewährung von Prozesskostenhilfe für die beabsichtigte Klage auf Entschädigung eine Verzögerungsrüge iSv § 198 Abs 5 Satz 1 GVG erhoben. 3 Nach § 198 Abs 1 Satz 1 GVG wird angemessen entschädigt , wer infolge unangemessener Dauer eines Gerichtsverfahrens als Verfahrensbeteiligter einen Nachteil erleidet. a ) Die Angemessenheit der Verfahrensdauer richtet sich gemäß § 198 Abs 1 Satz 2 GVG nach den Umständen des Einzelfalls , insbesondere nach der Schwierigkeit und Bedeutung des Verfahrens sowie nach dem Verhalten der Verfahrensbeteiligten und Dritter. Hierbei handelt es sich um eine beispielhafte , nicht abschließende Auflistung von Umständen , die für die Beurteilung der Angemessenheit besonders bedeutsam sind ( BT-Drs 17/3802 S 18 ). Weitere gewichtige Beurteilungskriterien sind die Verfahrensführung durch das Gericht sowie die zur Verfahrensbeschleunigung gegenläufigen Rechtsgüter der Gewährleistung der inhaltlichen Richtigkeit von Entscheidungen , der Beachtung der richterlichen Unabhängigkeit und des gesetzlichen Richters.""",
]
```
## 4. Use the pipeline to create outputs
```
empty_df = spark.createDataFrame([['']]).toDF('text')
pipeline_model = nlp_pipeline.fit(empty_df)
df = spark.createDataFrame(pd.DataFrame({'text': input_list}))
result = pipeline_model.transform(df)
```
## 5. Visualize results
Visualize outputs as data frame
```
from sparknlp_display import NerVisualizer
NerVisualizer().display(
result = result.collect()[0],
label_col = 'ner_chunk',
document_col = 'document'
)
```
| github_jupyter |
```
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torch.utils.data import Dataset, DataLoader
from torch.utils.tensorboard import SummaryWriter
torch.manual_seed(42)
class RNNRegressor(nn.Module):
def __init__(self, input_dim, hidden_dim, output_dim):
super(RNNRegressor, self).__init__()
self.input_dim = input_dim
self.hidden_dim = hidden_dim
self.output_dim = output_dim
self.i2h = nn.Linear(input_dim + hidden_dim, hidden_dim)
self.i2o = nn.Linear(input_dim + hidden_dim, output_dim)
self.tanh = nn.Tanh()
def forward(self, input, hidden):
#input = input.view(-1, input.shape[1])
# TODO: Modify code to accept batch tensors <loc, batch_nr, index>. Can add init hidden in here.
combined = torch.cat((input, hidden), 1)
hidden = self.i2h(combined)
output = self.i2o(combined)
output = self.tanh(output)
return output, hidden
def initHidden(self):
return torch.zeros(1, self.hidden_dim)
HIDDEN_DIM = 10
rnn = RNNRegressor(train_set.vocab_size, HIDDEN_DIM, 1)
writer = SummaryWriter('runs/RNN_playground')
writer.add_graph(rnn, (seq2tensor("ACGTT")[1], torch.zeros(1, HIDDEN_DIM)))
writer.close()
criterion = nn.MSELoss()
optimizer = optim.SGD(rnn.parameters(), lr=0.005)
def train(output_tensor, seq_tensor):
''''''
hidden = rnn.initHidden()
# zero the grad buffers
rnn.zero_grad()
optimizer.zero_grad()
# forward pass
for i in range(seq_tensor.shape[0]):
output, hidden = rnn(seq_tensor[i], hidden)
# compute loss and backward pass
loss = criterion(output, output_tensor)
loss.backward()
# update params
optimizer.step()
return output, loss.item()
train(torch.tensor([-0.0117]), seq2tensor("ACGTN"))
print(seq2tensor("ACGTN").shape, torch.tensor([-0.0118]).shape)
NUM_EPOCHS = 5
# TODO: not really minibatch for now
for epoch in range(NUM_EPOCHS):
running_loss = 0.0
for i, data in enumerate(train_loader, 0):
# get inputs
# TODO: Account for dtypes, otherwise get incompatible!
seq_tensor, expr = data
seq_tensor = seq_tensor[0]
expr = expr[0].view(1)
expr = expr.type(torch.FloatTensor)
# train on example
output, loss = train(expr[0], seq_tensor)
# print statistics
running_loss += loss
if i % 2000 == 1999: # print every 2000 mini-batches
print('[%d, %5d] loss: %.3f' %
(epoch + 1, i + 1, running_loss / 2000))
running_loss = 0.0
print('Finished Training')
# save model
PATH = './models/test_model'
torch.save(rnn.state_dict(), PATH)
# Predict loop
# correct = 0
# total = 0
# with torch.no_grad():
# for data in testloader:
# images, labels = data
# outputs = net(images)
# _, predicted = torch.max(outputs.data, 1)
# total += labels.size(0)
# correct += (predicted == labels).sum().item()
# print('Accuracy of the network on the 10000 test images: %d %%' % (
# 100 * correct / total))
```
| github_jupyter |
## Data Wrangling with Python: Intro to Pandas
Note: Notebook adapted from [here](https://github.com/EricElmoznino/lighthouse_pandas_tutorial/blob/master/pandas_tutorial.ipynb) & [here](https://github.com/sedv8808/LighthouseLabs/tree/main/W02D2) & from LHL's [21 Day Data Challenge](https://data-challenge.lighthouselabs.ca/start)
#### Instructor: Andrew Berry
#### Date: Aug 24, 2021
**Agenda:**
- Why Pandas?
- Pandas Basics
- Pandas Series vs. Pandas DataFrames
- .loc() vs. iloc()
- Pandas Advance
- Filtering
- Group bys
- Pandas Exercises
- Challenge 1
- Challenge 2
### Pandas: Why Pandas? What is it?
To do data anlaysis with Python, Pandas is a great tool to for dealing with data in a tabular and time series formats. Designed by Wes McKinney as an attempt to port R's dataframes to python.
- Python Package for working with **tables**
- Similar to SQL & Excel
- Faster
- More features to manipulate, transform, and aggregate data
- Easy to handle messy and missing data
- Great at working with large data files
- When combing with other Python libraries, it's fairly easy to create bautiful and customazied visuals. Easy integration with Matplotlib, Seaborn, Plotly.
- Easy integration with machine learning plugins (sckit-learn)
-----------
To read more about, Wes McKinney, the creator of Pandas, check out the article below.
1. https://qz.com/1126615/the-story-of-the-most-important-tool-in-data-science/
--------------
## Think of how we would try to represent a table in Python?
```
#A dicitonary of lists example
students = {
'student_id': [1, 2, 3, 4,5,6],
'name': ['Daenerys', 'Jon', 'Arya', 'Sansa', 'Eddard', 'Khal Drogo'],
'course_mark': [82, 100, 12, 76, 46, 20],
'species': ['cat', 'human', 'cat', 'human', 'human', 'human']
}
```
**What are some operations we might want to do on this data?**
- 1.Select a subset of columns
- 2.Filter out some rows based on an attribute
- 3.Group by some attribute
- 4.Compute some aggregate values within groups
- 5.Save to a file
How about we try out one of these to see how easy it is
### Try to return a table with the mean course mark per-species.
```
# Return a table with the mean course mark per-species
# Think about a SQL statment where we group by species with the average course mark
species_sums = {} #Tables of Sums
species_counts = {} #Count per Species
for i in range(len(students['species'])): #iterating over the rows
species = students['species'][i] #every row number I get species
course_mark = students['course_mark'][i] # and course mark
if species not in species_sums: #Intializing Species if not in list
species_sums[species] = 0
species_counts[species] = 0
species_sums[species] += course_mark #Add each course mark for each species
species_counts[species] += 1
species_means = {}
for species in species_sums: # for every unique species we found
species_means[species] = species_sums[species] / species_counts[species] #sum/count
species_means #return
```
- Did you like looking at is? Does this look fun to do?
- Super Tiring.
## Pandas Version
```
# Pandas Version
import pandas as pd
# Can take in a dictionry of list to instatiate a DataFrame
students = pd.DataFrame(students)
students
species_means = students[['species', 'course_mark']].groupby('species').mean()
#species_means = students.groupby('species')['course_mark'].mean()
species_means
```
### Dissecting the above code!
```
#Step 1: Filter out the columns we want to keep
students_filtered = students[['species','course_mark']]
students_filtered
# Step 2: Group by species column
students_grouped_by_species = students_filtered.groupby('species')
students_grouped_by_species
#Step 3: Specify how to aggregate the course-mark column
species_means = students_grouped_by_species.mean()
species_means
```
#### As shown, Pandas makes use of vectorized operations.
- Rather than use for-loops, we specify the operation that will apply to the structure as a whole (i.e. all the rows)
- By vectorizing, **the code becomes more concise and more readable**
- Pandas is optimized for vectorized operations (parallel vs. serial computation), which makes them **much faster**
- It is almost always possible to vectorize operations on Pandas data types
### Getting Started: Pandas Series & Pandas DataFrames
There are two Pandas data types of interest:
- Series (column)
- A pandas series is similar to an array but it has an index. The index is constant, and doesnt change through the operations we apply to the series.
- DataFrame (table)
- A pandas dataframe is an object that is similar to a collection of pandas series.
```
# One way to construct a Series
series = pd.Series([82, 100, 12, 76, 46, 20])
series
#We can specify some index when building a series.
grades = pd.Series([82, 100, 12, 76, 46, 20],
index = ['Daenerys', 'Jon', 'Arya', 'Sansa', 'Eddard', 'Khal Drogo'] )
grades
grades['Daenerys']
grades[0]
print("The values:", grades.values)
print("The indexes:", grades.index)
```
**Note:** The underlying index is still 0, 1, 2, 3.... and we can still index on that:
```
grades[2]
```
### Pandas DataFrames
```
# One way to construct a DataFrame
df = pd.DataFrame({
'name': ['Daenerys', 'Jon', 'Arya', 'Sansa'],
'course_mark': [82, 100, 12, 76],
'species': ['human', 'human', 'cat', 'human']},
index=[1412, 94, 9351, 14])
df
```
#### Reading a CSV file
We'll use the function `read_csv()` to load the data into our notebook
- The `read_csv()` function can read data from a locally saved file or from a URL
- We'll store the data as a variable `df_pokemon`
```
df_pokemon = pd.read_csv('pokemon.csv')
df_pokemon
```
**What do we see here?**
- Each row of the table is an observation, containing data of a single pokemon
```
df_pokemon.shape
```
For large DataFrames, it's often useful to display just the first few or last few rows:
```
#pd.options.display.max_rows = 15
df_pokemon.head(10)
df_pokemon.tail(10)
#df_pokemon.head?
```
> **Pro tip:**
> - To display the documentation for this method within Jupyter notebook, you can run the command `df_pokemon.head?` or press `Shift-Tab` within the parentheses of `df_pokemon.head()`
> - To see other methods available for the DataFrame, type `df_pokemon.` followed by `Tab` for auto-complete options
## Data at a Glance
`pandas` provides many ways to quickly and easily summarize your data:
- How many rows and columns are there?
- What are all the column names and what type of data is in each column?
- How many values are missing in each column or row?
- Numerical data: What is the average and range of the values?
- Text data: What are the unique values and how often does each occur?
### Peeking into the pokemon dataset
- Similar with getting familar with SQL tables, it is often a great idea to look at the pandas dataframes we are working with. Below are some of the basic methods to glance at a dataset.
```
#Getting the Columns
df_pokemon.columns
list_of_column = ['#', 'Name', 'Type 1', 'Type 2', 'Total', 'HP', 'Attack', 'Defense',
'Sp. Atk', 'Sp. Def', 'Speed', 'Generation', 'Legendary']
#Getting Summary Statistics
df_pokemon.describe()
df_pokemon[["Total","Attack"]].describe()
df_pokemon
list_columns = ['Name', 'Defense',
'Sp. Atk']
var_a = df_pokemon[list_columns].describe()
#var_a.round(2)
std_attack = df_pokemon['Attack'].std()
print(std_attack)
#Checking for Missing Data
df_pokemon.isnull().sum() / len(df_pokemon) * 100
```
## The .loc() vs .iloc() method
To select rows and columns at the same time, we use the syntax `.loc[<rows>, <columns>]`:
```
#Notice the square brackets on loc and the colon
df_pokemon.loc[10:20, ['Name']]
#Taking a slice of index values
# Getting more than one columns
df_pokemon.loc[10:14, ['Name',"Legendary",'Attack']]
#we can also feed in a list for the rows
df_pokemon.loc[[10,14,24,58,238], ['Name',"Legendary",'Attack']]
df_pokemon.head(3)
#We can also slice over range of column values
df_pokemon.loc[[10,14,24,58,238], 'Name':'Attack']
#Iloc is use for integer based indexing
df_pokemon.iloc[0:3,1:4]
```
### Modifying a Column or Creating a new column
Give a little description
```
df_pokemon.head(3)
df2 = df_pokemon.copy() #hard copy
df2['Total_Attack'] = df2['Attack'] + df2['Sp. Atk']
df2.head(3)
df2['Total'] = df2['Total'] * 2
df2['filler'] = True
#Modify an orginal
#Modify Data Frame with .loc() method
df2.loc[1, 'Name'] = 'Andrew'
```
### Sort_values() & value_counts()
1. ***df.sort_values()***
2. ***df.value_counts()***
The ***pandas.sort_values()*** allows us to reorder our dataframe in an ascending or descending order given a column for pandas to work from. This is similar to the excel sort function.
```python
import pandas as pd
df = pd.read_csv('random.csv')
df
df.sort_values(by=['some_column'], ascending = True)
```
In the above code snippet, we are sorting our *random.csv* pandas data frame by the column *some_column* in ascending order. To read more on the ***df.sort_values()*** function, read this [article](https://datatofish.com/sort-pandas-dataframe/).
The second function is ***df.value_counts()***, it allows us to count how many times a specific value/item occurred in the dataframe. This function is best used on a specific column on a data frame, ideally on a column representing categorical data. Categorical data refers to a statistical data type consisting of categorical variables.
```python
df['column'].value_counts()
```
To read more on some of the advanced functionalities of ***df.value_counts()***, please refer to the pandas documentation or this [article](https://towardsdatascience.com/getting-more-value-from-the-pandas-value-counts-aa17230907a6).
```
df2.head(10)
another_variable = df2.sort_values(by = 'Total_Attack', ascending = False).head(5)
df2.sort_values(by = ['Attack','Defense'], ascending = [True,False]).head(15).to_csv('modified.csv')
#Value_Counts
#pd.options.display.max_rows = 30
df2['Type 1'].value_counts(ascending = True)
df2['Type 1'].value_counts().sort_index()
#Just Unique Values
df2['Type 1'].unique()
#How many unique Values
df2['Type 1'].nunique()
```
### How to Query or Filter Data with Conditions?
- We can extract specific data from our dataframe based on a specific condition. We will be using the syntax below. Pandas will return a subset of the dataframe based on the given condition.
```python
df[<insert_condition>]
```
Conditions follow the generic boolean logic in Python. Below is a cheat sheet python boolean logic.
**Conditional Logic:**
Conditional logic refers to the execution of different actions based on whether a certain condition is met. In programming, these conditions are expressed by a set of symbols called **Boolean Operators**.
| Boolean Comparator | Example | Meaning |
|--------------------|---------|---------------------------------|
| > | x > y | x is greater than y |
| >= | x >= y | x is greater than or equal to y |
| < | x < y | x is less than y |
| <= | x <= y | x is less than or equal to y |
| != | x != y | x is not equal to y |
| == | x == y | x is equal to y |
```
#Step 1: Create a filter
#the_filter = df_pokemon['Total'] >= 300
the_filter = (df_pokemon['Total'] >= 300) & (df_pokemon['Legendary'] == True)
#Step 2: Apply Filter
#df_pokemon[the_filter]
df_pokemon[(df_pokemon['Total'] >= 300) & (df_pokemon['Legendary'] == True)]
#Finding Only Legendary Pokemons
```
### Grouping and Aggregation
Grouping and aggregation can be used to calculate statistics on groups in the data.
**Common Aggregation Functions**
- mean()
- median()
- sum()
- count()
```
df = df_pokemon.copy()
df.head(2)
df[['Type 1','Attack', 'Defense']].groupby('Type 1', as_index = False).mean()
```
- By default, `groupby()` assigns the variable that we're grouping on (in this case `Type 1`) to the index of the output data
- If we use the keyword argument `as_index=False`, the grouping variable is instead assigned to a regular column
- This can be useful in some situations, such as data visualization functions which expect the relevant variables to be in columns rather than the index
```
df[['Type 1','Attack', 'Defense','Legendary']].groupby(['Legendary','Type 1'], as_index = False).mean()
#pd.options.display.max_rows = 50
```
We can use the `agg` method to compute multiple aggregated statistics on our data, for example minimum and maximum country populations in each region:
```
df[['Attack','Type 1']].groupby('Type 1').agg(['min','max','mean'])
```
We can also use `agg` to compute different statistics for different columns:
```
agg_dict = {
'Attack': "mean",
'Defense': ['min','max']
}
new_df = df[['Attack','Defense','Type 1']].groupby('Type 1').agg(agg_dict)
new_df.reset_index()
```
### Challenge 1 (10 minutes)
Let's play around with Pandas on a more intricate dataset: a dataset on wines!
**Challenge 14 from the 21 Day Data Challenge**
Dot's neighbour said that he only likes wine from Stellenbosch, Bordeaux, and the Okanagan Valley, and that the sulfates can't be that high. The problem is, Dot can't really afford to spend tons of money on the wine. Dot's conditions for searching for wine are:
1. Sulfates cannot be higher than 0.6.
2. The price has to be less than $20.
Use the above conditions to filter the data for questions **2 and 3** below.
**Questions:**
1. Where is Stellenbosch, anyway? How many wines from Stellenbosch are there in the *entire dataset*?
2. *After filtering with the 2 conditions*, what is the average price of wine from the Bordeaux region?
3. *After filtering with the 2 conditions*, what is the least expensive wine that's of the highest quality from the Okanagan Valley?
**Stretch Question:**
1. What is the average price of wine from Stellenbosch, according to the entire unfiltered dataset?
**Note: Check the dataset to see if there are missing values; if there are, fill in missing values with the mean.**
```
#Write your Code Below
import pandas as pd
df = pd.read_csv('winequality-red_2.csv')
df = df.drop(columns = ['Unnamed: 0'])
df.head()
#Solutions
#Q1
df['region'].value_counts()
#Q2
filter_sulhpates = df['sulphates'] <= 0.6
filtered_df = df[filter_sulhpates]
filter_quality = filtered_df['price'] < 20
filtered_df = filtered_df[filter_quality]
filtered_df.groupby(['region']).mean()
#Answer is $11.300
#Q3
filter_region = df['region'] == 'Okanagan Valley'
filtered_df = filtered_df[filter_region]
filtered_df.sort_values(by=['quality', 'price'], ascending = [False,True])
```
### Challenge 2 (25 minutes)
**Challenge 21 from the 21DDC (Adapted)**
Dot wants to play retro video games with all their new friends! Help them figure out which games would be best.
Questions:
1. What is the top 5 best selling games released before the year 2000.
- **Note**: Use Global_Sales
2. Create a new column called Aggregate_Score, which returns the proportional average between Critic Score and User_Score based on Critic_Count and User_Count. Plot a horizontal bar chart of the top 5 highest rated games by Aggregate_Score, not published by Nintendo before the year 2000. From this bar chart, what is the highest rated game by Aggregate_Score?
- **Note**: Critic_Count should be filled with the mean. User_Count should be filled with the median.
#### In the exercise above, there is some missing values in the dataset. Look up the pandas documentation to figure out how to fill missing values in a column. You will be using the **fillna()** function.
```
df = pd.read_csv('video_games.csv')
df.head(5)
#Solution Q1
best_selling_2000_filter = df["Year_of_Release"] < 2000
best_selling_2000 = df[best_selling_2000_filter]
best_selling_2000.head(5)
#Solution Q2
#Step 1: Fill in missing values with the median
#Columns with missing values Critic_Count and User_Count
df['Critic_Count'].isnull().sum()
#Fill in with the mean
df['Critic_Count'] = df['Critic_Count'].fillna(value = df.Critic_Count.mean())
#Fill in with the median
df['User_Count'] = df['User_Count'].fillna(value = df.User_Count.median())
#Up the User_score
#Because the user_score is not on the same scale as the critic score
df['User_Score'] = df['User_Score'] * 10
#Create aggregate Score
df['Aggregate_Score'] = ((df['Critic_Score'] * df['Critic_Count']) + (df['User_Score'] * df['User_Count']))/(df['Critic_Count'] + df['User_Count'])
df["Aggregate_Score"].describe()
nintendo_filter_year = df["Year_of_Release"] < 2000
nintendo_filter_publisher = df["Publisher"] != 'Nintendo'
nintendo = df[nintendo_filter_year]
nintendo = nintendo[nintendo_filter_publisher]
nintendo.sort_values('Aggregate_Score', ascending = False).head(5)
```
# HINT
**How to create the Aggregate Score Column?**
\begin{equation*}
AggregateScore = \frac{(CriticCount * CriticScore)+(UserCount * UserScore)}{UserCount + CriticCount}
\end{equation*}
**Check Your Column Values**
The Critic_Score column is scored out of 100. The User_Score column is scored out of 10. You will need to modify one of the columns to match the other.
## Documentation
In the meantime, check out pandas the user guide in the [pandas documentation](https://pandas.pydata.org/docs/user_guide/index.html#user-guide).
-------
**Why should I use the documentation?**
On the job as a data scientist or data analyst, more often than not, you may find yourself looking up the documentation of a particular function or plugin you use. Don't worry if there are a few functions you don't know by heart. However, there are just too many to know! An essential skill is to learn how to navigate documentation and understand how to apply the examples to your work.
--------
Additional resources:
- To learn more about these topics, as well as other topics not covered here (e.g. reshaping, merging, additional subsetting methods, working with text data, etc.) check out [these introductory tutorials](https://pandas.pydata.org/docs/getting_started/index.html#getting-started) from the `pandas` documentation
- To learn more about subsetting your data, check out [this tutorial](https://pandas.pydata.org/docs/getting_started/intro_tutorials/03_subset_data.html#min-tut-03-subset)
- This [pandas cheatsheet](https://pandas.pydata.org/Pandas_Cheat_Sheet.pdf) may also be helpful as a reference.
| github_jupyter |
# Mask R-CNN Demo
A quick intro to using the pre-trained model to detect and segment objects.
```
import os
import sys
import random
import math
import numpy as np
import skimage.io
import matplotlib
import matplotlib.pyplot as plt
# Root directory of the project
ROOT_DIR = os.path.abspath("../")
# Import Mask RCNN
sys.path.append(ROOT_DIR) # To find local version of the library
from mrcnn import utils
import mrcnn.model as modellib
from mrcnn import visualize
# Import COCO config
sys.path.append(os.path.join(ROOT_DIR, "samples/coco/")) # To find local version
import coco
%matplotlib inline
# Directory to save logs and trained model
MODEL_DIR = os.path.join(ROOT_DIR, "logs")
# Local path to trained weights file
COCO_MODEL_PATH = os.path.join(ROOT_DIR, "mask_rcnn_coco.h5")
# Download COCO trained weights from Releases if needed
if not os.path.exists(COCO_MODEL_PATH):
utils.download_trained_weights(COCO_MODEL_PATH)
# Directory of images to run detection on
IMAGE_DIR = os.path.join(ROOT_DIR, "images")
```
## Configurations
We'll be using a model trained on the MS-COCO dataset. The configurations of this model are in the ```CocoConfig``` class in ```coco.py```.
For inferencing, modify the configurations a bit to fit the task. To do so, sub-class the ```CocoConfig``` class and override the attributes you need to change.
```
class InferenceConfig(coco.CocoConfig):
# Set batch size to 1 since we'll be running inference on
# one image at a time. Batch size = GPU_COUNT * IMAGES_PER_GPU
GPU_COUNT = 1
IMAGES_PER_GPU = 1
config = InferenceConfig()
config.display()
```
## Create Model and Load Trained Weights
```
# Create model object in inference mode.
model = modellib.MaskRCNN(mode="inference", model_dir=MODEL_DIR, config=config)
# Load weights trained on MS-COCO
model.load_weights(COCO_MODEL_PATH, by_name=True)
```
## Class Names
The model classifies objects and returns class IDs, which are integer value that identify each class. Some datasets assign integer values to their classes and some don't. For example, in the MS-COCO dataset, the 'person' class is 1 and 'teddy bear' is 88. The IDs are often sequential, but not always. The COCO dataset, for example, has classes associated with class IDs 70 and 72, but not 71.
To improve consistency, and to support training on data from multiple sources at the same time, our ```Dataset``` class assigns it's own sequential integer IDs to each class. For example, if you load the COCO dataset using our ```Dataset``` class, the 'person' class would get class ID = 1 (just like COCO) and the 'teddy bear' class is 78 (different from COCO). Keep that in mind when mapping class IDs to class names.
To get the list of class names, you'd load the dataset and then use the ```class_names``` property like this.
```
# Load COCO dataset
dataset = coco.CocoDataset()
dataset.load_coco(COCO_DIR, "train")
dataset.prepare()
# Print class names
print(dataset.class_names)
```
We don't want to require you to download the COCO dataset just to run this demo, so we're including the list of class names below. The index of the class name in the list represent its ID (first class is 0, second is 1, third is 2, ...etc.)
```
# COCO Class names
# Index of the class in the list is its ID. For example, to get ID of
# the teddy bear class, use: class_names.index('teddy bear')
class_names = ['BG', 'person', 'bicycle', 'car', 'motorcycle', 'airplane',
'bus', 'train', 'truck', 'boat', 'traffic light',
'fire hydrant', 'stop sign', 'parking meter', 'bench', 'bird',
'cat', 'dog', 'horse', 'sheep', 'cow', 'elephant', 'bear',
'zebra', 'giraffe', 'backpack', 'umbrella', 'handbag', 'tie',
'suitcase', 'frisbee', 'skis', 'snowboard', 'sports ball',
'kite', 'baseball bat', 'baseball glove', 'skateboard',
'surfboard', 'tennis racket', 'bottle', 'wine glass', 'cup',
'fork', 'knife', 'spoon', 'bowl', 'banana', 'apple',
'sandwich', 'orange', 'broccoli', 'carrot', 'hot dog', 'pizza',
'donut', 'cake', 'chair', 'couch', 'potted plant', 'bed',
'dining table', 'toilet', 'tv', 'laptop', 'mouse', 'remote',
'keyboard', 'cell phone', 'microwave', 'oven', 'toaster',
'sink', 'refrigerator', 'book', 'clock', 'vase', 'scissors',
'teddy bear', 'hair drier', 'toothbrush']
```
## Run Object Detection
```
# Load a random image from the images folder
file_names = next(os.walk(IMAGE_DIR))[2]
image = skimage.io.imread(os.path.join(IMAGE_DIR, random.choice(file_names)))
# Run detection
results = model.detect([image], verbose=1)
# Visualize results
r = results[0]
visualize.display_instances(image, r['rois'], r['masks'], r['class_ids'],
class_names, r['scores'])
```
| github_jupyter |
# Creating a Sentiment Analysis Web App
## Using PyTorch and SageMaker
_Deep Learning Nanodegree Program | Deployment_
---
Now that we have a basic understanding of how SageMaker works we will try to use it to construct a complete project from end to end. Our goal will be to have a simple web page which a user can use to enter a movie review. The web page will then send the review off to our deployed model which will predict the sentiment of the entered review.
## Instructions
Some template code has already been provided for you, and you will need to implement additional functionality to successfully complete this notebook. You will not need to modify the included code beyond what is requested. Sections that begin with '**TODO**' in the header indicate that you need to complete or implement some portion within them. Instructions will be provided for each section and the specifics of the implementation are marked in the code block with a `# TODO: ...` comment. Please be sure to read the instructions carefully!
In addition to implementing code, there will be questions for you to answer which relate to the task and your implementation. Each section where you will answer a question is preceded by a '**Question:**' header. Carefully read each question and provide your answer below the '**Answer:**' header by editing the Markdown cell.
> **Note**: Code and Markdown cells can be executed using the **Shift+Enter** keyboard shortcut. In addition, a cell can be edited by typically clicking it (double-click for Markdown cells) or by pressing **Enter** while it is highlighted.
## General Outline
Recall the general outline for SageMaker projects using a notebook instance.
1. Download or otherwise retrieve the data.
2. Process / Prepare the data.
3. Upload the processed data to S3.
4. Train a chosen model.
5. Test the trained model (typically using a batch transform job).
6. Deploy the trained model.
7. Use the deployed model.
For this project, you will be following the steps in the general outline with some modifications.
First, you will not be testing the model in its own step. You will still be testing the model, however, you will do it by deploying your model and then using the deployed model by sending the test data to it. One of the reasons for doing this is so that you can make sure that your deployed model is working correctly before moving forward.
In addition, you will deploy and use your trained model a second time. In the second iteration you will customize the way that your trained model is deployed by including some of your own code. In addition, your newly deployed model will be used in the sentiment analysis web app.
## Step 1: Downloading the data
As in the XGBoost in SageMaker notebook, we will be using the [IMDb dataset](http://ai.stanford.edu/~amaas/data/sentiment/)
> Maas, Andrew L., et al. [Learning Word Vectors for Sentiment Analysis](http://ai.stanford.edu/~amaas/data/sentiment/). In _Proceedings of the 49th Annual Meeting of the Association for Computational Linguistics: Human Language Technologies_. Association for Computational Linguistics, 2011.
```
%mkdir ../data
!wget -O ../data/aclImdb_v1.tar.gz http://ai.stanford.edu/~amaas/data/sentiment/aclImdb_v1.tar.gz
!tar -zxf ../data/aclImdb_v1.tar.gz -C ../data
```
## Step 2: Preparing and Processing the data
Also, as in the XGBoost notebook, we will be doing some initial data processing. The first few steps are the same as in the XGBoost example. To begin with, we will read in each of the reviews and combine them into a single input structure. Then, we will split the dataset into a training set and a testing set.
```
import os
import glob
def read_imdb_data(data_dir='../data/aclImdb'):
data = {}
labels = {}
for data_type in ['train', 'test']:
data[data_type] = {}
labels[data_type] = {}
for sentiment in ['pos', 'neg']:
data[data_type][sentiment] = []
labels[data_type][sentiment] = []
path = os.path.join(data_dir, data_type, sentiment, '*.txt')
files = glob.glob(path)
for f in files:
with open(f) as review:
data[data_type][sentiment].append(review.read())
# Here we represent a positive review by '1' and a negative review by '0'
labels[data_type][sentiment].append(1 if sentiment == 'pos' else 0)
assert len(data[data_type][sentiment]) == len(labels[data_type][sentiment]), \
"{}/{} data size does not match labels size".format(data_type, sentiment)
return data, labels
data, labels = read_imdb_data()
print("IMDB reviews: train = {} pos / {} neg, test = {} pos / {} neg".format(
len(data['train']['pos']), len(data['train']['neg']),
len(data['test']['pos']), len(data['test']['neg'])))
```
Now that we've read the raw training and testing data from the downloaded dataset, we will combine the positive and negative reviews and shuffle the resulting records.
```
from sklearn.utils import shuffle
def prepare_imdb_data(data, labels):
"""Prepare training and test sets from IMDb movie reviews."""
#Combine positive and negative reviews and labels
data_train = data['train']['pos'] + data['train']['neg']
data_test = data['test']['pos'] + data['test']['neg']
labels_train = labels['train']['pos'] + labels['train']['neg']
labels_test = labels['test']['pos'] + labels['test']['neg']
#Shuffle reviews and corresponding labels within training and test sets
data_train, labels_train = shuffle(data_train, labels_train)
data_test, labels_test = shuffle(data_test, labels_test)
# Return a unified training data, test data, training labels, test labets
return data_train, data_test, labels_train, labels_test
train_X, test_X, train_y, test_y = prepare_imdb_data(data, labels)
print("IMDb reviews (combined): train = {}, test = {}".format(len(train_X), len(test_X)))
```
Now that we have our training and testing sets unified and prepared, we should do a quick check and see an example of the data our model will be trained on. This is generally a good idea as it allows you to see how each of the further processing steps affects the reviews and it also ensures that the data has been loaded correctly.
```
print(train_X[100])
print(train_y[100])
```
The first step in processing the reviews is to make sure that any html tags that appear should be removed. In addition we wish to tokenize our input, that way words such as *entertained* and *entertaining* are considered the same with regard to sentiment analysis.
```
import nltk
from nltk.corpus import stopwords
from nltk.stem.porter import *
import re
from bs4 import BeautifulSoup
def review_to_words(review):
nltk.download("stopwords", quiet=True)
stemmer = PorterStemmer()
text = BeautifulSoup(review, "html.parser").get_text() # Remove HTML tags
text = re.sub(r"[^a-zA-Z0-9]", " ", text.lower()) # Convert to lower case
words = text.split() # Split string into words
words = [w for w in words if w not in stopwords.words("english")] # Remove stopwords
words = [PorterStemmer().stem(w) for w in words] # stem
return words
```
The `review_to_words` method defined above uses `BeautifulSoup` to remove any html tags that appear and uses the `nltk` package to tokenize the reviews. As a check to ensure we know how everything is working, try applying `review_to_words` to one of the reviews in the training set.
```
# TODO: Apply review_to_words to a review (train_X[100] or any other review)
review_to_words(train_X[100])
```
**Question:** Above we mentioned that `review_to_words` method removes html formatting and allows us to tokenize the words found in a review, for example, converting *entertained* and *entertaining* into *entertain* so that they are treated as though they are the same word. What else, if anything, does this method do to the input?
**Answer:** `review_to_words` does not only stem the words. It also removes stop words such as the articles `the`,`a`,`an` along with prepositions such as `and`,`to`,`from` and more. Moreover, it removes punctuations. The only issue with Stemming is that some words are not really accurate after the stemming (e.g. `pr` or `j`). However, if this is to happen systematically, it shouldn't be a problem.
The method below applies the `review_to_words` method to each of the reviews in the training and testing datasets. In addition it caches the results. This is because performing this processing step can take a long time. This way if you are unable to complete the notebook in the current session, you can come back without needing to process the data a second time.
```
import pickle
cache_dir = os.path.join("../cache", "sentiment_analysis") # where to store cache files
os.makedirs(cache_dir, exist_ok=True) # ensure cache directory exists
def preprocess_data(data_train, data_test, labels_train, labels_test,
cache_dir=cache_dir, cache_file="preprocessed_data.pkl"):
"""Convert each review to words; read from cache if available."""
# If cache_file is not None, try to read from it first
cache_data = None
if cache_file is not None:
try:
with open(os.path.join(cache_dir, cache_file), "rb") as f:
cache_data = pickle.load(f)
print("Read preprocessed data from cache file:", cache_file)
except:
pass # unable to read from cache, but that's okay
# If cache is missing, then do the heavy lifting
if cache_data is None:
# Preprocess training and test data to obtain words for each review
#words_train = list(map(review_to_words, data_train))
#words_test = list(map(review_to_words, data_test))
words_train = [review_to_words(review) for review in data_train]
words_test = [review_to_words(review) for review in data_test]
# Write to cache file for future runs
if cache_file is not None:
cache_data = dict(words_train=words_train, words_test=words_test,
labels_train=labels_train, labels_test=labels_test)
with open(os.path.join(cache_dir, cache_file), "wb") as f:
pickle.dump(cache_data, f)
print("Wrote preprocessed data to cache file:", cache_file)
else:
# Unpack data loaded from cache file
words_train, words_test, labels_train, labels_test = (cache_data['words_train'],
cache_data['words_test'], cache_data['labels_train'], cache_data['labels_test'])
return words_train, words_test, labels_train, labels_test
# Preprocess data
train_X, test_X, train_y, test_y = preprocess_data(train_X, test_X, train_y, test_y)
```
## Transform the data
In the XGBoost notebook we transformed the data from its word representation to a bag-of-words feature representation. For the model we are going to construct in this notebook we will construct a feature representation which is very similar. To start, we will represent each word as an integer. Of course, some of the words that appear in the reviews occur very infrequently and so likely don't contain much information for the purposes of sentiment analysis. The way we will deal with this problem is that we will fix the size of our working vocabulary and we will only include the words that appear most frequently. We will then combine all of the infrequent words into a single category and, in our case, we will label it as `1`.
Since we will be using a recurrent neural network, it will be convenient if the length of each review is the same. To do this, we will fix a size for our reviews and then pad short reviews with the category 'no word' (which we will label `0`) and truncate long reviews.
### (TODO) Create a word dictionary
To begin with, we need to construct a way to map words that appear in the reviews to integers. Here we fix the size of our vocabulary (including the 'no word' and 'infrequent' categories) to be `5000` but you may wish to change this to see how it affects the model.
> **TODO:** Complete the implementation for the `build_dict()` method below. Note that even though the vocab_size is set to `5000`, we only want to construct a mapping for the most frequently appearing `4998` words. This is because we want to reserve the special labels `0` for 'no word' and `1` for 'infrequent word'.
```
import numpy as np
from collections import Counter,OrderedDict
import operator
def build_dict(data, vocab_size = 5000):
"""Construct and return a dictionary mapping each of the most frequently appearing words to a unique integer."""
# TODO: Determine how often each word appears in `data`. Note that `data` is a list of sentences and that a
# sentence is a list of words.
# A dict storing the words that appear in the reviews along with how often they occur
temp_data = np.concatenate(data,axis=0)
word_counter = Counter(temp_data)
word_count = dict(word_counter)
# TODO: Sort the words found in `data` so that sorted_words[0] is the most frequently appearing word and
# sorted_words[-1] is the least frequently appearing word.
sorted_counts =sorted(word_count.items(), key=lambda x: x[1], reverse=True)
sorted_words = [word for word,_ in sorted_counts]
word_dict = {} # This is what we are building, a dictionary that translates words into integers
for idx, word in enumerate(sorted_words[:vocab_size - 2]): # The -2 is so that we save room for the 'no word'
word_dict[word] = idx + 2 # 'infrequent' labels
return word_dict
word_dict = build_dict(train_X)
```
**Question:** What are the five most frequently appearing (tokenized) words in the training set? Does it makes sense that these words appear frequently in the training set?
**Answer:** [movi,film,one,like,time] are the most frequently apprearing words in the training set. This makes sense as the reviews are about movies and we should be expecting people to express whether they like them or not.
```
# TODO: Use this space to determine the five most frequently appearing words in the training set.
temp_data = np.concatenate(train_X,axis=0)
word_counter = Counter(temp_data)
word_count = dict(word_counter)
sorted(word_count.items(), key=lambda x: x[1], reverse=True)[0:5]
```
### Save `word_dict`
Later on when we construct an endpoint which processes a submitted review we will need to make use of the `word_dict` which we have created. As such, we will save it to a file now for future use.
```
data_dir = '../data/pytorch' # The folder we will use for storing data
if not os.path.exists(data_dir): # Make sure that the folder exists
os.makedirs(data_dir)
with open(os.path.join(data_dir, 'word_dict.pkl'), "wb") as f:
pickle.dump(word_dict, f)
```
### Transform the reviews
Now that we have our word dictionary which allows us to transform the words appearing in the reviews into integers, it is time to make use of it and convert our reviews to their integer sequence representation, making sure to pad or truncate to a fixed length, which in our case is `500`.
```
def convert_and_pad(word_dict, sentence, pad=500):
NOWORD = 0 # We will use 0 to represent the 'no word' category
INFREQ = 1 # and we use 1 to represent the infrequent words, i.e., words not appearing in word_dict
working_sentence = [NOWORD] * pad
for word_index, word in enumerate(sentence[:pad]):
if word in word_dict:
working_sentence[word_index] = word_dict[word]
else:
working_sentence[word_index] = INFREQ
return working_sentence, min(len(sentence), pad)
def convert_and_pad_data(word_dict, data, pad=500):
result = []
lengths = []
for sentence in data:
converted, leng = convert_and_pad(word_dict, sentence, pad)
result.append(converted)
lengths.append(leng)
return np.array(result), np.array(lengths)
train_X, train_X_len = convert_and_pad_data(word_dict, train_X)
test_X, test_X_len = convert_and_pad_data(word_dict, test_X)
```
As a quick check to make sure that things are working as intended, check to see what one of the reviews in the training set looks like after having been processeed. Does this look reasonable? What is the length of a review in the training set?
```
# Use this cell to examine one of the processed reviews to make sure everything is working as intended.
train_X[0]
```
**Question:** In the cells above we use the `preprocess_data` and `convert_and_pad_data` methods to process both the training and testing set. Why or why not might this be a problem?
**Answer:** Since the word dictionary of the most frequently used words is built based on the training data, it's considered a form of leakage to use that same dictionary to transform and encode the testing set. However, the whole approach is to build the dictionary and freeze it such that we have consistent numerical representation across all datasets. Therefore, I would not change anything here as the results will not be consistent using different dictionaries across different datasets.
## Step 3: Upload the data to S3
As in the XGBoost notebook, we will need to upload the training dataset to S3 in order for our training code to access it. For now we will save it locally and we will upload to S3 later on.
### Save the processed training dataset locally
It is important to note the format of the data that we are saving as we will need to know it when we write the training code. In our case, each row of the dataset has the form `label`, `length`, `review[500]` where `review[500]` is a sequence of `500` integers representing the words in the review.
```
import pandas as pd
pd.concat([pd.DataFrame(train_y), pd.DataFrame(train_X_len), pd.DataFrame(train_X)], axis=1) \
.to_csv(os.path.join(data_dir, 'train.csv'), header=False, index=False)
```
### Uploading the training data
Next, we need to upload the training data to the SageMaker default S3 bucket so that we can provide access to it while training our model.
```
import sagemaker
sagemaker_session = sagemaker.Session()
bucket = sagemaker_session.default_bucket()
prefix = 'sagemaker/sentiment_rnn'
role = sagemaker.get_execution_role()
input_data = sagemaker_session.upload_data(path=data_dir, bucket=bucket, key_prefix=prefix)
```
**NOTE:** The cell above uploads the entire contents of our data directory. This includes the `word_dict.pkl` file. This is fortunate as we will need this later on when we create an endpoint that accepts an arbitrary review. For now, we will just take note of the fact that it resides in the data directory (and so also in the S3 training bucket) and that we will need to make sure it gets saved in the model directory.
## Step 4: Build and Train the PyTorch Model
In the XGBoost notebook we discussed what a model is in the SageMaker framework. In particular, a model comprises three objects
- Model Artifacts,
- Training Code, and
- Inference Code,
each of which interact with one another. In the XGBoost example we used training and inference code that was provided by Amazon. Here we will still be using containers provided by Amazon with the added benefit of being able to include our own custom code.
We will start by implementing our own neural network in PyTorch along with a training script. For the purposes of this project we have provided the necessary model object in the `model.py` file, inside of the `train` folder. You can see the provided implementation by running the cell below.
```
!pygmentize train/model.py
```
The important takeaway from the implementation provided is that there are three parameters that we may wish to tweak to improve the performance of our model. These are the embedding dimension, the hidden dimension and the size of the vocabulary. We will likely want to make these parameters configurable in the training script so that if we wish to modify them we do not need to modify the script itself. We will see how to do this later on. To start we will write some of the training code in the notebook so that we can more easily diagnose any issues that arise.
First we will load a small portion of the training data set to use as a sample. It would be very time consuming to try and train the model completely in the notebook as we do not have access to a gpu and the compute instance that we are using is not particularly powerful. However, we can work on a small bit of the data to get a feel for how our training script is behaving.
```
import torch
import torch.utils.data
# Read in only the first 250 rows
train_sample = pd.read_csv(os.path.join(data_dir, 'train.csv'), header=None, names=None, nrows=250)
# Turn the input pandas dataframe into tensors
train_sample_y = torch.from_numpy(train_sample[[0]].values).float().squeeze()
train_sample_X = torch.from_numpy(train_sample.drop([0], axis=1).values).long()
# Build the dataset
train_sample_ds = torch.utils.data.TensorDataset(train_sample_X, train_sample_y)
# Build the dataloader
train_sample_dl = torch.utils.data.DataLoader(train_sample_ds, batch_size=50)
```
### (TODO) Writing the training method
Next we need to write the training code itself. This should be very similar to training methods that you have written before to train PyTorch models. We will leave any difficult aspects such as model saving / loading and parameter loading until a little later.
```
def train(model, train_loader, epochs, optimizer, loss_fn, device):
for epoch in range(1, epochs + 1):
model.train()
total_loss = 0
for batch in train_loader:
batch_X, batch_y = batch
batch_X = batch_X.to(device)
batch_y = batch_y.to(device)
# TODO: Complete this train method to train the model provided.
optimizer.zero_grad()
output = model.forward(batch_X)
loss = loss_fn(output, batch_y)
loss.backward()
optimizer.step()
total_loss += loss.data.item()
print("Epoch: {}, BCELoss: {}".format(epoch, total_loss / len(train_loader)))
```
Supposing we have the training method above, we will test that it is working by writing a bit of code in the notebook that executes our training method on the small sample training set that we loaded earlier. The reason for doing this in the notebook is so that we have an opportunity to fix any errors that arise early when they are easier to diagnose.
```
import torch.optim as optim
from train.model import LSTMClassifier
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
model = LSTMClassifier(32, 100, 5000).to(device)
optimizer = optim.Adam(model.parameters())
loss_fn = torch.nn.BCELoss()
train(model, train_sample_dl, 5, optimizer, loss_fn, device)
```
In order to construct a PyTorch model using SageMaker we must provide SageMaker with a training script. We may optionally include a directory which will be copied to the container and from which our training code will be run. When the training container is executed it will check the uploaded directory (if there is one) for a `requirements.txt` file and install any required Python libraries, after which the training script will be run.
### (TODO) Training the model
When a PyTorch model is constructed in SageMaker, an entry point must be specified. This is the Python file which will be executed when the model is trained. Inside of the `train` directory is a file called `train.py` which has been provided and which contains most of the necessary code to train our model. The only thing that is missing is the implementation of the `train()` method which you wrote earlier in this notebook.
**TODO**: Copy the `train()` method written above and paste it into the `train/train.py` file where required.
The way that SageMaker passes hyperparameters to the training script is by way of arguments. These arguments can then be parsed and used in the training script. To see how this is done take a look at the provided `train/train.py` file.
```
from sagemaker.pytorch import PyTorch
estimator = PyTorch(entry_point="train.py",
source_dir="train",
role=role,
framework_version='0.4.0',
train_instance_count=1,
train_instance_type='ml.p2.xlarge',
hyperparameters={
'epochs': 10,
'hidden_dim': 200,
})
estimator.fit({'training': input_data})
```
## Step 5: Testing the model
As mentioned at the top of this notebook, we will be testing this model by first deploying it and then sending the testing data to the deployed endpoint. We will do this so that we can make sure that the deployed model is working correctly.
## Step 6: Deploy the model for testing
Now that we have trained our model, we would like to test it to see how it performs. Currently our model takes input of the form `review_length, review[500]` where `review[500]` is a sequence of `500` integers which describe the words present in the review, encoded using `word_dict`. Fortunately for us, SageMaker provides built-in inference code for models with simple inputs such as this.
There is one thing that we need to provide, however, and that is a function which loads the saved model. This function must be called `model_fn()` and takes as its only parameter a path to the directory where the model artifacts are stored. This function must also be present in the python file which we specified as the entry point. In our case the model loading function has been provided and so no changes need to be made.
**NOTE**: When the built-in inference code is run it must import the `model_fn()` method from the `train.py` file. This is why the training code is wrapped in a main guard ( ie, `if __name__ == '__main__':` )
Since we don't need to change anything in the code that was uploaded during training, we can simply deploy the current model as-is.
**NOTE:** When deploying a model you are asking SageMaker to launch an compute instance that will wait for data to be sent to it. As a result, this compute instance will continue to run until *you* shut it down. This is important to know since the cost of a deployed endpoint depends on how long it has been running for.
In other words **If you are no longer using a deployed endpoint, shut it down!**
**TODO:** Deploy the trained model.
```
# TODO: Deploy the trained model
predictor = estimator.deploy(initial_instance_count = 1, instance_type = 'ml.m4.xlarge')
```
## Step 7 - Use the model for testing
Once deployed, we can read in the test data and send it off to our deployed model to get some results. Once we collect all of the results we can determine how accurate our model is.
```
test_X = pd.concat([pd.DataFrame(test_X_len), pd.DataFrame(test_X)], axis=1)
# We split the data into chunks and send each chunk seperately, accumulating the results.
def predict(data, rows=512):
split_array = np.array_split(data, int(data.shape[0] / float(rows) + 1))
predictions = np.array([])
for array in split_array:
predictions = np.append(predictions, predictor.predict(array))
return predictions
predictions = predict(test_X.values)
predictions = [round(num) for num in predictions]
from sklearn.metrics import accuracy_score
accuracy_score(test_y, predictions)
```
**Question:** How does this model compare to the XGBoost model you created earlier? Why might these two models perform differently on this dataset? Which do *you* think is better for sentiment analysis?
**Answer:** The performance of this RNN model is comparable to the XGBoost model. However, this RNN model is is relatively very simple and it's not tuned yet. I am anticipating a better performance once tuning takes place or a more complex model is built for the RNN. For XGBoost, there is no more room for improvement as we already did the tuning for the very limited set of parameters. Therefore, I would recommend continuing with the RNN model for R&D.
### (TODO) More testing
We now have a trained model which has been deployed and which we can send processed reviews to and which returns the predicted sentiment. However, ultimately we would like to be able to send our model an unprocessed review. That is, we would like to send the review itself as a string. For example, suppose we wish to send the following review to our model.
```
test_review = 'The simplest pleasures in life are the best, and this film is one of them. Combining a rather basic storyline of love and adventure this movie transcends the usual weekend fair with wit and unmitigated charm.'
```
The question we now need to answer is, how do we send this review to our model?
Recall in the first section of this notebook we did a bunch of data processing to the IMDb dataset. In particular, we did two specific things to the provided reviews.
- Removed any html tags and stemmed the input
- Encoded the review as a sequence of integers using `word_dict`
In order process the review we will need to repeat these two steps.
**TODO**: Using the `review_to_words` and `convert_and_pad` methods from section one, convert `test_review` into a numpy array `test_data` suitable to send to our model. Remember that our model expects input of the form `review_length, review[500]`.
```
# TODO: Convert test_review into a form usable by the model and save the results in test_data
test_data = None
test_words = review_to_words(test_review)
test_numerical, length = convert_and_pad(word_dict, test_words)
test_data = np.array([[length] + test_numerical])
```
Now that we have processed the review, we can send the resulting array to our model to predict the sentiment of the review.
```
predictor.predict(test_data)
```
Since the return value of our model is close to `1`, we can be certain that the review we submitted is positive.
### Delete the endpoint
Of course, just like in the XGBoost notebook, once we've deployed an endpoint it continues to run until we tell it to shut down. Since we are done using our endpoint for now, we can delete it.
```
estimator.delete_endpoint()
```
## Step 6 (again) - Deploy the model for the web app
Now that we know that our model is working, it's time to create some custom inference code so that we can send the model a review which has not been processed and have it determine the sentiment of the review.
As we saw above, by default the estimator which we created, when deployed, will use the entry script and directory which we provided when creating the model. However, since we now wish to accept a string as input and our model expects a processed review, we need to write some custom inference code.
We will store the code that we write in the `serve` directory. Provided in this directory is the `model.py` file that we used to construct our model, a `utils.py` file which contains the `review_to_words` and `convert_and_pad` pre-processing functions which we used during the initial data processing, and `predict.py`, the file which will contain our custom inference code. Note also that `requirements.txt` is present which will tell SageMaker what Python libraries are required by our custom inference code.
When deploying a PyTorch model in SageMaker, you are expected to provide four functions which the SageMaker inference container will use.
- `model_fn`: This function is the same function that we used in the training script and it tells SageMaker how to load our model.
- `input_fn`: This function receives the raw serialized input that has been sent to the model's endpoint and its job is to de-serialize and make the input available for the inference code.
- `output_fn`: This function takes the output of the inference code and its job is to serialize this output and return it to the caller of the model's endpoint.
- `predict_fn`: The heart of the inference script, this is where the actual prediction is done and is the function which you will need to complete.
For the simple website that we are constructing during this project, the `input_fn` and `output_fn` methods are relatively straightforward. We only require being able to accept a string as input and we expect to return a single value as output. You might imagine though that in a more complex application the input or output may be image data or some other binary data which would require some effort to serialize.
### (TODO) Writing inference code
Before writing our custom inference code, we will begin by taking a look at the code which has been provided.
```
!pygmentize serve/predict.py
```
As mentioned earlier, the `model_fn` method is the same as the one provided in the training code and the `input_fn` and `output_fn` methods are very simple and your task will be to complete the `predict_fn` method. Make sure that you save the completed file as `predict.py` in the `serve` directory.
**TODO**: Complete the `predict_fn()` method in the `serve/predict.py` file.
### Deploying the model
Now that the custom inference code has been written, we will create and deploy our model. To begin with, we need to construct a new PyTorchModel object which points to the model artifacts created during training and also points to the inference code that we wish to use. Then we can call the deploy method to launch the deployment container.
**NOTE**: The default behaviour for a deployed PyTorch model is to assume that any input passed to the predictor is a `numpy` array. In our case we want to send a string so we need to construct a simple wrapper around the `RealTimePredictor` class to accomodate simple strings. In a more complicated situation you may want to provide a serialization object, for example if you wanted to sent image data.
```
from sagemaker.predictor import RealTimePredictor
from sagemaker.pytorch import PyTorchModel
class StringPredictor(RealTimePredictor):
def __init__(self, endpoint_name, sagemaker_session):
super(StringPredictor, self).__init__(endpoint_name, sagemaker_session, content_type='text/plain')
model = PyTorchModel(model_data=estimator.model_data,
role = role,
framework_version='0.4.0',
entry_point='predict.py',
source_dir='serve',
predictor_cls=StringPredictor)
predictor = model.deploy(initial_instance_count=1, instance_type='ml.m4.xlarge')
```
### Testing the model
Now that we have deployed our model with the custom inference code, we should test to see if everything is working. Here we test our model by loading the first `250` positive and negative reviews and send them to the endpoint, then collect the results. The reason for only sending some of the data is that the amount of time it takes for our model to process the input and then perform inference is quite long and so testing the entire data set would be prohibitive.
```
import glob
def test_reviews(data_dir='../data/aclImdb', stop=250):
results = []
ground = []
# We make sure to test both positive and negative reviews
for sentiment in ['pos', 'neg']:
path = os.path.join(data_dir, 'test', sentiment, '*.txt')
files = glob.glob(path)
files_read = 0
print('Starting ', sentiment, ' files')
# Iterate through the files and send them to the predictor
for f in files:
with open(f) as review:
# First, we store the ground truth (was the review positive or negative)
if sentiment == 'pos':
ground.append(1)
else:
ground.append(0)
# Read in the review and convert to 'utf-8' for transmission via HTTP
review_input = review.read().encode('utf-8')
# Send the review to the predictor and store the results
results.append(int(predictor.predict(review_input)))
# Sending reviews to our endpoint one at a time takes a while so we
# only send a small number of reviews
files_read += 1
if files_read == stop:
break
return ground, results
ground, results = test_reviews()
from sklearn.metrics import accuracy_score
accuracy_score(ground, results)
```
As an additional test, we can try sending the `test_review` that we looked at earlier.
```
predictor.predict(test_review)
```
Now that we know our endpoint is working as expected, we can set up the web page that will interact with it. If you don't have time to finish the project now, make sure to skip down to the end of this notebook and shut down your endpoint. You can deploy it again when you come back.
## Step 7 (again): Use the model for the web app
> **TODO:** This entire section and the next contain tasks for you to complete, mostly using the AWS console.
So far we have been accessing our model endpoint by constructing a predictor object which uses the endpoint and then just using the predictor object to perform inference. What if we wanted to create a web app which accessed our model? The way things are set up currently makes that not possible since in order to access a SageMaker endpoint the app would first have to authenticate with AWS using an IAM role which included access to SageMaker endpoints. However, there is an easier way! We just need to use some additional AWS services.
<img src="Web App Diagram.svg">
The diagram above gives an overview of how the various services will work together. On the far right is the model which we trained above and which is deployed using SageMaker. On the far left is our web app that collects a user's movie review, sends it off and expects a positive or negative sentiment in return.
In the middle is where some of the magic happens. We will construct a Lambda function, which you can think of as a straightforward Python function that can be executed whenever a specified event occurs. We will give this function permission to send and recieve data from a SageMaker endpoint.
Lastly, the method we will use to execute the Lambda function is a new endpoint that we will create using API Gateway. This endpoint will be a url that listens for data to be sent to it. Once it gets some data it will pass that data on to the Lambda function and then return whatever the Lambda function returns. Essentially it will act as an interface that lets our web app communicate with the Lambda function.
### Setting up a Lambda function
The first thing we are going to do is set up a Lambda function. This Lambda function will be executed whenever our public API has data sent to it. When it is executed it will receive the data, perform any sort of processing that is required, send the data (the review) to the SageMaker endpoint we've created and then return the result.
#### Part A: Create an IAM Role for the Lambda function
Since we want the Lambda function to call a SageMaker endpoint, we need to make sure that it has permission to do so. To do this, we will construct a role that we can later give the Lambda function.
Using the AWS Console, navigate to the **IAM** page and click on **Roles**. Then, click on **Create role**. Make sure that the **AWS service** is the type of trusted entity selected and choose **Lambda** as the service that will use this role, then click **Next: Permissions**.
In the search box type `sagemaker` and select the check box next to the **AmazonSageMakerFullAccess** policy. Then, click on **Next: Review**.
Lastly, give this role a name. Make sure you use a name that you will remember later on, for example `LambdaSageMakerRole`. Then, click on **Create role**.
#### Part B: Create a Lambda function
Now it is time to actually create the Lambda function.
Using the AWS Console, navigate to the AWS Lambda page and click on **Create a function**. When you get to the next page, make sure that **Author from scratch** is selected. Now, name your Lambda function, using a name that you will remember later on, for example `sentiment_analysis_func`. Make sure that the **Python 3.6** runtime is selected and then choose the role that you created in the previous part. Then, click on **Create Function**.
On the next page you will see some information about the Lambda function you've just created. If you scroll down you should see an editor in which you can write the code that will be executed when your Lambda function is triggered. In our example, we will use the code below.
```python
# We need to use the low-level library to interact with SageMaker since the SageMaker API
# is not available natively through Lambda.
import boto3
def lambda_handler(event, context):
# The SageMaker runtime is what allows us to invoke the endpoint that we've created.
runtime = boto3.Session().client('sagemaker-runtime')
# Now we use the SageMaker runtime to invoke our endpoint, sending the review we were given
response = runtime.invoke_endpoint(EndpointName = '**ENDPOINT NAME HERE**', # The name of the endpoint we created
ContentType = 'text/plain', # The data format that is expected
Body = event['body']) # The actual review
# The response is an HTTP response whose body contains the result of our inference
result = response['Body'].read().decode('utf-8')
return {
'statusCode' : 200,
'headers' : { 'Content-Type' : 'text/plain', 'Access-Control-Allow-Origin' : '*' },
'body' : result
}
```
Once you have copy and pasted the code above into the Lambda code editor, replace the `**ENDPOINT NAME HERE**` portion with the name of the endpoint that we deployed earlier. You can determine the name of the endpoint using the code cell below.
```
predictor.endpoint
```
Once you have added the endpoint name to the Lambda function, click on **Save**. Your Lambda function is now up and running. Next we need to create a way for our web app to execute the Lambda function.
### Setting up API Gateway
Now that our Lambda function is set up, it is time to create a new API using API Gateway that will trigger the Lambda function we have just created.
Using AWS Console, navigate to **Amazon API Gateway** and then click on **Get started**.
On the next page, make sure that **New API** is selected and give the new api a name, for example, `sentiment_analysis_api`. Then, click on **Create API**.
Now we have created an API, however it doesn't currently do anything. What we want it to do is to trigger the Lambda function that we created earlier.
Select the **Actions** dropdown menu and click **Create Method**. A new blank method will be created, select its dropdown menu and select **POST**, then click on the check mark beside it.
For the integration point, make sure that **Lambda Function** is selected and click on the **Use Lambda Proxy integration**. This option makes sure that the data that is sent to the API is then sent directly to the Lambda function with no processing. It also means that the return value must be a proper response object as it will also not be processed by API Gateway.
Type the name of the Lambda function you created earlier into the **Lambda Function** text entry box and then click on **Save**. Click on **OK** in the pop-up box that then appears, giving permission to API Gateway to invoke the Lambda function you created.
The last step in creating the API Gateway is to select the **Actions** dropdown and click on **Deploy API**. You will need to create a new Deployment stage and name it anything you like, for example `prod`.
You have now successfully set up a public API to access your SageMaker model. Make sure to copy or write down the URL provided to invoke your newly created public API as this will be needed in the next step. This URL can be found at the top of the page, highlighted in blue next to the text **Invoke URL**.
## Step 4: Deploying our web app
Now that we have a publicly available API, we can start using it in a web app. For our purposes, we have provided a simple static html file which can make use of the public api you created earlier.
In the `website` folder there should be a file called `index.html`. Download the file to your computer and open that file up in a text editor of your choice. There should be a line which contains **\*\*REPLACE WITH PUBLIC API URL\*\***. Replace this string with the url that you wrote down in the last step and then save the file.
Now, if you open `index.html` on your local computer, your browser will behave as a local web server and you can use the provided site to interact with your SageMaker model.
If you'd like to go further, you can host this html file anywhere you'd like, for example using github or hosting a static site on Amazon's S3. Once you have done this you can share the link with anyone you'd like and have them play with it too!
> **Important Note** In order for the web app to communicate with the SageMaker endpoint, the endpoint has to actually be deployed and running. This means that you are paying for it. Make sure that the endpoint is running when you want to use the web app but that you shut it down when you don't need it, otherwise you will end up with a surprisingly large AWS bill.
**TODO:** Make sure that you include the edited `index.html` file in your project submission.
Now that your web app is working, trying playing around with it and see how well it works.
**Question**: Give an example of a review that you entered into your web app. What was the predicted sentiment of your example review?
**Answer:**
A simple positive review has been tested on my local machine.
The call was successfully sent to the Gateway API and invoked the service.
The response is POSITIVE as expected.

### Delete the endpoint
Remember to always shut down your endpoint if you are no longer using it. You are charged for the length of time that the endpoint is running so if you forget and leave it on you could end up with an unexpectedly large bill.
```
predictor.delete_endpoint()
```
| github_jupyter |
# **Tansfer Learning for Classification of Horses and Humans**
## **Abstract**
Aim of the notebook is to demonstrate the use of the transfer learning for improving the model accuracy for real-world images.
```
import os
import tensorflow as tf
from tensorflow.keras import layers
from tensorflow.keras import Model
from os import getcwd
path_inception = f"{getcwd()}/../tmp2/inception_v3_weights_tf_dim_ordering_tf_kernels_notop.h5"
from tensorflow.keras.applications.inception_v3 import InceptionV3
local_weights_file = path_inception
pre_trained_model = InceptionV3(input_shape = (150, 150, 3),
include_top = False,
weights = None)
pre_trained_model.load_weights(local_weights_file)
for layer in pre_trained_model.layers:
layer.trainable = False
# Print the model summary
pre_trained_model.summary()
last_layer = pre_trained_model.get_layer('mixed7')
print('last layer output shape: ', last_layer.output_shape)
last_output = last_layer.output
# Defining a Callback class that stops training once accuracy reaches 97.0%
class myCallback(tf.keras.callbacks.Callback):
def on_epoch_end(self, epoch, logs={}):
if(logs.get('accuracy')>0.999):
print("\nReached 99.9% accuracy so cancelling training!")
self.model.stop_training = True
from tensorflow.keras.optimizers import RMSprop
# Flatten the output layer to 1 dimension
x = layers.Flatten()(last_output)
x = layers.Dense(1024, activation='relu')(x)
x = layers.Dropout(0.2)(x)
x = layers.Dense (1, activation='sigmoid')(x)
model = Model( pre_trained_model.input, x)
model.compile(optimizer = RMSprop(lr=0.0001),
loss = 'binary_crossentropy',
metrics = ['accuracy'])
model.summary()
# Get the Horse or Human dataset
path_horse_or_human = f"{getcwd()}/../tmp2/horse-or-human.zip"
# Get the Horse or Human Validation dataset
path_validation_horse_or_human = f"{getcwd()}/../tmp2/validation-horse-or-human.zip"
from tensorflow.keras.preprocessing.image import ImageDataGenerator
import os
import zipfile
import shutil
shutil.rmtree('/tmp')
local_zip = path_horse_or_human
zip_ref = zipfile.ZipFile(local_zip, 'r')
zip_ref.extractall('/tmp/training')
zip_ref.close()
local_zip = path_validation_horse_or_human
zip_ref = zipfile.ZipFile(local_zip, 'r')
zip_ref.extractall('/tmp/validation')
zip_ref.close()
train_dir = '/tmp/training'
validation_dir = '/tmp/validation'
train_horses_dir = os.path.join(train_dir, 'horses')
train_humans_dir = os.path.join(train_dir, 'humans')
validation_horses_dir = os.path.join(validation_dir, 'horses')
validation_humans_dir = os.path.join(validation_dir, 'humans')
train_horses_fnames = os.listdir(train_horses_dir)
train_humans_fnames = os.listdir(train_humans_dir)
validation_horses_fnames = os.listdir(validation_horses_dir)
validation_humans_fnames = os.listdir(validation_humans_dir)
print(len(train_horses_fnames))
print(len(train_humans_fnames))
print(len(validation_horses_fnames))
print(len(validation_humans_fnames))
train_datagen = ImageDataGenerator(rescale = 1./255.,
rotation_range = 40,
width_shift_range = 0.2,
height_shift_range = 0.2,
shear_range = 0.2,
zoom_range = 0.2,
horizontal_flip = True
)
test_datagen = ImageDataGenerator(
rescale = 1./255.
)
train_generator = train_datagen.flow_from_directory(
train_dir,
batch_size=64,
class_mode='binary',
target_size=(150,150)
)
validation_generator = test_datagen.flow_from_directory(
validation_dir,
batch_size=64,
class_mode='binary',
target_size=(150,150)
)
callbacks = myCallback()
history = model.fit_generator(
train_generator,
epochs=50,
validation_data=validation_generator,
callbacks=[callbacks]
)
%matplotlib inline
import matplotlib.pyplot as plt
acc = history.history['accuracy']
val_acc = history.history['val_accuracy']
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(len(acc))
plt.plot(epochs, acc, 'r', label='Training accuracy')
plt.plot(epochs, val_acc, 'b', label='Validation accuracy')
plt.title('Training and validation accuracy')
plt.legend(loc=0)
plt.figure()
plt.show()
```
## **Refrence**
https://www.coursera.org
https://www.tensorflow.org/
Copyright 2020 Abhishek Gargha Maheshwarappa
Permission is hereby granted, free of charge, to any person obtaining a copy of this software and associated documentation files (the "Software"), to deal in the Software without restriction, including without limitation the rights to use, copy, modify, merge, publish, distribute, sublicense, and/or sell copies of the Software, and to permit persons to whom the Software is furnished to do so, subject to the following conditions:
The above copyright notice and this permission notice shall be included in all copies or substantial portions of the Software.
THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE SOFTWARE.
| github_jupyter |
Let's design a LNA using Infineon's BFU520 transistor. First we need to import scikit-rf and a bunch of other utilities:
```
import numpy as np
import skrf
from skrf.media import DistributedCircuit
import skrf.frequency as freq
import skrf.network as net
import skrf.util
import matplotlib.pyplot as plt
%matplotlib inline
plt.rcParams['figure.figsize'] = [10, 10]
f = freq.Frequency(0.4, 2, 101)
tem = DistributedCircuit(f, z0=50)
# import the scattering parameters/noise data for the transistor
bjt = net.Network('BFU520_05V0_010mA_NF_SP.s2p').interpolate(f)
bjt
```
Let's plot the smith chart for it:
```
bjt.plot_s_smith()
```
Now let's calculate the source and load stablity curves.
I'm slightly misusing the `Network` type to plot the curves; normally the curves you pass in to `Network` should be a function of frequency, but it also works to draw these circles as long as you don't try to use any other functions on them
```
sqabs = lambda x: np.square(np.absolute(x))
delta = bjt.s11.s*bjt.s22.s - bjt.s12.s*bjt.s21.s
rl = np.absolute((bjt.s12.s * bjt.s21.s)/(sqabs(bjt.s22.s) - sqabs(delta)))
cl = np.conj(bjt.s22.s - delta*np.conj(bjt.s11.s))/(sqabs(bjt.s22.s) - sqabs(delta))
rs = np.absolute((bjt.s12.s * bjt.s21.s)/(sqabs(bjt.s11.s) - sqabs(delta)))
cs = np.conj(bjt.s11.s - delta*np.conj(bjt.s22.s))/(sqabs(bjt.s11.s) - sqabs(delta))
def calc_circle(c, r):
theta = np.linspace(0, 2*np.pi, 1000)
return c + r*np.exp(1.0j*theta)
for i, f in enumerate(bjt.f):
# decimate it a little
if i % 100 != 0:
continue
n = net.Network(name=str(f/1.e+9), s=calc_circle(cs[i][0, 0], rs[i][0, 0]))
n.plot_s_smith()
for i, f in enumerate(bjt.f):
# decimate it a little
if i % 100 != 0:
continue
n = net.Network(name=str(f/1.e+9), s=calc_circle(cl[i][0, 0], rl[i][0, 0]))
n.plot_s_smith()
```
So we can see that we need to avoid inductive loads near short circuit in the input matching network and high impedance inductive loads on the output.
Let's draw some constant noise circles. First we grab the noise parameters for our target frequency from the network model:
```
idx_915mhz = skrf.util.find_nearest_index(bjt.f, 915.e+6)
# we need the normalized equivalent noise and optimum source coefficient to calculate the constant noise circles
rn = bjt.rn[idx_915mhz]/50
gamma_opt = bjt.g_opt[idx_915mhz]
fmin = bjt.nfmin[idx_915mhz]
for nf_added in [0, 0.1, 0.2, 0.5]:
nf = 10**(nf_added/10) * fmin
N = (nf - fmin)*abs(1+gamma_opt)**2/(4*rn)
c_n = gamma_opt/(1+N)
r_n = 1/(1-N)*np.sqrt(N**2 + N*(1-abs(gamma_opt)**2))
n = net.Network(name=str(nf_added), s=calc_circle(c_n, r_n))
n.plot_s_smith()
print("the optimum source reflection coefficient is ", gamma_opt)
```
So we can see from the chart that just leaving the input at 50 ohms gets us under 0.1 dB of extra noise, which seems pretty good. I'm actually not sure that these actually correspond to the noise figure level increments I have listed up there, but the circles should at least correspond to increasing noise figures
So let's leave the input at 50 ohms and figure out how to match the output network to maximize gain and stability. Let's see what matching the load impedance with an unmatched input gives us:
```
gamma_s = 0.0
gamma_l = np.conj(bjt.s22.s - bjt.s21.s*gamma_s*bjt.s12.s/(1-bjt.s11.s*gamma_s))
gamma_l = gamma_l[idx_915mhz, 0, 0]
is_gamma_l_stable = np.absolute(gamma_l - cl[idx_915mhz]) > rl[idx_915mhz]
gamma_l, is_gamma_l_stable
```
This looks like it may be kind of close to the load instability circles, so it might make sense to pick a load point with less gain for more stability, or to pick a different source impedance with more noise.
But for now let's just build a matching network for this and see how it performs:
```
def calc_matching_network_vals(z1, z2):
flipped = np.real(z1) < np.real(z2)
if flipped:
z2, z1 = z1, z2
# cancel out the imaginary parts of both input and output impedances
z1_par = 0.0
if abs(np.imag(z1)) > 1e-6:
# parallel something to cancel out the imaginary part of
# z1's impedance
z1_par = 1/(-1j*np.imag(1/z1))
z1 = 1/(1./z1 + 1/z1_par)
z2_ser = 0.0
if abs(np.imag(z2)) > 1e-6:
z2_ser = -1j*np.imag(z2)
z2 = z2 + z2_ser
Q = np.sqrt((np.real(z1) - np.real(z2))/np.real(z2))
x1 = -1.j * np.real(z1)/Q
x2 = 1.j * np.real(z2)*Q
x1_tot = 1/(1/z1_par + 1/x1)
x2_tot = z2_ser + x2
if flipped:
return x2_tot, x1_tot
else:
return x1_tot, x2_tot
z_l = net.s2z(np.array([[[gamma_l]]]))[0,0,0]
# note that we're matching against the conjugate;
# this is because we want to see z_l from the BJT side
# if we plugged in z the matching network would make
# the 50 ohms look like np.conj(z) to match against it, so
# we use np.conj(z_l) so that it'll look like z_l from the BJT's side
z_par, z_ser = calc_matching_network_vals(np.conj(z_l), 50)
z_l, z_par, z_ser
```
Let's calculate what the component values are:
```
c_par = np.real(1/(2j*np.pi*915e+6*z_par))
l_ser = np.real(z_ser/(2j*np.pi*915e+6))
c_par, l_ser
```
The capacitance is kind of low but the inductance seems reasonable. Let's test it out:
```
output_network = tem.shunt_capacitor(c_par) ** tem.inductor(l_ser)
amplifier = bjt ** output_network
amplifier.plot_s_smith()
```
That looks pretty reasonable; let's take a look at the S21 to see what we got:
```
amplifier.s21.plot_s_db()
```
So about 18 dB gain; let's see what our noise figure is:
```
10*np.log10(amplifier.nf(50.)[idx_915mhz])
```
So 0.96 dB NF, which is reasonably close to the BJT tombstone optimal NF of 0.95 dB
| github_jupyter |
# Model Selection

## Model Selection
- The process of selecting the model among a collection of candidates machine learning models
### Problem type
- What kind of problem are you looking into?
- **Classification**: *Predict labels on data with predefined classes*
- Supervised Machine Learning
- **Clustering**: *Identify similarieties between objects and group them in clusters*
- Unsupervised Machine Learning
- **Regression**: *Predict continuous values*
- Supervised Machine Learning
- Resource: [Sklearn cheat sheet](https://scikit-learn.org/stable/tutorial/machine_learning_map/index.html)
### What is the "best" model?
- All models have some **predictive error**
- We should seek a model that is *good enough*
### Model Selection Techniques
- **Probabilistic Measures**: Scoring by performance and complexity of model.
- **Resampling Methods**: Splitting in sub-train and sub-test datasets and scoring by mean values of repeated runs.
```
import pandas as pd
data = pd.read_parquet('files/house_sales.parquet')
data.head()
data.describe()
data['SalePrice'].plot.hist(bins=20)
```
### Converting to Categories
- [`cut()`](https://pandas.pydata.org/docs/reference/api/pandas.cut.html) Bin values into discrete intervals.
- Data in bins based on data distribution.
- [`qcut()`](https://pandas.pydata.org/docs/reference/api/pandas.qcut.html) Quantile-based discretization function.
- Data in equal size bins
#### Invstigation
- Figure out why `cut` is not suitable for 3 bins here.
```
data['Target'] = pd.cut(data['SalePrice'], bins=3, labels=[1, 2, 3])
data['Target'].value_counts()/len(data)
data['Target'] = pd.qcut(data['SalePrice'], q=3, labels=[1, 2, 3])
data['Target'].value_counts()/len(data)
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC, LinearSVC
from sklearn.metrics import accuracy_score
X = data.drop(['SalePrice', 'Target'], axis=1).fillna(-1)
y = data['Target']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=.2, random_state=42)
svc = LinearSVC()
svc.fit(X_train, y_train)
y_pred = svc.predict(X_test)
accuracy_score(y_test, y_pred)
from sklearn.neighbors import KNeighborsClassifier
neigh = KNeighborsClassifier()
neigh.fit(X_train, y_train)
y_pred = neigh.predict(X_test)
accuracy_score(y_test, y_pred)
svc = SVC(kernel='rbf')
svc.fit(X_train, y_train)
y_pred = svc.predict(X_test)
accuracy_score(y_test, y_pred)
svc = SVC(kernel='sigmoid')
svc.fit(X_train, y_train)
y_pred = svc.predict(X_test)
accuracy_score(y_test, y_pred)
svc = SVC(kernel='poly', degree=5)
svc.fit(X_train, y_train)
y_pred = svc.predict(X_test)
accuracy_score(y_test, y_pred)
```
| github_jupyter |
```
import numpy as np
arr = np.load('MAPS.npy')
print(arr)
print(np.shape(arr))
arr2 = np.empty((20426, 88), dtype = int)
for i in range(arr.shape[0]):
for j in range(arr.shape[1]):
if arr[i,j]==False:
arr2[i,j]=int(0)
int(arr2[i,j])
elif arr[i,j]==True:
arr2[i,j]=int(1)
print(arr2)
!pip install midiutil
from midiutil.MidiFile import MIDIFile
mf = MIDIFile(1)
track = 0
time = 0
delta = 0.000005
mf.addTrackName(track, time, "Output")
mf.addTempo(track, time, 120)
channel = 0
volume = 100
duration = 0.01
for i in range(arr2.shape[0]):
time=time + i*delta
for j in range(arr2.shape[1]):
if arr[i,j] == 1:
pitch = j
mf.addNote(track, channel, pitch, time, duration, volume)
with open("output.mid", 'wb') as outf:
mf.writeFile(outf)
!pip install pretty_midi
import pretty_midi
import pandas as pd
path = "output.mid"
midi_data = pretty_midi.PrettyMIDI(path)
midi_list = []
pretty_midi.pretty_midi.MAX_TICK = 1e10
midi_data.tick_to_time(14325216)
for instrument in midi_data.instruments:
for note in instrument.notes:
start = note.start
end = note.end
pitch = note.pitch
velocity = note.velocity
midi_list.append([start, end, pitch, velocity, instrument.name])
midi_list = sorted(midi_list, key=lambda x: (x[0], x[2]))
df = pd.DataFrame(midi_list, columns=['Start', 'End', 'Pitch', 'Velocity', 'Instrument'])
print(df)
import matplotlib
import matplotlib.pyplot as plt
from matplotlib.patches import Rectangle
import numpy as np
fig, ax = plt.subplots()
i = 0
while(i<108934) :
start = float(midi_list[i][0])
pitch = float(midi_list[i][2])
duration = float(midi_list[i][1]-midi_list[i][0])
# if my_reader[i][4]=='Right Hand' :
# color1 = 'royalblue'
# else :
# color1 = 'darkorange'
rect = matplotlib.patches.Rectangle((start, pitch),duration, 1, ec='black', linewidth=10)
ax.add_patch(rect)
i+=1
# plt.xlabel("Time (seconds)", fontsize=150)
# plt.ylabel("Pitch", fontsize=150)
plt.xlim([0, 550])
plt.ylim([0, 88])
plt.grid(color='grey',linewidth=1)
plt.show()
```
ACTUAL
```
import pretty_midi
import pandas as pd
path = "MAPS.mid"
midi_data = pretty_midi.PrettyMIDI(path)
midi_list = []
pretty_midi.pretty_midi.MAX_TICK = 1e10
midi_data.tick_to_time(14325216)
for instrument in midi_data.instruments:
for note in instrument.notes:
start = note.start
end = note.end
pitch = note.pitch
velocity = note.velocity
midi_list.append([start, end, pitch, velocity, instrument.name])
midi_list = sorted(midi_list, key=lambda x: (x[0], x[2]))
df = pd.DataFrame(midi_list, columns=['Start', 'End', 'Pitch', 'Velocity', 'Instrument'])
print(df)
import matplotlib
import matplotlib.pyplot as plt
from matplotlib.patches import Rectangle
import numpy as np
fig, ax = plt.subplots()
i = 0
while(i<2200) :
start = float(midi_list[i][0])
pitch = float(midi_list[i][2])
duration = float(midi_list[i][1]-midi_list[i][0])
# if my_reader[i][4]=='Right Hand' :
# color1 = 'royalblue'
# else :
# color1 = 'darkorange'
rect = matplotlib.patches.Rectangle((start, pitch),duration, 1, ec='black', linewidth=10)
ax.add_patch(rect)
i+=1
# plt.xlabel("Time (seconds)", fontsize=150)
# plt.ylabel("Pitch", fontsize=150)
plt.xlim([0, 240])
plt.ylim([0, 88])
plt.grid(color='grey',linewidth=1)
plt.show()
```
| github_jupyter |
```
# Necessary imports
import warnings
warnings.filterwarnings('ignore')
import re
import os
import numpy as np
import scipy as sp
from scipy.sparse import csr_matrix
from sklearn import datasets
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.feature_extraction.text import TfidfTransformer
from sklearn.naive_bayes import MultinomialNB
from active_tester import ActiveTester
from active_tester.estimators.learned import Learned
from active_tester.estimators.naive import Naive
from active_tester.query_strategy.noisy_label_uncertainty import LabelUncertainty
from active_tester.query_strategy.classifier_uncertainty import ClassifierUncertainty
from active_tester.query_strategy.MCM import MCM
from active_tester.query_strategy.random import Random
from sklearn.metrics import accuracy_score
from active_tester.label_estimation.methods import oracle_one_label, no_oracle, oracle_multiple_labels
```
# Active Testing Using Text Data
This is an example of using the ActT library with a text dataset. To walk through this example, download __[a sentiment analysis dataset](https://archive.ics.uci.edu/ml/machine-learning-databases/00331/)__ from the UCI machine learning repository and place the contents in the text_data directory. Additionally, this tutorial follows Scikit Learn's steps on __[Working with Text Data](https://scikit-learn.org/stable/tutorial/text_analytics/working_with_text_data.html)__. Before we employ ActT, using the example dataset, we must preprocess the data to create textfiles for each sentence and to divide the dataset into a train and test set.
## Data Processing
Using the preprocessing scripts below, we will combine all of the files into one file containing all 3000 sentence. Then, we will separate the sentences into a test and training set containing the individual sentences as files, then place them in their respective class folders.
After the dataset is created, set `create_datasets` to `False` to avoid creating duplicate files.
```
create_datasets = False
# get rid of temporary files inserted to preserve directory structure
if create_datasets:
myfile = 'text_data/temp.txt'
if os.path.isfile(myfile):
os.remove(myfile)
myfile = 'train/positive/temp.txt'
if os.path.isfile(myfile):
os.remove(myfile)
myfile = 'train/negative/temp.txt'
if os.path.isfile(myfile):
os.remove(myfile)
myfile = 'test/positive/temp.txt'
if os.path.isfile(myfile):
os.remove(myfile)
myfile = 'test/negative/temp.txt'
if os.path.isfile(myfile):
os.remove(myfile)
if create_datasets:
#Combine all sentence files into one file
try:
sentences = open('sentences.txt', 'a')
#Renamed files with dashes
filenames = ['text_data/imdb_labelled.txt',
'text_data/amazon_cells_labelled.txt',
'text_data/yelp_labelled.txt']
for filename in filenames:
print(filename)
with open(filename) as file:
for line in file:
line = line.rstrip()
sentences.write(line + '\n')
except Exception:
print('File not found')
if create_datasets:
#Separate sentences into a test and training set
#Write each sentence to a file and place that file in its respective class folder
filename = 'sentences.txt'
with open(filename) as file:
count = 1
for line in file:
if count <= 2000:
line = line.rstrip()
if line[-1:] == '0':
input_file = open('train/negative/inputfile-' + str(count) + '.txt', 'a')
line = line[:-1]
line = line.rstrip()
input_file.write(line)
if line[-1:] == '1':
input_file = open('train/positive/inputfile-' + str(count) + '.txt', 'a')
line = line[:-1]
line = line.rstrip()
input_file.write(line)
if count > 2000:
line = line.rstrip()
if line[-1:] == '0':
input_file = open('test/negative/inputfile-' + str(count) + '.txt', 'a')
line = line[:-1]
line = line.rstrip()
input_file.write(line)
if line[-1:] == '1':
input_file = open('test/positive/inputfile-' + str(count) + '.txt', 'a')
line = line[:-1]
line = line.rstrip()
input_file.write(line)
count = count + 1
```
## Loading Data and Training a Model
Below, we load the training data, create term frequency features, and then fit a classifier to the data.
```
#Load training data from files
categories = ['positive', 'negative']
sent_data = datasets.load_files(container_path='train', categories=categories, shuffle=True)
X_train, y_train = sent_data.data, sent_data.target
#Extract features
count_vect = CountVectorizer()
X_train_counts = count_vect.fit_transform(X_train)
#Transform occurance matrix to a frequency matrix
tf_transformer = TfidfTransformer(use_idf=False).fit(X_train_counts)
X_train_tf = tf_transformer.transform(X_train_counts)
#Build a classifier
clf = MultinomialNB().fit(X_train_tf, sent_data.target)
```
Now, we transform the test dataset to use the same features, apply the classifier to the test dataset and compute the classifier's true accuracy.
```
#Load the test data from files
sent_data_test = datasets.load_files(container_path='test', categories=categories, shuffle=False)
X_test, y_test = sent_data_test.data, sent_data_test.target
#Extract features
X_test_counts = count_vect.transform(sent_data_test.data)
#Transform occurance matrix to a frequency matrix
X_test_tf = tf_transformer.transform(X_test_counts)
#Compute the true accuracy of the classifier
label_predictions = clf.predict(X_test_tf)
true_accuracy = accuracy_score(y_test, label_predictions)
```
## Using Active Tester
The following code creates a set of noisy labels, reshapes the true labels, and converts the test features to a dense array.
```
#Initialize key variables: X, Y_noisy, and vetted
Y_noisy = []
noisy_label_accuracy = 0.75
for i in range(len(y_test)):
if np.random.rand() < noisy_label_accuracy:
# noisy label is correct
Y_noisy.append(y_test[i])
else:
# noisy label is incorrect
Y_noisy.append(np.random.choice(np.delete(np.arange(2),y_test[i])))
Y_noisy = np.asarray(Y_noisy, dtype=int)
#Note that if your y_noisy array is shape (L,), you will need to reshape it to be (L,1)
Y_noisy = np.reshape(Y_noisy,(len(Y_noisy),1))
Y_ground_truth = np.reshape(y_test, (len(y_test), 1))
#Note that if using sklearn's transformer, you may recieve an error about a sparse
#matrix. Using scipy's sparse csr_matrix.toarray() method can resolve this issue
X = csr_matrix.toarray(X_test_tf)
```
Now to display the sentences to the vetter in an interactive session, we need to create a list of all the test data files. This will serve as raw input to the `query_vetted` method of `active_tester`.
```
#Create a list with all of the test data files to serve as the raw input to query vetted
file_list = []
sentence_dirs = os.path.join(os.getcwd(),'test')
for root, dirs, files in os.walk(sentence_dirs):
for name in files:
if name.endswith('.txt'):
local_path = os.path.join(root, name)
file_list.append(os.path.join(sentence_dirs, local_path))
```
Now, we are ready to estimate the performance of the classifier by querying the oracle.
```
#Active Tester with a Naive Estimator, Classifier Uncertainty Query Method, and Interactive Query Vetting
budget = 5
active_test = ActiveTester(Naive(metric=accuracy_score),
ClassifierUncertainty())
active_test.standardize_data(X=X,
classes=sent_data.target_names,
Y_noisy=Y_noisy)
active_test.gen_model_predictions(clf)
active_test.query_vetted(True, budget, raw=file_list)
active_test.test()
results = active_test.get_test_results()
# View the result and compare to the true accuracy
print('Test metric with budget of', budget,': ', results['tester_metric'])
print('True accuracy of classifier: ', true_accuracy)
```
## A Comparison of Query Strategies and Estimators
Below, we compare a couple of query strategies and estimators.
```
import matplotlib.pyplot as plt
abs_error_array = []
# Initialize the estimators
learned = Learned(metric=accuracy_score, estimation_method=oracle_multiple_labels)
naive = Naive(metric=accuracy_score)
estimator_list = {'Naive': naive, 'Learned': learned}
# Initialize a few query strategies
rand = Random()
classifier_uncertainty = ClassifierUncertainty()
mcm = MCM(estimation_method=oracle_multiple_labels)
query_strategy_list = {'Random': rand, 'Classifier Uncertainty': classifier_uncertainty,
'Most Common Mistake': mcm}
# Run active testing for each estimator-query pair, for a range of sample sizes
sample_sizes = [100, 200, 300, 400, 500]
for est_k, est_v in estimator_list.items():
for query_k, query_v in query_strategy_list.items():
abs_error_array = []
for i in sample_sizes:
at = ActiveTester(est_v, query_v)
#Set dataset and model values in the active tester object
at.standardize_data(X=X,
classes=sent_data.target_names,
Y_ground_truth=Y_ground_truth,
Y_noisy=Y_noisy)
at.gen_model_predictions(clf)
at.query_vetted(False, i)
at.test()
results = at.get_test_results()
abs_error_array.append(np.abs(results['tester_metric'] - true_accuracy))
plt.ylabel("Absolute Error")
plt.xlabel("Number Vetted")
plt.plot(sample_sizes, abs_error_array, label=est_k + '+' + query_k)
plt.legend(loc='best')
plt.title('Absolute Error vs Number Vetted')
plt.grid(True)
plt.show()
```
As you can see from the graph, the absolute error for the learned estimation method is smaller than for the naive method. There is not a large difference between the different query strategies.
| github_jupyter |
# Running Plato in Google's Colab Notebooks
## 1. Preparation
### Use Chrome broswer
Since Colab is a product from Google, to take the most advantage of it, Chrome is the most recommended broswer here.
### Activating GPU support
If you need GPU support in your project, you may activate it in Google Colab by clicking on `Runtime > Change runtime type` in the notebook menu and choosing `GPU` as the hardware accelerator. To check whether the GPU is available for computation, we import the deep learning framework [PyTorch](https://pytorch.org/):
```
import torch
torch.cuda.is_available()
```
If successful, the output of the cell above should print `True`.
### Use Google Drive
Since Google Colab removes all the files that you have downloaded or created when you end a session, the best option is to use GitHub to store your code, and Google Drive to store your datasets, logs, and anything else that would normally reside on your filesystem but wouldn’t be tracked by a git repo.
When you run the code below, you will need to click a link and follow a process that takes a few seconds. When the process is complete, all of your drive files will be available via ‘/root/drive’ on your Colab instance, and this will allow you to structure your projects in the same way you would if you were using a cloud server.
```
from google.colab import drive
drive.mount('/content/drive')
root_path = '/content/drive/My\ Drive'
%cd $root_path
```
## 2. Installing Plato with PyTorch
Clone Plato's public git repository on GitHub to your Google drive.
```
!git clone https://github.com/TL-System/plato
```
Then install the required Python packages:
```
!pip install -r $root_path/plato/requirements.txt -U
```
Get into the `plato` directory:
```
!chmod -R ugo+rx $root_path/plato/run
%cd $root_path/plato/
```
## 3. Running Plato
### Make sure you don’t get disconnected
Run the following cell when you plan to do a long training to avoid getting disconnected in the middle of it.
```
%%javascript
function ClickConnect(){
console.log("Working");
document.querySelector("colab-toolbar-button#connect").click()
}setInterval(ClickConnect,60000)
```
**Note:** Please use this responsibly. Getting booted from Colab is very annoying, but it is done to make resources available for others when you’re not actively using them.
### Setting up Weights and Biases
Support for logging using Weights and Biases (https://wandb.com) is built-in. It will prompt you to enter your key when starting your first run. If you don't wish to use Weights and Biases, set it to `offline`:
```
!wandb offline
```
### Running Plato in the Colab notebook
To start a federated learning training workload, run `run` from Plato's home directory. For example:
```
!./run -s 127.0.0.1:8000 -c ./configs/MNIST/fedavg_lenet5.yml
```
Here, `fedavg_lenet5.yml` is a sample configuration file that uses Federated Averaging as the federated learning algorithm, and LeNet5 as the model. Other configuration files under `plato/configs/` could also be used here.
### Running Plato in a terminal
It is strongly recommended and more convenient to run Plato in a terminal, preferably in Visual Studio Code. To do this, first sign up for a free account in [ngrok](https://ngrok.com), and then use your authentication token and your account password in the following code:
```
!pip install colab_ssh --upgrade
from getpass import getpass
ngrok_token = getpass('Your authentication token: ')
password = getpass('Your ngrok account password: ')
from colab_ssh import launch_ssh, init_git
launch_ssh(ngrok_token, password)
```
This will produce an SSH configuration for you to add to your Visual Studio Code setup, so that you can use **Remote-SSH: Connect to Host...** in Visual Studio Code to connect to this Colab instance. After your SSH connection is setup, you can use your instance just like any other remote virtual machine in the cloud. Detailed steps are:
1. Install the `Remote-SSH: Editing Configuration Files` extension in Visual Studio Code.
2. In Visual Studio Code, click on `View > Command Palette` in the menu (or use `Shift+Command+P`), and type `Remote-SSH: Add New SSH Host...`. It will ask you to enter SSH Connection Command. Enter `root@google_colab_ssh`.
3. Select the SSH configuration file to update, copy the conguration information you get after running the above cell into the selected SSH configuration file. The conguration information should be similar to
```
Host google_colab_ssh
HostName 0.tcp.ngrok.io
User root
Port <your port number>
```
Then save this configuration file.
4. Click on `View > Command Palette` again and type `Remote-SSH: Connect to Host...`. You should see the host `google_colab_ssh` you just added. Click it and Visual Studio will automatically open a new window for you, and prompt for your ngrok account password.
5. Enter your ngrok account password and you will be connected to the remote.
6. Open folder `/content/drive/MyDrive/plato/` and you are all set.
| github_jupyter |
# Tutorial 1: Instatiating a *scenario category*
In this tutorial, we will cover the following items:
1. Create *actor categories*, *activity categories*, and *physical thing categories*
2. Instantiate a *scenario category*
3. Show all tags of the *scenario category*
4. Use the `includes` function of a *scenario category*
5. Export the objects
```
# Before starting, let us do the necessary imports
import os
import json
from domain_model import ActorCategory, ActivityCategory, Constant, ScenarioCategory, \
Sinusoidal, Spline3Knots, StateVariable, PhysicalElementCategory, Tag, VehicleType, \
actor_category_from_json, scenario_category_from_json
```
## 1. Create *actor categories*, *activity categories*, and the *static physical thing categories*
In this tutorial, we will create a *scenario category* in which another vehicle changes lane such that it becomes the ego vehicle's leading vehicle. This is often referred to as a "cut-in scenario". The *scenario category* is depicted in the figure below. Here, the blue car represents the ego vehicle and the red car represents the vehicle that performs the cut in.
<img src="./examples/images/cut-in.png" alt="Cut in" width="400"/>
To create the *scenario category*, we first need to create the *actor categories*, *activity categories*, and the *physical things*. Let us start with the *actor categories*. Just like most objects, an *actor category* has a `name`, a `uid` (a unique ID), and `tags`. Additionally, an *actor category* has a `vehicle_type`.
In this implementation of the domain model, it is checked whether the correct types are used. For example, `name` must be a string. Similarly, `uid` must be an integer. `tags` must be a (possibly empty) list of type `Tag`. This is to ensure that only tags are chosen out of a predefined list. This is done for consistency, such that, for example, users do not use the tag "braking" at one time and "Braking" at another time. Note, however, that the disadvantage is that it might be very well possible that the list of possible tags is not complete, so if there is a good reason to add a `Tag` this should be allowed. Lastly, the `vehicle_type` must be of type `VehicleType`.
Now let us create the *actor categories*. For this example, we assume that both *actor categories* are "vehicles". Note that we can ignore the `uid` for now. When not `uid` is given, a unique ID is generated automatically. If no `tags` are provided, it will default to an empty list.
```
EGO_VEHICLE = ActorCategory(VehicleType.Vehicle, name="Ego vehicle",
tags=[Tag.EgoVehicle, Tag.RoadUserType_Vehicle])
TARGET_VEHICLE = ActorCategory(VehicleType.Vehicle, name="Target vehicle",
tags=[Tag.RoadUserType_Vehicle])
```
It is as simple as that. If it does not throw an error, you can be assured that a correct *actor category* is created. For example, if we would forget to add the brackets around the `Tag.RoadUserType_Vehicle` - such that it would not be a *list* of `Tag` - an error will be thrown:
```
# The following code results in an error!
# The error is captured as to show only the final error message.
try:
ActorCategory(VehicleType.Vehicle, name="Target vehicle", tags=Tag.RoadUserType_Vehicle)
except TypeError as error:
print(error)
```
Now let us create the *activity categories*:
```
FOLLOWING_LANE = ActivityCategory(Constant(), StateVariable.LATERAL_POSITION,
name="Following lane",
tags=[Tag.VehicleLateralActivity_GoingStraight])
CHANGING_LANE = ActivityCategory(Sinusoidal(), StateVariable.LATERAL_POSITION,
name="Changing lane",
tags=[Tag.VehicleLateralActivity_ChangingLane])
DRIVING_FORWARD = ActivityCategory(Spline3Knots(), StateVariable.SPEED,
name="Driving forward",
tags=[Tag.VehicleLongitudinalActivity_DrivingForward])
```
The last object we need to define before we can define the *scenario category* is the *static physical thing category*. A *scenario category* may contain multiple *physical things*, but for now we only define one that specifies the road layout. We assume that the scenario takes place at a straight motorway with multiple lanes:
```
MOTORWAY = PhysicalElementCategory(description="Motorway with multiple lanes",
name="Motorway",
tags=[Tag.RoadLayout_Straight,
Tag.RoadType_PrincipleRoad_Motorway])
```
## 2. Instantiate a *scenario category*
To define a *scenario category*, we need a description and a location to an image. After this, the static content of the scenario can be specified using the `set_physical_things` function. Next, to describe the dynamic content of the scenarios, the *actor categories* can be passed using the `set_actors` function and the *activity categories* can be passed using the `set_activities` function. Finally, using `set_acts`, it is described which activity is connected to which actor.
Note: It is possible that two actors perform the same activity. In this example, both the ego vehicle and the target vehicle are driving forward.
```
CUTIN = ScenarioCategory("./examples/images/cut-in.png",
description="Cut-in at the motorway",
name="Cut-in")
CUTIN.set_physical_elements([MOTORWAY])
CUTIN.set_actors([EGO_VEHICLE, TARGET_VEHICLE])
CUTIN.set_activities([FOLLOWING_LANE, CHANGING_LANE, DRIVING_FORWARD])
CUTIN.set_acts([(EGO_VEHICLE, DRIVING_FORWARD), (EGO_VEHICLE, FOLLOWING_LANE),
(TARGET_VEHICLE, DRIVING_FORWARD), (TARGET_VEHICLE, CHANGING_LANE)])
```
## 3. Show all tags of the *scenario category*
The tags should be used to define the *scenario category* in such a manner that also a computer can understand. However, we did not pass any tags to the *scenario category* itself. On the other hand, the attributes of the *scenario category* (in this case, the *physical things*, the *activity categories*, and the *actor categories*) have tags. Using the `derived_tags` function of the *scenario category*, these tags can be retrieved.
Running the `derived_tags` function returns a dictionary with (key,value) pairs. Each key is formatted as `<name>::<class>` and the corresponding value contains a list of tags that are associated to that particular object. For example, `Ego vehicle::ActorCategory` is a key and the corresponding tags are the tags that are passed when instantiating the ego vehicle (`EgoVehicle`) and the tags that are part of the *activity categories* that are connected with the ego vehicle (`GoingStraight` and `DrivingForward`).
```
CUTIN.derived_tags()
```
Another way - and possibly easier way - to show the tags, is to simply print the scenario category. Doing this will show the name, the description, and all tags of the scenario category.
```
print(CUTIN)
```
## 4. Use the *includes* function of a *scenario category*
A *scenario category* A includes another *scenario category* B if it comprises all scenarios that are comprised in B. Loosely said, this means that *scenario category* A is "more general" than *scenario category* B. To demonstrate this, let us first create another *scenario category*. The only different between the following *scenario category* is that the target vehicle comes from the left side of the ego vehicle. This means that the target vehicle performs a right lane change, whereas our previously defined *scenario category* did not define to which side the lane change was.
```
CHANGING_LANE_RIGHT = ActivityCategory(Sinusoidal(), StateVariable.LATERAL_POSITION,
name="Changing lane right",
tags=[Tag.VehicleLateralActivity_ChangingLane_Right])
CUTIN_LEFT = ScenarioCategory("./examples/images/cut-in.png",
description="Cut-in from the left at the motorway",
name="Cut-in from left")
CUTIN_LEFT.set_physical_elements([MOTORWAY])
CUTIN_LEFT.set_actors([EGO_VEHICLE, TARGET_VEHICLE])
CUTIN_LEFT.set_activities([FOLLOWING_LANE, CHANGING_LANE_RIGHT, DRIVING_FORWARD])
CUTIN_LEFT.set_acts([(EGO_VEHICLE, DRIVING_FORWARD), (EGO_VEHICLE, FOLLOWING_LANE),
(TARGET_VEHICLE, DRIVING_FORWARD), (TARGET_VEHICLE, CHANGING_LANE_RIGHT)])
```
To ensure ourselves that we correctly created a new *scenario category*, we can print the scenario category. Note the difference with the previously defined *scenario category*: now the target vehicle performs a right lane change (see the tag `VehicleLateralActivity_ChangingLane_Right`).
```
print(CUTIN_LEFT)
```
Because our original *scenario category* (`CUTIN`) is more general than the *scenario category* we just created (`CUTIN_LEFT`), we expect that `CUTIN` *includes* `CUTIN_LEFT`. In other words: because all "cut ins from the left" are also "cut ins", `CUTIN` *includes* `CUTIN_LEFT`.
The converse is not true: not all "cut ins" are "cut ins from the left".
Let's check it:
```
print(CUTIN.includes(CUTIN_LEFT)) # True
print(CUTIN_LEFT.includes(CUTIN)) # False
```
## 5. Export the objects
It would be cumbersome if one would be required to define a scenario category each time again. Luckily, there is an easy way to export the objects we have created.
Each object of this domain model comes with a `to_json` function and a `to_json_full` function. These functions return a dictionary that can be directly written to a .json file. The difference between `to_json` and `to_json_full` is that with `to_json`, rather than also returning the full dictionary of the attributes, only a reference (using the unique ID and the name) is returned. In case of the *physical thing*, *actor category*, and *activity category*, this does not make any difference. For the *scenario category*, however, this makes a difference.
To see this, let's see what the `to_json` function returns.
```
CUTIN.to_json()
```
As can be seen, the *physical thing category* (see `physical_thing_categories`) only returns the `name` and `uid`. This is not enough information for us if we would like to recreate the *physical thing category*. Therefore, for now we will use the `to_json_full` functionality.
Note, however, that if we would like to store the objects in a database, it would be better to have separate tables for *scenario categories*, *physical thing categories*, *activity categories*, and *actor categories*. In that case, the `to_json` function becomes handy. We will demonstrate this in a later tutorial.
Also note that Python has more efficient ways to store objects than through some json code. However, the reason to opt for the current approach is that this would be easily implementable in a database, such that it is easily possible to perform queries on the data. Again, the actual application of this goes beyond the current tutorial.
To save the returned dictionary to a .json file, we will use the external library `json`.
```
FILENAME = os.path.join("examples", "cutin_qualitative.json")
with open(FILENAME, "w") as FILE:
json.dump(CUTIN.to_json_full(), FILE, indent=4)
```
Let us also save the other *scenario category*, such that we can use it for a later tutorial.
```
FILENAME_CUTIN_LEFT = os.path.join("examples", "cutin_left_qualitative.json")
with open(FILENAME_CUTIN_LEFT, "w") as FILE:
json.dump(CUTIN_LEFT.to_json_full(), FILE, indent=4)
```
So how can we use this .json code to create the *scenario category*? As each object has a `to_json_full` function, for each object there is a `<class_name>_from_json` function. For the objects discussed in this toturial, we have:
- for a *physical thing category*: `physical_thing_category_from_json`
- for an *actor category*: `actor_category_from_json`
- for an *activity category*: `actvitiy_category_from_json`
- for a *model*: `model_from_json`
- for a *scenario category*: `scenario_category_from_json`
Each of these functions takes as input a dictionary that could be a potential output of its corresponding `to_json_full` function.
To demonstrate this, let's load the just created .json file and see if we can create a new *scenario category* from this.
```
with open(FILENAME, "r") as FILE:
CUTIN2 = scenario_category_from_json(json.load(FILE))
```
To see that this returns a similar *scenario category* as our previously created `CUTIN`, we can print the just created scenario category:
```
print(CUTIN2)
```
Note that although the just created *scenario category* is now similar to `CUTIN`, it is a different object in Python. That is, if we would change `CUTIN2`, that change will not apply to `CUTIN`.
You reached the end of the first tutorial. In the [next tutorial](./Tutorial%202%20Scenario.ipynb), we will see how we can instantiate a *scenario*.
| github_jupyter |
#### New to Plotly?
Plotly's Python library is free and open source! [Get started](https://plot.ly/python/getting-started/) by downloading the client and [reading the primer](https://plot.ly/python/getting-started/).
<br>You can set up Plotly to work in [online](https://plot.ly/python/getting-started/#initialization-for-online-plotting) or [offline](https://plot.ly/python/getting-started/#initialization-for-offline-plotting) mode, or in [jupyter notebooks](https://plot.ly/python/getting-started/#start-plotting-online).
<br>We also have a quick-reference [cheatsheet](https://images.plot.ly/plotly-documentation/images/python_cheat_sheet.pdf) (new!) to help you get started!
#### Creating a Plotly Grid
You can instantiate a grid with data by either uploading tabular data to Plotly or by creating a Plotly `grid` using the API. To upload the grid we will use `plotly.plotly.grid_ops.upload()`. It takes the following arguments:
- `grid` (Grid Object): the actual grid object that you are uploading.
- `filename` (str): name of the grid in your plotly account,
- `world_readable` (bool): if `True`, the grid is `public` and can be viewed by anyone in your files. If `False`, it is private and can only be viewed by you.
- `auto_open` (bool): if determines if the grid is opened in the browser or not.
You can run `help(py.grid_ops.upload)` for a more detailed description of these and all the arguments.
```
import plotly
import plotly.plotly as py
import plotly.tools as tls
import plotly.graph_objs as go
from plotly.grid_objs import Column, Grid
from datetime import datetime as dt
import numpy as np
from IPython.display import Image
column_1 = Column(['可以', '不可以', '随便'], '第一列')
column_2 = Column([1, 2, 3], '第二列') # Tabular data can be numbers, strings, or dates
grid = Grid([column_1, column_2])
url = py.grid_ops.upload(grid,
filename='grid_ex_'+str(dt.now()),
world_readable=True,
auto_open=False)
print(url)
```
#### View and Share your Grid
You can view your newly created grid at the `url`:
```
Image('view_grid_url.png')
```
You are also able to view the grid in your list of files inside your [organize folder](https://plot.ly/organize).
#### Upload Dataframes to Plotly
Along with uploading a grid, you can upload a Dataframe as well as convert it to raw data as a grid:
```
import plotly.plotly as py
import plotly.figure_factory as ff
import pandas as pd
df = pd.read_csv('https://raw.githubusercontent.com/plotly/datasets/master/2014_apple_stock.csv')
df_head = df.head()
table = ff.create_table(df_head)
py.iplot(table, filename='dataframe_ex_preview', oa)
grid = Grid([Column(df[column_name], column_name) for column_name in df.columns])
url = py.grid_ops.upload(grid, filename='dataframe_ex_'+str(dt.now()), world_readable=True, auto_open=True)
print(url)
```
#### Making Graphs from Grids
Plotly graphs are usually described with data embedded in them. For example, here we place `x` and `y` data directly into our `Histogram2dContour` object:
```
x = np.random.randn(1000)
y = np.random.randn(1000) + 1
data = [
go.Histogram2dContour(
x=x,
y=y
)
]
py.iplot(data, filename='Example 2D Histogram Contour')
```
We can also create graphs based off of references to columns of grids. Here, we'll upload several `column`s to our Plotly account:
```
column_1 = Column(np.random.randn(1000), 'column 1')
column_2 = Column(np.random.randn(1000)+1, 'column 2')
column_3 = Column(np.random.randn(1000)+2, 'column 3')
column_4 = Column(np.random.randn(1000)+3, 'column 4')
grid = Grid([column_1, column_2, column_3, column_4])
#url = py.grid_ops.upload(grid, filename='randn_int_offset_'+str(dt.now()))
url = py.grid_ops.upload(grid, filename='randn_int_offset')
print(url)
#Image('rand_int_histogram_view.png')
```
#### Make Graph from Raw Data
Instead of placing data into `x` and `y`, we'll place our Grid columns into `xsrc` and `ysrc`:
```
data = [
go.Histogram2dContour(
xsrc=grid[0],
ysrc=grid[1]
)
]
py.iplot(data, filename='2D Contour from Grid Data')
```
So, when you view the data, you'll see your original grid, not just the columns that compose this graph:
#### Attaching Meta Data to Grids
In [Plotly Enterprise](https://plot.ly/product/enterprise/), you can upload and assign free-form JSON `metadata` to any grid object. This means that you can keep all of your raw data in one place, under one grid.
If you update the original data source, in the workspace or with our API, all of the graphs that are sourced from it will be updated as well. You can make multiple graphs from a single Grid and you can make a graph from multiple grids. You can also add rows and columns to existing grids programatically.
```
meta = {
"Month": "November",
"Experiment ID": "d3kbd",
"Operator": "James Murphy",
"Initial Conditions": {
"Voltage": 5.5
}
}
#grid_url = py.grid_ops.upload(grid, filename='grid_with_metadata_'+str(dt.now()), meta=meta)
grid_url = py.grid_ops.upload(grid, filename='grid_with_metadata', meta=meta)
print(url)
#Image('grid_with_metadata.png')
```
#### Reference
```
help(py.grid_ops)
from IPython.display import display, HTML
display(HTML('<link href="//fonts.googleapis.com/css?family=Open+Sans:600,400,300,200|Inconsolata|Ubuntu+Mono:400,700" rel="stylesheet" type="text/css" />'))
display(HTML('<link rel="stylesheet" type="text/css" href="http://help.plot.ly/documentation/all_static/css/ipython-notebook-custom.css">'))
! pip install git+https://github.com/plotly/publisher.git --upgrade
import publisher
publisher.publish(
'grid-api.ipynb', 'python/data-api/', 'Upload Data to Plotly from Python',
'How to upload data to Plotly from Python with the Plotly Grid API.',
title = 'Plotly Data API', name = 'Plots from Grids', order = 5,
language='python', has_thumbnail='true', thumbnail='thumbnail/table.jpg', display_as='file_settings'
)
```
| github_jupyter |
# Python course Day 4
## Dictionaries
```
student = {"number": 570, "name":"Simon", "age":23, "height":165}
print(student)
print(student['name'])
print(student['age'])
my_list = {1: 23, 2:56, 3:78, 4:14, 5:67}
my_list[1]
my_list.keys()
my_list.values()
student.keys()
student.values()
student['number'] = 111
print(student)
student.items()
# Iterate over a list
numbers = [23,45,12,67,88,34,11]
for x in numbers:
print(x)
student.keys()
for k in student.keys():
print("student", k, student[k])
# initialize key and value with pairs from student dictionary
for key, value in student.items():
print(key , "--->", value)
print(student)
festival = 4
print(festival)
print(key)
# Iterate over two lists at a time
for x,y in zip(a,b):
print(x , ":", y)
test = zip(a,b)
type(test)
# Iterate over two lists at a time
a = [1,2,3,4,5]
b = [1,4,9,16,25]
c = [1,8,27,64,125]
for x,y,z in zip(a,b,c):
print(x , ":", y , "- ", z)
# items that do not have a corresponding item in the other list
# are ignored
a = [1,2,3,4,5,6,7]
b = [1,4,9,16,25]
for x,y in zip(a,b):
print(x , ":", y)
for x in numbers:
print(x)
for i in range(10):
print(i)
numbers
# Iterate over a list using index
for index in range(len(numbers)):
print(index , ":", numbers[index])
```
## List Comprehension
```
# Pythonic ways to create lists
# 1
numbers = []
for i in range(1,101):
numbers.append(i)
#1
'''
numbers contains all i's
such that
i takes value in range(1,101)
'''
numbers = [i for i in range(1, 101)]
print(numbers)
def square(num):
return num ** 2
square(5)
#2. call a function to make list of squares of numbers from 1-30
squared_numbers = [square(i) for i in range(1,31)]
print(squared_numbers)
#3) even numbers from 1 to 30
even_numbers = [i for i in range(1,31) if i%2 == 0]
print(even_numbers)
my_list = []
for i in range(1,31):
if i%2 == 0:
my_list.append(i)
print(my_list)
#4) squares of even numbers from 1 to 30
squared_even_numbers = [square(i) for i in range(1,31) if i%2 == 0]
print(squared_even_numbers)
#5) list of pairs
numbers_and_letters = [(chr(a),i) for a in range(65,68) for i in range(1,3)]
print(numbers_and_squares)
fun_list = []
for a in range(65,68):
for i in range(1,3):
fun_list.append((chr(a),i))
#print() # prints a new line
print(fun_list)
even_numbers
36 in even_numbers
35 in even_numbers
if 36 in even_numbers:
print("List contains 36")
even_numbers
all(even_numbers)
test = [True, True, False, True]
all(test)
not any(test)
even_numbers
import random
import math
math.factorial(6)
math.log2(16)
math.log10(1000)
math.pi
def fact(x):
if x == 0:
return 1
elif x < 0:
return -1
answer = 1
multiplier = 1
while multiplier <= x:
answer *= multiplier
multiplier += 1
return answer
fact(0)
fact(-5)
fact(4)
fact(6)
def fact_recur(x):
if x == 0:
return 1
if x < 0 :
return -1
return x * fact_recur(x-1)
fact_recur(5)
def fibo(n):
if n == 1:
return 0
if n == 2:
return 1
return fibo(n-1) + fibo(n-2)
fibo(2)
fibo(8)
fibo(9)
def simple_interest(principal, years, rate):
return (principal * years * rate ) /100
print(simple_interest(5000, 5, 2))
# Function with default argument
def simple_interest(principal, years, rate=2):
return (principal * years * rate ) /100
simple_interest(5000,5)
def simple_interest(principal=5000, years, rate=2):
return(principal * years * rate ) /100
def simple_interest(principal=5000, years=5, rate=2):
print("p = ", principal)
print("y = ", years)
print("r = ", rate)
return (principal * years * rate) / 100
simple_interest()
simple_interest(410)
simple_interest(410, 10)
# Call the function with keyword arguments/parameters
simple_interest(principal=7000, rate=10)
simple_interest(rate=3.4)
fun()
def fun():
print("fun")
gun()
def gun():
print("gun")
hun()
def hun():
print("hun")
def good():
print("good")
better()
# good() will cause error because better() function is not defined yet
def better():
print("better")
best()
def best():
print("best")
good()
```
| github_jupyter |
```
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
import nltk
%matplotlib inline
nltk.download_shell()
messages = [line.rstrip() for line in open('SMSSpamCollection')] ## Put in your dataset here
len(messages)
messages[50]
for msg_no, message in enumerate(messages[:10]):
print(msg_no, message)
print('\n')
messages = pd.read_csv('SMSSpamCollection', sep='\t', names=['Label', 'Message'])
messages.head()
messages.describe()
messages.groupby('Label').describe()
messages['Length'] = messages['Message'].apply(len)
messages.head()
plt.figure(figsize=(16,12))
sns.distplot(messages['Length'], bins=100, kde=False, color='black')
messages['Length'].describe()
messages[messages['Length'] == 910]['Message'].iloc[0]
messages.hist(column='Length', by='Label', bins=100, figsize=(16,8))
import string
from nltk.corpus import stopwords
def split_intoWords(msg):
## Firstly remove punctuation
noPunc = [char for char in msg if char not in string.punctuation]
## Then join the sepearate characters in a list
noPunc = ''.join(noPunc)
## Finally return only the significant words
return [word for word in noPunc.split() if word.lower() not in stopwords.words('english')]
messages['Message'].head(5).apply(split_intoWords)
from sklearn.feature_extraction.text import CountVectorizer
bow_transform = CountVectorizer(analyzer=split_intoWords).fit(messages['Message'])
print(len(bow_transform.vocabulary_))
messages_bow = bow_transform.transform(messages['Message'])
print('Shape of matrix: ',messages_bow.shape)
print('Non zero occurences: ',messages_bow.nnz)
sparsity = (100.0 * messages_bow.nnz / (messages_bow.shape[0] * messages_bow.shape[1]))
print('sparsity: {}'.format(sparsity))
from sklearn.feature_extraction.text import TfidfTransformer
tfidf_transform = TfidfTransformer().fit(messages_bow)
messages_tfidf = tfidf_transform.transform(messages_bow)
from sklearn.naive_bayes import MultinomialNB
spam_detect_model = MultinomialNB().fit(messages_tfidf, messages['Label'])
predictions = spam_detect_model.predict(messages_tfidf)
predictions
from sklearn.metrics import confusion_matrix, classification_report
confusion_matrix(messages['Label'], predictions)
print(classification_report(messages['Label'], predictions))
from sklearn.pipeline import Pipeline
from sklearn.ensemble import RandomForestClassifier
pipelineRf = Pipeline([
('bow', CountVectorizer(analyzer=split_intoWords)),
('tfidf', TfidfTransformer()),
('classifier', RandomForestClassifier())
])
```
# Now comparing with Random Forest Classifier instead of MultinomialNB.
# Stop here if you dont want to do the ahead steps
# Skip to 'save to csv' step
```
pipelineRf.fit(messages['Message'], messages['Label'])
predictionsRf = pipelineRf.predict(messages['Message'])
confusion_matrix(messages['Label'], predictionsRf)
print(classification_report(messages['Label'], predictionsRf))
predictionsRf
predictionsDf = pd.DataFrame(predictions, columns=['Naive Bayes Prediction'])
predictionsDf.head()
predictionsRfDf = pd.DataFrame(predictionsRf, columns=['Random Forest Predictions'])
predictionsRfDf.head()
messagesPred = pd.concat([messages, predictionsDf, predictionsRfDf], axis=1)
messagesPred
messagesPred.to_csv('predictions_spamOrHam_messages.csv', header=True, index_label='Index')
```
| github_jupyter |
# Using Hyperopt to optimize XGB model hyperparameters
## Importing the libraries and loading the data
```
#!pip install --upgrade tables
#!pip install eli5
#!pip install xgboost
#!pip install hyperopt
import numpy as np
import pandas as pd
import xgboost as xgb
from sklearn.metrics import mean_absolute_error as mae
from sklearn.model_selection import cross_val_score
from hyperopt import hp, fmin, tpe, STATUS_OK
import eli5
from eli5.sklearn import PermutationImportance
cd "/content/drive/My Drive/Colab Notebooks/dw_matrix_cars"
df = pd.read_hdf('data/car.h5')
df.shape
```
## Feature Engineering
```
SUFFIX_CAT = '_cat'
for feat in df.columns:
if isinstance(df[feat][0], list): continue
factorized_values = df[feat].factorize()[0]
if SUFFIX_CAT in feat:
df[feat] = factorized_values
else:
df[feat + SUFFIX_CAT] = factorized_values
df['param_rok-produkcji'] = df['param_rok-produkcji'].map(lambda x: -1 if str(x) == 'None' else int(x))
df['param_moc'] = df['param_moc'].map(lambda x: -1 if str(x) == 'None' else int(x.split(' ')[0]) )
df['param_pojemność-skokowa'] = df['param_pojemność-skokowa'].map(lambda x: -1 if str(x) == 'None' else int( str(x).split('cm')[0].replace(' ','')) )
def run_model(model, feats):
X = df[feats].values
y = df['price_value'].values
scores = cross_val_score(model, X, y, cv=3, scoring='neg_mean_absolute_error')
return np.mean(scores), np.std(scores)
feats = ['param_napęd_cat', 'param_rok-produkcji', 'param_stan_cat', 'param_skrzynia-biegów_cat', 'param_faktura-vat_cat', 'param_moc', 'param_marka-pojazdu_cat', 'feature_kamera-cofania_cat', 'param_typ_cat', 'param_pojemność-skokowa', 'seller_name_cat', 'feature_wspomaganie-kierownicy_cat', 'param_model-pojazdu_cat', 'param_wersja_cat', 'param_kod-silnika_cat', 'feature_system-start-stop_cat', 'feature_asystent-pasa-ruchu_cat', 'feature_czujniki-parkowania-przednie_cat', 'feature_łopatki-zmiany-biegów_cat', 'feature_regulowane-zawieszenie_cat']
xgb_params = {
'max_depth': 5,
'n_estimators': 50,
'learning_rate': 0.1,
'seed': 0
}
run_model(xgb.XGBRegressor(**xgb_params), feats)
```
## Hyperopt
```
def obj_func(params):
print("Training with params: ")
print(params)
mean_mae, score_std = run_model(xgb.XGBRegressor(**params), feats)
return {'loss': np.abs(mean_mae), 'status': STATUS_OK}
# space
xgb_reg_params = {
'learning_rate': hp.choice('learning_rate', np.arange(0.05, 0.31, 0.05)),
'max_depth': hp.choice('max_depth', np.arange(5, 16, 2, dtype=int)),
'subsample': hp.quniform('subsample', 0.5, 1, 0.05),
'colsample_bytree': hp.quniform('colsample_bytree', 0.5, 1, 0.05),
'objective': 'reg:squarederror',
'n_estimators': 100,
'seed': 0
}
# run
best = fmin(obj_func, xgb_reg_params, algo=tpe.suggest, max_evals=25)
best
```
| github_jupyter |
## Statistical Analysis
We have learned null hypothesis, and compared two-sample test to check whether two samples are the same or not
To add more to statistical analysis, the follwoing topics should be covered:
1- Approxite the histogram of data with combination of Gaussian (Normal) distribution functions:
Gaussian Mixture Model (GMM)
Kernel Density Estimation (KDE)
2- Correlation among features
## Review
Write a function that computes and plot histogram of a given data
Histogram is one method for estimating density
## What is Gaussian Mixture Model (GMM)?
GMM is a probabilistic model for representing normally distributed subpopulations within an overall population
<img src="Images/gmm_fig.png" width="300">
$p(x) = \sum_{i = 1}^{K} w_i \ \mathcal{N}(x \ | \ \mu_i,\ \sigma_i)$
$\sum_{i=1}^{K} w_i = 1$
https://brilliant.org/wiki/gaussian-mixture-model/
## Activity : Fit a GMM to a given data sample
Task:
1- Generate the concatination of the random variables as follows:
`x_1 = np.random.normal(-5, 1, 3000)
x_2 = np.random.normal(2, 3, 7000)
x = np.concatenate((x_1, x_2))`
2- Plot the histogram of `x`
3- Obtain the weights, mean and variances of each Gassuian
Steps needed:
`from sklearn import mixture
gmm = mixture.GaussianMixture(n_components=2)
gmm.fit(x.reshape(-1,1))`
```
import numpy as np
import matplotlib.pyplot as plt
from sklearn import mixture
# Generate data samples and plot its histogram
x_1 = np.random.normal(-5, 1, 3000)
x_2 = np.random.normal(2, 3, 7000)
x = np.concatenate((x_1, x_2))
plt.hist(x, bins=20, density=1)
plt.show()
# Define a GMM model and obtain its parameters
gmm = mixture.GaussianMixture(n_components=2)
gmm.fit(x.reshape(-1,1))
print(gmm.means_)
print(gmm.covariances_)
print(gmm.weights_)
```
## The GMM has learn the probability density function of our data sample
Lets the model generate sample from it model:
```
z = gmm.sample(10000)
plt.hist(z[0], bins=20, density=1)
plt.show()
```
## Kernel Density Estimation (KDE)
Kernel density estimation (KDE) is a non-parametric way to estimate the probability density function of a random variable. In other words the aim of KDE is to find probability density function (PDF) for a given dataset.
Approximate the pdf of dataset:
$p(x) = \frac{1}{Nh}\sum_{i = 1}^{N} \ K(\frac{x - x_i}{h})$
where $h$ is a bandwidth and $N$ is the number of data points
## Activity: Apply KDE on a given data sample
Task: Apply KDE on previous generated sample data `x`
Hint: use
`kde = KernelDensity(kernel='gaussian', bandwidth=0.6)`
```
from sklearn.neighbors import KernelDensity
kde = KernelDensity(kernel='gaussian', bandwidth=0.6)
kde.fit(x.reshape(-1,1))
s = np.linspace(np.min(x), np.max(x))
log_pdf = kde.score_samples(s.reshape(-1,1))
plt.plot(s, np.exp(log_pdf))
m = kde.sample(10000)
plt.hist(m, bins=20, density=1)
plt.show()
```
## KDE can learn handwitten digits distribution and generate new digits
http://scikit-learn.org/stable/auto_examples/neighbors/plot_digits_kde_sampling.html
## Correlation
Correlation is used to test relationships between quantitative variables
Some examples of data that have a high correlation:
1- Your caloric intake and your weight
2- The amount of time your study and your GPA
Question what is negative correlation?
Correlations are useful because we can find out what relationship variables have, we can make predictions about future behavior.
## Activity: Obtain the correlation among all features of iris dataset
1- Review the iris dataset. What are the features?
2- Eliminate two columns `['Id', 'Species']`
3- Compute the correlation among all features.
Hint: Use `df.corr()`
4- Plot the correlation by heatmap and corr plot in Seaborn -> `sns.heatmap`, `sns.corrplot`
5- Write a function that computes the correlation (Pearson formula)
Hint: https://en.wikipedia.org/wiki/Pearson_correlation_coefficient
6- Compare your answer with `scipy.stats.pearsonr` for any given two features
```
import pandas as pd
import numpy as np
import scipy.stats
import seaborn as sns
import scipy.stats
df = pd.read_csv('Iris.csv')
df = df.drop(columns=['Id', 'Species'])
sns.heatmap(df.corr(), annot=True)
def pearson_corr(x, y):
x_mean = np.mean(x)
y_mean = np.mean(y)
num = [(i - x_mean)*(j - y_mean) for i,j in zip(x,y)]
den_1 = [(i - x_mean)**2 for i in x]
den_2 = [(j - y_mean)**2 for j in y]
correlation_x_y = np.sum(num)/np.sqrt(np.sum(den_1))/np.sqrt(np.sum(den_2))
return correlation_x_y
print(pearson_corr(df['SepalLengthCm'], df['PetalLengthCm']))
print(scipy.stats.pearsonr(df['SepalLengthCm'], df['PetalLengthCm']))
```
| github_jupyter |
```
#default_exp data.transforms
#export
from fastai2.torch_basics import *
from fastai2.data.core import *
from fastai2.data.load import *
from fastai2.data.external import *
from sklearn.model_selection import train_test_split
from nbdev.showdoc import *
```
# Helper functions for processing data and basic transforms
> Functions for getting, splitting, and labeling data, as well as generic transforms
## Get, split, and label
For most data source creation we need functions to get a list of items, split them in to train/valid sets, and label them. fastai provides functions to make each of these steps easy (especially when combined with `fastai.data.blocks`).
### Get
First we'll look at functions that *get* a list of items (generally file names).
We'll use *tiny MNIST* (a subset of MNIST with just two classes, `7`s and `3`s) for our examples/tests throughout this page.
```
path = untar_data(URLs.MNIST_TINY)
(path/'train').ls()
# export
def _get_files(p, fs, extensions=None):
p = Path(p)
res = [p/f for f in fs if not f.startswith('.')
and ((not extensions) or f'.{f.split(".")[-1].lower()}' in extensions)]
return res
# export
def get_files(path, extensions=None, recurse=True, folders=None, followlinks=True):
"Get all the files in `path` with optional `extensions`, optionally with `recurse`, only in `folders`, if specified."
path = Path(path)
folders=L(folders)
extensions = setify(extensions)
extensions = {e.lower() for e in extensions}
if recurse:
res = []
for i,(p,d,f) in enumerate(os.walk(path, followlinks=followlinks)): # returns (dirpath, dirnames, filenames)
if len(folders) !=0 and i==0: d[:] = [o for o in d if o in folders]
else: d[:] = [o for o in d if not o.startswith('.')]
if len(folders) !=0 and i==0 and '.' not in folders: continue
res += _get_files(p, f, extensions)
else:
f = [o.name for o in os.scandir(path) if o.is_file()]
res = _get_files(path, f, extensions)
return L(res)
```
This is the most general way to grab a bunch of file names from disk. If you pass `extensions` (including the `.`) then returned file names are filtered by that list. Only those files directly in `path` are included, unless you pass `recurse`, in which case all child folders are also searched recursively. `folders` is an optional list of directories to limit the search to.
```
t3 = get_files(path/'train'/'3', extensions='.png', recurse=False)
t7 = get_files(path/'train'/'7', extensions='.png', recurse=False)
t = get_files(path/'train', extensions='.png', recurse=True)
test_eq(len(t), len(t3)+len(t7))
test_eq(len(get_files(path/'train'/'3', extensions='.jpg', recurse=False)),0)
test_eq(len(t), len(get_files(path, extensions='.png', recurse=True, folders='train')))
t
#hide
test_eq(len(get_files(path/'train'/'3', recurse=False)),346)
test_eq(len(get_files(path, extensions='.png', recurse=True, folders=['train', 'test'])),729)
test_eq(len(get_files(path, extensions='.png', recurse=True, folders='train')),709)
test_eq(len(get_files(path, extensions='.png', recurse=True, folders='training')),0)
```
It's often useful to be able to create functions with customized behavior. `fastai.data` generally uses functions named as CamelCase verbs ending in `er` to create these functions. `FileGetter` is a simple example of such a function creator.
```
#export
def FileGetter(suf='', extensions=None, recurse=True, folders=None):
"Create `get_files` partial function that searches path suffix `suf`, only in `folders`, if specified, and passes along args"
def _inner(o, extensions=extensions, recurse=recurse, folders=folders):
return get_files(o/suf, extensions, recurse, folders)
return _inner
fpng = FileGetter(extensions='.png', recurse=False)
test_eq(len(t7), len(fpng(path/'train'/'7')))
test_eq(len(t), len(fpng(path/'train', recurse=True)))
fpng_r = FileGetter(extensions='.png', recurse=True)
test_eq(len(t), len(fpng_r(path/'train')))
#export
image_extensions = set(k for k,v in mimetypes.types_map.items() if v.startswith('image/'))
#export
def get_image_files(path, recurse=True, folders=None):
"Get image files in `path` recursively, only in `folders`, if specified."
return get_files(path, extensions=image_extensions, recurse=recurse, folders=folders)
```
This is simply `get_files` called with a list of standard image extensions.
```
test_eq(len(t), len(get_image_files(path, recurse=True, folders='train')))
#export
def ImageGetter(suf='', recurse=True, folders=None):
"Create `get_image_files` partial function that searches path suffix `suf` and passes along `kwargs`, only in `folders`, if specified."
def _inner(o, recurse=recurse, folders=folders): return get_image_files(o/suf, recurse, folders)
return _inner
```
Same as `FileGetter`, but for image extensions.
```
test_eq(len(get_files(path/'train', extensions='.png', recurse=True, folders='3')),
len(ImageGetter( 'train', recurse=True, folders='3')(path)))
#export
def get_text_files(path, recurse=True, folders=None):
"Get text files in `path` recursively, only in `folders`, if specified."
return get_files(path, extensions=['.txt'], recurse=recurse, folders=folders)
#export
class ItemGetter(ItemTransform):
"Creates a proper transform that applies `itemgetter(i)` (even on a tuple)"
_retain = False
def __init__(self, i): self.i = i
def encodes(self, x): return x[self.i]
test_eq(ItemGetter(1)((1,2,3)), 2)
test_eq(ItemGetter(1)(L(1,2,3)), 2)
test_eq(ItemGetter(1)([1,2,3]), 2)
test_eq(ItemGetter(1)(np.array([1,2,3])), 2)
#export
class AttrGetter(ItemTransform):
"Creates a proper transform that applies `attrgetter(nm)` (even on a tuple)"
_retain = False
def __init__(self, nm, default=None): store_attr(self, 'nm,default')
def encodes(self, x): return getattr(x, self.nm, self.default)
test_eq(AttrGetter('shape')(torch.randn([4,5])), [4,5])
test_eq(AttrGetter('shape', [0])([4,5]), [0])
```
### Split
The next set of functions are used to *split* data into training and validation sets. The functions return two lists - a list of indices or masks for each of training and validation sets.
```
# export
def RandomSplitter(valid_pct=0.2, seed=None):
"Create function that splits `items` between train/val with `valid_pct` randomly."
def _inner(o):
if seed is not None: torch.manual_seed(seed)
rand_idx = L(int(i) for i in torch.randperm(len(o)))
cut = int(valid_pct * len(o))
return rand_idx[cut:],rand_idx[:cut]
return _inner
src = list(range(30))
f = RandomSplitter(seed=42)
trn,val = f(src)
assert 0<len(trn)<len(src)
assert all(o not in val for o in trn)
test_eq(len(trn), len(src)-len(val))
# test random seed consistency
test_eq(f(src)[0], trn)
```
Use scikit-learn train_test_split. This allow to *split* items in a stratified fashion (uniformely according to the ‘labels‘ distribution)
```
# export
def TrainTestSplitter(test_size=0.2, random_state=None, stratify=None, train_size=None, shuffle=True):
"Split `items` into random train and test subsets using sklearn train_test_split utility."
def _inner(o, **kwargs):
train, valid = train_test_split(range(len(o)), test_size=test_size, random_state=random_state, stratify=stratify, train_size=train_size, shuffle=shuffle)
return L(train), L(valid)
return _inner
src = list(range(30))
labels = [0] * 20 + [1] * 10
test_size = 0.2
f = TrainTestSplitter(test_size=test_size, random_state=42, stratify=labels)
trn,val = f(src)
assert 0<len(trn)<len(src)
assert all(o not in val for o in trn)
test_eq(len(trn), len(src)-len(val))
# test random seed consistency
test_eq(f(src)[0], trn)
# test labels distribution consistency
# there should be test_size % of zeroes and ones respectively in the validation set
test_eq(len([t for t in val if t < 20]) / 20, test_size)
test_eq(len([t for t in val if t > 20]) / 10, test_size)
#export
def IndexSplitter(valid_idx):
"Split `items` so that `val_idx` are in the validation set and the others in the training set"
def _inner(o):
train_idx = np.setdiff1d(np.array(range_of(o)), np.array(valid_idx))
return L(train_idx, use_list=True), L(valid_idx, use_list=True)
return _inner
items = list(range(10))
splitter = IndexSplitter([3,7,9])
test_eq(splitter(items),[[0,1,2,4,5,6,8],[3,7,9]])
# export
def _grandparent_idxs(items, name):
def _inner(items, name): return mask2idxs(Path(o).parent.parent.name == name for o in items)
return [i for n in L(name) for i in _inner(items,n)]
# export
def GrandparentSplitter(train_name='train', valid_name='valid'):
"Split `items` from the grand parent folder names (`train_name` and `valid_name`)."
def _inner(o):
return _grandparent_idxs(o, train_name),_grandparent_idxs(o, valid_name)
return _inner
fnames = [path/'train/3/9932.png', path/'valid/7/7189.png',
path/'valid/7/7320.png', path/'train/7/9833.png',
path/'train/3/7666.png', path/'valid/3/925.png',
path/'train/7/724.png', path/'valid/3/93055.png']
splitter = GrandparentSplitter()
test_eq(splitter(fnames),[[0,3,4,6],[1,2,5,7]])
fnames2 = fnames + [path/'test/3/4256.png', path/'test/7/2345.png', path/'valid/7/6467.png']
splitter = GrandparentSplitter(train_name=('train', 'valid'), valid_name='test')
test_eq(splitter(fnames2),[[0,3,4,6,1,2,5,7,10],[8,9]])
# export
def FuncSplitter(func):
"Split `items` by result of `func` (`True` for validation, `False` for training set)."
def _inner(o):
val_idx = mask2idxs(func(o_) for o_ in o)
return IndexSplitter(val_idx)(o)
return _inner
splitter = FuncSplitter(lambda o: Path(o).parent.parent.name == 'valid')
test_eq(splitter(fnames),[[0,3,4,6],[1,2,5,7]])
# export
def MaskSplitter(mask):
"Split `items` depending on the value of `mask`."
def _inner(o): return IndexSplitter(mask2idxs(mask))(o)
return _inner
items = list(range(6))
splitter = MaskSplitter([True,False,False,True,False,True])
test_eq(splitter(items),[[1,2,4],[0,3,5]])
# export
def FileSplitter(fname):
"Split `items` by providing file `fname` (contains names of valid items separated by newline)."
valid = Path(fname).read().split('\n')
def _func(x): return x.name in valid
def _inner(o): return FuncSplitter(_func)(o)
return _inner
with tempfile.TemporaryDirectory() as d:
fname = Path(d)/'valid.txt'
fname.write('\n'.join([Path(fnames[i]).name for i in [1,3,4]]))
splitter = FileSplitter(fname)
test_eq(splitter(fnames),[[0,2,5,6,7],[1,3,4]])
# export
def ColSplitter(col='is_valid'):
"Split `items` (supposed to be a dataframe) by value in `col`"
def _inner(o):
assert isinstance(o, pd.DataFrame), "ColSplitter only works when your items are a pandas DataFrame"
valid_idx = (o.iloc[:,col] if isinstance(col, int) else o[col]).values
return IndexSplitter(mask2idxs(valid_idx))(o)
return _inner
df = pd.DataFrame({'a': [0,1,2,3,4], 'b': [True,False,True,True,False]})
splits = ColSplitter('b')(df)
test_eq(splits, [[1,4], [0,2,3]])
#Works with strings or index
splits = ColSplitter(1)(df)
test_eq(splits, [[1,4], [0,2,3]])
# export
def RandomSubsetSplitter(train_sz, valid_sz, seed=None):
"Take randoms subsets of `splits` with `train_sz` and `valid_sz`"
assert 0 < train_sz < 1
assert 0 < valid_sz < 1
assert train_sz + valid_sz <= 1.
def _inner(o):
if seed is not None: torch.manual_seed(seed)
train_len,valid_len = int(len(o)*train_sz),int(len(o)*valid_sz)
idxs = L(int(i) for i in torch.randperm(len(o)))
return idxs[:train_len],idxs[train_len:train_len+valid_len]
return _inner
items = list(range(100))
valid_idx = list(np.arange(70,100))
splits = RandomSubsetSplitter(0.3, 0.1)(items)
test_eq(len(splits[0]), 30)
test_eq(len(splits[1]), 10)
```
### Label
The final set of functions is used to *label* a single item of data.
```
# export
def parent_label(o):
"Label `item` with the parent folder name."
return Path(o).parent.name
```
Note that `parent_label` doesn't have anything customize, so it doesn't return a function - you can just use it directly.
```
test_eq(parent_label(fnames[0]), '3')
test_eq(parent_label("fastai_dev/dev/data/mnist_tiny/train/3/9932.png"), '3')
[parent_label(o) for o in fnames]
#hide
#test for MS Windows when os.path.sep is '\\' instead of '/'
test_eq(parent_label(os.path.join("fastai_dev","dev","data","mnist_tiny","train", "3", "9932.png") ), '3')
# export
class RegexLabeller():
"Label `item` with regex `pat`."
def __init__(self, pat, match=False):
self.pat = re.compile(pat)
self.matcher = self.pat.match if match else self.pat.search
def __call__(self, o):
res = self.matcher(str(o))
assert res,f'Failed to find "{self.pat}" in "{o}"'
return res.group(1)
```
`RegexLabeller` is a very flexible function since it handles any regex search of the stringified item. Pass `match=True` to use `re.match` (i.e. check only start of string), or `re.search` otherwise (default).
For instance, here's an example the replicates the previous `parent_label` results.
```
f = RegexLabeller(fr'{os.path.sep}(\d){os.path.sep}')
test_eq(f(fnames[0]), '3')
[f(o) for o in fnames]
f = RegexLabeller(r'(\d*)', match=True)
test_eq(f(fnames[0].name), '9932')
#export
class ColReader():
"Read `cols` in `row` with potential `pref` and `suff`"
store_attrs = 'cols'
def __init__(self, cols, pref='', suff='', label_delim=None):
store_attr(self, 'suff,label_delim')
self.pref = str(pref) + os.path.sep if isinstance(pref, Path) else pref
self.cols = L(cols)
def _do_one(self, r, c):
o = r[c] if isinstance(c, int) else r[c] if c=='name' else getattr(r, c)
if len(self.pref)==0 and len(self.suff)==0 and self.label_delim is None: return o
if self.label_delim is None: return f'{self.pref}{o}{self.suff}'
else: return o.split(self.label_delim) if len(o)>0 else []
def __call__(self, o):
if len(self.cols) == 1: return self._do_one(o, self.cols[0])
return L(self._do_one(o, c) for c in self.cols)
@property
def name(self): return f"ColReader -- {attrdict(self, *self.store_attrs.split(','))}"
```
`cols` can be a list of column names or a list of indices (or a mix of both). If `label_delim` is passed, the result is split using it.
```
df = pd.DataFrame({'a': 'a b c d'.split(), 'b': ['1 2', '0', '', '1 2 3']})
f = ColReader('a', pref='0', suff='1')
test_eq([f(o) for o in df.itertuples()], '0a1 0b1 0c1 0d1'.split())
f = ColReader('b', label_delim=' ')
test_eq([f(o) for o in df.itertuples()], [['1', '2'], ['0'], [], ['1', '2', '3']])
df['a1'] = df['a']
f = ColReader(['a', 'a1'], pref='0', suff='1')
test_eq([f(o) for o in df.itertuples()], [L('0a1', '0a1'), L('0b1', '0b1'), L('0c1', '0c1'), L('0d1', '0d1')])
df = pd.DataFrame({'a': [L(0,1), L(2,3,4), L(5,6,7)]})
f = ColReader('a')
test_eq([f(o) for o in df.itertuples()], [L(0,1), L(2,3,4), L(5,6,7)])
df['name'] = df['a']
f = ColReader('name')
test_eq([f(df.iloc[0,:])], [L(0,1)])
```
## Categorize -
```
#export
class CategoryMap(CollBase):
"Collection of categories with the reverse mapping in `o2i`"
def __init__(self, col, sort=True, add_na=False, strict=False):
if is_categorical_dtype(col):
items = L(col.cat.categories, use_list=True)
#Remove non-used categories while keeping order
if strict: items = L(o for o in items if o in col.unique())
else:
if not hasattr(col,'unique'): col = L(col, use_list=True)
# `o==o` is the generalized definition of non-NaN used by Pandas
items = L(o for o in col.unique() if o==o)
if sort: items = items.sorted()
self.items = '#na#' + items if add_na else items
self.o2i = defaultdict(int, self.items.val2idx()) if add_na else dict(self.items.val2idx())
def map_objs(self,objs):
"Map `objs` to IDs"
return L(self.o2i[o] for o in objs)
def map_ids(self,ids):
"Map `ids` to objects in vocab"
return L(self.items[o] for o in ids)
def __eq__(self,b): return all_equal(b,self)
t = CategoryMap([4,2,3,4])
test_eq(t, [2,3,4])
test_eq(t.o2i, {2:0,3:1,4:2})
test_eq(t.map_objs([2,3]), [0,1])
test_eq(t.map_ids([0,1]), [2,3])
test_fail(lambda: t.o2i['unseen label'])
t = CategoryMap([4,2,3,4], add_na=True)
test_eq(t, ['#na#',2,3,4])
test_eq(t.o2i, {'#na#':0,2:1,3:2,4:3})
t = CategoryMap(pd.Series([4,2,3,4]), sort=False)
test_eq(t, [4,2,3])
test_eq(t.o2i, {4:0,2:1,3:2})
col = pd.Series(pd.Categorical(['M','H','L','M'], categories=['H','M','L'], ordered=True))
t = CategoryMap(col)
test_eq(t, ['H','M','L'])
test_eq(t.o2i, {'H':0,'M':1,'L':2})
col = pd.Series(pd.Categorical(['M','H','M'], categories=['H','M','L'], ordered=True))
t = CategoryMap(col, strict=True)
test_eq(t, ['H','M'])
test_eq(t.o2i, {'H':0,'M':1})
# export
class Categorize(Transform):
"Reversible transform of category string to `vocab` id"
loss_func,order,store_attrs=CrossEntropyLossFlat(),1,'vocab,add_na'
def __init__(self, vocab=None, sort=True, add_na=False):
store_attr(self, self.store_attrs+',sort')
self.vocab = None if vocab is None else CategoryMap(vocab, sort=sort, add_na=add_na)
def setups(self, dsets):
if self.vocab is None and dsets is not None: self.vocab = CategoryMap(dsets, sort=self.sort, add_na=self.add_na)
self.c = len(self.vocab)
def encodes(self, o): return TensorCategory(self.vocab.o2i[o])
def decodes(self, o): return Category (self.vocab [o])
@property
def name(self): return f"{super().name} -- {attrdict(self, *self.store_attrs.split(','))}"
#export
class Category(str, ShowTitle): _show_args = {'label': 'category'}
cat = Categorize()
tds = Datasets(['cat', 'dog', 'cat'], tfms=[cat])
test_eq(cat.vocab, ['cat', 'dog'])
test_eq(cat('cat'), 0)
test_eq(cat.decode(1), 'dog')
test_stdout(lambda: show_at(tds,2), 'cat')
cat = Categorize(add_na=True)
tds = Datasets(['cat', 'dog', 'cat'], tfms=[cat])
test_eq(cat.vocab, ['#na#', 'cat', 'dog'])
test_eq(cat('cat'), 1)
test_eq(cat.decode(2), 'dog')
test_stdout(lambda: show_at(tds,2), 'cat')
cat = Categorize(vocab=['dog', 'cat'], sort=False, add_na=True)
tds = Datasets(['cat', 'dog', 'cat'], tfms=[cat])
test_eq(cat.vocab, ['#na#', 'dog', 'cat'])
test_eq(cat('dog'), 1)
test_eq(cat.decode(2), 'cat')
test_stdout(lambda: show_at(tds,2), 'cat')
```
## Multicategorize -
```
# export
class MultiCategorize(Categorize):
"Reversible transform of multi-category strings to `vocab` id"
loss_func,order=BCEWithLogitsLossFlat(),1
def __init__(self, vocab=None, add_na=False): super().__init__(vocab=vocab,add_na=add_na)
def setups(self, dsets):
if not dsets: return
if self.vocab is None:
vals = set()
for b in dsets: vals = vals.union(set(b))
self.vocab = CategoryMap(list(vals), add_na=self.add_na)
def encodes(self, o): return TensorMultiCategory([self.vocab.o2i[o_] for o_ in o])
def decodes(self, o): return MultiCategory ([self.vocab [o_] for o_ in o])
#export
class MultiCategory(L):
def show(self, ctx=None, sep=';', color='black', **kwargs):
return show_title(sep.join(self.map(str)), ctx=ctx, color=color, **kwargs)
cat = MultiCategorize()
tds = Datasets([['b', 'c'], ['a'], ['a', 'c'], []], tfms=[cat])
test_eq(tds[3][0], TensorMultiCategory([]))
test_eq(cat.vocab, ['a', 'b', 'c'])
test_eq(cat(['a', 'c']), tensor([0,2]))
test_eq(cat([]), tensor([]))
test_eq(cat.decode([1]), ['b'])
test_eq(cat.decode([0,2]), ['a', 'c'])
test_stdout(lambda: show_at(tds,2), 'a;c')
# export
class OneHotEncode(Transform):
"One-hot encodes targets"
order,store_attrs=2,'c'
def __init__(self, c=None):
self.c = c
def setups(self, dsets):
if self.c is None: self.c = len(L(getattr(dsets, 'vocab', None)))
if not self.c: warn("Couldn't infer the number of classes, please pass a value for `c` at init")
def encodes(self, o): return TensorMultiCategory(one_hot(o, self.c).float())
def decodes(self, o): return one_hot_decode(o, None)
@property
def name(self): return f"{super().name} -- {attrdict(self, *self.store_attrs.split(','))}"
```
Works in conjunction with ` MultiCategorize` or on its own if you have one-hot encoded targets (pass a `vocab` for decoding and `do_encode=False` in this case)
```
_tfm = OneHotEncode(c=3)
test_eq(_tfm([0,2]), tensor([1.,0,1]))
test_eq(_tfm.decode(tensor([0,1,1])), [1,2])
tds = Datasets([['b', 'c'], ['a'], ['a', 'c'], []], [[MultiCategorize(), OneHotEncode()]])
test_eq(tds[1], [tensor([1.,0,0])])
test_eq(tds[3], [tensor([0.,0,0])])
test_eq(tds.decode([tensor([False, True, True])]), [['b','c']])
test_eq(type(tds[1][0]), TensorMultiCategory)
test_stdout(lambda: show_at(tds,2), 'a;c')
#hide
#test with passing the vocab
tds = Datasets([['b', 'c'], ['a'], ['a', 'c'], []], [[MultiCategorize(vocab=['a', 'b', 'c']), OneHotEncode()]])
test_eq(tds[1], [tensor([1.,0,0])])
test_eq(tds[3], [tensor([0.,0,0])])
test_eq(tds.decode([tensor([False, True, True])]), [['b','c']])
test_eq(type(tds[1][0]), TensorMultiCategory)
test_stdout(lambda: show_at(tds,2), 'a;c')
# export
class EncodedMultiCategorize(Categorize):
"Transform of one-hot encoded multi-category that decodes with `vocab`"
loss_func,order=BCEWithLogitsLossFlat(),1
def __init__(self, vocab):
super().__init__(vocab)
self.c = len(vocab)
def encodes(self, o): return TensorMultiCategory(tensor(o).float())
def decodes(self, o): return MultiCategory (one_hot_decode(o, self.vocab))
_tfm = EncodedMultiCategorize(vocab=['a', 'b', 'c'])
test_eq(_tfm([1,0,1]), tensor([1., 0., 1.]))
test_eq(type(_tfm([1,0,1])), TensorMultiCategory)
test_eq(_tfm.decode(tensor([False, True, True])), ['b','c'])
_tfm
#export
class RegressionSetup(Transform):
"Transform that floatifies targets"
loss_func,store_attrs=MSELossFlat(),'c'
def __init__(self, c=None):
self.c = c
def encodes(self, o): return tensor(o).float()
def decodes(self, o): return TitledFloat(o) if o.ndim==0 else TitledTuple(o_.item() for o_ in o)
def setups(self, dsets):
if self.c is not None: return
try: self.c = len(dsets[0]) if hasattr(dsets[0], '__len__') else 1
except: self.c = 0
@property
def name(self): return f"{super().name} -- {attrdict(self, *self.store_attrs.split(','))}"
_tfm = RegressionSetup()
dsets = Datasets([0, 1, 2], RegressionSetup)
test_eq(dsets.c, 1)
test_eq_type(dsets[0], (tensor(0.),))
dsets = Datasets([[0, 1, 2], [3,4,5]], RegressionSetup)
test_eq(dsets.c, 3)
test_eq_type(dsets[0], (tensor([0.,1.,2.]),))
#export
def get_c(dls):
if getattr(dls, 'c', False): return dls.c
if getattr(getattr(dls.train, 'after_item', None), 'c', False): return dls.train.after_item.c
if getattr(getattr(dls.train, 'after_batch', None), 'c', False): return dls.train.after_batch.c
vocab = getattr(dls, 'vocab', [])
if len(vocab) > 0 and is_listy(vocab[-1]): vocab = vocab[-1]
return len(vocab)
```
## End-to-end dataset example with MNIST
Let's show how to use those functions to grab the mnist dataset in a `Datasets`. First we grab all the images.
```
path = untar_data(URLs.MNIST_TINY)
items = get_image_files(path)
```
Then we split between train and validation depending on the folder.
```
splitter = GrandparentSplitter()
splits = splitter(items)
train,valid = (items[i] for i in splits)
train[:3],valid[:3]
```
Our inputs are images that we open and convert to tensors, our targets are labeled depending on the parent directory and are categories.
```
from PIL import Image
def open_img(fn:Path): return Image.open(fn).copy()
def img2tensor(im:Image.Image): return TensorImage(array(im)[None])
tfms = [[open_img, img2tensor],
[parent_label, Categorize()]]
train_ds = Datasets(train, tfms)
x,y = train_ds[3]
xd,yd = decode_at(train_ds,3)
test_eq(parent_label(train[3]),yd)
test_eq(array(Image.open(train[3])),xd[0].numpy())
ax = show_at(train_ds, 3, cmap="Greys", figsize=(1,1))
assert ax.title.get_text() in ('3','7')
test_fig_exists(ax)
```
## ToTensor -
```
#export
class ToTensor(Transform):
"Convert item to appropriate tensor class"
order = 5
```
## IntToFloatTensor -
```
# export
class IntToFloatTensor(Transform):
"Transform image to float tensor, optionally dividing by 255 (e.g. for images)."
order,store_attrs = 10,'div,div_mask' #Need to run after PIL transforms on the GPU
def __init__(self, div=255., div_mask=1):
store_attr(self, 'div,div_mask')
def encodes(self, o:TensorImage): return o.float().div_(self.div)
def encodes(self, o:TensorMask ): return o.long() // self.div_mask
def decodes(self, o:TensorImage): return ((o.clamp(0., 1.) * self.div).long()) if self.div else o
@property
def name(self): return f"{super().name} -- {attrdict(self, *self.store_attrs.split(','))}"
t = (TensorImage(tensor(1)),tensor(2).long(),TensorMask(tensor(3)))
tfm = IntToFloatTensor()
ft = tfm(t)
test_eq(ft, [1./255, 2, 3])
test_eq(type(ft[0]), TensorImage)
test_eq(type(ft[2]), TensorMask)
test_eq(ft[0].type(),'torch.FloatTensor')
test_eq(ft[1].type(),'torch.LongTensor')
test_eq(ft[2].type(),'torch.LongTensor')
```
## Normalization -
```
# export
def broadcast_vec(dim, ndim, *t, cuda=True):
"Make a vector broadcastable over `dim` (out of `ndim` total) by prepending and appending unit axes"
v = [1]*ndim
v[dim] = -1
f = to_device if cuda else noop
return [f(tensor(o).view(*v)) for o in t]
# export
@docs
class Normalize(Transform):
"Normalize/denorm batch of `TensorImage`"
parameters,order,store_attrs=L('mean', 'std'),99, 'mean,std,axes'
def __init__(self, mean=None, std=None, axes=(0,2,3)):
self.mean,self.std,self.axes = mean,std,axes
@classmethod
def from_stats(cls, mean, std, dim=1, ndim=4, cuda=True): return cls(*broadcast_vec(dim, ndim, mean, std, cuda=cuda))
def setups(self, dl:DataLoader):
if self.mean is None or self.std is None:
x,*_ = dl.one_batch()
self.mean,self.std = x.mean(self.axes, keepdim=True),x.std(self.axes, keepdim=True)+1e-7
def encodes(self, x:TensorImage): return (x-self.mean) / self.std
def decodes(self, x:TensorImage):
f = to_cpu if x.device.type=='cpu' else noop
return (x*f(self.std) + f(self.mean))
@property
def name(self): return f"{super().name} -- {attrdict(self, *self.store_attrs.split(','))}"
_docs=dict(encodes="Normalize batch", decodes="Denormalize batch")
mean,std = [0.5]*3,[0.5]*3
mean,std = broadcast_vec(1, 4, mean, std)
batch_tfms = [IntToFloatTensor(), Normalize.from_stats(mean,std)]
tdl = TfmdDL(train_ds, after_batch=batch_tfms, bs=4, device=default_device())
x,y = tdl.one_batch()
xd,yd = tdl.decode((x,y))
test_eq(x.type(), 'torch.cuda.FloatTensor' if default_device().type=='cuda' else 'torch.FloatTensor')
test_eq(xd.type(), 'torch.LongTensor')
test_eq(type(x), TensorImage)
test_eq(type(y), TensorCategory)
assert x.mean()<0.0
assert x.std()>0.5
assert 0<xd.float().mean()/255.<1
assert 0<xd.float().std()/255.<0.5
#hide
nrm = Normalize()
batch_tfms = [IntToFloatTensor(), nrm]
tdl = TfmdDL(train_ds, after_batch=batch_tfms, bs=4)
x,y = tdl.one_batch()
test_close(x.mean(), 0.0, 1e-4)
assert x.std()>0.9, x.std()
#Just for visuals
from fastai2.vision.core import *
tdl.show_batch((x,y))
x,y = torch.add(x,0),torch.add(y,0) #Lose type of tensors (to emulate predictions)
test_ne(type(x), TensorImage)
tdl.show_batch((x,y), figsize=(4,4)) #Check that types are put back by dl.
#TODO: make the above check a proper test
```
## Export -
```
#hide
from nbdev.export import notebook2script
notebook2script()
```
| github_jupyter |
```
import numpy as np
import pandas as pd
import torch
import torchvision
from torch.utils.data import Dataset, DataLoader
from torchvision import transforms, utils
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from matplotlib import pyplot as plt
%matplotlib inline
class MosaicDataset1(Dataset):
"""MosaicDataset dataset."""
def __init__(self, mosaic_list, mosaic_label,fore_idx):
"""
Args:
csv_file (string): Path to the csv file with annotations.
root_dir (string): Directory with all the images.
transform (callable, optional): Optional transform to be applied
on a sample.
"""
self.mosaic = mosaic_list
self.label = mosaic_label
self.fore_idx = fore_idx
def __len__(self):
return len(self.label)
def __getitem__(self, idx):
return self.mosaic[idx] , self.label[idx] , self.fore_idx[idx]
data = np.load("type4_data.npy",allow_pickle=True)
mosaic_list_of_images = data[0]["mosaic_list"]
mosaic_label = data[0]["mosaic_label"]
fore_idx = data[0]["fore_idx"]
batch = 250
msd = MosaicDataset1(mosaic_list_of_images, mosaic_label, fore_idx)
train_loader = DataLoader( msd,batch_size= batch ,shuffle=True)
class Focus_deep(nn.Module):
'''
deep focus network averaged at zeroth layer
input : elemental data
'''
def __init__(self,inputs,output,K,d):
super(Focus_deep,self).__init__()
self.inputs = inputs
self.output = output
self.K = K
self.d = d
self.linear1 = nn.Linear(self.inputs,50) #,self.output)
self.linear2 = nn.Linear(50,50)
self.linear3 = nn.Linear(50,self.output)
def forward(self,z):
batch = z.shape[0]
x = torch.zeros([batch,self.K],dtype=torch.float64)
y = torch.zeros([batch,50], dtype=torch.float64) # number of features of output
features = torch.zeros([batch,self.K,50],dtype=torch.float64)
x,y = x.to("cuda"),y.to("cuda")
features = features.to("cuda")
for i in range(self.K):
alp,ftrs = self.helper(z[:,i] ) # self.d*i:self.d*i+self.d
x[:,i] = alp[:,0]
features[:,i] = ftrs
log_x = F.log_softmax(x,dim=1) #log alpha
x = F.softmax(x,dim=1) # alphas
for i in range(self.K):
x1 = x[:,i]
y = y+torch.mul(x1[:,None],features[:,i]) # self.d*i:self.d*i+self.d
return y , x,log_x
def helper(self,x):
x = self.linear1(x)
x = F.relu(x)
x = self.linear2(x)
x1 = F.tanh(x)
x = F.relu(x)
x = self.linear3(x)
#print(x1.shape)
return x,x1
class Classification_deep(nn.Module):
'''
input : elemental data
deep classification module data averaged at zeroth layer
'''
def __init__(self,inputs,output):
super(Classification_deep,self).__init__()
self.inputs = inputs
self.output = output
self.linear1 = nn.Linear(self.inputs,50)
#self.linear2 = nn.Linear(50,50)
self.linear2 = nn.Linear(50,self.output)
def forward(self,x):
x = F.relu(self.linear1(x))
#x = F.relu(self.linear2(x))
x = self.linear2(x)
return x
criterion = nn.CrossEntropyLoss()
def my_cross_entropy(x, y,alpha,log_alpha,k):
loss = criterion(x,y)
b = -1.0* alpha * log_alpha
b = torch.mean(torch.sum(b,dim=1))
closs = loss
entropy = b
loss = (1-k)*loss + ((k)*b)
return loss,closs,entropy
def calculate_attn_loss(dataloader,what,where,k):
what.eval()
where.eval()
r_loss = 0
cc_loss = 0
cc_entropy = 0
alphas = []
lbls = []
pred = []
fidices = []
with torch.no_grad():
for i, data in enumerate(dataloader, 0):
inputs, labels,fidx = data
lbls.append(labels)
fidices.append(fidx)
inputs = inputs.double()
inputs, labels = inputs.to("cuda"),labels.to("cuda")
avg,alpha,log_alpha = where(inputs)
outputs = what(avg)
_, predicted = torch.max(outputs.data, 1)
pred.append(predicted.cpu().numpy())
alphas.append(alpha.cpu().numpy())
loss,closs,entropy = my_cross_entropy(outputs,labels,alpha,log_alpha,k)
r_loss += loss.item()
cc_loss += closs.item()
cc_entropy += entropy.item()
alphas = np.concatenate(alphas,axis=0)
pred = np.concatenate(pred,axis=0)
lbls = np.concatenate(lbls,axis=0)
fidices = np.concatenate(fidices,axis=0)
#print(alphas.shape,pred.shape,lbls.shape,fidices.shape)
analysis = analyse_data(alphas,lbls,pred,fidices)
return r_loss/i,cc_loss/i,cc_entropy/i,analysis
def analyse_data(alphas,lbls,predicted,f_idx):
'''
analysis data is created here
'''
batch = len(predicted)
amth,alth,ftpt,ffpt,ftpf,ffpf = 0,0,0,0,0,0
for j in range (batch):
focus = np.argmax(alphas[j])
if(alphas[j][focus] >= 0.5):
amth +=1
else:
alth +=1
if(focus == f_idx[j] and predicted[j] == lbls[j]):
ftpt += 1
elif(focus != f_idx[j] and predicted[j] == lbls[j]):
ffpt +=1
elif(focus == f_idx[j] and predicted[j] != lbls[j]):
ftpf +=1
elif(focus != f_idx[j] and predicted[j] != lbls[j]):
ffpf +=1
#print(sum(predicted==lbls),ftpt+ffpt)
return [ftpt,ffpt,ftpf,ffpf,amth,alth]
number_runs = 20
full_analysis = []
FTPT_analysis = pd.DataFrame(columns = ["FTPT","FFPT", "FTPF","FFPF"])
k = 0.005
r_loss = []
r_closs = []
r_centropy = []
for n in range(number_runs):
print("--"*40)
# instantiate focus and classification Model
torch.manual_seed(n)
where = Focus_deep(2,1,9,2).double()
torch.manual_seed(n)
what = Classification_deep(50,3).double()
where = where.to("cuda")
what = what.to("cuda")
# instantiate optimizer
optimizer_where = optim.Adam(where.parameters(),lr =0.001)#,momentum=0.9)
optimizer_what = optim.Adam(what.parameters(), lr=0.001)#,momentum=0.9)
#criterion = nn.CrossEntropyLoss()
acti = []
analysis_data = []
loss_curi = []
cc_loss_curi = []
cc_entropy_curi = []
epochs = 3000
# calculate zeroth epoch loss and FTPT values
running_loss,_,_,anlys_data = calculate_attn_loss(train_loader,what,where,k)
loss_curi.append(running_loss)
analysis_data.append(anlys_data)
print('epoch: [%d ] loss: %.3f' %(0,running_loss))
# training starts
for epoch in range(epochs): # loop over the dataset multiple times
ep_lossi = []
running_loss = 0.0
what.train()
where.train()
for i, data in enumerate(train_loader, 0):
# get the inputs
inputs, labels,_ = data
inputs = inputs.double()
inputs, labels = inputs.to("cuda"),labels.to("cuda")
# zero the parameter gradients
optimizer_where.zero_grad()
optimizer_what.zero_grad()
# forward + backward + optimize
avg, alpha,log_alpha = where(inputs)
outputs = what(avg)
loss,_,_ = my_cross_entropy( outputs,labels,alpha,log_alpha,k)
# print statistics
running_loss += loss.item()
loss.backward()
optimizer_where.step()
optimizer_what.step()
running_loss,ccloss,ccentropy,anls_data = calculate_attn_loss(train_loader,what,where,k)
analysis_data.append(anls_data)
print('epoch: [%d] loss: %.3f celoss: %.3f entropy: %.3f' %(epoch + 1,running_loss,ccloss,ccentropy))
loss_curi.append(running_loss) #loss per epoch
cc_loss_curi.append(ccloss)
cc_entropy_curi.append(ccentropy)
if running_loss<=0.01:
break
print('Finished Training run ' +str(n))
analysis_data = np.array(analysis_data)
FTPT_analysis.loc[n] = analysis_data[-1,:4]/30
full_analysis.append((epoch, analysis_data))
r_loss.append(np.array(loss_curi))
r_closs.append(np.array(cc_loss_curi))
r_centropy.append(np.array(cc_entropy_curi))
correct = 0
total = 0
with torch.no_grad():
for data in train_loader:
images, labels,_ = data
images = images.double()
images, labels = images.to("cuda"), labels.to("cuda")
avg, alpha,_ = where(images)
outputs = what(avg)
_, predicted = torch.max(outputs.data, 1)
total += labels.size(0)
correct += (predicted == labels).sum().item()
print('Accuracy of the network on the 3000 train images: %d %%' % ( 100 * correct / total))
a,b= full_analysis[0]
print(a)
cnt=1
for epoch, analysis_data in full_analysis:
analysis_data = np.array(analysis_data)
# print("="*20+"run ",cnt,"="*20)
plt.figure(figsize=(6,6))
plt.plot(np.arange(0,epoch+2,1),analysis_data[:,0],label="ftpt")
plt.plot(np.arange(0,epoch+2,1),analysis_data[:,1],label="ffpt")
plt.plot(np.arange(0,epoch+2,1),analysis_data[:,2],label="ftpf")
plt.plot(np.arange(0,epoch+2,1),analysis_data[:,3],label="ffpf")
plt.legend(loc='center left', bbox_to_anchor=(1, 0.5))
plt.title("Training trends for run "+str(cnt))
#plt.savefig("/content/drive/MyDrive/Research/alpha_analysis/100_300/k"+str(k)+"/"+"run"+str(cnt)+name+".png",bbox_inches="tight")
#plt.savefig("/content/drive/MyDrive/Research/alpha_analysis/100_300/k"+str(k)+"/"+"run"+str(cnt)+name+".pdf",bbox_inches="tight")
cnt+=1
# plt.figure(figsize=(6,6))
# plt.plot(np.arange(0,epoch+2,1),analysis_data[:,0],label="ftpt")
# plt.plot(np.arange(0,epoch+2,1),analysis_data[:,1],label="ffpt")
# plt.plot(np.arange(0,epoch+2,1),analysis_data[:,2],label="ftpf")
# plt.plot(np.arange(0,epoch+2,1),analysis_data[:,3],label="ffpf")
# plt.legend(loc='center left', bbox_to_anchor=(1, 0.5))
plt.plot(loss_curi)
np.mean(np.array(FTPT_analysis),axis=0)
FTPT_analysis.to_csv("type4_first_k_value_01_lr_001.csv",index=False)
```
```
FTPT_analysis
```
# Entropy
```
entropy_1 = r_centropy[11] # FTPT 100 ,FFPT 0 k value =0.01
loss_1 = r_loss[11]
ce_loss_1 = r_closs[11]
entropy_2 = r_centropy[16] # kvalue = 0 FTPT 99.96, FFPT 0.03
ce_loss_2 = r_closs[16]
# plt.plot(r_closs[1])
plt.plot(entropy_1,label = "entropy k_value=0.01")
plt.plot(loss_1,label = "overall k_value=0.01")
plt.plot(ce_loss_1,label = "ce kvalue = 0.01")
plt.plot(entropy_2,label = "entropy k_value = 0")
plt.plot(ce_loss_2,label = "ce k_value=0")
plt.legend(bbox_to_anchor=(1.05, 1), loc='upper left')
plt.savefig("second_layer.png")
```
| github_jupyter |
# TV Script Generation
In this project, you'll generate your own [Simpsons](https://en.wikipedia.org/wiki/The_Simpsons) TV scripts using RNNs. You'll be using part of the [Simpsons dataset](https://www.kaggle.com/wcukierski/the-simpsons-by-the-data) of scripts from 27 seasons. The Neural Network you'll build will generate a new TV script for a scene at [Moe's Tavern](https://simpsonswiki.com/wiki/Moe's_Tavern).
## Get the Data
The data is already provided for you. You'll be using a subset of the original dataset. It consists of only the scenes in Moe's Tavern. This doesn't include other versions of the tavern, like "Moe's Cavern", "Flaming Moe's", "Uncle Moe's Family Feed-Bag", etc..
```
"""
DON'T MODIFY ANYTHING IN THIS CELL
"""
import helper
data_dir = './data/simpsons/moes_tavern_lines.txt'
text = helper.load_data(data_dir)
# Ignore notice, since we don't use it for analysing the data
text = text[81:]
```
## Explore the Data
Play around with `view_sentence_range` to view different parts of the data.
```
view_sentence_range = (0, 10)
"""
DON'T MODIFY ANYTHING IN THIS CELL
"""
import numpy as np
print('Dataset Stats')
print('Roughly the number of unique words: {}'.format(len({word: None for word in text.split()})))
scenes = text.split('\n\n')
print('Number of scenes: {}'.format(len(scenes)))
sentence_count_scene = [scene.count('\n') for scene in scenes]
print('Average number of sentences in each scene: {}'.format(np.average(sentence_count_scene)))
sentences = [sentence for scene in scenes for sentence in scene.split('\n')]
print('Number of lines: {}'.format(len(sentences)))
word_count_sentence = [len(sentence.split()) for sentence in sentences]
print('Average number of words in each line: {}'.format(np.average(word_count_sentence)))
print()
print('The sentences {} to {}:'.format(*view_sentence_range))
print('\n'.join(text.split('\n')[view_sentence_range[0]:view_sentence_range[1]]))
```
## Implement Preprocessing Functions
The first thing to do to any dataset is preprocessing. Implement the following preprocessing functions below:
- Lookup Table
- Tokenize Punctuation
### Lookup Table
To create a word embedding, you first need to transform the words to ids. In this function, create two dictionaries:
- Dictionary to go from the words to an id, we'll call `vocab_to_int`
- Dictionary to go from the id to word, we'll call `int_to_vocab`
Return these dictionaries in the following tuple `(vocab_to_int, int_to_vocab)`
```
import numpy as np
import problem_unittests as tests
from collections import Counter
def create_lookup_tables(text):
"""
Create lookup tables for vocabulary
:param text: The text of tv scripts split into words
:return: A tuple of dicts (vocab_to_int, int_to_vocab)
"""
# TODO: Implement Function
# Create a counter to find unique words
words_count = Counter(text)
# Sort the words
sorted_words = sorted(words_count, key=words_count.get)
# Create vocab to int dictionary
vocab_to_int = { word: index for index, word in enumerate(sorted_words)}
# Create int to vocab dictionary
int_to_vocab = {index: word for word, index in vocab_to_int.items()}
return vocab_to_int, int_to_vocab
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
tests.test_create_lookup_tables(create_lookup_tables)
```
### Tokenize Punctuation
We'll be splitting the script into a word array using spaces as delimiters. However, punctuations like periods and exclamation marks make it hard for the neural network to distinguish between the word "bye" and "bye!".
Implement the function `token_lookup` to return a dict that will be used to tokenize symbols like "!" into "||Exclamation_Mark||". Create a dictionary for the following symbols where the symbol is the key and value is the token:
- Period ( . )
- Comma ( , )
- Quotation Mark ( " )
- Semicolon ( ; )
- Exclamation mark ( ! )
- Question mark ( ? )
- Left Parentheses ( ( )
- Right Parentheses ( ) )
- Dash ( -- )
- Return ( \n )
This dictionary will be used to token the symbols and add the delimiter (space) around it. This separates the symbols as it's own word, making it easier for the neural network to predict on the next word. Make sure you don't use a token that could be confused as a word. Instead of using the token "dash", try using something like "||dash||".
```
def token_lookup():
"""
Generate a dict to turn punctuation into a token.
:return: Tokenize dictionary where the key is the punctuation and the value is the token
"""
# TODO: Implement Function
token_dict = {'.': '||Period||',
',': '||Comma||',
'"': '||Quotation_Mark||',
';': '||Semicolon||',
'!': '||Exclamation_Mark||',
'?': '||Question_Mark||',
'(': '||Left_Parentheses||',
')': '||Right_Parentheses||',
'--': '||Dash||',
'\n': '||Return||'}
return token_dict
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
tests.test_tokenize(token_lookup)
```
## Preprocess all the data and save it
Running the code cell below will preprocess all the data and save it to file.
```
"""
DON'T MODIFY ANYTHING IN THIS CELL
"""
# Preprocess Training, Validation, and Testing Data
helper.preprocess_and_save_data(data_dir, token_lookup, create_lookup_tables)
```
# Check Point
This is your first checkpoint. If you ever decide to come back to this notebook or have to restart the notebook, you can start from here. The preprocessed data has been saved to disk.
```
"""
DON'T MODIFY ANYTHING IN THIS CELL
"""
import helper
import numpy as np
import problem_unittests as tests
int_text, vocab_to_int, int_to_vocab, token_dict = helper.load_preprocess()
```
## Build the Neural Network
You'll build the components necessary to build a RNN by implementing the following functions below:
- get_inputs
- get_init_cell
- get_embed
- build_rnn
- build_nn
- get_batches
### Check the Version of TensorFlow and Access to GPU
```
"""
DON'T MODIFY ANYTHING IN THIS CELL
"""
from distutils.version import LooseVersion
import warnings
import tensorflow as tf
# Check TensorFlow Version
assert LooseVersion(tf.__version__) >= LooseVersion('1.0'), 'Please use TensorFlow version 1.0 or newer'
print('TensorFlow Version: {}'.format(tf.__version__))
# Check for a GPU
if not tf.test.gpu_device_name():
warnings.warn('No GPU found. Please use a GPU to train your neural network.')
else:
print('Default GPU Device: {}'.format(tf.test.gpu_device_name()))
```
### Input
Implement the `get_inputs()` function to create TF Placeholders for the Neural Network. It should create the following placeholders:
- Input text placeholder named "input" using the [TF Placeholder](https://www.tensorflow.org/api_docs/python/tf/placeholder) `name` parameter.
- Targets placeholder
- Learning Rate placeholder
Return the placeholders in the following tuple `(Input, Targets, LearningRate)`
```
def get_inputs():
"""
Create TF Placeholders for input, targets, and learning rate.
:return: Tuple (input, targets, learning rate)
"""
# TODO: Implement Function
# Input placeholder
input = tf.placeholder(dtype=tf.int32, shape=[None, None], name='input')
# Targets placeholder
targets = tf.placeholder(dtype=tf.int32, shape=[None, None], name='targets')
# Learning rate placeholder
learning_rate = tf.placeholder(dtype=tf.float32, name='learning_rate')
return input, targets, learning_rate
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
tests.test_get_inputs(get_inputs)
```
### Build RNN Cell and Initialize
Stack one or more [`BasicLSTMCells`](https://www.tensorflow.org/api_docs/python/tf/contrib/rnn/BasicLSTMCell) in a [`MultiRNNCell`](https://www.tensorflow.org/api_docs/python/tf/contrib/rnn/MultiRNNCell).
- The Rnn size should be set using `rnn_size`
- Initalize Cell State using the MultiRNNCell's [`zero_state()`](https://www.tensorflow.org/api_docs/python/tf/contrib/rnn/MultiRNNCell#zero_state) function
- Apply the name "initial_state" to the initial state using [`tf.identity()`](https://www.tensorflow.org/api_docs/python/tf/identity)
Return the cell and initial state in the following tuple `(Cell, InitialState)`
```
def get_init_cell(batch_size, rnn_size):
"""
Create an RNN Cell and initialize it.
:param batch_size: Size of batches
:param rnn_size: Size of RNNs
:return: Tuple (cell, initialize state)
"""
# TODO: Implement Function
# Crete a basic LSTM cell (reason to use reuse param: https://github.com/tensorflow/tensorflow/issues/8191)
# Create a single MultiRNNCell
multi_cell = tf.contrib.rnn.MultiRNNCell([get_lstm_cell(rnn_size) for _ in range(2)])
#print((batch_size.shape))
# Initialize multicell state
initial_state = multi_cell.zero_state(batch_size, dtype=tf.float32)
# Provide a name for initial state
initial_state = tf.identity(initial_state, name='initial_state')
return multi_cell, initial_state
def get_lstm_cell(lstm_size):
return tf.contrib.rnn.BasicLSTMCell(num_units=lstm_size)
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
tests.test_get_init_cell(get_init_cell)
```
### Word Embedding
Apply embedding to `input_data` using TensorFlow. Return the embedded sequence.
```
def get_embed(input_data, vocab_size, embed_dim):
"""
Create embedding for <input_data>.
:param input_data: TF placeholder for text input.
:param vocab_size: Number of words in vocabulary.
:param embed_dim: Number of embedding dimensions
:return: Embedded input.
"""
# TODO: Implement Function
# Create embedding matrix(weight matrix) for the embedding layer
embeddings = tf.Variable(tf.random_uniform(shape=(vocab_size, embed_dim), minval= -0.1, maxval=0.1, dtype=tf.float32,
name='embeddings'))
# Create the lookup table using tf.nn.embedding_lookup method
embed = tf.nn.embedding_lookup(embeddings, input_data)
return embed
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
tests.test_get_embed(get_embed)
```
### Build RNN
You created a RNN Cell in the `get_init_cell()` function. Time to use the cell to create a RNN.
- Build the RNN using the [`tf.nn.dynamic_rnn()`](https://www.tensorflow.org/api_docs/python/tf/nn/dynamic_rnn)
- Apply the name "final_state" to the final state using [`tf.identity()`](https://www.tensorflow.org/api_docs/python/tf/identity)
Return the outputs and final_state state in the following tuple `(Outputs, FinalState)`
```
def build_rnn(cell, inputs):
"""
Create a RNN using a RNN Cell
:param cell: RNN Cell
:param inputs: Input text data
:return: Tuple (Outputs, Final State)
"""
# TODO: Implement Function
# Build the RNN using method tf.nn.dynamic_rnn()
outputs, final_state = tf.nn.dynamic_rnn(cell, inputs, dtype=tf.float32)
# Provide a name for the state
final_state = tf.identity(final_state, name='final_state')
return outputs, final_state
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
tests.test_build_rnn(build_rnn)
```
### Build the Neural Network
Apply the functions you implemented above to:
- Apply embedding to `input_data` using your `get_embed(input_data, vocab_size, embed_dim)` function.
- Build RNN using `cell` and your `build_rnn(cell, inputs)` function.
- Apply a fully connected layer with a linear activation and `vocab_size` as the number of outputs.
Return the logits and final state in the following tuple (Logits, FinalState)
```
def build_nn(cell, rnn_size, input_data, vocab_size, embed_dim):
"""
Build part of the neural network
:param cell: RNN cell
:param rnn_size: Size of rnns
:param input_data: Input data
:param vocab_size: Vocabulary size
:param embed_dim: Number of embedding dimensions
:return: Tuple (Logits, FinalState)
"""
# TODO: Implement Function
# Get the embed look up table
embed_look_up = get_embed(input_data=input_data, vocab_size=vocab_size, embed_dim=embed_dim)
# Build the RNN
outputs, final_state = build_rnn(cell, embed_look_up)
# Apply a fully connected layer with linear activation and vocab_size as the number of output
logits = tf.contrib.layers.fully_connected(outputs, vocab_size,
weights_initializer=tf.truncated_normal_initializer(stddev=0.1)
,activation_fn=None)
#print(logits.shape)
return logits, final_state
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
tests.test_build_nn(build_nn)
```
### Batches
Implement `get_batches` to create batches of input and targets using `int_text`. The batches should be a Numpy array with the shape `(number of batches, 2, batch size, sequence length)`. Each batch contains two elements:
- The first element is a single batch of **input** with the shape `[batch size, sequence length]`
- The second element is a single batch of **targets** with the shape `[batch size, sequence length]`
If you can't fill the last batch with enough data, drop the last batch.
For exmple, `get_batches([1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20], 3, 2)` would return a Numpy array of the following:
```
[
# First Batch
[
# Batch of Input
[[ 1 2], [ 7 8], [13 14]]
# Batch of targets
[[ 2 3], [ 8 9], [14 15]]
]
# Second Batch
[
# Batch of Input
[[ 3 4], [ 9 10], [15 16]]
# Batch of targets
[[ 4 5], [10 11], [16 17]]
]
# Third Batch
[
# Batch of Input
[[ 5 6], [11 12], [17 18]]
# Batch of targets
[[ 6 7], [12 13], [18 1]]
]
]
```
Notice that the last target value in the last batch is the first input value of the first batch. In this case, `1`. This is a common technique used when creating sequence batches, although it is rather unintuitive.
```
def get_batches(int_text, batch_size, seq_length):
"""
Return batches of input and target
:param int_text: Text with the words replaced by their ids
:param batch_size: The size of batch
:param seq_length: The length of sequence
:return: Batches as a Numpy array
"""
# TODO: Implement Function
n_batches = int(len(int_text) / (batch_size * seq_length))
# Drop the last few characters to make only full batches
xdata = np.array(int_text[: n_batches * batch_size * seq_length])
ydata = np.array(int_text[1: n_batches * batch_size * seq_length + 1])
ydata[-1] = xdata[0]
x_batches = np.split(xdata.reshape(batch_size, -1), n_batches, 1)
y_batches = np.split(ydata.reshape(batch_size, -1), n_batches, 1)
return np.array(list(zip(x_batches, y_batches)))
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
tests.test_get_batches(get_batches)
```
## Neural Network Training
### Hyperparameters
Tune the following parameters:
- Set `num_epochs` to the number of epochs.
- Set `batch_size` to the batch size.
- Set `rnn_size` to the size of the RNNs.
- Set `embed_dim` to the size of the embedding.
- Set `seq_length` to the length of sequence.
- Set `learning_rate` to the learning rate.
- Set `show_every_n_batches` to the number of batches the neural network should print progress.
```
# Number of Epochs
num_epochs = 50
# Batch Size
batch_size = 256
# RNN Size
rnn_size = 256
# Embedding Dimension Size
embed_dim = 300
# Sequence Length
seq_length = 15
# Learning Rate
learning_rate = 0.01
# Show stats for every n number of batches
show_every_n_batches = 5
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
save_dir = './save'
```
### Build the Graph
Build the graph using the neural network you implemented.
```
"""
DON'T MODIFY ANYTHING IN THIS CELL
"""
from tensorflow.contrib import seq2seq
train_graph = tf.Graph()
with train_graph.as_default():
vocab_size = len(int_to_vocab)
input_text, targets, lr = get_inputs()
input_data_shape = tf.shape(input_text)
cell, initial_state = get_init_cell(input_data_shape[0], rnn_size)
logits, final_state = build_nn(cell, rnn_size, input_text, vocab_size, embed_dim)
# Probabilities for generating words
probs = tf.nn.softmax(logits, name='probs')
print(probs.shape)
print(logits.shape)
# Loss function
cost = seq2seq.sequence_loss(
logits,
targets,
tf.ones([input_data_shape[0], input_data_shape[1]]))
# Optimizer
optimizer = tf.train.AdamOptimizer(lr)
# Gradient Clipping
gradients = optimizer.compute_gradients(cost)
capped_gradients = [(tf.clip_by_value(grad, -1., 1.), var) for grad, var in gradients if grad is not None]
train_op = optimizer.apply_gradients(capped_gradients)
```
## Train
Train the neural network on the preprocessed data. If you have a hard time getting a good loss, check the [forms](https://discussions.udacity.com/) to see if anyone is having the same problem.
```
"""
DON'T MODIFY ANYTHING IN THIS CELL
"""
batches = get_batches(int_text, batch_size, seq_length)
with tf.Session(graph=train_graph) as sess:
sess.run(tf.global_variables_initializer())
for epoch_i in range(num_epochs):
state = sess.run(initial_state, {input_text: batches[0][0]})
for batch_i, (x, y) in enumerate(batches):
#print("x = ", x)
#print("y = ", y)
feed = {
input_text: x,
targets: y,
initial_state: state,
lr: learning_rate}
train_loss, state, _ = sess.run([cost, final_state, train_op], feed)
# Show every <show_every_n_batches> batches
if (epoch_i * len(batches) + batch_i) % show_every_n_batches == 0:
print('Epoch {:>3} Batch {:>4}/{} train_loss = {:.3f}'.format(
epoch_i,
batch_i,
len(batches),
train_loss))
# Save Model
saver = tf.train.Saver()
saver.save(sess, save_dir)
print('Model Trained and Saved')
```
## Save Parameters
Save `seq_length` and `save_dir` for generating a new TV script.
```
"""
DON'T MODIFY ANYTHING IN THIS CELL
"""
# Save parameters for checkpoint
helper.save_params((seq_length, save_dir))
```
# Checkpoint
```
"""
DON'T MODIFY ANYTHING IN THIS CELL
"""
import tensorflow as tf
import numpy as np
import helper
import problem_unittests as tests
_, vocab_to_int, int_to_vocab, token_dict = helper.load_preprocess()
seq_length, load_dir = helper.load_params()
```
## Implement Generate Functions
### Get Tensors
Get tensors from `loaded_graph` using the function [`get_tensor_by_name()`](https://www.tensorflow.org/api_docs/python/tf/Graph#get_tensor_by_name). Get the tensors using the following names:
- "input:0"
- "initial_state:0"
- "final_state:0"
- "probs:0"
Return the tensors in the following tuple `(InputTensor, InitialStateTensor, FinalStateTensor, ProbsTensor)`
```
def get_tensors(loaded_graph):
"""
Get input, initial state, final state, and probabilities tensor from <loaded_graph>
:param loaded_graph: TensorFlow graph loaded from file
:return: Tuple (InputTensor, InitialStateTensor, FinalStateTensor, ProbsTensor)
"""
# TODO: Implement Function
input_tensor = loaded_graph.get_tensor_by_name(name='input:0')
initial_state_tensor = loaded_graph.get_tensor_by_name(name='initial_state:0')
final_state_tensor = loaded_graph.get_tensor_by_name(name='final_state:0')
probs_tensor = loaded_graph.get_tensor_by_name(name='probs:0')
return input_tensor, initial_state_tensor, final_state_tensor, probs_tensor
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
tests.test_get_tensors(get_tensors)
```
### Choose Word
Implement the `pick_word()` function to select the next word using `probabilities`.
```
def pick_word(probabilities, int_to_vocab):
"""
Pick the next word in the generated text
:param probabilities: Probabilites of the next word
:param int_to_vocab: Dictionary of word ids as the keys and words as the values
:return: String of the predicted word
"""
# TODO: Implement Function
#print(probabilities.shape[0])
#print(probabilities)
next_word = np.random.choice(len(probabilities), p=probabilities)
next_word = str(int_to_vocab[next_word])
return next_word
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
tests.test_pick_word(pick_word)
```
## Generate TV Script
This will generate the TV script for you. Set `gen_length` to the length of TV script you want to generate.
```
gen_length = 200
# homer_simpson, moe_szyslak, or Barney_Gumble
prime_word = 'moe_szyslak'
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
loaded_graph = tf.Graph()
with tf.Session(graph=loaded_graph) as sess:
# Load saved model
loader = tf.train.import_meta_graph(load_dir + '.meta')
loader.restore(sess, load_dir)
# Get Tensors from loaded model
input_text, initial_state, final_state, probs = get_tensors(loaded_graph)
# Sentences generation setup
gen_sentences = [prime_word + ':']
prev_state = sess.run(initial_state, {input_text: np.array([[1]])})
# Generate sentences
for n in range(gen_length):
# Dynamic Input
dyn_input = [[vocab_to_int[word] for word in gen_sentences[-seq_length:]]]
dyn_seq_length = len(dyn_input[0])
# debug
#print(len(dyn_input[0]))
# Get Prediction
probabilities, prev_state = sess.run(
[probs, final_state],
{input_text: dyn_input, initial_state: prev_state})
# debug
#print(probabilities.shape)
#print(type(probabilities))
#print(dyn_seq_length-1)
temp = np.squeeze(probabilities, axis=0)
#print(temp.shape)
temp = temp[dyn_seq_length - 1]
#print(temp.shape)
pred_word = pick_word(temp, int_to_vocab)
gen_sentences.append(pred_word)
# Remove tokens
tv_script = ' '.join(gen_sentences)
for key, token in token_dict.items():
ending = ' ' if key in ['\n', '(', '"'] else ''
tv_script = tv_script.replace(' ' + token.lower(), key)
tv_script = tv_script.replace('\n ', '\n')
tv_script = tv_script.replace('( ', '(')
print(tv_script)
```
# The TV Script is Nonsensical
It's ok if the TV script doesn't make any sense. We trained on less than a megabyte of text. In order to get good results, you'll have to use a smaller vocabulary or get more data. Luckly there's more data! As we mentioned in the begging of this project, this is a subset of [another dataset](https://www.kaggle.com/wcukierski/the-simpsons-by-the-data). We didn't have you train on all the data, because that would take too long. However, you are free to train your neural network on all the data. After you complete the project, of course.
# Submitting This Project
When submitting this project, make sure to run all the cells before saving the notebook. Save the notebook file as "dlnd_tv_script_generation.ipynb" and save it as a HTML file under "File" -> "Download as". Include the "helper.py" and "problem_unittests.py" files in your submission.
| github_jupyter |
# Parsing Inputs
In the chapter on [Grammars](Grammars.ipynb), we discussed how grammars can be
used to represent various languages. We also saw how grammars can be used to
generate strings of the corresponding language. Grammars can also perform the
reverse. That is, given a string, one can decompose the string into its
constituent parts that correspond to the parts of grammar used to generate it
– the _derivation tree_ of that string. These parts (and parts from other similar
strings) can later be recombined using the same grammar to produce new strings.
In this chapter, we use grammars to parse and decompose a given set of valid seed inputs into their corresponding derivation trees. This structural representation allows us to mutate, crossover, and recombine their parts in order to generate new valid, slightly changed inputs (i.e., fuzz)
```
from bookutils import YouTubeVideo
YouTubeVideo('2yS9EfBEirE')
```
**Prerequisites**
* You should have read the [chapter on grammars](Grammars.ipynb).
* An understanding of derivation trees from the [chapter on grammar fuzzer](GrammarFuzzer.ipynb)
is also required.
## Synopsis
<!-- Automatically generated. Do not edit. -->
To [use the code provided in this chapter](Importing.ipynb), write
```python
>>> from fuzzingbook.Parser import <identifier>
```
and then make use of the following features.
This chapter introduces `Parser` classes, parsing a string into a _derivation tree_ as introduced in the [chapter on efficient grammar fuzzing](GrammarFuzzer.ipynb). Two important parser classes are provided:
* [Parsing Expression Grammar parsers](#Parsing-Expression-Grammars) (`PEGParser`). These are very efficient, but limited to specific grammar structure. Notably, the alternatives represent *ordered choice*. That is, rather than choosing all rules that can potentially match, we stop at the first match that succeed.
* [Earley parsers](#Parsing-Context-Free-Grammars) (`EarleyParser`). These accept any kind of context-free grammars, and explore all parsing alternatives (if any).
Using any of these is fairly easy, though. First, instantiate them with a grammar:
```python
>>> from Grammars import US_PHONE_GRAMMAR
>>> us_phone_parser = EarleyParser(US_PHONE_GRAMMAR)
```
Then, use the `parse()` method to retrieve a list of possible derivation trees:
```python
>>> trees = us_phone_parser.parse("(555)987-6543")
>>> tree = list(trees)[0]
>>> display_tree(tree)
```

These derivation trees can then be used for test generation, notably for mutating and recombining existing inputs.

```
import bookutils
from typing import Dict, List, Tuple, Collection, Set, Iterable, Generator, cast
from Fuzzer import Fuzzer # minor dependendcy
from Grammars import EXPR_GRAMMAR, START_SYMBOL, RE_NONTERMINAL
from Grammars import is_valid_grammar, syntax_diagram, Grammar
from GrammarFuzzer import GrammarFuzzer, display_tree, tree_to_string, dot_escape
from GrammarFuzzer import DerivationTree
from ExpectError import ExpectError
from IPython.display import display
from Timer import Timer
```
## Why Parsing for Fuzzing?
Why would one want to parse existing inputs in order to fuzz? Let us illustrate the problem with an example. Here is a simple program that accepts a CSV file of vehicle details and processes this information.
```
def process_inventory(inventory):
res = []
for vehicle in inventory.split('\n'):
ret = process_vehicle(vehicle)
res.extend(ret)
return '\n'.join(res)
```
The CSV file contains details of one vehicle per line. Each row is processed in `process_vehicle()`.
```
def process_vehicle(vehicle):
year, kind, company, model, *_ = vehicle.split(',')
if kind == 'van':
return process_van(year, company, model)
elif kind == 'car':
return process_car(year, company, model)
else:
raise Exception('Invalid entry')
```
Depending on the kind of vehicle, the processing changes.
```
def process_van(year, company, model):
res = ["We have a %s %s van from %s vintage." % (company, model, year)]
iyear = int(year)
if iyear > 2010:
res.append("It is a recent model!")
else:
res.append("It is an old but reliable model!")
return res
def process_car(year, company, model):
res = ["We have a %s %s car from %s vintage." % (company, model, year)]
iyear = int(year)
if iyear > 2016:
res.append("It is a recent model!")
else:
res.append("It is an old but reliable model!")
return res
```
Here is a sample of inputs that the `process_inventory()` accepts.
```
mystring = """\
1997,van,Ford,E350
2000,car,Mercury,Cougar\
"""
print(process_inventory(mystring))
```
Let us try to fuzz this program. Given that the `process_inventory()` takes a CSV file, we can write a simple grammar for generating comma separated values, and generate the required CSV rows. For convenience, we fuzz `process_vehicle()` directly.
```
import string
CSV_GRAMMAR: Grammar = {
'<start>': ['<csvline>'],
'<csvline>': ['<items>'],
'<items>': ['<item>,<items>', '<item>'],
'<item>': ['<letters>'],
'<letters>': ['<letter><letters>', '<letter>'],
'<letter>': list(string.ascii_letters + string.digits + string.punctuation + ' \t\n')
}
```
We need some infrastructure first for viewing the grammar.
```
syntax_diagram(CSV_GRAMMAR)
```
We generate `1000` values, and evaluate the `process_vehicle()` with each.
```
gf = GrammarFuzzer(CSV_GRAMMAR, min_nonterminals=4)
trials = 1000
valid: List[str] = []
time = 0
for i in range(trials):
with Timer() as t:
vehicle_info = gf.fuzz()
try:
process_vehicle(vehicle_info)
valid.append(vehicle_info)
except:
pass
time += t.elapsed_time()
print("%d valid strings, that is GrammarFuzzer generated %f%% valid entries from %d inputs" %
(len(valid), len(valid) * 100.0 / trials, trials))
print("Total time of %f seconds" % time)
```
This is obviously not working. But why?
```
gf = GrammarFuzzer(CSV_GRAMMAR, min_nonterminals=4)
trials = 10
time = 0
for i in range(trials):
vehicle_info = gf.fuzz()
try:
print(repr(vehicle_info), end="")
process_vehicle(vehicle_info)
except Exception as e:
print("\t", e)
else:
print()
```
None of the entries will get through unless the fuzzer can produce either `van` or `car`.
Indeed, the reason is that the grammar itself does not capture the complete information about the format. So here is another idea. We modify the `GrammarFuzzer` to know a bit about our format.
```
import copy
import random
class PooledGrammarFuzzer(GrammarFuzzer):
def __init__(self, *args, **kwargs):
super().__init__(*args, **kwargs)
self._node_cache = {}
def update_cache(self, key, values):
self._node_cache[key] = values
def expand_node_randomly(self, node):
(symbol, children) = node
assert children is None
if symbol in self._node_cache:
if random.randint(0, 1) == 1:
return super().expand_node_randomly(node)
return copy.deepcopy(random.choice(self._node_cache[symbol]))
return super().expand_node_randomly(node)
```
Let us try again!
```
gf = PooledGrammarFuzzer(CSV_GRAMMAR, min_nonterminals=4)
gf.update_cache('<item>', [
('<item>', [('car', [])]),
('<item>', [('van', [])]),
])
trials = 10
time = 0
for i in range(trials):
vehicle_info = gf.fuzz()
try:
print(repr(vehicle_info), end="")
process_vehicle(vehicle_info)
except Exception as e:
print("\t", e)
else:
print()
```
At least we are getting somewhere! It would be really nice if _we could incorporate what we know about the sample data in our fuzzer._ In fact, it would be nice if we could _extract_ the template and valid values from samples, and use them in our fuzzing. How do we do that? The quick answer to this question is: Use a *parser*.
## Using a Parser
Generally speaking, a _parser_ is the part of a a program that processes (structured) input. The parsers we discuss in this chapter transform an input string into a _derivation tree_ (discussed in the [chapter on efficient grammar fuzzing](GrammarFuzzer.ipynb)). From a user's perspective, all it takes to parse an input is two steps:
1. Initialize the parser with a grammar, as in
```
parser = Parser(grammar)
```
2. Using the parser to retrieve a list of derivation trees:
```python
trees = parser.parse(input)
```
Once we have parsed a tree, we can use it just as the derivation trees produced from grammar fuzzing.
We discuss a number of such parsers, in particular
* [parsing expression grammar parsers](#Parsing-Expression-Grammars) (`PEGParser`), which are very efficient, but limited to specific grammar structure; and
* [Earley parsers](#Parsing-Context-Free-Grammars) (`EarleyParser`), which accept any kind of context-free grammars.
If you just want to _use_ parsers (say, because your main focus is testing), you can just stop here and move on [to the next chapter](LangFuzzer.ipynb), where we learn how to make use of parsed inputs to mutate and recombine them. If you want to _understand_ how parsers work, though, this chapter is right for you.
## An Ad Hoc Parser
As we saw in the previous section, programmers often have to extract parts of data that obey certain rules. For example, for *CSV* files, each element in a row is separated by *commas*, and multiple raws are used to store the data.
To extract the information, we write an ad hoc parser `simple_parse_csv()`.
```
def simple_parse_csv(mystring: str) -> DerivationTree:
children: List[DerivationTree] = []
tree = (START_SYMBOL, children)
for i, line in enumerate(mystring.split('\n')):
children.append(("record %d" % i, [(cell, [])
for cell in line.split(',')]))
return tree
```
We also change the default orientation of the graph to *left to right* rather than *top to bottom* for easier viewing using `lr_graph()`.
```
def lr_graph(dot):
dot.attr('node', shape='plain')
dot.graph_attr['rankdir'] = 'LR'
```
The `display_tree()` shows the structure of our CSV file after parsing.
```
tree = simple_parse_csv(mystring)
display_tree(tree, graph_attr=lr_graph)
```
This is of course simple. What if we encounter slightly more complexity? Again, another example from the Wikipedia.
```
mystring = '''\
1997,Ford,E350,"ac, abs, moon",3000.00\
'''
print(mystring)
```
We define a new annotation method `highlight_node()` to mark the nodes that are interesting.
```
def highlight_node(predicate):
def hl_node(dot, nid, symbol, ann):
if predicate(dot, nid, symbol, ann):
dot.node(repr(nid), dot_escape(symbol), fontcolor='red')
else:
dot.node(repr(nid), dot_escape(symbol))
return hl_node
```
Using `highlight_node()` we can highlight particular nodes that we were wrongly parsed.
```
tree = simple_parse_csv(mystring)
bad_nodes = {5, 6, 7, 12, 13, 20, 22, 23, 24, 25}
def hl_predicate(_d, nid, _s, _a): return nid in bad_nodes
highlight_err_node = highlight_node(hl_predicate)
display_tree(tree, log=False, node_attr=highlight_err_node,
graph_attr=lr_graph)
```
The marked nodes indicate where our parsing went wrong. We can of course extend our parser to understand quotes. First we define some of the helper functions `parse_quote()`, `find_comma()` and `comma_split()`
```
def parse_quote(string, i):
v = string[i + 1:].find('"')
return v + i + 1 if v >= 0 else -1
def find_comma(string, i):
slen = len(string)
while i < slen:
if string[i] == '"':
i = parse_quote(string, i)
if i == -1:
return -1
if string[i] == ',':
return i
i += 1
return -1
def comma_split(string):
slen = len(string)
i = 0
while i < slen:
c = find_comma(string, i)
if c == -1:
yield string[i:]
return
else:
yield string[i:c]
i = c + 1
```
We can update our `parse_csv()` procedure to use our advanced quote parser.
```
def parse_csv(mystring):
children = []
tree = (START_SYMBOL, children)
for i, line in enumerate(mystring.split('\n')):
children.append(("record %d" % i, [(cell, [])
for cell in comma_split(line)]))
return tree
```
Our new `parse_csv()` can now handle quotes correctly.
```
tree = parse_csv(mystring)
display_tree(tree, graph_attr=lr_graph)
```
That of course does not survive long:
```
mystring = '''\
1999,Chevy,"Venture \\"Extended Edition, Very Large\\"",,5000.00\
'''
print(mystring)
```
A few embedded quotes are sufficient to confuse our parser again.
```
tree = parse_csv(mystring)
bad_nodes = {4, 5}
display_tree(tree, node_attr=highlight_err_node, graph_attr=lr_graph)
```
Here is another record from that CSV file:
```
mystring = '''\
1996,Jeep,Grand Cherokee,"MUST SELL!
air, moon roof, loaded",4799.00
'''
print(mystring)
tree = parse_csv(mystring)
bad_nodes = {5, 6, 7, 8, 9, 10}
display_tree(tree, node_attr=highlight_err_node, graph_attr=lr_graph)
```
Fixing this would require modifying both inner `parse_quote()` and the outer `parse_csv()` procedures. We note that each of these features actually documented in the CSV [RFC 4180](https://tools.ietf.org/html/rfc4180)
Indeed, each additional improvement falls apart even with a little extra complexity. The problem becomes severe when one encounters recursive expressions. For example, JSON is a common alternative to CSV files for saving data. Similarly, one may have to parse data from an HTML table instead of a CSV file if one is getting the data from the web.
One might be tempted to fix it with a little more ad hoc parsing, with a bit of *regular expressions* thrown in. However, that is the [path to insanity](https://stackoverflow.com/a/1732454).
It is here that _formal parsers_ shine. The main idea is that, any given set of strings belong to a language, and these languages can be specified by their grammars (as we saw in the [chapter on grammars](Grammars.ipynb)). The great thing about grammars is that they can be _composed_. That is, one can introduce finer and finer details into an internal structure without affecting the external structure, and similarly, one can change the external structure without much impact on the internal structure.
## Grammars in Parsing
We briefly describe grammars in the context of parsing.
### Excursion: Grammars and Derivation Trees
A grammar, as you have read from the [chapter on grammars](Grammars.ipynb) is a set of _rules_ that explain how the start symbol can be expanded. Each rule has a name, also called a _nonterminal_, and a set of _alternative choices_ in how the nonterminal can be expanded.
```
A1_GRAMMAR: Grammar = {
"<start>": ["<expr>"],
"<expr>": ["<expr>+<expr>", "<expr>-<expr>", "<integer>"],
"<integer>": ["<digit><integer>", "<digit>"],
"<digit>": ["0", "1", "2", "3", "4", "5", "6", "7", "8", "9"]
}
syntax_diagram(A1_GRAMMAR)
```
In the above expression, the rule `<expr> : [<expr>+<expr>,<expr>-<expr>,<integer>]` corresponds to how the nonterminal `<expr>` might be expanded. The expression `<expr>+<expr>` corresponds to one of the alternative choices. We call this an _alternative_ expansion for the nonterminal `<expr>`. Finally, in an expression `<expr>+<expr>`, each of `<expr>`, `+`, and `<expr>` are _symbols_ in that expansion. A symbol could be either a nonterminal or a terminal symbol based on whether its expansion is available in the grammar.
Here is a string that represents an arithmetic expression that we would like to parse, which is specified by the grammar above:
```
mystring = '1+2'
```
The _derivation tree_ for our expression from this grammar is given by:
```
tree = ('<start>', [('<expr>',
[('<expr>', [('<integer>', [('<digit>', [('1', [])])])]),
('+', []),
('<expr>', [('<integer>', [('<digit>', [('2',
[])])])])])])
assert mystring == tree_to_string(tree)
display_tree(tree)
```
While a grammar can be used to specify a given language, there could be multiple
grammars that correspond to the same language. For example, here is another
grammar to describe the same addition expression.
```
A2_GRAMMAR: Grammar = {
"<start>": ["<expr>"],
"<expr>": ["<integer><expr_>"],
"<expr_>": ["+<expr>", "-<expr>", ""],
"<integer>": ["<digit><integer_>"],
"<integer_>": ["<integer>", ""],
"<digit>": ["0", "1", "2", "3", "4", "5", "6", "7", "8", "9"]
}
syntax_diagram(A2_GRAMMAR)
```
The corresponding derivation tree is given by:
```
tree = ('<start>', [('<expr>', [('<integer>', [('<digit>', [('1', [])]),
('<integer_>', [])]),
('<expr_>', [('+', []),
('<expr>',
[('<integer>',
[('<digit>', [('2', [])]),
('<integer_>', [])]),
('<expr_>', [])])])])])
assert mystring == tree_to_string(tree)
display_tree(tree)
```
Indeed, there could be different classes of grammars that
describe the same language. For example, the first grammar `A1_GRAMMAR`
is a grammar that sports both _right_ and _left_ recursion, while the
second grammar `A2_GRAMMAR` does not have left recursion in the
nonterminals in any of its productions, but contains _epsilon_ productions.
(An epsilon production is a production that has empty string in its right
hand side.)
### End of Excursion
### Excursion: Recursion
You would have noticed that we reuse the term `<expr>` in its own definition. Using the same nonterminal in its own definition is called *recursion*. There are two specific kinds of recursion one should be aware of in parsing, as we see in the next section.
#### Recursion
A grammar is _left recursive_ if any of its nonterminals are left recursive,
and a nonterminal is directly left-recursive if the left-most symbol of
any of its productions is itself.
```
LR_GRAMMAR: Grammar = {
'<start>': ['<A>'],
'<A>': ['<A>a', ''],
}
syntax_diagram(LR_GRAMMAR)
mystring = 'aaaaaa'
display_tree(
('<start>', [('<A>', [('<A>', [('<A>', []), ('a', [])]), ('a', [])]),
('a', [])]))
```
A grammar is indirectly left-recursive if any
of the left-most symbols can be expanded using their definitions to
produce the nonterminal as the left-most symbol of the expansion. The left
recursion is called a _hidden-left-recursion_ if during the series of
expansions of a nonterminal, one reaches a rule where the rule contains
the same nonterminal after a prefix of other symbols, and these symbols can
derive the empty string. For example, in `A1_GRAMMAR`, `<integer>` will be
considered hidden-left recursive if `<digit>` could derive an empty string.
Right recursive grammars are defined similarly.
Below is the derivation tree for the right recursive grammar that represents the same
language as that of `LR_GRAMMAR`.
```
RR_GRAMMAR: Grammar = {
'<start>': ['<A>'],
'<A>': ['a<A>', ''],
}
syntax_diagram(RR_GRAMMAR)
display_tree(('<start>', [('<A>', [
('a', []), ('<A>', [('a', []), ('<A>', [('a', []), ('<A>', [])])])])]
))
```
#### Ambiguity
To complicate matters further, there could be
multiple derivation trees – also called _parses_ – corresponding to the
same string from the same grammar. For example, a string `1+2+3` can be parsed
in two ways as we see below using the `A1_GRAMMAR`
```
mystring = '1+2+3'
tree = ('<start>',
[('<expr>',
[('<expr>', [('<expr>', [('<integer>', [('<digit>', [('1', [])])])]),
('+', []),
('<expr>', [('<integer>',
[('<digit>', [('2', [])])])])]), ('+', []),
('<expr>', [('<integer>', [('<digit>', [('3', [])])])])])])
assert mystring == tree_to_string(tree)
display_tree(tree)
tree = ('<start>',
[('<expr>', [('<expr>', [('<integer>', [('<digit>', [('1', [])])])]),
('+', []),
('<expr>',
[('<expr>', [('<integer>', [('<digit>', [('2', [])])])]),
('+', []),
('<expr>', [('<integer>', [('<digit>', [('3',
[])])])])])])])
assert tree_to_string(tree) == mystring
display_tree(tree)
```
There are many ways to resolve ambiguities. One approach taken by *Parsing Expression Grammars* explained in the next section is to specify a particular order of resolution, and choose the first one. Another approach is to simply return all possible derivation trees, which is the approach taken by *Earley parser* we develop later.
### End of Excursion
## A Parser Class
Next, we develop different parsers. To do that, we define a minimal interface for parsing that is obeyed by all parsers. There are two approaches to parsing a string using a grammar.
1. The traditional approach is to use a *lexer* (also called a *tokenizer* or a *scanner*) to first tokenize the incoming string, and feed the grammar one token at a time. The lexer is typically a smaller parser that accepts a *regular language*. The advantage of this approach is that the grammar used by the parser can eschew the details of tokenization. Further, one gets a shallow derivation tree at the end of the parsing which can be directly used for generating the *Abstract Syntax Tree*.
2. The second approach is to use a tree pruner after the complete parse. With this approach, one uses a grammar that incorporates complete details of the syntax. Next, the nodes corresponding to tokens are pruned and replaced with their corresponding strings as leaf nodes. The utility of this approach is that the parser is more powerful, and further there is no artificial distinction between *lexing* and *parsing*.
In this chapter, we use the second approach. This approach is implemented in the `prune_tree` method.
The *Parser* class we define below provides the minimal interface. The main methods that need to be implemented by the classes implementing this interface are `parse_prefix` and `parse`. The `parse_prefix` returns a tuple, which contains the index until which parsing was completed successfully, and the parse forest until that index. The method `parse` returns a list of derivation trees if the parse was successful.
```
class Parser:
"""Base class for parsing."""
def __init__(self, grammar: Grammar, *,
start_symbol: str = START_SYMBOL,
log: bool = False,
coalesce: bool = True,
tokens: Set[str] = set()) -> None:
"""Constructor.
`grammar` is the grammar to be used for parsing.
Keyword arguments:
`start_symbol` is the start symbol (default: '<start>').
`log` enables logging (default: False).
`coalesce` defines if tokens should be coalesced (default: True).
`tokens`, if set, is a set of tokens to be used."""
self._grammar = grammar
self._start_symbol = start_symbol
self.log = log
self.coalesce_tokens = coalesce
self.tokens = tokens
def grammar(self) -> Grammar:
"""Return the grammar of this parser."""
return self._grammar
def start_symbol(self) -> str:
"""Return the start symbol of this parser."""
return self._start_symbol
def parse_prefix(self, text: str) -> Tuple[int, Iterable[DerivationTree]]:
"""Return pair (cursor, forest) for longest prefix of text.
To be defined in subclasses."""
raise NotImplementedError
def parse(self, text: str) -> Iterable[DerivationTree]:
"""Parse `text` using the grammar.
Return an iterable of parse trees."""
cursor, forest = self.parse_prefix(text)
if cursor < len(text):
raise SyntaxError("at " + repr(text[cursor:]))
return [self.prune_tree(tree) for tree in forest]
def parse_on(self, text: str, start_symbol: str) -> Generator:
old_start = self._start_symbol
try:
self._start_symbol = start_symbol
yield from self.parse(text)
finally:
self._start_symbol = old_start
def coalesce(self, children: List[DerivationTree]) -> List[DerivationTree]:
last = ''
new_lst: List[DerivationTree] = []
for cn, cc in children:
if cn not in self._grammar:
last += cn
else:
if last:
new_lst.append((last, []))
last = ''
new_lst.append((cn, cc))
if last:
new_lst.append((last, []))
return new_lst
def prune_tree(self, tree: DerivationTree) -> DerivationTree:
name, children = tree
assert isinstance(children, list)
if self.coalesce_tokens:
children = self.coalesce(cast(List[DerivationTree], children))
if name in self.tokens:
return (name, [(tree_to_string(tree), [])])
else:
return (name, [self.prune_tree(c) for c in children])
```
### Excursion: Canonical Grammars
The `EXPR_GRAMMAR` we import from the [chapter on grammars](Grammars.ipynb) is oriented towards generation. In particular, the production rules are stored as strings. We need to massage this representation a little to conform to a _canonical representation_ where each token in a rule is represented separately. The `canonical` format uses separate tokens to represent each symbol in an expansion.
```
CanonicalGrammar = Dict[str, List[List[str]]]
import re
def single_char_tokens(grammar: Grammar) -> Dict[str, List[List[Collection[str]]]]:
g_ = {}
for key in grammar:
rules_ = []
for rule in grammar[key]:
rule_ = []
for token in rule:
if token in grammar:
rule_.append(token)
else:
rule_.extend(token)
rules_.append(rule_)
g_[key] = rules_
return g_
def canonical(grammar: Grammar) -> CanonicalGrammar:
def split(expansion):
if isinstance(expansion, tuple):
expansion = expansion[0]
return [token for token in re.split(
RE_NONTERMINAL, expansion) if token]
return {
k: [split(expression) for expression in alternatives]
for k, alternatives in grammar.items()
}
CE_GRAMMAR: CanonicalGrammar = canonical(EXPR_GRAMMAR)
CE_GRAMMAR
```
We also provide a convenience method for easier display of canonical grammars.
```
def recurse_grammar(grammar, key, order):
rules = sorted(grammar[key])
old_len = len(order)
for rule in rules:
for token in rule:
if token not in grammar: continue
if token not in order:
order.append(token)
new = order[old_len:]
for ckey in new:
recurse_grammar(grammar, ckey, order)
def show_grammar(grammar, start_symbol=START_SYMBOL):
order = [start_symbol]
recurse_grammar(grammar, start_symbol, order)
return {k: sorted(grammar[k]) for k in order}
show_grammar(CE_GRAMMAR)
```
We provide a way to revert a canonical expression.
```
def non_canonical(grammar):
new_grammar = {}
for k in grammar:
rules = grammar[k]
new_rules = []
for rule in rules:
new_rules.append(''.join(rule))
new_grammar[k] = new_rules
return new_grammar
non_canonical(CE_GRAMMAR)
```
It is easier to work with the `canonical` representation during parsing. Hence, we update our parser class to store the `canonical` representation also.
```
class Parser(Parser):
def __init__(self, grammar, **kwargs):
self._start_symbol = kwargs.get('start_symbol', START_SYMBOL)
self.log = kwargs.get('log', False)
self.tokens = kwargs.get('tokens', set())
self.coalesce_tokens = kwargs.get('coalesce', True)
canonical_grammar = kwargs.get('canonical', False)
if canonical_grammar:
self.cgrammar = single_char_tokens(grammar)
self._grammar = non_canonical(grammar)
else:
self._grammar = dict(grammar)
self.cgrammar = single_char_tokens(canonical(grammar))
# we do not require a single rule for the start symbol
if len(grammar.get(self._start_symbol, [])) != 1:
self.cgrammar['<>'] = [[self._start_symbol]]
```
We update the `prune_tree()` to account for the phony start symbol if it was insserted.
```
class Parser(Parser):
def prune_tree(self, tree):
name, children = tree
if name == '<>':
assert len(children) == 1
return self.prune_tree(children[0])
if self.coalesce_tokens:
children = self.coalesce(children)
if name in self.tokens:
return (name, [(tree_to_string(tree), [])])
else:
return (name, [self.prune_tree(c) for c in children])
```
### End of Excursion
## Parsing Expression Grammars
A _[Parsing Expression Grammar](http://bford.info/pub/lang/peg)_ (*PEG*) \cite{Ford2004} is a type of _recognition based formal grammar_ that specifies the sequence of steps to take to parse a given string.
A _parsing expression grammar_ is very similar to a _context-free grammar_ (*CFG*) such as the ones we saw in the [chapter on grammars](Grammars.ipynb). As in a CFG, a parsing expression grammar is represented by a set of nonterminals and corresponding alternatives representing how to match each. For example, here is a PEG that matches `a` or `b`.
```
PEG1 = {
'<start>': ['a', 'b']
}
```
However, unlike the _CFG_, the alternatives represent *ordered choice*. That is, rather than choosing all rules that can potentially match, we stop at the first match that succeed. For example, the below _PEG_ can match `ab` but not `abc` unlike a _CFG_ which will match both. (We call the sequence of ordered choice expressions *choice expressions* rather than alternatives to make the distinction from _CFG_ clear.)
```
PEG2 = {
'<start>': ['ab', 'abc']
}
```
Each choice in a _choice expression_ represents a rule on how to satisfy that particular choice. The choice is a sequence of symbols (terminals and nonterminals) that are matched against a given text as in a _CFG_.
Beyond the syntax of grammar definitions we have seen so far, a _PEG_ can also contain a few additional elements. See the exercises at the end of the chapter for additional information.
The PEGs model the typical practice in handwritten recursive descent parsers, and hence it may be considered more intuitive to understand.
### The Packrat Parser for Predicate Expression Grammars
Short of hand rolling a parser, _Packrat_ parsing is one of the simplest parsing techniques, and is one of the techniques for parsing PEGs.
The _Packrat_ parser is so named because it tries to cache all results from simpler problems in the hope that these solutions can be used to avoid re-computation later. We develop a minimal _Packrat_ parser next.
We derive from the `Parser` base class first, and we accept the text to be parsed in the `parse()` method, which in turn calls `unify_key()` with the `start_symbol`.
__Note.__ While our PEG parser can produce only a single unambiguous parse tree, other parsers can produce multiple parses for ambiguous grammars. Hence, we return a list of trees (in this case with a single element).
```
class PEGParser(Parser):
def parse_prefix(self, text):
cursor, tree = self.unify_key(self.start_symbol(), text, 0)
return cursor, [tree]
```
### Excursion: Implementing `PEGParser`
#### Unify Key
The `unify_key()` algorithm is simple. If given a terminal symbol, it tries to match the symbol with the current position in the text. If the symbol and text match, it returns successfully with the new parse index `at`.
If on the other hand, it was given a nonterminal, it retrieves the choice expression corresponding to the key, and tries to match each choice *in order* using `unify_rule()`. If **any** of the rules succeed in being unified with the given text, the parse is considered a success, and we return with the new parse index returned by `unify_rule()`.
```
class PEGParser(PEGParser):
"""Packrat parser for Parsing Expression Grammars (PEGs)."""
def unify_key(self, key, text, at=0):
if self.log:
print("unify_key: %s with %s" % (repr(key), repr(text[at:])))
if key not in self.cgrammar:
if text[at:].startswith(key):
return at + len(key), (key, [])
else:
return at, None
for rule in self.cgrammar[key]:
to, res = self.unify_rule(rule, text, at)
if res is not None:
return (to, (key, res))
return 0, None
mystring = "1"
peg = PEGParser(EXPR_GRAMMAR, log=True)
peg.unify_key('1', mystring)
mystring = "2"
peg.unify_key('1', mystring)
```
#### Unify Rule
The `unify_rule()` method is similar. It retrieves the tokens corresponding to the rule that it needs to unify with the text, and calls `unify_key()` on them in sequence. If **all** tokens are successfully unified with the text, the parse is a success.
```
class PEGParser(PEGParser):
def unify_rule(self, rule, text, at):
if self.log:
print('unify_rule: %s with %s' % (repr(rule), repr(text[at:])))
results = []
for token in rule:
at, res = self.unify_key(token, text, at)
if res is None:
return at, None
results.append(res)
return at, results
mystring = "0"
peg = PEGParser(EXPR_GRAMMAR, log=True)
peg.unify_rule(peg.cgrammar['<digit>'][0], mystring, 0)
mystring = "12"
peg.unify_rule(peg.cgrammar['<integer>'][0], mystring, 0)
mystring = "1 + 2"
peg = PEGParser(EXPR_GRAMMAR, log=False)
peg.parse(mystring)
```
The two methods are mutually recursive, and given that `unify_key()` tries each alternative until it succeeds, `unify_key` can be called multiple times with the same arguments. Hence, it is important to memoize the results of `unify_key`. Python provides a simple decorator `lru_cache` for memoizing any function call that has hashable arguments. We add that to our implementation so that repeated calls to `unify_key()` with the same argument get cached results.
This memoization gives the algorithm its name – _Packrat_.
```
from functools import lru_cache
class PEGParser(PEGParser):
@lru_cache(maxsize=None)
def unify_key(self, key, text, at=0):
if key not in self.cgrammar:
if text[at:].startswith(key):
return at + len(key), (key, [])
else:
return at, None
for rule in self.cgrammar[key]:
to, res = self.unify_rule(rule, text, at)
if res is not None:
return (to, (key, res))
return 0, None
```
We wrap initialization and calling of `PEGParser` in a method `parse()` already implemented in the `Parser` base class that accepts the text to be parsed along with the grammar.
### End of Excursion
Here are a few examples of our parser in action.
```
mystring = "1 + (2 * 3)"
peg = PEGParser(EXPR_GRAMMAR)
for tree in peg.parse(mystring):
assert tree_to_string(tree) == mystring
display(display_tree(tree))
mystring = "1 * (2 + 3.35)"
for tree in peg.parse(mystring):
assert tree_to_string(tree) == mystring
display(display_tree(tree))
```
One should be aware that while the grammar looks like a *CFG*, the language described by a *PEG* may be different. Indeed, only *LL(1)* grammars are guaranteed to represent the same language for both PEGs and other parsers. Behavior of PEGs for other classes of grammars could be surprising \cite{redziejowski2008}.
## Parsing Context-Free Grammars
### Problems with PEG
While _PEGs_ are simple at first sight, their behavior in some cases might be a bit unintuitive. For example, here is an example \cite{redziejowski2008}:
```
PEG_SURPRISE: Grammar = {
"<A>": ["a<A>a", "aa"]
}
```
When interpreted as a *CFG* and used as a string generator, it will produce strings of the form `aa, aaaa, aaaaaa` that is, it produces strings where the number of `a` is $ 2*n $ where $ n > 0 $.
```
strings = []
for nn in range(4):
f = GrammarFuzzer(PEG_SURPRISE, start_symbol='<A>')
tree = ('<A>', None)
for _ in range(nn):
tree = f.expand_tree_once(tree)
tree = f.expand_tree_with_strategy(tree, f.expand_node_min_cost)
strings.append(tree_to_string(tree))
display_tree(tree)
strings
```
However, the _PEG_ parser can only recognize strings of the form $2^n$
```
peg = PEGParser(PEG_SURPRISE, start_symbol='<A>')
for s in strings:
with ExpectError():
for tree in peg.parse(s):
display_tree(tree)
print(s)
```
This is not the only problem with _Parsing Expression Grammars_. While *PEGs* are expressive and the *packrat* parser for parsing them is simple and intuitive, *PEGs* suffer from a major deficiency for our purposes. *PEGs* are oriented towards language recognition, and it is not clear how to translate an arbitrary *PEG* to a *CFG*. As we mentioned earlier, a naive re-interpretation of a *PEG* as a *CFG* does not work very well. Further, it is not clear what is the exact relation between the class of languages represented by *PEG* and the class of languages represented by *CFG*. Since our primary focus is *fuzzing* – that is _generation_ of strings – , we next look at _parsers that can accept context-free grammars_.
The general idea of *CFG* parser is the following: Peek at the input text for the allowed number of characters, and use these, and our parser state to determine which rules can be applied to complete parsing. We next look at a typical *CFG* parsing algorithm, the Earley Parser.
### The Earley Parser
The Earley parser is a general parser that is able to parse any arbitrary *CFG*. It was invented by Jay Earley \cite{Earley1970} for use in computational linguistics. While its computational complexity is $O(n^3)$ for parsing strings with arbitrary grammars, it can parse strings with unambiguous grammars in $O(n^2)$ time, and all *[LR(k)](https://en.wikipedia.org/wiki/LR_parser)* grammars in linear time ($O(n)$ \cite{Leo1991}). Further improvements – notably handling epsilon rules – were invented by Aycock et al. \cite{Aycock2002}.
Note that one restriction of our implementation is that the start symbol can have only one alternative in its alternative expressions. This is not a restriction in practice because any grammar with multiple alternatives for its start symbol can be extended with a new start symbol that has the original start symbol as its only choice. That is, given a grammar as below,
```
grammar = {
'<start>': ['<A>', '<B>'],
...
}
```
one may rewrite it as below to conform to the *single-alternative* rule.
```
grammar = {
'<start>': ['<start_>'],
'<start_>': ['<A>', '<B>'],
...
}
```
Let us implement a class `EarleyParser`, again derived from `Parser` which implements an Earley parser.
### Excursion: Implementing `EarleyParser`
We first implement a simpler parser that is a parser for nearly all *CFGs*, but not quite. In particular, our parser does not understand _epsilon rules_ – rules that derive empty string. We show later how the parser can be extended to handle these.
We use the following grammar in our examples below.
```
SAMPLE_GRAMMAR: Grammar = {
'<start>': ['<A><B>'],
'<A>': ['a<B>c', 'a<A>'],
'<B>': ['b<C>', '<D>'],
'<C>': ['c'],
'<D>': ['d']
}
C_SAMPLE_GRAMMAR = canonical(SAMPLE_GRAMMAR)
syntax_diagram(SAMPLE_GRAMMAR)
```
The basic idea of Earley parsing is the following:
* Start with the alternative expressions corresponding to the START_SYMBOL. These represent the possible ways to parse the string from a high level. Essentially each expression represents a parsing path. Queue each expression in our set of possible parses of the string. The parsed index of an expression is the part of expression that has already been recognized. In the beginning of parse, the parsed index of all expressions is at the beginning. Further, each letter gets a queue of expressions that recognizes that letter at that point in our parse.
* Examine our queue of possible parses and check if any of them start with a nonterminal. If it does, then that nonterminal needs to be recognized from the input before the given rule can be parsed. Hence, add the alternative expressions corresponding to the nonterminal to the queue. Do this recursively.
* At this point, we are ready to advance. Examine the current letter in the input, and select all expressions that have that particular letter at the parsed index. These expressions can now advance one step. Advance these selected expressions by incrementing their parsed index and add them to the queue of expressions in line for recognizing the next input letter.
* If while doing these things, we find that any of the expressions have finished parsing, we fetch its corresponding nonterminal, and advance all expressions that have that nonterminal at their parsed index.
* Continue this procedure recursively until all expressions that we have queued for the current letter have been processed. Then start processing the queue for the next letter.
We explain each step in detail with examples in the coming sections.
The parser uses dynamic programming to generate a table containing a _forest of possible parses_ at each letter index – the table contains as many columns as there are letters in the input, and each column contains different parsing rules at various stages of the parse.
For example, given an input `adcd`, the Column 0 would contain the following:
```
<start> : ● <A> <B>
```
which is the starting rule that indicates that we are currently parsing the rule `<start>`, and the parsing state is just before identifying the symbol `<A>`. It would also contain the following which are two alternative paths it could take to complete the parsing.
```
<A> : ● a <B> c
<A> : ● a <A>
```
Column 1 would contain the following, which represents the possible completion after reading `a`.
```
<A> : a ● <B> c
<A> : a ● <A>
<B> : ● b <C>
<B> : ● <D>
<A> : ● a <B> c
<A> : ● a <A>
<D> : ● d
```
Column 2 would contain the following after reading `d`
```
<D> : d ●
<B> : <D> ●
<A> : a <B> ● c
```
Similarly, Column 3 would contain the following after reading `c`
```
<A> : a <B> c ●
<start> : <A> ● <B>
<B> : ● b <C>
<B> : ● <D>
<D> : ● d
```
Finally, Column 4 would contain the following after reading `d`, with the `●` at the end of the `<start>` rule indicating that the parse was successful.
```
<D> : d ●
<B> : <D> ●
<start> : <A> <B> ●
```
As you can see from above, we are essentially filling a table (a table is also called a **chart**) of entries based on each letter we read, and the grammar rules that can be applied. This chart gives the parser its other name -- Chart parsing.
#### Columns
We define the `Column` first. The `Column` is initialized by its own `index` in the input string, and the `letter` at that index. Internally, we also keep track of the states that are added to the column as the parsing progresses.
```
class Column:
def __init__(self, index, letter):
self.index, self.letter = index, letter
self.states, self._unique = [], {}
def __str__(self):
return "%s chart[%d]\n%s" % (self.letter, self.index, "\n".join(
str(state) for state in self.states if state.finished()))
```
The `Column` only stores unique `states`. Hence, when a new `state` is `added` to our `Column`, we check whether it is already known.
```
class Column(Column):
def add(self, state):
if state in self._unique:
return self._unique[state]
self._unique[state] = state
self.states.append(state)
state.e_col = self
return self._unique[state]
```
#### Items
An item represents a _parse in progress for a specific rule._ Hence the item contains the name of the nonterminal, and the corresponding alternative expression (`expr`) which together form the rule, and the current position of parsing in this expression -- `dot`.
**Note.** If you are familiar with [LR parsing](https://en.wikipedia.org/wiki/LR_parser), you will notice that an item is simply an `LR0` item.
```
class Item:
def __init__(self, name, expr, dot):
self.name, self.expr, self.dot = name, expr, dot
```
We also provide a few convenience methods. The method `finished()` checks if the `dot` has moved beyond the last element in `expr`. The method `advance()` produces a new `Item` with the `dot` advanced one token, and represents an advance of the parsing. The method `at_dot()` returns the current symbol being parsed.
```
class Item(Item):
def finished(self):
return self.dot >= len(self.expr)
def advance(self):
return Item(self.name, self.expr, self.dot + 1)
def at_dot(self):
return self.expr[self.dot] if self.dot < len(self.expr) else None
```
Here is how an item could be used. We first define our item
```
item_name = '<B>'
item_expr = C_SAMPLE_GRAMMAR[item_name][1]
an_item = Item(item_name, tuple(item_expr), 0)
```
To determine where the status of parsing, we use `at_dot()`
```
an_item.at_dot()
```
That is, the next symbol to be parsed is `<D>`
If we advance the item, we get another item that represents the finished parsing rule `<B>`.
```
another_item = an_item.advance()
another_item.finished()
```
#### States
For `Earley` parsing, the state of the parsing is simply one `Item` along with some meta information such as the starting `s_col` and ending column `e_col` for each state. Hence we inherit from `Item` to create a `State`.
Since we are interested in comparing states, we define `hash()` and `eq()` with the corresponding methods.
```
class State(Item):
def __init__(self, name, expr, dot, s_col, e_col=None):
super().__init__(name, expr, dot)
self.s_col, self.e_col = s_col, e_col
def __str__(self):
def idx(var):
return var.index if var else -1
return self.name + ':= ' + ' '.join([
str(p)
for p in [*self.expr[:self.dot], '|', *self.expr[self.dot:]]
]) + "(%d,%d)" % (idx(self.s_col), idx(self.e_col))
def copy(self):
return State(self.name, self.expr, self.dot, self.s_col, self.e_col)
def _t(self):
return (self.name, self.expr, self.dot, self.s_col.index)
def __hash__(self):
return hash(self._t())
def __eq__(self, other):
return self._t() == other._t()
def advance(self):
return State(self.name, self.expr, self.dot + 1, self.s_col)
```
The usage of `State` is similar to that of `Item`. The only difference is that it is used along with the `Column` to track the parsing state. For example, we initialize the first column as follows:
```
col_0 = Column(0, None)
item_tuple = tuple(*C_SAMPLE_GRAMMAR[START_SYMBOL])
start_state = State(START_SYMBOL, item_tuple, 0, col_0)
col_0.add(start_state)
start_state.at_dot()
```
The first column is then updated by using `add()` method of `Column`
```
sym = start_state.at_dot()
for alt in C_SAMPLE_GRAMMAR[sym]:
col_0.add(State(sym, tuple(alt), 0, col_0))
for s in col_0.states:
print(s)
```
#### The Parsing Algorithm
The _Earley_ algorithm starts by initializing the chart with columns (as many as there are letters in the input). We also seed the first column with a state representing the expression corresponding to the start symbol. In our case, the state corresponds to the start symbol with the `dot` at `0` is represented as below. The `●` symbol represents the parsing status. In this case, we have not parsed anything.
```
<start>: ● <A> <B>
```
We pass this partial chart to a method for filling the rest of the parse chart.
Before starting to parse, we seed the chart with the state representing the ongoing parse of the start symbol.
```
class EarleyParser(Parser):
"""Earley Parser. This parser can parse any context-free grammar."""
def __init__(self, grammar: Grammar, **kwargs) -> None:
super().__init__(grammar, **kwargs)
self.chart: List = [] # for type checking
def chart_parse(self, words, start):
alt = tuple(*self.cgrammar[start])
chart = [Column(i, tok) for i, tok in enumerate([None, *words])]
chart[0].add(State(start, alt, 0, chart[0]))
return self.fill_chart(chart)
```
The main parsing loop in `fill_chart()` has three fundamental operations. `predict()`, `scan()`, and `complete()`. We discuss `predict` next.
#### Predicting States
We have already seeded `chart[0]` with a state `[<A>,<B>]` with `dot` at `0`. Next, given that `<A>` is a nonterminal, we `predict` the possible parse continuations of this state. That is, it could be either `a <B> c` or `A <A>`.
The general idea of `predict()` is as follows: Say you have a state with name `<A>` from the above grammar, and expression containing `[a,<B>,c]`. Imagine that you have seen `a` already, which means that the `dot` will be on `<B>`. Below, is a representation of our parse status. The left hand side of ● represents the portion already parsed (`a`), and the right hand side represents the portion yet to be parsed (`<B> c`).
```
<A>: a ● <B> c
```
To recognize `<B>`, we look at the definition of `<B>`, which has different alternative expressions. The `predict()` step adds each of these alternatives to the set of states, with `dot` at `0`.
```
<A>: a ● <B> c
<B>: ● b c
<B>: ● <D>
```
In essence, the `predict()` method, when called with the current nonterminal, fetches the alternative expressions corresponding to this nonterminal, and adds these as predicted _child_ states to the _current_ column.
```
class EarleyParser(EarleyParser):
def predict(self, col, sym, state):
for alt in self.cgrammar[sym]:
col.add(State(sym, tuple(alt), 0, col))
```
To see how to use `predict`, we first construct the 0th column as before, and we assign the constructed column to an instance of the EarleyParser.
```
col_0 = Column(0, None)
col_0.add(start_state)
ep = EarleyParser(SAMPLE_GRAMMAR)
ep.chart = [col_0]
```
It should contain a single state -- `<start> at 0`
```
for s in ep.chart[0].states:
print(s)
```
We apply predict to fill out the 0th column, and the column should contain the possible parse paths.
```
ep.predict(col_0, '<A>', s)
for s in ep.chart[0].states:
print(s)
```
#### Scanning Tokens
What if rather than a nonterminal, the state contained a terminal symbol such as a letter? In that case, we are ready to make some progress. For example, consider the second state:
```
<B>: ● b c
```
We `scan` the next column's letter. Say the next token is `b`.
If the letter matches what we have, then create a new state by advancing the current state by one letter.
```
<B>: b ● c
```
This new state is added to the next column (i.e the column that has the matched letter).
```
class EarleyParser(EarleyParser):
def scan(self, col, state, letter):
if letter == col.letter:
col.add(state.advance())
```
As before, we construct the partial parse first, this time adding a new column so that we can observe the effects of `scan()`
```
ep = EarleyParser(SAMPLE_GRAMMAR)
col_1 = Column(1, 'a')
ep.chart = [col_0, col_1]
new_state = ep.chart[0].states[1]
print(new_state)
ep.scan(col_1, new_state, 'a')
for s in ep.chart[1].states:
print(s)
```
#### Completing Processing
When we advance, what if we actually `complete()` the processing of the current rule? If so, we want to update not just this state, but also all the _parent_ states from which this state was derived.
For example, say we have states as below.
```
<A>: a ● <B> c
<B>: b c ●
```
The state `<B>: b c ●` is now complete. So, we need to advance `<A>: a ● <B> c` one step forward.
How do we determine the parent states? Note from `predict` that we added the predicted child states to the _same_ column as that of the inspected state. Hence, we look at the starting column of the current state, with the same symbol `at_dot` as that of the name of the completed state.
For each such parent found, we advance that parent (because we have just finished parsing that non terminal for their `at_dot`) and add the new states to the current column.
```
class EarleyParser(EarleyParser):
def complete(self, col, state):
return self.earley_complete(col, state)
def earley_complete(self, col, state):
parent_states = [
st for st in state.s_col.states if st.at_dot() == state.name
]
for st in parent_states:
col.add(st.advance())
```
Here is an example of completed processing. First we complete the Column 0
```
ep = EarleyParser(SAMPLE_GRAMMAR)
col_1 = Column(1, 'a')
col_2 = Column(2, 'd')
ep.chart = [col_0, col_1, col_2]
ep.predict(col_0, '<A>', s)
for s in ep.chart[0].states:
print(s)
```
Then we use `scan()` to populate Column 1
```
for state in ep.chart[0].states:
if state.at_dot() not in SAMPLE_GRAMMAR:
ep.scan(col_1, state, 'a')
for s in ep.chart[1].states:
print(s)
for state in ep.chart[1].states:
if state.at_dot() in SAMPLE_GRAMMAR:
ep.predict(col_1, state.at_dot(), state)
for s in ep.chart[1].states:
print(s)
```
Then we use `scan()` again to populate Column 2
```
for state in ep.chart[1].states:
if state.at_dot() not in SAMPLE_GRAMMAR:
ep.scan(col_2, state, state.at_dot())
for s in ep.chart[2].states:
print(s)
```
Now, we can use `complete()`:
```
for state in ep.chart[2].states:
if state.finished():
ep.complete(col_2, state)
for s in ep.chart[2].states:
print(s)
```
#### Filling the Chart
The main driving loop in `fill_chart()` essentially calls these operations in order. We loop over each column in order.
* For each column, fetch one state in the column at a time, and check if the state is `finished`.
* If it is, then we `complete()` all the parent states depending on this state.
* If the state was not finished, we check to see if the state's current symbol `at_dot` is a nonterminal.
* If it is a nonterminal, we `predict()` possible continuations, and update the current column with these states.
* If it was not, we `scan()` the next column and advance the current state if it matches the next letter.
```
class EarleyParser(EarleyParser):
def fill_chart(self, chart):
for i, col in enumerate(chart):
for state in col.states:
if state.finished():
self.complete(col, state)
else:
sym = state.at_dot()
if sym in self.cgrammar:
self.predict(col, sym, state)
else:
if i + 1 >= len(chart):
continue
self.scan(chart[i + 1], state, sym)
if self.log:
print(col, '\n')
return chart
```
We now can recognize a given string as belonging to a language represented by a grammar.
```
ep = EarleyParser(SAMPLE_GRAMMAR, log=True)
columns = ep.chart_parse('adcd', START_SYMBOL)
```
The chart we printed above only shows completed entries at each index. The parenthesized expression indicates the column just before the first character was recognized, and the ending column.
Notice how the `<start>` nonterminal shows fully parsed status.
```
last_col = columns[-1]
for state in last_col.states:
if state.name == '<start>':
print(state)
```
Since `chart_parse()` returns the completed table, we now need to extract the derivation trees.
#### The Parse Method
For determining how far we have managed to parse, we simply look for the last index from `chart_parse()` where the `start_symbol` was found.
```
class EarleyParser(EarleyParser):
def parse_prefix(self, text):
self.table = self.chart_parse(text, self.start_symbol())
for col in reversed(self.table):
states = [
st for st in col.states if st.name == self.start_symbol()
]
if states:
return col.index, states
return -1, []
```
Here is the `parse_prefix()` in action.
```
ep = EarleyParser(SAMPLE_GRAMMAR)
cursor, last_states = ep.parse_prefix('adcd')
print(cursor, [str(s) for s in last_states])
```
The following is adapted from the excellent reference on Earley parsing by [Loup Vaillant](http://loup-vaillant.fr/tutorials/earley-parsing/).
Our `parse()` method is as follows. It depends on two methods `parse_forest()` and `extract_trees()` that will be defined next.
```
class EarleyParser(EarleyParser):
def parse(self, text):
cursor, states = self.parse_prefix(text)
start = next((s for s in states if s.finished()), None)
if cursor < len(text) or not start:
raise SyntaxError("at " + repr(text[cursor:]))
forest = self.parse_forest(self.table, start)
for tree in self.extract_trees(forest):
yield self.prune_tree(tree)
```
#### Parsing Paths
The `parse_paths()` method tries to unify the given expression in `named_expr` with the parsed string. For that, it extracts the last symbol in `named_expr` and checks if it is a terminal symbol. If it is, then it checks the chart at `til` to see if the letter corresponding to the position matches the terminal symbol. If it does, extend our start index by the length of the symbol.
If the symbol was a nonterminal symbol, then we retrieve the parsed states at the current end column index (`til`) that correspond to the nonterminal symbol, and collect the start index. These are the end column indexes for the remaining expression.
Given our list of start indexes, we obtain the parse paths from the remaining expression. If we can obtain any, then we return the parse paths. If not, we return an empty list.
```
class EarleyParser(EarleyParser):
def parse_paths(self, named_expr, chart, frm, til):
def paths(state, start, k, e):
if not e:
return [[(state, k)]] if start == frm else []
else:
return [[(state, k)] + r
for r in self.parse_paths(e, chart, frm, start)]
*expr, var = named_expr
starts = None
if var not in self.cgrammar:
starts = ([(var, til - len(var),
't')] if til > 0 and chart[til].letter == var else [])
else:
starts = [(s, s.s_col.index, 'n') for s in chart[til].states
if s.finished() and s.name == var]
return [p for s, start, k in starts for p in paths(s, start, k, expr)]
```
Here is the `parse_paths()` in action
```
print(SAMPLE_GRAMMAR['<start>'])
ep = EarleyParser(SAMPLE_GRAMMAR)
completed_start = last_states[0]
paths = ep.parse_paths(completed_start.expr, columns, 0, 4)
for path in paths:
print([list(str(s_) for s_ in s) for s in path])
```
That is, the parse path for `<start>` given the input `adcd` included recognizing the expression `<A><B>`. This was recognized by the two states: `<A>` from input(0) to input(2) which further involved recognizing the rule `a<B>c`, and the next state `<B>` from input(3) which involved recognizing the rule `<D>`.
#### Parsing Forests
The `parse_forest()` method takes the state which represents the completed parse, and determines the possible ways that its expressions corresponded to the parsed expression. For example, say we are parsing `1+2+3`, and the state has `[<expr>,+,<expr>]` in `expr`. It could have been parsed as either `[{<expr>:1+2},+,{<expr>:3}]` or `[{<expr>:1},+,{<expr>:2+3}]`.
```
class EarleyParser(EarleyParser):
def forest(self, s, kind, chart):
return self.parse_forest(chart, s) if kind == 'n' else (s, [])
def parse_forest(self, chart, state):
pathexprs = self.parse_paths(state.expr, chart, state.s_col.index,
state.e_col.index) if state.expr else []
return state.name, [[(v, k, chart) for v, k in reversed(pathexpr)]
for pathexpr in pathexprs]
ep = EarleyParser(SAMPLE_GRAMMAR)
result = ep.parse_forest(columns, last_states[0])
result
```
#### Extracting Trees
What we have from `parse_forest()` is a forest of trees. We need to extract a single tree from that forest. That is accomplished as follows.
(For now, we return the first available derivation tree. To do that, we need to extract the parse forest from the state corresponding to `start`.)
```
class EarleyParser(EarleyParser):
def extract_a_tree(self, forest_node):
name, paths = forest_node
if not paths:
return (name, [])
return (name, [self.extract_a_tree(self.forest(*p)) for p in paths[0]])
def extract_trees(self, forest):
yield self.extract_a_tree(forest)
```
We now verify that our parser can parse a given expression.
```
A3_GRAMMAR: Grammar = {
"<start>": ["<bexpr>"],
"<bexpr>": [
"<aexpr><gt><aexpr>", "<aexpr><lt><aexpr>", "<aexpr>=<aexpr>",
"<bexpr>=<bexpr>", "<bexpr>&<bexpr>", "<bexpr>|<bexpr>", "(<bexrp>)"
],
"<aexpr>":
["<aexpr>+<aexpr>", "<aexpr>-<aexpr>", "(<aexpr>)", "<integer>"],
"<integer>": ["<digit><integer>", "<digit>"],
"<digit>": ["0", "1", "2", "3", "4", "5", "6", "7", "8", "9"],
"<lt>": ['<'],
"<gt>": ['>']
}
syntax_diagram(A3_GRAMMAR)
mystring = '(1+24)=33'
parser = EarleyParser(A3_GRAMMAR)
for tree in parser.parse(mystring):
assert tree_to_string(tree) == mystring
display_tree(tree)
```
We now have a complete parser that can parse almost arbitrary *CFG*. There remains a small corner to fix -- the case of epsilon rules as we will see later.
#### Ambiguous Parsing
Ambiguous grammars are grammars that can produce multiple derivation trees for some given string. For example, the `A3_GRAMMAR` can parse `1+2+3` in two different ways – `[1+2]+3` and `1+[2+3]`.
Extracting a single tree might be reasonable for unambiguous parses. However, what if the given grammar produces ambiguity when given a string? We need to extract all derivation trees in that case. We enhance our `extract_trees()` method to extract multiple derivation trees.
```
import itertools as I
class EarleyParser(EarleyParser):
def extract_trees(self, forest_node):
name, paths = forest_node
if not paths:
yield (name, [])
for path in paths:
ptrees = [self.extract_trees(self.forest(*p)) for p in path]
for p in I.product(*ptrees):
yield (name, p)
```
As before, we verify that everything works.
```
mystring = '1+2'
parser = EarleyParser(A1_GRAMMAR)
for tree in parser.parse(mystring):
assert mystring == tree_to_string(tree)
display_tree(tree)
```
One can also use a `GrammarFuzzer` to verify that everything works.
```
gf = GrammarFuzzer(A1_GRAMMAR)
for i in range(5):
s = gf.fuzz()
print(i, s)
for tree in parser.parse(s):
assert tree_to_string(tree) == s
```
#### The Aycock Epsilon Fix
While parsing, one often requires to know whether a given nonterminal can derive an empty string. For example, in the following grammar A can derive an empty string, while B can't. The nonterminals that can derive an empty string are called _nullable_ nonterminals. For example, in the below grammar `E_GRAMMAR_1`, `<A>` is _nullable_, and since `<A>` is one of the alternatives of `<start>`, `<start>` is also _nullable_. But `<B>` is not _nullable_.
```
E_GRAMMAR_1: Grammar = {
'<start>': ['<A>', '<B>'],
'<A>': ['a', ''],
'<B>': ['b']
}
```
One of the problems with the original Earley implementation is that it does not handle rules that can derive empty strings very well. For example, the given grammar should match `a`
```
EPSILON = ''
E_GRAMMAR: Grammar = {
'<start>': ['<S>'],
'<S>': ['<A><A><A><A>'],
'<A>': ['a', '<E>'],
'<E>': [EPSILON]
}
syntax_diagram(E_GRAMMAR)
mystring = 'a'
parser = EarleyParser(E_GRAMMAR)
with ExpectError():
trees = parser.parse(mystring)
```
Aycock et al.\cite{Aycock2002} suggests a simple fix. Their idea is to pre-compute the `nullable` set and use it to advance the `nullable` states. However, before we do that, we need to compute the `nullable` set. The `nullable` set consists of all nonterminals that can derive an empty string.
Computing the `nullable` set requires expanding each production rule in the grammar iteratively and inspecting whether a given rule can derive the empty string. Each iteration needs to take into account new terminals that have been found to be `nullable`. The procedure stops when we obtain a stable result. This procedure can be abstracted into a more general method `fixpoint`.
##### Fixpoint
A `fixpoint` of a function is an element in the function's domain such that it is mapped to itself. For example, 1 is a `fixpoint` of square root because `squareroot(1) == 1`.
(We use `str` rather than `hash` to check for equality in `fixpoint` because the data structure `set`, which we would like to use as an argument has a good string representation but is not hashable).
```
def fixpoint(f):
def helper(arg):
while True:
sarg = str(arg)
arg_ = f(arg)
if str(arg_) == sarg:
return arg
arg = arg_
return helper
```
Remember `my_sqrt()` from [the first chapter](Intro_Testing.ipynb)? We can define `my_sqrt()` using fixpoint.
```
def my_sqrt(x):
@fixpoint
def _my_sqrt(approx):
return (approx + x / approx) / 2
return _my_sqrt(1)
my_sqrt(2)
```
##### Nullable
Similarly, we can define `nullable` using `fixpoint`. We essentially provide the definition of a single intermediate step. That is, assuming that `nullables` contain the current `nullable` nonterminals, we iterate over the grammar looking for productions which are `nullable` -- that is, productions where the entire sequence can yield an empty string on some expansion.
We need to iterate over the different alternative expressions and their corresponding nonterminals. Hence we define a `rules()` method converts our dictionary representation to this pair format.
```
def rules(grammar):
return [(key, choice)
for key, choices in grammar.items()
for choice in choices]
```
The `terminals()` method extracts all terminal symbols from a `canonical` grammar representation.
```
def terminals(grammar):
return set(token
for key, choice in rules(grammar)
for token in choice if token not in grammar)
def nullable_expr(expr, nullables):
return all(token in nullables for token in expr)
def nullable(grammar):
productions = rules(grammar)
@fixpoint
def nullable_(nullables):
for A, expr in productions:
if nullable_expr(expr, nullables):
nullables |= {A}
return (nullables)
return nullable_({EPSILON})
for key, grammar in {
'E_GRAMMAR': E_GRAMMAR,
'E_GRAMMAR_1': E_GRAMMAR_1
}.items():
print(key, nullable(canonical(grammar)))
```
So, once we have the `nullable` set, all that we need to do is, after we have called `predict` on a state corresponding to a nonterminal, check if it is `nullable` and if it is, advance and add the state to the current column.
```
class EarleyParser(EarleyParser):
def __init__(self, grammar, **kwargs):
super().__init__(grammar, **kwargs)
self.epsilon = nullable(self.cgrammar)
def predict(self, col, sym, state):
for alt in self.cgrammar[sym]:
col.add(State(sym, tuple(alt), 0, col))
if sym in self.epsilon:
col.add(state.advance())
mystring = 'a'
parser = EarleyParser(E_GRAMMAR)
for tree in parser.parse(mystring):
display_tree(tree)
```
To ensure that our parser does parse all kinds of grammars, let us try two more test cases.
```
DIRECTLY_SELF_REFERRING: Grammar = {
'<start>': ['<query>'],
'<query>': ['select <expr> from a'],
"<expr>": ["<expr>", "a"],
}
INDIRECTLY_SELF_REFERRING: Grammar = {
'<start>': ['<query>'],
'<query>': ['select <expr> from a'],
"<expr>": ["<aexpr>", "a"],
"<aexpr>": ["<expr>"],
}
mystring = 'select a from a'
for grammar in [DIRECTLY_SELF_REFERRING, INDIRECTLY_SELF_REFERRING]:
forest = EarleyParser(grammar).parse(mystring)
print('recognized', mystring)
try:
for tree in forest:
print(tree_to_string(tree))
except RecursionError as e:
print("Recursion error", e)
```
Why do we get recursion error here? The reason is that, our implementation of `extract_trees()` is eager. That is, it attempts to extract _all_ inner parse trees before it can construct the outer parse tree. When there is a self reference, this results in recursion. Here is a simple extractor that avoids this problem. The idea here is that we randomly and lazily choose a node to expand, which avoids the infinite recursion.
#### Tree Extractor
As you saw above, one of the problems with attempting to extract all trees is that the parse forest can consist of an infinite number of trees. So, here, we solve that problem by extracting one tree at a time.
```
class SimpleExtractor:
def __init__(self, parser, text):
self.parser = parser
cursor, states = parser.parse_prefix(text)
start = next((s for s in states if s.finished()), None)
if cursor < len(text) or not start:
raise SyntaxError("at " + repr(cursor))
self.my_forest = parser.parse_forest(parser.table, start)
def extract_a_node(self, forest_node):
name, paths = forest_node
if not paths:
return ((name, 0, 1), []), (name, [])
cur_path, i, length = self.choose_path(paths)
child_nodes = []
pos_nodes = []
for s, kind, chart in cur_path:
f = self.parser.forest(s, kind, chart)
postree, ntree = self.extract_a_node(f)
child_nodes.append(ntree)
pos_nodes.append(postree)
return ((name, i, length), pos_nodes), (name, child_nodes)
def choose_path(self, arr):
length = len(arr)
i = random.randrange(length)
return arr[i], i, length
def extract_a_tree(self):
pos_tree, parse_tree = self.extract_a_node(self.my_forest)
return self.parser.prune_tree(parse_tree)
```
Using it is as folows:
```
de = SimpleExtractor(EarleyParser(DIRECTLY_SELF_REFERRING), mystring)
for i in range(5):
tree = de.extract_a_tree()
print(tree_to_string(tree))
```
On the indirect reference:
```
ie = SimpleExtractor(EarleyParser(INDIRECTLY_SELF_REFERRING), mystring)
for i in range(5):
tree = ie.extract_a_tree()
print(tree_to_string(tree))
```
Note that the `SimpleExtractor` gives no guarantee of the uniqueness of the returned trees. This can however be fixed by keeping track of the particular nodes that were expanded from `pos_tree` variable, and hence, avoiding exploration of the same paths.
For implementing this, we extract the random stream passing into the `SimpleExtractor`, and use it to control which nodes are explored. Different exploration paths can then form a tree of nodes.
We start with the node definition for a single choice. The `self._chosen` is the current choice made, `self.next` holds the next choice done using `self._chosen`. The `self.total` holds the total number of choices that one can have in this node.
```
class ChoiceNode:
def __init__(self, parent, total):
self._p, self._chosen = parent, 0
self._total, self.next = total, None
def chosen(self):
assert not self.finished()
return self._chosen
def __str__(self):
return '%d(%s/%s %s)' % (self._i, str(self._chosen),
str(self._total), str(self.next))
def __repr__(self):
return repr((self._i, self._chosen, self._total))
def increment(self):
# as soon as we increment, next becomes invalid
self.next = None
self._chosen += 1
if self.finished():
if self._p is None:
return None
return self._p.increment()
return self
def finished(self):
return self._chosen >= self._total
```
Now we come to the enhanced `EnhancedExtractor()`.
```
class EnhancedExtractor(SimpleExtractor):
def __init__(self, parser, text):
super().__init__(parser, text)
self.choices = ChoiceNode(None, 1)
```
First we define `choose_path()` that given an array and a choice node, returns the element in array corresponding to the next choice node if it exists, or produces a new choice nodes, and returns that element.
```
class EnhancedExtractor(EnhancedExtractor):
def choose_path(self, arr, choices):
arr_len = len(arr)
if choices.next is not None:
if choices.next.finished():
return None, None, None, choices.next
else:
choices.next = ChoiceNode(choices, arr_len)
next_choice = choices.next.chosen()
choices = choices.next
return arr[next_choice], next_choice, arr_len, choices
```
We define `extract_a_node()` here. While extracting, we have a choice. Should we allow infinite forests, or should we have a finite number of trees with no direct recursion? A direct recursion is when there exists a parent node with the same nonterminal that parsed the same span. We choose here not to extract such trees. They can be added back after parsing.
This is a recursive procedure that inspects a node, extracts the path required to complete that node. A single path (corresponding to a nonterminal) may again be composed of a sequence of smaller paths. Such paths are again extracted using another call to `extract_a_node()` recursively.
What happens when we hit on one of the node recursions we want to avoid? In that case, we return the current choice node, which bubbles up to `extract_a_tree()`. That procedure increments the last choice, which in turn increments up the parents until we reach a choice node that still has options to explore.
What if we hit the end of choices for a particular choice node(i.e, we have exhausted paths that can be taken from a node)? In this case also, we return the current choice node, which bubbles up to `extract_a_tree()`.
That procedure increments the last choice, which bubbles up to the next choice that has some unexplored paths.
```
class EnhancedExtractor(EnhancedExtractor):
def extract_a_node(self, forest_node, seen, choices):
name, paths = forest_node
if not paths:
return (name, []), choices
cur_path, _i, _l, new_choices = self.choose_path(paths, choices)
if cur_path is None:
return None, new_choices
child_nodes = []
for s, kind, chart in cur_path:
if kind == 't':
child_nodes.append((s, []))
continue
nid = (s.name, s.s_col.index, s.e_col.index)
if nid in seen:
return None, new_choices
f = self.parser.forest(s, kind, chart)
ntree, newer_choices = self.extract_a_node(f, seen | {nid}, new_choices)
if ntree is None:
return None, newer_choices
child_nodes.append(ntree)
new_choices = newer_choices
return (name, child_nodes), new_choices
```
The `extract_a_tree()` is a depth first extractor of a single tree. It tries to extract a tree, and if the extraction returns `None`, it means that a particular choice was exhausted, or we hit on a recursion. In that case, we increment the choice, and explore a new path.
```
class EnhancedExtractor(EnhancedExtractor):
def extract_a_tree(self):
while not self.choices.finished():
parse_tree, choices = self.extract_a_node(self.my_forest, set(), self.choices)
choices.increment()
if parse_tree is not None:
return self.parser.prune_tree(parse_tree)
return None
```
Note that the `EnhancedExtractor` only extracts nodes that are not directly recursive. That is, if it finds a node with a nonterminal that covers the same span as that of a parent node with the same nonterminal, it skips the node.
```
ee = EnhancedExtractor(EarleyParser(INDIRECTLY_SELF_REFERRING), mystring)
i = 0
while True:
i += 1
t = ee.extract_a_tree()
if t is None: break
print(i, t)
s = tree_to_string(t)
assert s == mystring
istring = '1+2+3+4'
ee = EnhancedExtractor(EarleyParser(A1_GRAMMAR), istring)
i = 0
while True:
i += 1
t = ee.extract_a_tree()
if t is None: break
print(i, t)
s = tree_to_string(t)
assert s == istring
```
#### More Earley Parsing
A number of other optimizations exist for Earley parsers. A fast industrial strength Earley parser implementation is the [Marpa parser](https://jeffreykegler.github.io/Marpa-web-site/). Further, Earley parsing need not be restricted to character data. One may also parse streams (audio and video streams) \cite{qi2018generalized} using a generalized Earley parser.
### End of Excursion
Here are a few examples of the Earley parser in action.
```
mystring = "1 + (2 * 3)"
earley = EarleyParser(EXPR_GRAMMAR)
for tree in earley.parse(mystring):
assert tree_to_string(tree) == mystring
display(display_tree(tree))
mystring = "1 * (2 + 3.35)"
for tree in earley.parse(mystring):
assert tree_to_string(tree) == mystring
display(display_tree(tree))
```
In contrast to the `PEGParser`, above, the `EarleyParser` can handle arbitrary context-free grammars.
### Excursion: Testing the Parsers
While we have defined two parser variants, it would be nice to have some confirmation that our parses work well. While it is possible to formally prove that they work, it is much more satisfying to generate random grammars, their corresponding strings, and parse them using the same grammar.
```
def prod_line_grammar(nonterminals, terminals):
g = {
'<start>': ['<symbols>'],
'<symbols>': ['<symbol><symbols>', '<symbol>'],
'<symbol>': ['<nonterminals>', '<terminals>'],
'<nonterminals>': ['<lt><alpha><gt>'],
'<lt>': ['<'],
'<gt>': ['>'],
'<alpha>': nonterminals,
'<terminals>': terminals
}
if not nonterminals:
g['<nonterminals>'] = ['']
del g['<lt>']
del g['<alpha>']
del g['<gt>']
return g
syntax_diagram(prod_line_grammar(["A", "B", "C"], ["1", "2", "3"]))
def make_rule(nonterminals, terminals, num_alts):
prod_grammar = prod_line_grammar(nonterminals, terminals)
gf = GrammarFuzzer(prod_grammar, min_nonterminals=3, max_nonterminals=5)
name = "<%s>" % ''.join(random.choices(string.ascii_uppercase, k=3))
return (name, [gf.fuzz() for _ in range(num_alts)])
make_rule(["A", "B", "C"], ["1", "2", "3"], 3)
from Grammars import unreachable_nonterminals
def make_grammar(num_symbols=3, num_alts=3):
terminals = list(string.ascii_lowercase)
grammar = {}
name = None
for _ in range(num_symbols):
nonterminals = [k[1:-1] for k in grammar.keys()]
name, expansions = \
make_rule(nonterminals, terminals, num_alts)
grammar[name] = expansions
grammar[START_SYMBOL] = [name]
# Remove unused parts
for nonterminal in unreachable_nonterminals(grammar):
del grammar[nonterminal]
assert is_valid_grammar(grammar)
return grammar
make_grammar()
```
Now we verify if our arbitrary grammars can be used by the Earley parser.
```
for i in range(5):
my_grammar = make_grammar()
print(my_grammar)
parser = EarleyParser(my_grammar)
mygf = GrammarFuzzer(my_grammar)
s = mygf.fuzz()
print(s)
for tree in parser.parse(s):
assert tree_to_string(tree) == s
display_tree(tree)
```
With this, we have completed both implementation and testing of *arbitrary* CFG, which can now be used along with `LangFuzzer` to generate better fuzzing inputs.
### End of Excursion
## Background
Numerous parsing techniques exist that can parse a given string using a
given grammar, and produce corresponding derivation tree or trees. However,
some of these techniques work only on specific classes of grammars.
These classes of grammars are named after the specific kind of parser
that can accept grammars of that category. That is, the upper bound for
the capabilities of the parser defines the grammar class named after that
parser.
The *LL* and *LR* parsing are the main traditions in parsing. Here, *LL* means left-to-right, leftmost derivation, and it represents a top-down approach. On the other hand, and LR (left-to-right, rightmost derivation) represents a bottom-up approach. Another way to look at it is that LL parsers compute the derivation tree incrementally in *pre-order* while LR parsers compute the derivation tree in *post-order* \cite{pingali2015graphical}).
Different classes of grammars differ in the features that are available to
the user for writing a grammar of that class. That is, the corresponding
kind of parser will be unable to parse a grammar that makes use of more
features than allowed. For example, the `A2_GRAMMAR` is an *LL*
grammar because it lacks left recursion, while `A1_GRAMMAR` is not an
*LL* grammar. This is because an *LL* parser parses
its input from left to right, and constructs the leftmost derivation of its
input by expanding the nonterminals it encounters. If there is a left
recursion in one of these rules, an *LL* parser will enter an infinite loop.
Similarly, a grammar is LL(k) if it can be parsed by an LL parser with k lookahead token, and LR(k) grammar can only be parsed with LR parser with at least k lookahead tokens. These grammars are interesting because both LL(k) and LR(k) grammars have $O(n)$ parsers, and can be used with relatively restricted computational budget compared to other grammars.
The languages for which one can provide an *LL(k)* grammar is called *LL(k)* languages (where k is the minimum lookahead required). Similarly, *LR(k)* is defined as the set of languages that have an *LR(k)* grammar. In terms of languages, LL(k) $\subset$ LL(k+1) and LL(k) $\subset$ LR(k), and *LR(k)* $=$ *LR(1)*. All deterministic *CFLs* have an *LR(1)* grammar. However, there exist *CFLs* that are inherently ambiguous \cite{ogden1968helpful}, and for these, one can't provide an *LR(1)* grammar.
The other main parsing algorithms for *CFGs* are GLL \cite{scott2010gll}, GLR \cite{tomita1987efficient,tomita2012generalized}, and CYK \cite{grune2008parsing}.
The ALL(\*) (used by ANTLR) on the other hand is a grammar representation that uses *Regular Expression* like predicates (similar to advanced PEGs – see [Exercise](#Exercise-3:-PEG-Predicates)) rather than a fixed lookahead. Hence, ALL(\*) can accept a larger class of grammars than CFGs.
In terms of computational limits of parsing, the main CFG parsers have a complexity of $O(n^3)$ for arbitrary grammars. However, parsing with arbitrary *CFG* is reducible to boolean matrix multiplication \cite{Valiant1975} (and the reverse \cite{Lee2002}). This is at present bounded by $O(2^{23728639}$) \cite{LeGall2014}. Hence, worse case complexity for parsing arbitrary CFG is likely to remain close to cubic.
Regarding PEGs, the actual class of languages that is expressible in *PEG* is currently unknown. In particular, we know that *PEGs* can express certain languages such as $a^n b^n c^n$. However, we do not know if there exist *CFLs* that are not expressible with *PEGs*. In Section 2.3, we provided an instance of a counter-intuitive PEG grammar. While important for our purposes (we use grammars for generation of inputs) this is not a criticism of parsing with PEGs. PEG focuses on writing grammars for recognizing a given language, and not necessarily in interpreting what language an arbitrary PEG might yield. Given a Context-Free Language to parse, it is almost always possible to write a grammar for it in PEG, and given that 1) a PEG can parse any string in $O(n)$ time, and 2) at present we know of no CFL that can't be expressed as a PEG, and 3) compared with *LR* grammars, a PEG is often more intuitive because it allows top-down interpretation, when writing a parser for a language, PEGs should be under serious consideration.
## Synopsis
This chapter introduces `Parser` classes, parsing a string into a _derivation tree_ as introduced in the [chapter on efficient grammar fuzzing](GrammarFuzzer.ipynb). Two important parser classes are provided:
* [Parsing Expression Grammar parsers](#Parsing-Expression-Grammars) (`PEGParser`). These are very efficient, but limited to specific grammar structure. Notably, the alternatives represent *ordered choice*. That is, rather than choosing all rules that can potentially match, we stop at the first match that succeed.
* [Earley parsers](#Parsing-Context-Free-Grammars) (`EarleyParser`). These accept any kind of context-free grammars, and explore all parsing alternatives (if any).
Using any of these is fairly easy, though. First, instantiate them with a grammar:
```
from Grammars import US_PHONE_GRAMMAR
us_phone_parser = EarleyParser(US_PHONE_GRAMMAR)
```
Then, use the `parse()` method to retrieve a list of possible derivation trees:
```
trees = us_phone_parser.parse("(555)987-6543")
tree = list(trees)[0]
display_tree(tree)
```
These derivation trees can then be used for test generation, notably for mutating and recombining existing inputs.
```
# ignore
from ClassDiagram import display_class_hierarchy
# ignore
display_class_hierarchy([PEGParser, EarleyParser],
public_methods=[
Parser.parse,
Parser.__init__,
Parser.grammar,
Parser.start_symbol
],
types={
'DerivationTree': DerivationTree,
'Grammar': Grammar
},
project='fuzzingbook')
```
## Lessons Learned
* Grammars can be used to generate derivation trees for a given string.
* Parsing Expression Grammars are intuitive, and easy to implement, but require care to write.
* Earley Parsers can parse arbitrary Context Free Grammars.
## Next Steps
* Use parsed inputs to [recombine existing inputs](LangFuzzer.ipynb)
## Exercises
### Exercise 1: An Alternative Packrat
In the _Packrat_ parser, we showed how one could implement a simple _PEG_ parser. That parser kept track of the current location in the text using an index. Can you modify the parser so that it simply uses the current substring rather than tracking the index? That is, it should no longer have the `at` parameter.
**Solution.** Here is a possible solution:
```
class PackratParser(Parser):
def parse_prefix(self, text):
txt, res = self.unify_key(self.start_symbol(), text)
return len(txt), [res]
def parse(self, text):
remain, res = self.parse_prefix(text)
if remain:
raise SyntaxError("at " + res)
return res
def unify_rule(self, rule, text):
results = []
for token in rule:
text, res = self.unify_key(token, text)
if res is None:
return text, None
results.append(res)
return text, results
def unify_key(self, key, text):
if key not in self.cgrammar:
if text.startswith(key):
return text[len(key):], (key, [])
else:
return text, None
for rule in self.cgrammar[key]:
text_, res = self.unify_rule(rule, text)
if res:
return (text_, (key, res))
return text, None
mystring = "1 + (2 * 3)"
for tree in PackratParser(EXPR_GRAMMAR).parse(mystring):
assert tree_to_string(tree) == mystring
display_tree(tree)
```
### Exercise 2: More PEG Syntax
The _PEG_ syntax provides a few notational conveniences reminiscent of regular expressions. For example, it supports the following operators (letters `T` and `A` represents tokens that can be either terminal or nonterminal. `ε` is an empty string, and `/` is the ordered choice operator similar to the non-ordered choice operator `|`):
* `T?` represents an optional greedy match of T and `A := T?` is equivalent to `A := T/ε`.
* `T*` represents zero or more greedy matches of `T` and `A := T*` is equivalent to `A := T A/ε`.
* `T+` represents one or more greedy matches – equivalent to `TT*`
If you look at the three notations above, each can be represented in the grammar in terms of basic syntax.
Remember the exercise from [the chapter on grammars](Grammars.ipynb) that developed `define_ex_grammar()` that can represent grammars as Python code? extend `define_ex_grammar()` to `define_peg()` to support the above notational conveniences. The decorator should rewrite a given grammar that contains these notations to an equivalent grammar in basic syntax.
### Exercise 3: PEG Predicates
Beyond these notational conveniences, it also supports two predicates that can provide a powerful lookahead facility that does not consume any input.
* `T&A` represents an _And-predicate_ that matches `T` if `T` is matched, and it is immediately followed by `A`
* `T!A` represents a _Not-predicate_ that matches `T` if `T` is matched, and it is *not* immediately followed by `A`
Implement these predicates in our _PEG_ parser.
### Exercise 4: Earley Fill Chart
In the `Earley Parser`, `Column` class, we keep the states both as a `list` and also as a `dict` even though `dict` is ordered. Can you explain why?
**Hint**: see the `fill_chart` method.
**Solution.** Python allows us to append to a list in flight, while a dict, eventhough it is ordered does not allow that facility.
That is, the following will work
```python
values = [1]
for v in values:
values.append(v*2)
```
However, the following will result in an error
```python
values = {1:1}
for v in values:
values[v*2] = v*2
```
In the `fill_chart`, we make use of this facility to modify the set of states we are iterating on, on the fly.
### Exercise 5: Leo Parser
One of the problems with the original Earley parser is that while it can parse strings using arbitrary _Context Free Gramamrs_, its performance on right-recursive grammars is quadratic. That is, it takes $O(n^2)$ runtime and space for parsing with right-recursive grammars. For example, consider the parsing of the following string by two different grammars `LR_GRAMMAR` and `RR_GRAMMAR`.
```
mystring = 'aaaaaa'
```
To see the problem, we need to enable logging. Here is the logged version of parsing with the `LR_GRAMMAR`
```
result = EarleyParser(LR_GRAMMAR, log=True).parse(mystring)
for _ in result: pass # consume the generator so that we can see the logs
```
Compare that to the parsing of `RR_GRAMMAR` as seen below:
```
result = EarleyParser(RR_GRAMMAR, log=True).parse(mystring)
for _ in result: pass
```
As can be seen from the parsing log for each letter, the number of states with representation `<A>: a <A> ● (i, j)` increases at each stage, and these are simply a left over from the previous letter. They do not contribute anything more to the parse other than to simply complete these entries. However, they take up space, and require resources for inspection, contributing a factor of `n` in analysis.
Joop Leo \cite{Leo1991} found that this inefficiency can be avoided by detecting right recursion. The idea is that before starting the `completion` step, check whether the current item has a _deterministic reduction path_. If such a path exists, add a copy of the topmost element of the _deteministic reduction path_ to the current column, and return. If not, perform the original `completion` step.
**Definition 2.1**: An item is said to be on the deterministic reduction path above $[A \rightarrow \gamma., i]$ if it is $[B \rightarrow \alpha A ., k]$ with $[B \rightarrow \alpha . A, k]$ being the only item in $ I_i $ with the dot in front of A, or if it is on the deterministic reduction path above $[B \rightarrow \alpha A ., k]$. An item on such a path is called *topmost* one if there is no item on the deterministic reduction path above it\cite{Leo1991}.
Finding a _deterministic reduction path_ is as follows:
Given a complete state, represented by `<A> : seq_1 ● (s, e)` where `s` is the starting column for this rule, and `e` the current column, there is a _deterministic reduction path_ **above** it if two constraints are satisfied.
1. There exist a *single* item in the form `<B> : seq_2 ● <A> (k, s)` in column `s`.
2. That should be the *single* item in s with dot in front of `<A>`
The resulting item is of the form `<B> : seq_2 <A> ● (k, e)`, which is simply item from (1) advanced, and is considered above `<A>:.. (s, e)` in the deterministic reduction path.
The `seq_1` and `seq_2` are arbitrary symbol sequences.
This forms the following chain of links, with `<A>:.. (s_1, e)` being the child of `<B>:.. (s_2, e)` etc.
Here is one way to visualize the chain:
```
<C> : seq_3 <B> ● (s_3, e)
| constraints satisfied by <C> : seq_3 ● <B> (s_3, s_2)
<B> : seq_2 <A> ● (s_2, e)
| constraints satisfied by <B> : seq_2 ● <A> (s_2, s_1)
<A> : seq_1 ● (s_1, e)
```
Essentially, what we want to do is to identify potential deterministic right recursion candidates, perform completion on them, and *throw away the result*. We do this until we reach the top. See Grune et al.~\cite{grune2008parsing} for further information.
Note that the completions are in the same column (`e`), with each candidates with constraints satisfied
in further and further earlier columns (as shown below):
```
<C> : seq_3 ● <B> (s_3, s_2) --> <C> : seq_3 <B> ● (s_3, e)
|
<B> : seq_2 ● <A> (s_2, s_1) --> <B> : seq_2 <A> ● (s_2, e)
|
<A> : seq_1 ● (s_1, e)
```
Following this chain, the topmost item is the item `<C>:.. (s_3, e)` that does not have a parent. The topmost item needs to be saved is called a *transitive* item by Leo, and it is associated with the non-terminal symbol that started the lookup. The transitive item needs to be added to each column we inspect.
Here is the skeleton for the parser `LeoParser`.
```
class LeoParser(EarleyParser):
def complete(self, col, state):
return self.leo_complete(col, state)
def leo_complete(self, col, state):
detred = self.deterministic_reduction(state)
if detred:
col.add(detred.copy())
else:
self.earley_complete(col, state)
def deterministic_reduction(self, state):
raise NotImplementedError
```
Can you implement the `deterministic_reduction()` method to obtain the topmost element?
**Solution.** Here is a possible solution:
First, we update our `Column` class with the ability to add transitive items. Note that, while Leo asks the transitive to be added to the set $ I_k $ there is no actual requirement for the transitive states to be added to the `states` list. The transitive items are only intended for memoization and not for the `fill_chart()` method. Hence, we track them separately.
```
class Column(Column):
def __init__(self, index, letter):
self.index, self.letter = index, letter
self.states, self._unique, self.transitives = [], {}, {}
def add_transitive(self, key, state):
assert key not in self.transitives
self.transitives[key] = state
return self.transitives[key]
```
Remember the picture we drew of the deterministic path?
```
<C> : seq_3 <B> ● (s_3, e)
| constraints satisfied by <C> : seq_3 ● <B> (s_3, s_2)
<B> : seq_2 <A> ● (s_2, e)
| constraints satisfied by <B> : seq_2 ● <A> (s_2, s_1)
<A> : seq_1 ● (s_1, e)
```
We define a function `uniq_postdot()` that given the item `<A> := seq_1 ● (s_1, e)`, returns a `<B> : seq_2 ● <A> (s_2, s_1)` that satisfies the constraints mentioned in the above picture.
```
class LeoParser(LeoParser):
def uniq_postdot(self, st_A):
col_s1 = st_A.s_col
parent_states = [
s for s in col_s1.states if s.expr and s.at_dot() == st_A.name
]
if len(parent_states) > 1:
return None
matching_st_B = [s for s in parent_states if s.dot == len(s.expr) - 1]
return matching_st_B[0] if matching_st_B else None
lp = LeoParser(RR_GRAMMAR)
[(str(s), str(lp.uniq_postdot(s))) for s in columns[-1].states]
```
We next define the function `get_top()` that is the core of deterministic reduction which gets the topmost state above the current state (`A`).
```
class LeoParser(LeoParser):
def get_top(self, state_A):
st_B_inc = self.uniq_postdot(state_A)
if not st_B_inc:
return None
t_name = st_B_inc.name
if t_name in st_B_inc.e_col.transitives:
return st_B_inc.e_col.transitives[t_name]
st_B = st_B_inc.advance()
top = self.get_top(st_B) or st_B
return st_B_inc.e_col.add_transitive(t_name, top)
```
Once we have the machinery in place, `deterministic_reduction()` itself is simply a wrapper to call `get_top()`
```
class LeoParser(LeoParser):
def deterministic_reduction(self, state):
return self.get_top(state)
lp = LeoParser(RR_GRAMMAR)
columns = lp.chart_parse(mystring, lp.start_symbol())
[(str(s), str(lp.get_top(s))) for s in columns[-1].states]
```
Now, both LR and RR grammars should work within $O(n)$ bounds.
```
result = LeoParser(RR_GRAMMAR, log=True).parse(mystring)
for _ in result: pass
```
We verify the Leo parser with a few more right recursive grammars.
```
RR_GRAMMAR2 = {
'<start>': ['<A>'],
'<A>': ['ab<A>', ''],
}
mystring2 = 'ababababab'
result = LeoParser(RR_GRAMMAR2, log=True).parse(mystring2)
for _ in result: pass
RR_GRAMMAR3 = {
'<start>': ['c<A>'],
'<A>': ['ab<A>', ''],
}
mystring3 = 'cababababab'
result = LeoParser(RR_GRAMMAR3, log=True).parse(mystring3)
for _ in result: pass
RR_GRAMMAR4 = {
'<start>': ['<A>c'],
'<A>': ['ab<A>', ''],
}
mystring4 = 'ababababc'
result = LeoParser(RR_GRAMMAR4, log=True).parse(mystring4)
for _ in result: pass
RR_GRAMMAR5 = {
'<start>': ['<A>'],
'<A>': ['ab<B>', ''],
'<B>': ['<A>'],
}
mystring5 = 'abababab'
result = LeoParser(RR_GRAMMAR5, log=True).parse(mystring5)
for _ in result: pass
RR_GRAMMAR6 = {
'<start>': ['<A>'],
'<A>': ['a<B>', ''],
'<B>': ['b<A>'],
}
mystring6 = 'abababab'
result = LeoParser(RR_GRAMMAR6, log=True).parse(mystring6)
for _ in result: pass
RR_GRAMMAR7 = {
'<start>': ['<A>'],
'<A>': ['a<A>', 'a'],
}
mystring7 = 'aaaaaaaa'
result = LeoParser(RR_GRAMMAR7, log=True).parse(mystring7)
for _ in result: pass
```
We verify that our parser works correctly on `LR_GRAMMAR` too.
```
result = LeoParser(LR_GRAMMAR, log=True).parse(mystring)
for _ in result: pass
```
__Advanced:__ We have fixed the complexity bounds. However, because we are saving only the topmost item of a right recursion, we need to fix our parser to be aware of our fix while extracting parse trees. Can you fix it?
__Hint:__ Leo suggests simply transforming the Leo item sets to normal Earley sets, with the results from deterministic reduction expanded to their originals. For that, keep in mind the picture of constraint chain we drew earlier.
**Solution.** Here is a possible solution.
We first change the definition of `add_transitive()` so that results of deterministic reduction can be identified later.
```
class Column(Column):
def add_transitive(self, key, state):
assert key not in self.transitives
self.transitives[key] = TState(state.name, state.expr, state.dot,
state.s_col, state.e_col)
return self.transitives[key]
```
We also need a `back()` method to create the constraints.
```
class State(State):
def back(self):
return TState(self.name, self.expr, self.dot - 1, self.s_col, self.e_col)
```
We update `copy()` to make `TState` items instead.
```
class TState(State):
def copy(self):
return TState(self.name, self.expr, self.dot, self.s_col, self.e_col)
```
We now modify the `LeoParser` to keep track of the chain of constrains that we mentioned earlier.
```
class LeoParser(LeoParser):
def __init__(self, grammar, **kwargs):
super().__init__(grammar, **kwargs)
self._postdots = {}
```
Next, we update the `uniq_postdot()` so that it tracks the chain of links.
```
class LeoParser(LeoParser):
def uniq_postdot(self, st_A):
col_s1 = st_A.s_col
parent_states = [
s for s in col_s1.states if s.expr and s.at_dot() == st_A.name
]
if len(parent_states) > 1:
return None
matching_st_B = [s for s in parent_states if s.dot == len(s.expr) - 1]
if matching_st_B:
self._postdots[matching_st_B[0]._t()] = st_A
return matching_st_B[0]
return None
```
We next define a method `expand_tstate()` that, when given a `TState`, generates all the intermediate links that we threw away earlier for a given end column.
```
class LeoParser(LeoParser):
def expand_tstate(self, state, e):
if state._t() not in self._postdots:
return
c_C = self._postdots[state._t()]
e.add(c_C.advance())
self.expand_tstate(c_C.back(), e)
```
We define a `rearrange()` method to generate a reversed table where each column contains states that start at that column.
```
class LeoParser(LeoParser):
def rearrange(self, table):
f_table = [Column(c.index, c.letter) for c in table]
for col in table:
for s in col.states:
f_table[s.s_col.index].states.append(s)
return f_table
```
Here is the rearranged table. (Can you explain why the Column 0 has a large number of `<start>` items?)
```
ep = LeoParser(RR_GRAMMAR)
columns = ep.chart_parse(mystring, ep.start_symbol())
r_table = ep.rearrange(columns)
for col in r_table:
print(col, "\n")
```
We save the result of rearrange before going into `parse_forest()`.
```
class LeoParser(LeoParser):
def parse(self, text):
cursor, states = self.parse_prefix(text)
start = next((s for s in states if s.finished()), None)
if cursor < len(text) or not start:
raise SyntaxError("at " + repr(text[cursor:]))
self.r_table = self.rearrange(self.table)
forest = self.extract_trees(self.parse_forest(self.table, start))
for tree in forest:
yield self.prune_tree(tree)
```
Finally, during `parse_forest()`, we first check to see if it is a transitive state, and if it is, expand it to the original sequence of states using `traverse_constraints()`.
```
class LeoParser(LeoParser):
def parse_forest(self, chart, state):
if isinstance(state, TState):
self.expand_tstate(state.back(), state.e_col)
return super().parse_forest(chart, state)
```
This completes our implementation of `LeoParser`.
We check whether the previously defined right recursive grammars parse and return the correct parse trees.
```
result = LeoParser(RR_GRAMMAR).parse(mystring)
for tree in result:
assert mystring == tree_to_string(tree)
result = LeoParser(RR_GRAMMAR2).parse(mystring2)
for tree in result:
assert mystring2 == tree_to_string(tree)
result = LeoParser(RR_GRAMMAR3).parse(mystring3)
for tree in result:
assert mystring3 == tree_to_string(tree)
result = LeoParser(RR_GRAMMAR4).parse(mystring4)
for tree in result:
assert mystring4 == tree_to_string(tree)
result = LeoParser(RR_GRAMMAR5).parse(mystring5)
for tree in result:
assert mystring5 == tree_to_string(tree)
result = LeoParser(RR_GRAMMAR6).parse(mystring6)
for tree in result:
assert mystring6 == tree_to_string(tree)
result = LeoParser(RR_GRAMMAR7).parse(mystring7)
for tree in result:
assert mystring7 == tree_to_string(tree)
result = LeoParser(LR_GRAMMAR).parse(mystring)
for tree in result:
assert mystring == tree_to_string(tree)
RR_GRAMMAR8 = {
'<start>': ['<A>'],
'<A>': ['a<A>', 'a']
}
mystring8 = 'aa'
RR_GRAMMAR9 = {
'<start>': ['<A>'],
'<A>': ['<B><A>', '<B>'],
'<B>': ['b']
}
mystring9 = 'bbbbbbb'
result = LeoParser(RR_GRAMMAR8).parse(mystring8)
for tree in result:
print(repr(tree_to_string(tree)))
assert mystring8 == tree_to_string(tree)
result = LeoParser(RR_GRAMMAR9).parse(mystring9)
for tree in result:
print(repr(tree_to_string(tree)))
assert mystring9 == tree_to_string(tree)
```
### Exercise 6: Filtered Earley Parser
One of the problems with our Earley and Leo Parsers is that it can get stuck in infinite loops when parsing with grammars that contain token repetitions in alternatives. For example, consider the grammar below.
```
RECURSION_GRAMMAR: Grammar = {
"<start>": ["<A>"],
"<A>": ["<A>", "<A>aa", "AA", "<B>"],
"<B>": ["<C>", "<C>cc", "CC"],
"<C>": ["<B>", "<B>bb", "BB"]
}
```
With this grammar, one can produce an infinite chain of derivations of `<A>`, (direct recursion) or an infinite chain of derivations of `<B> -> <C> -> <B> ...` (indirect recursion). The problem is that, our implementation can get stuck trying to derive one of these infinite chains. One possibility is to use the `LazyExtractor`. Another, is to simply avoid generating such chains.
```
from ExpectError import ExpectTimeout
with ExpectTimeout(1, print_traceback=False):
mystring = 'AA'
parser = LeoParser(RECURSION_GRAMMAR)
tree, *_ = parser.parse(mystring)
assert tree_to_string(tree) == mystring
display_tree(tree)
```
Can you implement a solution such that any tree that contains such a chain is discarded?
**Solution.** Here is a possible solution.
```
class FilteredLeoParser(LeoParser):
def forest(self, s, kind, seen, chart):
return self.parse_forest(chart, s, seen) if kind == 'n' else (s, [])
def parse_forest(self, chart, state, seen=None):
if isinstance(state, TState):
self.expand_tstate(state.back(), state.e_col)
def was_seen(chain, s):
if isinstance(s, str):
return False
if len(s.expr) > 1:
return False
return s in chain
if len(state.expr) > 1: # things get reset if we have a non loop
seen = set()
elif seen is None: # initialization
seen = {state}
pathexprs = self.parse_paths(state.expr, chart, state.s_col.index,
state.e_col.index) if state.expr else []
return state.name, [[(s, k, seen | {s}, chart)
for s, k in reversed(pathexpr)
if not was_seen(seen, s)] for pathexpr in pathexprs]
```
With the `FilteredLeoParser`, we should be able to recover minimal parse trees in reasonable time.
```
mystring = 'AA'
parser = FilteredLeoParser(RECURSION_GRAMMAR)
tree, *_ = parser.parse(mystring)
assert tree_to_string(tree) == mystring
display_tree(tree)
mystring = 'AAaa'
parser = FilteredLeoParser(RECURSION_GRAMMAR)
tree, *_ = parser.parse(mystring)
assert tree_to_string(tree) == mystring
display_tree(tree)
mystring = 'AAaaaa'
parser = FilteredLeoParser(RECURSION_GRAMMAR)
tree, *_ = parser.parse(mystring)
assert tree_to_string(tree) == mystring
display_tree(tree)
mystring = 'CC'
parser = FilteredLeoParser(RECURSION_GRAMMAR)
tree, *_ = parser.parse(mystring)
assert tree_to_string(tree) == mystring
display_tree(tree)
mystring = 'BBcc'
parser = FilteredLeoParser(RECURSION_GRAMMAR)
tree, *_ = parser.parse(mystring)
assert tree_to_string(tree) == mystring
display_tree(tree)
mystring = 'BB'
parser = FilteredLeoParser(RECURSION_GRAMMAR)
tree, *_ = parser.parse(mystring)
assert tree_to_string(tree) == mystring
display_tree(tree)
mystring = 'BBccbb'
parser = FilteredLeoParser(RECURSION_GRAMMAR)
tree, *_ = parser.parse(mystring)
assert tree_to_string(tree) == mystring
display_tree(tree)
```
As can be seen, we are able to recover minimal parse trees without hitting on infinite chains.
### Exercise 7: Iterative Earley Parser
Recursive algorithms are quite handy in some cases but sometimes we might want to have iteration instead of recursion due to memory or speed problems.
Can you implement an iterative version of the `EarleyParser`?
__Hint:__ In general, you can use a stack to replace a recursive algorithm with an iterative one. An easy way to do this is pushing the parameters onto a stack instead of passing them to the recursive function.
**Solution.** Here is a possible solution.
First, we define `parse_paths()` that extract paths from a parsed expression, which is very similar to the original.
```
class IterativeEarleyParser(EarleyParser):
def parse_paths(self, named_expr_, chart, frm, til_):
return_paths = []
path_build_stack = [(named_expr_, til_, [])]
def iter_paths(path_prefix, path, start, k, e):
x = path_prefix + [(path, k)]
if not e:
return_paths.extend([x] if start == frm else [])
else:
path_build_stack.append((e, start, x))
while path_build_stack:
named_expr, til, path_prefix = path_build_stack.pop()
*expr, var = named_expr
starts = None
if var not in self.cgrammar:
starts = ([(var, til - len(var), 't')]
if til > 0 and chart[til].letter == var else [])
else:
starts = [(s, s.s_col.index, 'n') for s in chart[til].states
if s.finished() and s.name == var]
for s, start, k in starts:
iter_paths(path_prefix, s, start, k, expr)
return return_paths
```
Next we used these paths to recover the forest data structure using `parse_forest()`. Since `parse_forest()` does not recurse, we reuse the original definition. Next, we define `extract_a_tree()`
Now we are ready to extract trees from the forest using `extract_a_tree()`
```
class IterativeEarleyParser(IterativeEarleyParser):
def choose_a_node_to_explore(self, node_paths, level_count):
first, *rest = node_paths
return first
def extract_a_tree(self, forest_node_):
start_node = (forest_node_[0], [])
tree_build_stack = [(forest_node_, start_node[-1], 0)]
while tree_build_stack:
forest_node, tree, level_count = tree_build_stack.pop()
name, paths = forest_node
if not paths:
tree.append((name, []))
else:
new_tree = []
current_node = self.choose_a_node_to_explore(paths, level_count)
for p in reversed(current_node):
new_forest_node = self.forest(*p)
tree_build_stack.append((new_forest_node, new_tree, level_count + 1))
tree.append((name, new_tree))
return start_node
```
For now, we simply extract the first tree found.
```
class IterativeEarleyParser(IterativeEarleyParser):
def extract_trees(self, forest):
yield self.extract_a_tree(forest)
```
Let's see if it works with some of the grammars we have seen so far.
```
test_cases: List[Tuple[Grammar, str]] = [
(A1_GRAMMAR, '1-2-3+4-5'),
(A2_GRAMMAR, '1+2'),
(A3_GRAMMAR, '1+2+3-6=6-1-2-3'),
(LR_GRAMMAR, 'aaaaa'),
(RR_GRAMMAR, 'aa'),
(DIRECTLY_SELF_REFERRING, 'select a from a'),
(INDIRECTLY_SELF_REFERRING, 'select a from a'),
(RECURSION_GRAMMAR, 'AA'),
(RECURSION_GRAMMAR, 'AAaaaa'),
(RECURSION_GRAMMAR, 'BBccbb')
]
for i, (grammar, text) in enumerate(test_cases):
print(i, text)
tree, *_ = IterativeEarleyParser(grammar).parse(text)
assert text == tree_to_string(tree)
```
As can be seen, our `IterativeEarleyParser` is able to handle recursive grammars. However, it can only extract the first tree found. What should one do to get all possible parses? What we can do, is to keep track of options to explore at each `choose_a_node_to_explore()`. Next, capture in the nodes explored in a tree data structure, adding new paths each time a new leaf is expanded. See the `TraceTree` datastructure in the [chapter on Concolic fuzzing](ConcolicFuzzer.ipynb) for an example.
### Exercise 8: First Set of a Nonterminal
We previously gave a way to extract a the `nullable` (epsilon) set, which is often used for parsing.
Along with `nullable`, parsing algorithms often use two other sets [`first` and `follow`](https://en.wikipedia.org/wiki/Canonical_LR_parser#FIRST_and_FOLLOW_sets).
The first set of a terminal symbol is itself, and the first set of a nonterminal is composed of terminal symbols that can come at the beginning of any derivation
of that nonterminal. The first set of any nonterminal that can derive the empty string should contain `EPSILON`. For example, using our `A1_GRAMMAR`, the first set of both `<expr>` and `<start>` is `{0,1,2,3,4,5,6,7,8,9}`. The extraction first set for any self-recursive nonterminal is simple enough. One simply has to recursively compute the first set of the first element of its choice expressions. The computation of `first` set for a self-recursive nonterminal is tricky. One has to recursively compute the first set until one is sure that no more terminals can be added to the first set.
Can you implement the `first` set using our `fixpoint()` decorator?
**Solution.** The first set of all terminals is the set containing just themselves. So we initialize that first. Then we update the first set with rules that derive empty strings.
```
def firstset(grammar, nullable):
first = {i: {i} for i in terminals(grammar)}
for k in grammar:
first[k] = {EPSILON} if k in nullable else set()
return firstset_((rules(grammar), first, nullable))[1]
```
Finally, we rely on the `fixpoint` to update the first set with the contents of the current first set until the first set stops changing.
```
def first_expr(expr, first, nullable):
tokens = set()
for token in expr:
tokens |= first[token]
if token not in nullable:
break
return tokens
@fixpoint
def firstset_(arg):
(rules, first, epsilon) = arg
for A, expression in rules:
first[A] |= first_expr(expression, first, epsilon)
return (rules, first, epsilon)
firstset(canonical(A1_GRAMMAR), EPSILON)
```
### Exercise 9: Follow Set of a Nonterminal
The follow set definition is similar to the first set. The follow set of a nonterminal is the set of terminals that can occur just after that nonterminal is used in any derivation. The follow set of the start symbol is `EOF`, and the follow set of any nonterminal is the super set of first sets of all symbols that come after it in any choice expression.
For example, the follow set of `<expr>` in `A1_GRAMMAR` is the set `{EOF, +, -}`.
As in the previous exercise, implement the `followset()` using the `fixpoint()` decorator.
**Solution.** The implementation of `followset()` is similar to `firstset()`. We first initialize the follow set with `EOF`, get the epsilon and first sets, and use the `fixpoint()` decorator to iteratively compute the follow set until nothing changes.
```
EOF = '\0'
def followset(grammar, start):
follow = {i: set() for i in grammar}
follow[start] = {EOF}
epsilon = nullable(grammar)
first = firstset(grammar, epsilon)
return followset_((grammar, epsilon, first, follow))[-1]
```
Given the current follow set, one can update the follow set as follows:
```
@fixpoint
def followset_(arg):
grammar, epsilon, first, follow = arg
for A, expression in rules(grammar):
f_B = follow[A]
for t in reversed(expression):
if t in grammar:
follow[t] |= f_B
f_B = f_B | first[t] if t in epsilon else (first[t] - {EPSILON})
return (grammar, epsilon, first, follow)
followset(canonical(A1_GRAMMAR), START_SYMBOL)
```
### Exercise 10: A LL(1) Parser
As we mentioned previously, there exist other kinds of parsers that operate left-to-right with right most derivation (*LR(k)*) or left-to-right with left most derivation (*LL(k)*) with _k_ signifying the amount of lookahead the parser is permitted to use.
What should one do with the lookahead? That lookahead can be used to determine which rule to apply. In the case of an *LL(1)* parser, the rule to apply is determined by looking at the _first_ set of the different rules. We previously implemented `first_expr()` that takes a an expression, the set of `nullables`, and computes the first set of that rule.
If a rule can derive an empty set, then that rule may also be applicable if of sees the `follow()` set of the corresponding nonterminal.
#### Part 1: A LL(1) Parsing Table
The first part of this exercise is to implement the _parse table_ that describes what action to take for an *LL(1)* parser on seeing a terminal symbol on lookahead. The table should be in the form of a _dictionary_ such that the keys represent the nonterminal symbol, and the value should contain another dictionary with keys as terminal symbols and the particular rule to continue parsing as the value.
Let us illustrate this table with an example. The `parse_table()` method populates a `self.table` data structure that should conform to the following requirements:
```
class LL1Parser(Parser):
def parse_table(self):
self.my_rules = rules(self.cgrammar)
self.table = ... # fill in here to produce
def rules(self):
for i, rule in enumerate(self.my_rules):
print(i, rule)
def show_table(self):
ts = list(sorted(terminals(self.cgrammar)))
print('Rule Name\t| %s' % ' | '.join(t for t in ts))
for k in self.table:
pr = self.table[k]
actions = list(str(pr[t]) if t in pr else ' ' for t in ts)
print('%s \t| %s' % (k, ' | '.join(actions)))
```
On invocation of `LL1Parser(A2_GRAMMAR).show_table()`
It should result in the following table:
```
for i, r in enumerate(rules(canonical(A2_GRAMMAR))):
print("%d\t %s := %s" % (i, r[0], r[1]))
```
|Rule Name || + | - | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9|
|-----------||---|---|---|---|---|---|---|---|---|---|---|--|
|start || | | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0|
|expr || | | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1|
|expr_ || 2 | 3 | | | | | | | | | | |
|integer || | | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5|
|integer_ || 7 | 7 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6|
|digit || | | 8 | 9 |10 |11 |12 |13 |14 |15 |16 |17|
**Solution.** We define `predict()` as we explained before. Then we use the predicted rules to populate the parse table.
```
class LL1Parser(LL1Parser):
def predict(self, rulepair, first, follow, epsilon):
A, rule = rulepair
rf = first_expr(rule, first, epsilon)
if nullable_expr(rule, epsilon):
rf |= follow[A]
return rf
def parse_table(self):
self.my_rules = rules(self.cgrammar)
epsilon = nullable(self.cgrammar)
first = firstset(self.cgrammar, epsilon)
# inefficient, can combine the three.
follow = followset(self.cgrammar, self.start_symbol())
ptable = [(i, self.predict(rule, first, follow, epsilon))
for i, rule in enumerate(self.my_rules)]
parse_tbl = {k: {} for k in self.cgrammar}
for i, pvals in ptable:
(k, expr) = self.my_rules[i]
parse_tbl[k].update({v: i for v in pvals})
self.table = parse_tbl
ll1parser = LL1Parser(A2_GRAMMAR)
ll1parser.parse_table()
ll1parser.show_table()
```
#### Part 2: The Parser
Once we have the parse table, implementing the parser is as follows: Consider the first item from the sequence of tokens to parse, and seed the stack with the start symbol.
While the stack is not empty, extract the first symbol from the stack, and if the symbol is a terminal, verify that the symbol matches the item from the input stream. If the symbol is a nonterminal, use the symbol and input item to lookup the next rule from the parse table. Insert the rule thus found to the top of the stack. Keep track of the expressions being parsed to build up the parse table.
Use the parse table defined previously to implement the complete LL(1) parser.
**Solution.** Here is the complete parser:
```
class LL1Parser(LL1Parser):
def parse_helper(self, stack, inplst):
inp, *inplst = inplst
exprs = []
while stack:
val, *stack = stack
if isinstance(val, tuple):
exprs.append(val)
elif val not in self.cgrammar: # terminal
assert val == inp
exprs.append(val)
inp, *inplst = inplst or [None]
else:
if inp is not None:
i = self.table[val][inp]
_, rhs = self.my_rules[i]
stack = rhs + [(val, len(rhs))] + stack
return self.linear_to_tree(exprs)
def parse(self, inp):
self.parse_table()
k, _ = self.my_rules[0]
stack = [k]
return self.parse_helper(stack, inp)
def linear_to_tree(self, arr):
stack = []
while arr:
elt = arr.pop(0)
if not isinstance(elt, tuple):
stack.append((elt, []))
else:
# get the last n
sym, n = elt
elts = stack[-n:] if n > 0 else []
stack = stack[0:len(stack) - n]
stack.append((sym, elts))
assert len(stack) == 1
return stack[0]
ll1parser = LL1Parser(A2_GRAMMAR)
tree = ll1parser.parse('1+2')
display_tree(tree)
```
| github_jupyter |
<a href="http://landlab.github.io"><img style="float: left" src="../../landlab_header.png"></a>
# Using plotting tools associated with the Landlab NetworkSedimentTransporter component
<hr>
<small>For more Landlab tutorials, click here: <a href="https://landlab.readthedocs.io/en/latest/user_guide/tutorials.html">https://landlab.readthedocs.io/en/latest/user_guide/tutorials.html</a></small>
<hr>
This tutorial illustrates how to plot the results of the NetworkSedimentTransporter Landlab component using the `plot_network_and_parcels` tool.
In this example we will:
- create a simple instance of the NetworkSedimentTransporter using a *synthetic river network
- create a simple instance of the NetworkSedimentTransporter using an *input shapefile for the river network
- show options for setting the color and line widths of network links
- show options for setting the color of parcels (marked as dots on the network)
- show options for setting the size of parcels
- show options for plotting a subset of the parcels
- demonstrate changing the timestep plotted
- show an example combining many plotting controls
First, import the necessary libraries:
```
import warnings
warnings.filterwarnings('ignore')
import os
import pathlib
import matplotlib.pyplot as plt
import matplotlib.colors as colors
import numpy as np
from landlab import ExampleData
from landlab.components import FlowDirectorSteepest, NetworkSedimentTransporter
from landlab.data_record import DataRecord
from landlab.grid.network import NetworkModelGrid
from landlab.plot import plot_network_and_parcels
from landlab.io import read_shapefile
from matplotlib.colors import Normalize
```
## 1. Create and run the synthetic example of NST
First, we need to create an implementation of the Landlab NetworkModelGrid to plot. This example creates a synthetic grid, defining the location of each node and link.
```
y_of_node = (0, 100, 200, 200, 300, 400, 400, 125)
x_of_node = (0, 0, 100, -50, -100, 50, -150, -100)
nodes_at_link = ((1, 0), (2, 1), (1, 7), (3, 1), (3, 4), (4, 5), (4, 6))
grid1 = NetworkModelGrid((y_of_node, x_of_node), nodes_at_link)
grid1.at_node["bedrock__elevation"] = [0.0, 0.05, 0.2, 0.1, 0.25, 0.4, 0.8, 0.8]
grid1.at_node["topographic__elevation"] = [0.0, 0.05, 0.2, 0.1, 0.25, 0.4, 0.8, 0.8]
grid1.at_link["flow_depth"] = 2.5 * np.ones(grid1.number_of_links) # m
grid1.at_link["reach_length"] = 200*np.ones(grid1.number_of_links) # m
grid1.at_link["channel_width"] = 1*np.ones(grid1.number_of_links) # m
# element_id is the link on which the parcel begins.
element_id = np.repeat(np.arange(grid1.number_of_links),30)
element_id = np.expand_dims(element_id, axis=1)
volume = 0.1*np.ones(np.shape(element_id)) # (m3)
active_layer = np.ones(np.shape(element_id)) # 1= active, 0 = inactive
density = 2650 * np.ones(np.size(element_id)) # (kg/m3)
abrasion_rate = 0 * np.ones(np.size(element_id)) # (mass loss /m)
# Lognormal GSD
medianD = 0.05 # m
mu = np.log(medianD)
sigma = np.log(2) #assume that D84 = sigma*D50
np.random.seed(0)
D = np.random.lognormal(
mu,
sigma,
np.shape(element_id)
) # (m) the diameter of grains in each parcel
time_arrival_in_link = np.random.rand(np.size(element_id), 1)
location_in_link = np.random.rand(np.size(element_id), 1)
variables = {
"abrasion_rate": (["item_id"], abrasion_rate),
"density": (["item_id"], density),
"time_arrival_in_link": (["item_id", "time"], time_arrival_in_link),
"active_layer": (["item_id", "time"], active_layer),
"location_in_link": (["item_id", "time"], location_in_link),
"D": (["item_id", "time"], D),
"volume": (["item_id", "time"], volume)
}
items = {"grid_element": "link", "element_id": element_id}
parcels1 = DataRecord(
grid1,
items=items,
time=[0.0],
data_vars=variables,
dummy_elements={"link": [NetworkSedimentTransporter.OUT_OF_NETWORK]},
)
fd1 = FlowDirectorSteepest(grid1, "topographic__elevation")
fd1.run_one_step()
nst1 = NetworkSedimentTransporter(
grid1,
parcels1,
fd1,
bed_porosity=0.3,
g=9.81,
fluid_density=1000,
transport_method="WilcockCrowe",
)
timesteps = 10 # total number of timesteps
dt = 60 * 60 * 24 *1 # length of timestep (seconds)
for t in range(0, (timesteps * dt), dt):
nst1.run_one_step(dt)
```
## 2. Create and run an example of NST using a shapefile to define the network
First, we need to create an implementation of the Landlab NetworkModelGrid to plot. This example creates a grid based on a polyline shapefile.
```
datadir = ExampleData("io/shapefile", case="methow").base
shp_file = datadir / "MethowSubBasin.shp"
points_shapefile = datadir / "MethowSubBasin_Nodes_4.shp"
grid2 = read_shapefile(
shp_file,
points_shapefile=points_shapefile,
node_fields=["usarea_km2", "Elev_m"],
link_fields=["usarea_km2", "Length_m"],
link_field_conversion={"usarea_km2": "drainage_area", "Slope":"channel_slope", "Length_m":"reach_length"},
node_field_conversion={
"usarea_km2": "drainage_area",
"Elev_m": "topographic__elevation",
},
threshold=0.01,
)
grid2.at_node["bedrock__elevation"] = grid2.at_node["topographic__elevation"].copy()
grid2.at_link["channel_width"] = 1 * np.ones(grid2.number_of_links)
grid2.at_link["flow_depth"] = 0.9 * np.ones(grid2.number_of_links)
# element_id is the link on which the parcel begins.
element_id = np.repeat(np.arange(grid2.number_of_links), 50)
element_id = np.expand_dims(element_id, axis=1)
volume = 1*np.ones(np.shape(element_id)) # (m3)
active_layer = np.ones(np.shape(element_id)) # 1= active, 0 = inactive
density = 2650 * np.ones(np.size(element_id)) # (kg/m3)
abrasion_rate = 0 * np.ones(np.size(element_id)) # (mass loss /m)
# Lognormal GSD
medianD = 0.15 # m
mu = np.log(medianD)
sigma = np.log(2) #assume that D84 = sigma*D50
np.random.seed(0)
D = np.random.lognormal(
mu,
sigma,
np.shape(element_id)
) # (m) the diameter of grains in each parcel
time_arrival_in_link = np.random.rand(np.size(element_id), 1)
location_in_link = np.random.rand(np.size(element_id), 1)
variables = {
"abrasion_rate": (["item_id"], abrasion_rate),
"density": (["item_id"], density),
"time_arrival_in_link": (["item_id", "time"], time_arrival_in_link),
"active_layer": (["item_id", "time"], active_layer),
"location_in_link": (["item_id", "time"], location_in_link),
"D": (["item_id", "time"], D),
"volume": (["item_id", "time"], volume)
}
items = {"grid_element": "link", "element_id": element_id}
parcels2 = DataRecord(
grid2,
items=items,
time=[0.0],
data_vars=variables,
dummy_elements={"link": [NetworkSedimentTransporter.OUT_OF_NETWORK]},
)
fd2 = FlowDirectorSteepest(grid2, "topographic__elevation")
fd2.run_one_step()
nst2 = NetworkSedimentTransporter(
grid2,
parcels2,
fd2,
bed_porosity=0.3,
g=9.81,
fluid_density=1000,
transport_method="WilcockCrowe",
)
for t in range(0, (timesteps * dt), dt):
nst2.run_one_step(dt)
```
## 3. Options for link color and link line widths
The dictionary below (`link_color_options`) outlines 4 examples of link color and line width choices:
1. The default output of `plot_network_and_parcels`
2. Some simple modifications: the whole network is red, with a line width of 7, and no parcels.
3. Coloring links by an existing grid link attribute, in this case the total volume of sediment on the link (`grid.at_link.["sediment_total_volume"]`, which is created by the `NetworkSedimentTransporter`)
4. Similar to #3 above, but taking advantange of additional flexiblity in plotting
```
network_norm = Normalize(-1, 6) # see matplotlib.colors.Normalize
link_color_options = [
{# empty dictionary = defaults
},
{
"network_color":'r', # specify some simple modifications.
"network_linewidth":7,
"parcel_alpha":0 # make parcels transparent (not visible)
},
{
"link_attribute": "sediment_total_volume", # color links by an existing grid link attribute
"parcel_alpha":0
},
{
"link_attribute": "sediment_total_volume",
"network_norm": network_norm, # and normalize color scheme
"link_attribute_title": "Total Sediment Volume", # title on link color legend
"parcel_alpha":0,
"network_linewidth":3
}
]
```
Below, we implement these 4 plotting options, first for the synthetic network, and then for the shapefile-delineated network:
```
for grid, parcels in zip([grid1, grid2], [parcels1, parcels2]):
for l_opts in link_color_options:
fig = plot_network_and_parcels(
grid, parcels,
parcel_time_index=0, **l_opts)
plt.show()
```
In addition to plotting link coloring using an existing link attribute, we can pass any array of size link. In this example, we color links using an array of random values.
```
random_link = np.random.randn(grid2.size("link"))
l_opts = {
"link_attribute": random_link, # use an array of size link
"network_cmap": "jet", # change colormap
"network_norm": network_norm, # and normalize
"link_attribute_title": "A random number",
"parcel_alpha":0,
"network_linewidth":3
}
fig = plot_network_and_parcels(
grid2, parcels2,
parcel_time_index=0, **l_opts)
plt.show()
```
## 4. Options for parcel color
The dictionary below (`parcel_color_options`) outlines 4 examples of link color and line width choices:
1. The default output of `plot_network_and_parcels`
2. Some simple modifications: all parcels are red, with a parcel size of 10
3. Color parcels by an existing parcel attribute, in this case the sediment diameter of the parcel (`parcels1.dataset['D']`)
4. Color parcels by an existing parcel attribute, but change the colormap.
```
parcel_color_norm = Normalize(0, 1) # Linear normalization
parcel_color_norm2=colors.LogNorm(vmin=0.01, vmax=1)
parcel_color_options = [
{# empty dictionary = defaults
},
{
"parcel_color":'r', # specify some simple modifications.
"parcel_size":10
},
{
"parcel_color_attribute": "D", # existing parcel attribute.
"parcel_color_norm": parcel_color_norm,
"parcel_color_attribute_title":"Diameter [m]",
"parcel_alpha":1.0,
},
{
"parcel_color_attribute": "abrasion_rate", # silly example, does not vary in our example
"parcel_color_cmap": "bone",
},
]
for grid, parcels in zip([grid1, grid2], [parcels1, parcels2]):
for pc_opts in parcel_color_options:
fig = plot_network_and_parcels(
grid, parcels,
parcel_time_index=0, **pc_opts)
plt.show()
```
## 5. Options for parcel size
The dictionary below (`parcel_size_options`) outlines 4 examples of link color and line width choices:
1. The default output of `plot_network_and_parcels`
2. Set a uniform parcel size and color
3. Size parcels by an existing parcel attribute, in this case the sediment diameter (`parcels1.dataset['D']`), and making the parcel markers entirely opaque.
4. Normalize parcel size on a logarithmic scale, and change the default maximum and minimum parcel sizes.
```
parcel_size_norm = Normalize(0, 1)
parcel_size_norm2=colors.LogNorm(vmin=0.01, vmax=1)
parcel_size_options = [
{# empty dictionary = defaults
},
{
"parcel_color":'b', # specify some simple modifications.
"parcel_size":10
},
{
"parcel_size_attribute": "D", # use a parcel attribute.
"parcel_size_norm": parcel_color_norm,
"parcel_size_attribute_title":"Diameter [m]",
"parcel_alpha":1.0, # default parcel_alpha = 0.5
},
{
"parcel_size_attribute": "D",
"parcel_size_norm": parcel_size_norm2,
"parcel_size_min": 10, # default = 5
"parcel_size_max": 100, # default = 40
"parcel_alpha": 0.1
},
]
for grid, parcels in zip([grid1, grid2], [parcels1, parcels2]):
for ps_opts in parcel_size_options:
fig = plot_network_and_parcels(
grid, parcels,
parcel_time_index=0, **ps_opts)
plt.show()
```
## 6. Plotting a subset of the parcels
In some cases, we might want to plot only a subset of the parcels on the network. Below, we plot every 50th parcel in the `DataRecord`.
```
parcel_filter = np.zeros((parcels2.dataset.dims["item_id"]), dtype=bool)
parcel_filter[::50] = True
pc_opts= {
"parcel_color_attribute": "D", # a more complex normalization and a parcel filter.
"parcel_color_norm": parcel_color_norm2,
"parcel_color_attribute_title":"Diameter [m]",
"parcel_alpha": 1.0,
"parcel_size": 40,
"parcel_filter": parcel_filter
}
fig = plot_network_and_parcels(
grid2, parcels2,
parcel_time_index=0, **pc_opts
)
plt.show()
```
## 7. Select the parcel timestep to be plotted
As a default, `plot_network_and_parcels` plots parcel positions for the last timestep of the model run. However, `NetworkSedimentTransporter` tracks the motion of parcels for all timesteps. We can plot the location of parcels on the link at any timestep using `parcel_time_index`.
```
parcel_time_options = [0,4,7]
for grid, parcels in zip([grid1, grid2], [parcels1, parcels2]):
for pt_opts in parcel_time_options:
fig = plot_network_and_parcels(
grid, parcels,
parcel_size = 20,
parcel_alpha = 0.1,
parcel_time_index=pt_opts)
plt.show()
```
## 7. Combining network and parcel plotting options
Nothing will stop us from making all of the choices at once.
```
parcel_color_norm=colors.LogNorm(vmin=0.01, vmax=1)
parcel_filter = np.zeros((parcels2.dataset.dims["item_id"]), dtype=bool)
parcel_filter[::30] = True
fig = plot_network_and_parcels(grid2,
parcels2,
parcel_time_index=0,
parcel_filter=parcel_filter,
link_attribute="sediment_total_volume",
network_norm=network_norm,
network_linewidth=4,
network_cmap='bone_r',
parcel_alpha=1.0,
parcel_color_attribute="D",
parcel_color_norm=parcel_color_norm2,
parcel_size_attribute="D",
parcel_size_min=5,
parcel_size_max=150,
parcel_size_norm=parcel_size_norm,
parcel_size_attribute_title="D")
```
| github_jupyter |
The tanh-sinh (or double exponential) method.
We calculate an integral in the following fashion:
$$
I=\int_{-1}^{1} dx f(x) = \int_{-\infty}^{\infty} dt \; f(g(t)) \;g^{\prime}(t) \approx h \sum_{j=-N}^{N} w_j \; f(x_j)\; ,
$$
with $x_j= g(h \, t)$ and $w_j = g^{\prime}(h \, t) $. The functio $g(t)$ transorms the interval from $x \in [-1,1]$ to $t \in ({-\infty} , {\infty})$. The parameter $N$ is chosen so that $| w_j \; f(x_j) |< \epsilon$ (for $j>N$) with $\epsilon \equiv 10^{-p}$, with $p$ the precision leven (number of digits).
The method is called $\tanh-\sinh$ because we choose $g$ to be
$$
g(t)=\tanh \left(\dfrac{\pi}{2} \sinh(t) \right).
$$
This means that
$$
x_j = \tanh \left(\dfrac{\pi}{2} \sinh(h \; j ) \right)\\
w_j =\dfrac{ \dfrac{\pi}{2} \cosh(h \; j ) }{\cosh^2 \left(\dfrac{\pi}{2} \sinh(h \; j ) \right) }.
$$
It is worth mentioning that $x_j$ and $w_j$ can be computed once, and then just applied in a lot of integrals.
The error of the estimate is
$$
Err \approx h \left(\dfrac{h}{2 \pi}\right)^2 \sum_{j=-N}^{N}
\left[ \dfrac{d^2 \; g^{\prime}(t) f( g(t) ) }{dt} \right]_{t=h \, j}
$$
So, we start by choosing some N such that $|w_{N+1} f(\pm x_{N+1})| < \epsilon$.
Then, we calculate the integral and the error. if the error is acceptable (according to some tolerances
defined by the user) then the integral is returned. If the eror is large, then we update $h$ and $N$ as
$$
h \to h/2 \\
N \to 2N \; .
$$
Note, that once we have found $N$ suche that $|w_{N+1} f(\pm x_{N+1})| < \epsilon$, then by changing
$h \to h/2$, we need $N \to 2N$, so that $N \, h$ to be such that $|w_{N+1} f(\pm x_{N+1})| < \epsilon$
holds for the updated value of $h$.
Everything is based on [Wikipedia](https://en.wikipedia.org/wiki/Tanh-sinh_quadrature#Implementations) and [Bailey's paper](https://www.davidhbailey.com//dhbpapers/dhb-tanh-sinh.pdf).
```
import numpy as np
from numpy import tanh,sinh,cosh,pi,abs
#just for testing
from scipy.integrate import quad
class DoubleExp:
def g(self,t):
return tanh( pi/2. * sinh(t) )
def dgdt(self,t):
return pi/2. *cosh(t)/cosh( pi/2. * sinh(t) )**2.
def F(self,t):
#this will be used to determine the error
return self.func( self.g(t) )*self.dgdt(t)
def d2Fdt(self,t,_h=1e-8):
'''
This will give the second derivatives we need for the error estimation.
For the moment take derivatives numerically.
Later I will do the derivatives of g analytically, but for the moment should be fine.
'''
return (self.F(t+_h )- 2 * self.F(t ) + self.F(t -_h ))/(_h**2.)
def __init__(self,func,_exp=1,_exp_max=15,rtol=1e-5,atol=1e-5,p=10,Nmax=1000):
'''
func: function to be integrated in the interval [-1,1].
exp: initial value of h=2^-exp
exp_min: the minimum exp, with hmin= 2^{-exp_max}
p: precision.
Nmax=maximum number of evaluations
Note that x_{-j}=-x_j and w_{-j}=-w_j .
'''
self.func=func
self._exp=_exp
self._exp_max=_exp_max
self.h=2**-_exp
self.hmin=2**-_exp_max
self.rtol=rtol
self.atol=atol
self.eps=10**(-p)
#initialize N
self.N=0
self.N_init=False
#eval will tell us if we have already evaluated the integral for given N and h (no need to sum thingswe already have)
self.eval=True
self.h_stop=False
#initialize the integral and the error.
#As you update h and N, you need to add to the sum only new values produced
#Also, since h changes, multipy by h at the end of the evaluation.
self.integral=self.func( self.g(0) ) *self.dgdt(0)
self.err=self.d2Fdt(0)
def N_start(self):
'''
Find an appropriate N to start.
As you update h, just update N->N*2 (later we may use something better)
'''
#start from this.
tmp_N=self.N+1
while True:
#remember that x_j=-x_{-j}, w_j = w_{-j}
_x=self.g(self.h*tmp_N)
_w=self.dgdt(self.h*tmp_N)
_f1=_w*self.func(_x)
_f2= _w*self.func(-_x)
#Note that we want N to start as N>0. This way we make sure that N gets updated correctly
#(if N starts at 0, it's not going to be updated).
if abs(_f1)<self.eps and abs(_f2 )<self.eps and self.N>1:
self.eval=False
break
else:
self.integral+=_f1+_f2
self.err+=self.d2Fdt( tmp_N*self.h)
self.N=tmp_N
tmp_N+=1
def evaluate(self):
'''
Evaluate the integral for given h and N.
Also evaluate the error.
Note for later: since we update h->h/2, we just need to update the sum including only the new
addition we make. That is, you only calculate for odd j!
'''
j=1
while self.eval:
_x=self.g(self.h*j)
_w=self.dgdt(self.h*j)
self.integral+=_w*(self.func(_x) + self.func(-_x))
self.err+=self.d2Fdt( j*self.h)+self.d2Fdt( -j*self.h)
j+=2
if j>self.N-2:
self.eval=False
break
def h_control(self):
'''
Determines if the error is acceptable. If not, decrese h until it is (or hmin is found).
'''
abs_err=abs(self.err*self.h*(self.h/(2*pi))**2.)
_sc=self.atol + self.rtol*abs(self.integral)
if abs_err/_sc <1 :
self.h_stop=True
else:
if self.h<self.hmin:
self.h_stop=True
else:
self.h=self.h/2
self.N=self.N*2
self.eval=True
def integrate(self):
if self.N_init==False:
self.N_start()
while self.h_stop==False:
self.h_control()
self.evaluate()
self.eval=False
return (self.integral*self.h , abs(self.err*self.h*(self.h/(2*pi))**2.) )
def F(x):
# return (x**2-1)/(x**2+1)*1/(x**2+5)**0.5
# return 1/((1+x)**0.5 +(1-x)**0.5 +2 )
# return x**4*5*np.exp(-x**2/5.)
return np.exp(-x**2./1e-15)
DE=DoubleExp(func=F,_exp=10,_exp_max=50,p=20,rtol=1e-10,atol=1e-10)
DE.integrate()
quad(F,-1,1)
```
| github_jupyter |
```
# Autoreload packages in case they change.
%load_ext autoreload
%autoreload 2
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import os
import sys
import btk
import galsim
import warnings
```
# "Custom" tutorial
This tutorial is intended to showcase how to customize some elements of BTK, namely the sampling function, the surveys or the measure function. We encourage you to follow the intro tutorial first if you have not already done so.
## Table of contents
- [Custom sampling function](#custom_sampling_function)
- [Custom survey](#custom_survey)
- [Custom measure function](#custom_measure_function)
- [Custom target measure](#custom_target_measure)
## Custom sampling function
<a id='custom_sampling_function'></a>
The sampling function defines how galaxies are selected in the catalog and their positions in the blends. This is done by defining a custom class based on the `SamplingFunction` class, which will be called (like a function) when the blends are generated. The `__call__` method should normally only take as an argument the catalog (as an astropy table), and return a smaller astropy table containing the entries from the catalog corresponding to the galaxies, along with the shifts (in arcseconds) of the galaxies compared to the center of the image, in the columns "ra" and "dec".
Here is an example with the default sampling function.
```
class DefaultSampling(btk.sampling_functions.SamplingFunction):
"""Default sampling function used for producing blend tables."""
def __init__(self, max_number=2, stamp_size=24.0, maxshift=None):
"""
Args:
max_number (int): Defined in parent class
stamp_size (float): Size of the desired stamp.
maxshift (float): Magnitude of maximum value of shift. If None then it
is set as one-tenth the stamp size. (in arcseconds)
"""
super().__init__(max_number)
self.stamp_size = stamp_size
self.maxshift = maxshift if maxshift else self.stamp_size / 10.0
@property
def compatible_catalogs(self):
return "CatsimCatalog", "CosmosCatalog"
def __call__(self, table):
"""Applies default sampling to the input CatSim-like catalog and returns an
astropy table with entries corresponding to a blend centered close to postage
stamp center.
Function selects entries from input table that are brighter than 25.3 mag
in the i band. Number of objects per blend is set at a random integer
between 1 and Args.max_number. The blend table is then randomly sampled
entries from the table after selection cuts. The centers are randomly
distributed within 1/10th of the stamp size. Here even though the galaxies
are sampled from a CatSim catalog, their spatial location are not
representative of real blends.
Args:
table (astropy.table): Table containing entries corresponding to galaxies
from which to sample.
Returns:
Astropy.table with entries corresponding to one blend.
"""
number_of_objects = np.random.randint(1, self.max_number + 1)
(q,) = np.where(table["ref_mag"] <= 25.3)
blend_table = table[np.random.choice(q, size=number_of_objects)]
blend_table["ra"] = 0.0
blend_table["dec"] = 0.0
x_peak, y_peak = _get_random_center_shift(number_of_objects, self.maxshift)
blend_table["ra"] += x_peak
blend_table["dec"] += y_peak
if np.any(blend_table["ra"] > self.stamp_size / 2.0) or np.any(
blend_table["dec"] > self.stamp_size / 2.0
):
warnings.warn("Object center lies outside the stamp")
return blend_table
def _get_random_center_shift(num_objects, maxshift):
"""Returns random shifts in x and y coordinates between + and - max-shift in arcseconds.
Args:
num_objects (int): Number of x and y shifts to return.
Returns:
x_peak (float): random shift along the x axis
y_peak (float): random shift along the x axis
"""
x_peak = np.random.uniform(-maxshift, maxshift, size=num_objects)
y_peak = np.random.uniform(-maxshift, maxshift, size=num_objects)
return x_peak, y_peak
```
As you can see, this sampling function does 3 things: applying a magnitude cut to the catalog, selecting random galaxies uniformly (with a random number of galaxies, the maximum being specified at the initialization), and assigning them random uniform shifts.
Here is how we would write a sampling function for generating two galaxies, one bright and centered, the other faint and randomly shifted.
```
class PairSampling(btk.sampling_functions.SamplingFunction):
def __init__(self, stamp_size=24.0, maxshift=None):
super().__init__(2)
self.stamp_size = stamp_size
self.maxshift = maxshift if maxshift else self.stamp_size / 10.0
@property
def compatible_catalogs(self):
return "CatsimCatalog", "CosmosCatalog"
def __call__(self,table):
(q_bright,) = np.where(table["ref_mag"] <= 25.3)
(q_dim,) = np.where((table["ref_mag"] > 25.3) & (table["ref_mag"] <= 28))
indexes = [np.random.choice(q_bright),np.random.choice(q_dim)]
blend_table = table[indexes]
blend_table["ra"] = 0.0
blend_table["dec"] = 0.0
x_peak, y_peak = _get_random_center_shift(1, self.maxshift)
blend_table["ra"][1] += x_peak
blend_table["dec"][1] += y_peak
if np.any(blend_table["ra"] > self.stamp_size / 2.0) or np.any(
blend_table["dec"] > self.stamp_size / 2.0
):
warnings.warn("Object center lies outside the stamp")
return blend_table
```
You can try to write your own sampling function here if you wish.
Here is some code to test our new sampling function (please replace the first line if you wrote your own sampling function).
```
sampling_function = PairSampling()
catalog_name = "../data/sample_input_catalog.fits"
stamp_size = 24
survey = btk.survey.get_surveys("Rubin")
catalog = btk.catalog.CatsimCatalog.from_file(catalog_name)
draw_blend_generator = btk.draw_blends.CatsimGenerator(
catalog,
sampling_function,
survey,
stamp_size=stamp_size,
batch_size=5
)
batch = next(draw_blend_generator)
blend_images = batch['blend_images']
blend_list = batch['blend_list']
btk.plot_utils.plot_blends(blend_images, blend_list, limits=(30,90))
```
<a id='custom_survey'></a>
## Custom survey
<a id='custom_survey'></a>
The survey defines the observational parameters relative to the instrument and telescope making the observation; in particular, it serves to define the pixel scale, the number of bands, the noise level, the flux, and the PSF.
A number of surveys is provided with BTK, so most users will not need to define a new one; however you may want to add one, or to modify one (for example to use a custom PSF). Here we will detail how to do so.
A Survey is defined as a named tuple, that is a tuple where each slot has a name. Here are all the fields that a survey contains:
- name: Name of the survey
- pixel_scale: Pixel scale in arcseconds
- effective_area: Light-collecting area of the telescope; depending on the optics of the telescope this can be different from $\pi*r^2$, in the case of a Schmidt–Cassegrain telescope for instance.
- mirror_diameter: Diameter of the primary telescope, in meters (without accounting for an eventual missing area)
- airmass: Length of the optical path through atmosphere, relative to the zenith path length. An airmass of 1.2 means that light would travel the equivalent of 1.2 atmosphere when observing.
- zeropoint_airmass: airmass which was used when computing the zeropoints. If in doubt, set it to the same value as the airmass.
- filters: List of Filter objects, more on that below
The Filter object is, again, a named tuple, containing the informations relative to each filter; a single survey can contain multiple filters. Each filter contains:
- name: Name of the filter
- sky_brightness: brightness of the sky background, in mags/sq.arcsec
- exp_time: total exposure time, in seconds
- zeropoint: Magnitude of an object giving a measured flux of 1 electron per second
- extinction: exponential coefficient describing the absorption of light by the atmosphere.
- psf: PSF for the filter. This can be provided in two ways:
- Providing a Galsim PSF model, e.g. `galsim.Kolmogorov(fwhm)` or any convolution of such models.
- Providing a function which returns a Galsim model when called (with no arguments). This can be used when you
you want to randomize the PSF.
In the case of the default surveys, we only use the first possibility, computing the model using the get_psf function beforehand; those models have an atmospheric and an optical component.
Surveys are usually imported using `btk.survey.get_surveys(survey_names)`, which will create the Survey object(s) from a config file (currently, the implemented surveys are Rubin, HSC, HST, Euclid, DES and CFHT); it is also possible to create them directly in Python.
Here is the definition of the Rubin survey as an example. You may try changing the parameters if you wish to see the effects on the blends.
```
from btk.survey import Survey, Filter, get_psf
_central_wavelength = {
"u": 3592.13,
"g": 4789.98,
"r": 6199.52,
"i": 7528.51,
"z": 8689.83,
"y": 9674.05,
}
Rubin = btk.survey.Survey(
"Rubin",
pixel_scale=0.2,
effective_area=32.4,
mirror_diameter=8.36,
airmass=1.2,
zeropoint_airmass=1.2,
filters=[
btk.survey.Filter(
name="y",
psf=get_psf(
mirror_diameter=8.36,
effective_area=32.4,
filt_wavelength=_central_wavelength["y"],
fwhm=0.703,
),
sky_brightness=18.6,
exp_time=4800,
zeropoint=26.56,
extinction=0.138,
),
btk.survey.Filter(
name="z",
psf=get_psf(
mirror_diameter=8.36,
effective_area=32.4,
filt_wavelength=_central_wavelength["z"],
fwhm=0.725,
),
sky_brightness=19.6,
exp_time=4800,
zeropoint=27.39,
extinction=0.043,
),
btk.survey.Filter(
name="i",
psf=get_psf(
mirror_diameter=8.36,
effective_area=32.4,
filt_wavelength=_central_wavelength["i"],
fwhm=0.748,
),
sky_brightness=20.5,
exp_time=5520,
zeropoint=27.78,
extinction=0.07,
),
btk.survey.Filter(
name="r",
psf=get_psf(
mirror_diameter=8.36,
effective_area=32.4,
filt_wavelength=_central_wavelength["r"],
fwhm=0.781,
),
sky_brightness=21.2,
exp_time=5520,
zeropoint=28.10,
extinction=0.10,
),
btk.survey.Filter(
name="g",
psf=get_psf(
mirror_diameter=8.36,
effective_area=32.4,
filt_wavelength=_central_wavelength["g"],
fwhm=0.814,
),
sky_brightness=22.3,
exp_time=2400,
zeropoint=28.26,
extinction=0.163,
),
btk.survey.Filter(
name="u",
psf=get_psf(
mirror_diameter=8.36,
effective_area=32.4,
filt_wavelength=_central_wavelength["u"],
fwhm=0.859,
),
sky_brightness=22.9,
exp_time=1680,
zeropoint=26.40,
extinction=0.451,
),
],
)
sampling_function = btk.sampling_functions.DefaultSampling()
catalog_name = "../data/sample_input_catalog.fits"
stamp_size = 24
survey = Rubin
catalog = btk.catalog.CatsimCatalog.from_file(catalog_name)
draw_blend_generator = btk.draw_blends.CatsimGenerator(
catalog,
sampling_function,
survey,
stamp_size=stamp_size,
batch_size=5
)
batch = next(draw_blend_generator)
blend_images = batch['blend_images']
blend_list = batch['blend_list']
btk.plot_utils.plot_blends(blend_images, blend_list, limits=(30,90))
```
## Custom measure function
<a id='custom_measure_function'></a>
Users who wish to test their own algorithm using BTK should consider writing a measure function. Morally, a measure function takes in blends and return measurements, ie detections, segmentation and deblended images. It is then fed to a MeasureGenerator, which will apply the function for every blend in the batch.
More precisely, the measure function takes in two main arguments, named `batch` and `idx`; the first one contains the whole results from the DrawBlendsGenerator, while the second contains the id of the blend on which the measurement should be carried. This is done so that the user access to every relevant information, including the PSF and WCS which are defined per batch and not per blend.
The results should be returned as a dictionary, with entries:
- "catalog" containing the detections, as an astropy Table object with columns "x_peak" and "y_peak" containing the coordinates of the detection. The user may also include other measurements in it, even though they will not be covered by the metrics.
- "segmentation" containing the measured segmentation. It should be a boolean array with shape (n_objects,stamp_size,stamp_size) where n_objects is the number of detected objects (must be coherent with the "catalog" object). The i-th channel should have pixels corresponding to the i-th object set to True.
- "deblended_images" containing the deblended images. It should be an array with shape (n_objects, n_bands, stamp_size, stamp_size) where n_objects is the number of detected objects and n_bands the number of bands. If you set the channels_last option to True, it should instead be of shape (n_objects, stamp_size, stamp_size, n_bands).
Here is an example with the sep measure function:
```
import sep
def sep_measure(batch, idx, channels_last=False, surveys=None, sigma_noise=1.5, **kwargs):
"""Return detection, segmentation and deblending information with SEP.
NOTE: If this function is used with the multiresolution feature,
measurements will be carried on the first survey, and deblended images
or segmentations will not be returned.
Args:
batch (dict): Output of DrawBlendsGenerator object's `__next__` method.
idx (int): Index number of blend scene in the batch to preform
measurement on.
sigma_noise (float): Sigma threshold for detection against noise.
Returns:
dict with the centers of sources detected by SEP detection algorithm.
"""
channel_indx = 0 if not channels_last else -1
# multiresolution
if isinstance(batch["blend_images"], dict):
if surveys is None:
raise ValueError("surveys are required in order to use the MR feature.")
survey_name = surveys[0].name
image = batch["blend_images"][survey_name][idx]
avg_image = np.mean(image, axis=channel_indx)
wcs = batch["wcs"][survey_name]
# single-survey
else:
image = batch["blend_images"][idx]
avg_image = np.mean(image, axis=channel_indx)
wcs = batch["wcs"]
stamp_size = avg_image.shape[0]
bkg = sep.Background(avg_image)
catalog, segmentation = sep.extract(
avg_image, sigma_noise, err=bkg.globalrms, segmentation_map=True
)
n_objects = len(catalog)
segmentation_exp = np.zeros((n_objects, stamp_size, stamp_size), dtype=bool)
deblended_images = np.zeros((n_objects, *image.shape), dtype=image.dtype)
for i in range(n_objects):
seg_i = segmentation == i + 1
segmentation_exp[i] = seg_i
seg_i_reshaped = np.zeros((np.min(image.shape), stamp_size, stamp_size))
for j in range(np.min(image.shape)):
seg_i_reshaped[j] = seg_i
seg_i_reshaped = np.moveaxis(seg_i_reshaped, 0, np.argmin(image.shape))
deblended_images[i] = image * seg_i_reshaped
t = astropy.table.Table()
t["ra"], t["dec"] = wcs.pixel_to_world_values(catalog["x"], catalog["y"])
t["ra"] *= 3600 #Converting to arcseconds
t["dec"] *= 3600
# If multiresolution, return only the catalog
if isinstance(batch["blend_images"], dict):
return {"catalog": t}
else:
return {
"catalog": t,
"segmentation": segmentation_exp,
"deblended_images": deblended_images,
}
```
You can see that the function takes `batch` and `idx` as arguments, but also has a `channels_last` argument and some kwargs. You can either specify arguments or catch them with `kwargs.get()`, as is done with `sigma_noise` there. To pass those arguments to the function, you can use the measure_kwargs, as detailed later in this tutorial. The `channels_last` (specifying if the channels are the first or last dimension of the image) and the `survey` (BTK survey object) are always passed to the function (you can choose if you want to catch them with `kwargs.get()` or not).
In the multiresolution case, the segmentation and the deblended images should be dictionaries indexed by the surveys, each entry containing the results as for the single resolution case. The catalog field does not change, as the ra and dec are independent from the resolution; it will be automatically split in the MeasureGenerator to get several catalogs containing the pixel coordinates.
## Custom target measure
<a id='custom_target_measure'></a>
In order to evaluate the quality of reconstructed galaxy images, one may want to take a look at the actual measurements that will be carried on those images. The "target measures" refer to this kind of measurement, such as the shape or the photometric redshift, which will be done in a weak lensing pipeline. They are used in the metrics part to evaluate the deblended image, by making the measurements both on the deblended image and on the associated true isolated galaxy image and comparing the two. Be careful not to make the confusion with the measure functions, which correspond to making detections, segmentations and deblended images.
This can be achieved with the `target_meas` argument of the MetricsGenerator. To create a new target measure, you need to create a function with two arguments : the image on which the measurements will be done, and a second one corresponding to additional data that may be needed, including the PSF, the pixel scale, a band number on which the measurement should be done (if applicable), and a boolean for verbosity. The function should then return the measurement, either as a number for a single measurement or as a list if you measure several at the same time (e.g. the two components of ellipticity) ; in case there is an error it should return NaN or a list of NaNs. To pass the function to the MetricsGenerator, you need to put it in a dictionary indexed by the name you want to give to the target measure (e.g. "ellipticity" or "redshift").
The function will be ran on all the deblended images, and the results can be found in `metrics_results["reconstruction"][<measure function>][<name of the target measure>]`, or directly in the galaxy summary in a column with the name of the target measure. For each target measure, you will also have the results for the true galaxies under the key `<name of the target measure>_true`. Also, if your target measure has several outputs, they will be denoted `name0`, `name1`, ... and `name0_true`,... instead.
Let us see how it works through an example. First we instantiate a MeasureGenerator as usual.
```
catalog_name = "../data/sample_input_catalog.fits"
stamp_size = 24
survey = btk.survey.get_surveys("Rubin")
catalog = btk.catalog.CatsimCatalog.from_file(catalog_name)
draw_blend_generator = btk.draw_blends.CatsimGenerator(
catalog,
btk.sampling_functions.DefaultSampling(),
survey,
stamp_size=stamp_size,
batch_size=100
)
meas_generator = btk.measure.MeasureGenerator(btk.measure.sep_measure,draw_blend_generator)
```
Then we can define a target measure function. This one is builtin with BTK and uses the Galsim implementation of the KSB method to measure the ellipticity of the galaxy.
```
def meas_ksb_ellipticity(image, additional_params):
"""Utility function to measure ellipticity using the `galsim.hsm` package, with the KSB method.
Args:
image (np.array): Image of a single, isolated galaxy with shape (H, W).
additional_params (dict): Containing keys 'psf', 'pixel_scale' and 'meas_band_num'.
The psf should be a Galsim PSF model, and meas_band_num
an integer indicating the band in which the measurement
is done.
"""
meas_band_num = additional_params["meas_band_num"]
psf_image = galsim.Image(image.shape[1], image.shape[2])
psf_image = additional_params["psf"][meas_band_num].drawImage(psf_image)
pixel_scale = additional_params["pixel_scale"]
verbose = additional_params["verbose"]
gal_image = galsim.Image(image[meas_band_num, :, :])
gal_image.scale = pixel_scale
shear_est = "KSB"
res = galsim.hsm.EstimateShear(gal_image, psf_image, shear_est=shear_est, strict=False)
result = [res.corrected_g1, res.corrected_g2, res.observed_shape.e]
if res.error_message != "" and verbose:
print(
f"Shear measurement error: '{res.error_message }'. \
This error may happen for faint galaxies or inaccurate detections."
)
result = [np.nan, np.nan, np.nan]
return result
metrics_generator = btk.metrics.MetricsGenerator(meas_generator,
target_meas={"ellipticity":meas_ksb_ellipticity},
meas_band_num=2) # Note : the ellipticity will be computed in this band !
blend_results,meas_results,metrics_results = next(metrics_generator)
```
We can now see the results :
```
print("Raw metrics results for deblended images : ",metrics_results["reconstruction"]["sep_measure"]["ellipticity0"][:5])
print("Raw metrics results for true images : ",metrics_results["reconstruction"]["sep_measure"]["ellipticity0_true"][:5])
print(metrics_results["galaxy_summary"]["sep_measure"]["ellipticity0","ellipticity0_true"][:5])
```
As usual, we can use the interactive function to plot the results. In the case of target measures, you need to provide two additional arguments to have it work : a list of the names of the measures, and the interval in which they are comprised.
```
btk.plot_utils.plot_metrics_summary(metrics_results,interactive=True,
target_meas_keys=['ellipticity0','ellipticity1'],
target_meas_limits=[(-1, 1),(-1,1)])
```
| github_jupyter |
- Scipy의 stats 서브 패키지에 있는 binom 클래스는 이항 분포 클래스이다. n 인수와 p 인수를 사용하여 모수를 설정한다
```
N = 10
theta = 0.6
rv = sp.stats.binom(N, theta)
rv
```
- pmf 메서드를 사용하면, 확률 질량 함수 (pmf: probability mass function)를 계산할 수 있다.
```
%matplotlib inline
xx = np.arange(N + 1)
plt.bar(xx, rv.pmf(xx), align='center')
plt.ylabel('p(x)')
plt.title('binomial pmf')
plt.show()
```
- 시뮬레이션을 하려면 rvs 메서드를 사용한다.
```
np.random.seed(0)
x = rv.rvs(100)
x
sns.countplot(x)
plt.title("Binomial Distribution's Simulation")
plt.xlabel('Sample')
plt.show()
```
- 이론적인 확률 분포와 샘플의 확률 분포를 동시에 나타내려면 다음과 같은 코드를 사용한다.
```
y = np.bincount(x, minlength=N+1)/float(len(x))
df = pd.DataFrame({'Theory': rv.pmf(xx), 'simulation': y}).stack()
df = df.reset_index()
df.columns = ['values', 'type', 'ratio']
df.pivot('values', 'type', 'ratio')
df
sns.barplot(x='values', y='ratio', hue='type', data=df)
plt.show()
```
#### 연습 문제 1
- 이항 확률 분포의 모수가 다음과 같을 경우에 각각 샘플을 생성한 후, 기댓값과 분산을 구하고 앞의 예제와 같이 확률 밀도 함수와 비교한 카운트 플롯을 그린다.
- 샘풀의 갯수가 10개인 경우와 1000개인 경우에 대해 각각 위의 계산을 한다.
- 1. Theta = 0.5, N = 5
- 2. Theta = 0.9, N = 20
```
# 연습문제 1 - 1
N = 5
theta = 0.5
rv = sp.stats.binom(N, theta)
xx10 = np.arange(N + 1)
plt.bar(xx, rv.pmf(xx10), align='center')
plt.ylabel('P(x)')
plt.title('Binomail Distribution pmdf')
plt.show()
# sample 갯수 10개 일 때
np.random.seed(0)
x10 = rv.rvs(10)
sns.countplot(x10)
plt.title('binomail distribution Simulation 10')
plt.xlabel('values')
plt.show()
# sample 갯수가 1000개 일 때
x1000 = rv.rvs(1000)
sns.countplot(x1000)
plt.title('binomail distribution Simulation 10')
plt.xlabel('values')
plt.show()
y10 = np.bincount(x10, minlength = N + 1)/float(len(x10))
df = pd.DataFrame({'Theory': rv.pmf(xx10), 'Simulation': y10}).stack()
df = df.reset_index()
df.columns = ['values', 'type', 'ratio']
df.pivot('values', 'type', 'ratio')
sns.barplot(x='values', y='ratio', hue='type', data=df)
plt.show()
df
```
#### 샘플 갯수가 1000개일 경우에 theta = 0.9, N = 20
```
N = 20
theta = 0.9
rv = sp.stats.binom(N, theta)
xx = np.arange(N + 1)
plt.bar(xx, rv.pmf(xx), align = 'center')
plt.ylabel('P(x)')
plt.title('binomial pmf when N=20')
plt.show()
x1000 = rv.rvs(1000) # sample 1000개 생성
sns.countplot(x1000)
plt.title("Binomial Distribution's Simulation")
plt.xlabel('values')
plt.show()
y1000 = np.bincount(x1000, minlength = N + 1)/float(len(x1000))
df = pd.DataFrame({'Theory':rv.pmf(xx), 'Simulation': y1000}).stack()
df = df.reset_index()
df.columns = ['values', 'type', 'ratio']
df.pivot('values', 'type', 'ratio')
df
sns.barplot(x='values', y='ratio', hue='type', data=df)
plt.show()
```
| github_jupyter |
<table style="float:left; border:none">
<tr style="border:none; background-color: #ffffff">
<td style="border:none">
<a href="http://bokeh.pydata.org/">
<img
src="assets/bokeh-transparent.png"
style="width:50px"
>
</a>
</td>
<td style="border:none">
<h1>Bokeh Tutorial</h1>
</td>
</tr>
</table>
<div style="float:right;"><h2>07. Exporting and Embedding</h2></div>
So far we have seen how to generate interactive Bokeh output directly inline in Jupyter notbeooks. It also possible to embed interactive Bokeh plots and layouts in other contexts, such as standalone HTML files, or Jinja templates. Additionally, Bokeh can export plots to static (non-interactive) PNG and SVG formats.
We will look at all of these possibilities in this chapter. First we make the usual imports.
```
from bokeh.io import output_notebook, show
output_notebook()
```
And also load some data that will be used throughout this chapter
```
import pandas as pd
from bokeh.plotting import figure
from bokeh.sampledata.stocks import AAPL
df = pd.DataFrame(AAPL)
df['date'] = pd.to_datetime(df['date'])
```
# Embedding Interactive Content
To start we will look differnet ways of embedding live interactive Bokeh output in various situations.
## Displaying in the Notebook
The first way to embed Bokeh output is in the Jupyter Notebooks, as we have already, seen. As a reminder, the cell below will generate a plot inline as output, because we executed `output_notebook` above.
```
p = figure(plot_width=800, plot_height=250, x_axis_type="datetime")
p.line(df['date'], df['close'], color='navy', alpha=0.5)
show(p)
```
## Saving to an HTML File
It is also often useful to generate a standalone HTML script containing Bokeh content. This is accomplished by calling the `output_file(...)` function. It is especially common to do this from standard Python scripts, but here we see that it works in the notebook as well.
```
from bokeh.io import output_file, show
output_file("plot.html")
show(p) # save(p) will save without opening a new browser tab
```
In addition the inline plot above, you should also have seen a new browser tab open with the contents of the newly saved "plot.html" file. It is important to note that `output_file` initiates a *persistent mode of operation*. That is, all subsequent calls to show will generate output to the specified file. We can "reset" where output will go by calling `reset_output`:
```
from bokeh.io import reset_output
reset_output()
```
## Templating in HTML Documents
Another use case is to embed Bokeh content in a Jinja HTML template. We will look at a simple explicit case first, and then see how this technique might be used in a web app framework such as Flask.
The simplest way to embed standalone (i.e. not Bokeh server) content is to use the `components` function. This function takes a Bokeh object, and returns a `<script>` tag and `<div>` tag that can be put in any HTML tempate. The script will eecute and load the Bokeh content into the associated div.
The cells below show a complete example, including loading BokehJS JS and CSS resources in the temlpate.
```
import jinja2
from bokeh.embed import components
# IMPORTANT NOTE!! The version of BokehJS loaded in the template should match
# the version of Bokeh installed locally.
template = jinja2.Template("""
<!DOCTYPE html>
<html lang="en-US">
<link
href="http://cdn.pydata.org/bokeh/dev/bokeh-0.13.0.min.css"
rel="stylesheet" type="text/css"
>
<script
src="http://cdn.pydata.org/bokeh/dev/bokeh-0.13.0.min.js"
></script>
<body>
<h1>Hello Bokeh!</h1>
<p> Below is a simple plot of stock closing prices </p>
{{ script }}
{{ div }}
</body>
</html>
""")
p = figure(plot_width=800, plot_height=250, x_axis_type="datetime")
p.line(df['date'], df['close'], color='navy', alpha=0.5)
script, div = components(p)
from IPython.display import HTML
HTML(template.render(script=script, div=div))
```
Note that it is possible to pass multiple objects to a single call to `components`, in order to template multiple Bokeh objects at once. See the [User's Guide for components](https://bokeh.pydata.org/en/latest/docs/user_guide/embed.html#components) for more information.
Once we have the script and div from `components`, it is straighforward to serve a rendered page containing Bokeh content in a web application, e.g. a Flask app as shown below.
```
from flask import Flask
app = Flask(__name__)
@app.route('/')
def hello_bokeh():
return template.render(script=script, div=div)
# Uncomment to run the Flask Server. Use Kernel -> Interrupt from Notebook menubar to stop
#app.run(port=5050)
# EXERCISE: Create your own template (or modify the one above)
```
# Exporting Static Images
Sometimes it is desirable to produce static images of plots or other Bokeh output, without any interactive capabilities. Bokeh supports exports to PNG and SVG formats.
## PNG Export
Bokeh supports exporting a plot or layout to PNG image format with the `export_png` function. This function is alled with a Bokeh object to export, and a filename to write the PNG output to. Often the Bokeh object passed to `export_png` is a single plot, but it need not be. If a layout is exported, the entire lahyout is saved to one PNG image.
***Important Note:*** *the PNG export capability requires installing some additional optional dependencies. The simplest way to obtain them is via conda:*
conda install selenium phantomjs pillow
```
from bokeh.io import export_png
p = figure(plot_width=800, plot_height=250, x_axis_type="datetime")
p.line(df['date'], df['close'], color='navy', alpha=0.5)
export_png(p, filename="plot.png")
from IPython.display import Image
Image('plot.png')
# EXERCISE: Save a layout of plots (e.g. row or column) as SVG and see what happens
```
## SVG Export
Bokeh can also generate SVG output in the browser, instead of rendering to HTML canvas. This is accomplished by setting `output_backend='svg'` on a figure. This can be be used to generate SVGs in `output_file` HTML files, or in content emebdded with `components`. It can also be used with the `export_svgs` function to save `.svg` files. Note that an SVG is created for *each canvas*. It is not possible to capture entire layouts or widgets in SVG output.
***Important Note:*** *There a currently some known issue with SVG output, it may not work for all use-cases*
```
from bokeh.io import export_svgs
p = figure(plot_width=800, plot_height=250, x_axis_type="datetime", output_backend='svg')
p.line(df['date'], df['close'], color='navy', alpha=0.5)
export_svgs(p, filename="plot.svg")
from IPython.display import SVG
SVG('plot.svg')
# EXERCISE: Save a layout of plots (e.g. row or column) as SVG and see what happens
```
| github_jupyter |
```
import pandas as pd
import numpy as np
import pickle as pk
file_name = '1_min'
df = pd.read_csv(file_name + '.csv')
df['behavior'] = np.zeros(len(df)).astype(np.int)
intention_2_action_delay = 3000
acc_threshold = 1
# 0 for changing to left
# 1 for changing to right
# 2 for following
next_lane_change_time = dict()
next_lane_change_direct = dict()
next_vel_change_time = dict()
next_vel_change_direct = dict()
def classify_behavior(v_id, cur_time):
if next_lane_change_time[v_id] > -1 and next_lane_change_time[v_id] - cur_time < intention_2_action_delay:
return next_lane_change_direct[v_id]
return 2
# if next_vel_change_time[v_id] > -1 and next_vel_change_time[v_id] - r.Global_Time < intention_2_action_delay:
# return next_vel_change_direct[v_id] + 2
# return 4
lane_id = dict()
behavior_seq = dict()
behavior_seq_id = dict()
change_point = list()
cnt = np.zeros((5, 5))
for i in reversed(range(len(df))):
r = df.iloc[i]
v_id = r.Vehicle_ID
if v_id not in lane_id.keys():
lane_id[v_id] = r.Lane_ID
next_lane_change_time[v_id] = -1
next_vel_change_time[v_id] = -1
behavior_seq[v_id] = list()
if r.Lane_ID != lane_id[v_id]:
next_lane_change_time[v_id] = r.Global_Time
next_lane_change_direct[v_id] = int(r.Lane_ID < lane_id[v_id])
lane_id[v_id] = r.Lane_ID
# if abs(r.v_Acc) > acc_threshold:
# next_vel_change_time[v_id] = r.Global_Time
# next_vel_change_direct[v_id] = int(r.v_Acc > 0)
bhv = classify_behavior(v_id, r.Global_Time)
if len(behavior_seq[v_id])>0 and behavior_seq[v_id][-1] < 2 and bhv != behavior_seq[v_id][-1]:
change_point.append((v_id, behavior_seq_id[v_id]))
behavior_seq[v_id].append(bhv)
behavior_seq_id[v_id] = i
df.at[i,'behavior']= bhv
dT = 0.1
x = list()
y = list()
vehicles = dict()
show_up = set()
vel_sum = 0
for i in range(len(df)):
r = df.iloc[i]
v_id = r.Vehicle_ID
show_up.add(v_id)
if v_id not in vehicles.keys():
df.at[i,'lateral_acc'] = 0
df.at[i,'lateral_vel'] = 0
vehicles[v_id] = df.iloc[i].copy()
vel_sum += vehicles[v_id].v_Vel
else:
lateral_V = (r.Local_X - vehicles[v_id].Local_X) / dT
vel_sum -= vehicles[v_id].v_Vel
df.at[i,'lateral_acc'] = (lateral_V - vehicles[v_id]['lateral_vel']) /dT
df.at[i,'lateral_vel'] = lateral_V
vehicles[v_id] = df.iloc[i].copy()
vel_sum += vehicles[v_id].v_Vel
v_mean = vel_sum / len(vehicles)
df.at[i,'mean_vel'] = v_mean
#remove exited car after every moment
if i == len(df)-1 or r.Global_Time != df.iloc[i+1].Global_Time:
v_ids = list(vehicles.keys())
for v_id in v_ids:
if v_id not in show_up:
vel_sum -= vehicles[v_id].v_Vel
vehicles.pop(v_id)
show_up = set()
df[:10]
df.to_csv(file_name + '_labeled.csv')
for i in range((len(change_point)-1) // 10):
v_id, idx = change_point[i*10]
df[max(0,idx-5000):min(idx+15000,len(df))].to_csv('lane_changing_data/'+str(v_id)+'_'+str(idx)+'.csv')
len(change_point)
```
| github_jupyter |
```
from os.path import exists
import openpyxl
import os
import pandas as pd
import re
from collections import Counter
import streamlit as st
pd.set_option('display.max_colwidth',None)
result = 'searchoutput.csv'
if exists(result):
os.remove(result)
# 创建结果文件
wbResult = openpyxl.Workbook()
wsResult = wbResult.worksheets[0]
wsResult.append(['result'])
# 读取原表两次,一次用来进行建表输入,一次用来做对应的输入
wb = openpyxl.load_workbook('SourceDB.xlsx')
input_excel = 'SourceDB.xlsx'
data = pd.read_excel(input_excel)
ws = wb.worksheets[0]
# 原表空白部分用*填充
for k in range(1,ws.max_column+1):
for i in range(1,ws.max_row+1):
if ws.cell(row=i,column=k).value is None:
ws.cell(i,k,'****')
input_word = input("请输入搜索内容:").strip().lower()
# st.subheader('🐼[T.Q Knowledge Base]')
input_word1 = st.text_input('©TAILab|Last release:2022/3/3','')
input_word = input_word1.strip().lower()
input_word_exist = re.sub(u"([u4e00-\u9fa5\u0030-\u0039\u0041-\u005a\u0061-\u007a])","",input_word)
input_word = input_word.split()
result_list = []
for index,row in enumerate(ws.rows):
if index == 0:
continue
rs_list = list(map(lambda cell: cell.value, row))
list_str = "".join('%s' %id for id in rs_list).replace("\n"," ").replace("\n"," ").replace("\t"," ").replace("\r"," ").lower()
result_list.append([index, list_str])
def search_onebyone(input_word_exist, input_word_list, result_list):
new_list = []
dict_list = []
new_list_count = []
# 精确匹配
for i in range(len(result_list)):
for m in input_word_list:
pattern = m
regex = re.compile(pattern)
nz = regen.search(result_list[i][1])
if nz:
new_list.append([len(nz.group()),nz.stat(),result_list[i][0]-1])
new_list_count.append(result_list[i][0]-1)
new_list = sorted(new_list)
new_index = [x for _,_,x in new_list]
new_index = sorted(set(new_index),key=new_index.index)
# 计数,只有当输入的全部单词全部出现以后,才取出
dict_list.append([k for k,v in Counter(new_list_count).items() if v == len(input_word_list)])
for m in dict_list:
result_index = m
temp = [j for j in new_index if j in result_index]
return temp
result = search_onebyone(input_word_exist, input_word, result_list)
def display_highlighted_words(df, keywords):
head = """
<talbe>
<thead>
""" + \
"".join(["<th> %s </th>" % c for c in df.columns])\
+ """
</thead>
</table>"""
head = """
<table>
<thead>
<th> Keywords </th><th> Content </th>
</thead>
</table>
"""
for i,r in df.iterrows():
row = "<tr>"
for c in df.columns:
matches = []
for k in keywords:
for match in re.finditer(k, str(r[c])):
matches.append(match)
# reverse sorting
matches = sorted(matches, key = lambda x: x.start(), reverse=True)
# building HTML row
cell = str(r[c])
# print(cell)
for match in matches:
cell = cell[:match.start()] +\
"<span style='color:red;background-color:yellow'> %s </span>" % cell[match.start():match.end()] +\
cell[match.end():]
row += "<td> %s </td>" % cell
row += "</tr>"
head += row
head += "</tbody></table>"
return head
# htmlcode1 = display_highlighted_words(dftest, input_word)
# st.markdown(htmlcode1, unsafe_allow_html=True)
if len(input_word)>0:
display(data.loc[(x for x in result)])
data.loc[(x for x in result)].to_csv('searchoutput.csv', encoding= 'utf_8_sig')
```
| github_jupyter |
## Gaussian processes with genetic algorithm for the reconstruction of late-time Hubble data
This notebook uses Gaussian processes (GP) with the genetic algorithm (GA) to reconstruct the cosmic chronometers and supernovae data sets ([2106.08688](https://arxiv.org/abs/2106.08688)). We shall construct our own GP class and use it with the python package ``pygad`` (https://pygad.readthedocs.io/) for the GA.
References to the data can be found at the end of the notebook.
```
%matplotlib inline
import numpy as np
from numpy.random import uniform as unif
import matplotlib.pyplot as plt
import pygad
```
### 0. My GP class
Here is the GP class (written from scratch) that we shall use in this notebook.
```
class GP:
'''Class for making GP predictions.
rbf: k(r) = A^2 \exp(-r^2/(2l^2))
rq : k(r) = A^2 (1 + (r^2/(2 \alpha l^2)))^{-\alpha}
m52: k(r) = A^2 \exp(-\sqrt{5}r/l)
(1 + \sqrt{5}r/l + 5r^2/(3l^2))
mix: rbf + chy + m52
Input:
chromosome: list of kernel hyperparameters
'''
def __init__(self, chromosome):
self.C_rbf = chromosome[0] # rbf genes
self.l_rbf = chromosome[1]
self.n_rbf = chromosome[2]
self.C_rq = chromosome[3] # rq genes
self.l_rq = chromosome[4]
self.a_rq = chromosome[5]
self.n_rq = chromosome[6]
self.C_m52 = chromosome[7] # m52 genes
self.l_m52 = chromosome[8]
self.n_m52 = chromosome[9]
def kernel(self, x, y):
r = x - y
# rbf term
k_rbf = np.exp(-(r**2)/(2*(self.l_rbf**2)))
rbf_term = (self.C_rbf**2)*(k_rbf**self.n_rbf)
# rq term
r = x - y
R_sq = (r**2)/(2*(self.l_rq**2))
k_rq = 1/((1 + R_sq/self.a_rq)**self.a_rq)
rq_term = (self.C_rq**2)*(k_rq**self.n_rq)
# m52 term
X = np.sqrt(5)*np.abs(r)/self.l_m52
B = 1 + X + ((X**2)/3)
k_m52 = B*np.exp(-X)
m52_term = (self.C_m52**2)*(k_m52**self.n_m52)
return rbf_term + rq_term + m52_term
def k_plus_c_inv(self, Z, C):
k_ZZ = np.array([[self.kernel(z_i, z_j) \
for z_i in Z]
for z_j in Z])
return np.linalg.inv(k_ZZ + C)
def cov(self, Z, C, Zs):
'''Returns the covariance matrix at Zs.
Note: Zs must be an array.'''
kpc_inv = self.k_plus_c_inv(Z, C)
return np.array([[self.kernel(z_i, z_j) \
-(self.kernel(z_i, Z) @ \
kpc_inv @ \
self.kernel(Z, z_j)) \
for z_i in Zs] \
for z_j in Zs])
def var(self, Z, C, Zs):
'''Returns the variance at Zs.
Note: Zs must be an array.'''
kpc_inv = self.k_plus_c_inv(Z, C)
return np.array([self.kernel(zs, zs) \
-(self.kernel(zs, Z) @ \
kpc_inv @ \
self.kernel(Z, zs)) \
for zs in Zs])
def get_logmlike(self, Z, Y, C):
'''Returns the log-marginal likelihood.'''
kpc_inv = self.k_plus_c_inv(Z, C)
kpc = np.linalg.inv(kpc_inv)
kpc_det = np.linalg.det(kpc)
Ys = np.array([(self.kernel(zs, Z) @ kpc_inv \
@ Y) for zs in Z])
delta_y = Y
return -0.5*(delta_y @ kpc_inv @ delta_y) \
-0.5*np.log(kpc_det) \
-0.5*len(Z)*np.log(2*np.pi)
def predict(self, Z, Y, C, Zs, with_cov = False, \
k_as_cov = False):
kpc_inv = self.k_plus_c_inv(Z, C)
mean = np.array([(self.kernel(zs, Z) @ kpc_inv \
@ Y) for zs in Zs])
if with_cov == False:
var_zz = self.var(Z, C, Zs)
return {'z': Zs, 'Y': mean, \
'varY': var_zz}
elif (with_cov == True) and (k_as_cov == False):
cov_zz = self.cov(Z, C, Zs)
return {'z': Zs, 'Y': mean, \
'covY': cov_zz}
elif (with_cov == True) and (k_as_cov == True):
cov_zz = np.array([[self.kernel(z_i, z_j) \
for z_i in Zs] \
for z_j in Zs])
return {'z': Zs, 'Y': mean, \
'covY': cov_zz}
```
This will be used for both the cosmic chronometers (Section 1) and supernovae applications (Section 2).
### 1. Cosmic chronometers
Importing the cosmic chronometers data set.
```
cc_data = np.loadtxt('cc_data.txt')
z_cc = cc_data[:, 0]
Hz_cc = cc_data[:, 1]
sigHz_cc = cc_data[:, 2]
fig, ax = plt.subplots()
ax.errorbar(z_cc, Hz_cc, yerr = sigHz_cc,
fmt = 'ro', ecolor = 'k',
markersize = 7, capsize = 3)
ax.set_xlabel('$z$')
ax.set_ylabel('$H(z)$')
plt.show()
```
To use the GA, we setup the log-marginal likelihood as a fitness function. In addition, we consider a Bayesian-information type penalty to fine complex kernels.
```
n_data = len(z_cc)
def penalty(chromosome):
'''Identifies a penalty term to be factored in the fitness function
so that longer/more complex kernels will be given a due weight.'''
c_rbf = chromosome[0]
l_rbf = chromosome[1]
A_rbf = c_rbf*l_rbf
c_rq = chromosome[3]
l_rq = chromosome[4]
A_rq = c_rq*l_rq
c_m52 = chromosome[7]
l_m52 = chromosome[8]
A_m52 = c_m52*l_m52
# set threshold to A_X = c_x*l_x
A_th = 1e-3
k = 0
if A_rbf > A_th:
k += 3
if A_rq > A_th:
k += 4
if A_m52 > A_th:
k += 3
return k*np.log(n_data)/2
def get_fit(chromosome):
'''Evaluates the fitness of the indivial with chromosome'''
if all(hp > 0 for hp in chromosome) == True:
pnl = penalty(chromosome)
try:
gp = GP(chromosome)
lml = gp.get_logmlike(z_cc, Hz_cc,
np.diag(sigHz_cc**2))
return lml - pnl
except:
lml = -1000
return lml
else:
lml = -1000
return lml
def fitness_function(chromosome, chromosome_idx):
return get_fit(chromosome)
```
In the next line, we setup an equally uniform population of pure-bred kernels and a diverse set of kernels. It is interesting to see the evolution of the uniform population compared to one which is a lot more diverse.
```
pop_size = 1000 # population size
init_uni = []
for i in range(0, pop_size):
if i < int(pop_size/3):
init_uni.append([unif(0, 300), unif(0, 10), unif(0, 5),
0, 0, 0, 0, 0, 0, 0])
elif (i > int(pop_size/3)) and (i < int(2*pop_size/3)):
init_uni.append([0, 0, 0,
unif(0, 300), unif(0, 10), unif(0, 2), unif(0, 5),
0, 0, 0])
else:
init_uni.append([0, 0, 0, 0, 0, 0, 0,
unif(0, 300), unif(0, 10), unif(0, 5)])
init_uni = np.array(init_uni)
init_div = []
for i in range(0, pop_size):
init_div.append([unif(0, 300), unif(0, 10), unif(0, 5),
unif(0, 300), unif(0, 10), unif(0, 2), unif(0, 5),
unif(0, 300), unif(0, 10), unif(0, 5)])
init_div = np.array(init_div)
```
Given this, we prepare the parameters of the GA.
```
gene_space = [{'low': 0, 'high': 300}, {'low': 0, 'high': 10}, {'low': 0, 'high': 5}, # rbf lims
{'low': 0, 'high': 300}, {'low': 0, 'high': 10}, # chy lims
{'low': 0, 'high': 2}, {'low': 0, 'high': 5},
{'low': 0, 'high': 300}, {'low': 0, 'high': 10}, {'low': 0, 'high': 5}] # m52 lims
num_genes = 10 # length of chromosome
n_gen = 100 # number of generations
sel_rate = 0.3 # selection rate
# parent selection
parent_selection_type = "rws" # roulette wheel selection
keep_parents = int(sel_rate*pop_size)
num_parents_mating = int(sel_rate*pop_size)
# crossover
#crossover_type = "single_point"
#crossover_type = "two_points"
#crossover_type = "uniform"
crossover_type = "scattered"
crossover_prob = 1.0
# mutation type options: random, swap, inversion, scramble, adaptive
mutation_type = "random"
#mutation_type = "swap"
#mutation_type = "inversion"
#mutation_type = "scramble"
#mutation_type = "adaptive"
mutation_prob = 0.5
def callback_generation(ga_instance):
i_gen = ga_instance.generations_completed
if i_gen in [i for i in range(0, n_gen, int(n_gen*0.1))]:
last_best = ga_instance.best_solutions[-1]
print("generation = {generation}".format(generation = i_gen))
print("fitness = {fitness}".format(fitness = get_fit(last_best)))
```
The ``GA run`` is performed in the next line.
*The next two code runs may be skipped if output have already been saved. In this case, proceed to the loading lines.
```
# setup GA instance, for random initial pop.
ga_inst_uni_cc = pygad.GA(initial_population = init_uni,
num_genes = num_genes,
num_generations = n_gen,
num_parents_mating = num_parents_mating,
fitness_func = fitness_function,
parent_selection_type = parent_selection_type,
keep_parents = keep_parents,
crossover_type = crossover_type,
crossover_probability = crossover_prob,
mutation_type = mutation_type,
mutation_probability = mutation_prob,
mutation_by_replacement = True,
on_generation = callback_generation,
gene_space = gene_space,
save_best_solutions = True)
# perform GA run
ga_inst_uni_cc.run()
# save results
ga_inst_uni_cc.save('gp_ga_cc_uniform_init')
# best solution
solution = ga_inst_uni_cc.best_solutions[-1]
print("best chromosome: {solution}".format(solution = solution))
print("best fitness = {solution_fitness}".format(solution_fitness = \
get_fit(solution)))
```
Next run creates a GA instance with the same parameters as with the previous run, but a a diversified initial population.
```
ga_inst_div_cc = pygad.GA(initial_population = init_div,
num_genes = num_genes,
num_generations = n_gen,
num_parents_mating = num_parents_mating,
fitness_func = fitness_function,
parent_selection_type = parent_selection_type,
keep_parents = keep_parents,
crossover_type = crossover_type,
crossover_probability = crossover_prob,
mutation_type = mutation_type,
mutation_probability = mutation_prob,
mutation_by_replacement = True,
on_generation = callback_generation,
gene_space = gene_space,
save_best_solutions = True)
# perform GA run
ga_inst_div_cc.run()
# save results
ga_inst_div_cc.save('gp_ga_cc_diverse_init')
# best solution
solution = ga_inst_div_cc.best_solutions[-1]
print("best chromosome: {solution}".format(solution = solution))
print("best fitness = {solution_fitness}".format(solution_fitness = \
get_fit(solution)))
```
``Loading lines``
We can load the ``pygad`` results should they have been saved already in previous runs.
```
load_ga_uniform = pygad.load('gp_ga_cc_uniform_init')
load_ga_diverse = pygad.load('gp_ga_cc_diverse_init')
```
We can view the prediction based on this superior individual below.
```
# champion chromosomes
chr_1 = load_ga_uniform.best_solutions[-1]
chr_2 = load_ga_diverse.best_solutions[-1]
z_min = 0
z_max = 3
n_div = 1000
z_rec = np.linspace(z_min, z_max, n_div)
champs = {}
champs['uniform'] = {'chromosome': chr_1}
champs['diverse'] = {'chromosome': chr_2}
for champ in champs:
chromosome = champs[champ]['chromosome']
gp = GP(chromosome)
rec = gp.predict(z_cc, Hz_cc, np.diag(sigHz_cc**2),
z_rec)
Hz_rec, sigHz_rec = rec['Y'], np.sqrt(rec['varY'])
H0 = Hz_rec[0]
sigH0 = sigHz_rec[0]
# compute chi2
Hz = gp.predict(z_cc, Hz_cc, np.diag(sigHz_cc**2),
z_cc)['Y']
chi2 = np.sum(((Hz - Hz_cc)/sigHz_cc)**2)
# print GA measures
print(champ)
print('H0 =', np.round(H0, 1), '+/-', np.round(sigH0, 1))
print('log-marginal likelihood',
gp.get_logmlike(z_cc, Hz_cc, np.diag(sigHz_cc**2)))
print('penalty', penalty(chromosome))
print('fitness function', get_fit(chromosome))
print('chi^2', chi2)
print()
champs[champ]['z'] = z_rec
champs[champ]['Hz'] = Hz_rec
champs[champ]['sigHz'] = sigHz_rec
# plot champs' predictions
fig, ax = plt.subplots()
ax.errorbar(z_cc, Hz_cc, yerr = sigHz_cc,
fmt = 'kx', ecolor = 'k',
elinewidth = 1, capsize = 2, label = 'CC')
# color, line style, and hatch list
clst = ['b', 'r']
llst = ['-', '--']
hlst = ['|', '-']
for champ in champs:
i = list(champs.keys()).index(champ)
Hz_rec = champs[champ]['Hz']
sigHz_rec = champs[champ]['sigHz']
ax.plot(z_rec, Hz_rec, clst[i] + llst[i],
label = champ)
ax.fill_between(z_rec,
Hz_rec - 2*sigHz_rec,
Hz_rec + 2*sigHz_rec,
facecolor = clst[i], alpha = 0.2,
edgecolor = clst[i], hatch = hlst[i])
ax.set_xlabel('$z$')
ax.set_xlim(z_min, z_max)
ax.set_ylim(1, 370)
ax.set_ylabel('$H(z)$')
ax.legend(loc = 'upper left', prop = {'size': 9.5})
plt.show()
```
A plot of the generation vs fitness can also be shown.
```
fit_uni = [get_fit(c) for c in load_ga_uniform.best_solutions]
fit_div = [get_fit(c) for c in load_ga_diverse.best_solutions]
fig, ax = plt.subplots()
ax.plot(fit_uni, 'b-', label = 'uniform')
ax.plot(fit_div, 'r--', label = 'diverse')
ax.set_xlabel('generation')
ax.set_ylabel('best fitness')
ax.set_xlim(1, n_gen)
ax.set_ylim(-141.0, -140.5)
ax.legend(loc = 'lower right', prop = {'size': 9.5})
plt.show()
```
### 2. Supernovae Type Ia
In this section, we perform the GP reconstruction with the compressed Pantheon data set.
```
# load pantheon compressed m(z) data
loc_lcparam = 'lcparam_DS17f.txt'
loc_lcparam_sys = 'sys_DS17f.txt'
lcparam = np.loadtxt(loc_lcparam, usecols = (1, 4, 5))
lcparam_sys = np.loadtxt(loc_lcparam_sys, skiprows = 1)
# setup pantheon samples
z_ps = lcparam[:, 0]
logz_ps = np.log(z_ps)
mz_ps = lcparam[:, 1]
sigmz_ps = lcparam[:, 2]
# pantheon samples systematics
covmz_ps_sys = lcparam_sys.reshape(40, 40)
covmz_ps_tot = covmz_ps_sys + np.diag(sigmz_ps**2)
# plot data set
plt.errorbar(logz_ps, mz_ps,
yerr = np.sqrt(np.diag(covmz_ps_tot)),
fmt = 'kx', markersize = 4,
ecolor = 'red', elinewidth = 2, capsize = 2)
plt.xlabel('$\ln(z)$')
plt.ylabel('$m(z)$')
plt.show()
```
The fitness function, now taking in the SNe data set, is prepared below for the GA.
```
n_data = len(z_ps)
def get_fit(chromosome):
'''Evaluates the fitness of the indivial with chromosome'''
if all(hp > 0 for hp in chromosome) == True:
pnl = penalty(chromosome)
try:
gp = GP(chromosome)
lml = gp.get_logmlike(logz_ps, mz_ps,
covmz_ps_tot)
if np.isnan(lml) == False:
return lml - pnl
else:
return -1000
except:
lml = -1000
return lml
else:
lml = -1000
return lml
def fitness_function(chromosome, chromosome_idx):
return get_fit(chromosome)
```
Then, we setup the initial uniform and diverse kernel populations.
```
pop_size = 1000 # population size
init_uni = []
for i in range(0, pop_size):
if i < int(pop_size/3):
init_uni.append([unif(0, 200), unif(0, 100), unif(0, 5),
0, 0, 0, 0, 0, 0, 0])
elif (i > int(pop_size/3)) and (i < int(2*pop_size/3)):
init_uni.append([0, 0, 0,
unif(0, 200), unif(0, 100), unif(0, 2), unif(0, 5),
0, 0, 0])
else:
init_uni.append([0, 0, 0, 0, 0, 0, 0,
unif(0, 200), unif(0, 100), unif(0, 5)])
init_uni = np.array(init_uni)
init_div = []
for i in range(0, pop_size):
init_div.append([unif(0, 200), unif(0, 100), unif(0, 5),
unif(0, 200), unif(0, 100), unif(0, 2), unif(0, 5),
unif(0, 200), unif(0, 100), unif(0, 5)])
init_div = np.array(init_div)
```
The GA parameters can now be set for the SNe fitting.
```
gene_space = [{'low': 0, 'high': 200}, {'low': 0, 'high': 100}, {'low': 0, 'high': 5}, # rbf lims
{'low': 0, 'high': 200}, {'low': 0, 'high': 100}, # chy lims
{'low': 0, 'high': 2}, {'low': 0, 'high': 5},
{'low': 0, 'high': 200}, {'low': 0, 'high': 100}, {'low': 0, 'high': 5}] # m52 lims
num_genes = 10 # length of chromosome
n_gen = 100 # number of generations
sel_rate = 0.3 # selection rate
# parent selection
parent_selection_type = "rws" # roulette wheel selection
keep_parents = int(sel_rate*pop_size)
num_parents_mating = int(sel_rate*pop_size)
# crossover
#crossover_type = "single_point"
#crossover_type = "two_points"
#crossover_type = "uniform"
crossover_type = "scattered"
crossover_prob = 1.0
# mutation type options: random, swap, inversion, scramble, adaptive
mutation_type = "random"
#mutation_type = "swap"
#mutation_type = "inversion"
#mutation_type = "scramble"
#mutation_type = "adaptive"
mutation_prob = 0.5
```
Here are the ``GA runs``. We start with the uniform population.
*Skip the runs and jump ahead to loading lines if results have already been prepared.
```
ga_inst_uni_sn = pygad.GA(initial_population = init_uni,
num_genes = num_genes,
num_generations = n_gen,
num_parents_mating = num_parents_mating,
fitness_func = fitness_function,
parent_selection_type = parent_selection_type,
keep_parents = keep_parents,
crossover_type = crossover_type,
crossover_probability = crossover_prob,
mutation_type = mutation_type,
mutation_probability = mutation_prob,
mutation_by_replacement = True,
on_generation = callback_generation,
gene_space = gene_space,
save_best_solutions = True)
# perform GA run
ga_inst_uni_sn.run()
# save results
ga_inst_uni_sn.save('gp_ga_sn_uniform_init')
# best solution
solution = ga_inst_uni_sn.best_solutions[-1]
print("best chromosome: {solution}".format(solution = solution))
print("best fitness = {solution_fitness}".format(solution_fitness = \
get_fit(solution)))
```
Here is the GA run for a diversified initial population.
```
ga_inst_div_sn = pygad.GA(initial_population = init_div,
num_genes = num_genes,
num_generations = n_gen,
num_parents_mating = num_parents_mating,
fitness_func = fitness_function,
parent_selection_type = parent_selection_type,
keep_parents = keep_parents,
crossover_type = crossover_type,
crossover_probability = crossover_prob,
mutation_type = mutation_type,
mutation_probability = mutation_prob,
mutation_by_replacement = True,
on_generation = callback_generation,
gene_space = gene_space,
save_best_solutions = True)
# perform GA run
ga_inst_div_sn.run()
# save results
ga_inst_div_sn.save('gp_ga_sn_diverse_init')
# best solution
solution = ga_inst_div_sn.best_solutions[-1]
print("best chromosome: {solution}".format(solution = solution))
print("best fitness = {solution_fitness}".format(solution_fitness = \
get_fit(solution)))
```
``Load GA runs``
Saved ``pygad`` output can be accessed. This is done for the SNe runs below.
```
load_ga_uniform = pygad.load('gp_ga_sn_uniform_init')
load_ga_diverse = pygad.load('gp_ga_sn_diverse_init')
```
The GP reconstructions are shown below.
```
# champion chromosomes
chr_1 = load_ga_uniform.best_solutions[-1]
chr_2 = load_ga_diverse.best_solutions[-1]
z_min = 1e-5
z_max = 3
n_div = 1000
z_rec = np.logspace(np.log(z_min), np.log(z_max), n_div)
logz_rec = np.log(z_rec)
champs = {}
champs['uniform'] = {'chromosome': chr_1}
champs['diverse'] = {'chromosome': chr_2}
for champ in champs:
chromosome = champs[champ]['chromosome']
gp = GP(chromosome)
rec = gp.predict(logz_ps, mz_ps, covmz_ps_tot,
logz_rec)
mz_rec, sigmz_rec = rec['Y'], np.sqrt(rec['varY'])
# compute chi2
mz = gp.predict(logz_ps, mz_ps, covmz_ps_tot,
logz_ps)['Y']
cov_inv = np.linalg.inv(covmz_ps_tot)
delta_H = mz - mz_ps
chi2 = ( delta_H @ cov_inv @ delta_H )
# print GA measures
print(champ)
print('log-marginal likelihood',
gp.get_logmlike(logz_ps, mz_ps, covmz_ps_tot))
print('penalty', penalty(chromosome))
print('fitness function', get_fit(chromosome))
print('chi^2', chi2)
print()
champs[champ]['logz'] = logz_rec
champs[champ]['mz'] = mz_rec
champs[champ]['sigmz'] = sigmz_rec
# plot champs' predictions
fig, ax = plt.subplots()
ax.errorbar(logz_ps, mz_ps,
yerr = np.sqrt(np.diag(covmz_ps_tot)),
fmt = 'kx', ecolor = 'k',
elinewidth = 1, capsize = 2, label = 'SNe')
# color, line style, and hatch list
clst = ['b', 'r']
llst = ['-', '--']
hlst = ['|', '-']
for champ in champs:
i = list(champs.keys()).index(champ)
mz_rec = champs[champ]['mz']
sigmz_rec = champs[champ]['sigmz']
ax.plot(logz_rec, mz_rec, clst[i] + llst[i],
label = champ)
ax.fill_between(logz_rec,
mz_rec - 2*sigmz_rec,
mz_rec + 2*sigmz_rec,
facecolor = clst[i], alpha = 0.2,
edgecolor = clst[i], hatch = hlst[i])
ax.set_xlabel('$\ln(z)$')
ax.set_ylabel('$m(z)$')
ax.set_xlim(np.log(z_min), np.log(z_max))
ax.set_ylim(-10, 30)
ax.legend(loc = 'upper left', prop = {'size': 9.5})
plt.show()
```
Here is the fitness per generation for the GPs above.
```
fit_uni = [get_fit(c) for c in load_ga_uniform.best_solutions]
fit_div = [get_fit(c) for c in load_ga_diverse.best_solutions]
fig, ax = plt.subplots()
ax.plot(fit_uni, 'b-', label = 'uniform')
ax.plot(fit_div, 'r--', label = 'diverse')
ax.set_xlabel('generation')
ax.set_ylabel('best fitness')
ax.set_xlim(1, n_gen)
ax.set_ylim(41, 45)
ax.legend(loc = 'lower right', prop = {'size': 9.5})
plt.show()
```
### References
***Pantheon***: D. M. Scolnic et al., The Complete Light-curve Sample of Spectroscopically Confirmed SNe Ia
from Pan-STARRS1 and Cosmological Constraints from the Combined Pantheon Sample,
Astrophys. J. 859 (2018) 101 [[1710.00845](https://arxiv.org/abs/1710.00845)].
***Cosmic Chronometers***, from *various sources*:
(1) M. Moresco, L. Pozzetti, A. Cimatti, R. Jimenez, C. Maraston, L. Verde et al., A 6%
measurement of the Hubble parameter at z ∼ 0.45: direct evidence of the epoch of cosmic
re-acceleration, JCAP 05 (2016) 014 [[1601.01701](https://arxiv.org/abs/1601.01701)].
(2) M. Moresco, Raising the bar: new constraints on the Hubble parameter with cosmic
chronometers at z ∼ 2, Mon. Not. Roy. Astron. Soc. 450 (2015) L16 [[1503.01116](https://arxiv.org/abs/1503.01116)].
(3) C. Zhang, H. Zhang, S. Yuan, S. Liu, T.-J. Zhang and Y.-C. Sun, Four new observational H(z)
data from luminous red galaxies in the Sloan Digital Sky Survey data release seven, Research in
Astronomy and Astrophysics 14 (2014) 1221 [[1207.4541](https://arxiv.org/abs/1207.4541)].
(4) D. Stern, R. Jimenez, L. Verde, M. Kamionkowski and S. A. Stanford, Cosmic chronometers:
constraining the equation of state of dark energy. I: H(z) measurements, JCAP 2010 (2010)
008 [[0907.3149](https://arxiv.org/abs/0907.3149)].
(5) M. Moresco et al., Improved constraints on the expansion rate of the Universe up to z ˜1.1 from
the spectroscopic evolution of cosmic chronometers, JCAP 2012 (2012) 006 [[1201.3609](https://arxiv.org/abs/1201.3609)].
(6) Ratsimbazafy et al. Age-dating Luminous Red Galaxies observed with the Southern African
Large Telescope, Mon. Not. Roy. Astron. Soc. 467 (2017) 3239 [[1702.00418](https://arxiv.org/abs/1702.00418)].
| github_jupyter |
[](https://www.pythonista.io)
# Declaraciones y bloques de código.
## Flujo de ejecución del código.
El intérprete de Python es capaz de leer, evaluar y ejecutar una sucesión de instrucciones línea por línea de principio a fin. A esto se le conoce copmo flujo de ejecución de código.
Los lenguajes de programacion modernos pueden ejecutar o no porciones de código dependiendo de ciertas condiciones. Estas prociondes de código también se conocen como "bloques" y deben de ser delimitados sintácticamente.
Así como algunos lenguajes de programación identifican el final de una expresión mendiante el uso del punto y coma ```;```, también suelen delimitar bloques de código encerrándolos entre llaves ```{``` ```}```.
**Ejemplo:**
* El siguiente código ejemplifca el uso de llaves en un código simple de Javascript.
```javascript
for (let i = 1; i <= 10; i++) {
console.log(i);
}
console.log("Esta es la línea final.");
```
## Declaraciones.
Las declaraciones (statements) son expresiones capaces de contener a un bloque de código, las cuales se ejecutarán e incluso repetirán en caso de que se cumplan ciertas condiciones.
La inmensa mayoría de los lenguajes de programación utilizan a las declaraciones como parte fundamental de su estructura de código.
En el caso de Python, se colocan dos puntos ```:``` al final de la línea que define a una declaración y se indenta el código que pertence a dicha declaración.
```
<flujo principal>
...
...
<declaración>:
<bloque de código>
<flujo principal>
```
### Indentación.
Es una buena práctica entre programadores usar la indentación (dejar espacios o tabualdores antes de ingresar el código en una línea) como una regla de estilo a fin de poder identificar visualmente los bloques de código.
En el caso de Python , la indentación no sólo es una regla de estilo, sino un elemento sintáctico, por lo que en vez de encerrar un bloque de código entre llaves, un bloque de código se define indentándolo. El PEP-8 indica que la indentación correcta es de cuatro espacios y no se usan tabuladores.
**Ejemplo:**
* La siguiente celda ejemplifica del uso de indentación en Python para delimitar bloques de código.
```
for i in range (1, 11):
print(i)
print('Esta es la línea final.')
```
### Declaraciones anidadas.
Es muy común que el código incluya declaraciones dentro de otras declaraciones, por lo que para delimitar el códifgo dentro de una declaración anidada se utiliza la misma regla de indentación dejando 4 espacios adicionales.
**Ejemplo:**
```
'''Esta celda realizará una iteración de números en el rango
entre el ```1``` y ```10``` y mostrará un mensaje dependiendo
si el número es par o non.'''
for i in range (1, 11):
if i % 2 == 0:
print ('El número %d es par.' %i)
else:
print ('El número %d es non.' %i)
print('Esta es la línea final.')
```
<p style="text-align: center"><a rel="license" href="http://creativecommons.org/licenses/by/4.0/"><img alt="Licencia Creative Commons" style="border-width:0" src="https://i.creativecommons.org/l/by/4.0/80x15.png" /></a><br />Esta obra está bajo una <a rel="license" href="http://creativecommons.org/licenses/by/4.0/">Licencia Creative Commons Atribución 4.0 Internacional</a>.</p>
<p style="text-align: center">© José Luis Chiquete Valdivieso. 2021.</p>
| github_jupyter |
### Testing accuracy of RF classifier for lightly loaded, testing and training with all the rotational speeds
```
from jupyterthemes import get_themes
import jupyterthemes as jt
from jupyterthemes.stylefx import set_nb_theme
set_nb_theme('chesterish')
import pandas as pd
data_10=pd.read_csv(r'D:\Acads\BTP\Lightly Loaded\Train10hz.csv')
data_20=pd.read_csv(r'D:\Acads\BTP\Lightly Loaded\Train20hz.csv')
data_30=pd.read_csv(r'D:\Acads\BTP\Lightly Loaded\Train30Hz.csv')
data_15=pd.read_csv(r'D:\Acads\BTP\Lightly Loaded\Train15hz.csv')
data_25=pd.read_csv(r'D:\Acads\BTP\Lightly Loaded\Train25hz.csv')
data_35=pd.read_csv(r'D:\Acads\BTP\Lightly Loaded\Train35Hz.csv')
data_40=pd.read_csv(r'D:\Acads\BTP\Lightly Loaded\Train40Hz.csv')
data_10=data_10.head(44990)
data_15=data_15.head(44990)
data_20=data_20.head(44990)
data_25=data_25.head(44990)
data_30=data_30.head(44990)
data_35=data_35.head(44990)
data_40=data_40.head(44990)
data_25.head
#shuffling
data_20=data_20.sample(frac=1)
data_30=data_30.sample(frac=1)
data_40=data_40.sample(frac=1)
data_10=data_10.sample(frac=1)
data_15=data_15.sample(frac=1)
data_25=data_25.sample(frac=1)
data_35=data_35.sample(frac=1)
data_25.head
import sklearn as sk
```
### Assigning X and y for training
```
dataset_10=data_10.values
X_10= dataset_10[:,0:9]
print(X_10)
y_10=dataset_10[:,9]
print(y_10)
dataset_15=data_15.values
X_15= dataset_15[:,0:9]
print(X_15)
y_15=dataset_15[:,9]
print(y_15)
dataset_20=data_20.values
X_20= dataset_20[:,0:9]
print(X_20)
y_20=dataset_20[:,9]
print(y_20)
dataset_25=data_25.values
X_25= dataset_25[:,0:9]
print(X_25)
y_25=dataset_25[:,9]
print(y_25)
dataset_30=data_30.values
X_30= dataset_30[:,0:9]
print(X_30)
y_30=dataset_30[:,9]
print(y_30)
dataset_35=data_35.values
X_35= dataset_35[:,0:9]
print(X_35)
y_35=dataset_35[:,9]
print(y_35)
dataset_40=data_40.values
X_40= dataset_40[:,0:9]
print(X_40)
y_40=dataset_40[:,9]
print(y_40)
```
### Training Random Forest Classifier
```
from sklearn.ensemble import RandomForestClassifier
rf_10 = RandomForestClassifier(n_estimators = 1000, random_state = 42)
rf_10.fit(X_10, y_10);
from sklearn.ensemble import RandomForestClassifier
rf_15 = RandomForestClassifier(n_estimators = 1000, random_state = 42)
rf_15.fit(X_15, y_15);
from sklearn.ensemble import RandomForestClassifier
rf_20 = RandomForestClassifier(n_estimators = 1000, random_state = 42)
rf_20.fit(X_20, y_20);
from sklearn.ensemble import RandomForestClassifier
rf_25 = RandomForestClassifier(n_estimators = 1000, random_state = 42)
rf_25.fit(X_25, y_25);
from sklearn.ensemble import RandomForestClassifier
rf_30 = RandomForestClassifier(n_estimators = 1000, random_state = 42)
rf_30.fit(X_30, y_30);
from sklearn.ensemble import RandomForestClassifier
rf_35 = RandomForestClassifier(n_estimators = 1000, random_state = 42)
rf_35.fit(X_35, y_35);
from sklearn.ensemble import RandomForestClassifier
rf_40 = RandomForestClassifier(n_estimators = 1000, random_state = 42)
rf_40.fit(X_40, y_40);
```
### Importing Testing data
```
test_10=pd.read_csv(r'D:\Acads\BTP\Lightly Loaded\Test10hz.csv')
test_20=pd.read_csv(r'D:\Acads\BTP\Lightly Loaded\Test20hz.csv')
test_30=pd.read_csv(r'D:\Acads\BTP\Lightly Loaded\Test30Hz.csv')
test_15=pd.read_csv(r'D:\Acads\BTP\Lightly Loaded\Test15hz.csv')
test_25=pd.read_csv(r'D:\Acads\BTP\Lightly Loaded\Test25hz.csv')
test_35=pd.read_csv(r'D:\Acads\BTP\Lightly Loaded\Test35Hz.csv')
test_40=pd.read_csv(r'D:\Acads\BTP\Lightly Loaded\Test40Hz.csv')
test_10=test_10.head(99990)
test_15=test_15.head(99990)
test_20=test_20.head(99990)
test_25=test_25.head(99990)
test_30=test_30.head(99990)
test_35=test_35.head(99990)
test_40=test_40.head(99990)
#shuffling
test_20=test_20.sample(frac=1)
test_30=test_30.sample(frac=1)
test_40=test_40.sample(frac=1)
test_10=test_10.sample(frac=1)
test_15=test_15.sample(frac=1)
test_25=test_25.sample(frac=1)
test_35=test_35.sample(frac=1)
```
### Assigning X and y for testing
```
dataset_test_10 = test_10.values
X_test_10 = dataset_test_10[:,0:9]
print(X_test_10)
y_test_10= dataset_test_10[:,9]
print(y_test_10)
dataset_test_15 = test_15.values
X_test_15 = dataset_test_15[:,0:9]
print(X_test_15)
y_test_15= dataset_test_15[:,9]
print(y_test_15)
dataset_test_20 = test_20.values
X_test_20 = dataset_test_20[:,0:9]
print(X_test_20)
y_test_20= dataset_test_20[:,9]
print(y_test_20)
dataset_test_25 = test_25.values
X_test_25 = dataset_test_25[:,0:9]
print(X_test_25)
y_test_25= dataset_test_25[:,9]
print(y_test_25)
dataset_test_30 = test_30.values
X_test_30 = dataset_test_30[:,0:9]
print(X_test_30)
y_test_30= dataset_test_30[:,9]
print(y_test_30)
dataset_test_35 = test_35.values
X_test_35 = dataset_test_35[:,0:9]
print(X_test_35)
y_test_35= dataset_test_35[:,9]
print(y_test_35)
dataset_test_40 = test_40.values
X_test_40 = dataset_test_40[:,0:9]
print(X_test_40)
y_test_40= dataset_test_40[:,9]
print(y_test_40)
```
### Predictions with 10Hz Trained Model
```
import numpy as np
predictions_10 = rf_10.predict(X_test_10)
errors_10 = abs(predictions_10 - y_test_10)
print('Mean Absolute Error 10Hz with 10Hz:', round(np.mean(errors_10), 3), 'degrees.')
accuracy = 100 - np.mean(errors_10)
print('Accuracy:', round(accuracy, 3), '%.')
predictions_15 = rf_10.predict(X_test_15)
errors_15 = abs(predictions_15 - y_test_15)
print('Mean Absolute Error 15Hz with 10Hz:', round(np.mean(errors_15), 3), 'degrees.')
accuracy = 100 - np.mean(errors_15)
print('Accuracy:', round(accuracy, 3), '%.')
predictions_20 = rf_10.predict(X_test_20)
errors_20 = abs(predictions_20 - y_test_20)
print('Mean Absolute Error 20Hz with 10Hz:', round(np.mean(errors_20), 3), 'degrees.')
accuracy = 100 - np.mean(errors_20)
print('Accuracy:', round(accuracy, 3), '%.')
predictions_25 = rf_10.predict(X_test_25)
errors_25 = abs(predictions_25 - y_test_25)
print('Mean Absolute Error 25Hz with 10Hz:', round(np.mean(errors_25), 3), 'degrees.')
accuracy = 100 - np.mean(errors_25)
print('Accuracy:', round(accuracy, 3), '%.')
predictions_30 = rf_10.predict(X_test_30)
errors_30 = abs(predictions_30 - y_test_30)
print('Mean Absolute Error 30Hz with 10Hz:', round(np.mean(errors_30), 3), 'degrees.')
accuracy = 100 - np.mean(errors_30)
print('Accuracy:', round(accuracy, 3), '%.')
predictions_35 = rf_10.predict(X_test_35)
errors_35 = abs(predictions_35 - y_test_35)
print('Mean Absolute Error 35Hz with 10Hz:', round(np.mean(errors_35), 3), 'degrees.')
accuracy = 100 - np.mean(errors_35)
print('Accuracy:', round(accuracy, 3), '%.')
predictions_40 = rf_10.predict(X_test_40)
errors_40 = abs(predictions_40 - y_test_40)
print('Mean Absolute Error 40Hz with 10Hz:', round(np.mean(errors_40), 3), 'degrees.')
accuracy = 100 - np.mean(errors_40)
print('Accuracy:', round(accuracy, 3), '%.')
```
### Predictions with 15Hz model
```
predictions_10 = rf_15.predict(X_test_10)
errors_10 = abs(predictions_10 - y_test_10)
print('Mean Absolute Error 10Hz with 15Hz:', round(np.mean(errors_10), 3), 'degrees.')
accuracy = 100 - np.mean(errors_10)
print('Accuracy:', round(accuracy, 3), '%.')
predictions_15 = rf_15.predict(X_test_15)
errors_15 = abs(predictions_15 - y_test_15)
print('Mean Absolute Error 15Hz with 15Hz:', round(np.mean(errors_15), 3), 'degrees.')
accuracy = 100 - np.mean(errors_15)
print('Accuracy:', round(accuracy, 3), '%.')
predictions_20 = rf_15.predict(X_test_20)
errors_20 = abs(predictions_20 - y_test_20)
print('Mean Absolute Error 20Hz with 15Hz:', round(np.mean(errors_20), 3), 'degrees.')
accuracy = 100 - np.mean(errors_20)
print('Accuracy:', round(accuracy, 3), '%.')
predictions_25 = rf_15.predict(X_test_25)
errors_25 = abs(predictions_25 - y_test_25)
print('Mean Absolute Error 25Hz with 15Hz:', round(np.mean(errors_25), 3), 'degrees.')
accuracy = 100 - np.mean(errors_25)
print('Accuracy:', round(accuracy, 3), '%.')
predictions_30 = rf_15.predict(X_test_30)
errors_30 = abs(predictions_30 - y_test_30)
print('Mean Absolute Error 30Hz with 15Hz:', round(np.mean(errors_30), 3), 'degrees.')
accuracy = 100 - np.mean(errors_30)
print('Accuracy:', round(accuracy, 3), '%.')
predictions_35 = rf_15.predict(X_test_35)
errors_35 = abs(predictions_35 - y_test_35)
print('Mean Absolute Error 35Hz with 15Hz:', round(np.mean(errors_35), 3), 'degrees.')
accuracy = 100 - np.mean(errors_35)
print('Accuracy:', round(accuracy, 3), '%.')
predictions_40 = rf_15.predict(X_test_40)
errors_40 = abs(predictions_40 - y_test_40)
print('Mean Absolute Error 40Hz with 15Hz:', round(np.mean(errors_40), 3), 'degrees.')
accuracy = 100 - np.mean(errors_40)
print('Accuracy:', round(accuracy, 3), '%.')
```
### Predictions with 20Hz model
```
predictions_10 = rf_20.predict(X_test_10)
errors_10 = abs(predictions_10 - y_test_10)
print('Mean Absolute Error 10Hz with 20Hz:', round(np.mean(errors_10), 3), 'degrees.')
accuracy = 100 - np.mean(errors_10)
print('Accuracy:', round(accuracy, 3), '%.')
predictions_15 = rf_20.predict(X_test_15)
errors_15 = abs(predictions_15 - y_test_15)
print('Mean Absolute Error 15Hz with 20Hz:', round(np.mean(errors_15), 3), 'degrees.')
accuracy = 100 - np.mean(errors_15)
print('Accuracy:', round(accuracy, 3), '%.')
predictions_20 = rf_20.predict(X_test_20)
errors_20 = abs(predictions_20 - y_test_20)
print('Mean Absolute Error 20Hz with 20Hz:', round(np.mean(errors_20), 3), 'degrees.')
accuracy = 100 - np.mean(errors_20)
print('Accuracy:', round(accuracy, 3), '%.')
predictions_25 = rf_20.predict(X_test_25)
errors_25 = abs(predictions_25 - y_test_25)
print('Mean Absolute Error 25Hz with 20Hz:', round(np.mean(errors_25), 3), 'degrees.')
accuracy = 100 - np.mean(errors_25)
print('Accuracy:', round(accuracy, 3), '%.')
predictions_30 = rf_20.predict(X_test_30)
errors_30 = abs(predictions_30 - y_test_30)
print('Mean Absolute Error 30Hz with 20Hz:', round(np.mean(errors_30), 3), 'degrees.')
accuracy = 100 - np.mean(errors_30)
print('Accuracy:', round(accuracy, 3), '%.')
predictions_35 = rf_20.predict(X_test_35)
errors_35 = abs(predictions_35 - y_test_35)
print('Mean Absolute Error 35Hz with 20Hz:', round(np.mean(errors_35), 3), 'degrees.')
accuracy = 100 - np.mean(errors_35)
print('Accuracy:', round(accuracy, 3), '%.')
predictions_40 = rf_20.predict(X_test_40)
errors_40 = abs(predictions_40 - y_test_40)
print('Mean Absolute Error 40Hz with 20Hz:', round(np.mean(errors_40), 3), 'degrees.')
accuracy = 100 - np.mean(errors_40)
print('Accuracy:', round(accuracy, 3), '%.')
```
### Predictions with 25Hz model
```
predictions_10 = rf_25.predict(X_test_10)
errors_10 = abs(predictions_10 - y_test_10)
print('Mean Absolute Error 10Hz with 25Hz:', round(np.mean(errors_10), 3), 'degrees.')
accuracy = 100 - np.mean(errors_10)
print('Accuracy:', round(accuracy, 3), '%.')
predictions_15 = rf_25.predict(X_test_15)
errors_15 = abs(predictions_15 - y_test_15)
print('Mean Absolute Error 15Hz with 25Hz:', round(np.mean(errors_15), 3), 'degrees.')
accuracy = 100 - np.mean(errors_15)
print('Accuracy:', round(accuracy, 3), '%.')
predictions_20 = rf_25.predict(X_test_20)
errors_20 = abs(predictions_20 - y_test_20)
print('Mean Absolute Error 20Hz with 25Hz:', round(np.mean(errors_20), 3), 'degrees.')
accuracy = 100 - np.mean(errors_20)
print('Accuracy:', round(accuracy, 3), '%.')
predictions_25 = rf_25.predict(X_test_25)
errors_25 = abs(predictions_25 - y_test_25)
print('Mean Absolute Error 25Hz with 25Hz:', round(np.mean(errors_25), 3), 'degrees.')
accuracy = 100 - np.mean(errors_25)
print('Accuracy:', round(accuracy, 3), '%.')
predictions_30 = rf_25.predict(X_test_30)
errors_30 = abs(predictions_30 - y_test_30)
print('Mean Absolute Error 30Hz with 25Hz:', round(np.mean(errors_30), 3), 'degrees.')
accuracy = 100 - np.mean(errors_30)
print('Accuracy:', round(accuracy, 3), '%.')
predictions_35 = rf_25.predict(X_test_35)
errors_35 = abs(predictions_35 - y_test_35)
print('Mean Absolute Error 35Hz with 25Hz:', round(np.mean(errors_35), 3), 'degrees.')
accuracy = 100 - np.mean(errors_35)
print('Accuracy:', round(accuracy, 3), '%.')
predictions_40 = rf_25.predict(X_test_40)
errors_40 = abs(predictions_40 - y_test_40)
print('Mean Absolute Error 40Hz with 25Hz:', round(np.mean(errors_40), 3), 'degrees.')
accuracy = 100 - np.mean(errors_40)
print('Accuracy:', round(accuracy, 3), '%.')
```
### Predictions with 30Hz model
```
predictions_10 = rf_30.predict(X_test_10)
errors_10 = abs(predictions_10 - y_test_10)
print('Mean Absolute Error 10Hz with 30Hz:', round(np.mean(errors_10), 3), 'degrees.')
accuracy = 100 - np.mean(errors_10)
print('Accuracy:', round(accuracy, 3), '%.')
predictions_15 = rf_30.predict(X_test_15)
errors_15 = abs(predictions_15 - y_test_15)
print('Mean Absolute Error 15Hz with 30Hz:', round(np.mean(errors_15), 3), 'degrees.')
accuracy = 100 - np.mean(errors_15)
print('Accuracy:', round(accuracy, 3), '%.')
predictions_20 = rf_30.predict(X_test_20)
errors_20 = abs(predictions_20 - y_test_20)
print('Mean Absolute Error 20Hz with 30Hz:', round(np.mean(errors_20), 3), 'degrees.')
accuracy = 100 - np.mean(errors_20)
print('Accuracy:', round(accuracy, 3), '%.')
predictions_25 = rf_30.predict(X_test_25)
errors_25 = abs(predictions_25 - y_test_25)
print('Mean Absolute Error 25Hz with 30Hz:', round(np.mean(errors_25), 3), 'degrees.')
accuracy = 100 - np.mean(errors_25)
print('Accuracy:', round(accuracy, 3), '%.')
predictions_30 = rf_30.predict(X_test_30)
errors_30 = abs(predictions_30 - y_test_30)
print('Mean Absolute Error 30Hz with 30Hz:', round(np.mean(errors_30), 3), 'degrees.')
accuracy = 100 - np.mean(errors_30)
print('Accuracy:', round(accuracy, 3), '%.')
predictions_35 = rf_30.predict(X_test_35)
errors_35 = abs(predictions_35 - y_test_35)
print('Mean Absolute Error 35Hz with 30Hz:', round(np.mean(errors_35), 3), 'degrees.')
accuracy = 100 - np.mean(errors_35)
print('Accuracy:', round(accuracy, 3), '%.')
predictions_40 = rf_30.predict(X_test_40)
errors_40 = abs(predictions_40 - y_test_40)
print('Mean Absolute Error 40Hz with 30Hz:', round(np.mean(errors_40), 3), 'degrees.')
accuracy = 100 - np.mean(errors_40)
print('Accuracy:', round(accuracy, 3), '%.')
```
### Testing with 35Hz model
```
predictions_10 = rf_35.predict(X_test_10)
errors_10 = abs(predictions_10 - y_test_10)
print('Mean Absolute Error 10Hz with 35Hz:', round(np.mean(errors_10), 3), 'degrees.')
accuracy = 100 - np.mean(errors_10)
print('Accuracy:', round(accuracy, 3), '%.')
predictions_15 = rf_35.predict(X_test_15)
errors_15 = abs(predictions_15 - y_test_15)
print('Mean Absolute Error 15Hz with 35Hz:', round(np.mean(errors_15), 3), 'degrees.')
accuracy = 100 - np.mean(errors_15)
print('Accuracy:', round(accuracy, 3), '%.')
predictions_20 = rf_35.predict(X_test_20)
errors_20 = abs(predictions_20 - y_test_20)
print('Mean Absolute Error 20Hz with 35Hz:', round(np.mean(errors_20), 3), 'degrees.')
accuracy = 100 - np.mean(errors_20)
print('Accuracy:', round(accuracy, 3), '%.')
predictions_25 = rf_35.predict(X_test_25)
errors_25 = abs(predictions_25 - y_test_25)
print('Mean Absolute Error 25Hz with 35Hz:', round(np.mean(errors_25), 3), 'degrees.')
accuracy = 100 - np.mean(errors_25)
print('Accuracy:', round(accuracy, 3), '%.')
predictions_30 = rf_35.predict(X_test_30)
errors_30 = abs(predictions_30 - y_test_30)
print('Mean Absolute Error 30Hz with 35Hz:', round(np.mean(errors_30), 3), 'degrees.')
accuracy = 100 - np.mean(errors_30)
print('Accuracy:', round(accuracy, 3), '%.')
predictions_35 = rf_35.predict(X_test_35)
errors_35 = abs(predictions_35 - y_test_35)
print('Mean Absolute Error 35Hz with 35Hz:', round(np.mean(errors_35), 3), 'degrees.')
accuracy = 100 - np.mean(errors_35)
print('Accuracy:', round(accuracy, 3), '%.')
predictions_40 = rf_35.predict(X_test_40)
errors_40 = abs(predictions_40 - y_test_40)
print('Mean Absolute Error 40Hz with 35Hz:', round(np.mean(errors_40), 3), 'degrees.')
accuracy = 100 - np.mean(errors_40)
print('Accuracy:', round(accuracy, 3), '%.')
```
### Training with 40Hz model
```
predictions_10 = rf_35.predict(X_test_10)
errors_10 = abs(predictions_10 - y_test_10)
print('Mean Absolute Error 10Hz with 35Hz:', round(np.mean(errors_10), 3), 'degrees.')
accuracy = 100 - np.mean(errors_10)
print('Accuracy:', round(accuracy, 3), '%.')
predictions_15 = rf_35.predict(X_test_15)
errors_15 = abs(predictions_15 - y_test_15)
print('Mean Absolute Error 15Hz with 35Hz:', round(np.mean(errors_15), 3), 'degrees.')
accuracy = 100 - np.mean(errors_15)
print('Accuracy:', round(accuracy, 3), '%.')
predictions_20 = rf_35.predict(X_test_20)
errors_20 = abs(predictions_20 - y_test_20)
print('Mean Absolute Error 20Hz with 35Hz:', round(np.mean(errors_20), 3), 'degrees.')
accuracy = 100 - np.mean(errors_20)
print('Accuracy:', round(accuracy, 3), '%.')
predictions_20 = rf_35.predict(X_test_20)
errors_20 = abs(predictions_20 - y_test_20)
print('Mean Absolute Error 20Hz with 35Hz:', round(np.mean(errors_20), 3), 'degrees.')
accuracy = 100 - np.mean(errors_20)
print('Accuracy:', round(accuracy, 3), '%.')
predictions_25 = rf_35.predict(X_test_25)
errors_25 = abs(predictions_25 - y_test_25)
print('Mean Absolute Error 25Hz with 35Hz:', round(np.mean(errors_25), 3), 'degrees.')
accuracy = 100 - np.mean(errors_25)
print('Accuracy:', round(accuracy, 3), '%.')
predictions_30 = rf_35.predict(X_test_30)
errors_30 = abs(predictions_30 - y_test_30)
print('Mean Absolute Error 30Hz with 35Hz:', round(np.mean(errors_30), 3), 'degrees.')
accuracy = 100 - np.mean(errors_30)
print('Accuracy:', round(accuracy, 3), '%.')
predictions_35 = rf_35.predict(X_test_35)
errors_35 = abs(predictions_35 - y_test_35)
print('Mean Absolute Error 35Hz with 35Hz:', round(np.mean(errors_35), 3), 'degrees.')
accuracy = 100 - np.mean(errors_35)
print('Accuracy:', round(accuracy, 3), '%.')
predictions_40 = rf_35.predict(X_test_40)
errors_40 = abs(predictions_40 - y_test_40)
print('Mean Absolute Error 40Hz with 35Hz:', round(np.mean(errors_40), 3), 'degrees.')
accuracy = 100 - np.mean(errors_40)
print('Accuracy:', round(accuracy, 3), '%.')
```
| github_jupyter |
<div align="center">
<h1><img width="30" src="https://madewithml.com/static/images/rounded_logo.png"> <a href="https://madewithml.com/">Made With ML</a></h1>
Applied ML · MLOps · Production
<br>
Join 20K+ developers in learning how to responsibly <a href="https://madewithml.com/about/">deliver value</a> with ML.
<br>
</div>
<br>
<div align="center">
<a target="_blank" href="https://newsletter.madewithml.com"><img src="https://img.shields.io/badge/Subscribe-20K-brightgreen"></a>
<a target="_blank" href="https://github.com/GokuMohandas/MadeWithML"><img src="https://img.shields.io/github/stars/GokuMohandas/MadeWithML.svg?style=social&label=Star"></a>
<a target="_blank" href="https://www.linkedin.com/in/goku"><img src="https://img.shields.io/badge/style--5eba00.svg?label=LinkedIn&logo=linkedin&style=social"></a>
<a target="_blank" href="https://twitter.com/GokuMohandas"><img src="https://img.shields.io/twitter/follow/GokuMohandas.svg?label=Follow&style=social"></a>
<br>
🔥 Among the <a href="https://github.com/topics/deep-learning" target="_blank">top ML</a> repositories on GitHub
</div>
<br>
<hr>
# Neural Networks
In this lesson, we will explore multilayer perceptrons (MLPs) which are a basic type of neural network. We'll first motivate non-linear activation functions by trying to fit a linear model (logistic regression) on our non-linear spiral data. Then we'll implement an MLP using just NumPy and then with PyTorch.
<div align="left">
<a target="_blank" href="https://madewithml.com/courses/ml-foundations/neural-networks/"><img src="https://img.shields.io/badge/📖 Read-blog post-9cf"></a>
<a href="https://github.com/GokuMohandas/MadeWithML/blob/main/notebooks/08_Neural_Networks.ipynb" role="button"><img src="https://img.shields.io/static/v1?label=&message=View%20On%20GitHub&color=586069&logo=github&labelColor=2f363d"></a>
<a href="https://colab.research.google.com/github/GokuMohandas/MadeWithML/blob/main/notebooks/08_Neural_Networks.ipynb"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"></a>
</div>
# Overview
Our goal is to learn a model $\hat{y}$ that models $y$ given $X$ . You'll notice that neural networks are just extensions of the generalized linear methods we've seen so far but with non-linear activation functions since our data will be highly non-linear.
<div align="left">
<img src="https://raw.githubusercontent.com/GokuMohandas/MadeWithML/main/images/basics/neural-networks/mlp.png" width="500">
</div>
$z_1 = XW_1$
$a_1 = f(z_1)$
$z_2 = a_1W_2$
$\hat{y} = softmax(z_2)$ # classification
* $X$ = inputs | $\in \mathbb{R}^{NXD}$ ($D$ is the number of features)
* $W_1$ = 1st layer weights | $\in \mathbb{R}^{DXH}$ ($H$ is the number of hidden units in layer 1)
* $z_1$ = outputs from first layer $\in \mathbb{R}^{NXH}$
* $f$ = non-linear activation function
* $a_1$ = activation applied first layer's outputs | $\in \mathbb{R}^{NXH}$
* $W_2$ = 2nd layer weights | $\in \mathbb{R}^{HXC}$ ($C$ is the number of classes)
* $z_2$ = outputs from second layer $\in \mathbb{R}^{NXH}$
* $\hat{y}$ = prediction | $\in \mathbb{R}^{NXC}$ ($N$ is the number of samples)
* **Objective:** Predict the probability of class $y$ given the inputs $X$. Non-linearity is introduced to model the complex, non-linear data.
* **Advantages:**
* Can model non-linear patterns in the data really well.
* **Disadvantages:**
* Overfits easily.
* Computationally intensive as network increases in size.
* Not easily interpretable.
* **Miscellaneous:** Future neural network architectures that we'll see use the MLP as a modular unit for feed forward operations (affine transformation (XW) followed by a non-linear operation).
> We're going to leave out the bias terms $\beta$ to avoid further crowding the backpropagation calculations.
# Set up
```
import numpy as np
import random
SEED = 1234
# Set seed for reproducibility
np.random.seed(SEED)
random.seed(SEED)
```
## Load data
I created some non-linearly separable spiral data so let's go ahead and download it for our classification task.
```
import matplotlib.pyplot as plt
import pandas as pd
# Load data
url = "https://raw.githubusercontent.com/GokuMohandas/MadeWithML/main/datasets/spiral.csv"
df = pd.read_csv(url, header=0) # load
df = df.sample(frac=1).reset_index(drop=True) # shuffle
df.head()
# Data shapes
X = df[['X1', 'X2']].values
y = df['color'].values
print ("X: ", np.shape(X))
print ("y: ", np.shape(y))
# Visualize data
plt.title("Generated non-linear data")
colors = {'c1': 'red', 'c2': 'yellow', 'c3': 'blue'}
plt.scatter(X[:, 0], X[:, 1], c=[colors[_y] for _y in y], edgecolors='k', s=25)
plt.show()
```
## Split data
We'll shuffle our dataset (since it's ordered by class) and then create our data splits (stratified on class).
```
import collections
from sklearn.model_selection import train_test_split
TRAIN_SIZE = 0.7
VAL_SIZE = 0.15
TEST_SIZE = 0.15
def train_val_test_split(X, y, train_size):
"""Split dataset into data splits."""
X_train, X_, y_train, y_ = train_test_split(X, y, train_size=TRAIN_SIZE, stratify=y)
X_val, X_test, y_val, y_test = train_test_split(X_, y_, train_size=0.5, stratify=y_)
return X_train, X_val, X_test, y_train, y_val, y_test
# Create data splits
X_train, X_val, X_test, y_train, y_val, y_test = train_val_test_split(
X=X, y=y, train_size=TRAIN_SIZE)
print (f"X_train: {X_train.shape}, y_train: {y_train.shape}")
print (f"X_val: {X_val.shape}, y_val: {y_val.shape}")
print (f"X_test: {X_test.shape}, y_test: {y_test.shape}")
print (f"Sample point: {X_train[0]} → {y_train[0]}")
```
## Label encoding
In the previous lesson we wrote our own label encoder class to see the inner functions but this time we'll use scikit-learn [`LabelEncoder`](https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.LabelEncoder.html) class which does the same operations as ours.
```
from sklearn.preprocessing import LabelEncoder
# Output vectorizer
label_encoder = LabelEncoder()
# Fit on train data
label_encoder = label_encoder.fit(y_train)
classes = list(label_encoder.classes_)
print (f"classes: {classes}")
# Convert labels to tokens
print (f"y_train[0]: {y_train[0]}")
y_train = label_encoder.transform(y_train)
y_val = label_encoder.transform(y_val)
y_test = label_encoder.transform(y_test)
print (f"y_train[0]: {y_train[0]}")
# Class weights
counts = np.bincount(y_train)
class_weights = {i: 1.0/count for i, count in enumerate(counts)}
print (f"counts: {counts}\nweights: {class_weights}")
```
## Standardize data
We need to standardize our data (zero mean and unit variance) so a specific feature's magnitude doesn't affect how the model learns its weights. We're only going to standardize the inputs X because our outputs y are class values.
```
from sklearn.preprocessing import StandardScaler
# Standardize the data (mean=0, std=1) using training data
X_scaler = StandardScaler().fit(X_train)
# Apply scaler on training and test data (don't standardize outputs for classification)
X_train = X_scaler.transform(X_train)
X_val = X_scaler.transform(X_val)
X_test = X_scaler.transform(X_test)
# Check (means should be ~0 and std should be ~1)
print (f"X_test[0]: mean: {np.mean(X_test[:, 0], axis=0):.1f}, std: {np.std(X_test[:, 0], axis=0):.1f}")
print (f"X_test[1]: mean: {np.mean(X_test[:, 1], axis=0):.1f}, std: {np.std(X_test[:, 1], axis=0):.1f}")
```
# Linear model
Before we get to our neural network, we're going to motivate non-linear activation functions by implementing a generalized linear model (logistic regression). We'll see why linear models (with linear activations) won't suffice for our dataset.
```
import torch
# Set seed for reproducibility
torch.manual_seed(SEED)
```
## Model
```
from torch import nn
import torch.nn.functional as F
INPUT_DIM = X_train.shape[1] # X is 2-dimensional
HIDDEN_DIM = 100
NUM_CLASSES = len(classes) # 3 classes
class LinearModel(nn.Module):
def __init__(self, input_dim, hidden_dim, num_classes):
super(LinearModel, self).__init__()
self.fc1 = nn.Linear(input_dim, hidden_dim)
self.fc2 = nn.Linear(hidden_dim, num_classes)
def forward(self, x_in, apply_softmax=False):
z = self.fc1(x_in) # linear activation
y_pred = self.fc2(z)
if apply_softmax:
y_pred = F.softmax(y_pred, dim=1)
return y_pred
# Initialize model
model = LinearModel(input_dim=INPUT_DIM, hidden_dim=HIDDEN_DIM, num_classes=NUM_CLASSES)
print (model.named_parameters)
```
## Training
```
from torch.optim import Adam
LEARNING_RATE = 1e-2
NUM_EPOCHS = 10
BATCH_SIZE = 32
# Define Loss
class_weights_tensor = torch.Tensor(list(class_weights.values()))
loss_fn = nn.CrossEntropyLoss(weight=class_weights_tensor)
# Accuracy
def accuracy_fn(y_pred, y_true):
n_correct = torch.eq(y_pred, y_true).sum().item()
accuracy = (n_correct / len(y_pred)) * 100
return accuracy
# Optimizer
optimizer = Adam(model.parameters(), lr=LEARNING_RATE)
# Convert data to tensors
X_train = torch.Tensor(X_train)
y_train = torch.LongTensor(y_train)
X_val = torch.Tensor(X_val)
y_val = torch.LongTensor(y_val)
X_test = torch.Tensor(X_test)
y_test = torch.LongTensor(y_test)
# Training
for epoch in range(NUM_EPOCHS):
# Forward pass
y_pred = model(X_train)
# Loss
loss = loss_fn(y_pred, y_train)
# Zero all gradients
optimizer.zero_grad()
# Backward pass
loss.backward()
# Update weights
optimizer.step()
if epoch%1==0:
predictions = y_pred.max(dim=1)[1] # class
accuracy = accuracy_fn(y_pred=predictions, y_true=y_train)
print (f"Epoch: {epoch} | loss: {loss:.2f}, accuracy: {accuracy:.1f}")
```
## Evaluation
```
import json
import matplotlib.pyplot as plt
from sklearn.metrics import precision_recall_fscore_support
def get_performance(y_true, y_pred, classes):
"""Per-class performance metrics."""
# Performance
performance = {"overall": {}, "class": {}}
# Overall performance
metrics = precision_recall_fscore_support(y_true, y_pred, average="weighted")
performance["overall"]["precision"] = metrics[0]
performance["overall"]["recall"] = metrics[1]
performance["overall"]["f1"] = metrics[2]
performance["overall"]["num_samples"] = np.float64(len(y_true))
# Per-class performance
metrics = precision_recall_fscore_support(y_true, y_pred, average=None)
for i in range(len(classes)):
performance["class"][classes[i]] = {
"precision": metrics[0][i],
"recall": metrics[1][i],
"f1": metrics[2][i],
"num_samples": np.float64(metrics[3][i]),
}
return performance
# Predictions
y_prob = model(X_test, apply_softmax=True)
print (f"sample probability: {y_prob[0]}")
y_pred = y_prob.max(dim=1)[1]
print (f"sample class: {y_pred[0]}")
# Performance report
performance = get_performance(y_true=y_test, y_pred=y_pred, classes=classes)
print (json.dumps(performance, indent=2))
def plot_multiclass_decision_boundary(model, X, y):
x_min, x_max = X[:, 0].min() - 0.1, X[:, 0].max() + 0.1
y_min, y_max = X[:, 1].min() - 0.1, X[:, 1].max() + 0.1
xx, yy = np.meshgrid(np.linspace(x_min, x_max, 101), np.linspace(y_min, y_max, 101))
cmap = plt.cm.Spectral
X_test = torch.from_numpy(np.c_[xx.ravel(), yy.ravel()]).float()
y_pred = model(X_test, apply_softmax=True)
_, y_pred = y_pred.max(dim=1)
y_pred = y_pred.reshape(xx.shape)
plt.contourf(xx, yy, y_pred, cmap=plt.cm.Spectral, alpha=0.8)
plt.scatter(X[:, 0], X[:, 1], c=y, s=40, cmap=plt.cm.RdYlBu)
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
# Visualize the decision boundary
plt.figure(figsize=(12,5))
plt.subplot(1, 2, 1)
plt.title("Train")
plot_multiclass_decision_boundary(model=model, X=X_train, y=y_train)
plt.subplot(1, 2, 2)
plt.title("Test")
plot_multiclass_decision_boundary(model=model, X=X_test, y=y_test)
plt.show()
```
# Activation functions
Using the generalized linear method (logistic regression) yielded poor results because of the non-linearity present in our data yet our activation functions were linear. We need to use an activation function that can allow our model to learn and map the non-linearity in our data. There are many different options so let's explore a few.
```
# Fig size
plt.figure(figsize=(12,3))
# Data
x = torch.arange(-5., 5., 0.1)
# Sigmoid activation (constrain a value between 0 and 1.)
plt.subplot(1, 3, 1)
plt.title("Sigmoid activation")
y = torch.sigmoid(x)
plt.plot(x.numpy(), y.numpy())
# Tanh activation (constrain a value between -1 and 1.)
plt.subplot(1, 3, 2)
y = torch.tanh(x)
plt.title("Tanh activation")
plt.plot(x.numpy(), y.numpy())
# Relu (clip the negative values to 0)
plt.subplot(1, 3, 3)
y = F.relu(x)
plt.title("ReLU activation")
plt.plot(x.numpy(), y.numpy())
# Show plots
plt.show()
```
The ReLU activation function ($max(0,z)$) is by far the most widely used activation function for neural networks. But as you can see, each activation function has its own constraints so there are circumstances where you'll want to use different ones. For example, if we need to constrain our outputs between 0 and 1, then the sigmoid activation is the best choice.
> In some cases, using a ReLU activation function may not be sufficient. For instance, when the outputs from our neurons are mostly negative, the activation function will produce zeros. This effectively creates a "dying ReLU" and a recovery is unlikely. To mitigate this effect, we could lower the learning rate or use [alternative ReLU activations](https://medium.com/@danqing/a-practical-guide-to-relu-b83ca804f1f7), ex. leaky ReLU or parametric ReLU (PReLU), which have a small slope for negative neuron outputs.
# NumPy
Now let's create our multilayer perceptron (MLP) which is going to be exactly like the logistic regression model but with the activation function to map the non-linearity in our data.
> It's normal to find the math and code in this section slightly complex. You can still read each of the steps to build intuition for when we implement this using PyTorch.
Our goal is to learn a model 𝑦̂ that models 𝑦 given 𝑋 . You'll notice that neural networks are just extensions of the generalized linear methods we've seen so far but with non-linear activation functions since our data will be highly non-linear.
$z_1 = XW_1$
$a_1 = f(z_1)$
$z_2 = a_1W_2$
$\hat{y} = softmax(z_2)$ # classification
* $X$ = inputs | $\in \mathbb{R}^{NXD}$ ($D$ is the number of features)
* $W_1$ = 1st layer weights | $\in \mathbb{R}^{DXH}$ ($H$ is the number of hidden units in layer 1)
* $z_1$ = outputs from first layer $\in \mathbb{R}^{NXH}$
* $f$ = non-linear activation function
* $a_1$ = activation applied first layer's outputs | $\in \mathbb{R}^{NXH}$
* $W_2$ = 2nd layer weights | $\in \mathbb{R}^{HXC}$ ($C$ is the number of classes)
* $z_2$ = outputs from second layer $\in \mathbb{R}^{NXH}$
* $\hat{y}$ = prediction | $\in \mathbb{R}^{NXC}$ ($N$ is the number of samples)
## Initialize weights
1. Randomly initialize the model's weights $W$ (we'll cover more effective initialization strategies later in this lesson).
```
# Initialize first layer's weights
W1 = 0.01 * np.random.randn(INPUT_DIM, HIDDEN_DIM)
b1 = np.zeros((1, HIDDEN_DIM))
print (f"W1: {W1.shape}")
print (f"b1: {b1.shape}")
```
## Model
2. Feed inputs $X$ into the model to do the forward pass and receive the probabilities.
First we pass the inputs into the first layer.
* $z_1 = XW_1$
```
# z1 = [NX2] · [2X100] + [1X100] = [NX100]
z1 = np.dot(X_train, W1) + b1
print (f"z1: {z1.shape}")
```
Next we apply the non-linear activation function, ReLU ($max(0,z)$) in this case.
* $a_1 = f(z_1)$
```
# Apply activation function
a1 = np.maximum(0, z1) # ReLU
print (f"a_1: {a1.shape}")
```
We pass the activations to the second layer to get our logits.
* $z_2 = a_1W_2$
```
# Initialize second layer's weights
W2 = 0.01 * np.random.randn(HIDDEN_DIM, NUM_CLASSES)
b2 = np.zeros((1, NUM_CLASSES))
print (f"W2: {W2.shape}")
print (f"b2: {b2.shape}")
# z2 = logits = [NX100] · [100X3] + [1X3] = [NX3]
logits = np.dot(a1, W2) + b2
print (f"logits: {logits.shape}")
print (f"sample: {logits[0]}")
```
We'll apply the softmax function to normalize the logits and btain class probabilities.
* $\hat{y} = softmax(z_2)$
```
# Normalization via softmax to obtain class probabilities
exp_logits = np.exp(logits)
y_hat = exp_logits / np.sum(exp_logits, axis=1, keepdims=True)
print (f"y_hat: {y_hat.shape}")
print (f"sample: {y_hat[0]}")
```
## Loss
3. Compare the predictions $\hat{y}$ (ex. [0.3, 0.3, 0.4]) with the actual target values $y$ (ex. class 2 would look like [0, 0, 1]) with the objective (cost) function to determine loss $J$. A common objective function for classification tasks is cross-entropy loss.
* $J(\theta) = - \sum_i ln(\hat{y_i}) = - \sum_i ln (\frac{e^{X_iW_y}}{\sum_j e^{X_iW}}) $
```
# Loss
correct_class_logprobs = -np.log(y_hat[range(len(y_hat)), y_train])
loss = np.sum(correct_class_logprobs) / len(y_train)
```
## Gradients
4. Calculate the gradient of loss $J(\theta)$ w.r.t to the model weights.
The gradient of the loss w.r.t to $W_2$ is the same as the gradients from logistic regression since $\hat{y} = softmax(z_2)$.
* $\frac{\partial{J}}{\partial{W_{2j}}} = \frac{\partial{J}}{\partial{\hat{y}}}\frac{\partial{\hat{y}}}{\partial{W_{2j}}} = - \frac{1}{\hat{y}}\frac{\partial{\hat{y}}}{\partial{W_{2j}}} = - \frac{1}{\frac{e^{W_{2y}a_1}}{\sum_j e^{a_1W}}}\frac{\sum_j e^{a_1W}e^{a_1W_{2y}}0 - e^{a_1W_{2y}}e^{a_1W_{2j}}a_1}{(\sum_j e^{a_1W})^2} = \frac{a_1e^{a_1W_{2j}}}{\sum_j e^{a_1W}} = a_1\hat{y}$
* $\frac{\partial{J}}{\partial{W_{2y}}} = \frac{\partial{J}}{\partial{\hat{y}}}\frac{\partial{\hat{y}}}{\partial{W_{2y}}} = - \frac{1}{\hat{y}}\frac{\partial{\hat{y}}}{\partial{W_{2y}}} = - \frac{1}{\frac{e^{W_{2y}a_1}}{\sum_j e^{a_1W}}}\frac{\sum_j e^{a_1W}e^{a_1W_{2y}}a_1 - e^{a_1W_{2y}}e^{a_1W_{2y}}a_1}{(\sum_j e^{a_1W})^2} = \frac{1}{\hat{y}}(a_1\hat{y} - a_1\hat{y}^2) = a_1(\hat{y}-1)$
The gradient of the loss w.r.t $W_1$ is a bit trickier since we have to backpropagate through two sets of weights.
* $ \frac{\partial{J}}{\partial{W_1}} = \frac{\partial{J}}{\partial{\hat{y}}} \frac{\partial{\hat{y}}}{\partial{a_1}} \frac{\partial{a_1}}{\partial{z_1}} \frac{\partial{z_1}}{\partial{W_1}} = W_2(\partial{scores})(\partial{ReLU})X $
```
# dJ/dW2
dscores = y_hat
dscores[range(len(y_hat)), y_train] -= 1
dscores /= len(y_train)
dW2 = np.dot(a1.T, dscores)
db2 = np.sum(dscores, axis=0, keepdims=True)
# dJ/dW1
dhidden = np.dot(dscores, W2.T)
dhidden[a1 <= 0] = 0 # ReLu backprop
dW1 = np.dot(X_train.T, dhidden)
db1 = np.sum(dhidden, axis=0, keepdims=True)
```
## Update weights
5. Update the weights $W$ using a small learning rate $\alpha$. The updates will penalize the probability for the incorrect classes ($j$) and encourage a higher probability for the correct class ($y$).
* $W_i = W_i - \alpha\frac{\partial{J}}{\partial{W_i}}$
```
# Update weights
W1 += -LEARNING_RATE * dW1
b1 += -LEARNING_RATE * db1
W2 += -LEARNING_RATE * dW2
b2 += -LEARNING_RATE * db2
```
## Training
6. Repeat steps 2 - 4 until model performs well.
```
# Convert tensors to NumPy arrays
X_train = X_train.numpy()
y_train = y_train.numpy()
X_val = X_val.numpy()
y_val = y_val.numpy()
X_test = X_test.numpy()
y_test = y_test.numpy()
# Initialize random weights
W1 = 0.01 * np.random.randn(INPUT_DIM, HIDDEN_DIM)
b1 = np.zeros((1, HIDDEN_DIM))
W2 = 0.01 * np.random.randn(HIDDEN_DIM, NUM_CLASSES)
b2 = np.zeros((1, NUM_CLASSES))
# Training loop
for epoch_num in range(1000):
# First layer forward pass [NX2] · [2X100] = [NX100]
z1 = np.dot(X_train, W1) + b1
# Apply activation function
a1 = np.maximum(0, z1) # ReLU
# z2 = logits = [NX100] · [100X3] = [NX3]
logits = np.dot(a1, W2) + b2
# Normalization via softmax to obtain class probabilities
exp_logits = np.exp(logits)
y_hat = exp_logits / np.sum(exp_logits, axis=1, keepdims=True)
# Loss
correct_class_logprobs = -np.log(y_hat[range(len(y_hat)), y_train])
loss = np.sum(correct_class_logprobs) / len(y_train)
# show progress
if epoch_num%100 == 0:
# Accuracy
y_pred = np.argmax(logits, axis=1)
accuracy = np.mean(np.equal(y_train, y_pred))
print (f"Epoch: {epoch_num}, loss: {loss:.3f}, accuracy: {accuracy:.3f}")
# dJ/dW2
dscores = y_hat
dscores[range(len(y_hat)), y_train] -= 1
dscores /= len(y_train)
dW2 = np.dot(a1.T, dscores)
db2 = np.sum(dscores, axis=0, keepdims=True)
# dJ/dW1
dhidden = np.dot(dscores, W2.T)
dhidden[a1 <= 0] = 0 # ReLu backprop
dW1 = np.dot(X_train.T, dhidden)
db1 = np.sum(dhidden, axis=0, keepdims=True)
# Update weights
W1 += -1e0 * dW1
b1 += -1e0 * db1
W2 += -1e0 * dW2
b2 += -1e0 * db2
```
## Evaluation
```
class MLPFromScratch():
def predict(self, x):
z1 = np.dot(x, W1) + b1
a1 = np.maximum(0, z1)
logits = np.dot(a1, W2) + b2
exp_logits = np.exp(logits)
y_hat = exp_logits / np.sum(exp_logits, axis=1, keepdims=True)
return y_hat
# Evaluation
model = MLPFromScratch()
y_prob = model.predict(X_test)
y_pred = np.argmax(y_prob, axis=1)
# Performance report
performance = get_performance(y_true=y_test, y_pred=y_pred, classes=classes)
print (json.dumps(performance, indent=2))
def plot_multiclass_decision_boundary_numpy(model, X, y, savefig_fp=None):
"""Plot the multiclass decision boundary for a model that accepts 2D inputs.
Credit: https://cs231n.github.io/neural-networks-case-study/
Arguments:
model {function} -- trained model with function model.predict(x_in).
X {numpy.ndarray} -- 2D inputs with shape (N, 2).
y {numpy.ndarray} -- 1D outputs with shape (N,).
"""
# Axis boundaries
x_min, x_max = X[:, 0].min() - 0.1, X[:, 0].max() + 0.1
y_min, y_max = X[:, 1].min() - 0.1, X[:, 1].max() + 0.1
xx, yy = np.meshgrid(np.linspace(x_min, x_max, 101),
np.linspace(y_min, y_max, 101))
# Create predictions
x_in = np.c_[xx.ravel(), yy.ravel()]
y_pred = model.predict(x_in)
y_pred = np.argmax(y_pred, axis=1).reshape(xx.shape)
# Plot decision boundary
plt.contourf(xx, yy, y_pred, cmap=plt.cm.Spectral, alpha=0.8)
plt.scatter(X[:, 0], X[:, 1], c=y, s=40, cmap=plt.cm.RdYlBu)
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
# Plot
if savefig_fp:
plt.savefig(savefig_fp, format='png')
# Visualize the decision boundary
plt.figure(figsize=(12,5))
plt.subplot(1, 2, 1)
plt.title("Train")
plot_multiclass_decision_boundary_numpy(model=model, X=X_train, y=y_train)
plt.subplot(1, 2, 2)
plt.title("Test")
plot_multiclass_decision_boundary_numpy(model=model, X=X_test, y=y_test)
plt.show()
```
# PyTorch
## Model
We'll be using two linear layers along with PyTorch [Functional](https://pytorch.org/docs/stable/nn.functional.html) API's [ReLU](https://pytorch.org/docs/stable/nn.functional.html#torch.nn.functional.relu) operation.
```
class MLP(nn.Module):
def __init__(self, input_dim, hidden_dim, num_classes):
super(MLP, self).__init__()
self.fc1 = nn.Linear(input_dim, hidden_dim)
self.fc2 = nn.Linear(hidden_dim, num_classes)
def forward(self, x_in, apply_softmax=False):
z = F.relu(self.fc1(x_in)) # ReLU activaton function added!
y_pred = self.fc2(z)
if apply_softmax:
y_pred = F.softmax(y_pred, dim=1)
return y_pred
# Initialize model
model = MLP(input_dim=INPUT_DIM, hidden_dim=HIDDEN_DIM, num_classes=NUM_CLASSES)
print (model.named_parameters)
```
## Training
```
# Define Loss
class_weights_tensor = torch.Tensor(list(class_weights.values()))
loss_fn = nn.CrossEntropyLoss(weight=class_weights_tensor)
# Accuracy
def accuracy_fn(y_pred, y_true):
n_correct = torch.eq(y_pred, y_true).sum().item()
accuracy = (n_correct / len(y_pred)) * 100
return accuracy
# Optimizer
optimizer = Adam(model.parameters(), lr=LEARNING_RATE)
# Convert data to tensors
X_train = torch.Tensor(X_train)
y_train = torch.LongTensor(y_train)
X_val = torch.Tensor(X_val)
y_val = torch.LongTensor(y_val)
X_test = torch.Tensor(X_test)
y_test = torch.LongTensor(y_test)
# Training
for epoch in range(NUM_EPOCHS*10):
# Forward pass
y_pred = model(X_train)
# Loss
loss = loss_fn(y_pred, y_train)
# Zero all gradients
optimizer.zero_grad()
# Backward pass
loss.backward()
# Update weights
optimizer.step()
if epoch%10==0:
predictions = y_pred.max(dim=1)[1] # class
accuracy = accuracy_fn(y_pred=predictions, y_true=y_train)
print (f"Epoch: {epoch} | loss: {loss:.2f}, accuracy: {accuracy:.1f}")
```
## Evaluation
```
# Predictions
y_prob = model(X_test, apply_softmax=True)
y_pred = y_prob.max(dim=1)[1]
# Performance report
performance = get_performance(y_true=y_test, y_pred=y_pred, classes=classes)
print (json.dumps(performance, indent=2))
# Visualize the decision boundary
plt.figure(figsize=(12,5))
plt.subplot(1, 2, 1)
plt.title("Train")
plot_multiclass_decision_boundary(model=model, X=X_train, y=y_train)
plt.subplot(1, 2, 2)
plt.title("Test")
plot_multiclass_decision_boundary(model=model, X=X_test, y=y_test)
plt.show()
```
## Inference
```
# Inputs for inference
X_infer = pd.DataFrame([{'X1': 0.1, 'X2': 0.1}])
X_infer.head()
# Standardize
X_infer = X_scaler.transform(X_infer)
print (X_infer)
# Predict
y_infer = model(torch.Tensor(X_infer), apply_softmax=True)
prob, _class = y_infer.max(dim=1)
label = label_encoder.inverse_transform(_class.detach().numpy())[0]
print (f"The probability that you have {label} is {prob.detach().numpy()[0]*100.0:.0f}%")
```
# Initializing weights
So far we have been initializing weights with small random values and this isn't optimal for convergence during training. The objective is to have weights that are able to produce outputs that follow a similar distribution across all neurons. We can do this by enforcing weights to have unit variance prior the affine and non-linear operations.
> A popular method is to apply [xavier initialization](http://andyljones.tumblr.com/post/110998971763/an-explanation-of-xavier-initialization), which essentially initializes the weights to allow the signal from the data to reach deep into the network. You may be wondering why we don't do this for every forward pass and that's a great question. We'll look at more advanced strategies that help with optimization like batch/layer normalization, etc. in future lessons. Meanwhile you can check out other initializers [here](https://pytorch.org/docs/stable/nn.init.html).
```
from torch.nn import init
class MLP(nn.Module):
def __init__(self, input_dim, hidden_dim, num_classes):
super(MLP, self).__init__()
self.fc1 = nn.Linear(input_dim, hidden_dim)
self.fc2 = nn.Linear(hidden_dim, num_classes)
def init_weights(self):
init.xavier_normal(self.fc1.weight, gain=init.calculate_gain('relu'))
def forward(self, x_in, apply_softmax=False):
z = F.relu(self.fc1(x_in)) # ReLU activaton function added!
y_pred = self.fc2(z)
if apply_softmax:
y_pred = F.softmax(y_pred, dim=1)
return y_pred
```
# Dropout
A great technique to have our models generalize (perform well on test data) is to increase the size of your data but this isn't always an option. Fortuntely, there are methods like regularization and dropout that can help create a more robust model.
Dropout is a technique (used only during training) that allows us to zero the outputs of neurons. We do this for `dropout_p`% of the total neurons in each layer and it changes every batch. Dropout prevents units from co-adapting too much to the data and acts as a sampling strategy since we drop a different set of neurons each time.
<div align="left">
<img src="https://raw.githubusercontent.com/GokuMohandas/MadeWithML/main/images/basics/neural-networks/dropout.png" width="350">
</div>
* [Dropout: A Simple Way to Prevent Neural Networks from
Overfitting](http://jmlr.org/papers/volume15/srivastava14a/srivastava14a.pdf)
```
DROPOUT_P = 0.1 # % of the neurons that are dropped each pass
class MLP(nn.Module):
def __init__(self, input_dim, hidden_dim, dropout_p, num_classes):
super(MLP, self).__init__()
self.fc1 = nn.Linear(input_dim, hidden_dim)
self.dropout = nn.Dropout(dropout_p) # dropout
self.fc2 = nn.Linear(hidden_dim, num_classes)
def init_weights(self):
init.xavier_normal(self.fc1.weight, gain=init.calculate_gain('relu'))
def forward(self, x_in, apply_softmax=False):
z = F.relu(self.fc1(x_in))
z = self.dropout(z) # dropout
y_pred = self.fc2(z)
if apply_softmax:
y_pred = F.softmax(y_pred, dim=1)
return y_pred
# Initialize model
model = MLP(input_dim=INPUT_DIM, hidden_dim=HIDDEN_DIM,
dropout_p=DROPOUT_P, num_classes=NUM_CLASSES)
print (model.named_parameters)
```
# Overfitting
Though neural networks are great at capturing non-linear relationships they are highly susceptible to overfitting to the training data and failing to generalize on test data. Just take a look at the example below where we generate completely random data and are able to fit a model with [$2*N*C + D$](https://arxiv.org/abs/1611.03530) hidden units. The training performance is good (~70%) but the overfitting leads to very poor test performance. We'll be covering strategies to tackle overfitting in future lessons.
```
NUM_EPOCHS = 500
NUM_SAMPLES_PER_CLASS = 50
LEARNING_RATE = 1e-1
HIDDEN_DIM = 2 * NUM_SAMPLES_PER_CLASS * NUM_CLASSES + INPUT_DIM # 2*N*C + D
# Generate random data
X = np.random.rand(NUM_SAMPLES_PER_CLASS * NUM_CLASSES, INPUT_DIM)
y = np.array([[i]*NUM_SAMPLES_PER_CLASS for i in range(NUM_CLASSES)]).reshape(-1)
print ("X: ", format(np.shape(X)))
print ("y: ", format(np.shape(y)))
# Create data splits
X_train, X_val, X_test, y_train, y_val, y_test = train_val_test_split(
X=X, y=y, train_size=TRAIN_SIZE)
print (f"X_train: {X_train.shape}, y_train: {y_train.shape}")
print (f"X_val: {X_val.shape}, y_val: {y_val.shape}")
print (f"X_test: {X_test.shape}, y_test: {y_test.shape}")
print (f"Sample point: {X_train[0]} → {y_train[0]}")
# Standardize the inputs (mean=0, std=1) using training data
X_scaler = StandardScaler().fit(X_train)
X_train = X_scaler.transform(X_train)
X_val = X_scaler.transform(X_val)
X_test = X_scaler.transform(X_test)
# Convert data to tensors
X_train = torch.Tensor(X_train)
y_train = torch.LongTensor(y_train)
X_val = torch.Tensor(X_val)
y_val = torch.LongTensor(y_val)
X_test = torch.Tensor(X_test)
y_test = torch.LongTensor(y_test)
# Initialize model
model = MLP(input_dim=INPUT_DIM, hidden_dim=HIDDEN_DIM,
dropout_p=DROPOUT_P, num_classes=NUM_CLASSES)
print (model.named_parameters)
# Optimizer
optimizer = Adam(model.parameters(), lr=LEARNING_RATE)
# Training
for epoch in range(NUM_EPOCHS):
# Forward pass
y_pred = model(X_train)
# Loss
loss = loss_fn(y_pred, y_train)
# Zero all gradients
optimizer.zero_grad()
# Backward pass
loss.backward()
# Update weights
optimizer.step()
if epoch%20==0:
predictions = y_pred.max(dim=1)[1] # class
accuracy = accuracy_fn(y_pred=predictions, y_true=y_train)
print (f"Epoch: {epoch} | loss: {loss:.2f}, accuracy: {accuracy:.1f}")
# Predictions
y_prob = model(X_test, apply_softmax=True)
y_pred = y_prob.max(dim=1)[1]
# Performance report
performance = get_performance(y_true=y_test, y_pred=y_pred, classes=classes)
print (json.dumps(performance, indent=2))
# Visualize the decision boundary
plt.figure(figsize=(12,5))
plt.subplot(1, 2, 1)
plt.title("Train")
plot_multiclass_decision_boundary(model=model, X=X_train, y=y_train)
plt.subplot(1, 2, 2)
plt.title("Test")
plot_multiclass_decision_boundary(model=model, X=X_test, y=y_test)
plt.show()
```
It's important that we experiment, starting with simple models that underfit (high bias) and improve it towards a good fit. Starting with simple models (linear/logistic regression) let's us catch errors without the added complexity of more sophisticated models (neural networks).
<div align="left">
<img src="https://raw.githubusercontent.com/GokuMohandas/MadeWithML/main/images/basics/neural-networks/fit.png" width="700">
</div>
| github_jupyter |
# AWS. S3 Buckets
> 'Working with AWS S3 buckets'
- toc:true
- branch: master
- badges: false
- comments: false
- author: Alexandros Giavaras
- categories: [aws, s3-buckets, cloud-computing, data-storage, data-engineering, data-storage, boto3]
## Overview
In this notebook, we are going to have a brief view on AWS S3 storage. Concretely, we are going to discuss the following:
- How to create an AWS S3 Bucket
- How to upload and download items
- How to do multi-part file transfer
- How to generate pre-signed URLS.
- How to set up bucket policies
Moreover, we will work with AWS S3 buckets using the Boto3 Python package.
## S3 Buckets
AWS S3 is an object storage system. S3 stands for Simple Storage Service. By design, S3 has 11 9's of durability and stores data for millions of applications. S3 files are referred to as objects. You can find more information about S3 <a href="https://aws.amazon.com/s3/?p=ft&c=st&z=3">here</a> and <a href="https://docs.aws.amazon.com/AmazonS3/latest/userguide/Welcome.html">here</a>.
We will use the Boto3 Python package to interact with AWS S3; that is to create a bucket, upload and download files in the created bucket.
```
import logging
import boto3
from botocore.exceptions import ClientError
```
## Create S3 Bucket
```
# credentials to be used
AWS_ACCESS_KEY_ID = 'Use your own credentials'
AWS_SECRET_ACCESS_KEY = 'Use your own credentials'
# create a client for the resource we will use
s3_client = boto3.client('s3', region_name='us-west-2',
aws_access_key_id=AWS_ACCESS_KEY_ID,
aws_secret_access_key=AWS_SECRET_ACCESS_KEY)
location = {'LocationConstraint': 'us-west-2'}
s3_client.create_bucket(Bucket='coursera-s3-bucket',
CreateBucketConfiguration=location)
```
The response of the function all above is shown below:
```
{'ResponseMetadata': {'RequestId': '355VX5QNYSQBTSCM',
'HostId': '7jXN853VP175Fw/il1Zvx8UXkfRsdQRXH3VrAFOcCYZl4y2ZTF6zNPp6tXvwnpBGlmAKTCP9RFA=',
'HTTPStatusCode': 200,
'HTTPHeaders': {'x-amz-id-2': '7jXN853VP175Fw/il1Zvx8UXkfRsdQRXH3VrAFOcCYZl4y2ZTF6zNPp6tXvwnpBGlmAKTCP9RFA=',
'x-amz-request-id': '355VX5QNYSQBTSCM',
'date': 'Thu, 11 Nov 2021 11:01:14 GMT',
'location': 'http://coursera-s3-bucket.s3.amazonaws.com/',
'server': 'AmazonS3',
'content-length': '0'},
'RetryAttempts': 0},
'Location': 'http://coursera-s3-bucket.s3.amazonaws.com/'}
```
## Upload and object to a bucket
## Bucket policies
### Retrieve the policies attached to a bucket
```
result = 3_client.get_bucket_policy(Bucket='bucket-name')
```
The call above fails because by default there are no policies set. A bucket's policy can be set by calling the ```put_bucket_policy``` method. Moreover, a policy is defined in the same JSON format as an IAM policy.
The **Sid (statement ID)** is an optional identifier that you provide for the policy statement. You can assign a Sid value to each statement in a statement array.
The **Effect** element is required and specifies whether the statement results in an allow or an explicit deny. Valid values for Effect are Allow and Deny.
By default, access to resources is denied.
Use the **Principal** element in a policy to specify the principal that is allowed or denied access to a resource.
You can specify any of the following principals in a policy:
- AWS account and root user
- IAM users
- Federated users (using web identity or SAML federation)
- IAM roles
- Assumed-role sessions
- AWS services
- Anonymous users
The **Action** element describes the specific action or actions that will be allowed or denied.
We specify a value using a service namespace as an action prefix (iam, ec2, sqs, sns, s3, etc.) followed by the name of the action to allow or deny.
The **Resource** element specifies the object or objects that the statement covers. We specify a resource using an ARN. Amazon Resource Names (ARNs) uniquely identify AWS resources.
## CORS Configuration
```
response = s3_client.get_bucket_cors(Bucket=bucket_name)
print(response['CORSRules'])
cors_configuration = {
'CORSRules':[{'AllowHeaders':['Authorization'],
'AllowedMethods':['GET', 'PUT'],
'AllowedOrigins':['*'],
'ExposeHeaders':['GET', 'PUT'],
'MaxAgeSeconds':3000}
]
}
response = s3_client.put_bucket_cors(Bucket=bucket_name, CORSConfiguration=cors_configuration)
```
## References
1. <a href="https://aws.amazon.com/s3/?p=ft&c=st&z=3">AWS S3</a>
2. <a href="https://docs.aws.amazon.com/AmazonS3/latest/userguide/Welcome.html">What is Amazon S3?</a>
| github_jupyter |
```
%matplotlib inline
```
# Demo Axes Grid
Grid of 2x2 images with single or own colorbar.
```
import matplotlib.pyplot as plt
from mpl_toolkits.axes_grid1 import ImageGrid
plt.rcParams["mpl_toolkits.legacy_colorbar"] = False
def get_demo_image():
import numpy as np
from matplotlib.cbook import get_sample_data
f = get_sample_data("axes_grid/bivariate_normal.npy", asfileobj=False)
z = np.load(f)
# z is a numpy array of 15x15
return z, (-3, 4, -4, 3)
def demo_simple_grid(fig):
"""
A grid of 2x2 images with 0.05 inch pad between images and only
the lower-left axes is labeled.
"""
grid = ImageGrid(fig, 141, # similar to subplot(141)
nrows_ncols=(2, 2),
axes_pad=0.05,
label_mode="1",
)
Z, extent = get_demo_image()
for ax in grid:
ax.imshow(Z, extent=extent, interpolation="nearest")
# This only affects axes in first column and second row as share_all=False.
grid.axes_llc.set_xticks([-2, 0, 2])
grid.axes_llc.set_yticks([-2, 0, 2])
def demo_grid_with_single_cbar(fig):
"""
A grid of 2x2 images with a single colorbar
"""
grid = ImageGrid(fig, 142, # similar to subplot(142)
nrows_ncols=(2, 2),
axes_pad=0.0,
share_all=True,
label_mode="L",
cbar_location="top",
cbar_mode="single",
)
Z, extent = get_demo_image()
for ax in grid:
im = ax.imshow(Z, extent=extent, interpolation="nearest")
grid.cbar_axes[0].colorbar(im)
for cax in grid.cbar_axes:
cax.toggle_label(False)
# This affects all axes as share_all = True.
grid.axes_llc.set_xticks([-2, 0, 2])
grid.axes_llc.set_yticks([-2, 0, 2])
def demo_grid_with_each_cbar(fig):
"""
A grid of 2x2 images. Each image has its own colorbar.
"""
grid = ImageGrid(fig, 143, # similar to subplot(143)
nrows_ncols=(2, 2),
axes_pad=0.1,
label_mode="1",
share_all=True,
cbar_location="top",
cbar_mode="each",
cbar_size="7%",
cbar_pad="2%",
)
Z, extent = get_demo_image()
for ax, cax in zip(grid, grid.cbar_axes):
im = ax.imshow(Z, extent=extent, interpolation="nearest")
cax.colorbar(im)
cax.toggle_label(False)
# This affects all axes because we set share_all = True.
grid.axes_llc.set_xticks([-2, 0, 2])
grid.axes_llc.set_yticks([-2, 0, 2])
def demo_grid_with_each_cbar_labelled(fig):
"""
A grid of 2x2 images. Each image has its own colorbar.
"""
grid = ImageGrid(fig, 144, # similar to subplot(144)
nrows_ncols=(2, 2),
axes_pad=(0.45, 0.15),
label_mode="1",
share_all=True,
cbar_location="right",
cbar_mode="each",
cbar_size="7%",
cbar_pad="2%",
)
Z, extent = get_demo_image()
# Use a different colorbar range every time
limits = ((0, 1), (-2, 2), (-1.7, 1.4), (-1.5, 1))
for ax, cax, vlim in zip(grid, grid.cbar_axes, limits):
im = ax.imshow(Z, extent=extent, interpolation="nearest",
vmin=vlim[0], vmax=vlim[1])
cb = cax.colorbar(im)
cb.set_ticks((vlim[0], vlim[1]))
# This affects all axes because we set share_all = True.
grid.axes_llc.set_xticks([-2, 0, 2])
grid.axes_llc.set_yticks([-2, 0, 2])
fig = plt.figure(figsize=(10.5, 2.5))
fig.subplots_adjust(left=0.05, right=0.95)
demo_simple_grid(fig)
demo_grid_with_single_cbar(fig)
demo_grid_with_each_cbar(fig)
demo_grid_with_each_cbar_labelled(fig)
plt.show()
```
| github_jupyter |
#Importo librerie
```
import pandas as pd
import numpy as np
import concurrent.futures
import time
from requests.exceptions import ReadTimeout
!pip install -U -q PyDrive
from pydrive.auth import GoogleAuth
from pydrive.drive import GoogleDrive
from google.colab import auth
from oauth2client.client import GoogleCredentials
```
#Autenticazione Spotify API
```
!pip uninstall spotipy
!pip install spotipy
# autenticazione Spotify API con spotipy
import spotipy
from spotipy.oauth2 import SpotifyClientCredentials
auth_manager = SpotifyClientCredentials(client_id='caf57b996b464996bff50ab59186f265', client_secret='0bfcdbff8015426cae855b56b692f69b')
sp = spotipy.Spotify(auth_manager=auth_manager, requests_timeout=10)
```
#Importo dataset
```
# autenticazione google drive
auth.authenticate_user()
gauth = GoogleAuth()
gauth.credentials = GoogleCredentials.get_application_default()
drive = GoogleDrive(gauth)
# importo quarta parte del dataset --> 7087 datapoints
drive.CreateFile({'id':'1YAAvPUaPeBIddkuVzWgw7fhPPcT2uJTY'}).GetContentFile('billboard_dataset_unique.csv')
df_billboard = pd.read_csv("billboard_dataset_unique.csv").drop('Unnamed: 0',axis=1).iloc[21261:]
drive.CreateFile({'id':'1eOqgPk_izGXKIT5y6KfqPkmKWqBonVc0'}).GetContentFile('dataset2_X_billboard.csv')
df_songs = pd.read_csv("dataset2_X_billboard.csv").drop('Unnamed: 0',axis=1)
# df_billboard.iloc[:7087]
# df_billboard.iloc[7087:14174]
# df_billboard.iloc[14174:21261]
# df_billboard.iloc[21261:]
df_billboard.head()
df_billboard.shape
```
#Definizione funzioni
```
def print_exec_time(start):
print("Esecuzione completata in %.4f secondi" % (time.perf_counter()-start))
# funzione che effettua ricerca con Spotify API considerando i casi in cui nel campo 'artist' siano presenti più artisti (featuring)
def search_fix(artist, title):
artist_separators = ['%%%', ' Featuring', ' featuring', ' feat.', ' Feat.', ' feat', ' Feat', ' &', ' x', ' X', ' with', ' With', ', ', '/', ' duet', ' Duet', '+', ' and']
title_separators = ['%%%', ' (']
title_fix = ["%%%", "'s", "'"]
id = None
for x in artist_separators:
for y in title_separators:
for z in title_fix:
try:
id = sp.search(q='artist:'+artist.split(x)[0]+' track:'+title.split(y)[0].replace(z, ''), type='track', limit=1)['tracks']['items'][0]['id']
except IndexError:
pass
if(id != None):
break
if(id != None):
break
if(id != None):
break
return id
# funzione che prendendo una singola riga del Billboard dataset restituisce una lista con id, artista e titolo
# --> in caso di errore l'id viene impostato a None
def get_id(row):
artist = row[1]
title = row[0]
print("fetching id for %s by %s ..." % (title, artist))
try:
try:
id = sp.search(q='artist:'+artist+' track:'+title, type='track', limit=1)['tracks']['items'][0]['id']
except IndexError:
id = search_fix(artist, title)
except ReadTimeout:
id = None
if(id == None):
print('--> [error] %s by %s' % (title, artist))
return [id, artist, title]
# funzione che, preso un id, restituisce un array con le features (audio e non) della traccia corrispondente
def get_features(id):
print("fetching features for id: %s" % id)
# audio features
danceability = []
energy = []
key = []
loudness =[]
mode = []
speechiness = []
acousticness = []
instrumentalness = []
liveness = []
valence = []
tempo = []
duration_ms = []
audio_features_array = [danceability, energy, key, loudness, mode, speechiness,
acousticness, instrumentalness, liveness, valence, tempo, duration_ms]
# altre features
release_date = []
explicit = []
release_date.append(sp.track(id)['album']['release_date'])
explicit.append(sp.track(id)['explicit'])
audio_features = sp.audio_features(id)[0]
try:
# rimuovo campi non necessari
to_remove = ['type', 'id', 'uri', 'track_href', 'analysis_url', 'time_signature']
for rmv in to_remove:
audio_features.pop(rmv)
for i, feature in enumerate(audio_features.keys()):
audio_features_array[i].append(audio_features[feature])
except AttributeError:
print("--> [error] id = %s" % id)
for i in range(12):
audio_features_array[i].append(None)
audio_features_array.append(release_date)
audio_features_array.append(explicit)
return audio_features_array
```
#Integrazione dataset
##Recupero gli id del Billboard dataset
```
time_0 = time.perf_counter()
with concurrent.futures.ProcessPoolExecutor() as executor:
results = executor.map(get_id, df_billboard.values.tolist())
output = []
for result in results:
output.append(result)
print_exec_time(time_0)
# creo backup del billboard dataset
df_billboard_bak = df_billboard.copy()
# inserisco gli id ottenuti in una nuova colonna nel df_billboard
ids = np.array(output)[:,0]
df_billboard.insert(0, 'id', ids)
# calcolo percentuale di canzoni trovate
found_id = df_billboard.id.count()
x = (found_id / df_billboard.title.count()) * 100
print("Found ids = %d%%" % x)
# esporto su google drive
from google.colab import drive
# mounts the google drive to Colab Notebook
drive.mount('/content/drive',force_remount=True)
df_billboard.to_csv('/content/drive/My Drive/Colab Notebooks/datasets/billboard+ids_3.csv')
```
##Recupero audio features del Billboard dataset
```
# reimporto dataset billboard (con ids) + dataset principale
"""
drive.CreateFile({'id':'1fZzuYu-HXKP9HUeio-FL9P4eNygOQ0qq'}).GetContentFile('billboard+ids_0.csv')
df_billboard = pd.read_csv("billboard+ids_0.csv").drop('Unnamed: 0',axis=1)
drive.CreateFile({'id':'1eOqgPk_izGXKIT5y6KfqPkmKWqBonVc0'}).GetContentFile('dataset2_X_billboard.csv')
df_songs = pd.read_csv("dataset2_X_billboard.csv").drop('Unnamed: 0',axis=1)
"""
# elimino valori nulli (= id non trovati)
df_billboard = df_billboard.dropna()
# creo lista con gli id del dataset billboard
ids = list(df_billboard.id.array)
# creo lista degli id che non sono presenti nel dataset principale
time_0 = time.perf_counter()
ids_new = [id for id in ids if id not in list(df_songs.id.array)]
print_exec_time(time_0)
time_0 = time.perf_counter()
with concurrent.futures.ProcessPoolExecutor() as executor:
results = executor.map(get_features, ids_new)
output = []
for result in results:
output.append(result)
print_exec_time(time_0)
```
#Inserisco audio features nel dataset Billboard
```
num_datapoints = np.array(output).shape[0]
output = np.array(output).reshape((num_datapoints,14))
# creo backup df_billboard
df_billboard_bak = df_billboard.copy()
# filtro dataset billboard tenendo solo id nell'array 'ids_new', quindi quelli che non sono presenti nel dataset principale
df_billboard = df_billboard[df_billboard.id.isin(ids_new)]
to_insert = ['danceability',
'energy',
'key',
'loudness',
'mode',
'speechiness',
'acousticness',
'instrumentalness',
'liveness',
'valence',
'tempo',
'duration_ms',
'release_date',
'explicit']
for i, col in enumerate(output.T):
df_billboard.insert(4, to_insert[i], col)
# converto colonna 'release_date' in tipo datetime
df_billboard.release_date = pd.to_datetime(df_billboard.release_date,format="%Y-%m-%d",exact=False)
# inserisco colonna 'year'
year = df_billboard['release_date'].apply(lambda x: int(x.year))
df_billboard.insert(6, 'year', year)
# inserisco colonna 'popularity' --> nb: inizializzo a 0 perchè verrà rimossa
df_billboard.insert(17, 'popularity', np.zeros(df_billboard.shape[0]))
# inserisco colonna 'hit'
hit = np.ones(df_billboard.shape[0])
df_billboard.insert(3, 'hit', hit)
df_billboard.hit = df_billboard.hit.apply(int)
df_billboard.head()
```
#Esporto
```
# esporto in google drive
from google.colab import drive
# mounts the google drive to Colab Notebook
drive.mount('/content/drive',force_remount=True)
df_billboard.to_csv('/content/drive/My Drive/Colab Notebooks/datasets/billboard+features_3.csv')
```
| github_jupyter |
# Notebook use to check the result of the classifier, how well can you detect the nucleus .
You can click `shift` + `enter` to run one cell, you can also click run in top menu.
To run all the cells, you can click `kernel` and `Restart and run all` in the top menu.
```
# Some more magic so that the notebook will reload external python modules;
# see http://stackoverflow.com/questions/1907993/autoreload-of-modules-in-ipython
%load_ext autoreload
%autoreload 2
%reload_ext autoreload
%matplotlib inline
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = 8,8
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'
import numpy as np
import javabridge
import bioformats
from itkwidgets import view
from sklearn.externals import joblib
# Ignore warnings in notebook
import warnings
warnings.filterwarnings('ignore')
```
### The following path should direct to the folder "utils", on Window env it should have slash " / " and not backslash " \ " .
```
# Create a temporary python PATH to the module that we are using for the analysis
import sys
sys.path.insert(0, "/Users/Espenel/Desktop/Mini-Grant-Image-analysis/2018/Chloe/ChromosomeDetectionChloe/utils")
from chromosome_dsb import *
```
# Loading a typical image using bioformats
```
javabridge.start_vm(class_path=bioformats.JARS)
```
### In the path variable you should enter the path to your image of interest:
```
path = '/Users/Espenel/Desktop/Mini-Grant-Image-analysis/2018/Chloe/data_chloe/cku-exo1_002/2017-04-12_RAD51-HTP3_cku80-exo1_002_visit_13_D3D_ALX.dv'
```
## in the following cell in "channel" enter the the channel (starting from 0) where you will find the nucleus
```
img = load_data.load_bioformats(path, channel = 3, no_meta_direct = True)
img.shape
#view(visualization.convert_view(img))
```
# Sliding Window
### First need to load the classifier (clf) and scaler.
```
clf = joblib.load("/Users/Espenel/Desktop/Mini-Grant-Image-analysis/2018/Chloe/clf_scaler/clf")
scaler = joblib.load("/Users/Espenel/Desktop/Mini-Grant-Image-analysis/2018/Chloe/clf_scaler/scaler")
import time
tp1 = time.time()
result = search.rolling_window(img, clf, scaler)
tp2 = time.time()
print("It took {}sec to find the chromosomes in 1 Zstack".format(int(tp2-tp1)))
```
### Optionally you can create a Heat map with the probability at every pixel that there is a nucleus
```
#heat_map = visualization.heatmap(result)
#view(visualization.convert_view(heat_map))
```
### Max projection and check how the result looks like
```
proj = np.amax(img, axis=0)
```
### When boxes are overlapping, only keep the highest probability one.
Here you can adjust `probaThresh` and `overlaThresh`, if you find better parameters, you can change them in the function `batch.batch` in the `chromosome_dsb` folder.
```
box = search.non_max_suppression(result, probaThresh=0.8, overlapThresh=0.3)
import matplotlib.patches as patches
fig, ax = plt.subplots(1, 1, figsize=(10, 10))
ax.imshow(proj, vmax = 100000)
for rec in box:
rect = patches.Rectangle((rec[0],rec[1]),70,70,linewidth=3,edgecolor='y',facecolor='none')
# Add the patch to the Axes
ax.add_patch(rect)
plt.axis('off')
#plt.savefig('/Users/Espenel/Desktop/Mini-Grant-Image-analysis/2018/Chloe/data_chloe/fig.png', bbox_inches="tight", pad_inches=0)
```
# Save the result
```
#path = "/Users/Espenel/Desktop/Mini-Grant-Image-analysis/2018/Chloe/13/"
#load_data.save_file(path, "bbox_3D", box, model=False)
#load_data.save_file(path, "bbox_3D", binary, model=False)
```
| github_jupyter |
### Generator States
Let's look at a simple generator function:
```
def gen(s):
for c in s:
yield c
```
We create an generator object by calling the generator function:
```
g = gen('abc')
```
At this point the generator object is **created**, but we have not actually started running it. To do so, we call `next()`, which then starts running the function body until the first `yield` is encountered:
```
next(g)
```
Now the generator is **suspended**, waiting for us to call next again:
```
next(g)
```
Every time we call `next`, the generator function runs, or is in a **running** state until the next yield is encountered, or no more results are yielded and the function actually returns:
```
next(g)
next(g)
```
Once we exhaust the generator, we get a `StopIteration` exception, and we can think of the generator as being **closed**.
As we can see, a generator can be in one of four states:
* created
* running
* suspended
* closed
We can actually request the state of a generator programmatically by using the `inspect` module's `getgeneratorstate()` function:
```
from inspect import getgeneratorstate
g = gen('abc')
getgeneratorstate(g)
```
We can start running the generator by calling `next`:
```
next(g)
```
And the state is now:
```
getgeneratorstate(g)
```
Once we exhaust the generator:
```
next(g), next(g), next(g)
```
The generator is now in a closed state:
```
getgeneratorstate(g)
```
Now we haven't seen the running state - to do that we just need to print the state from inside the generator - but to do that we need to have a reference to the generator object itself. This is not that easy to do, so I'm going to cheat and assume that the generator object will be referenced by a global variable `global_gen`:
```
def gen(s):
for c in s:
print(getgeneratorstate(global_gen))
yield c
global_gen = gen('abc')
next(global_gen)
```
So a generator can be in these four very distinct states.
When the generator is created, it is not in a running or suspended state - it is simply in a **created** state.
We have to kick-off, or prime, the generator by calling `next` on it.
After the generator has yielded a value, it it is in **suspended** state.
Finally, once the generator **returns** (not yields), i.e. the StopIteration is raised, the generator is **closed**.
Finally it is really important to understand that when a `yield` is encountered, the generator is suspended **exactly** at that point, but not before it has evaluated the expression to the right of the yield statement so it can produce that value in the return value of the `next()` function.
To see this, let's write a simple function and a generator function as follows:
```
def square(i):
print(f'squaring {i}')
return i ** 2
def squares(n):
for i in range(n):
yield square(i)
print ('right after yield')
sq = squares(5)
next(sq)
```
As you can see `square(i)` was evaluated, **then** the value was yielded, and the genrator was suspended exactly at the point the `yield` statement was encountered:
```
next(sq)
```
As you can see, only now does the `right after yield` string get printed from our generator.
| github_jupyter |
```
import tkinter as tk
from tkinter import filedialog
from tkinter import *
from PIL import ImageTk, Image
# Load your model
model = load_model('Saved_model.h5') # Path to your model
# Initialise GUI
top=tk.Tk()
# Window dimensions (800x600)
top.geometry('800x600')
# Window title
top.title('Traffic sign classification')
# Window background color
top.configure(background='#CDCDCD')
# Window label
label=Label(top,background='#CDCDCD', font=('arial',15,'bold'))
# Sign image
sign_image = Label(top)
# Function to classify image
def classify(file_path):
global label_packed
# Open the image file path
image = Image.open(file_path)
# Resize the image
image = image.resize((30,30))
# Inserts a new axis that will appear at the axis position in the expanded array shape
image = np.expand_dims(image, axis=0)
# Convert to numpy array
image = np.array(image)
# Make prediction
pred = model.predict_classes([image])[0]
sign = classes[pred]
print(sign)
label.configure(foreground='#011638', text=sign)
# Function to show the "classify" button
def show_classify_button(file_path):
# Create the button
classify_b=Button(top,text="Classify Image",command=lambda: classify(file_path),padx=10,pady=5)
# Configure button colors
classify_b.configure(background='#364156', foreground='white',font=('arial',10,'bold'))
# Configure button place (location)
classify_b.place(relx=0.79,rely=0.46)
# Function to upload image
def upload_image():
try:
# Path of the image
file_path=filedialog.askopenfilename()
# Open file path
uploaded=Image.open(file_path)
uploaded.thumbnail(((top.winfo_width()/2.25),(top.winfo_height()/2.25)))
im=ImageTk.PhotoImage(uploaded)
sign_image.configure(image=im)
sign_image.image=im
label.configure(text='')
show_classify_button(file_path)
except:
pass
# Create "Upload" button
upload=Button(top,text="Upload an image",command=upload_image,padx=10,pady=5)
# "Upload" button colors and font
upload.configure(background='#364156', foreground='white',font=('arial',10,'bold'))
# Button location
upload.pack(side=BOTTOM,pady=50)
sign_image.pack(side=BOTTOM,expand=True)
label.pack(side=BOTTOM,expand=True)
# Window title text
heading = Label(top, text="Know Your Traffic Sign",pady=20, font=('arial',20,'bold'))
# Window colors
heading.configure(background='#CDCDCD',foreground='#364156')
heading.pack()
top.mainloop()
```
| github_jupyter |
# Notebook 2: Setup Domain
<img src="img/tab_start.png" alt="tab" style="width: 100px; margin:0;" />
Now that we have sshed into our virtual machine (as described in the 👈🏿 notebook [01-data-owners-login.ipynb](01-data-owners-login.ipynb)), let's move on to provision our Domain node.
**Note:** These steps are designed to work on a Ubuntu 20.04 VM however the steps for other linux versions or other OSes are very similar.
## Dependencies
PyGrid Domains require the following software dependencies to run:
- Docker (kubernetes is also available)
- Python 3.7+
- Git
## HAGrid CLI tool
We have a python command-line tool called `hagrid` which is capable of creating VMs as well as provisioning them.
However unfortunately a fresh Ubuntu 20.04 box does not include `pip` to install HAGrid.
## Step 1: Installing HAGrid
First, lets change to the `om` user.
<img src="img/tab_copy_run.png" alt="tab" style="width: 123px; margin:0;" />
```bash
sudo su - om
```
A fresh install of Ubuntu 20.04 does not come with `pip` installed, so lets quickly install!
<img src="img/tab_copy_run.png" alt="tab" style="width: 123px; margin:0;" />
```shell
sudo apt update && sudo apt install python3-pip
```
Once we have pip we can install HAGrid with `pip`.
<img src="img/tab_copy_run.png" alt="tab" style="width: 123px; margin:0;" />
```shell
pip install -U hagrid
```
<img src="img/tab_info.png" alt="tab" style="width: 100px; margin:0;" />
The first time you try to run HAGrid you might get an error `hagrid: command not found`, this usually means that the directory pip installed the HAGrid `console_scripts` is not in your path yet because you just installed pip. On Linux you can simply source the .profile file to update your paths:
<img src="img/tab_copy_run.png" alt="tab" style="width: 123px; margin:0;" />
```shell
. ~/.profile
```
## Step 2: Test HAGrid
Once HAGrid has installed you can simply type `hagrid` on the terminal to check if it is working.
<img src="img/tab_copy_run.png" alt="tab" style="width: 123px; margin:0;" />
```bash
hagrid
```
You should see the following table.

HAGrid checks if all dependencies required for provisioning a Domain or Network node are installed.
**Note**: We can see that *Docker* is already installed to speed up the demo. However HAGrid can install *Docker* for you when we provision with the `localhost` target.
## Step 3: Provisioning the Domain Node
You can now use HAGrid to provision the Domain node. Note this can be done outside the box or inside the box or even on your local machine, however the commands vary slightly.
<img src="img/tab_info.png" alt="tab" style="width: 100px; margin:0;" />
The HAGrid launch command follows the following format:
```
hagrid launch <node_type> <node_name> to <target_host>
```
**node_type**: In our case the default is implicitly a `domain` <br />
**target_host**: Since we are already logged into the VM we use `docker` <br />
**node_name**: is the name of the Domain and is an optional argument. If you don't specify a unique <node_name>, then HAGrid generates one automatically <br />
**--tag=latest**: this flag ensures we use the `latest` pre-built containers from `dockerhub` <br />
**--tail=false**: this flag launches everything in the background <br />
**NOTE**: You can run almost any `hagrid launch` command with `--cmd=true` and it will do a dry run, print commands instead of running them.
Since we're already logged into the VM and just want to provision our domain node, we will choose target to be `docker`.
<img src="img/tab_copy_run.png" alt="tab" style="width: 123px; margin:0;" />
```shell
hagrid launch to docker:80 --tag=latest --tail=false
```
When HAGrid is finished you should see all containers printing `Started` and the command prompt again.

## Step 4: Check if the Domain is up
The containers take a few moments to start up. To check if things are running we can:
- ask HAGrid
- check containers with ctop
### Ask HAGrid
<img src="img/tab_copy_run.png" alt="tab" style="width: 123px; margin:0;" />
```shell
hagrid check --wait
```
<img src="img/tab_info.png" alt="tab" style="width: 100px; margin:0;" />
When you first run this the API endpoint may not be finished starting, with the `--wait` flag hagrid will keep checking until they are all green.

### Step 5: Check in your Browser
<img src="img/tab_run.png" alt="tab" style="width: 100px; margin:0;" />
```
# autodetect the host_ip
from utils import auto_detect_domain_host_ip
DOMAIN_HOST_IP = auto_detect_domain_host_ip()
```
<img src="img/tab_do.png" alt="tab" style="width: 100px; margin:0;" />
```
print("Your Domain's Web Portal should now be ready:\n")
print("👇🏽 Click here to see PyGridUI")
print(f"http://{DOMAIN_HOST_IP}")
```
To login into the your domain you will need the following credentials:
- email address: We will use the email ([email protected]) set on domain creation
- password: We will use the password (changethis) set on domain creation

<img src="img/tab_finish.png" alt="tab" style="width: 100px; margin:0;" />
🙌🏽 Notebook Complete!
🖐 Raise your hand in Zoom
👉🏽 Then, click to continue to Notebook 3: [03-data-owners-upload-dataset.ipynb](03-data-owners-upload-dataset.ipynb)
<img src="img/tab_optional.png" alt="tab" style="width: 100px; margin:0;" />
### Inspect Containers
If you wish to view the individual containers and their logs there a great utility called `ctop` which allows you to work with docker containers on the command line easily.
We have pre-installed it for this demo so you can take it for a spin.
<img src="img/tab_copy_run.png" alt="tab" style="width: 123px; margin:0;" />
```shell
sudo ctop
```
You can use the arrow keys, enter and letter shortcuts to navigate around. You need to just press `q` (small letter q) to quit or exit from `ctop` session.
For information on `ctop` you can visit its [Github](https://github.com/bcicen/ctop) repo.

| github_jupyter |
# Importing libraries
```
import pandas as pd
import random
import numpy as np
from tensorflow.keras.preprocessing.text import Tokenizer
from tensorflow.keras.preprocessing.sequence import pad_sequences
from tensorflow.keras.utils import to_categorical
from tensorflow.keras import regularizers
import matplotlib.pyplot as plt
from itertools import combinations
from sklearn.preprocessing import LabelEncoder
from sklearn.preprocessing import OneHotEncoder
import re
from sklearn.model_selection import train_test_split
from gensim.models import Word2Vec
import tensorflow as tf
import csv
from keras.layers import Dense, Dropout, LSTM, Bidirectional
import matplotlib.pyplot as plt
import json
from operator import itemgetter
```
# Data loading and cleaning
```
Reddit_df = pd.read_csv("/home/ege/selenium/r_news.csv" )
contractions = pd.read_csv("/home/ege/Desktop/kaggle/NLP/archive/contractions.csv")
Reddit_df.dropna( inplace = True)
Reddit_df = Reddit_df[['r/news']]
Reddit_df.drop_duplicates(inplace = True)
Reddit_df.head()
with open('/home/ege/Desktop/kaggle/NLP/word_index.json', 'r') as fp:
tokens = json.load(fp)
```
# Defining preprocessing functions
```
def df_to_dict(data):
dictionary = dict()
col_names = data.columns
for _ in range(data.shape[0]):
dictionary[data[col_names[0]].iloc[_]] = data[col_names[1]].iloc[_]
return dictionary
def lower(data):
columns = data.columns
for col in columns:
data[col] = data[col].apply(str)
data[col] = data[col].str.lower()
return data
# Defining regex patterns.
urlPattern = r"((http://)[^ ]*|(https://)[^ ]*|(www\.)[^ ]*)"
userPattern = '@[^\s]+'
hashtagPattern = '#[^\s]+'
alphaPattern = "[^a-z0-9<>]"
sequencePattern = r"(.)\1\1+"
seqReplacePattern = r"\1\1"
# Defining regex for emojis
smileemoji = r"[8:=;]['`\-]?[)d]+"
sademoji = r"[8:=;]['`\-]?\(+"
neutralemoji = r"[8:=;]['`\-]?[\/|l*]"
lolemoji = r"[8:=;]['`\-]?p+"
def preprocess_data(news):
# Replace all URls with '<url>'
news = re.sub(urlPattern,'<url>',news )
# Replace @USERNAME to '<user>'.
news = re.sub(userPattern,'<user>', news)
# Replace 3 or more consecutive letters by 2 letter.
news = re.sub(sequencePattern, seqReplacePattern, news)
# Replace all emojis.
news = re.sub(r'<3', '<heart>', news)
news = re.sub(smileemoji, '<smile>', news)
news = re.sub(sademoji, '<sadface>', news)
news = re.sub(neutralemoji, '<neutralface>', news)
news = re.sub(lolemoji, '<lolface>', news)
for contraction, replacement in contractions_dict.items():
news = news.replace(contraction, replacement)
# Remove non-alphanumeric and symbols
news = re.sub(alphaPattern, ' ', news)
# Adding space on either side of '/' to seperate words (After replacing URLS).
news = re.sub(r'/', ' / ', news)
return news
def split_func(df):
data = df.values.tolist()
clean_list =[]
for sentences in data:
clean_list.append(sentences[0].split())
return clean_list
def tokenizer_based_on_json(data, tokens):
sentences = 0
word = 0
while True:
try:
data[sentences][word] = tokens[split_list[sentences][word]]
word += 1
if word == len(data[sentences]):
sentences += 1
word = 0
if sentences == len(data):
break
except:
data[sentences][word] = "<oov>"
return data
```
# Data preprocessing
```
Reddit_df = lower(Reddit_df)
contractions_dict = df_to_dict(contractions)
Reddit_df['r/news'] = Reddit_df['r/news'].apply(preprocess_data)
split_list = split_func(Reddit_df)
tokenized_list = tokenizer_based_on_json(split_list , tokens)
news_padded = pad_sequences(tokenized_list , maxlen= max([len(x) for x in tokenized_list]) ,
padding= 'post', truncating= 'post')
```
# Importing saved tensorflow model
```
model = tf.keras.models.load_model("/home/ege/saved_model/my_model")
```
# Predictions
```
predictions = model.predict(news_padded)
predictions_list = []
for pred in predictions:
if pred > 0.7:
predictions_list.append(1)
else:
predictions_list.append(0)
```
# Exploring predictions
```
print("negative news : " , predictions_list.count(0) , "positive news " , predictions_list.count(1))
fig = plt.figure()
ax = fig.add_axes([0,0,1,1])
labels = ['negative news', 'positive news']
numbers = [ predictions_list.count(0) , predictions_list.count(1)]
ax.bar(labels,numbers ,color = 'rg')
plt.show()
Poz_index = [i for i, x in enumerate(predictions_list) if x == 1]
Neg_index = [i for i, x in enumerate(predictions_list) if x == 0]
positive_news = []
negative_news = []
for poz in Poz_index:
positive_news.append(Reddit_df['r/news'].iloc[poz])
for neg in Neg_index:
negative_news.append(Reddit_df['r/news'].iloc[neg])
number_of_sentences = 7
print("-- Some negative news labeled by model -- " , "\n\n")
for sen in range(number_of_sentences):
print(sen+1 , negative_news[random.randrange(0,len(negative_news))],".")
number_of_sentences = 7
print("-- Some positive news labeled by model -- ", "\n\n")
for sen in range(number_of_sentences):
print( sen+1 , positive_news[random.randrange(0,len(positive_news))],".")
```
| github_jupyter |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.