code
stringlengths 2.5k
6.36M
| kind
stringclasses 2
values | parsed_code
stringlengths 0
404k
| quality_prob
float64 0
0.98
| learning_prob
float64 0.03
1
|
|---|---|---|---|---|
```
# best results when running `ocean events access`
import datetime
import time
import json
import requests
import logging
import urllib.parse
from IPython.display import display, IFrame, FileLink, Image
import pandas as pd
from ocean_cli.ocean import get_ocean
logging.getLogger().setLevel(logging.DEBUG)
alice = get_ocean('alice.ini')
if alice.balance().ocn < 1e18:
print('low balance, requesting 1 ocean (=1e18 drops)')
alice.tokens.request(alice.account, 1)
alice.balance()
bob = get_ocean('bob.ini')
bob.balance()
charlie = get_ocean('charlie.ini')
charlie.balance()
# publish url
did = bob.publish(name='put',
secret='https://i.giphy.com/media/3oEduQAsYcJKQH2XsI/giphy.webp',
price=100000000000000000)
did
# resolve did in ddo
ddo = bob.assets.resolve(did)
print(ddo.as_dictionary()['service'][0]['metadata']['base'])
# check permissions
print(alice.check_permissions(did))
print(alice.decrypt(did))
print(charlie.check_permissions(did))
# bob is provider
print(bob.check_permissions(did))# TODO: should be True!
# consume did
decrypted_url = alice.authorize(did)[2]['url']
Image(url=decrypted_url)
# similar result with check and decrypt
print(alice.check_permissions(did))
print(alice.decrypt(did))
print(charlie.check_permissions(did))
# bob is provider
print(bob.check_permissions(did))
print(f'{alice.balance().ocn/1e18} ocean (alice)')
print(f'{bob.balance().ocn/1e18} ocean (bob)')
# create notebook with snippet
from ocean_cli.api.notebook import create_notebook
print(create_notebook(did, name=f'notebook:{did}'))
# publish url with json
url = 'https://api.coingecko.com/api/v3/simple/price?ids=ocean-protocol&vs_currencies=EUR%2CUSD'
did_json = bob.publish(name='json', secret=url, price=2)
# decrypt url & consume json
decrypted_url = alice.authorize(did_json)[2]['url']
print(json.dumps(requests.get(decrypted_url).json(), indent=2, sort_keys=True))
# publish url with json
url = 'https://api.giphy.com/v1/gifs/random?api_key=0UTRbFtkMxAplrohufYco5IY74U8hOes&tag=fail&rating=pg-13'
did_random = bob.publish(name='img', secret=url, price=len(url))
# decrypt url, resolve payload
decrypted_url = alice.authorize(did_random)[2]['url']
try:
img = Image(url=requests.get(decrypted_url).json()['data']['images']['original']['url'])
display(img)
except TypeError as e:
print('pass / api throttle')
decrypted_url
# list last 10 assets
latest_dids = bob.assets.list()[-10:-1]
print(latest_dids)
# search assets for text
print(bob.search('img', pretty=True)[:10])
# publish csv
url = 'https://raw.githubusercontent.com/plotly/datasets/master/school_earnings.csv'
did_csv = bob.publish(name='csv', secret=url, price=len(url))
# consume csv
decrypted_url = alice.authorize(did_csv)[2]['url']
pd.read_csv(decrypted_url).describe()
# run `python -m http.server`
# serve files from localhost with encrypted url path
did_localhost = bob.publish(name='readme',
secret=[{'url': {'path': 'README.md'}}],
price=0,
service_endpoint='http://localhost:8000')
# order and consume request
response = alice.consume(did_localhost,
*alice.authorize(did_localhost),
method='api')
print(response.text)
# run `python proxy.py`
# publish proxy api with encrypted api token
did_api = bob.publish(name='api',
secret=[{'url': {
'path': 'docker/hello',
'qs': 'token=muchsecrettoken'
}}],
price=10000000,
service_endpoint='http://localhost:8080')
# alice cannot use someone elses authorization
# print(alice.consume(did_api, *bob.authorize(did_api), method='api'))
# consume api with token
print(alice.consume(did_api, *alice.authorize(did_api), method='api').json())
# run `python proxy.py` and encrypt api token
# publish proxy api with token
did_loc = bob.publish(name='locations:map:mallorca',
secret=[{'url': {
'path': 'locations/map',
'qs': f'token={"moresecrettoken"}'
f'&latitude={39.7}&longitude={3.0}&zoom={9}'
}}],
price=420000000,
service_endpoint='http://localhost:8080')
did_loc
# generate html with location heatmap
response = alice.consume(did_loc, *alice.authorize(did_loc), method='api')
# save html file locally
fn_html = f'{did_loc}.html'
with open(fn_html, 'w') as fid:
fid.write(response.content.decode())
# serve link
display(FileLink(f'./{fn_html}'))
# serve html in IFrame
IFrame(src=urllib.parse.quote_plus(fn_html), width=700, height=600)
# publish url of static HTML in cloud storage
url = "https://testocnfiles.blob.core.windows.net/testfiles/did%3Aop%3A287686641f1e4e01956b8403500c2f560516e52e72e1415fa040f613a3331259.html?sp=r&st=2019-06-24T19:29:47Z&se=2019-06-25T03:29:47Z&spr=https&sv=2018-03-28&sig=MPwu87X8MAXBCGZe4AWNVMYCchvnLAKkxIM2MbYTADU%3D&sr=b"
did_loc_service = bob.publish(name='put', secret=url, price=10)
# consume service in IFrame
IFrame(src=alice.authorize(did_loc_service)[2]['url'], width=700, height=600)
bob.search('"locations:map:mallorca"', pretty=True)
# run `python proxy.py` and encrypt api token
# publish proxy api with token
did_ani = bob.publish(name='locations:animation:mallorca',
secret=[{'url': {
'path': 'locations/animation',
'qs': f'token={"supersecrettoken"}'
f'&epochs={80}',
}}],
price=1000000000,
service_endpoint='http://localhost:8080')
did_ani
# generate html with location heatmap
response = alice.consume(did_ani, *alice.authorize(did_ani), method='api')
# save html file locally
fn_html = f'{did_ani}.html'
with open(fn_html, 'w') as fid:
fid.write(response.content.decode())
# display IFrame
display(FileLink(f'./{fn_html}'))
IFrame(src=urllib.parse.quote_plus(fn_html), width=700, height=600)
message = 'muchsecret'
signed_message = bob.keeper.sign_hash(message, bob.account)
bob.keeper.ec_recover(message, signed_message).lower() == bob.account.address.lower()
# publish proxy api with token
url = 'http://localhost:8080'
token = 'moresecrettoken'
did_gdr = bob.publish(name='gdrive:list',
secret=[{'url': {
'path': 'gdrive/list',
'qs': f'token={"ohsosecret"}'
f'&emailAddress={"[email protected]"}'
}}],
price=66666666666666,
service_endpoint=url)
# generate html with location heatmap
response = alice.consume(did_gdr, *alice.authorize(did_gdr), method='api')
response.json()
from ocean_cli.proxy.services import gdrive
file_id = gdrive.upload('data/img/paco.jpg')
did_gdr = bob.publish(name='gdrive:auth',
secret=[{'url': {
'path': 'gdrive/auth',
'qs': f'token={"secretisthewaytogoogle"}'
f'&fileId={file_id}'
f'&emailAddress={"[email protected]"}'
}}],
price=1234567,
service_endpoint='http://localhost:8080')
# share gdrive file with emailAddress
response = alice.consume(did_gdr, *alice.authorize(did_gdr), method='api')
response
alice.authorize(did_api)[2]['qs']
bob.agreements.
```
|
github_jupyter
|
# best results when running `ocean events access`
import datetime
import time
import json
import requests
import logging
import urllib.parse
from IPython.display import display, IFrame, FileLink, Image
import pandas as pd
from ocean_cli.ocean import get_ocean
logging.getLogger().setLevel(logging.DEBUG)
alice = get_ocean('alice.ini')
if alice.balance().ocn < 1e18:
print('low balance, requesting 1 ocean (=1e18 drops)')
alice.tokens.request(alice.account, 1)
alice.balance()
bob = get_ocean('bob.ini')
bob.balance()
charlie = get_ocean('charlie.ini')
charlie.balance()
# publish url
did = bob.publish(name='put',
secret='https://i.giphy.com/media/3oEduQAsYcJKQH2XsI/giphy.webp',
price=100000000000000000)
did
# resolve did in ddo
ddo = bob.assets.resolve(did)
print(ddo.as_dictionary()['service'][0]['metadata']['base'])
# check permissions
print(alice.check_permissions(did))
print(alice.decrypt(did))
print(charlie.check_permissions(did))
# bob is provider
print(bob.check_permissions(did))# TODO: should be True!
# consume did
decrypted_url = alice.authorize(did)[2]['url']
Image(url=decrypted_url)
# similar result with check and decrypt
print(alice.check_permissions(did))
print(alice.decrypt(did))
print(charlie.check_permissions(did))
# bob is provider
print(bob.check_permissions(did))
print(f'{alice.balance().ocn/1e18} ocean (alice)')
print(f'{bob.balance().ocn/1e18} ocean (bob)')
# create notebook with snippet
from ocean_cli.api.notebook import create_notebook
print(create_notebook(did, name=f'notebook:{did}'))
# publish url with json
url = 'https://api.coingecko.com/api/v3/simple/price?ids=ocean-protocol&vs_currencies=EUR%2CUSD'
did_json = bob.publish(name='json', secret=url, price=2)
# decrypt url & consume json
decrypted_url = alice.authorize(did_json)[2]['url']
print(json.dumps(requests.get(decrypted_url).json(), indent=2, sort_keys=True))
# publish url with json
url = 'https://api.giphy.com/v1/gifs/random?api_key=0UTRbFtkMxAplrohufYco5IY74U8hOes&tag=fail&rating=pg-13'
did_random = bob.publish(name='img', secret=url, price=len(url))
# decrypt url, resolve payload
decrypted_url = alice.authorize(did_random)[2]['url']
try:
img = Image(url=requests.get(decrypted_url).json()['data']['images']['original']['url'])
display(img)
except TypeError as e:
print('pass / api throttle')
decrypted_url
# list last 10 assets
latest_dids = bob.assets.list()[-10:-1]
print(latest_dids)
# search assets for text
print(bob.search('img', pretty=True)[:10])
# publish csv
url = 'https://raw.githubusercontent.com/plotly/datasets/master/school_earnings.csv'
did_csv = bob.publish(name='csv', secret=url, price=len(url))
# consume csv
decrypted_url = alice.authorize(did_csv)[2]['url']
pd.read_csv(decrypted_url).describe()
# run `python -m http.server`
# serve files from localhost with encrypted url path
did_localhost = bob.publish(name='readme',
secret=[{'url': {'path': 'README.md'}}],
price=0,
service_endpoint='http://localhost:8000')
# order and consume request
response = alice.consume(did_localhost,
*alice.authorize(did_localhost),
method='api')
print(response.text)
# run `python proxy.py`
# publish proxy api with encrypted api token
did_api = bob.publish(name='api',
secret=[{'url': {
'path': 'docker/hello',
'qs': 'token=muchsecrettoken'
}}],
price=10000000,
service_endpoint='http://localhost:8080')
# alice cannot use someone elses authorization
# print(alice.consume(did_api, *bob.authorize(did_api), method='api'))
# consume api with token
print(alice.consume(did_api, *alice.authorize(did_api), method='api').json())
# run `python proxy.py` and encrypt api token
# publish proxy api with token
did_loc = bob.publish(name='locations:map:mallorca',
secret=[{'url': {
'path': 'locations/map',
'qs': f'token={"moresecrettoken"}'
f'&latitude={39.7}&longitude={3.0}&zoom={9}'
}}],
price=420000000,
service_endpoint='http://localhost:8080')
did_loc
# generate html with location heatmap
response = alice.consume(did_loc, *alice.authorize(did_loc), method='api')
# save html file locally
fn_html = f'{did_loc}.html'
with open(fn_html, 'w') as fid:
fid.write(response.content.decode())
# serve link
display(FileLink(f'./{fn_html}'))
# serve html in IFrame
IFrame(src=urllib.parse.quote_plus(fn_html), width=700, height=600)
# publish url of static HTML in cloud storage
url = "https://testocnfiles.blob.core.windows.net/testfiles/did%3Aop%3A287686641f1e4e01956b8403500c2f560516e52e72e1415fa040f613a3331259.html?sp=r&st=2019-06-24T19:29:47Z&se=2019-06-25T03:29:47Z&spr=https&sv=2018-03-28&sig=MPwu87X8MAXBCGZe4AWNVMYCchvnLAKkxIM2MbYTADU%3D&sr=b"
did_loc_service = bob.publish(name='put', secret=url, price=10)
# consume service in IFrame
IFrame(src=alice.authorize(did_loc_service)[2]['url'], width=700, height=600)
bob.search('"locations:map:mallorca"', pretty=True)
# run `python proxy.py` and encrypt api token
# publish proxy api with token
did_ani = bob.publish(name='locations:animation:mallorca',
secret=[{'url': {
'path': 'locations/animation',
'qs': f'token={"supersecrettoken"}'
f'&epochs={80}',
}}],
price=1000000000,
service_endpoint='http://localhost:8080')
did_ani
# generate html with location heatmap
response = alice.consume(did_ani, *alice.authorize(did_ani), method='api')
# save html file locally
fn_html = f'{did_ani}.html'
with open(fn_html, 'w') as fid:
fid.write(response.content.decode())
# display IFrame
display(FileLink(f'./{fn_html}'))
IFrame(src=urllib.parse.quote_plus(fn_html), width=700, height=600)
message = 'muchsecret'
signed_message = bob.keeper.sign_hash(message, bob.account)
bob.keeper.ec_recover(message, signed_message).lower() == bob.account.address.lower()
# publish proxy api with token
url = 'http://localhost:8080'
token = 'moresecrettoken'
did_gdr = bob.publish(name='gdrive:list',
secret=[{'url': {
'path': 'gdrive/list',
'qs': f'token={"ohsosecret"}'
f'&emailAddress={"[email protected]"}'
}}],
price=66666666666666,
service_endpoint=url)
# generate html with location heatmap
response = alice.consume(did_gdr, *alice.authorize(did_gdr), method='api')
response.json()
from ocean_cli.proxy.services import gdrive
file_id = gdrive.upload('data/img/paco.jpg')
did_gdr = bob.publish(name='gdrive:auth',
secret=[{'url': {
'path': 'gdrive/auth',
'qs': f'token={"secretisthewaytogoogle"}'
f'&fileId={file_id}'
f'&emailAddress={"[email protected]"}'
}}],
price=1234567,
service_endpoint='http://localhost:8080')
# share gdrive file with emailAddress
response = alice.consume(did_gdr, *alice.authorize(did_gdr), method='api')
response
alice.authorize(did_api)[2]['qs']
bob.agreements.
| 0.273769 | 0.141222 |
# 随机梯度下降
:label:`sec_sgd`
但是,在前面的章节中,我们一直在训练过程中使用随机梯度下降,但没有解释它为什么起作用。为了澄清这一点,我们刚在 :numref:`sec_gd` 中描述了梯度下降的基本原则。在本节中,我们继续讨论
*更详细地说明随机梯度下降 *。
```
%matplotlib inline
import math
import torch
from d2l import torch as d2l
```
## 随机渐变更新
在深度学习中,目标函数通常是训练数据集中每个示例的损失函数的平均值。给定 $n$ 个示例的训练数据集,我们假设 $f_i(\mathbf{x})$ 是与指数 $i$ 的训练示例相比的损失函数,其中 $\mathbf{x}$ 是参数矢量。然后我们到达目标功能
$$f(\mathbf{x}) = \frac{1}{n} \sum_{i = 1}^n f_i(\mathbf{x}).$$
$\mathbf{x}$ 的目标函数的梯度计算为
$$\nabla f(\mathbf{x}) = \frac{1}{n} \sum_{i = 1}^n \nabla f_i(\mathbf{x}).$$
如果使用梯度下降,则每次独立变量迭代的计算成本为 $\mathcal{O}(n)$,随 $n$ 线性增长。因此,当训练数据集较大时,每次迭代的梯度下降成本将更高。
随机梯度下降 (SGD) 可降低每次迭代时的计算成本。在随机梯度下降的每次迭代中,我们随机统一采样一个指数 $i\in\{1,\ldots, n\}$ 以获取数据示例,并计算渐变 $\nabla f_i(\mathbf{x})$ 以更新 $\mathbf{x}$:
$$\mathbf{x} \leftarrow \mathbf{x} - \eta \nabla f_i(\mathbf{x}),$$
其中 $\eta$ 是学习率。我们可以看到,每次迭代的计算成本从梯度下降的 $\mathcal{O}(n)$ 降至常数 $\mathcal{O}(1)$。此外,我们要强调,随机梯度 $\nabla f_i(\mathbf{x})$ 是对完整梯度 $\nabla f(\mathbf{x})$ 的公正估计,因为
$$\mathbb{E}_i \nabla f_i(\mathbf{x}) = \frac{1}{n} \sum_{i = 1}^n \nabla f_i(\mathbf{x}) = \nabla f(\mathbf{x}).$$
这意味着,平均而言,随机梯度是对梯度的良好估计值。
现在,我们将把它与梯度下降进行比较,方法是向渐变添平均值 0 和方差 1 的随机噪声,以模拟随机渐变下降。
```
def f(x1, x2): # Objective function
return x1 ** 2 + 2 * x2 ** 2
def f_grad(x1, x2): # Gradient of the objective function
return 2 * x1, 4 * x2
def sgd(x1, x2, s1, s2, f_grad):
g1, g2 = f_grad(x1, x2)
# Simulate noisy gradient
g1 += torch.normal(0.0, 1, (1,))
g2 += torch.normal(0.0, 1, (1,))
eta_t = eta * lr()
return (x1 - eta_t * g1, x2 - eta_t * g2, 0, 0)
def constant_lr():
return 1
eta = 0.1
lr = constant_lr # Constant learning rate
d2l.show_trace_2d(f, d2l.train_2d(sgd, steps=50, f_grad=f_grad))
```
正如我们所看到的,随机梯度下降中变量的轨迹比我们在 :numref:`sec_gd` 中观察到的梯度下降中观察到的轨迹嘈杂得多。这是由于梯度的随机性质。也就是说,即使我们接近最低值,我们仍然受到通过 $\eta \nabla f_i(\mathbf{x})$ 的瞬间梯度所注入的不确定性的影响。即使经过 50 个步骤,质量仍然不那么好。更糟糕的是,经过额外的步骤,它不会改善(我们鼓励你尝试更多的步骤来确认这一点)。这给我们留下了唯一的选择:改变学习率 $\eta$。但是,如果我们选择太小,我们一开始就不会取得任何有意义的进展。另一方面,如果我们选择太大,我们将无法获得上文所述的好解决方案。解决这些相互冲突的目标的唯一方法是随着优化的进展动态 * 降低学习率 *。
这也是在 `sgd` 步长函数中添加学习率函数 `lr` 的原因。在上面的示例中,任何学习率调度功能都处于休眠状态,因为我们将关联的 `lr` 函数设置为恒定。
## 动态学习率
用时间相关的学习率 $\eta(t)$ 取代 $\eta$ 增加了控制优化算法收敛的复杂性。特别是,我们需要弄清 $\eta$ 应该有多快衰减。如果速度太快,我们将过早停止优化。如果我们减少速度太慢,我们会在优化上浪费太多时间。以下是随着时间推移调整 $\eta$ 时使用的一些基本策略(稍后我们将讨论更高级的策略):
$$
\begin{aligned}
\eta(t) & = \eta_i \text{ if } t_i \leq t \leq t_{i+1} && \text{piecewise constant} \\
\eta(t) & = \eta_0 \cdot e^{-\lambda t} && \text{exponential decay} \\
\eta(t) & = \eta_0 \cdot (\beta t + 1)^{-\alpha} && \text{polynomial decay}
\end{aligned}
$$
在第一个 * 分段常数 * 场景中,我们会降低学习率,例如,每当优化进度停顿时。这是训练深度网络的常见策略。或者,我们可以通过 * 指数衰减 * 来更积极地减少它。不幸的是,这往往会导致算法收敛之前过早停止。一个受欢迎的选择是 * 多项式衰变 * 与 $\alpha = 0.5$。在凸优化的情况下,有许多证据表明这种速率表现良好。
让我们看看指数衰减在实践中是什么样子。
```
def exponential_lr():
# Global variable that is defined outside this function and updated inside
global t
t += 1
return math.exp(-0.1 * t)
t = 1
lr = exponential_lr
d2l.show_trace_2d(f, d2l.train_2d(sgd, steps=1000, f_grad=f_grad))
```
正如预期的那样,参数的差异大大减少。但是,这是以未能融合到最佳解决方案 $\mathbf{x} = (0, 0)$ 为代价的。即使经过 1000 个迭代步骤,我们仍然离最佳解决方案很远。事实上,该算法根本无法收敛。另一方面,如果我们使用多项式衰减,其中学习率下降,步数的逆平方根,那么仅在 50 个步骤之后,收敛就会更好。
```
def polynomial_lr():
# Global variable that is defined outside this function and updated inside
global t
t += 1
return (1 + 0.1 * t) ** (-0.5)
t = 1
lr = polynomial_lr
d2l.show_trace_2d(f, d2l.train_2d(sgd, steps=50, f_grad=f_grad))
```
关于如何设置学习率,还有更多的选择。例如,我们可以从较小的利率开始,然后迅速上涨,然后再次降低,尽管速度更慢。我们甚至可以在较小和更大的学习率之间交替。这样的时间表有各种各样。现在,让我们专注于可以进行全面理论分析的学习率时间表,即凸环境下的学习率。对于一般的非凸问题,很难获得有意义的收敛保证,因为总的来说,最大限度地减少非线性非凸问题是 NP 困难的。有关调查,例如,请参阅 Tibshirani 2015 年的优秀 [讲义笔记](https://www.stat.cmu.edu/~ryantibs/convexopt-F15/lectures/26-nonconvex.pdf)。
## 凸目标的收敛性分析
以下对凸目标函数的随机梯度下降的收敛性分析是可选的,主要用于传达对问题的更多直觉。我们只限于最简单的证明之一 :cite:`Nesterov.Vial.2000`。存在着明显更先进的证明技术,例如,当客观功能表现特别好时。
假设所有 $\boldsymbol{\xi}$ 的目标函数 $f(\boldsymbol{\xi}, \mathbf{x})$ 在 $\mathbf{x}$ 中都是凸的。更具体地说,我们考虑随机梯度下降更新:
$$\mathbf{x}_{t+1} = \mathbf{x}_{t} - \eta_t \partial_\mathbf{x} f(\boldsymbol{\xi}_t, \mathbf{x}),$$
其中 $f(\boldsymbol{\xi}_t, \mathbf{x})$ 是培训实例 $f(\boldsymbol{\xi}_t, \mathbf{x})$ 的客观功能:$\boldsymbol{\xi}_t$ 从第 $t$ 步的某些分布中摘取,$\mathbf{x}$ 是模型参数。表示通过
$$R(\mathbf{x}) = E_{\boldsymbol{\xi}}[f(\boldsymbol{\xi}, \mathbf{x})]$$
预期风险和 $R^*$ 相对于 $\mathbf{x}$ 的最低风险。最后让 $\mathbf{x}^*$ 成为最小化器(我们假设它存在于定义 $\mathbf{x}$ 的域中)。在这种情况下,我们可以跟踪当前参数 $\mathbf{x}_t$ 当时 $\mathbf{x}_t$ 和风险最小化器 $\mathbf{x}^*$ 之间的距离,看看它是否随着时间的推移而改善:
$$\begin{aligned} &\|\mathbf{x}_{t+1} - \mathbf{x}^*\|^2 \\ =& \|\mathbf{x}_{t} - \eta_t \partial_\mathbf{x} f(\boldsymbol{\xi}_t, \mathbf{x}) - \mathbf{x}^*\|^2 \\ =& \|\mathbf{x}_{t} - \mathbf{x}^*\|^2 + \eta_t^2 \|\partial_\mathbf{x} f(\boldsymbol{\xi}_t, \mathbf{x})\|^2 - 2 \eta_t \left\langle \mathbf{x}_t - \mathbf{x}^*, \partial_\mathbf{x} f(\boldsymbol{\xi}_t, \mathbf{x})\right\rangle. \end{aligned}$$
:eqlabel:`eq_sgd-xt+1-xstar`
我们假设 $L_2$ 随机梯度 $\partial_\mathbf{x} f(\boldsymbol{\xi}_t, \mathbf{x})$ 的标准受到一定的 $L$ 的限制,因此我们有这个
$$\eta_t^2 \|\partial_\mathbf{x} f(\boldsymbol{\xi}_t, \mathbf{x})\|^2 \leq \eta_t^2 L^2.$$
:eqlabel:`eq_sgd-L`
我们最感兴趣的是 $\mathbf{x}_t$ 和 $\mathbf{x}^*$ 之间的距离如何变化 * 预期 *。事实上,对于任何具体的步骤序列,距离可能会增加,这取决于我们遇到的 $\boldsymbol{\xi}_t$。因此我们需要绑定点积。因为对于任何凸函数 $f$,它认为所有 $\mathbf{x}$ 和 $\mathbf{y}$ 的 $f(\mathbf{y}) \geq f(\mathbf{x}) + \langle f'(\mathbf{x}), \mathbf{y} - \mathbf{x} \rangle$ 和 $\mathbf{y}$,按凸度我们有
$$f(\boldsymbol{\xi}_t, \mathbf{x}^*) \geq f(\boldsymbol{\xi}_t, \mathbf{x}_t) + \left\langle \mathbf{x}^* - \mathbf{x}_t, \partial_{\mathbf{x}} f(\boldsymbol{\xi}_t, \mathbf{x}_t) \right\rangle.$$
:eqlabel:`eq_sgd-f-xi-xstar`
将不等式 :eqref:`eq_sgd-L` 和 :eqref:`eq_sgd-f-xi-xstar` 插入 :eqref:`eq_sgd-xt+1-xstar` 我们在时间 $t+1$ 时获得参数之间距离的边界,如下所示:
$$\|\mathbf{x}_{t} - \mathbf{x}^*\|^2 - \|\mathbf{x}_{t+1} - \mathbf{x}^*\|^2 \geq 2 \eta_t (f(\boldsymbol{\xi}_t, \mathbf{x}_t) - f(\boldsymbol{\xi}_t, \mathbf{x}^*)) - \eta_t^2 L^2.$$
:eqlabel:`eqref_sgd-xt-diff`
这意味着,只要当前亏损和最佳损失之间的差异超过 $\eta_t L^2/2$,我们就会取得进展。由于这种差异必然会收敛到零,因此学习率 $\eta_t$ 也需要 * 消失 *。
接下来,我们的预期超过 :eqref:`eqref_sgd-xt-diff`。这会产生
$$E\left[\|\mathbf{x}_{t} - \mathbf{x}^*\|^2\right] - E\left[\|\mathbf{x}_{t+1} - \mathbf{x}^*\|^2\right] \geq 2 \eta_t [E[R(\mathbf{x}_t)] - R^*] - \eta_t^2 L^2.$$
最后一步是对 $t \in \{1, \ldots, T\}$ 的不平等现象进行总结。自从总和望远镜以及通过掉低期我们获得的
$$\|\mathbf{x}_1 - \mathbf{x}^*\|^2 \geq 2 \left (\sum_{t=1}^T \eta_t \right) [E[R(\mathbf{x}_t)] - R^*] - L^2 \sum_{t=1}^T \eta_t^2.$$
:eqlabel:`eq_sgd-x1-xstar`
请注意,我们利用了 $\mathbf{x}_1$ 给出了,因此预期可以下降。最后定义
$$\bar{\mathbf{x}} \stackrel{\mathrm{def}}{=} \frac{\sum_{t=1}^T \eta_t \mathbf{x}_t}{\sum_{t=1}^T \eta_t}.$$
自
$$E\left(\frac{\sum_{t=1}^T \eta_t R(\mathbf{x}_t)}{\sum_{t=1}^T \eta_t}\right) = \frac{\sum_{t=1}^T \eta_t E[R(\mathbf{x}_t)]}{\sum_{t=1}^T \eta_t} = E[R(\mathbf{x}_t)],$$
根据延森的不平等性(设定为 $i=t$,$i=t$,$\alpha_i = \eta_t/\sum_{t=1}^T \eta_t$)和 $R$ 的凸度为 $R$,因此,
$$\sum_{t=1}^T \eta_t E[R(\mathbf{x}_t)] \geq \sum_{t=1}^T \eta_t E\left[R(\bar{\mathbf{x}})\right].$$
将其插入不平等性 :eqref:`eq_sgd-x1-xstar` 收益了限制
$$
\left[E[\bar{\mathbf{x}}]\right] - R^* \leq \frac{r^2 + L^2 \sum_{t=1}^T \eta_t^2}{2 \sum_{t=1}^T \eta_t},
$$
其中 $r^2 \stackrel{\mathrm{def}}{=} \|\mathbf{x}_1 - \mathbf{x}^*\|^2$ 受初始选择参数与最终结果之间的距离的约束。简而言之,收敛速度取决于随机梯度标准的限制方式($L$)以及初始参数值与最优性($r$)的距离($r$)。请注意,约束是按 $\bar{\mathbf{x}}$ 而不是 $\mathbf{x}_T$ 而不是 $\mathbf{x}_T$。情况就是这样,因为 $\bar{\mathbf{x}}$ 是优化路径的平滑版本。只要知道 $r, L$ 和 $T$,我们就可以选择学习率 $\eta = r/(L \sqrt{T})$。这个收益率为上限 $rL/\sqrt{T}$。也就是说,我们将汇率 $\mathcal{O}(1/\sqrt{T})$ 收敛到最佳解决方案。
## 随机梯度和有限样本
到目前为止,在谈论随机梯度下降时,我们玩得有点快而松散。我们假设我们从 $x_i$ 中绘制实例 $x_i$,通常使用来自某些发行版 $p(x, y)$ 的标签 $y_i$,我们用它来以某种方式更新模型参数。特别是,对于有限的样本数量,我们只是认为,某些函数 $\delta_{x_i}$ 和 $\delta_{y_i}$ 的离散分布 $p(x, y) = \frac{1}{n} \sum_{i=1}^n \delta_{x_i}(x) \delta_{y_i}(y)$ 和 $\delta_{y_i}$ 允许我们在其上执行随机梯度下降。
但是,这不是我们真正做的。在当前部分的玩具示例中,我们只是将噪音添加到其他非随机梯度上,也就是说,我们假装了对 $(x_i, y_i)$。事实证明,这是合理的(请参阅练习进行详细讨论)。更令人不安的是,在以前的所有讨论中,我们显然没有这样做。相反,我们遍历了所有实例 * 恰好一次 *。要了解为什么这更可取,请考虑反之,即我们从离散分布 * 中抽取 $n$ 个观测值 * 并带替换 *。随机选择一个元素 $i$ 的概率是 $1/n$。因此选择它 * 至少 * 一次就是
$$P(\mathrm{choose~} i) = 1 - P(\mathrm{omit~} i) = 1 - (1-1/n)^n \approx 1-e^{-1} \approx 0.63.$$
类似的推理表明,挑选一些样本(即训练示例)* 恰好一次 * 的概率是由
$${n \choose 1} \frac{1}{n} \left(1-\frac{1}{n}\right)^{n-1} = \frac{n}{n-1} \left(1-\frac{1}{n}\right)^{n} \approx e^{-1} \approx 0.37.$$
这导致与采样 * 不替换 * 相比,差异增加并降低数据效率。因此,在实践中我们执行后者(这是本书中的默认选择)。最后一点注意,重复穿过训练数据集会以 * 不同的 * 随机顺序遍历它。
## 摘要
* 对于凸出的问题,我们可以证明,对于广泛的学习率选择,随机梯度下降将收敛到最佳解决方案。
* 对于深度学习而言,情况通常并非如此。但是,对凸问题的分析使我们能够深入了解如何进行优化,即逐步降低学习率,尽管不是太快。
* 如果学习率太小或太大,就会出现问题。实际上,通常只有经过多次实验后才能找到合适的学习率。
* 当训练数据集中有更多示例时,计算渐变下降的每个迭代的成本更高,因此在这些情况下,首选随机梯度下降。
* 随机梯度下降的最佳性保证在非凸情况下一般不可用,因为需要检查的局部最小值数可能是指数级的。
## 练习
1. 尝试不同的学习速率计划以实现随机梯度下降和不同迭代次数。特别是,根据迭代次数的函数来绘制与最佳解 $(0, 0)$ 的距离。
1. 证明对于函数 $f(x_1, x_2) = x_1^2 + 2 x_2^2$ 而言,向梯度添加正常噪声等同于最小化损耗函数 $f(\mathbf{x}, \mathbf{w}) = (x_1 - w_1)^2 + 2 (x_2 - w_2)^2$,其中 $\mathbf{x}$ 是从正态分布中提取的。
1. 比较随机梯度下降的收敛性,当您从 $\{(x_1, y_1), \ldots, (x_n, y_n)\}$ 采样时使用替换方法进行采样时以及在不替换的情况下进行样品时
1. 如果某些渐变(或者更确切地说与之相关的某些坐标)始终比所有其他渐变都大,你将如何更改随机渐变下降求解器?
1. 假设是 $f(x) = x^2 (1 + \sin x)$。$f$ 有多少本地最小值?你能改变 $f$ 以尽量减少它需要评估所有本地最小值的方式吗?
[Discussions](https://discuss.d2l.ai/t/3838)
|
github_jupyter
|
%matplotlib inline
import math
import torch
from d2l import torch as d2l
def f(x1, x2): # Objective function
return x1 ** 2 + 2 * x2 ** 2
def f_grad(x1, x2): # Gradient of the objective function
return 2 * x1, 4 * x2
def sgd(x1, x2, s1, s2, f_grad):
g1, g2 = f_grad(x1, x2)
# Simulate noisy gradient
g1 += torch.normal(0.0, 1, (1,))
g2 += torch.normal(0.0, 1, (1,))
eta_t = eta * lr()
return (x1 - eta_t * g1, x2 - eta_t * g2, 0, 0)
def constant_lr():
return 1
eta = 0.1
lr = constant_lr # Constant learning rate
d2l.show_trace_2d(f, d2l.train_2d(sgd, steps=50, f_grad=f_grad))
def exponential_lr():
# Global variable that is defined outside this function and updated inside
global t
t += 1
return math.exp(-0.1 * t)
t = 1
lr = exponential_lr
d2l.show_trace_2d(f, d2l.train_2d(sgd, steps=1000, f_grad=f_grad))
def polynomial_lr():
# Global variable that is defined outside this function and updated inside
global t
t += 1
return (1 + 0.1 * t) ** (-0.5)
t = 1
lr = polynomial_lr
d2l.show_trace_2d(f, d2l.train_2d(sgd, steps=50, f_grad=f_grad))
| 0.59561 | 0.9601 |
```
%matplotlib inline
```
SyntaxError
===========
Example script with invalid Python syntax
```
"""
Remove line noise with ZapLine
==============================
Find a spatial filter to get rid of line noise [1]_.
Uses meegkit.dss_line().
References
----------
.. [1] de Cheveigné, A. (2019). ZapLine: A simple and effective method to
remove power line artifacts [Preprint]. https://doi.org/10.1101/782029
"""
# Authors: Maciej Szul <[email protected]>
# Nicolas Barascud <[email protected]>
import os
import matplotlib.pyplot as plt
import numpy as np
from meegkit import dss
from meegkit.utils import create_line_data, unfold
from scipy import signal
```
Line noise removal
=============================================================================
Remove line noise with dss_line()
-----------------------------------------------------------------------------
We first generate some noisy data to work with
```
sfreq = 250
fline = 50
nsamples = 10000
nchans = 10
data = create_line_data(n_samples=3 * nsamples, n_chans=nchans,
n_trials=1, fline=fline / sfreq, SNR=2)[0]
data = data[..., 0] # only take first trial
# Apply dss_line (ZapLine)
out, _ = dss.dss_line(data, fline, sfreq, nkeep=1)
```
Plot before/after
```
f, ax = plt.subplots(1, 2, sharey=True)
f, Pxx = signal.welch(data, sfreq, nperseg=500, axis=0, return_onesided=True)
ax[0].semilogy(f, Pxx)
f, Pxx = signal.welch(out, sfreq, nperseg=500, axis=0, return_onesided=True)
ax[1].semilogy(f, Pxx)
ax[0].set_xlabel('frequency [Hz]')
ax[1].set_xlabel('frequency [Hz]')
ax[0].set_ylabel('PSD [V**2/Hz]')
ax[0].set_title('before')
ax[1].set_title('after')
plt.show()
```
Remove line noise with dss_line_iter()
-----------------------------------------------------------------------------
We first load some noisy data to work with
```
data = np.load(os.path.join('..', 'tests', 'data', 'dss_line_data.npy'))
fline = 50
sfreq = 200
print(data.shape) # n_samples, n_chans, n_trials
# Apply dss_line(), removing only one component
out1, _ = dss.dss_line(data, fline, sfreq, nremove=1, nfft=400)
```
Now try dss_line_iter(). This applies dss_line() repeatedly until the
artifact is gone
```
out2, iterations = dss.dss_line_iter(data, fline, sfreq, nfft=400)
print(f'Removed {iterations} components')
```
Plot results with dss_line() vs. dss_line_iter()
```
f, ax = plt.subplots(1, 2, sharey=True)
f, Pxx = signal.welch(unfold(out1), sfreq, nperseg=200, axis=0,
return_onesided=True)
ax[0].semilogy(f, Pxx, lw=.5)
f, Pxx = signal.welch(unfold(out2), sfreq, nperseg=200, axis=0,
return_onesided=True)
ax[1].semilogy(f, Pxx, lw=.5)
ax[0].set_xlabel('frequency [Hz]')
ax[1].set_xlabel('frequency [Hz]')
ax[0].set_ylabel('PSD [V**2/Hz]')
ax[0].set_title('dss_line')
ax[1].set_title('dss_line_iter')
plt.tight_layout()
plt.show()
```
|
github_jupyter
|
%matplotlib inline
"""
Remove line noise with ZapLine
==============================
Find a spatial filter to get rid of line noise [1]_.
Uses meegkit.dss_line().
References
----------
.. [1] de Cheveigné, A. (2019). ZapLine: A simple and effective method to
remove power line artifacts [Preprint]. https://doi.org/10.1101/782029
"""
# Authors: Maciej Szul <[email protected]>
# Nicolas Barascud <[email protected]>
import os
import matplotlib.pyplot as plt
import numpy as np
from meegkit import dss
from meegkit.utils import create_line_data, unfold
from scipy import signal
sfreq = 250
fline = 50
nsamples = 10000
nchans = 10
data = create_line_data(n_samples=3 * nsamples, n_chans=nchans,
n_trials=1, fline=fline / sfreq, SNR=2)[0]
data = data[..., 0] # only take first trial
# Apply dss_line (ZapLine)
out, _ = dss.dss_line(data, fline, sfreq, nkeep=1)
f, ax = plt.subplots(1, 2, sharey=True)
f, Pxx = signal.welch(data, sfreq, nperseg=500, axis=0, return_onesided=True)
ax[0].semilogy(f, Pxx)
f, Pxx = signal.welch(out, sfreq, nperseg=500, axis=0, return_onesided=True)
ax[1].semilogy(f, Pxx)
ax[0].set_xlabel('frequency [Hz]')
ax[1].set_xlabel('frequency [Hz]')
ax[0].set_ylabel('PSD [V**2/Hz]')
ax[0].set_title('before')
ax[1].set_title('after')
plt.show()
data = np.load(os.path.join('..', 'tests', 'data', 'dss_line_data.npy'))
fline = 50
sfreq = 200
print(data.shape) # n_samples, n_chans, n_trials
# Apply dss_line(), removing only one component
out1, _ = dss.dss_line(data, fline, sfreq, nremove=1, nfft=400)
out2, iterations = dss.dss_line_iter(data, fline, sfreq, nfft=400)
print(f'Removed {iterations} components')
f, ax = plt.subplots(1, 2, sharey=True)
f, Pxx = signal.welch(unfold(out1), sfreq, nperseg=200, axis=0,
return_onesided=True)
ax[0].semilogy(f, Pxx, lw=.5)
f, Pxx = signal.welch(unfold(out2), sfreq, nperseg=200, axis=0,
return_onesided=True)
ax[1].semilogy(f, Pxx, lw=.5)
ax[0].set_xlabel('frequency [Hz]')
ax[1].set_xlabel('frequency [Hz]')
ax[0].set_ylabel('PSD [V**2/Hz]')
ax[0].set_title('dss_line')
ax[1].set_title('dss_line_iter')
plt.tight_layout()
plt.show()
| 0.848878 | 0.871365 |
# Quantile regression
This example page shows how to use ``statsmodels``' ``QuantReg`` class to replicate parts of the analysis published in
* Koenker, Roger and Kevin F. Hallock. "Quantile Regression". Journal of Economic Perspectives, Volume 15, Number 4, Fall 2001, Pages 143–156
We are interested in the relationship between income and expenditures on food for a sample of working class Belgian households in 1857 (the Engel data).
## Setup
We first need to load some modules and to retrieve the data. Conveniently, the Engel dataset is shipped with ``statsmodels``.
```
%matplotlib inline
import numpy as np
import pandas as pd
import statsmodels.api as sm
import statsmodels.formula.api as smf
import matplotlib.pyplot as plt
data = sm.datasets.engel.load_pandas().data
data.head()
```
## Least Absolute Deviation
The LAD model is a special case of quantile regression where q=0.5
```
mod = smf.quantreg("foodexp ~ income", data)
res = mod.fit(q=0.5)
print(res.summary())
```
## Visualizing the results
We estimate the quantile regression model for many quantiles between .05 and .95, and compare best fit line from each of these models to Ordinary Least Squares results.
### Prepare data for plotting
For convenience, we place the quantile regression results in a Pandas DataFrame, and the OLS results in a dictionary.
```
quantiles = np.arange(0.05, 0.96, 0.1)
def fit_model(q):
res = mod.fit(q=q)
return [q, res.params["Intercept"], res.params["income"]] + res.conf_int().loc[
"income"
].tolist()
models = [fit_model(x) for x in quantiles]
models = pd.DataFrame(models, columns=["q", "a", "b", "lb", "ub"])
ols = smf.ols("foodexp ~ income", data).fit()
ols_ci = ols.conf_int().loc["income"].tolist()
ols = dict(
a=ols.params["Intercept"], b=ols.params["income"], lb=ols_ci[0], ub=ols_ci[1]
)
print(models)
print(ols)
```
### First plot
This plot compares best fit lines for 10 quantile regression models to the least squares fit. As Koenker and Hallock (2001) point out, we see that:
1. Food expenditure increases with income
2. The *dispersion* of food expenditure increases with income
3. The least squares estimates fit low income observations quite poorly (i.e. the OLS line passes over most low income households)
```
x = np.arange(data.income.min(), data.income.max(), 50)
get_y = lambda a, b: a + b * x
fig, ax = plt.subplots(figsize=(8, 6))
for i in range(models.shape[0]):
y = get_y(models.a[i], models.b[i])
ax.plot(x, y, linestyle="dotted", color="grey")
y = get_y(ols["a"], ols["b"])
ax.plot(x, y, color="red", label="OLS")
ax.scatter(data.income, data.foodexp, alpha=0.2)
ax.set_xlim((240, 3000))
ax.set_ylim((240, 2000))
legend = ax.legend()
ax.set_xlabel("Income", fontsize=16)
ax.set_ylabel("Food expenditure", fontsize=16)
```
### Second plot
The dotted black lines form 95% point-wise confidence band around 10 quantile regression estimates (solid black line). The red lines represent OLS regression results along with their 95% confidence interval.
In most cases, the quantile regression point estimates lie outside the OLS confidence interval, which suggests that the effect of income on food expenditure may not be constant across the distribution.
```
n = models.shape[0]
p1 = plt.plot(models.q, models.b, color="black", label="Quantile Reg.")
p2 = plt.plot(models.q, models.ub, linestyle="dotted", color="black")
p3 = plt.plot(models.q, models.lb, linestyle="dotted", color="black")
p4 = plt.plot(models.q, [ols["b"]] * n, color="red", label="OLS")
p5 = plt.plot(models.q, [ols["lb"]] * n, linestyle="dotted", color="red")
p6 = plt.plot(models.q, [ols["ub"]] * n, linestyle="dotted", color="red")
plt.ylabel(r"$\beta_{income}$")
plt.xlabel("Quantiles of the conditional food expenditure distribution")
plt.legend()
plt.show()
```
|
github_jupyter
|
%matplotlib inline
import numpy as np
import pandas as pd
import statsmodels.api as sm
import statsmodels.formula.api as smf
import matplotlib.pyplot as plt
data = sm.datasets.engel.load_pandas().data
data.head()
mod = smf.quantreg("foodexp ~ income", data)
res = mod.fit(q=0.5)
print(res.summary())
quantiles = np.arange(0.05, 0.96, 0.1)
def fit_model(q):
res = mod.fit(q=q)
return [q, res.params["Intercept"], res.params["income"]] + res.conf_int().loc[
"income"
].tolist()
models = [fit_model(x) for x in quantiles]
models = pd.DataFrame(models, columns=["q", "a", "b", "lb", "ub"])
ols = smf.ols("foodexp ~ income", data).fit()
ols_ci = ols.conf_int().loc["income"].tolist()
ols = dict(
a=ols.params["Intercept"], b=ols.params["income"], lb=ols_ci[0], ub=ols_ci[1]
)
print(models)
print(ols)
x = np.arange(data.income.min(), data.income.max(), 50)
get_y = lambda a, b: a + b * x
fig, ax = plt.subplots(figsize=(8, 6))
for i in range(models.shape[0]):
y = get_y(models.a[i], models.b[i])
ax.plot(x, y, linestyle="dotted", color="grey")
y = get_y(ols["a"], ols["b"])
ax.plot(x, y, color="red", label="OLS")
ax.scatter(data.income, data.foodexp, alpha=0.2)
ax.set_xlim((240, 3000))
ax.set_ylim((240, 2000))
legend = ax.legend()
ax.set_xlabel("Income", fontsize=16)
ax.set_ylabel("Food expenditure", fontsize=16)
n = models.shape[0]
p1 = plt.plot(models.q, models.b, color="black", label="Quantile Reg.")
p2 = plt.plot(models.q, models.ub, linestyle="dotted", color="black")
p3 = plt.plot(models.q, models.lb, linestyle="dotted", color="black")
p4 = plt.plot(models.q, [ols["b"]] * n, color="red", label="OLS")
p5 = plt.plot(models.q, [ols["lb"]] * n, linestyle="dotted", color="red")
p6 = plt.plot(models.q, [ols["ub"]] * n, linestyle="dotted", color="red")
plt.ylabel(r"$\beta_{income}$")
plt.xlabel("Quantiles of the conditional food expenditure distribution")
plt.legend()
plt.show()
| 0.613121 | 0.990357 |
```
import sys
import torch
sys.path.insert(0, "/home/zaid/Source/ALBEF/models")
from models.vit import VisionTransformer
from transformers import BertForMaskedLM, AutoTokenizer, BertConfig
import torch
tokenizer = AutoTokenizer.from_pretrained('bert-base-uncased')
text = "this is a random image"
lm = BertForMaskedLM(BertConfig())
vm = VisionTransformer()
```
# How does ALBEF handle tokenization?
The captions in the input JSON fed into ALBEF are raw text. They are loaded into the [`pretrain_dataset`](https://sourcegraph.com/github.com/salesforce/ALBEF/-/blob/dataset/caption_dataset.py?L97) class, where the `pre_caption` function does some basic preprocessing.
It's then wrapped by a `create_dataset` function that doesn't alter the text data.
So, in summary, the dataset that comes out of `create_dataset` has `str` typed text data, not integer input ids.
The dataset then gets passed into a `create_loader` function, which also does not modify the text data.
The tokenization happens in the [`train`](https://sourcegraph.com/github.com/salesforce/ALBEF@9e9a5e952f72374c15cea02d3c34013554c86513/-/blob/Pretrain.py?L59) function.
```python
text_input = tokenizer(text, padding='longest', truncation=True, max_length=25, return_tensors="pt").to(device)
```
```
text = [
"this",
"this is",
"this is a",
"this is a random",
"this is a random image"
]
text_input = tokenizer(text, padding='longest', truncation=True, max_length=25, return_tensors="pt")
text_input
```
# How does sentence-pair tokenization look?
```
text_input = tokenizer.batch_encode_plus(list(zip(text, text)), padding='longest', truncation=True, max_length=50, return_tensors="pt")
text_input
```
The input ALBEF gets is a dictionary containing `input_ids` and the `attention_mask`. The attention mask covers all the non-pad tokens. In sentence-pair mode, there is no padding in between the sentences. The sentences are just separated by the `[SEP]` symbol.
# Constructing a sentence pair from ViT / word embeddings
The ViT output sequence is always the same length, and if stacked together, has no ragged edges. The sentences cannot be stacked together without padding.
```
image = torch.rand(3, 224, 224).unsqueeze(0)
vit_out = vm(image)
vit_out.shape
text = [
"this",
"this is",
"this is a",
"this is a random",
"this is a random image"
]
# Make a batch the same size as the amount of text.
img_batch = torch.vstack([vit_out] * len(text))
img_batch.shape
# Tokenize the text.
text_batch = tokenizer(text, padding='longest', truncation=True, max_length=25, return_tensors="pt", add_special_tokens=False)
text_batch
prefix = torch.ones(batch_size, 1, 1) * tokenizer.cls_token_id
separator = torch.ones(batch_size, 1, 1) * tokenizer.sep_token_id
eos = torch.ones(batch_size, 1, 1) * tokenizer.sep_token_id
```
The `input_embeds` keyword, which we will be passing data into, is filled from the `word_embeddings` layer if not provided (https://github.com/huggingface/transformers/blob/v4.15.0/src/transformers/models/bert/modeling_bert.py#L214).
```
lang_input_embeds = lm.embeddings.word_embeddings(text_batch['input_ids'])
prefix_embeds = lm.embeddings.word_embeddings(prefix.long()).squeeze(1)
sep_embeds = lm.embeddings.word_embeddings(separator.long()).squeeze(1)
eos_embeds = lm.embeddings.word_embeddings(eos.long()).squeeze(1)
model_input = torch.cat([prefix_embeds, img_batch, sep_embeds, lang_input_embeds, eos_embeds], dim=1)
lm.bert(inputs_embeds=model_input)
```
## Computing the token_type_id mask
```
sentence_pair = tokenizer.encode_plus(
text="this is some text",
text_pair="a second sentence, longer than the first",
padding='longest',
truncation=True,
max_length=25,
return_tensors="pt",
add_special_tokens=True
)
print(sentence_pair.input_ids)
print(sentence_pair.input_ids.shape)
print(sentence_pair.attention_mask)
print(sentence_pair.attention_mask.shape)
print(sentence_pair.token_type_ids)
print(sentence_pair.token_type_ids.shape)
```
|
github_jupyter
|
import sys
import torch
sys.path.insert(0, "/home/zaid/Source/ALBEF/models")
from models.vit import VisionTransformer
from transformers import BertForMaskedLM, AutoTokenizer, BertConfig
import torch
tokenizer = AutoTokenizer.from_pretrained('bert-base-uncased')
text = "this is a random image"
lm = BertForMaskedLM(BertConfig())
vm = VisionTransformer()
text_input = tokenizer(text, padding='longest', truncation=True, max_length=25, return_tensors="pt").to(device)
text = [
"this",
"this is",
"this is a",
"this is a random",
"this is a random image"
]
text_input = tokenizer(text, padding='longest', truncation=True, max_length=25, return_tensors="pt")
text_input
text_input = tokenizer.batch_encode_plus(list(zip(text, text)), padding='longest', truncation=True, max_length=50, return_tensors="pt")
text_input
image = torch.rand(3, 224, 224).unsqueeze(0)
vit_out = vm(image)
vit_out.shape
text = [
"this",
"this is",
"this is a",
"this is a random",
"this is a random image"
]
# Make a batch the same size as the amount of text.
img_batch = torch.vstack([vit_out] * len(text))
img_batch.shape
# Tokenize the text.
text_batch = tokenizer(text, padding='longest', truncation=True, max_length=25, return_tensors="pt", add_special_tokens=False)
text_batch
prefix = torch.ones(batch_size, 1, 1) * tokenizer.cls_token_id
separator = torch.ones(batch_size, 1, 1) * tokenizer.sep_token_id
eos = torch.ones(batch_size, 1, 1) * tokenizer.sep_token_id
lang_input_embeds = lm.embeddings.word_embeddings(text_batch['input_ids'])
prefix_embeds = lm.embeddings.word_embeddings(prefix.long()).squeeze(1)
sep_embeds = lm.embeddings.word_embeddings(separator.long()).squeeze(1)
eos_embeds = lm.embeddings.word_embeddings(eos.long()).squeeze(1)
model_input = torch.cat([prefix_embeds, img_batch, sep_embeds, lang_input_embeds, eos_embeds], dim=1)
lm.bert(inputs_embeds=model_input)
sentence_pair = tokenizer.encode_plus(
text="this is some text",
text_pair="a second sentence, longer than the first",
padding='longest',
truncation=True,
max_length=25,
return_tensors="pt",
add_special_tokens=True
)
print(sentence_pair.input_ids)
print(sentence_pair.input_ids.shape)
print(sentence_pair.attention_mask)
print(sentence_pair.attention_mask.shape)
print(sentence_pair.token_type_ids)
print(sentence_pair.token_type_ids.shape)
| 0.497559 | 0.856212 |
# 多层感知机
:label:`sec_mlp`
在 :numref:`chap_linear`中,
我们介绍了softmax回归( :numref:`sec_softmax`),
然后我们从零开始实现了softmax回归( :numref:`sec_softmax_scratch`),
接着使用高级API实现了算法( :numref:`sec_softmax_concise`),
并训练分类器从低分辨率图像中识别10类服装。
在这个过程中,我们学习了如何处理数据,如何将输出转换为有效的概率分布,
并应用适当的损失函数,根据模型参数最小化损失。
我们已经在简单的线性模型背景下掌握了这些知识,
现在我们可以开始对深度神经网络的探索,这也是本书主要涉及的一类模型。
## 隐藏层
我们在 :numref:`subsec_linear_model`中描述了仿射变换,
它是一种带有偏置项的线性变换。
首先,回想一下如 :numref:`fig_softmaxreg`中所示的softmax回归的模型架构。
该模型通过单个仿射变换将我们的输入直接映射到输出,然后进行softmax操作。
如果我们的标签通过仿射变换后确实与我们的输入数据相关,那么这种方法确实足够了。
但是,仿射变换中的*线性*是一个很强的假设。
### 线性模型可能会出错
例如,线性意味着*单调*假设:
任何特征的增大都会导致模型输出的增大(如果对应的权重为正),
或者导致模型输出的减小(如果对应的权重为负)。
有时这是有道理的。
例如,如果我们试图预测一个人是否会偿还贷款。
我们可以认为,在其他条件不变的情况下,
收入较高的申请人比收入较低的申请人更有可能偿还贷款。
但是,虽然收入与还款概率存在单调性,但它们不是线性相关的。
收入从0增加到5万,可能比从100万增加到105万带来更大的还款可能性。
处理这一问题的一种方法是对我们的数据进行预处理,
使线性变得更合理,如使用收入的对数作为我们的特征。
然而我们可以很容易找出违反单调性的例子。
例如,我们想要根据体温预测死亡率。
对于体温高于37摄氏度的人来说,温度越高风险越大。
然而,对于体温低于37摄氏度的人来说,温度越高风险就越低。
在这种情况下,我们也可以通过一些巧妙的预处理来解决问题。
例如,我们可以使用与37摄氏度的距离作为特征。
但是,如何对猫和狗的图像进行分类呢?
增加位置$(13, 17)$处像素的强度是否总是增加(或降低)图像描绘狗的似然?
对线性模型的依赖对应于一个隐含的假设,
即区分猫和狗的唯一要求是评估单个像素的强度。
在一个倒置图像后依然保留类别的世界里,这种方法注定会失败。
与我们前面的例子相比,这里的线性很荒谬,
而且我们难以通过简单的预处理来解决这个问题。
这是因为任何像素的重要性都以复杂的方式取决于该像素的上下文(周围像素的值)。
我们的数据可能会有一种表示,这种表示会考虑到我们在特征之间的相关交互作用。
在此表示的基础上建立一个线性模型可能会是合适的,
但我们不知道如何手动计算这么一种表示。
对于深度神经网络,我们使用观测数据来联合学习隐藏层表示和应用于该表示的线性预测器。
### 在网络中加入隐藏层
我们可以通过在网络中加入一个或多个隐藏层来克服线性模型的限制,
使其能处理更普遍的函数关系类型。
要做到这一点,最简单的方法是将许多全连接层堆叠在一起。
每一层都输出到上面的层,直到生成最后的输出。
我们可以把前$L-1$层看作表示,把最后一层看作线性预测器。
这种架构通常称为*多层感知机*(multilayer perceptron),通常缩写为*MLP*。
下面,我们以图的方式描述了多层感知机( :numref:`fig_mlp`)。

:label:`fig_mlp`
这个多层感知机有4个输入,3个输出,其隐藏层包含5个隐藏单元。
输入层不涉及任何计算,因此使用此网络产生输出只需要实现隐藏层和输出层的计算。
因此,这个多层感知机中的层数为2。
注意,这两个层都是全连接的。
每个输入都会影响隐藏层中的每个神经元,
而隐藏层中的每个神经元又会影响输出层中的每个神经元。
然而,正如 :numref:`subsec_parameterization-cost-fc-layers`所说,
具有全连接层的多层感知机的参数开销可能会高得令人望而却步。
即使在不改变输入或输出大小的情况下,
可能在参数节约和模型有效性之间进行权衡 :cite:`Zhang.Tay.Zhang.ea.2021`。
### 从线性到非线性
同之前的章节一样,
我们通过矩阵$\mathbf{X} \in \mathbb{R}^{n \times d}$
来表示$n$个样本的小批量,
其中每个样本具有$d$个输入特征。
对于具有$h$个隐藏单元的单隐藏层多层感知机,
用$\mathbf{H} \in \mathbb{R}^{n \times h}$表示隐藏层的输出,
称为*隐藏表示*(hidden representations)。
在数学或代码中,$\mathbf{H}$也被称为*隐藏层变量*(hidden-layer variable)
或*隐藏变量*(hidden variable)。
因为隐藏层和输出层都是全连接的,
所以我们有隐藏层权重$\mathbf{W}^{(1)} \in \mathbb{R}^{d \times h}$
和隐藏层偏置$\mathbf{b}^{(1)} \in \mathbb{R}^{1 \times h}$
以及输出层权重$\mathbf{W}^{(2)} \in \mathbb{R}^{h \times q}$
和输出层偏置$\mathbf{b}^{(2)} \in \mathbb{R}^{1 \times q}$。
形式上,我们按如下方式计算单隐藏层多层感知机的输出
$\mathbf{O} \in \mathbb{R}^{n \times q}$:
$$
\begin{aligned}
\mathbf{H} & = \mathbf{X} \mathbf{W}^{(1)} + \mathbf{b}^{(1)}, \\
\mathbf{O} & = \mathbf{H}\mathbf{W}^{(2)} + \mathbf{b}^{(2)}.
\end{aligned}
$$
注意在添加隐藏层之后,模型现在需要跟踪和更新额外的参数。
可我们能从中得到什么好处呢?
你可能会惊讶地发现:在上面定义的模型里,我们没有好处!
原因很简单:上面的隐藏单元由输入的仿射函数给出,
而输出(softmax操作前)只是隐藏单元的仿射函数。
仿射函数的仿射函数本身就是仿射函数,
但是我们之前的线性模型已经能够表示任何仿射函数。
我们可以证明这一等价性,即对于任意权重值,
我们只需合并隐藏层,便可产生具有参数
$\mathbf{W} = \mathbf{W}^{(1)}\mathbf{W}^{(2)}$
和$\mathbf{b} = \mathbf{b}^{(1)} \mathbf{W}^{(2)} + \mathbf{b}^{(2)}$
的等价单层模型:
$$
\mathbf{O} = (\mathbf{X} \mathbf{W}^{(1)} + \mathbf{b}^{(1)})\mathbf{W}^{(2)} + \mathbf{b}^{(2)} = \mathbf{X} \mathbf{W}^{(1)}\mathbf{W}^{(2)} + \mathbf{b}^{(1)} \mathbf{W}^{(2)} + \mathbf{b}^{(2)} = \mathbf{X} \mathbf{W} + \mathbf{b}.
$$
为了发挥多层架构的潜力,
我们还需要一个额外的关键要素:
在仿射变换之后对每个隐藏单元应用非线性的*激活函数*(activation function)$\sigma$。
激活函数的输出(例如,$\sigma(\cdot)$)被称为*活性值*(activations)。
一般来说,有了激活函数,就不可能再将我们的多层感知机退化成线性模型:
$$
\begin{aligned}
\mathbf{H} & = \sigma(\mathbf{X} \mathbf{W}^{(1)} + \mathbf{b}^{(1)}), \\
\mathbf{O} & = \mathbf{H}\mathbf{W}^{(2)} + \mathbf{b}^{(2)}.\\
\end{aligned}
$$
由于$\mathbf{X}$中的每一行对应于小批量中的一个样本,
出于记号习惯的考量,
我们定义非线性函数$\sigma$也以按行的方式作用于其输入,
即一次计算一个样本。
我们在 :numref:`subsec_softmax_vectorization`中
以相同的方式使用了softmax符号来表示按行操作。
但是在本节中,我们应用于隐藏层的激活函数通常不仅按行操作,也按元素操作。
这意味着在计算每一层的线性部分之后,我们可以计算每个活性值,
而不需要查看其他隐藏单元所取的值。对于大多数激活函数都是这样。
为了构建更通用的多层感知机,
我们可以继续堆叠这样的隐藏层,
例如$\mathbf{H}^{(1)} = \sigma_1(\mathbf{X} \mathbf{W}^{(1)} + \mathbf{b}^{(1)})$和$\mathbf{H}^{(2)} = \sigma_2(\mathbf{H}^{(1)} \mathbf{W}^{(2)} + \mathbf{b}^{(2)})$,
一层叠一层,从而产生更有表达能力的模型。
### 通用近似定理
多层感知机可以通过隐藏神经元,捕捉到输入之间复杂的相互作用,
这些神经元依赖于每个输入的值。
我们可以很容易地设计隐藏节点来执行任意计算。
例如,在一对输入上进行基本逻辑操作,多层感知机是通用近似器。
即使是网络只有一个隐藏层,给定足够的神经元和正确的权重,
我们可以对任意函数建模,尽管实际中学习该函数是很困难的。
你可能认为神经网络有点像C语言。
C语言和任何其他现代编程语言一样,能够表达任何可计算的程序。
但实际上,想出一个符合规范的程序才是最困难的部分。
而且,虽然一个单隐层网络能学习任何函数,
但并不意味着我们应该尝试使用单隐藏层网络来解决所有问题。
事实上,通过使用更深(而不是更广)的网络,我们可以更容易地逼近许多函数。
我们将在后面的章节中进行更细致的讨论。
## 激活函数
:label:`subsec_activation_functions`
*激活函数*(activation function)通过计算加权和并加上偏置来确定神经元是否应该被激活,
它们将输入信号转换为输出的可微运算。
大多数激活函数都是非线性的。
由于激活函数是深度学习的基础,下面(**简要介绍一些常见的激活函数**)。
```
%matplotlib inline
from mxnet import autograd, np, npx
from d2l import mxnet as d2l
npx.set_np()
```
### ReLU函数
最受欢迎的激活函数是*修正线性单元*(Rectified linear unit,*ReLU*),
因为它实现简单,同时在各种预测任务中表现良好。
[**ReLU提供了一种非常简单的非线性变换**]。
给定元素$x$,ReLU函数被定义为该元素与$0$的最大值:
(**$$\operatorname{ReLU}(x) = \max(x, 0).$$**)
通俗地说,ReLU函数通过将相应的活性值设为0,仅保留正元素并丢弃所有负元素。
为了直观感受一下,我们可以画出函数的曲线图。
正如从图中所看到,激活函数是分段线性的。
```
x = np.arange(-8.0, 8.0, 0.1)
x.attach_grad()
with autograd.record():
y = npx.relu(x)
d2l.plot(x, y, 'x', 'relu(x)', figsize=(5, 2.5))
```
当输入为负时,ReLU函数的导数为0,而当输入为正时,ReLU函数的导数为1。
注意,当输入值精确等于0时,ReLU函数不可导。
在此时,我们默认使用左侧的导数,即当输入为0时导数为0。
我们可以忽略这种情况,因为输入可能永远都不会是0。
这里引用一句古老的谚语,“如果微妙的边界条件很重要,我们很可能是在研究数学而非工程”,
这个观点正好适用于这里。
下面我们绘制ReLU函数的导数。
```
y.backward()
d2l.plot(x, x.grad, 'x', 'grad of relu', figsize=(5, 2.5))
```
使用ReLU的原因是,它求导表现得特别好:要么让参数消失,要么让参数通过。
这使得优化表现得更好,并且ReLU减轻了困扰以往神经网络的梯度消失问题(稍后将详细介绍)。
注意,ReLU函数有许多变体,包括*参数化ReLU*(Parameterized ReLU,*pReLU*)
函数 :cite:`He.Zhang.Ren.ea.2015`。
该变体为ReLU添加了一个线性项,因此即使参数是负的,某些信息仍然可以通过:
$$\operatorname{pReLU}(x) = \max(0, x) + \alpha \min(0, x).$$
### sigmoid函数
[**对于一个定义域在$\mathbb{R}$中的输入,
*sigmoid函数*将输入变换为区间(0, 1)上的输出**]。
因此,sigmoid通常称为*挤压函数*(squashing function):
它将范围(-inf, inf)中的任意输入压缩到区间(0, 1)中的某个值:
(**$$\operatorname{sigmoid}(x) = \frac{1}{1 + \exp(-x)}.$$**)
在最早的神经网络中,科学家们感兴趣的是对“激发”或“不激发”的生物神经元进行建模。
因此,这一领域的先驱可以一直追溯到人工神经元的发明者麦卡洛克和皮茨,他们专注于阈值单元。
阈值单元在其输入低于某个阈值时取值0,当输入超过阈值时取值1。
当人们逐渐关注到到基于梯度的学习时,
sigmoid函数是一个自然的选择,因为它是一个平滑的、可微的阈值单元近似。
当我们想要将输出视作二元分类问题的概率时,
sigmoid仍然被广泛用作输出单元上的激活函数
(你可以将sigmoid视为softmax的特例)。
然而,sigmoid在隐藏层中已经较少使用,
它在大部分时候被更简单、更容易训练的ReLU所取代。
在后面关于循环神经网络的章节中,我们将描述利用sigmoid单元来控制时序信息流的架构。
下面,我们绘制sigmoid函数。
注意,当输入接近0时,sigmoid函数接近线性变换。
```
with autograd.record():
y = npx.sigmoid(x)
d2l.plot(x, y, 'x', 'sigmoid(x)', figsize=(5, 2.5))
```
sigmoid函数的导数为下面的公式:
$$\frac{d}{dx} \operatorname{sigmoid}(x) = \frac{\exp(-x)}{(1 + \exp(-x))^2} = \operatorname{sigmoid}(x)\left(1-\operatorname{sigmoid}(x)\right).$$
sigmoid函数的导数图像如下所示。
注意,当输入为0时,sigmoid函数的导数达到最大值0.25;
而输入在任一方向上越远离0点时,导数越接近0。
```
y.backward()
d2l.plot(x, x.grad, 'x', 'grad of sigmoid', figsize=(5, 2.5))
```
### tanh函数
与sigmoid函数类似,
[**tanh(双曲正切)函数也能将其输入压缩转换到区间(-1, 1)上**]。
tanh函数的公式如下:
(**$$\operatorname{tanh}(x) = \frac{1 - \exp(-2x)}{1 + \exp(-2x)}.$$**)
下面我们绘制tanh函数。
注意,当输入在0附近时,tanh函数接近线性变换。
函数的形状类似于sigmoid函数,
不同的是tanh函数关于坐标系原点中心对称。
```
with autograd.record():
y = np.tanh(x)
d2l.plot(x, y, 'x', 'tanh(x)', figsize=(5, 2.5))
```
tanh函数的导数是:
$$\frac{d}{dx} \operatorname{tanh}(x) = 1 - \operatorname{tanh}^2(x).$$
tanh函数的导数图像如下所示。
当输入接近0时,tanh函数的导数接近最大值1。
与我们在sigmoid函数图像中看到的类似,
输入在任一方向上越远离0点,导数越接近0。
```
y.backward()
d2l.plot(x, x.grad, 'x', 'grad of tanh', figsize=(5, 2.5))
```
总结一下,我们现在了解了如何结合非线性函数来构建具有更强表达能力的多层神经网络架构。
顺便说一句,这些知识已经让你掌握了一个类似于1990年左右深度学习从业者的工具。
在某些方面,你比在20世纪90年代工作的任何人都有优势,
因为你可以利用功能强大的开源深度学习框架,只需几行代码就可以快速构建模型,
而以前训练这些网络需要研究人员编写数千行的C或Fortran代码。
## 小结
* 多层感知机在输出层和输入层之间增加一个或多个全连接隐藏层,并通过激活函数转换隐藏层的输出。
* 常用的激活函数包括ReLU函数、sigmoid函数和tanh函数。
## 练习
1. 计算pReLU激活函数的导数。
1. 证明一个仅使用ReLU(或pReLU)的多层感知机构造了一个连续的分段线性函数。
1. 证明$\operatorname{tanh}(x) + 1 = 2 \operatorname{sigmoid}(2x)$。
1. 假设我们有一个非线性单元,将它一次应用于一个小批量的数据。你认为这会导致什么样的问题?
[Discussions](https://discuss.d2l.ai/t/1797)
|
github_jupyter
|
%matplotlib inline
from mxnet import autograd, np, npx
from d2l import mxnet as d2l
npx.set_np()
x = np.arange(-8.0, 8.0, 0.1)
x.attach_grad()
with autograd.record():
y = npx.relu(x)
d2l.plot(x, y, 'x', 'relu(x)', figsize=(5, 2.5))
y.backward()
d2l.plot(x, x.grad, 'x', 'grad of relu', figsize=(5, 2.5))
with autograd.record():
y = npx.sigmoid(x)
d2l.plot(x, y, 'x', 'sigmoid(x)', figsize=(5, 2.5))
y.backward()
d2l.plot(x, x.grad, 'x', 'grad of sigmoid', figsize=(5, 2.5))
with autograd.record():
y = np.tanh(x)
d2l.plot(x, y, 'x', 'tanh(x)', figsize=(5, 2.5))
y.backward()
d2l.plot(x, x.grad, 'x', 'grad of tanh', figsize=(5, 2.5))
| 0.404507 | 0.902266 |
# 机器学习纳米学位
## 监督学习
## 项目2: 为*CharityML*寻找捐献者
欢迎来到机器学习工程师纳米学位的第二个项目!在此文件中,有些示例代码已经提供给你,但你还需要实现更多的功能让项目成功运行。除非有明确要求,你无须修改任何已给出的代码。以**'练习'**开始的标题表示接下来的代码部分中有你必须要实现的功能。每一部分都会有详细的指导,需要实现的部分也会在注释中以'TODO'标出。请仔细阅读所有的提示!
除了实现代码外,你还必须回答一些与项目和你的实现有关的问题。每一个需要你回答的问题都会以**'问题 X'**为标题。请仔细阅读每个问题,并且在问题后的**'回答'**文字框中写出完整的答案。我们将根据你对问题的回答和撰写代码所实现的功能来对你提交的项目进行评分。
>**提示:**Code 和 Markdown 区域可通过**Shift + Enter**快捷键运行。此外,Markdown可以通过双击进入编辑模式。
## 开始
在这个项目中,你将使用1994年美国人口普查收集的数据,选用几个监督学习算法以准确地建模被调查者的收入。然后,你将根据初步结果从中选择出最佳的候选算法,并进一步优化该算法以最好地建模这些数据。你的目标是建立一个能够准确地预测被调查者年收入是否超过50000美元的模型。这种类型的任务会出现在那些依赖于捐款而存在的非营利性组织。了解人群的收入情况可以帮助一个非营利性的机构更好地了解他们要多大的捐赠,或是否他们应该接触这些人。虽然我们很难直接从公开的资源中推断出一个人的一般收入阶层,但是我们可以(也正是我们将要做的)从其他的一些公开的可获得的资源中获得一些特征从而推断出该值。
这个项目的数据集来自[UCI机器学习知识库](https://archive.ics.uci.edu/ml/datasets/Census+Income)。这个数据集是由Ron Kohavi和Barry Becker在发表文章_"Scaling Up the Accuracy of Naive-Bayes Classifiers: A Decision-Tree Hybrid"_之后捐赠的,你可以在Ron Kohavi提供的[在线版本](https://www.aaai.org/Papers/KDD/1996/KDD96-033.pdf)中找到这个文章。我们在这里探索的数据集相比于原有的数据集有一些小小的改变,比如说移除了特征`'fnlwgt'` 以及一些遗失的或者是格式不正确的记录。
----
## 探索数据
运行下面的代码单元以载入需要的Python库并导入人口普查数据。注意数据集的最后一列`'income'`将是我们需要预测的列(表示被调查者的年收入会大于或者是最多50,000美元),人口普查数据中的每一列都将是关于被调查者的特征。
```
# 为这个项目导入需要的库
import numpy as np
import pandas as pd
from time import time
from IPython.display import display # 允许为DataFrame使用display()
# 导入附加的可视化代码visuals.py
import visuals as vs
# 为notebook提供更加漂亮的可视化
%matplotlib inline
# 导入人口普查数据
data = pd.read_csv("census.csv")
# 成功 - 显示第一条记录
display(data.head(n=1))
```
### 练习:数据探索
首先我们对数据集进行一个粗略的探索,我们将看看每一个类别里会有多少被调查者?并且告诉我们这些里面多大比例是年收入大于50,000美元的。在下面的代码单元中,你将需要计算以下量:
- 总的记录数量,`'n_records'`
- 年收入大于50,000美元的人数,`'n_greater_50k'`.
- 年收入最多为50,000美元的人数 `'n_at_most_50k'`.
- 年收入大于50,000美元的人所占的比例, `'greater_percent'`.
**提示:** 您可能需要查看上面的生成的表,以了解`'income'`条目的格式是什么样的。
```
# TODO:总的记录数
n_records = data.shape[0]
# TODO:被调查者的收入大于$50,000的人数
n_greater_50k = len(data[data.income == '>50K'])
# TODO:被调查者的收入最多为$50,000的人数
n_at_most_50k = len(data[data.income == '<=50K'])
# TODO:被调查者收入大于$50,000所占的比例
greater_percent = float(n_greater_50k) / n_records * 100
# 打印结果
print ("Total number of records: {}".format(n_records))
print ("Individuals making more than $50,000: {}".format(n_greater_50k))
print ("Individuals making at most $50,000: {}".format(n_at_most_50k))
print ("Percentage of individuals making more than $50,000: {:.2f}%".format(greater_percent))
```
----
## 准备数据
在数据能够被作为输入提供给机器学习算法之前,它经常需要被清洗,格式化,和重新组织 - 这通常被叫做**预处理**。幸运的是,对于这个数据集,没有我们必须处理的无效或丢失的条目,然而,由于某一些特征存在的特性我们必须进行一定的调整。这个预处理都可以极大地帮助我们提升几乎所有的学习算法的结果和预测能力。
### 获得特征和标签
`income` 列是我们需要的标签,记录一个人的年收入是否高于50K。 因此我们应该把他从数据中剥离出来,单独存放。
```
# 将数据切分成特征和对应的标签
income_raw = data['income']
features_raw = data.drop('income', axis = 1)
```
### 转换倾斜的连续特征
一个数据集有时可能包含至少一个靠近某个数字的特征,但有时也会有一些相对来说存在极大值或者极小值的不平凡分布的的特征。算法对这种分布的数据会十分敏感,并且如果这种数据没有能够很好地规一化处理会使得算法表现不佳。在人口普查数据集的两个特征符合这个描述:'`capital-gain'`和`'capital-loss'`。
运行下面的代码单元以创建一个关于这两个特征的条形图。请注意当前的值的范围和它们是如何分布的。
```
# 可视化 'capital-gain'和'capital-loss' 两个特征
vs.distribution(features_raw)
```
对于高度倾斜分布的特征如`'capital-gain'`和`'capital-loss'`,常见的做法是对数据施加一个<a href="https://en.wikipedia.org/wiki/Data_transformation_(statistics)">对数转换</a>,将数据转换成对数,这样非常大和非常小的值不会对学习算法产生负面的影响。并且使用对数变换显著降低了由于异常值所造成的数据范围异常。但是在应用这个变换时必须小心:因为0的对数是没有定义的,所以我们必须先将数据处理成一个比0稍微大一点的数以成功完成对数转换。
运行下面的代码单元来执行数据的转换和可视化结果。再次,注意值的范围和它们是如何分布的。
```
# 对于倾斜的数据使用Log转换
skewed = ['capital-gain', 'capital-loss']
features_raw[skewed] = data[skewed].apply(lambda x: np.log(x + 1))
# 可视化对数转换后 'capital-gain'和'capital-loss' 两个特征
vs.distribution(features_raw, transformed = True)
```
### 规一化数字特征
除了对于高度倾斜的特征施加转换,对数值特征施加一些形式的缩放通常会是一个好的习惯。在数据上面施加一个缩放并不会改变数据分布的形式(比如上面说的'capital-gain' or 'capital-loss');但是,规一化保证了每一个特征在使用监督学习器的时候能够被平等的对待。注意一旦使用了缩放,观察数据的原始形式不再具有它本来的意义了,就像下面的例子展示的。
运行下面的代码单元来规一化每一个数字特征。我们将使用[`sklearn.preprocessing.MinMaxScaler`](http://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.MinMaxScaler.html)来完成这个任务。
```
from sklearn.preprocessing import MinMaxScaler
# 初始化一个 scaler,并将它施加到特征上
scaler = MinMaxScaler()
numerical = ['age', 'education-num', 'capital-gain', 'capital-loss', 'hours-per-week']
features_raw[numerical] = scaler.fit_transform(data[numerical])
# 显示一个经过缩放的样例记录
display(features_raw.head(n = 5))
```
### 练习:数据预处理
从上面的**数据探索**中的表中,我们可以看到有几个属性的每一条记录都是非数字的。通常情况下,学习算法期望输入是数字的,这要求非数字的特征(称为类别变量)被转换。转换类别变量的一种流行的方法是使用**独热编码**方案。独热编码为每一个非数字特征的每一个可能的类别创建一个_“虚拟”_变量。例如,假设`someFeature`有三个可能的取值`A`,`B`或者`C`,。我们将把这个特征编码成`someFeature_A`, `someFeature_B`和`someFeature_C`.
| 特征X | | 特征X_A | 特征X_B | 特征X_C |
| :-: | | :-: | :-: | :-: |
| B | | 0 | 1 | 0 |
| C | ----> 独热编码 ----> | 0 | 0 | 1 |
| A | | 1 | 0 | 0 |
此外,对于非数字的特征,我们需要将非数字的标签`'income'`转换成数值以保证学习算法能够正常工作。因为这个标签只有两种可能的类别("<=50K"和">50K"),我们不必要使用独热编码,可以直接将他们编码分别成两个类`0`和`1`,在下面的代码单元中你将实现以下功能:
- 使用[`pandas.get_dummies()`](http://pandas.pydata.org/pandas-docs/stable/generated/pandas.get_dummies.html?highlight=get_dummies#pandas.get_dummies)对`'features_raw'`数据来施加一个独热编码。
- 将目标标签`'income_raw'`转换成数字项。
- 将"<=50K"转换成`0`;将">50K"转换成`1`。
```
# TODO:使用pandas.get_dummies()对'features_raw'数据进行独热编码
features = pd.get_dummies(features_raw)
# TODO:将'income_raw'编码成数字值
from sklearn import preprocessing
income = pd.Series(preprocessing.LabelEncoder().fit_transform(income_raw))
# 打印经过独热编码之后的特征数量
encoded = list(features.columns)
print ("{} total features after one-hot encoding.".format(len(encoded)))
# 移除下面一行的注释以观察编码的特征名字
print (encoded)
```
### 混洗和切分数据
现在所有的 _类别变量_ 已被转换成数值特征,而且所有的数值特征已被规一化。和我们一般情况下做的一样,我们现在将数据(包括特征和它们的标签)切分成训练和测试集。其中80%的数据将用于训练和20%的数据用于测试。然后再进一步把训练数据分为训练集和验证集,用来选择和优化模型。
运行下面的代码单元来完成切分。
```
# 导入 train_test_split
from sklearn.model_selection import train_test_split
# 将'features'和'income'数据切分成训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(features, income, test_size = 0.2, random_state = 0,
stratify = income)
# 将'X_train'和'y_train'进一步切分为训练集和验证集
X_train, X_val, y_train, y_val = train_test_split(X_train, y_train, test_size=0.2, random_state=0,
stratify = y_train)
# 显示切分的结果
print ("Training set has {} samples.".format(X_train.shape[0]))
print ("Validation set has {} samples.".format(X_val.shape[0]))
print ("Testing set has {} samples.".format(X_test.shape[0]))
```
----
## 评价模型性能
在这一部分中,我们将尝试四种不同的算法,并确定哪一个能够最好地建模数据。四种算法包含一个*天真的预测器* 和三个你选择的监督学习器。
### 评价方法和朴素的预测器
*CharityML*通过他们的研究人员知道被调查者的年收入大于\$50,000最有可能向他们捐款。因为这个原因*CharityML*对于准确预测谁能够获得\$50,000以上收入尤其有兴趣。这样看起来使用**准确率**作为评价模型的标准是合适的。另外,把*没有*收入大于\$50,000的人识别成年收入大于\$50,000对于*CharityML*来说是有害的,因为他想要找到的是有意愿捐款的用户。这样,我们期望的模型具有准确预测那些能够年收入大于\$50,000的能力比模型去**查全**这些被调查者*更重要*。我们能够使用**F-beta score**作为评价指标,这样能够同时考虑查准率和查全率:
$$ F_{\beta} = (1 + \beta^2) \cdot \frac{precision \cdot recall}{\left( \beta^2 \cdot precision \right) + recall} $$
尤其是,当 $\beta = 0.5$ 的时候更多的强调查准率,这叫做**F$_{0.5}$ score** (或者为了简单叫做F-score)。
### 问题 1 - 天真的预测器的性能
通过查看收入超过和不超过 \$50,000 的人数,我们能发现多数被调查者年收入没有超过 \$50,000。如果我们简单地预测说*“这个人的收入没有超过 \$50,000”*,我们就可以得到一个 准确率超过 50% 的预测。这样我们甚至不用看数据就能做到一个准确率超过 50%。这样一个预测被称作是天真的。通常对数据使用一个*天真的预测器*是十分重要的,这样能够帮助建立一个模型表现是否好的基准。 使用下面的代码单元计算天真的预测器的相关性能。将你的计算结果赋值给`'accuracy'`, `‘precision’`, `‘recall’` 和 `'fscore'`,这些值会在后面被使用,请注意这里不能使用scikit-learn,你需要根据公式自己实现相关计算。
*如果我们选择一个无论什么情况都预测被调查者年收入大于 \$50,000 的模型,那么这个模型在**验证集上**的准确率,查准率,查全率和 F-score是多少?*
```
#不能使用scikit-learn,你需要根据公式自己实现相关计算。
TP = float(len(y_val[y_val == 1]))
FP = float(len(y_val[y_val == 0]))
FN = 0
#TODO: 计算准确率
accuracy = float(TP)/len(y_val)
# TODO: 计算查准率 Precision
precision = TP/(TP+FP)
# TODO: 计算查全率 Recall
recall = TP/(TP+FN)
# TODO: 使用上面的公式,设置beta=0.5,计算F-score
fscore = (1+0.5**2)*((precision*recall)) / (0.5**2*precision+recall)
# 打印结果
print ("Naive Predictor on validation data: \n \
Accuracy score: {:.4f} \n \
Precision: {:.4f} \n \
Recall: {:.4f} \n \
F-score: {:.4f}".format(accuracy, precision, recall, fscore))
```
## 监督学习模型
### 问题 2 - 模型应用
你能够在 [`scikit-learn`](http://scikit-learn.org/stable/supervised_learning.html) 中选择以下监督学习模型
- 高斯朴素贝叶斯 (GaussianNB)
- 决策树 (DecisionTree)
- 集成方法 (Bagging, AdaBoost, Random Forest, Gradient Boosting)
- K近邻 (K Nearest Neighbors)
- 随机梯度下降分类器 (SGDC)
- 支撑向量机 (SVM)
- Logistic回归(LogisticRegression)
从上面的监督学习模型中选择三个适合我们这个问题的模型,并回答相应问题。
### 模型1
**模型名称**
回答:SVM
**描述一个该模型在真实世界的一个应用场景。(你需要为此做点研究,并给出你的引用出处)**
回答:人类行为认知的辨别,根据图像判断人物在做什么
**这个模型的优势是什么?他什么情况下表现最好?**
回答:丰富的核函数可以灵活解决回归问题和分类问题,当特征大于样本数且样本总数较小的时候表现优异
**这个模型的缺点是什么?什么条件下它表现很差?**
回答:当需要计算大量样本时丰富的核函数因为没有通用标准计算量大 且表现平平
**根据我们当前数据集的特点,为什么这个模型适合这个问题。**
回答:当前数据集含有大量特征 且样本总数适中 而且svm丰富的核函数可以很好的满足该项目需求
### 模型2
**模型名称**
回答:Random Forest
**描述一个该模型在真实世界的一个应用场景。(你需要为此做点研究,并给出你的引用出处)**
回答:随机森林分类器对土地覆盖进行分类
**这个模型的优势是什么?他什么情况下表现最好?**
回答:简单直观 便于理解 提前归一化 以及处理缺失值 可以解决任何类型的数据集 且不需要对数据预处理 通过网格搜索选择超参数 高泛化能力 当特征和样本数量比列保持平衡时表现优异
**这个模型的缺点是什么?什么条件下它表现很差?**
回答:容易过拟合 当某叶子结点发生变化时整体结构也发生变化 且当特征的样本比例不平衡的时候容易出现偏向
**根据我们当前数据集的特点,为什么这个模型适合这个问题。**
回答:特征唯独高 评估各个特征重要性 小范围噪声不会过拟合
### 模型3
**模型名称**
回答:K近邻 (K Nearest Neighbors)
**描述一个该模型在真实世界的一个应用场景。(你需要为此做点研究,并给出你的引用出处)**
回答:使用k近邻法估计和绘制森林林分密度,体积和覆盖类型
**这个模型的优势是什么?他什么情况下表现最好?**
回答:思想简单 容易理解 聚类效果较优
**这个模型的缺点是什么?什么条件下它表现很差?**
回答:对异常值敏感 提前判断K值 局部最优 复杂度高不易控制 迭代次数较多
**根据我们当前数据集的特点,为什么这个模型适合这个问题。**
回答:该项目数据适中且属于二分类为题
### 练习 - 创建一个训练和预测的流水线
为了正确评估你选择的每一个模型的性能,创建一个能够帮助你快速有效地使用不同大小的训练集并在验证集上做预测的训练和验证的流水线是十分重要的。
你在这里实现的功能将会在接下来的部分中被用到。在下面的代码单元中,你将实现以下功能:
- 从[`sklearn.metrics`](http://scikit-learn.org/stable/modules/classes.html#sklearn-metrics-metrics)中导入`fbeta_score`和`accuracy_score`。
- 用训练集拟合学习器,并记录训练时间。
- 对训练集的前300个数据点和验证集进行预测并记录预测时间。
- 计算预测训练集的前300个数据点的准确率和F-score。
- 计算预测验证集的准确率和F-score。
```
# TODO:从sklearn中导入两个评价指标 - fbeta_score和accuracy_score
from sklearn.metrics import fbeta_score, accuracy_score
def train_predict(learner, sample_size, X_train, y_train, X_val, y_val):
'''
inputs:
- learner: the learning algorithm to be trained and predicted on
- sample_size: the size of samples (number) to be drawn from training set
- X_train: features training set
- y_train: income training set
- X_val: features validation set
- y_val: income validation set
'''
results = {}
# TODO:使用sample_size大小的训练数据来拟合学习器
# TODO: Fit the learner to the training data using slicing with 'sample_size'
start = time() # 获得程序开始时间
learner = learner.fit(X_train[:sample_size], y_train[:sample_size])
end = time() # 获得程序结束时间
# TODO:计算训练时间
results['train_time'] = end - start
# TODO: 得到在验证集上的预测值
# 然后得到对前300个训练数据的预测结果
start = time() # 获得程序开始时间
predictions_val = learner.predict(X_val)
predictions_train = learner.predict(X_train[:300])
end = time() # 获得程序结束时间
# TODO:计算预测用时
results['pred_time'] = end - start
# TODO:计算在最前面的300个训练数据的准确率
results['acc_train'] = accuracy_score(y_test[:300], predictions_train)
# TODO:计算在验证上的准确率
results['acc_val'] = accuracy_score(y_val, predictions_val)
# TODO:计算在最前面300个训练数据上的F-score
results['f_train'] = fbeta_score(y_train[:300], predictions_train, beta=0.5)
# TODO:计算验证集上的F-score
results['f_val'] = fbeta_score(y_val, predictions_val, beta=0.5)
# 成功
print ("{} trained on {} samples.".format(learner.__class__.__name__, sample_size))
# 返回结果
return results
```
### 练习:初始模型的评估
在下面的代码单元中,您将需要实现以下功能:
- 导入你在前面讨论的三个监督学习模型。
- 初始化三个模型并存储在`'clf_A'`,`'clf_B'`和`'clf_C'`中。
- 使用模型的默认参数值,在接下来的部分中你将需要对某一个模型的参数进行调整。
- 设置`random_state` (如果有这个参数)。
- 计算1%, 10%, 100%的训练数据分别对应多少个数据点,并将这些值存储在`'samples_1'`, `'samples_10'`, `'samples_100'`中
**注意:**取决于你选择的算法,下面实现的代码可能需要一些时间来运行!
```
# TODO:从sklearn中导入三个监督学习模型
from sklearn.neighbors import KNeighborsClassifier
from sklearn.svm import SVC
from sklearn.ensemble import RandomForestClassifier
# TODO:初始化三个模型
clf_A = KNeighborsClassifier(n_neighbors=2)
clf_B = SVC(kernel='linear')
clf_C = RandomForestClassifier(random_state=0)
# TODO:计算1%, 10%, 100%的训练数据分别对应多少点
samples_1 = int(len(X_train) * 0.01)
samples_10 = int(len(X_train) * 0.10)
samples_100 = len(X_train)
# 收集学习器的结果
results = {}
for clf in [clf_A, clf_B, clf_C]:
clf_name = clf.__class__.__name__
results[clf_name] = {}
for i, samples in enumerate([samples_1, samples_10, samples_100]):
results[clf_name][i] = train_predict(clf, samples, X_train, y_train, X_val, y_val)
# 对选择的三个模型得到的评价结果进行可视化
vs.evaluate(results, accuracy, fscore)
```
----
## 提高效果
在这最后一节中,您将从三个有监督的学习模型中选择 *最好的* 模型来使用学生数据。你将在整个训练集(`X_train`和`y_train`)上使用网格搜索优化至少调节一个参数以获得一个比没有调节之前更好的 F-score。
### 问题 3 - 选择最佳的模型
*基于你前面做的评价,用一到两段话向 *CharityML* 解释这三个模型中哪一个对于判断被调查者的年收入大于 \$50,000 是最合适的。*
**提示:**你的答案应该包括评价指标,预测/训练时间,以及该算法是否适合这里的数据。
**回答:
从F-score来看,RandomForest在所有训练集上和1%、10%的验证集表现最好,SVM在100%的验证集表现最好
从准确度上来看,RandomForest在所有训练集上和1%、10%的验证集表现最好,SVM在100%的验证集表现最好
从训练时间上来看,SVM明显多与其他两种算法
从预测时间上来看,KNeighbors最多,SVM次之,RandomForest最少
KNeighbors由于初始点选择的问题可能会导致分类效果不固定
综上所述RandomForest综合表现较好,时间短分类准,我认为最合适,有调优的空间。如果不考虑时间SVM也有可能调出更优化的结果。
**
### 问题 4 - 用通俗的话解释模型
*用一到两段话,向 *CharityML* 用外行也听得懂的话来解释最终模型是如何工作的。你需要解释所选模型的主要特点。例如,这个模型是怎样被训练的,它又是如何做出预测的。避免使用高级的数学或技术术语,不要使用公式或特定的算法名词。*
**回答:**
训练
根据所有数据依次找到能最大区分当前数据的一个特征,进行数据分割,然后对分割的数据接着重复上述步骤,直到所有的特征都判断完,这样一系列的判断对应的结果为数据的类别,这样的判断构成的就是决策树
再多次执行上一步,每次执行的时候对样本进行随机有放回的抽样,构成多个不一样的决策树,这些决策树合并起来就是随机森林
预测
对于新来的样本,每个决策树做一个分类结果进行相等权重投票,然后以多数者投票的结果作为该样本的分类结果
### 练习:模型调优
调节选择的模型的参数。使用网格搜索(GridSearchCV)来至少调整模型的重要参数(至少调整一个),这个参数至少需尝试3个不同的值。你要使用整个训练集来完成这个过程。在接下来的代码单元中,你需要实现以下功能:
- 导入[`sklearn.model_selection.GridSearchCV`](http://scikit-learn.org/stable/modules/generated/sklearn.model_selection.GridSearchCV.html) 和 [`sklearn.metrics.make_scorer`](http://scikit-learn.org/stable/modules/generated/sklearn.metrics.make_scorer.html).
- 初始化你选择的分类器,并将其存储在`clf`中。
- 设置`random_state` (如果有这个参数)。
- 创建一个对于这个模型你希望调整参数的字典。
- 例如: parameters = {'parameter' : [list of values]}。
- **注意:** 如果你的学习器有 `max_features` 参数,请不要调节它!
- 使用`make_scorer`来创建一个`fbeta_score`评分对象(设置$\beta = 0.5$)。
- 在分类器clf上用'scorer'作为评价函数运行网格搜索,并将结果存储在grid_obj中。
- 用训练集(X_train, y_train)训练grid search object,并将结果存储在`grid_fit`中。
**注意:** 取决于你选择的参数列表,下面实现的代码可能需要花一些时间运行!
```
# TODO:导入'GridSearchCV', 'make_scorer'和其他一些需要的库
from sklearn.model_selection import GridSearchCV
from sklearn.metrics import make_scorer
# TODO:初始化分类器
clf = RandomForestClassifier(random_state=0)
# TODO:创建你希望调节的参数列表
parameters = {'n_estimators':[10,50,100,150]}
# TODO:创建一个fbeta_score打分对象
scorer = make_scorer(fbeta_score, beta=0.5)
# TODO:在分类器上使用网格搜索,使用'scorer'作为评价函数
grid_obj = GridSearchCV(clf, parameters, scorer)
# TODO:用训练数据拟合网格搜索对象并找到最佳参数
grid_obj.fit(X_train, y_train)
# 得到estimator
best_clf = grid_obj.best_estimator_
# 使用没有调优的模型做预测
predictions = (clf.fit(X_train, y_train)).predict(X_val)
best_predictions = best_clf.predict(X_val)
# 汇报调优后的模型
print ("best_clf\n------")
print (best_clf)
# 汇报调参前和调参后的分数
print ("\nUnoptimized model\n------")
print ("Accuracy score on validation data: {:.4f}".format(accuracy_score(y_val, predictions)))
print ("F-score on validation data: {:.4f}".format(fbeta_score(y_val, predictions, beta = 0.5)))
print ("\nOptimized Model\n------")
print ("Final accuracy score on the validation data: {:.4f}".format(accuracy_score(y_val, best_predictions)))
print ("Final F-score on the validation data: {:.4f}".format(fbeta_score(y_val, best_predictions, beta = 0.5)))
```
### 问题 5 - 最终模型评估
_你的最优模型在测试数据上的准确率和 F-score 是多少?这些分数比没有优化的模型好还是差?_
**注意:**请在下面的表格中填写你的结果,然后在答案框中提供讨论。
#### 结果:
| 评价指标 | 未优化的模型 | 优化的模型 |
| :------------: | :---------------: | :-------------: |
| 准确率 | 0.8389 | 0.8456 |
| F-score | 0.6812 | 0.6940 |
**回答:相比较没有优化的模型有少许提升**
----
## 特征的重要性
在数据上(比如我们这里使用的人口普查的数据)使用监督学习算法的一个重要的任务是决定哪些特征能够提供最强的预测能力。专注于少量的有效特征和标签之间的关系,我们能够更加简单地理解这些现象,这在很多情况下都是十分有用的。在这个项目的情境下这表示我们希望选择一小部分特征,这些特征能够在预测被调查者是否年收入大于\$50,000这个问题上有很强的预测能力。
选择一个有 `'feature_importance_'` 属性的scikit学习分类器(例如 AdaBoost,随机森林)。`'feature_importance_'` 属性是对特征的重要性排序的函数。在下一个代码单元中用这个分类器拟合训练集数据并使用这个属性来决定人口普查数据中最重要的5个特征。
### 问题 6 - 观察特征相关性
当**探索数据**的时候,它显示在这个人口普查数据集中每一条记录我们有十三个可用的特征。
_在这十三个记录中,你认为哪五个特征对于预测是最重要的,选择每个特征的理由是什么?你会怎样对他们排序?_
**回答:**
- 特征1:age 年龄的增长事业和收入也会增长
- 特征2:hours-per-week 理论上工作时间越多收入越高
- 特征3:captial-gain 拥有其他资本收益代表经济条件更好
- 特征4:martial-status 收入大雨50K说明拥有更好的承担能力
- 特征5:education-num 教育程度越高 越有可能高收入
### 练习 - 提取特征重要性
选择一个`scikit-learn`中有`feature_importance_`属性的监督学习分类器,这个属性是一个在做预测的时候根据所选择的算法来对特征重要性进行排序的功能。
在下面的代码单元中,你将要实现以下功能:
- 如果这个模型和你前面使用的三个模型不一样的话从sklearn中导入一个监督学习模型。
- 在整个训练集上训练一个监督学习模型。
- 使用模型中的 `'feature_importances_'`提取特征的重要性。
```
# TODO:导入一个有'feature_importances_'的监督学习模型
# TODO:在训练集上训练一个监督学习模型
model = best_clf
# TODO: 提取特征重要性
importances = model.feature_importances_
# 绘图best_clf
vs.feature_plot(importances, X_train, y_train)
```
### 问题 7 - 提取特征重要性
观察上面创建的展示五个用于预测被调查者年收入是否大于\$50,000最相关的特征的可视化图像。
_这五个特征的权重加起来是否超过了0.5?_<br>
_这五个特征和你在**问题 6**中讨论的特征比较怎么样?_<br>
_如果说你的答案和这里的相近,那么这个可视化怎样佐证了你的想法?_<br>
_如果你的选择不相近,那么为什么你觉得这些特征更加相关?_
**回答:0.24+0.12+0.10+0.07+0.06>0.5 基本一致。权重越高说明重要性越高**
### 特征选择
如果我们只是用可用特征的一个子集的话模型表现会怎么样?通过使用更少的特征来训练,在评价指标的角度来看我们的期望是训练和预测的时间会更少。从上面的可视化来看,我们可以看到前五个最重要的特征贡献了数据中**所有**特征中超过一半的重要性。这提示我们可以尝试去**减小特征空间**,简化模型需要学习的信息。下面代码单元将使用你前面发现的优化模型,并**只使用五个最重要的特征**在相同的训练集上训练模型。
```
# 导入克隆模型的功能
from sklearn.base import clone
# 减小特征空间
X_train_reduced = X_train[X_train.columns.values[(np.argsort(importances)[::-1])[:5]]]
X_val_reduced = X_val[X_val.columns.values[(np.argsort(importances)[::-1])[:5]]]
# 在前面的网格搜索的基础上训练一个“最好的”模型
clf_on_reduced = (clone(best_clf)).fit(X_train_reduced, y_train)
# 做一个新的预测
reduced_predictions = clf_on_reduced.predict(X_val_reduced)
# 对于每一个版本的数据汇报最终模型的分数
print ("Final Model trained on full data\n------")
print ("Accuracy on validation data: {:.4f}".format(accuracy_score(y_val, best_predictions)))
print ("F-score on validation data: {:.4f}".format(fbeta_score(y_val, best_predictions, beta = 0.5)))
print ("\nFinal Model trained on reduced data\n------")
print ("Accuracy on validation data: {:.4f}".format(accuracy_score(y_val, reduced_predictions)))
print ("F-score on validation data: {:.4f}".format(fbeta_score(y_val, reduced_predictions, beta = 0.5)))
```
### 问题 8 - 特征选择的影响
*最终模型在只是用五个特征的数据上和使用所有的特征数据上的 F-score 和准确率相比怎么样?*
*如果训练时间是一个要考虑的因素,你会考虑使用部分特征的数据作为你的训练集吗?*
**回答:**
| 评价指标 | 使用所有特征 | 使用部分特征 |
| :------------: | :---------------: | :-------------: |
| 准确率 | 0.8456 | 0.8333 |
| F-score | 0.6940 | 0.6678 |
使用部分特征和所有特征相比准确率和F1值出现了下降现象 如果考虑时间问题我会考虑使用部分特征 会缩短大量训练时间
### 问题 9 - 在测试集上测试你的模型
终于到了测试的时候,记住,测试集只能用一次。
*使用你最有信心的模型,在测试集上测试,计算出准确率和 F-score。*
*简述你选择这个模型的原因,并分析测试结果*
```
#TODO test your model on testing data and report accuracy and F score
res = best_clf.predict(X_test)
from sklearn.metrics import fbeta_score,accuracy_score
print('accuracy score:{}'.format(accuracy_score(y_test, res)))
print('fbeta score:{}'.format(fbeta_score(y_test, res, beta=0.5)))
```
> **注意:** 当你写完了所有的代码,并且回答了所有的问题。你就可以把你的 iPython Notebook 导出成 HTML 文件。你可以在菜单栏,这样导出**File -> Download as -> HTML (.html)**把这个 HTML 和这个 iPython notebook 一起做为你的作业提交。
|
github_jupyter
|
# 为这个项目导入需要的库
import numpy as np
import pandas as pd
from time import time
from IPython.display import display # 允许为DataFrame使用display()
# 导入附加的可视化代码visuals.py
import visuals as vs
# 为notebook提供更加漂亮的可视化
%matplotlib inline
# 导入人口普查数据
data = pd.read_csv("census.csv")
# 成功 - 显示第一条记录
display(data.head(n=1))
# TODO:总的记录数
n_records = data.shape[0]
# TODO:被调查者的收入大于$50,000的人数
n_greater_50k = len(data[data.income == '>50K'])
# TODO:被调查者的收入最多为$50,000的人数
n_at_most_50k = len(data[data.income == '<=50K'])
# TODO:被调查者收入大于$50,000所占的比例
greater_percent = float(n_greater_50k) / n_records * 100
# 打印结果
print ("Total number of records: {}".format(n_records))
print ("Individuals making more than $50,000: {}".format(n_greater_50k))
print ("Individuals making at most $50,000: {}".format(n_at_most_50k))
print ("Percentage of individuals making more than $50,000: {:.2f}%".format(greater_percent))
# 将数据切分成特征和对应的标签
income_raw = data['income']
features_raw = data.drop('income', axis = 1)
# 可视化 'capital-gain'和'capital-loss' 两个特征
vs.distribution(features_raw)
# 对于倾斜的数据使用Log转换
skewed = ['capital-gain', 'capital-loss']
features_raw[skewed] = data[skewed].apply(lambda x: np.log(x + 1))
# 可视化对数转换后 'capital-gain'和'capital-loss' 两个特征
vs.distribution(features_raw, transformed = True)
from sklearn.preprocessing import MinMaxScaler
# 初始化一个 scaler,并将它施加到特征上
scaler = MinMaxScaler()
numerical = ['age', 'education-num', 'capital-gain', 'capital-loss', 'hours-per-week']
features_raw[numerical] = scaler.fit_transform(data[numerical])
# 显示一个经过缩放的样例记录
display(features_raw.head(n = 5))
# TODO:使用pandas.get_dummies()对'features_raw'数据进行独热编码
features = pd.get_dummies(features_raw)
# TODO:将'income_raw'编码成数字值
from sklearn import preprocessing
income = pd.Series(preprocessing.LabelEncoder().fit_transform(income_raw))
# 打印经过独热编码之后的特征数量
encoded = list(features.columns)
print ("{} total features after one-hot encoding.".format(len(encoded)))
# 移除下面一行的注释以观察编码的特征名字
print (encoded)
# 导入 train_test_split
from sklearn.model_selection import train_test_split
# 将'features'和'income'数据切分成训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(features, income, test_size = 0.2, random_state = 0,
stratify = income)
# 将'X_train'和'y_train'进一步切分为训练集和验证集
X_train, X_val, y_train, y_val = train_test_split(X_train, y_train, test_size=0.2, random_state=0,
stratify = y_train)
# 显示切分的结果
print ("Training set has {} samples.".format(X_train.shape[0]))
print ("Validation set has {} samples.".format(X_val.shape[0]))
print ("Testing set has {} samples.".format(X_test.shape[0]))
#不能使用scikit-learn,你需要根据公式自己实现相关计算。
TP = float(len(y_val[y_val == 1]))
FP = float(len(y_val[y_val == 0]))
FN = 0
#TODO: 计算准确率
accuracy = float(TP)/len(y_val)
# TODO: 计算查准率 Precision
precision = TP/(TP+FP)
# TODO: 计算查全率 Recall
recall = TP/(TP+FN)
# TODO: 使用上面的公式,设置beta=0.5,计算F-score
fscore = (1+0.5**2)*((precision*recall)) / (0.5**2*precision+recall)
# 打印结果
print ("Naive Predictor on validation data: \n \
Accuracy score: {:.4f} \n \
Precision: {:.4f} \n \
Recall: {:.4f} \n \
F-score: {:.4f}".format(accuracy, precision, recall, fscore))
# TODO:从sklearn中导入两个评价指标 - fbeta_score和accuracy_score
from sklearn.metrics import fbeta_score, accuracy_score
def train_predict(learner, sample_size, X_train, y_train, X_val, y_val):
'''
inputs:
- learner: the learning algorithm to be trained and predicted on
- sample_size: the size of samples (number) to be drawn from training set
- X_train: features training set
- y_train: income training set
- X_val: features validation set
- y_val: income validation set
'''
results = {}
# TODO:使用sample_size大小的训练数据来拟合学习器
# TODO: Fit the learner to the training data using slicing with 'sample_size'
start = time() # 获得程序开始时间
learner = learner.fit(X_train[:sample_size], y_train[:sample_size])
end = time() # 获得程序结束时间
# TODO:计算训练时间
results['train_time'] = end - start
# TODO: 得到在验证集上的预测值
# 然后得到对前300个训练数据的预测结果
start = time() # 获得程序开始时间
predictions_val = learner.predict(X_val)
predictions_train = learner.predict(X_train[:300])
end = time() # 获得程序结束时间
# TODO:计算预测用时
results['pred_time'] = end - start
# TODO:计算在最前面的300个训练数据的准确率
results['acc_train'] = accuracy_score(y_test[:300], predictions_train)
# TODO:计算在验证上的准确率
results['acc_val'] = accuracy_score(y_val, predictions_val)
# TODO:计算在最前面300个训练数据上的F-score
results['f_train'] = fbeta_score(y_train[:300], predictions_train, beta=0.5)
# TODO:计算验证集上的F-score
results['f_val'] = fbeta_score(y_val, predictions_val, beta=0.5)
# 成功
print ("{} trained on {} samples.".format(learner.__class__.__name__, sample_size))
# 返回结果
return results
# TODO:从sklearn中导入三个监督学习模型
from sklearn.neighbors import KNeighborsClassifier
from sklearn.svm import SVC
from sklearn.ensemble import RandomForestClassifier
# TODO:初始化三个模型
clf_A = KNeighborsClassifier(n_neighbors=2)
clf_B = SVC(kernel='linear')
clf_C = RandomForestClassifier(random_state=0)
# TODO:计算1%, 10%, 100%的训练数据分别对应多少点
samples_1 = int(len(X_train) * 0.01)
samples_10 = int(len(X_train) * 0.10)
samples_100 = len(X_train)
# 收集学习器的结果
results = {}
for clf in [clf_A, clf_B, clf_C]:
clf_name = clf.__class__.__name__
results[clf_name] = {}
for i, samples in enumerate([samples_1, samples_10, samples_100]):
results[clf_name][i] = train_predict(clf, samples, X_train, y_train, X_val, y_val)
# 对选择的三个模型得到的评价结果进行可视化
vs.evaluate(results, accuracy, fscore)
# TODO:导入'GridSearchCV', 'make_scorer'和其他一些需要的库
from sklearn.model_selection import GridSearchCV
from sklearn.metrics import make_scorer
# TODO:初始化分类器
clf = RandomForestClassifier(random_state=0)
# TODO:创建你希望调节的参数列表
parameters = {'n_estimators':[10,50,100,150]}
# TODO:创建一个fbeta_score打分对象
scorer = make_scorer(fbeta_score, beta=0.5)
# TODO:在分类器上使用网格搜索,使用'scorer'作为评价函数
grid_obj = GridSearchCV(clf, parameters, scorer)
# TODO:用训练数据拟合网格搜索对象并找到最佳参数
grid_obj.fit(X_train, y_train)
# 得到estimator
best_clf = grid_obj.best_estimator_
# 使用没有调优的模型做预测
predictions = (clf.fit(X_train, y_train)).predict(X_val)
best_predictions = best_clf.predict(X_val)
# 汇报调优后的模型
print ("best_clf\n------")
print (best_clf)
# 汇报调参前和调参后的分数
print ("\nUnoptimized model\n------")
print ("Accuracy score on validation data: {:.4f}".format(accuracy_score(y_val, predictions)))
print ("F-score on validation data: {:.4f}".format(fbeta_score(y_val, predictions, beta = 0.5)))
print ("\nOptimized Model\n------")
print ("Final accuracy score on the validation data: {:.4f}".format(accuracy_score(y_val, best_predictions)))
print ("Final F-score on the validation data: {:.4f}".format(fbeta_score(y_val, best_predictions, beta = 0.5)))
# TODO:导入一个有'feature_importances_'的监督学习模型
# TODO:在训练集上训练一个监督学习模型
model = best_clf
# TODO: 提取特征重要性
importances = model.feature_importances_
# 绘图best_clf
vs.feature_plot(importances, X_train, y_train)
# 导入克隆模型的功能
from sklearn.base import clone
# 减小特征空间
X_train_reduced = X_train[X_train.columns.values[(np.argsort(importances)[::-1])[:5]]]
X_val_reduced = X_val[X_val.columns.values[(np.argsort(importances)[::-1])[:5]]]
# 在前面的网格搜索的基础上训练一个“最好的”模型
clf_on_reduced = (clone(best_clf)).fit(X_train_reduced, y_train)
# 做一个新的预测
reduced_predictions = clf_on_reduced.predict(X_val_reduced)
# 对于每一个版本的数据汇报最终模型的分数
print ("Final Model trained on full data\n------")
print ("Accuracy on validation data: {:.4f}".format(accuracy_score(y_val, best_predictions)))
print ("F-score on validation data: {:.4f}".format(fbeta_score(y_val, best_predictions, beta = 0.5)))
print ("\nFinal Model trained on reduced data\n------")
print ("Accuracy on validation data: {:.4f}".format(accuracy_score(y_val, reduced_predictions)))
print ("F-score on validation data: {:.4f}".format(fbeta_score(y_val, reduced_predictions, beta = 0.5)))
#TODO test your model on testing data and report accuracy and F score
res = best_clf.predict(X_test)
from sklearn.metrics import fbeta_score,accuracy_score
print('accuracy score:{}'.format(accuracy_score(y_test, res)))
print('fbeta score:{}'.format(fbeta_score(y_test, res, beta=0.5)))
| 0.208662 | 0.85555 |
```
import os
import time
import numpy as np
import matplotlib.pyplot as plt
import PIL
import torch
import torch.nn as nn
import torch.optim as optim
from torchvision import models
from torchvision.models import vgg16
from torchvision import datasets, transforms
print('pytorch version: {}'.format(torch.__version__))
print('GPU 사용 가능 여부: {}'.format(torch.cuda.is_available()))
device = "cuda" if torch.cuda.is_available() else "cpu" # GPU 사용 가능 여부에 따라 device 정보 저장
```
### 네트워크 설계 I (Pretrained 된 모델 사용 X)
### Front-end Module
```
import torch
import torch.nn as nn
def conv_relu(in_ch, out_ch, size=3, rate=1):
conv_relu = nn.Sequential(nn.Conv2d(in_channels=in_ch,
out_channels=out_ch,
kernel_size=3,
stride=1,
padding=rate,
dilation=rate),
nn.ReLU())
return conv_relu
class VGG16(nn.Module):
def __init__(self):
super(VGG16, self).__init__()
self.features1 = nn.Sequential(conv_relu(3, 64, 3, 1),
conv_relu(64, 64, 3, 1),
nn.MaxPool2d(2, stride=2, padding=0)) # 1/2
self.features2 = nn.Sequential(conv_relu(64, 128, 3, 1),
conv_relu(128, 128, 3, 1),
nn.MaxPool2d(2, stride=2, padding=0)) # 1/4
self.features3 = nn.Sequential(conv_relu(128, 256, 3, 1),
conv_relu(256, 256, 3, 1),
conv_relu(256, 256, 3, 1),
nn.MaxPool2d(2, stride=2, padding=0)) # 1/8
self.features4 = nn.Sequential(conv_relu(256, 512, 3, 1),
conv_relu(512, 512, 3, 1),
conv_relu(512, 512, 3, 1))
# and replace subsequent conv layer rate=2
self.features5 = nn.Sequential(conv_relu(512, 512, 3, 2),
conv_relu(512, 512, 3, 2),
conv_relu(512, 512, 3, 2))
def forward(self, x):
out = self.features1(x)
out = self.features2(out)
out = self.features3(out)
out = self.features4(out)
out = self.features5(out)
return out
class classifier(nn.Module):
def __init__(self, num_classes):
super(classifier, self).__init__()
self.classifier = nn.Sequential(conv_relu(512, 4096, 7, rate=4),
nn.Dropout2d(0.5),
conv_relu(4096, 4096, 1, 1),
nn.Dropout2d(0.5),
nn.Conv2d(4096, num_classes, 1)
)
def forward(self, x):
out = self.classifier(x)
return out
```
### Context Module
A context module is constructed based on the dilated convolution as below:

```
class BasicContextModule(nn.Module):
def __init__(self, num_classes):
super(BasicContextModule, self).__init__()
self.layer1 = nn.Sequential(conv_relu(num_classes, num_classes, 3, 1))
self.layer2 = nn.Sequential(conv_relu(num_classes, num_classes, 3, 1))
self.layer3 = nn.Sequential(conv_relu(num_classes, num_classes, 3, 2))
self.layer4 = nn.Sequential(conv_relu(num_classes, num_classes, 3, 4))
self.layer5 = nn.Sequential(conv_relu(num_classes, num_classes, 3, 8))
self.layer6 = nn.Sequential(conv_relu(num_classes, num_classes, 3, 16))
self.layer7 = nn.Sequential(conv_relu(num_classes, num_classes, 3, 1))
# No Truncation
self.layer8 = nn.Sequential(nn.Conv2d(num_classes, num_classes, 1, 1))
def forward(self, x):
out = self.layer1(x)
out = self.layer2(x)
out = self.layer3(x)
out = self.layer4(x)
out = self.layer5(x)
out = self.layer6(x)
out = self.layer7(x)
out = self.layer8(x)
return out
```
### DilatedNet
```
class DilatedNet(nn.Module):
def __init__(self, backbone, classifier, context_module):
super(DilatedNet, self).__init__()
self.backbone = backbone
self.classifier = classifier
self.context_module = context_module
self.deconv = nn.ConvTranspose2d(in_channels=21,
out_channels=21,
kernel_size=16,
stride=8,
padding=4)
def forward(self, x):
x = self.backbone(x)
x = self.classifier(x)
x = self.context_module(x)
x = self.deconv(x)
return x
# model output test
num_classes = 21
backbone = VGG16()
classifier = classifier(num_classes)
context_module = BasicContextModule(num_classes)
model = DilatedNet(backbone=backbone, classifier=classifier, context_module=context_module)
model.eval()
image = torch.randn(1, 3, 512, 512)
print("input:", image.shape)
print("output:", model(image).shape)
```
## CRF
```
import torch
import torch.nn as nn
from crfseg import CRF
model = nn.Sequential(
nn.Identity(), # your NN
CRF(n_spatial_dims=2)
)
batch_size, n_channels, spatial = 10, 3,(100, 100)
x = torch.zeros(batch_size, n_channels, *spatial)
log_proba = model(x)
```
### Reference
---
- [Dilated Convolution for Semantic Image Segmentation using caffe](https://github.com/fyu/dilation/blob/master/network.py)
|
github_jupyter
|
import os
import time
import numpy as np
import matplotlib.pyplot as plt
import PIL
import torch
import torch.nn as nn
import torch.optim as optim
from torchvision import models
from torchvision.models import vgg16
from torchvision import datasets, transforms
print('pytorch version: {}'.format(torch.__version__))
print('GPU 사용 가능 여부: {}'.format(torch.cuda.is_available()))
device = "cuda" if torch.cuda.is_available() else "cpu" # GPU 사용 가능 여부에 따라 device 정보 저장
import torch
import torch.nn as nn
def conv_relu(in_ch, out_ch, size=3, rate=1):
conv_relu = nn.Sequential(nn.Conv2d(in_channels=in_ch,
out_channels=out_ch,
kernel_size=3,
stride=1,
padding=rate,
dilation=rate),
nn.ReLU())
return conv_relu
class VGG16(nn.Module):
def __init__(self):
super(VGG16, self).__init__()
self.features1 = nn.Sequential(conv_relu(3, 64, 3, 1),
conv_relu(64, 64, 3, 1),
nn.MaxPool2d(2, stride=2, padding=0)) # 1/2
self.features2 = nn.Sequential(conv_relu(64, 128, 3, 1),
conv_relu(128, 128, 3, 1),
nn.MaxPool2d(2, stride=2, padding=0)) # 1/4
self.features3 = nn.Sequential(conv_relu(128, 256, 3, 1),
conv_relu(256, 256, 3, 1),
conv_relu(256, 256, 3, 1),
nn.MaxPool2d(2, stride=2, padding=0)) # 1/8
self.features4 = nn.Sequential(conv_relu(256, 512, 3, 1),
conv_relu(512, 512, 3, 1),
conv_relu(512, 512, 3, 1))
# and replace subsequent conv layer rate=2
self.features5 = nn.Sequential(conv_relu(512, 512, 3, 2),
conv_relu(512, 512, 3, 2),
conv_relu(512, 512, 3, 2))
def forward(self, x):
out = self.features1(x)
out = self.features2(out)
out = self.features3(out)
out = self.features4(out)
out = self.features5(out)
return out
class classifier(nn.Module):
def __init__(self, num_classes):
super(classifier, self).__init__()
self.classifier = nn.Sequential(conv_relu(512, 4096, 7, rate=4),
nn.Dropout2d(0.5),
conv_relu(4096, 4096, 1, 1),
nn.Dropout2d(0.5),
nn.Conv2d(4096, num_classes, 1)
)
def forward(self, x):
out = self.classifier(x)
return out
class BasicContextModule(nn.Module):
def __init__(self, num_classes):
super(BasicContextModule, self).__init__()
self.layer1 = nn.Sequential(conv_relu(num_classes, num_classes, 3, 1))
self.layer2 = nn.Sequential(conv_relu(num_classes, num_classes, 3, 1))
self.layer3 = nn.Sequential(conv_relu(num_classes, num_classes, 3, 2))
self.layer4 = nn.Sequential(conv_relu(num_classes, num_classes, 3, 4))
self.layer5 = nn.Sequential(conv_relu(num_classes, num_classes, 3, 8))
self.layer6 = nn.Sequential(conv_relu(num_classes, num_classes, 3, 16))
self.layer7 = nn.Sequential(conv_relu(num_classes, num_classes, 3, 1))
# No Truncation
self.layer8 = nn.Sequential(nn.Conv2d(num_classes, num_classes, 1, 1))
def forward(self, x):
out = self.layer1(x)
out = self.layer2(x)
out = self.layer3(x)
out = self.layer4(x)
out = self.layer5(x)
out = self.layer6(x)
out = self.layer7(x)
out = self.layer8(x)
return out
class DilatedNet(nn.Module):
def __init__(self, backbone, classifier, context_module):
super(DilatedNet, self).__init__()
self.backbone = backbone
self.classifier = classifier
self.context_module = context_module
self.deconv = nn.ConvTranspose2d(in_channels=21,
out_channels=21,
kernel_size=16,
stride=8,
padding=4)
def forward(self, x):
x = self.backbone(x)
x = self.classifier(x)
x = self.context_module(x)
x = self.deconv(x)
return x
# model output test
num_classes = 21
backbone = VGG16()
classifier = classifier(num_classes)
context_module = BasicContextModule(num_classes)
model = DilatedNet(backbone=backbone, classifier=classifier, context_module=context_module)
model.eval()
image = torch.randn(1, 3, 512, 512)
print("input:", image.shape)
print("output:", model(image).shape)
import torch
import torch.nn as nn
from crfseg import CRF
model = nn.Sequential(
nn.Identity(), # your NN
CRF(n_spatial_dims=2)
)
batch_size, n_channels, spatial = 10, 3,(100, 100)
x = torch.zeros(batch_size, n_channels, *spatial)
log_proba = model(x)
| 0.918891 | 0.785966 |
# 분산 분석 (ANOVA)
선형 회귀 분석의 결과가 어느 정도의 성능을 가지는지는 단순히 잔차 제곱합(RSS: Residula Sum of Square)으로 평가할 수 없다. 변수의 스케일이 달라지면 회귀 분석과 상관없이 잔차 제곱합도 같이 커지기 때문이다.
분산 분석(ANOVA:Analysis of Variance)은 종속 변수의 분산과 독립 변수의 분산간의 관계를 사용하여 선형 회귀 분석의 성능을 평가하고자 하는 방법이다. 분산 분석은 서로 다른 두 개의 선형 회귀 분석의 성능 비교에 응용할 수 있으며 독립 변수가 카테고리 변수인 경우 각 카테고리 값에 따른 영향을 정량적으로 분석하는데도 사용된다.
## 분산
$\bar{y}$를 종속 변수 $y$의 샘플 평균이라고 하자.
$$\bar{y}=\frac{1}{N}\sum_{i=1}^N y_i $$
종속 변수의 분산을 나타내는 TSS(total sum of square)라는 값을 정의한다.
$$\text{TSS} = \sum_i (y_i-\bar{y})^2$$
마찬가지로 회귀 분석에 의해 예측한 종속 변수의 분산을 나타내는 ESS(explained sum of squares),
$$\text{ESS}=\sum_i (\hat{y}_i -\bar{y})^2,$$
오차의 분산을 나타내는 RSS(residual sum of squares)도 정의한다.
$$\text{RSS}=\sum_i (y_i - \hat{y}_i)^2\,$$
이 때 이들 분산 간에는 다음과 같은 관계가 성립한다.
$$\text{TSS} = \text{ESS} + \text{RSS}$$
이는 다음과 같이 증명한다.
우선 회귀 분석으로 구한 가중치 벡터를 $\hat{w}$, 독립 변수(설명 변수) $x$에 의한 종속 변수의 추정값을 $\hat{y}$, 잔차를 $e$ 라고 하면 다음 식이 성립한다.
$$ y = X\hat{w} + e = \hat{y} + e $$
따라서
$$
y_i - \bar{y} = \hat{y}_i - \bar{y} + e_i = (x_i - \bar{x})\hat{w} + e_i
$$
를 벡터화하면
$$
y - \bar{y} = \hat{y} - \bar{y} + e_i = (X- \bar{X})\hat{w} + e
$$
여기에서 $\bar{X}$는 각 열이 $X$의 해당 열의 평균인 행렬이다.
이 식에 나온 $X-\bar{X}$와 잔차 $e$는 다음과 같은 독립 관계가 성립한다.
$$ X^Te = \bar{X}Te = 0 $$
이 식들을 정리하면 다음과 같다.
$$
\begin{eqnarray}
\text{TSS}
&=& (y - \bar{y})^T(y - \bar{y} ) \\
&=& (\hat{y} - \bar{y} + e)^T(\hat{y} - \bar{y} + e) \\
&=& (\hat{y} - \bar{y})^T(\hat{y} - \bar{y}) + e^Te + 2(\hat{y} - \bar{y})^Te \\
&=& (\hat{y} - \bar{y})^T(\hat{y} - \bar{y}) + e^Te + 2\hat{w}^T(X - \bar{X})^Te \\
&=& (\hat{y} - \bar{y})^T(\hat{y} - \bar{y}) + e^Te \\
&=& \text{ESS} + \text{RSS}
\end{eqnarray}
$$
## 결정 계수 (Coefficient of Determination)
위의 분산 관계식에서 다음과 같이 결정 계수(Coefficient of Determination) $R^2$를 정의할 수 있다.
$$R^2 \equiv 1 - \dfrac{\text{RSS}}{\text{TSS}}\ = \dfrac{\text{ESS}}{\text{TSS}}\ $$
분산 관계식과 모든 분산값이 0보다 크다는 점을 이용하면 $R^2$의 값은 다음과 같은 조건을 만족함을 알 수 있다.
$$0 \leq R^2 \leq 1$$
여기에서 $R^2$가 0이라는 것은 오차의 분산 RSS가 최대이고 회귀 분석 결과의 분산 ESS가 0인 경우이므로 회귀 분석의 결과가 아무런 의미가 없다는 뜻이다.
반대로 $R^2$가 1이라는 것은 오차의 분산 RSS가 0이고 회귀 분석 결과의 분산 ESS가 TSS와 같은 경우이므로 회귀 분석의 결과가 완벽하다는 뜻이다.
따라서 결정 계수값은 회귀 분석의 성능을 나타내는 수치라고 할 수 있다.
## F-검정
$R^2 = 0$인 경우에 다음 값은 F-분포를 따른다.
$$ \dfrac{R^2/(K-1)}{(1-R^2)(N-K)} \sim F(K-1, N-K) $$
따라서 이 값은 $R^2 = 0$인 귀무가설에 대한 검정 통계량으로 사용할 수 있다. 이러한 검정을 Loss-of-Fit test (Regression F-test)이라고 한다.
## 분산 분석표
분산 분석의 결과는 보통 다음과 같은 분산 분석표를 사용하여 표시한다.
| | source | degree of freedom | mean square | F statstics |
|-|-|-|-|-|
| Regression | $$\text{ESS}$$ | $$K-1$$ | $$s_{\hat{y}}^2 = \dfrac{\text{ESS}}{K-1}$$ | $$F$$ |
| Residual | $$\text{RSS}$$ | $$N-K$$ | $$s_e^2= \dfrac{\text{RSS}}{N-K}$$ |
| Total | $$\text{TSS}$$ | $$N-1$$ | $$s_y^2= \dfrac{\text{TSS}}{N-1}$$ |
| $R^2$ | $$\text{ESS} / \text{TSS}$$ |
statsmodels 에서는 다음과 같이 `anova_lm` 명령을 사용하여 분산 분석표를 출력할 수 있다. 다만 이 명령을 사용하기 위해서는 모형을 `from_formula` 메서드로 생성하여야 한다.
```
from sklearn.datasets import make_regression
X0, y, coef = make_regression(n_samples=100, n_features=1, noise=20, coef=True, random_state=0)
dfX0 = pd.DataFrame(X0, columns=["X"])
dfX = sm.add_constant(dfX0)
dfy = pd.DataFrame(y, columns=["Y"])
df = pd.concat([dfX, dfy], axis=1)
model = sm.OLS.from_formula("Y ~ X", data=df)
result = model.fit()
table = sm.stats.anova_lm(result)
table
```
## 다변수 분산 분석
독립 변수가 복수인 경우에는 각 독립 변수에 대한 F 검정 통계량을 구할 수 있다. 이 값은 각 변수만을 가진 복수의 모형의 성능을 비교하는 것과 같으므로 독립 변수의 영향력을 측정하는 것이 가능하다.
```
from sklearn.datasets import load_boston
boston = load_boston()
dfX0_boston = pd.DataFrame(boston.data, columns=boston.feature_names)
dfy_boston = pd.DataFrame(boston.target, columns=["MEDV"])
import statsmodels.api as sm
dfX_boston = sm.add_constant(dfX0_boston)
df_boston = pd.concat([dfX_boston, dfy_boston], axis=1)
model = sm.OLS.from_formula("MEDV ~ CRIM + ZN +INDUS + NOX + RM + AGE + DIS + RAD + TAX + PTRATIO + B + LSTAT + C(CHAS)", data=df_boston)
result = model.fit()
table = sm.stats.anova_lm(result)
table
```
|
github_jupyter
|
from sklearn.datasets import make_regression
X0, y, coef = make_regression(n_samples=100, n_features=1, noise=20, coef=True, random_state=0)
dfX0 = pd.DataFrame(X0, columns=["X"])
dfX = sm.add_constant(dfX0)
dfy = pd.DataFrame(y, columns=["Y"])
df = pd.concat([dfX, dfy], axis=1)
model = sm.OLS.from_formula("Y ~ X", data=df)
result = model.fit()
table = sm.stats.anova_lm(result)
table
from sklearn.datasets import load_boston
boston = load_boston()
dfX0_boston = pd.DataFrame(boston.data, columns=boston.feature_names)
dfy_boston = pd.DataFrame(boston.target, columns=["MEDV"])
import statsmodels.api as sm
dfX_boston = sm.add_constant(dfX0_boston)
df_boston = pd.concat([dfX_boston, dfy_boston], axis=1)
model = sm.OLS.from_formula("MEDV ~ CRIM + ZN +INDUS + NOX + RM + AGE + DIS + RAD + TAX + PTRATIO + B + LSTAT + C(CHAS)", data=df_boston)
result = model.fit()
table = sm.stats.anova_lm(result)
table
| 0.616705 | 0.983565 |
## The Variational Quantum Thermalizer
Author: Jack Ceroni
```
# Starts by importing all of the necessary dependencies
import pennylane as qml
from matplotlib import pyplot as plt
import numpy as np
from numpy import array
import scipy
from scipy.optimize import minimize
import random
import math
from tqdm import tqdm
import networkx as nx
import seaborn
```
### Introduction
In this Notebook, we will be discussing how to go about implementing and experimenting a recently proposed quantum algorithm called the **Variational Quantum Thermalizer**. Essentially, this algorithm is able to use a variational approach to reconstruct the thermal state of a given Hamiltonian at a given temperature. This is a task that is performed much more efficiently on a quantum device than a classical simulations performing the same calculations (for large enough systems). In fact, the original paper demonstrates that the VQT is actually a generalization of VQE, and as the effective "temperature" of our simulation approaches zero, our algorithm similarly approaches the VQE.
### The Idea
Before we actually jump into simulations of this algorithm, we will attempt to understand the mathematical and physical theory that makes this theory possible. For more background on variational quantum algorithms, and why VQE actually works, check out the other tutorials in the QML gallery (like [this one](https://pennylane.ai/qml/demos/tutorial_vqe.html)).
First off all, let us consider what we are actually trying to accomplish using this algorithm. We want to construct a **thermal state**, which is defined as:
<br>
$$\rho_\text{thermal} \ = \ \frac{e^{- H \beta / k_B}}{\text{Tr}(e^{- H \beta / k_B})} \ = \ \frac{e^{- H \beta / k_B}}{Z_{\beta}}$$
<br>
Where $H$ is the Hamiltonian of our system, $\beta \ = \ 1/T$, where $T$ is the temperature of our system, and $k_B$ is Boltzman's constant, which we will set to $1$ for the remainder of this Notebook.
The thermal state is the state of some quantum system, corresponding to some arbitrary Hamiltonian, such that the system is in **thermal equilibrium**. If we initialize some collection of particles at some arbitrary temperature, then over time, as entropy increases, the entire system approaches thermal equilibrium. The state of the system when it evolves into this thermal equilibrium is this thermal state. Knowing this state, allows us to in turn extract information about the system that we are studying, allowing to better understand the properties of materials/systems (for instance, superconductors, Bose-Hubbard models, etc.) **at thermal equilibrium**.
Inputed into our algorithm is an arbitrary Hamiltonian $H$, and our goal is to find $\rho_\text{thermal}$, or more specifically, the variational parameters that give us a state that is very "close" to $\rho_\text{thermal}$, as one does in any kind of variational quantum algorithm.
In order to do this, we will pick some "simple" mixed state to begin our process. This initial density matrix will be parametrized by a collection of parameters $\boldsymbol\theta$, which will describe the probabilities corresponding to different pure states. In this implementation of the algorithm, we will use the idea of a **factorized latent space** where the initial density matrix describing our quantum system in completely un-correlated. It is simply a tensor product of multiple $2 \times 2$, diagonal (in the computational basis) density matrices, each corresponding to one qubit. This works well for scalability of the algorithm, because instead of requiring $|\boldsymbol\theta| = 2^n$, for an $n$ qubit, diagonal density matrix, where we assign probabilities to each possible basis state, $|\theta| = n$, since for qubit $i$, we can assign probability $p_i(\theta_i)$ to $|0\rangle$, and $1 - p_i(\theta_i)$ to $|1\rangle$.
We will then sample from the probability distribution of measurements of different pure states. More concretely, if we have some initial mixed state:
<br>
$$\rho \ = \ \displaystyle\sum_{i} p_i |x_i\rangle \langle x_i|$$
<br>
Then the probability of our system being in state $|x_i\rangle$ is given by $p_i$. We repeatedly sample values of $x_i$ corresponding to pure states in the expansion of our "simple" mixed state and pass the corresponding $|x_i\rangle$ through a parametrized quantum circuit. We repeat this process, calculating the expectation value of the Hamiltonian with respect to the unitary-evolved density matrix. We then use this value along with the Von Neumann entropy of our state to create a **free energy cost function**, which is given by:
<br>
$$\mathcal{L}(\theta, \ \phi) \ = \ \beta \langle \hat{H} \rangle \ - \ S_\theta \ = \ \beta \ \text{Tr} (\hat{H} \ \rho_{\theta \phi}) \ - \ S_\theta \ = \ \beta \ \text{Tr}( \hat{H} \ \hat{U}(\phi) \rho_{\theta} \hat{U}(\phi)^{\dagger} ) \ - \ S_\theta$$
<br>
Where $\rho_\theta$ is the initial density matrix, $U(\phi)$ is the paramterized ansatz, and $S_\theta$ is the von Neumann entropy of $\rho_{\theta \phi}$. It is important to note that the von Neumann entropy of $\rho_{\theta \phi}$ is the same as the von Neumann entropy of $\phi_{\theta}$, since entropy is invariant under unitary transformations:
<br>
$$S(\rho') \ = \ - \text{Tr} (\rho' \log \rho') \ = \ - \text{Tr} ( U \rho U^{\dagger} \log (U \rho U^{\dagger})) \ = \ - \text{Tr} ( U \rho U^{\dagger} \log \rho) \ = \ - \text{Tr} ( U \rho \log \rho U^{\dagger}) \ = \ - \text{Tr} ( \rho \log \rho U^{\dagger} U) \ = \ - \text{Tr} ( \rho \log \rho) \ = \ S(\rho)$$
<br>
We repeat the algorithm with new parameters until we minimize free energy. Once we have done this, we have arrived at the thermal state. this comes from the fact that our free enrgy cost function is equivalent to the relative entropy between $\rho_{\theta \phi}$ and our target thermal state. Relative entropy is defined as:
<br>
$$D(\rho_1 || \rho_2) \ = \ \text{Tr} (\rho_1 \log \rho_1) \ - \ \text{Tr}(\rho_1 \log \rho_2)$$
<br>
If we let $\rho_1$ be $\rho_{\theta \phi}$ and $\rho_2$ be our thermal state, we get:
<br>
$$D(\rho_{\theta \phi} || \rho_{\text{Thermal}}) \ = \ -S_{\theta} \ - \ \text{Tr}(\rho_{\theta \phi} (-\beta \hat{H} \ - \ \log Z_{\beta})) \ = \ \beta \text{Tr} (\rho_{\theta \phi} \hat{H}) \ + \ \log Z_{\beta} \text{Tr}(\rho_{\theta \phi}) \ - \ S_{\theta} \ = \ \beta \langle \hat{H} \rangle \ - \ S_{\theta} \ + \ \log Z_{\beta} \ = \ \mathcal{L}(\theta, \ \phi) \ + \ \log Z_{\beta}$$
<br>
Since relative entropy must be positive, and is clearly $0$ when $\rho_{\theta \phi} \ = \ \rho_{\text{Thermal}}$, it follows that relative entropy, and hence $\mathcal{L}(\theta, \ \phi)$ (since it only differs from rleative entropy by an overall additive constant), are minimized when $\rho_{\theta \phi} \ = \ \rho_{\text{Thermal}}$. So, we know that we have to minimize $\mathcal{L}$ to find the thermal state. More specifically, when $\mathcal(\theta, \ \phi) \ = \ - \log Z_{\beta}$, then we have minimized the cost function and have found the thermal state.
For a diagramatic representation of how this works, check out Figure 3 from the [original VQT paper](https://arxiv.org/abs/1910.02071).
### The 3-Qubit Ising Model on a Line
We will begin by consdering the Ising model on a linear graph, for 3 qubits. This is a fairly simple model, and will act as a good test to see if the VQT is working as it is supposed to.
#### Numerical Calculation of Target State
We begin by calculating the target state numerically, so that it can be compared to the state our circuit prepares. We begin by defining a few fixed values that we will use throughout this example:
```
# Defines all necessary variables
beta = 0.5 #Note that B = 1/T
qubit = 3 # Number of qubits being used
qubits = range(qubit)
# Defines the device on which the simulation is run
dev = qml.device("default.qubit", wires=len(qubits))
```
The model that we are investigating lives on a linear graph, which we will construct using `networkx` for the purposes of eventually constructing our Hamiltonian:
```
# Creates the graph of interactions for the Heisenberg grid, then draws it
interaction_graph = nx.Graph()
interaction_graph.add_nodes_from(range(0, qubit))
interaction_graph.add_edges_from([(0, 1), (1, 2)])
nx.draw(interaction_graph)
```
Next, we can implemented a method that actually allows us to calculate the matrix form of our Hamiltonian (in the $Z$-basis). The Ising model Hamiltonian can be written as:
<br>
$$\hat{H} \ = \ \displaystyle\sum_{j} X_{j} X_{j + 1} \ + \ \displaystyle\sum_{i} Z_{i}$$
<br>
We can write this as a function, that returns the $n$-qubit matrix form of the Ising model Hamiltonian:
```
# Builds the Ising model Hamiltonian, for a given number of qubits and an interaction graph
def create_hamiltonian_matrix(n, graph):
pauli_x = np.array([[0, 1], [1, 0]])
pauli_y = np.array([[0, -1j], [1j, 0]])
pauli_z = np.array([[1, 0], [0, -1]])
identity = np.array([[1, 0], [0, 1]])
matrix = np.zeros((2**n, 2**n))
for i in graph.edges:
m = 1
for j in range(0, n):
if (j == i[0] or j == i[1]):
m = np.kron(m, pauli_x)
else:
m = np.kron(m, identity)
matrix = np.add(matrix, m)
for i in range(0, n):
m = 1
for j in range(0, n):
if (j == i):
m = np.kron(m, pauli_z)
else:
m = np.kron(m, identity)
matrix = np.add(matrix, m)
return matrix
# Constructs the Hamiltonian we will deal with in this simulation
ham_matrix = create_hamiltonian_matrix(qubit, interaction_graph)
print(ham_matrix)
```
With all of this done, all that is left to do is construct the target thermal state. We know that the thermal state is of the form:
<br>
$$\rho_{\text{thermal}} \ = \ \frac{e^{-\beta \hat{H}}}{Z_{\beta}}$$
<br>
Thus, we can calculate it by taking the matrix exponential of the Hamiltonian. The partition function can be found by simply taking the trace of the numerator (as it simply acts as a normalization factor). In addition to finding the thermal state, let's go one step further and also calculate the value of the cost function associated with this target state. Thus, we will have:
```
# Creates the target density matrix
def create_target(qubit, beta, ham, graph):
# Calculates the matrix form of the density matrix, by taking the exponential of the Hamiltonian
h = ham(qubit, graph)
y = -1*float(beta)*h
new_matrix = scipy.linalg.expm(np.array(y))
norm = np.trace(new_matrix)
final_target = (1/norm)*new_matrix
# Calculates the entropy, the expectation value, and the final cost
entropy = -1*np.trace(np.matmul(final_target, scipy.linalg.logm(final_target)))
ev = np.trace(np.matmul(final_target, h))
real_cost = beta*np.trace(np.matmul(final_target, h)) - entropy
# Prints the calculated values
print("Expectation Value: "+str(ev))
print("Entropy: "+str(entropy))
print("Final Cost: "+str(real_cost))
return final_target
```
Finally, we can calculate the thermal state corresponding to our Hamiltonian and inverse temperature, and visualize it using the `seaborn` data visualization library:
```
# Plots the final density matrix
final_density_matrix = create_target(qubit, beta, create_hamiltonian_matrix, interaction_graph)
seaborn.heatmap(abs(final_density_matrix))
```
#### Variational Quantum Thermalization of the Heisenberg Model
Now that we know exactly what our thermal state should look like, let's attempt to construct it with the VQT. Let's begin by constructing the classical probability distribution, which gives us the probabilities corresponding to each basis state in the expansion of our density matrix. As we discussed earlier in this Notebook, we will be using the factorized latent space model. We just have to decide how we will define each probability in the factorized space. We will let the probability associated with the $j$-th one-qubit system be:
<br>
$$p_{j}(\theta_{j}) \ = \ \frac{e^{\theta_j}}{e^{\theta_j} \ + \ 1}$$
<br>
The motivation behind this choice is the fact that this function has a range of $0$ to $1$, which is natural for defining probability without constraining our parameters. In addition, this function is called a sigmoid, and is a common choice as an activation function in machine learning methods. We can implement the sigmoid as:
```
# Creates the probability distribution according to the theta parameters
def sigmoid(x):
return (math.exp(x) / (math.exp(x) + 1))
```
From this, we can construct a function that actually constructs the probability distribution itself, which will be a function that returns a list of pairs of probabilities that correspond to each one-qubit system in the factorized latent space:
```
# Creates the probability distributions for each of the one-qubit systems
def prob_dist(params):
dist = []
for i in params:
dist.append([sigmoid(i), 1-sigmoid(i)])
return dist
```
Now, with this done, we have to define the quantum parts of our circuit. Befor any qubit register is passed through the variational circuit, we must prepare it in a given basis state. Thus, we can write a function that takes a list of bits, and returns a quantum circuit that prepares the corresponding basis state (in the computational basis):
```
#Creates the initialization unitary for each of the computational basis states
def create_v_gate(prep_state):
for i in range(0, len(prep_state)):
if (prep_state[i].val == 1):
qml.PauliX(wires=i)
```
All that is left to do before we construct the cost function is to construct the parametrized circuit, through which we pass our initial states. We will use a multi-layered ansatz, where each layer is composed of $RX$, $RZ$, and. $RY$ gates on each qubit, followed by exponentiated $CNOT$ gates placed between qubits that share an edge in the interaction graph. Our general single-qubit rotations can be implemented as:
```
# Creates the single rotational ansatz
def single_rotation(phi_params, q):
qml.RZ(phi_params[0], wires=q)
qml.RY(phi_params[1], wires=q)
qml.RX(phi_params[2], wires=q)
```
Putting this together with the $CNOT$ gates, we have a general ansatz of the form:
```
# Creates the ansatz circuit
def ansatz_circuit(params, qubits, layers, graph, param_number):
param_number = int(param_number.val)
number = param_number*qubit + len(graph.edges)
# Partitions the parameters into param lists
partition = []
for i in range(0, int((len(params)/number))):
partition.append(params[number*i:number*(i+1)])
qubits = range(qubit)
for j in range(0, depth):
# Implements the single qubit rotations
sq = partition[j][0:(number-len(graph.edges))]
for i in qubits:
single_rotation(sq[i*param_number:(i+1)*param_number], i)
# Implements the coupling layer of gates
for count, i in enumerate(graph.edges):
p = partition[j][(number-len(graph.edges)):number]
qml.CRX(p[count], wires=[i[0], i[1]])
```
There are a lot of variables floating around in this function. The `param_number` variable simply tells us how many unique parameters we assign to each application of the single-qubit rotation layer. We multiply this by the number of qubits, to get the total number of single-rotation parameters, and then add the number of edges in the interaction graph, which will also be the number of unique parameters needed for the $CNOT$ gates. With all of these components, we can define a function that acts as our quantum circuit, and pass it into a QNode:
```
# Defines the depth of the variational circuit
depth = 3
# Creates the quantum circuit
def quantum_circuit(params, qubits, sample, param_number):
# Prepares the initial basis state corresponding to the sample
create_v_gate(sample)
# Prepares the variational ansatz for the circuit
ansatz_circuit(params, qubits, depth, interaction_graph, param_number)
# Calculates the expectation value of the Hamiltonian, with respect to the preparred states
return qml.expval(qml.Hermitian(ham_matrix, wires=range(qubit)))
qnode = qml.QNode(quantum_circuit, dev)
# Tests and draws the QNode
results = qnode([1 for i in range(0, 12*depth)], qubits, [1, 0, 1, 0], 3)
print(qnode.draw())
```
There is one more thing we must do before implementing the cost function: writing a method that allows us to calculate the entropy of a state. Actually implementing a function that calculates the Von Neumann entropy is not too involved. We will take a probability distribution as our argument, each entry of which corresponds to the digonal elements of the $1$-qubit subsystems. The entropy of a collection of subsystems is the same as the sum of the entropies of the indiivdual systems, so we get:
```
#Calculate the Von Neumann entropy of the initial density matrices
def calculate_entropy(distribution):
total_entropy = []
for i in distribution:
total_entropy.append(-1*i[0]*np.log(i[0]) + -1*i[1]*np.log(i[1]))
#Returns an array of the entropy values of the different initial density matrices
return total_entropy
```
Finally, we define the cost function. More specifically, this is an **exact** version of the VQT cost function. Instead of sampling from our classical probability distribution, we simply calculate the probability corresponding to every basis state, and thus calculate the energy expectation exactly for each iteration. this is not how the VQT would work in the real world, for large systems where the number of basis states (and thus the size of the probability distribution) scales exponentially, but for small toy-models such as this, the exact form runs faster:
```
def exact_cost(params):
global iterations
# Separates the list of parameters
dist_params = params[0:qubit]
params = params[qubit:]
# Creates the probability distribution
distribution = prob_dist(dist_params)
# Generates a list of all computational basis states, of our qubit system
s = [[int(i) for i in list(bin(k)[2:].zfill(qubit))] for k in range(0, 2**qubit)]
# Passes each basis state through the variational circuit and multiplis the calculated energy EV with the associated probability from the distribution
final_cost = 0
for i in s:
result = qnode(params, qubits, i, 3)
for j in range(0, len(i)):
result = result*distribution[j][i[j]]
final_cost += result
# Calculates the entropy and the final cost function
entropy = calculate_entropy(distribution)
final_final_cost = beta*final_cost - sum(entropy)
if (iterations%50 == 0):
print("Cost at Step "+str(iterations)+": "+str(final_final_cost))
iterations += 1
return final_final_cost
```
Finally, we optimize the cost function:
```
# Creates the optimizer
iterations = 0
params = [random.randint(-100, 100)/100 for i in range(0, (12*depth)+qubit)]
out = minimize(exact_cost, x0=params, method="COBYLA", options={'maxiter':1000})
params = out['x']
print(out)
```
With our optimal parameters, we now wish to prepare the state to which they correspond, to see "how close" our prepared state is to the target state. This can be done by simply taking the optimal parameters, and passing each possible basis state through the variational circuit. Each corresponding probability is multiplied by the outer product of the resulting state with itself. Once we add these all together, we are left with the density matrix corresponding to the optimal parameters.
```
def prepare_state(params, device):
# Initializes the density matrix
final_density_matrix_2 = np.zeros((2**qubit, 2**qubit))
# Prepares the optimal parameters, creates the distribution and the bitstrings
dist_params = params[0:qubit]
unitary_params = params[qubit:]
distribution = prob_dist(dist_params)
s = [[int(i) for i in list(bin(k)[2:].zfill(qubit))] for k in range(0, 2**qubit)]
# Runs the circuit in the case of the optimal parameters, for each bitstring, and adds the result to the final density matrix
for i in s:
qnode(unitary_params, qubits, i, 3)
state = device.state
for j in range(0, len(i)):
state = np.sqrt(distribution[j][i[j]])*state
final_density_matrix_2 = np.add(final_density_matrix_2, np.outer(state, np.conj(state)))
return final_density_matrix_2
final_density_matrix_2 = prepare_state(params, dev)
```
Now, we need to asess how "close together" the prepared and target state are. The trace distance of two density matrices is a valid metric (a "distance function" with certain properties) on the space on density matrices defined by:
<br>
$$T(\rho, \ \sigma) \ = \ \frac{1}{2} \text{Tr} \sqrt{(\rho \ - \ \sigma)^{\dagger} (\rho \ - \ \sigma)}$$
<br>
We can implement this as a function, and compute the trace distance between the target and prepared states:
```
# Finds the trace distance between two density matrices
def trace_distance(one, two):
return 0.5*np.trace(np.absolute(np.add(one, -1*two)))
print("Final Trace Distance: "+str(trace_distance(final_density_matrix_2, final_density_matrix)))
```
This is pretty good! A trace distance close to $0$ means that the states are "close together", meaning that we prepared a good approximation of the thermal state. If you prefer a vision representation, we can plot the prepared state as a heatmap:
```
seaborn.heatmap(abs(final_density_matrix_2))
```
Then, we can compare it to the target:
```
seaborn.heatmap(abs(final_density_matrix))
```
As you can see, the two images are not completely the same, but there is definitely some resemblance between them!
### The 4-Qubit Heisenberg Model on a Square
Let's look at one more example of the VQT in action, this time, for a slightly more complicated model.
#### Numerical Calculation of Target State
As we did in the above example, we define our fixed values:
```
# Defines all necessary variables
beta = 1 #Note that B = 1/T
qubit = 4
qubits = range(qubit)
depth = 2
# Defines the device on which the simulation is run
dev2 = qml.device("default.qubit", wires=len(qubits))
```
This model lives on a square-shaped graph:
```
# Creates the graph of interactions for the Heisenberg grid, then draws it
interaction_graph = nx.Graph()
interaction_graph.add_nodes_from(range(0, qubit))
interaction_graph.add_edges_from([(0, 1), (2, 3), (0, 2), (1, 3)])
nx.draw(interaction_graph)
```
Recall that the two-dimensional Heiseberg model Hamiltonian can be written as:
<br>
$$\hat{H} \ = \ \displaystyle\sum_{(i, j) \in E} X_i X_{j} \ + \ Z_i Z_{j} \ + \ Y_i Y_{j}$$
<br>
With this knowledge, we have:
```
# Creates the target Hamiltonian matrix
def create_hamiltonian_matrix(n, graph):
pauli_x = np.array([[0, 1], [1, 0]])
pauli_y = np.array([[0, -1j], [1j, 0]])
pauli_z = np.array([[1, 0], [0, -1]])
identity = np.array([[1, 0], [0, 1]])
matrix = np.zeros((2**n, 2**n))
for i in graph.edges:
m = 1
for j in range(0, n):
if (j == i[0] or j == i[1]):
m = np.kron(pauli_x, m)
else:
m = np.kron(identity, m)
matrix = np.add(matrix, m)
for i in graph.edges:
m = 1
for j in range(0, n):
if (j == i[0] or j == i[1]):
m = np.kron(m, pauli_y)
else:
m = np.kron(m, identity)
matrix = np.add(matrix, m)
for i in graph.edges:
m = 1
for j in range(0, n):
if (j == i[0] or j == i[1]):
m = np.kron(m, pauli_z)
else:
m = np.kron(m, identity)
matrix = np.add(matrix, m)
return matrix
ham_matrix = create_hamiltonian_matrix(qubit, interaction_graph)
print(ham_matrix)
```
So this is the $Z$-basis matrix form of the Hamiltonian. We then calculate the thermal state at the inverse temperature defined above:
```
# Plots the final density matrix
final_density_matrix = create_target(qubit, beta, create_hamiltonian_matrix, interaction_graph)
seaborn.heatmap(abs(final_density_matrix))
```
We will use the same form of the latent space, ansatz, and cost function as above, thus only minor modifications need to be made. We must re-define our qnode, since we are now using a device with $4$ qubits rather than $3$:
```
# QNode
qnode = qml.QNode(quantum_circuit, dev2)
```
We then run our optimizer:
```
# Creates the optimizer
iterations = 0
params = [random.randint(-100, 100)/100 for i in range(0, (16*depth)+qubit)]
out = minimize(exact_cost, x0=params, method="COBYLA", options={'maxiter':1000})
params = out['x']
print(out)
```
With our optimal parameters, we can post-process our data. We start by calculating the matrix form of the density matrix we prepared:
```
# Prepares the density matrix
final_density_matrix_2 = prepare_state(params, dev2)
```
We then calculate the trace distance:
```
# Calculates the trace distance
print("Final Trace Distance: "+str(trace_distance(final_density_matrix_2, final_density_matrix)))
```
This is pretty good, but it could be better (most likely with a deeper ansatz and a more sophisticated optimizer, but to keep execution time relatively sohrt, we will not go down those avenues in this Notebook). To end off, let's visualize our two density matrices:
```
seaborn.heatmap(abs(final_density_matrix_2))
```
And we print the target:
```
seaborn.heatmap(abs(final_density_matrix))
```
### References
1. Verdon, G., Marks, J., Nanda, S., Leichenauer, S., & Hidary, J. (2019). Quantum Hamiltonian-Based Models and the Variational Quantum Thermalizer Algorithm. arXiv preprint [arXiv:1910.02071](https://arxiv.org/abs/1910.02071).
|
github_jupyter
|
# Starts by importing all of the necessary dependencies
import pennylane as qml
from matplotlib import pyplot as plt
import numpy as np
from numpy import array
import scipy
from scipy.optimize import minimize
import random
import math
from tqdm import tqdm
import networkx as nx
import seaborn
# Defines all necessary variables
beta = 0.5 #Note that B = 1/T
qubit = 3 # Number of qubits being used
qubits = range(qubit)
# Defines the device on which the simulation is run
dev = qml.device("default.qubit", wires=len(qubits))
# Creates the graph of interactions for the Heisenberg grid, then draws it
interaction_graph = nx.Graph()
interaction_graph.add_nodes_from(range(0, qubit))
interaction_graph.add_edges_from([(0, 1), (1, 2)])
nx.draw(interaction_graph)
# Builds the Ising model Hamiltonian, for a given number of qubits and an interaction graph
def create_hamiltonian_matrix(n, graph):
pauli_x = np.array([[0, 1], [1, 0]])
pauli_y = np.array([[0, -1j], [1j, 0]])
pauli_z = np.array([[1, 0], [0, -1]])
identity = np.array([[1, 0], [0, 1]])
matrix = np.zeros((2**n, 2**n))
for i in graph.edges:
m = 1
for j in range(0, n):
if (j == i[0] or j == i[1]):
m = np.kron(m, pauli_x)
else:
m = np.kron(m, identity)
matrix = np.add(matrix, m)
for i in range(0, n):
m = 1
for j in range(0, n):
if (j == i):
m = np.kron(m, pauli_z)
else:
m = np.kron(m, identity)
matrix = np.add(matrix, m)
return matrix
# Constructs the Hamiltonian we will deal with in this simulation
ham_matrix = create_hamiltonian_matrix(qubit, interaction_graph)
print(ham_matrix)
# Creates the target density matrix
def create_target(qubit, beta, ham, graph):
# Calculates the matrix form of the density matrix, by taking the exponential of the Hamiltonian
h = ham(qubit, graph)
y = -1*float(beta)*h
new_matrix = scipy.linalg.expm(np.array(y))
norm = np.trace(new_matrix)
final_target = (1/norm)*new_matrix
# Calculates the entropy, the expectation value, and the final cost
entropy = -1*np.trace(np.matmul(final_target, scipy.linalg.logm(final_target)))
ev = np.trace(np.matmul(final_target, h))
real_cost = beta*np.trace(np.matmul(final_target, h)) - entropy
# Prints the calculated values
print("Expectation Value: "+str(ev))
print("Entropy: "+str(entropy))
print("Final Cost: "+str(real_cost))
return final_target
# Plots the final density matrix
final_density_matrix = create_target(qubit, beta, create_hamiltonian_matrix, interaction_graph)
seaborn.heatmap(abs(final_density_matrix))
# Creates the probability distribution according to the theta parameters
def sigmoid(x):
return (math.exp(x) / (math.exp(x) + 1))
# Creates the probability distributions for each of the one-qubit systems
def prob_dist(params):
dist = []
for i in params:
dist.append([sigmoid(i), 1-sigmoid(i)])
return dist
#Creates the initialization unitary for each of the computational basis states
def create_v_gate(prep_state):
for i in range(0, len(prep_state)):
if (prep_state[i].val == 1):
qml.PauliX(wires=i)
# Creates the single rotational ansatz
def single_rotation(phi_params, q):
qml.RZ(phi_params[0], wires=q)
qml.RY(phi_params[1], wires=q)
qml.RX(phi_params[2], wires=q)
# Creates the ansatz circuit
def ansatz_circuit(params, qubits, layers, graph, param_number):
param_number = int(param_number.val)
number = param_number*qubit + len(graph.edges)
# Partitions the parameters into param lists
partition = []
for i in range(0, int((len(params)/number))):
partition.append(params[number*i:number*(i+1)])
qubits = range(qubit)
for j in range(0, depth):
# Implements the single qubit rotations
sq = partition[j][0:(number-len(graph.edges))]
for i in qubits:
single_rotation(sq[i*param_number:(i+1)*param_number], i)
# Implements the coupling layer of gates
for count, i in enumerate(graph.edges):
p = partition[j][(number-len(graph.edges)):number]
qml.CRX(p[count], wires=[i[0], i[1]])
# Defines the depth of the variational circuit
depth = 3
# Creates the quantum circuit
def quantum_circuit(params, qubits, sample, param_number):
# Prepares the initial basis state corresponding to the sample
create_v_gate(sample)
# Prepares the variational ansatz for the circuit
ansatz_circuit(params, qubits, depth, interaction_graph, param_number)
# Calculates the expectation value of the Hamiltonian, with respect to the preparred states
return qml.expval(qml.Hermitian(ham_matrix, wires=range(qubit)))
qnode = qml.QNode(quantum_circuit, dev)
# Tests and draws the QNode
results = qnode([1 for i in range(0, 12*depth)], qubits, [1, 0, 1, 0], 3)
print(qnode.draw())
#Calculate the Von Neumann entropy of the initial density matrices
def calculate_entropy(distribution):
total_entropy = []
for i in distribution:
total_entropy.append(-1*i[0]*np.log(i[0]) + -1*i[1]*np.log(i[1]))
#Returns an array of the entropy values of the different initial density matrices
return total_entropy
def exact_cost(params):
global iterations
# Separates the list of parameters
dist_params = params[0:qubit]
params = params[qubit:]
# Creates the probability distribution
distribution = prob_dist(dist_params)
# Generates a list of all computational basis states, of our qubit system
s = [[int(i) for i in list(bin(k)[2:].zfill(qubit))] for k in range(0, 2**qubit)]
# Passes each basis state through the variational circuit and multiplis the calculated energy EV with the associated probability from the distribution
final_cost = 0
for i in s:
result = qnode(params, qubits, i, 3)
for j in range(0, len(i)):
result = result*distribution[j][i[j]]
final_cost += result
# Calculates the entropy and the final cost function
entropy = calculate_entropy(distribution)
final_final_cost = beta*final_cost - sum(entropy)
if (iterations%50 == 0):
print("Cost at Step "+str(iterations)+": "+str(final_final_cost))
iterations += 1
return final_final_cost
# Creates the optimizer
iterations = 0
params = [random.randint(-100, 100)/100 for i in range(0, (12*depth)+qubit)]
out = minimize(exact_cost, x0=params, method="COBYLA", options={'maxiter':1000})
params = out['x']
print(out)
def prepare_state(params, device):
# Initializes the density matrix
final_density_matrix_2 = np.zeros((2**qubit, 2**qubit))
# Prepares the optimal parameters, creates the distribution and the bitstrings
dist_params = params[0:qubit]
unitary_params = params[qubit:]
distribution = prob_dist(dist_params)
s = [[int(i) for i in list(bin(k)[2:].zfill(qubit))] for k in range(0, 2**qubit)]
# Runs the circuit in the case of the optimal parameters, for each bitstring, and adds the result to the final density matrix
for i in s:
qnode(unitary_params, qubits, i, 3)
state = device.state
for j in range(0, len(i)):
state = np.sqrt(distribution[j][i[j]])*state
final_density_matrix_2 = np.add(final_density_matrix_2, np.outer(state, np.conj(state)))
return final_density_matrix_2
final_density_matrix_2 = prepare_state(params, dev)
# Finds the trace distance between two density matrices
def trace_distance(one, two):
return 0.5*np.trace(np.absolute(np.add(one, -1*two)))
print("Final Trace Distance: "+str(trace_distance(final_density_matrix_2, final_density_matrix)))
seaborn.heatmap(abs(final_density_matrix_2))
seaborn.heatmap(abs(final_density_matrix))
# Defines all necessary variables
beta = 1 #Note that B = 1/T
qubit = 4
qubits = range(qubit)
depth = 2
# Defines the device on which the simulation is run
dev2 = qml.device("default.qubit", wires=len(qubits))
# Creates the graph of interactions for the Heisenberg grid, then draws it
interaction_graph = nx.Graph()
interaction_graph.add_nodes_from(range(0, qubit))
interaction_graph.add_edges_from([(0, 1), (2, 3), (0, 2), (1, 3)])
nx.draw(interaction_graph)
# Creates the target Hamiltonian matrix
def create_hamiltonian_matrix(n, graph):
pauli_x = np.array([[0, 1], [1, 0]])
pauli_y = np.array([[0, -1j], [1j, 0]])
pauli_z = np.array([[1, 0], [0, -1]])
identity = np.array([[1, 0], [0, 1]])
matrix = np.zeros((2**n, 2**n))
for i in graph.edges:
m = 1
for j in range(0, n):
if (j == i[0] or j == i[1]):
m = np.kron(pauli_x, m)
else:
m = np.kron(identity, m)
matrix = np.add(matrix, m)
for i in graph.edges:
m = 1
for j in range(0, n):
if (j == i[0] or j == i[1]):
m = np.kron(m, pauli_y)
else:
m = np.kron(m, identity)
matrix = np.add(matrix, m)
for i in graph.edges:
m = 1
for j in range(0, n):
if (j == i[0] or j == i[1]):
m = np.kron(m, pauli_z)
else:
m = np.kron(m, identity)
matrix = np.add(matrix, m)
return matrix
ham_matrix = create_hamiltonian_matrix(qubit, interaction_graph)
print(ham_matrix)
# Plots the final density matrix
final_density_matrix = create_target(qubit, beta, create_hamiltonian_matrix, interaction_graph)
seaborn.heatmap(abs(final_density_matrix))
# QNode
qnode = qml.QNode(quantum_circuit, dev2)
# Creates the optimizer
iterations = 0
params = [random.randint(-100, 100)/100 for i in range(0, (16*depth)+qubit)]
out = minimize(exact_cost, x0=params, method="COBYLA", options={'maxiter':1000})
params = out['x']
print(out)
# Prepares the density matrix
final_density_matrix_2 = prepare_state(params, dev2)
# Calculates the trace distance
print("Final Trace Distance: "+str(trace_distance(final_density_matrix_2, final_density_matrix)))
seaborn.heatmap(abs(final_density_matrix_2))
seaborn.heatmap(abs(final_density_matrix))
| 0.617282 | 0.993216 |
(07:Releasing-and-versioning)=
# Releasing and versioning
<hr style="height:1px;border:none;color:#666;background-color:#666;" />
Previous chapters have focused on how to develop a Python package from scratch; by creating the Python source code, developing a testing framework, writing documentation, and then releasing it online via PyPI (if desired). This chapter now describes the next step in the packaging workflow — updating your package!
At any given time, your package's users (including you) will install a particular version of your package in a project. If you change the package's source code, their code could potentially break (imagine you change a module name, or remove a function argument a user was using). To solve this problem, developers assign a unique version number to each unique state of their package and release each new version independently. Most of the time, users will want to use the most up-to-date version of your package, but sometimes, they'll need to use an older version that is compatible with their project. Releasing versions is also an important way of communicating to your users that your package has changed (e.g, bugs have been fixed, new features have been added, etc.).
In this chapter, we'll walk through the process of creating and releasing new versions of your Python package.
(07:Version-numbering)=
## Version numbering
Versioning\index{versioning} is the process of adding unique identifiers to different versions of your package. The unique identifier you use may be name-based or number-based, but most Python packages use [semantic versioning](https://semver.org)\index{semantic versioning}. In semantic versioning, a version number consists of three integers A.B.C, where A is the "major" version, B is the "minor" version, and C is the "patch" version. The first version of a software usually starts at 0.1.0 and increments from there. We call an increment a "bump" and it consists of adding 1 to either the major, minor, or patch identifier as follows:
- **Patch** release\index{versioning!patch} (0.1.0 -> 0.1.**1**): patch releases are typically used for bug fixes which are backward compatible. Backward compatibility refers to the compatibility of your package with previous versions of itself. For example, if a user was using v0.1.0 of your package, they should be able to upgrade to v0.1.1 and have any code they previously wrote still work. It's fine to have so many patch releases that you need to use two digits (e.g., 0.1.27).
- **Minor** release\index{versioning!minor} (0.1.0 -> 0.**2**.0): a minor release typically includes larger bug fixes or new features which are backward compatible, for example, the addition of a new function. It's fine to have so many minor releases that you need to use two digits (e.g., 0.13.0).
- **Major** release\index{versioning!major} (0.1.0 -> **1**.0.0): release 1.0.0 is typically used for the first stable release of your package. After that, major releases are made for changes that are not backward compatible and may affect many users. Changes that are not backward compatible are called "breaking changes". For example, changing the name of one of the modules in your package would be a breaking change; if users upgraded to your new package, any code they'd written using the old module name would no longer work and they would have to change it.
Most of the time, you'll be making patch and minor releases. We'll discuss major releases, breaking changes\index{breaking change}, and how to deprecate package functionality (i.e., remove it) more in **{numref}`07:Breaking-changes-and-deprecating-package-functionality`**.
Even with the guidelines above, versioning a package can be a little subjective and requires you to use your best judgment. For example, small packages might make a patch release for each individual bug fixed or a minor release for each new feature added. In contrast, larger packages will often group multiple bug fixes into a single patch release or multiple features into a single minor release; because making a release for every individual change would result in an overwhelming and confusing amount of releases! {numref}`07-release-table` shows some practical examples of major, minor, and patch releases made for the Python software itself. To formalize the circumstances under which different kinds of releases should be made, some developers create a "version policy" document for their package; the `pandas` [version policy](https://pandas.pydata.org/docs/development/policies.html#version-policy) is a good example of this.
```{table} Examples of major, minor, and patch releases of the Python software.
:name: 07-release-table
|Release Type|Version Bump|Description|
|:--- |:--- | :--- |
|Major|2.X.X -> 3.0.0 ([December, 2008](https://www.python.org/downloads/release/python-300/))| This release included breaking changes, for example, `print()` became a function, and integer division resulted in creation of a float rather than an integer. Many built-in objects like dictionaries and strings also changed considerably, and many old features were removed in this release.|
|Minor|3.8.X -> 3.9.0 ([October, 2020](https://www.python.org/downloads/release/python-390/))| Many new features and optimizations were added in this release, for example, new string methods to remove prefixes (`.removeprefix()`) and suffixes (`.removesuffix()`) were added and a new parser was implemented for CPython (the engine that actually compiles and executes your Python code).|
|Patch|3.9.5 -> 3.9.6 ([June, 2021](https://www.python.org/downloads/release/python-396/))| This release contained many bug fixes and maintenance changes, for example, a confusing error message was updated in the `str.format()` method, the version of `pip` bundled with Python downloads was updated from 21.1.2 -> 21.1.3, and several parts of the documentation were updated.|
```
## Version bumping
While we'll discuss the full workflow for releasing a new version of your package in **{numref}`07:Checklist-for-releasing-a-new-package-version`**, we first want to dicuss version bumping. That is, how to increment the version of your package when you're preparing a new release. This can be done manually or automatically as we'll discuss in the sections below.
(07:Manual-version-bumping)=
### Manual version bumping
Once you've decided what the new version\index{versioning!manual} of your package will be (i.e., are you making a patch, minor, or major release) you need to update the package's version number in your source code. For a `poetry`-managed project\index{poetry}, that information is in the *`pyproject.toml`* file\index{pyproject.toml}. Consider the *`pyproject.toml`* file of the `pycounts` package we developed in **Chapter 3: {ref}`03:How-to-package-a-Python`**, and the top of which looks like this:
```{code-block} toml
---
emphasize-lines: 3
---
[tool.poetry]
name = "pycounts"
version = "0.1.0"
description = "Calculate word counts in a text file!"
authors = ["Tomas Beuzen"]
license = "MIT"
readme = "README.md"
...rest of file hidden...
```
Imagine we wanted to make a patch release of our package. We could simply change the `version` number manually in this file to "0.1.1" and many developers do take this manual approach. An alternative method is to use the `poetry version` command. The `poetry version` command can be used with the arguments `patch`, `minor` or `major` depending on how you want to update the version of your package. For example, to make a patch release, we could run the following at the command line:
```{tip}
If you're building the `pycounts` package with us in this book, you don't have to run the below command, it is just for demonstration purposes. We'll make a new version of `pycounts` later in this chapter.
```
```{prompt} bash \$ auto
$ poetry version patch
```
```md
Bumping version from 0.1.0 to 0.1.1
```
This command changes the `version` variable in the `pyproject.toml` file:
```{code-block} toml
---
emphasize-lines: 3
---
[tool.poetry]
name = "pycounts"
version = "0.1.1"
description = "Calculate word counts in a text file!"
authors = ["Tomas Beuzen"]
license = "MIT"
readme = "README.md"
...rest of file hidden...
```
(07:Automatic-version-bumping)=
### Automatic version bumping
In this book, we're interested in automating as much as possible of the packaging workflow. While the manual versioning approach described above in **{numref}`07:Manual-version-bumping`** is certainly used by many developers, we can do things more efficiently! To automate version bumping\index{versioning!automatic}, you'll need to be using a version control system like Git. If you are not using version control\index{version control} for your package, you can skip to **{numref}`07:Checklist-for-releasing-a-new-package-version`**.
[Python Semantic Release\index{versioning!Python Semantic Release}\index{Python Semantic Release} (PSR)](https://python-semantic-release.readthedocs.io/en/latest/) is a tool that can automatically bump version numbers based on keywords it finds in commit messages. The idea is to use a standardized commit message format and syntax which PSR can parse to determine how to increment the version number. The default commit message format used by PSR is the [Angular commit style](https://github.com/angular/angular.js/blob/master/DEVELOPERS.md#commit-message-format) which looks like this:
```md
<type>(optional scope): short summary in present tense
(optional body: explains motivation for the change)
(optional footer: note BREAKING CHANGES here, and issues to be closed)
```
`<type>` refers to the kind of change made and is usually one of:
- `feat`: A new feature.
- `fix`: A bug fix.
- `docs`: Documentation changes.
- `style`: Changes that do not affect the meaning of the code (white-space, formatting, missing semi-colons, etc).
- `refactor`: A code change that neither fixes a bug nor adds a feature.
- `perf`: A code change that improves performance.
- `test`: Changes to the test framework.
- `build`: Changes to the build process or tools.
`scope` is an optional keyword that provides context for where the change was made. It can be anything relevant to your package or development workflow (e.g., it could be the module or function name affected by the change).
Different text in the commit message will trigger PSR to make different kinds of releases:
- A `<type>` of `fix` triggers a patch version bump, e.g.;
```{prompt} bash \$ auto
$ git commit -m "fix(mod_plotting): fix confusing error message in \
plot_words"
```
- A `<type>` of `feat` triggers a minor version bump, e.g.;
```{prompt} bash \$ auto
$ git commit -m "feat(package): add example data and new module to \
package"
```
- The text `BREAKING CHANGE:` in the `footer` will trigger a major release, e.g.,
```{prompt} bash \$ auto
$ git commit -m "feat(mod_plotting): move code from plotting module \
to pycounts module
$
$ BREAKING CHANGE: plotting module wont exist after this release."
```
To use PSR we need to install and configure it. To install PSR as a development dependency of a `poetry`-managed project, you can use the following command:
```{prompt} bash \$ auto
$ poetry add --dev python-semantic-release
```
To configure PSR, we need to tell it where the version number of our package is stored. The package version is stored in the *`pyproject.toml`* file for a `poetry`-managed project. It exists as the variable `version` under the table `[tool.poetry]`. To tell PSR this, we need to add a new table to the *`pyproject.toml`* file called `[tool.semantic_release]` within which we specify that our `version_variable` is stored at `pyproject.toml:version`:
```toml
...rest of file hidden...
[tool.semantic_release]
version_variable = "pyproject.toml:version"
```
Finally, you can use the command `semantic-release version` at the command line to get PSR to automatically bump your package's version number. PSR will parse all the commit messages since the last tag of your package to determine what kind of version bump to make. For example, imagine the following three commit messages have been made since tag v0.1.0:
```md
1. "fix(mod_plotting): raise TypeError in plot_words"
2. "fix(mod_plotting): fix confusing error message in plot_words"
3. "feat(package): add example data and new module to package"
```
PSR will note that there are two "fix" and one "feat" keywords. "fix" triggers a patch release, but "feat" triggers a minor release, which trumps a patch release, so PSR would make a minor version bump from v0.1.0 to v0.2.0.
As a more practical demonstration of how PSR works, imagine we have a package at version 0.1.0, make a bug fix and commit our changes with the following message:
```{tip}
If you're building the `pycounts` package with us in this book, you don't have to run the below commands, they are just for demonstration purposes. We'll make a new version of `pycounts` later in this chapter.
```
```{prompt} bash \$ auto
$ git add src/pycounts/plotting.py
$ git commit -m "fix(code): change confusing error message in \
plotting.plot_words"
```
We then run `semantic-release version` to update our version number. In the command below, we'll specify the argument `-v DEBUG` to ask PSR to print extra information to the screen so we can get an inside look at how PSR works:
```{prompt} bash \$ auto
$ semantic-release version -v DEBUG
```
```md
Creating new version
debug: get_current_version_by_config_file()
debug: Parsing current version: path=PosixPath('pyproject.toml')
debug: Regex matched version: 0.1.0
debug: get_current_version_by_config_file -> 0.1.0
Current version: 0.1.0
debug: evaluate_version_bump('0.1.0', None)
debug: parse_commit_message('fix(code): change confusing error... )
debug: parse_commit_message -> ParsedCommit(bump=1, type='fix')
debug: Commits found since last release: 1
debug: evaluate_version_bump -> patch
debug: get_new_version('0.1.0', 'patch')
debug: get_new_version -> 0.1.1
debug: set_new_version('0.1.1')
debug: Writing new version number: path=PosixPath('pyproject.toml')
debug: set_new_version -> True
debug: commit_new_version('0.1.1')
debug: commit_new_version -> [main d82fa3f] 0.1.1
debug: Author: semantic-release <semantic-release>
debug: 1 file changed, 5 insertions(+), 1 deletion(-)
debug: tag_new_version('0.1.1')
debug: tag_new_version ->
Bumping with a patch version to 0.1.1
```
We can see that PSR found our commit messages, and decided that a patch release was necessary based on the text in the message. We can also see that command automatically updated the version number in the the *`pyproject.toml`* file and created a new version control tag for our package's source (we talked about tags in **{numref}`03:Tagging-a-package-release-with-version-control`**). In the next section we'll go through a real example of using PSR with our `pycounts` package.
(07:Checklist-for-releasing-a-new-package-version)=
## Checklist for releasing a new package version
Now that we know about versioning and how to increment the version\index{versioning} of our package, we're ready to run through a release checklist. We'll make a new minor release of the `pycounts` package we've been developing throughout this book, from v0.1.0 to v0.2.0, to demonstrate each step in the release checklist.
### Step 1: make changes to package source files
This is an obvious one, but before you can make a new release, you need to make the changes to your package's source that will comprise your new release!
Consider our `pycounts` package. We published the first release, v0.1.0, of our package in **Chapter 3: {ref}`03:How-to-package-a-Python`**. Since then, we've made a few changes. Specifically:
- In **Chapter 4: {ref}`04:Package-structure-and-distribution`** we added a new "datasets" module to our package along with some example data, a text file of the novel "Flatland" by Edwin Abbott{cite:p}`abbott1884`, that users could load to try out the functionality of our package.
- In **Chapter 5: {ref}`05:Testing`** we significantly upgraded our testing suite by adding several new unit, integration, and regression tests to the *`tests/test_pycounts.py`* file.
```{tip}
In practice, if you're using version control, changes are usually made to a package's source using [branches](https://git-scm.com/book/en/v2/Git-Branching-Branches-in-a-Nutshell). Branches isolate your changes so you can develop your package without affecting the existing, stable version. Only when you're happy with your changes do you merge them into the existing source.
```
### Step 2: document your changes
Before we make our new release, we should document everything we've changed in our changelog. For example, here's `pycounts`'s updated *`CHANGELOG.md`* file\index{documentation!changelog}:
```{tip}
We talked about changelog file format and content in **{numref}`06:Changelog`**.
```
```{code-block} md
---
emphasize-lines: 5
---
# Changelog
<!--next-version-placeholder-->
## v0.2.0 (10/09/2021)
### Feature
- Added new datasets modules to load example data
### Fix
- Check type of argument passed to `plotting.plot_words()`
### Tests
- Added new tests to all package modules in test_pycounts.py
## v0.1.0 (24/08/2021)
- First release of `pycounts`
```
If using version control, you should commit this change to make sure it becomes part of your release:
```{prompt} bash \$ auto
$ git add CHANGELOG.md
$ git commit -m "build: preparing for release v0.2.0"
$ git push
```
### Step 3: bump version number
Once your changes for the new release are ready, you need to bump the package version manually (**{numref}`07:Manual-version-bumping`**) or automatically with the PSR tool (**{numref}`07:Automatic-version-bumping`**).
We'll take the automatic route using PSR\index{versioning!Python Semantic Release}\index{Python Semantic Release} here, but if you're not using Git as a version control system, you'll need to do this step manually. The changes we made to `pycounts` described in the section above, constitute a minor release (we added a new feature to load example data and made some significant changes to our package's test framework). When we committed these changes in **{numref}`04:Version-control`** and **{numref}`05:Version-control`**, we did so with the following collection of commit messages:
```{prompt} bash \$ auto
$ git commit -m "feat: add example data and datasets module"
$ git commit -m "test: add additional tests for all modules"
$ git commit -m "fix: check input type to plot_words function"
```
As we discussed in **{numref}`07:Automatic-version-bumping`**, PSR can automatically parse these commit messages to increment our package version for us. If you haven't already, install PSR as a development dependency using `poetry`:
```{prompt} bash \$ auto
$ poetry add --dev python-semantic-release
```
This command updated our recorded package dependencies in `pyproject.toml` and `poetry.lock`, so we should commit those changes to version control before we update our package version:
```{prompt} bash \$ auto
$ git add pyproject.toml poetry.lock
$ git commit -m "build: add PSR as dev dependency"
$ git push
```
Now we can use PSR to automatically bump our package version with the `semantic-release version` command. If you want to see exactly what PSR found in your commit messages and why it decided to make a patch, minor, or major release, you can add the argument `-v DEBUG`.
```{attention}
Recall from **{numref}`07:Automatic-version-bumping`** that to use PSR, you need to tell it where your package's version number is stored by defining `version_variable = "pyproject.toml:version"` under the `[tool.semantic_release]` table in *`pyproject.toml`*.
```
```{prompt} bash \$ auto
$ semantic-release version
```
```md
Creating new version
Current version: 0.1.0
Bumping with a minor version to 0.2.0
```
This step automatically updated our package's version in the *`pyproject.toml`* file and created a new tag for our package, "v0.2.0", which you could view by typing `git tag --list` at the command line:
```{prompt} bash \$ auto
$ git tag --list
```
```md
v0.1.0
v0.2.0
```
### Step 4: run tests and build documentation
We've now prepped our package for release, but before we release it, it's important to check that its tests run and documentation builds successfully. To do this with our `pycounts` package, we should first install the package (we should re-install because as we've created a new version):
```{prompt} bash \$ auto
$ poetry install
```
```md
Installing the current project: pycounts (0.2.0)
```
Now we'll check that our tests are still passing and what their coverage is using `pytest` and `pytest-cov` (we discussed these tools in **Chapter 5: {ref}`05:Testing`**):
```{prompt} bash \$ auto
$ pytest tests/ --cov=pycounts
```
```md
========================= test session starts =========================
...
---------- coverage: platform darwin, python 3.9.6-final-0 -----------
Name Stmts Miss Cover
---------------------------------------------------
src/pycounts/__init__.py 2 0 100%
src/pycounts/data/__init__.py 0 0 100%
src/pycounts/datasets.py 5 0 100%
src/pycounts/plotting.py 12 0 100%
src/pycounts/pycounts.py 16 0 100%
---------------------------------------------------
TOTAL 35 0 100%
========================== 7 passed in 0.41s ==========================
```
Finally, to check that documentation still builds correctly you typically want to create the documentation from scratch, i.e., remove any existing built documentation in your package and then building it again. To do this, we first need to run `make clean --directory docs/` before running `make html --directory docs/` (we discussed building documentation with these commands in **Chapter 6: {ref}`06:Documentation`**). In the spirit of efficiency we can combine these two commands together like we do below:
```{prompt} bash \$ auto
$ make clean html --directory docs/
```
```md
Running Sphinx
...
build succeeded.
The HTML pages are in _build/html.
```
Looks like everything is working!
### Step 5: Tag a release with version control
For those using remote version control on GitHub (or similar), it's time to tag\index{version control!tag} a new release\index{version control!release} of your repository on GitHub\index{GitHub}. If you're not using version control, you can skip to the next section. We discussed how to tag a release and why we do this in **{numref}`03:Tagging-a-package-release-with-version-control`**. Recall that it's a two-step process:
1. Create a tag marking a specific point in a repository's history using the command `git tag`; and,
2. On GitHub, create a release of your repository based on the tag.
If using PSR to bump your package version, then step 1 was done automatically for you. If you didn't use PSR, you can make a tag manually using the following command:
```{prompt} bash \$ auto
$ git tag v0.2.0
```
You can now push any local commits and your new tag to GitHub with the following commands:
```{prompt} bash \$ auto
$ git push
$ git push --tags
```
After running those commands for our `pycounts` package, we can go to GitHub and navigate to the "Releases" tab to see our tag, as shown in {numref}`07-tag-fig`.
```{figure} images/07-tag.png
---
width: 100%
name: 07-tag-fig
alt: Tag of v0.2.0 of `pycounts` on GitHub.
---
Tag of v0.2.0 of `pycounts` on GitHub.
```
To create a release from this tag, click "Draft a new release". You can then identify the tag from which to create the release and optionally add a description of the release; often, this description links to the changelog, where changes have already been documented. {numref}`07-release-1-fig` shows the release of v0.2.0 of `pycounts` on GitHub.
```{figure} images/07-release-1.png
---
width: 100%
name: 07-release-1-fig
alt: Release v0.2.0 of `pycounts` on GitHub.
---
Release v0.2.0 of `pycounts` on GitHub.
```
### Step 6: build and release package to PyPI
It's now time to build the new distributions\index{distribution} for our package (i.e., the sdist and wheel — we talked about these in **{numref}`04:Package-distribution-and-installation`**). We can do that with `poetry` using the following command:
```{prompt} bash \$ auto
$ poetry build
```
```md
Building pycounts (0.2.0)
- Building sdist
- Built pycounts-0.2.0.tar.gz
- Building wheel
- Built pycounts-0.2.0-py3-none-any.whl
```
You can now use and share these distributions as you please, but most developers will want to upload them to PyPI, which is what we'll do here.
As discussed in **{numref}`03:Publishing-to-TestPyPI`**, it's good practice to release your package on [TestPyPI](https://test.pypi.org/) before PyPI\index{PyPI}, to test that everything is working as expected. We can do that with `poetry publish`:
```{prompt} bash \$ auto
$ poetry publish -r test-pypi
```
```{attention}
The above command assumes that you have added TestPyPI to the list of repositories `poetry` knows about via: `poetry config repositories.test-pypi https://test.pypi.org/legacy/`
```
Now you should be able to try and download your package from TestPyPI\index{TestPyPI} with the following command:
```{prompt} bash \$ auto
$ pip install --index-url https://test.pypi.org/simple/ pycounts
```
```{note}
By default `pip install` will search PyPI for the named package. The argument `--index-url` points `pip` to the TestPyPI index instead. If your package has dependencies that a developer did not upload to TestPyPI, you'll also need to tell `pip` that it can search for them on PyPI with the following argument: `--extra-index-url https://pypi.org/simple`.
```
If you're happy with how your newly versioned package is working, you can go ahead and publish to PyPI:
```{prompt} bash \$ auto
$ poetry publish
```
## Automating releases
As you've seen in this chapter, there are quite a few steps to go through in order to make a new release of a package. In **Chapter 8: {ref}`08:Continuous-integration-and-deployment`** we'll see how we can automate the entire release process, including running tests, building documentation, and publishing to TestPyPI and PyPI.
(07:Breaking-changes-and-deprecating-package-functionality)=
## Breaking changes and deprecating package functionality
As discussed earlier in the chapter, major version releases may come with backward incompatible changes, which we call "breaking changes\index{breaking change}". Breaking changes affect your package's user base. The impact and importance of breaking changes is directly proportional to the number of people using your package. That's not to say that you should avoid breaking changes — there are good reasons for making them, such as improving software design mistakes, improving functionality, or making code simpler and easier to use.
If you do need to make a breaking change, it is best to implement that change gradually, by providing adequate warning and advice to your package's user base through "deprecation\index{deprecation} warnings".
We can add a deprecation warning to our code by using the `warnings` [module](https://docs.python.org/3/library/warnings.html) from the Python standard library. For example, imagine that we want to remove the `get_flatland()` function from the `datasets` module of our `pycounts` package in the upcoming major v1.0.0 release. We can do this by adding a `FutureWarning` to our code, as shown in the *`datasets.py`* module below (we created this module back in **{numref}`04:Including-data-in-a-package`**).
```{tip}
If you've used any larger Python libraries before (such as `NumPy`, `Pandas` or `scikit-learn`) you probably have seen deprecation warnings before! On that note, these large, established Python libraries offer great resources for learning how to properly manage your own package — don't be afraid to check out their source code and history on GitHub.
```
```{code-block} python
---
emphasize-lines: 2, 9-10
---
from importlib import resources
import warnings
def get_flatland():
"""Get path to example "Flatland" [1]_ text file.
...rest of docstring hidden...
"""
warnings.warn("This function will be deprecated in v1.0.0.",
FutureWarning)
with resources.path("pycounts.data", "flatland.txt") as f:
data_file_path = f
return data_file_path
```
If we were to try and use this function now, we would see the `FutureWarning` printed to our output:
```{prompt} python >>> auto
>>> from pycounts.datasets import get_flatland
>>> flatland_path = get_flatland()
```
```md
FutureWarning: This function will be deprecated in v1.0.0.
```
A few other things to think about when making breaking changes:
- If you're changing a function significantly, consider keeping both the legacy version (with a deprecation warning) and new version of the function for a few releases to help users make a smoother transition to using the new function.
- If you're deprecating a lot of code, consider doing it in small increments over multiple releases.
- If your breaking change is a result of one of your package's dependencies changing, it is often better to warn your users that they require a newer version of a dependency rather than immediately making it a required dependency of your package.
- Documentation is key! Don't be afraid to be verbose about documenting breaking changes in your package's documentation and changelog.
|
github_jupyter
|
## Version bumping
While we'll discuss the full workflow for releasing a new version of your package in **{numref}`07:Checklist-for-releasing-a-new-package-version`**, we first want to dicuss version bumping. That is, how to increment the version of your package when you're preparing a new release. This can be done manually or automatically as we'll discuss in the sections below.
(07:Manual-version-bumping)=
### Manual version bumping
Once you've decided what the new version\index{versioning!manual} of your package will be (i.e., are you making a patch, minor, or major release) you need to update the package's version number in your source code. For a `poetry`-managed project\index{poetry}, that information is in the *`pyproject.toml`* file\index{pyproject.toml}. Consider the *`pyproject.toml`* file of the `pycounts` package we developed in **Chapter 3: {ref}`03:How-to-package-a-Python`**, and the top of which looks like this:
Imagine we wanted to make a patch release of our package. We could simply change the `version` number manually in this file to "0.1.1" and many developers do take this manual approach. An alternative method is to use the `poetry version` command. The `poetry version` command can be used with the arguments `patch`, `minor` or `major` depending on how you want to update the version of your package. For example, to make a patch release, we could run the following at the command line:
This command changes the `version` variable in the `pyproject.toml` file:
(07:Automatic-version-bumping)=
### Automatic version bumping
In this book, we're interested in automating as much as possible of the packaging workflow. While the manual versioning approach described above in **{numref}`07:Manual-version-bumping`** is certainly used by many developers, we can do things more efficiently! To automate version bumping\index{versioning!automatic}, you'll need to be using a version control system like Git. If you are not using version control\index{version control} for your package, you can skip to **{numref}`07:Checklist-for-releasing-a-new-package-version`**.
[Python Semantic Release\index{versioning!Python Semantic Release}\index{Python Semantic Release} (PSR)](https://python-semantic-release.readthedocs.io/en/latest/) is a tool that can automatically bump version numbers based on keywords it finds in commit messages. The idea is to use a standardized commit message format and syntax which PSR can parse to determine how to increment the version number. The default commit message format used by PSR is the [Angular commit style](https://github.com/angular/angular.js/blob/master/DEVELOPERS.md#commit-message-format) which looks like this:
`<type>` refers to the kind of change made and is usually one of:
- `feat`: A new feature.
- `fix`: A bug fix.
- `docs`: Documentation changes.
- `style`: Changes that do not affect the meaning of the code (white-space, formatting, missing semi-colons, etc).
- `refactor`: A code change that neither fixes a bug nor adds a feature.
- `perf`: A code change that improves performance.
- `test`: Changes to the test framework.
- `build`: Changes to the build process or tools.
`scope` is an optional keyword that provides context for where the change was made. It can be anything relevant to your package or development workflow (e.g., it could be the module or function name affected by the change).
Different text in the commit message will trigger PSR to make different kinds of releases:
- A `<type>` of `fix` triggers a patch version bump, e.g.;
```{prompt} bash \$ auto
$ git commit -m "fix(mod_plotting): fix confusing error message in \
plot_words"
```
- A `<type>` of `feat` triggers a minor version bump, e.g.;
```{prompt} bash \$ auto
$ git commit -m "feat(package): add example data and new module to \
package"
```
- The text `BREAKING CHANGE:` in the `footer` will trigger a major release, e.g.,
```{prompt} bash \$ auto
$ git commit -m "feat(mod_plotting): move code from plotting module \
to pycounts module
$
$ BREAKING CHANGE: plotting module wont exist after this release."
```
To use PSR we need to install and configure it. To install PSR as a development dependency of a `poetry`-managed project, you can use the following command:
To configure PSR, we need to tell it where the version number of our package is stored. The package version is stored in the *`pyproject.toml`* file for a `poetry`-managed project. It exists as the variable `version` under the table `[tool.poetry]`. To tell PSR this, we need to add a new table to the *`pyproject.toml`* file called `[tool.semantic_release]` within which we specify that our `version_variable` is stored at `pyproject.toml:version`:
Finally, you can use the command `semantic-release version` at the command line to get PSR to automatically bump your package's version number. PSR will parse all the commit messages since the last tag of your package to determine what kind of version bump to make. For example, imagine the following three commit messages have been made since tag v0.1.0:
PSR will note that there are two "fix" and one "feat" keywords. "fix" triggers a patch release, but "feat" triggers a minor release, which trumps a patch release, so PSR would make a minor version bump from v0.1.0 to v0.2.0.
As a more practical demonstration of how PSR works, imagine we have a package at version 0.1.0, make a bug fix and commit our changes with the following message:
We then run `semantic-release version` to update our version number. In the command below, we'll specify the argument `-v DEBUG` to ask PSR to print extra information to the screen so we can get an inside look at how PSR works:
We can see that PSR found our commit messages, and decided that a patch release was necessary based on the text in the message. We can also see that command automatically updated the version number in the the *`pyproject.toml`* file and created a new version control tag for our package's source (we talked about tags in **{numref}`03:Tagging-a-package-release-with-version-control`**). In the next section we'll go through a real example of using PSR with our `pycounts` package.
(07:Checklist-for-releasing-a-new-package-version)=
## Checklist for releasing a new package version
Now that we know about versioning and how to increment the version\index{versioning} of our package, we're ready to run through a release checklist. We'll make a new minor release of the `pycounts` package we've been developing throughout this book, from v0.1.0 to v0.2.0, to demonstrate each step in the release checklist.
### Step 1: make changes to package source files
This is an obvious one, but before you can make a new release, you need to make the changes to your package's source that will comprise your new release!
Consider our `pycounts` package. We published the first release, v0.1.0, of our package in **Chapter 3: {ref}`03:How-to-package-a-Python`**. Since then, we've made a few changes. Specifically:
- In **Chapter 4: {ref}`04:Package-structure-and-distribution`** we added a new "datasets" module to our package along with some example data, a text file of the novel "Flatland" by Edwin Abbott{cite:p}`abbott1884`, that users could load to try out the functionality of our package.
- In **Chapter 5: {ref}`05:Testing`** we significantly upgraded our testing suite by adding several new unit, integration, and regression tests to the *`tests/test_pycounts.py`* file.
### Step 2: document your changes
Before we make our new release, we should document everything we've changed in our changelog. For example, here's `pycounts`'s updated *`CHANGELOG.md`* file\index{documentation!changelog}:
If using version control, you should commit this change to make sure it becomes part of your release:
### Step 3: bump version number
Once your changes for the new release are ready, you need to bump the package version manually (**{numref}`07:Manual-version-bumping`**) or automatically with the PSR tool (**{numref}`07:Automatic-version-bumping`**).
We'll take the automatic route using PSR\index{versioning!Python Semantic Release}\index{Python Semantic Release} here, but if you're not using Git as a version control system, you'll need to do this step manually. The changes we made to `pycounts` described in the section above, constitute a minor release (we added a new feature to load example data and made some significant changes to our package's test framework). When we committed these changes in **{numref}`04:Version-control`** and **{numref}`05:Version-control`**, we did so with the following collection of commit messages:
As we discussed in **{numref}`07:Automatic-version-bumping`**, PSR can automatically parse these commit messages to increment our package version for us. If you haven't already, install PSR as a development dependency using `poetry`:
This command updated our recorded package dependencies in `pyproject.toml` and `poetry.lock`, so we should commit those changes to version control before we update our package version:
Now we can use PSR to automatically bump our package version with the `semantic-release version` command. If you want to see exactly what PSR found in your commit messages and why it decided to make a patch, minor, or major release, you can add the argument `-v DEBUG`.
This step automatically updated our package's version in the *`pyproject.toml`* file and created a new tag for our package, "v0.2.0", which you could view by typing `git tag --list` at the command line:
### Step 4: run tests and build documentation
We've now prepped our package for release, but before we release it, it's important to check that its tests run and documentation builds successfully. To do this with our `pycounts` package, we should first install the package (we should re-install because as we've created a new version):
Now we'll check that our tests are still passing and what their coverage is using `pytest` and `pytest-cov` (we discussed these tools in **Chapter 5: {ref}`05:Testing`**):
Finally, to check that documentation still builds correctly you typically want to create the documentation from scratch, i.e., remove any existing built documentation in your package and then building it again. To do this, we first need to run `make clean --directory docs/` before running `make html --directory docs/` (we discussed building documentation with these commands in **Chapter 6: {ref}`06:Documentation`**). In the spirit of efficiency we can combine these two commands together like we do below:
Looks like everything is working!
### Step 5: Tag a release with version control
For those using remote version control on GitHub (or similar), it's time to tag\index{version control!tag} a new release\index{version control!release} of your repository on GitHub\index{GitHub}. If you're not using version control, you can skip to the next section. We discussed how to tag a release and why we do this in **{numref}`03:Tagging-a-package-release-with-version-control`**. Recall that it's a two-step process:
1. Create a tag marking a specific point in a repository's history using the command `git tag`; and,
2. On GitHub, create a release of your repository based on the tag.
If using PSR to bump your package version, then step 1 was done automatically for you. If you didn't use PSR, you can make a tag manually using the following command:
You can now push any local commits and your new tag to GitHub with the following commands:
After running those commands for our `pycounts` package, we can go to GitHub and navigate to the "Releases" tab to see our tag, as shown in {numref}`07-tag-fig`.
To create a release from this tag, click "Draft a new release". You can then identify the tag from which to create the release and optionally add a description of the release; often, this description links to the changelog, where changes have already been documented. {numref}`07-release-1-fig` shows the release of v0.2.0 of `pycounts` on GitHub.
### Step 6: build and release package to PyPI
It's now time to build the new distributions\index{distribution} for our package (i.e., the sdist and wheel — we talked about these in **{numref}`04:Package-distribution-and-installation`**). We can do that with `poetry` using the following command:
You can now use and share these distributions as you please, but most developers will want to upload them to PyPI, which is what we'll do here.
As discussed in **{numref}`03:Publishing-to-TestPyPI`**, it's good practice to release your package on [TestPyPI](https://test.pypi.org/) before PyPI\index{PyPI}, to test that everything is working as expected. We can do that with `poetry publish`:
Now you should be able to try and download your package from TestPyPI\index{TestPyPI} with the following command:
If you're happy with how your newly versioned package is working, you can go ahead and publish to PyPI:
## Automating releases
As you've seen in this chapter, there are quite a few steps to go through in order to make a new release of a package. In **Chapter 8: {ref}`08:Continuous-integration-and-deployment`** we'll see how we can automate the entire release process, including running tests, building documentation, and publishing to TestPyPI and PyPI.
(07:Breaking-changes-and-deprecating-package-functionality)=
## Breaking changes and deprecating package functionality
As discussed earlier in the chapter, major version releases may come with backward incompatible changes, which we call "breaking changes\index{breaking change}". Breaking changes affect your package's user base. The impact and importance of breaking changes is directly proportional to the number of people using your package. That's not to say that you should avoid breaking changes — there are good reasons for making them, such as improving software design mistakes, improving functionality, or making code simpler and easier to use.
If you do need to make a breaking change, it is best to implement that change gradually, by providing adequate warning and advice to your package's user base through "deprecation\index{deprecation} warnings".
We can add a deprecation warning to our code by using the `warnings` [module](https://docs.python.org/3/library/warnings.html) from the Python standard library. For example, imagine that we want to remove the `get_flatland()` function from the `datasets` module of our `pycounts` package in the upcoming major v1.0.0 release. We can do this by adding a `FutureWarning` to our code, as shown in the *`datasets.py`* module below (we created this module back in **{numref}`04:Including-data-in-a-package`**).
If we were to try and use this function now, we would see the `FutureWarning` printed to our output:
| 0.898578 | 0.894421 |
```
import chex
import shinrl
import gym
import jax.numpy as jnp
import jax
```
# Create custom ShinEnv
This tutorial demonstrates how to create a custom environment.
We are going to implement the following simple two-state MDP.

You need to implement two classes,
1. A config class inheriting `shinrl.EnvConfig`
2. An env class inheriting `shinrl.ShinEnv`
## 1. Config
The config class is a dataclass inheriting `shinrl.EnvConfig`.
It holds hyperparameters of the environment.
```
@chex.dataclass
class ExampleConfig(shinrl.EnvConfig):
dS: int = 2 # number of states
dA: int = 2 # number of actions
discount: float = 0.99 # discount factor
horizon: int = 3 # environment horizon
```
## 2. Env
The main env class must inherit `shinrl.ShinEnv`.
The followings you need to implement (See details in [/home/rl-dqn/ShinRL-JAX/shinrl/envs/base/env.py](/home/rl-dqn/ShinRL-JAX/shinrl/envs/base/env.py)):
* **DefaultConfig** (ClassVariable): Default configuration of the environment.
* **dS** (property): Number of states.
* **dA** (property): Number of actions.
* **observation_space** (property): Gym observation space.
* **action_space** (property): Gym observation space.
* **init_probs** (function): A function that returns the probabilities of initial states.
* **transition** (function): Transition function of the MDP.
* **reward** (function): Reward function of the MDP.
* **observation** (function): Observation function of the MDP.
For continuous action space envs, you also need to implement:
* **continuous_action** (function): A function that converts a discrete action to a continuous action.
* **discrete_action** (function): A function that converts a continuous action to a discrete action.
```
class ExampleEnv(shinrl.ShinEnv):
DefaulatConfig = ExampleConfig
def __init__(self, config=None):
super().__init__(config)
@property
def dS(self) -> int:
return self.config.dS
@property
def dA(self) -> int:
return self.config.dA
@property
def observation_space(self):
return gym.spaces.Box(low=jnp.array([0, 0]), high=jnp.array([1., 1.]))
@property
def action_space(self):
return gym.spaces.Discrete(self.dA)
def init_probs(self):
return jnp.array([1.0, 0.0])
def transition(self, state, action):
next_state = jnp.array([0, 1], dtype=int)
all_probs = jnp.array([[[0.2, 0.8], [1.0, 0.0]], [[1.0, 0.0], [0.0, 1.0]]], dtype=float)
probs = all_probs[state, action]
return next_state, probs
def reward(self, state, action):
all_rews = jnp.array([[0.0, 0.0], [-1.0, 1.0]], dtype=float)
rew = all_rews[state, action]
return rew
def observation(self, state):
return jnp.array([state, state], dtype=float)
```
### env.mdp
These core functions (transition, reward, etc.) are automatically converted to matrix form and stored in env.mdp.
* env.mdp.**dS** (int): Number of states.
* env.mdp.**dA** (int): Number of actions.
* env.mdp.**obs_shape** (Shape): Observation shape.
* env.mdp.**obs_mat** (dS x (obs_shape) Array): Observation of all the states.
* env.mdp.**rew_mat** (dS x dA Array): Reward matrix.
* env.mdp.**tran_mat** ((dSxdA) x dS SparseMat): Tranition matrix.
* env.mdp.**init_probs** (dS Array): Probability of initial states.
* env.mdp.**discount (float): Discount factor.
These matrices are useful for analyzing the behavior (e.g., output of the Q-network) on the full state action space.
# What ShinEnv can do
Implemented ShinEnvs behaves like a usual gym.Env:
```
config = ExampleEnv.DefaulatConfig()
env = ExampleEnv(config)
env.reset()
for _ in range(10):
act = env.action_space.sample()
env.step(act)
```
ShinEnv also provides **oracle** methods that can compute exact quantities:
* `calc_q` computes a Q-value table containing all possible state-action pairs given a policy.
* `calc_optimal_q` computes the optimal Q-value table.
* `calc_visit` calculates state visitation frequency table, for a given policy.
* `calc_return` is a shortcut for computing exact undiscounted returns for a given policy.
```
# The optimal strategy is obously taking a=0 at s=0 and a=1 at s=1.
# You can verify that by calc_optimal_q method.
env.calc_optimal_q() # dS x dA array
# Compute the optimal undiscounted return
import distrax
optimal_q = env.calc_optimal_q() # dS x dA array
optimal_policy = distrax.Greedy(optimal_q).probs
env.calc_return(optimal_policy) # dS x dA array
# Compute the Q-values and return of an uniform policy
key = jax.random.PRNGKey(0)
dS, dA = env.dS, env.dA
policy = jax.random.uniform(key, (dS, dA))
policy = policy / policy.sum(axis=1, keepdims=True) # dS x dA uniform policy
env.calc_q(policy) # dS x dA array
env.calc_return(policy)
# Compute the state visitation frequency
env.calc_visit(policy) # dS x dA array
```
|
github_jupyter
|
import chex
import shinrl
import gym
import jax.numpy as jnp
import jax
@chex.dataclass
class ExampleConfig(shinrl.EnvConfig):
dS: int = 2 # number of states
dA: int = 2 # number of actions
discount: float = 0.99 # discount factor
horizon: int = 3 # environment horizon
class ExampleEnv(shinrl.ShinEnv):
DefaulatConfig = ExampleConfig
def __init__(self, config=None):
super().__init__(config)
@property
def dS(self) -> int:
return self.config.dS
@property
def dA(self) -> int:
return self.config.dA
@property
def observation_space(self):
return gym.spaces.Box(low=jnp.array([0, 0]), high=jnp.array([1., 1.]))
@property
def action_space(self):
return gym.spaces.Discrete(self.dA)
def init_probs(self):
return jnp.array([1.0, 0.0])
def transition(self, state, action):
next_state = jnp.array([0, 1], dtype=int)
all_probs = jnp.array([[[0.2, 0.8], [1.0, 0.0]], [[1.0, 0.0], [0.0, 1.0]]], dtype=float)
probs = all_probs[state, action]
return next_state, probs
def reward(self, state, action):
all_rews = jnp.array([[0.0, 0.0], [-1.0, 1.0]], dtype=float)
rew = all_rews[state, action]
return rew
def observation(self, state):
return jnp.array([state, state], dtype=float)
config = ExampleEnv.DefaulatConfig()
env = ExampleEnv(config)
env.reset()
for _ in range(10):
act = env.action_space.sample()
env.step(act)
# The optimal strategy is obously taking a=0 at s=0 and a=1 at s=1.
# You can verify that by calc_optimal_q method.
env.calc_optimal_q() # dS x dA array
# Compute the optimal undiscounted return
import distrax
optimal_q = env.calc_optimal_q() # dS x dA array
optimal_policy = distrax.Greedy(optimal_q).probs
env.calc_return(optimal_policy) # dS x dA array
# Compute the Q-values and return of an uniform policy
key = jax.random.PRNGKey(0)
dS, dA = env.dS, env.dA
policy = jax.random.uniform(key, (dS, dA))
policy = policy / policy.sum(axis=1, keepdims=True) # dS x dA uniform policy
env.calc_q(policy) # dS x dA array
env.calc_return(policy)
# Compute the state visitation frequency
env.calc_visit(policy) # dS x dA array
| 0.832713 | 0.917672 |
# Introduction to DSP with PYNQ
# 01: DSP & Python
> In this notebook we'll introduce some development tools for digital signal processing (DSP) using Python and JupyterLab. In our example application, we'll start by visualising some interesting signals — audio recordings of Scottish birds! We'll then use a few different analytical techniques to gain some understanding of these signals and finally process the audio to isolate a single type of bird.
## Inspecting our signal
In the assets folder there is an audio file, `birds.wav`. This was recorded by Stuart Fisher and released under [CC BY-NC-ND 2.5](https://creativecommons.org/licenses/by-nc-nd/2.5/); accessible [here](https://www.xeno-canto.org/28039).
Before we get into our signal processing at all, let's give it a listen. We can do that through our browser using IPython's rich set of display functions.
```
from IPython.display import Audio
Audio("assets/birds.wav")
```
OK, so what are we hearing? We've got two main subjects here:
1. The lower pitched bird (going "cuurloo!") is a Eurasian curlew
2. The higher pitched bird chatting away is a chaffinch
Just for context, here's what these birds look like:
<div style='max-width: 1005px;'>
<div style='width:45%; float:left; text-align:center;'>
<img src="assets/curlew.jpg"/>
<b>Curlew</b> <br/>Photo by Vedant Raju Kasambe <br/> <a href="https://creativecommons.org/licenses/by-sa/4.0/deed.en">Creative Commons Attribution-Share Alike 4.0</a>
</div>
<div style='width:45%; float:right; text-align:center;'>
<img src="assets/chaffinch.jpg"/>
<b>Chaffinch</b> <br/>Photo by Charles J Sharp <br/> <a href="https://creativecommons.org/licenses/by/3.0/deed.en">Creative Commons Attribution 3.0</a>
</div>
</div>
### Loading from disk
Let's get this audio file loaded in Python so we can perform some visualisation. We're going to make use of the [SciPy](https://www.scipy.org/) ecosystem for most of our signal processing in Python. To load the `.wav` file in to our environment as an array of samples, let's use SciPy's `wavfile` IO module.
```
from scipy.io import wavfile
fs, aud_in = wavfile.read("assets/birds.wav")
```
`wavfile.read` gives us two things: the sampling frequency of the signal (`fs`), and the raw samples as an array (`aud_in`). Let's check the sampling frequency.
```
fs
```
The sampling frequency of the recording is 44.1 kHz — the standard rate for CD quality audio. Now let's look at the format of the samples themselves. To start, what is the type of our sample array?
```
type(aud_in)
```
This is an N-dimensional array ('ndarray') from the NumPy package, that you'll remember from the introduction notebook.
Let's interrogate this array a little further. We should be aware of its length and the data type of each element:
```
len(aud_in)
aud_in.dtype
```
So each sample is a signed 16 bit integer, and we have over half a million samples in total! We can comfortably fit this in memory (it's just over 1 MB) but we will need to do some processing to visualise all of this data in a useful format.
### Plotting in the time domain
As a first investigation, let's plot only a short clip from the recording. We'll use [plotly_express](https://www.plotly.express/) here because it generates impressive, interactive plots with surprisingly small amounts of code. `plotly_express` expects input data to be given as a [pandas data frame](http://pandas.pydata.org/pandas-docs/stable/getting_started/overview.html#overview), so we'll need to do a little bit of conversion work upfront. We build up a frame with multiple columns (time and amplitude, in this case) and then we can efficiently traverse, sort, and search the data.
```
import pandas as pd
import numpy as np
def to_time_dataframe(samples, fs):
"""Create a pandas dataframe from an ndarray of 16-bit time domain samples"""
num_samples = len(samples)
sample_times = np.linspace(0, num_samples/fs, num_samples)
normalised_samples = samples / 2**15
return pd.DataFrame(dict(
amplitude = normalised_samples,
time = sample_times
))
```
Now that we can turn our sample array into a data frame, let's pass it to plotly_express to create a simple, time-domain plot. First let's make a theme for our plots.
```
# Derive a custom plotting template from `plotly_dark`
import plotly.io as pio
new_template = pio.templates['plotly_white']
new_template.update(dict(layout = dict(
width = 800,
autosize = False,
legend = dict(x=1.1),
paper_bgcolor = 'rgb(0,0,0,0)',
plot_bgcolor = 'rgb(0,0,0,0)',
)))
# Register new template as the default
pio.templates['light_plot'] = new_template
pio.templates.default = 'light_plot'
```
Now we can get plotly to plot a snippet of the audio, and it will be in the theme we described above.
```
import plotly_express as px
# Let's take a small subset of the recording
aud_clip = to_time_dataframe(aud_in, fs).query('0.3 < time < 0.718')
# Plot signal
px.line( # Make a line plot with...
aud_clip, # Data frame
x='time', y='amplitude', # Axes field names
labels = dict(amplitude='Normalised Amplitude', time='Time (s)'), # Axes label names
template='light_plot' # Appearance
)
```
This plot is interactive. Feel free to zoom in (click and drag) and pan around. You should be able to zoom in far enough to see the single sinusoidal cycles. Double click anywhere on the plot to zoom back out.
There is clearly some activity in this waveform, but it's hard to imagine what this should sound like from the time domain alone. Sure we can get a feel for the volume of the signal over time, but what are the different pitches/frequencies in this sound? Let's take a look at the same snippet in the frequency domain to find out.
### Plotting in the frequency domain
We can use SciPy to perform a Fast Fourier Transform (FFT) to convert our time domain signal into the frequency domain. The `fft` function performs an FFT for our input. Let's try this out on the small audio clip from above.
```
from scipy.fftpack import fft
def to_freq_dataframe(samples, fs):
"""Create a pandas dataframe from an ndarray frequency domain samples"""
sample_freqs = np.linspace(0, fs, len(samples))
return pd.DataFrame(dict(
amplitude = samples[0:int(len(samples)/2)],
freq = sample_freqs[0:int(len(samples)/2)]
))
# Take slice of full input
aud_clip_numpy = aud_in[int(0.3*fs): int(0.718*fs)]
# Perform FFT
NFFT = 2**14 # use a generous length here for maximum resolution
aud_clip_fft = np.abs(fft(aud_clip_numpy,NFFT))
# Plot FFT
px.line(
to_freq_dataframe(aud_clip_fft, fs),
x='freq', y='amplitude',
labels = dict(amplitude='Amplitude', freq='Freq (Hz)'),
template='light_plot'
)
```
There are a couple of features to note in the frequency domain that we had totally missed in the time domain:
1. *What a generous sampling rate!*
As the original sample rate is 44.1 kHz, the recording is able to represent any frequencies up to 22 kHz. However, there are no significant frequency components above 5 kHz so we could resample this signal to have about $\frac{1}{3}$ of the data and still retain almost all of the useful information. This should speed up calculations and reduce memory requirements.
2. *Bird identification!*
There are two clear and distinct signals: one at $\approx$ 1.7 kHz and one at $\approx$ 4 kHz. Go back and see just how difficult this is to identify in the time domain.
The lower frequency signal is from the curlew and the higher frequency is from the chaffinch. There is also some faint noise under 50 Hz from wind picked up by the microphone. It should be possible to employ some filtering to completely isolate one bird's sound from the other, but we'll get back to this later on in the notebook.
We've been able to glean more of an understanding of the signal's composition by using SciPy to view it the frequency domain. There's one final visualisation tool that we should employ here moving on — the spectrogram!
### Plotting as a spectrogram
The spectrogram can essentially give us a simultaneous view of both time and frequency by plotting how the FFT of the signal varies with time, with a spectrum of colours to represent signal amplitude.
These plots are a little more advanced, so we move away from `plotly_express` and use a lower-level plotly API.
```
import plotly.graph_objs as go
import plotly.offline as py
from scipy.signal import spectrogram, decimate
def plot_spectrogram(samples, fs, decimation_factor=3, max_heat=50, mode='2D'):
# Optionally decimate input
if decimation_factor>1:
samples_dec = decimate(samples, decimation_factor, zero_phase=True)
fs_dec = int(fs / decimation_factor)
else:
samples_dec = samples
fs_dec = fs
# Calculate spectrogram (an array of FFTs from small windows of our signal)
f_label, t_label, spec_data = spectrogram(
samples_dec, fs=fs_dec, mode="magnitude"
)
# Make a plotly heatmap/surface graph
layout = go.Layout(
height=500,
# 2D axis titles
xaxis=dict(title='Time (s)'),
yaxis=dict(title='Frequency (Hz)'),
# 3D axis titles
scene=dict(
xaxis=dict(title='Time (s)'),
yaxis=dict(title='Frequency (Hz)'),
zaxis=dict(title='Amplitude')
)
)
trace = go.Heatmap(
z=np.clip(spec_data,0,max_heat),
y=f_label,
x=t_label
) if mode=='2D' else go.Surface(
z=spec_data,
y=f_label,
x=t_label
)
py.iplot(dict(data=[trace], layout=layout))
plot_spectrogram(aud_in, fs, mode='2D')
```
Again, we can see the two bird noises quite distinctly — the curlew between 1.2 $\rightarrow$ 2.6 kHz and the chaffinch between 3 $\rightarrow$ 5 kHz. This time, however, we can see how these sounds change over time. The curlew has a smooth sweeping call followed by a short, constant tone while the chaffinch produces a more erratic spectrogram as it jumps between tones in quick succession.
Next we'll look at designing some filters from Python so we can isolate one of the birds.
## FIR filtering
We can use functions from SciPy's signal module to design some FIR filter coefficients and perform the filtering:
* `firwin` can design filter weights that meet a given spec — cut off frequencies, ripple, filter type...
* `freqz` helps us calculate the frequency response of the filter. Useful for checking the characteristics of the generated filter weights.
* `lfilter` actually performs the filtering of our signal.
>If you have used MATLAB these functions will feel familiar to you. One thing to note though is, unlike MATLAB, arrays (or lists) in Python are zero-indexed and array elements are referenced by square brackets, rather than parentheses.
### High-pass filter for chaffinch isolation
Let's start by designing a filter to isolate the chaffinch sounds. This should be a high-pass filter with the aim of suppressing all signals below 2.6 kHz approximately. To give ourselves some breathing space, we should ask for a filter with a cutoff frequency a little higher than 2.6 kHz; let's say 2.8 kHz.
```
from scipy.signal import freqz, firwin
nyq = fs / 2.0
taps = 99
# Design high-pass filter with cut-off at 2.8 kHz
hpf_coeffs = firwin(taps, 2800/nyq, pass_zero=False)
def plot_fir_response(coeffs, fs):
"""Plot the frequency magnitude response of a set of FIR filter weights"""
freqs, resp = freqz(coeffs, 1)
return px.line(
to_freq_dataframe(np.abs(resp), nyq),
x='freq', y='amplitude',
labels = dict(amplitude='Normalised amplitude', freq='Freq (Hz)'),
template='light_plot'
)
# Plot our filter's frequency response as a sanity check
plot_fir_response(hpf_coeffs, fs)
```
We'll also be using these coefficients in the next lab so let's save them to a file for later...
```
np.save('assets/hpf_coeffs.npy', hpf_coeffs)
```
So, we asked for a cut-off frequency of 2.8 kHz and we can use the cursor with the plot above to verify this. Hover over the trace at $\approx$0.5 amplitude and it should report that this point corresponds to 2.8 kHz.
Now it's time to use these filter coefficients to filter the original audio! Let's do this in software with `lfilter` just now, plot the resulting spectrogram, and save a `.wav` file for playback.
```
from scipy.signal import lfilter
# Filter audio
aud_hpf = lfilter(hpf_coeffs, 1.0, aud_in)
# Plot filtered audio
plot_spectrogram(aud_hpf, fs)
# Offer audio widget to hear filtered audio
wavfile.write('assets/hpf.wav', fs, np.array(aud_hpf, dtype=np.int16))
Audio('assets/hpf.wav')
```
Hopefully we can confirm both visually and aurally that we've isolated the chaffinch sounds from the curlew and the wind. Sounds pretty good!
>It is also possible to isolate the curlew, this time with a bandpass filter. If time permits, design and implement the filter using the techniques we've covered above and plot the results (check out the [documentation](https://docs.scipy.org/doc/scipy/reference/generated/scipy.signal.firwin.html) for the `firwin` function if you need help)
## Summary
We've reached the end of our first of two DSP notebooks, so let's quickly recap what we've covered:
* Using the JupyterLab and Python environment as a DSP prototyping platform:
+ Introducing the SciPy ecosystem, including the `scipy.signal` module for DSP operations and `numpy` for efficient arrays.
+ Visualisation with `plotly_express` and `pandas` data frames
* Using Python to inspect signals in the time and frequency domains
* Designing FIR filters with SciPy and verifying their frequency responses
* Performing FIR filtering in software
In the next notebook we will use the techniques learned here to interact with DSP IP on the FPGA. Using the power of PYNQ, we will then control this hardware directly from the notebook!
|
github_jupyter
|
from IPython.display import Audio
Audio("assets/birds.wav")
from scipy.io import wavfile
fs, aud_in = wavfile.read("assets/birds.wav")
fs
type(aud_in)
len(aud_in)
aud_in.dtype
import pandas as pd
import numpy as np
def to_time_dataframe(samples, fs):
"""Create a pandas dataframe from an ndarray of 16-bit time domain samples"""
num_samples = len(samples)
sample_times = np.linspace(0, num_samples/fs, num_samples)
normalised_samples = samples / 2**15
return pd.DataFrame(dict(
amplitude = normalised_samples,
time = sample_times
))
# Derive a custom plotting template from `plotly_dark`
import plotly.io as pio
new_template = pio.templates['plotly_white']
new_template.update(dict(layout = dict(
width = 800,
autosize = False,
legend = dict(x=1.1),
paper_bgcolor = 'rgb(0,0,0,0)',
plot_bgcolor = 'rgb(0,0,0,0)',
)))
# Register new template as the default
pio.templates['light_plot'] = new_template
pio.templates.default = 'light_plot'
import plotly_express as px
# Let's take a small subset of the recording
aud_clip = to_time_dataframe(aud_in, fs).query('0.3 < time < 0.718')
# Plot signal
px.line( # Make a line plot with...
aud_clip, # Data frame
x='time', y='amplitude', # Axes field names
labels = dict(amplitude='Normalised Amplitude', time='Time (s)'), # Axes label names
template='light_plot' # Appearance
)
from scipy.fftpack import fft
def to_freq_dataframe(samples, fs):
"""Create a pandas dataframe from an ndarray frequency domain samples"""
sample_freqs = np.linspace(0, fs, len(samples))
return pd.DataFrame(dict(
amplitude = samples[0:int(len(samples)/2)],
freq = sample_freqs[0:int(len(samples)/2)]
))
# Take slice of full input
aud_clip_numpy = aud_in[int(0.3*fs): int(0.718*fs)]
# Perform FFT
NFFT = 2**14 # use a generous length here for maximum resolution
aud_clip_fft = np.abs(fft(aud_clip_numpy,NFFT))
# Plot FFT
px.line(
to_freq_dataframe(aud_clip_fft, fs),
x='freq', y='amplitude',
labels = dict(amplitude='Amplitude', freq='Freq (Hz)'),
template='light_plot'
)
import plotly.graph_objs as go
import plotly.offline as py
from scipy.signal import spectrogram, decimate
def plot_spectrogram(samples, fs, decimation_factor=3, max_heat=50, mode='2D'):
# Optionally decimate input
if decimation_factor>1:
samples_dec = decimate(samples, decimation_factor, zero_phase=True)
fs_dec = int(fs / decimation_factor)
else:
samples_dec = samples
fs_dec = fs
# Calculate spectrogram (an array of FFTs from small windows of our signal)
f_label, t_label, spec_data = spectrogram(
samples_dec, fs=fs_dec, mode="magnitude"
)
# Make a plotly heatmap/surface graph
layout = go.Layout(
height=500,
# 2D axis titles
xaxis=dict(title='Time (s)'),
yaxis=dict(title='Frequency (Hz)'),
# 3D axis titles
scene=dict(
xaxis=dict(title='Time (s)'),
yaxis=dict(title='Frequency (Hz)'),
zaxis=dict(title='Amplitude')
)
)
trace = go.Heatmap(
z=np.clip(spec_data,0,max_heat),
y=f_label,
x=t_label
) if mode=='2D' else go.Surface(
z=spec_data,
y=f_label,
x=t_label
)
py.iplot(dict(data=[trace], layout=layout))
plot_spectrogram(aud_in, fs, mode='2D')
from scipy.signal import freqz, firwin
nyq = fs / 2.0
taps = 99
# Design high-pass filter with cut-off at 2.8 kHz
hpf_coeffs = firwin(taps, 2800/nyq, pass_zero=False)
def plot_fir_response(coeffs, fs):
"""Plot the frequency magnitude response of a set of FIR filter weights"""
freqs, resp = freqz(coeffs, 1)
return px.line(
to_freq_dataframe(np.abs(resp), nyq),
x='freq', y='amplitude',
labels = dict(amplitude='Normalised amplitude', freq='Freq (Hz)'),
template='light_plot'
)
# Plot our filter's frequency response as a sanity check
plot_fir_response(hpf_coeffs, fs)
np.save('assets/hpf_coeffs.npy', hpf_coeffs)
from scipy.signal import lfilter
# Filter audio
aud_hpf = lfilter(hpf_coeffs, 1.0, aud_in)
# Plot filtered audio
plot_spectrogram(aud_hpf, fs)
# Offer audio widget to hear filtered audio
wavfile.write('assets/hpf.wav', fs, np.array(aud_hpf, dtype=np.int16))
Audio('assets/hpf.wav')
| 0.843702 | 0.990533 |
# Gaussian Process for contouring
This week we are going to use a gaussian process for interpolating between sample points. All we need is `geopandas`, `numpy`, `matplotlib`, `itertools`, `contextily`, and a few modules from `sklearn`
First we will import our packages
```
import geopandas as gpd
import numpy as np
import matplotlib.pyplot as plt
from itertools import product
import contextily as ctx
%matplotlib inline
```
Then we will read in the same dataset we used in the Green's functions notebook.
```
data = gpd.read_file("geochemistry_subset.shp")
data.drop(
index=[3, 16], inplace=True
)
```
Now let's make the start of a grid from the x and y coordinates (min and max)
```
x_values = np.linspace(min(data.geometry.x), max(data.geometry.x), num=50)
y_values = np.linspace(min(data.geometry.y), max(data.geometry.y), num=50)
```
More work on creating our sample grid that we will interpolate to
```
xy = np.array(list(product(x_values, y_values)))
```
Next let's make a list with all the sample points and their x-y values
```
points = list(zip(data.geometry.x, data.geometry.y))
```
And while we are at it, let's make a `pandas` `Series` with the values we want to interpolate between points
```
values = data.qvalue
```
We have built our grid and now we want to use the `GaussianProcessRegressor` from `sklearn` with an `RBF` kernel to interpolate our data. A good background on Gaussian processes can be found [here](https://en.wikipedia.org/wiki/Gaussian_process) and [here](http://www.gaussianprocess.org/) and I love [this one](http://katbailey.github.io/post/gaussian-processes-for-dummies/). It took me quite a bit of reading to figure out what kernel I wanted to use and decided that `RBF` seemed easy enough to implement with `sklearn`. Let's go ahead and import the methods we need to fit the model
```
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import RBF
```
We will set our `RBF` kernel and choose some length scales, this took me some trial and error to figure out what was appropriate for the dataset
```
kernel = RBF(length_scale=1e2, length_scale_bounds=(3e4, 1e6))
```
Then we fit the `GaussianProcessRegressor` to the points and the values
```
gp = GaussianProcessRegressor(kernel=kernel)
gp.fit(points, values)
```
Now we want to predict the values at all the points on our grid. To do this we use `gp.predict` and feed in our grid, and we also want the mean squared error which is `MSE`
```
y_pred, MSE = gp.predict(xy, return_std=True)
```
Then we have to do some grid reshaping and prediction reshaping gymnastics to get things back into our spatial layout
```
X0, X1 = xy[:, 0].reshape(50, 50), xy[:, 1].reshape(50, 50)
predictions = np.reshape(y_pred, (50, 50))
error = np.reshape(MSE, (50, 50))
```
Then, just like last week we want to add a nice basemap using `contextily`
```
# this cell creates a function that grabs the stamen terrain tiles
def add_basemap(
ax, zoom, url="http://tile.stamen.com/terrain/tileZ/tileX/tileY.png"
):
xmin, xmax, ymin, ymax = ax.axis()
basemap, extent = ctx.bounds2img(
xmin, ymin, xmax, ymax, zoom=zoom, url=url
)
ax.imshow(basemap, extent=extent, interpolation="bilinear")
# restore original x/y limits
ax.axis((xmin, xmax, ymin, ymax))
```
We have predictions, a basemap, and our sample points, let's go ahead and plot it all up and see what we have
```
ax = data.plot(
column="qvalue",
vmin=0,
vmax=50,
figsize=(20, 10),
legend=True,
cmap="RdBu_r",
alpha=0.7,
edgecolor="k",
markersize=90,
zorder=2,
)
add_basemap(ax, zoom=9) # add our basemap to the plot
im = ax.pcolormesh(
X0,
X1,
predictions,
cmap="RdBu_r",
alpha=0.5,
vmin=0,
vmax=50,
edgecolor=(1.0, 1.0, 1.0, 1.0),
linewidth=0.01,
zorder=1,
)
plt.colorbar(im, ax=ax)
```
Since we have the `MSE` for the grid we can also plot that up as well and see how well things fit the spatial data
```
ax = data.plot(
vmin=0,
vmax=50,
figsize=(20, 10),
legend=True,
c="black",
alpha=0.7,
edgecolor="none",
markersize=90,
zorder=2,
)
ax.pcolormesh(
X0,
X1,
error,
cmap="RdBu_r",
alpha=0.5,
edgecolor=(1.0, 1.0, 1.0, 1.0),
linewidth=0.01,
zorder=1,
)
add_basemap(ax, zoom=9) # add our basemap to the plot
```
This notebook is licensed as CC-BY, use and share to your hearts content.
|
github_jupyter
|
import geopandas as gpd
import numpy as np
import matplotlib.pyplot as plt
from itertools import product
import contextily as ctx
%matplotlib inline
data = gpd.read_file("geochemistry_subset.shp")
data.drop(
index=[3, 16], inplace=True
)
x_values = np.linspace(min(data.geometry.x), max(data.geometry.x), num=50)
y_values = np.linspace(min(data.geometry.y), max(data.geometry.y), num=50)
xy = np.array(list(product(x_values, y_values)))
points = list(zip(data.geometry.x, data.geometry.y))
values = data.qvalue
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import RBF
kernel = RBF(length_scale=1e2, length_scale_bounds=(3e4, 1e6))
gp = GaussianProcessRegressor(kernel=kernel)
gp.fit(points, values)
y_pred, MSE = gp.predict(xy, return_std=True)
X0, X1 = xy[:, 0].reshape(50, 50), xy[:, 1].reshape(50, 50)
predictions = np.reshape(y_pred, (50, 50))
error = np.reshape(MSE, (50, 50))
# this cell creates a function that grabs the stamen terrain tiles
def add_basemap(
ax, zoom, url="http://tile.stamen.com/terrain/tileZ/tileX/tileY.png"
):
xmin, xmax, ymin, ymax = ax.axis()
basemap, extent = ctx.bounds2img(
xmin, ymin, xmax, ymax, zoom=zoom, url=url
)
ax.imshow(basemap, extent=extent, interpolation="bilinear")
# restore original x/y limits
ax.axis((xmin, xmax, ymin, ymax))
ax = data.plot(
column="qvalue",
vmin=0,
vmax=50,
figsize=(20, 10),
legend=True,
cmap="RdBu_r",
alpha=0.7,
edgecolor="k",
markersize=90,
zorder=2,
)
add_basemap(ax, zoom=9) # add our basemap to the plot
im = ax.pcolormesh(
X0,
X1,
predictions,
cmap="RdBu_r",
alpha=0.5,
vmin=0,
vmax=50,
edgecolor=(1.0, 1.0, 1.0, 1.0),
linewidth=0.01,
zorder=1,
)
plt.colorbar(im, ax=ax)
ax = data.plot(
vmin=0,
vmax=50,
figsize=(20, 10),
legend=True,
c="black",
alpha=0.7,
edgecolor="none",
markersize=90,
zorder=2,
)
ax.pcolormesh(
X0,
X1,
error,
cmap="RdBu_r",
alpha=0.5,
edgecolor=(1.0, 1.0, 1.0, 1.0),
linewidth=0.01,
zorder=1,
)
add_basemap(ax, zoom=9) # add our basemap to the plot
| 0.630457 | 0.990282 |
# Advanced CPP Buildsystem Override
In this example we will show how we can wrap a complex CPP project by extending the buildsystem defaults provided, which will give us flexibility to configure the required bindings.
If you are looking for a basic implementation of the C++ wrapper, you can get started with the ["Single file C++ Example"](https://docs.seldon.io/projects/seldon-core/en/latest/examples/cpp_simple.html).
You can read about how to configure your environment in the [CPP Wrapper documentation page](https://docs.seldon.io/projects/seldon-core/en/latest/cpp/README.html).
## Naming Conventions
In this example we will have full control on naming conventions.
More specifically there are a few key naming conventions that we need to consider:
* Python Module name
* Python Wrapper Class name
* C++ Library Name
As long as we keep these three key naming conventions in mind, we will have full flexibility on the entire build system.
For this project we will choose the following naming conventions:
* Python Module Name: `CustomSeldonPackage`
* Python Wrapper Class: `MyModelClass`
* C++ Library Name: `CustomSeldonPackage`
As you can see, the name of the Python Module and C++ Library can be the same.
## Wrapper Class
We will first start with the wrapper code of our example. We'll first create our file `Main.cpp` and we'll explain in detail each section below.
```
%%writefile Main.cpp
#include "seldon/SeldonModel.hpp"
class MyModelClass : public seldon::SeldonModelBase {
seldon::protos::SeldonMessage predict(seldon::protos::SeldonMessage &data) override {
return data;
}
};
SELDON_BIND_MODULE(CustomSeldonPackage, MyModelClass)
```
In this file we basically have to note the following key points:
* We import `"seldon/SeldonModel.hpp"` which is from the Seldon package
* We use our custom class name `"MyModelClass"`
* We extend the `SeldonModelBase` class which processes the protos for us
* We override the `predict()` function which provides the raw protos
* We register our class as `SELDON_BIND_MODULE` passing the package name and class name
## Buildsystem CMakeLists.txt
For the build system we have integrated with CMake, as this provides quite a lot of flexibility, and easy integration with external projects.
In this case below are the minimal configurations required in order for everything to work smoothly. The key components to note are:
* We fetch the seldon and pybind11 packages
* We register our C++ library with the name `CustomSeldonMessage`
* We bind the package with the seldon library
You are able to extend the points below as required.
```
%%writefile CMakeLists.txt
cmake_minimum_required(VERSION 3.4.1)
project(seldon_custom_model VERSION 0.0.1)
set(CMAKE_CXX_STANDARD 14)
find_package(seldon REQUIRED)
find_package(pybind11 REQUIRED)
pybind11_add_module(
CustomSeldonPackage
Main.cpp)
target_link_libraries(
CustomSeldonPackage PRIVATE
seldon::seldon)
```
# Environment Variables
The final component is to specify the environment variables.
FOr this we can either pass the env variable as a parameter to the `s2i` command below, or in this example we'll approach it by the other option which is creating an environment file in the `.s2i/environment` file.
The environment variable is `MODEL_NAME`, which should contain the name of your package and model.
In our case it is `CustomSeldonPackage.MyModelClass` as follows:
```
!mkdir -p .s2i/
%writefile .s2i/environment
MODEL_NAME = CustomSeldonPackage.MyModelClass
```
## (Optional) Extend CMake Config via Setup.py
In our case we won't have to pass any custom CMAKE parameters as we can configure everything through the `CMakeLists.txt`, but if you wish to modify how your C++ wrapper is packaged you can extend the setup.py file by following the details in the CPP Wrapper documentation page.
## Build Seldon Microservice
We can now build our seldon microservice using `s2i`:
```
!s2i build . seldonio/s2i-cpp-build:0.0.1 seldonio/advanced-cpp:0.1
```
## Test our model locally by running docker
```
!docker run --name "advanced_cpp" -d --rm -p 5000:5000 seldonio/advanced-cpp:0.1
```
### Send request (which should return the same value)
```
!curl -X POST -H 'Content-Type: application/json' \
-d '{"strData":"hello"}' \
http://localhost:5000/api/v1.0/predictions
```
### Clean up
```
!docker rm -f "advanced_cpp"
```
## Deploy to seldon
```
%%bash
kubectl apply -f - << END
apiVersion: machinelearning.seldon.io/v1
kind: SeldonDeployment
metadata:
name: advanced-cpp
spec:
predictors:
- componentSpecs:
- spec:
containers:
- image: seldonio/advanced-cpp:0.1
name: classifier
engineResources: {}
graph:
name: classifier
type: MODEL
name: default
replicas: 1
END
!curl -X POST -H 'Content-Type: application/json' \
-d '{"strData":"hello"}' \
http://localhost:80/seldon/default/advanced-cpp/api/v1.0/predictions
!kubectl delete sdep advanced-cpp
```
|
github_jupyter
|
%%writefile Main.cpp
#include "seldon/SeldonModel.hpp"
class MyModelClass : public seldon::SeldonModelBase {
seldon::protos::SeldonMessage predict(seldon::protos::SeldonMessage &data) override {
return data;
}
};
SELDON_BIND_MODULE(CustomSeldonPackage, MyModelClass)
%%writefile CMakeLists.txt
cmake_minimum_required(VERSION 3.4.1)
project(seldon_custom_model VERSION 0.0.1)
set(CMAKE_CXX_STANDARD 14)
find_package(seldon REQUIRED)
find_package(pybind11 REQUIRED)
pybind11_add_module(
CustomSeldonPackage
Main.cpp)
target_link_libraries(
CustomSeldonPackage PRIVATE
seldon::seldon)
!mkdir -p .s2i/
%writefile .s2i/environment
MODEL_NAME = CustomSeldonPackage.MyModelClass
!s2i build . seldonio/s2i-cpp-build:0.0.1 seldonio/advanced-cpp:0.1
!docker run --name "advanced_cpp" -d --rm -p 5000:5000 seldonio/advanced-cpp:0.1
!curl -X POST -H 'Content-Type: application/json' \
-d '{"strData":"hello"}' \
http://localhost:5000/api/v1.0/predictions
!docker rm -f "advanced_cpp"
%%bash
kubectl apply -f - << END
apiVersion: machinelearning.seldon.io/v1
kind: SeldonDeployment
metadata:
name: advanced-cpp
spec:
predictors:
- componentSpecs:
- spec:
containers:
- image: seldonio/advanced-cpp:0.1
name: classifier
engineResources: {}
graph:
name: classifier
type: MODEL
name: default
replicas: 1
END
!curl -X POST -H 'Content-Type: application/json' \
-d '{"strData":"hello"}' \
http://localhost:80/seldon/default/advanced-cpp/api/v1.0/predictions
!kubectl delete sdep advanced-cpp
| 0.295433 | 0.955899 |
```
import sys
sys.path.append('../../')
from pyspark.sql import SparkSession
from pyspark.ml import Pipeline
from sparknlp.annotator import *
from sparknlp.common import *
from sparknlp.base import *
import zipfile
import os
from pathlib import Path
import urllib.request
spark = SparkSession.builder \
.appName("ner")\
.master("local[1]")\
.config("spark.driver.memory","8G")\
.config("spark.driver.maxResultS1ize", "2G") \
.config("spark.jars.packages", "JohnSnowLabs:spark-nlp:2.0.1")\
.config("spark.kryoserializer.buffer.max", "500m")\
.getOrCreate()
```
1. Download CoNLL2003 dataset
2. Save 3 files eng.train, eng.testa, eng.testa, into working dir ./
```
# Example how to download CoNLL 2003 Dataset
def download_conll2003_file(file):
if not Path(file).is_file():
url = "https://raw.githubusercontent.com/patverga/torch-ner-nlp-from-scratch/master/data/conll2003/" + file
urllib.request.urlretrieve(url, file)
download_conll2003_file("eng.train")
download_conll2003_file("eng.testa")
download_conll2003_file("eng.testb")
```
3 Download Glove word embeddings
```
file = "glove.6B.zip"
if not Path("glove.6B.zip").is_file():
url = "http://nlp.stanford.edu/data/glove.6B.zip"
print("Start downoading Glove Word Embeddings. It will take some time, please wait...")
urllib.request.urlretrieve(url, "glove.6B.zip")
print("Downloading finished")
if not Path("glove.6B.100d.txt").is_file():
zip_ref = zipfile.ZipFile(file, 'r')
zip_ref.extractall("./")
zip_ref.close()
import time
def get_pipeline():
glove = WordEmbeddingsLookup()\
.setInputCols(["document", "token"])\
.setOutputCol("glove")\
.setEmbeddingsSource("glove.6B.100d.txt", 100, 2)
nerTagger = NerDLApproach()\
.setInputCols(["sentence", "token", "glove"])\
.setLabelColumn("label")\
.setOutputCol("ner")\
.setMaxEpochs(1)\
.setRandomSeed(0)\
.setVerbose(2)
converter = NerConverter()\
.setInputCols(["document", "token", "ner"])\
.setOutputCol("ner_span")
pipeline = Pipeline(
stages = [
glove,
nerTagger,
converter
])
return pipeline
def read_dataset(file):
print("Dataset Reading")
from sparknlp.dataset import CoNLL
conll = CoNLL()
start = time.time()
dataset = conll.readDataset(file)
print("Done, {}\n".format(time.time() - start))
return dataset
def train_model(file):
global spark
dataset = read_dataset(file)
print("Start fitting")
pipeline = get_pipeline()
return pipeline.fit(dataset)
from pyspark.sql.functions import col, udf, explode
def get_dataset_for_analysis(file, model):
global spark
print("Dataset Reading")
start = time.time()
dataset = read_dataset(file)
print("Done, {}\n".format(time.time() - start))
predicted = model.transform(dataset)
global annotation_schema
zip_annotations = udf(
lambda x, y: list(zip(x, y)),
ArrayType(StructType([
StructField("predicted", annotation_schema),
StructField("label", annotation_schema)
]))
)
return predicted\
.withColumn("result", zip_annotations("ner", "label"))\
.select(explode("result").alias("result"))\
.select(
col("result.predicted").alias("predicted"),
col("result.label").alias("label")
)
def printStat(label, correct, predicted, predictedCorrect):
prec = predictedCorrect / predicted if predicted > 0 else 0
rec = predictedCorrect / correct if correct > 0 else 0
f1 = (2*prec*rec)/(prec + rec) if prec + rec > 0 else 0
print("{}\t{}\t{}\t{}".format(label, prec, rec, f1))
def test_dataset(file, model, ignore_tokenize_misses=True):
global spark
started = time.time()
df = read_dataset(file)
transformed = model.transform(df).select("label", "ner")
labels = []
predictedLabels = []
for line in transformed.collect():
label = line[0]
ner = line[1]
ner = {(a["begin"], a["end"]):a["result"] for a in ner}
for a in label:
key = (a["begin"], a["end"])
label = a["result"].strip()
predictedLabel = ner.get(key, "O").strip()
if key not in ner and ignore_tokenize_misses:
continue
labels.append(label)
predictedLabels.append(predictedLabel)
correct = {}
predicted = {}
predictedCorrect = {}
print(len(labels))
for (lPredicted, lCorrect) in zip(predictedLabels, labels):
correct[lCorrect] = correct.get(lCorrect, 0) + 1
predicted[lPredicted] = predicted.get(lPredicted, 0) + 1
if lCorrect == lPredicted:
predictedCorrect[lPredicted] = predictedCorrect.get(lPredicted, 0) + 1
correct = { key: correct[key] for key in correct.keys() if key != 'O'}
predicted = { key: predicted[key] for key in predicted.keys() if key != 'O'}
predictedCorrect = { key: predictedCorrect[key] for key in predictedCorrect.keys() if key != 'O'}
tags = set(list(correct.keys()) + list(predicted.keys()))
print("label\tprec\trec\tf1")
totalCorrect = sum(correct.values())
totalPredicted = sum(predicted.values())
totalPredictedCorrect = sum(predictedCorrect.values())
printStat("Total", totalCorrect, totalPredicted, totalPredictedCorrect)
for label in tags:
printStat(label, correct.get(label, 0), predicted.get(label, 0), predictedCorrect.get(label, 0))
import os.path
folder = '.'
train_file = os.path.join(folder, "eng.train")
test_file_a = os.path.join(folder, "eng.testa")
test_file_b = os.path.join(folder, "eng.testb")
model = train_model(train_file)
print("\nQuality on training data")
test_dataset(train_file, model)
print("\n\nQuality on validation data")
test_dataset(test_file_a, model)
print("\n\nQuality on test data")
test_dataset(test_file_b, model)
df = get_dataset_for_analysis(test_file_a, model)
df.show()
get_pipeline().write().overwrite().save("./crf_pipeline")
model.write().overwrite().save("./crf_model")
from pyspark.ml import PipelineModel, Pipeline
Pipeline.read().load("./crf_pipeline")
sameModel = PipelineModel.read().load("./crf_model")
print("\nQuality on training data")
test_dataset(train_file, sameModel)
print("\n\nQuality on validation data")
test_dataset(test_file_a, sameModel)
print("\n\nQuality on test data")
test_dataset(test_file_b, sameModel)
```
|
github_jupyter
|
import sys
sys.path.append('../../')
from pyspark.sql import SparkSession
from pyspark.ml import Pipeline
from sparknlp.annotator import *
from sparknlp.common import *
from sparknlp.base import *
import zipfile
import os
from pathlib import Path
import urllib.request
spark = SparkSession.builder \
.appName("ner")\
.master("local[1]")\
.config("spark.driver.memory","8G")\
.config("spark.driver.maxResultS1ize", "2G") \
.config("spark.jars.packages", "JohnSnowLabs:spark-nlp:2.0.1")\
.config("spark.kryoserializer.buffer.max", "500m")\
.getOrCreate()
# Example how to download CoNLL 2003 Dataset
def download_conll2003_file(file):
if not Path(file).is_file():
url = "https://raw.githubusercontent.com/patverga/torch-ner-nlp-from-scratch/master/data/conll2003/" + file
urllib.request.urlretrieve(url, file)
download_conll2003_file("eng.train")
download_conll2003_file("eng.testa")
download_conll2003_file("eng.testb")
file = "glove.6B.zip"
if not Path("glove.6B.zip").is_file():
url = "http://nlp.stanford.edu/data/glove.6B.zip"
print("Start downoading Glove Word Embeddings. It will take some time, please wait...")
urllib.request.urlretrieve(url, "glove.6B.zip")
print("Downloading finished")
if not Path("glove.6B.100d.txt").is_file():
zip_ref = zipfile.ZipFile(file, 'r')
zip_ref.extractall("./")
zip_ref.close()
import time
def get_pipeline():
glove = WordEmbeddingsLookup()\
.setInputCols(["document", "token"])\
.setOutputCol("glove")\
.setEmbeddingsSource("glove.6B.100d.txt", 100, 2)
nerTagger = NerDLApproach()\
.setInputCols(["sentence", "token", "glove"])\
.setLabelColumn("label")\
.setOutputCol("ner")\
.setMaxEpochs(1)\
.setRandomSeed(0)\
.setVerbose(2)
converter = NerConverter()\
.setInputCols(["document", "token", "ner"])\
.setOutputCol("ner_span")
pipeline = Pipeline(
stages = [
glove,
nerTagger,
converter
])
return pipeline
def read_dataset(file):
print("Dataset Reading")
from sparknlp.dataset import CoNLL
conll = CoNLL()
start = time.time()
dataset = conll.readDataset(file)
print("Done, {}\n".format(time.time() - start))
return dataset
def train_model(file):
global spark
dataset = read_dataset(file)
print("Start fitting")
pipeline = get_pipeline()
return pipeline.fit(dataset)
from pyspark.sql.functions import col, udf, explode
def get_dataset_for_analysis(file, model):
global spark
print("Dataset Reading")
start = time.time()
dataset = read_dataset(file)
print("Done, {}\n".format(time.time() - start))
predicted = model.transform(dataset)
global annotation_schema
zip_annotations = udf(
lambda x, y: list(zip(x, y)),
ArrayType(StructType([
StructField("predicted", annotation_schema),
StructField("label", annotation_schema)
]))
)
return predicted\
.withColumn("result", zip_annotations("ner", "label"))\
.select(explode("result").alias("result"))\
.select(
col("result.predicted").alias("predicted"),
col("result.label").alias("label")
)
def printStat(label, correct, predicted, predictedCorrect):
prec = predictedCorrect / predicted if predicted > 0 else 0
rec = predictedCorrect / correct if correct > 0 else 0
f1 = (2*prec*rec)/(prec + rec) if prec + rec > 0 else 0
print("{}\t{}\t{}\t{}".format(label, prec, rec, f1))
def test_dataset(file, model, ignore_tokenize_misses=True):
global spark
started = time.time()
df = read_dataset(file)
transformed = model.transform(df).select("label", "ner")
labels = []
predictedLabels = []
for line in transformed.collect():
label = line[0]
ner = line[1]
ner = {(a["begin"], a["end"]):a["result"] for a in ner}
for a in label:
key = (a["begin"], a["end"])
label = a["result"].strip()
predictedLabel = ner.get(key, "O").strip()
if key not in ner and ignore_tokenize_misses:
continue
labels.append(label)
predictedLabels.append(predictedLabel)
correct = {}
predicted = {}
predictedCorrect = {}
print(len(labels))
for (lPredicted, lCorrect) in zip(predictedLabels, labels):
correct[lCorrect] = correct.get(lCorrect, 0) + 1
predicted[lPredicted] = predicted.get(lPredicted, 0) + 1
if lCorrect == lPredicted:
predictedCorrect[lPredicted] = predictedCorrect.get(lPredicted, 0) + 1
correct = { key: correct[key] for key in correct.keys() if key != 'O'}
predicted = { key: predicted[key] for key in predicted.keys() if key != 'O'}
predictedCorrect = { key: predictedCorrect[key] for key in predictedCorrect.keys() if key != 'O'}
tags = set(list(correct.keys()) + list(predicted.keys()))
print("label\tprec\trec\tf1")
totalCorrect = sum(correct.values())
totalPredicted = sum(predicted.values())
totalPredictedCorrect = sum(predictedCorrect.values())
printStat("Total", totalCorrect, totalPredicted, totalPredictedCorrect)
for label in tags:
printStat(label, correct.get(label, 0), predicted.get(label, 0), predictedCorrect.get(label, 0))
import os.path
folder = '.'
train_file = os.path.join(folder, "eng.train")
test_file_a = os.path.join(folder, "eng.testa")
test_file_b = os.path.join(folder, "eng.testb")
model = train_model(train_file)
print("\nQuality on training data")
test_dataset(train_file, model)
print("\n\nQuality on validation data")
test_dataset(test_file_a, model)
print("\n\nQuality on test data")
test_dataset(test_file_b, model)
df = get_dataset_for_analysis(test_file_a, model)
df.show()
get_pipeline().write().overwrite().save("./crf_pipeline")
model.write().overwrite().save("./crf_model")
from pyspark.ml import PipelineModel, Pipeline
Pipeline.read().load("./crf_pipeline")
sameModel = PipelineModel.read().load("./crf_model")
print("\nQuality on training data")
test_dataset(train_file, sameModel)
print("\n\nQuality on validation data")
test_dataset(test_file_a, sameModel)
print("\n\nQuality on test data")
test_dataset(test_file_b, sameModel)
| 0.422505 | 0.601184 |
## Synthetic Dataset Generation
Here we demonstrate how to use our `genalog` package to generate synthetic documents with custom image degradation and upload the documents to an Azure Blob Storage.
<p float="left">
<img src="static/labeled_synthetic_pipeline.png" width="900" />
</p>
## Dataset file structure
Our dataset follows this file structure:
```
<ROOT FOLDER>/ #eg. synthetic-image-root
<SRC_DATASET_NAME> #eg. CNN-Dailymail-Stories
│
│───shared/ #common files shared across different dataset versions
│ │───train/
│ │ │───clean_text/
│ │ │ │─0.txt
│ │ │ │─1.txt
│ │ │ └─...
│ │ └───clean_labels/
│ │ │─0.txt
│ │ │─1.txt
│ │ └─...
│ └───test/
│ │───clean_text/*.txt
│ └───clean_labels/*.txt
│
└───<VERSION_NAME>/ #e.g. hyphens_blur_heavy
│───train/
│ │─img/*.png #Degraded Images
│ │─ocr/*.json #json output files that are output of GROK
│ │─ocr_text/*.txt #text output retrieved from OCR Json Files
│ └─ocr_labels/*.txt #Aligned labels files in IOB format
│───test/
│ │─img/*.png #Degraded Images
│ │─ocr/*.json #json output files that are output of GROK
│ │─ocr_text/*.txt #text output retrieved from OCR Json Files
│ └─ocr_labels/*.txt #Aligned labels files in IOB format
│
│───layout.json #records page layout info (font-family,template name, etc)
│───degradation.json #records degradation parameters
│───ocr_metric.csv #records metrics on OCR noise across the dataset
└───substitution.json #records character substitution errors in the OCR'ed text.
```
## Source NER Dataset
This pipeline is designed to work with standard NER datasets like CoNLL 2003 and CoNLL 2012. You can downaload the source dataset from DeepAI: [CoNLL-2003](https://deepai.org/dataset/conll-2003-english)
**NOTE:** the source dataset has three separate columns of NER labels, we are only interested in the last column:
```
Source Desired (space-separted)
DOCSTART- -X- -X- O DOCSTART O
SOCCER NN B-NP O SOCCER O
- : O O - O
JAPAN NNP B-NP B-LOC JAPAN B-LOC
GET VB B-VP O GET O
LUCKY NNP B-NP O LUCKY O
WIN NNP I-NP O WIN O
, , O O , O
CHINA NNP B-NP B-PER CHINA B-PER
IN IN B-PP O IN O
SURPRISE DT B-NP O SURPRISE O
DEFEAT NN I-NP O DEFEAT O
... ...
```
Unfortunately, this preprocess step is out of the scope of this pipeline.
**TODO:** Add support for this or share the preprocessed dataset.
## Source Dataset Split
Before we can generate analog documents, we need text to populate the analog documents. To do so, we will split the source text into smaller text fragments. Here we have provided a script `genalog.text.splitter` to easily split NER datasets CoNLL-2003 and CoNLL-2012 in the following ways:
1. **Split dataset into smaller fragments**: each fragment is named as `<INDEX>.txt`
1. **Separate NER labels from document text**: NER labels will be stored in `clean_lables` folder and text in `clean_text` folder
```
INPUT_FILE_TEMPLATE = "/data/enki/datasets/CoNLL_2003_2012/CoNLL-<DATASET_YEAR>/CoNLL-<DATASET_YEAR>_<SUBSET>.txt"
OUTPUT_FOLDER_TEMPLATE = "/data/enki/datasets/synthetic_dataset/CoNLL_<DATASET_YEAR>_v3/shared/<SUBSET>/"
for year in ["2003", "2012"]:
for subset in ["test", "train"]:
# INPUT_FILE = "/data/enki/datasets/CoNLL_2003_2012/CoNLL-2012/CoNLL-2012_test.txt"
INPUT_FILE = INPUT_FILE_TEMPLATE.replace("<DATASET_YEAR>", year).replace("<SUBSET>", subset)
# OUTPUT_FOLDER = "/data/enki/datasets/synthetic_dataset/CoNLL_2012_v2/shared/test/"
OUTPUT_FOLDER = OUTPUT_FOLDER_TEMPLATE.replace("<DATASET_YEAR>", year).replace("<SUBSET>", subset)
print(f"Loading {INPUT_FILE} \nOutput to {OUTPUT_FOLDER}")
if year == "2003":
!python -m genalog.text.splitter $INPUT_FILE $OUTPUT_FOLDER --doc_sep="-DOCSTART-\tO"
else:
!python -m genalog.text.splitter $INPUT_FILE $OUTPUT_FOLDER
```
## Configurations
We will generate the synthetic dataset on your local disk first. You will need to specify the following CONSTANTS to locate where to store the dataset:
1. `ROOT_FOLDER`: root directory of the dataset, path can be relative to the location of this notebook.
1. `SRC_DATASET_NAME`: name of the source dataset from which the text used in the generation originates from
1. `SRC_TRAIN_SPLIT_PATH`: path of the train-split of the source dataset
1. `SRC_TEST_SPLIT_PATH`: path of the test-split of the source dataset
1. `VERSION_NAME`: version name of the generated dataset
You will also have to define the styles and degradation effects you will like to apply onto each generated document:
1. `STYLE_COMBINATIONS`: a dictionary defining the combination of styles to generate per text document (i.e. a copy of the same text document is generate per style combination). Example is shown below:
STYLE_COMBINATION = {
"language": ["en_US"],
"font_family": ["Segoe UI"],
"font_size": ["12px"],
"text_align": ["left"],
"hyphenate": [False],
}
You can expand the list of each style for more combinations
2. `DEGRADATIONS`: a list defining the sequence of degradation effects applied onto the synthetic images. Each element is a two-element tuple of which the first element is one of the method names from `genalog.degradation.effect` and the second element is the corresponding function keyword arguments.
DEGRADATIONS = [
("blur", {"radius": 3}),
("bleed_through", {"alpha": 0.8}),
("morphology", {"operation": "open", "kernel_shape": (3,3), "kernel_type": "ones"}),
]
The example above will apply degradation effects to synthetic images in the sequence of:
blur -> bleed_through -> morphological operation (open)
3. `HTML_TEMPLATE`: name of html template used to generate the synthetic images. The `genalog` package has the following default templates:
1. `columns.html.jinja`
2. `letter.html.jinja`
3. `text_block.html.jinja`
HTML_TEMPLATE = 'text_block.html.jinja'
```
from genalog.degradation.degrader import ImageState
ROOT_FOLDER = "/data/enki/datasets/synthetic_dataset/"
SRC_DATASET_NAME = "CoNLL_2003_v3"
VERSION_NAME = "hyphens_close_heavy"
SRC_TRAIN_SPLIT_PATH = ROOT_FOLDER + SRC_DATASET_NAME + "/shared/train/clean_text/"
SRC_TEST_SPLIT_PATH = ROOT_FOLDER + SRC_DATASET_NAME + "/shared/test/clean_text/"
DST_TRAIN_PATH = ROOT_FOLDER + SRC_DATASET_NAME + "/" + VERSION_NAME + "/train/"
DST_TEST_PATH = ROOT_FOLDER + SRC_DATASET_NAME + "/" + VERSION_NAME + "/test/"
STYLE_COMBINATIONS = {
"language": ["en_US"],
"font_family": ["Segeo UI"],
"font_size": ["12px"],
"text_align": ["justify"],
"hyphenate": [True],
}
DEGRADATIONS = [
## Stacking Degradations
("morphology", {"operation": "open", "kernel_shape":(9,9), "kernel_type":"plus"}),
("morphology", {"operation": "close", "kernel_shape":(9,1), "kernel_type":"ones"}),
("salt", {"amount": 0.9}),
("overlay", {
"src": ImageState.ORIGINAL_STATE,
"background": ImageState.CURRENT_STATE,
}),
("bleed_through", {
"src": ImageState.CURRENT_STATE,
"background": ImageState.ORIGINAL_STATE,
"alpha": 0.95,
"offset_x": -6,
"offset_y": -12,
}),
("pepper", {"amount": 0.001}),
("blur", {"radius": 5}),
("salt", {"amount": 0.1}),
]
HTML_TEMPLATE = "text_block.html.jinja"
IMG_RESOLUTION = 300 #dpi
print(f"Training set will be saved to: '{DST_TRAIN_PATH}'")
print(f"Testing set will be saved to: '{DST_TEST_PATH}'")
```
## Load in Text Documents
```
import glob
import os
train_text = sorted(glob.glob(SRC_TRAIN_SPLIT_PATH + "*.txt"))
test_text = sorted(glob.glob(SRC_TEST_SPLIT_PATH + "*.txt"))
print(f"Number of training text documents: {len(train_text)}")
print(f"Number of testing text documents: {len(test_text)}")
```
## Document Sample
```
from genalog.pipeline import AnalogDocumentGeneration
from IPython.core.display import Image, display
import timeit
import cv2
sample_file = test_text[0]
print(f"Sample Filename: {sample_file}")
doc_generation = AnalogDocumentGeneration(styles=STYLE_COMBINATIONS, degradations=DEGRADATIONS, resolution=IMG_RESOLUTION)
print(f"Avaliable Templates: {doc_generation.list_templates()}")
start_time = timeit.default_timer()
img_array = doc_generation.generate_img(sample_file, HTML_TEMPLATE, target_folder=None)
elapsed = timeit.default_timer() - start_time
print(f"Time to generate 1 documents: {elapsed:.3f} sec")
_, encoded_image = cv2.imencode('.png', img_array)
display(Image(data=encoded_image, width=600))
```
## Execute Generation
```
from genalog.pipeline import generate_dataset_multiprocess
# Generating test set
generate_dataset_multiprocess(
test_text, DST_TEST_PATH, STYLE_COMBINATIONS, DEGRADATIONS, HTML_TEMPLATE,
resolution=IMG_RESOLUTION, batch_size=5
)
from genalog.pipeline import generate_dataset_multiprocess
# Generating training set
generate_dataset_multiprocess(
train_text, DST_TRAIN_PATH, STYLE_COMBINATIONS, DEGRADATIONS, HTML_TEMPLATE,
resolution=IMG_RESOLUTION, batch_size=5
)
```
### Saving Dataset Configurations as .json
```
from genalog.pipeline import ImageStateEncoder
import json
layout_json_path = ROOT_FOLDER + SRC_DATASET_NAME + "/" + VERSION_NAME + "/layout.json"
degradation_json_path = ROOT_FOLDER + SRC_DATASET_NAME + "/" + VERSION_NAME + "/degradation.json"
layout = {
"style_combinations": STYLE_COMBINATIONS,
"img_resolution": IMG_RESOLUTION,
"html_templates": [HTML_TEMPLATE],
}
layout_js_str = json.dumps(layout, indent=2)
degrade_js_str = json.dumps(DEGRADATIONS, indent=2, cls=ImageStateEncoder)
with open(layout_json_path, "w") as f:
f.write(layout_js_str)
with open(degradation_json_path, "w") as f:
f.write(degrade_js_str)
print(f"Writing configs to {layout_json_path}")
print(f"Writing configs to {degradation_json_path}")
```
## Setup Azure Blob Client
We will use Azure Cognitive Service to run OCR on these synthetic images, and we will first upload the dataset to blob storage.
1. If you haven't already, setup new Azure resources
1. [Azure Blob Storage](https://azure.microsoft.com/en-us/services/storage/blobs/) (for storage)
1. [Azure Cognitive Search](https://azure.microsoft.com/en-us/services/search/) (for OCR results)
1. Create an `.secret` file with the environment variables that includes the names of you index, indexer, skillset, and datasource to create on the search service. Include keys to the blob that contains the documents you want to index, keys to the congnitive service and keys to you computer vision subscription and search service. In order to index more than 20 documents, you must have a computer services subscription. An example of one such `.secret` file is below:
```bash
SEARCH_SERVICE_NAME = "ocr-ner-pipeline"
SKILLSET_NAME = "ocrskillset"
INDEX_NAME = "ocrindex"
INDEXER_NAME = "ocrindexer"
DATASOURCE_NAME = <BLOB STORAGE ACCOUNT NAME>
DATASOURCE_CONTAINER_NAME = <BLOB CONTAINER NAME>
COMPUTER_VISION_ENDPOINT = "https://<YOUR ENDPOINT NAME>.cognitiveservices.azure.com/"
COMPUTER_VISION_SUBSCRIPTION_KEY = "<YOUR SUBSCRIPTION KEY>"
BLOB_NAME = "<YOUR BLOB STORAGE NAME>"
BLOB_KEY = "<YOUR BLOB KEY>"
SEARCH_SERVICE_KEY = "<YOUR SEARCH SERVICE KEY>"
COGNITIVE_SERVICE_KEY = "<YOUR COGNITIVE SERVICE KEY>"
```
```
from dotenv import load_dotenv
from genalog.ocr.blob_client import GrokBlobClient
# Setup variables and authenticate blob client
ROOT_FOLDER = "/data/enki/datasets/synthetic_dataset/"
SRC_DATASET_NAME = "CoNLL_2012_v3"
local_path = ROOT_FOLDER + SRC_DATASET_NAME
remote_path = SRC_DATASET_NAME
print(f"Uploadig from local_path: {local_path}")
print(f"Upload to remote_path: {remote_path}")
load_dotenv("../.secrets")
blob_client = GrokBlobClient.create_from_env_var()
```
## Upload Dataset to Azure Blob Storage
```
import time
# Python uploads can be slow.
# for very large datasets use azcopy: https://github.com/Azure/azure-storage-azcopy
start = time.time()
dest, res = blob_client.upload_images_to_blob(local_path, remote_path, use_async=True)
await res
print("time (mins): ", (time.time()-start)/60)
# Delete a remote folder on Blob
# blob_client.delete_blobs_folder("CoNLL_2003_v2_test")
```
## Run Indexer and Retrieve OCR results
Please note that this process can take a **long time**, but you can upload multiple dataset to Blob and run this once for all of them.
```
from genalog.ocr.rest_client import GrokRestClient
from dotenv import load_dotenv
load_dotenv("../.secrets")
grok_rest_client = GrokRestClient.create_from_env_var()
grok_rest_client.create_indexing_pipeline()
grok_rest_client.run_indexer()
# wait for indexer to finish
grok_rest_client.poll_indexer_till_complete()
```
## Download OCR Results
```
import os
# Downloading multiple dataset to local
remote_path = SRC_DATASET_NAME
local_path = ROOT_FOLDER + SRC_DATASET_NAME
versions = ["hyphens_all_heavy"]
version_prefix = ""
version_suffixes = [""]
print(f"Remote Path: {remote_path} \nLocal Path: {local_path} \nVersions: {versions}")
blob_img_paths_test = []
blob_img_paths_train = []
local_ocr_json_paths_test = []
local_ocr_json_paths_train = []
version_name = ""
for version in versions:
for weight in version_suffixes:
version_name = version_prefix + version + weight
blob_img_paths_test.append(os.path.join(remote_path, version_name, "test", "img"))
blob_img_paths_train.append(os.path.join(remote_path, version_name, "train", "img"))
local_ocr_json_paths_test.append(os.path.join(local_path, version_name, "test", "ocr"))
local_ocr_json_paths_train.append(os.path.join(local_path, version_name, "train", "ocr"))
print(f"Example Version Name: {version_name}")
# download OCR
for blob_path_test, blob_path_train, local_path_test, local_path_train in \
zip(blob_img_paths_test, blob_img_paths_train, \
local_ocr_json_paths_test, local_ocr_json_paths_train):
print(f"Downloading \nfrom remote path:'{blob_path_test} \n to local path:'{local_path_test}'")
await blob_client.get_ocr_json(blob_path_test, output_folder=local_path_test, use_async=True)
print(f"Downloading \nfrom remote path:'{blob_path_train} \n to local path:'{local_path_train}'")
await blob_client.get_ocr_json(blob_path_train, output_folder=local_path_train, use_async=True)
```
# Generate OCR metrics
```
import os
local_path = ROOT_FOLDER + SRC_DATASET_NAME
versions = ["hyphens_all_heavy"]
version_prefix = ""
version_suffixes = [""]
print(f"Local Path: {local_path} \nVersions: {versions}\n")
input_json_path_templates = []
output_metric_path = []
for version in versions:
for suffix in version_suffixes:
version_name = version_prefix + version + suffix
# Location depends on the input dataset
input_json_path_templates.append(os.path.join(local_path, version_name, "<test/train>/ocr"))
output_metric_path.append(os.path.join(local_path, version_name))
clean_text_path_template = os.path.join(local_path, "shared/<test/train>/clean_text")
csv_metric_name_template = "<test/train>_ocr_metrics.csv"
subs_json_name_template = "<test/train>_subtitutions.json"
avg_metric_name = "ocr_metrics.csv"
print(f"Loading \n'{clean_text_path_template}' \nand \n'{input_json_path_templates[0]}'...")
print(f"Saving to {output_metric_path}")
import sys
import json
import pandas as pd
from genalog.ocr.metrics import get_metrics, substitution_dict_to_json
for input_json_path_template, output_metric_path in zip(input_json_path_templates, output_metric_path):
subsets = ["train", "test"]
avg_stat = {subset: None for subset in subsets}
for subset in subsets:
clean_text_path = clean_text_path_template.replace("<test/train>", subset)
ocr_json_path = input_json_path_template.replace("<test/train>", subset)
csv_metric_name = csv_metric_name_template.replace("<test/train>", subset)
subs_json_name = subs_json_name_template.replace("<test/train>", subset)
output_csv_name = output_metric_path + "/" + csv_metric_name
output_json_name = output_metric_path + "/" + subs_json_name
print(f"Saving to '{output_csv_name}' \nand '{output_json_name}'")
df, subs, actions = get_metrics(clean_text_path, ocr_json_path, use_multiprocessing=True)
# Writing metrics on individual file
df.to_csv(output_csv_name)
json.dump(substitution_dict_to_json(subs), open(output_json_name, "w"))
# Getting average metrics
avg_stat[subset] = df.mean()
# Saving average metrics
avg_stat = pd.DataFrame(avg_stat)
output_avg_csv = os.path.join(output_metric_path, avg_metric_name)
avg_stat.to_csv(output_avg_csv)
print(f"Saving average metrics to {output_avg_csv}")
print(avg_stat[16:])
```
## Organize OCR'ed Text into IOB Format For Model Training Purpose
The last step in preparing the dataset is to format all the OCR'ed text and the NER label into a usable format for training. Our model consume data in IOB format, which is the same format used in the CoNLL datasets.
```
base_path = "/data/enki/datasets/synthetic_dataset/CoNLL_2012_v3"
versions = ["hyphens_all_heavy"]
version_prefix = ""
version_suffixes = [""]
version_names = []
for version in versions:
for suffix in version_suffixes:
version_names.append(version_prefix + version + suffix)
print(f"base_path: {base_path}\nversion_names: {version_names}")
for version in version_names:
!python -m genalog.text.conll_format $base_path $version --train_subset
```
## [Optional] Re-upload Local Dataset to Blob
We can re-upload the local copy of the dataset to Blob Storage to sync up the two copies
```
import os
local_dataset_to_sync = os.path.join(local_path)
blob_path = os.path.join(remote_path)
print(f"local_dataset_to_sync: {local_dataset_to_sync}\nblob_path: {blob_path}")
import time
# Python uploads can be slow.
# for very large datasets use azcopy: https://github.com/Azure/azure-storage-azcopy
start = time.time()
dest, res = blob_client.upload_images_to_blob(local_dataset_to_sync, blob_path, use_async=True)
await res
print("time (mins): ", (time.time()-start)/60)
```
|
github_jupyter
|
<ROOT FOLDER>/ #eg. synthetic-image-root
<SRC_DATASET_NAME> #eg. CNN-Dailymail-Stories
│
│───shared/ #common files shared across different dataset versions
│ │───train/
│ │ │───clean_text/
│ │ │ │─0.txt
│ │ │ │─1.txt
│ │ │ └─...
│ │ └───clean_labels/
│ │ │─0.txt
│ │ │─1.txt
│ │ └─...
│ └───test/
│ │───clean_text/*.txt
│ └───clean_labels/*.txt
│
└───<VERSION_NAME>/ #e.g. hyphens_blur_heavy
│───train/
│ │─img/*.png #Degraded Images
│ │─ocr/*.json #json output files that are output of GROK
│ │─ocr_text/*.txt #text output retrieved from OCR Json Files
│ └─ocr_labels/*.txt #Aligned labels files in IOB format
│───test/
│ │─img/*.png #Degraded Images
│ │─ocr/*.json #json output files that are output of GROK
│ │─ocr_text/*.txt #text output retrieved from OCR Json Files
│ └─ocr_labels/*.txt #Aligned labels files in IOB format
│
│───layout.json #records page layout info (font-family,template name, etc)
│───degradation.json #records degradation parameters
│───ocr_metric.csv #records metrics on OCR noise across the dataset
└───substitution.json #records character substitution errors in the OCR'ed text.
Source Desired (space-separted)
DOCSTART- -X- -X- O DOCSTART O
SOCCER NN B-NP O SOCCER O
- : O O - O
JAPAN NNP B-NP B-LOC JAPAN B-LOC
GET VB B-VP O GET O
LUCKY NNP B-NP O LUCKY O
WIN NNP I-NP O WIN O
, , O O , O
CHINA NNP B-NP B-PER CHINA B-PER
IN IN B-PP O IN O
SURPRISE DT B-NP O SURPRISE O
DEFEAT NN I-NP O DEFEAT O
... ...
INPUT_FILE_TEMPLATE = "/data/enki/datasets/CoNLL_2003_2012/CoNLL-<DATASET_YEAR>/CoNLL-<DATASET_YEAR>_<SUBSET>.txt"
OUTPUT_FOLDER_TEMPLATE = "/data/enki/datasets/synthetic_dataset/CoNLL_<DATASET_YEAR>_v3/shared/<SUBSET>/"
for year in ["2003", "2012"]:
for subset in ["test", "train"]:
# INPUT_FILE = "/data/enki/datasets/CoNLL_2003_2012/CoNLL-2012/CoNLL-2012_test.txt"
INPUT_FILE = INPUT_FILE_TEMPLATE.replace("<DATASET_YEAR>", year).replace("<SUBSET>", subset)
# OUTPUT_FOLDER = "/data/enki/datasets/synthetic_dataset/CoNLL_2012_v2/shared/test/"
OUTPUT_FOLDER = OUTPUT_FOLDER_TEMPLATE.replace("<DATASET_YEAR>", year).replace("<SUBSET>", subset)
print(f"Loading {INPUT_FILE} \nOutput to {OUTPUT_FOLDER}")
if year == "2003":
!python -m genalog.text.splitter $INPUT_FILE $OUTPUT_FOLDER --doc_sep="-DOCSTART-\tO"
else:
!python -m genalog.text.splitter $INPUT_FILE $OUTPUT_FOLDER
from genalog.degradation.degrader import ImageState
ROOT_FOLDER = "/data/enki/datasets/synthetic_dataset/"
SRC_DATASET_NAME = "CoNLL_2003_v3"
VERSION_NAME = "hyphens_close_heavy"
SRC_TRAIN_SPLIT_PATH = ROOT_FOLDER + SRC_DATASET_NAME + "/shared/train/clean_text/"
SRC_TEST_SPLIT_PATH = ROOT_FOLDER + SRC_DATASET_NAME + "/shared/test/clean_text/"
DST_TRAIN_PATH = ROOT_FOLDER + SRC_DATASET_NAME + "/" + VERSION_NAME + "/train/"
DST_TEST_PATH = ROOT_FOLDER + SRC_DATASET_NAME + "/" + VERSION_NAME + "/test/"
STYLE_COMBINATIONS = {
"language": ["en_US"],
"font_family": ["Segeo UI"],
"font_size": ["12px"],
"text_align": ["justify"],
"hyphenate": [True],
}
DEGRADATIONS = [
## Stacking Degradations
("morphology", {"operation": "open", "kernel_shape":(9,9), "kernel_type":"plus"}),
("morphology", {"operation": "close", "kernel_shape":(9,1), "kernel_type":"ones"}),
("salt", {"amount": 0.9}),
("overlay", {
"src": ImageState.ORIGINAL_STATE,
"background": ImageState.CURRENT_STATE,
}),
("bleed_through", {
"src": ImageState.CURRENT_STATE,
"background": ImageState.ORIGINAL_STATE,
"alpha": 0.95,
"offset_x": -6,
"offset_y": -12,
}),
("pepper", {"amount": 0.001}),
("blur", {"radius": 5}),
("salt", {"amount": 0.1}),
]
HTML_TEMPLATE = "text_block.html.jinja"
IMG_RESOLUTION = 300 #dpi
print(f"Training set will be saved to: '{DST_TRAIN_PATH}'")
print(f"Testing set will be saved to: '{DST_TEST_PATH}'")
import glob
import os
train_text = sorted(glob.glob(SRC_TRAIN_SPLIT_PATH + "*.txt"))
test_text = sorted(glob.glob(SRC_TEST_SPLIT_PATH + "*.txt"))
print(f"Number of training text documents: {len(train_text)}")
print(f"Number of testing text documents: {len(test_text)}")
from genalog.pipeline import AnalogDocumentGeneration
from IPython.core.display import Image, display
import timeit
import cv2
sample_file = test_text[0]
print(f"Sample Filename: {sample_file}")
doc_generation = AnalogDocumentGeneration(styles=STYLE_COMBINATIONS, degradations=DEGRADATIONS, resolution=IMG_RESOLUTION)
print(f"Avaliable Templates: {doc_generation.list_templates()}")
start_time = timeit.default_timer()
img_array = doc_generation.generate_img(sample_file, HTML_TEMPLATE, target_folder=None)
elapsed = timeit.default_timer() - start_time
print(f"Time to generate 1 documents: {elapsed:.3f} sec")
_, encoded_image = cv2.imencode('.png', img_array)
display(Image(data=encoded_image, width=600))
from genalog.pipeline import generate_dataset_multiprocess
# Generating test set
generate_dataset_multiprocess(
test_text, DST_TEST_PATH, STYLE_COMBINATIONS, DEGRADATIONS, HTML_TEMPLATE,
resolution=IMG_RESOLUTION, batch_size=5
)
from genalog.pipeline import generate_dataset_multiprocess
# Generating training set
generate_dataset_multiprocess(
train_text, DST_TRAIN_PATH, STYLE_COMBINATIONS, DEGRADATIONS, HTML_TEMPLATE,
resolution=IMG_RESOLUTION, batch_size=5
)
from genalog.pipeline import ImageStateEncoder
import json
layout_json_path = ROOT_FOLDER + SRC_DATASET_NAME + "/" + VERSION_NAME + "/layout.json"
degradation_json_path = ROOT_FOLDER + SRC_DATASET_NAME + "/" + VERSION_NAME + "/degradation.json"
layout = {
"style_combinations": STYLE_COMBINATIONS,
"img_resolution": IMG_RESOLUTION,
"html_templates": [HTML_TEMPLATE],
}
layout_js_str = json.dumps(layout, indent=2)
degrade_js_str = json.dumps(DEGRADATIONS, indent=2, cls=ImageStateEncoder)
with open(layout_json_path, "w") as f:
f.write(layout_js_str)
with open(degradation_json_path, "w") as f:
f.write(degrade_js_str)
print(f"Writing configs to {layout_json_path}")
print(f"Writing configs to {degradation_json_path}")
SEARCH_SERVICE_NAME = "ocr-ner-pipeline"
SKILLSET_NAME = "ocrskillset"
INDEX_NAME = "ocrindex"
INDEXER_NAME = "ocrindexer"
DATASOURCE_NAME = <BLOB STORAGE ACCOUNT NAME>
DATASOURCE_CONTAINER_NAME = <BLOB CONTAINER NAME>
COMPUTER_VISION_ENDPOINT = "https://<YOUR ENDPOINT NAME>.cognitiveservices.azure.com/"
COMPUTER_VISION_SUBSCRIPTION_KEY = "<YOUR SUBSCRIPTION KEY>"
BLOB_NAME = "<YOUR BLOB STORAGE NAME>"
BLOB_KEY = "<YOUR BLOB KEY>"
SEARCH_SERVICE_KEY = "<YOUR SEARCH SERVICE KEY>"
COGNITIVE_SERVICE_KEY = "<YOUR COGNITIVE SERVICE KEY>"
```
## Upload Dataset to Azure Blob Storage
## Run Indexer and Retrieve OCR results
Please note that this process can take a **long time**, but you can upload multiple dataset to Blob and run this once for all of them.
## Download OCR Results
# Generate OCR metrics
## Organize OCR'ed Text into IOB Format For Model Training Purpose
The last step in preparing the dataset is to format all the OCR'ed text and the NER label into a usable format for training. Our model consume data in IOB format, which is the same format used in the CoNLL datasets.
## [Optional] Re-upload Local Dataset to Blob
We can re-upload the local copy of the dataset to Blob Storage to sync up the two copies
| 0.399226 | 0.903337 |
# Lesson 3 Class Exercises: Pandas Part 1
With these class exercises we learn a few new things. When new knowledge is introduced you'll see the icon shown on the right:
<span style="float:right; margin-left:10px; clear:both;"></span>
## Reminder
The first checkin-in of the project is due next Tueday. After today, you should have everything you need to know to accomplish that first part.
## Get Started
Import the Numpy and Pandas packages
## Exercise 1: Import Iris Data
Import the Iris dataset made available to you in the last class period for the Numpy part2 exercises. Save it to a variable naemd `iris`. Print the first 5 rows and the dimensions to ensure it was read in properly.
Notice how much easier this was to import compared to the Numpy `genfromtxt`. We did not have to skip the headers, we did not have to specify the data type and we can have mixed data types in the same matrix.
## Exercise 2: Import Legislators Data
For portions of this notebook we will use a public dataset that contains all of the current legistators of the United States Congress. This dataset can be found [here](https://github.com/unitedstates/congress-legislators).
Import the data directly from this URL: https://theunitedstates.io/congress-legislators/legislators-current.csv
Save the data in a variable named `legistators`. Print the first 5 lines, and the dimensions.
## Exercise 3: Explore the Data
### Task 1
Print the column names of the legistators dataframe and explore the type of data in the data frame.
### Task 2
Show the datatypes of all of the columns in the legislator data. Do all of the data types seem appropriate for the data?
Show all of the datayptes in the iris dataframe
### Task 3
It's always important to know where the missing values are in your data. Are there any missing values in the legislators dataframe? How many per column?
Hint: we didn't learn how to find missing values in the lesson, but we can use the `isna()` function.
How about in the iris dataframe?
### Task 4
It is also important to know if you have any duplicatd rows. If you are performing statistcal analyses and you have duplicated entries they can affect the results. So, let's find out. Are there any duplicated rows in the legislators dataframe? Print then number of duplicates. If there are duplicates print the rows. What function could we used to find out if we have duplicated rows?
Do we have duplicated rows in the iris dataset? Print the number of duplicates? If there are duplicates print the rows.
If there are duplicated rows should we remove them or keep them?
### Task 5
It is important to also check that the range of values in our data matches expectations. For example, if we expect to have four species in our iris data, we should check that we see four species. How many political parties should we expect in the legislators data? If all we saw were a single part perhaps the data is incomplete.... Let's check. You can find out how many unique values there are per column using the `nunique` function. Try it for both the legislators and the iris data set.
What do you think? Do we see what we might expect? Are there fields where this type of check doesn't matter? In what fields might this type of exploration matter?
Check to see if you have all of the values expected for a given field. Pick a column you know should have a set number of values and print all of the unique values in that column. Do so for both the legislator and iris datasets.
## Exercise 5: Describe the data
For both the legislators and the iris data, get descriptive statistics for each numeric field.
## Exercise 6: Row Index Labels
For the legislator dataframe, let's change the row labels from numerical indexes to something more recognizable. Take a look at the columns of data, is there anything you might want to substitue as a row label? Pick one and set the index lables. Then print the top 5 rows to see if the index labels are present.
## Exercise 7: Indexing & Sampling
Randomly select 15 Republicans or Democrats (your choice) from the senate.
## Exercise 8: Dates
<span style="float:right; margin-left:10px; clear:both;"></span>
Let's learn something not covered in the Pandas 1 lesson regarding dates. We have the birthdates for each legislator, but they are in a String format. Let's convert it to a datetime object. We can do this using the `pd.to_datetime` function. Take a look at the online documentation to see how to use this function. Convert the `legislators['birthday']` column to a `datetime` object. Confirm that the column is now a datetime object.
Now that we have the birthdays in a `datetime` object, how can we calculate their age? Hint: we can use the `pd.Timestamp.now()` function to get a datetime object for this moment. Let's subtract the current time from their birthdays. Print the top 5 results.
Notice that the result of subtracting two `datetime` objects is a `timedelta` object. It contains the difference between two time values. The value we calculated therefore gives us the number of days old. However, we want the number of years.
To get the number of years we can divide the number of days old by the number of days in a year (i.e. 365). However, we need to extract out the days from the `datetime` object. To get this, the Pandas Series object has an accessor for extracting components of `datetime` objects and `timedelta` objects. It's named `dt` and it works for both. You can learn more about the attributes of this accessor at the [datetime objects page](https://pandas.pydata.org/pandas-docs/stable/reference/series.html#datetime-properties) and the [timedelta objects page](https://pandas.pydata.org/pandas-docs/stable/reference/series.html#timedelta-properties) by clicking. Take a moment to look over that documentation.
How would then extract the days in order to divide by 365 to get the years? Once you've figurd it out. Do so, convert the years to an integer and add the resulting series back into the legislator dataframe as a new column named `age`. Hint: use the [astype](https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.Series.astype.html) function of Pandas to convert the type.
Next, find the youngest, oldest and average age of all legislators
Who are the oldest and youngest legislators?
## Exercise 9: Indexing with loc and iloc
Reindex the legislators dataframe using the state, and find all legislators from your home state using the `loc` accessor.
Use the loc command to find all legislators from South Carolina and North Carolina
Use the loc command to retrieve all legislators from California, Oregon and Washington and only get their full name, state, party and age
## Exercise 10: Economics Data Example
### Task 1: Explore the data
Import the data from the [Lectures in Quantiatives Economics](https://github.com/QuantEcon/lecture-source-py) regarding minimum wages in countries round the world in US Dollars. You can view the data [here](https://github.com/QuantEcon/lecture-source-py/blob/master/source/_static/lecture_specific/pandas_panel/realwage.csv) and you can access the data file here: https://raw.githubusercontent.com/QuantEcon/lecture-source-py/master/source/_static/lecture_specific/pandas_panel/realwage.csv. Then perform the following
Import and print the first 5 lines of data to explore what is there.
Find the shape of the data.
List the column names.
Identify the data types. Do they match what you would expect?
Identify columns with missing values.
Identify if there are duplicated entires.
How many unique values per row are there. Do these look reasonable for the data type and what you know about what is stored in the column?
### Task 2: Explore More
Retrieve descriptive statistics for the data.
Identify all of the countries listed in the data.
Convert the time column to a datetime object.
Identify the time points that were used for data collection. How many years of data collection were there? What time of year were the data collected?
Because we only have one data point collected per year per country, simplify this by adding a new column with just the year. Print the first 5 rows to confirm the column was added.
There are two pay periods. Retrieve them in a list of just the two strings
### Task 3: Clean the data
We have no duplicates in this data so we do not need to consider removing those, but we do have missing values in the `value` column. Lets remove those. Check the dimensions afterwards to make sure they rows with missing values are gone.
### Task 4: Indexing
Use boolean indexing to retrieve the rows of annual salary in United States
Do we have enough data to calculate descriptive statistics for annual salary in the United States in 2016?
Use loc to calculate descriptive statistics for the hourly salary in the United States and then again separately for Ireland. Hint: you will have to set row indexes.
Now do the same for Annual salary
|
github_jupyter
|
# Lesson 3 Class Exercises: Pandas Part 1
With these class exercises we learn a few new things. When new knowledge is introduced you'll see the icon shown on the right:
<span style="float:right; margin-left:10px; clear:both;"></span>
## Reminder
The first checkin-in of the project is due next Tueday. After today, you should have everything you need to know to accomplish that first part.
## Get Started
Import the Numpy and Pandas packages
## Exercise 1: Import Iris Data
Import the Iris dataset made available to you in the last class period for the Numpy part2 exercises. Save it to a variable naemd `iris`. Print the first 5 rows and the dimensions to ensure it was read in properly.
Notice how much easier this was to import compared to the Numpy `genfromtxt`. We did not have to skip the headers, we did not have to specify the data type and we can have mixed data types in the same matrix.
## Exercise 2: Import Legislators Data
For portions of this notebook we will use a public dataset that contains all of the current legistators of the United States Congress. This dataset can be found [here](https://github.com/unitedstates/congress-legislators).
Import the data directly from this URL: https://theunitedstates.io/congress-legislators/legislators-current.csv
Save the data in a variable named `legistators`. Print the first 5 lines, and the dimensions.
## Exercise 3: Explore the Data
### Task 1
Print the column names of the legistators dataframe and explore the type of data in the data frame.
### Task 2
Show the datatypes of all of the columns in the legislator data. Do all of the data types seem appropriate for the data?
Show all of the datayptes in the iris dataframe
### Task 3
It's always important to know where the missing values are in your data. Are there any missing values in the legislators dataframe? How many per column?
Hint: we didn't learn how to find missing values in the lesson, but we can use the `isna()` function.
How about in the iris dataframe?
### Task 4
It is also important to know if you have any duplicatd rows. If you are performing statistcal analyses and you have duplicated entries they can affect the results. So, let's find out. Are there any duplicated rows in the legislators dataframe? Print then number of duplicates. If there are duplicates print the rows. What function could we used to find out if we have duplicated rows?
Do we have duplicated rows in the iris dataset? Print the number of duplicates? If there are duplicates print the rows.
If there are duplicated rows should we remove them or keep them?
### Task 5
It is important to also check that the range of values in our data matches expectations. For example, if we expect to have four species in our iris data, we should check that we see four species. How many political parties should we expect in the legislators data? If all we saw were a single part perhaps the data is incomplete.... Let's check. You can find out how many unique values there are per column using the `nunique` function. Try it for both the legislators and the iris data set.
What do you think? Do we see what we might expect? Are there fields where this type of check doesn't matter? In what fields might this type of exploration matter?
Check to see if you have all of the values expected for a given field. Pick a column you know should have a set number of values and print all of the unique values in that column. Do so for both the legislator and iris datasets.
## Exercise 5: Describe the data
For both the legislators and the iris data, get descriptive statistics for each numeric field.
## Exercise 6: Row Index Labels
For the legislator dataframe, let's change the row labels from numerical indexes to something more recognizable. Take a look at the columns of data, is there anything you might want to substitue as a row label? Pick one and set the index lables. Then print the top 5 rows to see if the index labels are present.
## Exercise 7: Indexing & Sampling
Randomly select 15 Republicans or Democrats (your choice) from the senate.
## Exercise 8: Dates
<span style="float:right; margin-left:10px; clear:both;"></span>
Let's learn something not covered in the Pandas 1 lesson regarding dates. We have the birthdates for each legislator, but they are in a String format. Let's convert it to a datetime object. We can do this using the `pd.to_datetime` function. Take a look at the online documentation to see how to use this function. Convert the `legislators['birthday']` column to a `datetime` object. Confirm that the column is now a datetime object.
Now that we have the birthdays in a `datetime` object, how can we calculate their age? Hint: we can use the `pd.Timestamp.now()` function to get a datetime object for this moment. Let's subtract the current time from their birthdays. Print the top 5 results.
Notice that the result of subtracting two `datetime` objects is a `timedelta` object. It contains the difference between two time values. The value we calculated therefore gives us the number of days old. However, we want the number of years.
To get the number of years we can divide the number of days old by the number of days in a year (i.e. 365). However, we need to extract out the days from the `datetime` object. To get this, the Pandas Series object has an accessor for extracting components of `datetime` objects and `timedelta` objects. It's named `dt` and it works for both. You can learn more about the attributes of this accessor at the [datetime objects page](https://pandas.pydata.org/pandas-docs/stable/reference/series.html#datetime-properties) and the [timedelta objects page](https://pandas.pydata.org/pandas-docs/stable/reference/series.html#timedelta-properties) by clicking. Take a moment to look over that documentation.
How would then extract the days in order to divide by 365 to get the years? Once you've figurd it out. Do so, convert the years to an integer and add the resulting series back into the legislator dataframe as a new column named `age`. Hint: use the [astype](https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.Series.astype.html) function of Pandas to convert the type.
Next, find the youngest, oldest and average age of all legislators
Who are the oldest and youngest legislators?
## Exercise 9: Indexing with loc and iloc
Reindex the legislators dataframe using the state, and find all legislators from your home state using the `loc` accessor.
Use the loc command to find all legislators from South Carolina and North Carolina
Use the loc command to retrieve all legislators from California, Oregon and Washington and only get their full name, state, party and age
## Exercise 10: Economics Data Example
### Task 1: Explore the data
Import the data from the [Lectures in Quantiatives Economics](https://github.com/QuantEcon/lecture-source-py) regarding minimum wages in countries round the world in US Dollars. You can view the data [here](https://github.com/QuantEcon/lecture-source-py/blob/master/source/_static/lecture_specific/pandas_panel/realwage.csv) and you can access the data file here: https://raw.githubusercontent.com/QuantEcon/lecture-source-py/master/source/_static/lecture_specific/pandas_panel/realwage.csv. Then perform the following
Import and print the first 5 lines of data to explore what is there.
Find the shape of the data.
List the column names.
Identify the data types. Do they match what you would expect?
Identify columns with missing values.
Identify if there are duplicated entires.
How many unique values per row are there. Do these look reasonable for the data type and what you know about what is stored in the column?
### Task 2: Explore More
Retrieve descriptive statistics for the data.
Identify all of the countries listed in the data.
Convert the time column to a datetime object.
Identify the time points that were used for data collection. How many years of data collection were there? What time of year were the data collected?
Because we only have one data point collected per year per country, simplify this by adding a new column with just the year. Print the first 5 rows to confirm the column was added.
There are two pay periods. Retrieve them in a list of just the two strings
### Task 3: Clean the data
We have no duplicates in this data so we do not need to consider removing those, but we do have missing values in the `value` column. Lets remove those. Check the dimensions afterwards to make sure they rows with missing values are gone.
### Task 4: Indexing
Use boolean indexing to retrieve the rows of annual salary in United States
Do we have enough data to calculate descriptive statistics for annual salary in the United States in 2016?
Use loc to calculate descriptive statistics for the hourly salary in the United States and then again separately for Ireland. Hint: you will have to set row indexes.
Now do the same for Annual salary
| 0.890634 | 0.988335 |
# Explore UK Crime Data with Pandas and GeoPandas
## Table of Contents
1. [Introduction to GeoPandas](#geopandas)<br>
2. [Getting ready](#ready)<br>
3. [London boroughs](#boroughs)<br>
2.1. [Load data](#load1)<br>
2.2. [Explore data](#explore1)<br>
4. [Crime data](#crime)<br>
3.1. [Load data](#load2)<br>
3.2. [Explore data](#explore2)<br>
5. [OSM data](#osm)<br>
4.1. [Load data](#load3)<br>
4.2. [Explore data](#explore3)<br>
```
import pandas as pd
import geopandas as gpd
from shapely.geometry import Point, LineString, Polygon
import matplotlib.pyplot as plt
from datetime import datetime
%matplotlib inline
```
<a id="geopandas"></a>
## 1. Introduction to GeoPandas
Hopefully you already know a little about Pandas. If you do not, please read through this [10 minute tutorial](http://pandas.pydata.org/pandas-docs/stable/getting_started/10min.html) or check out this [workshop](https://github.com/IBMDeveloperUK/pandas-workshop/blob/master/README.md).
A GeoDataSeries or GeoDataFrame is very similar to a Pandas DataFrame, but has an additional column with the geometry. You can load a file, or create your own:
```
df = pd.DataFrame({'city': ['London','Manchester','Birmingham','Leeds','Glasgow'],
'population': [9787426, 2553379, 2440986, 1777934, 1209143],
'area': [1737.9, 630.3, 598.9, 487.8, 368.5 ],
'latitude': [51.50853, 53.48095, 52.48142, 53.79648,55.86515],
'longitude': [-0.12574, -2.23743, -1.89983, -1.54785,-4.25763]})
df['geometry'] = list(zip(df.longitude, df.latitude))
df['geometry'] = df['geometry'].apply(Point)
cities = gpd.GeoDataFrame(df, geometry='geometry')
cities.head()
```
Creating a basic map is similar to creating a plot from a Pandas DataFrame:
```
cities.plot(column='population');
```
As `cities` is a DataFrame you can apply data manipulations, for instance:
```
cities['population'].mean()
```
Let's create a lines between 2 cities, and circles around some of the cities and store them as polygons:
```
london = cities.loc[cities['city'] == 'London', 'geometry'].squeeze()
manchester = cities.loc[cities['city'] == 'Manchester', 'geometry'].squeeze()
line = gpd.GeoSeries(LineString([london, manchester]))
line.plot();
cities2 = cities.copy()
cities2['geometry'] = cities2.buffer(1)
cities2 = cities2.drop([1, 2])
cities2.head()
cities2.plot();
```
And plot all of them together:
```
base = cities2.plot(color='lightblue', edgecolor='black')
cities.plot(ax=base, marker='o', color='red', markersize=10);
line.plot(ax=base);
cities3 = cities.copy()
cities3['geometry'] = cities3.buffer(2)
cities3 = cities3.drop([1, 2])
gpd.overlay(cities3, cities2, how='difference').plot();
```
### Spatial relationships
There are several functions to check geospatial relationships: `equals`, `contains`, `crosses`, `disjoint`,`intersects`,`overlaps`,`touches`,`within` and `covers`. These all use `shapely`: read more [here](https://shapely.readthedocs.io/en/stable/manual.html#predicates-and-relationships) and some more background [here](https://en.wikipedia.org/wiki/Spatial_relation).
A few examples:
```
cities2.contains(london)
cities2[cities2.contains(london)]
cities2[cities2.contains(manchester)]
```
The inverse of `contains`:
```
cities[cities.within(cities2)]
cities2[cities2.crosses(line)]
cities2[cities2.disjoint(london)]
```
<a id="ready"></a>
## 2. Getting ready
### 2.1. Add data to Cloud Object Store (COS)
The data for this workshop needs to be added to your project. Go to the GitHub repo and download the files in the [data folder](https://github.com/IBMDeveloperUK/geopandas-workshop/tree/master/data) to your machine.
Add the files in the data menu on the right of the notebook (click the 1010 button at the top right if you do not see this) into COS:
- boundaries.zip
- 2018-1-metropolitan-street.zip
- 2018-2-metropolitan-street.zip
- 2018-metropolitan-stop-and-search.zip
- london_inner_pois.zip
### 2.2. Project Access token
As the data files are not simple csv files, we need a little trick to load the data. The first thing you need is a project access token to programmatically access COS.
Click the 3 dots at the top of the notebook to insert the project token that you created earlier. This will create a new cell in the notebook that you will need to run first before continuing with the rest of the notebook. If you are sharing this notebook you should remove this cell, else anyone can use you Cloud Object Storage from this project.
> If you cannot find the new cell it is probably at the top of this notebook. Scroll up, run the cell and continue with section 2.3
### 2.3. Helper function to load data into notebook
The second thing you need to load data into the notebook is the below help function. Data will be copied to the local project space and loaded from there. The below helper function will do this for you.
```
# define the helper function
def download_file_to_local(project_filename, local_file_destination=None, project=None):
"""
Uses project-lib to get a bytearray and then downloads this file to local.
Requires a valid `project` object.
Args:
project_filename str: the filename to be passed to get_file
local_file_destination: the filename for the local file if different
Returns:
0 if everything worked
"""
project = project
# get the file
print("Attempting to get file {}".format(project_filename))
_bytes = project.get_file(project_filename).read()
# check for new file name, download the file
print("Downloading...")
if local_file_destination==None: local_file_destination = project_filename
with open(local_file_destination, 'wb') as f:
f.write(bytearray(_bytes))
print("Completed writing to {}".format(local_file_destination))
return 0
```
<a id="boroughs"></a>
## 2. London boroughs
There are various data sources out there, but [this one](https://data.london.gov.uk/dataset/2011-boundary-files) seemed most suitable as it contains a little more data than just the boundaries of the boroughs. A few files were combined together in the [data preparation notebook](https://github.com/IBMDeveloperUK/geopandas-workshop/blob/master/notebooks/prepare-uk-crime-data.ipynb), which makes this data quicker to load.
<a id="load1"></a>
### 2.1. Load data
Loading a shape file is easy with the use of the helper function from above that downloads the file to the local project space, and the `read_file` function from geopandas:
```
download_file_to_local('boundaries.zip', project=project)
boroughs = gpd.read_file("zip://./boundaries.zip")
!rm boundaries.zip
boroughs.head()
```
<a id="explore1"></a>
### 2.2. Explore data
To plot a basic map add `.plot()` to a geoDataFrame.
```
boroughs.plot();
```
LAD is Local Authority District. Adding a column will colour the map based on the classes in this column:
```
boroughs.plot(column='LAD11CD');
```
The boroughs are made up of many districts that you might want to combine. This can be done with `.dissolve()`:
```
lad = boroughs.dissolve(by='LAD11CD',aggfunc='sum')
lad.head()
lad.plot(column='HHOLDS');
```
<div class="alert alert-success">
<b>EXERCISE</b> <br/>
Explore the data:
<ul>
<li>Create a map of number of households (HHOLDS) by Middle-Level Super Output Area (MSOA11CD)</li>
<li>Change the colors with the <font face="Courier">cmap</font> option. Pick one of the colourmaps from https://matplotlib.org/users/colormaps.html</li>
<li>Add a legend with <font face="Courier">legend=True</font></li>
</ul>
</div>
```
# your answer (add as many cells as you need)
```
Hopefully your map is starting to look nice now! Remember these options, as you will need them again.
To see what I have come up with, uncomment the next two cells and run the cell to load the answer. Then run the cell once more to run the code. You will see that there are many more options to customize your map. These [matplotlib tutorials](https://matplotlib.org/tutorials/index.html) go through many more options.
```
# %load https://raw.githubusercontent.com/IBMDeveloperUK/geopandas-workshop/master/answers/answer1.py
# %load https://raw.githubusercontent.com/IBMDeveloperUK/geopandas-workshop/master/answers/answer2.py
```
## Coordinate system
Before moving on let's check the coordinate systems of the different data sets. They need to be the same to use them together. Check the range of coordinates with `.total_bounds`:
```
xmin, ymin, xmax, ymax = lad.total_bounds
print(xmin, ymin, xmax, ymax)
```
The coordinate reference system (CRS) determines how the two-dimensional (planar) coordinates of the geometry objects should be related to actual places on the (non-planar) earth.
```
lad.crs
```
These coordinates seem to be from the [National Grid](https://www.ordnancesurvey.co.uk/support/the-national-grid.html). If you want to learn more about coordinate systems, [this document](https://www.bnhs.co.uk/focuson/grabagridref/html/OSGB.pdf) from the Ordnance Survey gives a detailed overview.
Let's also quickly read one of the files with crime data to check the coordinates. This is a Pandas DataFrame so you cannot check the bounding box, but from the table below it is clear that the coordinates are different, they are latitudes and longitudes (Greenwich is 51.4934° N, 0.0098° E).
```
download_file_to_local('2018-metropolitan-stop-and-search.zip', project=project)
stop_search = pd.read_csv("./2018-metropolitan-stop-and-search.zip")
!rm 2018-metropolitan-stop-and-search.zip
stop_search.head()
```
It is possible to convert coordinates to a different system, but that is beyond the scope of this workshop.
Instead let's just find another map in the right coordinates. This [json file](https://skgrange.github.io/www/data/london_boroughs.json) is exactly what we need and it can be read directly from the url:
```
boroughs2 = gpd.read_file("https://skgrange.github.io/www/data/london_boroughs.json")
boroughs2.head()
boroughs2.plot();
```
<a id="crime"></a>
## 3. Crime data
The crime data is pre-processed in this [notebook](https://github.com/IBMDeveloperUK/geopandas-workshop/blob/master/notebooks/prepare-uk-crime-data.ipynb) so it is easier to read here. We will only look at data from 2018.
Data is downloaded from https://data.police.uk/ ([License](https://www.nationalarchives.gov.uk/doc/open-government-licence/version/3/))
<a id="load2"></a>
### 3.1. Load data
This dataset cannot be loaded into a geoDataFrame directly. Instead the data is loaded into a DataFrame and then converted:
```
download_file_to_local('2018-1-metropolitan-street.zip', project=project)
download_file_to_local('2018-2-metropolitan-street.zip', project=project)
street = pd.read_csv("./2018-1-metropolitan-street.zip")
street2 = pd.read_csv("./2018-2-metropolitan-street.zip")
street = street.append(street2)
download_file_to_local('2018-metropolitan-stop-and-search.zip', project=project)
stop_search = pd.read_csv("./2018-metropolitan-stop-and-search.zip")
```
Clean up of the local directory:
```
! rm *.zip
street.head()
stop_search.head()
```
#### Convert to geoDataFrames
```
street['coordinates'] = list(zip(street.Longitude, street.Latitude))
street['coordinates'] = street['coordinates'].apply(Point)
street = gpd.GeoDataFrame(street, geometry='coordinates')
street.head()
stop_search['coordinates'] = list(zip(stop_search.Longitude, stop_search.Latitude))
stop_search['coordinates'] = stop_search['coordinates'].apply(Point)
stop_search = gpd.GeoDataFrame(stop_search, geometry='coordinates')
stop_search.head()
```
<a id="explore2"></a>
### 3.2. Explore data
<div class="alert alert-success">
<b>EXERCISE</b> <br/>
Explore the data with Pandas. There are no right or wrong answers, the questions below give you some suggestions at what to look at. <br/>
<ul>
<li>How much data is there? Is this changing over time? Can you plot this? </li>
<li>Are there missing values? Should these rows be deleted? </li>
<li>Which columns of the datasets contain useful information? What kind of categories are there and are they all meaningful?</li>
<li>Which crimes occur most often? And near which location?</li>
<li>Is there anything you want to explore further or are curious about? Is there any data that you will need for this?</li>
<li>Notice anything odd about the latitude and longitudes? Read here how the data is anonymised: https://data.police.uk/about/.</li>
</ul>
</div>
```
# your data exploration (add as many cells as you need)
# %load https://raw.githubusercontent.com/IBMDeveloperUK/geopandas-workshop/master/answers/answer3.py
# %load https://raw.githubusercontent.com/IBMDeveloperUK/geopandas-workshop/master/answers/answer3b.py
# %load https://raw.githubusercontent.com/IBMDeveloperUK/geopandas-workshop/master/answers/answer4.py
# %load https://raw.githubusercontent.com/IBMDeveloperUK/geopandas-workshop/master/answers/answer5.py
# %load https://raw.githubusercontent.com/IBMDeveloperUK/geopandas-workshop/master/answers/answer6.py
```
* The number of stop and searches seems to go up. That is something you could investigate further. Is any of the categories increasing?
* Another interesting question is how the object of search and the outcome are related. Are there types of searches where nothing is found more frequently?
* In the original files there are also columns of gender, age range and ethnicity. If you want to explore this further you can change the code and re-process the data from this [notebook](https://github.com/IBMDeveloperUK/geopandas-workshop/blob/master/notebooks/prepare-uk-crime-data.ipynb) and use the full dataset.
* And how could you combine the two datasets?
### Spatial join
> The below solution was found [here](https://gis.stackexchange.com/questions/306674/geopandas-spatial-join-and-count) after googling for 'geopandas count points in polygon'
The `crs` needs to be the same for both GeoDataFrames.
```
print(boroughs2.crs)
print(stop_search.crs)
```
Add a borough to each point with a spatial join. This will add the `geometry` and other columns from `boroughs2` to the points in `stop_search`.
```
stop_search.crs = boroughs2.crs
dfsjoin = gpd.sjoin(boroughs2,stop_search)
dfsjoin.head()
```
Then aggregate this table by creating a [pivot table](https://jakevdp.github.io/PythonDataScienceHandbook/03.09-pivot-tables.html) where for each borough the number of types each of the categories in `Object of search` are counted. Then drop the pivot level and remove the index, so you can merge this new table back into the `boroughs2` DataFrame.
```
dfpivot = pd.pivot_table(dfsjoin,index='code',columns='Object of search',aggfunc={'Object of search':'count'})
dfpivot.columns = dfpivot.columns.droplevel()
dfpivot = dfpivot.reset_index()
dfpivot.head()
boroughs3 = boroughs2.merge(dfpivot, how='left',on='code')
boroughs3.head()
```
Let's make some maps!
```
fig, axs = plt.subplots(1, 2, figsize=(20,5))
p1=boroughs3.plot(column='Controlled drugs',ax=axs[0],cmap='Blues',legend=True);
axs[0].set_title('Controlled drugs', fontdict={'fontsize': '12', 'fontweight' : '5'});
p2=boroughs3.plot(column='Stolen goods',ax=axs[1], cmap='Reds',legend=True);
axs[1].set_title('Stolen goods', fontdict={'fontsize': '12', 'fontweight' : '5'});
```
<div class="alert alert-success">
<b>EXERCISE</b> <br/>
Explore the data with GeoPandas. Again there are no right or wrong answers, the questions below give you some suggestions at what to look at. <br/>
<ul>
<li>Improve the above maps. How many arrests are there in each borough? Use the above method but first select only the arrests using the column 'Outcome'. Can you plot this? </li>
<li>Are there changes over time? Is there a difference between months? Use `street` and look at Westminster or another borough where the crime rate seems higher. </li>
</ul>
</div>
```
# your data exploration (add as many cells as you need)
# %load https://raw.githubusercontent.com/IBMDeveloperUK/geopandas-workshop/master/answers/answer7.py
# %load https://raw.githubusercontent.com/IBMDeveloperUK/geopandas-workshop/master/answers/answer8.py
```
<a id="osm"></a>
## 4. OSM data
The Open Street Map data is also pre-processed in this [notebook]() so it is easier to read into this notebook.
Data is downloaded from http://download.geofabrik.de/europe/great-britain.html and more details decription of the data is [here](http://download.geofabrik.de/osm-data-in-gis-formats-free.pdf).
<a id="load3"></a>
### 4.1. Load data
```
download_file_to_local('london_inner_pois.zip', project=project)
pois = gpd.read_file("zip://./london_inner_pois.zip")
pois.head()
```
<a id="explore3"></a>
### 4.2. Explore data
```
pois.size
pois['fclass'].unique()
```
Count and plot the number of pubs by borough:
```
pubs = pois[pois['fclass']=='pub']
pubs2 = gpd.sjoin(boroughs2,pubs)
pubs3 = pd.pivot_table(pubs2,index='code_left',columns='fclass',aggfunc={'fclass':'count'})
pubs3.columns = pubs3.columns.droplevel()
pubs3 = pubs3.reset_index()
boroughs5 = boroughs2.merge(pubs3, left_on='code',right_on='code_left')
boroughs5.plot(column='pub',cmap='Blues',legend=True);
boroughs2.head()
```
<div class="alert alert-success">
<b>EXERCISE</b> <br/>
Explore the data further. Again there are no right or wrong answers, the questions below give you some suggestions at what to look at. <br/>
<ul>
<li> Is there a category of POIs that relates to the number of crimes? You might have to aggregate the data on a different more detailed level for this one. </li>
<li> Can you find if there is a category of POIs that related to the number of crimes? </li>
<li> Count the number of crimes around a certain POI. Choose a point and use the buffer function from the top of the notebook. But note that the crimes are anonymised, so the exact location is not given, only an approximation. </li>
</ul>
</div>
```
# answers
```
Hopefully you got an idea of the possibilities with geospatial data now. There is a lot more to explore with this data. Let me know if you find anything interesting! I am on Twitter as @MargrietGr.
### Author
Margriet Groenendijk is a Data & AI Developer Advocate for IBM. She develops and presents talks and workshops about data science and AI. She is active in the local developer communities through attending, presenting and organising meetups. She has a background in climate science where she explored large observational datasets of carbon uptake by forests during her PhD, and global scale weather and climate models as a postdoctoral fellow.
Copyright © 2019 IBM. This notebook and its source code are released under the terms of the MIT License.
|
github_jupyter
|
import pandas as pd
import geopandas as gpd
from shapely.geometry import Point, LineString, Polygon
import matplotlib.pyplot as plt
from datetime import datetime
%matplotlib inline
df = pd.DataFrame({'city': ['London','Manchester','Birmingham','Leeds','Glasgow'],
'population': [9787426, 2553379, 2440986, 1777934, 1209143],
'area': [1737.9, 630.3, 598.9, 487.8, 368.5 ],
'latitude': [51.50853, 53.48095, 52.48142, 53.79648,55.86515],
'longitude': [-0.12574, -2.23743, -1.89983, -1.54785,-4.25763]})
df['geometry'] = list(zip(df.longitude, df.latitude))
df['geometry'] = df['geometry'].apply(Point)
cities = gpd.GeoDataFrame(df, geometry='geometry')
cities.head()
cities.plot(column='population');
cities['population'].mean()
london = cities.loc[cities['city'] == 'London', 'geometry'].squeeze()
manchester = cities.loc[cities['city'] == 'Manchester', 'geometry'].squeeze()
line = gpd.GeoSeries(LineString([london, manchester]))
line.plot();
cities2 = cities.copy()
cities2['geometry'] = cities2.buffer(1)
cities2 = cities2.drop([1, 2])
cities2.head()
cities2.plot();
base = cities2.plot(color='lightblue', edgecolor='black')
cities.plot(ax=base, marker='o', color='red', markersize=10);
line.plot(ax=base);
cities3 = cities.copy()
cities3['geometry'] = cities3.buffer(2)
cities3 = cities3.drop([1, 2])
gpd.overlay(cities3, cities2, how='difference').plot();
cities2.contains(london)
cities2[cities2.contains(london)]
cities2[cities2.contains(manchester)]
cities[cities.within(cities2)]
cities2[cities2.crosses(line)]
cities2[cities2.disjoint(london)]
# define the helper function
def download_file_to_local(project_filename, local_file_destination=None, project=None):
"""
Uses project-lib to get a bytearray and then downloads this file to local.
Requires a valid `project` object.
Args:
project_filename str: the filename to be passed to get_file
local_file_destination: the filename for the local file if different
Returns:
0 if everything worked
"""
project = project
# get the file
print("Attempting to get file {}".format(project_filename))
_bytes = project.get_file(project_filename).read()
# check for new file name, download the file
print("Downloading...")
if local_file_destination==None: local_file_destination = project_filename
with open(local_file_destination, 'wb') as f:
f.write(bytearray(_bytes))
print("Completed writing to {}".format(local_file_destination))
return 0
download_file_to_local('boundaries.zip', project=project)
boroughs = gpd.read_file("zip://./boundaries.zip")
!rm boundaries.zip
boroughs.head()
boroughs.plot();
boroughs.plot(column='LAD11CD');
lad = boroughs.dissolve(by='LAD11CD',aggfunc='sum')
lad.head()
lad.plot(column='HHOLDS');
# your answer (add as many cells as you need)
# %load https://raw.githubusercontent.com/IBMDeveloperUK/geopandas-workshop/master/answers/answer1.py
# %load https://raw.githubusercontent.com/IBMDeveloperUK/geopandas-workshop/master/answers/answer2.py
xmin, ymin, xmax, ymax = lad.total_bounds
print(xmin, ymin, xmax, ymax)
lad.crs
download_file_to_local('2018-metropolitan-stop-and-search.zip', project=project)
stop_search = pd.read_csv("./2018-metropolitan-stop-and-search.zip")
!rm 2018-metropolitan-stop-and-search.zip
stop_search.head()
boroughs2 = gpd.read_file("https://skgrange.github.io/www/data/london_boroughs.json")
boroughs2.head()
boroughs2.plot();
download_file_to_local('2018-1-metropolitan-street.zip', project=project)
download_file_to_local('2018-2-metropolitan-street.zip', project=project)
street = pd.read_csv("./2018-1-metropolitan-street.zip")
street2 = pd.read_csv("./2018-2-metropolitan-street.zip")
street = street.append(street2)
download_file_to_local('2018-metropolitan-stop-and-search.zip', project=project)
stop_search = pd.read_csv("./2018-metropolitan-stop-and-search.zip")
! rm *.zip
street.head()
stop_search.head()
street['coordinates'] = list(zip(street.Longitude, street.Latitude))
street['coordinates'] = street['coordinates'].apply(Point)
street = gpd.GeoDataFrame(street, geometry='coordinates')
street.head()
stop_search['coordinates'] = list(zip(stop_search.Longitude, stop_search.Latitude))
stop_search['coordinates'] = stop_search['coordinates'].apply(Point)
stop_search = gpd.GeoDataFrame(stop_search, geometry='coordinates')
stop_search.head()
# your data exploration (add as many cells as you need)
# %load https://raw.githubusercontent.com/IBMDeveloperUK/geopandas-workshop/master/answers/answer3.py
# %load https://raw.githubusercontent.com/IBMDeveloperUK/geopandas-workshop/master/answers/answer3b.py
# %load https://raw.githubusercontent.com/IBMDeveloperUK/geopandas-workshop/master/answers/answer4.py
# %load https://raw.githubusercontent.com/IBMDeveloperUK/geopandas-workshop/master/answers/answer5.py
# %load https://raw.githubusercontent.com/IBMDeveloperUK/geopandas-workshop/master/answers/answer6.py
print(boroughs2.crs)
print(stop_search.crs)
stop_search.crs = boroughs2.crs
dfsjoin = gpd.sjoin(boroughs2,stop_search)
dfsjoin.head()
dfpivot = pd.pivot_table(dfsjoin,index='code',columns='Object of search',aggfunc={'Object of search':'count'})
dfpivot.columns = dfpivot.columns.droplevel()
dfpivot = dfpivot.reset_index()
dfpivot.head()
boroughs3 = boroughs2.merge(dfpivot, how='left',on='code')
boroughs3.head()
fig, axs = plt.subplots(1, 2, figsize=(20,5))
p1=boroughs3.plot(column='Controlled drugs',ax=axs[0],cmap='Blues',legend=True);
axs[0].set_title('Controlled drugs', fontdict={'fontsize': '12', 'fontweight' : '5'});
p2=boroughs3.plot(column='Stolen goods',ax=axs[1], cmap='Reds',legend=True);
axs[1].set_title('Stolen goods', fontdict={'fontsize': '12', 'fontweight' : '5'});
# your data exploration (add as many cells as you need)
# %load https://raw.githubusercontent.com/IBMDeveloperUK/geopandas-workshop/master/answers/answer7.py
# %load https://raw.githubusercontent.com/IBMDeveloperUK/geopandas-workshop/master/answers/answer8.py
download_file_to_local('london_inner_pois.zip', project=project)
pois = gpd.read_file("zip://./london_inner_pois.zip")
pois.head()
pois.size
pois['fclass'].unique()
pubs = pois[pois['fclass']=='pub']
pubs2 = gpd.sjoin(boroughs2,pubs)
pubs3 = pd.pivot_table(pubs2,index='code_left',columns='fclass',aggfunc={'fclass':'count'})
pubs3.columns = pubs3.columns.droplevel()
pubs3 = pubs3.reset_index()
boroughs5 = boroughs2.merge(pubs3, left_on='code',right_on='code_left')
boroughs5.plot(column='pub',cmap='Blues',legend=True);
boroughs2.head()
# answers
| 0.520253 | 0.977045 |
# Linear Support Vector Regressor with PolynomialFeatures
This Code template is for regression analysis using a Linear Support Vector Regressor(LinearSVR) based on the Support Vector Machine algorithm and feature transformation technique PolynomialFeatures in a pipeline. It provides a faster implementation than SVR but only considers the linear kernel.
### Required Packages
```
import warnings
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as se
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import make_pipeline
from sklearn.model_selection import train_test_split
from sklearn.svm import LinearSVR
from sklearn.metrics import r2_score, mean_absolute_error, mean_squared_error
warnings.filterwarnings('ignore')
```
### Initialization
Filepath of CSV file
```
#filepath
file_path=""
```
List of features which are required for model training .
```
#x_values
features=[]
```
Target feature for prediction.
```
#y_values
target=''
```
### Data fetching
Pandas is an open-source, BSD-licensed library providing high-performance, easy-to-use data manipulation and data analysis tools.
We will use panda's library to read the CSV file using its storage path.And we use the head function to display the initial row or entry.
```
df=pd.read_csv(file_path);
df.head()
```
### Feature Selections
It is the process of reducing the number of input variables when developing a predictive model. Used to reduce the number of input variables to both reduce the computational cost of modelling and, in some cases, to improve the performance of the model.
We will assign all the required input features to X and target/outcome to Y.
```
X=df[features]
Y=df[target]
```
### Data preprocessing
Since the majority of the machine learning models in the Sklearn library doesn't handle string category data and Null value, we have to explicitly remove or replace null values. The below snippet have functions, which removes the null value if any exists. And convert the string classes data in the datasets by encoding them to integer classes.
```
def NullClearner(df):
if(isinstance(df, pd.Series) and (df.dtype in ["float64","int64"])):
df.fillna(df.mean(),inplace=True)
return df
elif(isinstance(df, pd.Series)):
df.fillna(df.mode()[0],inplace=True)
return df
else:return df
def EncodeX(df):
return pd.get_dummies(df)
```
Calling preprocessing functions on the feature and target set.
```
x=X.columns.to_list()
for i in x:
X[i]=NullClearner(X[i])
X=EncodeX(X)
Y=NullClearner(Y)
X.head()
```
#### Correlation Map
In order to check the correlation between the features, we will plot a correlation matrix. It is effective in summarizing a large amount of data where the goal is to see patterns.
```
f,ax = plt.subplots(figsize=(18, 18))
matrix = np.triu(X.corr())
se.heatmap(X.corr(), annot=True, linewidths=.5, fmt= '.1f',ax=ax, mask=matrix)
plt.show()
```
### Data Splitting
The train-test split is a procedure for evaluating the performance of an algorithm. The procedure involves taking a dataset and dividing it into two subsets. The first subset is utilized to fit/train the model. The second subset is used for prediction. The main motive is to estimate the performance of the model on new data.
```
x_train,x_test,y_train,y_test=train_test_split(X,Y,test_size=0.2,random_state=123)#performing datasplitting
```
### Model
Support vector machines (SVMs) are a set of supervised learning methods used for classification, regression and outliers detection.
A Support Vector Machine is a discriminative classifier formally defined by a separating hyperplane. In other terms, for a given known/labelled data points, the SVM outputs an appropriate hyperplane that classifies the inputted new cases based on the hyperplane. In 2-Dimensional space, this hyperplane is a line separating a plane into two segments where each class or group occupied on either side.
LinearSVR is similar to SVR with kernel=’linear’. It has more flexibility in the choice of tuning parameters and is suited for large samples.
#### PolynomialFeatures:
Generate polynomial and interaction features.
Generate a new feature matrix consisting of all polynomial combinations of the features with degree less than or equal to the specified degree. For example, if an input sample is two dimensional and of the form [a, b], the degree-2 polynomial features are [1, a, b, a^2, ab, b^2].
for more ... [click here](https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.PolynomialFeatures.html)
#### Model Tuning Parameters
1. epsilon : float, default=0.0
> Epsilon parameter in the epsilon-insensitive loss function.
2. loss : {‘epsilon_insensitive’, ‘squared_epsilon_insensitive’}, default=’epsilon_insensitive’
> Specifies the loss function. ‘hinge’ is the standard SVM loss (used e.g. by the SVC class) while ‘squared_hinge’ is the square of the hinge loss. The combination of penalty='l1' and loss='hinge' is not supported.
3. C : float, default=1.0
> Regularization parameter. The strength of the regularization is inversely proportional to C. Must be strictly positive.
4. tol : float, default=1e-4
> Tolerance for stopping criteria.
5. dual : bool, default=True
> Select the algorithm to either solve the dual or primal optimization problem. Prefer dual=False when n_samples > n_features.
```
model=make_pipeline(PolynomialFeatures(),LinearSVR())
model.fit(x_train, y_train)
```
#### Model Accuracy
We will use the trained model to make a prediction on the test set.Then use the predicted value for measuring the accuracy of our model.
> **score**: The **score** function returns the coefficient of determination <code>R<sup>2</sup></code> of the prediction.
```
print("Accuracy score {:.2f} %\n".format(model.score(x_test,y_test)*100))
```
> **r2_score**: The **r2_score** function computes the percentage variablility explained by our model, either the fraction or the count of correct predictions.
> **mae**: The **mean abosolute error** function calculates the amount of total error(absolute average distance between the real data and the predicted data) by our model.
> **mse**: The **mean squared error** function squares the error(penalizes the model for large errors) by our model.
```
y_pred=model.predict(x_test)
print("R2 Score: {:.2f} %".format(r2_score(y_test,y_pred)*100))
print("Mean Absolute Error {:.2f}".format(mean_absolute_error(y_test,y_pred)))
print("Mean Squared Error {:.2f}".format(mean_squared_error(y_test,y_pred)))
```
#### Prediction Plot
First, we make use of a plot to plot the actual observations, with x_train on the x-axis and y_train on the y-axis.
For the regression line, we will use x_train on the x-axis and then the predictions of the x_train observations on the y-axis.
```
plt.figure(figsize=(14,10))
plt.plot(range(20),y_test[0:20], color = "green")
plt.plot(range(20),model.predict(x_test[0:20]), color = "red")
plt.legend(["Actual","prediction"])
plt.title("Predicted vs True Value")
plt.xlabel("Record number")
plt.ylabel(target)
plt.show()
```
#### Creator:Shreepad Nade , Github: [Profile](https://github.com/shreepad-nade)
|
github_jupyter
|
import warnings
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as se
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import make_pipeline
from sklearn.model_selection import train_test_split
from sklearn.svm import LinearSVR
from sklearn.metrics import r2_score, mean_absolute_error, mean_squared_error
warnings.filterwarnings('ignore')
#filepath
file_path=""
#x_values
features=[]
#y_values
target=''
df=pd.read_csv(file_path);
df.head()
X=df[features]
Y=df[target]
def NullClearner(df):
if(isinstance(df, pd.Series) and (df.dtype in ["float64","int64"])):
df.fillna(df.mean(),inplace=True)
return df
elif(isinstance(df, pd.Series)):
df.fillna(df.mode()[0],inplace=True)
return df
else:return df
def EncodeX(df):
return pd.get_dummies(df)
x=X.columns.to_list()
for i in x:
X[i]=NullClearner(X[i])
X=EncodeX(X)
Y=NullClearner(Y)
X.head()
f,ax = plt.subplots(figsize=(18, 18))
matrix = np.triu(X.corr())
se.heatmap(X.corr(), annot=True, linewidths=.5, fmt= '.1f',ax=ax, mask=matrix)
plt.show()
x_train,x_test,y_train,y_test=train_test_split(X,Y,test_size=0.2,random_state=123)#performing datasplitting
model=make_pipeline(PolynomialFeatures(),LinearSVR())
model.fit(x_train, y_train)
print("Accuracy score {:.2f} %\n".format(model.score(x_test,y_test)*100))
y_pred=model.predict(x_test)
print("R2 Score: {:.2f} %".format(r2_score(y_test,y_pred)*100))
print("Mean Absolute Error {:.2f}".format(mean_absolute_error(y_test,y_pred)))
print("Mean Squared Error {:.2f}".format(mean_squared_error(y_test,y_pred)))
plt.figure(figsize=(14,10))
plt.plot(range(20),y_test[0:20], color = "green")
plt.plot(range(20),model.predict(x_test[0:20]), color = "red")
plt.legend(["Actual","prediction"])
plt.title("Predicted vs True Value")
plt.xlabel("Record number")
plt.ylabel(target)
plt.show()
| 0.323487 | 0.992626 |
# Excitation Signals for Room Impulse Response Measurement
### Criteria
- Sufficient signal energy over the entire frequency range of interest
- Dynamic range
- Crest factor (peak-to-RMS value)
- Noise rejection (repetition and average, longer duration)
- Measurement duration
- Time variance
- Nonlinear distortion
#### _References_
* Müller, Swen, and Paulo Massarani. "Transfer-function measurement with sweeps." Journal of the Audio Engineering Society 49.6 (2001): 443-471.
[link](http://www.aes.org/e-lib/browse.cfm?elib=10189)
* Farina, Angelo. "Simultaneous measurement of impulse response and distortion with a swept-sine technique." Audio Engineering Society Convention 108. Audio Engineering Society, 2000.
[link](http://www.aes.org/e-lib/browse.cfm?elib=10211)
* Farina, Angelo. "Advancements in impulse response measurements by sine sweeps." Audio Engineering Society Convention 122. Audio Engineering Society, 2007.
[link](http://www.aes.org/e-lib/browse.cfm?elib=14106)
```
import tools
import numpy as np
from scipy.signal import chirp, max_len_seq, freqz, fftconvolve, resample
import matplotlib.pyplot as plt
import sounddevice as sd
%matplotlib inline
def crest_factor(x):
"""Peak-to-RMS value (crest factor) of the signal x
Parameter
---------
x : array_like
signal
"""
return np.max(np.abs(x)) / np.sqrt(np.mean(x**2))
def circular_convolve(x, y, outlen):
"""Circular convolution of x and y
Parameters
----------
x : array_like
Real-valued signal
y : array_like
Real-valued signal
outlen : int
Length of the output
"""
return np.fft.irfft(np.fft.rfft(x, n=outlen) * np.fft.rfft(y, n=outlen), n=outlen)
def plot_time_domain(x, fs=44100, ms=False):
time = np.arange(len(x)) / fs
timeunit = 's'
if ms:
time *= 1000
timeunit = 'ms'
fig = plt.figure()
plt.plot(time, x)
plt.xlabel('Time / {}'.format(timeunit))
return
def plot_freq_domain(x, fs=44100, khz=False):
Nf = len(x) // 2 + 1
freq = np.arange(Nf) / Nf * fs / 2
frequnit = 'Hz'
if khz:
freq /= 1000
frequnit = 'kHz'
fig = plt.figure()
plt.plot(freq, db(np.fft.rfft(x)))
plt.xscale('log')
plt.xlabel('Frequency / {}'.format(frequnit))
plt.ylabel('Magnitude / dB')
return
def compare_irs(h1, h2, ms=False):
t1 = np.arange(len(h1)) / fs
t2 = np.arange(len(h2)) / fs
timeunit = 's'
if ms:
t1 *= 1000
t2 *= 1000
timeunit = 'ms'
fig = plt.figure()
plt.plot(t1, h1, t2, h2)
plt.xlabel('Time / {}'.format(timeunit))
return
def compare_tfs(h1, h2, khz=False):
n1 = len(h1) // 2 + 1
n2 = len(h2) // 2 + 1
f1 = np.arange(n1) / n1 * fs / 2
f2 = np.arange(n2) / n2 * fs / 2
frequnit = 'Hz'
if khz:
freq /= 1000
frequnit = 'khz'
fig = plt.figure()
plt.plot(f1, db(np.fft.rfft(h1)), f2, db(np.fft.rfft(h2)))
plt.xscale('log')
plt.xlabel('Frequency / {}'.format(frequnit))
plt.ylabel('Magnitude / dB')
return
def pad_zeros(x, nzeros):
"""Append zeros at the end of the input sequence
"""
return np.pad(x, (0, nzeros), mode='constant', constant_values=0)
```
## Parameters
```
fs = 44100
dur = 1
L = int(np.ceil(dur * fs))
time = np.arange(L) / fs
```
## White Noise
Generate a random signal with normal (Gaussian) amplitude distribution. Use `numpy.random.randn` and normalize the amplitude with `tools.normalize`.
Let's listen to it.
Plot the signal in the time domain and in the frequency domain.
Is the signal really white?
What is the crest factor of a white noise?
Now feed the white noise to an unkown system `tools.blackbox` and save the output signal.
How do you think we can extract the impulse response of the system?
Try to compute the impulse response from the output signal.
Compare it with the actual impulse response which can be obtained by feeding an ideal impulse to `tools.blackbox`.
## Maximum Length Sequence
> Maximum-length sequences (MLSs) are binary sequences that can be generated very easily with an N-staged shift register and an XOR gate (with up to four inputs) connected with the shift register in such a way that all possible 2N states, minus the case "all 0," are run through. This can be accomplished by hardware with very few simple TTL ICs or by software with less than 20 lines of assembly code.
(Müller 2001)
```
nbit = int(np.ceil(np.log2(L)))
mls, _ = max_len_seq(nbit) # sequence of 0 and 1
mls = 2*mls - 1 # sequence of -1 and 1
```
Take a look at the signal in the time domain.
Examine the properties of the MLS
* frequency response
* crest factor
* simulate the impulse response measurement of `tools.blackbox`
* evaluate the obtained impulse response
In practive, the (digital) signal has to be converted into an analog signal by an audio interface?
Here, the process is simulated by oversampling the signal by a factor of 10.
Pay attention to the crest factor before and after upsampling.
```
upsample = 10
mls_up = resample(mls, num=len(mls) * upsample)
time = np.arange(len(mls)) / fs
time_up = np.arange(len(mls_up)) / fs / upsample
plt.figure(figsize=(10, 4))
plt.plot(time_up, mls_up, '-', label='Analog')
plt.plot(time, mls, '-', label='Digital')
plt.legend(loc='best')
plt.xlabel('Time / s')
plt.title('Crest factor {:.1f} -> {:.1f} dB'.format(db(crest_factor(mls)), db(crest_factor(mls_up))))
plt.figure(figsize=(10, 4))
plt.plot(time_up, mls_up, '-', label='Analog')
plt.plot(time, mls, 'o', label='Ditigal')
plt.xlim(0, 0.0025)
plt.legend(loc='best')
plt.xlabel('Time / s')
plt.title('Crest factor {:.1f} -> {:.1f} dB'.format(db(crest_factor(mls)), db(crest_factor(mls_up))));
```
## Linear Sweep
Generate a linear sweep with `lin_sweep`.
```
def lin_sweep(fstart, fstop, duration, fs):
"""Generation of a linear sweep signal.
Parameters
----------
fstart : int
Start frequency in Hz
fstop : int
Stop frequency in Hz
duration : float
Total length of signal in s
fs : int
Sampling frequency in Hz
Returns
-------
array_like
generated signal vector
Note that the stop frequency must not be greater than half the
sampling frequency (Nyquist-Shannon sampling theorem).
"""
if fstop > fs / 2:
raise ValueError("fstop must not be greater than fs/2")
t = np.arange(0, duration, 1 / fs)
excitation = np.sin(
2 * np.pi * ((fstop - fstart) /
(2 * duration) * t ** 2 + fstart * t))
# excitation = excitation - np.mean(excitation) # remove direct component
return excitation
fs = 44100
fstart =
fstop =
duration =
lsweep =
```
Examine the properties of linear sweeps
* spectrogram (Use `pyplot.specgram` with `NFFT=512` and `Fs=44100`)
* frequency response
* crest factor
* simulate the impulse response measurement of `tools.blackbox`
* evaluate the obtained impulse response
## Exponential Sweep
Generate a exponential sweep with `exp_sweep`.
```
def exp_sweep(fstart, fstop, duration, fs):
"""Generation of a exponential sweep signal.
Parameters
----------
fstart : int
Start frequency in Hz
fstop : int
Stop frequency
duration : float
Total length of signal in s
fs : int
Sampling frequency in Hz
Returns
-------
array_like
Generated signal vector
Note that the stop frequency must not be greater than half the
sampling frequency (Nyquist-Shannon sampling theorem).
"""
if fstop > fs / 2:
raise ValueError("fstop must not be greater than fs/2")
t = np.arange(0, duration, 1 / fs)
excitation = np.sin(2 * np.pi * duration *
fstart / np.log(fstop / fstart) *
(np.exp(t / duration * np.log(fstop / fstart)) - 1))
# excitation = excitation - np.mean(excitation) # remove direct component
return excitation
fs = 44100
fstart =
fstop =
duration =
esweep =
```
Examine the properties of linear sweeps
* spectrogram (Use `pyplot.specgram` with `NFFT=512` and `Fs=44100`)
* frequency response
* crest factor
* simulate the impulse response measurement of `tools.blackbox`
* evaluate the obtained impulse response
|
github_jupyter
|
import tools
import numpy as np
from scipy.signal import chirp, max_len_seq, freqz, fftconvolve, resample
import matplotlib.pyplot as plt
import sounddevice as sd
%matplotlib inline
def crest_factor(x):
"""Peak-to-RMS value (crest factor) of the signal x
Parameter
---------
x : array_like
signal
"""
return np.max(np.abs(x)) / np.sqrt(np.mean(x**2))
def circular_convolve(x, y, outlen):
"""Circular convolution of x and y
Parameters
----------
x : array_like
Real-valued signal
y : array_like
Real-valued signal
outlen : int
Length of the output
"""
return np.fft.irfft(np.fft.rfft(x, n=outlen) * np.fft.rfft(y, n=outlen), n=outlen)
def plot_time_domain(x, fs=44100, ms=False):
time = np.arange(len(x)) / fs
timeunit = 's'
if ms:
time *= 1000
timeunit = 'ms'
fig = plt.figure()
plt.plot(time, x)
plt.xlabel('Time / {}'.format(timeunit))
return
def plot_freq_domain(x, fs=44100, khz=False):
Nf = len(x) // 2 + 1
freq = np.arange(Nf) / Nf * fs / 2
frequnit = 'Hz'
if khz:
freq /= 1000
frequnit = 'kHz'
fig = plt.figure()
plt.plot(freq, db(np.fft.rfft(x)))
plt.xscale('log')
plt.xlabel('Frequency / {}'.format(frequnit))
plt.ylabel('Magnitude / dB')
return
def compare_irs(h1, h2, ms=False):
t1 = np.arange(len(h1)) / fs
t2 = np.arange(len(h2)) / fs
timeunit = 's'
if ms:
t1 *= 1000
t2 *= 1000
timeunit = 'ms'
fig = plt.figure()
plt.plot(t1, h1, t2, h2)
plt.xlabel('Time / {}'.format(timeunit))
return
def compare_tfs(h1, h2, khz=False):
n1 = len(h1) // 2 + 1
n2 = len(h2) // 2 + 1
f1 = np.arange(n1) / n1 * fs / 2
f2 = np.arange(n2) / n2 * fs / 2
frequnit = 'Hz'
if khz:
freq /= 1000
frequnit = 'khz'
fig = plt.figure()
plt.plot(f1, db(np.fft.rfft(h1)), f2, db(np.fft.rfft(h2)))
plt.xscale('log')
plt.xlabel('Frequency / {}'.format(frequnit))
plt.ylabel('Magnitude / dB')
return
def pad_zeros(x, nzeros):
"""Append zeros at the end of the input sequence
"""
return np.pad(x, (0, nzeros), mode='constant', constant_values=0)
fs = 44100
dur = 1
L = int(np.ceil(dur * fs))
time = np.arange(L) / fs
nbit = int(np.ceil(np.log2(L)))
mls, _ = max_len_seq(nbit) # sequence of 0 and 1
mls = 2*mls - 1 # sequence of -1 and 1
upsample = 10
mls_up = resample(mls, num=len(mls) * upsample)
time = np.arange(len(mls)) / fs
time_up = np.arange(len(mls_up)) / fs / upsample
plt.figure(figsize=(10, 4))
plt.plot(time_up, mls_up, '-', label='Analog')
plt.plot(time, mls, '-', label='Digital')
plt.legend(loc='best')
plt.xlabel('Time / s')
plt.title('Crest factor {:.1f} -> {:.1f} dB'.format(db(crest_factor(mls)), db(crest_factor(mls_up))))
plt.figure(figsize=(10, 4))
plt.plot(time_up, mls_up, '-', label='Analog')
plt.plot(time, mls, 'o', label='Ditigal')
plt.xlim(0, 0.0025)
plt.legend(loc='best')
plt.xlabel('Time / s')
plt.title('Crest factor {:.1f} -> {:.1f} dB'.format(db(crest_factor(mls)), db(crest_factor(mls_up))));
def lin_sweep(fstart, fstop, duration, fs):
"""Generation of a linear sweep signal.
Parameters
----------
fstart : int
Start frequency in Hz
fstop : int
Stop frequency in Hz
duration : float
Total length of signal in s
fs : int
Sampling frequency in Hz
Returns
-------
array_like
generated signal vector
Note that the stop frequency must not be greater than half the
sampling frequency (Nyquist-Shannon sampling theorem).
"""
if fstop > fs / 2:
raise ValueError("fstop must not be greater than fs/2")
t = np.arange(0, duration, 1 / fs)
excitation = np.sin(
2 * np.pi * ((fstop - fstart) /
(2 * duration) * t ** 2 + fstart * t))
# excitation = excitation - np.mean(excitation) # remove direct component
return excitation
fs = 44100
fstart =
fstop =
duration =
lsweep =
def exp_sweep(fstart, fstop, duration, fs):
"""Generation of a exponential sweep signal.
Parameters
----------
fstart : int
Start frequency in Hz
fstop : int
Stop frequency
duration : float
Total length of signal in s
fs : int
Sampling frequency in Hz
Returns
-------
array_like
Generated signal vector
Note that the stop frequency must not be greater than half the
sampling frequency (Nyquist-Shannon sampling theorem).
"""
if fstop > fs / 2:
raise ValueError("fstop must not be greater than fs/2")
t = np.arange(0, duration, 1 / fs)
excitation = np.sin(2 * np.pi * duration *
fstart / np.log(fstop / fstart) *
(np.exp(t / duration * np.log(fstop / fstart)) - 1))
# excitation = excitation - np.mean(excitation) # remove direct component
return excitation
fs = 44100
fstart =
fstop =
duration =
esweep =
| 0.894 | 0.939526 |
#### Libraries & UDFs
```
from ttictoc import Timer
import pickle
import json
from ast import literal_eval
import numpy as np
import pandas as pd
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.linear_model import SGDClassifier
from sklearn.model_selection import train_test_split, KFold, cross_val_score
from sklearn.metrics import accuracy_score, roc_auc_score, average_precision_score
base = '/Users/chuamelia/Google Drive/Spring 2020/Machine Learning/fake-review-detection-project/data/processed/dev/'
def load_obj(fname, base=base):
# This loads the pickled object.
with open(base + fname + '.pkl', 'rb') as f:
return pickle.load(f)
def writeJsonFile(fname, data, base=base):
with open(base + fname +'.json', 'w') as outfile:
json.dump(data, outfile)
print('Successfully written to {}'.format(fname))
def readJsonFile(fname, base=base):
with open(base + fname + '.json', 'r') as f:
data = json.load(f)
return data
def identity_tokenizer(tokens):
return tokens
def ClassifierMetrics (X_train, Y_train, X_test, Y_test, fitted_model):
Y_pred = fitted_model.predict(X_test)
Y_score = fitted_model.decision_function(X_test)
metrics = {'train_accuracy': fitted_model.score(X_train, Y_train),
'test_accuracy': fitted_model.score(X_test, Y_test),
'test_auc_pred': roc_auc_score(Y_test, Y_pred),
'test_auc_score': roc_auc_score(Y_test, Y_score),
'test_ap_pred': average_precision_score(Y_test, Y_pred),
'test_ap_score': average_precision_score(Y_test, Y_score)}
return metrics
```
#### Reading in Data
##### Lookup Tables
```
num_reviews_by_user = pd.read_csv(base + 'num_reviews_by_user.csv')
num_reviews_by_prod = pd.read_csv(base + 'num_reviews_by_prod.csv')
```
##### Construct Dev Set
```
dev_fname = '../../data/processed/dev/ac4119_dev_w_tokens.csv'
dev = pd.read_csv(dev_fname)
dev['token_review'] = dev['token_review'].apply(lambda x: literal_eval(x))
# Rationale:
# At train, you only have visibility to the training numbers to train your model
# However, at dev/test you will have the cumulative numbers as INPUT ONLY.
# We cannot use the cumulative number(s) to generate our model.
# But, realistic to use them as input during test/dev
dev_num_reviews_by_user = num_reviews_by_user[['user_id','cumulative_total_train_dev_test_reviews']]
dev_num_reviews_by_user.columns = ['user_id','num_user_reviews']
dev_num_reviews_by_prod = num_reviews_by_prod[['prod_id','cumulative_total_train_dev_test_reviews']]
dev_num_reviews_by_prod.columns = ['prod_id','num_prod_reviews']
dev = pd.merge(dev, dev_num_reviews_by_user , on='user_id', how='left')
dev = pd.merge(dev, dev_num_reviews_by_prod , on='prod_id', how='left')
def getTrainSet(i):
train_fname = '../../data/processed/dev/ac4119_train_set_{0}_w_tokens.csv'.format(i)
train = pd.read_csv(train_fname)
train['token_review'] = train['token_review'].apply(lambda x: literal_eval(x))
train_num_reviews_by_user = num_reviews_by_user[['user_id','train_num_reviews']]
train_num_reviews_by_user.columns = ['user_id','num_user_reviews']
train_num_reviews_by_prod = num_reviews_by_prod[['prod_id','train_num_reviews']]
train_num_reviews_by_prod.columns = ['prod_id','num_prod_reviews']
train = pd.merge(train, train_num_reviews_by_user , on='user_id', how='left')
train = pd.merge(train, train_num_reviews_by_prod , on='prod_id', how='left')
return train
```
#### Setting Pipeline
```
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.compose import make_column_transformer
feature_cols = ['rating', 'token_review', 'num_user_reviews', 'num_prod_reviews']
X_dev = dev[feature_cols].fillna(0)
Y_dev = dev['label']
def trainModel(params, X_train, Y_train):
# Defining tfidf params
tfidf_vectorizer = TfidfVectorizer(tokenizer=identity_tokenizer, decode_error='ignore',
stop_words='english',
lowercase=False, binary=True,
min_df=0.01)
# setting remainder to passthrough so that the remaining columns (i.e. rating) get included as-is
pipeline = Pipeline([
('transformer', make_column_transformer((StandardScaler(), ['num_user_reviews', 'num_prod_reviews']),
(tfidf_vectorizer, 'token_review'),
remainder = 'passthrough')),
('fitted_svm', SGDClassifier(**params)),
])
fitted_model = pipeline.fit(X_train, Y_train)
return fitted_model
```
### Grid Search
```
all_attempts = []
sets = [1,3]
losses = ['hinge', 'log', 'modified_huber', 'squared_hinge', 'perceptron']
alphas = [0.00001, 0.000001, 0.1, 1, 10]
sgd_params_combos = [(a,l,i) for a in alphas for l in losses for i in sets]
for p in sgd_params_combos:
a,l,i = p
train = getTrainSet(i)
feature_cols = ['rating', 'token_review', 'num_user_reviews', 'num_prod_reviews']
X_train = train[feature_cols].fillna(0)
Y_train = train['label']
# Defining model params
params = {'alpha': a,
'class_weight': 'balanced',
'loss': l,
'penalty': 'l2',
'random_state': 519}
fitted_model = trainModel(params, X_train, Y_train)
metrics = ClassifierMetrics(X_train, Y_train, X_dev, Y_dev, fitted_model)
model_attempt_details = {'params': params, 'metrics': metrics}
all_attempts.append(model_attempt_details)
# File name of the model attempts/results
fname = 'sgd_attempts_ac4119_202005119b'
writeJsonFile(fname, all_attempts)
all_attempts
```
### Apply to test set
```
test_fname = '../../data/processed/dev/ac4119_test_set_w_tokens.csv'
test = pd.read_csv(test_fname)
test_num_reviews_by_prod = num_reviews_by_prod[['prod_id','cumulative_total_train_dev_test_reviews']]
test_num_reviews_by_prod.columns = ['prod_id','num_prod_reviews']
test_num_reviews_by_user = num_reviews_by_user[['user_id','cumulative_total_train_dev_test_reviews']]
test_num_reviews_by_user.columns = ['user_id','num_user_reviews']
test = pd.merge(test, test_num_reviews_by_user , on='user_id', how='left')
test = pd.merge(test, test_num_reviews_by_prod , on='prod_id', how='left')
test['token_review'] = test['token_review'].apply(lambda x: literal_eval(x))
feature_cols = ['rating', 'token_review', 'num_user_reviews', 'num_prod_reviews']
X_test = test[feature_cols].fillna(0)
Y_test = test['label']
Y_pred = fitted_model.predict(X_test)
Y_score = fitted_model.decision_function(X_test)
len(Y_score)
test['Y_score'] = Y_score
test.head(5)
predictions = test[['ex_id', 'Y_score']].sort_values(by='ex_id', ascending=True)
predictions.head(5)
!pwd
fname = '/Users/chuamelia/Google Drive/Spring 2020/Machine Learning/fake-review-detection-project/predictions.csv'
predictions['Y_score'].to_csv(fname, header=False, index=False)
```
|
github_jupyter
|
from ttictoc import Timer
import pickle
import json
from ast import literal_eval
import numpy as np
import pandas as pd
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.linear_model import SGDClassifier
from sklearn.model_selection import train_test_split, KFold, cross_val_score
from sklearn.metrics import accuracy_score, roc_auc_score, average_precision_score
base = '/Users/chuamelia/Google Drive/Spring 2020/Machine Learning/fake-review-detection-project/data/processed/dev/'
def load_obj(fname, base=base):
# This loads the pickled object.
with open(base + fname + '.pkl', 'rb') as f:
return pickle.load(f)
def writeJsonFile(fname, data, base=base):
with open(base + fname +'.json', 'w') as outfile:
json.dump(data, outfile)
print('Successfully written to {}'.format(fname))
def readJsonFile(fname, base=base):
with open(base + fname + '.json', 'r') as f:
data = json.load(f)
return data
def identity_tokenizer(tokens):
return tokens
def ClassifierMetrics (X_train, Y_train, X_test, Y_test, fitted_model):
Y_pred = fitted_model.predict(X_test)
Y_score = fitted_model.decision_function(X_test)
metrics = {'train_accuracy': fitted_model.score(X_train, Y_train),
'test_accuracy': fitted_model.score(X_test, Y_test),
'test_auc_pred': roc_auc_score(Y_test, Y_pred),
'test_auc_score': roc_auc_score(Y_test, Y_score),
'test_ap_pred': average_precision_score(Y_test, Y_pred),
'test_ap_score': average_precision_score(Y_test, Y_score)}
return metrics
num_reviews_by_user = pd.read_csv(base + 'num_reviews_by_user.csv')
num_reviews_by_prod = pd.read_csv(base + 'num_reviews_by_prod.csv')
dev_fname = '../../data/processed/dev/ac4119_dev_w_tokens.csv'
dev = pd.read_csv(dev_fname)
dev['token_review'] = dev['token_review'].apply(lambda x: literal_eval(x))
# Rationale:
# At train, you only have visibility to the training numbers to train your model
# However, at dev/test you will have the cumulative numbers as INPUT ONLY.
# We cannot use the cumulative number(s) to generate our model.
# But, realistic to use them as input during test/dev
dev_num_reviews_by_user = num_reviews_by_user[['user_id','cumulative_total_train_dev_test_reviews']]
dev_num_reviews_by_user.columns = ['user_id','num_user_reviews']
dev_num_reviews_by_prod = num_reviews_by_prod[['prod_id','cumulative_total_train_dev_test_reviews']]
dev_num_reviews_by_prod.columns = ['prod_id','num_prod_reviews']
dev = pd.merge(dev, dev_num_reviews_by_user , on='user_id', how='left')
dev = pd.merge(dev, dev_num_reviews_by_prod , on='prod_id', how='left')
def getTrainSet(i):
train_fname = '../../data/processed/dev/ac4119_train_set_{0}_w_tokens.csv'.format(i)
train = pd.read_csv(train_fname)
train['token_review'] = train['token_review'].apply(lambda x: literal_eval(x))
train_num_reviews_by_user = num_reviews_by_user[['user_id','train_num_reviews']]
train_num_reviews_by_user.columns = ['user_id','num_user_reviews']
train_num_reviews_by_prod = num_reviews_by_prod[['prod_id','train_num_reviews']]
train_num_reviews_by_prod.columns = ['prod_id','num_prod_reviews']
train = pd.merge(train, train_num_reviews_by_user , on='user_id', how='left')
train = pd.merge(train, train_num_reviews_by_prod , on='prod_id', how='left')
return train
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.compose import make_column_transformer
feature_cols = ['rating', 'token_review', 'num_user_reviews', 'num_prod_reviews']
X_dev = dev[feature_cols].fillna(0)
Y_dev = dev['label']
def trainModel(params, X_train, Y_train):
# Defining tfidf params
tfidf_vectorizer = TfidfVectorizer(tokenizer=identity_tokenizer, decode_error='ignore',
stop_words='english',
lowercase=False, binary=True,
min_df=0.01)
# setting remainder to passthrough so that the remaining columns (i.e. rating) get included as-is
pipeline = Pipeline([
('transformer', make_column_transformer((StandardScaler(), ['num_user_reviews', 'num_prod_reviews']),
(tfidf_vectorizer, 'token_review'),
remainder = 'passthrough')),
('fitted_svm', SGDClassifier(**params)),
])
fitted_model = pipeline.fit(X_train, Y_train)
return fitted_model
all_attempts = []
sets = [1,3]
losses = ['hinge', 'log', 'modified_huber', 'squared_hinge', 'perceptron']
alphas = [0.00001, 0.000001, 0.1, 1, 10]
sgd_params_combos = [(a,l,i) for a in alphas for l in losses for i in sets]
for p in sgd_params_combos:
a,l,i = p
train = getTrainSet(i)
feature_cols = ['rating', 'token_review', 'num_user_reviews', 'num_prod_reviews']
X_train = train[feature_cols].fillna(0)
Y_train = train['label']
# Defining model params
params = {'alpha': a,
'class_weight': 'balanced',
'loss': l,
'penalty': 'l2',
'random_state': 519}
fitted_model = trainModel(params, X_train, Y_train)
metrics = ClassifierMetrics(X_train, Y_train, X_dev, Y_dev, fitted_model)
model_attempt_details = {'params': params, 'metrics': metrics}
all_attempts.append(model_attempt_details)
# File name of the model attempts/results
fname = 'sgd_attempts_ac4119_202005119b'
writeJsonFile(fname, all_attempts)
all_attempts
test_fname = '../../data/processed/dev/ac4119_test_set_w_tokens.csv'
test = pd.read_csv(test_fname)
test_num_reviews_by_prod = num_reviews_by_prod[['prod_id','cumulative_total_train_dev_test_reviews']]
test_num_reviews_by_prod.columns = ['prod_id','num_prod_reviews']
test_num_reviews_by_user = num_reviews_by_user[['user_id','cumulative_total_train_dev_test_reviews']]
test_num_reviews_by_user.columns = ['user_id','num_user_reviews']
test = pd.merge(test, test_num_reviews_by_user , on='user_id', how='left')
test = pd.merge(test, test_num_reviews_by_prod , on='prod_id', how='left')
test['token_review'] = test['token_review'].apply(lambda x: literal_eval(x))
feature_cols = ['rating', 'token_review', 'num_user_reviews', 'num_prod_reviews']
X_test = test[feature_cols].fillna(0)
Y_test = test['label']
Y_pred = fitted_model.predict(X_test)
Y_score = fitted_model.decision_function(X_test)
len(Y_score)
test['Y_score'] = Y_score
test.head(5)
predictions = test[['ex_id', 'Y_score']].sort_values(by='ex_id', ascending=True)
predictions.head(5)
!pwd
fname = '/Users/chuamelia/Google Drive/Spring 2020/Machine Learning/fake-review-detection-project/predictions.csv'
predictions['Y_score'].to_csv(fname, header=False, index=False)
| 0.521959 | 0.694406 |
  一般通过 urllib 或 requests 库发送 HTTP 请求,下面将分别介绍两个库的使用(笔者更倾向于使用 requests 库)。在正式开始前,先设置两个 url(分别进行 `get` 和 `post` 请求):
```
get_url = 'http://httpbin.org/get'
post_url = 'http://httpbin.org/post'
```
> `httpbin.org` 提供了简单的 HTTP 请求和响应服务
## 2.1 urllib
  `urllib` 是 python 内置的 HTTP 请求库,包含以下几个模块:
- urllib.request:请求模块
- urllib.error:异常处理模块
- urllib.parse:url 解析模块
- urllib.robotparser:`robots.txt` 解析模块
```
import socket
from urllib import request
from urllib import parse
from urllib import error
from urllib import robotparser
from http import cookiejar
```
### 2.1.1 request
  `request` 模块提供 `urlopen()` 方法打开 url,下面是一个简单的例子:
```
with request.urlopen('https://api.douban.com/v2/book/2224879') as f:
data = f.read() #获取网页内容
print('Status: {0} {1}'.format(f.status, f.reason)) #打印状态码和原因
print('Headers:')
for k, v in f.getheaders(): #打印响应头信息
print('\t{0}: {1}'.format(k, v))
print('Data:\n', data.decode('utf-8')) #打印网页内容
```
  在上面的例子中,首先通过 `urlopen()` 打开 url,接着通过 `read()`、`status`、 `getheaders()` 分别获取响应体内容、状态码和响应头信息。
  `urlopen()` 一般有 3 个常用参数:`url, data, timeout`,下面通过 `http://httpbin.org/post` 演示 `data` 参数的使用。
```
dict = {
'word': 'hello'
}
data = bytes(parse.urlencode(dict), encoding='utf8')
print(data)
response = request.urlopen(post_url, data=data)
print(response.read().decode('utf-8'))
```
  上面的例子中,先通过 `bytes(parse.urlencode())` 函数将 `dict` 的内容转换,接着将其添加到 `urlopen()`的 `data`参数中,这样就完成了一次 `POST` 请求。
> 在没有设置 `data` 参数时,默认以 `GET` 方法请求,反之则以 `POST` 方法请求
  当网络情况不好或者服务器端异常时,会出现请求慢或者请求异常的情况,因此需要给请求设置一个超时时间,而不是让程序一直在等待结果。例子如下:
```
try:
response = request.urlopen(get_url, timeout=0.1)
print(response.read().decode('utf-8'))
except Exception as e:
print(e)
```
  一般为了防范目标网站的反爬虫机制,会为请求设置一些 Headers 头部信息(如 `User-Agent`):
```
req = request.Request(url=get_url)
req.add_header('User-Agent', 'Mozilla/6.0 (iPhone; CPU iPhone OS 8_0 like Mac OS X) AppleWebKit/536.26 (KHTML, like Gecko) Version/8.0 Mobile/10A5376e Safari/8536.25')
with request.urlopen(req) as f:
print('Status: {0} {1}'.format(f.status, f.reason))
print('Data:\n', f.read().decode('utf-8'))
```
  除了通过 `add_header()` 方法添加头信息,还可以通过定义请求头字典,设置 `headers` 参数添加:
```
headers = {
'User-Agent': 'Mozilla/6.0 (iPhone; CPU iPhone OS 8_0 like Mac OS X) AppleWebKit/536.26 (KHTML, like Gecko) Version/8.0 Mobile/10A5376e Safari/8536.25'
}
req = request.Request(post_url, headers=headers, data=data)
with request.urlopen(req) as f:
print('Status: {0} {1}'.format(f.status, f.reason))
```
### 2.1.2 handler
  这里介绍两种 handler,分别是设置代理的 ProxyHandler 和处理 Cookie 的 HTTPCookiProcessor。
  网站会检测某段时间某个 IP 的访问次数,若访问次数过多,则会被禁止访问,这个时候就需要设置代理,urllib 通过 `request.ProxyHandler()` 可以设置代理:
```
proxy_handler = request.ProxyHandler({
'http': 'http://61.135.217.7',
'https': 'https://61.178.127.14'
})
opener = request.build_opener(proxy_handler)
with opener.open(post_url) as f:
print('Status: {0} {1}'.format(f.status, f.reason))
```
  可以通过 ProxyBasicAuthHandler 来处理代理的身份验证:
``` python
url = 'http://www.example.com/login.html'
proxy_handler = request.ProxyHandler({'http': 'http://www.example.com:3128/'})
proxy_auth_handler = request.ProxyBasicAuthHandler()
proxy_auth_handler.add_password('realm', 'host', 'username', 'password')
opener = request.build_opener(proxy_handler, proxy_auth_handler)
with opener.open(url) as f:
pass
```
  Cookie 中保存中我们常见的登录信息,有时候爬取网站需要携带 Cookie 信息访问,这里通过 `http.cookijar` 获取 Cookie 以及存储 Cookie:
```
cookie = cookiejar.CookieJar()
handler = request.HTTPCookieProcessor(cookie)
opener = request.build_opener(handler)
with opener.open('http://www.baidu.com'):
for item in cookie:
print(item.name + '=' + item.value)
```
### 2.1.3 error
  在 2.1.1 设置 `timeout` 参数时,借助了 `urllib.error` 模块进行异常处理。
```
try:
response = request.urlopen('http://www.pythonsite.com/', timeout=0.001)
except error.URLError as e:
print(type(e.reason))
if isinstance(e.reason, socket.timeout):
print('Time Out')
```
  在 `urllib.error` 中有两种异常错误:URLError 和 HTTPError。URLError 里只有一个属性—— `reason`,即抓异常的时候只能打印错误原因;而 HTTPError 里有三个属性:`code, reason, headers`,即抓异常的时候可以获得错误代码、错误原因、头信息三个信息,例子如下:
```
try:
response = request.urlopen('http://pythonsite.com/1111.html')
except error.HTTPError as e:
print(e.reason)
print(e.code)
print(e.headers)
except error.URLError as e:
print(e.reason)
else:
print('reqeust successfully')
```
### 2.1.4 parse
  `urllib.parse` 模块用于解析 url。其中 `urlparse()` 方法拆分 url:
```
result = parse.urlparse('http://www.baidu.com/index.html;user?id=5#comment')
print(result)
```
  `urlunparse()` 与之相反,用于拼接 url:
```
data = ['http', 'www.baidu.com', 'index.html', 'user', 'a=123', 'commit']
print(parse.urlunparse(data))
```
  `urljoin()` 也是用于拼接:
```
print(parse.urljoin('http://www.baidu.com', 'FAQ.html'))
```
  `urlencode()` 将字典转换为 url 参数:
```
params = {
'name': '尧德胜',
'age': 23,
}
base_url = 'http://www.baidu.com?'
print(base_url + parse.urlencode(params))
```
### 2.1.5 robotparser
  `urllib.robotparser` 模块用于解析 robots.txt(即 Robots 协议),下面以一个简单的例子来介绍:
> Robots 协议也称作爬虫协议,用于告知爬虫哪些页面可以抓取,一般放在网站的根目录下。
```
rp = robotparser.RobotFileParser() #创建 RobotFileParser 对象
rp.set_url('http://www.jianshu.com/robots.txt') #设置目标网站的 robots.txt 链接
rp.read() #读取 robots.txt 并解析
print(rp.can_fetch('*', 'https://www.jianshu.com/p/2b0ed045e535')) #判断网页是否可以被爬取
```
## 2.2 requests
  这一节介绍较 urllib 更为强大方便的 requests:
```
import requests
```
### 2.2.1 GET 请求
  urllib 的 `urlopen()` 方法实际上默认通过 `GET` 发送请求,而 requests 则以 `get()` 方法发送 `GET` 请求,更为明确:
```
with requests.get(get_url) as r:
print('Status: {0} {1}'.format(r.status_code, r.reason)) #打印状态码和原因
print('Encoding: {}'.format(r.encoding))
print('Headers: \n{}'.format(r.headers)) #打印响应头信息
print('Data: \n{}'.format(r.text)) #打印响应体内容
```
  通过观察,不难发现返回的数据格式为 JSON,可以通过 `json()` 方法将返回的 JSON 格式字符串转化为字典:
```
with requests.get(get_url) as r:
json = r.json()
print(json)
print(type(json))
```
  当需要对 `GET` 请求添加额外信息时,可以利用 `params` 参数:
```
data = {
'name': 'gaiusyao',
'id': '42'
}
with requests.get(get_url, params=data) as r:
print('Data: \n{}'.format(r.text))
```
  加入 `headers` 参数,设置请求头:
```
with requests.get(get_url, headers=headers) as r:
print('Status: {0} {1}'.format(r.status_code, r.reason))
```
### 2.2.2 POST 请求
  requests 发送 `POST` 请求是通过 `post()` 方法,与 urllib 相同的是,也需要设置 `data` 参数:
```
with requests.post(post_url, data = data) as r:
print('Status: {0} {1}'.format(r.status_code, r.reason))
print('Data: \n{}'.format(r.text))
```
### 2.2.3 响应
  发送请求后,将得到服务器端的响应,requests 除了 `text` 获取响应内容外,还有很多属性和方法:
```
res = requests.get('http://www.jianshu.com', headers=headers)
# 获取请求地址
res.url
# 获取状态码
res.status_code
# 获取头信息
res.headers
# 获取 Cookie
res.cookies
# 获取请求历史
res.history
```
### 2.2.4 Cookie
  先以一个简单的例子获取 Cookie:
```
with requests.get('http://www.jianshu.com', headers=headers) as r:
for k, v in r.cookies.items():
print('\t{0}: {1}'.format(k, v))
```
  可以将 Cookie 设置到 Headers 中,然后发送请求:
```
c_headers = {
'Cookie': '__yadk_uid=KJqOgEJ7RRTgmhU3x0gwXUmSB2SGF6Bv; remember_user_token=W1s2NTMzODI1XSwiJDJhJDExJGprOXAzcTQwQ09oUTQ1RW9GSEVCbi4iLCIxNTQxNzUzNTQzLjcyNTMxOCJd--c82c1473b9fb81ef55c8432ce297f13b41f223a8; sensorsdata2015jssdkcross=%7B%22distinct_id%22%3A%226533825%22%2C%22%24device_id%22%3A%221665ba3af58853-0563eb383564ca-5701631-1327104-1665ba3af5aaa9%22%2C%22props%22%3A%7B%22%24latest_traffic_source_type%22%3A%22%E7%9B%B4%E6%8E%A5%E6%B5%81%E9%87%8F%22%2C%22%24latest_referrer%22%3A%22%22%2C%22%24latest_referrer_host%22%3A%22%22%2C%22%24latest_search_keyword%22%3A%22%E6%9C%AA%E5%8F%96%E5%88%B0%E5%80%BC_%E7%9B%B4%E6%8E%A5%E6%89%93%E5%BC%80%22%7D%2C%22first_id%22%3A%221665ba3af58853-0563eb383564ca-5701631-1327104-1665ba3af5aaa9%22%7D; read_mode=day; default_font=font2; locale=zh-CN; _m7e_session=66694739e9ada77d06a7683f09d1f4ae; Hm_lvt_0c0e9d9b1e7d617b3e6842e85b9fb068=1541605221,1541686521,1541725091,1541843383; Hm_lpvt_0c0e9d9b1e7d617b3e6842e85b9fb068=1541855281',
'User-Agent': 'Mozilla/6.0 (iPhone; CPU iPhone OS 8_0 like Mac OS X) AppleWebKit/536.26 (KHTML, like Gecko) Version/8.0 Mobile/10A5376e Safari/8536.25'
}
with requests.get('http://www.jianshu.com', headers=c_headers) as r:
for k, v in r.cookies.items():
print('\t{0}: {1}'.format(k, v))
```
### 2.2.5 会话维持
  利用 `Session` 对象可以很方便地维持一个会话,且不用担心 Cookie 的问题:
```
with requests.Session() as s:
s.get('http://httpbin.org/cookies/set/number/12345678')
r = s.get('http://httpbin.org/cookies')
print(r.text)
requests.get('http://httpbin.org/cookies/set/number/123456789')
r = requests.get('http://httpbin.org/cookies')
print(r.text)
```
  如果不使用 Session 对象,在 `get('http://httpbin.org/cookies')` 这步,将无法获取之前设置的 Cookie。
### 2.2.6 代理设置
  通过设置 `proxies` 参数,可以设置代理:
```
proxies = {
'http': 'http://61.135.217.7',
'https': 'https://61.178.127.14'
}
with requests.get(get_url, proxies=proxies) as r:
print('Status: {0} {1}'.format(r.status_code, r.reason))
```
  若代理需要用到 HTTP Basic Auth,则可使用类似 `http://user:password@host:port` 这样的语法来部署代理。
### 2.2.7 超时设置
  requests 也是通过 `timeout` 参数来进行超时设置(不设置则会永久等待):
```
try:
with requests.get(get_url, timeout=1) as r:
print('Status: {0} {1}'.format(r.status_code, r.reason))
except Exception as e:
print(e)
```
  实际上请求分为连接和读取两个阶段,可以通过一个元组分别指定:
```
try:
with requests.get(get_url, timeout=(2, 4)) as r:
print('Status: {0} {1}'.format(r.status_code, r.reason))
except Exception as e:
print(e)
```
### 2.2.8 身份认证
  requests 自带身份认证功能:
``` python
r = requests.get('http://localhost:5000', auth=('username', 'password'))
print('Status: {0} {1}'.format(r.status_code, r.reason))
```
> 想了解更多参阅 [requests 官方文档](http://www.python-requests.org/en/master/)
|
github_jupyter
|
get_url = 'http://httpbin.org/get'
post_url = 'http://httpbin.org/post'
import socket
from urllib import request
from urllib import parse
from urllib import error
from urllib import robotparser
from http import cookiejar
with request.urlopen('https://api.douban.com/v2/book/2224879') as f:
data = f.read() #获取网页内容
print('Status: {0} {1}'.format(f.status, f.reason)) #打印状态码和原因
print('Headers:')
for k, v in f.getheaders(): #打印响应头信息
print('\t{0}: {1}'.format(k, v))
print('Data:\n', data.decode('utf-8')) #打印网页内容
dict = {
'word': 'hello'
}
data = bytes(parse.urlencode(dict), encoding='utf8')
print(data)
response = request.urlopen(post_url, data=data)
print(response.read().decode('utf-8'))
try:
response = request.urlopen(get_url, timeout=0.1)
print(response.read().decode('utf-8'))
except Exception as e:
print(e)
req = request.Request(url=get_url)
req.add_header('User-Agent', 'Mozilla/6.0 (iPhone; CPU iPhone OS 8_0 like Mac OS X) AppleWebKit/536.26 (KHTML, like Gecko) Version/8.0 Mobile/10A5376e Safari/8536.25')
with request.urlopen(req) as f:
print('Status: {0} {1}'.format(f.status, f.reason))
print('Data:\n', f.read().decode('utf-8'))
headers = {
'User-Agent': 'Mozilla/6.0 (iPhone; CPU iPhone OS 8_0 like Mac OS X) AppleWebKit/536.26 (KHTML, like Gecko) Version/8.0 Mobile/10A5376e Safari/8536.25'
}
req = request.Request(post_url, headers=headers, data=data)
with request.urlopen(req) as f:
print('Status: {0} {1}'.format(f.status, f.reason))
proxy_handler = request.ProxyHandler({
'http': 'http://61.135.217.7',
'https': 'https://61.178.127.14'
})
opener = request.build_opener(proxy_handler)
with opener.open(post_url) as f:
print('Status: {0} {1}'.format(f.status, f.reason))
  Cookie 中保存中我们常见的登录信息,有时候爬取网站需要携带 Cookie 信息访问,这里通过 `http.cookijar` 获取 Cookie 以及存储 Cookie:
### 2.1.3 error
  在 2.1.1 设置 `timeout` 参数时,借助了 `urllib.error` 模块进行异常处理。
  在 `urllib.error` 中有两种异常错误:URLError 和 HTTPError。URLError 里只有一个属性—— `reason`,即抓异常的时候只能打印错误原因;而 HTTPError 里有三个属性:`code, reason, headers`,即抓异常的时候可以获得错误代码、错误原因、头信息三个信息,例子如下:
### 2.1.4 parse
  `urllib.parse` 模块用于解析 url。其中 `urlparse()` 方法拆分 url:
  `urlunparse()` 与之相反,用于拼接 url:
  `urljoin()` 也是用于拼接:
  `urlencode()` 将字典转换为 url 参数:
### 2.1.5 robotparser
  `urllib.robotparser` 模块用于解析 robots.txt(即 Robots 协议),下面以一个简单的例子来介绍:
> Robots 协议也称作爬虫协议,用于告知爬虫哪些页面可以抓取,一般放在网站的根目录下。
## 2.2 requests
  这一节介绍较 urllib 更为强大方便的 requests:
### 2.2.1 GET 请求
  urllib 的 `urlopen()` 方法实际上默认通过 `GET` 发送请求,而 requests 则以 `get()` 方法发送 `GET` 请求,更为明确:
  通过观察,不难发现返回的数据格式为 JSON,可以通过 `json()` 方法将返回的 JSON 格式字符串转化为字典:
  当需要对 `GET` 请求添加额外信息时,可以利用 `params` 参数:
  加入 `headers` 参数,设置请求头:
### 2.2.2 POST 请求
  requests 发送 `POST` 请求是通过 `post()` 方法,与 urllib 相同的是,也需要设置 `data` 参数:
### 2.2.3 响应
  发送请求后,将得到服务器端的响应,requests 除了 `text` 获取响应内容外,还有很多属性和方法:
### 2.2.4 Cookie
  先以一个简单的例子获取 Cookie:
  可以将 Cookie 设置到 Headers 中,然后发送请求:
### 2.2.5 会话维持
  利用 `Session` 对象可以很方便地维持一个会话,且不用担心 Cookie 的问题:
  如果不使用 Session 对象,在 `get('http://httpbin.org/cookies')` 这步,将无法获取之前设置的 Cookie。
### 2.2.6 代理设置
  通过设置 `proxies` 参数,可以设置代理:
  若代理需要用到 HTTP Basic Auth,则可使用类似 `http://user:password@host:port` 这样的语法来部署代理。
### 2.2.7 超时设置
  requests 也是通过 `timeout` 参数来进行超时设置(不设置则会永久等待):
  实际上请求分为连接和读取两个阶段,可以通过一个元组分别指定:
### 2.2.8 身份认证
  requests 自带身份认证功能:
| 0.36625 | 0.850469 |
# Chapter 6: Basic algorithms: searching and sorting
##6.1 Introduction
The implementation of algorithms requires the use of different programming techniques to mainly represent, consume and produce data items.
* Data structures allow us to properly conceptualize the structure and organization of the data that is managed by our programs (as input, as intermediary results or as output).
* Functions allow us to fulfill two important requirements in any program:
* The DRY (Do not Repeat Yourself) principle.
* Improve the reusability of the code (implicitely including reliability if the function has been properly verified and validated).
* Improve the readability and understandibility of the code.
* Objects are a conceptualization of a domain in which we express data (attributes) and operations (functions) modelling entities (classes) that represent the relevant entities in both in the problem and solution domain.
These three elements allow us to manage the data is managed in a program and to implement business logic through functions and methods.
However, the functions or methods (in case of objects) that offer some capability usually implement some complex business logic that requires different types of algorithms.
There are different types of algorithms depending on the structure, their formal definition, their control flow or how they manage data. As an example, we can classify algorithms in a category as follows:
* **Recursive algorithms**: trying to solve a base case and, then, make a recursion to solve the general case. E.g. Factorial.
* **Dynamic programmign algorithms**: remembering past results (when there is an overlapping) and using them to find new resuls. E.g. Fibonacci numbers.
* **Backtracking algorithms**: trying to find a solution applying a depth-first recursive search until finding a solution. E.g. The famous $n$ queens.
* **Divide and conquer algorithms**: dividing the problem into smaller problems that can be then solved recursively to finally combine solutions and deliver a general solution. E.g. Binary search.
* **Greedy algorithms**: finding not just a solution but the best one. E.g. Count money using the fewest bills and coins.
* **Branch and bound algorithms**: calculating the probability of getting a solution for optimization problems. E.g. The famous TSP (Travelling salesman problem) problem.
* **Brute force algorithms**: testing all posible solutions until a satisfactory solution is found. It makes use of heuristics and optimization techniques. E.g. Break a password.
* **Randomized algorithms**: getting a solution by running a randomized number of times to make a decission. E.g. Quicksort and pivot selction.
The keypoint is how the algorithm tackle the solution of a problem and how the algorithm makes use of basic functionalities like searching and/or sorting to prepare the data and generate (intermediary and final) solutions.
That is why, it is necessary to know and govern basic algorithms for searching and sorting data under different data structures to be able to define and design more complex algorithms. In general, the design of algorithms makes use of different types of algorithms. In other words, more complex algorithms are built on top of other more basic algorithms.
For instance, an advanced artificial intelligence technique makes use of another type of algorithm (e.g. branch and bound) that, at the same time, makes use of other techniques such as searching and sorting. So, an algorithm relies on other layers of algorithms.
In this chapter, some basic searching (find an element in a collection) and sorting (ordering a collection of values) algorithms are presented. More specifically, the following algorithms are explained.
* Linear search.
* Binary search.
* Bubble sort.
* Insertion sort.
* Selection sort
Obviously, there are many other algorithms in both fields, and, this chapter only pretends to introduce the foundations of these techniques.
Furthermore, many programming languages and libraries are already providing these type of algorithms. However, it is important to know the foundations of these techniques to be able to design our own algorithms.
Finally, some introduction to the evaluation of algorithms in terms of time and space complexity is also outlined.
##6.2 Searching algorithms
We all know the notion search:
* There is a catalogue of items.
* There is a query.
* An algorithm tries to match the items according to this query.
* The results (positions or the items) are returned.
In the field of Computer Science and algorithms, searching is quite similar.
* Given a list of items and a target element, the searching function looks for the target element in the list of items and returns a value (the item, the position or a boolean value).
###6.2.1 Linear Search
####**Problem definition**
There are many cases in which we need to look for a value in some collection. For instance, given a person id and a list of students, the program shall return the student details.
In a more simple way, given a number and a collection of numbers, the program shall return whether the element exists within the collection.
* Given the list: [2,8,3,9]
* Target number: 2
* Result: True
####**Concept**
Linear search is the most basic technique for searching. Basically, it iterates over a collection until finding the target value. Then, there are different strategies:
* Find first.
* Find last.
* Find all.
In linear search, no assumption is taken (like elements must be sorted).
In regards to the time/temporal complexity, the linear search cannot be considered very efficient.
* Best case: $O(1)$, the first element visited by the algorithm is the target element.
* Worst case: $O(n)$, being $n$ the number of elements in the collection. For instance, if the last element is the target or if the target does not exist.
* Average case: $O(n)$, being $n$ the number of elements in the collection. Although the target can be found in any position between $(0,n)$ if it is not found in the first position, we can assume the algorithm will iterate over $n$ elements.
The notion of linearity for some algorithm is not generally bad. However, as the input grows the time to search will be also increased in linear time. So, an algorithm that can perfectly work for thousand of items, if the problem scales in one order of magnitude, the time can dramatically be increased.
In other algorithms with quadractic or event exponential time complexity, this situation is directly unsustainable and we should re-think our data structures and algorithms.
####**Application**
The linear search represents the basic and general algorithm for looking up elements in a collection.
It only requires a collection of items, a target (e.g. query or value) and strategy (first, last or all) and the algorithm will iterate over all the elements until finding the target.
* **Find first**:
>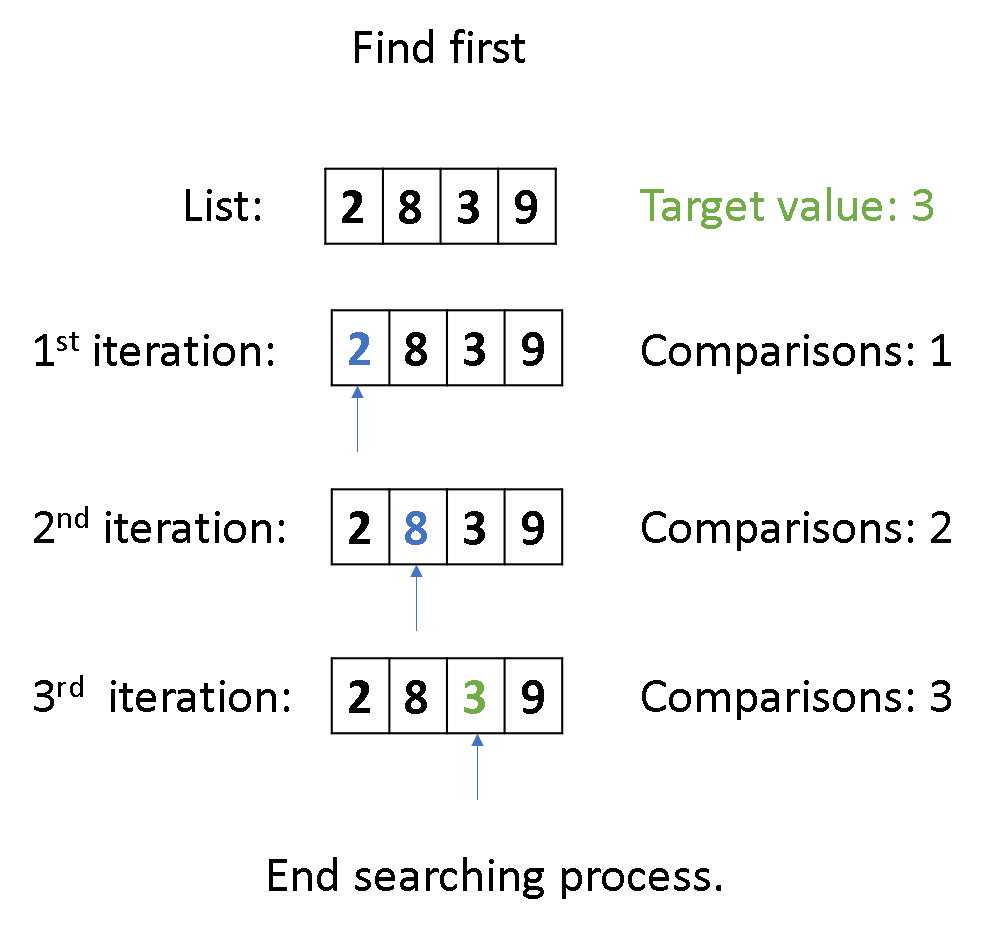
>Figure: Find first example.
* **Find last**:
>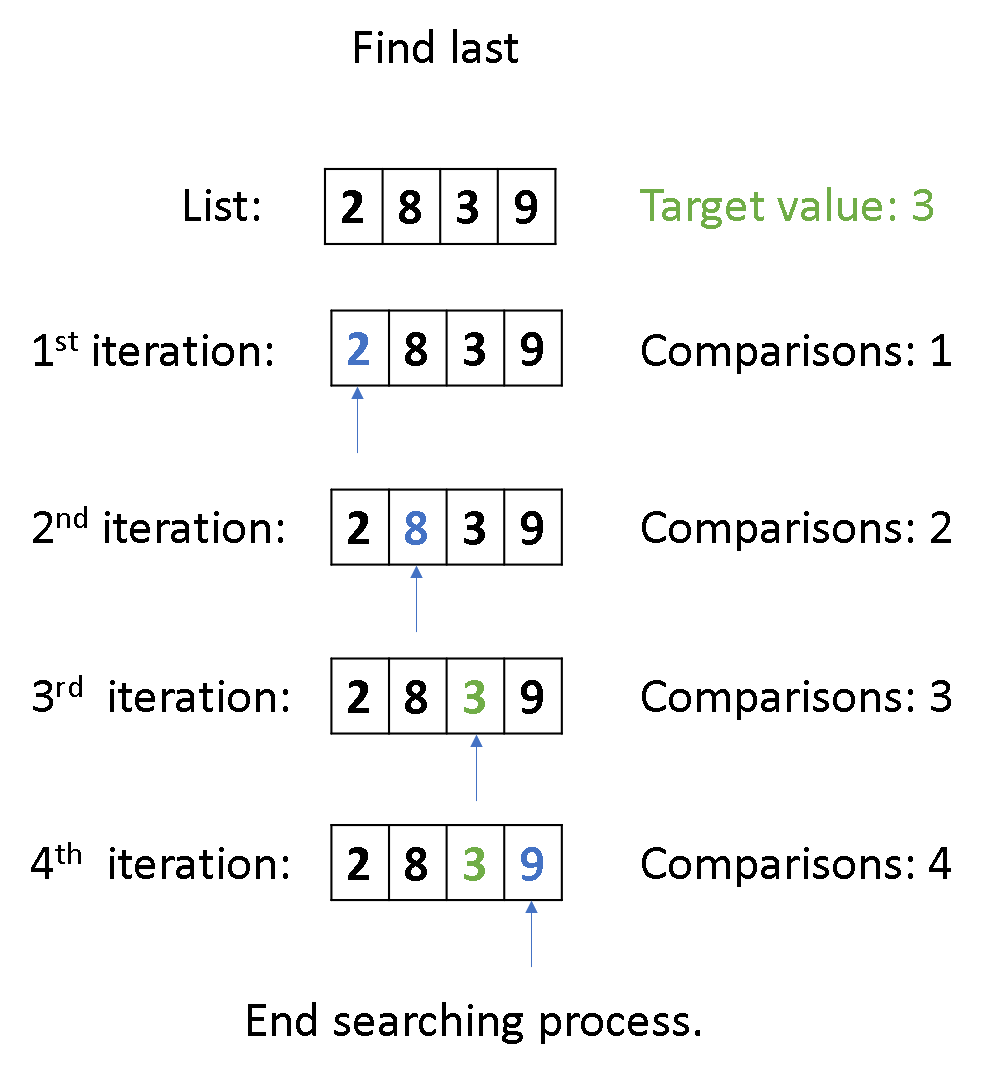
>Figure: Find last example.
* **Find all**:
>
>Figure: Find all example.
####**Python implementation**
Following, some examples of linear search are presented:
```
#Linear search examples
def linear_search_first(values, target):
found = False
i = 0
while not found and i<len(values):
found = values[i] == target
i += 1
return found
def linear_search_last(values, target):
found = False
i = len(values)-1
while not found and i>=0:
found = values[i] == target
i -= 1
return found
def linear_search_all(values, target):
i = 0
while i<len(values):
found = values[i] == target
if found:
print("Found at position: ",i)
i += 1
return
print(linear_search_first([2,8,3,9], 3))
print(linear_search_last([2,8,3,9], 3))
linear_search_all([2,8,3,9], 3)
```
####**Visual animations**
You can find some interesting visual representation of the algorithms in the following links:
* https://www.cs.usfca.edu/~galles/visualization/Search.html
* https://visualgo.net/en
###6.2.2 Binary Search
####**Problem definition**
Sometimes we face problems in which we can apply a technique of divide and conquer. In other words, we can reduce the solution space applying some rule.
For instance, if we have a deck of sorted cards and someone asks for some card, we can easily look up that card without checking all the cards. Try to think a bit in how you internally proceed:
1. You know the card you are looking for.
2. You know that the deck is sorted (perhaps is new).
3. You make an approximation to look up the target card.
4. If you are "lucky", you will match the card at the first attempt, otherwise, you will make an internal calculation to approximate where the card could be.
5. You will repeat the steps from 2 to 4 until getting the card.
In general, everybody will proceed in this manner (unless you have a lot of time to review all the cards). Here, the question is:
* What are we actually doing?
Basically, we are optimizing how we look up for an item by reducing the number of items we have to review. Since, the deck is sorted we can even discard part of the cards in each attempt.
As a simple experiment, try to sort a deck of cards and look for one specific card (measure the time). Afterwards, repeat the same experiment after shuffling the cards (measure the time again). Write down your feeling!
####**Concept**
Binary search or half-interval search is a kind of searching technique that is based in the previus concept:
* In each iteration, we reduce the possibilities by discarding half of the problem.
This technique works quite well for many problems but it has a very strong assumption: **the list must be sorted according to some criteria**. Furthemore, we need access to the elements using an index.
Given a list $l$ and a target value $v$, The algorithm works as folows:
* It takes two indexes: min and max. Initially, $min = 0$ and $max = len(l)$
* It calculates the middle, $(min-max)/2$ element of a list.
* It compares this element with the target element.
* If both are equal, then we have found $v$ and we can stop.
* If $v > l[middle]$, update index $min=middle+1$
* If $v < l[middle]$, update index $max=middle-1$
* The algorithm will stop if $min=max$ or $v$ is found.
In regards to the time/temporal complexity, the binary search is quite efficient (but we need a sorted list).
* Best case: $O(1)$, the first element visited by the algorithm is the target element.
* Worst case: $O(log\_n)$, being $n$ the number of elements in the collection. The $log$ complexity comes from the height of a full balanced binary tree (that is actually the intrinsic structure of calls that is generated).
* Average case: $O(log\_n)$, being $n$ the number of elements in the collection.
This algorithm represents a very good option if we have a sorted list.
####**Application**
As we have stated before, if we have searching problems containing a sorted collection with indexed access to elements, we can approach the problem with a binary search technique.
* **Binary search example**:
>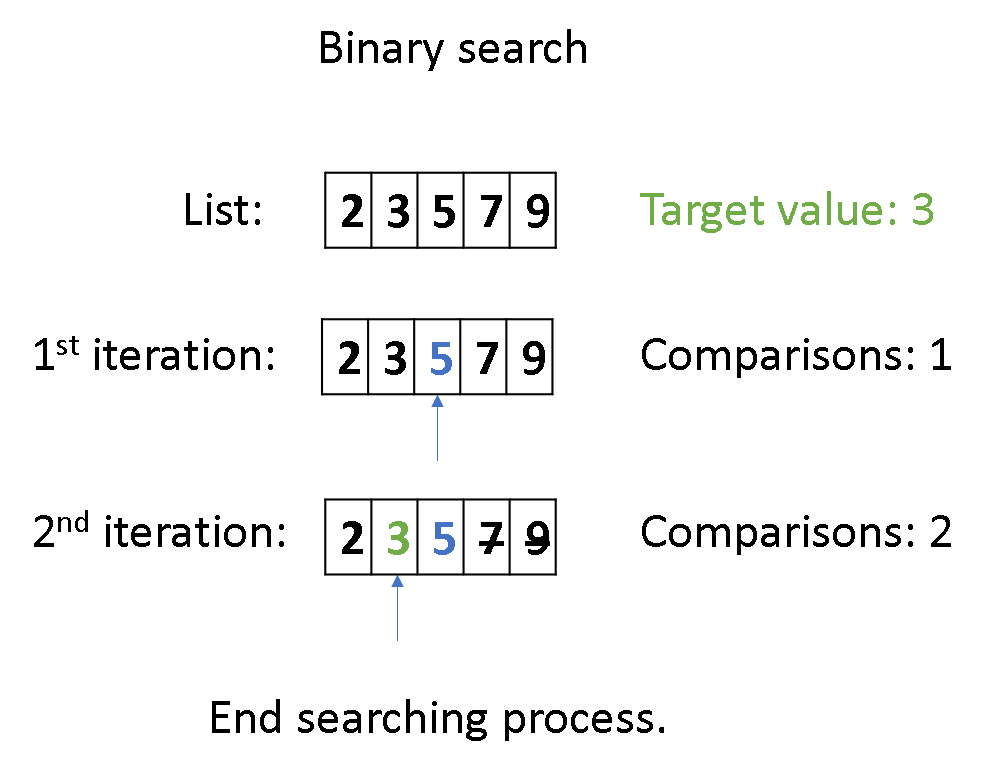
>Figure: Binary search example.
####**Python implementation**
```
#See animation: https://www.w3resource.com/python-exercises/data-structures-and-algorithms/python-search-and-sorting-exercise-1.php
def binary_search(values, target):
first = 0
last = len(values)-1
found = False
while first <= last and not found:
mid = (first + last)//2
if values[mid] == target:
found = True
else: #Discard half of the problem
if target < values[mid]:
last = mid - 1
else:
first = mid + 1
return found
print(binary_search([1,2,3,5,8], 6))
print(binary_search([1,2,3,5,8], 5))
```
##6.3 Sorting algorithms
As in searching, we all know the notion sorting a collection:
* There is a catalogue of items.
* There is some criteria to order the items.
* Al algorithm tries to swap elements until getting the proper order.
In the field of Computer Science and algorithms, sorting is quite similar.
* Given a list of items and some criteria (single or multiple), the sorting function looks for comparing the elements according to criteria and put them in the proper order.
The main consideration we need to know when sorting is that elements must be **comparable**. In practice, it means that we can apply the logical operators for comparison.
###6.3.1 The Bubble sort algorithm
####**Problem definition**
Let's suppose we have to generate a report of the list of students sorted by the family name in descending order. How can we approach this problem?
In general, we have to compare the items in the list, in this case family names, and swap them until we can ensure that the last element is sorted.
####**Concept**
The bubble sort is a very basic sorting algorithm based on comparing adjacent items and swap them if they are not in the proper order. The algorithm will repeat the process until all elements are sorted (and somehow have been compared each other).
In the following pseudo-code, the bubble sort algorithm is presented. The algorithm starts taking one element and compares it against all others swapping if necessary.
```
for i from 1 to N
for j from 0 to N-1
if a[j]>a[j+1]
swap(a[j], a[j+1])
```
In regards of time complexity, the bubble sort algorithm behaves with a very poor performance because it requires comparing all elements against all elements. In a list of $n$ elements, each element is compared against the other $n-1$ elements.
* Best, Worst and Average case: $O(n^2)$, being $n$ the number of elements in the list. In general, since we have two nested loops the time complexity can be calculated by multipliying the time complexity of the first loop ($n$) times the time complexity of the second loop ($n$).
However, there are variants of the bubble sort that tries to reduce the number of comparisons (and swaps) stopping when in one iteration there is no swap (the list is sorted). Anyway, the worst case time complexity still remains $O(n^2)$.
####**Application**
The application of the bubble sort algorithm is justified when we have to sort a small list of items, otherwise the time to sort will be dramatically increased and other algorithms should be considered.
* **Bubble sort example**:
>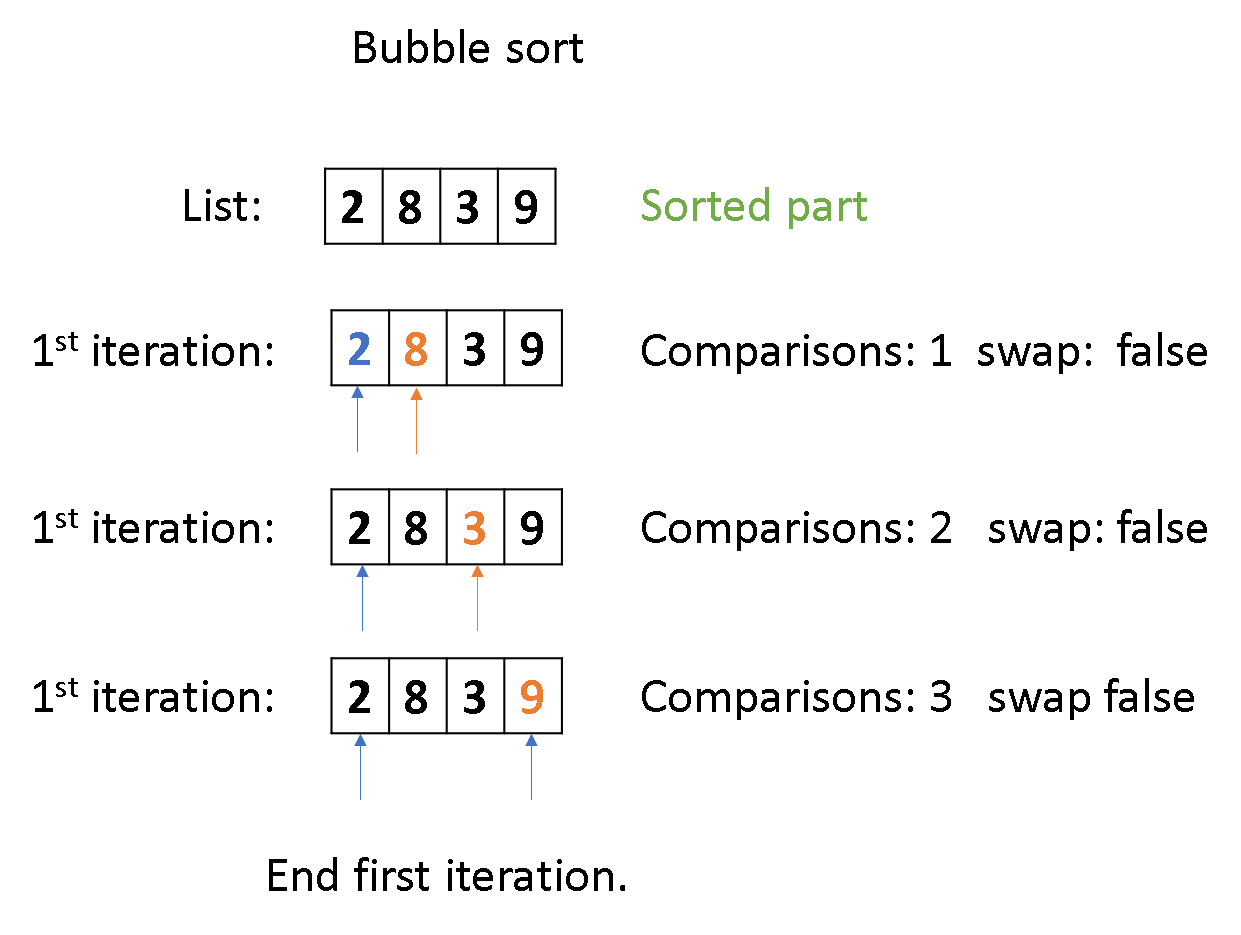
>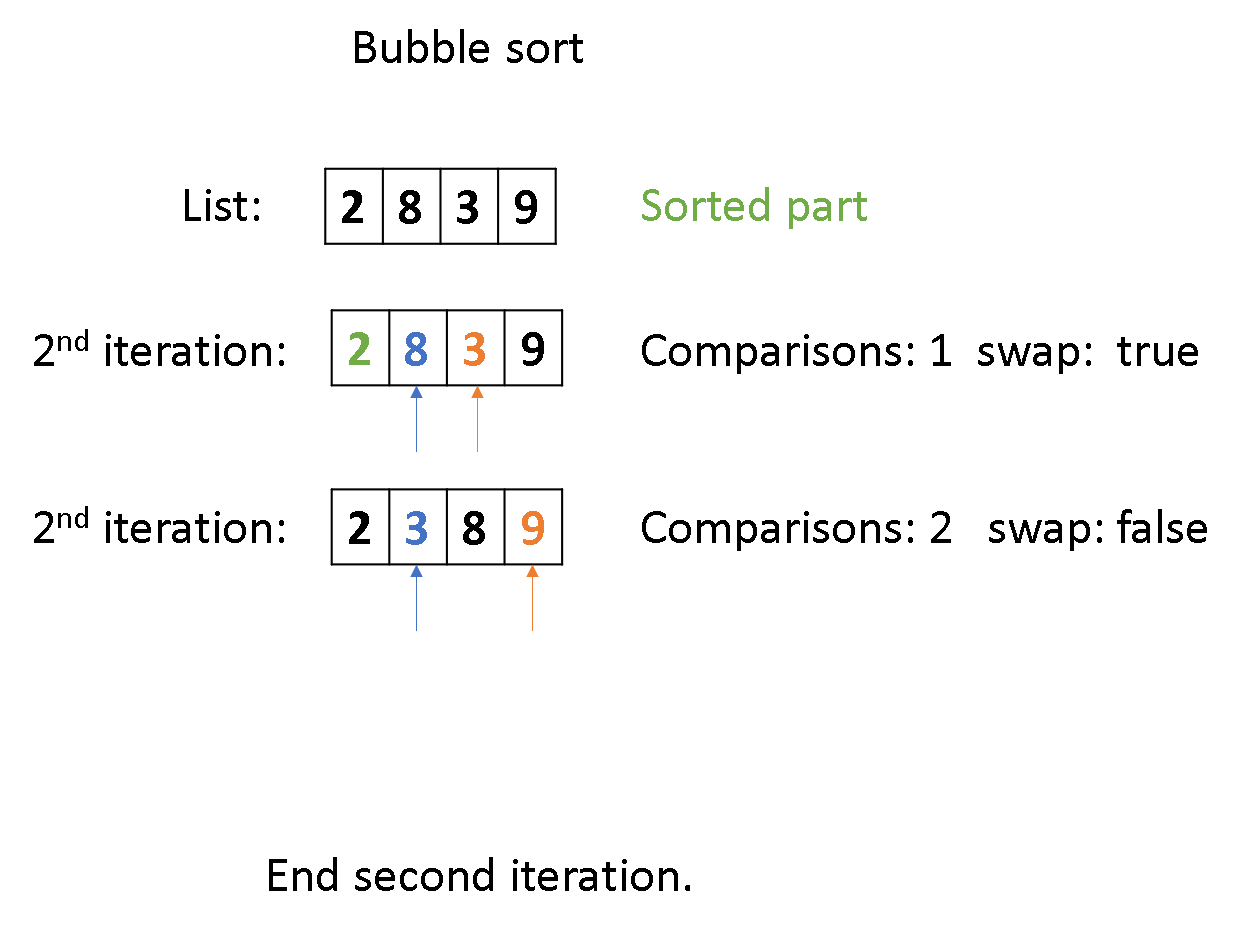
>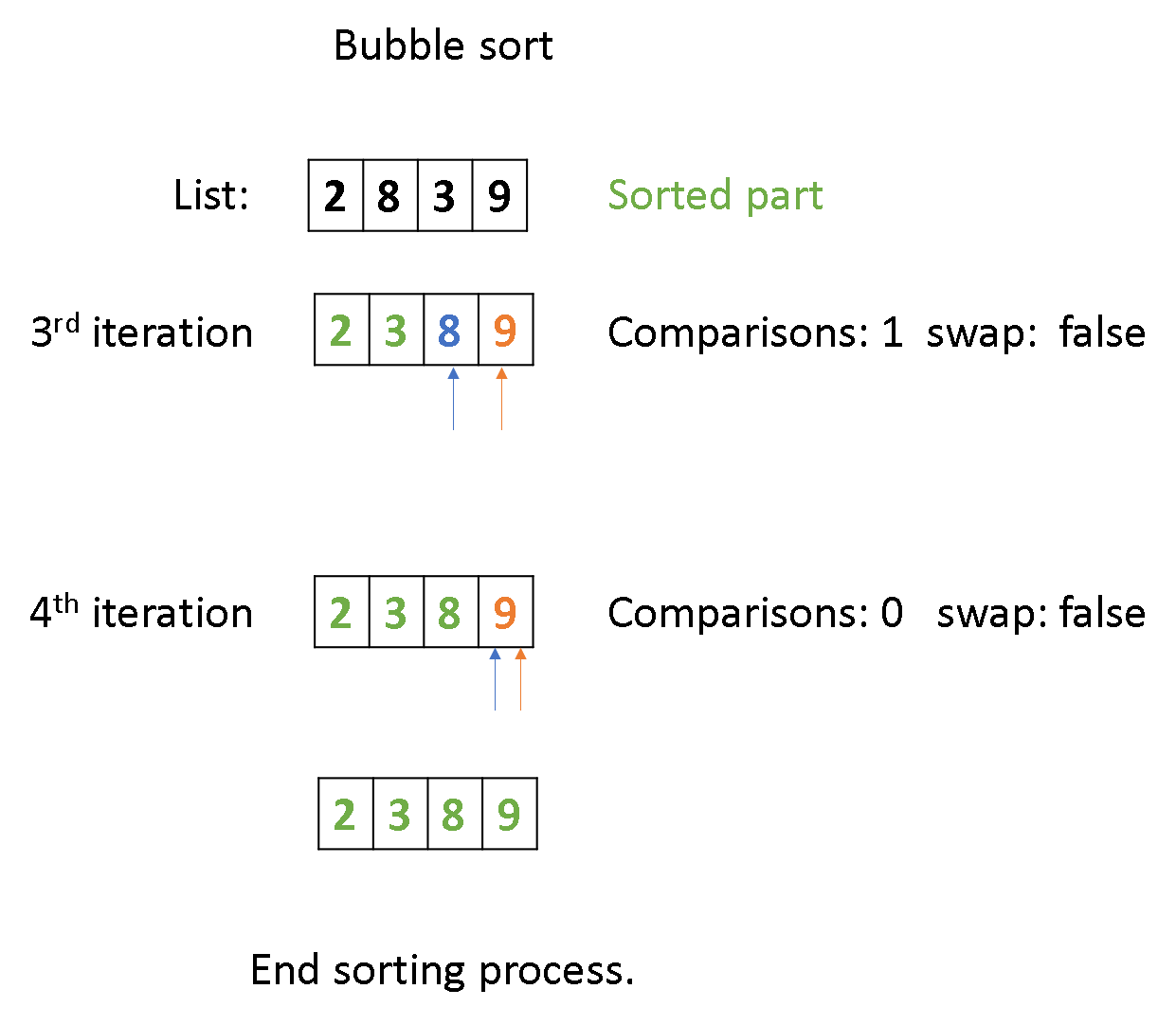
>Figure: Bubble sort example.
####**Python implementation**
```
#See more: https://www.w3resource.com/python-exercises/data-structures-and-algorithms/python-search-and-sorting-exercise-4.php
def bubble_sort(values):
n = len(values)
for i in range(n):
for j in range(n-i-1):
if values[j] > values[j+1]:
#Swap
values[j], values[j+1] = values[j+1], values[j]
values = [22, 8, 33, 12, 14, 43]
bubble_sort(values)
print(values)
```
###6.3.2 The Selection sort algorithm (only information)
####**Problem definition**
As we have introduced before, any time we have to sort a list of items according to some criteria, we should think in a sorting algorithm. If the list starts to become very large, we can optionally think in other algorithms rather than the bubble.
####**Concept**
The selection sort algorithm is a sorting algorithm that in each iteration looks for the minimum element in the right-hand side of the unsorted list and swap it with the element after the last sorted element (initially the first element).
Intrinsically, the algorithm generates two sublists (managed by an index): the sublist of sorted elements and the remaining list.
In the following pseudo-code, the selection sort algorithm is presented.
```
for i in len(lst):
min_index = i
for j in (i+1, max)
if lst[min_index] > key
min_index = j
swap(lst[min_index],lst[i])
```
In regards to the time/temporal complexity, the selection sort does not behave to much better in comparison to the bubble sort. It only tries to improve the number of swaps in the worst case.
* Best case, Worst case and Average case: $О(n^2)$ comparisons and $n$ swaps.
There are other variants of the selection sort that can improve the efficiency.
####**Application**
The main situation in which we should think in using the selection sort algorithm is when memory is limited since it does not required any extra resource to store temporary results.
* **Selection sort example**:
>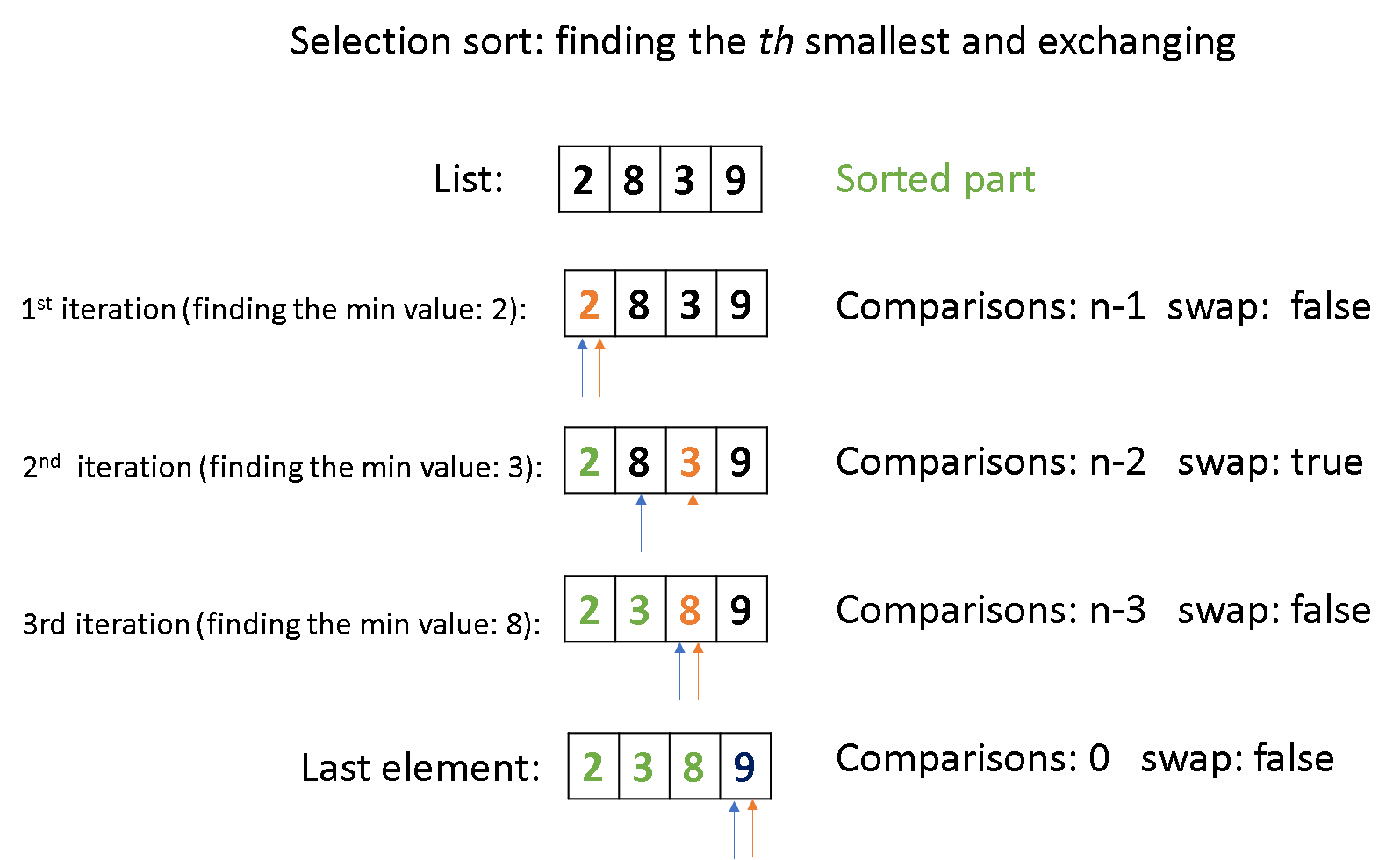
>Figure: Selection sort example.
####**Python implementation**
* Selection: "*Given a list, take the current element and exchange it with the smallest element on the right hand side of the current element.*"
```
def selection_sort(values):
n = len(values)
for i in range(n):
min_idx = i
for j in range(i+1, n):
if values[min_idx] > values[j]:
min_idx = j
#Swap with the minimum value position
values[i], values[min_idx] = values[min_idx], values[i]
values = [22, 8, 33, 12, 14, 43]
selection_sort(values)
print(values)
```
###6.3.3 The Insertion sort algorithm (only information)
####**Problem definition**
See problem definition before.
####**Concept**
The insertion sort algorithm is a sorting algorithm that in each iteration is building a sorted list by moving the elements until finding the right position.
In the following pseudo-code, the insertion sort algorithm is presented.
```
for i from 1 to N
key = a[i]
j = i - 1
while j >= 0 and a[j] > key
a[j+1] = a[j]
j = j - 1
a[j+1] = key
```
In regards to the time/temporal complexity, the insertion sort does not behave to much better in comparison to the previous ones.
* Best case: $О(n)$ comparisons and constant swaps.
* Worst case: $О(n^2)$ comparisons and swaps.
* Average case: $О(n^2)$ comparisons and swaps.
The insertion sort algorithm is quite simple and easy to implement, this is the main advantage.
####**Application**
The main situation in which we should think in using the insertion sort algorithm is again when the memory is limited.
* **Insertion sort example**:
>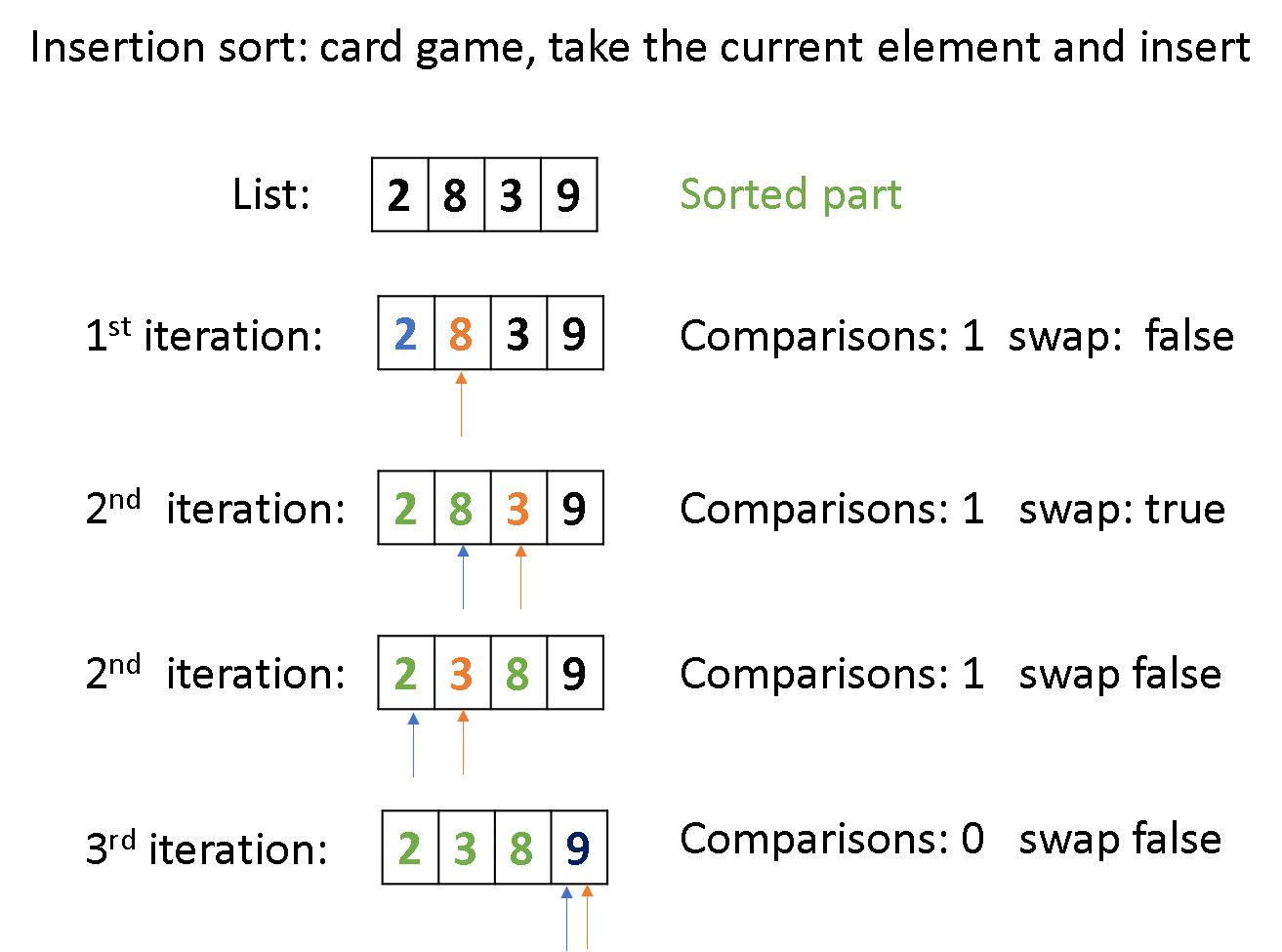
>Figure: Insertion sort example.
####**Python implementation**
* Insertion: "*Given a list, take the current element and insert it at the appropriate position of the list, adjusting the list every time you insert. It is similar to arranging the cards in a Card game.*"
```
def insertion_sort(values):
n = len(values)
for i in range(1, n):
key = values[i]
# Move elements of arr[0..i-1], that are greater than key, to one position ahead of their current position
j = i-1
while j >=0 and key < values[j] :
values[j+1] = values[j]
j -= 1
values[j+1] = key
values = [22, 8, 33, 12, 14, 43]
insertion_sort(values)
print(values)
```
##6.4 Evaluation of algorithms: time complexity
In computer science, time complexity refers to the amount of time required to execute an algorithm. Usually, it is estimated by counting the number of basic operations (constant execution time).
To express the time complexity of an algorithm, we use the Big O notation. This is a mathematical notation that describes the limiting behavior of a function when the argument tends towards a particular value or infinity. Its main application is the classification of algorithms depending on how the runtime increases when the input size grows.
There are some established time complexities, take a look to this [cheatsheet](https://www.bigocheatsheet.com/).
To evaluate the time complexity, we usually define three cases (best, worse and average). However, we should always consider the worst case to really provide a realistic value of the maximum execution time.
* Best case: represents the minimum amount of time required for inputs of a given size.
* Worst case: represents the maximum amount of time required for inputs of a given size.
* Average case: represents the average amount of time required for inputs of a given size.
>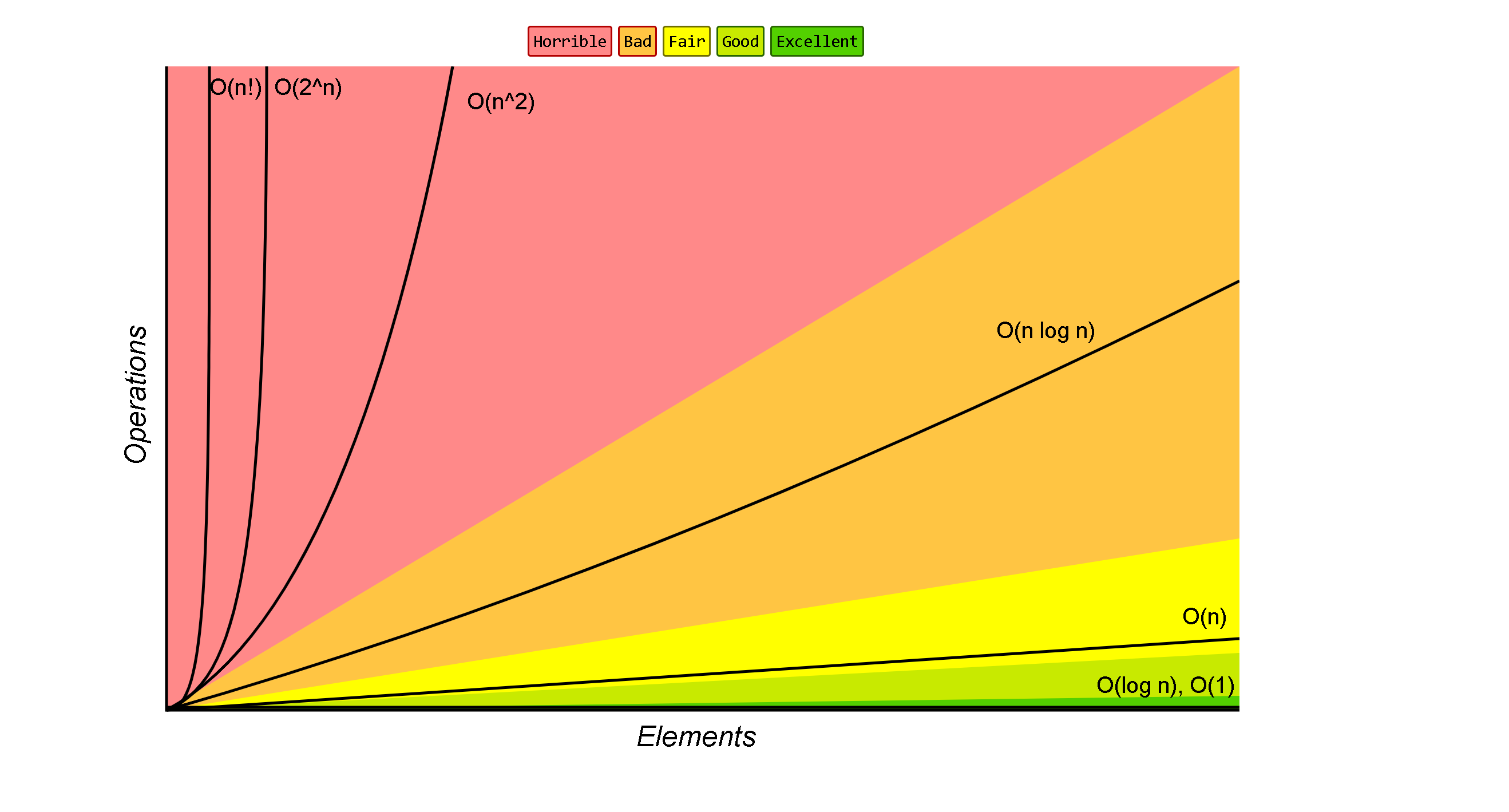
>Figure: Comparison of different complexities (source Big O cheatsheet).
The calculation of time complexity is an interesting and formal area in computer science. In this course, it is only necessary to know that there is a way of measuring and comparing the complexity of algorithms in terms of execution time.
Some typical time complexities can be calculated as follows:
* Constant: $O(1)$. In the following example, the number of instructions that are executed is constant (4) and does not depend on the input size.
```
a = 2
b = 3
c = a * b
print(c)
```
* Logarithmic: $O(log\_n)$. In the following example, the size of the problem is reduced in each iteration. We are discarding half of the problem in each step.
```
i = n
while i > n:
#Do constant operations
i = i // n
```
* Linear: $O(n)$. In the following example, the number of instructions to be executed will depend on the input size, $n$.
```
i = 0
while i < n:
#Do constant operations
i = i + 1
```
* Quadratic: $O(n^2)$. In the following example, the number of instructions to be executed will depend again on the input size, $n$. Nested loops are examples of quadratic complexities
```
for i in range(n):
for j in range (i):
#Do constant operations
```
In general, there are some rules to reduce the time complexity expressions and keep only an upper limit. For instance, if we have the following complexities, the estimations would be:
* $O(k)\to O(1)$
* $O(kn)\to O(n)$
* $O(n + m)\to O(n)$
* ...
* Which would be the time complexity of the next program?
```
for i in range(n):
print(i)
i = 0
while i<n:
print(i)
i = i + 1
```
Solution: the first loop iterates $n$ times performing one operation. Then, the second loop iterates again $n$ times performing 3 operations.
$n*1+n*2 = 3n, \to O(3n) \to O(n)$
##Relevant resources
* https://python-textbok.readthedocs.io/en/1.0/Sorting_and_Searching_Algorithms.html
* https://runestone.academy/runestone/books/published/pythonds/SortSearch/toctree.html
* https://www.oreilly.com/library/view/python-cookbook/0596001673/ch02.html
|
github_jupyter
|
#Linear search examples
def linear_search_first(values, target):
found = False
i = 0
while not found and i<len(values):
found = values[i] == target
i += 1
return found
def linear_search_last(values, target):
found = False
i = len(values)-1
while not found and i>=0:
found = values[i] == target
i -= 1
return found
def linear_search_all(values, target):
i = 0
while i<len(values):
found = values[i] == target
if found:
print("Found at position: ",i)
i += 1
return
print(linear_search_first([2,8,3,9], 3))
print(linear_search_last([2,8,3,9], 3))
linear_search_all([2,8,3,9], 3)
#See animation: https://www.w3resource.com/python-exercises/data-structures-and-algorithms/python-search-and-sorting-exercise-1.php
def binary_search(values, target):
first = 0
last = len(values)-1
found = False
while first <= last and not found:
mid = (first + last)//2
if values[mid] == target:
found = True
else: #Discard half of the problem
if target < values[mid]:
last = mid - 1
else:
first = mid + 1
return found
print(binary_search([1,2,3,5,8], 6))
print(binary_search([1,2,3,5,8], 5))
for i from 1 to N
for j from 0 to N-1
if a[j]>a[j+1]
swap(a[j], a[j+1])
#See more: https://www.w3resource.com/python-exercises/data-structures-and-algorithms/python-search-and-sorting-exercise-4.php
def bubble_sort(values):
n = len(values)
for i in range(n):
for j in range(n-i-1):
if values[j] > values[j+1]:
#Swap
values[j], values[j+1] = values[j+1], values[j]
values = [22, 8, 33, 12, 14, 43]
bubble_sort(values)
print(values)
for i in len(lst):
min_index = i
for j in (i+1, max)
if lst[min_index] > key
min_index = j
swap(lst[min_index],lst[i])
def selection_sort(values):
n = len(values)
for i in range(n):
min_idx = i
for j in range(i+1, n):
if values[min_idx] > values[j]:
min_idx = j
#Swap with the minimum value position
values[i], values[min_idx] = values[min_idx], values[i]
values = [22, 8, 33, 12, 14, 43]
selection_sort(values)
print(values)
for i from 1 to N
key = a[i]
j = i - 1
while j >= 0 and a[j] > key
a[j+1] = a[j]
j = j - 1
a[j+1] = key
def insertion_sort(values):
n = len(values)
for i in range(1, n):
key = values[i]
# Move elements of arr[0..i-1], that are greater than key, to one position ahead of their current position
j = i-1
while j >=0 and key < values[j] :
values[j+1] = values[j]
j -= 1
values[j+1] = key
values = [22, 8, 33, 12, 14, 43]
insertion_sort(values)
print(values)
a = 2
b = 3
c = a * b
print(c)
i = n
while i > n:
#Do constant operations
i = i // n
i = 0
while i < n:
#Do constant operations
i = i + 1
for i in range(n):
for j in range (i):
#Do constant operations
for i in range(n):
print(i)
i = 0
while i<n:
print(i)
i = i + 1
| 0.319865 | 0.993487 |
---
<div class="alert alert-success" data-title="">
<h2><i class="fa fa-tasks" aria-hidden="true"></i> 사이킷런을 사용한 당뇨병 혈당 예측
</h2>
</div>
<img src = "https://res.cloudinary.com/grohealth/image/upload/$wpsize_!_cld_full!,w_1200,h_630,c_scale/v1588094388/How-to-Bring-Down-High-Blood-Sugar-Levels-1.png" width = "700" >
이번 실습 시간에 다뤄볼 데이터는 당뇨병 관련 데이터 입니다.
- 당뇨병에 영향을 끼치는 여러 요소들 (X, Features)
- 혈당 (Y, Target)
## 데이터 살펴보기 (EDA)
### 데이터 불러오기
```
from sklearn.datasets import load_diabetes
diabetes = load_diabetes()
import pandas as pd
diabetes_df = pd.DataFrame(diabetes.data,
columns=diabetes.feature_names,
index=range(1,len(diabetes.data)+1))
diabetes_df['Target'] = diabetes.target
diabetes_df.head()
diabetes_df.shape
```
### 히트맵으로 상관관계 나타내기
```
import seaborn as sns
import matplotlib.pyplot as plt
# 변수들 간의 상관 계수를 구한다
ccol = ['age', 'sex', 'bmi', 'bp', 's1', 's2', 's3', 's4', 's5', 's6']
corrs = diabetes_df[ccol].corr()
# 상관 계수 값에 대한 히트맵을 그린다
# 매개변수 annot은 맵상에 값을 표시할 것인지의 여부를 지정한다
# 매개변수 annot_kws는 표시되는 값에 대한 추가 옵션이다.
sns.heatmap(corrs,annot=True,annot_kws={'size':10})
plt.show()
```
<div class="alert alert-success" data-title="">
<h2><i class="fa fa-tasks" aria-hidden="true"></i> 실제 데이터로 다중선형회귀 해보기
</h2>
</div>
```
# 데이터 프레임에서 독립변수와 종속변수를 다시 구분
X = diabetes_df.drop(['Target'],axis=1) # axis=1 열을 드랍 // axis=0 행을 드랍
y = diabetes_df['Target']
```
## 학습 평가 데이터 나누기
```python
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = \
train_test_split(X,y , test_size, train_size, random_state, shuffle, stratify)
```
- X, y : 분할시킬 데이터
- test_size : 테스트 데이터셋의 비율(float)이나 갯수(int) (default = 0.25)
- train_size : 학습 데이터셋의 비율(float)이나 갯수(int) (default = test_size의 나머지)
- shuffle : 셔플여부설정 (default = True)
- stratify : 지정한 Data의 비율을 유지 ex) Label Set인 Y가 25%의 0과 75%의 1로 이루어진 Binary -Set일 때, stratify=Y로 설정하면 나누어진 데이터셋들도 0과 1을 각각 25%, 75%로 유지한 채 분할된다.
```
# 학습용 및 검증용 데이터로 분리한다
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3,
random_state=42)
```
### random_state 에 대하여
- random_state : 데이터 분할시 셔플이 이루어지는데 이를 기억하기 위한 임의의 시드값 (int나 RandomState로 입력)
> 컴퓨터에서 random한 결과를 낼 시, 'Seed'라 부르는 특정한 시작으로 숫자를 지정합니다. 즉, 컴퓨터에서 random은 실제로 random이 아닙니다.
`random_sate`은 **학습데이터 평가데이터 분리할 때** 사용되며, 데이터셋을 무작위로 섞어서 분리하기 때문에 **시드값**이 필요합니다.
Ex) `random_state` = 1이라고 정의하는 경우, 시드값을 1로하는 무작위로 복원 추출된 데이터의 학습 결과와 그에 따라 결정된 변수들을 담아둡니다.
```
from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
```
## 평가
### 평가지표
- MAE(Mean Absolute Error): 실제 값과 예측값의 차이를 절대값으로 변환해 평균한 것.
- MSE(Mean Squared Error): 실제 값과 예측값의 차이를 제곱해 평균한 것.
- RMSE(Root Mean Squared Error): MSE에 루트를 씌워 값이 지나치게 커지는 것을 하고, 단위를 맞춰주는 것을 목표로 함.
- 이외에도.. MSLE, RMSLE 등의 평가지표가 많습니다.
```
from sklearn.metrics import mean_squared_error, r2_score, mean_absolute_error
import numpy as np
mse = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
mae = mean_absolute_error(y_test, y_pred)
rmse = np.sqrt(mse)
print('MSE: {:.3f}, MAE: {:.3f}, R2: {:.3f}, RMSE: {:.3f}'.format(mse, mae, r2,rmse ))
```
## CV 사용하기
```python
from sklearn.model_selection import KFold
from sklearn.model_selection import LeaveOneOut
from sklearn.model_selection import StratifiedKFold
from sklearn.model_selection import cross_val_score
```
```
from sklearn.model_selection import KFold
kfold = KFold()
from sklearn.model_selection import StratifiedKFold
skfold = StratifiedKFold()
from sklearn.model_selection import cross_val_score
kfold_result = cross_val_score(model, X,y,cv=kfold).mean()
kfold_result
skfold_result = cross_val_score(model, X,y,cv=skfold).mean()
skfold_result
```
|
github_jupyter
|
from sklearn.datasets import load_diabetes
diabetes = load_diabetes()
import pandas as pd
diabetes_df = pd.DataFrame(diabetes.data,
columns=diabetes.feature_names,
index=range(1,len(diabetes.data)+1))
diabetes_df['Target'] = diabetes.target
diabetes_df.head()
diabetes_df.shape
import seaborn as sns
import matplotlib.pyplot as plt
# 변수들 간의 상관 계수를 구한다
ccol = ['age', 'sex', 'bmi', 'bp', 's1', 's2', 's3', 's4', 's5', 's6']
corrs = diabetes_df[ccol].corr()
# 상관 계수 값에 대한 히트맵을 그린다
# 매개변수 annot은 맵상에 값을 표시할 것인지의 여부를 지정한다
# 매개변수 annot_kws는 표시되는 값에 대한 추가 옵션이다.
sns.heatmap(corrs,annot=True,annot_kws={'size':10})
plt.show()
# 데이터 프레임에서 독립변수와 종속변수를 다시 구분
X = diabetes_df.drop(['Target'],axis=1) # axis=1 열을 드랍 // axis=0 행을 드랍
y = diabetes_df['Target']
- X, y : 분할시킬 데이터
- test_size : 테스트 데이터셋의 비율(float)이나 갯수(int) (default = 0.25)
- train_size : 학습 데이터셋의 비율(float)이나 갯수(int) (default = test_size의 나머지)
- shuffle : 셔플여부설정 (default = True)
- stratify : 지정한 Data의 비율을 유지 ex) Label Set인 Y가 25%의 0과 75%의 1로 이루어진 Binary -Set일 때, stratify=Y로 설정하면 나누어진 데이터셋들도 0과 1을 각각 25%, 75%로 유지한 채 분할된다.
### random_state 에 대하여
- random_state : 데이터 분할시 셔플이 이루어지는데 이를 기억하기 위한 임의의 시드값 (int나 RandomState로 입력)
> 컴퓨터에서 random한 결과를 낼 시, 'Seed'라 부르는 특정한 시작으로 숫자를 지정합니다. 즉, 컴퓨터에서 random은 실제로 random이 아닙니다.
`random_sate`은 **학습데이터 평가데이터 분리할 때** 사용되며, 데이터셋을 무작위로 섞어서 분리하기 때문에 **시드값**이 필요합니다.
Ex) `random_state` = 1이라고 정의하는 경우, 시드값을 1로하는 무작위로 복원 추출된 데이터의 학습 결과와 그에 따라 결정된 변수들을 담아둡니다.
## 평가
### 평가지표
- MAE(Mean Absolute Error): 실제 값과 예측값의 차이를 절대값으로 변환해 평균한 것.
- MSE(Mean Squared Error): 실제 값과 예측값의 차이를 제곱해 평균한 것.
- RMSE(Root Mean Squared Error): MSE에 루트를 씌워 값이 지나치게 커지는 것을 하고, 단위를 맞춰주는 것을 목표로 함.
- 이외에도.. MSLE, RMSLE 등의 평가지표가 많습니다.
## CV 사용하기
| 0.577734 | 0.904861 |
# Stacked LSTMs for Time Series Classification
We'll now build a slightly deeper model by stacking two LSTM layers using the Quandl stock price data (see the stacked_lstm_with_feature_embeddings notebook for implementation details). Furthermore, we will include features that are not sequential in nature, namely indicator variables for identifying the equity and the month.
## Run inside docker container for GPU acceleration
See [tensorflow guide](https://www.tensorflow.org/install/docker) and more detailed [instructions](https://blog.sicara.com/tensorflow-gpu-opencv-jupyter-docker-10705b6cd1d)
`docker run -it -p 8889:8888 -v /path/to/machine-learning-for-trading/18_recurrent_neural_nets:/rnn --name tensorflow tensorflow/tensorflow:latest-gpu-py3 bash`
Inside docker container:
`jupyter notebook --ip 0.0.0.0 --no-browser --allow-root`
## Imports
```
%matplotlib inline
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from datetime import datetime, date
from sklearn.metrics import mean_squared_error, roc_auc_score
from sklearn.preprocessing import minmax_scale
from keras.callbacks import ModelCheckpoint, EarlyStopping
from keras.models import Sequential, Model
from keras.layers import Dense, LSTM, Input, concatenate, Embedding, Reshape
import keras
import keras.backend as K
import tensorflow as tf
sns.set_style('whitegrid')
np.random.seed(42)
K.clear_session()
```
## Data
Data produced by the notebook [build_dataset](00_build_dataset.ipynb).
```
data = pd.read_hdf('data.h5', 'returns_weekly')
data = data.drop([c for c in data.columns if str(c).startswith('year')], axis=1)
data.info()
```
## Train-test split
To respect the time series nature of the data, we set aside the data at the end of the sample as hold-out or test set. More specifically, we'll use the data for 2018.
```
window_size=52
ticker = 1
months = 12
n_tickers = data.ticker.nunique()
train_data = data[:'2016']
test_data = data['2017']
del data
```
For each train and test dataset, we generate a list with three input arrays containing the return series, the stock ticker (converted to integer values), and the month (as an integer), as shown here:
```
X_train = [
train_data.loc[:, list(range(1, window_size+1))].values.reshape(-1, window_size , 1),
train_data.ticker,
train_data.filter(like='month')
]
y_train = train_data.label
[x.shape for x in X_train], y_train.shape
# keep the last year for testing
X_test = [
test_data.loc[:, list(range(1, window_size+1))].values.reshape(-1, window_size , 1),
test_data.ticker,
test_data.filter(like='month')
]
y_test = test_data.label
[x.shape for x in X_test], y_test.shape
```
## Custom Metric
```
def roc_auc(y_true, y_pred):
# any tensorflow metric
value, update_op = tf.metrics.auc(y_true, y_pred)
# find all variables created for this metric
metric_vars = [i for i in tf.local_variables() if 'auc_roc' in i.name.split('/')[1]]
# Add metric variables to GLOBAL_VARIABLES collection.
# They will be initialized for new session.
for v in metric_vars:
tf.add_to_collection(tf.GraphKeys.GLOBAL_VARIABLES, v)
# force to update metric values
with tf.control_dependencies([update_op]):
value = tf.identity(value)
return value
# source: https://github.com/keras-team/keras/issues/3230
def auc(y_true, y_pred):
ptas = tf.stack([binary_PTA(y_true, y_pred, k) for k in np.linspace(0, 1, 1000)], axis=0)
pfas = tf.stack([binary_PFA(y_true, y_pred, k) for k in np.linspace(0, 1, 1000)], axis=0)
pfas = tf.concat([tf.ones((1,)), pfas], axis=0)
binSizes = -(pfas[1:] - pfas[:-1])
s = ptas * binSizes
return K.sum(s, axis=0)
def binary_PFA(y_true, y_pred, threshold=K.variable(value=0.5)):
"""prob false alert for binary classifier"""
y_pred = K.cast(y_pred >= threshold, 'float32')
# N = total number of negative labels
N = K.sum(1 - y_true)
# FP = total number of false alerts, alerts from the negative class labels
FP = K.sum(y_pred - y_pred * y_true)
return FP / (N + 1)
def binary_PTA(y_true, y_pred, threshold=K.variable(value=0.5)):
"""prob true alerts for binary classifier"""
y_pred = K.cast(y_pred >= threshold, 'float32')
# P = total number of positive labels
P = K.sum(y_true)
# TP = total number of correct alerts, alerts from the positive class labels
TP = K.sum(y_pred * y_true)
return TP / (P + 1)
```
## Define the Model Architecture
The functional API of Keras makes it easy to design architectures with multiple inputs and outputs. This example illustrates a network with three inputs, as follows:
- A two stacked LSTM layers with 25 and 10 units respectively
- An embedding layer that learns a 10-dimensional real-valued representation of the equities
- A one-hot encoded representation of the month
This can be constructed using just a few lines - see e.g.,
- the [general Keras documentation](https://keras.io/getting-started/sequential-model-guide/),
- the [LTSM documentation](https://keras.io/layers/recurrent/).
Make sure you are initializing your optimizer given the [keras-recommended approach for RNNs](https://keras.io/optimizers/)
We begin by defining the three inputs with their respective shapes, as described here:
```
returns = Input(shape=(window_size, n_features), name='Returns')
tickers = Input(shape=(1,), name='Tickers')
months = Input(shape=(12,), name='Months')
```
### LSTM Layers
To define stacked LSTM layers, we set the `return_sequences` keyword to `True`. This ensures that the first layer produces an output that conforms to the expected three-dimensional input format. Note that we also use dropout regularization and how the functional API passes the tensor outputs from one layer to the subsequent layer:
```
lstm1_units = 25
lstm2_units = 10
n_features = 1
lstm1 = LSTM(units=lstm1_units,
input_shape=(window_size, n_features),
name='LSTM1',
dropout=.2,
return_sequences=True)(returns)
lstm_model = LSTM(units=lstm2_units,
dropout=.2,
name='LSTM2')(lstm1)
```
### Embedding Layer
The embedding layer requires the `input_dim` keyword, which defines how many embeddings the layer will learn, the `output_dim` keyword, which defines the size of the embedding, and the `input_length` keyword to set the number of elements passed to the layer (here only one ticker per sample).
To combine the embedding layer with the LSTM layer and the months input, we need to reshape (or flatten) it, as follows:
```
ticker_embedding = Embedding(input_dim=n_tickers,
output_dim=10,
input_length=1)(tickers)
ticker_embedding = Reshape(target_shape=(10,))(ticker_embedding)
```
### Concatenate Model components
Now we can concatenate the three tensors and add fully-connected layers to learn a mapping from these learned time series, ticker, and month indicators to the outcome, a positive or negative return in the following week, as shown here:
```
merged = concatenate([lstm_model, ticker_embedding, months], name='Merged')
hidden_dense = Dense(10, name='FC1')(merged)
output = Dense(1, name='Output')(hidden_dense)
rnn = Model(inputs=[returns, tickers, months], outputs=output)
```
The summary lays out this slightly more sophisticated architecture with 29,371 parameters, as follows:
```
rnn.summary()
```
## Train the Model
We compile the model to compute a custom auc metric as follows:
```
rnn.compile(loss='binary_crossentropy',
optimizer='adam',
metrics=['accuracy', auc])
rnn_path = 'models/quandl.lstm_months_{}_{}.weights.best.hdf5'.format(lstm1_units, lstm2_units)
checkpointer = ModelCheckpoint(filepath=rnn_path,
monitor='val_loss',
save_best_only=True,
save_weights_only=True,
period=5)
early_stopping = EarlyStopping(monitor='val_loss',
patience=5,
restore_best_weights=True)
result = rnn.fit(X_train,
y_train,
epochs=50,
batch_size=32,
validation_data=(X_test, y_test),
callbacks=[checkpointer, early_stopping],
verbose=1)
```
Training stops after 18 epochs, producing a test area under the curve (AUC) of 0.63 for the best model with 13 rounds of training (each of which takes around an hour on a single GPU).
```
loss_history = pd.DataFrame(result.history)
loss_history
def which_metric(m):
return m.split('_')[-1]
loss_history.groupby(which_metric, axis=1).plot(figsize=(14, 6));
```
## Evaluate model performance
```
test_predict = pd.Series(rnn.predict(X_test).squeeze(), index=y_test.index)
roc_auc_score(y_score=test_predict, y_true=y_test)
rnn.load_weights(rnn_path)
test_predict = pd.Series(rnn.predict(X_test).squeeze(), index=y_test.index)
roc_auc_score(y_score=test_predict, y_true=y_test)
score
predictions = (test_predict.to_frame('prediction').assign(data='test')
.append(train_predict.to_frame('prediction').assign(data='train')))
predictions.info()
results = sp500_scaled.join(predictions).dropna()
results.info()
corr = {}
for run, df in results.groupby('data'):
corr[run] = df.SP500.corr(df.prediction)
sp500_scaled['Train Prediction'] = pd.Series(train_predict.squeeze(), index=y_train.index)
sp500_scaled['Test Prediction'] = pd.Series(test_predict.squeeze(), index=y_test.index)
training_error = np.sqrt(rnn.evaluate(X_train, y_train, verbose=0))
testing_error = np.sqrt(rnn.evaluate(X_test, y_test, verbose=0))
print('Training Error: {:.4f} | Test Error: {:.4f}'.format(training_error, testing_error))
sns.set_style('whitegrid')
```
|
github_jupyter
|
%matplotlib inline
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from datetime import datetime, date
from sklearn.metrics import mean_squared_error, roc_auc_score
from sklearn.preprocessing import minmax_scale
from keras.callbacks import ModelCheckpoint, EarlyStopping
from keras.models import Sequential, Model
from keras.layers import Dense, LSTM, Input, concatenate, Embedding, Reshape
import keras
import keras.backend as K
import tensorflow as tf
sns.set_style('whitegrid')
np.random.seed(42)
K.clear_session()
data = pd.read_hdf('data.h5', 'returns_weekly')
data = data.drop([c for c in data.columns if str(c).startswith('year')], axis=1)
data.info()
window_size=52
ticker = 1
months = 12
n_tickers = data.ticker.nunique()
train_data = data[:'2016']
test_data = data['2017']
del data
X_train = [
train_data.loc[:, list(range(1, window_size+1))].values.reshape(-1, window_size , 1),
train_data.ticker,
train_data.filter(like='month')
]
y_train = train_data.label
[x.shape for x in X_train], y_train.shape
# keep the last year for testing
X_test = [
test_data.loc[:, list(range(1, window_size+1))].values.reshape(-1, window_size , 1),
test_data.ticker,
test_data.filter(like='month')
]
y_test = test_data.label
[x.shape for x in X_test], y_test.shape
def roc_auc(y_true, y_pred):
# any tensorflow metric
value, update_op = tf.metrics.auc(y_true, y_pred)
# find all variables created for this metric
metric_vars = [i for i in tf.local_variables() if 'auc_roc' in i.name.split('/')[1]]
# Add metric variables to GLOBAL_VARIABLES collection.
# They will be initialized for new session.
for v in metric_vars:
tf.add_to_collection(tf.GraphKeys.GLOBAL_VARIABLES, v)
# force to update metric values
with tf.control_dependencies([update_op]):
value = tf.identity(value)
return value
# source: https://github.com/keras-team/keras/issues/3230
def auc(y_true, y_pred):
ptas = tf.stack([binary_PTA(y_true, y_pred, k) for k in np.linspace(0, 1, 1000)], axis=0)
pfas = tf.stack([binary_PFA(y_true, y_pred, k) for k in np.linspace(0, 1, 1000)], axis=0)
pfas = tf.concat([tf.ones((1,)), pfas], axis=0)
binSizes = -(pfas[1:] - pfas[:-1])
s = ptas * binSizes
return K.sum(s, axis=0)
def binary_PFA(y_true, y_pred, threshold=K.variable(value=0.5)):
"""prob false alert for binary classifier"""
y_pred = K.cast(y_pred >= threshold, 'float32')
# N = total number of negative labels
N = K.sum(1 - y_true)
# FP = total number of false alerts, alerts from the negative class labels
FP = K.sum(y_pred - y_pred * y_true)
return FP / (N + 1)
def binary_PTA(y_true, y_pred, threshold=K.variable(value=0.5)):
"""prob true alerts for binary classifier"""
y_pred = K.cast(y_pred >= threshold, 'float32')
# P = total number of positive labels
P = K.sum(y_true)
# TP = total number of correct alerts, alerts from the positive class labels
TP = K.sum(y_pred * y_true)
return TP / (P + 1)
returns = Input(shape=(window_size, n_features), name='Returns')
tickers = Input(shape=(1,), name='Tickers')
months = Input(shape=(12,), name='Months')
lstm1_units = 25
lstm2_units = 10
n_features = 1
lstm1 = LSTM(units=lstm1_units,
input_shape=(window_size, n_features),
name='LSTM1',
dropout=.2,
return_sequences=True)(returns)
lstm_model = LSTM(units=lstm2_units,
dropout=.2,
name='LSTM2')(lstm1)
ticker_embedding = Embedding(input_dim=n_tickers,
output_dim=10,
input_length=1)(tickers)
ticker_embedding = Reshape(target_shape=(10,))(ticker_embedding)
merged = concatenate([lstm_model, ticker_embedding, months], name='Merged')
hidden_dense = Dense(10, name='FC1')(merged)
output = Dense(1, name='Output')(hidden_dense)
rnn = Model(inputs=[returns, tickers, months], outputs=output)
rnn.summary()
rnn.compile(loss='binary_crossentropy',
optimizer='adam',
metrics=['accuracy', auc])
rnn_path = 'models/quandl.lstm_months_{}_{}.weights.best.hdf5'.format(lstm1_units, lstm2_units)
checkpointer = ModelCheckpoint(filepath=rnn_path,
monitor='val_loss',
save_best_only=True,
save_weights_only=True,
period=5)
early_stopping = EarlyStopping(monitor='val_loss',
patience=5,
restore_best_weights=True)
result = rnn.fit(X_train,
y_train,
epochs=50,
batch_size=32,
validation_data=(X_test, y_test),
callbacks=[checkpointer, early_stopping],
verbose=1)
loss_history = pd.DataFrame(result.history)
loss_history
def which_metric(m):
return m.split('_')[-1]
loss_history.groupby(which_metric, axis=1).plot(figsize=(14, 6));
test_predict = pd.Series(rnn.predict(X_test).squeeze(), index=y_test.index)
roc_auc_score(y_score=test_predict, y_true=y_test)
rnn.load_weights(rnn_path)
test_predict = pd.Series(rnn.predict(X_test).squeeze(), index=y_test.index)
roc_auc_score(y_score=test_predict, y_true=y_test)
score
predictions = (test_predict.to_frame('prediction').assign(data='test')
.append(train_predict.to_frame('prediction').assign(data='train')))
predictions.info()
results = sp500_scaled.join(predictions).dropna()
results.info()
corr = {}
for run, df in results.groupby('data'):
corr[run] = df.SP500.corr(df.prediction)
sp500_scaled['Train Prediction'] = pd.Series(train_predict.squeeze(), index=y_train.index)
sp500_scaled['Test Prediction'] = pd.Series(test_predict.squeeze(), index=y_test.index)
training_error = np.sqrt(rnn.evaluate(X_train, y_train, verbose=0))
testing_error = np.sqrt(rnn.evaluate(X_test, y_test, verbose=0))
print('Training Error: {:.4f} | Test Error: {:.4f}'.format(training_error, testing_error))
sns.set_style('whitegrid')
| 0.808029 | 0.948728 |
# Computational Assignment 1
**Assigned Tuesday, 1-22-19.**, **Due Tuesday, 1-29-19.**
Congratulations on installing the Jupyter Notebook! Welcomne to your first computational assignment!
Beyond using this as a tool to understand physical chemistry, python and notebooks are actually used widely in scientific analysis. Big data analysis especially uses python notebooks.
## Introduction to the notebook
If you double click on the text above, you will notice the look suddenly changes. Every section of the notebook, including the introductory text, is a technically a code entry. The text is written in a typesetting language called **Markdown**. To learn more see https://github.com/adam-p/markdown-here/wiki/Markdown-Cheatsheet
To run a code entry in the notebook, select the section you want to run and type
`shift+enter`
If you want to make notes on a notebook, you can press the plus sign in the toolbar above to creat a new entry. Then make sure to switch the menu that in the toolbar from **code** to **Markdown**.
We can also run calculations this way.
In the entry below, I haved typed
`123+3483`
Select the entry and type `shift+enter`
```
123+3483
```
Once you run an entry, the output is displayed on the screen, when applicable
Now try some arithmatic yourself in the blank entry below.
(Don't forget to hit `shift+enter` to run your calculation!)
```
917+215
```
## Introduction to programming and python
Python is a very powerful and intuitive modern programming language. It is easier to learn than many other languages. Because of the wide availability of libraries such **numpy** and **scipy** (among many others), it is very useful for scientific calculations.
In this section, we will cover some very basic concepts. I assuming that nearly everyone has little or no previous programming experience, which is common for most chemistry and biology students.
We will slowly build up to the skills we need to run complex calculations!
### Our first python code: "Hello World!"
The first thing we usually learn how to do is print a simple message to the output. Run the following entry.
```
print("Hello World!")
```
Print is function that takes in text as an argument and outputs that text.
A slightly more complicated example. Run the following entry
```
# This is a comment in python
# Set a variable
x = 1 + 7
# print the result of the variable
print(x)
```
The lines that begin with "#" are comments. They are not read by the notebook and do not affect the code. They are very useful to make your code human readable
This snippet of code set assigned the result of `1+7` to the variable `x` and then used `print` to output that value.
## Loops
One of the benifits of the computer is that it can run a calcualtion many times without having to manually type each line. The way that we do this is to use a **loop**.
```
# This is an example of a loop
# The colon is required on the first line
for i in (1,2,3,4):
# This indentation is required for loops
print ("Hello World, iteration",i)
```
### Explanation
1. The command `for` tells the code that this is a loop
2. The variable `i` is the counting variable. Everytime the loop runs, it will sequentially take on a different value from the list
3. The `(1,2,3)` is list of values.
Sometimes we need to run a loop many times or iterate over a large list of numbers. For this, the `range` command is useful
```
# The command range(a,b) creates a list of numbers from a to b
for i in range(-4,4):
print ("Hello World, iteration",i)
```
Note that the `range(a,b)` command makes a list that spans from `a` to `b-1`.
In the example above `range(-3,3`) makes a list that goes from -3 to 2
## Conditional Statements: IF
Many times we want the computer to do something after analyzing a logical statement. **If this is true, then do that**. These are called conditional statements
```
# Conditional example
a = 100
if (a>0):
#Like in the loop example, the indentation defines what happens in this
# block of the if statement
print("the number is positive")
elif (a<0):
print("the number is negative")
elif (a==0):
print("the number is zero")
```
Now we can try it again with a different value for `a`
```
# Conditional example again
a = -1234
if (a>0):
print("the number is positive")
elif (a<0):
print("the number is negative")
elif (a==0):
print("the number is zero")
```
Once more time
```
# Conditional example again
a = 0
if (a>0):
print("the number is positive")
elif (a<0):
print("the number is negative")
elif (a==0):
print("the number is zero")
```
## Bringing it all together
These can all be combined together to perform complicated actions. Note the indentation and colons. They matter.
### Combined Example
```
# A loop with an if statement
for i in range(-1,2):
print("Iteration",i)
if (i==0):
print("zero!")
```
# Exercise
Following the examples above, write a code snippet that uses the `range` command to scan from -10 to 10 and print whether the number is positive, negative, or zero.
**To turn this in, print this notebook and please make sure that your name is written on in.**
```
for i in range(-10,10):
if (i>0):
print("the number is positive")
elif (i<0):
print("the number is negative")
elif (i==0):
print("the number is zero")
```
|
github_jupyter
|
123+3483
917+215
print("Hello World!")
# This is a comment in python
# Set a variable
x = 1 + 7
# print the result of the variable
print(x)
# This is an example of a loop
# The colon is required on the first line
for i in (1,2,3,4):
# This indentation is required for loops
print ("Hello World, iteration",i)
# The command range(a,b) creates a list of numbers from a to b
for i in range(-4,4):
print ("Hello World, iteration",i)
# Conditional example
a = 100
if (a>0):
#Like in the loop example, the indentation defines what happens in this
# block of the if statement
print("the number is positive")
elif (a<0):
print("the number is negative")
elif (a==0):
print("the number is zero")
# Conditional example again
a = -1234
if (a>0):
print("the number is positive")
elif (a<0):
print("the number is negative")
elif (a==0):
print("the number is zero")
# Conditional example again
a = 0
if (a>0):
print("the number is positive")
elif (a<0):
print("the number is negative")
elif (a==0):
print("the number is zero")
# A loop with an if statement
for i in range(-1,2):
print("Iteration",i)
if (i==0):
print("zero!")
for i in range(-10,10):
if (i>0):
print("the number is positive")
elif (i<0):
print("the number is negative")
elif (i==0):
print("the number is zero")
| 0.118691 | 0.987946 |
# Web Scraping using BeautifulSoup
**BeautifulSoup**: Beautiful Soup is a Python package for parsing HTML and XML documents. It creates parse trees that is helpful to extract the data easily.<br>

```
from bs4 import BeautifulSoup
import requests
# Get The HTML
website = 'https://subslikescript.com/movie/Titanic-120338'
result = requests.get(website)
"""
content: It is the raw HTML content.
lxml: The HTML parser we want to use.
A really nice thing about the BeautifulSoup library is that it is built
on the top of the HTML parsing libraries like html5lib, lxml, html.parser, etc.
So BeautifulSoup object and specify the parser library can be created at the
same time.
"""
content = result.text
soup = BeautifulSoup(content, 'lxml')
"""
It gives the visual representation of the parse tree created from the raw
HTML content.
"""
print(soup.prettify())
# Locate the box that contains title and transcript
box = soup.find('article', class_='main-article')
# Locate title and transcript
"""
find() method returns the first matching element.
"""
title = box.find('h1').get_text()
transcript = box.find('div', class_='full-script').get_text(strip=True,
separator=' ')
# Export data in a text file with the "title" name.
with open(f'{title}.txt', 'w') as file:
file.write(transcript)
```
|
github_jupyter
|
from bs4 import BeautifulSoup
import requests
# Get The HTML
website = 'https://subslikescript.com/movie/Titanic-120338'
result = requests.get(website)
"""
content: It is the raw HTML content.
lxml: The HTML parser we want to use.
A really nice thing about the BeautifulSoup library is that it is built
on the top of the HTML parsing libraries like html5lib, lxml, html.parser, etc.
So BeautifulSoup object and specify the parser library can be created at the
same time.
"""
content = result.text
soup = BeautifulSoup(content, 'lxml')
"""
It gives the visual representation of the parse tree created from the raw
HTML content.
"""
print(soup.prettify())
# Locate the box that contains title and transcript
box = soup.find('article', class_='main-article')
# Locate title and transcript
"""
find() method returns the first matching element.
"""
title = box.find('h1').get_text()
transcript = box.find('div', class_='full-script').get_text(strip=True,
separator=' ')
# Export data in a text file with the "title" name.
with open(f'{title}.txt', 'w') as file:
file.write(transcript)
| 0.344554 | 0.418697 |

[](https://colab.research.google.com/github/JohnSnowLabs/spark-nlp-workshop/blob/master/jupyter/annotation/english/spark-nlp-basics/playground-dataFrames.ipynb)
## 0. Colab Setup
```
import os
# Install java
! apt-get update -qq
! apt-get install -y openjdk-8-jdk-headless -qq > /dev/null
os.environ["JAVA_HOME"] = "/usr/lib/jvm/java-8-openjdk-amd64"
os.environ["PATH"] = os.environ["JAVA_HOME"] + "/bin:" + os.environ["PATH"]
! java -version
# Install pyspark
! pip install --ignore-installed pyspark==2.4.4
# Install Spark NLP
! pip install --ignore-installed spark-nlp
import sparknlp
from sparknlp.base import *
from sparknlp.annotator import *
from pyspark.ml import Pipeline
spark = sparknlp.start()
document = DocumentAssembler().setInputCol('text').setOutputCol('document')
tokenizer = Tokenizer().setInputCols('document').setOutputCol('token')
pos = PerceptronModel.pretrained().setInputCols('document', 'token').setOutputCol('pos')
pipeline = Pipeline().setStages([document, tokenizer, pos])
data = spark.read.text('./sample-sentences-en.txt').toDF('text')
data.show(5)
model = pipeline.fit(data)
result = model.transform(data)
result.show(5)
stored = result\
.select('text', 'pos.begin', 'pos.end', 'pos.result', 'pos.metadata')\
.toDF('text', 'pos_begin', 'pos_end', 'pos_result', 'pos_meta')\
.cache()
stored.printSchema()
stored.show(5)
```
---------
## Spark SQL Functions
```
from pyspark.sql.functions import *
stored.filter(array_contains('pos_result', 'VBD')).show(5)
stored.withColumn('token_count', size('pos_result')).select('pos_result', 'token_count').show(5)
stored.select('text', array_max('pos_end')).show(5)
stored.withColumn('unique_pos', array_distinct('pos_result')).select('pos_result', 'unique_pos').show(5)
stored.groupBy(array_sort(array_distinct('pos_result'))).count().show(10)
```
----------------
### SQL Functions with `col`
```
from pyspark.sql.functions import col
stored.select(col('pos_meta').getItem(0).getItem('word')).show(5)
```
-------------
### Spark NLP Annotation UDFs
```
result.select('pos').show(1, truncate=False)
def nn_tokens(annotations):
nn_annotations = list(
filter(lambda annotation: annotation.result == 'NN', annotations)
)
return list(
map(lambda nn_annotation: nn_annotation.metadata['word'], nn_annotations)
)
from sparknlp.functions import *
from pyspark.sql.types import ArrayType, StringType
result.select(map_annotations(nn_tokens, ArrayType(StringType()))('pos').alias('nn_tokens')).show(truncate=False)
```
|
github_jupyter
|
import os
# Install java
! apt-get update -qq
! apt-get install -y openjdk-8-jdk-headless -qq > /dev/null
os.environ["JAVA_HOME"] = "/usr/lib/jvm/java-8-openjdk-amd64"
os.environ["PATH"] = os.environ["JAVA_HOME"] + "/bin:" + os.environ["PATH"]
! java -version
# Install pyspark
! pip install --ignore-installed pyspark==2.4.4
# Install Spark NLP
! pip install --ignore-installed spark-nlp
import sparknlp
from sparknlp.base import *
from sparknlp.annotator import *
from pyspark.ml import Pipeline
spark = sparknlp.start()
document = DocumentAssembler().setInputCol('text').setOutputCol('document')
tokenizer = Tokenizer().setInputCols('document').setOutputCol('token')
pos = PerceptronModel.pretrained().setInputCols('document', 'token').setOutputCol('pos')
pipeline = Pipeline().setStages([document, tokenizer, pos])
data = spark.read.text('./sample-sentences-en.txt').toDF('text')
data.show(5)
model = pipeline.fit(data)
result = model.transform(data)
result.show(5)
stored = result\
.select('text', 'pos.begin', 'pos.end', 'pos.result', 'pos.metadata')\
.toDF('text', 'pos_begin', 'pos_end', 'pos_result', 'pos_meta')\
.cache()
stored.printSchema()
stored.show(5)
from pyspark.sql.functions import *
stored.filter(array_contains('pos_result', 'VBD')).show(5)
stored.withColumn('token_count', size('pos_result')).select('pos_result', 'token_count').show(5)
stored.select('text', array_max('pos_end')).show(5)
stored.withColumn('unique_pos', array_distinct('pos_result')).select('pos_result', 'unique_pos').show(5)
stored.groupBy(array_sort(array_distinct('pos_result'))).count().show(10)
from pyspark.sql.functions import col
stored.select(col('pos_meta').getItem(0).getItem('word')).show(5)
result.select('pos').show(1, truncate=False)
def nn_tokens(annotations):
nn_annotations = list(
filter(lambda annotation: annotation.result == 'NN', annotations)
)
return list(
map(lambda nn_annotation: nn_annotation.metadata['word'], nn_annotations)
)
from sparknlp.functions import *
from pyspark.sql.types import ArrayType, StringType
result.select(map_annotations(nn_tokens, ArrayType(StringType()))('pos').alias('nn_tokens')).show(truncate=False)
| 0.498047 | 0.822688 |
# "Instability: Sliding Off a Hill"
> "A look at exponential growth in a simple dynamical system"
- toc: true
- branch: master
- badges: true
- comments: true
- categories: [physics, coronavirus]
- image: images/some_folder/your_image.png
- hide: true
- search_exclude: true
- metadata_key1: metadata_value1
- metadata_key2: metadata_value2
## Intro
Given that we often speak of “rolling off the top of a hill” as a metaphor for instability & subsequent exponential growth...**TODO: say more...**
(I’m sure the following problem is in a book somewhere, but I “made it up” today while thinking about instabilities, and was pleased at the compact form of the result. The factor of 1/2 at the start makes things cleaner later.)
## Problem
Show, for a particle starting at $x=0$ and constrained to slide frictionlessly along a parabola given by
$y = -\frac{1}{2}a x^2$, in the presence of a uniform downward vertical gravitational field $g$, that the $x-$component of its speed as a function of time is given by
$$v_x(t) = v_0 \cosh\left(t\sqrt{ga}\right),$$
where $v_0$ is the initial velocity.
**^^NO that's wrong. This result is incorrect. Will need to re-do this whole thing.**
## Solution
<details>
<summary>Click to expand!</summary>
**EDIT: I made a mistake in my derivation. Will need to re-do this whole thing.**
One may be tempted to start with Lagrange Multipliers, or a Hamiltonian approach, but I find that these just give you nonlinear ODEs that look kind of 'nasty,' but if you keep things 'simple' and just start wth Conservation of Energy, the solution's not bad!
$$ \frac{1}{2} m v_0^2 = \frac{1}{2}m v^2 + m g y.$$
Multiplying by $2/m$ and substituting for $y$ gives us
$$ v_0^2 = v^2 - g a x^2 $$
From this we get
$$ ga x^2 + v_0^2 = v^2 = ga \left( x^2 + {v_0^2\over ga}\right),$$
or
$$ v = \sqrt{ga}\sqrt{x^2 + b^2},$$
where we let $b \equiv v_0 / \sqrt{ga}$.
**The place where I made a mistake was next: "Since $ v = dx/dt$"** but that is not true, $v = ds/dt$ where $s$ is the tangential speed at any time. Woops. My other approaches with Lagrangians and Hamiltonians did this properly, which is why they produced equations that were so hard to solve! Ooops.
...The corrected solution ends up involving elliptic integrals! Not fun.
</details>
## Commentary
Sure, you could instead solve for the total speed (i.e., tangent to the parabola), or various other quantities, but none of these seemed to take on a ‘pleasing,’ compact form IMHO.
|
github_jupyter
|
# "Instability: Sliding Off a Hill"
> "A look at exponential growth in a simple dynamical system"
- toc: true
- branch: master
- badges: true
- comments: true
- categories: [physics, coronavirus]
- image: images/some_folder/your_image.png
- hide: true
- search_exclude: true
- metadata_key1: metadata_value1
- metadata_key2: metadata_value2
## Intro
Given that we often speak of “rolling off the top of a hill” as a metaphor for instability & subsequent exponential growth...**TODO: say more...**
(I’m sure the following problem is in a book somewhere, but I “made it up” today while thinking about instabilities, and was pleased at the compact form of the result. The factor of 1/2 at the start makes things cleaner later.)
## Problem
Show, for a particle starting at $x=0$ and constrained to slide frictionlessly along a parabola given by
$y = -\frac{1}{2}a x^2$, in the presence of a uniform downward vertical gravitational field $g$, that the $x-$component of its speed as a function of time is given by
$$v_x(t) = v_0 \cosh\left(t\sqrt{ga}\right),$$
where $v_0$ is the initial velocity.
**^^NO that's wrong. This result is incorrect. Will need to re-do this whole thing.**
## Solution
<details>
<summary>Click to expand!</summary>
**EDIT: I made a mistake in my derivation. Will need to re-do this whole thing.**
One may be tempted to start with Lagrange Multipliers, or a Hamiltonian approach, but I find that these just give you nonlinear ODEs that look kind of 'nasty,' but if you keep things 'simple' and just start wth Conservation of Energy, the solution's not bad!
$$ \frac{1}{2} m v_0^2 = \frac{1}{2}m v^2 + m g y.$$
Multiplying by $2/m$ and substituting for $y$ gives us
$$ v_0^2 = v^2 - g a x^2 $$
From this we get
$$ ga x^2 + v_0^2 = v^2 = ga \left( x^2 + {v_0^2\over ga}\right),$$
or
$$ v = \sqrt{ga}\sqrt{x^2 + b^2},$$
where we let $b \equiv v_0 / \sqrt{ga}$.
**The place where I made a mistake was next: "Since $ v = dx/dt$"** but that is not true, $v = ds/dt$ where $s$ is the tangential speed at any time. Woops. My other approaches with Lagrangians and Hamiltonians did this properly, which is why they produced equations that were so hard to solve! Ooops.
...The corrected solution ends up involving elliptic integrals! Not fun.
</details>
## Commentary
Sure, you could instead solve for the total speed (i.e., tangent to the parabola), or various other quantities, but none of these seemed to take on a ‘pleasing,’ compact form IMHO.
| 0.596198 | 0.771542 |
# MVTecAD Hazelnut の SimpleCNN による結果
## Preset
```
# default packages
import logging
import os
import pathlib
import typing as t
# third party packages
import IPython
import matplotlib.pyplot as plt
import torch
import torch.cuda as tc
import torch.nn as nn
import torch.utils.data as td
import torchvision.transforms as tv_transforms
# my packages
import src.data.dataset_torch as ds
import src.data.directories as directories
import src.data.mvtecad as mvtecad
import src.data.mvtecad_torch as mvtecad_torch
import src.models.cnn_ae as cnn_ae
IPython.get_ipython().run_line_magic("load_ext", "autoreload")
IPython.get_ipython().run_line_magic("autoreload", "2")
# logger
logger = logging.getLogger(__name__)
logging.basicConfig(level=logging.INFO)
def cd_project_root_() -> None:
"""ルートディレクトリをプロジェクトルートに移動."""
current = pathlib.Path().resolve()
if current.stem == "notebooks":
os.chdir(current.parent)
current = pathlib.Path().resolve()
logger.info(f"current path: {current}")
cd_project_root_()
USE_GPU = tc.is_available()
```
## Dataset
```
def create_dataset_() -> td.DataLoader:
batch_size = 8
num_workers = 4
transforms = tv_transforms.Compose(
[
tv_transforms.Resize((64, 64)),
tv_transforms.ToTensor(),
]
)
kind = mvtecad.Kind.HAZELNUT
dataset = mvtecad_torch.DatasetAE(kind, transforms, mode=ds.Mode.TRAIN)
dataloader = td.DataLoader(
dataset,
batch_size,
shuffle=False,
num_workers=num_workers,
pin_memory=True
)
return dataloader
DATALOADER = create_dataset_()
```
## Network
```
def create_network_() -> nn.Module:
network = cnn_ae.SimpleCBR(in_channels=3, out_channels=3)
network.load_state_dict(
torch.load(
directories.get_processed().joinpath(
"simple_cbr_mvtecad_hazelnut", "epoch=1"
)
)
)
if USE_GPU:
network = network.cuda()
network.eval()
return network
NETWORK = create_network_()
```
## Test
```
def show_images(batch: torch.Tensor, decode: torch.Tensor) -> None:
batch_cpu = batch.detach().cpu().numpy().transpose(0, 2, 3, 1)
decode_cpu = decode.detach().cpu().numpy().transpose(0, 2, 3, 1)
rows, cols = 2, batch_cpu.shape[0]
figsize = (4 * cols, 4 * rows)
fig, axes = plt.subplots(rows, cols, figsize=figsize)
for idx in range(cols):
ax = axes[0, idx]
ax.imshow(batch_cpu[idx])
ax = axes[1, idx]
ax.imshow(decode_cpu[idx])
plt.show()
fig.clf()
plt.close()
def test_() -> None:
with torch.no_grad():
for batch in DATALOADER:
if USE_GPU:
batch = batch.cuda()
output = NETWORK(batch)
show_images(batch, output)
break
test_()
```
|
github_jupyter
|
# default packages
import logging
import os
import pathlib
import typing as t
# third party packages
import IPython
import matplotlib.pyplot as plt
import torch
import torch.cuda as tc
import torch.nn as nn
import torch.utils.data as td
import torchvision.transforms as tv_transforms
# my packages
import src.data.dataset_torch as ds
import src.data.directories as directories
import src.data.mvtecad as mvtecad
import src.data.mvtecad_torch as mvtecad_torch
import src.models.cnn_ae as cnn_ae
IPython.get_ipython().run_line_magic("load_ext", "autoreload")
IPython.get_ipython().run_line_magic("autoreload", "2")
# logger
logger = logging.getLogger(__name__)
logging.basicConfig(level=logging.INFO)
def cd_project_root_() -> None:
"""ルートディレクトリをプロジェクトルートに移動."""
current = pathlib.Path().resolve()
if current.stem == "notebooks":
os.chdir(current.parent)
current = pathlib.Path().resolve()
logger.info(f"current path: {current}")
cd_project_root_()
USE_GPU = tc.is_available()
def create_dataset_() -> td.DataLoader:
batch_size = 8
num_workers = 4
transforms = tv_transforms.Compose(
[
tv_transforms.Resize((64, 64)),
tv_transforms.ToTensor(),
]
)
kind = mvtecad.Kind.HAZELNUT
dataset = mvtecad_torch.DatasetAE(kind, transforms, mode=ds.Mode.TRAIN)
dataloader = td.DataLoader(
dataset,
batch_size,
shuffle=False,
num_workers=num_workers,
pin_memory=True
)
return dataloader
DATALOADER = create_dataset_()
def create_network_() -> nn.Module:
network = cnn_ae.SimpleCBR(in_channels=3, out_channels=3)
network.load_state_dict(
torch.load(
directories.get_processed().joinpath(
"simple_cbr_mvtecad_hazelnut", "epoch=1"
)
)
)
if USE_GPU:
network = network.cuda()
network.eval()
return network
NETWORK = create_network_()
def show_images(batch: torch.Tensor, decode: torch.Tensor) -> None:
batch_cpu = batch.detach().cpu().numpy().transpose(0, 2, 3, 1)
decode_cpu = decode.detach().cpu().numpy().transpose(0, 2, 3, 1)
rows, cols = 2, batch_cpu.shape[0]
figsize = (4 * cols, 4 * rows)
fig, axes = plt.subplots(rows, cols, figsize=figsize)
for idx in range(cols):
ax = axes[0, idx]
ax.imshow(batch_cpu[idx])
ax = axes[1, idx]
ax.imshow(decode_cpu[idx])
plt.show()
fig.clf()
plt.close()
def test_() -> None:
with torch.no_grad():
for batch in DATALOADER:
if USE_GPU:
batch = batch.cuda()
output = NETWORK(batch)
show_images(batch, output)
break
test_()
| 0.704872 | 0.696862 |
# Using qucat programmatically
In this example we study a typical circuit QED system consisting of a transmon qubit coupled to a resonator.
The first step is to import the objects we will be needing from qucat.
```
# Import the circuit builder
from qucat import Network
# Import the circuit components
from qucat import L,J,C,R
import numpy as np
```
## Building the circuit
Note that the components (``R``, ``L``, ``C``, ``J``) accept node indexes as their two
first arguments,
here we will use the node ``0`` to designate ground. The last arguments should be
a label (``str``) or a value (``float``) or both, the order in which these
arguments are provided are unimportant.
For the moment, we will specify the value of all the components.
**Note: by default the junction is parametrized by its josephson inductance**
```
cir = Network([
C(0,1,100e-15), # Add a capacitor between nodes 0 and 1, with a value of 100fF
J(0,1,8e-9), # Add a josephson junction, the value is given as Josephson inductance
C(1,2,1e-15), # Add the coupling capacitor
C(2,0,100e-15), # Add the resonator capacitor
L(2,0,10e-9), # Add the resonator inductor
R(2,0,1e6) # Add the resonator resistor
])
```
This implements the following circuit, where we have also indexed the nodes, and we have fixed the value of $L_J$ to ``8e-9`` H
```
from IPython.display import Image
Image("graphics/transmon_LC_programmatically_1.png")
```
We now calculate the eigenfrequency, loss-rates, anharmonicity, and Kerr parameters of the circuit.
This can be done through the functions ``eigenfrequencies``, ``loss_rates``, ``anharmonicities`` and ``kerr``, which return the specified quantities for each mode, **ordered with increasing mode frequency**
## Calculating circuit parameters
### Eigen-frequencies
```
cir.eigenfrequencies()
```
This will return a list of the normal modes of the circuit, we can see they are seperated in frequency by 600 MHz, but we still do not which corresponds to the transmon, and which to the resonator.
To distinquish the two, we can calculate the anharmonicities of each mode.
### Anharmonicity
```
cir.anharmonicities()
```
The first (lowest frequency) mode, has a very small anharmonicity, whilst the second, has an anharmonicity of 191 MHz. The highest frequency mode thus corresponds to the transmon.
### Cross-Kerr or dispersive shift
In this regime of far detuning in frequency, the two modes will interact through a cross-Kerr or dispersive shift, which quantifies the amount by which one mode will shift if frequency if the other is populated with a photon.
We can access this by calculating the Kerr parameters ``K``. In this two dimensional array, the components ``K[i,j]`` correspond to the cross-Kerr interaction of mode ``i`` with mode ``j``.
```
K = cir.kerr()
print("%.2f kHz"%(K[0,1]/1e3))
```
From the above, we have found that the cross-Kerr interaction between these two modes is of about 670 kHz.
This should correspond to $2\sqrt{A_0A_1}$ where $A_i$ is the anharmonicity of mode $i$. Let's check that:
```
A = cir.anharmonicities()
print("%.2f kHz"%(2*np.sqrt(A[0]*A[1])/1e3))
```
### Loss rates
In the studied circuit, the only resistor is located in the resonator. In this regime of large frequency, detuning, we would thus expect the resonator to be more lossy than the transmon.
```
cir.loss_rates()
```
### $T_1$ times
When converting these rates to $T_1$ times, one should not forget the $2\pi$ in the conversion
```
T_1 = 1/cir.loss_rates()/2/np.pi
print(T_1)
```
All these relevant parameters (frequency, dissipation, anharmonicity and Kerr parameters) can be computed using a single function
```
cir.f_k_A_chi()
```
Using the option ``pretty_print = True`` a more readable summary can be printed
```
f,k,A,chi = cir.f_k_A_chi(pretty_print=True)
```
## Hamiltonian, and further analysis with QuTiP
### Generating a Hamiltonian
The Hamiltonian of the circuit, with the non-linearity of the Josephson junctions
Taylor-expanded, is given by
$\hat{H} = \sum_{m\in\text{modes}} hf_m\hat{a}_m^\dagger\hat{a}_m +\sum_j\sum_{2n\le\text{taylor}}E_j\frac{(-1)^{n+1}}{(2n)!}\left(\frac{\phi_{zpf,m,j}}{\phi_0}(\hat{a}_m^\dagger+\hat{a}_m)\right)^{2n}$
And in its construction, we have the freedom to choose the set of ``modes`` to include, the order of the Taylor expansion of the junction potential ``taylor``, and the number of excitations of each mode to consider.
```
# Compute hamiltonian (for h=1, so all energies are expressed in frequency units, not angular)
H = cir.hamiltonian(
modes = [0,1],# Include modes 0 and 1
taylor = 4,# Taylor the Josephson potential to the power 4
excitations = [8,10])# Consider 8 excitations in mode 0, 10 for mode 1
# QuTiP method which return the eigenergies of the system
ee = H.eigenenergies()
```
The first transition of the resonator is
```
print("%.3f GHz"%((ee[1]-ee[0])/1e9))
```
and of the transmon
```
print("%.3f GHz"%((ee[2]-ee[0])/1e9))
```
Notice the difference, especially for the transmon, with the corresponding normal-mode frequency calculated above. This is a consequence of the zero-point fluctuations entering the junction and changing the effective transition frequency.
Following first-order perturbation, the shift in transition frequency can be estimated from the anharmonicity $A_1$ and cross-kerr coupling $\chi_{0,1}$ and should be given by $-A_1-\chi_{0,1}/2$. We see below that we get fairly close (7 MHz) from the value obtained from the hamiltonian diagonalization.
```
f,k,A,K = cir.f_k_A_chi()
print("%.3f GHz"%((f[1]-A[1]-K[0,1]/2)/1e9))
```
### Open-system dynamics
A more elaborate use of QuTiP would be to compute the dynamics (for example with qutip.mesolve). The Hamiltonian and collapse operators to use are
```
# H is the Hamiltonian
H,a_m_list = cir.hamiltonian(modes = [0,1],taylor = 4,excitations = [5,5], return_ops = True)
# !!! which should be in angular frequencies for time-dependant simulations
H = 2.*np.pi*H
# c_ops are the collapse operators
# !!! which should be in angular frequencies for time-dependant simulations
k = cir.loss_rates()
c_ops = [np.sqrt(2*np.pi*k[0])*a_m_list[0],np.sqrt(2*np.pi*k[1])*a_m_list[1]]
```
## Sweeping a parameter
The most computationally expensive part of the
analysis is performed upon initializing the Network. To avoid doing this,
we have the option to enter a symbolic value for a component.
We will only provide a label ``L_J`` for the junction here,
and its value should be passed
as a keyword argument in subsequent function calls,
for example ``L_J=1e-9``.
```
cir = Network([
C(0,1,100e-15),
J(0,1,'L_J'),
C(1,2,1e-15),
C(2,0,100e-15),
L(2,0,10e-9),
R(2,0,1e6)
])
```
The implemented circuit, overlayed with the nodes, is:
```
from IPython.display import Image
Image("graphics/transmon_LC_programmatically_1.png")
```
Since the junction was created without a value,
we now have to specify it as a keyword argument
```
import matplotlib.pyplot as plt
# array of values for the josephson inductance
L_J = np.linspace(8e-9,12e-9,1001)
plt.plot(
L_J*1e9,# xaxis will be the inductance in units of nano-Henry
[cir.eigenfrequencies(L_J = x)/1e9 for x in L_J]) # yaxis an array of eigenfrequencies
# Add plot labels
plt.xlabel('L_J (nH)')
plt.ylabel('Normal mode frequency (GHz)')
# show the figure
plt.show()
```
|
github_jupyter
|
# Import the circuit builder
from qucat import Network
# Import the circuit components
from qucat import L,J,C,R
import numpy as np
cir = Network([
C(0,1,100e-15), # Add a capacitor between nodes 0 and 1, with a value of 100fF
J(0,1,8e-9), # Add a josephson junction, the value is given as Josephson inductance
C(1,2,1e-15), # Add the coupling capacitor
C(2,0,100e-15), # Add the resonator capacitor
L(2,0,10e-9), # Add the resonator inductor
R(2,0,1e6) # Add the resonator resistor
])
from IPython.display import Image
Image("graphics/transmon_LC_programmatically_1.png")
cir.eigenfrequencies()
cir.anharmonicities()
K = cir.kerr()
print("%.2f kHz"%(K[0,1]/1e3))
A = cir.anharmonicities()
print("%.2f kHz"%(2*np.sqrt(A[0]*A[1])/1e3))
cir.loss_rates()
T_1 = 1/cir.loss_rates()/2/np.pi
print(T_1)
cir.f_k_A_chi()
f,k,A,chi = cir.f_k_A_chi(pretty_print=True)
# Compute hamiltonian (for h=1, so all energies are expressed in frequency units, not angular)
H = cir.hamiltonian(
modes = [0,1],# Include modes 0 and 1
taylor = 4,# Taylor the Josephson potential to the power 4
excitations = [8,10])# Consider 8 excitations in mode 0, 10 for mode 1
# QuTiP method which return the eigenergies of the system
ee = H.eigenenergies()
print("%.3f GHz"%((ee[1]-ee[0])/1e9))
print("%.3f GHz"%((ee[2]-ee[0])/1e9))
f,k,A,K = cir.f_k_A_chi()
print("%.3f GHz"%((f[1]-A[1]-K[0,1]/2)/1e9))
# H is the Hamiltonian
H,a_m_list = cir.hamiltonian(modes = [0,1],taylor = 4,excitations = [5,5], return_ops = True)
# !!! which should be in angular frequencies for time-dependant simulations
H = 2.*np.pi*H
# c_ops are the collapse operators
# !!! which should be in angular frequencies for time-dependant simulations
k = cir.loss_rates()
c_ops = [np.sqrt(2*np.pi*k[0])*a_m_list[0],np.sqrt(2*np.pi*k[1])*a_m_list[1]]
cir = Network([
C(0,1,100e-15),
J(0,1,'L_J'),
C(1,2,1e-15),
C(2,0,100e-15),
L(2,0,10e-9),
R(2,0,1e6)
])
from IPython.display import Image
Image("graphics/transmon_LC_programmatically_1.png")
import matplotlib.pyplot as plt
# array of values for the josephson inductance
L_J = np.linspace(8e-9,12e-9,1001)
plt.plot(
L_J*1e9,# xaxis will be the inductance in units of nano-Henry
[cir.eigenfrequencies(L_J = x)/1e9 for x in L_J]) # yaxis an array of eigenfrequencies
# Add plot labels
plt.xlabel('L_J (nH)')
plt.ylabel('Normal mode frequency (GHz)')
# show the figure
plt.show()
| 0.639286 | 0.991724 |
```
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
from pathlib import Path
import seaborn as sns
import plotly.express as px
import functions as funcs
import pyemma as pm
from pandas.api.types import CategoricalDtype
import matplotlib as mpl
import numpy as np
import functions as funcs
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pymc3 as pm
import scipy as sp
import pickle
def zero_var(x):
if x.dtype=='object':
return np.unique(x).shape[0] == 1
else:
return np.var(x) < 1e-12
```
# Load data
```
data_dir = Path('/Volumes/REA/Data/fast_folders/')
```
Chosen lags and num_dom_procs are the specific values of markov lag time and number of dominant processes we're going to use in this analysis.
```
chosen_lags = pd.read_hdf('chosen_lag_times.h5', key='chosen_lags')
chosen_dom_procs = pd.read_hdf('chosen_num_dominant.h5', key='chosen_num_dominant')
```
# Load, subset and aggregate timescales
'timescales' contains all the timescale data. Subset the timescales for the specific lag and only keep the dominant timescales.
```
ts = pd.read_hdf('timescales.h5', key='timescales')
# Subset chosen lag time and number of implied timescales
lags_dict = dict(zip(chosen_lags['protein'], chosen_lags['lag']))
proc_dict = dict(zip(chosen_dom_procs['protein'], chosen_dom_procs['num_its']))
ts['choose_lag'] = ts['protein'].apply(lambda x: lags_dict[x])
ts['choose_k'] = ts['protein'].apply(lambda x: proc_dict[x])
ts = ts.loc[(ts.lag == ts.choose_lag) & (ts.num_its <= ts.choose_k+1), : ]
ts = ts.drop(columns=ts.filter(like='choose', axis=1).columns)
ts = ts.drop(columns=ts.columns[ts.apply(zero_var, axis=0)])
# aggregate
non_num_cols = list(ts.columns[ts.dtypes == 'object'])
agg_columns = ['protein', 'num_its', 'hp_index']
tmp = ts.groupby(agg_columns, as_index=False).median()
tmp2 = ts.groupby(agg_columns, as_index=False).first()
ts = tmp.merge(tmp2.loc[:, list(set(non_num_cols+agg_columns))], on=agg_columns, how='left')
ts = ts.drop(columns=['iteration'])
ts.rename(columns={'value': 'timescale'}, inplace=True)
ts.head()
```
## Load and aggregate VAMP scores
```
vamps = pd.read_hdf('vamps_and_hps.h5', key='vamps_hps')
vamps = vamps.drop(columns=vamps.columns[vamps.apply(zero_var, axis=0)])
non_num_cols = list(vamps.columns[vamps.dtypes == 'object'])
agg_columns = ['protein', 'hp_index']
tmp = vamps.groupby(agg_columns, as_index=False).median() # aggregate numeric columns
tmp2 = vamps.groupby(agg_columns, as_index=False).first() # aggregate all columns
vamps = tmp.merge(tmp2.loc[:, list(set(non_num_cols+agg_columns))], on=agg_columns, how='left')
vamps.rename(columns={'value': 'vamp'}, inplace=True)
vamps.head()
```
Check the number of cases is the same between the two datasets (ts contains many different timescales, so select the first one)
```
vamps.shape[0] == ts.loc[ts.num_its == 2, :].shape[0]
```
naming dictionary (for saving files)
```
prot_dict = dict((x[0][0], x[0][1]) for x in zip(vamps.loc[:, ['protein', 'protein_dir']].drop_duplicates().values))
```
## Calculate sensitivity to ouptuts
### Choose protein and feature
```
def fit(data, dep_var, ind_vars, formula, input_space):
# determin min/max values for scaling function
dep_range = np.array([data[dep_var].min(), data[dep_var].max()])
output_space = {'dep_var': dep_range}
var_space = input_space.copy()
var_space.update({dep_var: output_space['dep_var']})
# Create scaler
vs = funcs.create_grid(var_space)
vs_y, vs_X = funcs.create_dmatrices(vs, formula=formula)
_, scaler = funcs.scale_dmatrix(pd.concat([vs_y, vs_X], axis=1), scaler=None)
# Scale data
y, X = funcs.create_dmatrices(data, formula=formula)
data_s, _ = funcs.scale_dmatrix(pd.concat([y, X], axis=1), scaler=scaler)
# GP data and priors
dep_var_cols = [x for x in data_s.columns if dep_var in x]
ind_var_cols = [x for x in data_s.columns if np.any([y in x for y in ind_vars])]
y = data_s.loc[:, dep_var_cols]
X = data_s.loc[:, ind_var_cols]
l_prior = funcs.gamma(2, 0.5)
eta_prior = funcs.hcauchy(2)
sigma_prior = funcs.hcauchy(2)
gp, trace, model = funcs.fit_gp(y=y, X=X, # Data
l_prior=l_prior, eta_prior=eta_prior, sigma_prior=sigma_prior, # Priors
kernel_type='exponential', # Kernel
prop_Xu=None, # proportion of data points which are inducing variables.
bayes_kws=dict(draws=5000, tune=3000, chains=4, cores=4, target_accept=0.90)) # Bayes kws
results = {'gp': gp, 'trace': trace, 'model': model, 'data': data_s}
return results
def get_data(data_sets, dep_var, ind_vars, protein, feature, num_its=None, transform=None):
data = data_sets[dep_var].copy()
ix = (data.protein==protein) & (data.feature__value==feature)
if dep_var == 'timescale':
ix = ix & (data.num_its == num_its)
if feature == 'distances':
if transform is None:
raise ValueError('For distance feature you must specify a transform')
ix = ix & (data.distances__transform == transform)
data = data.loc[ix, [dep_var]+ind_vars]
return data
# feature = 'distances'
# feature_label = 'distances_linear'
# transform = 'linear'
# ind_vars = ['cluster__k', 'tica__dim', 'tica__lag', 'distances__scheme']
# input_space = {'tica__lag': np.array([1, 10, 100]), 'tica__dim': np.array([1, 5, 10]), 'cluster__k': np.array([10, 250, 500]),
# 'distances__scheme': np.array(['ca', 'closest-heavy'])}
# feature = 'dihedrals'
# feature_label = 'dihedrals'
# transform = None
# ind_vars = ['cluster__k', 'tica__dim', 'tica__lag']
# input_space = {'tica__lag': np.array([1, 10, 100]), 'tica__dim': np.array([1, 5, 10]), 'cluster__k': np.array([10, 250, 500])}
# feature = 'distances'
# feature_label = 'distances_logistic'
# transform = 'logistic'
# ind_vars = ['cluster__k', 'tica__dim', 'tica__lag', 'distances__scheme', 'distances__centre', 'distances__steepness']
# input_space = {'tica__lag': np.array([1, 10, 100]), 'tica__dim': np.array([1, 5, 10]), 'cluster__k': np.array([10, 250, 500]),
# 'distances__scheme': np.array(['ca', 'closest-heavy']),
# 'distances__centre': np.array([0.3, 1.5]),
# 'distances__steepness': np.array([0.1, 50])}
import warnings
warnings.simplefilter(action='ignore', category=FutureWarning)
out_dir = Path('sensitivities_exp_log_outcome')
out_dir.mkdir(exist_ok=True)
dep_vars = ['vamp', 'timescale']
data_sets = {'vamp': vamps, 'timescale': ts}
proteins = ts.protein.unique()
feature = 'distances'
feature_label = 'distances_linear'
transform = 'linear'
ind_vars = ['cluster__k', 'tica__dim', 'tica__lag', 'distances__scheme']
input_space = {'tica__lag': np.array([1, 10, 100]), 'tica__dim': np.array([1, 5, 10]), 'cluster__k': np.array([10, 250, 500]),
'distances__scheme': np.array(['ca', 'closest-heavy'])}
for protein in proteins:
dep_var = 'vamp'
filename = f"{prot_dict[protein]}_{feature_label}_{dep_var}_sensitivity.pkl"
print(filename)
formula = f"np.log({dep_var}) ~ 0 + " + ' + '.join(ind_vars)
data = get_data(data_sets, dep_var, ind_vars, protein, feature, transform=transform)
results = fit(data, dep_var, ind_vars, formula, input_space)
out_file = out_dir.joinpath(filename)
if out_file.exists():
raise RuntimeError(f'{out_file} already exists')
pickle.dump(file=out_file.open('wb'), obj=results)
dep_var = 'timescale'
formula = f"np.log({dep_var}) ~ 0 + " + ' + '.join(ind_vars)
max_its = proc_dict[protein]
for num_its in range(2, max_its+1):
filename = f"{prot_dict[protein]}_{feature_label}_{dep_var}_its_{num_its}_sensitivity.pkl"
print(filename)
data = get_data(data_sets, dep_var, ind_vars, protein, feature, num_its, transform=transform)
results = fit(data, dep_var, ind_vars, formula, input_space)
out_file = out_dir.joinpath(filename)
if out_file.exists():
raise RuntimeError(f'{out_file} already exists')
pickle.dump(file=out_file.open('wb'), obj=results)
```
|
github_jupyter
|
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
from pathlib import Path
import seaborn as sns
import plotly.express as px
import functions as funcs
import pyemma as pm
from pandas.api.types import CategoricalDtype
import matplotlib as mpl
import numpy as np
import functions as funcs
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pymc3 as pm
import scipy as sp
import pickle
def zero_var(x):
if x.dtype=='object':
return np.unique(x).shape[0] == 1
else:
return np.var(x) < 1e-12
data_dir = Path('/Volumes/REA/Data/fast_folders/')
chosen_lags = pd.read_hdf('chosen_lag_times.h5', key='chosen_lags')
chosen_dom_procs = pd.read_hdf('chosen_num_dominant.h5', key='chosen_num_dominant')
ts = pd.read_hdf('timescales.h5', key='timescales')
# Subset chosen lag time and number of implied timescales
lags_dict = dict(zip(chosen_lags['protein'], chosen_lags['lag']))
proc_dict = dict(zip(chosen_dom_procs['protein'], chosen_dom_procs['num_its']))
ts['choose_lag'] = ts['protein'].apply(lambda x: lags_dict[x])
ts['choose_k'] = ts['protein'].apply(lambda x: proc_dict[x])
ts = ts.loc[(ts.lag == ts.choose_lag) & (ts.num_its <= ts.choose_k+1), : ]
ts = ts.drop(columns=ts.filter(like='choose', axis=1).columns)
ts = ts.drop(columns=ts.columns[ts.apply(zero_var, axis=0)])
# aggregate
non_num_cols = list(ts.columns[ts.dtypes == 'object'])
agg_columns = ['protein', 'num_its', 'hp_index']
tmp = ts.groupby(agg_columns, as_index=False).median()
tmp2 = ts.groupby(agg_columns, as_index=False).first()
ts = tmp.merge(tmp2.loc[:, list(set(non_num_cols+agg_columns))], on=agg_columns, how='left')
ts = ts.drop(columns=['iteration'])
ts.rename(columns={'value': 'timescale'}, inplace=True)
ts.head()
vamps = pd.read_hdf('vamps_and_hps.h5', key='vamps_hps')
vamps = vamps.drop(columns=vamps.columns[vamps.apply(zero_var, axis=0)])
non_num_cols = list(vamps.columns[vamps.dtypes == 'object'])
agg_columns = ['protein', 'hp_index']
tmp = vamps.groupby(agg_columns, as_index=False).median() # aggregate numeric columns
tmp2 = vamps.groupby(agg_columns, as_index=False).first() # aggregate all columns
vamps = tmp.merge(tmp2.loc[:, list(set(non_num_cols+agg_columns))], on=agg_columns, how='left')
vamps.rename(columns={'value': 'vamp'}, inplace=True)
vamps.head()
vamps.shape[0] == ts.loc[ts.num_its == 2, :].shape[0]
prot_dict = dict((x[0][0], x[0][1]) for x in zip(vamps.loc[:, ['protein', 'protein_dir']].drop_duplicates().values))
def fit(data, dep_var, ind_vars, formula, input_space):
# determin min/max values for scaling function
dep_range = np.array([data[dep_var].min(), data[dep_var].max()])
output_space = {'dep_var': dep_range}
var_space = input_space.copy()
var_space.update({dep_var: output_space['dep_var']})
# Create scaler
vs = funcs.create_grid(var_space)
vs_y, vs_X = funcs.create_dmatrices(vs, formula=formula)
_, scaler = funcs.scale_dmatrix(pd.concat([vs_y, vs_X], axis=1), scaler=None)
# Scale data
y, X = funcs.create_dmatrices(data, formula=formula)
data_s, _ = funcs.scale_dmatrix(pd.concat([y, X], axis=1), scaler=scaler)
# GP data and priors
dep_var_cols = [x for x in data_s.columns if dep_var in x]
ind_var_cols = [x for x in data_s.columns if np.any([y in x for y in ind_vars])]
y = data_s.loc[:, dep_var_cols]
X = data_s.loc[:, ind_var_cols]
l_prior = funcs.gamma(2, 0.5)
eta_prior = funcs.hcauchy(2)
sigma_prior = funcs.hcauchy(2)
gp, trace, model = funcs.fit_gp(y=y, X=X, # Data
l_prior=l_prior, eta_prior=eta_prior, sigma_prior=sigma_prior, # Priors
kernel_type='exponential', # Kernel
prop_Xu=None, # proportion of data points which are inducing variables.
bayes_kws=dict(draws=5000, tune=3000, chains=4, cores=4, target_accept=0.90)) # Bayes kws
results = {'gp': gp, 'trace': trace, 'model': model, 'data': data_s}
return results
def get_data(data_sets, dep_var, ind_vars, protein, feature, num_its=None, transform=None):
data = data_sets[dep_var].copy()
ix = (data.protein==protein) & (data.feature__value==feature)
if dep_var == 'timescale':
ix = ix & (data.num_its == num_its)
if feature == 'distances':
if transform is None:
raise ValueError('For distance feature you must specify a transform')
ix = ix & (data.distances__transform == transform)
data = data.loc[ix, [dep_var]+ind_vars]
return data
# feature = 'distances'
# feature_label = 'distances_linear'
# transform = 'linear'
# ind_vars = ['cluster__k', 'tica__dim', 'tica__lag', 'distances__scheme']
# input_space = {'tica__lag': np.array([1, 10, 100]), 'tica__dim': np.array([1, 5, 10]), 'cluster__k': np.array([10, 250, 500]),
# 'distances__scheme': np.array(['ca', 'closest-heavy'])}
# feature = 'dihedrals'
# feature_label = 'dihedrals'
# transform = None
# ind_vars = ['cluster__k', 'tica__dim', 'tica__lag']
# input_space = {'tica__lag': np.array([1, 10, 100]), 'tica__dim': np.array([1, 5, 10]), 'cluster__k': np.array([10, 250, 500])}
# feature = 'distances'
# feature_label = 'distances_logistic'
# transform = 'logistic'
# ind_vars = ['cluster__k', 'tica__dim', 'tica__lag', 'distances__scheme', 'distances__centre', 'distances__steepness']
# input_space = {'tica__lag': np.array([1, 10, 100]), 'tica__dim': np.array([1, 5, 10]), 'cluster__k': np.array([10, 250, 500]),
# 'distances__scheme': np.array(['ca', 'closest-heavy']),
# 'distances__centre': np.array([0.3, 1.5]),
# 'distances__steepness': np.array([0.1, 50])}
import warnings
warnings.simplefilter(action='ignore', category=FutureWarning)
out_dir = Path('sensitivities_exp_log_outcome')
out_dir.mkdir(exist_ok=True)
dep_vars = ['vamp', 'timescale']
data_sets = {'vamp': vamps, 'timescale': ts}
proteins = ts.protein.unique()
feature = 'distances'
feature_label = 'distances_linear'
transform = 'linear'
ind_vars = ['cluster__k', 'tica__dim', 'tica__lag', 'distances__scheme']
input_space = {'tica__lag': np.array([1, 10, 100]), 'tica__dim': np.array([1, 5, 10]), 'cluster__k': np.array([10, 250, 500]),
'distances__scheme': np.array(['ca', 'closest-heavy'])}
for protein in proteins:
dep_var = 'vamp'
filename = f"{prot_dict[protein]}_{feature_label}_{dep_var}_sensitivity.pkl"
print(filename)
formula = f"np.log({dep_var}) ~ 0 + " + ' + '.join(ind_vars)
data = get_data(data_sets, dep_var, ind_vars, protein, feature, transform=transform)
results = fit(data, dep_var, ind_vars, formula, input_space)
out_file = out_dir.joinpath(filename)
if out_file.exists():
raise RuntimeError(f'{out_file} already exists')
pickle.dump(file=out_file.open('wb'), obj=results)
dep_var = 'timescale'
formula = f"np.log({dep_var}) ~ 0 + " + ' + '.join(ind_vars)
max_its = proc_dict[protein]
for num_its in range(2, max_its+1):
filename = f"{prot_dict[protein]}_{feature_label}_{dep_var}_its_{num_its}_sensitivity.pkl"
print(filename)
data = get_data(data_sets, dep_var, ind_vars, protein, feature, num_its, transform=transform)
results = fit(data, dep_var, ind_vars, formula, input_space)
out_file = out_dir.joinpath(filename)
if out_file.exists():
raise RuntimeError(f'{out_file} already exists')
pickle.dump(file=out_file.open('wb'), obj=results)
| 0.345989 | 0.904059 |
<a href="https://colab.research.google.com/github/abidshafee/AI-Hub-TTF-Projects/blob/master/Multi_horizon_Time_Series_Forecasting_with_TFTs.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Temporal Fusion Transformers for Multi-horizon Time Series Forecasting
## Introduction
This notebook demonstrates the use of the Temporal Fustion Transformer (TFT) for high-peformance mulit-horizon time series prediction, using a traffic forecasting example with data from the UCI PEMS-SF Repository.
We also show how to use TFT for two interpretability cases:
- Analyzing variable importance weights to identify signficant features for the prediction problem.
- Visualizing persistent temporal patterns learnt by the TFT using temporal self-attention weights.
A third use case is also presented in our companion notebook "Temporal Fusion Transfomers for Regime Identification in Time Series Data".
### Reference Paper
Bryan Lim, Sercan Arik, Nicolas Loeff and Tomas Pfister. "Temporal Fusion Transformers for Interpretable Multi-horizon Time Series Forecasting". Submitted, 2019.
##### Abstract
Multi-horizon forecasting problems often contain a complex mix of inputs -- including static (i.e. time-invariant) covariates, known future inputs, and other exogenous time series that are only observed historically -- without any prior information on how they interact with the target. While several deep learning models have been proposed for multi-step prediction, they typically comprise black-box models which do not account for the full range of inputs present in common scenarios. In this paper, we introduce the Temporal Fusion Transformer (TFT) -- a novel attention-based architecture which combines high-performance multi-horizon forecasting with interpretable insights into temporal dynamics. To learn temporal relationships at different scales, the TFT utilizes recurrent layers for local processing and interpretable self-attention layers for learning long-term dependencies. The TFT also uses specialized components for the judicious selection of relevant features and a series of gating layers to suppress unnecessary components, enabling high performance in a wide range of regimes. On a variety of real-world datasets, we demonstrate significant performance improvements over existing benchmarks, and showcase three practical interpretability use-cases of TFT.
# Preliminary Setup
### Package Installation
```
# Uses pip3 to install necessary packages
!pip3 install pyunpack wget patool plotly cufflinks --user
# Resets the IPython kernel to import the installed package.
import IPython
app = IPython.Application.instance()
app.kernel.do_shutdown(True)
```
|
github_jupyter
|
# Uses pip3 to install necessary packages
!pip3 install pyunpack wget patool plotly cufflinks --user
# Resets the IPython kernel to import the installed package.
import IPython
app = IPython.Application.instance()
app.kernel.do_shutdown(True)
| 0.385028 | 0.989612 |
```
from google.colab import drive
drive.mount('/content/drive')
import os
import pickle
import os, sys
import PIL
from PIL import Image
import numpy as np
from PIL import Image as im
import gdown
!pip install wandb
!git clone https://github.com/Healthcare-Robotics/bodies-at-rest.git
!/content/bodies-at-rest/PressurePose/download_real.sh
%cd /data_BR/real/S103
def load_pickle(pickle_file):
try:
with open(pickle_file, 'rb') as f:
pickle_data = pickle.load(f)
except UnicodeDecodeError as e:
with open(pickle_file, 'rb') as f:
pickle_data = pickle.load(f, encoding='latin1')
except Exception as e:
print('Unable to load data ', pickle_file, ':', e)
raise
return pickle_data
load_pickle("/data_BR/real/S103/prescribed.p")
%cd /content/bodies-at-rest/PressurePose
import os, sys
import pickle
path = "/data_BR/real/"
dirs = os.listdir(path)
Pose = []
for file in dirs:
with open(f'/data_BR/real/{file}/prescribed.p', 'rb') as f:
data1 = pickle.load(f, encoding='latin1')
Pose.extend(data1['RGB'])
with open(f'/data_BR/real/{file}/p_select.p', 'rb') as f:
data2 = pickle.load(f, encoding='latin1')
Pose.extend(data2['RGB'])
for i in range(0,1051):
Fig = im.fromarray(Pose[i])
b, g, r = Fig.split()
Fig = Image.merge("RGB", (r, g, b))
Fig.save(f'/content/dataset/{i}.png')
!git clone https://github.com/PeikeLi/Self-Correction-Human-Parsing.git
!pip install ninja
!mkdir input
!mkdir segment_output
!mkdir weight
from PIL import Image
from PIL import ImageEnhance
import cv2
for i in range(0,1051):
img = Image.open(f'/content/drive/MyDrive/Self-Correction-Human-Parsing/input/dataset/{i}.png')
img.show()
enhancer = ImageEnhance.Contrast(img)
enhancer.enhance(3).save(f'/content/drive/MyDrive/Self-Correction-Human-Parsing/input/dataset_color/{i}.png')
!python '/content/drive/MyDrive/Self-Correction-Human-Parsing/simple_extractor.py' --dataset 'pascal' --model-restore '/content/drive/MyDrive/Self-Correction-Human-Parsing/weight/exp-schp-201908270938-pascal-person-part.pth' --input-dir '/content/drive/MyDrive/Self-Correction-Human-Parsing/input/dataset/' --output-dir '/content/drive/MyDrive/Self-Correction-Human-Parsing/segment_output'
import os
import cv2
path = "/content/drive/MyDrive/Self-Correction-Human-Parsing/segment_output"
files = os.listdir(path)
traininfo = open('/content/drive/MyDrive/Self-Correction-Human-Parsing/datasets/dataset/train_id.txt', 'w')
valinfo= open('/content/drive/MyDrive/Self-Correction-Human-Parsing/datasets/dataset/val_id.txt', 'w')
for i, im in enumerate(files):
img = cv2.imread(os.path.join(path,im))
img_gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
img_gray[img_gray > 0] = 255
img_gray[img_gray == 0] = 0
_, tail = os.path.split(im)
name = tail.split('.')[0]
if i < 800:
cv2.imwrite(f"/content/drive/MyDrive/Self-Correction-Human-Parsing/datasets/dataset/train_img/{name}.jpg", img_gray)
traininfo.write(f"{name}")
traininfo.write('\n')
else:
cv2.imwrite(f"/content/drive/MyDrive/Self-Correction-Human-Parsing/datasets/dataset/val_img/{name}.jpg", img_gray)
valinfo.write(f"{name}")
valinfo.write('\n')
traininfo.close()
valinfo.close()
for i, im in enumerate(files):
img_rgb = cv2.imread(os.path.join(path, im))
img_gray = cv2.cvtColor(img_rgb, cv2.COLOR_BGR2GRAY)
img_gray[img_gray == 0] = 0
img_gray[img_gray == 15] = 1
img_gray[img_gray == 38] = 2
img_gray[img_gray == 53] = 3
img_gray[img_gray == 75] = 4
img_gray[img_gray == 90] = 5
img_gray[img_gray == 113] = 6
_, tail = os.path.split(im)
name = tail.split('.')[0]
if i < 800:
cv2.imwrite(f"/content/drive/MyDrive/Self-Correction-Human-Parsing/datasets/dataset/train_segment/{name}.png", img_gray)
else:
cv2.imwrite(f"/content/drive/MyDrive/Self-Correction-Human-Parsing/datasets/dataset/val_segment/{name}.png", img_gray)
import matplotlib.pyplot as plt
import cv2
fig = plt.figure(figsize=(10, 10))
img = cv2.imread("/content/drive/MyDrive/Self-Correction-Human-Parsing/input/dataset/167.png")
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
plt.subplot(141)
plt.imshow(img)
img1 = cv2.imread("/content/drive/MyDrive/Self-Correction-Human-Parsing/segment_output/167.png")
plt.subplot(142)
plt.imshow(img1)
!python train.py --data-dir '/content/drive/MyDrive/Self-Correction-Human-Parsing/datasets/dataset' --batch-size 3 --imagenet-pretrain '/content/drive/MyDrive/Self-Correction-Human-Parsing/weight/pretrain/pretrainrcrhzmamtmp' --num-classes 7 --epoch 10
```
|
github_jupyter
|
from google.colab import drive
drive.mount('/content/drive')
import os
import pickle
import os, sys
import PIL
from PIL import Image
import numpy as np
from PIL import Image as im
import gdown
!pip install wandb
!git clone https://github.com/Healthcare-Robotics/bodies-at-rest.git
!/content/bodies-at-rest/PressurePose/download_real.sh
%cd /data_BR/real/S103
def load_pickle(pickle_file):
try:
with open(pickle_file, 'rb') as f:
pickle_data = pickle.load(f)
except UnicodeDecodeError as e:
with open(pickle_file, 'rb') as f:
pickle_data = pickle.load(f, encoding='latin1')
except Exception as e:
print('Unable to load data ', pickle_file, ':', e)
raise
return pickle_data
load_pickle("/data_BR/real/S103/prescribed.p")
%cd /content/bodies-at-rest/PressurePose
import os, sys
import pickle
path = "/data_BR/real/"
dirs = os.listdir(path)
Pose = []
for file in dirs:
with open(f'/data_BR/real/{file}/prescribed.p', 'rb') as f:
data1 = pickle.load(f, encoding='latin1')
Pose.extend(data1['RGB'])
with open(f'/data_BR/real/{file}/p_select.p', 'rb') as f:
data2 = pickle.load(f, encoding='latin1')
Pose.extend(data2['RGB'])
for i in range(0,1051):
Fig = im.fromarray(Pose[i])
b, g, r = Fig.split()
Fig = Image.merge("RGB", (r, g, b))
Fig.save(f'/content/dataset/{i}.png')
!git clone https://github.com/PeikeLi/Self-Correction-Human-Parsing.git
!pip install ninja
!mkdir input
!mkdir segment_output
!mkdir weight
from PIL import Image
from PIL import ImageEnhance
import cv2
for i in range(0,1051):
img = Image.open(f'/content/drive/MyDrive/Self-Correction-Human-Parsing/input/dataset/{i}.png')
img.show()
enhancer = ImageEnhance.Contrast(img)
enhancer.enhance(3).save(f'/content/drive/MyDrive/Self-Correction-Human-Parsing/input/dataset_color/{i}.png')
!python '/content/drive/MyDrive/Self-Correction-Human-Parsing/simple_extractor.py' --dataset 'pascal' --model-restore '/content/drive/MyDrive/Self-Correction-Human-Parsing/weight/exp-schp-201908270938-pascal-person-part.pth' --input-dir '/content/drive/MyDrive/Self-Correction-Human-Parsing/input/dataset/' --output-dir '/content/drive/MyDrive/Self-Correction-Human-Parsing/segment_output'
import os
import cv2
path = "/content/drive/MyDrive/Self-Correction-Human-Parsing/segment_output"
files = os.listdir(path)
traininfo = open('/content/drive/MyDrive/Self-Correction-Human-Parsing/datasets/dataset/train_id.txt', 'w')
valinfo= open('/content/drive/MyDrive/Self-Correction-Human-Parsing/datasets/dataset/val_id.txt', 'w')
for i, im in enumerate(files):
img = cv2.imread(os.path.join(path,im))
img_gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
img_gray[img_gray > 0] = 255
img_gray[img_gray == 0] = 0
_, tail = os.path.split(im)
name = tail.split('.')[0]
if i < 800:
cv2.imwrite(f"/content/drive/MyDrive/Self-Correction-Human-Parsing/datasets/dataset/train_img/{name}.jpg", img_gray)
traininfo.write(f"{name}")
traininfo.write('\n')
else:
cv2.imwrite(f"/content/drive/MyDrive/Self-Correction-Human-Parsing/datasets/dataset/val_img/{name}.jpg", img_gray)
valinfo.write(f"{name}")
valinfo.write('\n')
traininfo.close()
valinfo.close()
for i, im in enumerate(files):
img_rgb = cv2.imread(os.path.join(path, im))
img_gray = cv2.cvtColor(img_rgb, cv2.COLOR_BGR2GRAY)
img_gray[img_gray == 0] = 0
img_gray[img_gray == 15] = 1
img_gray[img_gray == 38] = 2
img_gray[img_gray == 53] = 3
img_gray[img_gray == 75] = 4
img_gray[img_gray == 90] = 5
img_gray[img_gray == 113] = 6
_, tail = os.path.split(im)
name = tail.split('.')[0]
if i < 800:
cv2.imwrite(f"/content/drive/MyDrive/Self-Correction-Human-Parsing/datasets/dataset/train_segment/{name}.png", img_gray)
else:
cv2.imwrite(f"/content/drive/MyDrive/Self-Correction-Human-Parsing/datasets/dataset/val_segment/{name}.png", img_gray)
import matplotlib.pyplot as plt
import cv2
fig = plt.figure(figsize=(10, 10))
img = cv2.imread("/content/drive/MyDrive/Self-Correction-Human-Parsing/input/dataset/167.png")
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
plt.subplot(141)
plt.imshow(img)
img1 = cv2.imread("/content/drive/MyDrive/Self-Correction-Human-Parsing/segment_output/167.png")
plt.subplot(142)
plt.imshow(img1)
!python train.py --data-dir '/content/drive/MyDrive/Self-Correction-Human-Parsing/datasets/dataset' --batch-size 3 --imagenet-pretrain '/content/drive/MyDrive/Self-Correction-Human-Parsing/weight/pretrain/pretrainrcrhzmamtmp' --num-classes 7 --epoch 10
| 0.123432 | 0.068444 |
# Unit 5: Model-based Collaborative Filtering for **Rating** Prediction
In this unit, we change the approach towards CF from neighborhood-based to **model-based**. This means that we create and train a model for describing users and items instead of using the k nearest neighbors. The model parameters are latent representations for users and items.
Key to this idea is to compress the sparse interaction information of $R$ by finding two matrices $U$ and $V$ that by multiplication reconstruct $R$. The decomposition of $R$ into $U \times V$ is called _matrix factorization_ and we refer to $U$ as user latent factor matrix and $V$ as item latent factor matrix.
Compressing the sparse matrix into the product of two matrices means that the two remaining matrices are much smaller. This decrease in size is governed by the dimension of latent user/item vectors and symbolized by $d \in \mathbb{N}$. We choose $d$ to be much smaller than the number of items or users:
\begin{equation*}
\underset{m\times n}{\mathrm{R}} \approx \underset{m\times d}{U} \times \underset{d\times n}{V^T} \\
d \ll \min\{m, n\}
\end{equation*}
```
from collections import OrderedDict
import itertools
from typing import Dict, List, Tuple
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from recsys_training.data import Dataset
from recsys_training.evaluation import get_relevant_items
ml100k_ratings_filepath = '../../data/raw/ml-100k/u.data'
```
## Load Data
```
data = Dataset(ml100k_ratings_filepath)
data.rating_split(seed=42)
user_ratings = data.get_user_ratings()
```
## Initialize the user and item latent factors, i.e. the model parameters
```
seed = 42
m = data.n_users
n = data.n_items
d = 8
```
As we want to learn the user/item latent factors from rating data, we first randomly initialize them
```
np.random.seed(seed)
user_factors = np.random.normal(0, 1, (m, d))
item_factors = np.random.normal(0, 1, (n, d))
ratings = data.train_ratings[['user', 'item', 'rating']].sample(frac=1, random_state=seed)
np.dot(user_factors[1], item_factors[233])
```
## Training
We fit the model to the data with a technique called _minibatch gradient descent_.
This means that for a number of epochs, i.e. full passes through the training data (ratings), we randomly choose a small subset of ratings (our minibatch) holding user, item and rating for each instance. Then, we compute the rating prediction as the dot product of user and item latent vectors (also called embeddings) and compute the mean squared error between predicted and true rating. We derive this error for user and item latent vectors to obtain our partial derivatives. We subtract part of the gradient from our latent vectors to move into the direction of minimizing error, i.e. deviation between true values and predictions.
To keep track of the decreasing error, we compute the root mean squared error and print it.
```
epochs = 10
batch_size = 64
learning_rate = 0.01
num_batches = int(np.ceil(len(ratings) / batch_size))
rmse_trace = []
rmse_test_trace = []
```

**Task:** Implement `compute_gradients` that receives a minibatch and computes the gradients for user and item latent vectors involved.
```
def compute_gradients(ratings: np.array,
u: np.array,
v: np.array) -> Tuple[np.array, np.array]:
preds = np.sum(u * v, axis=1)
error = (ratings - preds).reshape(-1, 1)
u_grad = -2 * error * v
v_grad = -2 * error * u
return u_grad, v_grad
def get_rmse(rating, u, v) -> float:
pred = np.sum(u * v, axis=1)
error = rating - pred
rmse = np.sqrt(np.mean(error ** 2))
return rmse
for epoch in range(epochs):
for idx in range(num_batches):
minibatch = ratings.iloc[idx * batch_size:(idx + 1) * batch_size]
# deduct 1 as user ids are 1-indexed, but array is 0-indexed
user_embeds = user_factors[minibatch['user'].values - 1]
item_embeds = item_factors[minibatch['item'].values - 1]
user_grads, item_grads = compute_gradients(minibatch['rating'].values,
user_embeds,
item_embeds)
# update user and item factors
user_factors[minibatch['user'].values - 1] -= learning_rate * user_grads
item_factors[minibatch['item'].values - 1] -= learning_rate * item_grads
if not idx % 300:
rmse = get_rmse(minibatch['rating'].values,
user_embeds,
item_embeds)
rmse_test = get_rmse(data.test_ratings['rating'].values,
user_factors[data.test_ratings['user'].values - 1],
item_factors[data.test_ratings['user'].values - 1])
rmse_trace.append(rmse)
rmse_test_trace.append(rmse_test)
print(f"Epoch: {epoch:02d} - Batch: {idx:04d}, RMSE: {rmse:.3f}, Test RMSE: {rmse_test:.3f}")
plt.figure(figsize=(12,8))
plt.plot(range(len(rmse_trace)), rmse_trace, 'b--', label='Train')
plt.plot(range(len(rmse_test_trace)), rmse_test_trace, 'g--', label='Test')
plt.grid(True)
plt.legend()
plt.xlabel('Epoch')
plt.ylabel('RMSE')
plt.show()
```
### Using the model for Recommendations
We have now created a model to describe users and items in terms of latent vectors. We fitted them to reconstruct ratings by multiplication. So for obtaining recommendations we simply multiply user-item latent vectors we are interested in and see favorable combinations where predicted ratings, i.e. the products, are rather high.
Thus, before writing the `get_recommendations` we first implement `get_prediction`.

**Task:** Implement `get_prediction` for predicting ratings for a user and all items or a set of provided items. Remember to remove _known positives_.
```
def get_prediction(user,
user_ratings: Dict[int, Dict[int, float]] = user_ratings,
items: np.array = None,
data: object = data,
user_factors: np.array = user_factors,
item_factors: np.array = item_factors,
remove_known_pos: bool = True) -> Dict[int, Dict[str, float]]:
if items is None:
if remove_known_pos:
# Predict from unobserved items
known_items = np.array(list(user_ratings[user].keys()))
items = np.setdiff1d(data.items, known_items)
else:
items = np.array(data.items)
if type(items) == np.int64:
items = np.array([items])
user_embed = user_factors[user - 1].reshape(1, -1)
item_embeds = item_factors[items - 1].reshape(len(items), -1)
# use array-broadcasting
preds = np.sum(user_embed * item_embeds, axis=1)
sorting = np.argsort(preds)[::-1]
preds = {item: {'pred': pred} for item, pred in
zip(items[sorting], preds[sorting])}
return preds
item_predictions = get_prediction(1)
list(item_predictions.items())[:10]
def get_recommendations(user: int, N: int, remove_known_pos: bool = False) -> List[Tuple[int, Dict[str, float]]]:
predictions = get_prediction(user, remove_known_pos=remove_known_pos)
recommendations = []
for item, pred in predictions.items():
add_item = (item, pred)
recommendations.append(add_item)
if len(recommendations) == N:
break
return recommendations
recommendations = get_recommendations(1, 10)
recommendations
```
### Evaluation
```
N = 10
relevant_items = get_relevant_items(data.test_ratings)
users = relevant_items.keys()
prec_at_N = dict.fromkeys(data.users)
for user in users:
recommendations = get_recommendations(user, N, remove_known_pos=True)
recommendations = [val[0] for val in recommendations]
hits = np.intersect1d(recommendations,
relevant_items[user])
prec_at_N[user] = len(hits)/N
recommendations
np.mean([val for val in prec_at_N.values() if val is not None])
```
|
github_jupyter
|
from collections import OrderedDict
import itertools
from typing import Dict, List, Tuple
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from recsys_training.data import Dataset
from recsys_training.evaluation import get_relevant_items
ml100k_ratings_filepath = '../../data/raw/ml-100k/u.data'
data = Dataset(ml100k_ratings_filepath)
data.rating_split(seed=42)
user_ratings = data.get_user_ratings()
seed = 42
m = data.n_users
n = data.n_items
d = 8
np.random.seed(seed)
user_factors = np.random.normal(0, 1, (m, d))
item_factors = np.random.normal(0, 1, (n, d))
ratings = data.train_ratings[['user', 'item', 'rating']].sample(frac=1, random_state=seed)
np.dot(user_factors[1], item_factors[233])
epochs = 10
batch_size = 64
learning_rate = 0.01
num_batches = int(np.ceil(len(ratings) / batch_size))
rmse_trace = []
rmse_test_trace = []
def compute_gradients(ratings: np.array,
u: np.array,
v: np.array) -> Tuple[np.array, np.array]:
preds = np.sum(u * v, axis=1)
error = (ratings - preds).reshape(-1, 1)
u_grad = -2 * error * v
v_grad = -2 * error * u
return u_grad, v_grad
def get_rmse(rating, u, v) -> float:
pred = np.sum(u * v, axis=1)
error = rating - pred
rmse = np.sqrt(np.mean(error ** 2))
return rmse
for epoch in range(epochs):
for idx in range(num_batches):
minibatch = ratings.iloc[idx * batch_size:(idx + 1) * batch_size]
# deduct 1 as user ids are 1-indexed, but array is 0-indexed
user_embeds = user_factors[minibatch['user'].values - 1]
item_embeds = item_factors[minibatch['item'].values - 1]
user_grads, item_grads = compute_gradients(minibatch['rating'].values,
user_embeds,
item_embeds)
# update user and item factors
user_factors[minibatch['user'].values - 1] -= learning_rate * user_grads
item_factors[minibatch['item'].values - 1] -= learning_rate * item_grads
if not idx % 300:
rmse = get_rmse(minibatch['rating'].values,
user_embeds,
item_embeds)
rmse_test = get_rmse(data.test_ratings['rating'].values,
user_factors[data.test_ratings['user'].values - 1],
item_factors[data.test_ratings['user'].values - 1])
rmse_trace.append(rmse)
rmse_test_trace.append(rmse_test)
print(f"Epoch: {epoch:02d} - Batch: {idx:04d}, RMSE: {rmse:.3f}, Test RMSE: {rmse_test:.3f}")
plt.figure(figsize=(12,8))
plt.plot(range(len(rmse_trace)), rmse_trace, 'b--', label='Train')
plt.plot(range(len(rmse_test_trace)), rmse_test_trace, 'g--', label='Test')
plt.grid(True)
plt.legend()
plt.xlabel('Epoch')
plt.ylabel('RMSE')
plt.show()
def get_prediction(user,
user_ratings: Dict[int, Dict[int, float]] = user_ratings,
items: np.array = None,
data: object = data,
user_factors: np.array = user_factors,
item_factors: np.array = item_factors,
remove_known_pos: bool = True) -> Dict[int, Dict[str, float]]:
if items is None:
if remove_known_pos:
# Predict from unobserved items
known_items = np.array(list(user_ratings[user].keys()))
items = np.setdiff1d(data.items, known_items)
else:
items = np.array(data.items)
if type(items) == np.int64:
items = np.array([items])
user_embed = user_factors[user - 1].reshape(1, -1)
item_embeds = item_factors[items - 1].reshape(len(items), -1)
# use array-broadcasting
preds = np.sum(user_embed * item_embeds, axis=1)
sorting = np.argsort(preds)[::-1]
preds = {item: {'pred': pred} for item, pred in
zip(items[sorting], preds[sorting])}
return preds
item_predictions = get_prediction(1)
list(item_predictions.items())[:10]
def get_recommendations(user: int, N: int, remove_known_pos: bool = False) -> List[Tuple[int, Dict[str, float]]]:
predictions = get_prediction(user, remove_known_pos=remove_known_pos)
recommendations = []
for item, pred in predictions.items():
add_item = (item, pred)
recommendations.append(add_item)
if len(recommendations) == N:
break
return recommendations
recommendations = get_recommendations(1, 10)
recommendations
N = 10
relevant_items = get_relevant_items(data.test_ratings)
users = relevant_items.keys()
prec_at_N = dict.fromkeys(data.users)
for user in users:
recommendations = get_recommendations(user, N, remove_known_pos=True)
recommendations = [val[0] for val in recommendations]
hits = np.intersect1d(recommendations,
relevant_items[user])
prec_at_N[user] = len(hits)/N
recommendations
np.mean([val for val in prec_at_N.values() if val is not None])
| 0.655005 | 0.983231 |
<a href="http://cocl.us/pytorch_link_top">
<img src="https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/DL0110EN/notebook_images%20/Pytochtop.png" width="750" alt="IBM Product " />
</a>
<img src="https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/DL0110EN/notebook_images%20/cc-logo-square.png" width="200" alt="cognitiveclass.ai logo" />
<h1>Linear regression: Training and Validation Data</h1>
<h2>Table of Contents</h2>
<p>In this lab, you will perform early stopping and save the model that minimizes the total loss on the validation data for every iteration. <br><i>( <b>Note:</b> Early Stopping is a general term. We will focus on the variant where we use the validation data. You can also use a pre-determined number iterations</i>. )</p>
<ul>
<li><a href="#Makeup_Data">Make Some Data</a></li>
<li><a href="#LR_Loader_Cost">Create a Linear Regression Object, Data Loader and Criterion Function</a></li>
<li><a href="#Stop">Early Stopping and Saving the Mode</a></li>
<li><a href="#Result">View Results</a></li>
</ul>
<p>Estimated Time Needed: <strong>15 min</strong></p>
<hr>
<h2>Preparation</h2>
We'll need the following libraries, and set the random seed.
```
# Import the libraries and set random seed
from torch import nn
import torch
import numpy as np
import matplotlib.pyplot as plt
from torch import nn,optim
from torch.utils.data import Dataset, DataLoader
torch.manual_seed(1)
```
<!--Empty Space for separating topics-->
<h2 id="#Makeup_Data">Make Some Data</h2>
First let's create some artificial data, in a dataset class. The class will include the option to produce training data or validation data. The training data includes outliers.
```
# Create Data Class
class Data(Dataset):
# Constructor
def __init__(self, train = True):
if train == True:
self.x = torch.arange(-3, 3, 0.1).view(-1, 1)
self.f = -3 * self.x + 1
self.y = self.f + 0.1 * torch.randn(self.x.size())
self.len = self.x.shape[0]
if train == True:
self.y[50:] = 20
else:
self.x = torch.arange(-3, 3, 0.1).view(-1, 1)
self.y = -3 * self.x + 1
self.len = self.x.shape[0]
# Getter
def __getitem__(self, index):
return self.x[index], self.y[index]
# Get Length
def __len__(self):
return self.len
```
We create two objects, one that contains training data and a second that contains validation data, we will assume the training data has the outliers.
```
#Create train_data object and val_data object
train_data = Data()
val_data = Data(train = False)
```
We overlay the training points in red over the function that generated the data. Notice the outliers are at x=-3 and around x=2
```
# Plot the training data points
plt.plot(train_data.x.numpy(), train_data.y.numpy(), 'xr')
plt.plot(train_data.x.numpy(), train_data.f.numpy())
plt.show()
```
<!--Empty Space for separating topics-->
<h2 id="LR_Loader_Cost">Create a Linear Regression Class, Object, Data Loader, Criterion Function</h2>
Create linear regression model class.
```
# Create linear regression model class
from torch import nn
class linear_regression(nn.Module):
# Constructor
def __init__(self, input_size, output_size):
super(linear_regression, self).__init__()
self.linear = nn.Linear(input_size, output_size)
# Predition
def forward(self, x):
yhat = self.linear(x)
return yhat
```
Create the model object
```
# Create the model object
model = linear_regression(1, 1)
```
We create the optimizer, the criterion function and a Data Loader object.
```
# Create optimizer, cost function and data loader object
optimizer = optim.SGD(model.parameters(), lr = 0.1)
criterion = nn.MSELoss()
trainloader = DataLoader(dataset = train_data, batch_size = 1)
```
<!--Empty Space for separating topics-->
<h2 id="Stop">Early Stopping and Saving the Mode</h2>
Run several epochs of gradient descent and save the model that performs best on the validation data.
```
# Train the model
LOSS_TRAIN = []
LOSS_VAL = []
n=1;
min_loss = 1000
def train_model_early_stopping(epochs, min_loss):
for epoch in range(epochs):
for x, y in trainloader:
yhat = model(x)
loss = criterion(yhat, y)
optimizer.zero_grad()
loss.backward()
optimizer.step()
loss_train = criterion(model(train_data.x), train_data.y).data
loss_val = criterion(model(val_data.x), val_data.y).data
LOSS_TRAIN.append(loss_train)
LOSS_VAL.append(loss_val)
if loss_val < min_loss:
value = epoch
min_loss = loss_val
torch.save(model.state_dict(), 'best_model.pt')
train_model_early_stopping(20, min_loss)
```
<!--Empty Space for separating topics-->
<h2 id="Result">View Results</h2>
View the loss for every iteration on the training set and validation set.
```
# Plot the loss
plt.plot(LOSS_TRAIN, label = 'training loss')
plt.plot(LOSS_VAL, label = 'validation loss')
plt.xlabel("epochs")
plt.ylabel("Loss")
plt.legend(loc = 'upper right')
plt.show()
```
We will create a new linear regression object; we will use the parameters saved in the early stopping. The model must be the same input dimension and output dimension as the original model.
```
# Create a new linear regression model object
model_best = linear_regression(1, 1)
```
Load the model parameters <code>torch.load()</code>, then assign them to the object <code>model_best</code> using the method <code>load_state_dict</code>.
```
# Assign the best model to model_best
model_best.load_state_dict(torch.load('best_model.pt'))
```
Let's compare the prediction from the model obtained using early stopping and the model derived from using the maximum number of iterations.
```
plt.plot(model_best(val_data.x).data.numpy(), label = 'best model')
plt.plot(model(val_data.x).data.numpy(), label = 'maximum iterations')
plt.plot(val_data.y.numpy(), 'rx', label = 'true line')
plt.legend()
plt.show()
```
We can see the model obtained via early stopping fits the data points much better. For more variations of early stopping see:
Prechelt, Lutz.<i> "Early stopping-but when?." Neural Networks: Tricks of the trade. Springer, Berlin, Heidelberg, 1998. 55-69</i>.
<!--Empty Space for separating topics-->
<a href="http://cocl.us/pytorch_link_bottom">
<img src="https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/DL0110EN/notebook_images%20/notebook_bottom%20.png" width="750" alt="PyTorch Bottom" />
</a>
<h2>About the Authors:</h2>
<a href="https://www.linkedin.com/in/joseph-s-50398b136/">Joseph Santarcangelo</a> has a PhD in Electrical Engineering, his research focused on using machine learning, signal processing, and computer vision to determine how videos impact human cognition. Joseph has been working for IBM since he completed his PhD.
Other contributors: <a href="https://www.linkedin.com/in/michelleccarey/">Michelle Carey</a>, <a href="www.linkedin.com/in/jiahui-mavis-zhou-a4537814a">Mavis Zhou</a>
<hr>
Copyright © 2018 <a href="cognitiveclass.ai?utm_source=bducopyrightlink&utm_medium=dswb&utm_campaign=bdu">cognitiveclass.ai</a>. This notebook and its source code are released under the terms of the <a href="https://bigdatauniversity.com/mit-license/">MIT License</a>.
|
github_jupyter
|
# Import the libraries and set random seed
from torch import nn
import torch
import numpy as np
import matplotlib.pyplot as plt
from torch import nn,optim
from torch.utils.data import Dataset, DataLoader
torch.manual_seed(1)
# Create Data Class
class Data(Dataset):
# Constructor
def __init__(self, train = True):
if train == True:
self.x = torch.arange(-3, 3, 0.1).view(-1, 1)
self.f = -3 * self.x + 1
self.y = self.f + 0.1 * torch.randn(self.x.size())
self.len = self.x.shape[0]
if train == True:
self.y[50:] = 20
else:
self.x = torch.arange(-3, 3, 0.1).view(-1, 1)
self.y = -3 * self.x + 1
self.len = self.x.shape[0]
# Getter
def __getitem__(self, index):
return self.x[index], self.y[index]
# Get Length
def __len__(self):
return self.len
#Create train_data object and val_data object
train_data = Data()
val_data = Data(train = False)
# Plot the training data points
plt.plot(train_data.x.numpy(), train_data.y.numpy(), 'xr')
plt.plot(train_data.x.numpy(), train_data.f.numpy())
plt.show()
# Create linear regression model class
from torch import nn
class linear_regression(nn.Module):
# Constructor
def __init__(self, input_size, output_size):
super(linear_regression, self).__init__()
self.linear = nn.Linear(input_size, output_size)
# Predition
def forward(self, x):
yhat = self.linear(x)
return yhat
# Create the model object
model = linear_regression(1, 1)
# Create optimizer, cost function and data loader object
optimizer = optim.SGD(model.parameters(), lr = 0.1)
criterion = nn.MSELoss()
trainloader = DataLoader(dataset = train_data, batch_size = 1)
# Train the model
LOSS_TRAIN = []
LOSS_VAL = []
n=1;
min_loss = 1000
def train_model_early_stopping(epochs, min_loss):
for epoch in range(epochs):
for x, y in trainloader:
yhat = model(x)
loss = criterion(yhat, y)
optimizer.zero_grad()
loss.backward()
optimizer.step()
loss_train = criterion(model(train_data.x), train_data.y).data
loss_val = criterion(model(val_data.x), val_data.y).data
LOSS_TRAIN.append(loss_train)
LOSS_VAL.append(loss_val)
if loss_val < min_loss:
value = epoch
min_loss = loss_val
torch.save(model.state_dict(), 'best_model.pt')
train_model_early_stopping(20, min_loss)
# Plot the loss
plt.plot(LOSS_TRAIN, label = 'training loss')
plt.plot(LOSS_VAL, label = 'validation loss')
plt.xlabel("epochs")
plt.ylabel("Loss")
plt.legend(loc = 'upper right')
plt.show()
# Create a new linear regression model object
model_best = linear_regression(1, 1)
# Assign the best model to model_best
model_best.load_state_dict(torch.load('best_model.pt'))
plt.plot(model_best(val_data.x).data.numpy(), label = 'best model')
plt.plot(model(val_data.x).data.numpy(), label = 'maximum iterations')
plt.plot(val_data.y.numpy(), 'rx', label = 'true line')
plt.legend()
plt.show()
| 0.950146 | 0.959307 |
# Performance Evaluation on PWCLeaderboards dataset
This notebook runs AxCell on the **PWCLeaderboards** dataset.
For the pipeline to work we need a running elasticsearch instance. Run `docker-compose up -d` from the `axcell` repository to start a new instance.
```
from axcell.helpers.datasets import read_tables_annotations
from pathlib import Path
V1_URL = 'https://github.com/paperswithcode/axcell/releases/download/v1.0/'
PWC_LEADERBOARDS_URL = V1_URL + 'pwc-leaderboards.json.xz'
pwc_leaderboards = read_tables_annotations(PWC_LEADERBOARDS_URL)
# path to root directory containing e-prints
PWC_LEADERBOARDS_ROOT_PATH = Path('pwc-leaderboards')
PWC_LEADERBOARDS_ROOT_PATH = Path.home() / 'data/pwc-leaderboards'
SOURCES_PATH = PWC_LEADERBOARDS_ROOT_PATH / 'sources'
from axcell.helpers.paper_extractor import PaperExtractor
extract = PaperExtractor(PWC_LEADERBOARDS_ROOT_PATH)
%%time
from joblib import delayed, Parallel
# access extract from the global context to avoid serialization
def extract_single(file): return extract(file)
files = sorted([path for path in SOURCES_PATH.glob('**/*') if path.is_file()])
statuses = Parallel(backend='multiprocessing', n_jobs=-1)(delayed(extract_single)(file) for file in files)
assert statuses == ["success"] * 731
```
Download and unpack the archive with trained models (table type classifier, table segmentation), taxonomy and abbreviations.
```
MODELS_URL = V1_URL + 'models.tar.xz'
MODELS_ARCHIVE = 'models.tar.xz'
MODELS_PATH = Path('models')
from fastai.core import download_url
import tarfile
download_url(MODELS_URL, MODELS_ARCHIVE)
with tarfile.open(MODELS_ARCHIVE, 'r:*') as archive:
archive.extractall()
from axcell.helpers.results_extractor import ResultsExtractor
extract_results = ResultsExtractor(MODELS_PATH)
import pandas as pd
papers = []
our_taxonomy = set(extract_results.taxonomy.taxonomy)
gold_records = []
for _, paper in pwc_leaderboards.iterrows():
for table in paper.tables:
for record in table['records']:
r = dict(record)
r['arxiv_id'] = paper.arxiv_id
tdm = (record['task'], record['dataset'], record['metric'])
if tdm in our_taxonomy:
gold_records.append(r)
papers.append(paper.arxiv_id)
gold_records = pd.DataFrame(gold_records)
papers = sorted(set(papers))
from axcell.data.paper_collection import PaperCollection
pc = PaperCollection.from_files(PWC_LEADERBOARDS_ROOT_PATH / "papers")
pc = PaperCollection([pc.get_by_id(p) for p in papers])
%%time
from joblib import delayed, Parallel
def process_single(index):
extract_results = ResultsExtractor(MODELS_PATH)
return extract_results(pc[index])
results = Parallel(backend='multiprocessing', n_jobs=-1)(delayed(process_single)(index) for index in range(len(pc)))
predicted_records = []
for paper, records in zip(pc, results):
r = records.copy()
r['arxiv_id'] = paper.arxiv_no_version
predicted_records.append(r)
predicted_records = pd.concat(predicted_records)
predicted_records.to_json('axcell-predictions-on-pwc-leaderboards.json.xz', orient='records')
from axcell.helpers.evaluate import evaluate
evaluate(predicted_records, gold_records).style.format('{:.2%}')
```
|
github_jupyter
|
from axcell.helpers.datasets import read_tables_annotations
from pathlib import Path
V1_URL = 'https://github.com/paperswithcode/axcell/releases/download/v1.0/'
PWC_LEADERBOARDS_URL = V1_URL + 'pwc-leaderboards.json.xz'
pwc_leaderboards = read_tables_annotations(PWC_LEADERBOARDS_URL)
# path to root directory containing e-prints
PWC_LEADERBOARDS_ROOT_PATH = Path('pwc-leaderboards')
PWC_LEADERBOARDS_ROOT_PATH = Path.home() / 'data/pwc-leaderboards'
SOURCES_PATH = PWC_LEADERBOARDS_ROOT_PATH / 'sources'
from axcell.helpers.paper_extractor import PaperExtractor
extract = PaperExtractor(PWC_LEADERBOARDS_ROOT_PATH)
%%time
from joblib import delayed, Parallel
# access extract from the global context to avoid serialization
def extract_single(file): return extract(file)
files = sorted([path for path in SOURCES_PATH.glob('**/*') if path.is_file()])
statuses = Parallel(backend='multiprocessing', n_jobs=-1)(delayed(extract_single)(file) for file in files)
assert statuses == ["success"] * 731
MODELS_URL = V1_URL + 'models.tar.xz'
MODELS_ARCHIVE = 'models.tar.xz'
MODELS_PATH = Path('models')
from fastai.core import download_url
import tarfile
download_url(MODELS_URL, MODELS_ARCHIVE)
with tarfile.open(MODELS_ARCHIVE, 'r:*') as archive:
archive.extractall()
from axcell.helpers.results_extractor import ResultsExtractor
extract_results = ResultsExtractor(MODELS_PATH)
import pandas as pd
papers = []
our_taxonomy = set(extract_results.taxonomy.taxonomy)
gold_records = []
for _, paper in pwc_leaderboards.iterrows():
for table in paper.tables:
for record in table['records']:
r = dict(record)
r['arxiv_id'] = paper.arxiv_id
tdm = (record['task'], record['dataset'], record['metric'])
if tdm in our_taxonomy:
gold_records.append(r)
papers.append(paper.arxiv_id)
gold_records = pd.DataFrame(gold_records)
papers = sorted(set(papers))
from axcell.data.paper_collection import PaperCollection
pc = PaperCollection.from_files(PWC_LEADERBOARDS_ROOT_PATH / "papers")
pc = PaperCollection([pc.get_by_id(p) for p in papers])
%%time
from joblib import delayed, Parallel
def process_single(index):
extract_results = ResultsExtractor(MODELS_PATH)
return extract_results(pc[index])
results = Parallel(backend='multiprocessing', n_jobs=-1)(delayed(process_single)(index) for index in range(len(pc)))
predicted_records = []
for paper, records in zip(pc, results):
r = records.copy()
r['arxiv_id'] = paper.arxiv_no_version
predicted_records.append(r)
predicted_records = pd.concat(predicted_records)
predicted_records.to_json('axcell-predictions-on-pwc-leaderboards.json.xz', orient='records')
from axcell.helpers.evaluate import evaluate
evaluate(predicted_records, gold_records).style.format('{:.2%}')
| 0.667906 | 0.752559 |
## Markov Chain Monte Carlo
Suppose we wish to draw samples from the posterior distribution
$$
p(x) = \int_\theta p(x|\theta) p (\theta) d \theta
$$
and that the computation of the normalization factor is intractable, due to the high dimensionality of the problem.
**Markov Chain Monte Carlo** is a sampling method which scales well will the dimensionality of the sample space. Instead of directly sampling from $p(x)$, we sample from a Markov chain whose stationary distribution equals $p(x)$. The longer the chains, the more closely the distribution of the sample matches the target distribution.
### Hamiltonian Monte Carlo
### Example
Let's go back to the example from notebook 02:
$$weight \, | \, guess \sim \mathcal{N}(guess, 1)$$
$$ measurement \, | \, guess, weight \sim \mathcal{N}(weight, 0.75^2) $$
```
import torch
import pyro
import pyro.distributions as dist
pyro.set_rng_seed(1)
# define model
def scale(guess):
weight = pyro.sample("weight", dist.Normal(guess, 1.0))
measurement = pyro.sample("measurement", dist.Normal(weight, 0.75))
return measurement
```
Suppose that we observe a measurement of the object corresponding to 14 kg. We want to sample from the distribution of the weight given both the observation and an input knowledge `guess = 8.5`. In other words, we wish to infer the distribution
$$weight \, | \, guess, measurement=9.5 \sim ?$$
Pyro provides a method called `pyro.condition` that takes a model and a dictionary of observations and returns a new model which is fixed on the measurement observation.
```
# condition the model on a single observation
conditioned_scale = pyro.condition(scale, data={"measurement": torch.tensor(9.5)})
```
`conditioned_scale()` model could be equivalently defined as follows:
```
# using obs parameter
def conditioned_scale(guess):
weight = pyro.sample("weight", dist.Normal(guess, 1.))
measurement = pyro.sample("measurement", dist.Normal(weight, 1.), obs=9.5)
return measurement
```
Now that we have conditioned on an observation of measurement, we can perform inference.
This is an example of how you would write a posterior distribution on the conditioned scale model using MCMC.
```
from pyro.infer.mcmc import MCMC, HMC
hmc_kernel = HMC(model=conditioned_scale, step_size=0.9, num_steps=4)
mcmc = MCMC(hmc_kernel, num_samples=1000, warmup_steps=50)
# guess prior weight
data = 10.
posterior = mcmc.run(data)
mcmc.get_samples()['weight'].mean(0)
import matplotlib.pyplot as plt
import seaborn as sns
x = mcmc.get_samples()['weight']
sns.distplot(x)
plt.title("P(weight | measurement = 14)")
plt.xlabel("Weight")
plt.ylabel("#")
```
### Posterior predictive checking
## References
- [tutorial on deep probabilistic modeling](https://bookdown.org/robertness/causalml/docs/tutorial-on-deep-probabilitic-modeling-with-pyro.html)
|
github_jupyter
|
import torch
import pyro
import pyro.distributions as dist
pyro.set_rng_seed(1)
# define model
def scale(guess):
weight = pyro.sample("weight", dist.Normal(guess, 1.0))
measurement = pyro.sample("measurement", dist.Normal(weight, 0.75))
return measurement
# condition the model on a single observation
conditioned_scale = pyro.condition(scale, data={"measurement": torch.tensor(9.5)})
# using obs parameter
def conditioned_scale(guess):
weight = pyro.sample("weight", dist.Normal(guess, 1.))
measurement = pyro.sample("measurement", dist.Normal(weight, 1.), obs=9.5)
return measurement
from pyro.infer.mcmc import MCMC, HMC
hmc_kernel = HMC(model=conditioned_scale, step_size=0.9, num_steps=4)
mcmc = MCMC(hmc_kernel, num_samples=1000, warmup_steps=50)
# guess prior weight
data = 10.
posterior = mcmc.run(data)
mcmc.get_samples()['weight'].mean(0)
import matplotlib.pyplot as plt
import seaborn as sns
x = mcmc.get_samples()['weight']
sns.distplot(x)
plt.title("P(weight | measurement = 14)")
plt.xlabel("Weight")
plt.ylabel("#")
| 0.737536 | 0.991178 |
```
import os
import cv2
import warnings
import numpy as np
import pandas as pd
import seaborn as sns
import tensorflow as tf
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.metrics import confusion_matrix
from keras import backend as K
from keras import metrics
from sklearn.metrics import fbeta_score
from keras import optimizers
from keras.models import Sequential
from keras.preprocessing.image import ImageDataGenerator
from keras.layers import Dense, Dropout, Flatten, Conv2D, MaxPool2D, Activation, BatchNormalization
# Set seeds to make the experiment more reproducible.
from tensorflow import set_random_seed
from numpy.random import seed
set_random_seed(0)
seed(0)
%matplotlib inline
sns.set(style="whitegrid")
warnings.filterwarnings("ignore")
train = pd.read_csv('../input/train.csv')
labels = pd.read_csv('../input/labels.csv')
test = pd.read_csv('../input/sample_submission.csv')
print('Number of train samples: ', train.shape[0])
print('Number of test samples: ', test.shape[0])
print('Number of labels: ', labels.shape[0])
display(train.head())
display(labels.head())
train["id"] = train["id"].apply(lambda x:x+".png")
test["id"] = test["id"].apply(lambda x:x+".png")
```
### Model
```
# Model parameters
BATCH_SIZE = 64
EPOCHS = 50
LEARNING_RATE = 0.0001
HEIGHT = 64
WIDTH = 64
CANAL = 3
N_CLASSES = labels.shape[0]
classes = list(map(str, range(N_CLASSES)))
train_datagen=ImageDataGenerator(rescale=1./255, validation_split=0.2)
test_datagen = ImageDataGenerator(rescale=1./255)
train_generator=train_datagen.flow_from_dataframe(
dataframe=train,
directory="../input/train",
x_col="id",
y_col="attribute_ids",
batch_size=BATCH_SIZE,
shuffle=True,
class_mode="categorical",
classes=classes,
target_size=(HEIGHT, WIDTH),
subset='training')
valid_generator=train_datagen.flow_from_dataframe(
dataframe=train,
directory="../input/train",
x_col="id",
y_col="attribute_ids",
batch_size=BATCH_SIZE,
shuffle=True,
class_mode="categorical",
classes=classes,
target_size=(HEIGHT, WIDTH),
subset='validation')
test_generator = test_datagen.flow_from_dataframe(
dataframe=test,
directory = "../input/test",
x_col="id",
target_size=(HEIGHT, WIDTH),
batch_size=1,
shuffle=False,
class_mode=None)
def f2_score_thr(threshold=0.5):
def f2_score(y_true, y_pred):
beta = 2
y_pred = K.cast(K.greater(K.clip(y_pred, 0, 1), threshold), K.floatx())
true_positives = K.sum(K.clip(y_true * y_pred, 0, 1), axis=1)
predicted_positives = K.sum(K.clip(y_pred, 0, 1), axis=1)
possible_positives = K.sum(K.clip(y_true, 0, 1), axis=1)
precision = true_positives / (predicted_positives + K.epsilon())
recall = true_positives / (possible_positives + K.epsilon())
return K.mean(((1+beta**2)*precision*recall) / ((beta**2)*precision+recall+K.epsilon()))
return f2_score
model = Sequential()
model.add(Conv2D(32, (3, 3), padding='same', input_shape=(HEIGHT, WIDTH, CANAL)))
model.add(Activation('relu'))
model.add(Conv2D(32, (3, 3)))
model.add(Activation('relu'))
model.add(MaxPool2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
model.add(Conv2D(64, (3, 3), padding='same'))
model.add(Activation('relu'))
model.add(Conv2D(64, (3, 3)))
model.add(Activation('relu'))
model.add(MaxPool2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
model.add(Flatten())
model.add(Dense(1024))
model.add(Activation('relu'))
model.add(Dropout(0.5))
model.add(Dense(N_CLASSES, activation="sigmoid"))
optimizer = optimizers.adam(lr=LEARNING_RATE)
thresholds = [0.15, 0.2, 0.25, 0.3, 0.4, 0.5]
metrics = ["accuracy", "categorical_accuracy", f2_score_thr(0.15), f2_score_thr(0.2),
f2_score_thr(0.25), f2_score_thr(0.3), f2_score_thr(0.4), f2_score_thr(0.5)]
model.compile(optimizer=optimizer, loss="binary_crossentropy", metrics=metrics)
STEP_SIZE_TRAIN = train_generator.n//train_generator.batch_size
STEP_SIZE_VALID = valid_generator.n//valid_generator.batch_size
history = model.fit_generator(generator=train_generator,
steps_per_epoch=STEP_SIZE_TRAIN,
validation_data=valid_generator,
validation_steps=STEP_SIZE_VALID,
epochs=EPOCHS,
verbose=2)
```
### Model graph loss
```
sns.set_style("whitegrid")
fig, (ax1, ax2) = plt.subplots(1, 2, sharex='col', figsize=(20,7))
ax1.plot(history.history['loss'], label='Train loss')
ax1.plot(history.history['val_loss'], label='Validation loss')
ax1.legend(loc='best')
ax1.set_title('Loss')
ax2.plot(history.history['acc'], label='Train Accuracy')
ax2.plot(history.history['val_acc'], label='Validation accuracy')
ax2.legend(loc='best')
ax2.set_title('Accuracy')
plt.xlabel('Epochs')
sns.despine()
plt.show()
fig, axes = plt.subplots(3, 2, sharex='col', figsize=(20,7))
axes[0][0].plot(history.history['f2_score'], label='Train F2 Score')
axes[0][0].plot(history.history['val_f2_score'], label='Validation F2 Score')
axes[0][0].legend(loc='best')
axes[0][0].set_title('F2 Score threshold 0.15')
axes[0][1].plot(history.history['f2_score_1'], label='Train F2 Score')
axes[0][1].plot(history.history['val_f2_score_1'], label='Validation F2 Score')
axes[0][1].legend(loc='best')
axes[0][1].set_title('F2 Score threshold 0.2')
axes[1][0].plot(history.history['f2_score_2'], label='Train F2 Score')
axes[1][0].plot(history.history['val_f2_score_2'], label='Validation F2 Score')
axes[1][0].legend(loc='best')
axes[1][0].set_title('F2 Score threshold 0.25')
axes[1][1].plot(history.history['f2_score_3'], label='Train F2 Score')
axes[1][1].plot(history.history['val_f2_score_3'], label='Validation F2 Score')
axes[1][1].legend(loc='best')
axes[1][1].set_title('F2 Score threshold 0.3')
axes[2][0].plot(history.history['f2_score_4'], label='Train F2 Score')
axes[2][0].plot(history.history['val_f2_score_4'], label='Validation F2 Score')
axes[2][0].legend(loc='best')
axes[2][0].set_title('F2 Score threshold 0.4')
axes[2][1].plot(history.history['f2_score_5'], label='Train F2 Score')
axes[2][1].plot(history.history['val_f2_score_5'], label='Validation F2 Score')
axes[2][1].legend(loc='best')
axes[2][1].set_title('F2 Score threshold 0.5')
plt.xlabel('Epochs')
sns.despine()
plt.show()
```
### Find best threshold value
```
best_thr = 0
best_thr_val = history.history['val_f2_score'][-1]
for i in range(1, len(metrics)-2):
if best_thr_val < history.history['val_f2_score_%s' % i][-1]:
best_thr_val = history.history['val_f2_score_%s' % i][-1]
best_thr = 1
threshold = thresholds[best_thr]
```
### Apply model to test set and output predictions
```
test_generator.reset()
STEP_SIZE_TEST = test_generator.n//test_generator.batch_size
preds = model.predict_generator(test_generator, steps=STEP_SIZE_TEST)
labels = (train_generator.class_indices)
labels = dict((v,k) for k,v in labels.items())
predictions = []
for pred_ar in preds:
valid = ''
for idx, pred in enumerate(pred_ar):
if pred > threshold:
if len(valid) == 0:
valid += labels[idx]
else:
valid += (' %s' % labels[idx])
if len(valid) == 0:
valid = np.argmax(pred_ar)
predictions.append(valid)
filenames = test_generator.filenames
results = pd.DataFrame({'id':filenames, 'attribute_ids':predictions})
results['id'] = results['id'].map(lambda x: str(x)[:-4])
results.to_csv('submission.csv',index=False)
results.head(10)
```
|
github_jupyter
|
import os
import cv2
import warnings
import numpy as np
import pandas as pd
import seaborn as sns
import tensorflow as tf
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.metrics import confusion_matrix
from keras import backend as K
from keras import metrics
from sklearn.metrics import fbeta_score
from keras import optimizers
from keras.models import Sequential
from keras.preprocessing.image import ImageDataGenerator
from keras.layers import Dense, Dropout, Flatten, Conv2D, MaxPool2D, Activation, BatchNormalization
# Set seeds to make the experiment more reproducible.
from tensorflow import set_random_seed
from numpy.random import seed
set_random_seed(0)
seed(0)
%matplotlib inline
sns.set(style="whitegrid")
warnings.filterwarnings("ignore")
train = pd.read_csv('../input/train.csv')
labels = pd.read_csv('../input/labels.csv')
test = pd.read_csv('../input/sample_submission.csv')
print('Number of train samples: ', train.shape[0])
print('Number of test samples: ', test.shape[0])
print('Number of labels: ', labels.shape[0])
display(train.head())
display(labels.head())
train["id"] = train["id"].apply(lambda x:x+".png")
test["id"] = test["id"].apply(lambda x:x+".png")
# Model parameters
BATCH_SIZE = 64
EPOCHS = 50
LEARNING_RATE = 0.0001
HEIGHT = 64
WIDTH = 64
CANAL = 3
N_CLASSES = labels.shape[0]
classes = list(map(str, range(N_CLASSES)))
train_datagen=ImageDataGenerator(rescale=1./255, validation_split=0.2)
test_datagen = ImageDataGenerator(rescale=1./255)
train_generator=train_datagen.flow_from_dataframe(
dataframe=train,
directory="../input/train",
x_col="id",
y_col="attribute_ids",
batch_size=BATCH_SIZE,
shuffle=True,
class_mode="categorical",
classes=classes,
target_size=(HEIGHT, WIDTH),
subset='training')
valid_generator=train_datagen.flow_from_dataframe(
dataframe=train,
directory="../input/train",
x_col="id",
y_col="attribute_ids",
batch_size=BATCH_SIZE,
shuffle=True,
class_mode="categorical",
classes=classes,
target_size=(HEIGHT, WIDTH),
subset='validation')
test_generator = test_datagen.flow_from_dataframe(
dataframe=test,
directory = "../input/test",
x_col="id",
target_size=(HEIGHT, WIDTH),
batch_size=1,
shuffle=False,
class_mode=None)
def f2_score_thr(threshold=0.5):
def f2_score(y_true, y_pred):
beta = 2
y_pred = K.cast(K.greater(K.clip(y_pred, 0, 1), threshold), K.floatx())
true_positives = K.sum(K.clip(y_true * y_pred, 0, 1), axis=1)
predicted_positives = K.sum(K.clip(y_pred, 0, 1), axis=1)
possible_positives = K.sum(K.clip(y_true, 0, 1), axis=1)
precision = true_positives / (predicted_positives + K.epsilon())
recall = true_positives / (possible_positives + K.epsilon())
return K.mean(((1+beta**2)*precision*recall) / ((beta**2)*precision+recall+K.epsilon()))
return f2_score
model = Sequential()
model.add(Conv2D(32, (3, 3), padding='same', input_shape=(HEIGHT, WIDTH, CANAL)))
model.add(Activation('relu'))
model.add(Conv2D(32, (3, 3)))
model.add(Activation('relu'))
model.add(MaxPool2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
model.add(Conv2D(64, (3, 3), padding='same'))
model.add(Activation('relu'))
model.add(Conv2D(64, (3, 3)))
model.add(Activation('relu'))
model.add(MaxPool2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
model.add(Flatten())
model.add(Dense(1024))
model.add(Activation('relu'))
model.add(Dropout(0.5))
model.add(Dense(N_CLASSES, activation="sigmoid"))
optimizer = optimizers.adam(lr=LEARNING_RATE)
thresholds = [0.15, 0.2, 0.25, 0.3, 0.4, 0.5]
metrics = ["accuracy", "categorical_accuracy", f2_score_thr(0.15), f2_score_thr(0.2),
f2_score_thr(0.25), f2_score_thr(0.3), f2_score_thr(0.4), f2_score_thr(0.5)]
model.compile(optimizer=optimizer, loss="binary_crossentropy", metrics=metrics)
STEP_SIZE_TRAIN = train_generator.n//train_generator.batch_size
STEP_SIZE_VALID = valid_generator.n//valid_generator.batch_size
history = model.fit_generator(generator=train_generator,
steps_per_epoch=STEP_SIZE_TRAIN,
validation_data=valid_generator,
validation_steps=STEP_SIZE_VALID,
epochs=EPOCHS,
verbose=2)
sns.set_style("whitegrid")
fig, (ax1, ax2) = plt.subplots(1, 2, sharex='col', figsize=(20,7))
ax1.plot(history.history['loss'], label='Train loss')
ax1.plot(history.history['val_loss'], label='Validation loss')
ax1.legend(loc='best')
ax1.set_title('Loss')
ax2.plot(history.history['acc'], label='Train Accuracy')
ax2.plot(history.history['val_acc'], label='Validation accuracy')
ax2.legend(loc='best')
ax2.set_title('Accuracy')
plt.xlabel('Epochs')
sns.despine()
plt.show()
fig, axes = plt.subplots(3, 2, sharex='col', figsize=(20,7))
axes[0][0].plot(history.history['f2_score'], label='Train F2 Score')
axes[0][0].plot(history.history['val_f2_score'], label='Validation F2 Score')
axes[0][0].legend(loc='best')
axes[0][0].set_title('F2 Score threshold 0.15')
axes[0][1].plot(history.history['f2_score_1'], label='Train F2 Score')
axes[0][1].plot(history.history['val_f2_score_1'], label='Validation F2 Score')
axes[0][1].legend(loc='best')
axes[0][1].set_title('F2 Score threshold 0.2')
axes[1][0].plot(history.history['f2_score_2'], label='Train F2 Score')
axes[1][0].plot(history.history['val_f2_score_2'], label='Validation F2 Score')
axes[1][0].legend(loc='best')
axes[1][0].set_title('F2 Score threshold 0.25')
axes[1][1].plot(history.history['f2_score_3'], label='Train F2 Score')
axes[1][1].plot(history.history['val_f2_score_3'], label='Validation F2 Score')
axes[1][1].legend(loc='best')
axes[1][1].set_title('F2 Score threshold 0.3')
axes[2][0].plot(history.history['f2_score_4'], label='Train F2 Score')
axes[2][0].plot(history.history['val_f2_score_4'], label='Validation F2 Score')
axes[2][0].legend(loc='best')
axes[2][0].set_title('F2 Score threshold 0.4')
axes[2][1].plot(history.history['f2_score_5'], label='Train F2 Score')
axes[2][1].plot(history.history['val_f2_score_5'], label='Validation F2 Score')
axes[2][1].legend(loc='best')
axes[2][1].set_title('F2 Score threshold 0.5')
plt.xlabel('Epochs')
sns.despine()
plt.show()
best_thr = 0
best_thr_val = history.history['val_f2_score'][-1]
for i in range(1, len(metrics)-2):
if best_thr_val < history.history['val_f2_score_%s' % i][-1]:
best_thr_val = history.history['val_f2_score_%s' % i][-1]
best_thr = 1
threshold = thresholds[best_thr]
test_generator.reset()
STEP_SIZE_TEST = test_generator.n//test_generator.batch_size
preds = model.predict_generator(test_generator, steps=STEP_SIZE_TEST)
labels = (train_generator.class_indices)
labels = dict((v,k) for k,v in labels.items())
predictions = []
for pred_ar in preds:
valid = ''
for idx, pred in enumerate(pred_ar):
if pred > threshold:
if len(valid) == 0:
valid += labels[idx]
else:
valid += (' %s' % labels[idx])
if len(valid) == 0:
valid = np.argmax(pred_ar)
predictions.append(valid)
filenames = test_generator.filenames
results = pd.DataFrame({'id':filenames, 'attribute_ids':predictions})
results['id'] = results['id'].map(lambda x: str(x)[:-4])
results.to_csv('submission.csv',index=False)
results.head(10)
| 0.717111 | 0.639018 |
```
# Make sure were on ray 1.9
from ray.data.grouped_dataset import GroupedDataset
#tag::start-ray-local[]
import ray
ray.init(num_cpus=20) # In theory auto sensed, in practice... eh
#end::start-ray-local[]
#tag::local_fun[]
def hi():
import os
import socket
return f"Running on {socket.gethostname()} in pid {os.getpid()}"
#end::local_fun[]
hi()
#tag::remote_fun[]
@ray.remote
def remote_hi():
import os
import socket
return f"Running on {socket.gethostname()} in pid {os.getpid()}"
future = remote_hi.remote()
ray.get(future)
#end::remote_fun[]
#tag::sleepy_task_hello_world[]
import timeit
def slow_task(x):
import time
time.sleep(2) # Do something sciency/business
return x
@ray.remote
def remote_task(x):
return slow_task(x)
things = range(10)
very_slow_result = map(slow_task, things)
slowish_result = map(lambda x: remote_task.remote(x), things)
slow_time = timeit.timeit(lambda: list(very_slow_result), number=1)
fast_time = timeit.timeit(lambda: list(ray.get(list(slowish_result))), number=1)
print(f"In sequence {slow_time}, in parallel {fast_time}")
#end::sleepy_task_hello_world[]
slowish_result = map(lambda x: remote_task.remote(x), things)
ray.get(list(slowish_result))
# Note: if we were on a "real" cluster we'd have to do more magic to install it on all the nodes in the cluster.
!pip install bs4
#tag::mini_crawl_task[]
@ray.remote
def crawl(url, depth=0, maxdepth=1, maxlinks=4):
links = []
link_futures = []
import requests
from bs4 import BeautifulSoup
try:
f = requests.get(url)
links += [(url, f.text)]
if (depth > maxdepth):
return links # base case
soup = BeautifulSoup(f.text, 'html.parser')
c = 0
for link in soup.find_all('a'):
try:
c = c + 1
link_futures += [crawl.remote(link["href"], depth=(depth+1), maxdepth=maxdepth)]
# Don't branch too much were still in local mode and the web is big
if c > maxlinks:
break
except:
pass
for r in ray.get(link_futures):
links += r
return links
except requests.exceptions.InvalidSchema:
return [] # Skip non-web links
except requests.exceptions.MissingSchema:
return [] # Skip non-web links
ray.get(crawl.remote("http://holdenkarau.com/"))
#end::mini_crawl_task[]
#tag::actor[]
@ray.remote
class HelloWorld(object):
def __init__(self):
self.value = 0
def greet(self):
self.value += 1
return f"Hi user #{self.value}"
# Make an instance of the actor
hello_actor = HelloWorld.remote()
# Call the actor
print(ray.get(hello_actor.greet.remote()))
print(ray.get(hello_actor.greet.remote()))
#end::actor[]
#tag::ds[]
# Create a Dataset of URLS objects. We could also load this from a text file with ray.data.read_text()
urls = ray.data.from_items([
"https://github.com/scalingpythonml/scalingpythonml",
"https://github.com/ray-project/ray"])
def fetch_page(url):
import requests
f = requests.get(url)
return f.text
pages = urls.map(fetch_page)
# Look at a page to make sure it worked
pages.take(1)
#end:ds[]
#tag::ray_wordcount_on_ds[]
words = pages.flat_map(lambda x: x.split(" ")).map(lambda w: (w, 1))
grouped_words = words.groupby(lambda wc: wc[0])
#end::ray_wordcount_on_ds[]
word_counts = grouped_words.count()
word_counts.show()
```
|
github_jupyter
|
# Make sure were on ray 1.9
from ray.data.grouped_dataset import GroupedDataset
#tag::start-ray-local[]
import ray
ray.init(num_cpus=20) # In theory auto sensed, in practice... eh
#end::start-ray-local[]
#tag::local_fun[]
def hi():
import os
import socket
return f"Running on {socket.gethostname()} in pid {os.getpid()}"
#end::local_fun[]
hi()
#tag::remote_fun[]
@ray.remote
def remote_hi():
import os
import socket
return f"Running on {socket.gethostname()} in pid {os.getpid()}"
future = remote_hi.remote()
ray.get(future)
#end::remote_fun[]
#tag::sleepy_task_hello_world[]
import timeit
def slow_task(x):
import time
time.sleep(2) # Do something sciency/business
return x
@ray.remote
def remote_task(x):
return slow_task(x)
things = range(10)
very_slow_result = map(slow_task, things)
slowish_result = map(lambda x: remote_task.remote(x), things)
slow_time = timeit.timeit(lambda: list(very_slow_result), number=1)
fast_time = timeit.timeit(lambda: list(ray.get(list(slowish_result))), number=1)
print(f"In sequence {slow_time}, in parallel {fast_time}")
#end::sleepy_task_hello_world[]
slowish_result = map(lambda x: remote_task.remote(x), things)
ray.get(list(slowish_result))
# Note: if we were on a "real" cluster we'd have to do more magic to install it on all the nodes in the cluster.
!pip install bs4
#tag::mini_crawl_task[]
@ray.remote
def crawl(url, depth=0, maxdepth=1, maxlinks=4):
links = []
link_futures = []
import requests
from bs4 import BeautifulSoup
try:
f = requests.get(url)
links += [(url, f.text)]
if (depth > maxdepth):
return links # base case
soup = BeautifulSoup(f.text, 'html.parser')
c = 0
for link in soup.find_all('a'):
try:
c = c + 1
link_futures += [crawl.remote(link["href"], depth=(depth+1), maxdepth=maxdepth)]
# Don't branch too much were still in local mode and the web is big
if c > maxlinks:
break
except:
pass
for r in ray.get(link_futures):
links += r
return links
except requests.exceptions.InvalidSchema:
return [] # Skip non-web links
except requests.exceptions.MissingSchema:
return [] # Skip non-web links
ray.get(crawl.remote("http://holdenkarau.com/"))
#end::mini_crawl_task[]
#tag::actor[]
@ray.remote
class HelloWorld(object):
def __init__(self):
self.value = 0
def greet(self):
self.value += 1
return f"Hi user #{self.value}"
# Make an instance of the actor
hello_actor = HelloWorld.remote()
# Call the actor
print(ray.get(hello_actor.greet.remote()))
print(ray.get(hello_actor.greet.remote()))
#end::actor[]
#tag::ds[]
# Create a Dataset of URLS objects. We could also load this from a text file with ray.data.read_text()
urls = ray.data.from_items([
"https://github.com/scalingpythonml/scalingpythonml",
"https://github.com/ray-project/ray"])
def fetch_page(url):
import requests
f = requests.get(url)
return f.text
pages = urls.map(fetch_page)
# Look at a page to make sure it worked
pages.take(1)
#end:ds[]
#tag::ray_wordcount_on_ds[]
words = pages.flat_map(lambda x: x.split(" ")).map(lambda w: (w, 1))
grouped_words = words.groupby(lambda wc: wc[0])
#end::ray_wordcount_on_ds[]
word_counts = grouped_words.count()
word_counts.show()
| 0.522202 | 0.16807 |
# Credit Risk Resampling Techniques
```
import warnings
warnings.filterwarnings('ignore')
import numpy as np
import pandas as pd
from pathlib import Path
from collections import Counter
```
# Read the CSV and Perform Basic Data Cleaning
```
# load all of the data
file_path = Path('Resources/lending_data.csv')
loans_df = pd.read_csv(file_path)
loans_df.head()
from sklearn.preprocessing import LabelEncoder
# convert categorical data into binary data
le = LabelEncoder()
# homeowner column
le.fit(loans_df["homeowner"])
loans_df["homeowner"] = le.transform(loans_df["homeowner"])
# loan status column
le.fit(loans_df["loan_status"])
loans_df["loan_status"] = le.transform(loans_df["loan_status"])
loans_df.head()
```
# Split the Data into Training and Testing
```
# create the features
X = pd.get_dummies(loans_df.drop('loan_status', axis=1))
# create the target
y = loans_df["loan_status"]
X.describe()
# Check the balance of the target values
y.value_counts()
# Create X_train, X_test, y_train, y_test
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X,
y,
random_state=1,
stratify=y)
X_train.shape
```
# Simple Logistic Regression
```
from sklearn.linear_model import LogisticRegression
model = LogisticRegression(solver='lbfgs', random_state=1)
model.fit(X_train, y_train)
# Calculated the balanced accuracy score
from sklearn.metrics import balanced_accuracy_score
y_pred = model.predict(X_test)
balanced_accuracy_score(y_test, y_pred)
# Display the confusion matrix
from sklearn.metrics import confusion_matrix
confusion_matrix(y_test, y_pred)
# Print the imbalanced classification report
from imblearn.metrics import classification_report_imbalanced
print(classification_report_imbalanced(y_test, y_pred))
```
# Oversampling
In this section, you will compare two oversampling algorithms to determine which algorithm results in the best performance. You will oversample the data using the naive random oversampling algorithm and the SMOTE algorithm. For each algorithm, be sure to complete the folliowing steps:
1. View the count of the target classes using `Counter` from the collections library.
3. Use the resampled data to train a logistic regression model.
3. Calculate the balanced accuracy score from sklearn.metrics.
4. Print the confusion matrix from sklearn.metrics.
5. Generate a classication report using the `imbalanced_classification_report` from imbalanced-learn.
Note: Use a random state of 1 for each sampling algorithm to ensure consistency between tests
### Naive Random Oversampling
```
# Use RandomOverSampler to resample training data
from imblearn.over_sampling import RandomOverSampler
ros = RandomOverSampler(random_state=1)
X_resampled, y_resampled = ros.fit_resample(X_train, y_train)
Counter(y_resampled)
# Train the Logistic Regression model using the resampled data
from sklearn.linear_model import LogisticRegression
model = LogisticRegression(solver='lbfgs', random_state=1)
model.fit(X_resampled, y_resampled)
# Calculate the balanced accuracy score
from sklearn.metrics import balanced_accuracy_score
balanced_accuracy_score(y_test, y_pred)
# show the confusion matrix
from sklearn.metrics import confusion_matrix
y_pred = model.predict(X_test)
confusion_matrix(y_test, y_pred)
# Print the imbalanced classification report
from imblearn.metrics import classification_report_imbalanced
print(classification_report_imbalanced(y_test, y_pred))
```
### SMOTE Oversampling
```
# Resample the training data with SMOTE
from imblearn.over_sampling import SMOTE
X_resampled, y_resampled = SMOTE(random_state=1, sampling_strategy=1.0).fit_resample(
X_train, y_train
)
from collections import Counter
Counter(y_resampled)
# trrain the Logistic Regression model using the resampled data
model = LogisticRegression(solver='lbfgs', random_state=1)
model.fit(X_resampled, y_resampled)
# Calculate the balanced accuracy score
y_pred = model.predict(X_test)
balanced_accuracy_score(y_test, y_pred)
# show the confusion matrix
confusion_matrix(y_test, y_pred)
# print imbalanced classification report
print(classification_report_imbalanced(y_test, y_pred))
```
# Undersampling
In this section, you will test an undersampling algorithms to determine which algorithm results in the best performance compared to the oversampling algorithms above. You will undersample the data using the Cluster Centroids algorithm and complete the folliowing steps:
1. View the count of the target classes using `Counter` from the collections library.
3. Use the resampled data to train a logistic regression model.
3. Calculate the balanced accuracy score from sklearn.metrics.
4. Print the confusion matrix from sklearn.metrics.
5. Generate a classication report using the `imbalanced_classification_report` from imbalanced-learn.
Note: Use a random state of 1 for each sampling algorithm to ensure consistency between tests
```
# Resample the data using the ClusterCentroids resampler
from imblearn.under_sampling import ClusterCentroids
cc = ClusterCentroids(random_state=1)
X_resampled, y_resampled = cc.fit_resample(X_train, y_train)
Counter(y_resampled)
# Train the Logistic Regression model using the resampled data
from sklearn.linear_model import LogisticRegression
model = LogisticRegression(solver='lbfgs', random_state=1)
model.fit(X_resampled, y_resampled)
# Calculate the balanced accuracy score
from sklearn.metrics import balanced_accuracy_score
balanced_accuracy_score(y_test, y_pred)
# show confusion matrix
from sklearn.metrics import confusion_matrix
y_pred = model.predict(X_test)
confusion_matrix(y_test, y_pred)
# Print imbalanced classification report
from imblearn.metrics import classification_report_imbalanced
print(classification_report_imbalanced(y_test, y_pred))
```
# Combination (Over and Under) Sampling
In this section, you will test a combination over- and under-sampling algorithm to determine if the algorithm results in the best performance compared to the other sampling algorithms above. You will resample the data using the SMOTEENN algorithm and complete the folliowing steps:
1. View the count of the target classes using `Counter` from the collections library.
3. Use the resampled data to train a logistic regression model.
3. Calculate the balanced accuracy score from sklearn.metrics.
4. Print the confusion matrix from sklearn.metrics.
5. Generate a classication report using the `imbalanced_classification_report` from imbalanced-learn.
Note: Use a random state of 1 for each sampling algorithm to ensure consistency between tests
```
# Resample the training data with SMOTEENN
from imblearn.combine import SMOTEENN
sm = SMOTEENN(random_state=1)
X_resampled, y_resampled = sm.fit_resample(X_train, y_train)
Counter(y_resampled)
# Train the Logistic Regression model using the resampled data
from sklearn.linear_model import LogisticRegression
model = LogisticRegression(solver='lbfgs', random_state=1)
model.fit(X_resampled, y_resampled)
# Calculated the balanced accuracy score
from sklearn.metrics import balanced_accuracy_score
balanced_accuracy_score(y_test, y_pred)
# Display the confusion matrix
from sklearn.metrics import confusion_matrix
y_pred = model.predict(X_test)
confusion_matrix(y_test, y_pred)
# Print the imbalanced classification report
from imblearn.metrics import classification_report_imbalanced
print(classification_report_imbalanced(y_test, y_pred))
```
|
github_jupyter
|
import warnings
warnings.filterwarnings('ignore')
import numpy as np
import pandas as pd
from pathlib import Path
from collections import Counter
# load all of the data
file_path = Path('Resources/lending_data.csv')
loans_df = pd.read_csv(file_path)
loans_df.head()
from sklearn.preprocessing import LabelEncoder
# convert categorical data into binary data
le = LabelEncoder()
# homeowner column
le.fit(loans_df["homeowner"])
loans_df["homeowner"] = le.transform(loans_df["homeowner"])
# loan status column
le.fit(loans_df["loan_status"])
loans_df["loan_status"] = le.transform(loans_df["loan_status"])
loans_df.head()
# create the features
X = pd.get_dummies(loans_df.drop('loan_status', axis=1))
# create the target
y = loans_df["loan_status"]
X.describe()
# Check the balance of the target values
y.value_counts()
# Create X_train, X_test, y_train, y_test
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X,
y,
random_state=1,
stratify=y)
X_train.shape
from sklearn.linear_model import LogisticRegression
model = LogisticRegression(solver='lbfgs', random_state=1)
model.fit(X_train, y_train)
# Calculated the balanced accuracy score
from sklearn.metrics import balanced_accuracy_score
y_pred = model.predict(X_test)
balanced_accuracy_score(y_test, y_pred)
# Display the confusion matrix
from sklearn.metrics import confusion_matrix
confusion_matrix(y_test, y_pred)
# Print the imbalanced classification report
from imblearn.metrics import classification_report_imbalanced
print(classification_report_imbalanced(y_test, y_pred))
# Use RandomOverSampler to resample training data
from imblearn.over_sampling import RandomOverSampler
ros = RandomOverSampler(random_state=1)
X_resampled, y_resampled = ros.fit_resample(X_train, y_train)
Counter(y_resampled)
# Train the Logistic Regression model using the resampled data
from sklearn.linear_model import LogisticRegression
model = LogisticRegression(solver='lbfgs', random_state=1)
model.fit(X_resampled, y_resampled)
# Calculate the balanced accuracy score
from sklearn.metrics import balanced_accuracy_score
balanced_accuracy_score(y_test, y_pred)
# show the confusion matrix
from sklearn.metrics import confusion_matrix
y_pred = model.predict(X_test)
confusion_matrix(y_test, y_pred)
# Print the imbalanced classification report
from imblearn.metrics import classification_report_imbalanced
print(classification_report_imbalanced(y_test, y_pred))
# Resample the training data with SMOTE
from imblearn.over_sampling import SMOTE
X_resampled, y_resampled = SMOTE(random_state=1, sampling_strategy=1.0).fit_resample(
X_train, y_train
)
from collections import Counter
Counter(y_resampled)
# trrain the Logistic Regression model using the resampled data
model = LogisticRegression(solver='lbfgs', random_state=1)
model.fit(X_resampled, y_resampled)
# Calculate the balanced accuracy score
y_pred = model.predict(X_test)
balanced_accuracy_score(y_test, y_pred)
# show the confusion matrix
confusion_matrix(y_test, y_pred)
# print imbalanced classification report
print(classification_report_imbalanced(y_test, y_pred))
# Resample the data using the ClusterCentroids resampler
from imblearn.under_sampling import ClusterCentroids
cc = ClusterCentroids(random_state=1)
X_resampled, y_resampled = cc.fit_resample(X_train, y_train)
Counter(y_resampled)
# Train the Logistic Regression model using the resampled data
from sklearn.linear_model import LogisticRegression
model = LogisticRegression(solver='lbfgs', random_state=1)
model.fit(X_resampled, y_resampled)
# Calculate the balanced accuracy score
from sklearn.metrics import balanced_accuracy_score
balanced_accuracy_score(y_test, y_pred)
# show confusion matrix
from sklearn.metrics import confusion_matrix
y_pred = model.predict(X_test)
confusion_matrix(y_test, y_pred)
# Print imbalanced classification report
from imblearn.metrics import classification_report_imbalanced
print(classification_report_imbalanced(y_test, y_pred))
# Resample the training data with SMOTEENN
from imblearn.combine import SMOTEENN
sm = SMOTEENN(random_state=1)
X_resampled, y_resampled = sm.fit_resample(X_train, y_train)
Counter(y_resampled)
# Train the Logistic Regression model using the resampled data
from sklearn.linear_model import LogisticRegression
model = LogisticRegression(solver='lbfgs', random_state=1)
model.fit(X_resampled, y_resampled)
# Calculated the balanced accuracy score
from sklearn.metrics import balanced_accuracy_score
balanced_accuracy_score(y_test, y_pred)
# Display the confusion matrix
from sklearn.metrics import confusion_matrix
y_pred = model.predict(X_test)
confusion_matrix(y_test, y_pred)
# Print the imbalanced classification report
from imblearn.metrics import classification_report_imbalanced
print(classification_report_imbalanced(y_test, y_pred))
| 0.648355 | 0.956309 |
### Model Diagnostics in Python
In this notebook, you will be trying out some of the model diagnostics you saw from Sebastian, but in your case there will only be two cases - either admitted or not admitted.
First let's read in the necessary libraries and the dataset.
```
import numpy as np
import pandas as pd
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import confusion_matrix, precision_score, recall_score, accuracy_score
from sklearn.model_selection import train_test_split
np.random.seed(42)
df = pd.read_csv('./admissions.csv')
df.head()
```
`1.` Change prestige to dummy variable columns that are added to `df`. Then divide your data into training and test data. Create your test set as 20% of the data, and use a random state of 0. Your response should be the `admit` column. [Here](http://scikit-learn.org/stable/modules/generated/sklearn.model_selection.train_test_split.html) are the docs, which can also find with a quick google search if you get stuck.
```
df[['prest_1', 'prest_2', 'prest_3', 'prest_4']] = pd.get_dummies(df['prestige'])
X = df.drop(['admit', 'prestige', 'prest_1'] , axis=1)
y = df['admit']
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.20, random_state=0)
```
`2.` Now use [sklearn's Logistic Regression](http://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LogisticRegression.html) to fit a logistic model using `gre`, `gpa`, and 3 of your `prestige` dummy variables. For now, fit the logistic regression model without changing any of the hyperparameters.
The usual steps are:
* Instantiate
* Fit (on train)
* Predict (on test)
* Score (compare predict to test)
As a first score, obtain the [confusion matrix](http://scikit-learn.org/stable/modules/generated/sklearn.metrics.confusion_matrix.html). Then answer the first question below about how well your model performed on the test data.
```
log_mod = LogisticRegression()
log_mod.fit(X_train, y_train)
preds = log_mod.predict(X_test)
confusion_matrix(y_test, preds)
```
`3.` Now, try out a few additional metrics: [precision](http://scikit-learn.org/stable/modules/generated/sklearn.metrics.precision_score.html), [recall](http://scikit-learn.org/stable/modules/generated/sklearn.metrics.recall_score.html), and [accuracy](http://scikit-learn.org/stable/modules/generated/sklearn.metrics.accuracy_score.html) are all popular metrics, which you saw with Sebastian. You could compute these directly from the confusion matrix, but you can also use these built in functions in sklearn.
Another very popular set of metrics are [ROC curves and AUC](http://scikit-learn.org/stable/auto_examples/model_selection/plot_roc.html#sphx-glr-auto-examples-model-selection-plot-roc-py). These actually use the probability from the logistic regression models, and not just the label. [This](http://blog.yhat.com/posts/roc-curves.html) is also a great resource for understanding ROC curves and AUC.
Try out these metrics to answer the second quiz question below. I also provided the ROC plot below. The ideal case is for this to shoot all the way to the upper left hand corner. Again, these are discussed in more detail in the Machine Learning Udacity program.
```
precision_score(y_test, preds)
recall_score(y_test, preds)
accuracy_score(y_test, preds)
### Unless you install the ggplot library in the workspace, you will
### get an error when running this code!
from ggplot import *
from sklearn.metrics import roc_curve, auc
%matplotlib inline
preds = log_mod.predict_proba(X_test)[:,1]
fpr, tpr, _ = roc_curve(y_test, preds)
df = pd.DataFrame(dict(fpr=fpr, tpr=tpr))
ggplot(df, aes(x='fpr', y='tpr')) +\
geom_line() +\
geom_abline(linetype='dashed')
```


|
github_jupyter
|
import numpy as np
import pandas as pd
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import confusion_matrix, precision_score, recall_score, accuracy_score
from sklearn.model_selection import train_test_split
np.random.seed(42)
df = pd.read_csv('./admissions.csv')
df.head()
df[['prest_1', 'prest_2', 'prest_3', 'prest_4']] = pd.get_dummies(df['prestige'])
X = df.drop(['admit', 'prestige', 'prest_1'] , axis=1)
y = df['admit']
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.20, random_state=0)
log_mod = LogisticRegression()
log_mod.fit(X_train, y_train)
preds = log_mod.predict(X_test)
confusion_matrix(y_test, preds)
precision_score(y_test, preds)
recall_score(y_test, preds)
accuracy_score(y_test, preds)
### Unless you install the ggplot library in the workspace, you will
### get an error when running this code!
from ggplot import *
from sklearn.metrics import roc_curve, auc
%matplotlib inline
preds = log_mod.predict_proba(X_test)[:,1]
fpr, tpr, _ = roc_curve(y_test, preds)
df = pd.DataFrame(dict(fpr=fpr, tpr=tpr))
ggplot(df, aes(x='fpr', y='tpr')) +\
geom_line() +\
geom_abline(linetype='dashed')
| 0.419053 | 0.959383 |
# Tableau Visualization
<img align="right" style="padding-right:10px;" src="figures_wk8/data_visualization.png" width=500><br>
**Outline**
* What is Data Visualization?
- Why is data visualization so important?
- Different types of Data Visualization
* Getting started with Tableau
- Student License
* Connecting to our data
* Worksheet Tab
* Time to build a simple graph
* DJIA Demo
- Low_High_Close Graphic
- Duplicating an Existing Graphic
- Calculated Fields
* Building a Dashboard
* A Tableau Story
[Data Visualization Image Source](https://www.inc.com/anna-johansson/the-5-things-you-need-to-remember-when-relying-on-data-visualization.html)
## What is Data Visualization?
Data visualization is the graphical representation of information and data. By using visual elements like charts, graphs, and maps, data visualization tools provide an accessible way to see and understand trends, outliers, and patterns in data.
In the world of Big Data, data visualization tools and technologies are essential to analyze massive amounts of information and make data-driven decisions.
### Why is data visualization so important?
Our eyes are drawn to colors and patterns. We can quickly identify red from blue, square from circle. Our culture is visual, including everything from art and advertisements to TV and movies.
Data visualization is another form of visual art that grabs our interest and keeps our eyes on the message. When we see a chart, we quickly see trends and outliers. If we can see something, we internalize it quickly. It’s storytelling with a purpose. If you’ve ever stared at a massive spreadsheet of data and couldn’t see a trend, you know how much more effective a visualization can be.
<img align="center" style="padding-right:10px;" src="figures_wk8/viz_benefits.png" width=800><br>
### Different types of Data Visualization
When you think of data visualization, your first thought probably immediately goes to simple bar graphs or pie charts. While these may be an integral part of visualizing data and a common baseline for many data graphics, the right visualization must be paired with the right set of information. Simple graphs are only the tip of the iceberg. There’s a whole selection of visualization methods to present data in effective and interesting ways.
Below is a screenshot of a handy reference chart to help you with selecting the correct type of visualization for your data. <br>(pdf version located on WorldClass: Content -> Week8)<br>
<img align="center" style="padding-right:10px;" src="figures_wk8/chart_type.png" width=800><br>
Additionally, Tableau has collected [10 of the best examples of data visualization of all time](https://www.tableau.com/learn/articles/best-beautiful-data-visualization-examples), with examples that map historical conquests, analyze film scripts, reveal hidden causes of mortality, and more. Check these out!
References: <br>
https://www.tableau.com/learn/articles/data-visualization <br>
https://www.analyticsvidhya.com/learning-paths-data-science-business-analytics-business-intelligence-big-data/tableau-learning-path/
## Getting started with Tableau
Tableau offers everyone a [14-day trial subscription](https://www.tableau.com/products/trial). The trial version will be sufficient for this assignment.
### Student License
Tableau offers [students a one-year Tableau license for FREE](https://www.tableau.com/academic/students)!!!
<img align="center" style="padding-right:10px;" src="figures_wk8/get_started.png" width=600><br>
<div class="alert alert-block alert-danger">
<b>Important::</b> It can take a day or two to get your free license from Tableau. After you apply for a student license, you will be directed to a 14-day trial version and then you can apply your license once you receive it from Tableau.
</div>
Also, Tableau has a great [Getting Started tutorial](https://help.tableau.com/current/guides/get-started-tutorial/en-us/get-started-tutorial-home.htm) on their website. It's worth taking the time to go through this tutorial.
Once you have launched Tableau Desktop, you will be taken to the **Start Page**. <br>
<img align="center" style="padding-right:10px;" src="figures_wk8/start_page.png" width=700><br>
Let's stop and look at a couple of the key features on the Start page: <br>
In the upper left-hand corner of any Tableau page, click on the <b>Tableau icon</b> to switch you between the start page and your workspace. <br>
The **Connect** section is how you connect Tableau to your data. Tableau can connect to data that is:
<br>
- stored in a file, such as Microsoft Excel, PDF, Spatial files, and more. <br>
- stored on a server, such as Tableau Server, Microsoft SQL Server, Google Analytics, and more. <br>
- a data source that you’ve connected to before. <br>
Tableau supports the ability to connect to a wide range of data stored in a wide variety of places. The **Connect** pane lists the most common places that you might want to connect to, or click the More links to see more options. More on connecting to data sources in the Learning Library (in the top menu)
The <b>Open</b> will contain a list of existing workbooks that are available for you to open. If this is your first time working in Tableau, this section will most likely be empty.
The <b>Sample Workbooks</b> section contains sample dashboards and worksheets that come with your current version of Tableau.
The <b>Discover</b> section contains additional resources, available within Tableau. Here you will be able to view video tutorials, connect with others in forums and view the "Viz of the Week" to get ideas for building your great visualizations.
### Connecting to our data
On our WorldClass site in the Content -> Week8 section there is an data_wk8 folder. Make sure you have that folder downloaded and unzipped in a known location.
Let's connect to the DJIA_HistoricalPrices.csv dataset.
I clicked on **More** under the **Connect** section and was then presented with a navigation window to select my specific dataset.
<img align="center" style="padding-right:10px;" src="figures_wk8/select_data.png" width=500><br>
After you select your dataset, you will be shown a tabular view of your data.
This is where you could join multiple datasets together, filter your data or adjust your data prior to building a visualization.
<img align="center" style="padding-right:10px;" src="figures_wk8/data_view.png" width=700><br>
**Important:**
<img align="left" style="padding-right:10px;" src="figures_wk8/worksheet_button.png" width=200><br>
When you are satisfied with your data, you need to click on the orange worksheet tab at the bottom of the screen
### Worksheet Tab
In Tableau, the worksheet tab is where you will build your visualization.
<img align="left" style="padding-right:10px;" src="figures_wk8/worksheet_data_fields.png" width=200><br>
The left panel on the worksheet, is where you will access the individual data elements from within your dataset.
Let's view the different sections: <br>
 * Data Source: this is a very top and marked with the database icon. <br>
 * Roles: Tableau has two type of data element roles: Dimensions and Measures.<br>
  - Dimensions are categorical or qualitative data elements from your dataset<br>
  - Measures are numerical or quantitative data elements from your dataset<br>
 * Fields: the name of the data elements in your dataset<br>
 * Data Type: the specific type of the individual data field.<br>
<div class="alert alert-block alert-info">
<b>Helpful Hint::</b> In Tableau a shelf is another name for region or area within the worksheet.
</div>
<img align="left" style="padding-right:10px;" src="figures_wk8/columns_rows.png" width=200><br>
This is a topic that was a bit confusing for me at first, but I found this tip helpful in keeping things straight.
The data elements that you put on the **Columns** shelf relate to the x-axis of your graphic, and the **Rows** shelf relates to the x-axis for your graphic.
### Time to build a simple graph
To build your visual! You will need to drag and drop the individual fields from the left pane to the **Columns** shelf and **Rows** shelf.
Let's start by dragging **Date** to the **Columns** shelf and **Close** to the **Rows** shelf.
<img align="center" style="padding-right:10px;" src="figures_wk8/DJIA_1.png" width=500><br>
### Customize the data elements
<img align="left" style="padding-right:10px;" src="figures_wk8/DJIA_2b.png" width=200><br>
Well, it is a graph, but doesn't look like any DJIA graph that I've seen before. Let's see if we can improve things a bit.
First thing that I'll adjust is the **Columns**. Notice that when we dropped **Date** onto the **Columns** shelf, Tableau automatically aggregated our underlying datset at te *YEAR* level. I think I'd prefer to look at this data on a *DAILY* basis. To do this hover over the right end of the **Date** object and a down arrow should appear. Click on the down arrow and select **Day** from the list of options.
Next, we should probably do something to adjust the **Close** data element. Looking at the tick mark values,things seem really high to me. Again Tableau is trying to help us out and summed all the values within the **Close** data element to start our graph. We can change this by **Average** rather than **Sum**. this one a little bit tricky in that you have to click on the triangle next to the **Measure(Sum)** entry.
Here's what things look like now.
<img align="center" style="padding-right:10px;" src="figures_wk8/DJIA_2.png" width=500><br>
Hmmm.. Something still doesn't seem right.
The x-axis tick marks are implying that we only have one month of data. When in reality we have a years worth of data. (11/18/2016 through 11/16/2017). What Tableau has done here is to go through the dataset and summed all the data based on date within the month.
For example, for Day 1 - all of the months that had data for the 1st of the month, were summed togehter and then displayed.
So let's adjust our **Date** field again. This time let's select the options **More - > Custom**. I'm going to select **Month / Day / Year** from the drop-down list.
<img align="left" style="padding-right:10px;" src="figures_wk8/DJIA_3b.png" width=200>
<img align="left" style="padding-right:10px;" src="figures_wk8/DJIA_3.png" width=400><br>
That looks better! We have individual dates now! You should be able to scroll through all the individual dates within our dataset.
<img align="center" style="padding-right:10px;" src="figures_wk8/DJIA_4.png" width=500><br>
### DJIA Demo
I find it easier to learn if I have a target objective that I'm striving for, so let's apply that philosophy to our current Tableau exercise.
#### Low_High_Close Graphic
**Objective:** I'd like to build a graphic showing the range of the DJIA prices (low to high range)for every day within a given month and overlay the closing price on a daily basis.
Go ahead and remove the **Close** field from the **Rows** shelf. You can do this by right-clicking and selecting **Remove**.
I'm going to start by filtering our dataset down to one month. To do this, I'm going to drag **Date** from the left panel to the **Filters** shelf. The **Filter Fields** dialogue box will open up and I'll select **Month/Year** from this dialogue box and then click on **Next**. I'm going to select the month of **August 2017**.
<img align="left" style="padding-right:10px;" src="figures_wk8/Filter_Fields_2.png" width=400>
<img align="left" style="padding-right:10px;" src="figures_wk8/Filter_Fields.png" width=300><br>
Now we need to Add **Measure Values** for our graphic. To do this right click on **Measure Values** in the left panel. Select **Add to Sheet**
<img align="left" style="padding-right:10px;" src="figures_wk8/DJIA_6.png" width=300>
You will notice that a Measure Values section is opened up below the **Marks** shelf. All of the quantitative data elements are automatically added to this section. Remove all of the data elements except **Low** and **High**.
<img align="left" style="padding-right:10px;" src="figures_wk8/DJIA_6b.png" width=300><br>
Now drag **Measure Values** from the left panel to the **Rows** shelf. (You might need to remove **Measure Names** if it's already on the Rows shelf.)
<img align="center" style="padding-right:10px;" src="figures_wk8/DJIA_6c.png" width=400><br>
In the **Filters** shelf, notice that **Measure Names** has appeared. Right click on **Measure Names** in the **Filters** section, then select **Edit Filter**.
<img align="left" style="padding-right:10px;" src="figures_wk8/DJIA_6d.png" width=300>
Verify that only high and low are selected.<br>
<img align="left" style="padding-right:10px;" src="figures_wk8/DJIA_6e.png" width=300><br>
Now let's tell Tableau to use our newly created **Measure Names** as a way to create a color distinction in our graphic by dropping **Measure Names** from the left panel on **Colors** in the **Mark** shelf.
<img align="center" style="padding-right:10px;" src="figures_wk8/DJIA_7.png" width=500><br>
Last step, we can change the type f graph used to display our data. I'm going to select **Bar**. This is done witht he drop down at the top of the **Marks** section.
Tableau automatically determined that a Stacked Bar graph would be the best way to display this data. For the most part I agree, but I don't like the *additive* effect of stacking the low and high on top of each other. I'd rather see these two values stacked one in front of the other. To do this we need to change the focus of the graphic.
At the top of the Tableau window/screen, select **Analysis -> Stack Marks -> Off** from the toolbar across the top of your Tableau window.
<img align="center" style="padding-right:10px;" src="figures_wk8/DJIA_8.png" width=500><br>
I know, it doesn't look like we are making progress, but we are. Trust me!
The current issue is that the **High** values are blocking the **Low** values in the graphic. To fix this, we need to ensure that **Low** is first in the list of our **Measure Values** shelf. It's not, so I will drag **Low** above **High**
<img align="center" style="padding-right:10px;" src="figures_wk8/DJIA_9.png" width=500><br>
Getting better! I can see a hint of blue at the top of the orange bars.
Now we can adjust the range of the y-axis so we can see more of a distinction between the **Low** and **High** DJIA price each day.
To do this right click on the **Value** label along the y-axis. Select **Edit Axis**. I'll set:
* Range to be a **Fixed range between 21,500 and 22,200**.
* Y-axis Title to be **DJIA - Low and High Price**.
<img align="left" style="padding-right:10px;" src="figures_wk8/DJIA_10b.png" width=300> <br>
<img align="left" style="padding-right:10px;" src="figures_wk8/DJIA_10.png" width=400><br>
Here's what my graph looks like at this point.
<img align="center" style="padding-right:10px;" src="figures_wk8/DJIA_10c.png" width=500><br>
I want to turn-off the data values at the end of end bar in the chart. To do this we need to click on the **Label** icon in the **Marks** section
<img align="center" style="padding-right:10px;" src="figures_wk8/DJIA_10d.png" width=400><br>
Hmmm.. the x-axis still looks a bit too congested to me. I'm going to edit the **Date** in the **columns** shelf to be **Day**.
<img align="center" style="padding-right:10px;" src="figures_wk8/Hi_Low_Day.png" width=500><br>
### Adding a another data element
Moving right along, it's time to add **Close** to this graphic. To do this you will need to drag **Close** from the left panel to the right side of the existing graphic. Once you are near the right edge of the graphic you will see *a bolded dashed line appear along the right edge* of the existing graphic. You need to drop **Close** on that dashed line.
<img align="center" style="padding-right:10px;" src="figures_wk8/DJIA_11.png" width=700><br>
We are getting there... Just need to clean things up a bit. Let's start with adjusting the two sets of y-axes so that they are on the same scale with each other. Right click on the **Close** y-axis and select **Synchronize Axis**.
<img align="center" style="padding-right:10px;" src="figures_wk8/DJIA_12.png" width=500><br>
Well, now that the axes are in synch, we still have an issue that the bars for **Close** are covering up most of the graphic. We can fix this by changing the graphic type for the **Close** data elelment.
To do this go to the **Marks** shelf and click on **Close** (it should be bolded after you click on it). In this same shlef area, use the drop-down selector to change the graphic type for **Close** to **Line** from **Bar**. Make sure you are only adjusting the graphic type for **Close**.
Here's what our graphic will look like at this point.
<img align="center" style="padding-right:10px;" src="figures_wk8/DJIA_13.png" width=700><br>
Things are looking a lot better. But, I'm not too crazy about the default colors that Tableau selected.To adjust the color of the **Close** line, click on the **Color** icon in the **Marks** shelf. Make sure you are on the appropriate shelf.
<img align="center" style="padding-right:10px;" src="figures_wk8/DJIA_14b.png" width=400><br>
To adjust the colors for **Low** and **High**, we need to go to the very upper right corner of the worksheet space. You should see a **Measure Names** shelf. It is possible that the **Show Me** shelf is expanded and hiding the **Measure Names** shelf in this section of the worksheet. Collapse **Show Me** if necessary.
Click on **Measure Names** and then select the down arrow to the right of the name. Select **Edit Color** and adjust the colors to your preference. I'll set my colors as follows:
<img align="center" style="padding-right:10px;" src="figures_wk8/DJIA_14.png" width=400><br>
This graphic is really starting to take shape. However, I'm still a bit confused because I have no easy way to determine when the DJIA is trading or not trading. Since the markets are closed on weekends and holidays, I'd like to find a way to represent that.
Let's go back up to the **Columns** shelf and edit **Date** again. This time we will change the data element to be **Continuous**.
<img align="center" style="padding-right:10px;" src="figures_wk8/DJIA_15.png" width=400><br>
Time to put the final touches on this graphic.
Let's edit the x-axis and add a **Axis Title** of **Business Day**.
We should also clean up our second y-axis by changing that **Axis Title** to **Closing Price**.
Finally, we need to give our graphic a **Title**. To do this go to the **Sheet 1** shelf and click on the down arrow in the far upper right corner of this shelf area. Here is what I entered for my **Title**:
<img align="center" style="padding-right:10px;" src="figures_wk8/DJIA_16.png" width=500><br>
Pulling it all together, you should see a graphic that looks like this.
<img align="center" style="padding-right:10px;" src="figures_wk8/DJIA_17.png" width=600><br>
Congrats!! You have made your first Tableau graphic.
Make sure you rename your worksheet to be something meaningful and that you **SAVE** your work thus far.
Now we need to create a couple of additional graphics so that we can learn how to build a dashboard.
#### Duplicating an Existing Graphic
For our second graphic, I'm going to take the easy route and simply duplicate our existing worksheet and then adjust it from there.
**Objective:** Duplicate the August 2017 graphic and change the date range to another month within our dataset.
To do this right click on the worksheet tab and select **Duplicate**.
<img align="center" style="padding-right:10px;" src="figures_wk8/DJIA_18.png" width=300><br>
Make sure you are on the newly created worksheet. This would be a great time to rename the sheet to help keep things straight.
Let's adjust the date range to be another month. In the **Filters** shelf, select **Show Filter**.
<img align="center" style="padding-right:10px;" src="figures_wk8/DJIA_25.png" width=300><br>
The filter for this field will open ont he right side of the Tableau window.
<img align="center" style="padding-right:10px;" src="figures_wk8/DJIA_25b.png" width=300><br>
Remember where we adjusted the colors for our first graphic, now you should see a range selector for the **Date** data element. I'm going to change this to be the month of **April 2017**
<img align="center" style="padding-right:10px;" src="figures_wk8/DJIA_19.png" width=700><br>
Ummm... That's a bit troubling, where did the graphic go???
If we click on **Data Source** in the lower left corner, we can go back to the dataset itself and look to see what the range of values are for the month of April 2017.
Yup! that's our problem, we have the y-axis set to a **fixed** range that is greater than the possible range of values for the month of **April 2017**. Go ahead and adjust this range to be between **20,200 and 21,200**.
Look that graphic is back!
We should also adjust the graphic title to reflect the fact the we are looking at **April 2017**
<img align="center" style="padding-right:10px;" src="figures_wk8/DJIA_20.png" width=600><br>
### Calculated Fields
Let's make another graphic that uses **Calculated Fields**.
**Objective:** Display the market growth and decline on a per day basis for the month of August 2017.
We will start by duplicating the August 2017 graphic again. Rename the new worksheet to be reflective of the graphic.
We need to do a little cleanup before we really get started. This graphic has nothing to do with **Close**, so we will remove it from the **Rows** shelf.
We need to start by creating the **Calculated Field** since it's the subject of this graphic. Select **Create Calculated Field** under the **Analysis** tab with Tableau.
<img align="center" style="padding-right:10px;" src="figures_wk8/DJIA_26.png" width=600><br>
Let's create our **Calculated Field** by first naming the field, I used **Market Growth/Decline**.
The large blank space in this dialogue box is where you actually put the logic for your calculation. I'm going to define two states for my calculation:
* **Decline**: when the DJIA closes lower than where it opened for the day
* **Growth**: when the DJIA closes higher than where it opened for the day
This is what my **Calculated Field** looks like
<img align="center" style="padding-right:10px;" src="figures_wk8/DJIA_27.png" width=600><br>
If you look in the **Measures** shelf, you should see our newly created **Calculated Field**.
<img align="center" style="padding-right:10px;" src="figures_wk8/DJIA_28b.png" width=400><br>
We are going to use this claculated field as our color distinction data element. As before, we will drag "Market Growth/Decline" from the left panel to the **Color** are within the **Marks** shelf.
I'm also going to change the color selection that Tableau assigned to the values **Growth** (to be green) and **Decline** (to be red). Remember how to do this?
<img align="center" style="padding-right:10px;" src="figures_wk8/DJIA_28.png" width=400><br>
Time to switch things up a bit. I'd like the display per day be a bit more significant. I want to bound the bars in this graphic to show the difference between **Open** and **Close** only.
To do this, we will add the following data elements to the **Details** within the **Marks** shelf, remember to pull the fields from the left panel:
* **Date**: You will need to adjust the display type to by **Day** to match the **Columns** shelf
* **Open**
* **Close**
Final adjustment for **Marks**, I'm going to let Tableau sort out the best way to display this type of information, so I'll switch the graphic type to be **Automatic**.
Now it's time to tweak the rest of the graphic. The y-axis title isn't accurate now, so I'll change it to be **DJIA Price**. One last step, the overall title of the graphic is off a bit now too. So, I'll update that to be **DJIA Market Growth vs Decline** and leave the date range.
Here's what we have at this point.
<img align="center" style="padding-right:10px;" src="figures_wk8/DJIA_29.png" width=9900><br>
So what's going on with this graphic?
The green bars represent a day were the DJIA gained ground (closed higher than it opened). The red bars represent a market declining day (opened higher than it closed).
This is called a *Candlestick Bar* graph.
### Building a Dashboard
Okay, we now have three graphics to work with. Time to build a **Dashboard**
A dashboard is a consolidated display of many worksheets and related information in a single place. It is used to compare and monitor a variety of data simultaneously. The different data views are displayed all at once. Dashboards are shown as tabs at the bottom of the workbook and they usually get updated with the most recent data from the data source. While creating a dashboard, you can add views from any worksheet in the workbook along with many supporting objects such as text areas, web pages, and images.
Each view you add to the dashboard is connected to its corresponding worksheet. So when you modify the worksheet, the dashboard is updated and when you modify the view in the dashboard, the worksheet is updated.
<img align="left" style="padding-right:10px;" src="figures_wk8/DJIA_21.png" width=50><br>
To start building a dashboard, select the **Dashboard** icon along the bottom of your workbook.
This will open up the dashboard workspace for you. Don't worry this is the easy part.
<img align="left" style="padding-right:10px;" src="figures_wk8/DJIA_22.png" width=600><br>
You will notice that there is a **Sheets** shelf on the left side of the work space. Here you will find a list of all the available worksheets that you can add to your dashboard. I have the three worksheets that we have created together.
To build the **Dashboard** all you have to do is pick a worksheet and drag it onto the workspace. I'll start with our Market Growth/Decline graphic.
Now select one of the other graphics and drag it onto the workspace too. Tableau will show you shaded blocks that represent where you might consider locating that this worksheet. I decided to place my graphic with the April data below the Market Growth/Decline graphic.
One more to go. I'll now drag the graphic for the August 2017 data and drag it onto the workspace. I decide to split the space currently occupied by the Arpil graphic with the August graphic too. So now the two low_high_close graphics are sitting side-by-side.
Here's what my final result looks like.
<img align="left" style="padding-right:10px;" src="figures_wk8/DJIA_23.png" width=700><br>
### A Tableau Story
In Tableau, a **Story** is a sequence of graphics that work together to convey information. You can create stories to tell a data narrative, provide context, demonstrate how decisions relate to outcomes or to simply make a compelling case.
In short a Tableau **Story** is a collection of Dashboards and Worksheets that work together to tell a story about your data. This mimics a PowerPoint presentation, but is stored and powered through Tableau.
You can publish Tableau a **Dashboard** and **Story** to shre your insights with others.
<img align="left" style="padding-right:10px;" src="figures_wk8/DJIA_24.png" width=50><br>
To start building a dashboard, select the **Story** icon along the bottom of your workbook.
From here, you follow the same process as you did to build a **Dashboard**.
|
github_jupyter
|
# Tableau Visualization
<img align="right" style="padding-right:10px;" src="figures_wk8/data_visualization.png" width=500><br>
**Outline**
* What is Data Visualization?
- Why is data visualization so important?
- Different types of Data Visualization
* Getting started with Tableau
- Student License
* Connecting to our data
* Worksheet Tab
* Time to build a simple graph
* DJIA Demo
- Low_High_Close Graphic
- Duplicating an Existing Graphic
- Calculated Fields
* Building a Dashboard
* A Tableau Story
[Data Visualization Image Source](https://www.inc.com/anna-johansson/the-5-things-you-need-to-remember-when-relying-on-data-visualization.html)
## What is Data Visualization?
Data visualization is the graphical representation of information and data. By using visual elements like charts, graphs, and maps, data visualization tools provide an accessible way to see and understand trends, outliers, and patterns in data.
In the world of Big Data, data visualization tools and technologies are essential to analyze massive amounts of information and make data-driven decisions.
### Why is data visualization so important?
Our eyes are drawn to colors and patterns. We can quickly identify red from blue, square from circle. Our culture is visual, including everything from art and advertisements to TV and movies.
Data visualization is another form of visual art that grabs our interest and keeps our eyes on the message. When we see a chart, we quickly see trends and outliers. If we can see something, we internalize it quickly. It’s storytelling with a purpose. If you’ve ever stared at a massive spreadsheet of data and couldn’t see a trend, you know how much more effective a visualization can be.
<img align="center" style="padding-right:10px;" src="figures_wk8/viz_benefits.png" width=800><br>
### Different types of Data Visualization
When you think of data visualization, your first thought probably immediately goes to simple bar graphs or pie charts. While these may be an integral part of visualizing data and a common baseline for many data graphics, the right visualization must be paired with the right set of information. Simple graphs are only the tip of the iceberg. There’s a whole selection of visualization methods to present data in effective and interesting ways.
Below is a screenshot of a handy reference chart to help you with selecting the correct type of visualization for your data. <br>(pdf version located on WorldClass: Content -> Week8)<br>
<img align="center" style="padding-right:10px;" src="figures_wk8/chart_type.png" width=800><br>
Additionally, Tableau has collected [10 of the best examples of data visualization of all time](https://www.tableau.com/learn/articles/best-beautiful-data-visualization-examples), with examples that map historical conquests, analyze film scripts, reveal hidden causes of mortality, and more. Check these out!
References: <br>
https://www.tableau.com/learn/articles/data-visualization <br>
https://www.analyticsvidhya.com/learning-paths-data-science-business-analytics-business-intelligence-big-data/tableau-learning-path/
## Getting started with Tableau
Tableau offers everyone a [14-day trial subscription](https://www.tableau.com/products/trial). The trial version will be sufficient for this assignment.
### Student License
Tableau offers [students a one-year Tableau license for FREE](https://www.tableau.com/academic/students)!!!
<img align="center" style="padding-right:10px;" src="figures_wk8/get_started.png" width=600><br>
<div class="alert alert-block alert-danger">
<b>Important::</b> It can take a day or two to get your free license from Tableau. After you apply for a student license, you will be directed to a 14-day trial version and then you can apply your license once you receive it from Tableau.
</div>
Also, Tableau has a great [Getting Started tutorial](https://help.tableau.com/current/guides/get-started-tutorial/en-us/get-started-tutorial-home.htm) on their website. It's worth taking the time to go through this tutorial.
Once you have launched Tableau Desktop, you will be taken to the **Start Page**. <br>
<img align="center" style="padding-right:10px;" src="figures_wk8/start_page.png" width=700><br>
Let's stop and look at a couple of the key features on the Start page: <br>
In the upper left-hand corner of any Tableau page, click on the <b>Tableau icon</b> to switch you between the start page and your workspace. <br>
The **Connect** section is how you connect Tableau to your data. Tableau can connect to data that is:
<br>
- stored in a file, such as Microsoft Excel, PDF, Spatial files, and more. <br>
- stored on a server, such as Tableau Server, Microsoft SQL Server, Google Analytics, and more. <br>
- a data source that you’ve connected to before. <br>
Tableau supports the ability to connect to a wide range of data stored in a wide variety of places. The **Connect** pane lists the most common places that you might want to connect to, or click the More links to see more options. More on connecting to data sources in the Learning Library (in the top menu)
The <b>Open</b> will contain a list of existing workbooks that are available for you to open. If this is your first time working in Tableau, this section will most likely be empty.
The <b>Sample Workbooks</b> section contains sample dashboards and worksheets that come with your current version of Tableau.
The <b>Discover</b> section contains additional resources, available within Tableau. Here you will be able to view video tutorials, connect with others in forums and view the "Viz of the Week" to get ideas for building your great visualizations.
### Connecting to our data
On our WorldClass site in the Content -> Week8 section there is an data_wk8 folder. Make sure you have that folder downloaded and unzipped in a known location.
Let's connect to the DJIA_HistoricalPrices.csv dataset.
I clicked on **More** under the **Connect** section and was then presented with a navigation window to select my specific dataset.
<img align="center" style="padding-right:10px;" src="figures_wk8/select_data.png" width=500><br>
After you select your dataset, you will be shown a tabular view of your data.
This is where you could join multiple datasets together, filter your data or adjust your data prior to building a visualization.
<img align="center" style="padding-right:10px;" src="figures_wk8/data_view.png" width=700><br>
**Important:**
<img align="left" style="padding-right:10px;" src="figures_wk8/worksheet_button.png" width=200><br>
When you are satisfied with your data, you need to click on the orange worksheet tab at the bottom of the screen
### Worksheet Tab
In Tableau, the worksheet tab is where you will build your visualization.
<img align="left" style="padding-right:10px;" src="figures_wk8/worksheet_data_fields.png" width=200><br>
The left panel on the worksheet, is where you will access the individual data elements from within your dataset.
Let's view the different sections: <br>
 * Data Source: this is a very top and marked with the database icon. <br>
 * Roles: Tableau has two type of data element roles: Dimensions and Measures.<br>
  - Dimensions are categorical or qualitative data elements from your dataset<br>
  - Measures are numerical or quantitative data elements from your dataset<br>
 * Fields: the name of the data elements in your dataset<br>
 * Data Type: the specific type of the individual data field.<br>
<div class="alert alert-block alert-info">
<b>Helpful Hint::</b> In Tableau a shelf is another name for region or area within the worksheet.
</div>
<img align="left" style="padding-right:10px;" src="figures_wk8/columns_rows.png" width=200><br>
This is a topic that was a bit confusing for me at first, but I found this tip helpful in keeping things straight.
The data elements that you put on the **Columns** shelf relate to the x-axis of your graphic, and the **Rows** shelf relates to the x-axis for your graphic.
### Time to build a simple graph
To build your visual! You will need to drag and drop the individual fields from the left pane to the **Columns** shelf and **Rows** shelf.
Let's start by dragging **Date** to the **Columns** shelf and **Close** to the **Rows** shelf.
<img align="center" style="padding-right:10px;" src="figures_wk8/DJIA_1.png" width=500><br>
### Customize the data elements
<img align="left" style="padding-right:10px;" src="figures_wk8/DJIA_2b.png" width=200><br>
Well, it is a graph, but doesn't look like any DJIA graph that I've seen before. Let's see if we can improve things a bit.
First thing that I'll adjust is the **Columns**. Notice that when we dropped **Date** onto the **Columns** shelf, Tableau automatically aggregated our underlying datset at te *YEAR* level. I think I'd prefer to look at this data on a *DAILY* basis. To do this hover over the right end of the **Date** object and a down arrow should appear. Click on the down arrow and select **Day** from the list of options.
Next, we should probably do something to adjust the **Close** data element. Looking at the tick mark values,things seem really high to me. Again Tableau is trying to help us out and summed all the values within the **Close** data element to start our graph. We can change this by **Average** rather than **Sum**. this one a little bit tricky in that you have to click on the triangle next to the **Measure(Sum)** entry.
Here's what things look like now.
<img align="center" style="padding-right:10px;" src="figures_wk8/DJIA_2.png" width=500><br>
Hmmm.. Something still doesn't seem right.
The x-axis tick marks are implying that we only have one month of data. When in reality we have a years worth of data. (11/18/2016 through 11/16/2017). What Tableau has done here is to go through the dataset and summed all the data based on date within the month.
For example, for Day 1 - all of the months that had data for the 1st of the month, were summed togehter and then displayed.
So let's adjust our **Date** field again. This time let's select the options **More - > Custom**. I'm going to select **Month / Day / Year** from the drop-down list.
<img align="left" style="padding-right:10px;" src="figures_wk8/DJIA_3b.png" width=200>
<img align="left" style="padding-right:10px;" src="figures_wk8/DJIA_3.png" width=400><br>
That looks better! We have individual dates now! You should be able to scroll through all the individual dates within our dataset.
<img align="center" style="padding-right:10px;" src="figures_wk8/DJIA_4.png" width=500><br>
### DJIA Demo
I find it easier to learn if I have a target objective that I'm striving for, so let's apply that philosophy to our current Tableau exercise.
#### Low_High_Close Graphic
**Objective:** I'd like to build a graphic showing the range of the DJIA prices (low to high range)for every day within a given month and overlay the closing price on a daily basis.
Go ahead and remove the **Close** field from the **Rows** shelf. You can do this by right-clicking and selecting **Remove**.
I'm going to start by filtering our dataset down to one month. To do this, I'm going to drag **Date** from the left panel to the **Filters** shelf. The **Filter Fields** dialogue box will open up and I'll select **Month/Year** from this dialogue box and then click on **Next**. I'm going to select the month of **August 2017**.
<img align="left" style="padding-right:10px;" src="figures_wk8/Filter_Fields_2.png" width=400>
<img align="left" style="padding-right:10px;" src="figures_wk8/Filter_Fields.png" width=300><br>
Now we need to Add **Measure Values** for our graphic. To do this right click on **Measure Values** in the left panel. Select **Add to Sheet**
<img align="left" style="padding-right:10px;" src="figures_wk8/DJIA_6.png" width=300>
You will notice that a Measure Values section is opened up below the **Marks** shelf. All of the quantitative data elements are automatically added to this section. Remove all of the data elements except **Low** and **High**.
<img align="left" style="padding-right:10px;" src="figures_wk8/DJIA_6b.png" width=300><br>
Now drag **Measure Values** from the left panel to the **Rows** shelf. (You might need to remove **Measure Names** if it's already on the Rows shelf.)
<img align="center" style="padding-right:10px;" src="figures_wk8/DJIA_6c.png" width=400><br>
In the **Filters** shelf, notice that **Measure Names** has appeared. Right click on **Measure Names** in the **Filters** section, then select **Edit Filter**.
<img align="left" style="padding-right:10px;" src="figures_wk8/DJIA_6d.png" width=300>
Verify that only high and low are selected.<br>
<img align="left" style="padding-right:10px;" src="figures_wk8/DJIA_6e.png" width=300><br>
Now let's tell Tableau to use our newly created **Measure Names** as a way to create a color distinction in our graphic by dropping **Measure Names** from the left panel on **Colors** in the **Mark** shelf.
<img align="center" style="padding-right:10px;" src="figures_wk8/DJIA_7.png" width=500><br>
Last step, we can change the type f graph used to display our data. I'm going to select **Bar**. This is done witht he drop down at the top of the **Marks** section.
Tableau automatically determined that a Stacked Bar graph would be the best way to display this data. For the most part I agree, but I don't like the *additive* effect of stacking the low and high on top of each other. I'd rather see these two values stacked one in front of the other. To do this we need to change the focus of the graphic.
At the top of the Tableau window/screen, select **Analysis -> Stack Marks -> Off** from the toolbar across the top of your Tableau window.
<img align="center" style="padding-right:10px;" src="figures_wk8/DJIA_8.png" width=500><br>
I know, it doesn't look like we are making progress, but we are. Trust me!
The current issue is that the **High** values are blocking the **Low** values in the graphic. To fix this, we need to ensure that **Low** is first in the list of our **Measure Values** shelf. It's not, so I will drag **Low** above **High**
<img align="center" style="padding-right:10px;" src="figures_wk8/DJIA_9.png" width=500><br>
Getting better! I can see a hint of blue at the top of the orange bars.
Now we can adjust the range of the y-axis so we can see more of a distinction between the **Low** and **High** DJIA price each day.
To do this right click on the **Value** label along the y-axis. Select **Edit Axis**. I'll set:
* Range to be a **Fixed range between 21,500 and 22,200**.
* Y-axis Title to be **DJIA - Low and High Price**.
<img align="left" style="padding-right:10px;" src="figures_wk8/DJIA_10b.png" width=300> <br>
<img align="left" style="padding-right:10px;" src="figures_wk8/DJIA_10.png" width=400><br>
Here's what my graph looks like at this point.
<img align="center" style="padding-right:10px;" src="figures_wk8/DJIA_10c.png" width=500><br>
I want to turn-off the data values at the end of end bar in the chart. To do this we need to click on the **Label** icon in the **Marks** section
<img align="center" style="padding-right:10px;" src="figures_wk8/DJIA_10d.png" width=400><br>
Hmmm.. the x-axis still looks a bit too congested to me. I'm going to edit the **Date** in the **columns** shelf to be **Day**.
<img align="center" style="padding-right:10px;" src="figures_wk8/Hi_Low_Day.png" width=500><br>
### Adding a another data element
Moving right along, it's time to add **Close** to this graphic. To do this you will need to drag **Close** from the left panel to the right side of the existing graphic. Once you are near the right edge of the graphic you will see *a bolded dashed line appear along the right edge* of the existing graphic. You need to drop **Close** on that dashed line.
<img align="center" style="padding-right:10px;" src="figures_wk8/DJIA_11.png" width=700><br>
We are getting there... Just need to clean things up a bit. Let's start with adjusting the two sets of y-axes so that they are on the same scale with each other. Right click on the **Close** y-axis and select **Synchronize Axis**.
<img align="center" style="padding-right:10px;" src="figures_wk8/DJIA_12.png" width=500><br>
Well, now that the axes are in synch, we still have an issue that the bars for **Close** are covering up most of the graphic. We can fix this by changing the graphic type for the **Close** data elelment.
To do this go to the **Marks** shelf and click on **Close** (it should be bolded after you click on it). In this same shlef area, use the drop-down selector to change the graphic type for **Close** to **Line** from **Bar**. Make sure you are only adjusting the graphic type for **Close**.
Here's what our graphic will look like at this point.
<img align="center" style="padding-right:10px;" src="figures_wk8/DJIA_13.png" width=700><br>
Things are looking a lot better. But, I'm not too crazy about the default colors that Tableau selected.To adjust the color of the **Close** line, click on the **Color** icon in the **Marks** shelf. Make sure you are on the appropriate shelf.
<img align="center" style="padding-right:10px;" src="figures_wk8/DJIA_14b.png" width=400><br>
To adjust the colors for **Low** and **High**, we need to go to the very upper right corner of the worksheet space. You should see a **Measure Names** shelf. It is possible that the **Show Me** shelf is expanded and hiding the **Measure Names** shelf in this section of the worksheet. Collapse **Show Me** if necessary.
Click on **Measure Names** and then select the down arrow to the right of the name. Select **Edit Color** and adjust the colors to your preference. I'll set my colors as follows:
<img align="center" style="padding-right:10px;" src="figures_wk8/DJIA_14.png" width=400><br>
This graphic is really starting to take shape. However, I'm still a bit confused because I have no easy way to determine when the DJIA is trading or not trading. Since the markets are closed on weekends and holidays, I'd like to find a way to represent that.
Let's go back up to the **Columns** shelf and edit **Date** again. This time we will change the data element to be **Continuous**.
<img align="center" style="padding-right:10px;" src="figures_wk8/DJIA_15.png" width=400><br>
Time to put the final touches on this graphic.
Let's edit the x-axis and add a **Axis Title** of **Business Day**.
We should also clean up our second y-axis by changing that **Axis Title** to **Closing Price**.
Finally, we need to give our graphic a **Title**. To do this go to the **Sheet 1** shelf and click on the down arrow in the far upper right corner of this shelf area. Here is what I entered for my **Title**:
<img align="center" style="padding-right:10px;" src="figures_wk8/DJIA_16.png" width=500><br>
Pulling it all together, you should see a graphic that looks like this.
<img align="center" style="padding-right:10px;" src="figures_wk8/DJIA_17.png" width=600><br>
Congrats!! You have made your first Tableau graphic.
Make sure you rename your worksheet to be something meaningful and that you **SAVE** your work thus far.
Now we need to create a couple of additional graphics so that we can learn how to build a dashboard.
#### Duplicating an Existing Graphic
For our second graphic, I'm going to take the easy route and simply duplicate our existing worksheet and then adjust it from there.
**Objective:** Duplicate the August 2017 graphic and change the date range to another month within our dataset.
To do this right click on the worksheet tab and select **Duplicate**.
<img align="center" style="padding-right:10px;" src="figures_wk8/DJIA_18.png" width=300><br>
Make sure you are on the newly created worksheet. This would be a great time to rename the sheet to help keep things straight.
Let's adjust the date range to be another month. In the **Filters** shelf, select **Show Filter**.
<img align="center" style="padding-right:10px;" src="figures_wk8/DJIA_25.png" width=300><br>
The filter for this field will open ont he right side of the Tableau window.
<img align="center" style="padding-right:10px;" src="figures_wk8/DJIA_25b.png" width=300><br>
Remember where we adjusted the colors for our first graphic, now you should see a range selector for the **Date** data element. I'm going to change this to be the month of **April 2017**
<img align="center" style="padding-right:10px;" src="figures_wk8/DJIA_19.png" width=700><br>
Ummm... That's a bit troubling, where did the graphic go???
If we click on **Data Source** in the lower left corner, we can go back to the dataset itself and look to see what the range of values are for the month of April 2017.
Yup! that's our problem, we have the y-axis set to a **fixed** range that is greater than the possible range of values for the month of **April 2017**. Go ahead and adjust this range to be between **20,200 and 21,200**.
Look that graphic is back!
We should also adjust the graphic title to reflect the fact the we are looking at **April 2017**
<img align="center" style="padding-right:10px;" src="figures_wk8/DJIA_20.png" width=600><br>
### Calculated Fields
Let's make another graphic that uses **Calculated Fields**.
**Objective:** Display the market growth and decline on a per day basis for the month of August 2017.
We will start by duplicating the August 2017 graphic again. Rename the new worksheet to be reflective of the graphic.
We need to do a little cleanup before we really get started. This graphic has nothing to do with **Close**, so we will remove it from the **Rows** shelf.
We need to start by creating the **Calculated Field** since it's the subject of this graphic. Select **Create Calculated Field** under the **Analysis** tab with Tableau.
<img align="center" style="padding-right:10px;" src="figures_wk8/DJIA_26.png" width=600><br>
Let's create our **Calculated Field** by first naming the field, I used **Market Growth/Decline**.
The large blank space in this dialogue box is where you actually put the logic for your calculation. I'm going to define two states for my calculation:
* **Decline**: when the DJIA closes lower than where it opened for the day
* **Growth**: when the DJIA closes higher than where it opened for the day
This is what my **Calculated Field** looks like
<img align="center" style="padding-right:10px;" src="figures_wk8/DJIA_27.png" width=600><br>
If you look in the **Measures** shelf, you should see our newly created **Calculated Field**.
<img align="center" style="padding-right:10px;" src="figures_wk8/DJIA_28b.png" width=400><br>
We are going to use this claculated field as our color distinction data element. As before, we will drag "Market Growth/Decline" from the left panel to the **Color** are within the **Marks** shelf.
I'm also going to change the color selection that Tableau assigned to the values **Growth** (to be green) and **Decline** (to be red). Remember how to do this?
<img align="center" style="padding-right:10px;" src="figures_wk8/DJIA_28.png" width=400><br>
Time to switch things up a bit. I'd like the display per day be a bit more significant. I want to bound the bars in this graphic to show the difference between **Open** and **Close** only.
To do this, we will add the following data elements to the **Details** within the **Marks** shelf, remember to pull the fields from the left panel:
* **Date**: You will need to adjust the display type to by **Day** to match the **Columns** shelf
* **Open**
* **Close**
Final adjustment for **Marks**, I'm going to let Tableau sort out the best way to display this type of information, so I'll switch the graphic type to be **Automatic**.
Now it's time to tweak the rest of the graphic. The y-axis title isn't accurate now, so I'll change it to be **DJIA Price**. One last step, the overall title of the graphic is off a bit now too. So, I'll update that to be **DJIA Market Growth vs Decline** and leave the date range.
Here's what we have at this point.
<img align="center" style="padding-right:10px;" src="figures_wk8/DJIA_29.png" width=9900><br>
So what's going on with this graphic?
The green bars represent a day were the DJIA gained ground (closed higher than it opened). The red bars represent a market declining day (opened higher than it closed).
This is called a *Candlestick Bar* graph.
### Building a Dashboard
Okay, we now have three graphics to work with. Time to build a **Dashboard**
A dashboard is a consolidated display of many worksheets and related information in a single place. It is used to compare and monitor a variety of data simultaneously. The different data views are displayed all at once. Dashboards are shown as tabs at the bottom of the workbook and they usually get updated with the most recent data from the data source. While creating a dashboard, you can add views from any worksheet in the workbook along with many supporting objects such as text areas, web pages, and images.
Each view you add to the dashboard is connected to its corresponding worksheet. So when you modify the worksheet, the dashboard is updated and when you modify the view in the dashboard, the worksheet is updated.
<img align="left" style="padding-right:10px;" src="figures_wk8/DJIA_21.png" width=50><br>
To start building a dashboard, select the **Dashboard** icon along the bottom of your workbook.
This will open up the dashboard workspace for you. Don't worry this is the easy part.
<img align="left" style="padding-right:10px;" src="figures_wk8/DJIA_22.png" width=600><br>
You will notice that there is a **Sheets** shelf on the left side of the work space. Here you will find a list of all the available worksheets that you can add to your dashboard. I have the three worksheets that we have created together.
To build the **Dashboard** all you have to do is pick a worksheet and drag it onto the workspace. I'll start with our Market Growth/Decline graphic.
Now select one of the other graphics and drag it onto the workspace too. Tableau will show you shaded blocks that represent where you might consider locating that this worksheet. I decided to place my graphic with the April data below the Market Growth/Decline graphic.
One more to go. I'll now drag the graphic for the August 2017 data and drag it onto the workspace. I decide to split the space currently occupied by the Arpil graphic with the August graphic too. So now the two low_high_close graphics are sitting side-by-side.
Here's what my final result looks like.
<img align="left" style="padding-right:10px;" src="figures_wk8/DJIA_23.png" width=700><br>
### A Tableau Story
In Tableau, a **Story** is a sequence of graphics that work together to convey information. You can create stories to tell a data narrative, provide context, demonstrate how decisions relate to outcomes or to simply make a compelling case.
In short a Tableau **Story** is a collection of Dashboards and Worksheets that work together to tell a story about your data. This mimics a PowerPoint presentation, but is stored and powered through Tableau.
You can publish Tableau a **Dashboard** and **Story** to shre your insights with others.
<img align="left" style="padding-right:10px;" src="figures_wk8/DJIA_24.png" width=50><br>
To start building a dashboard, select the **Story** icon along the bottom of your workbook.
From here, you follow the same process as you did to build a **Dashboard**.
| 0.851706 | 0.985963 |
# Question 1 : Write a program to subtract two complex numbers in Python.
```
print("Subtraction of two complex numbers : ",(4+3j)-(3-7j))
```
# Question 2 : Write a program to find the fourth root of a number.
```
def fourth_root(x):
return x**(1/4)
num = int(input("Enter a number to find the fourth root: "))
print(fourth_root(num))
```
# Question 3: Write a program to swap two numbers in Python with the help of a temporary variable.
```
x = 5
y = 10
temp = x
x = y
y = temp
print('The value of x after swapping: {}'.format(x))
print('The value of y after swapping: {}'.format(y))
```
# Question 4: Write a program to swap two numbers in Python without using a temporary variable
```
x = 5
y = 10
x, y = y, x
print("x =", x)
print("y =", y)
```
# Question 5: Write a program to convert fahrenheit to kelvin and celsius both.
```
# Python program to convert temperature from
# Fahrenheit to Kelvin
F = int(input("Enter temperature in Fahrenheit: "))
Fahrenheit_to_Kelvin = 273.5 + ((F - 32.0) * (5.0/9.0))
print("Temperature in Kelvin = ", Fahrenheit_to_Kelvin,"K")
# Fahrenheit to Celsius
temp_F = int(input("Enter temperature in Fahrenheit: "))
Fahrenheit_to_Celsius = (5/9) * (temp_F - 32)
print("Temperature in Celsius = ", Fahrenheit_to_Celsius, "degree C")
```
# Question 6: Write a program to demonstrate all the available data types in Python. Hint: Use type() function.
```
x = 5
print(x)
print(type(x))
x = "Hello World"
print(x)
print(type(x))
x = 20.5
print(x)
print(type(x))
x = 1j
print(x)
print(type(x))
x = ["apple", "banana", "cherry"]
print(x)
print(type(x))
x = ("apple", "banana", "cherry")
print(x)
print(type(x))
x = range(6)
print(x)
print(type(x))
x = {"name" : "John", "age" : 36}
print(x)
print(type(x))
x = {"apple", "banana", "cherry"}
print(x)
print(type(x))
x = frozenset({"apple", "banana", "cherry"})
print(x)
print(type(x))
x = True
print(x)
print(type(x))
x = b"Hello"
print(x)
print(type(x))
x = bytearray(5)
print(x)
print(type(x))
x = memoryview(bytes(5))
print(x)
print(type(x))
```
# Question 7: Create a Markdown cell in jupyter and list the steps discussed in the session by Dr. Darshan Ingle sir to create Github profile and upload Githubs Assignment link.
1. GitHub is a place for building your profile which is used to push/upload your codes.
2. Signing in is just like creating an email account.
3. Create a repository named as LetsUpgrade AI-ML
4. Now we can upload our Jupyter notebook on the newly created repository by clicking on the upload file button.
5. 🔗Assignment Submission Link : https://bit.ly/aimlassignment
6. Fill the google form with the link mentioned above providing with the GitHub link for the uploaded assignment.
7. Before clicking on the submit button check the GitHub link whether it is visible or not / working or not.
8. Submit the assignment :)
|
github_jupyter
|
print("Subtraction of two complex numbers : ",(4+3j)-(3-7j))
def fourth_root(x):
return x**(1/4)
num = int(input("Enter a number to find the fourth root: "))
print(fourth_root(num))
x = 5
y = 10
temp = x
x = y
y = temp
print('The value of x after swapping: {}'.format(x))
print('The value of y after swapping: {}'.format(y))
x = 5
y = 10
x, y = y, x
print("x =", x)
print("y =", y)
# Python program to convert temperature from
# Fahrenheit to Kelvin
F = int(input("Enter temperature in Fahrenheit: "))
Fahrenheit_to_Kelvin = 273.5 + ((F - 32.0) * (5.0/9.0))
print("Temperature in Kelvin = ", Fahrenheit_to_Kelvin,"K")
# Fahrenheit to Celsius
temp_F = int(input("Enter temperature in Fahrenheit: "))
Fahrenheit_to_Celsius = (5/9) * (temp_F - 32)
print("Temperature in Celsius = ", Fahrenheit_to_Celsius, "degree C")
x = 5
print(x)
print(type(x))
x = "Hello World"
print(x)
print(type(x))
x = 20.5
print(x)
print(type(x))
x = 1j
print(x)
print(type(x))
x = ["apple", "banana", "cherry"]
print(x)
print(type(x))
x = ("apple", "banana", "cherry")
print(x)
print(type(x))
x = range(6)
print(x)
print(type(x))
x = {"name" : "John", "age" : 36}
print(x)
print(type(x))
x = {"apple", "banana", "cherry"}
print(x)
print(type(x))
x = frozenset({"apple", "banana", "cherry"})
print(x)
print(type(x))
x = True
print(x)
print(type(x))
x = b"Hello"
print(x)
print(type(x))
x = bytearray(5)
print(x)
print(type(x))
x = memoryview(bytes(5))
print(x)
print(type(x))
| 0.264263 | 0.968738 |
# Create PAO1 and PA14 compendia
This notebook is using the observation from the [exploratory notebook](../0_explore_data/cluster_by_accessory_gene.ipynb) to bin samples into PAO1 or PA14 compendia.
A sample is considered PAO1 if the median gene expression of PA14 accessory genes is 0 and PAO1 accessory genes in > 0.
Similarlty, a sample is considered PA14 if the median gene expression of PA14 accessory genes is > 0 and PAO1 accessory genes in 0.
```
%load_ext autoreload
%autoreload 2
%matplotlib inline
import os
import pandas as pd
import seaborn as sns
from textwrap import fill
import matplotlib.pyplot as plt
from scripts import paths, utils
# User param
# same_threshold: if median accessory expression of PAO1 samples > same_threshold then this sample is binned as PAO1
# 25 threshold based on comparing expression of PAO1 SRA-labeled samples vs non-PAO1 samples
same_threshold = 25
# opp_threshold: if median accessory expression of PA14 samples < opp_threshold then this sample is binned as PAO1
# 25 threshold based on previous plot (eye-balling trying to avoid samples
# on the diagonal of explore_data/cluster_by_accessory_gene.ipynb plot)
opp_threshold = 25
```
## Load data
The expression data being used is described in the [paper](link TBD) with source code [here](https://github.com/hoganlab-dartmouth/pa-seq-compendia)
```
# Expression data files
pao1_expression_filename = paths.PAO1_GE
pa14_expression_filename = paths.PA14_GE
# File containing table to map sample id to strain name
sample_to_strain_filename = paths.SAMPLE_TO_STRAIN
# Load expression data
pao1_expression = pd.read_csv(pao1_expression_filename, sep="\t", index_col=0, header=0)
pa14_expression = pd.read_csv(pa14_expression_filename, sep="\t", index_col=0, header=0)
# Load metadata
# Set index to experiment id, which is what we will use to map to expression data
sample_to_strain_table_full = pd.read_csv(sample_to_strain_filename, index_col=2)
```
## Get core and accessory annotations
```
# Annotations are from BACTOME
# Gene ids from PAO1 are annotated with the homologous PA14 gene id and vice versa
pao1_annot_filename = paths.GENE_PAO1_ANNOT
pa14_annot_filename = paths.GENE_PA14_ANNOT
core_acc_dict = utils.get_my_core_acc_genes(
pao1_annot_filename, pa14_annot_filename, pao1_expression, pa14_expression
)
pao1_acc = core_acc_dict["acc_pao1"]
pa14_acc = core_acc_dict["acc_pa14"]
```
## Format expression data
Format index to only include experiment id. This will be used to map to expression data and SRA labels later
```
# Format expression data indices so that values can be mapped to `sample_to_strain_table`
pao1_index_processed = pao1_expression.index.str.split(".").str[0]
pa14_index_processed = pa14_expression.index.str.split(".").str[0]
print(
f"No. of samples processed using PAO1 reference after filtering: {pao1_expression.shape}"
)
print(
f"No. of samples processed using PA14 reference after filtering: {pa14_expression.shape}"
)
pao1_expression.index = pao1_index_processed
pa14_expression.index = pa14_index_processed
pao1_expression.head()
pa14_expression.head()
# Save pre-binned expression data
pao1_expression.to_csv(paths.PAO1_PREBIN_COMPENDIUM, sep="\t")
pa14_expression.to_csv(paths.PA14_PREBIN_COMPENDIUM, sep="\t")
```
## Bin samples as PAO1 or PA14
```
# Create accessory df
# accessory gene ids | median accessory expression | strain label
# PAO1
pao1_acc_expression = pao1_expression[pao1_acc]
pao1_acc_expression["median_acc_expression"] = pao1_acc_expression.median(axis=1)
# PA14
pa14_acc_expression = pa14_expression[pa14_acc]
pa14_acc_expression["median_acc_expression"] = pa14_acc_expression.median(axis=1)
pao1_acc_expression.head()
# Merge PAO1 and PA14 accessory dataframes
pao1_pa14_acc_expression = pao1_acc_expression.merge(
pa14_acc_expression,
left_index=True,
right_index=True,
suffixes=["_pao1", "_pa14"],
)
pao1_pa14_acc_expression.head()
# Find PAO1 samples
pao1_binned_ids = list(
pao1_pa14_acc_expression.query(
"median_acc_expression_pao1>@same_threshold & median_acc_expression_pa14<@opp_threshold"
).index
)
# Find PA14 samples
pa14_binned_ids = list(
pao1_pa14_acc_expression.query(
"median_acc_expression_pao1<@opp_threshold & median_acc_expression_pa14>@same_threshold"
).index
)
# Check that there are no samples that are binned as both PAO1 and PA14
shared_pao1_pa14_binned_ids = list(set(pao1_binned_ids).intersection(pa14_binned_ids))
assert len(shared_pao1_pa14_binned_ids) == 0
```
## Format SRA annotations
```
# Since experiments have multiple runs there are duplicated experiment ids in the index
# We will need to remove these so that the count calculations are accurate
sample_to_strain_table_full_processed = sample_to_strain_table_full[
~sample_to_strain_table_full.index.duplicated(keep="first")
]
assert (
len(sample_to_strain_table_full.index.unique())
== sample_to_strain_table_full_processed.shape[0]
)
# Aggregate boolean labels into a single strain label
aggregated_label = []
for exp_id in list(sample_to_strain_table_full_processed.index):
if sample_to_strain_table_full_processed.loc[exp_id, "PAO1"].all() == True:
aggregated_label.append("PAO1")
elif sample_to_strain_table_full_processed.loc[exp_id, "PA14"].all() == True:
aggregated_label.append("PA14")
elif sample_to_strain_table_full_processed.loc[exp_id, "PAK"].all() == True:
aggregated_label.append("PAK")
elif (
sample_to_strain_table_full_processed.loc[exp_id, "ClinicalIsolate"].all()
== True
):
aggregated_label.append("Clinical Isolate")
else:
aggregated_label.append("NA")
sample_to_strain_table_full_processed["Strain type"] = aggregated_label
sample_to_strain_table = sample_to_strain_table_full_processed["Strain type"].to_frame()
sample_to_strain_table.head()
```
## Save pre-binned data with median accessory expression
This dataset will be used for Georgia's manuscript, which describes how we generated these compendia
```
# Select columns with median accessory expression
pao1_pa14_acc_expression_select = pao1_pa14_acc_expression[
["median_acc_expression_pao1", "median_acc_expression_pa14"]
]
pao1_pa14_acc_expression_select.head()
# Add SRA strain type
pao1_pa14_acc_expression_label = pao1_pa14_acc_expression_select.merge(
sample_to_strain_table, left_index=True, right_index=True
)
# Rename column
pao1_pa14_acc_expression_label = pao1_pa14_acc_expression_label.rename(
{"Strain type": "SRA label"}, axis=1
)
pao1_pa14_acc_expression_label.head()
# Add our binned label
pao1_pa14_acc_expression_label["Our label"] = "NA"
pao1_pa14_acc_expression_label.loc[pao1_binned_ids, "Our label"] = "PAO1-like"
pao1_pa14_acc_expression_label.loc[pa14_binned_ids, "Our label"] = "PA14-like"
pao1_pa14_acc_expression_label.head()
# Confirm dimensions
pao1_expression_prebin_filename = paths.PAO1_PREBIN_COMPENDIUM
pa14_expression_prebin_filename = paths.PA14_PREBIN_COMPENDIUM
pao1_expression_prebin = pd.read_csv(
pao1_expression_prebin_filename, sep="\t", index_col=0, header=0
)
pa14_expression_prebin = pd.read_csv(
pa14_expression_prebin_filename, sep="\t", index_col=0, header=0
)
# he two expression prebins are because the same samples were mapped to 2 different references (PAO1 and a PA14 reference.
# This assertion is to make sure that the number of samples is the same in both, which it is.
# This assertion is also testing that when we added information about our accessory gene expression
# and labels we retained the same number of samples, which we did.
assert (
pao1_expression_prebin.shape[0]
== pa14_expression_prebin.shape[0]
== pao1_pa14_acc_expression_label.shape[0]
)
# Save
pao1_pa14_acc_expression_label.to_csv(
"prebinned_compendia_acc_expression.tsv", sep="\t"
)
```
## Create compendia
Create PAO1 and PA14 compendia
```
# Get expression data
# Note: reindexing needed here instead of .loc since samples from expression data
# were filtered out for low counts, but these samples still exist in log files
pao1_expression_binned = pao1_expression.loc[pao1_binned_ids]
pa14_expression_binned = pa14_expression.loc[pa14_binned_ids]
assert len(pao1_binned_ids) == pao1_expression_binned.shape[0]
assert len(pa14_binned_ids) == pa14_expression_binned.shape[0]
# Label samples with SRA annotations
# pao1_expression_label = pao1_expression_binned.join(
# sample_to_strain_table, how='left')
pao1_expression_label = pao1_expression_binned.merge(
sample_to_strain_table, left_index=True, right_index=True
)
pa14_expression_label = pa14_expression_binned.merge(
sample_to_strain_table, left_index=True, right_index=True
)
print(pao1_expression_label.shape)
pao1_expression_label.head()
print(pa14_expression_label.shape)
pa14_expression_label.head()
assert pao1_expression_binned.shape[0] == pao1_expression_label.shape[0]
assert pa14_expression_binned.shape[0] == pa14_expression_label.shape[0]
sample_to_strain_table["Strain type"].value_counts()
```
Looks like our binned compendium sizes is fairly close in number to what SRA annotates
## Quick comparison
Quick check comparing our binned labels compared with SRA annotations
```
pao1_expression_label["Strain type"].value_counts()
```
**Manually check that these PA14 are mislabeled**
* Clinical ones can be removed by increasing threshold
```
pa14_expression_label["Strain type"].value_counts()
```
## Check
Manually look up the samples we binned as PAO1 but SRA labeled as PA14. Are these cases of samples being mislabeled?
```
pao1_expression_label[pao1_expression_label["Strain type"] == "PA14"]
```
Note: These are the 7 PA14 labeled samples using threshold of 0
Most samples appear to be mislabeled:
* SRX5099522: https://www.ncbi.nlm.nih.gov/sra/?term=SRX5099522
* SRX5099523: https://www.ncbi.nlm.nih.gov/sra/?term=SRX5099523
* SRX5099524: https://www.ncbi.nlm.nih.gov/sra/?term=SRX5099524
* SRX5290921: https://www.ncbi.nlm.nih.gov/sra/?term=SRX5290921
* SRX5290922: https://www.ncbi.nlm.nih.gov/sra/?term=SRX5290922
Two samples appear to be PA14 samples treated with antimicrobial manuka honey.
* SRX7423386: https://www.ncbi.nlm.nih.gov/sra/?term=SRX7423386
* SRX7423388: https://www.ncbi.nlm.nih.gov/sra/?term=SRX7423388
```
pa14_label_pao1_binned_ids = list(
pao1_expression_label[pao1_expression_label["Strain type"] == "PA14"].index
)
pao1_pa14_acc_expression.loc[
pa14_label_pao1_binned_ids,
["median_acc_expression_pao1", "median_acc_expression_pa14"],
]
# Save compendia with SRA label
pao1_expression_label.to_csv(paths.PAO1_COMPENDIUM_LABEL, sep="\t")
pa14_expression_label.to_csv(paths.PA14_COMPENDIUM_LABEL, sep="\t")
# Save compendia without SRA label
pao1_expression_binned.to_csv(paths.PAO1_COMPENDIUM, sep="\t")
pa14_expression_binned.to_csv(paths.PA14_COMPENDIUM, sep="\t")
# Save processed metadata table
sample_to_strain_table.to_csv(paths.SAMPLE_TO_STRAIN_PROCESSED, sep="\t")
```
|
github_jupyter
|
%load_ext autoreload
%autoreload 2
%matplotlib inline
import os
import pandas as pd
import seaborn as sns
from textwrap import fill
import matplotlib.pyplot as plt
from scripts import paths, utils
# User param
# same_threshold: if median accessory expression of PAO1 samples > same_threshold then this sample is binned as PAO1
# 25 threshold based on comparing expression of PAO1 SRA-labeled samples vs non-PAO1 samples
same_threshold = 25
# opp_threshold: if median accessory expression of PA14 samples < opp_threshold then this sample is binned as PAO1
# 25 threshold based on previous plot (eye-balling trying to avoid samples
# on the diagonal of explore_data/cluster_by_accessory_gene.ipynb plot)
opp_threshold = 25
# Expression data files
pao1_expression_filename = paths.PAO1_GE
pa14_expression_filename = paths.PA14_GE
# File containing table to map sample id to strain name
sample_to_strain_filename = paths.SAMPLE_TO_STRAIN
# Load expression data
pao1_expression = pd.read_csv(pao1_expression_filename, sep="\t", index_col=0, header=0)
pa14_expression = pd.read_csv(pa14_expression_filename, sep="\t", index_col=0, header=0)
# Load metadata
# Set index to experiment id, which is what we will use to map to expression data
sample_to_strain_table_full = pd.read_csv(sample_to_strain_filename, index_col=2)
# Annotations are from BACTOME
# Gene ids from PAO1 are annotated with the homologous PA14 gene id and vice versa
pao1_annot_filename = paths.GENE_PAO1_ANNOT
pa14_annot_filename = paths.GENE_PA14_ANNOT
core_acc_dict = utils.get_my_core_acc_genes(
pao1_annot_filename, pa14_annot_filename, pao1_expression, pa14_expression
)
pao1_acc = core_acc_dict["acc_pao1"]
pa14_acc = core_acc_dict["acc_pa14"]
# Format expression data indices so that values can be mapped to `sample_to_strain_table`
pao1_index_processed = pao1_expression.index.str.split(".").str[0]
pa14_index_processed = pa14_expression.index.str.split(".").str[0]
print(
f"No. of samples processed using PAO1 reference after filtering: {pao1_expression.shape}"
)
print(
f"No. of samples processed using PA14 reference after filtering: {pa14_expression.shape}"
)
pao1_expression.index = pao1_index_processed
pa14_expression.index = pa14_index_processed
pao1_expression.head()
pa14_expression.head()
# Save pre-binned expression data
pao1_expression.to_csv(paths.PAO1_PREBIN_COMPENDIUM, sep="\t")
pa14_expression.to_csv(paths.PA14_PREBIN_COMPENDIUM, sep="\t")
# Create accessory df
# accessory gene ids | median accessory expression | strain label
# PAO1
pao1_acc_expression = pao1_expression[pao1_acc]
pao1_acc_expression["median_acc_expression"] = pao1_acc_expression.median(axis=1)
# PA14
pa14_acc_expression = pa14_expression[pa14_acc]
pa14_acc_expression["median_acc_expression"] = pa14_acc_expression.median(axis=1)
pao1_acc_expression.head()
# Merge PAO1 and PA14 accessory dataframes
pao1_pa14_acc_expression = pao1_acc_expression.merge(
pa14_acc_expression,
left_index=True,
right_index=True,
suffixes=["_pao1", "_pa14"],
)
pao1_pa14_acc_expression.head()
# Find PAO1 samples
pao1_binned_ids = list(
pao1_pa14_acc_expression.query(
"median_acc_expression_pao1>@same_threshold & median_acc_expression_pa14<@opp_threshold"
).index
)
# Find PA14 samples
pa14_binned_ids = list(
pao1_pa14_acc_expression.query(
"median_acc_expression_pao1<@opp_threshold & median_acc_expression_pa14>@same_threshold"
).index
)
# Check that there are no samples that are binned as both PAO1 and PA14
shared_pao1_pa14_binned_ids = list(set(pao1_binned_ids).intersection(pa14_binned_ids))
assert len(shared_pao1_pa14_binned_ids) == 0
# Since experiments have multiple runs there are duplicated experiment ids in the index
# We will need to remove these so that the count calculations are accurate
sample_to_strain_table_full_processed = sample_to_strain_table_full[
~sample_to_strain_table_full.index.duplicated(keep="first")
]
assert (
len(sample_to_strain_table_full.index.unique())
== sample_to_strain_table_full_processed.shape[0]
)
# Aggregate boolean labels into a single strain label
aggregated_label = []
for exp_id in list(sample_to_strain_table_full_processed.index):
if sample_to_strain_table_full_processed.loc[exp_id, "PAO1"].all() == True:
aggregated_label.append("PAO1")
elif sample_to_strain_table_full_processed.loc[exp_id, "PA14"].all() == True:
aggregated_label.append("PA14")
elif sample_to_strain_table_full_processed.loc[exp_id, "PAK"].all() == True:
aggregated_label.append("PAK")
elif (
sample_to_strain_table_full_processed.loc[exp_id, "ClinicalIsolate"].all()
== True
):
aggregated_label.append("Clinical Isolate")
else:
aggregated_label.append("NA")
sample_to_strain_table_full_processed["Strain type"] = aggregated_label
sample_to_strain_table = sample_to_strain_table_full_processed["Strain type"].to_frame()
sample_to_strain_table.head()
# Select columns with median accessory expression
pao1_pa14_acc_expression_select = pao1_pa14_acc_expression[
["median_acc_expression_pao1", "median_acc_expression_pa14"]
]
pao1_pa14_acc_expression_select.head()
# Add SRA strain type
pao1_pa14_acc_expression_label = pao1_pa14_acc_expression_select.merge(
sample_to_strain_table, left_index=True, right_index=True
)
# Rename column
pao1_pa14_acc_expression_label = pao1_pa14_acc_expression_label.rename(
{"Strain type": "SRA label"}, axis=1
)
pao1_pa14_acc_expression_label.head()
# Add our binned label
pao1_pa14_acc_expression_label["Our label"] = "NA"
pao1_pa14_acc_expression_label.loc[pao1_binned_ids, "Our label"] = "PAO1-like"
pao1_pa14_acc_expression_label.loc[pa14_binned_ids, "Our label"] = "PA14-like"
pao1_pa14_acc_expression_label.head()
# Confirm dimensions
pao1_expression_prebin_filename = paths.PAO1_PREBIN_COMPENDIUM
pa14_expression_prebin_filename = paths.PA14_PREBIN_COMPENDIUM
pao1_expression_prebin = pd.read_csv(
pao1_expression_prebin_filename, sep="\t", index_col=0, header=0
)
pa14_expression_prebin = pd.read_csv(
pa14_expression_prebin_filename, sep="\t", index_col=0, header=0
)
# he two expression prebins are because the same samples were mapped to 2 different references (PAO1 and a PA14 reference.
# This assertion is to make sure that the number of samples is the same in both, which it is.
# This assertion is also testing that when we added information about our accessory gene expression
# and labels we retained the same number of samples, which we did.
assert (
pao1_expression_prebin.shape[0]
== pa14_expression_prebin.shape[0]
== pao1_pa14_acc_expression_label.shape[0]
)
# Save
pao1_pa14_acc_expression_label.to_csv(
"prebinned_compendia_acc_expression.tsv", sep="\t"
)
# Get expression data
# Note: reindexing needed here instead of .loc since samples from expression data
# were filtered out for low counts, but these samples still exist in log files
pao1_expression_binned = pao1_expression.loc[pao1_binned_ids]
pa14_expression_binned = pa14_expression.loc[pa14_binned_ids]
assert len(pao1_binned_ids) == pao1_expression_binned.shape[0]
assert len(pa14_binned_ids) == pa14_expression_binned.shape[0]
# Label samples with SRA annotations
# pao1_expression_label = pao1_expression_binned.join(
# sample_to_strain_table, how='left')
pao1_expression_label = pao1_expression_binned.merge(
sample_to_strain_table, left_index=True, right_index=True
)
pa14_expression_label = pa14_expression_binned.merge(
sample_to_strain_table, left_index=True, right_index=True
)
print(pao1_expression_label.shape)
pao1_expression_label.head()
print(pa14_expression_label.shape)
pa14_expression_label.head()
assert pao1_expression_binned.shape[0] == pao1_expression_label.shape[0]
assert pa14_expression_binned.shape[0] == pa14_expression_label.shape[0]
sample_to_strain_table["Strain type"].value_counts()
pao1_expression_label["Strain type"].value_counts()
pa14_expression_label["Strain type"].value_counts()
pao1_expression_label[pao1_expression_label["Strain type"] == "PA14"]
pa14_label_pao1_binned_ids = list(
pao1_expression_label[pao1_expression_label["Strain type"] == "PA14"].index
)
pao1_pa14_acc_expression.loc[
pa14_label_pao1_binned_ids,
["median_acc_expression_pao1", "median_acc_expression_pa14"],
]
# Save compendia with SRA label
pao1_expression_label.to_csv(paths.PAO1_COMPENDIUM_LABEL, sep="\t")
pa14_expression_label.to_csv(paths.PA14_COMPENDIUM_LABEL, sep="\t")
# Save compendia without SRA label
pao1_expression_binned.to_csv(paths.PAO1_COMPENDIUM, sep="\t")
pa14_expression_binned.to_csv(paths.PA14_COMPENDIUM, sep="\t")
# Save processed metadata table
sample_to_strain_table.to_csv(paths.SAMPLE_TO_STRAIN_PROCESSED, sep="\t")
| 0.7011 | 0.953405 |
<a name="top"></a>Overview: Standard libraries
===
* [The Python standard library](#standard)
* [Importing modules](#importieren)
* [Maths](#math)
* [Files and folders](#ospath)
* [Statistics and random numbers](#statistics)
* [Exercise 06: Standard libraries](#uebung06)
**Learning Goals:** After this lecture you
* know how to import functions from other modules
* can use the ```math``` module for complex mathematical calculations
* understand how to manipulate folders and files using the ```os.path``` module
* have an idea how to do statistics with the ```statistics``` module
<a name="standard"></a>The Python standard library
===
<a name="importieren"></a>Importing modules
---
We already know a few functions, which are pre-built into Python. As you have seen they are very helpful, as for example:
* ```print()```
* ```sum()```
* ```len()```
* ...
You can find a list of directly available functions here: https://docs.python.org/2/library/functions.html
Additionally, there are a number of _standard libraries_ in python, which automatically get installed together with Python. This means, you already have these libraries on the computer (or in our case - the jupyter notebook).
However, the functionalities provided are rather specific, so the libraries are not automatically _included_ in every script you write.
Thus, if you want to use a function from a part of the standard libraries (_modules_) you have to _import_ that module first.
[top](#top)
<a name="math"></a>Maths
---
A standard example is the ```math``` module. It contains a number of helpful functions (for doing advanced maths), for example ```sin()``` and ```cos()```. To import a module in Python we use the ```import``` keyword:
```
# we import the modul, from now on we can use it in this entire script
import math
```
We access functions of the module by using a "module.function" syntax:
```
math.sin(3)
result = math.cos(math.pi)
print(result)
```
##### Documentation
You'd assume that ```math``` includes functions like sine, cosine, absolute value or such to do appropriate rounding.
If you're interested in what else ```math``` contains, you should take a look at the online-documentation dof the module:
Documentation of ```math```: https://docs.python.org/3/library/math.html
Alternatively, we can get help on single functions directly in the notebook:
```
help(math.cos)
? math.cos
```
[top](#top)
<a name="ospath"></a>Files and folders
---
The ```os``` module allows us to interact with the files and folders in the operating system on which Python is running (```os``` - **o**perating **s**ystem):
```
import os
```
Using ```os``` we can, for example, get the information on the path to our current working directory (the directory, in which _this notebook_ is located):
```
path = os.getcwd() # [c]urrent [w]orking [d]irectory, cwd
# the return vaule of 'os.getcwd()' is a string containing the path
print(path)
```
We can also get a list of the files in our working directory:
```
# os.listdir returns a list containing strings of file names
files = os.listdir(path)
# note: a number of hidden files are shown as well
# hidden files have a name that starts with a point
print(files)
```
Now we are going to create a few new files. Since we want to keep a tidy directory, we first create a new folder to hold these files:
```
new_folder_name = 'my_folder'
os.mkdir(new_folder_name)
print(os.listdir(path))
```
Since we want our new files to go into the new folder, we have to update the path we are using. To do this, we use a _sub-module_ of ```os```, called ```os.path```:
```
path = os.path.join(path, new_folder_name)
print(path)
```
Since we don't want to have to write ```os.path.join()``` every time we want to modify a path, we're going to import the function ```join()``` directly into the global namespace of our script:
```
from os.path import join
```
Now we can interact with files, and for example open them in the script, write something into them and then close them again (we don't even need the module ```os``` for that). If we try to open a file that does not exist, the computer throws an error:
```
filename = 'my_file.txt'
open(join(path,filename))
```
To solve this problem, we pass an additional argument ot the ```open``` function, which tells it we want to **w**rite into the file (and by logical extention, if no file exists, to create it):
```
# passing w (short for write) to 'open()' allows it
# to write into a file and create the file if it does not exist
open(os.path.join(path, filename), 'w')
# remove the file again:
os.remove(join(path, filename))
```
Now let's automatically create a number of files. To do this, we put the functions we used before into a loop:
```
# loop over i 0 to 10
for i in range(10):
# create a file name based on a static string and i
file_name = 'file_{}.txt'.format(i)
# create a file with the name 'file_path' in the directory 'path'
open(join(path, file_name), 'w')
```
We can also modify these file names automatically:
```
file_names = os.listdir(path)
print(file_names)
# note: we should not touch any hidden files!
# iterate over the files in 'path'
# we use enumerate() to get an index
# which we use for the new file name
for i, name in enumerate(file_names):
# we only want to touch files that end in '.txt'
if name.endswith('.txt'):
# create a new name
new_name = '2017-06-11_{}.txt'.format(i)
# we use rename(old_path, new_path) to rename the files
os.rename(join(path, name), join(path,new_name))
# IMPORTANT: always pass the entire path to the file!
```
[top](#top)
<a name="statistics"></a>Statistics and random numbers
---
The standard libraries also include basic functionality for statistics and random numbers. You can find the documentation of these two modules here:
* ```statistics```: https://docs.python.org/3/library/statistics.html
* ```random```: https://docs.python.org/3/library/random.html
```
import random
import statistics
```
We can, for example, create a list of random integer numbers:
```
# use list-comprehension to create ten random
# integers between 0 and 10 and save them in a list
random_numbers = [random.randint(0,10) for i in range(10)]
# every execution of this cell produces different random numbers
print(random_numbers)
```
We can also do a bit of statistics and look at the mean median and standard deviation of the numbers
```
# create ten lists of random integers
for i in range(10):
# create a list of ten integers in -10 to 10
numbers = [random.randint(-10,10) for i in range(10)]
mean = statistics.mean(numbers) # Mean
std = statistics.stdev(numbers) # Standard deviation
median = statistics.median(numbers) # Median
# display the results neatly formated
print('mean: {}, stdev: {}, median: {}'\
.format(mean, std, median))
```
[top](#top)
<a name="uebung06"></a>Exercise 06: Standard libraries
===
1. **Math**
1. Read the documentation of ```math``` to understand how to convert from degrees to radians and vice versa. Convert $\pi$, $\pi/2$ and $2\pi$ to degrees and $100^\circ$, $200^\circ$ and $300^\circ$ to radians.
2. Given are the coordinates of the corners of a triangle:
$A = (0,0); \quad B = (3,0); \quad C = (4,2)$.
Write a function, which accepts the $(x,y)$ coordinates of two corners and then calculates the length of the distance between the corners. Use the ```math``` module.
3. Use your function to calculate the lengths of all the edges $a, b, c$ of the triangle.
4. **(Optional)** Also calculate the opposite angles $\alpha, \beta, \gamma$ of the triangle.
Hint: Law of cosines https://en.wikipedia.org/wiki/Law_of_cosines
2. **Files and folders**
1. Create a new directory using ```mkdir()```.
2. Find the path to the this directory and save it in a variable.
3. Automatically create 5 new .txt files and 5 new .csv files in your new directory.
4. Automatically rename theses files. Use different names depending on whether the file is .csv or .txt.
5. **(Optional)** Automatically create a directory for every week in June. In every directory, create a file for every day of the week which the directory represents. Use the specific date of the file as its name (e.g. 2017-06-01 for the 1. Juni 2017).
6. **(Optional)** Investigate, how to write from a script into a file. Test the concept on a .txt file.
7. **(Optional)** Write the appropriate date into each of the file you created for June.
3. **Statistics and random numbers**
1. Create a list with a random length $\in [5,10]$ filled with random integers.
2. Take a look at the ```shuffle()``` function of the ```random``` module and use it to mix the order of the elements of the list.
3. **(Optional)**: Create a copy of the list. Write a function, which mixes the copy, compares it to the original and returns ```True``` if they are the same, ```False``` else.
4. **(Optional)** Write a loop, which shuffels the list N times. How long does it take until the copy randomly has the same order as the original? How does the number of necessary iterations depend on the length of the list?
[top](#top)
|
github_jupyter
|
* ```sum()```
* ```len()```
* ...
You can find a list of directly available functions here: https://docs.python.org/2/library/functions.html
Additionally, there are a number of _standard libraries_ in python, which automatically get installed together with Python. This means, you already have these libraries on the computer (or in our case - the jupyter notebook).
However, the functionalities provided are rather specific, so the libraries are not automatically _included_ in every script you write.
Thus, if you want to use a function from a part of the standard libraries (_modules_) you have to _import_ that module first.
[top](#top)
<a name="math"></a>Maths
---
A standard example is the ```math``` module. It contains a number of helpful functions (for doing advanced maths), for example ```sin()``` and ```cos()```. To import a module in Python we use the ```import``` keyword:
We access functions of the module by using a "module.function" syntax:
##### Documentation
You'd assume that ```math``` includes functions like sine, cosine, absolute value or such to do appropriate rounding.
If you're interested in what else ```math``` contains, you should take a look at the online-documentation dof the module:
Documentation of ```math```: https://docs.python.org/3/library/math.html
Alternatively, we can get help on single functions directly in the notebook:
[top](#top)
<a name="ospath"></a>Files and folders
---
The ```os``` module allows us to interact with the files and folders in the operating system on which Python is running (```os``` - **o**perating **s**ystem):
Using ```os``` we can, for example, get the information on the path to our current working directory (the directory, in which _this notebook_ is located):
We can also get a list of the files in our working directory:
Now we are going to create a few new files. Since we want to keep a tidy directory, we first create a new folder to hold these files:
Since we want our new files to go into the new folder, we have to update the path we are using. To do this, we use a _sub-module_ of ```os```, called ```os.path```:
Since we don't want to have to write ```os.path.join()``` every time we want to modify a path, we're going to import the function ```join()``` directly into the global namespace of our script:
Now we can interact with files, and for example open them in the script, write something into them and then close them again (we don't even need the module ```os``` for that). If we try to open a file that does not exist, the computer throws an error:
To solve this problem, we pass an additional argument ot the ```open``` function, which tells it we want to **w**rite into the file (and by logical extention, if no file exists, to create it):
Now let's automatically create a number of files. To do this, we put the functions we used before into a loop:
We can also modify these file names automatically:
[top](#top)
<a name="statistics"></a>Statistics and random numbers
---
The standard libraries also include basic functionality for statistics and random numbers. You can find the documentation of these two modules here:
* ```statistics```: https://docs.python.org/3/library/statistics.html
* ```random```: https://docs.python.org/3/library/random.html
We can, for example, create a list of random integer numbers:
We can also do a bit of statistics and look at the mean median and standard deviation of the numbers
| 0.807195 | 0.981471 |
Step 1: build a surface water network. You can "pickle" this, so it doesn't need to be repeated.
n = swn.SurfaceWaterNetwork.from_lines(gdf.geometry)
n.to_pickle("surface-water-network.pkl")
# then in a later session, skip the above and just do:
n = swn.SurfaceWaterNetwork.from_pickle("surface-water-network.pkl")
Step 2: load a MF6 model, then find the intersections:
sim = flopy.mf6.MFSimulation.load(...)
m = sim.get_model(...)
nm = swn.SwnMf6.from_swn_flopy(n, m)
Most of the results will be in the nm.reaches property, but other reach datasets will need to be specified, including "man", "rbth", "rgrd", "rhk", "rtp", and "rwid". There are two methods to format the PACKAGEDATA:
nm.flopy_packagedata
nm.write_packagedata("packagedata.dat")
Similar with CONNECTIONDATA:
nm.flopy_connectiondata
nm.write_connectiondata("connectiondata.dat")
There are a few "helper" methods to sort out things like "set_reach_slope" based on a few methods. One missing one is "set_reach_elevation" or whatever to make the reaches fit in the layer and/or move the layer elevations to fit the stream.
And lastly, there is no PERIOD data yet. I'm working on this, which is holding up the merge.
```
import geopandas
import os
import swn
import flopy
import numpy as np
import time
```
# SW network pickle
#only do this once... takes forever... then load pickle
gdb_dir = 'D:\modelling\data'
gdb_fname = 'nzRec2_v5.gdb'
gdb_path = os.path.join(gdb_dir, gdb_fname)
# Read national data of streams
gdf_lines = geopandas.read_file(gdb_path, layer='riverlines')
gdf_lines.set_index('nzsegment', inplace=True, verify_integrity=True)
gdf_ws = geopandas.read_file(gdb_path, layer='rec2ws')
gdf_ws.set_index('nzsegment', inplace=True, verify_integrity=True)
# Convert MultiLineString -> LineString
lines = gdf_lines.geometry.apply(lambda x: x.geoms[0]) #what is geoms[0]
polygons = gdf_ws.geometry.apply(lambda x: x.geoms[0])
#ni_lines = gdf_lines.loc[gdf_lines.index < 10000000, "geometry"]
# requires reindex otherwise failure in core.from_lines
t0=time.time()
n = swn.SurfaceWaterNetwork.from_lines(lines,polygons.reindex(index=lines.index))
print(time.time()-t0)
n.to_pickle("surface-water-network.pkl")
# get the pickle
```
n = swn.SurfaceWaterNetwork.from_pickle("surface-water-network.pkl")
```
# Load MF6 model
```
os.getcwd()
sim_ws=os.path.join('..','zmodels','20210622_simulation','wairau_240_3')
model_name='wairau_240_3'
sim=flopy.mf6.MFSimulation.load(sim_ws=sim_ws)
gwf=sim.get_model(model_name)
```
## spatial reference for model
```
#sr=flopy.utils.reference.SpatialReference.from_gridspec(os.path.join(sim_ws,model_name+'.grid.spc'))
#gwf.dis.xorigin=sr.xul
#gwf.dis.yorigin=sr.yul-np.sum(gwf.dis.delr.data)
#gwf.dis.write()
# this also takes forever
t0=time.time()
ngwf = swn.SwnMf6.from_swn_flopy(n, gwf)
print(time.time()-t0)
# https://modflow6.readthedocs.io/en/latest/_mf6io/gwf-sfr.html?highlight=ustrf#block-packagedata
# started from sagehen example, tweaked
# can do ngwf.default_packagedata() now?
d={'rwid':10.0,'rbth':1.0,'man':0.04,'ustrf':1.0,'ndv': 0}
for k in ["man", "rbth", "rwid"]:
ngwf.reaches[k]=d[k]
```
# was taking much time to fail with no zcoord, now takes 1.2 sec
t0=time.time()
#zcoord_ab or grid_top
try:
ngwf.set_reach_slope(method='zcoord_ab')
except:
print(time.time()-t0)
```
# check for nans, should have been fixed, taken care of
ngwf.set_reach_slope(method='grid_top')
#ngwf.set_reach_data_from_array('rtp',gwf.dis.top.array)
ngwf.reaches['rgrd']=
ngwf.reaches
ngwf.set_reach_data_from_array('rhk',gwf.npf.k.array[0])
ngwf.reaches
n.segments
n.segments.to_csv(os.path.join(sim_ws,'znseg_mf6rch.csv'))
mask=[s for s in n.segments.index if (len(n.segments.loc[s,'from_segnums'])==0) & (n.segments.loc[s,'to_segnum']==0)]
len(mask)
n.segments.drop(mask,inplace=True)
len(n.segments)
help(n.remove)
# There are two methods to format the PACKAGEDATA:
ngwf.flopy_packagedata
ngwf.write_packagedata(os.path.join(sim_ws,model_name+'.sfr.reach.dat'))
#Similar with CONNECTIONDATA:
ngwf.flopy_connectiondata
ngwf.write_connectiondata(os.path.join(sim_ws,model_name+'.sfr.connection.dat'))
sfr=flopy.mf6.ModflowGwfsfr(gwf,packagedata={'filename':model_name+'.sfr.reach.dat'},
connectiondata={'filename':model_name+'.sfr.connection.dat'},
nreaches=len(ngwf.reaches),budget_filerecord=model_name + "_sfr.bud",
save_flows=True)
#gwf.register_package(sfr)
sfr.write()
gwf.write()
help(ngwf)
```
# write shapefile, but not sfr info from grid intersection
```
swn.file.gdf_to_shapefile(n.segments, 'segments.shp')
```
|
github_jupyter
|
import geopandas
import os
import swn
import flopy
import numpy as np
import time
n = swn.SurfaceWaterNetwork.from_pickle("surface-water-network.pkl")
os.getcwd()
sim_ws=os.path.join('..','zmodels','20210622_simulation','wairau_240_3')
model_name='wairau_240_3'
sim=flopy.mf6.MFSimulation.load(sim_ws=sim_ws)
gwf=sim.get_model(model_name)
#sr=flopy.utils.reference.SpatialReference.from_gridspec(os.path.join(sim_ws,model_name+'.grid.spc'))
#gwf.dis.xorigin=sr.xul
#gwf.dis.yorigin=sr.yul-np.sum(gwf.dis.delr.data)
#gwf.dis.write()
# this also takes forever
t0=time.time()
ngwf = swn.SwnMf6.from_swn_flopy(n, gwf)
print(time.time()-t0)
# https://modflow6.readthedocs.io/en/latest/_mf6io/gwf-sfr.html?highlight=ustrf#block-packagedata
# started from sagehen example, tweaked
# can do ngwf.default_packagedata() now?
d={'rwid':10.0,'rbth':1.0,'man':0.04,'ustrf':1.0,'ndv': 0}
for k in ["man", "rbth", "rwid"]:
ngwf.reaches[k]=d[k]
# check for nans, should have been fixed, taken care of
ngwf.set_reach_slope(method='grid_top')
#ngwf.set_reach_data_from_array('rtp',gwf.dis.top.array)
ngwf.reaches['rgrd']=
ngwf.reaches
ngwf.set_reach_data_from_array('rhk',gwf.npf.k.array[0])
ngwf.reaches
n.segments
n.segments.to_csv(os.path.join(sim_ws,'znseg_mf6rch.csv'))
mask=[s for s in n.segments.index if (len(n.segments.loc[s,'from_segnums'])==0) & (n.segments.loc[s,'to_segnum']==0)]
len(mask)
n.segments.drop(mask,inplace=True)
len(n.segments)
help(n.remove)
# There are two methods to format the PACKAGEDATA:
ngwf.flopy_packagedata
ngwf.write_packagedata(os.path.join(sim_ws,model_name+'.sfr.reach.dat'))
#Similar with CONNECTIONDATA:
ngwf.flopy_connectiondata
ngwf.write_connectiondata(os.path.join(sim_ws,model_name+'.sfr.connection.dat'))
sfr=flopy.mf6.ModflowGwfsfr(gwf,packagedata={'filename':model_name+'.sfr.reach.dat'},
connectiondata={'filename':model_name+'.sfr.connection.dat'},
nreaches=len(ngwf.reaches),budget_filerecord=model_name + "_sfr.bud",
save_flows=True)
#gwf.register_package(sfr)
sfr.write()
gwf.write()
help(ngwf)
swn.file.gdf_to_shapefile(n.segments, 'segments.shp')
| 0.228329 | 0.734334 |
```
# Reload all src modules every time before executing the Python code typed
%load_ext autoreload
%autoreload 2
import os
import cProfile
import pandas as pd
import geopandas as geopd
import numpy as np
import multiprocessing as mp
import re
import gzip
try:
import cld3
except ModuleNotFoundError:
pass
import pycld2
from pyproj import Transformer
from shapely.geometry import Polygon
from shapely.geometry import Point
import matplotlib.cm as cm
import matplotlib.pyplot as plt
import descartes
import folium
import src.utils.geometry as geo
import src.data.shp_extract as shp_extract
import src.data.tweets_cells_counts as tweets_counts
import src.data.text_process as text_process
import src.data.access as data_access
import src.visualization.grid_viz as grid_viz
import src.data.user_filters as ufilters
from dotenv import load_dotenv
load_dotenv()
pd.reset_option("display.max_rows")
```
Too small 'places' data: BO, TN
Limited 'places' data: LT: 69 and EE: 252 (only large cities), HK: 21 (only districts),
mixed distribution?
```
data_dir_path = os.environ['DATA_DIR']
tweets_files_format = 'tweets_2015_2018_{}.json.gz'
places_files_format = 'places_2015_2018_{}.json.gz'
ssh_domain = os.environ['IFISC_DOMAIN']
ssh_username = os.environ['IFISC_USERNAME']
country_codes = ('BO', 'CA', 'CH', 'EE', 'ES', 'FR', 'HK','ID', 'LT', 'LV',
'MY', 'PE', 'RO', 'SG', 'TN', 'UA')
latlon_proj = 'epsg:4326'
xy_proj = 'epsg:3857'
external_data_dir = '../data/external/'
fig_dir = '../reports/figures'
cc = 'CH'
```
## Getting data
```
data_dir_path = os.environ['DATA_DIR']
tweets_files_format = 'tweets_{}_{}_{}.json.gz'
places_files_format = 'places_{}_{}_{}.json.gz'
ssh_domain = os.environ['IFISC_DOMAIN']
ssh_username = os.environ['IFISC_USERNAME']
project_data_dir = os.path.join('..', 'data')
external_data_dir = os.path.join(project_data_dir, 'external')
interim_data_dir = os.path.join(project_data_dir, 'interim')
processed_data_dir = os.path.join(project_data_dir, 'processed')
cell_data_path_format = os.path.join(processed_data_dir,
'{}_cell_data_cc={}_cell_size={}m.geojson')
latlon_proj = 'epsg:4326'
LANGS_DICT = dict([(lang[1],lang[0].lower().capitalize())
for lang in pycld2.LANGUAGES])
cc= 'SG'
region = None
# region = 'Cataluña'
with open(os.path.join(external_data_dir, 'countries.json')) as f:
countries_study_data = json.load(f)
if region:
area_dict = countries_study_data[cc]['regions'][region]
else:
area_dict = countries_study_data[cc]
fig_dir = os.path.join('..', 'reports', 'figures', cc)
if not os.path.exists(fig_dir):
os.makedirs(os.path.join(fig_dir, 'counts'))
os.makedirs(os.path.join(fig_dir, 'prop'))
xy_proj = area_dict['xy_proj']
cc_timezone = area_dict['timezone']
plot_langs_list = area_dict['local_langs']
min_poly_area = area_dict.get('min_poly_area') or 0.1
max_place_area = area_dict.get('max_place_area') or 1e9 # linked to cell size and places data
valid_uids_path = os.path.join(interim_data_dir, f'valid_uids_{cc}.csv')
tweets_file_path = os.path.join(data_dir_path, tweets_files_format.format(cc))
chunk_size = 100000
raw_tweets_df_generator = data_access.yield_json(tweets_file_path,
ssh_domain=ssh_domain, ssh_username=ssh_username, chunk_size=chunk_size, compression='gzip')
for i,raw_tweets_df in enumerate(raw_tweets_df_generator):
break
raw_tweets_df_generator.close()
ratio_coords = len(raw_tweets_df.loc[raw_tweets_df['coordinates'].notnull()]) / chunk_size
print('{:.1%} of tweets have exact coordinates data'.format(ratio_coords))
nr_users = len(raw_tweets_df['uid'].unique())
print('There are {} distinct users in the dataset'.format(nr_users))
raw_tweets_df.head()
places_file_path = os.path.join(data_dir_path, places_files_format.format(cc))
shapefile_name = 'CNTR_RG_01M_2016_4326.shp'
shapefile_path = os.path.join(external_data_dir, shapefile_name, shapefile_name)
shape_df = geopd.read_file(shapefile_path)
shape_df = shape_df.loc[shape_df['FID'] == cc]
raw_places_df = data_access.return_json(places_file_path,
ssh_domain=ssh_domain, ssh_username=ssh_username, compression='gzip')
raw_places_df.head()
```
Get most frequent, small enough place: if most frequent -> select it, if within more frequent bigger place -> select it,
If not small enough place, discard the user
```
print(raw_tweets_df.info())
```
The "I'm at \<place\>" from Foursquare are also there, and they all have 'source' = <a href="http://foursquare.com" rel="nofollow">Foursquare</a>. Tweetbot is an app for regular users, it's not related to bot users.
```
tweets_df = raw_tweets_df[['text', 'id', 'lang', 'place_id', 'coordinates', 'uid', 'created_at']]
tweets_df = tweets_df.rename(columns={'lang': 'twitter_lang'})
null_reply_id = 'e39d05b72f25767869d44391919434896bb055772d7969f74472032b03bc18418911f3b0e6dd47ff8f3b2323728225286c3cb36914d28dc7db40bdd786159c0a'
raw_tweets_df.loc[raw_tweets_df['in_reply_to_status_id'] == null_reply_id,
['in_reply_to_status_id', 'in_reply_to_screen_name', 'in_reply_to_user_id']] = None
tweets_df['source'] = raw_tweets_df['source'].str.extract(r'>(.+)</a>', expand=False)
tweets_df['source'].value_counts().head(20)
a = raw_tweets_df[raw_tweets_df['source'].str.contains('tweetmyjobs')]
a = (a.drop(columns=['in_reply_to_status_id', 'id', 'source',
'in_reply_to_screen_name', 'in_reply_to_user_id', 'quoted_status_id'])
.sort_values(by=['uid', 'created_at']))
pd.set_option("display.max_rows", None)
a[a['uid'] == '066669353196d994d624138aa1ef4aafd892ed8e1e6e65532a39ecc7e6129b829bdbf8ea2b53b11f93a74cb7d1a3e1aa537d0c060be02778b37550d70a77a80d']
```
## First tests on single df
```
ref_year = 2015
nr_consec_months = 3
tweets_file_path = os.path.join(data_dir_path, tweets_files_format.format(cc))
raw_tweets_df_generator = data_access.yield_json(tweets_file_path,
ssh_domain=ssh_domain, ssh_username=ssh_username, chunk_size=1000000, compression='gzip')
agg_tweeted_months_users = pd.DataFrame([], columns=['uid', 'month', 'count'])
tweets_df_list = []
for raw_tweets_df in raw_tweets_df_generator:
tweets_df_list.append(raw_tweets_df)
agg_tweeted_months_users = ufilters.inc_months_activity(
agg_tweeted_months_users, raw_tweets_df)
raw_tweets_df_generator.close()
local_uid_series = ufilters.consec_months(agg_tweeted_months_users)
ref_year = 2015
nr_consec_months = 3
tweeted_months_users = pd.DataFrame([], columns=['uid', 'month', 'count'])
tweeted_months_users = ufilters.inc_months_activity(
tweeted_months_users, tweets_df)
local_uid_series = ufilters.consec_months(tweeted_months_users)
raw_tweets_df['lang'].value_counts().head(10)
raw_tweets_df.join(local_uid_series, on='uid', how='inner')['lang'].value_counts().head(10)
tweets_file_path = os.path.join(data_dir_path, tweets_files_format.format(cc))
raw_tweets_df_generator = data_access.yield_json(tweets_file_path,
ssh_domain=ssh_domain, ssh_username=ssh_username, chunk_size=1000000, compression='gzip')
for raw_tweets_df in raw_tweets_df_generator:
filtered_tweets_df = pd.DataFrame(local_uid_series)
```
## Language detection
### Detected languages
- Languages possibly detected by CLD:
```
lang_with_code = dict(pycld2.LANGUAGES)
detected_lang_with_code = [(lang, lang_with_code[lang]) for lang in pycld2.DETECTED_LANGUAGES]
print(detected_lang_with_code)
```
- Languages possibly detected by Twitter (see 'lang' in https://support.gnip.com/apis/powertrack2.0/rules.html#Operators):
Amharic - am
Arabic - ar
Armenian - hy
Bengali - bn
Bulgarian - bg
Burmese - my
Chinese - zh
Czech - cs
Danish - da
Dutch - nl
English - en
Estonian - et
Finnish - fi
French - fr
Georgian - ka
German - de
Greek - el
Gujarati - gu
Haitian - ht
Hebrew - iw
Hindi - hi
Hungarian - hu
Icelandic - is
Indonesian - in
Italian - it
Japanese - ja
Kannada - kn
Khmer - km
Korean - ko
Lao - lo
Latvian - lv
Lithuanian - lt
Malayalam - ml
Maldivian - dv
Marathi - mr
Nepali - ne
Norwegian - no
Oriya - or
Panjabi - pa
Pashto - ps
Persian - fa
Polish - pl
Portuguese - pt
Romanian - ro
Russian - ru
Serbian - sr
Sindhi - sd
Sinhala - si
Slovak - sk
Slovenian - sl
Sorani Kurdish - ckb
Spanish - es
Swedish - sv
Tagalog - tl
Tamil - ta
Telugu - te
Thai - th
Tibetan - bo
Turkish - tr
Ukrainian - uk
Urdu - ur
Uyghur - ug
Vietnamese - vi
Welsh - cy
```
tweets_lang_df = text_process.lang_detect(tweets_df, text_col='text', min_nr_words=4, cld='pycld2')
tweets_lang_df.head()
cld_langs = tweets_lang_df['cld_lang'].unique()
cld_langs.sort()
print('Languages detected by cld: {}'.format(cld_langs))
twitter_langs = tweets_lang_df['twitter_lang'].unique()
twitter_langs.sort()
print('Languages detected by twitter: {}'.format(twitter_langs))
tweets_lang_df['twitter_lang'].value_counts().head(10)
tweets_lang_df['cld_lang'].value_counts().head(10)
```
French case, corsican is unreliably detected by CLD for French tweets, however seems pretty accurate when twitter_lang='it'
Mandarin (zh) is not detected well by cld: example of a run on a chunk: 5300 tweets in Mandarin detected by twitter, and only 2300 by cld. However, there are also a good number of false positives from twitter (looking roughly at the data by hand). There notably seems to be a problem with repeated logograms: just having "haha" messes with the whole translation
### Multilingual users
```
groupby_user_lang = tweets_lang_df.loc[tweets_lang_df['twitter_lang'] != 'und'].groupby(['uid', 'twitter_lang'])
count_tweets_by_user_lang = groupby_user_lang.size()
count_langs_by_user_df = count_tweets_by_user_lang.groupby('uid').transform('size')
multiling_users_df = count_tweets_by_user_lang.loc[count_langs_by_user_df > 1]
pd.DataFrame(multiling_users_df)
pd.set_option("display.max_rows", 100)
multiling_users_list = [x[0] for x in multiling_users_df.index.values]
tweets_lang_df[tweets_lang_df['uid'].isin(multiling_users_list)].sort_values(by=['uid', 'cld_lang'])[
['uid', 'filtered_text', 'cld_lang', 'twitter_lang', 'created_at']]
```
## Places into geodf and join on tweets
Calculate the area to discard bbox which are too large? Problem: need to project first, which is expensive
```
tweets_to_loc_df = tweets_lang_df.loc[tweets_lang_df['coordinates'].isnull()]
crs = {'init': latlon_proj}
places_df = raw_places_df[['id', 'bounding_box', 'name', 'place_type']]
geometry = places_df['bounding_box'].apply(lambda x: Polygon(x['coordinates'][0]))
places_geodf = geopd.GeoDataFrame(places_df, crs=crs, geometry=geometry)
places_geodf = places_geodf.set_index('id')
places_geodf = places_geodf.drop(columns=['bounding_box'])
places_geodf['area'] = places_geodf.geometry.to_crs(xy_proj).area
tweets_final_df = tweets_to_loc_df.join(places_geodf, on='place_id', how='left')
tweets_final_df.head(10)
```
### Corsican?
```
tweets_final_df.loc[(tweets_final_df['cld_lang'] =='co') & (tweets_final_df['twitter_lang'] =='it')]
```
CLD sensitive to letter repetitions made to insist: can put threshold if more than 3 consecutive same letter, bring it down to 2, it seems to improve prediction on example
Usually twitter's prediction seems better...
```
tweets_final_df[tweets_final_df['cld_lang'] != tweets_final_df['twitter_lang']].drop(columns=['id'])
```
### Swiss German?
```
zurich_id = places_geodf.loc[places_geodf['name']=='Zurich', 'geometry'].index[0]
# places_in_zurich = places_geodf
places_in_zurich = places_geodf.loc[places_geodf.within(places_geodf.loc[zurich_id, 'geometry'])]
places_in_zurich
tweets_in_zurich = tweets_final_df.join(places_in_zurich, on='place_id', rsuffix='_place')
print(tweets_in_zurich['cld_lang'].value_counts().head())
print(tweets_in_zurich['twitter_lang'].value_counts().head())
tweets_in_zurich.loc[(tweets_in_zurich['cld_lang']=='un') & (tweets_in_zurich['twitter_lang']=='de'),
'filtered_text']
```
Mostly mixed languages not detected by twitter it seems:
```
tweets_in_zurich.loc[tweets_in_zurich['twitter_lang']=='und',
'filtered_text']
```
## groupbys and stuff
```
def get_mean_time(df, dt_col):
t_series_in_sec_of_day = df['hour']*3600 + df['minute']*60 + df['second']
return pd.to_timedelta(int(t_series_in_sec_of_day.mean()), unit='s')
tweets_df = raw_tweets_df.copy()
# Speeds up the process to extract the hour, min and sec first
tweets_df['hour'] = tweets_df['created_at'].dt.hour
tweets_df['minute'] = tweets_df['created_at'].dt.minute
tweets_df['second'] = tweets_df['created_at'].dt.second
groupby_user_place = tweets_df.groupby(['uid', 'place_id'])
count_tweets_by_user_place = groupby_user_place.size()
count_tweets_by_user_place.rename('count', inplace=True)
mean_time_by_user_place = groupby_user_place.apply(lambda df: get_mean_time(df, 'created_at'))
mean_time_by_user_place.rename('avg time', inplace=True)
# transform to keep same size, so as to be able to have a matching boolean Series of same size as
# original df to select users with more than one place for example:
count_places_by_user_df = count_tweets_by_user_place.groupby('uid').transform('size')
agg_data_df = pd.concat([count_tweets_by_user_place, mean_time_by_user_place], axis=1)
count_tweets_by_user_place_geodf = agg_data_df.join(places_geodf, on='place_id')
count_tweets_by_user_place_geodf.head()
cProfile.run("groupby_user_place.apply(lambda df: get_mean_time(df, 'created_at'))")
count_tweets_by_user_place_geodf.loc[count_places_by_user_df > 1]
```
Add new chunk to cumulative data:
```
count_tweets_by_user_place_geodf = count_tweets_by_user_place_geodf.join(
count_tweets_by_user_place_geodf['count'],
on=['uid', 'place_id'], how='outer', rsuffix='_new')
count_tweets_by_user_place_geodf['count'] += count_tweets_by_user_place_geodf['count_new']
count_tweets_by_user_place_geodf.drop(columns=['count_new'], inplace=True)
count_tweets_by_user_place_geodf
```
|
github_jupyter
|
# Reload all src modules every time before executing the Python code typed
%load_ext autoreload
%autoreload 2
import os
import cProfile
import pandas as pd
import geopandas as geopd
import numpy as np
import multiprocessing as mp
import re
import gzip
try:
import cld3
except ModuleNotFoundError:
pass
import pycld2
from pyproj import Transformer
from shapely.geometry import Polygon
from shapely.geometry import Point
import matplotlib.cm as cm
import matplotlib.pyplot as plt
import descartes
import folium
import src.utils.geometry as geo
import src.data.shp_extract as shp_extract
import src.data.tweets_cells_counts as tweets_counts
import src.data.text_process as text_process
import src.data.access as data_access
import src.visualization.grid_viz as grid_viz
import src.data.user_filters as ufilters
from dotenv import load_dotenv
load_dotenv()
pd.reset_option("display.max_rows")
data_dir_path = os.environ['DATA_DIR']
tweets_files_format = 'tweets_2015_2018_{}.json.gz'
places_files_format = 'places_2015_2018_{}.json.gz'
ssh_domain = os.environ['IFISC_DOMAIN']
ssh_username = os.environ['IFISC_USERNAME']
country_codes = ('BO', 'CA', 'CH', 'EE', 'ES', 'FR', 'HK','ID', 'LT', 'LV',
'MY', 'PE', 'RO', 'SG', 'TN', 'UA')
latlon_proj = 'epsg:4326'
xy_proj = 'epsg:3857'
external_data_dir = '../data/external/'
fig_dir = '../reports/figures'
cc = 'CH'
data_dir_path = os.environ['DATA_DIR']
tweets_files_format = 'tweets_{}_{}_{}.json.gz'
places_files_format = 'places_{}_{}_{}.json.gz'
ssh_domain = os.environ['IFISC_DOMAIN']
ssh_username = os.environ['IFISC_USERNAME']
project_data_dir = os.path.join('..', 'data')
external_data_dir = os.path.join(project_data_dir, 'external')
interim_data_dir = os.path.join(project_data_dir, 'interim')
processed_data_dir = os.path.join(project_data_dir, 'processed')
cell_data_path_format = os.path.join(processed_data_dir,
'{}_cell_data_cc={}_cell_size={}m.geojson')
latlon_proj = 'epsg:4326'
LANGS_DICT = dict([(lang[1],lang[0].lower().capitalize())
for lang in pycld2.LANGUAGES])
cc= 'SG'
region = None
# region = 'Cataluña'
with open(os.path.join(external_data_dir, 'countries.json')) as f:
countries_study_data = json.load(f)
if region:
area_dict = countries_study_data[cc]['regions'][region]
else:
area_dict = countries_study_data[cc]
fig_dir = os.path.join('..', 'reports', 'figures', cc)
if not os.path.exists(fig_dir):
os.makedirs(os.path.join(fig_dir, 'counts'))
os.makedirs(os.path.join(fig_dir, 'prop'))
xy_proj = area_dict['xy_proj']
cc_timezone = area_dict['timezone']
plot_langs_list = area_dict['local_langs']
min_poly_area = area_dict.get('min_poly_area') or 0.1
max_place_area = area_dict.get('max_place_area') or 1e9 # linked to cell size and places data
valid_uids_path = os.path.join(interim_data_dir, f'valid_uids_{cc}.csv')
tweets_file_path = os.path.join(data_dir_path, tweets_files_format.format(cc))
chunk_size = 100000
raw_tweets_df_generator = data_access.yield_json(tweets_file_path,
ssh_domain=ssh_domain, ssh_username=ssh_username, chunk_size=chunk_size, compression='gzip')
for i,raw_tweets_df in enumerate(raw_tweets_df_generator):
break
raw_tweets_df_generator.close()
ratio_coords = len(raw_tweets_df.loc[raw_tweets_df['coordinates'].notnull()]) / chunk_size
print('{:.1%} of tweets have exact coordinates data'.format(ratio_coords))
nr_users = len(raw_tweets_df['uid'].unique())
print('There are {} distinct users in the dataset'.format(nr_users))
raw_tweets_df.head()
places_file_path = os.path.join(data_dir_path, places_files_format.format(cc))
shapefile_name = 'CNTR_RG_01M_2016_4326.shp'
shapefile_path = os.path.join(external_data_dir, shapefile_name, shapefile_name)
shape_df = geopd.read_file(shapefile_path)
shape_df = shape_df.loc[shape_df['FID'] == cc]
raw_places_df = data_access.return_json(places_file_path,
ssh_domain=ssh_domain, ssh_username=ssh_username, compression='gzip')
raw_places_df.head()
print(raw_tweets_df.info())
tweets_df = raw_tweets_df[['text', 'id', 'lang', 'place_id', 'coordinates', 'uid', 'created_at']]
tweets_df = tweets_df.rename(columns={'lang': 'twitter_lang'})
null_reply_id = 'e39d05b72f25767869d44391919434896bb055772d7969f74472032b03bc18418911f3b0e6dd47ff8f3b2323728225286c3cb36914d28dc7db40bdd786159c0a'
raw_tweets_df.loc[raw_tweets_df['in_reply_to_status_id'] == null_reply_id,
['in_reply_to_status_id', 'in_reply_to_screen_name', 'in_reply_to_user_id']] = None
tweets_df['source'] = raw_tweets_df['source'].str.extract(r'>(.+)</a>', expand=False)
tweets_df['source'].value_counts().head(20)
a = raw_tweets_df[raw_tweets_df['source'].str.contains('tweetmyjobs')]
a = (a.drop(columns=['in_reply_to_status_id', 'id', 'source',
'in_reply_to_screen_name', 'in_reply_to_user_id', 'quoted_status_id'])
.sort_values(by=['uid', 'created_at']))
pd.set_option("display.max_rows", None)
a[a['uid'] == '066669353196d994d624138aa1ef4aafd892ed8e1e6e65532a39ecc7e6129b829bdbf8ea2b53b11f93a74cb7d1a3e1aa537d0c060be02778b37550d70a77a80d']
ref_year = 2015
nr_consec_months = 3
tweets_file_path = os.path.join(data_dir_path, tweets_files_format.format(cc))
raw_tweets_df_generator = data_access.yield_json(tweets_file_path,
ssh_domain=ssh_domain, ssh_username=ssh_username, chunk_size=1000000, compression='gzip')
agg_tweeted_months_users = pd.DataFrame([], columns=['uid', 'month', 'count'])
tweets_df_list = []
for raw_tweets_df in raw_tweets_df_generator:
tweets_df_list.append(raw_tweets_df)
agg_tweeted_months_users = ufilters.inc_months_activity(
agg_tweeted_months_users, raw_tweets_df)
raw_tweets_df_generator.close()
local_uid_series = ufilters.consec_months(agg_tweeted_months_users)
ref_year = 2015
nr_consec_months = 3
tweeted_months_users = pd.DataFrame([], columns=['uid', 'month', 'count'])
tweeted_months_users = ufilters.inc_months_activity(
tweeted_months_users, tweets_df)
local_uid_series = ufilters.consec_months(tweeted_months_users)
raw_tweets_df['lang'].value_counts().head(10)
raw_tweets_df.join(local_uid_series, on='uid', how='inner')['lang'].value_counts().head(10)
tweets_file_path = os.path.join(data_dir_path, tweets_files_format.format(cc))
raw_tweets_df_generator = data_access.yield_json(tweets_file_path,
ssh_domain=ssh_domain, ssh_username=ssh_username, chunk_size=1000000, compression='gzip')
for raw_tweets_df in raw_tweets_df_generator:
filtered_tweets_df = pd.DataFrame(local_uid_series)
lang_with_code = dict(pycld2.LANGUAGES)
detected_lang_with_code = [(lang, lang_with_code[lang]) for lang in pycld2.DETECTED_LANGUAGES]
print(detected_lang_with_code)
tweets_lang_df = text_process.lang_detect(tweets_df, text_col='text', min_nr_words=4, cld='pycld2')
tweets_lang_df.head()
cld_langs = tweets_lang_df['cld_lang'].unique()
cld_langs.sort()
print('Languages detected by cld: {}'.format(cld_langs))
twitter_langs = tweets_lang_df['twitter_lang'].unique()
twitter_langs.sort()
print('Languages detected by twitter: {}'.format(twitter_langs))
tweets_lang_df['twitter_lang'].value_counts().head(10)
tweets_lang_df['cld_lang'].value_counts().head(10)
groupby_user_lang = tweets_lang_df.loc[tweets_lang_df['twitter_lang'] != 'und'].groupby(['uid', 'twitter_lang'])
count_tweets_by_user_lang = groupby_user_lang.size()
count_langs_by_user_df = count_tweets_by_user_lang.groupby('uid').transform('size')
multiling_users_df = count_tweets_by_user_lang.loc[count_langs_by_user_df > 1]
pd.DataFrame(multiling_users_df)
pd.set_option("display.max_rows", 100)
multiling_users_list = [x[0] for x in multiling_users_df.index.values]
tweets_lang_df[tweets_lang_df['uid'].isin(multiling_users_list)].sort_values(by=['uid', 'cld_lang'])[
['uid', 'filtered_text', 'cld_lang', 'twitter_lang', 'created_at']]
tweets_to_loc_df = tweets_lang_df.loc[tweets_lang_df['coordinates'].isnull()]
crs = {'init': latlon_proj}
places_df = raw_places_df[['id', 'bounding_box', 'name', 'place_type']]
geometry = places_df['bounding_box'].apply(lambda x: Polygon(x['coordinates'][0]))
places_geodf = geopd.GeoDataFrame(places_df, crs=crs, geometry=geometry)
places_geodf = places_geodf.set_index('id')
places_geodf = places_geodf.drop(columns=['bounding_box'])
places_geodf['area'] = places_geodf.geometry.to_crs(xy_proj).area
tweets_final_df = tweets_to_loc_df.join(places_geodf, on='place_id', how='left')
tweets_final_df.head(10)
tweets_final_df.loc[(tweets_final_df['cld_lang'] =='co') & (tweets_final_df['twitter_lang'] =='it')]
tweets_final_df[tweets_final_df['cld_lang'] != tweets_final_df['twitter_lang']].drop(columns=['id'])
zurich_id = places_geodf.loc[places_geodf['name']=='Zurich', 'geometry'].index[0]
# places_in_zurich = places_geodf
places_in_zurich = places_geodf.loc[places_geodf.within(places_geodf.loc[zurich_id, 'geometry'])]
places_in_zurich
tweets_in_zurich = tweets_final_df.join(places_in_zurich, on='place_id', rsuffix='_place')
print(tweets_in_zurich['cld_lang'].value_counts().head())
print(tweets_in_zurich['twitter_lang'].value_counts().head())
tweets_in_zurich.loc[(tweets_in_zurich['cld_lang']=='un') & (tweets_in_zurich['twitter_lang']=='de'),
'filtered_text']
tweets_in_zurich.loc[tweets_in_zurich['twitter_lang']=='und',
'filtered_text']
def get_mean_time(df, dt_col):
t_series_in_sec_of_day = df['hour']*3600 + df['minute']*60 + df['second']
return pd.to_timedelta(int(t_series_in_sec_of_day.mean()), unit='s')
tweets_df = raw_tweets_df.copy()
# Speeds up the process to extract the hour, min and sec first
tweets_df['hour'] = tweets_df['created_at'].dt.hour
tweets_df['minute'] = tweets_df['created_at'].dt.minute
tweets_df['second'] = tweets_df['created_at'].dt.second
groupby_user_place = tweets_df.groupby(['uid', 'place_id'])
count_tweets_by_user_place = groupby_user_place.size()
count_tweets_by_user_place.rename('count', inplace=True)
mean_time_by_user_place = groupby_user_place.apply(lambda df: get_mean_time(df, 'created_at'))
mean_time_by_user_place.rename('avg time', inplace=True)
# transform to keep same size, so as to be able to have a matching boolean Series of same size as
# original df to select users with more than one place for example:
count_places_by_user_df = count_tweets_by_user_place.groupby('uid').transform('size')
agg_data_df = pd.concat([count_tweets_by_user_place, mean_time_by_user_place], axis=1)
count_tweets_by_user_place_geodf = agg_data_df.join(places_geodf, on='place_id')
count_tweets_by_user_place_geodf.head()
cProfile.run("groupby_user_place.apply(lambda df: get_mean_time(df, 'created_at'))")
count_tweets_by_user_place_geodf.loc[count_places_by_user_df > 1]
count_tweets_by_user_place_geodf = count_tweets_by_user_place_geodf.join(
count_tweets_by_user_place_geodf['count'],
on=['uid', 'place_id'], how='outer', rsuffix='_new')
count_tweets_by_user_place_geodf['count'] += count_tweets_by_user_place_geodf['count_new']
count_tweets_by_user_place_geodf.drop(columns=['count_new'], inplace=True)
count_tweets_by_user_place_geodf
| 0.264738 | 0.671659 |
#### IWSLT English MLM
This notebook shows a simple example of how to use the transformer provided by this repo for MLM.
We will use the IWSLT 2016 En dataset.
This is similar to BERT, except missing some other training tricks, such as NSP.
```
import numpy as np
from torchtext import data, datasets
from torchtext.data import get_tokenizer
import spacy
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.optim import Adam
import sys
sys.path.append("..")
from model.EncoderDecoder import TransformerEncoder
from model.utils import device, Batch, BasicIterator
from model.opt import NoamOpt
from model.Layers import Linear
import time
from collections import Counter
```
##### The below does some basic data preprocessing and filtering, in addition to setting special tokens.
```
tok = get_tokenizer("moses")
PAD = "<pad>"
SOS = "<sos>"
EOS = "<eos>"
en_field = data.Field(tokenize=tok, pad_token=PAD, init_token=SOS, eos_token=EOS)
d = data.TabularDataset(".data/iwslt/de-en/train.en", format="csv", fields=[("text", en_field)],
csv_reader_params={"delimiter":'\n'})
MIN_FREQ = 4
en_field.build_vocab(d.text, min_freq=MIN_FREQ, specials=["<mask>"])
```
##### The batch_size_fn helps deal with dynamic batch size for the torchtext iterator
##### The BasicIterator class helps with dynamic batching too, making sure batches are tightly grouped with minimal padding.
```
global max_text_in_batch
def batch_size_fn(new, count, _):
global max_text_in_batch
if count == 1:
max_text_in_batch = 0
max_text_in_batch = max(max_text_in_batch, len(new.text))
return count * max_text_in_batch
train_loader = BasicIterator(d, batch_size=1100, device=torch.device("cuda"),
repeat=False, sort_key=lambda x: (len(x.text)),
batch_size_fn=batch_size_fn, train=True)
```
##### Single step over entire dataset, with tons of gradient accumulation to get batch sizes big enough for stable training.
```
def train_step(dataloader):
i = 0
loss = 0
total_loss = 0
for batch in dataloader:
# Only take a step every 20th batch
if (i + 1) % 20 == 0:
optimizer.step()
optimizer.zero_grad()
loss, _, _ = transformer.mask_forward_and_return_loss(criterion, batch.text, .15)
loss.backward()
total_loss += loss.item()
i += 1
return total_loss / i
```
#### Creating the pseudoBERT:
Subclassing the TransformerEncoder class allows us to implement a forward_and_return_loss_function easily, and requires nothing else before being fully functional.
The TransformerEncoder class handles embedding and the transformer encoder layers itself, we simply need to follow it up with a single Linear layer. The masking is a bit complex, but should be understandable with the below comments.
The goal of MLM is to randomly mask tokens, then train a model to predict what the ground truth token actually is. This is a hard task that requires good understanding of language itself.
We use the utils.Batch object to automatically create padding masks.
```
class MLM(TransformerEncoder):
def __init__(self, input_vocab_size,embedding_dim,
n_layers,hidden_dim,n_heads,dropout_rate,
pad_idx,mask_idx,):
super(MLM, self).__init__(input_vocab_size,embedding_dim, n_layers,
hidden_dim,n_heads,dropout_rate,pad_idx,)
self.pad_idx = pad_idx
self.mask_idx = mask_idx
self.fc1 = Linear(embedding_dim, input_vocab_size)
def mask_forward_and_return_loss(self, criterion, seq, mask_rate):
"""
Pass input through transformer encoder and returns loss, handles masking for
both MLM and padding automagically
Args:
criterion: torch.nn.functional loss function of choice
sources: source sequences, [seq_len, bs]
mask_rate: masking rate for non-padding tokens
Returns:
loss, transformer output, mask
"""
# count number of tokens that are padding
number_of_pad_tokens = torch.sum(
torch.where(seq == self.pad_idx, torch.ones_like(seq),
torch.zeros_like(seq)
).float())
# Don't mask pad tokens, scale mask ratio up accordingly
num_tokens = np.prod(seq.size())
# clamp to prevent errors if there are a huge amount of padding
# tokens in a given batch (> 70%)
true_masking_rate = torch.clamp((1 / (1 - (number_of_pad_tokens / num_tokens))) * mask_rate, 0, 1)
bernoulli_probabilities = torch.zeros_like(seq) + true_masking_rate
masking_mask = torch.bernoulli(bernoulli_probabilities).long().to(device)
masked_seq = torch.where(torch.logical_and((seq != self.pad_idx), (masking_mask == 1)),
(torch.ones_like(seq) * self.mask_idx).to(device), seq)
batch = Batch(masked_seq, None, self.pad_idx)
out = self.forward(batch.src.to(device), batch.src_mask.to(device))
out = self.fc1(out.transpose(0, 1)).transpose(0, 1)
# zeroing out token predictions on non-masked tokens
out = out * masking_mask.unsqueeze(-1)
loss = criterion(
out.contiguous().view(-1, out.size(-1)),
# ((A-1) @ M) + 1 = A is 1 where B is 0, and otherwise unchanged
# This makes loss only depend on masked tokens, like BERT
(((seq-1) * masking_mask) + 1).contiguous().view(-1),
ignore_index=self.pad_idx,
)
return loss, out, masking_mask
```
##### Here we instantiate the model and set hyperparameters. Note: this MLM model is extremely small for ease of recreating experiments.
```
input_vocab_size = len(en_field.vocab)
embedding_dim = 512
n_layers = 4
hidden_dim = 1024
n_heads = 4
dropout_rate = .1
pad_idx = 1
mask_idx = 4
transformer = MLM(input_vocab_size, embedding_dim, n_layers, hidden_dim,
n_heads, dropout_rate, pad_idx, mask_idx).to(device)
adamopt = torch.optim.Adam(transformer.parameters(), lr=0, betas=(0.9, 0.98), eps=1e-9)
optimizer = NoamOpt(embedding_dim, 1, 2000, adamopt)
criterion = F.cross_entropy
# optimization is unstable without this step
for p in transformer.parameters():
if p.dim() > 1:
nn.init.xavier_uniform_(p)
```
#### Let's run 5 epochs over the entire dataset, printing loss once per epoch.
```
true_start = time.time()
for i in range(5):
transformer.train()
t = time.time()
loss = train_step(train_loader)
print("Epoch {}. Loss: {}, ".format((i+1), str(loss)[:5], int(time.time() - t)))
print("Total time (s): {}, Last epoch time (s): {}".format(int(time.time()- true_start), int(time.time() - t)))
torch.save(transformer, "basic_MLM.pt")
```
##### Let's go ahead and process some random example sentences not in the training data, and vizualize the results.
```
transformer.eval()
inp = en_field.process([tok("Now, if we all played football, this wouldn't be an issue."),
tok("I don't really agree with you, honestly"),
tok("Not all who wander are lost.")]).to(device)
_, pred, mask = transformer.mask_forward_and_return_loss(criterion, inp, .20)
pred = pred.transpose(0, 1)
mask = mask.transpose(0, 1)
```
##### Simple code for visualization. Let's check out how our model did.
```
def visualize_model_predictions(inp, pred, mask):
print("Sentence:", end=" ")
for i in range(len(inp)):
if en_field.vocab.itos[inp[i]] == "<eos>":
break
if mask[i] == 1:
print("<" + en_field.vocab.itos[pred[i]] + " | " + en_field.vocab.itos[inp[i]] + ">", end = " ")
else:
print(en_field.vocab.itos[inp[i]], end = " ")
print("\n")
```
##### Masked tokens are surrounded by < >. The word on the left is the prediction, the word on the right is the ground truth. They're seperated by a |.
##### Despite being a small model, the predictions are fairly accurate.
```
for i in range(len(inp.T)):
visualize_model_predictions(
inp.transpose(0, 1)[i].tolist(),
torch.argmax(pred[i], dim=-1).tolist(),
mask[i])
```
|
github_jupyter
|
import numpy as np
from torchtext import data, datasets
from torchtext.data import get_tokenizer
import spacy
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.optim import Adam
import sys
sys.path.append("..")
from model.EncoderDecoder import TransformerEncoder
from model.utils import device, Batch, BasicIterator
from model.opt import NoamOpt
from model.Layers import Linear
import time
from collections import Counter
tok = get_tokenizer("moses")
PAD = "<pad>"
SOS = "<sos>"
EOS = "<eos>"
en_field = data.Field(tokenize=tok, pad_token=PAD, init_token=SOS, eos_token=EOS)
d = data.TabularDataset(".data/iwslt/de-en/train.en", format="csv", fields=[("text", en_field)],
csv_reader_params={"delimiter":'\n'})
MIN_FREQ = 4
en_field.build_vocab(d.text, min_freq=MIN_FREQ, specials=["<mask>"])
global max_text_in_batch
def batch_size_fn(new, count, _):
global max_text_in_batch
if count == 1:
max_text_in_batch = 0
max_text_in_batch = max(max_text_in_batch, len(new.text))
return count * max_text_in_batch
train_loader = BasicIterator(d, batch_size=1100, device=torch.device("cuda"),
repeat=False, sort_key=lambda x: (len(x.text)),
batch_size_fn=batch_size_fn, train=True)
def train_step(dataloader):
i = 0
loss = 0
total_loss = 0
for batch in dataloader:
# Only take a step every 20th batch
if (i + 1) % 20 == 0:
optimizer.step()
optimizer.zero_grad()
loss, _, _ = transformer.mask_forward_and_return_loss(criterion, batch.text, .15)
loss.backward()
total_loss += loss.item()
i += 1
return total_loss / i
class MLM(TransformerEncoder):
def __init__(self, input_vocab_size,embedding_dim,
n_layers,hidden_dim,n_heads,dropout_rate,
pad_idx,mask_idx,):
super(MLM, self).__init__(input_vocab_size,embedding_dim, n_layers,
hidden_dim,n_heads,dropout_rate,pad_idx,)
self.pad_idx = pad_idx
self.mask_idx = mask_idx
self.fc1 = Linear(embedding_dim, input_vocab_size)
def mask_forward_and_return_loss(self, criterion, seq, mask_rate):
"""
Pass input through transformer encoder and returns loss, handles masking for
both MLM and padding automagically
Args:
criterion: torch.nn.functional loss function of choice
sources: source sequences, [seq_len, bs]
mask_rate: masking rate for non-padding tokens
Returns:
loss, transformer output, mask
"""
# count number of tokens that are padding
number_of_pad_tokens = torch.sum(
torch.where(seq == self.pad_idx, torch.ones_like(seq),
torch.zeros_like(seq)
).float())
# Don't mask pad tokens, scale mask ratio up accordingly
num_tokens = np.prod(seq.size())
# clamp to prevent errors if there are a huge amount of padding
# tokens in a given batch (> 70%)
true_masking_rate = torch.clamp((1 / (1 - (number_of_pad_tokens / num_tokens))) * mask_rate, 0, 1)
bernoulli_probabilities = torch.zeros_like(seq) + true_masking_rate
masking_mask = torch.bernoulli(bernoulli_probabilities).long().to(device)
masked_seq = torch.where(torch.logical_and((seq != self.pad_idx), (masking_mask == 1)),
(torch.ones_like(seq) * self.mask_idx).to(device), seq)
batch = Batch(masked_seq, None, self.pad_idx)
out = self.forward(batch.src.to(device), batch.src_mask.to(device))
out = self.fc1(out.transpose(0, 1)).transpose(0, 1)
# zeroing out token predictions on non-masked tokens
out = out * masking_mask.unsqueeze(-1)
loss = criterion(
out.contiguous().view(-1, out.size(-1)),
# ((A-1) @ M) + 1 = A is 1 where B is 0, and otherwise unchanged
# This makes loss only depend on masked tokens, like BERT
(((seq-1) * masking_mask) + 1).contiguous().view(-1),
ignore_index=self.pad_idx,
)
return loss, out, masking_mask
input_vocab_size = len(en_field.vocab)
embedding_dim = 512
n_layers = 4
hidden_dim = 1024
n_heads = 4
dropout_rate = .1
pad_idx = 1
mask_idx = 4
transformer = MLM(input_vocab_size, embedding_dim, n_layers, hidden_dim,
n_heads, dropout_rate, pad_idx, mask_idx).to(device)
adamopt = torch.optim.Adam(transformer.parameters(), lr=0, betas=(0.9, 0.98), eps=1e-9)
optimizer = NoamOpt(embedding_dim, 1, 2000, adamopt)
criterion = F.cross_entropy
# optimization is unstable without this step
for p in transformer.parameters():
if p.dim() > 1:
nn.init.xavier_uniform_(p)
true_start = time.time()
for i in range(5):
transformer.train()
t = time.time()
loss = train_step(train_loader)
print("Epoch {}. Loss: {}, ".format((i+1), str(loss)[:5], int(time.time() - t)))
print("Total time (s): {}, Last epoch time (s): {}".format(int(time.time()- true_start), int(time.time() - t)))
torch.save(transformer, "basic_MLM.pt")
transformer.eval()
inp = en_field.process([tok("Now, if we all played football, this wouldn't be an issue."),
tok("I don't really agree with you, honestly"),
tok("Not all who wander are lost.")]).to(device)
_, pred, mask = transformer.mask_forward_and_return_loss(criterion, inp, .20)
pred = pred.transpose(0, 1)
mask = mask.transpose(0, 1)
def visualize_model_predictions(inp, pred, mask):
print("Sentence:", end=" ")
for i in range(len(inp)):
if en_field.vocab.itos[inp[i]] == "<eos>":
break
if mask[i] == 1:
print("<" + en_field.vocab.itos[pred[i]] + " | " + en_field.vocab.itos[inp[i]] + ">", end = " ")
else:
print(en_field.vocab.itos[inp[i]], end = " ")
print("\n")
for i in range(len(inp.T)):
visualize_model_predictions(
inp.transpose(0, 1)[i].tolist(),
torch.argmax(pred[i], dim=-1).tolist(),
mask[i])
| 0.708818 | 0.900486 |
# Clustering Text Documents Using K-Means
We use publicly available dataset consists of 20 news groups(categories). In order to perform k-means, we need to convert text into numbers, which is done with the help TF-IDF. TF-IDF determines the importance of the words based on its frequency. These features are fed to K-means algorithm to do clustering. In order to perform pre-processing, we use NLTK library for tokenization and lemmatization/stemming
```
from __future__ import division
import sklearn
from sklearn.datasets import fetch_20newsgroups
from sklearn.feature_extraction.text import TfidfTransformer, TfidfVectorizer
from sklearn.cluster import KMeans
from sklearn.preprocessing import Normalizer
from sklearn import metrics
import string
from string import punctuation
import pandas as pd
import numpy as np
import re
import nltk
from nltk.tokenize import word_tokenize, sent_tokenize
from nltk.corpus import stopwords
from nltk.stem import PorterStemmer
from nltk.stem import WordNetLemmatizer
import matplotlib.pyplot as plt
import itertools
%matplotlib inline
```
### TfidfVectorizer
Convert a collection of raw documents to a matrix of TF-IDF features.
Equivalent to CountVectorizer followed by TfidfTransformer.
# Steps
## Stages:
i. Pre-processing of the dataset
ii. Creation of Term Document Matrix
iii. TF-IDF (Term Frequency – Inverse Document Frequency) Normalization
iv. K-Means Clustering using Euclidean Distances (sklearn by default uses Euclidean distances)
v. Auto-Tagging based on Cluster Centers
### Stage 1: (Pre-processing)
i. Removing punctuations
ii. Transforming to lower case
iii. Grammatically tagging sentences and removing pre-identified stop phrases (Chunking)
iv. Removing numbers from the document
v. Stripping any excess white spaces
vi. Removing generic words of the English language viz. determiners, articles, conjunctions and other parts of speech.
vii. Document Stemming which reduces each word to its root using Porter’s stemming algorithm.
```
training_set = fetch_20newsgroups(subset='train', shuffle=True)
target = training_set.target
print len(training_set.data)
df = pd.DataFrame(training_set.data, columns=["data"])
df["targets"] = target
df.head(10)
```
# Determine distribution of classes
```
df.groupby('targets').count()
# print one sample of data
print df["data"][0]
```
## Text Normalization
Since dataset contains many non-relevant words therefore we do pre-processing so that our algorithm can classify the data efficiently.
### Pre-processing steps:
i. Lemmatization / Stemming
ii. Sentence Tokenization
iii. Word Tokenization
iv. Remove punctuations and contractions
v. Apply Regex expressions to remove unwanted words(such as numbers i.e. A45 )
```
class text_normalization:
def __init__(self):
self.punctuations = list(punctuation)
self.stemmer = PorterStemmer()
self.lemma = WordNetLemmatizer()
self.contractions = {"'nt":"not", "'ll": " will","'d":"would" ,"'re":"are", "'ve":"have", "'m":"am", "'s":"is"}
'''
This function takes text as input
and returns list of tokenized words(punctuations not included)
'''
def word_tokenizer(self,text):
self.word_tokenize_list = []
for word in word_tokenize(text):
result = 0
#find words containing numbers i.e A45, or 45
result = re.findall(r'([a-z]|[A-Z])(\d)|(\d)', word)
findUrl = re.findall(r'([a-z])(\.com)', word)
findBlankWords = re.findall(r'(([a-z])(__))|(__)([a-z])', word)
findBlanks = re.findall(r'(__)', word)
if word in self.contractions:
self.word_tokenize_list.append(self.contractions[word])
elif len(findBlankWords) > 0 or len(findBlanks) > 0:
continue
elif len(result) > 0:
continue
elif len(findUrl) > 0:
# print "word ", word
continue
elif len(word) < 3:
continue
elif word in self.punctuations:
continue
else:
self.word_tokenize_list.append(word)
return self.word_tokenize_list
'''
This function takes text as input
and returns list of tokenized sentences
'''
def sentence_tokenizer(self,sentence):
self.sentence_tokenize_list = sent_tokenize(sentence)
return self.sentence_tokenize_list
'''
This function takes tokenized sentence as input
and returns lemma of tokenized sentence
1. First sentences from text are tokenized
2. Then, words from sentences are tokenized
3. Lemmatizer of words is determined
'''
def lemmatizer(self, sentences):
sentences = re.sub(r'([a-z]|[A-Z])(_)', r'\1', sentences)
sentences = re.sub(r'(_)([a-z]|[A-Z])', r'\2', sentences)
token_sent = self.sentence_tokenizer(sentences)
token_sent = token_sent[1:len(token_sent)-1]
token_word = [self.word_tokenizer(token_sent[i]) for i in range(len(token_sent))]
lemmatizedSentences = []
for noOfSent in range(len(token_word)):
stem = [(self.lemma.lemmatize((token_word[noOfSent][words]))) for words in range(len(token_word[noOfSent]))]
stem = " ".join(stem)
lemmatizedSentences.append(stem)
lemmatizedSentences = " ".join(lemmatizedSentences)
return lemmatizedSentences
def porter_stemmer(self,sentence):
token_sent = self.sentence_tokenizer(sentence)
token_word = [self.word_tokenizer(token_sent[i]) for i in range(len(token_sent))]
stemizedSentences = []
for no_of_sent in range(len(token_word)):
stem = [(self.stemmer.stem((token_word[no_of_sent][words]))) for words in range(len(token_word[no_of_sent]))]
stem = " ".join(stem)
stemizedSentences.append(stem)
stemizedSentences = " ".join(stemizedSentences)
return stemizedSentences
```
# Create a dataframe with two classes only
Although there are 20 categories of the documents but for simplicity we just take documents of 2 categories. Furthermore, we only consider total 100 examples for the training and testing of the algorithm
```
TwoClassesFrame = pd.DataFrame(columns=['examples', 'labels'])
count = 0
for i, t in df.iterrows():
if df["targets"][i] < 2:
# print df['data'][i]
TwoClassesFrame.loc[count, 'examples'] = df['data'][i]
TwoClassesFrame.loc[count, 'labels'] = df['targets'][i]
count += 1
if count > 100:
break
TwoClassesFrame
```
# Pre-processing
```
TextNormalization = text_normalization()
# Do prepreprocessing
for row, name in TwoClassesFrame.iterrows():
sentence = TwoClassesFrame.loc[row, 'examples']
TwoClassesFrame.loc[row, 'examples'] = TextNormalization.lemmatizer(sentence)
# Print example after pre-processing
print TwoClassesFrame["examples"][0]
```
## Extract features using TF-IDF
```
TwoClassesVectors = TfidfVectorizer(stop_words='english', lowercase=True)
X_twoClasses = TwoClassesVectors.fit_transform(TwoClassesFrame["examples"])
```
## Fit the KMeans Model on the documents
```
K = 2
model_twoClasses = KMeans(n_clusters=K, max_iter=100, n_init=1, n_jobs=3)
model_twoClasses.fit(X_twoClasses)
```
## Evaluation of the Model
```
predicted = (model_twoClasses.labels_)
predicted = predicted.tolist()
true_labels = TwoClassesFrame["labels"]
true_labels = true_labels.tolist()
misclassified = 0
for i in range(len(predicted)):
if predicted[i] != true_labels[i]:
misclassified += 1
print "misclassified ", str(misclassified) + " Out of " + str(len(true_labels))
print "Total percentage of misclassification ", (misclassified/len(true_labels))*100
```
## Confusion Matrix
```
confusion_Matrix = sklearn.metrics.confusion_matrix(predicted,true_labels)
confusion_Matrix
class_names = [training_set.target_names[0], training_set.target_names[1]]
# code taken from scipty
def plot_confusion_matrix(cm, classes,
normalize=False,
title='Confusion matrix',
cmap=plt.cm.Blues):
"""
This function prints and plots the confusion matrix.
Normalization can be applied by setting `normalize=True`.
"""
if normalize:
cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
print("Normalized confusion matrix")
else:
print('Confusion matrix, without normalization')
print(cm)
plt.imshow(cm, interpolation='nearest', cmap=cmap)
plt.title(title)
plt.colorbar()
tick_marks = np.arange(len(classes))
plt.xticks(tick_marks, classes, rotation=45)
plt.yticks(tick_marks, classes)
fmt = '.2f' if normalize else 'd'
thresh = cm.max() / 2.
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i, format(cm[i, j], fmt),
horizontalalignment="center",
color="white" if cm[i, j] > thresh else "black")
plt.tight_layout()
plt.ylabel('True label')
plt.xlabel('Predicted label')
# Plot non-normalized confusion matrix
plt.figure()
plot_confusion_matrix(confusion_Matrix, classes=class_names,
title='Confusion matrix, without normalization')
```
### Conclusion
The total accuracy achieved is around 70% after evaluating on 2 categories from the news dataset. However, this performance can be increased if pre-processing can be further improved as some data contains lot of irrelevant information due to which algorithm fails to achieve optimal solution.
This performance varies based on the initialization of K-means algorithm
|
github_jupyter
|
from __future__ import division
import sklearn
from sklearn.datasets import fetch_20newsgroups
from sklearn.feature_extraction.text import TfidfTransformer, TfidfVectorizer
from sklearn.cluster import KMeans
from sklearn.preprocessing import Normalizer
from sklearn import metrics
import string
from string import punctuation
import pandas as pd
import numpy as np
import re
import nltk
from nltk.tokenize import word_tokenize, sent_tokenize
from nltk.corpus import stopwords
from nltk.stem import PorterStemmer
from nltk.stem import WordNetLemmatizer
import matplotlib.pyplot as plt
import itertools
%matplotlib inline
training_set = fetch_20newsgroups(subset='train', shuffle=True)
target = training_set.target
print len(training_set.data)
df = pd.DataFrame(training_set.data, columns=["data"])
df["targets"] = target
df.head(10)
df.groupby('targets').count()
# print one sample of data
print df["data"][0]
class text_normalization:
def __init__(self):
self.punctuations = list(punctuation)
self.stemmer = PorterStemmer()
self.lemma = WordNetLemmatizer()
self.contractions = {"'nt":"not", "'ll": " will","'d":"would" ,"'re":"are", "'ve":"have", "'m":"am", "'s":"is"}
'''
This function takes text as input
and returns list of tokenized words(punctuations not included)
'''
def word_tokenizer(self,text):
self.word_tokenize_list = []
for word in word_tokenize(text):
result = 0
#find words containing numbers i.e A45, or 45
result = re.findall(r'([a-z]|[A-Z])(\d)|(\d)', word)
findUrl = re.findall(r'([a-z])(\.com)', word)
findBlankWords = re.findall(r'(([a-z])(__))|(__)([a-z])', word)
findBlanks = re.findall(r'(__)', word)
if word in self.contractions:
self.word_tokenize_list.append(self.contractions[word])
elif len(findBlankWords) > 0 or len(findBlanks) > 0:
continue
elif len(result) > 0:
continue
elif len(findUrl) > 0:
# print "word ", word
continue
elif len(word) < 3:
continue
elif word in self.punctuations:
continue
else:
self.word_tokenize_list.append(word)
return self.word_tokenize_list
'''
This function takes text as input
and returns list of tokenized sentences
'''
def sentence_tokenizer(self,sentence):
self.sentence_tokenize_list = sent_tokenize(sentence)
return self.sentence_tokenize_list
'''
This function takes tokenized sentence as input
and returns lemma of tokenized sentence
1. First sentences from text are tokenized
2. Then, words from sentences are tokenized
3. Lemmatizer of words is determined
'''
def lemmatizer(self, sentences):
sentences = re.sub(r'([a-z]|[A-Z])(_)', r'\1', sentences)
sentences = re.sub(r'(_)([a-z]|[A-Z])', r'\2', sentences)
token_sent = self.sentence_tokenizer(sentences)
token_sent = token_sent[1:len(token_sent)-1]
token_word = [self.word_tokenizer(token_sent[i]) for i in range(len(token_sent))]
lemmatizedSentences = []
for noOfSent in range(len(token_word)):
stem = [(self.lemma.lemmatize((token_word[noOfSent][words]))) for words in range(len(token_word[noOfSent]))]
stem = " ".join(stem)
lemmatizedSentences.append(stem)
lemmatizedSentences = " ".join(lemmatizedSentences)
return lemmatizedSentences
def porter_stemmer(self,sentence):
token_sent = self.sentence_tokenizer(sentence)
token_word = [self.word_tokenizer(token_sent[i]) for i in range(len(token_sent))]
stemizedSentences = []
for no_of_sent in range(len(token_word)):
stem = [(self.stemmer.stem((token_word[no_of_sent][words]))) for words in range(len(token_word[no_of_sent]))]
stem = " ".join(stem)
stemizedSentences.append(stem)
stemizedSentences = " ".join(stemizedSentences)
return stemizedSentences
TwoClassesFrame = pd.DataFrame(columns=['examples', 'labels'])
count = 0
for i, t in df.iterrows():
if df["targets"][i] < 2:
# print df['data'][i]
TwoClassesFrame.loc[count, 'examples'] = df['data'][i]
TwoClassesFrame.loc[count, 'labels'] = df['targets'][i]
count += 1
if count > 100:
break
TwoClassesFrame
TextNormalization = text_normalization()
# Do prepreprocessing
for row, name in TwoClassesFrame.iterrows():
sentence = TwoClassesFrame.loc[row, 'examples']
TwoClassesFrame.loc[row, 'examples'] = TextNormalization.lemmatizer(sentence)
# Print example after pre-processing
print TwoClassesFrame["examples"][0]
TwoClassesVectors = TfidfVectorizer(stop_words='english', lowercase=True)
X_twoClasses = TwoClassesVectors.fit_transform(TwoClassesFrame["examples"])
K = 2
model_twoClasses = KMeans(n_clusters=K, max_iter=100, n_init=1, n_jobs=3)
model_twoClasses.fit(X_twoClasses)
predicted = (model_twoClasses.labels_)
predicted = predicted.tolist()
true_labels = TwoClassesFrame["labels"]
true_labels = true_labels.tolist()
misclassified = 0
for i in range(len(predicted)):
if predicted[i] != true_labels[i]:
misclassified += 1
print "misclassified ", str(misclassified) + " Out of " + str(len(true_labels))
print "Total percentage of misclassification ", (misclassified/len(true_labels))*100
confusion_Matrix = sklearn.metrics.confusion_matrix(predicted,true_labels)
confusion_Matrix
class_names = [training_set.target_names[0], training_set.target_names[1]]
# code taken from scipty
def plot_confusion_matrix(cm, classes,
normalize=False,
title='Confusion matrix',
cmap=plt.cm.Blues):
"""
This function prints and plots the confusion matrix.
Normalization can be applied by setting `normalize=True`.
"""
if normalize:
cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
print("Normalized confusion matrix")
else:
print('Confusion matrix, without normalization')
print(cm)
plt.imshow(cm, interpolation='nearest', cmap=cmap)
plt.title(title)
plt.colorbar()
tick_marks = np.arange(len(classes))
plt.xticks(tick_marks, classes, rotation=45)
plt.yticks(tick_marks, classes)
fmt = '.2f' if normalize else 'd'
thresh = cm.max() / 2.
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i, format(cm[i, j], fmt),
horizontalalignment="center",
color="white" if cm[i, j] > thresh else "black")
plt.tight_layout()
plt.ylabel('True label')
plt.xlabel('Predicted label')
# Plot non-normalized confusion matrix
plt.figure()
plot_confusion_matrix(confusion_Matrix, classes=class_names,
title='Confusion matrix, without normalization')
| 0.388618 | 0.916857 |
# Simulation and figure generation for differential correlation
```
import scipy.stats as stats
import scipy.sparse as sparse
from scipy.stats import norm, gamma, poisson, nbinom
import numpy as np
from mixedvines.copula import Copula, GaussianCopula, ClaytonCopula, \
FrankCopula
from mixedvines.mixedvine import MixedVine
import matplotlib.pyplot as plt
import itertools
import pandas as pd
import scanpy as sc
%matplotlib inline
import imp
import seaborn as sns
import sys
sys.path.append('/home/mkim7/Github/scrna-parameter-estimation/examples/simulation/')
import simulate as sim
data_path = '/data/parameter_estimation/interferon_data/'
import sys
sys.path.append('/home/mkim7/Github/scrna-parameter-estimation/scmemo')
import scmemo, utils
import matplotlib as mpl
mpl.rcParams['pdf.fonttype'] = 42
mpl.rcParams['ps.fonttype'] = 42
import matplotlib.pylab as pylab
params = {'legend.fontsize': 'medium',
'axes.labelsize': 'medium',
'axes.titlesize':'medium',
'figure.titlesize':'medium',
'xtick.labelsize':'small',
'ytick.labelsize':'small'}
pylab.rcParams.update(params)
```
### Function for converting params
```
def convert_params(mu, theta):
"""
Convert mean/dispersion parameterization of a negative binomial to the ones scipy supports
See https://en.wikipedia.org/wiki/Negative_binomial_distribution#Alternative_formulations
"""
r = theta
var = mu + 1 / r * mu ** 2
p = (var - mu) / var
return r, 1 - p
```
### Function for plotting 2D discrete scatter plots
```
def plot_2d_discrete(data, size_multiplier=10, offset=0.0):
""" Plotting discrete 2D data according to the frequency. """
df = pd.DataFrame(data).groupby([0, 1]).size().reset_index(name='count')
df['log_count'] = np.log(df['count'])
plt.scatter(df[0]+offset, df[1]+offset, s=df['log_count']*size_multiplier)
```
### Simulation
```
def simulate_correlated_data(corr, size=1000):
dim = 2 # Dimension
vine = MixedVine(dim)
vine.set_marginal(0, nbinom(*convert_params(3, 10)))
vine.set_marginal(1, nbinom(*convert_params(3, 10)))
vine.set_copula(1, 0, GaussianCopula(corr))
samples = vine.rvs(size)
return samples.astype(int)
def simulate_dropout(
true_counts,
q,
q_sq):
"""
:true_counts: True counts
:q: first moment of the dropout probability
:q_sq: second moment of the dropout probability
Simulate the beta-binomial dropout.
"""
m = q
v = q_sq - q**2
alpha = m*(m*(1-m)/v - 1)
beta = (1-m)*(m*(1-m)/v - 1)
qs = stats.beta.rvs(alpha, beta, size=true_counts.shape[0])
return qs, stats.binom.rvs(true_counts, np.vstack([qs for i in range(true_counts.shape[1])]).T)
def create_simulated_anndata(samples):
N = samples.shape[0]
obs_df = pd.DataFrame()
obs_df['n_counts'] = [1e10 for i in range(N)]
#obs_df['cell_type'] = label
values = samples
adata = sc.AnnData(
values,
var=pd.DataFrame(index=['gene_' + str(i) for i in range(1, n_genes+1)]),
obs=obs_df)
return adata
N = 20000
n_genes=2
p = 0.1
noise_level = 0.2049755522580501
p_sq = (noise_level+1)*p**2
samples_A = simulate_correlated_data(0.7, size=N)
samples_B = simulate_correlated_data(0.01, size=N)
qs_A, obs_samples_A = simulate_dropout(samples_A, p, p_sq)
qs_B, obs_samples_B = simulate_dropout(samples_B, p, p_sq)
adata = create_simulated_anndata(np.vstack([obs_samples_A, obs_samples_B]))
adata.obs['cell_type'] = ['A' for i in range(N)] + ['B' for i in range(N)]
```
### Estimate correlation
```
imp.reload(scmemo)
estimator = scmemo.SingleCellEstimator(
adata=adata,
group_label='cell_type',
n_umis_column='n_counts',
num_permute=100000,
beta=p)
estimator.beta_sq = p_sq
estimator.compute_observed_moments()
estimator.estimate_1d_parameters()
estimator.estimate_2d_parameters(
gene_list_1=['gene_1'],
gene_list_2=['gene_2'])
estimator.compute_confidence_intervals_1d(
groups=['A','B'],
groups_to_compare=[('A', 'B')])
estimator.compute_confidence_intervals_2d(
gene_list_1=['gene_1'],
gene_list_2=['gene_2'],
groups=['A', 'B'],
groups_to_compare=[('A', 'B')])
```
### Plotting simulation results
```
def line_from_correlation(corr, corr_ci, x, y, mu_x, mu_y, sigma_x, sigma_y, color_order):
# mu_x = x.mean()
# mu_y = y.mean()
# sigma_x = x.std()
# sigma_y = y.std()
beta_up = sigma_y/sigma_x*(corr + corr_ci)
alpha_up = mu_y - beta_up*mu_x
beta = sigma_y/sigma_x*(corr)
alpha = mu_y - beta*mu_x
beta_down = sigma_y/sigma_x*(corr - corr_ci)
alpha_down = mu_y - beta_down*mu_x
x_range = np.arange(x.min(), 7, 0.1)
up = beta_up*x_range + alpha_up
line = beta*x_range + alpha
down = beta_down*x_range + alpha_down
plt.fill_between(x_range, up, down, alpha=0.3, color=sns.color_palette()[color_order])
plt.plot(x_range, line, color=sns.color_palette()[color_order])
print(stats.pearsonr(samples_A[:, 0], samples_A[:, 1]))
print(stats.pearsonr(samples_B[:, 0], samples_B[:, 1]))
print(stats.pearsonr(obs_samples_A[:, 0], obs_samples_A[:, 1]))
print(stats.pearsonr(obs_samples_B[:, 0], obs_samples_B[:, 1]))
print(estimator.parameters['A']['corr'][0, 1])
print(estimator.parameters['B']['corr'][0, 1])
%matplotlib inline
plt.figure(figsize=(6.5, 1.5))
plt.subplots_adjust(left=None, bottom=None, right=None, top=None, wspace=0.45,
hspace=None)
plt.subplot(1, 2, 1);
plot_2d_discrete(samples_A, 1, 0.15)
plot_2d_discrete(samples_B, 1, -0.15)
plt.xlim(-1, 13)
plt.ylim(-1, 13)
plt.ylabel('True expression \n of gene B');
plt.xlabel('True expression of gene A');
plt.subplot(1, 2, 2);
plot_2d_discrete(obs_samples_A, 1, 0.1)
plot_2d_discrete(obs_samples_B, 1, -0.1)
line_from_correlation(
corr=estimator.parameters['A']['corr'][0, 1],
corr_ci=estimator.parameters_confidence_intervals['A']['corr'][0, 1],
x=obs_samples_A[:, 0],
y=obs_samples_A[:, 1],
mu_x=estimator.parameters['A']['mean'][0],
mu_y=estimator.parameters['A']['mean'][1],
sigma_x=estimator.estimated_central_moments['A']['second'][0],
sigma_y=estimator.estimated_central_moments['A']['second'][1],
color_order=0
)
line_from_correlation(
corr=estimator.parameters['B']['corr'][0, 1],
corr_ci=estimator.parameters_confidence_intervals['B']['corr'][0, 1],
x=obs_samples_B[:, 0],
y=obs_samples_B[:, 1],
mu_x=estimator.parameters['B']['mean'][0],
mu_y=estimator.parameters['B']['mean'][1],
sigma_x=estimator.estimated_central_moments['B']['second'][0],
sigma_y=estimator.estimated_central_moments['B']['second'][1],
color_order=1
)
plt.ylabel('Observed expression \n of gene B');
plt.xlabel('Observed expression of gene A');
#plt.tight_layout()
plt.savefig('diff_cor.pdf', bbox_inches='tight')
```
|
github_jupyter
|
import scipy.stats as stats
import scipy.sparse as sparse
from scipy.stats import norm, gamma, poisson, nbinom
import numpy as np
from mixedvines.copula import Copula, GaussianCopula, ClaytonCopula, \
FrankCopula
from mixedvines.mixedvine import MixedVine
import matplotlib.pyplot as plt
import itertools
import pandas as pd
import scanpy as sc
%matplotlib inline
import imp
import seaborn as sns
import sys
sys.path.append('/home/mkim7/Github/scrna-parameter-estimation/examples/simulation/')
import simulate as sim
data_path = '/data/parameter_estimation/interferon_data/'
import sys
sys.path.append('/home/mkim7/Github/scrna-parameter-estimation/scmemo')
import scmemo, utils
import matplotlib as mpl
mpl.rcParams['pdf.fonttype'] = 42
mpl.rcParams['ps.fonttype'] = 42
import matplotlib.pylab as pylab
params = {'legend.fontsize': 'medium',
'axes.labelsize': 'medium',
'axes.titlesize':'medium',
'figure.titlesize':'medium',
'xtick.labelsize':'small',
'ytick.labelsize':'small'}
pylab.rcParams.update(params)
def convert_params(mu, theta):
"""
Convert mean/dispersion parameterization of a negative binomial to the ones scipy supports
See https://en.wikipedia.org/wiki/Negative_binomial_distribution#Alternative_formulations
"""
r = theta
var = mu + 1 / r * mu ** 2
p = (var - mu) / var
return r, 1 - p
def plot_2d_discrete(data, size_multiplier=10, offset=0.0):
""" Plotting discrete 2D data according to the frequency. """
df = pd.DataFrame(data).groupby([0, 1]).size().reset_index(name='count')
df['log_count'] = np.log(df['count'])
plt.scatter(df[0]+offset, df[1]+offset, s=df['log_count']*size_multiplier)
def simulate_correlated_data(corr, size=1000):
dim = 2 # Dimension
vine = MixedVine(dim)
vine.set_marginal(0, nbinom(*convert_params(3, 10)))
vine.set_marginal(1, nbinom(*convert_params(3, 10)))
vine.set_copula(1, 0, GaussianCopula(corr))
samples = vine.rvs(size)
return samples.astype(int)
def simulate_dropout(
true_counts,
q,
q_sq):
"""
:true_counts: True counts
:q: first moment of the dropout probability
:q_sq: second moment of the dropout probability
Simulate the beta-binomial dropout.
"""
m = q
v = q_sq - q**2
alpha = m*(m*(1-m)/v - 1)
beta = (1-m)*(m*(1-m)/v - 1)
qs = stats.beta.rvs(alpha, beta, size=true_counts.shape[0])
return qs, stats.binom.rvs(true_counts, np.vstack([qs for i in range(true_counts.shape[1])]).T)
def create_simulated_anndata(samples):
N = samples.shape[0]
obs_df = pd.DataFrame()
obs_df['n_counts'] = [1e10 for i in range(N)]
#obs_df['cell_type'] = label
values = samples
adata = sc.AnnData(
values,
var=pd.DataFrame(index=['gene_' + str(i) for i in range(1, n_genes+1)]),
obs=obs_df)
return adata
N = 20000
n_genes=2
p = 0.1
noise_level = 0.2049755522580501
p_sq = (noise_level+1)*p**2
samples_A = simulate_correlated_data(0.7, size=N)
samples_B = simulate_correlated_data(0.01, size=N)
qs_A, obs_samples_A = simulate_dropout(samples_A, p, p_sq)
qs_B, obs_samples_B = simulate_dropout(samples_B, p, p_sq)
adata = create_simulated_anndata(np.vstack([obs_samples_A, obs_samples_B]))
adata.obs['cell_type'] = ['A' for i in range(N)] + ['B' for i in range(N)]
imp.reload(scmemo)
estimator = scmemo.SingleCellEstimator(
adata=adata,
group_label='cell_type',
n_umis_column='n_counts',
num_permute=100000,
beta=p)
estimator.beta_sq = p_sq
estimator.compute_observed_moments()
estimator.estimate_1d_parameters()
estimator.estimate_2d_parameters(
gene_list_1=['gene_1'],
gene_list_2=['gene_2'])
estimator.compute_confidence_intervals_1d(
groups=['A','B'],
groups_to_compare=[('A', 'B')])
estimator.compute_confidence_intervals_2d(
gene_list_1=['gene_1'],
gene_list_2=['gene_2'],
groups=['A', 'B'],
groups_to_compare=[('A', 'B')])
def line_from_correlation(corr, corr_ci, x, y, mu_x, mu_y, sigma_x, sigma_y, color_order):
# mu_x = x.mean()
# mu_y = y.mean()
# sigma_x = x.std()
# sigma_y = y.std()
beta_up = sigma_y/sigma_x*(corr + corr_ci)
alpha_up = mu_y - beta_up*mu_x
beta = sigma_y/sigma_x*(corr)
alpha = mu_y - beta*mu_x
beta_down = sigma_y/sigma_x*(corr - corr_ci)
alpha_down = mu_y - beta_down*mu_x
x_range = np.arange(x.min(), 7, 0.1)
up = beta_up*x_range + alpha_up
line = beta*x_range + alpha
down = beta_down*x_range + alpha_down
plt.fill_between(x_range, up, down, alpha=0.3, color=sns.color_palette()[color_order])
plt.plot(x_range, line, color=sns.color_palette()[color_order])
print(stats.pearsonr(samples_A[:, 0], samples_A[:, 1]))
print(stats.pearsonr(samples_B[:, 0], samples_B[:, 1]))
print(stats.pearsonr(obs_samples_A[:, 0], obs_samples_A[:, 1]))
print(stats.pearsonr(obs_samples_B[:, 0], obs_samples_B[:, 1]))
print(estimator.parameters['A']['corr'][0, 1])
print(estimator.parameters['B']['corr'][0, 1])
%matplotlib inline
plt.figure(figsize=(6.5, 1.5))
plt.subplots_adjust(left=None, bottom=None, right=None, top=None, wspace=0.45,
hspace=None)
plt.subplot(1, 2, 1);
plot_2d_discrete(samples_A, 1, 0.15)
plot_2d_discrete(samples_B, 1, -0.15)
plt.xlim(-1, 13)
plt.ylim(-1, 13)
plt.ylabel('True expression \n of gene B');
plt.xlabel('True expression of gene A');
plt.subplot(1, 2, 2);
plot_2d_discrete(obs_samples_A, 1, 0.1)
plot_2d_discrete(obs_samples_B, 1, -0.1)
line_from_correlation(
corr=estimator.parameters['A']['corr'][0, 1],
corr_ci=estimator.parameters_confidence_intervals['A']['corr'][0, 1],
x=obs_samples_A[:, 0],
y=obs_samples_A[:, 1],
mu_x=estimator.parameters['A']['mean'][0],
mu_y=estimator.parameters['A']['mean'][1],
sigma_x=estimator.estimated_central_moments['A']['second'][0],
sigma_y=estimator.estimated_central_moments['A']['second'][1],
color_order=0
)
line_from_correlation(
corr=estimator.parameters['B']['corr'][0, 1],
corr_ci=estimator.parameters_confidence_intervals['B']['corr'][0, 1],
x=obs_samples_B[:, 0],
y=obs_samples_B[:, 1],
mu_x=estimator.parameters['B']['mean'][0],
mu_y=estimator.parameters['B']['mean'][1],
sigma_x=estimator.estimated_central_moments['B']['second'][0],
sigma_y=estimator.estimated_central_moments['B']['second'][1],
color_order=1
)
plt.ylabel('Observed expression \n of gene B');
plt.xlabel('Observed expression of gene A');
#plt.tight_layout()
plt.savefig('diff_cor.pdf', bbox_inches='tight')
| 0.568416 | 0.898277 |
```
#load packages
import numpy as np
import pandas as pd
import scipy
from PIL import Image
import glob
import os
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import MultiLabelBinarizer
import matplotlib.pyplot as plt
from pandarallel import pandarallel
%matplotlib inline
import tensorflow as tf
from tensorflow.keras.layers import Dense, Dropout, Flatten, Activation, Conv2D, MaxPooling2D, GlobalAveragePooling2D
from tensorflow.keras.models import Sequential, Model, load_model
from tensorflow.keras.optimizers import Adam, SGD
from tensorflow.keras.preprocessing.image import img_to_array, load_img
from tensorflow.keras import utils
from tensorflow.keras.applications.inception_v3 import InceptionV3
#grab file path names
image_paths = glob.glob("../data/movie-genre-from-its-poster/SampleMoviePosters/*.jpg")
image_ids = []
for path in image_paths:
start = path.rfind("/") +1
end = len(path) - 4
image_ids.append(path[start:end])
len(image_paths)
df_movie = pd.read_csv("../data/movie-genre-from-its-poster/MovieGenre.csv", encoding = "ISO-8859-1")
df_movie.shape
df_movie.head(1)
df_movie_sample = df_movie[df_movie["imdbId"].isin(image_ids)]
df_movie_sample = df_movie_sample.drop_duplicates(subset=['imdbId'], keep="last")
df_movie_sample.shape
df_movie_sample['Genre']
```
### Apply tuple in parallel
```
def convert_tuple(list):
return tuple(i for i in list)
pandarallel.initialize()
df_movie_sample["Genre"] = df_movie_sample["Genre"].str.split("|")
# df_movie_sample["Genre"] = df_movie_sample["Genre"].parallel_apply(convert_tuple)
target = df_movie_sample['Genre']
X = df_movie_sample.drop("Genre", axis =1)
y = df_movie_sample["Genre"]
mlb = MultiLabelBinarizer()
y = mlb.fit_transform(y)
target_key = mlb.classes_
images = []
for img in image_paths:
try:
img = load_img(img, target_size=(256,256))
img = img_to_array(img)
img = np.expand_dims(img, axis=0)
images.append(img)
except:
pass
images = np.vstack(images)
# images = np.array([img_to_array(
# load_img(img, target_size=(256,256))
# ) for img in image_paths])
images = images.astype('float32')/255.0
#sample image
plt.imshow(images[2]);
plt.grid(True);
plt.xticks([]);
plt.yticks([]);
target_labels = target_key
total_classes = len(set(target_labels))
print("number of genre:", total_classes)
df_movie.loc[942]
len(image_ids)
images.shape
y.shape
X_train, X_valid, y_train, y_valid = train_test_split(images, y,
random_state=42)
model = Sequential()
model.add(Conv2D(32, (3, 3), input_shape=(256, 256, 3)))
model.add(Activation('relu')) # this is just different syntax for specifying the activation function
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Conv2D(32, (3, 3)))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Conv2D(64, (3, 3)))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Flatten())
model.add(Dense(64))
model.add(Activation('relu'))
model.add(Dropout(0.5))
model.add(Dense(total_classes))
model.add(Activation('sigmoid'))
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
model.summary()
history = model.fit(X_train, y_train, epochs=5, validation_data=(X_valid, y_valid))
img_test_predict = np.reshape(images[4], (1, 256, 256, 3))
def poster_classification(img, target_key=target_key, model=model):
proba = model.predict(img)[0]
idxs = np.argsort(proba)[::-1][:2]
print("Poster Prediction")
for (i, j) in enumerate(idxs):
label = "{}: {:.2f}%".format(target_key[j], proba[j] * 100)
for (label, p) in zip(target_key, proba):
if p >= .1:
print("{}: {:.2f}%".format(label, p * 100))
plt.imshow(img[0]);
plt.grid(True);
plt.xticks([]);
plt.yticks([]);
def poster_classification_database(idx=7, images=images, target=target, target_key=target_key, model=model):
img = np.reshape(images[idx], (1, 256, 256, 3))
proba = model.predict(img)[0]
idxs = np.argsort(proba)[::-1][:2]
print("Poster Prediction")
for (i, j) in enumerate(idxs):
label = "{}: {:.2f}%".format(target_key[j], proba[j] * 100)
for (label, p) in zip(target_key, proba):
if p >= .1:
print("{}: {:.2f}%".format(label, p * 100))
plt.imshow(img[0]);
plt.grid(True);
plt.xticks([]);
plt.yticks([]);
print("")
print(f"True poster genre:{target.iloc[idx]}")
poster_classification(img_test_predict)
poster_classification_database(54)
poster_classification_database(278)
```
|
github_jupyter
|
#load packages
import numpy as np
import pandas as pd
import scipy
from PIL import Image
import glob
import os
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import MultiLabelBinarizer
import matplotlib.pyplot as plt
from pandarallel import pandarallel
%matplotlib inline
import tensorflow as tf
from tensorflow.keras.layers import Dense, Dropout, Flatten, Activation, Conv2D, MaxPooling2D, GlobalAveragePooling2D
from tensorflow.keras.models import Sequential, Model, load_model
from tensorflow.keras.optimizers import Adam, SGD
from tensorflow.keras.preprocessing.image import img_to_array, load_img
from tensorflow.keras import utils
from tensorflow.keras.applications.inception_v3 import InceptionV3
#grab file path names
image_paths = glob.glob("../data/movie-genre-from-its-poster/SampleMoviePosters/*.jpg")
image_ids = []
for path in image_paths:
start = path.rfind("/") +1
end = len(path) - 4
image_ids.append(path[start:end])
len(image_paths)
df_movie = pd.read_csv("../data/movie-genre-from-its-poster/MovieGenre.csv", encoding = "ISO-8859-1")
df_movie.shape
df_movie.head(1)
df_movie_sample = df_movie[df_movie["imdbId"].isin(image_ids)]
df_movie_sample = df_movie_sample.drop_duplicates(subset=['imdbId'], keep="last")
df_movie_sample.shape
df_movie_sample['Genre']
def convert_tuple(list):
return tuple(i for i in list)
pandarallel.initialize()
df_movie_sample["Genre"] = df_movie_sample["Genre"].str.split("|")
# df_movie_sample["Genre"] = df_movie_sample["Genre"].parallel_apply(convert_tuple)
target = df_movie_sample['Genre']
X = df_movie_sample.drop("Genre", axis =1)
y = df_movie_sample["Genre"]
mlb = MultiLabelBinarizer()
y = mlb.fit_transform(y)
target_key = mlb.classes_
images = []
for img in image_paths:
try:
img = load_img(img, target_size=(256,256))
img = img_to_array(img)
img = np.expand_dims(img, axis=0)
images.append(img)
except:
pass
images = np.vstack(images)
# images = np.array([img_to_array(
# load_img(img, target_size=(256,256))
# ) for img in image_paths])
images = images.astype('float32')/255.0
#sample image
plt.imshow(images[2]);
plt.grid(True);
plt.xticks([]);
plt.yticks([]);
target_labels = target_key
total_classes = len(set(target_labels))
print("number of genre:", total_classes)
df_movie.loc[942]
len(image_ids)
images.shape
y.shape
X_train, X_valid, y_train, y_valid = train_test_split(images, y,
random_state=42)
model = Sequential()
model.add(Conv2D(32, (3, 3), input_shape=(256, 256, 3)))
model.add(Activation('relu')) # this is just different syntax for specifying the activation function
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Conv2D(32, (3, 3)))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Conv2D(64, (3, 3)))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Flatten())
model.add(Dense(64))
model.add(Activation('relu'))
model.add(Dropout(0.5))
model.add(Dense(total_classes))
model.add(Activation('sigmoid'))
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
model.summary()
history = model.fit(X_train, y_train, epochs=5, validation_data=(X_valid, y_valid))
img_test_predict = np.reshape(images[4], (1, 256, 256, 3))
def poster_classification(img, target_key=target_key, model=model):
proba = model.predict(img)[0]
idxs = np.argsort(proba)[::-1][:2]
print("Poster Prediction")
for (i, j) in enumerate(idxs):
label = "{}: {:.2f}%".format(target_key[j], proba[j] * 100)
for (label, p) in zip(target_key, proba):
if p >= .1:
print("{}: {:.2f}%".format(label, p * 100))
plt.imshow(img[0]);
plt.grid(True);
plt.xticks([]);
plt.yticks([]);
def poster_classification_database(idx=7, images=images, target=target, target_key=target_key, model=model):
img = np.reshape(images[idx], (1, 256, 256, 3))
proba = model.predict(img)[0]
idxs = np.argsort(proba)[::-1][:2]
print("Poster Prediction")
for (i, j) in enumerate(idxs):
label = "{}: {:.2f}%".format(target_key[j], proba[j] * 100)
for (label, p) in zip(target_key, proba):
if p >= .1:
print("{}: {:.2f}%".format(label, p * 100))
plt.imshow(img[0]);
plt.grid(True);
plt.xticks([]);
plt.yticks([]);
print("")
print(f"True poster genre:{target.iloc[idx]}")
poster_classification(img_test_predict)
poster_classification_database(54)
poster_classification_database(278)
| 0.493164 | 0.65339 |
# GRR Colab
```
%load_ext grr_colab.ipython_extension
import grr_colab
```
Specifying GRR Colab flags:
```
grr_colab.flags.FLAGS.set_default('grr_http_api_endpoint', 'http://localhost:8000/')
grr_colab.flags.FLAGS.set_default('grr_admin_ui_url', 'http://localhost:8000/')
grr_colab.flags.FLAGS.set_default('grr_auth_api_user', 'admin')
grr_colab.flags.FLAGS.set_default('grr_auth_password', 'admin')
```
## Magics API
GRR magics allow to search for clients and then to choose a single client to work with. The results of magics are represented as pandas dataframes unless they are primitives.
### Searching clients
You can search for clients by specifying username, hostname, client labels etc. The results are sorted by the last seen column.
```
df = %grr_search_clients -u admin
df[['online', 'online.pretty', 'client_id', 'last_seen_ago', 'last_seen_at.pretty']]
```
There is a shortcut for searching for online only clients directly so that you don't need to filter the dataframe.
```
df = %grr_search_online_clients -u admin
df[['online', 'online.pretty', 'client_id', 'last_seen_ago', 'last_seen_at.pretty']]
```
Every datetime field has two representations: the original one that is microseconds and the pretty one that is pandas timestamp.
```
df[['last_seen_at', 'last_seen_at.pretty']]
```
### Setting current clients
To work with a client you need to select a client first. It means that you are able to work only with a single client simultaneously using magic commands (there is no such restriction for Python API). To set a client you need either a hostname (works in case of one client set up for that hostname) or a client ID which you can get from the search clients dataframe.
```
client_id = df['client_id'][0]
%grr_set_client -c {client_id}
%grr_id
```
An attempt to set a client with a hostname that has multiple clients will lead to an exception.
### Requesting approvals
If you don't have valid approvals for the selected client, you will get an error while attempting to run a flow on it. You can request an approval with magic commands specifying the reason and list of approvers.
```
%grr_request_approval -r "For testing" -a admin
```
This function will not wait until the approval is granted. If you need your code to wait until it's granted, use `grr_request_approval_and_wait` instead.
### Exploring filesystem
In addition to the selected client, working directory is also saved. It means that you can use relative paths instead of absolute. Note that the existence of directories is not checked and you will not get an error if you try to cd into directory that does not exist.
Initially you are in the root directory.
```
%grr_pwd
%grr_cd tmp/foo/bar
%grr_pwd
%grr_cd ../baz
%grr_pwd
```
You can ls the current directory and any other directories specified by relative and absolute paths.
**Note**. The most file-related magics start flows and fetch live data from the client. It means that the client has to be online in order for them to work.
```
df = %grr_ls
df
```
Stat mode has two representations: number and UNIX-style:
```
df[['st_mode', 'st_mode.pretty']]
%grr_ls ../baz/dir2
%grr_ls /tmp/foo
```
To see some metadata of a file you can just call `grr_stat` function.
```
%grr_stat file1
```
You can use globbing for stat:
```
%grr_stat "file*"
```
You can print the first bytes of a file:
```
%grr_head file1 -c 30
```
Alghough there is no offset in original bash `head` command you can specify offset in `grr_head`:
```
%grr_head file1 -c 30 -o 20
```
Some of the functions like `grr_head` and `grr_ls` have `--cached` (`-C` for short) option which indicates that no calls to the client should be performed. In this case the data will be fetched from the cached data on the server. Server cached data is updated only during calls to the client so it is not always up-to-date but accessing it is way faster.
```
%grr_ls /tmp/foo/baz -C
%grr_head file1 -C
```
Grepping files is also possible. `--fixed-string` (`-F` for short) option indicates that pattern to search for is not a regular expression. `--hex-string` (`-X` for short) option allows to pass hex strings as a pattern.
```
%grr_grep "line" file1
%grr_grep -F "line" file1
%grr_grep -X "6c696e65" file1
```
There is a shortcut for `--fixed-strings` option. Globbing is also available here.
```
%grr_fgrep "line" "file*"
%grr_fgrep -X "6c696e65" file1
```
If the file is too large and you'd like to download it then use `wget`:
```
%grr_wget file1
```
You can also download a cached version:
```
%grr_wget file1 -C
```
You can specify path type with `--path-type` flag (`-P` for short) for all filesystem related magics. The available values are `os` (default), `tsk`, `ntfs`, `registry`.
```
%grr_ls -P os -C
```
### System information
Names of the functions are the same as in bash for simplicity.
Printing hostname of the client:
```
%grr_hostname
```
Getting network interfaces info:
```
ifaces = %grr_ifconfig
```
For mac address fields there are also two columns: one with the original bytes type but not representable and pretty one with string representation of mac address.
```
ifaces[['mac_address', 'mac_address.pretty']][1:]
```
If a field contains a collection then the cell in the dataframe is represented as another dataframe. IP address fields also have two representations.
```
ifaces['addresses'][1]
```
For `uname` command only two options are available: `--machine` that prints the machine architecture and `--kernel-release`.
```
%grr_uname -m
%grr_uname -r
```
To get the client summary you can simply call interrogate flow.
```
df = %grr_interrogate
df[['client_id', 'system_info.system', 'system_info.machine']]
```
There is also possible to get info about processes that are running on client machine:
```
ps = %grr_ps
ps[:5]
```
To fetch some system information you can also use osquery. Osquery tables are also converted to dataframes.
```
%grr_osqueryi "SELECT pid, name, cmdline, state, nice, threads FROM processes WHERE pid >= 440 and pid < 600;"
```
Running YARA for scanning processes is also available.
```
import os
pid = os.getpid()
data = "dadasdasdasdjaskdakdaskdakjdkjadkjakjjdsgkngksfkjadsjnfandankjd"
rule = 'rule TextExample {{ strings: $text_string = "{data}" condition: $text_string }}'.format(data=data)
df = %grr_yara '{rule}' -p {pid}
df[['process.pid', 'process.name', 'process.exe']]
```
### Configuring flow timeout
The default flow timeout is 30 seconds. It's time the function waits for a flow to complete. You can configure this timeout with `grr_set_flow_timeout` specifying number of seconds to wait. For examples, this will set the timeout to a minute:
```
%grr_set_flow_timeout 60
```
To tell functions to wait for the flows forever until they are completed:
```
%grr_set_no_flow_timeout
```
To set timeout to default value of 30 seconds:
```
%grr_set_default_flow_timeout
```
Setting timeout to 0 tells functions not to wait at all and exit immediately after the flow starts.
```
%grr_set_flow_timeout 0
```
In case timeout is exceeded (or you set 0 timeout) you will se such error with a link to Admin UI.
### Collecting artifacts
You can first list all the artifacts that you can collect:
```
df = %grr_list_artifacts
df[:2]
```
To collect an artifact you just need to provide its name:
```
%grr_collect "DebianVersion"
```
## Python API
### Getting a client
Using Python API you can work with multiple clients simultaneously. You don't need to select a client to work with, instead you simply get a client object.
Use `search` method to search for clients. You can specify `ip`, `mac`, `host`, `version`, `user`, and `labels` search criteria. As a result you will get a list of client objects so that you can pick one of them to work with.
```
clients = grr_colab.Client.search(user='admin')
clients
clients[0].id
```
If you know a client ID or a hostname (in case there is one client installed for this hostname) you can get a client object using one of these values:
```
client = grr_colab.Client.with_id('C.dc3782aeab2c5b4c')
```
### Client properties
There is a bunch of simple client properties to get some info about the client. Unlike magic API this API returns objects but not dataframes for non-primitive values.
Getting the client ID:
```
client.id
```
Getting the client hostname:
```
client.hostname
```
Getting network interfaces info:
```
client.ifaces[1:]
client.ifaces[1].ifname
```
This is a collection of interface objects so you can iterate over it and access interface object fields:
```
for iface in client.ifaces:
print(iface.ifname)
```
Getting the knowledge base for the client:
You can also access its fields:
```
client.knowledgebase
client.knowledgebase.os_release
```
Getting an architecture of a machine that client runs on:
```
client.arch
```
Getting kernel version string:
```
client.kernel
```
Getting a list of labels that are associated with this client:
```
client.labels
```
First seen and last seen times are saved as datetime objects:
```
client.first_seen
client.last_seen
```
### Requesting approvals
As in magics API here you also need to request an approval before running flows on a client. To do this simply call `request_approval` method providing a reason for the approval and list of approvers.
```
client.request_approval(approvers=['admin'], reason='Test reason')
```
This method does not wait until the approval is granted. If you need to wait, use `request_approval_and_wait` method that has the same signature.
### Running flows
To set the flow timeout use `set_flow_timeout` function. 30 seconds is the default value. 0 means exit immediately after the flow started. You can also reset timeout and set it to a default value of 30 seconds.
```
# Wait forever
grr_colab.set_no_flow_timeout()
# Exit immediately
grr_colab.set_flow_timeout(0)
# Wait for one minute
grr_colab.set_flow_timeout(60)
#Wait for 30 seconds
grr_colab.set_default_flow_timeout()
```
Below are examples of flows that you can run.
Interrogating a client:
```
summary = client.interrogate()
summary.system_info.system
```
Listing processes on a client:
```
ps = client.ps()
ps[:1]
ps[0]
ps[0].exe
```
Listing files in a directory. Here you need to provide the absolute path to the directory because there is no state.
```
files = client.ls('/tmp/foo/baz')
files
for f in files:
print(f.pathspec.path)
```
Recursive listing of a directory is also possible. To do this specify the max depth of the recursion.
```
files = client.ls('/tmp/foo', max_depth=3)
files
for f in files:
print(f.pathspec.path)
```
Globbing files:
```
files = client.glob('/tmp/foo/baz/file*')
files
```
Grepping files with regular expressions:
```
matches = client.grep(path='/tmp/foo/baz/file*', pattern=b'line')
matches
for match in matches:
print(match.pathspec.path, match.offset, match.data)
matches = client.grep(path='/tmp/foo/baz/file*', pattern=b'\x6c\x69\x6e\x65')
matches
```
Grepping files by exact match:
```
matches = client.fgrep(path='/tmp/foo/baz/file*', literal=b'line')
matches
```
Downloading files:
```
client.wget('/tmp/foo/baz/file1')
```
Osquerying a client:
```
table = client.osquery('SELECT pid, name, nice FROM processes WHERE pid < 5')
table
header = ' '.join(str(col.name).rjust(10) for col in table.header.columns)
print(header)
print('-' * len(header))
for row in table.rows:
print(' '.join(map(lambda _: _.rjust(10), row.values)))
```
Listing artifacts:
```
artifacts = grr_colab.list_artifacts()
artifacts[0]
```
To collect an artifact you just need to provide its name:
```
client.collect('DebianVersion')
```
Running YARA:
```
import os
pid = os.getpid()
data = "dadasdasdasdjaskdakdaskdakjdkjadkjakjjdsgkngksfkjadsjnfandankjd"
rule = 'rule TextExample {{ strings: $text_string = "{data}" condition: $text_string }}'.format(data=data)
matches = client.yara(rule, pids=[pid])
print(matches[0].process.pid, matches[0].process.name)
```
### Working with files
You can read and seek files interacting with them like fith usual python files.
```
with client.open('/tmp/foo/baz/file1') as f:
print(f.readline())
with client.open('/tmp/foo/baz/file1') as f:
for line in f:
print(line)
with client.open('/tmp/foo/baz/file1') as f:
print(f.read(22))
f.seek(0)
print(f.read(22))
print(f.read())
```
### Cached data
To fetch server cached data use `cached` property of a client object.
You can list files in directory (recursively also) and read and download files as above:
```
files = client.cached.ls('/tmp/foo/baz')
files
files = client.cached.ls('/tmp/foo/baz', max_depth=2)
files
with client.cached.open('/tmp/foo/baz/file1') as f:
for line in f:
print(line)
client.cached.wget('/tmp/foo/baz/file1')
```
You can also refresh filesystem metadata that is cached on the server by calling `refresh` method (that will refresh the contents of the directory and not its subdirectories):
```
client.cached.refresh('/tmp/foo/baz')
```
To refresh a directory recursively specify `max_depth` parameter:
```
client.cached.refresh('/tmp/foo/baz', max_depth=2)
### Path types
```
To specify path type, just use one of the client properties: `client.os` (the same as just using `client`), `client.tsk`, `client.ntfs`, `client.registry`.
```
client.os.ls('/tmp/foo')
client.os.cached.ls('/tmp/foo')
```
|
github_jupyter
|
%load_ext grr_colab.ipython_extension
import grr_colab
grr_colab.flags.FLAGS.set_default('grr_http_api_endpoint', 'http://localhost:8000/')
grr_colab.flags.FLAGS.set_default('grr_admin_ui_url', 'http://localhost:8000/')
grr_colab.flags.FLAGS.set_default('grr_auth_api_user', 'admin')
grr_colab.flags.FLAGS.set_default('grr_auth_password', 'admin')
df = %grr_search_clients -u admin
df[['online', 'online.pretty', 'client_id', 'last_seen_ago', 'last_seen_at.pretty']]
df = %grr_search_online_clients -u admin
df[['online', 'online.pretty', 'client_id', 'last_seen_ago', 'last_seen_at.pretty']]
df[['last_seen_at', 'last_seen_at.pretty']]
client_id = df['client_id'][0]
%grr_set_client -c {client_id}
%grr_id
%grr_request_approval -r "For testing" -a admin
%grr_pwd
%grr_cd tmp/foo/bar
%grr_pwd
%grr_cd ../baz
%grr_pwd
df = %grr_ls
df
df[['st_mode', 'st_mode.pretty']]
%grr_ls ../baz/dir2
%grr_ls /tmp/foo
%grr_stat file1
%grr_stat "file*"
%grr_head file1 -c 30
%grr_head file1 -c 30 -o 20
%grr_ls /tmp/foo/baz -C
%grr_head file1 -C
%grr_grep "line" file1
%grr_grep -F "line" file1
%grr_grep -X "6c696e65" file1
%grr_fgrep "line" "file*"
%grr_fgrep -X "6c696e65" file1
%grr_wget file1
%grr_wget file1 -C
%grr_ls -P os -C
%grr_hostname
ifaces = %grr_ifconfig
ifaces[['mac_address', 'mac_address.pretty']][1:]
ifaces['addresses'][1]
%grr_uname -m
%grr_uname -r
df = %grr_interrogate
df[['client_id', 'system_info.system', 'system_info.machine']]
ps = %grr_ps
ps[:5]
%grr_osqueryi "SELECT pid, name, cmdline, state, nice, threads FROM processes WHERE pid >= 440 and pid < 600;"
import os
pid = os.getpid()
data = "dadasdasdasdjaskdakdaskdakjdkjadkjakjjdsgkngksfkjadsjnfandankjd"
rule = 'rule TextExample {{ strings: $text_string = "{data}" condition: $text_string }}'.format(data=data)
df = %grr_yara '{rule}' -p {pid}
df[['process.pid', 'process.name', 'process.exe']]
%grr_set_flow_timeout 60
%grr_set_no_flow_timeout
%grr_set_default_flow_timeout
%grr_set_flow_timeout 0
df = %grr_list_artifacts
df[:2]
%grr_collect "DebianVersion"
clients = grr_colab.Client.search(user='admin')
clients
clients[0].id
client = grr_colab.Client.with_id('C.dc3782aeab2c5b4c')
client.id
client.hostname
client.ifaces[1:]
client.ifaces[1].ifname
for iface in client.ifaces:
print(iface.ifname)
client.knowledgebase
client.knowledgebase.os_release
client.arch
client.kernel
client.labels
client.first_seen
client.last_seen
client.request_approval(approvers=['admin'], reason='Test reason')
# Wait forever
grr_colab.set_no_flow_timeout()
# Exit immediately
grr_colab.set_flow_timeout(0)
# Wait for one minute
grr_colab.set_flow_timeout(60)
#Wait for 30 seconds
grr_colab.set_default_flow_timeout()
summary = client.interrogate()
summary.system_info.system
ps = client.ps()
ps[:1]
ps[0]
ps[0].exe
files = client.ls('/tmp/foo/baz')
files
for f in files:
print(f.pathspec.path)
files = client.ls('/tmp/foo', max_depth=3)
files
for f in files:
print(f.pathspec.path)
files = client.glob('/tmp/foo/baz/file*')
files
matches = client.grep(path='/tmp/foo/baz/file*', pattern=b'line')
matches
for match in matches:
print(match.pathspec.path, match.offset, match.data)
matches = client.grep(path='/tmp/foo/baz/file*', pattern=b'\x6c\x69\x6e\x65')
matches
matches = client.fgrep(path='/tmp/foo/baz/file*', literal=b'line')
matches
client.wget('/tmp/foo/baz/file1')
table = client.osquery('SELECT pid, name, nice FROM processes WHERE pid < 5')
table
header = ' '.join(str(col.name).rjust(10) for col in table.header.columns)
print(header)
print('-' * len(header))
for row in table.rows:
print(' '.join(map(lambda _: _.rjust(10), row.values)))
artifacts = grr_colab.list_artifacts()
artifacts[0]
client.collect('DebianVersion')
import os
pid = os.getpid()
data = "dadasdasdasdjaskdakdaskdakjdkjadkjakjjdsgkngksfkjadsjnfandankjd"
rule = 'rule TextExample {{ strings: $text_string = "{data}" condition: $text_string }}'.format(data=data)
matches = client.yara(rule, pids=[pid])
print(matches[0].process.pid, matches[0].process.name)
with client.open('/tmp/foo/baz/file1') as f:
print(f.readline())
with client.open('/tmp/foo/baz/file1') as f:
for line in f:
print(line)
with client.open('/tmp/foo/baz/file1') as f:
print(f.read(22))
f.seek(0)
print(f.read(22))
print(f.read())
files = client.cached.ls('/tmp/foo/baz')
files
files = client.cached.ls('/tmp/foo/baz', max_depth=2)
files
with client.cached.open('/tmp/foo/baz/file1') as f:
for line in f:
print(line)
client.cached.wget('/tmp/foo/baz/file1')
client.cached.refresh('/tmp/foo/baz')
client.cached.refresh('/tmp/foo/baz', max_depth=2)
### Path types
client.os.ls('/tmp/foo')
client.os.cached.ls('/tmp/foo')
| 0.182571 | 0.780788 |
```
#Author Jeffrey Tang
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import tensorflow as tf
from tensorflow import keras
import re
import random
import warnings
from time import time
from collections import defaultdict
import spacy
import logging
logging.basicConfig(format="%(levelname)s - %(asctime)s: %(message)s", datefmt= '%H:%M:%S', level=logging.INFO)
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.naive_bayes import MultinomialNB
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.tree import DecisionTreeClassifier
from xgboost import XGBClassifier
from sklearn.metrics import roc_auc_score, confusion_matrix, plot_confusion_matrix, plot_precision_recall_curve
warnings.simplefilter("ignore")
#Data Preprocessing
df = pd.read_csv('stack overflow data.csv')
df
df.info()
#df['Category']=pd.get_dummies(df['Y'])
df2 = pd.get_dummies(df['Y'])
df2
df['Y'] = df['Y'].map({'LQ_CLOSE':0, 'LQ_EDIT': 1, 'HQ':2})
sns.countplot(x='HQ',data=df2)
df['text'] = df['Title'] + ' ' + df['Body']
df = df.drop(['Id', 'Title', 'CreationDate'], axis = 1)
df
nlp = spacy.load('en', disable=['ner', 'parser'])
def cleaning(doc):
#remove stopwords + Lemmitze them
txt = [token.lemma_ for token in doc if not token.is_stop]
if len(txt)>2:
return ' '.join(txt)
init_cleaning = (re.sub("[^A-Za-z]+",' ',str(row)).lower() for row in df['text'])
t = time()
txt = [cleaning(doc) for doc in nlp.pipe(init_cleaning,batch_size=5000,n_threads=-1)]
print('Time too clean up everything: {} mins'.format(round((time() - t)/60,2)))
df_clean = pd.DataFrame({'clean':txt})
df_clean = df_clean.dropna().drop_duplicates()
df_clean.shape
from sklearn.model_selection import train_test_split
X=df['text'].values
y=df['Y'].values
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20, shuffle=True)
X_train
from sklearn.feature_extraction.text import TfidfVectorizer
#Vectorization
vectorizer = TfidfVectorizer()
X_train = vectorizer.fit_transform(X_train)
X_test = vectorizer.transform(X_test)
X_test
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Activation, Dropout
model = Sequential()
model.add(Dense(units=8270,activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(units=4000,activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(units=1000,activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(units=400,activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(units=1,activation='sigmoid'))
model.compile(loss='binary_crossentropy', optimizer='adam')
from tensorflow.keras.callbacks import EarlyStopping
early_stop = EarlyStopping(monitor='val_loss', mode='min', verbose=1, patience=10)
model.fit(x=X_train,y=y_train,epochs=40,validation_data=(X_test, y_test), verbose=1,callbacks=[early_stop])
```
|
github_jupyter
|
#Author Jeffrey Tang
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import tensorflow as tf
from tensorflow import keras
import re
import random
import warnings
from time import time
from collections import defaultdict
import spacy
import logging
logging.basicConfig(format="%(levelname)s - %(asctime)s: %(message)s", datefmt= '%H:%M:%S', level=logging.INFO)
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.naive_bayes import MultinomialNB
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.tree import DecisionTreeClassifier
from xgboost import XGBClassifier
from sklearn.metrics import roc_auc_score, confusion_matrix, plot_confusion_matrix, plot_precision_recall_curve
warnings.simplefilter("ignore")
#Data Preprocessing
df = pd.read_csv('stack overflow data.csv')
df
df.info()
#df['Category']=pd.get_dummies(df['Y'])
df2 = pd.get_dummies(df['Y'])
df2
df['Y'] = df['Y'].map({'LQ_CLOSE':0, 'LQ_EDIT': 1, 'HQ':2})
sns.countplot(x='HQ',data=df2)
df['text'] = df['Title'] + ' ' + df['Body']
df = df.drop(['Id', 'Title', 'CreationDate'], axis = 1)
df
nlp = spacy.load('en', disable=['ner', 'parser'])
def cleaning(doc):
#remove stopwords + Lemmitze them
txt = [token.lemma_ for token in doc if not token.is_stop]
if len(txt)>2:
return ' '.join(txt)
init_cleaning = (re.sub("[^A-Za-z]+",' ',str(row)).lower() for row in df['text'])
t = time()
txt = [cleaning(doc) for doc in nlp.pipe(init_cleaning,batch_size=5000,n_threads=-1)]
print('Time too clean up everything: {} mins'.format(round((time() - t)/60,2)))
df_clean = pd.DataFrame({'clean':txt})
df_clean = df_clean.dropna().drop_duplicates()
df_clean.shape
from sklearn.model_selection import train_test_split
X=df['text'].values
y=df['Y'].values
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20, shuffle=True)
X_train
from sklearn.feature_extraction.text import TfidfVectorizer
#Vectorization
vectorizer = TfidfVectorizer()
X_train = vectorizer.fit_transform(X_train)
X_test = vectorizer.transform(X_test)
X_test
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Activation, Dropout
model = Sequential()
model.add(Dense(units=8270,activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(units=4000,activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(units=1000,activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(units=400,activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(units=1,activation='sigmoid'))
model.compile(loss='binary_crossentropy', optimizer='adam')
from tensorflow.keras.callbacks import EarlyStopping
early_stop = EarlyStopping(monitor='val_loss', mode='min', verbose=1, patience=10)
model.fit(x=X_train,y=y_train,epochs=40,validation_data=(X_test, y_test), verbose=1,callbacks=[early_stop])
| 0.528533 | 0.260002 |
# Modely s optimalizáciou hyperparametrov
```
import pandas as pd
import nltk
from nltk.corpus import stopwords
from sklearn import tree
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn import metrics
from sklearn.tree import export_graphviz
from graphviz import Source
from IPython.display import Image
import seaborn as sns
from sklearn.model_selection import GridSearchCV
from sklearn.pipeline import Pipeline
import matplotlib.pyplot as plt
data = "finalne_data.csv"
df_final = pd.read_csv(data)
df_final.dropna(inplace = True)
df_final.info()
# Funkcia pre zrealizovanie GridSearch
def gridsearch(vectorizer, X_train, Y_train, X_test, Y_test):
pipeline = Pipeline([
('vect', vectorizer),
('clf', DecisionTreeClassifier()),
])
scoring = ['accuracy', 'precision_macro']
param_dict = {
"vect__max_features":range(10,200,20),
"clf__criterion":['gini', 'entropy'],
}
# Funkcia GridSearchCV
grid_search = GridSearchCV(pipeline, param_dict, cv=10, scoring=scoring, n_jobs=-1, verbose=1, refit='accuracy')
grid_search.fit(X_train, Y_train)
pred = grid_search.predict(X_test)
df_results = pd.concat([pd.DataFrame(grid_search.cv_results_["params"]),pd.DataFrame(grid_search.cv_results_["mean_test_accuracy"], columns=["Accuracy"])], axis=1)
display(df_results)
vectorizer = grid_search.best_estimator_.named_steps["vect"]
clf = grid_search.best_estimator_.named_steps["clf"]
features = vectorizer.get_feature_names()
feature_importances = clf.feature_importances_
data = {'feature':features, 'feature_importance':feature_importances}
df_features = pd.DataFrame(data)
df_features = df_features.sort_values('feature_importance', ascending = False).reset_index(drop = True)
display(df_features[:20])
fig = plt.figure(figsize =(16, 8))
plt.bar(df_features['feature'][:10], df_features['feature_importance'][:10])
plt.xlabel("Features")
plt.ylabel("Feature importance")
plt.show()
# Najlepšie výsledky
print(grid_search.best_params_)
print("Best score: %f" % grid_search.best_score_)
print("Accuracy: %f" % metrics.accuracy_score(Y_test, pred))
print("Precision: %f" % metrics.precision_score(Y_test, pred, average="macro"))
print("Recall: %f\n" % metrics.recall_score(Y_test, pred, average="macro"))
```
# CountVectorizer
```
def grid_count_vect(data, stopword):
if stopword == 1:
vectorizer = CountVectorizer(stop_words=stopwords.words('english'))
elif stopword == 0:
vectorizer = CountVectorizer()
X = data
y = df_final.label
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=1)
gridsearch(vectorizer, X_train, y_train, X_test, y_test)
```
## Title
```
grid_count_vect(df_final.title, 1)
grid_count_vect(df_final.title_stem, 0)
grid_count_vect(df_final.title_lemm, 0)
grid_count_vect(df_final.title_hypernym, 0)
```
## Text
```
grid_count_vect(df_final.text, 1)
grid_count_vect(df_final.text_stem, 0)
grid_count_vect(df_final.text_lemm, 0)
grid_count_vect(df_final.text_hypernym, 0)
```
## Title + Text
```
grid_count_vect(df_final.title_text, 1)
grid_count_vect(df_final.title_text_stem, 0)
grid_count_vect(df_final.title_text_lemm, 0)
grid_count_vect(df_final.title_text_hypernym, 0)
```
# TfidfVectorizer
```
def grid_tfidf_vect(data, stopword):
if stopword == 1:
vectorizer = TfidfVectorizer(stop_words=stopwords.words('english'))
elif stopword == 0:
vectorizer = TfidfVectorizer()
X = data
y = df_final.label
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=1)
gridsearch(vectorizer, X_train, y_train, X_test, y_test)
```
## Title
```
grid_tfidf_vect(df_final.title, 1)
grid_tfidf_vect(df_final.title_stem, 0)
grid_tfidf_vect(df_final.title_lemm, 0)
grid_tfidf_vect(df_final.title_hypernym, 0)
```
## Text
```
grid_tfidf_vect(df_final.text, 1)
grid_tfidf_vect(df_final.text_stem, 0)
grid_tfidf_vect(df_final.text_lemm, 0)
grid_tfidf_vect(df_final.text_hypernym, 0)
```
## Title + Text
```
grid_tfidf_vect(df_final.title_text, 1)
grid_tfidf_vect(df_final.title_text_stem, 0)
grid_tfidf_vect(df_final.title_text_lemm, 0)
grid_tfidf_vect(df_final.title_text_hypernym, 0)
```
|
github_jupyter
|
import pandas as pd
import nltk
from nltk.corpus import stopwords
from sklearn import tree
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn import metrics
from sklearn.tree import export_graphviz
from graphviz import Source
from IPython.display import Image
import seaborn as sns
from sklearn.model_selection import GridSearchCV
from sklearn.pipeline import Pipeline
import matplotlib.pyplot as plt
data = "finalne_data.csv"
df_final = pd.read_csv(data)
df_final.dropna(inplace = True)
df_final.info()
# Funkcia pre zrealizovanie GridSearch
def gridsearch(vectorizer, X_train, Y_train, X_test, Y_test):
pipeline = Pipeline([
('vect', vectorizer),
('clf', DecisionTreeClassifier()),
])
scoring = ['accuracy', 'precision_macro']
param_dict = {
"vect__max_features":range(10,200,20),
"clf__criterion":['gini', 'entropy'],
}
# Funkcia GridSearchCV
grid_search = GridSearchCV(pipeline, param_dict, cv=10, scoring=scoring, n_jobs=-1, verbose=1, refit='accuracy')
grid_search.fit(X_train, Y_train)
pred = grid_search.predict(X_test)
df_results = pd.concat([pd.DataFrame(grid_search.cv_results_["params"]),pd.DataFrame(grid_search.cv_results_["mean_test_accuracy"], columns=["Accuracy"])], axis=1)
display(df_results)
vectorizer = grid_search.best_estimator_.named_steps["vect"]
clf = grid_search.best_estimator_.named_steps["clf"]
features = vectorizer.get_feature_names()
feature_importances = clf.feature_importances_
data = {'feature':features, 'feature_importance':feature_importances}
df_features = pd.DataFrame(data)
df_features = df_features.sort_values('feature_importance', ascending = False).reset_index(drop = True)
display(df_features[:20])
fig = plt.figure(figsize =(16, 8))
plt.bar(df_features['feature'][:10], df_features['feature_importance'][:10])
plt.xlabel("Features")
plt.ylabel("Feature importance")
plt.show()
# Najlepšie výsledky
print(grid_search.best_params_)
print("Best score: %f" % grid_search.best_score_)
print("Accuracy: %f" % metrics.accuracy_score(Y_test, pred))
print("Precision: %f" % metrics.precision_score(Y_test, pred, average="macro"))
print("Recall: %f\n" % metrics.recall_score(Y_test, pred, average="macro"))
def grid_count_vect(data, stopword):
if stopword == 1:
vectorizer = CountVectorizer(stop_words=stopwords.words('english'))
elif stopword == 0:
vectorizer = CountVectorizer()
X = data
y = df_final.label
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=1)
gridsearch(vectorizer, X_train, y_train, X_test, y_test)
grid_count_vect(df_final.title, 1)
grid_count_vect(df_final.title_stem, 0)
grid_count_vect(df_final.title_lemm, 0)
grid_count_vect(df_final.title_hypernym, 0)
grid_count_vect(df_final.text, 1)
grid_count_vect(df_final.text_stem, 0)
grid_count_vect(df_final.text_lemm, 0)
grid_count_vect(df_final.text_hypernym, 0)
grid_count_vect(df_final.title_text, 1)
grid_count_vect(df_final.title_text_stem, 0)
grid_count_vect(df_final.title_text_lemm, 0)
grid_count_vect(df_final.title_text_hypernym, 0)
def grid_tfidf_vect(data, stopword):
if stopword == 1:
vectorizer = TfidfVectorizer(stop_words=stopwords.words('english'))
elif stopword == 0:
vectorizer = TfidfVectorizer()
X = data
y = df_final.label
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=1)
gridsearch(vectorizer, X_train, y_train, X_test, y_test)
grid_tfidf_vect(df_final.title, 1)
grid_tfidf_vect(df_final.title_stem, 0)
grid_tfidf_vect(df_final.title_lemm, 0)
grid_tfidf_vect(df_final.title_hypernym, 0)
grid_tfidf_vect(df_final.text, 1)
grid_tfidf_vect(df_final.text_stem, 0)
grid_tfidf_vect(df_final.text_lemm, 0)
grid_tfidf_vect(df_final.text_hypernym, 0)
grid_tfidf_vect(df_final.title_text, 1)
grid_tfidf_vect(df_final.title_text_stem, 0)
grid_tfidf_vect(df_final.title_text_lemm, 0)
grid_tfidf_vect(df_final.title_text_hypernym, 0)
| 0.558327 | 0.656452 |
<h1><center>K-Means: A macroscopic investigation using Python</center></h1>
In Machine Learning, the types of <b>Learning</b> can broadly be classified into three types: <b>1. Supervised Learning, 2. Unsupervised Learning and 3. Semi-supervised Learning</b>. Algorithms belonging to the family of <b>Unsupervised Learning</b> have no variable to predict tied to the data. Instead of having an output, the data only has an input which would be multiple variables that describe the data. This is where clustering comes in.
Clustering is the task of grouping together a set of objects in a way that objects in the same cluster are more similar to each other than to objects in other clusters. Similarity is an amount that reflects the strength of relationship between two data objects. Clustering is mainly used for exploratory data mining. Clustering has manifold usage in many fields such as machine learning, pattern recognition, image analysis, information retrieval, bio-informatics, data compression, and computer graphics.
However, this post tries to unravel the inner workings of K-Means, a very popular clustering technique. There's also a very good DataCamp post on K-Means which explains the types of clustering (hard and soft clustering), types of clustering methods (connectivity, centroid, distribution and density) with a case study. K-Means will help you to tackle unlabeled datasets (i.e. the datasets that do not have any class-labels) and draw your own inferences from them with ease.
K-Means falls under the category of centroid-based clustering. A centroid is a data point (imaginary or real) at the center of a cluster. In centroid-based clustering, clusters are represented by a central vector or a centroid. This centroid might not necessarily be a member of the dataset. Centroid-baes clustering is an iterative clustering algorithm in which the notion of similarity is derived by how close a data point is to the centroid of the cluster.
<h2>In this post you will get to know about:</h2>
* The inner workings of K-Means algorithm
* A simple case study of K-Means in Python
* Disadvantages of K-Means
* Further readings on K-Means
So, let's dissect the operations of K-Means.
<h3>The inner workings of K-Means algorithm:</h3>
To do this, you will need a sample dataset (training set):
<center><table border = "1">
<tr>
<th>Objects</th>
<th>X</th>
<th>Y</th>
<th>Z</th>
</tr>
<tr>
<td>OB-1</td>
<td>1</td>
<td>4</td>
<td>1</td>
</tr>
<tr>
<td>OB-2</td>
<td>1</td>
<td>2</td>
<td>2</td>
</tr>
<tr>
<td>OB-3</td>
<td>1</td>
<td>4</td>
<td>2</td>
</tr>
<tr>
<td>OB-4</td>
<td>2</td>
<td>1</td>
<td>2</td>
</tr>
<tr>
<td>OB-5</td>
<td>1</td>
<td>1</td>
<td>1</td>
</tr>
<tr>
<td>OB-6</td>
<td>2</td>
<td>4</td>
<td>2</td>
</tr>
<tr>
<td>OB-7</td>
<td>1</td>
<td>1</td>
<td>2</td>
</tr>
<tr>
<td>OB-8</td>
<td>2</td>
<td>1</td>
<td>1</td>
</tr>
</table></center>
The sample dataset contains 8 objects with their X, Y and Z coordinates. Your task is to cluster these objects into two clusters (here you define the value of K (of K-Means) i.e. to be 2).
So, the algorithm works by:
<ul>
<li>Taking any two centroids (as you took 2 as K hence the number of centroids also 2) in its account initially. </li>
<li>After choosing the centroids, (say C1 and C2) the data points (coordinates here) are assigned to any of the Clusters (let’s take centroids = clusters for the time being) depending upon the distance between them and the centroids. </li>
<li>Assume that the algorithm chose OB-2 (1,2,2) and OB-6 (2,4,2) as centroids and cluster 1 and cluster 2 as well. </li>
<li>For measuring the distances, you take the following distance measurement function (also termed as similarity measurement function):</li>
</ul>
<b>$d = |x2 – x1| + | y2 – y1| + |z2 – z1|$ </b> (This is also known as <b>Taxicab distance</b> or <b>Manhattan distance</b>), where d is distance measurement between two objects, (x1,y1,z1) and (x2,y2,z2) are the X, Y and Z coordinates of any two objects taken for distance measurement. <br><br>
Feel free to check out other distance measurement functions like [Euclidean Distance, Cosine Distance](https:///arxiv.org/ftp/arxiv/papers/1405/1405.7471.pdf) etc. <br><br>
The following table shows the calculation of distances (using the above distance measurement function) between the objects and centroids (OB-2 and OB-6): <br><br>
<center><table border = "1">
<tr>
<th>Objects</th>
<th>X</th>
<th>Y</th>
<th>Z</th>
<th>Distance from C1(1,2,2)</th>
<th>Distance from C2(2,4,2)</th>
</tr>
<tr>
<td>OB-1</td>
<td>1</td>
<td>4</td>
<td>1</td>
<td>3</td>
<td>2</td>
</tr>
<tr>
<td>OB-2</td>
<td>1</td>
<td>2</td>
<td>2</td>
<td>0</td>
<td>3</td>
</tr>
<tr>
<td>OB-3</td>
<td>1</td>
<td>4</td>
<td>2</td>
<td>2</td>
<td>1</td>
</tr>
<tr>
<td>OB-4</td>
<td>2</td>
<td>1</td>
<td>2</td>
<td>2</td>
<td>3</td>
</tr>
<tr>
<td>OB-5</td>
<td>1</td>
<td>1</td>
<td>1</td>
<td>2</td>
<td>5</td>
</tr>
<tr>
<td>OB-6</td>
<td>2</td>
<td>4</td>
<td>2</td>
<td>3</td>
<td>0</td>
</tr>
<tr>
<td>OB-7</td>
<td>1</td>
<td>1</td>
<td>2</td>
<td>1</td>
<td>4</td>
</tr>
<tr>
<td>OB-8</td>
<td>2</td>
<td>1</td>
<td>1</td>
<td>3</td>
<td>4</td>
</tr>
</table></center>
<ul>
<li>The objects are clustered based on their distances between the centroids. An object which has a shorter distance between a centroid (say C1) than the other centroid (say C2) will fall into the cluster of C1. After the initial pass of clustering, the clustered objects will look something like the following: </li></ul><br><br>
<center><table border = "1">
<tr><th>Cluster 1</th>
</tr>
<tr>
<td>OB-2</td>
</tr>
<tr>
<td>OB-4</td>
</tr>
<tr>
<td>OB-5</td>
</tr>
<tr>
<td>OB-7</td>
</tr>
<tr>
<td>OB-8</td>
</tr>
</table><br>
<table border = "1">
<tr><th>Cluster 2</th>
</tr>
<tr>
<td>OB-1</td>
</tr>
<tr>
<td>OB-3</td>
</tr>
<tr>
<td>OB-6</td>
</tr>
</table></center>
<br><br>
<ul><li>
Now the algorithm will continue updating cluster centroids (i.e the coordinates) until they cannot be updated anymore (more on when it cannot be updated later). The updation takes place in the following manner: </li></ul>
<center>(($\sum_{i=1}^n xi$)/n , ($\sum_{i=1}^n yi$)/n , ($\sum_{i=1}^n zi$)/n) (where n = number of objects belonging to that particular cluster) </center><br>
So, following this rule the updated cluster 1 will be ((1+2+1+1+2)/5, (2+1+1+1+1)/5,(2+2+1+2+1)/5) = (1.4,1.2,1.6). And for cluster 2 it will be ((1+1+2)/3, (4+4+4)/3, (1+2+2)/3) = (1.33, 4, 1.66).
After this, the algorithm again starts finding the distances between the data points and newly derived cluster centroids. So the new distances will be like following: <br>
<center><table border = "1">
<tr>
<th>Objects</th>
<th>X</th>
<th>Y</th>
<th>Z</th>
<th>Distance from C1(1.4,1.2,1.6)</th>
<th>Distance from C2(1.33, 4, 1.66)</th>
</tr>
<tr>
<td>OB-1</td>
<td>1</td>
<td>4</td>
<td>1</td>
<td>3.8</td>
<td>1</td>
</tr>
<tr>
<td>OB-2</td>
<td>1</td>
<td>2</td>
<td>2</td>
<td>1.6</td>
<td>2.66</td>
</tr>
<tr>
<td>OB-3</td>
<td>1</td>
<td>4</td>
<td>2</td>
<td>3.6</td>
<td>0.66</td>
</tr>
<tr>
<td>OB-4</td>
<td>2</td>
<td>1</td>
<td>2</td>
<td>1.2</td>
<td>4</td>
</tr>
<tr>
<td>OB-5</td>
<td>1</td>
<td>1</td>
<td>1</td>
<td>1.2</td>
<td>4</td>
</tr>
<tr>
<td>OB-6</td>
<td>2</td>
<td>4</td>
<td>2</td>
<td>3.8</td>
<td>1</td>
</tr>
<tr>
<td>OB-7</td>
<td>1</td>
<td>1</td>
<td>2</td>
<td>1</td>
<td>3.66</td>
</tr>
<tr>
<td>OB-8</td>
<td>2</td>
<td>1</td>
<td>1</td>
<td>1.4</td>
<td>4.33</td>
</tr>
</table></center>
<br>The new assignments of the objects with respect to the updated clusters will be:
<br><br>
<center><table border = "1">
<tr><th>Cluster 1</th>
</tr>
<tr>
<td>OB-2</td>
</tr>
<tr>
<td>OB-4</td>
</tr>
<tr>
<td>OB-5</td>
</tr>
<tr>
<td>OB-7</td>
</tr>
<tr>
<td>OB-8</td>
</tr>
</table><br>
<table border = "1">
<tr><th>Cluster 2</th>
</tr>
<tr>
<td>OB-1</td>
</tr>
<tr>
<td>OB-3</td>
</tr>
<tr>
<td>OB-6</td>
</tr>
</table></center>
<br>
This is where the algorithm and no more updates the centroids. Because there is no change in the current cluster formation, it is the same as the previous formation.
Now when, you are done with the cluster formation with K-Means you may apply it to some data the algorithm has not seen before (what you call a Test set). Let's generate that:
<br><br>
<center><table border = "1">
<tr>
<th>Objects</th>
<th>X</th>
<th>Y</th>
<th>Z</th>
</tr>
<tr>
<td>OB-1</td>
<td>2</td>
<td>4</td>
<td>1</td>
</tr>
<tr>
<td>OB-2</td>
<td>2</td>
<td>2</td>
<td>2</td>
</tr>
<tr>
<td>OB-3</td>
<td>1</td>
<td>2</td>
<td>1</td>
</tr>
<tr>
<td>OB-4</td>
<td>2</td>
<td>2</td>
<td>1</td>
</tr>
</table></center>
<br>
After applying K-means on the above dataset, the final clusters will be:
<center>
<table border = "1">
<tr><th>Cluster 1</th>
</tr>
<tr>
<td>OB-2</td>
</tr>
<tr>
<td>OB-3</td>
</tr>
<tr>
<td>OB-4</td>
</tr>
</table> <br>
<table border = "1">
<tr><th>Cluster 2</th>
</tr>
<tr>
<td>OB-1</td>
</tr>
</table></center> <br>
Any application of an algorithm is incomplete if one is not sure about its performance. Now, in order to know how well the K-Means algorithm is performing there are certain metrics to consider. Some of these metrics are:
<ul>
<li>Adjusted rand index</li>
<li>Mutual information based scoring</li>
<li>Homogeneity, completeness and v-measure</li>
</ul>
Now that you have got familiar with the inner mechanics of K-Means let's see K-Means live in action.
<h3>A simple case study of K-Means in Python:</h3>
For the implementation part you will be using Titanic dataset (available [here](https://www.kaggle.com/c/titanic)). Before proceeding with it, I would like to discuss some facts about the data itself. The sinking of the RMS Titanic is one of the most infamous shipwrecks in history. On April 15, 1912, during her maiden voyage, the Titanic sank after colliding with an iceberg, killing 1502 out of 2224 passengers and crew. This sensational tragedy shocked the international community and led to better safety regulations for ships.
One of the reasons that the shipwreck led to such loss of life was that there were not enough lifeboats for the passengers and crew. Although there was some element of luck involved in surviving the sinking, some groups of people were more likely to survive than others, such as women, children, and the upper-class.
Now talking about the dataset, the training set contains several records about the passengers of Titanic (hence the name of the dataset). It has 12 features capturing information about passernger_class, port_of_Embarkation, passenger_fare etc. The dataset's label is <b>survival</b> which denotes the survivial status of a particular passenger. Your task is to cluster the records into two i.e. the ones who survived and the ones who did not.
You might be thinking it is a labelled dataset, how can it be used for a clustering task. Ofcourse, it can be used! You just have to drop the 'survival' column from the dataset and make it unlabelled. It's the task of K-Means to cluster the records of the datasets if they survived or not.
```
# Dependencies
import pandas as pd
import numpy as np
from sklearn.cluster import KMeans
from sklearn.preprocessing import LabelEncoder
from sklearn.preprocessing import MinMaxScaler
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
```
You have imported all the dependencies that you will need in the course. Now, you will load the dataset.
```
# Load the train and test datasets to create two DataFrames
train_url = "http://s3.amazonaws.com/assets.datacamp.com/course/Kaggle/train.csv"
train = pd.read_csv(train_url)
test_url = "http://s3.amazonaws.com/assets.datacamp.com/course/Kaggle/test.csv"
test = pd.read_csv(test_url)
```
Let's preview the kind of data you will be working with.
```
# Print some samples from both the train and test DataFrames
print("***** Train_Set *****")
print(train.head())
print("\n")
print("***** Test_Set *****")
print(test.head())
# Get some initial statistics of both the train and test DataFrames using pandas describe() method
print("***** Train_Set *****")
print(train.describe())
print("\n")
print("***** Test_Set *****")
print(test.describe())
```
So, from the above outputs you definitely got to know about the features of the dataset and some basic statistics of it. I will list the feature names for you:
```
print(train.columns.values)
```
It is very important to note that not all machine learning algorithms support missing values in the data that you are feeding to them. K-Means being one of them. So we need to handle the missing values present in the data. Let's first see where are the values missing:
```
# For the train set
train.isna().head()
# For the test set
test.isna().head()
```
Let's get the total number of missing values in both of the datasets.
```
# Let's see the number of total missing values
print("*****In the train set*****")
print(train.isna().sum())
print("\n")
print("*****In the test set*****")
print(test.isna().sum())
```
So, you can see in the train set in the columns Age, Cabin and Embarked there are missing values and in the test set Age and Cabin columns contain missing values.
There are a couple of ways to handle missing values:
- Remove rows with missing values
- Impute missing values
I prefer the latter one because if you remove the rows with missing values it can cause insufficiency in the data which in turn results in inefficient training of the machine learning model.
Now, there are several ways you can perform the imputation:
- A constant value that has meaning within the domain, such as 0, distinct from all other values.
- A value from another randomly selected record.
- A mean, median or mode value for the column.
- A value estimated by another machine learning model.
Any imputation performed on the train set will have to be performed on test data in the future when predictions are needed from the final machine learning model. This needs to be taken into consideration when choosing how to impute the missing values.
Pandas provides the fillna() function for replacing missing values with a specific value. Let's apply that with <b>Mean Imputation</b>.
```
# Fill missing values with mean column values in the train set
train.fillna(train.mean(), inplace=True)
# Fill missing values with mean column values in the test set
test.fillna(test.mean(), inplace=True)
```
Now that you have imputed the missing values in the dataset, it's time to see if the dataset still has any missing values.
```
# Let's see if you have any missing value now in the train set
print(train.isna().sum())
# Let's see if you have any missing value now in the test set
print(test.isna().sum())
```
Yes, you can see there are still some missing values in Cabin and Embarked columns. It happened because the values are non-numeric there. In order to perform the imputation the values need to be in numeric form. There are ways to convert a non-numeric value to a numeric one. More on this later.
Let's do some more analytics in order to understand the data better. Understanding is really required in order to perform any Machine Learning task. Let's start with finding out which features are categorical and which are numerical.
- Categorical: Survived, Sex, and Embarked. Ordinal: Pclass.
- Continuous: Age, Fare. Discrete: SibSp, Parch.
Two features are left out which are not listed above in any of the categories. Yes, you guessed it right, <b>Ticket</b> and <b>Cabin</b>. Ticket is a mix of numeric and alphanumeric data types. Cabin is alphanumeric. Let see some sample values.
```
train['Ticket'].head()
train['Cabin'].head()
```
Let's see the survival count of passengers with respect to the following features:
- Pclass
- Sex
- SibSp
- Parch
Let's do that one by one:
```
# Survival count w.r.t Pclass
train[['Pclass', 'Survived']].groupby(['Pclass'], as_index=False).mean().sort_values(by='Survived', ascending=False)
# Survival count w.r.t Sex
train[["Sex", "Survived"]].groupby(['Sex'], as_index=False).mean().sort_values(by='Survived', ascending=False)
```
<h4>You can see the survival count of female passengers is significantly higher than male ones.</h4>
```
# Survival count w.r.t SibSp
train[["SibSp", "Survived"]].groupby(['SibSp'], as_index=False).mean().sort_values(by='Survived', ascending=False)
```
Now its time for some quick plotting. Let's first plot the graph of "Age vs. Survived":
```
g = sns.FacetGrid(train, col='Survived')
g.map(plt.hist, 'Age', bins=20)
```
Its time to see how Pclass and Survived features are related each with a graph:
```
grid = sns.FacetGrid(train, col='Survived', row='Pclass', size=2.2, aspect=1.6)
grid.map(plt.hist, 'Age', alpha=.5, bins=20)
grid.add_legend();
```
Enough of visualization and analytics for now! Now let's actually build K-Means model with the train set. But before that you will need some data preprocessing also. You can see all the feature values are not of same type. Some of them are numerical and some of them are not. In order to ease the computation, you will feed all numerical data to the model. Let's see the data types of different features that you have:
```
train.info()
```
So, you can see that the following features are non-numeric:
- Name
- Sex
- Ticket
- Cabin
- Embarked
Before converting them into numeric ones, you might want to do some feature engineering, i.e. features like Name, Ticket, Cabin and Embarked do not have any impact on the survival status of the passengers. Often, it is better to train your model with only significant features than to train it all the features including unnecessary ones. It not only helps in efficient modelling, but also the training of the model can happen in much lesser time. Although, feature engineering is a whole field of study itself, I will encourage you to dig it further. But for this tutorial, know that the features Name, Ticket, Cabin and Embarked can be dropped and they will not have significant impact on the training of the K-Means model.
```
train = train.drop(['Name','Ticket', 'Cabin','Embarked'], axis=1)
test = test.drop(['Name','Ticket', 'Cabin','Embarked'], axis=1)
```
Now that the dropping part is done let's convert the 'Sex' feature to a numerical one (only 'Sex' is remaining now which is a non-numeric feature). You will do this using a technique called [Label Encoding](http://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.LabelEncoder.html).
```
labelEncoder = LabelEncoder()
labelEncoder.fit(train['Sex'])
labelEncoder.fit(test['Sex'])
train['Sex'] = labelEncoder.transform(train['Sex'])
test['Sex'] = labelEncoder.transform(test['Sex'])
# Let's investigate if you have non-numeric data anymore
train.info()
test.info()
# Note that the test set does not have Survived feature
```
<h3>Brilliant!</h3>
Looks like you are good to go to train your K-Means model now.
```
# Let's first drop the Survival column from the data
X = np.array(train.drop(['Survived'], 1).astype(float))
y = np.array(train['Survived'])
# Let's finally review what all features you are going to feed to K-Means
train.info()
# Let's build the K-Means model now
kmeans = KMeans(n_clusters=2) # You want cluster the passenger records into 2: Survived or Not survived
kmeans.fit(X)
```
You can see all the other parameters of the model other than <b>n_clusters</b> also.
```
# Let's see how well the model is doing i.e. what is its percentage of clustering the passenger records correctly
correct = 0
for i in range(len(X)):
predict_me = np.array(X[i].astype(float))
predict_me = predict_me.reshape(-1, len(predict_me))
prediction = kmeans.predict(predict_me)
if prediction[0] == y[i]:
correct += 1
print(correct/len(X))
```
That is nice for the first go. Your model was able to cluster correctly with a 50% (accuracy of your model). But in order to enhance the performance of the model you could tweak some parameters of the model itself. I will list some of these parameters which the scikit-learn implementation of K-Means provides:
- algorithm
- max_iter
- n_jobs
<br><br>
Let's tweak the values of these parameters and see if there is a change in the result.
In the [scikit-learn documentation](http://scikit-learn.org/stable/modules/generated/sklearn.cluster.KMeans.html), you will find a solid information about these parameters which you should dig further.
```
kmeans = kmeans = KMeans(n_clusters=2, max_iter=600, algorithm = 'auto')
kmeans.fit(X)
correct = 0
for i in range(len(X)):
predict_me = np.array(X[i].astype(float))
predict_me = predict_me.reshape(-1, len(predict_me))
prediction = kmeans.predict(predict_me)
if prediction[0] == y[i]:
correct += 1
print(correct/len(X))
```
You can see a decrease in the score. One of the reasons being you have not scaled the values of the different features that you are feeding to the model. The features in the dataset contain different ranges of values. So, what happens is a small change in a feature does not affect the other feature. So, it is also important to scale the values of the features to a same range.
Let's do that now and for this experiment you are going to take 0 - 1 as the uniform value range across all the features.
```
scaler = MinMaxScaler()
X_scaled = scaler.fit_transform(X)
kmeans.fit(X_scaled)
correct = 0
for i in range(len(X)):
predict_me = np.array(X[i].astype(float))
predict_me = predict_me.reshape(-1, len(predict_me))
prediction = kmeans.predict(predict_me)
if prediction[0] == y[i]:
correct += 1
print(correct/len(X))
```
Great! You can see an instant 12% increase in the score.
So far you were able to load your data, preprocess it accordingly, do a little bit of feature engineering and finally you were able to make a K-Means model and see it in action.
Now, let's discuss K-Means's limitations.
<h3>Disadvantages of K-Means:</h3>
Now that you have a fairly good idea on how K-Means algorithm works let's discuss some its disadvantages.
The biggest disadvantage is that K-Means requires you to pre-specify the number of clusters (k). However, for the Titanic dataset, you had some domain knowledge available that told you the number of people who survived in the shipwreck. This might not always be the case with real world datasets. Hierarchical clustering is an alternative approach that does not require a particular choice of clusters. An additional disadvantage of k-means is that it is sensitive to outliers and different results can occur if you change the ordering of the data.
K-Means is a lazy learner where generalization of the training data is delayed until a query is made to the system. Which means K-Means starts working only when you trigger it to, thus lazy learning methods can construct a different approximation or result to the target function for each encountered query. It is a good method for online learning, but it requires a possibly large amount of memory to store the data, and each request involves starting the identification of a local model from scratch.
<h3>Further readings on K-Means:</h3>
So, in this tutorial you scratched the surface of one of the most popular clustering techniques - K-Means. You learnt its inner mechanics, you implemented it using the Titanic Dataset in Python. You also got a fair idea of its disadvantages. Following are some points which I would like to leave for you to investigate further on K-Means:
* Apply K-Means on a real-life dataset and share your findings. You will find many real life datasets in UCI machine learning repository, Kaggle etc. The datasets may require a lot of Data preprocessing which is another field of study itself.
* After applying K-Means measure its performance with the metrics that I mentioned in the reference.
* Apply different distance measurement functions mentioned above and examine how the results are getting changed. It will help you to choose the right set of parameters for K-Means algorithm for the given task.
* Investigate on how to choose the right value of 'K'. There is no direct method for choosing K's value. However, there are a number of articles on the internet which will tell you what to do about it. My favorite among them is [this one](https://www.datascience.com/blog/k-means-clustering).
* Finally study some beautiful business applications of K-Means including research papers that use K-Means.
|
github_jupyter
|
# Dependencies
import pandas as pd
import numpy as np
from sklearn.cluster import KMeans
from sklearn.preprocessing import LabelEncoder
from sklearn.preprocessing import MinMaxScaler
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
# Load the train and test datasets to create two DataFrames
train_url = "http://s3.amazonaws.com/assets.datacamp.com/course/Kaggle/train.csv"
train = pd.read_csv(train_url)
test_url = "http://s3.amazonaws.com/assets.datacamp.com/course/Kaggle/test.csv"
test = pd.read_csv(test_url)
# Print some samples from both the train and test DataFrames
print("***** Train_Set *****")
print(train.head())
print("\n")
print("***** Test_Set *****")
print(test.head())
# Get some initial statistics of both the train and test DataFrames using pandas describe() method
print("***** Train_Set *****")
print(train.describe())
print("\n")
print("***** Test_Set *****")
print(test.describe())
print(train.columns.values)
# For the train set
train.isna().head()
# For the test set
test.isna().head()
# Let's see the number of total missing values
print("*****In the train set*****")
print(train.isna().sum())
print("\n")
print("*****In the test set*****")
print(test.isna().sum())
# Fill missing values with mean column values in the train set
train.fillna(train.mean(), inplace=True)
# Fill missing values with mean column values in the test set
test.fillna(test.mean(), inplace=True)
# Let's see if you have any missing value now in the train set
print(train.isna().sum())
# Let's see if you have any missing value now in the test set
print(test.isna().sum())
train['Ticket'].head()
train['Cabin'].head()
# Survival count w.r.t Pclass
train[['Pclass', 'Survived']].groupby(['Pclass'], as_index=False).mean().sort_values(by='Survived', ascending=False)
# Survival count w.r.t Sex
train[["Sex", "Survived"]].groupby(['Sex'], as_index=False).mean().sort_values(by='Survived', ascending=False)
# Survival count w.r.t SibSp
train[["SibSp", "Survived"]].groupby(['SibSp'], as_index=False).mean().sort_values(by='Survived', ascending=False)
g = sns.FacetGrid(train, col='Survived')
g.map(plt.hist, 'Age', bins=20)
grid = sns.FacetGrid(train, col='Survived', row='Pclass', size=2.2, aspect=1.6)
grid.map(plt.hist, 'Age', alpha=.5, bins=20)
grid.add_legend();
train.info()
train = train.drop(['Name','Ticket', 'Cabin','Embarked'], axis=1)
test = test.drop(['Name','Ticket', 'Cabin','Embarked'], axis=1)
labelEncoder = LabelEncoder()
labelEncoder.fit(train['Sex'])
labelEncoder.fit(test['Sex'])
train['Sex'] = labelEncoder.transform(train['Sex'])
test['Sex'] = labelEncoder.transform(test['Sex'])
# Let's investigate if you have non-numeric data anymore
train.info()
test.info()
# Note that the test set does not have Survived feature
# Let's first drop the Survival column from the data
X = np.array(train.drop(['Survived'], 1).astype(float))
y = np.array(train['Survived'])
# Let's finally review what all features you are going to feed to K-Means
train.info()
# Let's build the K-Means model now
kmeans = KMeans(n_clusters=2) # You want cluster the passenger records into 2: Survived or Not survived
kmeans.fit(X)
# Let's see how well the model is doing i.e. what is its percentage of clustering the passenger records correctly
correct = 0
for i in range(len(X)):
predict_me = np.array(X[i].astype(float))
predict_me = predict_me.reshape(-1, len(predict_me))
prediction = kmeans.predict(predict_me)
if prediction[0] == y[i]:
correct += 1
print(correct/len(X))
kmeans = kmeans = KMeans(n_clusters=2, max_iter=600, algorithm = 'auto')
kmeans.fit(X)
correct = 0
for i in range(len(X)):
predict_me = np.array(X[i].astype(float))
predict_me = predict_me.reshape(-1, len(predict_me))
prediction = kmeans.predict(predict_me)
if prediction[0] == y[i]:
correct += 1
print(correct/len(X))
scaler = MinMaxScaler()
X_scaled = scaler.fit_transform(X)
kmeans.fit(X_scaled)
correct = 0
for i in range(len(X)):
predict_me = np.array(X[i].astype(float))
predict_me = predict_me.reshape(-1, len(predict_me))
prediction = kmeans.predict(predict_me)
if prediction[0] == y[i]:
correct += 1
print(correct/len(X))
| 0.631026 | 0.976243 |
# Prepare Outputs CSV
* Then filter to the "downtown" list
```
import os
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
```
## Read in Pano Metadata
```
df_meta = pd.read_csv('gsv_metadata.csv')
print(df_meta.shape)
df_meta['img_id'] = df_meta['name'].str.strip('.json')
meta_keep_cols = ['img_id', 'lat', 'long', 'date']
df_meta = df_meta[meta_keep_cols]
df_meta.head()
df_meta[['lat', 'long']].describe()
```
## Images that we Still Have
```
import s3fs
import boto3
fs = s3fs.S3FileSystem()
s3_image_bucket = 's3://streetview-w210'
gsv_images_dir = os.path.join(s3_image_bucket, 'gsv')
# See what is in the folder
gsv_images_paths = [filename for filename in fs.ls(gsv_images_dir) if '.jpg' in filename]
# Extract just the imgid and heading
gsv_imgid_heading = [os.path.basename(filename).strip('.jpg') for filename in gsv_images_paths]
print(len(gsv_imgid_heading))
gsv_imgid_heading[0:10]
df_s3_img = pd.DataFrame({'imgid_heading' : gsv_imgid_heading})
df_s3_img.head()
df_s3_img[['imgid', 'heading']] = df_s3_img['imgid_heading'].str.split('_', expand = True)
df_s3_img.head()
df_all_in_s3 = df_s3_img.merge(df_meta, how = 'inner', left_on = 'imgid', right_on = 'img_id')
print(df_all_in_s3.shape)
df_all_in_s3 = df_all_in_s3[['imgid_heading', 'img_id', 'heading', 'lat', 'long', 'date']]
df_all_in_s3.head()
df_all_in_s3.to_csv('metadata_all_imgid_ins3.csv', index = False)
```
# Create a subset List of Downtown Images
* Upper Left Corner = 43.053415 x -87.919210
* Lower Right Corner = 43.025648 x -87.883629
```
downtown_mask = ((43.025648 <= df_meta['lat']) & (df_meta['lat'] <= 43.05315) & (-87.919210 <= df_meta['long']) & (df_meta['long'] <= -87.883629))
df_downtown = df_meta[downtown_mask]
print(df_downtown.shape)
fig = plt.figure()
ax = fig.add_subplot()
x = df_downtown['long']
y = df_downtown['lat']
plt.plot(x, y, marker = '.', ls = 'None')
df_downtown.head()
```
## Concatenate with the list of images that actually exists with an inner merge
```
df_downtown_img = df_downtown.merge(df_s3_img, how = 'inner', left_on = 'img_id', right_on = 'imgid')
print(df_downtown_img.shape)
df_downtown_img.head()
fig = plt.figure()
ax = fig.add_subplot()
x = df_downtown_img['long']
y = df_downtown_img['lat']
plt.plot(x, y, marker = '.', ls = 'None')
df_downtown_img.columns
df_downtown_img = df_downtown_img[['imgid_heading', 'img_id', 'heading', 'lat', 'long', 'date']]
df_downtown_img.head()
df_downtown_img.to_csv('downtown_imgid_heading_ins3.csv', index = False)
```
|
github_jupyter
|
import os
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
df_meta = pd.read_csv('gsv_metadata.csv')
print(df_meta.shape)
df_meta['img_id'] = df_meta['name'].str.strip('.json')
meta_keep_cols = ['img_id', 'lat', 'long', 'date']
df_meta = df_meta[meta_keep_cols]
df_meta.head()
df_meta[['lat', 'long']].describe()
import s3fs
import boto3
fs = s3fs.S3FileSystem()
s3_image_bucket = 's3://streetview-w210'
gsv_images_dir = os.path.join(s3_image_bucket, 'gsv')
# See what is in the folder
gsv_images_paths = [filename for filename in fs.ls(gsv_images_dir) if '.jpg' in filename]
# Extract just the imgid and heading
gsv_imgid_heading = [os.path.basename(filename).strip('.jpg') for filename in gsv_images_paths]
print(len(gsv_imgid_heading))
gsv_imgid_heading[0:10]
df_s3_img = pd.DataFrame({'imgid_heading' : gsv_imgid_heading})
df_s3_img.head()
df_s3_img[['imgid', 'heading']] = df_s3_img['imgid_heading'].str.split('_', expand = True)
df_s3_img.head()
df_all_in_s3 = df_s3_img.merge(df_meta, how = 'inner', left_on = 'imgid', right_on = 'img_id')
print(df_all_in_s3.shape)
df_all_in_s3 = df_all_in_s3[['imgid_heading', 'img_id', 'heading', 'lat', 'long', 'date']]
df_all_in_s3.head()
df_all_in_s3.to_csv('metadata_all_imgid_ins3.csv', index = False)
downtown_mask = ((43.025648 <= df_meta['lat']) & (df_meta['lat'] <= 43.05315) & (-87.919210 <= df_meta['long']) & (df_meta['long'] <= -87.883629))
df_downtown = df_meta[downtown_mask]
print(df_downtown.shape)
fig = plt.figure()
ax = fig.add_subplot()
x = df_downtown['long']
y = df_downtown['lat']
plt.plot(x, y, marker = '.', ls = 'None')
df_downtown.head()
df_downtown_img = df_downtown.merge(df_s3_img, how = 'inner', left_on = 'img_id', right_on = 'imgid')
print(df_downtown_img.shape)
df_downtown_img.head()
fig = plt.figure()
ax = fig.add_subplot()
x = df_downtown_img['long']
y = df_downtown_img['lat']
plt.plot(x, y, marker = '.', ls = 'None')
df_downtown_img.columns
df_downtown_img = df_downtown_img[['imgid_heading', 'img_id', 'heading', 'lat', 'long', 'date']]
df_downtown_img.head()
df_downtown_img.to_csv('downtown_imgid_heading_ins3.csv', index = False)
| 0.191177 | 0.602208 |
# Mixup / Label smoothing
```
%load_ext autoreload
%autoreload 2
%matplotlib inline
from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = "all"
#export
from exp.nb_10 import *
path = datasets.untar_data(datasets.URLs.IMAGENETTE_160)
tfms = [make_rgb, ResizeFixed(128), to_byte_tensor, to_float_tensor]
bs = 64
il = ImageList.from_files(path, tfms=tfms)
sd = SplitData.split_by_func(il, partial(grandparent_splitter, valid_name='val'))
ll = label_by_func(sd, parent_labeler, proc_y=CategoryProcessor())
data = ll.to_databunch(bs, c_in=3, c_out=10, num_workers=4)
```
## Mixup
### What is mixup?
As the name kind of suggests, the authors of the [mixup article](https://arxiv.org/abs/1710.09412) propose to train the model on a mix of the pictures of the training set. Let's say we're on CIFAR10 for instance, then instead of feeding the model the raw images, we take two (which could be in the same class or not) and do a linear combination of them: in terms of tensor it's
``` python
new_image = t * image1 + (1-t) * image2
```
where t is a float between 0 and 1. Then the target we assign to that image is the same combination of the original targets:
``` python
new_target = t * target1 + (1-t) * target2
```
assuming your targets are one-hot encoded (which isn't the case in pytorch usually). And that's as simple as this.
```
img1 = PIL.Image.open(ll.train.x.items[0])
img1
img2 = PIL.Image.open(ll.train.x.items[4000])
img2
mixed_up = ll.train.x[0] * 0.3 + ll.train.x[4000] * 0.7
mixed_up.shape
plt.imshow(mixed_up.permute(1,2,0));
import numpy as np
a = np.arange(12).reshape(3,4)
a
torch.tensor(a).permute(1,0)
a.transpose()
a.swapaxes(0,-1)
# reduce
a;a.shape
np.add.reduce(a, 0)
np.add.reduce(a, 1)
X = np.arange(8).reshape((2,2,2))
X
np.add.reduce(X, 0)
np.add.reduce(X, 1)
np.add.reduce(X, 2)
mixed_up.shape
mixed_up.permute(1,2,0).shape
plt.imshow(mixed_up.permute(1,2,0))
```
French horn or tench? The right answer is 70% french horn and 30% tench ;)
### Implementation
The implementation relies on something called the *beta distribution* which in turns uses something which Jeremy still finds mildly terrifying called the *gamma function*. To get over his fears, Jeremy reminds himself that *gamma* is just a factorial function that (kinda) interpolates nice and smoothly to non-integers too. How it does that exactly isn't important...
```
# PyTorch has a log-gamma but not a gamma, so we'll create one
Γ = lambda x: x.lgamma().exp()
```
NB: If you see math symbols you don't know you can google them like this: [Γ function](https://www.google.com/search?q=Γ+function).
If you're not used to typing unicode symbols, on Mac type <kbd>ctrl</kbd>-<kbd>cmd</kbd>-<kbd>space</kbd> to bring up a searchable emoji box. On Linux you can use the [compose key](https://help.ubuntu.com/community/ComposeKey). On Windows you can also use a compose key, but you first need to install [WinCompose](https://github.com/samhocevar/wincompose). By default the <kbd>compose</kbd> key is the right-hand <kbd>Alt</kbd> key.
You can search for symbol names in WinCompose. The greek letters are generally <kbd>compose</kbd>-<kbd>\*</kbd>-<kbd>letter</kbd> (where *letter* is, for instance, <kbd>a</kbd> to get greek α alpha).
```
facts = [math.factorial(i) for i in range(7)]
plt.plot(range(7), facts, 'ro')
plt.plot(torch.linspace(0,6), Γ(torch.linspace(0,6)+1))
plt.legend(['factorial','Γ']);
torch.linspace(0,0.9,10)
```
In the original article, the authors suggested three things:
1. Create two separate dataloaders and draw a batch from each at every iteration to mix them up
2. Draw a t value following a beta distribution with a parameter α (0.4 is suggested in their article)
3. Mix up the two batches with the same value t.
4. Use one-hot encoded targets
Why the beta distribution with the same parameters α? Well it looks like this:
```
_,axs = plt.subplots(1,2, figsize=(12,4))
x = torch.linspace(0,1, 100)
for α,ax in zip([0.1,0.8], axs):
α = tensor(α)
# y = (x.pow(α-1) * (1-x).pow(α-1)) / (gamma_func(α ** 2) / gamma_func(α))
y = (x**(α-1) * (1-x)**(α-1)) / (Γ(α)**2 / Γ(2*α))
ax.plot(x,y)
ax.set_title(f"α={α:.1}")
```
With a low `α`, we pick values close to 0. and 1. with a high probability, and the values in the middle all have the same kind of probability. With a greater `α`, 0. and 1. get a lower probability .
While the approach above works very well, it's not the fastest way we can do this. The main point that slows down this process is wanting two different batches at every iteration (which means loading twice the amount of images and applying to them the other data augmentation function). To avoid this slow down, we can be a little smarter and mixup a batch with a shuffled version of itself (this way the images mixed up are still different). This was a trick suggested in the MixUp paper.
Then pytorch was very careful to avoid one-hot encoding targets when it could, so it seems a bit of a drag to undo this. Fortunately for us, if the loss is a classic cross-entropy, we have
```python
loss(output, new_target) = t * loss(output, target1) + (1-t) * loss(output, target2)
```
so we won't one-hot encode anything and just compute those two losses then do the linear combination.
Using the same parameter t for the whole batch also seemed a bit inefficient. In our experiments, we noticed that the model can train faster if we draw a different t for every image in the batch (both options get to the same result in terms of accuracy, it's just that one arrives there more slowly).
The last trick we have to apply with this is that there can be some duplicates with this strategy: let's say or shuffle say to mix image0 with image1 then image1 with image0, and that we draw t=0.1 for the first, and t=0.9 for the second. Then
```python
image0 * 0.1 + shuffle0 * (1-0.1) = image0 * 0.1 + image1 * 0.9
image1 * 0.9 + shuffle1 * (1-0.9) = image1 * 0.9 + image0 * 0.1
```
will be the same. Of course, we have to be a bit unlucky but in practice, we saw there was a drop in accuracy by using this without removing those near-duplicates. To avoid them, the tricks is to replace the vector of parameters we drew by
``` python
t = max(t, 1-t)
```
The beta distribution with the two parameters equal is symmetric in any case, and this way we insure that the biggest coefficient is always near the first image (the non-shuffled batch).
In `Mixup` we have handle loss functions that have an attribute `reduction` (like `nn.CrossEntropy()`). To deal with the `reduction=None` with various types of loss function without modifying the actual loss function outside of the scope we need to perform those operations with no reduction, we create a context manager:
```
#export
class NoneReduce():
def __init__(self, loss_func):
self.loss_func,self.old_red = loss_func,None
def __enter__(self):
if hasattr(self.loss_func, 'reduction'):
self.old_red = getattr(self.loss_func, 'reduction')
setattr(self.loss_func, 'reduction', 'none')
return self.loss_func
else: return partial(self.loss_func, reduction='none')
def __exit__(self, type, value, traceback):
if self.old_red is not None: setattr(self.loss_func, 'reduction', self.old_red)
```
Then we can use it in `MixUp`:
```
#export
from torch.distributions.beta import Beta
def unsqueeze(input, dims):
for dim in listify(dims): input = torch.unsqueeze(input, dim)
return input
def reduce_loss(loss, reduction='mean'):
return loss.mean() if reduction=='mean' else loss.sum() if reduction=='sum' else loss
#export
class MixUp(Callback):
_order = 90 #Runs after normalization and cuda
def __init__(self, α:float=0.4): self.distrib = Beta(tensor([α]), tensor([α]))
def begin_fit(self): self.old_loss_func,self.run.loss_func = self.run.loss_func,self.loss_func
def begin_batch(self):
if not self.in_train: return #Only mixup things during training
λ = self.distrib.sample((self.yb.size(0),)).squeeze().to(self.xb.device)
λ = torch.stack([λ, 1-λ], 1)
self.λ = unsqueeze(λ.max(1)[0], (1,2,3))
shuffle = torch.randperm(self.yb.size(0)).to(self.xb.device)
xb1,self.yb1 = self.xb[shuffle],self.yb[shuffle]
self.run.xb = lin_comb(self.xb, xb1, self.λ)
def after_fit(self): self.run.loss_func = self.old_loss_func
def loss_func(self, pred, yb):
if not self.in_train: return self.old_loss_func(pred, yb)
with NoneReduce(self.old_loss_func) as loss_func:
loss1 = loss_func(pred, yb)
loss2 = loss_func(pred, self.yb1)
loss = lin_comb(loss1, loss2, self.λ)
return reduce_loss(loss, getattr(self.old_loss_func, 'reduction', 'mean'))
nfs = [32,64,128,256,512]
def get_learner(nfs, data, lr, layer, loss_func=F.cross_entropy,
cb_funcs=None, opt_func=optim.SGD, **kwargs):
model = get_cnn_model(data, nfs, layer, **kwargs)
init_cnn(model)
return Learner(model, data, loss_func, lr=lr, cb_funcs=cb_funcs, opt_func=opt_func)
cbfs = [partial(AvgStatsCallback,accuracy),
CudaCallback,
ProgressCallback,
partial(BatchTransformXCallback, norm_imagenette),
MixUp]
learn = get_learner(nfs, data, 0.4, conv_layer, cb_funcs=cbfs)
learn.fit(1)
```
Questions: How does softmax interact with all this? Should we jump straight from mixup to inference?
## Label smoothing
Another regularization technique that's often used is label smoothing. It's designed to make the model a little bit less certain of it's decision by changing a little bit its target: instead of wanting to predict 1 for the correct class and 0 for all the others, we ask it to predict `1-ε` for the correct class and `ε` for all the others, with `ε` a (small) positive number and N the number of classes. This can be written as:
$$loss = (1-ε) ce(i) + ε \sum ce(j) / N$$
where `ce(x)` is cross-entropy of `x` (i.e. $-\log(p_{x})$), and `i` is the correct class. This can be coded in a loss function:
```
#export
class LabelSmoothingCrossEntropy(nn.Module):
def __init__(self, ε:float=0.1, reduction='mean'):
super().__init__()
self.ε,self.reduction = ε,reduction
def forward(self, output, target):
c = output.size()[-1]
log_preds = F.log_softmax(output, dim=-1)
loss = reduce_loss(-log_preds.sum(dim=-1), self.reduction)
nll = F.nll_loss(log_preds, target, reduction=self.reduction)
return lin_comb(loss/c, nll, self.ε)
```
Note: we implement the various reduction attributes so that it plays nicely with MixUp after.
```
cbfs = [partial(AvgStatsCallback,accuracy),
CudaCallback,
ProgressCallback,
partial(BatchTransformXCallback, norm_imagenette)]
learn = get_learner(nfs, data, 0.4, conv_layer, cb_funcs=cbfs, loss_func=LabelSmoothingCrossEntropy())
learn.fit(1)
```
And we can check our loss function `reduction` attribute hasn't changed outside of the training loop:
```
assert learn.loss_func.reduction == 'mean'
```
## Export
```
!./notebook2script.py 10b_mixup_label_smoothing.ipynb
```
|
github_jupyter
|
%load_ext autoreload
%autoreload 2
%matplotlib inline
from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = "all"
#export
from exp.nb_10 import *
path = datasets.untar_data(datasets.URLs.IMAGENETTE_160)
tfms = [make_rgb, ResizeFixed(128), to_byte_tensor, to_float_tensor]
bs = 64
il = ImageList.from_files(path, tfms=tfms)
sd = SplitData.split_by_func(il, partial(grandparent_splitter, valid_name='val'))
ll = label_by_func(sd, parent_labeler, proc_y=CategoryProcessor())
data = ll.to_databunch(bs, c_in=3, c_out=10, num_workers=4)
where t is a float between 0 and 1. Then the target we assign to that image is the same combination of the original targets:
assuming your targets are one-hot encoded (which isn't the case in pytorch usually). And that's as simple as this.
French horn or tench? The right answer is 70% french horn and 30% tench ;)
### Implementation
The implementation relies on something called the *beta distribution* which in turns uses something which Jeremy still finds mildly terrifying called the *gamma function*. To get over his fears, Jeremy reminds himself that *gamma* is just a factorial function that (kinda) interpolates nice and smoothly to non-integers too. How it does that exactly isn't important...
NB: If you see math symbols you don't know you can google them like this: [Γ function](https://www.google.com/search?q=Γ+function).
If you're not used to typing unicode symbols, on Mac type <kbd>ctrl</kbd>-<kbd>cmd</kbd>-<kbd>space</kbd> to bring up a searchable emoji box. On Linux you can use the [compose key](https://help.ubuntu.com/community/ComposeKey). On Windows you can also use a compose key, but you first need to install [WinCompose](https://github.com/samhocevar/wincompose). By default the <kbd>compose</kbd> key is the right-hand <kbd>Alt</kbd> key.
You can search for symbol names in WinCompose. The greek letters are generally <kbd>compose</kbd>-<kbd>\*</kbd>-<kbd>letter</kbd> (where *letter* is, for instance, <kbd>a</kbd> to get greek α alpha).
In the original article, the authors suggested three things:
1. Create two separate dataloaders and draw a batch from each at every iteration to mix them up
2. Draw a t value following a beta distribution with a parameter α (0.4 is suggested in their article)
3. Mix up the two batches with the same value t.
4. Use one-hot encoded targets
Why the beta distribution with the same parameters α? Well it looks like this:
With a low `α`, we pick values close to 0. and 1. with a high probability, and the values in the middle all have the same kind of probability. With a greater `α`, 0. and 1. get a lower probability .
While the approach above works very well, it's not the fastest way we can do this. The main point that slows down this process is wanting two different batches at every iteration (which means loading twice the amount of images and applying to them the other data augmentation function). To avoid this slow down, we can be a little smarter and mixup a batch with a shuffled version of itself (this way the images mixed up are still different). This was a trick suggested in the MixUp paper.
Then pytorch was very careful to avoid one-hot encoding targets when it could, so it seems a bit of a drag to undo this. Fortunately for us, if the loss is a classic cross-entropy, we have
so we won't one-hot encode anything and just compute those two losses then do the linear combination.
Using the same parameter t for the whole batch also seemed a bit inefficient. In our experiments, we noticed that the model can train faster if we draw a different t for every image in the batch (both options get to the same result in terms of accuracy, it's just that one arrives there more slowly).
The last trick we have to apply with this is that there can be some duplicates with this strategy: let's say or shuffle say to mix image0 with image1 then image1 with image0, and that we draw t=0.1 for the first, and t=0.9 for the second. Then
will be the same. Of course, we have to be a bit unlucky but in practice, we saw there was a drop in accuracy by using this without removing those near-duplicates. To avoid them, the tricks is to replace the vector of parameters we drew by
The beta distribution with the two parameters equal is symmetric in any case, and this way we insure that the biggest coefficient is always near the first image (the non-shuffled batch).
In `Mixup` we have handle loss functions that have an attribute `reduction` (like `nn.CrossEntropy()`). To deal with the `reduction=None` with various types of loss function without modifying the actual loss function outside of the scope we need to perform those operations with no reduction, we create a context manager:
Then we can use it in `MixUp`:
Questions: How does softmax interact with all this? Should we jump straight from mixup to inference?
## Label smoothing
Another regularization technique that's often used is label smoothing. It's designed to make the model a little bit less certain of it's decision by changing a little bit its target: instead of wanting to predict 1 for the correct class and 0 for all the others, we ask it to predict `1-ε` for the correct class and `ε` for all the others, with `ε` a (small) positive number and N the number of classes. This can be written as:
$$loss = (1-ε) ce(i) + ε \sum ce(j) / N$$
where `ce(x)` is cross-entropy of `x` (i.e. $-\log(p_{x})$), and `i` is the correct class. This can be coded in a loss function:
Note: we implement the various reduction attributes so that it plays nicely with MixUp after.
And we can check our loss function `reduction` attribute hasn't changed outside of the training loop:
## Export
| 0.606498 | 0.923592 |
```
from IPython.display import Image
Image('../../Python_probability_statistics_machine_learning_2E.png',width=200)
```
<!-- new sections -->
<!-- Ensemble learning -->
<!-- - Machine Learning Flach, Ch.11 -->
<!-- - Machine Learning Mohri, pp.135- -->
<!-- - Data Mining Witten, Ch. 8 -->
With the exception of the random forest, we have so far considered machine
learning models as stand-alone entities. Combinations of models that jointly
produce a classification are known as *ensembles*. There are two main
methodologies that create ensembles: *bagging* and *boosting*.
## Bagging
Bagging refers to bootstrap aggregating, where bootstrap here is the same as we
discussed in the section [ch:stats:sec:boot](#ch:stats:sec:boot). Basically,
we resample the data with replacement and then train a classifier on the newly
sampled data. Then, we combine the outputs of each of the individual
classifiers using a majority-voting scheme (for discrete outputs) or a weighted
average (for continuous outputs). This combination is particularly effective
for models that are easily influenced by a single data element. The resampling
process means that these elements cannot appear in every bootstrapped
training set so that some of the models will not suffer these effects. This
makes the so-computed combination of outputs less volatile. Thus, bagging
helps reduce the collective variance of individual high-variance models.
To get a sense of bagging, let's suppose we have a two-dimensional plane that
is partitioned into two regions with the following boundary: $y=-x+x^2$.
Pairs of $(x_i,y_i)$ points above this boundary are labeled one and points
below are labeled zero. [Figure](#fig:ensemble_001) shows the two regions
with the nonlinear separating boundary as the black curved line.
<!-- dom:FIGURE: [fig-machine_learning/ensemble_001.png, width=500 frac=0.75] Two regions in the plane are separated by a nonlinear boundary. The training data is sampled from this plane. The objective is to correctly classify the so-sampled data. <div id="fig:ensemble_001"></div> -->
<!-- begin figure -->
<div id="fig:ensemble_001"></div>
<p>Two regions in the plane are separated by a nonlinear boundary. The training data is sampled from this plane. The objective is to correctly classify the so-sampled data.</p>
<img src="fig-machine_learning/ensemble_001.png" width=500>
<!-- end figure -->
The problem is to take samples from each of these regions
and classify them correctly using a perceptron (see the section [ch:ml:sec:perceptron](#ch:ml:sec:perceptron)). A perceptron
is the simplest possible linear classifier that finds a line
in the plane to separate two purported categories. Because
the separating boundary is nonlinear, there is no way that
the perceptron can completely solve this problem. The
following code sets up the perceptron available in
Scikit-learn.
```
from sklearn.linear_model import Perceptron
p=Perceptron()
p
```
The training data and the resulting perceptron separating boundary
are shown in [Figure](#fig:ensemble_002). The circles and crosses are the
sampled training data and the gray separating line is the perceptron's
separating boundary between the two categories. The black squares are those
elements in the training data that the perceptron mis-classified. Because the
perceptron can only produce linear separating boundaries, and the boundary in
this case is non-linear, the perceptron makes mistakes near where the
boundary curves. The next step is to see how bagging can
improve upon this by using multiple perceptrons.
<!-- dom:FIGURE: [fig-machine_learning/ensemble_002.png, width=500 frac=0.75] The perceptron finds the best linear boundary between the two classes. <div id="fig:ensemble_002"></div> -->
<!-- begin figure -->
<div id="fig:ensemble_002"></div>
<p>The perceptron finds the best linear boundary between the two classes.</p>
<img src="fig-machine_learning/ensemble_002.png" width=500>
<!-- end figure -->
The following code sets up the bagging classifier in Scikit-learn. Here we
select only three perceptrons. [Figure](#fig:ensemble_003) shows each of the
three individual classifiers and the final bagged classifer in the panel on the
bottom right. As before, the black circles indicate misclassifications in the
training data. Joint classifications are determined by majority voting.
```
from sklearn.ensemble import BaggingClassifier
bp = BaggingClassifier(Perceptron(),max_samples=0.50,n_estimators=3)
bp
```
<!-- dom:FIGURE: [fig-machine_learning/ensemble_003.png, width=500 frac=0.85] Each panel with the single gray line is one of the perceptrons used for the ensemble bagging classifier on the lower right. <div id="fig:ensemble_003"></div> -->
<!-- begin figure -->
<div id="fig:ensemble_003"></div>
<p>Each panel with the single gray line is one of the perceptrons used for the ensemble bagging classifier on the lower right.</p>
<img src="fig-machine_learning/ensemble_003.png" width=500>
<!-- end figure -->
The `BaggingClassifier` can estimate its own out-of-sample error if passed the
`oob_score=True` flag upon construction. This keeps track of which samples were
used for training and which were not, and then estimates the out-of-sample
error using those samples that were unused in training. The `max_samples`
keyword argument specifies the number of items from the training set to use for
the base classifier. The smaller the `max_samples` used in the bagging
classifier, the better the out-of-sample error estimate, but at the cost of
worse in-sample performance. Of course, this depends on the overall number of
samples and the degrees-of-freedom in each individual classifier. The
VC-dimension surfaces again!
## Boosting
As we discussed, bagging is particularly effective for individual high-variance
classifiers because the final majority-vote tends to smooth out the individual
classifiers and produce a more stable collaborative solution. On the other
hand, boosting is particularly effective for high-bias classifiers that are
slow to adjust to new data. On the one hand, boosting is similiar to bagging in
that it uses a majority-voting (or averaging for numeric prediction) process at
the end; and it also combines individual classifiers of the same type. On the
other hand, boosting is serially iterative, whereas the individual classifiers
in bagging can be trained in parallel. Boosting uses the misclassifications of
prior iterations to influence the training of the next iterative classifier by
weighting those misclassifications more heavily in subsequent steps. This means
that, at every step, boosting focuses more and more on specific
misclassifications up to that point, letting the prior classifications
be carried by earlier iterations.
The primary implementation for boosting in Scikit-learn is the Adaptive
Boosting (*AdaBoost*) algorithm, which does classification
(`AdaBoostClassifier`) and regression (`AdaBoostRegressor`). The first step in
the basic AdaBoost algorithm is to initialize the weights over each of the
training set indicies, $D_0(i)=1/n$ where there are $n$ elements in the
training set. Note that this creates a discrete uniform distribution over the
*indicies*, not over the training data $\lbrace (x_i,y_i) \rbrace$ itself. In
other words, if there are repeated elements in the training data, then each
gets its own weight. The next step is to train the base classifer $h_k$ and
record the classification error at the $k^{th}$ iteration, $\epsilon_k$. Two
factors can next be calculated using $\epsilon_k$,
$$
\alpha_k = \frac{1}{2}\log \frac{1-\epsilon_k}{\epsilon_k}
$$
and the normalization factor,
$$
Z_k = 2 \sqrt{ \epsilon_k (1- \epsilon_k) }
$$
For the next step, the weights over the training data are updated as
in the following,
$$
D_{k+1}(i) = \frac{1}{Z_k} D_k(i)\exp{(-\alpha_k y_i h_k(x_i))}
$$
The final classification result is assembled using the $\alpha_k$
factors, $g = \sgn(\sum_{k} \alpha_k h_k)$.
To re-do the problem above using boosting with perceptrons, we set up the
AdaBoost classifier in the following,
```
from sklearn.ensemble import AdaBoostClassifier
clf=AdaBoostClassifier(Perceptron(),n_estimators=3,
algorithm='SAMME',
learning_rate=0.5)
clf
```
The `learning_rate` above controls how aggressively the weights are
updated. The resulting classification boundaries for the embedded perceptrons
are shown in [Figure](#fig:ensemble_004). Compare this to the lower right
panel in [Figure](#fig:ensemble_003). The performance for both cases is about
the same.
<!-- dom:FIGURE: [fig-machine_learning/ensemble_004.png, width=500 frac=0.75] The individual perceptron classifiers embedded in the AdaBoost classifier are shown along with the mis-classified points (in black). Compare this to the lower right panel of [Figure](#fig:ensemble_003). <div id="fig:ensemble_004"></div> -->
<!-- begin figure -->
<div id="fig:ensemble_004"></div>
<p>The individual perceptron classifiers embedded in the AdaBoost classifier are shown along with the mis-classified points (in black). Compare this to the lower right panel of [Figure](#fig:ensemble_003).</p>
<img src="fig-machine_learning/ensemble_004.png" width=500>
<!-- end figure -->
|
github_jupyter
|
from IPython.display import Image
Image('../../Python_probability_statistics_machine_learning_2E.png',width=200)
from sklearn.linear_model import Perceptron
p=Perceptron()
p
from sklearn.ensemble import BaggingClassifier
bp = BaggingClassifier(Perceptron(),max_samples=0.50,n_estimators=3)
bp
from sklearn.ensemble import AdaBoostClassifier
clf=AdaBoostClassifier(Perceptron(),n_estimators=3,
algorithm='SAMME',
learning_rate=0.5)
clf
| 0.691289 | 0.990385 |
# Bootstrapping Without Re-training
## Setup
Suppose we have a model $f: \mathcal X \to [0, 1]$ which predicts probabilities for some binary classificaiton problem with labels in $\mathcal Y = \{0, 1\}$, and we have some test set $D_\text{test} = \mathbf{X} \in \mathcal X^{N_{\text{data}}}, \mathbf{y} \in \mathcal Y^{N_{\text{data}}}$. We want to assess the efficacy of our classifier. So, we generate a bunch of probabilities $\mathbf p = f(\mathbf{X})$, $\mathbf p \in [0, 1]^{N_\text{data}}$. We also have some _single_ threshold $t$ that we use for prediction, such that we form $\hat{y}_i = \begin{cases} 1 & \text{if } p_i > t \\ 0 & \text{otherwise.}\end{cases}$. Ultimately, now we have a set of _triples_ of probabilities and labels $(p_i, \hat{y}_i, y_i)$ for $0 \le i < N_\text{data}$.
We could just compute our evaluation on these straight-away. However, that would be silly -- we need variance! So instead, we decide (potentially erroneously) to do what we'll call in this notebook _bootstrapping_ (this may or may not be what is canonically meant by "bootstrapping"), by which I concretely mean that for $K$ iterations (where typically $K$ is large, e.g., $K >> 100$) we will choose a number of samples $N_\text{bootstrap}$ (which will _typically_ be $N_\text{data}$, but I'll allow the framework to be general so that we can disentangle their effects) from this set of triples randomly, independently, and with replacement, then compute some evaluation metric of interest on this $N_\text{bootstrap}$ subset. Over our $K$ samples, we can then compute confidence intervlas, means, variances, etc. With this setup, let's analyze a few concrete evaluation metrics we might care about.
## Dead Simple Evaluation Metrics
### Confusion Matrix Elements
Let's consider the confusion matrix elements _on the raw, original dataset_; in particular, the number of true positives, $TP$ (`TP`) which is the number of times $y_i = 1$ and $\hat{y}_i = 1$, the number of false positives, $FP$ (`FP`), which is the number of times $y_i = 0$ and $\hat{y}_i = 1$, the number of true negatives, $TN$ (`TN`), which is the number of times $y_i = 0$ and $\hat{y}_i = 0$, and the number of false negatives, $FN$ (`FN`), which is the number of times $y_i = 1$ and $\hat{y}_i = 0$. We'll add one more, which the number of "correct" points, $C$ (`C`), which is the number of points where $\hat{y}_i = y_i$. Mathematically:
* $TP = \sum_{i=0}^{N_\text{data} - 1} \mathbb{1}_{y_i = 1} \cdot \mathbb{1}_{\hat{y}_i = 1}$
* $FP = \sum_{i=0}^{N_\text{data} - 1} \mathbb{1}_{y_i = 0} \cdot \mathbb{1}_{\hat{y}_i = 1}$
* $TN = \sum_{i=0}^{N_\text{data} - 1} \mathbb{1}_{y_i = 0} \cdot \mathbb{1}_{\hat{y}_i = 0}$
* $FN = \sum_{i=0}^{N_\text{data} - 1} \mathbb{1}_{y_i = 1} \cdot \mathbb{1}_{\hat{y}_i = 0}$
* $C = TP + TN = \sum_{i=0}^{N_\text{data}-1} \mathbb{1}_{y_i = \hat{y}_i}$
What happens to our estimates of these metrics under bootstrapping? Do we gain any insight into the variance we can expect for these numbers?
Well, note that any individual draw of our bootstrap process (e.g., any draw of a triple $(p^{(b)}, \hat{y}^{(b)}, y^{(b)})$ from our original set of triples during a bootstrap sample) is a draw from the empirical distribution of the dataset. Which means that as exactly $\frac{TP}{N_\text{data}}$ proportion of the samples have $\hat{y} = y = 1$, we see that this sample will output $\mathbb{1}_{y^{(b)} = 1} \cdot \mathbb{1}_{\hat{y}^{(b)} = 1} = 1$ according _precisely_ to a Bernoulli random variable with parameter given by $\frac{TP}{N_\text{data}}$. This holds as well for $FP$, $TN$, $FN$, and $C$ (all at their own proper rates).
Thus, the induced number of true/false positives/negatives or the overall number of correct points under bootstrapping (for any given sample of the set of $K$ total bootstrap samples) therefore should follow a simple _binomial_ distribution with parameters (assume we are talking about true positives without loss of generality) of probability $p$ given by $\frac{TP}{N_\text{data}}$ and number of samples $N$ given by $N_\text{bootstrap}$. Thus, any derived property over the bootstrap samples should (provided $K$ is large) be determined simply by $TP$, $N_\text{data}$, and $N_\text{bootstrap}$. Thus the variance here has _minimal_ dependence on our model $f$.
Note that this immediately offers insight into the measure "accuracy" as well, which is simply given by $\frac{C}{N}$ (where $N$ is the size of the dataset, either $N_\text{data}$ or $N_\text{bootstrap}$ depending).
### Compound Elements
Ok, so accuracy, $TP$, $FP$, $TN$, $FN$ and so on are all easy. But what about $TPR$, $FPR$, $TNR$, $FNR$? Recall that these rates are compounds:
* $TPR = \frac{TP}{TP + FN} = \frac{TP}{\sum_{i=0}^{N_\text{data}-1} \mathbb{1}_{y_i = 1}}$
We can make this more analytical by considering breaking down our sampling problem. Let $PR = \frac{\sum_{i=0}^{N_\text{data}-1} \mathbb{1}_{y_i = 1}}{N_\text{data}}$ and $NR = 1- PR = \frac{\sum_{i=0}^{N_\text{data}-1} \mathbb{1}_{y_i = 0}}{N_\text{data}}$ be the positive and negative rate of our original dataset. With this parameter in mind, we can re-visit our original sampling procedure as, rather than sampling at random uniformly from the overall set of triples, we first choose wheter to sample a positive or negative example (with probability $PR$ v. $NR$), then within that choose to sample a predicted positive or predicted negative sample (with probability $TPR$ v. $FNR$ -OR- $FPR$ v. $TNR$).
Under this setting, it is clear that the probability our observed $TPR$ takes on value $\frac{m}{n}$ is given by:
$$p(TPR_\text{obs} = \frac{m}{n} = p(P_\text{obs} = n \text{ AND } TP_\text{obs} = m)$$
But,
$$ p(P_\text{obs} = n \text{ AND } TP_\text{obs} = m) = p(P_\text{obs} = n) p(TP_\text{obs} = m | P_\text{obs} = n)$$
The former probability in this product is given by a binomial random variable with parameters $PR$ and $N_\text{bootstrap}$. The second is given by $0$ if $m > n$ and a binomial random variable with parameters $TPR$ and $n$. Recall the probability of an $q, S$ binomial random variable taking on value $x$ is given by $P_{x} = {S \choose x} q^{x} (1-q)^{S-x}$.
Thus, the probability for us is:
$$p\left(TPR_\text{obs} = \frac{TP_\text{obs}}{P_\text{obs}}\right) = \left(
{N_\text{bootstrap} \choose P_\text{obs}} PR^{P_\text{obs}}(1-PR)^{N_\text{bootstrap} - P_\text{obs}}
\right) \cdot \left(
{P_\text{obs} \choose TP_\text{obs}} TPR^{TP_\text{obs}}(1-TPR)^{P_\text{obs} - TP_\text{obs}}
\right)$$
## AUROC
This one is... tougher. The formulation of interest to us here is that the AUROC is the probability that a randomly sampled positive example will be given an assigned probability that is higher than a randomly sampled negative example. The reason this is tricky is because when we take our bootstrap sample we sample at the level of individual data points, not pairs.
Note that the number of pairs of points $(i, j)$ such that $y_i = 1$ and $y_j = 0$ is precisely given by $P * N$ (or, in the bootstrap sampled, $P_\text{obs} * N_\text{obs}$). But, as everything is either $P$ or $N$, we can also rewrite this as $P (1 - P) = P - P**2$.
This is our denominator in the AUROC calculation. The numerator is given by the number of pairs of points $(i, j)$ such that both $y_i = 1, y_j = 0$ _and_ that $p_i > p_j$.
$$
p\left(\text{AUROC}_\text{obs} = \frac{R}{P_\text{obs}(1-P_\text{obs})}\right)
= p\left(\left.\text{AUROC}_\text{obs} = \frac{R}{P_\text{obs}(1-P_\text{obs})}\right| P_\text{obs} \right) \cdot p(P_\text{obs})
$$
$$ p\left(\text{AUROC}_\text{obs} = \frac{R}{P_\text{obs}(1-P_\text{obs})}\right)
= p\left(\left.\text{AUROC}_\text{obs} = \frac{R}{P_\text{obs}(1-P_\text{obs})}\right| P_\text{obs} \right) \cdot
\left(
{N_\text{bootstrap} \choose P_\text{obs}} PR^{P_\text{obs}}(1-PR)^{N_\text{bootstrap} - P_\text{obs}}
\right)
$$
|
github_jupyter
|
# Bootstrapping Without Re-training
## Setup
Suppose we have a model $f: \mathcal X \to [0, 1]$ which predicts probabilities for some binary classificaiton problem with labels in $\mathcal Y = \{0, 1\}$, and we have some test set $D_\text{test} = \mathbf{X} \in \mathcal X^{N_{\text{data}}}, \mathbf{y} \in \mathcal Y^{N_{\text{data}}}$. We want to assess the efficacy of our classifier. So, we generate a bunch of probabilities $\mathbf p = f(\mathbf{X})$, $\mathbf p \in [0, 1]^{N_\text{data}}$. We also have some _single_ threshold $t$ that we use for prediction, such that we form $\hat{y}_i = \begin{cases} 1 & \text{if } p_i > t \\ 0 & \text{otherwise.}\end{cases}$. Ultimately, now we have a set of _triples_ of probabilities and labels $(p_i, \hat{y}_i, y_i)$ for $0 \le i < N_\text{data}$.
We could just compute our evaluation on these straight-away. However, that would be silly -- we need variance! So instead, we decide (potentially erroneously) to do what we'll call in this notebook _bootstrapping_ (this may or may not be what is canonically meant by "bootstrapping"), by which I concretely mean that for $K$ iterations (where typically $K$ is large, e.g., $K >> 100$) we will choose a number of samples $N_\text{bootstrap}$ (which will _typically_ be $N_\text{data}$, but I'll allow the framework to be general so that we can disentangle their effects) from this set of triples randomly, independently, and with replacement, then compute some evaluation metric of interest on this $N_\text{bootstrap}$ subset. Over our $K$ samples, we can then compute confidence intervlas, means, variances, etc. With this setup, let's analyze a few concrete evaluation metrics we might care about.
## Dead Simple Evaluation Metrics
### Confusion Matrix Elements
Let's consider the confusion matrix elements _on the raw, original dataset_; in particular, the number of true positives, $TP$ (`TP`) which is the number of times $y_i = 1$ and $\hat{y}_i = 1$, the number of false positives, $FP$ (`FP`), which is the number of times $y_i = 0$ and $\hat{y}_i = 1$, the number of true negatives, $TN$ (`TN`), which is the number of times $y_i = 0$ and $\hat{y}_i = 0$, and the number of false negatives, $FN$ (`FN`), which is the number of times $y_i = 1$ and $\hat{y}_i = 0$. We'll add one more, which the number of "correct" points, $C$ (`C`), which is the number of points where $\hat{y}_i = y_i$. Mathematically:
* $TP = \sum_{i=0}^{N_\text{data} - 1} \mathbb{1}_{y_i = 1} \cdot \mathbb{1}_{\hat{y}_i = 1}$
* $FP = \sum_{i=0}^{N_\text{data} - 1} \mathbb{1}_{y_i = 0} \cdot \mathbb{1}_{\hat{y}_i = 1}$
* $TN = \sum_{i=0}^{N_\text{data} - 1} \mathbb{1}_{y_i = 0} \cdot \mathbb{1}_{\hat{y}_i = 0}$
* $FN = \sum_{i=0}^{N_\text{data} - 1} \mathbb{1}_{y_i = 1} \cdot \mathbb{1}_{\hat{y}_i = 0}$
* $C = TP + TN = \sum_{i=0}^{N_\text{data}-1} \mathbb{1}_{y_i = \hat{y}_i}$
What happens to our estimates of these metrics under bootstrapping? Do we gain any insight into the variance we can expect for these numbers?
Well, note that any individual draw of our bootstrap process (e.g., any draw of a triple $(p^{(b)}, \hat{y}^{(b)}, y^{(b)})$ from our original set of triples during a bootstrap sample) is a draw from the empirical distribution of the dataset. Which means that as exactly $\frac{TP}{N_\text{data}}$ proportion of the samples have $\hat{y} = y = 1$, we see that this sample will output $\mathbb{1}_{y^{(b)} = 1} \cdot \mathbb{1}_{\hat{y}^{(b)} = 1} = 1$ according _precisely_ to a Bernoulli random variable with parameter given by $\frac{TP}{N_\text{data}}$. This holds as well for $FP$, $TN$, $FN$, and $C$ (all at their own proper rates).
Thus, the induced number of true/false positives/negatives or the overall number of correct points under bootstrapping (for any given sample of the set of $K$ total bootstrap samples) therefore should follow a simple _binomial_ distribution with parameters (assume we are talking about true positives without loss of generality) of probability $p$ given by $\frac{TP}{N_\text{data}}$ and number of samples $N$ given by $N_\text{bootstrap}$. Thus, any derived property over the bootstrap samples should (provided $K$ is large) be determined simply by $TP$, $N_\text{data}$, and $N_\text{bootstrap}$. Thus the variance here has _minimal_ dependence on our model $f$.
Note that this immediately offers insight into the measure "accuracy" as well, which is simply given by $\frac{C}{N}$ (where $N$ is the size of the dataset, either $N_\text{data}$ or $N_\text{bootstrap}$ depending).
### Compound Elements
Ok, so accuracy, $TP$, $FP$, $TN$, $FN$ and so on are all easy. But what about $TPR$, $FPR$, $TNR$, $FNR$? Recall that these rates are compounds:
* $TPR = \frac{TP}{TP + FN} = \frac{TP}{\sum_{i=0}^{N_\text{data}-1} \mathbb{1}_{y_i = 1}}$
We can make this more analytical by considering breaking down our sampling problem. Let $PR = \frac{\sum_{i=0}^{N_\text{data}-1} \mathbb{1}_{y_i = 1}}{N_\text{data}}$ and $NR = 1- PR = \frac{\sum_{i=0}^{N_\text{data}-1} \mathbb{1}_{y_i = 0}}{N_\text{data}}$ be the positive and negative rate of our original dataset. With this parameter in mind, we can re-visit our original sampling procedure as, rather than sampling at random uniformly from the overall set of triples, we first choose wheter to sample a positive or negative example (with probability $PR$ v. $NR$), then within that choose to sample a predicted positive or predicted negative sample (with probability $TPR$ v. $FNR$ -OR- $FPR$ v. $TNR$).
Under this setting, it is clear that the probability our observed $TPR$ takes on value $\frac{m}{n}$ is given by:
$$p(TPR_\text{obs} = \frac{m}{n} = p(P_\text{obs} = n \text{ AND } TP_\text{obs} = m)$$
But,
$$ p(P_\text{obs} = n \text{ AND } TP_\text{obs} = m) = p(P_\text{obs} = n) p(TP_\text{obs} = m | P_\text{obs} = n)$$
The former probability in this product is given by a binomial random variable with parameters $PR$ and $N_\text{bootstrap}$. The second is given by $0$ if $m > n$ and a binomial random variable with parameters $TPR$ and $n$. Recall the probability of an $q, S$ binomial random variable taking on value $x$ is given by $P_{x} = {S \choose x} q^{x} (1-q)^{S-x}$.
Thus, the probability for us is:
$$p\left(TPR_\text{obs} = \frac{TP_\text{obs}}{P_\text{obs}}\right) = \left(
{N_\text{bootstrap} \choose P_\text{obs}} PR^{P_\text{obs}}(1-PR)^{N_\text{bootstrap} - P_\text{obs}}
\right) \cdot \left(
{P_\text{obs} \choose TP_\text{obs}} TPR^{TP_\text{obs}}(1-TPR)^{P_\text{obs} - TP_\text{obs}}
\right)$$
## AUROC
This one is... tougher. The formulation of interest to us here is that the AUROC is the probability that a randomly sampled positive example will be given an assigned probability that is higher than a randomly sampled negative example. The reason this is tricky is because when we take our bootstrap sample we sample at the level of individual data points, not pairs.
Note that the number of pairs of points $(i, j)$ such that $y_i = 1$ and $y_j = 0$ is precisely given by $P * N$ (or, in the bootstrap sampled, $P_\text{obs} * N_\text{obs}$). But, as everything is either $P$ or $N$, we can also rewrite this as $P (1 - P) = P - P**2$.
This is our denominator in the AUROC calculation. The numerator is given by the number of pairs of points $(i, j)$ such that both $y_i = 1, y_j = 0$ _and_ that $p_i > p_j$.
$$
p\left(\text{AUROC}_\text{obs} = \frac{R}{P_\text{obs}(1-P_\text{obs})}\right)
= p\left(\left.\text{AUROC}_\text{obs} = \frac{R}{P_\text{obs}(1-P_\text{obs})}\right| P_\text{obs} \right) \cdot p(P_\text{obs})
$$
$$ p\left(\text{AUROC}_\text{obs} = \frac{R}{P_\text{obs}(1-P_\text{obs})}\right)
= p\left(\left.\text{AUROC}_\text{obs} = \frac{R}{P_\text{obs}(1-P_\text{obs})}\right| P_\text{obs} \right) \cdot
\left(
{N_\text{bootstrap} \choose P_\text{obs}} PR^{P_\text{obs}}(1-PR)^{N_\text{bootstrap} - P_\text{obs}}
\right)
$$
| 0.86319 | 0.985787 |
[](https://pythonista.io)
# Atributos de identificación *id* y *class*.
Es muy común que un elemento o un conjunto de elementos dentro de un documento HTML sean diferenciados del resto de los elementos.
## El atributo *id*.
Es posible distinguir a un elemento específico dentro de un documento HTML mediante el atributo *id*. Dicho atributo permite asignar un identificador único a un elemento.
La sintaxis para asignar un identificador único a un elemento es al siguiente:
```html
<(elemento) id="(identificador)">
...
...
</(elemento)>
```
## El atributo *class*.
El atributo *class* permite agrupar a diversos elementos dentro de un documento HTML mediante un identificador compartido.
No es necesario que los elementos que comparten el identificador definido por el atributo *class* sean del mismo tipo.
```html
<(elemento_1) class="(identificador de clase)">
...
...
</(elemento_1)>
...
...
<(elemento_2) class="(identificador de clase)">
...
...
</(elemento_2)>
...
...
<(elemento_n) class="(identificador de clase)">
...
...
</(elemento_n)>
```
## Uso de los atributos *id* y *class* en la aplicación de reglas de estilo.
Uno de los usos más comunes de los atributos de identificación *id* y *class* es la de la aplicación de estilos.
Las hojas de estilo se estudiarán más adelante. Sin embargo, con la finalidad de ilustrar el uso de los atributos *id* y *class* adelantaremos algunos conceptos.
### Selectores.
Los selectores en una hoja de estilo perimten aplicar ciertas reglas de estilo (color, tamaño, fuente tipográfica, etc.) a un objeto dentro de un documento HTML.
El selector de un elemento con un atributo *id* específico se denota mediante la siguiente sintaxis:
``` css
#(identificador)
```
El selector de uno o varios elementos que comparten un atributo *class* específico se denota mediante la siguiente sintaxis:
``` css
.(identificador de clase)
```
**Ejemplo:**
El siguiente código incluye el elemento *<style*>, el cual contiene las definición de estilos aplicable al elemento con el atributo *id="parrafo"* y a todos los elementos que tengan el atributo *class="estilo"*.
Las reglas de estilo se aplicarán exclusivamente a los elementos que contengan los atributos definidos.
``` html
<!DOCTYPE html>
<html>
<head>
<title>Ejemplo de id y class</title>
<meta charset="UTF-8">
<meta name="description" content="Apuntes Pythonista">
<meta autor="josech">
<style>
#parrafo
{
font-size: 1.5em;
font-style: bold;
color: red;
}
.estilo
{
font-style: italic;
color: green;
}
</style>
</head>
<body>
<p>Este es un ejemplo del uso de los atributos <em>id</em> y <em>class</em>.</p>
<h2> Ejemplo de uso del atributo <em>id</em>.</h2>
<p>El elemento <id> permite asignar un nombre único a un elemento de HTML.</p>
<p id="parrafo">Puede diferenciar a un elemento de otros.</p>
<h2>Ejemplo de uso del atributo <em>class</em>.</h2>
<p>El atributo <em>class</em> puede asignar un identificador a más de un elemento de HTML.<br/>Esto es útil para.</p>
<ul>
<li class="estilo">Homogenizar los atributos de grupos de elementos en un documento.</li>
<li>Permitir recopilar imformación de dichos elementos a partir del código.</li>
</ul>
<p class="estilo">El atributo class puede ser utilizado incluso en elementos de tipo distinto.</p>
</body>
</html>
```
El resultado se puede apreciar en el documento [ejemplos/ejemplo_id_class.html](ejemplos/ejemplo_id_class.html).
<p style="text-align: center"><a rel="license" href="http://creativecommons.org/licenses/by/4.0/"><img alt="Licencia Creative Commons" style="border-width:0" src="https://i.creativecommons.org/l/by/4.0/80x15.png" /></a><br />Esta obra está bajo una <a rel="license" href="http://creativecommons.org/licenses/by/4.0/">Licencia Creative Commons Atribución 4.0 Internacional</a>.</p>
<p style="text-align: center">© José Luis Chiquete Valdivieso. 2018.</p>
|
github_jupyter
|
<(elemento) id="(identificador)">
...
...
</(elemento)>
<(elemento_1) class="(identificador de clase)">
...
...
</(elemento_1)>
...
...
<(elemento_2) class="(identificador de clase)">
...
...
</(elemento_2)>
...
...
<(elemento_n) class="(identificador de clase)">
...
...
</(elemento_n)>
El selector de uno o varios elementos que comparten un atributo *class* específico se denota mediante la siguiente sintaxis:
**Ejemplo:**
El siguiente código incluye el elemento *<style*>, el cual contiene las definición de estilos aplicable al elemento con el atributo *id="parrafo"* y a todos los elementos que tengan el atributo *class="estilo"*.
Las reglas de estilo se aplicarán exclusivamente a los elementos que contengan los atributos definidos.
| 0.244904 | 0.896478 |
<img src="images/utfsm.png" alt="" width="200px" align="right"/>
# USM Numérica
## Errores en Python
### Objetivos
1. Aprender a diagosticar y solucionar errores comunes en python.
2. Aprender técnicas comunes de debugging.
## 0.1 Instrucciones
Las instrucciones de instalación y uso de un ipython notebook se encuentran en el siguiente [link](link).
Después de descargar y abrir el presente notebook, recuerden:
* Desarrollar los problemas de manera secuencial.
* Guardar constantemente con *`Ctr-S`* para evitar sorpresas.
* Reemplazar en las celdas de código donde diga *`FIX_ME`* por el código correspondiente.
* Ejecutar cada celda de código utilizando *`Ctr-Enter`*
## 0.2 Licenciamiento y Configuración
Ejecutar la siguiente celda mediante *`Ctr-S`*.
```
"""
IPython Notebook v4.0 para python 3.0
Librerías adicionales: IPython, pdb
Contenido bajo licencia CC-BY 4.0. Código bajo licencia MIT.
(c) Sebastian Flores, Christopher Cooper, Alberto Rubio, Pablo Bunout.
"""
# Configuración para recargar módulos y librerías dinámicamente
%reload_ext autoreload
%autoreload 2
# Configuración para graficos en línea
%matplotlib inline
# Configuración de estilo
from IPython.core.display import HTML
HTML(open("./style/style.css", "r").read())
```
## Contenido
1. Introducción
2. Técnicas de debugging.
## Sobre el Notebook
Existen 4 desafíos:
* En todos los casos, documenten lo encontrado. Escriban como un #comentario o """comentario""" los errores que vayan detectando.
* En el desafío 1: Ejecute la celda, lea el output y arregle el código. Comente los 5 errores en la misma celda.
* En el desafío 2: Ejecute la celda y encuentre los errores utilizando print. Comente los 3 errores en la misma celda.
* En el desafío 3: Ejecute el archivo ./mat281_code/desafio_3.py, y encuentre los 3 errores utilizando pdb.set_trace()
* En el desafío 4: Ejecute el archivo ./mat281_code/desafio_4.py, y encuentre los 3 errores utilizando IPython.embed()
## 1. Introducción
**Debugging**: Eliminación de errores de un programa computacional.
* Fácilmente 40-60% del tiempo utilizado en la creación de un programa.
* Ningún programa está excento de bugs/errores.
* Imposible garantizar utilización 100% segura por parte del usuario.
* Programas computaciones tienen inconsistencias/errores de implementación.
* ¡Hardware también puede tener errores!
## 1. Introducción
**¿Porqué se le llama bugs?**
Existen registros en la correspondencia de Thomas Edisson, en 1848, hablaba de **bugs** para referirse a errores en sus inventos. El término se utilizaba ocasionalmente en el dominio informático. En 1947, el ordenador Mark II presentaba un error. Al buscar el origen del error, los técnicos encontraron una polilla, que se había introducido en la máquina.
<img src="images/bug.jpg" alt="" width="600px" align="middle"/>
Toda la historia en el siguiente [enlace a wikipedia (ingles)](https://en.wikipedia.org/wiki/Software_bug).
## 2. Técnicas para Debug
1. Leer output entregado por python para posibles errores
2. Utilizando **print**
3. Utilizando **pdb**: **p**ython **d**ebu**g**ger
4. Lanzamiento condicional de **Ipython embed**
## 2.1 Debug: Leer output de errores
Cuando el programa no funciona y entrega un error normalmente es fácil solucionarlo.
El mensaje de error entregará: la línea donde se detecta el error y el tipo de error.
**PROS**:
* Explicativo
* Fácil de detectar y reparar
**CONTRA**:
* No todos los errores arrojan error, particularmente los errores conceptuales.
## 2.1.1 Lista de errores comunes
Los errores más comunes en un programa son los siguientes:
* SyntaxError:
* Parentésis no cierran adecuadamente.
* Faltan comillas en un string.
* Falta dos puntos para definir un bloque if-elif-ese, una función, o un ciclo.
* NameError:
* Se está usando una variable que no existe (nombre mal escrito o se define después de donde es utilizada)
* Todavía no se ha definido la función o variable.
* No se ha importado el módulo requerido
* IOError: El archivo a abrir no existe.
* KeyError: La llave no existe en el diccionario.
* TypeError: La función no puede aplicarse sobre el objeto.
* IndentationError: Los bloques de código no están bien definidos. Revisar la indentación.
Un error clásico y que es dificil de detectar es la **asignación involuntaria**: Escribir $a=b$ cuando realmente se quiere testear la igualdad $a==b$.
## Desafío 1
Arregle el siguiente programa en python para que funcione. Contiene 5 errores. Anote los errores como comentarios en el código.
Al ejecutar sin errores, debería regresar el valor 0.333384348536
```
import numpy as np
def promedio_positivo(a):
pos_mean = a[a>0].mean()
return pos_mean
N = 100
x = np.linspace(-1,1,N)
y = 0.5 - x**2 # No cambiar esta linea
print(promedio_positivo(y))
# Error 1:
# Error 2:
# Error 3:
# Error 4:
# Error 5:
```
## 2.2 Debug: Utilización de print
Utilizar **print** es la técnica más sencilla y habitual, apropiada si los errores son sencillos.
**PRO**:
* Fácil y rápido de implementar.
* Permite inspeccionar valores de variable a lo largo de todo un programa
**CONTRA**:
* Requiere escribir expresiones más complicadas para estudiar más de una variable simultáneamente.
* Impresión no ayuda para estudiar datos multidimensionales (arreglos, matrices, diccionarios grandes).
* Eliminacion de múltiples print puede ser compleja en programa grande.
* Inapropiado si la ejecución del programa tarde demasiado (por ejemplo si tiene que leer un archivo de disco), pues habitualmente se van insertando prints a lo largo de varias ejecuciones "persiguiendo" el valor de una variable.
#### Consejo
Si se desea inspeccionar la variable mi_variable_con_error, utilice
print("!!!" + str(mi_variable_con_error))
o bien
print(mi_variable_con_error) #!!!
De esa forma será más facil ver en el output donde está la variable impresa, y luego de solucionar el bug, será también más fácil eliminar las expresiones print que han sido insertadas para debugear (no se confundirá con los print que sí son necesarios y naturales al programa).
## Desafío 2
Detecte porqué el programa se comporta de manera inadecuada, utilizando print donde parezca adecuado.
No elimine los print que usted haya introducido, sólo coméntelos con #.
Arregle el desperfecto e indique con un comentario en el código donde estaba el error.
```
def fibonacci(n):
"""
Debe regresar la lista con los primeros n numeros de fibonacci.
Para n<1, regresar [].
Para n=1, regresar [1].
Para n=2, regresar [1,1].
Para n=3, regresar [1,1,2].
Para n=4, regresar [1,1,2,3].
Y sucesivamente
"""
a = 1
b = 1
fib = [a,b]
count = 2
if n<1:
return []
if n=1:
return [1]
while count <= n:
aux = a
a = b
b = aux + b
count += 1
fib.append(aux)
return fib
print "fibonacci(-1):", fibonacci(-1) # Deberia ser []
print "fibonacci(0):", fibonacci(0) # Deberia ser []
print "fibonacci(1):", fibonacci(1) # Deberia ser [1]
print "fibonacci(2):", fibonacci(2) # Deberia ser [1,1]
print "fibonacci(3):", fibonacci(3) # Deberia ser [1,1,2]
print "fibonacci(5):", fibonacci(5) # Deberia ser [1,1,2,3,5]
print "fibonacci(10):", fibonacci(10) # Deberia ser ...
"""
ERRORES DETECTADOS:
1)
2)
3)
"""
```
## 2.3 Debug: Utilización de pdb
Python trae un debugger por defecto: pdb (**p**ython **d**e**b**ugger), que guarda similaridades con gdb (el debugger de C).
**PRO**:
* Permite inspeccionar el estado real de la máquina en un instante dado.
* Permite ejecutar las instrucciones siguientes.
**CONTRA**:
* Requiere conocer comandos.
* No tiene completación por tabulación como IPython.
El funcionamiento de pdb similar a los breakpoints en matlab.
Se debe realizar lo siguiente:
1. Importar la librería
import pdb
2. Solicitar que se ejecute la inspección en las líneas que potencialmente tienen el error. Para ello es necesario insertar en una nueva línea, con el alineamiento adecuado, lo siguiente:
pdb.set_trace()
3. Ejecutar el programa como se realizaría normalmente:
$ python mi_programa_con_error.py
Al realizar las acciones anteriores, pdb ejecuta todas las instrucciones hasta el primer pdb.set_trace() y regresa el terminal al usuario, para que inspeccione las variables y revise el código. Los comandos principales a memorizar son:
* **n + Enter**: Permite ejecutar la siguiente instrucción (línea).
* **c + Enter**: Permite continar la ejecución del programa, hasta el próximo pdb.set_trace() o el final del programa.
* **l + Enter**: Permite ver qué línea esta actualmente en ejecución.
* **p mi_variable + Enter**: Imprime la variable mi_variable.
* **Enter**: Ejecuta la última accion realizada en pdb.
## 2.3.1 Ejemplo
Ejecute el archivo ./mat281_code/ejemplo_pdb.py y siga las instrucciones que obtendrá:
$ python ./mat281_code/ejemplo_pdb.py
## Desafío 3
Utilice **pdb** para debuggear el archivo ***./mat281_code/desafio_3.py***.
El desafío 3 consiste en hallar 3 errores en la implementación defectuosa del método de la secante:
[link wikipedia](https://es.wikipedia.org/wiki/M%C3%A9todo_de_la_secante)
Instrucciones:
* Después de utilizar **pdb.set_trace()** no borre la línea creada, solo coméntela con **#** para poder revisar su utilización.
* Anote en la celda a continuación los errores que ha encontrado en el archivo **./mat281_code/desafio_3.py**
```
# Desafio 3 - Errores encontrados en ./mat281_code/desafio_3.py
"""
Se detectaron los siguientes errores:
1- FIX ME - COMENTAR AQUI
2- FIX ME - COMENTAR AQUI
3- FIX ME - COMENTAR AQUI
"""
```
## 2.4 Debug: Utilización de IPython
**PRO**:
* Permite inspeccionar el estado real de la máquina en un instante dado.
* Permite calcular cualquier expresión, de manera sencilla.
* Permite graficar, imprimir matrices, etc.
* Tiene completación por tabulación de IPython.
* Tiene todo el poder de IPython (%who, %whos, etc.)
**CONTRA**:
* No permite avanzar a la próxima instrucción como n+Enter en pdb.
El funcionamiento de IPython es el siguiente:
1. Importar la librería
import IPython
2. Solicitar que se ejecute la inspección en las líneas que potencialmente tienen el error. Para ello es necesario insertar en una nueva línea, con el alineamiento adecuado, lo siguiente:
IPython.embed()
3. Ejecutar el programa como se realizaría normalmente:
$ python mi_programa_con_error.py
Al realizar las acciones anteriores, python ejecuta todas las instrucciones hasta el primer IPython.embed() y regresa el terminal interactivo IPython al usuario en el punto seleccionado, para que inspeccione las variables y revise el código.
Para salir de IPython es necesario utilizar ***Ctr+d***.
## 2.3.1 Ejemplo
Ejecute el archivo **./mat281_code/ejemplo_ipython.py** y siga las instrucciones que obtendrá:
$ python ./mat281_code/ejemplo_ipython.py
## Desafío 4
Utilice **IPython** para debuggear el archivo ***./mat281_code/desafio_4.py***.
El desafío 4 consiste en reparar una implementación defectuosa del método de bisección:
[link wikipedia](https://es.wikipedia.org/wiki/M%C3%A9todo_de_bisecci%C3%B3n)
Instrucciones:
* Después de utilizar **IPython.embed()** no borre la línea, solo coméntela con # para poder revisar su utilización.
* Anote en la celda a continuación los errores que ha encontrado en el archivo **./mat281_code/desafio_4.py**
```
# Desafio 4 - Errores encontrados en ./mat281_code/desafio_4.py
"""
Se detectaron los siguientes errores:
1- FIX ME - COMENTAR AQUI
2- FIX ME - COMENTAR AQUI
3- FIX ME - COMENTAR AQUI
"""
```
## Resumen
El siguiente [blog](http://pythonforbiologists.com/index.php/29-common-beginner-python-errors-on-one-page/) tiene una imagen que resume gran parte de los errores más comunes:
<img src="images/errores.png" alt="" width="1200px" align="middle"/>
|
github_jupyter
|
"""
IPython Notebook v4.0 para python 3.0
Librerías adicionales: IPython, pdb
Contenido bajo licencia CC-BY 4.0. Código bajo licencia MIT.
(c) Sebastian Flores, Christopher Cooper, Alberto Rubio, Pablo Bunout.
"""
# Configuración para recargar módulos y librerías dinámicamente
%reload_ext autoreload
%autoreload 2
# Configuración para graficos en línea
%matplotlib inline
# Configuración de estilo
from IPython.core.display import HTML
HTML(open("./style/style.css", "r").read())
import numpy as np
def promedio_positivo(a):
pos_mean = a[a>0].mean()
return pos_mean
N = 100
x = np.linspace(-1,1,N)
y = 0.5 - x**2 # No cambiar esta linea
print(promedio_positivo(y))
# Error 1:
# Error 2:
# Error 3:
# Error 4:
# Error 5:
def fibonacci(n):
"""
Debe regresar la lista con los primeros n numeros de fibonacci.
Para n<1, regresar [].
Para n=1, regresar [1].
Para n=2, regresar [1,1].
Para n=3, regresar [1,1,2].
Para n=4, regresar [1,1,2,3].
Y sucesivamente
"""
a = 1
b = 1
fib = [a,b]
count = 2
if n<1:
return []
if n=1:
return [1]
while count <= n:
aux = a
a = b
b = aux + b
count += 1
fib.append(aux)
return fib
print "fibonacci(-1):", fibonacci(-1) # Deberia ser []
print "fibonacci(0):", fibonacci(0) # Deberia ser []
print "fibonacci(1):", fibonacci(1) # Deberia ser [1]
print "fibonacci(2):", fibonacci(2) # Deberia ser [1,1]
print "fibonacci(3):", fibonacci(3) # Deberia ser [1,1,2]
print "fibonacci(5):", fibonacci(5) # Deberia ser [1,1,2,3,5]
print "fibonacci(10):", fibonacci(10) # Deberia ser ...
"""
ERRORES DETECTADOS:
1)
2)
3)
"""
# Desafio 3 - Errores encontrados en ./mat281_code/desafio_3.py
"""
Se detectaron los siguientes errores:
1- FIX ME - COMENTAR AQUI
2- FIX ME - COMENTAR AQUI
3- FIX ME - COMENTAR AQUI
"""
# Desafio 4 - Errores encontrados en ./mat281_code/desafio_4.py
"""
Se detectaron los siguientes errores:
1- FIX ME - COMENTAR AQUI
2- FIX ME - COMENTAR AQUI
3- FIX ME - COMENTAR AQUI
"""
| 0.270384 | 0.939803 |
Download employee_reviews.csv from https://www.kaggle.com/petersunga/google-amazon-facebook-employee-reviews
```
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
# show plots
%matplotlib inline
from scipy import stats
from keras.datasets import imdb
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import LSTM, Dropout
from keras.layers.embeddings import Embedding
from keras.preprocessing import sequence
from keras.preprocessing.text import Tokenizer
import numpy as np
from sklearn.model_selection import train_test_split
# fix random seed for reproducibility
numpy.random.seed(7)
# keep the top n words, zero the rest
# this is used for tokenizer and embedding
top_words = 5000
def tidy_count(df,groupbyvars):
stats = df.groupby(groupbyvars).size().\
reset_index().rename(columns={0: 'n'}).sort_values('n',ascending=False)
stats['percent'] = stats['n'] / sum(stats['n'])
return(stats)
```
https://machinelearningmastery.com/sequence-classification-lstm-recurrent-neural-networks-python-keras/
```
# Load data
reviews = pd.read_csv('employee_reviews.csv')
reviews['overall-ratings'] = reviews['overall-ratings'].astype(int) # convert to int
# Create binary flag for if the review was positive (4+)
reviews['pos_ovr'] = False
reviews.loc[reviews['overall-ratings'] >= 4,'pos_ovr'] = True
tidy_count(reviews,'pos_ovr')
#reviews.dtypes
reviews.sample(3)
reviews_sample = reviews.sample(n=10000,random_state=42)
# CV split
X_train, X_test, y_train, y_test = train_test_split(reviews_sample['pros'] + ' ' + reviews_sample['cons'], reviews_sample['pos_ovr'],
test_size=0.33, random_state=42)
tkizer = Tokenizer(num_words=top_words) # initialize
# fit the tokenizer object on the documents
tkizer.fit_on_texts(X_train.tolist() + X_test.tolist())
# Tokenize into sequences
X_train_tokens = tkizer.texts_to_sequences(X_train)
X_test_tokens = tkizer.texts_to_sequences(X_test)
# Find word count for each document
token_lengths = [len(x) for x in X_train_tokens] + [len(x) for x in X_test_tokens]
```
Plot the number of words in each document
```
sns.distplot(token_lengths, hist=False, rug=False)
plt.xlim(0, 500)
len(X_train)
#tkizer.word_index
# truncate and pad input sequences
max_review_length = 300 # maximum number of words we look at in a review
X_train_pad = sequence.pad_sequences(X_train_tokens, maxlen=max_review_length)
X_test_pad = sequence.pad_sequences(X_test_tokens, maxlen=max_review_length)
# create the model
embedding_vecor_length = 32
model = Sequential()
model.add(Embedding(top_words, embedding_vecor_length, input_length=max_review_length))
#model.add(Dropout(0.2))
model.add(LSTM(100,dropout=0.5, recurrent_dropout=0.5))
model.add(Dense(1, activation='sigmoid'))
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
print(model.summary())
model.fit(X_train_pad, y_train, validation_data=(X_test_pad, y_test), epochs=10, batch_size=128)
```
|
github_jupyter
|
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
# show plots
%matplotlib inline
from scipy import stats
from keras.datasets import imdb
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import LSTM, Dropout
from keras.layers.embeddings import Embedding
from keras.preprocessing import sequence
from keras.preprocessing.text import Tokenizer
import numpy as np
from sklearn.model_selection import train_test_split
# fix random seed for reproducibility
numpy.random.seed(7)
# keep the top n words, zero the rest
# this is used for tokenizer and embedding
top_words = 5000
def tidy_count(df,groupbyvars):
stats = df.groupby(groupbyvars).size().\
reset_index().rename(columns={0: 'n'}).sort_values('n',ascending=False)
stats['percent'] = stats['n'] / sum(stats['n'])
return(stats)
# Load data
reviews = pd.read_csv('employee_reviews.csv')
reviews['overall-ratings'] = reviews['overall-ratings'].astype(int) # convert to int
# Create binary flag for if the review was positive (4+)
reviews['pos_ovr'] = False
reviews.loc[reviews['overall-ratings'] >= 4,'pos_ovr'] = True
tidy_count(reviews,'pos_ovr')
#reviews.dtypes
reviews.sample(3)
reviews_sample = reviews.sample(n=10000,random_state=42)
# CV split
X_train, X_test, y_train, y_test = train_test_split(reviews_sample['pros'] + ' ' + reviews_sample['cons'], reviews_sample['pos_ovr'],
test_size=0.33, random_state=42)
tkizer = Tokenizer(num_words=top_words) # initialize
# fit the tokenizer object on the documents
tkizer.fit_on_texts(X_train.tolist() + X_test.tolist())
# Tokenize into sequences
X_train_tokens = tkizer.texts_to_sequences(X_train)
X_test_tokens = tkizer.texts_to_sequences(X_test)
# Find word count for each document
token_lengths = [len(x) for x in X_train_tokens] + [len(x) for x in X_test_tokens]
sns.distplot(token_lengths, hist=False, rug=False)
plt.xlim(0, 500)
len(X_train)
#tkizer.word_index
# truncate and pad input sequences
max_review_length = 300 # maximum number of words we look at in a review
X_train_pad = sequence.pad_sequences(X_train_tokens, maxlen=max_review_length)
X_test_pad = sequence.pad_sequences(X_test_tokens, maxlen=max_review_length)
# create the model
embedding_vecor_length = 32
model = Sequential()
model.add(Embedding(top_words, embedding_vecor_length, input_length=max_review_length))
#model.add(Dropout(0.2))
model.add(LSTM(100,dropout=0.5, recurrent_dropout=0.5))
model.add(Dense(1, activation='sigmoid'))
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
print(model.summary())
model.fit(X_train_pad, y_train, validation_data=(X_test_pad, y_test), epochs=10, batch_size=128)
| 0.861989 | 0.788705 |
# Programmatically retrieving information about simulation tools registered with BioSimulators
[BioSimulators](https://biosimulators.org) contains extensive information about simulation software tools. This includes information about the model formats (e.g., CellML, SBML), modeling frameworks (e.g., flux balance, logical, ordinary differential equations), simulation types (e.g., steady-state, time course), and algorithms (e.g., CVODE, SSA) supported by each tool. This information can be helpful for finding an appropriate simulation tool for a specific project and for using simulation tools, especially with the [Simulation Experiment Description Markup Langauge (SED-ML)](http://sed-ml.org/).
This information can be retrieved using [BioSimulators' REST API](https://api.biosimulators.org). This API returns information about simulation tools in [JavaScript Object Notation (JSON)](https://www.json.org/) format. The schemas that BioSimulators uses are described in the [documentation](https://api.biosimulators.org) for the API. The API follows the [OpenAPI](https://swagger.io/specification/) standards.
These schemas utilize several ontologies:
* Funding agencies: [FunderRegistry](https://www.crossref.org/services/funder-registry/)
* Modeling frameworks: [Systems Biology Ontology (SBO)](https://wwwdev.ebi.ac.uk/sbo/)
* Modeling formats: [EDAM](https://edamontology.org/page) and [SED-ML model language URNs](https://sed-ml.org/urns.html)
* Output dimensions: [Semanticscience Integrated Ontology (SIO)](https://semanticscience.org/)
* Outputs of implicit simulation variables: [SED-ML symbol URNs](https://sed-ml.org/urns.html)
* Programming languages: [Linguist](https://github.com/github/linguist)
* Simulation algorithms, their parameters, and their outputs: [Kinetic Simulation Algorithm Ontology (KiSAO)](https://github.com/SED-ML/KiSAO)
* Software licenses: [Software Package Data Exchange (SPDX)](https://spdx.org/licenses)
This tutorial illustrates how to programmatically retrieve information about simulation tools for BioSimulators' REST API. Please see the other tools for more information about using simulation tools to execute individual simulations and entire simulation projects.
## 1. Retrieve a list of the simulation tools registered with BioSimulators
Import the [`requests`](https://docs.python-requests.org/en/latest/) package to run HTTP requests to BioSimulators' API.
```
import requests
```
The https://api.biosimulators.org/simulators/latest endpoint provides a list of all of the registered simulation tools and information about their most recent versions. Next, use the requests package to query this endpoint.
```
response = requests.get('https://api.biosimulators.org/simulators/latest')
```
Run the `raise_for_status` method to check that the request succeeded.
```
response.raise_for_status()
```
Call the `json` method to get the data returned by BioSimulators' API.
```
simulators = {simulator['id']: simulator for simulator in response.json()}
```
Get one simulation tool.
```
simulator = simulators['cobrapy']
```
Print out information about the tool
```
import yaml
print(yaml.dump(simulator))
```
## 2. Find the validated simulation tools that provide Python APIs
```
simulators_with_apis = {}
for id, simulator in simulators.items():
if simulator['biosimulators']['validated'] and simulator.get('pythonApi', None):
simulators_with_apis[id] = simulator
print(sorted(simulators_with_apis.keys()))
```
## 3. Find the simulation tools that support a particular model format (e.g. SBML, [EDAM:format_2585](https://www.ebi.ac.uk/ols/ontologies/edam/terms?iri=http%3A%2F%2Fedamontology.org%2Fformat_2585))
```
sbml_simulators = {}
for id, simulator in simulators_with_apis.items():
for algorithm in simulator['algorithms']:
for model_format in algorithm['modelFormats']:
if model_format['id'] == 'format_2585':
sbml_simulators[id] = simulator
print(sorted(sbml_simulators.keys()))
```
## 4. Find the simulation tools that support a particular modeling framework (e.g. ODE, [SBO:0000293](https://www.ebi.ac.uk/sbo/main/SBO:0000293))
```
ode_simulators = {}
for id, simulator in simulators_with_apis.items():
for algorithm in simulator['algorithms']:
for model_format in algorithm['modelingFrameworks']:
if model_format['id'] == 'SBO_0000293':
ode_simulators[id] = simulator
print(sorted(ode_simulators.keys()))
```
## 5. Find the simulation tools that support a particular type of simulation or analysis (e.g. SED-ML uniform time course, `SedUniformTimeCourseSimulation`)
```
time_course_simulators = {}
for id, simulator in simulators_with_apis.items():
for algorithm in simulator['algorithms']:
if 'SedUniformTimeCourseSimulation' in algorithm['simulationTypes']:
time_course_simulators[id] = simulator
print(sorted(time_course_simulators.keys()))
```
## 6. Find the simulation tools that support a particular algorithm (e.g. CVODE, [KISAO_0000019](https://www.ebi.ac.uk/ols/ontologies/kisao/terms?iri=http%3A%2F%2Fwww.biomodels.net%2Fkisao%2FKISAO%23KISAO_0000019))
```
cvode_simulators = {}
for id, simulator in simulators_with_apis.items():
for algorithm in simulator['algorithms']:
if algorithm['kisaoId']['id'] == 'KISAO_0000019':
cvode_simulators[id] = simulator
print(sorted(cvode_simulators.keys()))
```
## 7. Get a specific simulation tool such as [COPASI](http://copasi.org/)
```
copasi = simulators['copasi']
```
## 8. Get the algorithms implemented by the tool
```
algorithms = {}
for algorithm in copasi['algorithms']:
kisao_id = algorithm['kisaoId']['id']
algorithms[kisao_id] = algorithm
print(sorted(algorithms.keys()))
```
## 9. Get a specific algorithm implemented by the tool, such as LSODA, [KISAO_0000560](https://www.ebi.ac.uk/ols/ontologies/kisao/terms?iri=http%3A%2F%2Fwww.biomodels.net%2Fkisao%2FKISAO%23KISAO_0000560))
```
lsoda = algorithms['KISAO_0000560']
```
## 10. Get additional information about the algorithm from the KiSAO ontology
```
from kisao import Kisao
kisao = Kisao()
term = kisao.get_term(lsoda['kisaoId']['id'])
print(term.name)
```
## 11. Get the parameters of the algorithm and their names, data types, and default values
```
parameters = {}
for parameter in lsoda['parameters']:
parameters[parameter['kisaoId']['id']] = {
'name': kisao.get_term(parameter['kisaoId']['id']).name,
'type': parameter['type'],
'value': parameter['value'],
}
print(yaml.dump(parameters))
```
## 12. Get the model changes supported by the implementation of the algorithm by the tool
```
print(yaml.dump(algorithm['modelChangePatterns']))
```
## 13. Get the observables supported by the implementation of the algorithm by the tool
```
print(yaml.dump(algorithm['outputVariablePatterns']))
```
## 14. Get more information about model formats and modeling frameworks
Information about all of the ontologies used by BioSimulators is available from [BioSimulations' ontology REST API](https://api.biosimulations.org/). Documentation is available inline at this URL. The API can be queried as illustrated below to retrieve information about specific terms, such as the Systems Biology Markup Language (SBML) ([EDAM:format_2585](https://www.ebi.ac.uk/ols/ontologies/edam/terms?iri=http%3A%2F%2Fedamontology.org%2Fformat_2585)) and ordinary differential equations (ODES) ([SBO_0000293](https://www.ebi.ac.uk/ols/ontologies/sbo/terms?iri=http%3A%2F%2Fbiomodels.net%2FSBO%2FSBO_0000293)).
```
response = requests.get('https://api.biosimulations.org/ontologies/EDAM/format_2585')
response.raise_for_status()
print(yaml.dump(response.json()))
response = requests.get('https://api.biosimulations.org/ontologies/SBO/SBO_0000293')
response.raise_for_status()
print(yaml.dump(response.json()))
```
```
import importlib
api = importlib.import_module(copasi['pythonApi']['module'])
```
## 16. Use the API for the simulator to get its version and the available version of the tool
```
print(api.__version__)
print(api.get_simulator_version())
```
|
github_jupyter
|
import requests
response = requests.get('https://api.biosimulators.org/simulators/latest')
response.raise_for_status()
simulators = {simulator['id']: simulator for simulator in response.json()}
simulator = simulators['cobrapy']
import yaml
print(yaml.dump(simulator))
simulators_with_apis = {}
for id, simulator in simulators.items():
if simulator['biosimulators']['validated'] and simulator.get('pythonApi', None):
simulators_with_apis[id] = simulator
print(sorted(simulators_with_apis.keys()))
sbml_simulators = {}
for id, simulator in simulators_with_apis.items():
for algorithm in simulator['algorithms']:
for model_format in algorithm['modelFormats']:
if model_format['id'] == 'format_2585':
sbml_simulators[id] = simulator
print(sorted(sbml_simulators.keys()))
ode_simulators = {}
for id, simulator in simulators_with_apis.items():
for algorithm in simulator['algorithms']:
for model_format in algorithm['modelingFrameworks']:
if model_format['id'] == 'SBO_0000293':
ode_simulators[id] = simulator
print(sorted(ode_simulators.keys()))
time_course_simulators = {}
for id, simulator in simulators_with_apis.items():
for algorithm in simulator['algorithms']:
if 'SedUniformTimeCourseSimulation' in algorithm['simulationTypes']:
time_course_simulators[id] = simulator
print(sorted(time_course_simulators.keys()))
cvode_simulators = {}
for id, simulator in simulators_with_apis.items():
for algorithm in simulator['algorithms']:
if algorithm['kisaoId']['id'] == 'KISAO_0000019':
cvode_simulators[id] = simulator
print(sorted(cvode_simulators.keys()))
copasi = simulators['copasi']
algorithms = {}
for algorithm in copasi['algorithms']:
kisao_id = algorithm['kisaoId']['id']
algorithms[kisao_id] = algorithm
print(sorted(algorithms.keys()))
lsoda = algorithms['KISAO_0000560']
from kisao import Kisao
kisao = Kisao()
term = kisao.get_term(lsoda['kisaoId']['id'])
print(term.name)
parameters = {}
for parameter in lsoda['parameters']:
parameters[parameter['kisaoId']['id']] = {
'name': kisao.get_term(parameter['kisaoId']['id']).name,
'type': parameter['type'],
'value': parameter['value'],
}
print(yaml.dump(parameters))
print(yaml.dump(algorithm['modelChangePatterns']))
print(yaml.dump(algorithm['outputVariablePatterns']))
response = requests.get('https://api.biosimulations.org/ontologies/EDAM/format_2585')
response.raise_for_status()
print(yaml.dump(response.json()))
response = requests.get('https://api.biosimulations.org/ontologies/SBO/SBO_0000293')
response.raise_for_status()
print(yaml.dump(response.json()))
import importlib
api = importlib.import_module(copasi['pythonApi']['module'])
print(api.__version__)
print(api.get_simulator_version())
| 0.2359 | 0.987289 |
```
import torch.utils.data as utils
import torch.nn.functional as F
import torch
import torch.nn as nn
from torch.autograd import Variable
from torch.nn.parameter import Parameter
import numpy as np
import pandas as pd
import math
import time
import matplotlib.pyplot as plt
%matplotlib inline
print(torch.__version__)
def PrepareDataset(speed_matrix, BATCH_SIZE = 40, seq_len = 10, pred_len = 1, train_propotion = 0.7, valid_propotion = 0.2):
""" Prepare training and testing datasets and dataloaders.
Convert speed/volume/occupancy matrix to training and testing dataset.
The vertical axis of speed_matrix is the time axis and the horizontal axis
is the spatial axis.
Args:
speed_matrix: a Matrix containing spatial-temporal speed data for a network
seq_len: length of input sequence
pred_len: length of predicted sequence
Returns:
Training dataloader
Testing dataloader
"""
time_len = speed_matrix.shape[0]
max_speed = speed_matrix.max().max()
speed_matrix = speed_matrix / max_speed
speed_sequences, speed_labels = [], []
for i in range(time_len - seq_len - pred_len):
speed_sequences.append(speed_matrix.iloc[i:i+seq_len].values)
speed_labels.append(speed_matrix.iloc[i+seq_len:i+seq_len+pred_len].values)
speed_sequences, speed_labels = np.asarray(speed_sequences), np.asarray(speed_labels)
# shuffle and split the dataset to training and testing datasets
sample_size = speed_sequences.shape[0]
index = np.arange(sample_size, dtype = int)
np.random.shuffle(index)
train_index = int(np.floor(sample_size * train_propotion))
valid_index = int(np.floor(sample_size * ( train_propotion + valid_propotion)))
train_data, train_label = speed_sequences[:train_index], speed_labels[:train_index]
valid_data, valid_label = speed_sequences[train_index:valid_index], speed_labels[train_index:valid_index]
test_data, test_label = speed_sequences[valid_index:], speed_labels[valid_index:]
train_data, train_label = torch.Tensor(train_data), torch.Tensor(train_label)
valid_data, valid_label = torch.Tensor(valid_data), torch.Tensor(valid_label)
test_data, test_label = torch.Tensor(test_data), torch.Tensor(test_label)
train_dataset = utils.TensorDataset(train_data, train_label)
valid_dataset = utils.TensorDataset(valid_data, valid_label)
test_dataset = utils.TensorDataset(test_data, test_label)
train_dataloader = utils.DataLoader(train_dataset, batch_size = BATCH_SIZE, shuffle=True, drop_last = True)
valid_dataloader = utils.DataLoader(valid_dataset, batch_size = BATCH_SIZE, shuffle=True, drop_last = True)
test_dataloader = utils.DataLoader(test_dataset, batch_size = BATCH_SIZE, shuffle=True, drop_last = True)
return train_dataloader, valid_dataloader, test_dataloader, max_speed
if __name__ == "__main__":
# data = 'inrix'
data = 'loop'
directory = '../../Data_Warehouse/Data_network_traffic/'
if data == 'inrix':
speed_matrix = pd.read_pickle( directory + 'inrix_seattle_speed_matrix_2012')
A = np.load(directory + 'INRIX_Seattle_2012_A.npy')
FFR_5min = np.load(directory + 'INRIX_Seattle_2012_reachability_free_flow_5min.npy')
FFR_10min = np.load(directory + 'INRIX_Seattle_2012_reachability_free_flow_10min.npy')
FFR_15min = np.load(directory + 'INRIX_Seattle_2012_reachability_free_flow_15min.npy')
FFR_20min = np.load(directory + 'INRIX_Seattle_2012_reachability_free_flow_20min.npy')
FFR_25min = np.load(directory + 'INRIX_Seattle_2012_reachability_free_flow_25min.npy')
FFR = [FFR_5min, FFR_10min, FFR_15min, FFR_20min, FFR_25min]
elif data == 'loop':
speed_matrix = pd.read_pickle( directory + 'speed_matrix_2015')
A = np.load( directory + 'Loop_Seattle_2015_A.npy')
FFR_5min = np.load( directory + 'Loop_Seattle_2015_reachability_free_flow_5min.npy')
FFR_10min = np.load( directory + 'Loop_Seattle_2015_reachability_free_flow_10min.npy')
FFR_15min = np.load( directory + 'Loop_Seattle_2015_reachability_free_flow_15min.npy')
FFR_20min = np.load( directory + 'Loop_Seattle_2015_reachability_free_flow_20min.npy')
FFR_25min = np.load( directory + 'Loop_Seattle_2015_reachability_free_flow_25min.npy')
FFR = [FFR_5min, FFR_10min, FFR_15min, FFR_20min, FFR_25min]
train_dataloader, valid_dataloader, test_dataloader, max_speed = PrepareDataset(speed_matrix)
inputs, labels = next(iter(train_dataloader))
[batch_size, step_size, fea_size] = inputs.size()
input_dim = fea_size
hidden_dim = fea_size
output_dim = fea_size
def TrainModel(model, train_dataloader, valid_dataloader, learning_rate = 1e-5, num_epochs = 300, patience = 10, min_delta = 0.00001):
inputs, labels = next(iter(train_dataloader))
[batch_size, step_size, fea_size] = inputs.size()
input_dim = fea_size
hidden_dim = fea_size
output_dim = fea_size
model.cuda()
loss_MSE = torch.nn.MSELoss()
loss_L1 = torch.nn.L1Loss()
learning_rate = 1e-5
optimizer = torch.optim.RMSprop(model.parameters(), lr = learning_rate)
use_gpu = torch.cuda.is_available()
interval = 100
losses_train = []
losses_valid = []
losses_epochs_train = []
losses_epochs_valid = []
cur_time = time.time()
pre_time = time.time()
# Variables for Early Stopping
is_best_model = 0
patient_epoch = 0
for epoch in range(num_epochs):
# print('Epoch {}/{}'.format(epoch, num_epochs - 1))
# print('-' * 10)
trained_number = 0
valid_dataloader_iter = iter(valid_dataloader)
losses_epoch_train = []
losses_epoch_valid = []
for data in train_dataloader:
inputs, labels = data
if inputs.shape[0] != batch_size:
continue
if use_gpu:
inputs, labels = Variable(inputs.cuda()), Variable(labels.cuda())
else:
inputs, labels = Variable(inputs), Variable(labels)
model.zero_grad()
outputs = model(inputs)
loss_train = loss_MSE(outputs, torch.squeeze(labels))
losses_train.append(loss_train.data)
losses_epoch_train.append(loss_train.data)
optimizer.zero_grad()
loss_train.backward()
optimizer.step()
# validation
try:
inputs_val, labels_val = next(valid_dataloader_iter)
except StopIteration:
valid_dataloader_iter = iter(valid_dataloader)
inputs_val, labels_val = next(valid_dataloader_iter)
if use_gpu:
inputs_val, labels_val = Variable(inputs_val.cuda()), Variable(labels_val.cuda())
else:
inputs_val, labels_val = Variable(inputs_val), Variable(labels_val)
outputs_val= model(inputs_val)
loss_valid = loss_MSE(outputs_val, torch.squeeze(labels_val))
losses_valid.append(loss_valid.data)
losses_epoch_valid.append(loss_valid.data)
# output
trained_number += 1
avg_losses_epoch_train = sum(losses_epoch_train) / float(len(losses_epoch_train))
avg_losses_epoch_valid = sum(losses_epoch_valid) / float(len(losses_epoch_valid))
losses_epochs_train.append(avg_losses_epoch_train)
losses_epochs_valid.append(avg_losses_epoch_valid)
# Early Stopping
if epoch == 0:
is_best_model = 1
best_model = model
min_loss_epoch_valid = 10000.0
if avg_losses_epoch_valid < min_loss_epoch_valid:
min_loss_epoch_valid = avg_losses_epoch_valid
else:
if min_loss_epoch_valid - avg_losses_epoch_valid > min_delta:
is_best_model = 1
best_model = model
min_loss_epoch_valid = avg_losses_epoch_valid
patient_epoch = 0
else:
is_best_model = 0
patient_epoch += 1
if patient_epoch >= patience:
print('Early Stopped at Epoch:', epoch)
break
# Print training parameters
cur_time = time.time()
print('Epoch: {}, train_loss: {}, valid_loss: {}, time: {}, best model: {}'.format( \
epoch, \
np.around(avg_losses_epoch_train, decimals=8),\
np.around(avg_losses_epoch_valid, decimals=8),\
np.around([cur_time - pre_time] , decimals=2),\
is_best_model) )
pre_time = cur_time
return best_model, [losses_train, losses_valid, losses_epochs_train, losses_epochs_valid]
def TestModel(model, test_dataloader, max_speed):
inputs, labels = next(iter(test_dataloader))
[batch_size, step_size, fea_size] = inputs.size()
cur_time = time.time()
pre_time = time.time()
use_gpu = torch.cuda.is_available()
loss_MSE = torch.nn.MSELoss()
loss_L1 = torch.nn.MSELoss()
tested_batch = 0
losses_mse = []
losses_l1 = []
for data in test_dataloader:
inputs, labels = data
if inputs.shape[0] != batch_size:
continue
if use_gpu:
inputs, labels = Variable(inputs.cuda()), Variable(labels.cuda())
else:
inputs, labels = Variable(inputs), Variable(labels)
# rnn.loop()
hidden = model.initHidden(batch_size)
outputs = None
outputs = model(inputs)
loss_MSE = torch.nn.MSELoss()
loss_L1 = torch.nn.L1Loss()
loss_mse = loss_MSE(outputs, torch.squeeze(labels))
loss_l1 = loss_L1(outputs, torch.squeeze(labels))
losses_mse.append(loss_mse.cpu().data.numpy())
losses_l1.append(loss_l1.cpu().data.numpy())
tested_batch += 1
if tested_batch % 1000 == 0:
cur_time = time.time()
print('Tested #: {}, loss_l1: {}, loss_mse: {}, time: {}'.format( \
tested_batch * batch_size, \
np.around([loss_l1.data[0]], decimals=8), \
np.around([loss_mse.data[0]], decimals=8), \
np.around([cur_time - pre_time], decimals=8) ) )
pre_time = cur_time
losses_l1 = np.array(losses_l1)
losses_mse = np.array(losses_mse)
mean_l1 = np.mean(losses_l1) * max_speed
std_l1 = np.std(losses_l1) * max_speed
print('Tested: L1_mean: {}, L1_std : {}'.format(mean_l1, std_l1))
return [losses_l1, losses_mse, mean_l1, std_l1]
class LSTM(nn.Module):
def __init__(self, input_size, cell_size, hidden_size, output_last = True):
"""
cell_size is the size of cell_state.
hidden_size is the size of hidden_state, or say the output_state of each step
"""
super(LSTM, self).__init__()
self.cell_size = cell_size
self.hidden_size = hidden_size
self.fl = nn.Linear(input_size + hidden_size, hidden_size)
self.il = nn.Linear(input_size + hidden_size, hidden_size)
self.ol = nn.Linear(input_size + hidden_size, hidden_size)
self.Cl = nn.Linear(input_size + hidden_size, hidden_size)
self.output_last = output_last
def step(self, input, Hidden_State, Cell_State):
combined = torch.cat((input, Hidden_State), 1)
f = F.sigmoid(self.fl(combined))
i = F.sigmoid(self.il(combined))
o = F.sigmoid(self.ol(combined))
C = F.tanh(self.Cl(combined))
Cell_State = f * Cell_State + i * C
Hidden_State = o * F.tanh(Cell_State)
return Hidden_State, Cell_State
def forward(self, inputs):
batch_size = inputs.size(0)
time_step = inputs.size(1)
Hidden_State, Cell_State = self.initHidden(batch_size)
if self.output_last:
for i in range(time_step):
Hidden_State, Cell_State = self.step(torch.squeeze(inputs[:,i:i+1,:]), Hidden_State, Cell_State)
return Hidden_State
else:
outputs = None
for i in range(time_step):
Hidden_State, Cell_State = self.step(torch.squeeze(inputs[:,i:i+1,:]), Hidden_State, Cell_State)
if outputs is None:
outputs = Hidden_State.unsqueeze(1)
else:
outputs = torch.cat((outputs, Hidden_State.unsqueeze(1)), 1)
return outputs
def initHidden(self, batch_size):
use_gpu = torch.cuda.is_available()
if use_gpu:
Hidden_State = Variable(torch.zeros(batch_size, self.hidden_size).cuda())
Cell_State = Variable(torch.zeros(batch_size, self.hidden_size).cuda())
return Hidden_State, Cell_State
else:
Hidden_State = Variable(torch.zeros(batch_size, self.hidden_size))
Cell_State = Variable(torch.zeros(batch_size, self.hidden_size))
return Hidden_State, Cell_State
class ConvLSTM(nn.Module):
def __init__(self, input_size, cell_size, hidden_size, output_last = True):
"""
cell_size is the size of cell_state.
hidden_size is the size of hidden_state, or say the output_state of each step
"""
super(ConvLSTM, self).__init__()
self.cell_size = cell_size
self.hidden_size = hidden_size
self.fl = nn.Linear(input_size + hidden_size, hidden_size)
self.il = nn.Linear(input_size + hidden_size, hidden_size)
self.ol = nn.Linear(input_size + hidden_size, hidden_size)
self.Cl = nn.Linear(input_size + hidden_size, hidden_size)
self.conv = nn.Conv1d(1, hidden_size, hidden_size)
self.output_last = output_last
def step(self, input, Hidden_State, Cell_State):
conv = self.conv(input)
combined = torch.cat((conv, Hidden_State), 1)
f = F.sigmoid(self.fl(combined))
i = F.sigmoid(self.il(combined))
o = F.sigmoid(self.ol(combined))
C = F.tanh(self.Cl(combined))
Cell_State = f * Cell_State + i * C
Hidden_State = o * F.tanh(Cell_State)
return Hidden_State, Cell_State
def forward(self, inputs):
batch_size = inputs.size(0)
time_step = inputs.size(1)
Hidden_State, Cell_State = self.initHidden(batch_size)
if self.output_last:
for i in range(time_step):
Hidden_State, Cell_State = self.step(torch.squeeze(inputs[:,i:i+1,:]), Hidden_State, Cell_State)
return Hidden_State
else:
outputs = None
for i in range(time_step):
Hidden_State, Cell_State = self.step(torch.squeeze(inputs[:,i:i+1,:]), Hidden_State, Cell_State)
if outputs is None:
outputs = Hidden_State.unsqueeze(1)
else:
outputs = torch.cat((outputs, Hidden_State.unsqueeze(1)), 1)
return outputs
def initHidden(self, batch_size):
use_gpu = torch.cuda.is_available()
if use_gpu:
Hidden_State = Variable(torch.zeros(batch_size, self.hidden_size).cuda())
Cell_State = Variable(torch.zeros(batch_size, self.hidden_size).cuda())
return Hidden_State, Cell_State
else:
Hidden_State = Variable(torch.zeros(batch_size, self.hidden_size))
Cell_State = Variable(torch.zeros(batch_size, self.hidden_size))
return Hidden_State, Cell_State
class LocalizedSpectralGraphConvolution(nn.Module):
def __init__(self, A, K):
super(LocalizedSpectralGraphConvolution, self).__init__()
self.K = K
self.A = A.cuda()
feature_size = A.shape[0]
self.D = torch.diag(torch.sum(self.A, dim=0)).cuda()
I = torch.eye(feature_size,feature_size).cuda()
self.L = I - torch.inverse(torch.sqrt(self.D)).matmul(self.A).matmul(torch.inverse(torch.sqrt(self.D)))
L_temp = I
for i in range(K):
L_temp = torch.matmul(L_temp, self.L)
if i == 0:
self.L_tensor = torch.unsqueeze(L_temp, 2)
else:
self.L_tensor = torch.cat((self.L_tensor, torch.unsqueeze(L_temp, 2)), 2)
self.L_tensor = Variable(self.L_tensor.cuda(), requires_grad=False)
self.params = Parameter(torch.FloatTensor(K).cuda())
stdv = 1. / math.sqrt(K)
for i in range(K):
self.params[i].data.uniform_(-stdv, stdv)
def forward(self, input):
x = input
conv = x.matmul( torch.sum(self.params.expand_as(self.L_tensor) * self.L_tensor, 2) )
return conv
class LocalizedSpectralGraphConvolutionalLSTM(nn.Module):
def __init__(self, K, A, feature_size, Clamp_A=True, output_last = True):
'''
Args:
K: K-hop graph
A: adjacency matrix
FFR: free-flow reachability matrix
feature_size: the dimension of features
Clamp_A: Boolean value, clamping all elements of A between 0. to 1.
'''
super(LocalizedSpectralGraphConvolutionalLSTM, self).__init__()
self.feature_size = feature_size
self.hidden_size = feature_size
self.K = K
self.A = A
self.gconv = LocalizedSpectralGraphConvolution(A, K)
hidden_size = self.feature_size
input_size = self.feature_size + hidden_size
self.fl = nn.Linear(input_size, hidden_size)
self.il = nn.Linear(input_size, hidden_size)
self.ol = nn.Linear(input_size, hidden_size)
self.Cl = nn.Linear(input_size, hidden_size)
self.output_last = output_last
def step(self, input, Hidden_State, Cell_State):
# conv_sample_start = time.time()
conv = F.relu(self.gconv(input))
# conv_sample_end = time.time()
# print('conv_sample:', (conv_sample_end - conv_sample_start))
combined = torch.cat((conv, Hidden_State), 1)
f = F.sigmoid(self.fl(combined))
i = F.sigmoid(self.il(combined))
o = F.sigmoid(self.ol(combined))
C = F.tanh(self.Cl(combined))
Cell_State = f * Cell_State + i * C
Hidden_State = o * F.tanh(Cell_State)
return Hidden_State, Cell_State
def Bi_torch(self, a):
a[a < 0] = 0
a[a > 0] = 1
return a
def forward(self, inputs):
batch_size = inputs.size(0)
time_step = inputs.size(1)
Hidden_State, Cell_State = self.initHidden(batch_size)
outputs = None
for i in range(time_step):
Hidden_State, Cell_State = self.step(torch.squeeze(inputs[:,i:i+1,:]), Hidden_State, Cell_State)
if outputs is None:
outputs = Hidden_State.unsqueeze(1)
else:
outputs = torch.cat((outputs, Hidden_State.unsqueeze(1)), 1)
# print(type(outputs))
if self.output_last:
return outputs[:,-1,:]
else:
return outputs
def initHidden(self, batch_size):
use_gpu = torch.cuda.is_available()
if use_gpu:
Hidden_State = Variable(torch.zeros(batch_size, self.hidden_size).cuda())
Cell_State = Variable(torch.zeros(batch_size, self.hidden_size).cuda())
return Hidden_State, Cell_State
else:
Hidden_State = Variable(torch.zeros(batch_size, self.hidden_size))
Cell_State = Variable(torch.zeros(batch_size, self.hidden_size))
return Hidden_State, Cell_State
def reinitHidden(self, batch_size, Hidden_State_data, Cell_State_data):
use_gpu = torch.cuda.is_available()
if use_gpu:
Hidden_State = Variable(Hidden_State_data.cuda(), requires_grad=True)
Cell_State = Variable(Cell_State_data.cuda(), requires_grad=True)
return Hidden_State, Cell_State
else:
Hidden_State = Variable(Hidden_State_data, requires_grad=True)
Cell_State = Variable(Cell_State_data, requires_grad=True)
return Hidden_State, Cell_State
class SpectralGraphConvolution(nn.Module):
def __init__(self, A):
super(SpectralGraphConvolution, self).__init__()
feature_size = A.shape[0]
self.A = A
self.D = torch.diag(torch.sum(self.A, dim=0))
self.L = D - A
self.param = Parameter(torch.FloatTensor(feature_size).cuda())
stdv = 1. / math.sqrt(feature_size)
self.param.data.uniform_(-stdv, stdv)
self.e, self.v = torch.eig(L_, eigenvectors=True)
self.vt = torch.t(self.v)
self.v = Variable(self.v.cuda(), requires_grad=False)
self.vt = Variable(self.vt.cuda(), requires_grad=False)
def forward(self, input):
x = input
conv_sample_start = time.time()
conv = x.matmul(self.v.matmul(torch.diag(self.param)).matmul(self.vt))
conv_sample_end = time.time()
print('conv_sample:', (conv_sample_end - conv_sample_start))
return conv
class SpectralGraphConvolutionalLSTM(nn.Module):
def __init__(self, K, A, feature_size, Clamp_A=True, output_last = True):
'''
Args:
K: K-hop graph
A: adjacency matrix
FFR: free-flow reachability matrix
feature_size: the dimension of features
Clamp_A: Boolean value, clamping all elements of A between 0. to 1.
'''
super(SpectralGraphConvolutionalLSTM, self).__init__()
self.feature_size = feature_size
self.hidden_size = feature_size
self.K = K
self.A = A
self.gconv = SpectralGraphConvolution(A)
hidden_size = self.feature_size
input_size = self.feature_size + hidden_size
self.fl = nn.Linear(input_size, hidden_size)
self.il = nn.Linear(input_size, hidden_size)
self.ol = nn.Linear(input_size, hidden_size)
self.Cl = nn.Linear(input_size, hidden_size)
self.output_last = output_last
def step(self, input, Hidden_State, Cell_State):
conv_sample_start = time.time()
conv = self.gconv(input)
conv_sample_end = time.time()
print('conv_sample:', (conv_sample_end - conv_sample_start))
combined = torch.cat((conv, Hidden_State), 1)
f = F.sigmoid(self.fl(combined))
i = F.sigmoid(self.il(combined))
o = F.sigmoid(self.ol(combined))
C = F.tanh(self.Cl(combined))
Cell_State = f * Cell_State + i * C
Hidden_State = o * F.tanh(Cell_State)
return Hidden_State, Cell_State
def Bi_torch(self, a):
a[a < 0] = 0
a[a > 0] = 1
return a
def forward(self, inputs):
batch_size = inputs.size(0)
time_step = inputs.size(1)
Hidden_State, Cell_State = self.initHidden(batch_size)
outputs = None
train_sample_start = time.time()
for i in range(time_step):
Hidden_State, Cell_State = self.step(torch.squeeze(inputs[:,i:i+1,:]), Hidden_State, Cell_State)
if outputs is None:
outputs = Hidden_State.unsqueeze(1)
else:
outputs = torch.cat((outputs, Hidden_State.unsqueeze(1)), 1)
train_sample_end = time.time()
print('train sample:' , (train_sample_end - train_sample_start))
if self.output_last:
return outputs[:,-1,:]
else:
return outputs
def initHidden(self, batch_size):
use_gpu = torch.cuda.is_available()
if use_gpu:
Hidden_State = Variable(torch.zeros(batch_size, self.hidden_size).cuda())
Cell_State = Variable(torch.zeros(batch_size, self.hidden_size).cuda())
return Hidden_State, Cell_State
else:
Hidden_State = Variable(torch.zeros(batch_size, self.hidden_size))
Cell_State = Variable(torch.zeros(batch_size, self.hidden_size))
return Hidden_State, Cell_State
def reinitHidden(self, batch_size, Hidden_State_data, Cell_State_data):
use_gpu = torch.cuda.is_available()
if use_gpu:
Hidden_State = Variable(Hidden_State_data.cuda(), requires_grad=True)
Cell_State = Variable(Cell_State_data.cuda(), requires_grad=True)
return Hidden_State, Cell_State
else:
Hidden_State = Variable(Hidden_State_data, requires_grad=True)
Cell_State = Variable(Cell_State_data, requires_grad=True)
return Hidden_State, Cell_State
class GraphConvolutionalLSTM(nn.Module):
def __init__(self, K, A, FFR, feature_size, Clamp_A=True, output_last = True):
'''
Args:
K: K-hop graph
A: adjacency matrix
FFR: free-flow reachability matrix
feature_size: the dimension of features
Clamp_A: Boolean value, clamping all elements of A between 0. to 1.
'''
super(GraphConvolutionalLSTM, self).__init__()
self.feature_size = feature_size
self.hidden_size = feature_size
self.K = K
self.A_list = [] # Adjacency Matrix List
A = torch.FloatTensor(A)
A_temp = torch.eye(feature_size,feature_size)
for i in range(K):
A_temp = torch.matmul(A_temp, torch.Tensor(A))
if Clamp_A:
# confine elements of A
A_temp = torch.clamp(A_temp, max = 1.)
self.A_list.append(torch.mul(A_temp, torch.Tensor(FFR)))
# self.A_list.append(A_temp)
# a length adjustable Module List for hosting all graph convolutions
self.gc_list = nn.ModuleList([FilterLinear(feature_size, feature_size, self.A_list[i], bias=False) for i in range(K)])
hidden_size = self.feature_size
input_size = self.feature_size * K
self.fl = nn.Linear(input_size + hidden_size, hidden_size)
self.il = nn.Linear(input_size + hidden_size, hidden_size)
self.ol = nn.Linear(input_size + hidden_size, hidden_size)
self.Cl = nn.Linear(input_size + hidden_size, hidden_size)
# initialize the neighbor weight for the cell state
self.Neighbor_weight = Parameter(torch.FloatTensor(feature_size))
stdv = 1. / math.sqrt(feature_size)
self.Neighbor_weight.data.uniform_(-stdv, stdv)
self.output_last = output_last
def step(self, input, Hidden_State, Cell_State):
x = input
gc = self.gc_list[0](x)
for i in range(1, self.K):
gc = torch.cat((gc, self.gc_list[i](x)), 1)
combined = torch.cat((gc, Hidden_State), 1)
f = F.sigmoid(self.fl(combined))
i = F.sigmoid(self.il(combined))
o = F.sigmoid(self.ol(combined))
C = F.tanh(self.Cl(combined))
NC = torch.mul(Cell_State, torch.mv(Variable(self.A_list[-1], requires_grad=False).cuda(), self.Neighbor_weight))
Cell_State = f * NC + i * C
Hidden_State = o * F.tanh(Cell_State)
return Hidden_State, Cell_State, gc
def Bi_torch(self, a):
a[a < 0] = 0
a[a > 0] = 1
return a
def forward(self, inputs):
batch_size = inputs.size(0)
time_step = inputs.size(1)
Hidden_State, Cell_State = self.initHidden(batch_size)
outputs = None
for i in range(time_step):
Hidden_State, Cell_State, gc = self.step(torch.squeeze(inputs[:,i:i+1,:]), Hidden_State, Cell_State)
if outputs is None:
outputs = Hidden_State.unsqueeze(1)
else:
outputs = torch.cat((outputs, Hidden_State.unsqueeze(1)), 1)
if self.output_last:
return outputs[:,-1,:]
else:
return outputs
def initHidden(self, batch_size):
use_gpu = torch.cuda.is_available()
if use_gpu:
Hidden_State = Variable(torch.zeros(batch_size, self.hidden_size).cuda())
Cell_State = Variable(torch.zeros(batch_size, self.hidden_size).cuda())
return Hidden_State, Cell_State
else:
Hidden_State = Variable(torch.zeros(batch_size, self.hidden_size))
Cell_State = Variable(torch.zeros(batch_size, self.hidden_size))
return Hidden_State, Cell_State
def reinitHidden(self, batch_size, Hidden_State_data, Cell_State_data):
use_gpu = torch.cuda.is_available()
if use_gpu:
Hidden_State = Variable(Hidden_State_data.cuda(), requires_grad=True)
Cell_State = Variable(Cell_State_data.cuda(), requires_grad=True)
return Hidden_State, Cell_State
else:
Hidden_State = Variable(Hidden_State_data, requires_grad=True)
Cell_State = Variable(Cell_State_data, requires_grad=True)
return Hidden_State, Cell_State
lstm = LSTM(input_dim, hidden_dim, output_dim, output_last = True)
lstm, lstm_loss = TrainModel(lstm, train_dataloader, valid_dataloader, num_epochs = 1)
lstm_test = TestModel(lstm, test_dataloader, max_speed )
K = 64
Clamp_A = False
lsgclstm = LocalizedSpectralGraphConvolutionalLSTM(K, torch.Tensor(A), A.shape[0], Clamp_A=Clamp_A, output_last = True)
lsgclstm, lsgclstm_loss = TrainModel(lsgclstm, train_dataloader, valid_dataloader, num_epochs = 1)
lsgclstm_test = TestModel(lsgclstm, test_dataloader, max_speed )
K = 3
back_length = 3
Clamp_A = False
sgclstm = SpectralGraphConvolutionalLSTM(K, torch.Tensor(A), A.shape[0], Clamp_A=Clamp_A, output_last = True)
sgclstm, sgclstm_loss = TrainModel(sgclstm, train_dataloader, valid_dataloader, num_epochs = 1)
sgclstm_test = TestModel(sgclstm, test_dataloader, max_speed )
K = 3
back_length = 3
Clamp_A = False
gclstm = GraphConvolutionalLSTM(K, torch.Tensor(A), FFR[back_length], A.shape[0], Clamp_A=Clamp_A, output_last = True)
gclstm, gclstm_loss = TrainModel(gclstm, train_dataloader, valid_dataloader, num_epochs = 1)
gclstm_test = TestModel(gclstm, test_dataloader, max_speed )
rnn_val_loss = np.asarray(rnn_loss[3])
lstm_val_loss = np.asarray(lstm_loss[3])
hgclstm_val_loss = np.asarray(gclstm_loss[3])
lsgclstm_val_loss = np.asarray(lsgclstm_loss[3])
sgclstm_val_loss = np.asarray(sgclstm_loss[3])
lstm_val_loss = np.load('lstm_val_loss.npy')
hgclstm_val_loss = np.load('hgclstm_val_loss.npy')
lsgclstm_val_loss = np.load('lsgclstm_val_loss.npy')
sgclstm_val_loss = np.load('sgclstm_val_loss.npy')
# np.save('lstm_val_loss', lstm_val_loss)
# np.save('hgclstm_val_loss', gclstm_val_loss)
# np.save('lsgclstm_val_loss', lsgclstm_val_loss)
# np.save('sgclstm_val_loss', sgclstm_val_loss)
fig, ax = plt.subplots()
plt.plot(np.arange(1, len(lstm_val_loss) + 1), lstm_val_loss, label = 'LSTM')
plt.plot(np.arange(1, len(sgclstm_val_loss) + 1), sgclstm_val_loss, label = 'SGC+LSTM')
plt.plot(np.arange(1, len(lsgclstm_val_loss) + 1), lsgclstm_val_loss, label = 'LSGC+LSTM')
plt.plot(np.arange(1, len(hgclstm_val_loss) + 1),hgclstm_val_loss, label = 'HGC-LSTM')
plt.ylim((6 * 0.0001, 0.0019))
plt.xticks(fontsize = 12)
plt.yticks(fontsize = 12)
plt.yscale('log')
plt.ylabel('Validation Loss (MSE)', fontsize=12)
plt.xlabel('Epoch', fontsize=12)
# plt.gca().invert_xaxis()
plt.legend(fontsize=14)
plt.grid(True, which='both')
plt.savefig('Validation_loss.png', dpi=300, bbox_inches = 'tight', pad_inches=0.1)
```
|
github_jupyter
|
import torch.utils.data as utils
import torch.nn.functional as F
import torch
import torch.nn as nn
from torch.autograd import Variable
from torch.nn.parameter import Parameter
import numpy as np
import pandas as pd
import math
import time
import matplotlib.pyplot as plt
%matplotlib inline
print(torch.__version__)
def PrepareDataset(speed_matrix, BATCH_SIZE = 40, seq_len = 10, pred_len = 1, train_propotion = 0.7, valid_propotion = 0.2):
""" Prepare training and testing datasets and dataloaders.
Convert speed/volume/occupancy matrix to training and testing dataset.
The vertical axis of speed_matrix is the time axis and the horizontal axis
is the spatial axis.
Args:
speed_matrix: a Matrix containing spatial-temporal speed data for a network
seq_len: length of input sequence
pred_len: length of predicted sequence
Returns:
Training dataloader
Testing dataloader
"""
time_len = speed_matrix.shape[0]
max_speed = speed_matrix.max().max()
speed_matrix = speed_matrix / max_speed
speed_sequences, speed_labels = [], []
for i in range(time_len - seq_len - pred_len):
speed_sequences.append(speed_matrix.iloc[i:i+seq_len].values)
speed_labels.append(speed_matrix.iloc[i+seq_len:i+seq_len+pred_len].values)
speed_sequences, speed_labels = np.asarray(speed_sequences), np.asarray(speed_labels)
# shuffle and split the dataset to training and testing datasets
sample_size = speed_sequences.shape[0]
index = np.arange(sample_size, dtype = int)
np.random.shuffle(index)
train_index = int(np.floor(sample_size * train_propotion))
valid_index = int(np.floor(sample_size * ( train_propotion + valid_propotion)))
train_data, train_label = speed_sequences[:train_index], speed_labels[:train_index]
valid_data, valid_label = speed_sequences[train_index:valid_index], speed_labels[train_index:valid_index]
test_data, test_label = speed_sequences[valid_index:], speed_labels[valid_index:]
train_data, train_label = torch.Tensor(train_data), torch.Tensor(train_label)
valid_data, valid_label = torch.Tensor(valid_data), torch.Tensor(valid_label)
test_data, test_label = torch.Tensor(test_data), torch.Tensor(test_label)
train_dataset = utils.TensorDataset(train_data, train_label)
valid_dataset = utils.TensorDataset(valid_data, valid_label)
test_dataset = utils.TensorDataset(test_data, test_label)
train_dataloader = utils.DataLoader(train_dataset, batch_size = BATCH_SIZE, shuffle=True, drop_last = True)
valid_dataloader = utils.DataLoader(valid_dataset, batch_size = BATCH_SIZE, shuffle=True, drop_last = True)
test_dataloader = utils.DataLoader(test_dataset, batch_size = BATCH_SIZE, shuffle=True, drop_last = True)
return train_dataloader, valid_dataloader, test_dataloader, max_speed
if __name__ == "__main__":
# data = 'inrix'
data = 'loop'
directory = '../../Data_Warehouse/Data_network_traffic/'
if data == 'inrix':
speed_matrix = pd.read_pickle( directory + 'inrix_seattle_speed_matrix_2012')
A = np.load(directory + 'INRIX_Seattle_2012_A.npy')
FFR_5min = np.load(directory + 'INRIX_Seattle_2012_reachability_free_flow_5min.npy')
FFR_10min = np.load(directory + 'INRIX_Seattle_2012_reachability_free_flow_10min.npy')
FFR_15min = np.load(directory + 'INRIX_Seattle_2012_reachability_free_flow_15min.npy')
FFR_20min = np.load(directory + 'INRIX_Seattle_2012_reachability_free_flow_20min.npy')
FFR_25min = np.load(directory + 'INRIX_Seattle_2012_reachability_free_flow_25min.npy')
FFR = [FFR_5min, FFR_10min, FFR_15min, FFR_20min, FFR_25min]
elif data == 'loop':
speed_matrix = pd.read_pickle( directory + 'speed_matrix_2015')
A = np.load( directory + 'Loop_Seattle_2015_A.npy')
FFR_5min = np.load( directory + 'Loop_Seattle_2015_reachability_free_flow_5min.npy')
FFR_10min = np.load( directory + 'Loop_Seattle_2015_reachability_free_flow_10min.npy')
FFR_15min = np.load( directory + 'Loop_Seattle_2015_reachability_free_flow_15min.npy')
FFR_20min = np.load( directory + 'Loop_Seattle_2015_reachability_free_flow_20min.npy')
FFR_25min = np.load( directory + 'Loop_Seattle_2015_reachability_free_flow_25min.npy')
FFR = [FFR_5min, FFR_10min, FFR_15min, FFR_20min, FFR_25min]
train_dataloader, valid_dataloader, test_dataloader, max_speed = PrepareDataset(speed_matrix)
inputs, labels = next(iter(train_dataloader))
[batch_size, step_size, fea_size] = inputs.size()
input_dim = fea_size
hidden_dim = fea_size
output_dim = fea_size
def TrainModel(model, train_dataloader, valid_dataloader, learning_rate = 1e-5, num_epochs = 300, patience = 10, min_delta = 0.00001):
inputs, labels = next(iter(train_dataloader))
[batch_size, step_size, fea_size] = inputs.size()
input_dim = fea_size
hidden_dim = fea_size
output_dim = fea_size
model.cuda()
loss_MSE = torch.nn.MSELoss()
loss_L1 = torch.nn.L1Loss()
learning_rate = 1e-5
optimizer = torch.optim.RMSprop(model.parameters(), lr = learning_rate)
use_gpu = torch.cuda.is_available()
interval = 100
losses_train = []
losses_valid = []
losses_epochs_train = []
losses_epochs_valid = []
cur_time = time.time()
pre_time = time.time()
# Variables for Early Stopping
is_best_model = 0
patient_epoch = 0
for epoch in range(num_epochs):
# print('Epoch {}/{}'.format(epoch, num_epochs - 1))
# print('-' * 10)
trained_number = 0
valid_dataloader_iter = iter(valid_dataloader)
losses_epoch_train = []
losses_epoch_valid = []
for data in train_dataloader:
inputs, labels = data
if inputs.shape[0] != batch_size:
continue
if use_gpu:
inputs, labels = Variable(inputs.cuda()), Variable(labels.cuda())
else:
inputs, labels = Variable(inputs), Variable(labels)
model.zero_grad()
outputs = model(inputs)
loss_train = loss_MSE(outputs, torch.squeeze(labels))
losses_train.append(loss_train.data)
losses_epoch_train.append(loss_train.data)
optimizer.zero_grad()
loss_train.backward()
optimizer.step()
# validation
try:
inputs_val, labels_val = next(valid_dataloader_iter)
except StopIteration:
valid_dataloader_iter = iter(valid_dataloader)
inputs_val, labels_val = next(valid_dataloader_iter)
if use_gpu:
inputs_val, labels_val = Variable(inputs_val.cuda()), Variable(labels_val.cuda())
else:
inputs_val, labels_val = Variable(inputs_val), Variable(labels_val)
outputs_val= model(inputs_val)
loss_valid = loss_MSE(outputs_val, torch.squeeze(labels_val))
losses_valid.append(loss_valid.data)
losses_epoch_valid.append(loss_valid.data)
# output
trained_number += 1
avg_losses_epoch_train = sum(losses_epoch_train) / float(len(losses_epoch_train))
avg_losses_epoch_valid = sum(losses_epoch_valid) / float(len(losses_epoch_valid))
losses_epochs_train.append(avg_losses_epoch_train)
losses_epochs_valid.append(avg_losses_epoch_valid)
# Early Stopping
if epoch == 0:
is_best_model = 1
best_model = model
min_loss_epoch_valid = 10000.0
if avg_losses_epoch_valid < min_loss_epoch_valid:
min_loss_epoch_valid = avg_losses_epoch_valid
else:
if min_loss_epoch_valid - avg_losses_epoch_valid > min_delta:
is_best_model = 1
best_model = model
min_loss_epoch_valid = avg_losses_epoch_valid
patient_epoch = 0
else:
is_best_model = 0
patient_epoch += 1
if patient_epoch >= patience:
print('Early Stopped at Epoch:', epoch)
break
# Print training parameters
cur_time = time.time()
print('Epoch: {}, train_loss: {}, valid_loss: {}, time: {}, best model: {}'.format( \
epoch, \
np.around(avg_losses_epoch_train, decimals=8),\
np.around(avg_losses_epoch_valid, decimals=8),\
np.around([cur_time - pre_time] , decimals=2),\
is_best_model) )
pre_time = cur_time
return best_model, [losses_train, losses_valid, losses_epochs_train, losses_epochs_valid]
def TestModel(model, test_dataloader, max_speed):
inputs, labels = next(iter(test_dataloader))
[batch_size, step_size, fea_size] = inputs.size()
cur_time = time.time()
pre_time = time.time()
use_gpu = torch.cuda.is_available()
loss_MSE = torch.nn.MSELoss()
loss_L1 = torch.nn.MSELoss()
tested_batch = 0
losses_mse = []
losses_l1 = []
for data in test_dataloader:
inputs, labels = data
if inputs.shape[0] != batch_size:
continue
if use_gpu:
inputs, labels = Variable(inputs.cuda()), Variable(labels.cuda())
else:
inputs, labels = Variable(inputs), Variable(labels)
# rnn.loop()
hidden = model.initHidden(batch_size)
outputs = None
outputs = model(inputs)
loss_MSE = torch.nn.MSELoss()
loss_L1 = torch.nn.L1Loss()
loss_mse = loss_MSE(outputs, torch.squeeze(labels))
loss_l1 = loss_L1(outputs, torch.squeeze(labels))
losses_mse.append(loss_mse.cpu().data.numpy())
losses_l1.append(loss_l1.cpu().data.numpy())
tested_batch += 1
if tested_batch % 1000 == 0:
cur_time = time.time()
print('Tested #: {}, loss_l1: {}, loss_mse: {}, time: {}'.format( \
tested_batch * batch_size, \
np.around([loss_l1.data[0]], decimals=8), \
np.around([loss_mse.data[0]], decimals=8), \
np.around([cur_time - pre_time], decimals=8) ) )
pre_time = cur_time
losses_l1 = np.array(losses_l1)
losses_mse = np.array(losses_mse)
mean_l1 = np.mean(losses_l1) * max_speed
std_l1 = np.std(losses_l1) * max_speed
print('Tested: L1_mean: {}, L1_std : {}'.format(mean_l1, std_l1))
return [losses_l1, losses_mse, mean_l1, std_l1]
class LSTM(nn.Module):
def __init__(self, input_size, cell_size, hidden_size, output_last = True):
"""
cell_size is the size of cell_state.
hidden_size is the size of hidden_state, or say the output_state of each step
"""
super(LSTM, self).__init__()
self.cell_size = cell_size
self.hidden_size = hidden_size
self.fl = nn.Linear(input_size + hidden_size, hidden_size)
self.il = nn.Linear(input_size + hidden_size, hidden_size)
self.ol = nn.Linear(input_size + hidden_size, hidden_size)
self.Cl = nn.Linear(input_size + hidden_size, hidden_size)
self.output_last = output_last
def step(self, input, Hidden_State, Cell_State):
combined = torch.cat((input, Hidden_State), 1)
f = F.sigmoid(self.fl(combined))
i = F.sigmoid(self.il(combined))
o = F.sigmoid(self.ol(combined))
C = F.tanh(self.Cl(combined))
Cell_State = f * Cell_State + i * C
Hidden_State = o * F.tanh(Cell_State)
return Hidden_State, Cell_State
def forward(self, inputs):
batch_size = inputs.size(0)
time_step = inputs.size(1)
Hidden_State, Cell_State = self.initHidden(batch_size)
if self.output_last:
for i in range(time_step):
Hidden_State, Cell_State = self.step(torch.squeeze(inputs[:,i:i+1,:]), Hidden_State, Cell_State)
return Hidden_State
else:
outputs = None
for i in range(time_step):
Hidden_State, Cell_State = self.step(torch.squeeze(inputs[:,i:i+1,:]), Hidden_State, Cell_State)
if outputs is None:
outputs = Hidden_State.unsqueeze(1)
else:
outputs = torch.cat((outputs, Hidden_State.unsqueeze(1)), 1)
return outputs
def initHidden(self, batch_size):
use_gpu = torch.cuda.is_available()
if use_gpu:
Hidden_State = Variable(torch.zeros(batch_size, self.hidden_size).cuda())
Cell_State = Variable(torch.zeros(batch_size, self.hidden_size).cuda())
return Hidden_State, Cell_State
else:
Hidden_State = Variable(torch.zeros(batch_size, self.hidden_size))
Cell_State = Variable(torch.zeros(batch_size, self.hidden_size))
return Hidden_State, Cell_State
class ConvLSTM(nn.Module):
def __init__(self, input_size, cell_size, hidden_size, output_last = True):
"""
cell_size is the size of cell_state.
hidden_size is the size of hidden_state, or say the output_state of each step
"""
super(ConvLSTM, self).__init__()
self.cell_size = cell_size
self.hidden_size = hidden_size
self.fl = nn.Linear(input_size + hidden_size, hidden_size)
self.il = nn.Linear(input_size + hidden_size, hidden_size)
self.ol = nn.Linear(input_size + hidden_size, hidden_size)
self.Cl = nn.Linear(input_size + hidden_size, hidden_size)
self.conv = nn.Conv1d(1, hidden_size, hidden_size)
self.output_last = output_last
def step(self, input, Hidden_State, Cell_State):
conv = self.conv(input)
combined = torch.cat((conv, Hidden_State), 1)
f = F.sigmoid(self.fl(combined))
i = F.sigmoid(self.il(combined))
o = F.sigmoid(self.ol(combined))
C = F.tanh(self.Cl(combined))
Cell_State = f * Cell_State + i * C
Hidden_State = o * F.tanh(Cell_State)
return Hidden_State, Cell_State
def forward(self, inputs):
batch_size = inputs.size(0)
time_step = inputs.size(1)
Hidden_State, Cell_State = self.initHidden(batch_size)
if self.output_last:
for i in range(time_step):
Hidden_State, Cell_State = self.step(torch.squeeze(inputs[:,i:i+1,:]), Hidden_State, Cell_State)
return Hidden_State
else:
outputs = None
for i in range(time_step):
Hidden_State, Cell_State = self.step(torch.squeeze(inputs[:,i:i+1,:]), Hidden_State, Cell_State)
if outputs is None:
outputs = Hidden_State.unsqueeze(1)
else:
outputs = torch.cat((outputs, Hidden_State.unsqueeze(1)), 1)
return outputs
def initHidden(self, batch_size):
use_gpu = torch.cuda.is_available()
if use_gpu:
Hidden_State = Variable(torch.zeros(batch_size, self.hidden_size).cuda())
Cell_State = Variable(torch.zeros(batch_size, self.hidden_size).cuda())
return Hidden_State, Cell_State
else:
Hidden_State = Variable(torch.zeros(batch_size, self.hidden_size))
Cell_State = Variable(torch.zeros(batch_size, self.hidden_size))
return Hidden_State, Cell_State
class LocalizedSpectralGraphConvolution(nn.Module):
def __init__(self, A, K):
super(LocalizedSpectralGraphConvolution, self).__init__()
self.K = K
self.A = A.cuda()
feature_size = A.shape[0]
self.D = torch.diag(torch.sum(self.A, dim=0)).cuda()
I = torch.eye(feature_size,feature_size).cuda()
self.L = I - torch.inverse(torch.sqrt(self.D)).matmul(self.A).matmul(torch.inverse(torch.sqrt(self.D)))
L_temp = I
for i in range(K):
L_temp = torch.matmul(L_temp, self.L)
if i == 0:
self.L_tensor = torch.unsqueeze(L_temp, 2)
else:
self.L_tensor = torch.cat((self.L_tensor, torch.unsqueeze(L_temp, 2)), 2)
self.L_tensor = Variable(self.L_tensor.cuda(), requires_grad=False)
self.params = Parameter(torch.FloatTensor(K).cuda())
stdv = 1. / math.sqrt(K)
for i in range(K):
self.params[i].data.uniform_(-stdv, stdv)
def forward(self, input):
x = input
conv = x.matmul( torch.sum(self.params.expand_as(self.L_tensor) * self.L_tensor, 2) )
return conv
class LocalizedSpectralGraphConvolutionalLSTM(nn.Module):
def __init__(self, K, A, feature_size, Clamp_A=True, output_last = True):
'''
Args:
K: K-hop graph
A: adjacency matrix
FFR: free-flow reachability matrix
feature_size: the dimension of features
Clamp_A: Boolean value, clamping all elements of A between 0. to 1.
'''
super(LocalizedSpectralGraphConvolutionalLSTM, self).__init__()
self.feature_size = feature_size
self.hidden_size = feature_size
self.K = K
self.A = A
self.gconv = LocalizedSpectralGraphConvolution(A, K)
hidden_size = self.feature_size
input_size = self.feature_size + hidden_size
self.fl = nn.Linear(input_size, hidden_size)
self.il = nn.Linear(input_size, hidden_size)
self.ol = nn.Linear(input_size, hidden_size)
self.Cl = nn.Linear(input_size, hidden_size)
self.output_last = output_last
def step(self, input, Hidden_State, Cell_State):
# conv_sample_start = time.time()
conv = F.relu(self.gconv(input))
# conv_sample_end = time.time()
# print('conv_sample:', (conv_sample_end - conv_sample_start))
combined = torch.cat((conv, Hidden_State), 1)
f = F.sigmoid(self.fl(combined))
i = F.sigmoid(self.il(combined))
o = F.sigmoid(self.ol(combined))
C = F.tanh(self.Cl(combined))
Cell_State = f * Cell_State + i * C
Hidden_State = o * F.tanh(Cell_State)
return Hidden_State, Cell_State
def Bi_torch(self, a):
a[a < 0] = 0
a[a > 0] = 1
return a
def forward(self, inputs):
batch_size = inputs.size(0)
time_step = inputs.size(1)
Hidden_State, Cell_State = self.initHidden(batch_size)
outputs = None
for i in range(time_step):
Hidden_State, Cell_State = self.step(torch.squeeze(inputs[:,i:i+1,:]), Hidden_State, Cell_State)
if outputs is None:
outputs = Hidden_State.unsqueeze(1)
else:
outputs = torch.cat((outputs, Hidden_State.unsqueeze(1)), 1)
# print(type(outputs))
if self.output_last:
return outputs[:,-1,:]
else:
return outputs
def initHidden(self, batch_size):
use_gpu = torch.cuda.is_available()
if use_gpu:
Hidden_State = Variable(torch.zeros(batch_size, self.hidden_size).cuda())
Cell_State = Variable(torch.zeros(batch_size, self.hidden_size).cuda())
return Hidden_State, Cell_State
else:
Hidden_State = Variable(torch.zeros(batch_size, self.hidden_size))
Cell_State = Variable(torch.zeros(batch_size, self.hidden_size))
return Hidden_State, Cell_State
def reinitHidden(self, batch_size, Hidden_State_data, Cell_State_data):
use_gpu = torch.cuda.is_available()
if use_gpu:
Hidden_State = Variable(Hidden_State_data.cuda(), requires_grad=True)
Cell_State = Variable(Cell_State_data.cuda(), requires_grad=True)
return Hidden_State, Cell_State
else:
Hidden_State = Variable(Hidden_State_data, requires_grad=True)
Cell_State = Variable(Cell_State_data, requires_grad=True)
return Hidden_State, Cell_State
class SpectralGraphConvolution(nn.Module):
def __init__(self, A):
super(SpectralGraphConvolution, self).__init__()
feature_size = A.shape[0]
self.A = A
self.D = torch.diag(torch.sum(self.A, dim=0))
self.L = D - A
self.param = Parameter(torch.FloatTensor(feature_size).cuda())
stdv = 1. / math.sqrt(feature_size)
self.param.data.uniform_(-stdv, stdv)
self.e, self.v = torch.eig(L_, eigenvectors=True)
self.vt = torch.t(self.v)
self.v = Variable(self.v.cuda(), requires_grad=False)
self.vt = Variable(self.vt.cuda(), requires_grad=False)
def forward(self, input):
x = input
conv_sample_start = time.time()
conv = x.matmul(self.v.matmul(torch.diag(self.param)).matmul(self.vt))
conv_sample_end = time.time()
print('conv_sample:', (conv_sample_end - conv_sample_start))
return conv
class SpectralGraphConvolutionalLSTM(nn.Module):
def __init__(self, K, A, feature_size, Clamp_A=True, output_last = True):
'''
Args:
K: K-hop graph
A: adjacency matrix
FFR: free-flow reachability matrix
feature_size: the dimension of features
Clamp_A: Boolean value, clamping all elements of A between 0. to 1.
'''
super(SpectralGraphConvolutionalLSTM, self).__init__()
self.feature_size = feature_size
self.hidden_size = feature_size
self.K = K
self.A = A
self.gconv = SpectralGraphConvolution(A)
hidden_size = self.feature_size
input_size = self.feature_size + hidden_size
self.fl = nn.Linear(input_size, hidden_size)
self.il = nn.Linear(input_size, hidden_size)
self.ol = nn.Linear(input_size, hidden_size)
self.Cl = nn.Linear(input_size, hidden_size)
self.output_last = output_last
def step(self, input, Hidden_State, Cell_State):
conv_sample_start = time.time()
conv = self.gconv(input)
conv_sample_end = time.time()
print('conv_sample:', (conv_sample_end - conv_sample_start))
combined = torch.cat((conv, Hidden_State), 1)
f = F.sigmoid(self.fl(combined))
i = F.sigmoid(self.il(combined))
o = F.sigmoid(self.ol(combined))
C = F.tanh(self.Cl(combined))
Cell_State = f * Cell_State + i * C
Hidden_State = o * F.tanh(Cell_State)
return Hidden_State, Cell_State
def Bi_torch(self, a):
a[a < 0] = 0
a[a > 0] = 1
return a
def forward(self, inputs):
batch_size = inputs.size(0)
time_step = inputs.size(1)
Hidden_State, Cell_State = self.initHidden(batch_size)
outputs = None
train_sample_start = time.time()
for i in range(time_step):
Hidden_State, Cell_State = self.step(torch.squeeze(inputs[:,i:i+1,:]), Hidden_State, Cell_State)
if outputs is None:
outputs = Hidden_State.unsqueeze(1)
else:
outputs = torch.cat((outputs, Hidden_State.unsqueeze(1)), 1)
train_sample_end = time.time()
print('train sample:' , (train_sample_end - train_sample_start))
if self.output_last:
return outputs[:,-1,:]
else:
return outputs
def initHidden(self, batch_size):
use_gpu = torch.cuda.is_available()
if use_gpu:
Hidden_State = Variable(torch.zeros(batch_size, self.hidden_size).cuda())
Cell_State = Variable(torch.zeros(batch_size, self.hidden_size).cuda())
return Hidden_State, Cell_State
else:
Hidden_State = Variable(torch.zeros(batch_size, self.hidden_size))
Cell_State = Variable(torch.zeros(batch_size, self.hidden_size))
return Hidden_State, Cell_State
def reinitHidden(self, batch_size, Hidden_State_data, Cell_State_data):
use_gpu = torch.cuda.is_available()
if use_gpu:
Hidden_State = Variable(Hidden_State_data.cuda(), requires_grad=True)
Cell_State = Variable(Cell_State_data.cuda(), requires_grad=True)
return Hidden_State, Cell_State
else:
Hidden_State = Variable(Hidden_State_data, requires_grad=True)
Cell_State = Variable(Cell_State_data, requires_grad=True)
return Hidden_State, Cell_State
class GraphConvolutionalLSTM(nn.Module):
def __init__(self, K, A, FFR, feature_size, Clamp_A=True, output_last = True):
'''
Args:
K: K-hop graph
A: adjacency matrix
FFR: free-flow reachability matrix
feature_size: the dimension of features
Clamp_A: Boolean value, clamping all elements of A between 0. to 1.
'''
super(GraphConvolutionalLSTM, self).__init__()
self.feature_size = feature_size
self.hidden_size = feature_size
self.K = K
self.A_list = [] # Adjacency Matrix List
A = torch.FloatTensor(A)
A_temp = torch.eye(feature_size,feature_size)
for i in range(K):
A_temp = torch.matmul(A_temp, torch.Tensor(A))
if Clamp_A:
# confine elements of A
A_temp = torch.clamp(A_temp, max = 1.)
self.A_list.append(torch.mul(A_temp, torch.Tensor(FFR)))
# self.A_list.append(A_temp)
# a length adjustable Module List for hosting all graph convolutions
self.gc_list = nn.ModuleList([FilterLinear(feature_size, feature_size, self.A_list[i], bias=False) for i in range(K)])
hidden_size = self.feature_size
input_size = self.feature_size * K
self.fl = nn.Linear(input_size + hidden_size, hidden_size)
self.il = nn.Linear(input_size + hidden_size, hidden_size)
self.ol = nn.Linear(input_size + hidden_size, hidden_size)
self.Cl = nn.Linear(input_size + hidden_size, hidden_size)
# initialize the neighbor weight for the cell state
self.Neighbor_weight = Parameter(torch.FloatTensor(feature_size))
stdv = 1. / math.sqrt(feature_size)
self.Neighbor_weight.data.uniform_(-stdv, stdv)
self.output_last = output_last
def step(self, input, Hidden_State, Cell_State):
x = input
gc = self.gc_list[0](x)
for i in range(1, self.K):
gc = torch.cat((gc, self.gc_list[i](x)), 1)
combined = torch.cat((gc, Hidden_State), 1)
f = F.sigmoid(self.fl(combined))
i = F.sigmoid(self.il(combined))
o = F.sigmoid(self.ol(combined))
C = F.tanh(self.Cl(combined))
NC = torch.mul(Cell_State, torch.mv(Variable(self.A_list[-1], requires_grad=False).cuda(), self.Neighbor_weight))
Cell_State = f * NC + i * C
Hidden_State = o * F.tanh(Cell_State)
return Hidden_State, Cell_State, gc
def Bi_torch(self, a):
a[a < 0] = 0
a[a > 0] = 1
return a
def forward(self, inputs):
batch_size = inputs.size(0)
time_step = inputs.size(1)
Hidden_State, Cell_State = self.initHidden(batch_size)
outputs = None
for i in range(time_step):
Hidden_State, Cell_State, gc = self.step(torch.squeeze(inputs[:,i:i+1,:]), Hidden_State, Cell_State)
if outputs is None:
outputs = Hidden_State.unsqueeze(1)
else:
outputs = torch.cat((outputs, Hidden_State.unsqueeze(1)), 1)
if self.output_last:
return outputs[:,-1,:]
else:
return outputs
def initHidden(self, batch_size):
use_gpu = torch.cuda.is_available()
if use_gpu:
Hidden_State = Variable(torch.zeros(batch_size, self.hidden_size).cuda())
Cell_State = Variable(torch.zeros(batch_size, self.hidden_size).cuda())
return Hidden_State, Cell_State
else:
Hidden_State = Variable(torch.zeros(batch_size, self.hidden_size))
Cell_State = Variable(torch.zeros(batch_size, self.hidden_size))
return Hidden_State, Cell_State
def reinitHidden(self, batch_size, Hidden_State_data, Cell_State_data):
use_gpu = torch.cuda.is_available()
if use_gpu:
Hidden_State = Variable(Hidden_State_data.cuda(), requires_grad=True)
Cell_State = Variable(Cell_State_data.cuda(), requires_grad=True)
return Hidden_State, Cell_State
else:
Hidden_State = Variable(Hidden_State_data, requires_grad=True)
Cell_State = Variable(Cell_State_data, requires_grad=True)
return Hidden_State, Cell_State
lstm = LSTM(input_dim, hidden_dim, output_dim, output_last = True)
lstm, lstm_loss = TrainModel(lstm, train_dataloader, valid_dataloader, num_epochs = 1)
lstm_test = TestModel(lstm, test_dataloader, max_speed )
K = 64
Clamp_A = False
lsgclstm = LocalizedSpectralGraphConvolutionalLSTM(K, torch.Tensor(A), A.shape[0], Clamp_A=Clamp_A, output_last = True)
lsgclstm, lsgclstm_loss = TrainModel(lsgclstm, train_dataloader, valid_dataloader, num_epochs = 1)
lsgclstm_test = TestModel(lsgclstm, test_dataloader, max_speed )
K = 3
back_length = 3
Clamp_A = False
sgclstm = SpectralGraphConvolutionalLSTM(K, torch.Tensor(A), A.shape[0], Clamp_A=Clamp_A, output_last = True)
sgclstm, sgclstm_loss = TrainModel(sgclstm, train_dataloader, valid_dataloader, num_epochs = 1)
sgclstm_test = TestModel(sgclstm, test_dataloader, max_speed )
K = 3
back_length = 3
Clamp_A = False
gclstm = GraphConvolutionalLSTM(K, torch.Tensor(A), FFR[back_length], A.shape[0], Clamp_A=Clamp_A, output_last = True)
gclstm, gclstm_loss = TrainModel(gclstm, train_dataloader, valid_dataloader, num_epochs = 1)
gclstm_test = TestModel(gclstm, test_dataloader, max_speed )
rnn_val_loss = np.asarray(rnn_loss[3])
lstm_val_loss = np.asarray(lstm_loss[3])
hgclstm_val_loss = np.asarray(gclstm_loss[3])
lsgclstm_val_loss = np.asarray(lsgclstm_loss[3])
sgclstm_val_loss = np.asarray(sgclstm_loss[3])
lstm_val_loss = np.load('lstm_val_loss.npy')
hgclstm_val_loss = np.load('hgclstm_val_loss.npy')
lsgclstm_val_loss = np.load('lsgclstm_val_loss.npy')
sgclstm_val_loss = np.load('sgclstm_val_loss.npy')
# np.save('lstm_val_loss', lstm_val_loss)
# np.save('hgclstm_val_loss', gclstm_val_loss)
# np.save('lsgclstm_val_loss', lsgclstm_val_loss)
# np.save('sgclstm_val_loss', sgclstm_val_loss)
fig, ax = plt.subplots()
plt.plot(np.arange(1, len(lstm_val_loss) + 1), lstm_val_loss, label = 'LSTM')
plt.plot(np.arange(1, len(sgclstm_val_loss) + 1), sgclstm_val_loss, label = 'SGC+LSTM')
plt.plot(np.arange(1, len(lsgclstm_val_loss) + 1), lsgclstm_val_loss, label = 'LSGC+LSTM')
plt.plot(np.arange(1, len(hgclstm_val_loss) + 1),hgclstm_val_loss, label = 'HGC-LSTM')
plt.ylim((6 * 0.0001, 0.0019))
plt.xticks(fontsize = 12)
plt.yticks(fontsize = 12)
plt.yscale('log')
plt.ylabel('Validation Loss (MSE)', fontsize=12)
plt.xlabel('Epoch', fontsize=12)
# plt.gca().invert_xaxis()
plt.legend(fontsize=14)
plt.grid(True, which='both')
plt.savefig('Validation_loss.png', dpi=300, bbox_inches = 'tight', pad_inches=0.1)
| 0.787073 | 0.69867 |
# Independent Component Analysis Lab
In this notebook, we'll use Independent Component Analysis to retrieve original signals from three observations each of which contains a different mix of the original signals. This is the same problem explained in the ICA video.
## Dataset
Let's begin by looking at the dataset we have. We have three WAVE files, each of which is a mix, as we've mentioned. If you haven't worked with audio files in python before, that's okay, they basically boil down to being lists of floats.
Let's begin by loading our first audio file, **[ICA mix 1.wav](ICA mix 1.wav)** [click to listen to the file]:
```
import numpy as np
import wave
# Read the wave file
mix_1_wave = wave.open('ICA mix 1.wav','r')
```
Let's peak at the parameters of the wave file to learn more about it
```
mix_1_wave.getparams()
```
So this file has only channel (so it's mono sound). It has a frame rate of 44100, which means each second of sound is represented by 44100 integers (integers because the file is in the common PCM 16-bit format). The file has a total of 264515 integers/frames, which means its length in seconds is:
```
264515/44100
```
Let's extract the frames of the wave file, which will be a part of the dataset we'll run ICA against:
```
# Extract Raw Audio from Wav File
signal_1_raw = mix_1_wave.readframes(-1)
signal_1 = np.fromstring(signal_1_raw, 'Int16')
```
signal_1 is now a list of ints representing the sound contained in the first file.
```
'length: ', len(signal_1) , 'first 100 elements: ',signal_1[:100]
```
If we plot this array as a line graph, we'll get the familiar wave form representation:
```
import matplotlib.pyplot as plt
fs = mix_1_wave.getframerate()
timing = np.linspace(0, len(signal_1)/fs, num=len(signal_1))
plt.figure(figsize=(12,2))
plt.title('Recording 1')
plt.plot(timing,signal_1, c="#3ABFE7")
plt.ylim(-35000, 35000)
plt.show()
```
In the same way, we can now load the other two wave files, **[ICA mix 2.wav](ICA mix 2.wav)** and **[ICA mix 3.wav](ICA mix 3.wav)**
```
mix_2_wave = wave.open('ICA mix 2.wav','r')
#Extract Raw Audio from Wav File
signal_raw_2 = mix_2_wave.readframes(-1)
signal_2 = np.fromstring(signal_raw_2, 'Int16')
mix_3_wave = wave.open('ICA mix 3.wav','r')
#Extract Raw Audio from Wav File
signal_raw_3 = mix_3_wave.readframes(-1)
signal_3 = np.fromstring(signal_raw_3, 'Int16')
plt.figure(figsize=(12,2))
plt.title('Recording 2')
plt.plot(timing,signal_2, c="#3ABFE7")
plt.ylim(-35000, 35000)
plt.show()
plt.figure(figsize=(12,2))
plt.title('Recording 3')
plt.plot(timing,signal_3, c="#3ABFE7")
plt.ylim(-35000, 35000)
plt.show()
```
Now that we've read all three files, we're ready to [zip](https://docs.python.org/3/library/functions.html#zip) them to create our dataset.
* Create dataset ```X``` by zipping signal_1, signal_2, and signal_3 into a single list
```
X = list(zip(signal_1, signal_2, signal_3))
# Let's peak at what X looks like
X[:10]
```
We are now ready to run ICA to try to retrieve the original signals.
* Import sklearn's [FastICA](http://scikit-learn.org/stable/modules/generated/sklearn.decomposition.FastICA.html) module
* Initialize FastICA look for three components
* Run the FastICA algorithm using fit_transform on dataset X
```
# DONE: Import FastICA
from sklearn.decomposition import FastICA
# DONE: Initialize FastICA with n_components=3
ica = FastICA(n_components=3)
# TODO: Run the FastICA algorithm using fit_transform on dataset X
ica_result = ica.fit_transform(X)
```
```ica_result``` now contains the result of FastICA, which we hope are the original signals. It's in the shape:
```
ica_result.shape
```
Let's split into separate signals and look at them
```
result_signal_1 = ica_result[:,0]
result_signal_2 = ica_result[:,1]
result_signal_3 = ica_result[:,2]
```
Let's plot to see how the wave forms look
```
# Plot Independent Component #1
plt.figure(figsize=(12,2))
plt.title('Independent Component #1')
plt.plot(result_signal_1, c="#df8efd")
plt.ylim(-0.010, 0.010)
plt.show()
# Plot Independent Component #2
plt.figure(figsize=(12,2))
plt.title('Independent Component #2')
plt.plot(result_signal_2, c="#87de72")
plt.ylim(-0.010, 0.010)
plt.show()
# Plot Independent Component #3
plt.figure(figsize=(12,2))
plt.title('Independent Component #3')
plt.plot(result_signal_3, c="#f65e97")
plt.ylim(-0.010, 0.010)
plt.show()
```
Do some of these look like musical wave forms?
The best way to confirm the result is to listen to resulting files. So let's save as wave files and verify. But before we do that, we'll have to:
* convert them to integer (so we can save as PCM 16-bit Wave files), otherwise only some media players would be able to play them and others won't
* Map the values to the appropriate range for int16 audio. That range is between -32768 and +32767. A basic mapping can be done by multiplying by 32767.
* The sounds will be a little faint, we can increase the volume by multiplying by a value like 100
```
from scipy.io import wavfile
# Convert to int, map the appropriate range, and increase the volume a little bit
result_signal_1_int = np.int16(result_signal_1*32767*100)
result_signal_2_int = np.int16(result_signal_2*32767*100)
result_signal_3_int = np.int16(result_signal_3*32767*100)
# Write wave files
wavfile.write("result_signal_1.wav", fs, result_signal_1_int)
wavfile.write("result_signal_2.wav", fs, result_signal_2_int)
wavfile.write("result_signal_3.wav", fs, result_signal_3_int)
```
The resulting files we have now are: [note: make sure to lower the volume on your speakers first, just in case some problem caused the file to sound like static]
* [result_signal_1.wav](result_signal_1.wav)
* [result_signal_2.wav](result_signal_2.wav)
* [result_signal_3.wav](result_signal_3.wav)
Music:
* Piano - The Carnival of the Animals - XIII. The Swan (Solo piano version). Performer: Markus Staab
* Cello - Cello Suite no. 3 in C, BWV 1009 - I. Prelude. Performer: European Archive
|
github_jupyter
|
import numpy as np
import wave
# Read the wave file
mix_1_wave = wave.open('ICA mix 1.wav','r')
mix_1_wave.getparams()
264515/44100
# Extract Raw Audio from Wav File
signal_1_raw = mix_1_wave.readframes(-1)
signal_1 = np.fromstring(signal_1_raw, 'Int16')
'length: ', len(signal_1) , 'first 100 elements: ',signal_1[:100]
import matplotlib.pyplot as plt
fs = mix_1_wave.getframerate()
timing = np.linspace(0, len(signal_1)/fs, num=len(signal_1))
plt.figure(figsize=(12,2))
plt.title('Recording 1')
plt.plot(timing,signal_1, c="#3ABFE7")
plt.ylim(-35000, 35000)
plt.show()
mix_2_wave = wave.open('ICA mix 2.wav','r')
#Extract Raw Audio from Wav File
signal_raw_2 = mix_2_wave.readframes(-1)
signal_2 = np.fromstring(signal_raw_2, 'Int16')
mix_3_wave = wave.open('ICA mix 3.wav','r')
#Extract Raw Audio from Wav File
signal_raw_3 = mix_3_wave.readframes(-1)
signal_3 = np.fromstring(signal_raw_3, 'Int16')
plt.figure(figsize=(12,2))
plt.title('Recording 2')
plt.plot(timing,signal_2, c="#3ABFE7")
plt.ylim(-35000, 35000)
plt.show()
plt.figure(figsize=(12,2))
plt.title('Recording 3')
plt.plot(timing,signal_3, c="#3ABFE7")
plt.ylim(-35000, 35000)
plt.show()
X = list(zip(signal_1, signal_2, signal_3))
# Let's peak at what X looks like
X[:10]
# DONE: Import FastICA
from sklearn.decomposition import FastICA
# DONE: Initialize FastICA with n_components=3
ica = FastICA(n_components=3)
# TODO: Run the FastICA algorithm using fit_transform on dataset X
ica_result = ica.fit_transform(X)
ica_result.shape
result_signal_1 = ica_result[:,0]
result_signal_2 = ica_result[:,1]
result_signal_3 = ica_result[:,2]
# Plot Independent Component #1
plt.figure(figsize=(12,2))
plt.title('Independent Component #1')
plt.plot(result_signal_1, c="#df8efd")
plt.ylim(-0.010, 0.010)
plt.show()
# Plot Independent Component #2
plt.figure(figsize=(12,2))
plt.title('Independent Component #2')
plt.plot(result_signal_2, c="#87de72")
plt.ylim(-0.010, 0.010)
plt.show()
# Plot Independent Component #3
plt.figure(figsize=(12,2))
plt.title('Independent Component #3')
plt.plot(result_signal_3, c="#f65e97")
plt.ylim(-0.010, 0.010)
plt.show()
from scipy.io import wavfile
# Convert to int, map the appropriate range, and increase the volume a little bit
result_signal_1_int = np.int16(result_signal_1*32767*100)
result_signal_2_int = np.int16(result_signal_2*32767*100)
result_signal_3_int = np.int16(result_signal_3*32767*100)
# Write wave files
wavfile.write("result_signal_1.wav", fs, result_signal_1_int)
wavfile.write("result_signal_2.wav", fs, result_signal_2_int)
wavfile.write("result_signal_3.wav", fs, result_signal_3_int)
| 0.554229 | 0.978219 |
### Техники оптимизации С++ программ.
<br />
##### Как настроить машину под измерение performance
* Очистите ваш компьютер от стороннего софта настолько насколько это возможно (хотя бы на время замеров)
* Никаких баз данных
* Ваших личных крутящихся nginx
* Антивирусов
* Лишних демонов / сервисов
* Фоновых обновлений
* Чтения email-ов
* Открытых IDE
* Вы должны быть единственным залогиненным пользователем на машине
* В BOIS отключите Intel SpeedStep / SpeedShift / TurboBoost technologies
* сказать пару слов об этих технологиях и почему они влияют
* [Disable hyper threading](https://www.pcmag.com/article/314585/how-to-disable-hyperthreading)
* сказать пару слов что такое hyper threading и почему он влияет
* [Disable CPU scaling](https://askubuntu.com/questions/3924/disable-ondemand-cpu-scaling-daemon/3927) (linux, [doc](https://www.kernel.org/doc/Documentation/cpu-freq/governors.txt))
* Disable [address space randomization](https://en.wikipedia.org/wiki/Address_space_layout_randomization)
```sh
echo 0 | sudo tee /proc/sys/kernel/randomize_va_space
```
* Ни в коем случае не запускайте измерялку из IDE (Visual Studio цепляется к программе и отслеживает её состояние), запускайте через консоль.
* Привяжите процесс к ядру (лучше, ненулевому физ. ядру). Для linux есть команда `taskset`, в windows можно поковыряться в диспетчере.
```sh
taskset -c 2 myprogram
```
* Измеряйте только release-борку (-O2 / -O3), debug-версию измерять нет смысла (почти).
Для ознакомления:
* https://github.com/ivafanas/sltbench/blob/master/doc/howtobenchmark.md
* https://easyperf.net/blog/2019/08/02/Perf-measurement-environment-on-Linux
<br />
##### Уровни оптимизации компилятора
gcc / clang:
https://gcc.gnu.org/onlinedocs/gcc/Optimize-Options.html
* `-O0` - без оптимизаций (для отладки)
* `-O1` - набор оптимизаций 1
* `-O2` - набор оптимизаций 1 + набор оптимизаций 2
* `-O3` - набор оптимизаций 1 + набор оптимизаций 2 + набор оптимизаций 3
Чем выше `On`, тем больше время компиляции, но эффективнее код
(на самом деле it depends)
Дополнительные варианты:
* `-Os` - сфокусироваться на оптимизации размера бинарного файла вместо скорости выполнения
* `-Ofast` = `-O3` + `-ffast-math` - ослабить требования к математическим вычислениям - не выполнять все требования IEEE (может ускорить вычислительные алгоритмы, но программист должен поклясться на крови полуночных русалок, что урезанных требований и меньшей точности достаточно)
Закинуть это код в godbolt, показать какой ассемблер генерирует компилятор для последнего gcc и clang на разных уровнях оптимизаций:
```c++
#include <vector>
int sum(const std::vector<int>& x)
{
int rv = 0;
for (int v : x)
rv += v;
return rv;
}
```
<br />
msvc:
https://docs.microsoft.com/en-us/cpp/build/reference/o-options-optimize-code?view=vs-2019
Аналоги: `/Od`, `/O1`, `/O2`, `/Os` + доп. варинты (см. ссылку)
<br />
##### Профилировка на примере домашнего задания
**Visual studio:** Показать пример профилировки и просмотра результатов на msvc
<br />
<u>Замечание:</u> выполнять домашнее задание нужно на конфигурации `clang++-8 -stdlib=libc++ -O2 -std=c++17`.
Чтобы установить clang и libc++ на ubuntu (если они ещё не установлены), выполните следующие команды:
```sh
sudo apt-get install clang-8
sudo apt-get install libc++-dev
sudo apt-get install libc++abi-dev
```
<br />
**встроенный профилировщик в clang/gcc:**
Скрипт запуска встроенного в clang/gcc профилировщика:
```sh
echo "cleanup"
rm -f gmon.out
rm -f analysis.txt
rm -f a.out
echo "compile"
clang++-8 -pg -O2 reference.cpp -stdlib=libc++ -std=c++17
echo "running"
./a.out
echo "analyze"
gprof a.out gmon.out > analysis.txt
```
<br />
**google perf:**
Предустановки для инструмента google perf:
```sh
sudo apt-get install google-perftools libgoogle-perftools-dev
sudo apt-get install kcachegrind
```
Прогон google perf:
```sh
echo "cleanup"
rm -f a.out
rm -f cpu_profile
rm -f callgrind
echo "compile"
clang++-8 -O2 reference.cpp -std=c++17 -stdlib=libc++
echo "run with profile"
LD_PRELOAD=/usr/lib/x86_64-linux-gnu/libprofiler.so CPUPROFILE=cpu_profile CPUPROFILE_FREQUENCY=5000 ./a.out
echo "analyze"
# google-pprof --gv a.out cpu_profile # X
# google-pprof --web a.out cpu_profile # browser
# google-pprof --test a.out cpu_profile # console
google-pprof --callgrind a.out cpu_profile > callgrind && kcachegrind callgrind
```
<br />
##### Модель памяти

<br />

Дополнительно рассказать про кешлайны, многопоточность и разреженность
<br />
Немного хардкорных ссылок:
* [performance tuning guide for RHEL](https://access.redhat.com/documentation/en-us/red_hat_enterprise_linux/6/html/performance_tuning_guide/index)
* [how to benchmark code time execution on Intel](https://www.intel.com/content/dam/www/public/us/en/documents/white-papers/ia-32-ia-64-benchmark-code-execution-paper.pdf)
|
github_jupyter
|
echo 0 | sudo tee /proc/sys/kernel/randomize_va_space
taskset -c 2 myprogram
<br />
msvc:
https://docs.microsoft.com/en-us/cpp/build/reference/o-options-optimize-code?view=vs-2019
Аналоги: `/Od`, `/O1`, `/O2`, `/Os` + доп. варинты (см. ссылку)
<br />
##### Профилировка на примере домашнего задания
**Visual studio:** Показать пример профилировки и просмотра результатов на msvc
<br />
<u>Замечание:</u> выполнять домашнее задание нужно на конфигурации `clang++-8 -stdlib=libc++ -O2 -std=c++17`.
Чтобы установить clang и libc++ на ubuntu (если они ещё не установлены), выполните следующие команды:
<br />
**встроенный профилировщик в clang/gcc:**
Скрипт запуска встроенного в clang/gcc профилировщика:
<br />
**google perf:**
Предустановки для инструмента google perf:
Прогон google perf:
| 0.26086 | 0.930868 |
# Scheduling Multipurpose Batch Processes using State-Task Networks
Keywords: cbc usage, state-task networks, gdp, disjunctive programming, batch processes
The State-Task Network (STN) is an approach to modeling multipurpose batch process for the purpose of short term scheduling. It was first developed by Kondili, et al., in 1993, and subsequently developed and extended by others.
## Imports
```
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from IPython.display import display, HTML
import shutil
import sys
import os.path
if not shutil.which("pyomo"):
!pip install -q pyomo
assert(shutil.which("pyomo"))
if not (shutil.which("cbc") or os.path.isfile("cbc")):
if "google.colab" in sys.modules:
!apt-get install -y -qq coinor-cbc
else:
try:
!conda install -c conda-forge coincbc
except:
pass
assert(shutil.which("cbc") or os.path.isfile("cbc"))
from pyomo.environ import *
```
## References
Floudas, C. A., & Lin, X. (2005). Mixed integer linear programming in process scheduling: Modeling, algorithms, and applications. Annals of Operations Research, 139(1), 131-162.
Harjunkoski, I., Maravelias, C. T., Bongers, P., Castro, P. M., Engell, S., Grossmann, I. E., ... & Wassick, J. (2014). Scope for industrial applications of production scheduling models and solution methods. Computers & Chemical Engineering, 62, 161-193.
Kondili, E., Pantelides, C. C., & Sargent, R. W. H. (1993). A general algorithm for short-term scheduling of batch operations—I. MILP formulation. Computers & Chemical Engineering, 17(2), 211-227.
Méndez, C. A., Cerdá, J., Grossmann, I. E., Harjunkoski, I., & Fahl, M. (2006). State-of-the-art review of optimization methods for short-term scheduling of batch processes. Computers & Chemical Engineering, 30(6), 913-946.
Shah, N., Pantelides, C. C., & Sargent, R. W. H. (1993). A general algorithm for short-term scheduling of batch operations—II. Computational issues. Computers & Chemical Engineering, 17(2), 229-244.
Wassick, J. M., & Ferrio, J. (2011). Extending the resource task network for industrial applications. Computers & chemical engineering, 35(10), 2124-2140.
## Example (Kondili, et al., 1993)
A state-task network is a graphical representation of the activities in a multiproduct batch process. The representation includes the minimum details needed for short term scheduling of batch operations.
A well-studied example due to Kondili (1993) is shown below. Other examples are available in the references cited above.
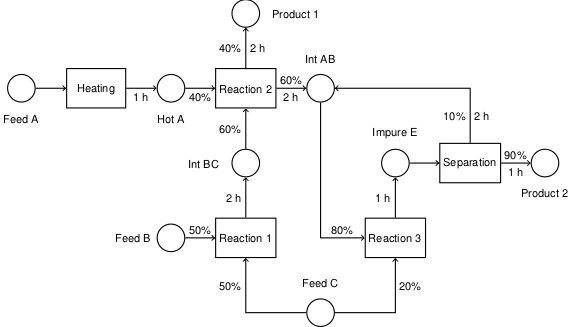
Each circular node in the diagram designates material in a particular state. The materials are generally held in suitable vessels with a known capacity. The relevant information for each state is the initial inventory, storage capacity, and the unit price of the material in each state. The price of materials in intermediate states may be assigned penalities in order to minimize the amount of work in progress.
The rectangular nodes denote process tasks. When scheduled for execution, each task is assigned an appropriate piece of equipment, and assigned a batch of material according to the incoming arcs. Each incoming arc begins at a state where the associated label indicates the mass fraction of the batch coming from that particular state. Outgoing arcs indicate the disposition of the batch to product states. The outgoing are labels indicate the fraction of the batch assigned to each product state, and the time necessary to produce that product.
Not shown in the diagram is the process equipment used to execute the tasks. A separate list of process units is available, each characterized by a capacity and list of tasks which can be performed in that unit.
### Exercise
Read this reciped for Hollandaise Sauce: http://www.foodnetwork.com/recipes/tyler-florence/hollandaise-sauce-recipe-1910043. Assume the available equipment consists of one sauce pan and a double-boiler on a stove. Draw a state-task network outlining the basic steps in the recipe.
## Encoding the STN data
The basic data structure specifies the states, tasks, and units comprising a state-task network. The intention is for all relevant problem data to be contained in a single JSON-like structure.
```
# planning horizon
H = 10
Kondili = {
# time grid
'TIME': range(0, H+1),
# states
'STATES': {
'Feed_A' : {'capacity': 500, 'initial': 500, 'price': 0},
'Feed_B' : {'capacity': 500, 'initial': 500, 'price': 0},
'Feed_C' : {'capacity': 500, 'initial': 500, 'price': 0},
'Hot_A' : {'capacity': 100, 'initial': 0, 'price': -100},
'Int_AB' : {'capacity': 200, 'initial': 0, 'price': -100},
'Int_BC' : {'capacity': 150, 'initial': 0, 'price': -100},
'Impure_E' : {'capacity': 100, 'initial': 0, 'price': -100},
'Product_1': {'capacity': 500, 'initial': 0, 'price': 10},
'Product_2': {'capacity': 500, 'initial': 0, 'price': 10},
},
# state-to-task arcs indexed by (state, task)
'ST_ARCS': {
('Feed_A', 'Heating') : {'rho': 1.0},
('Feed_B', 'Reaction_1'): {'rho': 0.5},
('Feed_C', 'Reaction_1'): {'rho': 0.5},
('Feed_C', 'Reaction_3'): {'rho': 0.2},
('Hot_A', 'Reaction_2'): {'rho': 0.4},
('Int_AB', 'Reaction_3'): {'rho': 0.8},
('Int_BC', 'Reaction_2'): {'rho': 0.6},
('Impure_E', 'Separation'): {'rho': 1.0},
},
# task-to-state arcs indexed by (task, state)
'TS_ARCS': {
('Heating', 'Hot_A') : {'dur': 1, 'rho': 1.0},
('Reaction_2', 'Product_1'): {'dur': 2, 'rho': 0.4},
('Reaction_2', 'Int_AB') : {'dur': 2, 'rho': 0.6},
('Reaction_1', 'Int_BC') : {'dur': 2, 'rho': 1.0},
('Reaction_3', 'Impure_E') : {'dur': 1, 'rho': 1.0},
('Separation', 'Int_AB') : {'dur': 2, 'rho': 0.1},
('Separation', 'Product_2'): {'dur': 1, 'rho': 0.9},
},
# unit data indexed by (unit, task)
'UNIT_TASKS': {
('Heater', 'Heating') : {'Bmin': 0, 'Bmax': 100, 'Cost': 1, 'vCost': 0, 'Tclean': 0},
('Reactor_1', 'Reaction_1'): {'Bmin': 0, 'Bmax': 80, 'Cost': 1, 'vCost': 0, 'Tclean': 0},
('Reactor_1', 'Reaction_2'): {'Bmin': 0, 'Bmax': 80, 'Cost': 1, 'vCost': 0, 'Tclean': 0},
('Reactor_1', 'Reaction_3'): {'Bmin': 0, 'Bmax': 80, 'Cost': 1, 'vCost': 0, 'Tclean': 0},
('Reactor_2', 'Reaction_1'): {'Bmin': 0, 'Bmax': 80, 'Cost': 1, 'vCost': 0, 'Tclean': 0},
('Reactor_2', 'Reaction_2'): {'Bmin': 0, 'Bmax': 80, 'Cost': 1, 'vCost': 0, 'Tclean': 0},
('Reactor_2', 'Reaction_3'): {'Bmin': 0, 'Bmax': 80, 'Cost': 1, 'vCost': 0, 'Tclean': 0},
('Still', 'Separation'): {'Bmin': 0, 'Bmax': 200, 'Cost': 1, 'vCost': 0, 'Tclean': 0},
},
}
STN = Kondili
H = 16
Hydrolubes = {
# time grid
'TIME': range(0, H+1),
# states
'STATES': {
'Feed_A' : {'capacity': 500, 'initial': 500, 'price': 0},
'Feed_B' : {'capacity': 500, 'initial': 500, 'price': 0},
'Feed_C' : {'capacity': 500, 'initial': 500, 'price': 0},
'Hot_A' : {'capacity': 100, 'initial': 0, 'price': -100},
'Int_AB' : {'capacity': 200, 'initial': 0, 'price': -100},
'Int_BC' : {'capacity': 150, 'initial': 0, 'price': -100},
'Impure_E' : {'capacity': 100, 'initial': 0, 'price': -100},
'Product_1': {'capacity': 500, 'initial': 0, 'price': 10},
'Product_2': {'capacity': 500, 'initial': 0, 'price': 10},
},
# state-to-task arcs indexed by (state, task)
'ST_ARCS': {
('Feed_A', 'Heating') : {'rho': 1.0},
('Feed_B', 'Reaction_1'): {'rho': 0.5},
('Feed_C', 'Reaction_1'): {'rho': 0.5},
('Feed_C', 'Reaction_3'): {'rho': 0.2},
('Hot_A', 'Reaction_2'): {'rho': 0.4},
('Int_AB', 'Reaction_3'): {'rho': 0.8},
('Int_BC', 'Reaction_2'): {'rho': 0.6},
('Impure_E', 'Separation'): {'rho': 1.0},
},
# task-to-state arcs indexed by (task, state)
'TS_ARCS': {
('Heating', 'Hot_A') : {'dur': 1, 'rho': 1.0},
('Reaction_2', 'Product_1'): {'dur': 2, 'rho': 0.4},
('Reaction_2', 'Int_AB') : {'dur': 2, 'rho': 0.6},
('Reaction_1', 'Int_BC') : {'dur': 2, 'rho': 1.0},
('Reaction_3', 'Impure_E') : {'dur': 1, 'rho': 1.0},
('Separation', 'Int_AB') : {'dur': 2, 'rho': 0.1},
('Separation', 'Product_2'): {'dur': 1, 'rho': 0.9},
},
# unit data indexed by (unit, task)
'UNIT_TASKS': {
('Heater', 'Heating') : {'Bmin': 0, 'Bmax': 100, 'Cost': 1, 'vCost': 0, 'Tclean': 0},
('Reactor_1', 'Reaction_1'): {'Bmin': 0, 'Bmax': 80, 'Cost': 1, 'vCost': 0, 'Tclean': 0},
('Reactor_1', 'Reaction_2'): {'Bmin': 0, 'Bmax': 80, 'Cost': 1, 'vCost': 0, 'Tclean': 0},
('Reactor_1', 'Reaction_3'): {'Bmin': 0, 'Bmax': 80, 'Cost': 1, 'vCost': 0, 'Tclean': 0},
('Reactor_2', 'Reaction_1'): {'Bmin': 0, 'Bmax': 80, 'Cost': 1, 'vCost': 0, 'Tclean': 0},
('Reactor_2', 'Reaction_2'): {'Bmin': 0, 'Bmax': 80, 'Cost': 1, 'vCost': 0, 'Tclean': 0},
('Reactor_2', 'Reaction_3'): {'Bmin': 0, 'Bmax': 80, 'Cost': 1, 'vCost': 0, 'Tclean': 0},
('Still', 'Separation'): {'Bmin': 0, 'Bmax': 200, 'Cost': 1, 'vCost': 0, 'Tclean': 0},
},
}
STN = Hydrolubes
```
### Setting a time grid
The following computations can be done on any time grid, including real-valued time points. TIME is a list of time points commencing at 0.
## Creating a Pyomo model
The following Pyomo model closely follows the development in Kondili, et al. (1993). In particular, the first step in the model is to process the STN data to create sets as given in Kondili.
One important difference from Kondili is the adoption of a more natural time scale that starts at $t = 0$ and extends to $t = H$ (rather than from 1 to H+1).
A second difference is the introduction of an additional decision variable denoted by $Q_{j,t}$ indicating the amount of material in unit $j$ at time $t$. A material balance then reads
\begin{align*}
Q_{jt} & = Q_{j(t-1)} + \sum_{i\in I_j}B_{ijt} - \sum_{i\in I_j}\sum_{\substack{s \in \bar{S}_i\\s\ni t-P_{is} \geq 0}}\bar{\rho}_{is}B_{ij(t-P_{is})} \qquad \forall j,t
\end{align*}
Following Kondili's notation, $I_j$ is the set of tasks that can be performed in unit $j$, and $\bar{S}_i$ is the set of states fed by task $j$. We assume the units are empty at the beginning and end of production period, i.e.,
\begin{align*}
Q_{j(-1)} & = 0 \qquad \forall j \\
Q_{j,H} & = 0 \qquad \forall j
\end{align*}
The unit allocation constraints are written the full backward aggregation method described by Shah (1993). The allocation constraint reads
\begin{align*}
\sum_{i \in I_j} \sum_{t'=t}^{t-p_i+1} W_{ijt'} & \leq 1 \qquad \forall j,t
\end{align*}
Each processing unit $j$ is tagged with a minimum and maximum capacity, $B_{ij}^{min}$ and $B_{ij}^{max}$, respectively, denoting the minimum and maximum batch sizes for each task $i$. A minimum capacity may be needed to cover heat exchange coils in a reactor or mixing blades in a blender, for example. The capacity may depend on the nature of the task being performed. These constraints are written
\begin{align*}
B_{ij}^{min}W_{ijt} & \leq B_{ijt} \leq B_{ij}^{max}W_{ijt} \qquad \forall j, \forall i\in I_j, \forall t
\end{align*}
### Characterization of tasks
```
STATES = STN['STATES']
ST_ARCS = STN['ST_ARCS']
TS_ARCS = STN['TS_ARCS']
UNIT_TASKS = STN['UNIT_TASKS']
TIME = STN['TIME']
H = max(TIME)
# set of tasks
TASKS = set([i for (j,i) in UNIT_TASKS])
# S[i] input set of states which feed task i
S = {i: set() for i in TASKS}
for (s,i) in ST_ARCS:
S[i].add(s)
# S_[i] output set of states fed by task i
S_ = {i: set() for i in TASKS}
for (i,s) in TS_ARCS:
S_[i].add(s)
# rho[(i,s)] input fraction of task i from state s
rho = {(i,s): ST_ARCS[(s,i)]['rho'] for (s,i) in ST_ARCS}
# rho_[(i,s)] output fraction of task i to state s
rho_ = {(i,s): TS_ARCS[(i,s)]['rho'] for (i,s) in TS_ARCS}
# P[(i,s)] time for task i output to state s
P = {(i,s): TS_ARCS[(i,s)]['dur'] for (i,s) in TS_ARCS}
# p[i] completion time for task i
p = {i: max([P[(i,s)] for s in S_[i]]) for i in TASKS}
# K[i] set of units capable of task i
K = {i: set() for i in TASKS}
for (j,i) in UNIT_TASKS:
K[i].add(j)
```
### Characterization of states
```
# T[s] set of tasks receiving material from state s
T = {s: set() for s in STATES}
for (s,i) in ST_ARCS:
T[s].add(i)
# set of tasks producing material for state s
T_ = {s: set() for s in STATES}
for (i,s) in TS_ARCS:
T_[s].add(i)
# C[s] storage capacity for state s
C = {s: STATES[s]['capacity'] for s in STATES}
```
### Characterization of units
```
UNITS = set([j for (j,i) in UNIT_TASKS])
# I[j] set of tasks performed with unit j
I = {j: set() for j in UNITS}
for (j,i) in UNIT_TASKS:
I[j].add(i)
# Bmax[(i,j)] maximum capacity of unit j for task i
Bmax = {(i,j):UNIT_TASKS[(j,i)]['Bmax'] for (j,i) in UNIT_TASKS}
# Bmin[(i,j)] minimum capacity of unit j for task i
Bmin = {(i,j):UNIT_TASKS[(j,i)]['Bmin'] for (j,i) in UNIT_TASKS}
```
### Pyomo model
```
TIME = np.array(TIME)
model = ConcreteModel()
# W[i,j,t] 1 if task i starts in unit j at time t
model.W = Var(TASKS, UNITS, TIME, domain=Boolean)
# B[i,j,t,] size of batch assigned to task i in unit j at time t
model.B = Var(TASKS, UNITS, TIME, domain=NonNegativeReals)
# S[s,t] inventory of state s at time t
model.S = Var(STATES.keys(), TIME, domain=NonNegativeReals)
# Q[j,t] inventory of unit j at time t
model.Q = Var(UNITS, TIME, domain=NonNegativeReals)
# Objective function
# project value
model.Value = Var(domain=NonNegativeReals)
model.valuec = Constraint(expr = model.Value == sum([STATES[s]['price']*model.S[s,H] for s in STATES]))
# project cost
model.Cost = Var(domain=NonNegativeReals)
model.costc = Constraint(expr = model.Cost == sum([UNIT_TASKS[(j,i)]['Cost']*model.W[i,j,t] +
UNIT_TASKS[(j,i)]['vCost']*model.B[i,j,t] for i in TASKS for j in K[i] for t in TIME]))
model.obj = Objective(expr = model.Value - model.Cost, sense = maximize)
# Constraints
model.cons = ConstraintList()
# a unit can only be allocated to one task
for j in UNITS:
for t in TIME:
lhs = 0
for i in I[j]:
for tprime in TIME:
if tprime >= (t-p[i]+1-UNIT_TASKS[(j,i)]['Tclean']) and tprime <= t:
lhs += model.W[i,j,tprime]
model.cons.add(lhs <= 1)
# state capacity constraint
model.sc = Constraint(STATES.keys(), TIME, rule = lambda model, s, t: model.S[s,t] <= C[s])
# state mass balances
for s in STATES.keys():
rhs = STATES[s]['initial']
for t in TIME:
for i in T_[s]:
for j in K[i]:
if t >= P[(i,s)]:
rhs += rho_[(i,s)]*model.B[i,j,max(TIME[TIME <= t-P[(i,s)]])]
for i in T[s]:
rhs -= rho[(i,s)]*sum([model.B[i,j,t] for j in K[i]])
model.cons.add(model.S[s,t] == rhs)
rhs = model.S[s,t]
# unit capacity constraints
for t in TIME:
for j in UNITS:
for i in I[j]:
model.cons.add(model.W[i,j,t]*Bmin[i,j] <= model.B[i,j,t])
model.cons.add(model.B[i,j,t] <= model.W[i,j,t]*Bmax[i,j])
# unit mass balances
for j in UNITS:
rhs = 0
for t in TIME:
rhs += sum([model.B[i,j,t] for i in I[j]])
for i in I[j]:
for s in S_[i]:
if t >= P[(i,s)]:
rhs -= rho_[(i,s)]*model.B[i,j,max(TIME[TIME <= t-P[(i,s)]])]
model.cons.add(model.Q[j,t] == rhs)
rhs = model.Q[j,t]
# unit terminal condition
model.tc = Constraint(UNITS, rule = lambda model, j: model.Q[j,H] == 0)
SolverFactory('cbc').solve(model).write()
```
## Analysis
### Profitability
```
print("Value of State Inventories = {0:12.2f}".format(model.Value()))
print(" Cost of Unit Assignments = {0:12.2f}".format(model.Cost()))
print(" Net Objective = {0:12.2f}".format(model.Value() - model.Cost()))
```
### Unit assignment
```
UnitAssignment = pd.DataFrame({j:[None for t in TIME] for j in UNITS}, index=TIME)
for t in TIME:
for j in UNITS:
for i in I[j]:
for s in S_[i]:
if t-p[i] >= 0:
if model.W[i,j,max(TIME[TIME <= t-p[i]])]() > 0:
UnitAssignment.loc[t,j] = None
for i in I[j]:
if model.W[i,j,t]() > 0:
UnitAssignment.loc[t,j] = (i,model.B[i,j,t]())
UnitAssignment
```
### State inventories
```
pd.DataFrame([[model.S[s,t]() for s in STATES.keys()] for t in TIME], columns = STATES.keys(), index = TIME)
plt.figure(figsize=(10,6))
for (s,idx) in zip(STATES.keys(),range(0,len(STATES.keys()))):
plt.subplot(ceil(len(STATES.keys())/3),3,idx+1)
tlast,ylast = 0,STATES[s]['initial']
for (t,y) in zip(list(TIME),[model.S[s,t]() for t in TIME]):
plt.plot([tlast,t,t],[ylast,ylast,y],'b')
#plt.plot([tlast,t],[ylast,y],'b.',ms=10)
tlast,ylast = t,y
plt.ylim(0,1.1*C[s])
plt.plot([0,H],[C[s],C[s]],'r--')
plt.title(s)
plt.tight_layout()
```
### Unit batch inventories
```
pd.DataFrame([[model.Q[j,t]() for j in UNITS] for t in TIME], columns = UNITS, index = TIME)
```
### Gannt chart
```
plt.figure(figsize=(12,6))
gap = H/500
idx = 1
lbls = []
ticks = []
for j in sorted(UNITS):
idx -= 1
for i in sorted(I[j]):
idx -= 1
ticks.append(idx)
lbls.append("{0:s} -> {1:s}".format(j,i))
plt.plot([0,H],[idx,idx],lw=20,alpha=.3,color='y')
for t in TIME:
if model.W[i,j,t]() > 0:
plt.plot([t+gap,t+p[i]-gap], [idx,idx],'b', lw=20, solid_capstyle='butt')
txt = "{0:.2f}".format(model.B[i,j,t]())
plt.text(t+p[i]/2, idx, txt, color='white', weight='bold', ha='center', va='center')
plt.xlim(0,H)
plt.gca().set_yticks(ticks)
plt.gca().set_yticklabels(lbls);
```
## Trace of events and states
```
sep = '\n--------------------------------------------------------------------------------------------\n'
print(sep)
print("Starting Conditions")
print(" Initial Inventories:")
for s in STATES.keys():
print(" {0:10s} {1:6.1f} kg".format(s,STATES[s]['initial']))
units = {j:{'assignment':'None', 't':0} for j in UNITS}
for t in TIME:
print(sep)
print("Time =",t,"hr")
print(" Instructions:")
for j in UNITS:
units[j]['t'] += 1
# transfer from unit to states
for i in I[j]:
for s in S_[i]:
if t-P[(i,s)] >= 0:
amt = rho_[(i,s)]*model.B[i,j,max(TIME[TIME <= t - P[(i,s)]])]()
if amt > 0:
print(" Transfer", amt, "kg from", j, "to", s)
for j in UNITS:
# release units from tasks
for i in I[j]:
if t-p[i] >= 0:
if model.W[i,j,max(TIME[TIME <= t-p[i]])]() > 0:
print(" Release", j, "from", i)
units[j]['assignment'] = 'None'
units[j]['t'] = 0
# assign units to tasks
for i in I[j]:
if model.W[i,j,t]() > 0:
print(" Assign", j, "with capacity", Bmax[(i,j)], "kg to task",i,"for",p[i],"hours")
units[j]['assignment'] = i
units[j]['t'] = 1
# transfer from states to starting tasks
for i in I[j]:
for s in S[i]:
amt = rho[(i,s)]*model.B[i,j,t]()
if amt > 0:
print(" Transfer", amt,"kg from", s, "to", j)
print("\n Inventories are now:")
for s in STATES.keys():
print(" {0:10s} {1:6.1f} kg".format(s,model.S[s,t]()))
print("\n Unit Assignments are now:")
for j in UNITS:
if units[j]['assignment'] != 'None':
fmt = " {0:s} performs the {1:s} task with a {2:.2f} kg batch for hour {3:f} of {4:f}"
i = units[j]['assignment']
print(fmt.format(j,i,model.Q[j,t](),units[j]['t'],p[i]))
print(sep)
print('Final Conditions')
print(" Final Inventories:")
for s in STATES.keys():
print(" {0:10s} {1:6.1f} kg".format(s,model.S[s,H]()))
```
|
github_jupyter
|
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from IPython.display import display, HTML
import shutil
import sys
import os.path
if not shutil.which("pyomo"):
!pip install -q pyomo
assert(shutil.which("pyomo"))
if not (shutil.which("cbc") or os.path.isfile("cbc")):
if "google.colab" in sys.modules:
!apt-get install -y -qq coinor-cbc
else:
try:
!conda install -c conda-forge coincbc
except:
pass
assert(shutil.which("cbc") or os.path.isfile("cbc"))
from pyomo.environ import *
# planning horizon
H = 10
Kondili = {
# time grid
'TIME': range(0, H+1),
# states
'STATES': {
'Feed_A' : {'capacity': 500, 'initial': 500, 'price': 0},
'Feed_B' : {'capacity': 500, 'initial': 500, 'price': 0},
'Feed_C' : {'capacity': 500, 'initial': 500, 'price': 0},
'Hot_A' : {'capacity': 100, 'initial': 0, 'price': -100},
'Int_AB' : {'capacity': 200, 'initial': 0, 'price': -100},
'Int_BC' : {'capacity': 150, 'initial': 0, 'price': -100},
'Impure_E' : {'capacity': 100, 'initial': 0, 'price': -100},
'Product_1': {'capacity': 500, 'initial': 0, 'price': 10},
'Product_2': {'capacity': 500, 'initial': 0, 'price': 10},
},
# state-to-task arcs indexed by (state, task)
'ST_ARCS': {
('Feed_A', 'Heating') : {'rho': 1.0},
('Feed_B', 'Reaction_1'): {'rho': 0.5},
('Feed_C', 'Reaction_1'): {'rho': 0.5},
('Feed_C', 'Reaction_3'): {'rho': 0.2},
('Hot_A', 'Reaction_2'): {'rho': 0.4},
('Int_AB', 'Reaction_3'): {'rho': 0.8},
('Int_BC', 'Reaction_2'): {'rho': 0.6},
('Impure_E', 'Separation'): {'rho': 1.0},
},
# task-to-state arcs indexed by (task, state)
'TS_ARCS': {
('Heating', 'Hot_A') : {'dur': 1, 'rho': 1.0},
('Reaction_2', 'Product_1'): {'dur': 2, 'rho': 0.4},
('Reaction_2', 'Int_AB') : {'dur': 2, 'rho': 0.6},
('Reaction_1', 'Int_BC') : {'dur': 2, 'rho': 1.0},
('Reaction_3', 'Impure_E') : {'dur': 1, 'rho': 1.0},
('Separation', 'Int_AB') : {'dur': 2, 'rho': 0.1},
('Separation', 'Product_2'): {'dur': 1, 'rho': 0.9},
},
# unit data indexed by (unit, task)
'UNIT_TASKS': {
('Heater', 'Heating') : {'Bmin': 0, 'Bmax': 100, 'Cost': 1, 'vCost': 0, 'Tclean': 0},
('Reactor_1', 'Reaction_1'): {'Bmin': 0, 'Bmax': 80, 'Cost': 1, 'vCost': 0, 'Tclean': 0},
('Reactor_1', 'Reaction_2'): {'Bmin': 0, 'Bmax': 80, 'Cost': 1, 'vCost': 0, 'Tclean': 0},
('Reactor_1', 'Reaction_3'): {'Bmin': 0, 'Bmax': 80, 'Cost': 1, 'vCost': 0, 'Tclean': 0},
('Reactor_2', 'Reaction_1'): {'Bmin': 0, 'Bmax': 80, 'Cost': 1, 'vCost': 0, 'Tclean': 0},
('Reactor_2', 'Reaction_2'): {'Bmin': 0, 'Bmax': 80, 'Cost': 1, 'vCost': 0, 'Tclean': 0},
('Reactor_2', 'Reaction_3'): {'Bmin': 0, 'Bmax': 80, 'Cost': 1, 'vCost': 0, 'Tclean': 0},
('Still', 'Separation'): {'Bmin': 0, 'Bmax': 200, 'Cost': 1, 'vCost': 0, 'Tclean': 0},
},
}
STN = Kondili
H = 16
Hydrolubes = {
# time grid
'TIME': range(0, H+1),
# states
'STATES': {
'Feed_A' : {'capacity': 500, 'initial': 500, 'price': 0},
'Feed_B' : {'capacity': 500, 'initial': 500, 'price': 0},
'Feed_C' : {'capacity': 500, 'initial': 500, 'price': 0},
'Hot_A' : {'capacity': 100, 'initial': 0, 'price': -100},
'Int_AB' : {'capacity': 200, 'initial': 0, 'price': -100},
'Int_BC' : {'capacity': 150, 'initial': 0, 'price': -100},
'Impure_E' : {'capacity': 100, 'initial': 0, 'price': -100},
'Product_1': {'capacity': 500, 'initial': 0, 'price': 10},
'Product_2': {'capacity': 500, 'initial': 0, 'price': 10},
},
# state-to-task arcs indexed by (state, task)
'ST_ARCS': {
('Feed_A', 'Heating') : {'rho': 1.0},
('Feed_B', 'Reaction_1'): {'rho': 0.5},
('Feed_C', 'Reaction_1'): {'rho': 0.5},
('Feed_C', 'Reaction_3'): {'rho': 0.2},
('Hot_A', 'Reaction_2'): {'rho': 0.4},
('Int_AB', 'Reaction_3'): {'rho': 0.8},
('Int_BC', 'Reaction_2'): {'rho': 0.6},
('Impure_E', 'Separation'): {'rho': 1.0},
},
# task-to-state arcs indexed by (task, state)
'TS_ARCS': {
('Heating', 'Hot_A') : {'dur': 1, 'rho': 1.0},
('Reaction_2', 'Product_1'): {'dur': 2, 'rho': 0.4},
('Reaction_2', 'Int_AB') : {'dur': 2, 'rho': 0.6},
('Reaction_1', 'Int_BC') : {'dur': 2, 'rho': 1.0},
('Reaction_3', 'Impure_E') : {'dur': 1, 'rho': 1.0},
('Separation', 'Int_AB') : {'dur': 2, 'rho': 0.1},
('Separation', 'Product_2'): {'dur': 1, 'rho': 0.9},
},
# unit data indexed by (unit, task)
'UNIT_TASKS': {
('Heater', 'Heating') : {'Bmin': 0, 'Bmax': 100, 'Cost': 1, 'vCost': 0, 'Tclean': 0},
('Reactor_1', 'Reaction_1'): {'Bmin': 0, 'Bmax': 80, 'Cost': 1, 'vCost': 0, 'Tclean': 0},
('Reactor_1', 'Reaction_2'): {'Bmin': 0, 'Bmax': 80, 'Cost': 1, 'vCost': 0, 'Tclean': 0},
('Reactor_1', 'Reaction_3'): {'Bmin': 0, 'Bmax': 80, 'Cost': 1, 'vCost': 0, 'Tclean': 0},
('Reactor_2', 'Reaction_1'): {'Bmin': 0, 'Bmax': 80, 'Cost': 1, 'vCost': 0, 'Tclean': 0},
('Reactor_2', 'Reaction_2'): {'Bmin': 0, 'Bmax': 80, 'Cost': 1, 'vCost': 0, 'Tclean': 0},
('Reactor_2', 'Reaction_3'): {'Bmin': 0, 'Bmax': 80, 'Cost': 1, 'vCost': 0, 'Tclean': 0},
('Still', 'Separation'): {'Bmin': 0, 'Bmax': 200, 'Cost': 1, 'vCost': 0, 'Tclean': 0},
},
}
STN = Hydrolubes
STATES = STN['STATES']
ST_ARCS = STN['ST_ARCS']
TS_ARCS = STN['TS_ARCS']
UNIT_TASKS = STN['UNIT_TASKS']
TIME = STN['TIME']
H = max(TIME)
# set of tasks
TASKS = set([i for (j,i) in UNIT_TASKS])
# S[i] input set of states which feed task i
S = {i: set() for i in TASKS}
for (s,i) in ST_ARCS:
S[i].add(s)
# S_[i] output set of states fed by task i
S_ = {i: set() for i in TASKS}
for (i,s) in TS_ARCS:
S_[i].add(s)
# rho[(i,s)] input fraction of task i from state s
rho = {(i,s): ST_ARCS[(s,i)]['rho'] for (s,i) in ST_ARCS}
# rho_[(i,s)] output fraction of task i to state s
rho_ = {(i,s): TS_ARCS[(i,s)]['rho'] for (i,s) in TS_ARCS}
# P[(i,s)] time for task i output to state s
P = {(i,s): TS_ARCS[(i,s)]['dur'] for (i,s) in TS_ARCS}
# p[i] completion time for task i
p = {i: max([P[(i,s)] for s in S_[i]]) for i in TASKS}
# K[i] set of units capable of task i
K = {i: set() for i in TASKS}
for (j,i) in UNIT_TASKS:
K[i].add(j)
# T[s] set of tasks receiving material from state s
T = {s: set() for s in STATES}
for (s,i) in ST_ARCS:
T[s].add(i)
# set of tasks producing material for state s
T_ = {s: set() for s in STATES}
for (i,s) in TS_ARCS:
T_[s].add(i)
# C[s] storage capacity for state s
C = {s: STATES[s]['capacity'] for s in STATES}
UNITS = set([j for (j,i) in UNIT_TASKS])
# I[j] set of tasks performed with unit j
I = {j: set() for j in UNITS}
for (j,i) in UNIT_TASKS:
I[j].add(i)
# Bmax[(i,j)] maximum capacity of unit j for task i
Bmax = {(i,j):UNIT_TASKS[(j,i)]['Bmax'] for (j,i) in UNIT_TASKS}
# Bmin[(i,j)] minimum capacity of unit j for task i
Bmin = {(i,j):UNIT_TASKS[(j,i)]['Bmin'] for (j,i) in UNIT_TASKS}
TIME = np.array(TIME)
model = ConcreteModel()
# W[i,j,t] 1 if task i starts in unit j at time t
model.W = Var(TASKS, UNITS, TIME, domain=Boolean)
# B[i,j,t,] size of batch assigned to task i in unit j at time t
model.B = Var(TASKS, UNITS, TIME, domain=NonNegativeReals)
# S[s,t] inventory of state s at time t
model.S = Var(STATES.keys(), TIME, domain=NonNegativeReals)
# Q[j,t] inventory of unit j at time t
model.Q = Var(UNITS, TIME, domain=NonNegativeReals)
# Objective function
# project value
model.Value = Var(domain=NonNegativeReals)
model.valuec = Constraint(expr = model.Value == sum([STATES[s]['price']*model.S[s,H] for s in STATES]))
# project cost
model.Cost = Var(domain=NonNegativeReals)
model.costc = Constraint(expr = model.Cost == sum([UNIT_TASKS[(j,i)]['Cost']*model.W[i,j,t] +
UNIT_TASKS[(j,i)]['vCost']*model.B[i,j,t] for i in TASKS for j in K[i] for t in TIME]))
model.obj = Objective(expr = model.Value - model.Cost, sense = maximize)
# Constraints
model.cons = ConstraintList()
# a unit can only be allocated to one task
for j in UNITS:
for t in TIME:
lhs = 0
for i in I[j]:
for tprime in TIME:
if tprime >= (t-p[i]+1-UNIT_TASKS[(j,i)]['Tclean']) and tprime <= t:
lhs += model.W[i,j,tprime]
model.cons.add(lhs <= 1)
# state capacity constraint
model.sc = Constraint(STATES.keys(), TIME, rule = lambda model, s, t: model.S[s,t] <= C[s])
# state mass balances
for s in STATES.keys():
rhs = STATES[s]['initial']
for t in TIME:
for i in T_[s]:
for j in K[i]:
if t >= P[(i,s)]:
rhs += rho_[(i,s)]*model.B[i,j,max(TIME[TIME <= t-P[(i,s)]])]
for i in T[s]:
rhs -= rho[(i,s)]*sum([model.B[i,j,t] for j in K[i]])
model.cons.add(model.S[s,t] == rhs)
rhs = model.S[s,t]
# unit capacity constraints
for t in TIME:
for j in UNITS:
for i in I[j]:
model.cons.add(model.W[i,j,t]*Bmin[i,j] <= model.B[i,j,t])
model.cons.add(model.B[i,j,t] <= model.W[i,j,t]*Bmax[i,j])
# unit mass balances
for j in UNITS:
rhs = 0
for t in TIME:
rhs += sum([model.B[i,j,t] for i in I[j]])
for i in I[j]:
for s in S_[i]:
if t >= P[(i,s)]:
rhs -= rho_[(i,s)]*model.B[i,j,max(TIME[TIME <= t-P[(i,s)]])]
model.cons.add(model.Q[j,t] == rhs)
rhs = model.Q[j,t]
# unit terminal condition
model.tc = Constraint(UNITS, rule = lambda model, j: model.Q[j,H] == 0)
SolverFactory('cbc').solve(model).write()
print("Value of State Inventories = {0:12.2f}".format(model.Value()))
print(" Cost of Unit Assignments = {0:12.2f}".format(model.Cost()))
print(" Net Objective = {0:12.2f}".format(model.Value() - model.Cost()))
UnitAssignment = pd.DataFrame({j:[None for t in TIME] for j in UNITS}, index=TIME)
for t in TIME:
for j in UNITS:
for i in I[j]:
for s in S_[i]:
if t-p[i] >= 0:
if model.W[i,j,max(TIME[TIME <= t-p[i]])]() > 0:
UnitAssignment.loc[t,j] = None
for i in I[j]:
if model.W[i,j,t]() > 0:
UnitAssignment.loc[t,j] = (i,model.B[i,j,t]())
UnitAssignment
pd.DataFrame([[model.S[s,t]() for s in STATES.keys()] for t in TIME], columns = STATES.keys(), index = TIME)
plt.figure(figsize=(10,6))
for (s,idx) in zip(STATES.keys(),range(0,len(STATES.keys()))):
plt.subplot(ceil(len(STATES.keys())/3),3,idx+1)
tlast,ylast = 0,STATES[s]['initial']
for (t,y) in zip(list(TIME),[model.S[s,t]() for t in TIME]):
plt.plot([tlast,t,t],[ylast,ylast,y],'b')
#plt.plot([tlast,t],[ylast,y],'b.',ms=10)
tlast,ylast = t,y
plt.ylim(0,1.1*C[s])
plt.plot([0,H],[C[s],C[s]],'r--')
plt.title(s)
plt.tight_layout()
pd.DataFrame([[model.Q[j,t]() for j in UNITS] for t in TIME], columns = UNITS, index = TIME)
plt.figure(figsize=(12,6))
gap = H/500
idx = 1
lbls = []
ticks = []
for j in sorted(UNITS):
idx -= 1
for i in sorted(I[j]):
idx -= 1
ticks.append(idx)
lbls.append("{0:s} -> {1:s}".format(j,i))
plt.plot([0,H],[idx,idx],lw=20,alpha=.3,color='y')
for t in TIME:
if model.W[i,j,t]() > 0:
plt.plot([t+gap,t+p[i]-gap], [idx,idx],'b', lw=20, solid_capstyle='butt')
txt = "{0:.2f}".format(model.B[i,j,t]())
plt.text(t+p[i]/2, idx, txt, color='white', weight='bold', ha='center', va='center')
plt.xlim(0,H)
plt.gca().set_yticks(ticks)
plt.gca().set_yticklabels(lbls);
sep = '\n--------------------------------------------------------------------------------------------\n'
print(sep)
print("Starting Conditions")
print(" Initial Inventories:")
for s in STATES.keys():
print(" {0:10s} {1:6.1f} kg".format(s,STATES[s]['initial']))
units = {j:{'assignment':'None', 't':0} for j in UNITS}
for t in TIME:
print(sep)
print("Time =",t,"hr")
print(" Instructions:")
for j in UNITS:
units[j]['t'] += 1
# transfer from unit to states
for i in I[j]:
for s in S_[i]:
if t-P[(i,s)] >= 0:
amt = rho_[(i,s)]*model.B[i,j,max(TIME[TIME <= t - P[(i,s)]])]()
if amt > 0:
print(" Transfer", amt, "kg from", j, "to", s)
for j in UNITS:
# release units from tasks
for i in I[j]:
if t-p[i] >= 0:
if model.W[i,j,max(TIME[TIME <= t-p[i]])]() > 0:
print(" Release", j, "from", i)
units[j]['assignment'] = 'None'
units[j]['t'] = 0
# assign units to tasks
for i in I[j]:
if model.W[i,j,t]() > 0:
print(" Assign", j, "with capacity", Bmax[(i,j)], "kg to task",i,"for",p[i],"hours")
units[j]['assignment'] = i
units[j]['t'] = 1
# transfer from states to starting tasks
for i in I[j]:
for s in S[i]:
amt = rho[(i,s)]*model.B[i,j,t]()
if amt > 0:
print(" Transfer", amt,"kg from", s, "to", j)
print("\n Inventories are now:")
for s in STATES.keys():
print(" {0:10s} {1:6.1f} kg".format(s,model.S[s,t]()))
print("\n Unit Assignments are now:")
for j in UNITS:
if units[j]['assignment'] != 'None':
fmt = " {0:s} performs the {1:s} task with a {2:.2f} kg batch for hour {3:f} of {4:f}"
i = units[j]['assignment']
print(fmt.format(j,i,model.Q[j,t](),units[j]['t'],p[i]))
print(sep)
print('Final Conditions')
print(" Final Inventories:")
for s in STATES.keys():
print(" {0:10s} {1:6.1f} kg".format(s,model.S[s,H]()))
| 0.307878 | 0.897291 |
# Valuación de opciones asiáticas
- Las opciones que tratamos la clase pasada dependen sólo del valor del precio del subyacente $S_t$, en el instante que se ejerce.
- Cambios bruscos en el precio, cambian que la opción esté *in the money* a estar *out the money*.
- **Posibilidad de evitar esto** $\longrightarrow$ suscribir un contrato sobre el valor promedio del precio del subyacente.
- **Opciones exóticas**: opciones cuya estructura de resultados es diferente a la de las opciones tradicionales, y que han surgido con la intención, bien de **abaratar el coste de las primas** de dichas opciones tradicionales, o bien, para ajustarse más adecuadamente a determinadas situaciones.
> 
> Referencia: ver información adicional acerca de las distintas opciones exóticas en el siguiente enlace: [link](http://rabida.uhu.es/dspace/bitstream/handle/10272/5546/Opciones_exoticas.pdf?sequence=2)
- <font color ='red'> Puede proveer protección contra fluctuaciones extremas del precio en mercados volátiles. </font>
- **Nombre**: Banco Trust de Tokio ofreció este tipo de opciones
### Justificación
- Debido a que los contratos que solo dependen del precio final del subyacente son más vulnerables a cambios repentinos de gran tamaño o manipulación de precios, las opciones asiáticas son menos sensibles a dichos fenómenos (menos riesgosas).
- Algunos agentes prefieren opciones asiáticas como instrumentos de cobertura, ya que pueden estar expuestos a la evolución del subyacente en un intervalo de tiempo.
- Son más baratas que sus contrapartes **plain vanilla** $\longrightarrow$ la volatilidad del promedio por lo general será menor que la del subyacente. **Menor sensibilidad de la opción ante cambios en el subyacente que para una opción vanilla con el mismo vencimiento.**
> Información adicional: **[link](https://reader.elsevier.com/reader/sd/pii/S0186104216300304?token=FE78324CCB90A9B00930E308E5369EB593916F99C8F78EA9190DF9F8FFF55547D8EB557F77801D84C6E01FE63B92F9A3)**
### ¿Dónde se negocian?
- Mercados OTC (Over the Counter / Independientes).
- Las condiciones para el cálculo matemático del promedio y otras condiciones son especificadas en el contrato. Lo que las hace un poco más “personalizables”.
Existen diversos tipos de opciones asiáticas y se clasiflcan de acuerdo con lo siguiente.
1. La media que se utiliza puede ser **aritmética** o geométrica.
- Media aritmética: $$ \bar x = \frac{1}{n}\sum_{i=1}^{n} x_i$$
- Media geométrica: $$ {\bar {x}}={\sqrt[{n}]{\prod _{i=1}^{n}{x_{i}}}}={\sqrt[{n}]{x_{1}\cdot x_{2}\cdots x_{n}}}$$
* **Ventajas**:
- Considera todos los valores de la distribución.
- Es menos sensible que la media aritmética a los valores extremos.
* **Desventajas**
- Es de significado estadístico menos intuitivo que la media aritmética.
- Su cálculo es más difícil.
- Si un valor $x_i = 0$ entonces la media geométrica se anula o no queda determinada.
La media aritmética de un conjunto de números positivos siempre es igual o superior a la media geométrica:
$$
\sqrt[n]{x_1 \cdot x_2 \dots x_n} \le \frac{x_1+ \dots + x_n}{n}
$$
2. Media se calcula para $S_t \longrightarrow$ "Precio de ejercicio fijo". Media se calcula para precio de ejercicio $\longrightarrow$ "Precio de ejercicio flotante".
3. Si la opción sólo se puede ejercer al final del tiempo del contrato se dice que es asiática de tipo europeo o **euroasiática**, y si puede ejercer en cualquier instante, durante la vigencia del contrato se denomina **asiática de tipo americano.**
Los tipos de opciones euroasiáticas son:
- Call con precio de ejercicio fijo, función de pago: $\max\{A-K,0\}$.
- Put con precio de ejercicio fijo, función de pago: $\max\{K-A,0\}$.
- Call con precio de ejercicio flotante, función de pago: $\max\{S_T-A,0\}$.
- Put con precio de ejercicio flotante, función de pago: $\max\{A-S_T,0\}$.
Donde $A$ es el promedio del precio del subyacente.
$$\text{Promedio aritmético} \quad A={1\over T} \int_0^TS_tdt$$
$$\text{Promedio geométrico} \quad A=\exp\Big({1\over T} \int_0^T Ln(S_t) dt\Big)$$
De aquí en adelante denominaremos **Asiática** $\longrightarrow$ Euroasiática y se analizará el call asiático con **K Fijo**.
Se supondrá un solo activo con riesgo, cuyos proceso de precios $\{S_t | t\in [0,T]\}$ satisface un movimiento browniano geométrico, en un mercado que satisface las suposiciones del modelo de Black y Scholes.
__Suposiciones del modelo__:
- El precio del activo sigue un movimiento browniano geométrico.
$$\frac{dS_t}{S_t}=\mu dt + \sigma dW_t,\quad 0\leq t \leq T, S_0 >0$$
- El comercio puede tener lugar continuamente sin ningún costo de transacción o impuestos.
- Se permite la venta en corto y los activos son perfectamente divisibles. Por lo tanto, se pueden vender activos que no son propios y se puede comprar y vender cualquier número (no necesariamente un número entero) de los activos subyacentes.
- La tasa de interés libre de riesgo continuamente compuesta es constante.
- Los inversores pueden pedir prestado o prestar a la misma tasa de interés sin riesgo.
- No hay oportunidades de arbitraje sin riesgo. De ello se deduce que todas las carteras libres de riesgo deben obtener el mismo rendimiento.
Recordemos que bajo esta medida de probabilidad, $P^*$, denominada de riesgo neutro, bajo la cual el precio del activo, $S_t$, satisface:
$$dS_t = rS_tdt+\sigma S_tdW_t,\quad 0\leq t \leq T, S_0 >0$$
Para un call asiático de promedio aritmético y con precio de ejercicios fijo, está dado por
$$\max \{A(T)-K,0\} = (A(T)-K)_+$$
con $A(x)={1\over x} \int_0^x S_u du$
Se puede ver que el valor en el tiempo t de la opción call asiática está dado por:
$$ V_t(K) = e^{-r(T-t)}E^*[(A(T)-K)_+]$$
Para el caso de interés, *Valución de la opción*, donde $t_0=0$ y $t=0$, se tiene:
$$\textbf{Valor call asiático}\longrightarrow V_0(K)=e^{-rT}E\Bigg[ \Big({1\over T} \int_0^T S_u du -K\Big)_+\Bigg]$$
## Usando Monte Carlo
Para usar este método es necesario que se calcule el promedio $S_u$ en el intervalo $[0,T]$. Para esto se debe aproximar el valor de la integral por los siguiente dos métodos.
Para los dos esquemas se dividirá el intervalo $[0,T]$ en N subintervalos de igual longitud, $h={T\over N}$, esto determina los tiempos $t_0,t_1,\cdots,t_{N-1},t_N $, en donde $t_i=ih$ para $i=0,1,\cdots,N$
### 1. Sumas de Riemann
$$\int_0^T S_u du \approx h \sum_{i=0}^{n-1} S_{t_i}$$
De este modo, si con el método de Monte Carlo se generan $M$ trayectorias, entonces
la aproximación de el valor del call asiático estaría dada por:
$$\hat V_0^{(1)}= {e^{-rT} \over M} \sum_{j=1}^{M} \Bigg({1\over N} \sum_{i=0}^{N-1} S_{t_i}-K \Bigg)_+$$
### 2. Mejorando la aproximación de las sumas de Riemann (esquema del trapecio)

Desarrollando la exponencial en serie de taylor y suponiendo que $h$ es pequeña, sólo se conservan los términos de orden uno, se tiene la siguiente aproximación:
$$\int_0^T S_u du \approx {h \over 2}\sum_{i=0}^{N-1}S_{t_i}(2+rh+(W_{t_{i+1}}-W_{t_i})\sigma)$$
Reemplazando esta aproximación en el precio del call, se tiene la siguiente estimación:
$$\hat V_0^{(2)}= {e^{-rT} \over M} \sum_{j=1}^{M} \Bigg({h\over 2T} \sum_{i=0}^{N-1} S_{t_i}(2+rh+(W_{t_{i+1}}-W_{t_i})\sigma)-K \Bigg)_+$$
**recordar que $h = \frac{T}{N}$**
> **Referencia**:
http://mat.izt.uam.mx/mat/documentos/notas%20de%20clase/cfenaoe3.pdf
## Ejemplo
Como caso de prueba se seleccionó el de un call asiático con precio inicial, $S_0 = 100$, precio de ejercicio $K = 100$, tasa libre de riesgo $r = 0.10$, volatilidad $\sigma = 0.20$ y $T = 1$ año. Cuyo precio es $\approx 7.04$.
```
#importar los paquetes que se van a usar
import pandas as pd
import pandas_datareader.data as web
import numpy as np
import datetime
import matplotlib.pyplot as plt
import scipy.stats as st
import seaborn as sns
%matplotlib inline
#algunas opciones para Pandas
pd.set_option('display.notebook_repr_html', True)
pd.set_option('display.max_columns', 9)
pd.set_option('display.max_rows', 10)
pd.set_option('display.width', 78)
pd.set_option('precision', 3)
# Programar la solución de la ecuación de Black-Scholes
# St = S0*exp((r-sigma^2/2)*t+ sigma*DeltaW)
np.random.seed(5555)
NbTraj = 2
NbStep = 100
S0 = 100
r = 0.10
sigma = 0.2
K = 100
DeltaT = 1 / NbStep
SqDeltaT = np.sqrt(DeltaT)
DeltaW = np.random.randn(NbStep - 1, NbTraj) * SqDeltaT
nu = r-sigma**2/2
increments = nu*DeltaT + sigma * DeltaW
# Ln St = Ln S0 + (r-sigma^2/2)*t+ sigma*DeltaW)
concat = np.concatenate([np.log(S0)*np.ones([NbStep, 1]), increments], axis=1)
LogSt = np.cumsum(concat, axis=1)
St = np.exp(LogSt)
def BSprices(mu,sigma,S0,NbTraj,NbStep):
"""
Expresión de la solución de la ecuación de Black-Scholes
St = S0*exp((r-sigma^2/2)*t+ sigma*DeltaW)
Parámetros
---------
mu : Tasa libre de riesgo
sigma : Desviación estándar de los rendimientos
S0 : Precio inicial del activo subyacente
NbTraj: Cantidad de trayectorias a simular
NbStep: Número de días a simular
"""
# Datos para la fórmula de St
nu = mu-(sigma**2)/2
DeltaT = 1/NbStep
SqDeltaT = np.sqrt(DeltaT)
DeltaW = SqDeltaT*np.random.randn(NbTraj,NbStep-1)
# Se obtiene --> Ln St = Ln S0+ nu*DeltaT + sigma*DeltaW
increments = nu*DeltaT + sigma*DeltaW
concat = np.concatenate((np.log(S0)*np.ones([NbTraj,1]),increments),axis=1)
# Se utiliza cumsum por que se quiere simular los precios iniciando desde S0
LogSt = np.cumsum(concat,axis=1)
# Se obtienen los precios simulados para los NbStep fijados
St = np.exp(LogSt)
# Vector con la cantidad de días simulados
t = np.arange(0,NbStep)
return St.T,t
def calc_daily_ret(closes):
return np.log(closes/closes.shift(1)).iloc[1:]
np.random.seed(5555)
NbTraj = 2
NbStep = 100
S0 = 100
r = 0.10
sigma = 0.2
K = 100
# Resolvemos la ecuación de black scholes para obtener los precios
St,t = BSprices(r,sigma,S0,NbTraj,NbStep)
# t = t*NbStep
prices = pd.DataFrame(St,index=t)
prices
# Graficamos los precios simulados
ax = prices.plot(label='precios originales')#plt.plot(t,St,label='precios')
# Explorar el funcionamiento de la función expanding y rolling para ver cómo calcular el promedio
# y graficar sus diferencias
Average_t = prices.expanding(1, axis=0).mean()
Average_t_roll = prices.rolling(window=20).mean()
Average_t.plot(ax=ax)
Average_t_roll.plot(ax=ax)
plt.legend()
(1.5+3)/2, 2.333*2-1.5
data
# Ilustración función rolling y expanding
data = pd.DataFrame([
['a', 1],
['a', 2],
['a', 4],
['b', 5],
], columns = ['category', 'value'])
print('expanding\n',data.value.expanding(2).sum())
print('rolling\n',data.value.rolling(window=2).sum())
# Ilustración resultado función expanding
pan = pd.DataFrame(np.matrix([[1,2,3],[4,5,6],[7,8,9],[1,1,1]]))
pan.expanding(1,axis=0).mean()
```
## Valuación opciones asiáticas
### 1. Método sumas de Riemann
```
#### Sumas de Riemann
# Strike
strike = K
# Tiempo de cierre del contrato
T = 1
# Valuación de la opción
call = pd.DataFrame({'Prima_asiatica':
np.exp(-r*T) * np.fmax(Average_t - strike, 0).mean(axis=1)}, index=t)
call.plot()
print('La prima estimada usando %i trayectorias es: %2.2f'%(NbTraj,call.iloc[-1].Prima_asiatica))
# intervalos de confianza
confianza = 0.95
sigma_est = call.sem().Prima_asiatica
mean_est = call.iloc[-1].Prima_asiatica
i1 = st.t.interval(confianza, NbTraj - 1, loc=mean_est, scale=sigma_est)
i2 = st.norm.interval(confianza, loc=mean_est, scale=sigma_est)
print('El intervalor de confianza usando t-dist es:', i1)
print('El intervalor de confianza usando norm-dist es:', i2)
call.iloc[-1].Prima
```
Ahora hagamos pruebas variando la cantidad de trayectorias `NbTraj` y la cantidad de números de puntos `NbStep` para ver como aumenta la precisión del método. Primero creemos una función que realice la aproximación de Riemann
```
# Función donde se almacenan todos los resultados
def Riemann_approach(K:'Strike price',r:'Tasa libre de riesgo',S0:'Precio inicial',
NbTraj:'Número trayectorias',NbStep:'Cantidad de pasos a simular',
sigma:'Volatilidad',T:'Tiempo de cierre del contrato en años',
flag=None):
# Resolvemos la ecuación de black scholes para obtener los precios
St,t = BSprices(r,sigma,S0,NbTraj,NbStep)
# Almacenamos los precios en un dataframe
prices = pd.DataFrame(St,index=t)
# Obtenemos los precios promedios
Average_t = prices.expanding().mean()
# Definimos el dataframe de strikes
strike = K
# Calculamos el call de la opción según la formula obtenida para Sumas de Riemann
call = pd.DataFrame({'Prima': np.exp(-r*T) \
*np.fmax(Average_t - strike, 0).mean(axis=1)}, index=t)
# intervalos de confianza
confianza = 0.95
sigma_est = call.sem().Prima
mean_est = call.iloc[-1].Prima
i1 = st.norm.interval(confianza, loc=mean_est, scale=sigma_est)
# return np.array([call.iloc[-1].Prima,i1[0],i1[1]])
# if flag==True:
# # calcular intervarlo
# return call, intervalo
# else
return call.iloc[-1].Prima
```
## Ejemplo
Valuar la siguiente opción asiática con los siguientes datos $S_0= 100$, $r=0.10$, $\sigma=0.2$, $K=100$, $T=1$ en años, usando la siguiente combinación de trayectorias y número de pasos:
```
NbTraj = [1000, 10000, 20000]
NbStep = [10, 50, 100]
# Visualización de datos
filas = ['Nbtray = %i' %i for i in NbTraj]
col = ['NbStep = %i' %i for i in NbStep]
df = pd.DataFrame(index=filas,columns=col)
df
# Resolverlo acá
S0 = 100
r = 0.10
sigma = 0.2
K = 100
T = 1
df.loc[:, :] = list(map(lambda N_tra: list(map(lambda N_ste: Riemann_approach(K, r, S0, N_tra, N_ste, sigma, T), NbStep)),
NbTraj))
df
```
# Tarea
Implementar el método de esquemas del trapecio, para valuar la opción call y put asiática con precio inicial, $S_0 = 100$, precio de ejercicio $K = 100$, tasa libre de riesgo $r = 0.10$, volatilidad $\sigma = 0.20$ y $T = 1$ año. Cuyo precio es $\approx 7.04$. Realizar la simulación en base a la siguiente tabla:

Observe que en esta tabla se encuentran los intervalos de confianza de la aproximación obtenida y además el tiempo de simulación que tarda en encontrar la respuesta cada método.
- Se debe entonces realizar una simulación para la misma cantidad de trayectorias y número de pasos y construir una Dataframe de pandas para reportar todos los resultados obtenidos.**(70 puntos)**
- Compare los resultados obtenidos con los resultados arrojados por la función `Riemann_approach`. Concluya. **(30 puntos)**
Se habilitará un enlace en canvas donde se adjuntará los resultados de dicha tarea
>**Nota:** Para generar índices de manera como se especifica en la tabla referirse a:
> - https://pandas.pydata.org/pandas-docs/stable/user_guide/advanced.html
> - https://jakevdp.github.io/PythonDataScienceHandbook/03.05-hierarchical-indexing.html
> - https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.MultiIndex.html
<script>
$(document).ready(function(){
$('div.prompt').hide();
$('div.back-to-top').hide();
$('nav#menubar').hide();
$('.breadcrumb').hide();
$('.hidden-print').hide();
});
</script>
<footer id="attribution" style="float:right; color:#808080; background:#fff;">
Created with Jupyter by Oscar David Jaramillo Z.
</footer>
|
github_jupyter
|
#importar los paquetes que se van a usar
import pandas as pd
import pandas_datareader.data as web
import numpy as np
import datetime
import matplotlib.pyplot as plt
import scipy.stats as st
import seaborn as sns
%matplotlib inline
#algunas opciones para Pandas
pd.set_option('display.notebook_repr_html', True)
pd.set_option('display.max_columns', 9)
pd.set_option('display.max_rows', 10)
pd.set_option('display.width', 78)
pd.set_option('precision', 3)
# Programar la solución de la ecuación de Black-Scholes
# St = S0*exp((r-sigma^2/2)*t+ sigma*DeltaW)
np.random.seed(5555)
NbTraj = 2
NbStep = 100
S0 = 100
r = 0.10
sigma = 0.2
K = 100
DeltaT = 1 / NbStep
SqDeltaT = np.sqrt(DeltaT)
DeltaW = np.random.randn(NbStep - 1, NbTraj) * SqDeltaT
nu = r-sigma**2/2
increments = nu*DeltaT + sigma * DeltaW
# Ln St = Ln S0 + (r-sigma^2/2)*t+ sigma*DeltaW)
concat = np.concatenate([np.log(S0)*np.ones([NbStep, 1]), increments], axis=1)
LogSt = np.cumsum(concat, axis=1)
St = np.exp(LogSt)
def BSprices(mu,sigma,S0,NbTraj,NbStep):
"""
Expresión de la solución de la ecuación de Black-Scholes
St = S0*exp((r-sigma^2/2)*t+ sigma*DeltaW)
Parámetros
---------
mu : Tasa libre de riesgo
sigma : Desviación estándar de los rendimientos
S0 : Precio inicial del activo subyacente
NbTraj: Cantidad de trayectorias a simular
NbStep: Número de días a simular
"""
# Datos para la fórmula de St
nu = mu-(sigma**2)/2
DeltaT = 1/NbStep
SqDeltaT = np.sqrt(DeltaT)
DeltaW = SqDeltaT*np.random.randn(NbTraj,NbStep-1)
# Se obtiene --> Ln St = Ln S0+ nu*DeltaT + sigma*DeltaW
increments = nu*DeltaT + sigma*DeltaW
concat = np.concatenate((np.log(S0)*np.ones([NbTraj,1]),increments),axis=1)
# Se utiliza cumsum por que se quiere simular los precios iniciando desde S0
LogSt = np.cumsum(concat,axis=1)
# Se obtienen los precios simulados para los NbStep fijados
St = np.exp(LogSt)
# Vector con la cantidad de días simulados
t = np.arange(0,NbStep)
return St.T,t
def calc_daily_ret(closes):
return np.log(closes/closes.shift(1)).iloc[1:]
np.random.seed(5555)
NbTraj = 2
NbStep = 100
S0 = 100
r = 0.10
sigma = 0.2
K = 100
# Resolvemos la ecuación de black scholes para obtener los precios
St,t = BSprices(r,sigma,S0,NbTraj,NbStep)
# t = t*NbStep
prices = pd.DataFrame(St,index=t)
prices
# Graficamos los precios simulados
ax = prices.plot(label='precios originales')#plt.plot(t,St,label='precios')
# Explorar el funcionamiento de la función expanding y rolling para ver cómo calcular el promedio
# y graficar sus diferencias
Average_t = prices.expanding(1, axis=0).mean()
Average_t_roll = prices.rolling(window=20).mean()
Average_t.plot(ax=ax)
Average_t_roll.plot(ax=ax)
plt.legend()
(1.5+3)/2, 2.333*2-1.5
data
# Ilustración función rolling y expanding
data = pd.DataFrame([
['a', 1],
['a', 2],
['a', 4],
['b', 5],
], columns = ['category', 'value'])
print('expanding\n',data.value.expanding(2).sum())
print('rolling\n',data.value.rolling(window=2).sum())
# Ilustración resultado función expanding
pan = pd.DataFrame(np.matrix([[1,2,3],[4,5,6],[7,8,9],[1,1,1]]))
pan.expanding(1,axis=0).mean()
#### Sumas de Riemann
# Strike
strike = K
# Tiempo de cierre del contrato
T = 1
# Valuación de la opción
call = pd.DataFrame({'Prima_asiatica':
np.exp(-r*T) * np.fmax(Average_t - strike, 0).mean(axis=1)}, index=t)
call.plot()
print('La prima estimada usando %i trayectorias es: %2.2f'%(NbTraj,call.iloc[-1].Prima_asiatica))
# intervalos de confianza
confianza = 0.95
sigma_est = call.sem().Prima_asiatica
mean_est = call.iloc[-1].Prima_asiatica
i1 = st.t.interval(confianza, NbTraj - 1, loc=mean_est, scale=sigma_est)
i2 = st.norm.interval(confianza, loc=mean_est, scale=sigma_est)
print('El intervalor de confianza usando t-dist es:', i1)
print('El intervalor de confianza usando norm-dist es:', i2)
call.iloc[-1].Prima
# Función donde se almacenan todos los resultados
def Riemann_approach(K:'Strike price',r:'Tasa libre de riesgo',S0:'Precio inicial',
NbTraj:'Número trayectorias',NbStep:'Cantidad de pasos a simular',
sigma:'Volatilidad',T:'Tiempo de cierre del contrato en años',
flag=None):
# Resolvemos la ecuación de black scholes para obtener los precios
St,t = BSprices(r,sigma,S0,NbTraj,NbStep)
# Almacenamos los precios en un dataframe
prices = pd.DataFrame(St,index=t)
# Obtenemos los precios promedios
Average_t = prices.expanding().mean()
# Definimos el dataframe de strikes
strike = K
# Calculamos el call de la opción según la formula obtenida para Sumas de Riemann
call = pd.DataFrame({'Prima': np.exp(-r*T) \
*np.fmax(Average_t - strike, 0).mean(axis=1)}, index=t)
# intervalos de confianza
confianza = 0.95
sigma_est = call.sem().Prima
mean_est = call.iloc[-1].Prima
i1 = st.norm.interval(confianza, loc=mean_est, scale=sigma_est)
# return np.array([call.iloc[-1].Prima,i1[0],i1[1]])
# if flag==True:
# # calcular intervarlo
# return call, intervalo
# else
return call.iloc[-1].Prima
NbTraj = [1000, 10000, 20000]
NbStep = [10, 50, 100]
# Visualización de datos
filas = ['Nbtray = %i' %i for i in NbTraj]
col = ['NbStep = %i' %i for i in NbStep]
df = pd.DataFrame(index=filas,columns=col)
df
# Resolverlo acá
S0 = 100
r = 0.10
sigma = 0.2
K = 100
T = 1
df.loc[:, :] = list(map(lambda N_tra: list(map(lambda N_ste: Riemann_approach(K, r, S0, N_tra, N_ste, sigma, T), NbStep)),
NbTraj))
df
| 0.243193 | 0.959307 |
```
import os
from keras import regularizers
from keras.layers import Dense, Input
from keras.models import Model
import mne
import numpy as np
raw_dir = 'D:\\NING - spindle\\training set\\'
os.chdir(raw_dir)
import matplotlib.pyplot as plt
%matplotlib inline
raw_names = ['suj11_l2nap_day2.fif','suj11_l5nap_day1.fif',
'suj12_l2nap_day1.fif','suj12_l5nap_day2.fif',
'suj13_l2nap_day2.fif','suj13_l5nap_day1.fif',
'suj14_l2nap_day2.fif','suj14_l5nap_day1.fif',
'suj15_l2nap_day1.fif','suj15_l5nap_day2.fif',
'suj16_l2nap_day2.fif','suj16_l5nap_day1.fif']
epochs = []
for ii,raw_name in enumerate(raw_names):
raw = mne.io.read_raw_fif(raw_name)
duration = 5 # 5 seconds
events = mne.make_fixed_length_events(raw,id=1,duration=duration,)
epoch=mne.Epochs(raw,events,tmin=0,tmax=duration,preload=True,
proj=False).resample(128)
epoch=epoch.pick_channels(epoch.ch_names[:-2])
if ii == 0:
epochs = epoch.get_data()
else:
epochs = np.concatenate([epochs,epoch.get_data()])
raw.close()
epochs.shape
from sklearn.model_selection import train_test_split
x_train,x_test = train_test_split(epochs)
x_train = x_train.astype('float32').reshape(x_train.shape[0],-1)
x_train /= np.max(x_train)
x_test = x_test.astype('float32').reshape(x_test.shape[0],-1)
x_test /= np.max(x_test)
input_shape = x_train.shape[1]
# this is the size of our encoded representations
encoding_dim = 32
input_img = Input(shape=(input_shape,))
encoded = Dense(256, activation='relu', activity_regularizer=regularizers.l1(10e-5))(input_img)
encoded = Dense(128, activation='relu')(encoded)
encoded = Dense(64, activation='relu')(encoded)
decoded = Dense(128, activation='relu')(encoded)
decoded = Dense(256, activation='relu')(decoded)
decoded = Dense(input_shape, activation='sigmoid')(decoded)
autoencoder = Model(input=input_img, output=decoded)
# this model maps an input to its encoded representation
encoder = Model(input=input_img, output=encoded)
# create a placeholder for an encoded (32-dimensional) input
encoded_input_1 = Input(shape=(64,))
encoded_input_2 = Input(shape=(128,))
encoded_input_3 = Input(shape=(256,))
# retrieve the last layer of the autoencoder model
decoder_layer_1 = autoencoder.layers[-3]
decoder_layer_2 = autoencoder.layers[-2]
decoder_layer_3 = autoencoder.layers[-1]
# create the decoder model
decoder_1 = Model(input = encoded_input_1, output = decoder_layer_1(encoded_input_1))
decoder_2 = Model(input = encoded_input_2, output = decoder_layer_2(encoded_input_2))
decoder_3 = Model(input = encoded_input_3, output = decoder_layer_3(encoded_input_3))
autoencoder.compile(optimizer='adam', loss='mean_squared_error')
autoencoder.fit(x_train, x_train,
epochs=2000,
batch_size=512,
shuffle=True,
validation_data=(x_test, x_test))
#a=autoencoder.predict(x_test)
n = 1
fig, ax = plt.subplots(nrows=2,figsize=(8,8))
_=ax[0].plot(x_test[n].reshape(61,640))
_=ax[1].plot(a[n].reshape(61,640))
```
|
github_jupyter
|
import os
from keras import regularizers
from keras.layers import Dense, Input
from keras.models import Model
import mne
import numpy as np
raw_dir = 'D:\\NING - spindle\\training set\\'
os.chdir(raw_dir)
import matplotlib.pyplot as plt
%matplotlib inline
raw_names = ['suj11_l2nap_day2.fif','suj11_l5nap_day1.fif',
'suj12_l2nap_day1.fif','suj12_l5nap_day2.fif',
'suj13_l2nap_day2.fif','suj13_l5nap_day1.fif',
'suj14_l2nap_day2.fif','suj14_l5nap_day1.fif',
'suj15_l2nap_day1.fif','suj15_l5nap_day2.fif',
'suj16_l2nap_day2.fif','suj16_l5nap_day1.fif']
epochs = []
for ii,raw_name in enumerate(raw_names):
raw = mne.io.read_raw_fif(raw_name)
duration = 5 # 5 seconds
events = mne.make_fixed_length_events(raw,id=1,duration=duration,)
epoch=mne.Epochs(raw,events,tmin=0,tmax=duration,preload=True,
proj=False).resample(128)
epoch=epoch.pick_channels(epoch.ch_names[:-2])
if ii == 0:
epochs = epoch.get_data()
else:
epochs = np.concatenate([epochs,epoch.get_data()])
raw.close()
epochs.shape
from sklearn.model_selection import train_test_split
x_train,x_test = train_test_split(epochs)
x_train = x_train.astype('float32').reshape(x_train.shape[0],-1)
x_train /= np.max(x_train)
x_test = x_test.astype('float32').reshape(x_test.shape[0],-1)
x_test /= np.max(x_test)
input_shape = x_train.shape[1]
# this is the size of our encoded representations
encoding_dim = 32
input_img = Input(shape=(input_shape,))
encoded = Dense(256, activation='relu', activity_regularizer=regularizers.l1(10e-5))(input_img)
encoded = Dense(128, activation='relu')(encoded)
encoded = Dense(64, activation='relu')(encoded)
decoded = Dense(128, activation='relu')(encoded)
decoded = Dense(256, activation='relu')(decoded)
decoded = Dense(input_shape, activation='sigmoid')(decoded)
autoencoder = Model(input=input_img, output=decoded)
# this model maps an input to its encoded representation
encoder = Model(input=input_img, output=encoded)
# create a placeholder for an encoded (32-dimensional) input
encoded_input_1 = Input(shape=(64,))
encoded_input_2 = Input(shape=(128,))
encoded_input_3 = Input(shape=(256,))
# retrieve the last layer of the autoencoder model
decoder_layer_1 = autoencoder.layers[-3]
decoder_layer_2 = autoencoder.layers[-2]
decoder_layer_3 = autoencoder.layers[-1]
# create the decoder model
decoder_1 = Model(input = encoded_input_1, output = decoder_layer_1(encoded_input_1))
decoder_2 = Model(input = encoded_input_2, output = decoder_layer_2(encoded_input_2))
decoder_3 = Model(input = encoded_input_3, output = decoder_layer_3(encoded_input_3))
autoencoder.compile(optimizer='adam', loss='mean_squared_error')
autoencoder.fit(x_train, x_train,
epochs=2000,
batch_size=512,
shuffle=True,
validation_data=(x_test, x_test))
#a=autoencoder.predict(x_test)
n = 1
fig, ax = plt.subplots(nrows=2,figsize=(8,8))
_=ax[0].plot(x_test[n].reshape(61,640))
_=ax[1].plot(a[n].reshape(61,640))
| 0.631594 | 0.455622 |
数据网站,https://www.temperaturerecord.org
下载数据
```
> wget https://www.climatelevels.org/files/temperature_dataset.xlsx
```
## Library
```
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import torch
import torch.nn as nn
from torch.autograd import Variable
from sklearn.preprocessing import MinMaxScaler
```
## Data Plot
```
data = pd.read_csv('data/temperature_dataset.csv')
training_set = data.iloc[:,-2:-1].values
y = [i[0] for i in training_set]
x = [i[0] for i in data.iloc[:,1:2].values]
# print(timeline)
plt.plot(x, y, )
plt.show()
```
## Dataloading
```
def sliding_windows(data, seq_length):
x = []
y = []
for i in range(len(data)-seq_length-1):
_x = data[i:(i+seq_length)]
_y = data[i+seq_length]
x.append(_x)
y.append(_y)
return np.array(x),np.array(y)
sc = MinMaxScaler()
training_data = sc.fit_transform(training_set)
# print(training_set)
# print(training_data)
seq_length = 4
x, y = sliding_windows(training_data, seq_length)
train_size = int(len(y) * 0.67)
test_size = len(y) - train_size
dataX = Variable(torch.Tensor(np.array(x)))
dataY = Variable(torch.Tensor(np.array(y)))
trainX = Variable(torch.Tensor(np.array(x[0:train_size])))
trainY = Variable(torch.Tensor(np.array(y[0:train_size])))
testX = Variable(torch.Tensor(np.array(x[train_size:len(x)])))
testY = Variable(torch.Tensor(np.array(y[train_size:len(y)])))
# print(training_data)
# print(trainX)
# print(trainY)
```
## Model
```
class LSTM(nn.Module):
def __init__(self, num_classes, input_size, hidden_size, num_layers):
super(LSTM, self).__init__()
self.num_classes = num_classes
self.num_layers = num_layers
self.input_size = input_size
self.hidden_size = hidden_size
self.seq_length = seq_length
self.lstm = nn.LSTM(input_size=input_size, hidden_size=hidden_size,
num_layers=num_layers, batch_first=True)
self.fc = nn.Linear(hidden_size, num_classes)
def forward(self, x):
h_0 = Variable(torch.zeros(
self.num_layers, x.size(0), self.hidden_size))
c_0 = Variable(torch.zeros(
self.num_layers, x.size(0), self.hidden_size))
# Propagate input through LSTM
ula, (h_out, _) = self.lstm(x, (h_0, c_0))
h_out = h_out.view(-1, self.hidden_size)
out = self.fc(h_out)
return out
```
## Training
```
num_epochs = 2000
learning_rate = 0.01
input_size = 1
hidden_size = 2
num_layers = 1
num_classes = 1
lstm = LSTM(num_classes, input_size, hidden_size, num_layers)
criterion = torch.nn.MSELoss() # mean-squared error for regression
optimizer = torch.optim.Adam(lstm.parameters(), lr=learning_rate)
#optimizer = torch.optim.SGD(lstm.parameters(), lr=learning_rate)
# Train the model
for epoch in range(num_epochs):
outputs = lstm(trainX)
optimizer.zero_grad()
# obtain the loss function
loss = criterion(outputs, trainY)
loss.backward()
optimizer.step()
if epoch % 100 == 0:
print("Epoch: %d, loss: %1.5f" % (epoch, loss.item()))
```
## Testing for Global CO2 Monthly Dataset
```
lstm.eval()
train_predict = lstm(dataX)
data_predict = train_predict.data.numpy()
dataY_plot = dataY.data.numpy()
data_predict = sc.inverse_transform(data_predict)
dataY_plot = sc.inverse_transform(dataY_plot)
plt.axvline(x=train_size, c='r', linestyle='--')
plt.plot(dataY_plot)
plt.plot(data_predict)
plt.suptitle('Time-Series Prediction')
plt.show()
```
|
github_jupyter
|
> wget https://www.climatelevels.org/files/temperature_dataset.xlsx
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import torch
import torch.nn as nn
from torch.autograd import Variable
from sklearn.preprocessing import MinMaxScaler
data = pd.read_csv('data/temperature_dataset.csv')
training_set = data.iloc[:,-2:-1].values
y = [i[0] for i in training_set]
x = [i[0] for i in data.iloc[:,1:2].values]
# print(timeline)
plt.plot(x, y, )
plt.show()
def sliding_windows(data, seq_length):
x = []
y = []
for i in range(len(data)-seq_length-1):
_x = data[i:(i+seq_length)]
_y = data[i+seq_length]
x.append(_x)
y.append(_y)
return np.array(x),np.array(y)
sc = MinMaxScaler()
training_data = sc.fit_transform(training_set)
# print(training_set)
# print(training_data)
seq_length = 4
x, y = sliding_windows(training_data, seq_length)
train_size = int(len(y) * 0.67)
test_size = len(y) - train_size
dataX = Variable(torch.Tensor(np.array(x)))
dataY = Variable(torch.Tensor(np.array(y)))
trainX = Variable(torch.Tensor(np.array(x[0:train_size])))
trainY = Variable(torch.Tensor(np.array(y[0:train_size])))
testX = Variable(torch.Tensor(np.array(x[train_size:len(x)])))
testY = Variable(torch.Tensor(np.array(y[train_size:len(y)])))
# print(training_data)
# print(trainX)
# print(trainY)
class LSTM(nn.Module):
def __init__(self, num_classes, input_size, hidden_size, num_layers):
super(LSTM, self).__init__()
self.num_classes = num_classes
self.num_layers = num_layers
self.input_size = input_size
self.hidden_size = hidden_size
self.seq_length = seq_length
self.lstm = nn.LSTM(input_size=input_size, hidden_size=hidden_size,
num_layers=num_layers, batch_first=True)
self.fc = nn.Linear(hidden_size, num_classes)
def forward(self, x):
h_0 = Variable(torch.zeros(
self.num_layers, x.size(0), self.hidden_size))
c_0 = Variable(torch.zeros(
self.num_layers, x.size(0), self.hidden_size))
# Propagate input through LSTM
ula, (h_out, _) = self.lstm(x, (h_0, c_0))
h_out = h_out.view(-1, self.hidden_size)
out = self.fc(h_out)
return out
num_epochs = 2000
learning_rate = 0.01
input_size = 1
hidden_size = 2
num_layers = 1
num_classes = 1
lstm = LSTM(num_classes, input_size, hidden_size, num_layers)
criterion = torch.nn.MSELoss() # mean-squared error for regression
optimizer = torch.optim.Adam(lstm.parameters(), lr=learning_rate)
#optimizer = torch.optim.SGD(lstm.parameters(), lr=learning_rate)
# Train the model
for epoch in range(num_epochs):
outputs = lstm(trainX)
optimizer.zero_grad()
# obtain the loss function
loss = criterion(outputs, trainY)
loss.backward()
optimizer.step()
if epoch % 100 == 0:
print("Epoch: %d, loss: %1.5f" % (epoch, loss.item()))
lstm.eval()
train_predict = lstm(dataX)
data_predict = train_predict.data.numpy()
dataY_plot = dataY.data.numpy()
data_predict = sc.inverse_transform(data_predict)
dataY_plot = sc.inverse_transform(dataY_plot)
plt.axvline(x=train_size, c='r', linestyle='--')
plt.plot(dataY_plot)
plt.plot(data_predict)
plt.suptitle('Time-Series Prediction')
plt.show()
| 0.772531 | 0.938124 |
___
<a href='https://github.com/ai-vithink'> <img src='https://avatars1.githubusercontent.com/u/41588940?s=200&v=4' /></a>
___
# Regression Plots
Seaborn has many built-in capabilities for regression plots, however we won't really discuss regression until the machine learning section of the course, so we will only cover the **lmplot()** function for now.
**lmplot** allows you to display linear models, but it also conveniently allows you to split up those plots based off of features, as well as coloring the hue based off of features.
Let's explore how this works:
```
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
from IPython.display import HTML
HTML('''<script>
code_show_err=false;
function code_toggle_err() {
if (code_show_err){
$('div.output_stderr').hide();
} else {
$('div.output_stderr').show();
}
code_show_err = !code_show_err
}
$( document ).ready(code_toggle_err);
</script>
To toggle on/off output_stderr, click <a href="javascript:code_toggle_err()">here</a>.''')
# To hide warnings, which won't change the desired outcome.
%%HTML
<style type="text/css">
table.dataframe td, table.dataframe th {
border: 3px black solid !important;
color: black !important;
}
# For having gridlines
import warnings
warnings.filterwarnings("ignore")
sns.set_style('darkgrid')
tips = sns.load_dataset('tips')
tips.head()
# Simple linear plot using lmplot
# Feature you want on x axis vs the feature on y axis
sns.lmplot(x='total_bill', y='tip', data=tips)
# Gives us a scatter plot with linear fit on top of it.
sns.lmplot(x = 'total_bill', y = 'tip',data = tips,hue ="sex")
```
* Hue to have some separation based off of a categorical label/feature/column.
* Gives us 2 scatter plots and 2 linear fits.
* It tells us male and females have almost same linear fit on basis of total_bill vs tip given.
* Also we can pass in matplotlib style markers and marker types
### Working with Markers
lmplot kwargs get passed through to **regplot** which is a more general form of lmplot(). regplot has a scatter_kws parameter that gets passed to plt.scatter. So you want to set the s parameter in that dictionary, which corresponds (a bit confusingly) to the squared markersize. In other words you end up passing a dictionary with the base matplotlib arguments, in this case, s for size of a scatter plot. In general, you probably won't remember this off the top of your head, but instead reference the documentation.
```
sns.lmplot(x = 'total_bill', y = 'tip',data = tips,hue ="sex",markers=['o','v'])
# List of markers = [] passed as hue has 2 elements.
# If the plot is small for you then we can pass in a scatter_kws parameter to sns, which makes use of matplotlib internally.
# Seaborn calls matplotlib under the hood, and we can affect matplotlib from seaborn by passing parameter as dict.
sns.lmplot(x = 'total_bill', y = 'tip',data = tips,hue ="sex",markers=['o','v'],scatter_kws={"s":100})
# See how marker size increases. s stands for size.
# Reference these in documentation, though this degree of modification is not needed everyday.
```
## Using a Grid
We can add more variable separation through columns and rows with the use of a grid. Just indicate this with the col or row arguments:
```
# Instead of separating by hue we can also use a grid.
sns.lmplot(x = 'total_bill', y = 'tip',data = tips,col='sex')
# col gives us 2 separate columns separated by sex category instead of separation by colour as we do using hue.
# Similarly we can do grids of row and col simultaneouly as well in the following manner
sns.lmplot(x = 'total_bill', y = 'tip',data = tips,col='sex',row='time')
# If you want to plot even more labels then we can use hue with row and col as well simultaneously resulting in :
sns.lmplot(x = 'total_bill', y = 'tip',data = tips,col='day',row='time',hue='sex')
# Too much info, try eliminating something.
sns.lmplot(x = 'total_bill', y = 'tip',data = tips,col='day',hue='sex')
# Better now, but size and aspect looks odd and hard to read.
```
## Aspect and Size
Seaborn figures can have their size and aspect ratio adjusted with the **size** and **aspect** parameters:
```
# We can change ratio of height and width called aspect
sns.lmplot(x = 'total_bill', y = 'tip',data = tips,col='day',hue='sex',aspect=0.6,size=8)
# Much better but still font-size looks kinda small right ?
```
* NOTE : For more advanced features like setting the marker size, or changing marker type, please refer the documentation.
* [Documentation Regression Plot - Seaborn](https://seaborn.pydata.org/generated/seaborn.regplot.html)
# Up Next : Font Size, Styling, Colour etc.
|
github_jupyter
|
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
from IPython.display import HTML
HTML('''<script>
code_show_err=false;
function code_toggle_err() {
if (code_show_err){
$('div.output_stderr').hide();
} else {
$('div.output_stderr').show();
}
code_show_err = !code_show_err
}
$( document ).ready(code_toggle_err);
</script>
To toggle on/off output_stderr, click <a href="javascript:code_toggle_err()">here</a>.''')
# To hide warnings, which won't change the desired outcome.
%%HTML
<style type="text/css">
table.dataframe td, table.dataframe th {
border: 3px black solid !important;
color: black !important;
}
# For having gridlines
import warnings
warnings.filterwarnings("ignore")
sns.set_style('darkgrid')
tips = sns.load_dataset('tips')
tips.head()
# Simple linear plot using lmplot
# Feature you want on x axis vs the feature on y axis
sns.lmplot(x='total_bill', y='tip', data=tips)
# Gives us a scatter plot with linear fit on top of it.
sns.lmplot(x = 'total_bill', y = 'tip',data = tips,hue ="sex")
sns.lmplot(x = 'total_bill', y = 'tip',data = tips,hue ="sex",markers=['o','v'])
# List of markers = [] passed as hue has 2 elements.
# If the plot is small for you then we can pass in a scatter_kws parameter to sns, which makes use of matplotlib internally.
# Seaborn calls matplotlib under the hood, and we can affect matplotlib from seaborn by passing parameter as dict.
sns.lmplot(x = 'total_bill', y = 'tip',data = tips,hue ="sex",markers=['o','v'],scatter_kws={"s":100})
# See how marker size increases. s stands for size.
# Reference these in documentation, though this degree of modification is not needed everyday.
# Instead of separating by hue we can also use a grid.
sns.lmplot(x = 'total_bill', y = 'tip',data = tips,col='sex')
# col gives us 2 separate columns separated by sex category instead of separation by colour as we do using hue.
# Similarly we can do grids of row and col simultaneouly as well in the following manner
sns.lmplot(x = 'total_bill', y = 'tip',data = tips,col='sex',row='time')
# If you want to plot even more labels then we can use hue with row and col as well simultaneously resulting in :
sns.lmplot(x = 'total_bill', y = 'tip',data = tips,col='day',row='time',hue='sex')
# Too much info, try eliminating something.
sns.lmplot(x = 'total_bill', y = 'tip',data = tips,col='day',hue='sex')
# Better now, but size and aspect looks odd and hard to read.
# We can change ratio of height and width called aspect
sns.lmplot(x = 'total_bill', y = 'tip',data = tips,col='day',hue='sex',aspect=0.6,size=8)
# Much better but still font-size looks kinda small right ?
| 0.457137 | 0.949669 |
# 14 Linear Algebra – Students (1)
## Motivating problem: Two masses on three strings
Two masses $M_1$ and $M_2$ are hung from a horizontal rod with length $L$ in such a way that a rope of length $L_1$ connects the left end of the rod to $M_1$, a rope of length $L_2$ connects $M_1$ and $M_2$, and a rope of length $L_3$ connects $M_2$ to the right end of the rod. The system is at rest (in equilibrium under gravity).

Find the angles that the ropes make with the rod and the tension forces in the ropes.
In class we derived the equations that govern this problem – see [14_String_Problem_lecture_notes (PDF)](14_String_Problem_lecture_notes.pdf).
We can represent the problem as system of nine coupled non-linear equations:
$$
\mathbf{f}(\mathbf{x}) = 0
$$
### Summary of equations to be solved
Treat $\sin\theta_i$ and $\cos\theta_i$ together with $T_i$, $1\leq i \leq 3$, as unknowns that have to simultaneously fulfill the nine equations
\begin{align}
-T_1 \cos\theta_1 + T_2\cos\theta_2 &= 0\\
T_1 \sin\theta_1 - T_2\sin\theta_2 - W_1 &= 0\\
-T_2\cos\theta_2 + T_3\cos\theta_3 &= 0\\
T_2\sin\theta_2 + T_3\sin\theta_3 - W_2 &= 0\\
L_1\cos\theta_1 + L_2\cos\theta_2 + L_3\cos\theta_3 - L &= 0\\
-L_1\sin\theta_1 - L_2\sin\theta_2 + L_3\sin\theta_3 &= 0\\
\sin^2\theta_1 + \cos^2\theta_1 - 1 &= 0\\
\sin^2\theta_2 + \cos^2\theta_2 - 1 &= 0\\
\sin^2\theta_3 + \cos^2\theta_3 - 1 &= 0
\end{align}
Consider the nine equations a vector function $\mathbf{f}$ that takes a 9-vector $\mathbf{x}$ of the unknowns as argument:
\begin{align}
\mathbf{f}(\mathbf{x}) &= 0\\
\mathbf{x} &= \left(\begin{array}{c}
x_0 \\ x_1 \\ x_2 \\
x_3 \\ x_4 \\ x_5 \\
x_6 \\ x_7 \\ x_8
\end{array}\right)
=
\left(\begin{array}{c}
\sin\theta_1 \\ \sin\theta_2 \\ \sin\theta_3 \\
\cos\theta_1 \\ \cos\theta_2 \\ \cos\theta_3 \\
T_1 \\ T_2 \\ T_3
\end{array}\right) \\
\mathbf{L} &= \left(\begin{array}{c}
L \\ L_1 \\ L_2 \\ L_3
\end{array}\right), \quad
\mathbf{W} = \left(\begin{array}{c}
W_1 \\ W_2
\end{array}\right)
\end{align}
In more detail:
\begin{align}
f_1(\mathbf{x}) &= -x_6 x_3 + x_7 x_4 &= 0\\
f_2(\mathbf{x}) &= x_6 x_0 - x_7 x_1 - W_1 & = 0\\
\dots\\
f_8(\mathbf{x}) &= x_2^2 + x_5^2 - 1 &=0
\end{align}
We generalize the *Newton-Raphson algorithm* from the [last lecture](http://asu-compmethodsphysics-phy494.github.io/ASU-PHY494//2017/03/16/13_Root_finding/) to $n$ dimensions:
## General Newton-Raphson algorithm
Given a trial vector $\mathbf{x}$, the correction $\Delta\mathbf{x}$ can be derived from the Taylor expansion
$$
f_i(\mathbf{x} + \Delta\mathbf{x}) = f_i(\mathbf{x}) + \sum_{j=1}^{n} \left.\frac{\partial f_i}{\partial x_j}\right|_{\mathbf{x}} \, \Delta x_j + \dots
$$
or in full vector notation
\begin{align}
\mathbf{f}(\mathbf{x} + \Delta\mathbf{x}) &= \mathbf{f}(\mathbf{x}) + \left.\frac{d\mathbf{f}}{d\mathbf{x}}\right|_{\mathbf{x}} \Delta\mathbf{x} + \dots\\
&= \mathbf{f}(\mathbf{x}) + \mathsf{J}(\mathbf{x}) \Delta\mathbf{x} + \dots
\end{align}
where $\mathsf{J}(\mathbf{x})$ is the *[Jacobian](http://mathworld.wolfram.com/Jacobian.html)* matrix of $\mathbf{f}$ at $\mathbf{x}$, the generalization of the derivative to multivariate vector functions.
Solve
$$
\mathbf{f}(\mathbf{x} + \Delta\mathbf{x}) = 0
$$
i.e.,
$$
\mathsf{J}(\mathbf{x}) \Delta\mathbf{x} = -\mathbf{f}(\mathbf{x})
$$
for the correction $\Delta x$
$$
\Delta\mathbf{x} = -\mathsf{J}(\mathbf{x})^{-1} \mathbf{f}(\mathbf{x})
$$
which has the same form as the 1D Newton-Raphson correction $\Delta x = -f'(x)^{-1} f(x)$.
These are *matrix equations* (we linearized the problem). One can either explicitly solve for the unknown vector $\Delta\mathbf{x}$ with the inverse matrix of the Jacobian or use other methods to solve the coupled system of linear equations of the general form
$$
\mathsf{A} \mathbf{x} = \mathbf{b}.
$$
## Linear algebra with `numpy.linalg`
```
import numpy as np
np.linalg?
```
### System of coupled linear equations
Solve the coupled system of linear equations of the general form
$$
\mathsf{A} \mathbf{x} = \mathbf{b}.
$$
```
A = np.array([
[1, 0, 0],
[0, 1, 0],
[0, 0, 2]
])
b = np.array([1, 0, 1])
```
What does this system of equations look like?
```
for i in range(A.shape[0]):
terms = []
for j in range(A.shape[1]):
terms.append("{1} x[{0}]".format(i, A[i, j]))
print(" + ".join(terms), "=", b[i])
```
Now solve it with `numpy.linalg.solve`:
Test that it satisfies the original equation:
$$
\mathsf{A} \mathbf{x} - \mathbf{b} = 0
$$
#### Activity: Solving matrix equations
With
$$
\mathsf{A}_1 = \left(\begin{array}{ccc}
+4 & -2 & +1\\
+3 & +6 & -4\\
+2 & +1 & +8
\end{array}\right)
$$
and
$$
\mathbf{b}_1 = \left(\begin{array}{c}
+12 \\ -25 \\ +32
\end{array}\right), \quad
\mathbf{b}_2 = \left(\begin{array}{c}
+4 \\ -1 \\ +36
\end{array}\right), \quad
$$
solve for $\mathbf{x}_i$
$$
\mathsf{A}_1 \mathbf{x}_i = \mathbf{b}_i
$$
and *check the correctness of your answer*.
### Matrix inverse
In order to solve directly we need the inverse of $\mathsf{A}$:
$$
\mathsf{A}\mathsf{A}^{-1} = \mathsf{A}^{-1}\mathsf{A} = \mathsf{1}
$$
Then
$$
\mathbf{x} = \mathsf{A}^{-1} \mathbf{b}
$$
If the inverse exists, `numpy.linalg.inv()` can calculate it:
Check that it behaves like an inverse:
Now solve the coupled equations directly:
#### Activity: Solving coupled equations with the inverse matrix
1. Compute the inverse of $\mathsf{A}_1$ and *check the correctness*.
2. Compute $\mathbf{x}_1$ and $\mathbf{x}_2$ with $\mathsf{A}_1^{-1}$ and check the correctness of your answers.
### Eigenvalue problems
The equation
\begin{gather}
\mathsf{A} \mathbf{x}_i = \lambda_i \mathbf{x}_i
\end{gather}
is the **eigenvalue problem** and a solution provides the eigenvalues $\lambda_i$ and corresponding eigenvectors $x_i$ that satisfy the equation.
#### Example 1: Principal axes of a square
The principle axes of the [moment of inertia tensor](https://en.wikipedia.org/wiki/Moment_of_inertia#The_inertia_tensor) are defined through the eigenvalue problem
$$
\mathsf{I} \mathbf{\omega}_i = \lambda_i \mathbf{\omega}_i
$$
The principal axes are the $\mathbf{\omega}_i$.
```
Isquare = np.array([[2/3, -1/4], [-1/4, 2/3]])
```
Note that the eigenvectors are `omegas[:, i]`! You can transpose so that axis 0 is the eigenvector index:
Test:
$$
(\mathsf{I} - \lambda_i \mathsf{1}) \mathbf{\omega}_i = 0
$$
#### Example 2: Spin in a magnetic field
In quantum mechanics, a spin 1/2 particle is represented by a spinor $\chi$, a 2-component vector. The Hamiltonian operator for a stationary spin 1/2 particle in a homogenous magnetic field $B_y$ is
$$
\mathsf{H} = -\gamma \mathsf{S}_y B_y = -\gamma B_y \frac{\hbar}{2} \mathsf{\sigma_y}
= \hbar \omega \left( \begin{array}{cc} 0 & -i \\ i & 0 \end{array}\right)
$$
Determine the *eigenvalues* and *eigenstates*
$$
\mathsf{H} \mathbf{\chi} = E \mathbf{\chi}
$$
of the spin 1/2 particle.
(To make this a purely numerical problem, divide through by $\hbar\omega$, i.e. calculate $E/\hbar\omega$.)
Normalize the eigenvectors:
$$
\hat\chi = \frac{1}{\sqrt{\chi^\dagger \cdot \chi}} \chi
$$
#### Activity: eigenvalues
Find the eigenvalues and eigenvectors of
$$
\mathsf{A}_2 = \left(\begin{array}{ccc}
-2 & +2 & -3\\
+2 & +1 & -6\\
-1 & -2 & +0
\end{array}\right)
$$
Are the eigenvectors normalized?
Check your results.
|
github_jupyter
|
import numpy as np
np.linalg?
A = np.array([
[1, 0, 0],
[0, 1, 0],
[0, 0, 2]
])
b = np.array([1, 0, 1])
for i in range(A.shape[0]):
terms = []
for j in range(A.shape[1]):
terms.append("{1} x[{0}]".format(i, A[i, j]))
print(" + ".join(terms), "=", b[i])
Isquare = np.array([[2/3, -1/4], [-1/4, 2/3]])
| 0.100095 | 0.994347 |
# Funciones
## Función
**Función.** Una función en `Python` es una pieza de código reutilizable que solo se ejecuta cuando es llamada.
Se define usando la palabra reservada `def` y estructura general es la siguiente:
```
def nombre_función(input1, input2, ..., inputn):
cuerpo de la función
return output
```
**Observación.** La instrucción `return` finaliza la ejecución de la función y devuelve el resultado que se indica a continuación. Si no se indicase nada, la función finalizaría, pero no retornaría nada.
Como hemos visto, en general, las funciones constan de 3 partes:
- **Inputs (parámetros o argumentos).** Son los valores que le pasamos como entrada a la función.
- **Cuerpo.** Son todas las operaciones que lleva a cabo la función.
- **Output.** Es el resultado que devuelve la función.
**Observación.** Los parámetros son variables internas de la función. Si probásemos a ejecutar una de dichas variables en el entorno global, nos saltaría un error.
Con lo visto anteriormente, a la hora de construir una función hay que hacerse las siguientes preguntas:
- ¿Qué datos necesita conocer la función? (inputs)
- ¿Qué hace la función? (cuerpo)
- ¿Qué devuelve? (output)
**Observación.** Los inputs y el output son opcionales: podemos definir una función sin necesidad de proporcionarle inputs y sin que nos devuelva nada.
Una vez definida una función, para llamarla utilizamos su nombre seguido de paréntesis:
```
def mi_primera_funcion():
print("Hola")
mi_primera_funcion()
```
Hemos dicho que tanto los inputs como el output son opcionales. Veamos algunos ejemplos con diferentes casos.
---
#### Ejemplo 1
Veamos otro ejemplo que no necesite ningún parámetro y no nos devuelva nada, tal y como ocurría con `mi_primera_funcion()`
```
def holaMundo():
print("Hola mundo")
holaMundo()
# Esta función, cuando es llamada, imprime "Hola mundo", pero no devuelve nada.
```
---
#### Ejemplo 2
Veamos un ejemplo de función que no necesita ningún input, pero que devuelve un output. Por ejemplo, una función que nos devuelve "¡Buenos días!"
```
# Declaramos la función:
def buenosDias():
return "Buenos días"
# Llamamos a la función:
buenosDias()
```
Como nos devuelve el saludo, lo podemos guardar en una variable, que será de tipo string
```
buenosDias = buenosDias()
print(buenosDias)
print(type(buenosDias))
```
---
#### Ejemplo 3
Veamos ahora un ejemplo de función que no nos devuelva nada, pero que sí toma algún parámetro
```
def buenos_dias(nombre):
print("¡Buenos días, {}!".format(nombre))
buenos_dias(nombre = "Nacho")
# La función recibe un nombre por parámetro y muestra por pantalla el resultado con el nombre indicado.
```
---
#### Ejemplo 4
Por último, vamos a crear una función que nos calcule la división entera de dos números y nos retorne el cociente y el resto.
```
def division_entera(x, y):
q = x // y
r = x % y
return q, r
```
Esta función, a la que hemos llamado `division_entera`, calcula el cociente y el resto de dos números cualesquiera y devuelve como resultado esos dos números calculados.
Utilicemos ahora nuestra función para calcular el cociente y el resto de la división $41 \div 7$
```
division_entera(x = 41, y = 7)
division_entera(y = 7, x = 41)
division_entera(41, 7)
```
Al llamar a la función e indicarle por parámetros `x = 41` e `y = 7`, hemos obtenido como resultado la tupla `(5, 6)`. El significado de dicho resulatdo es que el cociente entero de $41\div 7$ es 5, mientras que el resto es $6$. Efectivamente
$$41 = 7\cdot 5 + 6$$
También podríamos guardar en variables diferentes los resultados que nos devuelve nuestra función, para poder trabajar con ellos en el entorno global
```
cociente, resto = division_entera(x = 41, y = 7)
print(cociente)
print(resto)
print(41 == 7 * cociente + resto)
```
## Parámetros
Por defecto, una función debe ser llamada con el número correcto de argumentos. Esto es, si la función espera 2 argumentos, tenemos que llamar a la función con esos 2 argumentos. Ni más, ni menos.
```
def nombre_completo(nombre, apellido):
print("El nombre completo es: ", nombre, apellido)
nombre_completo("Ana", "García")
```
Si intentamos llamar a la función `complete_name()` pasando 1 solo parámetro o 3 parámetros, entonces la función devuelve error.
### Número arbitrario de argumentos
Si no sabemos el número de parámetros que van a ser introducidos, entonces añadimos un asterisco `*` previo al nombre del parámetro en la definición de la función. Los valores introducidos serán guardados en una tupla.
```
def suma_num(*numeros):
suma = 0
for n in numeros:
suma += n
return suma
suma_num(1, 2, 3)
suma_num(2, 4, 613, 8, 10)
```
### Número arbitrario de claves de argumento
Hasta ahora hemos visto que al pasar valores por parámetro a la función, podemos hacerlo con la sintaxis `clave_argumento = valor` o directamente pasar por parámetro el valor siguiendo el orden posicional de la definición de la función:
```
def nombre_completo(nombre, apellido):
print("El nombre completo es: ", nombre, apellido)
nombre_completo("Pedro", "Aguado")
```
En realidad, los nombres completos pueden tener dos o incluso más apellidos, pero no sabemos si el usuario tiene 1 o 2 o más. Entones, podemos añadir dos asteriscos `**` antes del nombre del parámetro para así poder introducir tantos como queramos sin que salte error
```
def nombre_completo(nombre, **apellido):
print("El nombre completo es: {}".format(nombre), end = " " )
for i in apellido.items():
print("{}".format(i[1]), end = " ")
nombre_completo(nombre = "Luis", apellido1 = "Pérez", apellido2 = "López")
```
### Parámetros por defecto
Hemos visto que una función en `Python` puede tener o no parámetros.
En caso de tener, podemos indicar que alguno tenga un valor por defecto.
La función `diff()` calcula la diferencia entre los dos números que introducimos por parámetros. Podemos hacer que el sustraendo por defecto valga 1 del siguiente modo:
```
def diff(x, y = 1):
return x - y
diff(613)
```
## Docstring
**Docstring.** Son comentarios explicativos que ayudan a comprender el funcionamiento de una función.
- Van entre triple comilla doble
- Pueden ser multilínea
- Se sitúan al principio de la definición de la función
Retomando el ejemplo de la división entera, podríamos utilizar docstring del siguiente modo:
```
def division_entera(x, y):
"""
Esta función calcula el cociente y el resto
de la división entera de x entre y.
Argumentos:
x(int): dividendo
y(int): divisor distinto de cero.
"""
q = x // y
r = x % y
return q, r
```
Con la ayuda del método `.__doc__` podemos acceder directamente a la información indicada en el docstring de una función
```
print(division_entera.__doc__)
```
## Variables de una función
Dentro de una función en `Python` existen dos tipos de variables:
- **Variable local.** Aquella que es creada y solamente existe dentro de la función.
- **Variable global.** Aquella que es creada en el entorno global.
Dada la siguiente función:
```
def operaciones_aritmeticas(x, y):
sum = x + y
diff = x - y
mult = x * y
div = x / y
return {"suma": sum,
"resta": diff,
"producto": mult,
"division": div}
```
Si nosotros queremos imprimir por ejemplo el valor que toma la variable `mult` en el entorno global nos saltará un error, pues esta variable no existe a nivel global porque no ha sido declarada en dicho entorno ya que solamente ha sido declarada a nivel local, dentro de la función `operaciones_aritmeticas()`.
```
print(operaciones_aritmeticas(5, 3))
```
Si se diese el caso de que sí hubiese sido definida la variable `mult` en el entorno global, como lo que ocurre en el siguiente bloque de código, por mucho que la variable local tenga el mimso nombre y por mucho que ejecutemos la función, el valor de la variable global no se ve modificado
```
mult = 10
print(operaciones_aritmeticas(x = 5, y = 3))
print(mult)
```
Si dentro de una función utilizamos la palabra reservada `global` a una variable local, ésta automáticamente pasa a ser una variable global previamente definida.
Veamos un ejemplo de función que nos devuelve el siguiente número del entero `n` definido en el entorno global:
```
n = 7
def next_n():
global n
return n + 1
next_n()
```
### Paso por copia vs. paso por referencia
Dependiendo del tipo de dato que pasemos por parámetro a la función, podemos diferenciar entre
- **Paso por copia.** Se crea una copia local de la variable dentro de la función.
- **Paso por referencia.** Se maneja directamente la variable y los cambios realizados dentro de la función afectan también a nivel global.
En general, los tipos de datos básicos como enteros, en coma flotante, strings o booleanos se pasan por copia, mientras que estructuras de datos como listas, diccionarios, conjuntos o tuplas u otros objetos se pasan por referencia.
Un ejemplo de paso por copia sería
```
def double_value(n):
n = n*2
return n
num = 5
print(double_value(num))
print(num)
```
Un ejemplo de paso por referencia sería
```
def double_values(ns):
for i, n in enumerate(ns):
ns[i] *= 2
return ns
nums = [1, 2, 3, 4, 5]
print(double_values(nums))
print(nums)
```
## Funciones más complejas
Las funciones pueden ser más completas, pues admiten tanto operadores de decisión como de iteración.
Volviendo al ejemplo 4, la función creada claramente es muy sencilla, pues suponemos que el usuario va a introducir por parámetros números enteros.
**Ejercicio.** Mejora la función `division_entera()` para que
- Compruebe que los números introducidos son enteros. En caso de no ser así, indicar que se ha tomado la parte entera de los valores introducidos.
- Realice la división entera del mayor parámetro (en valor absoluto) entre el menor parámetro. Esto es, si el usuario introduce `x = -2` e `y = -10`, como 10 > 2, entonces la función debe llevar a cabo la división entera de -10 entre -2.
- Imprima por pantalla una frase indicando la división realizada y el cociente y el resto obtenidos.
- Devuelva el cociente y el resto a modo de tupla
```
def division_entera(x, y):
ints = (x == int(x)) and (y == int(y))
if not ints:
x = int(x)
y = int(y)
print("Se tomarán como parámetro las partes enteras de los valores introducidos")
if abs(x) >= abs(y):
q = x // y
r = x % y
print(f"Se ha realizado la división de {x} entre {y}, el resultado es: cociente = {q} y el resto {r}")
else:
q = y // x
r = y % x
print(f"Se ha realizado la división de {y} entre {x}, el resultado es: cociente = {q} y el resto {r}")
return q, r
division_entera(-10.3, -5)
division_entera(-3, 19)
```
---
#### Ejemplo 5
Veamos una función que dado un número, nos dice si éste es positivo, negativo o vale 0.
```
def signo(num):
"""
Función que dado un número devuelve el signo positivo
negativo o cero del mismo.
Argumentos:
num(int): Número del cual queremos hallar su signo.
Returns:
signo(str): string positivo, negativo o cero.
"""
if num > 0:
return "Positivo"
elif num < 0:
return "Negativo"
else:
return "Cero"
print(signo(3.1415))
print(signo(-100))
print(signo(0))
```
---
#### Ejemplo 6
Veamos ahora una función que contiene un bucle `for` y que dado un número entero, nos imprime su tabla de multiplicar con sus 10 primeros múltiplos y nos devuelve una lista con todos esos múltiplos:
```
def multiplication_table10(num):
"""
Dado un número entero, imprimimos su tabla de multiplicar con
los 10 primeros múltiplos y devolvemos una lista de los múltiplos.
Args:
num (int): valor del cual vamos a calcular sus tabla de multiplicar
Returns:
multiples (list): lista con los 10 primeros múltiplos de num
"""
multiples = []
print("La tabla de multiplicar del {}:".format(num))
for i in range(1, 11):
multiple = num * i
print("{} x {} = {}".format(num, i, multiple))
multiples.append(multiple)
return multiples
multiples7 = multiplication_table10(7)
print(multiples7)
```
Vamos ahora a mejorar la función `multiplication_table10()` para que si el usuario decide introducir un número que no sea entero, nuestra función le avise y le explique el error que está cometiendo:
```
def multiplication_table10(num):
"""
Dado un número entero, primero comprovamos si es entero.
Si no lo es, no devolvemos nada.
Si lo es, imprimimos su tabla de multiplicar con los 10
primeros múltiplos y devolvemos una lista de los múltiplos.
Args:
num (int): valor del cual vamos a calcular sus 10 primeros múltiplos
Returns:
multiples (list): lista con los 10 primeros múltiplos de num
"""
if type(num) != type(1):
print("El número introducido no es entero")
return
multiples = []
print("La tabla de multiplicar del {}:".format(num))
for i in range(1, 11):
multiple = num * i
print("{} x {} = {}".format(num, i, multiple))
multiples.append(multiple)
return multiples
multiples3 = multiplication_table10(num = 3)
print(multiples3)
multiples_float = multiplication_table10(num = "3.7")
print(multiples_float)
```
---
#### Ejemplo 7
Creemos ahora una función que dada una frase acabada en punto, nos devuelva si contiene o no la letra "a" haciendo uso de un bucle `while`
```
def contains_a(sentence):
i = 0
while sentence[i] != ".":
if sentence[i] == "a":
return True
i += 1
return False
contains_a("El erizo es bonito.")
contains_a("El elefante es gigante.")
```
**Ejercicio.** Generaliza la función `contains_a()` a una función llamada contains_letter() que devuelva si una frase cualquiera (no necesariamente acabada en punto) contiene o no la letra indicada también por el usuario. Tienes que hacerlo únicamente con operadores de decisión e iteración. No vale usar ningún método existente de `string`.
```
def contains_letter(sentence, letter):
for c in sentence:
if c == letter:
return True
return False
contains_letter("Mi amigo es muy inteligente, pero un poco pesado", "t")
```
---
## Funciones recursivas
**Función recursiva.** Es una función que se llama a sí misma.
**¡Cuidado!** Hay que tener mucho cuidado con este tipo de funciones porque podemos caer en un bucle infinito. Es decir, que la función no acabara nunca de ejecutarse.
Una función recursiva que entraría en bucle infinito sería la siguiente.
```
def powers(x, n):
print(x ** n)
powers(x, n + 1)
```
¿Por qué decimos que entra en bulce infinito? Pues porque solo parará si nosotros interrumpimos la ejecución.
Esto se debe a que no le hemos indicado un caso de parada a la función, denominado caso final.
**Caso final.** Es el caso que indica cuándo debe romperse la recursión. Hay que indicarlo siempre para no caer en un bucle infinito.
En el caso de la función `powers()`, podemos indicar como caso final cuando el valor resultante supere 1000000. Lo indicamos con un `if`
```
def powers(x, n):
if x ** n > 1000000:
return x ** n
print(x ** n)
powers(x, n + 1)
powers(2, 1)
```
---
#### Ejemplo 8
Veamos ahora un ejemplo clásico de función recursiva que funciona correctamente.
Queremos una función que nos imprima el término $i$-ésimo de la sucesión de Fibonacci. Es decir, nosotros le indicamos el índice del término y la función nos devuelve el valor de dicho término.
La sucesión de Fibonacci es
$$1, 1, 2, 3, 5, 8, 13,\dots$$
Es decir, cada término se obtiene de la suma de los dos anteriores.
$$F_0 = F_1 = 1$$
$$F_n = F_{n-1} + F_{n-2}, n\geq 2$$
Con lo cual, la función que queremos y a la que hemos llamado `Fibonacci()` es:
```
def Fibonacci(index):
if index == 0 or index == 1:
return 1
return Fibonacci(index - 1) + Fibonacci(index - 2)
Fibonacci(index = 7)
Fibonacci(30)
```
## Funciones helper
Al igual que las funciones pueden llamarse a sí mismas, también pueden llamar a otras funciones.
**Función helper.** Es una función cuyo propósito es evitar la repetición de código.
Si nos dan la siguiente función
```
def sign_sum(x, y):
if x + y > 0:
print("El resultado de sumar {} más {} es positivo".format(x, y))
elif x + y == 0:
print("El resultado de sumar {} más {} es cero".format(x, y))
else:
print("El resultado de sumar {} más {} es negativo".format(x, y))
sign_sum(5, 4)
sign_sum(3, -3)
sign_sum(1, -8)
```
Vemos que el `print` se repite salvo por la última palabra.
Podríamos pensar en crear la función helper siguiente:
```
def helper_print(x, y, sign):
print("El resultado de sumar {} más {} es {}.".format(x, y, sign))
```
Si utilizamos la función helper, la función `sign_sum()` quedaría modificada del siguiente modo:
```
def sign_sum(x, y):
if x + y > 0:
helper_print(x, y, "positivo")
elif x + y == 0:
helper_print(x, y, "cero")
else:
helper_print(x, y, "negativo")
sign_sum(5, 4)
sign_sum(3, -3)
sign_sum(1, -8)
```
Con lo cual ya no hay código repetido.
Y como se puede observar, la función original funciona correctamente.
# Funciones `lambda`
## Funciones `lambda`
Son un tipo especial de funciones de `Python` que tienen la sintaxis siguiente
```
lambda parámetros: expresión
```
- Son útiles para ejecutar funciones en una sola línea
- Pueden tomar cualquier número de argumentos
- Tienen una limitación: solamente pueden contener una expresión
Veamos algunos ejemplos
---
#### Ejemplo 1
Función que dado un número, le suma 10 puntos más:
```
plus10 = lambda x: x + 10
plus10(5)
```
---
#### Ejemplo 2
Función que calcula el producto de dos números:
```
prod = lambda x, y: x * y
prod(5, 10)
```
---
#### Ejemplo 3
Función que dados 3 números, calcula el discriminante de la ecuación de segundo grado.
Recordemos que dada una ecuación de segundo grado de la forma $$ax^2 + bx + c = 0$$
el discriminante es $$\triangle = b^2-4ac$$
y dependiendo de su signo, nos indica cuantas soluciones reales va a tener la ecuación:
- Si $\triangle > 0$, entonces hay dos soluciones diferentes
- Si $\triangle = 0$, entonces hay dos soluciones que son iguales
- Si $\triangle < 0$, entonces no hay solución
```
discriminante = lambda a, b, c: b ** 2 - 4 * a * c
discriminante(1, 2, 1) # Se corresponde a la ecuación x^2 + 2x + 1 = 0, cuya única solución es x = -1
```
## La función `filter()`
- Aplica una función a todos los elementos de un objeto iterable
- Devuelve un objeto generador, de ahí que usamos la función `list()` para convertirlo a lista
- Como output, devuelve los elementos para los cuales el aplicar la función ha devuelto `True`
Con la ayuda de las funciones `lambda`, apliquemos `filter()` para quedarnos con los números múltiplos de 7 de la siguiente lista llamada `nums`
```
nums = [49, 57, 62, 147, 2101, 22]
list(filter(lambda x: (x % 7 == 0), nums))
```
La función proporcionada a `filter()` no tiene por qué ser `lambda`, sino que puede ser una ya existente, o bien una creada por nosotros mismos.
Con las siguientes líneas de código vamos a obtener todas las palabras cuya tercera letra sea `s` haciendo uso de `filter()` y la función creada `third_letter_is_s()`:
```
def third_letter_is_s(word):
return word[2] == "s"
words = ["castaña", "astronomía", "masa", "bolígrafo", "mando", "tostada"]
list(filter(third_letter_is_s, words))
```
## La función `reduce()`
- Aplica continuamente una misma función a los elementos de un objeto iterable
1. Aplica la función a los primeros dos elementos
2. Aplica la función al resultado del paso anterior y el tercer elemento
3. Aplica la función al resultado del paso anterior y el cuarto elemento
4. Sigue así hasta que solo queda un elemento
- Devuelve el valor resultante
Con la ayuda de las funciones `lambda`, apliquemos `reduce()` para calcular el producto de todos los elementos de una lista
```
from functools import reduce
nums = [1, 2, 3, 4, 5, 6]
reduce(lambda x, y: x * y, nums)
```
De nuevo, la función proporcionada a `reduce()` no tiene por qué ser `lambda`, sino que puede ser una ya existente o bien, una creada por nosotros mismos.
Con las siguientes líneas de código, vamos a obtener el máximo de una lista dada, haciendo uso de `reduce()` y la función creada `bigger_than()`:
```
def bigger_than(a, b):
if a > b:
return a
return b
bigger_than(14, 7)
nums = [-10, 5, 7, -3, 16, -30, 2, 33]
reduce(bigger_than, nums)
```
## La función `map()`
- Aplica una misma función a todos los elementos de un objeto iterable
- Devuelve un objeto generador, de ahí que usemos la función `list()` para convertirlo a lista
- Como output, devuelve el resultado de aplicar la función a cada elemento
Con la ayuda de las funciones `lambda`, apliquemos `map()` para calcular las longitudes de las siguientes palabras
```
words = ["zapato", "amigo", "yoyo", "barco", "xilófono", "césped"]
list(map(lambda w: len(w), words))
```
Sin embargo, para este caso en concreto no haría falta usar funciones `lambda`, pues podríamos hacer directamente
```
list(map(len, words))
```
## La función `sorted()`
- Ordena los elementos del objeto iterable que indiquemos de acuerdo a la función que pasemos por parámetro
- Como output, devuelve una permutación del objeto iterable ordenado según la función indicada
Con la ayuda de las funciones `lambda`, apliquemos `sorted()` para ordenar la lista `words` en función de las longitudes de las palabras en orden descendente.
```
words = ["zapato", "amigo", "yoyo", "barco", "xilófono", "césped"]
sorted(words, key = lambda x: len(x), reverse = True)
```
**Observación.** Si quisiésemos ordenar en orden ascendente, simplemente tendríamos que indicar `reverse = False`, que al ser el valor por defecto, bastaría con omitir dicho parámetro.
**Observación.** Si el tipo de objeto a ser ordenado es un string y no indicamos parámetro `key`, entonces se ordenan por defecto: orden alfabético ascendente.
```
sorted(words, key = len)
sorted(words)
```
|
github_jupyter
|
def nombre_función(input1, input2, ..., inputn):
cuerpo de la función
return output
def mi_primera_funcion():
print("Hola")
mi_primera_funcion()
def holaMundo():
print("Hola mundo")
holaMundo()
# Esta función, cuando es llamada, imprime "Hola mundo", pero no devuelve nada.
# Declaramos la función:
def buenosDias():
return "Buenos días"
# Llamamos a la función:
buenosDias()
buenosDias = buenosDias()
print(buenosDias)
print(type(buenosDias))
def buenos_dias(nombre):
print("¡Buenos días, {}!".format(nombre))
buenos_dias(nombre = "Nacho")
# La función recibe un nombre por parámetro y muestra por pantalla el resultado con el nombre indicado.
def division_entera(x, y):
q = x // y
r = x % y
return q, r
division_entera(x = 41, y = 7)
division_entera(y = 7, x = 41)
division_entera(41, 7)
cociente, resto = division_entera(x = 41, y = 7)
print(cociente)
print(resto)
print(41 == 7 * cociente + resto)
def nombre_completo(nombre, apellido):
print("El nombre completo es: ", nombre, apellido)
nombre_completo("Ana", "García")
def suma_num(*numeros):
suma = 0
for n in numeros:
suma += n
return suma
suma_num(1, 2, 3)
suma_num(2, 4, 613, 8, 10)
def nombre_completo(nombre, apellido):
print("El nombre completo es: ", nombre, apellido)
nombre_completo("Pedro", "Aguado")
def nombre_completo(nombre, **apellido):
print("El nombre completo es: {}".format(nombre), end = " " )
for i in apellido.items():
print("{}".format(i[1]), end = " ")
nombre_completo(nombre = "Luis", apellido1 = "Pérez", apellido2 = "López")
def diff(x, y = 1):
return x - y
diff(613)
def division_entera(x, y):
"""
Esta función calcula el cociente y el resto
de la división entera de x entre y.
Argumentos:
x(int): dividendo
y(int): divisor distinto de cero.
"""
q = x // y
r = x % y
return q, r
print(division_entera.__doc__)
def operaciones_aritmeticas(x, y):
sum = x + y
diff = x - y
mult = x * y
div = x / y
return {"suma": sum,
"resta": diff,
"producto": mult,
"division": div}
print(operaciones_aritmeticas(5, 3))
mult = 10
print(operaciones_aritmeticas(x = 5, y = 3))
print(mult)
n = 7
def next_n():
global n
return n + 1
next_n()
def double_value(n):
n = n*2
return n
num = 5
print(double_value(num))
print(num)
def double_values(ns):
for i, n in enumerate(ns):
ns[i] *= 2
return ns
nums = [1, 2, 3, 4, 5]
print(double_values(nums))
print(nums)
def division_entera(x, y):
ints = (x == int(x)) and (y == int(y))
if not ints:
x = int(x)
y = int(y)
print("Se tomarán como parámetro las partes enteras de los valores introducidos")
if abs(x) >= abs(y):
q = x // y
r = x % y
print(f"Se ha realizado la división de {x} entre {y}, el resultado es: cociente = {q} y el resto {r}")
else:
q = y // x
r = y % x
print(f"Se ha realizado la división de {y} entre {x}, el resultado es: cociente = {q} y el resto {r}")
return q, r
division_entera(-10.3, -5)
division_entera(-3, 19)
def signo(num):
"""
Función que dado un número devuelve el signo positivo
negativo o cero del mismo.
Argumentos:
num(int): Número del cual queremos hallar su signo.
Returns:
signo(str): string positivo, negativo o cero.
"""
if num > 0:
return "Positivo"
elif num < 0:
return "Negativo"
else:
return "Cero"
print(signo(3.1415))
print(signo(-100))
print(signo(0))
def multiplication_table10(num):
"""
Dado un número entero, imprimimos su tabla de multiplicar con
los 10 primeros múltiplos y devolvemos una lista de los múltiplos.
Args:
num (int): valor del cual vamos a calcular sus tabla de multiplicar
Returns:
multiples (list): lista con los 10 primeros múltiplos de num
"""
multiples = []
print("La tabla de multiplicar del {}:".format(num))
for i in range(1, 11):
multiple = num * i
print("{} x {} = {}".format(num, i, multiple))
multiples.append(multiple)
return multiples
multiples7 = multiplication_table10(7)
print(multiples7)
def multiplication_table10(num):
"""
Dado un número entero, primero comprovamos si es entero.
Si no lo es, no devolvemos nada.
Si lo es, imprimimos su tabla de multiplicar con los 10
primeros múltiplos y devolvemos una lista de los múltiplos.
Args:
num (int): valor del cual vamos a calcular sus 10 primeros múltiplos
Returns:
multiples (list): lista con los 10 primeros múltiplos de num
"""
if type(num) != type(1):
print("El número introducido no es entero")
return
multiples = []
print("La tabla de multiplicar del {}:".format(num))
for i in range(1, 11):
multiple = num * i
print("{} x {} = {}".format(num, i, multiple))
multiples.append(multiple)
return multiples
multiples3 = multiplication_table10(num = 3)
print(multiples3)
multiples_float = multiplication_table10(num = "3.7")
print(multiples_float)
def contains_a(sentence):
i = 0
while sentence[i] != ".":
if sentence[i] == "a":
return True
i += 1
return False
contains_a("El erizo es bonito.")
contains_a("El elefante es gigante.")
def contains_letter(sentence, letter):
for c in sentence:
if c == letter:
return True
return False
contains_letter("Mi amigo es muy inteligente, pero un poco pesado", "t")
def powers(x, n):
print(x ** n)
powers(x, n + 1)
def powers(x, n):
if x ** n > 1000000:
return x ** n
print(x ** n)
powers(x, n + 1)
powers(2, 1)
def Fibonacci(index):
if index == 0 or index == 1:
return 1
return Fibonacci(index - 1) + Fibonacci(index - 2)
Fibonacci(index = 7)
Fibonacci(30)
def sign_sum(x, y):
if x + y > 0:
print("El resultado de sumar {} más {} es positivo".format(x, y))
elif x + y == 0:
print("El resultado de sumar {} más {} es cero".format(x, y))
else:
print("El resultado de sumar {} más {} es negativo".format(x, y))
sign_sum(5, 4)
sign_sum(3, -3)
sign_sum(1, -8)
def helper_print(x, y, sign):
print("El resultado de sumar {} más {} es {}.".format(x, y, sign))
def sign_sum(x, y):
if x + y > 0:
helper_print(x, y, "positivo")
elif x + y == 0:
helper_print(x, y, "cero")
else:
helper_print(x, y, "negativo")
sign_sum(5, 4)
sign_sum(3, -3)
sign_sum(1, -8)
lambda parámetros: expresión
plus10 = lambda x: x + 10
plus10(5)
prod = lambda x, y: x * y
prod(5, 10)
discriminante = lambda a, b, c: b ** 2 - 4 * a * c
discriminante(1, 2, 1) # Se corresponde a la ecuación x^2 + 2x + 1 = 0, cuya única solución es x = -1
nums = [49, 57, 62, 147, 2101, 22]
list(filter(lambda x: (x % 7 == 0), nums))
def third_letter_is_s(word):
return word[2] == "s"
words = ["castaña", "astronomía", "masa", "bolígrafo", "mando", "tostada"]
list(filter(third_letter_is_s, words))
from functools import reduce
nums = [1, 2, 3, 4, 5, 6]
reduce(lambda x, y: x * y, nums)
def bigger_than(a, b):
if a > b:
return a
return b
bigger_than(14, 7)
nums = [-10, 5, 7, -3, 16, -30, 2, 33]
reduce(bigger_than, nums)
words = ["zapato", "amigo", "yoyo", "barco", "xilófono", "césped"]
list(map(lambda w: len(w), words))
list(map(len, words))
words = ["zapato", "amigo", "yoyo", "barco", "xilófono", "césped"]
sorted(words, key = lambda x: len(x), reverse = True)
sorted(words, key = len)
sorted(words)
| 0.468304 | 0.984501 |
# Moon Phase
```
import datetime as dt
def julian(year, month, day):
a = (14 - month) / 12.0
y = year + 4800 - a
m = (12 * a) - 3 + month
return (
day + (153 * m + 2) / 5.0 + (365 * y) + y / 4.0 - y / 100.0 + y / 400.0 - 32045
)
moon_phase = {
1.84566: "🌑", # new
5.53699: "🌒", # waxing crescent
9.22831: "🌓", # first quarter
12.91963: "🌔", # waxing gibbous
16.61096: "🌕", # full
20.30228: "🌖", # waning gibbous
23.99361: "🌗", # last quarter
27.68493: "🌘", # waning crescent
27.68494: "🌑", # new
}
now = dt.datetime.now()
phase = (julian(now.year, now.month, now.day) - julian(2000, 1, 6)) % 29.530588853
moon_phase.get([k for k in moon_phase.keys() if phase < k][0],'chyba')
moon_phase.get(list(filter(lambda x: phase<x,moon_phase))[0])
def greet_me(**kwargs):
for key, value in kwargs.items():
print(f"{key} = {value}")
greet_me(name1="nodes",name2="yesod")
```
# Merge Dictionaries
The `.update()` method is called from the primary dictionary and accepts another dictionary as an argument.
## Drawback: is not an expression and needs a temporary variable
```
d1 = { "first_name": "Jonathan",
"last_name": "Hsu"
}
d1.update({"first_name": "Jet", "age": 15})
d1
```
## double-asterisk operator
An alternative is the double-asterisk operator, which is used to unpack dictionaries:
```
d2 = { "first_name": "Li",
"age": 25
}
{ **d1, **d2 }
```
## Union Operators To dict
[PEP 584 -- Add Union Operators To dict](https://www.python.org/dev/peps/pep-0584/)
Remember, these operators will only be available in Python 3.9 and above so make sure you add the appropriate version validation to your code.
```
d1 = { "first_name": "Jonathan", "last_name": "Hsu" }
d2 = { "first_name": "Jet", "age": 15 }
d3 = d1 | d2
myDict = { "first_name": "Jonathan", "last_name": "Hsu" }
myDict |= {"first_name": "Jet", "age": 15}
```
# math
$$
f(x) = {\frac {\sin(x)}{(x)}}
$$
```
# Configure plotting in Jupyter
from matplotlib import pyplot as plt
%matplotlib inline
plt.rcParams.update({
'figure.figsize': (9, 9),
})
"""
'axes.spines.right': False,
'axes.spines.left': False,
'axes.spines.top': False,
'axes.spines.bottom': False})
"""
import numpy as np
x = np.linspace(-6*np.pi,6*np.pi)
print(len(x))
f = x*x
plt.plot(x,f)
%matplotlib inline
import matplotlib
from matplotlib import pyplot as plt
plt.rcParams.update({'figure.figsize': (12, 12),})
x = np.linspace(-6*np.pi, 6*np.pi, 6*32)
f = np.sin(x)/x
plt.plot(x,f, label=r'$f(x) = {\frac {\sin(x)}{(x)}}$')
plt.title(r'$f(x) = {\frac {\sin(x)}{(x)}}$')
plt.legend(frameon=False)
plt.plot((x[0],x[-1]),(0,0), '--', color='grey', linewidth=1.2) # x = 0
plt.plot((0,0),(min(f),max(f)), '--', color='grey', linewidth=1.2) # y = 0
plt.grid()
def format_func(value, tick_number):
# find number of multiples of pi/2
N = int(np.round(2 * value / np.pi))
if N == 0:
return "0"
elif N == 1:
return r"$\pi/2$"
elif N == 2:
return r"$\pi$"
elif N % 2 > 0:
return r"${0}\pi/2$".format(N)
else:
return r"${0}\pi$".format(N // 2)
fig,ax = plt.subplots()
ax.grid()
ax.xaxis.set_major_formatter(plt.FuncFormatter(format_func))
ax.plot(x,f, linewidth=4, label=r'$f(x) = {\frac {\sin(x)}{(x)}}$')
plt.Line2D([0,1],[0,1])
x = np.linspace(-5,5,100)
print(len(x))
f = 1/x
plt.plot(x,f, '-', linewidth=2)
x = np.linspace(-5,5,100)
f = 1/(x*x)
plt.plot(x,f, '-', linewidth=2, )
```
|
github_jupyter
|
import datetime as dt
def julian(year, month, day):
a = (14 - month) / 12.0
y = year + 4800 - a
m = (12 * a) - 3 + month
return (
day + (153 * m + 2) / 5.0 + (365 * y) + y / 4.0 - y / 100.0 + y / 400.0 - 32045
)
moon_phase = {
1.84566: "🌑", # new
5.53699: "🌒", # waxing crescent
9.22831: "🌓", # first quarter
12.91963: "🌔", # waxing gibbous
16.61096: "🌕", # full
20.30228: "🌖", # waning gibbous
23.99361: "🌗", # last quarter
27.68493: "🌘", # waning crescent
27.68494: "🌑", # new
}
now = dt.datetime.now()
phase = (julian(now.year, now.month, now.day) - julian(2000, 1, 6)) % 29.530588853
moon_phase.get([k for k in moon_phase.keys() if phase < k][0],'chyba')
moon_phase.get(list(filter(lambda x: phase<x,moon_phase))[0])
def greet_me(**kwargs):
for key, value in kwargs.items():
print(f"{key} = {value}")
greet_me(name1="nodes",name2="yesod")
d1 = { "first_name": "Jonathan",
"last_name": "Hsu"
}
d1.update({"first_name": "Jet", "age": 15})
d1
d2 = { "first_name": "Li",
"age": 25
}
{ **d1, **d2 }
d1 = { "first_name": "Jonathan", "last_name": "Hsu" }
d2 = { "first_name": "Jet", "age": 15 }
d3 = d1 | d2
myDict = { "first_name": "Jonathan", "last_name": "Hsu" }
myDict |= {"first_name": "Jet", "age": 15}
# Configure plotting in Jupyter
from matplotlib import pyplot as plt
%matplotlib inline
plt.rcParams.update({
'figure.figsize': (9, 9),
})
"""
'axes.spines.right': False,
'axes.spines.left': False,
'axes.spines.top': False,
'axes.spines.bottom': False})
"""
import numpy as np
x = np.linspace(-6*np.pi,6*np.pi)
print(len(x))
f = x*x
plt.plot(x,f)
%matplotlib inline
import matplotlib
from matplotlib import pyplot as plt
plt.rcParams.update({'figure.figsize': (12, 12),})
x = np.linspace(-6*np.pi, 6*np.pi, 6*32)
f = np.sin(x)/x
plt.plot(x,f, label=r'$f(x) = {\frac {\sin(x)}{(x)}}$')
plt.title(r'$f(x) = {\frac {\sin(x)}{(x)}}$')
plt.legend(frameon=False)
plt.plot((x[0],x[-1]),(0,0), '--', color='grey', linewidth=1.2) # x = 0
plt.plot((0,0),(min(f),max(f)), '--', color='grey', linewidth=1.2) # y = 0
plt.grid()
def format_func(value, tick_number):
# find number of multiples of pi/2
N = int(np.round(2 * value / np.pi))
if N == 0:
return "0"
elif N == 1:
return r"$\pi/2$"
elif N == 2:
return r"$\pi$"
elif N % 2 > 0:
return r"${0}\pi/2$".format(N)
else:
return r"${0}\pi$".format(N // 2)
fig,ax = plt.subplots()
ax.grid()
ax.xaxis.set_major_formatter(plt.FuncFormatter(format_func))
ax.plot(x,f, linewidth=4, label=r'$f(x) = {\frac {\sin(x)}{(x)}}$')
plt.Line2D([0,1],[0,1])
x = np.linspace(-5,5,100)
print(len(x))
f = 1/x
plt.plot(x,f, '-', linewidth=2)
x = np.linspace(-5,5,100)
f = 1/(x*x)
plt.plot(x,f, '-', linewidth=2, )
| 0.430147 | 0.867822 |
<a href="https://colab.research.google.com/github/Irene-kim/Cyberbullying-Detection-for-Women-/blob/master/codes)without_ELMo.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
from google.colab import drive
drive.mount('/content/gdrive')
%tensorflow_version 1.x
import numpy as np
import pandas as pd
import os
import random
import matplotlib.pyplot as plt
%matplotlib inline
from sklearn.metrics import classification_report, confusion_matrix
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import train_test_split
from tensorflow.keras.wrappers.scikit_learn import KerasRegressor
from tensorflow.keras.preprocessing.text import Tokenizer
from tensorflow.keras.preprocessing.sequence import pad_sequences
from tensorflow.keras.wrappers.scikit_learn import KerasClassifier
from tensorflow.keras.layers import BatchNormalization, Dropout
import re
from tensorflow.keras.layers import SimpleRNN, Embedding, Dense, LSTM, Bidirectional
from tensorflow.keras.models import Sequential
import tensorflow as tf
from keras import backend as K
from sklearn.metrics import roc_curve, roc_auc_score, auc
# seed = 2, 42, 123, 1208, 1996
os.environ["CUDA_DEVICE_ORDER"] = "PCI_BUS_ID"
os.environ["CUDA_VISIBLE_DEVICES"] = ""
seed = 42
random.seed(seed) # Python
np.random.seed(seed) # numpy
# tf.random.set_seed(seed) # over Tensorflow 2.0
tf.set_random_seed(seed) # below Tensorflow
os.environ['PYTHONHASHSEED'] = str(seed)
base_path = r'/content/gdrive/My Drive/Sk/categories'
file_path = os.path.join(base_path, "Cyberbullying.csv")
df = pd.read_csv(file_path)
df = df[['Cyberbullying', 'Text']]
print(len(df))
df[:6]
def cleanText(text):
text = text.strip().replace("\n", " ").replace("\r", " ")
text = text.strip().replace('\x80', "").replace('\x80', "")
text = re.sub(r'^https?:\/\/.*[\r\n]*', '', text, flags=re.MULTILINE)
text = re.sub(r'[,!@#$%^&*)(|/><";:.?\'\\}{]',"",text)
text = text.lower()
text = re.sub(r'(.)\1+', r'\1\1', text)
text = re.sub("’", "'", text)
return text
df['Text'] = df['Text'].apply(cleanText)
filter = df['Text'] != ""
df = df[filter]
#df[50:60]
df['Text'].nunique()
df.drop_duplicates(subset=['Text'], inplace=True)
#print(df.iloc[50:75])
input_data = df['Text']
output_data = df['Cyberbullying']
tokenizer = Tokenizer()
tokenizer.fit_on_texts(input_data)
input_data = tokenizer.texts_to_sequences(input_data)
print(input_data)
word_to_index = tokenizer.word_index
print(word_to_index)
vocab_size = len(word_to_index) + 1
print('total number of tokens: {}'.format((vocab_size)))
print('max len : %d' % max(len(l) for l in input_data))
print('avg len : %f' % (sum(map(len, input_data))/len(input_data)))
max_len = 285
input_data = pad_sequences(input_data, maxlen = max_len)
print("train data size(shape): ", input_data.shape)
#input_data[54]
input_train, input_test, output_train, output_test = train_test_split(input_data, output_data, test_size=0.2, random_state=seed)
output_train.head(3)
input_train, input_val, output_train, output_val = train_test_split(input_train, output_train, test_size=0.25, random_state = seed)
print(input_train.shape)
print(input_test.shape)
print(output_train.shape)
print(output_test.shape)
print(input_test)
def f1(y_true, y_pred):
def recall(y_true, y_pred):
true_positives = K.sum(K.round(K.clip(y_true * y_pred, 0, 1)))
possible_positives = K.sum(K.round(K.clip(y_true, 0, 1)))
recall = true_positives / (possible_positives + K.epsilon())
return recall
def precision(y_true, y_pred):
true_positives = K.sum(K.round(K.clip(y_true * y_pred, 0, 1)))
predicted_positives = K.sum(K.round(K.clip(y_pred, 0, 1)))
precision = true_positives / (predicted_positives + K.epsilon())
return precision
precision = precision(y_true, y_pred)
recall = recall(y_true, y_pred)
return 2*((precision*recall)/(precision+recall+K.epsilon()))
def simple_model():
model = Sequential()
model.add(Embedding(vocab_size, 32))
model.add(Dropout(0.25))
model.add(SimpleRNN(64))
model.add(Dropout(0.50))
model.add(Dense(1, activation='sigmoid'))
model.compile(optimizer='adam', loss='binary_crossentropy', metrics=['acc', f1])
return model
def lstm_model():
model = Sequential()
model.add(Embedding(vocab_size, 32))
model.add(Dropout(0.25))
model.add((LSTM(64)))
model.add(Dropout(0.50))
model.add(Dense(1, activation='sigmoid'))
model.compile(optimizer='adam', loss='binary_crossentropy', metrics=['acc', f1])
return model
def bilstm_model():
model = Sequential()
model.add(Embedding(vocab_size, 32))
model.add(Dropout(0.25))
model.add(Bidirectional(LSTM(64)))
model.add(Dropout(0.50))
model.add(Dense(1, activation='sigmoid'))
model.compile(optimizer='adam', loss='binary_crossentropy', metrics=['acc', f1])
return model
model = bilstm_model()
model.summary()
history = model.fit(input_train, output_train, epochs=4, batch_size=32, validation_data = (input_val, output_val), verbose=1)
y_pred = model.evaluate(input_test, output_test)
y_pred
y_pred = model.predict(input_test)
#Error Check
#output_test[840:850]
#prediction = y_pred > 0.5
#prediction[840:850]
fpr_keras, tpr_keras, thresholds_keras = roc_curve(output_test, y_pred)
auc_keras = auc(fpr_keras, tpr_keras)
auc_keras
plt.figure(1)
plt.plot([0, 1], [0, 1], 'k--')
plt.plot(fpr_keras, tpr_keras, label='SimpleRNN (area = {:.3f})'.format(auc_keras))
plt.plot([0,1], [0,1], color='orange', linestyle='--')
plt.xticks(np.arange(0.0, 1.1, step=0.1))
plt.xlabel("Flase Positive Rate", fontsize=12)
plt.yticks(np.arange(0.0, 1.1, step=0.1))
plt.ylabel("True Positive Rate", fontsize=12)
plt.title('ROC Curve Analysis', fontweight='bold', fontsize=15)
plt.legend(prop={'size':9}, loc='lower right')
plt.show()
#plt.savefig(".jpg")
y_pred_binary = []
for pred in y_pred:
if pred > 0.5:
y_pred_binary.append(1)
else:
y_pred_binary.append(0)
print(classification_report(output_test, y_pred_binary, labels=[0, 1]))
from sklearn.metrics import classification_report, confusion_matrix , f1_score, precision_score, recall_score
print(precision_score(output_test, y_pred_binary , average="macro"))
print(recall_score(output_test, y_pred_binary , average="macro"))
print(f1_score(output_test, y_pred_binary , average="macro"))
tn, fp, fn, tp = confusion_matrix(output_test, y_pred_binary).ravel()
(tn, fp, fn, tp)
```
|
github_jupyter
|
from google.colab import drive
drive.mount('/content/gdrive')
%tensorflow_version 1.x
import numpy as np
import pandas as pd
import os
import random
import matplotlib.pyplot as plt
%matplotlib inline
from sklearn.metrics import classification_report, confusion_matrix
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import train_test_split
from tensorflow.keras.wrappers.scikit_learn import KerasRegressor
from tensorflow.keras.preprocessing.text import Tokenizer
from tensorflow.keras.preprocessing.sequence import pad_sequences
from tensorflow.keras.wrappers.scikit_learn import KerasClassifier
from tensorflow.keras.layers import BatchNormalization, Dropout
import re
from tensorflow.keras.layers import SimpleRNN, Embedding, Dense, LSTM, Bidirectional
from tensorflow.keras.models import Sequential
import tensorflow as tf
from keras import backend as K
from sklearn.metrics import roc_curve, roc_auc_score, auc
# seed = 2, 42, 123, 1208, 1996
os.environ["CUDA_DEVICE_ORDER"] = "PCI_BUS_ID"
os.environ["CUDA_VISIBLE_DEVICES"] = ""
seed = 42
random.seed(seed) # Python
np.random.seed(seed) # numpy
# tf.random.set_seed(seed) # over Tensorflow 2.0
tf.set_random_seed(seed) # below Tensorflow
os.environ['PYTHONHASHSEED'] = str(seed)
base_path = r'/content/gdrive/My Drive/Sk/categories'
file_path = os.path.join(base_path, "Cyberbullying.csv")
df = pd.read_csv(file_path)
df = df[['Cyberbullying', 'Text']]
print(len(df))
df[:6]
def cleanText(text):
text = text.strip().replace("\n", " ").replace("\r", " ")
text = text.strip().replace('\x80', "").replace('\x80', "")
text = re.sub(r'^https?:\/\/.*[\r\n]*', '', text, flags=re.MULTILINE)
text = re.sub(r'[,!@#$%^&*)(|/><";:.?\'\\}{]',"",text)
text = text.lower()
text = re.sub(r'(.)\1+', r'\1\1', text)
text = re.sub("’", "'", text)
return text
df['Text'] = df['Text'].apply(cleanText)
filter = df['Text'] != ""
df = df[filter]
#df[50:60]
df['Text'].nunique()
df.drop_duplicates(subset=['Text'], inplace=True)
#print(df.iloc[50:75])
input_data = df['Text']
output_data = df['Cyberbullying']
tokenizer = Tokenizer()
tokenizer.fit_on_texts(input_data)
input_data = tokenizer.texts_to_sequences(input_data)
print(input_data)
word_to_index = tokenizer.word_index
print(word_to_index)
vocab_size = len(word_to_index) + 1
print('total number of tokens: {}'.format((vocab_size)))
print('max len : %d' % max(len(l) for l in input_data))
print('avg len : %f' % (sum(map(len, input_data))/len(input_data)))
max_len = 285
input_data = pad_sequences(input_data, maxlen = max_len)
print("train data size(shape): ", input_data.shape)
#input_data[54]
input_train, input_test, output_train, output_test = train_test_split(input_data, output_data, test_size=0.2, random_state=seed)
output_train.head(3)
input_train, input_val, output_train, output_val = train_test_split(input_train, output_train, test_size=0.25, random_state = seed)
print(input_train.shape)
print(input_test.shape)
print(output_train.shape)
print(output_test.shape)
print(input_test)
def f1(y_true, y_pred):
def recall(y_true, y_pred):
true_positives = K.sum(K.round(K.clip(y_true * y_pred, 0, 1)))
possible_positives = K.sum(K.round(K.clip(y_true, 0, 1)))
recall = true_positives / (possible_positives + K.epsilon())
return recall
def precision(y_true, y_pred):
true_positives = K.sum(K.round(K.clip(y_true * y_pred, 0, 1)))
predicted_positives = K.sum(K.round(K.clip(y_pred, 0, 1)))
precision = true_positives / (predicted_positives + K.epsilon())
return precision
precision = precision(y_true, y_pred)
recall = recall(y_true, y_pred)
return 2*((precision*recall)/(precision+recall+K.epsilon()))
def simple_model():
model = Sequential()
model.add(Embedding(vocab_size, 32))
model.add(Dropout(0.25))
model.add(SimpleRNN(64))
model.add(Dropout(0.50))
model.add(Dense(1, activation='sigmoid'))
model.compile(optimizer='adam', loss='binary_crossentropy', metrics=['acc', f1])
return model
def lstm_model():
model = Sequential()
model.add(Embedding(vocab_size, 32))
model.add(Dropout(0.25))
model.add((LSTM(64)))
model.add(Dropout(0.50))
model.add(Dense(1, activation='sigmoid'))
model.compile(optimizer='adam', loss='binary_crossentropy', metrics=['acc', f1])
return model
def bilstm_model():
model = Sequential()
model.add(Embedding(vocab_size, 32))
model.add(Dropout(0.25))
model.add(Bidirectional(LSTM(64)))
model.add(Dropout(0.50))
model.add(Dense(1, activation='sigmoid'))
model.compile(optimizer='adam', loss='binary_crossentropy', metrics=['acc', f1])
return model
model = bilstm_model()
model.summary()
history = model.fit(input_train, output_train, epochs=4, batch_size=32, validation_data = (input_val, output_val), verbose=1)
y_pred = model.evaluate(input_test, output_test)
y_pred
y_pred = model.predict(input_test)
#Error Check
#output_test[840:850]
#prediction = y_pred > 0.5
#prediction[840:850]
fpr_keras, tpr_keras, thresholds_keras = roc_curve(output_test, y_pred)
auc_keras = auc(fpr_keras, tpr_keras)
auc_keras
plt.figure(1)
plt.plot([0, 1], [0, 1], 'k--')
plt.plot(fpr_keras, tpr_keras, label='SimpleRNN (area = {:.3f})'.format(auc_keras))
plt.plot([0,1], [0,1], color='orange', linestyle='--')
plt.xticks(np.arange(0.0, 1.1, step=0.1))
plt.xlabel("Flase Positive Rate", fontsize=12)
plt.yticks(np.arange(0.0, 1.1, step=0.1))
plt.ylabel("True Positive Rate", fontsize=12)
plt.title('ROC Curve Analysis', fontweight='bold', fontsize=15)
plt.legend(prop={'size':9}, loc='lower right')
plt.show()
#plt.savefig(".jpg")
y_pred_binary = []
for pred in y_pred:
if pred > 0.5:
y_pred_binary.append(1)
else:
y_pred_binary.append(0)
print(classification_report(output_test, y_pred_binary, labels=[0, 1]))
from sklearn.metrics import classification_report, confusion_matrix , f1_score, precision_score, recall_score
print(precision_score(output_test, y_pred_binary , average="macro"))
print(recall_score(output_test, y_pred_binary , average="macro"))
print(f1_score(output_test, y_pred_binary , average="macro"))
tn, fp, fn, tp = confusion_matrix(output_test, y_pred_binary).ravel()
(tn, fp, fn, tp)
| 0.536799 | 0.7335 |
# "The Hitchhiker's Guide to Neural Networks - An Introduction"
> "An introduction to neural networks for beginners."
- toc: false
- branch: master
- author: Yashvardhan Jain
- badges: false
- comments: false
- categories: [deep learning]
- image: images/post1_main.jpg
- hide: false
- search_exclude: true
> **Don't Panic!**
If you’re one of those people who has been bitten by the bug of “Deep Learning” and wants to learn how to build the neural networks that power deep learning, you have come to the right place(probably?). In this article, I will try to teach you how to build a neural network and also, answer questions as to why we do what we do and why it all works. This will be a long in-depth article, so grab your popcorn, turn up your music and let’s get started.
**Quick Tip:** It would be more beneficial if you crank up your IDE and code along.
## What is a neural network?
> “…a computing system made up of a number of simple, highly interconnected processing elements, which process information by their dynamic state response to external inputs.” — Dr. Robert Hecht-Nielsen
In simpler terms, neural networks (or Artificial Neural Networks) are computing systems that are loosely modeled after the biological neurons in our brains.
>A neural network can be represented as a graph of multiple interconnected nodes where each connection can be fine-tuned to control how much impact a certain input has on the overall output.

**Few points about a neural network:**
1. A single node in this network along with its input and output, may be referred to as a ‘Perceptron’.
2. The network shown above is a 2-layer network because we do not count the input layer, by convention.
3. The number of nodes in any layer can vary.
4. The number of hidden layers can vary too. We can even create a network that has no hidden layers. Although one must keep in mind that just because we can, doesn’t mean we should.
5. It’s vital to set up your neural network model perfectly before running it, otherwise you may end up imploding the entire Multiverse! Not really.
If it is still a bit unclear as to what a neural network is, it would only get clearer when we actually build one and see how it works. So, let me stop with the boring theory, and let’s dive into some code.
---
We will be using Python 3 and NumPy to build our neural network. We use Python 3 because it’s cool (read:popular and has a lot of superpowers in the form of packages and frameworks for machine learning). And NumPy is a scientific computing package for Python that makes it easier to implement a lot of Math (read:makes our lives a bit easier and simpler).
We will not be using the overly used and super boring “Housing Price Prediction” dataset for our tutorial. Instead, we will be using “Kaggle’s Titanic: Machine Learning from Disaster” dataset to predict who on the sinking Titanic would have survived.
**Quick Tip:** *If you don’t know this already, [Kaggle](https://www.kaggle.com) is a paradise for machine learners. It hosts machine learning competitions, tutorials and has thousands of funky datasets that you can use to do cool machine learning stuff. Do check it out!*
## What will we be building?
We will be building a 2-Layer neural network with the following specs:
1. Number of input nodes = Number of input features = 6
2. Number of nodes in the hidden layer = 4
3. Number of Output nodes = 1
4. Type of output = Binary (0 — Dead, 1 — Survived)
## What is our dataset?
The dataset consists of certain details about the passengers aboard the RMS Titanic as well as whether or not they survived. Before going further, I would recommend you clone the github repository (or simply download the files)from [here](https://github.com/J-Yash/The-hitchhiker-s-guide-to-neural-networks-an-introduction.git).
**Note:** You can either type the code as we go. Or simply open the *“first neural network.py”* file that you just downloaded along with the dataset. I would recommend you type.
The **train.csv** file contains the following details( along with what they mean):
1. PassengerId : A unique ID to identify each Passenger in our dataset
2. Embarked : Port of Embarkation (C = Cherbourg; Q = Queenstown; S = Southampton)
3. Pclass : Ticket Class
4. Name : Name of the passenger
5. Sex : Sex/Gender of the passenger
6. Age : Age of the passenger
7. SibSp : Number of siblings/spouses aboard the Titanic
8. Parch : Number of parents/children aboard the Titanic
9. Ticket : Ticket Number
10. Fare : Passenger Fare
11. Cabin : Cabin Number
12. Survived : Whether or not they survived (0 = No; 1 = Yes)
The details numbered **1** through **11** are called the *attributes* or *features* of our dataset thus, forming the input of our model. The detail number **12** is called the *output* of our dataset. By convention, *features* are represented by *X* whereas the *output* is represented by *Y*.
Finally, take out your wand so we could conjure up our neural network. And if you’re a mere muggle like me, then your laptop will just do fine.
And now, let the coding begin.
```python
import math
import os
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
```
The above code imports all the packages and dependencies that we will need. **Pandas** is a data analysis package for python and will help us in reading our data from the file. **Matplotlib** is a package for data visualization and will let us plot graphs.
```python
def preprocess():
# Reading data from the CSV file
data = pd.read_csv(os.path.join(
os.path.dirname(
__file__), 'train.csv'),
header=0, delimiter=",", quoting=3)
#Converting data from Pandas DataFrame to Numpy Arrays
data_np = data.values[:, [0, 1, 4, 5, 6, 7, 11]]
X = data_np[:, 1:]
Y = data_np[:, [0]]
# Converting string values into numeric values
for i in range(X.shape[0]):
if X[i][1] == 'male':
X[i][1] = 1
else:
X[i][1] = 2
if X[i][5] == 'C':
X[i][5] = 1
elif X[i][5] == 'Q':
X[i][5] = 2
else:
X[i][5] = 3
if math.isnan(X[i][2]):
X[i][2] = 0
else:
X[i][2] = int(X[i][2])
# Creating training and test sets
X_train = np.array(X[:624, :].T, dtype=np.float64)
X_train[2, :] = X_train[2, :]/max(X_train[2, :])#Normalizing Age
Y_train = np.array(Y[:624, :].T, dtype=np.float64)
X_test = np.array(X[624:891, :].T, dtype=np.float64)
X_test[2, :] = X_test[2, :]/max(X_test[2, :]) # Normalizing Age
Y_test = np.array(Y[624:891, :].T, dtype=np.float64)
return X_train, Y_train, X_test, Y_test
```
Phew! That’s a lot of code and we haven’t even started building our neural net. A lot of tutorials choose to skip this step and give you the data that can be easily used in our neural network model. But I feel that this is an extremely important step. And hence, I chose to include this **preprocessing** step into this tutorial. So what exactly is happening? Here’s what.
The function `def preprocess()` reads the data from the ‘train.csv’ file that we downloaded and creates a Pandas DataFrame, which is a data structure Pandas provides. (No need to worry too much about Pandas and DataFrames right now)
We take our data from the Pandas DataFrame and create a NumPy array. `X` is a NumPy array that contains our attributes and `Y` is a NumPy array that contains our outputs. Also, instead of using all the data from the file, we only use 6 attributes, namely(along with their changed representations):
1. Pclass
2. Sex : 1 for male; 2 for female
3. Age
4. Sibsp
5. Parch
6. Embarked : 1 for C; 2 for Q; 3 for S
We convert all the data of type string into float values. We represent string values with some numeric value. **WHY?** *This is done because neural networks take only numeric values as inputs. We can’t use strings as inputs. That is the reason why all the data is converted into integer/float values.*
Finally, we divide our data into training and test sets. The dataset contains a total of 891 examples. So we divide our data as:
1. **Training Set** ~ 70% of data (624 examples)
2. **Test Set** ~ 30% of data (267 examples)
`X_train` and `Y_train` contain the training input and training output respectively.
`X_test` and `Y_test` contain the test input and test output respectively.
The Test Sets contain whether or not the passenger survived.
> Now, the question that you might be asking is, “What just happened? Why did we just divide our data into training and test sets? What is the need for this? What exactly are training and test sets? Why isn’t Pizza good for our health???”
To be completely honest, I really don’t know the answer to that last question. I’m sorry. But I can help you with the other questions.
Before we try to understand the need for different training and test sets, we need to understand what exactly does a neural network does?
> A Neural Network finds (or tries to) the correlation between the inputs and the output.
So we train the network on a bunch of data, and the network finds the correlation between the input(attributes) and the output. But how do we know that the network will **generalize** well? How can we make sure that the network will be able to make predictions (correlate) new data that it has never seen before?
When you study for your Defence Against the Dark Arts exam at Hogwarts, how do they know that you actually understand the subject matter? Sure, you can answer the ten questions at the back of the chapter because you have studied those questions. But, can you answer new questions based on the same chapter? Can you answer the questions that you have never seen before, but are based on the same subject matter? How do they find that out? What do they do? They **Test** you. In your final exam.
In the same way, we use test set to check whether or not our network generalizes well. We train our network on the training set. And then, we test our network on the test data which is completely new to our network. This test data tells us how well our model generalizes.
> The goal of the test set is to give you an unbiased estimate of the performance of your final network.
Generally, we use 70% of the total available data as the training data, and the rest 30% as the test data. This, of course, is not a strict rule and is changed according to the circumstances.
**Note:** Additionally, there is a “Hold Out Cross Validation Set” or “Development Set”. This set is used to check which model works best. Validation set (also called dev set) is an extremely important aspect and it’s creation/use is considered an important practice in Machine Learning. I omitted this from this tutorial for reasons only Lord Voldemort knows (Ok! I got a bit lazy).
Now let’s move forward.
```python
def weight_initialization(number_of_hidden_nodes):
# For the hidden layer
W1 = np.random.randn(number_of_hidden_nodes, 6)
# A [4x6] weight matrix
b1 = np.zeros([number_of_hidden_nodes, 1]) # A [4x1] bias matrix
# For the output layer
W2 = np.random.randn(1, number_of_hidden_nodes)
# A [1x4] weight matrix
b2 = np.zeros([1, 1]) # A [1x1] bias matrix
return W1, b1, W2, b2
```
The function `def weight_initialization()` initializes our weights and biases for the hidden layer and the output layer. `W1` and `W2` are the weights for the hidden layer and the output layer respectively. `b1` and `b2` are the biases for the hidden layer and the output layer respectively. `W1`, `W2`, `b1`, `b2` are NumPy matrices. But, how do we know what the dimensions of these matrices will be?
Dimensions are as follows:
1. W⁰ = (n⁰, n¹)
2. b⁰ = (n⁰, 1)
where; 0 = Current Layer, 1 = Previous Layer, n = Number of nodes
Since, we are creating a 2-Layer neural network with 6 input nodes, 4 hidden nodes and 1 output node, we use the dimensions as shown in the code.
**Why initialize the weights with random values, instead of initializing with zeros (like bias)?**
We initialize the weights with random values in order to **break symmetry**. If we initialize all the weights with the same value (0 or 1), then the signal that will go into each node in the hidden layers will be similar. For example, if we initialize all our weights as 1, then each node gets a signal that is equal to the sum of all the inputs. If we initialize all the weights as 0, then all the nodes will get a signal of 0. Why does this happen? Because the neural network works on the following equation:
> _**Y = W*X + b**_
## But wait, what exactly is weight and bias?
Weight and bias can be looked upon as two knobs that we have access to. Quite like the volume button in our TV, weight and bias can be turned up or turned down. They can be used to control how much effect a certain input will have on the final output. There is an exact relationship between the weight and the error in our prediction, which can be derived mathematically. We won’t go into the math of it, but simply put, weight and bias let us control the impact of each input on the output and hence, let us reduce the total error in our network, thereby increasing the accuracy of the network.
Moving on.
```python
def forward_propagation(W1, b1, W2, b2, X):
Z1 = np.dot(W1, X) + b1 # Analogous to Y = W*X + b
A1 = sigmoid(Z1)
Z2 = np.dot(W2, A1) + b2
A2 = sigmoid(Z2)
return A2, A1
```
The function `def forward_propagation()` defines the forward propagation step of our learning. So what’s happening here?
`Z1` gives us the output of the dot product of weights with the inputs (and added bias). The `sigmoid()` **activation function** is then applied to these outputs, which gives us `A1`. This `A1` acts as the input to the second layer(output layer) and same steps are repeated. The final output is stored in `A2`.
This is what forward propagation is. We propagate through the network and apply our mathematical magic to the inputs. We use our weights and biases to control the impact of each input on the final output.
## But what is an activation function?
An activation function is used on the output of each node in order to introduce some non-linearity in our outputs. It is important to introduce non-linearity because without it, a neural network would just act as a single layer perceptron, no matter how many layers it has. There are several different types of activation functions like sigmoid, ReLu, tanh etc. Sigmoid function gives us the output between 0 and 1. This is useful for binary classification since we can get the probability of each output.
Once we have done the forward propagation step, it’s time to calculate by how much we missed the actual outputs i.e. the error/loss. Therefore, we compute the cost of the network, which is basically a mean of the loss/error for each training example.
```python
def compute_cost(A2, Y):
cost = -(np.sum(np.multiply(
Y, np.log(A2)) + np.multiply(
1-Y, np.log(1-A2)))/Y.shape[1])
return cost
```
The `def compute_cost()` function calculates the cost of our network. Now remember, do not panic! That one line is loaded so take your time understanding what it is really doing. The formula for computing cost is:
> cost = -1/m\[summation(y*log(y’) + (1-y)*log(1-y’))\]
where; m=total number of output examples, y=actual output value, y’=predicted output value
Once we have computed the cost, we start with our dark magic of backpropagation and gradient descent.
```python
def back_propagation_and_weight_updation(
A2, A1, X_train, W2, W1, b2, b1,
learning_rate=0.01):
dZ2 = A2 - Y_train
dW2 = np.dot(dZ2, A1.T)/X_train.shape[1]
db2 = np.sum(dZ2, axis=1, keepdims=True)/X_train.shape[1]
dZ1 = np.dot(W2.T, dZ2) * (1 - np.power(A1, 2))
dW1 = np.dot(dZ1, X_train.T)/X_train.shape[1]
db1 = np.sum(dZ1, axis=1, keepdims=True)/X_train.shape[1]
W1 = W1 - learning_rate * dW1
b1 = b1 - learning_rate * db1
W2 = W2 - learning_rate * dW2
b2 = b2 - learning_rate * db2
return W1, W2, b1, b2
```
The `def back_propagation_and_weight_updation()` function is our backpropagation and weight updation step. Well, duh.
## So what is backpropagation?
Backpropagation step is used to find out how much each parameter affected the error. What was the contribution of each parameter in the total cost of our network. This step is the most Calculus-heavy step because we need to calculate the gradients of the final cost function with respect to the inner parameters(Weight and bias). For example, `dW2` means the partial derivative(gradient) of the final cost function with respect to `W2`(which is the weights of output layer).
If this part seems scary, and you are as terrified of calculus as most people, don’t worry. Modern frameworks like Tensorflow, Pytorch etc. calculate these derivatives on their own.
So by backpropagation, we find out `dW1`, `dW2`, `db1`, `db2` which tell us by how much we should change our weights and biases in order to reduce the error, thereby reducing the cost of our network. And so we update our weights and biases.
## So what is Gradient Descent?
Iterating over the network again and again, we keep on reducing our cost of the network by going over the forward propagation and backpropagation step again and again. This iterative reduction of cost in order to find the minimum value for the cost function, is called Gradient Descent.
## And what is `learning_rate`?
`learning_rate` is a **hyperparameter** that is used to control the speed and steps of gradient descent. We can tune this hyperparameter to make our gradient descent faster or slower in order to avoid mainly two problems:
1. Overshooting : This means, we have jumped over the minima and are now stuck in a limbo. The value of cost function will go haywire and increase and decrease and do all sorts of things but won’t reach the global minima.
2. Super long training time : The network takes so long to train that your body turns into a skeleton.
To prevent these two conditions from happening, we use the learning rate which is one of the many hyperparameters.
So that’s it, that’s all we have to do to train a network. After this, we use different evaluation metrics to test how good our network performs. And then, if we’re feeling fancy, we can use graphs to visualize what we have done.
So, tying all these function together, we write the final function.
```python
if __name__ == "__main__":
# STEP 1: LOADING AND PREPROCESSING DATA
X_train, Y_train, X_test, Y_test = preprocess()
# STEP 2: INITIALIZING WEIGHTS AND BIASES
number_of_hidden_nodes = 4
W1, b1, W2, b2 = weight_initialization(
number_of_hidden_nodes)
# Setting the number of iterations for gradient descent
num_of_iterations = 50000
all_costs = []
for i in range(0, num_of_iterations):
# STEP 3: FORWARD PROPAGATION
A2, A1 = forward_propagation(W1, b1, W2, b2, X_train)
# STEP 4: COMPUTING COST
cost = compute_cost(A2, Y_train)
all_costs.append(cost)
# STEP 5: BACKPROPAGATION AND PARAMETER UPDATTION
W1, W2, b1, b2 = back_propagation_and_weight_updation(
A2, A1,X_train, W2, W1, b2, b1)
if i % 1000 == 0:
print("Cost after iteration "+str(i)+": "+str(cost))
# STEP 6: EVALUATION METRICS
# To Show accuracy of our training set
A2, _ = forward_propagation(W1, b1, W2, b2, X_train)
pred = (A2 > 0.5)
print('Accuracy for training set: %d' % float((
np.dot(Y_train, pred.T) + np.dot(
1-Y_train, 1-pred.T))/float(Y_train.size)*100) + '%')
# To show accuracy of our test set
A2, _ = forward_propagation(W1, b1, W2, b2, X_test)
pred = (A2 > 0.5)
print('Accuracy for test set: %d' % float((
np.dot(Y_test, pred.T) + np.dot(
1-Y_test, 1-pred.T))/float(Y_test.size)*100) + '%')
# STEP 7: VISUALIZING EVALUATION METRICS
# Plot graph for gradient descent
plt.plot(np.squeeze(all_costs))
plt.ylabel('Cost')
plt.xlabel('Number of Iterations')
plt.show()
```
We do 50,000 iterations of our training. `num_of_iterations` is also a hyperparameter. Once trained, we calculate the accuracy of our trained network on the training data. This comes out to be 79%.
Then we check how good our network is at generalizing by using our test data. This accuracy hits 81%.
The cost function decreases as shown in the following graph. Because graphs are cool!

As you can see, the cost of our network reduces drastically at first and then reduces slowly, before being plateaued.
**Note:** When you run this code on your machine, your graph might be a bit different because weights are initialized randomly. But still, you will get a nearly 80% accuracy on your training and test sets.
So, we are able to predict who would have survived the sinking of the RMS Titanic with an 81% accuracy. Not bad for a simple 2-layer model. **Congratulations. You have built your very first neural network.**
> You’re a Wizard now!
Modern frameworks like Tensorflow and PyTorch do a lot of things for us and make it easier to build deep learning models. But it is important to understand what exactly is going on behind-the-scenes. I hope you found this article useful. And understand neural networks a bit better than you did before reading this article.
_**Do-it-Yourself:** Try changing the hyperparameters(learning rate, number of iterations, and number of hidden nodes) to see how it affects the network. Also, try changing the activation function in `A1` from `sigmoid` to `tanh`._
_Now, how do we improve this network? How do we make this better? There are a lot of tips, tricks and techniques that can be used and you can learn about them at the University of Internet._
|
github_jupyter
|
import math
import os
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
def preprocess():
# Reading data from the CSV file
data = pd.read_csv(os.path.join(
os.path.dirname(
__file__), 'train.csv'),
header=0, delimiter=",", quoting=3)
#Converting data from Pandas DataFrame to Numpy Arrays
data_np = data.values[:, [0, 1, 4, 5, 6, 7, 11]]
X = data_np[:, 1:]
Y = data_np[:, [0]]
# Converting string values into numeric values
for i in range(X.shape[0]):
if X[i][1] == 'male':
X[i][1] = 1
else:
X[i][1] = 2
if X[i][5] == 'C':
X[i][5] = 1
elif X[i][5] == 'Q':
X[i][5] = 2
else:
X[i][5] = 3
if math.isnan(X[i][2]):
X[i][2] = 0
else:
X[i][2] = int(X[i][2])
# Creating training and test sets
X_train = np.array(X[:624, :].T, dtype=np.float64)
X_train[2, :] = X_train[2, :]/max(X_train[2, :])#Normalizing Age
Y_train = np.array(Y[:624, :].T, dtype=np.float64)
X_test = np.array(X[624:891, :].T, dtype=np.float64)
X_test[2, :] = X_test[2, :]/max(X_test[2, :]) # Normalizing Age
Y_test = np.array(Y[624:891, :].T, dtype=np.float64)
return X_train, Y_train, X_test, Y_test
The function `def weight_initialization()` initializes our weights and biases for the hidden layer and the output layer. `W1` and `W2` are the weights for the hidden layer and the output layer respectively. `b1` and `b2` are the biases for the hidden layer and the output layer respectively. `W1`, `W2`, `b1`, `b2` are NumPy matrices. But, how do we know what the dimensions of these matrices will be?
Dimensions are as follows:
1. W⁰ = (n⁰, n¹)
2. b⁰ = (n⁰, 1)
where; 0 = Current Layer, 1 = Previous Layer, n = Number of nodes
Since, we are creating a 2-Layer neural network with 6 input nodes, 4 hidden nodes and 1 output node, we use the dimensions as shown in the code.
**Why initialize the weights with random values, instead of initializing with zeros (like bias)?**
We initialize the weights with random values in order to **break symmetry**. If we initialize all the weights with the same value (0 or 1), then the signal that will go into each node in the hidden layers will be similar. For example, if we initialize all our weights as 1, then each node gets a signal that is equal to the sum of all the inputs. If we initialize all the weights as 0, then all the nodes will get a signal of 0. Why does this happen? Because the neural network works on the following equation:
> _**Y = W*X + b**_
## But wait, what exactly is weight and bias?
Weight and bias can be looked upon as two knobs that we have access to. Quite like the volume button in our TV, weight and bias can be turned up or turned down. They can be used to control how much effect a certain input will have on the final output. There is an exact relationship between the weight and the error in our prediction, which can be derived mathematically. We won’t go into the math of it, but simply put, weight and bias let us control the impact of each input on the output and hence, let us reduce the total error in our network, thereby increasing the accuracy of the network.
Moving on.
The function `def forward_propagation()` defines the forward propagation step of our learning. So what’s happening here?
`Z1` gives us the output of the dot product of weights with the inputs (and added bias). The `sigmoid()` **activation function** is then applied to these outputs, which gives us `A1`. This `A1` acts as the input to the second layer(output layer) and same steps are repeated. The final output is stored in `A2`.
This is what forward propagation is. We propagate through the network and apply our mathematical magic to the inputs. We use our weights and biases to control the impact of each input on the final output.
## But what is an activation function?
An activation function is used on the output of each node in order to introduce some non-linearity in our outputs. It is important to introduce non-linearity because without it, a neural network would just act as a single layer perceptron, no matter how many layers it has. There are several different types of activation functions like sigmoid, ReLu, tanh etc. Sigmoid function gives us the output between 0 and 1. This is useful for binary classification since we can get the probability of each output.
Once we have done the forward propagation step, it’s time to calculate by how much we missed the actual outputs i.e. the error/loss. Therefore, we compute the cost of the network, which is basically a mean of the loss/error for each training example.
The `def compute_cost()` function calculates the cost of our network. Now remember, do not panic! That one line is loaded so take your time understanding what it is really doing. The formula for computing cost is:
> cost = -1/m\[summation(y*log(y’) + (1-y)*log(1-y’))\]
where; m=total number of output examples, y=actual output value, y’=predicted output value
Once we have computed the cost, we start with our dark magic of backpropagation and gradient descent.
The `def back_propagation_and_weight_updation()` function is our backpropagation and weight updation step. Well, duh.
## So what is backpropagation?
Backpropagation step is used to find out how much each parameter affected the error. What was the contribution of each parameter in the total cost of our network. This step is the most Calculus-heavy step because we need to calculate the gradients of the final cost function with respect to the inner parameters(Weight and bias). For example, `dW2` means the partial derivative(gradient) of the final cost function with respect to `W2`(which is the weights of output layer).
If this part seems scary, and you are as terrified of calculus as most people, don’t worry. Modern frameworks like Tensorflow, Pytorch etc. calculate these derivatives on their own.
So by backpropagation, we find out `dW1`, `dW2`, `db1`, `db2` which tell us by how much we should change our weights and biases in order to reduce the error, thereby reducing the cost of our network. And so we update our weights and biases.
## So what is Gradient Descent?
Iterating over the network again and again, we keep on reducing our cost of the network by going over the forward propagation and backpropagation step again and again. This iterative reduction of cost in order to find the minimum value for the cost function, is called Gradient Descent.
## And what is `learning_rate`?
`learning_rate` is a **hyperparameter** that is used to control the speed and steps of gradient descent. We can tune this hyperparameter to make our gradient descent faster or slower in order to avoid mainly two problems:
1. Overshooting : This means, we have jumped over the minima and are now stuck in a limbo. The value of cost function will go haywire and increase and decrease and do all sorts of things but won’t reach the global minima.
2. Super long training time : The network takes so long to train that your body turns into a skeleton.
To prevent these two conditions from happening, we use the learning rate which is one of the many hyperparameters.
So that’s it, that’s all we have to do to train a network. After this, we use different evaluation metrics to test how good our network performs. And then, if we’re feeling fancy, we can use graphs to visualize what we have done.
So, tying all these function together, we write the final function.
| 0.761804 | 0.984396 |
<a href="https://colab.research.google.com/github/portkata/KataGo/blob/master/JBX2010_template_60bKatago_bot_1po_OGS.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
Please click "COPY to Drive" on top and save as your own copy first. Please also download the required Config files from Github. https://github.com/JBX2010/KataGo_Colab/
1. Please first check what GPU is allocated by Colab by clicking the command line below.
```
!nvidia-smi
```
2. Building KataGo and gtp2ogs. Please switch CUDA/OPENCL depending on the GPU allocated. Search KATAGO_BACKEND = "OPENCL" and update accordingly. For T4 recommend to use CUDA. For P100, P4 and K80 recommend to use OPENCL.
```
KATAGO_BACKEND="CUDA"
%cd /content
!apt install sudo
!sudo apt remove cmake
!sudo apt purge --auto-remove cmake
!mkdir ~/temp
%cd ~/temp
!wget https://cmake.org/files/v3.12/cmake-3.12.3-Linux-x86_64.sh
!sudo mkdir /opt/cmake
!sudo sh cmake-3.12.3-Linux-x86_64.sh --prefix=/opt/cmake --skip-license
!sudo rm -R /usr/local/bin/cmake
!sudo ln -s /opt/cmake/bin/cmake /usr/local/bin/cmake
%cd /content
!apt-get update
!add-apt-repository -y ppa:ubuntu-toolchain-r/test
!apt-get -y install gcc-8 g++-8 zlib1g-dev libzip-dev libboost-filesystem-dev libgoogle-perftools-dev
!update-alternatives --install /usr/bin/gcc gcc /usr/bin/gcc-8 40 --slave /usr/bin/g++ g++ /usr/bin/g++-8
!apt-get install curl
!curl -sL https://deb.nodesource.com/setup_13.x | -E bash -
!apt-get install -y nodejs
!npm install -g gtp2ogs
%cd /content
!mkdir testtt
%cd /content/testtt
!git clone -b devel https://github.com/online-go/gtp2ogs
%cd /content/testtt/gtp2ogs
!git branch
!sudo cp -rf * /usr/lib/node_modules/gtp2ogs/
%cd /usr/lib/node_modules/gtp2ogs/
!npm install
%cd /content
!git clone https://github.com/lightvector/KataGo.git
!cd /content/KataGo/cpp/ && cmake . -DBUILD_MCTS=1 -DUSE_BACKEND=$KATAGO_BACKEND && make
!cd /content/KataGo/cpp/ && wget https://github.com/portkata/KataGo/releases/download/v0.1/60.bin.gz
!cd /content/KataGo/cpp/ && gunzip 60.bin.gz
!cd /content/KataGo/cpp/ && mv 60.bin 60e.bin
!cd /content/KataGo/cpp/ && wget https://github.com/portkata/KataGo/releases/download/v.01/t1p1v1.cfg.gz
!cd /content/KataGo/cpp/ && gunzip t1p1v1.cfg.gz
!cd /content/KataGo/cpp/ && wget http://res.yikeweiqi.com/yklinker/yk-linker.zip
!cd /content/KataGo/cpp/ && unzip yk-linker.zip
```
In the above commands, if you want to update the 60b net from the default pre-release one in this script to a stronger one, replace the github address in the following line
```
!cd /content/KataGo/cpp/ && wget https://github.com/portkata/KataGo/releases/download/v0.1/60.bin.gz
```
with the address for the updated net. then in the line below, replace "60.bin.gz" with the name of the updated net. Then in the next line below, replace the 60 in "60.bin" with the updated net name, but leave the "60e.bin" as is.
3. Run Bot on OGS https://online-go.com/ . Please update your ogsBotName and your ogsBotAPIKey in below command. Finally click command below to start you bot. You will need to logon to https://online-go.com/ with your local pc or smart phone to see how your bot runs... Enjoy!
```
!nodejs /usr/lib/node_modules/gtp2ogs/gtp2ogs.js --username <bot_username> --apikey <api_key> --ogspv KataGo --persist --maxconnectedgames 4 --noautohandicapranked --maxhandicap 1 --speeds live --greeting "I use 1 playout. The first move takes 10 seconds. Then it should be very quick. Good luck in Go and all you do today" -- /content/KataGo/cpp/katago gtp -model /content/KataGo/cpp/60e.bin -config /content/KataGo/cpp/t1p1v1.cfg
```
# 4a. (Optional) copy and paste the function below in browser console and press enter to prevent disconnect when browser is inactive
```
setInterval(ClickConnect,60000)
function ClickConnect(){
console.log("Clicked on connect button");
document.querySelector("colab-connect-button").click()
}
setInterval(ClickConnect,60000)
```
4b. (Optional) Upload pre-tuned P100 OPENCL tunning file can save sometime on the KataGo initialization and may help enhance Bot Strength (IF GPU is P100). File name: tune6_gpuTeslaP100PCIE16GB_x19_y19_c256_mv8.txt . Please upload to the same /KataGo/cpp folder and then click below command.
```
%cd /root/
!mkdir .katago
%cd /root/.katago/
!mkdir opencltuning
!mv /content/KataGo/cpp/tune6_gpuTeslaP100PCIE16GB_x19_y19_c256_mv8.txt /root/.katago/opencltuning/tune6_gpuTeslaP100PCIE16GB_x19_y19_c256_mv8.txt
```
5. (Optional) KataGo GPU BenchMark testing and Configuration fine tunning (This probably doesn't work as written).
```
!cd /content/KataGo/cpp/ && ./katago benchmark -v 3200 -tune -model 60e.bin -config gtp_example.cfg
```
|
github_jupyter
|
!nvidia-smi
KATAGO_BACKEND="CUDA"
%cd /content
!apt install sudo
!sudo apt remove cmake
!sudo apt purge --auto-remove cmake
!mkdir ~/temp
%cd ~/temp
!wget https://cmake.org/files/v3.12/cmake-3.12.3-Linux-x86_64.sh
!sudo mkdir /opt/cmake
!sudo sh cmake-3.12.3-Linux-x86_64.sh --prefix=/opt/cmake --skip-license
!sudo rm -R /usr/local/bin/cmake
!sudo ln -s /opt/cmake/bin/cmake /usr/local/bin/cmake
%cd /content
!apt-get update
!add-apt-repository -y ppa:ubuntu-toolchain-r/test
!apt-get -y install gcc-8 g++-8 zlib1g-dev libzip-dev libboost-filesystem-dev libgoogle-perftools-dev
!update-alternatives --install /usr/bin/gcc gcc /usr/bin/gcc-8 40 --slave /usr/bin/g++ g++ /usr/bin/g++-8
!apt-get install curl
!curl -sL https://deb.nodesource.com/setup_13.x | -E bash -
!apt-get install -y nodejs
!npm install -g gtp2ogs
%cd /content
!mkdir testtt
%cd /content/testtt
!git clone -b devel https://github.com/online-go/gtp2ogs
%cd /content/testtt/gtp2ogs
!git branch
!sudo cp -rf * /usr/lib/node_modules/gtp2ogs/
%cd /usr/lib/node_modules/gtp2ogs/
!npm install
%cd /content
!git clone https://github.com/lightvector/KataGo.git
!cd /content/KataGo/cpp/ && cmake . -DBUILD_MCTS=1 -DUSE_BACKEND=$KATAGO_BACKEND && make
!cd /content/KataGo/cpp/ && wget https://github.com/portkata/KataGo/releases/download/v0.1/60.bin.gz
!cd /content/KataGo/cpp/ && gunzip 60.bin.gz
!cd /content/KataGo/cpp/ && mv 60.bin 60e.bin
!cd /content/KataGo/cpp/ && wget https://github.com/portkata/KataGo/releases/download/v.01/t1p1v1.cfg.gz
!cd /content/KataGo/cpp/ && gunzip t1p1v1.cfg.gz
!cd /content/KataGo/cpp/ && wget http://res.yikeweiqi.com/yklinker/yk-linker.zip
!cd /content/KataGo/cpp/ && unzip yk-linker.zip
!nodejs /usr/lib/node_modules/gtp2ogs/gtp2ogs.js --username <bot_username> --apikey <api_key> --ogspv KataGo --persist --maxconnectedgames 4 --noautohandicapranked --maxhandicap 1 --speeds live --greeting "I use 1 playout. The first move takes 10 seconds. Then it should be very quick. Good luck in Go and all you do today" -- /content/KataGo/cpp/katago gtp -model /content/KataGo/cpp/60e.bin -config /content/KataGo/cpp/t1p1v1.cfg
%cd /root/
!mkdir .katago
%cd /root/.katago/
!mkdir opencltuning
!mv /content/KataGo/cpp/tune6_gpuTeslaP100PCIE16GB_x19_y19_c256_mv8.txt /root/.katago/opencltuning/tune6_gpuTeslaP100PCIE16GB_x19_y19_c256_mv8.txt
!cd /content/KataGo/cpp/ && ./katago benchmark -v 3200 -tune -model 60e.bin -config gtp_example.cfg
| 0.194139 | 0.4953 |
<a href="https://colab.research.google.com/github/tbbcoach/DS-Unit-2-Linear-Models/blob/master/Copy_of_LS_DS_214_solution.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
Lambda School Data Science
*Unit 2, Sprint 1, Module 4*
---
```
%%capture
import sys
# If you're on Colab:
if 'google.colab' in sys.modules:
DATA_PATH = 'https://raw.githubusercontent.com/LambdaSchool/DS-Unit-2-Linear-Models/master/data/'
!pip install category_encoders==2.*
# If you're working locally:
else:
DATA_PATH = '../data/'
```
# Module Project: Logistic Regression
Do you like burritos? 🌯 You're in luck then, because in this project you'll create a model to predict whether a burrito is `'Great'`.
The dataset for this assignment comes from [Scott Cole](https://srcole.github.io/100burritos/), a San Diego-based data scientist and burrito enthusiast.
## Directions
The tasks for this project are the following:
- **Task 1:** Import `csv` file using `wrangle` function.
- **Task 2:** Conduct exploratory data analysis (EDA), and modify `wrangle` function .
- **Task 3:** Split data into feature matrix `X` and target vector `y`.
- **Task 4:** Split feature matrix `X` and target vector `y` into training and test sets.
- **Task 5:** Establish the baseline accuracy score for your dataset.
- **Task 6:** Build `model_logr` using a pipeline that includes three transfomers and `LogisticRegression` predictor. Train model on `X_train` and `X_test`.
- **Task 7:** Calculate the training and test accuracy score for your model.
- **Task 8:** Create a horizontal bar chart showing the 10 most influencial features for your model.
- **Task 9:** Demonstrate and explain the differences between `model_lr.predict()` and `model_lr.predict_proba()`.
**Note**
You should limit yourself to the following libraries:
- `category_encoders`
- `matplotlib`
- `pandas`
- `sklearn`
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from category_encoders import OneHotEncoder
from sklearn.linear_model import LinearRegression
from sklearn.impute import SimpleImputer
from sklearn.preprocessing import StandardScaler
```
# I. Wrangle Data
```
def wrangle(filepath):
# Import w/ DateTimeIndex
df = pd.read_csv(filepath, parse_dates=['Date'],
index_col='Date')
# Drop unrated burritos
df.dropna(subset=['overall'], inplace=True)
# Derive binary classification target:
# We define a 'Great' burrito as having an
# overall rating of 4 or higher, on a 5 point scale
df['Great'] = (df['overall'] >= 4).astype(int)
# Drop high cardinality categoricals
df = df.drop(columns=['Notes', 'Location', 'Address', 'URL'])
# Drop columns to prevent "leakage"
df = df.drop(columns=['Rec', 'overall'])
# binary_cols = ['Unreliable', 'NonSD', 'Beef', 'Pico', 'Guac', 'Cheese', 'Fries',
# 'Sour cream', 'Pork', 'Chicken', 'Shrimp', 'Fish', 'Rice', 'Beans',
# 'Lettuce', 'Tomato', 'Bell peper', 'Carrots', 'Cabbage', 'Sauce',
# 'Salsa.1', 'Cilantro', 'Onion', 'Taquito', 'Pineapple', 'Ham',
# 'Chile relleno', 'Nopales', 'Lobster', 'Queso', 'Egg', 'Mushroom',
# 'Bacon', 'Sushi', 'Avocado', 'Corn', 'Zucchini', 'Chips']
#convert values to 1's and 0's
df.fillna(0, inplace=True)
df.replace({'x': 1}, inplace=True)
df.replace({'X': 1}, inplace=True)
# df[binary_cols].applymap(lambda x: 1 if type(x)==str else 0).head(10)
#also have to define which columns are in 'binary_cols.
return df
filepath = DATA_PATH + 'burritos/burritos.csv'
```
**Task 1:** Use the above `wrangle` function to import the `burritos.csv` file into a DataFrame named `df`.
```
df = wrangle(filepath)
df.head()
```
During your exploratory data analysis, note that there are several columns whose data type is `object` but that seem to be a binary encoding. For example, `df['Beef'].head()` returns:
```
0 x
1 x
2 NaN
3 x
4 x
Name: Beef, dtype: object
```
**Task 2:** Change the `wrangle` function so that these columns are properly encoded as `0` and `1`s. Be sure your code handles upper- and lowercase `X`s, and `NaN`s.
```
# Conduct your exploratory data analysis here
# And modify the `wrangle` function above.
df.info()
```
If you explore the `'Burrito'` column of `df`, you'll notice that it's a high-cardinality categorical feature. You'll also notice that there's a lot of overlap between the categories.
**Stretch Goal:** Change the `wrangle` function above so that it engineers four new features: `'california'`, `'asada'`, `'surf'`, and `'carnitas'`. Each row should have a `1` or `0` based on the text information in the `'Burrito'` column. For example, here's how the first 5 rows of the dataset would look.
| **Burrito** | **california** | **asada** | **surf** | **carnitas** |
| :---------- | :------------: | :-------: | :------: | :----------: |
| California | 1 | 0 | 0 | 0 |
| California | 1 | 0 | 0 | 0 |
| Carnitas | 0 | 0 | 0 | 1 |
| Carne asada | 0 | 1 | 0 | 0 |
| California | 1 | 0 | 0 | 0 |
**Note:** Be sure to also drop the `'Burrito'` once you've engineered your new features.
```
# Conduct your exploratory data analysis here
# And modify the `wrangle` function above.
df.head()
```
# II. Split Data
**Task 3:** Split your dataset into the feature matrix `X` and the target vector `y`. You want to predict `'Great'`.
```
target = 'Great'
X = df.drop(columns= target)
y = df[target]
y.shape, X.shape
```
**Task 4:** Split `X` and `y` into a training set (`X_train`, `y_train`) and a test set (`X_test`, `y_test`).
- Your training set should include data from 2016 through 2017.
- Your test set should include data from 2018 and later.
```
cutoff = '2018'
mask = X.index < cutoff
X_train, y_train = X.loc[mask], y.loc[mask]
X_test, y_test = X.loc[~mask], y.loc[~mask]
X_train.shape, y_train.shape, X_test.shape, y_test.shape
```
# III. Establish Baseline
**Task 5:** Since this is a **classification** problem, you should establish a baseline accuracy score. Figure out what is the majority class in `y_train` and what percentage of your training observations it represents.
```
y_train.value_counts(normalize=True) * 100
majority_class = y_train.mode()[0]
y_pred = [majority_class] * len(y_train)
from sklearn.metrics import accuracy_score
baseline_acc = accuracy_score(y_train, y_pred)
print(y_train.value_counts(normalize=True))
print('Baseline Accuracy Score:', baseline_acc)
```
# IV. Build Model
**Task 6:** Build a `Pipeline` named `model_logr`, and fit it to your training data. Your pipeline should include:
- a `OneHotEncoder` transformer for categorical features,
- a `SimpleImputer` transformer to deal with missing values,
- a [`StandarScaler`](https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.StandardScaler.html) transfomer (which often improves performance in a logistic regression model), and
- a `LogisticRegression` predictor.
```
from sklearn.pipeline import make_pipeline
from sklearn.linear_model import LogisticRegression
model_logr = make_pipeline(
OneHotEncoder(use_cat_names=True),
SimpleImputer(),
StandardScaler(),
LogisticRegression()
)
model_logr.fit(X_train, y_train)
#print('Accuracy from pipeling', model_logr.score(X_remain, y_train))
```
# IV. Check Metrics
**Task 7:** Calculate the training and test accuracy score for `model_lr`.
```
training_acc = model_logr.score(X_train, y_train)
test_acc = model_logr.score(X_test, y_test)
print('Training MAE:', training_acc)
print('Test MAE:', test_acc)
```
# V. Communicate Results
**Task 8:** Create a horizontal barchart that plots the 10 most important coefficients for `model_lr`, sorted by absolute value.
**Note:** Since you created your model using a `Pipeline`, you'll need to use the [`named_steps`](https://scikit-learn.org/stable/modules/generated/sklearn.pipeline.Pipeline.html) attribute to access the coefficients in your `LogisticRegression` predictor. Be sure to look at the shape of the coefficients array before you combine it with the feature names.
```
# Create your horizontal barchart here.
coefficients = model_logr.named_steps['logisticregression'].coef_[0]
features = model_logr.named_steps['onehotencoder'].get_feature_names()
feat_imp = pd.Series(coefficients, index=features).sort_values(key=abs)
feat_imp.tail(10).plot(kind='barh');
```
There is more than one way to generate predictions with `model_lr`. For instance, you can use [`predict`](https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LogisticRegression.html?highlight=logisticregression) or [`predict_proba`](https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LogisticRegression.html?highlight=logisticregression#sklearn.linear_model.LogisticRegression.predict_proba).
**Task 9:** Generate predictions for `X_test` using both `predict` and `predict_proba`. Then below, write a summary of the differences in the output for these two methods. You should answer the following questions:
- What data type do `predict` and `predict_proba` output?
- What are the shapes of their different output?
- What numerical values are in the output?
- What do those numerical values represent?
```
# Write code here to explore the differences between `predict` and `predict_proba`.
np.round(model_logr.predict_proba(X_test)), np.round(model_logr.predict(X_test))
```
**Give your written answer here:**
```Predict gives the prediction for which class might occur based on features - in this case whether a burrito was great or not. Predict_proba gives the probably of a feature being 1 or 0
Predict gives the prediction for which class might occur based on features - in this case whether a burrito was great or not. Predict_proba gives the probably of a feature being 1 or 0
```
|
github_jupyter
|
%%capture
import sys
# If you're on Colab:
if 'google.colab' in sys.modules:
DATA_PATH = 'https://raw.githubusercontent.com/LambdaSchool/DS-Unit-2-Linear-Models/master/data/'
!pip install category_encoders==2.*
# If you're working locally:
else:
DATA_PATH = '../data/'
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from category_encoders import OneHotEncoder
from sklearn.linear_model import LinearRegression
from sklearn.impute import SimpleImputer
from sklearn.preprocessing import StandardScaler
def wrangle(filepath):
# Import w/ DateTimeIndex
df = pd.read_csv(filepath, parse_dates=['Date'],
index_col='Date')
# Drop unrated burritos
df.dropna(subset=['overall'], inplace=True)
# Derive binary classification target:
# We define a 'Great' burrito as having an
# overall rating of 4 or higher, on a 5 point scale
df['Great'] = (df['overall'] >= 4).astype(int)
# Drop high cardinality categoricals
df = df.drop(columns=['Notes', 'Location', 'Address', 'URL'])
# Drop columns to prevent "leakage"
df = df.drop(columns=['Rec', 'overall'])
# binary_cols = ['Unreliable', 'NonSD', 'Beef', 'Pico', 'Guac', 'Cheese', 'Fries',
# 'Sour cream', 'Pork', 'Chicken', 'Shrimp', 'Fish', 'Rice', 'Beans',
# 'Lettuce', 'Tomato', 'Bell peper', 'Carrots', 'Cabbage', 'Sauce',
# 'Salsa.1', 'Cilantro', 'Onion', 'Taquito', 'Pineapple', 'Ham',
# 'Chile relleno', 'Nopales', 'Lobster', 'Queso', 'Egg', 'Mushroom',
# 'Bacon', 'Sushi', 'Avocado', 'Corn', 'Zucchini', 'Chips']
#convert values to 1's and 0's
df.fillna(0, inplace=True)
df.replace({'x': 1}, inplace=True)
df.replace({'X': 1}, inplace=True)
# df[binary_cols].applymap(lambda x: 1 if type(x)==str else 0).head(10)
#also have to define which columns are in 'binary_cols.
return df
filepath = DATA_PATH + 'burritos/burritos.csv'
df = wrangle(filepath)
df.head()
0 x
1 x
2 NaN
3 x
4 x
Name: Beef, dtype: object
# Conduct your exploratory data analysis here
# And modify the `wrangle` function above.
df.info()
# Conduct your exploratory data analysis here
# And modify the `wrangle` function above.
df.head()
target = 'Great'
X = df.drop(columns= target)
y = df[target]
y.shape, X.shape
cutoff = '2018'
mask = X.index < cutoff
X_train, y_train = X.loc[mask], y.loc[mask]
X_test, y_test = X.loc[~mask], y.loc[~mask]
X_train.shape, y_train.shape, X_test.shape, y_test.shape
y_train.value_counts(normalize=True) * 100
majority_class = y_train.mode()[0]
y_pred = [majority_class] * len(y_train)
from sklearn.metrics import accuracy_score
baseline_acc = accuracy_score(y_train, y_pred)
print(y_train.value_counts(normalize=True))
print('Baseline Accuracy Score:', baseline_acc)
from sklearn.pipeline import make_pipeline
from sklearn.linear_model import LogisticRegression
model_logr = make_pipeline(
OneHotEncoder(use_cat_names=True),
SimpleImputer(),
StandardScaler(),
LogisticRegression()
)
model_logr.fit(X_train, y_train)
#print('Accuracy from pipeling', model_logr.score(X_remain, y_train))
training_acc = model_logr.score(X_train, y_train)
test_acc = model_logr.score(X_test, y_test)
print('Training MAE:', training_acc)
print('Test MAE:', test_acc)
# Create your horizontal barchart here.
coefficients = model_logr.named_steps['logisticregression'].coef_[0]
features = model_logr.named_steps['onehotencoder'].get_feature_names()
feat_imp = pd.Series(coefficients, index=features).sort_values(key=abs)
feat_imp.tail(10).plot(kind='barh');
# Write code here to explore the differences between `predict` and `predict_proba`.
np.round(model_logr.predict_proba(X_test)), np.round(model_logr.predict(X_test))
| 0.407216 | 0.975343 |
From:
- [BERT Fine-Tuning Tutorial with PyTorch · Chris McCormick](http://mccormickml.com/2019/07/22/BERT-fine-tuning/)
- [huggingface/pytorch-transformers: 👾 A library of state-of-the-art pretrained models for Natural Language Processing (NLP)](https://github.com/huggingface/pytorch-transformers)
Fine-Tuning:
- Easy Training: recommend 2-4 epochs on a special NLP task
- Less Data
- Good Results
```
import torch
from torch.utils.data import TensorDataset, DataLoader, RandomSampler, SequentialSampler
from keras.preprocessing.sequence import pad_sequences
from sklearn.model_selection import train_test_split
from pytorch_transformers import BertTokenizer, BertConfig
from pytorch_transformers import BertForSequenceClassification, BertModel
from pytorch_transformers.optimization import AdamW, WarmupLinearSchedule
from tqdm import tqdm, trange
import pandas as pd
import io
import os
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
```
## Data
```bash
# download glue data
$ git clone https://gist.github.com/60c2bdb54d156a41194446737ce03e2e.git download_glue_repo
$ python download_glue_repo/download_glue_data.py --data_dir='glue_data'
```
```
# [The Corpus of Linguistic Acceptability (CoLA)](https://nyu-mll.github.io/CoLA/)
data_path = "cola_public/raw/"
train_path = os.path.join(data_path, "in_domain_train.tsv")
df = pd.read_csv(train_path, delimiter='\t', header=None,
names=['sentence_source', 'label', 'label_notes', 'sentence'])
df.sample(5)
sentences = df.sentence.values
sentences = ["[CLS] " + sentence + " [SEP]" for sentence in sentences]
labels = df.label.values
```
## Input
```
# The default download path is ~/.cache
tokenizer = BertTokenizer.from_pretrained("bert-base-uncased", do_lower_case=True)
tokenized_texts = [tokenizer.tokenize(sent) for sent in sentences]
print ("Tokenize the first sentence:")
print (tokenized_texts[0])
tokenizer.tokenize("i love you")
tokenizer.vocab_size
```
Format:
- input ids: index in BERT tokenizer vocabulary
- segment mask: a sequence of 1s and 0s used to identify whether the input is one sentence or two sentences.
- attention mask: a sequence of 1s and 0s, with 1s for input tokens and 0s for padding ones.
- labels: a single 0 or 1
```
MAX_LEN = 16
input_ids = pad_sequences([tokenizer.convert_tokens_to_ids(s) for s in tokenized_texts],
maxlen=MAX_LEN, dtype="long", truncating="post", padding="post")
# "post" means padding or truncating at the end of the sequence.
attn_masks = []
for seq in input_ids:
seq_mask = [float(i>0) for i in seq]
attn_masks.append(seq_mask)
len(attn_masks)
len(input_ids)
train_inputs, validation_inputs, train_labels, validation_labels = train_test_split(
input_ids, labels, random_state=2018, test_size=0.1)
train_masks, validation_masks, _, _ = train_test_split(
attn_masks, input_ids, random_state=2018, test_size=0.1)
train_inputs = torch.tensor(train_inputs)
validation_inputs = torch.tensor(validation_inputs)
train_labels = torch.tensor(train_labels)
validation_labels = torch.tensor(validation_labels)
train_masks = torch.tensor(train_masks)
validation_masks = torch.tensor(validation_masks)
batch_size = 32
train_data = TensorDataset(train_inputs, train_masks, train_labels)
train_sampler = RandomSampler(train_data)
train_dataloader = DataLoader(train_data, sampler=train_sampler, batch_size=batch_size)
validation_data = TensorDataset(validation_inputs, validation_masks, validation_labels)
validation_sampler = SequentialSampler(validation_data)
validation_dataloader = DataLoader(validation_data, sampler=validation_sampler, batch_size=batch_size)
train_inputs.shape
train_labels.shape
```
## Model
```
# need to download the base uncased model, 420M
# The default download path is ~/.cache
model1 = BertForSequenceClassification.from_pretrained("bert-base-uncased", num_labels=2)
model2 = BertModel.from_pretrained("bert-base-uncased", num_labels=2)
input_ids = torch.tensor(tokenizer.encode("Hello, my dog is cute")).unsqueeze(0) # Batch size 1
outputs1 = model1(input_ids)
outputs2 = model2(input_ids)
outputs1
encoder_out, text_cls = outputs2
encoder_out.unsqueeze(1)
model1.config
model2.config
```
Hyperparamters recommended:
- Batch size: 16, 32
- Learning rate (Adam): 5e-5, 3e-5, 2e-5
- Number of epochs: 2, 3, 4
```
param_optimizer = list(model.named_parameters())
no_decay = ['bias', 'gamma', 'beta']
optimizer_grouped_parameters = [
{'params': [p for n, p in param_optimizer if not any(nd in n for nd in no_decay)],
'weight_decay_rate': 0.01},
{'params': [p for n, p in param_optimizer if any(nd in n for nd in no_decay)],
'weight_decay_rate': 0.0}
]
optimizer = AdamW(optimizer_grouped_parameters, lr=2e-5)
num_train_optimization_steps = int(len(train_data) / batch_size / 1) * 4
scheduler = WarmupLinearSchedule(optimizer, warmup_steps=100, t_total=num_train_optimization_steps)
```
## Train
```
def flat_accuracy(preds, labels):
pred_flat = np.argmax(preds, axis=1).flatten()
labels_flat = labels.flatten()
return np.sum(pred_flat == labels_flat) / len(labels_flat)
train_loss_set = []
# Number of training epochs (authors recommend between 2 and 4)
epochs = 4
# trange is a tqdm wrapper around the normal python range
for _ in trange(epochs, desc="Epoch"):
# Training
# Set our model to training mode (as opposed to evaluation mode)
model.train()
# Tracking variables
tr_loss = 0
nb_tr_examples, nb_tr_steps = 0, 0
# Train the data for one epoch
for step, batch in enumerate(train_dataloader):
# Add batch to GPU
# batch = tuple(t.to(device) for t in batch)
# Unpack the inputs from our dataloader
b_input_ids, b_input_mask, b_labels = batch
# Clear out the gradients (by default they accumulate)
optimizer.zero_grad()
# Forward pass
outputs = model(b_input_ids, token_type_ids=None, attention_mask=b_input_mask, labels=b_labels)
loss = outputs[0]
train_loss_set.append(loss.item())
# Backward pass
loss.backward()
# Update parameters and take a step using the computed gradient
optimizer.step()
scheduler.step()
# Update tracking variables
tr_loss += loss.item()
nb_tr_examples += b_input_ids.size(0)
nb_tr_steps += 1
print("Train loss: {}".format(tr_loss/nb_tr_steps))
# Validation
# Put model in evaluation mode to evaluate loss on the validation set
model.eval()
# Tracking variables
eval_loss, eval_accuracy = 0, 0
nb_eval_steps, nb_eval_examples = 0, 0
# Evaluate data for one epoch
for batch in validation_dataloader:
# Add batch to GPU
# batch = tuple(t.to(device) for t in batch)
# Unpack the inputs from our dataloader
b_input_ids, b_input_mask, b_labels = batch
# Telling the model not to compute or store gradients, saving memory and speeding up validation
with torch.no_grad():
# Forward pass, calculate logit predictions
logits = model(b_input_ids, token_type_ids=None, attention_mask=b_input_mask)
# Move logits and labels to CPU
logits = logits.detach().cpu().numpy()
label_ids = b_labels.to('cpu').numpy()
tmp_eval_accuracy = flat_accuracy(logits, label_ids)
eval_accuracy += tmp_eval_accuracy
nb_eval_steps += 1
print("Validation Accuracy: {}".format(eval_accuracy/nb_eval_steps))
plt.figure(figsize=(15,8))
plt.title("Training loss")
plt.xlabel("Batch")
plt.ylabel("Loss")
plt.plot(train_loss_set)
plt.show()
```
|
github_jupyter
|
import torch
from torch.utils.data import TensorDataset, DataLoader, RandomSampler, SequentialSampler
from keras.preprocessing.sequence import pad_sequences
from sklearn.model_selection import train_test_split
from pytorch_transformers import BertTokenizer, BertConfig
from pytorch_transformers import BertForSequenceClassification, BertModel
from pytorch_transformers.optimization import AdamW, WarmupLinearSchedule
from tqdm import tqdm, trange
import pandas as pd
import io
import os
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
# download glue data
$ git clone https://gist.github.com/60c2bdb54d156a41194446737ce03e2e.git download_glue_repo
$ python download_glue_repo/download_glue_data.py --data_dir='glue_data'
# [The Corpus of Linguistic Acceptability (CoLA)](https://nyu-mll.github.io/CoLA/)
data_path = "cola_public/raw/"
train_path = os.path.join(data_path, "in_domain_train.tsv")
df = pd.read_csv(train_path, delimiter='\t', header=None,
names=['sentence_source', 'label', 'label_notes', 'sentence'])
df.sample(5)
sentences = df.sentence.values
sentences = ["[CLS] " + sentence + " [SEP]" for sentence in sentences]
labels = df.label.values
# The default download path is ~/.cache
tokenizer = BertTokenizer.from_pretrained("bert-base-uncased", do_lower_case=True)
tokenized_texts = [tokenizer.tokenize(sent) for sent in sentences]
print ("Tokenize the first sentence:")
print (tokenized_texts[0])
tokenizer.tokenize("i love you")
tokenizer.vocab_size
MAX_LEN = 16
input_ids = pad_sequences([tokenizer.convert_tokens_to_ids(s) for s in tokenized_texts],
maxlen=MAX_LEN, dtype="long", truncating="post", padding="post")
# "post" means padding or truncating at the end of the sequence.
attn_masks = []
for seq in input_ids:
seq_mask = [float(i>0) for i in seq]
attn_masks.append(seq_mask)
len(attn_masks)
len(input_ids)
train_inputs, validation_inputs, train_labels, validation_labels = train_test_split(
input_ids, labels, random_state=2018, test_size=0.1)
train_masks, validation_masks, _, _ = train_test_split(
attn_masks, input_ids, random_state=2018, test_size=0.1)
train_inputs = torch.tensor(train_inputs)
validation_inputs = torch.tensor(validation_inputs)
train_labels = torch.tensor(train_labels)
validation_labels = torch.tensor(validation_labels)
train_masks = torch.tensor(train_masks)
validation_masks = torch.tensor(validation_masks)
batch_size = 32
train_data = TensorDataset(train_inputs, train_masks, train_labels)
train_sampler = RandomSampler(train_data)
train_dataloader = DataLoader(train_data, sampler=train_sampler, batch_size=batch_size)
validation_data = TensorDataset(validation_inputs, validation_masks, validation_labels)
validation_sampler = SequentialSampler(validation_data)
validation_dataloader = DataLoader(validation_data, sampler=validation_sampler, batch_size=batch_size)
train_inputs.shape
train_labels.shape
# need to download the base uncased model, 420M
# The default download path is ~/.cache
model1 = BertForSequenceClassification.from_pretrained("bert-base-uncased", num_labels=2)
model2 = BertModel.from_pretrained("bert-base-uncased", num_labels=2)
input_ids = torch.tensor(tokenizer.encode("Hello, my dog is cute")).unsqueeze(0) # Batch size 1
outputs1 = model1(input_ids)
outputs2 = model2(input_ids)
outputs1
encoder_out, text_cls = outputs2
encoder_out.unsqueeze(1)
model1.config
model2.config
param_optimizer = list(model.named_parameters())
no_decay = ['bias', 'gamma', 'beta']
optimizer_grouped_parameters = [
{'params': [p for n, p in param_optimizer if not any(nd in n for nd in no_decay)],
'weight_decay_rate': 0.01},
{'params': [p for n, p in param_optimizer if any(nd in n for nd in no_decay)],
'weight_decay_rate': 0.0}
]
optimizer = AdamW(optimizer_grouped_parameters, lr=2e-5)
num_train_optimization_steps = int(len(train_data) / batch_size / 1) * 4
scheduler = WarmupLinearSchedule(optimizer, warmup_steps=100, t_total=num_train_optimization_steps)
def flat_accuracy(preds, labels):
pred_flat = np.argmax(preds, axis=1).flatten()
labels_flat = labels.flatten()
return np.sum(pred_flat == labels_flat) / len(labels_flat)
train_loss_set = []
# Number of training epochs (authors recommend between 2 and 4)
epochs = 4
# trange is a tqdm wrapper around the normal python range
for _ in trange(epochs, desc="Epoch"):
# Training
# Set our model to training mode (as opposed to evaluation mode)
model.train()
# Tracking variables
tr_loss = 0
nb_tr_examples, nb_tr_steps = 0, 0
# Train the data for one epoch
for step, batch in enumerate(train_dataloader):
# Add batch to GPU
# batch = tuple(t.to(device) for t in batch)
# Unpack the inputs from our dataloader
b_input_ids, b_input_mask, b_labels = batch
# Clear out the gradients (by default they accumulate)
optimizer.zero_grad()
# Forward pass
outputs = model(b_input_ids, token_type_ids=None, attention_mask=b_input_mask, labels=b_labels)
loss = outputs[0]
train_loss_set.append(loss.item())
# Backward pass
loss.backward()
# Update parameters and take a step using the computed gradient
optimizer.step()
scheduler.step()
# Update tracking variables
tr_loss += loss.item()
nb_tr_examples += b_input_ids.size(0)
nb_tr_steps += 1
print("Train loss: {}".format(tr_loss/nb_tr_steps))
# Validation
# Put model in evaluation mode to evaluate loss on the validation set
model.eval()
# Tracking variables
eval_loss, eval_accuracy = 0, 0
nb_eval_steps, nb_eval_examples = 0, 0
# Evaluate data for one epoch
for batch in validation_dataloader:
# Add batch to GPU
# batch = tuple(t.to(device) for t in batch)
# Unpack the inputs from our dataloader
b_input_ids, b_input_mask, b_labels = batch
# Telling the model not to compute or store gradients, saving memory and speeding up validation
with torch.no_grad():
# Forward pass, calculate logit predictions
logits = model(b_input_ids, token_type_ids=None, attention_mask=b_input_mask)
# Move logits and labels to CPU
logits = logits.detach().cpu().numpy()
label_ids = b_labels.to('cpu').numpy()
tmp_eval_accuracy = flat_accuracy(logits, label_ids)
eval_accuracy += tmp_eval_accuracy
nb_eval_steps += 1
print("Validation Accuracy: {}".format(eval_accuracy/nb_eval_steps))
plt.figure(figsize=(15,8))
plt.title("Training loss")
plt.xlabel("Batch")
plt.ylabel("Loss")
plt.plot(train_loss_set)
plt.show()
| 0.832407 | 0.949106 |
# Ensemble Models
## Hypertuning
## Imports
```
## Basic Imports
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
# NLP processing
import spacy
nlp = spacy.load('en_core_web_sm')
# sklearn models
from sklearn.metrics import accuracy_score, classification_report, confusion_matrix
from sklearn.feature_extraction.text import TfidfVectorizer, CountVectorizer
from sklearn.ensemble import RandomForestClassifier, GradientBoostingClassifier
from sklearn.model_selection import RandomizedSearchCV, GridSearchCV
from sklearn.model_selection import train_test_split
from sklearn.pipeline import Pipeline
```
## Constants
```
# File path
SAMPLE_PATH = '..\data\clean\electronics_sample.csv'
# Dtypes and data column
DTYPES = {
'overall':np.int16,
'vote':np.int64,
'verified':bool,
'reviewText':object,
'summary':object
}
```
## Functions
```
# preprocessing text
def lemma(text):
doc = nlp(text)
return " ".join([token.lemma_ for token in doc if token.is_alpha and token.lemma_ != '-PRON-'])
```
## Load data
```
## Loading Data
df = pd.read_csv(SAMPLE_PATH, dtype=DTYPES, parse_dates=[2]).dropna()
df.head()
df.info()
sns.countplot(x='overall', data=df)
plt.show()
# Getting read of reviews that include information about the number of stars or
# those below 6 words
war_1 = df.reviewText.str.contains('one star')
war_2 = df.reviewText.str.contains('two star')
war_3 = df.reviewText.str.contains('three star')
war_4 = df.reviewText.str.contains('four star')
war_5 = df.reviewText.str.contains('five star')
war_6 = (df.reviewText.str.split().str.len() > 5)
mask = (~war_1 & ~war_2 & ~war_3 & ~war_4 & ~war_5 & war_6)
df = df[mask]
df.info()
```
## Baseline Model
```
X = df['reviewText']
y = df['overall']-1
X_train, X_test, y_train, y_test = train_test_split(X, y,
stratify=y,
test_size=0.2,
random_state=42)
# creating tfidf model
tfidf = TfidfVectorizer(min_df=0.01, max_df=0.99, ngram_range=(1,2), stop_words='english')
X_train_tfidf = tfidf.fit_transform(X_train)
X_test_tfidf = tfidf.transform(X_test)
print('Vocabulary Size: ', len(tfidf.get_feature_names()))
gb = GradientBoostingClassifier(n_estimators=100, max_depth=20)
gb.fit(X_train_tfidf, y_train)
gb.score(X_test_tfidf, y_test)
y_test_pred_gb = gb.predict(X_test_tfidf)
cl_report_gb = pd.DataFrame(classification_report(y_test, y_test_pred_gb, output_dict=True)).T
display(cl_report_gb)
cm_gb = confusion_matrix(y_test, y_test_pred_gb, normalize='true')
sns.heatmap(cm_gb, cmap='Greens',
yticklabels=range(1,6),
xticklabels=range(1,6),
annot=True,
fmt='.2f'
)
plt.show()
```
## Hyperparameter Tuning
## Informed Search - Coarse to Fine
### Randomized Search to Grid Search
```
# Creating Pipeline
steps = [('vectorizer', TfidfVectorizer()),
('classifier', GradientBoostingClassifier())]
pipe = Pipeline(steps)
params = {#'vectorizer': [TfidfVectorizer(), CountVectorizer()],
'vectorizer__max_df':[0.8,0.9,0.99,1.],
'vectorizer__min_df':[0.001, 0.01, 0.],
'vectorizer__max_features':[1_000, 10_000],
'vectorizer__ngram_range':[(1,1),(1,2)],
#'classifier': [RandomForestClassifier(), GradientBoostingClassifier()],
'classifier__n_estimators':[100,200,500],
'classifier__max_depth':[5,8,10,20,50,100],
'classifier__max_features':[0.4,0.6,0.8,1.],
'classifier__subsample':[0.4,0.6,0.8,1.]
}
search = RandomizedSearchCV(pipe,
param_distributions=params,
n_iter=50,
cv=3)
results = pd.read_csv('../data/rand_search_result.csv', index_col=0)
results.sort_values(by='rank_test_score').head()
sns.scatterplot(x='param_vectorizer__ngram_range',y='mean_test_score',data=results, alpha=0.7)
plt.show()
sns.scatterplot(x='param_vectorizer__min_df',y='mean_test_score',data=results)
plt.show()
sns.scatterplot(x='param_vectorizer__max_df',y='mean_test_score',data=results)
plt.show()
sns.scatterplot(x='param_vectorizer__max_features',y='mean_test_score',data=results)
plt.show()
sns.scatterplot(x='param_classifier__subsample',y='mean_test_score',color='green', data=results)
plt.show()
sns.scatterplot(x='param_classifier__max_features',y='mean_test_score',color='green', data=results)
plt.show()
sns.scatterplot(x='param_classifier__max_depth',y='mean_test_score',color='green', data=results)
plt.show()
sns.scatterplot(x='param_classifier__n_estimators',y='mean_test_score',color='green', data=results)
plt.show()
params = {#'vectorizer': [TfidfVectorizer(), CountVectorizer()],
'vectorizer__max_df':[1.],
'vectorizer__min_df':[0.001, 0.01],
'vectorizer__max_features':[1_000, 2_000],
'vectorizer__ngram_range':[(1,1)],
#'classifier': [RandomForestClassifier(), GradientBoostingClassifier()],
'classifier__n_estimators':[100],
'classifier__max_depth':[4,6],
'classifier__max_features':[0.4,0.6],
'classifier__subsample':[0.6]
}
search_grid = GridSearchCV(pipe,
param_grid=params,
cv=3)
search_grid.fit(X_train[:5_000], y_train[:5_000])
grid_results = pd.DataFrame(search_grid.cv_results_)
grid_results.sort_values(by='rank_test_score')[['params','mean_test_score','std_test_score']]
search_grid.best_params_
model = search_grid.best_estimator_
model.fit(X_train, y_train)
y_test_pred = model.predict(X_test)
cl_report = pd.DataFrame(classification_report(y_test, y_test_pred, output_dict=True)).T
display(cl_report)
cm = confusion_matrix(y_test, y_test_pred, normalize='true')
sns.heatmap(cm, cmap='Reds',
yticklabels=range(1,6),
xticklabels=range(1,6),
annot=True,
fmt='.2f'
)
plt.show()
# saving the model
import pickle
# save the model to disk
filename = '../models/gbt_model.sav'
pickle.dump(model, open(filename, 'wb'))
# load the model from disk
loaded_model = pickle.load(open(filename, 'rb'))
result = loaded_model.score(X_test, y_test)
print(result)
```
|
github_jupyter
|
## Basic Imports
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
# NLP processing
import spacy
nlp = spacy.load('en_core_web_sm')
# sklearn models
from sklearn.metrics import accuracy_score, classification_report, confusion_matrix
from sklearn.feature_extraction.text import TfidfVectorizer, CountVectorizer
from sklearn.ensemble import RandomForestClassifier, GradientBoostingClassifier
from sklearn.model_selection import RandomizedSearchCV, GridSearchCV
from sklearn.model_selection import train_test_split
from sklearn.pipeline import Pipeline
# File path
SAMPLE_PATH = '..\data\clean\electronics_sample.csv'
# Dtypes and data column
DTYPES = {
'overall':np.int16,
'vote':np.int64,
'verified':bool,
'reviewText':object,
'summary':object
}
# preprocessing text
def lemma(text):
doc = nlp(text)
return " ".join([token.lemma_ for token in doc if token.is_alpha and token.lemma_ != '-PRON-'])
## Loading Data
df = pd.read_csv(SAMPLE_PATH, dtype=DTYPES, parse_dates=[2]).dropna()
df.head()
df.info()
sns.countplot(x='overall', data=df)
plt.show()
# Getting read of reviews that include information about the number of stars or
# those below 6 words
war_1 = df.reviewText.str.contains('one star')
war_2 = df.reviewText.str.contains('two star')
war_3 = df.reviewText.str.contains('three star')
war_4 = df.reviewText.str.contains('four star')
war_5 = df.reviewText.str.contains('five star')
war_6 = (df.reviewText.str.split().str.len() > 5)
mask = (~war_1 & ~war_2 & ~war_3 & ~war_4 & ~war_5 & war_6)
df = df[mask]
df.info()
X = df['reviewText']
y = df['overall']-1
X_train, X_test, y_train, y_test = train_test_split(X, y,
stratify=y,
test_size=0.2,
random_state=42)
# creating tfidf model
tfidf = TfidfVectorizer(min_df=0.01, max_df=0.99, ngram_range=(1,2), stop_words='english')
X_train_tfidf = tfidf.fit_transform(X_train)
X_test_tfidf = tfidf.transform(X_test)
print('Vocabulary Size: ', len(tfidf.get_feature_names()))
gb = GradientBoostingClassifier(n_estimators=100, max_depth=20)
gb.fit(X_train_tfidf, y_train)
gb.score(X_test_tfidf, y_test)
y_test_pred_gb = gb.predict(X_test_tfidf)
cl_report_gb = pd.DataFrame(classification_report(y_test, y_test_pred_gb, output_dict=True)).T
display(cl_report_gb)
cm_gb = confusion_matrix(y_test, y_test_pred_gb, normalize='true')
sns.heatmap(cm_gb, cmap='Greens',
yticklabels=range(1,6),
xticklabels=range(1,6),
annot=True,
fmt='.2f'
)
plt.show()
# Creating Pipeline
steps = [('vectorizer', TfidfVectorizer()),
('classifier', GradientBoostingClassifier())]
pipe = Pipeline(steps)
params = {#'vectorizer': [TfidfVectorizer(), CountVectorizer()],
'vectorizer__max_df':[0.8,0.9,0.99,1.],
'vectorizer__min_df':[0.001, 0.01, 0.],
'vectorizer__max_features':[1_000, 10_000],
'vectorizer__ngram_range':[(1,1),(1,2)],
#'classifier': [RandomForestClassifier(), GradientBoostingClassifier()],
'classifier__n_estimators':[100,200,500],
'classifier__max_depth':[5,8,10,20,50,100],
'classifier__max_features':[0.4,0.6,0.8,1.],
'classifier__subsample':[0.4,0.6,0.8,1.]
}
search = RandomizedSearchCV(pipe,
param_distributions=params,
n_iter=50,
cv=3)
results = pd.read_csv('../data/rand_search_result.csv', index_col=0)
results.sort_values(by='rank_test_score').head()
sns.scatterplot(x='param_vectorizer__ngram_range',y='mean_test_score',data=results, alpha=0.7)
plt.show()
sns.scatterplot(x='param_vectorizer__min_df',y='mean_test_score',data=results)
plt.show()
sns.scatterplot(x='param_vectorizer__max_df',y='mean_test_score',data=results)
plt.show()
sns.scatterplot(x='param_vectorizer__max_features',y='mean_test_score',data=results)
plt.show()
sns.scatterplot(x='param_classifier__subsample',y='mean_test_score',color='green', data=results)
plt.show()
sns.scatterplot(x='param_classifier__max_features',y='mean_test_score',color='green', data=results)
plt.show()
sns.scatterplot(x='param_classifier__max_depth',y='mean_test_score',color='green', data=results)
plt.show()
sns.scatterplot(x='param_classifier__n_estimators',y='mean_test_score',color='green', data=results)
plt.show()
params = {#'vectorizer': [TfidfVectorizer(), CountVectorizer()],
'vectorizer__max_df':[1.],
'vectorizer__min_df':[0.001, 0.01],
'vectorizer__max_features':[1_000, 2_000],
'vectorizer__ngram_range':[(1,1)],
#'classifier': [RandomForestClassifier(), GradientBoostingClassifier()],
'classifier__n_estimators':[100],
'classifier__max_depth':[4,6],
'classifier__max_features':[0.4,0.6],
'classifier__subsample':[0.6]
}
search_grid = GridSearchCV(pipe,
param_grid=params,
cv=3)
search_grid.fit(X_train[:5_000], y_train[:5_000])
grid_results = pd.DataFrame(search_grid.cv_results_)
grid_results.sort_values(by='rank_test_score')[['params','mean_test_score','std_test_score']]
search_grid.best_params_
model = search_grid.best_estimator_
model.fit(X_train, y_train)
y_test_pred = model.predict(X_test)
cl_report = pd.DataFrame(classification_report(y_test, y_test_pred, output_dict=True)).T
display(cl_report)
cm = confusion_matrix(y_test, y_test_pred, normalize='true')
sns.heatmap(cm, cmap='Reds',
yticklabels=range(1,6),
xticklabels=range(1,6),
annot=True,
fmt='.2f'
)
plt.show()
# saving the model
import pickle
# save the model to disk
filename = '../models/gbt_model.sav'
pickle.dump(model, open(filename, 'wb'))
# load the model from disk
loaded_model = pickle.load(open(filename, 'rb'))
result = loaded_model.score(X_test, y_test)
print(result)
| 0.520009 | 0.832237 |
# Creating an advanced interactive map with Bokeh
This page demonstrates, how it is possible to visualize any kind of geometries (normal geometries + Multi-geometries) in Bokeh and add a legend into the map which is one of the key elements of a good map.
```
from bokeh.palettes import YlOrRd as palette #Spectral6 as palette
from bokeh.plotting import figure, save
from bokeh.models import ColumnDataSource, HoverTool, LogColorMapper
from bokeh.palettes import RdYlGn10 as palette
import geopandas as gpd
import pysal as ps
import numpy as np
# Filepaths
fp = r"/home/geo/data/TravelTimes_to_5975375_RailwayStation.shp"
roads_fp = r"/home/geo/data/roads.shp"
metro_fp = r"/home/geo/data/metro.shp"
# Read the data with Geopandas
data = gpd.read_file(fp)
roads = gpd.read_file(roads_fp)
metro = gpd.read_file(metro_fp)
# Ensure that the CRS is the same than in the all layers
data['geometry'] = data['geometry'].to_crs(epsg=3067)
roads['geometry'] = roads['geometry'].to_crs(epsg=3067)
metro['geometry'] = metro['geometry'].to_crs(epsg=3067)
```
- Next, let's create a set of functions that are used for getting the x and y coordinates of the geometries. Shapefiles etc. can often have Multi-geometries (MultiLineStrings etc.), thus we need to handle those as well which makes things slightly more complicated. It is always a good practice to slice your functions into small pieces which is what we have done here:
```
def getXYCoords(geometry, coord_type):
""" Returns either x or y coordinates from geometry coordinate sequence. Used with LineString and Polygon geometries."""
if coord_type == 'x':
return geometry.coords.xy[0]
elif coord_type == 'y':
return geometry.coords.xy[1]
def getPolyCoords(geometry, coord_type):
""" Returns Coordinates of Polygon using the Exterior of the Polygon."""
ext = geometry.exterior
return getXYCoords(ext, coord_type)
def getLineCoords(geometry, coord_type):
""" Returns Coordinates of Linestring object."""
return getXYCoords(geometry, coord_type)
def getPointCoords(geometry, coord_type):
""" Returns Coordinates of Point object."""
if coord_type == 'x':
return geometry.x
elif coord_type == 'y':
return geometry.y
def multiGeomHandler(multi_geometry, coord_type, geom_type):
"""
Function for handling multi-geometries. Can be MultiPoint, MultiLineString or MultiPolygon.
Returns a list of coordinates where all parts of Multi-geometries are merged into a single list.
Individual geometries are separated with np.nan which is how Bokeh wants them.
# Bokeh documentation regarding the Multi-geometry issues can be found here (it is an open issue)
# https://github.com/bokeh/bokeh/issues/2321
"""
for i, part in enumerate(multi_geometry):
# On the first part of the Multi-geometry initialize the coord_array (np.array)
if i == 0:
if geom_type == "MultiPoint":
coord_arrays = np.append(getPointCoords(part, coord_type), np.nan)
elif geom_type == "MultiLineString":
coord_arrays = np.append(getLineCoords(part, coord_type), np.nan)
elif geom_type == "MultiPolygon":
coord_arrays = np.append(getPolyCoords(part, coord_type), np.nan)
else:
if geom_type == "MultiPoint":
coord_arrays = np.concatenate([coord_arrays, np.append(getPointCoords(part, coord_type), np.nan)])
elif geom_type == "MultiLineString":
coord_arrays = np.concatenate([coord_arrays, np.append(getLineCoords(part, coord_type), np.nan)])
elif geom_type == "MultiPolygon":
coord_arrays = np.concatenate([coord_arrays, np.append(getPolyCoords(part, coord_type), np.nan)])
# Return the coordinates
return coord_arrays
def getCoords(row, geom_col, coord_type):
"""
Returns coordinates ('x' or 'y') of a geometry (Point, LineString or Polygon) as a list (if geometry is LineString or Polygon).
Can handle also MultiGeometries.
"""
# Get geometry
geom = row[geom_col]
# Check the geometry type
gtype = geom.geom_type
# "Normal" geometries
# -------------------
if gtype == "Point":
return getPointCoords(geom, coord_type)
elif gtype == "LineString":
return list( getLineCoords(geom, coord_type) )
elif gtype == "Polygon":
return list( getPolyCoords(geom, coord_type) )
# Multi geometries
# ----------------
else:
return list( multiGeomHandler(geom, coord_type, gtype) )
```
- Now we can apply our functions and calculate the x and y coordinates of any kind of geometry by using the same function, i.e. `getCoords()`.
```
# Calculate the x and y coordinates of the grid
data['x'] = data.apply(getCoords, geom_col="geometry", coord_type="x", axis=1)
data['y'] = data.apply(getCoords, geom_col="geometry", coord_type="y", axis=1)
# Calculate the x and y coordinates of the roads
roads['x'] = roads.apply(getCoords, geom_col="geometry", coord_type="x", axis=1)
roads['y'] = roads.apply(getCoords, geom_col="geometry", coord_type="y", axis=1)
# Calculate the x and y coordinates of metro
metro['x'] = metro.apply(getCoords, geom_col="geometry", coord_type="x", axis=1)
metro['y'] = metro.apply(getCoords, geom_col="geometry", coord_type="y", axis=1)
```
- Next, we need to classify the travel time values into 5 minute intervals using Pysal's user defined classifier. We also create legend labels for the classes.
```
# Replace No Data values (-1) with large number (999)
data = data.replace(-1, 999)
# Classify our travel times into 5 minute classes until 200 minutes
# Create a list of values where minumum value is 5, maximum value is 200 and step is 5.
breaks = [x for x in range(5, 200, 5)]
classifier = ps.User_Defined.make(bins=breaks)
pt_classif = data[['pt_r_tt']].apply(classifier)
car_classif = data[['car_r_t']].apply(classifier)
# Rename columns
pt_classif.columns = ['pt_r_tt_ud']
car_classif.columns = ['car_r_t_ud']
# Join back to main data
data = data.join(pt_classif)
data = data.join(car_classif)
# Create names for the legend (until 60 minutes)
upper_limit = 60
step = 5
# This will produce: ["0-5", "5-10", "10-15", ... , "60 <"]
names = ["%s-%s " % (x-5, x) for x in range(step, upper_limit, step)]
# Add legend label for over 60
names.append("%s <" % upper_limit)
# Assign legend names for the classes
data['label_pt'] = None
data['label_car'] = None
for i in range(len(names)):
# Update rows where class is i
data.loc[data['pt_r_tt_ud'] == i, 'label_pt'] = names[i]
data.loc[data['car_r_t_ud'] == i, 'label_car'] = names[i]
# Update all cells that didn't get any value with "60 <"
data['label_pt'] = data['label_pt'].fillna("%s <" % upper_limit)
data['label_car'] = data['label_car'].fillna("%s <" % upper_limit)
```
- Finally, we can visualize our layers with Bokeh, add a legend for travel times and add HoverTools for Destination Point and the grid values (travel times)
```
# Select only necessary columns for our plotting to keep the amount of data minumum
df = data[['x', 'y', 'pt_r_tt_ud', 'pt_r_tt', 'car_r_t', 'from_id', 'label_pt']]
dfsource = ColumnDataSource(data=df)
# Exclude geometry from roads as well
rdf = roads[['x', 'y']]
rdfsource = ColumnDataSource(data=rdf)
# Exclude geometry from metro as well
mdf = metro[['x','y']]
mdfsource = ColumnDataSource(data=mdf)
TOOLS = "pan,wheel_zoom,box_zoom,reset,save"
# Flip the colors in color palette
palette.reverse()
color_mapper = LogColorMapper(palette=palette)
p = figure(title="Travel times to Helsinki city center by public transportation", tools=TOOLS,
plot_width=650, plot_height=500, active_scroll = "wheel_zoom" )
# Do not add grid line
p.grid.grid_line_color = None
# Add polygon grid and a legend for it
grid = p.patches('x', 'y', source=dfsource, name="grid",
fill_color={'field': 'pt_r_tt_ud', 'transform': color_mapper},
fill_alpha=1.0, line_color="black", line_width=0.03, legend="label_pt")
# Add roads
r = p.multi_line('x', 'y', source=rdfsource, color="grey")
# Add metro
m = p.multi_line('x', 'y', source=mdfsource, color="red")
# Modify legend location
p.legend.location = "top_right"
p.legend.orientation = "vertical"
# Insert a circle on top of the Central Railway Station (coords in EurefFIN-TM35FIN)
station_x = 385752.214
station_y = 6672143.803
circle = p.circle(x=[station_x], y=[station_y], name="point", size=6, color="yellow")
# Add two separate hover tools for the data
phover = HoverTool(renderers=[circle])
phover.tooltips=[("Destination", "Railway Station")]
ghover = HoverTool(renderers=[grid])
ghover.tooltips=[("YKR-ID", "@from_id"),
("PT time", "@pt_r_tt"),
("Car time", "@car_r_t"),
]
p.add_tools(ghover)
p.add_tools(phover)
# Output filepath to HTML
output_file = r"/home/geo/accessibility_map_Helsinki.html"
# Save the map
save(p, output_file);
```
|
github_jupyter
|
from bokeh.palettes import YlOrRd as palette #Spectral6 as palette
from bokeh.plotting import figure, save
from bokeh.models import ColumnDataSource, HoverTool, LogColorMapper
from bokeh.palettes import RdYlGn10 as palette
import geopandas as gpd
import pysal as ps
import numpy as np
# Filepaths
fp = r"/home/geo/data/TravelTimes_to_5975375_RailwayStation.shp"
roads_fp = r"/home/geo/data/roads.shp"
metro_fp = r"/home/geo/data/metro.shp"
# Read the data with Geopandas
data = gpd.read_file(fp)
roads = gpd.read_file(roads_fp)
metro = gpd.read_file(metro_fp)
# Ensure that the CRS is the same than in the all layers
data['geometry'] = data['geometry'].to_crs(epsg=3067)
roads['geometry'] = roads['geometry'].to_crs(epsg=3067)
metro['geometry'] = metro['geometry'].to_crs(epsg=3067)
def getXYCoords(geometry, coord_type):
""" Returns either x or y coordinates from geometry coordinate sequence. Used with LineString and Polygon geometries."""
if coord_type == 'x':
return geometry.coords.xy[0]
elif coord_type == 'y':
return geometry.coords.xy[1]
def getPolyCoords(geometry, coord_type):
""" Returns Coordinates of Polygon using the Exterior of the Polygon."""
ext = geometry.exterior
return getXYCoords(ext, coord_type)
def getLineCoords(geometry, coord_type):
""" Returns Coordinates of Linestring object."""
return getXYCoords(geometry, coord_type)
def getPointCoords(geometry, coord_type):
""" Returns Coordinates of Point object."""
if coord_type == 'x':
return geometry.x
elif coord_type == 'y':
return geometry.y
def multiGeomHandler(multi_geometry, coord_type, geom_type):
"""
Function for handling multi-geometries. Can be MultiPoint, MultiLineString or MultiPolygon.
Returns a list of coordinates where all parts of Multi-geometries are merged into a single list.
Individual geometries are separated with np.nan which is how Bokeh wants them.
# Bokeh documentation regarding the Multi-geometry issues can be found here (it is an open issue)
# https://github.com/bokeh/bokeh/issues/2321
"""
for i, part in enumerate(multi_geometry):
# On the first part of the Multi-geometry initialize the coord_array (np.array)
if i == 0:
if geom_type == "MultiPoint":
coord_arrays = np.append(getPointCoords(part, coord_type), np.nan)
elif geom_type == "MultiLineString":
coord_arrays = np.append(getLineCoords(part, coord_type), np.nan)
elif geom_type == "MultiPolygon":
coord_arrays = np.append(getPolyCoords(part, coord_type), np.nan)
else:
if geom_type == "MultiPoint":
coord_arrays = np.concatenate([coord_arrays, np.append(getPointCoords(part, coord_type), np.nan)])
elif geom_type == "MultiLineString":
coord_arrays = np.concatenate([coord_arrays, np.append(getLineCoords(part, coord_type), np.nan)])
elif geom_type == "MultiPolygon":
coord_arrays = np.concatenate([coord_arrays, np.append(getPolyCoords(part, coord_type), np.nan)])
# Return the coordinates
return coord_arrays
def getCoords(row, geom_col, coord_type):
"""
Returns coordinates ('x' or 'y') of a geometry (Point, LineString or Polygon) as a list (if geometry is LineString or Polygon).
Can handle also MultiGeometries.
"""
# Get geometry
geom = row[geom_col]
# Check the geometry type
gtype = geom.geom_type
# "Normal" geometries
# -------------------
if gtype == "Point":
return getPointCoords(geom, coord_type)
elif gtype == "LineString":
return list( getLineCoords(geom, coord_type) )
elif gtype == "Polygon":
return list( getPolyCoords(geom, coord_type) )
# Multi geometries
# ----------------
else:
return list( multiGeomHandler(geom, coord_type, gtype) )
# Calculate the x and y coordinates of the grid
data['x'] = data.apply(getCoords, geom_col="geometry", coord_type="x", axis=1)
data['y'] = data.apply(getCoords, geom_col="geometry", coord_type="y", axis=1)
# Calculate the x and y coordinates of the roads
roads['x'] = roads.apply(getCoords, geom_col="geometry", coord_type="x", axis=1)
roads['y'] = roads.apply(getCoords, geom_col="geometry", coord_type="y", axis=1)
# Calculate the x and y coordinates of metro
metro['x'] = metro.apply(getCoords, geom_col="geometry", coord_type="x", axis=1)
metro['y'] = metro.apply(getCoords, geom_col="geometry", coord_type="y", axis=1)
# Replace No Data values (-1) with large number (999)
data = data.replace(-1, 999)
# Classify our travel times into 5 minute classes until 200 minutes
# Create a list of values where minumum value is 5, maximum value is 200 and step is 5.
breaks = [x for x in range(5, 200, 5)]
classifier = ps.User_Defined.make(bins=breaks)
pt_classif = data[['pt_r_tt']].apply(classifier)
car_classif = data[['car_r_t']].apply(classifier)
# Rename columns
pt_classif.columns = ['pt_r_tt_ud']
car_classif.columns = ['car_r_t_ud']
# Join back to main data
data = data.join(pt_classif)
data = data.join(car_classif)
# Create names for the legend (until 60 minutes)
upper_limit = 60
step = 5
# This will produce: ["0-5", "5-10", "10-15", ... , "60 <"]
names = ["%s-%s " % (x-5, x) for x in range(step, upper_limit, step)]
# Add legend label for over 60
names.append("%s <" % upper_limit)
# Assign legend names for the classes
data['label_pt'] = None
data['label_car'] = None
for i in range(len(names)):
# Update rows where class is i
data.loc[data['pt_r_tt_ud'] == i, 'label_pt'] = names[i]
data.loc[data['car_r_t_ud'] == i, 'label_car'] = names[i]
# Update all cells that didn't get any value with "60 <"
data['label_pt'] = data['label_pt'].fillna("%s <" % upper_limit)
data['label_car'] = data['label_car'].fillna("%s <" % upper_limit)
# Select only necessary columns for our plotting to keep the amount of data minumum
df = data[['x', 'y', 'pt_r_tt_ud', 'pt_r_tt', 'car_r_t', 'from_id', 'label_pt']]
dfsource = ColumnDataSource(data=df)
# Exclude geometry from roads as well
rdf = roads[['x', 'y']]
rdfsource = ColumnDataSource(data=rdf)
# Exclude geometry from metro as well
mdf = metro[['x','y']]
mdfsource = ColumnDataSource(data=mdf)
TOOLS = "pan,wheel_zoom,box_zoom,reset,save"
# Flip the colors in color palette
palette.reverse()
color_mapper = LogColorMapper(palette=palette)
p = figure(title="Travel times to Helsinki city center by public transportation", tools=TOOLS,
plot_width=650, plot_height=500, active_scroll = "wheel_zoom" )
# Do not add grid line
p.grid.grid_line_color = None
# Add polygon grid and a legend for it
grid = p.patches('x', 'y', source=dfsource, name="grid",
fill_color={'field': 'pt_r_tt_ud', 'transform': color_mapper},
fill_alpha=1.0, line_color="black", line_width=0.03, legend="label_pt")
# Add roads
r = p.multi_line('x', 'y', source=rdfsource, color="grey")
# Add metro
m = p.multi_line('x', 'y', source=mdfsource, color="red")
# Modify legend location
p.legend.location = "top_right"
p.legend.orientation = "vertical"
# Insert a circle on top of the Central Railway Station (coords in EurefFIN-TM35FIN)
station_x = 385752.214
station_y = 6672143.803
circle = p.circle(x=[station_x], y=[station_y], name="point", size=6, color="yellow")
# Add two separate hover tools for the data
phover = HoverTool(renderers=[circle])
phover.tooltips=[("Destination", "Railway Station")]
ghover = HoverTool(renderers=[grid])
ghover.tooltips=[("YKR-ID", "@from_id"),
("PT time", "@pt_r_tt"),
("Car time", "@car_r_t"),
]
p.add_tools(ghover)
p.add_tools(phover)
# Output filepath to HTML
output_file = r"/home/geo/accessibility_map_Helsinki.html"
# Save the map
save(p, output_file);
| 0.750278 | 0.939913 |
<a href="https://colab.research.google.com/github/probml/probml-notebooks/blob/main/notebooks/genmo_types_implicit_explicit.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Types of models: implicit or explicit models
Author: Mihaela Rosca
We use a simple example below (a mixture of Gaussians in 1 dimension) to exemplify the different between explicit generative models (with an associated density which we can query) and implicit generative models (which have an associated density but which we cannot query for likelhoods, but we can sample from it).
```
import random
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
import scipy
sns.set(rc={"lines.linewidth": 2.8}, font_scale=2)
sns.set_style("whitegrid")
# We implement our own very simple mixture, relying on scipy for the mixture
# components.
class SimpleGaussianMixture(object):
def __init__(self, mixture_weights, mixture_components):
self.mixture_weights = mixture_weights
self.mixture_components = mixture_components
def sample(self, num_samples):
# First sample from the mixture
mixture_choices = np.random.choice(range(0, len(self.mixture_weights)),
p=self.mixture_weights, size=num_samples)
# And then sample from the chosen mixture
return np.array(
[self.mixture_components[mixture_choice].rvs(size=1)
for mixture_choice in mixture_choices])
def pdf(self, x):
value = 0.
for index, weight in enumerate(self.mixture_weights):
# Assuming using scipy distributions for components
value += weight * self.mixture_components[index].pdf(x)
return value
mix = 0.4
mixture_weight = [mix, 1.-mix]
mixture_components = [scipy.stats.norm(loc=-1, scale=0.1), scipy.stats.norm(loc=1, scale=0.5)]
mixture = SimpleGaussianMixture(mixture_weight, mixture_components)
mixture.sample(10)
mixture.pdf([10, 1])
data_samples = mixture.sample(30)
len(data_samples)
data_samples
plt.figure()
plt.plot(data_samples, [0] * len(data_samples), 'ro', ms=10, label='data')
plt.axis('off')
plt.ylim(-1, 2)
plt.xticks([])
plt.yticks([])
# Use another set of samples to exemplify samples from the model
data_samples2 = mixture.sample(30)
```
## Implicit generative model
An implicit generative model only provides us with samples. Here for simplicity, we use a different set of samples obtained from the data distribution (i.e, we assume a perfect model).
```
plt.figure(figsize=(12,8))
plt.plot(data_samples, [0] * len(data_samples), 'ro', ms=12, label='data')
plt.plot(data_samples2, [0] * len(data_samples), 'bd', ms=10, alpha=0.7, label='model samples')
plt.axis('off')
# plt.ylim(-0.2, 2)
# plt.xlim(-2, 3)
plt.xticks([])
plt.yticks([])
plt.legend(framealpha=0.)
```
## Explicit generative models
An explicit generative model allows us to query for likelihoods under the learned distribution for points in the input space of the data. Here too we assume a perfect model in the plot, by using the data distribution pdf.
```
plt.figure(figsize=(12,8))
plt.plot(data_samples, [0] * len(data_samples), 'ro', ms=12, label='data')
x_vals = np.linspace(-2., 3., int(1e4))
pdf_vals = mixture.pdf(x_vals)
plt.plot(x_vals, pdf_vals, linewidth=4, label='model density')
plt.axis('off')
plt.ylim(-0.2, 2)
plt.xlim(-2, 3)
plt.xticks([])
plt.yticks([])
plt.legend(framealpha=0)
```
|
github_jupyter
|
import random
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
import scipy
sns.set(rc={"lines.linewidth": 2.8}, font_scale=2)
sns.set_style("whitegrid")
# We implement our own very simple mixture, relying on scipy for the mixture
# components.
class SimpleGaussianMixture(object):
def __init__(self, mixture_weights, mixture_components):
self.mixture_weights = mixture_weights
self.mixture_components = mixture_components
def sample(self, num_samples):
# First sample from the mixture
mixture_choices = np.random.choice(range(0, len(self.mixture_weights)),
p=self.mixture_weights, size=num_samples)
# And then sample from the chosen mixture
return np.array(
[self.mixture_components[mixture_choice].rvs(size=1)
for mixture_choice in mixture_choices])
def pdf(self, x):
value = 0.
for index, weight in enumerate(self.mixture_weights):
# Assuming using scipy distributions for components
value += weight * self.mixture_components[index].pdf(x)
return value
mix = 0.4
mixture_weight = [mix, 1.-mix]
mixture_components = [scipy.stats.norm(loc=-1, scale=0.1), scipy.stats.norm(loc=1, scale=0.5)]
mixture = SimpleGaussianMixture(mixture_weight, mixture_components)
mixture.sample(10)
mixture.pdf([10, 1])
data_samples = mixture.sample(30)
len(data_samples)
data_samples
plt.figure()
plt.plot(data_samples, [0] * len(data_samples), 'ro', ms=10, label='data')
plt.axis('off')
plt.ylim(-1, 2)
plt.xticks([])
plt.yticks([])
# Use another set of samples to exemplify samples from the model
data_samples2 = mixture.sample(30)
plt.figure(figsize=(12,8))
plt.plot(data_samples, [0] * len(data_samples), 'ro', ms=12, label='data')
plt.plot(data_samples2, [0] * len(data_samples), 'bd', ms=10, alpha=0.7, label='model samples')
plt.axis('off')
# plt.ylim(-0.2, 2)
# plt.xlim(-2, 3)
plt.xticks([])
plt.yticks([])
plt.legend(framealpha=0.)
plt.figure(figsize=(12,8))
plt.plot(data_samples, [0] * len(data_samples), 'ro', ms=12, label='data')
x_vals = np.linspace(-2., 3., int(1e4))
pdf_vals = mixture.pdf(x_vals)
plt.plot(x_vals, pdf_vals, linewidth=4, label='model density')
plt.axis('off')
plt.ylim(-0.2, 2)
plt.xlim(-2, 3)
plt.xticks([])
plt.yticks([])
plt.legend(framealpha=0)
| 0.850593 | 0.986244 |
# Advanced Recommender Systems with Python
Welcome to the code notebook for creating Advanced Recommender Systems with Python. This is an optional lecture notebook for you to check out. Currently there is no video for this lecture because of the level of mathematics used and the heavy use of SciPy here.
Recommendation Systems usually rely on larger data sets and specifically need to be organized in a particular fashion. Because of this, we won't have a project to go along with this topic, instead we will have a more intensive walkthrough process on creating a recommendation system with Python with the same Movie Lens Data Set.
*Note: The actual mathematics behind recommender systems is pretty heavy in Linear Algebra.*
___
## Methods Used
Two most common types of recommender systems are **Content-Based** and **Collaborative Filtering (CF)**.
* Collaborative filtering produces recommendations based on the knowledge of users’ attitude to items, that is it uses the "wisdom of the crowd" to recommend items.
* Content-based recommender systems focus on the attributes of the items and give you recommendations based on the similarity between them.
## Collaborative Filtering
In general, Collaborative filtering (CF) is more commonly used than content-based systems because it usually gives better results and is relatively easy to understand (from an overall implementation perspective). The algorithm has the ability to do feature learning on its own, which means that it can start to learn for itself what features to use.
CF can be divided into **Memory-Based Collaborative Filtering** and **Model-Based Collaborative filtering**.
In this tutorial, we will implement Model-Based CF by using singular value decomposition (SVD) and Memory-Based CF by computing cosine similarity.
## The Data
We will use famous MovieLens dataset, which is one of the most common datasets used when implementing and testing recommender engines. It contains 100k movie ratings from 943 users and a selection of 1682 movies.
You can download the dataset [here](http://files.grouplens.org/datasets/movielens/ml-100k.zip) or just use the u.data file that is already included in this folder.
____
## Getting Started
Let's import some libraries we will need:
```
import numpy as np
import pandas as pd
```
We can then read in the **u.data** file, which contains the full dataset. You can read a brief description of the dataset [here](http://files.grouplens.org/datasets/movielens/ml-100k-README.txt).
Note how we specify the separator argument for a Tab separated file.
```
column_names = ['user_id', 'item_id', 'rating', 'timestamp']
df = pd.read_csv('u.data', sep='\t', names=column_names)
```
Let's take a quick look at the data.
```
df.head()
```
Note how we only have the item_id, not the movie name. We can use the Movie_ID_Titles csv file to grab the movie names and merge it with this dataframe:
```
movie_titles = pd.read_csv("Movie_Id_Titles")
movie_titles.head()
```
Then merge the dataframes:
```
df = pd.merge(df,movie_titles,on='item_id')
df.head()
```
Now let's take a quick look at the number of unique users and movies.
```
n_users = df.user_id.nunique()
n_items = df.item_id.nunique()
print('Num. of Users: '+ str(n_users))
print('Num of Movies: '+str(n_items))
```
## Train Test Split
Recommendation Systems by their very nature are very difficult to evaluate, but we will still show you how to evaluate them in this tutorial. In order to do this, we'll split our data into two sets. However, we won't do our classic X_train,X_test,y_train,y_test split. Instead we can actually just segement the data into two sets of data:
```
from sklearn.cross_validation import train_test_split
train_data, test_data = train_test_split(df, test_size=0.25)
```
## Memory-Based Collaborative Filtering
Memory-Based Collaborative Filtering approaches can be divided into two main sections: **user-item filtering** and **item-item filtering**.
A *user-item filtering* will take a particular user, find users that are similar to that user based on similarity of ratings, and recommend items that those similar users liked.
In contrast, *item-item filtering* will take an item, find users who liked that item, and find other items that those users or similar users also liked. It takes items and outputs other items as recommendations.
* *Item-Item Collaborative Filtering*: “Users who liked this item also liked …”
* *User-Item Collaborative Filtering*: “Users who are similar to you also liked …”
In both cases, you create a user-item matrix which built from the entire dataset.
Since we have split the data into testing and training we will need to create two ``[943 x 1682]`` matrices (all users by all movies).
The training matrix contains 75% of the ratings and the testing matrix contains 25% of the ratings.
Example of user-item matrix:
<img class="aligncenter size-thumbnail img-responsive" src="http://s33.postimg.org/ay0ty90fj/BLOG_CCA_8.png" alt="blog8"/>
After you have built the user-item matrix you calculate the similarity and create a similarity matrix.
The similarity values between items in *Item-Item Collaborative Filtering* are measured by observing all the users who have rated both items.
<img class="aligncenter size-thumbnail img-responsive" style="max-width:100%; width: 50%; max-width: none" src="http://s33.postimg.org/i522ma83z/BLOG_CCA_10.png"/>
For *User-Item Collaborative Filtering* the similarity values between users are measured by observing all the items that are rated by both users.
<img class="aligncenter size-thumbnail img-responsive" style="max-width:100%; width: 50%; max-width: none" src="http://s33.postimg.org/mlh3z3z4f/BLOG_CCA_11.png"/>
A distance metric commonly used in recommender systems is *cosine similarity*, where the ratings are seen as vectors in ``n``-dimensional space and the similarity is calculated based on the angle between these vectors.
Cosine similiarity for users *a* and *m* can be calculated using the formula below, where you take dot product of the user vector *$u_k$* and the user vector *$u_a$* and divide it by multiplication of the Euclidean lengths of the vectors.
<img class="aligncenter size-thumbnail img-responsive" src="https://latex.codecogs.com/gif.latex?s_u^{cos}(u_k,u_a)=\frac{u_k&space;\cdot&space;u_a&space;}{&space;\left&space;\|&space;u_k&space;\right&space;\|&space;\left&space;\|&space;u_a&space;\right&space;\|&space;}&space;=\frac{\sum&space;x_{k,m}x_{a,m}}{\sqrt{\sum&space;x_{k,m}^2\sum&space;x_{a,m}^2}}"/>
To calculate similarity between items *m* and *b* you use the formula:
<img class="aligncenter size-thumbnail img-responsive" src="https://latex.codecogs.com/gif.latex?s_u^{cos}(i_m,i_b)=\frac{i_m&space;\cdot&space;i_b&space;}{&space;\left&space;\|&space;i_m&space;\right&space;\|&space;\left&space;\|&space;i_b&space;\right&space;\|&space;}&space;=\frac{\sum&space;x_{a,m}x_{a,b}}{\sqrt{\sum&space;x_{a,m}^2\sum&space;x_{a,b}^2}}
"/>
Your first step will be to create the user-item matrix. Since you have both testing and training data you need to create two matrices.
```
#Create two user-item matrices, one for training and another for testing
train_data_matrix = np.zeros((n_users, n_items))
for line in train_data.itertuples():
train_data_matrix[line[1]-1, line[2]-1] = line[3]
test_data_matrix = np.zeros((n_users, n_items))
for line in test_data.itertuples():
test_data_matrix[line[1]-1, line[2]-1] = line[3]
```
You can use the [pairwise_distances](http://scikit-learn.org/stable/modules/generated/sklearn.metrics.pairwise.pairwise_distances.html) function from sklearn to calculate the cosine similarity. Note, the output will range from 0 to 1 since the ratings are all positive.
```
from sklearn.metrics.pairwise import pairwise_distances
user_similarity = pairwise_distances(train_data_matrix, metric='cosine')
item_similarity = pairwise_distances(train_data_matrix.T, metric='cosine')
```
Next step is to make predictions. You have already created similarity matrices: `user_similarity` and `item_similarity` and therefore you can make a prediction by applying following formula for user-based CF:
<img class="aligncenter size-thumbnail img-responsive" src="https://latex.codecogs.com/gif.latex?\hat{x}_{k,m}&space;=&space;\bar{x}_{k}&space;+&space;\frac{\sum\limits_{u_a}&space;sim_u(u_k,&space;u_a)&space;(x_{a,m}&space;-&space;\bar{x_{u_a}})}{\sum\limits_{u_a}|sim_u(u_k,&space;u_a)|}"/>
You can look at the similarity between users *k* and *a* as weights that are multiplied by the ratings of a similar user *a* (corrected for the average rating of that user). You will need to normalize it so that the ratings stay between 1 and 5 and, as a final step, sum the average ratings for the user that you are trying to predict.
The idea here is that some users may tend always to give high or low ratings to all movies. The relative difference in the ratings that these users give is more important than the absolute values. To give an example: suppose, user *k* gives 4 stars to his favourite movies and 3 stars to all other good movies. Suppose now that another user *t* rates movies that he/she likes with 5 stars, and the movies he/she fell asleep over with 3 stars. These two users could have a very similar taste but treat the rating system differently.
When making a prediction for item-based CF you don't need to correct for users average rating since query user itself is used to do predictions.
<img class="aligncenter size-thumbnail img-responsive" src="https://latex.codecogs.com/gif.latex?\hat{x}_{k,m}&space;=&space;\frac{\sum\limits_{i_b}&space;sim_i(i_m,&space;i_b)&space;(x_{k,b})&space;}{\sum\limits_{i_b}|sim_i(i_m,&space;i_b)|}"/>
```
def predict(ratings, similarity, type='user'):
if type == 'user':
mean_user_rating = ratings.mean(axis=1)
#You use np.newaxis so that mean_user_rating has same format as ratings
ratings_diff = (ratings - mean_user_rating[:, np.newaxis])
pred = mean_user_rating[:, np.newaxis] + similarity.dot(ratings_diff) / np.array([np.abs(similarity).sum(axis=1)]).T
elif type == 'item':
pred = ratings.dot(similarity) / np.array([np.abs(similarity).sum(axis=1)])
return pred
item_prediction = predict(train_data_matrix, item_similarity, type='item')
user_prediction = predict(train_data_matrix, user_similarity, type='user')
```
### Evaluation
There are many evaluation metrics but one of the most popular metric used to evaluate accuracy of predicted ratings is *Root Mean Squared Error (RMSE)*.
<img src="https://latex.codecogs.com/gif.latex?RMSE&space;=\sqrt{\frac{1}{N}&space;\sum&space;(x_i&space;-\hat{x_i})^2}" title="RMSE =\sqrt{\frac{1}{N} \sum (x_i -\hat{x_i})^2}" />
You can use the [mean_square_error](http://scikit-learn.org/stable/modules/generated/sklearn.metrics.mean_squared_error.html) (MSE) function from `sklearn`, where the RMSE is just the square root of MSE. To read more about different evaluation metrics you can take a look at [this article](http://research.microsoft.com/pubs/115396/EvaluationMetrics.TR.pdf).
Since you only want to consider predicted ratings that are in the test dataset, you filter out all other elements in the prediction matrix with `prediction[ground_truth.nonzero()]`.
```
from sklearn.metrics import mean_squared_error
from math import sqrt
def rmse(prediction, ground_truth):
prediction = prediction[ground_truth.nonzero()].flatten()
ground_truth = ground_truth[ground_truth.nonzero()].flatten()
return sqrt(mean_squared_error(prediction, ground_truth))
print('User-based CF RMSE: ' + str(rmse(user_prediction, test_data_matrix)))
print('Item-based CF RMSE: ' + str(rmse(item_prediction, test_data_matrix)))
```
Memory-based algorithms are easy to implement and produce reasonable prediction quality.
The drawback of memory-based CF is that it doesn't scale to real-world scenarios and doesn't address the well-known cold-start problem, that is when new user or new item enters the system. Model-based CF methods are scalable and can deal with higher sparsity level than memory-based models, but also suffer when new users or items that don't have any ratings enter the system. I would like to thank Ethan Rosenthal for his [post](http://blog.ethanrosenthal.com/2015/11/02/intro-to-collaborative-filtering/) about Memory-Based Collaborative Filtering.
# Model-based Collaborative Filtering
Model-based Collaborative Filtering is based on **matrix factorization (MF)** which has received greater exposure, mainly as an unsupervised learning method for latent variable decomposition and dimensionality reduction. Matrix factorization is widely used for recommender systems where it can deal better with scalability and sparsity than Memory-based CF. The goal of MF is to learn the latent preferences of users and the latent attributes of items from known ratings (learn features that describe the characteristics of ratings) to then predict the unknown ratings through the dot product of the latent features of users and items.
When you have a very sparse matrix, with a lot of dimensions, by doing matrix factorization you can restructure the user-item matrix into low-rank structure, and you can represent the matrix by the multiplication of two low-rank matrices, where the rows contain the latent vector. You fit this matrix to approximate your original matrix, as closely as possible, by multiplying the low-rank matrices together, which fills in the entries missing in the original matrix.
Let's calculate the sparsity level of MovieLens dataset:
```
sparsity=round(1.0-len(df)/float(n_users*n_items),3)
print('The sparsity level of MovieLens100K is ' + str(sparsity*100) + '%')
```
To give an example of the learned latent preferences of the users and items: let's say for the MovieLens dataset you have the following information: _(user id, age, location, gender, movie id, director, actor, language, year, rating)_. By applying matrix factorization the model learns that important user features are _age group (under 10, 10-18, 18-30, 30-90)_, _location_ and _gender_, and for movie features it learns that _decade_, _director_ and _actor_ are most important. Now if you look into the information you have stored, there is no such feature as the _decade_, but the model can learn on its own. The important aspect is that the CF model only uses data (user_id, movie_id, rating) to learn the latent features. If there is little data available model-based CF model will predict poorly, since it will be more difficult to learn the latent features.
Models that use both ratings and content features are called **Hybrid Recommender Systems** where both Collaborative Filtering and Content-based Models are combined. Hybrid recommender systems usually show higher accuracy than Collaborative Filtering or Content-based Models on their own: they are capable to address the cold-start problem better since if you don't have any ratings for a user or an item you could use the metadata from the user or item to make a prediction.
### SVD
A well-known matrix factorization method is **Singular value decomposition (SVD)**. Collaborative Filtering can be formulated by approximating a matrix `X` by using singular value decomposition. The winning team at the Netflix Prize competition used SVD matrix factorization models to produce product recommendations, for more information I recommend to read articles: [Netflix Recommendations: Beyond the 5 stars](http://techblog.netflix.com/2012/04/netflix-recommendations-beyond-5-stars.html) and [Netflix Prize and SVD](http://buzzard.ups.edu/courses/2014spring/420projects/math420-UPS-spring-2014-gower-netflix-SVD.pdf).
The general equation can be expressed as follows:
<img src="https://latex.codecogs.com/gif.latex?X=USV^T" title="X=USV^T" />
Given `m x n` matrix `X`:
* *`U`* is an *`(m x r)`* orthogonal matrix
* *`S`* is an *`(r x r)`* diagonal matrix with non-negative real numbers on the diagonal
* *V^T* is an *`(r x n)`* orthogonal matrix
Elements on the diagnoal in `S` are known as *singular values of `X`*.
Matrix *`X`* can be factorized to *`U`*, *`S`* and *`V`*. The *`U`* matrix represents the feature vectors corresponding to the users in the hidden feature space and the *`V`* matrix represents the feature vectors corresponding to the items in the hidden feature space.
<img class="aligncenter size-thumbnail img-responsive" style="max-width:100%; width: 50%; max-width: none" src="http://s33.postimg.org/kwgsb5g1b/BLOG_CCA_5.png"/>
Now you can make a prediction by taking dot product of *`U`*, *`S`* and *`V^T`*.
<img class="aligncenter size-thumbnail img-responsive" style="max-width:100%; width: 50%; max-width: none" src="http://s33.postimg.org/ch9lcm6pb/BLOG_CCA_4.png"/>
```
import scipy.sparse as sp
from scipy.sparse.linalg import svds
#get SVD components from train matrix. Choose k.
u, s, vt = svds(train_data_matrix, k = 20)
s_diag_matrix=np.diag(s)
X_pred = np.dot(np.dot(u, s_diag_matrix), vt)
print('User-based CF MSE: ' + str(rmse(X_pred, test_data_matrix)))
```
Carelessly addressing only the relatively few known entries is highly prone to overfitting. SVD can be very slow and computationally expensive. More recent work minimizes the squared error by applying alternating least square or stochastic gradient descent and uses regularization terms to prevent overfitting. Alternating least square and stochastic gradient descent methods for CF will be covered in the next tutorials.
Review:
* We have covered how to implement simple **Collaborative Filtering** methods, both memory-based CF and model-based CF.
* **Memory-based models** are based on similarity between items or users, where we use cosine-similarity.
* **Model-based CF** is based on matrix factorization where we use SVD to factorize the matrix.
* Building recommender systems that perform well in cold-start scenarios (where little data is available on new users and items) remains a challenge. The standard collaborative filtering method performs poorly is such settings.
## Looking for more?
If you want to tackle your own recommendation system analysis, check out these data sets. Note: The files are quite large in most cases, not all the links may stay up to host the data, but the majority of them still work. Or just Google for your own data set!
**Movies Recommendation:**
MovieLens - Movie Recommendation Data Sets http://www.grouplens.org/node/73
Yahoo! - Movie, Music, and Images Ratings Data Sets http://webscope.sandbox.yahoo.com/catalog.php?datatype=r
Jester - Movie Ratings Data Sets (Collaborative Filtering Dataset) http://www.ieor.berkeley.edu/~goldberg/jester-data/
Cornell University - Movie-review data for use in sentiment-analysis experiments http://www.cs.cornell.edu/people/pabo/movie-review-data/
**Music Recommendation:**
Last.fm - Music Recommendation Data Sets http://www.dtic.upf.edu/~ocelma/MusicRecommendationDataset/index.html
Yahoo! - Movie, Music, and Images Ratings Data Sets http://webscope.sandbox.yahoo.com/catalog.php?datatype=r
Audioscrobbler - Music Recommendation Data Sets http://www-etud.iro.umontreal.ca/~bergstrj/audioscrobbler_data.html
Amazon - Audio CD recommendations http://131.193.40.52/data/
**Books Recommendation:**
Institut für Informatik, Universität Freiburg - Book Ratings Data Sets http://www.informatik.uni-freiburg.de/~cziegler/BX/
Food Recommendation:
Chicago Entree - Food Ratings Data Sets http://archive.ics.uci.edu/ml/datasets/Entree+Chicago+Recommendation+Data
Merchandise Recommendation:
**Healthcare Recommendation:**
Nursing Home - Provider Ratings Data Set http://data.medicare.gov/dataset/Nursing-Home-Compare-Provider-Ratings/mufm-vy8d
Hospital Ratings - Survey of Patients Hospital Experiences http://data.medicare.gov/dataset/Survey-of-Patients-Hospital-Experiences-HCAHPS-/rj76-22dk
**Dating Recommendation:**
www.libimseti.cz - Dating website recommendation (collaborative filtering) http://www.occamslab.com/petricek/data/
Scholarly Paper Recommendation:
National University of Singapore - Scholarly Paper Recommendation http://www.comp.nus.edu.sg/~sugiyama/SchPaperRecData.html
# Great Job!
|
github_jupyter
|
import numpy as np
import pandas as pd
column_names = ['user_id', 'item_id', 'rating', 'timestamp']
df = pd.read_csv('u.data', sep='\t', names=column_names)
df.head()
movie_titles = pd.read_csv("Movie_Id_Titles")
movie_titles.head()
df = pd.merge(df,movie_titles,on='item_id')
df.head()
n_users = df.user_id.nunique()
n_items = df.item_id.nunique()
print('Num. of Users: '+ str(n_users))
print('Num of Movies: '+str(n_items))
from sklearn.cross_validation import train_test_split
train_data, test_data = train_test_split(df, test_size=0.25)
#Create two user-item matrices, one for training and another for testing
train_data_matrix = np.zeros((n_users, n_items))
for line in train_data.itertuples():
train_data_matrix[line[1]-1, line[2]-1] = line[3]
test_data_matrix = np.zeros((n_users, n_items))
for line in test_data.itertuples():
test_data_matrix[line[1]-1, line[2]-1] = line[3]
from sklearn.metrics.pairwise import pairwise_distances
user_similarity = pairwise_distances(train_data_matrix, metric='cosine')
item_similarity = pairwise_distances(train_data_matrix.T, metric='cosine')
def predict(ratings, similarity, type='user'):
if type == 'user':
mean_user_rating = ratings.mean(axis=1)
#You use np.newaxis so that mean_user_rating has same format as ratings
ratings_diff = (ratings - mean_user_rating[:, np.newaxis])
pred = mean_user_rating[:, np.newaxis] + similarity.dot(ratings_diff) / np.array([np.abs(similarity).sum(axis=1)]).T
elif type == 'item':
pred = ratings.dot(similarity) / np.array([np.abs(similarity).sum(axis=1)])
return pred
item_prediction = predict(train_data_matrix, item_similarity, type='item')
user_prediction = predict(train_data_matrix, user_similarity, type='user')
from sklearn.metrics import mean_squared_error
from math import sqrt
def rmse(prediction, ground_truth):
prediction = prediction[ground_truth.nonzero()].flatten()
ground_truth = ground_truth[ground_truth.nonzero()].flatten()
return sqrt(mean_squared_error(prediction, ground_truth))
print('User-based CF RMSE: ' + str(rmse(user_prediction, test_data_matrix)))
print('Item-based CF RMSE: ' + str(rmse(item_prediction, test_data_matrix)))
sparsity=round(1.0-len(df)/float(n_users*n_items),3)
print('The sparsity level of MovieLens100K is ' + str(sparsity*100) + '%')
import scipy.sparse as sp
from scipy.sparse.linalg import svds
#get SVD components from train matrix. Choose k.
u, s, vt = svds(train_data_matrix, k = 20)
s_diag_matrix=np.diag(s)
X_pred = np.dot(np.dot(u, s_diag_matrix), vt)
print('User-based CF MSE: ' + str(rmse(X_pred, test_data_matrix)))
| 0.52683 | 0.991456 |
```
import tensorflow as tf
print(tf.__version__)
```
在深度学习中,我们通常会频繁地对数据进行操作。作为动手学深度学习的基础,本节将介绍如何对内存中的数据进行操作。
在tensorflow中,tensor是一个类,也是存储和变换数据的主要工具。如果你之前用过NumPy,你会发现tensor和NumPy的多维数组非常类似。然而,tensor提供GPU计算和自动求梯度等更多功能,这些使tensor更加适合深度学习。
## 2.2.1 Create NDArray
我们先介绍NDArray的最基本功能,我们用arange函数创建一个行向量。
```
x = tf.constant(range(12))
print(x.shape)
x
```
这时返回了一个tensor实例,其中包含了从0开始的12个连续整数。
我们可以通过shape属性来获取tensor实例的形状。
```
x.shape
```
我们也能够通过len得到tensor实例中元素(element)的总数。
```
len(x)
```
下面使用reshape函数把行向量x的形状改为(3, 4),也就是一个3行4列的矩阵,并记作X。除了形状改变之外,X中的元素保持不变。
```
X = tf.reshape(x,(3,4))
X
```
注意X属性中的形状发生了变化。上面x.reshape((3, 4))也可写成x.reshape((-1, 4))或x.reshape((3, -1))。由于x的元素个数是已知的,这里的-1是能够通过元素个数和其他维度的大小推断出来的。
接下来,我们创建一个各元素为0,形状为(2, 3, 4)的张量。实际上,之前创建的向量和矩阵都是特殊的张量。
```
tf.zeros((2,3,4))
```
类似地,我们可以创建各元素为1的张量。
```
tf.ones((3,4))
```
我们也可以通过Python的列表(list)指定需要创建的tensor中每个元素的值。
```
Y = tf.constant([[2,1,4,3],[1,2,3,4],[4,3,2,1]])
Y
```
有些情况下,我们需要随机生成tensor中每个元素的值。下面我们创建一个形状为(3, 4)的tensor。它的每个元素都随机采样于均值为0、标准差为1的正态分布。
```
tf.random.normal(shape=[3,4], mean=0, stddev=1)
```
## 2.2.2 arithmetic ops
tensor支持大量的运算符(operator)。例如,我们可以对之前创建的两个形状为(3, 4)的tensor做按元素加法。所得结果形状不变。
```
X + Y
```
按元素乘法:
```
X * Y
```
按元素除法:
```
X / Y
```
按元素做指数运算:
```
Y = tf.cast(Y, tf.float32)
tf.exp(Y)
```
除了按元素计算外,我们还可以使用matmul函数做矩阵乘法。下面将X与Y的转置做矩阵乘法。由于X是3行4列的矩阵,Y转置为4行3列的矩阵,因此两个矩阵相乘得到3行3列的矩阵。
```
Y = tf.cast(Y, tf.int32)
tf.matmul(X, tf.transpose(Y))
```
我们也可以将多个tensor连结(concatenate)。下面分别在行上(维度0,即形状中的最左边元素)和列上(维度1,即形状中左起第二个元素)连结两个矩阵。可以看到,输出的第一个tensor在维度0的长度( 6 )为两个输入矩阵在维度0的长度之和( 3+3 ),而输出的第二个tensor在维度1的长度( 8 )为两个输入矩阵在维度1的长度之和( 4+4 )。
```
tf.concat([X,Y],axis = 0), tf.concat([X,Y],axis = 1)
```
使用条件判断式可以得到元素为0或1的新的tensor。以X == Y为例,如果X和Y在相同位置的条件判断为真(值相等),那么新的tensor在相同位置的值为1;反之为0。
```
tf.equal(X,Y)
```
对tensor中的所有元素求和得到只有一个元素的tensor。
```
tf.reduce_sum(X)
X = tf.cast(X, tf.float32)
tf.norm(X)
```
## 2.2.3 broadcasting
前面我们看到如何对两个形状相同的tensor做按元素运算。当对两个形状不同的tensor按元素运算时,可能会触发广播(broadcasting)机制:先适当复制元素使这两个tensor形状相同后再按元素运算。
定义两个tensor:
```
A = tf.reshape(tf.constant(range(3)), (3,1))
B = tf.reshape(tf.constant(range(2)), (1,2))
A, B
```
由于A和B分别是3行1列和1行2列的矩阵,如果要计算A + B,那么A中第一列的3个元素被广播(复制)到了第二列,而B中第一行的2个元素被广播(复制)到了第二行和第三行。如此,就可以对2个3行2列的矩阵按元素相加。
```
A + B
```
## 2.2.4 indexing
在tensor中,索引(index)代表了元素的位置。tensor的索引从0开始逐一递增。例如,一个3行2列的矩阵的行索引分别为0、1和2,列索引分别为0和1。
在下面的例子中,我们指定了tensor的行索引截取范围[1:3]。依据左闭右开指定范围的惯例,它截取了矩阵X中行索引为1和2的两行。
```
X[1:3]
```
我们可以指定tensor中需要访问的单个元素的位置,如矩阵中行和列的索引,并为该元素重新赋值。
```
X = tf.Variable(X)
X[1,2].assign(9)
```
当然,我们也可以截取一部分元素,并为它们重新赋值。在下面的例子中,我们为行索引为1的每一列元素重新赋值。
```
X = tf.Variable(X)
X
X[1:2,:].assign(tf.ones(X[1:2,:].shape, dtype = tf.float32)*12)
```
## 2.2.5 saving memory
在前面的例子里我们对每个操作新开内存来存储运算结果。举个例子,即使像Y = X + Y这样的运算,我们也会新开内存,然后将Y指向新内存。为了演示这一点,我们可以使用Python自带的id函数:如果两个实例的ID一致,那么它们所对应的内存地址相同;反之则不同。
```
X = tf.Variable(X)
Y = tf.cast(Y, dtype=tf.float32)
before = id(Y)
Y = Y + X
id(Y) == before
```
如果想指定结果到特定内存,我们可以使用前面介绍的索引来进行替换操作。在下面的例子中,我们先通过zeros_like创建和Y形状相同且元素为0的tensor,记为Z。接下来,我们把X + Y的结果通过[:]写进Z对应的内存中。
```
Z = tf.Variable(tf.zeros_like(Y))
before = id(Z)
Z[:].assign(X + Y)
id(Z) == before
```
实际上,上例中我们还是为X + Y开了临时内存来存储计算结果,再复制到Z对应的内存。如果想避免这个临时内存开销,我们可以使用运算符全名函数中的out参数。
```
Z = tf.add(X, Y)
id(Z) == before
```
如果X的值在之后的程序中不会复用,我们也可以用 X[:] = X + Y 或者 X += Y 来减少运算的内存开销。
```
before = id(X)
X.assign_add(Y)
id(X) == before
```
## 2.2.6 trans between numpy
我们可以通过array函数和asnumpy函数令数据在NDArray和NumPy格式之间相互变换。下面将NumPy实例变换成tensor实例。
```
import numpy as np
P = np.ones((2,3))
D = tf.constant(P)
D
```
再将NDArray实例变换成NumPy实例。
```
np.array(D)
```
|
github_jupyter
|
import tensorflow as tf
print(tf.__version__)
x = tf.constant(range(12))
print(x.shape)
x
x.shape
len(x)
X = tf.reshape(x,(3,4))
X
tf.zeros((2,3,4))
tf.ones((3,4))
Y = tf.constant([[2,1,4,3],[1,2,3,4],[4,3,2,1]])
Y
tf.random.normal(shape=[3,4], mean=0, stddev=1)
X + Y
X * Y
X / Y
Y = tf.cast(Y, tf.float32)
tf.exp(Y)
Y = tf.cast(Y, tf.int32)
tf.matmul(X, tf.transpose(Y))
tf.concat([X,Y],axis = 0), tf.concat([X,Y],axis = 1)
tf.equal(X,Y)
tf.reduce_sum(X)
X = tf.cast(X, tf.float32)
tf.norm(X)
A = tf.reshape(tf.constant(range(3)), (3,1))
B = tf.reshape(tf.constant(range(2)), (1,2))
A, B
A + B
X[1:3]
X = tf.Variable(X)
X[1,2].assign(9)
X = tf.Variable(X)
X
X[1:2,:].assign(tf.ones(X[1:2,:].shape, dtype = tf.float32)*12)
X = tf.Variable(X)
Y = tf.cast(Y, dtype=tf.float32)
before = id(Y)
Y = Y + X
id(Y) == before
Z = tf.Variable(tf.zeros_like(Y))
before = id(Z)
Z[:].assign(X + Y)
id(Z) == before
Z = tf.add(X, Y)
id(Z) == before
before = id(X)
X.assign_add(Y)
id(X) == before
import numpy as np
P = np.ones((2,3))
D = tf.constant(P)
D
np.array(D)
| 0.49585 | 0.983118 |
```
%matplotlib inline
from matplotlib import style
style.use('fivethirtyeight')
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import datetime as dt
from numpy import mean
```
# Reflect Tables into SQLAlchemy ORM
```
# Python SQL toolkit and Object Relational Mapper
import sqlalchemy
from sqlalchemy.ext.automap import automap_base
from sqlalchemy.orm import Session
from sqlalchemy import create_engine, func, inspect
# create engine to hawaii.sqlite
engine = create_engine("sqlite:///Resources/hawaii.sqlite")
# reflect an existing database into a new model
Base=automap_base()
# reflect the tables
Base.prepare(engine, reflect=True)
# View all of the classes that automap found
Base.classes.keys()
# Save references to each table
Measurements=Base.classes.measurement
Station=Base.classes.station
# Create our session (link) from Python to the DB
session=Session(engine)
```
# Exploratory Precipitation Analysis
```
first_row = session.query(Measurements).first()
first_row.__dict__
first_row = session.query(Station).first()
first_row.__dict__
# Find the most recent date in the data set.
recent_date=session.query(Measurements.date)\
.order_by(Measurements.date.desc()).first()
#convert query result into date
date_time = dt.datetime.strptime(recent_date[0], '%Y-%m-%d')
#get date ranges for quey
date1=date_time.date()
date2=date1-dt.timedelta(days=365)
print(f"{date1} - {date2}")
# Design a query to retrieve the last 12 months of precipitation data and plot the results.
prcp=session.query(Measurements.date, Measurements.prcp)\
.order_by(Measurements.date.desc())\
.filter(Measurements.date<= date1)\
.filter(Measurements.date >= date2)\
.all()
prcp
# Starting from the most recent data point in the database.
# Calculate the date one year from the last date in data set.
# Perform a query to retrieve the data and precipitation scores
# Save the query results as a Pandas DataFrame
precipitation=pd.DataFrame(prcp)
precipitation
#set the index to the date colum
precipitation.dropna(inplace=True)
precipitation.set_index('date', inplace=True)
# Sort the dataframe by date
precipitation.sort_values('date',ascending= True, inplace=True)
precipitation
# Use Pandas Plotting with Matplotlib to plot the data
precipitation.reset_index(inplace=True)
date_list=[]
date_list.append(date2.strftime('%Y-%m-%d'))
d=date2
for x in range(12):
d= d+dt.timedelta(days=28)
s=d.strftime('%Y-%m-%d')
date_list.append(s)
# Use Pandas Plotting with Matplotlib to plot the data
plt.figure(figsize=(10,6))
pyplot_bar=plt.bar(precipitation['date'], precipitation['prcp'], width= 3)
ax = plt.gca()
ax.set_xticks(date_list)
plt.xticks(rotation='vertical')
plt.title('Honolulu precipitation')
plt.xlabel('date')
plt.ylabel('Precipitation')
plt.show()
# Use Pandas to calcualte the summary statistics for the precipitation data
precipitation.describe()
```
# Exploratory Station Analysis
```
# Design a query to calculate the total number stations in the dataset
stations = session.query(Station.station).count()
stations
# Design a query to find the most active stations (i.e. what stations have the most rows?)
# List the stations and the counts in descending order.
count_ = func.count('*')
most_active_station = session.query(Measurements.station, count_)\
.group_by(Measurements.station)\
.order_by(count_.desc())\
.all()
most_active_station
# Using the most active station id from the previous query, calculate the lowest, highest, and average temperature.
station=session.query(Station.name)\
.filter(Station.station == 'USC00519281').all()
min_temp=session.query(func.min(Measurements.tobs))\
.filter(Measurements.station =='USC00519281')\
.all()
max_temp=session.query(func.max(Measurements.tobs))\
.filter(Measurements.station =='USC00519281')\
.all()
avg_temp=session.query(func.avg(Measurements.tobs))\
.filter(Measurements.station =='USC00519281')\
.all()
print(f"station: {station[0][0]}\nMin temperature: {min_temp[0][0]} ºF\n\
Max temperature: {max_temp[0][0]} ºF\nAvg Temperature: {avg_temp[0][0]} ºF")
# Using the most active station id
# Query the last 12 months of temperature observation data for this station and plot the results as a histogram
temp=session.query(Measurements.date, Measurements.tobs)\
.filter(Measurements.station =='USC00519281')\
.filter(Measurements.date<=date1)\
.filter(Measurements.date >=date2)\
.all()
temp=pd.DataFrame(temp)
temp.head()
x = temp['tobs']
plt.hist(x, bins = 12)
plt.xticks(rotation='vertical')
plt.title('WAIHEE Temperature Observation Data (TOBS)')
plt.xlabel('Temperature')
plt.ylabel('Frequency')
plt.show()
```
# Close session
```
# Close Session
session.close()
```
|
github_jupyter
|
%matplotlib inline
from matplotlib import style
style.use('fivethirtyeight')
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import datetime as dt
from numpy import mean
# Python SQL toolkit and Object Relational Mapper
import sqlalchemy
from sqlalchemy.ext.automap import automap_base
from sqlalchemy.orm import Session
from sqlalchemy import create_engine, func, inspect
# create engine to hawaii.sqlite
engine = create_engine("sqlite:///Resources/hawaii.sqlite")
# reflect an existing database into a new model
Base=automap_base()
# reflect the tables
Base.prepare(engine, reflect=True)
# View all of the classes that automap found
Base.classes.keys()
# Save references to each table
Measurements=Base.classes.measurement
Station=Base.classes.station
# Create our session (link) from Python to the DB
session=Session(engine)
first_row = session.query(Measurements).first()
first_row.__dict__
first_row = session.query(Station).first()
first_row.__dict__
# Find the most recent date in the data set.
recent_date=session.query(Measurements.date)\
.order_by(Measurements.date.desc()).first()
#convert query result into date
date_time = dt.datetime.strptime(recent_date[0], '%Y-%m-%d')
#get date ranges for quey
date1=date_time.date()
date2=date1-dt.timedelta(days=365)
print(f"{date1} - {date2}")
# Design a query to retrieve the last 12 months of precipitation data and plot the results.
prcp=session.query(Measurements.date, Measurements.prcp)\
.order_by(Measurements.date.desc())\
.filter(Measurements.date<= date1)\
.filter(Measurements.date >= date2)\
.all()
prcp
# Starting from the most recent data point in the database.
# Calculate the date one year from the last date in data set.
# Perform a query to retrieve the data and precipitation scores
# Save the query results as a Pandas DataFrame
precipitation=pd.DataFrame(prcp)
precipitation
#set the index to the date colum
precipitation.dropna(inplace=True)
precipitation.set_index('date', inplace=True)
# Sort the dataframe by date
precipitation.sort_values('date',ascending= True, inplace=True)
precipitation
# Use Pandas Plotting with Matplotlib to plot the data
precipitation.reset_index(inplace=True)
date_list=[]
date_list.append(date2.strftime('%Y-%m-%d'))
d=date2
for x in range(12):
d= d+dt.timedelta(days=28)
s=d.strftime('%Y-%m-%d')
date_list.append(s)
# Use Pandas Plotting with Matplotlib to plot the data
plt.figure(figsize=(10,6))
pyplot_bar=plt.bar(precipitation['date'], precipitation['prcp'], width= 3)
ax = plt.gca()
ax.set_xticks(date_list)
plt.xticks(rotation='vertical')
plt.title('Honolulu precipitation')
plt.xlabel('date')
plt.ylabel('Precipitation')
plt.show()
# Use Pandas to calcualte the summary statistics for the precipitation data
precipitation.describe()
# Design a query to calculate the total number stations in the dataset
stations = session.query(Station.station).count()
stations
# Design a query to find the most active stations (i.e. what stations have the most rows?)
# List the stations and the counts in descending order.
count_ = func.count('*')
most_active_station = session.query(Measurements.station, count_)\
.group_by(Measurements.station)\
.order_by(count_.desc())\
.all()
most_active_station
# Using the most active station id from the previous query, calculate the lowest, highest, and average temperature.
station=session.query(Station.name)\
.filter(Station.station == 'USC00519281').all()
min_temp=session.query(func.min(Measurements.tobs))\
.filter(Measurements.station =='USC00519281')\
.all()
max_temp=session.query(func.max(Measurements.tobs))\
.filter(Measurements.station =='USC00519281')\
.all()
avg_temp=session.query(func.avg(Measurements.tobs))\
.filter(Measurements.station =='USC00519281')\
.all()
print(f"station: {station[0][0]}\nMin temperature: {min_temp[0][0]} ºF\n\
Max temperature: {max_temp[0][0]} ºF\nAvg Temperature: {avg_temp[0][0]} ºF")
# Using the most active station id
# Query the last 12 months of temperature observation data for this station and plot the results as a histogram
temp=session.query(Measurements.date, Measurements.tobs)\
.filter(Measurements.station =='USC00519281')\
.filter(Measurements.date<=date1)\
.filter(Measurements.date >=date2)\
.all()
temp=pd.DataFrame(temp)
temp.head()
x = temp['tobs']
plt.hist(x, bins = 12)
plt.xticks(rotation='vertical')
plt.title('WAIHEE Temperature Observation Data (TOBS)')
plt.xlabel('Temperature')
plt.ylabel('Frequency')
plt.show()
# Close Session
session.close()
| 0.722331 | 0.872293 |
```
# NBVAL_SKIP
%matplotlib inline
import logging
logging.basicConfig(level=logging.CRITICAL)
# NBVAL_SKIP
import torch
import pytorch3d
from pytorch3d.ops import sample_points_from_meshes
```
# Creating Protein Meshes in Graphein & 3D Visualisation
Graphein provides functionality to create meshes of protein surfaces. The mesh computation is handled under the hood by PyMol to produce `.obj` files, which are handled by many geometric analysis libraries (such as PyTorch3D). We'll create a few protein meshes, convert them to PyTorch3D objects and visualises them. Again, there is a high-level and low-level API for convenience.
## High-level API
### Config
Again, we use a config object to manage global configurations.
* `pymol_command_line_options`: String of additional pymol command line options when launching. A full list can be found [here](https://www.pymolwiki.org/index.php/Command_Line_Options). The default options, `"-cKq"`, do:
* `c`: launch in command-line only mode for batch processing
* `K`: keep alive: when running without a GUI, don't quit after the input
is exhausted
* `q`: supress startup message
* `pymol_commands` : List of string pymol commands to execute. You can use these to configure the exact mesh you wish to construct. A reference to these can be found [here](https://pymol.org/pymol-command-ref.html)
```
from graphein.protein.config import ProteinMeshConfig
config = ProteinMeshConfig()
config.dict()
```
### Building a mesh
Let's build a mesh!
```
# NBVAL_SKIP
from graphein.protein.meshes import create_mesh
verts, faces, aux = create_mesh(pdb_code="3eiy", config=config)
print(verts, faces, aux)
```
In order to visualise these tensors containing vertices, faces and aux data, we convert them into a PyTorch3D `Mesh` object
```
# NBVAL_SKIP
from graphein.protein.meshes import convert_verts_and_face_to_mesh
m = convert_verts_and_face_to_mesh(verts, faces)
from graphein.protein.visualisation import plot_pointcloud
plot_pointcloud(m, title="my first mesh")
```
## Modifying Mesh Parameters
Let's see what happens if we play around with some of the parameters and make a smoother mesh using
```
# NBVAL_SKIP
pymol_commands = {"pymol_commands": ["hide cartoon",
"set solvent_radius, 10",
"alter all, vdw=4",
"sort",
"set surface_quality, 1",
"show surface"]}
config = ProteinMeshConfig(**pymol_commands)
verts, faces, aux = create_mesh(pdb_code="3eiy", config=config)
m = convert_verts_and_face_to_mesh(verts, faces)
plot_pointcloud(m, title="my second mesh")
```
## Using PyMol for 3D Visualisation
We also provide a wrapper for pymol (based on [IPyMol](https://github.com/cxhernandez/ipymol) developed by [@cxhernandez](https://github.com/cxhernandez))
```
# NBVAL_SKIP
from graphein.utils.pymol import viewer as pymol
pymol.fetch("3eiy")
pymol.display()
```
|
github_jupyter
|
# NBVAL_SKIP
%matplotlib inline
import logging
logging.basicConfig(level=logging.CRITICAL)
# NBVAL_SKIP
import torch
import pytorch3d
from pytorch3d.ops import sample_points_from_meshes
from graphein.protein.config import ProteinMeshConfig
config = ProteinMeshConfig()
config.dict()
# NBVAL_SKIP
from graphein.protein.meshes import create_mesh
verts, faces, aux = create_mesh(pdb_code="3eiy", config=config)
print(verts, faces, aux)
# NBVAL_SKIP
from graphein.protein.meshes import convert_verts_and_face_to_mesh
m = convert_verts_and_face_to_mesh(verts, faces)
from graphein.protein.visualisation import plot_pointcloud
plot_pointcloud(m, title="my first mesh")
# NBVAL_SKIP
pymol_commands = {"pymol_commands": ["hide cartoon",
"set solvent_radius, 10",
"alter all, vdw=4",
"sort",
"set surface_quality, 1",
"show surface"]}
config = ProteinMeshConfig(**pymol_commands)
verts, faces, aux = create_mesh(pdb_code="3eiy", config=config)
m = convert_verts_and_face_to_mesh(verts, faces)
plot_pointcloud(m, title="my second mesh")
# NBVAL_SKIP
from graphein.utils.pymol import viewer as pymol
pymol.fetch("3eiy")
pymol.display()
| 0.448668 | 0.891952 |
# Introduction to Python - part 1
Author: Manuel Dalcastagnè. This work is licensed under a CC Attribution 3.0 Unported license (http://creativecommons.org/licenses/by/3.0/).
Original material, "Introduction to Python programming", was created by J.R. Johansson under the CC Attribution 3.0 Unported license (http://creativecommons.org/licenses/by/3.0/) and can be found at https://github.com/jrjohansson/scientific-python-lectures.
## Python program files and some general rules
* Python code is usually stored in text files with the file ending "`.py`":
myprogram.py
* To run our Python program from the command line we use:
$ python myprogram.py
* Every line in a Python program file is assumed to be a Python statement, except comment lines which start with `#`:
# this is a comment
* Remark: **multiline comments do not exist in Python!**
* Differently from other languages, statements of code do not require any punctuation like `;` at the end of rows
* Code blocks of flow controls do not require curly brackets `{}`; in contrast, they are defined using code indentation (`tab`)
* Conditions of flow controls do not require round brackets `()`
* Python does not require a `main` function to run a program; we can define that, but it is not mandatory
## Variables and types
### Names
Variable names in Python can contain alphanumerical characters `a-z`, `A-Z`, `0-9` and some special characters such as `_`. Normal variable names must start with a letter.
By convention, variable names start with a lower-case letter, and Class names start with a capital letter.
In addition, there are a number of Python keywords that cannot be used as variable names. These keywords are:
and, as, assert, break, class, continue, def, del, elif, else, except,
exec, finally, for, from, global, if, import, in, is, lambda, not, or,
pass, print, raise, return, try, while, with, yield
### Variable assignment
The assignment operator in Python is `=`, and it can be used to create new variables or assign values to already existing ones:
```
# variable assignments
x = 1.0
my_variable = 12.2
```
However, a variable has a type associated with it. The type is derived from the assigned value.
```
type(x)
```
If we assign a new value to a variable, its type changes.
```
x = 1
type(x)
```
### Fundamental data types
```
# integers
x = 1
type(x)
# float
x = 1.0
type(x)
# boolean
b1 = True
b2 = False
type(b1)
# complex numbers: note the use of `j` to specify the imaginary part
x = 1.0 - 1.0j
type(x)
# string
s = "Hello world"
type(s)
```
Strings can be seen as sequences of characters, although the character data type is not supported in Python.
```
# length of the string: the number of characters
len(s)
```
#### Data slicing
We can index characters in a string using `[]`, but **heads up MATLAB users:** indexing starts at 0! Moreover, we can extract a part of a string using the syntax `[start:stop]` (data slicing), which extracts characters between index `start` and `stop` -1:
```
s[0:5]
```
If we omit either of `start` or `stop` from `[start:stop]`, the default is the beginning and the end of the string, respectively:
```
s[:5]
s[6:]
```
#### How to print and format strings
```
print("str1", 1.0, False, -1) # The print statement converts all arguments to strings
print("str1" + "str2", "is not", False) # strings added with + are concatenated without space
# alternative way to format a string
s3 = 'value1 = {0}, value2 = {1}'.format(3.1415, "Hello")
print(s3)
# how to print a float number up to a certain number of decimals
print("{0:.4f}".format(5.78678387))
```
Python has a very rich set of functions for text processing. See for example http://docs.python.org/3/library/string.html for more information.
#### Type utility functions
The module `types` contains a number of functions that can be used to test if variables are of certain types:
```
import types
x = 1.0
# check if the variable x is a float
type(x) is float
# check if the variable x is an int
type(x) is int
```
The module `types` contains also functions to convert variables from a type to another (**type casting**):
```
x = 1.5
print(x, type(x))
x = int(x)
print(x, type(x))
```
## Operators
Arithmetic operators: `+`, `-`, `*`, `/`, `//` (integer division), `%` (modulo), `**` (power)
```
1 + 2, 1 - 2, 1 * 2, 2 / 4
1.0 + 2.0, 1.0 - 2.0, 1.0 * 2.0, 2.0 / 4.0
7.0 // 3.0, 7.0 % 3.0
7 // 3, 7 % 3
2 ** 3
```
Boolean operators: `and`, `not`, `or`
```
True and False
not False
True or False
```
Comparison operators: `>`, `<`, `>=`, `<=`, `==` (equality), `is` (identity)
```
2 > 1, 2 < 1
2 >= 2, 2 <= 1
# equality
[1,2] == [1,2]
# identity
l1 = l2 = [1,2]
l1 is l2
# identity
l1 = [1,2]
l2 = [1,2]
l1 is l2
```
When testing for identity, we are asking Python if an object is the same as another one. If you come from C or C++, you can think of the identity as an operator to check if the pointers of two objects are pointing to the same memory address.
In Python identities of objects are integers which are guaranteed to be unique for the lifetime of objects, and they can be found by using the `id()` function.
```
id(l1), id(l2), id(10)
```
## Basic data structures: List, Set, Tuple and Dictionary
### List
Lists are collections of ordered elements, where elements can be of different types and duplicate elements are allowed.
The syntax for creating lists in Python is `[...]`:
```
l = [1,2,3,4]
print(type(l))
print(l)
```
We can use the same slicing techniques to manipulate lists as we could use on strings:
```
print(l)
print(l[1:3])
```
Lists play a very important role in Python. For example they are used in loops and other flow control structures (discussed below). There are a number of convenient functions for generating lists of various types, for example the `range` function:
```
start = 1
stop = 10
step = 1
# range generates an iterator, which can be converted to a list using 'list(...)'.
list(range(start, stop, step))
list(range(1,20,1))
```
#### Adding, modifying and removing elements in lists
```
# create a new empty list
l = []
# append an element to the end of a list using `append`
l.append("A")
l.append("B")
l.append("C")
print(l)
# modify lists by assigning new values to elements in the list.
l[1] = "D"
l[2] = "E"
print(l)
# remove first element with specific value using 'remove'
l.remove("A")
print(l)
```
See `help(list)` for more details, or read the online documentation.
```
help(list)
```
### Set
Sets are collections of unordered elements, where elements can be of different types and duplicate elements are not allowed.
The syntax for creating sets in Python is `{...}`:
```
l = {1,2,3,4}
print(type(l))
print(l)
```
Set elements are not ordered, so we can not use slicing techniques or access elements using indexes.
#### Adding and removing elements in sets
```
# create a new empty set
l = set()
# add an element to the set using `add`
l.add("A")
l.add("B")
l.add("C")
print(l)
#Remove first element with specific value using 'remove'
l.remove("A")
print(l)
```
See `help(set)` for more details, or read the online documentation.
### Dictionary
Dictionaries are collections of ordered elements, where each element is a key-value pair and keys-values can be of different types.
The syntax for dictionaries is `{key1 : value1, ...}`:
```
params = {"parameter1" : 1.0,
"parameter2" : 2.0,
"parameter3" : 3.0,}
print(type(params))
print(params)
# add a new element with key = "parameter4" and value = 4.0
params["parameter4"] = 4.0
print(params)
```
#### Adding and removing elements in dictionaries
```
# create a new empty dictionary
params = {}
# add an element to the set using `add`
params.update({"A": 1})
params.update({"B": 2})
params.update({"C": 3})
print(params)
#Remove the element with key = "parameter4" using 'pop'
params.pop("C")
print(params)
```
See `help(dict)` for more details, or read the online documentation.
### Tuples
Tuples are collections of ordered elements, where each element can be of different types. However, once created, tuples cannot be modified.
In Python, tuples are created using the syntax `(..., ..., ...)`:
```
point = (10, 20)
print(type(point))
print(point[1])
```
See `help(tuple)` for more details, or read the online documentation.
## Control Flow
### Conditional statements: if, elif, else
The Python syntax for conditional execution of code uses the keywords `if`, `elif` (else if), `else`:
```
x = 10
# round parenthesis for conditions are not necessary
if (x==5):
print("statement1 is True")
elif x==10:
print("statement2 is True")
else:
print("statement1 and statement2 are False")
```
For the first time, we found a peculiar aspect of the Python language: **blocks are defined by their indentation level (usually a tab).**
In many languages blocks are defined by curly brakets `{ }`, and the level of indentation is optional. In contrast, in Python we have to be careful to indent our code correctly or else we will get syntax errors.
#### Other examples:
```
statement1 = statement2 = True
if statement1:
if statement2:
print("both statement1 and statement2 are True")
statement1 = False
if statement1:
print("printed if statement1 is True")
print("still inside the if block")
if statement1:
print("printed if statement1 is True")
print("now outside the if block")
```
### Loops: for, while
In Python, there are two types of loops: `for` and `while`.
#### `for` loop
The `for` loop iterates over the elements of the list, and executes the code block once for each element of the list:
```
for x in [1,2,3]:
print(x)
```
Any kind of list can be used in the `for` loop. For example:
```
for x in range(4):
print(x)
for x in range(-1,3):
print(x)
```
To iterate over key-value pairs of a dictionary:
```
params = {"parameter1" : 1.0,
"parameter2" : 2.0,
"parameter3" : 3.0,}
for key,value in params.items():
print(key + " = " + str(value))
```
Sometimes it is useful to have access to the indices of the values when iterating over a list. We can use the `enumerate` function for this:
```
for idx, x in enumerate(range(-3,3)):
print(idx, x)
```
Loops can be interrupted, using the `break` command:
```
for i in range(1,5):
if i==3:
break
print(i)
```
#### `while` loop
The `while` loop iterates until its boolean condition is satisfied (so equal to True), and it executes the code block once for each iteration. Be careful to write the code so that the condition will be satisfied at a certain point, otherwise it will loop forever!
```
i = 0
while i < 5:
print(i)
i = i + 1
print("done")
```
**If something goes wrong and you enter an infinite loop**, the only solution is to kill the process. In Jupiter Notebook, go to the main dashboard and select the Running tab: then pick the notebook which is stuck and press Shutdown. In the Python interpreter, press CTRL + C twice.
# EXERCISE 1:
Given a list of integers, without using any package or built-in function, compute and print:
- mean of the list
- number of negative and positive numbers in the list
- two lists that contain positives and negatives in the original list
```
input = [-2,2,-3,3,10]
```
# EXERCISE 2:
Given a list of integers, without using any package or built-in function, compute and print:
- a dictionary where:
- keys are unique numbers contained in the list
- values count the occurrencies of unique numbers in the list
TIP: you can use dictionary functions
```
input = [1,2,3,4,2,3,1,2,3,4,2,1,3]
```
This notebook can be found at: https://tinyurl.com/introml-nb1
|
github_jupyter
|
# variable assignments
x = 1.0
my_variable = 12.2
type(x)
x = 1
type(x)
# integers
x = 1
type(x)
# float
x = 1.0
type(x)
# boolean
b1 = True
b2 = False
type(b1)
# complex numbers: note the use of `j` to specify the imaginary part
x = 1.0 - 1.0j
type(x)
# string
s = "Hello world"
type(s)
# length of the string: the number of characters
len(s)
s[0:5]
s[:5]
s[6:]
print("str1", 1.0, False, -1) # The print statement converts all arguments to strings
print("str1" + "str2", "is not", False) # strings added with + are concatenated without space
# alternative way to format a string
s3 = 'value1 = {0}, value2 = {1}'.format(3.1415, "Hello")
print(s3)
# how to print a float number up to a certain number of decimals
print("{0:.4f}".format(5.78678387))
import types
x = 1.0
# check if the variable x is a float
type(x) is float
# check if the variable x is an int
type(x) is int
x = 1.5
print(x, type(x))
x = int(x)
print(x, type(x))
1 + 2, 1 - 2, 1 * 2, 2 / 4
1.0 + 2.0, 1.0 - 2.0, 1.0 * 2.0, 2.0 / 4.0
7.0 // 3.0, 7.0 % 3.0
7 // 3, 7 % 3
2 ** 3
True and False
not False
True or False
2 > 1, 2 < 1
2 >= 2, 2 <= 1
# equality
[1,2] == [1,2]
# identity
l1 = l2 = [1,2]
l1 is l2
# identity
l1 = [1,2]
l2 = [1,2]
l1 is l2
id(l1), id(l2), id(10)
l = [1,2,3,4]
print(type(l))
print(l)
print(l)
print(l[1:3])
start = 1
stop = 10
step = 1
# range generates an iterator, which can be converted to a list using 'list(...)'.
list(range(start, stop, step))
list(range(1,20,1))
# create a new empty list
l = []
# append an element to the end of a list using `append`
l.append("A")
l.append("B")
l.append("C")
print(l)
# modify lists by assigning new values to elements in the list.
l[1] = "D"
l[2] = "E"
print(l)
# remove first element with specific value using 'remove'
l.remove("A")
print(l)
help(list)
l = {1,2,3,4}
print(type(l))
print(l)
# create a new empty set
l = set()
# add an element to the set using `add`
l.add("A")
l.add("B")
l.add("C")
print(l)
#Remove first element with specific value using 'remove'
l.remove("A")
print(l)
params = {"parameter1" : 1.0,
"parameter2" : 2.0,
"parameter3" : 3.0,}
print(type(params))
print(params)
# add a new element with key = "parameter4" and value = 4.0
params["parameter4"] = 4.0
print(params)
# create a new empty dictionary
params = {}
# add an element to the set using `add`
params.update({"A": 1})
params.update({"B": 2})
params.update({"C": 3})
print(params)
#Remove the element with key = "parameter4" using 'pop'
params.pop("C")
print(params)
point = (10, 20)
print(type(point))
print(point[1])
x = 10
# round parenthesis for conditions are not necessary
if (x==5):
print("statement1 is True")
elif x==10:
print("statement2 is True")
else:
print("statement1 and statement2 are False")
statement1 = statement2 = True
if statement1:
if statement2:
print("both statement1 and statement2 are True")
statement1 = False
if statement1:
print("printed if statement1 is True")
print("still inside the if block")
if statement1:
print("printed if statement1 is True")
print("now outside the if block")
for x in [1,2,3]:
print(x)
for x in range(4):
print(x)
for x in range(-1,3):
print(x)
params = {"parameter1" : 1.0,
"parameter2" : 2.0,
"parameter3" : 3.0,}
for key,value in params.items():
print(key + " = " + str(value))
for idx, x in enumerate(range(-3,3)):
print(idx, x)
for i in range(1,5):
if i==3:
break
print(i)
i = 0
while i < 5:
print(i)
i = i + 1
print("done")
input = [-2,2,-3,3,10]
input = [1,2,3,4,2,3,1,2,3,4,2,1,3]
| 0.376165 | 0.926304 |
# Using TensorRT to Optimize Caffe Models in Python
TensorRT 4.0 includes support for a Python API to load in and optimize Caffe models, which can then be executed and stored.
First, we import TensorRT.
```
import tensorrt as trt
```
We use PyCUDA to transfer data to/from the GPU and NumPy to store data.
```
import pycuda.driver as cuda
import pycuda.autoinit
import numpy as np
```
For this example, we also want to import `pillow` (an image processing library) and `randint`.
```
from random import randint
from PIL import Image
from matplotlib.pyplot import imshow #to show test case
```
Since we are converting a Caffe model, we also need to use the `caffeparser` located in `tensorrt.parsers`.
```
from tensorrt import parsers
```
Typically, the first thing you will do is create a logger, which is used extensively during the model conversion and inference process. We provide a simple logger implementation in `tensorrt.infer.ConsoleLogger`, but you can define your own as well.
```
G_LOGGER = trt.infer.ConsoleLogger(trt.infer.LogSeverity.ERROR)
```
Now, we define some constants for our model, which we will use to classify digits from the MNIST dataset.
```
INPUT_LAYERS = ['data']
OUTPUT_LAYERS = ['prob']
INPUT_H = 28
INPUT_W = 28
OUTPUT_SIZE = 10
```
We now define data paths. Please change these to reflect where you placed the data included with the samples.
```
MODEL_PROTOTXT = './data/mnist/mnist.prototxt'
CAFFE_MODEL = './data/mnist/mnist.caffemodel'
DATA = './data/mnist/'
IMAGE_MEAN = './data/mnist/mnist_mean.binaryproto'
```
The first step is to create our engine. The Python API provides utilities to make this simpler. Here, we use the caffe model converter utility in `tensorrt.utils`. We provide a logger, a path to the model prototxt, the model file, the max batch size, the max workspace size, the output layer(s) and the data type of the weights.
```
engine = trt.utils.caffe_to_trt_engine(G_LOGGER,
MODEL_PROTOTXT,
CAFFE_MODEL,
1,
1 << 20,
OUTPUT_LAYERS,
trt.infer.DataType.FLOAT)
```
Now let's generate a test case for our engine.
```
rand_file = randint(0,9)
path = DATA + str(rand_file) + '.pgm'
im = Image.open(path)
%matplotlib inline
imshow(np.asarray(im))
arr = np.array(im)
img = arr.ravel()
print("Test Case: " + str(rand_file))
```
We now need to apply the mean to the input image; we have this stored in a .binaryproto file which can be read by the caffeparser.
```
parser = parsers.caffeparser.create_caffe_parser()
mean_blob = parser.parse_binary_proto(IMAGE_MEAN)
parser.destroy()
#NOTE: This is different than the C++ API, you must provide the size of the data
mean = mean_blob.get_data(INPUT_W ** 2)
data = np.empty([INPUT_W ** 2])
for i in range(INPUT_W ** 2):
data[i] = float(img[i]) - mean[i]
mean_blob.destroy()
```
Now we need to create a runtime for inference and create a context for our engine.
```
runtime = trt.infer.create_infer_runtime(G_LOGGER)
context = engine.create_execution_context()
```
Now we can run inference. We first make sure our data is in the correct datatype (FP32 for this model). Then, we allocate an empty array on the CPU to store our results from inference.
```
assert(engine.get_nb_bindings() == 2)
#convert input data to Float32
img = img.astype(np.float32)
#create output array to receive data
output = np.empty(OUTPUT_SIZE, dtype = np.float32)
```
Now, we allocate memory on the GPU with PyCUDA and register it with the engine. The size of the allocations is the size of the input/expected output * the batch size.
```
d_input = cuda.mem_alloc(1 * img.size * img.dtype.itemsize)
d_output = cuda.mem_alloc(1 * output.size * output.dtype.itemsize)
```
The engine needs bindings provided as pointers to the GPU memory. PyCUDA lets us do this for memory allocations by casting those allocations to ints.
```
bindings = [int(d_input), int(d_output)]
```
We then create a cuda stream to run inference.
```
stream = cuda.Stream()
```
Now we transfer the data to the GPU, run inference and the copy the results back.
```
#transfer input data to device
cuda.memcpy_htod_async(d_input, img, stream)
#execute model
context.enqueue(1, bindings, stream.handle, None)
#transfer predictions back
cuda.memcpy_dtoh_async(output, d_output, stream)
#syncronize threads
stream.synchronize()
```
We can run `np.argmax` to get a prediction.
```
print("Test Case: " + str(rand_file))
print ("Prediction: " + str(np.argmax(output)))
```
We can also write our engine to a file to use later.
```
trt.utils.write_engine_to_file("./data/mnist/new_mnist.engine", engine.serialize())
```
You can load this engine later by using `tensorrt.utils.load_engine`.
```
new_engine = trt.utils.load_engine(G_LOGGER, "./data/mnist/new_mnist.engine")
```
Finally, we clean up our context, engine and runtime
```
context.destroy()
engine.destroy()
new_engine.destroy()
runtime.destroy()
```
|
github_jupyter
|
import tensorrt as trt
import pycuda.driver as cuda
import pycuda.autoinit
import numpy as np
from random import randint
from PIL import Image
from matplotlib.pyplot import imshow #to show test case
from tensorrt import parsers
G_LOGGER = trt.infer.ConsoleLogger(trt.infer.LogSeverity.ERROR)
INPUT_LAYERS = ['data']
OUTPUT_LAYERS = ['prob']
INPUT_H = 28
INPUT_W = 28
OUTPUT_SIZE = 10
MODEL_PROTOTXT = './data/mnist/mnist.prototxt'
CAFFE_MODEL = './data/mnist/mnist.caffemodel'
DATA = './data/mnist/'
IMAGE_MEAN = './data/mnist/mnist_mean.binaryproto'
engine = trt.utils.caffe_to_trt_engine(G_LOGGER,
MODEL_PROTOTXT,
CAFFE_MODEL,
1,
1 << 20,
OUTPUT_LAYERS,
trt.infer.DataType.FLOAT)
rand_file = randint(0,9)
path = DATA + str(rand_file) + '.pgm'
im = Image.open(path)
%matplotlib inline
imshow(np.asarray(im))
arr = np.array(im)
img = arr.ravel()
print("Test Case: " + str(rand_file))
parser = parsers.caffeparser.create_caffe_parser()
mean_blob = parser.parse_binary_proto(IMAGE_MEAN)
parser.destroy()
#NOTE: This is different than the C++ API, you must provide the size of the data
mean = mean_blob.get_data(INPUT_W ** 2)
data = np.empty([INPUT_W ** 2])
for i in range(INPUT_W ** 2):
data[i] = float(img[i]) - mean[i]
mean_blob.destroy()
runtime = trt.infer.create_infer_runtime(G_LOGGER)
context = engine.create_execution_context()
assert(engine.get_nb_bindings() == 2)
#convert input data to Float32
img = img.astype(np.float32)
#create output array to receive data
output = np.empty(OUTPUT_SIZE, dtype = np.float32)
d_input = cuda.mem_alloc(1 * img.size * img.dtype.itemsize)
d_output = cuda.mem_alloc(1 * output.size * output.dtype.itemsize)
bindings = [int(d_input), int(d_output)]
stream = cuda.Stream()
#transfer input data to device
cuda.memcpy_htod_async(d_input, img, stream)
#execute model
context.enqueue(1, bindings, stream.handle, None)
#transfer predictions back
cuda.memcpy_dtoh_async(output, d_output, stream)
#syncronize threads
stream.synchronize()
print("Test Case: " + str(rand_file))
print ("Prediction: " + str(np.argmax(output)))
trt.utils.write_engine_to_file("./data/mnist/new_mnist.engine", engine.serialize())
new_engine = trt.utils.load_engine(G_LOGGER, "./data/mnist/new_mnist.engine")
context.destroy()
engine.destroy()
new_engine.destroy()
runtime.destroy()
| 0.355104 | 0.979687 |
# Riskfolio-Lib Tutorial:
<br>__[Financionerioncios](https://financioneroncios.wordpress.com)__
<br>__[Orenji](https://www.orenj-i.net)__
<br>__[Riskfolio-Lib](https://riskfolio-lib.readthedocs.io/en/latest/)__
<br>__[Dany Cajas](https://www.linkedin.com/in/dany-cajas/)__
<a href='https://ko-fi.com/B0B833SXD' target='_blank'><img height='36' style='border:0px;height:36px;' src='https://cdn.ko-fi.com/cdn/kofi1.png?v=2' border='0' alt='Buy Me a Coffee at ko-fi.com' /></a>
## Tutorial 36: Mean Tail Gini Range Optimization
## 1. Downloading the data:
```
import numpy as np
import pandas as pd
import yfinance as yf
import warnings
warnings.filterwarnings("ignore")
pd.options.display.float_format = '{:.4%}'.format
# Date range
start = '2016-01-01'
end = '2019-12-30'
# Tickers of assets
assets = ['JCI', 'TGT', 'CMCSA', 'CPB', 'MO', 'APA', 'MMC', 'JPM',
'ZION', 'PSA', 'BAX', 'BMY', 'LUV', 'PCAR', 'TXT', 'TMO',
'DE', 'MSFT', 'HPQ', 'SEE', 'VZ', 'CNP', 'NI', 'T', 'BA']
assets.sort()
# Downloading data
data = yf.download(assets, start = start, end = end)
data = data.loc[:,('Adj Close', slice(None))]
data.columns = assets
# Calculating returns
Y = data[assets].pct_change().dropna()
Y = Y.iloc[-300:,:]
display(Y.head())
```
## 2. Estimating Mean Tail Gini Range Portfolios
The Tail Gini Range is an specific case of the OWA portfolio model proposed by __[Cajas (2021)](https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3988927)__ .
It is recommended to use MOSEK to optimize Tail Gini Range, due to it requires more computing power for the number of constraints and variables the model use.
Instructions to install MOSEK are in this __[link](https://docs.mosek.com/9.2/install/installation.html)__, is better to install using Anaconda. Also you will need a license, I recommend you that ask for an academic license __[here](https://www.mosek.com/products/academic-licenses/)__.
### 2.1 Calculating the portfolio that optimize return/Tail Gini Range ratio.
```
import riskfolio as rp
import mosek
# Building the portfolio object
port = rp.Portfolio(returns=Y)
# Calculating optimum portfolio
# Select method and estimate input parameters:
method_mu='hist' # Method to estimate expected returns based on historical data.
method_cov='hist' # Method to estimate covariance matrix based on historical data.
port.assets_stats(method_mu=method_mu, method_cov=method_cov, d=0.94)
# Estimate optimal portfolio:
port.solvers = ['MOSEK'] # It is recommended to use mosek when optimizing GMD
port.sol_params = {'MOSEK': {'mosek_params': {mosek.iparam.num_threads: 2}}}
port.alpha = 0.05
port.beta = 0.05
model ='Classic' # Could be Classic (historical), BL (Black Litterman) or FM (Factor Model)
rm = 'TGRG' # Risk measure used, this time will be Tail Gini Range
obj = 'Sharpe' # Objective function, could be MinRisk, MaxRet, Utility or Sharpe
hist = True # Use historical scenarios for risk measures that depend on scenarios
rf = 0 # Risk free rate
l = 0 # Risk aversion factor, only useful when obj is 'Utility'
w = port.optimization(model=model, rm=rm, obj=obj, rf=rf, l=l, hist=hist)
display(w.T)
```
### 2.2 Plotting portfolio composition
```
# Plotting the composition of the portfolio
ax = rp.plot_pie(w=w,
title='Sharpe Mean - Tail Gini Range',
others=0.05,
nrow=25,
cmap = "tab20",
height=6,
width=10,
ax=None)
```
### 2.3 Plotting range risk measures
```
ax = rp.plot_range(returns=Y,
w=w,
alpha=0.05,
a_sim=100,
beta=None,
b_sim=None,
bins=50,
height=6,
width=10,
ax=None)
```
### 2.4 Calculate efficient frontier
```
points = 40 # Number of points of the frontier
frontier = port.efficient_frontier(model=model, rm=rm, points=points, rf=rf, hist=hist)
display(frontier.T.head())
# Plotting the efficient frontier
label = 'Max Risk Adjusted Return Portfolio' # Title of point
mu = port.mu # Expected returns
cov = port.cov # Covariance matrix
returns = port.returns # Returns of the assets
ax = rp.plot_frontier(w_frontier=frontier, mu=mu, cov=cov, returns=returns, rm=rm,
rf=rf, alpha=0.05, cmap='viridis', w=w, label=label,
marker='*', s=16, c='r', height=6, width=10, ax=None)
# Plotting efficient frontier composition
ax = rp.plot_frontier_area(w_frontier=frontier, cmap="tab20", height=6, width=10, ax=None)
```
## 3. Estimating Risk Parity Portfolios for Tail Gini Range
### 3.1 Calculating the risk parity portfolio for Tail Gini Range.
```
b = None # Risk contribution constraints vector
w_rp = port.rp_optimization(model=model, rm=rm, rf=rf, b=b, hist=hist)
display(w_rp.T)
```
### 3.2 Plotting portfolio composition
```
ax = rp.plot_pie(w=w_rp, title='Risk Parity Tail Gini Range', others=0.05, nrow=25, cmap = "tab20",
height=6, width=10, ax=None)
```
### 3.3 Plotting Risk Composition
```
ax = rp.plot_risk_con(w_rp, cov=port.cov, returns=port.returns, rm=rm, rf=0, alpha=0.05,
color="tab:blue", height=6, width=10, ax=None)
```
|
github_jupyter
|
import numpy as np
import pandas as pd
import yfinance as yf
import warnings
warnings.filterwarnings("ignore")
pd.options.display.float_format = '{:.4%}'.format
# Date range
start = '2016-01-01'
end = '2019-12-30'
# Tickers of assets
assets = ['JCI', 'TGT', 'CMCSA', 'CPB', 'MO', 'APA', 'MMC', 'JPM',
'ZION', 'PSA', 'BAX', 'BMY', 'LUV', 'PCAR', 'TXT', 'TMO',
'DE', 'MSFT', 'HPQ', 'SEE', 'VZ', 'CNP', 'NI', 'T', 'BA']
assets.sort()
# Downloading data
data = yf.download(assets, start = start, end = end)
data = data.loc[:,('Adj Close', slice(None))]
data.columns = assets
# Calculating returns
Y = data[assets].pct_change().dropna()
Y = Y.iloc[-300:,:]
display(Y.head())
import riskfolio as rp
import mosek
# Building the portfolio object
port = rp.Portfolio(returns=Y)
# Calculating optimum portfolio
# Select method and estimate input parameters:
method_mu='hist' # Method to estimate expected returns based on historical data.
method_cov='hist' # Method to estimate covariance matrix based on historical data.
port.assets_stats(method_mu=method_mu, method_cov=method_cov, d=0.94)
# Estimate optimal portfolio:
port.solvers = ['MOSEK'] # It is recommended to use mosek when optimizing GMD
port.sol_params = {'MOSEK': {'mosek_params': {mosek.iparam.num_threads: 2}}}
port.alpha = 0.05
port.beta = 0.05
model ='Classic' # Could be Classic (historical), BL (Black Litterman) or FM (Factor Model)
rm = 'TGRG' # Risk measure used, this time will be Tail Gini Range
obj = 'Sharpe' # Objective function, could be MinRisk, MaxRet, Utility or Sharpe
hist = True # Use historical scenarios for risk measures that depend on scenarios
rf = 0 # Risk free rate
l = 0 # Risk aversion factor, only useful when obj is 'Utility'
w = port.optimization(model=model, rm=rm, obj=obj, rf=rf, l=l, hist=hist)
display(w.T)
# Plotting the composition of the portfolio
ax = rp.plot_pie(w=w,
title='Sharpe Mean - Tail Gini Range',
others=0.05,
nrow=25,
cmap = "tab20",
height=6,
width=10,
ax=None)
ax = rp.plot_range(returns=Y,
w=w,
alpha=0.05,
a_sim=100,
beta=None,
b_sim=None,
bins=50,
height=6,
width=10,
ax=None)
points = 40 # Number of points of the frontier
frontier = port.efficient_frontier(model=model, rm=rm, points=points, rf=rf, hist=hist)
display(frontier.T.head())
# Plotting the efficient frontier
label = 'Max Risk Adjusted Return Portfolio' # Title of point
mu = port.mu # Expected returns
cov = port.cov # Covariance matrix
returns = port.returns # Returns of the assets
ax = rp.plot_frontier(w_frontier=frontier, mu=mu, cov=cov, returns=returns, rm=rm,
rf=rf, alpha=0.05, cmap='viridis', w=w, label=label,
marker='*', s=16, c='r', height=6, width=10, ax=None)
# Plotting efficient frontier composition
ax = rp.plot_frontier_area(w_frontier=frontier, cmap="tab20", height=6, width=10, ax=None)
b = None # Risk contribution constraints vector
w_rp = port.rp_optimization(model=model, rm=rm, rf=rf, b=b, hist=hist)
display(w_rp.T)
ax = rp.plot_pie(w=w_rp, title='Risk Parity Tail Gini Range', others=0.05, nrow=25, cmap = "tab20",
height=6, width=10, ax=None)
ax = rp.plot_risk_con(w_rp, cov=port.cov, returns=port.returns, rm=rm, rf=0, alpha=0.05,
color="tab:blue", height=6, width=10, ax=None)
| 0.792906 | 0.936692 |
# Session 12: Model selection and cross-validation
In this combined teaching module and exercise set we will investigate how to optimize the choice of hyperparameters using model validation and cross validation. As an aside, we will see how to build machine learning models using a formalized pipeline from preprocessed (i.e. tidy) data to a model.
We import our standard stuff. Notice that we are not interested in seeing the convergence warning in scikit-learn so we suppress them for now.
```
import warnings
from sklearn.exceptions import ConvergenceWarning
warnings.filterwarnings(action='ignore', category=ConvergenceWarning)
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
```
### Intro and recap
We begin with a brief review of important concepts and an overview of this module.
```
from IPython.display import YouTubeVideo
YouTubeVideo('9gkjahx_SWo', width=640, height=360)
```
### Bias and variance - a tradeoff
What is the cause of over- and underfitting? The video below explains that there are two concepts, bias and variance that explain thse two issues.
```
YouTubeVideo('YjC3mQLhWH8', width=640, height=360)
```
### Model building with pipelines
A powerful tool for making and applying models are pipelines, which allows to combine different preprocessing and model procedures into one. This has many advantages, mainly being more safe but also has the added side effect being more code-efficient.
```
YouTubeVideo('dGhqOx9jj7k', width=640, height=360)
```
> **Ex. 12.1.0:** Begin by reloading the housing dataset from Ex. 11.2.0 using the code below.
```
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
cal_house = fetch_california_housing()
X = pd.DataFrame(data=cal_house['data'],
columns=cal_house['feature_names'])\
.iloc[:,:-2]
y = cal_house['target']
```
> **Ex. 12.1.1:** Construct a model building pipeline which
> 1. adds polynomial features of degree 3 without bias;
> 1. scales the features to mean zero and unit std.
>> *Hint:* a modelling pipeline can be constructed with `make_pipeline` from `sklearn.pipeline`.
```
# [Answer to Ex. 12.1.1]
```
# Model selection and validation
### Simple validation
In machine learning, we have two types of parameters: those that are learned from
the training data, for example, the weights in logistic regression, and the parameters
of a learning algorithm that are optimized separately. The latter are the tuning
parameters, also called *hyperparameters*, of a model, for example, the regularization
parameter in logistic regression or the depth parameter of a decision tree.
Below we investigate how we can choose optimal hyperparameters.
```
YouTubeVideo('NrIBv9ApX_8', width=640, height=360)
```
In what follows we will regard the "train" (aka. development, non-test) data for two purposes.
- First we are interested in getting a credible measure of models under different hyperparameters to perform a model selection.
- Then with the selected model we estimate/train it on all the training data.
> **Ex. 12.1.2:** Make a for loop with 10 iterations where you:
1. Split the input data into, train (also know as development) and test where the test sample should be one third. (Set a new random state for each iteration of the loop, so each iteration makes a different split).
2. Further split the training (aka development) data into to even sized bins; the first data is for training models and the other is for validating them. (Therefore these data sets are often called training and validation)
3. Train a linear regression model with sub-training data. Compute the RMSE for out-of-sample predictions for both the test data and the validation data. Save the RMSE.
> You should now have a 10x2 DataFrame with 10 RMSE from both the test data set and the train data set. Compute descriptive statistics of RMSE for the out-of-sample predictions on test and validation data. Are they simular?
> They hopefuly are pretty simular. This shows us, that we can split the train data, and use this to fit the model.
>> *Hint*: you can reuse any code used to solve exercises 11.2.X.
```
# [Answer to Ex. 12.1.2]
```
> **Ex. 12.1.3:** Construct a model building pipeline which
> 1. adds polynomial features of degree 3 without bias;
> 1. scales the features to mean zero and unit std.
> 1. estimates a Lasso model
```
# [Answer to Ex. 12.1.3]
```
### Cross validation
The simple validation procedure that we outlined above has one disadvantage: it only uses parts of the *development* data for validation. In the video below we present a refined approach that uses all the *development* for validation.
```
YouTubeVideo('m4qR8L65fKQ', width=640, height=360)
```
When we want to optimize over both normal parameters and hyperparameteres we do this using nested loops (two-layered cross validation). In outer loop we vary the hyperparameters, and then in the inner loop we do cross validation for the model with the specific selection of hyperparameters. This way we can find the model, with the lowest mean MSE.
> **Ex. 12.1.4:**
Run a Lasso regression using the Pipeline from `Ex 12.1.2`. In the outer loop searching through the lambdas specified below.
In the inner loop make *5 fold cross validation* on the selected model and store the average MSE for each fold. Which lambda, from the selection below, gives the lowest test MSE?
```python
lambdas = np.logspace(-4, 4, 12)
```
*Hint:* `KFold` in `sklearn.model_selection` may be useful.
```
# [Answer to Ex. 12.1.4]
```
### Tools for model selection
Below we review three useful tools for performing model selection. The first tool, the learning curve, can be used to assess whether there is over- and underfitting.
```
YouTubeVideo('Ii8UZW8PYlI', width=640, height=360)
```
The next tool, the validation curve, helps to make perform automated model selection and to visualize the process of model selection.
```
YouTubeVideo('xabvOCSGQx4', width=640, height=360)
```
When we have more than one hyperparameter, we need to find the combination of optimal hyperparameters. In the video below we see how to do that for *elastic net*, which has both L1 and L2 regularization.
```
YouTubeVideo('J0tt-j3CSlA', width=640, height=360)
```
> **Ex. 12.1.5:** __Automated Cross Validation in one dimension__
Now we want to repeat exercise 12.1.4 in a more automated fasion.
When you are doing cross validation with one hyperparameter, you can automate the process by using `validation_curve` from `sklearn.model_selection`. Use this function to search through the values of lambda, and find the value of lambda, which give the lowest test error.
> check if you got the same output for the manual implementation (Ex. 12.1.3) and the automated implementation (Ex. 12.1.4)
> BONUS: Plot the average MSE-test and MSE-train against the different values of lambda. (*Hint*: Use logarithmic axes, and lambda as index)
```
# [Answer to Ex. 12.1.5]
```
When you have *more than one* hyperparameter, you will want to fit the model to all the possible combinations of hyperparameters. This is done in an approch called `Grid Search`, which is implementet in `sklearn.model_selection` as `GridSearchCV`
> **Ex. 12.1.6:** To get to know `Grid Search` we want to implement in one dimension. Using `GridSearchCV` implement the Lasso, with the same lambdas as before (`lambdas = np.logspace(-4, 4, 12)`), 10-fold CV and (negative) mean squared error as the scoring variable. Which value of Lambda gives the lowest test error?
```
# [Answer to Ex. 12.1.6]
```
> **Ex. 12.1.7 BONUS** Expand the Lasso pipe from the last excercise with a Principal Component Analisys (PCA), and expand the Grid Search to searching in two dimensions (both along the values of lambda and the values of principal components (n_components)). Is `n_components` a hyperparameter? Which hyperparameters does the Grid Search select as the best?
> NB. This might take a while to calculate.
```
# [Answer to Ex. 12.1.7]
```
> **Ex. 12.1.8 BONUS** repeat the previous now with RandomizedSearchCV with 20 iterations.
```
# [Answer to Ex. 12.1.8]
```
> **Ex. 12.1.9 BONUS** read about nested cross validation. How might we implement this in answer 12.1.6?
```
# [Answer to Ex. 12.1.9]
```
|
github_jupyter
|
import warnings
from sklearn.exceptions import ConvergenceWarning
warnings.filterwarnings(action='ignore', category=ConvergenceWarning)
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
from IPython.display import YouTubeVideo
YouTubeVideo('9gkjahx_SWo', width=640, height=360)
YouTubeVideo('YjC3mQLhWH8', width=640, height=360)
YouTubeVideo('dGhqOx9jj7k', width=640, height=360)
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
cal_house = fetch_california_housing()
X = pd.DataFrame(data=cal_house['data'],
columns=cal_house['feature_names'])\
.iloc[:,:-2]
y = cal_house['target']
# [Answer to Ex. 12.1.1]
YouTubeVideo('NrIBv9ApX_8', width=640, height=360)
# [Answer to Ex. 12.1.2]
# [Answer to Ex. 12.1.3]
YouTubeVideo('m4qR8L65fKQ', width=640, height=360)
*Hint:* `KFold` in `sklearn.model_selection` may be useful.
### Tools for model selection
Below we review three useful tools for performing model selection. The first tool, the learning curve, can be used to assess whether there is over- and underfitting.
The next tool, the validation curve, helps to make perform automated model selection and to visualize the process of model selection.
When we have more than one hyperparameter, we need to find the combination of optimal hyperparameters. In the video below we see how to do that for *elastic net*, which has both L1 and L2 regularization.
> **Ex. 12.1.5:** __Automated Cross Validation in one dimension__
Now we want to repeat exercise 12.1.4 in a more automated fasion.
When you are doing cross validation with one hyperparameter, you can automate the process by using `validation_curve` from `sklearn.model_selection`. Use this function to search through the values of lambda, and find the value of lambda, which give the lowest test error.
> check if you got the same output for the manual implementation (Ex. 12.1.3) and the automated implementation (Ex. 12.1.4)
> BONUS: Plot the average MSE-test and MSE-train against the different values of lambda. (*Hint*: Use logarithmic axes, and lambda as index)
When you have *more than one* hyperparameter, you will want to fit the model to all the possible combinations of hyperparameters. This is done in an approch called `Grid Search`, which is implementet in `sklearn.model_selection` as `GridSearchCV`
> **Ex. 12.1.6:** To get to know `Grid Search` we want to implement in one dimension. Using `GridSearchCV` implement the Lasso, with the same lambdas as before (`lambdas = np.logspace(-4, 4, 12)`), 10-fold CV and (negative) mean squared error as the scoring variable. Which value of Lambda gives the lowest test error?
> **Ex. 12.1.7 BONUS** Expand the Lasso pipe from the last excercise with a Principal Component Analisys (PCA), and expand the Grid Search to searching in two dimensions (both along the values of lambda and the values of principal components (n_components)). Is `n_components` a hyperparameter? Which hyperparameters does the Grid Search select as the best?
> NB. This might take a while to calculate.
> **Ex. 12.1.8 BONUS** repeat the previous now with RandomizedSearchCV with 20 iterations.
> **Ex. 12.1.9 BONUS** read about nested cross validation. How might we implement this in answer 12.1.6?
| 0.795102 | 0.994467 |
```
import sys
sys.path.append("../")
```
## Analysis of n - we are keeping mean time of arrival as 100 and T_k as 1000 milliseconds
```
import pandas as pd
mean_percent_longest_chain = []
mean_orphans_received = []
mean_blocks = []
x_axis = []
df = pd.read_csv("../final_results/results_1.dump")
df['percent_reaching_longest_chain'] = df['<in longest chain>']*100/df["<peer's blocks>"]
df
mean_percent_longest_chain.append(df['percent_reaching_longest_chain'].mean())
mean_orphans_received.append(df['<orphans received>'].mean())
mean_blocks.append(df["<peer's blocks>"].mean())
x = 1000
x_axis.append(x)
```
## When tk = 100000
```
df = pd.read_csv("../final_results/results_2.dump")
df['percent_reaching_longest_chain'] = df['<in longest chain>']*100/df["<peer's blocks>"]
df
mean_percent_longest_chain.append(df['percent_reaching_longest_chain'].mean())
mean_orphans_received.append(df['<orphans received>'].mean())
mean_blocks.append(df["<peer's blocks>"].mean())
x = 10000
x_axis.append(x)
x = 100
x_axis.append(x)
df = pd.read_csv("../final_results/results_3.dump")
df['percent_reaching_longest_chain'] = df['<in longest chain>']*100/df["<peer's blocks>"]
df
mean_percent_longest_chain.append(df['percent_reaching_longest_chain'].mean())
mean_orphans_received.append(df['<orphans received>'].mean())
mean_blocks.append(df["<peer's blocks>"].mean())
mean_percent_longest_chain = [mean_percent_longest_chain[i] for i in [2,0,1]]
mean_orphans_received = [mean_orphans_received[i] for i in [2, 0, 1]]
mean_blocks = [mean_blocks[i] for i in [2, 0, 1]]
mean_percent_longest_chain
from matplotlib import pyplot as plt
plt.plot(x_axis, mean_percent_longest_chain, label = 'Mean of percent reaching longest chain')
plt.plot(x_axis, mean_orphans_received, label = 'Mean of orphans received')
plt.plot(x_axis, mean_blocks, label = 'Mean of number of blocks generateed')
plt.xlabel("T_k")
plt.ylabel("Property")
plt.title("Analysis of T_k")
plt.legend()
plt.show()
x_axis = [100,1000, 10000]
mean_percent_longest_chain[2] = 100
plt.plot(x_axis, mean_percent_longest_chain, label = 'Mean of percent reaching longest chain')
plt.plot(x_axis, mean_orphans_received, label = 'Mean of orphans received')
plt.plot(x_axis, mean_blocks, label = 'Mean of number of blocks generateed')
plt.xlabel("T_k")
plt.ylabel("Property")
plt.title("Analysis of T_k")
plt.legend()
plt.show()
mean_percent_longest_chain = []
mean_orphans_received = []
mean_blocks = []
x_axis = []
df = pd.read_csv("../final_results/results_4.dump")
df['percent_reaching_longest_chain'] = df['<in longest chain>']*100/df["<peer's blocks>"]
df
mean_percent_longest_chain.append(df['percent_reaching_longest_chain'].mean())
mean_orphans_received.append(df['<orphans received>'].mean())
mean_blocks.append(df["<peer's blocks>"].mean())
x_axis.append(0.25)
df
df = pd.read_csv("../final_results/results_5.dump")
df['percent_reaching_longest_chain'] = df['<in longest chain>']*100/df["<peer's blocks>"]
mean_percent_longest_chain.append(df['percent_reaching_longest_chain'].mean())
mean_orphans_received.append(df['<orphans received>'].mean())
mean_blocks.append(df["<peer's blocks>"].mean())
x_axis.append(0.5)
df
df = pd.read_csv("../final_results/results_6.dump")
df['percent_reaching_longest_chain'] = df['<in longest chain>']*100/df["<peer's blocks>"]
mean_percent_longest_chain.append(df['percent_reaching_longest_chain'].mean())
mean_orphans_received.append(df['<orphans received>'].mean())
mean_blocks.append(df["<peer's blocks>"].mean())
x_axis.append(0.5)
df
x_axis[2] = 0.75
plt.plot(x_axis, mean_percent_longest_chain, label = 'Mean of percent reaching longest chain')
plt.plot(x_axis, mean_orphans_received, label = 'Mean of orphans received')
plt.plot(x_axis, mean_blocks, label = 'Mean of number of blocks generateed')
plt.xlabel("% having lower mean time for T_k")
plt.ylabel("Property")
plt.title("Analysis of T_k")
plt.legend()
plt.show()
```
## For % z
```
mean_percent_longest_chain = []
mean_orphans_received = []
mean_blocks = []
x_axis = []
df = pd.read_csv("../final_results/results_7.dump")
df['percent_reaching_longest_chain'] = df['<in longest chain>']*100/df["<peer's blocks>"]
df
mean_percent_longest_chain.append(df['percent_reaching_longest_chain'].mean())
mean_orphans_received.append(df['<orphans received>'].mean())
mean_blocks.append(df["<peer's blocks>"].mean())
x_axis.append(0.25)
df
df = pd.read_csv("../final_results/results_5.dump")
df['percent_reaching_longest_chain'] = df['<in longest chain>']*100/df["<peer's blocks>"]
mean_percent_longest_chain.append(df['percent_reaching_longest_chain'].mean())
mean_orphans_received.append(df['<orphans received>'].mean())
mean_blocks.append(df["<peer's blocks>"].mean())
x_axis.append(0.5)
df
df = pd.read_csv("../final_results/results_6.dump")
df['percent_reaching_longest_chain'] = df['<in longest chain>']*100/df["<peer's blocks>"]
mean_percent_longest_chain.append(df['percent_reaching_longest_chain'].mean())
mean_orphans_received.append(df['<orphans received>'].mean())
mean_blocks.append(df["<peer's blocks>"].mean())
x_axis.append(0.5)
df
x_axis[2] = 0.75
plt.plot(x_axis, mean_percent_longest_chain, label = 'Mean of percent reaching longest chain')
plt.plot(x_axis, mean_orphans_received, label = 'Mean of orphans received')
plt.plot(x_axis, mean_blocks, label = 'Mean of number of blocks generateed')
plt.xlabel("% having lower mean time for T_k")
plt.ylabel("Property")
plt.title("Analysis of T_k")
plt.legend()
plt.show()
mean_percent_longest_chain = []
mean_orphans_received = []
mean_blocks = []
x_axis = []
df = pd.read_csv("../final_results/results_4.dump")
df['percent_reaching_longest_chain'] = df['<in longest chain>']*100/df["<peer's blocks>"]
df
mean_percent_longest_chain.append(df['percent_reaching_longest_chain'].mean())
mean_orphans_received.append(df['<orphans received>'].mean())
mean_blocks.append(df["<peer's blocks>"].mean())
x_axis.append(0.25)
df
df = pd.read_csv("../final_results/results_5.dump")
df['percent_reaching_longest_chain'] = df['<in longest chain>']*100/df["<peer's blocks>"]
mean_percent_longest_chain.append(df['percent_reaching_longest_chain'].mean())
mean_orphans_received.append(df['<orphans received>'].mean())
mean_blocks.append(df["<peer's blocks>"].mean())
x_axis.append(0.5)
df
df = pd.read_csv("../final_results/results_6.dump")
df['percent_reaching_longest_chain'] = df['<in longest chain>']*100/df["<peer's blocks>"]
mean_percent_longest_chain.append(df['percent_reaching_longest_chain'].mean())
mean_orphans_received.append(df['<orphans received>'].mean())
mean_blocks.append(df["<peer's blocks>"].mean())
x_axis.append(0.5)
df
x_axis[2] = 0.75
plt.plot(x_axis, mean_percent_longest_chain, label = 'Mean of percent reaching longest chain')
plt.plot(x_axis, mean_orphans_received, label = 'Mean of orphans received')
plt.plot(x_axis, mean_blocks, label = 'Mean of number of blocks generateed')
plt.xlabel("% having lower mean time for T_k")
plt.ylabel("Property")
plt.title("Analysis of T_k")
plt.legend()
plt.show()
mean_percent_longest_chain = []
mean_orphans_received = []
mean_blocks = []
x_axis = []
df = pd.read_csv("../final_results/results_10.dump")
df['percent_reaching_longest_chain'] = df['<in longest chain>']*100/df["<peer's blocks>"]
df
mean_percent_longest_chain.append(df['percent_reaching_longest_chain'].mean())
mean_orphans_received.append(df['<orphans received>'].mean())
mean_blocks.append(df["<peer's blocks>"].mean())
x_axis.append(10)
df
df = pd.read_csv("../final_results/results_11.dump")
df['percent_reaching_longest_chain'] = df['<in longest chain>']*100/df["<peer's blocks>"]
mean_percent_longest_chain.append(df['percent_reaching_longest_chain'].mean())
mean_orphans_received.append(df['<orphans received>'].mean())
mean_blocks.append(df["<peer's blocks>"].mean())
x_axis.append(100)
df
df = pd.read_csv("../final_results/results_12.dump")
df['percent_reaching_longest_chain'] = df['<in longest chain>']*100/df["<peer's blocks>"]
mean_percent_longest_chain.append(df['percent_reaching_longest_chain'].mean())
mean_orphans_received.append(df['<orphans received>'].mean())
mean_blocks.append(df["<peer's blocks>"].mean())
x_axis.append(50)
df
plt.plot(x_axis, mean_percent_longest_chain, label = 'Mean of percent reaching longest chain')
plt.plot(x_axis, mean_orphans_received, label = 'Mean of orphans received')
plt.plot(x_axis, mean_blocks, label = 'Mean of number of blocks generateed')
plt.xlabel("N")
plt.ylabel("Property")
plt.title("Value of n")
plt.legend()
plt.show()
```
|
github_jupyter
|
import sys
sys.path.append("../")
import pandas as pd
mean_percent_longest_chain = []
mean_orphans_received = []
mean_blocks = []
x_axis = []
df = pd.read_csv("../final_results/results_1.dump")
df['percent_reaching_longest_chain'] = df['<in longest chain>']*100/df["<peer's blocks>"]
df
mean_percent_longest_chain.append(df['percent_reaching_longest_chain'].mean())
mean_orphans_received.append(df['<orphans received>'].mean())
mean_blocks.append(df["<peer's blocks>"].mean())
x = 1000
x_axis.append(x)
df = pd.read_csv("../final_results/results_2.dump")
df['percent_reaching_longest_chain'] = df['<in longest chain>']*100/df["<peer's blocks>"]
df
mean_percent_longest_chain.append(df['percent_reaching_longest_chain'].mean())
mean_orphans_received.append(df['<orphans received>'].mean())
mean_blocks.append(df["<peer's blocks>"].mean())
x = 10000
x_axis.append(x)
x = 100
x_axis.append(x)
df = pd.read_csv("../final_results/results_3.dump")
df['percent_reaching_longest_chain'] = df['<in longest chain>']*100/df["<peer's blocks>"]
df
mean_percent_longest_chain.append(df['percent_reaching_longest_chain'].mean())
mean_orphans_received.append(df['<orphans received>'].mean())
mean_blocks.append(df["<peer's blocks>"].mean())
mean_percent_longest_chain = [mean_percent_longest_chain[i] for i in [2,0,1]]
mean_orphans_received = [mean_orphans_received[i] for i in [2, 0, 1]]
mean_blocks = [mean_blocks[i] for i in [2, 0, 1]]
mean_percent_longest_chain
from matplotlib import pyplot as plt
plt.plot(x_axis, mean_percent_longest_chain, label = 'Mean of percent reaching longest chain')
plt.plot(x_axis, mean_orphans_received, label = 'Mean of orphans received')
plt.plot(x_axis, mean_blocks, label = 'Mean of number of blocks generateed')
plt.xlabel("T_k")
plt.ylabel("Property")
plt.title("Analysis of T_k")
plt.legend()
plt.show()
x_axis = [100,1000, 10000]
mean_percent_longest_chain[2] = 100
plt.plot(x_axis, mean_percent_longest_chain, label = 'Mean of percent reaching longest chain')
plt.plot(x_axis, mean_orphans_received, label = 'Mean of orphans received')
plt.plot(x_axis, mean_blocks, label = 'Mean of number of blocks generateed')
plt.xlabel("T_k")
plt.ylabel("Property")
plt.title("Analysis of T_k")
plt.legend()
plt.show()
mean_percent_longest_chain = []
mean_orphans_received = []
mean_blocks = []
x_axis = []
df = pd.read_csv("../final_results/results_4.dump")
df['percent_reaching_longest_chain'] = df['<in longest chain>']*100/df["<peer's blocks>"]
df
mean_percent_longest_chain.append(df['percent_reaching_longest_chain'].mean())
mean_orphans_received.append(df['<orphans received>'].mean())
mean_blocks.append(df["<peer's blocks>"].mean())
x_axis.append(0.25)
df
df = pd.read_csv("../final_results/results_5.dump")
df['percent_reaching_longest_chain'] = df['<in longest chain>']*100/df["<peer's blocks>"]
mean_percent_longest_chain.append(df['percent_reaching_longest_chain'].mean())
mean_orphans_received.append(df['<orphans received>'].mean())
mean_blocks.append(df["<peer's blocks>"].mean())
x_axis.append(0.5)
df
df = pd.read_csv("../final_results/results_6.dump")
df['percent_reaching_longest_chain'] = df['<in longest chain>']*100/df["<peer's blocks>"]
mean_percent_longest_chain.append(df['percent_reaching_longest_chain'].mean())
mean_orphans_received.append(df['<orphans received>'].mean())
mean_blocks.append(df["<peer's blocks>"].mean())
x_axis.append(0.5)
df
x_axis[2] = 0.75
plt.plot(x_axis, mean_percent_longest_chain, label = 'Mean of percent reaching longest chain')
plt.plot(x_axis, mean_orphans_received, label = 'Mean of orphans received')
plt.plot(x_axis, mean_blocks, label = 'Mean of number of blocks generateed')
plt.xlabel("% having lower mean time for T_k")
plt.ylabel("Property")
plt.title("Analysis of T_k")
plt.legend()
plt.show()
mean_percent_longest_chain = []
mean_orphans_received = []
mean_blocks = []
x_axis = []
df = pd.read_csv("../final_results/results_7.dump")
df['percent_reaching_longest_chain'] = df['<in longest chain>']*100/df["<peer's blocks>"]
df
mean_percent_longest_chain.append(df['percent_reaching_longest_chain'].mean())
mean_orphans_received.append(df['<orphans received>'].mean())
mean_blocks.append(df["<peer's blocks>"].mean())
x_axis.append(0.25)
df
df = pd.read_csv("../final_results/results_5.dump")
df['percent_reaching_longest_chain'] = df['<in longest chain>']*100/df["<peer's blocks>"]
mean_percent_longest_chain.append(df['percent_reaching_longest_chain'].mean())
mean_orphans_received.append(df['<orphans received>'].mean())
mean_blocks.append(df["<peer's blocks>"].mean())
x_axis.append(0.5)
df
df = pd.read_csv("../final_results/results_6.dump")
df['percent_reaching_longest_chain'] = df['<in longest chain>']*100/df["<peer's blocks>"]
mean_percent_longest_chain.append(df['percent_reaching_longest_chain'].mean())
mean_orphans_received.append(df['<orphans received>'].mean())
mean_blocks.append(df["<peer's blocks>"].mean())
x_axis.append(0.5)
df
x_axis[2] = 0.75
plt.plot(x_axis, mean_percent_longest_chain, label = 'Mean of percent reaching longest chain')
plt.plot(x_axis, mean_orphans_received, label = 'Mean of orphans received')
plt.plot(x_axis, mean_blocks, label = 'Mean of number of blocks generateed')
plt.xlabel("% having lower mean time for T_k")
plt.ylabel("Property")
plt.title("Analysis of T_k")
plt.legend()
plt.show()
mean_percent_longest_chain = []
mean_orphans_received = []
mean_blocks = []
x_axis = []
df = pd.read_csv("../final_results/results_4.dump")
df['percent_reaching_longest_chain'] = df['<in longest chain>']*100/df["<peer's blocks>"]
df
mean_percent_longest_chain.append(df['percent_reaching_longest_chain'].mean())
mean_orphans_received.append(df['<orphans received>'].mean())
mean_blocks.append(df["<peer's blocks>"].mean())
x_axis.append(0.25)
df
df = pd.read_csv("../final_results/results_5.dump")
df['percent_reaching_longest_chain'] = df['<in longest chain>']*100/df["<peer's blocks>"]
mean_percent_longest_chain.append(df['percent_reaching_longest_chain'].mean())
mean_orphans_received.append(df['<orphans received>'].mean())
mean_blocks.append(df["<peer's blocks>"].mean())
x_axis.append(0.5)
df
df = pd.read_csv("../final_results/results_6.dump")
df['percent_reaching_longest_chain'] = df['<in longest chain>']*100/df["<peer's blocks>"]
mean_percent_longest_chain.append(df['percent_reaching_longest_chain'].mean())
mean_orphans_received.append(df['<orphans received>'].mean())
mean_blocks.append(df["<peer's blocks>"].mean())
x_axis.append(0.5)
df
x_axis[2] = 0.75
plt.plot(x_axis, mean_percent_longest_chain, label = 'Mean of percent reaching longest chain')
plt.plot(x_axis, mean_orphans_received, label = 'Mean of orphans received')
plt.plot(x_axis, mean_blocks, label = 'Mean of number of blocks generateed')
plt.xlabel("% having lower mean time for T_k")
plt.ylabel("Property")
plt.title("Analysis of T_k")
plt.legend()
plt.show()
mean_percent_longest_chain = []
mean_orphans_received = []
mean_blocks = []
x_axis = []
df = pd.read_csv("../final_results/results_10.dump")
df['percent_reaching_longest_chain'] = df['<in longest chain>']*100/df["<peer's blocks>"]
df
mean_percent_longest_chain.append(df['percent_reaching_longest_chain'].mean())
mean_orphans_received.append(df['<orphans received>'].mean())
mean_blocks.append(df["<peer's blocks>"].mean())
x_axis.append(10)
df
df = pd.read_csv("../final_results/results_11.dump")
df['percent_reaching_longest_chain'] = df['<in longest chain>']*100/df["<peer's blocks>"]
mean_percent_longest_chain.append(df['percent_reaching_longest_chain'].mean())
mean_orphans_received.append(df['<orphans received>'].mean())
mean_blocks.append(df["<peer's blocks>"].mean())
x_axis.append(100)
df
df = pd.read_csv("../final_results/results_12.dump")
df['percent_reaching_longest_chain'] = df['<in longest chain>']*100/df["<peer's blocks>"]
mean_percent_longest_chain.append(df['percent_reaching_longest_chain'].mean())
mean_orphans_received.append(df['<orphans received>'].mean())
mean_blocks.append(df["<peer's blocks>"].mean())
x_axis.append(50)
df
plt.plot(x_axis, mean_percent_longest_chain, label = 'Mean of percent reaching longest chain')
plt.plot(x_axis, mean_orphans_received, label = 'Mean of orphans received')
plt.plot(x_axis, mean_blocks, label = 'Mean of number of blocks generateed')
plt.xlabel("N")
plt.ylabel("Property")
plt.title("Value of n")
plt.legend()
plt.show()
| 0.238905 | 0.700178 |
### Example 4: Burgers' equation
Now that we have seen how to construct the non-linear convection and diffusion examples, we can combine them to form Burgers' equations. We again create a set of coupled equations which are actually starting to form quite complicated stencil expressions, even if we are only using a low-order discretisations.
Let's start with the definition fo the governing equations:
$$ \frac{\partial u}{\partial t} + u \frac{\partial u}{\partial x} + v \frac{\partial u}{\partial y} = \nu \; \left(\frac{\partial ^2 u}{\partial x^2} + \frac{\partial ^2 u}{\partial y^2}\right)$$
$$ \frac{\partial v}{\partial t} + u \frac{\partial v}{\partial x} + v \frac{\partial v}{\partial y} = \nu \; \left(\frac{\partial ^2 v}{\partial x^2} + \frac{\partial ^2 v}{\partial y^2}\right)$$
The discretized and rearranged form then looks like this:
\begin{aligned}
u_{i,j}^{n+1} &= u_{i,j}^n - \frac{\Delta t}{\Delta x} u_{i,j}^n (u_{i,j}^n - u_{i-1,j}^n) - \frac{\Delta t}{\Delta y} v_{i,j}^n (u_{i,j}^n - u_{i,j-1}^n) \\
&+ \frac{\nu \Delta t}{\Delta x^2}(u_{i+1,j}^n-2u_{i,j}^n+u_{i-1,j}^n) + \frac{\nu \Delta t}{\Delta y^2} (u_{i,j+1}^n - 2u_{i,j}^n + u_{i,j+1}^n)
\end{aligned}
\begin{aligned}
v_{i,j}^{n+1} &= v_{i,j}^n - \frac{\Delta t}{\Delta x} u_{i,j}^n (v_{i,j}^n - v_{i-1,j}^n) - \frac{\Delta t}{\Delta y} v_{i,j}^n (v_{i,j}^n - v_{i,j-1}^n) \\
&+ \frac{\nu \Delta t}{\Delta x^2}(v_{i+1,j}^n-2v_{i,j}^n+v_{i-1,j}^n) + \frac{\nu \Delta t}{\Delta y^2} (v_{i,j+1}^n - 2v_{i,j}^n + v_{i,j+1}^n)
\end{aligned}
Great. Now before we look at the Devito implementation, let's re-create the NumPy-based implementation form the original.
```
from examples.cfd import plot_field, init_hat
import numpy as np
%matplotlib inline
# Some variable declarations
nx = 41
ny = 41
nt = 120
c = 1
dx = 2. / (nx - 1)
dy = 2. / (ny - 1)
sigma = .0009
nu = 0.01
dt = sigma * dx * dy / nu
#NBVAL_IGNORE_OUTPUT
# Assign initial conditions
u = np.empty((nx, ny))
v = np.empty((nx, ny))
init_hat(field=u, dx=dx, dy=dy, value=2.)
init_hat(field=v, dx=dx, dy=dy, value=2.)
plot_field(u)
#NBVAL_IGNORE_OUTPUT
for n in range(nt + 1): ##loop across number of time steps
un = u.copy()
vn = v.copy()
u[1:-1, 1:-1] = (un[1:-1, 1:-1] -
dt / dx * un[1:-1, 1:-1] *
(un[1:-1, 1:-1] - un[1:-1, 0:-2]) -
dt / dy * vn[1:-1, 1:-1] *
(un[1:-1, 1:-1] - un[0:-2, 1:-1]) +
nu * dt / dx**2 *
(un[1:-1,2:] - 2 * un[1:-1, 1:-1] + un[1:-1, 0:-2]) +
nu * dt / dy**2 *
(un[2:, 1:-1] - 2 * un[1:-1, 1:-1] + un[0:-2, 1:-1]))
v[1:-1, 1:-1] = (vn[1:-1, 1:-1] -
dt / dx * un[1:-1, 1:-1] *
(vn[1:-1, 1:-1] - vn[1:-1, 0:-2]) -
dt / dy * vn[1:-1, 1:-1] *
(vn[1:-1, 1:-1] - vn[0:-2, 1:-1]) +
nu * dt / dx**2 *
(vn[1:-1, 2:] - 2 * vn[1:-1, 1:-1] + vn[1:-1, 0:-2]) +
nu * dt / dy**2 *
(vn[2:, 1:-1] - 2 * vn[1:-1, 1:-1] + vn[0:-2, 1:-1]))
u[0, :] = 1
u[-1, :] = 1
u[:, 0] = 1
u[:, -1] = 1
v[0, :] = 1
v[-1, :] = 1
v[:, 0] = 1
v[:, -1] = 1
plot_field(u)
```
Nice, our wave looks just like the original. Now we shall attempt to write our entire Burgers' equation operator in a single cell - but before we can demonstrate this, there is one slight problem.
The diffusion term in our equation requires a second-order space discretisation on our velocity fields, which we set through the `TimeFunction` constructor for $u$ and $v$. The `TimeFunction` objects will store this dicretisation information and use it as default whenever we use the shorthand notations for derivative, like `u.dxl` or `u.dyl`. For the advection term, however, we want to use a first-order discretisation, which we now have to create by hand when combining terms with different stencil discretisations. To illustrate let's consider the following example:
```
from devito import Grid, TimeFunction, first_derivative, left
grid = Grid(shape=(nx, ny), extent=(2., 2.))
x, y = grid.dimensions
t = grid.stepping_dim
u1 = TimeFunction(name='u1', grid=grid, space_order=1)
print("Space order 1:\n%s\n" % u1.dxl)
u2 = TimeFunction(name='u2', grid=grid, space_order=2)
print("Space order 2:\n%s\n" % u2.dxl)
# We use u2 to create the explicit first-order derivative
u1_dx = first_derivative(u2, dim=x, side=left, order=1)
print("Explicit space order 1:\n%s\n" % u1_dx)
```
Ok, so by constructing derivative terms explicitly we again have full control of the spatial discretisation - the power of symbolic computation. Armed with that trick, we can now build and execute our advection-diffusion operator from scratch in one cell.
```
#NBVAL_IGNORE_OUTPUT
from sympy import solve
from devito import Operator, Constant, Eq, INTERIOR
# Define our velocity fields and initialise with hat function
u = TimeFunction(name='u', grid=grid, space_order=2)
v = TimeFunction(name='v', grid=grid, space_order=2)
init_hat(field=u.data[0], dx=dx, dy=dy, value=2.)
init_hat(field=v.data[0], dx=dx, dy=dy, value=2.)
# Write down the equations with explicit backward differences
a = Constant(name='a')
u_dx = first_derivative(u, dim=x, side=left, order=1)
u_dy = first_derivative(u, dim=y, side=left, order=1)
v_dx = first_derivative(v, dim=x, side=left, order=1)
v_dy = first_derivative(v, dim=y, side=left, order=1)
eq_u = Eq(u.dt + u*u_dx + v*u_dy, a*u.laplace, region=INTERIOR)
eq_v = Eq(v.dt + u*v_dx + v*v_dy, a*v.laplace, region=INTERIOR)
# Let SymPy rearrange our stencils to form the update expressions
stencil_u = solve(eq_u, u.forward)[0]
stencil_v = solve(eq_v, v.forward)[0]
update_u = Eq(u.forward, stencil_u)
update_v = Eq(v.forward, stencil_v)
# Create Dirichlet BC expressions using the low-level API
bc_u = [Eq(u.indexed[t+1, 0, y], 1.)] # left
bc_u += [Eq(u.indexed[t+1, nx-1, y], 1.)] # right
bc_u += [Eq(u.indexed[t+1, x, ny-1], 1.)] # top
bc_u += [Eq(u.indexed[t+1, x, 0], 1.)] # bottom
bc_v = [Eq(v.indexed[t+1, 0, y], 1.)] # left
bc_v += [Eq(v.indexed[t+1, nx-1, y], 1.)] # right
bc_v += [Eq(v.indexed[t+1, x, ny-1], 1.)] # top
bc_v += [Eq(v.indexed[t+1, x, 0], 1.)] # bottom
# Create the operator
op = Operator([update_u, update_v] + bc_u + bc_v)
# Execute the operator for a number of timesteps
op(time=nt, dt=dt, a=nu)
plot_field(u.data[0])
```
|
github_jupyter
|
from examples.cfd import plot_field, init_hat
import numpy as np
%matplotlib inline
# Some variable declarations
nx = 41
ny = 41
nt = 120
c = 1
dx = 2. / (nx - 1)
dy = 2. / (ny - 1)
sigma = .0009
nu = 0.01
dt = sigma * dx * dy / nu
#NBVAL_IGNORE_OUTPUT
# Assign initial conditions
u = np.empty((nx, ny))
v = np.empty((nx, ny))
init_hat(field=u, dx=dx, dy=dy, value=2.)
init_hat(field=v, dx=dx, dy=dy, value=2.)
plot_field(u)
#NBVAL_IGNORE_OUTPUT
for n in range(nt + 1): ##loop across number of time steps
un = u.copy()
vn = v.copy()
u[1:-1, 1:-1] = (un[1:-1, 1:-1] -
dt / dx * un[1:-1, 1:-1] *
(un[1:-1, 1:-1] - un[1:-1, 0:-2]) -
dt / dy * vn[1:-1, 1:-1] *
(un[1:-1, 1:-1] - un[0:-2, 1:-1]) +
nu * dt / dx**2 *
(un[1:-1,2:] - 2 * un[1:-1, 1:-1] + un[1:-1, 0:-2]) +
nu * dt / dy**2 *
(un[2:, 1:-1] - 2 * un[1:-1, 1:-1] + un[0:-2, 1:-1]))
v[1:-1, 1:-1] = (vn[1:-1, 1:-1] -
dt / dx * un[1:-1, 1:-1] *
(vn[1:-1, 1:-1] - vn[1:-1, 0:-2]) -
dt / dy * vn[1:-1, 1:-1] *
(vn[1:-1, 1:-1] - vn[0:-2, 1:-1]) +
nu * dt / dx**2 *
(vn[1:-1, 2:] - 2 * vn[1:-1, 1:-1] + vn[1:-1, 0:-2]) +
nu * dt / dy**2 *
(vn[2:, 1:-1] - 2 * vn[1:-1, 1:-1] + vn[0:-2, 1:-1]))
u[0, :] = 1
u[-1, :] = 1
u[:, 0] = 1
u[:, -1] = 1
v[0, :] = 1
v[-1, :] = 1
v[:, 0] = 1
v[:, -1] = 1
plot_field(u)
from devito import Grid, TimeFunction, first_derivative, left
grid = Grid(shape=(nx, ny), extent=(2., 2.))
x, y = grid.dimensions
t = grid.stepping_dim
u1 = TimeFunction(name='u1', grid=grid, space_order=1)
print("Space order 1:\n%s\n" % u1.dxl)
u2 = TimeFunction(name='u2', grid=grid, space_order=2)
print("Space order 2:\n%s\n" % u2.dxl)
# We use u2 to create the explicit first-order derivative
u1_dx = first_derivative(u2, dim=x, side=left, order=1)
print("Explicit space order 1:\n%s\n" % u1_dx)
#NBVAL_IGNORE_OUTPUT
from sympy import solve
from devito import Operator, Constant, Eq, INTERIOR
# Define our velocity fields and initialise with hat function
u = TimeFunction(name='u', grid=grid, space_order=2)
v = TimeFunction(name='v', grid=grid, space_order=2)
init_hat(field=u.data[0], dx=dx, dy=dy, value=2.)
init_hat(field=v.data[0], dx=dx, dy=dy, value=2.)
# Write down the equations with explicit backward differences
a = Constant(name='a')
u_dx = first_derivative(u, dim=x, side=left, order=1)
u_dy = first_derivative(u, dim=y, side=left, order=1)
v_dx = first_derivative(v, dim=x, side=left, order=1)
v_dy = first_derivative(v, dim=y, side=left, order=1)
eq_u = Eq(u.dt + u*u_dx + v*u_dy, a*u.laplace, region=INTERIOR)
eq_v = Eq(v.dt + u*v_dx + v*v_dy, a*v.laplace, region=INTERIOR)
# Let SymPy rearrange our stencils to form the update expressions
stencil_u = solve(eq_u, u.forward)[0]
stencil_v = solve(eq_v, v.forward)[0]
update_u = Eq(u.forward, stencil_u)
update_v = Eq(v.forward, stencil_v)
# Create Dirichlet BC expressions using the low-level API
bc_u = [Eq(u.indexed[t+1, 0, y], 1.)] # left
bc_u += [Eq(u.indexed[t+1, nx-1, y], 1.)] # right
bc_u += [Eq(u.indexed[t+1, x, ny-1], 1.)] # top
bc_u += [Eq(u.indexed[t+1, x, 0], 1.)] # bottom
bc_v = [Eq(v.indexed[t+1, 0, y], 1.)] # left
bc_v += [Eq(v.indexed[t+1, nx-1, y], 1.)] # right
bc_v += [Eq(v.indexed[t+1, x, ny-1], 1.)] # top
bc_v += [Eq(v.indexed[t+1, x, 0], 1.)] # bottom
# Create the operator
op = Operator([update_u, update_v] + bc_u + bc_v)
# Execute the operator for a number of timesteps
op(time=nt, dt=dt, a=nu)
plot_field(u.data[0])
| 0.715325 | 0.987387 |
# Inputs and outputs
## Outputs
When a cell of a Jupyter Notebook is executed, the return value (the result) of the last statement is printed below the cell. However,
if the last statement does not have a return value (e.g. assigning a value to a variable does not have one), there will be no
output.
Thus, working with this kind of output has two drawbacks: First, only the result of the last statement is given as output. Second, if the last statement does not have a return value, there is no output at all!
Using the Python function `print()`, it is possible overcome these drawbacks. The argument within the paranthesis will be printed as output below the cell. (There will be a complete chapter about functions. Just briefly: A function consists of a function name (here *print*) followed by a pair of paranthesis. Within these paranthesis there can be one or several arguments, which are separated by commas.)
```
print("Hello")
print(42)
name = "Joey"
print(name)
```
The desired output is passed to the `print()` function as an argument. It is also possible to provide multiple parameters to
the `print` function. In this case the parameters must be separated by a comma (`,`).
```
name = "Joey"
lastname = "Ramone"
print(name, lastname)
```
# Inputs
Remember the exercise to calculate the surface area and volume of a cuboid? Calculating the values for a new cuboid has
been quite tedious so far.
Each time you need to:
- Go to the cell of the notebook and change the Python program
- Execute the cell again
It would be much better if the program asked for the data to be processed as *input*. The Python program should be
independent of specific values. The specific values should be provided as input to the program. This is the classic
structure of a program according to the IPO principle: input → processing → output
### The `input()` function
The `input()` function can be used to read input from the user. A typical call of the function `input()` is:
```python
i = input("Please enter a number:")
print(i)
```
```
i = input("Please insert a number: ")
print(i)
```
The function `input()` first outputs the given argument *("Please ...")*. After that, the function waits for an input
from the user. The user enters a value and finishes the input with the return key (enter key). The entered value is
assigned to the variable `i`.
### Exercise
Write a program that uses `input()` to retrieve values for first name, last name, and email address. Output the entered
values afterwards.
### Exercise 2
Write a program that uses `input()` to accept two numbers from a user and output the sum and the product of both numbers.
Expected form of the output:
The sum is 30.
The product is 225.
|
github_jupyter
|
print("Hello")
print(42)
name = "Joey"
print(name)
name = "Joey"
lastname = "Ramone"
print(name, lastname)
i = input("Please enter a number:")
print(i)
i = input("Please insert a number: ")
print(i)
| 0.119344 | 0.992809 |
# Predicting Boston Housing Prices
## Using XGBoost in SageMaker (Batch Transform)
_Deep Learning Nanodegree Program | Deployment_
---
As an introduction to using SageMaker's High Level Python API we will look at a relatively simple problem. Namely, we will use the [Boston Housing Dataset](https://www.cs.toronto.edu/~delve/data/boston/bostonDetail.html) to predict the median value of a home in the area of Boston Mass.
The documentation for the high level API can be found on the [ReadTheDocs page](http://sagemaker.readthedocs.io/en/latest/)
## General Outline
Typically, when using a notebook instance with SageMaker, you will proceed through the following steps. Of course, not every step will need to be done with each project. Also, there is quite a lot of room for variation in many of the steps, as you will see throughout these lessons.
1. Download or otherwise retrieve the data.
2. Process / Prepare the data.
3. Upload the processed data to S3.
4. Train a chosen model.
5. Test the trained model (typically using a batch transform job).
6. Deploy the trained model.
7. Use the deployed model.
In this notebook we will only be covering steps 1 through 5 as we just want to get a feel for using SageMaker. In later notebooks we will talk about deploying a trained model in much more detail.
## Step 0: Setting up the notebook
We begin by setting up all of the necessary bits required to run our notebook. To start that means loading all of the Python modules we will need.
```
%matplotlib inline
import os
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_boston
import sklearn.model_selection
```
In addition to the modules above, we need to import the various bits of SageMaker that we will be using.
```
import sagemaker
from sagemaker import get_execution_role
from sagemaker.amazon.amazon_estimator import get_image_uri
from sagemaker.predictor import csv_serializer
# This is an object that represents the SageMaker session that we are currently operating in. This
# object contains some useful information that we will need to access later such as our region.
session = sagemaker.Session()
# This is an object that represents the IAM role that we are currently assigned. When we construct
# and launch the training job later we will need to tell it what IAM role it should have. Since our
# use case is relatively simple we will simply assign the training job the role we currently have.
role = get_execution_role()
```
## Step 1: Downloading the data
Fortunately, this dataset can be retrieved using sklearn and so this step is relatively straightforward.
```
boston = load_boston()
```
## Step 2: Preparing and splitting the data
Given that this is clean tabular data, we don't need to do any processing. However, we do need to split the rows in the dataset up into train, test and validation sets.
```
# First we package up the input data and the target variable (the median value) as pandas dataframes. This
# will make saving the data to a file a little easier later on.
X_bos_pd = pd.DataFrame(boston.data, columns=boston.feature_names)
Y_bos_pd = pd.DataFrame(boston.target)
# We split the dataset into 2/3 training and 1/3 testing sets.
X_train, X_test, Y_train, Y_test = sklearn.model_selection.train_test_split(X_bos_pd, Y_bos_pd, test_size=0.33)
# Then we split the training set further into 2/3 training and 1/3 validation sets.
X_train, X_val, Y_train, Y_val = sklearn.model_selection.train_test_split(X_train, Y_train, test_size=0.33)
```
## Step 3: Uploading the data files to S3
When a training job is constructed using SageMaker, a container is executed which performs the training operation. This container is given access to data that is stored in S3. This means that we need to upload the data we want to use for training to S3. In addition, when we perform a batch transform job, SageMaker expects the input data to be stored on S3. We can use the SageMaker API to do this and hide some of the details.
### Save the data locally
First we need to create the test, train and validation csv files which we will then upload to S3.
```
# This is our local data directory. We need to make sure that it exists.
data_dir = '../data/boston'
if not os.path.exists(data_dir):
os.makedirs(data_dir)
# We use pandas to save our test, train and validation data to csv files. Note that we make sure not to include header
# information or an index as this is required by the built in algorithms provided by Amazon. Also, for the train and
# validation data, it is assumed that the first entry in each row is the target variable.
X_test.to_csv(os.path.join(data_dir, 'test.csv'), header=False, index=False)
pd.concat([Y_val, X_val], axis=1).to_csv(os.path.join(data_dir, 'validation.csv'), header=False, index=False)
pd.concat([Y_train, X_train], axis=1).to_csv(os.path.join(data_dir, 'train.csv'), header=False, index=False)
```
### Upload to S3
Since we are currently running inside of a SageMaker session, we can use the object which represents this session to upload our data to the 'default' S3 bucket. Note that it is good practice to provide a custom prefix (essentially an S3 folder) to make sure that you don't accidentally interfere with data uploaded from some other notebook or project.
```
prefix = 'boston-xgboost-HL'
test_location = session.upload_data(os.path.join(data_dir, 'test.csv'), key_prefix=prefix)
val_location = session.upload_data(os.path.join(data_dir, 'validation.csv'), key_prefix=prefix)
train_location = session.upload_data(os.path.join(data_dir, 'train.csv'), key_prefix=prefix)
```
## Step 4: Train the XGBoost model
Now that we have the training and validation data uploaded to S3, we can construct our XGBoost model and train it. We will be making use of the high level SageMaker API to do this which will make the resulting code a little easier to read at the cost of some flexibility.
To construct an estimator, the object which we wish to train, we need to provide the location of a container which contains the training code. Since we are using a built in algorithm this container is provided by Amazon. However, the full name of the container is a bit lengthy and depends on the region that we are operating in. Fortunately, SageMaker provides a useful utility method called `get_image_uri` that constructs the image name for us.
To use the `get_image_uri` method we need to provide it with our current region, which can be obtained from the session object, and the name of the algorithm we wish to use. In this notebook we will be using XGBoost however you could try another algorithm if you wish. The list of built in algorithms can be found in the list of [Common Parameters](https://docs.aws.amazon.com/sagemaker/latest/dg/sagemaker-algo-docker-registry-paths.html).
```
# As stated above, we use this utility method to construct the image name for the training container.
container = get_image_uri(session.boto_region_name, 'xgboost')
# Now that we know which container to use, we can construct the estimator object.
xgb = sagemaker.estimator.Estimator(container, # The image name of the training container
role, # The IAM role to use (our current role in this case)
train_instance_count=1, # The number of instances to use for training
train_instance_type='ml.m4.xlarge', # The type of instance to use for training
output_path='s3://{}/{}/output'.format(session.default_bucket(), prefix),
# Where to save the output (the model artifacts)
sagemaker_session=session) # The current SageMaker session
```
Before asking SageMaker to begin the training job, we should probably set any model specific hyperparameters. There are quite a few that can be set when using the XGBoost algorithm, below are just a few of them. If you would like to change the hyperparameters below or modify additional ones you can find additional information on the [XGBoost hyperparameter page](https://docs.aws.amazon.com/sagemaker/latest/dg/xgboost_hyperparameters.html)
```
xgb.set_hyperparameters(max_depth=5,
eta=0.2,
gamma=4,
min_child_weight=6,
subsample=0.8,
objective='reg:linear',
early_stopping_rounds=10,
num_round=200)
```
Now that we have our estimator object completely set up, it is time to train it. To do this we make sure that SageMaker knows our input data is in csv format and then execute the `fit` method.
```
# This is a wrapper around the location of our train and validation data, to make sure that SageMaker
# knows our data is in csv format.
s3_input_train = sagemaker.s3_input(s3_data=train_location, content_type='csv')
s3_input_validation = sagemaker.s3_input(s3_data=val_location, content_type='csv')
xgb.fit({'train': s3_input_train, 'validation': s3_input_validation})
```
## Step 5: Test the model
Now that we have fit our model to the training data, using the validation data to avoid overfitting, we can test our model. To do this we will make use of SageMaker's Batch Transform functionality. To start with, we need to build a transformer object from our fit model.
```
xgb_transformer = xgb.transformer(instance_count = 1, instance_type = 'ml.m4.xlarge')
```
Next we ask SageMaker to begin a batch transform job using our trained model and applying it to the test data we previously stored in S3. We need to make sure to provide SageMaker with the type of data that we are providing to our model, in our case `text/csv`, so that it knows how to serialize our data. In addition, we need to make sure to let SageMaker know how to split our data up into chunks if the entire data set happens to be too large to send to our model all at once.
Note that when we ask SageMaker to do this it will execute the batch transform job in the background. Since we need to wait for the results of this job before we can continue, we use the `wait()` method. An added benefit of this is that we get some output from our batch transform job which lets us know if anything went wrong.
```
xgb_transformer.transform(test_location, content_type='text/csv', split_type='Line')
xgb_transformer.wait()
```
Now that the batch transform job has finished, the resulting output is stored on S3. Since we wish to analyze the output inside of our notebook we can use a bit of notebook magic to copy the output file from its S3 location and save it locally.
```
!aws s3 cp --recursive $xgb_transformer.output_path $data_dir
```
To see how well our model works we can create a simple scatter plot between the predicted and actual values. If the model was completely accurate the resulting scatter plot would look like the line $x=y$. As we can see, our model seems to have done okay but there is room for improvement.
```
Y_pred = pd.read_csv(os.path.join(data_dir, 'test.csv.out'), header=None)
plt.scatter(Y_test, Y_pred)
plt.xlabel("Median Price")
plt.ylabel("Predicted Price")
plt.title("Median Price vs Predicted Price")
```
## Optional: Clean up
The default notebook instance on SageMaker doesn't have a lot of excess disk space available. As you continue to complete and execute notebooks you will eventually fill up this disk space, leading to errors which can be difficult to diagnose. Once you are completely finished using a notebook it is a good idea to remove the files that you created along the way. Of course, you can do this from the terminal or from the notebook hub if you would like. The cell below contains some commands to clean up the created files from within the notebook.
```
# First we will remove all of the files contained in the data_dir directory
!rm $data_dir/*
# And then we delete the directory itself
!rmdir $data_dir
```
|
github_jupyter
|
%matplotlib inline
import os
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_boston
import sklearn.model_selection
import sagemaker
from sagemaker import get_execution_role
from sagemaker.amazon.amazon_estimator import get_image_uri
from sagemaker.predictor import csv_serializer
# This is an object that represents the SageMaker session that we are currently operating in. This
# object contains some useful information that we will need to access later such as our region.
session = sagemaker.Session()
# This is an object that represents the IAM role that we are currently assigned. When we construct
# and launch the training job later we will need to tell it what IAM role it should have. Since our
# use case is relatively simple we will simply assign the training job the role we currently have.
role = get_execution_role()
boston = load_boston()
# First we package up the input data and the target variable (the median value) as pandas dataframes. This
# will make saving the data to a file a little easier later on.
X_bos_pd = pd.DataFrame(boston.data, columns=boston.feature_names)
Y_bos_pd = pd.DataFrame(boston.target)
# We split the dataset into 2/3 training and 1/3 testing sets.
X_train, X_test, Y_train, Y_test = sklearn.model_selection.train_test_split(X_bos_pd, Y_bos_pd, test_size=0.33)
# Then we split the training set further into 2/3 training and 1/3 validation sets.
X_train, X_val, Y_train, Y_val = sklearn.model_selection.train_test_split(X_train, Y_train, test_size=0.33)
# This is our local data directory. We need to make sure that it exists.
data_dir = '../data/boston'
if not os.path.exists(data_dir):
os.makedirs(data_dir)
# We use pandas to save our test, train and validation data to csv files. Note that we make sure not to include header
# information or an index as this is required by the built in algorithms provided by Amazon. Also, for the train and
# validation data, it is assumed that the first entry in each row is the target variable.
X_test.to_csv(os.path.join(data_dir, 'test.csv'), header=False, index=False)
pd.concat([Y_val, X_val], axis=1).to_csv(os.path.join(data_dir, 'validation.csv'), header=False, index=False)
pd.concat([Y_train, X_train], axis=1).to_csv(os.path.join(data_dir, 'train.csv'), header=False, index=False)
prefix = 'boston-xgboost-HL'
test_location = session.upload_data(os.path.join(data_dir, 'test.csv'), key_prefix=prefix)
val_location = session.upload_data(os.path.join(data_dir, 'validation.csv'), key_prefix=prefix)
train_location = session.upload_data(os.path.join(data_dir, 'train.csv'), key_prefix=prefix)
# As stated above, we use this utility method to construct the image name for the training container.
container = get_image_uri(session.boto_region_name, 'xgboost')
# Now that we know which container to use, we can construct the estimator object.
xgb = sagemaker.estimator.Estimator(container, # The image name of the training container
role, # The IAM role to use (our current role in this case)
train_instance_count=1, # The number of instances to use for training
train_instance_type='ml.m4.xlarge', # The type of instance to use for training
output_path='s3://{}/{}/output'.format(session.default_bucket(), prefix),
# Where to save the output (the model artifacts)
sagemaker_session=session) # The current SageMaker session
xgb.set_hyperparameters(max_depth=5,
eta=0.2,
gamma=4,
min_child_weight=6,
subsample=0.8,
objective='reg:linear',
early_stopping_rounds=10,
num_round=200)
# This is a wrapper around the location of our train and validation data, to make sure that SageMaker
# knows our data is in csv format.
s3_input_train = sagemaker.s3_input(s3_data=train_location, content_type='csv')
s3_input_validation = sagemaker.s3_input(s3_data=val_location, content_type='csv')
xgb.fit({'train': s3_input_train, 'validation': s3_input_validation})
xgb_transformer = xgb.transformer(instance_count = 1, instance_type = 'ml.m4.xlarge')
xgb_transformer.transform(test_location, content_type='text/csv', split_type='Line')
xgb_transformer.wait()
!aws s3 cp --recursive $xgb_transformer.output_path $data_dir
Y_pred = pd.read_csv(os.path.join(data_dir, 'test.csv.out'), header=None)
plt.scatter(Y_test, Y_pred)
plt.xlabel("Median Price")
plt.ylabel("Predicted Price")
plt.title("Median Price vs Predicted Price")
# First we will remove all of the files contained in the data_dir directory
!rm $data_dir/*
# And then we delete the directory itself
!rmdir $data_dir
| 0.499268 | 0.989378 |
# Tarea 6. Distribución óptima de capital y selección de portafolios.
<img style="float: right; margin: 0px 0px 15px 15px;" src="https://upload.wikimedia.org/wikipedia/en/f/f3/SML-chart.png" width="400px" height="400px" />
**Resumen.**
> En esta tarea, tendrás la oportunidad de aplicar los conceptos y las herramientas que aprendimos en el módulo 3. Específicamente, utilizarás técnicas de optimización media-varianza para construir la frontera de mínima varianza, encontrar el mejor portafolio sobre la frontera mínima varianza, y finalmente, identificar la asignación óptima de capital para un inversionista dado su nivel de averisón al riesgo.
**Criterio de revisión.**
> Se te calificará de acuerdo a los resultados finales que reportes, basados en tu análisis.
**Antes de comenzar.**
> Por favor, copiar y pegar este archivo en otra ubicación. Antes de comenzar, nombrarlo *Tarea6_ApellidoNombre*, sin acentos y sin espacios; por ejemplo, en mi caso el archivo se llamaría *Tarea6_JimenezEsteban*. Resolver todos los puntos en dicho archivo y subir en este espacio.
## 1. Datos (10 puntos)
Considere los siguientes datos de bonos, índice de acciones, mercados desarrollados, mercados emergentes, fondos privados, activos reales y activos libres de riesgo:
```
# Importamos pandas y numpy
import pandas as pd
import numpy as np
# Resumen en base anual de rendimientos esperados y volatilidades
annual_ret_summ = pd.DataFrame(columns=['Bonos', 'Acciones', 'Desarrollado', 'Emergente', 'Privados', 'Real', 'Libre_riesgo'], index=['Media', 'Volatilidad'])
annual_ret_summ.loc['Media'] = np.array([0.0400, 0.1060, 0.0830, 0.1190, 0.1280, 0.0620, 0.0300])
annual_ret_summ.loc['Volatilidad'] = np.array([0.0680, 0.2240, 0.2210, 0.3000, 0.2310, 0.0680, None])
annual_ret_summ.round(4)
# Matriz de correlación
corr = pd.DataFrame(data= np.array([[1.0000, 0.4000, 0.2500, 0.2000, 0.1500, 0.2000],
[0.4000, 1.0000, 0.7000, 0.6000, 0.7000, 0.2000],
[0.2500, 0.7000, 1.0000, 0.7500, 0.6000, 0.1000],
[0.2000, 0.6000, 0.7500, 1.0000, 0.2500, 0.1500],
[0.1500, 0.7000, 0.6000, 0.2500, 1.0000, 0.3000],
[0.2000, 0.2000, 0.1000, 0.1500, 0.3000, 1.0000]]),
columns=annual_ret_summ.columns[:-1], index=annual_ret_summ.columns[:-1])
corr.round(4)
```
1. Graficar en el espacio de rendimiento esperado contra volatilidad cada uno de los activos (10 puntos).
## 2. Hallando portafolios sobre la frontera de mínima varianza (35 puntos)
Usando los datos del punto anterior:
1. Halle los pesos del portafolio de mínima varianza considerando todos los activos riesgosos. También reportar claramente el rendimiento esperado, volatilidad y cociente de Sharpe para dicho portafolio (15 puntos).
2. Halle los pesos del portafolio EMV considerando todos los activos riesgosos. También reportar claramente el rendimiento esperado, volatilidad y cociente de Sharpe para dicho portafolio (15 puntos).
3. Halle la covarianza y la correlación entre los dos portafolios hallados (5 puntos)
## 3. Frontera de mínima varianza y LAC (30 puntos)
Con los portafolios que se encontraron en el punto anterior (de mínima varianza y EMV):
1. Construya la frontera de mínima varianza calculando el rendimiento esperado y volatilidad para varias combinaciones de los anteriores portafolios. Reportar dichas combinaciones en un DataFrame incluyendo pesos, rendimiento, volatilidad y cociente de Sharpe (15 puntos).
2. También construya la línea de asignación de capital entre el activo libre de riesgo y el portafolio EMV. Reportar las combinaciones de estos activos en un DataFrame incluyendo pesos, rendimiento, volatilidad y cociente de Sharpe (15 puntos).
## 4. Gráficos y conclusiones (25 puntos)
1. Usando todos los datos obtenidos, grafique:
- los activos individuales,
- portafolio de mínima varianza,
- portafolio eficiente en media-varianza (EMV),
- frontera de mínima varianza, y
- línea de asignación de capital,
en el espacio de rendimiento (eje $y$) vs. volatilidad (eje $x$). Asegúrese de etiquetar todo y poner distintos colores para diferenciar los distintos elementos en su gráfico (15 puntos).
2. Suponga que usted está aconsejando a un cliente cuyo coeficiente de aversión al riesgo resultó ser 4. ¿Qué asignación de capital le sugeriría?, ¿qué significa su resultado?(10 puntos)
<script>
$(document).ready(function(){
$('div.prompt').hide();
$('div.back-to-top').hide();
$('nav#menubar').hide();
$('.breadcrumb').hide();
$('.hidden-print').hide();
});
</script>
<footer id="attribution" style="float:right; color:#808080; background:#fff;">
Created with Jupyter by Esteban Jiménez Rodríguez.
</footer>
|
github_jupyter
|
# Importamos pandas y numpy
import pandas as pd
import numpy as np
# Resumen en base anual de rendimientos esperados y volatilidades
annual_ret_summ = pd.DataFrame(columns=['Bonos', 'Acciones', 'Desarrollado', 'Emergente', 'Privados', 'Real', 'Libre_riesgo'], index=['Media', 'Volatilidad'])
annual_ret_summ.loc['Media'] = np.array([0.0400, 0.1060, 0.0830, 0.1190, 0.1280, 0.0620, 0.0300])
annual_ret_summ.loc['Volatilidad'] = np.array([0.0680, 0.2240, 0.2210, 0.3000, 0.2310, 0.0680, None])
annual_ret_summ.round(4)
# Matriz de correlación
corr = pd.DataFrame(data= np.array([[1.0000, 0.4000, 0.2500, 0.2000, 0.1500, 0.2000],
[0.4000, 1.0000, 0.7000, 0.6000, 0.7000, 0.2000],
[0.2500, 0.7000, 1.0000, 0.7500, 0.6000, 0.1000],
[0.2000, 0.6000, 0.7500, 1.0000, 0.2500, 0.1500],
[0.1500, 0.7000, 0.6000, 0.2500, 1.0000, 0.3000],
[0.2000, 0.2000, 0.1000, 0.1500, 0.3000, 1.0000]]),
columns=annual_ret_summ.columns[:-1], index=annual_ret_summ.columns[:-1])
corr.round(4)
| 0.228156 | 0.913252 |
# Keras Word Embeddings
```
%load_ext autoreload
%autoreload 2
from keras.models import load_model
from keras.models import Sequential, load_model
from keras.layers import LSTM, Dense, Dropout, Embedding, Masking
from keras.optimizers import Adam
from keras.utils import Sequence
from keras.preprocessing.text import Tokenizer
from sklearn.utils import shuffle
from IPython.display import HTML
from itertools import chain
from keras.utils import plot_model
import numpy as np
import pandas as pd
import random
import json
import re
RANDOM_STATE = 50
TRAIN_FRACTION = 0.7
from IPython.core.interactiveshell import InteractiveShell
from IPython.display import HTML
InteractiveShell.ast_node_interactivity = 'all'
import warnings
warnings.filterwarnings('ignore', category = RuntimeWarning)
warnings.filterwarnings('ignore', category = UserWarning)
import pandas as pd
import numpy as np
from utils import get_data, get_embeddings, find_closest
```
# Fetch Training Data
* Using patent abstracts from patent search for neural network
* 3000+ patents total
```
data = pd.read_csv('../data/neural_network_patent_query.csv')
data.head()
training_dict, word_idx, idx_word, sequences = get_data('../data/neural_network_patent_query.csv', training_len = 50)
```
* Sequences of text are represented as integers
* `word_idx` maps words to integers
* `idx_word` maps integers to words
* Features are integer sequences of length 50
* Label is next word in sequence
* Labels are one-hot encoded
```
training_dict['X_train'][:2]
training_dict['y_train'][:2]
for i, sequence in enumerate(training_dict['X_train'][:2]):
text = []
for idx in sequence:
text.append(idx_word[idx])
print('Features: ' + ' '.join(text) + '\n')
print('Label: ' + idx_word[np.argmax(training_dict['y_train'][i])] + '\n')
```
# Make Recurrent Neural Network
* Embedding dimension = 100
* 64 LSTM cells in one layer
* Dropout and recurrent dropout for regularization
* Fully connected layer with 64 units on top of LSTM
* 'relu' activation
* Drop out for regularization
* Output layer produces prediction for each word
* 'softmax' activation
* Adam optimizer with defaults
* Categorical cross entropy loss
* Monitor accuracy
```
from keras.models import Sequential, load_model
from keras.layers import LSTM, Dense, Dropout, Embedding, Masking, Bidirectional
from keras.optimizers import Adam
from keras.utils import plot_model
model = Sequential()
# Embedding layer
model.add(
Embedding(
input_dim=len(word_idx) + 1,
output_dim=100,
weights=None,
trainable=True))
# Recurrent layer
model.add(
LSTM(
64, return_sequences=False, dropout=0.1,
recurrent_dropout=0.1))
# Fully connected layer
model.add(Dense(64, activation='relu'))
# Dropout for regularization
model.add(Dropout(0.5))
# Output layer
model.add(Dense(len(word_idx) + 1, activation='softmax'))
# Compile the model
model.compile(
optimizer='adam', loss='categorical_crossentropy', metrics=['accuracy'])
model.summary()
h = model.fit(training_dict['X_train'], training_dict['y_train'], epochs=5, batch_size=2048,
validation_data = (training_dict['X_valid'], training_dict['y_valid']), verbose=1)
print('Model Performance: Log Loss and Accuracy on training data')
model.evaluate(training_dict['X_train'], training_dict['y_train'], batch_size = 2048)
print('\nModel Performance: Log Loss and Accuracy on validation data')
model.evaluate(training_dict['X_valid'], training_dict['y_valid'], batch_size = 2048)
```
# Inspect Embeddings
As a final piece of model inspection, we can look at the embeddings and find the words closest to a query word in the embedding space. This gives us an idea of what the network has learned.
```
embeddings = get_embeddings(model)
embeddings.shape
```
Each word in the vocabulary is now represented as a 100-dimensional vector. This could be reduced to 2 or 3 dimensions for visualization. It can also be used to find the closest word to a query word.
```
find_closest('network', embeddings, word_idx, idx_word)
find_closest('web', embeddings, word_idx, idx_word)
```
|
github_jupyter
|
%load_ext autoreload
%autoreload 2
from keras.models import load_model
from keras.models import Sequential, load_model
from keras.layers import LSTM, Dense, Dropout, Embedding, Masking
from keras.optimizers import Adam
from keras.utils import Sequence
from keras.preprocessing.text import Tokenizer
from sklearn.utils import shuffle
from IPython.display import HTML
from itertools import chain
from keras.utils import plot_model
import numpy as np
import pandas as pd
import random
import json
import re
RANDOM_STATE = 50
TRAIN_FRACTION = 0.7
from IPython.core.interactiveshell import InteractiveShell
from IPython.display import HTML
InteractiveShell.ast_node_interactivity = 'all'
import warnings
warnings.filterwarnings('ignore', category = RuntimeWarning)
warnings.filterwarnings('ignore', category = UserWarning)
import pandas as pd
import numpy as np
from utils import get_data, get_embeddings, find_closest
data = pd.read_csv('../data/neural_network_patent_query.csv')
data.head()
training_dict, word_idx, idx_word, sequences = get_data('../data/neural_network_patent_query.csv', training_len = 50)
training_dict['X_train'][:2]
training_dict['y_train'][:2]
for i, sequence in enumerate(training_dict['X_train'][:2]):
text = []
for idx in sequence:
text.append(idx_word[idx])
print('Features: ' + ' '.join(text) + '\n')
print('Label: ' + idx_word[np.argmax(training_dict['y_train'][i])] + '\n')
from keras.models import Sequential, load_model
from keras.layers import LSTM, Dense, Dropout, Embedding, Masking, Bidirectional
from keras.optimizers import Adam
from keras.utils import plot_model
model = Sequential()
# Embedding layer
model.add(
Embedding(
input_dim=len(word_idx) + 1,
output_dim=100,
weights=None,
trainable=True))
# Recurrent layer
model.add(
LSTM(
64, return_sequences=False, dropout=0.1,
recurrent_dropout=0.1))
# Fully connected layer
model.add(Dense(64, activation='relu'))
# Dropout for regularization
model.add(Dropout(0.5))
# Output layer
model.add(Dense(len(word_idx) + 1, activation='softmax'))
# Compile the model
model.compile(
optimizer='adam', loss='categorical_crossentropy', metrics=['accuracy'])
model.summary()
h = model.fit(training_dict['X_train'], training_dict['y_train'], epochs=5, batch_size=2048,
validation_data = (training_dict['X_valid'], training_dict['y_valid']), verbose=1)
print('Model Performance: Log Loss and Accuracy on training data')
model.evaluate(training_dict['X_train'], training_dict['y_train'], batch_size = 2048)
print('\nModel Performance: Log Loss and Accuracy on validation data')
model.evaluate(training_dict['X_valid'], training_dict['y_valid'], batch_size = 2048)
embeddings = get_embeddings(model)
embeddings.shape
find_closest('network', embeddings, word_idx, idx_word)
find_closest('web', embeddings, word_idx, idx_word)
| 0.705684 | 0.679335 |
Sveučilište u Zagrebu
Fakultet elektrotehnike i računarstva
## Strojno učenje 2020/2021
http://www.fer.unizg.hr/predmet/su
------------------------------
### Laboratorijska vježba 2: Linearni diskriminativni modeli i logistička regresija
*Verzija: 1.4
Zadnji put ažurirano: 22. 10. 2020.*
(c) 2015-2020 Jan Šnajder, Domagoj Alagić
Rok za predaju: **2. studenog 2020. u 06:00h**
------------------------------
### Upute
Prva laboratorijska vježba sastoji se od šest zadataka. U nastavku slijedite upute navedene u ćelijama s tekstom. Rješavanje vježbe svodi se na **dopunjavanje ove bilježnice**: umetanja ćelije ili više njih **ispod** teksta zadatka, pisanja odgovarajućeg kôda te evaluiranja ćelija.
Osigurajte da u potpunosti **razumijete** kôd koji ste napisali. Kod predaje vježbe, morate biti u stanju na zahtjev asistenta (ili demonstratora) preinačiti i ponovno evaluirati Vaš kôd. Nadalje, morate razumjeti teorijske osnove onoga što radite, u okvirima onoga što smo obradili na predavanju. Ispod nekih zadataka možete naći i pitanja koja služe kao smjernice za bolje razumijevanje gradiva (**nemojte pisati** odgovore na pitanja u bilježnicu). Stoga se nemojte ograničiti samo na to da riješite zadatak, nego slobodno eksperimentirajte. To upravo i jest svrha ovih vježbi.
Vježbe trebate raditi **samostalno** ili u **tandemu**. Možete se konzultirati s drugima o načelnom načinu rješavanja, ali u konačnici morate sami odraditi vježbu. U protivnome vježba nema smisla.
```
# Učitaj osnovne biblioteke...
import sklearn
import matplotlib.pyplot as plt
%pylab inline
def plot_2d_clf_problem(X, y, h=None):
'''
Plots a two-dimensional labeled dataset (X,y) and, if function h(x) is given,
the decision surfaces.
'''
assert X.shape[1] == 2, "Dataset is not two-dimensional"
if h!=None :
# Create a mesh to plot in
r = 0.04 # mesh resolution
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, r),
np.arange(y_min, y_max, r))
XX=np.c_[xx.ravel(), yy.ravel()]
try:
Z_test = h(XX)
if Z_test.shape == ():
# h returns a scalar when applied to a matrix; map explicitly
Z = np.array(list(map(h,XX)))
else :
Z = Z_test
except ValueError:
# can't apply to a matrix; map explicitly
Z = np.array(list(map(h,XX)))
# Put the result into a color plot
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, cmap=plt.cm.Pastel1)
# Plot the dataset
plt.scatter(X[:,0],X[:,1], c=y, cmap=plt.cm.tab20b, marker='o', s=50);
```
## Zadatci
### 1. Linearna regresija kao klasifikator
U prvoj laboratorijskoj vježbi koristili smo model linearne regresije za, naravno, regresiju. Međutim, model linearne regresije može se koristiti i za **klasifikaciju**. Iako zvuči pomalo kontraintuitivno, zapravo je dosta jednostavno. Naime, cilj je naučiti funkciju $f(\mathbf{x})$ koja za negativne primjere predviđa vrijednost $1$, dok za pozitivne primjere predviđa vrijednost $0$. U tom slučaju, funkcija $f(\mathbf{x})=0.5$ predstavlja granicu između klasa, tj. primjeri za koje vrijedi $h(\mathbf{x})\geq 0.5$ klasificiraju se kao pozitivni, dok se ostali klasificiraju kao negativni.
Klasifikacija pomoću linearne regresije implementirana je u razredu [`RidgeClassifier`](http://scikit-learn.org/stable/modules/generated/sklearn.linear_model.RidgeClassifier.html). U sljedećim podzadatcima **istrenirajte** taj model na danim podatcima i **prikažite** dobivenu granicu između klasa. Pritom isključite regularizaciju ($\alpha = 0$, odnosno `alpha=0`). Također i ispišite **točnost** vašeg klasifikacijskog modela (smijete koristiti funkciju [`metrics.accuracy_score`](http://scikit-learn.org/stable/modules/generated/sklearn.metrics.accuracy_score.html)). Skupove podataka vizualizirajte korištenjem pomoćne funkcije ``plot_clf_problem(X, y, h=None)`` koja je dana na početku ove bilježnice. `X` i `y` predstavljaju ulazne primjere i oznake, dok `h` predstavlja funkciju predikcije modela (npr. `model.predict`).
U ovom zadatku cilj je razmotriti kako se klasifikacijski model linearne regresije ponaša na linearno odvojim i neodvojivim podatcima.
```
from sklearn.linear_model import LinearRegression, RidgeClassifier
from sklearn.metrics import accuracy_score
```
### (a)
Prvo, isprobajte *ugrađeni* model na linearno odvojivom skupu podataka `seven` ($N=7$).
```
seven_X = np.array([[2,1], [2,3], [1,2], [3,2], [5,2], [5,4], [6,3]])
seven_y = np.array([1, 1, 1, 1, 0, 0, 0])
clf1a = RidgeClassifier(alpha=0)
clf1a.fit(seven_X, seven_y)
print("Accuracy score: {}".format(accuracy_score(seven_y, clf1a.predict(seven_X))))
plot_2d_clf_problem(seven_X, seven_y, h=clf1a.predict)
```
Kako bi se uvjerili da se u isprobanoj implementaciji ne radi o ničemu doli o običnoj linearnoj regresiji, napišite kôd koji dolazi do jednakog rješenja korištenjem isključivo razreda [`LinearRegression`](http://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LinearRegression.html). Funkciju za predikciju, koju predajete kao treći argument `h` funkciji `plot_2d_clf_problem`, možete definirati lambda-izrazom: `lambda x : model.predict(x) >= 0.5`.
```
clf1a_reg = LinearRegression()
clf1a_reg.fit(seven_X, seven_y)
print("Accuracy score: {}".format(accuracy_score(seven_y, clf1a_reg.predict(seven_X) > 0.5)))
plot_2d_clf_problem(seven_X, seven_y, h=lambda x : clf1a_reg.predict(x) >= 0.5)
```
**Q:** Kako bi bila definirana granica između klasa ako bismo koristili oznake klasa $-1$ i $1$ umjesto $0$ i $1$?
### (b)
Probajte isto na linearno odvojivom skupu podataka `outlier` ($N=8$):
```
outlier_X = np.append(seven_X, [[12,8]], axis=0)
outlier_y = np.append(seven_y, 0)
clf1b = LinearRegression()
clf1b.fit(outlier_X, outlier_y)
print("Accuracy score: {}".format(accuracy_score(outlier_y, clf1b.predict(outlier_X) > .5)))
plot_2d_clf_problem(outlier_X, outlier_y, h=lambda x: clf1b.predict(x) > .5)
```
**Q:** Zašto model ne ostvaruje potpunu točnost iako su podatci linearno odvojivi?
### (c)
Završno, probajte isto na linearno neodvojivom skupu podataka `unsep` ($N=8$):
```
unsep_X = np.append(seven_X, [[2,2]], axis=0)
unsep_y = np.append(seven_y, 0)
clf1c = LinearRegression()
clf1c.fit(unsep_X, unsep_y)
print("Accuracy score: {}".format(accuracy_score(unsep_y, clf1c.predict(unsep_X) > .5)))
plot_2d_clf_problem(unsep_X, unsep_y, h=lambda x: clf1c.predict(x) >= 0.5)
```
**Q:** Očito je zašto model nije u mogućnosti postići potpunu točnost na ovom skupu podataka. Međutim, smatrate li da je problem u modelu ili u podacima? Argumentirajte svoj stav.
### 2. Višeklasna klasifikacija
Postoji više načina kako se binarni klasifikatori mogu se upotrijebiti za višeklasnu klasifikaciju. Najčešće se koristi shema tzv. **jedan-naspram-ostali** (engl. *one-vs-rest*, OVR), u kojoj se trenira po jedan klasifikator $h_j$ za svaku od $K$ klasa. Svaki klasifikator $h_j$ trenira se da razdvaja primjere klase $j$ od primjera svih drugih klasa, a primjer se klasificira u klasu $j$ za koju je $h_j(\mathbf{x})$ maksimalan.
Pomoću funkcije [`datasets.make_classification`](http://scikit-learn.org/stable/modules/generated/sklearn.datasets.make_classification.html) generirajte slučajan dvodimenzijski skup podataka od tri klase i prikažite ga koristeći funkciju `plot_2d_clf_problem`. Radi jednostavnosti, pretpostavite da nema redundantnih značajki te da je svaka od klasa "zbijena" upravo u jednu grupu.
```
from sklearn.datasets import make_classification
X, y = make_classification(n_features=2, n_redundant=0, n_clusters_per_class=1, n_classes=3)
plot_2d_clf_problem(X, y)
```
Trenirajte tri binarna klasifikatora, $h_1$, $h_2$ i $h_3$ te prikažite granice između klasa (tri grafikona). Zatim definirajte $h(\mathbf{x})=\mathrm{argmax}_j h_j(\mathbf{x})$ (napišite svoju funkciju `predict` koja to radi) i prikažite granice između klasa za taj model. Zatim se uvjerite da biste identičan rezultat dobili izravno primjenom modela `RidgeClassifier`, budući da taj model za višeklasan problem zapravo interno implementira shemu jedan-naspram-ostali.
**Q:** Alternativna shema jest ona zvana **jedan-naspram-jedan** (engl, *one-vs-one*, OVO). Koja je prednost sheme OVR nad shemom OVO? A obratno?
```
# y == 0
h1_y = (y == 0).astype(int)
h1 = LinearRegression()
h1.fit(X, h1_y)
plt.title('h1')
plot_2d_clf_problem(X, y, h=lambda x: h1.predict(x) >= .5)
plt.show()
# y == 1
h2_y = (y == 1).astype(int)
h2 = LinearRegression()
h2.fit(X, h2_y)
plt.title('h2')
plot_2d_clf_problem(X, y, h=lambda x: h2.predict(x) >= .5)
plt.show()
# y == 1
h3_y = (y == 2).astype(int)
h3 = LinearRegression()
h3.fit(X, h3_y)
plt.title('h3')
plot_2d_clf_problem(X, y, h=lambda x: h3.predict(x) >= .5)
plt.show()
def ovr_predict(hs, X):
predictions = np.array(list(map(lambda h: h.predict(X), hs)))
return np.argmax(predictions, axis=0)
plt.title('OVR')
plot_2d_clf_problem(X, y, h=lambda x: ovr_predict([h1, h2, h3], x))
plt.show()
clf2 = RidgeClassifier(alpha=0)
clf2.fit(X, y)
plt.title('RidgeClassifier')
plot_2d_clf_problem(X, y, h=clf2.predict)
plt.show()
```
### 3. Logistička regresija
Ovaj zadatak bavi se probabilističkim diskriminativnim modelom, **logističkom regresijom**, koja je, unatoč nazivu, klasifikacijski model.
Logistička regresija tipičan je predstavnik tzv. **poopćenih linearnih modela** koji su oblika: $h(\mathbf{x})=f(\mathbf{w}^\intercal\tilde{\mathbf{x}})$. Logistička funkcija za funkciju $f$ koristi tzv. **logističku** (sigmoidalnu) funkciju $\sigma (x) = \frac{1}{1 + \textit{exp}(-x)}$.
### (a)
Definirajte logističku (sigmoidalnu) funkciju $\mathrm{sigm}(x)=\frac{1}{1+\exp(-\alpha x)}$ i prikažite je za $\alpha\in\{1,2,4\}$.
```
def sigmoid(x, alpha=1):
return 1 / (1 + np.exp(-alpha * x))
fig, axes = plt.subplots(1, 3)
fig.set_size_inches(15, 5)
x = np.linspace(-5, 5)
for i, alpha in enumerate([1, 2, 4]):
axes[i].set_title('alpha = {}'.format(alpha))
axes[i].plot(x, sigmoid(x, alpha))
plt.show()
```
**Q**: Zašto je sigmoidalna funkcija prikladan izbor za aktivacijsku funkciju poopćenoga linearnog modela?
</br>
**Q**: Kakav utjecaj ima faktor $\alpha$ na oblik sigmoide? Što to znači za model logističke regresije (tj. kako izlaz modela ovisi o normi vektora težina $\mathbf{w}$)?
### (b)
Implementirajte funkciju
> `lr_train(X, y, eta=0.01, max_iter=2000, alpha=0, epsilon=0.0001, trace=False)`
za treniranje modela logističke regresije gradijentnim spustom (*batch* izvedba). Funkcija uzima označeni skup primjera za učenje (matrica primjera `X` i vektor oznaka `y`) te vraća $(n+1)$-dimenzijski vektor težina tipa `ndarray`. Ako je `trace=True`, funkcija dodatno vraća listu (ili matricu) vektora težina $\mathbf{w}^0,\mathbf{w}^1,\dots,\mathbf{w}^k$ generiranih kroz sve iteracije optimizacije, od 0 do $k$. Optimizaciju treba provoditi dok se ne dosegne `max_iter` iteracija, ili kada razlika u pogrešci unakrsne entropije između dviju iteracija padne ispod vrijednosti `epsilon`. Parametar `alpha` predstavlja faktor L2-regularizacije.
Preporučamo definiranje pomoćne funkcije `lr_h(x,w)` koja daje predikciju za primjer `x` uz zadane težine `w`. Također, preporučamo i funkciju `cross_entropy_error(X,y,w)` koja izračunava pogrešku unakrsne entropije modela na označenom skupu `(X,y)` uz te iste težine.
**NB:** Obratite pozornost na to da je način kako su definirane oznake ($\{+1,-1\}$ ili $\{1,0\}$) kompatibilan s izračunom funkcije gubitka u optimizacijskome algoritmu.
```
from numpy import linalg
def lr_h(x, w):
return sigmoid(np.dot(x, w[1:]) + w[0])
def cross_entropy_error(X, y, w, alpha=0):
return ((1 / X.shape[0]) * np.sum(-y * np.log(lr_h(X, w)) - (1 - y) * np.log(1 - lr_h(X, w))) + (alpha / 2) * w[:1].T * w[:1])[0]
def lr_train(X, y, eta=0.01, max_iter=2000, alpha=0, epsilon=0.0001, trace=False, verbose=True):
y = (y == 1).astype(int)
weights_trace = []
last_err = 0
w = np.zeros((X.shape[1] + 1))
for i in range(max_iter):
if trace:
weights_trace.append(np.copy(w))
err = cross_entropy_error(X, y, w, alpha)
if i % 100 == 0 and verbose:
print('Iteration: {}, Error = {}'.format(i, err))
if abs(err - last_err) < epsilon:
print('Stopped at iteration number {}.'.format(i))
break
last_err = err
w0grad = 0
wgrad = np.zeros((X.shape[1]))
for j, sample in enumerate(X):
h = lr_h(sample, w)
w0grad += h - y[j]
wgrad += (h - y[j]) * sample
w[0] -= eta * w0grad
w[1:] = w[1:] * (1 - alpha * eta) - eta * wgrad
if trace:
return np.array(weights_trace)
else:
return w
```
### (c)
Koristeći funkciju `lr_train`, trenirajte model logističke regresije na skupu `seven`, prikažite dobivenu granicu između klasa te izračunajte pogrešku unakrsne entropije.
**NB:** Pripazite da modelu date dovoljan broj iteracija.
```
w = lr_train(seven_X, seven_y)
plot_2d_clf_problem(seven_X, seven_y, h=lambda x: lr_h(x, w) >= 0.5)
```
**Q:** Koji kriterij zaustavljanja je aktiviran?
**Q:** Zašto dobivena pogreška unakrsne entropije nije jednaka nuli?
**Q:** Kako biste utvrdili da je optimizacijski postupak doista pronašao hipotezu koja minimizira pogrešku učenja? O čemu to ovisi?
**Q:** Na koji način biste preinačili kôd ako biste htjeli da se optimizacija izvodi stohastičkim gradijentnim spustom (*online learning*)?
### (d)
Prikažite na jednom grafikonu pogrešku unakrsne entropije (očekivanje logističkog gubitka) i pogrešku klasifikacije (očekivanje gubitka 0-1) na skupu `seven` kroz iteracije optimizacijskog postupka. Koristite trag težina funkcije `lr_train` iz zadatka (b) (opcija `trace=True`). Na drugom grafikonu prikažite pogrešku unakrsne entropije kao funkciju broja iteracija za različite stope učenja, $\eta\in\{0.005,0.01,0.05,0.1\}$.
```
from sklearn.metrics import zero_one_loss
ws = lr_train(seven_X, seven_y, trace=True)
fig, axes = plt.subplots(1, 2)
fig.set_size_inches(15, 5)
axes[0].set_title('Cross entropy error vs zero one error')
axes[0].plot(range(len(ws)), [cross_entropy_error(seven_X, seven_y, w) for w in ws], label='Cross entropy error')
axes[0].plot(range(len(ws)), [zero_one_loss(seven_y, lr_h(seven_X, w) >= 0.5) for w in ws], label='Zero one error')
axes[0].legend()
axes[1].set_title('Cross entropy losses over iterations')
for eta in [0.005, 0.01, 0.05, 0.1]:
eta_ws = lr_train(seven_X, seven_y, trace=True, eta=eta, verbose=False)
axes[1].plot(range(len(eta_ws)), [cross_entropy_error(seven_X, seven_y, w) for w in eta_ws], label='eta: {}'.format(eta))
axes[1].legend()
plt.show()
```
**Q:** Zašto je pogreška unakrsne entropije veća od pogreške klasifikacije? Je li to uvijek slučaj kod logističke regresije i zašto?
**Q:** Koju stopu učenja $\eta$ biste odabrali i zašto?
### (e)
Upoznajte se s klasom [`linear_model.LogisticRegression`](http://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LogisticRegression.html) koja implementira logističku regresiju. Usporedite rezultat modela na skupu `seven` s rezultatom koji dobivate pomoću vlastite implementacije algoritma.
**NB:** Kako ugrađena implementacija koristi naprednije verzije optimizacije funkcije, vrlo je vjerojatno da Vam se rješenja neće poklapati, ali generalne performanse modela bi trebale. Ponovno, pripazite na broj iteracija i snagu regularizacije.
```
from sklearn.linear_model import LogisticRegression
clf3_e = LogisticRegression(max_iter=2000, penalty='none', tol=0.0001)
clf3_e.fit(seven_X, seven_y)
plot_2d_clf_problem(seven_X, seven_y, h=clf3_e.predict)
```
### 4. Analiza logističke regresije
### (a)
Koristeći ugrađenu implementaciju logističke regresije, provjerite kako se logistička regresija nosi s vrijednostima koje odskaču. Iskoristite skup `outlier` iz prvog zadatka. Prikažite granicu između klasa.
```
clf4_a = LogisticRegression(max_iter=2000, penalty='none', tol=0.0001)
clf4_a.fit(outlier_X, outlier_y)
plot_2d_clf_problem(outlier_X, outlier_y, h=clf4_a.predict)
```
**Q:** Zašto se rezultat razlikuje od onog koji je dobio model klasifikacije linearnom regresijom iz prvog zadatka?
### (b)
Trenirajte model logističke regresije na skupu `seven` te na dva odvojena grafikona prikažite, kroz iteracije optimizacijskoga algoritma, (1) izlaz modela $h(\mathbf{x})$ za svih sedam primjera te (2) vrijednosti težina $w_0$, $w_1$, $w_2$.
```
ws = lr_train(seven_X, seven_y, trace=True)
fig, axes = plt.subplots(1, 2)
fig.set_size_inches(15, 5)
axes[0].set_title('Sample probabilities over iterations')
for i in range(len(seven_X)):
preds = []
for w in ws:
preds.append(lr_h(seven_X[i], w))
axes[0].plot(range(len(ws)), preds, label='Sample {}'.format(i))
axes[0].legend()
axes[1].set_title('Weights over iterations')
axes[1].plot(range(len(ws)), [w[0] for w in ws], label='Weight 0')
axes[1].plot(range(len(ws)), [w[1] for w in ws], label='Weight 1')
axes[1].plot(range(len(ws)), [w[2] for w in ws], label='Weight 2')
axes[1].legend()
plt.show()
```
### (c)
Ponovite eksperiment iz podzadatka (b) koristeći linearno neodvojiv skup podataka `unsep` iz prvog zadatka.
```
ws = lr_train(unsep_X, unsep_y, epsilon=1e-6, trace=True)
plot_2d_clf_problem(unsep_X, unsep_y, h=lambda x: lr_h(x, ws[-1]) >= 0.5)
fig, axes = plt.subplots(1, 2)
fig.set_size_inches(15, 5)
axes[0].set_title('Sample probabilities over iterations')
for i in range(len(unsep_X)):
preds = []
for w in ws:
preds.append(lr_h(unsep_X[i], w))
axes[0].plot(range(len(ws)), preds, label='Sample {}'.format(i))
axes[0].legend()
axes[1].set_title('Weights over iterations')
axes[1].plot(range(len(ws)), [w[0] for w in ws], label='Weight 0')
axes[1].plot(range(len(ws)), [w[1] for w in ws], label='Weight 1')
axes[1].plot(range(len(ws)), [w[2] for w in ws], label='Weight 2')
axes[1].legend()
plt.show()
```
**Q:** Usporedite grafikone za slučaj linearno odvojivih i linearno neodvojivih primjera te komentirajte razliku.
### 5. Regularizirana logistička regresija
Trenirajte model logističke regresije na skupu `seven` s različitim faktorima L2-regularizacije, $\alpha\in\{0,1,10,100\}$. Prikažite na dva odvojena grafikona (1) pogrešku unakrsne entropije te (2) L2-normu vektora $\mathbf{w}$ kroz iteracije optimizacijskog algoritma.
```
from numpy.linalg import norm
fig, axes = plt.subplots(1, 2)
fig.set_size_inches(15, 5)
axes[0].set_title('Cross entropy errors over iterations')
axes[1].set_title('L2 norm over iterations')
for alpha in [0, 1, 10, 100]:
ws = lr_train(seven_X, seven_y, alpha=alpha, trace=True, verbose=False, epsilon=0)
axes[0].plot(range(len(ws)), [cross_entropy_error(seven_X, seven_y, w) for w in ws], label='alpha = {}'.format(alpha))
axes[1].plot(range(len(ws)), [norm(w[1:]) for w in ws], label='alpha = {}'.format(alpha))
axes[0].legend()
axes[1].legend()
plt.show()
```
**Q:** Jesu li izgledi krivulja očekivani i zašto?
**Q:** Koju biste vrijednost za $\alpha$ odabrali i zašto?
### 6. Logistička regresija s funkcijom preslikavanja
Proučite funkciju [`datasets.make_classification`](http://scikit-learn.org/stable/modules/generated/sklearn.datasets.make_classification.html). Generirajte i prikažite dvoklasan skup podataka s ukupno $N=100$ dvodimenzijskih ($n=2)$ primjera, i to sa dvije grupe po klasi (`n_clusters_per_class=2`). Malo je izgledno da će tako generiran skup biti linearno odvojiv, međutim to nije problem jer primjere možemo preslikati u višedimenzijski prostor značajki pomoću klase [`preprocessing.PolynomialFeatures`](http://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.PolynomialFeatures.html), kao što smo to učinili kod linearne regresije u prvoj laboratorijskoj vježbi. Trenirajte model logističke regresije koristeći za preslikavanje u prostor značajki polinomijalnu funkciju stupnja $d=2$ i stupnja $d=3$. Prikažite dobivene granice između klasa. Možete koristiti svoju implementaciju, ali se radi brzine preporuča koristiti `linear_model.LogisticRegression`. Regularizacijski faktor odaberite po želji.
**NB:** Kao i ranije, za prikaz granice između klasa koristite funkciju `plot_2d_clf_problem`. Funkciji kao argumente predajte izvorni skup podataka, a preslikavanje u prostor značajki napravite unutar poziva funkcije `h` koja čini predikciju, na sljedeći način:
```
from sklearn.preprocessing import PolynomialFeatures
#plot_2d_clf_problem(X, y, lambda x : model.predict(poly.transform(x))
from sklearn.datasets import make_classification
X, y = make_classification(n_samples=100, n_features=2, n_redundant=0, n_clusters_per_class=2, n_classes=2)
poly1 = PolynomialFeatures(2)
poly2 = PolynomialFeatures(3)
C = .5
clf1 = LogisticRegression(C=C)
clf2 = LogisticRegression(C=C)
clf1.fit(poly1.fit_transform(X), y)
clf2.fit(poly2.fit_transform(X), y)
plot_2d_clf_problem(X, y, lambda x : clf1.predict(poly1.transform(x)))
plt.show()
plot_2d_clf_problem(X, y, lambda x : clf2.predict(poly2.transform(x)))
plt.show()
```
**Q:** Koji biste stupanj polinoma upotrijebili i zašto? Je li taj odabir povezan s odabirom regularizacijskog faktora $\alpha$? Zašto?
|
github_jupyter
|
# Učitaj osnovne biblioteke...
import sklearn
import matplotlib.pyplot as plt
%pylab inline
def plot_2d_clf_problem(X, y, h=None):
'''
Plots a two-dimensional labeled dataset (X,y) and, if function h(x) is given,
the decision surfaces.
'''
assert X.shape[1] == 2, "Dataset is not two-dimensional"
if h!=None :
# Create a mesh to plot in
r = 0.04 # mesh resolution
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, r),
np.arange(y_min, y_max, r))
XX=np.c_[xx.ravel(), yy.ravel()]
try:
Z_test = h(XX)
if Z_test.shape == ():
# h returns a scalar when applied to a matrix; map explicitly
Z = np.array(list(map(h,XX)))
else :
Z = Z_test
except ValueError:
# can't apply to a matrix; map explicitly
Z = np.array(list(map(h,XX)))
# Put the result into a color plot
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, cmap=plt.cm.Pastel1)
# Plot the dataset
plt.scatter(X[:,0],X[:,1], c=y, cmap=plt.cm.tab20b, marker='o', s=50);
from sklearn.linear_model import LinearRegression, RidgeClassifier
from sklearn.metrics import accuracy_score
seven_X = np.array([[2,1], [2,3], [1,2], [3,2], [5,2], [5,4], [6,3]])
seven_y = np.array([1, 1, 1, 1, 0, 0, 0])
clf1a = RidgeClassifier(alpha=0)
clf1a.fit(seven_X, seven_y)
print("Accuracy score: {}".format(accuracy_score(seven_y, clf1a.predict(seven_X))))
plot_2d_clf_problem(seven_X, seven_y, h=clf1a.predict)
clf1a_reg = LinearRegression()
clf1a_reg.fit(seven_X, seven_y)
print("Accuracy score: {}".format(accuracy_score(seven_y, clf1a_reg.predict(seven_X) > 0.5)))
plot_2d_clf_problem(seven_X, seven_y, h=lambda x : clf1a_reg.predict(x) >= 0.5)
outlier_X = np.append(seven_X, [[12,8]], axis=0)
outlier_y = np.append(seven_y, 0)
clf1b = LinearRegression()
clf1b.fit(outlier_X, outlier_y)
print("Accuracy score: {}".format(accuracy_score(outlier_y, clf1b.predict(outlier_X) > .5)))
plot_2d_clf_problem(outlier_X, outlier_y, h=lambda x: clf1b.predict(x) > .5)
unsep_X = np.append(seven_X, [[2,2]], axis=0)
unsep_y = np.append(seven_y, 0)
clf1c = LinearRegression()
clf1c.fit(unsep_X, unsep_y)
print("Accuracy score: {}".format(accuracy_score(unsep_y, clf1c.predict(unsep_X) > .5)))
plot_2d_clf_problem(unsep_X, unsep_y, h=lambda x: clf1c.predict(x) >= 0.5)
from sklearn.datasets import make_classification
X, y = make_classification(n_features=2, n_redundant=0, n_clusters_per_class=1, n_classes=3)
plot_2d_clf_problem(X, y)
# y == 0
h1_y = (y == 0).astype(int)
h1 = LinearRegression()
h1.fit(X, h1_y)
plt.title('h1')
plot_2d_clf_problem(X, y, h=lambda x: h1.predict(x) >= .5)
plt.show()
# y == 1
h2_y = (y == 1).astype(int)
h2 = LinearRegression()
h2.fit(X, h2_y)
plt.title('h2')
plot_2d_clf_problem(X, y, h=lambda x: h2.predict(x) >= .5)
plt.show()
# y == 1
h3_y = (y == 2).astype(int)
h3 = LinearRegression()
h3.fit(X, h3_y)
plt.title('h3')
plot_2d_clf_problem(X, y, h=lambda x: h3.predict(x) >= .5)
plt.show()
def ovr_predict(hs, X):
predictions = np.array(list(map(lambda h: h.predict(X), hs)))
return np.argmax(predictions, axis=0)
plt.title('OVR')
plot_2d_clf_problem(X, y, h=lambda x: ovr_predict([h1, h2, h3], x))
plt.show()
clf2 = RidgeClassifier(alpha=0)
clf2.fit(X, y)
plt.title('RidgeClassifier')
plot_2d_clf_problem(X, y, h=clf2.predict)
plt.show()
def sigmoid(x, alpha=1):
return 1 / (1 + np.exp(-alpha * x))
fig, axes = plt.subplots(1, 3)
fig.set_size_inches(15, 5)
x = np.linspace(-5, 5)
for i, alpha in enumerate([1, 2, 4]):
axes[i].set_title('alpha = {}'.format(alpha))
axes[i].plot(x, sigmoid(x, alpha))
plt.show()
from numpy import linalg
def lr_h(x, w):
return sigmoid(np.dot(x, w[1:]) + w[0])
def cross_entropy_error(X, y, w, alpha=0):
return ((1 / X.shape[0]) * np.sum(-y * np.log(lr_h(X, w)) - (1 - y) * np.log(1 - lr_h(X, w))) + (alpha / 2) * w[:1].T * w[:1])[0]
def lr_train(X, y, eta=0.01, max_iter=2000, alpha=0, epsilon=0.0001, trace=False, verbose=True):
y = (y == 1).astype(int)
weights_trace = []
last_err = 0
w = np.zeros((X.shape[1] + 1))
for i in range(max_iter):
if trace:
weights_trace.append(np.copy(w))
err = cross_entropy_error(X, y, w, alpha)
if i % 100 == 0 and verbose:
print('Iteration: {}, Error = {}'.format(i, err))
if abs(err - last_err) < epsilon:
print('Stopped at iteration number {}.'.format(i))
break
last_err = err
w0grad = 0
wgrad = np.zeros((X.shape[1]))
for j, sample in enumerate(X):
h = lr_h(sample, w)
w0grad += h - y[j]
wgrad += (h - y[j]) * sample
w[0] -= eta * w0grad
w[1:] = w[1:] * (1 - alpha * eta) - eta * wgrad
if trace:
return np.array(weights_trace)
else:
return w
w = lr_train(seven_X, seven_y)
plot_2d_clf_problem(seven_X, seven_y, h=lambda x: lr_h(x, w) >= 0.5)
from sklearn.metrics import zero_one_loss
ws = lr_train(seven_X, seven_y, trace=True)
fig, axes = plt.subplots(1, 2)
fig.set_size_inches(15, 5)
axes[0].set_title('Cross entropy error vs zero one error')
axes[0].plot(range(len(ws)), [cross_entropy_error(seven_X, seven_y, w) for w in ws], label='Cross entropy error')
axes[0].plot(range(len(ws)), [zero_one_loss(seven_y, lr_h(seven_X, w) >= 0.5) for w in ws], label='Zero one error')
axes[0].legend()
axes[1].set_title('Cross entropy losses over iterations')
for eta in [0.005, 0.01, 0.05, 0.1]:
eta_ws = lr_train(seven_X, seven_y, trace=True, eta=eta, verbose=False)
axes[1].plot(range(len(eta_ws)), [cross_entropy_error(seven_X, seven_y, w) for w in eta_ws], label='eta: {}'.format(eta))
axes[1].legend()
plt.show()
from sklearn.linear_model import LogisticRegression
clf3_e = LogisticRegression(max_iter=2000, penalty='none', tol=0.0001)
clf3_e.fit(seven_X, seven_y)
plot_2d_clf_problem(seven_X, seven_y, h=clf3_e.predict)
clf4_a = LogisticRegression(max_iter=2000, penalty='none', tol=0.0001)
clf4_a.fit(outlier_X, outlier_y)
plot_2d_clf_problem(outlier_X, outlier_y, h=clf4_a.predict)
ws = lr_train(seven_X, seven_y, trace=True)
fig, axes = plt.subplots(1, 2)
fig.set_size_inches(15, 5)
axes[0].set_title('Sample probabilities over iterations')
for i in range(len(seven_X)):
preds = []
for w in ws:
preds.append(lr_h(seven_X[i], w))
axes[0].plot(range(len(ws)), preds, label='Sample {}'.format(i))
axes[0].legend()
axes[1].set_title('Weights over iterations')
axes[1].plot(range(len(ws)), [w[0] for w in ws], label='Weight 0')
axes[1].plot(range(len(ws)), [w[1] for w in ws], label='Weight 1')
axes[1].plot(range(len(ws)), [w[2] for w in ws], label='Weight 2')
axes[1].legend()
plt.show()
ws = lr_train(unsep_X, unsep_y, epsilon=1e-6, trace=True)
plot_2d_clf_problem(unsep_X, unsep_y, h=lambda x: lr_h(x, ws[-1]) >= 0.5)
fig, axes = plt.subplots(1, 2)
fig.set_size_inches(15, 5)
axes[0].set_title('Sample probabilities over iterations')
for i in range(len(unsep_X)):
preds = []
for w in ws:
preds.append(lr_h(unsep_X[i], w))
axes[0].plot(range(len(ws)), preds, label='Sample {}'.format(i))
axes[0].legend()
axes[1].set_title('Weights over iterations')
axes[1].plot(range(len(ws)), [w[0] for w in ws], label='Weight 0')
axes[1].plot(range(len(ws)), [w[1] for w in ws], label='Weight 1')
axes[1].plot(range(len(ws)), [w[2] for w in ws], label='Weight 2')
axes[1].legend()
plt.show()
from numpy.linalg import norm
fig, axes = plt.subplots(1, 2)
fig.set_size_inches(15, 5)
axes[0].set_title('Cross entropy errors over iterations')
axes[1].set_title('L2 norm over iterations')
for alpha in [0, 1, 10, 100]:
ws = lr_train(seven_X, seven_y, alpha=alpha, trace=True, verbose=False, epsilon=0)
axes[0].plot(range(len(ws)), [cross_entropy_error(seven_X, seven_y, w) for w in ws], label='alpha = {}'.format(alpha))
axes[1].plot(range(len(ws)), [norm(w[1:]) for w in ws], label='alpha = {}'.format(alpha))
axes[0].legend()
axes[1].legend()
plt.show()
from sklearn.preprocessing import PolynomialFeatures
#plot_2d_clf_problem(X, y, lambda x : model.predict(poly.transform(x))
from sklearn.datasets import make_classification
X, y = make_classification(n_samples=100, n_features=2, n_redundant=0, n_clusters_per_class=2, n_classes=2)
poly1 = PolynomialFeatures(2)
poly2 = PolynomialFeatures(3)
C = .5
clf1 = LogisticRegression(C=C)
clf2 = LogisticRegression(C=C)
clf1.fit(poly1.fit_transform(X), y)
clf2.fit(poly2.fit_transform(X), y)
plot_2d_clf_problem(X, y, lambda x : clf1.predict(poly1.transform(x)))
plt.show()
plot_2d_clf_problem(X, y, lambda x : clf2.predict(poly2.transform(x)))
plt.show()
| 0.623721 | 0.836688 |
```
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
import omegaconf
import torch
import torch.optim as optim
import mbrl.models as models
import mbrl.util.replay_buffer as replay_buffer
device = torch.device("cuda:0")
%load_ext autoreload
%autoreload 2
%matplotlib inline
mpl.rcParams['figure.facecolor'] = 'white'
num_points = 10000
x_data = np.linspace(-12, 12, num_points)
y_data = np.sin(x_data)
train_size = 2000
val_size = 200
x_train = np.zeros(2 * train_size)
y_train = np.zeros(2 * train_size)
x_val = np.zeros(2 * val_size)
y_val = np.zeros(2 * val_size)
# Half with lower noise
train_val_idx_1 = np.random.choice(list(range(1200, 3500)),
size=train_size + val_size,
replace=False)
mag = 0.05
x_train[:train_size] = x_data[train_val_idx_1[:train_size]]
y_train[:train_size] = y_data[train_val_idx_1[:train_size]] + mag * np.random.randn(train_size)
x_val[:val_size] = x_data[train_val_idx_1[train_size:]]
y_val[:val_size] = y_data[train_val_idx_1[train_size:]] + mag * np.random.randn(val_size)
# Half with higher noise
train_val_idx_2 = np.random.choice(list(range(6500, 8800)),
size=train_size + val_size,
replace=False)
mag = 0.20
x_train[train_size:] = x_data[train_val_idx_2[:train_size]]
y_train[train_size:] = y_data[train_val_idx_2[:train_size]] + mag * np.random.randn(train_size)
x_val[val_size:] = x_data[train_val_idx_2[train_size:]]
y_val[val_size:] = y_data[train_val_idx_2[train_size:]] + mag * np.random.randn(val_size)
plt.figure(figsize=(16, 8))
plt.plot(x_data, y_data, x_train, y_train, '.', x_val, y_val, 'o', markersize=4)
plt.show()
train_size *=2
val_size *= 2
# ReplayBuffer generates its own training/validation split, but in this example we want to
# keep the split generated above, so instead we use two replay buffers.
num_members = 5
train_buffer = replay_buffer.ReplayBuffer(train_size, (1,), (0,))
val_buffer = replay_buffer.ReplayBuffer(val_size, (1,), (0,))
for i in range(train_size):
train_buffer.add(x_train[i], 0, y_train[i], 0, False)
for i in range(val_size):
val_buffer.add(x_val[i], 0, y_val[i], 0, False)
train_dataset, _ = train_buffer.get_iterators(
2048, 0, train_ensemble=True, ensemble_size=num_members, shuffle_each_epoch=True)
val_dataset, _ = train_buffer.get_iterators(2048, 0, train_ensemble=False)
num_members = 5
member_cfg = omegaconf.OmegaConf.create({
"_target_": "mbrl.models.GaussianMLP",
"device": "cuda:0",
"in_size": 1,
"out_size": 1,
"num_layers": 3,
"hid_size": 64,
"use_silu": True
})
ensemble = models.BasicEnsemble(num_members, device, member_cfg)
wrapper = models.OneDTransitionRewardModel(ensemble, target_is_delta=False, normalize=True, learned_rewards=False)
wrapper.update_normalizer(train_buffer.get_all())
trainer = models.ModelTrainer(wrapper, optim_lr=0.003, weight_decay=5e-5)
train_losses, val_losses = trainer.train(train_dataset, val_dataset, num_epochs=500, patience=100)
fig, ax = plt.subplots(2, 1, figsize=(16, 8))
ax[0].plot(train_losses)
ax[0].set_xlabel("epoch")
ax[0].set_ylabel("train loss (gaussian nll)")
ax[1].plot(val_losses)
ax[1].set_xlabel("epoch")
ax[1].set_ylabel("val loss (mse)")
plt.show()
x_tensor = torch.from_numpy(x_data).unsqueeze(1).float().to(device)
x_tensor = wrapper.input_normalizer.normalize(x_tensor)
with torch.no_grad():
y_pred, y_pred_logvar = ensemble(x_tensor)
y_pred = y_pred[..., 0]
y_pred_logvar = y_pred_logvar[..., 0]
y_var_epi = y_pred.var(dim=0).cpu().numpy()
y_var = y_pred_logvar.exp()
y_pred = y_pred.mean(dim=0).cpu().numpy()
y_var_ale = y_var.mean(dim=0).cpu().numpy()
y_std = np.sqrt(y_var_epi + y_var_ale)
plt.figure(figsize=(16, 8))
plt.plot(x_data, y_data, 'r')
plt.plot(x_train, y_train, '.', markersize=0.9)
plt.plot(x_data, y_pred, 'b-', markersize=4)
plt.fill_between(x_data, y_pred, y_pred + 2 * y_std, color='b', alpha=0.2)
plt.fill_between(x_data, y_pred - 2 * y_std, y_pred, color='b', alpha=0.2)
plt.axis([-12, 12, -2.5, 2.5])
plt.show()
```
|
github_jupyter
|
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
import omegaconf
import torch
import torch.optim as optim
import mbrl.models as models
import mbrl.util.replay_buffer as replay_buffer
device = torch.device("cuda:0")
%load_ext autoreload
%autoreload 2
%matplotlib inline
mpl.rcParams['figure.facecolor'] = 'white'
num_points = 10000
x_data = np.linspace(-12, 12, num_points)
y_data = np.sin(x_data)
train_size = 2000
val_size = 200
x_train = np.zeros(2 * train_size)
y_train = np.zeros(2 * train_size)
x_val = np.zeros(2 * val_size)
y_val = np.zeros(2 * val_size)
# Half with lower noise
train_val_idx_1 = np.random.choice(list(range(1200, 3500)),
size=train_size + val_size,
replace=False)
mag = 0.05
x_train[:train_size] = x_data[train_val_idx_1[:train_size]]
y_train[:train_size] = y_data[train_val_idx_1[:train_size]] + mag * np.random.randn(train_size)
x_val[:val_size] = x_data[train_val_idx_1[train_size:]]
y_val[:val_size] = y_data[train_val_idx_1[train_size:]] + mag * np.random.randn(val_size)
# Half with higher noise
train_val_idx_2 = np.random.choice(list(range(6500, 8800)),
size=train_size + val_size,
replace=False)
mag = 0.20
x_train[train_size:] = x_data[train_val_idx_2[:train_size]]
y_train[train_size:] = y_data[train_val_idx_2[:train_size]] + mag * np.random.randn(train_size)
x_val[val_size:] = x_data[train_val_idx_2[train_size:]]
y_val[val_size:] = y_data[train_val_idx_2[train_size:]] + mag * np.random.randn(val_size)
plt.figure(figsize=(16, 8))
plt.plot(x_data, y_data, x_train, y_train, '.', x_val, y_val, 'o', markersize=4)
plt.show()
train_size *=2
val_size *= 2
# ReplayBuffer generates its own training/validation split, but in this example we want to
# keep the split generated above, so instead we use two replay buffers.
num_members = 5
train_buffer = replay_buffer.ReplayBuffer(train_size, (1,), (0,))
val_buffer = replay_buffer.ReplayBuffer(val_size, (1,), (0,))
for i in range(train_size):
train_buffer.add(x_train[i], 0, y_train[i], 0, False)
for i in range(val_size):
val_buffer.add(x_val[i], 0, y_val[i], 0, False)
train_dataset, _ = train_buffer.get_iterators(
2048, 0, train_ensemble=True, ensemble_size=num_members, shuffle_each_epoch=True)
val_dataset, _ = train_buffer.get_iterators(2048, 0, train_ensemble=False)
num_members = 5
member_cfg = omegaconf.OmegaConf.create({
"_target_": "mbrl.models.GaussianMLP",
"device": "cuda:0",
"in_size": 1,
"out_size": 1,
"num_layers": 3,
"hid_size": 64,
"use_silu": True
})
ensemble = models.BasicEnsemble(num_members, device, member_cfg)
wrapper = models.OneDTransitionRewardModel(ensemble, target_is_delta=False, normalize=True, learned_rewards=False)
wrapper.update_normalizer(train_buffer.get_all())
trainer = models.ModelTrainer(wrapper, optim_lr=0.003, weight_decay=5e-5)
train_losses, val_losses = trainer.train(train_dataset, val_dataset, num_epochs=500, patience=100)
fig, ax = plt.subplots(2, 1, figsize=(16, 8))
ax[0].plot(train_losses)
ax[0].set_xlabel("epoch")
ax[0].set_ylabel("train loss (gaussian nll)")
ax[1].plot(val_losses)
ax[1].set_xlabel("epoch")
ax[1].set_ylabel("val loss (mse)")
plt.show()
x_tensor = torch.from_numpy(x_data).unsqueeze(1).float().to(device)
x_tensor = wrapper.input_normalizer.normalize(x_tensor)
with torch.no_grad():
y_pred, y_pred_logvar = ensemble(x_tensor)
y_pred = y_pred[..., 0]
y_pred_logvar = y_pred_logvar[..., 0]
y_var_epi = y_pred.var(dim=0).cpu().numpy()
y_var = y_pred_logvar.exp()
y_pred = y_pred.mean(dim=0).cpu().numpy()
y_var_ale = y_var.mean(dim=0).cpu().numpy()
y_std = np.sqrt(y_var_epi + y_var_ale)
plt.figure(figsize=(16, 8))
plt.plot(x_data, y_data, 'r')
plt.plot(x_train, y_train, '.', markersize=0.9)
plt.plot(x_data, y_pred, 'b-', markersize=4)
plt.fill_between(x_data, y_pred, y_pred + 2 * y_std, color='b', alpha=0.2)
plt.fill_between(x_data, y_pred - 2 * y_std, y_pred, color='b', alpha=0.2)
plt.axis([-12, 12, -2.5, 2.5])
plt.show()
| 0.608943 | 0.594728 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.