text
stringlengths 2.5k
6.39M
| kind
stringclasses 3
values |
|---|---|
## Libraries
```
import pandas as pd
import numpy as np
import scipy.stats as stat
from math import sqrt
from mlgear.utils import show, display_columns
from surveyweights import normalize_weights, run_weighting_iteration
def margin_of_error(n=None, sd=None, p=None, type='proportion', interval_size=0.95):
z_lookup = {0.8: 1.28, 0.85: 1.44, 0.9: 1.65, 0.95: 1.96, 0.99: 2.58}
if interval_size not in z_lookup.keys():
raise ValueError('{} not a valid `interval_size` - must be {}'.format(interval_size,
', '.join(list(z_lookup.keys()))))
if type == 'proportion':
se = sqrt(p * (1 - p)) / sqrt(n)
elif type == 'continuous':
se = sd / sqrt(n)
else:
raise ValueError('{} not a valid `type` - must be proportion or continuous')
z = z_lookup[interval_size]
return se * z
def print_pct(pct, digits=0):
pct = pct * 100
pct = np.round(pct, digits)
if pct >= 100:
if digits == 0:
val = '>99.0%'
else:
val = '>99.'
for d in range(digits - 1):
val += '9'
val += '9%'
elif pct <= 0:
if digits == 0:
val = '<0.1%'
else:
val = '<0.'
for d in range(digits - 1):
val += '0'
val += '1%'
else:
val = '{}%'.format(pct)
return val
def calc_result(biden_vote, trump_vote, n, interval=0.8):
GENERAL_POLLING_ERROR = 5.0
N_SIMS = 100000
biden_moe = margin_of_error(n=n, p=biden_vote/100, interval_size=interval)
trump_moe = margin_of_error(n=n, p=trump_vote/100, interval_size=interval)
undecided = (100 - biden_vote - trump_vote) / 2
biden_mean = biden_vote + undecided * 0.25
biden_raw_moe = biden_moe * 100
biden_allocate_undecided = undecided * 0.4
biden_margin = biden_raw_moe + biden_allocate_undecided + GENERAL_POLLING_ERROR
trump_mean = trump_vote + undecided * 0.25
trump_raw_moe = trump_moe * 100
trump_allocate_undecided = undecided * 0.4
trump_margin = trump_raw_moe + trump_allocate_undecided + GENERAL_POLLING_ERROR
cdf_value = 0.5 + 0.5 * interval
normed_sigma = stat.norm.ppf(cdf_value)
biden_sigma = biden_margin / 100 / normed_sigma
biden_sims = np.random.normal(biden_mean / 100, biden_sigma, N_SIMS)
trump_sigma = trump_margin / 100 / normed_sigma
trump_sims = np.random.normal(trump_mean / 100, trump_sigma, N_SIMS)
chance_pass = np.sum([sim[0] > sim[1] for sim in zip(biden_sims, trump_sims)]) / N_SIMS
low, high = np.percentile(biden_sims - trump_sims, [20, 80]) * 100
return {'mean': biden_mean - trump_mean, 'high': high, 'low': low, 'n': n,
'raw_moe': biden_raw_moe + trump_raw_moe,
'margin': (biden_margin + trump_margin) / 2,
'sigma': (biden_sigma + trump_sigma) / 2,
'chance_pass': chance_pass}
def print_result(mean, high, low, n, raw_moe, margin, sigma, chance_pass):
mean = np.round(mean, 1)
first = np.round(high, 1)
second = np.round(low, 1)
sigma = np.round(sigma * 100, 1)
raw_moe = np.round(raw_moe, 1)
margin = np.round(margin, 1)
chance_pass = print_pct(chance_pass, 1)
if second < first:
_ = first
first = second
second = _
if second > 100:
second = 100
if first < -100:
first = -100
print(('Result Biden {} (80% CI: {} to {}) (Weighted N={}) (raw_moe={}pts, margin={}pts, '
'sigma={}pts) (Biden {} likely to win)').format(mean,
first,
second,
n,
raw_moe,
margin,
sigma,
chance_pass))
print(('Biden {} (80% CI: {} to {}) ({} Biden)').format(mean,
first,
second,
chance_pass))
print('-')
def calc_result_sen(dem_vote, rep_vote, n, interval=0.8):
GENERAL_POLLING_ERROR = 5.0
N_SIMS = 100000
dem_moe = margin_of_error(n=n, p=dem_vote/100, interval_size=interval)
rep_moe = margin_of_error(n=n, p=rep_vote/100, interval_size=interval)
undecided = 100 - dem_vote - rep_vote
dem_mean = dem_vote + undecided * 0.25
dem_raw_moe = dem_moe * 100
dem_allocate_undecided = undecided * 0.4
dem_margin = dem_raw_moe + dem_allocate_undecided + GENERAL_POLLING_ERROR
rep_mean = rep_vote + undecided * 0.25
rep_raw_moe = rep_moe * 100
rep_allocate_undecided = undecided * 0.4
rep_margin = rep_raw_moe + rep_allocate_undecided + GENERAL_POLLING_ERROR
cdf_value = 0.5 + 0.5 * interval
normed_sigma = stat.norm.ppf(cdf_value)
dem_sigma = dem_margin / 100 / normed_sigma
dem_sims = np.random.normal(dem_mean / 100, dem_sigma, N_SIMS)
rep_sigma = rep_margin / 100 / normed_sigma
rep_sims = np.random.normal(rep_mean / 100, rep_sigma, N_SIMS)
chance_pass = np.sum([sim[0] > sim[1] for sim in zip(dem_sims, rep_sims)]) / N_SIMS
low, high = np.percentile(dem_sims - rep_sims, [20, 80]) * 100
return {'mean': dem_mean - rep_mean, 'high': high, 'low': low, 'n': n,
'raw_moe': dem_raw_moe + rep_raw_moe,
'margin': (dem_margin + rep_margin) / 2,
'sigma': (dem_sigma + rep_sigma) / 2,
'chance_pass': chance_pass}
def print_result_sen(mean, high, low, n, raw_moe, margin, sigma, chance_pass):
mean = np.round(mean, 1)
first = np.round(high, 1)
second = np.round(low, 1)
sigma = np.round(sigma * 100, 1)
raw_moe = np.round(raw_moe, 1)
margin = np.round(margin, 1)
chance_pass = print_pct(chance_pass, 1)
if second < first:
_ = first
first = second
second = _
if second > 100:
second = 100
if first < -100:
first = -100
print(('Result Dem Sen {} (80% CI: {} to {}) (Weighted N={}) (raw_moe={}pts, margin={}pts, '
'sigma={}pts) (Dem Sen {} likely to win)').format(mean,
first,
second,
n,
raw_moe,
margin,
sigma,
chance_pass))
print(('Dem {} (80% CI: {} to {}) ({} Dem)').format(mean,
first,
second,
chance_pass))
print('-')
```
## Load Processed Data
```
survey = pd.read_csv('responses_processed_national_weighted.csv').fillna('Not presented')
```
## State Presidential Models
```
POTUS_CENSUS = {'Alabama': {'Hillary Clinton': 0.3436, 'Donald Trump': 0.6208},
'Alaska': {'Hillary Clinton': 0.3655, 'Donald Trump': 0.5128},
'Arizona': {'Hillary Clinton': 0.4513, 'Donald Trump': 0.4867},
'Arkansas': {'Hillary Clinton': 0.3365, 'Donald Trump': 0.6057},
'California': {'Hillary Clinton': 0.6173, 'Donald Trump': 0.3162},
'Colorado': {'Hillary Clinton': 0.4816, 'Donald Trump': 0.4325},
'Connecticut': {'Hillary Clinton': 0.5457, 'Donald Trump': 0.4093},
'Delaware': {'Hillary Clinton': 0.531, 'Donald Trump': 0.417},
'Washington DC': {'Hillary Clinton': 0.905, 'Donald Trump': 0.016},
'Florida': {'Hillary Clinton': 0.478, 'Donald Trump': 0.490},
'Georgia': {'Hillary Clinton': 0.456, 'Donald Trump': 0.508},
'Hawaii': {'Hillary Clinton': 0.622, 'Donald Trump': 0.300},
'Idaho': {'Hillary Clinton': 0.275, 'Donald Trump': 0.593},
'Illinois': {'Hillary Clinton': 0.558, 'Donald Trump': 0.379},
'Indiana': {'Hillary Clinton': 0.379, 'Donald Trump': 0.511},
'Iowa': {'Hillary Clinton': 0.417, 'Donald Trump': 0.512},
'Kansas': {'Hillary Clinton': 0.361, 'Donald Trump': 0.567},
'Kentucky': {'Hillary Clinton': 0.327, 'Donald Trump': 0.625},
'Louisiana': {'Hillary Clinton': 0.385, 'Donald Trump': 0.581},
'Maine': {'Hillary Clinton': 0.478, 'Donald Trump': 0.449},
'Maryland': {'Hillary Clinton': 0.603, 'Donald Trump': 0.339},
'Massachusetts': {'Hillary Clinton': 0.600, 'Donald Trump': 0.328},
'Michigan': {'Hillary Clinton': 0.473, 'Donald Trump': 0.475},
'Minnesota': {'Hillary Clinton': 0.464, 'Donald Trump': 0.449},
'Mississippi': {'Hillary Clinton': 0.401, 'Donald Trump': 0.579},
'Missouri': {'Hillary Clinton': 0.401, 'Donald Trump': 0.579},
'Montana': {'Hillary Clinton': 0.381, 'Donald Trump': 0.562},
'Nebraska': {'Hillary Clinton': 0.337, 'Donald Trump': 0.588},
'Nevada': {'Hillary Clinton': 0.479, 'Donald Trump': 0.455},
'New Hampshire': {'Hillary Clinton': 0.470, 'Donald Trump': 0.466},
'New Jersey': {'Hillary Clinton': 0.555, 'Donald Trump': 0.414},
'New Mexico': {'Hillary Clinton': 0.483, 'Donald Trump': 0.404},
'New York': {'Hillary Clinton': 0.590, 'Donald Trump': 0.365},
'North Carolina': {'Hillary Clinton': 0.462, 'Donald Trump': 0.498},
'North Dakota': {'Hillary Clinton': 0.272, 'Donald Trump': 0.630},
'Ohio': {'Hillary Clinton': 0.436, 'Donald Trump': 0.517},
'Oklahoma': {'Hillary Clinton': 0.289, 'Donald Trump': 0.653},
'Oregon': {'Hillary Clinton': 0.501, 'Donald Trump': 0.391},
'Pennsylvania': {'Hillary Clinton': 0.475, 'Donald Trump': 0.481},
'Rhode Island': {'Hillary Clinton': 0.544, 'Donald Trump': 0.389},
'South Carolina': {'Hillary Clinton': 0.407, 'Donald Trump': 0.549},
'South Dakota': {'Hillary Clinton': 0.317, 'Donald Trump': 0.615},
'Tennessee': {'Hillary Clinton': 0.347, 'Donald Trump': 0.607},
'Texas': {'Hillary Clinton': 0.432, 'Donald Trump': 0.522},
'Utah': {'Hillary Clinton': 0.275, 'Donald Trump': 0.454},
'Vermont': {'Hillary Clinton': 0.567, 'Donald Trump': 0.303},
'Virginia': {'Hillary Clinton': 0.497, 'Donald Trump': 0.444},
'Washington': {'Hillary Clinton': 0.525, 'Donald Trump': 0.368},
'West Virginia': {'Hillary Clinton': 0.264, 'Donald Trump': 0.685},
'Wisconsin': {'Hillary Clinton': 0.465, 'Donald Trump': 0.472},
'Wyoming': {'Hillary Clinton': 0.216, 'Donald Trump': 0.674 }}
for state in POTUS_CENSUS.keys():
print('## {} ##'.format(state.upper()))
state_survey = survey.copy()
potus_census = {'vote2016': POTUS_CENSUS[state].copy()}
potus_census['vote2016']['Other'] = 1 - potus_census['vote2016']['Hillary Clinton'] - potus_census['vote2016']['Donald Trump']
output = run_weighting_iteration(state_survey, census=potus_census, weigh_on=['vote2016'], verbose=0)
potus_weights = output['weights']['vote2016']
potus_weights = state_survey['vote2016'].astype(str).replace(potus_weights)
state_survey['weight'] = normalize_weights(state_survey['weight'] * potus_weights)
state_survey['lv_weight'] = normalize_weights(state_survey['weight'] * state_survey['lv_index'])
options = ['Donald Trump', 'Hillary Clinton', 'Other']
survey_ = state_survey.loc[state_survey['vote2016'].isin(options)].copy()
survey_['weight'] = normalize_weights(survey_['weight'])
survey_['rv_weight'] = normalize_weights(survey_['rv_weight'])
survey_['lv_weight'] = normalize_weights(survey_['lv_weight'])
lv_weighted_n = int(np.round(survey_['lv_weight'].apply(lambda w: 1 if w > 1 else w).sum()))
votes = survey_['vote2016'].value_counts(normalize=True) * survey_.groupby('vote2016')['lv_weight'].mean() * 100
votes = votes[options] * (100 / votes[options].sum())
raw_result = potus_census['vote2016']['Hillary Clinton'] - potus_census['vote2016']['Donald Trump']
print('Raw result: {}'.format(np.round(raw_result * 100, 1)))
print(votes)
options = ['Joe Biden, the Democrat', 'Donald Trump, the Republican', 'Another candidate', 'Not decided']
survey_ = state_survey.loc[state_survey['vote_trump_biden'].isin(options)].copy()
survey_['weight'] = normalize_weights(survey_['weight'])
survey_['lv_weight'] = normalize_weights(survey_['lv_weight'])
votes = survey_['vote_trump_biden'].value_counts(normalize=True) * survey_.groupby('vote_trump_biden')['lv_weight'].mean() * 100
votes = votes[options] * (100 / votes[options].sum())
print(votes)
print('-')
print_result(**calc_result(biden_vote=votes['Joe Biden, the Democrat'],
trump_vote=votes['Donald Trump, the Republican'],
n=lv_weighted_n))
print('-')
```
## State Models (Alt Weights, Post-Hoc)
```
for state in POTUS_CENSUS.keys():
print('## {} ##'.format(state.upper()))
state_survey = survey.copy()
potus_census = {'vote2016': POTUS_CENSUS[state].copy()}
potus_census['vote2016']['Other'] = 1 - potus_census['vote2016']['Hillary Clinton'] - potus_census['vote2016']['Donald Trump']
output = run_weighting_iteration(state_survey, census=potus_census, weigh_on=['vote2016'], verbose=0)
potus_weights = output['weights']['vote2016']
potus_weights = state_survey['vote2016'].astype(str).replace(potus_weights)
state_survey['weight'] = normalize_weights(state_survey['weight'] * potus_weights)
state_survey['lv_weight'] = normalize_weights(state_survey['weight'] * state_survey['lv_index'])
state_survey['lv_weight_alt'] = state_survey['lv_weight']
state_survey.loc[(~state_survey['voted2016']) & (state_survey['vote_trump_biden'] == 'Donald Trump, the Republican'), 'lv_weight_alt'] *= 1.662
state_survey['lv_weight_alt'] = normalize_weights(state_survey['lv_weight_alt'])
options = ['Joe Biden, the Democrat', 'Donald Trump, the Republican', 'Another candidate', 'Not decided']
survey_ = state_survey.loc[state_survey['vote_trump_biden'].isin(options)].copy()
survey_['lv_weight_alt'] = normalize_weights(survey_['lv_weight_alt'])
votes = survey_['vote_trump_biden'].value_counts(normalize=True) * survey_.groupby('vote_trump_biden')['lv_weight_alt'].mean() * 100
votes = votes[options] * (100 / votes[options].sum())
print(votes)
print('-')
print_result(**calc_result(biden_vote=votes['Joe Biden, the Democrat'],
trump_vote=votes['Donald Trump, the Republican'],
n=lv_weighted_n))
print('-')
```
## Senate Models
```
SENATE_STATES = ['Alabama', 'Alaska', 'Arizona', 'Arkansas', 'Colorado', 'Delaware', 'Georgia',
'Idaho', 'Illinois', 'Iowa', 'Kansas', 'Kentucky', 'Louisiana', 'Maine',
'Massachusetts', 'Michigan', 'Minnesota', 'Mississippi', 'Montana', 'Nebraska',
'New Hampshire', 'New Jersey', 'New Mexico', 'North Carolina', 'Oklahoma',
'Oregon', 'Rhode Island', 'South Carolina', 'South Dakota', 'Tennessee',
'Texas', 'Virginia', 'West Virginia', 'Wyoming']
for state in SENATE_STATES:
print('## {} ##'.format(state.upper()))
state_survey = survey.copy()
potus_census = {'vote2016': POTUS_CENSUS[state].copy()}
potus_census['vote2016']['Other'] = 1 - potus_census['vote2016']['Hillary Clinton'] - potus_census['vote2016']['Donald Trump']
output = run_weighting_iteration(state_survey, census=potus_census, weigh_on=['vote2016'], verbose=0)
potus_weights = output['weights']['vote2016']
potus_weights = state_survey['vote2016'].astype(str).replace(potus_weights)
state_survey['weight'] = normalize_weights(state_survey['weight'] * potus_weights)
state_survey['lv_weight'] = normalize_weights(state_survey['weight'] * state_survey['lv_index'])
options = ['A Democratic candidate', 'A Republican candidate', 'Another candidate', 'Not decided']
survey_ = state_survey.loc[state_survey['vote_senate'].isin(options)].copy()
survey_['weight'] = normalize_weights(survey_['weight'])
survey_['lv_weight'] = normalize_weights(survey_['lv_weight'])
votes = survey_['vote_senate'].value_counts(normalize=True) * survey_.groupby('vote_senate')['lv_weight'].mean() * 100
votes = votes[options] * (100 / votes[options].sum())
print(votes)
print('-')
print_result_sen(**calc_result_sen(dem_vote=votes['A Democratic candidate'],
rep_vote=votes['A Republican candidate'],
n=lv_weighted_n))
print('-')
```
|
github_jupyter
|
# Live Twitter Sentiments for Cryptocurrencies
Plot the evolution in time of the tweets sentiment for a cryptocurrency. We will use the *tweepy*'s streaming to see the live evolution of the Twitter sentiments for the cryptocurrencies.
* *Inputs*: currency keywords to seach in Twitter, number of tweets to analyse the sentiement, plot update interval in seconds (default = 1.0 seconds).
* *Output*: Plot with sentiment analysis and the mean in time for a specific cryptocurrency.
* *Note*: The free Twitter plan lets you download *100 Tweets per search*, and you can search Tweets from the previous seven days. *Please check the limits of getting tweets per day or month before to use this script!*
### Requirements
* *Language*: Python 3.*
* *Dependencies*: tweepy = retrieve tweets using APIs; json = handling the API results, textblob = text operations and sentiment analysis, re = text processing, matplotlib = plots, numpy = numerical calculations, IPython = interactive plots into notebooks
* *Other tools*: Textblog Corpora for text processing: *python -m textblob.download_corpora*
## How to use
Complete your twitter API credential and your crypto keywords, number of tweets and run the entire notebook.
## Step 1: Import the python dependencies
```
import time, json, re
from tweepy import Stream
from tweepy import OAuthHandler
from tweepy.streaming import StreamListener
from textblob import TextBlob
import matplotlib.pyplot as plt
import numpy as np
from IPython.display import clear_output
%matplotlib inline
```
## Step 2: Define your data
You need to define the keywords, number of tweets, the update interval, and your twitter API keys. Your can define the key here or read them from a JSON file.
```
# YOUR preference (to complete)
keywords = ["Bitcoin", 'BTC'] # a set of keywords for a crypto
noTweets = 10 # number of tweets/connections
secUpdate = 1.0 # update interval in seconds
# YOUR Twitter API information (to complete)
# if you have a local file with your info, ommit these lines
CONSUMER_KEY = 'YOUR DATA'
CONSUMER_SECRET = 'YOUR DATA'
ACCESS_TOKEN = 'YOUR DATA'
ACCESS_SECRET = 'YOUR DATA'
# Setting a JSON of your credentials (to complete)
creds = {"CONSUMER_KEY": CONSUMER_KEY, "CONSUMER_SECRET": CONSUMER_SECRET,
"ACCESS_TOKEN": ACCESS_TOKEN, "ACCESS_SECRET": ACCESS_SECRET}
# If you didnt define above, load credentials from json file
# (overwrite creds with data from file if available)
try:
print('-> Reading Twitter API credentials from file ... ')
with open("twitter_credentials.json", "r") as file:
creds = json.load(file)
print('Done!')
except:
print('! There is no twitter API credential file! Using the information you defined above!')
```
## Step 3: Define a custom class for Twitter streaming
We will use some variables as globals in order to input parameters from the main code (currency keywords to seach in Twitter, number of tweets to analyse the sentiement, plot refresh time) and to fill list with tweets sentiment, times of the sentiment analysis and means of the sentiments at a specific time. These list will be used to interactivelly plot the evolution of the sentiment and the mean of sentiments.
```
class listener(StreamListener):
def on_data(self,data):
global initime # to calculate the time of analysis
global inidatetime # to print the initial datetime
global count # counting the tweets
global t # list with the time of sentiment analysis
global sent # list with sentiments at moments t
global sentMeans # list of sentiment means at different time
global keywords # external - list with keywords for a crypto
global noTweets # external - number of tweets to get with your twitter API
global secUpdate # external - number of seconds to update the plot
# update the list for analysis time
currTime = int(time.time()-initime)
t.append(currTime)
# get the tweet data
all_data=json.loads(data)
# encode to unicode for different types of characters
tweet=all_data["text"].encode("utf-8")
# remove URLs from tweets
tweet = re.sub(r"http\S+", "", str(tweet))
# remove strange characters from the tweet
tweet=" ".join(re.findall("[a-zA-Z]+", str(tweet)))
# strip the spaces from the tweet
blob=TextBlob(tweet.strip())
# count the tweets
count=count+1
# update the list for sentiments and the means at different time
sent.append(blob.sentiment.polarity)
sentMeans.append(np.mean(sent))
# Plotting sentiment analysis in time for a cryptocurrency
# clear the plot
clear_output(wait=True)
# set axis, labels
plt.xlabel('Time')
plt.ylabel('Twitter sentiment')
# set grid
plt.grid()
# print the current mean of sentiments
print('Live Twitter sentiment analysis for cryptocurrencies')
print('**********************************************************************')
print('From: '+str(inidatetime)+' To: '+str(time.ctime()))
print('Sentiment Mean for '+str(keywords)+': '+str(np.mean(sent)))
# plot sentiments and means in time
plt.plot(t,sent, t,sentMeans)
# add legend
plt.legend(['Sentiment', 'Sentiment Mean'],loc='center left', bbox_to_anchor=(1, 0.5))
# plotting
plt.show()
# wait for update
plt.pause(secUpdate) # wait 1 sec!
# if we have the number of tweets, end the script
if count==noTweets:
return False
else:
return True
def on_error(self,status):
print(status)
```
## Step 4: Run the Twitter stream for sentiment analysis
Initialize all the variables and use the tweets stream for sentiment analysis plotting:
```
# Define external variables to be used inside the streaming class
t = [0] # list with time
sent = [0] # list with tweets sentiment in time
sentMeans = [0] # list with means of sentiment in time
count=0 # curent number of tweet
initime=time.time() # to calculate the time
inidatetime = time.ctime() # initial date time in readable format
# setup the twitter screaming
auth=OAuthHandler(creds['CONSUMER_KEY'],creds['CONSUMER_SECRET'])
auth.set_access_token(creds['ACCESS_TOKEN'],creds['ACCESS_SECRET'])
# start the stream with tweets using your keyworks
twitterStream = Stream(auth, listener(count))
twitterStream.filter(track=keywords)
```
### Hint
You can use this notebook for any twitter search, not limited to the cryptocurrencies!
Hf!
2018@muntisa
|
github_jupyter
|
### AD470 - Module 7 Introduction to Deep LearningProgramming Assignment
#### Andrew Boyer
#### Brandan Owens
```
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import scipy.io
from sklearn.preprocessing import StandardScaler
import tensorflow
from tensorflow import keras
from tensorflow.keras import layers
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
from sklearn.model_selection import train_test_split
```
#### Q.1(a) Use pandas to read in the dataset “Churn_Modelling.csv”
```
churn_df = pd.read_csv("../dataFiles/Churn_Modelling.csv")
churn_df.columns
```
#### (b) Create the following bar plots.
```
sns.countplot(data = churn_df, x = 'Exited' )
sns.countplot(data = churn_df , x = 'Geography', hue = 'Exited')
sns.barplot(data=churn_df , x= 'Geography', y= 'Balance')
```
#### (c) From the dataframe, find the percentage of people who exited, and the percentage of people who did not exit.
```
churn_df['Exited'].value_counts()/churn_df['Exited'].count()*100
```
#### (d) Check for any missing values in the dataframe.
```
churn_df.isnull().values.any()
```
#### (e) Define X and y
```
X = churn_df.drop(['RowNumber', 'CustomerId', 'Surname', 'Exited'], axis=1)
y = churn_df['Exited']
```
#### (f) Get dummies for all categorical variables of X, remember to set drop_first = True.
```
X = pd.get_dummies(X, drop_first = True)
X
```
#### (g) Split the dataset into training set and test set. test_size=0.2, random_state=0
```
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
```
#### (h) Use the following codes to do the feature scaling on the training and test sets. (Standardize all numerical variables by subtracting the means and dividing each variable by its standard deviation.)
```
sc_x = StandardScaler()
X_train = pd.DataFrame(sc_x.fit_transform(X_train), columns=X.columns.values)
X_test = pd.DataFrame(sc_x.transform(X_test), columns=X.columns.values)
```
#### (i) Build a 4-layer neural network.
```
#model = keras.Sequential([
# layers.Dense(6, activation='relu', input_shape=[11]),
# layers.Dense(12, activation='relu'),
# layers.Dense(24, activation='relu'),
# layers.Dense(1, activation='sigmoid'),
#])
model = Sequential()
model.add(Dense(6, input_shape=(11,), activation='relu'))
model.add(Dense(12, activation='relu'))
model.add(Dense(24, activation='relu'))
model.add(Dense(1, activation='sigmoid'))
model.summary()
```
#### (j) Compile the neural network.
```
model.compile(optimizer='adam',
loss = 'binary_crossentropy',
metrics=['accuracy'])
#model.summary()
#x_partial_train = X_train[:100]
#y_partial_train = y_train[:100]
#x_val = X_train[100:]
#y_val = y_train[100:]
```
#### (k) Fit the model on training set. Set the batch_size =10, run for 100 epochs.
```
history = model.fit(
X_train, y_train,
validation_data=(X_test,y_test),
epochs=100,
batch_size =10,
)
```
#### (l) Evaluate the model on test set.
```
test_loss, test_acc = model.evaluate(X_test, y_test, verbose=2)
history_dict = history.history
loss_values = history_dict['loss']
val_loss_values = history_dict['val_loss']
epochs = range(1, len(loss_values) + 1)
plt.plot(epochs, loss_values, 'bo', label='Training Loss')
plt.plot(epochs, val_loss_values, 'b', label='Validation Loss')
plt.title('Training and Validation Loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.show()
acc = history_dict['accuracy']
val_acc = history_dict['val_accuracy']
plt.plot(epochs, acc, 'bo', label='Training Accuracy')
plt.plot(epochs, val_acc, 'b', label='Validation Accuracy')
plt.title('Training and Validation Accuracy')
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.legend()
plt.show()
```
#### (m) Finally, predict the probability of y = Exited on the test set.
```
prediction = model.predict(X_test)
print(prediction)
new_pred = (prediction > 0.6)
true_count = np.count_nonzero(new_pred)
print(true_count/new_pred.size)
print("% of employees that have a 60% or greater chance of leaving the company")
```
#### Q.2 (a) Download the file 'natural_images.zip', and extra the files.
```
import zipfile
local_zip = "../dataFiles/natural_images.zip"
zip_ref = zipfile.ZipFile(local_zip, 'r')
zip_ref.extractall('natural_images')
```
#### (b) Use os.listdir to create a list of labels.
```
os.listdir("natural_images")
```
#### (c) Display the first 5 images of each class.
```
from IPython.display import Image, display
display(Image( image file))
```
#### (d) Create the following barplot.
#### (e) Use cv2.imread() to convert images into numpy array (X). Then, use cv2.resize(), so that each image has the size (32,32) Create an array which contains the label of each image (Y).
#### (f) Print the shape of images (X) and shape of labels (Y).
#### (g) Standardize X by dividing X by 255.
#### (h) Use LabelEncoder() to encode Y. Use to_categorical() covert Y into categorical numpy array.
#### (i) Split the data into training set and test set. test_size = 0.33, random_state = 46.
#### (j) But a CNN model- first layer is Conv2D, filters =32, kernel_size = (5,5), activation = relu.- second layer is MaxPool2D, pool_size = (2,2)- third layer is Conv2D, filters =64, kernel_size = (3,3), activation = relu.- fourth layer is MaxPool2D, pool_size = (2,2)- fifth layer to flatten the tensors.- sixth layer is Dense, output shape = 256, activation = relu.- seventh layer is Dense, output shape = 8, activation = softmax.
#### (k) Compile the modelloss='categorical_crossentropy', optimizer='adam', metrics=['accuracy']
#### (l) fit the model, epochs = 25, validation_split = 0.2
#### (m)Plot the change in loss score on training set and validation set over epochs.
#### (n) Plot the change in accuracy on training set and validation set over epochs.
#### (o) Retrain the model using the entire training set and set epochs = 5. Evaluate the model on the test set.
|
github_jupyter
|
```
#IMPORT SEMUA LIBARARY
#IMPORT LIBRARY PANDAS
import pandas as pd
#IMPORT LIBRARY UNTUK POSTGRE
from sqlalchemy import create_engine
import psycopg2
#IMPORT LIBRARY CHART
from matplotlib import pyplot as plt
from matplotlib import style
#IMPORT LIBRARY BASE PATH
import os
import io
#IMPORT LIBARARY PDF
from fpdf import FPDF
#IMPORT LIBARARY CHART KE BASE64
import base64
#IMPORT LIBARARY EXCEL
import xlsxwriter
#FUNGSI UNTUK MENGUPLOAD DATA DARI CSV KE POSTGRESQL
def uploadToPSQL(columns, table, filePath, engine):
#FUNGSI UNTUK MEMBACA CSV
df = pd.read_csv(
os.path.abspath(filePath),
names=columns,
keep_default_na=False
)
#APABILA ADA FIELD KOSONG DISINI DIFILTER
df.fillna('')
#MENGHAPUS COLUMN YANG TIDAK DIGUNAKAN
del df['kategori']
del df['jenis']
del df['pengiriman']
del df['satuan']
#MEMINDAHKAN DATA DARI CSV KE POSTGRESQL
df.to_sql(
table,
engine,
if_exists='replace'
)
#DIHITUNG APABILA DATA YANG DIUPLOAD BERHASIL, MAKA AKAN MENGEMBALIKAN KELUARAN TRUE(BENAR) DAN SEBALIKNYA
if len(df) == 0:
return False
else:
return True
#FUNGSI UNTUK MEMBUAT CHART, DATA YANG DIAMBIL DARI DATABASE DENGAN MENGGUNAKAN ORDER DARI TANGGAL DAN JUGA LIMIT
#DISINI JUGA MEMANGGIL FUNGSI MAKEEXCEL DAN MAKEPDF
def makeChart(host, username, password, db, port, table, judul, columns, filePath, name, subjudul, limit, negara, basePath):
#TEST KONEKSI DATABASE
try:
#KONEKSI KE DATABASE
connection = psycopg2.connect(user=username,password=password,host=host,port=port,database=db)
cursor = connection.cursor()
#MENGAMBL DATA DARI TABLE YANG DIDEFINISIKAN DIBAWAH, DAN DIORDER DARI TANGGAL TERAKHIR
#BISA DITAMBAHKAN LIMIT SUPAYA DATA YANG DIAMBIL TIDAK TERLALU BANYAK DAN BERAT
postgreSQL_select_Query = "SELECT * FROM "+table+" ORDER BY tanggal ASC LIMIT " + str(limit)
cursor.execute(postgreSQL_select_Query)
mobile_records = cursor.fetchall()
uid = []
lengthx = []
lengthy = []
#MELAKUKAN LOOPING ATAU PERULANGAN DARI DATA YANG SUDAH DIAMBIL
#KEMUDIAN DATA TERSEBUT DITEMPELKAN KE VARIABLE DIATAS INI
for row in mobile_records:
uid.append(row[0])
lengthx.append(row[1])
if row[2] == "":
lengthy.append(float(0))
else:
lengthy.append(float(row[2]))
#FUNGSI UNTUK MEMBUAT CHART
#bar
style.use('ggplot')
fig, ax = plt.subplots()
#MASUKAN DATA ID DARI DATABASE, DAN JUGA DATA TANGGAL
ax.bar(uid, lengthy, align='center')
#UNTUK JUDUL CHARTNYA
ax.set_title(judul)
ax.set_ylabel('Total')
ax.set_xlabel('Tanggal')
ax.set_xticks(uid)
#TOTAL DATA YANG DIAMBIL DARI DATABASE, DIMASUKAN DISINI
ax.set_xticklabels((lengthx))
b = io.BytesIO()
#CHART DISIMPAN KE FORMAT PNG
plt.savefig(b, format='png', bbox_inches="tight")
#CHART YANG SUDAH DIJADIKAN PNG, DISINI DICONVERT KE BASE64
barChart = base64.b64encode(b.getvalue()).decode("utf-8").replace("\n", "")
#CHART DITAMPILKAN
plt.show()
#line
#MASUKAN DATA DARI DATABASE
plt.plot(lengthx, lengthy)
plt.xlabel('Tanggal')
plt.ylabel('Total')
#UNTUK JUDUL CHARTNYA
plt.title(judul)
plt.grid(True)
l = io.BytesIO()
#CHART DISIMPAN KE FORMAT PNG
plt.savefig(l, format='png', bbox_inches="tight")
#CHART YANG SUDAH DIJADIKAN PNG, DISINI DICONVERT KE BASE64
lineChart = base64.b64encode(l.getvalue()).decode("utf-8").replace("\n", "")
#CHART DITAMPILKAN
plt.show()
#pie
#UNTUK JUDUL CHARTNYA
plt.title(judul)
#MASUKAN DATA DARI DATABASE
plt.pie(lengthy, labels=lengthx, autopct='%1.1f%%',
shadow=True, startangle=180)
plt.axis('equal')
p = io.BytesIO()
#CHART DISIMPAN KE FORMAT PNG
plt.savefig(p, format='png', bbox_inches="tight")
#CHART YANG SUDAH DIJADIKAN PNG, DISINI DICONVERT KE BASE64
pieChart = base64.b64encode(p.getvalue()).decode("utf-8").replace("\n", "")
#CHART DITAMPILKAN
plt.show()
#MENGAMBIL DATA DARI CSV YANG DIGUNAKAN SEBAGAI HEADER DARI TABLE UNTUK EXCEL DAN JUGA PDF
header = pd.read_csv(
os.path.abspath(filePath),
names=columns,
keep_default_na=False
)
#MENGHAPUS COLUMN YANG TIDAK DIGUNAKAN
header.fillna('')
del header['tanggal']
del header['total']
#MEMANGGIL FUNGSI EXCEL
makeExcel(mobile_records, header, name, limit, basePath)
#MEMANGGIL FUNGSI PDF
makePDF(mobile_records, header, judul, barChart, lineChart, pieChart, name, subjudul, limit, basePath)
#JIKA GAGAL KONEKSI KE DATABASE, MASUK KESINI UNTUK MENAMPILKAN ERRORNYA
except (Exception, psycopg2.Error) as error :
print (error)
#KONEKSI DITUTUP
finally:
if(connection):
cursor.close()
connection.close()
#FUNGSI MAKEEXCEL GUNANYA UNTUK MEMBUAT DATA YANG BERASAL DARI DATABASE DIJADIKAN FORMAT EXCEL TABLE F2
#PLUGIN YANG DIGUNAKAN ADALAH XLSXWRITER
def makeExcel(datarow, dataheader, name, limit, basePath):
#MEMBUAT FILE EXCEL
workbook = xlsxwriter.Workbook(basePath+'jupyter/BLOOMBERG/SektorHargaInflasi/excel/'+name+'.xlsx')
#MENAMBAHKAN WORKSHEET PADA FILE EXCEL TERSEBUT
worksheet = workbook.add_worksheet('sheet1')
#SETINGAN AGAR DIBERIKAN BORDER DAN FONT MENJADI BOLD
row1 = workbook.add_format({'border': 2, 'bold': 1})
row2 = workbook.add_format({'border': 2})
#MENJADIKAN DATA MENJADI ARRAY
data=list(datarow)
isihead=list(dataheader.values)
header = []
body = []
#LOOPING ATAU PERULANGAN, KEMUDIAN DATA DITAMPUNG PADA VARIABLE DIATAS
for rowhead in dataheader:
header.append(str(rowhead))
for rowhead2 in datarow:
header.append(str(rowhead2[1]))
for rowbody in isihead[1]:
body.append(str(rowbody))
for rowbody2 in data:
body.append(str(rowbody2[2]))
#MEMASUKAN DATA DARI VARIABLE DIATAS KE DALAM COLUMN DAN ROW EXCEL
for col_num, data in enumerate(header):
worksheet.write(0, col_num, data, row1)
for col_num, data in enumerate(body):
worksheet.write(1, col_num, data, row2)
#FILE EXCEL DITUTUP
workbook.close()
#FUNGSI UNTUK MEMBUAT PDF YANG DATANYA BERASAL DARI DATABASE DIJADIKAN FORMAT EXCEL TABLE F2
#PLUGIN YANG DIGUNAKAN ADALAH FPDF
def makePDF(datarow, dataheader, judul, bar, line, pie, name, subjudul, lengthPDF, basePath):
#FUNGSI UNTUK MENGATUR UKURAN KERTAS, DISINI MENGGUNAKAN UKURAN A4 DENGAN POSISI LANDSCAPE
pdf = FPDF('L', 'mm', [210,297])
#MENAMBAHKAN HALAMAN PADA PDF
pdf.add_page()
#PENGATURAN UNTUK JARAK PADDING DAN JUGA UKURAN FONT
pdf.set_font('helvetica', 'B', 20.0)
pdf.set_xy(145.0, 15.0)
#MEMASUKAN JUDUL KE DALAM PDF
pdf.cell(ln=0, h=2.0, align='C', w=10.0, txt=judul, border=0)
#PENGATURAN UNTUK UKURAN FONT DAN JUGA JARAK PADDING
pdf.set_font('arial', '', 14.0)
pdf.set_xy(145.0, 25.0)
#MEMASUKAN SUB JUDUL KE PDF
pdf.cell(ln=0, h=2.0, align='C', w=10.0, txt=subjudul, border=0)
#MEMBUAT GARIS DI BAWAH SUB JUDUL
pdf.line(10.0, 30.0, 287.0, 30.0)
pdf.set_font('times', '', 10.0)
pdf.set_xy(17.0, 37.0)
#PENGATURAN UNTUK UKURAN FONT DAN JUGA JARAK PADDING
pdf.set_font('Times','',10.0)
#MENGAMBIL DATA HEADER PDF YANG SEBELUMNYA SUDAH DIDEFINISIKAN DIATAS
datahead=list(dataheader.values)
pdf.set_font('Times','B',12.0)
pdf.ln(0.5)
th1 = pdf.font_size
#MEMBUAT TABLE PADA PDF, DAN MENAMPILKAN DATA DARI VARIABLE YANG SUDAH DIKIRIM
pdf.cell(100, 2*th1, "Kategori", border=1, align='C')
pdf.cell(177, 2*th1, datahead[0][0], border=1, align='C')
pdf.ln(2*th1)
pdf.cell(100, 2*th1, "Jenis", border=1, align='C')
pdf.cell(177, 2*th1, datahead[0][1], border=1, align='C')
pdf.ln(2*th1)
pdf.cell(100, 2*th1, "Pengiriman", border=1, align='C')
pdf.cell(177, 2*th1, datahead[0][2], border=1, align='C')
pdf.ln(2*th1)
pdf.cell(100, 2*th1, "Satuan", border=1, align='C')
pdf.cell(177, 2*th1, datahead[0][3], border=1, align='C')
pdf.ln(2*th1)
#PENGATURAN PADDING
pdf.set_xy(17.0, 75.0)
#PENGATURAN UNTUK UKURAN FONT DAN JUGA JARAK PADDING
pdf.set_font('Times','B',11.0)
data=list(datarow)
epw = pdf.w - 2*pdf.l_margin
col_width = epw/(lengthPDF+1)
#PENGATURAN UNTUK JARAK PADDING
pdf.ln(0.5)
th = pdf.font_size
#MEMASUKAN DATA HEADER YANG DIKIRIM DARI VARIABLE DIATAS KE DALAM PDF
pdf.cell(50, 2*th, str("Negara"), border=1, align='C')
for row in data:
pdf.cell(40, 2*th, str(row[1]), border=1, align='C')
pdf.ln(2*th)
#MEMASUKAN DATA ISI YANG DIKIRIM DARI VARIABLE DIATAS KE DALAM PDF
pdf.set_font('Times','B',10.0)
pdf.set_font('Arial','',9)
pdf.cell(50, 2*th, negara, border=1, align='C')
for row in data:
pdf.cell(40, 2*th, str(row[2]), border=1, align='C')
pdf.ln(2*th)
#MENGAMBIL DATA CHART, KEMUDIAN CHART TERSEBUT DIJADIKAN PNG DAN DISIMPAN PADA DIRECTORY DIBAWAH INI
#BAR CHART
bardata = base64.b64decode(bar)
barname = basePath+'jupyter/BLOOMBERG/SektorHargaInflasi/img/'+name+'-bar.png'
with open(barname, 'wb') as f:
f.write(bardata)
#LINE CHART
linedata = base64.b64decode(line)
linename = basePath+'jupyter/BLOOMBERG/SektorHargaInflasi/img/'+name+'-line.png'
with open(linename, 'wb') as f:
f.write(linedata)
#PIE CHART
piedata = base64.b64decode(pie)
piename = basePath+'jupyter/BLOOMBERG/SektorHargaInflasi/img/'+name+'-pie.png'
with open(piename, 'wb') as f:
f.write(piedata)
#PENGATURAN UNTUK UKURAN FONT DAN JUGA JARAK PADDING
pdf.set_xy(17.0, 75.0)
col = pdf.w - 2*pdf.l_margin
widthcol = col/3
#MEMANGGIL DATA GAMBAR DARI DIREKTORY DIATAS
pdf.image(barname, link='', type='',x=8, y=100, w=widthcol)
pdf.set_xy(17.0, 75.0)
col = pdf.w - 2*pdf.l_margin
pdf.image(linename, link='', type='',x=103, y=100, w=widthcol)
pdf.set_xy(17.0, 75.0)
col = pdf.w - 2*pdf.l_margin
pdf.image(piename, link='', type='',x=195, y=100, w=widthcol)
pdf.ln(2*th)
#MEMBUAT FILE PDF
pdf.output(basePath+'jupyter/BLOOMBERG/SektorHargaInflasi/pdf/'+name+'.pdf', 'F')
#DISINI TEMPAT AWAL UNTUK MENDEFINISIKAN VARIABEL VARIABEL SEBELUM NANTINYA DIKIRIM KE FUNGSI
#PERTAMA MANGGIL FUNGSI UPLOADTOPSQL DULU, KALAU SUKSES BARU MANGGIL FUNGSI MAKECHART
#DAN DI MAKECHART MANGGIL FUNGSI MAKEEXCEL DAN MAKEPDF
#DEFINISIKAN COLUMN BERDASARKAN FIELD CSV
columns = [
"kategori",
"jenis",
"tanggal",
"total",
"pengiriman",
"satuan",
]
#UNTUK NAMA FILE
name = "SektorHargaInflasi3_3"
#VARIABLE UNTUK KONEKSI KE DATABASE
host = "localhost"
username = "postgres"
password = "1234567890"
port = "5432"
database = "bloomberg_SektorHargaInflasi"
table = name.lower()
#JUDUL PADA PDF DAN EXCEL
judul = "Data Sektor Harga Inflasi"
subjudul = "Badan Perencanaan Pembangunan Nasional"
#LIMIT DATA UNTUK SELECT DI DATABASE
limitdata = int(8)
#NAMA NEGARA UNTUK DITAMPILKAN DI EXCEL DAN PDF
negara = "Indonesia"
#BASE PATH DIRECTORY
basePath = 'C:/Users/ASUS/Documents/bappenas/'
#FILE CSV
filePath = basePath+ 'data mentah/BLOOMBERG/SektorHargaInflasi/' +name+'.csv';
#KONEKSI KE DATABASE
engine = create_engine('postgresql://'+username+':'+password+'@'+host+':'+port+'/'+database)
#MEMANGGIL FUNGSI UPLOAD TO PSQL
checkUpload = uploadToPSQL(columns, table, filePath, engine)
#MENGECEK FUNGSI DARI UPLOAD PSQL, JIKA BERHASIL LANJUT MEMBUAT FUNGSI CHART, JIKA GAGAL AKAN MENAMPILKAN PESAN ERROR
if checkUpload == True:
makeChart(host, username, password, database, port, table, judul, columns, filePath, name, subjudul, limitdata, negara, basePath)
else:
print("Error When Upload CSV")
```
|
github_jupyter
|
# Jupyter UX Survey 2015 - Initial Sandbox
* Goal: Start looking at how we can surface insights from the data.
* Description: https://github.com/jupyter/surveys/tree/master/surveys/2015-12-notebook-ux
* Data: https://raw.githubusercontent.com/jupyter/surveys/master/surveys/2015-12-notebook-ux/20160115235816-SurveyExport.csv
## Initial Questions
### To what audiences is the Jupyter Community trying to cater?
* New to the practice of "data science"
* Experienced audience not using jupyter
* Existing audience
### How can we boil down the free text to "themes"?
* Remove stop words and find key terms to do some frequency counts
* Read and tag everything manually, then analyze the tags
* Overlap between responses to the various questions
* Apply coccurence grouping to the text
* Throw text at the alchemy Keyword Extraction API and see what it pulls out
* Bin short vs long and analyze separately
### What roles do the survey respondant fill? And in what fields / industries do they fill those roles?
See the [Roles]() section down below.
### Generally, what themes do we see across the free-text responses?
See the [Themes]() in hinderances section for an initial approach on how to find and expand on sets of themes for one particular question. We think we can apply this to the other questions as well.
### What themes do we see across the free-text responses but within the role/industry categories?
e.g., Is it always software developers that are asking for IDE features vs hard scientists asking for collaboration features?
We took an initial approach on rolling up the roles into a smaller set of categories. We then looked at mapping the requests for vim/emacs and ide feature to the software engineering related roles. It turns out that these requests seem to cross roles, and are not specific to software engineers. More of the responses for emacs/vim, in fact, came from respondants from the hard sciences (e.g. physicist, computational biologist, etc.)
This led us to believe that we should not assume certain roles are certain hinderances, but rather try to visualize if there are any hot-spots between roles and hinderance themes. It may turn out, we hypothesize, that the roles have little to do with the hinderances and that the themes are cross cutting. Or not.
We plan to create heatmap-like plots, one per question. On one axis we will have the role categories and on the other we will have the themes we identify within the responses for that question. After creating these plots for all questions, we'll also create similar plots where we substitute industry, years in role, # of notebook consumers, frequency of use, etc. on one of the axes and keep the themes on the other.
### What shortcodes can we use to refer to the questions?
Assume we roll up the answers into single columns:
* how_often
* how_long
* hinderance
* integrated
* how_run
* workflow_needs_addressed
* workflow_needs_not_addressed
* pleasant_aspects
* difficult_aspects
* features_changes
* first_experience_enhancements
* keywords
* role
* years_in_role
* industry
* notebook_consumers
```
%matplotlib inline
import warnings
warnings.simplefilter('ignore')
import pandas as pd
import matplotlib.pyplot as plt
pd.set_option('max_colwidth', 1000)
df = pd.read_csv('../20160115235816-SurveyExport.csv')
df.columns
```
## Themes in the hinderances
Let's start with the hinderances question and figure out the process first. Then we can apply it to the other free form text responses (we think).
```
hinder = df['What, if anything, hinders you from making Jupyter Notebook an even more regular part of your workflow?']
```
How many non-null responses are there?
```
hinder.isnull().value_counts()
```
Clear out the nulls.
```
hinder = hinder.dropna()
```
How much did people write?
```
char_lengths = hinder.apply(lambda response: len(response))
fig, ax = plt.subplots(figsize=(11, 7))
char_lengths.hist(bins=100, ax=ax)
ax.set_title('Character count histogram')
```
We should definitely look at the longest responses. These are people who might have felt very strongly about what they were writing.
```
for row in hinder[char_lengths > 1400]:
print(row)
print()
```
Now just to get the constrast, let's look at some of the shortest responses.
```
hinder[char_lengths < 100].sample(20)
```
From reading a bunch of random samples of the shortest responses, we've got a list of ideas that we think we can search for across all of the responses in order to judge how common the themes are.
* Nothing
* UX / navigation / mobile / paradigm
* IDE / debug / editor familiarity / comfort zone / keys
* Setup / learning / getting started / perceived lack of skills
* Inertia
* Colleagues / peer pressure
* Version control / git / history / tracking / provenance
* Collaboration / export / sharing
* Integration / missing languages / extensibility
Before we do, let's look at a few "medium-length" responses too for good measure.
```
for x in list(hinder[(char_lengths < 300) & (char_lengths > 100)].sample(20)):
print(x)
print()
```
We can add a few themes to the list we created above (which we'll replicate here to keep growing it as we go, because, history):
* Nothing
* UX / navigation / mobile / paradigm
* IDE / debug / editor familiarity / comfort zone / keys
* Setup / learning / getting started / perceived lack of skills / community / documentation
* Inertia
* Colleagues / peer pressure
* Version control / git / history / tracking / provenance
* Collaboration / export / sharing / dirt simple deploy
* Customization / personalization
* Reuse / modularization
* Integration / missing languages / extensibility
```
keywords = ['git', 'version control', 'history', 'track', 'checkpoint', 'save']
def keywords_or(text):
for keyword in keywords:
if keyword in text:
return text
return None
results = hinder.map(keywords_or)
len(results.dropna())
results.dropna()
```
Moving forward, here's a semi-automatic procedure we can follow for identifying themes across questions:
1. Take a random sample of question responses
2. Write down common theme keywords
3. Search back through the responses using the theme keywords
4. Expand the set of keywords with other words seen in the search results
5. Repeat for all themes and questions
Later, we can use a fully automated topic modeling approach to validate our manually generated themes.
## Roles
We want to pull out the major roles that people self-identified as filling when they use Jupyter Notebook.
```
roles_df = df[['What is your primary role when using Jupyter Notebook (e.g., student,\xa0astrophysicist, financial modeler, business manager, etc.)?']]
roles_df = roles.dropna()
```
We're renaming the column for brevity only.
```
roles_df.columns = ['role']
```
Some basic normalization. TODO: do more later.
```
roles_df['role_norm'] = roles_df.role.str.lower()
```
For now, we're going to look at the top 20 and see what industries they support from the other columns
```
roles_df.role_norm.value_counts()
```
## Industry vs Role
```
len(df['Industry #1:What industries does your role and analytical work support (e.g., Journalism, IT, etc.)?'].dropna())
len(df['Industry #2:What industries does your role and analytical work support (e.g., Journalism, IT, etc.)?'].dropna())
len(df['Industry #3:What industries does your role and analytical work support (e.g., Journalism, IT, etc.)?'].dropna())
industry_df = df[
['Industry #1:What industries does your role and analytical work support (e.g., Journalism, IT, etc.)?',
'Industry #2:What industries does your role and analytical work support (e.g., Journalism, IT, etc.)?',
'Industry #3:What industries does your role and analytical work support (e.g., Journalism, IT, etc.)?',
'What is your primary role when using Jupyter Notebook (e.g., student,\xa0astrophysicist, financial modeler, business manager, etc.)?'
]
]
industry_df.columns = ['industry1', 'industry2', 'industry3', 'role']
industry_df = industry_df.dropna(how='all')
top_roles = roles_df.role_norm.value_counts()[:20]
top_industry_df = industry_df[industry_df.role.isin(top_roles.index)]
top_industry_df[top_industry_df.role == 'data analyst']
```
## Example: Software Engineering Role
We want to see if software engineers (or related roles) are the ones asking about IDE-like features.
```
software_roles = ['engineer', 'software engineer', 'developer', 'software developer', 'programmer']
role_hinder_df = pd.merge(roles_df, hinder_df, left_index=True, right_index=True)
role_hinder_df = role_hinder_df.ix[:, 1:]
role_hinder_df[role_hinder_df.role_norm.isin(software_roles)]
tmp_df = role_hinder_df.dropna()
tmp_df[tmp_df.ix[:, 1].str.contains('emacs|vim', case=False)]
tmp_df[tmp_df.ix[:, 1].str.contains('\W+ide\W+', case=False)]
```
## Years in Role vs Role Name
```
years_in_role = df.ix[:, 32]
years_in_role.value_counts()
how_long = df.ix[:, 5]
how_long.value_counts()
using_vs_role = df[[5, 32]]
using_vs_role.columns = ['how_long_using', 'how_long_role']
pd.crosstab(using_vs_role.how_long_role, using_vs_role.how_long_using)
```
|
github_jupyter
|
<a href="https://colab.research.google.com/github/Nadda1004/Intro_Machine_learning/blob/main/W1_D1_ML_HeuristicModel.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Predicting Rain in Seattle
Seattle is one of the rainiest places in the world. Even so, it is worth asking the question 'will it rain tomorrow.' Imagine you are headed to sleep at a hotel in downtown Seattle.
The next days activities are supposed to include walking around outside most of the day. You want to know if it will rain or not (you don't really care how much rain just a simple yes or no will do), which will greatly impact what you choose to wear and carry around (like an umbrella).
Build a heuristic model to predict if it will rain tomorrow.
## Our Data
```
import pandas as pd
df = pd.read_csv('https://raw.githubusercontent.com/gumdropsteve/datasets/master/seattle_weather_1948-2017.csv')
df
df.info()
#since the ds is representing the date but its not in date time format i will convert it to datetime format
df.ds = pd.to_datetime(df['ds'])
df.info()
df.head()
import numpy as np
# what % of days did it rain?
rainy = (df.rain.value_counts()[1] / df.shape[0]) * 100
print('The Percenatge of Rained Days {:.3f}%'.format(rainy))
# what values are seen in the prcp column
df.prcp.value_counts()
import matplotlib.pyplot as plt
plt.figure(figsize=(15,7))
df.prcp.plot.hist(bins = 20).set(title = 'Values Range in Prcp');
# show me a histogram of prcp < 2
plt.figure(figsize=(15,7))
df.loc[df.prcp < 2].prcp.plot.hist(bins = 20).set(title = 'Values < 2 in Prcp');
```
#### Check for Missing Values and Outliers
```
# how many null values does each column have?
df.isnull().sum()
# show me the null rows
df.loc[df.isnull().any(axis=1)]
# drop the null rows and update the dataframe
df1 = df.dropna()
df1
import seaborn as sns
# make a box plot
plt.figure(figsize=(15,7))
sns.boxplot(data=df1).set(title = 'Boxplot for all columns');
# show me some outler values from tmax or tmin
plt.figure(figsize=(15,7))
sns.boxplot(data=[df1.tmin , df1.tmax]).set(title = 'Boxplot for minimum temperature and maximum temperature' );
plt.xlabel('Min and Max Temp');
# make an sns pairplot with hue='rain'
sns.pairplot(data = df1 , hue = 'rain');
# bonus challenge
# plot prcp by day (ds on x axis)
plt.figure(figsize=(40,10))
sns.lineplot(x = df1.ds , y = df1.prcp).set(title = 'Prcp Values Over The Years');
```
## Set up a basic model to make predicitons
First, split the data...
```
from sklearn.model_selection import train_test_split
X = df1[['prcp', 'tmax', 'tmin']] # all the values you want to help predict the target value
y = df1.rain.astype(np.int32) # the target value
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.7)
```
Bring in a model now...
```
from sklearn.linear_model import LogisticRegression
# logistic regression is a classifier, for our case, True (1) or False (0)
lr = LogisticRegression()
lr
lr.fit(X=X_train, y=y_train)
# predict the y values from X test data
lr.predict(X_test)
preds = lr.predict(X_test)
# how'd your model score?
from sklearn.metrics import accuracy_score
accuracy_score(y_test, preds) * 100
```
|
github_jupyter
|
## UCI SMS Spam Collection Dataset
* **Input**: sms textual content. **Target**: ham or spam
* **data representation**: each sms is repesented with a **fixed-length vector of word indexes**. A word index lookup is generated from the vocabulary list.
* **words embedding**: A word embedding (dense vector) is learnt for each word. That is, each sms is presented as a matrix of (document-word-count, word-embedding-size)
* **convolution layer**: Apply filter(s) to the word-embedding matrix, before input to the fully-connected NN
* **train-data.tsv, valid-datat.tsv**, and **vocab_list.tsv** are prepared and saved in 'data/sms-spam'
```
import tensorflow as tf
from tensorflow import data
from datetime import datetime
import multiprocessing
import shutil
print(tf.__version__)
MODEL_NAME = 'sms-class-model-01'
TRAIN_DATA_FILES_PATTERN = 'data/sms-spam/train-*.tsv'
VALID_DATA_FILES_PATTERN = 'data/sms-spam/valid-*.tsv'
VOCAB_LIST_FILE = 'data/sms-spam/vocab_list.tsv'
N_WORDS_FILE = 'data/sms-spam/n_words.tsv'
RESUME_TRAINING = False
MULTI_THREADING = True
```
## 1. Define Dataset Metadata
```
MAX_DOCUMENT_LENGTH = 100
PAD_WORD = '#=KS=#'
HEADER = ['class', 'sms']
HEADER_DEFAULTS = [['NA'], ['NA']]
TEXT_FEATURE_NAME = 'sms'
TARGET_NAME = 'class'
WEIGHT_COLUNM_NAME = 'weight'
TARGET_LABELS = ['spam', 'ham']
with open(N_WORDS_FILE) as file:
N_WORDS = int(file.read())+2
print(N_WORDS)
```
## 2. Define Data Input Function
### a. TSV parsing logic
```
def parse_tsv_row(tsv_row):
columns = tf.decode_csv(tsv_row, record_defaults=HEADER_DEFAULTS, field_delim='\t')
features = dict(zip(HEADER, columns))
target = features.pop(TARGET_NAME)
# giving more weight to "spam" records are the are only 13% of the training set
features[WEIGHT_COLUNM_NAME] = tf.cond( tf.equal(target,'spam'), lambda: 6.6, lambda: 1.0 )
return features, target
```
### b. Data pipeline input function
```
def parse_label_column(label_string_tensor):
table = tf.contrib.lookup.index_table_from_tensor(tf.constant(TARGET_LABELS))
return table.lookup(label_string_tensor)
def input_fn(files_name_pattern, mode=tf.estimator.ModeKeys.EVAL,
skip_header_lines=0,
num_epochs=1,
batch_size=200):
shuffle = True if mode == tf.estimator.ModeKeys.TRAIN else False
num_threads = multiprocessing.cpu_count() if MULTI_THREADING else 1
buffer_size = 2 * batch_size + 1
print("")
print("* data input_fn:")
print("================")
print("Input file(s): {}".format(files_name_pattern))
print("Batch size: {}".format(batch_size))
print("Epoch Count: {}".format(num_epochs))
print("Mode: {}".format(mode))
print("Thread Count: {}".format(num_threads))
print("Shuffle: {}".format(shuffle))
print("================")
print("")
file_names = tf.matching_files(files_name_pattern)
dataset = data.TextLineDataset(filenames=file_names)
dataset = dataset.skip(skip_header_lines)
if shuffle:
dataset = dataset.shuffle(buffer_size)
dataset = dataset.map(lambda tsv_row: parse_tsv_row(tsv_row),
num_parallel_calls=num_threads)
dataset = dataset.batch(batch_size)
dataset = dataset.repeat(num_epochs)
dataset = dataset.prefetch(buffer_size)
iterator = dataset.make_one_shot_iterator()
features, target = iterator.get_next()
return features, parse_label_column(target)
```
## 3. Define Model Function
```
def process_text(text_feature):
# Load vocabolary lookup table to map word => word_id
vocab_table = tf.contrib.lookup.index_table_from_file(vocabulary_file=VOCAB_LIST_FILE,
num_oov_buckets=1, default_value=-1)
# Get text feature
smss = text_feature
# Split text to words -> this will produce sparse tensor with variable-lengthes (word count) entries
words = tf.string_split(smss)
# Convert sparse tensor to dense tensor by padding each entry to match the longest in the batch
dense_words = tf.sparse_tensor_to_dense(words, default_value=PAD_WORD)
# Convert word to word_ids via the vocab lookup table
word_ids = vocab_table.lookup(dense_words)
# Create a word_ids padding
padding = tf.constant([[0,0],[0,MAX_DOCUMENT_LENGTH]])
# Pad all the word_ids entries to the maximum document length
word_ids_padded = tf.pad(word_ids, padding)
word_id_vector = tf.slice(word_ids_padded, [0,0], [-1, MAX_DOCUMENT_LENGTH])
# Return the final word_id_vector
return word_id_vector
def model_fn(features, labels, mode, params):
hidden_units = params.hidden_units
output_layer_size = len(TARGET_LABELS)
embedding_size = params.embedding_size
window_size = params.window_size
stride = int(window_size/2)
filters = params.filters
# word_id_vector
word_id_vector = process_text(features[TEXT_FEATURE_NAME])
# print("word_id_vector: {}".format(word_id_vector)) # (?, MAX_DOCUMENT_LENGTH)
# layer to take each word_id and convert it into vector (embeddings)
word_embeddings = tf.contrib.layers.embed_sequence(word_id_vector, vocab_size=N_WORDS,
embed_dim=embedding_size)
#print("word_embeddings: {}".format(word_embeddings)) # (?, MAX_DOCUMENT_LENGTH, embbeding_size)
# convolution
words_conv = tf.layers.conv1d(word_embeddings, filters=filters, kernel_size=window_size,
strides=stride, padding='SAME', activation=tf.nn.relu)
#print("words_conv: {}".format(words_conv)) # (?, MAX_DOCUMENT_LENGTH/stride, filters)
words_conv_shape = words_conv.get_shape()
dim = words_conv_shape[1] * words_conv_shape[2]
input_layer = tf.reshape(words_conv,[-1, dim])
#print("input_layer: {}".format(input_layer)) # (?, (MAX_DOCUMENT_LENGTH/stride)*filters)
if hidden_units is not None:
# Create a fully-connected layer-stack based on the hidden_units in the params
hidden_layers = tf.contrib.layers.stack(inputs=input_layer,
layer=tf.contrib.layers.fully_connected,
stack_args= hidden_units,
activation_fn=tf.nn.relu)
# print("hidden_layers: {}".format(hidden_layers)) # (?, last-hidden-layer-size)
else:
hidden_layers = input_layer
# Connect the output layer (logits) to the hidden layer (no activation fn)
logits = tf.layers.dense(inputs=hidden_layers,
units=output_layer_size,
activation=None)
# print("logits: {}".format(logits)) # (?, output_layer_size)
# Provide an estimator spec for `ModeKeys.PREDICT`.
if mode == tf.estimator.ModeKeys.PREDICT:
probabilities = tf.nn.softmax(logits)
predicted_indices = tf.argmax(probabilities, 1)
# Convert predicted_indices back into strings
predictions = {
'class': tf.gather(TARGET_LABELS, predicted_indices),
'probabilities': probabilities
}
export_outputs = {
'prediction': tf.estimator.export.PredictOutput(predictions)
}
# Provide an estimator spec for `ModeKeys.PREDICT` modes.
return tf.estimator.EstimatorSpec(mode,
predictions=predictions,
export_outputs=export_outputs)
# weights
weights = features[WEIGHT_COLUNM_NAME]
# Calculate loss using softmax cross entropy
loss = tf.losses.sparse_softmax_cross_entropy(
logits=logits, labels=labels,
weights=weights
)
tf.summary.scalar('loss', loss)
if mode == tf.estimator.ModeKeys.TRAIN:
# Create Optimiser
optimizer = tf.train.AdamOptimizer(params.learning_rate)
# Create training operation
train_op = optimizer.minimize(
loss=loss, global_step=tf.train.get_global_step())
# Provide an estimator spec for `ModeKeys.TRAIN` modes.
return tf.estimator.EstimatorSpec(mode=mode,
loss=loss,
train_op=train_op)
if mode == tf.estimator.ModeKeys.EVAL:
probabilities = tf.nn.softmax(logits)
predicted_indices = tf.argmax(probabilities, 1)
# Return accuracy and area under ROC curve metrics
labels_one_hot = tf.one_hot(
labels,
depth=len(TARGET_LABELS),
on_value=True,
off_value=False,
dtype=tf.bool
)
eval_metric_ops = {
'accuracy': tf.metrics.accuracy(labels, predicted_indices, weights=weights),
'auroc': tf.metrics.auc(labels_one_hot, probabilities, weights=weights)
}
# Provide an estimator spec for `ModeKeys.EVAL` modes.
return tf.estimator.EstimatorSpec(mode,
loss=loss,
eval_metric_ops=eval_metric_ops)
def create_estimator(run_config, hparams):
estimator = tf.estimator.Estimator(model_fn=model_fn,
params=hparams,
config=run_config)
print("")
print("Estimator Type: {}".format(type(estimator)))
print("")
return estimator
```
## 4. Run Experiment
### a. Set HParam and RunConfig
```
TRAIN_SIZE = 4179
NUM_EPOCHS = 10
BATCH_SIZE = 250
EVAL_AFTER_SEC = 60
TOTAL_STEPS = int((TRAIN_SIZE/BATCH_SIZE)*NUM_EPOCHS)
hparams = tf.contrib.training.HParams(
num_epochs = NUM_EPOCHS,
batch_size = BATCH_SIZE,
embedding_size = 3,
window_size = 3,
filters = 2,
hidden_units=None, #[8],
max_steps = TOTAL_STEPS,
learning_rate = 0.01
)
model_dir = 'trained_models/{}'.format(MODEL_NAME)
run_config = tf.estimator.RunConfig(
log_step_count_steps=5000,
tf_random_seed=19830610,
model_dir=model_dir
)
print(hparams)
print("Model Directory:", run_config.model_dir)
print("")
print("Dataset Size:", TRAIN_SIZE)
print("Batch Size:", BATCH_SIZE)
print("Steps per Epoch:",TRAIN_SIZE/BATCH_SIZE)
print("Total Steps:", TOTAL_STEPS)
print("That is 1 evaluation step after each",EVAL_AFTER_SEC,"training seconds")
```
### b. Define serving function
```
def serving_input_fn():
receiver_tensor = {
'sms': tf.placeholder(tf.string, [None]),
}
features = {
key: tensor
for key, tensor in receiver_tensor.items()
}
return tf.estimator.export.ServingInputReceiver(
features, receiver_tensor)
```
### c. Define TrainSpec and EvaluSpec
```
train_spec = tf.estimator.TrainSpec(
input_fn = lambda: input_fn(
TRAIN_DATA_FILES_PATTERN,
mode = tf.estimator.ModeKeys.TRAIN,
num_epochs=hparams.num_epochs,
batch_size=hparams.batch_size
),
max_steps=hparams.max_steps,
hooks=None
)
eval_spec = tf.estimator.EvalSpec(
input_fn = lambda: input_fn(
VALID_DATA_FILES_PATTERN,
mode=tf.estimator.ModeKeys.EVAL,
batch_size=hparams.batch_size
),
exporters=[tf.estimator.LatestExporter(
name="predict", # the name of the folder in which the model will be exported to under export
serving_input_receiver_fn=serving_input_fn,
exports_to_keep=1,
as_text=True)],
steps=None,
throttle_secs = EVAL_AFTER_SEC
)
```
### d. Run Experiment via train_and_evaluate
```
if not RESUME_TRAINING:
print("Removing previous artifacts...")
shutil.rmtree(model_dir, ignore_errors=True)
else:
print("Resuming training...")
tf.logging.set_verbosity(tf.logging.INFO)
time_start = datetime.utcnow()
print("Experiment started at {}".format(time_start.strftime("%H:%M:%S")))
print(".......................................")
estimator = create_estimator(run_config, hparams)
tf.estimator.train_and_evaluate(
estimator=estimator,
train_spec=train_spec,
eval_spec=eval_spec
)
time_end = datetime.utcnow()
print(".......................................")
print("Experiment finished at {}".format(time_end.strftime("%H:%M:%S")))
print("")
time_elapsed = time_end - time_start
print("Experiment elapsed time: {} seconds".format(time_elapsed.total_seconds()))
```
## 5. Evaluate the Model
```
TRAIN_SIZE = 4179
TEST_SIZE = 1393
train_input_fn = lambda: input_fn(files_name_pattern= TRAIN_DATA_FILES_PATTERN,
mode= tf.estimator.ModeKeys.EVAL,
batch_size= TRAIN_SIZE)
test_input_fn = lambda: input_fn(files_name_pattern= VALID_DATA_FILES_PATTERN,
mode= tf.estimator.ModeKeys.EVAL,
batch_size= TEST_SIZE)
estimator = create_estimator(run_config, hparams)
train_results = estimator.evaluate(input_fn=train_input_fn, steps=1)
print()
print("######################################################################################")
print("# Train Measures: {}".format(train_results))
print("######################################################################################")
test_results = estimator.evaluate(input_fn=test_input_fn, steps=1)
print()
print("######################################################################################")
print("# Test Measures: {}".format(test_results))
print("######################################################################################")
```
## 6. Predict Using Serving Function
```
import os
export_dir = model_dir +"/export/predict/"
saved_model_dir = export_dir + "/" + os.listdir(path=export_dir)[-1]
print(saved_model_dir)
print("")
predictor_fn = tf.contrib.predictor.from_saved_model(
export_dir = saved_model_dir,
signature_def_key="prediction"
)
output = predictor_fn(
{
'sms':[
'ok, I will be with you in 5 min. see you then',
'win 1000 cash free of charge promo hot deal sexy',
'hot girls sexy tonight call girls waiting call chat'
]
}
)
print(output)
```
|
github_jupyter
|
# $\lambda$对CMA性能影响研究
<link rel="stylesheet" href="http://yandex.st/highlightjs/6.2/styles/googlecode.min.css">
<script src="http://code.jquery.com/jquery-1.7.2.min.js"></script>
<script src="http://yandex.st/highlightjs/6.2/highlight.min.js"></script>
<script>hljs.initHighlightingOnLoad();</script>
<script type="text/javascript">
$(document).ready(function(){
$("h2,h3,h4,h5,h6").each(function(i,item){
var tag = $(item).get(0).localName;
$(item).attr("id","wow"+i);
$("#category").append('<a class="new'+tag+'" href="#wow'+i+'">'+$(this).text()+'</a></br>');
$(".newh2").css("margin-left",0);
$(".newh3").css("margin-left",20);
$(".newh4").css("margin-left",40);
$(".newh5").css("margin-left",60);
$(".newh6").css("margin-left",80);
});
});
</script>
<div id="category"></div>
**摘要**: $\lambda$大小影响单次计算时间,根据文档合理的$\lambda$在[5,2n+10]之间,Hansen给出的推荐值为$4+3\times \lfloor ln(N) \rfloor$,本文固定mu=0.5,sigma=0.3,根据不同的$\lambda$对不同函数绘图分析.
### 第一阶段测试
* 函数:[rosen,bukin,griewank]
* 最小值:[0,6.82,0]
* 维度:[130]
* $\lambda$:[5,18,20,50,80,110,140]
```
%pylab inline
import pandas as pd
from pandas import Series, DataFrame
import pickle
plt.rc('figure', figsize=(12, 8))
with open("data.tl",'r') as f:
result_list=pickle.load(f)
def convertdic(result_list):
res=[{}]
for row in result_list:
for i,d in enumerate(res):
if row[-1] not in d.keys():
d[row[-1]]=row[:-1]
break
if i==len(res)-1:
res.append({row[-1]:row[:-1]})
break
return res
def draw(title,tail):
bs=[row[:tail] for row in result_list if row[tail]==title]
bs=np.array(bs)
lmax=max(bs[:,-1])
bs=bs/bs.max(0)
bs=bs*[1,1,1,1,lmax]
bs=convertdic(bs)
df=DataFrame(bs[0],index=['countiter','countevals','result','time(s)'])
df=df.stack().unstack(0)
df.columns.name='values'
df.index.name='lambda'
df.plot(kind='bar',stacked=False,colormap='jet',alpha=0.9,title=title,figsize=(12,8));
df.plot(kind='area',stacked=False,colormap='jet',alpha=0.5,title=title,figsize=(12,8),xticks=np.arange(5,lmax,10));
def drawSigmaLines(t,xl):
sigmas=[[row[-3],row[-1]] for row in result_list if row[-2]==t]
ss=map(list,zip(*sigmas))[1]
M=max(map(len,ss))
for s in sigmas:
for i in range(M-len(s[1])):
s[1].append(None)
df1=DataFrame({s[0]:s[1] for s in sigmas})
df1.columns.name='sigma'
df1.index.name='lambda'
df1.plot(title=t,fontsize=10,linewidth=2,alpha=0.8,colormap='rainbow',xlim=(0,xl))
#bukin函数
draw('bukin',-1)
#rosen函数
draw('rosen',-1)
#griwank函数
draw('griewank',-1)
```
### 第二阶段测试
* 函数:[sphere,cigar,elli]
* 最小值:[0,0,0]
* 维度:[208]
* $\lambda$:[5,10,14,18,20,22,26,60,100,140,180,220]
```
with open("data1.tl",'r') as f:
result_list=pickle.load(f)
#sphere函数
draw('sphere',-2)
drawSigmaLines('sphere',300)
#cigar函数
draw('cigar',-2)
drawSigmaLines('cigar',300)
#elli函数
draw('elli',-2)
drawSigmaLines('elli',300)
```
|
github_jupyter
|
# Graphing network packets
This notebook currently relies on HoloViews 1.9 or above. Run `conda install -c ioam/label/dev holoviews` to install it.
## Preparing data
The data source comes from a publicly available network forensics repository: http://www.netresec.com/?page=PcapFiles. The selected file is https://download.netresec.com/pcap/maccdc-2012/maccdc2012_00000.pcap.gz.
```
tcpdump -qns 0 -r maccdc2012_00000.pcap | grep tcp > maccdc2012_00000.txt
```
For example, here is a snapshot of the resulting output:
```
09:30:07.780000 IP 192.168.202.68.8080 > 192.168.24.100.1038: tcp 1380
09:30:07.780000 IP 192.168.24.100.1038 > 192.168.202.68.8080: tcp 0
09:30:07.780000 IP 192.168.202.68.8080 > 192.168.24.100.1038: tcp 1380
09:30:07.780000 IP 192.168.202.68.8080 > 192.168.24.100.1038: tcp 1380
09:30:07.780000 IP 192.168.27.100.37877 > 192.168.204.45.41936: tcp 0
09:30:07.780000 IP 192.168.24.100.1038 > 192.168.202.68.8080: tcp 0
09:30:07.780000 IP 192.168.202.68.8080 > 192.168.24.100.1038: tcp 1380
09:30:07.780000 IP 192.168.202.68.8080 > 192.168.24.100.1038: tcp 1380
09:30:07.780000 IP 192.168.202.68.8080 > 192.168.24.100.1038: tcp 1380
09:30:07.780000 IP 192.168.202.68.8080 > 192.168.24.100.1038: tcp 1380
```
Given the directional nature of network traffic and the numerous ports per node, we will simplify the graph by treating traffic between nodes as undirected and ignorning the distinction between ports. The graph edges will have weights represented by the total number of bytes across both nodes in either direction.
```
python pcap_to_parquet.py maccdc2012_00000.txt
```
The resulting output will be two Parquet dataframes, `maccdc2012_nodes.parq` and `maccdc2012_edges.parq`.
## Loading data
```
import holoviews as hv
import networkx as nx
import dask.dataframe as dd
from holoviews.operation.datashader import (
datashade, dynspread, directly_connect_edges, bundle_graph, stack
)
from holoviews.element.graphs import layout_nodes
from datashader.layout import random_layout
from colorcet import fire
hv.extension('bokeh')
%opts RGB Graph Nodes [bgcolor='black' width=800 height=800 xaxis=None yaxis=None]
edges_df = dd.read_parquet('../data/maccdc2012_full_edges.parq').compute()
edges_df = edges_df.reset_index(drop=True)
graph = hv.Graph(edges_df)
len(edges_df)
```
## Edge bundling & layouts
Datashader and HoloViews provide support for a number of different graph layouts including circular, force atlas and random layouts. Since large graphs with thousands of edges can become quite messy when plotted datashader also provides functionality to bundle the edges.
#### Circular layout
By default the HoloViews Graph object lays out nodes using a circular layout. Once we have declared the ``Graph`` object we can simply apply the ``bundle_graph`` operation. We also overlay the datashaded graph with the nodes, letting us identify each node by hovering.
```
%%opts Nodes (size=5)
circular = bundle_graph(graph)
pad = dict(x=(-1.2, 1.2), y=(-1.2, 1.2))
datashade(circular, width=800, height=800) * circular.nodes.redim.range(**pad)
```
#### Force Atlas 2 layout
For other graph layouts you can use the ``layout_nodes`` operation supplying the datashader or NetworkX layout function. Here we will use the ``nx.spring_layout`` function based on the [Fruchterman-Reingold](https://en.wikipedia.org/wiki/Force-directed_graph_drawing) algorithm. Instead of bundling the edges we may also use the directly_connect_edges function:
```
%%opts Nodes (size=5)
forceatlas = directly_connect_edges(layout_nodes(graph, layout=nx.spring_layout))
pad = dict(x=(-.5, 1.3), y=(-.5, 1.3))
datashade(forceatlas, width=800, height=800) * forceatlas.nodes.redim.range(**pad)
```
#### Random layout
Datashader also provides a number of layout functions in case you don't want to depend on NetworkX:
```
%%opts Nodes (size=5)
random = bundle_graph(layout_nodes(graph, layout=random_layout))
pad = dict(x=(-.05, 1.05), y=(-0.05, 1.05))
datashade(random, width=800, height=800) * random.nodes.redim.range(**pad)
```
## Showing nodes with active traffic
To select just nodes with active traffic we will split the dataframe of bundled paths and then apply ``select`` on the new Graph to select just those edges with a weight of more than 10,000. By overlaying the sub-graph of high traffic edges we can take advantage of the interactive hover and tap features that bokeh provides while still revealing the full datashaded graph in the background.
```
%%opts Graph (edge_line_color='white' edge_hover_line_color='blue')
pad = dict(x=(-1.2, 1.2), y=(-1.2, 1.2))
datashade(circular, width=800, height=800) * circular.select(weight=(10000, None)).redim.range(**pad)
```
## Highlight TCP and UDP traffic
Using the same selection features we can highlight TCP and UDP connections separately again by overlaying it on top of the full datashaded graph. The edges can be revealed over the highlighted nodes and by setting an alpha level we can also reveal connections with both TCP (blue) and UDP (red) connections in purple.
```
%%opts Graph (edge_alpha=0 edge_hover_alpha=0.5 edge_nonselection_alpha=0 node_size=8 node_alpha=0.5) [color_index='weight' inspection_policy='edges']
udp_style = dict(edge_hover_line_color='red', node_hover_size=20, node_fill_color='red', edge_selection_line_color='red')
tcp_style = dict(edge_hover_line_color='blue', node_fill_color='blue', edge_selection_line_color='blue')
udp = forceatlas.select(protocol='udp', weight=(10000, None)).opts(style=udp_style)
tcp = forceatlas.select(protocol='icmp', weight=(10000, None)).opts(style=tcp_style)
datashade(forceatlas, width=800, height=800, normalization='log', cmap=['black', 'white']) * tcp * udp
```
## Coloring by protocol
As we have already seen we can easily apply selection to the ``Graph`` objects. We can use this functionality to select by protocol, datashade the subgraph for each protocol and assign each a different color and finally stack the resulting datashaded layers:
```
from bokeh.palettes import Blues9, Reds9, Greens9
ranges = dict(x_range=(-.5, 1.6), y_range=(-.5, 1.6), width=800, height=800)
protocols = [('tcp', Blues9), ('udp', Reds9), ('icmp', Greens9)]
shaded = hv.Overlay([datashade(forceatlas.select(protocol=p), cmap=cmap, **ranges)
for p, cmap in protocols]).collate()
stack(shaded * dynspread(datashade(forceatlas.nodes, cmap=['white'], **ranges)), link_inputs=True)
```
## Selecting the highest targets
With a bit of help from pandas we can also extract the twenty most targetted nodes and overlay them on top of the datashaded plot:
```
%%opts RGB [width=800 height=800] Nodes (size=8)
target_counts = list(edges_df.groupby('target').count().sort_values('weight').iloc[-20:].index.values)
(datashade(forceatlas, cmap=fire[128:]) * datashade(forceatlas.nodes, cmap=['cyan']) *
forceatlas.nodes.select(index=target_counts))
```
|
github_jupyter
|
```
# Copyright 2021 Google LLC
# Use of this source code is governed by an MIT-style
# license that can be found in the LICENSE file or at
# https://opensource.org/licenses/MIT.
# Notebook authors: Kevin P. Murphy ([email protected])
# and Mahmoud Soliman ([email protected])
# This notebook reproduces figures for chapter 15 from the book
# "Probabilistic Machine Learning: An Introduction"
# by Kevin Murphy (MIT Press, 2021).
# Book pdf is available from http://probml.ai
```
<a href="https://opensource.org/licenses/MIT" target="_parent"><img src="https://img.shields.io/github/license/probml/pyprobml"/></a>
<a href="https://colab.research.google.com/github/probml/pml-book/blob/main/pml1/figure_notebooks/chapter15_neural_networks_for_sequences_figures.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
## Figure 15.1:<a name='15.1'></a> <a name='rnn'></a>
Recurrent neural network (RNN) for generating a variable length output sequence $\mathbf y _ 1:T $ given an optional fixed length input vector $\mathbf x $.
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.1.png" width="256"/>
## Figure 15.2:<a name='15.2'></a> <a name='rnnTimeMachine'></a>
Example output of length 500 generated from a character level RNN when given the prefix ``the''. We use greedy decoding, in which the most likely character at each step is computed, and then fed back into the model. The model is trained on the book \em The Time Machine by H. G. Wells.
To reproduce this figure, click the open in colab button: <a href="https://colab.research.google.com/github/probml/probml-notebooks/blob/master/notebooks-d2l/rnn_torch.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
## Figure 15.3:<a name='15.3'></a> <a name='imageCaptioning'></a>
Illustration of a CNN-RNN model for image captioning. The pink boxes labeled ``LSTM'' refer to a specific kind of RNN that we discuss in \cref sec:LSTM . The pink boxes labeled $W_ \text emb $ refer to embedding matrices for the (sampled) one-hot tokens, so that the input to the model is a real-valued vector. From https://bit.ly/2FKnqHm . Used with kind permission of Yunjey Choi.
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.3.pdf" width="256"/>
## Figure 15.4:<a name='15.4'></a> <a name='rnnBiPool'></a>
(a) RNN for sequence classification. (b) Bi-directional RNN for sequence classification.
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.4_A.png" width="256"/>
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.4_B.png" width="256"/>
## Figure 15.5:<a name='15.5'></a> <a name='biRNN'></a>
(a) RNN for transforming a sequence to another, aligned sequence. (b) Bi-directional RNN for the same task.
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.5_A.png" width="256"/>
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.5_B.png" width="256"/>
## Figure 15.6:<a name='15.6'></a> <a name='deepRNN'></a>
Illustration of a deep RNN. Adapted from Figure 9.3.1 of <a href='#dive'>[Zha+20]</a> .
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.6.png" width="256"/>
## Figure 15.7:<a name='15.7'></a> <a name='seq2seq'></a>
Encoder-decoder RNN architecture for mapping sequence $\mathbf x _ 1:T $ to sequence $\mathbf y _ 1:T' $.
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.7.png" width="256"/>
## Figure 15.8:<a name='15.8'></a> <a name='NMT'></a>
(a) Illustration of a seq2seq model for translating English to French. The - character represents the end of a sentence. From Figure 2.4 of <a href='#Luong2016thesis'>[Luo16]</a> . Used with kind permission of Minh-Thang Luong. (b) Illustration of greedy decoding. The most likely French word at each step is highlighted in green, and then fed in as input to the next step of the decoder. From Figure 2.5 of <a href='#Luong2016thesis'>[Luo16]</a> . Used with kind permission of Minh-Thang Luong.
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.8_A.png" width="256"/>
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.8_B.png" width="256"/>
## Figure 15.9:<a name='15.9'></a> <a name='BPTT'></a>
An RNN unrolled (vertically) for 3 time steps, with the target output sequence and loss node shown explicitly. From Figure 8.7.2 of <a href='#dive'>[Zha+20]</a> . Used with kind permission of Aston Zhang.
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.9.png" width="256"/>
## Figure 15.10:<a name='15.10'></a> <a name='GRU'></a>
Illustration of a GRU. Adapted from Figure 9.1.3 of <a href='#dive'>[Zha+20]</a> .
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.10.png" width="256"/>
## Figure 15.11:<a name='15.11'></a> <a name='LSTM'></a>
Illustration of an LSTM. Adapted from Figure 9.2.4 of <a href='#dive'>[Zha+20]</a> .
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.11.png" width="256"/>
## Figure 15.12:<a name='15.12'></a> <a name='stsProb'></a>
Conditional probabilities of generating each token at each step for two different sequences. From Figures 9.8.1--9.8.2 of <a href='#dive'>[Zha+20]</a> . Used with kind permission of Aston Zhang.
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.12_A.png" width="256"/>
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.12_B.png" width="256"/>
## Figure 15.13:<a name='15.13'></a> <a name='beamSearch'></a>
Illustration of beam search using a beam of size $K=2$. The vocabulary is $\mathcal Y = \ A,B,C,D,E\ $, with size $V=5$. We assume the top 2 symbols at step 1 are A,C. At step 2, we evaluate $p(y_1=A,y_2=y)$ and $p(y_1=C,y_2=y)$ for each $y \in \mathcal Y $. This takes $O(K V)$ time. We then pick the top 2 partial paths, which are $(y_1=A,y_2=B)$ and $(y_1=C,y_2=E)$, and continue in the obvious way. Adapted from Figure 9.8.3 of <a href='#dive'>[Zha+20]</a> .
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.13.png" width="256"/>
## Figure 15.14:<a name='15.14'></a> <a name='textCNN'></a>
Illustration of the TextCNN model for binary sentiment classification. Adapted from Figure 15.3.5 of <a href='#dive'>[Zha+20]</a> .
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.14.png" width="256"/>
## Figure 15.15:<a name='15.15'></a> <a name='wavenet'></a>
Illustration of the wavenet model using dilated (atrous) convolutions, with dilation factors of 1, 2, 4 and 8. From Figure 3 of <a href='#wavenet'>[Aar+16]</a> . Used with kind permission of Aaron van den Oord.
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.15.png" width="256"/>
## Figure 15.16:<a name='15.16'></a> <a name='attention'></a>
Attention computes a weighted average of a set of values, where the weights are derived by comparing the query vector to a set of keys. From Figure 10.3.1 of <a href='#dive'>[Zha+20]</a> . Used with kind permission of Aston Zhang.
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.16.pdf" width="256"/>
## Figure 15.17:<a name='15.17'></a> <a name='attenRegression'></a>
Kernel regression in 1d. (a) Kernel weight matrix. (b) Resulting predictions on a dense grid of test points.
To reproduce this figure, click the open in colab button: <a href="https://colab.research.google.com/github/probml/probml-notebooks/blob/master/notebooks/kernel_regression_attention.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.17_A.png" width="256"/>
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.17_B.png" width="256"/>
## Figure 15.18:<a name='15.18'></a> <a name='seq2seqAttn'></a>
Illustration of seq2seq with attention for English to French translation. Used with kind permission of Minh-Thang Luong.
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.18.png" width="256"/>
## Figure 15.19:<a name='15.19'></a> <a name='translationHeatmap'></a>
Illustration of the attention heatmaps generated while translating two sentences from Spanish to English. (a) Input is ``hace mucho frio aqui.'', output is ``it is very cold here.''. (b) Input is ``¿todavia estan en casa?'', output is ``are you still at home?''. Note that when generating the output token ``home'', the model should attend to the input token ``casa'', but in fact it seems to attend to the input token ``?''.
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.19_A.png" width="256"/>
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.19_B.png" width="256"/>
## Figure 15.20:<a name='15.20'></a> <a name='EHR'></a>
Example of an electronic health record. In this example, 24h after admission to the hospital, the RNN classifier predicts the risk of death as 19.9\%; the patient ultimately died 10 days after admission. The ``relevant'' keywords from the input clinical notes are shown in red, as identified by an attention mechanism. From Figure 3 of <a href='#Rajkomar2018'>[Alv+18]</a> . Used with kind permission of Alvin Rakomar.
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.20.png" width="256"/>
## Figure 15.21:<a name='15.21'></a> <a name='SNLI'></a>
Illustration of sentence pair entailment classification using an MLP with attention to align the premise (``I do need sleep'') with the hypothesis (``I am tired''). White squares denote active attention weights, blue squares are inactive. (We are assuming hard 0/1 attention for simplicity.) From Figure 15.5.2 of <a href='#dive'>[Zha+20]</a> . Used with kind permission of Aston Zhang.
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.21.png" width="256"/>
## Figure 15.22:<a name='15.22'></a> <a name='showAttendTell'></a>
Image captioning using attention. (a) Soft attention. Generates ``a woman is throwing a frisbee in a park''. (b) Hard attention. Generates ``a man and a woman playing frisbee in a field''. From Figure 6 of <a href='#showAttendTell'>[Kel+15]</a> . Used with kind permission of Kelvin Xu.
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.22_A.png" width="256"/>
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.22_B.png" width="256"/>
## Figure 15.23:<a name='15.23'></a> <a name='transformerTranslation'></a>
Illustration of how encoder self-attention for the word ``it'' differs depending on the input context. From https://ai.googleblog.com/2017/08/transformer-novel-neural-network.html . Used with kind permission of Jakob Uszkoreit.
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.23.png" width="256"/>
## Figure 15.24:<a name='15.24'></a> <a name='multiHeadAttn'></a>
Multi-head attention. Adapted from Figure 9.3.3 of <a href='#dive'>[Zha+20]</a> .
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.24.png" width="256"/>
## Figure 15.25:<a name='15.25'></a> <a name='positionalEncodingSinusoids'></a>
(a) Positional encoding matrix for a sequence of length $n=60$ and an embedding dimension of size $d=32$. (b) Basis functions for columsn 6 to 9.
To reproduce this figure, click the open in colab button: <a href="https://colab.research.google.com/github/probml/probml-notebooks/blob/master/notebooks-d2l/positional_encoding.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.25_A.png" width="256"/>
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.25_B.png" width="256"/>
## Figure 15.26:<a name='15.26'></a> <a name='transformer'></a>
The transformer. From <a href='#Weng2018attention'>[Lil18]</a> . Used with kind permission of Lilian Weng. Adapted from Figures 1--2 of <a href='#Vaswani2017'>[Ash+17]</a> .
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.26.png" width="256"/>
## Figure 15.27:<a name='15.27'></a> <a name='attentionBakeoff'></a>
Comparison of (1d) CNNs, RNNs and self-attention models. From Figure 10.6.1 of <a href='#dive'>[Zha+20]</a> . Used with kind permission of Aston Zhang.
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.27.png" width="256"/>
## Figure 15.28:<a name='15.28'></a> <a name='VIT'></a>
The Vision Transformer (ViT) model. This treats an image as a set of input patches. The input is prepended with the special CLASS embedding vector (denoted by *) in location 0. The class label for the image is derived by applying softmax to the final ouput encoding at location 0. From Figure 1 of <a href='#ViT'>[Ale+21]</a> . Used with kind permission of Alexey Dosovitskiy
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.28.png" width="256"/>
## Figure 15.29:<a name='15.29'></a> <a name='transformers_taxonomy'></a>
Venn diagram presenting the taxonomy of different efficient transformer architectures. From <a href='#Tay2020transformers'>[Yi+20]</a> . Used with kind permission of Yi Tay.
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.29.pdf" width="256"/>
## Figure 15.30:<a name='15.30'></a> <a name='rand_for_fast_atten'></a>
Attention matrix $\mathbf A $ rewritten as a product of two lower rank matrices $\mathbf Q ^ \prime $ and $(\mathbf K ^ \prime )^ \mkern -1.5mu\mathsf T $ with random feature maps $\boldsymbol \phi (\mathbf q _i) \in \mathbb R ^M$ and $\boldsymbol \phi (\mathbf v _k) \in \mathbb R ^M$ for the corresponding queries/keys stored in the rows/columns. Used with kind permission of Krzysztof Choromanski.
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.30.png" width="256"/>
## Figure 15.31:<a name='15.31'></a> <a name='fatten'></a>
Decomposition of the attention matrix $\mathbf A $ can be leveraged to improve attention computations via matrix associativity property. To compute $\mathbf AV $, we first calculate $\mathbf G =(\mathbf k ^ \prime )^ \mkern -1.5mu\mathsf T \mathbf V $ and then $\mathbf q ^ \prime \mathbf G $, resulting in linear in $N$ space and time complexity. Used with kind permission of Krzysztof Choromanski.
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.31.png" width="256"/>
## Figure 15.32:<a name='15.32'></a> <a name='elmo'></a>
Illustration of ELMo bidrectional language model. Here $y_t=x_ t+1 $ when acting as the target for the forwards LSTM, and $y_t = x_ t-1 $ for the backwards LSTM. (We add \text \em bos \xspace and \text \em eos \xspace sentinels to handle the edge cases.) From <a href='#Weng2019LM'>[Lil19]</a> . Used with kind permission of Lilian Weng.
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.32.png" width="256"/>
## Figure 15.33:<a name='15.33'></a> <a name='GPT'></a>
Illustration of (a) BERT and (b) GPT. $E_t$ is the embedding vector for the input token at location $t$, and $T_t$ is the output target to be predicted. From Figure 3 of <a href='#bert'>[Jac+19]</a> . Used with kind permission of Ming-Wei Chang.
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.33_A.png" width="256"/>
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.33_B.png" width="256"/>
## Figure 15.34:<a name='15.34'></a> <a name='bertEmbedding'></a>
Illustration of how a pair of input sequences, denoted A and B, are encoded before feeding to BERT. From Figure 14.8.2 of <a href='#dive'>[Zha+20]</a> . Used with kind permission of Aston Zhang.
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.34.png" width="256"/>
## Figure 15.35:<a name='15.35'></a> <a name='bert-tasks'></a>
Illustration of how BERT can be used for different kinds of supervised NLP tasks. (a) Single sentence classification (e.g., sentiment analysis); (b) Sentence-pair classification (e.g., textual entailment); (d) Single sentence tagging (e.g., shallow parsing); (d) Question answering. From Figure 4 of <a href='#bert'>[Jac+19]</a> . Used with kind permission of Ming-Wei Chang.
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.35_A.png" width="256"/>
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.35_B.png" width="256"/>
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.35_C.png" width="256"/>
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.35_D.png" width="256"/>
## Figure 15.36:<a name='15.36'></a> <a name='T5'></a>
Illustration of how the T5 model (``Text-to-text Transfer Transformer'') can be used to perform multiple NLP tasks, such as translating English to German; determining if a sentence is linguistic valid or not ( \bf CoLA stands for ``Corpus of Linguistic Acceptability''); determining the degree of semantic similarity ( \bf STSB stands for ``Semantic Textual Similarity Benchmark''); and abstractive summarization. From Figure 1 of <a href='#T5'>[Col+19]</a> . Used with kind permission of Colin Raffel.
```
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
!git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
%cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
%reload_ext autoreload
%autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
```
<img src="https://github.com/probml/pml-book/raw/main/pml1/figures/Figure_15.36.png" width="256"/>
## References:
<a name='wavenet'>[Aar+16]</a> V. Aaron, D. Sander, Z. Heiga, S. Karen, V. Oriol, G. Alex, K. Nal, S. Andrew and K. Koray. "WaveNet: A Generative Model for Raw Audio". abs/1609.03499 (2016). arXiv: 1609.03499
<a name='ViT'>[Ale+21]</a> D. Alexey, B. Lucas, K. A. Dirk, Z. Xiaohua, U. T. Mostafa, M. Matthias, H. G. Sylvain, U. Jakob and H. Neil. "An Image is Worth 16x16 Words: Transformers for ImageRecognition at Scale". (2021).
<a name='Rajkomar2018'>[Alv+18]</a> R. Alvin, O. Eyal, C. Kai, D. A. Nissan, H. Michaela, L. PeterJ, L. LiuXiaobing, M. Jake, S. Mimi, S. Patrik, Y. Hector, Z. Kun, Z. Yi, F. Gerardo, D. GavinE, I. Jamie, L. Quoc, L. K. Alexander, T. Justin, W. De, W. James, W. Jimbo, L. Dana, V. L, C. Katherine, P. Michael, M. MadabushiSrinivasan, S. NigamH, B. AtulJ, H. D, C. Claire, C. GregS and D. Jeffrey. "Scalable and accurate deep learning with electronic healthrecords". In: NPJ Digit Med (2018).
<a name='Vaswani2017'>[Ash+17]</a> V. Ashish, S. Noam, P. Niki, U. Jakob, J. Llion, G. AidanN, K. KaiserLukasz and P. Illia. "Attention Is All You Need". (2017).
<a name='T5'>[Col+19]</a> R. Colin, S. Noam, R. Adam, L. LeeKatherine, N. Sharan, M. Michael, Z. ZhouYanqi, L. Wei and L. PeterJ. "Exploring the Limits of Transfer Learning with a UnifiedText-to-Text Transformer". abs/1910.10683 (2019). arXiv: 1910.10683
<a name='bert'>[Jac+19]</a> D. Jacob, C. Ming-Wei, L. Kenton and T. ToutanovaKristina. "BERT: Pre-training of Deep Bidirectional Transformers forLanguage Understanding". (2019).
<a name='showAttendTell'>[Kel+15]</a> X. Kelvin, B. JimmyLei, K. Ryan, C. K. Aaron, S. Ruslan, Z. S and B. Yoshua. "Show, Attend and Tell: Neural Image Caption Generation withVisual Attention". (2015).
<a name='Weng2018attention'>[Lil18]</a> W. Lilian "Attention? Attention!". In: lilianweng.github.io/lil-log (2018).
<a name='Weng2019LM'>[Lil19]</a> W. Lilian "Generalized Language Models". In: lilianweng.github.io/lil-log (2019).
<a name='Luong2016thesis'>[Luo16]</a> M. Luong "Neural machine translation". (2016).
<a name='Tay2020transformers'>[Yi+20]</a> T. Yi, D. Mostafa, B. Dara and M. MetzlerDonald. "Efficient Transformers: A Survey". abs/2009.06732 (2020). arXiv: 2009.06732
<a name='dive'>[Zha+20]</a> A. Zhang, Z. Lipton, M. Li and A. Smola. "Dive into deep learning". (2020).
|
github_jupyter
|
**Introduction to Python**<br/>
Prof. Dr. Jan Kirenz <br/>
Hochschule der Medien Stuttgart
<h1>Table of Contents<span class="tocSkip"></span></h1>
<div class="toc"><ul class="toc-item"><li><span><a href="#Import-data" data-toc-modified-id="Import-data-1"><span class="toc-item-num">1 </span>Import data</a></span></li><li><span><a href="#Data-tidying" data-toc-modified-id="Data-tidying-2"><span class="toc-item-num">2 </span>Data tidying</a></span></li></ul></div>
```
import pandas as pd
```
To get more information about the Pandas syntax, download the [Pandas code cheat sheet](https://pandas.pydata.org/Pandas_Cheat_Sheet.pdf)
### Import data
```
# Import data from GitHub (or from your local computer)
df = pd.read_csv("https://raw.githubusercontent.com/kirenz/datasets/master/wage.csv")
```
### Data tidying
First of all we want to get an overview of the data
```
# show the head (first few observations in the df)
df.head(3)
# show metadata (take a look at the level of measurement)
df.info()
```
---
**Some notes on data types (level of measurement):**
If we need to transform variables into a **numerical format**, we can transfrom the data with pd.to_numeric [see Pandas documenation](https://pandas.pydata.org/pandas-docs/stable/generated/pandas.to_numeric.html):
If the data contains strings, we need to replace them with NaN (not a number). Otherwise we get an error message. Therefore, use errors='coerce' ...
* pandas.to_numeric(arg, errors='coerce', downcast=None)
* errors : {‘ignore’, ‘raise’, ‘coerce’}, default ‘raise’
* If ‘raise’, then invalid parsing will raise an exception
* If ‘coerce’, then invalid parsing will be set as NaN
* If ‘ignore’, then invalid parsing will return the input
To change data into **categorical** format, you can use the following codes:
df['variable'] = pd.Categorical(df['variable'])
If the data is ordinal, we use pandas [CategoricalDtype](https://pandas.pydata.org/pandas-docs/stable/categorical.html)
---
```
# show all columns in the data
df.columns
# rename variable "education" to "edu"
df = df.rename(columns={"education": "edu"})
# check levels and frequency of edu
df['edu'].value_counts()
```
Convert `edu` to ordinal variable with pandas [CategoricalDtype](https://pandas.pydata.org/pandas-docs/stable/categorical.html)
```
from pandas.api.types import CategoricalDtype
# convert to ordinal variable
cat_edu = CategoricalDtype(categories=
['1. < HS Grad',
'2. HS Grad',
'3. Some College',
'4. College Grad',
'5. Advanced Degree'],
ordered=True)
df.edu = df.edu.astype(cat_edu)
```
Now convert `race ` to a categorical variable
```
# convert to categorical variable
df['race'] = pd.Categorical(df['race'])
```
Take a look at the metadata (what happend to `edu` and `race`)?
```
df.info()
```
|
github_jupyter
|
## Series
```
import pandas as pd
import numpy as np
import random
first_series = pd.Series([1,2,3, np.nan ,"hello"])
first_series
series = pd.Series([1,2,3, np.nan ,"hello"], index = ['A','B','C','Unknown','String'])
series
#indexing the Series with custom values
dict = {"Python": "Fun", "C++": "Outdated","Coding":"Hmm.."}
series = pd.Series(dict)
series
# Dict to pandas Series
series[['Coding','Python']]
series.index
series.values
series.describe()
#Series is a mutable data structures and you can easily change any item’s value:
series['Coding'] = 'Awesome'
series
# add new values:
series['Java'] = 'Okay'
series
# If it is necessary to apply any mathematical operation to Series items, you may done it like below:
num_series = pd.Series([1,2,3,4,5,6,None])
num_series_changed = num_series/2
num_series_changed
# NULL/NaN checking can be performed with isnull() and notnull().
print(series.isnull())
print(num_series.notnull())
print(num_series_changed.notnull())
```
## DataFrames
```
data = {'year': [1990, 1994, 1998, 2002, 2006, 2010, 2014],
'winner': ['Germany', 'Brazil', 'France', 'Brazil','Italy', 'Spain', 'Germany'],
'runner-up': ['Argentina', 'Italy', 'Brazil','Germany', 'France', 'Netherlands', 'Argentina'],
'final score': ['1-0', '0-0 (pen)', '3-0', '2-0', '1-1 (pen)', '1-0', '1-0'] }
world_cup = pd.DataFrame(data, columns=['year', 'winner', 'runner-up', 'final score'])
world_cup
# Another way to set a DataFrame is the using of Python list of dictionaries:
data_2 = [{'year': 1990, 'winner': 'Germany', 'runner-up': 'Argentina', 'final score': '1-0'},
{'year': 1994, 'winner': 'Brazil', 'runner-up': 'Italy', 'final score': '0-0 (pen)'},
{'year': 1998, 'winner': 'France', 'runner-up': 'Brazil', 'final score': '3-0'},
{'year': 2002, 'winner': 'Brazil', 'runner-up': 'Germany', 'final score': '2-0'},
{'year': 2006, 'winner': 'Italy','runner-up': 'France', 'final score': '1-1 (pen)'},
{'year': 2010, 'winner': 'Spain', 'runner-up': 'Netherlands', 'final score': '1-0'},
{'year': 2014, 'winner': 'Germany', 'runner-up': 'Argentina', 'final score': '1-0'}
]
world_cup = pd.DataFrame(data_2)
world_cup
print("First 2 Rows: ",end="\n\n")
print (world_cup.head(2),end="\n\n")
print ("Last 2 Rows : ",end="\n\n")
print (world_cup.tail(2),end="\n\n")
print("Using slicing : ",end="\n\n")
print (world_cup[2:4])
```
### CSV
#### Reading:
`df = pd.read_csv("path\to\the\csv\file\for\reading")`
#### Writing:
`df.to_csv("path\to\the\folder\where\you\want\save\csv\file")`
### TXT file(s)
(txt file can be read as a CSV file with other separator (delimiter); we suppose below that columns are separated by tabulation):
#### Reading:
`df = pd.read_csv("path\to\the\txt\file\for\reading", sep='\t')`
#### Writing:
`df.to_csv("path\to\the\folder\where\you\want\save\txt\file", sep='\t')`
### JSON files
(an open-standard format that uses human-readable text to transmit data objects consisting of attribute–value pairs. It is the most common data format used for asynchronous browser/server communication. By its view it is very similar to Python dictionary)
#### Reading:
`df = pd.read_json("path\to\the\json\file\for\reading", sep='\t')`
#### Writing:
`df.to_json("path\to\the\folder\where\you\want\save\json\file", sep='\t')`
```
# To write world_cup Dataframe to a CSV File
world_cup.to_csv("worldcup.csv")
# To save CSV file without index use index=False attribute
print("File Written!",end="\n\n")
#To check if it was written
import os
print(os.path.exists('worldcup.csv'))
# reading from it in a new dataframe df
df = pd.read_csv('worldcup.csv')
print(df.head())
# We can also load the data without index as :
df = pd.read_csv('worldcup.csv',index_col=0)
print(df)
movies=pd.read_csv("data/movies.csv",encoding = "ISO-8859-1")
# encoding is added only for this specific dataset because it gave error with utf-8
movies['release_date'] = movies['release_date'].map(pd.to_datetime)
print(movies.head(20))
#print(movies.describe())
movies_rating = movies['rating']
# Here we are showing only one column, i.e. a Series
print ('type:', type(movies_rating))
movies_rating.head()
# Filtering data
# Let's display only women
movies_user_female = movies[movies['gender']=='F']
print(movies_user_female.head())
#to see all the different values possible for a given column
occupation_list = movies['occupation']
print(occupation_list)
```
### Work with indexes and MultiIndex option
```
import random
indexes = [random.randrange(0,100) for i in range(5)]
data = [{i:random.randint(0,10) for i in 'ABCDE'} for i in range(5)]
df = pd.DataFrame(data, index=[1,2,3,4,5])
df
movies_user_gender_male = movies[movies['gender']=='M']
movies_user_gender_male_dup = movies_user_gender_male.drop_duplicates(keep=False)
print(movies_user_gender_male.head())
# From this we can clearly see age has missing value and that from 100,000 the data reduced to 74260,
# due to filtering and removing duplicates
#gender = female and age between 30 and 40
gender_required = ['F']
filtered_df = movies[((movies['gender'] == 'F') & (movies['age'] > 30) & (movies['age'] <40))]
filtered_df
```
#### Note
In the above fragment you HAVE TO ADD parantheses to each and every argument that is being compared else you will get an error.
As you can see after filtering result tables (i.e. DataFrames) have non-ordered indexes. To fix this trouble you may write the following:
```
filtered_df = filtered_df.reset_index()
filtered_df.head(10)
# set 'user_id' 'movie_id' as index
filtered_df_new = filtered_df.set_index(['user_id','movie_id'])
filtered_df_new.head(10)
# Note that set_index takes only a list as an argument to it.
# if you remove the [] then only the first argument is set as the index.
# By default, `set_index()` returns a new DataFrame.
# so you’ll have to specify if you’d like the changes to occur in place.
# Here we used filtered_df_new to get the new dataframe and now see the type of filtererd_df_new
print(type(filtered_df_new.index))
```
Notice here that we now have a new sort of 'index' which is `MultiIndex`, which contains information about indexing of DataFrame and allows manipulating with this data.
```
filtered_df_new.index.names
# Gives you the names of the two index values we set as a FrozenList
```
Method `get_level_values()` allows to get all values for the corresponding index level.
`get_level_values(0)` corresponds to 'user_id' and `get_level_values(1)` corresponds to 'movie_id'
```
print(filtered_df_new.index.get_level_values(0))
print(filtered_df_new.index.get_level_values(1))
```
### Selection by label and position
Object selection in pandas is now supported by three types of multi-axis indexing.
* `.loc` works on labels in the index;
* `.iloc` works on the positions in the index (so it only takes integers);
The sequence of the following examples demonstrates how we can manipulate with DataFrame’s rows.
At first let’s get the first row of movies:
```
movies.loc[0]
movies.loc[1:3]
```
If you want to return specific columns then you have to specify them as a separate argument of .loc
```
movies.loc[1:3 , 'movie_title']
movies.loc[1:5 , ['movie_title','age','gender']]
# If more than one column is to be selected then you have to give the second argument of .loc as a list
# movies.iloc[1:5 , ['movie_title','age','gender']]
# Gives error as iloc only uses integer values
movies.iloc[0]
movies.iloc[1:5]
# movies.select(lambda x: x%2==0).head() is the same as :
movies.loc[movies.index.map(lambda x: x%2==0)].head()
# .select() has been deprecated for now and will be completely removed in future updates so use .loc
```
## Working with Missing Data
Pandas primarily uses the value np.nan to represent missing data (in table missed/empty value are marked by NaN). It is by default not included in computations. Missing data creates many issues at mathematical or computational tasks with DataFrames and Series and it’s important to know how fight with these values.
```
ages = movies['age']
sum(ages)
```
This is because there are so many cases where Age isn't given and hence takes on the value of np.nan.
We can use `fillna()`a very effecient pandas method for filling missing values
```
ages = movies['age'].fillna(0)
sum(ages)
```
This fills all the values with 0 and calculates the sum.
To remain only rows with non-null values you can use method `dropna()`
```
ages = movies['age'].dropna()
sum(ages)
movies_nonnull = movies.dropna()
movies_nonnull.head(20)
#14th value was dropped because it had a missing value in a column
movies_notnull = movies.dropna(how='all',subset=['age','occupation'])
#Drops all nan values from movies belonging to age and occupation
movies_notnull.info()
#Notice how age and occupation now have nearly 6000 lesser values
```
Thus, if `how='all'`, we get DataFrame, where all values in both columns from subset are NaN.
If `how='any'`, we get DataFrame, where at least one contains NaN.
```
movies.describe()
```
At first, let’s find all unique dates in `‘release_date’` column of `movies` and then select only dates in range lower than 1995.
```
movies['release_date'] = movies['release_date'].map(pd.to_datetime)
# We map it to_datetime as pandas has a set way to deal with dates and then we can effectively work with dates.
unique_dates = movies['release_date'].drop_duplicates().dropna()
# Drops duplicates and nan values
unique_dates
# find dates with year lower/equal than 1995
unique_dates_1 = filter(lambda x: x.year <= 1995, unique_dates)
# filter() takes two arguments. First one should return only boolean values and the second one is the variable over which ititerates over.
# This basically takes unique_dates and uses the lambda function (here, it returns bool values) and filters True cases.
unique_dates_1
```
Here we have used `drop_duplicates()` method to select only `unique` Series values. Then we can filter `movies` with respect to `release_date` condition. Each `datetime` Python object possesses with attributes `year`, `month`, `day`, etc. allowing to extract values of year, month, day, etc. from the date. We call the new DataFrame as `old_movies`.
```
old_movies = movies[movies['release_date'].isin(unique_dates_1)]
old_movies.head()
```
Now we may filter DataFrame `old_movies` by `age` and `rating`. Lets’ drop `timestamp`, `zip_code`
```
# get all users with age less than 25 that rated old movies higher than 3
old_movies_watch = old_movies[(old_movies['age']<25) & (old_movies['rating']>3)]
# Drop timestamp and zip_code
old_movies_watch = old_movies_watch.drop(['timestamp', 'zip_code'],axis=1)
old_movies_watch.head()
```
`Pandas` has support for accelerating certain types of binary numerical and boolean operations using the `numexpr `library (it uses smart chunking, caching, and multiple cores) and the `bottleneck` libraries (is a set of specialized cython routines that are especially fast when dealing with arrays that have NaNs). It allows one to increase pandas functionality a lot. This advantage is shown for some boolean and calculation operations. To count the time elapsed on operation performing we will use the decorator
```
# this function counts the time for a particular operation
def timer(func):
from datetime import datetime
def wrapper(*args):
start = datetime.now()
func(*args)
end = datetime.now()
return 'elapsed time = {' + str(end - start)+'}'
return wrapper
import random
n = 100
# generate rangon datasets
df_1 = pd.DataFrame({'col :'+str(i):[random.randint(-100,100) for j in range(n)]for i in range(n)})
# here we pass a dictionary to the DataFrame() constructor.
# The key is "col : i" where i can take random values and the value for those keys is i.
df_2 = pd.DataFrame({'col :'+str(i):[random.randint(-100,100) for j in range(n)] for i in range(n)})
@timer
def direct_comparison(df_1, df_2):
bool_df = pd.DataFrame({'col_{}'.format(i): [True for j in range(n)] for i in range(n)})
for i in range(len(df_1.index)):
for j in range(len(df_1.loc[i])):
if df_1.loc[i, df_1.columns[j]] >= df_2.loc[i, df_2.columns[j]]:
bool_df.loc[i,bool_df.columns[j]] = False
return bool_df
@timer
def pandas_comparison(df_1, df_2):
return df_1 < df_2
print ('direct_comparison:', (direct_comparison(df_1, df_2)))
print ('pandas_comparison:', (pandas_comparison(df_1, df_2)))
```
As you can see, the difference in speed is too noticeable.
Besides, pandas possesses methods `eq` (equal), `ne` (not equal), `lt` (less then), `gt` (greater than), `le` (less or equal) and `ge` (greater or equal) for simplifying boolean comparison
## Matrix Addition
```
df = pd.DataFrame({'A':[1,2,3],'B':[-2,-3,-4],"C":[7,8,9]})
dfa = pd.DataFrame({'A':[1,2,3],'D':[6,7,8],"C":[12,12,12]})
dfc = df + dfa
dfc
df.le(dfa)
```
You can also apply the reductions: `empty`, `any()`, `all()`, and `bool()` to provide a way to summarize a boolean result:
```
(df<0).all()
# here horyzontal direction for comparison is taking into account and we check all row’s items
(df < 0).all(axis=1)
# here vertical direction for comparison is taking into
# account and we check if just one column’s item satisfies the condition
(df < 0).any()
# here we check if all DataFrame's items satisfy the condition
(df < 0).any().any()
# here we check if DataFrame no one element
df.empty
```
### Descriptive Statistics
|Function|Description|
|--|-------------------------------|
|abs|absolute value|
|count|number of non-null observations|
|cumsum|cumulative sum (a sequence of partial sums of a given sequence)|
|sum|sum of values|
|mean|mean of values|
|mad|mean absolute deviation|
|median|arithmetic median of values|
|min|minimum value|
|max|maximum value|
|mode|mode|
|prod|product of values|
|std|unbiased standard deviation|
|var|unbiased variance|
```
print("Sum : ", movies['age'].sum())
print(df)
print("Mean : ")
print(df.mean())
print("\nMean of all Mean Values: ")
print(df.mean().mean())
print("\nMedian: ")
print(df.median())
print("\nStandard Deviation: ")
print(df.std())
print("\nVariance: ")
print(df.var())
print("\nMax: ")
print(df.max())
```
## Function Applications
When you need to make some transformations with some column’s or row’s elements, then method `map` will be helpful (it works like pure Python function `map()` ). But there is also possibility to apply some function to each DataFrame element (not to a column or a row) – method `apply(map)` aids in this case.
```
movies.loc[:, (movies.dtypes == np.int64) | (movies.dtypes == np.float64)].apply(np.mean)
# This calculates the mean of all the columns present in movies
# to print mean of all row values in movies :
movies.loc[:,(movies.dtypes==np.int64) | (movies.dtypes==np.float64)].apply(np.mean, axis = 1)
```
### Remember
The attribute axis define the horizontal `(axis=1)` or vertical direction for calculations `(axis=0)`
### Groupby with Dictionary
```
import numpy as np
import pandas as pd
d = {'id':[1,2,3],
'Column 1.1':[14,15,16],
'Column 1.2':[10,10,10],
'Column 1.3':[1,4,5],
'Column 2.1':[1,2,3],
'Column 2.2':[10,10,10],
}
df = pd.DataFrame(d)
df
groupby_dict = {'Column 1.1':'Column 1','Column 1.2':'Column 1','Column 1.3':'Column 1','Column 2.1':'Column 2','Column 2.2':'Column 2'}
df = df.set_index('id')
df=df.groupby(groupby_dict,axis=1).min()
df
import numpy as np
import pandas as pd
dict = {
"ID":[1,2,3],
"Movies":["The Godfather","Fight Club","Casablanca"],
"Week_1_Viewers":[30,30,40],
"Week_2_Viewers":[60,40,80],
"Week_3_Viewers":[40,20,20]
};
df = pd.DataFrame(dict);
df
mapping = {"Week_1_Viewers":"Total_Viewers",
"Week_2_Viewers":"Total_Viewers",
"Week_3_Viewers":"Total_Viewers",
"Movies":"Movies"
}
df = df.set_index('ID')
df=df.groupby(mapping,axis=1).sum()
df
```
### Breaking up a String into columns using regex
```
dict = {'movie_data':['The Godfather 1972 9.2',
'Bird Box 2018 6.8',
'Fight Club 1999 8.8']
}
df = pd.DataFrame(dict)
df
df['Name'] = df['movie_data'].str.extract('(\w*\s\w*)', expand=True)
df['Year'] = df['movie_data'].str.extract('(\d\d\d\d)', expand=True)
df['Rating'] = df['movie_data'].str.extract('(\d\.\d)', expand=True)
df
import re
movie_data = ["Name:The Godfather Year: 1972 Rating: 9.2",
"Name:Bird Box Year: 2018 Rating: 6.8",
"Name:Fight Club Year: 1999 Rating: 8.8"]
movies={"Name":[],
"Year":[],
"Rating":[]}
for item in movie_data:
name_field = re.search("Name:.*",item)
if name_field is not None:
name = re.search('\w*\s\w*',name_field.group())
else:
name = None
movies["Name"].append(name.group())
year_field = re.search("Year: .*",item)
if year_field is not None:
year = re.search('\s\d\d\d\d',year_field.group())
else:
year = None
movies["Year"].append(year.group().strip())
rating_field = re.search("Rating: .*",item)
if rating_field is not None:
rating = re.search('\s\d.\d',rating_field.group())
else:
rating - None
movies["Rating"].append(rating.group().strip())
movies
df = pd.DataFrame(movies)
df
```
### Ranking Rows in Pandas
```
import pandas as pd
movies = {'Name': ['The Godfather', 'Bird Box', 'Fight Club'],
'Year': ['1972', '2018', '1999'],
'Rating': ['9.2', '6.8', '8.8']}
df = pd.DataFrame(movies)
df
df['Rating_Rank'] = df['Rating'].rank(ascending=1)
df
df =df.set_index('Rating_Rank')
df
df.sort_index()
# Example 2
import pandas as pd
student_details = {'Name':['Raj','Raj','Raj','Aravind','Aravind','Aravind','John','John','John','Arjun','Arjun','Arjun'],
'Subject':['Maths','Physics','Chemistry','Maths','Physics','Chemistry','Maths','Physics','Chemistry','Maths','Physics','Chemistry'],
'Marks':[80,90,75,60,40,60,80,55,100,90,75,70]
}
df = pd.DataFrame(student_details)
df
df['Mark_Rank'] = df['Marks'].rank(ascending=0)
df = df.set_index('Mark_Rank')
df
df = df.sort_index()
df
```
|
github_jupyter
|
# [Module 2.2] 세이지 메이커 인퍼런스
본 워크샵의 모든 노트북은 `conda_python3` 추가 패키지를 설치하고 모두 이 커널 에서 작업 합니다.
- 1. 배포 준비
- 2. 로컬 앤드포인트 생성
- 3. 로컬 추론
---
이전 노트북에서 인퍼런스 테스트를 완료한 티펙트를 가져옵니다.
```
%store -r artifact_path
```
# 1. 배포 준비
```
print("artifact_path: ", artifact_path)
import sagemaker
sagemaker_session = sagemaker.Session()
bucket = sagemaker_session.default_bucket()
prefix = "sagemaker/DEMO-pytorch-cnn-cifar10"
role = sagemaker.get_execution_role()
```
## 테스트 데이터 세트 로딩
- 로컬에서 저장된 데이터를 가져와서 데이터를 변환 합니다.
- batch_size 만큼 데이터를 로딩하는 데이터 로더를 정의 합니다.
```
import numpy as np
import torchvision, torch
import torchvision.transforms as transforms
from source.utils_cifar import imshow, classes
transform = transforms.Compose(
[transforms.ToTensor(), transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))]
)
testset = torchvision.datasets.CIFAR10(
root='../data', train=False, download=False, transform=transform
)
test_loader = torch.utils.data.DataLoader(
testset, batch_size=4, shuffle=False, num_workers=2
)
# get some random training images
dataiter = iter(test_loader)
images, labels = dataiter.next()
# show images
imshow(torchvision.utils.make_grid(images))
# print labels
print(" ".join("%9s" % classes[labels[j]] for j in range(4)))
```
# 2. 엔드포인트 생성
- 이 과정은 세이지 메이커 엔드포인트를 생성합니다.
```
import os
import time
import sagemaker
from sagemaker.pytorch.model import PyTorchModel
role = sagemaker.get_execution_role()
%%time
endpoint_name = "sagemaker-endpoint-cifar10-classifier-{}".format(int(time.time()))
sm_pytorch_model = PyTorchModel(model_data=artifact_path,
role=role,
entry_point='inference.py',
source_dir = 'source',
framework_version='1.8.1',
py_version='py3',
model_server_workers=1,
)
sm_predictor = sm_pytorch_model.deploy(instance_type='ml.p2.xlarge',
initial_instance_count=1,
endpoint_name=endpoint_name,
wait=True,
)
```
# 3. 로컬 추론
- 준비된 입력 데이터로 로컬 엔드포인트에서 추론
# 엔드 포인트 추론
```
# print images
imshow(torchvision.utils.make_grid(images))
print("GroundTruth: ", " ".join("%4s" % classes[labels[j]] for j in range(4)))
outputs = sm_predictor.predict(images.numpy())
_, predicted = torch.max(torch.from_numpy(np.array(outputs)), 1)
print("Predicted: ", " ".join("%4s" % classes[predicted[j]] for j in range(4)))
```
# Clean-up
위의 엔드포인트를 삭제 합니다.
```
sm_predictor.delete_endpoint()
```
|
github_jupyter
|
```
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from plotnine import *
```
Leitura e visualização dos dados:
```
#carregar os dados no dataframe
df = pd.read_csv('movie_metadata.csv')
df.head()
df.shape
df.dtypes
list(df.columns)
```
Análise Exploratória
```
df['color'].value_counts()
df.drop('color', axis=1, inplace=True)
#verificando se existem valores faltantes nos dados
df.isna().any()
df.isna().sum()
df.dropna(axis=0, subset=['director_name', 'num_critic_for_reviews',
'duration','director_facebook_likes','actor_3_facebook_likes',
'actor_2_name','actor_1_facebook_likes','actor_1_name','actor_3_name',
'facenumber_in_poster','num_user_for_reviews','language','country',
'actor_2_facebook_likes','plot_keywords', 'title_year'],inplace=True)
df.shape
#classificação indicativa do filme, ex. R = livre
df['content_rating'].value_counts()
#preencher os valores faltantes dos outros filmes com a indicação livre
df['content_rating'].fillna('R', inplace = True)
#valores de tamanho de tela
df['aspect_ratio'].value_counts()
#substituindo os valores faltantes dos tamanhos de tela pela mediana dos valores
df['aspect_ratio'].fillna(df['aspect_ratio'].median(), inplace=True)
#substituindo os valores faltantes dos orçamentos dos filmes pela mediana dos valores
df['budget'].fillna(df['budget'].median(), inplace=True)
#substituindo os valores faltantes dos faturamentos dos filmes pela mediana dos valores
df['gross'].fillna(df['gross'].median(), inplace=True)
df.isna().sum()
#ter cuidado e verifiacr os dados duplicados pois eles por estarem em maiores quantidades enviesam o modelo
df.duplicated().sum()
#removendo as duplicatas
df.drop_duplicates(inplace=True)
df.shape
#verificando quais os valores da coluna 'language'
df['language'].value_counts()
df.drop('language', axis=1, inplace=True)
df['country'].value_counts()
df.drop('country', axis=1, inplace=True)
df.shape
#criando uma nova coluna na tabela
df['Profit'] = df['budget'].sub(df['gross'], axis=0)
df.head()
df['Profit_Percentage'] = (df['Profit']/df['gross'])*100
df.head()
#salvar tudo o que fiz até agora
df.to_csv('dados_imdb_dandaraleit.csv', index=False)
```
Visualização dos dados
```
#criando gráfico de correlaciona lucro e nota do IMDB
ggplot(aes(x='imdb_score', y='Profit'), data=df) +\
geom_line() +\
stat_smooth(colour='blue', span=1)
#criando gráfico de correlaciona likes no facebook do filme e nota do IMDB
(ggplot(df)+\
aes(x='imdb_score', y='movie_facebook_likes') +\
geom_line() +\
labs(title='Nota no IMDB vs likes no facebook do filme', x='Nota no IMDB', y='Likes no facebook')
)
#gráfico dos 20 filmes com melhor nota com relação aos atores principais
plt.figure(figsize=(10,8))
df= df.sort_values(by ='imdb_score' , ascending=False)
df2=df.head(20)
ax=sns.pointplot(df2['actor_1_name'], df2['imdb_score'], hue=df2['movie_title'])
ax.set_xticklabels(ax.get_xticklabels(), rotation=40, ha="right")
plt.tight_layout()
plt.show()
```
Preparação dos dados
```
#retirando algumas colunas com dados categóricos
df.drop(columns=['director_name', 'actor_1_name', 'actor_2_name',
'actor_3_name', 'plot_keywords', 'movie_title'], axis=1, inplace=True)
#verificando os valores da coluna 'genre'
df['genres'].value_counts()
df.drop('genres', axis=1, inplace=True)
#retirando as colunas criadas
df.drop(columns=['Profit', 'Profit_Percentage'], axis=1, inplace=True)
#verificando se existem colunas fortemente correlacionadas // Método corr, usando mapa de calor
import numpy as np
corr = df.corr()
sns.set_context("notebook", font_scale=1.0, rc={"lines.linewidth": 2.5})
plt.figure(figsize=(13,7))
mask = np.zeros_like(corr)
mask[np.triu_indices_from(mask, 1)] = True
a = sns.heatmap(corr,mask=mask, annot=True, fmt='.2f')
rotx = a.set_xticklabels(a.get_xticklabels(), rotation=90)
roty = a.set_yticklabels(a.get_yticklabels(), rotation=30)
#criando uma nova coluna combinando as duas colunas muito correlacionadas
df['Other_actors_facebook_likes'] = df['actor_2_facebook_likes'] + df['actor_3_facebook_likes']
#removendo as colunas
df.drop(columns=['actor_2_facebook_likes', 'actor_3_facebook_likes',
'cast_total_facebook_likes'], axis=1, inplace=True)
#criando uma nova coluna combinando as duas colunas muito correlacionadas // Razão entre o número de críticas por reviews e o número de usuários que fizeram reviews
df['critic_review_ratio'] = df['num_critic_for_reviews']/df['num_user_for_reviews']
df.drop(columns=['num_critic_for_reviews', 'num_user_for_reviews'], axis=1, inplace=True)
#verificando se ainda existem colunas fortemente correlacionadas
corr = df.corr()
sns.set_context("notebook", font_scale=1.0, rc={"lines.linewidth": 2.5})
plt.figure(figsize=(13,7))
mask = np.zeros_like(corr)
mask[np.triu_indices_from(mask, 1)] = True
a = sns.heatmap(corr,mask=mask, annot=True, fmt='.2f')
rotx = a.set_xticklabels(a.get_xticklabels(), rotation=90)
roty = a.set_yticklabels(a.get_yticklabels(), rotation=30)
#categorizando os valores de nota do imdb
df['imdb_binned_score']=pd.cut(df['imdb_score'], bins=[0,4,6,8,10], right=True, labels=False)+1
df.head()
#criando novas colunas para transformar os valores categóricos de 'content rating' (classificação indicativa)
#em valores numéricos
df = pd.get_dummies(data = df, columns=['content_rating'], prefix=['content_rating'], drop_first=True)
df.head()
df.to_csv('dados_imdb_com_nota.csv', index=False)
```
Fornecer os dados escolhidos para o modelo a ser treinado e ver os resultados que ele vai prever. Aprendizado Supervisionado
```
#escolhendo as colunas do dataframe que serão nossos valores de entrada para o modelo
X=pd.DataFrame(columns=['duration','director_facebook_likes','actor_1_facebook_likes','gross',
'num_voted_users','facenumber_in_poster','budget','title_year','aspect_ratio',
'movie_facebook_likes','Other_actors_facebook_likes','critic_review_ratio',
'content_rating_G','content_rating_GP',
'content_rating_M','content_rating_NC-17','content_rating_Not Rated',
'content_rating_PG','content_rating_PG-13','content_rating_Passed',
'content_rating_R','content_rating_TV-14','content_rating_TV-G',
'content_rating_TV-PG','content_rating_Unrated','content_rating_X'],data=df)
#escolhendo a(s) coluna(s) do dataframe que serão a resposta do modelo
y = pd.DataFrame(columns=['imdb_binned_score'], data=df)
#importando o pacote de divisão dos dados em treinamento e teste
from sklearn.model_selection import train_test_split
#dividindo os dados em treinamento e teste
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
#normalizando os dados
from sklearn.preprocessing import StandardScaler
sc_X = StandardScaler()
X_train = sc_X.fit_transform(X_train)
X_test = sc_X.transform(X_test)
X.isna().sum()
```
Utilização de modelo de regressão logística. Ele tenta descobrir uma função matemática que simule a distribuição dos dados. Modelo mais simples, disponível no sklearning.
```
#importando, configurando e treinando o modelo de regressão
from sklearn.linear_model import LogisticRegression
logit =LogisticRegression(verbose=1, max_iter=1000)
logit.fit(X_train,np.ravel(y_train,order='C'))
y_pred=logit.predict(X_test)
#verificando os valores preditos
y_pred
#importando o pacote de métricas e calculando a matriz de confusão
from sklearn import metrics
cnf_matrix = metrics.confusion_matrix(y_test, y_pred)
#código para melhor visualização da matriz de confusão
#alternativa:
# print(cnf_matrix)
import itertools
def plot_confusion_matrix(cm, classes,
normalize=False,
title='Confusion matrix',
cmap=plt.cm.Blues):
"""
This function prints and plots the confusion matrix.
Normalization can be applied by setting `normalize=True`.
"""
if normalize:
cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
plt.imshow(cm, interpolation='nearest', cmap=cmap)
plt.title(title)
plt.colorbar()
tick_marks = np.arange(len(classes))
plt.xticks(tick_marks, classes, rotation=45)
plt.yticks(tick_marks, classes)
fmt = '.2f' if normalize else 'd'
thresh = cm.max() / 2.
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i, format(cm[i, j], fmt),
horizontalalignment="center",
color="white" if cm[i, j] > thresh else "black")
plt.ylabel('True label')
plt.xlabel('Predicted label')
plt.tight_layout()
#imprimindo a matriz de confusão
plot_confusion_matrix(cnf_matrix, classes=['1','2', '3', '4'],
title='Matriz de confusão não normalizada', normalize=False)
```
Modelo de Machine Learn não se dá muito bem com dados desbalanceados, ou seja, quando se tem mais dados de uma categoria, ela é que vai ser melhor prevista, como por exemplo a categoria 3 de filmes bons, foi da qual mais o modelo se aproximou, será que é esta categoria que tem mais dados? Vamos ver abaixo.
P.s: Como fazer para balancear?
```
#verificando quantos valores existem de cada categoria em 'imdb_binned_score'
df['imdb_binned_score'].value_counts()
#métricas finais, outro modo de olhar o número de amostras de cada categoria/classe
print(metrics.classification_report(y_test, y_pred, target_names=['1','2', '3', '4']))
#importante o pacote para salvar o modelo
import pickle
#definindo em qual caminho vamos salvar o modelo em uma variável para ficar mais organizado. ex: modelo_treinado.
modelo_treinado = 'modelo_imdb.sav'
#salvando o modelo
pickle.dump(logit, open(modelo_treinado, 'wb'))
#carregando o modelo treinado
modelo_carregado = pickle.load(open(modelo_treinado, 'rb'))
#Olhando o conteúdo de um vetor de teste
X_test[0]
#fazendo predição do novo dado com o modelo carregado
modelo_carregado.predict([X_test[0]])
```
O resultado deu que os filmes com os valores mais acima testados estão dentro da categoria de filme 3 (acima), que se traduz em filmes bons.
|
github_jupyter
|
# 使用PyNative进行神经网络的训练调试体验
[](https://gitee.com/mindspore/docs/blob/master/docs/notebook/mindspore_debugging_in_pynative_mode.ipynb)
## 概述
在神经网络训练过程中,数据是否按照自己设计的神经网络运行,是使用者非常关心的事情,如何去查看数据是怎样经过神经网络,并产生变化的呢?这时候需要AI框架提供一个功能,方便使用者将计算图中的每一步变化拆开成单个算子或者深层网络拆分成多个单层来调试观察,了解分析数据在经过算子或者计算层后的变化情况,MindSpore在设计之初就提供了这样的功能模式--`PyNative_MODE`,与此对应的是`GRAPH_MODE`,他们的特点分别如下:
- PyNative模式:也称动态图模式,将神经网络中的各个算子逐一下发执行,方便用户编写和调试神经网络模型。
- Graph模式:也称静态图模式或者图模式,将神经网络模型编译成一整张图,然后下发执行。该模式利用图优化等技术提高运行性能,同时有助于规模部署和跨平台运行。
默认情况下,MindSpore处于Graph模式,可以通过`context.set_context(mode=context.PYNATIVE_MODE)`切换为PyNative模式;同样地,MindSpore处于PyNative模式时,可以通过`context.set_context(mode=context.GRAPH_MODE)`切换为Graph模式。
<br/>本次体验我们将使用一张手写数字图片跑完单次训练,在PyNative模式下,将数据在训练中经过每层神经网络的变化情况打印出来,并计算对应的loss值以及梯度值`grads`,整体流程如下:
1. 环境准备,设置PyNative模式。
2. 数据集准备,并取用单张图片数据。
3. 构建神经网络并设置每层断点打印数据。
4. 构建梯度计算函数。
5. 执行神经网络训练,查看网络各参数梯度。
> 本文档适用于GPU和Ascend环境。
## 环境准备
使用`context.set_context`将模式设置成`PYNATIVE_MODE`。
```
from mindspore import context
context.set_context(mode=context.PYNATIVE_MODE, device_target="GPU")
```
## 数据准备
### 数据集的下载
以下示例代码将数据集下载并解压到指定位置。
```
import os
import requests
requests.packages.urllib3.disable_warnings()
def download_dataset(dataset_url, path):
filename = dataset_url.split("/")[-1]
save_path = os.path.join(path, filename)
if os.path.exists(save_path):
return
if not os.path.exists(path):
os.makedirs(path)
res = requests.get(dataset_url, stream=True, verify=False)
with open(save_path, "wb") as f:
for chunk in res.iter_content(chunk_size=512):
if chunk:
f.write(chunk)
print("The {} file is downloaded and saved in the path {} after processing".format(os.path.basename(dataset_url), path))
train_path = "datasets/MNIST_Data/train"
test_path = "datasets/MNIST_Data/test"
download_dataset("https://mindspore-website.obs.myhuaweicloud.com/notebook/datasets/mnist/train-labels-idx1-ubyte", train_path)
download_dataset("https://mindspore-website.obs.myhuaweicloud.com/notebook/datasets/mnist/train-images-idx3-ubyte", train_path)
download_dataset("https://mindspore-website.obs.myhuaweicloud.com/notebook/datasets/mnist/t10k-labels-idx1-ubyte", test_path)
download_dataset("https://mindspore-website.obs.myhuaweicloud.com/notebook/datasets/mnist/t10k-images-idx3-ubyte", test_path)
```
下载的数据集文件的目录结构如下:
```text
./datasets/MNIST_Data
├── test
│ ├── t10k-images-idx3-ubyte
│ └── t10k-labels-idx1-ubyte
└── train
├── train-images-idx3-ubyte
└── train-labels-idx1-ubyte
```
### 数据集的增强操作
下载下来后的数据集,需要通过`mindspore.dataset`处理成适用于MindSpore框架的数据,再使用一系列框架中提供的工具进行数据增强操作来适应LeNet网络的数据处理需求。
```
import mindspore.dataset.vision.c_transforms as CV
import mindspore.dataset.transforms.c_transforms as C
from mindspore.dataset.vision import Inter
from mindspore import dtype as mstype
import mindspore.dataset as ds
import numpy as np
def create_dataset(data_path, batch_size=32, repeat_size=1,
num_parallel_workers=1):
""" create dataset for train or test
Args:
data_path (str): Data path
batch_size (int): The number of data records in each group
repeat_size (int): The number of replicated data records
num_parallel_workers (int): The number of parallel workers
"""
# define dataset
mnist_ds = ds.MnistDataset(data_path)
# define some parameters needed for data enhancement and rough justification
resize_height, resize_width = 32, 32
rescale = 1.0 / 255.0
shift = 0.0
rescale_nml = 1 / 0.3081
shift_nml = -1 * 0.1307 / 0.3081
# according to the parameters, generate the corresponding data enhancement method
resize_op = CV.Resize((resize_height, resize_width), interpolation=Inter.LINEAR)
rescale_nml_op = CV.Rescale(rescale_nml, shift_nml)
rescale_op = CV.Rescale(rescale, shift)
hwc2chw_op = CV.HWC2CHW()
type_cast_op = C.TypeCast(mstype.int32)
# using map method to apply operations to a dataset
mnist_ds = mnist_ds.map(operations=type_cast_op, input_columns="label", num_parallel_workers=num_parallel_workers)
mnist_ds = mnist_ds.map(operations=resize_op, input_columns="image", num_parallel_workers=num_parallel_workers)
mnist_ds = mnist_ds.map(operations=rescale_op, input_columns="image", num_parallel_workers=num_parallel_workers)
mnist_ds = mnist_ds.map(operations=rescale_nml_op, input_columns="image", num_parallel_workers=num_parallel_workers)
mnist_ds = mnist_ds.map(operations=hwc2chw_op, input_columns="image", num_parallel_workers=num_parallel_workers)
# process the generated dataset
buffer_size = 10000
mnist_ds = mnist_ds.shuffle(buffer_size=buffer_size)
mnist_ds = mnist_ds.batch(batch_size, drop_remainder=True)
mnist_ds = mnist_ds.repeat(repeat_size)
return mnist_ds
```
### 数据图片的提取
本次体验我们只需要一张图片进行训练体验,所以随机选取`batch`中的第一张图片`image`和下标`label`。
```
from mindspore import Tensor
import matplotlib.pyplot as plt
train_data_path = "./datasets/MNIST_Data/train/"
ms_dataset = create_dataset(train_data_path)
dict_data = ms_dataset.create_dict_iterator()
data = next(dict_data)
images = data["image"].asnumpy()
labels = data["label"].asnumpy()
print(images.shape)
count = 1
for i in images:
plt.subplot(4, 8, count)
plt.imshow(np.squeeze(i))
plt.title('num:%s'%labels[count-1])
plt.xticks([])
count += 1
plt.axis("off")
plt.show()
```
当前batch的image数据如上图,后面的体验将提取第一张图片进行训练操作。
### 定义图像显示函数
定义一个图像显示函数`image_show`,插入LeNet5的前面4层神经网络中抽取图像数据并显示。
```
def image_show(x):
count = 1
x = x.asnumpy()
number = x.shape[1]
sqrt_number = int(np.sqrt(number))
for i in x[0]:
plt.subplot(sqrt_number, int(number/sqrt_number), count)
plt.imshow(i)
count += 1
plt.show()
```
## 构建神经网络LeNet5
在`construct`中使用`image_show`,查看每层网络后的图片变化。
> 这里只抽取了图片显示,想要查看具体的数值,可以按照自己的需要进行`print(x)`。
```
import mindspore.nn as nn
import mindspore.ops as ops
from mindspore import dtype as mstype
from mindspore.common.initializer import Normal
class LeNet5(nn.Cell):
"""Lenet network structure."""
# define the operator required
def __init__(self, num_class=10, num_channel=1):
super(LeNet5, self).__init__()
self.conv1 = nn.Conv2d(num_channel, 6, 5, pad_mode='valid')
self.conv2 = nn.Conv2d(6, 16, 5, pad_mode='valid')
self.fc1 = nn.Dense(16 * 5 * 5, 120, weight_init=Normal(0.02))
self.fc2 = nn.Dense(120, 84, weight_init=Normal(0.02))
self.fc3 = nn.Dense(84, num_class, weight_init=Normal(0.02))
self.relu = nn.ReLU()
self.max_pool2d = nn.MaxPool2d(kernel_size=2, stride=2)
self.flatten = nn.Flatten()
self.switch = 1
def construct(self, x):
x = self.conv1(x)
if self.switch > 0:
print("The first layer: convolution layer")
image_show(x)
x = self.relu(x)
x = self.max_pool2d(x)
if self.switch > 0:
print("The second layer: pool layer")
image_show(x)
x = self.conv2(x)
if self.switch > 0:
print("The third layer: convolution layer")
image_show(x)
x = self.relu(x)
x = self.max_pool2d(x)
if self.switch > 0:
print("The fourth layer: pool layer")
image_show(x)
x = self.flatten(x)
x = self.relu(self.fc1(x))
x = self.relu(self.fc2(x))
x = self.fc3(x)
self.switch -= 1
return x
network = LeNet5()
print("layer conv1:", network.conv1)
print("*"*40)
print("layer fc1:", network.fc1)
```
## 构建计算梯度函数GradWrap
构建梯度下降求值函数,该函数可计算网络中所有权重的梯度。
```
from mindspore import Tensor, ParameterTuple
class GradWrap(nn.Cell):
""" GradWrap definition """
def __init__(self, network):
super(GradWrap, self).__init__(auto_prefix=False)
self.network = network
self.weights = ParameterTuple(filter(lambda x: x.requires_grad, network.get_parameters()))
def construct(self, x, label):
weights = self.weights
return ops.GradOperation(get_by_list=True)(self.network, weights)(x, label)
```
## 执行训练函数
可以从网络中查看当前`batch`中第一张图片`image`的数据在神经网络中的变化,经过神经网络后,计算出其loss值,再根据loss值求参数的偏导即神经网络的梯度值,最后将梯度和loss进行优化。
- image:为当前batch的第一张图片。
- output:表示图片数据经过当前网络训练后生成的值,其张量为(1,10)。
```
from mindspore.nn import WithLossCell, Momentum
net = LeNet5()
optimizer = Momentum(filter(lambda x: x.requires_grad, net.get_parameters()), 0.1, 0.9)
criterion = nn.SoftmaxCrossEntropyWithLogits(sparse=True, reduction='mean')
net_with_criterion = WithLossCell(net, criterion)
train_network = GradWrap(net_with_criterion)
train_network.set_train()
image = images[0][0]
image = image.reshape((1, 1, 32, 32))
plt.imshow(np.squeeze(image))
plt.show()
input_data = Tensor(np.array(image).astype(np.float32))
label = Tensor(np.array([labels[0]]).astype(np.int32))
output = net(Tensor(input_data))
```
将第一层卷积层、第二层池化层、第三层卷积层和第四层池化层的图像特征打印出来后,直观地看到随着深度的增加,图像特征几乎无法用肉眼识别,但是机器可以用这些特征进行学习和识别,后续的全连接层为二维数组,无法图像显示,但可以打印出数据查看,由于数据量过大此处就不打印了,用户可以根据需求选择打印。
### 求loss值和梯度值,并进行优化
先求得loss值,后再根据loss值求梯度(偏导函数值),使用优化器`optimizer`进行优化。
- `loss_output`:即为loss值。
- `grads`:即网络中每层权重的梯度。
- `net_params`:即网络中每层权重的名称,用户可执行`print(net_params)`自行打印。
- `success`:优化参数。
```
loss_output = criterion(output, label)
grads = train_network(input_data, label)
net_params = net.trainable_params()
for i, grad in enumerate(grads):
print("{}:".format(net_params[i].name), grad.shape)
success = optimizer(grads)
loss = loss_output.asnumpy()
print("Loss_value:", loss)
```
具体每层权重的参数有多少,从打印出来的梯度张量能够看到,对应的梯度值用户可以自行选择打印。
## 总结
本次体验我们将MindSpore的数据增强后,使用了`create_dict_iterator`转化成字典,再单独取出来;使用PyNative模式将神经网络分层单独调试,提取并观察数据;用`WithLossCell`在PyNative模式下计算loss值;构造梯度函数`GradWrap`将神经网络中各个权重的梯度计算出来,以上就是本次的全部体验内容。
|
github_jupyter
|
<a href="https://colab.research.google.com/github/RachitBansal/AppliancePower_TimeSeries/blob/master/ARIMA_Ukdale.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
from google.colab import drive
drive.mount('/content/drive',force_remount=True)
from sklearn.externals import joblib
import numpy as np
import matplotlib.pyplot as plt
eq = input("Enter equipment: ")
train_x = np.load(file='./drive/My Drive/ukdale_'+eq+'_x.npy')
train_y = np.load(file='./drive/My Drive/ukdale_'+eq+'_y.npy')
test_y = np.load(file='./drive/My Drive/ukdale_'+eq+'_ty.npy')
test_x = np.load(file='./drive/My Drive/ukdale_'+eq+'_tx.npy')
from pandas import datetime
import pandas as pd
# series = joblib.load("hour_resampled_data.pkl")
# sample = series
# sample = np.array(sample)
# sample = sample[3000:4500,1:2]
# series = np.array(series)
# series = series[:3000,1:2]
# print(series.shape)
# series = pd.DataFrame(series)
# #series.drop(axis = "index")
# print(series.head())
# equipment = int(input('equipment: '))
series = test_x[:3000, 0]
plt.plot(series)
plt.show()
from pandas import read_csv
from pandas import datetime
from matplotlib import pyplot
from pandas.plotting import autocorrelation_plot
# series = read_csv('shampoo-sales.csv', header=0, parse_dates=[0], index_col=0, squeeze=True, date_parser=parser)
autocorrelation_plot(series)
pyplot.show()
from pandas import datetime
from pandas import DataFrame
from statsmodels.tsa.arima_model import ARIMA
from matplotlib import pyplot
import numpy as np
def parser(x):
return datetime.strptime('190'+x, '%Y-%m')
# series = read_csv('shampoo-sales.csv', header=0, parse_dates=[0], index_col=0, squeeze=True, date_parser=parser)
# fit model
series = np.array(series)
model = ARIMA(series, order=(5,1,0))
model_fit = model.fit(disp=0)
print(model_fit.summary())
# plot residual errors
residuals = DataFrame(model_fit.resid)
residuals.plot()
pyplot.show()
residuals.plot(kind='kde')
pyplot.show()
print(residuals.describe())
from pandas import datetime
from matplotlib import pyplot
from statsmodels.tsa.arima_model import ARIMA
from sklearn.metrics import mean_squared_error,mean_absolute_error
# equipment = 3
len(list(train_x[0].reshape(-1)))
history = list(train_x[0].reshape(-1))
for i in range(train_x.shape[0] - 1):
history.append(train_x[i+1][-1])
plt.plot(history)
history = list(train_x[0].reshape(-1))
for i in range(1000):
history.append(train_x[-1000+i][-1])
# history.append(x for x in test_x[0].reshape(-1))
model = ARIMA(history, order=(5,1,0))
model_fit = model.fit(disp=0)
history = list(test_x[0].reshape(-1))
predictions = []
# history = [x for x in test_x[i].reshape(-1) for i in range(1000)]
for t in range(1000):
model = ARIMA(history, order=(5,1,0))
model_fit = model.fit(disp=0)
output = model_fit.forecast()
yhat = output[0]
predictions.append(yhat)
obs = test_y[t][0][0]
history.append(obs)
if(t%50==0):
print('predicted=%f, expected=%f' % (yhat, obs))
predictions = np.array(predictions)
print(predictions.shape)
print(test_y.shape)
error = mean_squared_error(test_y[:1000].reshape(-1), predictions)
print('Test MSE: %.3f' % error)
print("RMSE : %.3f"%(np.sqrt(error)))
print("MAE : %.3f"%(mean_absolute_error(test_y[:1000].reshape(-1),predictions)))
# plot
pyplot.plot(test_y[:1000].reshape(-1))
pyplot.plot(predictions)
np.save(arr = np.array(predictions), file = './drive/My Drive/arima_ukdale_preds_1000_eq'+eq+'.npy')
import time
t1 = time.time()
times = []
for t in range(50):
model = ARIMA(history[t], order=(5,1,0))
model_fit = model.fit(disp=0)
t1 = time.time()
output = model_fit.forecast()
t2 = time.time()
times.append(t2-t1)
print(times)
print(sum(times))
def mean_abs_pct_error(actual_values, forecast_values):
err=0
actual_values = pd.DataFrame(actual_values)
forecast_values = pd.DataFrame(forecast_values)
for i in range(len(forecast_values)):
err += np.abs(actual_values.values[i] - forecast_values.values[i])/actual_values.values[i]
return err[0] * 100/len(forecast_values)
mean_abs_pct_error(test,predictions)
```
|
github_jupyter
|
```
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# http://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
import sys
print(sys.version)
##################
# Imports #
##################
# import the podaac package
import podaac.podaac as podaac
# import the podaac_utils package
import podaac.podaac_utils as utils
# import the mcc package
import podaac.mcc as mcc
#######################
# Class instantiation #
#######################
# then create an instance of the Podaac class
p = podaac.Podaac()
# then create an instance of the PodaacUtils class
u = utils.PodaacUtils()
# then create an instance of the MCC class
m = mcc.MCC()
###########################################
# Lets look at some convenience functions #
###########################################
print(u.list_all_available_extract_granule_dataset_ids())
print(u.list_all_available_extract_granule_dataset_short_names())
print(u.list_all_available_granule_search_dataset_ids())
print(u.list_all_available_granule_search_dataset_short_names())
print(u.list_available_granule_search_level2_dataset_ids())
print(u.list_available_granule_search_level2_dataset_short_names())
# Now lets take a look at using the results from above to interact with the PO.DAAC Webservices
########################
# PO.DAAC Web Services #
########################
# First lets retrieve dataset metadata
print(p.dataset_metadata(dataset_id='PODAAC-GHMG2-2PO01'))
# Lets try searching for datasets
print(p.dataset_search(keyword='modis'))
# Now retrieve dataset variables
print(p.dataset_variables(dataset_id='PODAAC-GHMDA-2PJ02'))
# Now extracting an individual granule
print(p.extract_l4_granule(dataset_id='PODAAC-AQR50-3YVAS'))
# Now retrieving granule metadata
print(p.granule_metadata(dataset_id='PODAAC-GHMG2-2PO01'), granule_name='20120912-MSG02-OSDPD-L2P-MSG02_0200Z-v01.nc')
from IPython.display import Image
from IPython.core.display import HTML
result = p.granule_preview(dataset_id='PODAAC-ASOP2-25X01')
# Additionally, we can search metadata for list of granules archived within the last 24 hours in Datacasting format.
print(p.last24hours_datacasting_granule_md(dataset_id='PODAAC-AQR50-3YVAS'))
# Now Searching for Granules
print(p.granule_search(dataset_id='PODAAC-ASOP2-25X01',bbox='0,0,180,90',start_time='2013-01-01T01:30:00Z',end_time='2014-01-01T00:00:00Z',start_index='1', pretty='True'))
######################################################
# Working with Metadata Compliance Webservices (mcc) #
######################################################
# Compliance Check a Local File
print(m.check_local_file(acdd_version='1.3', gds2_parameters='L4', file_upload='../podaac/tests/ascat_20130719_230600_metopa_35024_eps_o_250_2200_ovw.l2_subsetted_.nc', response='json'))
# Compliance Check a Remote File
print(m.check_remote_file(checkers='CF', url_upload='http://test.opendap.org/opendap/data/ncml/agg/dated/CG2006158_120000h_usfc.nc', response='json'))
# Thank you for trying out podaacpy
# That concludes the quick start. Hopefully this has been helpful in providing an overview
# of the main podaacpy features. If you have any issues with this document then please register
# them at the issue tracker - https://github.com/nasa/podaacpy/issues
# Please use labels to classify your issue.
# Thanks,
# Lewis John McGibbney
```
|
github_jupyter
|
```
import numpy as np
import sklearn
import os
import pandas as pd
import scipy
from sklearn.linear_model import LinearRegression
import sklearn
import matplotlib.pyplot as plt
import torch
import torch.nn as nn
import torch.nn.functional as F
import random
from torchvision import datasets, transforms
import copy
#!pip install line_profiler
os.chdir("/content/drive/MyDrive/Winter_Research")
```
### Load Data
```
master_df = pd.read_csv("Sentinel2_Traffic/Traffic_Data/5_state_traffic.csv")
master_df = master_df.set_index("Unnamed: 0")
CA_x, CA_y = [], []
KS_x, KS_y = [], []
MT_x, MT_y = [], []
TX_x, TX_y = [], []
OH_x, OH_y = [], []
states = {"CA" : [CA_x, CA_y, "Roi_1"],
"KS" : [KS_x, KS_y, "Roi_2"],
"MT" : [MT_x, MT_y, "Roi_3"],
"TX" : [TX_x, TX_y, "Roi_4"],
"OH" : [OH_x, OH_y, "Roi_5"]}
for st in ["CA", "KS", "MT", "TX", "OH"]:
path = "Rois/" + states[st][2] + "/greedy_a/"
imgs = os.listdir(path)
for img in imgs:
date = img.split('.')[0]
photo = np.loadtxt(path + img).reshape(-1, 7, 3)
if photo[pd.isnull(photo)].shape[0] == 0:
print("waasss", photo.shape[0])
if st == "CA" and photo.shape[0] != 72264:
continue
if st == "KS" and photo.shape[0] != 69071:
continue
if st == "MT" and photo.shape[0] != 72099:
continue
if st == "TX" and photo.shape[0] != 71764:
continue
if st == "OH" and photo.shape[0] != 62827:
continue
if date in list(master_df.index):
if not pd.isna(master_df.loc[date][st]):
states[st][0].append(photo)
states[st][1].append(master_df.loc[date][st])
len(states['CA'][0])
states
for s in ["CA", "KS", "MT", "TX", "OH"]:
for i in range(len(states[s][0])):
states[s][0][i] = states[s][0][i][:8955]
def load(states, mean_bal_x=True, mean_bal_y=True):
img_st = []
y = []
for s in states:
val = np.array(states[s][0])
if mean_bal_x:
img_st.append((val - np.mean(val, axis=0)) / np.mean(val, axis=0))
else:
img_st.append(val)
for i in states[s][1]:
if mean_bal_y:
y.append((i - np.mean(states[s][1])) / np.mean(states[s][1]))
else:
y.append(i)
X = np.concatenate(img_st)
return X, y
X, y = load(states, mean_bal_x=False, mean_bal_y=False)
print(len(X), len(y))
def load_some(states):
img_st = []
y = []
for s in states:
if s == "MT":
continue
img_st.append(np.array(states[s][0]))
for i in states[s][1]:
y.append(i)
X = np.concatenate(img_st)
return np.array(X), np.array(y)
def load_MT(states):
img_st = np.array(states["MT"][0])
y_test = []
for i in states["MT"][1]:
y_test.append(i)
return img_st, np.array(y_test)
def load_some_augment(X, y):
new_imgs = []
new_y = []
for i in range(X.shape[0]):
a = random.randint(0, X.shape[0] - 1)
b = random.randint(0, X.shape[0] - 1)
new_imgs.append(mush(X[a], X[b]))
new_y.append(y[a] + y[b])
return np.array(new_imgs), np.array(new_y)
def mush(img_a, img_b):
new_img = np.zeros((img_a.shape[0] + img_b.shape[0], 7, 3))
buffer = int((img_a.shape[0] + 0.5) // 8)
# print(buffer)
for i in range(0, img_a.shape[0]*2, buffer*2):
# print(i)
# print(img_a[i // 2: i // 2 + buffer, :, :].shape)
if (i // 2) + buffer > img_a.shape[0]:
buffer = img_a.shape[0] - (i // 2)
new_img[i: i + buffer, :, :] = img_a[i // 2: i // 2 + buffer, :, :]
new_img[i + buffer: i + 2 * buffer, :, :] = img_b[i // 2: i // 2 + buffer, :, :]
return new_img
#X, y = load_some_augment(X, y)
# X_test, y_test = load_MT(states)
# X_test, y_test = augment(X_test)
# y_test
# X_test = np.concatenate((X_test, X_test), axis=1)
# y_test = y_test + y_test
def augment(X, y):
new_imgs = []
new_y = []
for i in range(X.shape[0]):
new_y.extend([y[i]]*4)
#OG
#new_imgs.append(X[i]) #1
#Chunk Half
chunk1 = X[i][:X[i].shape[0] // 3, :, :]
chunk2 = X[i][X[i].shape[0] // 3 : 2 * X[i].shape[0] // 3, :, :]
chunk3 = X[i][2 * X[i].shape[0] // 3 :, :, :]
chunks = {0 : chunk1, 1 : chunk2, 2 : chunk3}
# for order in [(0, 1, 2), (0, 2, 1)]: #, (1, 0, 2), (1, 2, 0), (2, 1, 0), (2, 0, 1)
# new_img = np.zeros(X[i].shape)
# new_img[:X[i].shape[0] // 3, :, :] = chunks[order[0]]
# new_img[X[i].shape[0] // 3 : 2 * X[i].shape[0] // 3, :, :] = chunks[order[1]]
# new_img[2 * X[i].shape[0] // 3 :, :, :] = chunks[order[2]]
new_img = X[i]
new_imgs.append(new_img)
new_imgs.append(np.flip(new_img, axis=0))
new_imgs.append(np.flip(new_img, axis=1))
new_imgs.append(np.flip(np.flip(new_img, axis=0), axis=1))
return np.array(new_imgs), np.array(new_y)
# Can't sugment befoire split
# X, y = load_some(states)
# X, y = augment(X, y)
# print(X.shape, y.shape)
# y_baseline = np.loadtxt("Baseline_Y.csv", delimiter=',')
print(torch.cuda.device_count())
cuda0 = torch.device('cuda:0')
#Train, test, val, split
# 41
#Just MT version
X_train_t, X_test, y_train_t, y_test = sklearn.model_selection.train_test_split(X, y, test_size=0.2, random_state=41)
# X_train_t = X
# y_train_t = y
X_train, X_val, y_train, y_val = sklearn.model_selection.train_test_split(X_train_t, y_train_t, test_size=0.1, random_state=41)
X_train, y_train = augment(X_train, y_train)
#To tensors
X_train = torch.as_tensor(X_train, device=cuda0, dtype=torch.float)
X_test = torch.as_tensor(X_test, device=cuda0, dtype=torch.float)
X_val = torch.as_tensor(X_val, device=cuda0, dtype=torch.float)
y_train = torch.as_tensor(y_train, device=cuda0, dtype=torch.float)
y_val = torch.as_tensor(y_val, device=cuda0, dtype=torch.float)
y_test = torch.as_tensor(y_test, device=cuda0, dtype=torch.float)
#Reshape y
y_train = y_train.reshape(y_train.shape[0], 1)
y_test = y_test.reshape(y_test.shape[0], 1)
y_val = y_val.reshape(y_val.shape[0], 1)
print(X_train.shape, y_train.shape, X_val.shape, y_val.shape, X_test.shape, y_test.shape)
X_train = X_train.permute(0, 3, 1, 2)
X_val = X_val.permute(0, 3, 1, 2)
X_test = X_test.permute(0, 3, 1, 2)
```
# PyTorch Model
```
del model
X_train.shape
# OG 3 ==> 10, reg layer, 10 ==> 10, flatten, ==> 100, 100==> 50, 50 ==> 1
class Net(nn.Module):
def __init__(self):
super().__init__()
self.conv1 = nn.Conv2d(in_channels=3, out_channels=10, kernel_size=3, stride=1, padding=1)
self.reg = nn.BatchNorm2d(10)
self.relu1 = nn.ReLU()
#self.reg = nn.Dropout(p=0.8)
self.conv2 = nn.Conv2d(in_channels=10, out_channels=3, kernel_size=3, stride=1, padding=1)
# self.reg = nn.BatchNorm2d(3)
self.relu2 = nn.ReLU()
# self.pool = nn.MaxPool2d(kernel_size=2)
# self.conv3 = nn.Conv2d(in_channels=20, out_channels=10, kernel_size=3, stride=1, padding=1)
# self.reg = nn.BatchNorm2d(10)
# self.relu3 = nn.ReLU()
# self.conv4 = nn.Conv2d(in_channels=50, out_channels=10, kernel_size=3, stride=1, padding=1)
# self.relu4 = nn.ReLU()
# self.conv5 = nn.Conv2d(in_channels=10, out_channels=100, kernel_size=3, stride=1, padding=1)
# self.relu5 = nn.ReLU()
self.fc1 = nn.Linear(in_features=(125370 // 2)*3, out_features=100) # 100
self.relu6 = nn.ReLU()
self.fc2 = nn.Linear(in_features=100, out_features=50) #100 -> 50
self.relu7 = nn.ReLU()
self.fc3 = nn.Linear(in_features=50, out_features=1)
# self.relu8 = nn.ReLU()
# self.fc4 = nn.Linear(in_features=20, out_features=1)
def forward(self, input):
output = self.conv1(input)
output = self.relu1(output)
output = self.reg(output)
output = self.conv2(output)
output = self.relu2(output)
# output = self.conv3(output)
# output = self.relu3(output)
# output = self.pool(output)
# output = self.conv3(output)
# output = self.relu3(output)
# output = self.conv4(output)
# output = self.relu4(output)
# output = self.conv4(output)
# output = self.relu4(output)
#print(output.shape)
output = output.reshape(-1, (125370 // 2)*3)
#print(output.shape)
output = self.fc1(output)
output = self.relu6(output)
#print(output.shape)
output = self.fc2(output)
output = self.relu7(output)
output = self.fc3(output)
# output = self.relu8(output)
# output = self.fc4(output)
#print(output.shape)
return output
model = Net()
model = model.cuda()
torch.cuda.empty_cache()
X_train.shape
batches_x = []
batches_y = []
batch_size = 10
for i in range(0, X_train.shape[0], batch_size):
batches_x.append(X_train[i:i+batch_size])
batches_y.append(y_train[i:i+batch_size])
batches_x[0].shape
del optimizer
del criterion
# del model
torch.cuda.empty_cache()
criterion = nn.MSELoss()
model.to('cuda:0')
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)
train_loss = []
val_loss = []
def init_weights(m):
if type(m) == nn.Linear:
torch.nn.init.xavier_uniform(m.weight)
m.bias.data.fill_(0.01)
model.apply(init_weights)
best_model = model
min_val = 1e9
loss_arr = []
epochs = 100
for i in range(epochs):
model.train()
loss_tot = 0
#for j in range(X_train.shape[0]):
for batch_x, batch_y in zip(batches_x, batches_y):
# print(batch_x.shape)
y_hat = model.forward(batch_x)
#print("y_hat", y_hat.shape, y_hat)
#print("y_train", y_train)
#break
loss = criterion(y_hat, batch_y)
loss_arr.append(loss)
loss_tot += loss.item()
optimizer.zero_grad()
loss.backward()
optimizer.step()
with torch.no_grad():
model.eval()
y_hat_t = model.forward(X_val)
loss_v = criterion(y_hat_t, y_val)
val_loss.append(loss_v.item())
if loss_v.item() < min_val:
print("new_best")
min_val = loss_v.item()
best_model = copy.deepcopy(model)
if i % 5 == 0:
print(f'Epoch: {i} Train Loss: {loss_tot // len(batches_x)} " Val Loss: "{loss_v}')
train_loss.append(int(loss_tot // len(batches_x)))
min_val
preds = []
model.eval()
with torch.no_grad():
y_hat_t = best_model.forward(X_test)
loss = criterion(y_hat_t, y_test)
val_loss.append(loss.item())
print(loss.item())
#preds.append(y_hat.argmax().item())
PATH = "models/augmented_test_115k.tar"
torch.save(model.state_dict(), PATH)
print(y_test)
plt.plot(range(len(train_loss[10:])), train_loss[4:])
plt.plot(range(len(val_loss[4:])), val_loss[4:])
plt.legend(["Train Loss", "Val Loss"])
plt.xlabel("Epoch")
plt.ylabel("MSE Loss")
#plt.savefig("Train_Test.png")
plt.show()
x_temp = y_test.cpu()
y_temp = y_hat_t.cpu()
# print(y_temp)
# for i in range(y_temp.shape[0]):
# if y_temp[i] > 5000:
# print(x_temp.shape)
# x_temp = torch.cat([x_temp[0:i, :], x_temp[i+1:, :]])
# y_temp = torch.cat([y_temp[0:i, :], y_temp[i+1:, :]])
# break
x_plot = np.array(y_temp)
y_plot = np.array(x_temp)
new_x = np.array(x_plot).reshape(-1,1)
new_y = np.array(y_plot)
fit = LinearRegression().fit(new_x, new_y)
score = fit.score(new_x, new_y)
plt.xlabel("Prediction")
plt.ylabel("Actual Traffic")
print(score)
plt.scatter(new_x, new_y)
axes = plt.gca()
x_vals = np.array(axes.get_xlim())
y_vals = x_vals
plt.plot(x_vals, y_vals, '--')
# plt.savefig("Aug_batch_r2_0.85_mse_97k.png")
plt.show()
```
0.8731882702459102 MSE--123
0.8591212743652898
0.8662367216836014
0.873
0.889 MSE-99
R^2 = 0.911 MSE == 79 num 4
num 5 R^2 0.922 MSE == 82,000
num 11 R^2 == 0.93 MSE = 60
```
# 0.945, 0.830
# MSE 88, 914, 76
#0.950
#MSE 63,443
X_test
y_hat
torch.cuda.memory_summary(device=0, abbreviated=False)
import gc
for obj in gc.get_objects():
try:
if torch.is_tensor(obj) or (hasattr(obj, 'data') and torch.is_tensor(obj.data)):
print(type(obj), obj.size())
except:
pass
s = y_train[y_train[:, 1] == 5]
s
np.mean(s[:, 0])
preds = {}
for i in range(1, 6):
select = y_train[y_train[:, 1] == i]
preds[i] = np.mean(select[:, 0])
preds
y_test
x = []
y = []
mse = 0
for i in range(y_test.shape[0]):
x.append(preds[y_test[i][1]])
y.append(y_test[i][0])
mse += (preds[y_test[i][1]] - y_test[i][0])**2
mse / len(y_test)
x_plot = np.array(x)
y_plot = np.array(y)
new_x = np.array(x_plot).reshape(-1,1)
new_y = np.array(y_plot)
fit = LinearRegression().fit(new_x, new_y)
score = fit.score(new_x, new_y)
plt.xlabel("Prediction")
plt.ylabel("Actual Traffic")
print(score)
plt.scatter(new_x, new_y)
axes = plt.gca()
x_vals = np.array(axes.get_xlim())
y_vals = x_vals
plt.plot(x_vals, y_vals, '--')
plt.savefig("Baseline.png")
plt.show()
# 0.873
# 99098
```
|
github_jupyter
|
```
%load_ext autoreload
%autoreload 2
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
import warnings
warnings.filterwarnings('ignore')
```
## Introduction
```
from IPython.display import YouTubeVideo
YouTubeVideo(id="BYOK12I9vgI", width="100%")
```
In this chapter, we will look at bipartite graphs and their applications.
## What are bipartite graphs?
As the name suggests,
bipartite have two (bi) node partitions (partite).
In other words, we can assign nodes to one of the two partitions.
(By contrast, all of the graphs that we have seen before are _unipartite_:
they only have a single partition.)
### Rules for bipartite graphs
With unipartite graphs, you might remember a few rules that apply.
Firstly, nodes and edges belong to a _set_.
This means the node set contains only unique members,
i.e. no node can be duplicated.
The same applies for the edge set.
On top of those two basic rules, bipartite graphs add an additional rule:
Edges can only occur between nodes of **different** partitions.
In other words, nodes within the same partition
are not allowed to be connected to one another.
### Applications of bipartite graphs
Where do we see bipartite graphs being used?
Here's one that is very relevant to e-commerce,
which touches our daily lives:
> We can model customer purchases of products using a bipartite graph.
> Here, the two node sets are **customer** nodes and **product** nodes,
> and edges indicate that a customer $C$ purchased a product $P$.
On the basis of this graph, we can do interesting analyses,
such as finding customers that are similar to one another
on the basis of their shared product purchases.
Can you think of other situations
where a bipartite graph model can be useful?
## Dataset
Here's another application in crime analysis,
which is relevant to the example that we will use in this chapter:
> This bipartite network contains persons
> who appeared in at least one crime case
> as either a suspect, a victim, a witness
> or both a suspect and victim at the same time.
> A left node represents a person and a right node represents a crime.
> An edge between two nodes shows that
> the left node was involved in the crime
> represented by the right node.
This crime dataset was also sourced from Konect.
```
from nams import load_data as cf
G = cf.load_crime_network()
for n, d in G.nodes(data=True):
G.nodes[n]["degree"] = G.degree(n)
```
If you inspect the nodes,
you will see that they contain a special metadata keyword: `bipartite`.
This is a special keyword that NetworkX can use
to identify nodes of a given partition.
### Visualize the crime network
To help us get our bearings right, let's visualize the crime network.
```
import nxviz as nv
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(7, 7))
nv.circos(G, sort_by="degree", group_by="bipartite", node_color_by="bipartite", node_enc_kwargs={"size_scale": 3})
```
### Exercise: Extract each node set
A useful thing to be able to do
is to extract each partition's node set.
This will become handy when interacting with
NetworkX's bipartite algorithms later on.
> Write a function that extracts all of the nodes
> from specified node partition.
> It should also raise a plain Exception
> if no nodes exist in that specified partition.
> (as a precuation against users putting in invalid partition names).
```
import networkx as nx
def extract_partition_nodes(G: nx.Graph, partition: str):
nodeset = [_ for _, _ in _______ if ____________]
if _____________:
raise Exception(f"No nodes exist in the partition {partition}!")
return nodeset
from nams.solutions.bipartite import extract_partition_nodes
# Uncomment the next line to see the answer.
# extract_partition_nodes??
```
## Bipartite Graph Projections
In a bipartite graph, one task that can be useful to do
is to calculate the projection of a graph onto one of its nodes.
What do we mean by the "projection of a graph"?
It is best visualized using this figure:
```
from nams.solutions.bipartite import draw_bipartite_graph_example, bipartite_example_graph
from nxviz import annotate
import matplotlib.pyplot as plt
bG = bipartite_example_graph()
pG = nx.bipartite.projection.projected_graph(bG, "abcd")
ax = draw_bipartite_graph_example()
plt.sca(ax[0])
annotate.parallel_labels(bG, group_by="bipartite")
plt.sca(ax[1])
annotate.arc_labels(pG)
```
As shown in the figure above, we start first with a bipartite graph with two node sets,
the "alphabet" set and the "numeric" set.
The projection of this bipartite graph onto the "alphabet" node set
is a graph that is constructed such that it only contains the "alphabet" nodes,
and edges join the "alphabet" nodes because they share a connection to a "numeric" node.
The red edge on the right
is basically the red path traced on the left.
### Computing graph projections
How does one compute graph projections using NetworkX?
Turns out, NetworkX has a `bipartite` submodule,
which gives us all of the facilities that we need
to interact with bipartite algorithms.
First of all, we need to check that the graph
is indeed a bipartite graph.
NetworkX provides a function for us to do so:
```
from networkx.algorithms import bipartite
bipartite.is_bipartite(G)
```
Now that we've confirmed that the graph is indeed bipartite,
we can use the NetworkX bipartite submodule functions
to generate the bipartite projection onto one of the node partitions.
First off, we need to extract nodes from a particular partition.
```
person_nodes = extract_partition_nodes(G, "person")
crime_nodes = extract_partition_nodes(G, "crime")
```
Next, we can compute the projection:
```
person_graph = bipartite.projected_graph(G, person_nodes)
crime_graph = bipartite.projected_graph(G, crime_nodes)
```
And with that, we have our projected graphs!
Go ahead and inspect them:
```
list(person_graph.edges(data=True))[0:5]
list(crime_graph.edges(data=True))[0:5]
```
Now, what is the _interpretation_ of these projected graphs?
- For `person_graph`, we have found _individuals who are linked by shared participation (whether witness or suspect) in a crime._
- For `crime_graph`, we have found _crimes that are linked by shared involvement by people._
Just by this graph, we already can find out pretty useful information.
Let's use an exercise that leverages what you already know
to extract useful information from the projected graph.
### Exercise: find the crime(s) that have the most shared connections with other crimes
> Find crimes that are most similar to one another
> on the basis of the number of shared connections to individuals.
_Hint: This is a degree centrality problem!_
```
import pandas as pd
def find_most_similar_crimes(cG: nx.Graph):
"""
Find the crimes that are most similar to other crimes.
"""
dcs = ______________
return ___________________
from nams.solutions.bipartite import find_most_similar_crimes
find_most_similar_crimes(crime_graph)
```
### Exercise: find the individual(s) that have the most shared connections with other individuals
> Now do the analogous thing for individuals!
```
def find_most_similar_people(pG: nx.Graph):
"""
Find the persons that are most similar to other persons.
"""
dcs = ______________
return ___________________
from nams.solutions.bipartite import find_most_similar_people
find_most_similar_people(person_graph)
```
## Weighted Projection
Though we were able to find out which graphs were connected with one another,
we did not record in the resulting projected graph
the **strength** by which the two nodes were connected.
To preserve this information, we need another function:
```
weighted_person_graph = bipartite.weighted_projected_graph(G, person_nodes)
list(weighted_person_graph.edges(data=True))[0:5]
```
### Exercise: Find the people that can help with investigating a `crime`'s `person`.
Let's pretend that we are a detective trying to solve a crime,
and that we right now need to find other individuals
who were not implicated in the same _exact_ crime as an individual was,
but who might be able to give us information about that individual
because they were implicated in other crimes with that individual.
> Implement a function that takes in a bipartite graph `G`, a string `person` and a string `crime`,
> and returns a list of other `person`s that were **not** implicated in the `crime`,
> but were connected to the `person` via other crimes.
> It should return a _ranked list_,
> based on the **number of shared crimes** (from highest to lowest)
> because the ranking will help with triage.
```
list(G.neighbors('p1'))
def find_connected_persons(G, person, crime):
# Step 0: Check that the given "person" and "crime" are connected.
if _____________________________:
raise ValueError(f"Graph does not have a connection between {person} and {crime}!")
# Step 1: calculate weighted projection for person nodes.
person_nodes = ____________________________________
person_graph = bipartite.________________________(_, ____________)
# Step 2: Find neighbors of the given `person` node in projected graph.
candidate_neighbors = ___________________________________
# Step 3: Remove candidate neighbors from the set if they are implicated in the given crime.
for p in G.neighbors(crime):
if ________________________:
_____________________________
# Step 4: Rank-order the candidate neighbors by number of shared connections.
_________ = []
## You might need a for-loop here
return pd.DataFrame(__________).sort_values("________", ascending=False)
from nams.solutions.bipartite import find_connected_persons
find_connected_persons(G, 'p2', 'c10')
```
## Degree Centrality
The degree centrality metric is something we can calculate for bipartite graphs.
Recall that the degree centrality metric is the number of neighbors of a node
divided by the total number of _possible_ neighbors.
In a unipartite graph, the denominator can be the total number of nodes less one
(if self-loops are not allowed)
or simply the total number of nodes (if self loops _are_ allowed).
### Exercise: What is the denominator for bipartite graphs?
Think about it for a moment, then write down your answer.
```
from nams.solutions.bipartite import bipartite_degree_centrality_denominator
from nams.functions import render_html
render_html(bipartite_degree_centrality_denominator())
```
### Exercise: Which `persons` are implicated in the most number of crimes?
> Find the `persons` (singular or plural) who are connected to the most number of crimes.
To do so, you will need to use `nx.bipartite.degree_centrality`,
rather than the regular `nx.degree_centrality` function.
`nx.bipartite.degree_centrality` requires that you pass in
a node set from one of the partitions
so that it can correctly partition nodes on the other set.
What is returned, though, is the degree centrality
for nodes in both sets.
Here is an example to show you how the function is used:
```python
dcs = nx.bipartite.degree_centrality(my_graph, nodes_from_one_partition)
```
```
def find_most_crime_person(G, person_nodes):
dcs = __________________________
return ___________________________
from nams.solutions.bipartite import find_most_crime_person
find_most_crime_person(G, person_nodes)
```
## Solutions
Here are the solutions to the exercises above.
```
from nams.solutions import bipartite
import inspect
print(inspect.getsource(bipartite))
```
|
github_jupyter
|
# Predict Model
The aim of this notebook is to assess how well our [logistic regression classifier](../models/LR.csv) generalizes to unseen data. We will accomplish this by using the Matthew's Correlation Coefficient (MCC) to evaluate it's predictive performance on the test set. Following this, we will determine which features the classifier deems most important in the classification of a physicist as a Nobel Laureate. Finally, we will use our model to predict the most likely Physics Nobel Prize Winners in 2018.
```
import ast
import numpy as np
import pandas as pd
from sklearn.externals import joblib
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import classification_report
from sklearn.metrics import confusion_matrix
from sklearn.metrics import matthews_corrcoef
from src.features.features_utils import convert_categoricals_to_numerical
from src.features.features_utils import convert_target_to_numerical
from src.models.metrics_utils import confusion_matrix_to_dataframe
from src.models.metrics_utils import print_matthews_corrcoef
from src.visualization.visualization_utils import plot_logistic_regression_odds_ratio
```
## Reading in the Data
First let's read in the classifier parameters and metadata that we saved in order to reconstruct the classifier.
```
classifier_params = pd.read_csv('../models/LR.csv', squeeze=True, index_col=0)
classifier_params
```
Next let's read in the training, validation and test features and targets. We make sure to convert the categorical fields to a numerical form that is suitable for building machine learning models.
```
train_features = pd.read_csv('../data/processed/train-features.csv')
X_train = convert_categoricals_to_numerical(train_features)
X_train.head()
train_target = pd.read_csv('../data/processed/train-target.csv', index_col='full_name', squeeze=True)
y_train = convert_target_to_numerical(train_target)
y_train.head()
validation_features = pd.read_csv('../data/processed/validation-features.csv')
X_validation = convert_categoricals_to_numerical(validation_features)
X_validation.head()
validation_target = pd.read_csv('../data/processed/validation-target.csv', index_col='full_name',
squeeze=True)
y_validation = convert_target_to_numerical(validation_target)
y_validation.head()
test_features = pd.read_csv('../data/processed/test-features.csv')
X_test = convert_categoricals_to_numerical(test_features)
X_test.head()
test_target = pd.read_csv('../data/processed/test-target.csv', index_col='full_name', squeeze=True)
y_test = convert_target_to_numerical(test_target)
y_test.head()
```
## Retraining on the Training and Validation Data
It makes sense to retrain the model on both the training and validation data so that we can obtain as good a predictive performance as possible. So let's combine the training and validation features and targets, reconstruct the classifier and retrain the model.
```
X_train_validation = X_train.append(X_validation)
assert(len(X_train_validation) == len(X_train) + len(X_validation))
X_train_validation.head()
y_train_validation = y_train.append(y_validation)
assert(len(y_train_validation) == len(y_train) + len(y_validation))
y_train_validation.head()
classifier = LogisticRegression(**ast.literal_eval(classifier_params.params))
classifier.fit(X_train_validation, y_train_validation)
```
## Predicting on the Test Data
Here comes the moment of truth! We will soon see just how good the model is by predicting on the test data. However, first it makes sense to look at the performance of our "naive" [baseline model](5.0-baseline-model.ipynb) on the test data. Recall that this is a model that predicts the physicist is a laureate whenever the number of workplaces is at least 2.
```
y_train_pred = X_train_validation.num_workplaces_at_least_2
y_test_pred = X_test.num_workplaces_at_least_2
mcc_train_validation = matthews_corrcoef(y_train_validation, y_train_pred)
mcc_test = matthews_corrcoef(y_test, y_test_pred)
name = 'Baseline Classifier'
print_matthews_corrcoef(mcc_train_validation, name, data_label='train + validation')
print_matthews_corrcoef(mcc_test, name, data_label='test')
```
Unsurprisingly, this classifier exhibits very poor performance on the test data. We see evidence of the covariate shift again here due to the relatively large difference in the test and train + validation MCCs. Either physicists started working in more workplaces in general, or the records of where physicists have worked are better in modern times. The confusion matrix and classification report indicate that the classifier is poor in terms of both precision and recall when identifying laureates.
```
display(confusion_matrix_to_dataframe(confusion_matrix(y_test, y_test_pred)))
print(classification_report(y_test, y_test_pred))
```
OK let's see how our logistic regression model does on the test data.
```
y_train_pred = (classifier.predict_proba(X_train_validation)[:, 1] > ast.literal_eval(
classifier_params.threshold)).astype('int64')
y_test_pred = (classifier.predict_proba(X_test)[:, 1] > ast.literal_eval(
classifier_params.threshold)).astype('int64')
mcc_train_validation = matthews_corrcoef(y_train_validation, y_train_pred)
mcc_test = matthews_corrcoef(y_test, y_test_pred)
print_matthews_corrcoef(mcc_train_validation, classifier_params.name, data_label='train + validation')
print_matthews_corrcoef(mcc_test, classifier_params.name, data_label='test')
```
This classifier performs much better on the test data than the baseline classifier. Again we are discussing its performance in relative and not absolute terms. There is very little in the literature, even as a rule of thumb, saying what the expected MCC is for a "good performing classifier" as it is very dependent on the context and usage. As we noted before, predicting Physics Nobel Laureates is a difficult task due to the many complex factors involved, so we certainly should not be expecting stellar performance from *any* classifier. This includes both machine classifiers, either machine-learning-based or rules-based, and human classifiers without inside knowledge. However, let us try and get off the fence just a little now.
The MCC is a [contingency matrix](https://en.wikipedia.org/wiki/Contingency_table) method of calculating the [Pearson product-moment correlation coefficient](https://en.wikipedia.org/wiki/Pearson_correlation_coefficient) and so it has the [same interpretation](https://stats.stackexchange.com/questions/118219/how-to-interpret-matthews-correlation-coefficient-mcc). If the values in the link are to be believed, then our classifier has a "moderate positive relationship" with the target. This [statistical guide](https://statistics.laerd.com/statistical-guides/pearson-correlation-coefficient-statistical-guide.php ) also seems to agree with this assessment. However, we can easily find examples that indicate there is a [low positive correlation](https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3576830/) or a [weak uphill (positive) linear relationship](https://www.dummies.com/education/math/statistics/how-to-interpret-a-correlation-coefficient-r/) between the classifier's predictions and the target.
So should we conclude that the classifier has a low or moderate performance? Asking this question is missing the purpose of this study. Instead we should ask, based on the classifier's performance, would we be willing to make recommendations to the Nobel Committee, about any biases that may be present when deciding Physics Laureates? We can see from the confusion matrix and classification report that although this classifier has reasonable recall of laureates, it is contaminated by too many false postives. Or in other words, it is not precise enough. As a result, the answer to the question is very likely no.
```
display(confusion_matrix_to_dataframe(confusion_matrix(y_test, y_test_pred)))
print(classification_report(y_test, y_test_pred))
```
## Most Important Features
Out of interest, let's determine the features that are most important to the prediction by looking at the coefficients of the logistic regression model. Each coefficient represents the impact that the *presence* vs. *absence* of a predictor has on the [log odds ratio](https://en.wikipedia.org/wiki/Odds_ratio#Role_in_logistic_regression) of a physicist being classified as a laureate. The change in [odds ratio](https://en.wikipedia.org/wiki/Odds_ratio) for each predictor can can simply be computed by exponentiating its associated coefficient. The top fifteen most important features are plotted in the chart below.
```
top_n = 15
ax = plot_logistic_regression_odds_ratio(classifier.coef_, top_n=top_n, columns=X_train_validation.columns,
title='Top {} most important features in prediction of Physics Nobel Laureates'.format(top_n))
ax.figure.set_size_inches(10, 8)
```
By far the most important feature is being an experimental physicist. This matches with what we observed during the [exploratory data analysis](4.0-exploratory-data-analysis.ipynb). Next comes having at least one physics laureate doctoral student and then living for at least 65-79 years. We also saw during the exploratory data analysis that the later also seemed to have a big effect in distinguishing laureates from their counterparts. Some of the other interesting top features are being a citizen of France or Switzerland, working at [Bell Labs](https://en.wikipedia.org/wiki/Bell_Labs#Discoveries_and_developments) or [The University of Cambridge](https://en.wikipedia.org/wiki/List_of_Nobel_laureates_by_university_affiliation#University_of_Cambridge_(2nd)), being an alumnus in Asia and having at least two alma mater.
## Prediction of 2018 Physics Nobel Laureates
Now let us use the logistic regression model to predict the 2018 Physics Nobel Laureates. A maximum of three physicists can be awarded the prize in any one year. However, to give ourselves more of a fighting chance, we will instead try to predict the ten most likely winners. Let's start by forming the feature and target dataframes of living physicists (i.e the union of the validation and test sets) as the Nobel Prize cannot be awarded posthumously.
```
X_validation_test = X_validation.append(X_test)
assert(len(X_validation_test) == len(X_validation) + len(X_test))
X_validation_test.head()
y_validation_test = y_validation.append(y_test)
assert(len(y_validation_test) == len(y_validation) + len(y_test))
y_validation_test.head()
```
Recall that *John Bardeen* is the only [double laureate in Physics](https://www.nobelprize.org/prizes/facts/facts-on-the-nobel-prize-in-physics/), so although it is possible to receive the Nobel Prize in Physics multiple times, it is extremely rare. So let's drop previous Physics Laureates from the dataframe. This will make the list far more interesting as it will not be polluted by previous laureates.
```
X_eligible = X_validation_test.drop(y_validation_test[y_validation_test == 1].index)
assert(len(X_eligible) == len(X_validation_test) - len(y_validation_test[y_validation_test == 1]))
X_eligible.head()
```
According to our model, these are the ten most likely winners of 2018 Physics Nobel Prize:
```
physicist_win_probabilites = pd.Series(
classifier.predict_proba(X_eligible)[:, 1], index=X_eligible.index).sort_values(ascending=False)
physicist_win_probabilites[:10]
```
The list contains some great and very interesting physicists who have won numerous of the top prizes in physics. We'll leave you to check out their Wikipedia articles for some more information on them. However, a few are worth discussing now. Without doubt the most infamous is [Jocelyn Bell Burnell](https://en.wikipedia.org/wiki/Jocelyn_Bell_Burnell) who, as a postgraduate student, co-discovered the first radio pulsars in 1967. Her Wikipedia article says:
"The discovery was recognised by the award of the 1974 Nobel Prize in Physics, but despite the fact that she was the first to observe the pulsars, Bell was excluded from the recipients of the prize.
The paper announcing the discovery of pulsars had five authors. Bell's thesis supervisor Antony Hewish was listed first, Bell second. Hewish was awarded the Nobel Prize, along with the astronomer Martin Ryle. Many prominent astronomers criticised Bell's omission, including Sir Fred Hoyle."
You can read more about her in her Wikipedia article and further details about other [Nobel Physics Prize controversies](https://en.wikipedia.org/wiki/Nobel_Prize_controversies#Physics).
[Vera Rubin](https://en.wikipedia.org/wiki/Vera_Rubin) was an American astronomer who's research provided evidence of the existence of [dark matter](https://en.wikipedia.org/wiki/Dark_matter). According to her Wikipedia article, she "never won the Nobel Prize, though physicists such as Lisa Randall and Emily Levesque have argued that this was an oversight." Unfortunately she died on 25 December 2016 and is no longer eligible for the award. Recall that the list contains some deceased physicists due to the lag in updates of dbPedia data from Wikipedia. *Peter Mansfield*, who is also on the list, is deceased too.
[Manfred Eigen](https://en.wikipedia.org/wiki/Manfred_Eigen) actually won the 1967 Nobel Prize in Chemistry for work on measuring fast chemical reactions.
The actual winners of the [2018 Nobel Prize in Physics](https://www.nobelprize.org/prizes/physics/2018/summary/) were [Gérard Mourou](https://en.wikipedia.org/wiki/G%C3%A9rard_Mourou), [Arthur Ashkin](https://en.wikipedia.org/wiki/Arthur_Ashkin) and [Donna Strickland](https://en.wikipedia.org/wiki/Donna_Strickland). Our model actually had zero chance of predicting them as they were never in the original [list of physicists](../data/raw/physicists.txt) scraped from Wikipedia! Obviously they are now deemed famous enough to have been added to Wikipedia since.
```
('Gérard Mourou' in physicist_win_probabilites,
'Arthur Ashkin' in physicist_win_probabilites,
'Donna Strickland' in physicist_win_probabilites)
```
So should we declare this part of the study as an epic failure as we were unable to identify the winners? No not quite. Closer inspection reveals many interesting characteristics of the three winners that are related to the top features in our predictive model:
- *Gérard Mourou* is an experimental physicist, a citizen of France, 74 years of age (i.e. years lived group 65-79), has at least one physics laureate doctoral student (i.e. *Donna Strickland*) and has 3 alma mater.
- *Arthur Ashkin* is an experimental physicist, worked at Bell Labs and has 2 alma mater.
- *Donna Strickland* is an experimental physicist and has 2 alma mater.
Maybe this is a pure coincidence, but more likely, there are patterns in the data that the model has found. Whether or not these characteristics can be attributed to biases in the [Nobel Physics Prize nomination and selection process](https://www.nobelprize.org/nomination/physics/) is another matter, as correlation does not necessarily imply causation.
This section was a lot of fun and quite informative about the logistic regression classifier, however, it was not possible without cheating. Look closely to see if you can spot the cheating!
## Model Deployment
It makes sense to retrain the model on *all* the data so that we can obtain as good a predictive performance as possible. So let's go ahead and do this now.
```
X_train_validation_test = X_train_validation.append(X_test)
assert(len(X_train_validation_test) == len(X_train_validation) + len(X_test))
X_train_validation_test.head()
y_train_validation_test = y_train_validation.append(y_test)
assert(len(y_train_validation_test) == len(y_train_validation) + len(y_test))
y_train_validation_test.head()
classifier.fit(X_train_validation_test, y_train_validation_test)
```
Due to the short training time, it is possible in this study to always recreate the logistic regression classifier from the [model template](../models/LR.csv) that we persisted. Every time we want to use the model to make predictions on new data, it is easy enough to retrain the model first. However, if we had more data and longer training times, this would be rather cumbersome. In such a case, if we were deploying the model, which we are not for the reasons mentioned above, it would make sense to actually persist the trained model. Nonetheless, for completeness, let's persist the model.
```
joblib.dump(classifier, '../models/LR.joblib')
```
As a sanity check let's load the model and make sure that we get the same results as before.
```
classifier_check = joblib.load('../models/LR.joblib')
np.testing.assert_allclose(classifier.predict_proba(X_train_validation_test),
classifier_check.predict_proba(X_train_validation_test))
```
Great, everything looks good.
Although persisting the model suffers from the [compatibility and security issues](https://stackabuse.com/scikit-learn-save-and-restore-models/#compatibilityissues) mentioned previously, we have the [model template](../models/LR.csv) that allows us to reconstruct the classifier for future python, library and model versions. This mitigates the compatibility risk. We can also mitigate the security risk by only restoring the model from *trusted* or *authenticated* sources.
|
github_jupyter
|
```
from kbc_pul.project_info import project_dir as kbc_e_metrics_project_dir
import os
from typing import List, Dict, Set, Optional
import numpy as np
import pandas as pd
from artificial_bias_experiments.evaluation.confidence_comparison.df_utils import ColumnNamesInfo
from artificial_bias_experiments.known_prop_scores.dataset_generation_file_naming import \
get_root_dir_experiment_noisy_propensity_scores
from kbc_pul.confidence_naming import ConfidenceEnum
from kbc_pul.observed_data_generation.sar_two_subject_groups.sar_two_subject_groups_prop_scores import \
PropScoresTwoSARGroups
from artificial_bias_experiments.noisy_prop_scores.sar_two_subject_groups.experiment_info import \
NoisyPropScoresSARExperimentInfo
from artificial_bias_experiments.noisy_prop_scores.sar_two_subject_groups.noisy_prop_scores_sar_two_groups_loading import \
load_df_noisy_prop_scores_two_groups
from pathlib import Path
from pylo.language.lp import Clause as PyloClause
```
# Noisy SAR 2 groups - paper table
```
dataset_name="yago3_10"
is_pca_version: bool = False
true_prop_score_in_filter = 0.5
true_prop_score_other_list = [0.3, .7]
# true_prop_scores = PropScoresTwoSARGroups(
# in_filter=true_prop_score_in_filter,
# other=true_prop_score_other
# )
noisy_prop_score_in_filter: float = true_prop_score_in_filter
noisy_prop_score_not_in_filter_list: List[float] = [0.1, 0.2, .3, .4, .5, .6, .7, .8, .9, 1]
root_experiment_dir: str = os.path.join(
get_root_dir_experiment_noisy_propensity_scores(),
'sar_two_subject_groups',
dataset_name
)
path_root_experiment_dir = Path(root_experiment_dir)
true_prop_score_other_to_df_map: Dict[float, pd.DataFrame] = dict()
df_list_complete: List[pd.DataFrame] = []
for true_prop_score_other in true_prop_score_other_list:
true_prop_scores = PropScoresTwoSARGroups(
in_filter=true_prop_score_in_filter,
other=true_prop_score_other
)
# df_list: List[pd.DataFrame] = []
for target_rel_path in path_root_experiment_dir.iterdir():
if target_rel_path.is_dir():
for filter_dir in target_rel_path.iterdir():
if filter_dir.is_dir():
target_relation = target_rel_path.name
filter_relation = filter_dir.name
print(f"{target_relation} - {filter_relation}")
try:
experiment_info = NoisyPropScoresSARExperimentInfo(
dataset_name=dataset_name,
target_relation=target_relation,
filter_relation=filter_relation,
true_prop_scores=true_prop_scores,
noisy_prop_score_in_filter=noisy_prop_score_in_filter,
noisy_prop_score_not_in_filter_list=noisy_prop_score_not_in_filter_list,
is_pca_version=is_pca_version
)
df_rule_wrappers_tmp = load_df_noisy_prop_scores_two_groups(
experiment_info=experiment_info
)
df_list_complete.append(df_rule_wrappers_tmp)
except Exception as err:
print(err)
df_rule_wrappers_all_targets: pd.DataFrame = pd.concat(df_list_complete, axis=0)
# true_prop_score_other_to_df_map[true_prop_score_other] = df_for_true_prop_score_other
df_rule_wrappers_all_targets.head()
df_rule_wrappers_all_targets.columns
column_names_logistics: List[str] = [
'target_relation',
'filter_relation',
'true_prop_scores_in_filter', 'true_prop_scores_not_in_filter',
'noisy_prop_scores_in_filter', 'noisy_prop_scores_not_in_filter',
'random_trial_index',
"Rule"
]
other_columns = [col for col in df_rule_wrappers_all_targets.columns if col not in column_names_logistics]
resorted_columns = column_names_logistics + other_columns
df_rule_wrappers_all_targets = df_rule_wrappers_all_targets[resorted_columns]
df_rule_wrappers_all_targets.head()
df_rule_wrappers_all_targets.rename(
columns={
'true_prop_scores_in_filter': "true_filter",
'true_prop_scores_not_in_filter': "true_other",
'noisy_prop_scores_in_filter': "noisy_filter", 'noisy_prop_scores_not_in_filter': "noisy_other",
},
inplace=True,
errors="ignore"
)
column_names_logistics: List[str] = [
'target_relation',
'filter_relation',
'true_filter', 'true_other',
'noisy_filter', 'noisy_other',
'random_trial_index',
"Rule"
]
df_rule_wrappers_all_targets.head()
```
## 2. Only keep a subset of rules
### 2.1. Only keep the non-recursive rules; drop recursive rules
```
from kbc_pul.data_structures.rule_wrapper import get_pylo_rule_from_string, is_pylo_rule_recursive
def is_rule_recursive(rule_string: str) -> bool:
pylo_rule: PyloClause = get_pylo_rule_from_string(rule_string)
is_rule_recursive = is_pylo_rule_recursive(pylo_rule)
return is_rule_recursive
mask_recursive_rules = df_rule_wrappers_all_targets.apply(
lambda row: is_rule_recursive(row["Rule"]),
axis=1
)
print(len(df_rule_wrappers_all_targets))
df_rule_wrappers_all_targets: pd.DataFrame = df_rule_wrappers_all_targets[~mask_recursive_rules]
print(len(df_rule_wrappers_all_targets))
```
### 2.3 Drop the Pair-positive columns (both directions)
```
df_rule_wrappers_all_targets.drop(
[ConfidenceEnum.TRUE_CONF_BIAS_YS_ZERO_S_TO_O.value,
ConfidenceEnum.TRUE_CONF_BIAS_YS_ZERO_O_TO_S.value],
axis=1,
inplace=True,
errors='ignore'
)
df_rule_wrappers_all_targets.head()
```
### 2.4 Drop the IPW-PCA columns (both directions)
```
df_rule_wrappers_all_targets.drop(
[ConfidenceEnum.IPW_PCA_CONF_S_TO_O.value,
ConfidenceEnum.IPW_PCA_CONF_O_TO_S.value],
axis=1,
inplace=True,
errors='ignore'
)
df_rule_wrappers_all_targets.head()
```
### 2.4 Drop the $c_{q}=0.5$ column
```
df_rule_wrappers_all_targets.drop(
["true_filter", "noisy_filter"],
axis=1,
inplace=True,
errors='ignore'
)
column_names_logistics = [
col for col in column_names_logistics
if col != "true_filter"
and col != "noisy_filter"
]
df_rule_wrappers_all_targets.head()
group_by_list = [
"target_relation",
"filter_relation",
'true_other',
'noisy_other',
"Rule",
"random_trial_index"
]
df_count_trials: pd.DataFrame = df_rule_wrappers_all_targets[
[
"target_relation",
"filter_relation",
'true_other',
'noisy_other',
"Rule",
"random_trial_index"
]
].groupby(
[
"target_relation",
"filter_relation",
'true_other',
'noisy_other',
"Rule",
]
).count().reset_index()
df_less_than_ten_trials: pd.DataFrame = df_count_trials[df_count_trials["random_trial_index"].values != 10]
df_less_than_ten_trials
df_rule_wrappers_all_targets = df_rule_wrappers_all_targets[
~(
(df_rule_wrappers_all_targets["target_relation"] == "isaffiliatedto")
&
(df_rule_wrappers_all_targets["filter_relation"] == "wasbornin")
&
(df_rule_wrappers_all_targets["Rule"]=="isaffiliatedto(A,B) :- playsfor(A,B)")
)
]
df_rule_wrappers_all_targets.head()
```
**Now, we have the full dataframe**
****
## Calculate $[conf(R) - \widehat{conf}(R)]$
```
true_conf: ConfidenceEnum = ConfidenceEnum.TRUE_CONF
conf_estimators_list: List[ConfidenceEnum] = [
ConfidenceEnum.CWA_CONF,
ConfidenceEnum.ICW_CONF,
ConfidenceEnum.PCA_CONF_S_TO_O,
ConfidenceEnum.PCA_CONF_O_TO_S,
ConfidenceEnum.IPW_CONF,
]
all_confs_list: List[ConfidenceEnum] = [ConfidenceEnum.TRUE_CONF ] + conf_estimators_list
column_names_all_confs: List[str] = [
conf.get_name()
for conf in all_confs_list
]
df_rule_wrappers_all_targets = df_rule_wrappers_all_targets[
column_names_logistics + column_names_all_confs
]
df_rule_wrappers_all_targets.head()
df_conf_estimators_true_other = df_rule_wrappers_all_targets[
df_rule_wrappers_all_targets["true_other"] == df_rule_wrappers_all_targets["noisy_other"]
]
df_conf_estimators_true_other.head()
column_names_info =ColumnNamesInfo(
true_conf=true_conf,
column_name_true_conf=true_conf.get_name(),
conf_estimators=conf_estimators_list,
column_names_conf_estimators=[
col.get_name()
for col in conf_estimators_list
],
column_names_logistics=column_names_logistics
)
def get_df_rulewise_squared_diffs_between_true_conf_and_conf_estimator(
df_rule_wrappers: pd.DataFrame,
column_names_info: ColumnNamesInfo
) -> pd.DataFrame:
df_rulewise_diffs_between_true_conf_and_conf_estimator: pd.DataFrame = df_rule_wrappers[
column_names_info.column_names_logistics
]
col_name_estimator: str
for col_name_estimator in column_names_info.column_names_conf_estimators:
df_rulewise_diffs_between_true_conf_and_conf_estimator \
= df_rulewise_diffs_between_true_conf_and_conf_estimator.assign(
**{
col_name_estimator: (
(df_rule_wrappers[column_names_info.column_name_true_conf]
- df_rule_wrappers[col_name_estimator]) ** 2
)
}
)
return df_rulewise_diffs_between_true_conf_and_conf_estimator
df_conf_squared_errors: pd.DataFrame = get_df_rulewise_squared_diffs_between_true_conf_and_conf_estimator(
df_rule_wrappers=df_rule_wrappers_all_targets,
column_names_info = column_names_info
)
df_conf_squared_errors.head()
```
## AVERAGE the PCA(S) and PCA(O)
```
df_conf_squared_errors["PCA"] = (
(
df_conf_squared_errors[ConfidenceEnum.PCA_CONF_S_TO_O.value]
+
df_conf_squared_errors[ConfidenceEnum.PCA_CONF_O_TO_S.value]
) / 2
)
df_conf_squared_errors.head()
df_conf_squared_errors = df_conf_squared_errors.drop(
columns=[
ConfidenceEnum.PCA_CONF_S_TO_O.value
+
ConfidenceEnum.PCA_CONF_O_TO_S.value
],
axis=1,
errors='ignore'
)
df_conf_squared_errors.head()
```
# Now start averaging
```
df_conf_squared_errors_avg_over_trials: pd.DataFrame = df_conf_squared_errors.groupby(
by=["target_relation", "filter_relation", 'true_other', "noisy_other", "Rule"],
sort=True,
as_index=False
).mean()
df_conf_squared_errors_avg_over_trials.head()
df_conf_squared_errors_avg_over_trials_and_rules: pd.DataFrame = df_conf_squared_errors_avg_over_trials.groupby(
by=["target_relation", "filter_relation", 'true_other', "noisy_other",],
sort=True,
as_index=False
).mean()
df_conf_squared_errors_avg_over_trials_and_rules.head()
len(df_conf_squared_errors_avg_over_trials_and_rules)
```
### How many $p$, $q$ combinations are there?
```
df_p_and_q = df_conf_squared_errors_avg_over_trials_and_rules[["target_relation", "filter_relation"]].drop_duplicates()
df_p_and_q.head()
len(df_p_and_q)
df_conf_errors_avg_over_trials_and_rules_and_q: pd.DataFrame = df_conf_squared_errors_avg_over_trials_and_rules.groupby(
by=["target_relation", 'true_other', "noisy_other",],
sort=True,
as_index=False
).mean()
df_conf_errors_avg_over_trials_and_rules_and_q.head()
len(df_conf_errors_avg_over_trials_and_rules_and_q)
```
## Subset of noisy_other
```
first_true_label_freq_to_include = 0.3
second_true_label_freq_to_include = 0.7
true_label_frequencies_set: Set[float] = {
first_true_label_freq_to_include, second_true_label_freq_to_include,
}
true_label_frequency_to_estimate_map: Dict[float, Set[float]] = dict()
label_frequency_est_diff: float = 0.1
label_frequencies_to_keep: Set[float] = set(true_label_frequencies_set)
for true_label_freq in true_label_frequencies_set:
true_label_frequency_to_estimate_map[true_label_freq] = {
round(true_label_freq - label_frequency_est_diff, 1),
round(true_label_freq + label_frequency_est_diff, 1)
}
label_frequencies_to_keep.update(true_label_frequency_to_estimate_map[true_label_freq])
df_conf_errors_avg_over_trials_and_rules_and_q_c_subset = df_conf_errors_avg_over_trials_and_rules_and_q[
df_conf_errors_avg_over_trials_and_rules_and_q["noisy_other"].isin(label_frequencies_to_keep)
]
df_conf_errors_avg_over_trials_and_rules_and_q_c_subset.head()
len(df_conf_errors_avg_over_trials_and_rules_and_q_c_subset)
```
## Count the rules per $p$
```
df_n_rules_per_target = df_rule_wrappers_all_targets[["target_relation", "Rule"]].groupby(
by=['target_relation'],
# sort=True,
# as_index=False
)["Rule"].nunique().to_frame().reset_index().rename(
columns={"Rule" : "# rules"}
)
df_n_rules_per_target.head()
```
****
# Format pretty table
Goal:
* put smallest value per row in BOLT
* per target: mean_value 0.3 / 0.4
```
true_label_freq_to_noisy_to_df_map: Dict[float, Dict[float, pd.DataFrame]] = dict()
for true_label_freq in true_label_frequencies_set:
df_true_tmp: pd.DataFrame = df_conf_errors_avg_over_trials_and_rules_and_q_c_subset[
df_conf_errors_avg_over_trials_and_rules_and_q_c_subset["true_other"] == true_label_freq
]
noisy_label_freq_to_df_map = dict()
true_label_freq_to_noisy_to_df_map[true_label_freq] = noisy_label_freq_to_df_map
df_true_and_noisy_tmp = df_true_tmp[
df_true_tmp["noisy_other"] == true_label_freq
]
noisy_label_freq_to_df_map[true_label_freq] = df_true_and_noisy_tmp[
[col for col in df_true_and_noisy_tmp.columns if col != "noisy_other" and col != "true_other"]
]
for noisy_label_freq in true_label_frequency_to_estimate_map[true_label_freq]:
df_true_and_noisy_tmp = df_true_tmp[
df_true_tmp["noisy_other"] == noisy_label_freq
]
noisy_label_freq_to_df_map[noisy_label_freq] = df_true_and_noisy_tmp[
[col for col in df_true_and_noisy_tmp.columns if col != "noisy_other" and col != "true_other"]
]
true_label_freq_to_noisy_to_df_map[first_true_label_freq_to_include][0.2].head()
from typing import Iterator
true_label_freq_to_df_map = dict()
label_freq_estimators: Iterator[float]
for true_label_freq in true_label_frequencies_set:
noisy_to_df_map: Dict[float, pd.DataFrame] = true_label_freq_to_noisy_to_df_map[true_label_freq]
df_true_label_freq: pd.DataFrame = noisy_to_df_map[true_label_freq]
lower_est: float = round(true_label_freq - label_frequency_est_diff, 1)
higher_est: float = round(true_label_freq + label_frequency_est_diff, 1)
df_lower: pd.DataFrame = noisy_to_df_map[lower_est][
['target_relation', ConfidenceEnum.IPW_CONF.value]
].rename(
columns={
ConfidenceEnum.IPW_CONF.value: f"{ConfidenceEnum.IPW_CONF.value}_lower"
}
)
df_true_label_freq = pd.merge(
left=df_true_label_freq,
right=df_lower,
on="target_relation"
)
df_higher = noisy_to_df_map[higher_est][
['target_relation', ConfidenceEnum.IPW_CONF.value]
].rename(
columns={
ConfidenceEnum.IPW_CONF.value: f"{ConfidenceEnum.IPW_CONF.value}_higher"
}
)
df_true_label_freq = pd.merge(
left=df_true_label_freq,
right=df_higher,
on="target_relation"
)
true_label_freq_to_df_map[true_label_freq] = df_true_label_freq
true_label_freq_to_df_map[0.3].head()
for key, df in true_label_freq_to_df_map.items():
true_label_freq_to_df_map[key] = df.drop(
columns=["random_trial_index"],
axis=1,
errors='ignore'
)
df_one_row_per_target = pd.merge(
left=true_label_freq_to_df_map[first_true_label_freq_to_include],
right=true_label_freq_to_df_map[second_true_label_freq_to_include],
on="target_relation",
suffixes=(f"_{first_true_label_freq_to_include}", f"_{second_true_label_freq_to_include}")
)
df_one_row_per_target.head()
```
## What is the smallest value?
```
all_values: np.ndarray = df_one_row_per_target[
[ col
for col in df_one_row_per_target.columns
if col != "target_relation"
]
].values
min_val = np.amin(all_values)
min_val
min_val * 10000
max_val = np.amax(all_values)
max_val
max_val * 10000
df_one_row_per_target.head() * 10000
df_one_row_per_target.dtypes
exponent = 4
multiplication_factor = 10 ** exponent
multiplication_factor
df_one_row_per_target[
df_one_row_per_target.select_dtypes(include=['number']).columns
] *= multiplication_factor
df_one_row_per_target
df_one_row_per_target.head()
```
## Output files definitions
```
dir_latex_table: str = os.path.join(
kbc_e_metrics_project_dir,
"paper_latex_tables",
'known_prop_scores',
'sar_two_groups'
)
if not os.path.exists(dir_latex_table):
os.makedirs(dir_latex_table)
filename_tsv_rule_stats = os.path.join(
dir_latex_table,
"conf_error_stats_v3.tsv"
)
filename_tsv_single_row_summary = os.path.join(
dir_latex_table,
"noisy_sar_two_groups_single_row_summary.tsv"
)
```
## Create single-row summary
```
df_one_row_in_total: pd.Series = df_one_row_per_target.mean(
)
df_one_row_in_total
df_n_rules_per_target.head()
df_one_row_in_total["# rules"] = int(df_n_rules_per_target["# rules"].sum())
df_one_row_in_total
type(df_one_row_in_total)
df_one_row_in_total.to_csv(
filename_tsv_single_row_summary,
sep = "\t",
header=None
)
```
### Now create a pretty table
```
column_names_info.column_names_conf_estimators
simplified_column_names_conf_estimators = ['CWA', 'PCA', 'ICW', 'IPW',]
multi_index_columns = [
("$p$", ""),
("\# rules", "")
]
from itertools import product
# conf_upper_cols = column_names_info.column_names_conf_estimators + [
# f"{ConfidenceEnum.IPW_CONF.value} " + "($\Delta c=-" + f"{label_frequency_est_diff}" + "$)",
# f"{ConfidenceEnum.IPW_CONF.value} " + "($\Delta c=" + f"{label_frequency_est_diff}" + "$)",
# ]
conf_upper_cols = simplified_column_names_conf_estimators + [
f"{ConfidenceEnum.IPW_CONF.value} " + "($-\Delta$)",
f"{ConfidenceEnum.IPW_CONF.value} " + "($+\Delta$)",
]
c_subcols = ["$c_{\\neg q}=0.3$", "$c_{\\neg q}=0.7$"]
multi_index_columns = multi_index_columns + list(product(c_subcols, conf_upper_cols))
# multi_index_list
multi_index_columns = pd.MultiIndex.from_tuples(multi_index_columns)
multi_index_columns
rule_counter: int = 1
rule_str_to_rule_id_map: Dict[str, int] = {}
float_precision: int = 1
col_name_conf_estimator: str
pretty_rows: List[List] = []
row_index: int
row: pd.Series
# columns_to_use = [
# "$p$",
# "\# rules"
# ] + column_names_info.column_names_conf_estimators + [
# f"{ConfidenceEnum.IPW_CONF.value} " + "($\Delta c=-" + f"{label_frequency_est_diff}" + "$)",
# f"{ConfidenceEnum.IPW_CONF.value} " + "($\Delta c=" + f"{label_frequency_est_diff}" + "$)",
# ]
LabelFreq = float
def get_dict_with_smallest_estimator_per_label_freq(row: pd.Series) -> Dict[LabelFreq, Set[str]]:
# Find estimator with smallest mean value for label frequency###################
label_freq_to_set_of_smallest_est_map: Dict[LabelFreq, Set[str]] = dict()
for label_freq in [first_true_label_freq_to_include, second_true_label_freq_to_include]:
o_set_of_col_names_with_min_value: Optional[Set[str]] = None
o_current_smallest_value: Optional[float] = None
# Find smallest squared error
for col_name_conf_estimator in simplified_column_names_conf_estimators:
current_val: float = row[f"{col_name_conf_estimator}_{label_freq}"]
# print(current_val)
if o_set_of_col_names_with_min_value is None or o_current_smallest_value > current_val:
o_set_of_col_names_with_min_value = {col_name_conf_estimator}
o_current_smallest_value = current_val
elif current_val == o_current_smallest_value:
o_set_of_col_names_with_min_value.update(col_name_conf_estimator)
label_freq_to_set_of_smallest_est_map[label_freq] = o_set_of_col_names_with_min_value
return label_freq_to_set_of_smallest_est_map
def format_value_depending_on_whether_it_is_smallest(
value: float,
is_smallest: bool,
float_precision: float,
use_si: bool = False
)-> str:
if is_smallest:
if not use_si:
formatted_value = "$\\bm{" + f"{value:0.{float_precision}f}" + "}$"
# formatted_value = "$\\bm{" + f"{value:0.{float_precision}e}" + "}$"
else:
formatted_value = "\\textbf{$" + f"\\num[round-precision={float_precision},round-mode=figures,scientific-notation=true]"+\
"{"+ str(value) + "}"+ "$}"
else:
if not use_si:
formatted_value = f"${value:0.{float_precision}f}$"
# formatted_value = f"${value:0.{float_precision}e}$"
else:
formatted_value = "$" + f"\\num[round-precision={float_precision},round-mode=figures,scientific-notation=true]"+\
"{"+ str(value) + "}"+ "$"
return formatted_value
estimator_columns = simplified_column_names_conf_estimators + [
f"{ConfidenceEnum.IPW_CONF.value}_lower",
f"{ConfidenceEnum.IPW_CONF.value}_higher"
]
# For each row, i.e. for each target relation
for row_index, row in df_one_row_per_target.iterrows():
# Find estimator with smallest mean value for label frequency###################
label_freq_to_set_of_smallest_est_map: Dict[float, Set[str]] = get_dict_with_smallest_estimator_per_label_freq(
row=row
)
##################################################################################
# Construct the new row
######################
target_relation = row["target_relation"]
nb_of_rules = df_n_rules_per_target[df_n_rules_per_target['target_relation'] == target_relation][
"# rules"
].iloc[0]
new_row: List[str] = [
target_relation,
nb_of_rules
]
# For each Confidence estimator, get the value at c 0.3 and 0.7
# for col_name_conf_estimator in estimator_columns:
# mean_val_03:float = row[f"{col_name_conf_estimator}_0.3"]
# mean_val_07:float = row[f"{col_name_conf_estimator}_0.7"]
#
# new_row_value = (
# format_value_depending_on_whether_it_is_smallest(
# value=mean_val_03,
# is_smallest=col_name_conf_estimator == label_freq_to_smallest_est_map[0.3],
# float_precision=float_precision
# )
# + " / "
# + format_value_depending_on_whether_it_is_smallest(
# value=mean_val_07,
# is_smallest=col_name_conf_estimator == label_freq_to_smallest_est_map[0.7],
# float_precision=float_precision
# )
# )
# new_row.append(new_row_value)
for col_name_conf_estimator in estimator_columns:
mean_val_03:float = row[f"{col_name_conf_estimator}_{first_true_label_freq_to_include}"]
new_row_value_03 = format_value_depending_on_whether_it_is_smallest(
value=mean_val_03,
is_smallest=(
col_name_conf_estimator in label_freq_to_set_of_smallest_est_map[first_true_label_freq_to_include]
),
float_precision=float_precision
)
new_row.append(new_row_value_03)
for col_name_conf_estimator in estimator_columns:
mean_val_07:float = row[f"{col_name_conf_estimator}_{second_true_label_freq_to_include}"]
new_row_value_07 = format_value_depending_on_whether_it_is_smallest(
value=mean_val_07,
is_smallest=(
col_name_conf_estimator in label_freq_to_set_of_smallest_est_map[second_true_label_freq_to_include]
),
float_precision=float_precision
)
new_row.append(new_row_value_07)
pretty_rows.append(new_row)
df_pretty: pd.DataFrame = pd.DataFrame(
data=pretty_rows,
columns=multi_index_columns
)
df_pretty.head()
df_pretty: pd.DataFrame = df_pretty.sort_values(
by=["$p$"]
)
df_pretty.head()
```
# To file
```
# dir_latex_table: str = os.path.join(
# kbc_e_metrics_project_dir,
# "paper_latex_tables",
# 'known_prop_scores',
# 'scar'
# )
#
# if not os.path.exists(dir_latex_table):
# os.makedirs(dir_latex_table)
filename_latex_table: str = os.path.join(
dir_latex_table,
"confidence-error-table-sar-two-subject-groups-agg-per-p.tex"
)
filename_tsv_table: str = os.path.join(
dir_latex_table,
"confidence-error-table-sar-two-subject-groups-agg-per-p.tsv"
)
with open(filename_latex_table, "w") as latex_ofile:
with pd.option_context("max_colwidth", 1000):
latex_ofile.write(
df_pretty.to_latex(
column_format="lr|lllllll|lllllll",
index=False,
float_format="{:0.3f}".format,
escape=False,
# caption="$[widehat{conf}-conf]^2$ for SCAR. "
# "std=standard confidence, "
# "PCA (S) = PCA confidence with $s$ as domain, "
# "PCA (O) = PCA confidence with $o$ as domain, "
# "IPW = PCA confidence with $\hat{e}=e$, "
# "IPW +/- $" + f"{label_frequency_est_diff:0.1}" + "$ = IPW confidence with $\hat{e}=e+/-" + f"{label_frequency_est_diff:0.1}" + "$."
)
)
with open(filename_tsv_table, "w") as tsv_ofile:
tsv_ofile.write(df_pretty.to_csv(
index=False,
sep="\t"
))
print(filename_latex_table)
```
|
github_jupyter
|
```
# %gui qt
import numpy as np
import mne
import pickle
import sys
import os
# import matplotlib
from multiprocessing import Pool
from tqdm import tqdm
import matplotlib.pyplot as plt
# import vispy
# print(vispy.sys_info())
# BASE_DIR = os.path.dirname(os.path.dirname(os.path.abspath(__file__)))
# sys.path.append(BASE_DIR)
%matplotlib inline
mne.utils.set_config('MNE_USE_CUDA', 'true')
mne.cuda.init_cuda(verbose=True)
baseFolder='./pickled-avg'
files=[f for f in os.listdir(baseFolder) if not f.startswith('.')]
data=pickle.load(open('pickled-avg/OpenBCISession_2020-02-14_11-09-00-SEVEN', 'rb'))
data[0]
#Naming system for blocks into integers
bloc={
"sync":1,
"baseline":2,
"stressor":3,
"survey":4,
"rest":5,
"slowBreath":6,
"paced":7
}
def createMNEObj(data, name='Empty'):
#Create Metadata
sampling_rate = 125
channel_names = ['Fp1', 'Fp2', 'C3', 'C4', 'P7', 'P8', 'O1', 'O2', 'F7', 'F8', 'F3', 'F4', 'T7', 'T8', 'P3', 'P4',
'time', 'bpm', 'ibi', 'sdnn', 'sdsd', 'rmssd', 'pnn20', 'pnn50', 'hr_mad', 'sd1', 'sd2', 's', 'sd1/sd2', 'breathingrate', 'segment_indices1', 'segment_indices2', 'block']
channel_types = ['eeg', 'eeg', 'eeg', 'eeg', 'eeg', 'eeg', 'eeg', 'eeg', 'eeg', 'eeg', 'eeg', 'eeg', 'eeg', 'eeg', 'eeg', 'eeg',
'misc', 'misc', 'misc', 'misc', 'misc', 'misc', 'misc', 'misc', 'misc', 'misc', 'misc', 'misc', 'misc', 'misc', 'misc', 'misc', 'stim']
n_channels = len(channel_types)
info = mne.create_info(ch_names=channel_names, sfreq=sampling_rate, ch_types=channel_types)
info['description'] = name
print(info)
transformed = []
start=-1.0
for i in range(len(data)):
add=[]
add=data[i][1:17]
# print(data[i][19].keys())
if start==-1:
start=data[i][18].hour*3600 + data[i][18].minute*60 + data[i][18].second + data[i][18].microsecond/1000
add.append(0.0)
else:
tim=data[i][18].hour*3600 + data[i][18].minute*60 + data[i][18].second + data[i][18].microsecond/1000
add.append(tim-start)
# add.append(str(data[i][18].hour)+':'+str(data[i][18].minute)+':'+str(data[i][18].second)+':'+str(int(data[i][18].microsecond/1000)))
# try:
add.append(data[i][19]['bpm'])
# except Exception as e:
# print(e, i)
# print(data[i][19])
# print(len(data))
add.append(data[i][19]['ibi'])
add.append(data[i][19]['sdnn'])
add.append(data[i][19]['sdsd'])
add.append(data[i][19]['rmssd'])
add.append(data[i][19]['pnn20'])
add.append(data[i][19]['pnn50'])
add.append(data[i][19]['hr_mad'])
add.append(data[i][19]['sd1'])
add.append(data[i][19]['sd2'])
add.append(data[i][19]['s'])
add.append(data[i][19]['sd1/sd2'])
add.append(data[i][19]['breathingrate'])
add.append(data[i][19]['segment_indices'][0])
add.append(data[i][19]['segment_indices'][1])
add.append(bloc[data[i][20]])
transformed.append(np.array(add))
transformed=np.array(transformed)
print(transformed[0])
#have to convert rows to columns to fit MNE structure
transformed=transformed.transpose()
print(transformed[0], transformed[1], transformed[2], transformed[3])
print(len(transformed[0]))
loaded=mne.io.RawArray(transformed, info)
return loaded
raw=createMNEObj(data)
raw[1][]
data
np.transpose(np.transpose(data))
def filt(ind):
name=files[ind]
data=pickle.load(open('pickled-avg/'+name, 'rb'))
# if ind==1:
# pbar = tqdm(total=len(data), position=ind)
raw=createMNEObj(data)
print('Created object')
montage = mne.channels.make_standard_montage('easycap-M1')
raw.set_montage(montage, raise_if_subset=False)
mne.io.Raw.filter(raw,l_freq=0.5,h_freq=None)
print('Done filtering')
tem=np.transpose(data)
# for i in tqdm(range(len(data))):
# if ind==1:
# pbar.update(1)
# data[i][k+1]=raw[k][0][0][i]
for k in range(0, 16):
tem[k+1]=raw[k][0][0]
data=np.transpose(tem)
pickle.dump(data, open('pickled-high/'+name, "wb" ) )
filt(1)
p = Pool(18)
master=p.map(filt, range(len(files)))
data=pickle.load(open('pickled-filt/OpenBCISession_2020-02-14_11-09-00-SEVEN', 'rb'))
data[0]
```
|
github_jupyter
|
# Hyperparameter Optimization [xgboost](https://github.com/dmlc/xgboost)
What the options there're for tuning?
* [GridSearch](http://scikit-learn.org/stable/modules/grid_search.html)
* [RandomizedSearch](http://scikit-learn.org/stable/modules/generated/sklearn.grid_search.RandomizedSearchCV.html)
All right!
Xgboost has about 20 params:
1. base_score
2. **colsample_bylevel**
3. **colsample_bytree**
4. **gamma**
5. **learning_rate**
6. **max_delta_step**
7. **max_depth**
8. **min_child_weight**
9. missing
10. **n_estimators**
11. nthread
12. **objective**
13. **reg_alpha**
14. **reg_lambda**
15. **scale_pos_weight**
16. **seed**
17. silent
18. **subsample**
Let's for tuning will be use 12 of them them with 5-10 possible values, so... there're 12^5 - 12^10 possible cases.
If you will check one case in 10s, for **12^5** you need **30 days** for **12^10** about **20K** years :).
This is too long.. but there's a thid option - **Bayesan optimisation**.
```
import pandas as pd
import xgboost as xgb
import numpy as np
import seaborn as sns
from hyperopt import hp
from hyperopt import hp, fmin, tpe, STATUS_OK, Trials
%matplotlib inline
train = pd.read_csv('bike.csv')
train['datetime'] = pd.to_datetime( train['datetime'] )
train['day'] = train['datetime'].map(lambda x: x.day)
```
## Modeling
```
def assing_test_samples(data, last_training_day=0.3, seed=1):
days = data.day.unique()
np.random.seed(seed)
np.random.shuffle(days)
test_days = days[: int(len(days) * 0.3)]
data['is_test'] = data.day.isin(test_days)
def select_features(data):
columns = data.columns[ (data.dtypes == np.int64) | (data.dtypes == np.float64) | (data.dtypes == np.bool) ].values
return [feat for feat in columns if feat not in ['count', 'casual', 'registered'] and 'log' not in feat ]
def get_X_y(data, target_variable):
features = select_features(data)
X = data[features].values
y = data[target_variable].values
return X,y
def train_test_split(train, target_variable):
df_train = train[train.is_test == False]
df_test = train[train.is_test == True]
X_train, y_train = get_X_y(df_train, target_variable)
X_test, y_test = get_X_y(df_test, target_variable)
return X_train, X_test, y_train, y_test
def fit_and_predict(train, model, target_variable):
X_train, X_test, y_train, y_test = train_test_split(train, target_variable)
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
return (y_test, y_pred)
def post_pred(y_pred):
y_pred[y_pred < 0] = 0
return y_pred
def rmsle(y_true, y_pred, y_pred_only_positive=True):
if y_pred_only_positive: y_pred = post_pred(y_pred)
diff = np.log(y_pred+1) - np.log(y_true+1)
mean_error = np.square(diff).mean()
return np.sqrt(mean_error)
assing_test_samples(train)
def etl_datetime(df):
df['year'] = df['datetime'].map(lambda x: x.year)
df['month'] = df['datetime'].map(lambda x: x.month)
df['hour'] = df['datetime'].map(lambda x: x.hour)
df['minute'] = df['datetime'].map(lambda x: x.minute)
df['dayofweek'] = df['datetime'].map(lambda x: x.dayofweek)
df['weekend'] = df['datetime'].map(lambda x: x.dayofweek in [5,6])
etl_datetime(train)
train['{0}_log'.format('count')] = train['count'].map(lambda x: np.log2(x) )
for name in ['registered', 'casual']:
train['{0}_log'.format(name)] = train[name].map(lambda x: np.log2(x+1) )
```
## Tuning hyperparmeters using Bayesian optimization algorithms
```
def objective(space):
model = xgb.XGBRegressor(
max_depth = space['max_depth'],
n_estimators = int(space['n_estimators']),
subsample = space['subsample'],
colsample_bytree = space['colsample_bytree'],
learning_rate = space['learning_rate'],
reg_alpha = space['reg_alpha']
)
X_train, X_test, y_train, y_test = train_test_split(train, 'count')
eval_set = [( X_train, y_train), ( X_test, y_test)]
(_, registered_pred) = fit_and_predict(train, model, 'registered_log')
(_, casual_pred) = fit_and_predict(train, model, 'casual_log')
y_test = train[train.is_test == True]['count']
y_pred = (np.exp2(registered_pred) - 1) + (np.exp2(casual_pred) -1)
score = rmsle(y_test, y_pred)
print "SCORE:", score
return{'loss':score, 'status': STATUS_OK }
space ={
'max_depth': hp.quniform("x_max_depth", 2, 20, 1),
'n_estimators': hp.quniform("n_estimators", 100, 1000, 1),
'subsample': hp.uniform ('x_subsample', 0.8, 1),
'colsample_bytree': hp.uniform ('x_colsample_bytree', 0.1, 1),
'learning_rate': hp.uniform ('x_learning_rate', 0.01, 0.1),
'reg_alpha': hp.uniform ('x_reg_alpha', 0.1, 1)
}
trials = Trials()
best = fmin(fn=objective,
space=space,
algo=tpe.suggest,
max_evals=15,
trials=trials)
print(best)
```
## Links
1. http://hyperopt.github.io/hyperopt/
2. https://districtdatalabs.silvrback.com/parameter-tuning-with-hyperopt
3. http://fastml.com/optimizing-hyperparams-with-hyperopt/
4. https://github.com/Far0n/xgbfi
|
github_jupyter
|
##### Copyright 2020 The TensorFlow Hub Authors.
```
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
```
<table class="tfo-notebook-buttons" align="left">
<td>
<a target="_blank" href="https://www.tensorflow.org/tutorials/text/solve_glue_tasks_using_bert_on_tpu"><img src="https://www.tensorflow.org/images/tf_logo_32px.png" />View on TensorFlow.org</a>
</td>
<td>
<a target="_blank" href="https://colab.research.google.com/github/tensorflow/docs/blob/master/site/en/tutorials/text/solve_glue_tasks_using_bert_on_tpu.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
</td>
<td>
<a target="_blank" href="https://github.com/tensorflow/docs/blob/master/site/en/tutorials/text/solve_glue_tasks_using_bert_on_tpu.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View on GitHub</a>
</td>
<td>
<a href="https://storage.googleapis.com/tensorflow_docs/docs/site/en/tutorials/text/solve_glue_tasks_using_bert_on_tpu.ipynb"><img src="https://www.tensorflow.org/images/download_logo_32px.png" />Download notebook</a>
</td>
<td>
<a href="https://tfhub.dev/google/collections/bert/1"><img src="https://www.tensorflow.org/images/hub_logo_32px.png" />See TF Hub model</a>
</td>
</table>
# Solve GLUE tasks using BERT on TPU
BERT can be used to solve many problems in natural language processing. You will learn how to fine-tune BERT for many tasks from the [GLUE benchmark](https://gluebenchmark.com/):
1. [CoLA](https://nyu-mll.github.io/CoLA/) (Corpus of Linguistic Acceptability): Is the sentence grammatically correct?
1. [SST-2](https://nlp.stanford.edu/sentiment/index.html) (Stanford Sentiment Treebank): The task is to predict the sentiment of a given sentence.
1. [MRPC](https://www.microsoft.com/en-us/download/details.aspx?id=52398) (Microsoft Research Paraphrase Corpus): Determine whether a pair of sentences are semantically equivalent.
1. [QQP](https://data.quora.com/First-Quora-Dataset-Release-Question-Pairs) (Quora Question Pairs2): Determine whether a pair of questions are semantically equivalent.
1. [MNLI](http://www.nyu.edu/projects/bowman/multinli/) (Multi-Genre Natural Language Inference): Given a premise sentence and a hypothesis sentence, the task is to predict whether the premise entails the hypothesis (entailment), contradicts the hypothesis (contradiction), or neither (neutral).
1. [QNLI](https://rajpurkar.github.io/SQuAD-explorer/)(Question-answering Natural Language Inference): The task is to determine whether the context sentence contains the answer to the question.
1. [RTE](https://aclweb.org/aclwiki/Recognizing_Textual_Entailment)(Recognizing Textual Entailment): Determine if a sentence entails a given hypothesis or not.
1. [WNLI](https://cs.nyu.edu/faculty/davise/papers/WinogradSchemas/WS.html)(Winograd Natural Language Inference): The task is to predict if the sentence with the pronoun substituted is entailed by the original sentence.
This tutorial contains complete end-to-end code to train these models on a TPU. You can also run this notebook on a GPU, by changing one line (described below).
In this notebook, you will:
- Load a BERT model from TensorFlow Hub
- Choose one of GLUE tasks and download the dataset
- Preprocess the text
- Fine-tune BERT (examples are given for single-sentence and multi-sentence datasets)
- Save the trained model and use it
Key point: The model you develop will be end-to-end. The preprocessing logic will be included in the model itself, making it capable of accepting raw strings as input.
Note: This notebook should be run using a TPU. In Colab, choose **Runtime -> Change runtime type** and verify that a **TPU** is selected.
## Setup
You will use a separate model to preprocess text before using it to fine-tune BERT. This model depends on [tensorflow/text](https://github.com/tensorflow/text), which you will install below.
```
!pip install -q -U tensorflow-text
```
You will use the AdamW optimizer from [tensorflow/models](https://github.com/tensorflow/models) to fine-tune BERT, which you will install as well.
```
!pip install -q -U tf-models-official
!pip install -U tfds-nightly
import os
import tensorflow as tf
import tensorflow_hub as hub
import tensorflow_datasets as tfds
import tensorflow_text as text # A dependency of the preprocessing model
import tensorflow_addons as tfa
from official.nlp import optimization
import numpy as np
tf.get_logger().setLevel('ERROR')
```
Next, configure TFHub to read checkpoints directly from TFHub's Cloud Storage buckets. This is only recomended when running TFHub models on TPU.
Without this setting TFHub would download the compressed file and extract the checkpoint locally. Attempting to load from these local files will fail with following Error:
```
InvalidArgumentError: Unimplemented: File system scheme '[local]' not implemented
```
This is because the [TPU can only read directly from Cloud Storage buckets](https://cloud.google.com/tpu/docs/troubleshooting#cannot_use_local_filesystem).
Note: This setting is automatic in Colab.
```
os.environ["TFHUB_MODEL_LOAD_FORMAT"]="UNCOMPRESSED"
```
### Connect to the TPU worker
The following code connects to the TPU worker and changes TensorFlow's default device to the CPU device on the TPU worker. It also defines a TPU distribution strategy that you will use to distribute model training onto the 8 separate TPU cores available on this one TPU worker. See TensorFlow's [TPU guide](https://www.tensorflow.org/guide/tpu) for more information.
```
import os
if os.environ['COLAB_TPU_ADDR']:
cluster_resolver = tf.distribute.cluster_resolver.TPUClusterResolver(tpu='grpc://' + os.environ['COLAB_TPU_ADDR'])
tf.config.experimental_connect_to_cluster(cluster_resolver)
tf.tpu.experimental.initialize_tpu_system(cluster_resolver)
strategy = tf.distribute.TPUStrategy(cluster_resolver)
print('Using TPU')
elif tf.test.is_gpu_available():
strategy = tf.distribute.MirroredStrategy()
print('Using GPU')
else:
raise ValueError('Running on CPU is not recomended.')
```
## Loading models from TensorFlow Hub
Here you can choose which BERT model you will load from TensorFlow Hub and fine-tune.
There are multiple BERT models available to choose from.
- [BERT-Base](https://tfhub.dev/tensorflow/bert_en_uncased_L-12_H-768_A-12/3), [Uncased](https://tfhub.dev/tensorflow/bert_en_uncased_L-12_H-768_A-12/3) and [seven more models](https://tfhub.dev/google/collections/bert/1) with trained weights released by the original BERT authors.
- [Small BERTs](https://tfhub.dev/google/collections/bert/1) have the same general architecture but fewer and/or smaller Transformer blocks, which lets you explore tradeoffs between speed, size and quality.
- [ALBERT](https://tfhub.dev/google/collections/albert/1): four different sizes of "A Lite BERT" that reduces model size (but not computation time) by sharing parameters between layers.
- [BERT Experts](https://tfhub.dev/google/collections/experts/bert/1): eight models that all have the BERT-base architecture but offer a choice between different pre-training domains, to align more closely with the target task.
- [Electra](https://tfhub.dev/google/collections/electra/1) has the same architecture as BERT (in three different sizes), but gets pre-trained as a discriminator in a set-up that resembles a Generative Adversarial Network (GAN).
- BERT with Talking-Heads Attention and Gated GELU [[base](https://tfhub.dev/tensorflow/talkheads_ggelu_bert_en_base/1), [large](https://tfhub.dev/tensorflow/talkheads_ggelu_bert_en_large/1)] has two improvements to the core of the Transformer architecture.
See the model documentation linked above for more details.
In this tutorial, you will start with BERT-base. You can use larger and more recent models for higher accuracy, or smaller models for faster training times. To change the model, you only need to switch a single line of code (shown below). All of the differences are encapsulated in the SavedModel you will download from TensorFlow Hub.
```
#@title Choose a BERT model to fine-tune
bert_model_name = 'bert_en_uncased_L-12_H-768_A-12' #@param ["bert_en_uncased_L-12_H-768_A-12", "bert_en_uncased_L-24_H-1024_A-16", "bert_en_wwm_uncased_L-24_H-1024_A-16", "bert_en_cased_L-12_H-768_A-12", "bert_en_cased_L-24_H-1024_A-16", "bert_en_wwm_cased_L-24_H-1024_A-16", "bert_multi_cased_L-12_H-768_A-12", "small_bert/bert_en_uncased_L-2_H-128_A-2", "small_bert/bert_en_uncased_L-2_H-256_A-4", "small_bert/bert_en_uncased_L-2_H-512_A-8", "small_bert/bert_en_uncased_L-2_H-768_A-12", "small_bert/bert_en_uncased_L-4_H-128_A-2", "small_bert/bert_en_uncased_L-4_H-256_A-4", "small_bert/bert_en_uncased_L-4_H-512_A-8", "small_bert/bert_en_uncased_L-4_H-768_A-12", "small_bert/bert_en_uncased_L-6_H-128_A-2", "small_bert/bert_en_uncased_L-6_H-256_A-4", "small_bert/bert_en_uncased_L-6_H-512_A-8", "small_bert/bert_en_uncased_L-6_H-768_A-12", "small_bert/bert_en_uncased_L-8_H-128_A-2", "small_bert/bert_en_uncased_L-8_H-256_A-4", "small_bert/bert_en_uncased_L-8_H-512_A-8", "small_bert/bert_en_uncased_L-8_H-768_A-12", "small_bert/bert_en_uncased_L-10_H-128_A-2", "small_bert/bert_en_uncased_L-10_H-256_A-4", "small_bert/bert_en_uncased_L-10_H-512_A-8", "small_bert/bert_en_uncased_L-10_H-768_A-12", "small_bert/bert_en_uncased_L-12_H-128_A-2", "small_bert/bert_en_uncased_L-12_H-256_A-4", "small_bert/bert_en_uncased_L-12_H-512_A-8", "small_bert/bert_en_uncased_L-12_H-768_A-12", "albert_en_base", "albert_en_large", "albert_en_xlarge", "albert_en_xxlarge", "electra_small", "electra_base", "experts_pubmed", "experts_wiki_books", "talking-heads_base", "talking-heads_large"]
map_name_to_handle = {
'bert_en_uncased_L-12_H-768_A-12':
'https://tfhub.dev/tensorflow/bert_en_uncased_L-12_H-768_A-12/3',
'bert_en_uncased_L-24_H-1024_A-16':
'https://tfhub.dev/tensorflow/bert_en_uncased_L-24_H-1024_A-16/3',
'bert_en_wwm_uncased_L-24_H-1024_A-16':
'https://tfhub.dev/tensorflow/bert_en_wwm_uncased_L-24_H-1024_A-16/3',
'bert_en_cased_L-12_H-768_A-12':
'https://tfhub.dev/tensorflow/bert_en_cased_L-12_H-768_A-12/3',
'bert_en_cased_L-24_H-1024_A-16':
'https://tfhub.dev/tensorflow/bert_en_cased_L-24_H-1024_A-16/3',
'bert_en_wwm_cased_L-24_H-1024_A-16':
'https://tfhub.dev/tensorflow/bert_en_wwm_cased_L-24_H-1024_A-16/3',
'bert_multi_cased_L-12_H-768_A-12':
'https://tfhub.dev/tensorflow/bert_multi_cased_L-12_H-768_A-12/3',
'small_bert/bert_en_uncased_L-2_H-128_A-2':
'https://tfhub.dev/tensorflow/small_bert/bert_en_uncased_L-2_H-128_A-2/1',
'small_bert/bert_en_uncased_L-2_H-256_A-4':
'https://tfhub.dev/tensorflow/small_bert/bert_en_uncased_L-2_H-256_A-4/1',
'small_bert/bert_en_uncased_L-2_H-512_A-8':
'https://tfhub.dev/tensorflow/small_bert/bert_en_uncased_L-2_H-512_A-8/1',
'small_bert/bert_en_uncased_L-2_H-768_A-12':
'https://tfhub.dev/tensorflow/small_bert/bert_en_uncased_L-2_H-768_A-12/1',
'small_bert/bert_en_uncased_L-4_H-128_A-2':
'https://tfhub.dev/tensorflow/small_bert/bert_en_uncased_L-4_H-128_A-2/1',
'small_bert/bert_en_uncased_L-4_H-256_A-4':
'https://tfhub.dev/tensorflow/small_bert/bert_en_uncased_L-4_H-256_A-4/1',
'small_bert/bert_en_uncased_L-4_H-512_A-8':
'https://tfhub.dev/tensorflow/small_bert/bert_en_uncased_L-4_H-512_A-8/1',
'small_bert/bert_en_uncased_L-4_H-768_A-12':
'https://tfhub.dev/tensorflow/small_bert/bert_en_uncased_L-4_H-768_A-12/1',
'small_bert/bert_en_uncased_L-6_H-128_A-2':
'https://tfhub.dev/tensorflow/small_bert/bert_en_uncased_L-6_H-128_A-2/1',
'small_bert/bert_en_uncased_L-6_H-256_A-4':
'https://tfhub.dev/tensorflow/small_bert/bert_en_uncased_L-6_H-256_A-4/1',
'small_bert/bert_en_uncased_L-6_H-512_A-8':
'https://tfhub.dev/tensorflow/small_bert/bert_en_uncased_L-6_H-512_A-8/1',
'small_bert/bert_en_uncased_L-6_H-768_A-12':
'https://tfhub.dev/tensorflow/small_bert/bert_en_uncased_L-6_H-768_A-12/1',
'small_bert/bert_en_uncased_L-8_H-128_A-2':
'https://tfhub.dev/tensorflow/small_bert/bert_en_uncased_L-8_H-128_A-2/1',
'small_bert/bert_en_uncased_L-8_H-256_A-4':
'https://tfhub.dev/tensorflow/small_bert/bert_en_uncased_L-8_H-256_A-4/1',
'small_bert/bert_en_uncased_L-8_H-512_A-8':
'https://tfhub.dev/tensorflow/small_bert/bert_en_uncased_L-8_H-512_A-8/1',
'small_bert/bert_en_uncased_L-8_H-768_A-12':
'https://tfhub.dev/tensorflow/small_bert/bert_en_uncased_L-8_H-768_A-12/1',
'small_bert/bert_en_uncased_L-10_H-128_A-2':
'https://tfhub.dev/tensorflow/small_bert/bert_en_uncased_L-10_H-128_A-2/1',
'small_bert/bert_en_uncased_L-10_H-256_A-4':
'https://tfhub.dev/tensorflow/small_bert/bert_en_uncased_L-10_H-256_A-4/1',
'small_bert/bert_en_uncased_L-10_H-512_A-8':
'https://tfhub.dev/tensorflow/small_bert/bert_en_uncased_L-10_H-512_A-8/1',
'small_bert/bert_en_uncased_L-10_H-768_A-12':
'https://tfhub.dev/tensorflow/small_bert/bert_en_uncased_L-10_H-768_A-12/1',
'small_bert/bert_en_uncased_L-12_H-128_A-2':
'https://tfhub.dev/tensorflow/small_bert/bert_en_uncased_L-12_H-128_A-2/1',
'small_bert/bert_en_uncased_L-12_H-256_A-4':
'https://tfhub.dev/tensorflow/small_bert/bert_en_uncased_L-12_H-256_A-4/1',
'small_bert/bert_en_uncased_L-12_H-512_A-8':
'https://tfhub.dev/tensorflow/small_bert/bert_en_uncased_L-12_H-512_A-8/1',
'small_bert/bert_en_uncased_L-12_H-768_A-12':
'https://tfhub.dev/tensorflow/small_bert/bert_en_uncased_L-12_H-768_A-12/1',
'albert_en_base':
'https://tfhub.dev/tensorflow/albert_en_base/2',
'albert_en_large':
'https://tfhub.dev/tensorflow/albert_en_large/2',
'albert_en_xlarge':
'https://tfhub.dev/tensorflow/albert_en_xlarge/2',
'albert_en_xxlarge':
'https://tfhub.dev/tensorflow/albert_en_xxlarge/2',
'electra_small':
'https://tfhub.dev/google/electra_small/2',
'electra_base':
'https://tfhub.dev/google/electra_base/2',
'experts_pubmed':
'https://tfhub.dev/google/experts/bert/pubmed/2',
'experts_wiki_books':
'https://tfhub.dev/google/experts/bert/wiki_books/2',
'talking-heads_base':
'https://tfhub.dev/tensorflow/talkheads_ggelu_bert_en_base/1',
'talking-heads_large':
'https://tfhub.dev/tensorflow/talkheads_ggelu_bert_en_large/1',
}
map_model_to_preprocess = {
'bert_en_uncased_L-24_H-1024_A-16':
'https://tfhub.dev/tensorflow/bert_en_uncased_preprocess/3',
'bert_en_uncased_L-12_H-768_A-12':
'https://tfhub.dev/tensorflow/bert_en_uncased_preprocess/3',
'bert_en_wwm_cased_L-24_H-1024_A-16':
'https://tfhub.dev/tensorflow/bert_en_cased_preprocess/3',
'bert_en_cased_L-24_H-1024_A-16':
'https://tfhub.dev/tensorflow/bert_en_cased_preprocess/3',
'bert_en_cased_L-12_H-768_A-12':
'https://tfhub.dev/tensorflow/bert_en_cased_preprocess/3',
'bert_en_wwm_uncased_L-24_H-1024_A-16':
'https://tfhub.dev/tensorflow/bert_en_uncased_preprocess/3',
'small_bert/bert_en_uncased_L-2_H-128_A-2':
'https://tfhub.dev/tensorflow/bert_en_uncased_preprocess/3',
'small_bert/bert_en_uncased_L-2_H-256_A-4':
'https://tfhub.dev/tensorflow/bert_en_uncased_preprocess/3',
'small_bert/bert_en_uncased_L-2_H-512_A-8':
'https://tfhub.dev/tensorflow/bert_en_uncased_preprocess/3',
'small_bert/bert_en_uncased_L-2_H-768_A-12':
'https://tfhub.dev/tensorflow/bert_en_uncased_preprocess/3',
'small_bert/bert_en_uncased_L-4_H-128_A-2':
'https://tfhub.dev/tensorflow/bert_en_uncased_preprocess/3',
'small_bert/bert_en_uncased_L-4_H-256_A-4':
'https://tfhub.dev/tensorflow/bert_en_uncased_preprocess/3',
'small_bert/bert_en_uncased_L-4_H-512_A-8':
'https://tfhub.dev/tensorflow/bert_en_uncased_preprocess/3',
'small_bert/bert_en_uncased_L-4_H-768_A-12':
'https://tfhub.dev/tensorflow/bert_en_uncased_preprocess/3',
'small_bert/bert_en_uncased_L-6_H-128_A-2':
'https://tfhub.dev/tensorflow/bert_en_uncased_preprocess/3',
'small_bert/bert_en_uncased_L-6_H-256_A-4':
'https://tfhub.dev/tensorflow/bert_en_uncased_preprocess/3',
'small_bert/bert_en_uncased_L-6_H-512_A-8':
'https://tfhub.dev/tensorflow/bert_en_uncased_preprocess/3',
'small_bert/bert_en_uncased_L-6_H-768_A-12':
'https://tfhub.dev/tensorflow/bert_en_uncased_preprocess/3',
'small_bert/bert_en_uncased_L-8_H-128_A-2':
'https://tfhub.dev/tensorflow/bert_en_uncased_preprocess/3',
'small_bert/bert_en_uncased_L-8_H-256_A-4':
'https://tfhub.dev/tensorflow/bert_en_uncased_preprocess/3',
'small_bert/bert_en_uncased_L-8_H-512_A-8':
'https://tfhub.dev/tensorflow/bert_en_uncased_preprocess/3',
'small_bert/bert_en_uncased_L-8_H-768_A-12':
'https://tfhub.dev/tensorflow/bert_en_uncased_preprocess/3',
'small_bert/bert_en_uncased_L-10_H-128_A-2':
'https://tfhub.dev/tensorflow/bert_en_uncased_preprocess/3',
'small_bert/bert_en_uncased_L-10_H-256_A-4':
'https://tfhub.dev/tensorflow/bert_en_uncased_preprocess/3',
'small_bert/bert_en_uncased_L-10_H-512_A-8':
'https://tfhub.dev/tensorflow/bert_en_uncased_preprocess/3',
'small_bert/bert_en_uncased_L-10_H-768_A-12':
'https://tfhub.dev/tensorflow/bert_en_uncased_preprocess/3',
'small_bert/bert_en_uncased_L-12_H-128_A-2':
'https://tfhub.dev/tensorflow/bert_en_uncased_preprocess/3',
'small_bert/bert_en_uncased_L-12_H-256_A-4':
'https://tfhub.dev/tensorflow/bert_en_uncased_preprocess/3',
'small_bert/bert_en_uncased_L-12_H-512_A-8':
'https://tfhub.dev/tensorflow/bert_en_uncased_preprocess/3',
'small_bert/bert_en_uncased_L-12_H-768_A-12':
'https://tfhub.dev/tensorflow/bert_en_uncased_preprocess/3',
'bert_multi_cased_L-12_H-768_A-12':
'https://tfhub.dev/tensorflow/bert_multi_cased_preprocess/3',
'albert_en_base':
'https://tfhub.dev/tensorflow/albert_en_preprocess/2',
'albert_en_large':
'https://tfhub.dev/tensorflow/albert_en_preprocess/2',
'albert_en_xlarge':
'https://tfhub.dev/tensorflow/albert_en_preprocess/2',
'albert_en_xxlarge':
'https://tfhub.dev/tensorflow/albert_en_preprocess/2',
'electra_small':
'https://tfhub.dev/tensorflow/bert_en_uncased_preprocess/3',
'electra_base':
'https://tfhub.dev/tensorflow/bert_en_uncased_preprocess/3',
'experts_pubmed':
'https://tfhub.dev/tensorflow/bert_en_uncased_preprocess/3',
'experts_wiki_books':
'https://tfhub.dev/tensorflow/bert_en_uncased_preprocess/3',
'talking-heads_base':
'https://tfhub.dev/tensorflow/bert_en_uncased_preprocess/3',
'talking-heads_large':
'https://tfhub.dev/tensorflow/bert_en_uncased_preprocess/3',
}
tfhub_handle_encoder = map_name_to_handle[bert_model_name]
tfhub_handle_preprocess = map_model_to_preprocess[bert_model_name]
print(f'BERT model selected : {tfhub_handle_encoder}')
print(f'Preprocessing model auto-selected: {tfhub_handle_preprocess}')
```
## Preprocess the text
On the [Classify text with BERT colab](https://www.tensorflow.org/tutorials/text/classify_text_with_bert) the preprocessing model is used directly embedded with the BERT encoder.
This tutorial demonstrates how to do preprocessing as part of your input pipeline for training, using Dataset.map, and then merge it into the model that gets exported for inference. That way, both training and inference can work from raw text inputs, although the TPU itself requires numeric inputs.
TPU requirements aside, it can help performance have preprocessing done asynchronously in an input pipeline (you can learn more in the [tf.data performance guide](https://www.tensorflow.org/guide/data_performance)).
This tutorial also demonstrates how to build multi-input models, and how to adjust the sequence length of the inputs to BERT.
Let's demonstrate the preprocessing model.
```
bert_preprocess = hub.load(tfhub_handle_preprocess)
tok = bert_preprocess.tokenize(tf.constant(['Hello TensorFlow!']))
print(tok)
```
Each preprocessing model also provides a method,`.bert_pack_inputs(tensors, seq_length)`, which takes a list of tokens (like `tok` above) and a sequence length argument. This packs the inputs to create a dictionary of tensors in the format expected by the BERT model.
```
text_preprocessed = bert_preprocess.bert_pack_inputs([tok, tok], tf.constant(20))
print('Shape Word Ids : ', text_preprocessed['input_word_ids'].shape)
print('Word Ids : ', text_preprocessed['input_word_ids'][0, :16])
print('Shape Mask : ', text_preprocessed['input_mask'].shape)
print('Input Mask : ', text_preprocessed['input_mask'][0, :16])
print('Shape Type Ids : ', text_preprocessed['input_type_ids'].shape)
print('Type Ids : ', text_preprocessed['input_type_ids'][0, :16])
```
Here are some details to pay attention to:
- `input_mask` The mask allows the model to cleanly differentiate between the content and the padding. The mask has the same shape as the `input_word_ids`, and contains a 1 anywhere the `input_word_ids` is not padding.
- `input_type_ids` has the same shape of `input_mask`, but inside the non-padded region, contains a 0 or a 1 indicating which sentence the token is a part of.
Next, you will create a preprocessing model that encapsulates all this logic. Your model will take strings as input, and return appropriately formatted objects which can be passed to BERT.
Each BERT model has a specific preprocessing model, make sure to use the proper one described on the BERT's model documentation.
Note: BERT adds a "position embedding" to the token embedding of each input, and these come from a fixed-size lookup table. That imposes a max seq length of 512 (which is also a practical limit, due to the quadratic growth of attention computation). For this colab 128 is good enough.
```
def make_bert_preprocess_model(sentence_features, seq_length=128):
"""Returns Model mapping string features to BERT inputs.
Args:
sentence_features: a list with the names of string-valued features.
seq_length: an integer that defines the sequence length of BERT inputs.
Returns:
A Keras Model that can be called on a list or dict of string Tensors
(with the order or names, resp., given by sentence_features) and
returns a dict of tensors for input to BERT.
"""
input_segments = [
tf.keras.layers.Input(shape=(), dtype=tf.string, name=ft)
for ft in sentence_features]
# Tokenize the text to word pieces.
bert_preprocess = hub.load(tfhub_handle_preprocess)
tokenizer = hub.KerasLayer(bert_preprocess.tokenize, name='tokenizer')
segments = [tokenizer(s) for s in input_segments]
# Optional: Trim segments in a smart way to fit seq_length.
# Simple cases (like this example) can skip this step and let
# the next step apply a default truncation to approximately equal lengths.
truncated_segments = segments
# Pack inputs. The details (start/end token ids, dict of output tensors)
# are model-dependent, so this gets loaded from the SavedModel.
packer = hub.KerasLayer(bert_preprocess.bert_pack_inputs,
arguments=dict(seq_length=seq_length),
name='packer')
model_inputs = packer(truncated_segments)
return tf.keras.Model(input_segments, model_inputs)
```
Let's demonstrate the preprocessing model. You will create a test with two sentences input (input1 and input2). The output is what a BERT model would expect as input: `input_word_ids`, `input_masks` and `input_type_ids`.
```
test_preprocess_model = make_bert_preprocess_model(['my_input1', 'my_input2'])
test_text = [np.array(['some random test sentence']),
np.array(['another sentence'])]
text_preprocessed = test_preprocess_model(test_text)
print('Keys : ', list(text_preprocessed.keys()))
print('Shape Word Ids : ', text_preprocessed['input_word_ids'].shape)
print('Word Ids : ', text_preprocessed['input_word_ids'][0, :16])
print('Shape Mask : ', text_preprocessed['input_mask'].shape)
print('Input Mask : ', text_preprocessed['input_mask'][0, :16])
print('Shape Type Ids : ', text_preprocessed['input_type_ids'].shape)
print('Type Ids : ', text_preprocessed['input_type_ids'][0, :16])
```
Let's take a look at the model's structure, paying attention to the two inputs you just defined.
```
tf.keras.utils.plot_model(test_preprocess_model)
```
To apply the preprocessing in all the inputs from the dataset, you will use the `map` function from the dataset. The result is then cached for [performance](https://www.tensorflow.org/guide/data_performance#top_of_page).
```
AUTOTUNE = tf.data.AUTOTUNE
def load_dataset_from_tfds(in_memory_ds, info, split, batch_size,
bert_preprocess_model):
is_training = split.startswith('train')
dataset = tf.data.Dataset.from_tensor_slices(in_memory_ds[split])
num_examples = info.splits[split].num_examples
if is_training:
dataset = dataset.shuffle(num_examples)
dataset = dataset.repeat()
dataset = dataset.batch(batch_size)
dataset = dataset.map(lambda ex: (bert_preprocess_model(ex), ex['label']))
dataset = dataset.cache().prefetch(buffer_size=AUTOTUNE)
return dataset, num_examples
```
## Define your model
You are now ready to define your model for sentence or sentence pair classification by feeding the preprocessed inputs through the BERT encoder and putting a linear classifier on top (or other arrangement of layers as you prefer), and using dropout for regularization.
Note: Here the model will be defined using the [Keras functional API](https://www.tensorflow.org/guide/keras/functional)
```
def build_classifier_model(num_classes):
inputs = dict(
input_word_ids=tf.keras.layers.Input(shape=(None,), dtype=tf.int32),
input_mask=tf.keras.layers.Input(shape=(None,), dtype=tf.int32),
input_type_ids=tf.keras.layers.Input(shape=(None,), dtype=tf.int32),
)
encoder = hub.KerasLayer(tfhub_handle_encoder, trainable=True, name='encoder')
net = encoder(inputs)['pooled_output']
net = tf.keras.layers.Dropout(rate=0.1)(net)
net = tf.keras.layers.Dense(num_classes, activation=None, name='classifier')(net)
return tf.keras.Model(inputs, net, name='prediction')
```
Let's try running the model on some preprocessed inputs.
```
test_classifier_model = build_classifier_model(2)
bert_raw_result = test_classifier_model(text_preprocessed)
print(tf.sigmoid(bert_raw_result))
```
Let's take a look at the model's structure. You can see the three BERT expected inputs.
```
tf.keras.utils.plot_model(test_classifier_model)
```
## Choose a task from GLUE
You are going to use a TensorFlow DataSet from the [GLUE](https://www.tensorflow.org/datasets/catalog/glue) benchmark suite.
Colab lets you download these small datasets to the local filesystem, and the code below reads them entirely into memory, because the separate TPU worker host cannot access the local filesystem of the colab runtime.
For bigger datasets, you'll need to create your own [Google Cloud Storage](https://cloud.google.com/storage) bucket and have the TPU worker read the data from there. You can learn more in the [TPU guide](https://www.tensorflow.org/guide/tpu#input_datasets).
It's recommended to start with the CoLa dataset (for single sentence) or MRPC (for multi sentence) since these are small and don't take long to fine tune.
```
tfds_name = 'glue/cola' #@param ['glue/cola', 'glue/sst2', 'glue/mrpc', 'glue/qqp', 'glue/mnli', 'glue/qnli', 'glue/rte', 'glue/wnli']
tfds_info = tfds.builder(tfds_name).info
sentence_features = list(tfds_info.features.keys())
sentence_features.remove('idx')
sentence_features.remove('label')
available_splits = list(tfds_info.splits.keys())
train_split = 'train'
validation_split = 'validation'
test_split = 'test'
if tfds_name == 'glue/mnli':
validation_split = 'validation_matched'
test_split = 'test_matched'
num_classes = tfds_info.features['label'].num_classes
num_examples = tfds_info.splits.total_num_examples
print(f'Using {tfds_name} from TFDS')
print(f'This dataset has {num_examples} examples')
print(f'Number of classes: {num_classes}')
print(f'Features {sentence_features}')
print(f'Splits {available_splits}')
with tf.device('/job:localhost'):
# batch_size=-1 is a way to load the dataset into memory
in_memory_ds = tfds.load(tfds_name, batch_size=-1, shuffle_files=True)
# The code below is just to show some samples from the selected dataset
print(f'Here are some sample rows from {tfds_name} dataset')
sample_dataset = tf.data.Dataset.from_tensor_slices(in_memory_ds[train_split])
labels_names = tfds_info.features['label'].names
print(labels_names)
print()
sample_i = 1
for sample_row in sample_dataset.take(5):
samples = [sample_row[feature] for feature in sentence_features]
print(f'sample row {sample_i}')
for sample in samples:
print(sample.numpy())
sample_label = sample_row['label']
print(f'label: {sample_label} ({labels_names[sample_label]})')
print()
sample_i += 1
```
The dataset also determines the problem type (classification or regression) and the appropriate loss function for training.
```
def get_configuration(glue_task):
loss = tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True)
if glue_task is 'glue/cola':
metrics = tfa.metrics.MatthewsCorrelationCoefficient()
else:
metrics = tf.keras.metrics.SparseCategoricalAccuracy(
'accuracy', dtype=tf.float32)
return metrics, loss
```
## Train your model
Finally, you can train the model end-to-end on the dataset you chose.
### Distribution
Recall the set-up code at the top, which has connected the colab runtime to
a TPU worker with multiple TPU devices. To distribute training onto them, you will create and compile your main Keras model within the scope of the TPU distribution strategy. (For details, see [Distributed training with Keras](https://www.tensorflow.org/tutorials/distribute/keras).)
Preprocessing, on the other hand, runs on the CPU of the worker host, not the TPUs, so the Keras model for preprocessing as well as the training and validation datasets mapped with it are built outside the distribution strategy scope. The call to `Model.fit()` will take care of distributing the passed-in dataset to the model replicas.
Note: The single TPU worker host already has the resource objects (think: a lookup table) needed for tokenization. Scaling up to multiple workers requires use of `Strategy.experimental_distribute_datasets_from_function` with a function that loads the preprocessing model separately onto each worker.
### Optimizer
Fine-tuning follows the optimizer set-up from BERT pre-training (as in [Classify text with BERT](https://www.tensorflow.org/tutorials/text/classify_text_with_bert)): It uses the AdamW optimizer with a linear decay of a notional initial learning rate, prefixed with a linear warm-up phase over the first 10% of training steps (`num_warmup_steps`). In line with the BERT paper, the initial learning rate is smaller for fine-tuning (best of 5e-5, 3e-5, 2e-5).
```
epochs = 3
batch_size = 32
init_lr = 2e-5
print(f'Fine tuning {tfhub_handle_encoder} model')
bert_preprocess_model = make_bert_preprocess_model(sentence_features)
with strategy.scope():
# metric have to be created inside the strategy scope
metrics, loss = get_configuration(tfds_name)
train_dataset, train_data_size = load_dataset_from_tfds(
in_memory_ds, tfds_info, train_split, batch_size, bert_preprocess_model)
steps_per_epoch = train_data_size // batch_size
num_train_steps = steps_per_epoch * epochs
num_warmup_steps = num_train_steps // 10
validation_dataset, validation_data_size = load_dataset_from_tfds(
in_memory_ds, tfds_info, validation_split, batch_size,
bert_preprocess_model)
validation_steps = validation_data_size // batch_size
classifier_model = build_classifier_model(num_classes)
optimizer = optimization.create_optimizer(
init_lr=init_lr,
num_train_steps=num_train_steps,
num_warmup_steps=num_warmup_steps,
optimizer_type='adamw')
classifier_model.compile(optimizer=optimizer, loss=loss, metrics=[metrics])
classifier_model.fit(
x=train_dataset,
validation_data=validation_dataset,
steps_per_epoch=steps_per_epoch,
epochs=epochs,
validation_steps=validation_steps)
```
## Export for inference
You will create a final model that has the preprocessing part and the fine-tuned BERT we've just created.
At inference time, preprocessing needs to be part of the model (because there is no longer a separate input queue as for training data that does it). Preprocessing is not just computation; it has its own resources (the vocab table) that must be attached to the Keras Model that is saved for export.
This final assembly is what will be saved.
You are going to save the model on colab and later you can download to keep it for the future (**View -> Table of contents -> Files**).
```
main_save_path = './my_models'
bert_type = tfhub_handle_encoder.split('/')[-2]
saved_model_name = f'{tfds_name.replace("/", "_")}_{bert_type}'
saved_model_path = os.path.join(main_save_path, saved_model_name)
preprocess_inputs = bert_preprocess_model.inputs
bert_encoder_inputs = bert_preprocess_model(preprocess_inputs)
bert_outputs = classifier_model(bert_encoder_inputs)
model_for_export = tf.keras.Model(preprocess_inputs, bert_outputs)
print(f'Saving {saved_model_path}')
# Save everything on the Colab host (even the variables from TPU memory)
save_options = tf.saved_model.SaveOptions(experimental_io_device='/job:localhost')
model_for_export.save(saved_model_path, include_optimizer=False, options=save_options)
```
## Test the model
The final step is testing the results of your exported model.
Just to make some comparison, let's reload the model and test it using some inputs from the test split from the dataset.
Note: The test is done on the colab host, not the TPU worker that it has connected to, so it appears below with explicit device placements. You can omit those when loading the SavedModel elsewhere.
```
with tf.device('/job:localhost'):
reloaded_model = tf.saved_model.load(saved_model_path)
#@title Utility methods
def prepare(record):
model_inputs = [[record[ft]] for ft in sentence_features]
return model_inputs
def prepare_serving(record):
model_inputs = {ft: record[ft] for ft in sentence_features}
return model_inputs
def print_bert_results(test, bert_result, dataset_name):
bert_result_class = tf.argmax(bert_result, axis=1)[0]
if dataset_name == 'glue/cola':
print(f'sentence: {test[0].numpy()}')
if bert_result_class == 1:
print(f'This sentence is acceptable')
else:
print(f'This sentence is unacceptable')
elif dataset_name == 'glue/sst2':
print(f'sentence: {test[0]}')
if bert_result_class == 1:
print(f'This sentence has POSITIVE sentiment')
else:
print(f'This sentence has NEGATIVE sentiment')
elif dataset_name == 'glue/mrpc':
print(f'sentence1: {test[0]}')
print(f'sentence2: {test[1]}')
if bert_result_class == 1:
print(f'Are a paraphrase')
else:
print(f'Are NOT a paraphrase')
elif dataset_name == 'glue/qqp':
print(f'question1: {test[0]}')
print(f'question2: {test[1]}')
if bert_result_class == 1:
print(f'Questions are similar')
else:
print(f'Questions are NOT similar')
elif dataset_name == 'glue/mnli':
print(f'premise : {test[0]}')
print(f'hypothesis: {test[1]}')
if bert_result_class == 1:
print(f'This premise is NEUTRAL to the hypothesis')
elif bert_result_class == 2:
print(f'This premise CONTRADICTS the hypothesis')
else:
print(f'This premise ENTAILS the hypothesis')
elif dataset_name == 'glue/qnli':
print(f'question: {test[0]}')
print(f'sentence: {test[1]}')
if bert_result_class == 1:
print(f'The question is NOT answerable by the sentence')
else:
print(f'The question is answerable by the sentence')
elif dataset_name == 'glue/rte':
print(f'sentence1: {test[0]}')
print(f'sentence2: {test[1]}')
if bert_result_class == 1:
print(f'Sentence1 DOES NOT entails sentence2')
else:
print(f'Sentence1 entails sentence2')
elif dataset_name == 'glue/wnli':
print(f'sentence1: {test[0]}')
print(f'sentence2: {test[1]}')
if bert_result_class == 1:
print(f'Sentence1 DOES NOT entails sentence2')
else:
print(f'Sentence1 entails sentence2')
print(f'Bert raw results:{bert_result[0]}')
print()
```
### Test
```
with tf.device('/job:localhost'):
test_dataset = tf.data.Dataset.from_tensor_slices(in_memory_ds[test_split])
for test_row in test_dataset.shuffle(1000).map(prepare).take(5):
if len(sentence_features) == 1:
result = reloaded_model(test_row[0])
else:
result = reloaded_model(list(test_row))
print_bert_results(test_row, result, tfds_name)
```
If you want to use your model on [TF Serving](https://www.tensorflow.org/tfx/guide/serving), remember that it will call your SavedModel through one of its named signatures. Notice there are some small differences in the input. In Python, you can test them as follows:
```
with tf.device('/job:localhost'):
serving_model = reloaded_model.signatures['serving_default']
for test_row in test_dataset.shuffle(1000).map(prepare_serving).take(5):
result = serving_model(**test_row)
# The 'prediction' key is the classifier's defined model name.
print_bert_results(list(test_row.values()), result['prediction'], tfds_name)
```
You did it! Your saved model could be used for serving or simple inference in a process, with a simpler api with less code and easier to maintain.
## Next Steps
Now that you've tried one of the base BERT models, you can try other ones to achieve more accuracy or maybe with smaller model versions.
You can also try in other datasets.
|
github_jupyter
|
# Open, Re-usable Deep Learning Components on the Web
## Learning objectives
- Use [ImJoy](https://imjoy.io/#/) web-based imaging components
- Create a JavaScript-based ImJoy plugin
- Create a Python-based ImJoy plugin
*See also:* the [I2K 2020 Tutorial: ImJoying Interactive Bioimage Analysis
with Deep Learning, ImageJ.JS &
Friends](https://www.janelia.org/sites/default/files/You%20%2B%20Janelia/Conferences/10.pdf)
ImJoy is a plugin powered hybrid computing platform for deploying deep learning applications such as advanced image analysis tools.
ImJoy runs on mobile and desktop environment cross different operating systems, plugins can run in the browser, localhost, remote and cloud servers.
With ImJoy, delivering Deep Learning tools to the end users is simple and easy thanks to
its flexible plugin system and sharable plugin URL. Developer can easily add rich and interactive web interfaces to existing Python code.
<img src="https://github.com/imjoy-team/ImJoy/raw/master/docs/assets/imjoy-overview.jpg" width="600px"></img>
Checkout the documentation for how to get started and more details
for how to develop ImJoy plugins: [ImJoy Docs](https://imjoy.io/docs)
## Key Features of ImJoy
* Minimal and flexible plugin powered web application
* Server-less progressive web application with offline support
* Support mobile devices
* Rich and interactive user interface powered by web technologies
- use any existing web design libraries
- Rendering multi-dimensional data in 3D with webGL, Three.js etc.
* Easy-to-use workflow composition
* Isolated workspaces for grouping plugins
* Self-contained plugin prototyping and development
- Built-in code editor, no extra IDE is needed for development
* Powerful and extendable computational backends for browser, local and cloud computing
- Support Javascript, native Python and web Python
- Concurrent plugin execution through asynchronous programming
- Run Python plugins in the browser with Webassembly
- Browser plugins are isolated with secured sandboxes
- Support `async/await` syntax for Python3 and Javascript
- Support Conda virtual environments and pip packages for Python
- Support libraries hosted on Github or CDNs for javascript
- Easy plugin deployment and sharing through GitHub or Gist
- Deploying your own plugin repository to Github
* Native support for n-dimensional arrays and tensors
- Support ndarrays from Numpy for data exchange
**ImJoy greatly accelerates the development and dissemination of new tools.** You can develop plugins in ImJoy, deploy the plugin file to Github, and share the plugin URL through social networks. Users can then use it by a single click, even on a mobile phone
<a href="https://imjoy.io/#/app?p=imjoy-team/example-plugins:Skin-Lesion-Analyzer" target="_blank">
<img src="https://github.com/imjoy-team/ImJoy/raw/master/docs/assets/imjoy-sharing.jpg" width="500px"></img>
</a>
Examine the ImJoy extension in the notebook toolbar

```
#ciskip
# Create an ImJoy plugin in Python that uses itk-vtk-viewer to visualize images
import imageio
import numpy as np
from imjoy_rpc import api
class ImJoyPlugin():
def setup(self):
api.log('plugin initialized')
async def run(self, ctx):
viewer = await api.showDialog(src="https://kitware.github.io/itk-vtk-viewer/app/")
# show a 3D volume
image_array = np.random.randint(0, 255, [10,10,10], dtype='uint8')
# show a 2D image
# image_array = imageio.imread('imageio:chelsea.png')
await viewer.setImage(image_array)
api.export(ImJoyPlugin())
# Create a JavaScript ImJoy plugin
from IPython.display import HTML
my_plugin_source = HTML('''
<docs lang="markdown">
[TODO: write documentation for this plugin.]
</docs>
<config lang="json">
{
"name": "Untitled Plugin",
"type": "window",
"tags": [],
"ui": "",
"version": "0.1.0",
"cover": "",
"description": "[TODO: describe this plugin with one sentence.]",
"icon": "extension",
"inputs": null,
"outputs": null,
"api_version": "0.1.8",
"env": "",
"permissions": [],
"requirements": [],
"dependencies": [],
"defaults": {"w": 20, "h": 10}
}
</config>
<script lang="javascript">
class ImJoyPlugin {
async setup() {
api.log('initialized')
}
async run(ctx) {
}
}
api.export(new ImJoyPlugin())
</script>
<window lang="html">
<div>
<p>
Hello World
</p>
</div>
</window>
<style lang="css">
</style>
''')
#ciskip
# Register the plugin
from imjoy_rpc import api
class ImJoyPlugin():
async def setup(self):
pass
async def run(self, ctx):
# for regular plugin
# p = await api.getPlugin(my_plugin_source)
# or for window plugin
# await api.createWindow(src=my_plugin_source)
await api.showDialog(src=my_plugin_source)
api.export(ImJoyPlugin())
```
## Exercises
Try out plugins from the [ImJoy reference plugin repository](https://imjoy.io/repo/).
|
github_jupyter
|
# Autonomous driving - Car detection
Welcome to your week 3 programming assignment. You will learn about object detection using the very powerful YOLO model. Many of the ideas in this notebook are described in the two YOLO papers: Redmon et al., 2016 (https://arxiv.org/abs/1506.02640) and Redmon and Farhadi, 2016 (https://arxiv.org/abs/1612.08242).
**You will learn to**:
- Use object detection on a car detection dataset
- Deal with bounding boxes
Run the following cell to load the packages and dependencies that are going to be useful for your journey!
```
import argparse
import os
import matplotlib.pyplot as plt
from matplotlib.pyplot import imshow
import scipy.io
import scipy.misc
import numpy as np
import pandas as pd
import PIL
import tensorflow as tf
from keras import backend as K
from keras.layers import Input, Lambda, Conv2D
from keras.models import load_model, Model
from yolo_utils import read_classes, read_anchors, generate_colors, preprocess_image, draw_boxes, scale_boxes
from yad2k.models.keras_yolo import yolo_head, yolo_boxes_to_corners, preprocess_true_boxes, yolo_loss, yolo_body
%matplotlib inline
```
**Important Note**: As you can see, we import Keras's backend as K. This means that to use a Keras function in this notebook, you will need to write: `K.function(...)`.
## 1 - Problem Statement
You are working on a self-driving car. As a critical component of this project, you'd like to first build a car detection system. To collect data, you've mounted a camera to the hood (meaning the front) of the car, which takes pictures of the road ahead every few seconds while you drive around.
<center>
<video width="400" height="200" src="nb_images/road_video_compressed2.mp4" type="video/mp4" controls>
</video>
</center>
<caption><center> Pictures taken from a car-mounted camera while driving around Silicon Valley. <br> We would like to especially thank [drive.ai](https://www.drive.ai/) for providing this dataset! Drive.ai is a company building the brains of self-driving vehicles.
</center></caption>
<img src="nb_images/driveai.png" style="width:100px;height:100;">
You've gathered all these images into a folder and have labelled them by drawing bounding boxes around every car you found. Here's an example of what your bounding boxes look like.
<img src="nb_images/box_label.png" style="width:500px;height:250;">
<caption><center> <u> **Figure 1** </u>: **Definition of a box**<br> </center></caption>
If you have 80 classes that you want YOLO to recognize, you can represent the class label $c$ either as an integer from 1 to 80, or as an 80-dimensional vector (with 80 numbers) one component of which is 1 and the rest of which are 0. The video lectures had used the latter representation; in this notebook, we will use both representations, depending on which is more convenient for a particular step.
In this exercise, you will learn how YOLO works, then apply it to car detection. Because the YOLO model is very computationally expensive to train, we will load pre-trained weights for you to use.
## 2 - YOLO
YOLO ("you only look once") is a popular algoritm because it achieves high accuracy while also being able to run in real-time. This algorithm "only looks once" at the image in the sense that it requires only one forward propagation pass through the network to make predictions. After non-max suppression, it then outputs recognized objects together with the bounding boxes.
### 2.1 - Model details
First things to know:
- The **input** is a batch of images of shape (m, 608, 608, 3)
- The **output** is a list of bounding boxes along with the recognized classes. Each bounding box is represented by 6 numbers $(p_c, b_x, b_y, b_h, b_w, c)$ as explained above. If you expand $c$ into an 80-dimensional vector, each bounding box is then represented by 85 numbers.
We will use 5 anchor boxes. So you can think of the YOLO architecture as the following: IMAGE (m, 608, 608, 3) -> DEEP CNN -> ENCODING (m, 19, 19, 5, 85).
Lets look in greater detail at what this encoding represents.
<img src="nb_images/architecture.png" style="width:700px;height:400;">
<caption><center> <u> **Figure 2** </u>: **Encoding architecture for YOLO**<br> </center></caption>
If the center/midpoint of an object falls into a grid cell, that grid cell is responsible for detecting that object.
Since we are using 5 anchor boxes, each of the 19 x19 cells thus encodes information about 5 boxes. Anchor boxes are defined only by their width and height.
For simplicity, we will flatten the last two last dimensions of the shape (19, 19, 5, 85) encoding. So the output of the Deep CNN is (19, 19, 425).
<img src="nb_images/flatten.png" style="width:700px;height:400;">
<caption><center> <u> **Figure 3** </u>: **Flattening the last two last dimensions**<br> </center></caption>
Now, for each box (of each cell) we will compute the following elementwise product and extract a probability that the box contains a certain class.
<img src="nb_images/probability_extraction.png" style="width:700px;height:400;">
<caption><center> <u> **Figure 4** </u>: **Find the class detected by each box**<br> </center></caption>
Here's one way to visualize what YOLO is predicting on an image:
- For each of the 19x19 grid cells, find the maximum of the probability scores (taking a max across both the 5 anchor boxes and across different classes).
- Color that grid cell according to what object that grid cell considers the most likely.
Doing this results in this picture:
<img src="nb_images/proba_map.png" style="width:300px;height:300;">
<caption><center> <u> **Figure 5** </u>: Each of the 19x19 grid cells colored according to which class has the largest predicted probability in that cell.<br> </center></caption>
Note that this visualization isn't a core part of the YOLO algorithm itself for making predictions; it's just a nice way of visualizing an intermediate result of the algorithm.
Another way to visualize YOLO's output is to plot the bounding boxes that it outputs. Doing that results in a visualization like this:
<img src="nb_images/anchor_map.png" style="width:200px;height:200;">
<caption><center> <u> **Figure 6** </u>: Each cell gives you 5 boxes. In total, the model predicts: 19x19x5 = 1805 boxes just by looking once at the image (one forward pass through the network)! Different colors denote different classes. <br> </center></caption>
In the figure above, we plotted only boxes that the model had assigned a high probability to, but this is still too many boxes. You'd like to filter the algorithm's output down to a much smaller number of detected objects. To do so, you'll use non-max suppression. Specifically, you'll carry out these steps:
- Get rid of boxes with a low score (meaning, the box is not very confident about detecting a class)
- Select only one box when several boxes overlap with each other and detect the same object.
### 2.2 - Filtering with a threshold on class scores
You are going to apply a first filter by thresholding. You would like to get rid of any box for which the class "score" is less than a chosen threshold.
The model gives you a total of 19x19x5x85 numbers, with each box described by 85 numbers. It'll be convenient to rearrange the (19,19,5,85) (or (19,19,425)) dimensional tensor into the following variables:
- `box_confidence`: tensor of shape $(19 \times 19, 5, 1)$ containing $p_c$ (confidence probability that there's some object) for each of the 5 boxes predicted in each of the 19x19 cells.
- `boxes`: tensor of shape $(19 \times 19, 5, 4)$ containing $(b_x, b_y, b_h, b_w)$ for each of the 5 boxes per cell.
- `box_class_probs`: tensor of shape $(19 \times 19, 5, 80)$ containing the detection probabilities $(c_1, c_2, ... c_{80})$ for each of the 80 classes for each of the 5 boxes per cell.
**Exercise**: Implement `yolo_filter_boxes()`.
1. Compute box scores by doing the elementwise product as described in Figure 4. The following code may help you choose the right operator:
```python
a = np.random.randn(19*19, 5, 1)
b = np.random.randn(19*19, 5, 80)
c = a * b # shape of c will be (19*19, 5, 80)
```
2. For each box, find:
- the index of the class with the maximum box score ([Hint](https://keras.io/backend/#argmax)) (Be careful with what axis you choose; consider using axis=-1)
- the corresponding box score ([Hint](https://keras.io/backend/#max)) (Be careful with what axis you choose; consider using axis=-1)
3. Create a mask by using a threshold. As a reminder: `([0.9, 0.3, 0.4, 0.5, 0.1] < 0.4)` returns: `[False, True, False, False, True]`. The mask should be True for the boxes you want to keep.
4. Use TensorFlow to apply the mask to box_class_scores, boxes and box_classes to filter out the boxes we don't want. You should be left with just the subset of boxes you want to keep. ([Hint](https://www.tensorflow.org/api_docs/python/tf/boolean_mask))
Reminder: to call a Keras function, you should use `K.function(...)`.
```
# GRADED FUNCTION: yolo_filter_boxes
def yolo_filter_boxes(box_confidence, boxes, box_class_probs, threshold = .6):
"""Filters YOLO boxes by thresholding on object and class confidence.
Arguments:
box_confidence -- tensor of shape (19, 19, 5, 1)
boxes -- tensor of shape (19, 19, 5, 4)
box_class_probs -- tensor of shape (19, 19, 5, 80)
threshold -- real value, if [ highest class probability score < threshold], then get rid of the corresponding box
Returns:
scores -- tensor of shape (None,), containing the class probability score for selected boxes
boxes -- tensor of shape (None, 4), containing (b_x, b_y, b_h, b_w) coordinates of selected boxes
classes -- tensor of shape (None,), containing the index of the class detected by the selected boxes
Note: "None" is here because you don't know the exact number of selected boxes, as it depends on the threshold.
For example, the actual output size of scores would be (10,) if there are 10 boxes.
"""
# print(box_confidence.get_shape())
# Step 1: Compute box scores
### START CODE HERE ### (≈ 1 line)
box_scores = box_confidence*box_class_probs
#print(box_scores.get_shape())
### END CODE HERE ###
# Step 2: Find the box_classes thanks to the max box_scores, keep track of the corresponding score
### START CODE HERE ### (≈ 2 lines)
box_classes = K.argmax(box_scores,axis = -1)
#print(box_classes.get_shape())
box_class_scores = K.max(box_scores,axis = -1)
#print(box_class_scores.get_shape())
### END CODE HERE ###
# Step 3: Create a filtering mask based on "box_class_scores" by using "threshold". The mask should have the
# same dimension as box_class_scores, and be True for the boxes you want to keep (with probability >= threshold)
### START CODE HERE ### (≈ 1 line)
filtering_mask = box_class_scores>=threshold
#print(filtering_mask.get_shape())
### END CODE HERE ###
# Step 4: Apply the mask to scores, boxes and classes
### START CODE HERE ### (≈ 3 lines)
scores = tf.boolean_mask(box_class_scores,filtering_mask)
boxes = tf.boolean_mask(boxes,filtering_mask)
classes = tf.boolean_mask(box_classes,filtering_mask)
### END CODE HERE ###
return scores, boxes, classes
with tf.Session() as test_a:
box_confidence = tf.random_normal([19, 19, 5, 1], mean=1, stddev=4, seed = 1)
boxes = tf.random_normal([19, 19, 5, 4], mean=1, stddev=4, seed = 1)
box_class_probs = tf.random_normal([19, 19, 5, 80], mean=1, stddev=4, seed = 1)
scores, boxes, classes = yolo_filter_boxes(box_confidence, boxes, box_class_probs, threshold = 0.5)
print("scores[2] = " + str(scores[2].eval()))
print("boxes[2] = " + str(boxes[2].eval()))
print("classes[2] = " + str(classes[2].eval()))
print("scores.shape = " + str(scores.shape))
print("boxes.shape = " + str(boxes.shape))
print("classes.shape = " + str(classes.shape))
```
**Expected Output**:
<table>
<tr>
<td>
**scores[2]**
</td>
<td>
10.7506
</td>
</tr>
<tr>
<td>
**boxes[2]**
</td>
<td>
[ 8.42653275 3.27136683 -0.5313437 -4.94137383]
</td>
</tr>
<tr>
<td>
**classes[2]**
</td>
<td>
7
</td>
</tr>
<tr>
<td>
**scores.shape**
</td>
<td>
(?,)
</td>
</tr>
<tr>
<td>
**boxes.shape**
</td>
<td>
(?, 4)
</td>
</tr>
<tr>
<td>
**classes.shape**
</td>
<td>
(?,)
</td>
</tr>
</table>
### 2.3 - Non-max suppression ###
Even after filtering by thresholding over the classes scores, you still end up a lot of overlapping boxes. A second filter for selecting the right boxes is called non-maximum suppression (NMS).
<img src="nb_images/non-max-suppression.png" style="width:500px;height:400;">
<caption><center> <u> **Figure 7** </u>: In this example, the model has predicted 3 cars, but it's actually 3 predictions of the same car. Running non-max suppression (NMS) will select only the most accurate (highest probabiliy) one of the 3 boxes. <br> </center></caption>
Non-max suppression uses the very important function called **"Intersection over Union"**, or IoU.
<img src="nb_images/iou.png" style="width:500px;height:400;">
<caption><center> <u> **Figure 8** </u>: Definition of "Intersection over Union". <br> </center></caption>
**Exercise**: Implement iou(). Some hints:
- In this exercise only, we define a box using its two corners (upper left and lower right): (x1, y1, x2, y2) rather than the midpoint and height/width.
- To calculate the area of a rectangle you need to multiply its height (y2 - y1) by its width (x2 - x1)
- You'll also need to find the coordinates (xi1, yi1, xi2, yi2) of the intersection of two boxes. Remember that:
- xi1 = maximum of the x1 coordinates of the two boxes
- yi1 = maximum of the y1 coordinates of the two boxes
- xi2 = minimum of the x2 coordinates of the two boxes
- yi2 = minimum of the y2 coordinates of the two boxes
In this code, we use the convention that (0,0) is the top-left corner of an image, (1,0) is the upper-right corner, and (1,1) the lower-right corner.
```
# GRADED FUNCTION: iou
def iou(box1, box2):
"""Implement the intersection over union (IoU) between box1 and box2
Arguments:
box1 -- first box, list object with coordinates (x1, y1, x2, y2)
box2 -- second box, list object with coordinates (x1, y1, x2, y2)
"""
# Calculate the (y1, x1, y2, x2) coordinates of the intersection of box1 and box2. Calculate its Area.
### START CODE HERE ### (≈ 5 lines)
# print(type(box1))
#print(box1[0])
xi1 = np.maximum(box1[0],box2[0])
yi1 = np.maximum(box1[1],box2[1])
xi2 = np.minimum(box1[2],box2[2])
yi2 = np.minimum(box1[3],box2[3])
inter_area = (yi2-yi1)*(xi2-xi1)
### END CODE HERE ###
# Calculate the Union area by using Formula: Union(A,B) = A + B - Inter(A,B)
### START CODE HERE ### (≈ 3 lines)
box1_area = (box1[3]-box1[1])*(box1[2]-box1[0])
box2_area = (box2[3]-box2[1])*(box2[2]-box2[0])
union_area = box1_area + box2_area - inter_area
### END CODE HERE ###
# compute the IoU
### START CODE HERE ### (≈ 1 line)
iou = inter_area/union_area
### END CODE HERE ###
return iou
box1 = (2, 1, 4, 3)
box2 = (1, 2, 3, 4)
print("iou = " + str(iou(box1, box2)))
```
**Expected Output**:
<table>
<tr>
<td>
**iou = **
</td>
<td>
0.14285714285714285
</td>
</tr>
</table>
You are now ready to implement non-max suppression. The key steps are:
1. Select the box that has the highest score.
2. Compute its overlap with all other boxes, and remove boxes that overlap it more than `iou_threshold`.
3. Go back to step 1 and iterate until there's no more boxes with a lower score than the current selected box.
This will remove all boxes that have a large overlap with the selected boxes. Only the "best" boxes remain.
**Exercise**: Implement yolo_non_max_suppression() using TensorFlow. TensorFlow has two built-in functions that are used to implement non-max suppression (so you don't actually need to use your `iou()` implementation):
- [tf.image.non_max_suppression()](https://www.tensorflow.org/api_docs/python/tf/image/non_max_suppression)
- [K.gather()](https://www.tensorflow.org/api_docs/python/tf/gather)
```
# GRADED FUNCTION: yolo_non_max_suppression
def yolo_non_max_suppression(scores, boxes, classes, max_boxes = 10, iou_threshold = 0.5):
"""
Applies Non-max suppression (NMS) to set of boxes
Arguments:
scores -- tensor of shape (None,), output of yolo_filter_boxes()
boxes -- tensor of shape (None, 4), output of yolo_filter_boxes() that have been scaled to the image size (see later)
classes -- tensor of shape (None,), output of yolo_filter_boxes()
max_boxes -- integer, maximum number of predicted boxes you'd like
iou_threshold -- real value, "intersection over union" threshold used for NMS filtering
Returns:
scores -- tensor of shape (, None), predicted score for each box
boxes -- tensor of shape (4, None), predicted box coordinates
classes -- tensor of shape (, None), predicted class for each box
Note: The "None" dimension of the output tensors has obviously to be less than max_boxes. Note also that this
function will transpose the shapes of scores, boxes, classes. This is made for convenience.
"""
max_boxes_tensor = K.variable(max_boxes, dtype='int32') # tensor to be used in tf.image.non_max_suppression()
K.get_session().run(tf.variables_initializer([max_boxes_tensor])) # initialize variable max_boxes_tensor
# Use tf.image.non_max_suppression() to get the list of indices corresponding to boxes you keep
### START CODE HERE ### (≈ 1 line)
nms_indices = tf.image.non_max_suppression(boxes,scores,max_boxes_tensor,iou_threshold)
### END CODE HERE ###
# Use K.gather() to select only nms_indices from scores, boxes and classes
### START CODE HERE ### (≈ 3 lines)
scores = tf.gather(scores,nms_indices)
boxes = tf.gather(boxes,nms_indices)
classes = tf.gather(classes,nms_indices)
### END CODE HERE ###
return scores, boxes, classes
with tf.Session() as test_b:
scores = tf.random_normal([54,], mean=1, stddev=4, seed = 1)
boxes = tf.random_normal([54, 4], mean=1, stddev=4, seed = 1)
classes = tf.random_normal([54,], mean=1, stddev=4, seed = 1)
scores, boxes, classes = yolo_non_max_suppression(scores, boxes, classes)
print("scores[2] = " + str(scores[2].eval()))
print("boxes[2] = " + str(boxes[2].eval()))
print("classes[2] = " + str(classes[2].eval()))
print("scores.shape = " + str(scores.eval().shape))
print("boxes.shape = " + str(boxes.eval().shape))
print("classes.shape = " + str(classes.eval().shape))
```
**Expected Output**:
<table>
<tr>
<td>
**scores[2]**
</td>
<td>
6.9384
</td>
</tr>
<tr>
<td>
**boxes[2]**
</td>
<td>
[-5.299932 3.13798141 4.45036697 0.95942086]
</td>
</tr>
<tr>
<td>
**classes[2]**
</td>
<td>
-2.24527
</td>
</tr>
<tr>
<td>
**scores.shape**
</td>
<td>
(10,)
</td>
</tr>
<tr>
<td>
**boxes.shape**
</td>
<td>
(10, 4)
</td>
</tr>
<tr>
<td>
**classes.shape**
</td>
<td>
(10,)
</td>
</tr>
</table>
### 2.4 Wrapping up the filtering
It's time to implement a function taking the output of the deep CNN (the 19x19x5x85 dimensional encoding) and filtering through all the boxes using the functions you've just implemented.
**Exercise**: Implement `yolo_eval()` which takes the output of the YOLO encoding and filters the boxes using score threshold and NMS. There's just one last implementational detail you have to know. There're a few ways of representing boxes, such as via their corners or via their midpoint and height/width. YOLO converts between a few such formats at different times, using the following functions (which we have provided):
```python
boxes = yolo_boxes_to_corners(box_xy, box_wh)
```
which converts the yolo box coordinates (x,y,w,h) to box corners' coordinates (x1, y1, x2, y2) to fit the input of `yolo_filter_boxes`
```python
boxes = scale_boxes(boxes, image_shape)
```
YOLO's network was trained to run on 608x608 images. If you are testing this data on a different size image--for example, the car detection dataset had 720x1280 images--this step rescales the boxes so that they can be plotted on top of the original 720x1280 image.
Don't worry about these two functions; we'll show you where they need to be called.
```
# GRADED FUNCTION: yolo_eval
def yolo_eval(yolo_outputs, image_shape = (720., 1280.), max_boxes=10, score_threshold=.6, iou_threshold=.5):
"""
Converts the output of YOLO encoding (a lot of boxes) to your predicted boxes along with their scores, box coordinates and classes.
Arguments:
yolo_outputs -- output of the encoding model (for image_shape of (608, 608, 3)), contains 4 tensors:
box_confidence: tensor of shape (None, 19, 19, 5, 1)
box_xy: tensor of shape (None, 19, 19, 5, 2)
box_wh: tensor of shape (None, 19, 19, 5, 2)
box_class_probs: tensor of shape (None, 19, 19, 5, 80)
image_shape -- tensor of shape (2,) containing the input shape, in this notebook we use (608., 608.) (has to be float32 dtype)
max_boxes -- integer, maximum number of predicted boxes you'd like
score_threshold -- real value, if [ highest class probability score < threshold], then get rid of the corresponding box
iou_threshold -- real value, "intersection over union" threshold used for NMS filtering
Returns:
scores -- tensor of shape (None, ), predicted score for each box
boxes -- tensor of shape (None, 4), predicted box coordinates
classes -- tensor of shape (None,), predicted class for each box
"""
### START CODE HERE ###
# Retrieve outputs of the YOLO model (≈1 line)
box_confidence, box_xy, box_wh, box_class_probs = yolo_outputs
# Convert boxes to be ready for filtering functions
boxes = yolo_boxes_to_corners(box_xy, box_wh)
# Use one of the functions you've implemented to perform Score-filtering with a threshold of score_threshold (≈1 line)
scores, boxes, classes = yolo_filter_boxes(box_confidence,boxes,box_class_probs,score_threshold)
# Scale boxes back to original image shape.
boxes = scale_boxes(boxes, image_shape)
# Use one of the functions you've implemented to perform Non-max suppression with a threshold of iou_threshold (≈1 line)
scores, boxes, classes = yolo_non_max_suppression(scores,boxes,classes,max_boxes,iou_threshold)
### END CODE HERE ###
return scores, boxes, classes
with tf.Session() as test_b:
yolo_outputs = (tf.random_normal([19, 19, 5, 1], mean=1, stddev=4, seed = 1),
tf.random_normal([19, 19, 5, 2], mean=1, stddev=4, seed = 1),
tf.random_normal([19, 19, 5, 2], mean=1, stddev=4, seed = 1),
tf.random_normal([19, 19, 5, 80], mean=1, stddev=4, seed = 1))
scores, boxes, classes = yolo_eval(yolo_outputs)
print("scores[2] = " + str(scores[2].eval()))
print("boxes[2] = " + str(boxes[2].eval()))
print("classes[2] = " + str(classes[2].eval()))
print("scores.shape = " + str(scores.eval().shape))
print("boxes.shape = " + str(boxes.eval().shape))
print("classes.shape = " + str(classes.eval().shape))
```
**Expected Output**:
<table>
<tr>
<td>
**scores[2]**
</td>
<td>
138.791
</td>
</tr>
<tr>
<td>
**boxes[2]**
</td>
<td>
[ 1292.32971191 -278.52166748 3876.98925781 -835.56494141]
</td>
</tr>
<tr>
<td>
**classes[2]**
</td>
<td>
54
</td>
</tr>
<tr>
<td>
**scores.shape**
</td>
<td>
(10,)
</td>
</tr>
<tr>
<td>
**boxes.shape**
</td>
<td>
(10, 4)
</td>
</tr>
<tr>
<td>
**classes.shape**
</td>
<td>
(10,)
</td>
</tr>
</table>
<font color='blue'>
**Summary for YOLO**:
- Input image (608, 608, 3)
- The input image goes through a CNN, resulting in a (19,19,5,85) dimensional output.
- After flattening the last two dimensions, the output is a volume of shape (19, 19, 425):
- Each cell in a 19x19 grid over the input image gives 425 numbers.
- 425 = 5 x 85 because each cell contains predictions for 5 boxes, corresponding to 5 anchor boxes, as seen in lecture.
- 85 = 5 + 80 where 5 is because $(p_c, b_x, b_y, b_h, b_w)$ has 5 numbers, and and 80 is the number of classes we'd like to detect
- You then select only few boxes based on:
- Score-thresholding: throw away boxes that have detected a class with a score less than the threshold
- Non-max suppression: Compute the Intersection over Union and avoid selecting overlapping boxes
- This gives you YOLO's final output.
## 3 - Test YOLO pretrained model on images
In this part, you are going to use a pretrained model and test it on the car detection dataset. As usual, you start by **creating a session to start your graph**. Run the following cell.
```
sess = K.get_session()
```
### 3.1 - Defining classes, anchors and image shape.
Recall that we are trying to detect 80 classes, and are using 5 anchor boxes. We have gathered the information about the 80 classes and 5 boxes in two files "coco_classes.txt" and "yolo_anchors.txt". Let's load these quantities into the model by running the next cell.
The car detection dataset has 720x1280 images, which we've pre-processed into 608x608 images.
```
class_names = read_classes("model_data/coco_classes.txt")
anchors = read_anchors("model_data/yolo_anchors.txt")
image_shape = (720., 1280.)
```
### 3.2 - Loading a pretrained model
Training a YOLO model takes a very long time and requires a fairly large dataset of labelled bounding boxes for a large range of target classes. You are going to load an existing pretrained Keras YOLO model stored in "yolo.h5". (These weights come from the official YOLO website, and were converted using a function written by Allan Zelener. References are at the end of this notebook. Technically, these are the parameters from the "YOLOv2" model, but we will more simply refer to it as "YOLO" in this notebook.) Run the cell below to load the model from this file.
```
yolo_model = load_model("model_data/yolo.h5")
```
This loads the weights of a trained YOLO model. Here's a summary of the layers your model contains.
```
yolo_model.summary()
```
**Note**: On some computers, you may see a warning message from Keras. Don't worry about it if you do--it is fine.
**Reminder**: this model converts a preprocessed batch of input images (shape: (m, 608, 608, 3)) into a tensor of shape (m, 19, 19, 5, 85) as explained in Figure (2).
### 3.3 - Convert output of the model to usable bounding box tensors
The output of `yolo_model` is a (m, 19, 19, 5, 85) tensor that needs to pass through non-trivial processing and conversion. The following cell does that for you.
```
yolo_outputs = yolo_head(yolo_model.output, anchors, len(class_names))
```
You added `yolo_outputs` to your graph. This set of 4 tensors is ready to be used as input by your `yolo_eval` function.
### 3.4 - Filtering boxes
`yolo_outputs` gave you all the predicted boxes of `yolo_model` in the correct format. You're now ready to perform filtering and select only the best boxes. Lets now call `yolo_eval`, which you had previously implemented, to do this.
```
scores, boxes, classes = yolo_eval(yolo_outputs, image_shape)
```
### 3.5 - Run the graph on an image
Let the fun begin. You have created a (`sess`) graph that can be summarized as follows:
1. <font color='purple'> yolo_model.input </font> is given to `yolo_model`. The model is used to compute the output <font color='purple'> yolo_model.output </font>
2. <font color='purple'> yolo_model.output </font> is processed by `yolo_head`. It gives you <font color='purple'> yolo_outputs </font>
3. <font color='purple'> yolo_outputs </font> goes through a filtering function, `yolo_eval`. It outputs your predictions: <font color='purple'> scores, boxes, classes </font>
**Exercise**: Implement predict() which runs the graph to test YOLO on an image.
You will need to run a TensorFlow session, to have it compute `scores, boxes, classes`.
The code below also uses the following function:
```python
image, image_data = preprocess_image("images/" + image_file, model_image_size = (608, 608))
```
which outputs:
- image: a python (PIL) representation of your image used for drawing boxes. You won't need to use it.
- image_data: a numpy-array representing the image. This will be the input to the CNN.
**Important note**: when a model uses BatchNorm (as is the case in YOLO), you will need to pass an additional placeholder in the feed_dict {K.learning_phase(): 0}.
```
def predict(sess, image_file):
"""
Runs the graph stored in "sess" to predict boxes for "image_file". Prints and plots the preditions.
Arguments:
sess -- your tensorflow/Keras session containing the YOLO graph
image_file -- name of an image stored in the "images" folder.
Returns:
out_scores -- tensor of shape (None, ), scores of the predicted boxes
out_boxes -- tensor of shape (None, 4), coordinates of the predicted boxes
out_classes -- tensor of shape (None, ), class index of the predicted boxes
Note: "None" actually represents the number of predicted boxes, it varies between 0 and max_boxes.
"""
# Preprocess your image
image, image_data = preprocess_image("images/" + image_file, model_image_size = (608, 608))
# Run the session with the correct tensors and choose the correct placeholders in the feed_dict.
# You'll need to use feed_dict={yolo_model.input: ... , K.learning_phase(): 0})
### START CODE HERE ### (≈ 1 line)
out_scores, out_boxes, out_classes = sess.run([scores, boxes, classes], feed_dict={yolo_model.input: image_data, K.learning_phase(): 0})
### END CODE HERE ###
# Print predictions info
print('Found {} boxes for {}'.format(len(out_boxes), image_file))
# Generate colors for drawing bounding boxes.
colors = generate_colors(class_names)
# Draw bounding boxes on the image file
draw_boxes(image, out_scores, out_boxes, out_classes, class_names, colors)
# Save the predicted bounding box on the image
image.save(os.path.join("out", image_file), quality=90)
# Display the results in the notebook
output_image = scipy.misc.imread(os.path.join("out", image_file))
imshow(output_image)
return out_scores, out_boxes, out_classes
```
Run the following cell on the "test.jpg" image to verify that your function is correct.
```
out_scores, out_boxes, out_classes = predict(sess, "test.jpg")
```
**Expected Output**:
<table>
<tr>
<td>
**Found 7 boxes for test.jpg**
</td>
</tr>
<tr>
<td>
**car**
</td>
<td>
0.60 (925, 285) (1045, 374)
</td>
</tr>
<tr>
<td>
**car**
</td>
<td>
0.66 (706, 279) (786, 350)
</td>
</tr>
<tr>
<td>
**bus**
</td>
<td>
0.67 (5, 266) (220, 407)
</td>
</tr>
<tr>
<td>
**car**
</td>
<td>
0.70 (947, 324) (1280, 705)
</td>
</tr>
<tr>
<td>
**car**
</td>
<td>
0.74 (159, 303) (346, 440)
</td>
</tr>
<tr>
<td>
**car**
</td>
<td>
0.80 (761, 282) (942, 412)
</td>
</tr>
<tr>
<td>
**car**
</td>
<td>
0.89 (367, 300) (745, 648)
</td>
</tr>
</table>
The model you've just run is actually able to detect 80 different classes listed in "coco_classes.txt". To test the model on your own images:
1. Click on "File" in the upper bar of this notebook, then click "Open" to go on your Coursera Hub.
2. Add your image to this Jupyter Notebook's directory, in the "images" folder
3. Write your image's name in the cell above code
4. Run the code and see the output of the algorithm!
If you were to run your session in a for loop over all your images. Here's what you would get:
<center>
<video width="400" height="200" src="nb_images/pred_video_compressed2.mp4" type="video/mp4" controls>
</video>
</center>
<caption><center> Predictions of the YOLO model on pictures taken from a camera while driving around the Silicon Valley <br> Thanks [drive.ai](https://www.drive.ai/) for providing this dataset! </center></caption>
<font color='blue'>
**What you should remember**:
- YOLO is a state-of-the-art object detection model that is fast and accurate
- It runs an input image through a CNN which outputs a 19x19x5x85 dimensional volume.
- The encoding can be seen as a grid where each of the 19x19 cells contains information about 5 boxes.
- You filter through all the boxes using non-max suppression. Specifically:
- Score thresholding on the probability of detecting a class to keep only accurate (high probability) boxes
- Intersection over Union (IoU) thresholding to eliminate overlapping boxes
- Because training a YOLO model from randomly initialized weights is non-trivial and requires a large dataset as well as lot of computation, we used previously trained model parameters in this exercise. If you wish, you can also try fine-tuning the YOLO model with your own dataset, though this would be a fairly non-trivial exercise.
**References**: The ideas presented in this notebook came primarily from the two YOLO papers. The implementation here also took significant inspiration and used many components from Allan Zelener's github repository. The pretrained weights used in this exercise came from the official YOLO website.
- Joseph Redmon, Santosh Divvala, Ross Girshick, Ali Farhadi - [You Only Look Once: Unified, Real-Time Object Detection](https://arxiv.org/abs/1506.02640) (2015)
- Joseph Redmon, Ali Farhadi - [YOLO9000: Better, Faster, Stronger](https://arxiv.org/abs/1612.08242) (2016)
- Allan Zelener - [YAD2K: Yet Another Darknet 2 Keras](https://github.com/allanzelener/YAD2K)
- The official YOLO website (https://pjreddie.com/darknet/yolo/)
**Car detection dataset**:
<a rel="license" href="http://creativecommons.org/licenses/by/4.0/"><img alt="Creative Commons License" style="border-width:0" src="https://i.creativecommons.org/l/by/4.0/88x31.png" /></a><br /><span xmlns:dct="http://purl.org/dc/terms/" property="dct:title">The Drive.ai Sample Dataset</span> (provided by drive.ai) is licensed under a <a rel="license" href="http://creativecommons.org/licenses/by/4.0/">Creative Commons Attribution 4.0 International License</a>. We are especially grateful to Brody Huval, Chih Hu and Rahul Patel for collecting and providing this dataset.
|
github_jupyter
|
<a href="https://colab.research.google.com/github/Aditya-Singla/Banknote-Authentication/blob/master/Banknote_authentication.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
**Importing the libraries**
```
import pandas as pd
import numpy as np
```
**Uploading the dataset**
```
dataset = pd.read_csv('Bank note authentication.csv')
X = dataset.iloc[:,:-1].values
y = dataset.iloc[:,-1].values
```
**No missing values** (*as specified by the source* https://archive.ics.uci.edu/ml/datasets/banknote+authentication )
**Splitting the dataset into training set and test set**
```
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(X, y, test_size =0.2, random_state =0 )
```
*Checking* training and test sets
```
print(x_train)
print(y_train)
print(x_test)
print(y_test)
print(y_test)
```
**Feature Scaling** (**NOT** required for the *independent variable*)
```
from sklearn.preprocessing import StandardScaler
x_sc = StandardScaler()
x_train_sc = x_sc.fit_transform(x_train)
x_test_sc = x_sc.fit_transform(x_test)
```
*Checking* feature scaling
```
print(x_train_sc)
```
**Logistic Regression**
```
from sklearn.linear_model import LogisticRegression
classifier_lr = LogisticRegression(random_state=0)
classifier_lr.fit(x_train_sc,y_train)
y_predict_lr = classifier_lr.predict(x_test_sc)
```
**Evaluating** Logistic Regeression
```
from sklearn.metrics import confusion_matrix, accuracy_score, roc_auc_score
cm_lr = confusion_matrix(y_test,y_predict_lr)
print(cm_lr)
accuracy_score(y_test,y_predict_lr)
auc_score_lr = roc_auc_score(y_test,y_predict_lr)
print(auc_score_lr)
```
**Evaluating** K-Cross Validation Score
```
from sklearn.model_selection import cross_val_score
accuracy_lr = cross_val_score(classifier_lr, x_train_sc, y_train, cv=10 )
print( 'Accuracy:{:.2f}%'.format(accuracy_lr.mean()*100))
print( 'Standard Deviation: {:.2f}%'.format(accuracy_lr.std()*100))
```
**K Nearest Neighbors**
```
from sklearn.neighbors import KNeighborsClassifier
classifier_knn = KNeighborsClassifier(n_neighbors = 5, metric = 'minkowski',p=2)
classifier_knn.fit(x_train_sc,y_train)
y_predict_knn = classifier_knn.predict(x_test_sc)
```
**Evaluating** K Nearest Neighbors
```
cm_knn = confusion_matrix(y_test, y_predict_knn)
print(cm_knn)
accuracy_score(y_test,y_predict_knn)
auc_score_knn = roc_auc_score(y_test,y_predict_knn)
print(auc_score_knn)
```
**Evaluating** K-Cross Validation Score
```
from sklearn.model_selection import cross_val_score
accuracy_knn = cross_val_score(classifier_knn, x_train_sc, y_train, cv=10 )
print( 'Accuracy:{:.2f}%'.format(accuracy_knn.mean()*100))
print( 'Standard Deviation: {:.2f}%'.format(accuracy_knn.std()*100))
```
**Support Vector Machines (Kernel SVM)**
```
from sklearn.svm import SVC
classifier_svm = SVC(kernel ='rbf', random_state = 20)
classifier_svm.fit(x_train_sc,y_train)
y_predict_svm = classifier_svm.predict(x_test_sc)
```
**Evaluating** Kernel SVM
```
cm_svm = confusion_matrix(y_test,y_predict_svm)
print(cm_svm)
accuracy_score(y_test,y_predict_svm)
auc_score_svm = roc_auc_score(y_test,y_predict_svm)
print(auc_score_svm)
```
**Evaluating** K-Cross Validation Score
```
accuracy_svm = cross_val_score(classifier_svm, x_train_sc, y_train, cv=10 )
print( 'Accuracy:{:.2f}%'.format(accuracy_svm.mean()*100))
print( 'Standard Deviation: {:.2f}%'.format(accuracy_svm.std()*100))
```
**Naive-Bayes Classification**
```
from sklearn.naive_bayes import GaussianNB
classifier_nb = GaussianNB()
classifier_nb.fit(x_train_sc, y_train)
y_predict_nb = classifier_nb.predict(x_test_sc)
```
**Evaluating** Naive Bayes
```
cm_nb = confusion_matrix(y_test, y_predict_nb)
print (cm_nb)
accuracy_score(y_test, y_predict_nb)
auc_score_nb = roc_auc_score(y_test,y_predict_nb)
print(auc_score_nb)
```
**Evaluating** K-Cross Validation Score
```
accuracy_nb = cross_val_score(classifier_nb, x_train_sc, y_train, cv=10 )
print( 'Accuracy:{:.2f}%'.format(accuracy_nb.mean()*100))
print( 'Standard Deviation: {:.2f}%'.format(accuracy_nb.std()*100))
```
**Decision Tree Classification**
```
from sklearn.tree import DecisionTreeClassifier
classifier_dt = DecisionTreeClassifier(criterion='entropy',random_state=0)
classifier_dt.fit(x_train_sc, y_train)
y_predict_dt = classifier_dt.predict(x_test_sc)
```
**Evaluating** Decision Tree Classifier
```
cm_dt = confusion_matrix(y_test, y_predict_dt)
print (cm_dt)
accuracy_score(y_test, y_predict_dt)
auc_score_dt = roc_auc_score(y_test,y_predict_dt)
print(auc_score_dt)
```
**Evaluating** K-Cross Validation Score
```
accuracy_dt = cross_val_score(classifier_dt, x_train_sc, y_train, cv=10 )
print( 'Accuracy:{:.2f}%'.format(accuracy_dt.mean()*100))
print( 'Standard Deviation: {:.2f}%'.format(accuracy_dt.std()*100))
```
**Random Forest Classification**
```
from sklearn.ensemble import RandomForestClassifier
classifier_rf = RandomForestClassifier(n_estimators=100, criterion='entropy',random_state=0)
classifier_rf.fit(x_train_sc, y_train)
y_predict_rf = classifier_rf.predict(x_test_sc)
```
**Evaluating** Random Forest Classifier
```
cm_rf = confusion_matrix(y_test, y_predict_rf)
print (cm_rf)
accuracy_score(y_test, y_predict_rf)
auc_score_rf = roc_auc_score(y_test,y_predict_rf)
print(auc_score_rf)
```
**Evaluating** K-Cross Validation Score
```
accuracy_rf = cross_val_score(classifier_rf, x_train_sc, y_train, cv=10 )
print( 'Accuracy:{:.2f}%'.format(accuracy_rf.mean()*100))
print( 'Standard Deviation: {:.2f}%'.format(accuracy_rf.std()*100))
```
**Neural Network Classifier**
P.S. This is just for fun!
```
from sklearn.neural_network import MLPClassifier
classifier_neural_network = MLPClassifier(random_state=0)
classifier_neural_network.fit(x_train_sc,y_train)
y_predict_neural_network = classifier_neural_network.predict(x_test_sc)
```
**Evaluating** Neural Network
```
cm_neural_network = confusion_matrix(y_test, y_predict_neural_network)
print(cm_neural_network)
accuracy_score(y_test, y_predict_neural_network)
auc_score_neural_network = roc_auc_score(y_test,y_predict_neural_network)
print(auc_score_neural_network)
```
**Evaluating** K-Cross Validation Score
```
accuracy_neural_network = cross_val_score(classifier_neural_network, x_train_sc, y_train, cv=10 )
print( 'Accuracy:{:.2f}%'.format(accuracy_neural_network.mean()*100))
print( 'Standard Deviation: {:.2f}%'.format(accuracy_neural_network.std()*100))
```
*Neural Network* model as well as *Kernel SVM* gave us the best overall accuracy of 99.27% !!
Well, no tuning is necessary as the accuracy has already pretty much reached the maximum.
|
github_jupyter
|
# A Char-RNN Implementation in Tensorflow
*This notebook is slightly modified from https://colab.research.google.com/drive/13Vr3PrDg7cc4OZ3W2-grLSVSf0RJYWzb, with the following changes:*
* Main parameters defined at the start instead of middle
* Run all works, because of the added upload_custom_data parameter
* Training time specified in minutes instead of steps, for time-constrained classroom use
---
CharRNN was a well known generative text model (character level LSTM) created by Andrej Karpathy. It allowed easy training and generation of arbitrary text with many hilarious results:
* Music: abc notation
<https://highnoongmt.wordpress.com/2015/05/22/lisls-stis-recurrent-neural-networks-for-folk-music-generation/>,
* Irish folk music
<https://soundcloud.com/seaandsailor/sets/char-rnn-composes-irish-folk-music>-
* Obama speeches
<https://medium.com/@samim/obama-rnn-machine-generated-political-speeches-c8abd18a2ea0>-
* Eminem lyrics
<https://soundcloud.com/mrchrisjohnson/recurrent-neural-shady>- (NSFW ;-))
* Research awards
<http://karpathy.github.io/2015/05/21/rnn-effectiveness/#comment-2073825449>-
* TED Talks
<https://medium.com/@samim/ted-rnn-machine-generated-ted-talks-3dd682b894c0>-
* Movie Titles <http://www.cs.toronto.edu/~graves/handwriting.html>
This notebook contains a reimplementation in Tensorflow. It will let you input a file containing the text you want your generator to mimic, train your model, see the results, and save it for future use.
To get started, start running the cells in order, following the instructions at each step. You will need a sizable text file (try at least 1 MB of text) when prompted to upload one. For exploration you can also use the provided text corpus taken from Shakespeare's works.
The training cell saves a checkpoint every 30 seconds, so you can check the output of your network and not lose any progress.
## Outline
This notebook will guide you through the following steps. Roughly speaking, these will be our steps:
* Upload some data
* Set some training parameters (you can just use the defaults for now)
* Define our Model, training loss function, and data input manager
* Train on a cloud GPU
* Save out model and use it to generate some new text.
Design of the RNN is inspired by [this github project](https://github.com/sherjilozair/char-rnn-tensorflow) which was based on Andrej Karpathy's [char-rnn](https://github.com/karpathy/char-rnn). If you'd like to learn more, Andrej's [blog post](http://karpathy.github.io/2015/05/21/rnn-effectiveness/) is a great place to start.
### Imports and Values Needed to Run this Code
```
%tensorflow_version 1.x
from __future__ import absolute_import, print_function, division
from google.colab import files
from collections import Counter, defaultdict
from copy import deepcopy
from IPython.display import clear_output
from random import randint
import json
import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf
CHECKPOINT_DIR = './checkpoints/' #Checkpoints are temporarily kept here.
TEXT_ENCODING = 'utf-8'
```
### Let's define our training parameters.
Feel free to leave these untouched at their default values and just run this cell as is. Later, you can come back here and experiment wth these.
These parameters are just for training. Further down at the inference step, we'll define parameters for the text-generation step.
```
#The most common parameters to change
upload_custom_data = False #if false, use the default Shakespeare data
training_time_minutes = 2 #change this depending on how much time you have
#Neural network and optimization default parameters that usually work ok
num_layers = 2
state_size = 256
batch_size = 64
sequence_length = 256
steps_per_epoch = 500
learning_rate = 0.002
learning_rate_decay = 0.95
gradient_clipping = 5.0
```
### Get the training data.
We can either download the works of Shakespeare to train on or upload our own plain text file that we will be training on.
```
if not upload_custom_data:
shakespeare_url = "https://ocw.mit.edu/ans7870/6/6.006/s08/lecturenotes/files/t8.shakespeare.txt"
import urllib
file_contents = urllib.urlopen(shakespeare_url).read()
file_name = "shakespeare"
file_contents = file_contents[10501:] # Skip headers and start at content
print("An excerpt: \n", file_contents[:664])
if upload_custom_data:
uploaded = files.upload()
if type(uploaded) is not dict: uploaded = uploaded.files ## Deal with filedit versions
file_bytes = uploaded[uploaded.keys()[0]]
utf8_string = file_bytes.decode(TEXT_ENCODING)
file_contents = utf8_string if files else ''
file_name = uploaded.keys()[0]
print("An excerpt: \n", file_contents[:664])
```
## Set up the recurrent LSTM network
Before we can do anything, we have to define what our neural network looks like. This next cell creates a class which will contain the tensorflow graph and training parameters that make up the network.
```
class RNN(object):
"""Represents a Recurrent Neural Network using LSTM cells.
Attributes:
num_layers: The integer number of hidden layers in the RNN.
state_size: The size of the state in each LSTM cell.
num_classes: Number of output classes. (E.g. 256 for Extended ASCII).
batch_size: The number of training sequences to process per step.
sequence_length: The number of chars in a training sequence.
batch_index: Index within the dataset to start the next batch at.
on_gpu_sequences: Generates the training inputs for a single batch.
on_gpu_targets: Generates the training labels for a single batch.
input_symbol: Placeholder for a single label for use during inference.
temperature: Used when sampling outputs. A higher temperature will yield
more variance; a lower one will produce the most likely outputs. Value
should be between 0 and 1.
initial_state: The LSTM State Tuple to initialize the network with. This
will need to be set to the new_state computed by the network each cycle.
logits: Unnormalized probability distribution for the next predicted
label, for each timestep in each sequence.
output_labels: A [batch_size, 1] int32 tensor containing a predicted
label for each sequence in a batch. Only generated in infer mode.
"""
def __init__(self,
rnn_num_layers=1,
rnn_state_size=128,
num_classes=256,
rnn_batch_size=1,
rnn_sequence_length=1):
self.num_layers = rnn_num_layers
self.state_size = rnn_state_size
self.num_classes = num_classes
self.batch_size = rnn_batch_size
self.sequence_length = rnn_sequence_length
self.batch_shape = (self.batch_size, self.sequence_length)
print("Built LSTM: ",
self.num_layers ,self.state_size ,self.num_classes ,
self.batch_size ,self.sequence_length ,self.batch_shape)
def build_training_model(self, dropout_rate, data_to_load):
"""Sets up an RNN model for running a training job.
Args:
dropout_rate: The rate at which weights may be forgotten during training.
data_to_load: A numpy array of containing the training data, with each
element in data_to_load being an integer representing a label. For
example, for Extended ASCII, values may be 0 through 255.
Raises:
ValueError: If mode is data_to_load is None.
"""
if data_to_load is None:
raise ValueError('To continue, you must upload training data.')
inputs = self._set_up_training_inputs(data_to_load)
self._build_rnn(inputs, dropout_rate)
def build_inference_model(self):
"""Sets up an RNN model for generating a sequence element by element.
"""
self.input_symbol = tf.placeholder(shape=[1, 1], dtype=tf.int32)
self.temperature = tf.placeholder(shape=(), dtype=tf.float32,
name='temperature')
self.num_options = tf.placeholder(shape=(), dtype=tf.int32,
name='num_options')
self._build_rnn(self.input_symbol, 0.0)
self.temperature_modified_logits = tf.squeeze(
self.logits, 0) / self.temperature
#for beam search
self.normalized_probs = tf.nn.softmax(self.logits)
self.output_labels = tf.multinomial(self.temperature_modified_logits,
self.num_options)
def _set_up_training_inputs(self, data):
self.batch_index = tf.placeholder(shape=(), dtype=tf.int32)
batch_input_length = self.batch_size * self.sequence_length
input_window = tf.slice(tf.constant(data, dtype=tf.int32),
[self.batch_index],
[batch_input_length + 1])
self.on_gpu_sequences = tf.reshape(
tf.slice(input_window, [0], [batch_input_length]), self.batch_shape)
self.on_gpu_targets = tf.reshape(
tf.slice(input_window, [1], [batch_input_length]), self.batch_shape)
return self.on_gpu_sequences
def _build_rnn(self, inputs, dropout_rate):
"""Generates an RNN model using the passed functions.
Args:
inputs: int32 Tensor with shape [batch_size, sequence_length] containing
input labels.
dropout_rate: A floating point value determining the chance that a weight
is forgotten during evaluation.
"""
# Alias some commonly used functions
dropout_wrapper = tf.contrib.rnn.DropoutWrapper
lstm_cell = tf.contrib.rnn.LSTMCell
multi_rnn_cell = tf.contrib.rnn.MultiRNNCell
self._cell = multi_rnn_cell(
[dropout_wrapper(lstm_cell(self.state_size), 1.0, 1.0 - dropout_rate)
for _ in range(self.num_layers)])
self.initial_state = self._cell.zero_state(self.batch_size, tf.float32)
embedding = tf.get_variable('embedding',
[self.num_classes, self.state_size])
embedding_input = tf.nn.embedding_lookup(embedding, inputs)
output, self.new_state = tf.nn.dynamic_rnn(self._cell, embedding_input,
initial_state=self.initial_state)
self.logits = tf.contrib.layers.fully_connected(output, self.num_classes,
activation_fn=None)
```
###Define your loss function
Loss is a measure of how well the neural network is modeling the data distribution.
Pass in your logits and the targets you're training against. In this case, target_weights is a set of multipliers that will put higher emphasis on certain outputs. In this notebook, we'll give all outputs equal importance.
```
def get_loss(logits, targets, target_weights):
with tf.name_scope('loss'):
return tf.contrib.seq2seq.sequence_loss(
logits,
targets,
target_weights,
average_across_timesteps=True)
```
### Define your optimizer
This tells Tensorflow how to reduce the loss. We will use the popular [ADAM algorithm](https://www.tensorflow.org/api_docs/python/tf/train/AdamOptimizer)
```
def get_optimizer(loss, initial_learning_rate, gradient_clipping, global_step,
decay_steps, decay_rate):
with tf.name_scope('optimizer'):
computed_learning_rate = tf.train.exponential_decay(
initial_learning_rate,
global_step,
decay_steps,
decay_rate,
staircase=True)
optimizer = tf.train.AdamOptimizer(computed_learning_rate)
trained_vars = tf.trainable_variables()
gradients, _ = tf.clip_by_global_norm(
tf.gradients(loss, trained_vars),
gradient_clipping)
training_op = optimizer.apply_gradients(
zip(gradients, trained_vars),
global_step=global_step)
return training_op, computed_learning_rate
```
### This class will let us view the progress of our training as it progresses.
```
class LossPlotter(object):
def __init__(self, history_length):
self.global_steps = []
self.losses = []
self.averaged_loss_x = []
self.averaged_loss_y = []
self.history_length = history_length
def draw_plots(self):
self._update_averages(self.global_steps, self.losses,
self.averaged_loss_x, self.averaged_loss_y)
plt.title('Average Loss Over Time')
plt.xlabel('Global Step')
plt.ylabel('Loss')
plt.plot(self.averaged_loss_x, self.averaged_loss_y, label='Loss/Time (Avg)')
plt.plot()
plt.plot(self.global_steps, self.losses,
label='Loss/Time (Last %d)' % self.history_length,
alpha=.1, color='r')
plt.plot()
plt.legend()
plt.show()
plt.title('Loss for the last 100 Steps')
plt.xlabel('Global Step')
plt.ylabel('Loss')
plt.plot(self.global_steps, self.losses,
label='Loss/Time (Last %d)' % self.history_length, color='r')
plt.plot()
plt.legend()
plt.show()
# The notebook will be slowed down at the end of training if we plot the
# entire history of raw data. Plot only the last 100 steps of raw data,
# and the average of each 100 batches. Don't keep unused data.
self.global_steps = []
self.losses = []
self.learning_rates = []
def log_step(self, global_step, loss):
self.global_steps.append(global_step)
self.losses.append(loss)
def _update_averages(self, x_list, y_list,
averaged_data_x, averaged_data_y):
averaged_data_x.append(x_list[-1])
averaged_data_y.append(sum(y_list) / self.history_length)
```
## Now, we're going to start training our model.
This could take a while, so you might want to grab a coffee. Every 30 seconds of training, we're going to save a checkpoint to make sure we don't lose our progress. To monitor the progress of your training, feel free to stop the training every once in a while and run the inference cell to generate text with your model!
First, we will need to turn the plain text file into arrays of tokens (and, later, back). To do this we will use this token mapper helper class:
```
import string
class TokenMapper(object):
def __init__(self):
self.token_mapping = {}
self.reverse_token_mapping = {}
def buildFromData(self, utf8_string, limit=0.00004):
print("Build token dictionary.")
total_num = len(utf8_string)
sorted_tokens = sorted(Counter(utf8_string.decode('utf8')).items(),
key=lambda x: -x[1])
# Filter tokens: Only allow printable characters (not control chars) and
# limit to ones that are resonably common, i.e. skip strange esoteric
# characters in order to reduce the dictionary size.
filtered_tokens = filter(lambda t: t[0] in string.printable or
float(t[1])/total_num > limit, sorted_tokens)
tokens, counts = zip(*filtered_tokens)
self.token_mapping = dict(zip(tokens, range(len(tokens))))
for c in string.printable:
if c not in self.token_mapping:
print("Skipped token for: ", c)
self.reverse_token_mapping = {
val: key for key, val in self.token_mapping.items()}
print("Created dictionary: %d tokens"%len(self.token_mapping))
def mapchar(self, char):
if char in self.token_mapping:
return self.token_mapping[char]
else:
return self.token_mapping[' ']
def mapstring(self, utf8_string):
return [self.mapchar(c) for c in utf8_string]
def maptoken(self, token):
return self.reverse_token_mapping[token]
def maptokens(self, int_array):
return ''.join([self.reverse_token_mapping[c] for c in int_array])
def size(self):
return len(self.token_mapping)
def alphabet(self):
return ''.join([k for k,v in sorted(self.token_mapping.items(),key=itemgetter(1))])
def print(self):
for k,v in sorted(self.token_mapping.items(),key=itemgetter(1)): print(k, v)
def save(self, path):
with open(path, 'wb') as json_file:
json.dump(self.token_mapping, json_file)
def restore(self, path):
with open(path, 'r') as json_file:
self.token_mapping = {}
self.token_mapping.update(json.load(json_file))
self.reverse_token_mapping = {val: key for key, val in self.token_mapping.items()}
```
Now convert the raw input into a list of tokens.
```
# Clean the checkpoint directory and make a fresh one
!rm -rf {CHECKPOINT_DIR}
!mkdir {CHECKPOINT_DIR}
!ls -lt
chars_in_batch = (sequence_length * batch_size)
file_len = len(file_contents)
unique_sequential_batches = file_len // chars_in_batch
mapper = TokenMapper()
mapper.buildFromData(file_contents)
mapper.save(''.join([CHECKPOINT_DIR, 'token_mapping.json']))
input_values = mapper.mapstring(file_contents)
```
###First, we'll build our neural network and add our training operations to the Tensorflow graph.
If you're continuing training after testing your generator, run the next three cells.
```
tf.reset_default_graph()
config = tf.ConfigProto()
config.gpu_options.allow_growth = True
print('Constructing model...')
model = RNN(
rnn_num_layers=num_layers,
rnn_state_size=state_size,
num_classes=mapper.size(),
rnn_batch_size=batch_size,
rnn_sequence_length=sequence_length)
model.build_training_model(0.05, np.asarray(input_values))
print('Constructed model successfully.')
print('Setting up training session...')
neutral_target_weights = tf.constant(
np.ones(model.batch_shape),
tf.float32
)
loss = get_loss(model.logits, model.on_gpu_targets, neutral_target_weights)
global_step = tf.get_variable('global_step', shape=(), trainable=False,
dtype=tf.int32)
training_step, computed_learning_rate = get_optimizer(
loss,
learning_rate,
gradient_clipping,
global_step,
steps_per_epoch,
learning_rate_decay
)
```
The supervisor will manage the training flow and checkpointing.
```
# Create a supervisor that will checkpoint the model in the CHECKPOINT_DIR
sv = tf.train.Supervisor(
logdir=CHECKPOINT_DIR,
global_step=global_step,
save_model_secs=30)
print('Training session ready.')
```
###This next cell will begin the training cycle.
First, we will attempt to pick up training where we left off, if a previous checkpoint exists, then continue the training process.
```
from datetime import datetime
start_time = datetime.now()
with sv.managed_session(config=config) as sess:
print('Training supervisor successfully initialized all variables.')
if not file_len:
raise ValueError('To continue, you must upload training data.')
elif file_len < chars_in_batch:
raise ValueError('To continue, you must upload a larger set of data.')
plotter = LossPlotter(100)
step_number = sess.run(global_step)
zero_state = sess.run([model.initial_state])
max_batch_index = (unique_sequential_batches - 1) * chars_in_batch
while not sv.should_stop() and (datetime.now()-start_time).seconds/60 < training_time_minutes:
feed_dict = {
model.batch_index: randint(0, max_batch_index),
model.initial_state: zero_state
}
[_, _, training_loss, step_number, current_learning_rate, _] = sess.run(
[model.on_gpu_sequences,
model.on_gpu_targets,
loss,
global_step,
computed_learning_rate,
training_step],
feed_dict)
plotter.log_step(step_number, training_loss)
if step_number % 100 == 0:
clear_output(True)
plotter.draw_plots()
print('Latest checkpoint is: %s' %
tf.train.latest_checkpoint(CHECKPOINT_DIR))
print('Learning Rate is: %f' %
current_learning_rate)
if step_number % 10 == 0:
print('global step %d, loss=%f' % (step_number, training_loss))
clear_output(True)
print('Training completed in HH:MM:SS = ', datetime.now()-start_time)
print('Latest checkpoint is: %s' %
tf.train.latest_checkpoint(CHECKPOINT_DIR))
```
## Now, we're going to generate some text!
Here, we'll use the **Beam Search** algorithm to generate some text with our trained model. Beam Search picks N possible next options from each of the current options at every step. This way, if the generator picks an item leading to a bad decision down the line, it can toss the bad result out and keep going with a more likely one.
```
class BeamSearchCandidate(object):
"""Represents a node within the search space during Beam Search.
Attributes:
state: The resulting RNN state after the given sequence has been generated.
sequence: The sequence of selections leading to this node.
probability: The probability of the sequence occurring, computed as the sum
of the probabilty of each character in the sequence at its respective
step.
"""
def __init__(self, init_state, sequence, probability):
self.state = init_state
self.sequence = sequence
self.probability = probability
def search_from(self, tf_sess, rnn_model, temperature, num_options):
"""Expands the num_options most likely next elements in the sequence.
Args:
tf_sess: The Tensorflow session containing the rnn_model.
rnn_model: The RNN to use to generate the next element in the sequence.
temperature: Modifies the probabilities of each character, placing
more emphasis on higher probabilities as the value approaches 0.
num_options: How many potential next options to expand from this one.
Returns: A list of BeamSearchCandidate objects descended from this node.
"""
expanded_set = []
feed = {rnn_model.input_symbol: np.array([[self.sequence[-1]]]),
rnn_model.initial_state: self.state,
rnn_model.temperature: temperature,
rnn_model.num_options: num_options}
[predictions, probabilities, new_state] = tf_sess.run(
[rnn_model.output_labels,
rnn_model.normalized_probs,
rnn_model.new_state], feed)
# Get the indices of the num_beams next picks
picks = [predictions[0][x] for x in range(len(predictions[0]))]
for new_char in picks:
new_seq = deepcopy(self.sequence)
new_seq.append(new_char)
expanded_set.append(
BeamSearchCandidate(new_state, new_seq,
probabilities[0][0][new_char] + self.probability))
return expanded_set
def __eq__(self, other):
return self.sequence == other.sequence
def __ne__(self, other):
return not self.__eq__(other)
def __hash__(self):
return hash(self.sequence())
def beam_search_generate_sequence(tf_sess, rnn_model, primer, temperature=0.85,
termination_condition=None, num_beams=5):
"""Implements a sequence generator using Beam Search.
Args:
tf_sess: The Tensorflow session containing the rnn_model.
rnn_model: The RNN to use to generate the next element in the sequence.
temperature: Controls how 'Creative' the generated sequence is. Values
close to 0 tend to generate the most likely sequence, while values
closer to 1 generate more original sequences. Acceptable values are
within (0, 1].
termination_condition: A function taking one parameter, a list of
integers, that returns True when a condition is met that signals to the
RNN to return what it has generated so far.
num_beams: The number of possible sequences to keep at each step of the
generation process.
Returns: A list of at most num_beams BeamSearchCandidate objects.
"""
candidates = []
rnn_current_state = sess.run([rnn_model.initial_state])
#Initialize the state for the primer
for primer_val in primer[:-1]:
feed = {rnn_model.input_symbol: np.array([[primer_val]]),
rnn_model.initial_state: rnn_current_state
}
[rnn_current_state] = tf_sess.run([rnn_model.new_state], feed)
candidates.append(BeamSearchCandidate(rnn_current_state, primer, num_beams))
while True not in [termination_condition(x.sequence) for x in candidates]:
new_candidates = []
for candidate in candidates:
expanded_candidates = candidate.search_from(
tf_sess, rnn_model, temperature, num_beams)
for new in expanded_candidates:
if new not in new_candidates:
#do not reevaluate duplicates
new_candidates.append(new)
candidates = sorted(new_candidates,
key=lambda x: x.probability, reverse=True)[:num_beams]
return [c for c in candidates if termination_condition(c.sequence)]
```
Input something to start your generated text with, and set how characters long you want the text to be.
"Creativity" refers to how much emphasis your neural network puts on matching a pattern. If you notice looping in the output, try raising this value. If your output seems too random, try lowering it a bit.
If the results don't look too great in general, run the three training cells again for a bit longer. The lower your loss, the more closely your generated text will match the training data.
```
tf.reset_default_graph()
config = tf.ConfigProto()
config.gpu_options.allow_growth = True
sess = tf.InteractiveSession(config=config)
model = RNN(
rnn_num_layers=num_layers,
rnn_state_size=state_size,
num_classes=mapper.size(),
rnn_batch_size=1,
rnn_sequence_length=1)
model.build_inference_model()
sess.run(tf.global_variables_initializer())
saver = tf.train.Saver(tf.global_variables())
ckpt = tf.train.latest_checkpoint(CHECKPOINT_DIR)
saver.restore(sess, ckpt)
def gen(start_with, pred, creativity):
int_array = mapper.mapstring(start_with)
candidates = beam_search_generate_sequence(
sess, model, int_array, temperature=creativity,
termination_condition=pred,
num_beams=1)
gentext = mapper.maptokens(candidates[0].sequence)
return gentext
def lengthlimit(n):
return lambda text: len(text)>n
def sentences(n):
return lambda text: mapper.maptokens(text).count(".")>=n
def paragraph():
return lambda text: mapper.maptokens(text).count("\n")>0
length_of_generated_text = 2000
creativity = 0.85 # Should be greater than 0 but less than 1
print(gen(" ANTONIO: Who is it ?", lengthlimit(length_of_generated_text), creativity))
```
## Let's save a copy of our trained RNN so we can do all kinds of cool things with it later.
```
save_model_to_drive = False ## Set this to true to save directly to Google Drive.
def save_model_hyperparameters(path):
with open(path, 'w') as json_file:
model_params = {
'num_layers': model.num_layers,
'state_size': model.state_size,
'num_classes': model.num_classes
}
json.dump(model_params, json_file)
def save_to_drive(title, content):
# Install the PyDrive wrapper & import libraries.
!pip install -U -q PyDrive
from pydrive.auth import GoogleAuth
from pydrive.drive import GoogleDrive
from google.colab import auth
from oauth2client.client import GoogleCredentials
# Authenticate and create the PyDrive client.
auth.authenticate_user()
gauth = GoogleAuth()
gauth.credentials = GoogleCredentials.get_application_default()
drive = GoogleDrive(gauth)
newfile = drive.CreateFile({'title': title})
newfile.SetContentFile(content)
newfile.Upload()
print('Uploaded file with ID %s as %s'% (newfile.get('id'),
archive_name))
archive_name = ''.join([file_name,'_seedbank_char-rnn.zip'])
latest_model = tf.train.latest_checkpoint(CHECKPOINT_DIR).split('/')[2]
checkpoints_archive_path = ''.join(['./exports/',archive_name])
if not latest_model:
raise ValueError('You must train a model before you can export one.')
%system mkdir exports
%rm -f {checkpoints_archive_path}
mapper.save(''.join([CHECKPOINT_DIR, 'token_mapping.json']))
save_model_hyperparameters(''.join([CHECKPOINT_DIR, 'model_attributes.json']))
%system zip '{checkpoints_archive_path}' -@ '{CHECKPOINT_DIR}checkpoint' \
'{CHECKPOINT_DIR}token_mapping.json' \
'{CHECKPOINT_DIR}model_attributes.json' \
'{CHECKPOINT_DIR}{latest_model}.'*
if save_model_to_drive:
save_to_drive(archive_name, checkpoints_archive_path)
else:
files.download(checkpoints_archive_path)
```
|
github_jupyter
|
##### Copyright 2020 The TensorFlow Authors.
```
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
```
# Recurrent Neural Networks (RNN) with Keras
<table class="tfo-notebook-buttons" align="left">
<td>
<a target="_blank" href="https://www.tensorflow.org/guide/keras/rnn"><img src="https://www.tensorflow.org/images/tf_logo_32px.png" />View on TensorFlow.org</a>
</td>
<td>
<a target="_blank" href="https://colab.research.google.com/github/tensorflow/docs/blob/snapshot-keras/site/en/guide/keras/rnn.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
</td>
<td>
<a target="_blank" href="https://github.com/keras-team/keras-io/blob/master/guides/working_with_rnns.py"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View source on GitHub</a>
</td>
<td>
<a href="https://storage.googleapis.com/tensorflow_docs/docs/site/en/guide/keras/rnn.ipynb"><img src="https://www.tensorflow.org/images/download_logo_32px.png" />Download notebook</a>
</td>
</table>
## Introduction
Recurrent neural networks (RNN) are a class of neural networks that is powerful for
modeling sequence data such as time series or natural language.
Schematically, a RNN layer uses a `for` loop to iterate over the timesteps of a
sequence, while maintaining an internal state that encodes information about the
timesteps it has seen so far.
The Keras RNN API is designed with a focus on:
- **Ease of use**: the built-in `keras.layers.RNN`, `keras.layers.LSTM`,
`keras.layers.GRU` layers enable you to quickly build recurrent models without
having to make difficult configuration choices.
- **Ease of customization**: You can also define your own RNN cell layer (the inner
part of the `for` loop) with custom behavior, and use it with the generic
`keras.layers.RNN` layer (the `for` loop itself). This allows you to quickly
prototype different research ideas in a flexible way with minimal code.
## Setup
```
import numpy as np
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
```
## Built-in RNN layers: a simple example
There are three built-in RNN layers in Keras:
1. `keras.layers.SimpleRNN`, a fully-connected RNN where the output from previous
timestep is to be fed to next timestep.
2. `keras.layers.GRU`, first proposed in
[Cho et al., 2014](https://arxiv.org/abs/1406.1078).
3. `keras.layers.LSTM`, first proposed in
[Hochreiter & Schmidhuber, 1997](https://www.bioinf.jku.at/publications/older/2604.pdf).
In early 2015, Keras had the first reusable open-source Python implementations of LSTM
and GRU.
Here is a simple example of a `Sequential` model that processes sequences of integers,
embeds each integer into a 64-dimensional vector, then processes the sequence of
vectors using a `LSTM` layer.
```
model = keras.Sequential()
# Add an Embedding layer expecting input vocab of size 1000, and
# output embedding dimension of size 64.
model.add(layers.Embedding(input_dim=1000, output_dim=64))
# Add a LSTM layer with 128 internal units.
model.add(layers.LSTM(128))
# Add a Dense layer with 10 units.
model.add(layers.Dense(10))
model.summary()
```
Built-in RNNs support a number of useful features:
- Recurrent dropout, via the `dropout` and `recurrent_dropout` arguments
- Ability to process an input sequence in reverse, via the `go_backwards` argument
- Loop unrolling (which can lead to a large speedup when processing short sequences on
CPU), via the `unroll` argument
- ...and more.
For more information, see the
[RNN API documentation](https://keras.io/api/layers/recurrent_layers/).
## Outputs and states
By default, the output of a RNN layer contains a single vector per sample. This vector
is the RNN cell output corresponding to the last timestep, containing information
about the entire input sequence. The shape of this output is `(batch_size, units)`
where `units` corresponds to the `units` argument passed to the layer's constructor.
A RNN layer can also return the entire sequence of outputs for each sample (one vector
per timestep per sample), if you set `return_sequences=True`. The shape of this output
is `(batch_size, timesteps, units)`.
```
model = keras.Sequential()
model.add(layers.Embedding(input_dim=1000, output_dim=64))
# The output of GRU will be a 3D tensor of shape (batch_size, timesteps, 256)
model.add(layers.GRU(256, return_sequences=True))
# The output of SimpleRNN will be a 2D tensor of shape (batch_size, 128)
model.add(layers.SimpleRNN(128))
model.add(layers.Dense(10))
model.summary()
```
In addition, a RNN layer can return its final internal state(s). The returned states
can be used to resume the RNN execution later, or
[to initialize another RNN](https://arxiv.org/abs/1409.3215).
This setting is commonly used in the
encoder-decoder sequence-to-sequence model, where the encoder final state is used as
the initial state of the decoder.
To configure a RNN layer to return its internal state, set the `return_state` parameter
to `True` when creating the layer. Note that `LSTM` has 2 state tensors, but `GRU`
only has one.
To configure the initial state of the layer, just call the layer with additional
keyword argument `initial_state`.
Note that the shape of the state needs to match the unit size of the layer, like in the
example below.
```
encoder_vocab = 1000
decoder_vocab = 2000
encoder_input = layers.Input(shape=(None,))
encoder_embedded = layers.Embedding(input_dim=encoder_vocab, output_dim=64)(
encoder_input
)
# Return states in addition to output
output, state_h, state_c = layers.LSTM(64, return_state=True, name="encoder")(
encoder_embedded
)
encoder_state = [state_h, state_c]
decoder_input = layers.Input(shape=(None,))
decoder_embedded = layers.Embedding(input_dim=decoder_vocab, output_dim=64)(
decoder_input
)
# Pass the 2 states to a new LSTM layer, as initial state
decoder_output = layers.LSTM(64, name="decoder")(
decoder_embedded, initial_state=encoder_state
)
output = layers.Dense(10)(decoder_output)
model = keras.Model([encoder_input, decoder_input], output)
model.summary()
```
## RNN layers and RNN cells
In addition to the built-in RNN layers, the RNN API also provides cell-level APIs.
Unlike RNN layers, which processes whole batches of input sequences, the RNN cell only
processes a single timestep.
The cell is the inside of the `for` loop of a RNN layer. Wrapping a cell inside a
`keras.layers.RNN` layer gives you a layer capable of processing batches of
sequences, e.g. `RNN(LSTMCell(10))`.
Mathematically, `RNN(LSTMCell(10))` produces the same result as `LSTM(10)`. In fact,
the implementation of this layer in TF v1.x was just creating the corresponding RNN
cell and wrapping it in a RNN layer. However using the built-in `GRU` and `LSTM`
layers enable the use of CuDNN and you may see better performance.
There are three built-in RNN cells, each of them corresponding to the matching RNN
layer.
- `keras.layers.SimpleRNNCell` corresponds to the `SimpleRNN` layer.
- `keras.layers.GRUCell` corresponds to the `GRU` layer.
- `keras.layers.LSTMCell` corresponds to the `LSTM` layer.
The cell abstraction, together with the generic `keras.layers.RNN` class, make it
very easy to implement custom RNN architectures for your research.
## Cross-batch statefulness
When processing very long sequences (possibly infinite), you may want to use the
pattern of **cross-batch statefulness**.
Normally, the internal state of a RNN layer is reset every time it sees a new batch
(i.e. every sample seen by the layer is assumed to be independent of the past). The
layer will only maintain a state while processing a given sample.
If you have very long sequences though, it is useful to break them into shorter
sequences, and to feed these shorter sequences sequentially into a RNN layer without
resetting the layer's state. That way, the layer can retain information about the
entirety of the sequence, even though it's only seeing one sub-sequence at a time.
You can do this by setting `stateful=True` in the constructor.
If you have a sequence `s = [t0, t1, ... t1546, t1547]`, you would split it into e.g.
```
s1 = [t0, t1, ... t100]
s2 = [t101, ... t201]
...
s16 = [t1501, ... t1547]
```
Then you would process it via:
```python
lstm_layer = layers.LSTM(64, stateful=True)
for s in sub_sequences:
output = lstm_layer(s)
```
When you want to clear the state, you can use `layer.reset_states()`.
> Note: In this setup, sample `i` in a given batch is assumed to be the continuation of
sample `i` in the previous batch. This means that all batches should contain the same
number of samples (batch size). E.g. if a batch contains `[sequence_A_from_t0_to_t100,
sequence_B_from_t0_to_t100]`, the next batch should contain
`[sequence_A_from_t101_to_t200, sequence_B_from_t101_to_t200]`.
Here is a complete example:
```
paragraph1 = np.random.random((20, 10, 50)).astype(np.float32)
paragraph2 = np.random.random((20, 10, 50)).astype(np.float32)
paragraph3 = np.random.random((20, 10, 50)).astype(np.float32)
lstm_layer = layers.LSTM(64, stateful=True)
output = lstm_layer(paragraph1)
output = lstm_layer(paragraph2)
output = lstm_layer(paragraph3)
# reset_states() will reset the cached state to the original initial_state.
# If no initial_state was provided, zero-states will be used by default.
lstm_layer.reset_states()
```
### RNN State Reuse
<a id="rnn_state_reuse"></a>
The recorded states of the RNN layer are not included in the `layer.weights()`. If you
would like to reuse the state from a RNN layer, you can retrieve the states value by
`layer.states` and use it as the
initial state for a new layer via the Keras functional API like `new_layer(inputs,
initial_state=layer.states)`, or model subclassing.
Please also note that sequential model might not be used in this case since it only
supports layers with single input and output, the extra input of initial state makes
it impossible to use here.
```
paragraph1 = np.random.random((20, 10, 50)).astype(np.float32)
paragraph2 = np.random.random((20, 10, 50)).astype(np.float32)
paragraph3 = np.random.random((20, 10, 50)).astype(np.float32)
lstm_layer = layers.LSTM(64, stateful=True)
output = lstm_layer(paragraph1)
output = lstm_layer(paragraph2)
existing_state = lstm_layer.states
new_lstm_layer = layers.LSTM(64)
new_output = new_lstm_layer(paragraph3, initial_state=existing_state)
```
## Bidirectional RNNs
For sequences other than time series (e.g. text), it is often the case that a RNN model
can perform better if it not only processes sequence from start to end, but also
backwards. For example, to predict the next word in a sentence, it is often useful to
have the context around the word, not only just the words that come before it.
Keras provides an easy API for you to build such bidirectional RNNs: the
`keras.layers.Bidirectional` wrapper.
```
model = keras.Sequential()
model.add(
layers.Bidirectional(layers.LSTM(64, return_sequences=True), input_shape=(5, 10))
)
model.add(layers.Bidirectional(layers.LSTM(32)))
model.add(layers.Dense(10))
model.summary()
```
Under the hood, `Bidirectional` will copy the RNN layer passed in, and flip the
`go_backwards` field of the newly copied layer, so that it will process the inputs in
reverse order.
The output of the `Bidirectional` RNN will be, by default, the sum of the forward layer
output and the backward layer output. If you need a different merging behavior, e.g.
concatenation, change the `merge_mode` parameter in the `Bidirectional` wrapper
constructor. For more details about `Bidirectional`, please check
[the API docs](https://www.tensorflow.org/api_docs/python/tf/keras/layers/Bidirectional/).
## Performance optimization and CuDNN kernels
In TensorFlow 2.0, the built-in LSTM and GRU layers have been updated to leverage CuDNN
kernels by default when a GPU is available. With this change, the prior
`keras.layers.CuDNNLSTM/CuDNNGRU` layers have been deprecated, and you can build your
model without worrying about the hardware it will run on.
Since the CuDNN kernel is built with certain assumptions, this means the layer **will
not be able to use the CuDNN kernel if you change the defaults of the built-in LSTM or
GRU layers**. E.g.:
- Changing the `activation` function from `tanh` to something else.
- Changing the `recurrent_activation` function from `sigmoid` to something else.
- Using `recurrent_dropout` > 0.
- Setting `unroll` to True, which forces LSTM/GRU to decompose the inner
`tf.while_loop` into an unrolled `for` loop.
- Setting `use_bias` to False.
- Using masking when the input data is not strictly right padded (if the mask
corresponds to strictly right padded data, CuDNN can still be used. This is the most
common case).
For the detailed list of constraints, please see the documentation for the
[LSTM](https://www.tensorflow.org/api_docs/python/tf/keras/layers/LSTM/) and
[GRU](https://www.tensorflow.org/api_docs/python/tf/keras/layers/GRU/) layers.
### Using CuDNN kernels when available
Let's build a simple LSTM model to demonstrate the performance difference.
We'll use as input sequences the sequence of rows of MNIST digits (treating each row of
pixels as a timestep), and we'll predict the digit's label.
```
batch_size = 64
# Each MNIST image batch is a tensor of shape (batch_size, 28, 28).
# Each input sequence will be of size (28, 28) (height is treated like time).
input_dim = 28
units = 64
output_size = 10 # labels are from 0 to 9
# Build the RNN model
def build_model(allow_cudnn_kernel=True):
# CuDNN is only available at the layer level, and not at the cell level.
# This means `LSTM(units)` will use the CuDNN kernel,
# while RNN(LSTMCell(units)) will run on non-CuDNN kernel.
if allow_cudnn_kernel:
# The LSTM layer with default options uses CuDNN.
lstm_layer = keras.layers.LSTM(units, input_shape=(None, input_dim))
else:
# Wrapping a LSTMCell in a RNN layer will not use CuDNN.
lstm_layer = keras.layers.RNN(
keras.layers.LSTMCell(units), input_shape=(None, input_dim)
)
model = keras.models.Sequential(
[
lstm_layer,
keras.layers.BatchNormalization(),
keras.layers.Dense(output_size),
]
)
return model
```
Let's load the MNIST dataset:
```
mnist = keras.datasets.mnist
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train, x_test = x_train / 255.0, x_test / 255.0
sample, sample_label = x_train[0], y_train[0]
```
Let's create a model instance and train it.
We choose `sparse_categorical_crossentropy` as the loss function for the model. The
output of the model has shape of `[batch_size, 10]`. The target for the model is an
integer vector, each of the integer is in the range of 0 to 9.
```
model = build_model(allow_cudnn_kernel=True)
model.compile(
loss=keras.losses.SparseCategoricalCrossentropy(from_logits=True),
optimizer="sgd",
metrics=["accuracy"],
)
model.fit(
x_train, y_train, validation_data=(x_test, y_test), batch_size=batch_size, epochs=1
)
```
Now, let's compare to a model that does not use the CuDNN kernel:
```
noncudnn_model = build_model(allow_cudnn_kernel=False)
noncudnn_model.set_weights(model.get_weights())
noncudnn_model.compile(
loss=keras.losses.SparseCategoricalCrossentropy(from_logits=True),
optimizer="sgd",
metrics=["accuracy"],
)
noncudnn_model.fit(
x_train, y_train, validation_data=(x_test, y_test), batch_size=batch_size, epochs=1
)
```
When running on a machine with a NVIDIA GPU and CuDNN installed,
the model built with CuDNN is much faster to train compared to the
model that uses the regular TensorFlow kernel.
The same CuDNN-enabled model can also be used to run inference in a CPU-only
environment. The `tf.device` annotation below is just forcing the device placement.
The model will run on CPU by default if no GPU is available.
You simply don't have to worry about the hardware you're running on anymore. Isn't that
pretty cool?
```
import matplotlib.pyplot as plt
with tf.device("CPU:0"):
cpu_model = build_model(allow_cudnn_kernel=True)
cpu_model.set_weights(model.get_weights())
result = tf.argmax(cpu_model.predict_on_batch(tf.expand_dims(sample, 0)), axis=1)
print(
"Predicted result is: %s, target result is: %s" % (result.numpy(), sample_label)
)
plt.imshow(sample, cmap=plt.get_cmap("gray"))
```
## RNNs with list/dict inputs, or nested inputs
Nested structures allow implementers to include more information within a single
timestep. For example, a video frame could have audio and video input at the same
time. The data shape in this case could be:
`[batch, timestep, {"video": [height, width, channel], "audio": [frequency]}]`
In another example, handwriting data could have both coordinates x and y for the
current position of the pen, as well as pressure information. So the data
representation could be:
`[batch, timestep, {"location": [x, y], "pressure": [force]}]`
The following code provides an example of how to build a custom RNN cell that accepts
such structured inputs.
### Define a custom cell that supports nested input/output
See [Making new Layers & Models via subclassing](https://www.tensorflow.org/guide/keras/custom_layers_and_models/)
for details on writing your own layers.
```
class NestedCell(keras.layers.Layer):
def __init__(self, unit_1, unit_2, unit_3, **kwargs):
self.unit_1 = unit_1
self.unit_2 = unit_2
self.unit_3 = unit_3
self.state_size = [tf.TensorShape([unit_1]), tf.TensorShape([unit_2, unit_3])]
self.output_size = [tf.TensorShape([unit_1]), tf.TensorShape([unit_2, unit_3])]
super(NestedCell, self).__init__(**kwargs)
def build(self, input_shapes):
# expect input_shape to contain 2 items, [(batch, i1), (batch, i2, i3)]
i1 = input_shapes[0][1]
i2 = input_shapes[1][1]
i3 = input_shapes[1][2]
self.kernel_1 = self.add_weight(
shape=(i1, self.unit_1), initializer="uniform", name="kernel_1"
)
self.kernel_2_3 = self.add_weight(
shape=(i2, i3, self.unit_2, self.unit_3),
initializer="uniform",
name="kernel_2_3",
)
def call(self, inputs, states):
# inputs should be in [(batch, input_1), (batch, input_2, input_3)]
# state should be in shape [(batch, unit_1), (batch, unit_2, unit_3)]
input_1, input_2 = tf.nest.flatten(inputs)
s1, s2 = states
output_1 = tf.matmul(input_1, self.kernel_1)
output_2_3 = tf.einsum("bij,ijkl->bkl", input_2, self.kernel_2_3)
state_1 = s1 + output_1
state_2_3 = s2 + output_2_3
output = (output_1, output_2_3)
new_states = (state_1, state_2_3)
return output, new_states
def get_config(self):
return {"unit_1": self.unit_1, "unit_2": unit_2, "unit_3": self.unit_3}
```
### Build a RNN model with nested input/output
Let's build a Keras model that uses a `keras.layers.RNN` layer and the custom cell
we just defined.
```
unit_1 = 10
unit_2 = 20
unit_3 = 30
i1 = 32
i2 = 64
i3 = 32
batch_size = 64
num_batches = 10
timestep = 50
cell = NestedCell(unit_1, unit_2, unit_3)
rnn = keras.layers.RNN(cell)
input_1 = keras.Input((None, i1))
input_2 = keras.Input((None, i2, i3))
outputs = rnn((input_1, input_2))
model = keras.models.Model([input_1, input_2], outputs)
model.compile(optimizer="adam", loss="mse", metrics=["accuracy"])
```
### Train the model with randomly generated data
Since there isn't a good candidate dataset for this model, we use random Numpy data for
demonstration.
```
input_1_data = np.random.random((batch_size * num_batches, timestep, i1))
input_2_data = np.random.random((batch_size * num_batches, timestep, i2, i3))
target_1_data = np.random.random((batch_size * num_batches, unit_1))
target_2_data = np.random.random((batch_size * num_batches, unit_2, unit_3))
input_data = [input_1_data, input_2_data]
target_data = [target_1_data, target_2_data]
model.fit(input_data, target_data, batch_size=batch_size)
```
With the Keras `keras.layers.RNN` layer, You are only expected to define the math
logic for individual step within the sequence, and the `keras.layers.RNN` layer
will handle the sequence iteration for you. It's an incredibly powerful way to quickly
prototype new kinds of RNNs (e.g. a LSTM variant).
For more details, please visit the [API docs](https://https://www.tensorflow.org/api_docs/python/tf/keras/layers/RNN/).
|
github_jupyter
|
(tune-mnist-keras)=
# Using Keras & TensorFlow with Tune
```{image} /images/tf_keras_logo.jpeg
:align: center
:alt: Keras & TensorFlow Logo
:height: 120px
:target: https://keras.io
```
```{contents}
:backlinks: none
:local: true
```
## Example
```
import argparse
import os
from filelock import FileLock
from tensorflow.keras.datasets import mnist
import ray
from ray import tune
from ray.tune.schedulers import AsyncHyperBandScheduler
from ray.tune.integration.keras import TuneReportCallback
def train_mnist(config):
# https://github.com/tensorflow/tensorflow/issues/32159
import tensorflow as tf
batch_size = 128
num_classes = 10
epochs = 12
with FileLock(os.path.expanduser("~/.data.lock")):
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train, x_test = x_train / 255.0, x_test / 255.0
model = tf.keras.models.Sequential(
[
tf.keras.layers.Flatten(input_shape=(28, 28)),
tf.keras.layers.Dense(config["hidden"], activation="relu"),
tf.keras.layers.Dropout(0.2),
tf.keras.layers.Dense(num_classes, activation="softmax"),
]
)
model.compile(
loss="sparse_categorical_crossentropy",
optimizer=tf.keras.optimizers.SGD(lr=config["lr"], momentum=config["momentum"]),
metrics=["accuracy"],
)
model.fit(
x_train,
y_train,
batch_size=batch_size,
epochs=epochs,
verbose=0,
validation_data=(x_test, y_test),
callbacks=[TuneReportCallback({"mean_accuracy": "accuracy"})],
)
def tune_mnist(num_training_iterations):
sched = AsyncHyperBandScheduler(
time_attr="training_iteration", max_t=400, grace_period=20
)
analysis = tune.run(
train_mnist,
name="exp",
scheduler=sched,
metric="mean_accuracy",
mode="max",
stop={"mean_accuracy": 0.99, "training_iteration": num_training_iterations},
num_samples=10,
resources_per_trial={"cpu": 2, "gpu": 0},
config={
"threads": 2,
"lr": tune.uniform(0.001, 0.1),
"momentum": tune.uniform(0.1, 0.9),
"hidden": tune.randint(32, 512),
},
)
print("Best hyperparameters found were: ", analysis.best_config)
if __name__ == "__main__":
parser = argparse.ArgumentParser()
parser.add_argument(
"--smoke-test", action="store_true", help="Finish quickly for testing"
)
parser.add_argument(
"--server-address",
type=str,
default=None,
required=False,
help="The address of server to connect to if using " "Ray Client.",
)
args, _ = parser.parse_known_args()
if args.smoke_test:
ray.init(num_cpus=4)
elif args.server_address:
ray.init(f"ray://{args.server_address}")
tune_mnist(num_training_iterations=5 if args.smoke_test else 300)
```
## More Keras and TensorFlow Examples
- {doc}`/tune/examples/includes/pbt_memnn_example`: Example of training a Memory NN on bAbI with Keras using PBT.
- {doc}`/tune/examples/includes/tf_mnist_example`: Converts the Advanced TF2.0 MNIST example to use Tune
with the Trainable. This uses `tf.function`.
Original code from tensorflow: https://www.tensorflow.org/tutorials/quickstart/advanced
- {doc}`/tune/examples/includes/pbt_tune_cifar10_with_keras`:
A contributed example of tuning a Keras model on CIFAR10 with the PopulationBasedTraining scheduler.
|
github_jupyter
|
#### Implementation of Distributional paper for 1-dimensional games, such as Cartpole.
- https://arxiv.org/abs/1707.06887
<br>
Please note: The 2 dimensional image state requires a lot of memory capacity (~50GB) due to the buffer size of 1,000,000 as in DQN paper.
So, one might want to train an agent with a smaller size (this may cause a lower performance).
#### Please NOTE,
The code lines different from Vanila DQN are annotated with '*/*/*/'.
So, by searching '*/*/*/', you can find these lines.
```
import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
import gym
import numpy as np
import time
import os
import cv2
import matplotlib.pyplot as plt
from IPython.display import clear_output
class QNetwork(nn.Module):
def __init__(self, input_dim, action_dim, rand_seed=False,
conv_channel_1=32, conv_channel_2=64, conv_channel_3=128,
kernel_1=3, kernel_2=3, kernel_3=3,
stride_1=2, stride_2=2, stride_3=1, n_atoms=51):
super(QNetwork, self).__init__()
self.action_dim = action_dim
self.n_atoms = n_atoms
self.Conv1 = nn.Conv2d(input_dim[0], conv_channel_1, (kernel_1,kernel_1), stride=stride_1)
self.Conv2 = nn.Conv2d(conv_channel_1, conv_channel_2, (kernel_2,kernel_2), stride=stride_2)
self.Conv3 = nn.Conv2d(conv_channel_2, conv_channel_3, (kernel_3,kernel_3), stride=stride_3)
def calculate_conv2d_size(size, kernel_size, stride):
return (size - (kernel_size - 1) - 1) // stride + 1
w, h = input_dim[1], input_dim[2]
convw = calculate_conv2d_size(calculate_conv2d_size(calculate_conv2d_size(w,kernel_1,stride_1),
kernel_2,stride_2),
kernel_3,stride_3)
convh = calculate_conv2d_size(calculate_conv2d_size(calculate_conv2d_size(h,kernel_1,stride_1),
kernel_2,stride_2),
kernel_3,stride_3)
linear_input_size = convw * convh * conv_channel_3
# */*/*/
self.fc1 = nn.Linear(linear_input_size, 512)
self.fc2 = nn.Linear(512, action_dim*n_atoms)
self.relu = nn.ReLU()
# */*/*/
def forward(self, x):
x = self.relu(self.Conv1(x))
x = self.relu(self.Conv2(x))
x = self.relu(self.Conv3(x))
x = x.reshape(x.shape[0], -1)
# */*/*/
Q = self.fc2(self.relu(self.fc1(x))).view(-1, self.action_dim, self.n_atoms)
return F.softmax(Q, dim=2) # Shape: (batch_size, action_dim, n_atoms)
# */*/*/
if __name__ == '__main__':
state_size = (4, 84, 84)
action_size = 10
net = QNetwork(state_size, action_size,
conv_channel_1=32, conv_channel_2=64, conv_channel_3=64)
test = torch.randn(size=(64, 4, 84, 84))
print(net)
print("Network output: ", net(test).shape)
class ReplayBuffer:
""" Experience Replay Buffer in DQN paper """
def __init__(self,
buffer_size: ('int: total size of the Replay Buffer'),
input_dim: ('tuple: a dimension of input data. Ex) (3, 84, 84)'),
batch_size: ('int: a batch size when updating')):
# To check if input image has 3 channels
assert len(input_dim)==3, "The state dimension should be 3-dim! (CHxWxH). Please check if input_dim is right"
self.batch_size = batch_size
self.buffer_size = buffer_size
self.save_count, self.current_size = 0, 0
# One can choose either np.zeros or np.ones.
# The reason using np.ones here is for checking the total memory occupancy of the buffer.
self.state_buffer = np.ones((buffer_size, input_dim[0], input_dim[1], input_dim[2]),
dtype=np.uint8) # data type is np.int8 for saving the memory
self.action_buffer = np.ones(buffer_size, dtype=np.uint8)
self.reward_buffer = np.ones(buffer_size, dtype=np.float32)
self.next_state_buffer = np.ones((buffer_size, input_dim[0], input_dim[1], input_dim[2]),
dtype=np.uint8)
self.done_buffer = np.ones(buffer_size, dtype=np.uint8)
def __len__(self):
return self.current_size
def store(self,
state: np.ndarray,
action: int,
reward: float,
next_state: np.ndarray,
done: int):
self.state_buffer[self.save_count] = state
self.action_buffer[self.save_count] = action
self.reward_buffer[self.save_count] = reward
self.next_state_buffer[self.save_count] = next_state
self.done_buffer[self.save_count] = done
# self.save_count is an index when storing transitions into the replay buffer
self.save_count = (self.save_count + 1) % self.buffer_size
# self.current_size is an indication for how many transitions is stored
self.current_size = min(self.current_size+1, self.buffer_size)
def batch_load(self):
# Selecting samples randomly with a size of self.batch_size
indices = np.random.randint(self.current_size, size=self.batch_size)
return dict(
states=self.state_buffer[indices],
actions=self.action_buffer[indices],
rewards=self.reward_buffer[indices],
next_states=self.next_state_buffer[indices],
dones=self.done_buffer[indices])
class Agent:
def __init__(self,
env: 'Environment',
input_frame: ('int: The number of channels of input image'),
input_dim: ('int: The width and height of pre-processed input image'),
training_frames: ('int: The total number of training frames'),
skipped_frame: ('int: The number of skipped frames in the environment'),
eps_decay: ('float: Epsilon Decay_rate'),
gamma: ('float: Discount Factor'),
update_freq: ('int: Behavior Network Update Frequency'),
target_update_freq: ('int: Target Network Update Frequency'),
update_type: ('str: Update type for target network. Hard or Soft')='hard',
soft_update_tau: ('float: Soft update ratio')=None,
batch_size: ('int: Update batch size')=32,
buffer_size: ('int: Replay buffer size')=1000000,
update_start_buffer_size: ('int: Update starting buffer size')=50000,
learning_rate: ('float: Learning rate')=0.0004,
eps_min: ('float: Epsilon Min')=0.1,
eps_max: ('float: Epsilon Max')=1.0,
device_num: ('int: GPU device number')=0,
rand_seed: ('int: Random seed')=None,
plot_option: ('str: Plotting option')=False,
model_path: ('str: Model saving path')='./',
trained_model_path: ('str: Trained model path')='',
# */*/*/
n_atoms: ('int: The number of atoms')=51,
Vmax: ('int: The maximum Q value')=10,
Vmin: ('int: The minimum Q value')=-10):
# */*/*/
self.action_dim = env.action_space.n
self.device = torch.device(f'cuda:{device_num}' if torch.cuda.is_available() else 'cpu')
self.model_path = model_path
self.env = env
self.input_frames = input_frame
self.input_dim = input_dim
self.training_frames = training_frames
self.skipped_frame = skipped_frame
self.epsilon = eps_max
self.eps_decay = eps_decay
self.eps_min = eps_min
self.gamma = gamma
self.update_freq = update_freq
self.target_update_freq = target_update_freq
self.update_cnt = 0
self.update_type = update_type
self.tau = soft_update_tau
self.batch_size = batch_size
self.buffer_size = buffer_size
self.update_start = update_start_buffer_size
self.seed = rand_seed
self.plot_option = plot_option
# */*/*/
self.n_atoms = n_atoms
self.Vmin = Vmin
self.Vmax = Vmax
self.dz = (Vmax - Vmin) / (n_atoms - 1)
self.support = torch.linspace(Vmin, Vmax, n_atoms).to(self.device)
self.expanded_support = self.support.expand((batch_size, self.action_dim, n_atoms)).to(self.device)
self.q_behave = QNetwork((self.input_frames, self.input_dim, self.input_dim), self.action_dim, n_atoms=self.n_atoms).to(self.device)
self.q_target = QNetwork((self.input_frames, self.input_dim, self.input_dim), self.action_dim, n_atoms=self.n_atoms).to(self.device)
# */*/*/
if trained_model_path: # load a trained model if existing
self.q_behave.load_state_dict(torch.load(trained_model_path))
print("Trained model is loaded successfully.")
# Initialize target network parameters with behavior network parameters
self.q_target.load_state_dict(self.q_behave.state_dict())
self.q_target.eval()
self.optimizer = optim.Adam(self.q_behave.parameters(), lr=learning_rate)
self.memory = ReplayBuffer(self.buffer_size, (self.input_frames, self.input_dim, self.input_dim), self.batch_size)
def select_action(self, state: 'Must be pre-processed in the same way as updating current Q network. See def _compute_loss'):
if np.random.random() < self.epsilon:
return np.zeros(self.action_dim), self.env.action_space.sample()
else:
# if normalization is applied to the image such as devision by 255, MUST be expressed 'state/255' below.
with torch.no_grad():
state = torch.FloatTensor(state).to(self.device).unsqueeze(0)/255
# */*/*/
Qs = self.q_behave(state)*self.expanded_support[0]
Expected_Qs = Qs.sum(2)
# */*/*/
action = Expected_Qs.argmax(1)
# return Q-values and action (Q-values are not required for implementing algorithms. This is just for checking Q-values for each state. Not must-needed)
return Expected_Qs.detach().cpu().numpy()[0], action.detach().item()
def processing_resize_and_gray(self, frame):
''' Convert images to gray scale and resize '''
frame = cv2.cvtColor(frame, cv2.COLOR_RGB2GRAY)
frame = cv2.resize(frame, dsize=(self.input_dim, self.input_dim)).reshape(self.input_dim, self.input_dim).astype(np.uint8)
return frame
def get_init_state(self):
''' return an initial state with a dimension of (self.input_frames, self.input_dim, self.input_dim) '''
init_state = np.zeros((self.input_frames, self.input_dim, self.input_dim))
init_frame = self.env.reset()
init_state[0] = self.processing_resize_and_gray(init_frame)
for i in range(1, self.input_frames):
action = self.env.action_space.sample()
for j in range(self.skipped_frame-1):
state, _, _, _ = self.env.step(action)
state, _, _, _ = self.env.step(action)
init_state[i] = self.processing_resize_and_gray(state)
return init_state
def get_state(self, state, action, skipped_frame=0):
''' return reward, next_state, done '''
next_state = np.zeros((self.input_frames, self.input_dim, self.input_dim))
for i in range(len(state)-1):
next_state[i] = state[i+1]
rewards = 0
dones = 0
for _ in range(skipped_frame-1):
state, reward, done, _ = self.env.step(action)
rewards += reward # reward accumulates for the case that rewards occur while skipping
dones += int(done)
state, reward, done, _ = self.env.step(action)
next_state[-1] = self.processing_resize_and_gray(state)
rewards += reward
dones += int(done)
return rewards, next_state, dones
def store(self, state, action, reward, next_state, done):
self.memory.store(state, action, reward, next_state, done)
def update_behavior_q_net(self):
# update behavior q network with a batch
batch = self.memory.batch_load()
loss = self._compute_loss(batch)
self.optimizer.zero_grad()
loss.backward()
self.optimizer.step()
return loss.item()
def target_soft_update(self):
''' target network is updated with Soft Update. tau is a hyperparameter for the updating ratio betweeen target and behavior network '''
for target_param, current_param in zip(self.q_target.parameters(), self.q_behave.parameters()):
target_param.data.copy_(self.tau*current_param.data + (1.0-self.tau)*target_param.data)
def target_hard_update(self):
''' target network is updated with Hard Update '''
self.update_cnt = (self.update_cnt+1) % self.target_update_freq
if self.update_cnt==0:
self.q_target.load_state_dict(self.q_behave.state_dict())
def train(self):
tic = time.time()
losses = []
scores = []
epsilons = []
avg_scores = [[-10000]] # As an initial score, set an arbitrary score of an episode.
score = 0
print("Storing initial buffer..")
state = self.get_init_state()
for frame_idx in range(1, self.update_start+1):
# Store transitions into the buffer until the number of 'self.update_start' transitions is stored
_, action = self.select_action(state)
reward, next_state, done = self.get_state(state, action, skipped_frame=self.skipped_frame)
self.store(state, action, reward, next_state, done)
state = next_state
if done: state = self.get_init_state()
print("Done. Start learning..")
history_store = []
for frame_idx in range(1, self.training_frames+1):
Qs, action = self.select_action(state)
reward, next_state, done = self.get_state(state, action, skipped_frame=self.skipped_frame)
self.store(state, action, reward, next_state, done)
history_store.append([state, Qs, action, reward, next_state, done]) # history_store is for checking an episode later. Not must-needed.
if (frame_idx % self.update_freq) == 0:
loss = self.update_behavior_q_net()
score += reward
losses.append(loss)
if self.update_type=='hard': self.target_hard_update()
elif self.update_type=='soft': self.target_soft_update()
if done:
# For saving and plotting when an episode is done.
scores.append(score)
if np.mean(scores[-10:]) > max(avg_scores):
torch.save(self.q_behave.state_dict(), self.model_path+'{}_Score:{}.pt'.format(frame_idx, np.mean(scores[-10:])))
training_time = round((time.time()-tic)/3600, 1)
np.save(self.model_path+'{}_history_Score_{}_{}hrs.npy'.format(frame_idx, score, training_time), np.array(history_store))
print(" | Model saved. Recent scores: {}, Training time: {}hrs".format(scores[-10:], training_time), ' /'.join(os.getcwd().split('/')[-3:]))
avg_scores.append(np.mean(scores[-10:]))
if self.plot_option=='inline':
scores.append(score)
epsilons.append(self.epsilon)
self._plot(frame_idx, scores, losses, epsilons)
else:
print(score, end='\r')
score=0
state = self.get_init_state()
history_store = []
else: state = next_state
self._epsilon_step()
print("Total training time: {}(hrs)".format((time.time()-tic)/3600))
def _epsilon_step(self):
''' Controlling epsilon decay. Here is the same as DQN paper, linearly decaying rate. '''
self.epsilon = max(self.epsilon-self.eps_decay, 0.1)
def _compute_loss(self, batch: "Dictionary (S, A, R', S', Dones)"):
''' Compute loss. If normalization is used, it must be applied to both 'state' and 'next_state'. ex) state/255 '''
states = torch.FloatTensor(batch['states']).to(self.device) / 255
next_states = torch.FloatTensor(batch['next_states']).to(self.device) / 255
actions = torch.LongTensor(batch['actions']).to(self.device)
rewards = torch.FloatTensor(batch['rewards'].reshape(-1, 1)).to(self.device)
dones = torch.FloatTensor(batch['dones'].reshape(-1, 1)).to(self.device)
# */*/*/
log_behave_Q_dist = self.q_behave(states)[range(self.batch_size), actions].log()
with torch.no_grad():
# Computing projected distribution for a categorical loss
behave_next_Q_dist = self.q_behave(next_states)
next_actions = torch.sum(behave_next_Q_dist*self.expanded_support, 2).argmax(1)
target_next_Q_dist = self.q_target(next_states)[range(self.batch_size), next_actions] # Double DQN.
Tz = rewards + self.gamma*(1 - dones)*self.expanded_support[:,0]
Tz.clamp_(self.Vmin, self.Vmax)
b = (Tz - self.Vmin) / self.dz
l = b.floor().long()
u = b.ceil().long()
l[(l==u) & (u>0)] -= 1 # avoiding the case when floor index and ceil index have the same values
u[(u==0) & (l==0)] += 1 # (because it causes target_next_Q_dist's value to be counted as zero)
batch_init_indices = torch.linspace(0, (self.batch_size-1)*self.n_atoms, self.batch_size).long().unsqueeze(1).expand(self.batch_size, self.n_atoms).to(self.device)
proj_dist = torch.zeros(self.batch_size, self.n_atoms).to(self.device)
proj_dist.view(-1).index_add_(0, (l+batch_init_indices).view(-1), (target_next_Q_dist*(u-b)).view(-1))
proj_dist.view(-1).index_add_(0, (u+batch_init_indices).view(-1), (target_next_Q_dist*(b-l)).view(-1))
# Compute KL divergence between two distributions
loss = torch.sum(-proj_dist*log_behave_Q_dist, 1).mean()
# */*/*/
return loss
def _plot(self, frame_idx, scores, losses, epsilons):
clear_output(True)
plt.figure(figsize=(20, 5), facecolor='w')
plt.subplot(131)
plt.title('frame %s. score: %s' % (frame_idx, np.mean(scores[-10:])))
plt.plot(scores)
plt.subplot(132)
plt.title('loss')
plt.plot(losses)
plt.subplot(133)
plt.title('epsilons')
plt.plot(epsilons)
plt.show()
```
#### Configurations


```
env_list = {
0: "CartPole-v0",
1: "CartPole-v2",
2: "LunarLander-v2",
3: "Breakout-v4",
4: "BreakoutDeterministic-v4",
5: "BreakoutNoFrameskip-v4",
6: "BoxingDeterministic-v4",
7: "PongDeterministic-v4",
}
env_name = env_list[6]
env = gym.make(env_name)
# Same input size as in DQN paper.
input_dim = 84
input_frame = 4
print("env_name", env_name)
print(env.unwrapped.get_action_meanings(), env.action_space.n)
# starting to update Q-network until ReplayBuffer is filled with the number of samples = update_start_buffer_size
update_start_buffer_size = 10000
# total training frames
training_frames = 10000000
# epsilon for exploration
eps_max = 1.0
eps_min = 0.1
eps_decay = 1/1000000
# gamma (used decaying future rewards)
gamma = 0.99
# size of ReplayBuffer
buffer_size = int(1e6) # this is the same size of the paper
# buffer_size = int(1.5e5) # if don't have an enough memory capacity, lower the value like this. But this may cause a bad training performance.
# update batch size
batch_size = 32
learning_rate = 0.0001 # In the paper, they use RMSProp and learning rate 0.00025. In this notebook, the Adam is used with lr=0.0001.
# updating Q-network with 'soft' or 'hard' updating method
update_freq = 4
update_type = 'hard'
soft_update_tau = 0.002
# target network update frequency (applied when it takes 'hard' update).
# 10000 means the target network is updated once while the behavior network is updated 10000 times.
target_update_freq = 10000
# assign skipped_frame to be 0
# because the word 'Deterministic' in the name 'BoxingDeterministic' means it automatically skips 4 frames in the game.
# assign skipped_frame to be 0 when selecting games such as "BreakoutNoFrameskip".
skipped_frame = 0
# cuda device
device_num = 0
# choose plotting option.
# 'inline' - plots status in jupyter notebook
# 'False' - it prints only reward of the episode
plot_options = {1: 'inline', 2: False}
plot_option = plot_options[2]
# */*/*/
n_atoms = 51
Vmax = 10
Vmin = -10
# */*/*/
# The path for saving a trained model.
rand_seed = None
rand_name = ('').join(map(str, np.random.randint(10, size=(3,))))
folder_name = os.getcwd().split('/')[-1]
model_name = 'Test'
model_save_path = f'./model_save/{model_name}/'
if not os.path.exists('./model_save/'):
os.mkdir('./model_save/')
if not os.path.exists(model_save_path):
os.mkdir(model_save_path)
print("model_save_path:", model_save_path)
trained_model_path = ''
agent = Agent(
env,
input_frame,
input_dim,
training_frames,
skipped_frame,
eps_decay,
gamma,
update_freq,
target_update_freq,
update_type,
soft_update_tau,
batch_size,
buffer_size,
update_start_buffer_size,
learning_rate,
eps_min,
eps_max,
device_num,
rand_seed,
plot_option,
model_save_path,
trained_model_path,
n_atoms,
Vmax,
Vmin
)
agent.train()
```
#### An example of results
Storing initial buffer..
Done. Start learning..
| Model saved. Recent scores: [1.0], Training time: 0.0hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [1.0, -1.0, 2.0, -2.0, 5.0, 2.0], Training time: 0.0hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [2.0, -2.0, 5.0, 2.0, 0.0, 0.0, -2.0, 3.0, 2.0, 6.0], Training time: 0.0hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [3.0, 3.0, -2.0, -4.0, 6.0, -1.0, -5.0, 4.0, 6.0, 7.0], Training time: 0.0hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [4.0, 6.0, 7.0, -4.0, -2.0, -6.0, 1.0, 3.0, 4.0, 6.0], Training time: 0.1hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [6.0, 7.0, -4.0, -2.0, -6.0, 1.0, 3.0, 4.0, 6.0, 9.0], Training time: 0.1hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [7.0, 1.0, 6.0, 5.0, 5.0, 0.0, -2.0, -1.0, 2.0, 5.0], Training time: 0.1hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [-4.0, 10.0, 9.0, -10.0, 9.0, -2.0, -5.0, 6.0, 7.0, 11.0], Training time: 0.3hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [10.0, 9.0, -10.0, 9.0, -2.0, -5.0, 6.0, 7.0, 11.0, 1.0], Training time: 0.3hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [6.0, 1.0, 8.0, -1.0, 2.0, 3.0, 1.0, 7.0, 6.0, 14.0], Training time: 0.3hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [7.0, 6.0, 14.0, 1.0, 3.0, -1.0, 8.0, 4.0, -4.0, 14.0], Training time: 0.3hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [6.0, 14.0, 1.0, 3.0, -1.0, 8.0, 4.0, -4.0, 14.0, 9.0], Training time: 0.3hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [6.0, -4.0, -2.0, 27.0, 1.0, 4.0, 5.0, 1.0, 13.0, 10.0], Training time: 0.7hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [27.0, 1.0, 4.0, 5.0, 1.0, 13.0, 10.0, 1.0, 1.0, 16.0], Training time: 0.7hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [1.0, 10.0, 13.0, 19.0, 1.0, 6.0, 4.0, 8.0, 12.0, 13.0], Training time: 1.1hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [10.0, 13.0, 19.0, 1.0, 6.0, 4.0, 8.0, 12.0, 13.0, 10.0], Training time: 1.1hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [5.0, 3.0, 7.0, 18.0, -1.0, 13.0, 9.0, 10.0, 29.0, 8.0], Training time: 1.3hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [3.0, 7.0, 18.0, -1.0, 13.0, 9.0, 10.0, 29.0, 8.0, 18.0], Training time: 1.3hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [7.0, 18.0, -1.0, 13.0, 9.0, 10.0, 29.0, 8.0, 18.0, 8.0], Training time: 1.3hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [13.0, 9.0, 10.0, 29.0, 8.0, 18.0, 8.0, -1.0, 16.0, 27.0], Training time: 1.3hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [16.0, 27.0, 8.0, 11.0, 2.0, 19.0, 13.0, 19.0, 12.0, 15.0], Training time: 1.3hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [14.0, 11.0, 9.0, 11.0, 20.0, 16.0, 7.0, 13.0, 13.0, 37.0], Training time: 1.4hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [18.0, 7.0, 19.0, 15.0, 5.0, 9.0, 18.0, 29.0, 18.0, 18.0], Training time: 1.6hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [15.0, 11.0, 9.0, 33.0, 5.0, 30.0, 12.0, 17.0, 23.0, 15.0], Training time: 1.7hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [14.0, 22.0, 6.0, 13.0, 16.0, 15.0, 24.0, 28.0, 8.0, 29.0], Training time: 1.9hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [22.0, 6.0, 13.0, 16.0, 15.0, 24.0, 28.0, 8.0, 29.0, 18.0], Training time: 1.9hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [20.0, 16.0, 31.0, 23.0, 24.0, 18.0, 8.0, 15.0, 12.0, 14.0], Training time: 2.5hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [27.0, 5.0, 27.0, 2.0, 11.0, 19.0, 17.0, 20.0, 23.0, 31.0], Training time: 2.5hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [19.0, 20.0, 20.0, 18.0, 10.0, 37.0, 12.0, 9.0, 25.0, 15.0], Training time: 2.7hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [27.0, 8.0, 34.0, 22.0, 17.0, 2.0, 31.0, 13.0, 7.0, 25.0], Training time: 2.8hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [14.0, 18.0, 27.0, 21.0, 22.0, 9.0, -2.0, 28.0, 30.0, 26.0], Training time: 2.8hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [17.0, 23.0, 9.0, 40.0, 9.0, 26.0, 10.0, 26.0, 10.0, 29.0], Training time: 3.0hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [23.0, 9.0, 40.0, 9.0, 26.0, 10.0, 26.0, 10.0, 29.0, 19.0], Training time: 3.0hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [11.0, 23.0, 17.0, 13.0, 19.0, 37.0, 21.0, 26.0, 20.0, 16.0], Training time: 3.0hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [23.0, 17.0, 13.0, 19.0, 37.0, 21.0, 26.0, 20.0, 16.0, 25.0], Training time: 3.0hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [8.0, 25.0, 19.0, 10.0, 27.0, 14.0, 26.0, 39.0, 22.0, 35.0], Training time: 3.2hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [25.0, 19.0, 10.0, 27.0, 14.0, 26.0, 39.0, 22.0, 35.0, 37.0], Training time: 3.2hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [19.0, 10.0, 27.0, 14.0, 26.0, 39.0, 22.0, 35.0, 37.0, 26.0], Training time: 3.2hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [10.0, 27.0, 14.0, 26.0, 39.0, 22.0, 35.0, 37.0, 26.0, 33.0], Training time: 3.2hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [27.0, 14.0, 26.0, 39.0, 22.0, 35.0, 37.0, 26.0, 33.0, 12.0], Training time: 3.2hrs MacaronRL /Value_Based /C51
| Model saved. Recent scores: [39.0, 22.0, 35.0, 37.0, 26.0, 33.0, 12.0, 6.0, 26.0, 39.0], Training time: 3.2hrs MacaronRL /Value_Based /C51
|
github_jupyter
|
# RadarCOVID-Report
## Data Extraction
```
import datetime
import logging
import os
import shutil
import tempfile
import textwrap
import uuid
import dataframe_image as dfi
import matplotlib.ticker
import numpy as np
import pandas as pd
import seaborn as sns
%matplotlib inline
sns.set()
matplotlib.rcParams['figure.figsize'] = (15, 6)
extraction_datetime = datetime.datetime.utcnow()
extraction_date = extraction_datetime.strftime("%Y-%m-%d")
extraction_previous_datetime = extraction_datetime - datetime.timedelta(days=1)
extraction_previous_date = extraction_previous_datetime.strftime("%Y-%m-%d")
extraction_date_with_hour = datetime.datetime.utcnow().strftime("%Y-%m-%d@%H")
```
### COVID-19 Cases
```
confirmed_df = pd.read_csv("https://covid19tracking.narrativa.com/csv/confirmed.csv")
radar_covid_countries = {"Spain"}
# radar_covid_regions = { ... }
confirmed_df = confirmed_df[confirmed_df["Country_EN"].isin(radar_covid_countries)]
# confirmed_df = confirmed_df[confirmed_df["Region"].isin(radar_covid_regions)]
# set(confirmed_df.Region.tolist()) == radar_covid_regions
confirmed_country_columns = list(filter(lambda x: x.startswith("Country_"), confirmed_df.columns))
confirmed_regional_columns = confirmed_country_columns + ["Region"]
confirmed_df.drop(columns=confirmed_regional_columns, inplace=True)
confirmed_df = confirmed_df.sum().to_frame()
confirmed_df.tail()
confirmed_df.reset_index(inplace=True)
confirmed_df.columns = ["sample_date_string", "cumulative_cases"]
confirmed_df.sort_values("sample_date_string", inplace=True)
confirmed_df["new_cases"] = confirmed_df.cumulative_cases.diff()
confirmed_df["rolling_mean_new_cases"] = confirmed_df.new_cases.rolling(7).mean()
confirmed_df.tail()
extraction_date_confirmed_df = \
confirmed_df[confirmed_df.sample_date_string == extraction_date]
extraction_previous_date_confirmed_df = \
confirmed_df[confirmed_df.sample_date_string == extraction_previous_date].copy()
if extraction_date_confirmed_df.empty and \
not extraction_previous_date_confirmed_df.empty:
extraction_previous_date_confirmed_df["sample_date_string"] = extraction_date
extraction_previous_date_confirmed_df["new_cases"] = \
extraction_previous_date_confirmed_df.rolling_mean_new_cases
extraction_previous_date_confirmed_df["cumulative_cases"] = \
extraction_previous_date_confirmed_df.new_cases + \
extraction_previous_date_confirmed_df.cumulative_cases
confirmed_df = confirmed_df.append(extraction_previous_date_confirmed_df)
confirmed_df.tail()
confirmed_df[["new_cases", "rolling_mean_new_cases"]].plot()
```
### Extract API TEKs
```
from Modules.RadarCOVID import radar_covid
exposure_keys_df = radar_covid.download_last_radar_covid_exposure_keys(days=14)
exposure_keys_df[[
"sample_date_string", "source_url", "region", "key_data"]].head()
exposure_keys_summary_df = \
exposure_keys_df.groupby(["sample_date_string"]).key_data.nunique().to_frame()
exposure_keys_summary_df.sort_index(ascending=False, inplace=True)
exposure_keys_summary_df.rename(columns={"key_data": "tek_count"}, inplace=True)
exposure_keys_summary_df.head()
```
### Dump API TEKs
```
tek_list_df = exposure_keys_df[["sample_date_string", "key_data"]].copy()
tek_list_df["key_data"] = tek_list_df["key_data"].apply(str)
tek_list_df.rename(columns={
"sample_date_string": "sample_date",
"key_data": "tek_list"}, inplace=True)
tek_list_df = tek_list_df.groupby(
"sample_date").tek_list.unique().reset_index()
tek_list_df["extraction_date"] = extraction_date
tek_list_df["extraction_date_with_hour"] = extraction_date_with_hour
tek_list_df.drop(columns=["extraction_date", "extraction_date_with_hour"]).to_json(
"Data/TEKs/Current/RadarCOVID-TEKs.json",
lines=True, orient="records")
tek_list_df.drop(columns=["extraction_date_with_hour"]).to_json(
"Data/TEKs/Daily/RadarCOVID-TEKs-" + extraction_date + ".json",
lines=True, orient="records")
tek_list_df.to_json(
"Data/TEKs/Hourly/RadarCOVID-TEKs-" + extraction_date_with_hour + ".json",
lines=True, orient="records")
tek_list_df.head()
```
### Load TEK Dumps
```
import glob
def load_extracted_teks(mode, limit=None) -> pd.DataFrame:
extracted_teks_df = pd.DataFrame()
paths = list(reversed(sorted(glob.glob(f"Data/TEKs/{mode}/RadarCOVID-TEKs-*.json"))))
if limit:
paths = paths[:limit]
for path in paths:
logging.info(f"Loading TEKs from '{path}'...")
iteration_extracted_teks_df = pd.read_json(path, lines=True)
extracted_teks_df = extracted_teks_df.append(
iteration_extracted_teks_df, sort=False)
return extracted_teks_df
```
### Daily New TEKs
```
daily_extracted_teks_df = load_extracted_teks(mode="Daily", limit=14)
daily_extracted_teks_df.head()
tek_list_df = daily_extracted_teks_df.groupby("extraction_date").tek_list.apply(
lambda x: set(sum(x, []))).reset_index()
tek_list_df = tek_list_df.set_index("extraction_date").sort_index(ascending=True)
tek_list_df.head()
new_tek_df = tek_list_df.diff().tek_list.apply(
lambda x: len(x) if not pd.isna(x) else None).to_frame().reset_index()
new_tek_df.rename(columns={
"tek_list": "new_tek_count",
"extraction_date": "sample_date_string",}, inplace=True)
new_tek_df.head()
new_tek_devices_df = daily_extracted_teks_df.copy()
new_tek_devices_df["new_sample_extraction_date"] = \
pd.to_datetime(new_tek_devices_df.sample_date) + datetime.timedelta(1)
new_tek_devices_df["extraction_date"] = pd.to_datetime(new_tek_devices_df.extraction_date)
new_tek_devices_df = new_tek_devices_df[
new_tek_devices_df.new_sample_extraction_date == new_tek_devices_df.extraction_date]
new_tek_devices_df.head()
new_tek_devices_df.set_index("extraction_date", inplace=True)
new_tek_devices_df = new_tek_devices_df.tek_list.apply(lambda x: len(set(x))).to_frame()
new_tek_devices_df.reset_index(inplace=True)
new_tek_devices_df.rename(columns={
"extraction_date": "sample_date_string",
"tek_list": "new_tek_devices"}, inplace=True)
new_tek_devices_df["sample_date_string"] = new_tek_devices_df.sample_date_string.dt.strftime("%Y-%m-%d")
new_tek_devices_df.head()
```
### Hourly New TEKs
```
hourly_extracted_teks_df = load_extracted_teks(mode="Hourly", limit=24)
hourly_extracted_teks_df.head()
hourly_tek_list_df = hourly_extracted_teks_df.groupby("extraction_date_with_hour").tek_list.apply(
lambda x: set(sum(x, []))).reset_index()
hourly_tek_list_df = hourly_tek_list_df.set_index("extraction_date_with_hour").sort_index(ascending=True)
hourly_new_tek_df = hourly_tek_list_df.diff().tek_list.apply(
lambda x: len(x) if not pd.isna(x) else None).to_frame().reset_index()
hourly_new_tek_df.rename(columns={
"tek_list": "new_tek_count"}, inplace=True)
hourly_new_tek_df.tail()
hourly_new_tek_devices_df = hourly_extracted_teks_df.copy()
hourly_new_tek_devices_df["new_sample_extraction_date"] = \
pd.to_datetime(hourly_new_tek_devices_df.sample_date) + datetime.timedelta(1)
hourly_new_tek_devices_df["extraction_date"] = pd.to_datetime(hourly_new_tek_devices_df.extraction_date)
hourly_new_tek_devices_df = hourly_new_tek_devices_df[
hourly_new_tek_devices_df.new_sample_extraction_date == hourly_new_tek_devices_df.extraction_date]
hourly_new_tek_devices_df.set_index("extraction_date_with_hour", inplace=True)
hourly_new_tek_devices_df_ = pd.DataFrame()
for i, chunk_df in hourly_new_tek_devices_df.groupby("extraction_date"):
chunk_df = chunk_df.copy()
chunk_df.sort_index(inplace=True)
chunk_tek_count_df = chunk_df.tek_list.apply(lambda x: len(set(x)))
chunk_df = chunk_tek_count_df.diff().fillna(chunk_tek_count_df).to_frame()
hourly_new_tek_devices_df_ = hourly_new_tek_devices_df_.append(chunk_df)
hourly_new_tek_devices_df = hourly_new_tek_devices_df_
hourly_new_tek_devices_df.reset_index(inplace=True)
hourly_new_tek_devices_df.rename(columns={
"tek_list": "new_tek_devices"}, inplace=True)
hourly_new_tek_devices_df.tail()
hourly_summary_df = hourly_new_tek_df.merge(
hourly_new_tek_devices_df, on=["extraction_date_with_hour"], how="outer")
hourly_summary_df["datetime_utc"] = pd.to_datetime(
hourly_summary_df.extraction_date_with_hour, format="%Y-%m-%d@%H")
hourly_summary_df.set_index("datetime_utc", inplace=True)
hourly_summary_df.tail()
```
### Data Merge
```
result_summary_df = exposure_keys_summary_df.merge(new_tek_df, on=["sample_date_string"], how="outer")
result_summary_df.head()
result_summary_df = result_summary_df.merge(new_tek_devices_df, on=["sample_date_string"], how="outer")
result_summary_df.head()
result_summary_df = result_summary_df.merge(confirmed_df, on=["sample_date_string"], how="left")
result_summary_df.head()
result_summary_df["tek_count_per_new_case"] = \
result_summary_df.tek_count / result_summary_df.rolling_mean_new_cases
result_summary_df["new_tek_count_per_new_case"] = \
result_summary_df.new_tek_count / result_summary_df.rolling_mean_new_cases
result_summary_df["new_tek_devices_per_new_case"] = \
result_summary_df.new_tek_devices / result_summary_df.rolling_mean_new_cases
result_summary_df["new_tek_count_per_new_tek_device"] = \
result_summary_df.new_tek_count / result_summary_df.new_tek_devices
result_summary_df.head()
result_summary_df["sample_date"] = pd.to_datetime(result_summary_df.sample_date_string)
result_summary_df.set_index("sample_date", inplace=True)
result_summary_df = result_summary_df.sort_index(ascending=False)
```
## Report Results
### Summary Table
```
result_summary_df_ = result_summary_df.copy()
result_summary_df = result_summary_df[[
"tek_count",
"new_tek_count",
"new_cases",
"rolling_mean_new_cases",
"tek_count_per_new_case",
"new_tek_count_per_new_case",
"new_tek_devices",
"new_tek_devices_per_new_case",
"new_tek_count_per_new_tek_device"]]
result_summary_df
```
### Summary Plots
```
summary_ax_list = result_summary_df[[
"rolling_mean_new_cases",
"tek_count",
"new_tek_count",
"new_tek_devices",
"new_tek_count_per_new_tek_device",
"new_tek_devices_per_new_case"
]].sort_index(ascending=True).plot.bar(
title="Summary", rot=45, subplots=True, figsize=(15, 22))
summary_ax_list[-1].yaxis.set_major_formatter(matplotlib.ticker.PercentFormatter(1.0))
```
### Hourly Summary Plots
```
hourly_summary_ax_list = hourly_summary_df.plot.bar(
title="Last 24h Summary", rot=45, subplots=True)
```
### Publish Results
```
def get_temporary_image_path() -> str:
return os.path.join(tempfile.gettempdir(), str(uuid.uuid4()) + ".png")
def save_temporary_plot_image(ax):
if isinstance(ax, np.ndarray):
ax = ax[0]
media_path = get_temporary_image_path()
ax.get_figure().savefig(media_path)
return media_path
def save_temporary_dataframe_image(df):
media_path = get_temporary_image_path()
dfi.export(df, media_path)
return media_path
summary_plots_image_path = save_temporary_plot_image(ax=summary_ax_list)
summary_table_image_path = save_temporary_dataframe_image(df=result_summary_df)
hourly_summary_plots_image_path = save_temporary_plot_image(ax=hourly_summary_ax_list)
```
### Save Results
```
report_resources_path_prefix = "Data/Resources/Current/RadarCOVID-Report-"
result_summary_df.to_csv(report_resources_path_prefix + "Summary-Table.csv")
result_summary_df.to_html(report_resources_path_prefix + "Summary-Table.html")
_ = shutil.copyfile(summary_plots_image_path, report_resources_path_prefix + "Summary-Plots.png")
_ = shutil.copyfile(summary_table_image_path, report_resources_path_prefix + "Summary-Table.png")
_ = shutil.copyfile(hourly_summary_plots_image_path, report_resources_path_prefix + "Hourly-Summary-Plots.png")
report_daily_url_pattern = \
"https://github.com/pvieito/RadarCOVID-Report/blob/master/Notebooks/" \
"RadarCOVID-Report/{report_type}/RadarCOVID-Report-{report_date}.ipynb"
report_daily_url = report_daily_url_pattern.format(
report_type="Daily", report_date=extraction_date)
report_hourly_url = report_daily_url_pattern.format(
report_type="Hourly", report_date=extraction_date_with_hour)
```
### Publish on README
```
with open("Data/Templates/README.md", "r") as f:
readme_contents = f.read()
summary_table_html = result_summary_df.to_html()
readme_contents = readme_contents.format(
summary_table_html=summary_table_html,
report_url_with_hour=report_hourly_url,
extraction_date_with_hour=extraction_date_with_hour)
with open("README.md", "w") as f:
f.write(readme_contents)
```
### Publish on Twitter
```
enable_share_to_twitter = os.environ.get("RADARCOVID_REPORT__ENABLE_PUBLISH_ON_TWITTER")
github_event_name = os.environ.get("GITHUB_EVENT_NAME")
if enable_share_to_twitter and github_event_name == "schedule":
import tweepy
twitter_api_auth_keys = os.environ["RADARCOVID_REPORT__TWITTER_API_AUTH_KEYS"]
twitter_api_auth_keys = twitter_api_auth_keys.split(":")
auth = tweepy.OAuthHandler(twitter_api_auth_keys[0], twitter_api_auth_keys[1])
auth.set_access_token(twitter_api_auth_keys[2], twitter_api_auth_keys[3])
api = tweepy.API(auth)
summary_plots_media = api.media_upload(summary_plots_image_path)
summary_table_media = api.media_upload(summary_table_image_path)
hourly_summary_plots_media = api.media_upload(hourly_summary_plots_image_path)
media_ids = [
summary_plots_media.media_id,
summary_table_media.media_id,
hourly_summary_plots_media.media_id,
]
extraction_date_result_summary_df = \
result_summary_df[result_summary_df.index == extraction_date]
extraction_date_result_hourly_summary_df = \
hourly_summary_df[hourly_summary_df.extraction_date_with_hour == extraction_date_with_hour]
new_teks = extraction_date_result_summary_df.new_tek_count.sum().astype(int)
new_teks_last_hour = extraction_date_result_hourly_summary_df.new_tek_count.sum().astype(int)
new_devices = extraction_date_result_summary_df.new_tek_devices.sum().astype(int)
new_devices_last_hour = extraction_date_result_hourly_summary_df.new_tek_devices.sum().astype(int)
new_tek_count_per_new_tek_device = \
extraction_date_result_summary_df.new_tek_count_per_new_tek_device.sum()
new_tek_devices_per_new_case = \
extraction_date_result_summary_df.new_tek_devices_per_new_case.sum()
status = textwrap.dedent(f"""
Report Update – {extraction_date_with_hour}
#ExposureNotification #RadarCOVID
Shared Diagnoses Day Summary:
- New TEKs: {new_teks} ({new_teks_last_hour:+d} last hour)
- New Devices: {new_devices} ({new_devices_last_hour:+d} last hour, {new_tek_count_per_new_tek_device:.2} TEKs/device)
- Usage Ratio: {new_tek_devices_per_new_case:.2%} devices/case
Report Link: {report_hourly_url}
""")
status = status.encode(encoding="utf-8")
api.update_status(status=status, media_ids=media_ids)
```
|
github_jupyter
|
```
import tensorflow as tf
from tensorflow.keras.preprocessing.image import load_img, img_to_array
from tensorflow.keras.models import Sequential, load_model
from tensorflow.keras.layers import Dense, Flatten, Conv2D, MaxPooling2D
from tensorflow.keras.callbacks import ModelCheckpoint, EarlyStopping
import os
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import cv2
print("Tensorflow Version:",tf.__version__)
```
### INDEX
[1.- LOAD DATA USING IMAGE GENREATORS](#1)
[2.-Create a CNN From Scracth](#2)
<a id='1'></a>
## 1.- LOAD DATA USING IMAGE GENREATORS
```
### Initiate an instnace of ImagaDataGenerator ###
## More in Data Augmentation:
## https://towardsdatascience.com/exploring-image-data-augmentation-with-keras-and-tensorflow-a8162d89b844
path = "Data_set_eye" # Dataset Path
###################################### Create Data Generator ##############################################################
image_generator = tf.keras.preprocessing.image.ImageDataGenerator(validation_split=0.2, # Split for Test/Validation
height_shift_range=0.2, # Height Shift
brightness_range=(0.5, 1.), # Brightness
rescale=0.9, # Rescale
)
############################################## TRAINING DATASET ##############################################################
train_dataset = image_generator.flow_from_directory(batch_size=32, # Batch Size
directory=path, # Directory
shuffle=True, # Shuffle images
target_size=(100, 100), # Resize to 100x100
color_mode="rgb", # Set RGB as default
subset="training", # Set Subset to Training
class_mode='categorical' # Set Data to Categoriacal
)
############################################## TESTING DATASET ##############################################################
validation_dataset = image_generator.flow_from_directory(batch_size=32, # Batch Size
directory=path, # Directory
shuffle=True, # Shuffle images
target_size=(100, 100), # Resize to 100x100
subset="validation", # Set Subset to Validation
color_mode="rgb", # Set RGB as default
class_mode='categorical') # Set Data to Categoriacal
```
### 1.1.- Calculate Steps that have to be taken every epoch
```
val_steps = validation_dataset.n // validation_dataset.batch_size # Steps in an epoch Validation Data
train_steps = train_dataset.n // train_dataset.batch_size # Steps in an epoch for Traninning Data
###################################### INFROM THE USER ABOUT THE STEPS #####################################################
print(f"Train steps per epoch: {train_steps}") # Steps in an epoch for Traninning Data
print(f"Validation steps per epoch: {val_steps}") # Steps in an epoch Validation Data
```
### 1.2.- Get tha labels for each class
```
#### All the labels are stored in Lables.txt file ######
path = "Data_set_eye/Labels.txt" # Path for Label txt file
with open(path,"r") as handler: # Open txt file
labels = handler.read().splitlines() # Create a list based on every new line
print(labels) # Show the labels
```
<br>
<br>
<a id='2'></a>
# 2.-Create a CNN From Scracth
```
def get_new_model(rate=0.5):
"""
Convolutional Neural Network with Droput
"""
############################### NEURAL NETWORK ARCHITECTURE ############################################
model = tf.keras.Sequential()
model.add(tf.keras.Input(shape=((100, 100, 3))))
model.add(tf.keras.layers.Conv2D(filters=16,kernel_size=(3,3),activation="relu",padding="same",name="conv_1"))
model.add(tf.keras.layers.Dropout(rate))
model.add(tf.keras.layers.Conv2D(filters=16,kernel_size=(3,3),activation="relu",padding="same",name="conv_2"))
model.add(tf.keras.layers.Dropout(rate))
model.add(tf.keras.layers.Conv2D(filters=8,kernel_size=(3,3),activation="relu",padding="same",name="conv_3"))
model.add(tf.keras.layers.Dropout(rate))
model.add(tf.keras.layers.MaxPooling2D(pool_size=(8,8),name="pool_1"))
model.add(tf.keras.layers.Flatten(name="flatten"))
model.add(tf.keras.layers.Dense(units=64,activation="relu",name="dense_1"))
model.add(tf.keras.layers.Dense(units=64,activation="relu",name="dense_2"))
model.add(tf.keras.layers.Dense(units=64,activation="relu",name="dense_3"))
model.add(tf.keras.layers.Dense(units=4,activation="softmax",name="dense_4"))
########################### Compilation of CNN ########################################################
model.compile(optimizer='adam',loss='categorical_crossentropy',metrics=['accuracy'])
return model
def get_test_accuracy(model,data,steps,**kwargs):
"""Test model classification accuracy"""
test_loss, test_acc = model.evaluate_generator(data,steps,**kwargs)
print('accuracy: {acc:0.3f}'.format(acc=test_acc))
def get_checkpoint_best_only():
"""
- saves only the weights that generate the highest validation (testing) accuracy
"""
path = r'C:\Users\Eduardo\Documents\CARRERA\8vo_semestre\BIO_4\Lab\3_Silla_de_ruedas\Python\Weights_eyes\weights'# path to save model
checkpoint = tf.keras.callbacks.ModelCheckpoint(filepath=path, save_best_only=True,save_weights_only=True,verbose=2)
return checkpoint
def get_early_stopping():
"""
This function should return an EarlyStopping callback that stops training when
the validation (testing) accuracy has not improved in the last 5 epochs.
EarlyStopping callback with the correct 'monitor' and 'patience'
"""
return tf.keras.callbacks.EarlyStopping(monitor='accuracy',min_delta=0.01,patience=5,mode="max")
def plot_learning(history):
"""PLOT LEARNING CUVRVES """
figrue, ax = plt.subplots(1,2,figsize=(15,6)) # Create Figure
ax[0].set_title("Loss Vs Epochs") # Set Title
ax[0].plot(history.history['loss'],label=" Trainining Loss") # Plot Training Loss
ax[0].plot(history.history['val_loss'],label="Validation Loss") # Plot Validation Loss
ax[0].legend() # Print Labels in plot
ax[1].set_title("Accuracy Vs Epochs") # Set Title
ax[1].plot(history.history['accuracy'],label=" Trainining Accurcacy") # Plot Training Accuracy
ax[1].plot(history.history['val_accuracy'],label="Validation Accurcacy") # Plot Validation Accuracy
ax[1].legend() # Print Labels in plot
plt.show() # Show plot
## THERE IS NOTHING TO RETURN ##
model = get_new_model() # Initiate Model
get_test_accuracy(model,validation_dataset,val_steps) # Test intial Accruacy (without Trainning)
model.summary() # Get Model Architecture
```
### 2.1 Train Model
```
checkpoint_best_only = get_checkpoint_best_only() # Get best only save
early_stopping = get_early_stopping() # Get Early stopping
callbacks = [checkpoint_best_only, early_stopping] # Put callbacks in a list
### Train model using the callbacks ##
history = model.fit(train_dataset, # Data generator for Training
steps_per_epoch =train_steps, # Steps in an epoch of Training Data
validation_data = validation_dataset, # Data Generator for Validation
validation_steps=val_steps, # Steps in a epoch of Validation Data
epochs=40,callbacks=callbacks # Callbacks
)
plot_learning(history) # Plot learning curves at the end
img = cv2.imread('Data_Set/Back/Back112.jpg') # Get image
img = cv2.imread('Data_Set/Right/Right68.jpg') # Get Right
img = cv2.imread('Data_Set/Left/Left59.jpg') # Left
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB )
prediction = model.predict(img[np.newaxis,...]) # Make Prediction
y_predict = np.argmax(prediction) # Get Maximum Probability
print(labels[y_predict])
```
### 2.2 Test Model in Video
```
## This is just an example to ilustrate how to use Haar Cascades in order to detect objects (LIVE) ##
face = cv2.CascadeClassifier('Haarcascade/haarcascade_frontalface_default.xml') # Face Haar Cascade loading
eye = cv2.CascadeClassifier('Haarcascade/haarcascade_eye.xml') # Eye Haar Cascade Loading
vid = cv2.VideoCapture(0) # Define a video capture object
status = True # Initalize status
width = 100 # Width
height = 100 # Height
dimensions=(width,height) # Dimenssions
font = cv2.FONT_HERSHEY_SIMPLEX
while(status):
status, frame = vid.read() # Capture the video frame by frame
frame2 = np.copy(frame) # Copy frame
gray = cv2.cvtColor(frame, cv2.COLOR_BGR2GRAY) # Convert to gray scale
face_info = face.detectMultiScale(gray, 1.3, 5) # Get face infromation
if face_info != (): # If face was capture
(x,y,w,h) = face_info[0] # unpack information
cv2.rectangle(frame,(x,y),(x+w,y+h),(255,255,0),1) # Draw rectangle
eye_info = eye.detectMultiScale(gray) # eye info
if eye_info != ():
(x,y,w,h) = eye_info[0] # unpack information
cv2.rectangle(frame,(x,y),(x+w,y+h),(255,0,255),1)
cropped_face_color = frame2[y:y+h, x:x+w] # Crop face (color)
res = cv2.resize(cropped_face_color,dimensions, interpolation=cv2.INTER_AREA) # Resize
res = cv2.cvtColor(res, cv2.COLOR_BGR2RGB ) # Convert to RGB
prediction = model.predict(res[np.newaxis,...]) # Make Prediction
y_predict = np.argmax(prediction) # Get Maximum Probability
y_prediction_text = labels[y_predict] # Get Text of prediction
cv2.putText(frame,y_prediction_text,(20,20), font, 1,(255,255,0),2)
cv2.imshow('frame', frame) # Display the resulting frame
wait_key = cv2.waitKey(1) & 0xFF # Store Waitkey object
if wait_key == ord('q'): # If q is pressed
break # Break while loop
vid.release() # After the loop release the cap object
cv2.destroyAllWindows() # Destroy all the windows
```
<br>
<br>
<a id='2'></a>
# 2.- Use Transfer Learning

```
from keras.applications.vgg16 import VGG16
from keras.applications.vgg16 import preprocess_input
image_size = [100,100,3] # Add image size we wish to train Data with
### Intiate VGG16 ###
vgg = VGG16(input_shape=image_size, # Input Shape
weights='imagenet', # Dataset used to train weights
include_top=False # Do not include Top
)
##### MAKE ALL LAYERS UNTRAINABLE ###
maximum = 7
i=0
for layer in vgg.layers: # Iterate over layers
if i < maximum: # if layer index is less than the one we specified
layer.trainable = False # Make layer untrianable
i+=1
vgg.layers # Print VGG Layers
vgg.layers[6].trainable
x = Flatten()(vgg.output)
prediction = Dense(4,activation="softmax")(x)
model2 = tf.keras.models.Model(inputs=vgg.input,outputs=prediction)
model2.compile(optimizer='adam',loss='categorical_crossentropy',metrics=['accuracy'])
model2.summary()
#history = model2.fit(train_dataset,steps_per_epoch=train_steps,epochs=4)
history = model2.fit(train_dataset, # Data generator for Training
steps_per_epoch =train_steps, # Steps in an epoch of Training Data
validation_data = validation_dataset, # Data Generator for Validation
validation_steps=val_steps, # Steps in a epoch of Validation Data
epochs=10)
plot_learning(history)
## This is just an example to ilustrate how to use Haar Cascades in order to detect objects (LIVE) ##
face = cv2.CascadeClassifier('Haarcascade/haarcascade_frontalface_default.xml') # Face Haar Cascade loading
eye = cv2.CascadeClassifier('Haarcascade/haarcascade_eye.xml') # Eye Haar Cascade Loading
vid = cv2.VideoCapture(0) # Define a video capture object
status = True # Initalize status
width = 100 # Width
height = 100 # Height
dimensions=(width,height) # Dimenssions
font = cv2.FONT_HERSHEY_SIMPLEX
while(status): # Iterate while status is true
status, frame = vid.read() # Capture the video frame by frame
gray = cv2.cvtColor(frame, cv2.COLOR_BGR2GRAY) # Convert to gray scale
face_info = face.detectMultiScale(gray, 1.3, 5) # Get face infromation
for (x,y,w,h) in face_info: # Iterate over this information
cv2.rectangle(frame,(x,y),(x+w,y+h),(255,255,0),1) # Draw rectangle
cropped_face_color = frame[y:y+h, x:x+w] # Crop face (color)
if face_info != (): # If face was capture
res = cv2.resize(cropped_face_color,dimensions, interpolation=cv2.INTER_AREA) # Resize
prediction = model2.predict(res[np.newaxis,...]) # Make Prediction
y_predict = np.argmax(prediction) # Get Maximum Probability
y_prediction_text = labels[y_predict] # Get Text of prediction
cv2.putText(frame,y_prediction_text,(20,20), font, 1,(255,255,0),2)
cv2.imshow('frame', frame) # Display the resulting frame
wait_key = cv2.waitKey(1) & 0xFF # Store Waitkey object
if wait_key == ord('q'): # If q is pressed
break # Break while loop
vid.release() # After the loop release the cap object
cv2.destroyAllWindows() # Destroy all the windows
```
|
github_jupyter
|
<img align="right" src="images/tf-small.png" width="128"/>
<img align="right" src="images/phblogo.png" width="128"/>
<img align="right" src="images/dans.png"/>
---
Start with [convert](https://nbviewer.jupyter.org/github/annotation/banks/blob/master/programs/convert.ipynb)
---
# Getting data from online repos
We show the various automatic ways by which you can get data that is out there on GitHub to your computer.
The work horse is the function `checkoutRepo()` in `tf.applib.repo`.
Text-Fabric uses this function for all operations where data flows from GitHub to your computer.
There are quite some options, and here we explain all the `checkout` options, i.e. the selection of
data from the history.
See also the [documentation](https://annotation.github.io/text-fabric/tf/advanced/repo.html).
```
%load_ext autoreload
%autoreload 2
```
## Leading example
We use markdown display from IPython purely for presentation.
It is not needed to run `checkoutRepo()`.
```
from tf.advanced.helpers import dm
from tf.advanced.repo import checkoutRepo
```
We work with our tiny example TF app: `banks`.
```
ORG = "annotation"
REPO = "banks"
MAIN = "tf"
MOD = "sim/tf"
```
`MAIN`points to the main data, `MOD` points to a module of data: the similarity feature.
## Presenting the results
The function `do()` just formats the results of a `checkoutRepo()` run.
The result of such a run, after the progress messages, is a tuple.
For the explanation of the tuple, read the [docs](https://annotation.github.io/text-fabric/tf/advanced/repo.html).
```
def do(task):
md = f"""
commit | release | local | base | subdir
--- | --- | --- | --- | ---
`{task[0]}` | `{task[1]}` | `{task[2]}` | `{task[3]}` | `{task[4]}`
"""
dm(md)
```
## All the checkout options
We discuss the meaning and effects of the values you can pass to the `checkout` option.
### `clone`
> Look whether the appropriate folder exists under your `~/github` directory.
This is merely a check whether your data exists in the expected location.
* No online checks take place.
* No data is moved or copied.
**NB**: you cannot select releases and commits in your *local* GitHub clone.
The data will be used as it is found on your file system.
**When to use**
> If you are developing new feature data.
When you develop your data in a repository, your development is private as long as you
do not push to GitHub.
You can test your data, even without locally committing your data.
But, if you are ready to share your data, everything is in place, and you only
have to commit and push, and pass the location on github to others, like
```
myorg/myrepo/subfolder
```
```
do(checkoutRepo(org=ORG, repo=REPO, folder=MAIN, version="0.2", checkout="clone"))
```
We show what happens if you do not have a local github clone in `~/github`.
```
%%sh
mv ~/github/annotation/banks/tf ~/github/annotation/banks/tfxxx
do(checkoutRepo(org=ORG, repo=REPO, folder=MAIN, version="0.2", checkout="clone"))
```
Note that no attempt is made to retrieve online data.
```
%%sh
mv ~/github/annotation/banks/tfxxx ~/github/annotation/banks/tf
```
### `local`
> Look whether the appropriate folder exists under your `~/text-fabric-data` directory.
This is merely a check whether your data exists in the expected location.
* No online checks take place.
* No data is moved or copied.
**When to use**
> If you are using data created and shared by others, and if the data
is already on your system.
You can be sure that no updates are downloaded, and that everything works the same as the last time
you ran your program.
If you do not already have the data, you have to pass `latest` or `hot` or `''` which will be discussed below.
```
do(checkoutRepo(org=ORG, repo=REPO, folder=MAIN, version="0.2", checkout="local"))
```
You see this data because earlier I have downloaded release `v2.0`, which is a tag for
the commit with hash `9713e71c18fd296cf1860d6411312f9127710ba7`.
If you do not have any corresponding data in your `~/text-fabric-data`, you get this:
```
%%sh
mv ~/text-fabric-data/annotation/banks/tf ~/text-fabric-data/annotation/banks/tfxxx
do(checkoutRepo(org=ORG, repo=REPO, folder=MAIN, version="0.2", checkout="local"))
%%sh
mv ~/text-fabric-data/annotation/banks/tfxxx ~/text-fabric-data/annotation/banks/tf
```
### `''` (default)
This is about when you omit the `checkout` parameter, or pass `''` to it.
The destination for local data is your `~/text-fabric-data` folder.
If you have already a local copy of the data, that will be used.
If not:
> Note that if your local data is outdated, no new data will be downloaded.
You need `latest` or `hot` for that.
But what is the latest online copy? In this case we mean:
* the latest *release*, and from that release an appropriate attached zip file
* but if there is no such zip file, we take the files from the corresponding commit
* but if there is no release at all, we take the files from the *latest commit*.
**When to use**
> If you need data created/shared by other people and you want to be sure that you always have the
same copy that you initially downloaded.
* If the data provider makes releases after important modifications, you will get those.
* If the data provider is experimenting after the latest release, and commits them to GitHub,
you do not get those.
However, with `hot`, you `can` get the latest commit, to be discussed below.
```
do(checkoutRepo(org=ORG, repo=REPO, folder=MAIN, version="0.2", checkout=""))
```
Note that no data has been downloaded, because it has detected that there is already local data on your computer.
If you do not have any checkout of this data on your computer, the data will be downloaded.
```
%%sh
rm -rf ~/text-fabric-data/annotation/banks/tf
do(checkoutRepo(org=ORG, repo=REPO, folder=MAIN, version="0.2", checkout=""))
```
#### Note about versions and releases
The **version** of the data is not necessarily the same concept as the **release** of it.
It is possible to keep the versions and the releases strictly parallel,
but in text conversion workflows it can be handy to make a distinction between them,
e.g. as follows:
> the version is a property of the input data
> the release is a property of the output data
When you create data from sources using conversion algorithms,
you want to increase the version if you get new input data, e.g. as a result of corrections
made by the author.
But if you modify your conversion algorithm, while still running it on the same input data,
you may release the new output data as a **new release** of the **same version**.
Likewise, when the input data stays the same, but you have corrected typos in the metadata,
you can make a **new release** of the **same version** of the data.
The conversion delivers the features under a specific version,
and Text-Fabric supports those versions: users of TF can select the version they work with.
Releases are made in the version control system (git and GitHub).
The part of Text-Fabric that auto-downloads data is aware of releases.
But once the data has been downloaded in place, there is no machinery in Text-Fabric to handle
different releases.
Yet the release tag and commit hash are passed on to the point where it comes to recording
the provenance of the data.
#### Download a different version
We download version `0.1` of the data.
```
do(checkoutRepo(org=ORG, repo=REPO, folder=MAIN, version="0.1", checkout=""))
```
Several observations:
* we obtained the older version from the *latest* release, which is still release `v2.0`
* the download looks different from when we downloaded version `0.2`;
this is because the data producer has zipped the `0.2` data and has attached it to release `v2.0`,
but he forgot, or deliberately refused, to attach version `0.1` to that release;
so it has been retrieved directly from the files in the corresponding commit, which is
`9713e71c18fd296cf1860d6411312f9127710ba7`.
For the verification, an online check is needed. The verification consists of checking the release tag and/or commit hash.
If there is no online connection, you get this:
```
%%sh
networksetup -setairportpower en0 off
do(checkoutRepo(org=ORG, repo=REPO, folder=MAIN, version="0.1", checkout="latest"))
```
or if you do not have local data:
```
%%sh
mv ~/text-fabric-data/annotation/banks/tf/0.1 ~/text-fabric-data/annotation/banks/tf/0.1xxx
do(checkoutRepo(org=ORG, repo=REPO, folder=MAIN, version="0.1", checkout="latest"))
%%sh
mv ~/text-fabric-data/annotation/banks/tf/0.1xxx ~/text-fabric-data/annotation/banks/tf/0.1
%%sh
networksetup -setairportpower en0 on
```
### `latest`
> The latest online release will be identified,
and if you do not have that copy locally, it will be downloaded.
**When to use**
> If you need data created/shared by other people and you want to be sure that you always have the
latest *stable* version of that data, unreleased data is not good enough.
One of the difference with `checkout=''` is that if there are no releases, you will not get data.
```
do(checkoutRepo(org=ORG, repo=REPO, folder=MAIN, version="0.2", checkout="latest"))
```
There is no sim/tf data in any release commit, so if we look it up, it should fail.
```
do(checkoutRepo(org=ORG, repo=REPO, folder=MOD, version="0.2", checkout="latest"))
```
But with `checkout=''` it will only be found if you do not have local data already:
```
do(checkoutRepo(org=ORG, repo=REPO, folder=MOD, version="0.2", checkout=""))
```
In that case there is only one way: `hot`:
```
do(checkoutRepo(org=ORG, repo=REPO, folder=MOD, version="0.2", checkout="hot"))
```
### `hot`
> The latest online commit will be identified,
and if you do not have that copy locally, it will be downloaded.
**When to use**
> If you need data created/shared by other people and you want to be sure that you always have the
latest version of that data, whether released or not.
The difference with `checkout=''` is that if there are releases,
you will now get data that may be newer than the latest release.
```
do(checkoutRepo(org=ORG, repo=REPO, folder=MAIN, version="0.2", checkout="hot"))
```
Observe that data has been downloaded, and that we have now data corresponding to a different commit hash,
and not corresponding to a release.
If we now ask for the latest *stable* data, the data will be downloaded anew.
```
do(checkoutRepo(org=ORG, repo=REPO, folder=MAIN, version="0.2", checkout="latest"))
```
### `v1.0` a specific release
> Look for a specific online release to get data from.
**When to use**
> When you want to replicate something, and need data from an earlier point in the history.
```
do(checkoutRepo(org=ORG, repo=REPO, folder=MAIN, version="0.1", checkout="v1.0"))
```
We might try to get version `0.2` from this release.
```
do(checkoutRepo(org=ORG, repo=REPO, folder=MAIN, version="0.2", checkout="v1.0"))
```
At that early point in the history there is not yet a version `0.2` of the data.
### `a81746c` a specific commit
> Look for a specific online commit to get data from.
**When to use**
> When you want to replicate something, and need data from an earlier point in the history, and there is no
release for that commit.
```
do(
checkoutRepo(
org=ORG,
repo=REPO,
folder=MAIN,
version="0.1",
checkout="a81746c5f9627637db4dae04c2d5348bda9e511a",
)
)
```
## *source* and *dest*: an alternative for `~/github` and `~/text-fabric-data`
Everything so far uses the hard-wired `~/github` and `~/text-fabric-data` directories.
But you can change that:
* pass *source* as a replacement for `~/github`.
* pass *dest* as a replacement for `~/text-fabric-data`.
**When to use**
> if you do not want to interfere with the `~/text-fabric-data` directory.
Text-Fabric manages the `~/text-fabric-data` directory,
and if you are experimenting outside Text-Fabric
you may not want to touch its data directory.
> if you want to clone data into your `~/github` directory.
Normally, TF uses your `~/github` directory as a source of information,
and never writes into it.
But if you explicitly pass `dest=~/github`, things change: downloads will
arrive under `~/github`. Use this with care.
> if you work with cloned data outside your `~/github` directory,
you can let the system look in *source* instead of `~/github`.
We customize source and destination directories:
* we put them both under `~/Downloads`
* we give them different names
```
MY_GH = "~/Downloads/repoclones"
MY_TFD = "~/Downloads/textbase"
```
Download a fresh copy of the data to `~/Downloads/textbase` instead.
```
do(
checkoutRepo(
org=ORG,
repo=REPO,
folder=MAIN,
version="0.2",
checkout="",
source=MY_GH,
dest=MY_TFD,
)
)
```
Lookup the same data locally.
```
do(
checkoutRepo(
org=ORG,
repo=REPO,
folder=MAIN,
version="0.2",
checkout="",
source=MY_GH,
dest=MY_TFD,
)
)
```
We copy the local github data to the custom location:
```
%%sh
mkdir -p ~/Downloads/repoclones/annotation
cp -R ~/github/annotation/banks ~/Downloads/repoclones/annotation/banks
```
Lookup the data in this alternative directory.
```
do(
checkoutRepo(
org=ORG,
repo=REPO,
folder=MAIN,
version="0.2",
checkout="clone",
source=MY_GH,
dest=MY_TFD,
)
)
```
Note that the directory trees under the customised *source* and *dest* locations have exactly the same shape as before.
## Conclusion
With the help of `checkoutRepo()` you will be able to make local copies of online data in an organized way.
This will help you when
* you use other people's data
* develop your own data
* share and publish your data
* go back in history.
---
All chapters:
* [use](use.ipynb)
* [share](share.ipynb)
* [app](app.ipynb)
* *repo*
* [compose](compose.ipynb)
---
|
github_jupyter
|
# Text Mining DocSouth Slave Narrative Archive
---
*Note:* This is the first in [a series of documents and notebooks](https://jeddobson.github.io/textmining-docsouth/) that will document and evaluate various machine learning and text mining tools for use in literary studies. These notebooks form the practical and critical archive of my book-in-progress, _Digital Humanities and the Search for a Method_. I have published a critique of some existing methods (Dobson 2015) that takes up some of these concerns and provides some theoretical background for my account of computational methods as used within the humanities. Each notebook displays code, data, results, interpretation, and critique. I attempt to provide as much explanation of the individual steps and documentation (along with citations of related papers) of the concepts and justification of choices made.
### Revision Date and Notes:
- 05/10/2017: Initial version ([email protected])
- 08/29/2017: Updated to automatically assign labels and reduced to two classes/periods.
### KNearest Neighbor (kNN) period classification of texts
The following Jupyter cells show a very basic classification task using the [kNN](https://en.wikipedia.org/wiki/K-nearest_neighbors_algorithm) algorithm as implemented in Python and with the [scikit-learn](http://scikit-learn.org/) package.
A simple check to see if the dates in the table of contents ("toc.csv") for the DocSouth ["North American Slave Narratives"](http://docsouth.unc.edu/neh/) can be converted to an integer (date as year) is used to assign one of these two classes:
- antebellum: prior to 1865
- postbellum: after 1865
These period categories are rough and by no means not perfect. Publication year may have little relation to the content of the text, the source for the vectorizing process and eventual categorization. These dates are what Matthew Jockers calls, within the digital humanities context, catalog metadata (Jockers 2013, 35-62). Recently, critics have challenged such divisions (Marrs 2015) that are central to the understanding of field of nineteenth-century American literary studies with concepts like "transbellum" that might be capable of helping to better understand works that address the Civil War and its attendant anxities through the "long nineteenth century." The majority of the texts included in the DocSouth archive are first-person autobiographical narratives of lives lived during the antebellum and Civil War years and published in the years leading up to, including, and after the war.
### Complete (Labeled) Dataset
|class|count|
|---|---|
|antebellum|143|
|postbellum|109|
|unknown or ambiguous|40|
There are 252 texts with four digit years and eighteen texts with ambiguous or unknown publication dates. This script will attempt to classify these texts into one of these two periods following the "fitting" of the labeled training texts. I split the 252 texts with known and certain publication dates into two groups: a training set and a testing test. After "fitting" the training set and establishing the neighbors, the code attempts to categorize the testing set. Many questions can and should be asked about the creation of the training set and the labeling of the data. This labeling practice introduces many subjective decisions into what is perceived as an objective (machine and algorithmically generated) process (Dobson 2015, Gillespie 2016).
### Training Data Set
The training set (the first 252 texts, preserving the order in "toc.csv") over-represents the antebellum period and may account for the ability of the classifier to make good predictions for this class.
|class|count|
|---|---|
|antebellum|96|
|postbellum|81|
### Test Data Set
The "testing" dataset is used to validate the classifier. This dataset contains seventy-five texts with known year of publication. This dataset, like the training dataset, overrepresents the antebellum period.
|class|count|
|---|---|
|antebellum|47|
|postbellum|28|
#### Text Pre-processing
The texts are all used/imported as found in the zip file provided by the DocSouth ["North American Slave Narratives"](http://docsouth.unc.edu/neh/) collection. The texts have been encoded in a combination of UTF-8 Unicode and ASCII. Scikit-learn's HashingVectorizer performs some additional pre-processing and that will be examined in the sections below.
#### kNN Background
The kNN algorithm is a non-parametric algorithm, meaning that it does not require detailed knowledge of the input data and its distribution (Cover and Hart 1967). This algorithm is known as reliable and it is quite simple, especially when compared to some of the more complex machine learning algorithms used as present, to implement and understand. It was originally conceived of as a response to what is called a “discrimination problem”: the categorization of a large number of input points into discrete "boxes." Data are eventually organized into categories, in the case of this script, the three categories of antebellum, postbellum, and twentieth-century.
The algorithm functions in space and produces each input text as a "neighbor" and has each text "vote" for membership into parcellated neighborhoods. Cover and Hart explain: "If the number of samples is large it makes good sense to use, instead of the single nearest neighbor, the majority vote of the nearest k neighbors" (22). The following code uses the value of "12" for the number of neighbors or the 'k' of kNN.
The kNN algorithm may give better results for smaller numbers of classes. The performance of particular implementation of kNN and the feature selection algorithm (HashingVectorizer) was better with just the antebellum and postbellum class. Alternative boundaries for the classes (year markers) might also improve results.
#### Feature Selection
While it is non-parametics, the kNN algorithm does require a set of features in order to categorize the input data, the texts. This script operates according to the _"bag of words"_ method in which each text is treated not as a narrative but a collection of unordered and otherwise undiferentiated words. This means that multiple word phrases (aka ngrams) are ignored and much meaning will be removed from the comparative method because of a loss of context.
In order to select the features by which a text can be compared to another, we need some sort of method that can produce numerical data. I have selected the HashingVectorizer, which is a fast method to generate a list of words/tokens from a file. This returns a numpy compressed sparse row (CSR) matrix that scikit-learn will use in the creation of the neighborhood "map."
The HashingVectorizer removes a standard 318 English-language stop words and by default does not alter or remove any accents or accented characters in the encoded (UTF-8) format. It also converts all words to lowercase, potentially introducing false positives.
**Issues with HashingVectorizer** This vectorizer works well, but it limits the questions we can ask after it has been run. We cannot, for example, interrogate why a certain text might have been misclassified by examining the words/tokens returned by the vectorizer. This is because the HashingVectorizer returns only indices to features and does not keep the string representation of specific words.
```
# load required packages
import sys, os
import re
import operator
import nltk
from nltk import pos_tag, ne_chunk
from nltk.tokenize import wordpunct_tokenize
import seaborn as sn
%matplotlib inline
# load local library
sys.path.append("lib")
import docsouth_utils
# each dictionary entry in the 'list' object returned by load_narratives
# contains the following keys:
# 'author' = Author of the text (first name, last name)
# 'title' = Title of the text
# 'year' = Year published as integer or False if not simple four-digit year
# 'file' = Filename of text
# 'text' = NLTK Text object
neh_slave_archive = docsouth_utils.load_narratives()
# establish two simple classes for kNN classification
# the "date" field has already been converted to an integer
# all texts published before 1865, we'll call "antebellum"
# "postbellum" for those after.
period_classes=list()
for entry in neh_slave_archive:
file = ' '.join(entry['text'])
if entry['year'] != False and entry['year'] < 1865:
period_classes.append([file,"antebellum"])
if entry['year'] != False and entry['year'] > 1865:
period_classes.append([file,"postbellum"])
# create labels and filenames
labels=[i[1] for i in period_classes]
files=[i[0] for i in period_classes]
# create training and test datasets by leaving out the
# last 100 files with integer dates from the toc for testing.
test_size=100
train_labels=labels[:-test_size]
train_files=files[:-test_size]
# the last set of texts (test_size) are the "test" dataset (for validation)
test_labels=labels[-test_size:]
test_files=files[-test_size:]
from sklearn.feature_extraction.text import HashingVectorizer
from sklearn.neighbors import KNeighborsClassifier
from sklearn import metrics
# intialize the vectorizer using occurance counts normalized as
# token frequencies: norm=l2
vectorizer = HashingVectorizer(lowercase=True,
stop_words='english',
norm='l2',
non_negative=True)
training_data = vectorizer.fit_transform(train_files)
test_data=vectorizer.transform(test_files)
# display file counts
print("training data:")
for period in ['postbellum', 'antebellum']:
print(" ",period,":",train_labels.count(period))
print("test data:")
for period in ['postbellum', 'antebellum']:
print(" ",period,":",test_labels.count(period))
# run kNN and fit training data
knn = KNeighborsClassifier(n_neighbors=13)
knn.fit(training_data,train_labels)
# Predict results from the test data and check accuracy
pred = knn.predict(test_data)
score = metrics.accuracy_score(test_labels, pred)
print("accuracy: %0.3f" % score)
print(metrics.classification_report(test_labels, pred))
print("confusion matrix:")
print(metrics.confusion_matrix(test_labels, pred))
# Produce visualization of confusion matrix
sn.heatmap(metrics.confusion_matrix(test_labels, pred),annot=True,cmap='Blues',fmt='g')
```
## Prediction of unclassified data
The following cell loads and vectorizes (using the above HashingVectorizing method, with the exact same parameters used for the training set) and tests against the trained classifier, all the algorithmically uncategorized and ambiguously dated (in the toc.csv) input files.
### Partial list of Unspecified or Ambiguous Publication Dates
|File|Date|
|---|---|
|church-hatcher-hatcher.txt|c1908|
|fpn-jacobs-jacobs.txt|1861,c1860
|neh-aga-aga.txt|[1846]|
|neh-anderson-anderson.txt|1854?|
|neh-brownj-brownj.txt|1856,c1865
|neh-carolinatwin-carolinatwin.txt|[between 1902 and 1912]|
|neh-delaney-delaney.txt|[189?]|
|neh-equiano1-equiano1.txt|[1789]|
|neh-equiano2-equiano2.txt|[1789]|
|neh-henry-henry.txt|[1872]|
|neh-jonestom-jones.txt|[185-?]|
|neh-latta-latta.txt|[1903]|
|neh-leewilliam-lee.txt|c1918|
|neh-millie-christine-millie-christine.txt|[18--?]|
|neh-parkerh-parkerh.txt|186?|
|neh-pomp-pomp.txt|1795|
|neh-washstory-washin.txt|c1901|
|neh-white-white.txt|[c1849]|
```
# predict class or period membership for all texts without
# four digit years
for entry in neh_slave_archive:
if entry['year'] == False:
print(entry['author'],", ",entry['title'])
print(" ",knn.predict(vectorizer.transform([entry['file']])))
```
## Works Cited
Cover T.M. and P. E. Hart. 1967. "Nearest Neighbor Pattern Classification." _IEEE Transactions on Information Theory_ 13, no. 1: 21-27.
Dobson, James E. 2015. [“Can an Algorithm be Disturbed? Machine Learning, Intrinsic Criticism, and the Digital Humanities.”](https://mla.hcommons.org/deposits/item/mla:313/) _College Literature_ 42, no. 4: 543-564.
Gillespie, Tarleton. 2016. “Algorithm.” In _Digital Keywords: A Vocabulary of Information Society and Culture_. Edited by Benjamin Peters. Princeton: Princeton University Press.
Jockers, Matthew. 2013. _Macroanalysis: Digital Methods & Literary History_ Urbana: University of Illinois Press.
Marrs, Cody. 2015. _Nineteenth-Century American Literature and the Long Civil War_. New York: Cambridge University Press.
|
github_jupyter
|
## 1. The NIST Special Publication 800-63B
<p>If you – 50 years ago – needed to come up with a secret password you were probably part of a secret espionage organization or (more likely) you were pretending to be a spy when playing as a kid. Today, many of us are forced to come up with new passwords <em>all the time</em> when signing into sites and apps. As a password <em>inventeur</em> it is your responsibility to come up with good, hard-to-crack passwords. But it is also in the interest of sites and apps to make sure that you use good passwords. The problem is that it's really hard to define what makes a good password. However, <em>the National Institute of Standards and Technology</em> (NIST) knows what the second best thing is: To make sure you're at least not using a <em>bad</em> password. </p>
<p>In this notebook, we will go through the rules in <a href="https://pages.nist.gov/800-63-3/sp800-63b.html">NIST Special Publication 800-63B</a> which details what checks a <em>verifier</em> (what the NIST calls a second party responsible for storing and verifying passwords) should perform to make sure users don't pick bad passwords. We will go through the passwords of users from a fictional company and use python to flag the users with bad passwords. But us being able to do this already means the fictional company is breaking one of the rules of 800-63B:</p>
<blockquote>
<p>Verifiers SHALL store memorized secrets in a form that is resistant to offline attacks. Memorized secrets SHALL be salted and hashed using a suitable one-way key derivation function.</p>
</blockquote>
<p>That is, never save users' passwords in plaintext, always encrypt the passwords! Keeping this in mind for the next time we're building a password management system, let's load in the data.</p>
<p><em>Warning: The list of passwords and the fictional user database both contain <strong>real</strong> passwords leaked from <strong>real</strong> websites. These passwords have not been filtered in any way and include words that are explicit, derogatory and offensive.</em></p>
```
# Importing the pandas module
import pandas as pd
# Loading in datasets/users.csv
users = pd.read_csv('datasets/users.csv')
# Printing out how many users we've got
print(users)
# Taking a look at the 12 first users
users.head(12)
```
## 2. Passwords should not be too short
<p>If we take a look at the first 12 users above we already see some bad passwords. But let's not get ahead of ourselves and start flagging passwords <em>manually</em>. What is the first thing we should check according to the NIST Special Publication 800-63B?</p>
<blockquote>
<p>Verifiers SHALL require subscriber-chosen memorized secrets to be at least 8 characters in length.</p>
</blockquote>
<p>Ok, so the passwords of our users shouldn't be too short. Let's start by checking that!</p>
```
# Calculating the lengths of users' passwords
import pandas as pd
users = pd.read_csv('datasets/users.csv')
users['length'] = users.password.str.len()
users['too_short'] = users['length'] < 8
print(users['too_short'].sum())
# Taking a look at the 12 first rows
users.head(12)
```
## 3. Common passwords people use
<p>Already this simple rule flagged a couple of offenders among the first 12 users. Next up in Special Publication 800-63B is the rule that</p>
<blockquote>
<p>verifiers SHALL compare the prospective secrets against a list that contains values known to be commonly-used, expected, or compromised.</p>
<ul>
<li>Passwords obtained from previous breach corpuses.</li>
<li>Dictionary words.</li>
<li>Repetitive or sequential characters (e.g. ‘aaaaaa’, ‘1234abcd’).</li>
<li>Context-specific words, such as the name of the service, the username, and derivatives thereof.</li>
</ul>
</blockquote>
<p>We're going to check these in order and start with <em>Passwords obtained from previous breach corpuses</em>, that is, websites where hackers have leaked all the users' passwords. As many websites don't follow the NIST guidelines and encrypt passwords there now exist large lists of the most popular passwords. Let's start by loading in the 10,000 most common passwords which I've taken from <a href="https://github.com/danielmiessler/SecLists/tree/master/Passwords">here</a>.</p>
```
# Reading in the top 10000 passwords
common_passwords = pd.read_csv("datasets/10_million_password_list_top_10000.txt",
header=None,
squeeze=True)
# Taking a look at the top 20
common_passwords.head(20)
```
## 4. Passwords should not be common passwords
<p>The list of passwords was ordered, with the most common passwords first, and so we shouldn't be surprised to see passwords like <code>123456</code> and <code>qwerty</code> above. As hackers also have access to this list of common passwords, it's important that none of our users use these passwords!</p>
<p>Let's flag all the passwords in our user database that are among the top 10,000 used passwords.</p>
```
# Flagging the users with passwords that are common passwords
users['common_password'] = users['password'].isin(common_passwords)
# Counting and printing the number of users using common passwords
print(users['common_password'].sum())
# Taking a look at the 12 first rows
users.head(12)
```
## 5. Passwords should not be common words
<p>Ay ay ay! It turns out many of our users use common passwords, and of the first 12 users there are already two. However, as most common passwords also tend to be short, they were already flagged as being too short. What is the next thing we should check?</p>
<blockquote>
<p>Verifiers SHALL compare the prospective secrets against a list that contains [...] dictionary words.</p>
</blockquote>
<p>This follows the same logic as before: It is easy for hackers to check users' passwords against common English words and therefore common English words make bad passwords. Let's check our users' passwords against the top 10,000 English words from <a href="https://github.com/first20hours/google-10000-english">Google's Trillion Word Corpus</a>.</p>
```
# Reading in a list of the 10000 most common words
words = pd.read_csv("datasets/google-10000-english.txt", header=None,
squeeze=True)
# Flagging the users with passwords that are common words
users['common_word'] = users['password'].str.lower().isin(words)
# Counting and printing the number of users using common words as passwords
print(users['common_word'].sum())
# Taking a look at the 12 first rows
users.head(12)
```
## 6. Passwords should not be your name
<p>It turns out many of our passwords were common English words too! Next up on the NIST list:</p>
<blockquote>
<p>Verifiers SHALL compare the prospective secrets against a list that contains [...] context-specific words, such as the name of the service, the username, and derivatives thereof.</p>
</blockquote>
<p>Ok, so there are many things we could check here. One thing to notice is that our users' usernames consist of their first names and last names separated by a dot. For now, let's just flag passwords that are the same as either a user's first or last name.</p>
```
# Extracting first and last names into their own columns
users['first_name'] = users['user_name'].str.extract(r'(^\w+)', expand=False)
users['last_name'] = users['user_name'].str.extract(r'(\w+$)', expand=False)
# Flagging the users with passwords that matches their names
users['uses_name'] = (users['password'] == users['first_name']) | (users['password'] == users['last_name'])
# Counting and printing the number of users using names as passwords
print(users['uses_name'].count())
# Taking a look at the 12 first rows
users.head(12)
```
## 7. Passwords should not be repetitive
<p>Milford Hubbard (user number 12 above), what where you thinking!? Ok, so the last thing we are going to check is a bit tricky:</p>
<blockquote>
<p>verifiers SHALL compare the prospective secrets [so that they don't contain] repetitive or sequential characters (e.g. ‘aaaaaa’, ‘1234abcd’).</p>
</blockquote>
<p>This is tricky to check because what is <em>repetitive</em> is hard to define. Is <code>11111</code> repetitive? Yes! Is <code>12345</code> repetitive? Well, kind of. Is <code>13579</code> repetitive? Maybe not..? To check for <em>repetitiveness</em> can be arbitrarily complex, but here we're only going to do something simple. We're going to flag all passwords that contain 4 or more repeated characters.</p>
```
### Flagging the users with passwords with >= 4 repeats
users['too_many_repeats'] = users['password'].str.contains(r'(.)\1\1\1')
# Taking a look at the users with too many repeats
users.head(12)
```
## 8. All together now!
<p>Now we have implemented all the basic tests for bad passwords suggested by NIST Special Publication 800-63B! What's left is just to flag all bad passwords and maybe to send these users an e-mail that strongly suggests they change their password.</p>
```
# Flagging all passwords that are bad
users['bad_password'] = (users['too_short'])|(users['common_password'])|(users['common_word'])|(users['uses_name'])|(users['too_many_repeats'])
# Counting and printing the number of bad passwords
print(sum(users['bad_password']))
# Looking at the first 25 bad passwords
users[users['bad_password']==True]['password'].head(25)
```
## 9. Otherwise, the password should be up to the user
<p>In this notebook, we've implemented the password checks recommended by the NIST Special Publication 800-63B. It's certainly possible to better implement these checks, for example, by using a longer list of common passwords. Also note that the NIST checks in no way guarantee that a chosen password is good, just that it's not obviously bad.</p>
<p>Apart from the checks we've implemented above the NIST is also clear with what password rules should <em>not</em> be imposed:</p>
<blockquote>
<p>Verifiers SHOULD NOT impose other composition rules (e.g., requiring mixtures of different character types or prohibiting consecutively repeated characters) for memorized secrets. Verifiers SHOULD NOT require memorized secrets to be changed arbitrarily (e.g., periodically).</p>
</blockquote>
<p>So the next time a website or app tells you to "include both a number, symbol and an upper and lower case character in your password" you should send them a copy of <a href="https://pages.nist.gov/800-63-3/sp800-63b.html">NIST Special Publication 800-63B</a>.</p>
```
# Enter a password that passes the NIST requirements
# PLEASE DO NOT USE AN EXISTING PASSWORD HERE
new_password = "test@2019"
```
|
github_jupyter
|
##### Copyright 2019 The TensorFlow Authors.
```
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
```
<table class="tfo-notebook-buttons" align="left">
<td>
<a target="_blank" href="https://www.tensorflow.org/guide/keras/custom_callback"><img src="https://www.tensorflow.org/images/tf_logo_32px.png" />View on TensorFlow.org</a>
</td>
<td>
<a target="_blank" href="https://colab.research.google.com/github/tensorflow/docs/blob/master/site/en/guide/keras/custom_callback.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
</td>
<td>
<a target="_blank" href="https://github.com/tensorflow/docs/blob/master/site/en/guide/keras/custom_callback.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View source on GitHub</a>
</td>
<td>
<a href="https://storage.googleapis.com/tensorflow_docs/docs/site/en/guide/keras/custom_callback.ipynb"><img src="https://www.tensorflow.org/images/download_logo_32px.png" />Download notebook</a>
</td>
</table>
# Writing custom Keras callbacks
A custom callback is a powerful tool to customize the behavior of a Keras model during training, evaluation, or inference, including reading/changing the Keras model. Examples include `tf.keras.callbacks.TensorBoard` where the training progress and results can be exported and visualized with TensorBoard, or `tf.keras.callbacks.ModelCheckpoint` where the model is automatically saved during training, and more. In this guide, you will learn what Keras callback is, when it will be called, what it can do, and how you can build your own. Towards the end of this guide, there will be demos of creating a couple of simple callback applications to get you started on your custom callback.
## Setup
```
from __future__ import absolute_import, division, print_function, unicode_literals
try:
# %tensorflow_version only exists in Colab.
%tensorflow_version 2.x
except Exception:
pass
import tensorflow as tf
```
## Introduction to Keras callbacks
In Keras, `Callback` is a python class meant to be subclassed to provide specific functionality, with a set of methods called at various stages of training (including batch/epoch start and ends), testing, and predicting. Callbacks are useful to get a view on internal states and statistics of the model during training. You can pass a list of callbacks (as the keyword argument `callbacks`) to any of `tf.keras.Model.fit()`, `tf.keras.Model.evaluate()`, and `tf.keras.Model.predict()` methods. The methods of the callbacks will then be called at different stages of training/evaluating/inference.
To get started, let's import tensorflow and define a simple Sequential Keras model:
```
# Define the Keras model to add callbacks to
def get_model():
model = tf.keras.Sequential()
model.add(tf.keras.layers.Dense(1, activation = 'linear', input_dim = 784))
model.compile(optimizer=tf.keras.optimizers.RMSprop(lr=0.1), loss='mean_squared_error', metrics=['mae'])
return model
```
Then, load the MNIST data for training and testing from Keras datasets API:
```
# Load example MNIST data and pre-process it
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data()
x_train = x_train.reshape(60000, 784).astype('float32') / 255
x_test = x_test.reshape(10000, 784).astype('float32') / 255
```
Now, define a simple custom callback to track the start and end of every batch of data. During those calls, it prints the index of the current batch.
```
import datetime
class MyCustomCallback(tf.keras.callbacks.Callback):
def on_train_batch_begin(self, batch, logs=None):
print('Training: batch {} begins at {}'.format(batch, datetime.datetime.now().time()))
def on_train_batch_end(self, batch, logs=None):
print('Training: batch {} ends at {}'.format(batch, datetime.datetime.now().time()))
def on_test_batch_begin(self, batch, logs=None):
print('Evaluating: batch {} begins at {}'.format(batch, datetime.datetime.now().time()))
def on_test_batch_end(self, batch, logs=None):
print('Evaluating: batch {} ends at {}'.format(batch, datetime.datetime.now().time()))
```
Providing a callback to model methods such as `tf.keras.Model.fit()` ensures the methods are called at those stages:
```
model = get_model()
_ = model.fit(x_train, y_train,
batch_size=64,
epochs=1,
steps_per_epoch=5,
verbose=0,
callbacks=[MyCustomCallback()])
```
## Model methods that take callbacks
Users can supply a list of callbacks to the following `tf.keras.Model` methods:
#### [`fit()`](https://www.tensorflow.org/versions/r2.0/api_docs/python/tf/keras/Model#fit), [`fit_generator()`](https://www.tensorflow.org/versions/r2.0/api_docs/python/tf/keras/Model#fit_generator)
Trains the model for a fixed number of epochs (iterations over a dataset, or data yielded batch-by-batch by a Python generator).
#### [`evaluate()`](https://www.tensorflow.org/versions/r2.0/api_docs/python/tf/keras/Model#evaluate), [`evaluate_generator()`](https://www.tensorflow.org/versions/r2.0/api_docs/python/tf/keras/Model#evaluate_generator)
Evaluates the model for given data or data generator. Outputs the loss and metric values from the evaluation.
#### [`predict()`](https://www.tensorflow.org/versions/r2.0/api_docs/python/tf/keras/Model#predict), [`predict_generator()`](https://www.tensorflow.org/versions/r2.0/api_docs/python/tf/keras/Model#predict_generator)
Generates output predictions for the input data or data generator.
```
_ = model.evaluate(x_test, y_test, batch_size=128, verbose=0, steps=5,
callbacks=[MyCustomCallback()])
```
## An overview of callback methods
### Common methods for training/testing/predicting
For training, testing, and predicting, following methods are provided to be overridden.
#### `on_(train|test|predict)_begin(self, logs=None)`
Called at the beginning of `fit`/`evaluate`/`predict`.
#### `on_(train|test|predict)_end(self, logs=None)`
Called at the end of `fit`/`evaluate`/`predict`.
#### `on_(train|test|predict)_batch_begin(self, batch, logs=None)`
Called right before processing a batch during training/testing/predicting. Within this method, `logs` is a dict with `batch` and `size` available keys, representing the current batch number and the size of the batch.
#### `on_(train|test|predict)_batch_end(self, batch, logs=None)`
Called at the end of training/testing/predicting a batch. Within this method, `logs` is a dict containing the stateful metrics result.
### Training specific methods
In addition, for training, following are provided.
#### on_epoch_begin(self, epoch, logs=None)
Called at the beginning of an epoch during training.
#### on_epoch_end(self, epoch, logs=None)
Called at the end of an epoch during training.
### Usage of `logs` dict
The `logs` dict contains the loss value, and all the metrics at the end of a batch or epoch. Example includes the loss and mean absolute error.
```
class LossAndErrorPrintingCallback(tf.keras.callbacks.Callback):
def on_train_batch_end(self, batch, logs=None):
print('For batch {}, loss is {:7.2f}.'.format(batch, logs['loss']))
def on_test_batch_end(self, batch, logs=None):
print('For batch {}, loss is {:7.2f}.'.format(batch, logs['loss']))
def on_epoch_end(self, epoch, logs=None):
print('The average loss for epoch {} is {:7.2f} and mean absolute error is {:7.2f}.'.format(epoch, logs['loss'], logs['mae']))
model = get_model()
_ = model.fit(x_train, y_train,
batch_size=64,
steps_per_epoch=5,
epochs=3,
verbose=0,
callbacks=[LossAndErrorPrintingCallback()])
```
Similarly, one can provide callbacks in `evaluate()` calls.
```
_ = model.evaluate(x_test, y_test, batch_size=128, verbose=0, steps=20,
callbacks=[LossAndErrorPrintingCallback()])
```
## Examples of Keras callback applications
The following section will guide you through creating simple Callback applications.
### Early stopping at minimum loss
First example showcases the creation of a `Callback` that stops the Keras training when the minimum of loss has been reached by mutating the attribute `model.stop_training` (boolean). Optionally, the user can provide an argument `patience` to specfify how many epochs the training should wait before it eventually stops.
`tf.keras.callbacks.EarlyStopping` provides a more complete and general implementation.
```
import numpy as np
class EarlyStoppingAtMinLoss(tf.keras.callbacks.Callback):
"""Stop training when the loss is at its min, i.e. the loss stops decreasing.
Arguments:
patience: Number of epochs to wait after min has been hit. After this
number of no improvement, training stops.
"""
def __init__(self, patience=0):
super(EarlyStoppingAtMinLoss, self).__init__()
self.patience = patience
# best_weights to store the weights at which the minimum loss occurs.
self.best_weights = None
def on_train_begin(self, logs=None):
# The number of epoch it has waited when loss is no longer minimum.
self.wait = 0
# The epoch the training stops at.
self.stopped_epoch = 0
# Initialize the best as infinity.
self.best = np.Inf
def on_epoch_end(self, epoch, logs=None):
current = logs.get('loss')
if np.less(current, self.best):
self.best = current
self.wait = 0
# Record the best weights if current results is better (less).
self.best_weights = self.model.get_weights()
else:
self.wait += 1
if self.wait >= self.patience:
self.stopped_epoch = epoch
self.model.stop_training = True
print('Restoring model weights from the end of the best epoch.')
self.model.set_weights(self.best_weights)
def on_train_end(self, logs=None):
if self.stopped_epoch > 0:
print('Epoch %05d: early stopping' % (self.stopped_epoch + 1))
model = get_model()
_ = model.fit(x_train, y_train,
batch_size=64,
steps_per_epoch=5,
epochs=30,
verbose=0,
callbacks=[LossAndErrorPrintingCallback(), EarlyStoppingAtMinLoss()])
```
### Learning rate scheduling
One thing that is commonly done in model training is changing the learning rate as more epochs have passed. Keras backend exposes get_value api which can be used to set the variables. In this example, we're showing how a custom Callback can be used to dymanically change the learning rate.
Note: this is just an example implementation see `callbacks.LearningRateScheduler` and `keras.optimizers.schedules` for more general implementations.
```
class LearningRateScheduler(tf.keras.callbacks.Callback):
"""Learning rate scheduler which sets the learning rate according to schedule.
Arguments:
schedule: a function that takes an epoch index
(integer, indexed from 0) and current learning rate
as inputs and returns a new learning rate as output (float).
"""
def __init__(self, schedule):
super(LearningRateScheduler, self).__init__()
self.schedule = schedule
def on_epoch_begin(self, epoch, logs=None):
if not hasattr(self.model.optimizer, 'lr'):
raise ValueError('Optimizer must have a "lr" attribute.')
# Get the current learning rate from model's optimizer.
lr = float(tf.keras.backend.get_value(self.model.optimizer.lr))
# Call schedule function to get the scheduled learning rate.
scheduled_lr = self.schedule(epoch, lr)
# Set the value back to the optimizer before this epoch starts
tf.keras.backend.set_value(self.model.optimizer.lr, scheduled_lr)
print('\nEpoch %05d: Learning rate is %6.4f.' % (epoch, scheduled_lr))
LR_SCHEDULE = [
# (epoch to start, learning rate) tuples
(3, 0.05), (6, 0.01), (9, 0.005), (12, 0.001)
]
def lr_schedule(epoch, lr):
"""Helper function to retrieve the scheduled learning rate based on epoch."""
if epoch < LR_SCHEDULE[0][0] or epoch > LR_SCHEDULE[-1][0]:
return lr
for i in range(len(LR_SCHEDULE)):
if epoch == LR_SCHEDULE[i][0]:
return LR_SCHEDULE[i][1]
return lr
model = get_model()
_ = model.fit(x_train, y_train,
batch_size=64,
steps_per_epoch=5,
epochs=15,
verbose=0,
callbacks=[LossAndErrorPrintingCallback(), LearningRateScheduler(lr_schedule)])
```
### Standard Keras callbacks
Be sure to check out the existing Keras callbacks by [visiting the api doc](https://www.tensorflow.org/versions/r2.0/api_docs/python/tf/keras/callbacks). Applications include logging to CSV, saving the model, visualizing on TensorBoard and a lot more.
|
github_jupyter
|
```
from torchvision import transforms
from torch.utils.data import Dataset, DataLoader
import torch
from torch import optim
from torch.autograd import Variable
import numpy as np
import os
import math
from torch import nn
from sklearn.metrics import confusion_matrix
import matplotlib.pyplot as plt
import itertools
import random
from sklearn import preprocessing
from scipy import io
os.environ["CUDA_VISIBLE_DEVICES"] = "0"
```
## DataLoader
```
### handle the dataset
class TorchDataset(Dataset):
def __init__(self, trs_file, label_file, trace_num, trace_offset, trace_length):
self.trs_file = trs_file
self.label_file = label_file
self.trace_num = trace_num
self.trace_offset = trace_offset
self.trace_length = trace_length
self.ToTensor = transforms.ToTensor()
def __getitem__(self, i):
index = i % self.trace_num
trace = self.trs_file[index,:]
label = self.label_file[index]
trace = trace[self.trace_offset:self.trace_offset+self.trace_length]
trace = np.reshape(trace,(1,-1))
trace = self.ToTensor(trace)
trace = np.reshape(trace, (1,-1))
label = torch.tensor(label, dtype=torch.long)
return trace.float(), label
def __len__(self):
return self.trace_num
### data loader for training
def load_training(batch_size, kwargs):
data = TorchDataset(**kwargs)
train_loader = torch.utils.data.DataLoader(data, batch_size=batch_size, shuffle=True, drop_last=True, num_workers=1, pin_memory=True)
return train_loader
### data loader for testing
def load_testing(batch_size, kwargs):
data = TorchDataset(**kwargs)
test_loader = torch.utils.data.DataLoader(data, batch_size=batch_size, shuffle=False, drop_last=True, num_workers=1, pin_memory=True)
return test_loader
```
## Arrays and Functions
```
Sbox = [99, 124, 119, 123, 242, 107, 111, 197, 48, 1, 103, 43, 254, 215, 171, 118, 202, 130, 201, 125, 250, 89, 71,
240, 173, 212, 162, 175, 156, 164, 114, 192, 183, 253, 147, 38, 54, 63, 247, 204, 52, 165, 229, 241, 113, 216,
49, 21, 4, 199, 35, 195, 24, 150, 5, 154, 7, 18, 128, 226, 235, 39, 178, 117, 9, 131, 44, 26, 27, 110, 90, 160,
82, 59, 214, 179, 41, 227, 47, 132, 83, 209, 0, 237, 32, 252, 177, 91, 106, 203, 190, 57, 74, 76, 88, 207, 208,
239, 170, 251, 67, 77, 51, 133, 69, 249, 2, 127, 80, 60, 159, 168, 81, 163, 64, 143, 146, 157, 56, 245, 188,
182, 218, 33, 16, 255, 243, 210, 205, 12, 19, 236, 95, 151, 68, 23, 196, 167, 126, 61, 100, 93, 25, 115, 96,
129, 79, 220, 34, 42, 144, 136, 70, 238, 184, 20, 222, 94, 11, 219, 224, 50, 58, 10, 73, 6, 36, 92, 194, 211,
172, 98, 145, 149, 228, 121, 231, 200, 55, 109, 141, 213, 78, 169, 108, 86, 244, 234, 101, 122, 174, 8, 186,
120, 37, 46, 28, 166, 180, 198, 232, 221, 116, 31, 75, 189, 139, 138, 112, 62, 181, 102, 72, 3, 246, 14, 97,
53, 87, 185, 134, 193, 29, 158, 225, 248, 152, 17, 105, 217, 142, 148, 155, 30, 135, 233, 206, 85, 40, 223, 140,
161, 137, 13, 191, 230, 66, 104, 65, 153, 45, 15, 176, 84, 187, 22]
InvSbox = [82, 9, 106, 213, 48, 54, 165, 56, 191, 64, 163, 158, 129, 243, 215, 251, 124, 227, 57, 130, 155, 47, 255, 135,
52, 142, 67, 68, 196, 222, 233, 203, 84, 123, 148, 50, 166, 194, 35, 61,238, 76, 149, 11, 66, 250, 195, 78, 8,
46, 161, 102, 40, 217, 36, 178, 118, 91, 162, 73, 109, 139, 209, 37, 114, 248, 246, 100, 134, 104, 152, 22, 212,
164, 92, 204, 93, 101, 182, 146, 108, 112, 72, 80, 253, 237, 185, 218, 94, 21, 70, 87, 167, 141, 157, 132, 144,
216, 171, 0, 140, 188, 211, 10, 247, 228, 88, 5, 184, 179, 69, 6, 208, 44, 30, 143, 202, 63, 15, 2, 193, 175, 189,
3, 1, 19, 138, 107, 58, 145, 17, 65, 79, 103, 220, 234, 151, 242, 207, 206, 240, 180, 230, 115, 150, 172, 116, 34,
231, 173, 53, 133, 226, 249, 55, 232, 28, 117, 223, 110, 71, 241, 26, 113, 29, 41, 197, 137, 111, 183, 98, 14, 170,
24,190, 27, 252, 86, 62, 75, 198, 210, 121, 32, 154, 219, 192, 254, 120, 205, 90, 244, 31, 221, 168, 51, 136, 7,
199, 49, 177, 18, 16, 89, 39, 128, 236, 95, 96, 81, 127, 169, 25, 181,74, 13, 45, 229, 122, 159, 147, 201, 156,
239, 160, 224, 59, 77, 174, 42, 245, 176, 200, 235, 187, 60, 131, 83, 153, 97, 23, 43, 4, 126, 186, 119, 214, 38,
225, 105, 20, 99, 85, 33,12, 125]
HW_byte = [0, 1, 1, 2, 1, 2, 2, 3, 1, 2, 2, 3, 2, 3, 3, 4, 1, 2, 2, 3, 2, 3, 3, 4, 2, 3, 3, 4, 3, 4, 4, 5, 1, 2, 2,
3, 2, 3, 3, 4, 2, 3, 3, 4, 3, 4, 4, 5, 2, 3, 3, 4, 3, 4, 4, 5, 3, 4, 4, 5, 4, 5, 5, 6, 1, 2, 2, 3, 2, 3,
3, 4, 2, 3, 3, 4, 3, 4, 4, 5, 2, 3, 3, 4, 3, 4, 4, 5, 3, 4, 4, 5, 4, 5, 5, 6, 2, 3, 3, 4, 3, 4, 4, 5, 3,
4, 4, 5, 4, 5, 5, 6, 3, 4, 4, 5, 4, 5, 5, 6, 4, 5, 5, 6, 5, 6, 6, 7, 1, 2, 2, 3, 2, 3, 3, 4, 2, 3, 3, 4,
3, 4, 4, 5, 2, 3, 3, 4, 3, 4, 4, 5, 3, 4, 4, 5, 4, 5, 5, 6, 2, 3, 3, 4, 3, 4, 4, 5, 3, 4, 4, 5, 4, 5, 5,
6, 3, 4, 4, 5, 4, 5, 5, 6, 4, 5, 5, 6, 5, 6, 6, 7, 2, 3, 3, 4, 3, 4, 4, 5, 3, 4, 4, 5, 4, 5, 5, 6, 3, 4,
4, 5, 4, 5, 5, 6, 4, 5, 5, 6, 5, 6, 6, 7, 3, 4, 4, 5, 4, 5, 5, 6, 4, 5, 5, 6, 5, 6, 6, 7, 4, 5, 5, 6, 5,
6, 6, 7, 5, 6, 6, 7, 6, 7, 7, 8]
### To train a network
def train(epoch, model, freeze_BN = False):
"""
- epoch : the current epoch
- model : the current model
- freeze_BN : whether to freeze batch normalization layers
"""
if freeze_BN:
model.eval() # enter eval mode to freeze batch normalization layers
else:
model.train() # enter training mode
# Instantiate the Iterator
iter_source = iter(source_train_loader)
# get the number of batches
num_iter = len(source_train_loader)
clf_criterion = nn.CrossEntropyLoss()
# train on each batch of data
for i in range(1, num_iter+1):
source_data, source_label = iter_source.next()
if cuda:
source_data, source_label = source_data.cuda(), source_label.cuda()
source_data, source_label = Variable(source_data), Variable(source_label)
optimizer.zero_grad()
source_preds = model(source_data)
preds = source_preds.data.max(1, keepdim=True)[1]
correct_batch = preds.eq(source_label.data.view_as(preds)).sum()
loss = clf_criterion(source_preds, source_label)
# optimzie the cross-entropy loss
loss.backward()
optimizer.step()
if i % log_interval == 0:
print('Train Epoch {}: [{}/{} ({:.0f}%)]\tLoss: {:.6f}\tAcc: {:.6f}%'.format(
epoch, i * len(source_data), len(source_train_loader) * batch_size,
100. * i / len(source_train_loader), loss.data, float(correct_batch) * 100. /batch_size))
### validation
def validation(model):
# enter evaluation mode
model.eval()
valid_loss = 0
# the number of correct prediction
correct_valid = 0
clf_criterion = nn.CrossEntropyLoss()
for data, label in source_valid_loader:
if cuda:
data, label = data.cuda(), label.cuda()
data, label = Variable(data), Variable(label)
valid_preds = model(data)
# sum up batch loss
valid_loss += clf_criterion(valid_preds, label)
# get the index of the max probability
pred = valid_preds.data.max(1)[1]
# get the number of correct prediction
correct_valid += pred.eq(label.data.view_as(pred)).cpu().sum()
valid_loss /= len(source_valid_loader)
valid_acc = 100. * correct_valid / len(source_valid_loader.dataset)
print('Validation: loss: {:.4f}, accuracy: {}/{} ({:.6f}%)'.format(
valid_loss.data, correct_valid, len(source_valid_loader.dataset),
valid_acc))
return valid_loss, valid_acc
### test/attack
def test(model, device_id, disp_GE=True, model_flag='pretrained'):
"""
- model : the current model
- device_id : id of the tested device
- disp_GE : whether to attack/calculate guessing entropy (GE)
- model_flag : a string for naming GE result
"""
# enter evaluation mode
model.eval()
test_loss = 0
# the number of correct prediction
correct = 0
epoch = 0
clf_criterion = nn.CrossEntropyLoss()
if device_id == source_device_id: # attack on the source domain
test_num = source_test_num
test_loader = source_test_loader
real_key = real_key_01
else: # attack on the target domain
test_num = target_test_num
test_loader = target_test_loader
real_key = real_key_02
# Initialize the prediction and label lists(tensors)
predlist=torch.zeros(0,dtype=torch.long, device='cpu')
lbllist=torch.zeros(0,dtype=torch.long, device='cpu')
test_preds_all = torch.zeros((test_num, class_num), dtype=torch.float, device='cpu')
for data, label in test_loader:
if cuda:
data, label = data.cuda(), label.cuda()
data, label = Variable(data), Variable(label)
test_preds = model(data)
# sum up batch loss
test_loss += clf_criterion(test_preds, label)
# get the index of the max probability
pred = test_preds.data.max(1)[1]
# get the softmax results for attack/showing guessing entropy
softmax = nn.Softmax(dim=1)
test_preds_all[epoch*batch_size:(epoch+1)*batch_size, :] =softmax(test_preds)
# get the predictions (predlist) and real labels (lbllist) for showing confusion matrix
predlist=torch.cat([predlist,pred.view(-1).cpu()])
lbllist=torch.cat([lbllist,label.view(-1).cpu()])
# get the number of correct prediction
correct += pred.eq(label.data.view_as(pred)).cpu().sum()
epoch += 1
test_loss /= len(test_loader)
print('Target test loss: {:.4f}, Target test accuracy: {}/{} ({:.2f}%)\n'.format(
test_loss.data, correct, len(test_loader.dataset),
100. * correct / len(test_loader.dataset)))
# get the confusion matrix
confusion_mat = confusion_matrix(lbllist.numpy(), predlist.numpy())
# show the confusion matrix
plot_sonfusion_matrix(confusion_mat, classes = range(class_num))
# show the guessing entropy and success rate
if disp_GE:
plot_guessing_entropy(test_preds_all.numpy(), real_key, device_id, model_flag)
### fine-tune a pre-trained model
def CDP_train(epoch, model):
"""
- epoch : the current epoch
- model : the current model
"""
# enter evaluation mode to freeze the BN and dropout (if have) layer when fine-tuning
model.eval()
# Instantiate the Iterator for source tprofiling traces
iter_source = iter(source_train_loader)
# Instantiate the Iterator for target traces
iter_target = iter(target_finetune_loader)
num_iter_target = len(target_finetune_loader)
finetune_trace_all = torch.zeros((num_iter_target, batch_size, 1, trace_length))
for i in range(num_iter_target):
finetune_trace_all[i,:,:,:], _ = iter_target.next()
# get the number of batches
num_iter = len(source_train_loader)
clf_criterion = nn.CrossEntropyLoss()
# train on each batch of data
for i in range(1, num_iter+1):
# get traces and labels for source domain
source_data, source_label = iter_source.next()
# get traces for target domain
target_data = finetune_trace_all[(i-1)%num_iter_target,:,:,:]
if cuda:
source_data, source_label = source_data.cuda(), source_label.cuda()
target_data = target_data.cuda()
source_data, source_label = Variable(source_data), Variable(source_label)
target_data = Variable(target_data)
optimizer.zero_grad()
# get predictions and MMD loss
source_preds, mmd_loss = model(source_data, target_data)
preds = source_preds.data.max(1, keepdim=True)[1]
# get classification loss on source doamin
clf_loss = clf_criterion(source_preds, source_label)
# the total loss function
loss = clf_loss + lambda_*mmd_loss
# optimzie the total loss
loss.backward()
optimizer.step()
if i % log_interval == 0:
print('Train Epoch {}: [{}/{} ({:.0f}%)]\ttotal_loss: {:.6f}\tclf_loss: {:.6f}\tmmd_loss: {:.6f}'.format(
epoch, i * len(source_data), len(source_train_loader) * batch_size,
100. * i / len(source_train_loader), loss.data, clf_loss.data, mmd_loss.data))
### Validation for fine-tuning phase
def CDP_validation(model):
# enter evaluation mode
clf_criterion = nn.CrossEntropyLoss()
model.eval()
# Instantiate the Iterator for source validation traces
iter_source = iter(source_valid_loader)
# Instantiate the Iterator for target traces
iter_target = iter(target_finetune_loader)
num_iter_target = len(target_finetune_loader)
finetune_trace_all = torch.zeros((num_iter_target, batch_size, 1, trace_length))
for i in range(num_iter_target):
finetune_trace_all[i,:,:,:], _ = iter_target.next()
# get the number of batches
num_iter = len(source_valid_loader)
# the classification loss
total_clf_loss = 0
# the MMD loss
total_mmd_loss = 0
# the total loss
total_loss = 0
# the number of correct prediction
correct = 0
for i in range(1, num_iter+1):
# get traces and labels for source domain
source_data, source_label = iter_source.next()
# get traces for target domain
target_data = finetune_trace_all[(i-1)%num_iter_target,:,:,:]
if cuda:
source_data, source_label = source_data.cuda(), source_label.cuda()
target_data = target_data.cuda()
source_data, source_label = Variable(source_data), Variable(source_label)
target_data = Variable(target_data)
valid_preds, mmd_loss = model(source_data, target_data)
clf_loss = clf_criterion(valid_preds, source_label)
# sum up batch loss
loss = clf_loss + lambda_*mmd_loss
total_clf_loss += clf_loss
total_mmd_loss += mmd_loss
total_loss += loss
# get the index of the max probability
pred = valid_preds.data.max(1)[1]
correct += pred.eq(source_label.data.view_as(pred)).cpu().sum()
total_loss /= len(source_valid_loader)
total_clf_loss /= len(source_valid_loader)
total_mmd_loss /= len(source_valid_loader)
print('Validation: total_loss: {:.4f}, clf_loss: {:.4f}, mmd_loss: {:.4f}, accuracy: {}/{} ({:.2f}%)'.format(
total_loss.data, total_clf_loss, total_mmd_loss, correct, len(source_valid_loader.dataset),
100. * correct / len(source_valid_loader.dataset)))
return total_loss
### kernel function
def guassian_kernel(source, target, kernel_mul=2.0, kernel_num=5, fix_sigma=None):
"""
- source : source data
- target : target data
- kernel_mul : multiplicative step of bandwidth (sigma)
- kernel_num : the number of guassian kernels
- fix_sigma : use a fix value of bandwidth
"""
n_samples = int(source.size()[0])+int(target.size()[0])
total = torch.cat([source, target], dim=0)
total0 = total.unsqueeze(0).expand(int(total.size(0)), \
int(total.size(0)), \
int(total.size(1)))
total1 = total.unsqueeze(1).expand(int(total.size(0)), \
int(total.size(0)), \
int(total.size(1)))
# |x-y|
L2_distance = ((total0-total1)**2).sum(2)
# bandwidth
if fix_sigma:
bandwidth = fix_sigma
else:
bandwidth = torch.sum(L2_distance.data) / (n_samples**2-n_samples)
# take the current bandwidth as the median value, and get a list of bandwidths (for example, when bandwidth is 1, we get [0.25,0.5,1,2,4]).
bandwidth /= kernel_mul ** (kernel_num // 2)
bandwidth_list = [bandwidth * (kernel_mul**i) for i in range(kernel_num)]
#exp(-|x-y|/bandwidth)
kernel_val = [torch.exp(-L2_distance / bandwidth_temp) for \
bandwidth_temp in bandwidth_list]
# return the final kernel matrix
return sum(kernel_val)
### MMD loss function based on guassian kernels
def mmd_rbf(source, target, kernel_mul=2.0, kernel_num=5, fix_sigma=None):
"""
- source : source data
- target : target data
- kernel_mul : multiplicative step of bandwidth (sigma)
- kernel_num : the number of guassian kernels
- fix_sigma : use a fix value of bandwidth
"""
loss = 0.0
batch_size = int(source.size()[0])
kernels = guassian_kernel(source, target,kernel_mul=kernel_mul,kernel_num=kernel_num, fix_sigma=fix_sigma)
XX = kernels[:batch_size, :batch_size] # Source<->Source
YY = kernels[batch_size:, batch_size:] # Target<->Target
XY = kernels[:batch_size, batch_size:] # Source<->Target
YX = kernels[batch_size:, :batch_size] # Target<->Source
loss = torch.mean(XX + YY - XY -YX)
return loss
### show the guessing entropy and success rate
def plot_guessing_entropy(preds, real_key, device_id, model_flag):
"""
- preds : the probability for each class (n*256 for a byte, n*9 for Hamming weight)
- real_key : the key of the target device
- device_id : id of the target device
- model_flag : a string for naming GE result
"""
# GE/SR is averaged over 100 attacks
num_averaged = 100
# max trace num for attack
trace_num_max = 5000
# the step trace num increases
step = 1
if trace_num_max > 400 and trace_num_max < 1000:
step = 2
if trace_num_max >= 1000 and trace_num_max < 5000:
step = 4
if trace_num_max >= 5000 and trace_num_max < 10000:
step = 5
guessing_entropy = np.zeros((num_averaged, int(trace_num_max/step)))
success_flag = np.zeros((num_averaged, int(trace_num_max/step)))
if device_id == target_device_id: # attack on the target domain
ciphertext = ciphertexts_target
elif device_id == source_device_id: # attack on the source domain
ciphertext = ciphertexts_source
# try to attack multiples times for average
for time in range(num_averaged):
# select the attack traces randomly
random_index = list(range(ciphertext.shape[0]))
random.shuffle(random_index)
random_index = random_index[0:trace_num_max]
# initialize score matrix
score_mat = np.zeros((trace_num_max, 256))
for key_guess in range(0, 256):
for i in range(0, trace_num_max):
temp = int(ciphertext[random_index[i], 1]) ^ key_guess
initialState = InvSbox[temp]
media_value = initialState ^ int(ciphertext[random_index[i], 5])
if labeling_method == 'identity':
label = media_value
elif labeling_method == 'hw':
label = HW_byte[media_value]
score_mat[i, key_guess] = preds[random_index[i], label]
score_mat = np.log(score_mat+1e-40)
for i in range(0, trace_num_max, step):
log_likelihood = np.sum(score_mat[0:i+1,:], axis=0)
ranked = np.argsort(log_likelihood)[::-1]
guessing_entropy[time,int(i/step)] = list(ranked).index(real_key)
if list(ranked).index(real_key) == 0:
success_flag[time, int(i/step)] = 1
guessing_entropy = np.mean(guessing_entropy,axis=0)
plt.figure(figsize=(12,4))
plt.subplot(1, 2, 1)
x = range(0, trace_num_max, step)
p1, = plt.plot(x, guessing_entropy[0:int(trace_num_max/step)],color='red')
plt.xlabel('Number of trace')
plt.ylabel('Guessing entropy')
#np.save('./results/entropy_'+ labeling_method + '_{}_to_{}_'.format(source_device_id, device_id) + model_flag, guessing_entropy)
plt.subplot(1, 2, 2)
success_flag = np.sum(success_flag, axis=0)
success_rate = success_flag/num_averaged
p2, = plt.plot(x, success_rate[0:int(trace_num_max/step)], color='red')
plt.xlabel('Number of trace')
plt.ylabel('Success rate')
plt.show()
#np.save('./results/success_rate_' + labeling_method + '_{}_to_{}_'.format(source_device_id, device_id) + model_flag, success_rate)
### show the confusion matrix
def plot_sonfusion_matrix(cm, classes, normalize=False, title='Confusion matrix',cmap=plt.cm.Blues):
plt.imshow(cm, interpolation='nearest', cmap=cmap)
plt.title(title)
plt.colorbar()
plt.ylim((len(classes)-0.5, -0.5))
plt.tight_layout()
plt.ylabel('True label')
plt.xlabel('Predict label')
plt.show()
```
# Setups
```
source_device_id = 1
target_device_id = 2
# roundkeys of the three devices are : 0x21, 0xCD, 0x8F
real_key_01 = 0x21 # key of the source domain
real_key_02 = 0xCD # key of the target domain
lambda_ = 0.05 # Penalty coefficient
labeling_method = 'identity' # labeling of trace
preprocess = 'horizontal_standardization' # preprocess method
batch_size = 200
total_epoch = 200
finetune_epoch = 15 # epoch number for fine-tuning
lr = 0.001 # learning rate
log_interval = 50 # epoch interval to log training information
train_num = 85000
valid_num = 5000
source_test_num = 9900
target_finetune_num = 200
target_test_num = 9400
trace_offset = 0
trace_length = 1000
source_file_path = './Data/device1/'
target_file_path = './Data/device2/'
no_cuda =False
cuda = not no_cuda and torch.cuda.is_available()
seed = 8
torch.manual_seed(seed)
if cuda:
torch.cuda.manual_seed(seed)
if labeling_method == 'identity':
class_num = 256
elif labeling_method == 'hw':
class_num = 9
# to load traces and labels
X_train_source = np.load(source_file_path + 'X_train.npy')
Y_train_source = np.load(source_file_path + 'Y_train.npy')
X_attack_source = np.load(source_file_path + 'X_attack.npy')
Y_attack_source = np.load(source_file_path + 'Y_attack.npy')
X_attack_target = np.load(target_file_path + 'X_attack.npy')
Y_attack_target = np.load(target_file_path + 'Y_attack.npy')
# to load ciphertexts
ciphertexts_source = np.load(source_file_path + 'ciphertexts_attack.npy')
ciphertexts_target = np.load(target_file_path + 'ciphertexts_attack.npy')
ciphertexts_target = ciphertexts_target[target_finetune_num:target_finetune_num+target_test_num]
# preprocess of traces
if preprocess == 'horizontal_standardization':
mn = np.repeat(np.mean(X_train_source, axis=1, keepdims=True), X_train_source.shape[1], axis=1)
std = np.repeat(np.std(X_train_source, axis=1, keepdims=True), X_train_source.shape[1], axis=1)
X_train_source = (X_train_source - mn)/std
mn = np.repeat(np.mean(X_attack_source, axis=1, keepdims=True), X_attack_source.shape[1], axis=1)
std = np.repeat(np.std(X_attack_source, axis=1, keepdims=True), X_attack_source.shape[1], axis=1)
X_attack_source = (X_attack_source - mn)/std
mn = np.repeat(np.mean(X_attack_target, axis=1, keepdims=True), X_attack_target.shape[1], axis=1)
std = np.repeat(np.std(X_attack_target, axis=1, keepdims=True), X_attack_target.shape[1], axis=1)
X_attack_target = (X_attack_target - mn)/std
elif preprocess == 'horizontal_scaling':
scaler = preprocessing.MinMaxScaler(feature_range=(-1, 1)).fit(X_train_source.T)
X_train_source = scaler.transform(X_train_source.T).T
scaler = preprocessing.MinMaxScaler(feature_range=(-1, 1)).fit(X_attack_source.T)
X_attack_source = scaler.transform(X_attack_source.T).T
scaler = preprocessing.MinMaxScaler(feature_range=(-1, 1)).fit(X_attack_target.T)
X_attack_target = scaler.transform(X_attack_target.T).T
# parameters of data loader
kwargs_source_train = {
'trs_file': X_train_source[0:train_num,:],
'label_file': Y_train_source[0:train_num],
'trace_num':train_num,
'trace_offset':trace_offset,
'trace_length':trace_length,
}
kwargs_source_valid = {
'trs_file': X_train_source[train_num:train_num+valid_num,:],
'label_file': Y_train_source[train_num:train_num+valid_num],
'trace_num':valid_num,
'trace_offset':trace_offset,
'trace_length':trace_length,
}
kwargs_source_test = {
'trs_file': X_attack_source,
'label_file': Y_attack_source,
'trace_num':source_test_num,
'trace_offset':trace_offset,
'trace_length':trace_length,
}
kwargs_target_finetune = {
'trs_file': X_attack_target[0:target_finetune_num,:],
'label_file': Y_attack_target[0:target_finetune_num],
'trace_num':target_finetune_num,
'trace_offset':trace_offset,
'trace_length':trace_length,
}
kwargs_target = {
'trs_file': X_attack_target[target_finetune_num:target_finetune_num+target_test_num, :],
'label_file': Y_attack_target[target_finetune_num:target_finetune_num+target_test_num],
'trace_num':target_test_num,
'trace_offset':trace_offset,
'trace_length':trace_length,
}
source_train_loader = load_training(batch_size, kwargs_source_train)
source_valid_loader = load_training(batch_size, kwargs_source_valid)
source_test_loader = load_testing(batch_size, kwargs_source_test)
target_finetune_loader = load_training(batch_size, kwargs_target_finetune)
target_test_loader = load_testing(batch_size, kwargs_target)
print('Load data complete!')
```
# Model
```
### the pre-trained model
class Net(nn.Module):
def __init__(self, num_classes=class_num):
super(Net, self).__init__()
# the encoder part
self.features = nn.Sequential(
nn.Conv1d(1, 8, kernel_size=1),
nn.SELU(),
nn.BatchNorm1d(8),
nn.AvgPool1d(kernel_size=2, stride=2),
nn.Conv1d(8, 16, kernel_size=11),
nn.SELU(),
nn.BatchNorm1d(16),
nn.AvgPool1d(kernel_size=11, stride=11),
nn.Conv1d(16, 32, kernel_size=2),
nn.SELU(),
nn.BatchNorm1d(32),
nn.AvgPool1d(kernel_size=3, stride=3),
nn.Flatten()
)
# the fully-connected layer 1
self.classifier_1 = nn.Sequential(
nn.Linear(448, 2),
nn.SELU(),
)
# the output layer
self.final_classifier = nn.Sequential(
nn.Linear(2, num_classes)
)
# how the network runs
def forward(self, input):
x = self.features(input)
x = x.view(x.size(0), -1)
x = self.classifier_1(x)
output = self.final_classifier(x)
return output
### the fine-tuning model
class CDP_Net(nn.Module):
def __init__(self, num_classes=class_num):
super(CDP_Net, self).__init__()
# the encoder part
self.features = nn.Sequential(
nn.Conv1d(1, 8, kernel_size=1),
nn.SELU(),
nn.BatchNorm1d(8),
nn.AvgPool1d(kernel_size=2, stride=2),
nn.Conv1d(8, 16, kernel_size=11),
nn.SELU(),
nn.BatchNorm1d(16),
nn.AvgPool1d(kernel_size=11, stride=11),
nn.Conv1d(16, 32, kernel_size=2),
nn.SELU(),
nn.BatchNorm1d(32),
nn.AvgPool1d(kernel_size=3, stride=3),
nn.Flatten()
)
# the fully-connected layer 1
self.classifier_1 = nn.Sequential(
nn.Linear(448, 2),
nn.SELU(),
)
# the output layer
self.final_classifier = nn.Sequential(
nn.Linear(2, num_classes)
)
# how the network runs
def forward(self, source, target):
mmd_loss = 0
#source data flow
source = self.features(source)
source_0 = source.view(source.size(0), -1)
source_1 = self.classifier_1(source_0)
#target data flow
target = self.features(target)
target = target.view(target.size(0), -1)
mmd_loss += mmd_rbf(source_0, target)
target = self.classifier_1(target)
mmd_loss += mmd_rbf(source_1, target)
result = self.final_classifier(source_1)
return result, mmd_loss
```
## Performance of the pre-trained model
```
# create a network
model = Net(num_classes=class_num)
print('Construct model complete')
if cuda:
model.cuda()
# load the pre-trained network
checkpoint = torch.load('./models/pre-trained_device{}.pth'.format(source_device_id))
pretrained_dict = checkpoint['model_state_dict']
model_dict = pretrained_dict
model.load_state_dict(model_dict)
# evaluate the pre-trained model on source and target domain
with torch.no_grad():
print('Result on source device:')
test(model, source_device_id, model_flag='pretrained_source')
print('Result on target device:')
test(model, target_device_id, model_flag='pretrained_target')
```
## Cross-Device Profiling: fine-tune 15 epochs
```
# create a network
CDP_model = CDP_Net(num_classes=class_num)
print('Construct model complete')
if cuda:
CDP_model.cuda()
# initialize a big enough loss number
min_loss = 1000
# load the pre-trained model
checkpoint = torch.load('./models/pre-trained_device{}.pth'.format(source_device_id))
pretrained_dict = checkpoint['model_state_dict']
CDP_model.load_state_dict(pretrained_dict)
optimizer = optim.Adam([
{'params': CDP_model.features.parameters()},
{'params': CDP_model.classifier_1.parameters()},
{'params': CDP_model.final_classifier.parameters()}
], lr=lr)
# restore the optimizer state
optimizer.load_state_dict(checkpoint['optimizer_state_dict'])
for epoch in range(1, finetune_epoch + 1):
print(f'Train Epoch {epoch}:')
CDP_train(epoch, CDP_model)
with torch.no_grad():
valid_loss = CDP_validation(CDP_model)
# save the model that achieves the lowest validation loss
if valid_loss < min_loss:
min_loss = valid_loss
torch.save({
'epoch': epoch,
'model_state_dict': CDP_model.state_dict(),
'optimizer_state_dict': optimizer.state_dict()
}, './models/best_valid_loss_finetuned_device{}_to_{}.pth'.format(source_device_id, target_device_id))
torch.save({
'epoch': epoch,
'model_state_dict': CDP_model.state_dict(),
'optimizer_state_dict': optimizer.state_dict()
}, './models/last_valid_loss_finetuned_device{}_to_{}.pth'.format(source_device_id, target_device_id))
```
## Performance of the fine-tuned model
```
# create a network
model = Net(num_classes=class_num)
print('Construct model complete')
if cuda:
model.cuda()
# load the fine-tuned model
checkpoint = torch.load('./models/best_valid_loss_finetuned_device{}_to_{}.pth'.format(source_device_id, target_device_id))
finetuned_dict = checkpoint['model_state_dict']
model.load_state_dict(finetuned_dict)
print('Results after fine-tuning:')
# evaluate the fine-tuned model on source and target domain
with torch.no_grad():
print('Result on source device:')
test(model, source_device_id, model_flag='finetuned_source')
print('Result on target device:')
test(model, target_device_id, model_flag='finetuned_target')
```
|
github_jupyter
|
# Facial Keypoint Detection
This project will be all about defining and training a convolutional neural network to perform facial keypoint detection, and using computer vision techniques to transform images of faces. The first step in any challenge like this will be to load and visualize the data you'll be working with.
Let's take a look at some examples of images and corresponding facial keypoints.
<img src='images/key_pts_example.png' width=50% height=50%/>
Facial keypoints (also called facial landmarks) are the small magenta dots shown on each of the faces in the image above. In each training and test image, there is a single face and **68 keypoints, with coordinates (x, y), for that face**. These keypoints mark important areas of the face: the eyes, corners of the mouth, the nose, etc. These keypoints are relevant for a variety of tasks, such as face filters, emotion recognition, pose recognition, and so on. Here they are, numbered, and you can see that specific ranges of points match different portions of the face.
<img src='images/landmarks_numbered.jpg' width=30% height=30%/>
---
## Load and Visualize Data
The first step in working with any dataset is to become familiar with your data; you'll need to load in the images of faces and their keypoints and visualize them! This set of image data has been extracted from the [YouTube Faces Dataset](https://www.cs.tau.ac.il/~wolf/ytfaces/), which includes videos of people in YouTube videos. These videos have been fed through some processing steps and turned into sets of image frames containing one face and the associated keypoints.
#### Training and Testing Data
This facial keypoints dataset consists of 5770 color images. All of these images are separated into either a training or a test set of data.
* 3462 of these images are training images, for you to use as you create a model to predict keypoints.
* 2308 are test images, which will be used to test the accuracy of your model.
The information about the images and keypoints in this dataset are summarized in CSV files, which we can read in using `pandas`. Let's read the training CSV and get the annotations in an (N, 2) array where N is the number of keypoints and 2 is the dimension of the keypoint coordinates (x, y).
---
```
# import the required libraries
import glob
import os
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
import cv2
key_pts_frame = pd.read_csv('data/training_frames_keypoints.csv')
n = 0
image_name = key_pts_frame.iloc[n, 0]
key_pts = key_pts_frame.iloc[n, 1:].as_matrix()
key_pts = key_pts.astype('float').reshape(-1, 2)
print('Image name: ', image_name)
print('Landmarks shape: ', key_pts.shape)
print('First 4 key pts: {}'.format(key_pts[:4]))
# print out some stats about the data
print('Number of images: ', key_pts_frame.shape[0])
```
## Look at some images
Below, is a function `show_keypoints` that takes in an image and keypoints and displays them. As you look at this data, **note that these images are not all of the same size**, and neither are the faces! To eventually train a neural network on these images, we'll need to standardize their shape.
```
def show_keypoints(image, key_pts):
"""Show image with keypoints"""
plt.imshow(image)
plt.scatter(key_pts[:, 0], key_pts[:, 1], s=20, marker='.', c='m')
# Display a few different types of images by changing the index n
# select an image by index in our data frame
n = 0
image_name = key_pts_frame.iloc[n, 0]
key_pts = key_pts_frame.iloc[n, 1:].as_matrix()
key_pts = key_pts.astype('float').reshape(-1, 2)
plt.figure(figsize=(5, 5))
image_show = mpimg.imread(os.path.join('data/training/', image_name));
show_keypoints(image_show, key_pts)
plt.show()
print("image shape: ", image_show.shape)
```
## Dataset class and Transformations
To prepare our data for training, we'll be using PyTorch's Dataset class. Much of this this code is a modified version of what can be found in the [PyTorch data loading tutorial](http://pytorch.org/tutorials/beginner/data_loading_tutorial.html).
#### Dataset class
``torch.utils.data.Dataset`` is an abstract class representing a
dataset. This class will allow us to load batches of image/keypoint data, and uniformly apply transformations to our data, such as rescaling and normalizing images for training a neural network.
Your custom dataset should inherit ``Dataset`` and override the following
methods:
- ``__len__`` so that ``len(dataset)`` returns the size of the dataset.
- ``__getitem__`` to support the indexing such that ``dataset[i]`` can
be used to get the i-th sample of image/keypoint data.
Let's create a dataset class for our face keypoints dataset. We will
read the CSV file in ``__init__`` but leave the reading of images to
``__getitem__``. This is memory efficient because all the images are not
stored in the memory at once but read as required.
A sample of our dataset will be a dictionary
``{'image': image, 'keypoints': key_pts}``. Our dataset will take an
optional argument ``transform`` so that any required processing can be
applied on the sample. We will see the usefulness of ``transform`` in the
next section.
```
from torch.utils.data import Dataset, DataLoader
class FacialKeypointsDataset(Dataset):
"""Face Landmarks dataset."""
def __init__(self, csv_file, root_dir, transform=None):
"""
Args:
csv_file (string): Path to the csv file with annotations.
root_dir (string): Directory with all the images.
transform (callable, optional): Optional transform to be applied
on a sample.
"""
self.key_pts_frame = pd.read_csv(csv_file)
self.root_dir = root_dir
self.transform = transform
def __len__(self):
return len(self.key_pts_frame)
def __getitem__(self, idx):
image_name = os.path.join(self.root_dir,
self.key_pts_frame.iloc[idx, 0])
image = mpimg.imread(image_name)
# if image has an alpha color channel, get rid of it
if(image.shape[2] == 4):
image = image[:,:,0:3]
key_pts = self.key_pts_frame.iloc[idx, 1:].as_matrix()
key_pts = key_pts.astype('float').reshape(-1, 2)
sample = {'image': image, 'keypoints': key_pts}
if self.transform:
sample = self.transform(sample)
return sample
```
Now that we've defined this class, let's instantiate the dataset and display some images.
```
# Construct the dataset
face_dataset = FacialKeypointsDataset(csv_file='data/training_frames_keypoints.csv',
root_dir='data/training/')
# print some stats about the dataset
print('Length of dataset: ', len(face_dataset))
# Display a few of the images from the dataset
num_to_display = 3
for i in range(num_to_display):
# define the size of images
fig = plt.figure(figsize=(20,10))
# randomly select a sample
rand_i = np.random.randint(0, len(face_dataset))
sample = face_dataset[rand_i]
# print the shape of the image and keypoints
print(i, sample['image'].shape, sample['keypoints'].shape)
ax = plt.subplot(1, num_to_display, i + 1)
ax.set_title('Sample #{}'.format(i))
# Using the same display function, defined earlier
show_keypoints(sample['image'], sample['keypoints'])
```
## Transforms
Now, the images above are not of the same size, and neural networks often expect images that are standardized; a fixed size, with a normalized range for color ranges and coordinates, and (for PyTorch) converted from numpy lists and arrays to Tensors.
Therefore, we will need to write some pre-processing code.
Let's create four transforms:
- ``Normalize``: to convert a color image to grayscale values with a range of [0,1] and normalize the keypoints to be in a range of about [-1, 1]
- ``Rescale``: to rescale an image to a desired size.
- ``RandomCrop``: to crop an image randomly.
- ``ToTensor``: to convert numpy images to torch images.
We will write them as callable classes instead of simple functions so
that parameters of the transform need not be passed everytime it's
called. For this, we just need to implement ``__call__`` method and
(if we require parameters to be passed in), the ``__init__`` method.
We can then use a transform like this:
tx = Transform(params)
transformed_sample = tx(sample)
Observe below how these transforms are generally applied to both the image and its keypoints.
```
import torch
from torchvision import transforms, utils
# tranforms
class Normalize(object):
"""Convert a color image to grayscale and normalize the color range to [0,1]."""
def __call__(self, sample):
image, key_pts = sample['image'], sample['keypoints']
image_copy = np.copy(image)
key_pts_copy = np.copy(key_pts)
# convert image to grayscale
image_copy = cv2.cvtColor(image, cv2.COLOR_RGB2GRAY)
# scale color range from [0, 255] to [0, 1]
image_copy= image_copy/255.0
# scale keypoints to be centered around 0 with a range of [-1, 1]
# mean = 100, sqrt = 50, so, pts should be (pts - 100)/50
key_pts_copy = (key_pts_copy - 100)/50.0
return {'image': image_copy, 'keypoints': key_pts_copy}
class Rescale(object):
"""Rescale the image in a sample to a given size.
Args:
output_size (tuple or int): Desired output size. If tuple, output is
matched to output_size. If int, smaller of image edges is matched
to output_size keeping aspect ratio the same.
"""
def __init__(self, output_size):
assert isinstance(output_size, (int, tuple))
self.output_size = output_size
def __call__(self, sample):
image, key_pts = sample['image'], sample['keypoints']
h, w = image.shape[:2]
if isinstance(self.output_size, int):
if h > w:
new_h, new_w = self.output_size * h / w, self.output_size
else:
new_h, new_w = self.output_size, self.output_size * w / h
else:
new_h, new_w = self.output_size
new_h, new_w = int(new_h), int(new_w)
img = cv2.resize(image, (new_w, new_h))
# scale the pts, too
key_pts = key_pts * [new_w / w, new_h / h]
return {'image': img, 'keypoints': key_pts}
class RandomCrop(object):
"""Crop randomly the image in a sample.
Args:
output_size (tuple or int): Desired output size. If int, square crop
is made.
"""
def __init__(self, output_size):
assert isinstance(output_size, (int, tuple))
if isinstance(output_size, int):
self.output_size = (output_size, output_size)
else:
assert len(output_size) == 2
self.output_size = output_size
def __call__(self, sample):
image, key_pts = sample['image'], sample['keypoints']
h, w = image.shape[:2]
new_h, new_w = self.output_size
top = np.random.randint(0, h - new_h)
left = np.random.randint(0, w - new_w)
image = image[top: top + new_h,
left: left + new_w]
key_pts = key_pts - [left, top]
return {'image': image, 'keypoints': key_pts}
class ToTensor(object):
"""Convert ndarrays in sample to Tensors."""
def __call__(self, sample):
image, key_pts = sample['image'], sample['keypoints']
# if image has no grayscale color channel, add one
if(len(image.shape) == 2):
# add that third color dim
image = image.reshape(image.shape[0], image.shape[1], 1)
# swap color axis because
# numpy image: H x W x C
# torch image: C X H X W
image = image.transpose((2, 0, 1))
return {'image': torch.from_numpy(image),
'keypoints': torch.from_numpy(key_pts)}
```
## Test out the transforms
Let's test these transforms out to make sure they behave as expected. As you look at each transform, note that, in this case, **order does matter**. For example, you cannot crop a image using a value smaller than the original image (and the orginal images vary in size!), but, if you first rescale the original image, you can then crop it to any size smaller than the rescaled size.
```
# test out some of these transforms
rescale = Rescale(100)
crop = RandomCrop(50)
composed = transforms.Compose([Rescale(250),
RandomCrop(224)])
# apply the transforms to a sample image
test_num = 500
sample = face_dataset[test_num]
fig = plt.figure()
for i, tx in enumerate([rescale, crop, composed]):
transformed_sample = tx(sample)
ax = plt.subplot(1, 3, i + 1)
plt.tight_layout()
ax.set_title(type(tx).__name__)
show_keypoints(transformed_sample['image'], transformed_sample['keypoints'])
plt.show()
```
## Create the transformed dataset
Apply the transforms in order to get grayscale images of the same shape. Verify that your transform works by printing out the shape of the resulting data (printing out a few examples should show you a consistent tensor size).
```
# define the data tranform
# order matters! i.e. rescaling should come before a smaller crop
data_transform = transforms.Compose([Rescale(250),
RandomCrop(224),
Normalize(),
ToTensor()])
# create the transformed dataset
transformed_dataset = FacialKeypointsDataset(csv_file='data/training_frames_keypoints.csv',
root_dir='data/training/',
transform=data_transform)
# print some stats about the transformed data
print('Number of images: ', len(transformed_dataset))
# make sure the sample tensors are the expected size
for i in range(5):
sample = transformed_dataset[i]
print(i, sample['image'].size(), sample['keypoints'].size())
```
## Data Iteration and Batching
Right now, we are iterating over this data using a ``for`` loop, but we are missing out on a lot of PyTorch's dataset capabilities, specifically the abilities to:
- Batch the data
- Shuffle the data
- Load the data in parallel using ``multiprocessing`` workers.
``torch.utils.data.DataLoader`` is an iterator which provides all these
features, and we'll see this in use in the *next* notebook, Notebook 2, when we load data in batches to train a neural network!
---
## Ready to Train!
Now that you've seen how to load and transform our data, you're ready to build a neural network to train on this data.
In the next notebook, you'll be tasked with creating a CNN for facial keypoint detection.
|
github_jupyter
|
# Simple Use Cases
Simulus is a discrete-event simulator in Python. This document is to demonstrate how to run simulus via a few examples. This is not a tutorial. For that, use [Simulus Tutorial](simulus-tutorial.ipynb). All the examples shown in this guide can be found under the `examples/demos` directory in the simulus source-code distribution.
It's really simple to install simulus. Assuming you have installed pip, you can simply do the following to install simulus:
```
pip install simulus
```
If you don't have administrative privilege to install packages on your machine, you can install it in the per-user managed location using:
```
pip install --user simulus
```
If all are fine at this point, you can simply import the module 'simulus' to start using the simulator.
```
import simulus
```
### Use Case #1: Direct Event Scheduling
One can schedule functions to be executed at designated simulation time. The functions in this case are called event handlers (using the discrete-event simulation terminology).
```
# %load "../examples/demos/case-1.py"
import simulus
# An event handler is a user-defined function; in this case, we take
# one positional argument 'sim', and place all keyworded arguments in
# the dictionary 'params'
def myfunc(sim, **params):
print(str(sim.now) + ": myfunc() runs with params=" + str(params))
# schedule the next event 10 seconds from now
sim.sched(myfunc, sim, **params, offset=10)
# create an anonymous simulator
sim1 = simulus.simulator()
# schedule the first event at 10 seconds
sim1.sched(myfunc, sim1, until=10, msg="hello world", value=100)
# advance simulation until 100 seconds
sim1.run(until=100)
print("simulator.run() ends at " + str(sim1.now))
# we can advance simulation for another 50 seconds
sim1.run(offset=50)
print("simulator.run() ends at " + str(sim1.now))
```
### Use Case #2: Simulation Process
A simulation process is an independent thread of execution. A process can be blocked and therefore advances its simulation time either by sleeping for some duration of time or by being blocked from synchronization primitives (such as semaphores).
```
# %load "../examples/demos/case-2.py"
import simulus
# A process for simulus is a python function with two parameters:
# the first parameter is the simulator, and the second parameter is
# the dictionary containing user-defined parameters for the process
def myproc(sim, intv, id):
print(str(sim.now) + ": myproc(%d) runs with intv=%r" % (id, intv))
while True:
# suspend the process for some time
sim.sleep(intv)
print(str(sim.now) + ": myproc(%d) resumes execution" % id)
# create an anonymous simulator
sim2 = simulus.simulator()
# start a process 100 seconds from now
sim2.process(myproc, sim2, 10, 0, offset=100)
# start another process 5 seconds from now
sim2.process(myproc, sim2, 20, 1, offset=5)
# advance simulation until 200 seconds
sim2.run(until=200)
print("simulator.run() ends at " + str(sim2.now))
sim2.run(offset=50)
print("simulator.run() ends at " + str(sim2.now))
```
### Use Case #3: Process Synchronization with Semaphores
We illustrate the use of semaphore in the context of a classic producer-consumer problem. We are simulating a single-server queue (M/M/1) here.
```
# %load "../examples/demos/case-3.py"
import simulus
from random import seed, expovariate
from statistics import mean, median, stdev
# make it repeatable
seed(12345)
# configuration of the single server queue: the mean inter-arrival
# time, and the mean service time
cfg = {"mean_iat":1, "mean_svc":0.8}
# keep the time of job arrivals, starting services, and departures
arrivals = []
starts = []
finishes = []
# the producer process waits for some random time from an
# exponential distribution, and increments the semaphore
# to represent a new item being produced, and then repeats
def producer(sim, mean_iat, sem):
while True:
iat = expovariate(1.0/mean_iat)
sim.sleep(iat)
#print("%g: job arrives (iat=%g)" % (sim.now, iat))
arrivals.append(sim.now)
sem.signal()
# the consumer process waits for the semaphore (it decrements
# the value and blocks if the value is non-positive), waits for
# some random time from another exponential distribution, and
# then repeats
def consumer(sim, mean_svc, sem):
while True:
sem.wait()
#print("%g: job starts service" % sim.now)
starts.append(sim.now)
svc = expovariate(1.0/mean_svc)
sim.sleep(svc)
#print("%g: job departs (svc=%g)" % (sim.now, svc))
finishes.append(sim.now)
# create an anonymous simulator
sim3 = simulus.simulator()
# create a semaphore with initial value of zero
sem = sim3.semaphore(0)
# start the producer and consumer processes
sim3.process(producer, sim3, cfg['mean_iat'], sem)
sim3.process(consumer, sim3, cfg['mean_svc'], sem)
# advance simulation until 100 seconds
sim3.run(until=1000)
print("simulator.run() ends at " + str(sim3.now))
# calculate and output statistics
print(f'Results: jobs=arrivals:{len(arrivals)}, starts:{len(starts)}, finishes:{len(finishes)}')
waits = [start - arrival for arrival, start in zip(arrivals, starts)]
totals = [finish - arrival for arrival, finish in zip(arrivals, finishes)]
print(f'Wait Time: mean={mean(waits):.1f}, stdev={stdev(waits):.1f}, median={median(waits):.1f}. max={max(waits):.1f}')
print(f'Total Time: mean={mean(totals):.1f}, stdev={stdev(totals):.1f}, median={median(totals):.1f}. max={max(totals):.1f}')
my_lambda = 1.0/cfg['mean_iat'] # mean arrival rate
my_mu = 1.0/cfg['mean_svc'] # mean service rate
my_rho = my_lambda/my_mu # server utilization
my_lq = my_rho*my_rho/(1-my_rho) # number in queue
my_wq = my_lq/my_lambda # wait in queue
my_w = my_wq+1/my_mu # wait in system
print(f'Theoretical Results: mean wait time = {my_wq:.1f}, mean total time = {my_w:.1f}')
```
### Use Case #4: Dynamic Processes
We continue with the previous example. At the time, rathar than using semaphores, we can achieve exactly the same results by dynamically creating processes.
```
# %load "../examples/demos/case-4.py"
import simulus
from random import seed, expovariate
from statistics import mean, median, stdev
# make it repeatable
seed(12345)
# configuration of the single server queue: the mean inter-arrival
# time, and the mean service time
cfg = {"mean_iat":1, "mean_svc":0.8}
# keep the time of job arrivals, starting services, and departures
arrivals = []
starts = []
finishes = []
# we keep the account of the number of jobs in the system (those who
# have arrived but not yet departed); this is used to indicate whether
# there's a consumer process currently running; the value is more than
# 1, we don't need to create a new consumer process
jobs_in_system = 0
# the producer process waits for some random time from an exponential
# distribution to represent a new item being produced, creates a
# consumer process when necessary to represent the item being
# consumed, and then repeats
def producer(sim, mean_iat, mean_svc):
global jobs_in_system
while True:
iat = expovariate(1.0/mean_iat)
sim.sleep(iat)
#print("%g: job arrives (iat=%g)" % (sim.now, iat))
arrivals.append(sim.now)
jobs_in_system += 1
if jobs_in_system <= 1:
sim.process(consumer, sim, mean_svc)
# the consumer process waits for the semaphore (it decrements
# the value and blocks if the value is non-positive), waits for
# some random time from another exponential distribution, and
# then repeats
def consumer(sim, mean_svc):
global jobs_in_system
while jobs_in_system > 0:
#print("%g: job starts service" % sim.now)
starts.append(sim.now)
svc = expovariate(1.0/mean_svc)
sim.sleep(svc)
#print("%g: job departs (svc=%g)" % (sim.now, svc))
finishes.append(sim.now)
jobs_in_system -= 1
# create an anonymous simulator
sim3 = simulus.simulator()
# start the producer process only
sim3.process(producer, sim3, cfg['mean_iat'], cfg['mean_svc'])
# advance simulation until 100 seconds
sim3.run(until=1000)
print("simulator.run() ends at " + str(sim3.now))
# calculate and output statistics
print(f'Results: jobs=arrival:{len(arrivals)}, starts:{len(starts)}, finishes:{len(finishes)}')
waits = [start - arrival for arrival, start in zip(arrivals, starts)]
totals = [finish - arrival for arrival, finish in zip(arrivals, finishes)]
print(f'Wait Time: mean={mean(waits):.1f}, stdev={stdev(waits):.1f}, median={median(waits):.1f}. max={max(waits):.1f}')
print(f'Total Time: mean={mean(totals):.1f}, stdev={stdev(totals):.1f}, median={median(totals):.1f}. max={max(totals):.1f}')
my_lambda = 1.0/cfg['mean_iat'] # mean arrival rate
my_mu = 1.0/cfg['mean_svc'] # mean service rate
my_rho = my_lambda/my_mu # server utilization
my_lq = my_rho*my_rho/(1-my_rho) # number in queue
my_wq = my_lq/my_lambda # wait in queue
my_w = my_wq+1/my_mu # wait in system
print(f'Theoretical Results: mean wait time = {my_wq:.1f}, mean total time = {my_w:.1f}')
```
|
github_jupyter
|
##### Copyright 2019 The TensorFlow Authors.
```
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
```
# Custom training with tf.distribute.Strategy
<table class="tfo-notebook-buttons" align="left">
<td>
<a target="_blank" href="https://www.tensorflow.org/tutorials/distribute/custom_training"><img src="https://www.tensorflow.org/images/tf_logo_32px.png" />View on TensorFlow.org</a>
</td>
<td>
<a target="_blank" href="https://colab.research.google.com/github/tensorflow/docs/blob/master/site/en/tutorials/distribute/custom_training.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
</td>
<td>
<a target="_blank" href="https://github.com/tensorflow/docs/blob/master/site/en/tutorials/distribute/custom_training.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View source on GitHub</a>
</td>
<td>
<a href="https://storage.googleapis.com/tensorflow_docs/docs/site/en/tutorials/distribute/custom_training.ipynb"><img src="https://www.tensorflow.org/images/download_logo_32px.png" />Download notebook</a>
</td>
</table>
This tutorial demonstrates how to use [`tf.distribute.Strategy`](https://www.tensorflow.org/guide/distributed_training) with custom training loops. We will train a simple CNN model on the fashion MNIST dataset. The fashion MNIST dataset contains 60000 train images of size 28 x 28 and 10000 test images of size 28 x 28.
We are using custom training loops to train our model because they give us flexibility and a greater control on training. Moreover, it is easier to debug the model and the training loop.
```
from __future__ import absolute_import, division, print_function, unicode_literals
# Import TensorFlow
try:
# %tensorflow_version only exists in Colab.
%tensorflow_version 2.x
except Exception:
pass
import tensorflow as tf
# Helper libraries
import numpy as np
import os
print(tf.__version__)
```
## Download the fashion MNIST dataset
```
fashion_mnist = tf.keras.datasets.fashion_mnist
(train_images, train_labels), (test_images, test_labels) = fashion_mnist.load_data()
# Adding a dimension to the array -> new shape == (28, 28, 1)
# We are doing this because the first layer in our model is a convolutional
# layer and it requires a 4D input (batch_size, height, width, channels).
# batch_size dimension will be added later on.
train_images = train_images[..., None]
test_images = test_images[..., None]
# Getting the images in [0, 1] range.
train_images = train_images / np.float32(255)
test_images = test_images / np.float32(255)
```
## Create a strategy to distribute the variables and the graph
How does `tf.distribute.MirroredStrategy` strategy work?
* All the variables and the model graph is replicated on the replicas.
* Input is evenly distributed across the replicas.
* Each replica calculates the loss and gradients for the input it received.
* The gradients are synced across all the replicas by summing them.
* After the sync, the same update is made to the copies of the variables on each replica.
Note: You can put all the code below inside a single scope. We are dividing it into several code cells for illustration purposes.
```
# If the list of devices is not specified in the
# `tf.distribute.MirroredStrategy` constructor, it will be auto-detected.
strategy = tf.distribute.MirroredStrategy()
print ('Number of devices: {}'.format(strategy.num_replicas_in_sync))
```
## Setup input pipeline
Export the graph and the variables to the platform-agnostic SavedModel format. After your model is saved, you can load it with or without the scope.
```
BUFFER_SIZE = len(train_images)
BATCH_SIZE_PER_REPLICA = 64
GLOBAL_BATCH_SIZE = BATCH_SIZE_PER_REPLICA * strategy.num_replicas_in_sync
EPOCHS = 10
```
Create the datasets and distribute them:
```
train_dataset = tf.data.Dataset.from_tensor_slices((train_images, train_labels)).shuffle(BUFFER_SIZE).batch(GLOBAL_BATCH_SIZE)
test_dataset = tf.data.Dataset.from_tensor_slices((test_images, test_labels)).batch(GLOBAL_BATCH_SIZE)
train_dist_dataset = strategy.experimental_distribute_dataset(train_dataset)
test_dist_dataset = strategy.experimental_distribute_dataset(test_dataset)
```
## Create the model
Create a model using `tf.keras.Sequential`. You can also use the Model Subclassing API to do this.
```
def create_model():
model = tf.keras.Sequential([
tf.keras.layers.Conv2D(32, 3, activation='relu'),
tf.keras.layers.MaxPooling2D(),
tf.keras.layers.Conv2D(64, 3, activation='relu'),
tf.keras.layers.MaxPooling2D(),
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(64, activation='relu'),
tf.keras.layers.Dense(10)
])
return model
# Create a checkpoint directory to store the checkpoints.
checkpoint_dir = './training_checkpoints'
checkpoint_prefix = os.path.join(checkpoint_dir, "ckpt")
```
## Define the loss function
Normally, on a single machine with 1 GPU/CPU, loss is divided by the number of examples in the batch of input.
*So, how should the loss be calculated when using a `tf.distribute.Strategy`?*
* For an example, let's say you have 4 GPU's and a batch size of 64. One batch of input is distributed
across the replicas (4 GPUs), each replica getting an input of size 16.
* The model on each replica does a forward pass with its respective input and calculates the loss. Now, instead of dividing the loss by the number of examples in its respective input (BATCH_SIZE_PER_REPLICA = 16), the loss should be divided by the GLOBAL_BATCH_SIZE (64).
*Why do this?*
* This needs to be done because after the gradients are calculated on each replica, they are synced across the replicas by **summing** them.
*How to do this in TensorFlow?*
* If you're writing a custom training loop, as in this tutorial, you should sum the per example losses and divide the sum by the GLOBAL_BATCH_SIZE:
`scale_loss = tf.reduce_sum(loss) * (1. / GLOBAL_BATCH_SIZE)`
or you can use `tf.nn.compute_average_loss` which takes the per example loss,
optional sample weights, and GLOBAL_BATCH_SIZE as arguments and returns the scaled loss.
* If you are using regularization losses in your model then you need to scale
the loss value by number of replicas. You can do this by using the `tf.nn.scale_regularization_loss` function.
* Using `tf.reduce_mean` is not recommended. Doing so divides the loss by actual per replica batch size which may vary step to step.
* This reduction and scaling is done automatically in keras `model.compile` and `model.fit`
* If using `tf.keras.losses` classes (as in the example below), the loss reduction needs to be explicitly specified to be one of `NONE` or `SUM`. `AUTO` and `SUM_OVER_BATCH_SIZE` are disallowed when used with `tf.distribute.Strategy`. `AUTO` is disallowed because the user should explicitly think about what reduction they want to make sure it is correct in the distributed case. `SUM_OVER_BATCH_SIZE` is disallowed because currently it would only divide by per replica batch size, and leave the dividing by number of replicas to the user, which might be easy to miss. So instead we ask the user do the reduction themselves explicitly.
```
with strategy.scope():
# Set reduction to `none` so we can do the reduction afterwards and divide by
# global batch size.
loss_object = tf.keras.losses.SparseCategoricalCrossentropy(
from_logits=True,
reduction=tf.keras.losses.Reduction.NONE)
def compute_loss(labels, predictions):
per_example_loss = loss_object(labels, predictions)
return tf.nn.compute_average_loss(per_example_loss, global_batch_size=GLOBAL_BATCH_SIZE)
```
## Define the metrics to track loss and accuracy
These metrics track the test loss and training and test accuracy. You can use `.result()` to get the accumulated statistics at any time.
```
with strategy.scope():
test_loss = tf.keras.metrics.Mean(name='test_loss')
train_accuracy = tf.keras.metrics.SparseCategoricalAccuracy(
name='train_accuracy')
test_accuracy = tf.keras.metrics.SparseCategoricalAccuracy(
name='test_accuracy')
```
## Training loop
```
# model and optimizer must be created under `strategy.scope`.
with strategy.scope():
model = create_model()
optimizer = tf.keras.optimizers.Adam()
checkpoint = tf.train.Checkpoint(optimizer=optimizer, model=model)
with strategy.scope():
def train_step(inputs):
images, labels = inputs
with tf.GradientTape() as tape:
predictions = model(images, training=True)
loss = compute_loss(labels, predictions)
gradients = tape.gradient(loss, model.trainable_variables)
optimizer.apply_gradients(zip(gradients, model.trainable_variables))
train_accuracy.update_state(labels, predictions)
return loss
def test_step(inputs):
images, labels = inputs
predictions = model(images, training=False)
t_loss = loss_object(labels, predictions)
test_loss.update_state(t_loss)
test_accuracy.update_state(labels, predictions)
with strategy.scope():
# `experimental_run_v2` replicates the provided computation and runs it
# with the distributed input.
@tf.function
def distributed_train_step(dataset_inputs):
per_replica_losses = strategy.experimental_run_v2(train_step,
args=(dataset_inputs,))
return strategy.reduce(tf.distribute.ReduceOp.SUM, per_replica_losses,
axis=None)
@tf.function
def distributed_test_step(dataset_inputs):
return strategy.experimental_run_v2(test_step, args=(dataset_inputs,))
for epoch in range(EPOCHS):
# TRAIN LOOP
total_loss = 0.0
num_batches = 0
for x in train_dist_dataset:
total_loss += distributed_train_step(x)
num_batches += 1
train_loss = total_loss / num_batches
# TEST LOOP
for x in test_dist_dataset:
distributed_test_step(x)
if epoch % 2 == 0:
checkpoint.save(checkpoint_prefix)
template = ("Epoch {}, Loss: {}, Accuracy: {}, Test Loss: {}, "
"Test Accuracy: {}")
print (template.format(epoch+1, train_loss,
train_accuracy.result()*100, test_loss.result(),
test_accuracy.result()*100))
test_loss.reset_states()
train_accuracy.reset_states()
test_accuracy.reset_states()
```
Things to note in the example above:
* We are iterating over the `train_dist_dataset` and `test_dist_dataset` using a `for x in ...` construct.
* The scaled loss is the return value of the `distributed_train_step`. This value is aggregated across replicas using the `tf.distribute.Strategy.reduce` call and then across batches by summing the return value of the `tf.distribute.Strategy.reduce` calls.
* `tf.keras.Metrics` should be updated inside `train_step` and `test_step` that gets executed by `tf.distribute.Strategy.experimental_run_v2`.
*`tf.distribute.Strategy.experimental_run_v2` returns results from each local replica in the strategy, and there are multiple ways to consume this result. You can do `tf.distribute.Strategy.reduce` to get an aggregated value. You can also do `tf.distribute.Strategy.experimental_local_results` to get the list of values contained in the result, one per local replica.
## Restore the latest checkpoint and test
A model checkpointed with a `tf.distribute.Strategy` can be restored with or without a strategy.
```
eval_accuracy = tf.keras.metrics.SparseCategoricalAccuracy(
name='eval_accuracy')
new_model = create_model()
new_optimizer = tf.keras.optimizers.Adam()
test_dataset = tf.data.Dataset.from_tensor_slices((test_images, test_labels)).batch(GLOBAL_BATCH_SIZE)
@tf.function
def eval_step(images, labels):
predictions = new_model(images, training=False)
eval_accuracy(labels, predictions)
checkpoint = tf.train.Checkpoint(optimizer=new_optimizer, model=new_model)
checkpoint.restore(tf.train.latest_checkpoint(checkpoint_dir))
for images, labels in test_dataset:
eval_step(images, labels)
print ('Accuracy after restoring the saved model without strategy: {}'.format(
eval_accuracy.result()*100))
```
## Alternate ways of iterating over a dataset
### Using iterators
If you want to iterate over a given number of steps and not through the entire dataset you can create an iterator using the `iter` call and explicity call `next` on the iterator. You can choose to iterate over the dataset both inside and outside the tf.function. Here is a small snippet demonstrating iteration of the dataset outside the tf.function using an iterator.
```
with strategy.scope():
for _ in range(EPOCHS):
total_loss = 0.0
num_batches = 0
train_iter = iter(train_dist_dataset)
for _ in range(10):
total_loss += distributed_train_step(next(train_iter))
num_batches += 1
average_train_loss = total_loss / num_batches
template = ("Epoch {}, Loss: {}, Accuracy: {}")
print (template.format(epoch+1, average_train_loss, train_accuracy.result()*100))
train_accuracy.reset_states()
```
### Iterating inside a tf.function
You can also iterate over the entire input `train_dist_dataset` inside a tf.function using the `for x in ...` construct or by creating iterators like we did above. The example below demonstrates wrapping one epoch of training in a tf.function and iterating over `train_dist_dataset` inside the function.
```
with strategy.scope():
@tf.function
def distributed_train_epoch(dataset):
total_loss = 0.0
num_batches = 0
for x in dataset:
per_replica_losses = strategy.experimental_run_v2(train_step,
args=(x,))
total_loss += strategy.reduce(
tf.distribute.ReduceOp.SUM, per_replica_losses, axis=None)
num_batches += 1
return total_loss / tf.cast(num_batches, dtype=tf.float32)
for epoch in range(EPOCHS):
train_loss = distributed_train_epoch(train_dist_dataset)
template = ("Epoch {}, Loss: {}, Accuracy: {}")
print (template.format(epoch+1, train_loss, train_accuracy.result()*100))
train_accuracy.reset_states()
```
### Tracking training loss across replicas
Note: As a general rule, you should use `tf.keras.Metrics` to track per-sample values and avoid values that have been aggregated within a replica.
We do *not* recommend using `tf.metrics.Mean` to track the training loss across different replicas, because of the loss scaling computation that is carried out.
For example, if you run a training job with the following characteristics:
* Two replicas
* Two samples are processed on each replica
* Resulting loss values: [2, 3] and [4, 5] on each replica
* Global batch size = 4
With loss scaling, you calculate the per-sample value of loss on each replica by adding the loss values, and then dividing by the global batch size. In this case: `(2 + 3) / 4 = 1.25` and `(4 + 5) / 4 = 2.25`.
If you use `tf.metrics.Mean` to track loss across the two replicas, the result is different. In this example, you end up with a `total` of 3.50 and `count` of 2, which results in `total`/`count` = 1.75 when `result()` is called on the metric. Loss calculated with `tf.keras.Metrics` is scaled by an additional factor that is equal to the number of replicas in sync.
### Guide and examples
Here are some examples for using distribution strategy with custom training loops:
1. [Distributed training guide](../../guide/distributed_training)
2. [DenseNet](https://github.com/tensorflow/examples/blob/master/tensorflow_examples/models/densenet/distributed_train.py) example using `MirroredStrategy`.
1. [BERT](https://github.com/tensorflow/models/blob/master/official/nlp/bert/run_classifier.py) example trained using `MirroredStrategy` and `TPUStrategy`.
This example is particularly helpful for understanding how to load from a checkpoint and generate periodic checkpoints during distributed training etc.
2. [NCF](https://github.com/tensorflow/models/blob/master/official/recommendation/ncf_keras_main.py) example trained using `MirroredStrategy` that can be enabled using the `keras_use_ctl` flag.
3. [NMT](https://github.com/tensorflow/examples/blob/master/tensorflow_examples/models/nmt_with_attention/distributed_train.py) example trained using `MirroredStrategy`.
More examples listed in the [Distribution strategy guide](../../guide/distributed_training.ipynb#examples_and_tutorials)
## Next steps
Try out the new `tf.distribute.Strategy` API on your models.
|
github_jupyter
|
```
%matplotlib inline
import adaptive
import matplotlib.pyplot as plt
import pycqed as pq
import numpy as np
from pycqed.measurement import measurement_control
import pycqed.measurement.detector_functions as det
from qcodes import station
station = station.Station()
```
## Setting up the mock device
Measurements are controlled through the `MeasurementControl` usually instantiated as `MC`
```
from pycqed.instrument_drivers.virtual_instruments.mock_device import Mock_Device
MC = measurement_control.MeasurementControl('MC',live_plot_enabled=True, verbose=True)
MC.station = station
station.add_component(MC)
mock_device = Mock_Device('mock_device')
mock_device.mw_pow(-20)
mock_device.res_freq(7.400023457e9)
mock_device.cw_noise_level(.0005)
mock_device.acq_delay(.05)
```
## Measuring a resonator using the conventional method
Points are chosen on a linspace of 100 points. This is enough to identify the location of the resonator.
```
freqs = np.linspace(7.39e9, 7.41e9, 100)
d = det.Function_Detector(mock_device.S21,value_names=['Magn', 'Phase'],
value_units=['V', 'deg'])
MC.set_sweep_function(mock_device.mw_freq)
MC.set_sweep_points(freqs)
MC.set_detector_function(d)
dat=MC.run('test')
```
## Using 1D adaptive sampler from the MC
This can also be done using an adaptive `Leaner1D` object, chosing 100 points optimally in the interval.
```
mock_device.acq_delay(.05)
d = det.Function_Detector(mock_device.S21, value_names=['Magn', 'Phase'], value_units=['V', 'deg'])
MC.set_sweep_function(mock_device.mw_freq)
MC.set_detector_function(d)
MC.set_adaptive_function_parameters({'adaptive_function': adaptive.Learner1D,
'goal':lambda l: l.npoints>100,
'bounds':(7.39e9, 7.41e9)})
dat = MC.run(mode='adaptive')
from pycqed.analysis import measurement_analysis as ma
# ma.Homodyne_Analysis(close_fig=False, label='M')
```
## Two D learner
The learner can also be used to adaptively sample a 2D /heatmap type experiment.
However, currently we do not have easy plotting function for that and we still need to rely on the adaptive Learner plotting methods.
It would be great to have this working with a realtime pyqtgraph based plotting window so that we can use this without the notebooks.
```
d = det.Function_Detector(mock_device.S21, value_names=['Magn', 'Phase'], value_units=['V', 'deg'])
MC.set_sweep_function(mock_device.mw_freq)
MC.set_sweep_function_2D(mock_device.mw_pow)
MC.set_detector_function(d)
MC.set_adaptive_function_parameters({'adaptive_function': adaptive.Learner2D,
'goal':lambda l: l.npoints>20*20,
'bounds':((7.398e9, 7.402e9),
(-20, -10))})
dat = MC.run(mode='adaptive')
# Required to be able to use the fancy interpolating plot
adaptive.notebook_extension()
MC.learner.plot(tri_alpha=.1)
```
|
github_jupyter
|
```
import numpy as np
import pandas as pd
import time
import psutil
import matplotlib.pyplot as plt
import numpy as np
# We create a very simple data set with 5 data items in it.
size= 5
# mu, sigma = 100, 5000 # mean and standard deviation
# error=np.random.normal(mu, sigma, size)
x1 = np.arange(0, size)
# x2 = np.arange(1, size)
x2 = np.arange(5, 5+size)
# y = 2.5*x1 + error
y1=2.5 * x1
y2 =-1 *x2
# y = 2*x1 + 10* x2
x = []
for i in range(size):
x.append(np.array([x1[i],x2[i]]))
y = y1 + y2
print(x)
print(y)
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib as mpl
from mpl_toolkits.mplot3d import Axes3D
import numpy as np
import matplotlib.pyplot as plt
mpl.rcParams['legend.fontsize'] = 10
fig = plt.figure()
ax = fig.gca(projection='3d')
x1 = np.arange(0, size)
# x2 = np.arange(1, size)
x2 = np.arange(5, 5+size)
ax.scatter3D(x1, x2, y, label='parametric curve')
ax.legend()
plt.show()
learningRate = 0.01
num_iteration = 300
# This is our regression coefficients.
beta=np.zeros(2)
n = float(size)
# print("Sample size", n)
# Let's start with main iterative part of gradient descent algorithm
for i in range(num_iteration):
# Calculate the prediction with current regression coefficients.
cost = 0
m_gradient = 0
for j in range(size):
y_prediction = np.dot(beta , x[j])
# We compute costs just for monitoring
cost += ( y[j] - y_prediction)**2
# calculate gradients. sum the gradients for all rows
m_gradient += x[j] * (y[j] - y_prediction)
m_gradient = (-1.0/n)* m_gradient
print(i , "beta = ", beta, " Cost=", cost)
# update the weights - Regression Coefficients
beta = beta - learningRate * m_gradient
x1 = np.arange(0, size)
# x2 = np.arange(1, size)
x2 = np.arange(5, 5+size)
x3 = np.arange(2, 2+size)
# y = 2.5*x1 + error
y1=2.5 * x1
y2 =-1 *x2
y3 = 1*x3
# y = 2*x1 + 10* x2
x = []
for i in range(size):
x.append(np.array([x1[i],x2[i],x3[i]]))
y = y1+y2+y3
# plt.plot(x1, y, 'o', markersize=2)
# plt.show()
print(x)
# print(x2)
# print(error)
print(y)
learningRate = 0.01
num_iteration = 100
# Now we have 3 variables.
beta = np.zeros(3)
n = float(size)
# print("Sample size", n)
# Let's start with main iterative part of gradient descent algorithm
for i in range(num_iteration):
# Calculate the prediction with current regression coefficients.
cost = 0
m_gradient = 0
for j in range(size):
y_prediction = np.dot(beta, x[j])
# We compute costs just for monitoring
cost += ( y[j] - y_prediction)**2
# calculate gradients.
m_gradient += x[j] * (y[j] - y_prediction)
m_gradient = (-1.0/n)* m_gradient
print(i , "beta=", beta, " Cost=", cost)
# update the weights - Regression Coefficients
beta = beta - learningRate * m_gradient
```
|
github_jupyter
|
## Purpose: Get the stats for pitching per year (1876-2019).
```
# import dependencies.
import time
import pandas as pd
from splinter import Browser
from bs4 import BeautifulSoup as bs
!which chromedriver
# set up driver.
executable_path = {"executable_path": "/usr/local/bin/chromedriver"}
browser = Browser("chrome", **executable_path, headless=False)
# Grab the data into lists.
pitching_data = []
for year in range(2019, 1875, -1):
year = str(year)
url = "http://mlb.mlb.com/stats/sortable.jsp#elem=%5Bobject+Object%5D&tab_level=child&click_text=Sortable+Team+pitching&game_type='R'&season="+year+"&season_type=ANY&league_code='MLB'§ionType=st&statType=pitching&page=1&ts=1564260727128&playerType=QUALIFIER&sportCode='mlb'&split=&team_id=&active_sw=&position='1'&page_type=SortablePlayer&sortOrder='desc'&sortColumn=avg&results=&perPage=50&timeframe=&last_x_days=&extended=0"
browser.visit(url)
html = browser.html
soup = bs(html, "html.parser")
a = soup.find("tbody")
time.sleep(20)
for tr in a:
team_data = {}
team_data["year"] = year
team_data["team"] = tr.find("td", class_="dg-team_full").text
team_data["W"] = tr.find("td", class_="dg-w").text
team_data["L"] = tr.find("td", class_="dg-l").text
team_data["ERA"] = tr.find("td", class_="dg-era").text
team_data["G1"] = tr.find("td", class_="dg-g").text
team_data["GS"] = tr.find("td", class_="dg-gs").text
team_data["SV"] = tr.find("td", class_="dg-sv").text
team_data["SVO"] = tr.find("td", class_="dg-svo").text
team_data["IP"] = tr.find("td", class_="dg-ip").text
team_data["H1"] = tr.find("td", class_="dg-h").text
team_data["R1"] = tr.find("td", class_="dg-r").text
team_data["ER"] = tr.find("td", class_="dg-er").text
team_data["HR1"] = tr.find("td", class_="dg-hr").text
team_data["BB1"] = tr.find("td", class_="dg-bb").text
team_data["SO1"] = tr.find("td", class_="dg-so").text
team_data["WHIP"] = tr.find("td", class_="dg-whip").text
team_data["CG"] = tr.find("td", class_="dg-cg").text
team_data["SHO"] = tr.find("td", class_="dg-sho").text
team_data["HB"] = tr.find("td", class_="dg-hb").text
team_data["IBB1"] = tr.find("td", class_="dg-ibb").text
team_data["GF"] = tr.find("td", class_="dg-gf").text
team_data["HLD"] = tr.find("td", class_="dg-hld").text
team_data["GIDP"] = tr.find("td", class_="dg-gidp").text
team_data["GO1"] = tr.find("td", class_="dg-go").text
team_data["AO1"] = tr.find("td", class_="dg-ao").text
team_data["WP"] = tr.find("td", class_="dg-wp").text
team_data["BK"] = tr.find("td", class_="dg-bk").text
team_data["SB1"] = tr.find("td", class_="dg-sb").text
team_data["CS1"] = tr.find("td", class_="dg-cs").text
team_data["PK"] = tr.find("td", class_="dg-pk").text
team_data["TBF"] = tr.find("td", class_="dg-tbf").text
team_data["NP"] = tr.find("td", class_="dg-np").text
team_data["WPCT"] = tr.find("td", class_="dg-wpct").text
team_data["GO_AO1"] = tr.find("td", class_="dg-go_ao").text
team_data["OBP1"] = tr.find("td", class_="dg-obp").text
team_data["SLG1"] = tr.find("td", class_="dg-slg").text
team_data["OPS"] = tr.find("td", class_="dg-ops").text
pitching_data.append(team_data)
team_data = {}
pitching_data = pd.DataFrame(pitching_data)
pitching_data.head()
pitching_data.to_csv("../Resources/pitching_data.csv")
```
|
github_jupyter
|
<div class="alert alert-block alert-info">
<font size="6"><b><center> Section 2</font></center>
<br>
<font size="6"><b><center> Fully-Connected, Feed-Forward Neural Network Examples </font></center>
</div>
# Example 1: A feedforward network with one hidden layer using torch.nn and simulated data
In developing (and training) a feedforward neural network, the developer needs to make many decisions, many of which are required when developing more complicated neural networks, such as CNN and RNN:
- the depth of the network (i.e. number of layer)
- the width of the network (i.e. number of hidden units per layer)
- the type of nonlinear activation function applied in each hidden layer
- the type of activation function applied in the output layer
- the loss function
- the optimization algorithms
- the regularization technique (*which we will consider in Section 3*)
- number of epoch and batch size
Our first example uses simulated data, which has the advantage that we define our own data generating mechanism and can observe how a neural network can approximate the mechanism.
----
## Simulate and Visualize Data
Let's first consider an example with one explanatory variable.
<br><br>
The output is related to the input using the following function
$$y_i = 3x_{i,1} + x^2 exp(x_{i,1}) + \epsilon_i$$
where $\epsilon$ is an independently and identically distributed (i.i.d.) random variable and $i = 1,2,\dots,n$ is an index of examples (or observations)
```
# In the following example, n=100
import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
n = 100 # number of examples (or observations)
# Generate a set of n random numbers from a standard normal distribution
epsilon = np.random.randn(n)
# Generate a set of n random numbers from a uniform[0,1] distribution
x1 = np.random.uniform(0,1,n)
# Create the data generating mechanism
y = 3*x1 + np.power(x1,2)*np.exp(x1) + epsilon
stats.describe(y)
stats.describe(x1)
fig = plt.figure(figsize=(12,8))
plt.subplot(2, 2, 1)
sns.set()
#ax = sns.distplot(x1)
plt.hist(x1)
plt.subplot(2, 2, 2)
plt.scatter(x1, y)
```
**Note: Before training, `numpy array` needs to be converted to `PyTorch's tensors`**
```
type(x1)
print(x1.shape)
print(y.shape)
# convert numpy array to tensor in shape of input size
import torch
x1 = torch.from_numpy(x1.reshape(-1,1)).float()
y = torch.from_numpy(y.reshape(-1,1)).float()
print(x1.shape)
print(y.shape)
```
## Create a network: First Attempt
* Specify a network
* Define a loss function and choose an optimization algorithm
* Train the network
Our first network is a linear regression model
### Create a linear regression model
```
from __future__ import print_function
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.autograd import Variable
class LinearNet(nn.Module):
def __init__(self):
super(LinearNet, self).__init__()
self.linearlayer1 = torch.nn.Linear(1, 1)
def forward(self, x):
y_pred = self.linearlayer1(x)
return y_pred
linearNet = LinearNet()
print(linearNet)
```
### Define Loss Function and Optimization Algorithm
```
# Define Optimizer and Loss Function
optimizer = torch.optim.SGD(linearNet.parameters(), lr=0.01)
loss_func = torch.nn.MSELoss()
```
### Model training and print losses
```
X = Variable(x1)
y_data = Variable(y)
for epoch in range(500):
y_pred = linearNet(X)
loss = torch.sqrt(loss_func(y_pred, y_data))
optimizer.zero_grad()
loss.backward()
optimizer.step()
# Plot the prediction and print out the loss
if epoch in [0,99,299,399,499]:
print(epoch)
plt.cla()
plt.scatter(x1.data.numpy(), y.data.numpy())
#plt.plot(x.data.numpy(), y_pred.data.numpy(), 'r-', lw=2)
plt.scatter(x1.data.numpy(), y_pred.data.numpy())
plt.text(0.7, -1, 'Loss=%.4f' % loss.data.numpy(), fontdict={'size': 14, 'color': 'red'})
plt.pause(0.1)
plt.show()
```
## Create a Network: 2nd Attempt
### Define a Feed-forward network with 1 hidden layer
**Let's insert a computational graph here**
```
from __future__ import print_function
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.autograd import Variable
class ffNet(nn.Module):
def __init__(self):
super(ffNet, self).__init__()
self.linearCombo1 = torch.nn.Linear(1, 4) # z1 = W1*x1 + b1
self.linearCombo2 = torch.nn.Linear(4, 1) # z2 = W2*h1 + b2
self.relu = torch.nn.ReLU()
def forward(self, x):
h1 = self.relu(self.linearCombo1(x)) # the ReLU (non-linear activation function) is applied to the linear combination of the weights and input (x1)
y_pred = self.linearCombo2(h1)
return y_pred
ffnet = ffNet()
print(ffnet)
```
### Define loss function and optimization algorithm
```
# Define Optimizer and Loss Function
optimizer = torch.optim.SGD(ffnet.parameters(), lr=0.01)
loss_func = torch.nn.MSELoss()
```
### Model Training
```
X = Variable(x1)
y_data = Variable(y)
for epoch in range(500):
y_pred = ffnet(X)
loss = loss_func(y_pred, y_data)
optimizer.zero_grad()
loss.backward()
optimizer.step()
if epoch in [0,99,299,399,499]:
print(epoch)
plt.cla()
plt.scatter(x1.data.numpy(), y.data.numpy())
plt.scatter(x1.data.numpy(), y_pred.data.numpy())
#plt.plot(x.data.numpy(), y_pred.data.numpy(), 'r-', lw=2)
plt.text(0.5, 0, 'Loss=%.4f' % loss.data.numpy(), fontdict={'size': 10, 'color': 'red'})
plt.pause(0.1)
plt.show()
```
## Create a Network: 3rd Attempt
### Define a Feed-forward network with 2 hidden layers
```
from __future__ import print_function
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.autograd import Variable
class ffNet(nn.Module):
def __init__(self):
super(ffNet, self).__init__()
self.linearlayer1 = torch.nn.Linear(1, 8)
self.linearlayer2 = torch.nn.Linear(8, 4)
self.linearlayer3 = torch.nn.Linear(4, 1)
self.relu = torch.nn.ReLU()
def forward(self, x):
out1 = self.relu(self.linearlayer1(x))
out2 = self.relu(self.linearlayer2(out1))
y_pred = self.linearlayer3(out2)
return y_pred
ffnet2 = ffNet()
print(ffnet2)
```
### Define loss function and optimization algorithm
```
# Define Optimizer and Loss Function
optimizer = torch.optim.SGD(ffnet2.parameters(), lr=0.01)
loss_func = torch.nn.MSELoss()
```
### Model Training
```
X = Variable(x1)
y_data = Variable(y)
for epoch in range(500):
y_pred = ffnet2(X)
loss = loss_func(y_pred, y_data)
optimizer.zero_grad()
loss.backward()
optimizer.step()
if epoch in [0,99,299,399,499,999]:
print(epoch)
plt.cla()
plt.scatter(x1.data.numpy(), y.data.numpy())
#plt.plot(x.data.numpy(), y_pred.data.numpy(), 'r', lw=1)
plt.scatter(x1.data.numpy(), y_pred.data.numpy())
plt.text(0.5, 0, 'Loss=%.4f' % loss.data.numpy(), fontdict={'size': 10, 'color': 'red'})
plt.pause(0.1)
plt.show()
```
# Lab 2
**Review modeling attempt 1 - 3 and design a network to improve the existing results.**
|
github_jupyter
|
# Exploring datastructures for dataset
A Pandas exploration. Find the best datastructure to explore and transform the dataset (both training and test dataframes). Use case:
- find all numerical features (filtering)
- transform all numerical features (e.g. take square)
- replace NaN values for a numerical feature
- plot distribution for a column in the training dataset
```
import sys
import os
import pandas as pd
import seaborn as sns
sys.path.insert(1, os.path.join(sys.path[0], '..')) # add parent directory to path
import samlib
```
## Using `samlib.DataSet`
Original approach used in `data_exploration_numerical_features`
- class that contains 3 dataframes attributes (train, test, df, where df is the full dataframe
- whenever df is updated, the train and test frames are updated
This allows to work with the training dataset, and to update/transform the full dataset if necessary, so that the transformation is also applied to the test dataframe that will be needed for the final prediction.
```
raw_train = pd.read_csv('../data/train_prepared_light.csv')
raw_test = pd.read_csv('../data/test_prepared_light.csv')
ds = samlib.DataSet(raw_train, raw_test)
is_num = ds.dtypes != object
dfnum = ds.df.loc[:, is_num]
dfnum.head()
ds.apply(lambda df: df.loc[:, is_num]**2, inplace=True)
ds.df.head()
ds.df.MasVnrArea.isnull().sum()
ds.df.loc[ds.df.MasVnrArea.isnull(), 'MasVnrArea'] = 0
ds.df.MasVnrArea.isnull().sum()
sns.distplot(ds.train.GrLivArea)
```
Works but not so great because requires a new dependency (samlib) and a different way of working compared to Pandas. Need to learn the behaviour of the DataSet class, and remember to use the `apply` method otherwise the `train` and `test` sets are *not* going to be kept in sync (for example when assigning to a slice of `ds.df`)
## Using an extra categorical `dataset` column
```
traindf = raw_train.copy()
testdf = raw_test.copy()
traindf['dataset'] = 'train'
testdf['dataset'] = 'test'
df = pd.concat([traindf, testdf])
```
Then we can filter using the value of the `dataset` column
```
train = df['dataset'] == 'train'
test = ~train
df[train].head()
df[test].head()
is_num = df.dtypes != object
dfnum = df.loc[:, is_num]
dfnum.head()
df.loc[:, is_num] = dfnum **2
df.head()
df.MasVnrArea.isnull().sum()
df.loc[df.MasVnrArea.isnull(), 'MasVnrArea'] = 0
df.MasVnrArea.isnull().sum()
sns.distplot(df.loc[train, 'GrLivArea'])
```
Works quite well but takes a bit of work to setup and requires to keep two boolean series (`train` and `test`) to filter the dataset whenever needed. An improvement over `samlib.DataSet` though.
## Using Panel object
```
panel = pd.Panel({'train':raw_train.copy(), 'test': raw_test.copy()})
panel.train.head()
panel.test.head()
```
The above is very nice, but unfortunately a panel isn't a dataframe so we can't really get a view of the full data. Also we seem to have lost all the data types:
```
is_num = panel.train.dtypes != object
any(is_num)
```
So we must keep the raw data if we want to filter the numerical columns :-(
```
is_num = raw_train.dtypes != object
numpanel = panel.loc[:, :, is_num]
numpanel
numpanel.train.head()
```
Finally this raises an error!
```
try:
panel.loc[:, :, is_num] = panel.loc[:, :, is_num]**2
except NotImplementedError as err:
print('raises NotImplementedError: ', err)
```
Looked promising initially but not really workable as we can't assign an indexer with a Panel yet. We really need a dataframe object.
## Using multi-index on rows
```
traindf = raw_train.copy()
testdf = raw_test.copy()
df = pd.concat([traindf, testdf], keys=('train', 'test'))
df.head()
df.tail()
```
The test and train datasets can be accessed by filtering the index. Nice but not quite as compact as `df[train]`, though we don't need the extra `train` (and `test`) masks.
```
df.loc['train'].head()
is_num = df.dtypes != object
dfnum = df.loc[:, is_num]
dfnum.head()
df.loc[:, is_num] = dfnum **2
df.head()
df.MasVnrArea.isnull().sum()
df.loc[df.MasVnrArea.isnull(), 'MasVnrArea'] = 0
df.MasVnrArea.isnull().sum()
sns.distplot(df.GrLivArea.train)
```
Another way of doing it
```
sns.distplot(df.loc['train', 'GrLivArea'])
```
Works very well.
## Using multi-index on columns (swapped levels)
Swap the levels to fix the issue with filtering on features in the column multi-index case.
```
traindf = raw_train.copy()
testdf = raw_test.copy()
df = pd.concat([traindf, testdf], axis=1, keys=('train','test')).swaplevel(axis=1)
df.sort_index(axis=1, inplace=True) # needed otherwise we get in trouble for slicing
df.head()
df.tail()
```
The test and train datasets can be accessed by filtering the index. Nice but not quite as compact as `df[train]`, though we don't need the extra `train` (and `test`) masks.
```
df.xs('train', level=1, axis=1).head() # or use IndexSlice
```
We must also deal with the extra index level when filtering, but it's not too bad.
```
is_num = df.dtypes != object
dfnum = df.loc[:, is_num]
dfnum.head()
df.loc[:, is_num] = dfnum **2
df.head()
```
Getting nulls and setting nulls (without fillna) is a little tricky. Boolean indexing is (by definition) meant to work over rows, not rows *and columns. We can use boolean arrays with DataFrame.mask though. But this is definitely something to keep in mind when using multi indexing over columns.
```
df.MasVnrArea = df.MasVnrArea.mask(df.MasVnrArea.isnull(), 0)
df.MasVnrArea.tail()
```
Visualizing the training dataset is pretty easy.
```
sns.distplot(df.GrLivArea.train)
```
## Using multi-index on columns
Makes it easier to filter on dataset (train or test) and has the advantage of being a dataframe.
```
traindf = raw_train.copy()
testdf = raw_test.copy()
df = pd.concat([traindf, testdf], axis=1, keys=('train','test'))
df.head()
df.tail()
```
The test and train datasets can be accessed by filtering the index. Nice but not quite as compact as `df[train]`, though we don't need the extra `train` (and `test`) masks.
```
df.train.head()
```
We must also deal with the extra index level when filtering, but it's not too bad.
```
is_num = df.dtypes != object
dfnum = df.loc[:, is_num]
dfnum.head()
df.loc[:, is_num] = dfnum **2
df.head()
```
Definitely harder to slice accross columns. It's possible (unlike with panels), but hard (requires pd.IndexSlice).
```
df.loc[:, pd.IndexSlice[:, 'MasVnrArea']].isnull().sum()
```
You can also use a cross section to get the data more easily, but you can't use this for sssignments
```
df.xs('MasVnrArea', axis=1, level=1).head()
df.loc[:, pd.IndexSlice[:, 'MasVnrArea']] = 0
df.loc[:, pd.IndexSlice[:, 'MasVnrArea']].isnull().sum()
```
Visualizing the training dataset is pretty easy.
```
sns.distplot(df.train.GrLivArea)
```
## Using dataset type as label
** Method 1: add columns then use set_index **
```
traindf = raw_train.copy()
testdf = raw_test.copy()
traindf['Dataset'] = 'train'
testdf['Dataset'] = 'test'
df = pd.concat([traindf, testdf])
df.set_index('Dataset').head()
```
** Method 2: use concat and droplevel **
```
traindf = raw_train.copy()
testdf = raw_test.copy()
df = pd.concat([traindf, testdf], keys=('train', 'test'))
df.index = df.index.droplevel(1)
df.head()
df.tail()
```
The test and train datasets can be accessed by using `loc` .
```
df.loc['train'].head()
```
Filtering columns is very easy
```
is_num = df.dtypes != object
dfnum = df.loc[:, is_num]
dfnum.head()
df.loc[:, is_num] = dfnum **2
df.head()
df.MasVnrArea.isnull().sum()
df.loc[df.MasVnrArea.isnull(), 'MasVnrArea'] = 0
df.MasVnrArea.isnull().sum()
sns.distplot(df.GrLivArea.train)
```
Another way of doing it
```
sns.distplot(df.loc['train', 'GrLivArea'])
```
## Discussion
### Samlib
- Pros: does most of what we need pretty easily
- Cons: third party dependency, hackish, introduces new structure with weird behaviour (assining to a slice doesn't update training and test datasets)
- Score: 2/5
### Extra categorical `dataset` column
- Pros: works very well and syntax is compact
- Cons: a bit long to setup, requires to maintain mask variables `test` and `train` alongside the data.
- Score; 4/5
### Panel
doesn't work
### Multi-index on rows
- Pros: excellent, easy to filter on colums and on dataset
- Cons: none
- Score: 5/5
### Multi-index on columns
- Pros: easy to filter on train/test sets
- Cons: hard to transform features for both datasets + would be weird if train and test sets have widely different numbers of indices
- Score: 1/5
### Dataset label
- Pros: index is not a multi index
- Cons: a bit hard to setup and index looks a bit weird as all samples have the same index
- Score: 4/5
## Conclusion
Use `pd.concat([traindf, testdf], keys=['train', 'test'])` to merge the datasets into one dataframe while making it easy to visualize/process features on only the training dataset.
|
github_jupyter
|
## 10.4 딥러닝 기반 Q-Learning을 이용하는 강화학습
- 관련 패키지 불러오기
```
# 기본 패키지
import numpy as np
import random
from collections import deque
import matplotlib.pyplot as plt
# 강화학습 환경 패키지
import gym
# 인공지능 패키지: 텐서플로, 케라스
# 호환성을 위해 텐스플로에 포함된 케라스를 불러옴
import tensorflow as tf # v2.4.1 at 7/25/2021
from tensorflow import keras # v2.4.0 at 7/25/2021
from tensorflow.keras import Model, Input
from tensorflow.keras.layers import Dense
from tensorflow.keras.optimizers import Adam
```
- Q 함수를 위한 뉴럴넷 구성하기
```
def create_q_model(num_states, num_actions):
inputs = Input(shape=(num_states,))
layer = Dense(32, activation="relu")(inputs)
layer = Dense(16, activation="relu")(layer)
action = Dense(num_actions, activation="linear")(layer)
return Model(inputs=inputs, outputs=action)
model = create_q_model(4,2)
model.summary()
```
- Q함수 뉴럴넷의 학습에 필요한 코드 작성
```
def get_env_model(id='MountainCar-v0'):
env = gym.make(id)
num_states = env.observation_space.shape[0]
num_actions = env.action_space.n
model = create_q_model(num_states, num_actions)
return env, model
def train(model, env):
state_size = env.observation_space.shape[0]
action_size = env.action_space.n
states = np.zeros((10,state_size), dtype=np.float32)
with tf.GradientTape() as tape:
predicts = model(states)
env, model = get_env_model()
train(model, env)
print('Simple processing used in training is completed!')
env_cartpole = gym.make('CartPole-v1')
print('CartPole-v1: ', env_cartpole.observation_space.shape, env_cartpole.action_space.n)
env_mountaincar = gym.make('MountainCar-v0')
print('MountainCar-v0: ', env_mountaincar.observation_space.shape, env_mountaincar.action_space.n)
class World_00:
def __init__(self):
self.get_env_model()
def get_env_model(self):
self.env = gym.make('MountainCar-v0')
self.num_states = env.observation_space.shape[0]
self.num_actions = env.action_space.n
self.model = create_q_model(self.num_states, self.num_actions)
# print(self.model.summary())
def train(self):
states = np.zeros((10,self.num_states), dtype=np.float32)
with tf.GradientTape() as tape:
predicts = self.model(states)
new_world = World_00()
new_world.train()
print('Simple processing used in training is completed!')
def env_test_model_memory(memory, env, model, n_episodes=1000,
flag_render=False):
for e in range(n_episodes):
done = False
score = 0
s = env.reset()
while not done:
s_array = np.array(s).reshape((1,-1))
Qsa = model.predict(s_array)[0]
a = np.argmax(Qsa)
next_s, r, done, _ = env.step(a)
if flag_render:
env.render()
score += r
memory.append([s,a,r,next_s,done])
print(f'Episode: {e:5d} --> Score: {score:3.1f}')
print('Notice that the max score is set to 500.0 in CartPole-v1')
def list_rotate(l):
return list(zip(*l))
class World_01(World_00):
def __init__(self):
World_00.__init__(self)
self.memory = deque(maxlen=2000)
self.N_batch = 64
self.t_model = create_q_model(self.num_states, self.num_actions)
self.discount_factor = 0.99
self.learning_rate = 0.001
self.optimizer = Adam(lr=self.learning_rate)
def trial(self, flag_render=False):
env_test_model_memory(self.memory, self.env,
self.model, n_episodes=10, flag_render=flag_render)
print(len(self.memory))
def train_memory(self):
if len(self.memory) >= self.N_batch:
memory_batch = random.sample(self.memory, self.N_batch)
s_l,a_l,r_l,next_s_l,done_l = [np.array(x) for x in list_rotate(memory_batch)]
model_w = self.model.trainable_variables
with tf.GradientTape() as tape:
Qsa_pred_l = self.model(s_l.astype(np.float32))
a_l_onehot = tf.one_hot(a_l, self.num_actions)
Qs_a_pred_l = tf.reduce_sum(a_l_onehot * Qsa_pred_l,
axis=1)
Qsa_tpred_l = self.t_model(next_s_l.astype(np.float32))
Qsa_tpred_l = tf.stop_gradient(Qsa_tpred_l)
max_Q_next_s_a_l = np.amax(Qsa_tpred_l, axis=-1)
Qs_a_l = r_l + (1 - done_l) * self.discount_factor * max_Q_next_s_a_l
loss = tf.reduce_mean(tf.square(Qs_a_l - Qs_a_pred_l))
grads = tape.gradient(loss, model_w)
self.optimizer.apply_gradients(zip(grads, model_w))
new_world = World_01()
new_world.trial()
new_world.train_memory()
new_world.env.close()
print('Completed!')
class World_02(World_01):
def __init__(self):
World_01.__init__(self)
self.epsilon = 0.2
def update_t_model(self):
self.t_model.set_weights(self.model.get_weights())
def best_action(self, s):
if random.random() <= self.epsilon:
return random.randrange(self.num_actions)
else:
s_array = np.array(s).reshape((1,-1))
Qsa = self.model.predict(s_array)[0]
return np.argmax(Qsa)
def trials(self, n_episodes=100, flag_render=False):
memory = self.memory
env = self.env
model = self.model
score_l = []
for e in range(n_episodes):
done = False
score = 0
s = env.reset()
while not done:
a = self.best_action(s)
next_s, r, done, _ = env.step(a)
if flag_render:
env.render()
score += r
memory.append([s,a,r,next_s,done])
# self.train_memory()
s = next_s
self.train_memory()
self.update_t_model()
print(f'Episode: {e:5d} --> Score: {score:3.1f}')
score_l.append(score)
return score_l
new_world = World_02()
score_l = new_world.trials(n_episodes=50)
new_world.env.close()
np.save('score_l.npy', score_l)
```
---
### 전체코드 (분할 버전)
```
l = [[1,2],[3,4],[5,6]]
list(zip(*l))
# 기본 패키지
import numpy as np
import random
from collections import deque
import matplotlib.pyplot as plt
# 강화학습 환경 패키지
import gym
# 인공지능 패키지: 텐서플로, 케라스
# 호환성을 위해 텐스플로에 포함된 케라스를 불러옴
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import Model, Input
from tensorflow.keras.layers import Dense
from tensorflow.keras.optimizers import Adam
def create_q_model(num_states, num_actions):
inputs = Input(shape=(num_states,))
layer = Dense(32, activation="relu")(inputs)
layer = Dense(16, activation="relu")(layer)
action = Dense(num_actions, activation="linear")(layer)
return Model(inputs=inputs, outputs=action)
def list_rotate(l):
return list(zip(*l))
class WorldFull():
def __init__(self):
self.get_env_model() #?
self.memory = deque(maxlen=2000)
self.N_batch = 64
self.t_model = create_q_model(self.num_states, self.num_actions)
self.discount_factor = 0.99
self.learning_rate = 0.001
self.optimizer = Adam(lr=self.learning_rate)
self.epsilon = 0.2
def get_env_model(self):
self.env = gym.make('CartPole-v1')
self.num_states = self.env.observation_space.shape[0]
self.num_actions = self.env.action_space.n
self.model = create_q_model(self.num_states, self.num_actions)
def update_t_model(self):
self.t_model.set_weights(self.model.get_weights())
def best_action(self, s):
if random.random() <= self.epsilon:
return random.randrange(self.num_actions)
else:
s_array = np.array(s).reshape((1,-1))
Qsa = self.model.predict(s_array)[0]
return np.argmax(Qsa)
def train_memory(self):
if len(self.memory) >= self.N_batch:
memory_batch = random.sample(self.memory, self.N_batch)
s_l,a_l,r_l,next_s_l,done_l = [np.array(x) for x in list_rotate(memory_batch)]
model_w = self.model.trainable_variables
with tf.GradientTape() as tape:
Qsa_pred_l = self.model(s_l.astype(np.float32))
a_l_onehot = tf.one_hot(a_l, self.num_actions)
Qs_a_pred_l = tf.reduce_sum(a_l_onehot * Qsa_pred_l,
axis=1)
Qsa_tpred_l = self.t_model(next_s_l.astype(np.float32))
Qsa_tpred_l = tf.stop_gradient(Qsa_tpred_l)
max_Q_next_s_a_l = np.amax(Qsa_tpred_l, axis=-1)
Qs_a_l = r_l + (1 - done_l) * self.discount_factor * max_Q_next_s_a_l
loss = tf.reduce_mean(tf.square(Qs_a_l - Qs_a_pred_l))
grads = tape.gradient(loss, model_w)
self.optimizer.apply_gradients(zip(grads, model_w))
def trials(self, n_episodes=100, flag_render=False):
memory = self.memory
env = self.env
model = self.model
score_l = []
for e in range(n_episodes):
done = False
score = 0
s = env.reset()
while not done:
a = self.best_action(s)
next_s, r, done, _ = env.step(a)
if flag_render:
env.render()
score += r
memory.append([s,a,r,next_s,done])
# self.train_memory()
s = next_s
self.train_memory()
self.update_t_model()
print(f'Episode: {e:5d} --> Score: {score:3.1f}')
score_l.append(score)
return score_l
new_world = WorldFull()
score_l = new_world.trials(n_episodes=100)
new_world.env.close()
np.save('score_l.npy', score_l)
print('Job completed!')
plt.plot(score_l)
plt.title("Deep Q-Learning for Cartpole")
plt.xlabel("Episode")
plt.ylabel("Score")
plt.plot(score_l)
plt.title("Deep Q-Learning for Cartpole")
plt.xlabel("Episode")
plt.ylabel("Score")
```
---
### 전체코드
```
"""
ENV: MoutainCar
- 2nd hidden layer: 16 --> 32
"""
# 기본 패키지
import numpy as np
import random
from collections import deque
import matplotlib.pyplot as plt
# 강화학습 환경 패키지
import gym
# 인공지능 패키지: 텐서플로, 케라스
# 호환성을 위해 텐스플로에 포함된 케라스를 불러옴
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import Model, Input
from tensorflow.keras.layers import Dense
from tensorflow.keras.optimizers import Adam
def create_q_model(num_states, num_actions):
inputs = Input(shape=(num_states,))
layer = Dense(32, activation="relu")(inputs)
layer = Dense(32, activation="relu")(layer)
action = Dense(num_actions, activation="linear")(layer)
return Model(inputs=inputs, outputs=action)
def list_rotate(l):
return list(zip(*l))
class WorldFull():
def __init__(self):
self.get_env_model() #?
self.memory = deque(maxlen=2000)
self.N_batch = 64
self.t_model = create_q_model(self.num_states, self.num_actions)
self.discount_factor = 0.99
self.learning_rate = 0.001
self.optimizer = Adam(lr=self.learning_rate)
self.epsilon = 0.05
def get_env_model(self):
self.env = gym.make('MountainCar-v0')
self.num_states = self.env.observation_space.shape[0]
self.num_actions = self.env.action_space.n
self.model = create_q_model(self.num_states, self.num_actions)
def update_t_model(self):
self.t_model.set_weights(self.model.get_weights())
def best_action(self, s):
if random.random() <= self.epsilon:
return random.randrange(self.num_actions)
else:
s_array = np.array(s).reshape((1,-1))
Qsa = self.model.predict(s_array)[0]
return np.argmax(Qsa)
def train_memory(self):
if len(self.memory) >= self.N_batch:
memory_batch = random.sample(self.memory, self.N_batch)
s_l,a_l,r_l,next_s_l,done_l = [np.array(x) for x in list_rotate(memory_batch)]
model_w = self.model.trainable_variables
with tf.GradientTape() as tape:
Qsa_pred_l = self.model(s_l.astype(np.float32))
a_l_onehot = tf.one_hot(a_l, self.num_actions)
Qs_a_pred_l = tf.reduce_sum(a_l_onehot * Qsa_pred_l,
axis=1)
Qsa_tpred_l = self.t_model(next_s_l.astype(np.float32))
Qsa_tpred_l = tf.stop_gradient(Qsa_tpred_l)
max_Q_next_s_a_l = np.amax(Qsa_tpred_l, axis=-1)
Qs_a_l = r_l + (1 - done_l) * self.discount_factor * max_Q_next_s_a_l
loss = tf.reduce_mean(tf.square(Qs_a_l - Qs_a_pred_l))
grads = tape.gradient(loss, model_w)
self.optimizer.apply_gradients(zip(grads, model_w))
def trials(self, n_episodes=100, flag_render=False):
memory = self.memory
env = self.env
model = self.model
score_l = []
for e in range(n_episodes):
done = False
score = 0
s = env.reset()
while not done:
a = self.best_action(s)
next_s, r, done, _ = env.step(a)
if flag_render:
env.render()
score += r
memory.append([s,a,r,next_s,done])
# self.train_memory()
s = next_s
self.train_memory()
self.update_t_model()
print(f'Episode: {e:5d} --> Score: {score:3.1f}')
score_l.append(score)
return score_l
new_world = WorldFull()
score_l = new_world.trials(n_episodes=100)
new_world.env.close()
np.save('score_l.npy', score_l)
print('Job completed!')
plt.plot(score_l)
plt.title("Deep Q-Learning for Cartpole")
plt.xlabel("Episode")
plt.ylabel("Score")
```
|
github_jupyter
|
# **Swin Transformer: Hierarchical Vision Transformer using Shifted Windows**
**Swin Transformer (ICCV 2021 best paper award (Marr Prize))**
**Authors {v-zeliu1,v-yutlin,yuecao,hanhu,v-yixwe,zhez,stevelin,bainguo}@microsoft.com**
**Official Github**: https://github.com/microsoft/Swin-Transformer
---
**Edited By Su Hyung Choi - [Computer Vision Paper Reviews]**
**[Github: @JonyChoi]** https://github.com/jonychoi/Computer-Vision-Paper-Reviews
Edited Jan 4 2022
---
## **About Swin Transformer**
```
# --------------------------------------------------------
# Swin Transformer
# Copyright (c) 2021 Microsoft
# Licensed under The MIT License [see LICENSE for details]
# Written by Ze Liu
# --------------------------------------------------------
import torch
import torch.nn as nn
import torch.utils.checkpoint as checkpoint
from timm.models.layers import DropPath, to_2tuple, trunc_normal_
class Mlp(nn.Module):
def __init__(self, in_features, hidden_features=None, out_features=None, act_layer=nn.GELU, drop=0.):
super().__init__()
out_features = out_features or in_features
hidden_features = hidden_features or in_features
self.fc1 = nn.Linear(in_features, hidden_features)
self.act = act_layer()
self.fc2 = nn.Linear(hidden_features, out_features)
self.drop = nn.Dropout(drop)
def forward(self, x):
x = self.fc1(x)
x = self.act(x)
x = self.drop(x)
x = self.fc2(x)
x = self.drop(x)
return x
def window_partition(x, window_size):
"""
Args:
x: (B, H, W, C)
window_size (int): window size
Returns:
windows: (num_windows*B, window_size, window_size, C)
"""
B, H, W, C = x.shape
x = x.view(B, H // window_size, window_size, W // window_size, window_size, C)
windows = x.permute(0, 1, 3, 2, 4, 5).contiguous().view(-1, window_size, window_size, C)
return windows
def window_reverse(windows, window_size, H, W):
"""
Args:
windows: (num_windows*B, window_size, window_size, C)
window_size (int): Window size
H (int): Height of image
W (int): Width of image
Returns:
x: (B, H, W, C)
"""
B = int(windows.shape[0] / (H * W / window_size / window_size))
x = windows.view(B, H // window_size, W // window_size, window_size, window_size, -1)
x = x.permute(0, 1, 3, 2, 4, 5).contiguous().view(B, H, W, -1)
return x
class WindowAttention(nn.Module):
r""" Window based multi-head self attention (W-MSA) module with relative position bias.
It supports both of shifted and non-shifted window.
Args:
dim (int): Number of input channels.
window_size (tuple[int]): The height and width of the window.
num_heads (int): Number of attention heads.
qkv_bias (bool, optional): If True, add a learnable bias to query, key, value. Default: True
qk_scale (float | None, optional): Override default qk scale of head_dim ** -0.5 if set
attn_drop (float, optional): Dropout ratio of attention weight. Default: 0.0
proj_drop (float, optional): Dropout ratio of output. Default: 0.0
"""
def __init__(self, dim, window_size, num_heads, qkv_bias=True, qk_scale=None, attn_drop=0., proj_drop=0.):
super().__init__()
self.dim = dim
self.window_size = window_size # Wh, Ww
self.num_heads = num_heads
head_dim = dim // num_heads
self.scale = qk_scale or head_dim ** -0.5
# define a parameter table of relative position bias
self.relative_position_bias_table = nn.Parameter(
torch.zeros((2 * window_size[0] - 1) * (2 * window_size[1] - 1), num_heads)) # 2*Wh-1 * 2*Ww-1, nH
# get pair-wise relative position index for each token inside the window
coords_h = torch.arange(self.window_size[0])
coords_w = torch.arange(self.window_size[1])
coords = torch.stack(torch.meshgrid([coords_h, coords_w])) # 2, Wh, Ww
coords_flatten = torch.flatten(coords, 1) # 2, Wh*Ww
relative_coords = coords_flatten[:, :, None] - coords_flatten[:, None, :] # 2, Wh*Ww, Wh*Ww
relative_coords = relative_coords.permute(1, 2, 0).contiguous() # Wh*Ww, Wh*Ww, 2
relative_coords[:, :, 0] += self.window_size[0] - 1 # shift to start from 0
relative_coords[:, :, 1] += self.window_size[1] - 1
relative_coords[:, :, 0] *= 2 * self.window_size[1] - 1
relative_position_index = relative_coords.sum(-1) # Wh*Ww, Wh*Ww
self.register_buffer("relative_position_index", relative_position_index)
self.qkv = nn.Linear(dim, dim * 3, bias=qkv_bias)
self.attn_drop = nn.Dropout(attn_drop)
self.proj = nn.Linear(dim, dim)
self.proj_drop = nn.Dropout(proj_drop)
trunc_normal_(self.relative_position_bias_table, std=.02)
self.softmax = nn.Softmax(dim=-1)
def forward(self, x, mask=None):
"""
Args:
x: input features with shape of (num_windows*B, N, C)
mask: (0/-inf) mask with shape of (num_windows, Wh*Ww, Wh*Ww) or None
"""
B_, N, C = x.shape
qkv = self.qkv(x).reshape(B_, N, 3, self.num_heads, C // self.num_heads).permute(2, 0, 3, 1, 4)
q, k, v = qkv[0], qkv[1], qkv[2] # make torchscript happy (cannot use tensor as tuple)
q = q * self.scale
attn = (q @ k.transpose(-2, -1))
relative_position_bias = self.relative_position_bias_table[self.relative_position_index.view(-1)].view(
self.window_size[0] * self.window_size[1], self.window_size[0] * self.window_size[1], -1) # Wh*Ww,Wh*Ww,nH
relative_position_bias = relative_position_bias.permute(2, 0, 1).contiguous() # nH, Wh*Ww, Wh*Ww
attn = attn + relative_position_bias.unsqueeze(0)
if mask is not None:
nW = mask.shape[0]
attn = attn.view(B_ // nW, nW, self.num_heads, N, N) + mask.unsqueeze(1).unsqueeze(0)
attn = attn.view(-1, self.num_heads, N, N)
attn = self.softmax(attn)
else:
attn = self.softmax(attn)
attn = self.attn_drop(attn)
x = (attn @ v).transpose(1, 2).reshape(B_, N, C)
x = self.proj(x)
x = self.proj_drop(x)
return x
def extra_repr(self) -> str:
return f'dim={self.dim}, window_size={self.window_size}, num_heads={self.num_heads}'
def flops(self, N):
# calculate flops for 1 window with token length of N
flops = 0
# qkv = self.qkv(x)
flops += N * self.dim * 3 * self.dim
# attn = (q @ k.transpose(-2, -1))
flops += self.num_heads * N * (self.dim // self.num_heads) * N
# x = (attn @ v)
flops += self.num_heads * N * N * (self.dim // self.num_heads)
# x = self.proj(x)
flops += N * self.dim * self.dim
return flops
class SwinTransformerBlock(nn.Module):
r""" Swin Transformer Block.
Args:
dim (int): Number of input channels.
input_resolution (tuple[int]): Input resulotion.
num_heads (int): Number of attention heads.
window_size (int): Window size.
shift_size (int): Shift size for SW-MSA.
mlp_ratio (float): Ratio of mlp hidden dim to embedding dim.
qkv_bias (bool, optional): If True, add a learnable bias to query, key, value. Default: True
qk_scale (float | None, optional): Override default qk scale of head_dim ** -0.5 if set.
drop (float, optional): Dropout rate. Default: 0.0
attn_drop (float, optional): Attention dropout rate. Default: 0.0
drop_path (float, optional): Stochastic depth rate. Default: 0.0
act_layer (nn.Module, optional): Activation layer. Default: nn.GELU
norm_layer (nn.Module, optional): Normalization layer. Default: nn.LayerNorm
"""
def __init__(self, dim, input_resolution, num_heads, window_size=7, shift_size=0,
mlp_ratio=4., qkv_bias=True, qk_scale=None, drop=0., attn_drop=0., drop_path=0.,
act_layer=nn.GELU, norm_layer=nn.LayerNorm):
super().__init__()
self.dim = dim
self.input_resolution = input_resolution
self.num_heads = num_heads
self.window_size = window_size
self.shift_size = shift_size
self.mlp_ratio = mlp_ratio
if min(self.input_resolution) <= self.window_size:
# if window size is larger than input resolution, we don't partition windows
self.shift_size = 0
self.window_size = min(self.input_resolution)
assert 0 <= self.shift_size < self.window_size, "shift_size must in 0-window_size"
self.norm1 = norm_layer(dim)
self.attn = WindowAttention(
dim, window_size=to_2tuple(self.window_size), num_heads=num_heads,
qkv_bias=qkv_bias, qk_scale=qk_scale, attn_drop=attn_drop, proj_drop=drop)
self.drop_path = DropPath(drop_path) if drop_path > 0. else nn.Identity()
self.norm2 = norm_layer(dim)
mlp_hidden_dim = int(dim * mlp_ratio)
self.mlp = Mlp(in_features=dim, hidden_features=mlp_hidden_dim, act_layer=act_layer, drop=drop)
if self.shift_size > 0:
# calculate attention mask for SW-MSA
H, W = self.input_resolution
img_mask = torch.zeros((1, H, W, 1)) # 1 H W 1
h_slices = (slice(0, -self.window_size),
slice(-self.window_size, -self.shift_size),
slice(-self.shift_size, None))
w_slices = (slice(0, -self.window_size),
slice(-self.window_size, -self.shift_size),
slice(-self.shift_size, None))
cnt = 0
for h in h_slices:
for w in w_slices:
img_mask[:, h, w, :] = cnt
cnt += 1
mask_windows = window_partition(img_mask, self.window_size) # nW, window_size, window_size, 1
mask_windows = mask_windows.view(-1, self.window_size * self.window_size)
attn_mask = mask_windows.unsqueeze(1) - mask_windows.unsqueeze(2)
attn_mask = attn_mask.masked_fill(attn_mask != 0, float(-100.0)).masked_fill(attn_mask == 0, float(0.0))
else:
attn_mask = None
self.register_buffer("attn_mask", attn_mask)
def forward(self, x):
H, W = self.input_resolution
B, L, C = x.shape
assert L == H * W, "input feature has wrong size"
shortcut = x
x = self.norm1(x)
x = x.view(B, H, W, C)
# cyclic shift
if self.shift_size > 0:
shifted_x = torch.roll(x, shifts=(-self.shift_size, -self.shift_size), dims=(1, 2))
else:
shifted_x = x
# partition windows
x_windows = window_partition(shifted_x, self.window_size) # nW*B, window_size, window_size, C
x_windows = x_windows.view(-1, self.window_size * self.window_size, C) # nW*B, window_size*window_size, C
# W-MSA/SW-MSA
attn_windows = self.attn(x_windows, mask=self.attn_mask) # nW*B, window_size*window_size, C
# merge windows
attn_windows = attn_windows.view(-1, self.window_size, self.window_size, C)
shifted_x = window_reverse(attn_windows, self.window_size, H, W) # B H' W' C
# reverse cyclic shift
if self.shift_size > 0:
x = torch.roll(shifted_x, shifts=(self.shift_size, self.shift_size), dims=(1, 2))
else:
x = shifted_x
x = x.view(B, H * W, C)
# FFN
x = shortcut + self.drop_path(x)
x = x + self.drop_path(self.mlp(self.norm2(x)))
return x
def extra_repr(self) -> str:
return f"dim={self.dim}, input_resolution={self.input_resolution}, num_heads={self.num_heads}, " \
f"window_size={self.window_size}, shift_size={self.shift_size}, mlp_ratio={self.mlp_ratio}"
def flops(self):
flops = 0
H, W = self.input_resolution
# norm1
flops += self.dim * H * W
# W-MSA/SW-MSA
nW = H * W / self.window_size / self.window_size
flops += nW * self.attn.flops(self.window_size * self.window_size)
# mlp
flops += 2 * H * W * self.dim * self.dim * self.mlp_ratio
# norm2
flops += self.dim * H * W
return flops
class PatchMerging(nn.Module):
r""" Patch Merging Layer.
Args:
input_resolution (tuple[int]): Resolution of input feature.
dim (int): Number of input channels.
norm_layer (nn.Module, optional): Normalization layer. Default: nn.LayerNorm
"""
def __init__(self, input_resolution, dim, norm_layer=nn.LayerNorm):
super().__init__()
self.input_resolution = input_resolution
self.dim = dim
self.reduction = nn.Linear(4 * dim, 2 * dim, bias=False)
self.norm = norm_layer(4 * dim)
def forward(self, x):
"""
x: B, H*W, C
"""
H, W = self.input_resolution
B, L, C = x.shape
assert L == H * W, "input feature has wrong size"
assert H % 2 == 0 and W % 2 == 0, f"x size ({H}*{W}) are not even."
x = x.view(B, H, W, C)
x0 = x[:, 0::2, 0::2, :] # B H/2 W/2 C
x1 = x[:, 1::2, 0::2, :] # B H/2 W/2 C
x2 = x[:, 0::2, 1::2, :] # B H/2 W/2 C
x3 = x[:, 1::2, 1::2, :] # B H/2 W/2 C
x = torch.cat([x0, x1, x2, x3], -1) # B H/2 W/2 4*C
x = x.view(B, -1, 4 * C) # B H/2*W/2 4*C
x = self.norm(x)
x = self.reduction(x)
return x
def extra_repr(self) -> str:
return f"input_resolution={self.input_resolution}, dim={self.dim}"
def flops(self):
H, W = self.input_resolution
flops = H * W * self.dim
flops += (H // 2) * (W // 2) * 4 * self.dim * 2 * self.dim
return flops
class BasicLayer(nn.Module):
""" A basic Swin Transformer layer for one stage.
Args:
dim (int): Number of input channels.
input_resolution (tuple[int]): Input resolution.
depth (int): Number of blocks.
num_heads (int): Number of attention heads.
window_size (int): Local window size.
mlp_ratio (float): Ratio of mlp hidden dim to embedding dim.
qkv_bias (bool, optional): If True, add a learnable bias to query, key, value. Default: True
qk_scale (float | None, optional): Override default qk scale of head_dim ** -0.5 if set.
drop (float, optional): Dropout rate. Default: 0.0
attn_drop (float, optional): Attention dropout rate. Default: 0.0
drop_path (float | tuple[float], optional): Stochastic depth rate. Default: 0.0
norm_layer (nn.Module, optional): Normalization layer. Default: nn.LayerNorm
downsample (nn.Module | None, optional): Downsample layer at the end of the layer. Default: None
use_checkpoint (bool): Whether to use checkpointing to save memory. Default: False.
"""
def __init__(self, dim, input_resolution, depth, num_heads, window_size,
mlp_ratio=4., qkv_bias=True, qk_scale=None, drop=0., attn_drop=0.,
drop_path=0., norm_layer=nn.LayerNorm, downsample=None, use_checkpoint=False):
super().__init__()
self.dim = dim
self.input_resolution = input_resolution
self.depth = depth
self.use_checkpoint = use_checkpoint
# build blocks
self.blocks = nn.ModuleList([
SwinTransformerBlock(dim=dim, input_resolution=input_resolution,
num_heads=num_heads, window_size=window_size,
shift_size=0 if (i % 2 == 0) else window_size // 2,
mlp_ratio=mlp_ratio,
qkv_bias=qkv_bias, qk_scale=qk_scale,
drop=drop, attn_drop=attn_drop,
drop_path=drop_path[i] if isinstance(drop_path, list) else drop_path,
norm_layer=norm_layer)
for i in range(depth)])
# patch merging layer
if downsample is not None:
self.downsample = downsample(input_resolution, dim=dim, norm_layer=norm_layer)
else:
self.downsample = None
def forward(self, x):
for blk in self.blocks:
if self.use_checkpoint:
x = checkpoint.checkpoint(blk, x)
else:
x = blk(x)
if self.downsample is not None:
x = self.downsample(x)
return x
def extra_repr(self) -> str:
return f"dim={self.dim}, input_resolution={self.input_resolution}, depth={self.depth}"
def flops(self):
flops = 0
for blk in self.blocks:
flops += blk.flops()
if self.downsample is not None:
flops += self.downsample.flops()
return flops
class PatchEmbed(nn.Module):
r""" Image to Patch Embedding
Args:
img_size (int): Image size. Default: 224.
patch_size (int): Patch token size. Default: 4.
in_chans (int): Number of input image channels. Default: 3.
embed_dim (int): Number of linear projection output channels. Default: 96.
norm_layer (nn.Module, optional): Normalization layer. Default: None
"""
def __init__(self, img_size=224, patch_size=4, in_chans=3, embed_dim=96, norm_layer=None):
super().__init__()
img_size = to_2tuple(img_size)
patch_size = to_2tuple(patch_size)
patches_resolution = [img_size[0] // patch_size[0], img_size[1] // patch_size[1]]
self.img_size = img_size
self.patch_size = patch_size
self.patches_resolution = patches_resolution
self.num_patches = patches_resolution[0] * patches_resolution[1]
self.in_chans = in_chans
self.embed_dim = embed_dim
self.proj = nn.Conv2d(in_chans, embed_dim, kernel_size=patch_size, stride=patch_size)
if norm_layer is not None:
self.norm = norm_layer(embed_dim)
else:
self.norm = None
def forward(self, x):
B, C, H, W = x.shape
# FIXME look at relaxing size constraints
assert H == self.img_size[0] and W == self.img_size[1], \
f"Input image size ({H}*{W}) doesn't match model ({self.img_size[0]}*{self.img_size[1]})."
x = self.proj(x).flatten(2).transpose(1, 2) # B Ph*Pw C
if self.norm is not None:
x = self.norm(x)
return x
def flops(self):
Ho, Wo = self.patches_resolution
flops = Ho * Wo * self.embed_dim * self.in_chans * (self.patch_size[0] * self.patch_size[1])
if self.norm is not None:
flops += Ho * Wo * self.embed_dim
return flops
class SwinTransformer(nn.Module):
r""" Swin Transformer
A PyTorch impl of : `Swin Transformer: Hierarchical Vision Transformer using Shifted Windows` -
https://arxiv.org/pdf/2103.14030
Args:
img_size (int | tuple(int)): Input image size. Default 224
patch_size (int | tuple(int)): Patch size. Default: 4
in_chans (int): Number of input image channels. Default: 3
num_classes (int): Number of classes for classification head. Default: 1000
embed_dim (int): Patch embedding dimension. Default: 96
depths (tuple(int)): Depth of each Swin Transformer layer.
num_heads (tuple(int)): Number of attention heads in different layers.
window_size (int): Window size. Default: 7
mlp_ratio (float): Ratio of mlp hidden dim to embedding dim. Default: 4
qkv_bias (bool): If True, add a learnable bias to query, key, value. Default: True
qk_scale (float): Override default qk scale of head_dim ** -0.5 if set. Default: None
drop_rate (float): Dropout rate. Default: 0
attn_drop_rate (float): Attention dropout rate. Default: 0
drop_path_rate (float): Stochastic depth rate. Default: 0.1
norm_layer (nn.Module): Normalization layer. Default: nn.LayerNorm.
ape (bool): If True, add absolute position embedding to the patch embedding. Default: False
patch_norm (bool): If True, add normalization after patch embedding. Default: True
use_checkpoint (bool): Whether to use checkpointing to save memory. Default: False
"""
def __init__(self, img_size=224, patch_size=4, in_chans=3, num_classes=1000,
embed_dim=96, depths=[2, 2, 6, 2], num_heads=[3, 6, 12, 24],
window_size=7, mlp_ratio=4., qkv_bias=True, qk_scale=None,
drop_rate=0., attn_drop_rate=0., drop_path_rate=0.1,
norm_layer=nn.LayerNorm, ape=False, patch_norm=True,
use_checkpoint=False, **kwargs):
super().__init__()
self.num_classes = num_classes
self.num_layers = len(depths)
self.embed_dim = embed_dim
self.ape = ape
self.patch_norm = patch_norm
self.num_features = int(embed_dim * 2 ** (self.num_layers - 1))
self.mlp_ratio = mlp_ratio
# split image into non-overlapping patches
self.patch_embed = PatchEmbed(
img_size=img_size, patch_size=patch_size, in_chans=in_chans, embed_dim=embed_dim,
norm_layer=norm_layer if self.patch_norm else None)
num_patches = self.patch_embed.num_patches
patches_resolution = self.patch_embed.patches_resolution
self.patches_resolution = patches_resolution
# absolute position embedding
if self.ape:
self.absolute_pos_embed = nn.Parameter(torch.zeros(1, num_patches, embed_dim))
trunc_normal_(self.absolute_pos_embed, std=.02)
self.pos_drop = nn.Dropout(p=drop_rate)
# stochastic depth
dpr = [x.item() for x in torch.linspace(0, drop_path_rate, sum(depths))] # stochastic depth decay rule
# build layers
self.layers = nn.ModuleList()
for i_layer in range(self.num_layers):
layer = BasicLayer(dim=int(embed_dim * 2 ** i_layer),
input_resolution=(patches_resolution[0] // (2 ** i_layer),
patches_resolution[1] // (2 ** i_layer)),
depth=depths[i_layer],
num_heads=num_heads[i_layer],
window_size=window_size,
mlp_ratio=self.mlp_ratio,
qkv_bias=qkv_bias, qk_scale=qk_scale,
drop=drop_rate, attn_drop=attn_drop_rate,
drop_path=dpr[sum(depths[:i_layer]):sum(depths[:i_layer + 1])],
norm_layer=norm_layer,
downsample=PatchMerging if (i_layer < self.num_layers - 1) else None,
use_checkpoint=use_checkpoint)
self.layers.append(layer)
self.norm = norm_layer(self.num_features)
self.avgpool = nn.AdaptiveAvgPool1d(1)
self.head = nn.Linear(self.num_features, num_classes) if num_classes > 0 else nn.Identity()
self.apply(self._init_weights)
def _init_weights(self, m):
if isinstance(m, nn.Linear):
trunc_normal_(m.weight, std=.02)
if isinstance(m, nn.Linear) and m.bias is not None:
nn.init.constant_(m.bias, 0)
elif isinstance(m, nn.LayerNorm):
nn.init.constant_(m.bias, 0)
nn.init.constant_(m.weight, 1.0)
@torch.jit.ignore
def no_weight_decay(self):
return {'absolute_pos_embed'}
@torch.jit.ignore
def no_weight_decay_keywords(self):
return {'relative_position_bias_table'}
def forward_features(self, x):
x = self.patch_embed(x)
if self.ape:
x = x + self.absolute_pos_embed
x = self.pos_drop(x)
for layer in self.layers:
x = layer(x)
x = self.norm(x) # B L C
x = self.avgpool(x.transpose(1, 2)) # B C 1
x = torch.flatten(x, 1)
return x
def forward(self, x):
x = self.forward_features(x)
x = self.head(x)
return x
def flops(self):
flops = 0
flops += self.patch_embed.flops()
for i, layer in enumerate(self.layers):
flops += layer.flops()
flops += self.num_features * self.patches_resolution[0] * self.patches_resolution[1] // (2 ** self.num_layers)
flops += self.num_features * self.num_classes
return flops
```
|
github_jupyter
|
```
import os
os.environ['CUDA_VISIBLE_DEVICES'] = '2'
import pickle
import numpy as np
import pandas as pd
import skimage.io as io
import matplotlib.pyplot as plt
%matplotlib inline
import tensorflow as tf
import keras
from keras.applications import ResNet50
from keras.applications.resnet50 import preprocess_input
from keras.models import Model
from keras.layers import GlobalAveragePooling2D, Dense, Dropout, Activation, Input, Lambda, BatchNormalization
from keras.optimizers import Adam
from keras.utils import to_categorical
from imgaug import augmenters as iaa
from datetime import datetime
# %load keras_utils.py
import keras
import numpy as np
import skimage.io as io
class DataGenerator(keras.utils.Sequence):
'Generates data for Keras'
def __init__(self, list_IDs, labels, center_IDs=None, batch_size=32, dim=(256,256,3), shuffle=True, img_preprocess=None, img_aug = None):
'Initialization'
self.dim = dim
self.batch_size = batch_size
self.labels = labels
self.list_IDs = list_IDs
self.center_IDs = center_IDs
self.n_classes = labels.shape[1]
self.shuffle = shuffle
self.on_epoch_end()
self.indexes = list(range(0, len(self.list_IDs)))
self.img_aug = img_aug
self.img_preprocess = img_preprocess
def __len__(self):
'Denotes the number of batches per epoch'
return int(np.floor(len(self.list_IDs) / self.batch_size))
def __getitem__(self, index):
'Generate one batch of data'
# Generate indexes of the batch
indexes = self.indexes[index*self.batch_size:min((index+1)*self.batch_size, len(self.list_IDs))]
'Generates data containing batch_size samples' # X : (n_samples, *dim, n_channels)
# Initialization
X = np.empty((self.batch_size, *self.dim))
Y = np.empty((self.batch_size, self.n_classes), dtype=int)
M = np.empty((self.batch_size), dtype=int)
# Generate data
for i, ID in enumerate(indexes):
# Store sample
X[i,] = io.imread(self.list_IDs[ID]).astype(float)
# Store class
Y[i,] = self.labels[ID]
if self.img_aug is not None:
X = self.img_aug.augment_images(X.astype(np.uint8))
X = self.__data_preprocess(X.astype(float))
if self.center_IDs is None:
return X, Y
else:
for i, ID in enumerate(indexes):
M[i] = self.center_IDs[ID]
return [X,M], [Y,M]
def on_epoch_end(self):
'Updates indexes after each epoch'
self.indexes = np.arange(len(self.list_IDs))
if self.shuffle == True:
np.random.shuffle(self.indexes)
def __data_preprocess(self, img):
if self.img_preprocess is None:
processed_img = img/255.0
else:
processed_img = self.img_preprocess(img)
return processed_img
FLAG_savedir = '/home/put_data/moth/metadata/5_fold/'
FLAG_sfold = 5
idx_fold = 4
FLAG_hidden = 1024
FLAG_dropout = 0.0
FLAG_base_model = 'ResNet50'
FLAG_batch_size = 32
X = pd.read_csv('/home/put_data/moth/metadata/1121_updated_metadata_flickr_summary_used_final.csv',index_col=0)
X.head()
with open(os.path.join('/home/put_data/moth/metadata/1121_Y_mean_dict.pickle'), 'rb') as handle:
Y_dict = pickle.load(handle)
FLAG_model_save = '/home/put_data/moth/code/cmchang/regression/fullcrop_dp{0}_newaug-rmhue+old_species_keras_resnet_fold_{1}_{2}'.format(int(FLAG_dropout*100), datetime.now().strftime('%Y%m%d'),
idx_fold)
if not os.path.exists(FLAG_model_save):
os.makedirs(FLAG_model_save)
print('directory: {}'.format(FLAG_model_save))
X['img_rmbg_path'] = X.Number.apply(lambda x: '/home/put_data/moth/data/whole_crop/'+str(x)+'.png')
plt.imshow(io.imread(X.img_rmbg_path[0]))
sel = list()
for i in range(X.shape[0]):
if os.path.exists(X['img_rmbg_path'][i]):
sel.append(True)
else:
sel.append(False)
X = X[sel]
Xtrain = X[(X.Species.duplicated() == False)]
Xsplit = X[(X.Species.duplicated() == True)]
print("Unique: {0}; Duplicate: {1}".format(Xtrain.shape, Xsplit.shape))
from sklearn.model_selection import train_test_split
Xmerge, Xtest = train_test_split(Xsplit, test_size = 0.2, random_state=0)
Xtrain = pd.concat([Xtrain, Xmerge])
Ytrain = np.vstack(Xtrain['Species'].apply(lambda x: Y_dict[x]))
Ytest = np.vstack(Xtest['Species'].apply(lambda x: Y_dict[x]))
print('Xtrain.shape: {0}, Ytrain.shape: {1}'.format(Xtrain.shape, Ytrain.shape))
print('Xtest.shape: {0}, Ytest.shape: {1}'.format(Xtest.shape, Ytest.shape))
Xtrain.to_csv(os.path.join(FLAG_model_save,'train.csv'), index=False)
Xtest.to_csv(os.path.join(FLAG_model_save,'test.csv'), index=False)
sometimes = lambda aug: iaa.Sometimes(0.5, aug)
augseq = iaa.Sequential([
iaa.Fliplr(0.5)
,sometimes(iaa.Affine(
scale={"x": (0.9, 1.1), "y": (0.9, 1.1)}, # scale images to 80-120% of their size, individually per axis
translate_percent={"x": (-0.1, 0.1), "y": (-0.1, 0.1)}, # translate by -20 to +20 percent (per axis)
rotate=(-30, 30), # rotate by -45 to +45 degrees
cval=255 # if mode is constant, use a cval between 0 and 255
))
])
# Parameters
input_shape = (256, 256, 3)
n_classes = Ytest.shape[1]
batch_size = FLAG_batch_size
isCenterloss = False
from keras.regularizers import l2
img_input = Input(shape=input_shape)
extractor = ResNet50(input_tensor=img_input, include_top=False, weights='imagenet', pooling='avg')
x1 = Dense(FLAG_hidden)(extractor.output)
x1 = BatchNormalization()(x1)
x1 = Activation(activation='relu')(x1)
output = Dense(n_classes, activation='linear', name='output_layer')(x1)
train_params = {'dim': input_shape,
'batch_size': FLAG_batch_size,
'shuffle': True,
'img_aug': augseq,
'img_preprocess': tf.contrib.keras.applications.resnet50.preprocess_input}
valid_params = {'dim': input_shape,
'batch_size': FLAG_batch_size,
'shuffle': False,
'img_aug': None,
'img_preprocess': tf.contrib.keras.applications.resnet50.preprocess_input}
model = Model(inputs=img_input, outputs=output)
model.compile(optimizer=Adam(lr=5e-5, beta_1=0.5),
loss="mean_squared_error")
# Generators
training_generator = DataGenerator(list_IDs = list(Xtrain['img_rmbg_path']), labels = Ytrain, center_IDs = None, **train_params)
validation_generator = DataGenerator(list_IDs = list(Xtest['img_rmbg_path']), labels = Ytest, center_IDs = None, **valid_params)
model.summary()
csv_logger = keras.callbacks.CSVLogger(os.path.join(FLAG_model_save, 'training.log'))
checkpoint = keras.callbacks.ModelCheckpoint(os.path.join(FLAG_model_save, 'model.h5'),
monitor='val_loss',
verbose=1,
save_best_only=True,
save_weights_only=False,
mode='min',
period=1)
earlystop = keras.callbacks.EarlyStopping(monitor='val_loss', mode='min',patience=20,min_delta=0.01)
# Train model on dataset
model.fit_generator(generator=training_generator,
validation_data=validation_generator,
steps_per_epoch=Xtrain.shape[0]/FLAG_batch_size,
validation_steps=Xtest.shape[0]/FLAG_batch_size,
epochs=200,
callbacks=[csv_logger, checkpoint, earlystop])
loss = pd.read_table(csv_logger.filename, delimiter=',')
plt.plot(loss.epoch, loss.loss, label='loss')
plt.plot(loss.epoch, loss.val_loss, label='val_loss')
plt.legend()
plt.xlabel('epoch')
plt.ylabel('MSE')
plt.savefig(os.path.join(FLAG_model_save, 'loss.png'))
best_epoch = np.argmin(loss.val_loss)
header = 'model_save,base_model,batch_size,hidden,dropout,epoch,loss,val_loss\n'
row = '{0},{1},{2},{3},{4},{5},{6:.4f},{7:.4f}\n'.format(FLAG_model_save,
FLAG_base_model,
FLAG_batch_size,
FLAG_hidden,
FLAG_dropout,
best_epoch,
loss.iloc[best_epoch]['loss'],
loss.iloc[best_epoch]['val_loss'])
if os.path.exists('result_summary.csv'):
with open('result_summary.csv','a') as myfile:
myfile.write(row)
else:
with open('result_summary.csv','w') as myfile:
myfile.write(header)
myfile.write(row)
```
### evaluation over validation dataset
```
from keras.models import load_model
model = load_model(os.path.join(FLAG_model_save,'model.h5'))
TestImg = list()
for i in range(Xtest.shape[0]):
img = io.imread(list(Xtest['img_rmbg_path'])[i])
TestImg.append(img)
TestImg = np.stack(TestImg)
TestInput = preprocess_input(TestImg.astype(float))
Pred = model.predict(TestInput)
from sklearn.metrics import mean_squared_error, mean_absolute_error
from scipy.stats import pearsonr
plt.scatter(Ytest, Pred, s=0.7)
plt.xlabel('true')
plt.ylabel('pred')
plt.title('rmse={0:.4f}, cor={1:.4f}'.format(np.sqrt(mean_squared_error(y_true=Ytest, y_pred=Pred)),
pearsonr(Ytest, Pred)[0][0]))
plt.savefig(os.path.join(FLAG_model_save, 'scatter_per_img.png'))
result = pd.DataFrame({'Species':Xtest.Species,
'pred':Pred.reshape(-1),
'true':Ytest.reshape(-1)})
result.to_csv(os.path.join(FLAG_model_save, 'predictions.csv'), index=False)
```
### by species
```
Xtest = Xtest.reset_index()
Xtest.drop(columns='index', inplace=True)
Ytest = np.vstack(Xtest['Species'].apply(lambda x: Y_dict[x]))
df_species_group = Xtest.groupby('Species').apply(
lambda g: pd.Series({
'indices': g.index.tolist(),
# 'Alt_class': g['Alt_class'].unique().tolist()[0]
}))
df_species_group = df_species_group.sample(frac=1).reset_index()
display(df_species_group.head())
species_ypred = list()
species_ytest = list()
for i in range(len(df_species_group)):
tidx = df_species_group.iloc[i][1]
species_ypred.append(np.mean(Pred[tidx], axis=0))
species_ytest.append(np.mean(Ytest[tidx], axis=0))
species_ypred = np.stack(species_ypred)
species_ytest = np.stack(species_ytest)
plt.scatter(species_ytest, species_ypred, s=0.7)
plt.xlabel('true')
plt.ylabel('pred')
plt.title('rmse={0:.4f}, cor={1:.4f}'.format(mean_squared_error(y_true=species_ytest, y_pred=species_ypred)**0.5,
pearsonr(species_ytest, species_ypred)[0][0]))
plt.savefig(os.path.join(FLAG_model_save, 'scatter_per_species.png'))
result = pd.DataFrame({'Species':df_species_group.Species,
'pred':species_ypred.reshape(-1),
'true':species_ytest.reshape(-1)})
result.to_csv(os.path.join(FLAG_model_save, 'predictions_species.csv'), index=False)
```
|
github_jupyter
|
```
import os
os.environ['GOOGLE_APPLICATION_CREDENTIALS'] = '/home/husein/t5/prepare/mesolitica-tpu.json'
os.environ['CUDA_VISIBLE_DEVICES'] = ''
from bigbird import modeling
from bigbird import utils
import tensorflow as tf
import numpy as np
import sentencepiece as spm
vocab = '/home/husein/b2b/sp10m.cased.t5.model'
sp = spm.SentencePieceProcessor()
sp.Load(vocab)
class Encoder:
def __init__(self, sp):
self.sp = sp
self.vocab_size = sp.GetPieceSize() + 100
def encode(self, s):
return self.sp.EncodeAsIds(s)
def decode(self, ids, strip_extraneous=False):
return self.sp.DecodeIds(list(ids))
encoder = Encoder(sp)
top_p = tf.placeholder(tf.float32, None, name = 'top_p')
temperature = tf.placeholder(tf.float32, None, name = 'temperature')
bert_config = {
# transformer basic configs
'attention_probs_dropout_prob': 0.1,
'hidden_act': 'relu',
'hidden_dropout_prob': 0.1,
'hidden_size': 512,
'initializer_range': 0.02,
'intermediate_size': 3072,
'max_position_embeddings': 4096,
'max_encoder_length': 2048,
'max_decoder_length': 512,
'num_attention_heads': 8,
'num_hidden_layers': 6,
'type_vocab_size': 2,
'scope': 'pegasus',
'use_bias': False,
'rescale_embedding': True,
'vocab_model_file': None,
# sparse mask configs
'attention_type': 'block_sparse',
'norm_type': 'prenorm',
'block_size': 64,
'num_rand_blocks': 3,
'vocab_size': 32128,
'beam_size': 1,
'alpha': 1.0,
'couple_encoder_decoder': False,
'num_warmup_steps': 10000,
'learning_rate': 0.1,
'label_smoothing': 0.0,
'optimizer': 'Adafactor',
'use_tpu': True,
'top_p': top_p,
'temperature': temperature
}
model = modeling.TransformerModel(bert_config)
X = tf.placeholder(tf.int32, [None, None])
r = model(X, training = False)
r
logits = tf.identity(r[0][2], name = 'logits')
logits
files = tf.gfile.Glob('gs://mesolitica-tpu-general/t2t-summarization-v2/data/seq2*')
batch_size = 4
data_fields = {
'inputs': tf.VarLenFeature(tf.int64),
'targets': tf.VarLenFeature(tf.int64),
}
data_len = {
'inputs': 2048,
'targets': 1024,
}
def parse(serialized_example):
features = tf.parse_single_example(
serialized_example, features = data_fields
)
for k in features.keys():
features[k] = features[k].values
features[k] = tf.pad(
features[k], [[0, data_len[k] - tf.shape(features[k])[0]]]
)
features[k].set_shape((data_len[k]))
return features
def _decode_record(example, name_to_features):
"""Decodes a record to a TensorFlow example."""
# tf.Example only supports tf.int64, but the TPU only supports tf.int32.
# So cast all int64 to int32.
for name in list(example.keys()):
t = example[name]
if t.dtype == tf.int64:
t = tf.to_int32(t)
example[name] = t
return example
d = tf.data.TFRecordDataset(files)
d = d.map(parse, num_parallel_calls = 32)
d = d.apply(
tf.contrib.data.map_and_batch(
lambda record: _decode_record(record, data_fields),
batch_size = batch_size,
num_parallel_batches = 4,
drop_remainder = True,
)
)
d = d.make_one_shot_iterator().get_next()
d
import tensorflow as tf
ckpt_path = tf.train.latest_checkpoint('gs://mesolitica-tpu-general/bigbird-summarization-small')
ckpt_path
sess = tf.InteractiveSession()
sess.run(tf.global_variables_initializer())
r_ = sess.run(d)
encoder.decode(r_['inputs'][0].tolist())
encoder.decode(r_['targets'][0].tolist())
# import re
# import collections
# def get_assignment_map_from_checkpoint(tvars, init_checkpoint):
# """Compute the union of the current variables and checkpoint variables."""
# assignment_map = {}
# initialized_variable_names = {}
# name_to_variable = collections.OrderedDict()
# for var in tvars:
# name = var.name
# m = re.match('^(.*):\\d+$', name)
# if m is not None:
# name = m.group(1)
# name_to_variable[name] = var
# init_vars = tf.train.list_variables(init_checkpoint)
# assignment_map = collections.OrderedDict()
# for x in init_vars:
# (name, var) = (x[0], x[1])
# l = 'pegasus/' + name
# l = l.replace('embeddings/weights', 'embeddings/word_embeddings')
# l = l.replace('self/output', 'output')
# l = l.replace('ffn/dense_1', 'output/dense')
# l = l.replace('ffn', 'intermediate')
# l = l.replace('memory_attention/output', 'attention/encdec_output')
# l = l.replace('memory_attention', 'attention/encdec')
# if l not in name_to_variable:
# continue
# assignment_map[name] = name_to_variable[l]
# initialized_variable_names[l + ':0'] = 1
# return (assignment_map, initialized_variable_names)
# t = tf.trainable_variables()
# assignment_map, initialized_variable_names = get_assignment_map_from_checkpoint(t, ckpt_path)
saver = tf.train.Saver()
saver.restore(sess, ckpt_path)
# var_lists = tf.get_collection(tf.GraphKeys.TRAINABLE_VARIABLES)
# saver = tf.train.Saver(var_list = var_lists)
# saver.restore(sess, 'gs://mesolitica-tpu-general/bigbird-summarization-small/model.ckpt-0')
import re
from unidecode import unidecode
def cleaning(string):
return re.sub(r'[ ]+', ' ', unidecode(string.replace('\n', ' '))).strip()
string = """
KUALA LUMPUR: Hakim Mahkamah Tinggi, Mohd Nazlan Mohd Ghazali menyifatkan kes penyelewengan dana RM42 juta milik SRC International Sdn Bhd dihadapi Datuk Seri Najib Razak adalah kesalahan salah guna kedudukan, pecah amanah jenayah dan pengubahan wang haram yang paling teruk.
Mohd Nazlan yang mensabitkan Najib terhadap kesemua tujuh tuduhan dan memerintahkan bekas Perdana Menteri itu dipenjara 12 tahun, dan didenda RM210 juta, berkata ia bukan sahaja disebabkan oleh alasan bagaimana jenayah itu dilakukan, malah kes berprofil tinggi berkenaan turut membabitkan sejumlah wang yang sangat besar.
Melalui alasan penghakiman penuh setebal 801 muka surat itu, Mohd Nazlan, berkata kes terbabit mempunyai elemen yang memberikan kesan ke atas kepentingan awam kerana dana RM42 juta itu adalah milik Kementerian Kewangan (Diperbadankan) (MKD) yang berkemungkinan berasal daripada dana pencen Kumpulan Wang Persaraan (Diperbadankan) (KWAP) berjumlah RM4 bilion.
"Dan yang paling penting ia membabitkan individu yang pada ketika itu berada dalam pada tertinggi dalam kerajaan," katanya.
Pada 28 Julai lalu, Mohd Nazlan memerintahkan Najib dipenjarakan 10 tahun masing-masing bagi tiga tuduhan pecah amanah wang RM42 juta milik SRC.
Hakim turut memerintahkan Najib dipenjara 12 tahun dan denda RM210 juta (jika gagal bayar, lima tahun penjara) bagi tuduhan menyalahgunakan kedudukan.
Bagi tuduhan pengubahan wang haram pula, Mohd Nazlan memerintahkan Najib dipenjara 10 tahun bagi setiap tuduhan.
Sementara itu, Mohd Nazlan berkata, Najib selaku tertuduh tidak menunjukkan penyesalan, malah mempertahankan pembelaan beliau tidak mengetahui mengenai wang RM42 juta milik SRC itu dalam rayuannya bagi diringankan hukuman.
"Tetapi saya tidak boleh menafikan beliau adalah Perdana Menteri negara ini dan tidak boleh mempersoalkan sumbangannya untuk kebaikan dan kesejahteraan masyarakat dalam pelbagai cara kerana beliau adalah Perdana Menteri selama sembilan tahun.
"Sejarah politik akan terus diperdebatkan sama ada dari segi keseimbangan, beliau melakukan lebih banyak kebaikan daripada keburukan.
"Walau apa pun, ia adalah tidak selari dengan idea sesebuah pentadbiran negara yang bersih daripada rasuah yang tidak boleh bertolak ansur dengan sebarang penyalahgunaan kuasa," katanya.
Mahkamah Rayuan menetapkan pada 15 Oktober ini bagi pengurusan kes rayuan Najib terhadap sabitan dan hukuman terhadapnya.
"""
string2 = """
Gabungan parti Warisan, Pakatan Harapan, dan Upko hari ini mendedahkan calon-calon masing-masing untuk pilihan raya negeri Sabah, tetapi ketika pengumuman itu berlangsung, perwakilan PKR di dewan itu dilihat ‘gelisah’ seperti ‘tidak senang duduk’.
Sekumpulan anggota PKR kemudian dilihat meninggalkan dewan di Pusat Konvensyen Antarabangsa Sabah di Kota Kinabalu selepas berbincang dengan ketua PKR Sabah Christina Liew.
Semakan senarai-senarai calon berkenaan mendapati PKR hanya memperolehi separuh daripada jumlah kerusi yang diharapkan.
Semalam, PKR Sabah mengumumkan akan bertanding di 14 kerusi tetapi ketika Presiden Warisan Shafie Apdal mengumumkan calon gabungan tersebut hari ini, PKR hanya diberikan tujuh kerusi untuk bertanding.
Kerusi yang diberikan adalah Api-Api, Inanam, Tempasuk, Tamparuli, Matunggong, Klias, dan Sook.
Klias dan Sook adalah dua kerusi yang diberikan kepada PKR, sementara lima kerusi selebihnya pernah ditandingi oleh PKR pada pilihan raya umum 2018.
Dalam pengumuman PKR Sabah semalam, parti itu menjangkakan Warisan akan turut menyerahkan kerusi Kemabong, Membakut, dan Petagas kepada mereka.
Walau bagaimanapun, Warisan menyerahkan kerusi Kemabong kepada Upko dan mengekalkan bertanding untuk kerusi Membakut dan Petagas.
PKR juga menuntut empat daripada 13 kerusi baru yang diperkenalkan iaitu Segama, Limbahau, Sungai Manila, dan Pintasan tetapi Warisan membolot semua kerusi itu.
Sebagai pertukaran untuk kerusi yang diintainya, PKR bersedia untuk menyerahkan kerusi Kadaimaian, Kuala Penyu, dan Karanaan. Namun, ini dijangka tidak akan berlaku memandangkan parti tersebut tidak berpuas hati dengan agihan kerusi seperti yang diharapkan itu.
Selepas perwakilan dari PKR dan Liew keluar dari dewan tersebut, wartawan kemudian menyusuri Liew untuk mendapatkan penjelasannya.
Walau bagaimanapun, Liew enggan memberikan sebarang komen dan berkata bahawa dia ingin ke tandas.
Liew dan perwakilan PKR kemudian tidak kembali ke dalam dewan tersebut.
Apabila calon pilihan raya yang diumumkan diminta naik ke atas pentas untuk sesi bergambar, Liew tidak kelihatan.
Bilangan kerusi yang ditandingi oleh PKR kali ini hanya kurang satu kerusi daripada yang ditandingi parti itu pada PRU 2018.
Dalam perkembangan berkaitan, DAP dan Amanah dikatakan tidak mempunyai sebarang masalah dengan kerusi yang diberikan untuk PRN Sabah.
Sementara itu, Presiden Upko Madius Tangau enggan mengulas adakah dia berpuas hati dengan agihan kerusi tersebut. Madius kekal di majlis tersebut sehingga ia berakhir.
Partinya diberikan 12 kerusi, iaitu lebih tujuh kerusi berbanding PRU lalu.
DAP dan Amanah akan bertanding di bawah logo Warisan sementara PKR dan Upko akan menggunakan logo masing-masing.
DAP akan bertanding di tujuh kerusi, jumlah yang sama seperti yang mereka tandingi pada PRU lalu, sementara Amanah diberi satu kerusi.
Warisan akan bertanding sebanyak 54 kerusi.
Perkembangan terbaru ini mungkin mencetuskan pergeseran di antara PKR dan Warisan. PKR boleh memilih untuk bertanding di lebih banyak kerusi daripada 14 yang dituntutnya manakala Warisan juga boleh bertanding di kerusi sekutunya.
Barisan pemimpin tertinggi PKR dan Warisan hanya mempunyai dua hari sebelum hari penamaan calon pada Sabtu untuk mengurangkan pergeseran.
"""
string3 = """
Penubuhan universiti sukan seperti diutarakan Ketua Unit Sukan Kementerian Pengajian Tinggi, Dr Pekan Ramli dan disokong Pakar Pembangunan Sukan dan Reakreasi Luar, Universiti Pendidikan Sultan Idris (UPSI), Prof Dr Md Amin Md Taaf seperti disiarkan akhbar ini, memberikan sinar harapan kepada kewujudan institusi sedemikian.
Ia menjadi impian atlet negara untuk mengejar kejayaan dalam bidang sukan dan kecemerlangan dalam akademik untuk menjamin masa depan lebih baik apabila bersara daripada arena sukan kelak.
Pelbagai pandangan, idea, kaedah, bukti dan cadangan dilontarkan pakar berikutan pentingnya universiti sukan yang akan memberi impak besar sama ada pada peringkat kebangsaan mahupun antarabangsa.
Negara lain sudah lama meraih laba dengan kewujudan universiti sukan seperti China, Korea, Japan, Taiwan, India dan Vietnam. Mereka menghasilkan atlet universiti yang mempamerkan keputusan cemerlang pada peringkat tinggi seperti Sukan Olimpik, Kejohanan Dunia dan Sukan Asia.
Justeru, kejayaan mereka perlu dijadikan rujukan demi memajukan sukan tanah air. Jika kita merujuk pendekatan Asia, kewujudan universiti sukan penting dan memberi kesan positif dalam melonjakkan prestasi sukan lebih optimum.
Namun, jika kita melihat pendekatan Eropah, universiti sukan bukan antara organisasi atau institusi penting yang diberi perhatian dalam menyumbang kepada pemenang pingat.
Antara isu dalam universiti sukan ialah kos tinggi, lokasi, prasarana sukan, pertindihan kursus dengan universiti sedia ada dan impak terhadap dunia sukan negara hingga mengundang persoalan kewajaran dan kerelevanan penubuhannya.
Namun sebagai bekas atlet memanah negara dan Olympian (OLY) di Sukan Olimpik 2004 di Athens, Greece serta bekas pelajar Sekolah Sukan Bukit Jalil hingga berjaya dalam dunia akademik, saya mendapati terdapat beberapa faktor sering menjadi halangan dalam rutin harian mereka.
Antaranya, faktor masa yang terpaksa bergegas menghadiri kuliah selepas tamat sesi latihan yang mengambil masa 15 hingga 20 minit dengan menunggang motosikal; kereta (20-30 minit) atau pengangkutan disediakan Majlis Sukan Negara (MSN) ke Universiti Putra Malaysia (UPM).
Jika mereka menuntut di Universiti Teknologi MARA (UiTM) atau Universiti Malaya (UM), ia mungkin lebih lama.
Walaupun di universiti tersedia dengan kemudahan kolej dan kemudahan sukan, mereka memilih pulang ke MSN untuk menjalani latihan bersama pasukan dan jurulatih di padang atau gelanggang latihan rasmi.
Ini berlanjutan selagi bergelar atlet negara yang perlu memastikan prestasi sentiasa meningkat dari semasa ke semasa tanpa mengabaikan tugas sebagai pelajar.
Alangkah baiknya jika sebahagian Sekolah Sukan Bukit Jalil itu sendiri dijadikan Kolej atau Universiti Sukan Malaysia kerana lengkap dari segi kemudahan prasarana sukannya dan proses pengajaran dan pembelajaran (PdP) dalam bidang Sains Sukan, Kejurulatihan, Pendidikan Jasmani dan setaraf dengannya.
Pengambilan setiap semester pula hanya terhad kepada atlet berstatus kebangsaan dan antarabangsa sahaja supaya hasrat melahirkan lebih ramai atlet bertaraf Olimpik mudah direalisasikan.
Contohnya, bekas atlet lompat bergalah negara, Roslinda Samsu yang juga pemenang pingat perak Sukan Asia Doha 2006 dan Penerima Anugerah Khas Majlis Anugerah Sukan KPT 2012, terpaksa mengambil masa lebih kurang sembilan tahun untuk menamatkan ijazah Sarjana Muda Pendidikan Jasmani di UPM sepanjang 14 tahun terbabit dalam sukan olahraga.
Sepanjang tempoh bergelar atlet kebangsaan dan mahasiswa, beliau juga memenangi pingat Emas Sukan SEA empat siri berturut-turut pada 2005, 2007, 2009 dan 2011.
Begitu juga atlet kebangsaan seperti Leong Mun Yee (UPM); Pandalela Renong (UM); Bryan Nickson Lomas (UM); Cheng Chu Sian (UPM); Marbawi Sulaiman (UiTM) dan Norasheela Khalid (UPM).
Jika disenaraikan, mungkin lebih ramai lagi. Namun, pernah terlintas di fikiran mengapa hanya atlet dari sukan terjun yang dapat memenangi pingat di Sukan Olimpik? Bagaimana dengan atlet lain yang juga layak secara merit? Apakah kekangan atau masalah dihadapi sebagai atlet dan mahasiswa?
Adakah kewujudan universiti sukan akan memberi impak besar kepada kemajuan sukan negara? Jika dirancang dan diatur dengan cekap dan sistematik, ia perkara tidak mustahil dicapai.
"""
cleaning(string2)
pad_sequences = tf.keras.preprocessing.sequence.pad_sequences
encoded = encoder.encode(f'ringkasan: {cleaning(string2)}') + [1]
s = pad_sequences([encoded], padding='post', maxlen = 2048)
%%time
l = sess.run(r[0][2], feed_dict = {X: s, top_p: 0.0, temperature: 0.0})
encoder.decode(l[0].tolist())
saver = tf.train.Saver(tf.trainable_variables())
saver.save(sess, 'output/model.ckpt')
strings = ','.join(
[
n.name
for n in tf.get_default_graph().as_graph_def().node
if ('Variable' in n.op
or 'Placeholder' in n.name
or 'top_p' in n.name
or 'temperature' in n.name
or 'logits' in n.name
or 'alphas' in n.name
or 'self/Softmax' in n.name)
and 'adam' not in n.name
and 'beta' not in n.name
and 'global_step' not in n.name
and 'gradients' not in n.name
]
)
strings.split(',')
def freeze_graph(model_dir, output_node_names):
if not tf.gfile.Exists(model_dir):
raise AssertionError(
"Export directory doesn't exists. Please specify an export "
'directory: %s' % model_dir
)
checkpoint = tf.train.get_checkpoint_state(model_dir)
input_checkpoint = checkpoint.model_checkpoint_path
absolute_model_dir = '/'.join(input_checkpoint.split('/')[:-1])
output_graph = absolute_model_dir + '/frozen_model.pb'
clear_devices = True
with tf.Session(graph = tf.Graph()) as sess:
saver = tf.train.import_meta_graph(
input_checkpoint + '.meta', clear_devices = clear_devices
)
saver.restore(sess, input_checkpoint)
output_graph_def = tf.graph_util.convert_variables_to_constants(
sess,
tf.get_default_graph().as_graph_def(),
output_node_names.split(','),
)
with tf.gfile.GFile(output_graph, 'wb') as f:
f.write(output_graph_def.SerializeToString())
print('%d ops in the final graph.' % len(output_graph_def.node))
freeze_graph('output', strings)
from tensorflow.tools.graph_transforms import TransformGraph
transforms = ['add_default_attributes',
'remove_nodes(op=Identity, op=CheckNumerics, op=Dropout)',
'fold_batch_norms',
'fold_old_batch_norms',
'quantize_weights(fallback_min=-10, fallback_max=10)',
'strip_unused_nodes',
'sort_by_execution_order']
pb = 'output/frozen_model.pb'
input_graph_def = tf.GraphDef()
with tf.gfile.FastGFile(pb, 'rb') as f:
input_graph_def.ParseFromString(f.read())
inputs = ['Placeholder', 'top_p', 'temperature']
transformed_graph_def = TransformGraph(input_graph_def,
inputs,
['logits'], transforms)
with tf.gfile.GFile(f'{pb}.quantized', 'wb') as f:
f.write(transformed_graph_def.SerializeToString())
def load_graph(frozen_graph_filename, **kwargs):
with tf.gfile.GFile(frozen_graph_filename, 'rb') as f:
graph_def = tf.GraphDef()
graph_def.ParseFromString(f.read())
# https://github.com/onnx/tensorflow-onnx/issues/77#issuecomment-445066091
# to fix import T5
for node in graph_def.node:
if node.op == 'RefSwitch':
node.op = 'Switch'
for index in xrange(len(node.input)):
if 'moving_' in node.input[index]:
node.input[index] = node.input[index] + '/read'
elif node.op == 'AssignSub':
node.op = 'Sub'
if 'use_locking' in node.attr:
del node.attr['use_locking']
elif node.op == 'AssignAdd':
node.op = 'Add'
if 'use_locking' in node.attr:
del node.attr['use_locking']
elif node.op == 'Assign':
node.op = 'Identity'
if 'use_locking' in node.attr:
del node.attr['use_locking']
if 'validate_shape' in node.attr:
del node.attr['validate_shape']
if len(node.input) == 2:
node.input[0] = node.input[1]
del node.input[1]
with tf.Graph().as_default() as graph:
tf.import_graph_def(graph_def)
return graph
g = load_graph('output/frozen_model.pb')
x = g.get_tensor_by_name('import/Placeholder:0')
top_p = g.get_tensor_by_name('import/top_p:0')
temperature = g.get_tensor_by_name('import/temperature:0')
logits = g.get_tensor_by_name('import/logits:0')
test_sess = tf.InteractiveSession(graph = g)
%%time
l = test_sess.run(logits, feed_dict = {x: s, top_p: 0.0, temperature: 0.0})
encoder.decode([i for i in l[0].tolist() if i > 0])
g = load_graph('output/frozen_model.pb.quantized')
x = g.get_tensor_by_name('import/Placeholder:0')
top_p = g.get_tensor_by_name('import/top_p:0')
temperature = g.get_tensor_by_name('import/temperature:0')
logits = g.get_tensor_by_name('import/logits:0')
test_sess = tf.InteractiveSession(graph = g)
%%time
l = test_sess.run(logits, feed_dict = {x: s, top_p: 0.0, temperature: 0.0})
encoder.decode([i for i in l[0].tolist() if i > 0])
```
|
github_jupyter
|
# Objective
Import the FAF freight matrices provided with FAF into AequilibraE's matrix format
## Input data
* FAF: https://faf.ornl.gov/fafweb/
* Matrices: https://faf.ornl.gov/fafweb/Data/FAF4.4_HiLoForecasts.zip
* Zones System: http://www.census.gov/econ/cfs/AboutGeographyFiles/CFS_AREA_shapefile_010215.zip
* FAF User Guide: https://faf.ornl.gov/fafweb/data/FAF4%20User%20Guide.pdf
* The blog post (with data): http://www.xl-optim.com/matrix-api-and-multi-class-assignment
# The code
We import all libraries we will need, including the AequilibraE, after putting it in our Python path
```
import sys
# On Linux
# sys.path.append('/home/pedro/.qgis2/python/plugins/AequilibraE')
# On Windows
sys.path.append('C:/Users/Pedro/.qgis2/python/plugins/AequilibraE')
import pandas as pd
import numpy as np
import os
from aequilibrae.matrix import AequilibraeMatrix
from scipy.sparse import coo_matrix
```
Now we set all the paths for files and parameters we need
```
data_folder = 'Y:/ALL DATA/DATA/Pedro/Professional/Data/USA/FAF/4.4'
data_file = 'FAF4.4_HiLoForecasts.csv'
sctg_names_file = 'sctg_codes.csv' # Simplified to 50 characters, which is AequilibraE's limit
output_folder = data_folder
```
We import the the matrices
```
matrices = pd.read_csv(os.path.join(data_folder, data_file), low_memory=False)
print matrices.head(10)
```
We import the sctg codes
```
sctg_names = pd.read_csv(os.path.join(data_folder, sctg_names_file), low_memory=False)
sctg_names.set_index('Code', inplace=True)
sctg_descr = list(sctg_names['Commodity Description'])
print sctg_names.head(5)
```
We now process the matrices to collect all the data we need, such as:
* the list of zones
* CSTG codes
* Matrices/scenarios we are importing
```
# lists the zones
all_zones = np.array(sorted(list(set( list(matrices.dms_orig.unique()) + list(matrices.dms_dest.unique())))))
# Count them and create a 0-based index
num_zones = all_zones.shape[0]
idx = np.arange(num_zones)
# Creates the indexing dataframes
origs = pd.DataFrame({"from_index": all_zones, "from":idx})
dests = pd.DataFrame({"to_index": all_zones, "to":idx})
# adds the new index columns to the pandas dataframe
matrices = matrices.merge(origs, left_on='dms_orig', right_on='from_index', how='left')
matrices = matrices.merge(dests, left_on='dms_dest', right_on='to_index', how='left')
# Lists sctg codes and all the years/scenarios we have matrices for
mat_years = [x for x in matrices.columns if 'tons' in x]
sctg_codes = matrices.sctg2.unique()
```
We now import one matrix for each year, saving all the SCTG codes as different matrix cores in our zoning system
```
# aggregate the matrix according to the relevant criteria
agg_matrix = matrices.groupby(['from', 'to', 'sctg2'])[mat_years].sum()
# returns the indices
agg_matrix.reset_index(inplace=True)
for y in mat_years:
mat = AequilibraeMatrix()
kwargs = {'file_name': os.path.join(output_folder, y + '.aem'),
'zones': num_zones,
'matrix_names': sctg_descr}
mat.create_empty(**kwargs)
mat.index[:] = all_zones[:]
# for all sctg codes
for i in sctg_names.index:
prod_name = sctg_names['Commodity Description'][i]
mat_filtered_sctg = agg_matrix[agg_matrix.sctg2 == i]
m = coo_matrix((mat_filtered_sctg[y], (mat_filtered_sctg['from'], mat_filtered_sctg['to'])),
shape=(num_zones, num_zones)).toarray().astype(np.float64)
mat.matrix[prod_name][:,:] = m[:,:]
```
|
github_jupyter
|
```
%matplotlib widget
import os
import sys
sys.path.insert(0, os.getenv('HOME')+'/pycode/MscThesis/')
import pandas as pd
from amftrack.util import get_dates_datetime, get_dirname, get_plate_number, get_postion_number,get_begin_index
import ast
from amftrack.plotutil import plot_t_tp1
from scipy import sparse
from datetime import datetime
from amftrack.pipeline.functions.node_id import orient
import pickle
import scipy.io as sio
from pymatreader import read_mat
from matplotlib import colors
import cv2
import imageio
import matplotlib.pyplot as plt
import numpy as np
from skimage.filters import frangi
from skimage import filters
from random import choice
import scipy.sparse
import os
from amftrack.pipeline.functions.extract_graph import from_sparse_to_graph, generate_nx_graph, sparse_to_doc
from skimage.feature import hessian_matrix_det
from amftrack.pipeline.functions.experiment_class_surf import Experiment, Edge, Node, Hyphae, plot_raw_plus
from amftrack.pipeline.paths.directory import run_parallel, find_state, directory_scratch, directory_project
from amftrack.notebooks.analysis.util import *
from scipy import stats
from scipy.ndimage.filters import uniform_filter1d
from statsmodels.stats import weightstats as stests
from amftrack.pipeline.functions.hyphae_id_surf import get_pixel_growth_and_new_children
from collections import Counter
from IPython.display import clear_output
from amftrack.notebooks.analysis.data_info import *
from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = "all"
plt.rcParams.update({
"font.family": "verdana",
'font.weight' : 'normal',
'font.size': 20})
from amftrack.plotutil import plot_node_skel
lapse = 60
exp = get_exp((38,131,131+lapse),directory_project)
exp2 = Experiment(38,directory_project)
exp2.copy(exp)
exp = exp2
def transform_skeleton_final_for_show(skeleton_doc,Rot,trans):
skeleton_transformed={}
transformed_keys = np.round(np.transpose(np.dot(Rot,np.transpose(np.array(list(skeleton_doc.keys())))))+trans).astype(np.int)
i=0
for pixel in list(transformed_keys):
i+=1
skeleton_transformed[(pixel[0],pixel[1])]=1
skeleton_transformed_sparse=sparse.lil_matrix((27000, 60000))
for pixel in list(skeleton_transformed.keys()):
i+=1
skeleton_transformed_sparse[(pixel[0],pixel[1])]=1
return(skeleton_transformed_sparse)
def get_skeleton_non_aligned(exp,boundaries,t,directory):
i = t
plate = exp.plate
listdir=os.listdir(directory)
dates = exp.dates
date =dates [i]
directory_name = get_dirname(date, plate)
path_snap=directory+directory_name
skel = read_mat(path_snap+'/Analysis/skeleton.mat')
skelet = skel['skeleton']
skelet = sparse_to_doc(skelet)
# Rot= skel['R']
# trans = skel['t']
skel_aligned = transform_skeleton_final_for_show(skelet,np.array([[1,0],[0,1]]),np.array([0,0]))
output = skel_aligned[boundaries[2]:boundaries[3],boundaries[0]:boundaries[1]].todense()
kernel = np.ones((5,5),np.uint8)
output = cv2.dilate(output.astype(np.uint8),kernel,iterations = 1)
return(output)
from amftrack.util import get_skeleton
def plot_raw_plus_random(exp,compress=5,ranges = 1000):
t0 = choice(range(exp.ts))
node_ch = choice([node for node in exp.nodes if node.is_in(t0) and node.degree(t0)==1])
# node_ch = choice(exp.nodes)
# t0 = choice(node_ch.ts())
node_ch.show_source_image(t0,t0+1)
for index,t in enumerate([t0,t0+1]):
date = exp.dates[t]
anchor_time = t0
center = node_ch.pos(anchor_time)[1],node_ch.pos(anchor_time)[0]
window = (center[0]-ranges,center[0]+ranges,center[1]-ranges,center[1]+ranges)
skelet= get_skeleton_non_aligned(exp,window,t,exp.directory)
tips = [node.label for node in exp.nodes if t in node.ts() and node.degree(t) ==1 and node.pos(t)[1]>=window[0]-ranges and node.pos(t)[1]<=window[1]+ranges and node.pos(t)[0]>=window[2]-ranges and node.pos(t)[0]<=window[3]+ranges]
junction = [node.label for node in exp.nodes if t in node.ts() and node.degree(t) >=2 and node.pos(t)[1]>=window[0]-ranges and node.pos(t)[1]<=window[1]+ranges and node.pos(t)[0]>=window[2]-ranges and node.pos(t)[0]<=window[3]+ranges]
directory_name = get_dirname(date,exp.plate)
path_snap = exp.directory + directory_name
skel = read_mat(path_snap + "/Analysis/skeleton_pruned_realigned.mat")
Rot = skel["R"]
trans = skel["t"]
im = read_mat(path_snap+'/Analysis/raw_image.mat')['raw']
size = 8
fig = plt.figure(figsize = (9,9))
ax = fig.add_subplot(111)
ax.imshow(im[(window[2]//compress):(window[3]//compress),(window[0]//compress):(window[1]//compress)])
ax.imshow(cv2.resize(skelet,(2*ranges//compress,2*ranges//compress)),alpha = 0.2)
shift=(window[2],window[0])
greys = [1,0.5]
for i,node_list in enumerate([tips,junction]):
grey = greys[i]
bbox = dict(boxstyle="circle", fc=colors.rgb2hex((grey, grey, grey)))
# ax.text(right, top, time,
# horizontalalignment='right',
# verticalalignment='bottom',
# transform=ax.transAxes,color='white')
for node in node_list:
# print(self.positions[ts[i]])
if node in exp.positions[t].keys():
xs,ys = exp.positions[t][node]
rottrans = np.dot(np.linalg.inv(Rot), np.array([xs, ys] - trans))
ys, xs = round(rottrans[0]), round(rottrans[1])
tex = ax.text(
(xs - shift[1]) // compress,
(ys - shift[0]) // compress,
str(node),
ha="center",
va="center",
size=size,
bbox=bbox,
)
plt.show()
plt.close('all')
plot_raw_plus_random(exp,compress=5,ranges = 700)
```
|
github_jupyter
|
# Data Labelling Analysis (DLA) Dataset C
```
#import libraries
import warnings
warnings.filterwarnings("ignore")
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
import os
print('Libraries imported!!')
#define directory of functions and actual directory
HOME_PATH = '' #home path of the project
FUNCTIONS_DIR = 'EVALUATION FUNCTIONS/RESEMBLANCE'
ACTUAL_DIR = os.getcwd()
#change directory to functions directory
os.chdir(HOME_PATH + FUNCTIONS_DIR)
#import functions for data labelling analisys
from data_labelling import mix_data
from data_labelling import split_data
from data_labelling import DataPreProcessor
from data_labelling import ClassificationModels
#change directory to actual directory
os.chdir(ACTUAL_DIR)
print('Functions imported!!')
```
## 1. Read real and synthetic datasets
In this part real and synthetic datasets are read.
```
#Define global variables
DATA_TYPES = ['Real','GM','SDV','CTGAN','WGANGP']
SYNTHESIZERS = ['GM','SDV','CTGAN','WGANGP']
FILEPATHS = {'Real' : HOME_PATH + 'REAL DATASETS/TRAIN DATASETS/C_Obesity_Data_Real_Train.csv',
'GM' : HOME_PATH + 'SYNTHETIC DATASETS/GM/C_Obesity_Data_Synthetic_GM.csv',
'SDV' : HOME_PATH + 'SYNTHETIC DATASETS/SDV/C_Obesity_Data_Synthetic_SDV.csv',
'CTGAN' : HOME_PATH + 'SYNTHETIC DATASETS/CTGAN/C_Obesity_Data_Synthetic_CTGAN.csv',
'WGANGP' : HOME_PATH + 'SYNTHETIC DATASETS/WGANGP/C_Obesity_Data_Synthetic_WGANGP.csv'}
categorical_columns = ['Gender','family_history_with_overweight','FAVC','CAEC','SMOKE','SCC','CALC','MTRANS','Obesity_level']
data = dict()
#iterate over all datasets filepaths and read each dataset
for name, path in FILEPATHS.items() :
data[name] = pd.read_csv(path)
for col in categorical_columns :
data[name][col] = data[name][col].astype('category')
data
```
## 2. Mix real data with synthetic data
```
mixed_data = dict()
for name in SYNTHESIZERS :
mixed_data[name] = mix_data(data['Real'], data[name])
mixed_data
```
- 0 for real data
- 1 for synthetic data
## 2. Split train and test data
```
train_len = 0.8
train_data = dict()
test_data = dict()
for name in SYNTHESIZERS :
print(name)
train_data[name], test_data[name] = split_data(mixed_data[name], train_len)
print(train_data[name].shape, test_data[name].shape)
print('Train data', train_data[name].groupby('Label').size())
print('Test data', test_data[name].groupby('Label').size())
print('##############################################')
```
## 3. Train Classifiers
```
categorical_columns = ['Gender','family_history_with_overweight','FAVC','CAEC','SMOKE','SCC','CALC','MTRANS','Obesity_level']
numerical_columns = ['Age','Height','Weight','FCVC','NCP','CH2O','FAF','TUE']
categories = [np.array([0, 1]), np.array([0, 1]), np.array([0, 1]), np.array([0, 1, 2, 3]), np.array([0, 1]),
np.array([0, 1]), np.array([0, 1, 2, 3]), np.array([0, 1, 2, 3, 4]), np.array([0, 1, 2, 3, 4, 5, 6])]
#initialize classifiers
classifiers_all = dict()
data_preprocessors = dict()
target = 'Label'
for name in SYNTHESIZERS :
print(name)
classifiers_all[name] = ClassificationModels()
data_preprocessors[name] = DataPreProcessor(categorical_columns, numerical_columns, categories)
x_train = data_preprocessors[name].preprocess_train_data(train_data[name].iloc[:, train_data[name].columns != target])
y_train = train_data[name].loc[:, target]
classifiers_all[name].train_classifiers(x_train, y_train)
print('####################################################')
```
## 5. Evaluate Classifiers
```
results_all = dict()
for name in SYNTHESIZERS :
print(name)
x_test = data_preprocessors[name].preprocess_test_data(test_data[name].loc[:, test_data[name].columns != target])
print(x_test.shape)
y_test = test_data[name].loc[:, target]
classifiers_all[name].evaluate_classifiers(x_test, y_test)
print('####################################################')
```
## 6. Analyse models results
```
fig, axs = plt.subplots(nrows=1, ncols=4, figsize=(8, 2.5))
axs_idxs = [[0,0], [0,1], [1,0], [1,1]]
axs_idxs = [0, 1, 2, 3]
idx = dict(zip(SYNTHESIZERS,axs_idxs))
for name in SYNTHESIZERS :
ax_plot = axs[idx[name]]
classifiers_all[name].plot_classification_metrics(ax_plot)
ax_plot.set_title(name, fontsize=10)
plt.tight_layout()
fig.savefig('DATA LABELLING RESULTS/CLASSIFICATION_METRICS.svg', bbox_inches='tight')
```
|
github_jupyter
|
# Validation
This notebook contains examples of some of the simulations that have been used to validate Disimpy's functionality by comparing the simulated signals to analytical solutions and signals generated by other simulators. Here, we simulate free diffusion and restricted diffusion inside cylinders and spheres.
```
# Import the required packages and modules
import os
import pickle
import numpy as np
import matplotlib.pyplot as plt
from disimpy import gradients, simulations, substrates, utils
from disimpy.gradients import GAMMA
# Define the simulation parameters
n_walkers = int(1e6) # Number of random walkers
n_t = int(1e3) # Number of time points
diffusivity = 2e-9 # In SI units (m^2/s)
```
## Free diffusion
In the case of free diffusion, the analytical expression for the signal is $S = S_0 \exp(-bD)$, where $S_0$ is the signal without diffusion-weighting, $b$ is the b-value, and $D$ is the diffusivity.
```
# Create a Stejskal-Tanner gradient array with ∆ = 40 ms and δ = 30 ms
T = 70e-3
gradient = np.zeros((1, 700, 3))
gradient[0, 1:300, 0] = 1
gradient[0, -300:-1, 0] = -1
bs = np.linspace(1, 3e9, 100)
gradient = np.concatenate([gradient for _ in bs], axis=0)
dt = T / (gradient.shape[1] - 1)
gradient, dt = gradients.interpolate_gradient(gradient, dt, n_t)
gradient = gradients.set_b(gradient, dt, bs)
# Show the waveform of the measurement with the highest b-value
fig, ax = plt.subplots(1, figsize=(7, 4))
for i in range(3):
ax.plot(np.linspace(0, T, n_t), gradient[-1, :, i])
ax.legend(['G$_x$', 'G$_y$', 'G$_z$'])
ax.set_xlabel('Time (s)')
ax.set_ylabel('Gradient magnitude (T/m)')
plt.show()
# Run the simulation
substrate = substrates.free()
signals = simulations.simulation(
n_walkers, diffusivity, gradient, dt, substrate)
# Plot the results
fig, ax = plt.subplots(1, figsize=(7, 4))
ax.plot(bs, np.exp(-bs * diffusivity), color='tab:orange')
ax.scatter(bs, signals / n_walkers, s=10, marker='o')
ax.legend(['Analytical signal', 'Simulated signal'])
ax.set_xlabel('b (ms/μm$^2$)')
ax.set_ylabel('S/S$_0$')
ax.set_yscale('log')
plt.show()
```
## Restricted diffusion and comparison to MISST
Here, diffusion inside cylinders and spheres is simulated and the signals are compared to those calculated with [MISST](http://mig.cs.ucl.ac.uk/index.php?n=Tutorial.MISST) that uses matrix operators to calculate the time evolution of the diffusion signal inside simple geometries. The cylinder is simulated using a triangular mesh and the sphere as an analytically defined surface.
```
# Load and show the cylinder mesh used in the simulations
mesh_path = os.path.join(
os.path.dirname(simulations.__file__), 'tests', 'cylinder_mesh_closed.pkl')
with open(mesh_path, 'rb') as f:
example_mesh = pickle.load(f)
faces = example_mesh['faces']
vertices = example_mesh['vertices']
cylinder_substrate = substrates.mesh(
vertices, faces, periodic=True, init_pos='intra')
utils.show_mesh(cylinder_substrate)
# Run the simulation
signals = simulations.simulation(
n_walkers, diffusivity, gradient, dt, cylinder_substrate)
# Load MISST signals
tests_dir = os.path.join(os.path.dirname(gradients.__file__), 'tests')
misst_signals = np.loadtxt(os.path.join(tests_dir,
'misst_cylinder_signal_smalldelta_30ms_bigdelta_40ms_radius_5um.txt'))
# Plot the results
fig, ax = plt.subplots(1, figsize=(7, 4))
ax.scatter(bs, signals / n_walkers, s=10, marker='o')
ax.scatter(bs, misst_signals, s=10, marker='.')
ax.set_xlabel('b (ms/μm$^2$)')
ax.set_ylabel('S/S$_0$')
ax.legend(['Disimpy', 'MISST'])
ax.set_title('Diffusion in a cylinder')
ax.set_yscale('log')
plt.show()
# Run the simulation
sphere_substrate = substrates.sphere(5e-6)
signals = simulations.simulation(
n_walkers, diffusivity, gradient, dt, sphere_substrate)
# Load MISST signals
tests_dir = os.path.join(os.path.dirname(gradients.__file__), 'tests')
misst_signals = np.loadtxt(os.path.join(tests_dir,
'misst_sphere_signal_smalldelta_30ms_bigdelta_40ms_radius_5um.txt'))
# Plot the results
fig, ax = plt.subplots(1, figsize=(7, 4))
ax.scatter(bs, signals / n_walkers, s=10, marker='o')
ax.scatter(bs, misst_signals, s=10, marker='.')
ax.set_xlabel('b (ms/μm$^2$)')
ax.set_ylabel('S/S$_0$')
ax.legend(['Disimpy', 'MISST'])
ax.set_title('Diffusion in a sphere')
ax.set_yscale('log')
plt.show()
```
## Signal diffraction pattern
In the case of restricted diffusion in a cylinder perpendicular to the direction of the diffusion encoding gradient with short pulses and long diffusion time, the signal minimum occurs at $0.61 · 2 · \pi/r$, where $r$ is the cylinder radius. Details are provided by [Avram et al](https://doi.org/10.1002/nbm.1277), for example.
```
# Create a Stejskal-Tanner gradient array with ∆ = 0.5 s and δ = 0.1 ms
T = 501e-3
gradient = np.zeros((1, n_t, 3))
gradient[0, 1:2, 0] = 1
gradient[0, -2:-1, 0] = -1
dt = T / (gradient.shape[1] - 1)
bs = np.linspace(1, 1e11, 250)
gradient = np.concatenate([gradient for _ in bs], axis=0)
gradient = gradients.set_b(gradient, dt, bs)
q = gradients.calc_q(gradient, dt)
qs = np.max(np.linalg.norm(q, axis=2), axis=1)
# Show the waveform of the measurement with the highest b-value
fig, ax = plt.subplots(1, figsize=(7, 4))
for i in range(3):
ax.plot(np.linspace(0, T, n_t), gradient[-1, :, i])
ax.legend(['G$_x$', 'G$_y$', 'G$_z$'])
ax.set_xlabel('Time (s)')
ax.set_ylabel('Gradient magnitude (T/m)')
plt.show()
# Run the simulation
radius = 10e-6
substrate = substrates.cylinder(
radius=radius, orientation=np.array([0., 0., 1.]))
signals = simulations.simulation(
n_walkers, diffusivity, gradient, dt, substrate)
# Plot the results
fig, ax = plt.subplots(1, figsize=(7, 4))
ax.scatter(1e-6 * qs, signals / n_walkers, s=10, marker='o')
minimum = 1e-6 * .61 * 2 * np.pi / radius
ax.plot([minimum, minimum], [0, 1], ls='--', lw=2, color='tab:orange')
ax.legend(['Analytical minimum', 'Simulated signal'])
ax.set_xlabel('q (μm$^{-1}$)')
ax.set_ylabel('S/S$_0$')
ax.set_yscale('log')
ax.set_ylim([1e-4, 1])
ax.set_xlim([0, max(1e-6 * qs)])
plt.show()
```
|
github_jupyter
|
## Dependencies
```
import json, warnings, shutil
from jigsaw_utility_scripts import *
from transformers import TFXLMRobertaModel, XLMRobertaConfig
from tensorflow.keras.models import Model
from tensorflow.keras import optimizers, metrics, losses, layers
from tensorflow.keras.callbacks import EarlyStopping, ModelCheckpoint
from transformers import TFAutoModel, AutoTokenizer
warnings.filterwarnings("ignore")
```
## TPU configuration
```
strategy, tpu = set_up_strategy()
print("REPLICAS: ", strategy.num_replicas_in_sync)
AUTO = tf.data.experimental.AUTOTUNE
```
# Load data
```
# database_base_path = '/kaggle/input/jigsaw-dataset-split-pb-roberta-large-192/'
# k_fold = pd.read_csv(database_base_path + '5-fold.csv')
# valid_df = pd.read_csv("/kaggle/input/jigsaw-multilingual-toxic-comment-classification/validation.csv", usecols=['comment_text', 'toxic', 'lang'])
# print('Train set samples: %d' % len(k_fold))
# print('Validation set samples: %d' % len(valid_df))
# display(k_fold.head())
# # Unzip files
# !tar -xvf /kaggle/input/jigsaw-dataset-split-pb-roberta-large-192/fold_1.tar.gz
# # !tar -xvf /kaggle/input/jigsaw-dataset-split-pb-roberta-large-192/fold_2.tar.gz
# # !tar -xvf /kaggle/input/jigsaw-dataset-split-pb-roberta-large-192/fold_3.tar.gz
# # !tar -xvf /kaggle/input/jigsaw-dataset-split-pb-roberta-large-192/fold_4.tar.gz
# # !tar -xvf /kaggle/input/jigsaw-dataset-split-pb-roberta-large-192/fold_5.tar.gz
```
# Model parameters
```
base_path = '/kaggle/input/jigsaw-transformers/XLM-RoBERTa/'
config = {
"MAX_LEN": 192,
"BATCH_SIZE": 16 * strategy.num_replicas_in_sync,
"EPOCHS": 2,
"LEARNING_RATE": 1e-5,
"ES_PATIENCE": 1,
"N_FOLDS": 1,
"base_model_path": base_path + 'tf-xlm-roberta-large-tf_model.h5',
"config_path": base_path + 'xlm-roberta-large-config.json'
}
with open('config.json', 'w') as json_file:
json.dump(json.loads(json.dumps(config)), json_file)
```
# Model
```
# module_config = XLMRobertaConfig.from_pretrained(config['config_path'], output_hidden_states=False)
# def model_fn(MAX_LEN):
# input_ids = layers.Input(shape=(MAX_LEN,), dtype=tf.int32, name='input_ids')
# base_model = TFXLMRobertaModel.from_pretrained(config['base_model_path'], config=module_config)
# sequence_output = base_model({'input_ids': input_ids})
# last_state = sequence_output[0]
# cls_token = last_state[:, 0, :]
# output = layers.Dense(1, activation='sigmoid', name='output')(cls_token)
# model = Model(inputs=input_ids, outputs=output)
# model.compile(optimizers.Adam(lr=config['LEARNING_RATE']),
# loss=losses.BinaryCrossentropy(),
# metrics=[metrics.BinaryAccuracy(), metrics.AUC()])
# return model
```
# Train
```
# history_list = []
# for n_fold in range(config['N_FOLDS']):
# tf.tpu.experimental.initialize_tpu_system(tpu)
# print('\nFOLD: %d' % (n_fold+1))
# # Load data
# base_data_path = 'fold_%d/' % (n_fold+1)
# x_train = np.load(base_data_path + 'x_train.npy')
# y_train = np.load(base_data_path + 'y_train.npy')
# x_valid = np.load(base_data_path + 'x_valid.npy')
# x_valid_ml = np.load(database_base_path + 'x_valid.npy')
# y_valid_ml = np.load(database_base_path + 'y_valid.npy')
# step_size = x_train.shape[0] // config['BATCH_SIZE']
# ### Delete data dir
# shutil.rmtree(base_data_path)
# # Train model
# model_path = 'model_fold_%d.h5' % (n_fold+1)
# es = EarlyStopping(monitor='val_loss', mode='min', patience=config['ES_PATIENCE'],
# restore_best_weights=True, verbose=1)
# checkpoint = ModelCheckpoint(model_path, monitor='val_loss', mode='min',
# save_best_only=True, save_weights_only=True, verbose=1)
# with strategy.scope():
# model = model_fn(config['MAX_LEN'])
# history = model.fit(get_training_dataset(x_train, y_train, config['BATCH_SIZE'], AUTO),
# validation_data=(get_validation_dataset(x_valid_ml, y_valid_ml, config['BATCH_SIZE'], AUTO)),
# callbacks=[checkpoint, es],
# epochs=config['EPOCHS'],
# steps_per_epoch=step_size,
# verbose=1).history
# history_list.append(history)
# # Make predictions
# train_preds = model.predict(get_test_dataset(x_train, config['BATCH_SIZE'], AUTO))
# valid_preds = model.predict(get_test_dataset(x_valid, config['BATCH_SIZE'], AUTO))
# valid_ml_preds = model.predict(get_test_dataset(x_valid_ml, config['BATCH_SIZE'], AUTO))
# k_fold.loc[k_fold['fold_%d' % (n_fold+1)] == 'train', 'pred_%d' % (n_fold+1)] = np.round(train_preds)
# k_fold.loc[k_fold['fold_%d' % (n_fold+1)] == 'validation', 'pred_%d' % (n_fold+1)] = np.round(valid_preds)
# valid_df['pred_%d' % (n_fold+1)] = np.round(valid_ml_preds)
```
## Model loss graph
```
# sns.set(style="whitegrid")
# for n_fold in range(config['N_FOLDS']):
# print('Fold: %d' % (n_fold+1))
# plot_metrics(history_list[n_fold])
```
# Model evaluation
```
# display(evaluate_model(k_fold, config['N_FOLDS']).style.applymap(color_map))
```
# Confusion matrix
```
# for n_fold in range(config['N_FOLDS']):
# print('Fold: %d' % (n_fold+1))
# train_set = k_fold[k_fold['fold_%d' % (n_fold+1)] == 'train']
# validation_set = k_fold[k_fold['fold_%d' % (n_fold+1)] == 'validation']
# plot_confusion_matrix(train_set['toxic'], train_set['pred_%d' % (n_fold+1)],
# validation_set['toxic'], validation_set['pred_%d' % (n_fold+1)])
```
# Model evaluation by language
```
# display(evaluate_model_lang(valid_df, config['N_FOLDS']).style.applymap(color_map))
```
# Visualize predictions
```
# pd.set_option('max_colwidth', 120)
# display(k_fold[['comment_text', 'toxic'] + [c for c in k_fold.columns if c.startswith('pred')]].head(15))
def regular_encode(texts, tokenizer, maxlen=512):
enc_di = tokenizer.batch_encode_plus(
texts,
return_attention_masks=False,
return_token_type_ids=False,
pad_to_max_length=True,
max_length=maxlen
)
return np.array(enc_di['input_ids'])
def build_model(transformer, max_len=512):
input_word_ids = layers.Input(shape=(max_len,), dtype=tf.int32, name="input_word_ids")
sequence_output = transformer(input_word_ids)[0]
cls_token = sequence_output[:, 0, :]
out = layers.Dense(1, activation='sigmoid')(cls_token)
model = Model(inputs=input_word_ids, outputs=out)
model.compile(optimizers.Adam(lr=1e-5), loss='binary_crossentropy', metrics=['accuracy'])
return model
AUTO = tf.data.experimental.AUTOTUNE
# Configuration
EPOCHS = 2
BATCH_SIZE = 16 * strategy.num_replicas_in_sync
MAX_LEN = 192
MODEL = 'jplu/tf-xlm-roberta-large'
tokenizer = AutoTokenizer.from_pretrained(MODEL)
train1 = pd.read_csv("/kaggle/input/jigsaw-multilingual-toxic-comment-classification/jigsaw-toxic-comment-train.csv")
train2 = pd.read_csv("/kaggle/input/jigsaw-multilingual-toxic-comment-classification/jigsaw-unintended-bias-train.csv")
train2.toxic = train2.toxic.round().astype(int)
valid = pd.read_csv('/kaggle/input/jigsaw-multilingual-toxic-comment-classification/validation.csv')
test = pd.read_csv('/kaggle/input/jigsaw-multilingual-toxic-comment-classification/test.csv')
sub = pd.read_csv('/kaggle/input/jigsaw-multilingual-toxic-comment-classification/sample_submission.csv')
# Combine train1 with a subset of train2
train = pd.concat([
train1[['comment_text', 'toxic']],
train2[['comment_text', 'toxic']].query('toxic==1'),
train2[['comment_text', 'toxic']].query('toxic==0').sample(n=100000, random_state=0)
])
x_train = regular_encode(train.comment_text.values, tokenizer, maxlen=MAX_LEN)
x_valid = regular_encode(valid.comment_text.values, tokenizer, maxlen=MAX_LEN)
x_test = regular_encode(test.content.values, tokenizer, maxlen=MAX_LEN)
y_train = train.toxic.values
y_valid = valid.toxic.values
train_dataset = (
tf.data.Dataset
.from_tensor_slices((x_train, y_train))
.repeat()
.shuffle(2048)
.batch(BATCH_SIZE)
.prefetch(AUTO)
)
valid_dataset = (
tf.data.Dataset
.from_tensor_slices((x_valid, y_valid))
.batch(BATCH_SIZE)
.cache()
.prefetch(AUTO)
)
test_dataset = (
tf.data.Dataset
.from_tensor_slices(x_test)
.batch(BATCH_SIZE)
)
module_config = XLMRobertaConfig.from_pretrained(config['config_path'], output_hidden_states=False)
with strategy.scope():
# transformer_layer = TFAutoModel.from_pretrained(config['base_model_path'])
transformer_layer = TFXLMRobertaModel.from_pretrained(config['base_model_path'], config=module_config)
model = build_model(transformer_layer, max_len=MAX_LEN)
model.summary()
n_steps = x_train.shape[0] // BATCH_SIZE
train_history = model.fit(
train_dataset,
steps_per_epoch=n_steps,
validation_data=valid_dataset,
epochs=EPOCHS
)
n_steps = x_valid.shape[0] // BATCH_SIZE
train_history_2 = model.fit(
valid_dataset.repeat(),
steps_per_epoch=n_steps,
epochs=EPOCHS
)
sub['toxic'] = model.predict(test_dataset, verbose=1)
sub.to_csv('submission.csv', index=False)
```
|
github_jupyter
|
```
from __future__ import division, print_function
import os
import sys
from collections import OrderedDict
# Third-party
import astropy.coordinates as coord
import astropy.units as u
import matplotlib as mpl
import matplotlib.pyplot as pl
import numpy as np
pl.style.use('apw-notebook')
%matplotlib inline
# Custom
import gala.dynamics as gd
import gala.integrate as gi
import gala.potential as gp
from gala.units import galactic
from scipy.misc import factorial
# from ophiuchus import barred_mw, static_mw
import ophiuchus.potential as op
plotpath = "/Users/adrian/projects/ophiuchus-paper/figures/"
if not os.path.exists(plotpath):
os.mkdir(plotpath)
barred_mw = op.load_potential("barred_mw_4")
static_mw = op.load_potential("static_mw")
# transform from H&O 1992 coefficients to Lowing 2011 coefficients
nlms = np.array([[0,0,0],
[1,0,0],
[2,0,0],
[3,0,0],
[0,2,0],
[1,2,0],
[2,2,0],
[0,2,2],
[1,2,2],
[2,2,2],
[0,4,0],
[1,4,0],
[0,4,2],
[1,4,2],
[0,4,4],
[1,4,4],
[0,6,0],
[0,6,2],
[0,6,4],
[0,6,6]])
_Snlm = np.array([1.509,-0.086,-0.033,-0.02,-2.606,
-0.221,-0.001,0.665,0.129,0.006,6.406,
1.295,-0.66,-0.14,0.044,-0.012,-5.859,
0.984,-0.03,0.001])
NEW_S = _Snlm.copy()
for i,(n,l,m) in zip(range(len(_Snlm)), nlms):
if l != 0:
fac = np.sqrt(4*np.pi) * np.sqrt((2*l+1) / (4*np.pi) * factorial(l-m) / factorial(l+m))
NEW_S[i] /= fac
nmax = 3
lmax = 6
Snlm = np.zeros((nmax+1,lmax+1,lmax+1))
for (n,l,m),A in zip(nlms,NEW_S):
Snlm[n,l,m] = A
static_mw
barred_mw
# barpars = barred_mw.parameters.copy()
# barpars['halo']['q_z'] = 1.
# barpars['spheroid']['c'] = 0.2
# barpars['spheroid']['m'] = 5E9
# barpars['disk']['m'] = 4E10
# barpars['bar']['r_s'] = 1.2
# barpars['bar']['m'] = barpars['bar']['m']
# barred_mw = op.OphiuchusPotential(**barpars)
# stapars = static_mw.parameters.copy()
# stapars['halo']['q_z'] = 1.
# stapars['spheroid']['c'] = 0.3
# stapars['spheroid']['m'] = 1.2E10
# stapars['disk']['m'] = 6E10
# static_mw = op.OphiuchusPotential(**stapars)
potential_classes = OrderedDict()
potential_classes['disk'] = gp.MiyamotoNagaiPotential
potential_classes['halo'] = gp.FlattenedNFWPotential
potential_classes['bar'] = op.WangZhaoBarPotential
potential_classes['spheroid'] = gp.HernquistPotential
(0.19*u.kpc/u.Myr).to(u.km/u.s)
```
---
### Mass profile
```
ix = 0
xyz = np.zeros((3,128))
xyz[ix] = np.linspace(0.,10.,xyz.shape[1])
for pot in [static_mw, barred_mw]:
Menc = pot.mass_enclosed(xyz)
pl.loglog(xyz[ix], Menc, marker='')
pl.axvline(1)
pl.axhline(1E10)
```
---
```
def density_on_grid(potential, t=0., grid_lim=(-15,15), ngrid=128):
grid = np.linspace(grid_lim[0], grid_lim[1], ngrid)
xyz = np.vstack(map(np.ravel, np.meshgrid(grid,grid,grid)))
# val = np.zeros((ngrid*ngrid*ngrid,))
val = potential.density(xyz, t=t).value
val[np.isnan(val)] = val[np.isfinite(val)].min()
val[val < 0] = 1.
gridx = xyz[0].reshape(ngrid,ngrid,ngrid)[:,:,0]
gridy = xyz[1].reshape(ngrid,ngrid,ngrid)[:,:,0]
return gridx, gridy, val
ngrid = 128
xx,yy,barred_dens = density_on_grid(barred_mw, ngrid=ngrid)
xx,yy,static_dens = density_on_grid(static_mw, ngrid=ngrid)
```
## Surface density plots
```
def side_by_side_surface_dens(xx, yy, dens):
ngrid = xx.shape[0]
fig,axes = pl.subplots(1, 2, figsize=(8,4),
sharex=True, sharey=True)
axes[0].pcolormesh(xx, yy, dens.reshape(ngrid,ngrid,ngrid).sum(axis=2),
cmap='Greys_r',
norm=mpl.colors.LogNorm(),
vmin=1E7, vmax=5E9)
axes[0].text(-8., 0, r"$\odot$", ha='center', va='center', fontsize=18, color='w')
axes[1].pcolormesh(xx, yy, dens.reshape(ngrid,ngrid,ngrid).sum(axis=0).T,
cmap='Greys_r',
norm=mpl.colors.LogNorm(),
vmin=1E7, vmax=5E9)
axes[0].set_xlim(xx.min(), xx.max())
axes[0].set_ylim(yy.min(), yy.max())
# TODO: fix the damn aspect ratio
# for ax in axes:
# ax.set_aspect('equal')
fig.tight_layout()
return fig
fig = side_by_side_surface_dens(xx, yy, barred_dens)
fig = side_by_side_surface_dens(xx, yy, static_dens)
```
## Contour plots
```
def side_by_side_contour_plots(xx, yy, dens, levels=10**np.arange(7,12,0.25)):
ngrid = xx.shape[0]
fig,axes = pl.subplots(1,2,figsize=(7.8,4),sharex=True,sharey=True)
im = axes[0].contour(xx, yy, dens.reshape(ngrid,ngrid,ngrid).sum(axis=2),
colors='k',
levels=levels,
rasterized=True)
axes[0].text(-8., 0, r"$\odot$", ha='center', va='center', fontsize=18)
_ = axes[1].contour(xx, yy, dens.reshape(ngrid,ngrid,ngrid).sum(axis=1).T,
colors='k',
levels=levels,
rasterized=True)
# fig.subplots_adjust(bottom=0.2, right=0.85, wspace=0.25)
for ax in axes:
ax.xaxis.set_ticks([-10,0,10])
ax.yaxis.set_ticks([-10,0,10])
axes[0].set_xlabel("$x$ [kpc]")
axes[0].set_ylabel("$y$ [kpc]")
axes[1].set_xlabel("$y$ [kpc]")
axes[1].set_ylabel("$z$ [kpc]")
axes[0].set_xlim(xx.min(), xx.max())
axes[0].set_ylim(yy.min(), yy.max())
fig.tight_layout()
return fig
barred_fig = side_by_side_contour_plots(xx, yy, barred_dens)
static_fig = side_by_side_contour_plots(xx, yy, static_dens)
# barred_fig.savefig(os.path.join(plotpath, "barred-surface-density-contour.pdf"), bbox_inches='tight')
# barred_fig.savefig(os.path.join(plotpath, "barred-surface-density-contour.png"), dpi=400, bbox_inches='tight')
# static_fig.savefig(os.path.join(plotpath, "static-surface-density-contour.pdf"), bbox_inches='tight')
# static_fig.savefig(os.path.join(plotpath, "static-surface-density-contour.png"), dpi=400, bbox_inches='tight')
```
## Portail et al. (2015)
```
ngrid = 65
grid = np.linspace(-2,2,ngrid)
xyz = np.vstack(map(np.ravel, np.meshgrid(grid,grid,grid)))
val2 = np.zeros((ngrid*ngrid*ngrid,))
# for k in potentials.keys():
# val += potentials[k].density(xyz)
val2 += potentials['bar'].density(xyz)
val2[np.isnan(val2)] = val2[np.isfinite(val2)].max()
surf_dens = (val2.reshape(ngrid,ngrid,ngrid).sum(axis=1).T*u.Msun/(u.kpc**2)/ngrid).to(u.Msun/u.pc**2)
pl.figure(figsize=(6,3))
pl.contourf(xyz[0].reshape(ngrid,ngrid,ngrid)[:,:,0],
xyz[1].reshape(ngrid,ngrid,ngrid)[:,:,0],
surf_dens.value,
norm=mpl.colors.LogNorm(),
levels=np.logspace(1., 4, 8),
cmap='Blues')
# cmap='Greys_r',
# norm=mpl.colors.LogNorm(),
# vmin=5E8, vmax=5E10)
pl.xlim(-2,2)
pl.ylim(-1.1,1.1)
pl.colorbar()
pl.tight_layout()
```
## Circular velocity curve
```
def circ_vel_plot(potential, name):
""" name = barred, static """
rr = np.linspace(0.1, 20., 1024)
xyz = np.zeros((3, len(rr)))
xyz[0] = rr
potentials = OrderedDict()
for k,P in potential_classes.items():
potentials[k] = P(units=galactic, **potential.parameters[k])
# vcirc = (np.sqrt(potential.G * potential.mass_enclosed(xyz) / rr)*u.kpc/u.Myr).to(u.km/u.s).value
vcirc = (np.sqrt(potential.G * np.sum([p.mass_enclosed(xyz) for p in potentials.values()], axis=0) / rr)*u.kpc/u.Myr).to(u.km/u.s).value
fig,ax = pl.subplots(1,1,figsize=(6,5))
ax.plot(rr, vcirc, marker='', lw=3.)
styles = dict(
halo=dict(lw=2, ls='-.'),
bar=dict(lw=3., ls=':'),
spheroid=dict(lw=3., ls=':'),
disk=dict(lw=2., ls='--')
)
for k,p in potentials.items():
if k != 'halo' and potential.parameters[k]['m'] == 0:
continue
if k == 'bar':
continue
if name == 'static':
disk_other = 'Spher'
elif name == 'barred':
disk_other = 'Bar+Spher'
vc = (np.sqrt(potential.G * p.mass_enclosed(xyz).value / rr)*u.kpc/u.Myr).to(u.km/u.s).value
if name == 'barred' and k == 'spheroid':
menc_sph = p.mass_enclosed(xyz)
p = potentials['bar']
vc = (np.sqrt(potential.G * (menc_sph + p.mass_enclosed(xyz)).value / rr)*u.kpc/u.Myr).to(u.km/u.s).value
label = 'Bar+Spheroid'
else:
label = k.capitalize()
ax.plot(rr, vc, marker='', label=label, **styles[k])
if name == 'barred':
vc = (np.sqrt(potential.G * (potentials['spheroid'].mass_enclosed(xyz)+potentials['bar'].mass_enclosed(xyz)+potentials['disk'].mass_enclosed(xyz)).value / rr)*u.kpc/u.Myr).to(u.km/u.s).value
ax.plot(rr, vc, marker='', label='Disk+Bar+Spher', lw=2.)
else:
vc = (np.sqrt(potential.G * (potentials['spheroid'].mass_enclosed(xyz)+potentials['disk'].mass_enclosed(xyz)).value / rr)*u.kpc/u.Myr).to(u.km/u.s).value
ax.set_xlabel("$R$ [kpc]")
ax.set_ylabel(r"$v_c$ [${\rm km}\,{\rm s}^{-1}$]")
ax.legend(loc='upper right', fontsize=12)
ax.set_ylim(0,300)
# ax.set_ylim(150,300)
# ax.axhline(220, alpha=0.2, lw=1.)
# ax.axvline(8., color='#cccccc', lw=2., zorder=-100)
rcolor = '#dddddd'
rect = mpl.patches.Rectangle((0.,215), rr.max(), 20., zorder=-100, color=rcolor)
ax.add_patch(rect)
rect2 = mpl.patches.Rectangle((8.,0), 0.3, ax.get_ylim()[1], zorder=-100, color=rcolor)
ax.add_patch(rect2)
fig.tight_layout()
return fig
fig = circ_vel_plot(barred_mw, 'barred')
# fig.savefig(os.path.join(plotpath, "barred-circ-vel.pdf"))
# fig.savefig(os.path.join(plotpath, "barred-circ-vel.png"), dpi=400)
fig = circ_vel_plot(static_mw, name='static')
# fig.savefig(os.path.join(plotpath, "static-circ-vel.pdf"))
# fig.savefig(os.path.join(plotpath, "static-circ-vel.png"), dpi=400)
```
## A new figure with all four panels
```
fig,axes = pl.subplots(2,2,figsize=(9,8.5),sharex='col')
# Circular velocity
styles = dict(
halo=dict(lw=2, ls='-.'),
bar=dict(lw=3., ls=':'),
spheroid=dict(lw=3., ls=':'),
disk=dict(lw=2., ls='--')
)
# Contour
levels = 10**np.arange(7,12,0.25)
rr = np.linspace(0.1, 22., 1024)
fac = static_mw.G / rr
xyz = np.zeros((3, len(rr)))
xyz[0] = rr
for i,(name,pot,dens) in enumerate(zip(['barred','static'], [barred_mw, static_mw],[barred_dens, static_dens])):
# Circular velocity
ax = axes[i,0]
potentials = OrderedDict()
for k,P in potential_classes.items():
potentials[k] = P(units=galactic, **pot.parameters[k])
# vcirc = (np.sqrt(potential.G * potential.mass_enclosed(xyz) / rr)*u.kpc/u.Myr).to(u.km/u.s).value
vcirc = (np.sqrt(pot.G * np.sum([p.mass_enclosed(xyz) for p in potentials.values()], axis=0) / rr)*u.kpc/u.Myr)\
.to(u.km/u.s).value
ax.plot(rr, vcirc, marker='', lw=3.)
menc = dict()
for k,p in potentials.items():
menc[k] = p.mass_enclosed(xyz)
# Halo
vc = np.sqrt(fac * menc['halo'].value)
ax.plot(rr, (vc*u.kpc/u.Myr).to(u.km/u.s),
marker='', label='Halo', **styles['halo'])
# disk, etc.
if name == 'static':
vc = np.sqrt(fac * (menc['disk']+menc['spheroid']).value)
ax.plot(rr, (vc*u.kpc/u.Myr).to(u.km/u.s),
marker='', label='Disk+Sph', **styles['disk'])
elif name == 'barred':
vc = np.sqrt(fac * (menc['disk']+menc['spheroid']+menc['bar']).value)
ax.plot(rr, (vc*u.kpc/u.Myr).to(u.km/u.s),
marker='', label='Disk+Sph+Bar', **styles['disk'])
ax.legend(loc='upper right', fontsize=12)
ax.set_ylim(0,300)
# ax.set_ylim(150,300)
# ax.axhline(220, alpha=0.2, lw=1.)
# ax.axvline(8., color='#cccccc', lw=2., zorder=-100)
rcolor = '#dddddd'
rect = mpl.patches.Rectangle((0.,215), rr.max(), 22., zorder=-100, color=rcolor)
ax.add_patch(rect)
rect2 = mpl.patches.Rectangle((8.,0), 0.3, ax.get_ylim()[1], zorder=-100, color=rcolor)
ax.add_patch(rect2)
# Surface density
ngrid = xx.shape[0]
ax = axes[i,1]
im = ax.contour(xx, yy, dens.reshape(ngrid,ngrid,ngrid).sum(axis=2),
colors='k', levels=levels, rasterized=True)
ax.text(-8., 0, r"$\odot$", ha='center', va='center', fontsize=18)
ax.xaxis.set_ticks([-10,0,10])
ax.yaxis.set_ticks([-10,0,10])
ax.set_xlim(xx.min(), xx.max())
ax.set_ylim(yy.min(), yy.max())
if i == 0:
ax = axes[0,0]
ax.text(8.4, 40, r'$R_\odot$', fontsize=18, color='#666666')
# ax.annotate(r'$R_\odot$', xy=(8.3, 50), xytext=(12, 75.),
# fontsize=18,
# xycoords='data', textcoords='data',
# arrowprops=dict(arrowstyle="fancy",
# fc="0.6", ec="none",
# patchB=rect2,
# connectionstyle="angle3,angleA=0,angleB=90"),
# )
axes[0,0].text(1, 260, "Barred", fontsize=24, fontstyle='italic', ha='left')
axes[1,0].text(1, 260, "Static", fontsize=24, fontstyle='italic', ha='left')
axes[1,0].set_xlabel("$R$ [kpc]")
axes[1,1].set_xlabel("$x$ [kpc]")
axes[0,0].set_ylabel(r"$v_c$ [${\rm km}\,{\rm s}^{-1}$]")
axes[1,0].set_ylabel(r"$v_c$ [${\rm km}\,{\rm s}^{-1}$]")
axes[0,0].set_xlim(0,22)
axes[0,1].set_ylabel("$y$ [kpc]")
axes[1,1].set_ylabel("$y$ [kpc]")
axes[0,1].yaxis.set_label_position('right')
axes[1,1].yaxis.set_label_position('right')
axes[0,1].yaxis.tick_right()
axes[1,1].yaxis.tick_right()
axes[1,1].set_aspect('equal')
fig.tight_layout()
# fig.savefig(os.path.join(plotpath, "potentials-four.pdf"))
# fig.savefig(os.path.join(plotpath, "potentials-four.png"), dpi=400)
```
---
### What direction is it rotating? I hope clockwise...
```
pot = op.WangZhaoBarPotential(**barred_mw.parameters['bar'])
T = (2*np.pi/(60*u.km/u.s/u.kpc)).to(u.Myr).value
for time in np.linspace(0.,T/4,4):
xx,yy,_dens = density_on_grid(pot, t=time, ngrid=64)
fig = side_by_side_surface_dens(xx, yy, _dens)
```
---
```
pars = barred_mw.parameters['bar'].copy()
pars['alpha'] = 0.
pot = op.WangZhaoBarPotential(**pars)
X = np.linspace(-15,15,256)
_xyz = np.zeros((X.size,3))
_xyz[:,0] = X
along_x = pot.acceleration(_xyz)[:,0]
_xyz = np.zeros((X.size,3))
_xyz[:,1] = X
along_y = pot.acceleration(_xyz)[:,1]
pl.plot(X, np.abs(along_x))
pl.plot(X, np.abs(along_y))
engrid = 32
derp = np.linspace(-15,15,engrid)
xy = np.vstack(map(np.ravel, np.meshgrid(derp,derp))).T
xyz = np.zeros((len(xy),3))
xyz[:,[0,2]] = xy
dens = pot.density(xyz, t=0)
dens[np.isnan(dens)] = dens[np.isfinite(dens)].max()
xx = xyz[:,0].reshape(engrid,engrid)
yy = xyz[:,2].reshape(engrid,engrid)
pl.figure(figsize=(5,5))
pl.contour(xx, yy, dens.reshape(engrid,engrid),
colors='k', rasterized=True)
```
|
github_jupyter
|
## Basic core
This module contains all the basic functions we need in other modules of the fastai library (split with [`torch_core`](/torch_core.html#torch_core) that contains the ones requiring pytorch). Its documentation can easily be skipped at a first read, unless you want to know what a given function does.
```
from fastai.gen_doc.nbdoc import *
from fastai.core import *
```
## Global constants
`default_cpus = min(16, num_cpus())` <div style="text-align: right"><a href="https://github.com/fastai/fastai/blob/master/fastai/core.py#L45">[source]</a></div>
## Check functions
```
show_doc(has_arg)
```
Examples for two [`fastai.core`](/core.html#core) functions. Docstring shown before calling [`has_arg`](/core.html#has_arg) for reference
```
has_arg(download_url,'url')
has_arg(index_row,'x')
has_arg(index_row,'a')
show_doc(ifnone)
param,alt_param = None,5
ifnone(param,alt_param)
param,alt_param = None,[1,2,3]
ifnone(param,alt_param)
show_doc(is1d)
two_d_array = np.arange(12).reshape(6,2)
print( two_d_array )
print( is1d(two_d_array) )
is1d(two_d_array.flatten())
show_doc(is_listy)
```
Check if `x` is a `Collection`. `Tuple` or `List` qualify
```
some_data = [1,2,3]
is_listy(some_data)
some_data = (1,2,3)
is_listy(some_data)
some_data = 1024
print( is_listy(some_data) )
print( is_listy( [some_data] ) )
some_data = dict([('a',1),('b',2),('c',3)])
print( some_data )
print( some_data.keys() )
print( is_listy(some_data) )
print( is_listy(some_data.keys()) )
print( is_listy(list(some_data.keys())) )
show_doc(is_tuple)
```
Check if `x` is a `tuple`.
```
print( is_tuple( [1,2,3] ) )
print( is_tuple( (1,2,3) ) )
```
## Collection related functions
```
show_doc(arange_of)
arange_of([5,6,7])
type(arange_of([5,6,7]))
show_doc(array)
array([1,2,3])
```
Note that after we call the generator, we do not reset. So the [`array`](/core.html#array) call has 5 less entries than it would if we ran from the start of the generator.
```
def data_gen():
i = 100.01
while i<200:
yield i
i += 1.
ex_data_gen = data_gen()
for _ in range(5):
print(next(ex_data_gen))
array(ex_data_gen)
ex_data_gen_int = data_gen()
array(ex_data_gen_int,dtype=int) #Cast output to int array
show_doc(arrays_split)
data_a = np.arange(15)
data_b = np.arange(15)[::-1]
mask_a = (data_a > 10)
print(data_a)
print(data_b)
print(mask_a)
arrays_split(mask_a,data_a)
np.vstack([data_a,data_b]).transpose().shape
arrays_split(mask_a,np.vstack([data_a,data_b]).transpose()) #must match on dimension 0
show_doc(chunks)
```
You can transform a `Collection` into an `Iterable` of 'n' sized chunks by calling [`chunks`](/core.html#chunks):
```
data = [0,1,2,3,4,5,6,7,8,9]
for chunk in chunks(data, 2):
print(chunk)
for chunk in chunks(data, 3):
print(chunk)
show_doc(df_names_to_idx)
ex_df = pd.DataFrame.from_dict({"a":[1,1,1],"b":[2,2,2]})
print(ex_df)
df_names_to_idx('b',ex_df)
show_doc(extract_kwargs)
key_word_args = {"a":2,"some_list":[1,2,3],"param":'mean'}
key_word_args
(extracted_val,remainder) = extract_kwargs(['param'],key_word_args)
print( extracted_val,remainder )
show_doc(idx_dict)
idx_dict(['a','b','c'])
show_doc(index_row)
data = [0,1,2,3,4,5,6,7,8,9]
index_row(data,4)
index_row(pd.Series(data),7)
data_df = pd.DataFrame([data[::-1],data]).transpose()
data_df
index_row(data_df,7)
show_doc(listify)
to_match = np.arange(12)
listify('a',to_match)
listify('a',5)
listify(77.1,3)
listify( (1,2,3) )
listify((1,2,3),('a','b','c'))
show_doc(random_split)
```
Splitting is done here with `random.uniform()` so you may not get the exact split percentage for small data sets
```
data = np.arange(20).reshape(10,2)
data.tolist()
random_split(0.20,data.tolist())
random_split(0.20,pd.DataFrame(data))
show_doc(range_of)
range_of([5,4,3])
range_of(np.arange(10)[::-1])
show_doc(series2cat)
data_df = pd.DataFrame.from_dict({"a":[1,1,1,2,2,2],"b":['f','e','f','g','g','g']})
data_df
data_df['b']
series2cat(data_df,'b')
data_df['b']
series2cat(data_df,'a')
data_df['a']
show_doc(split_kwargs_by_func)
key_word_args = {'url':'http://fast.ai','dest':'./','new_var':[1,2,3],'testvalue':42}
split_kwargs_by_func(key_word_args,download_url)
show_doc(to_int)
to_int(3.1415)
data = [1.2,3.4,7.25]
to_int(data)
show_doc(uniqueify)
uniqueify( pd.Series(data=['a','a','b','b','f','g']) )
```
## Files management and downloads
```
show_doc(download_url)
show_doc(find_classes)
show_doc(join_path)
show_doc(join_paths)
show_doc(loadtxt_str)
show_doc(save_texts)
```
## Multiprocessing
```
show_doc(num_cpus)
show_doc(parallel)
show_doc(partition)
show_doc(partition_by_cores)
```
## Data block API
```
show_doc(ItemBase, title_level=3)
```
All items used in fastai should subclass this. Must have a [`data`](/tabular.data.html#tabular.data) field that will be used when collating in mini-batches.
```
show_doc(ItemBase.apply_tfms)
show_doc(ItemBase.show)
```
The default behavior is to set the string representation of this object as title of `ax`.
```
show_doc(Category, title_level=3)
```
Create a [`Category`](/core.html#Category) with an `obj` of index [`data`](/tabular.data.html#tabular.data) in a certain classes list.
```
show_doc(EmptyLabel, title_level=3)
show_doc(MultiCategory, title_level=3)
```
Create a [`MultiCategory`](/core.html#MultiCategory) with an `obj` that is a collection of labels. [`data`](/tabular.data.html#tabular.data) corresponds to the one-hot encoded labels and `raw` is a list of associated string.
```
show_doc(FloatItem)
```
## Others
```
show_doc(camel2snake)
camel2snake('DeviceDataLoader')
show_doc(even_mults)
```
In linear scales each element is equidistant from its neighbors:
```
# from 1 to 10 in 5 steps
t = np.linspace(1, 10, 5)
t
for i in range(len(t) - 1):
print(t[i+1] - t[i])
```
In logarithmic scales, each element is a multiple of the previous entry:
```
t = even_mults(1, 10, 5)
t
# notice how each number is a multiple of its predecessor
for i in range(len(t) - 1):
print(t[i+1] / t[i])
show_doc(func_args)
func_args(download_url)
```
Additionally, [`func_args`](/core.html#func_args) can be used with functions that do not belong to the fastai library
```
func_args(np.linspace)
show_doc(noop)
```
Return `x`.
```
# object is returned as-is
noop([1,2,3])
show_doc(one_hot)
```
One-hot encoding is a standard machine learning technique. Assume we are dealing with a 10-class classification problem and we are supplied a list of labels:
```
y = [1, 4, 4, 5, 7, 9, 2, 4, 0]
jekyll_note("""y is zero-indexed, therefore its first element (1) belongs to class 2, its second element (4) to class 5 and so on.""")
len(y)
```
y can equivalently be expressed as a matrix of 9 rows and 10 columns, where each row represents one element of the original y.
```
for label in y:
print(one_hot(label, 10))
show_doc(show_some)
# select 3 elements from a list
some_data = show_some([10, 20, 30, 40, 50], 3)
some_data
type(some_data)
# the separator can be changed
some_data = show_some([10, 20, 30, 40, 50], 3, sep = '---')
some_data
some_data[:-3]
```
[`show_some`](/core.html#show_some) can take as input any class with \_\_len\_\_ and \_\_getitem\_\_
```
class Any(object):
def __init__(self, data):
self.data = data
def __len__(self):
return len(self.data)
def __getitem__(self,i):
return self.data[i]
some_other_data = Any('nice')
show_some(some_other_data, 2)
show_doc(subplots)
show_doc(text2html_table)
```
## Undocumented Methods - Methods moved below this line will intentionally be hidden
## New Methods - Please document or move to the undocumented section
```
show_doc(is_dict)
```
|
github_jupyter
|
<a href="https://colab.research.google.com/github/denikn/Machine-Learning-MIT-Assignment/blob/main/Week%2002%20-%20Perceptrons/Week02_Homework_02.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
#MIT 6.036 Spring 2019: Homework 2#
This colab notebook provides code and a framework for problems 7-10 of [the homework](https://openlearninglibrary.mit.edu/courses/course-v1:MITx+6.036+1T2019/courseware/Week2/week2_homework/1). You can work out your solutions here, then submit your results back on the homework page when ready.
## <section>**Setup**</section>
First, download the code distribution for this homework that contains test cases and helper functions (such as `positive`).
Run the next code block to download and import the code for this lab.
```
!rm -f code_for_hw02.py*
!wget --no-check-certificate --quiet https://introml_oll.odl.mit.edu/6.036/static/homework/hw02/code_for_hw02.py
from code_for_hw02 import *
help(tidy_plot)
```
```
def test(a):
return a + 53
def methodB(a):
return test(a)
def someMethod():
test = 7
return methodB(test + 3)
someMethod()
```
# <section>**7) Implement perceptron**</section>
Implement [the perceptron algorithm](https://lms.mitx.mit.edu/courses/course-v1:MITx+6.036+2019_Spring/courseware/Week2/perceptron/2), where
* `data` is a numpy array of dimension $d$ by $n$
* `labels` is numpy array of dimension $1$ by $n$
* `params` is a dictionary specifying extra parameters to this algorithm; your algorithm should run a number of iterations equal to $T$
* `hook` is either None or a function that takes the tuple `(th, th0)` as an argument and displays the separator graphically. We won't be testing this in the Tutor, but it will help you in debugging on your own machine.
It should return a tuple of $\theta$ (a $d$ by 1 array) and $\theta_0$ (a 1 by 1 array).
We have given you some data sets in the code file for you to test your implementation.
Your function should initialize all parameters to 0, then run through the data, in the order it is given, performing an update to the parameters whenever the current parameters would make a mistake on that data point. Perform $T$ iterations through the data.
```
import numpy as np
import numpy as np
# x is dimension d by 1
# th is dimension d by 1
# th0 is dimension 1 by 1
# return 1 by 1 matrix of +1, 0, -1
def positive(x, th, th0):
return np.sign(th.T@x + th0)
# Perceptron algorithm with offset.
# data is dimension d by n
# labels is dimension 1 by n
# T is a positive integer number of steps to run
# Perceptron algorithm with offset.
# data is dimension d by n
# labels is dimension 1 by n
# T is a positive integer number of steps to run
def perceptron(data, labels, params = {}, hook = None):
# if T not in params, default to 100
T = params.get('T', 100)
(d, n) = data.shape
theta = np.zeros((d, 1)); theta_0 = np.zeros((1, 1))
for t in range(T):
for i in range(n):
x = data[:,i:i+1]
y = labels[:,i:i+1]
if y * positive(x, theta, theta_0) <= 0.0:
theta = theta + y * x
theta_0 = theta_0 + y
if hook: hook((theta, theta_0))
return theta, theta_0
test_perceptron(perceptron)
```
# <section>8) Implement averaged perceptron</section>
Regular perceptron can be somewhat sensitive to the most recent examples that it sees. Instead, averaged perceptron produces a more stable output by outputting the average value of `th` and `th0` across all iterations.
Implement averaged perceptron with the same spec as regular perceptron, and using the pseudocode below as a guide.
<pre>
procedure averaged_perceptron({(x^(i), y^(i)), i=1,...n}, T)
th = 0 (d by 1); th0 = 0 (1 by 1)
ths = 0 (d by 1); th0s = 0 (1 by 1)
for t = 1,...,T do:
for i = 1,...,n do:
if y^(i)(th . x^(i) + th0) <= 0 then
th = th + y^(i)x^(i)
th0 = th0 + y^(i)
ths = ths + th
th0s = th0s + th0
return ths/(nT), th0s/(nT)
</pre>
```
import numpy as np
# x is dimension d by 1
# th is dimension d by 1
# th0 is dimension 1 by 1
# return 1 by 1 matrix of +1, 0, -1
def positive(x, th, th0):
return np.sign(th.T@x + th0)
def averaged_perceptron(data, labels, params = {}, hook = None):
T = params.get('T', 100)
(d, n) = data.shape
theta = np.zeros((d, 1)); theta_0 = np.zeros((1, 1))
theta_sum = theta.copy()
theta_0_sum = theta_0.copy()
for t in range(T):
for i in range(n):
x = data[:,i:i+1]
y = labels[:,i:i+1]
if y * positive(x, theta, theta_0) <= 0.0:
theta = theta + y * x
theta_0 = theta_0 + y
if hook: hook((theta, theta_0))
theta_sum = theta_sum + theta
theta_0_sum = theta_0_sum + theta_0
theta_avg = theta_sum / (T*n)
theta_0_avg = theta_0_sum / (T*n)
if hook: hook((theta_avg, theta_0_avg))
return theta_avg, theta_0_avg
test_averaged_perceptron(averaged_perceptron)
```
# 9) Implement evaluation strategies
## 9.1) Evaluating a classifier
To evaluate a classifier, we are interested in how well it performs on data that it wasn't trained on. Construct a testing procedure that uses a training data set, calls a learning algorithm to get a linear separator (a tuple of $\theta, \theta_0$), and then reports the percentage correct on a new testing set as a float between 0. and 1..
The learning algorithm is passed as a function that takes a data array and a labels vector. Your evaluator should be able to interchangeably evaluate `perceptron` or `averaged_perceptron` (or future algorithms with the same spec), depending on what is passed through the `learner` parameter.
The `eval_classifier` function should accept the following parameters:
* <tt>learner</tt> - a function, such as perceptron or averaged_perceptron
* <tt>data_train</tt> - training data
* <tt>labels_train</tt> - training labels
* <tt>data_test</tt> - test data
* <tt>labels_test</tt> - test labels
Assume that you have available the function `score` from HW 1, which takes inputs:
* <tt>data</tt>: a <tt>d</tt> by <tt>n</tt> array of floats (representing <tt>n</tt> data points in <tt>d</tt> dimensions)
* <tt>labels</tt>: a <tt>1</tt> by <tt>n</tt> array of elements in <tt>(+1, -1)</tt>, representing target labels
* <tt>th</tt>: a <tt>d</tt> by <tt>1</tt> array of floats that together with
* <tt>th0</tt>: a single scalar or 1 by 1 array, represents a hyperplane
and returns 1 by 1 matrix with an integer indicating number of data points correct for the separator.
```
import numpy as np
def eval_classifier(learner, data_train, labels_train, data_test, labels_test):
th, th0 = learner(data_train, labels_train)
return score(data_test, labels_test, th, th0)/data_test.shape[1]
test_eval_classifier(eval_classifier,perceptron)
```
## <subsection>9.2) Evaluating a learning algorithm using a data source</subsection>
Construct a testing procedure that takes a learning algorithm and a data source as input and runs the learning algorithm multiple times, each time evaluating the resulting classifier as above. It should report the overall average classification accuracy.
You can use our implementation of `eval_classifier` as above.
Write the function `eval_learning_alg` that takes:
* <tt>learner</tt> - a function, such as perceptron or averaged_perceptron
* <tt>data_gen</tt> - a data generator, call it with a desired data set size; returns a tuple (data, labels)
* <tt>n_train</tt> - the size of the learning sets
* <tt>n_test</tt> - the size of the test sets
* <tt>it</tt> - the number of iterations to average over
and returns the average classification accuracy as a float between 0. and 1..
** Note: Be sure to generate your training data and then testing data in that order, to ensure that the pseudorandomly generated data matches that in the test code. **
```
import numpy as np
def eval_learning_alg(learner, data_gen, n_train, n_test, it):
score_sum = 0
for i in range(it):
data_train, labels_train = data_gen(n_train)
data_test, labels_test = data_gen(n_test)
score_sum += eval_classifier(learner, data_train, labels_train,
data_test, labels_test)
return score_sum/it
test_eval_learning_alg(eval_learning_alg,perceptron)
```
## <subsection>9.3) Evaluating a learning algorithm with a fixed dataset</subsection>
Cross-validation is a strategy for evaluating a learning algorithm, using a single training set of size $n$. Cross-validation takes in a learning algorithm $L$, a fixed data set $\mathcal{D}$, and a parameter $k$. It will run the learning algorithm $k$ different times, then evaluate the accuracy of the resulting classifier, and ultimately return the average of the accuracies over each of the $k$ "runs" of $L$. It is structured like this:
<pre><code>divide D into k parts, as equally as possible; call them D_i for i == 0 .. k-1
# be sure the data is shuffled in case someone put all the positive examples first in the data!
for j from 0 to k-1:
D_minus_j = union of all the datasets D_i, except for D_j
h_j = L(D_minus_j)
score_j = accuracy of h_j measured on D_j
return average(score0, ..., score(k-1))
</code></pre>
So, each time, it trains on $k−1$ of the pieces of the data set and tests the resulting hypothesis on the piece that was not used for training.
When $k=n$, it is called *leave-one-out cross validation*.
Implement cross validation **assuming that the input data is shuffled already** so that the positives and negatives are distributed randomly. If the size of the data does not evenly divide by k, split the data into n % k sub-arrays of size n//k + 1 and the rest of size n//k. (Hint: You can use <a href="https://docs.scipy.org/doc/numpy/reference/generated/numpy.array_split.html">numpy.array_split</a>
and <a href="https://docs.scipy.org/doc/numpy/reference/generated/numpy.concatenate.html">numpy.concatenate</a> with axis arguments to split and rejoin the data as you desire.)
Note: In Python, n//k indicates integer division, e.g. 2//3 gives 0 and 4//3 gives 1.
```
import numpy as np
def xval_learning_alg(learner, data, labels, k):
s_data = np.array_split(data, k, axis=1)
s_labels = np.array_split(labels, k, axis=1)
score_sum = 0
for i in range(k):
data_train = np.concatenate(s_data[:i] + s_data[i+1:], axis=1)
labels_train = np.concatenate(s_labels[:i] + s_labels[i+1:], axis=1)
data_test = np.array(s_data[i])
labels_test = np.array(s_labels[i])
score_sum += eval_classifier(learner, data_train, labels_train,
data_test, labels_test)
return score_sum/k
test_xval_learning_alg(xval_learning_alg,perceptron)
```
## 10) Testing
In this section, we compare the effectiveness of perceptron and averaged perceptron on some data that are not necessarily linearly separable.
Use your `eval_learning_alg` and the `gen_flipped_lin_separable` generator in the code file to evaluate the accuracy of `perceptron` vs. a`veraged_perceptron`. `gen_flipped_lin_separable` can be called with an integer to return a data set and labels. Note that this generates linearly separable data and then "flips" the labels with some specified probability (the argument pflip); so most of the results will not be linearly separable. You can also specifiy pflip in the call to the generator. You should use the default values of th and th_0 to retain consistency with the Tutor.
Run enough trials so that you can confidently predict the accuracy of these algorithms on new data from that same generator; assume training/test sets on the order of 20 points. The Tutor will check that your answer is within 0.025 of the answer we got using the same generator.
```
print(eval_learning_alg(perceptron, gen_flipped_lin_separable(pflip=.1), 20, 20, 5))
```
|
github_jupyter
|
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
```
## PIN computation
To compute the PIN of a given day, we need to optimize the product of the likelihood computed on each time interval in the day.
In particular we fix a time interval of 5 minutes to discretize time, and since we are dealing with the dta of a single trade day we only comppute the corresponding PIN, without further analysis of its time evolution.
Note that this problem must be approached by taking particular care about the optimization method choosen. We tested all the methods from scipy.optimize.minimize for bounded problems, both gradient-based and gredient-free, but most of the results exhibited high dependence on the initial guess for the set of parameters. We then choose to apply powell method, which is a gradient-free method, since it is the only one which actually exhibits an evolution and results to be unbiased by the initial point.
```
def likelihood(x, bid, ask, T): #x = [alpha, delta, eps, mu]
"""
likelihood function for the model
args:
x: parameters of the model
bid: observation of the bid side
ask: observation of the ask side
T: time bins
"""
#compute likelihood with Ealsy's (15) notation
from scipy.stats import poisson
likelihood = (1-x[0])*poisson.pmf(k=bid,mu=x[2]*T)*poisson.pmf(k=ask,mu=x[2]*T)+\
+x[0]*x[1]*poisson.pmf(k=bid,mu=x[2]*T)*poisson.pmf(k=ask,mu=(x[2]+x[3])*T)+\
+x[0]*(1-x[1])*poisson.pmf(k=bid,mu=(x[2]+x[3])*T)*poisson.pmf(k=ask,mu=x[2]*T)
return likelihood
def loss (x, bid, ask, T):
"""
loss function for the model
args:
x: parameters of the model (to train)
bid: list of observations of the bid side
ask: list of observations of the ask side
T: time bin width (assumed the same for each bin)
"""
prod=[]
#restricting the loss function to values which do not kill the output
for b, a in zip(bid, ask):
l=likelihood(x, b, a, T)
if l>0: prod.append(l)
else: continue
return -np.prod(prod)
from scipy.optimize import minimize
from tqdm import tqdm
from datetime import timedelta
time_delta = timedelta(minutes=1)
occurrences = pd.read_csv("../data_cleaned/occurrences.csv")
np.random.seed(0)
r=minimize(loss, x0=np.random.uniform(size=4),#
args=(occurrences['bid_observations'], occurrences['ask_observations'], time_delta.total_seconds()),
method='powell', bounds=[(0, 1), (0, 1), (0, None), (0, None)])
params = {'alpha': r.x[0], 'delta': r.x[0], 'eps': r.x[0], 'mu': r.x[0]}
PIN = params['alpha']*params['mu']/(params['alpha']*params['mu']+2*params['eps'])
print('PIN: {:.2f}'.format(PIN))
print('alpha: {:.2f}'.format(params['alpha']))
print('delta: {:.2f}'.format(params['delta']))
```
|
github_jupyter
|
```
import cartopy.crs as ccrs
import xarray as xr
import matplotlib.pyplot as plt
import numpy as np
from itertools import product
import pandas as pd
import os
import time
from datetime import timedelta
import rasterio.warp as rasteriowarp
SATELLITE_DATA_PATH = os.path.expanduser('~/data/EUMETSAT/reprojected_subsetted/')
PV_DATA_FILENAME = os.path.expanduser('~/data/pvoutput.org/UK_PV_timeseries_batch.nc')
PV_METADATA_FILENAME = os.path.expanduser('~/data/pvoutput.org/UK_PV_metadata.csv')
DST_CRS = {
'ellps': 'WGS84',
'proj': 'tmerc', # Transverse Mercator
'units': 'm' # meters
}
# Geospatial boundary in Transverse Mercator projection (meters)
SOUTH = 5513500
NORTH = 6613500
WEST = -889500
EAST = 410500
```
## Load and convert PV metadata
```
pv_metadata = pd.read_csv(PV_METADATA_FILENAME, index_col='system_id')
pv_metadata.dropna(subset=['longitude', 'latitude'], how='any', inplace=True)
# Convert lat lons to Transverse Mercator
pv_metadata['x'], pv_metadata['y'] = rasteriowarp.transform(
src_crs={'init': 'EPSG:4326'},
dst_crs=DST_CRS,
xs=pv_metadata['longitude'].values,
ys=pv_metadata['latitude'].values)
# Filter 3 PV systems which apparently aren't in the UK!
pv_metadata = pv_metadata[
(pv_metadata.x >= WEST) &
(pv_metadata.x <= EAST) &
(pv_metadata.y <= NORTH) &
(pv_metadata.y >= SOUTH)]
len(pv_metadata)
```
## Load and normalise PV power data
```
%%time
pv_power = xr.load_dataset(PV_DATA_FILENAME)
pv_power_selected = pv_power.loc[dict(datetime=slice('2018-06-01', '2019-07-01'))]
pv_power_df = pv_power_selected.to_dataframe().dropna(axis='columns', how='all')
pv_power_df = pv_power_df.clip(lower=0, upper=5E7)
pv_power_df.columns = [np.int64(col) for col in pv_power_df.columns]
pv_power_df = pv_power_df.tz_localize('Europe/London').tz_convert('UTC')
del pv_power
del pv_power_selected
# A bit of hand-crafted cleaning
# TODO: Is this still relevant?
pv_power_df[30248][:'2019-01-03'] = np.NaN
# Scale to the range [0, 1]
pv_power_df -= pv_power_df.min()
pv_power_df /= pv_power_df.max()
# Drop systems which are producing over night
NIGHT_YIELD_THRESHOLD = 0.4
night_hours = list(range(21, 24)) + list(range(0, 4))
bad_systems = np.where(
(pv_power_df[pv_power_df.index.hour.isin(night_hours)] > NIGHT_YIELD_THRESHOLD).sum()
)[0]
bad_systems = pv_power_df.columns[bad_systems]
print(len(bad_systems), 'bad systems found.')
#ax = pv_power_df[bad_systems].plot(figsize=(40, 10), alpha=0.5)
#ax.set_title('Bad PV systems');
pv_power_df.drop(bad_systems, axis='columns', inplace=True)
%%time
# Interpolate up to 15 minutes ahead.
pv_power_df = pv_power_df.interpolate(limit=3)
# Sort the columns
pv_power_df = pv_power_df[np.sort(pv_power_df.columns)]
len(pv_power_df.columns)
#pv_power_df.plot(figsize=(40, 10), alpha=0.5, legend=False);
# Sort the metadata in the same order as the PV power data
pv_metadata = pv_metadata.reindex(pv_power_df.columns, axis='index')
pv_power_df.head()
```
## Load satellite data
```
from glob import glob
from torch.utils.data import Dataset
RECTANGLE_WIDTH = 128000 # in meters
RECTANGLE_HEIGHT = RECTANGLE_WIDTH
def get_rectangle(data_array, time, centre_x, centre_y, width=RECTANGLE_WIDTH, height=RECTANGLE_HEIGHT):
half_width = width / 2
half_height = height / 2
north = centre_y + half_height
south = centre_y - half_height
east = centre_x + half_width
west = centre_x - half_width
data = data_array.loc[dict(
x=slice(west, east),
y=slice(north, south))]
MEAN = 20.444992
STD = 8.766013
data = data - MEAN
data = data / STD
return data
class SatelliteLoader(Dataset):
"""
Attributes:
index: pd.Series which maps from UTC datetime to full filename of satellite data.
_data_array_cache: The last lazily opened xr.DataArray that __getitem__ was asked to open.
Useful so that we don't have to re-open the DataArray if we're asked to get
data from the same file on several different calls.
"""
def __init__(self, file_pattern):
self._load_sat_index(file_pattern)
self._data_array_cache = None
self._last_filename_requested = None
def __getitem__(self, dt):
sat_filename = self.index[dt]
if self._data_array_cache is None or sat_filename != self._last_filename_requested:
self._data_array_cache = xr.open_dataarray(sat_filename)
self._last_filename_requested = sat_filename
return self._data_array_cache
def close(self):
if self._data_array_cache is not None:
self._data_array_cache.close()
def __len__(self):
return len(self.index)
def _load_sat_index(self, file_pattern):
"""Opens all satellite files in `file_pattern` and loads all their datetime indicies into self.index."""
sat_filenames = glob(file_pattern)
sat_filenames.sort()
n_filenames = len(sat_filenames)
sat_index = []
for i_filename, sat_filename in enumerate(sat_filenames):
if i_filename % 10 == 0 or i_filename == (n_filenames - 1):
print('\r {:5d} of {:5d}'.format(i_filename + 1, n_filenames), end='', flush=True)
data_array = xr.open_dataarray(sat_filename, drop_variables=['x', 'y'])
sat_index.extend([(sat_filename, t) for t in data_array.time.values])
sat_index = pd.DataFrame(sat_index, columns=['filename', 'datetime']).set_index('datetime').squeeze()
self.index = sat_index.tz_localize('UTC')
def get_rectangles_for_all_data(self, centre_x, centre_y, width=RECTANGLE_WIDTH, height=RECTANGLE_HEIGHT):
"""Iterate through all satellite filenames and load rectangle of imagery."""
sat_filenames = np.sort(np.unique(self.index.values))
for sat_filename in sat_filenames:
data_array = xr.open_dataarray(sat_filename)
yield get_rectangle(data_array, time, centre_x, centre_y, width, height)
def get_rectangle(self, time, centre_x, centre_y, width=RECTANGLE_WIDTH, height=RECTANGLE_HEIGHT):
data_array = self[time]
return get_rectangle(data_array, time, centre_x, centre_y, width, height)
%%time
sat_loader = SatelliteLoader(os.path.join(SATELLITE_DATA_PATH, '*.nc'))
print()
len(sat_loader)
# Test get rectangle
dt = pd.Timestamp('2019-02-21 10:15')
pv_system_id = pv_metadata.index[1]
x, y = pv_metadata.loc[pv_system_id][['x', 'y']]
%%time
sat_data = sat_loader.get_rectangle(time=dt, centre_x=x, centre_y=y) #, width=512000, height=512000)
fig = plt.figure(figsize=(10, 10))
crs = ccrs.TransverseMercator()
ax = plt.axes(projection=crs)
ax.coastlines(resolution='10m', alpha=0.5, color='pink')
img = sat_data.isel(time=10).plot.imshow(ax=ax, cmap='gray', origin='upper', add_colorbar=True)
path_collection = ax.scatter(x=x, y=y, alpha=0.7)
import pvlib
from pvlib.location import Location
location = Location(
latitude=pv_metadata['latitude'][pv_system_id],
longitude=pv_metadata['longitude'][pv_system_id],
tz='UTC',
name=pv_metadata['system_name'][pv_system_id])
location
fig, ax = plt.subplots(figsize=(20, 7))
pv_data_to_plot = pv_power_df[pv_system_id][dt - timedelta(hours=48):dt + timedelta(hours=48)]
ax.plot(pv_data_to_plot, label='PV yield')
#ax.plot((dt, dt), (0, 1), linewidth=1, color='black', label='datetime of image above')
ax.set_title(dt)
ax.set_ylim((0, 1))
ax2 = ax.twinx()
clearsky = location.get_clearsky(pv_data_to_plot.index)
lines = ax2.plot(clearsky)
for line, label in zip(lines, clearsky.columns):
line.set_label(label);
ax2.legend(loc='upper left');
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torch.utils.data import DataLoader
from collections import OrderedDict
%%time
# Load all satellite data rectangles into RAM
dims = OrderedDict()
dims['time'] = sat_loader.index.index.values
dims['y'] = sat_data.y
dims['x'] = sat_data.x
shape = [len(values) for values in dims.values()]
print('Creating huge numpy array!', flush=True)
data = np.zeros(shape, dtype=np.float16)
print('Setting to NaN', flush=True)
data[:, :, :] = np.NaN
print('Creating huge DataArray!', flush=True)
sat_data_master = xr.DataArray(
data,
coords=dims,
dims=dims.keys(),
name='HRV')
del data, dims, shape
for data_array in sat_loader.get_rectangles_for_all_data(centre_x=x, centre_y=y):
print('\r', data_array.time.values[0], flush=True, end='')
sat_data_master.loc[data_array.time.values, :, :] = data_array
print()
sat_data_master = sat_data_master.dropna(dim='time', how='any')
# Align with PV
pv_data = pv_power_df[pv_system_id].dropna()
sat_data_index = pd.DatetimeIndex(sat_data_master.time.values, tz='UTC')
datetime_index = pv_data.index.intersection(sat_data_index)
len(datetime_index)
datetime_index.tz
sat_data_master = sat_data_master.loc[datetime_index.tz_convert(None)]
pv_data = pv_data[datetime_index]
pv_data_cuda = torch.cuda.HalfTensor(pv_data.values[:, np.newaxis])
pv_data_cuda.shape
sat_data_master_cuda = torch.cuda.HalfTensor(sat_data_master.values[:, np.newaxis])
sat_data_master_cuda.shape
torch.cuda.get_device_name(0)
print('{:,.0f} MB CUDA memory allocated.'.format(torch.cuda.memory_allocated() / 1E6))
# Split train & test by days
days = np.unique(datetime_index.date)
len(days)
# Use every 5th day for testing
testing_days = days[::5]
len(testing_days)
training_days = np.array(list(set(days) - set(testing_days)))
training_days = np.sort(training_days)
len(training_days)
def get_index_into_datetime_index(training_or_testing_days):
return np.where(pd.Series(datetime_index.date).isin(training_or_testing_days))[0]
training_index = get_index_into_datetime_index(training_days)
testing_index = get_index_into_datetime_index(testing_days)
assert not set(training_index).intersection(testing_index)
len(training_index), len(testing_index)
hours_of_day = datetime_index.hour.values.astype(np.float32)
hours_of_day -= hours_of_day.mean()
hours_of_day /= hours_of_day.std()
hours_of_day = torch.cuda.HalfTensor(hours_of_day[:, np.newaxis])
clearsky = location.get_clearsky(datetime_index)
clearsky -= clearsky.mean()
clearsky /= clearsky.std()
clearsky = torch.cuda.HalfTensor(clearsky.values)
class Net(nn.Module):
def __init__(self, dropout_proportion=0.1):
super(Net, self).__init__()
self.conv1 = nn.Conv2d(in_channels=1, out_channels=12, kernel_size=5)
self.pool = nn.MaxPool2d(kernel_size=2, stride=2)
self.conv2 = nn.Conv2d(in_channels=12, out_channels=16, kernel_size=5)
HOURS_OF_DAY_CHANNELS = 1
CLEARSKY_CHANNELS = 3
self.fc1 = nn.Linear(16 * 29 * 29, 120)
self.fc2 = nn.Linear(120 + HOURS_OF_DAY_CHANNELS + CLEARSKY_CHANNELS, 84)
self.fc3 = nn.Linear(84, 1)
self.dropout_layer = nn.Dropout(p=dropout_proportion)
def forward(self, x, hour_of_day, clearsky):
#x = self.dropout_layer(x)
x = self.pool(F.relu(self.conv1(x)))
# x is now <batch_size>, 6, 62, 62.
# 62 is 124 / 2. 124 is the 128-dim input - 4
x = self.dropout_layer(x)
x = self.pool(F.relu(self.conv2(x)))
# x is now <batch_size>, 16, 29, 29
x = x.view(-1, 16 * 29 * 29)
# x is now <batch_size>, 16 x 29 x 29
x = self.dropout_layer(x)
x = F.relu(self.fc1(x))
x = self.dropout_layer(x)
x = torch.cat((x, hour_of_day, clearsky), dim=1)
x = F.relu(self.fc2(x))
x = self.fc3(x)
return x
net = Net().cuda().half()
optimizer = optim.SGD(net.parameters(), lr=0.01)
loss_func = nn.MSELoss()
mae_loss_func = nn.L1Loss()
train_losses = []
train_mae_losses = []
test_losses = []
test_mae_losses = []
%%time
STATS_PERIOD = 1000
TRAINING_BATCH_SIZE = 128
TESTING_BATCH_SIZE = 256
TESTING_BATCH_INDEX = testing_index[:TESTING_BATCH_SIZE]
TESTING_INPUTS = sat_data_master_cuda[TESTING_BATCH_INDEX]
TESTING_TARGET = pv_data_cuda[TESTING_BATCH_INDEX]
TESTING_HOURS_OF_DAY = hours_of_day[TESTING_BATCH_INDEX]
TESTING_CLEARSKY = clearsky[TESTING_BATCH_INDEX]
running_train_loss = 0.0
running_train_mae = 0.0
t0 = time.time()
training_index_len_minus_1 = len(training_index)-1
for i_batch in range(20000 * 4 * 3):
print('\rBatch: {:4d}'.format(i_batch + 1), end='', flush=True)
# Create batch
batch_index = np.random.randint(low=0, high=training_index_len_minus_1, size=TRAINING_BATCH_SIZE)
batch_index = training_index[batch_index]
inputs = sat_data_master_cuda[batch_index]
hours_of_day_for_batch = hours_of_day[batch_index]
clearsky_for_batch = clearsky[batch_index]
target = pv_data_cuda[batch_index]
# zero the parameter gradients
optimizer.zero_grad()
# forward + backward + optimize
net.train()
outputs = net(inputs, hours_of_day_for_batch, clearsky_for_batch)
train_loss = loss_func(outputs, target)
train_loss.backward()
optimizer.step()
running_train_loss += train_loss.item()
# MAE
train_mae = mae_loss_func(outputs, target)
running_train_mae += train_mae.item()
# print statistics
if i_batch % STATS_PERIOD == STATS_PERIOD - 1: # print every STATS_PERIOD mini-batches
t1 = time.time()
# Train loss
mean_train_loss = running_train_loss / STATS_PERIOD
train_losses.append(mean_train_loss)
mean_train_mae = running_train_mae / STATS_PERIOD
train_mae_losses.append(mean_train_mae)
# Test loss
net.eval()
test_outputs = net(TESTING_INPUTS, TESTING_HOURS_OF_DAY, TESTING_CLEARSKY)
test_loss = loss_func(test_outputs, TESTING_TARGET).item()
test_losses.append(test_loss)
test_mae = mae_loss_func(test_outputs, TESTING_TARGET).item()
test_mae_losses.append(test_mae)
print(
'\n time = {:.2f} milli seconds per batch.\n'
' train loss = {:8.5f}\n'
' train MAE = {:8.5f}\n'
' test loss = {:8.5f}\n'
' test MAE = {:8.5f}'.format(
((t1 - t0) / STATS_PERIOD) * 1000,
mean_train_loss,
mean_train_mae,
test_loss,
test_mae
))
running_train_loss = 0.0
running_train_mae = 0.0
t0 = time.time()
print('Finished Training')
fig, (ax1, ax2) = plt.subplots(nrows=2, sharex=True, figsize=(20, 10))
ax1.plot(test_losses, label='testing')
ax1.plot(train_losses, label='training')
ax1.set_title('MSE (training objective)')
ax1.set_ylabel('MSE')
ax1.legend()
ax2.plot(test_mae_losses, label='testing')
ax2.plot(train_mae_losses, label='training')
ax2.set_title('MAE')
ax2.set_ylabel('MAE')
ax2.legend();
# Get MAPE across entire testing dataset :)
net.eval()
start_i = 0
mae_on_all_testset = []
while start_i < len(testing_index) - 1:
end_i = start_i + TESTING_BATCH_SIZE
test_index_batch = testing_index[start_i:end_i]
start_i = end_i
inputs = sat_data_master_cuda[test_index_batch]
testing_hour_of_day = hours_of_day[test_index_batch]
testing_clearsky = clearsky[test_index_batch]
target = pv_data_cuda[test_index_batch]
output = net(inputs, testing_hour_of_day, testing_clearsky)
mae = mae_loss_func(output, target).item()
mae_on_all_testset.append(mae)
np.mean(mae_on_all_testset)
%%time
# Plot some results!
#batch_index = np.random.randint(low=0, high=len(testing_index)-1, size=BATCH_SIZE)
START = 500
batch_index = range(START, START+TESTING_BATCH_SIZE + 512)
batch_index = testing_index[batch_index]
inputs = sat_data_master_cuda[batch_index]
testing_hour_of_day = hours_of_day[batch_index]
testing_clearsky = clearsky[batch_index]
target = pv_data_cuda[batch_index]
net.eval()
output = net(inputs, testing_hour_of_day, testing_clearsky)
i = 30
plt.imshow(
inputs[i, 0].to(device=torch.device('cpu'), dtype=torch.float32),
origin='upper')
output[i, 0].detach().cpu()
target[i, 0].detach().cpu()
fig, (ax1, ax2, ax3) = plt.subplots(nrows=3, figsize=(13,10))
#dt_index = datetime_index[batch_index]
ax1.set_title('5-minutely data')
ax1.plot(output[:, 0].detach().cpu(), label='net output')
ax1.plot(target[:, 0].detach().cpu(), label='target')
ax2.set_title('Hourly rolling means')
ax2.plot(pd.Series(output[:, 0].detach().cpu()).rolling(12, center=True).mean().values, label='net output (hourly rolling mean)')
ax2.plot(pd.Series(target[:, 0].detach().cpu()).rolling(12, center=True).mean().values, label='target (hourly rolling mean)')
ax3.plot(testing_clearsky.detach().cpu())
ax3.set_title('Clearsky irradiance (scaled to have mean=0 and std=1)')
ax1.legend()
ax2.legend()
ax1.set_ylabel('PV yield')
ax2.set_ylabel('PV yield')
ax3.set_xlabel('timestep (5 minutes between timesteps)')
fig.tight_layout();
np.unique(datetime_index[batch_index].date)
```
|
github_jupyter
|
# Stochastic Volatility model
## Imports & Settings
```
import warnings
warnings.filterwarnings('ignore')
%matplotlib inline
from pathlib import Path
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib.ticker import FuncFormatter
import seaborn as sns
import pymc3 as pm
from pymc3.distributions.timeseries import GaussianRandomWalk
sns.set_style('whitegrid')
# model_path = Path('models')
```
## Model assumptions
Asset prices have time-varying volatility (variance of day over day `returns`). In some periods, returns are highly variable, while in others very stable. Stochastic volatility models model this with a latent volatility variable, modeled as a stochastic process. The following model is similar to the one described in the No-U-Turn Sampler paper, Hoffman (2011) p21.
$$\begin{align*}
\sigma &\sim \text{Exponential}(50)\\
\nu &\sim \text{Exponential}(.1)\\
s_i &\sim \text{Normal}(s_{i-1}, \sigma^{-2})\\
\log(r_i) &\sim t(\nu, 0, \exp(-2 s_i))
\end{align*}$$
Here, $r$ is the daily return series and $s$ is the latent log volatility process.
## Get Return Data
First we load some daily returns of the S&P 500.
```
prices = pd.read_hdf('../data/assets.h5', key='sp500/stooq').loc['2000':, 'close']
log_returns = np.log(prices).diff().dropna()
ax = log_returns.plot(figsize=(15, 4),
title='S&P 500 | Daily Log Returns',
rot=0)
ax.yaxis.set_major_formatter(FuncFormatter(lambda y, _: '{:.0%}'.format(y)))
sns.despine()
plt.tight_layout();
```
As you can see, the volatility seems to change over time quite a bit while clustering around certain time-periods, most notably the 2009 financial crash.
## Specify Model in PyMC3
Specifying the model in `PyMC3` mirrors its statistical specification.
```
with pm.Model() as model:
step_size = pm.Exponential('sigma', 50.)
s = GaussianRandomWalk('s', sd=step_size,
shape=len(log_returns))
nu = pm.Exponential('nu', .1)
r = pm.StudentT('r', nu=nu,
lam=pm.math.exp(-2*s),
observed=log_returns)
pm.model_to_graphviz(model)
```
## Fit Model
For this model, the full maximum a posteriori (MAP) point is degenerate and has infinite density. NUTS, however, gives the correct posterior.
```
with model:
trace = pm.sample(tune=2000,
draws=5000,
chains=4,
cores=1,
target_accept=.9)
```
Optionally, persist result as pickle:
```
# with open('model_vol.pkl', 'wb') as buff:
# pickle.dump({'model': model, 'trace': trace}, buff)
```
## Evaluate results
### Trace Plot
```
pm.traceplot(trace, varnames=['sigma', 'nu']);
```
Looking at the returns over time and overlaying the estimated standard deviation we can see how the model tracks the volatility over time.
### In-Sample Predictions
```
pm.trace_to_dataframe(trace).info()
fig, ax = plt.subplots(figsize=(15, 5))
log_returns.plot(ax=ax, lw=.5, xlim=('2000', '2020'), rot=0,
title='In-Sample Fit of Stochastic Volatility Model')
ax.plot(log_returns.index, np.exp(trace[s]).T, 'r', alpha=.03, lw=.5);
ax.set(xlabel='Time', ylabel='Returns')
ax.legend(['S&P 500 (log returns)', 'Stochastic Volatility Model'])
ax.yaxis.set_major_formatter(FuncFormatter(lambda y, _: '{:.0%}'.format(y)))
sns.despine()
fig.tight_layout();
```
|
github_jupyter
|
<h1>Table of Contents<span class="tocSkip"></span></h1>
<div class="toc"><ul class="toc-item"><li><span><a href="#Explainability-with-Amazon-SageMaker-Debugger" data-toc-modified-id="Explainability-with-Amazon-SageMaker-Debugger-1">Explainability with Amazon SageMaker Debugger</a></span><ul class="toc-item"><li><span><a href="#Introduction-" data-toc-modified-id="Introduction--1.1">Introduction <a id="intro"></a></a></span><ul class="toc-item"><li><span><a href="#Saving-tensors" data-toc-modified-id="Saving-tensors-1.1.1">Saving model parameters</a></span></li><li><span><a href="#Analysis" data-toc-modified-id="Analysis-1.1.2">Analysis</a></span></li></ul></li><li><span><a href="#Section-1---Setup-" data-toc-modified-id="Section-1---Setup--1.2">Section 1 - Setup <a id="setup"></a></a></span><ul class="toc-item"><li><span><a href="#1.1-Import-necessary-libraries" data-toc-modified-id="1.1-Import-necessary-libraries-1.2.1">1.1 Import necessary libraries</a></span></li><li><span><a href="#1.2-AWS-region-and--IAM-Role" data-toc-modified-id="1.2-AWS-region-and--IAM-Role-1.2.2">1.2 AWS region and IAM Role</a></span></li><li><span><a href="#1.3-S3-bucket-and-prefix-to-hold-training-data,-debugger-information-and-model-artifact" data-toc-modified-id="1.3-S3-bucket-and-prefix-to-hold-training-data,-debugger-information-and-model-artifact-1.2.3">1.3 S3 bucket and prefix to hold training data, debugger information and model artifact</a></span></li></ul></li><li><span><a href="#Section-2---Data-preparation-" data-toc-modified-id="Section-2---Data-preparation--1.3">Section 2 - Data preparation <a id="prep-data"></a></a></span></li><li><span><a href="#Section-3---Train-XGBoost-model-in-Amazon-SageMaker-with--debugger-enabled.-" data-toc-modified-id="Section-3---Train-XGBoost-model-in-Amazon-SageMaker-with--debugger-enabled.--1.4">Section 3 - Train XGBoost model in Amazon SageMaker with debugger enabled. <a id="train"></a></a></span><ul class="toc-item"><li><span><a href="#3.1-Install-the-'smdebug'-open-source-library" data-toc-modified-id="3.1-Install-the-'smdebug'-open-source-library-1.4.1">3.1 Install the 'smdebug' open source library</a></span></li><li><span><a href="#3.2-Build-the-XGBoost-container" data-toc-modified-id="3.2-Build-the-XGBoost-container-1.4.2">3.2 Build the XGBoost container</a></span></li><li><span><a href="#3.3-Enabling-Debugger-in-Estimator-object" data-toc-modified-id="3.3-Enabling-Debugger-in-Estimator-object-1.4.3">3.3 Enabling Debugger in Estimator object</a></span><ul class="toc-item"><li><span><a href="#DebuggerHookConfig" data-toc-modified-id="DebuggerHookConfig-1.4.3.1">DebuggerHookConfig</a></span></li><li><span><a href="#Rules" data-toc-modified-id="Rules-1.4.3.2">Rules</a></span></li></ul></li><li><span><a href="#3.4-Result" data-toc-modified-id="3.4-Result-1.4.4">3.4 Result</a></span></li><li><span><a href="#3.5-Check-the-status-of-the-Rule-Evaluation-Job" data-toc-modified-id="3.5-Check-the-status-of-the-Rule-Evaluation-Job-1.4.5">3.5 Check the status of the Rule Evaluation Job</a></span></li></ul></li><li><span><a href="#Section-4---Analyze-debugger-output-" data-toc-modified-id="Section-4---Analyze-debugger-output--1.5">Section 4 - Analyze debugger output <a id="analyze-debugger-ouput"></a></a></span><ul class="toc-item"><li><span><a href="#Retrieving-and-Analyzing-tensors" data-toc-modified-id="Retrieving-and-Analyzing-tensors-1.5.1">Retrieving and Analyzing model parameters</a></span></li><li><span><a href="#Plot-Performance-metrics" data-toc-modified-id="Plot-Performance-metrics-1.5.2">Plot Performance metrics</a></span></li><li><span><a href="#Feature-importance" data-toc-modified-id="Feature-importance-1.5.3">Feature importance</a></span></li><li><span><a href="#SHAP" data-toc-modified-id="SHAP-1.5.4">SHAP</a></span></li><li><span><a href="#Global-explanations" data-toc-modified-id="Global-explanations-1.5.5">Global explanations</a></span></li><li><span><a href="#Local-explanations" data-toc-modified-id="Local-explanations-1.5.6">Local explanations</a></span><ul class="toc-item"><li><span><a href="#Force-plot" data-toc-modified-id="Force-plot-1.5.6.1">Force plot</a></span></li><li><span><a href="#Stacked-force-plot" data-toc-modified-id="Stacked-force-plot-1.5.6.2">Stacked force plot</a></span></li></ul></li><li><span><a href="#Outliers" data-toc-modified-id="Outliers-1.5.7">Outliers</a></span></li></ul></li><li><span><a href="#Conclusion" data-toc-modified-id="Conclusion-1.6">Conclusion</a></span></li></ul></li></ul></div>
# Explainability with Amazon SageMaker Debugger
_**Explain a XGBoost model that predicts an individual's income**_
This notebook demonstrates how to use Amazon SageMaker Debugger to capture the feature importance and SHAP values for a XGBoost model.
*This notebook was created and tested on an ml.t2.medium notebook instance.*
## Introduction <a id='intro'></a>
Amazon SageMaker Debugger is the capability of Amazon SageMaker that allows debugging machine learning training. The capability helps you monitor the training jobs in near real time using rules and alert you once it has detected inconsistency in training.
Using Amazon SageMaker Debugger is a two step process: Saving model parameters and Analysis.
Let's look at each one of them closely.
### Saving model parameters
In machine learning process, model parameters are updated every forward and backward pass and can describe the state of the training job at any particular instant in an ML lifecycle. Amazon SageMaker Debugger allows you to capture the model parameters and save them for analysis. Although XGBoost is not a deep learning algorithm, Amazon SageMaker Debugger is highly customizable and can help you interpret results by saving insightful metrics. For example, performance metrics or the importance of features at different frequencies. Refer to [SageMaker Debugger documentation](https://docs.aws.amazon.com/sagemaker/latest/dg/debugger-configuration.html) for details on how to save the metrics you want.
The saved model parameters in this notebook include feature importance and SHAP values for all features in the dataset. The feature importance and SHAP values are what we will use to provide local and global explainability.
### Analysis
After the model parameters are saved, perform automatic analysis by running debugging ***Rules***.
On a very broad level, a rule is Python code used to detect certain conditions during training.
Some of the conditions that a data scientist training an algorithm may care about are monitoring for gradients getting too large or too small, detecting overfitting, and so on.
Amazon SageMaker Debugger comes pre-packaged with certain rules that can be invoked on Amazon SageMaker. Users can also write their own rules using the Amazon SageMaker Debugger APIs.
For more information about automatic analysis using a rule, see the [rules documentation](https://github.com/awslabs/sagemaker-debugger/blob/master/docs/analysis.md).
## Section 1 - Setup <a id='setup'></a>
In this section, we will import the necessary libraries, setup variables and examine dataset used. that was used to train the XGBoost model to predict an individual's income.
Let's start by specifying:
* The AWS region used to host your model.
* The IAM role associated with this SageMaker notebook instance.
* The S3 bucket used to store the data used to train the model, save debugger information during training and the trained model artifact.
<font color='red'>**Important**</font>: To use the new Debugger features, you need to upgrade the SageMaker Python SDK and the SMDebug libary. In the following cell, change the third line to `install_needed=True` and run to upgrade the libraries.
```
import sys
import IPython
install_needed = False # Set to True to upgrade
if install_needed:
print("installing deps and restarting kernel")
!{sys.executable} -m pip install -U sagemaker
!{sys.executable} -m pip install -U smdebug
IPython.Application.instance().kernel.do_shutdown(True)
```
### 1.1 Import necessary libraries
```
import boto3
import sagemaker
import os
import pandas as pd
from sagemaker import get_execution_role
```
### 1.2 AWS region and IAM Role
```
region = boto3.Session().region_name
print("AWS Region: {}".format(region))
role = get_execution_role()
print("RoleArn: {}".format(role))
```
### 1.3 S3 bucket and prefix to hold training data, debugger information, and model artifact
```
bucket = sagemaker.Session().default_bucket()
prefix = "DEMO-smdebug-xgboost-adult-income-prediction"
```
## Section 2 - Data preparation <a id='prep-data'></a>
We'll be using the [Adult Census dataset](https://archive.ics.uci.edu/ml/datasets/adult) for this exercise.
This data was extracted from the [1994 Census bureau database](http://www.census.gov/en.html) by Ronny Kohavi and Barry Becker (Data Mining and Visualization, Silicon Graphics), with the task being to predict if an individual person makes over 50K a year.
We'll be using the [SHAP](https://github.com/slundberg/shap) library to perform visual analysis. The library contains the dataset pre-loaded which we will utilize here.
```
!python -m pip install shap
import shap
X, y = shap.datasets.adult()
X_display, y_display = shap.datasets.adult(display=True)
feature_names = list(X.columns)
feature_names
# create a train/test split
from sklearn.model_selection import train_test_split # For splitting the dataset
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=7)
X_train_display = X_display.loc[X_train.index]
train = pd.concat(
[pd.Series(y_train, index=X_train.index, name="Income>50K", dtype=int), X_train], axis=1
)
test = pd.concat(
[pd.Series(y_test, index=X_test.index, name="Income>50K", dtype=int), X_test], axis=1
)
# Use 'csv' format to store the data
# The first column is expected to be the output column
train.to_csv("train.csv", index=False, header=False)
test.to_csv("validation.csv", index=False, header=False)
boto3.Session().resource("s3").Bucket(bucket).Object(
os.path.join(prefix, "data/train.csv")
).upload_file("train.csv")
boto3.Session().resource("s3").Bucket(bucket).Object(
os.path.join(prefix, "data/validation.csv")
).upload_file("validation.csv")
```
## Section 3 - Train XGBoost model in Amazon SageMaker with debugger enabled. <a id='train'></a>
Now train an XGBoost model with Amazon SageMaker Debugger enabled and monitor the training jobs. This is done using the Amazon SageMaker Estimator API. While the training job is running, use Amazon SageMaker Debugger API to access saved model parameters in real time and visualize them. You can rely on Amazon SageMaker Debugger to take care of downloading a fresh set of model parameters every time you query for them.
Amazon SageMaker Debugger is available in Amazon SageMaker XGBoost container version 0.90-2 or later. If you want to use XGBoost with Amazon SageMaker Debugger, you have to specify `repo_version='0.90-2'` in the `get_image_uri` function.
### 3.2 Build the XGBoost container
Amazon SageMaker Debugger is available in Amazon SageMaker XGBoost container version 0.90-2 or later.
```
container = sagemaker.image_uris.retrieve("xgboost", region, "0.90-2")
base_job_name = "demo-smdebug-xgboost-adult-income-prediction-classification"
bucket_path = "s3://{}".format(bucket)
hyperparameters = {
"max_depth": "5",
"eta": "0.2",
"gamma": "4",
"min_child_weight": "6",
"subsample": "0.7",
"silent": "0",
"objective": "binary:logistic",
"num_round": "51",
}
save_interval = 5
```
### 3.3 Enabling Debugger in Estimator object
#### DebuggerHookConfig
Enabling Amazon SageMaker Debugger in training job can be accomplished by adding its configuration into Estimator object constructor:
```python
from sagemaker.debugger import DebuggerHookConfig, CollectionConfig
estimator = Estimator(
...,
debugger_hook_config = DebuggerHookConfig(
s3_output_path="s3://{bucket_name}/{location_in_bucket}", # Required
collection_configs=[
CollectionConfig(
name="metrics",
parameters={
"save_interval": "10"
}
)
]
)
)
```
Here, the `DebuggerHookConfig` object instructs `Estimator` what data we are interested in.
Two parameters are provided in the example:
- `s3_output_path`: Points to an S3 bucket where you intend to store model parameters. Amount of data saved depends on multiple factors, major ones are training job, data set, model, frequency of saving model parameters. This S3 bucket should be in your AWS account so that you have full access to control over the stored data. **Note**: The S3 bucket should be originally created in the same Region where your training job is running, otherwise you might run into problems with cross-Region access.
- `collection_configs`: It enumerates named collections of model parameters to save. Collections are a convenient way to organize relevant model parameters under same umbrella to make it easy to navigate them during analysis. In this particular example, you are interested in a single collection named metrics. You also configured Amazon SageMaker Debugger to save metrics every 10 iterations. See [Collection](https://github.com/awslabs/sagemaker-debugger/blob/master/docs/api.md#collection) documentation for all parameters that are supported by Collections and DebuggerConfig documentation for more details about all parameters DebuggerConfig supports.
#### Rules
Enabling Rules in training job can be accomplished by adding the `rules` configuration into Estimator object constructor.
- `rules`: This parameter will accept a list of rules you want to evaluate against training jobs.
For rules, Amazon SageMaker Debugger supports two types:
- SageMaker Rules: These are rules specially curated by the data science and engineering teams in Amazon SageMaker which you can opt to evaluate against your training job.
- Custom Rules: You can optionally choose to write your own rule as a Python source file and have it evaluated against your training job.
To provide Amazon SageMaker Debugger to evaluate this rule, you would have to provide the S3 location of the rule source and the evaluator image.
In this example, you will use a Amazon SageMaker's LossNotDecreasing rule, which helps you identify if you are running into a situation where the training loss is not going down.
```python
from sagemaker.debugger import rule_configs, Rule
estimator = Estimator(
...,
rules=[
Rule.sagemaker(
rule_configs.loss_not_decreasing(),
rule_parameters={
"collection_names": "metrics",
"num_steps": "10",
},
),
],
)
```
- `rule_parameters`: In this parameter, you provide the runtime values of the parameter in your constructor.
You can still choose to pass in other values which may be necessary for your rule to be evaluated.
In this example, you will use Amazon SageMaker's LossNotDecreasing rule to monitor the `metircs` collection.
The rule will alert you if the loss value in the `metrics` collection has not decreased for more than 10 steps.
```
from sagemaker.debugger import rule_configs, Rule, DebuggerHookConfig, CollectionConfig
from sagemaker.estimator import Estimator
xgboost_estimator = Estimator(
role=role,
base_job_name=base_job_name,
instance_count=1,
instance_type="ml.m5.4xlarge",
image_uri=container,
hyperparameters=hyperparameters,
max_run=1800,
debugger_hook_config=DebuggerHookConfig(
s3_output_path=bucket_path, # Required
collection_configs=[
CollectionConfig(name="metrics", parameters={"save_interval": str(save_interval)}),
CollectionConfig(
name="feature_importance", parameters={"save_interval": str(save_interval)}
),
CollectionConfig(name="full_shap", parameters={"save_interval": str(save_interval)}),
CollectionConfig(name="average_shap", parameters={"save_interval": str(save_interval)}),
],
),
rules=[
Rule.sagemaker(
rule_configs.loss_not_decreasing(),
rule_parameters={
"collection_names": "metrics",
"num_steps": str(save_interval * 2),
},
),
],
)
```
With the next step, start a training job by using the Estimator object you created above. This job is started in an asynchronous, non-blocking way. This means that control is passed back to the notebook and further commands can be run while the training job is progressing.
```
from sagemaker.session import TrainingInput
train_input = TrainingInput(
"s3://{}/{}/{}".format(bucket, prefix, "data/train.csv"), content_type="csv"
)
validation_input = TrainingInput(
"s3://{}/{}/{}".format(bucket, prefix, "data/validation.csv"), content_type="csv"
)
xgboost_estimator.fit(
{"train": train_input, "validation": validation_input},
# This is a fire and forget event. By setting wait=False, you submit the job to run in the background.
# Amazon SageMaker starts one training job and release control to next cells in the notebook.
# Follow this notebook to see status of the training job.
wait=False,
)
```
### 3.4 Result
As a result of the above command, Amazon SageMaker starts **one training job and one rule job** for you. The first one is the job that produces the model parameters to be analyzed. The second one analyzes the model parameters to check if `train-error` and `validation-error` are not decreasing at any point during training.
Check the status of the training job below.
After your training job is started, Amazon SageMaker starts a rule-execution job to run the LossNotDecreasing rule.
The cell below will block till the training job is complete.
```
import time
for _ in range(36):
job_name = xgboost_estimator.latest_training_job.name
client = xgboost_estimator.sagemaker_session.sagemaker_client
description = client.describe_training_job(TrainingJobName=job_name)
training_job_status = description["TrainingJobStatus"]
rule_job_summary = xgboost_estimator.latest_training_job.rule_job_summary()
rule_evaluation_status = rule_job_summary[0]["RuleEvaluationStatus"]
print(
"Training job status: {}, Rule Evaluation Status: {}".format(
training_job_status, rule_evaluation_status
)
)
if training_job_status in ["Completed", "Failed"]:
break
time.sleep(10)
```
### 3.5 Check the status of the Rule Evaluation Job
To get the rule evaluation job that Amazon SageMaker started for you, run the command below. The results show you the `RuleConfigurationName`, `RuleEvaluationJobArn`, `RuleEvaluationStatus`, `StatusDetails`, and `RuleEvaluationJobArn`.
If the model parameters meet a rule evaluation condition, the rule execution job throws a client error with `RuleEvaluationConditionMet`.
The logs of the rule evaluation job are available in the Cloudwatch Logstream `/aws/sagemaker/ProcessingJobs` with `RuleEvaluationJobArn`.
You can see that once the rule execution job starts, it identifies the loss not decreasing situation in the training job, it raises the `RuleEvaluationConditionMet` exception, and it ends the job.
```
xgboost_estimator.latest_training_job.rule_job_summary()
```
## Section 4 - Analyze debugger output <a id='analyze-debugger-ouput'></a>
Now that you've trained the system, analyze the data. Here, you focus on after-the-fact analysis.
You import a basic analysis library, which defines the concept of trial, which represents a single training run.
### Retrieving and Analyzing tensors
Before getting to analysis, here are some notes on concepts being used in Amazon SageMaker Debugger that help with analysis.
- ***Trial*** - Object that is a centerpiece of the SageMaker Debugger API when it comes to getting access to model parameters. It is a top level abstract that represents a single run of a training job. All model parameters emitted by a training job are associated with its trial.
- ***Tensor*** - Object that represents model parameters, such as weights, gradients, accuracy, and loss, that are saved during training job.
For more details on aforementioned concepts as well as on SageMaker Debugger API in general (including examples) see [SageMaker Debugger Analysis API](https://github.com/awslabs/sagemaker-debugger/blob/master/docs/analysis.md) documentation.
In the following code cell, use a ***Trial*** to access model parameters. You can do that by inspecting currently running training job and extract necessary parameters from its debug configuration to instruct SageMaker Debugger where the data you are looking for is located. Keep in mind the following:
- model parameters are being stored in your own S3 bucket to which you can navigate and manually inspect its content if desired.
- You might notice a slight delay before trial object is created. This is normal as SageMaker Debugger monitors the corresponding bucket and waits until model parameters to appear. The delay is introduced by less than instantaneous upload of model parameters from a training container to your S3 bucket.
```
from smdebug.trials import create_trial
s3_output_path = xgboost_estimator.latest_job_debugger_artifacts_path()
trial = create_trial(s3_output_path)
```
You can list all model parameters that you want to analyze. Each one of these names is the name of a model parameter. The name is a combination of the feature name, which in these cases, is auto-assigned by XGBoost, and whether it's an evaluation metric, feature importance, or SHAP value.
```
trial.tensor_names()
```
For each model parameter, we can get the values at all saved steps.
```
trial.tensor("average_shap/f1").values()
```
### Plot Performance metrics
You can also create a simple function that visualizes the training and validation errors as the training progresses.
The error should get smaller over time, as the system converges to a good solution.
```
from itertools import islice
import matplotlib.pyplot as plt
import re
MAX_PLOTS = 35
def get_data(trial, tname):
"""
For the given tensor name, walks though all the iterations
for which you have data and fetches the values.
Returns the set of steps and the values.
"""
tensor = trial.tensor(tname)
steps = tensor.steps()
vals = [tensor.value(s) for s in steps]
return steps, vals
def match_tensor_name_with_feature_name(tensor_name, feature_names=feature_names):
feature_tag = tensor_name.split("/")
for ifeat, feature_name in enumerate(feature_names):
if feature_tag[-1] == "f{}".format(str(ifeat)):
return feature_name
return tensor_name
def plot_collection(trial, collection_name, regex=".*", figsize=(8, 6)):
"""
Takes a `trial` and a collection name, and
plots all tensors that match the given regex.
"""
fig, ax = plt.subplots(figsize=figsize)
tensors = trial.collection(collection_name).tensor_names
matched_tensors = [t for t in tensors if re.match(regex, t)]
for tensor_name in islice(matched_tensors, MAX_PLOTS):
steps, data = get_data(trial, tensor_name)
ax.plot(steps, data, label=match_tensor_name_with_feature_name(tensor_name))
ax.legend(loc="center left", bbox_to_anchor=(1, 0.5))
ax.set_xlabel("Iteration")
plot_collection(trial, "metrics")
```
### Feature importance
You can also visualize the feature priorities as determined by
[xgboost.get_score()](https://xgboost.readthedocs.io/en/latest/python/python_api.html#xgboost.Booster.get_score).
If you instructed Estimator to log the `feature_importance` collection, all importance types supported by `xgboost.get_score()` will be available in the collection.
```
def plot_feature_importance(trial, importance_type="weight"):
SUPPORTED_IMPORTANCE_TYPES = ["weight", "gain", "cover", "total_gain", "total_cover"]
if importance_type not in SUPPORTED_IMPORTANCE_TYPES:
raise ValueError(f"{importance_type} is not one of the supported importance types.")
plot_collection(trial, "feature_importance", regex=f"feature_importance/{importance_type}/.*")
plot_feature_importance(trial, importance_type="cover")
```
### SHAP
[SHAP](https://github.com/slundberg/shap) (SHapley Additive exPlanations) is
another approach to explain the output of machine learning models.
SHAP values represent a feature's contribution to a change in the model output.
You instructed Estimator to log the average SHAP values in this example so the SHAP values (as calculated by [xgboost.predict(pred_contribs=True)](https://xgboost.readthedocs.io/en/latest/python/python_api.html#xgboost.Booster.predict)) will be available the `average_shap` collection.
```
plot_collection(trial, "average_shap")
```
### Global explanations
Global explanatory methods allow understanding the model and its feature contributions in aggregate over multiple datapoints. Here we show an aggregate bar plot that plots the mean absolute SHAP value for each feature.
Specifically, the below plot indicates that the value of relationship (Wife=5, Husband=4, Own-child=3, Other-relative=2, Unmarried=1, Not-in-family=0) plays the most important role in predicting the income probability being higher than 50K.
```
shap_values = trial.tensor("full_shap/f0").value(trial.last_complete_step)
shap_no_base = shap_values[:, :-1]
shap_base_value = shap_values[0, -1]
shap.summary_plot(shap_no_base, plot_type="bar", feature_names=feature_names)
shap_base_value
```
The detailed summary plot below can provide more context over the above bar chart. It tells which features are most important and, in addition, their range of effects over the dataset. The color allows us to match how changes in the value of a feature effect the change in prediction.
The 'red' indicates higher value of the feature and 'blue' indicates lower (normalized over the features). This allows conclusions such as 'increase in age leads to higher log odds for prediction, eventually leading to `True` predictions more often.
```
shap.summary_plot(shap_no_base, X_train)
```
### Local explanations
Local explainability aims to explain model behavior for a fixed input point. This can be used for either auditing models before deployment or to provide explanations for specific inference predictions.
```
shap.initjs()
```
#### Force plot
A force plot explanation shows how features are contributing to push the model output from the base value (the average model output over the dataset) to the model output. Features pushing the prediction higher are shown in **red**, those pushing the prediction lower are in **blue**.
Plot below indicates that for this particular data point the prediction probability (0.48) is higher than the average (~0.2) primarily because this person is in a relationship (`Relationship = Wife`), and to smaller degree because of the higher-than-average age. Similarly the model reduces the probability due specific `Sex` and `Race` values indicating existence of bias in model behavior (possibly due to bias in the data).
```
shap.force_plot(
shap_base_value,
shap_no_base[100, :],
X_train_display.iloc[100, :],
link="logit",
matplotlib=False,
)
```
#### Stacked force plot
SHAP allows stacking multiple force-plots after rotating 90 degress to understand the explanations for multiple datapoints. If Javascript is enabled, then in the notebook this plot is interactive, allowing understanding the change in output for each feature independently. This stacking of force plots provides a balance between local and global explainability.
```
import numpy as np
N_ROWS = shap_no_base.shape[0]
N_SAMPLES = min(100, N_ROWS)
sampled_indices = np.random.randint(N_ROWS, size=N_SAMPLES)
shap.force_plot(
shap_base_value,
shap_no_base[sampled_indices, :],
X_train_display.iloc[sampled_indices, :],
link="logit",
)
```
### Outliers
Outliers are extreme values that deviate from other observations on data. It's useful to understand the influence of various features for outlier predictions to determine if it's a novelty, an experimental error, or a shortcoming in the model.
Here we show force plot for prediction outliers that are on either side of the baseline value.
```
# top outliers
from scipy import stats
N_OUTLIERS = 3 # number of outliers on each side of the tail
shap_sum = np.sum(shap_no_base, axis=1)
z_scores = stats.zscore(shap_sum)
outlier_indices = (np.argpartition(z_scores, -N_OUTLIERS)[-N_OUTLIERS:]).tolist()
outlier_indices += (np.argpartition(z_scores, N_OUTLIERS)[:N_OUTLIERS]).tolist()
for fig_index, outlier_index in enumerate(outlier_indices, start=1):
shap.force_plot(
shap_base_value,
shap_no_base[outlier_index, :],
X_train_display.iloc[outlier_index, :],
matplotlib=False,
link="logit",
)
```
## Conclusion
This notebook discussed the importance of explainability for improved ML
adoption and. We introduced the Amazon SageMaker Debugger capability with built-in
model parameter collections to enable model explainability.
The notebook walked you through training an ML model for a financial services use case
of individual income prediction. We further analyzed the global and local
explanations of the model by visualizing the captured model parameters.
|
github_jupyter
|
# Метод сопряжённых градиентов (Conjugate gradient method): гадкий утёнок
## На прошлом занятии...
1. Методы спуска
2. Направление убывания
3. Градиентный метод
4. Правила выбора шага
5. Теоремы сходимости
6. Эксперименты
## Система линейных уравнений vs. задача безусловной минимизации
Рассмотрим задачу
$$
\min_{x \in \mathbb{R}^n} \frac{1}{2}x^{\top}Ax - b^{\top}x,
$$
где $A \in \mathbb{S}^n_{++}$.
Из необходимого условия экстремума имеем
$$
Ax^* = b
$$
Также обозначим $f'(x_k) = Ax_k - b = r_k$
## Как решить систему $Ax = b$?
- Прямые методы основаны на матричных разложениях:
- Плотная матрица $A$: для размерностей не больше нескольких тысяч
- Разреженная (sparse) матрица $A$: для размерностей порядка $10^4 - 10^5$
- Итерационные методы: хороши во многих случаях, единственный подход для задач с размерностью $ > 10^6$
## Немного истории...
M. Hestenes и E. Stiefel предложили *метод сопряжённых градиентов* для решения систем линейных уравнений в 1952 году как **прямой** метод.
Также долгое время считалось, что метод представляет только теоретический интерес поскольку
- метод сопряжённых градиентов не работает на логарифмической линейке
- метод сопряжённых градиентов имеет небольшое преимущество перед исключением Гаусса при вычислениях на калькуляторе
- для вычислений на "human computers" слишком много обменов данными
<img src="./human_computer.jpeg">
Метод сопряжённых градиентов необходимо рассматривать как **итерационный метод**, то есть останавливаться до точной сходимости!
Подробнее [здесь](https://www.siam.org/meetings/la09/talks/oleary.pdf)
## Метод сопряжённых направлений
В градиентном спуске направления убывания - анти-градиенты, но для функций с плохо обусловленным гессианом сходимость **медленная**.
**Идея:** двигаться вдоль направлений, которые гарантируют сходимость за $n$ шагов.
**Определение.** Множество ненулевых векторов $\{p_0, \ldots, p_l\}$ называется *сопряжённым* относительно матрицы $A \in \mathbb{S}^n_{++}$, если
$$
p^{\top}_iAp_j = 0, \qquad i \neq j
$$
**Утверждение.** Для любой $x_0 \in \mathbb{R}^n$ последовательность $\{x_k\}$, генерируемая методом сопряжённых направлений, сходится к решению системы $Ax = b$ максимум за $n$ шагов.
```python
def ConjugateDirections(x0, A, b, p):
x = x0
r = A.dot(x) - b
for i in range(len(p)):
alpha = - (r.dot(p[i])) / (p[i].dot(A.dot(p[i])))
x = x + alpha * p[i]
r = A.dot(x) - b
return x
```
### Примеры сопряжённых направлений
- Собственные векторы матрицы $A$
- Для любого набора из $n$ векторов можно провести аналог ортогонализации Грама-Шмидта и получить сопряжённые направления
**Вопрос:** что такое ортогонализация Грама-Шмидта? :)
### Геометрическая интерпретация (Mathematics Stack Exchange)
<center><img src="./cg.png" ></center>
## Метод сопряжённых градиентов
**Идея:** новое направление $p_k$ ищется в виде $p_k = -r_k + \beta_k p_{k-1}$, где $\beta_k$ выбирается, исходя из требования сопряжённости $p_k$ и $p_{k-1}$:
$$
\beta_k = \dfrac{p^{\top}_{k-1}Ar_k}{p^{\top}_{k-1}Ap_{k-1}}
$$
Таким образом, для получения следующего сопряжённого направления $p_k$ необходимо хранить только сопряжённое направление $p_{k-1}$ и остаток $r_k$ с предыдущей итерации.
**Вопрос:** как находить размер шага $\alpha_k$?
## Сопряжённость сопряжённых градиентов
**Теорема**
Пусть после $k$ итераций $x_k \neq x^*$. Тогда
- $\langle r_k, r_i \rangle = 0, \; i = 1, \ldots k - 1$
- $\mathtt{span}(r_0, \ldots, r_k) = \mathtt{span}(r_0, Ar_0, \ldots, A^kr_0)$
- $\mathtt{span}(p_0, \ldots, p_k) = \mathtt{span}(r_0, Ar_0, \ldots, A^kr_0)$
- $p_k^{\top}Ap_i = 0$, $i = 1,\ldots,k-1$
### Теоремы сходимости
**Теорема 1.** Если матрица $A$ имеет только $r$ различных собственных значений, то метод сопряжённых градиентов cойдётся за $r$ итераций.
**Теорема 2.** Имеет место следующая оценка сходимости
$$
\| x_{k} - x^* \|_A \leq 2\left( \dfrac{\sqrt{\kappa(A)} - 1}{\sqrt{\kappa(A)} + 1} \right)^k \|x_0 - x^*\|_A,
$$
где $\|x\|_A = x^{\top}Ax$ и $\kappa(A) = \frac{\lambda_1(A)}{\lambda_n(A)}$ - число обусловленности матрицы $A$, $\lambda_1(A) \geq ... \geq \lambda_n(A)$ - собственные значения матрицы $A$
**Замечание:** сравните коэффициент геометрической прогрессии с аналогом в градиентном спуске.
### Интерпретации метода сопряжённых градиентов
- Градиентный спуск в пространстве $y = Sx$, где $S = [p_0, \ldots, p_n]$, в котором матрица $A$ становится диагональной (или единичной в случае ортонормированности сопряжённых направлений)
- Поиск оптимального решения в [Крыловском подпространстве](https://stanford.edu/class/ee364b/lectures/conj_grad_slides.pdf) $\mathcal{K}_k(A) = \{b, Ab, A^2b, \ldots A^{k-1}b\}$
$$
x_k = \arg\min_{x \in \mathcal{K}_k} f(x)
$$
- Однако естественный базис Крыловского пространства неортогональный и, более того, **плохо обусловлен**.
**Упражнение** Проверьте численно, насколько быстро растёт обусловленность матрицы из векторов $\{b, Ab, ... \}$
- Поэтому его необходимо ортогонализовать, что и происходит в методе сопряжённых градиентов
### Основное свойство
$$
A^{-1}b \in \mathcal{K}_n(A)
$$
Доказательство
- Теорема Гамильтона-Кэли: $p(A) = 0$, где $p(\lambda) = \det(A - \lambda I)$
- $p(A)b = A^nb + a_1A^{n-1}b + \ldots + a_{n-1}Ab + a_n b = 0$
- $A^{-1}p(A)b = A^{n-1}b + a_1A^{n-2}b + \ldots + a_{n-1}b + a_nA^{-1}b = 0$
- $A^{-1}b = -\frac{1}{a_n}(A^{n-1}b + a_1A^{n-2}b + \ldots + a_{n-1}b)$
### Сходимость по функции и по аргументу
- Решение: $x^* = A^{-1}b$
- Минимум функции:
$$
f^* = \frac{1}{2}b^{\top}A^{-\top}AA^{-1}b - b^{\top}A^{-1}b = -\frac{1}{2}b^{\top}A^{-1}b = -\frac{1}{2}\|x^*\|^2_A
$$
- Оценка сходимости по функции:
$$
f(x) - f^* = \frac{1}{2}x^{\top}Ax - b^{\top}x + \frac{1}{2}\|x^*\|_A^2 =\frac{1}{2}\|x\|_A^2 - x^{\top}Ax^* + \frac{1}{2}\|x^*\|_A^2 = \frac{1}{2}\|x - x^*\|_A^2
$$
### Доказательство сходимости
- $x_k$ лежит в $\mathcal{K}_k$
- $x_k = \sum\limits_{i=1}^k c_i A^{i-1}b = p(A)b$, где $p(x)$ некоторый полином степени не выше $k-1$
- $x_k$ минимизирует $f$ на $\mathcal{K}_k$, отсюда
$$
2(f_k - f^*) = \inf_{x \in \mathcal{K}_k} \|x - x^* \|^2_A = \inf_{\mathrm{deg}(p) < k} \|(p(A) - A^{-1})b\|^2_A
$$
- Спектральное разложение $A = U\Lambda U^*$ даёт
$$
2(f_k - f^*) = \inf_{\mathrm{deg}(p) < k} \|(p(\Lambda) - \Lambda^{-1})d\|^2_{\Lambda} = \inf_{\mathrm{deg}(p) < k} \sum_{i=1}^n\frac{d_i^2 (\lambda_ip(\lambda_i) - 1)^2}{\lambda_i} = \inf_{\mathrm{deg}(q) \leq k, q(0) = 1} \sum_{i=1}^n\frac{d_i^2 q(\lambda_i)^2}{\lambda_i}
$$
- Сведём задачу к поиску некоторого многочлена
$$
f_k - f^* \leq \left(\sum_{i=1}^n \frac{d_i^2}{2\lambda_i}\right) \inf_{\mathrm{deg}(q) \leq k, q(0) = 1}\left(\max_{i=1,\ldots,n} q(\lambda_i)^2 \right) = \frac{1}{2}\|x^*\|^2_A \inf_{\mathrm{deg}(q) \leq k, q(0) = 1}\left(\max_{i=1,\ldots,n} q(\lambda_i)^2 \right)
$$
- Пусть $A$ имеет $m$ различных собственных значений, тогда для
$$
r(y) = \frac{(-1)^m}{\lambda_1 \cdot \ldots \cdot \lambda_m}(y - \lambda_i)\cdot \ldots \cdot (y - \lambda_m)
$$
выполнено $\mathrm{deg}(r) = m$ и $r(0) = 1$
- Значение для оптимального полинома степени не выше $k$ оценим сверху значением для полинома $r$ степени $m$
$$
0 \leq f_k - f^* \leq \frac{1}{2}\|x^*\|_A^2 \max_{i=1,\ldots,m} r(\lambda_i) = 0
$$
- Метод сопряжённых градиентов сошёлся за $m$ итераций
### Улучшенная версия метода сопряжённых градиентов
На практике используются следующие формулы для шага $\alpha_k$ и коэффициента $\beta_{k}$:
$$
\alpha_k = \dfrac{r^{\top}_k r_k}{p^{\top}_{k}Ap_{k}} \qquad \beta_k = \dfrac{r^{\top}_k r_k}{r^{\top}_{k-1} r_{k-1}}
$$
**Вопрос:** чем они лучше базовой версии?
### Псевдокод метода сопряжённых градиентов
```python
def ConjugateGradientQuadratic(x0, A, b, eps):
r = A.dot(x0) - b
p = -r
while np.linalg.norm(r) > eps:
alpha = r.dot(r) / p.dot(A.dot(p))
x = x + alpha * p
r_next = r + alpha * A.dot(p)
beta = r_next.dot(r_next) / r.dot(r)
p = -r_next + beta * p
r = r_next
return x
```
## Метод сопряжённых градиентов для неквадратичной функции
**Идея:** использовать градиенты $f'(x_k)$ неквадратичной функции вместо остатков $r_k$ и линейный поиск шага $\alpha_k$ вместо аналитического вычисления. Получим метод Флетчера-Ривса.
```python
def ConjugateGradientFR(f, gradf, x0, eps):
x = x0
grad = gradf(x)
p = -grad
while np.linalg.norm(gradf(x)) > eps:
alpha = StepSearch(x, f, gradf, **kwargs)
x = x + alpha * p
grad_next = gradf(x)
beta = grad_next.dot(grad_next) / grad.dot(grad)
p = -grad_next + beta * p
grad = grad_next
if restart_condition:
p = -gradf(x)
return x
```
### Теорема сходимости
**Теорема.** Пусть
- множество уровней $\mathcal{L}$ ограничено
- существует $\gamma > 0$: $\| f'(x) \|_2 \leq \gamma$ для $x \in \mathcal{L}$
Тогда
$$
\lim_{j \to \infty} \| f'(x_{k_j}) \|_2 = 0
$$
### Перезапуск (restart)
1. Для ускорения метода сопряжённых градиентов используют технику перезапусков: удаление ранее накопленной истории и перезапуск метода с текущей точки, как будто это точка $x_0$
2. Существуют разные условия, сигнализирующие о том, что надо делать перезапуск, например
- $k = n$
- $\dfrac{|\langle f'(x_k), f'(x_{k-1}) \rangle |}{\| f'(x_k) \|_2^2} \geq \nu \approx 0.1$
3. Можно показать (см. Nocedal, Wright Numerical Optimization, Ch. 5, p. 125), что запуск метода Флетчера-Ривза без использования перезапусков на некоторых итерациях может приводить к крайне медленной сходимости!
4. Метод Полака-Рибьера и его модификации лишены подобного недостатка.
### Комментарии
- Замечательная методичка "An Introduction to the Conjugate Gradient Method Without the Agonizing Pain" размещена [тут](https://www.cs.cmu.edu/~quake-papers/painless-conjugate-gradient.pdf)
- Помимо метода Флетчера-Ривса существуют другие способы вычисления $\beta_k$: метод Полака-Рибьера, метод Хестенса-Штифеля...
- Для метода сопряжённых градиентов требуется 4 вектора: каких?
- Самой дорогой операцией является умножение матрицы на вектор
## Эксперименты
### Квадратичная целевая функция
```
import numpy as np
n = 100
# Random
A = np.random.randn(n, n)
A = A.T.dot(A)
# Clustered eigenvalues
# A = np.diagflat([np.ones(n//4), 10 * np.ones(n//4), 100*np.ones(n//4), 1000* np.ones(n//4)])
# U = np.random.rand(n, n)
# Q, _ = np.linalg.qr(U)
# A = Q.dot(A).dot(Q.T)
# A = (A + A.T) * 0.5
print("A is normal matrix: ||AA* - A*A|| =", np.linalg.norm(A.dot(A.T) - A.T.dot(A)))
b = np.random.randn(n)
# Hilbert matrix
# A = np.array([[1.0 / (i+j - 1) for i in range(1, n+1)] for j in range(1, n+1)]) + 1e-3 * np.eye(n)
# b = np.ones(n)
f = lambda x: 0.5 * x.dot(A.dot(x)) - b.dot(x)
grad_f = lambda x: A.dot(x) - b
x0 = np.zeros(n)
```
#### Распределение собственных значений
```
%matplotlib inline
import matplotlib.pyplot as plt
plt.rc("text", usetex=True)
plt.rc("font", family='serif')
import seaborn as sns
sns.set_context("talk")
eigs = np.linalg.eigvalsh(A)
cond_A = np.linalg.cond(A)
print((np.sqrt(cond_A) - 1) / (np.sqrt(cond_A) + 1))
print((cond_A - 1) / (cond_A + 1))
plt.semilogy(np.unique(eigs))
plt.ylabel("Eigenvalues", fontsize=20)
plt.xticks(fontsize=18)
_ = plt.yticks(fontsize=18)
```
#### Правильный ответ
```
import scipy.optimize as scopt
def callback(x, array):
array.append(x)
scopt_cg_array = []
scopt_cg_callback = lambda x: callback(x, scopt_cg_array)
x = scopt.minimize(f, x0, method="CG", jac=grad_f, callback=scopt_cg_callback)
x = x.x
print("||f'(x*)|| =", np.linalg.norm(A.dot(x) - b))
print("f* =", f(x))
```
#### Реализация метода сопряжённых градиентов
```
def ConjugateGradientQuadratic(x0, A, b, tol=1e-8, callback=None):
x = x0
r = A.dot(x0) - b
p = -r
while np.linalg.norm(r) > tol:
alpha = r.dot(r) / p.dot(A.dot(p))
x = x + alpha * p
if callback is not None:
callback(x)
r_next = r + alpha * A.dot(p)
beta = r_next.dot(r_next) / r.dot(r)
p = -r_next + beta * p
r = r_next
return x
import liboptpy.unconstr_solvers as methods
import liboptpy.step_size as ss
print("\t CG quadratic")
cg_quad = methods.fo.ConjugateGradientQuad(A, b)
x_cg = cg_quad.solve(x0, max_iter=1000, tol=1e-7, disp=True)
print("\t Gradient Descent")
gd = methods.fo.GradientDescent(f, grad_f, ss.ExactLineSearch4Quad(A, b))
x_gd = gd.solve(x0, tol=1e-7, disp=True)
print("Condition number of A =", abs(max(eigs)) / abs(min(eigs)))
```
#### График сходимости
```
plt.figure(figsize=(8,6))
plt.semilogy([np.linalg.norm(grad_f(x)) for x in cg_quad.get_convergence()], label=r"$\|f'(x_k)\|^{CG}_2$", linewidth=2)
plt.semilogy([np.linalg.norm(grad_f(x)) for x in scopt_cg_array[:5000]], label=r"$\|f'(x_k)\|^{CG_{PR}}_2$", linewidth=2)
plt.semilogy([np.linalg.norm(grad_f(x)) for x in gd.get_convergence()], label=r"$\|f'(x_k)\|^{G}_2$", linewidth=2)
plt.legend(loc="best", fontsize=20)
plt.xlabel(r"Iteration number, $k$", fontsize=20)
plt.ylabel("Convergence rate", fontsize=20)
plt.xticks(fontsize=18)
_ = plt.yticks(fontsize=18)
print([np.linalg.norm(grad_f(x)) for x in cg_quad.get_convergence()])
plt.figure(figsize=(8,6))
plt.plot([f(x) for x in cg_quad.get_convergence()], label=r"$f(x^{CG}_k)$", linewidth=2)
plt.plot([f(x) for x in scopt_cg_array], label=r"$f(x^{CG_{PR}}_k)$", linewidth=2)
plt.plot([f(x) for x in gd.get_convergence()], label=r"$f(x^{G}_k)$", linewidth=2)
plt.legend(loc="best", fontsize=20)
plt.xlabel(r"Iteration number, $k$", fontsize=20)
plt.ylabel("Function value", fontsize=20)
plt.xticks(fontsize=18)
_ = plt.yticks(fontsize=18)
```
### Неквадратичная функция
```
import numpy as np
import sklearn.datasets as skldata
import scipy.special as scspec
n = 300
m = 1000
X, y = skldata.make_classification(n_classes=2, n_features=n, n_samples=m, n_informative=n//3)
C = 1
def f(w):
return np.linalg.norm(w)**2 / 2 + C * np.mean(np.logaddexp(np.zeros(X.shape[0]), -y * X.dot(w)))
def grad_f(w):
denom = scspec.expit(-y * X.dot(w))
return w - C * X.T.dot(y * denom) / X.shape[0]
# f = lambda x: -np.sum(np.log(1 - A.T.dot(x))) - np.sum(np.log(1 - x*x))
# grad_f = lambda x: np.sum(A.dot(np.diagflat(1 / (1 - A.T.dot(x)))), axis=1) + 2 * x / (1 - np.power(x, 2))
x0 = np.zeros(n)
print("Initial function value = {}".format(f(x0)))
print("Initial gradient norm = {}".format(np.linalg.norm(grad_f(x0))))
```
#### Реализация метода Флетчера-Ривса
```
def ConjugateGradientFR(f, gradf, x0, num_iter=100, tol=1e-8, callback=None, restart=False):
x = x0
grad = gradf(x)
p = -grad
it = 0
while np.linalg.norm(gradf(x)) > tol and it < num_iter:
alpha = utils.backtracking(x, p, method="Wolfe", beta1=0.1, beta2=0.4, rho=0.5, f=f, grad_f=gradf)
if alpha < 1e-18:
break
x = x + alpha * p
if callback is not None:
callback(x)
grad_next = gradf(x)
beta = grad_next.dot(grad_next) / grad.dot(grad)
p = -grad_next + beta * p
grad = grad_next.copy()
it += 1
if restart and it % restart == 0:
grad = gradf(x)
p = -grad
return x
```
#### График сходимости
```
import scipy.optimize as scopt
import liboptpy.restarts as restarts
n_restart = 60
tol = 1e-5
max_iter = 600
scopt_cg_array = []
scopt_cg_callback = lambda x: callback(x, scopt_cg_array)
x = scopt.minimize(f, x0, tol=tol, method="CG", jac=grad_f, callback=scopt_cg_callback, options={"maxiter": max_iter})
x = x.x
print("\t CG by Polak-Rebiere")
print("Norm of garient = {}".format(np.linalg.norm(grad_f(x))))
print("Function value = {}".format(f(x)))
print("\t CG by Fletcher-Reeves")
cg_fr = methods.fo.ConjugateGradientFR(f, grad_f, ss.Backtracking("Wolfe", rho=0.9, beta1=0.1, beta2=0.4, init_alpha=1.))
x = cg_fr.solve(x0, tol=tol, max_iter=max_iter, disp=True)
print("\t CG by Fletcher-Reeves with restart n")
cg_fr_rest = methods.fo.ConjugateGradientFR(f, grad_f, ss.Backtracking("Wolfe", rho=0.9, beta1=0.1, beta2=0.4,
init_alpha=1.), restarts.Restart(n // n_restart))
x = cg_fr_rest.solve(x0, tol=tol, max_iter=max_iter, disp=True)
print("\t Gradient Descent")
gd = methods.fo.GradientDescent(f, grad_f, ss.Backtracking("Wolfe", rho=0.9, beta1=0.1, beta2=0.4, init_alpha=1.))
x = gd.solve(x0, max_iter=max_iter, tol=tol, disp=True)
plt.figure(figsize=(8, 6))
plt.semilogy([np.linalg.norm(grad_f(x)) for x in cg_fr.get_convergence()], label=r"$\|f'(x_k)\|^{CG_{FR}}_2$ no restart", linewidth=2)
plt.semilogy([np.linalg.norm(grad_f(x)) for x in cg_fr_rest.get_convergence()], label=r"$\|f'(x_k)\|^{CG_{FR}}_2$ restart", linewidth=2)
plt.semilogy([np.linalg.norm(grad_f(x)) for x in scopt_cg_array], label=r"$\|f'(x_k)\|^{CG_{PR}}_2$", linewidth=2)
plt.semilogy([np.linalg.norm(grad_f(x)) for x in gd.get_convergence()], label=r"$\|f'(x_k)\|^{G}_2$", linewidth=2)
plt.legend(loc="best", fontsize=16)
plt.xlabel(r"Iteration number, $k$", fontsize=20)
plt.ylabel("Convergence rate", fontsize=20)
plt.xticks(fontsize=18)
_ = plt.yticks(fontsize=18)
```
#### Время выполнения
```
%timeit scopt.minimize(f, x0, method="CG", tol=tol, jac=grad_f, options={"maxiter": max_iter})
%timeit cg_fr.solve(x0, tol=tol, max_iter=max_iter)
%timeit cg_fr_rest.solve(x0, tol=tol, max_iter=max_iter)
%timeit gd.solve(x0, tol=tol, max_iter=max_iter)
```
## Резюме
1. Сопряжённые направления
2. Метод сопряжённых градиентов
3. Сходимость
4. Эксперименты
|
github_jupyter
|
# Reading Data
## Connect to store (using sina local file)
First let's create an empty database with you as a single user
In a real application only admin user should have write permission to the file
```
import os
import sys
import shlex
from subprocess import Popen, PIPE
import kosh
kosh_example_sql_file = "kosh_example_read.sql"
# Create a new store (erase if exists)
store = kosh.create_new_db(kosh_example_sql_file)
```
## Adding datasets to the store
Let's add a dataset and associate hdf5 file with it.
```
dataset = store.create()
dataset.associate("../tests/baselines/node_extracts2/node_extracts2.hdf5", mime_type="hdf5", absolute_path=False)
```
## Querying Data
In Kosh data retrievable are called "features"
Let's see which feature are associated with this dataset:
```
features = dataset.list_features()
print(features)
```
Let's get more information on a specific features
```
info = dataset.describe_feature("node/metrics_5")
print(info)
```
## Opening Data
We might want to simply acces the URI (to add ata to it for example).
for this we will need the *id* of the associated_uri
```
associated_id = dataset.search(mime_type="hdf5", ids_only=True)[0]
h5_file = dataset.open(associated_id)
h5_file
```
## Getting Data
Let's access this feature by calling the `get_execution_graph()` function.
This returns a Kosh representation of how to get to a feature's data.
Note that is just a representation (a path) to the data, not the data itself.
```
feature = dataset.get_execution_graph("node/metrics_5")
feature
```
This can be shorten as:
```
feature = dataset["node/metrics_5"]
feature
```
This gives us a handle to this feature's data, no data has actually been read yet.
Let's retrieve the data by calling the `traverse` function. This will connect the feature's origin (uri) to the data, applying any *transformer* or *operator* to it (see other notebooks to learn about these)
```
data = feature.traverse()
print(data)
```
Which is equivalent to:
```
data = feature()
print(data)
```
This is equivalent of what versions 1.1 and below used to do:
```
data = dataset.get("node/metrics_5")
print(data)
```
Note that you can also slice the feature directly
```
data = feature[:]
print(data)
# If you know the dims you can select by value and/or indices
print(dataset.describe_feature("node/metrics_1"))
feature2 = dataset["node/metrics_1"]
data2 = feature2(cycles=slice(0,1), elements=[17, 15])
print(data2.shape)
```
## Associating Multiple Sources
Let's add an image file
```
dataset.associate("../share/icons/png/Kosh_Logo_K_blue.png", mime_type="png", absolute_path=False)
dataset.list_features()
img = dataset["image"]
print(img[:].shape)
try:
import matplotlib.pyplot as plt
%matplotlib inline
plt.imshow(img[...,-1]) # Plot last channel
except ImportError:
print("You will need matplotlib to plot the picture")
```
We can also retrieve the png as the raw binary data
```
raw = img(format="bytes")
len(raw), type(raw)
```
We can associate many image files but this leads to duplicate "image" feature
```
# let's remove hdf5 for clarity
dataset.dissociate("../tests/baselines/node_extracts2/node_extracts2.hdf5", absolute_path=False)
dataset.list_features()
```
Now let's associate a second image file
```
dataset.associate("../share/icons/png/Kosh_Logo_K_orange.png", mime_type="png", absolute_path=False)
dataset.list_features() # URI is now added to feature to disambiguate them
dataset.describe_feature("image_@_../share/icons/png/Kosh_Logo_K_orange.png")
try:
plt.imshow(dataset.get("image_@_../share/icons/png/Kosh_Logo_K_orange.png")) # Plot last channel
except Exception:
print("With matplotlib you would have seen a ")
```
|
github_jupyter
|
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_openml
data = fetch_openml(data_id=1590, as_frame=True)
X = pd.get_dummies(data.data)
y_true = (data.target == '>50K') * 1
sex = data.data[['sex', 'race']]
sex.value_counts()
from fairlearn.metrics import group_summary
from sklearn.metrics import accuracy_score
from sklearn.tree import DecisionTreeClassifier
classifier = DecisionTreeClassifier(min_samples_leaf=10, max_depth=4)
classifier.fit(X, y_true)
y_pred = classifier.predict(X)
#group_summary(accuracy_score, y_true, y_pred, sensitive_features=sex)
from fairlearn.metrics import selection_rate_group_summary
#selection_rate_group_summary(y_true, y_pred, sensitive_features=sex)
from fairlearn.widget import FairlearnDashboard
FairlearnDashboard(sensitive_features=sex,
sensitive_feature_names=['sex', 'race'],
y_true=y_true,
y_pred={"initial model": y_pred})
```
Can we find intersectional discrimination with Fairlearn?
```
import numpy as np
X = pd.DataFrame(np.random.randint(0, high=2, size=(100, 3), dtype='l'), columns=['sex', 'race', 'Y'])
X['cnt'] = 1
counts = X.groupby(['sex', 'race']).Y.count()
f = lambda x: [np.random.choice([0,1], 17, p=[0.65, 0.35])[0] for _ in range(x)]
X.at[(X['sex'] == 1) & (X['race'] == 1),'result'] = f(counts.loc[1,1])
X.groupby(['sex', 'race']).agg({'result':'sum', 'Y':['sum', 'count']})
# now let's create a biased scoring function
```
Idea: first sample from the biased distribution p_bias, then calculate the expectancy value of the unbiased distribution p_0 and caluculate how much you need to bias p_0 to get the exectancy of value of the unbiased distribution p_0 -> p_correction
```
X[(X[['sex', 'race']] == 1).all(1)].shape
X.groupby(['sex', 'race']).agg({'result':'sum', 'Y':['sum', 'count']}).loc[[1]*len()]
a = tuple([1 for _ in range(len(counts.index.levels))])
a
counts.loc[a]
def biased_score(df, sensitive_cols, biased_prob):
#todo make this agnostic of specific columns
counts = df.groupby(sensitive_cols).agg({sensitive_cols[0]:'sum'})
indexer = tuple([1 for _ in range(len(counts.index.levels))])
df[(df[sensitive_cols] == 1).all(axis=1)]['result'] = np.random.choice([0,1], counts.loc[indexer].values, p=[biased_prob, 1-biased_prob])
return df
type(counts)
biased_score(X, ['sex', 'race'], 0.3)
def shift_prop(counts, expected_distribution):
expected_values = counts.sum() * expected_distribution
counts.sum()
counts
counts.loc[1,:].sum()
i = 1000003054
i
i = i + 1
a = i * 3
i = 2
i
i == 2
type(i)
type("adfaserer")
"1" == 1
```
|
github_jupyter
|
#### New to Plotly?
Plotly's Python library is free and open source! [Get started](https://plotly.com/python/getting-started/) by downloading the client and [reading the primer](https://plotly.com/python/getting-started/).
<br>You can set up Plotly to work in [online](https://plotly.com/python/getting-started/#initialization-for-online-plotting) or [offline](https://plotly.com/python/getting-started/#initialization-for-offline-plotting) mode, or in [jupyter notebooks](https://plotly.com/python/getting-started/#start-plotting-online).
<br>We also have a quick-reference [cheatsheet](https://images.plot.ly/plotly-documentation/images/python_cheat_sheet.pdf) (new!) to help you get started!
#### Version Check
Note: Ternary Plots are available in version 1.9.10+
Run pip install plotly --upgrade to update your Plotly version
```
import plotly
plotly.__version__
```
### Basic Ternary Plot with Markers
```
import plotly.plotly as py
import plotly.graph_objs as go
rawData = [
{'journalist':75,'developer':25,'designer':0,'label':'point 1'},
{'journalist':70,'developer':10,'designer':20,'label':'point 2'},
{'journalist':75,'developer':20,'designer':5,'label':'point 3'},
{'journalist':5,'developer':60,'designer':35,'label':'point 4'},
{'journalist':10,'developer':80,'designer':10,'label':'point 5'},
{'journalist':10,'developer':90,'designer':0,'label':'point 6'},
{'journalist':20,'developer':70,'designer':10,'label':'point 7'},
{'journalist':10,'developer':20,'designer':70,'label':'point 8'},
{'journalist':15,'developer':5,'designer':80,'label':'point 9'},
{'journalist':10,'developer':10,'designer':80,'label':'point 10'},
{'journalist':20,'developer':10,'designer':70,'label':'point 11'},
];
def makeAxis(title, tickangle):
return {
'title': title,
'titlefont': { 'size': 20 },
'tickangle': tickangle,
'tickfont': { 'size': 15 },
'tickcolor': 'rgba(0,0,0,0)',
'ticklen': 5,
'showline': True,
'showgrid': True
}
data = [{
'type': 'scatterternary',
'mode': 'markers',
'a': [i for i in map(lambda x: x['journalist'], rawData)],
'b': [i for i in map(lambda x: x['developer'], rawData)],
'c': [i for i in map(lambda x: x['designer'], rawData)],
'text': [i for i in map(lambda x: x['label'], rawData)],
'marker': {
'symbol': 100,
'color': '#DB7365',
'size': 14,
'line': { 'width': 2 }
},
}]
layout = {
'ternary': {
'sum': 100,
'aaxis': makeAxis('Journalist', 0),
'baxis': makeAxis('<br>Developer', 45),
'caxis': makeAxis('<br>Designer', -45)
},
'annotations': [{
'showarrow': False,
'text': 'Simple Ternary Plot with Markers',
'x': 0.5,
'y': 1.3,
'font': { 'size': 15 }
}]
}
fig = {'data': data, 'layout': layout}
py.iplot(fig, validate=False)
```
#### Reference
See https://plotly.com/python/reference/#scatterternary for more information and chart attribute options!
```
from IPython.display import display, HTML
display(HTML('<link href="//fonts.googleapis.com/css?family=Open+Sans:600,400,300,200|Inconsolata|Ubuntu+Mono:400,700" rel="stylesheet" type="text/css" />'))
display(HTML('<link rel="stylesheet" type="text/css" href="http://help.plot.ly/documentation/all_static/css/ipython-notebook-custom.css">'))
! pip install git+https://github.com/plotly/publisher.git --upgrade
import publisher
publisher.publish(
'ternary.ipynb', 'python/ternary-plots/', 'Python Ternary Plots | plotly',
'How to make Ternary plots in Python with Plotly.',
name = 'Ternary Plots',
thumbnail='thumbnail/ternary.jpg', language='python',
page_type='example_index', has_thumbnail='true', display_as='scientific', order=9,
ipynb= '~notebook_demo/39')
```
|
github_jupyter
|
# **PARAMETER FITTING DETAILED EXAMPLE**
This provides a detailed example of parameter fitting using the python-based tool ``SBstoat``.
Details about the tool can be found at in this [github repository](https://github.com/sys-bio/SBstoat).
# Preliminaries
```
IS_COLAB = True
if IS_COLAB:
!pip install -q SBstoat
!pip install -q tellurium
pass
# Python packages used in this chapter
import matplotlib.pyplot as plt
import numpy as np
import os
import pandas as pd
import urllib.request # use this library to download file from GitHub
import tellurium as te
from SBstoat.namedTimeseries import NamedTimeseries, TIME
from SBstoat.modelFitter import ModelFitter
import SBstoat
```
# Constants and Helper Functions
```
def getSharedCodes(moduleName):
"""
Obtains common codes from the github repository.
Parameters
----------
moduleName: str
name of the python module in the src directory
"""
if IS_COLAB:
url = "https://github.com/sys-bio/network-modeling-summer-school-2021/raw/main/src/%s.py" % moduleName
local_python = "python.py"
_, _ = urllib.request.urlretrieve(url=url, filename=local_python)
else:
local_python = "../../src/%s.py" % moduleName
with open(local_python, "r") as fd:
codeStr = "".join(fd.readlines())
print(codeStr)
exec(codeStr, globals())
# Acquire codes
getSharedCodes("util")
# TESTS
assert(isinstance(LINEAR_PATHWAY_DF, pd.DataFrame))
def plotTS(ts, title=""):
"""
Plots columns in a timeseries.
Parameters
----------
ts: NamedTimeseries
"""
p = plt.plot(ts[TIME], ts[ts.colnames])
_ = plt.legend(p, ts.colnames, bbox_to_anchor=(1.05, 1), loc='upper left')
_ = plt.title(title)
```
# Running SBstoat
``SBstoat`` is a python package intended to simplify the programmatic aspects of fitting. The package provides handles the programming details
of the interactions between the optimization codes (``lmfit``) and ``tellurium`` simulations.
The required inputs to ``SBstoat`` are:
- the model for which parameter values are being estimated;
- observational data; and
- specification of the parameters, their value ranges, and initial values.
For the linear pathway model, we ``LINEAR_PATHWAY_MODEL`` and ``LINEAR_PATHWAY_DF`` for the model and data, respectively.
The description of the paarameters is done using a python dictionary, as shown below.
```
# Name, minimal value, initial value, and maximum value of each parameter
LINEAR_PATHWAY_PARAMETERS = [
SBstoat.Parameter("k1", lower=1, value=50, upper=100),
SBstoat.Parameter("k2", lower=1, value=50, upper=100),
SBstoat.Parameter("k3", lower=1, value=50, upper=100),
SBstoat.Parameter("k4", lower=1, value=50, upper=100),
]
```
The python class ``ModelFitter`` does fitting for ``SBstoat``. Details of using this can be found below.
```
?ModelFitter
fitter = ModelFitter(LINEAR_PATHWAY_MODEL,
NamedTimeseries(dataframe=LINEAR_PATHWAY_DF),
parametersToFit=LINEAR_PATHWAY_PARAMETERS)
fitter.fitModel()
```
``SBstoat`` provides a textual report of the results of the fit.
```
print(fitter.reportFit())
```
The report is in three sections.
The first section contains measures of the fit quality. The most commonly used measures are chi-square and reduced chai-square.
We want both of these to be "small", although small is relative.
These measures are most useful when comparing different fit results.
The "Variables" section gives parameter estimates. We se that the estimates obtained are fairly close to
the true values in the original models.
The final section provides information about the relationships between parameter estimates. This can be useful
in models where the structure of the model makes it difficult to separate one parameter from another.
In these cases, there will be a large correlation between parameter (absolute) parameter values.
``SBstoat`` provides many plots to aid in understanding the fitting results.
You can see these by typing in a Jupyter code cell ``fitter.pl`` and then pressing the tab key.
Arguably the most useful is ``plotFitAll``, which, for each floating species (column in observed data), plots the fitted and observed values.
This is shown below.
```
fitter.plotFitAll(figsize=(20, 5), numCol=5, color=["red", "blue"], titlePosition=(0.5, 1.05))
```
These fits seem to be quite consistent with the observed data, with the possible exception of ``S5``.
In the latter case, there is considerable variability that likely makes a good fit more difficult.
```
# See the options for plotFitAll
?fitter.plotFitAll
```
If you are interested in a more complete analysis of the residuals, use ``plotResidualsAll``.
```
fitter.plotResidualsAll(figsize=(20, 10))
```
# Workflow for fitting the Linear Pathway Model
Although ``SBstoat`` eliminates the burden of programming details, fitting is often complex.
This is because of the complexity of the fitting surface, as illustrated earlier in this chaper.
This section illustrates how to use ``SBstoat`` to explore complex fitting surfaces.
``SBstoat`` allows you to explore fitting along three dimensions.
1. **Fitting surface**. The fitting surface changes based on the following:
a. the selection of float species (columns in the observed data) that we attempt to fit;
b. the time span we fit over
1. **Optimization Algorithms**. As we noted previously, gradient descent is fast, but it only works well for convex fitting surfaces. We might want to try both gradient descent and differential evolution to see which works best for our model. Also, some optimization algorithms are stochastic, and so the search strategy may also choose to run
the same algorithm multiple times. Finally, it may be desirable to do multiple optimizations in succession, using the results of the $n-1$-st to be the starting point for the $n$-th.
1. **Search start & scope**. This refers to the initial values of parameter values and the range of parameter values that are explored.
In the following explorations of the above dimensions of parameter fitting, we use the above workflow that consists of:
1. Select a subset of the observed data based on a specified time span (in this case, just ending time)
1. Construct a fitter for the linear pathway, observed data, columns to consider in fitting, the fitting methods, and parameter ranges/initial values.
1. Fit the model.
1. Print the fitting report.
1. Plot observed and fitted values.
This workflow is encapsulated in the the function ``doFit``.
The arguments of the function have default that reproduce the
results in the previous section.
```
def doFit(selectedColumns=None,
endTime=10,
fitterMethods=["differential_evolution", "leastsq"],
parametersToFit=LINEAR_PATHWAY_PARAMETERS,
isTest=False):
"""
Encapsulates the workflow to fit the linear pathway model.
Parameters
----------
selectedColumns: list-str
endTime: int
fitterMethods: list-str
parametersToFit: list-SBstoat.Parameter
isTest: bool
Test mode
Returns
-------
ModelFitter
"""
model = te.loada(LINEAR_PATHWAY_MODEL)
observedTS = NamedTimeseries(dataframe=LINEAR_PATHWAY_DF)
# Find the last index to use
lastIdx = len([t for t in observedTS[TIME] if t <= endTime])
observedTS = observedTS[:lastIdx]
# Construct the fitter and do the fit
fitter = ModelFitter(model, observedTS, selectedColumns=selectedColumns,
fitterMethods=fitterMethods,
parametersToFit=parametersToFit)
fitter.fitModel()
if not isTest:
print(fitter.reportFit())
fitter.plotFitAll(figsize=(20, 5), numCol=5, color=["red", "blue"],
titlePosition=(0.5, 1.05))
return fitter
# TESTS
result = doFit(isTest=True)
assert(isinstance(fitter, ModelFitter))
doFit()
```
## Fitting Surface
We begin by exploring the effect of the fitting surface.
We can control the fitting surface in two ways. The first is by the selection of columns that are matched with observational data.
For example, suppose that we only consider ``S5`` and so the fitting surface is residuals
from fitting ``S5``.
```
doFit(selectedColumns=["S5"])
```
We see that we get poor estimates for most of the parameters, something that we can check because we know the true values of the parameters (``k1=1``, ``k2=2``, ``k3=3``, ``k4=4``).
Another consideration is to focus on a subset of the dynamics. Below, we only consider through 2 seconds.
```
doFit(endTime=2)
```
This improved the quality of the fit. We see this visually in the above plots and also in the significant reduction in chi-square. A lot of this improvement
is a result of not inluding regions of high variability in observed values for ``S5``.
## Optimization Algorithms
The main consideration here is the choice of optimization algorithms.
Any valid ``method`` for ``lmfit`` can be used, and multiple methods can be used in combination. We illustrate this below.
```
# Fit with Levenberg-Marquardt
doFit(fitterMethods=["leastsq"])
# Fit with differential evolution
doFit(fitterMethods=["differential_evolution"])
# Fit with differential evolution and then Levenberg-Marquardt
doFit(fitterMethods=["differential_evolution", "leastsq"])
```
For this model, we see that Levenberg-Marquardt works better than differential evolution, and doing the two in combination offers no benefit.
## Search Start & Scope
Where we start the search and how far we search depends on the ranges of parameter values and the specification of initial values.
This is specified by the ``parameterDct`` argument to ``ModelFitter``. This argument defaults to ``LINEAR_PATHWAY_PARAMETER_DCT``.
If we create a bad parameter range, then we get very poor fits. Below, we start the search with a negative value for each parameter.
Note that the observed values appear to be constant because of the large scale of the fitted values.
```
parametersToFit = [
SBstoat.Parameter("k1", lower=-11, value=-1, upper=1),
SBstoat.Parameter("k2", lower=-11, value=-1, upper=1),
SBstoat.Parameter("k3", lower=-11, value=-1, upper=1),
SBstoat.Parameter("k4", lower=-11, value=-1, upper=1),
]
doFit(parametersToFit=parametersToFit)
```
# Exercise
This exercise is about fitting parameters in the Wolf model for glycolytic oscillations.
The model is ``WOLF_MODEL`` and the observational data for this model are ``WOLF_DF``.
1. Implement a ``doFit`` function that encapsulates the workflow for the Wolf model.
1. Try fitting the model using ``WOLF_PARAMETERS``. First try ``leastSquares`` (a graident descent method) and then ``differential_evolution``. How did the two methods differ as to fitting time and quality? Why? What would you try next to get better fits?
1. Limit the parameter values so that the upper value is twice the true value. Try fits using leastsqs and differential evolution.
|
github_jupyter
|
```
"""
Script of petro-inversion of gravity over TKC
Notes:
This version of the script uses data with less noises
but still invert with a higher assumed noise level.
This is equivalent to increase the chi-factor.
This has been needed in order to fit both geophysical
and petrophysical data set.
"""
# Script of petro-inversion of gravity over TKC
import SimPEG.PF as PF
from SimPEG import *
from SimPEG.Utils import io_utils
import matplotlib
import time as tm
import mpl_toolkits.mplot3d as a3
import matplotlib.colors as colors
import matplotlib.pyplot as plt
import scipy as sp
from scipy.interpolate import NearestNDInterpolator
from sklearn.mixture import GaussianMixture
import numpy as np
import copy
import pickle
from pymatsolver import PardisoSolver
%matplotlib inline
matplotlib.rcParams['font.size'] = 14
import seaborn
import sys
sys.path.append('../../../')
from DO27_Utils import *
# Nicer plot
seaborn.set()
# Reproducible Science
np.random.seed(518936)
# We first need to create a susceptibility model.
# Based on a set of parametric surfaces representing TKC,
# we use VTK to discretize the 3-D space.
# Reproducible Science
np.random.seed(518936)
# Load Mesh
mesh = Mesh.load_mesh('../../../Forward/mesh_inverse')
# Define no-data-value
ndv = -100
# Load topography file in UBC format and find the active cells
# Import Topo
model_dir = '../../../Geology_Surfaces/'
topofile = model_dir + 'TKCtopo.dat'
topo = np.genfromtxt(topofile, skip_header=1)
# Find the active cells
actv = Utils.surface2ind_topo(mesh, topo, gridLoc='N')
# Create active map to go from reduce set to full
actvMap = Maps.InjectActiveCells(mesh, actv, ndv)
print("Active cells created from topography!")
# Load data
survey = io_utils.readUBCgravityObservations(
"../../../Forward/GRAV_noisydata.obs"
)
# Now that we have a survey we can build the linear system ...
nactv = np.int(np.sum(actv))
# Creat reduced identity map
idenMap = Maps.IdentityMap(nP=nactv)
# Create the forward model operator
prob = PF.Gravity.GravityIntegral(mesh, rhoMap=idenMap, actInd=actv)
# Pair the survey and problem
survey.pair(prob)
# If you formed the sensitivity gravity matrix before, you can load it here
#G = np.load('../../../Forward/G_Grav_Inverse.npy')
#prob._G = G
# Define noise level
std = 0.01
eps = 0.
survey.std = std
survey.eps = eps
# **Inverse problem**
# Petro Inversion
# It is potential fields, so we will need to push the inverison down
# Create distance weights from our linera forward operator
# rxLoc = survey.srcField.rxList[0].locs
# wr = PF.Magnetics.get_dist_wgt(mesh, rxLoc, actv, 3., np.min(mesh.hx)/4.)
# wr = wr**2.
wr = np.sum(prob.G**2., axis=0)**0.5
wr = (wr / np.max(wr))
#Initial model
m0 = np.ones(idenMap.nP) * -1e-4
# Load ground-truth models for comparison
model_grav = mesh.readModelUBC(
'../../../Forward/model_grav.den'
)
geomodel = mesh.readModelUBC(
'../../../Forward/geomodel'
)
model_grav = model_grav[model_grav != -100.]
# Load petrophysics
clf = pickle.load(open('../../../Petrophysics/gmm_density.p','rb'))
n = clf.n_components
# wires map
wires = Maps.Wires(('m', m0.shape[0]))
# PGI Regularization
reg = Regularization.MakeSimplePetroRegularization(
GMmref=clf,
GMmodel=clf,
mesh=mesh,
wiresmap=wires,
maplist=[idenMap],
mref=m0,
indActive=actv,
alpha_s=1.0, alpha_x=1.0, alpha_y=1.0, alpha_z=1.0,
alpha_xx=0., alpha_yy=0., alpha_zz=0.,
cell_weights_list=[wr]
)
reg.mrefInSmooth = False
reg.approx_gradient = True
reg.objfcts[0].evaltype = 'approx'
# Data misfit
dmis = DataMisfit.l2_DataMisfit(survey)
# Assign flat uncertainties of 0.01mGal
wd = np.ones(len(survey.dobs)) * 0.01
dmis.W = 1 / wd
# Optimization scheme
opt = Optimization.ProjectedGNCG(
maxIter=50, lower=-1., upper=0., maxIterLS=20, maxIterCG=100, tolCG=1e-3
)
#Create inverse problem
invProb = InvProblem.BaseInvProblem(dmis, reg, opt)
# Add directives to the inversion
# Smoothness weights
Alphas = Directives.AlphasSmoothEstimate_ByEig(
alpha0_ratio=1.,
ninit=10, verbose=True
)
# Beta initialization
beta = Directives.BetaEstimate_ByEig(beta0_ratio=1., ninit=10)
#Beta Schedule
betaIt = Directives.PetroBetaReWeighting(
verbose=True, rateCooling=5., rateWarming=1.,
tolerance=0.1, UpdateRate=1,
ratio_in_cooling=False,
progress=0.2,
update_prior_confidence=False,
progress_gamma_cooling=1.,
ratio_in_gamma_cooling=False,
alphadir_rateCooling=1.,
kappa_rateCooling=1.,
nu_rateCooling=1.,
)
# Targets misfits
targets = Directives.PetroTargetMisfit(verbose=True)
# Include mref in Smoothness
MrefInSmooth = Directives.AddMrefInSmooth(
wait_till_stable=True,
verbose=True
)
# GMM, mref and Ws updates
petrodir = Directives.GaussianMixtureUpdateModel(
keep_ref_fixed_in_Smooth=True,
verbose=False,
nu=1e8,
kappa=1e8,
alphadir=1e8
)
# Pre-conditioner
update_Jacobi = Directives.UpdatePreconditioner()
# Create inversion
inv = Inversion.BaseInversion(
invProb,
directiveList=[
Alphas, beta,
petrodir, targets,
betaIt, MrefInSmooth, update_Jacobi
]
)
vmin, vmax = -1.2,0
plt.plot(
np.linspace(vmin, vmax, 100), np.exp(
clf.score_samples(np.linspace(vmin, vmax, 100)[:, np.newaxis])
),
color='blue'
)
plt.plot(
np.linspace(vmin, vmax, 100), (
clf.predict(np.linspace(vmin, vmax, 100)[:, np.newaxis])
),
color='red'
)
plt.show()
# Run inversion...
mcluster = inv.run(m0)
# Get the final model back to full space
m_petro = actvMap * mcluster
m_petro[m_petro == ndv] = np.nan
# Plot the recoverd models
mesh = Mesh.TensorMesh([mesh.hx, mesh.hy, mesh.hz], x0="CCN")
npad = 10
X, Y = np.meshgrid(mesh.vectorCCx[npad:-npad:2], mesh.vectorCCy[npad:-npad:2])
vmin, vmax = -1.2, 0.1
fig, ax = plt.subplots(3, 1, figsize=(10, 12))
ax = Utils.mkvc(ax)
mesh.plotSlice(
m_petro, ax=ax[0], normal='Y',
clim=np.r_[vmin, vmax], pcolorOpts={'cmap':'viridis'}
)
ax[0].set_aspect('equal')
ax[0].set_title('Petro model')
dat_true = mesh.plotSlice(
actvMap*model_grav, ax=ax[1], normal='Y',
clim=np.r_[vmin, vmax], pcolorOpts={'cmap':'viridis'}
)
ax[1].set_aspect('equal')
ax[1].set_title('True model')
pos = ax[1].get_position()
cbarax = fig.add_axes(
[pos.x0 - 0.15, pos.y0, pos.width * 0.1, pos.height * 0.75]
) # the parameters are the specified position you set
cb = fig.colorbar(
dat_true[0], cax=cbarax, orientation="vertical",
ax=ax[1], ticks=np.linspace(vmin, vmax, 4)
)
mcluster = m_petro[~np.isnan(m_petro)]
ax[2].hist(mcluster, bins=100, density=True)
ax[2].plot(
np.linspace(vmin, vmax, 100), np.exp(
clf.score_samples(np.linspace(vmin, vmax, 100)[:, np.newaxis])
),
color='blue'
)
ax[2].plot(
np.linspace(vmin, vmax, 100), np.exp(
reg.objfcts[0].GMmodel.score_samples(np.linspace(vmin, vmax, 100)[:, np.newaxis])
),
color='k'
)
ax[2].set_ylim([0., 5.])
plt.show()
```
|
github_jupyter
|
<a href="https://colab.research.google.com/github/mrdbourke/tensorflow-deep-learning/blob/main/07_food_vision_milestone_project_1.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# 07. Milestone Project 1: 🍔👁 Food Vision Big™
In the previous notebook ([transfer learning part 3: scaling up](https://github.com/mrdbourke/tensorflow-deep-learning/blob/main/06_transfer_learning_in_tensorflow_part_3_scaling_up.ipynb)) we built Food Vision mini: a transfer learning model which beat the original results of the [Food101 paper](https://data.vision.ee.ethz.ch/cvl/datasets_extra/food-101/) with only 10% of the data.
But you might be wondering, what would happen if we used all the data?
Well, that's what we're going to find out in this notebook!
We're going to be building Food Vision Big™, using all of the data from the Food101 dataset.
Yep. All 75,750 training images and 25,250 testing images.
And guess what...
This time **we've got the goal of beating [DeepFood](https://www.researchgate.net/publication/304163308_DeepFood_Deep_Learning-Based_Food_Image_Recognition_for_Computer-Aided_Dietary_Assessment)**, a 2016 paper which used a Convolutional Neural Network trained for 2-3 days to achieve 77.4% top-1 accuracy.
> 🔑 **Note:** **Top-1 accuracy** means "accuracy for the top softmax activation value output by the model" (because softmax ouputs a value for every class, but top-1 means only the highest one is evaluated). **Top-5 accuracy** means "accuracy for the top 5 softmax activation values output by the model", in other words, did the true label appear in the top 5 activation values? Top-5 accuracy scores are usually noticeably higher than top-1.
| | 🍔👁 Food Vision Big™ | 🍔👁 Food Vision mini |
|-----|-----|-----|
| Dataset source | TensorFlow Datasets | Preprocessed download from Kaggle |
| Train data | 75,750 images | 7,575 images |
| Test data | 25,250 images | 25,250 images |
| Mixed precision | Yes | No |
| Data loading | Performanant tf.data API | TensorFlow pre-built function |
| Target results | 77.4% top-1 accuracy (beat [DeepFood paper](https://arxiv.org/abs/1606.05675)) | 50.76% top-1 accuracy (beat [Food101 paper](https://data.vision.ee.ethz.ch/cvl/datasets_extra/food-101/static/bossard_eccv14_food-101.pdf)) |
*Table comparing difference between Food Vision Big (this notebook) versus Food Vision mini (previous notebook).*
Alongside attempting to beat the DeepFood paper, we're going to learn about two methods to significantly improve the speed of our model training:
1. Prefetching
2. Mixed precision training
But more on these later.
## What we're going to cover
* Using TensorFlow Datasets to download and explore data
* Creating preprocessing function for our data
* Batching & preparing datasets for modelling (**making our datasets run fast**)
* Creating modelling callbacks
* Setting up **mixed precision training**
* Building a feature extraction model (see [transfer learning part 1: feature extraction](https://github.com/mrdbourke/tensorflow-deep-learning/blob/main/04_transfer_learning_in_tensorflow_part_1_feature_extraction.ipynb))
* Fine-tuning the feature extraction model (see [transfer learning part 2: fine-tuning](https://github.com/mrdbourke/tensorflow-deep-learning/blob/main/05_transfer_learning_in_tensorflow_part_2_fine_tuning.ipynb))
* Viewing training results on TensorBoard
## How you should approach this notebook
You can read through the descriptions and the code (it should all run, except for the cells which error on purpose), but there's a better option.
Write all of the code yourself.
Yes. I'm serious. Create a new notebook, and rewrite each line by yourself. Investigate it, see if you can break it, why does it break?
You don't have to write the text descriptions but writing the code yourself is a great way to get hands-on experience.
Don't worry if you make mistakes, we all do. The way to get better and make less mistakes is to write more code.
> 📖 **Resource:** See the full set of course materials on GitHub: https://github.com/mrdbourke/tensorflow-deep-learning
## Check GPU
For this notebook, we're going to be doing something different.
We're going to be using mixed precision training.
Mixed precision training was introduced in [TensorFlow 2.4.0](https://blog.tensorflow.org/2020/12/whats-new-in-tensorflow-24.html) (a very new feature at the time of writing).
What does **mixed precision training** do?
Mixed precision training uses a combination of single precision (float32) and half-preicison (float16) data types to speed up model training (up 3x on modern GPUs).
We'll talk about this more later on but in the meantime you can read the [TensorFlow documentation on mixed precision](https://www.tensorflow.org/guide/mixed_precision) for more details.
For now, before we can move forward if we want to use mixed precision training, we need to make sure the GPU powering our Google Colab instance (if you're using Google Colab) is compataible.
For mixed precision training to work, you need access to a GPU with a compute compability score of 7.0+.
Google Colab offers P100, K80 and T4 GPUs, however, **the P100 and K80 aren't compatible with mixed precision training**.
Therefore before we proceed we need to make sure we have **access to a Tesla T4 GPU in our Google Colab instance**.
If you're not using Google Colab, you can find a list of various [Nvidia GPU compute capabilities on Nvidia's developer website](https://developer.nvidia.com/cuda-gpus#compute).
> 🔑 **Note:** If you run the cell below and see a P100 or K80, try going to to Runtime -> Factory Reset Runtime (note: this will remove any saved variables and data from your Colab instance) and then retry to get a T4.
>
> **You can still run the code *without* a GPU capable of mixed precision** (it'll just be a little slower).
```
# If using Google Colab, this should output "Tesla T4" otherwise,
# you won't be able to use mixed precision training
!nvidia-smi -L
```
Since mixed precision training was introduced in TensorFlow 2.4.0, make sure you've got at least TensorFlow 2.4.0+.
```
# Hide warning logs (see: https://stackoverflow.com/a/38645250/7900723)
import os
os.environ["TF_CPP_MIN_LOG_LEVEL"] = "3"
# Check TensorFlow version (should be 2.4.0+)
import tensorflow as tf
print(tf.__version__)
```
## Get helper functions
We've created a series of helper functions throughout the previous notebooks in the course. Instead of rewriting them (tedious), we'll import the [`helper_functions.py`](https://github.com/mrdbourke/tensorflow-deep-learning/blob/main/extras/helper_functions.py) file from the GitHub repo.
```
# Get helper functions file
if not os.path.exists("helper_functions.py"):
print("Downloading helper functions...")
!wget https://raw.githubusercontent.com/mrdbourke/tensorflow-deep-learning/main/extras/helper_functions.py
else:
print("Helper functions file already exists, skipping download...")
# Import series of helper functions for the notebook (we've created/used these in previous notebooks)
from helper_functions import create_tensorboard_callback, plot_loss_curves, compare_historys
```
## Use TensorFlow Datasets to Download Data
In previous notebooks, we've downloaded our food images (from the [Food101 dataset](https://www.kaggle.com/dansbecker/food-101/home)) from Google Storage.
And this is a typical workflow you'd use if you're working on your own datasets.
However, there's another way to get datasets ready to use with TensorFlow.
For many of the most popular datasets in the machine learning world (often referred to and used as benchmarks), you can access them through [TensorFlow Datasets (TFDS)](https://www.tensorflow.org/datasets/overview).
What is **TensorFlow Datasets**?
A place for prepared and ready-to-use machine learning datasets.
Why use TensorFlow Datasets?
* Load data already in Tensors
* Practice on well established datasets
* Experiment with differet data loading techniques (like we're going to use in this notebook)
* Experiment with new TensorFlow features quickly (such as mixed precision training)
Why *not* use TensorFlow Datasets?
* The datasets are static (they don't change, like your real-world datasets would)
* Might not be suited for your particular problem (but great for experimenting)
To begin using TensorFlow Datasets we can import it under the alias `tfds`.
```
# Get TensorFlow Datasets
import tensorflow_datasets as tfds
```
To find all of the available datasets in TensorFlow Datasets, you can use the `list_builders()` method.
After doing so, we can check to see if the one we're after (`"food101"`) is present.
```
# List available datasets
datasets_list = tfds.list_builders() # get all available datasets in TFDS
print("food101" in datasets_list) # is the dataset we're after available?
```
Beautiful! It looks like the dataset we're after is available (note there are plenty more available but we're on Food101).
To get access to the Food101 dataset from the TFDS, we can use the [`tfds.load()`](https://www.tensorflow.org/datasets/api_docs/python/tfds/load) method.
In particular, we'll have to pass it a few parameters to let it know what we're after:
* `name` (str) : the target dataset (e.g. `"food101"`)
* `split` (list, optional) : what splits of the dataset we're after (e.g. `["train", "validation"]`)
* the `split` parameter is quite tricky. See [the documentation for more](https://github.com/tensorflow/datasets/blob/master/docs/splits.md).
* `shuffle_files` (bool) : whether or not to shuffle the files on download, defaults to `False`
* `as_supervised` (bool) : `True` to download data samples in tuple format (`(data, label)`) or `False` for dictionary format
* `with_info` (bool) : `True` to download dataset metadata (labels, number of samples, etc)
> 🔑 **Note:** Calling the `tfds.load()` method will start to download a target dataset to disk if the `download=True` parameter is set (default). This dataset could be 100GB+, so make sure you have space.
```
# Load in the data (takes about 5-6 minutes in Google Colab)
(train_data, test_data), ds_info = tfds.load(name="food101", # target dataset to get from TFDS
split=["train", "validation"], # what splits of data should we get? note: not all datasets have train, valid, test
shuffle_files=True, # shuffle files on download?
as_supervised=True, # download data in tuple format (sample, label), e.g. (image, label)
with_info=True) # include dataset metadata? if so, tfds.load() returns tuple (data, ds_info)
```
Wonderful! After a few minutes of downloading, we've now got access to entire Food101 dataset (in tensor format) ready for modelling.
Now let's get a little information from our dataset, starting with the class names.
Getting class names from a TensorFlow Datasets dataset requires downloading the "`dataset_info`" variable (by using the `as_supervised=True` parameter in the `tfds.load()` method, **note:** this will only work for supervised datasets in TFDS).
We can access the class names of a particular dataset using the `dataset_info.features` attribute and accessing `names` attribute of the the `"label"` key.
```
# Features of Food101 TFDS
ds_info.features
# Get class names
class_names = ds_info.features["label"].names
class_names[:10]
```
### Exploring the Food101 data from TensorFlow Datasets
Now we've downloaded the Food101 dataset from TensorFlow Datasets, how about we do what any good data explorer should?
In other words, "visualize, visualize, visualize".
Let's find out a few details about our dataset:
* The shape of our input data (image tensors)
* The datatype of our input data
* What the labels of our input data look like (e.g. one-hot encoded versus label-encoded)
* Do the labels match up with the class names?
To do, let's take one sample off the training data (using the [`.take()` method](https://www.tensorflow.org/api_docs/python/tf/data/Dataset#take)) and explore it.
```
# Take one sample off the training data
train_one_sample = train_data.take(1) # samples are in format (image_tensor, label)
```
Because we used the `as_supervised=True` parameter in our `tfds.load()` method above, data samples come in the tuple format structure `(data, label)` or in our case `(image_tensor, label)`.
```
# What does one sample of our training data look like?
train_one_sample
```
Let's loop through our single training sample and get some info from the `image_tensor` and `label`.
```
# Output info about our training sample
for image, label in train_one_sample:
print(f"""
Image shape: {image.shape}
Image dtype: {image.dtype}
Target class from Food101 (tensor form): {label}
Class name (str form): {class_names[label.numpy()]}
""")
```
Because we set the `shuffle_files=True` parameter in our `tfds.load()` method above, running the cell above a few times will give a different result each time.
Checking these you might notice some of the images have different shapes, for example `(512, 342, 3)` and `(512, 512, 3)` (height, width, color_channels).
Let's see what one of the image tensors from TFDS's Food101 dataset looks like.
```
# What does an image tensor from TFDS's Food101 look like?
image
# What are the min and max values?
tf.reduce_min(image), tf.reduce_max(image)
```
Alright looks like our image tensors have values of between 0 & 255 (standard red, green, blue colour values) and the values are of data type `unit8`.
We might have to preprocess these before passing them to a neural network. But we'll handle this later.
In the meantime, let's see if we can plot an image sample.
### Plot an image from TensorFlow Datasets
We've seen our image tensors in tensor format, now let's really adhere to our motto.
"Visualize, visualize, visualize!"
Let's plot one of the image samples using [`matplotlib.pyplot.imshow()`](https://matplotlib.org/stable/api/_as_gen/matplotlib.pyplot.imshow.html) and set the title to target class name.
```
# Plot an image tensor
import matplotlib.pyplot as plt
plt.imshow(image)
plt.title(class_names[label.numpy()]) # add title to image by indexing on class_names list
plt.axis(False);
```
Delicious!
Okay, looks like the Food101 data we've got from TFDS is similar to the datasets we've been using in previous notebooks.
Now let's preprocess it and get it ready for use with a neural network.
## Create preprocessing functions for our data
In previous notebooks, when our images were in folder format we used the method [`tf.keras.preprocessing.image_dataset_from_directory()`](https://www.tensorflow.org/api_docs/python/tf/keras/preprocessing/image_dataset_from_directory) to load them in.
Doing this meant our data was loaded into a format ready to be used with our models.
However, since we've downloaded the data from TensorFlow Datasets, there are a couple of preprocessing steps we have to take before it's ready to model.
More specifically, our data is currently:
* In `uint8` data type
* Comprised of all differnet sized tensors (different sized images)
* Not scaled (the pixel values are between 0 & 255)
Whereas, models like data to be:
* In `float32` data type
* Have all of the same size tensors (batches require all tensors have the same shape, e.g. `(224, 224, 3)`)
* Scaled (values between 0 & 1), also called normalized
To take care of these, we'll create a `preprocess_img()` function which:
* Resizes an input image tensor to a specified size using [`tf.image.resize()`](https://www.tensorflow.org/api_docs/python/tf/image/resize)
* Converts an input image tensor's current datatype to `tf.float32` using [`tf.cast()`](https://www.tensorflow.org/api_docs/python/tf/cast)
> 🔑 **Note:** Pretrained EfficientNetBX models in [`tf.keras.applications.efficientnet`](https://www.tensorflow.org/api_docs/python/tf/keras/applications/efficientnet) (what we're going to be using) have rescaling built-in. But for many other model architectures you'll want to rescale your data (e.g. get its values between 0 & 1). This could be incorporated inside your "`preprocess_img()`" function (like the one below) or within your model as a [`tf.keras.layers.experimental.preprocessing.Rescaling`](https://www.tensorflow.org/api_docs/python/tf/keras/layers/experimental/preprocessing/Rescaling) layer.
```
# Make a function for preprocessing images
def preprocess_img(image, label, img_shape=224):
"""
Converts image datatype from 'uint8' -> 'float32' and reshapes image to
[img_shape, img_shape, color_channels]
"""
image = tf.image.resize(image, [img_shape, img_shape]) # reshape to img_shape
return tf.cast(image, tf.float32), label # return (float32_image, label) tuple
```
Our `preprocess_img()` function above takes image and label as input (even though it does nothing to the label) because our dataset is currently in the tuple structure `(image, label)`.
Let's try our function out on a target image.
```
# Preprocess a single sample image and check the outputs
preprocessed_img = preprocess_img(image, label)[0]
print(f"Image before preprocessing:\n {image[:2]}...,\nShape: {image.shape},\nDatatype: {image.dtype}\n")
print(f"Image after preprocessing:\n {preprocessed_img[:2]}...,\nShape: {preprocessed_img.shape},\nDatatype: {preprocessed_img.dtype}")
```
Excellent! Looks like our `preprocess_img()` function is working as expected.
The input image gets converted from `uint8` to `float32` and gets reshaped from its current shape to `(224, 224, 3)`.
How does it look?
```
# We can still plot our preprocessed image as long as we
# divide by 255 (for matplotlib capatibility)
plt.imshow(preprocessed_img/255.)
plt.title(class_names[label])
plt.axis(False);
```
All this food visualization is making me hungry. How about we start preparing to model it?
## Batch & prepare datasets
Before we can model our data, we have to turn it into batches.
Why?
Because computing on batches is memory efficient.
We turn our data from 101,000 image tensors and labels (train and test combined) into batches of 32 image and label pairs, thus enabling it to fit into the memory of our GPU.
To do this in effective way, we're going to be leveraging a number of methods from the [`tf.data` API](https://www.tensorflow.org/api_docs/python/tf/data).
> 📖 **Resource:** For loading data in the most performant way possible, see the TensorFlow docuemntation on [Better performance with the tf.data API](https://www.tensorflow.org/guide/data_performance).
Specifically, we're going to be using:
* [`map()`](https://www.tensorflow.org/api_docs/python/tf/data/Dataset#map) - maps a predefined function to a target dataset (e.g. `preprocess_img()` to our image tensors)
* [`shuffle()`](https://www.tensorflow.org/api_docs/python/tf/data/Dataset#shuffle) - randomly shuffles the elements of a target dataset up `buffer_size` (ideally, the `buffer_size` is equal to the size of the dataset, however, this may have implications on memory)
* [`batch()`](https://www.tensorflow.org/api_docs/python/tf/data/Dataset#batch) - turns elements of a target dataset into batches (size defined by parameter `batch_size`)
* [`prefetch()`](https://www.tensorflow.org/api_docs/python/tf/data/Dataset#prefetch) - prepares subsequent batches of data whilst other batches of data are being computed on (improves data loading speed but costs memory)
* Extra: [`cache()`](https://www.tensorflow.org/api_docs/python/tf/data/Dataset#cache) - caches (saves them for later) elements in a target dataset, saving loading time (will only work if your dataset is small enough to fit in memory, standard Colab instances only have 12GB of memory)
Things to note:
- Can't batch tensors of different shapes (e.g. different image sizes, need to reshape images first, hence our `preprocess_img()` function)
- `shuffle()` keeps a buffer of the number you pass it images shuffled, ideally this number would be all of the samples in your training set, however, if your training set is large, this buffer might not fit in memory (a fairly large number like 1000 or 10000 is usually suffice for shuffling)
- For methods with the `num_parallel_calls` parameter available (such as `map()`), setting it to`num_parallel_calls=tf.data.AUTOTUNE` will parallelize preprocessing and significantly improve speed
- Can't use `cache()` unless your dataset can fit in memory
Woah, the above is alot. But once we've coded below, it'll start to make sense.
We're going to through things in the following order:
```
Original dataset (e.g. train_data) -> map() -> shuffle() -> batch() -> prefetch() -> PrefetchDataset
```
This is like saying,
> "Hey, map this preprocessing function across our training dataset, then shuffle a number of elements before batching them together and make sure you prepare new batches (prefetch) whilst the model is looking through the current batch".
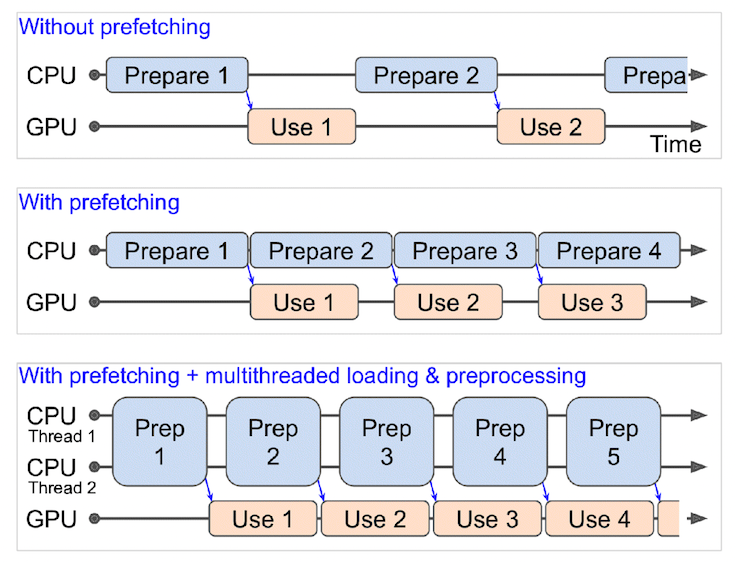
*What happens when you use prefetching (faster) versus what happens when you don't use prefetching (slower). **Source:** Page 422 of [Hands-On Machine Learning with Scikit-Learn, Keras & TensorFlow Book by Aurélien Géron](https://www.oreilly.com/library/view/hands-on-machine-learning/9781492032632/).*
```
# Map preprocessing function to training data (and paralellize)
train_data = train_data.map(map_func=preprocess_img, num_parallel_calls=tf.data.AUTOTUNE)
# Shuffle train_data and turn it into batches and prefetch it (load it faster)
train_data = train_data.shuffle(buffer_size=1000).batch(batch_size=32).prefetch(buffer_size=tf.data.AUTOTUNE)
# Map prepreprocessing function to test data
test_data = test_data.map(preprocess_img, num_parallel_calls=tf.data.AUTOTUNE)
# Turn test data into batches (don't need to shuffle)
test_data = test_data.batch(32).prefetch(tf.data.AUTOTUNE)
```
And now let's check out what our prepared datasets look like.
```
train_data, test_data
```
Excellent! Looks like our data is now in tutples of `(image, label)` with datatypes of `(tf.float32, tf.int64)`, just what our model is after.
> 🔑 **Note:** You can get away without calling the `prefetch()` method on the end of your datasets, however, you'd probably see significantly slower data loading speeds when building a model. So most of your dataset input pipelines should end with a call to [`prefecth()`](https://www.tensorflow.org/api_docs/python/tf/data/Dataset#prefetch).
Onward.
## Create modelling callbacks
Since we're going to be training on a large amount of data and training could take a long time, it's a good idea to set up some modelling callbacks so we be sure of things like our model's training logs being tracked and our model being checkpointed (saved) after various training milestones.
To do each of these we'll use the following callbacks:
* [`tf.keras.callbacks.TensorBoard()`](https://www.tensorflow.org/api_docs/python/tf/keras/callbacks/TensorBoard) - allows us to keep track of our model's training history so we can inspect it later (**note:** we've created this callback before have imported it from `helper_functions.py` as `create_tensorboard_callback()`)
* [`tf.keras.callbacks.ModelCheckpoint()`](https://www.tensorflow.org/api_docs/python/tf/keras/callbacks/ModelCheckpoint) - saves our model's progress at various intervals so we can load it and resuse it later without having to retrain it
* Checkpointing is also helpful so we can start fine-tuning our model at a particular epoch and revert back to a previous state if fine-tuning offers no benefits
```
# Create TensorBoard callback (already have "create_tensorboard_callback()" from a previous notebook)
from helper_functions import create_tensorboard_callback
# Create ModelCheckpoint callback to save model's progress
checkpoint_path = "model_checkpoints/cp.ckpt" # saving weights requires ".ckpt" extension
model_checkpoint = tf.keras.callbacks.ModelCheckpoint(checkpoint_path,
montior="val_accuracy", # save the model weights with best validation accuracy
save_best_only=True, # only save the best weights
save_weights_only=True, # only save model weights (not whole model)
verbose=1) # don't print out whether or not model is being saved
```
## Setup mixed precision training
We touched on mixed precision training above.
However, we didn't quite explain it.
Normally, tensors in TensorFlow default to the float32 datatype (unless otherwise specified).
In computer science, float32 is also known as [single-precision floating-point format](https://en.wikipedia.org/wiki/Single-precision_floating-point_format). The 32 means it usually occupies 32 bits in computer memory.
Your GPU has a limited memory, therefore it can only handle a number of float32 tensors at the same time.
This is where mixed precision training comes in.
Mixed precision training involves using a mix of float16 and float32 tensors to make better use of your GPU's memory.
Can you guess what float16 means?
Well, if you thought since float32 meant single-precision floating-point, you might've guessed float16 means [half-precision floating-point format](https://en.wikipedia.org/wiki/Half-precision_floating-point_format). And if you did, you're right! And if not, no trouble, now you know.
For tensors in float16 format, each element occupies 16 bits in computer memory.
So, where does this leave us?
As mentioned before, when using mixed precision training, your model will make use of float32 and float16 data types to use less memory where possible and in turn run faster (using less memory per tensor means more tensors can be computed on simultaneously).
As a result, using mixed precision training can improve your performance on modern GPUs (those with a compute capability score of 7.0+) by up to 3x.
For a more detailed explanation, I encourage you to read through the [TensorFlow mixed precision guide](https://www.tensorflow.org/guide/mixed_precision) (I'd highly recommend at least checking out the summary).

*Because mixed precision training uses a combination of float32 and float16 data types, you may see up to a 3x speedup on modern GPUs.*
> 🔑 **Note:** If your GPU doesn't have a score of over 7.0+ (e.g. P100 in Colab), mixed precision won't work (see: ["Supported Hardware"](https://www.tensorflow.org/guide/mixed_precision#supported_hardware) in the mixed precision guide for more).
> 📖 **Resource:** If you'd like to learn more about precision in computer science (the detail to which a numerical quantity is expressed by a computer), see the [Wikipedia page](https://en.wikipedia.org/wiki/Precision_(computer_science)) (and accompanying resources).
Okay, enough talk, let's see how we can turn on mixed precision training in TensorFlow.
The beautiful thing is, the [`tensorflow.keras.mixed_precision`](https://www.tensorflow.org/api_docs/python/tf/keras/mixed_precision/) API has made it very easy for us to get started.
First, we'll import the API and then use the [`set_global_policy()`](https://www.tensorflow.org/api_docs/python/tf/keras/mixed_precision/set_global_policy) method to set the *dtype policy* to `"mixed_float16"`.
```
# Turn on mixed precision training
from tensorflow.keras import mixed_precision
mixed_precision.set_global_policy(policy="mixed_float16") # set global policy to mixed precision
```
Nice! As long as the GPU you're using has a compute capability of 7.0+ the cell above should run without error.
Now we can check the global dtype policy (the policy which will be used by layers in our model) using the [`mixed_precision.global_policy()`](https://www.tensorflow.org/api_docs/python/tf/keras/mixed_precision/global_policy) method.
```
mixed_precision.global_policy() # should output "mixed_float16"
```
Great, since the global dtype policy is now `"mixed_float16"` our model will automatically take advantage of float16 variables where possible and in turn speed up training.
## Build feature extraction model
Callbacks: ready to roll.
Mixed precision: turned on.
Let's build a model.
Because our dataset is quite large, we're going to move towards fine-tuning an existing pretrained model (EfficienetNetB0).
But before we get into fine-tuning, let's set up a feature-extraction model.
Recall, the typical order for using transfer learning is:
1. Build a feature extraction model (replace the top few layers of a pretrained model)
2. Train for a few epochs with lower layers frozen
3. Fine-tune if necessary with multiple layers unfrozen
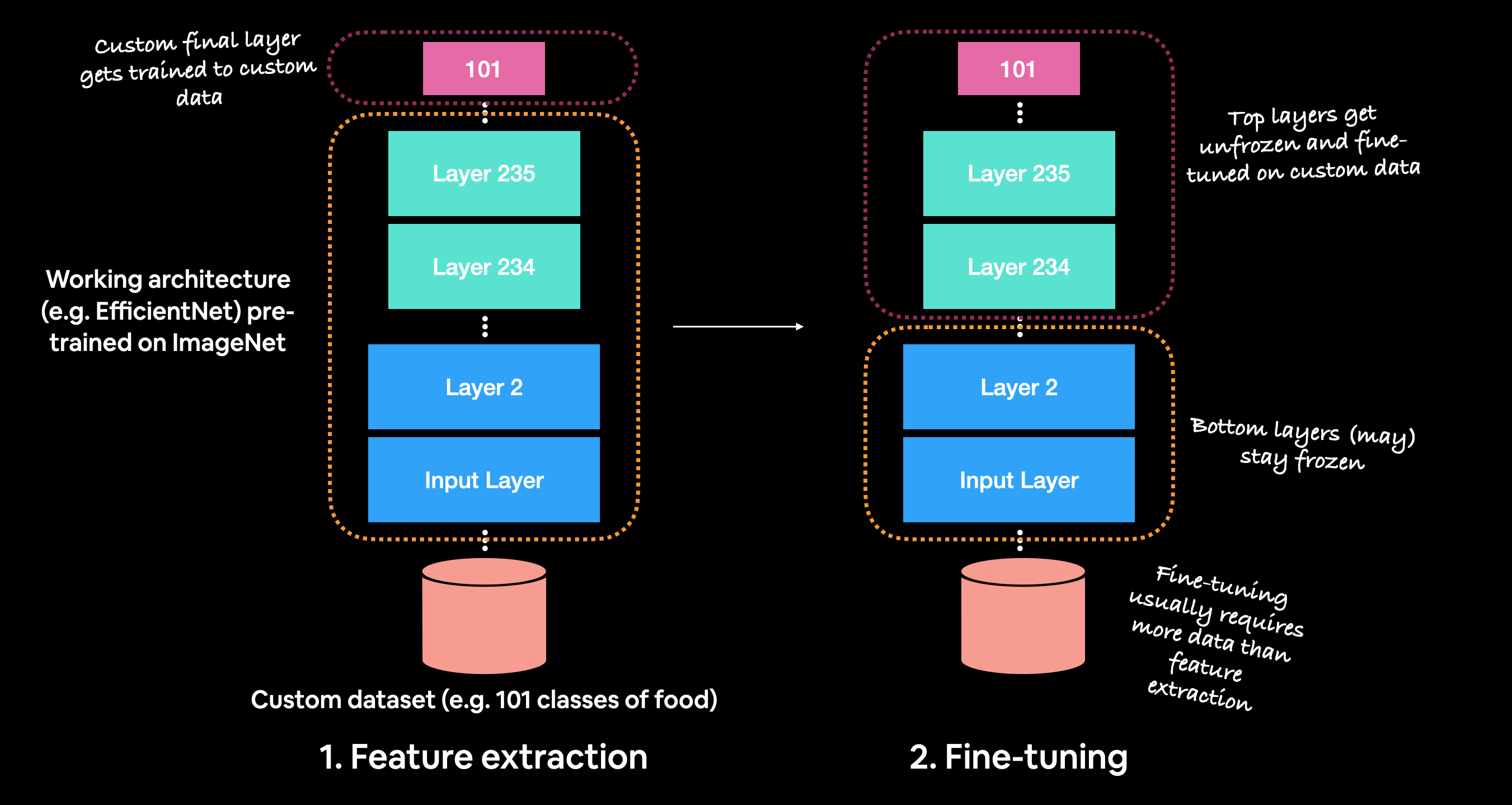
*Before fine-tuning, it's best practice to train a feature extraction model with custom top layers.*
To build the feature extraction model (covered in [Transfer Learning in TensorFlow Part 1: Feature extraction](https://github.com/mrdbourke/tensorflow-deep-learning/blob/main/04_transfer_learning_in_tensorflow_part_1_feature_extraction.ipynb)), we'll:
* Use `EfficientNetB0` from [`tf.keras.applications`](https://www.tensorflow.org/api_docs/python/tf/keras/applications) pre-trained on ImageNet as our base model
* We'll download this without the top layers using `include_top=False` parameter so we can create our own output layers
* Freeze the base model layers so we can use the pre-learned patterns the base model has found on ImageNet
* Put together the input, base model, pooling and output layers in a [Functional model](https://keras.io/guides/functional_api/)
* Compile the Functional model using the Adam optimizer and [sparse categorical crossentropy](https://www.tensorflow.org/api_docs/python/tf/keras/losses/SparseCategoricalCrossentropy) as the loss function (since our labels **aren't** one-hot encoded)
* Fit the model for 3 epochs using the TensorBoard and ModelCheckpoint callbacks
> 🔑 **Note:** Since we're using mixed precision training, our model needs a separate output layer with a hard-coded `dtype=float32`, for example, `layers.Activation("softmax", dtype=tf.float32)`. This ensures the outputs of our model are returned back to the float32 data type which is more numerically stable than the float16 datatype (important for loss calculations). See the ["Building the model"](https://www.tensorflow.org/guide/mixed_precision#building_the_model) section in the TensorFlow mixed precision guide for more.

*Turning mixed precision on in TensorFlow with 3 lines of code.*
```
from tensorflow.keras import layers
from tensorflow.keras.layers.experimental import preprocessing
# Create base model
input_shape = (224, 224, 3)
base_model = tf.keras.applications.EfficientNetB0(include_top=False)
base_model.trainable = False # freeze base model layers
# Create Functional model
inputs = layers.Input(shape=input_shape, name="input_layer", dtype=tf.float16)
# Note: EfficientNetBX models have rescaling built-in but if your model didn't you could have a layer like below
# x = preprocessing.Rescaling(1./255)(x)
x = base_model(inputs, training=False) # set base_model to inference mode only
x = layers.GlobalAveragePooling2D(name="pooling_layer")(x)
x = layers.Dense(len(class_names))(x) # want one output neuron per class
# Separate activation of output layer so we can output float32 activations
outputs = layers.Activation("softmax", dtype=tf.float32, name="softmax_float32")(x)
model = tf.keras.Model(inputs, outputs)
# Compile the model
model.compile(loss="sparse_categorical_crossentropy", # Use sparse_categorical_crossentropy when labels are *not* one-hot
optimizer=tf.keras.optimizers.Adam(),
metrics=["accuracy"])
# Check out our model
model.summary()
```
## Checking layer dtype policies (are we using mixed precision?)
Model ready to go!
Before we said the mixed precision API will automatically change our layers' dtype policy's to whatever the global dtype policy is (in our case it's `"mixed_float16"`).
We can check this by iterating through our model's layers and printing layer attributes such as `dtype` and `dtype_policy`.
```
# Check the dtype_policy attributes of layers in our model
for layer in model.layers:
print(layer.name, layer.trainable, layer.dtype, layer.dtype_policy) # Check the dtype policy of layers
```
Going through the above we see:
* `layer.name` (str) : a layer's human-readable name, can be defined by the `name` parameter on construction
* `layer.trainable` (bool) : whether or not a layer is trainable (all of our layers are trainable except the efficientnetb0 layer since we set it's `trainable` attribute to `False`
* `layer.dtype` : the data type a layer stores its variables in
* `layer.dtype_policy` : the data type a layer computes in
> 🔑 **Note:** A layer can have a dtype of `float32` and a dtype policy of `"mixed_float16"` because it stores its variables (weights & biases) in `float32` (more numerically stable), however it computes in `float16` (faster).
We can also check the same details for our model's base model.
```
# Check the layers in the base model and see what dtype policy they're using
for layer in model.layers[1].layers[:20]: # only check the first 20 layers to save output space
print(layer.name, layer.trainable, layer.dtype, layer.dtype_policy)
```
> 🔑 **Note:** The mixed precision API automatically causes layers which can benefit from using the `"mixed_float16"` dtype policy to use it. It also prevents layers which shouldn't use it from using it (e.g. the normalization layer at the start of the base model).
## Fit the feature extraction model
Now that's one good looking model. Let's fit it to our data shall we?
Three epochs should be enough for our top layers to adjust their weights enough to our food image data.
To save time per epoch, we'll also only validate on 15% of the test data.
```
# Fit the model with callbacks
history_101_food_classes_feature_extract = model.fit(train_data,
epochs=3,
steps_per_epoch=len(train_data),
validation_data=test_data,
validation_steps=int(0.15 * len(test_data)),
callbacks=[create_tensorboard_callback("training_logs",
"efficientnetb0_101_classes_all_data_feature_extract"),
model_checkpoint])
```
Nice, looks like our feature extraction model is performing pretty well. How about we evaluate it on the whole test dataset?
```
# Evaluate model (unsaved version) on whole test dataset
results_feature_extract_model = model.evaluate(test_data)
results_feature_extract_model
```
And since we used the `ModelCheckpoint` callback, we've got a saved version of our model in the `model_checkpoints` directory.
Let's load it in and make sure it performs just as well.
## Load and evaluate checkpoint weights
We can load in and evaluate our model's checkpoints by:
1. Cloning our model using [`tf.keras.models.clone_model()`](https://www.tensorflow.org/api_docs/python/tf/keras/models/clone_model) to make a copy of our feature extraction model with reset weights.
2. Calling the `load_weights()` method on our cloned model passing it the path to where our checkpointed weights are stored.
3. Calling `evaluate()` on the cloned model with loaded weights.
A reminder, checkpoints are helpful for when you perform an experiment such as fine-tuning your model. In the case you fine-tune your feature extraction model and find it doesn't offer any improvements, you can always revert back to the checkpointed version of your model.
```
# Clone the model we created (this resets all weights)
cloned_model = tf.keras.models.clone_model(model)
cloned_model.summary()
!ls model_checkpoints/
# Where are our checkpoints stored?
checkpoint_path
# Load checkpointed weights into cloned_model
cloned_model.load_weights(checkpoint_path)
```
Each time you make a change to your model (including loading weights), you have to recompile.
```
# Compile cloned_model (with same parameters as original model)
cloned_model.compile(loss="sparse_categorical_crossentropy",
optimizer=tf.keras.optimizers.Adam(),
metrics=["accuracy"])
# Evalaute cloned model with loaded weights (should be same score as trained model)
results_cloned_model_with_loaded_weights = cloned_model.evaluate(test_data)
```
Our cloned model with loaded weight's results should be very close to the feature extraction model's results (if the cell below errors, something went wrong).
```
# Loaded checkpoint weights should return very similar results to checkpoint weights prior to saving
import numpy as np
assert np.isclose(results_feature_extract_model, results_cloned_model_with_loaded_weights).all() # check if all elements in array are close
```
Cloning the model preserves `dtype_policy`'s of layers (but doesn't preserve weights) so if we wanted to continue fine-tuning with the cloned model, we could and it would still use the mixed precision dtype policy.
```
# Check the layers in the base model and see what dtype policy they're using
for layer in cloned_model.layers[1].layers[:20]: # check only the first 20 layers to save space
print(layer.name, layer.trainable, layer.dtype, layer.dtype_policy)
```
## Save the whole model to file
We can also save the whole model using the [`save()`](https://www.tensorflow.org/api_docs/python/tf/keras/Model#save) method.
Since our model is quite large, you might want to save it to Google Drive (if you're using Google Colab) so you can load it in for use later.
> 🔑 **Note:** Saving to Google Drive requires mounting Google Drive (go to Files -> Mount Drive).
```
# ## Saving model to Google Drive (optional)
# # Create save path to drive
# save_dir = "drive/MyDrive/tensorflow_course/food_vision/07_efficientnetb0_feature_extract_model_mixed_precision/"
# # os.makedirs(save_dir) # Make directory if it doesn't exist
# # Save model
# model.save(save_dir)
```
We can also save it directly to our Google Colab instance.
> 🔑 **Note:** Google Colab storage is ephemeral and your model will delete itself (along with any other saved files) when the Colab session expires.
```
# Save model locally (if you're using Google Colab, your saved model will Colab instance terminates)
save_dir = "07_efficientnetb0_feature_extract_model_mixed_precision"
model.save(save_dir)
```
And again, we can check whether or not our model saved correctly by loading it in and evaluating it.
```
# Load model previously saved above
loaded_saved_model = tf.keras.models.load_model(save_dir)
```
Loading a `SavedModel` also retains all of the underlying layers `dtype_policy` (we want them to be `"mixed_float16"`).
```
# Check the layers in the base model and see what dtype policy they're using
for layer in loaded_saved_model.layers[1].layers[:20]: # check only the first 20 layers to save output space
print(layer.name, layer.trainable, layer.dtype, layer.dtype_policy)
# Check loaded model performance (this should be the same as results_feature_extract_model)
results_loaded_saved_model = loaded_saved_model.evaluate(test_data)
results_loaded_saved_model
# The loaded model's results should equal (or at least be very close) to the model's results prior to saving
# Note: this will only work if you've instatiated results variables
import numpy as np
assert np.isclose(results_feature_extract_model, results_loaded_saved_model).all()
```
That's what we want! Our loaded model performing as it should.
> 🔑 **Note:** We spent a fair bit of time making sure our model saved correctly because training on a lot of data can be time-consuming, so we want to make sure we don't have to continaully train from scratch.
## Preparing our model's layers for fine-tuning
Our feature-extraction model is showing some great promise after three epochs. But since we've got so much data, it's probably worthwhile that we see what results we can get with fine-tuning (fine-tuning usually works best when you've got quite a large amount of data).
Remember our goal of beating the [DeepFood paper](https://arxiv.org/pdf/1606.05675.pdf)?
They were able to achieve 77.4% top-1 accuracy on Food101 over 2-3 days of training.
Do you think fine-tuning will get us there?
Let's find out.
To start, let's load in our saved model.
> 🔑 **Note:** It's worth remembering a traditional workflow for fine-tuning is to freeze a pre-trained base model and then train only the output layers for a few iterations so their weights can be updated inline with your custom data (feature extraction). And then unfreeze a number or all of the layers in the base model and continue training until the model stops improving.
Like all good cooking shows, I've saved a model I prepared earlier (the feature extraction model from above) to Google Storage.
We can download it to make sure we're using the same model going forward.
```
# Download the saved model from Google Storage
!wget https://storage.googleapis.com/ztm_tf_course/food_vision/07_efficientnetb0_feature_extract_model_mixed_precision.zip
# Unzip the SavedModel downloaded from Google Stroage
!mkdir downloaded_gs_model # create new dir to store downloaded feature extraction model
!unzip 07_efficientnetb0_feature_extract_model_mixed_precision.zip -d downloaded_gs_model
# Load and evaluate downloaded GS model
tf.get_logger().setLevel('INFO') # hide warning logs
loaded_gs_model = tf.keras.models.load_model("downloaded_gs_model/07_efficientnetb0_feature_extract_model_mixed_precision")
# Get a summary of our downloaded model
loaded_gs_model.summary()
```
And now let's make sure our loaded model is performing as expected.
```
# How does the loaded model perform?
results_loaded_gs_model = loaded_gs_model.evaluate(test_data)
results_loaded_gs_model
```
Great, our loaded model is performing as expected.
When we first created our model, we froze all of the layers in the base model by setting `base_model.trainable=False` but since we've loaded in our model from file, let's check whether or not the layers are trainable or not.
```
# Are any of the layers in our model frozen?
for layer in loaded_gs_model.layers:
layer.trainable = True # set all layers to trainable
print(layer.name, layer.trainable, layer.dtype, layer.dtype_policy) # make sure loaded model is using mixed precision dtype_policy ("mixed_float16")
```
Alright, it seems like each layer in our loaded model is trainable. But what if we got a little deeper and inspected each of the layers in our base model?
> 🤔 **Question:** *Which layer in the loaded model is our base model?*
Before saving the Functional model to file, we created it with five layers (layers below are 0-indexed):
0. The input layer
1. The pre-trained base model layer (`tf.keras.applications.EfficientNetB0`)
2. The pooling layer
3. The fully-connected (dense) layer
4. The output softmax activation (with float32 dtype)
Therefore to inspect our base model layer, we can access the `layers` attribute of the layer at index 1 in our model.
```
# Check the layers in the base model and see what dtype policy they're using
for layer in loaded_gs_model.layers[1].layers[:20]:
print(layer.name, layer.trainable, layer.dtype, layer.dtype_policy)
```
Wonderful, it looks like each layer in our base model is trainable (unfrozen) and every layer which should be using the dtype policy `"mixed_policy16"` is using it.
Since we've got so much data (750 images x 101 training classes = 75750 training images), let's keep all of our base model's layers unfrozen.
> 🔑 **Note:** If you've got a small amount of data (less than 100 images per class), you may want to only unfreeze and fine-tune a small number of layers in the base model at a time. Otherwise, you risk overfitting.
## A couple more callbacks
We're about to start fine-tuning a deep learning model with over 200 layers using over 100,000 (75k+ training, 25K+ testing) images, which means our model's training time is probably going to be much longer than before.
> 🤔 **Question:** *How long does training take?*
It could be a couple of hours or in the case of the [DeepFood paper](https://arxiv.org/pdf/1606.05675.pdf) (the baseline we're trying to beat), their best performing model took 2-3 days of training time.
You will really only know how long it'll take once you start training.
> 🤔 **Question:** *When do you stop training?*
Ideally, when your model stops improving. But again, due to the nature of deep learning, it can be hard to know when exactly a model will stop improving.
Luckily, there's a solution: the [`EarlyStopping` callback](https://www.tensorflow.org/api_docs/python/tf/keras/callbacks/EarlyStopping).
The `EarlyStopping` callback monitors a specified model performance metric (e.g. `val_loss`) and when it stops improving for a specified number of epochs, automatically stops training.
Using the `EarlyStopping` callback combined with the `ModelCheckpoint` callback saving the best performing model automatically, we could keep our model training for an unlimited number of epochs until it stops improving.
Let's set both of these up to monitor our model's `val_loss`.
```
# Setup EarlyStopping callback to stop training if model's val_loss doesn't improve for 3 epochs
early_stopping = tf.keras.callbacks.EarlyStopping(monitor="val_loss", # watch the val loss metric
patience=3) # if val loss decreases for 3 epochs in a row, stop training
# Create ModelCheckpoint callback to save best model during fine-tuning
checkpoint_path = "fine_tune_checkpoints/"
model_checkpoint = tf.keras.callbacks.ModelCheckpoint(checkpoint_path,
save_best_only=True,
monitor="val_loss")
```
Woohoo! Fine-tuning callbacks ready.
If you're planning on training large models, the `ModelCheckpoint` and `EarlyStopping` are two callbacks you'll want to become very familiar with.
We're almost ready to start fine-tuning our model but there's one more callback we're going to implement: [`ReduceLROnPlateau`](https://www.tensorflow.org/api_docs/python/tf/keras/callbacks/ReduceLROnPlateau).
Remember how the learning rate is the most important model hyperparameter you can tune? (if not, treat this as a reminder).
Well, the `ReduceLROnPlateau` callback helps to tune the learning rate for you.
Like the `ModelCheckpoint` and `EarlyStopping` callbacks, the `ReduceLROnPlateau` callback montiors a specified metric and when that metric stops improving, it reduces the learning rate by a specified factor (e.g. divides the learning rate by 10).
> 🤔 **Question:** *Why lower the learning rate?*
Imagine having a coin at the back of the couch and you're trying to grab with your fingers.
Now think of the learning rate as the size of the movements your hand makes towards the coin.
The closer you get, the smaller you want your hand movements to be, otherwise the coin will be lost.
Our model's ideal performance is the equivalent of grabbing the coin. So as training goes on and our model gets closer and closer to it's ideal performance (also called **convergence**), we want the amount it learns to be less and less.
To do this we'll create an instance of the `ReduceLROnPlateau` callback to monitor the validation loss just like the `EarlyStopping` callback.
Once the validation loss stops improving for two or more epochs, we'll reduce the learning rate by a factor of 5 (e.g. `0.001` to `0.0002`).
And to make sure the learning rate doesn't get too low (and potentially result in our model learning nothing), we'll set the minimum learning rate to `1e-7`.
```
# Creating learning rate reduction callback
reduce_lr = tf.keras.callbacks.ReduceLROnPlateau(monitor="val_loss",
factor=0.2, # multiply the learning rate by 0.2 (reduce by 5x)
patience=2,
verbose=1, # print out when learning rate goes down
min_lr=1e-7)
```
Learning rate reduction ready to go!
Now before we start training, we've got to recompile our model.
We'll use sparse categorical crossentropy as the loss and since we're fine-tuning, we'll use a 10x lower learning rate than the Adam optimizers default (`1e-4` instead of `1e-3`).
```
# Compile the model
loaded_gs_model.compile(loss="sparse_categorical_crossentropy", # sparse_categorical_crossentropy for labels that are *not* one-hot
optimizer=tf.keras.optimizers.Adam(0.0001), # 10x lower learning rate than the default
metrics=["accuracy"])
```
Okay, model compiled.
Now let's fit it on all of the data.
We'll set it up to run for up to 100 epochs.
Since we're going to be using the `EarlyStopping` callback, it might stop before reaching 100 epochs.
> 🔑 **Note:** Running the cell below will set the model up to fine-tune all of the pre-trained weights in the base model on all of the Food101 data. Doing so with **unoptimized** data pipelines and **without** mixed precision training will take a fairly long time per epoch depending on what type of GPU you're using (about 15-20 minutes on Colab GPUs). But don't worry, **the code we've written above will ensure it runs much faster** (more like 4-5 minutes per epoch).
```
# Start to fine-tune (all layers)
history_101_food_classes_all_data_fine_tune = loaded_gs_model.fit(train_data,
epochs=100, # fine-tune for a maximum of 100 epochs
steps_per_epoch=len(train_data),
validation_data=test_data,
validation_steps=int(0.15 * len(test_data)), # validation during training on 15% of test data
callbacks=[create_tensorboard_callback("training_logs", "efficientb0_101_classes_all_data_fine_tuning"), # track the model training logs
model_checkpoint, # save only the best model during training
early_stopping, # stop model after X epochs of no improvements
reduce_lr]) # reduce the learning rate after X epochs of no improvements
```
> 🔑 **Note:** If you didn't use mixed precision or use techniques such as [`prefetch()`](https://www.tensorflow.org/api_docs/python/tf/data/Dataset#prefetch) in the *Batch & prepare datasets* section, your model fine-tuning probably takes up to 2.5-3x longer per epoch (see the output below for an example).
| | Prefetch and mixed precision | No prefetch and no mixed precision |
|-----|-----|-----|
| Time per epoch | ~280-300s | ~1127-1397s |
*Results from fine-tuning Food Vision Big™ on Food101 dataset using an EfficienetNetB0 backbone using a Google Colab Tesla T4 GPU.*
```
Saving TensorBoard log files to: training_logs/efficientB0_101_classes_all_data_fine_tuning/20200928-013008
Epoch 1/100
2368/2368 [==============================] - 1397s 590ms/step - loss: 1.2068 - accuracy: 0.6820 - val_loss: 1.1623 - val_accuracy: 0.6894
Epoch 2/100
2368/2368 [==============================] - 1193s 504ms/step - loss: 0.9459 - accuracy: 0.7444 - val_loss: 1.1549 - val_accuracy: 0.6872
Epoch 3/100
2368/2368 [==============================] - 1143s 482ms/step - loss: 0.7848 - accuracy: 0.7838 - val_loss: 1.0402 - val_accuracy: 0.7142
Epoch 4/100
2368/2368 [==============================] - 1127s 476ms/step - loss: 0.6599 - accuracy: 0.8149 - val_loss: 0.9599 - val_accuracy: 0.7373
```
*Example fine-tuning time for non-prefetched data as well as non-mixed precision training (~2.5-3x longer per epoch).*
Let's make sure we save our model before we start evaluating it.
```
# # Save model to Google Drive (optional)
# loaded_gs_model.save("/content/drive/MyDrive/tensorflow_course/food_vision/07_efficientnetb0_fine_tuned_101_classes_mixed_precision/")
# Save model locally (note: if you're using Google Colab and you save your model locally, it will be deleted when your Google Colab session ends)
loaded_gs_model.save("07_efficientnetb0_fine_tuned_101_classes_mixed_precision")
```
Looks like our model has gained a few performance points from fine-tuning, let's evaluate on the whole test dataset and see if managed to beat the [DeepFood paper's](https://arxiv.org/abs/1606.05675) result of 77.4% accuracy.
```
# Evaluate mixed precision trained loaded model
results_loaded_gs_model_fine_tuned = loaded_gs_model.evaluate(test_data)
results_loaded_gs_model_fine_tuned
```
Woohoo!!!! It looks like our model beat the results mentioned in the DeepFood paper for Food101 (DeepFood's 77.4% top-1 accuracy versus our ~79% top-1 accuracy).
## Download fine-tuned model from Google Storage
As mentioned before, training models can take a significant amount of time.
And again, like any good cooking show, here's something we prepared earlier...
It's a fine-tuned model exactly like the one we trained above but it's saved to Google Storage so it can be accessed, imported and evaluated.
```
# Download and evaluate fine-tuned model from Google Storage
!wget https://storage.googleapis.com/ztm_tf_course/food_vision/07_efficientnetb0_fine_tuned_101_classes_mixed_precision.zip
```
The downloaded model comes in zip format (`.zip`) so we'll unzip it into the Google Colab instance.
```
# Unzip fine-tuned model
!mkdir downloaded_fine_tuned_gs_model # create separate directory for fine-tuned model downloaded from Google Storage
!unzip 07_efficientnetb0_fine_tuned_101_classes_mixed_precision -d downloaded_fine_tuned_gs_model
```
Now we can load it using the [`tf.keras.models.load_model()`](https://www.tensorflow.org/tutorials/keras/save_and_load) method and get a summary (it should be the exact same as the model we created above).
```
# Load in fine-tuned model from Google Storage and evaluate
loaded_fine_tuned_gs_model = tf.keras.models.load_model("downloaded_fine_tuned_gs_model/07_efficientnetb0_fine_tuned_101_classes_mixed_precision")
# Get a model summary (same model architecture as above)
loaded_fine_tuned_gs_model.summary()
```
Finally, we can evaluate our model on the test data (this requires the `test_data` variable to be loaded.
```
# Note: Even if you're loading in the model from Google Storage, you will still need to load the test_data variable for this cell to work
results_downloaded_fine_tuned_gs_model = loaded_fine_tuned_gs_model.evaluate(test_data)
results_downloaded_fine_tuned_gs_model
```
Excellent! Our saved model is performing as expected (better results than the DeepFood paper!).
Congrautlations! You should be excited! You just trained a computer vision model with competitive performance to a research paper and in far less time (our model took ~20 minutes to train versus DeepFood's quoted 2-3 days).
In other words, you brought Food Vision life!
If you really wanted to step things up, you could try using the [`EfficientNetB4`](https://www.tensorflow.org/api_docs/python/tf/keras/applications/EfficientNetB4) model (a larger version of `EfficientNetB0`). At at the time of writing, the EfficientNet family has the [state of the art classification results](https://paperswithcode.com/sota/fine-grained-image-classification-on-food-101) on the Food101 dataset.
> 📖 **Resource:** To see which models are currently performing the best on a given dataset or problem type as well as the latest trending machine learning research, be sure to check out [paperswithcode.com](http://paperswithcode.com/) and [sotabench.com](https://sotabench.com/).
## View training results on TensorBoard
Since we tracked our model's fine-tuning training logs using the `TensorBoard` callback, let's upload them and inspect them on TensorBoard.dev.
```
# !tensorboard dev upload --logdir ./training_logs \
# --name "Fine-tuning EfficientNetB0 on all Food101 Data" \
# --description "Training results for fine-tuning EfficientNetB0 on Food101 Data with learning rate 0.0001" \
```
Viewing at our [model's training curves on TensorBoard.dev](https://tensorboard.dev/experiment/2KINdYxgSgW2bUg7dIvevw/), it looks like our fine-tuning model gains boost in performance but starts to overfit as training goes on.
See the training curves on TensorBoard.dev here: https://tensorboard.dev/experiment/2KINdYxgSgW2bUg7dIvevw/
To fix this, in future experiments, we might try things like:
* A different iteration of `EfficientNet` (e.g. `EfficientNetB4` instead of `EfficientNetB0`).
* Unfreezing less layers of the base model and training them rather than unfreezing the whole base model in one go.
You can also view and delete past experiments on TensorBoard.dev with the following commands.
```
# View past TensorBoard experiments
# !tensorboard dev list
# Delete past TensorBoard experiments
# !tensorboard dev delete --experiment_id YOUR_EXPERIMENT_ID
# Example
# !tensorboard dev delete --experiment_id OAE6KXizQZKQxDiqI3cnUQ
```
## Exercises
1. Use the same evaluation techniques on the large-scale Food Vision model as you did in the previous notebook ([Transfer Learning Part 3: Scaling up](https://github.com/mrdbourke/tensorflow-deep-learning/blob/main/06_transfer_learning_in_tensorflow_part_3_scaling_up.ipynb)). More specifically, it would be good to see:
* A confusion matrix between all of the model's predictions and true labels.
* A graph showing the f1-scores of each class.
* A visualization of the model making predictions on various images and comparing the predictions to the ground truth.
* For example, plot a sample image from the test dataset and have the title of the plot show the prediction, the prediction probability and the ground truth label.
2. Take 3 of your own photos of food and use the Food Vision model to make predictions on them. How does it go? Share your images/predictions with the other students.
3. Retrain the model (feature extraction and fine-tuning) we trained in this notebook, except this time use [`EfficientNetB4`](https://www.tensorflow.org/api_docs/python/tf/keras/applications/EfficientNetB4) as the base model instead of `EfficientNetB0`. Do you notice an improvement in performance? Does it take longer to train? Are there any tradeoffs to consider?
4. Name one important benefit of mixed precision training, how does this benefit take place?
## Extra-curriculum
* Read up on learning rate scheduling and the [learning rate scheduler callback](https://www.tensorflow.org/api_docs/python/tf/keras/callbacks/LearningRateScheduler). What is it? And how might it be helpful to this project?
* Read up on TensorFlow data loaders ([improving TensorFlow data loading performance](https://www.tensorflow.org/guide/data_performance)). Is there anything we've missed? What methods you keep in mind whenever loading data in TensorFlow? Hint: check the summary at the bottom of the page for a gret round up of ideas.
* Read up on the documentation for [TensorFlow mixed precision training](https://www.tensorflow.org/guide/mixed_precision). What are the important things to keep in mind when using mixed precision training?
|
github_jupyter
|
# CPSC 330 hw7
```
import numpy as np
import pandas as pd
### BEGIN SOLUTION
from sklearn.impute import SimpleImputer
from sklearn.compose import ColumnTransformer
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler, OrdinalEncoder, OneHotEncoder
from sklearn.linear_model import Ridge
from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import GridSearchCV, RandomizedSearchCV
from sklearn.metrics import r2_score
### END SOLUTION
```
## Instructions
rubric={points:5}
Follow the [homework submission instructions](https://github.students.cs.ubc.ca/cpsc330-2019w-t2/home/blob/master/docs/homework_instructions.md).
## Exercise 1: time series prediction
In this exercise we'll be looking at a [dataset of avocado prices](https://www.kaggle.com/neuromusic/avocado-prices). You should start by downloading the dataset. As usual, please do not commit it to your repos.
```
df = pd.read_csv("avocado.csv", parse_dates=["Date"], index_col=0)
df.head()
df.shape
df["Date"].min()
df["Date"].max()
```
It looks like the data ranges from the start of 2015 to March 2018 (~2 years ago), for a total of 3.25 years or so. Let's split the data so that we have a 6 months of test data.
```
split_date = '20170925'
df_train = df[df["Date"] <= split_date]
df_test = df[df["Date"] > split_date]
assert len(df_train) + len(df_test) == len(df)
```
#### 1(a)
rubric={points:3}
In the Rain is Australia dataset from Lecture 16, we had different measurements for each Location. What about this dataset: for which categorical feature(s), if any, do we have separate measurements? Justify your answer by referencing the dataset.
### BEGIN SOLUTION
```
df.sort_values(by="Date").head()
```
From the above, we definitely see measurements on the same day at different regresion. Let's now group by region.
```
df.sort_values(by=["region", "Date"]).head()
```
From the above we see that, even in Albany, we have two measurements on the same date. This seems to be due to the type of avocado.
```
df.sort_values(by=["region", "type", "Date"]).head()
```
Great, now we have a sequence of dates with a single row per date. So, the answer is that we have a separate timeseries for each combination of `region` and `type`.
### END SOLUTION
#### 1(b)
rubric={points:3}
In the Rain in Australia dataset, the measurements were generally equally spaced but with some exceptions. How about with this dataset? Justify your answer by referencing the dataset.
### BEGIN SOLUTION
I think it's not unreasonable to do this on `df` rather than `df_train`, but either way is fine.
```
for name, group in df.groupby(['region', 'type']):
print("%-40s %s" % (name, group["Date"].sort_values().diff().min()))
for name, group in df.groupby(['region', 'type']):
print("%-40s %s" % (name, group["Date"].sort_values().diff().max()))
```
It looks almost perfect - just organic avocados in WestTexNewMexico seems to be missing a couple measurements.
```
name
group["Date"].sort_values().diff().value_counts()
```
So, in one case there's a 2-week jump, and in one cast there's a 3-week jump.
```
group["Date"].sort_values().reset_index(drop=True).diff().sort_values()
```
We can see the anomalies occur at index 48 and 127. (Note: I had to `reset_index` because the index was not unique to each row.)
```
group["Date"].sort_values().reset_index(drop=True)[45:50]
```
We can spot the first anomaly: a 2-week jump from Nov 29, 2015 to Dec 13, 2015.
```
group["Date"].sort_values().reset_index(drop=True)[125:130]
```
And we can spot the second anomaly: a 3-week jump from June 11, 2017 to July 2, 2017.
### END SOLUTION
#### 1(c)
rubric={points:1}
In the Rain is Australia dataset, each location was a different place in Australia. For this dataset, look at the names of the regions. Do you think the regions are also all distinct, or are there overlapping regions? Justify your answer by referencing the data.
### BEGIN SOLUTION
```
df["region"].unique()
```
There seems to be a hierarchical structure here: `TotalUS` is split into bigger regions like `West`, `Southeast`, `Northeast`, `Midsouth`; and `California` is split into cities like `Sacramento`, `SanDiego`, `LosAngeles`. It's a bit hard to figure out what's going on.
```
df.query("region == 'TotalUS' and type == 'conventional' and Date == '20150104'")["Total Volume"].values[0]
df.query("region != 'TotalUS' and type == 'conventional' and Date == '20150104'")["Total Volume"].sum()
```
Since the individual regions sum up to more than the total US, it seems that some of the other regions are double-counted, which is consistent with a hierarchical structure. For example, Los Angeles is probalby double counted because it's within `LosAngeles` but also within `California`. What a mess!
### END SOLUTION
We will use the entire dataset despite any location-based weirdness uncovered in the previous part.
We will be trying to forecast the avocado price, which is the `AveragePrice` column. The function below is adapted from Lecture 16, with some improvements.
```
def create_lag_feature(df, orig_feature, lag, groupby, new_feature_name=None, clip=False):
"""
Creates a new feature that's a lagged version of an existing one.
NOTE: assumes df is already sorted by the time columns and has unique indices.
Parameters
----------
df : pandas.core.frame.DataFrame
The dataset.
orig_feature : str
The column name of the feature we're copying
lag : int
The lag; negative lag means values from the past, positive lag means values from the future
groupby : list
Column(s) to group by in case df contains multiple time series
new_feature_name : str
Override the default name of the newly created column
clip : bool
If True, remove rows with a NaN values for the new feature
Returns
-------
pandas.core.frame.DataFrame
A new dataframe with the additional column added.
"""
if new_feature_name is None:
if lag < 0:
new_feature_name = "%s_lag%d" % (orig_feature, -lag)
else:
new_feature_name = "%s_ahead%d" % (orig_feature, lag)
new_df = df.assign(**{new_feature_name : np.nan})
for name, group in new_df.groupby(groupby):
if lag < 0: # take values from the past
new_df.loc[group.index[-lag:],new_feature_name] = group.iloc[:lag][orig_feature].values
else: # take values from the future
new_df.loc[group.index[:-lag], new_feature_name] = group.iloc[lag:][orig_feature].values
if clip:
new_df = new_df.dropna(subset=[new_feature_name])
return new_df
```
We first sort our dataframe properly:
```
df_sort = df.sort_values(by=["region", "type", "Date"]).reset_index(drop=True)
df_sort
```
We then call `create_lag_feature`. This creates a new column in the dataset `AveragePriceNextWeek`, which is the following week's `AveragePrice`. We have set `clip=True` which means it will remove rows where the target would be missing.
```
df_hastarget = create_lag_feature(df_sort, "AveragePrice", +1, ["region", "type"], "AveragePriceNextWeek", clip=True)
df_hastarget
```
I will now split the data:
```
df_train = df_hastarget[df_hastarget["Date"] <= split_date]
df_test = df_hastarget[df_hastarget["Date"] > split_date]
```
#### 1(d)
rubric={points:1}
Why was it reasonable for me to do this operation _before_ splitting the data, despite the fact that this usually constitutes a violation of the Golden Rule?
### BEGIN SOLUTION
Because we were only looking at the dates and creating the future feature. The difference is that the very last time point in our training set now contains the average price from the first time point in our test set. This is a realistic scenario if we wre actually using this model to forecast, so it's not a major concern.
### END SOLUTION
#### 1(e)
rubric={points:1}
Next we will want to build some models to forecast the average avocado price a week in advance. Before we start with any ML, let's try a baseline: just predicting the previous week's `AveragePrice`. What $R^2$ do you get with this approach?
### BEGIN SOLUTION
```
r2_score(df_train["AveragePriceNextWeek"], df_train["AveragePrice"])
r2_score(df_test["AveragePriceNextWeek"], df_test["AveragePrice"])
```
Interesting that this is a less effective prediction strategy in the later part of the dataset. I guess that means the price was fluctuating more in late 2017 / early 2018?
### END SOLUTION
#### 1(f)
rubric={points:10}
Build some models to forecast the average avocado price. Experiment with a few approachs for encoding the date. Justify the decisions you make. Which approach worked best? Report your test score and briefly discuss your results.
Benchmark: you should be able to achieve $R^2$ of at least 0.79 on the test set. I got to 0.80, but not beyond that. Let me know if you do better!
Note: because we only have 2 splits here, we need to be a bit wary of overfitting on the test set. Try not to test on it a ridiculous number of times. If you are interested in some proper ways of dealing with this, see for example sklearn's [TimeSeriesSplit](https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.TimeSeriesSplit.html), which is like cross-validation for time series data.
### BEGIN SOLUTION
```
df_train.head()
(df_train.loc[:, "Small Bags": "XLarge Bags"].sum(axis=1) - df_train["Total Bags"]).abs().max()
```
It seems that `Total Bags` is (approximately) the sum of the other 3 bag features, so I will drop `Total Bags`.
```
(df_train.loc[:, "4046": "4770"].sum(axis=1) - df_train["Total Volume"]).abs().max()
```
It seems that `Total Volume` is _not_ the sum of the 3 avocado types, so I will keep all 4 columns.
```
df_train.info()
```
It seems there are no null values, so I will not do any imputation.
Will plot a single time series for exploration purposes:
```
df_train.query("region == 'TotalUS'").set_index("Date").groupby("type")["AveragePrice"].plot(legend=True);
df_train.query("region == 'TotalUS' and type == 'conventional'").plot(x="Date", y="Total Volume");
```
We see some seasonality in the total volume, but not much in the average price - interesting.
I will not scale the `AveragePrice` because I am not scaling `AveragePriceNextWeek` either, and it may be helpful to keep them the same. Alternatively, it may have been effective to predict the _change_ in price instead of next's week's price.
```
numeric_features = ["Total Volume", "4046", "4225", "4770", "Small Bags", "Large Bags", "XLarge Bags", "year"]
categorical_features = ["type", "region"]
keep_features = ["AveragePrice"]
drop_features = ["Date", "Total Bags"]
target_feature = "AveragePriceNextWeek"
```
Next, I grab the `preprocess_features` function from Lecture 16, with a minor modification to allow un-transformed features via `keep_features`:
```
def preprocess_features(df_train, df_test,
numeric_features,
categorical_features,
keep_features,
drop_features,
target_feature):
all_features = numeric_features + categorical_features + keep_features + drop_features + [target_feature]
if set(df_train.columns) != set(all_features):
print("Missing columns", set(df_train.columns) - set(all_features))
print("Extra columns", set(all_features) - set(df_train.columns))
raise Exception("Columns do not match")
# Put the columns in the order we want
df_train = df_train[all_features]
df_test = df_test[all_features]
numeric_transformer = Pipeline([
('imputer', SimpleImputer(strategy='median')),
('scaler', StandardScaler())
])
categorical_transformer = Pipeline([
('imputer', SimpleImputer(strategy='most_frequent')),
('onehot', OneHotEncoder(sparse=False, drop='first'))
])
preprocessor = ColumnTransformer([
('numeric', numeric_transformer, numeric_features),
('categorical', categorical_transformer, categorical_features)
], remainder='passthrough')
preprocessor.fit(df_train);
if len(categorical_features) > 0:
ohe = preprocessor.named_transformers_['categorical'].named_steps['onehot']
ohe_feature_names = list(ohe.get_feature_names(categorical_features))
new_columns = numeric_features + ohe_feature_names + keep_features + drop_features + [target_feature]
else:
new_columns = all_features
X_train_enc = pd.DataFrame(preprocessor.transform(df_train), index=df_train.index, columns=new_columns)
X_test_enc = pd.DataFrame(preprocessor.transform(df_test), index=df_test.index, columns=new_columns)
X_train_enc = X_train_enc.drop(columns=drop_features + [target_feature])
X_test_enc = X_test_enc.drop( columns=drop_features + [target_feature])
y_train = df_train[target_feature]
y_test = df_test[ target_feature]
return X_train_enc, y_train, X_test_enc, y_test
df_train_enc, y_train, df_test_enc, y_test = preprocess_features(df_train, df_test,
numeric_features,
categorical_features,
keep_features,
drop_features,
target_feature)
df_train_enc.head()
lr = Ridge()
lr.fit(df_train_enc, y_train);
lr.score(df_train_enc, y_train)
lr.score(df_test_enc, y_test)
lr_coef = pd.DataFrame(data=np.squeeze(lr.coef_), index=df_train_enc.columns, columns=["Coef"])
lr_coef.sort_values(by="Coef", ascending=False)
```
This is not a very impressive showing. We're doing almost the same as the baseline.
Let's see if encoding the date helps at all. We'll try to OHE the month.
```
df_train_month = df_train.assign(Month=df_train["Date"].apply(lambda x: x.month))
df_test_month = df_test.assign( Month=df_test[ "Date"].apply(lambda x: x.month))
df_train_month_enc, y_train, df_test_month_enc, y_test = preprocess_features(df_train_month, df_test_month,
numeric_features,
categorical_features + ["Month"],
keep_features,
drop_features,
target_feature)
df_train_month_enc.head()
lr = Ridge()
lr.fit(df_train_month_enc, y_train);
lr.score(df_train_month_enc, y_train)
lr.score(df_test_month_enc, y_test)
```
A tiny bit better.
```
pd.DataFrame(data=np.squeeze(lr.coef_), index=df_train_month_enc.columns, columns=["Coef"]).sort_values(by="Coef", ascending=False)
```
Let's add some lag features. I'm arbitrarily deciding on 4 lags for `AveragePrice` (the most important feature).
```
def add_lags(df):
df = create_lag_feature(df, "AveragePrice", -1, ["region", "type"])
df = create_lag_feature(df, "AveragePrice", -2, ["region", "type"])
df = create_lag_feature(df, "AveragePrice", -3, ["region", "type"])
df = create_lag_feature(df, "AveragePrice", -4, ["region", "type"])
return df
df_train_month_lag = add_lags(df_train_month)
df_test_month_lag = add_lags(df_test_month)
df_train_month_lag
df_train_month_lag_enc, y_train, df_test_month_lag_enc, y_test = preprocess_features(df_train_month_lag, df_test_month_lag,
numeric_features + ["AveragePrice_lag1", "AveragePrice_lag2", "AveragePrice_lag3", "AveragePrice_lag4"],
categorical_features + ["Month"],
keep_features,
drop_features,
target_feature)
lr = Ridge()
lr.fit(df_train_month_lag_enc, y_train);
lr.score(df_train_month_lag_enc, y_train)
lr.score(df_test_month_lag_enc, y_test)
```
This did not seem to help.
```
pd.DataFrame(data=np.squeeze(lr.coef_), index=df_train_month_lag_enc.columns, columns=["Coef"]).sort_values(by="Coef", ascending=False)
```
We can also try a random forest:
```
rf = RandomForestRegressor()
rf.fit(df_train_month_lag_enc, y_train);
rf.score(df_train_month_lag_enc, y_train)
rf.score(df_test_month_lag_enc, y_test)
```
For the random forest it may be helpful to model the difference between today and tomorrow. The linear model does not care about this because it just corresponds to changing the coefficient corresponding to `AveragePrice` by 1, but for the random forest it may help:
```
rf = RandomForestRegressor()
rf.fit(df_train_month_lag_enc, y_train - df_train_month_lag_enc["AveragePrice"]);
r2_score(y_train, rf.predict(df_train_month_lag_enc) + df_train_month_lag_enc["AveragePrice"])
r2_score(y_test, rf.predict(df_test_month_lag_enc) + df_test_month_lag_enc["AveragePrice"])
```
This massively overfits when we do this shifting. Let's try a simpler model...
```
rf = RandomForestRegressor(max_depth=8)
rf.fit(df_train_month_lag_enc, y_train - df_train_month_lag_enc["AveragePrice"]);
r2_score(y_train, rf.predict(df_train_month_lag_enc) + df_train_month_lag_enc["AveragePrice"])
r2_score(y_test, rf.predict(df_test_month_lag_enc) + df_test_month_lag_enc["AveragePrice"])
```
Doesn't realy help.
Also, we can just confirm that this shifting has no effect on the linear model (well, a small effect because it's `Ridge` instead of `LinearRegression`, but small):
```
lr = Ridge()
lr.fit(df_train_month_lag_enc, y_train - df_train_month_lag_enc["AveragePrice"]);
r2_score(y_train, lr.predict(df_train_month_lag_enc) + df_train_month_lag_enc["AveragePrice"])
r2_score(y_test, lr.predict(df_test_month_lag_enc) + df_test_month_lag_enc["AveragePrice"])
```
Indeed, this is essentially the same score we had before.
Overall, adding the month helped, but adding the lagged price was surprisingly unhelpful. Perhaps lagged version of other features would have been better, or other representations of the time of year, or dealing with the regions and avocado types a bit more carefully.
### END SOLUTION
#### 1(g)
rubric={points:3}
We talked a little bit about _seasonality_, which is the idea of a periodic component to the time series. For example, in Lecture 16 we attempted to capture this by encoding the month. Something we didn't discuss is _trends_, which are long-term variations in the quantity of interest. Aside from the effects of climate change, the amount of rain in Australia is likely to vary during the year but less likely to have long-term trends over the years. Avocado prices, on the other hand, could easily exhibit trends: for example avocados may just cost more in 2020 than they did in 2015.
Briefly discuss in ~1 paragraph: to what extent, if any, was your model above able to account for seasonality? What about trends?
### BEGIN SOLUTION
I tried to take seasonality into account by having the month as an OHE variable. As far as trends are concerned, the year is also a numeric variable in the model, so it could learn that the price in 2017 is higher than in 2015, say. However, there are very few years in the training set (2015, 16, 17), so that is not a lot of data to learn from. Perhaps including the number of months since the start of the dataset, or something like that, would enable the model to do a bit better with trends. Nonetheless, extrapolating is very hard so we can't necessarily trust our models' handing of trend.
```
pd.DataFrame(data=np.squeeze(lr.coef_), index=df_train_month_lag_enc.columns, columns=["Coef"]).loc["year"]
```
It seems that our linear model learned a small positive trend for the year. It would be cool to use SHAP and see what the random forest is doing.
### END SOLUTION
## Exercise 2: very short answer questions
Each question is worth 2 points.
#### 2(a)
rubric={points:4}
The following questions pertain to Lecture 16 on time series data:
1. Sometimes a time series has missing time points or, worse, time points that are unequally spaced in general. Give an example of a real world situation where the time series data would have unequally spaced time points.
2. In class we discussed two approaches to using temporal information: encoding the date as one or more features, and creating lagged versions of features. Which of these (one/other/both/neither) two approaches would struggle with unequally spaced time points? Briefly justify your answer.
### BEGIN SOLUTION
1. Many many examples: credit card transactions, log files, basically any situation where the frequency of the measurements could not be chosen by the person taking the measurements.
2. Encoding the date as, e.g. OHE month works just fine with unequally spaced points. However, the lag features are more problematic, because the "previous" measurement will be a different length of time away in each case.
### END SOLUTION
#### 2(b)
rubric={points:10}
The following questions pertain to Lecture 17 on survival analysis. We'll consider the use case of customer churn analysis.
1. What is the problem with simply labeling customers are "churned" or "not churned" and using standard supervised learning techniques, as we did in hw4?
2. Consider customer A who just joined last week vs. customer B who has been with the service for a year. Who do you expect will leave the service first: probably customer A, probably customer B, or we don't have enough information to answer? (This is a bit tricky - it's OK if you don't know the answer, but try to argue your case.)
3. One of the true/false questions from class was: "If a customer is censored after 5 months with the service, then all customers are censored after 5 months (i.e. no values of `tenure` above 5)." What is the answer if all customers joined the service at the same time? Briefly explain.
4. One of the true/false questions from class was: "If a customer is censored after 5 months with the service, then all customers are censored after 5 months (i.e. no values of `tenure` above 5)." What is the answer if customers did not necessarily join the service at the same time? Briefly explain.
5. If a customer's survival function is almost flat during a certain period, how do we interpret that?
### BEGIN SOLUTION
1. The "not churned" are censored - we don't know if they will churn shortly or in a long time. These people have the same label and our model will be impacted negatively.
2. Not enough information - it depends! Imagine a subscription service where you have to pay a starter fee after a month and then pay a huge fee after a year. Well, customer B just paid that huge fee and will probably stay a while, whereas customer A may leave before paying the huge fee, so customer A will probably leave first. But imagine a service where people are more and more likely to leave every day, e.g. a movie service with only 100 movies, so you can run out easily. In that case customer B will probably leave first.
3. True. If all started at the same time, and a customer is censored after 5 months, that means they all started 5 months ago and are all censored after 5 months.
4. False. That particular customer started 5 months ago, but you may have another customer who started much longer ago.
5. The customer is very unlikely to leave during that period.
### END SOLUTION
#### 2(c)
rubric={points:10}
The following questions pertain to Lecture 18 on clustering.
1. What's the main difference between unsupervised and supervised learning?
2. When choosing $k$ in $k$-means, why not just choose the $k$ that leads to the smallest inertia (sum of squared distances within clusters)?
3. You decide to use clustering for _outlier detection_; that is, to detect instances that are very atypical compared to all the rest. How might you do this with $k$-means?
4. You decide to use clustering for _outlier detection_; that is, to detect instances that are very atypical compared to all the rest. How might you do this with DBSCAN?
5. For hierarchical clustering, we briefly discussed a few different methods for merging clusters: single linkage, average linkage, etc. Why do we have this added complication here - can't we just minimize distance like we did with $k$-means?
### BEGIN SOLUTION
1. Supervised has target values ($y$), unsupervised does not.
2. Because inertia decreases with $k$, so you'd just choose $k=n$, which is not interesting.
3. Look for examples that are very far away from their cluster mean.
4. Look for examples that were not assigned to any cluster.
5. With $k$-means we had to find the distance between a point and a cluster mean. Here, we need to find the distance between two clusters, and, importantly, we have no cluster means. So it's ambiguous how to definite distance between two clusters.
### END SOLUTION
|
github_jupyter
|
# Candlestick Hanging Man
https://www.investopedia.com/articles/active-trading/040914/understanding-hanging-man-optimistic-candlestick-pattern.asp
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import talib
import warnings
warnings.filterwarnings("ignore")
# yahoo finance is used to fetch data
import yfinance as yf
yf.pdr_override()
# input
symbol = 'AMD'
start = '2018-01-01'
end = '2021-10-08'
# Read data
df = yf.download(symbol,start,end)
# View Columns
df.head()
```
## Candlestick with Hanging Man
```
from matplotlib import dates as mdates
import datetime as dt
dfc = df.copy()
dfc['VolumePositive'] = dfc['Open'] < dfc['Adj Close']
#dfc = dfc.dropna()
dfc = dfc.reset_index()
dfc['Date'] = pd.to_datetime(dfc['Date'])
dfc['Date'] = dfc['Date'].apply(mdates.date2num)
dfc.head()
from mplfinance.original_flavor import candlestick_ohlc
fig = plt.figure(figsize=(14,10))
ax = plt.subplot(2, 1, 1)
candlestick_ohlc(ax,dfc.values, width=0.5, colorup='g', colordown='r', alpha=1.0)
ax.xaxis_date()
ax.xaxis.set_major_formatter(mdates.DateFormatter('%d-%m-%Y'))
ax.grid(True, which='both')
ax.minorticks_on()
axv = ax.twinx()
colors = dfc.VolumePositive.map({True: 'g', False: 'r'})
axv.bar(dfc.Date, dfc['Volume'], color=colors, alpha=0.4)
axv.axes.yaxis.set_ticklabels([])
axv.set_ylim(0, 3*df.Volume.max())
ax.set_title('Stock '+ symbol +' Closing Price')
ax.set_ylabel('Price')
hanging_man = talib.CDLHANGINGMAN(df['Open'], df['High'], df['Low'], df['Close'])
hanging_man = hanging_man[hanging_man != 0]
df['hanging_man'] = talib.CDLHANGINGMAN(df['Open'], df['High'], df['Low'], df['Close'])
df.loc[df['hanging_man'] !=0]
df['Adj Close'].loc[df['hanging_man'] !=0]
df['Adj Close'].loc[df['hanging_man'] !=0].index
hanging_man
hanging_man.index
df
fig = plt.figure(figsize=(20,16))
ax = plt.subplot(2, 1, 1)
candlestick_ohlc(ax,dfc.values, width=0.5, colorup='g', colordown='r', alpha=1.0)
ax.xaxis_date()
ax.xaxis.set_major_formatter(mdates.DateFormatter('%d-%m-%Y'))
ax.grid(True, which='both')
ax.minorticks_on()
axv = ax.twinx()
ax.plot_date(df['Adj Close'].loc[df['hanging_man'] !=0].index, df['Adj Close'].loc[df['hanging_man'] !=0],
'Dc', # marker style 'o', color 'g'
fillstyle='none', # circle is not filled (with color)
ms=10.0)
colors = dfc.VolumePositive.map({True: 'g', False: 'r'})
axv.bar(dfc.Date, dfc['Volume'], color=colors, alpha=0.4)
axv.axes.yaxis.set_ticklabels([])
axv.set_ylim(0, 3*df.Volume.max())
ax.set_title('Stock '+ symbol +' Closing Price')
ax.set_ylabel('Price')
```
## Plot Certain dates
```
df = df['2021-07-01':'2021-08-01']
dfc = df.copy()
dfc['VolumePositive'] = dfc['Open'] < dfc['Adj Close']
#dfc = dfc.dropna()
dfc = dfc.reset_index()
dfc['Date'] = pd.to_datetime(dfc['Date'])
dfc['Date'] = dfc['Date'].apply(mdates.date2num)
dfc.head()
fig = plt.figure(figsize=(20,16))
ax = plt.subplot(2, 1, 1)
ax.set_facecolor('black')
candlestick_ohlc(ax,dfc.values, width=0.5, colorup='tan', colordown='gold', alpha=1.0)
ax.xaxis_date()
ax.xaxis.set_major_formatter(mdates.DateFormatter('%d-%m-%Y'))
#ax.grid(True, which='both')
#ax.minorticks_on()
axv = ax.twinx()
ax.plot_date(df['Adj Close'].loc[df['hanging_man'] !=0].index, df['Adj Close'].loc[df['hanging_man'] !=0],
'dr', # marker style 'o', color 'g'
fillstyle='none', # circle is not filled (with color)
ms=20.0)
colors = dfc.VolumePositive.map({True: 'tan', False: 'gold'})
axv.bar(dfc.Date, dfc['Volume'], color=colors, alpha=0.4)
axv.axes.yaxis.set_ticklabels([])
axv.set_ylim(0, 3*df.Volume.max())
ax.set_title('Stock '+ symbol +' Closing Price')
ax.set_ylabel('Price')
```
# Highlight Candlestick
```
from matplotlib.dates import date2num
from datetime import datetime
fig = plt.figure(figsize=(20,16))
ax = plt.subplot(2, 1, 1)
candlestick_ohlc(ax,dfc.values, width=0.5, colorup='g', colordown='r', alpha=1.0)
ax.xaxis_date()
ax.xaxis.set_major_formatter(mdates.DateFormatter('%d-%m-%Y'))
#ax.grid(True, which='both')
#ax.minorticks_on()
axv = ax.twinx()
ax.axvspan(date2num(datetime(2021,7,19)), date2num(datetime(2021,7,21)),
label="Hanging Man Bearish",color="red", alpha=0.3)
ax.legend()
colors = dfc.VolumePositive.map({True: 'g', False: 'r'})
axv.bar(dfc.Date, dfc['Volume'], color=colors, alpha=0.4)
axv.axes.yaxis.set_ticklabels([])
axv.set_ylim(0, 3*df.Volume.max())
ax.set_title('Stock '+ symbol +' Closing Price')
ax.set_ylabel('Price')
```
|
github_jupyter
|
# Clonamos el repositorio para obtener los dataSet
```
!git clone https://github.com/joanby/ia-course.git
```
# Damos acceso a nuestro Drive
```
from google.colab import drive
drive.mount('/content/drive')
```
# Test it
```
!ls '/content/drive/My Drive'
```
#Google colab tools
```
from google.colab import files # Para manejar los archivos y, por ejemplo, exportar a su navegador
import glob # Para manejar los archivos y, por ejemplo, exportar a su navegador
from google.colab import drive # Montar tu Google drive
```
# Instalar dependencias de Renderizado, tarda alrededor de 45 segundos
```
!apt-get update > /dev/null 2>&1
!apt-get install python-opengl -y > /dev/null 2>&1
!apt install xvfb -y --fix-missing > /dev/null 2>&1
!apt-get install ffmpeg > /dev/null 2>&1
!apt-get install x11-utils > /dev/null 2>&1
!apt-get install pyglet > /dev/null 2>&1
```
# Instalar OpenAi Gym
```
!pip install gym pyvirtualdisplay > /dev/null 2>&1
!pip install piglet > /dev/null 2>&1
!pip install 'gym[box2d]' > /dev/null 2>&1
#por si quieres algun environment en concreto
#!pip install atari_py > /dev/null 2>&1
#!pip install gym[atari] > /dev/null 2>&1
```
# Todos los imports necesarios en google colab y helpers para poder visualizar OpenAi
```
import gym
from gym import logger as gymlogger
from gym.wrappers import Monitor
gymlogger.set_level(40) #error only
import numpy as np
import random
import matplotlib
import matplotlib.pyplot as plt
%matplotlib inline
import math
import glob
import io
import base64
from IPython.display import HTML
from IPython import display as ipythondisplay
```
# Activamos una vista, seria como crear un plot de una grafica en python
```
from pyvirtualdisplay import Display
display = Display(visible=0, size=(1400, 900)) #Puedes modificar el high and width de la pantalla
display.start()
```
# Este código crea una pantalla virtual para dibujar imágenes del juego.
## Si se ejecuta localmente, simplemente ignóralo
```
import os
if type(os.environ.get('DISPLAY')) is not str or \
len(os.environ.get('DISPLAY')) == 0:
!bash ../xvfb start
%env DISPLAY=:1
```
# Funciones de utilidad para permitir la grabación de video del ambiente del gimnasio y su visualización
## Para habilitar la visualizacion por pantalla , tan solo haz "**environment = wrap_env(environment)**", por ejemplo: **environment = wrap_env(gym.make("MountainCar-v0"))**
```
import io
import glob
import base64
from IPython.display import HTML
from IPython import display as ipythondisplay
def show_video():
mp4list = glob.glob('video/*.mp4')
if len(mp4list) > 0:
mp4 = mp4list[0]
video = io.open(mp4, 'r+b').read()
encoded = base64.b64encode(video)
content = ipythondisplay.display(HTML(data='''
<video alt="test" autoplay loop controls style="height: 400px;">
<source src="data:video/mp4;base64,{0}" type="video/mp4" />
</video>
'''.format(encoded.decode('ascii'))))
else:
print("Couldn't find video")
def wrap_env(env):
env = gym.wrappers.Monitor(env, './video', force=True)
return env
```
# Nuestro Script
```
environment = wrap_env(gym.make("Qbert-v0"))
from gym.spaces import *
import sys
# Box -> R^n (x1,x2,x3,...,xn), xi [low, high]
#gym.spaces.Box(low = -10, high = 10, shape = (2,)) # (x,y), -10<x,y<10
# Discrete -> Números enteros entre 0 y n-1, {0,1,2,3,...,n-1}
#gym.spaces.Discrete(5) # {0,1,2,3,4}
#Dict -> Diccionario de espacios más complejos
#gym.spaces.Dict({
# "position": gym.spaces.Discrete(3), #{0,1,2}
# "velocity": gym.spaces.Discrete(2) #{0,1}
# })
# Multi Binary -> {T,F}^n (x1,x2,x3,...xn), xi {T,F}
# gym.spaces.MultiBinary(3)# (x,y,z), x,y,z = T|F
# Multi Discreto -> {a,a+1,a+2..., b}^m
#gym.spaces.MultiDiscrete([-10,10],[0,1])
# Tuple -> Producto de espacios simples
#gym.spaces.Tuple((gym.spaces.Discrete(3), gym.spaces.Discrete(2)))#{0,1,2}x{0,1}
# prng -> Random Seed
def print_spaces(space):
print(space)
if isinstance(space, Box):#Comprueba si el space subministrado es de tipo Box
print("\n Cota inferior: ", space.low)
print("\n Cota superior: ", space.high)
```
# main
```
sys.argv=['self.py','CartPole-v0'] #Aqui Cambia el nombre para ver el environment
if __name__ == "__main__":
environment = gym.make(sys.argv[1]) ## El usuario debe llamar al script con el nombre del entorno como parámetro
print("Espacio de estados:")
print_spaces(environment.observation_space)
print("Espacio de acciones: ")
print_spaces(environment.action_space)
try:
print("Descripción de las acciones: ", environment.unwrapped.get_action_meanings())
except AttributeError:
pass
```
|
github_jupyter
|
# Inferential Statistics III - Bayesian
## Introduction
In the last two subunits, you've encountered two schools for performing inference from samples. The Frequentist school calls upon a body of theory established over the past couple of centuries or so. Under certain assumptions and conditions, this allows us to calculate what we would expect to see if an experiment were to be repeated again and again and again. The expected value of the average of a sample is one such statistic we can calculate a result for, even if the originating distribution is far from normal. The bootstrap school, on the other hand, literally does (virtually) run that experiment again and again and again and empirically observes the multitude of outcomes. It then empirically calculates a statistic of interest. While this can be for exactly the same statistics that frequentism calculates (e.g. the mean of a sample) this empirical approach can also perform inference on statistics that do not have well known sampling distributions. Because of the requirement to repeat many, many redraws (with replacement) from the sample, this approach only became feasible with modern computing power.
And thus we come to the Bayesian school of inference. Here we frame our probabilities not so much in terms of "how many times would I expect this event to occur if the experiment were to be rerun many times" but rather in terms of "what is my belief in the likelihood of this event occurring?" In a Bayesian probabilistic programming context, we can build models for systems and then let the data tell us how likely certain values for our model parameters are. This can be a very useful way to incorporate prior knowledge and deal with limited data. It can just be more than a _little_ fiddly to produce a good model!
## Medical charge data set
For the final mini-project of the stats unit, you'll once again return tot he medical charge data you've used for the other mini-projects. Previously, we considered whether we believed that the actual average(non-insured) charge had fallen below a certain threshold.
The hospital is now reviewing its financial resiliency plan, which requires a model for revenue under a range of conditions that include the number of patients treated. Its current model is based on a confidence interval for the mean, and scaling that by different numbers of patients for each scenario. This approach has a number of limitations, most acutely the breakdown of the central limit theorem for low patient volumes; the current model does not do a good job of reflecting the variability in revenue you would see as the number of cases drops. A bootstrap approach would return samples of the same size as the original. Taking subsamples would restrict the sampling to the values already present in the original sample and would not do a good job of representing the actual variability you might see. What is needed is a better model of individual charges.
So the problem here is that we want to model the distribution of individual charges and _we also really want to be able to capture our uncertainty about that distribution_ so we can better capture the range of values we might see. This naturally leads us to a powerful, probabilistic approach — we'll use the pymc3 library to perform Bayesian inference.
### Loading the data and performing an initial view
```
import pandas as pd
import numpy as np
import pymc3 as pm
import pymc3 as pm
import pandas as pd
import numpy as np
from numpy.random import seed
import matplotlib.pyplot as plt
from scipy.stats import gamma
# there has been some incompatibilty between theano and numpy, if you encounter
# an error with the latest packages from anaconda, then the included
# package-list-txt should allow you to create a conda environment with compatible
# packages.
medical = pd.read_csv('insurance2.csv')
medical.head()
insurance = medical.charges[medical.insuranceclaim == 1]
no_insurance = medical.charges[medical.insuranceclaim == 0]
n_ins = len(insurance)
n_no_ins = len(no_insurance)
_ = plt.hist(insurance, bins=30, alpha=0.5, label='insurance claim')
_ = plt.hist(no_insurance, bins=30, alpha=0.5, label='not insurance claim')
_ = plt.xlabel('Charge amount')
_ = plt.ylabel('Frequency')
_ = plt.legend()
```
We may suspect from the above that there is some sort of exponential-like distribution at play here. The charges that were not insurance claims seem most like this. The insurance claim charges may possibly be multimodal. The gamma distribution may be applicable and we could test this for the distribution of charges that weren't insurance claims first. Developing our new method for the easiest looking case first is a common and sound approach that can demonstrate a minimum viable solution/product and get, or keep, stakeholders on board.
### Initial parameter estimation
An initial guess for the gamma distribution's $\alpha$ and $\beta$ parameters can be made as described [here](https://wiki.analytica.com/index.php?title=Gamma_distribution).
```
alpha_est = np.mean(no_insurance)**2 / np.var(no_insurance)
beta_est = np.var(no_insurance) / np.mean(no_insurance)
alpha_est, beta_est
```
### Initial simulation
Let's draw the same number of random variates from this distribution and compare to our observed data.
```
seed(47)
no_ins_model_rvs = gamma(alpha_est, scale=beta_est).rvs(n_no_ins)
_ = plt.hist(no_ins_model_rvs, bins=30, alpha=0.5, label='simulated')
_ = plt.hist(no_insurance, bins=30, alpha=0.5, label='observed')
_ = plt.xlabel('Charge amount')
_ = plt.ylabel('Frequency')
_ = plt.legend()
```
Well it doesn't look too bad! We're not a million miles off. But can we do better? We have a plausible form for the distribution of charge amounts and potential values for that distribution's parameters so we can already draw random variates from that distribution to perform simulations. But we don't know if we have a _best_ estimate for the population parameters, and we also only have a single estimate each for $\alpha$ and $\beta$; we aren't capturing our uncertainty in their values. Can we take a Bayesian inference approach to estimate the parameters?
### Creating a PyMC3 model
```
# PyMC3 Gamma seems to use rate = 1/beta
rate_est = 1/beta_est
# Initial parameter estimates we'll use below
alpha_est, rate_est
```
__Q:__ You are now going to create your own PyMC3 model!
1. Use an [exponential](https://docs.pymc.io/api/distributions/continuous.html#pymc3.distributions.continuous.Exponential) prior for alpha. Call this stochastic variable `alpha_`.
2. Similarly, use an exponential prior for the rate ([$1/\beta$](https://wiki.analytica.com/index.php?title=Gamma_distribution)) parameter in PyMC3's [Gamma](https://docs.pymc.io/api/distributions/continuous.html#pymc3.distributions.continuous.Gamma). Call this stochastic variable `rate_` (but it will be supplied as `pm.Gamma`'s `beta` parameter). Hint: to set up a prior with an exponential distribution for $x$ where you have an initial estimate for $x$ of $x_0$, use a scale parameter of $1/x_0$.
5. Create your Gamma distribution with your `alpha_` and `rate_` stochastic variables and the observed data.
6. Perform 10000 draws.
Hint: you may find it helpful to work backwards. Start with your `pm.Gamma`, and note the required stochastic variables `alpha` and `beta`. Then, before that, you need to create those stochastic variables using `pm.Exponential` and the correct parameters.
__A:__
```
with pm.Model() as model:
alpha_ = pm.Exponential('alpha_', 1/alpha_est)
rate_ = pm.Exponential('rate_', 1/rate_est) #beta = 1/rate
no_insurance_charge = pm.Gamma('no_insurance_charge', alpha=alpha_, beta=rate_, observed = no_insurance)
trace = pm.sample(10000)
trace
```
If you get a warning about acceptance probability not matching the target, and that it's around 0.88 when it should be close to 0.8, don't worry. We encourage you to read up on this and see if you can adjust the parameters and/or arguments to pm.sample, but if your model runs without any additional warnings or errors then you should be doing great!
__Q:__ Explore your posteriors for $\alpha$ and $\beta$ (from the trace).
* Calculate the 95% credible interval for $\alpha$ and $\beta$.
* Plot your posterior values of $\alpha$ and $\beta$ (both line plots and histograms).
* Mark your CIs on the histograms.
* Do they look okay? What would bad plots look like?
__A:__
```
#95% Confidence Interval for Alpha:
alpha_mean = np.mean(trace.alpha_)
print(f"Alpha Mean is {alpha_mean}")
confi_alpha_lower, confi_alpha_upper= np.percentile(trace.alpha_, [2.5, 97.5])
print(f"Confidence Intreval for Alpha is {confi_alpha_lower} & {confi_alpha_upper}")
#95% Confidence Interval for Beta:
beta_mean = 1/np.mean(trace.rate_) #Beta mean = 1/rate mean
print(f"Beta Mean is {beta_mean}")
confi_beta_lower, confi_beta_upper = 1/np.percentile(trace.rate_, [2.5, 97.5])
print(f"Confidence Interval for Beta is {confi_beta_lower} and {confi_beta_upper}")
#Histogram and Line plots for Alpha Posterior Values:
_ = plt.hist(trace.alpha_, bins = 30, edgecolor = 'black')
_ = plt.axvline(alpha_mean, color= 'red')
_ = plt.axvline(confi_alpha_lower, color = 'gold', linestyle= '-.')
_ = plt.axvline(confi_alpha_upper, color = 'gold', linestyle= '-.')
_ = plt.xlabel('Alpha_')
_ = plt.ylabel('Count')
_ = plt.title('Alpha Posterior Values')
#Histogram and Line Plots for Beta Posterior Values:
_ = plt.hist(1/trace.rate_, bins = 30, edgecolor = 'black')
_ = plt.axvline(beta_mean, color= 'red')
_ = plt.axvline(confi_beta_lower, color = 'gold', linestyle= '-.')
_ = plt.axvline(confi_beta_upper, color = 'gold', linestyle= '-.')
_ = plt.xlabel('Beta_')
_ = plt.ylabel('Count')
_ = plt.title('Beta Posterior Values')
```
__Q:__ Play around with some of the built-in diagnostic plots for your model. We suggest at least checking out the traceplot for alpha and beta. How do they look?
__A:__
```
#TracePlot:
_ = pm.traceplot(trace)
```
Traceplots for alpha and beta looks similar
__Q:__ Take your best shot at a new simulated sequence of medical charges using scipy.stat's gamma distribution. Don't forget the difference between functions that take $\beta$ and functions that use $1/\beta$ for the scale parameter. Simulate a data set the same size as the number of observations in the data and overlay the two histograms (simulated and observed).
__A:__
```
#Using Scipy Stats:
seed(47)
best_shot_simulated = gamma(alpha_mean, scale = beta_mean).rvs(n_no_ins)
#Overlay Histogram:
_ = plt.hist(best_shot_simulated, bins=30, alpha = 0.5, label ='Simulated')
_ = plt.hist(no_insurance, bins = 30, alpha = 0.5, label = 'Observed')
_ = plt.legend()
_ = plt.xlabel('Non Insured Charges')
_ = plt.ylabel('Count')
_ = plt.title('Overlay of Simluated and Observed Non Insured Charges')
```
Similar to initial simulation
## Summary
In this exercise, we have postulated a distribution to describe the individual charge amounts for non-insured cases. This distribution has two required parameters, which we do not know, but we used PyMC3 to perform Bayesian inference to find our level of "belief" in a range of values for them. We then used the average parameter values to create one simulated data set of the same size as the original, but the distribution of our posteriors for these parameters will allow us to perform simulations of any sample size we desire and for a range of scenarios of different $\alpha$ and $\beta$. This could be a powerful tool to model different financial conditions for the hospital.
Well done making it through this tricky subject. Starting think Bayesian _and_ starting to get to grips with something like PyMC3 is no easy task. As a data scientist, the most important thing is to be aware that this statistical approach exists, though you may not actually use this approach as much as you use the other approaches you've learned about. Still, we encourage you to think of ways that this approach could apply to the work that you do in this course and throughout your career.
|
github_jupyter
|
# Gated PixelCNN receptive fields
Hi everybody!
In this notebook, we will analyse the Gated PixelCNN's block receptive field. Diferent of the original PixelCNN, we expect that the blocks of the Gated PixelCNN do not create blind spots that limit the information flow of the previous pixel in order to model the density probability function.
Let's start!
First, we define the masked convolutions involved in the Gated PixelCNN as presented in the post.
*Note: Here we are using float64 to get more precise values of the gradients and avoid false values.
```
import random as rn
import matplotlib
import matplotlib.pyplot as plt
from matplotlib.ticker import FixedLocator
import numpy as np
import tensorflow as tf
from tensorflow import keras
from tensorflow import nn
from tensorflow.keras import initializers
from tensorflow.keras.utils import Progbar
tf.keras.backend.set_floatx('float64')
class MaskedConv2D(keras.layers.Layer):
"""Convolutional layers with masks extended to work with Gated PixelCNN.
Convolutional layers with simple implementation of masks type A and B for
autoregressive models. Extended version to work with the verticala and horizontal
stacks from the Gated PixelCNN model.
Arguments:
mask_type: one of `"V"`, `"A"` or `"B".`
filters: Integer, the dimensionality of the output space (i.e. the number of output
filters in the convolution).
kernel_size: An integer or tuple/list of 2 integers, specifying the height and width
of the 2D convolution window.
Can be a single integer to specify the same value for all spatial dimensions.
strides: An integer or tuple/list of 2 integers, specifying the strides of the
convolution along the height and width.
Can be a single integer to specify the same value for all spatial dimensions.
Specifying any stride value != 1 is incompatible with specifying any
`dilation_rate` value != 1.
padding: one of `"valid"` or `"same"` (case-insensitive).
kernel_initializer: Initializer for the `kernel` weights matrix.
bias_initializer: Initializer for the bias vector.
"""
def __init__(self,
mask_type,
filters,
kernel_size,
strides=1,
padding='same',
kernel_initializer='glorot_uniform',
bias_initializer='zeros'):
super(MaskedConv2D, self).__init__()
assert mask_type in {'A', 'B', 'V'}
self.mask_type = mask_type
self.filters = filters
if isinstance(kernel_size, int):
kernel_size = (kernel_size, kernel_size)
self.kernel_size = kernel_size
self.strides = strides
self.padding = padding.upper()
self.kernel_initializer = initializers.get(kernel_initializer)
self.bias_initializer = initializers.get(bias_initializer)
def build(self, input_shape):
kernel_h, kernel_w = self.kernel_size
self.kernel = self.add_weight('kernel',
shape=(kernel_h,
kernel_w,
int(input_shape[-1]),
self.filters),
initializer=self.kernel_initializer,
trainable=True)
self.bias = self.add_weight('bias',
shape=(self.filters,),
initializer=self.bias_initializer,
trainable=True)
mask = np.ones(self.kernel.shape, dtype=np.float64)
# Get centre of the filter for even or odd dimensions
if kernel_h % 2 != 0:
center_h = kernel_h // 2
else:
center_h = (kernel_h - 1) // 2
if kernel_w % 2 != 0:
center_w = kernel_w // 2
else:
center_w = (kernel_w - 1) // 2
if self.mask_type == 'V':
mask[center_h + 1:, :, :, :] = 0.
else:
mask[:center_h, :, :] = 0.
mask[center_h, center_w + (self.mask_type == 'B'):, :, :] = 0.
mask[center_h + 1:, :, :] = 0.
self.mask = tf.constant(mask, dtype=tf.float64, name='mask')
def call(self, input):
masked_kernel = tf.math.multiply(self.mask, self.kernel)
x = nn.conv2d(input,
masked_kernel,
strides=[1, self.strides, self.strides, 1],
padding=self.padding)
x = nn.bias_add(x, self.bias)
return x
```
Then, we define th eblock implementation.
```
class GatedBlock(tf.keras.Model):
""" Gated block that compose Gated PixelCNN."""
def __init__(self, mask_type, filters, kernel_size):
super(GatedBlock, self).__init__(name='')
self.mask_type = mask_type
self.vertical_conv = MaskedConv2D(mask_type='V',
filters=2 * filters,
kernel_size=kernel_size)
self.horizontal_conv = MaskedConv2D(mask_type=mask_type,
filters=2 * filters,
kernel_size=(1, kernel_size))
self.padding = keras.layers.ZeroPadding2D(padding=((1, 0), 0))
self.cropping = keras.layers.Cropping2D(cropping=((0, 1), 0))
self.v_to_h_conv = keras.layers.Conv2D(filters=2 * filters, kernel_size=1)
self.horizontal_output = keras.layers.Conv2D(filters=filters, kernel_size=1)
def _gate(self, x):
tanh_preactivation, sigmoid_preactivation = tf.split(x, 2, axis=-1)
return tf.nn.tanh(tanh_preactivation) * tf.nn.sigmoid(sigmoid_preactivation)
def call(self, input_tensor):
v = input_tensor[0]
h = input_tensor[1]
vertical_preactivation = self.vertical_conv(v)
# Shifting vertical stack feature map down before feed into horizontal stack to
# ensure causality
v_to_h = self.padding(vertical_preactivation)
v_to_h = self.cropping(v_to_h)
v_to_h = self.v_to_h_conv(v_to_h)
horizontal_preactivation = self.horizontal_conv(h)
v_out = self._gate(vertical_preactivation)
horizontal_preactivation = horizontal_preactivation + v_to_h
h_activated = self._gate(horizontal_preactivation)
h_activated = self.horizontal_output(h_activated)
if self.mask_type == 'A':
h_out = h_activated
elif self.mask_type == 'B':
h_out = h + h_activated
return v_out, h_out
```
In order to analyse grow the receptive field grows along the layers, we will start analysing 1 block.
```
height = 10
width = 10
n_channel = 1
data = tf.random.normal((1, height, width, n_channel))
inputs = keras.layers.Input(shape=(height, width, n_channel))
v, h = GatedBlock(mask_type='A', filters=1, kernel_size=3)([inputs, inputs])
model = tf.keras.Model(inputs=inputs, outputs=h)
def plot_receptive_field(model, data):
with tf.GradientTape() as tape:
tape.watch(data)
prediction = model(data)
loss = prediction[:,5,5,0]
gradients = tape.gradient(loss, data)
gradients = np.abs(gradients.numpy().squeeze())
gradients = (gradients > 0).astype('float64')
gradients[5, 5] = 0.5
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
plt.xticks(np.arange(0, 10, step=1))
plt.yticks(np.arange(0, 10, step=1))
ax.xaxis.set_minor_locator(FixedLocator(np.arange(0.5, 10.5, step=1)))
ax.yaxis.set_minor_locator(FixedLocator(np.arange(0.5, 10.5, step=1)))
plt.grid(which="minor")
plt.imshow(gradients, vmin=0, vmax=1)
plt.show()
plot_receptive_field(model, data)
```
Excellent! Like we expected the block considered all the previous blocks in the same row of the analyssed pixel, and the two rows over it.
Note that this receptive field is different from the original PixelCNN. In the original PixelCNN only one row over the analysed pixel influenced in its prediction (when using one masked convolution). In the Gated PixelCNN, the authors used a vertical stack with effective area of 2x3 per vertical convolution. This is not a problem, since the considered pixels still being the ones in past positions. We believe the main coice for this format is to implement an efficient way to apply the masked convolutions without using masking (which we will discuss in future posts).
For the next step, we wll verify a model with 2, 3, 4, and 5 layers
```
inputs = keras.layers.Input(shape=(height, width, n_channel))
v, h = GatedBlock(mask_type='A', filters=1, kernel_size=3)([inputs, inputs])
v, h = GatedBlock(mask_type='B', filters=1, kernel_size=3)([v, h])
model = tf.keras.Model(inputs=inputs, outputs=h)
plot_receptive_field(model, data)
inputs = keras.layers.Input(shape=(height, width, n_channel))
v, h = GatedBlock(mask_type='A', filters=1, kernel_size=3)([inputs, inputs])
v, h = GatedBlock(mask_type='B', filters=1, kernel_size=3)([v, h])
v, h = GatedBlock(mask_type='B', filters=1, kernel_size=3)([v, h])
model = tf.keras.Model(inputs=inputs, outputs=h)
plot_receptive_field(model, data)
inputs = keras.layers.Input(shape=(height, width, n_channel))
v, h = GatedBlock(mask_type='A', filters=1, kernel_size=3)([inputs, inputs])
v, h = GatedBlock(mask_type='B', filters=1, kernel_size=3)([v, h])
v, h = GatedBlock(mask_type='B', filters=1, kernel_size=3)([v, h])
v, h = GatedBlock(mask_type='B', filters=1, kernel_size=3)([v, h])
model = tf.keras.Model(inputs=inputs, outputs=h)
plot_receptive_field(model, data)
inputs = keras.layers.Input(shape=(height, width, n_channel))
v, h = GatedBlock(mask_type='A', filters=1, kernel_size=3)([inputs, inputs])
v, h = GatedBlock(mask_type='B', filters=1, kernel_size=3)([v, h])
v, h = GatedBlock(mask_type='B', filters=1, kernel_size=3)([v, h])
v, h = GatedBlock(mask_type='B', filters=1, kernel_size=3)([v, h])
v, h = GatedBlock(mask_type='B', filters=1, kernel_size=3)([v, h])
model = tf.keras.Model(inputs=inputs, outputs=h)
plot_receptive_field(model, data)
```
As you can notice, the Gated PixelCNN does not create blind spots when adding more and more layers.
|
github_jupyter
|
<img src='https://certificate.tpq.io/quantsdev_banner_color.png' width="250px" align="right">
# Reinforcement Learning
© Dr Yves J Hilpisch | The Python Quants GmbH
[quants@dev Discord Server](https://discord.gg/uJPtp9Awaj) | [@quants_dev](https://twitter.com/quants_dev) | <a href="mailto:[email protected]">[email protected]</a>
<img src="https://hilpisch.com/aiif_cover_shadow.png" width="300px" align="left">
## Imports
```
import os
import math
import random
import numpy as np
import pandas as pd
from pylab import plt, mpl
plt.style.use('seaborn')
mpl.rcParams['font.family'] = 'serif'
np.set_printoptions(precision=4, suppress=True)
os.environ['PYTHONHASHSEED'] = '0'
%config InlineBackend.figure_format = 'svg'
import warnings as w
w.simplefilter('ignore')
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '4'
import tensorflow as tf
from tensorflow import keras
from keras.layers import Dense, Dropout
from keras.models import Sequential
from sklearn.metrics import accuracy_score
from tensorflow.python.framework.ops import disable_eager_execution
disable_eager_execution()
def set_seeds(seed=100):
random.seed(seed)
np.random.seed(seed)
tf.random.set_seed(seed)
env.seed(seed)
env.action_space.seed(100)
```
## Improved Finance Environment
```
class observation_space:
def __init__(self, n):
self.shape = (n,)
class action_space:
def __init__(self, n):
self.n = n
def seed(self, seed):
pass
def sample(self):
return random.randint(0, self.n - 1)
class Finance:
url = 'http://hilpisch.com/aiif_eikon_eod_data.csv'
def __init__(self, symbol, features, window, lags,
leverage=1, min_performance=0.85,
start=0, end=None, mu=None, std=None):
self.symbol = symbol
self.features = features
self.n_features = len(features)
self.window = window
self.lags = lags
self.leverage = leverage
self.min_performance = min_performance
self.start = start
self.end = end
self.mu = mu
self.std = std
self.observation_space = observation_space(self.lags)
self.action_space = action_space(2)
self._get_data()
self._prepare_data()
def _get_data(self):
self.raw = pd.read_csv(self.url, index_col=0,
parse_dates=True).dropna()
def _prepare_data(self):
self.data = pd.DataFrame(self.raw[self.symbol])
self.data = self.data.iloc[self.start:]
self.data['r'] = np.log(self.data / self.data.shift(1))
self.data.dropna(inplace=True)
self.data['s'] = self.data[self.symbol].rolling(
self.window).mean()
self.data['m'] = self.data['r'].rolling(self.window).mean()
self.data['v'] = self.data['r'].rolling(self.window).std()
self.data.dropna(inplace=True)
if self.mu is None:
self.mu = self.data.mean()
self.std = self.data.std()
self.data_ = (self.data - self.mu) / self.std
self.data_['d'] = np.where(self.data['r'] > 0, 1, 0)
self.data_['d'] = self.data_['d'].astype(int)
if self.end is not None:
self.data = self.data.iloc[:self.end - self.start]
self.data_ = self.data_.iloc[:self.end - self.start]
def _get_state(self):
return self.data_[self.features].iloc[self.bar -
self.lags:self.bar]
def seed(self, seed):
random.seed(seed)
np.random.seed(seed)
def reset(self):
self.treward = 0
self.accuracy = 0
self.performance = 1
self.bar = self.lags
state = self.data_[self.features].iloc[self.bar-
self.lags:self.bar]
return state.values
def step(self, action):
correct = action == self.data_['d'].iloc[self.bar]
ret = self.data['r'].iloc[self.bar] * self.leverage
reward_1 = 1 if correct else 0
reward_2 = abs(ret) if correct else -abs(ret)
self.treward += reward_1
self.bar += 1
self.accuracy = self.treward / (self.bar - self.lags)
self.performance *= math.exp(reward_2)
if self.bar >= len(self.data):
done = True
elif reward_1 == 1:
done = False
elif (self.performance < self.min_performance and
self.bar > self.lags + 15):
done = True
else:
done = False
state = self._get_state()
info = {}
return state.values, reward_1 + reward_2 * 252, done, info
env = Finance('EUR=', ['EUR=', 'r', 'v'], window=10, lags=5)
a = env.action_space.sample()
a
env.reset()
env.step(a)
```
## Improved Financial QL Agent
```
from collections import deque
class FQLAgent:
def __init__(self, hidden_units, learning_rate, learn_env, valid_env, dropout=True):
self.learn_env = learn_env
self.valid_env = valid_env
self.dropout = dropout
self.epsilon = 1.0
self.epsilon_min = 0.1
self.epsilon_decay = 0.98
self.learning_rate = learning_rate
self.gamma = 0.95
self.batch_size = 128
self.max_treward = 0
self.trewards = list()
self.averages = list()
self.performances = list()
self.aperformances = list()
self.vperformances = list()
self.memory = deque(maxlen=2000)
self.model = self._build_model(hidden_units, learning_rate)
def _build_model(self, hu, lr):
model = Sequential()
model.add(Dense(hu, input_shape=(
self.learn_env.lags, self.learn_env.n_features),
activation='relu'))
if self.dropout:
model.add(Dropout(0.3, seed=100))
model.add(Dense(hu, activation='relu'))
if self.dropout:
model.add(Dropout(0.3, seed=100))
model.add(Dense(2, activation='linear'))
model.compile(
loss='mse',
optimizer=keras.optimizers.RMSprop(learning_rate=lr)
)
return model
def act(self, state):
if random.random() <= self.epsilon:
return self.learn_env.action_space.sample()
action = self.model.predict(state)[0, 0]
return np.argmax(action)
def replay(self):
batch = random.sample(self.memory, self.batch_size)
for state, action, reward, next_state, done in batch:
if not done:
reward += self.gamma * np.amax(
self.model.predict(next_state)[0, 0])
target = self.model.predict(state)
target[0, 0, action] = reward
self.model.fit(state, target, epochs=1,
verbose=False)
if self.epsilon > self.epsilon_min:
self.epsilon *= self.epsilon_decay
def learn(self, episodes):
for e in range(1, episodes + 1):
state = self.learn_env.reset()
state = np.reshape(state, [1, self.learn_env.lags,
self.learn_env.n_features])
for _ in range(10000):
action = self.act(state)
next_state, reward, done, info = \
self.learn_env.step(action)
next_state = np.reshape(next_state,
[1, self.learn_env.lags,
self.learn_env.n_features])
self.memory.append([state, action, reward,
next_state, done])
state = next_state
if done:
treward = _ + 1
self.trewards.append(treward)
av = sum(self.trewards[-25:]) / 25
perf = self.learn_env.performance
self.averages.append(av)
self.performances.append(perf)
self.aperformances.append(
sum(self.performances[-25:]) / 25)
self.max_treward = max(self.max_treward, treward)
templ = 'episode: {:2d}/{} | treward: {:4d} | '
templ += 'perf: {:5.3f} | av: {:5.1f} | max: {:4d}'
print(templ.format(e, episodes, treward, perf,
av, self.max_treward), end='\r')
break
self.validate(e, episodes)
if len(self.memory) > self.batch_size:
self.replay()
print()
def validate(self, e, episodes):
state = self.valid_env.reset()
state = np.reshape(state, [1, self.valid_env.lags,
self.valid_env.n_features])
for _ in range(10000):
action = np.argmax(self.model.predict(state)[0, 0])
next_state, reward, done, info = self.valid_env.step(action)
state = np.reshape(next_state, [1, self.valid_env.lags,
self.valid_env.n_features])
if done:
treward = _ + 1
perf = self.valid_env.performance
self.vperformances.append(perf)
if e % 20 == 0:
templ = 71 * '='
templ += '\nepisode: {:2d}/{} | VALIDATION | '
templ += 'treward: {:4d} | perf: {:5.3f} | '
templ += 'eps: {:.2f}\n'
templ += 71 * '='
print(templ.format(e, episodes, treward,
perf, self.epsilon))
break
symbol = 'EUR='
features = ['r', 's', 'm', 'v']
a = 0
b = 2000
c = 500
learn_env = Finance(symbol, features, window=10, lags=6,
leverage=1, min_performance=0.85,
start=a, end=a + b, mu=None, std=None)
learn_env.data.info()
valid_env = Finance(symbol, features, window=learn_env.window,
lags=learn_env.lags, leverage=learn_env.leverage,
min_performance=learn_env.min_performance,
start=a + b, end=a + b + c,
mu=learn_env.mu, std=learn_env.std)
valid_env.data.info()
set_seeds(100)
agent = FQLAgent(48, 0.0001, learn_env, valid_env, True)
episodes = 61
%time agent.learn(episodes)
agent.epsilon
plt.figure(figsize=(10, 6))
x = range(1, len(agent.averages) + 1)
y = np.polyval(np.polyfit(x, agent.averages, deg=3), x)
plt.plot(agent.averages, label='moving average')
plt.plot(x, y, 'r--', label='regression')
plt.xlabel('episodes')
plt.ylabel('total reward')
plt.legend();
plt.figure(figsize=(10, 6))
x = range(1, len(agent.performances) + 1)
y = np.polyval(np.polyfit(x, agent.performances, deg=3), x)
y_ = np.polyval(np.polyfit(x, agent.vperformances, deg=3), x)
plt.plot(agent.performances[:], label='training')
plt.plot(agent.vperformances[:], label='validation')
plt.plot(x, y, 'r--', label='regression (train)')
plt.plot(x, y_, 'r-.', label='regression (valid)')
plt.xlabel('episodes')
plt.ylabel('gross performance')
plt.legend();
```
<img src="https://certificate.tpq.io/quantsdev_banner_color.png" alt="quants@dev" width="35%" align="right" border="0"><br>
[quants@dev Discord Server](https://discord.gg/uJPtp9Awaj) | [@quants_dev](https://twitter.com/quants_dev) | <a href="mailto:[email protected]">[email protected]</a>
|
github_jupyter
|
# The importance of constraints
Constraints determine which potential adversarial examples are valid inputs to the model. When determining the efficacy of an attack, constraints are everything. After all, an attack that looks very powerful may just be generating nonsense. Or, perhaps more nefariously, an attack may generate a real-looking example that changes the original label of the input. That's why you should always clearly define the *constraints* your adversarial examples must meet.
[](https://colab.research.google.com/github/QData/TextAttack/blob/master/docs/2notebook/2_Constraints.ipynb)
[](https://github.com/QData/TextAttack/blob/master/docs/2notebook/2_Constraints.ipynb)
### Classes of constraints
TextAttack evaluates constraints using methods from three groups:
- **Overlap constraints** determine if a perturbation is valid based on character-level analysis. For example, some attacks are constrained by edit distance: a perturbation is only valid if it perturbs some small number of characters (or fewer).
- **Grammaticality constraints** filter inputs based on syntactical information. For example, an attack may require that adversarial perturbations do not introduce grammatical errors.
- **Semantic constraints** try to ensure that the perturbation is semantically similar to the original input. For example, we may design a constraint that uses a sentence encoder to encode the original and perturbed inputs, and enforce that the sentence encodings be within some fixed distance of one another. (This is what happens in subclasses of `textattack.constraints.semantics.sentence_encoders`.)
### A new constraint
To add our own constraint, we need to create a subclass of `textattack.constraints.Constraint`. We can implement one of two functions, either `_check_constraint` or `_check_constraint_many`:
- `_check_constraint` determines whether candidate `TokenizedText` `transformed_text`, transformed from `current_text`, fulfills a desired constraint. It returns either `True` or `False`.
- `_check_constraint_many` determines whether each of a list of candidates `transformed_texts` fulfill the constraint relative to `current_text`. This is here in case your constraint can be vectorized. If not, just implement `_check_constraint`, and `_check_constraint` will be executed for each `(transformed_text, current_text)` pair.
### A custom constraint
For fun, we're going to see what happens when we constrain an attack to only allow perturbations that substitute out a named entity for another. In linguistics, a **named entity** is a proper noun, the name of a person, organization, location, product, etc. Named Entity Recognition is a popular NLP task (and one that state-of-the-art models can perform quite well).
### NLTK and Named Entity Recognition
**NLTK**, the Natural Language Toolkit, is a Python package that helps developers write programs that process natural language. NLTK comes with predefined algorithms for lots of linguistic tasks– including Named Entity Recognition.
First, we're going to write a constraint class. In the `_check_constraints` method, we're going to use NLTK to find the named entities in both `current_text` and `transformed_text`. We will only return `True` (that is, our constraint is met) if `transformed_text` has substituted one named entity in `current_text` for another.
Let's import NLTK and download the required modules:
```
import nltk
nltk.download('punkt') # The NLTK tokenizer
nltk.download('maxent_ne_chunker') # NLTK named-entity chunker
nltk.download('words') # NLTK list of words
```
### NLTK NER Example
Here's an example of using NLTK to find the named entities in a sentence:
```
sentence = ('In 2017, star quarterback Tom Brady led the Patriots to the Super Bowl, '
'but lost to the Philadelphia Eagles.')
# 1. Tokenize using the NLTK tokenizer.
tokens = nltk.word_tokenize(sentence)
# 2. Tag parts of speech using the NLTK part-of-speech tagger.
tagged = nltk.pos_tag(tokens)
# 3. Extract entities from tagged sentence.
entities = nltk.chunk.ne_chunk(tagged)
print(entities)
```
It looks like `nltk.chunk.ne_chunk` gives us an `nltk.tree.Tree` object where named entities are also `nltk.tree.Tree` objects within that tree. We can take this a step further and grab the named entities from the tree of entities:
```
# 4. Filter entities to just named entities.
named_entities = [entity for entity in entities if isinstance(entity, nltk.tree.Tree)]
print(named_entities)
```
### Caching with `@functools.lru_cache`
A little-known feature of Python 3 is `functools.lru_cache`, a decorator that allows users to easily cache the results of a function in an LRU cache. We're going to be using the NLTK library quite a bit to tokenize, parse, and detect named entities in sentences. These sentences might repeat themselves. As such, we'll use this decorator to cache named entities so that we don't have to perform this expensive computation multiple times.
### Putting it all together: getting a list of Named Entity Labels from a sentence
Now that we know how to tokenize, parse, and detect named entities using NLTK, let's put it all together into a single helper function. Later, when we implement our constraint, we can query this function to easily get the entity labels from a sentence. We can even use `@functools.lru_cache` to try and speed this process up.
```
import functools
@functools.lru_cache(maxsize=2**14)
def get_entities(sentence):
tokens = nltk.word_tokenize(sentence)
tagged = nltk.pos_tag(tokens)
# Setting `binary=True` makes NLTK return all of the named
# entities tagged as NNP instead of detailed tags like
#'Organization', 'Geo-Political Entity', etc.
entities = nltk.chunk.ne_chunk(tagged, binary=True)
return entities.leaves()
```
And let's test our function to make sure it works:
```
sentence = 'Jack Black starred in the 2003 film classic "School of Rock".'
get_entities(sentence)
```
We flattened the tree of entities, so the return format is a list of `(word, entity type)` tuples. For non-entities, the `entity_type` is just the part of speech of the word. `'NNP'` is the indicator of a named entity (a proper noun, according to NLTK). Looks like we identified three named entities here: 'Jack' and 'Black', 'School', and 'Rock'. as a 'GPE'. (Seems that the labeler thinks Rock is the name of a place, a city or something.) Whatever technique NLTK uses for named entity recognition may be a bit rough, but it did a pretty decent job here!
### Creating our NamedEntityConstraint
Now that we know how to detect named entities using NLTK, let's create our custom constraint.
```
from textattack.constraints import Constraint
class NamedEntityConstraint(Constraint):
""" A constraint that ensures `transformed_text` only substitutes named entities from `current_text` with other named entities.
"""
def _check_constraint(self, transformed_text, current_text):
transformed_entities = get_entities(transformed_text.text)
current_entities = get_entities(current_text.text)
# If there aren't named entities, let's return False (the attack
# will eventually fail).
if len(current_entities) == 0:
return False
if len(current_entities) != len(transformed_entities):
# If the two sentences have a different number of entities, then
# they definitely don't have the same labels. In this case, the
# constraint is violated, and we return False.
return False
else:
# Here we compare all of the words, in order, to make sure that they match.
# If we find two words that don't match, this means a word was swapped
# between `current_text` and `transformed_text`. That word must be a named entity to fulfill our
# constraint.
current_word_label = None
transformed_word_label = None
for (word_1, label_1), (word_2, label_2) in zip(current_entities, transformed_entities):
if word_1 != word_2:
# Finally, make sure that words swapped between `x` and `x_adv` are named entities. If
# they're not, then we also return False.
if (label_1 not in ['NNP', 'NE']) or (label_2 not in ['NNP', 'NE']):
return False
# If we get here, all of the labels match up. Return True!
return True
```
### Testing our constraint
We need to create an attack and a dataset to test our constraint on. We went over all of this in the transformations tutorial, so let's gloss over this part for now.
```
# Import the model
import transformers
from textattack.models.tokenizers import AutoTokenizer
from textattack.models.wrappers import HuggingFaceModelWrapper
model = transformers.AutoModelForSequenceClassification.from_pretrained("textattack/albert-base-v2-yelp-polarity")
tokenizer = AutoTokenizer("textattack/albert-base-v2-yelp-polarity")
model_wrapper = HuggingFaceModelWrapper(model, tokenizer)
# Create the goal function using the model
from textattack.goal_functions import UntargetedClassification
goal_function = UntargetedClassification(model_wrapper)
# Import the dataset
from textattack.datasets import HuggingFaceDataset
dataset = HuggingFaceDataset("yelp_polarity", None, "test")
from textattack.transformations import WordSwapEmbedding
from textattack.search_methods import GreedySearch
from textattack.shared import Attack
from textattack.constraints.pre_transformation import RepeatModification, StopwordModification
# We're going to the `WordSwapEmbedding` transformation. Using the default settings, this
# will try substituting words with their neighbors in the counter-fitted embedding space.
transformation = WordSwapEmbedding(max_candidates=15)
# We'll use the greedy search method again
search_method = GreedySearch()
# Our constraints will be the same as Tutorial 1, plus the named entity constraint
constraints = [RepeatModification(),
StopwordModification(),
NamedEntityConstraint(False)]
# Now, let's make the attack using these parameters.
attack = Attack(goal_function, constraints, transformation, search_method)
print(attack)
```
Now, let's use our attack. We're going to attack samples until we achieve 5 successes. (There's a lot to check here, and since we're using a greedy search over all potential word swap positions, each sample will take a few minutes. This will take a few hours to run on a single core.)
```
from textattack.loggers import CSVLogger # tracks a dataframe for us.
from textattack.attack_results import SuccessfulAttackResult
results_iterable = attack.attack_dataset(dataset)
logger = CSVLogger(color_method='html')
num_successes = 0
while num_successes < 5:
result = next(results_iterable)
if isinstance(result, SuccessfulAttackResult):
logger.log_attack_result(result)
num_successes += 1
print(f'{num_successes} of 5 successes complete.')
```
Now let's visualize our 5 successes in color:
```
import pandas as pd
pd.options.display.max_colwidth = 480 # increase column width so we can actually read the examples
from IPython.core.display import display, HTML
display(HTML(logger.df[['original_text', 'perturbed_text']].to_html(escape=False)))
```
### Conclusion
Our constraint seems to have done its job: it filtered out attacks that did not swap out a named entity for another, according to the NLTK named entity detector. However, we can see some problems inherent in the detector: it often thinks the first word of a given sentence is a named entity, probably due to capitalization.
We did manage to produce some nice adversarial examples! "Sigh" beacame "Inahles" and the prediction shifted from negative to positive.
|
github_jupyter
|
```
import os
import glob
import pandas as pd
import numpy as np
from tqdm import tqdm
import pickle
from copy import copy
sources_with_data_text = os.path.join('data', 'sources_with_data.txt')
with open (sources_with_data_text, mode='r') as f:
lines = f.readlines()
#check we closed the file
assert f.closed
#strip the spaces at the end
lines = [l.strip() for l in lines]
#keep only CVEs and drop the rest
lines = [l for l in lines if 'CVE' in l]
unique_cve = (set(lines))
print("Found {} unique CVEs in {}".format(len(unique_cve), sources_with_data_text))
def load_obj(path ):
with open(path, 'rb') as f:
return pickle.load(f)
#create list of dicts
broadcom_arr=[]
for file in tqdm(glob.glob('broadcom_dicts/*.pkl')):
obj = load_obj(file)
#if array is not empty
if obj['CVE']:
broadcom_arr.extend(obj['CVE'])
broadcom_cve = (set(broadcom_arr))
print("Found {} unique CVEs in {}".format(len(broadcom_cve), 'broadcom dicts'))
cve_in_wild = copy(broadcom_cve)
cve_in_wild.update(unique_cve)
#cve_in_wild = list(cve_in_wild)
print("Found {} unique CVEs overll".format(len(cve_in_wild)))
#fix some inconsistencies in data collection
#manual fixes
cve_in_wild = [cve.replace('1)', '') for cve in cve_in_wild]
cve_in_wild = [cve.replace('service', '') for cve in cve_in_wild]
cve_in_wild = [cve.replace('3)', '') for cve in cve_in_wild]
cve_in_wild = [cve.replace('_3', '') for cve in cve_in_wild]
cve_in_wild = [cve for cve in cve_in_wild if len(cve)>=11]
cve_in_wild = [cve.replace('(', '') for cve in cve_in_wild]
cve_in_wild = [cve.replace(')', '') for cve in cve_in_wild]
## more manual fixes to corrupted data
cve_in_wild = [cve.replace('CVE2019-7278', 'CVE-2019-7278') for cve in cve_in_wild]
cve_in_wild = [cve.replace('2CVE-2006-3643', 'CVE-2006-3643') for cve in cve_in_wild]
cve_in_wild = [cve.replace('CVE2019-7279', 'CVE-2019-7279') for cve in cve_in_wild]
cve_in_wild = [cve.replace('CVE-2018_16858', 'CVE-2018-16858') for cve in cve_in_wild]
cve_in_wild = [cve.replace('CVE 2014-6278', 'CVE-2014-6278') for cve in cve_in_wild]
cve_in_wild = [cve.replace('CVE-209-18935', 'CVE-2019-18935') for cve in cve_in_wild]
cve_in_wild = [cve.replace('CVE_2009-3729', 'CVE-2009-3729') for cve in cve_in_wild]
cve_in_wild = [cve.replace('CVE-20190-11539', 'CVE-2019-11539') for cve in cve_in_wild]
cve_in_wild = [cve.replace('CVE-2190-11539', 'CVE-2019-11539') for cve in cve_in_wild]
dates = set([x.split('-')[1] for x in cve_in_wild])
for x in cve_in_wild:
if '2190' in x:
print(x)
dates
print("First exploit was recorded in {}".format(min(dates)))
print("Last exploit was recorded in {}".format(max(dates)))
target_cve_dict = {}
df_nvd = pd.read_csv(os.path.join('data', 'nvdcve_combined.csv'))
for cve in df_nvd['ID']:
if cve in cve_in_wild:
target_cve_dict[cve] = 1
else:
target_cve_dict[cve] = 0
df_target = pd.DataFrame.from_dict(target_cve_dict, orient='index', columns=['in_the_wild'])
df_target['ID'] = df_target.index
df_target = df_target.reset_index(drop=True)
#rearrange
df_target = df_target[['ID', 'in_the_wild']]
df_target.head()
df_target['in_the_wild'].mean()
dates = []
```
|
github_jupyter
|
<script async src="https://www.googletagmanager.com/gtag/js?id=UA-59152712-8"></script>
<script>
window.dataLayer = window.dataLayer || [];
function gtag(){dataLayer.push(arguments);}
gtag('js', new Date());
gtag('config', 'UA-59152712-8');
</script>
# `GiRaFFE_NRPy`: Main Driver
## Author: Patrick Nelson
<a id='intro'></a>
**Notebook Status:** <font color=Red><b> Validation in progress </b></font>
**Validation Notes:** This code assembles the various parts needed for GRFFE evolution in order.
### NRPy+ Source Code for this module:
* [GiRaFFE_NRPy/GiRaFFE_NRPy_Main_Driver.py](../../edit/in_progress/GiRaFFE_NRPy/GiRaFFE_NRPy_Main_Driver.py)
### Other critical files (in alphabetical order):
* [GiRaFFE_NRPy/Afield_flux.py](../../edit/in_progress/GiRaFFE_NRPy/Afield_flux.py) [\[**tutorial**\]](Tutorial-GiRaFFE_NRPy-Afield_flux.ipynb) Generates the expressions to find the flux term of the induction equation.
* [GiRaFFE_NRPy/GiRaFFE_NRPy_A2B.py](../../edit/in_progress/GiRaFFE_NRPy/GiRaFFE_NRPy_A2B.py) [\[**tutorial**\]](Tutorial-GiRaFFE_NRPy-A2B.ipynb) Generates the driver to compute the magnetic field from the vector potential/
* [GiRaFFE_NRPy/GiRaFFE_NRPy_BCs.py](../../edit/in_progress/GiRaFFE_NRPy/GiRaFFE_NRPy_BCs.py) [\[**tutorial**\]](Tutorial-GiRaFFE_NRPy-BCs.ipynb) Generates the code to apply boundary conditions to the vector potential, scalar potential, and three-velocity.
* [GiRaFFE_NRPy/GiRaFFE_NRPy_C2P_P2C.py](../../edit/in_progress/GiRaFFE_NRPy/GiRaFFE_NRPy_C2P_P2C.py) [\[**tutorial**\]](Tutorial-GiRaFFE_NRPy-C2P_P2C.ipynb) Generates the conservative-to-primitive and primitive-to-conservative solvers.
* [GiRaFFE_NRPy/GiRaFFE_NRPy_Metric_Face_Values.py](../../edit/in_progress/GiRaFFE_NRPy/GiRaFFE_NRPy_Metric_Face_Values.py) [\[**tutorial**\]](Tutorial-GiRaFFE_NRPy-Metric_Face_Values.ipynb) Generates code to interpolate metric gridfunctions to cell faces.
* [GiRaFFE_NRPy/GiRaFFE_NRPy_PPM.py](../../edit/in_progress/GiRaFFE_NRPy/GiRaFFE_NRPy_PPM.py) [\[**tutorial**\]](Tutorial-GiRaFFE_NRPy-PPM.ipynb) Genearates code to reconstruct primitive variables on cell faces.
* [GiRaFFE_NRPy/GiRaFFE_NRPy_Source_Terms.py](../../edit/in_progress/GiRaFFE_NRPy/GiRaFFE_NRPy_Source_Terms.py) [\[**tutorial**\]](Tutorial-GiRaFFE_NRPy-Source_Terms.ipynb) Genearates code to compute the $\tilde{S}_i$ source term.
* [GiRaFFE_NRPy/Stilde_flux.py](../../edit/in_progress/GiRaFFE_NRPy/Stilde_flux.py) [\[**tutorial**\]](Tutorial-GiRaFFE_NRPy-Stilde_flux.ipynb) Generates the expressions to find the flux term of the Poynting flux evolution equation.
* [../GRFFE/equations.py](../../edit/GRFFE/equations.py) [\[**tutorial**\]](../Tutorial-GRFFE_Equations-Cartesian.ipynb) Generates code necessary to compute the source terms.
* [../GRHD/equations.py](../../edit/GRHD/equations.py) [\[**tutorial**\]](../Tutorial-GRHD_Equations-Cartesian.ipynb) Generates code necessary to compute the source terms.
## Introduction:
Having written all the various algorithms that will go into evolving the GRFFE equations forward through time, we are ready to write a start-to-finish module to do so. However, to help keep things more organized, we will first create a dedicated module to assemble the various functions we need to run, in order, to perform the evolution. This will reduce the length of the standalone C code, improving that notebook's readability.
<a id='prelim'></a>
# Table of Contents
$$\label{prelim}$$
During a given RK substep, we will perform the following steps in this order, based on the order used in the original `GiRaFFE`:
0. [Step 0](#prelim): Preliminaries
1. [Step 1](#rhs): Calculate the right-hand sides
1. [Step 1.a](#parenthetical): Calculate the portion of the gauge terms for $A_k$, $(\alpha \Phi - \beta^j A_j)$ and $\Phi$, $(\alpha\sqrt{\gamma}A^j - \beta^j [\sqrt{\gamma} \Phi])$ *inside* the parentheses to be finite-differenced.
* **GRFFE/equations.py**, **GRHD/equations.py**
1. [Step 1.b](#source): Calculate the source terms of $\partial_t A_i$, $\partial_t \tilde{S}_i$, and $\partial_t [\sqrt{\gamma} \Phi]$ right-hand sides
* **GRFFE/equations.py**, **GRHD/equations.py**, **GiRaFFE_NRPy/GiRaFFE_NRPy_Source_Terms**
1. [Step 1.c](#flux): Calculate the Flux terms
* In each direction:
* Interpolate the metric gridfunctions to cell faces
* **GiRaFFE_NRPy/GiRaFFE_NRPy_Metric_Face_Values.py**
* Reconstruct primitives $\bar{v}^i$ and $B^i$ on cell faces with the piecewise-parabolic method
* **GiRaFFE_NRPy/GiRaFFE_NRPy_PPM.py**
* Compute the fluxes of $\tilde{S}_i$ and $A_i$ and add the appropriate combinations to the evolution equation right-hand sides
* **GiRaFFE_NRPy/Stilde_flux.py**, **GiRaFFE_NRPy/Afield_flux.py**
1. [Step 2](#poststep): Recover the primitive variables and apply boundary conditions (post-step)
1. [Step 2.a](#potential_bc): Apply boundary conditions to $A_i$ and $\sqrt{\gamma} \Phi$
* **GiRaFFE_NRPy/GiRaFFE_NRPy_BCs.py**
1. [Step 2.b](#a2b): Compute $B^i$ from $A_i$
* **GiRaFFE_NRPy/GiRaFFE_NRPy_A2B.py**
1. [Step 2.c](#c2p): Run the Conservative-to-Primitive solver
* This applies fixes to $\tilde{S}_i$, then computes $\bar{v}^i$. A current sheet prescription is then applied to $\bar{v}^i$, and $\tilde{S}_i$ is recomputed to be consistent.
* **GiRaFFE_NRPy/GiRaFFE_NRPy_C2P_P2C.py**
1. [Step 2.d](#velocity_bc): Apply outflow boundary conditions to $\bar{v}^i$
* **GiRaFFE_NRPy/GiRaFFE_NRPy_BCs.py**
1. [Step 3](#write_out): Write out the C code function
1. [Step 3](#code_validation): Self-Validation against `GiRaFFE_NRPy_Main_Drive.py`
1. [Step 5](#latex_pdf_output): Output this notebook to $\LaTeX$-formatted PDF file
<a id='prelim'></a>
# Step 0: Preliminaries \[Back to [top](#toc)\]
$$\label{prelim}$$
We begin by importing the NRPy+ core functionality. We also import the Levi-Civita symbol, the GRHD module, and the GRFFE module.
```
# Step 0: Add NRPy's directory to the path
# https://stackoverflow.com/questions/16780014/import-file-from-parent-directory
import os,sys
nrpy_dir_path = os.path.join("..")
if nrpy_dir_path not in sys.path:
sys.path.append(nrpy_dir_path)
from outputC import * # NRPy+: Core C code output module
import finite_difference as fin # NRPy+: Finite difference C code generation module
import NRPy_param_funcs as par # NRPy+: Parameter interface
import grid as gri # NRPy+: Functions having to do with numerical grids
import loop as lp # NRPy+: Generate C code loops
import indexedexp as ixp # NRPy+: Symbolic indexed expression (e.g., tensors, vectors, etc.) support
import reference_metric as rfm # NRPy+: Reference metric support
import cmdline_helper as cmd # NRPy+: Multi-platform Python command-line interface
thismodule = "GiRaFFE_NRPy_Main_Driver"
par.set_parval_from_str("grid::GridFuncMemAccess","ETK")
par.set_parval_from_str("finite_difference::FD_CENTDERIVS_ORDER",2)
out_dir = os.path.join("GiRaFFE_standalone_Ccodes")
cmd.mkdir(out_dir)
CoordSystem = "Cartesian"
par.set_parval_from_str("reference_metric::CoordSystem",CoordSystem)
rfm.reference_metric() # Create ReU, ReDD needed for rescaling B-L initial data, generating BSSN RHSs, etc.
# Default Kreiss-Oliger dissipation strength
default_KO_strength = 0.1
diss_strength = par.Cparameters("REAL", thismodule, "diss_strength", default_KO_strength)
outCparams = "outCverbose=False,CSE_sorting=none"
```
<a id='rhs'></a>
# Step 1: Calculate the right-hand sides \[Back to [top](#toc)\]
$$\label{rhs}$$
<a id='parenthetical'></a>
In the method of lines using Runge-Kutta methods, each timestep involves several "RK substeps" during which we will run the same set of function calls. These can be divided into two groups: one in which the RHSs themselves are calculated, and a second in which boundary conditions are applied and auxiliary variables updated (the post-step). Here, we focus on that first group.
## Step 1.a: Calculate the portion of the gauge terms for $A_k$, $(\alpha \Phi - \beta^j A_j)$ and $\Phi$, $(\alpha\sqrt{\gamma}A^j - \beta^j [\sqrt{\gamma} \Phi])$ *inside* the parentheses to be finite-differenced. \[Back to [top](#toc)\]
$$\label{parenthetical}$$
The source terms of our evolution equations consist of two terms that are derivatives of some parenthetical quantity. We can save some effort and execution time (at the cost of memory needed) by computing these parentheticals, storing them, and then finite-differencing that stored variable. For more information, see the notebook for the [implementation](Tutorial-GiRaFFE_NRPy-Source_Terms.ipynb) and the [validation](Tutorial-Start_to_Finish_UnitTest-GiRaFFE_NRPy-Source_Terms.ipynb), as well as [Tutorial-GRFFE_Equations-Cartesian](../Tutorial-GRFFE_Equations-Cartesian.ipynb) and [Tutorial-GRHD_Equations-Cartesian](../Tutorial-GRHD_Equations-Cartesian.ipynb) for the terms themselves.
```
import GRHD.equations as GRHD # NRPy+: Generate general relativistic hydrodynamics equations
import GRFFE.equations as GRFFE # NRPy+: Generate general relativisitic force-free electrodynamics equations
gammaDD = ixp.register_gridfunctions_for_single_rank2("AUXEVOL","gammaDD","sym01",DIM=3)
betaU = ixp.register_gridfunctions_for_single_rank1("AUXEVOL","betaU",DIM=3)
alpha = gri.register_gridfunctions("AUXEVOL","alpha")
AD = ixp.register_gridfunctions_for_single_rank1("EVOL","AD")
BU = ixp.register_gridfunctions_for_single_rank1("AUXEVOL","BU")
ValenciavU = ixp.register_gridfunctions_for_single_rank1("AUXEVOL","ValenciavU")
psi6Phi = gri.register_gridfunctions("EVOL","psi6Phi")
StildeD = ixp.register_gridfunctions_for_single_rank1("EVOL","StildeD")
PhievolParenU = ixp.register_gridfunctions_for_single_rank1("AUXEVOL","PhievolParenU",DIM=3)
AevolParen = gri.register_gridfunctions("AUXEVOL","AevolParen")
GRHD.compute_sqrtgammaDET(gammaDD)
GRFFE.compute_AD_source_term_parenthetical_for_FD(GRHD.sqrtgammaDET,betaU,alpha,psi6Phi,AD)
GRFFE.compute_psi6Phi_rhs_parenthetical(gammaDD,GRHD.sqrtgammaDET,betaU,alpha,AD,psi6Phi)
parens_to_print = [\
lhrh(lhs=gri.gfaccess("auxevol_gfs","AevolParen"),rhs=GRFFE.AevolParen),\
lhrh(lhs=gri.gfaccess("auxevol_gfs","PhievolParenU0"),rhs=GRFFE.PhievolParenU[0]),\
lhrh(lhs=gri.gfaccess("auxevol_gfs","PhievolParenU1"),rhs=GRFFE.PhievolParenU[1]),\
lhrh(lhs=gri.gfaccess("auxevol_gfs","PhievolParenU2"),rhs=GRFFE.PhievolParenU[2]),\
]
subdir = "RHSs"
cmd.mkdir(os.path.join(out_dir, subdir))
desc = "Calculate quantities to be finite-differenced for the GRFFE RHSs"
name = "calculate_parentheticals_for_RHSs"
outCfunction(
outfile = os.path.join(out_dir,subdir,name+".h"), desc=desc, name=name,
params ="const paramstruct *restrict params,const REAL *restrict in_gfs,REAL *restrict auxevol_gfs",
body = fin.FD_outputC("returnstring",parens_to_print,params=outCparams).replace("IDX4","IDX4S"),
loopopts ="AllPoints",
rel_path_for_Cparams=os.path.join("../"))
```
<a id='source'></a>
## Step 1.b: Calculate the source terms of $\partial_t A_i$, $\partial_t \tilde{S}_i$, and $\partial_t [\sqrt{\gamma} \Phi]$ right-hand sides \[Back to [top](#toc)\]
$$\label{source}$$
With the parentheticals stored in memory from the previous step, we can now now calculate the terms on the RHS of $A_i$ and $[\sqrt{\gamma} \Phi]$ that involve the derivatives of those terms. We also compute the other term in the RHS of $[\sqrt{\gamma} \Phi]$, which is a straightforward damping term.
```
xi_damping = par.Cparameters("REAL",thismodule,"xi_damping",0.1)
GRFFE.compute_psi6Phi_rhs_damping_term(alpha,psi6Phi,xi_damping)
AevolParen_dD = ixp.declarerank1("AevolParen_dD",DIM=3)
PhievolParenU_dD = ixp.declarerank2("PhievolParenU_dD","nosym",DIM=3)
A_rhsD = ixp.zerorank1()
psi6Phi_rhs = GRFFE.psi6Phi_damping
for i in range(3):
A_rhsD[i] += -AevolParen_dD[i]
psi6Phi_rhs += -PhievolParenU_dD[i][i]
# Add Kreiss-Oliger dissipation to the GRFFE RHSs:
# psi6Phi_dKOD = ixp.declarerank1("psi6Phi_dKOD")
# AD_dKOD = ixp.declarerank2("AD_dKOD","nosym")
# for i in range(3):
# psi6Phi_rhs += diss_strength*psi6Phi_dKOD[i]*rfm.ReU[i] # ReU[i] = 1/scalefactor_orthog_funcform[i]
# for j in range(3):
# A_rhsD[j] += diss_strength*AD_dKOD[j][i]*rfm.ReU[i] # ReU[i] = 1/scalefactor_orthog_funcform[i]
RHSs_to_print = [\
lhrh(lhs=gri.gfaccess("rhs_gfs","AD0"),rhs=A_rhsD[0]),\
lhrh(lhs=gri.gfaccess("rhs_gfs","AD1"),rhs=A_rhsD[1]),\
lhrh(lhs=gri.gfaccess("rhs_gfs","AD2"),rhs=A_rhsD[2]),\
lhrh(lhs=gri.gfaccess("rhs_gfs","psi6Phi"),rhs=psi6Phi_rhs),\
]
desc = "Calculate AD gauge term and psi6Phi RHSs"
name = "calculate_AD_gauge_psi6Phi_RHSs"
source_Ccode = outCfunction(
outfile = "returnstring", desc=desc, name=name,
params ="const paramstruct *params,const REAL *in_gfs,const REAL *auxevol_gfs,REAL *rhs_gfs",
body = fin.FD_outputC("returnstring",RHSs_to_print,params=outCparams).replace("IDX4","IDX4S"),
loopopts ="InteriorPoints",
rel_path_for_Cparams=os.path.join("../")).replace("= NGHOSTS","= NGHOSTS_A2B").replace("NGHOSTS+Nxx0","Nxx_plus_2NGHOSTS0-NGHOSTS_A2B").replace("NGHOSTS+Nxx1","Nxx_plus_2NGHOSTS1-NGHOSTS_A2B").replace("NGHOSTS+Nxx2","Nxx_plus_2NGHOSTS2-NGHOSTS_A2B")
# Note the above .replace() functions. These serve to expand the loop range into the ghostzones, since
# the second-order FD needs fewer than some other algorithms we use do.
with open(os.path.join(out_dir,subdir,name+".h"),"w") as file:
file.write(source_Ccode)
```
We also need to compute the source term of the $\tilde{S}_i$ evolution equation. This term involves derivatives of the four metric, so we can save some effort here by taking advantage of the interpolations done of the metric gridfunctions to the cell faces, which will allow us to take a finite-difference derivative with the accuracy of a higher order and the computational cost of a lower order. However, it will require some more complicated coding, detailed in [Tutorial-GiRaFFE_NRPy-Source_Terms](Tutorial-GiRaFFE_NRPy-Source_Terms.ipynb)
```
import GiRaFFE_NRPy.GiRaFFE_NRPy_Source_Terms as source
# Declare this symbol:
sqrt4pi = par.Cparameters("REAL",thismodule,"sqrt4pi","sqrt(4.0*M_PI)")
source.write_out_functions_for_StildeD_source_term(os.path.join(out_dir,subdir),outCparams,gammaDD,betaU,alpha,
ValenciavU,BU,sqrt4pi)
```
<a id='flux'></a>
## Step 1.c: Calculate the Flux terms \[Back to [top](#toc)\]
$$\label{flux}$$
Now, we will compute the flux terms of $\partial_t A_i$ and $\partial_t \tilde{S}_i$. To do so, we will first need to interpolate the metric gridfunctions to cell faces and to reconstruct the primitives on the cell faces using the code detailed in [Tutorial-GiRaFFE_NRPy-Metric_Face_Values](Tutorial-GiRaFFE_NRPy-Metric_Face_Values.ipynb) and in [Tutorial-GiRaFFE_NRPy-PPM](Tutorial-GiRaFFE_NRPy-PPM.ipynb).
```
subdir = "FCVAL"
cmd.mkdir(os.path.join(out_dir, subdir))
import GiRaFFE_NRPy.GiRaFFE_NRPy_Metric_Face_Values as FCVAL
FCVAL.GiRaFFE_NRPy_FCVAL(os.path.join(out_dir,subdir))
subdir = "PPM"
cmd.mkdir(os.path.join(out_dir, subdir))
import GiRaFFE_NRPy.GiRaFFE_NRPy_PPM as PPM
PPM.GiRaFFE_NRPy_PPM(os.path.join(out_dir,subdir))
```
Here, we will write the function to compute the electric field contribution to the induction equation RHS. This is coded with documentation in [Tutorial-GiRaFFE_NRPy-Afield_flux](Tutorial-GiRaFFE_NRPy-Afield_flux.ipynb). The electric field in the $i^{\rm th}$ direction, it will contribute to the $j^{\rm th}$ and $k^{\rm th}$ component of the electric field. That is, in Cartesian coordinates, the component $x$ of the electric field will be the average of the values computed on the cell faces in the $\pm y$- and $\pm z$-directions, and so forth for the other components. This ultimately results in the six functions we create below.
```
import GiRaFFE_NRPy.Afield_flux as Af
# We will pass values of the gridfunction on the cell faces into the function. This requires us
# to declare them as C parameters in NRPy+. We will denote this with the _face infix/suffix.
alpha_face = gri.register_gridfunctions("AUXEVOL","alpha_face")
gamma_faceDD = ixp.register_gridfunctions_for_single_rank2("AUXEVOL","gamma_faceDD","sym01")
beta_faceU = ixp.register_gridfunctions_for_single_rank1("AUXEVOL","beta_faceU")
# We'll need some more gridfunctions, now, to represent the reconstructions of BU and ValenciavU
# on the right and left faces
Valenciav_rU = ixp.register_gridfunctions_for_single_rank1("AUXEVOL","Valenciav_rU",DIM=3)
B_rU = ixp.register_gridfunctions_for_single_rank1("AUXEVOL","B_rU",DIM=3)
Valenciav_lU = ixp.register_gridfunctions_for_single_rank1("AUXEVOL","Valenciav_lU",DIM=3)
B_lU = ixp.register_gridfunctions_for_single_rank1("AUXEVOL","B_lU",DIM=3)
subdir = "RHSs"
Af.generate_Afield_flux_function_files(out_dir,subdir,alpha_face,gamma_faceDD,beta_faceU,\
Valenciav_rU,B_rU,Valenciav_lU,B_lU,True)
```
We must do something similar here, albeit a bit simpler. For instance, the $x$ component of $\partial_t \tilde{S}_i$ will be a finite difference of the flux throught the faces in the $\pm x$ direction; for further detail, see [Tutorial-GiRaFFE_NRPy-Stilde_flux](Tutorial-GiRaFFE_NRPy-Stilde_flux.ipynb).
```
import GiRaFFE_NRPy.Stilde_flux as Sf
subdir = "RHSs"
Sf.generate_C_code_for_Stilde_flux(os.path.join(out_dir,subdir), True, alpha_face,gamma_faceDD,beta_faceU,
Valenciav_rU,B_rU,Valenciav_lU,B_lU,sqrt4pi)
```
<a id='poststep'></a>
# Step 2: Recover the primitive variables and apply boundary conditions \[Back to [top](#toc)\]
$$\label{poststep}$$
With the RHSs computed, we can now recover the primitive variables, which are the Valencia three-velocity $\bar{v}^i$ and the magnetic field $B^i$. We can also apply boundary conditions to the vector potential and velocity. By doing this at each RK substep, we can help ensure the accuracy of the following substeps.
<a id='potential_bc'></a>
## Step 2.a: Apply boundary conditions to $A_i$ and $\sqrt{\gamma} \Phi$ \[Back to [top](#toc)\]
$$\label{potential_bc}$$
First, we will apply boundary conditions to the vector potential, $A_i$, and the scalar potential $\sqrt{\gamma} \Phi$. The file we generate here contains both functions we need for BCs, as documented in [Tutorial-GiRaFFE_NRPy-BCs](Tutorial-GiRaFFE_NRPy-BCs.ipynb).
```
subdir = "boundary_conditions"
cmd.mkdir(os.path.join(out_dir,subdir))
import GiRaFFE_NRPy.GiRaFFE_NRPy_BCs as BC
BC.GiRaFFE_NRPy_BCs(os.path.join(out_dir,subdir))
```
<a id='a2b'></a>
## Step 2.b: Compute $B^i$ from $A_i$ \[Back to [top](#toc)\]
$$\label{a2b}$$
Now, we will calculate the magnetic field as the curl of the vector potential at all points in our domain; this requires care to be taken in the ghost zones, which is detailed in [Tutorial-GiRaFFE_NRPy-A2B](Tutorial-GiRaFFE_NRPy-A2B.ipynb).
```
subdir = "A2B"
cmd.mkdir(os.path.join(out_dir,subdir))
import GiRaFFE_NRPy.GiRaFFE_NRPy_A2B as A2B
A2B.GiRaFFE_NRPy_A2B(os.path.join(out_dir,subdir),gammaDD,AD,BU)
```
<a id='c2p'></a>
## Step 2.c: Run the Conservative-to-Primitive solver \[Back to [top](#toc)\]
$$\label{c2p}$$
With these functions, we apply fixes to the Poynting flux, and use that to update the three-velocity. Then, we apply our current sheet prescription to the velocity, and recompute the Poynting flux to agree with the now-fixed velocity. More detail can be found in [Tutorial-GiRaFFE_NRPy-C2P_P2C](Tutorial-GiRaFFE_NRPy-C2P_P2C.ipynb).
```
import GiRaFFE_NRPy.GiRaFFE_NRPy_C2P_P2C as C2P_P2C
C2P_P2C.GiRaFFE_NRPy_C2P(StildeD,BU,gammaDD,betaU,alpha)
values_to_print = [\
lhrh(lhs=gri.gfaccess("in_gfs","StildeD0"),rhs=C2P_P2C.outStildeD[0]),\
lhrh(lhs=gri.gfaccess("in_gfs","StildeD1"),rhs=C2P_P2C.outStildeD[1]),\
lhrh(lhs=gri.gfaccess("in_gfs","StildeD2"),rhs=C2P_P2C.outStildeD[2]),\
lhrh(lhs=gri.gfaccess("auxevol_gfs","ValenciavU0"),rhs=C2P_P2C.ValenciavU[0]),\
lhrh(lhs=gri.gfaccess("auxevol_gfs","ValenciavU1"),rhs=C2P_P2C.ValenciavU[1]),\
lhrh(lhs=gri.gfaccess("auxevol_gfs","ValenciavU2"),rhs=C2P_P2C.ValenciavU[2])\
]
subdir = "C2P"
cmd.mkdir(os.path.join(out_dir,subdir))
desc = "Apply fixes to \tilde{S}_i and recompute the velocity to match with current sheet prescription."
name = "GiRaFFE_NRPy_cons_to_prims"
outCfunction(
outfile = os.path.join(out_dir,subdir,name+".h"), desc=desc, name=name,
params ="const paramstruct *params,REAL *xx[3],REAL *auxevol_gfs,REAL *in_gfs",
body = fin.FD_outputC("returnstring",values_to_print,params=outCparams).replace("IDX4","IDX4S"),
loopopts ="AllPoints,Read_xxs",
rel_path_for_Cparams=os.path.join("../"))
# TINYDOUBLE = par.Cparameters("REAL",thismodule,"TINYDOUBLE",1e-100)
C2P_P2C.GiRaFFE_NRPy_P2C(gammaDD,betaU,alpha, ValenciavU,BU, sqrt4pi)
values_to_print = [\
lhrh(lhs=gri.gfaccess("in_gfs","StildeD0"),rhs=C2P_P2C.StildeD[0]),\
lhrh(lhs=gri.gfaccess("in_gfs","StildeD1"),rhs=C2P_P2C.StildeD[1]),\
lhrh(lhs=gri.gfaccess("in_gfs","StildeD2"),rhs=C2P_P2C.StildeD[2]),\
]
desc = "Recompute StildeD after current sheet fix to Valencia 3-velocity to ensure consistency between conservative & primitive variables."
name = "GiRaFFE_NRPy_prims_to_cons"
outCfunction(
outfile = os.path.join(out_dir,subdir,name+".h"), desc=desc, name=name,
params ="const paramstruct *params,REAL *auxevol_gfs,REAL *in_gfs",
body = fin.FD_outputC("returnstring",values_to_print,params=outCparams).replace("IDX4","IDX4S"),
loopopts ="AllPoints",
rel_path_for_Cparams=os.path.join("../"))
```
<a id='velocity_bc'></a>
## Step 2.d: Apply outflow boundary conditions to $\bar{v}^i$ \[Back to [top](#toc)\]
$$\label{velocity_bc}$$
Now, we can apply outflow boundary conditions to the Valencia three-velocity. This specific type of boundary condition helps avoid numerical error "flowing" into our grid.
This function has already been generated [above](#potential_bc).
<a id='write_out'></a>
# Step 3: Write out the C code function \[Back to [top](#toc)\]
$$\label{write_out}$$
Now, we have generated all the functions we will need for the `GiRaFFE` evolution. So, we will now assemble our evolution driver. This file will first `#include` all of the files we just generated for easy access. Then, we will write a function that calls these functions in the correct order, iterating over the flux directions as necessary.
```
%%writefile $out_dir/GiRaFFE_NRPy_Main_Driver.h
// Structure to track ghostzones for PPM:
typedef struct __gf_and_gz_struct__ {
REAL *gf;
int gz_lo[4],gz_hi[4];
} gf_and_gz_struct;
// Some additional constants needed for PPM:
const int VX=0,VY=1,VZ=2,BX=3,BY=4,BZ=5;
const int NUM_RECONSTRUCT_GFS = 6;
// Include ALL functions needed for evolution
#include "RHSs/calculate_parentheticals_for_RHSs.h"
#include "RHSs/calculate_AD_gauge_psi6Phi_RHSs.h"
#include "PPM/reconstruct_set_of_prims_PPM_GRFFE_NRPy.c"
#include "FCVAL/interpolate_metric_gfs_to_cell_faces.h"
#include "RHSs/calculate_StildeD0_source_term.h"
#include "RHSs/calculate_StildeD1_source_term.h"
#include "RHSs/calculate_StildeD2_source_term.h"
#include "../calculate_E_field_flat_all_in_one.h"
#include "RHSs/calculate_Stilde_flux_D0.h"
#include "RHSs/calculate_Stilde_flux_D1.h"
#include "RHSs/calculate_Stilde_flux_D2.h"
#include "boundary_conditions/GiRaFFE_boundary_conditions.h"
#include "A2B/driver_AtoB.h"
#include "C2P/GiRaFFE_NRPy_cons_to_prims.h"
#include "C2P/GiRaFFE_NRPy_prims_to_cons.h"
void override_BU_with_old_GiRaFFE(const paramstruct *restrict params,REAL *restrict auxevol_gfs,const int n) {
#include "set_Cparameters.h"
char filename[100];
sprintf(filename,"BU0_override-%08d.bin",n);
FILE *out2D = fopen(filename, "rb");
fread(auxevol_gfs+BU0GF*Nxx_plus_2NGHOSTS0*Nxx_plus_2NGHOSTS1*Nxx_plus_2NGHOSTS2,
sizeof(double),Nxx_plus_2NGHOSTS0*Nxx_plus_2NGHOSTS1*Nxx_plus_2NGHOSTS2,out2D);
fclose(out2D);
sprintf(filename,"BU1_override-%08d.bin",n);
out2D = fopen(filename, "rb");
fread(auxevol_gfs+BU1GF*Nxx_plus_2NGHOSTS0*Nxx_plus_2NGHOSTS1*Nxx_plus_2NGHOSTS2,
sizeof(double),Nxx_plus_2NGHOSTS0*Nxx_plus_2NGHOSTS1*Nxx_plus_2NGHOSTS2,out2D);
fclose(out2D);
sprintf(filename,"BU2_override-%08d.bin",n);
out2D = fopen(filename, "rb");
fread(auxevol_gfs+BU2GF*Nxx_plus_2NGHOSTS0*Nxx_plus_2NGHOSTS1*Nxx_plus_2NGHOSTS2,
sizeof(double),Nxx_plus_2NGHOSTS0*Nxx_plus_2NGHOSTS1*Nxx_plus_2NGHOSTS2,out2D);
fclose(out2D);
}
void GiRaFFE_NRPy_RHSs(const paramstruct *restrict params,REAL *restrict auxevol_gfs,const REAL *restrict in_gfs,REAL *restrict rhs_gfs) {
#include "set_Cparameters.h"
// First thing's first: initialize the RHSs to zero!
#pragma omp parallel for
for(int ii=0;ii<Nxx_plus_2NGHOSTS0*Nxx_plus_2NGHOSTS1*Nxx_plus_2NGHOSTS2*NUM_EVOL_GFS;ii++) {
rhs_gfs[ii] = 0.0;
}
// Next calculate the easier source terms that don't require flux directions
// This will also reset the RHSs for each gf at each new timestep.
calculate_parentheticals_for_RHSs(params,in_gfs,auxevol_gfs);
calculate_AD_gauge_psi6Phi_RHSs(params,in_gfs,auxevol_gfs,rhs_gfs);
// Now, we set up a bunch of structs of pointers to properly guide the PPM algorithm.
// They also count the number of ghostzones available.
gf_and_gz_struct in_prims[NUM_RECONSTRUCT_GFS], out_prims_r[NUM_RECONSTRUCT_GFS], out_prims_l[NUM_RECONSTRUCT_GFS];
int which_prims_to_reconstruct[NUM_RECONSTRUCT_GFS],num_prims_to_reconstruct;
const int Nxxp2NG012 = Nxx_plus_2NGHOSTS0*Nxx_plus_2NGHOSTS1*Nxx_plus_2NGHOSTS2;
REAL *temporary = auxevol_gfs + Nxxp2NG012*AEVOLPARENGF; //We're not using this anymore
// This sets pointers to the portion of auxevol_gfs containing the relevant gridfunction.
int ww=0;
in_prims[ww].gf = auxevol_gfs + Nxxp2NG012*VALENCIAVU0GF;
out_prims_r[ww].gf = auxevol_gfs + Nxxp2NG012*VALENCIAV_RU0GF;
out_prims_l[ww].gf = auxevol_gfs + Nxxp2NG012*VALENCIAV_LU0GF;
ww++;
in_prims[ww].gf = auxevol_gfs + Nxxp2NG012*VALENCIAVU1GF;
out_prims_r[ww].gf = auxevol_gfs + Nxxp2NG012*VALENCIAV_RU1GF;
out_prims_l[ww].gf = auxevol_gfs + Nxxp2NG012*VALENCIAV_LU1GF;
ww++;
in_prims[ww].gf = auxevol_gfs + Nxxp2NG012*VALENCIAVU2GF;
out_prims_r[ww].gf = auxevol_gfs + Nxxp2NG012*VALENCIAV_RU2GF;
out_prims_l[ww].gf = auxevol_gfs + Nxxp2NG012*VALENCIAV_LU2GF;
ww++;
in_prims[ww].gf = auxevol_gfs + Nxxp2NG012*BU0GF;
out_prims_r[ww].gf = auxevol_gfs + Nxxp2NG012*B_RU0GF;
out_prims_l[ww].gf = auxevol_gfs + Nxxp2NG012*B_LU0GF;
ww++;
in_prims[ww].gf = auxevol_gfs + Nxxp2NG012*BU1GF;
out_prims_r[ww].gf = auxevol_gfs + Nxxp2NG012*B_RU1GF;
out_prims_l[ww].gf = auxevol_gfs + Nxxp2NG012*B_LU1GF;
ww++;
in_prims[ww].gf = auxevol_gfs + Nxxp2NG012*BU2GF;
out_prims_r[ww].gf = auxevol_gfs + Nxxp2NG012*B_RU2GF;
out_prims_l[ww].gf = auxevol_gfs + Nxxp2NG012*B_LU2GF;
ww++;
// Prims are defined AT ALL GRIDPOINTS, so we set the # of ghostzones to zero:
for(int i=0;i<NUM_RECONSTRUCT_GFS;i++) for(int j=1;j<=3;j++) { in_prims[i].gz_lo[j]=0; in_prims[i].gz_hi[j]=0; }
// Left/right variables are not yet defined, yet we set the # of gz's to zero by default:
for(int i=0;i<NUM_RECONSTRUCT_GFS;i++) for(int j=1;j<=3;j++) { out_prims_r[i].gz_lo[j]=0; out_prims_r[i].gz_hi[j]=0; }
for(int i=0;i<NUM_RECONSTRUCT_GFS;i++) for(int j=1;j<=3;j++) { out_prims_l[i].gz_lo[j]=0; out_prims_l[i].gz_hi[j]=0; }
ww=0;
which_prims_to_reconstruct[ww]=VX; ww++;
which_prims_to_reconstruct[ww]=VY; ww++;
which_prims_to_reconstruct[ww]=VZ; ww++;
which_prims_to_reconstruct[ww]=BX; ww++;
which_prims_to_reconstruct[ww]=BY; ww++;
which_prims_to_reconstruct[ww]=BZ; ww++;
num_prims_to_reconstruct=ww;
// In each direction, perform the PPM reconstruction procedure.
// Then, add the fluxes to the RHS as appropriate.
for(int flux_dirn=0;flux_dirn<3;flux_dirn++) {
// In each direction, interpolate the metric gfs (gamma,beta,alpha) to cell faces.
interpolate_metric_gfs_to_cell_faces(params,auxevol_gfs,flux_dirn+1);
// Then, reconstruct the primitive variables on the cell faces.
// This function is housed in the file: "reconstruct_set_of_prims_PPM_GRFFE_NRPy.c"
reconstruct_set_of_prims_PPM_GRFFE_NRPy(params, auxevol_gfs, flux_dirn+1, num_prims_to_reconstruct,
which_prims_to_reconstruct, in_prims, out_prims_r, out_prims_l, temporary);
// For example, if flux_dirn==0, then at gamma_faceDD00(i,j,k) represents gamma_{xx}
// at (i-1/2,j,k), Valenciav_lU0(i,j,k) is the x-component of the velocity at (i-1/2-epsilon,j,k),
// and Valenciav_rU0(i,j,k) is the x-component of the velocity at (i-1/2+epsilon,j,k).
if(flux_dirn==0) {
// Next, we calculate the source term for StildeD. Again, this also resets the rhs_gfs array at
// each new timestep.
calculate_StildeD0_source_term(params,auxevol_gfs,rhs_gfs);
// Now, compute the electric field on each face of a cell and add it to the RHSs as appropriate
//calculate_E_field_D0_right(params,auxevol_gfs,rhs_gfs);
//calculate_E_field_D0_left(params,auxevol_gfs,rhs_gfs);
// Finally, we calculate the flux of StildeD and add the appropriate finite-differences
// to the RHSs.
calculate_Stilde_flux_D0(params,auxevol_gfs,rhs_gfs);
}
else if(flux_dirn==1) {
calculate_StildeD1_source_term(params,auxevol_gfs,rhs_gfs);
//calculate_E_field_D1_right(params,auxevol_gfs,rhs_gfs);
//calculate_E_field_D1_left(params,auxevol_gfs,rhs_gfs);
calculate_Stilde_flux_D1(params,auxevol_gfs,rhs_gfs);
}
else {
calculate_StildeD2_source_term(params,auxevol_gfs,rhs_gfs);
//calculate_E_field_D2_right(params,auxevol_gfs,rhs_gfs);
//calculate_E_field_D2_left(params,auxevol_gfs,rhs_gfs);
calculate_Stilde_flux_D2(params,auxevol_gfs,rhs_gfs);
}
for(int count=0;count<=1;count++) {
// This function is written to be general, using notation that matches the forward permutation added to AD2,
// i.e., [F_HLL^x(B^y)]_z corresponding to flux_dirn=0, count=1.
// The SIGN parameter is necessary because
// -E_z(x_i,y_j,z_k) = 0.25 ( [F_HLL^x(B^y)]_z(i+1/2,j,k)+[F_HLL^x(B^y)]_z(i-1/2,j,k)
// -[F_HLL^y(B^x)]_z(i,j+1/2,k)-[F_HLL^y(B^x)]_z(i,j-1/2,k) )
// Note the negative signs on the reversed permutation terms!
// By cyclically permuting with flux_dirn, we
// get contributions to the other components, and by incrementing count, we get the backward permutations:
// Let's suppose flux_dirn = 0. Then we will need to update Ay (count=0) and Az (count=1):
// flux_dirn=count=0 -> AD0GF+(flux_dirn+1+count)%3 = AD0GF + (0+1+0)%3=AD1GF <- Updating Ay!
// (flux_dirn)%3 = (0)%3 = 0 Vx
// (flux_dirn-count+2)%3 = (0-0+2)%3 = 2 Vz . Inputs Vx, Vz -> SIGN = -1 ; 2.0*((REAL)count)-1.0=-1 check!
// flux_dirn=0,count=1 -> AD0GF+(flux_dirn+1+count)%3 = AD0GF + (0+1+1)%3=AD2GF <- Updating Az!
// (flux_dirn)%3 = (0)%3 = 0 Vx
// (flux_dirn-count+2)%3 = (0-1+2)%3 = 1 Vy . Inputs Vx, Vy -> SIGN = +1 ; 2.0*((REAL)count)-1.0=2-1=+1 check!
// Let's suppose flux_dirn = 1. Then we will need to update Az (count=0) and Ax (count=1):
// flux_dirn=1,count=0 -> AD0GF+(flux_dirn+1+count)%3 = AD0GF + (1+1+0)%3=AD2GF <- Updating Az!
// (flux_dirn)%3 = (1)%3 = 1 Vy
// (flux_dirn-count+2)%3 = (1-0+2)%3 = 0 Vx . Inputs Vy, Vx -> SIGN = -1 ; 2.0*((REAL)count)-1.0=-1 check!
// flux_dirn=count=1 -> AD0GF+(flux_dirn+1+count)%3 = AD0GF + (1+1+1)%3=AD0GF <- Updating Ax!
// (flux_dirn)%3 = (1)%3 = 1 Vy
// (flux_dirn-count+2)%3 = (1-1+2)%3 = 2 Vz . Inputs Vy, Vz -> SIGN = +1 ; 2.0*((REAL)count)-1.0=2-1=+1 check!
// Let's suppose flux_dirn = 2. Then we will need to update Ax (count=0) and Ay (count=1):
// flux_dirn=2,count=0 -> AD0GF+(flux_dirn+1+count)%3 = AD0GF + (2+1+0)%3=AD0GF <- Updating Ax!
// (flux_dirn)%3 = (2)%3 = 2 Vz
// (flux_dirn-count+2)%3 = (2-0+2)%3 = 1 Vy . Inputs Vz, Vy -> SIGN = -1 ; 2.0*((REAL)count)-1.0=-1 check!
// flux_dirn=2,count=1 -> AD0GF+(flux_dirn+1+count)%3 = AD0GF + (2+1+1)%3=AD1GF <- Updating Ay!
// (flux_dirn)%3 = (2)%3 = 2 Vz
// (flux_dirn-count+2)%3 = (2-1+2)%3 = 0 Vx . Inputs Vz, Vx -> SIGN = +1 ; 2.0*((REAL)count)-1.0=2-1=+1 check!
calculate_E_field_flat_all_in_one(params,
&auxevol_gfs[IDX4ptS(VALENCIAV_RU0GF+(flux_dirn)%3, 0)],&auxevol_gfs[IDX4ptS(VALENCIAV_RU0GF+(flux_dirn-count+2)%3, 0)],
&auxevol_gfs[IDX4ptS(VALENCIAV_LU0GF+(flux_dirn)%3, 0)],&auxevol_gfs[IDX4ptS(VALENCIAV_LU0GF+(flux_dirn-count+2)%3, 0)],
&auxevol_gfs[IDX4ptS(B_RU0GF +(flux_dirn)%3, 0)],&auxevol_gfs[IDX4ptS(B_RU0GF +(flux_dirn-count+2)%3, 0)],
&auxevol_gfs[IDX4ptS(B_LU0GF +(flux_dirn)%3, 0)],&auxevol_gfs[IDX4ptS(B_LU0GF +(flux_dirn-count+2)%3, 0)],
&auxevol_gfs[IDX4ptS(B_RU0GF +(flux_dirn-count+2)%3, 0)],
&auxevol_gfs[IDX4ptS(B_LU0GF +(flux_dirn-count+2)%3, 0)],
&rhs_gfs[IDX4ptS(AD0GF+(flux_dirn+1+count)%3,0)], 2.0*((REAL)count)-1.0, flux_dirn);
}
}
}
void GiRaFFE_NRPy_post_step(const paramstruct *restrict params,REAL *xx[3],REAL *restrict auxevol_gfs,REAL *restrict evol_gfs,const int n) {
// First, apply BCs to AD and psi6Phi. Then calculate BU from AD
apply_bcs_potential(params,evol_gfs);
driver_A_to_B(params,evol_gfs,auxevol_gfs);
//override_BU_with_old_GiRaFFE(params,auxevol_gfs,n);
// Apply fixes to StildeD, then recompute the velocity at the new timestep.
// Apply the current sheet prescription to the velocities
GiRaFFE_NRPy_cons_to_prims(params,xx,auxevol_gfs,evol_gfs);
// Then, recompute StildeD to be consistent with the new velocities
//GiRaFFE_NRPy_prims_to_cons(params,auxevol_gfs,evol_gfs);
// Finally, apply outflow boundary conditions to the velocities.
apply_bcs_velocity(params,auxevol_gfs);
}
```
<a id='code_validation'></a>
# Step 4: Self-Validation against `GiRaFFE_NRPy_Main_Drive.py` \[Back to [top](#toc)\]
$$\label{code_validation}$$
To validate the code in this tutorial we check for agreement between the files
1. that were generated in this tutorial and
1. those that are generated in the module `GiRaFFE_NRPy_Main_Driver.py`
```
gri.glb_gridfcs_list = []
# Define the directory that we wish to validate against:
valdir = os.path.join("GiRaFFE_validation_Ccodes")
cmd.mkdir(valdir)
import GiRaFFE_NRPy.GiRaFFE_NRPy_Main_Driver as md
md.GiRaFFE_NRPy_Main_Driver_generate_all(valdir)
```
With both sets of codes generated, we can now compare them against each other.
```
import difflib
import sys
print("Printing difference between original C code and this code...")
# Open the files to compare
files = ["GiRaFFE_NRPy_Main_Driver.h",
"RHSs/calculate_parentheticals_for_RHSs.h",
"RHSs/calculate_AD_gauge_psi6Phi_RHSs.h",
"PPM/reconstruct_set_of_prims_PPM_GRFFE_NRPy.c",
"PPM/loop_defines_reconstruction_NRPy.h",
"FCVAL/interpolate_metric_gfs_to_cell_faces.h",
"RHSs/calculate_StildeD0_source_term.h",
"RHSs/calculate_StildeD1_source_term.h",
"RHSs/calculate_StildeD2_source_term.h",
"RHSs/calculate_E_field_D0_right.h",
"RHSs/calculate_E_field_D0_left.h",
"RHSs/calculate_E_field_D1_right.h",
"RHSs/calculate_E_field_D1_left.h",
"RHSs/calculate_E_field_D2_right.h",
"RHSs/calculate_E_field_D2_left.h",
"RHSs/calculate_Stilde_flux_D0.h",
"RHSs/calculate_Stilde_flux_D1.h",
"RHSs/calculate_Stilde_flux_D2.h",
"boundary_conditions/GiRaFFE_boundary_conditions.h",
"A2B/driver_AtoB.h",
"C2P/GiRaFFE_NRPy_cons_to_prims.h",
"C2P/GiRaFFE_NRPy_prims_to_cons.h"]
for file in files:
print("Checking file " + file)
with open(os.path.join(valdir,file)) as file1, open(os.path.join(out_dir,file)) as file2:
# Read the lines of each file
file1_lines = file1.readlines()
file2_lines = file2.readlines()
num_diffs = 0
for line in difflib.unified_diff(file1_lines, file2_lines, fromfile=os.path.join(valdir,file), tofile=os.path.join(out_dir,file)):
sys.stdout.writelines(line)
num_diffs = num_diffs + 1
if num_diffs == 0:
print("No difference. TEST PASSED!")
else:
print("ERROR: Disagreement found with .py file. See differences above.")
sys.exit(1)
```
<a id='latex_pdf_output'></a>
# Step 4: Output this notebook to $\LaTeX$-formatted PDF file \[Back to [top](#toc)\]
$$\label{latex_pdf_output}$$
The following code cell converts this Jupyter notebook into a proper, clickable $\LaTeX$-formatted PDF file. After the cell is successfully run, the generated PDF may be found in the root NRPy+ tutorial directory, with filename
[Tutorial-GiRaFFE_NRPy_Main_Driver](TTutorial-GiRaFFE_NRPy_Main_Driver.pdf) (Note that clicking on this link may not work; you may need to open the PDF file through another means.)
```
import cmdline_helper as cmd # NRPy+: Multi-platform Python command-line interface
cmd.output_Jupyter_notebook_to_LaTeXed_PDF("Tutorial-GiRaFFE_NRPy_Main_Driver")
```
|
github_jupyter
|
```
# Visualization of the KO Gold Standard from:
# Miraldi et al. (2018) "Leveraging chromatin accessibility data for transcriptional regulatory network inference in Th17 Cells"
# TO START: In the menu above, choose "Cell" --> "Run All", and network + heatmap will load
# NOTE: Default limits networks to TF-TF edges in top 1 TF / gene model (.93 quantile), to see the full
# network hit "restore" (in the drop-down menu in cell below) and set threshold to 0 and hit "threshold"
# You can search for gene names in the search box below the network (hit "Match"), and find regulators ("targeted by")
# Change "canvas" to "SVG" (drop-down menu in cell below) to enable drag interactions with nodes & labels
# Change "SVG" to "canvas" to speed up layout operations
# More info about jp_gene_viz and user interface instructions are available on Github:
# https://github.com/simonsfoundation/jp_gene_viz/blob/master/doc/dNetwork%20widget%20overview.ipynb
# directory containing gene expression data and network folder
directory = "."
# folder containing networks
netPath = 'Networks'
# network file name
networkFile = 'KO75_KOrk_1norm_sp.tsv'
# title for network figure
netTitle = 'KO Gold Standard'
# name of gene expression file
expressionFile = 'Th0_Th17_48hTh.txt'
# column of gene expression file to color network nodes
rnaSampleOfInt = 'Th17(48h)'
# edge cutoff, TF KO edges from Yosef et al. (2013) Nature. and Ciofani et al. (2012) Cell. are not on comparable scales
edgeCutoff = 0
import sys
if ".." not in sys.path:
sys.path.append("..")
from jp_gene_viz import dNetwork
dNetwork.load_javascript_support()
# from jp_gene_viz import multiple_network
from jp_gene_viz import LExpression
LExpression.load_javascript_support()
# Load network linked to gene expression data
L = LExpression.LinkedExpressionNetwork()
L.show()
# Load Network and Heatmap
L.load_network(directory + '/' + netPath + '/' + networkFile)
L.load_heatmap(directory + '/' + expressionFile)
N = L.network
N.set_title(netTitle)
N.threshhold_slider.value = edgeCutoff
N.apply_click(None)
N.draw()
# Add labels to nodes
N.labels_button.value=True
N.restore_click()
# Limit to TFs only, remove unconnected TFs, choose and set network layout
N.tf_only_click()
N.connected_only_click()
N.layout_dropdown.value = 'fruchterman_reingold'
N.layout_click()
# Interact with Heatmap
# Limit genes in heatmap to network genes
L.gene_click(None)
# Z-score heatmap values
L.expression.transform_dropdown.value = 'Z score'
L.expression.apply_transform()
# Choose a column in the heatmap (e.g., 48h Th17) to color nodes
L.expression.col = rnaSampleOfInt
L.condition_click(None)
# Switch SVG layout to get line colors, then switch back to faster canvas mode
N.force_svg(None)
```
|
github_jupyter
|
# SMIB system as in Milano's book example 8.1
```
%matplotlib widget
import numpy as np
import matplotlib.pyplot as plt
import scipy.optimize as sopt
import ipywidgets
from pydae import ssa
import json
```
## Import system module
```
from smib_milano_ex8p1_4ord_avr import smib_milano_ex8p1_4ord_avr_class
```
## Instantiate system
```
syst = smib_milano_ex8p1_4ord_avr_class()
```
## Initialize the system (backward and foreward)
```
events=[{'p_t':0.8, 'v_t':1.1, 'K_a':500, 'T_e':0.1}]
syst.initialize(events,xy0=1)
syst.save_0()
syst.report_u()
syst.report_x()
syst.report_y()
```
## Simulation
```
syst = smib_milano_ex8p1_4ord_avr_class()
events=[{'p_t':0.8, 'v_t':1.0, 'K_a':400, 'T_e':0.5, 'H':6}]
syst.initialize(events,xy0=1)
events=[{'t_end':1.0},
{'t_end':15.0, 'p_m':0.8, 'v_ref':1.05}
]
syst.simulate(events,xy0='prev');
plt.close('all')
fig, axes = plt.subplots(nrows=2,ncols=2, figsize=(10, 5), frameon=False, dpi=50)
axes[0,0].plot(syst.T, syst.get_values('omega'), label=f'$\omega$')
axes[0,1].plot(syst.T, syst.get_values('v_t'), label=f'$v_t$')
axes[1,0].plot(syst.T, syst.get_values('p_t'), label=f'$p_t$')
axes[1,1].plot(syst.T, syst.get_values('q_t'), label=f'$q_t$')
```
## Run in two time intervals
```
events=[{'t_end':1.0}]
syst.run(events)
events=[{'t_end':2.0}]
syst.run(events)
syst.get_value('omega')
events=[{'p_t':0.8, 'v_t':1.0, 'K_a':400, 'T_e':0.5}]
syst.initialize(events,xy0=1)
ssa.eval_A(syst)
ssa.damp_report(syst)
syst.get_value('p_m')
Ts_control = 0.010
times = np.arange(0.0,10,Ts_control)
# Calculate second references
events=[{'P_t':0.9, 'Q_t':0.0}]
syst.initialize(events,xy0=1.0)
x_ref = np.copy(syst.struct[0].x)
v_f_ref = syst.struct[0]['v_f']
p_m_ref = syst.struct[0]['p_m']
# Calculate initial references
events=[{'P_t':0.0, 'Q_t':0.0}]
syst.initialize(events,xy0=1.0)
x_0 = np.copy(syst.struct[0].x)
v_f_0 = syst.get_value('v_f')
p_m_0 = syst.get_value('p_m')
# Control design
ssa.eval_ss(syst)
Q = np.eye(syst.N_x)*100
R = np.eye(syst.N_u)
K = ctrl.place(syst.A,syst.B,[-2.0+1j*6,-2.0-1j*6,-100,-101])
K,S,E = ctrl.lqr(syst.A,syst.B,Q,R)
Ad,Bd = ssa.discretise_time(syst.A,syst.B,Ts_control)
Kd,S,E = ssa.dlqr(Ad,Bd,Q,R)
for t in times:
x = np.copy(syst.struct[0].x)
v_f = v_f_0
p_m = p_m_0
if t>1.0:
u_ctrl = K*(x_ref - x)
p_m = p_m_ref + u_ctrl[0]
v_f = v_f_ref + u_ctrl[1]
events=[{'t_end':t,'v_f':v_f,'p_m':p_m}]
syst.run(events)
syst.post();
plt.close('all')
fig, axes = plt.subplots(nrows=2,ncols=2, figsize=(10, 5), frameon=False, dpi=50)
axes[0,0].plot(syst.T, syst.get_values('omega'), label=f'$\omega$')
axes[0,1].plot(syst.T, syst.get_values('v_1'), label=f'$v_1$')
axes[1,0].plot(syst.T, syst.get_values('P_t'), label=f'$P_t$')
axes[1,1].plot(syst.T, syst.get_values('Q_t'), label=f'$Q_t$')
ssa.eval_ss(syst)
from scipy.signal import ss2tf,lti,bode
num,den =ss2tf(syst.A,syst.B,syst.C,syst.D,input=0)
G = lti(num[1],den)
w, mag, phase = G.bode()
plt.figure()
plt.semilogx(w, mag) # Bode magnitude plot
plt.figure()
plt.semilogx(w, phase) # Bode phase plot
plt.show()
events=[{'t_end':1.0,'P_t':0.8, 'Q_t':0.5},
{'t_end':10.0, 'p_m':0.9}
]
syst.simulate(events,xy0=1.0);
syst.inputs_run_list
0.01/6
syst.B
syst.struct[0]['Fu']
```
|
github_jupyter
|
# Week 2 - Data handling
The Python modules `pandas` and `numpy` are useful libraries to handle datasets and apply basic operations on them.
Some of the things we learnt in week 1 using native Python (e.g. accessing, working with and writing data files, and performing operations on them) can be easily achieved using `pandas` instead. `pandas` offers data structures and operations for manipulating different types of datasets - see [documentation](https://pandas.pydata.org/).
We will only cover `pandas` today, however feel free to explore `numpy` in parallel at your own pace e.g. following [this tutorial](https://numpy.org/devdocs/user/quickstart.html) and combining it with continuing to learn `pandas`.
### Aims
- Gain familiarity using `pandas` to handle datasets
- Create, read and write data
- Select a subset of variables (columns)
- Filter rows based on their values
- Sort datasets
- Create new columns or modify existing ones
- Summarise and collapse values in one or more columns to a single summary value
- Handle missing data
- Merge datasets
### Installing pandas
The module `pandas` does not come by default as part of the default Anaconda installation. In order to install it in your system, launch the "Anaconda Prompt (Anaconda3)" program and run the following command: `conda install pandas`. Once the command finishes execution, `pandas` will be installed in your system
<img src="../img/az_conda_prompt.png" width="400">
**Note:** if you have any issues installing `pandas`, please get in touch with one of the trainers after the lecture
### Loading pandas
Once installed, you can import it e.g. using the alias `pd` as follows:
```
import pandas as pd
```
### Reading datasets with `pandas`
We are going to use the METABRIC dataset `metabric_clinical_and_expression_data.csv` containing information about breast cancer patients as we did in week 1.
Pandas allows importing data from various file formats such as csv, xls, json, sql ...
To read a csv file, use the method `.read_csv()`:
```
metabric = pd.read_csv("../data/metabric_clinical_and_expression_data.csv")
metabric
print(metabric)
```
If you forget to include `../data/` above, or if you include it but your copy of the file is saved somewhere else, you will get an error that ends with a line like this: `FileNotFoundError: File b'metabric_clinical_and_expression_data.csv' does not exist`
Generally, rows in a `DataFrame` are the **observations** (patients in the case of METABRIC) whereas columns are known as the observed **variables** (Cohort, Age_at_diagnosis ...).
Looking at the column on the far left, you can see the row names of the DataFrame `metabric` assigned using the known 0-based indexing used in Python.
Note that the `.read_csv()` method is not limited to reading csv files. For example, you can also read Tab Separated Value (TSV) files by adding the argument `sep='\t'`.
### Exploring data
The pandas DataFrame object borrows features from the well-known R's `data.frame` or SQL's `table`. They are 2-dimensional tables whose columns can contain different data types (e.g. boolean, integer, float, categorical/factor). Both the rows and columns are indexed, and can be referred to by number or name.
An index in a DataFrame refers to the position of an element in the data structure. Using the `.info()` method, we can view basic information about our DataFrame object:
```
metabric.info()
```
As expected, our object is a `DataFrame` (or, to use the full name that Python uses to refer to it internally, a `pandas.core.frame.DataFrame`).
```
type(metabric)
```
It has 1904 rows (the patients) and 32 columns. The columns consist of integer, floats and strings (object). It uses almost 500 KB of memory.
As mentioned, a DataFrame is a Python object or data structure, which means it can have **Attributes** and **Methods**.
**Attributes** contain information about the object. You can access them to learn more about the contents of your DataFrame. To do this, use the object variable name `metabric` followed by the attribute name, separated by a `.`. Do not use any () to access attributes.
For example, the types of data contained in the columns are stored in the `.dtypes` attribute:
```
metabric.dtypes
```
You can access the dimensions of your DataFrame using the `.shape` attribute. The first value is the number of rows, and the second the number of columns:
```
metabric.shape
```
The row and column names can be accessed using the attributes `.index` and `.columns` respectively:
```
metabric.index
metabric.columns
```
If you'd like to transpose `metabric` use the attribute `T`:
```
metabric.T
```
**Methods** are functions that are associated with a DataFrame. Because they are functions, you do use () to call them, and can have arguments added inside the parentheses to control their behaviour. For example, the `.info()` command we executed previously was a method.
The `.head()` method prints the first few rows of the table, while the `.tail()` method prints the last few rows:
```
metabric.head()
metabric.head(3)
metabric.tail()
```
The `.describe()` method computes summary statistics for the columns (including the count, mean, median, and std):
```
metabric.describe()
```
In general you can find which **Attributes** and **Methods** are available for your DataFrame using the function `dir()`:
```
dir(metabric)
```
We often want to calculate summary statistics grouped by subsets or attributes within fields of our data. For example, we might want to calculate the average survival time for patients with an advanced tumour stage.
There are two ways to access columns in a DataFrame. The first is using the name of the DataFrame `metabric` followed by a `.` and then followed by the name of the column. The second is using square brackets:
```
metabric.Survival_time
metabric['Survival_time']
```
We can also compute metrics on specific columns or on the entire DataFrame:
```
metabric['Survival_time'].mean()
metabric['Survival_time'].std()
metabric.mean()
```
### Selecting columns and rows
The [pandas cheat sheet](https://pandas.pydata.org/Pandas_Cheat_Sheet.pdf) can be very helpful for recalling basic pandas operations.
To select rows and columns in a DataFrame, we use square brackets `[ ]`. There are two ways to do this: with **positional** indexing, which uses index numbers, and **label-based** indexing which uses column or row names.
To select the first three rows using their numeric index:
```
metabric[:3]
```
The colon `:` defines a range as we saw with slicing lists in week 1.
To select one column using its name:
```
metabric['Mutation_count']
```
And we can combine the two like this:
```
metabric[:3]['Mutation_count']
```
However the following does not work:
```
metabric[:3,'Mutation_count']
```
To do **positional** indexing for both rows and columns, use `.iloc[]`. The first argument is the numeric index of the rows, and the second the numeric index of the columns:
```
metabric.iloc[:3,2]
```
For **label-based** indexing, use `.loc[]` with the column and row names:
```
metabric.loc[:3,"Age_at_diagnosis"]
```
**Note**: because the rows have numeric indices in this DataFrame, we may think that selecting rows with `.iloc[]` and `.loc[]` is same. As observed above, this is not the case.
If you'd like to select more than one row:
```
metabric.loc[:3, ['Cohort', 'Chemotherapy']]
metabric.loc[:3, 'Cohort':'Chemotherapy']
```
### Filtering rows
You can choose rows from a DataFrame that match some specified criteria. The criteria are based on values of variables and can make use of comparison operators such as `==`, `>`, `<` and `!=`.
For example, to filter `metabric` so that it only contains observations for those patients who died of breast cancer:
```
metabric[metabric.Vital_status=="Died of Disease"]
```
To filter based on more than one condition, you can use the operators `&` (and), `|` (or).
```
metabric[(metabric.Vital_status=="Died of Disease") & (metabric.Age_at_diagnosis>70)]
```
For categorical variables e.g. `Vital_status` or `Cohort`, it may be useful to count how many occurrences there is for each category:
```
metabric['Vital_status'].unique()
metabric['Vital_status'].value_counts()
```
To filter by more than one category, use the `.isin()` method.
```
metabric[metabric.Vital_status.isin(['Died of Disease', 'Died of Other Causes'])]
metabric['Cohort'].value_counts()
```
To tabulate two categorical variables just like `table` in R, use the function `.crosstab()`:
```
pd.crosstab(metabric['Vital_status'], metabric['Cohort'])
```
### Define new columns
To obtain the age of the patient today `Age_today` (new column) based on the `Age_at_diagnosis` (years) and the `Survival_time` (days), you can do the following:
```
metabric['Age_today'] = metabric['Age_at_diagnosis'] + metabric['Survival_time']/365
metabric
```
### Sort data
To sort the entire DataFrame according to one of the columns, we can use the `.sort_values()` method. We can store the sorted DataFrame using a new variable name such as `metabric_sorted`:
```
metabric_sorted = metabric.sort_values('Tumour_size')
metabric_sorted
metabric_sorted.iloc[0]
metabric_sorted.loc[0]
```
We can also sort the DataFrame in descending order:
```
metabric_sorted = metabric.sort_values('Tumour_size', ascending=False)
metabric_sorted
```
### Missing data
Pandas primarily uses `NaN` to represent missing data, which are by default not included in computations.
The `.info()` method shown above already gave us a way to find columns containing missing data:
```
metabric.info()
```
To get the locations where values are missing:
```
pd.isna(metabric)
metabric.isnull()
```
To drop any rows containing at least one column with missing data:
```
metabric.dropna()
```
However, from the other way around, to rather remove columns with at least one row with missing data, you need to use the 'axis' argument:
```
metabric.dropna(axis=1)
```
Define in which columns to look for missing values before dropping the row:
```
metabric.dropna(subset = ["Tumour_size"])
metabric.dropna(subset = ["Tumour_size", "Tumour_stage"])
```
Filling missing data:
```
metabric.fillna(value=0)
metabric.fillna(value={'Tumour_size':0, 'Tumour_stage':5})
```
### Grouping
Grouping patients by Cohort and then applying the `.mean()` function to the resulting groups:
```
metabric.groupby('Cohort')
metabric.groupby('Cohort').mean()
```
Grouping by multiple columns forms a hierarchical index, and again we can apply the `.mean()` function:
```
metabric.groupby(['Cohort', 'Vital_status']).mean()
```
### Pivoting
In some cases, you may want to re-structure your existing DataFrame. The function `.pivot_table()` is useful for this:
```
import numpy as np
df = pd.DataFrame({'A': ['one', 'one', 'two', 'three'] * 3, 'B': ['A', 'B', 'C'] * 4, 'C': ['foo', 'foo', 'foo', 'bar', 'bar', 'bar'] * 2, 'D': np.random.randn(12), 'E': np.random.randn(12)})
df
pd.pivot_table(df, values='D', index=['A', 'B'], columns=['C'])
```
### Merge datasets
You can concatenate DataFrames using the function `concat()`:
```
metabric_cohort1 = metabric[metabric["Cohort"]==1]
metabric_cohort1
metabric_cohort2 = metabric[metabric["Cohort"]==2]
metabric_cohort2
pd.concat([metabric_cohort1,metabric_cohort2])
```
Or join datasets using the function `.merge()`:
```
left = pd.DataFrame({'key': ['foo', 'foo'], 'lval': [1, 2]})
left
right = pd.DataFrame({'key': ['foo', 'foo'], 'rval': [4, 5]})
right
pd.merge(left, right, on='key')
```
A final example:
```
left = pd.DataFrame({'key': ['foo', 'bar'], 'lval': [1, 2]})
left
right = pd.DataFrame({'key': ['foo', 'bar'], 'rval': [4, 5]})
right
pd.merge(left, right, on='key')
```
## Assignment
1. Write python commands using pandas to learn how to output tables as follows:
- Read the dataset `metabric_clinical_and_expression_data.csv` and store its summary statistics into a new variable called `metabric_summary`.
- Just like the `.read_csv()` method allows reading data from a file, `pandas` provides a `.to_csv()` method to write `DataFrames` to files. Write your summary statistics object into a file called `metabric_summary.csv`. You can use `help(metabric.to_csv)` to get information on how to use this function.
- Use the help information to modify the previous step so that you can generate a Tab Separated Value (TSV) file instead
- Similarly, explore the method `to_excel()` to output an excel spreadsheet containing summary statistics
2. Write python commands to perform basic statistics in the metabric dataset and answer the following questions:
- Read the dataset `metabric_clinical_and_expression_data.csv` into a variable e.g. `metabric`.
- Calculate mean tumour size of patients grouped by vital status and tumour stage
- Find the cohort of patients and tumour stage where the average expression of genes TP53 and FOXA1 is the highest
- Do patients with greater tumour size live longer? How about patients with greater tumour stage? How about greater Nottingham_prognostic_index?
3. Review the section on missing data presented in the lecture. Consulting the [user's guide section dedicated to missing data](https://pandas.pydata.org/pandas-docs/stable/user_guide/missing_data.html) and any other materials as necessary use the functionality provided by pandas to answer the following questions:
- Which variables (columns) of the metabric dataset have missing data?
- Find the patients ids who have missing tumour size and/or missing mutation count data. Which cohorts do they belong to?
- For the patients identified to have missing tumour size data for each cohort, calculate the average tumour size of the patients with tumour size data available within the same cohort to fill in the missing data
|
github_jupyter
|
```
import numpy as np
import pandas as pd
import os
import matplotlib.pyplot as plt
from fastai.vision import *
import torch
#from mrnet_orig import *
from mrnet_itemlist import *
#from ipywidgets import interact, Dropdown, IntSlider
%matplotlib notebook
plt.style.use('grayscale')
# run tree on my data to see its data structure
! tree -d ..
data_path = Path('../data24') # /data24 contains interpolated data where each case-plane has 24 slices
caselist = MRNetCaseList.from_folder(path=data_path)
type(caselist)
caselist.items[:5] # items are Case numbers as 4-character strings
caselist.inner_df # at this point, inner_df is an empty attribute, returning None, since caselist was
```
Construct a DataFrame with labels linked to cases. First, do just the "Abnormal" label.
```
train_abnl = pd.read_csv(data_path/'train-abnormal.csv', header=None,
names=['Case', 'Abnormal'],
dtype={'Case': str, 'Abnormal': np.int64})
valid_abnl = pd.read_csv(data_path/'valid-abnormal.csv', header=None,
names=['Case', 'Abnormal'],
dtype={'Case': str, 'Abnormal': np.int64})
abnl = train_abnl.append(valid_abnl, ignore_index=True)
caselist.link_label_df(df=abnl)
caselist.inner_df
```
Now can label from inner_df associated to CaseList.
```
casesplit = caselist.split_by_folder()
ll = casesplit.label_from_df()
len(ll.train), len(ll.valid)
casesplit.valid
case = casesplit.train.get(0)
case.data.shape
```
At this point we have a correctly labeled dataset. It would be possible to do various types of transformations and augmentation on the data, or could convert into a data bunch. Will implement custom transformations/augmentations later.
Can just call `.databunch()` on the labeled list to create a `DataBunch`.
```
data = ll.databunch(bs=8)
data.show_batch(4)
x,y = data.one_batch(DatasetType.Train, True, True)
x.shape, y.shape
smpl = grab_idx(x, 2)
smpl.shape, type(smpl)
```
Calling `.reconstruct` on the PyTorch Tensor returns the same kind of thing as the `.get` method, which in this context is an `MRNetCase`, which we can then display.
```
tst = data.train_ds.x.reconstruct(smpl)
type(tst)
tst
tst.data.shape
fig, ax = plt.subplots(1, 1, figsize=(10,10))
ax.imshow(tst.data[2, 11, :, :])
plt.show()
```
### Minimal training example
- [x] import necessary libraries (fastai, mrnet_itemlist)
- [x] https://docs.fast.ai/data_block.html
- [x] 1 provide inputs
- [x] 2 split data into training and validation sets
- [x] 3 label the inputs
- [ ] 4 what transforms to apply (none for now)
- [ ] 5 how to add test set (none for now)
- [x] 6 how to wrap in dataloaders and create the databunch
|
github_jupyter
|
Sascha Spors,
Professorship Signal Theory and Digital Signal Processing,
Institute of Communications Engineering (INT),
Faculty of Computer Science and Electrical Engineering (IEF),
University of Rostock, Germany
# Tutorial Digital Signal Processing
**Correlation**,
Winter Semester 2021/22 (Course #24505)
- lecture: https://github.com/spatialaudio/digital-signal-processing-lecture
- tutorial: https://github.com/spatialaudio/digital-signal-processing-exercises
Feel free to contact lecturer [email protected]
WIP...
```
# most common used packages for DSP, have a look into other scipy submodules
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
from scipy import signal
def my_xcorr2(x, y, scaleopt='none'):
N = len(x)
M = len(y)
kappa = np.arange(0, N+M-1) - (M-1)
ccf = signal.correlate(x, y, mode='full', method='auto')
if N == M:
if scaleopt == 'none' or scaleopt == 'raw':
ccf /= 1
elif scaleopt == 'biased' or scaleopt == 'bias':
ccf /= N
elif scaleopt == 'unbiased' or scaleopt == 'unbias':
ccf /= (N - np.abs(kappa))
elif scaleopt == 'coeff' or scaleopt == 'normalized':
ccf /= np.sqrt(np.sum(x**2) * np.sum(y**2))
else:
print('scaleopt unknown: we leave output unnormalized')
return kappa, ccf
if True: # test my_xcorr with simple example
x = np.array([0, 1, 0, 0, 0])
y = np.array([1, 0, 0])
# plot my_xcorr2(x, y) vs. my_xcorr2(y, x)
plt.figure(figsize=(9, 2))
plt.subplot(1, 2, 1)
kappa_xy, ccf_xy = my_xcorr2(x, y)
plt.stem(kappa_xy, ccf_xy, basefmt='C0:', use_line_collection=True)
plt.xlabel(r'$\kappa$')
plt.ylabel(r'$\varphi_{xy}[\kappa]$')
plt.title('cross correlation between x and y')
plt.grid(True)
plt.subplot(1, 2, 2)
kappa_yx, ccf_yx = my_xcorr2(y, x)
plt.stem(kappa_yx, ccf_yx, basefmt='C0:', use_line_collection=True)
plt.xlabel(r'$\kappa$')
plt.ylabel(r'$\varphi_{yx}[\kappa]$')
plt.title('cross correlation between y and x')
plt.grid(True)
```
## Normalization schemes for cross correlation of finite length signals
check cross correlation
- of a cosine and a sine signal
- of a normal pdf process that exhibits some repetition
```
case_str = 'cos_sin'
case_str = 'normal_pdf'
if case_str == 'cos_sin':
Nt = 200 # number of samples for a full period
x = np.cos(2*np.pi/Nt * 1 * np.arange(0, Nt)) * 2
y = np.sin(2*np.pi/Nt * 1 * np.arange(0, Nt)) * 2
elif case_str == 'normal_pdf':
Nt = 20000
loc, scale = 2, np.sqrt(2) # mu, sigma
x = scale * np.random.randn(Nt) + loc
y = np.roll(x,-7500) # process similarity for offset of 7500 samples
plt.figure(figsize=(8,6))
plt.subplot(2,2,1)
kappa, ccf = my_xcorr2(x, y, scaleopt='none')
plt.plot(kappa, ccf)
plt.ylabel(r'$\varphi_{xy}[\kappa]$')
plt.title('raw CCF(x,y)')
plt.grid(True)
plt.subplot(2,2,2)
kappa, ccf = my_xcorr2(x, y, scaleopt='biased')
plt.plot(kappa, ccf)
plt.title('biased CCF(x,y)')
plt.grid(True)
plt.subplot(2,2,3)
kappa, ccf = my_xcorr2(x, y, scaleopt='unbiased')
plt.plot(kappa, ccf)
plt.xlabel(r'$\kappa$')
plt.ylabel(r'$\varphi_{xy}[\kappa]$')
plt.title('unbiased CCF(x,y)')
plt.grid(True)
plt.subplot(2,2,4)
kappa, ccf = my_xcorr2(x, y, scaleopt='coeff')
plt.plot(kappa, ccf)
plt.xlabel(r'$\kappa$')
plt.title('normalized CCF(x,y)')
plt.grid(True)
# check that the unbiased estimate of the CCF represents the theoretical
# result best in comparison to the other normalization schemes, at least
# for the chosen examples
```
# **Copyright**
The notebooks are provided as [Open Educational Resources](https://en.wikipedia.org/wiki/Open_educational_resources). Feel free to use the notebooks for your own purposes. The text is licensed under [Creative Commons Attribution 4.0](https://creativecommons.org/licenses/by/4.0/), the code of the IPython examples under the [MIT license](https://opensource.org/licenses/MIT). Please attribute the work as follows: *Frank Schultz, Digital Signal Processing - A Tutorial Featuring Computational Examples* with the URL https://github.com/spatialaudio/digital-signal-processing-exercises
|
github_jupyter
|

<h2 align='center'>Data Literacy through Sports Analytics</h2>
<h3 align='center'>Southern Alberta Teachers' Convention 2021</h3>
<h3 align='center'>Tina Leard (Cybera)<br>
Michael Lamoureux (University of Calgary)</h3><br>
<h4 align='center'> Slides at: https://tinyurl.com/callysto-data </h4>

<center><img src='./images/ccby.png' alt="CC BY logo" width='300' /></center>
<p><center><a href='https://creativecommons.org/licenses/by/4.0/' target='_blank'>CC BY</a>:<br>
This license allows reusers to distribute, remix, adapt, and build upon the material in any medium or format,<br>
so long as attribution is given to the creator.
</center></p>
```
import numpy as np
import pandas as pd
from pandas import read_csv
import plotly.graph_objects as go
import plotly.express as px
from plotly import subplots
from plotly.offline import download_plotlyjs, plot,iplot
import cufflinks as cf
cf.go_offline()
from IPython.display import YouTubeVideo
from ipysheet import sheet, cell, cell_range
%matplotlib inline
```
# Overview
- Data literacy via sports
- The learning progression
- Examples of learning and data analysis
- Professional soccer
- Ice hockey
- Field hockey
- Python, Jupyter, and Callysto
<center><img src='./images/data_literacy.png' alt='data literacy' width='85%' /></center>
#### Content and context
(Alberta Education, 2000, 2007, updated 2016, 2017)
## Example: professional soccer event data
```
df_soccer = pd.read_csv("https://raw.githubusercontent.com/metrica-sports/sample-data/master/data/Sample_Game_1/Sample_Game_1_RawEventsData.csv"); df_soccer
```
**Home team passes, second half**
```
df_soccer.loc[lambda df: (df['Team'] == 'Home') & (df['Period'] == 2) & (df['Type'] == 'PASS'), :] \
.iplot(kind="scatter",x = "Start X", y = "Start Y", mode = "markers")
```
## Bridging expert to novice
## Data visualization learning progression
<img src='./images/creating_scaffolding.png' alt='scaffolding' width='95%' />
## Data visualization learning progression
<img src='./images/creating_adapting.png' alt='adapting' width='95%' />
Communicating mathemtical reasoning (Alberta Education, 2007, updated 2016)
## Data gathering learning progression
<br>
<center><img src='./images/data_gathering.png' alt='data gathering' width='85%' /></center>
<br><br><br>Source: <a href='http://oceansofdata.org/sites/oceansofdata.org/files/pervasive-and-persistent-understandings-01-14.pdf' target='_blank'>Pervasive and Persistent Understandings about Data</a>, Kastens (2014)
## Authentic learning approach
- Learning design based on interdisciplinary<br>
connections and real-world examples
- Industry-aligned data science analysis process
- Python, an all-purpose programming language
- Jupyter notebook, a free industry-standard tool for data scientists
- CallystoHub, free cloud computing
## Athlete development
### U15 training to train
- Promotes tactical strategies for in-game decision making, reading the situation and inferring
- Focuses on the team and the process
- Situates personal goals within a team approach
### U18 training to compete
- Emphasizes individual technical and position-specific training
## Youth sports analytics
Online communication,<br>
sometimes through shared video analysis spaces
Video replay during games and training
Post–game video analysis, limitted statistics
## Learning design and flexibility
<br>
<img src='./images/flexibility.png' alt='adapting' width='90%' />
## Two data examples
1. Import a csv file and use a Python spreadsheet<br>to create shot maps (ice hockey)
2. Gather data from video to analyze and make decisions (field hockey)
## Data example 1:
## Using IIHF World Junior Championship data to create graphs and a shot map
## Defining ice hockey net zones:<br> What factors can lead to scoring?
<!--USA Hockey Goaltender Basics https://www.usahockeygoaltending.com/page/show/890039-stance-->
||
|-|-|
|<img src='./images/hockey_net_zones.png' width='100%'/>|<img src='https://cdn.hockeycanada.ca/hockey-canada/Team-Canada/Men/Under-18/2014-15/2014-15_goalie_camp.jpg?q=60' />|
||<a href='https://www.hockeycanada.ca/en-ca/news/34-goaltenders-invited-to-2014-poe-camp' target='_blank'>Image source: Hockey Canada</a>|
```
%%html
<h2>Data source IIHF: Shot charts</h2><br>
<iframe width="1200" height="600" src="https://www.iihf.com/pdf/503/ihm503a13_77a_3_0" frameborder="0" ></iframe>
```
## Tally chart
<img src='./images/hockey_tally.png' alt='tally chart' width='85%' />
## Generating a csv file
Zone,Austria,Canada,Czech_Republic,Finland,Germany,Russia,Switzerland,Slovakia,Sweden,USA,Total<br>
one,0,7,0,3,2,0,0,0,3,3,18<br>
two,0,1,1,0,1,0,0,0,0,0,3<br>
three,0,5,0,2,2,4,1,0,3,6,23<br>
four,0,4,3,2,1,1,0,1,0,3,15<br>
five,0,1,0,2,1,0,0,0,0,0,4<br>
six,1,1,2,4,0,2,0,1,0,2,13<br>
seven,0,6,0,1,3,3,1,1,0,9,24<br>
eight,0,5,1,2,2,3,1,2,3,2,21<br>
nine,0,3,3,0,2,3,2,0,5,0,18<br>
## Exploring scoring on net zones
```
hockey_goals_df = pd.read_csv('./data/hockey_goals.csv')
hockey_goals_df.head(9)
```
### What do measures of central tendency<br>tell us about the total goals per net zone?
```
hockey_goals_df['Total'].sum()
hockey_goals_df['Total'].min()
hockey_goals_df['Total'].max()
scatter_hockey_goals_df = px.scatter(hockey_goals_df,x="Zone",y="Total",title="Total goals per net zone")
scatter_hockey_goals_df.show()
hockey_goals_df['Total'].mean()
hockey_goals_df['Total'].median()
hockey_goals_df['Total'].mode()
```
### Which net zones score above the median?
```
hockey_goals_df = hockey_goals_df.sort_values('Total', ascending=False)
hockey_goals_df
bar_hockey_goals_df = px.bar(hockey_goals_df,
x="Zone", y="Total")
bar_hockey_goals_df.update_layout(title_text='Total goals by net zone')
```
### What connections exist between<br>goalie position and scoring?
```
hockey_goals_df = pd.read_csv('./data/hockey_goals.csv')
hockey_goals_df.Total
spread_sheet_hockey_net = sheet(rows=3, columns=3)
my_cells_net = cell_range([[18,3,23],[15,4,13],[24,21,18]],row_start=0,col_start=0,numeric_format="int")
figure_hockey_net = go.Figure(data=go.Heatmap(
z =list(reversed(my_cells_net.value)),
type = 'heatmap',
colorscale = 'greys',opacity = 1.0))
axis_template = dict(range = [0,5], autorange = True,
showgrid = False, zeroline = False,
showticklabels = False,
ticks = '' )
figure_hockey_net.update_layout(margin = dict(t=50,r=200,b=200,l=200),
xaxis = axis_template,
yaxis = axis_template,
showlegend = False,
width = 800, height = 500, title="Ice hockey net zones",
autosize = True )
# Add image in the background
nLanes = 3
nZones = 3
figure_hockey_net.add_layout_image(
dict(
source="images/hockey_net.png",
xref="x",
yref="y",
x=-0.5,
y=-.5 + nLanes, #this adjusts the placement of the image
sizex=nZones,
sizey=nLanes,
sizing="fill",
opacity=1.0,
layer="above")
)
# changes in my_cells should trigger this function
def calculate(change):
figure_hockey_net.update_traces(z=list(reversed(my_cells_net.value)))
my_cells_net.observe(calculate, 'value')
spread_sheet_hockey_net
139
figure_hockey_net.update() # Click the keys "Shift-return" to update the figure
```
## Data example 2:
## Analyzing youth field hockey data to make decisions
<center><img src='./images/learning_cycle1.png' alt="Learning design and context" width='90%' /></center>
#### Learning design and context notes
The context is physical education, and the content is statistics. Within physical education, in-game skills, fair play, teamwork, and goal setting are integrated. Those outcomes can be applied to in-game decision making. The goal setting can also be part of the communication resulting from the data analysis. When considering in-game decision making, we can define an action as the result of a decision. Decision making is part of a learning cycle that incorporates a technological feedback loop.
(Field Hokcey Alberta, 2020; Field Hockey Canada, 2020; Alberta Education, 2000)
<center><img src='./images/learning_cycle5.png' alt="Learning cycle" width='90%' /></center>
#### Learning cycle notes
The real situation occurs on the field where a decision is made and an action is executed. Then, the athlete forms a mental representation, processing occurs, and a real model is formed. The real model is integrated into the computational model, which results in a technological feedback, then a connection is made back into game play.
(Butler & Winne, 1995; Cleary & Zimmerman, 2001; Hadwin et al., 2017; Leard & Hadwin, 2001)
<center><img src='./images/computational_thinking.png' alt="Computationl thinking" width='90%' /></center>
<a href="https://app.lucidchart.com/documents/view/8e3186f7-bdfe-46af-9c7f-9c426b80d083">Connecting data literacy and sports</a>
#### Computational modelling and data literacy notes
The definition of computational thinking can vary.
Computational thinking is math reasoning combined with critical thinking plus the power of computers. We can use computers to do work more efficiently for us, like compute thousands of lines of data.
Under that definition of computational thinking, we can apply computational thinking strategies. The foundational process is decomposing to look for patterns. We can use computer programming to design algorithms to look for patterns. With these algorithms, we can infer through abstractions.
The abstractions can be in the form of computational models: data visualizations (including graphs from the curriculum), data analyses, and simulations of probability models. The data visualizations can extend beyond the curriculum to support math reasoning.
(Berikan & Özdemir, 2019; Gadanidis, 2020; Guadalupe & Gómez-Blancarte, 2019; Leard & Hadwin, 2001)
<center><img src='./images/analysis_process.png' alt="Data science analysis process" width='90%' /></center>
#### Data science analysis process notes
This data science analysis process was modified from how expert data scientists analyze data and aligned to several provincial curricula.
There are six steps:
1. Understand the problem. What questions are we trying to answer?
2. Gather the data. Find the data sources, with the extension of big data sets.
3. Organize the data so we can explore it, usually in the form of a table.
4. Explore the data to create computational models. Usually, there is more than one model. Look for evidence to answer our questions.
5. Interpret the data through inferences. Explain how the evidence answers our questions.
6. Communicate the results. In the context of sports analytics, the communication might be within a team to decide tactical strategies for game play.
(Alberta Education, 2007, updated 2016; Ferri, 2006; Leard & Hadwin, 2001; Manitoba Education and Training, 2020; Ontario Ministry of Education, 2020)
<center><img src='./images/collective.png' alt="Collective decision making" width='90%' /></center>
#### Learning cycle notes
How the individual makes decisions within the collective responsibilities and actions of the team can be considered. In-game decision making involves in-game communication with team members, with each athlete referring to their own real model.
While in-game decision making will always produce a real model, athletes also need to decide when it is appropriate to connect the real model to the computational model and integrate that connection back into game play.
(BC Ministry of Education, 2020; Hadwin et al., 2017; Leard & Hadwin, 2001)
<center><img src='./images/models.png' alt="Models" width='90%' /></center>
#### Real model and computational model notes
How the individual makes decisions within the collective responsibilities and actions of the team can be considered. In-game decision making involves in-game communication with team members, with each athlete referring to their own real model.
While in-game decision making will always produce a real model, athletes also need to decide when it is appropriate to connect the real model to the computational model and integrate that connection back into game play.
(Field Hockey Canada, 2020)
<center><img src='./images/data_literacy_sports.png' alt="Connecting data literacy and sports" width='90%' /></center>
<center><img src='./images/field_hockey_game.png' alt="Field hockey" width='90%' /></center>
<center><img src='./images/understand1.png' alt="Understand actions" width='90%' /></center>
(Field Hockey Alberta, 2020; Field Hockey Canada, 2020)
<center><img src='./images/actions.png' alt="Understand viewpoints" width='90%' /></center>
```
print ('Passes received')
YouTubeVideo('mIwiiJO7Rk4?start=2893&end=2915', width='600', height='355')
```
<center><img src='./images/gather4.png' alt="Gather" width='90%' /></center>
<center><img src='./images/collection_passing.png' alt="Passing" width='90%' /></center>
## 3. Organize
```
possession_time_df = read_csv('data/field_hockey_possession_time.csv')
possession_time_df.head(8)
```
## 4. Explore
How does ball possession affect outcomes?
```
bar_possession_time_df = px.bar(possession_time_df,x="Possession Time (seconds)",y="Quarter",title="Possession per quarter<br>Home 2 shots on net (Q3); Away 1 shot on net (Q1)",color="Team")
bar_possession_time_df.update_layout(autosize=False, width=600, height=400)
lanes_home_passes_df = read_csv('data/field_hockey_lanes_home_passes.csv')
lanes_home_passes_df.head()
circle_lanes_home_passes_df = px.pie(lanes_home_passes_df,values="Count",names="Action",title="Passes received, intercepted, and missed for Home team")
circle_lanes_home_passes_df.show()
bar_lanes_home_passes_df = px.bar(lanes_home_passes_df,
x="Quarter", y="Count", color="Action", title="Passes per quarter for Home team")
bar_lanes_home_passes_df.update_layout(barmode='stack', xaxis={'categoryorder':'array', 'categoryarray':['first','second','third','fourth']})
```
## 4. Explore passes received
What stays the same and what changes?
```
lanes_home_passes_received_df = lanes_home_passes_df[lanes_home_passes_df['Action']=='pass received']
lanes_home_passes_received_df.head()
bar_lanes_home_passes_received_df = px.bar(lanes_home_passes_received_df,
x="Quarter", y="Count", color="Lane", text="Lane", title="Passes received in lanes per quarter for Home team")
bar_lanes_home_passes_received_df.update_layout(barmode='stack', xaxis={'categoryorder':'array', 'categoryarray':['first','second','third','fourth']})
df_passes_home = pd.read_csv('data/field_hockey_home_passes.csv'); df_passes_home
df_temp_1 = df_passes_home.loc[lambda df: (df['Phase of Play'] == 'attack') &(df['Quarter'] == 'first') ];
df_temp_2 = df_passes_home.loc[lambda df: (df['Phase of Play'] == 'attack') &(df['Quarter'] == 'second') ];
df_temp_3 = df_passes_home.loc[lambda df: (df['Phase of Play'] == 'attack') &(df['Quarter'] == 'third') ];
df_temp_4 = df_passes_home.loc[lambda df: (df['Phase of Play'] == 'attack') &(df['Quarter'] == 'fourth') ];
#import plotly.tools as tls
fig_all = subplots.make_subplots(rows=1, cols=4)
fig_1 = df_temp_1.iplot(kind='heatmap', colorscale='blues', x='Lane', y='Zone', z='Count' , asFigure=True)
fig_2 = df_temp_2.iplot(kind='heatmap', colorscale='blues', x='Lane', y='Zone', z='Count' , asFigure=True)
fig_3 = df_temp_3.iplot(kind='heatmap', colorscale='blues', x='Lane', y='Zone', z='Count' , asFigure=True)
fig_4 = df_temp_4.iplot(kind='heatmap', colorscale='blues', x='Lane', y='Zone', z='Count' , asFigure=True)
fig_all.append_trace(fig_1['data'][0], 1, 1)
fig_all.append_trace(fig_2['data'][0], 1, 2)
fig_all.append_trace(fig_3['data'][0], 1, 3)
fig_all.append_trace(fig_4['data'][0], 1, 4)
fig_all.update_xaxes(showticklabels = False, linecolor='black')
fig_all.update_yaxes(showticklabels = False, linecolor='black')
iplot(fig_all)
```
#### Passes in left outside lane of the opponent's net
|||||
|---|---|---|---|
|**Q1: 29%** (14/49)|**Q2: 41%** (13/32)|**Q3: 38%** (16/42)|**Q4: 28%** (8/29)|
```
df_passes_home.loc[lambda df: (df['Lane'] == 1) &(df['Phase of Play'] == 'attack') &(df['Quarter']== 'first') ].sum()
14/49
```
## 5. Interpret<br> How can the data exploration inform decision making?
> - Considering the role of passing versus carrying the ball
> - Keeping the ball out of the zone near the net
> - Attacking on the outer lanes, especially toward the left side of the opponent's net
# The technology in this talk
- **Jupyter** notebooks, **Python** programming, **Pandas** for data
- Free to teachers and students
- **Callysto.ca** project (CanCode, Cybera, PIMS)
- This slideshow **IS** a Jupyter notebook! (take a tour)
## Callysto resources
- <a href="https://www.callysto.ca/starter-kit/">Callysto starter kit</a> Getting started
- <a href="https://courses.callysto.ca">courses.callysto.ca</a> Online courses
- <a href="https://www.callysto.ca/weekly-data-visualization/">Weekly data visualizations</a> Quick activities
<center><a href='https://www.callysto.ca/learning-modules/'><img src='./images/learning_modules.png' target='_blank' alt="Callysto learning modules" width='90%' /></a></center>
<center>All free, all open source, aimed at teachers and students</center>
<p><center>Contact us at <a href="mailto:[email protected]">[email protected]</a><br>
for in-class workshops, virtual hackathons...<br>
<a href="https://twitter.com/callysto_canada">@callysto_canada</a><br>
<a href="https://callysto.ca">callysto.ca</a><br>
<a href="https://www.youtube.com/channel/UCPdq1SYKA42EZBvUlNQUAng">YouTube</a>
</center></p>
## Thank you for your attention!
<center><img src='./images/callysto_logo.png' alt="Callysto logo" width='80%' /></center>
<center><img src='./images/callysto_partners2.png' alt='Callysto partners' width='80%' /></center>
### References
Alberta Education. (2000). *Physical education* [Program of Studies]. https://education.alberta.ca/media/160191/phys2000.pdf
Alberta Education. (2007, updated 2016). *Mathematics kindergarten to grade 9* [Program of Studies]. https://education.alberta.ca/media/3115252/2016_k_to_9_math_pos.pdf
Alberta Education. (2017). *Career and Ttechnology foundations* [Program of Studies]. https://education.alberta.ca/media/3795641/ctf-program-of-studies-jan-4-2019.pdf
BC Ministry of Education. (2020). *BC's digital literacy framework*. https://www2.gov.bc.ca/assets/gov/education/kindergarten-to-grade-12/teach/teaching-tools/digital-literacy-framework.pdf
Berikan, B., & Özdemir, S. (2019). Investigating “problem-solving with datasets” as an implementation of computational thinking: A literature review. *Journal of Educational Computing Research, 58*(2), 502–534. https://doi.org/10.1177/0735633119845694
Butler, D. L., & Winne, P. H. (1995). Feedback and self-regulated learning: A theoretical synthesis. *Review of Educational Research, 65*(3), 245–281. https://doi.org/10.3102/00346543065003245
Cleary, T. J., & Zimmerman, B. J. (2001). Self-regulation differences during athletic practice by experts, non-experts, and novices. *I Journal of Applied Sport Psychology, 13*(2), 185–206. https://doi.org/10.1080/104132001753149883
Ferri, R. B. (2006). Theoretical and empirical differentiations of phases in the modelling process. *ZDM, 38*(2), 86–95. https://doi.org/10.1007/bf02655883
Field Hockey Alberta (2020). *Tactical Seminars*. http://www.fieldhockey.ab.ca/content/tactical-seminars
Field Hockey Canada (2020). *Ahead of the Game*. http://www.fieldhockey.ca/ahead-of-the-game-field-hockey-canada-webinar-series/
Gadanidis, G. (2020, September 2). *Shifting from computational thinking to computational modelling in math education* [Online plenary talk]. Changing the Culture 2020, Pacific Institute for the Mathematical Sciences.
Guadalupe, T. & Gómez-Blancarte, A. (2019). Assessment of informal and formal inferential reasoning: A critical research review. *Statistics Education Research Journal, 18*, 8-25. https://www.researchgate.net/publication/335057564_ASSESSMENT_OF_INFORMAL_AND_FORMAL_INFERENTIAL_REASONING_A_CRITICAL_RESEARCH_REVIEW
Hadwin, A., Järvelä, S., & Miller, M. (2017). Self-Regulation, Co-Regulation, and Shared Regulation in Collaborative Learning Environments. *Handbook of Self-Regulation of Learning and Performance*, 83–106. https://doi.org/10.4324/9781315697048-6
Kastens, K. (2014). *Pervasive and Persistent Understandings about Data*. Oceans of Data Institute. http://oceansofdata.org/sites/oceansofdata.org/files/pervasive-and-persistent-understandings-01-14.pdf
Leard, T., & Hadwin, A. F. (2001, May). *Analyzing logfile data to produce navigation profiles of studying as self-regulated learning* [Paper presentaion]. Canadian Society for the Study of Education, Quebec City, Quebec, Canada.
Manitoba Education and Training (2020). *Literacy with ICT across the curriculum: A model for 21st century learning from K-12*. https://www.edu.gov.mb.ca/k12/tech/lict/index.html
Ontario Ministry of Education. (2020). *The Ontario curriculum grades 1‐8: Mathematics* [Program of Studies]. https://www.dcp.edu.gov.on.ca/en/curriculum/elementary-mathematics
|
github_jupyter
|
# Prepare Superresolution Training Data with eo-learn
There are many examples and resources for training superresolution networks on (satellite) imagery:
- [MDL4EO](https://mdl4eo.irstea.fr/2019/03/29/enhancement-of-sentinel-2-images-at-1-5m/)
- [ElementAI HighRes-Net](https://github.com/ElementAI/HighRes-net)
- [Fast.ai superresolution](https://github.com/fastai/course-v3/blob/master/nbs/dl1/lesson7-superres.ipynb)
We'll show you how to use `eo-learn` to prepare data for these tasks (and an example of training the network with `fastai`)
First you'll need to download the [Spacenet Challenge: Paris Data](https://spacenetchallenge.github.io/AOI_Lists/AOI_3_Paris.html). We're using this to get high resolution image chips.
```
from os import path as op
from glob import glob
import datetime
from eolearn.io import ImportFromTiff, SentinelHubInputTask
from eolearn.core import FeatureType, LinearWorkflow, EOTask
from sentinelhub import BBox, CRS, DataSource
from PIL import Image
import numpy as np
from tqdm import tqdm
spacenet_images = glob('AOI_3_Paris_Train/RGB-PanSharpen/*.tif')
# Import the Spacenet chips into EOPatches, as a feature called "spacenet"
input_task = ImportFromTiff((FeatureType.DATA_TIMELESS, 'spacenet'))
# Add Sentinel 2 L2A to our EOPatches covering the same area
time_interval = ('2017-02-28', '2017-04-01') # roughly matching the spacenet dates
add_l2a = SentinelHubInputTask(
data_source=DataSource.SENTINEL2_L2A,
bands=['B04','B03','B02'],
bands_feature=(FeatureType.DATA, 'TRUE-COLOR-S2-L2A'),
additional_data=[(FeatureType.MASK, 'dataMask', 'IS_VALID'), (FeatureType.DATA, 'SCL')],
maxcc=.1,
time_difference=datetime.timedelta(hours=2),
max_threads=3,
resolution=(10,10)
)
# Save the Spacenet and Sentinel images in separate folders. Resize our images when saving
BIG_SIZE = (256, 256)
SMALL_SIZE = (64, 64)
INPUT_FOLDER = 'input'
TARGET_FOLDER = 'target'
class CustomSave(EOTask):
def execute(self, eopatch, image_name=None):
# if we don't have enough data, don't save
spacenet_array = eopatch.data_timeless['spacenet']
data_pct = (np.count_nonzero(spacenet_array) / spacenet_array.size)
if data_pct < 0.9:
return eopatch
# resize images, rescale to 8bit
sentinel_array = eopatch.data[layer][0]
sentinel_array_8bit = (sentinel_array * 255.).astype(np.uint8)
sentinel_img = Image.fromarray(sentinel_array_8bit).resize(SMALL_SIZE, resample=Image.BILINEAR)
sentinel_img.save(op.join(INPUT_FOLDER, f'{image_name}.png'))
spacenet_array_8bit = ((spacenet_array - np.min(spacenet_array, axis=(0, 1))) / (np.max(spacenet_array, axis=(0, 1)) - np.min(spacenet_array, axis=(0, 1))) * 255).astype(np.uint8)
spacenet_image = Image.fromarray(spacenet_array_8bit).resize(BIG_SIZE, resample=Image.BILINEAR)
spacenet_image.save(op.join(TARGET_FOLDER, f'{image_name}.png'))
return eopatch
custom_save = CustomSave()
# Create this as a EOWorkflow to run over all the images
prepare_data = LinearWorkflow(
input_task,
add_l2a,
custom_save
)
# Execute the workflow
pbar = tqdm(total=len(spacenet_images))
for image in spacenet_images:
image_name = op.splitext(op.basename(image))[0].replace('RGB-PanSharpen_AOI_3_Paris_', '')
workflow_input = {
input_task: dict(filename=image),
add_l1c: dict(time_interval=time_interval),
custom_save: dict(image_name=image_name)
}
prepare_data.execute(workflow_input)
pbar.update(1)
```
|
github_jupyter
|
**Chapter 6 – Decision Trees**
_This notebook contains all the sample code and solutions to the exercises in chapter 6._
<table align="left">
<td>
<a target="_blank" href="https://colab.research.google.com/github/ageron/handson-ml/blob/master/06_decision_trees.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
</td>
</table>
**Warning**: this is the code for the 1st edition of the book. Please visit https://github.com/ageron/handson-ml2 for the 2nd edition code, with up-to-date notebooks using the latest library versions.
# Setup
First, let's make sure this notebook works well in both python 2 and 3, import a few common modules, ensure MatplotLib plots figures inline and prepare a function to save the figures:
```
# To support both python 2 and python 3
from __future__ import division, print_function, unicode_literals
# Common imports
import numpy as np
import os
# to make this notebook's output stable across runs
np.random.seed(42)
# To plot pretty figures
%matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rc('axes', labelsize=14)
mpl.rc('xtick', labelsize=12)
mpl.rc('ytick', labelsize=12)
# Where to save the figures
PROJECT_ROOT_DIR = "."
CHAPTER_ID = "decision_trees"
IMAGES_PATH = os.path.join(PROJECT_ROOT_DIR, "images", CHAPTER_ID)
os.makedirs(IMAGES_PATH, exist_ok=True)
def save_fig(fig_id, tight_layout=True, fig_extension="png", resolution=300):
path = os.path.join(IMAGES_PATH, fig_id + "." + fig_extension)
print("Saving figure", fig_id)
if tight_layout:
plt.tight_layout()
plt.savefig(path, format=fig_extension, dpi=resolution)
```
# Training and visualizing
```
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
iris = load_iris()
X = iris.data[:, 2:] # petal length and width
y = iris.target
tree_clf = DecisionTreeClassifier(max_depth=2, random_state=42)
tree_clf.fit(X, y)
from sklearn.tree import export_graphviz
def image_path(fig_id):
return os.path.join(IMAGES_PATH, fig_id)
export_graphviz(
tree_clf,
out_file=image_path("iris_tree.dot"),
feature_names=iris.feature_names[2:],
class_names=iris.target_names,
rounded=True,
filled=True
)
from matplotlib.colors import ListedColormap
def plot_decision_boundary(clf, X, y, axes=[0, 7.5, 0, 3], iris=True, legend=False, plot_training=True):
x1s = np.linspace(axes[0], axes[1], 100)
x2s = np.linspace(axes[2], axes[3], 100)
x1, x2 = np.meshgrid(x1s, x2s)
X_new = np.c_[x1.ravel(), x2.ravel()]
y_pred = clf.predict(X_new).reshape(x1.shape)
custom_cmap = ListedColormap(['#fafab0','#9898ff','#a0faa0'])
plt.contourf(x1, x2, y_pred, alpha=0.3, cmap=custom_cmap)
if not iris:
custom_cmap2 = ListedColormap(['#7d7d58','#4c4c7f','#507d50'])
plt.contour(x1, x2, y_pred, cmap=custom_cmap2, alpha=0.8)
if plot_training:
plt.plot(X[:, 0][y==0], X[:, 1][y==0], "yo", label="Iris-Setosa")
plt.plot(X[:, 0][y==1], X[:, 1][y==1], "bs", label="Iris-Versicolor")
plt.plot(X[:, 0][y==2], X[:, 1][y==2], "g^", label="Iris-Virginica")
plt.axis(axes)
if iris:
plt.xlabel("Petal length", fontsize=14)
plt.ylabel("Petal width", fontsize=14)
else:
plt.xlabel(r"$x_1$", fontsize=18)
plt.ylabel(r"$x_2$", fontsize=18, rotation=0)
if legend:
plt.legend(loc="lower right", fontsize=14)
plt.figure(figsize=(8, 4))
plot_decision_boundary(tree_clf, X, y)
plt.plot([2.45, 2.45], [0, 3], "k-", linewidth=2)
plt.plot([2.45, 7.5], [1.75, 1.75], "k--", linewidth=2)
plt.plot([4.95, 4.95], [0, 1.75], "k:", linewidth=2)
plt.plot([4.85, 4.85], [1.75, 3], "k:", linewidth=2)
plt.text(1.40, 1.0, "Depth=0", fontsize=15)
plt.text(3.2, 1.80, "Depth=1", fontsize=13)
plt.text(4.05, 0.5, "(Depth=2)", fontsize=11)
save_fig("decision_tree_decision_boundaries_plot")
plt.show()
```
# Predicting classes and class probabilities
```
tree_clf.predict_proba([[5, 1.5]])
tree_clf.predict([[5, 1.5]])
```
# Sensitivity to training set details
```
X[(X[:, 1]==X[:, 1][y==1].max()) & (y==1)] # widest Iris-Versicolor flower
not_widest_versicolor = (X[:, 1]!=1.8) | (y==2)
X_tweaked = X[not_widest_versicolor]
y_tweaked = y[not_widest_versicolor]
tree_clf_tweaked = DecisionTreeClassifier(max_depth=2, random_state=40)
tree_clf_tweaked.fit(X_tweaked, y_tweaked)
plt.figure(figsize=(8, 4))
plot_decision_boundary(tree_clf_tweaked, X_tweaked, y_tweaked, legend=False)
plt.plot([0, 7.5], [0.8, 0.8], "k-", linewidth=2)
plt.plot([0, 7.5], [1.75, 1.75], "k--", linewidth=2)
plt.text(1.0, 0.9, "Depth=0", fontsize=15)
plt.text(1.0, 1.80, "Depth=1", fontsize=13)
save_fig("decision_tree_instability_plot")
plt.show()
from sklearn.datasets import make_moons
Xm, ym = make_moons(n_samples=100, noise=0.25, random_state=53)
deep_tree_clf1 = DecisionTreeClassifier(random_state=42)
deep_tree_clf2 = DecisionTreeClassifier(min_samples_leaf=4, random_state=42)
deep_tree_clf1.fit(Xm, ym)
deep_tree_clf2.fit(Xm, ym)
plt.figure(figsize=(11, 4))
plt.subplot(121)
plot_decision_boundary(deep_tree_clf1, Xm, ym, axes=[-1.5, 2.5, -1, 1.5], iris=False)
plt.title("No restrictions", fontsize=16)
plt.subplot(122)
plot_decision_boundary(deep_tree_clf2, Xm, ym, axes=[-1.5, 2.5, -1, 1.5], iris=False)
plt.title("min_samples_leaf = {}".format(deep_tree_clf2.min_samples_leaf), fontsize=14)
save_fig("min_samples_leaf_plot")
plt.show()
angle = np.pi / 180 * 20
rotation_matrix = np.array([[np.cos(angle), -np.sin(angle)], [np.sin(angle), np.cos(angle)]])
Xr = X.dot(rotation_matrix)
tree_clf_r = DecisionTreeClassifier(random_state=42)
tree_clf_r.fit(Xr, y)
plt.figure(figsize=(8, 3))
plot_decision_boundary(tree_clf_r, Xr, y, axes=[0.5, 7.5, -1.0, 1], iris=False)
plt.show()
np.random.seed(6)
Xs = np.random.rand(100, 2) - 0.5
ys = (Xs[:, 0] > 0).astype(np.float32) * 2
angle = np.pi / 4
rotation_matrix = np.array([[np.cos(angle), -np.sin(angle)], [np.sin(angle), np.cos(angle)]])
Xsr = Xs.dot(rotation_matrix)
tree_clf_s = DecisionTreeClassifier(random_state=42)
tree_clf_s.fit(Xs, ys)
tree_clf_sr = DecisionTreeClassifier(random_state=42)
tree_clf_sr.fit(Xsr, ys)
plt.figure(figsize=(11, 4))
plt.subplot(121)
plot_decision_boundary(tree_clf_s, Xs, ys, axes=[-0.7, 0.7, -0.7, 0.7], iris=False)
plt.subplot(122)
plot_decision_boundary(tree_clf_sr, Xsr, ys, axes=[-0.7, 0.7, -0.7, 0.7], iris=False)
save_fig("sensitivity_to_rotation_plot")
plt.show()
```
# Regression trees
```
# Quadratic training set + noise
np.random.seed(42)
m = 200
X = np.random.rand(m, 1)
y = 4 * (X - 0.5) ** 2
y = y + np.random.randn(m, 1) / 10
from sklearn.tree import DecisionTreeRegressor
tree_reg = DecisionTreeRegressor(max_depth=2, random_state=42)
tree_reg.fit(X, y)
from sklearn.tree import DecisionTreeRegressor
tree_reg1 = DecisionTreeRegressor(random_state=42, max_depth=2)
tree_reg2 = DecisionTreeRegressor(random_state=42, max_depth=3)
tree_reg1.fit(X, y)
tree_reg2.fit(X, y)
def plot_regression_predictions(tree_reg, X, y, axes=[0, 1, -0.2, 1], ylabel="$y$"):
x1 = np.linspace(axes[0], axes[1], 500).reshape(-1, 1)
y_pred = tree_reg.predict(x1)
plt.axis(axes)
plt.xlabel("$x_1$", fontsize=18)
if ylabel:
plt.ylabel(ylabel, fontsize=18, rotation=0)
plt.plot(X, y, "b.")
plt.plot(x1, y_pred, "r.-", linewidth=2, label=r"$\hat{y}$")
plt.figure(figsize=(11, 4))
plt.subplot(121)
plot_regression_predictions(tree_reg1, X, y)
for split, style in ((0.1973, "k-"), (0.0917, "k--"), (0.7718, "k--")):
plt.plot([split, split], [-0.2, 1], style, linewidth=2)
plt.text(0.21, 0.65, "Depth=0", fontsize=15)
plt.text(0.01, 0.2, "Depth=1", fontsize=13)
plt.text(0.65, 0.8, "Depth=1", fontsize=13)
plt.legend(loc="upper center", fontsize=18)
plt.title("max_depth=2", fontsize=14)
plt.subplot(122)
plot_regression_predictions(tree_reg2, X, y, ylabel=None)
for split, style in ((0.1973, "k-"), (0.0917, "k--"), (0.7718, "k--")):
plt.plot([split, split], [-0.2, 1], style, linewidth=2)
for split in (0.0458, 0.1298, 0.2873, 0.9040):
plt.plot([split, split], [-0.2, 1], "k:", linewidth=1)
plt.text(0.3, 0.5, "Depth=2", fontsize=13)
plt.title("max_depth=3", fontsize=14)
save_fig("tree_regression_plot")
plt.show()
export_graphviz(
tree_reg1,
out_file=image_path("regression_tree.dot"),
feature_names=["x1"],
rounded=True,
filled=True
)
tree_reg1 = DecisionTreeRegressor(random_state=42)
tree_reg2 = DecisionTreeRegressor(random_state=42, min_samples_leaf=10)
tree_reg1.fit(X, y)
tree_reg2.fit(X, y)
x1 = np.linspace(0, 1, 500).reshape(-1, 1)
y_pred1 = tree_reg1.predict(x1)
y_pred2 = tree_reg2.predict(x1)
plt.figure(figsize=(11, 4))
plt.subplot(121)
plt.plot(X, y, "b.")
plt.plot(x1, y_pred1, "r.-", linewidth=2, label=r"$\hat{y}$")
plt.axis([0, 1, -0.2, 1.1])
plt.xlabel("$x_1$", fontsize=18)
plt.ylabel("$y$", fontsize=18, rotation=0)
plt.legend(loc="upper center", fontsize=18)
plt.title("No restrictions", fontsize=14)
plt.subplot(122)
plt.plot(X, y, "b.")
plt.plot(x1, y_pred2, "r.-", linewidth=2, label=r"$\hat{y}$")
plt.axis([0, 1, -0.2, 1.1])
plt.xlabel("$x_1$", fontsize=18)
plt.title("min_samples_leaf={}".format(tree_reg2.min_samples_leaf), fontsize=14)
save_fig("tree_regression_regularization_plot")
plt.show()
```
# Exercise solutions
## 1. to 6.
See appendix A.
## 7.
_Exercise: train and fine-tune a Decision Tree for the moons dataset._
a. Generate a moons dataset using `make_moons(n_samples=10000, noise=0.4)`.
Adding `random_state=42` to make this notebook's output constant:
```
from sklearn.datasets import make_moons
X, y = make_moons(n_samples=10000, noise=0.4, random_state=42)
```
b. Split it into a training set and a test set using `train_test_split()`.
```
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
```
c. Use grid search with cross-validation (with the help of the `GridSearchCV` class) to find good hyperparameter values for a `DecisionTreeClassifier`. Hint: try various values for `max_leaf_nodes`.
```
from sklearn.model_selection import GridSearchCV
params = {'max_leaf_nodes': list(range(2, 100)), 'min_samples_split': [2, 3, 4]}
grid_search_cv = GridSearchCV(DecisionTreeClassifier(random_state=42), params, n_jobs=-1, verbose=1, cv=3)
grid_search_cv.fit(X_train, y_train)
grid_search_cv.best_estimator_
```
d. Train it on the full training set using these hyperparameters, and measure your model's performance on the test set. You should get roughly 85% to 87% accuracy.
By default, `GridSearchCV` trains the best model found on the whole training set (you can change this by setting `refit=False`), so we don't need to do it again. We can simply evaluate the model's accuracy:
```
from sklearn.metrics import accuracy_score
y_pred = grid_search_cv.predict(X_test)
accuracy_score(y_test, y_pred)
```
## 8.
_Exercise: Grow a forest._
a. Continuing the previous exercise, generate 1,000 subsets of the training set, each containing 100 instances selected randomly. Hint: you can use Scikit-Learn's `ShuffleSplit` class for this.
```
from sklearn.model_selection import ShuffleSplit
n_trees = 1000
n_instances = 100
mini_sets = []
rs = ShuffleSplit(n_splits=n_trees, test_size=len(X_train) - n_instances, random_state=42)
for mini_train_index, mini_test_index in rs.split(X_train):
X_mini_train = X_train[mini_train_index]
y_mini_train = y_train[mini_train_index]
mini_sets.append((X_mini_train, y_mini_train))
```
b. Train one Decision Tree on each subset, using the best hyperparameter values found above. Evaluate these 1,000 Decision Trees on the test set. Since they were trained on smaller sets, these Decision Trees will likely perform worse than the first Decision Tree, achieving only about 80% accuracy.
```
from sklearn.base import clone
forest = [clone(grid_search_cv.best_estimator_) for _ in range(n_trees)]
accuracy_scores = []
for tree, (X_mini_train, y_mini_train) in zip(forest, mini_sets):
tree.fit(X_mini_train, y_mini_train)
y_pred = tree.predict(X_test)
accuracy_scores.append(accuracy_score(y_test, y_pred))
np.mean(accuracy_scores)
```
c. Now comes the magic. For each test set instance, generate the predictions of the 1,000 Decision Trees, and keep only the most frequent prediction (you can use SciPy's `mode()` function for this). This gives you _majority-vote predictions_ over the test set.
```
Y_pred = np.empty([n_trees, len(X_test)], dtype=np.uint8)
for tree_index, tree in enumerate(forest):
Y_pred[tree_index] = tree.predict(X_test)
from scipy.stats import mode
y_pred_majority_votes, n_votes = mode(Y_pred, axis=0)
```
d. Evaluate these predictions on the test set: you should obtain a slightly higher accuracy than your first model (about 0.5 to 1.5% higher). Congratulations, you have trained a Random Forest classifier!
```
accuracy_score(y_test, y_pred_majority_votes.reshape([-1]))
```
|
github_jupyter
|
# Train DynUNet on Decathlon datasets
This tutorial shows how to train 3D segmentation tasks on all the 10 decathlon datasets with `DynUNet`.
Refer to papers:
`Automated Design of Deep Learning Methods for Biomedical Image Segmentation <https://arxiv.org/abs/1904.08128>`
`nnU-Net: Self-adapting Framework for U-Net-Based Medical Image Segmentation <https://arxiv.org/abs/1809.10486>`
[](https://colab.research.google.com/github/Project-MONAI/tutorials/blob/master/modules/dynunet_tutorial.ipynb)
## Setup environment
```
%pip install -q "monai[itk, ignite, tqdm]"
%pip install -q matplotlib
%matplotlib inline
```
## Setup imports
```
# Copyright 2020 MONAI Consortium
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
# http://www.apache.org/licenses/LICENSE-2.0
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
import os
import logging
import ignite
import matplotlib.pyplot as plt
import torch
import torch.nn as nn
import numpy as np
from monai.apps import DecathlonDataset
from monai.config import print_config
from monai.data import DataLoader
from monai.engines import SupervisedTrainer
from monai.handlers import MeanDice, StatsHandler
from monai.inferers import SimpleInferer
from monai.losses import DiceLoss
from monai.networks.nets import DynUNet
from monai.transforms import (
AsDiscreted,
Compose,
LoadNiftid,
AddChanneld,
CropForegroundd,
Spacingd,
Orientationd,
SpatialPadd,
NormalizeIntensityd,
RandCropByPosNegLabeld,
RandZoomd,
CastToTyped,
RandGaussianNoised,
RandGaussianSmoothd,
RandScaleIntensityd,
RandFlipd,
ToTensord,
)
print_config()
```
## Select Decathlon task
The Decathlon dataset contains 10 tasks, this dynUNet tutorial can support all of them.
Just need to select task ID and other parameters will be automatically selected.
(Tested task 04 locally, epoch time is 8 secs on V100 GPU and best metrics is 0.8828 at epoch: 70)
```
task_id = "04"
task_name = {
"01": "Task01_BrainTumour",
"02": "Task02_Heart",
"03": "Task03_Liver",
"04": "Task04_Hippocampus",
"05": "Task05_Prostate",
"06": "Task06_Lung",
"07": "Task07_Pancreas",
"08": "Task08_HepaticVessel",
"09": "Task09_Spleen",
"10": "Task10_Colon",
}
patch_size = {
"01": [128, 128, 128],
"02": [160, 192, 80],
"03": [128, 128, 128],
"04": [40, 56, 40],
"05": [320, 256, 20],
"06": [192, 160, 80],
"07": [224, 224, 40],
"08": [192, 192, 64],
"09": [192, 160, 64],
"10": [192, 160, 56],
}
spacing = {
"01": [1.0, 1.0, 1.0],
"02": [1.25, 1.25, 1.37],
"03": [0.77, 0.77, 1],
"04": [1.0, 1.0, 1.0],
"05": [0.62, 0.62, 3.6],
"06": [0.79, 0.79, 1.24],
"07": [0.8, 0.8, 2.5],
"08": [0.8, 0.8, 1.5],
"09": [0.79, 0.79, 1.6],
"10": [0.78, 0.78, 3],
}
```
## Setup data directory
You can specify a directory with the `MONAI_DATA_DIRECTORY` environment variable.
This allows you to save results and reuse downloads.
If not specified a temporary directory will be used.
```
directory = os.environ.get("MONAI_DATA_DIRECTORY")
root_dir = tempfile.mkdtemp() if directory is None else directory
print(root_dir)
```
## Define train and validation transforms
```
train_transform = Compose(
[
LoadNiftid(keys=["image", "label"]),
AddChanneld(keys=["image", "label"]),
CropForegroundd(keys=["image", "label"], source_key="image"),
Spacingd(
keys=["image", "label"],
pixdim=spacing[task_id],
mode=("bilinear", "nearest"),
),
Orientationd(keys=["image", "label"], axcodes="RAS"),
SpatialPadd(keys=["image", "label"], spatial_size=patch_size[task_id]),
NormalizeIntensityd(keys=["image"], nonzero=False, channel_wise=True),
RandCropByPosNegLabeld(
keys=["image", "label"],
label_key="label",
spatial_size=patch_size[task_id],
pos=1,
neg=1,
num_samples=1,
image_key="image",
image_threshold=0,
),
RandZoomd(
keys=["image", "label"],
min_zoom=0.9,
max_zoom=1.2,
mode=("trilinear", "nearest"),
align_corners=(True, None),
prob=0.16,
),
CastToTyped(keys=["image", "label"], dtype=(np.float32, np.uint8)),
RandGaussianNoised(keys=["image"], std=0.01, prob=0.15),
RandGaussianSmoothd(
keys=["image"],
sigma_x=(0.5, 1.15),
sigma_y=(0.5, 1.15),
sigma_z=(0.5, 1.15),
prob=0.15,
),
RandScaleIntensityd(keys=["image"], factors=0.3, prob=0.15),
RandFlipd(["image", "label"], spatial_axis=[0, 1, 2], prob=0.5),
ToTensord(keys=["image", "label"]),
]
)
val_transform = Compose(
[
LoadNiftid(keys=["image", "label"]),
AddChanneld(keys=["image", "label"]),
CropForegroundd(keys=["image", "label"], source_key="image"),
Spacingd(
keys=["image", "label"],
pixdim=spacing[task_id],
mode=("bilinear", "nearest"),
),
Orientationd(keys=["image", "label"], axcodes="RAS"),
SpatialPadd(keys=["image", "label"], spatial_size=patch_size[task_id]),
NormalizeIntensityd(keys=["image"], nonzero=False, channel_wise=True),
CastToTyped(keys=["image", "label"], dtype=(np.float32, np.uint8)),
ToTensord(keys=["image", "label"]),
]
)
```
## Load data by MONAI DecathlonDataset
```
train_ds = DecathlonDataset(
root_dir=root_dir,
task=task_name[task_id],
transform=train_transform,
section="training",
download=False,
num_workers=4,
)
train_loader = DataLoader(train_ds, batch_size=2, shuffle=True, num_workers=1)
val_ds = DecathlonDataset(
root_dir=root_dir,
task=task_name[task_id],
transform=val_transform,
section="validation",
download=False,
num_workers=4,
)
val_loader = DataLoader(val_ds, batch_size=1, shuffle=False, num_workers=1)
```
## Visualize batch of data to check images and labels
```
for i in range(2):
image, label = val_ds[i]["image"], val_ds[i]["label"]
plt.figure("check", (12, 8))
plt.subplot(1, 2, 1)
plt.title("image")
plt.imshow(image[0, :, :, 10].detach().cpu(), cmap="gray")
plt.subplot(1, 2, 2)
plt.title("label")
plt.imshow(label[0, :, :, 10].detach().cpu())
plt.show()
```
## Customize loss function
Here we combine Dice loss and Cross Entropy loss.
```
class CrossEntropyLoss(nn.Module):
def __init__(self):
super().__init__()
self.loss = nn.CrossEntropyLoss()
def forward(self, y_pred, y_true):
# CrossEntropyLoss target needs to have shape (B, D, H, W)
# Target from pipeline has shape (B, 1, D, H, W)
y_true = torch.squeeze(y_true, dim=1).long()
return self.loss(y_pred, y_true)
class DiceCELoss(nn.Module):
def __init__(self):
super().__init__()
self.dice = DiceLoss(to_onehot_y=True, softmax=True)
self.cross_entropy = CrossEntropyLoss()
def forward(self, y_pred, y_true):
dice = self.dice(y_pred, y_true)
cross_entropy = self.cross_entropy(y_pred, y_true)
return dice + cross_entropy
```
## Initialize training components
```
device = torch.device("cuda:0")
loss = DiceCELoss()
learning_rate = 0.01
max_epochs = 200
sizes, spacings = patch_size[task_id], spacing[task_id]
properties = val_ds.get_properties(keys=["labels", "modality"])
n_class, in_channels = len(properties["labels"]), len(properties["modality"])
best_dice, best_epoch = (n_class - 1) * [0], (n_class - 1) * [0]
strides, kernels = [], []
while True:
spacing_ratio = [sp / min(spacings) for sp in spacings]
stride = [2 if ratio <= 2 and size >= 8 else 1 for (ratio, size) in zip(spacing_ratio, sizes)]
kernel = [3 if ratio <= 2 else 1 for ratio in spacing_ratio]
if all(s == 1 for s in stride):
break
sizes = [i / j for i, j in zip(sizes, stride)]
spacings = [i * j for i, j in zip(spacings, stride)]
kernels.append(kernel)
strides.append(stride)
strides.insert(0, len(spacings) * [1])
kernels.append(len(spacings) * [3])
net = DynUNet(
spatial_dims=3,
in_channels=in_channels,
out_channels=n_class,
kernel_size=kernels,
strides=strides,
upsample_kernel_size=strides[1:],
norm_name="instance",
deep_supervision=True,
deep_supr_num=2,
res_block=False,
).to(device)
optimizer = torch.optim.SGD(net.parameters(), lr=learning_rate, momentum=0.95)
scheduler = torch.optim.lr_scheduler.LambdaLR(
optimizer, lr_lambda=lambda epoch: (1 - epoch / max_epochs) ** 0.9
)
```
## MONAI evaluator
Here we customized the forward computation, so need to define `_iteration` function.
```
from monai.engines import SupervisedEvaluator
from monai.handlers import StatsHandler, CheckpointSaver, MeanDice
from monai.inferers import SlidingWindowInferer
val_handlers = [
StatsHandler(output_transform=lambda x: None),
CheckpointSaver(save_dir="./runs/", save_dict={"net": net}, save_key_metric=True),
]
val_post_transform = Compose(
[AsDiscreted(keys=("pred", "label"), argmax=(True, False), to_onehot=True, n_classes=n_class)]
)
# Define customized evaluator
class DynUNetEvaluator(SupervisedEvaluator):
def _iteration(self, engine, batchdata):
inputs, targets = self.prepare_batch(batchdata)
inputs, targets = inputs.to(engine.state.device), targets.to(engine.state.device)
flip_inputs = torch.flip(inputs, dims=(2, 3, 4))
def _compute_pred():
pred = self.inferer(inputs, self.network)
flip_pred = torch.flip(self.inferer(flip_inputs, self.network), dims=(2, 3, 4))
return (pred + flip_pred) / 2
# execute forward computation
self.network.eval()
with torch.no_grad():
if self.amp:
with torch.cuda.amp.autocast():
predictions = _compute_pred()
else:
predictions = _compute_pred()
return {"image": inputs, "label": targets, "pred": predictions}
evaluator = DynUNetEvaluator(
device=device,
val_data_loader=val_loader,
network=net,
inferer=SlidingWindowInferer(roi_size=patch_size[task_id], sw_batch_size=4, overlap=0.5),
post_transform=val_post_transform,
key_val_metric={
"val_mean_dice": MeanDice(
include_background=False,
output_transform=lambda x: (x["pred"], x["label"]),
)
},
val_handlers=val_handlers,
amp=True,
)
```
## MONAI trainer
Here we customized loss computation progress, so need to define `_iteration` function.
```
from torch.nn.functional import interpolate
from monai.engines import SupervisedTrainer
from monai.inferers import SimpleInferer
from monai.handlers import LrScheduleHandler, ValidationHandler, StatsHandler
train_handlers = [
LrScheduleHandler(lr_scheduler=scheduler, print_lr=True),
ValidationHandler(validator=evaluator, interval=2, epoch_level=True),
StatsHandler(tag_name="train_loss", output_transform=lambda x: x["loss"]),
]
# define customized trainer
class DynUNetTrainer(SupervisedTrainer):
def _iteration(self, engine, batchdata):
inputs, targets = self.prepare_batch(batchdata)
inputs, targets = inputs.to(engine.state.device), targets.to(engine.state.device)
def _compute_loss(preds, label):
labels = [label] + [interpolate(label, pred.shape[2:]) for pred in preds[1:]]
return sum([0.5 ** i * self.loss_function(p, l) for i, (p, l) in enumerate(zip(preds, labels))])
self.network.train()
self.optimizer.zero_grad()
if self.amp and self.scaler is not None:
with torch.cuda.amp.autocast():
predictions = self.inferer(inputs, self.network)
loss = _compute_loss(predictions, targets)
self.scaler.scale(loss).backward()
self.scaler.step(self.optimizer)
self.scaler.update()
else:
predictions = self.inferer(inputs, self.network)
loss = _compute_loss(predictions, targets).mean()
loss.backward()
self.optimizer.step()
return {"image": inputs, "label": targets, "pred": predictions, "loss": loss.item()}
trainer = DynUNetTrainer(
device=device,
max_epochs=max_epochs,
train_data_loader=train_loader,
network=net,
optimizer=optimizer,
loss_function=loss,
inferer=SimpleInferer(),
post_transform=None,
key_train_metric=None,
train_handlers=train_handlers,
amp=True,
)
```
## Execute training with workflows
```
import logging
import sys
logging.basicConfig(stream=sys.stdout, level=logging.INFO)
trainer.run()
```
## Cleanup data directory
Remove directory if a temporary was used.
```
if directory is None:
shutil.rmtree(root_dir)
```
|
github_jupyter
|
##### Function "print" for prints the specified message to the screen, or other standard output device
```
print(5+5)
print("Hello World")
print(TRUE)
----------------------
```
##### R is case sensitive
```
print("Me")
#Not same with
print("ME")
print("01")
#Not same with
print("1")
----------------------
```
###### "c" Function for makes continues number
```
c(1,2,3,4,5,6,7,8,9,10)
#Same with
c(1:10)
----------------------
```
##### Variable in R
```
a <- "Hello World"
b <- 57
print(a)
print(b)
----------------------
```
##### Making Vector in R
```
Vector <- c(51,45,67)
print(Vector)
----------------------
```
##### Continues Vector and Manual Vector
```
manual <- c(10,11,12,13,14,15,16,17,18,19,20)
#Same with
vector <- c(10:20)
print(manual)
print(vector)
----------------------
```
##### Vector can contains text
```
vector <- c("I","Love","You")
print(vector)
----------------------
```
##### Vector Indexing
```
vector <- c(80,85,87,83,82,98,93,100)
print(vector[[2]]) #Print index number 2 from left
print(vector[6]) #Print index number 6 from left
print(vector[5:8]) #Print index number 5 to 8 from left
----------------------
```
##### Named Vector
```
named <- c(language="R",machine_learning="Yes",data_mining="Yes")
print(named)
print(named["machine_learning"]) #Print object named "machine_learning"
----------------------
```
##### List
```
alist <- list("I","am",100,"%","Human")
print(alist)
----------------------
```
##### List Indexing
```
alist <- list("I","am",100,"%","Human")
print(alist[3]) #Print index number 3
print(alist[1:4]) #Print index number 1 to 4
----------------------
```
##### Data Frame in R
```
jumlah_mahasiswa <- c(450,670,490,421,577)
fakultas <- c("Teknik Pertanian","Sistem Informasi","Statistika","Matematika","Ilmu Komputer")
dataframe <- data.frame(fakultas,jumlah_mahasiswa)
print(dataframe)
----------------------
```
##### Taking column from data frame
```
jumlah_mahasiswa <- c(450,670,490,421,577)
fakultas <- c("Teknik Pertanian","Sistem Informasi","Statistika","Matematika","Ilmu Komputer")
dataframe <- data.frame(fakultas,jumlah_mahasiswa)
dataframe$fakultas
dataframe$jumlah_mahasiswa
----------------------
```
##### Making chart with ggplot2
```
library(ggplot2) #Importing ggplot2 library
jumlah_mahasiswa <- c(450,670,490,421,577)
fakultas <- c("Teknik Pertanian","Sistem Informasi","Statistika","Matematika","Ilmu Komputer")
dataframe <- data.frame(prodi,jumlah_mahasiswa)
plot <- ggplot(dataframe,aes(x=fakultas,y=jumlah_mahasiswa,fill=fakultas))
plot <- plot + geom_bar(width=0.9,stat="identity")
plot
----------------------
```
##### Adding title and other informations
```
library(ggplot2) #Importing ggplot2 library
jumlah_mahasiswa <- c(450,670,490,421,577)
fakultas <- c("Teknik Pertanian","Sistem Informasi","Statistika","Matematika","Ilmu Komputer")
dataframe <- data.frame(prodi,jumlah_mahasiswa)
plot <- ggplot(dataframe,aes(x=fakultas,y=jumlah_mahasiswa,fill=fakultas))
plot <- plot + geom_bar(width=0.9,stat="identity")
plot <- plot + ggtitle("Grafik Jumlah Mahasiswa Terhadap Fakultas") #Adding title
plot <- plot + xlab("Fakultas") #Adding bottom information
plot <- plot + ylab("Jumlah Mahasiswa") # Adding side information
plot
----------------------
```
##### Reading .xlsx file in R
```
library(openxlsx) #Importing library for reading .xlsx file
read <- read.xlsx("https://academy.dqlab.id/dataset/mahasiswa.xlsx",sheet = "Sheet 1")
read
----------------------
```
##### Making graph from .xlsx file
```
library(openxlsx) #Importing library for reading .xlsx file
read <- read.xlsx("https://academy.dqlab.id/dataset/mahasiswa.xlsx",sheet = "Sheet 1")
plot <- ggplot(read,aes(x=Fakultas,y=JUMLAH,fill=Fakultas))
plot <- plot + geom_bar(width=0.9,stat="identity")
plot
```
Learning Source : www.dqlab.id
|
github_jupyter
|
##### Copyright 2019 The TensorFlow Authors.
Licensed under the Apache License, Version 2.0 (the "License");
```
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
```
# Pix2Pix
<table class="tfo-notebook-buttons" align="left">
<td>
<a target="_blank" href="https://www.tensorflow.org/tutorials/generative/pix2pix"><img src="https://www.tensorflow.org/images/tf_logo_32px.png" />View on TensorFlow.org</a>
</td>
<td>
<a target="_blank" href="https://colab.research.google.com/github/tensorflow/docs/blob/master/site/en/tutorials/generative/pix2pix.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
</td>
<td>
<a target="_blank" href="https://github.com/tensorflow/docs/blob/master/site/en/tutorials/generative/pix2pix.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View source on GitHub</a>
</td>
<td>
<a href="https://storage.googleapis.com/tensorflow_docs/docs/site/en/tutorials/generative/pix2pix.ipynb"><img src="https://www.tensorflow.org/images/download_logo_32px.png" />Download notebook</a>
</td>
</table>
This notebook demonstrates image to image translation using conditional GAN's, as described in [Image-to-Image Translation with Conditional Adversarial Networks](https://arxiv.org/abs/1611.07004). Using this technique we can colorize black and white photos, convert google maps to google earth, etc. Here, we convert building facades to real buildings.
In example, we will use the [CMP Facade Database](http://cmp.felk.cvut.cz/~tylecr1/facade/), helpfully provided by the [Center for Machine Perception](http://cmp.felk.cvut.cz/) at the [Czech Technical University in Prague](https://www.cvut.cz/). To keep our example short, we will use a preprocessed [copy](https://people.eecs.berkeley.edu/~tinghuiz/projects/pix2pix/datasets/) of this dataset, created by the authors of the [paper](https://arxiv.org/abs/1611.07004) above.
Each epoch takes around 15 seconds on a single V100 GPU.
Below is the output generated after training the model for 200 epochs.


## Import TensorFlow and other libraries
```
import tensorflow as tf
import os
import time
from matplotlib import pyplot as plt
from IPython import display
!pip install -U tensorboard
```
## Load the dataset
You can download this dataset and similar datasets from [here](https://people.eecs.berkeley.edu/~tinghuiz/projects/pix2pix/datasets). As mentioned in the [paper](https://arxiv.org/abs/1611.07004) we apply random jittering and mirroring to the training dataset.
* In random jittering, the image is resized to `286 x 286` and then randomly cropped to `256 x 256`
* In random mirroring, the image is randomly flipped horizontally i.e left to right.
```
_URL = 'https://people.eecs.berkeley.edu/~tinghuiz/projects/pix2pix/datasets/facades.tar.gz'
path_to_zip = tf.keras.utils.get_file('facades.tar.gz',
origin=_URL,
extract=True)
PATH = os.path.join(os.path.dirname(path_to_zip), 'facades/')
BUFFER_SIZE = 400
BATCH_SIZE = 1
IMG_WIDTH = 256
IMG_HEIGHT = 256
def load(image_file):
image = tf.io.read_file(image_file)
image = tf.image.decode_jpeg(image)
w = tf.shape(image)[1]
w = w // 2
real_image = image[:, :w, :]
input_image = image[:, w:, :]
input_image = tf.cast(input_image, tf.float32)
real_image = tf.cast(real_image, tf.float32)
return input_image, real_image
inp, re = load(PATH+'train/100.jpg')
# casting to int for matplotlib to show the image
plt.figure()
plt.imshow(inp/255.0)
plt.figure()
plt.imshow(re/255.0)
def resize(input_image, real_image, height, width):
input_image = tf.image.resize(input_image, [height, width],
method=tf.image.ResizeMethod.NEAREST_NEIGHBOR)
real_image = tf.image.resize(real_image, [height, width],
method=tf.image.ResizeMethod.NEAREST_NEIGHBOR)
return input_image, real_image
def random_crop(input_image, real_image):
stacked_image = tf.stack([input_image, real_image], axis=0)
cropped_image = tf.image.random_crop(
stacked_image, size=[2, IMG_HEIGHT, IMG_WIDTH, 3])
return cropped_image[0], cropped_image[1]
# normalizing the images to [-1, 1]
def normalize(input_image, real_image):
input_image = (input_image / 127.5) - 1
real_image = (real_image / 127.5) - 1
return input_image, real_image
@tf.function()
def random_jitter(input_image, real_image):
# resizing to 286 x 286 x 3
input_image, real_image = resize(input_image, real_image, 286, 286)
# randomly cropping to 256 x 256 x 3
input_image, real_image = random_crop(input_image, real_image)
if tf.random.uniform(()) > 0.5:
# random mirroring
input_image = tf.image.flip_left_right(input_image)
real_image = tf.image.flip_left_right(real_image)
return input_image, real_image
```
As you can see in the images below
that they are going through random jittering
Random jittering as described in the paper is to
1. Resize an image to bigger height and width
2. Randomly crop to the target size
3. Randomly flip the image horizontally
```
plt.figure(figsize=(6, 6))
for i in range(4):
rj_inp, rj_re = random_jitter(inp, re)
plt.subplot(2, 2, i+1)
plt.imshow(rj_inp/255.0)
plt.axis('off')
plt.show()
def load_image_train(image_file):
input_image, real_image = load(image_file)
input_image, real_image = random_jitter(input_image, real_image)
input_image, real_image = normalize(input_image, real_image)
return input_image, real_image
def load_image_test(image_file):
input_image, real_image = load(image_file)
input_image, real_image = resize(input_image, real_image,
IMG_HEIGHT, IMG_WIDTH)
input_image, real_image = normalize(input_image, real_image)
return input_image, real_image
```
## Input Pipeline
```
train_dataset = tf.data.Dataset.list_files(PATH+'train/*.jpg')
train_dataset = train_dataset.map(load_image_train,
num_parallel_calls=tf.data.experimental.AUTOTUNE)
train_dataset = train_dataset.shuffle(BUFFER_SIZE)
train_dataset = train_dataset.batch(BATCH_SIZE)
test_dataset = tf.data.Dataset.list_files(PATH+'test/*.jpg')
test_dataset = test_dataset.map(load_image_test)
test_dataset = test_dataset.batch(BATCH_SIZE)
```
## Build the Generator
* The architecture of generator is a modified U-Net.
* Each block in the encoder is (Conv -> Batchnorm -> Leaky ReLU)
* Each block in the decoder is (Transposed Conv -> Batchnorm -> Dropout(applied to the first 3 blocks) -> ReLU)
* There are skip connections between the encoder and decoder (as in U-Net).
```
OUTPUT_CHANNELS = 3
def downsample(filters, size, apply_batchnorm=True):
initializer = tf.random_normal_initializer(0., 0.02)
result = tf.keras.Sequential()
result.add(
tf.keras.layers.Conv2D(filters, size, strides=2, padding='same',
kernel_initializer=initializer, use_bias=False))
if apply_batchnorm:
result.add(tf.keras.layers.BatchNormalization())
result.add(tf.keras.layers.LeakyReLU())
return result
down_model = downsample(3, 4)
down_result = down_model(tf.expand_dims(inp, 0))
print (down_result.shape)
def upsample(filters, size, apply_dropout=False):
initializer = tf.random_normal_initializer(0., 0.02)
result = tf.keras.Sequential()
result.add(
tf.keras.layers.Conv2DTranspose(filters, size, strides=2,
padding='same',
kernel_initializer=initializer,
use_bias=False))
result.add(tf.keras.layers.BatchNormalization())
if apply_dropout:
result.add(tf.keras.layers.Dropout(0.5))
result.add(tf.keras.layers.ReLU())
return result
up_model = upsample(3, 4)
up_result = up_model(down_result)
print (up_result.shape)
def Generator():
inputs = tf.keras.layers.Input(shape=[256,256,3])
down_stack = [
downsample(64, 4, apply_batchnorm=False), # (bs, 128, 128, 64)
downsample(128, 4), # (bs, 64, 64, 128)
downsample(256, 4), # (bs, 32, 32, 256)
downsample(512, 4), # (bs, 16, 16, 512)
downsample(512, 4), # (bs, 8, 8, 512)
downsample(512, 4), # (bs, 4, 4, 512)
downsample(512, 4), # (bs, 2, 2, 512)
downsample(512, 4), # (bs, 1, 1, 512)
]
up_stack = [
upsample(512, 4, apply_dropout=True), # (bs, 2, 2, 1024)
upsample(512, 4, apply_dropout=True), # (bs, 4, 4, 1024)
upsample(512, 4, apply_dropout=True), # (bs, 8, 8, 1024)
upsample(512, 4), # (bs, 16, 16, 1024)
upsample(256, 4), # (bs, 32, 32, 512)
upsample(128, 4), # (bs, 64, 64, 256)
upsample(64, 4), # (bs, 128, 128, 128)
]
initializer = tf.random_normal_initializer(0., 0.02)
last = tf.keras.layers.Conv2DTranspose(OUTPUT_CHANNELS, 4,
strides=2,
padding='same',
kernel_initializer=initializer,
activation='tanh') # (bs, 256, 256, 3)
x = inputs
# Downsampling through the model
skips = []
for down in down_stack:
x = down(x)
skips.append(x)
skips = reversed(skips[:-1])
# Upsampling and establishing the skip connections
for up, skip in zip(up_stack, skips):
x = up(x)
x = tf.keras.layers.Concatenate()([x, skip])
x = last(x)
return tf.keras.Model(inputs=inputs, outputs=x)
generator = Generator()
tf.keras.utils.plot_model(generator, show_shapes=True, dpi=64)
gen_output = generator(inp[tf.newaxis,...], training=False)
plt.imshow(gen_output[0,...])
```
* **Generator loss**
* It is a sigmoid cross entropy loss of the generated images and an **array of ones**.
* The [paper](https://arxiv.org/abs/1611.07004) also includes L1 loss which is MAE (mean absolute error) between the generated image and the target image.
* This allows the generated image to become structurally similar to the target image.
* The formula to calculate the total generator loss = gan_loss + LAMBDA * l1_loss, where LAMBDA = 100. This value was decided by the authors of the [paper](https://arxiv.org/abs/1611.07004).
The training procedure for the generator is shown below:
```
LAMBDA = 100
def generator_loss(disc_generated_output, gen_output, target):
gan_loss = loss_object(tf.ones_like(disc_generated_output), disc_generated_output)
# mean absolute error
l1_loss = tf.reduce_mean(tf.abs(target - gen_output))
total_gen_loss = gan_loss + (LAMBDA * l1_loss)
return total_gen_loss, gan_loss, l1_loss
```
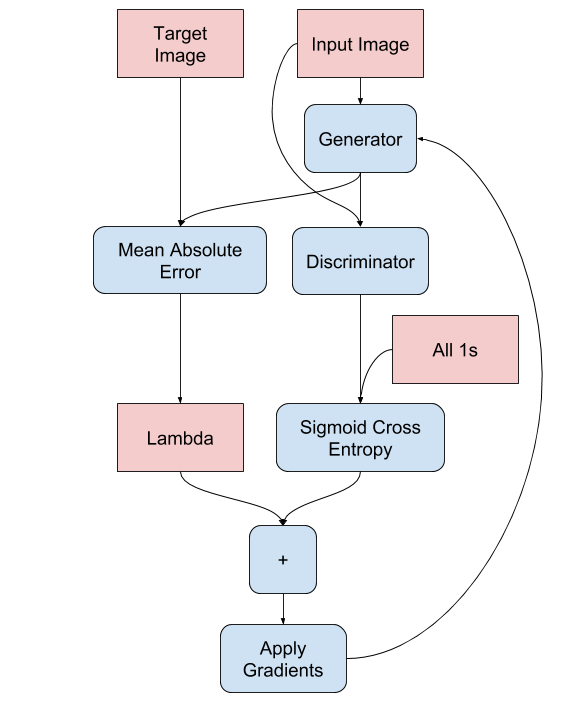
## Build the Discriminator
* The Discriminator is a PatchGAN.
* Each block in the discriminator is (Conv -> BatchNorm -> Leaky ReLU)
* The shape of the output after the last layer is (batch_size, 30, 30, 1)
* Each 30x30 patch of the output classifies a 70x70 portion of the input image (such an architecture is called a PatchGAN).
* Discriminator receives 2 inputs.
* Input image and the target image, which it should classify as real.
* Input image and the generated image (output of generator), which it should classify as fake.
* We concatenate these 2 inputs together in the code (`tf.concat([inp, tar], axis=-1)`)
```
def Discriminator():
initializer = tf.random_normal_initializer(0., 0.02)
inp = tf.keras.layers.Input(shape=[256, 256, 3], name='input_image')
tar = tf.keras.layers.Input(shape=[256, 256, 3], name='target_image')
x = tf.keras.layers.concatenate([inp, tar]) # (bs, 256, 256, channels*2)
down1 = downsample(64, 4, False)(x) # (bs, 128, 128, 64)
down2 = downsample(128, 4)(down1) # (bs, 64, 64, 128)
down3 = downsample(256, 4)(down2) # (bs, 32, 32, 256)
zero_pad1 = tf.keras.layers.ZeroPadding2D()(down3) # (bs, 34, 34, 256)
conv = tf.keras.layers.Conv2D(512, 4, strides=1,
kernel_initializer=initializer,
use_bias=False)(zero_pad1) # (bs, 31, 31, 512)
batchnorm1 = tf.keras.layers.BatchNormalization()(conv)
leaky_relu = tf.keras.layers.LeakyReLU()(batchnorm1)
zero_pad2 = tf.keras.layers.ZeroPadding2D()(leaky_relu) # (bs, 33, 33, 512)
last = tf.keras.layers.Conv2D(1, 4, strides=1,
kernel_initializer=initializer)(zero_pad2) # (bs, 30, 30, 1)
return tf.keras.Model(inputs=[inp, tar], outputs=last)
discriminator = Discriminator()
tf.keras.utils.plot_model(discriminator, show_shapes=True, dpi=64)
disc_out = discriminator([inp[tf.newaxis,...], gen_output], training=False)
plt.imshow(disc_out[0,...,-1], vmin=-20, vmax=20, cmap='RdBu_r')
plt.colorbar()
```
**Discriminator loss**
* The discriminator loss function takes 2 inputs; **real images, generated images**
* real_loss is a sigmoid cross entropy loss of the **real images** and an **array of ones(since these are the real images)**
* generated_loss is a sigmoid cross entropy loss of the **generated images** and an **array of zeros(since these are the fake images)**
* Then the total_loss is the sum of real_loss and the generated_loss
```
loss_object = tf.keras.losses.BinaryCrossentropy(from_logits=True)
def discriminator_loss(disc_real_output, disc_generated_output):
real_loss = loss_object(tf.ones_like(disc_real_output), disc_real_output)
generated_loss = loss_object(tf.zeros_like(disc_generated_output), disc_generated_output)
total_disc_loss = real_loss + generated_loss
return total_disc_loss
```
The training procedure for the discriminator is shown below.
To learn more about the architecture and the hyperparameters you can refer the [paper](https://arxiv.org/abs/1611.07004).
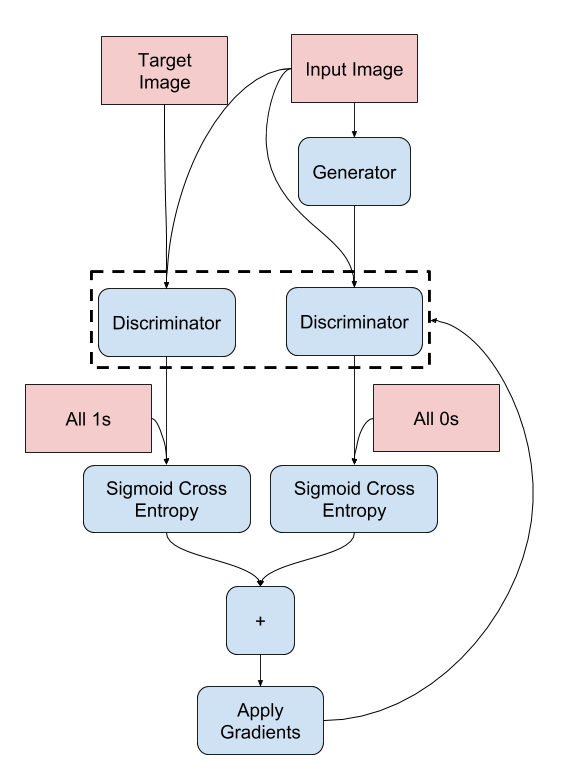
## Define the Optimizers and Checkpoint-saver
```
generator_optimizer = tf.keras.optimizers.Adam(2e-4, beta_1=0.5)
discriminator_optimizer = tf.keras.optimizers.Adam(2e-4, beta_1=0.5)
checkpoint_dir = './training_checkpoints'
checkpoint_prefix = os.path.join(checkpoint_dir, "ckpt")
checkpoint = tf.train.Checkpoint(generator_optimizer=generator_optimizer,
discriminator_optimizer=discriminator_optimizer,
generator=generator,
discriminator=discriminator)
```
## Generate Images
Write a function to plot some images during training.
* We pass images from the test dataset to the generator.
* The generator will then translate the input image into the output.
* Last step is to plot the predictions and **voila!**
Note: The `training=True` is intentional here since
we want the batch statistics while running the model
on the test dataset. If we use training=False, we will get
the accumulated statistics learned from the training dataset
(which we don't want)
```
def generate_images(model, test_input, tar):
prediction = model(test_input, training=True)
plt.figure(figsize=(15,15))
display_list = [test_input[0], tar[0], prediction[0]]
title = ['Input Image', 'Ground Truth', 'Predicted Image']
for i in range(3):
plt.subplot(1, 3, i+1)
plt.title(title[i])
# getting the pixel values between [0, 1] to plot it.
plt.imshow(display_list[i] * 0.5 + 0.5)
plt.axis('off')
plt.show()
for example_input, example_target in test_dataset.take(1):
generate_images(generator, example_input, example_target)
```
## Training
* For each example input generate an output.
* The discriminator receives the input_image and the generated image as the first input. The second input is the input_image and the target_image.
* Next, we calculate the generator and the discriminator loss.
* Then, we calculate the gradients of loss with respect to both the generator and the discriminator variables(inputs) and apply those to the optimizer.
* Then log the losses to TensorBoard.
```
EPOCHS = 150
import datetime
log_dir="logs/"
summary_writer = tf.summary.create_file_writer(
log_dir + "fit/" + datetime.datetime.now().strftime("%Y%m%d-%H%M%S"))
@tf.function
def train_step(input_image, target, epoch):
with tf.GradientTape() as gen_tape, tf.GradientTape() as disc_tape:
gen_output = generator(input_image, training=True)
disc_real_output = discriminator([input_image, target], training=True)
disc_generated_output = discriminator([input_image, gen_output], training=True)
gen_total_loss, gen_gan_loss, gen_l1_loss = generator_loss(disc_generated_output, gen_output, target)
disc_loss = discriminator_loss(disc_real_output, disc_generated_output)
generator_gradients = gen_tape.gradient(gen_total_loss,
generator.trainable_variables)
discriminator_gradients = disc_tape.gradient(disc_loss,
discriminator.trainable_variables)
generator_optimizer.apply_gradients(zip(generator_gradients,
generator.trainable_variables))
discriminator_optimizer.apply_gradients(zip(discriminator_gradients,
discriminator.trainable_variables))
with summary_writer.as_default():
tf.summary.scalar('gen_total_loss', gen_total_loss, step=epoch)
tf.summary.scalar('gen_gan_loss', gen_gan_loss, step=epoch)
tf.summary.scalar('gen_l1_loss', gen_l1_loss, step=epoch)
tf.summary.scalar('disc_loss', disc_loss, step=epoch)
```
The actual training loop:
* Iterates over the number of epochs.
* On each epoch it clears the display, and runs `generate_images` to show it's progress.
* On each epoch it iterates over the training dataset, printing a '.' for each example.
* It saves a checkpoint every 20 epochs.
```
def fit(train_ds, epochs, test_ds):
for epoch in range(epochs):
start = time.time()
display.clear_output(wait=True)
for example_input, example_target in test_ds.take(1):
generate_images(generator, example_input, example_target)
print("Epoch: ", epoch)
# Train
for n, (input_image, target) in train_ds.enumerate():
print('.', end='')
if (n+1) % 100 == 0:
print()
train_step(input_image, target, epoch)
print()
# saving (checkpoint) the model every 20 epochs
if (epoch + 1) % 20 == 0:
checkpoint.save(file_prefix = checkpoint_prefix)
print ('Time taken for epoch {} is {} sec\n'.format(epoch + 1,
time.time()-start))
checkpoint.save(file_prefix = checkpoint_prefix)
```
This training loop saves logs you can easily view in TensorBoard to monitor the training progress. Working locally you would launch a separate tensorboard process. In a notebook, if you want to monitor with TensorBoard it's easiest to launch the viewer before starting the training.
To launch the viewer paste the following into a code-cell:
```
#docs_infra: no_execute
%load_ext tensorboard
%tensorboard --logdir {log_dir}
```
Now run the training loop:
```
fit(train_dataset, EPOCHS, test_dataset)
```
If you want to share the TensorBoard results _publicly_ you can upload the logs to [TensorBoard.dev](https://tensorboard.dev/) by copying the following into a code-cell.
Note: This requires a Google account.
```
!tensorboard dev upload --logdir {log_dir}
```
Caution: This command does not terminate. It's designed to continuously upload the results of long-running experiments. Once your data is uploaded you need to stop it using the "interrupt execution" option in your notebook tool.
You can view the [results of a previous run](https://tensorboard.dev/experiment/lZ0C6FONROaUMfjYkVyJqw) of this notebook on [TensorBoard.dev](https://tensorboard.dev/).
TensorBoard.dev is a managed experience for hosting, tracking, and sharing ML experiments with everyone.
It can also included inline using an `<iframe>`:
```
display.IFrame(
src="https://tensorboard.dev/experiment/lZ0C6FONROaUMfjYkVyJqw",
width="100%",
height="1000px")
```
Interpreting the logs from a GAN is more subtle than a simple classification or regression model. Things to look for::
* Check that neither model has "won". If either the `gen_gan_loss` or the `disc_loss` gets very low it's an indicator that this model is dominating the other, and you are not successfully training the combined model.
* The value `log(2) = 0.69` is a good reference point for these losses, as it indicates a perplexity of 2: That the discriminator is on average equally uncertain about the two options.
* For the `disc_loss` a value below `0.69` means the discriminator is doing better than random, on the combined set of real+generated images.
* For the `gen_gan_loss` a value below `0.69` means the generator i doing better than random at foolding the descriminator.
* As training progresses the `gen_l1_loss` should go down.
## Restore the latest checkpoint and test
```
!ls {checkpoint_dir}
# restoring the latest checkpoint in checkpoint_dir
checkpoint.restore(tf.train.latest_checkpoint(checkpoint_dir))
```
## Generate using test dataset
```
# Run the trained model on a few examples from the test dataset
for inp, tar in test_dataset.take(5):
generate_images(generator, inp, tar)
```
|
github_jupyter
|
# Managing Throwing and Catching and Exceptions
In this workbook, we're going to work with a sample that describes a cashier's till at a store. We'll look at what happens when the cashier makes change for orders, the exceptions thrown and the danger they create.
First, let's describe the `Till` class
```
public class Till
{
private int OneDollarBills;
private int FiveDollarBills;
private int TenDollarBills;
private int TwentyDollarBills;
public Till(int ones, int fives, int tens = 0, int twenties = 0) =>
(OneDollarBills, FiveDollarBills, TenDollarBills, TwentyDollarBills) =
(ones, fives, tens, twenties);
public void MakeChange(int cost, int twenties, int tens = 0, int fives = 0, int ones = 0)
{
TwentyDollarBills += twenties;
TenDollarBills += tens;
FiveDollarBills += fives;
OneDollarBills += ones;
int amountPaid = twenties * 20 + tens * 10 + fives * 5 + ones;
int changeNeeded = amountPaid - cost;
if (changeNeeded < 0)
throw new InvalidOperationException("Not enough money provided");
Console.WriteLine("Cashier Returns:");
while ((changeNeeded > 19) && (TwentyDollarBills > 0))
{
TwentyDollarBills--;
changeNeeded -= 20;
Console.WriteLine("\t A twenty");
}
while ((changeNeeded > 9) && (TenDollarBills > 0))
{
TenDollarBills--;
changeNeeded -= 10;
Console.WriteLine("\t A tenner");
}
while ((changeNeeded > 4) && (FiveDollarBills > 0))
{
FiveDollarBills--;
changeNeeded -= 5;
Console.WriteLine("\t A fiver");
}
while ((changeNeeded > 0) && (OneDollarBills > 0))
{
OneDollarBills--;
changeNeeded--;
Console.WriteLine("\t A one");
}
if (changeNeeded > 0)
throw new InvalidOperationException("Can't make change. Do you have anything smaller?");
}
public void LogTillStatus()
{
Console.WriteLine("The till currently has:");
Console.WriteLine($"{TwentyDollarBills * 20} in twenties");
Console.WriteLine($"{TenDollarBills * 10} in tens");
Console.WriteLine($"{FiveDollarBills * 5} in fives");
Console.WriteLine($"{OneDollarBills} in ones");
Console.WriteLine();
}
public override string ToString() =>
$"The till has {TwentyDollarBills * 20 + TenDollarBills * 10 + FiveDollarBills * 5 + OneDollarBills} dollars";
}
```
Now that we have our `Till`, let's set up our scenario to experiment with.
```
// TheBank is our cashier's till we are working with and we'll give it some cash to start with
var theBank = new Till(ones: 50, fives: 20, tens: 10, twenties: 5);
var expectedTotal = 50 * 1 + 20 * 5 + 10 * 10 + 5 * 20;
theBank.LogTillStatus();
Console.WriteLine(theBank);
Console.WriteLine($"Expected till value: {expectedTotal}");
```
Now that we have set an initial value for the contents of `TheBank`, let's start working with customers and making change.
We'll define a number of transactions to run through `TheBank` and also setup a random number generator to give us the feeling of random items being purchased and we'll make change for those customers
```
int transactions = 2;
var valueGenerator = new Random((int)DateTime.Now.Ticks);
while (transactions-- > 0)
{
int itemCost = valueGenerator.Next(2, 50);
int numOnes = itemCost % 2;
int numFives = (itemCost % 10 > 7) ? 1 : 0;
int numTens = (itemCost % 20 > 13) ? 1 : 0;
int numTwenties = (itemCost < 20) ? 1 : 2;
try
{
Console.WriteLine($"Customer making a ${itemCost} purchase");
Console.WriteLine($"\t Using {numTwenties} twenties");
Console.WriteLine($"\t Using {numTens} tenners");
Console.WriteLine($"\t Using {numFives} fivers");
Console.WriteLine($"\t Using {numOnes} silver dollar coins");
theBank.MakeChange(itemCost, numTwenties, numTens, numFives, numOnes);
expectedTotal += itemCost;
}
catch (InvalidOperationException e)
{
Console.WriteLine($"Could not make transaction: {e.Message}");
}
Console.WriteLine(theBank);
Console.WriteLine($"Expected till value: {expectedTotal}");
Console.WriteLine(" ------------------------------------------");
}
```
|
github_jupyter
|
# Consume deployed webservice via REST
Demonstrates the usage of a deployed model via plain REST.
REST is language-agnostic, so you should be able to query from any REST-capable programming language.
## Configuration
```
from environs import Env
env = Env(expand_vars=True)
env.read_env("foundation.env")
env.read_env("service-principals.env")
# image to test
IMAGE_TO_TEST = "mnist_fashion/04_consumption/random_test_images/random-test-image-9629.png"
# endpoint of the scoring webservice
SCORING_URI = "<add your own scoring REST endpoint here>"
# auth method, either "Token", "Keys" or "None".
# also specify additional values depending on auth method
AUTH_METHOD = "Keys"
if AUTH_METHOD == "Keys":
AUTH_KEY = "<add your own key here>"
elif AUTH_METHOD == "Token":
REGION = "eastus"
SUBSCRIPTION_ID = env("SUBSCRIPTION_ID")
RESOURCE_GROUP = env("RESOURCE_GROUP")
WORKSPACE_NAME = env("WORKSPACE_NAME")
SERVICE_NAME = "mnist-fashion-service"
CONSUME_MODEL_SP_TENANT_ID = env("CONSUME_MODEL_SP_TENANT_ID")
CONSUME_MODEL_SP_CLIENT_ID = env("CONSUME_MODEL_SP_CLIENT_ID")
CONSUME_MODEL_SP_CLIENT_SECRET = env("CONSUME_MODEL_SP_CLIENT_SECRET")
elif AUTH_METHOD == "None":
pass
```
## Load a random image and plot it
```
import matplotlib.pyplot as plt
from PIL import Image
image = Image.open(IMAGE_TO_TEST)
plt.figure()
plt.imshow(image)
plt.colorbar()
plt.grid(False)
plt.show()
```
## Invoke the webservice and show result
```
import requests
import json
# --- get input data
input_data = open(IMAGE_TO_TEST, "rb").read()
# alternatively for JSON input
#input_data = json.dumps({"x": 4711})
# --- get headers
# Content-Type
# for binary data
headers = {"Content-Type": "application/octet-stream"}
# alternatively for JSON data
#headers = {"Content-Type": "application/json"}
# Authorization
if AUTH_METHOD == "Token":
# get an access token for the service principal to access Azure
azure_access_token = requests.post(
f"https://login.microsoftonline.com/{CONSUME_MODEL_SP_TENANT_ID}/oauth2/token",
headers={"Content-Type": "application/x-www-form-urlencoded"},
data="grant_type=client_credentials"
+ "&resource=https%3A%2F%2Fmanagement.azure.com%2F"
+ f"&client_id={CONSUME_MODEL_SP_CLIENT_ID}"
+ f"&client_secret={CONSUME_MODEL_SP_CLIENT_SECRET}",
).json()["access_token"]
# use that token to get another token for accessing the webservice
# note: the token is only valid for a certain period of time.
# after that time, a new token has to be used. the logic
# to do this, is not implemented here yet. you can check
# the current time against the refresh after time to know
# if a new token is required. refreshAfter and expiryOn
# are UNIX timestamps. use time.time() to get the current
# timestamp.
token_response = requests.post(
f"https://{REGION}.modelmanagement.azureml.net/modelmanagement/v1.0/subscriptions/{SUBSCRIPTION_ID}/resourceGroups/{RESOURCE_GROUP}/providers/Microsoft.MachineLearningServices/workspaces/{WORKSPACE_NAME}/services/{SERVICE_NAME}/token",
headers={"Authorization": f"Bearer {azure_access_token}"}
).json()
access_token = token_response["accessToken"]
access_token_refresh_after = int(token_response["refreshAfter"])
access_token_expiry_on = int(token_response["expiryOn"])
# finally, use that token to access the webservice
headers["Authorization"] = f"Bearer {access_token}"
if AUTH_METHOD == "Keys":
headers["Authorization"] = f"Bearer {AUTH_KEY}"
if AUTH_METHOD == "None":
# do nothing
pass
# --- make request and display response
response = requests.post(SCORING_URI, input_data, headers=headers, verify=True)
print(response.json())
```
|
github_jupyter
|
# Calculate China-Z Index (CZI) with Python
China Z-Index (CZI) is extensively used by National Climate Centre (NCC) of China to monitor drought conditions throughout
the country (Wu et al., 2001; Dogan et al., 2012). CZI assumes that precipitation data follow the Pearson Type III distribution and is related to Wilson–Hilferty cube-root transformation (Wilson and Hilferty, 1931) from chi-square variable to the Z-scale (Kendall and Stuart, 1977).
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
```
## Prepare data
```
data = pd.read_csv('data/prcphq.046037.month.txt', sep=r"\s+",
skiprows=1, usecols=[1, 2],
parse_dates=True,
index_col = 0,
names=['Date', 'Rain'])
```
## Calculate six-monthly CZI
Here we use all years as a reference period to calculate monthly long-term normals. ZSI = (p-pm)/s
```
data['Rain_6'] = data['Rain'].rolling(6).sum()
df_6mon = data[['Rain_6']].dropna()
df_6mon['CZI'] = np.nan
for imon in np.arange(1, 13):
sinds = df_6mon.index.month==imon
x = df_6mon[sinds]
zsi = (x -x.mean())/x.std()
cs = np.power(zsi, 3)/len(x)
czi = 6.0/cs*np.power((cs/2.0*zsi + 1.0), 1.0/3.0)-6.0/cs + cs/6.0
df_6mon.loc[sinds, 'CZI'] = czi.values[:,0]
data['CZI'] = df_6mon['CZI']
del df_6mon
data.head(7)
```
## Visualize
```
ax = data['CZI'].plot(figsize=(15, 7), )
ax.axhline(1, linestyle='--', color='g')
ax.axhline(-1, linestyle='--', color='r')
ax.set_title('Six-Monthly China-Z Index', fontsize=16)
ax.set_xlim(data.index.min(), data.index.max())
ax.set_ylim(-3, 3)
data.head(12)
data.Rain_6.plot(figsize=(15, 7),)
```
## Summary and discussion
NCC computes CZI only for 1-month time step. However, CZI could be computed for five time steps i.e. 1-, 3-, 6-, 9- and 12-month time step.
Many studies comparing the CZI with that of SPI and Z-score reported similar results (Wu et al., 2001; Morid et al., 2006).
Further, Wu et al. (2001) suggested that because of simplicity in calculating drought severity at monthly time step using CZI, it can be preferred over SPI, where rainfall data are often incomplete.
## References
Dogan, S., Berktay, A., Singh, V.P., 2012. Comparison of multi-monthly rainfall-based drought severity indices, with application to semi-arid Konya closed basin, Turkey. J. Hydrol. 470–471, 255–268.
Kendall, M.G.; Stuart, A. The Advanced Theory of Statistics; Charles Griffin & Company-High Wycombe: London, UK, 1997; pp. 400–401.
Morid, S., Smakhtin, V., Moghaddasi, M., 2006. Comparison of seven meteorological indices for drought monitoring in Iran. Int. J. Climatol. 26, 971–985.
Wilson, E.B., Hilferty, M.M., 1931. The Distribution of Chi-Square. Proc. Natl. Acad. Sci. USA 17, 684–688.
Wu, H., Hayes, M.J., Weiss, A., Hu, Q.I., 2001. An evaluation of the standardized precipitation index, the china-Zindex and the statistical Z-Score. Int. J. Climatol.21, 745–758. http://dx.doi.org/10.1002/joc.658.
|
github_jupyter
|
```
import os
import sys
sys.path.append(f'{os.environ["HOME"]}/Projects/planckClusters/catalogs')
from load_catalogs import load_PSZcatalog
from tqdm import tqdm_notebook
data = load_PSZcatalog()
PS1_dir = f'{os.environ["HOME"]}/Projects/planckClusters/data/extern/PS1'
SDSS_dir = f'{os.environ["HOME"]}/Projects/planckClusters/data/extern/SDSS'
DECaLS_dir = f'{os.environ["HOME"]}/Projects/planckClusters/data/extern/DECaLS'
DES_dir = f'{os.environ["HOME"]}/Projects/planckClusters/data/extern/DES'
outpath = './data_full_new'
for name in tqdm_notebook(data['NAME'], total=len(data['NAME'])):
name = name.replace(' ', '_')
if not os.path.exists(f'{outpath}/{name}'):
continue
if os.path.isdir(f'{PS1_dir}/{name}'):
relpath = os.path.relpath(f'{PS1_dir}/{name}', f'{outpath}/{name}')
target_files = ['_PS1stack_g.fits', '_PS1stack_r.fits', '_PS1stack_i.fits',
'_PS1stack_z.fits', '_PS1stack_y.fits', '_PS1stack_irg.tiff']
for file in target_files:
try:
os.symlink(f'{PS1_dir}/{name}/{name}{file}',
f'{outpath}/{name}/{name}{file}')
except FileExistsError:
pass
if os.path.isdir(f'{SDSS_dir}/{name}'):
relpath = os.path.relpath(f'{SDSS_dir}/{name}', f'{outpath}/{name}')
target_files = ['_SDSSstack_g.fits', '_SDSSstack_r.fits', '_SDSSstack_i.fits',
'_SDSSstack_z.fits', '_SDSSstack_irg.tiff']
for file in target_files:
try:
os.symlink(f'{SDSS_dir}/{name}/{name}{file}',
f'{outpath}/{name}/{name}{file}')
except FileExistsError:
pass
if os.path.isdir(f'{DECaLS_dir}/{name}'):
relpath = os.path.relpath(f'{DECaLS_dir}/{name}', f'{outpath}/{name}')
target_files = ['_DECaLSstack_r.fits', '_DECaLSstack.jpg']
for file in target_files:
try:
os.symlink(f'{DECaLS_dir}/{name}/{name}{file}',
f'{outpath}/{name}/{name}{file}')
except FileExistsError:
pass
if os.path.isdir(f'{DES_dir}/{name}'):
relpath = os.path.relpath(f'{DES_dir}/{name}', f'{outpath}/{name}')
target_files = ['_DESstack_r.fits', '_DESstack.jpg']
for file in target_files:
try:
os.symlink(f'{DES_dir}/{name}/{name}{file}',
f'{outpath}/{name}/{name}{file}')
except FileExistsError:
pass
```
|
github_jupyter
|
# Keras mnist LeNet-5 v2
**此项目为测试修改版的LeNet-5**
- 目前达到$0.9929$的准确率
```
%matplotlib inline
import os
import PIL
import pickle
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import tensorflow as tf
import keras
from IPython import display
from functools import partial
from sklearn.preprocessing import normalize
from keras import backend
from keras.utils import np_utils, plot_model
from keras.callbacks import TensorBoard, ModelCheckpoint
from keras.callbacks import LearningRateScheduler, ReduceLROnPlateau
from keras.preprocessing.image import ImageDataGenerator
from keras.models import load_model
from keras.models import Sequential, Model
from keras.layers import Dense, Conv2D, MaxPool2D, Input, AveragePooling2D
from keras.layers import Activation, Dropout, Flatten, BatchNormalization
import warnings
warnings.filterwarnings('ignore')
np.random.seed(42)
```
## 准备数据
```
file_path = r"I:\Dataset\mnist\all_mnist_data.csv"
mnist_data = pd.read_csv(file_path)
idx = np.random.permutation(len(mnist_data))
train_data = mnist_data.iloc[idx[: 60000]]
test_data = mnist_data.iloc[idx[60000: ]]
X_train = np.array(train_data.drop('0', axis=1)).reshape(-1, 28, 28, 1).astype("float32")
X_test = np.array(test_data.drop('0', axis=1)).reshape(-1, 28, 28, 1).astype("float32")
y_train = np.array(train_data['0'])
y_test = np.array(test_data['0'])
y_train = np_utils.to_categorical(y_train)
y_test = np_utils.to_categorical(y_test)
x_train = X_train[10000:]
t_train = y_train[10000:]
x_val = X_train[:10000]
t_val = y_train[:10000]
print("\nimgs of trainset : ", x_train.shape)
print("labels of trainset : ", t_train.shape)
print("imgs of valset : ", x_val.shape)
print("labels of valset : ", t_val.shape)
print("imgs of testset : ", X_test.shape)
print("labels of testset : ", y_test.shape)
```
## 搭建模型
```
def myCNN():
model = Sequential()
model.add(Conv2D(filters=16,
kernel_size=(5, 5),
padding='same',
input_shape=(28, 28, 1),
activation='relu',
name='conv2d_1'))
model.add(MaxPool2D(pool_size=(2, 2), name='max_pool2d_1'))
model.add(Conv2D(filters=36,
kernel_size=(5, 5),
padding='same',
input_shape=(14, 14, 1),
activation='relu',
name='conv2d_2'))
model.add(MaxPool2D(pool_size=(2, 2), name='max_pool2d_2'))
model.add(Dropout(0.25, name='dropout_1'))
model.add(Flatten(name='flatten_1'))
model.add(Dense(128, activation='relu', name='dense_1'))
model.add(Dropout(0.5, name='dropout_2'))
model.add(Dense(10, activation='softmax', name='dense_2'))
return model
model = myCNN()
model.summary()
```
### 计算资源的分配
```
config = tf.ConfigProto()
config.gpu_options.per_process_gpu_memory_fraction = 0.2
sess = tf.Session(config=config)
backend.set_session(sess)
```
### 训练
```
"""训练模型并保存模型及训练历史
保存模型单独创建一个子文件夹modeldir, 保存训练历史则为单个文件hisfile"""
models_name = "Keras_mnist_LeNet-5_v2" # 模型名称的公共前缀
factor_list = [""] # 此次调参的变量列表
model_list = [] # 模型名称列表
for i in range(len(factor_list)):
modelname = models_name + factor_list[i] + ".h5"
model_list.append(modelname)
# 创建模型保存子目录modeldir
if not os.path.isdir("saved_models"):
os.mkdir("saved_models")
modeldir = r"saved_models"
# 创建训练历史保存目录
if not os.path.isdir("train_history"):
os.mkdir("train_history")
# 设置训练历史文件路径
hisfile = r"train_history\Keras_mnist_LeNet-5_v2.train_history"
# 每个模型及其对应的训练历史作为键值对{modelname: train_history}
# train_history为字典,含四个key,代表train和val的loss和acc
model_train_history = dict()
# 开始训练
epochs=100
batch_size = 32
steps_per_epoch=1250
for i in range(len(model_list)):
model = myCNN()
modelname = model_list[i]
modelpath = os.path.join(modeldir, modelname)
train_his = np.array([]).reshape(-1, 2)
val_his = np.array([]).reshape(-1, 2)
datagen = ImageDataGenerator()
datagen.fit(x_train)
model.compile(loss="categorical_crossentropy",
optimizer=keras.optimizers.Adam(),
metrics=["accuracy"])
print("\ntraining model : ", modelname)
ck_epoch, max_val_acc = 0, 0.0
for epoch in range(epochs+1):
i = 0
tr_his = []
for X, y in datagen.flow(x_train, t_train, batch_size=batch_size):
his = model.train_on_batch(X, y)
tr_his.append(his)
i += 1
if i >= steps_per_epoch: break
tr = np.mean(tr_his, axis=0)
val = model.evaluate(x_val, t_val, verbose=0)
train_his = np.vstack((train_his, tr))
val_his = np.vstack((val_his, val))
if epoch<10 or epoch%5==0:
print("%4d epoch: train acc: %8f loss: %8f val acc: %8f loss: %8f"%(epoch, tr[1], tr[0], val[1], val[0]))
# 设置保存模型
if val[1] > max_val_acc:
model.save(modelpath)
print("val acc improved from %6f to %6f"%(max_val_acc, val[1]))
max_val_acc = val[1]
ck_epoch = epoch
model_train_history[modelname] = {"acc": train_his[:, 1], "val_acc": val_his[:, 1],
"loss": train_his[:, 0], "val_loss": val_his[:, 0]}
"""保存训练历史"""
fo = open(hisfile, 'wb')
pickle.dump(model_train_history, fo)
fo.close()
```
### 可视化训练过程
```
def show_train_history(saved_history, his_img_file):
modelnames = sorted(list(saved_history.keys()))
train = ["acc", "loss"]
val = ["val_acc", "val_loss"]
"""作loss和acc两个图"""
fig, ax = plt.subplots(1, 2, figsize=(16, 5))
ax = ax.flatten()
color_add = 0.9/len(saved_history)
for i in range(2):
c = 0.05
for j in range(len(saved_history)):
modelname = modelnames[j]
train_history = saved_history[modelname]
ax[i].plot(train_history[train[i]],
color=(0, 1-c, 0),
linestyle="-",
label="train_"+modelname[21:-3])
ax[i].plot(train_history[val[i]],
color=(c, 0, 1-c),
linestyle="-",
label="val_"+modelname[21:-3])
c += color_add
ax[i].set_title('Train History')
ax[i].set_ylabel(train[i])
ax[i].set_xlabel('Epoch')
ax[0].legend(loc="lower right")
ax[1].legend(loc="upper right")
ax[0].set_ylim(0.9, 1.0)
ax[1].set_ylim(0, 0.2)
plt.suptitle("LeNet-5_v2")
print("saved img: ", his_img_file)
plt.savefig(his_img_file)
plt.show()
"""载入训练历史并可视化, 并且保存图片"""
if not os.path.isdir("his_img"):
os.mkdir("his_img")
his_img_file = r"his_img\LeNet-5_v2.png"
fo2 = open(hisfile, "rb")
saved_history1 = pickle.load(fo2)
show_train_history(saved_history1, his_img_file)
```
## 在测试集上测试
```
smodel = load_model(modelpath)
print("test model: ", os.path.basename(modelpath))
loss, acc = smodel.evaluate(X_test, y_test)
print("test :acc: %.4f"%(acc))
```
|
github_jupyter
|
<a href="https://colab.research.google.com/github/krmiddlebrook/intro_to_deep_learning/blob/master/machine_learning/lesson%203%20-%20Neural%20Networks/intro-to-neural-networks.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Intro to Neural Networks
<figure><img src='https://mk0analyticsindf35n9.kinstacdn.com/wp-content/uploads/2018/12/nural-network-banner.gif' width='70%'></img><figcaption>A Feed Forward Neural Network</figcaption>
</figure>
In the previous lesson, we introduced the softmax regression method to solve multi-class classification tasks, implementing a classifer to recognize 10 handwritten digits from the MNIST digits dataset.
We've come a long way and covered many concepts throughout this series, with each lesson building on the previous material. We've learned how to clean data, create linear models (via linear regression), coerce model outputs into a valid probability distribution (via logistic and softmax regression), train models using Sklearn and Tensorflow, apply the appropriate loss function, and to minimize it with respect to our model's parameters (via optimization algorithms). Now that we have a healthy understanding of these concepts in the context of simple linear models, we are ready to explore neural networks--one of the most exciting and successful methods in modern machine learning!
In this lesson, we describe deep linear neural networks at a high level, focusing on their structure, and demonstrate how to build one using Tensorflow.
To make this lesson more approachable, we don't cover every detail about neural networks here, but we aim to provide enough information for you to create your own neural networks and to inspire you to explore deep learning in more detail.
Lesson roadmap:
- High level introduction to *neural networks*.
- Building neural networks in Python - recreating the feed forward neural network model in 3Blue1Brown's excellent video [But what is a Neural Network? | Deep learning, chapter 1](https://www.youtube.com/watch?v=aircAruvnKk&t=436s) and training it to classify handwritten digits. As you will see, this simple feed forward neural network achieves impressive results.
## Neural Networks
Although neural networks only recently became popular, they've been around for quite some time. In fact, they first appeared in machine learning research way back in the late 1950s! But they didn't become popular until after 2012, when researchers built a neural network to classify different kinds of labeled images, achieving groundbreaking results (see [ImageNet Classification with Deep Convolutional
Neural Networks](http://papers.nips.cc/paper/4824-imagenet-classification-with-deep-convolutional-neural-networks.pdf)). Since then, neural networks have become widely used in machine learning. Neural networks are successful, in part, because they can effectively learn representations of complex data (e.g., images, text, sound, tabular, etc.), especially given enough data and computing power.
At a high level, there are three fundemental types of neural networks: 1) encoders, 2) decoders, or 3) a combination of both. We will focus on *encoders*.
Encoder networks take in some input data (i.e., images, texts, sounds, etc.) and output *predictions*, just like the linear models we've been working with. The simplest type of neural networks are called feed forward neural networks (FFNNs), and they consist of many *layers* of *neurons* each *fully-connected* to those in the layer below (from which they receive input) and those above (which they, in turn, influence).
FFNNs may sound complex right now, but hang in there. In many ways FFNNs are the superpowered version of the linear models we already know about. Like the linear models we've discussed (linear/logistic/softmax regression), neural networks can be configured to solve different kinds of tasks: either *regression* or *classification*.
Here are some quick facts about neural networks:
- They are effective models for learning to represent complex data (like images, text, sound, tabular, etc.).
- Encoder-based networks, which take input data and output predictions, are probably the most common neural networks - they are useful for classification and regression tasks
- Feed forward neural networks (FFNNs) are the simplest type of neural network. They consist of many *layers* of *neurons* each *fully-connected* to those in the layer below (from which they receive input) and those above (which they, in turn, influence).
- FFNNs are like linear models on steriods. They have many more parameters than simple linear models, which enables them to learn more complex relationships from the input data.
- Even though FFNNs are the simplest kind of neural network, they can be very effective.
**Challenge:** What are two tasks that you think encoder networks might be at good at solving?
### Feed Forward Neural Networks
<figure><img src='https://thumbs.gfycat.com/WeepyConcreteGemsbok-size_restricted.gif' width='100%'></img><figcaption>A Feed Forward Neural Network | <em>Source: <a href='https://www.youtube.com/watch?v=aircAruvnKk&t=436s'>3Blue1Brown - But what is a Neural Network? Deep Learning Part 1</a></em></figcaption>
</figure>
Did you watch the [3Blue1Brown video on neural networks](https://www.youtube.com/watch?v=aircAruvnKk&t=436s)? If you haven't yet, I highly recommend checking it out (feel free to rewatch it too, it's a great overview of neural networks). I'll frequently be referencing important concepts that the video talks about.
In the following sections, we will summarize the key concepts behind neural networks. First, we describe the motivation and inspiration behind neural networks. Then, we dive into the structure of neural networks, outlining a few critical pieces that make them work.
*Note, we describe these concepts from the perspective of a feed forward neural network. That said, the fundemental ideas discussed generalize to almost every type of neural network.*
#### Neural Networks: Neural Network $=$ Brain?
<figure><img src='https://github.com/BreakoutMentors/Data-Science-and-Machine-Learning/blob/master/images/neural-network-brain-pizza-yoda-analogy.png?raw=true' width='75%'></img><figcaption>"Pizza, I like" - Yoda</figcaption>
</figure>
No, neural networks $\neq$ brains.
While neural networks don't actually operate like brains, they were inspired by them.
Let's consider an extremely oversimplified version of the brain. The brain is an organ that uses neurons to process information and make decisions. The neurons are what the brain uses to process data (i.e., information about the world). When some piece of data is sent to a neuron it activates (or dpesn't). The magnitude/strength (i.e., positive or negative) of the activation triggers other groups of neurons to activate (or not). Eventually, this process outputs a decision--based on a combination of the prior triggers and activations--as a response to the input data. As an example, let's say there is a pizza in the kitchen and my nose picks up the scent. The smell of freshly baked dough and melted cheese activates my "I'm hungry neurons". Eventually, I can't ignore these neurons any longer, so I run to the kitchen and eat some pizza.
#### Neural Networks: Neurons
<figure><img src='https://github.com/BreakoutMentors/Data-Science-and-Machine-Learning/blob/master/images/neuron-3blue1brown.png?raw=true' width='75%'></img><figcaption>Neural Networks: Neuron | <em>Source: <a href='https://www.youtube.com/watch?v=aircAruvnKk&t=436s'>3Blue1Brown - But what is a Neural Network? Deep Learning Part 1</a></em></figcaption>
</figure>
**Neurons** are at the core of neural networks (after all, they are practically in the name). At a high level, a neuron holds a corresponding value (i.e., number) called an **activation**. The activation can be represented by a tiny value, a large value, or a value somewhere in between. A neuron is "lit up" (i.e., activated) when its corresponding activation is large, and it is "dim" (i.e., not very activated) when its activation is small. Connecting this to the pizza example, my "I'm hungry neurons" lit up after I smelled the pizza in the kitchen.
#### Neural Networks: Layers
<figure><img src='https://miro.medium.com/max/1280/1*_nTmA2RowzQBCqI9BVtmEQ.gif' width='75%'></img><figcaption>The Neural Network's Secret Sauce: Stacking Layers | <em>Source: <a href='https://www.youtube.com/watch?v=aircAruvnKk&t=436s'>3Blue1Brown - But what is a Neural Network? Deep Learning Part 1</a></em></figcaption>
</figure>
The secret sauce driving neural networks is the technique of *stacking layers*. At a high level, this method enables the neural network to learn an effective representation of the data. The layers that are in between the input layer and the output layer are called *hidden layers*.
A **layer** is composed of a set of **neurons**. We can manually configure the number of neurons we want to have in each layer, except for in the first and last ones. When we add more neurons and layers to the model, we add more parameters (weights and biases) to it. As a result, larger models (models with many parameters) can be computationally expensive, but very effective. This creates a trade-off between computation effeciency and model representation ability (making smaller models as effective as bigger ones is an active area of research).
For classification tasks, the number of neurons in the last layer is determined by the number of categories/classes in the dataset. While in regression tasks, there is generally only one neurons in the final layer, since we are predicting a continuous value (e.g., the happiness score for a particular country).
**Challenge:** In the above figure (from previous cell), how many layers are in the neural network? How many are hidden layers? How many neurons are in the first layer? How many are in the last layer?
#### Neural Networks: Weights & Activation Functions
<figure><img src='https://thumbs.gfycat.com/BabyishGeneralFruitfly-size_restricted.gif' width='65%'></img><figcaption>Calculating a Neuron's Activation: Connections and Weights (1) | <em>Source: <a href='https://www.youtube.com/watch?v=aircAruvnKk&t=436s'>3Blue1Brown - But what is a Neural Network? Deep Learning Part 1</a></em></figcaption>
</figure>
<figure><img src='https://thumbs.gfycat.com/GlitteringCavernousGoosefish-small.gif' width='65%'></img><figcaption>Calculating a Neuron's Activation: Connections and Weights (2)| <em>Source: <a href='https://www.youtube.com/watch?v=aircAruvnKk&t=436s'>3Blue1Brown - But what is a Neural Network? Deep Learning Part 1</a></em></figcaption>
</figure>
Neural networks pass information through the network using connections between pairs of neurons in adjacent layers. Each connection has a corresponding **weight** parameter that is learned during the model training phase. As shown in the figure above, the activation of a neuron in a subsequent layer is determined by the *weighted sum* of the weights and activations of the neurons in the previous layer (i.e., connections). A **bias** term is added at the end of the weighted sum to control how large/small a neuron's weighted sum must be to activate. Before the neuron receives a final activation value, the weighted sum is *squeezed* by an **activation function**.
Activation functions and parameters (weights and biases)may sound intimidating. Fortunately, you already know a lot about these concepts: 1) the *sigmoid* and *softmax* logit functions are examples of activation functions, 2) linear models (linear/logistic/softmax) use the same *weighted sum* method to activate neurons in subsequent layers, the difference is these networks only have one layer after the input.
As you may remember from the logistic and softmax lessons, these logit functions convert the inputs to a valid probability space. An activation function, more generally, can be defined as any function that transforms the neuron output. It is common to choose an activation function that normalizes the input between 0 and 1 or -1 and 1.
Activation functions play a critical role in building effective deep neural networks. They can help the network converge quickly (find the right parameters) and improve the model's overall performance.
In the diagrams above, the second layer has one neuron. This neuron is connected to every other neuron in the previous layer. Consequently, it has 784 connections plus one bias term. That's a lot of number crunching! For this reason, we generally select activation functions that can be computed effeciently (quickly).
<figure><img src='https://github.com/BreakoutMentors/Data-Science-and-Machine-Learning/blob/master/images/sigmoid-activation-3Blue1Brown.png?raw=true' width='65%'></img><figcaption>Calculating a Neuron's Activation: Sigmoid Activation Function (2)| <em>Source: <a href='https://www.youtube.com/watch?v=aircAruvnKk&t=436s'>3Blue1Brown - But what is a Neural Network? Deep Learning Part 1</a></em></figcaption>
</figure>
So far we've only discussed connections and activations in the context of one neuron in a subsequent layer. But, most layers have many neurons. The good news is, we calculate neuron activations in the same way as before. The bad news is, we have to repeat the calculation process many times over. For example, in the diagrams below we see that all 16 neurons in the 2nd layer are connected to every other neuron in the 1st layer (i.e., 784 neurons). Thus, we need to perform $784\times16$ weights $ + 16$ biases calculations to get the activations for the 16 neurons in the 2nd layer. Doing this by hand would be way too difficult, but luckily, we can make computers do most of the heavy lifting.
<figure><img src='https://github.com/BreakoutMentors/Data-Science-and-Machine-Learning/blob/master/images/2-layer-weights-biases-connections-3Blue1Brown.png?raw=true' width='65%'></img><figcaption>Calculating a Neuron's Activation: Sigmoid Activation Function (2) | <em>Source: <a href='https://www.youtube.com/watch?v=aircAruvnKk&t=436s'>3Blue1Brown - But what is a Neural Network? Deep Learning Part 1</a></em></figcaption>
</figure>
**Challenge:** In the below neural network diagram, how many weights and biases are there between the 2nd layer and the 3rd layer? How many total weights and biases are there in the entire network? Hint: all neurons are connected to every other neuron in the previous layer.
<figure><img src='https://thumbs.gfycat.com/DeadlyDeafeningAtlanticblackgoby-poster.jpg' width='65%'></img><figcaption>A Neural Network: Total Weights & Biases | <em>Source: <a href='https://www.youtube.com/watch?v=aircAruvnKk&t=436s'>3Blue1Brown - But what is a Neural Network? Deep Learning Part 1</a></em></figcaption>
</figure>
## Building a Neural Network: Summary
Now that we know a little about neural networks, it's time to make our own! In this section, we demonstrate how to build a neural network in Python using Tensorflow. Specifically, we implement the neural network from 3Blue1Brown's video [But what is a Neural Network? Deep Learning Part 1](https://www.youtube.com/watch?v=aircAruvnKk&t=436s) to classify 10 types of handwritten digits from the MNIST dataset. Before we start, let's summarize what we know so far about neural networks:
- *Stacking layers* is their secret sauce - enabling the model to learn an effective representations of the data (most of the time).
- Layers are comprised of *neurons*. We configure the number of neurons in *hidden layers*.
- Neurons hold a corresponding *activation* - large activations "light up" neurons.
- The activations of neurons are determined by the weighted sum of their *connections* with the previous layer's neurons - quantified by *weights* and a *bias* term. The resulting output is then squeezed by an *activation function* such as the *sigmoid* function.
- For classification tasks, the number of neurons in the last layer corresponds to the number of classes/categories in the dataset.
Now, it's time to make our first neural network!
### Classification of Handwritten Digits with a Feed Forward Neural Network
<figure><img src='https://thumbs.gfycat.com/ViciousUnnaturalAmethystsunbird-max-1mb.gif' width='75%'></img><figcaption>A Neural Network: Total Weights & Biases | <em>Source: <a href='https://www.youtube.com/watch?v=aircAruvnKk&t=436s'>3Blue1Brown - But what is a Neural Network? Deep Learning Part 1</a></em></figcaption>
</figure>
In this section, we will recreate the feed forward neural network (FFNN) from 3Blue1Brown's video [But what is a Neural Network? Deep Learning Part 1](https://www.youtube.com/watch?v=aircAruvnKk&t=436s) and use it to classify handwritten digits from the MNIST dataset. This process involves several steps: 1) [loading the dataset](#-Step-1:-Loading-the-Dataset), 2) [building the model](#-Step-2:-Building-the-Model), 3) [training the model](#-Step-3:-Training-the-Model), 4) [testing the model](#-Step-4:-Testing-the-Model).
### Prerequisites: Google Colab + building neural networks in python
We recommend that you run this this notebook in the cloud on Google Colab, if you're not already doing so. It's the simplest way to get started. Google Colab gives you free access to specialized compute resources called [GPUs](https://en.wikipedia.org/wiki/Graphics_processing_unit) and [TPUs](https://en.wikipedia.org/wiki/Tensor_processing_unit). In modern machine learning these resources are frequently used because they significantly speed up model training compared to using [CPUs](https://en.wikipedia.org/wiki/Central_processing_unit) (your computer is probably using CPUs). At a high level, GPUs and TPUs are special types of computer chips that excel at performing computations on large matrices. They perform mathematical matrix operations like multiplication, addition, subtraction, etc. at a much higher rate (i.e., speed) than CPUs.
Native Python code won't run on GPUs and TPUs because they use specialized operating system *kernels*. We could convert our code to a language that these kernals can understand, but that would be a very tedious and frustrating process. Fortunately, there are several open-source Python libraries exist that do the heavy lifting for us. In particular, the two most popular open-source libraries are [PyTorch](https://pytorch.org/) and [Tensorflow](https://www.tensorflow.org/). These libraries enable us to build custom neural networks in Python that can run on GPUs and TPUs!
In this lesson we will use Tensorflow because it is a bit easier to use (while you are learning about neural networks) and it comes preinstalled in Google Colab. It is also possible to [install TensorFlow locally](https://www.tensorflow.org/install/). But, the simple solution is normally best (i.e., use Google Colab).
[tf.keras](https://www.tensorflow.org/guide/keras) is the simplest way to build and train neural network models in TensorFlow, so we will use it throughout this lessons.
Note that there's [tf.keras](https://www.tensorflow.org/guide/keras) (comes with TensorFlow) and there's [Keras](https://keras.io/) (standalone). You should be using [tf.keras](https://www.tensorflow.org/guide/keras) because 1) it comes with TensorFlow so you don't need to install anything extra and 2) it comes with powerful TensorFlow-specific features.
Lastly, to accelerate model training time, you may want to run this notebook on a GPU in Google Colab. To do this, click on the "Runtime" tab in the top left corner of the notebook, click "Change runtime type", and select the "GPU" option under "Hardware accelerator".
```
# TensorFlow and tf.keras
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras.layers import Input, Flatten, Dense
# Commonly used modules
import numpy as np
import os
import sys
# Images, plots, display, and visualization
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
import cv2
import IPython
from six.moves import urllib
print('Tensorflow version:', tf.__version__)
```
### Step 1: Loading the Dataset
The MNIST dataset contains 70k grayscale images of handwritten digits at a resolution of $28 \times 28$ pixels. Our goal is to build a classification model to take one of these images as input and predict the most likely digit contained in the image (along with a relative confidence about the prediction):
<figure><img src="https://i.imgur.com/ITrm9x4.png" width="65%"><figcaption><em>Source: <a href="https://deeplearning.mit.edu/">MIT Deep Learning</a></em></figcaption></figure>
Loading the dataset will return four NumPy arrays:
* The `train_images` and `train_labels` arrays are the *training set*—the data the model uses to learn.
* The `test_images` and `test_labels` arrays are the *test set*--the data the model is tested on.
The images are $28\times28$ NumPy arrays (i.e., the x variables), with pixel values ranging between 0 and 255. The *labels* (i.e., y variable) are an array of integers, ranging from 0 to 9. We will use *one-hot encoding* (the technique we learned about in the logistic regression lesson) to convert these labels to vectors (i.e., arrays with mostly 0s and a 1 at the index that corresponds to the data sample's digit category). We also need to *normalize* the input images by subtracting the mean and standard deviation of the pixels. Normalizing the data encourages our model to learn more generalizable features and helps it perform better on outside data. The final data processing step is "flattening" the $28\times28$ image pixel matrices into $784 \times 1$ arrays. We reshape the image matrices into arrays because our model expects the input to be a tensor with $784$ features.
Now, let's load the data!
```
# Model / data parameters
num_classes = 10
input_shape = (-1, 28*28) # this will be used to reshape the 28x28 image pixel matrices into 784 pixel vectors
# the data, split between train and test sets
(train_images, train_labels), (test_images, test_labels) = keras.datasets.mnist.load_data()
# Normalize train/test images
train_images = train_images.astype("float32")
test_images = test_images.astype("float32")
mean = train_images.mean()
std = train_images.std()
train_images -= mean
train_images /= std
test_images -= mean
test_images /= std
print(f'normalized images mean and std pixel values: {round(train_images.mean(), 4)}, {round(train_images.std(), 4)}')
# Flatten the images.
train_images = train_images.reshape(input_shape)
test_images = test_images.reshape(input_shape)
print("train_images shape:", train_images.shape)
print(train_images.shape[0], "train samples")
print(test_images.shape[0], "test samples")
# convert class vectors to binary class matrices (i.e., "one-hot encode" the y labels)
train_labels = keras.utils.to_categorical(train_labels, num_classes)
test_labels = keras.utils.to_categorical(test_labels, num_classes)
```
Let's display the first 5 images from the *training set* and display the class name below each image.
```
plt.figure(figsize=(10,2))
for i in range(5):
plt.subplot(1,5,i+1)
plt.xticks([])
plt.yticks([])
plt.grid(False)
plt.imshow(train_images[i].reshape(28, 28), cmap=plt.cm.binary)
plt.xlabel(np.argmax(train_labels[i]))
```
#### Step 2: Building the Model
Remember that the secret sauce of neural networks is *stacking layers*? In code, we take advantage of this secret sauce by constructing several layers and combining them to create a neural network model. Building the model is a two step process that involves 1) stacking layers together using `keras.Sequential`, 2) configuring the loss function, optimizer, and metrics to monitor the model using the keras `compile` method. Loss functions, optimizers, and metrics aren't formally discussed in this lesson. Don't worry too much about them for now. They will be described in detail in a future lesson. The goal of this lesson is to introduce the underlying structure of neural networks, and demonstrate how to build/train/test one in Python. Nonetheless, a quick summary about loss functions, optimizers, and metrics can't hurt:
* **Loss function** - measures how accurate the model is during training, we want to minimize the value this function returns using an optimization method.
* **Optimizer** - defines the optimization method to use to update the model's weights based on the data it sees and its loss function.
* **Metrics** - monitors the model using a set of user-defined metrics; metrics are calculated at the end of every train and test cycle.
**Building the Model - Step 1: Stacking Layers with `keras.Sequential`**
The [3Blue1Brown video](https://www.youtube.com/watch?v=aircAruvnKk&t=436s) used a feed forward neural network with 2 hidden layers to classify handwritten digits. To recreate this neural network, first we need to build a model that 1) takes 784 image pixel feature vectors as input, 2) has 2 hidden layers with 16 neurons and the sigmoid activation function, and 3) includes a final layer with 10 neurons (i.e., there are 10 digit classes so we need 10 neurons) and the *softmax* activation function. The softmax activation function normalizes the activations for the output neurons such that:
- every activation is between 0 and 1
- the sum of all activations is 1
Notice that the softmax activation is similar to the sigmoid activation--neuron activations are squeezed between 0 and 1. Softmax differs from sigmoid by constraining the sum of all activations to 1. For multi-class classification problems, where multiple categories/classes are present in the y variable, it is common to use the softmax activation (or a varient) in the final layer. This is because the softmax activation enables us to treat the final neuron activations as confidence values (i.e., probabilities). The neuron with the largest activation is selected as the category/class prediction.
Let's see what this looks like in Python code.
```
# step 1: stack model layers using keras.Sequential
model = keras.Sequential([
Input(shape=input_shape[1]), # each input is a 784 feature pixel vector
Dense(16, activation="relu"), # hidden layer 1
Dense(16, activation='relu'), # hidden layer 2
Dense(num_classes, activation="softmax"), # final output layer
])
# print the model summary to see its structure and the number of parameters (i.e., weights and biases)
print(model.summary())
```
**Building the Model - Step 2: Configuring the Loss Function, Optimizer, & Metrics with the Keras `compile` Method**
The model structure is defined in step 1, so most of the building process is finished. But, we still need to configure the model's loss function, optimizer, and metrics using the keras `compile` method. We will use binary cross entropy (BCE) for the loss function, the Adam optimization method, and monitor accuracy, precision, and recall of the model.
```
# step 2: configure the loss function, optimizer, and model metrics
model.compile(loss="categorical_crossentropy", # BCE loss
optimizer="adam", # Adam optimization
metrics=["accuracy", keras.metrics.Precision(), keras.metrics.Recall()] # monitor metrics
)
```
Now, we can train the model!
#### Step 3: Training the Model
Training the neural network model requires the following steps:
1. Feed the training data to the model—in this example, the `train_images` and `train_labels` arrays.
2. The model learns to associate images and labels.
3. We ask the model to make predictions on a test set—in this example, the `test_images` array. We verify that the predictions match the labels from the `test_labels` array.
We call the `model.fit` method to train the model—the model is "fit" to the training data:
```
# fit the model to the data; train for 20 epochs, use batch size 128, and 10% of the training data
# for validation to model performance during training, and configure the early stopping callback
batch_size = 128
epochs = 20
history = model.fit(train_images,
train_labels,
batch_size=batch_size,
epochs=epochs,
validation_split=0.1)
```
**Challenge:** As the model is trained, the loss and metrics are displayed. What is the final precision score on the training data?
Now that we finished training, let's view the results. We'll use the Pandas library to store the training history in a dataframe.
```
# store the training history in a dataframe
hist = pd.DataFrame(history.history)
hist['epoch'] = history.epoch
# see what the hist dataframe looks like
hist
```
Now, let's plot the loss function measure on the training and validation sets. The validation set is used to prevent overfitting ([learn more about it here](https://www.tensorflow.org/tutorials/keras/overfit_and_underfit)). However, because our network is small, the training converges (i.e., reaches an optimal loss value) without noticeably overfitting the data as the plot shows.
```
def plot_loss():
plt.figure()
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.plot(hist['epoch'], hist['loss'], label='Train Error')
plt.plot(hist['epoch'], hist['val_loss'], label = 'Val Error')
plt.legend()
plt.ylim([0,max(hist['loss'].max()+0.2, hist['val_loss'].max()+0.2)])
plot_loss()
```
Now, let's plot accuracy metric on the training and validation set. Similar to the loss metric, we expect the validation accuracy to be a bit lower than the training accuracy. If the validation accuracy is noticeably different than the training one, we might want to do some more analysis. When the validation accuracy is much lower than the training accuracy, the model could be overfitting. When the it is much higher than the training accuracy, the model could be underfitting (this happens less often). However, the plot suggests the model is not overfitting/underfitting the data.
```
def plot_accuracy():
plt.figure()
plt.xlabel('Epoch')
plt.ylabel('Accuracy')
plt.plot(hist['epoch'], hist['accuracy'], label='Train Accuracy')
plt.plot(hist['epoch'], hist['val_accuracy'], label = 'Val Accuracy')
plt.legend()
plt.ylim([0,1])
plot_accuracy()
```
#### Step 4: Testing the Model
Our results on the training and validation data look promising, but we want to know whether our model performs well on unknown data. For this, we compare how the model performs on the test dataset:
```
print(test_images.shape)
test_loss, test_acc, test_prec, test_rec = model.evaluate(test_images, test_labels)
print('Test accuracy:', test_acc)
```
Let's take a look at a few sample that the network classified incorrectly.
```
predictions = np.argmax(model.predict(test_images, batch_size=32), axis=-1)
is_correct = predictions == np.argmax(test_labels, axis=-1)
misclassified_indices = np.argwhere(is_correct == False)
def plot_misclassified(imgs, labels, preds, misclassified_indices, n=5):
plt.figure(figsize=(10,3))
for i, idx in enumerate(misclassified_indices[:n]):
plt.subplot(1, n, i+1)
plt.xticks([])
plt.yticks([])
plt.imshow(imgs[idx].reshape(28, 28), cmap=plt.cm.binary)
plt.xlabel(f'True: {np.argmax(labels[idx])}, Pred: {preds[idx][0]}')
plot_misclassified(test_images, test_labels, predictions, misclassified_indices)
```
We can see that some of these digits are hard to recognize, even for a human!
Often times, the accuracy on the test dataset is a little less than the accuracy on the training dataset. Small differences are ok, but we don't want the test results to differ significantly from the training results--this suggests the model is overfitting/underfitting.
**Challenge:** Do you think the difference between the training accuracy and the testing accuracy is significant? Is the model overfitting? Is it underfitting? Are the misclassify images justifiably misclassified (i.e., does it make sense that the model misclassified them)?
## Recap
You made it! We covered a lot of material in this lesson. Don't worry if it doesn't all make sense yet. The concepts will become more intuitive as you practice building, training, and testing your own neural network models.
Let's summarize what we learned about neural networks:
- Neural Networks are popular and successful machine learning models that can learn effective representations from data (i.e., images, text, sound). They can and *classification* tasks (see [Part 2](#-Part-2:-Classification-of-MNIST-Digits-with-Convolutional-Neural-Networks)), and also to generate images, text, videos, and sound.
- Special libraries like Tensorflow and Pytorch enable us to build neural networks in Python and train them on accelerated hardware like GPUs and TPUs.
- Several steps are involved in making an effective neural network:
1. Loading the dataset
2. Building the model--stacking several layers and configuring the loss function, optimizer, and metrics.
3. Training the model--fitting the model on the training data.
4. Evaluating/Testing the model--evaluating the model on the testing data.
- Once a model is trained, it can be used to make predictions on outside data (see [Part 2, Step 5](#-Step-5:-Make-predictions-on-outside-data)).
#### Acknowlegements
- [MIT Deep Learning Basics](https://www.youtube.com/watch?v=O5xeyoRL95U&list=PLrAXtmErZgOeiKm4sgNOknGvNjby9efdf)
- [Dive into Deep Learning](https://d2l.ai/index.html)
```
```
|
github_jupyter
|
# Building your Deep Neural Network: Step by Step
Welcome to your week 4 assignment (part 1 of 2)! You have previously trained a 2-layer Neural Network (with a single hidden layer). This week, you will build a deep neural network, with as many layers as you want!
- In this notebook, you will implement all the functions required to build a deep neural network.
- In the next assignment, you will use these functions to build a deep neural network for image classification.
**After this assignment you will be able to:**
- Use non-linear units like ReLU to improve your model
- Build a deeper neural network (with more than 1 hidden layer)
- Implement an easy-to-use neural network class
**Notation**:
- Superscript $[l]$ denotes a quantity associated with the $l^{th}$ layer.
- Example: $a^{[L]}$ is the $L^{th}$ layer activation. $W^{[L]}$ and $b^{[L]}$ are the $L^{th}$ layer parameters.
- Superscript $(i)$ denotes a quantity associated with the $i^{th}$ example.
- Example: $x^{(i)}$ is the $i^{th}$ training example.
- Lowerscript $i$ denotes the $i^{th}$ entry of a vector.
- Example: $a^{[l]}_i$ denotes the $i^{th}$ entry of the $l^{th}$ layer's activations).
Let's get started!
### <font color='darkblue'> Updates to Assignment <font>
#### If you were working on a previous version
* The current notebook filename is version "4a".
* You can find your work in the file directory as version "4".
* To see the file directory, click on the Coursera logo at the top left of the notebook.
#### List of Updates
* compute_cost unit test now includes tests for Y = 0 as well as Y = 1. This catches a possible bug before students get graded.
* linear_backward unit test now has a more complete unit test that catches a possible bug before students get graded.
## 1 - Packages
Let's first import all the packages that you will need during this assignment.
- [numpy](www.numpy.org) is the main package for scientific computing with Python.
- [matplotlib](http://matplotlib.org) is a library to plot graphs in Python.
- dnn_utils provides some necessary functions for this notebook.
- testCases provides some test cases to assess the correctness of your functions
- np.random.seed(1) is used to keep all the random function calls consistent. It will help us grade your work. Please don't change the seed.
```
import numpy as np
import h5py
import matplotlib.pyplot as plt
from testCases_v4a import *
from dnn_utils_v2 import sigmoid, sigmoid_backward, relu, relu_backward
%matplotlib inline
plt.rcParams['figure.figsize'] = (5.0, 4.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'
%load_ext autoreload
%autoreload 2
np.random.seed(1)
```
## 2 - Outline of the Assignment
To build your neural network, you will be implementing several "helper functions". These helper functions will be used in the next assignment to build a two-layer neural network and an L-layer neural network. Each small helper function you will implement will have detailed instructions that will walk you through the necessary steps. Here is an outline of this assignment, you will:
- Initialize the parameters for a two-layer network and for an $L$-layer neural network.
- Implement the forward propagation module (shown in purple in the figure below).
- Complete the LINEAR part of a layer's forward propagation step (resulting in $Z^{[l]}$).
- We give you the ACTIVATION function (relu/sigmoid).
- Combine the previous two steps into a new [LINEAR->ACTIVATION] forward function.
- Stack the [LINEAR->RELU] forward function L-1 time (for layers 1 through L-1) and add a [LINEAR->SIGMOID] at the end (for the final layer $L$). This gives you a new L_model_forward function.
- Compute the loss.
- Implement the backward propagation module (denoted in red in the figure below).
- Complete the LINEAR part of a layer's backward propagation step.
- We give you the gradient of the ACTIVATE function (relu_backward/sigmoid_backward)
- Combine the previous two steps into a new [LINEAR->ACTIVATION] backward function.
- Stack [LINEAR->RELU] backward L-1 times and add [LINEAR->SIGMOID] backward in a new L_model_backward function
- Finally update the parameters.
<img src="images/final outline.png" style="width:800px;height:500px;">
<caption><center> **Figure 1**</center></caption><br>
**Note** that for every forward function, there is a corresponding backward function. That is why at every step of your forward module you will be storing some values in a cache. The cached values are useful for computing gradients. In the backpropagation module you will then use the cache to calculate the gradients. This assignment will show you exactly how to carry out each of these steps.
## 3 - Initialization
You will write two helper functions that will initialize the parameters for your model. The first function will be used to initialize parameters for a two layer model. The second one will generalize this initialization process to $L$ layers.
### 3.1 - 2-layer Neural Network
**Exercise**: Create and initialize the parameters of the 2-layer neural network.
**Instructions**:
- The model's structure is: *LINEAR -> RELU -> LINEAR -> SIGMOID*.
- Use random initialization for the weight matrices. Use `np.random.randn(shape)*0.01` with the correct shape.
- Use zero initialization for the biases. Use `np.zeros(shape)`.
```
# GRADED FUNCTION: initialize_parameters
def initialize_parameters(n_x, n_h, n_y):
"""
Argument:
n_x -- size of the input layer
n_h -- size of the hidden layer
n_y -- size of the output layer
Returns:
parameters -- python dictionary containing your parameters:
W1 -- weight matrix of shape (n_h, n_x)
b1 -- bias vector of shape (n_h, 1)
W2 -- weight matrix of shape (n_y, n_h)
b2 -- bias vector of shape (n_y, 1)
"""
np.random.seed(1)
### START CODE HERE ### (≈ 4 lines of code)
W1 = np.random.randn(n_h,n_x) * 0.01
b1 = np.zeros(shape=(n_h,1))
W2 = np.random.randn(n_y,n_h) * 0.01
b2 = np.zeros(shape=(n_y,1))
### END CODE HERE ###
assert(W1.shape == (n_h, n_x))
assert(b1.shape == (n_h, 1))
assert(W2.shape == (n_y, n_h))
assert(b2.shape == (n_y, 1))
parameters = {"W1": W1,
"b1": b1,
"W2": W2,
"b2": b2}
return parameters
parameters = initialize_parameters(3,2,1)
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))
```
**Expected output**:
<table style="width:80%">
<tr>
<td> **W1** </td>
<td> [[ 0.01624345 -0.00611756 -0.00528172]
[-0.01072969 0.00865408 -0.02301539]] </td>
</tr>
<tr>
<td> **b1**</td>
<td>[[ 0.]
[ 0.]]</td>
</tr>
<tr>
<td>**W2**</td>
<td> [[ 0.01744812 -0.00761207]]</td>
</tr>
<tr>
<td> **b2** </td>
<td> [[ 0.]] </td>
</tr>
</table>
### 3.2 - L-layer Neural Network
The initialization for a deeper L-layer neural network is more complicated because there are many more weight matrices and bias vectors. When completing the `initialize_parameters_deep`, you should make sure that your dimensions match between each layer. Recall that $n^{[l]}$ is the number of units in layer $l$. Thus for example if the size of our input $X$ is $(12288, 209)$ (with $m=209$ examples) then:
<table style="width:100%">
<tr>
<td> </td>
<td> **Shape of W** </td>
<td> **Shape of b** </td>
<td> **Activation** </td>
<td> **Shape of Activation** </td>
<tr>
<tr>
<td> **Layer 1** </td>
<td> $(n^{[1]},12288)$ </td>
<td> $(n^{[1]},1)$ </td>
<td> $Z^{[1]} = W^{[1]} X + b^{[1]} $ </td>
<td> $(n^{[1]},209)$ </td>
<tr>
<tr>
<td> **Layer 2** </td>
<td> $(n^{[2]}, n^{[1]})$ </td>
<td> $(n^{[2]},1)$ </td>
<td>$Z^{[2]} = W^{[2]} A^{[1]} + b^{[2]}$ </td>
<td> $(n^{[2]}, 209)$ </td>
<tr>
<tr>
<td> $\vdots$ </td>
<td> $\vdots$ </td>
<td> $\vdots$ </td>
<td> $\vdots$</td>
<td> $\vdots$ </td>
<tr>
<tr>
<td> **Layer L-1** </td>
<td> $(n^{[L-1]}, n^{[L-2]})$ </td>
<td> $(n^{[L-1]}, 1)$ </td>
<td>$Z^{[L-1]} = W^{[L-1]} A^{[L-2]} + b^{[L-1]}$ </td>
<td> $(n^{[L-1]}, 209)$ </td>
<tr>
<tr>
<td> **Layer L** </td>
<td> $(n^{[L]}, n^{[L-1]})$ </td>
<td> $(n^{[L]}, 1)$ </td>
<td> $Z^{[L]} = W^{[L]} A^{[L-1]} + b^{[L]}$</td>
<td> $(n^{[L]}, 209)$ </td>
<tr>
</table>
Remember that when we compute $W X + b$ in python, it carries out broadcasting. For example, if:
$$ W = \begin{bmatrix}
j & k & l\\
m & n & o \\
p & q & r
\end{bmatrix}\;\;\; X = \begin{bmatrix}
a & b & c\\
d & e & f \\
g & h & i
\end{bmatrix} \;\;\; b =\begin{bmatrix}
s \\
t \\
u
\end{bmatrix}\tag{2}$$
Then $WX + b$ will be:
$$ WX + b = \begin{bmatrix}
(ja + kd + lg) + s & (jb + ke + lh) + s & (jc + kf + li)+ s\\
(ma + nd + og) + t & (mb + ne + oh) + t & (mc + nf + oi) + t\\
(pa + qd + rg) + u & (pb + qe + rh) + u & (pc + qf + ri)+ u
\end{bmatrix}\tag{3} $$
**Exercise**: Implement initialization for an L-layer Neural Network.
**Instructions**:
- The model's structure is *[LINEAR -> RELU] $ \times$ (L-1) -> LINEAR -> SIGMOID*. I.e., it has $L-1$ layers using a ReLU activation function followed by an output layer with a sigmoid activation function.
- Use random initialization for the weight matrices. Use `np.random.randn(shape) * 0.01`.
- Use zeros initialization for the biases. Use `np.zeros(shape)`.
- We will store $n^{[l]}$, the number of units in different layers, in a variable `layer_dims`. For example, the `layer_dims` for the "Planar Data classification model" from last week would have been [2,4,1]: There were two inputs, one hidden layer with 4 hidden units, and an output layer with 1 output unit. This means `W1`'s shape was (4,2), `b1` was (4,1), `W2` was (1,4) and `b2` was (1,1). Now you will generalize this to $L$ layers!
- Here is the implementation for $L=1$ (one layer neural network). It should inspire you to implement the general case (L-layer neural network).
```python
if L == 1:
parameters["W" + str(L)] = np.random.randn(layer_dims[1], layer_dims[0]) * 0.01
parameters["b" + str(L)] = np.zeros((layer_dims[1], 1))
```
```
# GRADED FUNCTION: initialize_parameters_deep
def initialize_parameters_deep(layer_dims):
"""
Arguments:
layer_dims -- python array (list) containing the dimensions of each layer in our network
Returns:
parameters -- python dictionary containing your parameters "W1", "b1", ..., "WL", "bL":
Wl -- weight matrix of shape (layer_dims[l], layer_dims[l-1])
bl -- bias vector of shape (layer_dims[l], 1)
"""
np.random.seed(3)
parameters = {}
L = len(layer_dims) # number of layers in the network
for l in range(1, L):
### START CODE HERE ### (≈ 2 lines of code)
parameters['W' + str(l)] = np.random.randn(layer_dims[l],layer_dims[l-1]) * 0.01
parameters['b' + str(l)] = np.zeros((layer_dims[l],1))
### END CODE HERE ###
assert(parameters['W' + str(l)].shape == (layer_dims[l], layer_dims[l-1]))
assert(parameters['b' + str(l)].shape == (layer_dims[l], 1))
return parameters
parameters = initialize_parameters_deep([5,4,3])
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))
```
**Expected output**:
<table style="width:80%">
<tr>
<td> **W1** </td>
<td>[[ 0.01788628 0.0043651 0.00096497 -0.01863493 -0.00277388]
[-0.00354759 -0.00082741 -0.00627001 -0.00043818 -0.00477218]
[-0.01313865 0.00884622 0.00881318 0.01709573 0.00050034]
[-0.00404677 -0.0054536 -0.01546477 0.00982367 -0.01101068]]</td>
</tr>
<tr>
<td>**b1** </td>
<td>[[ 0.]
[ 0.]
[ 0.]
[ 0.]]</td>
</tr>
<tr>
<td>**W2** </td>
<td>[[-0.01185047 -0.0020565 0.01486148 0.00236716]
[-0.01023785 -0.00712993 0.00625245 -0.00160513]
[-0.00768836 -0.00230031 0.00745056 0.01976111]]</td>
</tr>
<tr>
<td>**b2** </td>
<td>[[ 0.]
[ 0.]
[ 0.]]</td>
</tr>
</table>
## 4 - Forward propagation module
### 4.1 - Linear Forward
Now that you have initialized your parameters, you will do the forward propagation module. You will start by implementing some basic functions that you will use later when implementing the model. You will complete three functions in this order:
- LINEAR
- LINEAR -> ACTIVATION where ACTIVATION will be either ReLU or Sigmoid.
- [LINEAR -> RELU] $\times$ (L-1) -> LINEAR -> SIGMOID (whole model)
The linear forward module (vectorized over all the examples) computes the following equations:
$$Z^{[l]} = W^{[l]}A^{[l-1]} +b^{[l]}\tag{4}$$
where $A^{[0]} = X$.
**Exercise**: Build the linear part of forward propagation.
**Reminder**:
The mathematical representation of this unit is $Z^{[l]} = W^{[l]}A^{[l-1]} +b^{[l]}$. You may also find `np.dot()` useful. If your dimensions don't match, printing `W.shape` may help.
```
# GRADED FUNCTION: linear_forward
def linear_forward(A, W, b):
"""
Implement the linear part of a layer's forward propagation.
Arguments:
A -- activations from previous layer (or input data): (size of previous layer, number of examples)
W -- weights matrix: numpy array of shape (size of current layer, size of previous layer)
b -- bias vector, numpy array of shape (size of the current layer, 1)
Returns:
Z -- the input of the activation function, also called pre-activation parameter
cache -- a python tuple containing "A", "W" and "b" ; stored for computing the backward pass efficiently
"""
### START CODE HERE ### (≈ 1 line of code)
Z = (np.dot(W,A) + b)
### END CODE HERE ###
assert(Z.shape == (W.shape[0], A.shape[1]))
cache = (A, W, b)
return Z, cache
A, W, b = linear_forward_test_case()
Z, linear_cache = linear_forward(A, W, b)
print("Z = " + str(Z))
```
**Expected output**:
<table style="width:35%">
<tr>
<td> **Z** </td>
<td> [[ 3.26295337 -1.23429987]] </td>
</tr>
</table>
### 4.2 - Linear-Activation Forward
In this notebook, you will use two activation functions:
- **Sigmoid**: $\sigma(Z) = \sigma(W A + b) = \frac{1}{ 1 + e^{-(W A + b)}}$. We have provided you with the `sigmoid` function. This function returns **two** items: the activation value "`a`" and a "`cache`" that contains "`Z`" (it's what we will feed in to the corresponding backward function). To use it you could just call:
``` python
A, activation_cache = sigmoid(Z)
```
- **ReLU**: The mathematical formula for ReLu is $A = RELU(Z) = max(0, Z)$. We have provided you with the `relu` function. This function returns **two** items: the activation value "`A`" and a "`cache`" that contains "`Z`" (it's what we will feed in to the corresponding backward function). To use it you could just call:
``` python
A, activation_cache = relu(Z)
```
For more convenience, you are going to group two functions (Linear and Activation) into one function (LINEAR->ACTIVATION). Hence, you will implement a function that does the LINEAR forward step followed by an ACTIVATION forward step.
**Exercise**: Implement the forward propagation of the *LINEAR->ACTIVATION* layer. Mathematical relation is: $A^{[l]} = g(Z^{[l]}) = g(W^{[l]}A^{[l-1]} +b^{[l]})$ where the activation "g" can be sigmoid() or relu(). Use linear_forward() and the correct activation function.
```
# GRADED FUNCTION: linear_activation_forward
def linear_activation_forward(A_prev, W, b, activation):
"""
Implement the forward propagation for the LINEAR->ACTIVATION layer
Arguments:
A_prev -- activations from previous layer (or input data): (size of previous layer, number of examples)
W -- weights matrix: numpy array of shape (size of current layer, size of previous layer)
b -- bias vector, numpy array of shape (size of the current layer, 1)
activation -- the activation to be used in this layer, stored as a text string: "sigmoid" or "relu"
Returns:
A -- the output of the activation function, also called the post-activation value
cache -- a python tuple containing "linear_cache" and "activation_cache";
stored for computing the backward pass efficiently
"""
if activation == "sigmoid":
# Inputs: "A_prev, W, b". Outputs: "A, activation_cache".
### START CODE HERE ### (≈ 2 lines of code)
Z, linear_cache = linear_forward(A_prev,W,b)
A, activation_cache = sigmoid(Z)
### END CODE HERE ###
elif activation == "relu":
# Inputs: "A_prev, W, b". Outputs: "A, activation_cache".
### START CODE HERE ### (≈ 2 lines of code)
Z, linear_cache = linear_forward(A_prev,W,b)
A, activation_cache = relu(Z)
### END CODE HERE ###
assert (A.shape == (W.shape[0], A_prev.shape[1]))
cache = (linear_cache, activation_cache)
return A, cache
A_prev, W, b = linear_activation_forward_test_case()
A, linear_activation_cache = linear_activation_forward(A_prev, W, b, activation = "sigmoid")
print("With sigmoid: A = " + str(A))
A, linear_activation_cache = linear_activation_forward(A_prev, W, b, activation = "relu")
print("With ReLU: A = " + str(A))
```
**Expected output**:
<table style="width:35%">
<tr>
<td> **With sigmoid: A ** </td>
<td > [[ 0.96890023 0.11013289]]</td>
</tr>
<tr>
<td> **With ReLU: A ** </td>
<td > [[ 3.43896131 0. ]]</td>
</tr>
</table>
**Note**: In deep learning, the "[LINEAR->ACTIVATION]" computation is counted as a single layer in the neural network, not two layers.
### d) L-Layer Model
For even more convenience when implementing the $L$-layer Neural Net, you will need a function that replicates the previous one (`linear_activation_forward` with RELU) $L-1$ times, then follows that with one `linear_activation_forward` with SIGMOID.
<img src="images/model_architecture_kiank.png" style="width:600px;height:300px;">
<caption><center> **Figure 2** : *[LINEAR -> RELU] $\times$ (L-1) -> LINEAR -> SIGMOID* model</center></caption><br>
**Exercise**: Implement the forward propagation of the above model.
**Instruction**: In the code below, the variable `AL` will denote $A^{[L]} = \sigma(Z^{[L]}) = \sigma(W^{[L]} A^{[L-1]} + b^{[L]})$. (This is sometimes also called `Yhat`, i.e., this is $\hat{Y}$.)
**Tips**:
- Use the functions you had previously written
- Use a for loop to replicate [LINEAR->RELU] (L-1) times
- Don't forget to keep track of the caches in the "caches" list. To add a new value `c` to a `list`, you can use `list.append(c)`.
```
# GRADED FUNCTION: L_model_forward
def L_model_forward(X, parameters):
"""
Implement forward propagation for the [LINEAR->RELU]*(L-1)->LINEAR->SIGMOID computation
Arguments:
X -- data, numpy array of shape (input size, number of examples)
parameters -- output of initialize_parameters_deep()
Returns:
AL -- last post-activation value
caches -- list of caches containing:
every cache of linear_activation_forward() (there are L-1 of them, indexed from 0 to L-1)
"""
caches = []
A = X
L = len(parameters) // 2 # number of layers in the neural network
# Implement [LINEAR -> RELU]*(L-1). Add "cache" to the "caches" list.
for l in range(1, L):
A_prev = A
### START CODE HERE ### (≈ 2 lines of code)
A, cache = linear_activation_forward(A_prev,
parameters['W' + str(l)],
parameters['b' + str(l)],
activation='relu')
caches.append(cache)
### END CODE HERE ###
# Implement LINEAR -> SIGMOID. Add "cache" to the "caches" list.
### START CODE HERE ### (≈ 2 lines of code)
AL, cache = linear_activation_forward(A,
parameters['W' + str(L)],
parameters['b' + str(L)],
activation='sigmoid')
caches.append(cache)
### END CODE HERE ###
assert(AL.shape == (1,X.shape[1]))
return AL, caches
X, parameters = L_model_forward_test_case_2hidden()
AL, caches = L_model_forward(X, parameters)
print("AL = " + str(AL))
print("Length of caches list = " + str(len(caches)))
```
<table style="width:50%">
<tr>
<td> **AL** </td>
<td > [[ 0.03921668 0.70498921 0.19734387 0.04728177]]</td>
</tr>
<tr>
<td> **Length of caches list ** </td>
<td > 3 </td>
</tr>
</table>
Great! Now you have a full forward propagation that takes the input X and outputs a row vector $A^{[L]}$ containing your predictions. It also records all intermediate values in "caches". Using $A^{[L]}$, you can compute the cost of your predictions.
## 5 - Cost function
Now you will implement forward and backward propagation. You need to compute the cost, because you want to check if your model is actually learning.
**Exercise**: Compute the cross-entropy cost $J$, using the following formula: $$-\frac{1}{m} \sum\limits_{i = 1}^{m} (y^{(i)}\log\left(a^{[L] (i)}\right) + (1-y^{(i)})\log\left(1- a^{[L](i)}\right)) \tag{7}$$
```
# GRADED FUNCTION: compute_cost
def compute_cost(AL, Y):
"""
Implement the cost function defined by equation (7).
Arguments:
AL -- probability vector corresponding to your label predictions, shape (1, number of examples)
Y -- true "label" vector (for example: containing 0 if non-cat, 1 if cat), shape (1, number of examples)
Returns:
cost -- cross-entropy cost
"""
m = Y.shape[1]
# Compute loss from aL and y.
### START CODE HERE ### (≈ 1 lines of code)
cost = -(1/m) * (np.sum(np.multiply(Y,np.log(AL)) + np.multiply((1 - Y),np.log(1 - AL))))
### END CODE HERE ###
cost = np.squeeze(cost) # To make sure your cost's shape is what we expect (e.g. this turns [[17]] into 17).
assert(cost.shape == ())
return cost
Y, AL = compute_cost_test_case()
print("cost = " + str(compute_cost(AL, Y)))
```
**Expected Output**:
<table>
<tr>
<td>**cost** </td>
<td> 0.2797765635793422</td>
</tr>
</table>
## 6 - Backward propagation module
Just like with forward propagation, you will implement helper functions for backpropagation. Remember that back propagation is used to calculate the gradient of the loss function with respect to the parameters.
**Reminder**:
<img src="images/backprop_kiank.png" style="width:650px;height:250px;">
<caption><center> **Figure 3** : Forward and Backward propagation for *LINEAR->RELU->LINEAR->SIGMOID* <br> *The purple blocks represent the forward propagation, and the red blocks represent the backward propagation.* </center></caption>
<!--
For those of you who are expert in calculus (you don't need to be to do this assignment), the chain rule of calculus can be used to derive the derivative of the loss $\mathcal{L}$ with respect to $z^{[1]}$ in a 2-layer network as follows:
$$\frac{d \mathcal{L}(a^{[2]},y)}{{dz^{[1]}}} = \frac{d\mathcal{L}(a^{[2]},y)}{{da^{[2]}}}\frac{{da^{[2]}}}{{dz^{[2]}}}\frac{{dz^{[2]}}}{{da^{[1]}}}\frac{{da^{[1]}}}{{dz^{[1]}}} \tag{8} $$
In order to calculate the gradient $dW^{[1]} = \frac{\partial L}{\partial W^{[1]}}$, you use the previous chain rule and you do $dW^{[1]} = dz^{[1]} \times \frac{\partial z^{[1]} }{\partial W^{[1]}}$. During the backpropagation, at each step you multiply your current gradient by the gradient corresponding to the specific layer to get the gradient you wanted.
Equivalently, in order to calculate the gradient $db^{[1]} = \frac{\partial L}{\partial b^{[1]}}$, you use the previous chain rule and you do $db^{[1]} = dz^{[1]} \times \frac{\partial z^{[1]} }{\partial b^{[1]}}$.
This is why we talk about **backpropagation**.
!-->
Now, similar to forward propagation, you are going to build the backward propagation in three steps:
- LINEAR backward
- LINEAR -> ACTIVATION backward where ACTIVATION computes the derivative of either the ReLU or sigmoid activation
- [LINEAR -> RELU] $\times$ (L-1) -> LINEAR -> SIGMOID backward (whole model)
### 6.1 - Linear backward
For layer $l$, the linear part is: $Z^{[l]} = W^{[l]} A^{[l-1]} + b^{[l]}$ (followed by an activation).
Suppose you have already calculated the derivative $dZ^{[l]} = \frac{\partial \mathcal{L} }{\partial Z^{[l]}}$. You want to get $(dW^{[l]}, db^{[l]}, dA^{[l-1]})$.
<img src="images/linearback_kiank.png" style="width:250px;height:300px;">
<caption><center> **Figure 4** </center></caption>
The three outputs $(dW^{[l]}, db^{[l]}, dA^{[l-1]})$ are computed using the input $dZ^{[l]}$.Here are the formulas you need:
$$ dW^{[l]} = \frac{\partial \mathcal{J} }{\partial W^{[l]}} = \frac{1}{m} dZ^{[l]} A^{[l-1] T} \tag{8}$$
$$ db^{[l]} = \frac{\partial \mathcal{J} }{\partial b^{[l]}} = \frac{1}{m} \sum_{i = 1}^{m} dZ^{[l](i)}\tag{9}$$
$$ dA^{[l-1]} = \frac{\partial \mathcal{L} }{\partial A^{[l-1]}} = W^{[l] T} dZ^{[l]} \tag{10}$$
**Exercise**: Use the 3 formulas above to implement linear_backward().
```
# GRADED FUNCTION: linear_backward
def linear_backward(dZ, cache):
"""
Implement the linear portion of backward propagation for a single layer (layer l)
Arguments:
dZ -- Gradient of the cost with respect to the linear output (of current layer l)
cache -- tuple of values (A_prev, W, b) coming from the forward propagation in the current layer
Returns:
dA_prev -- Gradient of the cost with respect to the activation (of the previous layer l-1), same shape as A_prev
dW -- Gradient of the cost with respect to W (current layer l), same shape as W
db -- Gradient of the cost with respect to b (current layer l), same shape as b
"""
A_prev, W, b = cache
m = A_prev.shape[1]
### START CODE HERE ### (≈ 3 lines of code)
dW = 1/m * (np.dot(dZ,A_prev.T))
db = 1/m * (np.sum(dZ,axis = 1,keepdims = True))
dA_prev = np.dot(W.T,dZ)
### END CODE HERE ###
assert (dA_prev.shape == A_prev.shape)
assert (dW.shape == W.shape)
assert (db.shape == b.shape)
return dA_prev, dW, db
# Set up some test inputs
dZ, linear_cache = linear_backward_test_case()
dA_prev, dW, db = linear_backward(dZ, linear_cache)
print ("dA_prev = "+ str(dA_prev))
print ("dW = " + str(dW))
print ("db = " + str(db))
```
** Expected Output**:
```
dA_prev =
[[-1.15171336 0.06718465 -0.3204696 2.09812712]
[ 0.60345879 -3.72508701 5.81700741 -3.84326836]
[-0.4319552 -1.30987417 1.72354705 0.05070578]
[-0.38981415 0.60811244 -1.25938424 1.47191593]
[-2.52214926 2.67882552 -0.67947465 1.48119548]]
dW =
[[ 0.07313866 -0.0976715 -0.87585828 0.73763362 0.00785716]
[ 0.85508818 0.37530413 -0.59912655 0.71278189 -0.58931808]
[ 0.97913304 -0.24376494 -0.08839671 0.55151192 -0.10290907]]
db =
[[-0.14713786]
[-0.11313155]
[-0.13209101]]
```
### 6.2 - Linear-Activation backward
Next, you will create a function that merges the two helper functions: **`linear_backward`** and the backward step for the activation **`linear_activation_backward`**.
To help you implement `linear_activation_backward`, we provided two backward functions:
- **`sigmoid_backward`**: Implements the backward propagation for SIGMOID unit. You can call it as follows:
```python
dZ = sigmoid_backward(dA, activation_cache)
```
- **`relu_backward`**: Implements the backward propagation for RELU unit. You can call it as follows:
```python
dZ = relu_backward(dA, activation_cache)
```
If $g(.)$ is the activation function,
`sigmoid_backward` and `relu_backward` compute $$dZ^{[l]} = dA^{[l]} * g'(Z^{[l]}) \tag{11}$$.
**Exercise**: Implement the backpropagation for the *LINEAR->ACTIVATION* layer.
```
# GRADED FUNCTION: linear_activation_backward
def linear_activation_backward(dA, cache, activation):
"""
Implement the backward propagation for the LINEAR->ACTIVATION layer.
Arguments:
dA -- post-activation gradient for current layer l
cache -- tuple of values (linear_cache, activation_cache) we store for computing backward propagation efficiently
activation -- the activation to be used in this layer, stored as a text string: "sigmoid" or "relu"
Returns:
dA_prev -- Gradient of the cost with respect to the activation (of the previous layer l-1), same shape as A_prev
dW -- Gradient of the cost with respect to W (current layer l), same shape as W
db -- Gradient of the cost with respect to b (current layer l), same shape as b
"""
linear_cache, activation_cache = cache
if activation == "relu":
### START CODE HERE ### (≈ 2 lines of code)
dZ = relu_backward(dA,activation_cache)
dA_prev, dW, db = linear_backward(dZ,linear_cache)
### END CODE HERE ###
elif activation == "sigmoid":
### START CODE HERE ### (≈ 2 lines of code)
dZ = sigmoid_backward(dA,activation_cache)
dA_prev, dW, db = linear_backward(dZ,linear_cache)
### END CODE HERE ###
return dA_prev, dW, db
dAL, linear_activation_cache = linear_activation_backward_test_case()
dA_prev, dW, db = linear_activation_backward(dAL, linear_activation_cache, activation = "sigmoid")
print ("sigmoid:")
print ("dA_prev = "+ str(dA_prev))
print ("dW = " + str(dW))
print ("db = " + str(db) + "\n")
dA_prev, dW, db = linear_activation_backward(dAL, linear_activation_cache, activation = "relu")
print ("relu:")
print ("dA_prev = "+ str(dA_prev))
print ("dW = " + str(dW))
print ("db = " + str(db))
```
**Expected output with sigmoid:**
<table style="width:100%">
<tr>
<td > dA_prev </td>
<td >[[ 0.11017994 0.01105339]
[ 0.09466817 0.00949723]
[-0.05743092 -0.00576154]] </td>
</tr>
<tr>
<td > dW </td>
<td > [[ 0.10266786 0.09778551 -0.01968084]] </td>
</tr>
<tr>
<td > db </td>
<td > [[-0.05729622]] </td>
</tr>
</table>
**Expected output with relu:**
<table style="width:100%">
<tr>
<td > dA_prev </td>
<td > [[ 0.44090989 0. ]
[ 0.37883606 0. ]
[-0.2298228 0. ]] </td>
</tr>
<tr>
<td > dW </td>
<td > [[ 0.44513824 0.37371418 -0.10478989]] </td>
</tr>
<tr>
<td > db </td>
<td > [[-0.20837892]] </td>
</tr>
</table>
### 6.3 - L-Model Backward
Now you will implement the backward function for the whole network. Recall that when you implemented the `L_model_forward` function, at each iteration, you stored a cache which contains (X,W,b, and z). In the back propagation module, you will use those variables to compute the gradients. Therefore, in the `L_model_backward` function, you will iterate through all the hidden layers backward, starting from layer $L$. On each step, you will use the cached values for layer $l$ to backpropagate through layer $l$. Figure 5 below shows the backward pass.
<img src="images/mn_backward.png" style="width:450px;height:300px;">
<caption><center> **Figure 5** : Backward pass </center></caption>
** Initializing backpropagation**:
To backpropagate through this network, we know that the output is,
$A^{[L]} = \sigma(Z^{[L]})$. Your code thus needs to compute `dAL` $= \frac{\partial \mathcal{L}}{\partial A^{[L]}}$.
To do so, use this formula (derived using calculus which you don't need in-depth knowledge of):
```python
dAL = - (np.divide(Y, AL) - np.divide(1 - Y, 1 - AL)) # derivative of cost with respect to AL
```
You can then use this post-activation gradient `dAL` to keep going backward. As seen in Figure 5, you can now feed in `dAL` into the LINEAR->SIGMOID backward function you implemented (which will use the cached values stored by the L_model_forward function). After that, you will have to use a `for` loop to iterate through all the other layers using the LINEAR->RELU backward function. You should store each dA, dW, and db in the grads dictionary. To do so, use this formula :
$$grads["dW" + str(l)] = dW^{[l]}\tag{15} $$
For example, for $l=3$ this would store $dW^{[l]}$ in `grads["dW3"]`.
**Exercise**: Implement backpropagation for the *[LINEAR->RELU] $\times$ (L-1) -> LINEAR -> SIGMOID* model.
```
# GRADED FUNCTION: L_model_backward
def L_model_backward(AL, Y, caches):
"""
Implement the backward propagation for the [LINEAR->RELU] * (L-1) -> LINEAR -> SIGMOID group
Arguments:
AL -- probability vector, output of the forward propagation (L_model_forward())
Y -- true "label" vector (containing 0 if non-cat, 1 if cat)
caches -- list of caches containing:
every cache of linear_activation_forward() with "relu" (it's caches[l], for l in range(L-1) i.e l = 0...L-2)
the cache of linear_activation_forward() with "sigmoid" (it's caches[L-1])
Returns:
grads -- A dictionary with the gradients
grads["dA" + str(l)] = ...
grads["dW" + str(l)] = ...
grads["db" + str(l)] = ...
"""
grads = {}
L = len(caches) # the number of layers
m = AL.shape[1]
Y = Y.reshape(AL.shape) # after this line, Y is the same shape as AL
# Initializing the backpropagation
### START CODE HERE ### (1 line of code)
dAL = - (np.divide(Y, AL) - np.divide(1 - Y, 1 - AL))
### END CODE HERE ###
# Lth layer (SIGMOID -> LINEAR) gradients. Inputs: "dAL, current_cache". Outputs: "grads["dAL-1"], grads["dWL"], grads["dbL"]
### START CODE HERE ### (approx. 2 lines)
current_cache = caches[L-1]
grads["dA" + str(L-1)], grads["dW" + str(L)], grads["db" + str(L)] = linear_activation_backward(dAL,current_cache,activation="sigmoid")
### END CODE HERE ###
# Loop from l=L-2 to l=0
for l in reversed(range(L-1)):
# lth layer: (RELU -> LINEAR) gradients.
# Inputs: "grads["dA" + str(l + 1)], current_cache". Outputs: "grads["dA" + str(l)] , grads["dW" + str(l + 1)] , grads["db" + str(l + 1)]
### START CODE HERE ### (approx. 5 lines)
current_cache = caches[l]
dA_prev_temp, dW_temp, db_temp = linear_activation_backward(grads["dA" + str(l+1)],current_cache,activation='relu')
grads["dA" + str(l)] = dA_prev_temp
grads["dW" + str(l + 1)] = dW_temp
grads["db" + str(l + 1)] = db_temp
### END CODE HERE ###
return grads
AL, Y_assess, caches = L_model_backward_test_case()
grads = L_model_backward(AL, Y_assess, caches)
print_grads(grads)
```
**Expected Output**
<table style="width:60%">
<tr>
<td > dW1 </td>
<td > [[ 0.41010002 0.07807203 0.13798444 0.10502167]
[ 0. 0. 0. 0. ]
[ 0.05283652 0.01005865 0.01777766 0.0135308 ]] </td>
</tr>
<tr>
<td > db1 </td>
<td > [[-0.22007063]
[ 0. ]
[-0.02835349]] </td>
</tr>
<tr>
<td > dA1 </td>
<td > [[ 0.12913162 -0.44014127]
[-0.14175655 0.48317296]
[ 0.01663708 -0.05670698]] </td>
</tr>
</table>
### 6.4 - Update Parameters
In this section you will update the parameters of the model, using gradient descent:
$$ W^{[l]} = W^{[l]} - \alpha \text{ } dW^{[l]} \tag{16}$$
$$ b^{[l]} = b^{[l]} - \alpha \text{ } db^{[l]} \tag{17}$$
where $\alpha$ is the learning rate. After computing the updated parameters, store them in the parameters dictionary.
**Exercise**: Implement `update_parameters()` to update your parameters using gradient descent.
**Instructions**:
Update parameters using gradient descent on every $W^{[l]}$ and $b^{[l]}$ for $l = 1, 2, ..., L$.
```
# GRADED FUNCTION: update_parameters
def update_parameters(parameters, grads, learning_rate):
"""
Update parameters using gradient descent
Arguments:
parameters -- python dictionary containing your parameters
grads -- python dictionary containing your gradients, output of L_model_backward
Returns:
parameters -- python dictionary containing your updated parameters
parameters["W" + str(l)] = ...
parameters["b" + str(l)] = ...
"""
L = len(parameters) // 2 # number of layers in the neural network
# Update rule for each parameter. Use a for loop.
### START CODE HERE ### (≈ 3 lines of code)
for l in range(L):
parameters["W" + str(l+1)] -= (learning_rate * grads["dW" + str(l+1)])
parameters["b" + str(l+1)] -= (learning_rate * grads["db" + str(l+1)])
### END CODE HERE ###
return parameters
parameters, grads = update_parameters_test_case()
parameters = update_parameters(parameters, grads, 0.1)
print ("W1 = "+ str(parameters["W1"]))
print ("b1 = "+ str(parameters["b1"]))
print ("W2 = "+ str(parameters["W2"]))
print ("b2 = "+ str(parameters["b2"]))
```
**Expected Output**:
<table style="width:100%">
<tr>
<td > W1 </td>
<td > [[-0.59562069 -0.09991781 -2.14584584 1.82662008]
[-1.76569676 -0.80627147 0.51115557 -1.18258802]
[-1.0535704 -0.86128581 0.68284052 2.20374577]] </td>
</tr>
<tr>
<td > b1 </td>
<td > [[-0.04659241]
[-1.28888275]
[ 0.53405496]] </td>
</tr>
<tr>
<td > W2 </td>
<td > [[-0.55569196 0.0354055 1.32964895]]</td>
</tr>
<tr>
<td > b2 </td>
<td > [[-0.84610769]] </td>
</tr>
</table>
## 7 - Conclusion
Congrats on implementing all the functions required for building a deep neural network!
We know it was a long assignment but going forward it will only get better. The next part of the assignment is easier.
In the next assignment you will put all these together to build two models:
- A two-layer neural network
- An L-layer neural network
You will in fact use these models to classify cat vs non-cat images!
|
github_jupyter
|
<img align="center" style="max-width: 1000px" src="banner.png">
<img align="right" style="max-width: 200px; height: auto" src="hsg_logo.png">
## Lab 02 - "Artificial Neural Networks"
Machine Learning, University of St. Gallen, Spring Term 2022
The lab environment of the "Coding and Artificial Intelligence" IEMBA course at the University of St. Gallen (HSG) is based on Jupyter Notebooks (https://jupyter.org), which allow to perform a variety of statistical evaluations and data analyses.
In this lab, we will learn how to implement, train, and apply our first **Artificial Neural Network (ANN)** using a Python library named `PyTorch`. The `PyTorch` library is an open-source machine learning library for Python, used for a variety of applications such as image classification and natural language processing. We will use the implemented neural network to learn to again classify images of fashion articles from the **Fashion-MNIST** dataset.
The figure below illustrates a high-level view of the machine learning process we aim to establish in this lab:
<img align="center" style="max-width: 700px" src="classification.png">
As always, pls. don't hesitate to ask all your questions either during the lab, post them in our CANVAS (StudyNet) forum (https://learning.unisg.ch), or send us an email (using the course email).
## 1. Lab Objectives:
After today's lab, you should be able to:
> 1. Understand the basic concepts, intuitions and major building blocks of **Artificial Neural Networks (ANNs)**.
> 2. Know how to use Python's **PyTorch library** to train and evaluate neural network based models.
> 3. Understand how to apply neural networks to **classify images** of handwritten digits.
> 4. Know how to **interpret the detection results** of the network as well as its **reconstruction loss**.
Before we start let's watch a motivational video:
```
from IPython.display import YouTubeVideo
# Official Intro | GTC 2017 | I AM AI"
# YouTubeVideo('SUNPrR4o5ZA', width=800, height=400)
```
## 2. Setup of the Jupyter Notebook Environment
Similar to the previous labs, we need to import a couple of Python libraries that allow for data analysis and data visualization. We will mostly use the `PyTorch`, `Numpy`, `Scikit-Learn`, `Matplotlib` and the `Seaborn` and a few utility libraries throughout this lab:
```
# import standard python libraries
import os, urllib, io
from datetime import datetime
import numpy as np
```
Import the Python machine / deep learning libraries:
```
# import the PyTorch deep learning libary
import torch, torchvision
import torch.nn.functional as F
from torch import nn, optim
```
Import the sklearn classification metrics:
```
# import sklearn classification evaluation library
from sklearn import metrics
from sklearn.metrics import classification_report, confusion_matrix
```
Import Python plotting libraries:
```
# import matplotlib, seaborn, and PIL data visualization libary
import matplotlib.pyplot as plt
import seaborn as sns
from PIL import Image
```
Enable notebook matplotlib inline plotting:
```
%matplotlib inline
```
Import `Google's GDrive` connector and mount your `GDrive` directories:
```
# import the Google Colab GDrive connector
from google.colab import drive
# mount GDrive inside the Colab notebook
drive.mount('/content/drive')
```
Create a structure of `Colab` Notebook sub-directories inside of `GDrive` to to store the data and the trained neural network models:
```
# create Colab Notebooks directory
notebook_directory = '/content/drive/MyDrive/Colab Notebooks'
if not os.path.exists(notebook_directory): os.makedirs(notebook_directory)
# create data sub-directory inside the Colab Notebooks directory
data_directory = '/content/drive/MyDrive/Colab Notebooks/data_fmnist'
if not os.path.exists(data_directory): os.makedirs(data_directory)
# create models sub-directory inside the Colab Notebooks directory
models_directory = '/content/drive/MyDrive/Colab Notebooks/models_fmnist'
if not os.path.exists(models_directory): os.makedirs(models_directory)
```
Set a random `seed` value to obtain reproducable results:
```
# init deterministic seed
seed_value = 1234
np.random.seed(seed_value) # set numpy seed
torch.manual_seed(seed_value) # set pytorch seed CPU
```
Google Colab provides the use of free GPUs for running notebooks. However, if you just execute this notebook as is, it will use your device's CPU. To run the lab on a GPU, got to `Runtime` > `Change runtime type` and set the Runtime type to `GPU` in the drop-down. Running this lab on a CPU is fine, but you will find that GPU computing is faster. *CUDA* indicates that the lab is being run on GPU.
Enable GPU computing by setting the device flag and init a CUDA seed:
```
# set cpu or gpu enabled device
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu').type
# init deterministic GPU seed
torch.cuda.manual_seed(seed_value)
# log type of device enabled
print('[LOG] notebook with {} computation enabled'.format(str(device)))
```
Let's determine if we have access to a GPU provided by e.g. `Google's Colab` environment:
```
!nvidia-smi
```
## 3. Dataset Download and Data Assessment
The **Fashion-MNIST database** is a large database of Zalando articles that is commonly used for training various image processing systems. The database is widely used for training and testing in the field of machine learning. Let's have a brief look into a couple of sample images contained in the dataset:
<img align="center" style="max-width: 700px; height: 300px" src="FashionMNIST.png">
Source: https://www.kaggle.com/c/insar-fashion-mnist-challenge
Further details on the dataset can be obtained via Zalando research's [github page](https://github.com/zalandoresearch/fashion-mnist).
The **Fashion-MNIST database** is an image dataset of Zalando's article images, consisting of in total 70,000 images.
The dataset is divided into a set of **60,000 training examples** and a set of **10,000 evaluation examples**. Each example is a **28x28 grayscale image**, associated with a **label from 10 classes**. Zalando created this dataset with the intention of providing a replacement for the popular **MNIST** handwritten digits dataset. It is a useful addition as it is a bit more complex, but still very easy to use. It shares the same image size and train/test split structure as MNIST, and can therefore be used as a drop-in replacement. It requires minimal efforts on preprocessing and formatting the distinct images.
Let's download, transform and inspect the training images of the dataset. Therefore, let's first define the directory in which we aim to store the training data:
```
train_path = data_directory + '/train_fmnist'
```
Now, let's download the training data accordingly:
```
# define pytorch transformation into tensor format
transf = torchvision.transforms.Compose([torchvision.transforms.ToTensor()])
# download and transform training images
fashion_mnist_train_data = torchvision.datasets.FashionMNIST(root=train_path, train=True, transform=transf, download=True)
```
Verify the number of training images downloaded:
```
# determine the number of training data images
len(fashion_mnist_train_data)
```
Furthermore, let's inspect a couple of the downloaded training images:
```
# select and set a (random) image id
image_id = 3000
# retrieve image exhibiting the image id
fashion_mnist_train_data[image_id]
```
Ok, that doesn't seem right :). Let's now seperate the image from its label information:
```
fashion_mnist_train_image, fashion_mnist_train_label = fashion_mnist_train_data[image_id]
```
We can verify the label that our selected image has:
```
fashion_mnist_train_label
```
Ok, we know that the numerical label is 6. Each image is associated with a label from 0 to 9, and this number represents one of the fashion items. So what does 6 mean? Is 6 a bag? A pullover? The order of the classes can be found on Zalando research's [github page](https://github.com/zalandoresearch/fashion-mnist). We need to map each numerical label to its fashion item, which will be useful throughout the lab:
```
fashion_classes = {0: 'T-shirt/top',
1: 'Trouser',
2: 'Pullover',
3: 'Dress',
4: 'Coat',
5: 'Sandal',
6: 'Shirt',
7: 'Sneaker',
8: 'Bag',
9: 'Ankle boot'}
```
So, we can determine the fashion item that the label represents:
```
fashion_classes[fashion_mnist_train_label]
```
Great, let's now visually inspect our sample image:
```
# define tensor to image transformation
trans = torchvision.transforms.ToPILImage()
# set image plot title
plt.title('Example: {}, Label: {}'.format(str(image_id), fashion_classes[fashion_mnist_train_label]))
# plot mnist handwritten digit sample
plt.imshow(trans(fashion_mnist_train_image), cmap='gray')
```
Fantastic, right? Let's now define the directory in which we aim to store the evaluation data:
```
eval_path = data_directory + '/eval_fmnist'
```
And download the evaluation data accordingly:
```
# define pytorch transformation into tensor format
transf = torchvision.transforms.Compose([torchvision.transforms.ToTensor()])
# download and transform training images
fashion_mnist_eval_data = torchvision.datasets.FashionMNIST(root=eval_path, train=False, transform=transf, download=True)
```
Let's also verify the number of evaluation images downloaded:
```
# determine the number of evaluation data images
len(fashion_mnist_eval_data)
```
## 4. Neural Network Implementation
In this section we, will implement the architecture of the **neural network** we aim to utilize to learn a model that is capable to classify the 28x28 pixel FashionMNIST images of fashion items. However, before we start the implementation let's briefly revisit the process to be established. The following cartoon provides a birds-eye view:
<img align="center" style="max-width: 1000px" src="https://github.com/HSG-AIML/LabGSERM/blob/main/lab_04/process.png?raw=1">
### 4.1 Implementation of the Neural Network Architecture
The neural network, which we name **'FashionMNISTNet'** consists of three **fully-connected layers** (including an “input layer” and two hidden layers). Furthermore, the **FashionMNISTNet** should encompass the following number of neurons per layer: 100 (layer 1), 50 (layer 2) and 10 (layer 3). Meaning the first layer consists of 100 neurons, the second layer of 50 neurons and third layer of 10 neurons (the number of digit classes we aim to classify.
We will now start implementing the network architecture as a separate Python class. Implementing the network architectures as a **separate class** in Python is good practice in deep learning projects. It will allow us to create and train several instances of the same neural network architecture. This provides us, for example, the opportunity to evaluate different initializations of the network parameters or train models using distinct datasets.
```
# implement the MNISTNet network architecture
class FashionMNISTNet(nn.Module):
# define the class constructor
def __init__(self):
# call super class constructor
super(FashionMNISTNet, self).__init__()
# specify fully-connected (fc) layer 1 - in 28*28, out 100
self.linear1 = nn.Linear(28*28, 100, bias=True) # the linearity W*x+b
self.relu1 = nn.ReLU(inplace=True) # the non-linearity
# specify fc layer 2 - in 100, out 50
self.linear2 = nn.Linear(100, 50, bias=True) # the linearity W*x+b
self.relu2 = nn.ReLU(inplace=True) # the non-linarity
# specify fc layer 3 - in 50, out 10
self.linear3 = nn.Linear(50, 10) # the linearity W*x+b
# add a softmax to the last layer
self.logsoftmax = nn.LogSoftmax(dim=1) # the softmax
# define network forward pass
def forward(self, images):
# reshape image pixels
x = images.view(-1, 28*28)
# define fc layer 1 forward pass
x = self.relu1(self.linear1(x))
# define fc layer 2 forward pass
x = self.relu2(self.linear2(x))
# define layer 3 forward pass
x = self.logsoftmax(self.linear3(x))
# return forward pass result
return x
```
You may have noticed, when reviewing the implementation above, that we applied an additional operator, referred to as **'Softmax'** to the third layer of our neural network.
The **softmax function**, also known as the normalized exponential function, is a function that takes as input a vector of K real numbers, and normalizes it into a probability distribution consisting of K probabilities.
That is, prior to applying softmax, some vector components could be negative, or greater than one; and might not sum to 1; but after application of the softmax, each component will be in the interval $(0,1)$, and the components will add up to 1, so that they can be interpreted as probabilities. In general, the softmax function $\sigma :\mathbb {R} ^{K}\to \mathbb {R} ^{K}$ is defined by the formula:
<center> $\sigma (\mathbf {z} )_{i}=\ln ({e^{z_{i}} / \sum _{j=1}^{K}e^{z_{j}}})$ </center>
for $i = 1, …, K$ and ${\mathbf {z}}=(z_{1},\ldots ,z_{K})\in \mathbb {R} ^{K}$ (Source: https://en.wikipedia.org/wiki/Softmax_function ).
Let's have a look at the simplified three-class example below. The scores of the distinct predicted classes $c_i$ are computed from the forward propagation of the network. We then take the softmax and obtain the probabilities as shown:
<img align="center" style="max-width: 800px" src="https://github.com/HSG-AIML/LabGSERM/blob/main/lab_04/softmax.png?raw=1">
The output of the softmax describes the probability (or if you may, the confidence) of the neural network that a particular sample belongs to a certain class. Thus, for the first example above, the neural network assigns a confidence of 0.49 that it is a 'three', 0.49 that it is a 'four', and 0.03 that it is an 'eight'. The same goes for each of the samples above.
Now, that we have implemented our first neural network we are ready to instantiate a network model to be trained:
```
model = FashionMNISTNet()
```
Let's push the initialized `FashionMNISTNet` model to the computing `device` that is enabled:
```
model = model.to(device)
```
Let's double check if our model was deployed to the GPU if available:
```
!nvidia-smi
```
Once the model is initialized, we can visualize the model structure and review the implemented network architecture by execution of the following cell:
```
# print the initialized architectures
print('[LOG] FashionMNISTNet architecture:\n\n{}\n'.format(model))
```
Looks like intended? Brilliant! Finally, let's have a look into the number of model parameters that we aim to train in the next steps of the notebook:
```
# init the number of model parameters
num_params = 0
# iterate over the distinct parameters
for param in model.parameters():
# collect number of parameters
num_params += param.numel()
# print the number of model paramters
print('[LOG] Number of to be trained FashionMNISTNet model parameters: {}.'.format(num_params))
```
Ok, our "simple" FashionMNISTNet model already encompasses an impressive number 84'060 model parameters to be trained.
### 4.2 Specification of the Neural Network Loss Function
Now that we have implemented the **FashionMNISTNet** we are ready to train the network. However, prior to starting the training, we need to define an appropriate loss function. Remember, we aim to train our model to learn a set of model parameters $\theta$ that minimize the classification error of the true class $c^{i}$ of a given handwritten digit image $x^{i}$ and its predicted class $\hat{c}^{i} = f_\theta(x^{i})$ as faithfully as possible.
Thereby, the training objective is to learn a set of optimal model parameters $\theta^*$ that optimize $\arg\min_{\theta} \|C - f_\theta(X)\|$ over all training images in the FashionMNIST dataset. To achieve this optimization objective, one typically minimizes a loss function $\mathcal{L_{\theta}}$ as part of the network training. In this lab we use the **'Negative Log Likelihood (NLL)'** loss, defined by:
<center> $\mathcal{L}^{NLL}_{\theta} (c_i, \hat c_i) = - \frac{1}{N} \sum_{i=1}^N \log (\hat{c}_i) $, </center>
for a set of $n$-FashionMNIST images $x^{i}$, $i=1,...,n$ and their respective predicted class labels $\hat{c}^{i}$. This is summed for all the correct classes.
Let's have a look at a brief example:
<img align="center" style="max-width: 900px" src="./loss.png">
As we see in the example, we first compute class predictions for each class. We normalize the predictions with a softmax over all classes, so that we end up with 'probabilities' (that's what comes out of the NN).
To compute the loss, we pick the predicted probability of the true class $\hat{c}_i$ and take the log of it. As the probabilities are on [0,1], the log of them are on [-$\infty$,0]. To maximize the probability of the true class $\hat{c}_i$, we have to maximize $log(\hat{c}_i)$. Due to the softmax, the predicted probabilties of all classes $c_i$ sum to 1: $\sum_i c_i = 1$. Therefore, by maximizing the probability of the true class $\hat{c}_i$, we minimize the probabilities of all the other (wrong) classes.
In ML, it has become common to minimize an 'error' or 'loss' term. Therfore, we sum over the log-likelihoods and take the negative of it. Small values (close to $0$) here translate to high values in true class probability.
During training the **NLL** loss will penalize models that result in a high classification error between the predicted class labels $\hat{c}^{i}$ and their respective true class label $c^{i}$. Luckily, an implementation of the NLL loss is already available in PyTorch! It can be instantiated "off-the-shelf" via the execution of the following PyTorch command:
```
# define the optimization criterion / loss function
nll_loss = nn.NLLLoss()
```
Let's also push the initialized `nll_loss` computation to the computing `device` that is enabled:
```
nll_loss = nll_loss.to(device)
```
## 5. Neural Network Model Training
In this section, we will train our neural network model (as implemented in the section above) using the transformed images of fashion items. More specifically, we will have a detailed look into the distinct training steps as well as how to monitor the training progress.
### 5.1. Preparing the Network Training
So far, we have pre-processed the dataset, implemented the ANN and defined the classification error. Let's now start to train a corresponding model for **20 epochs** and a **mini-batch size of 128** FashionMNIST images per batch. This implies that the whole dataset will be fed to the ANN 20 times in chunks of 128 images yielding to **469 mini-batches** (60.000 images / 128 images per mini-batch) per epoch.
```
# specify the training parameters
num_epochs = 20 # number of training epochs
mini_batch_size = 128 # size of the mini-batches
```
Based on the loss magnitude of a certain mini-batch PyTorch automatically computes the gradients. But even better, based on the gradient, the library also helps us in the optimization and update of the network parameters $\theta$.
We will use the **Stochastic Gradient Descent (SGD) optimization** and set the learning-rate $l = 0.001$. Each mini-batch step the optimizer will update the model parameters $\theta$ values according to the degree of classification error (the MSE loss).
```
# define learning rate and optimization strategy
learning_rate = 0.001
optimizer = optim.SGD(params=model.parameters(), lr=learning_rate)
```
Now that we have successfully implemented and defined the three ANN building blocks let's take some time to review the `FashionMNISTNet` model definition as well as the `loss`. Please, read the above code and comments carefully and don't hesitate to let us know any questions you might have.
Furthermore, lets specify and instantiate a corresponding PyTorch data loader that feeds the image tensors to our neural network:
```
fashion_mnist_train_dataloader = torch.utils.data.DataLoader(fashion_mnist_train_data, batch_size=mini_batch_size, shuffle=True)
```
### 5.2. Running the Network Training
Finally, we start training the model. The detailed training procedure for each mini-batch is performed as follows:
>1. do a forward pass through the FashionMNISTNet network,
>2. compute the negative log likelihood classification error $\mathcal{L}^{NLL}_{\theta}(c^{i};\hat{c}^{i})$,
>3. do a backward pass through the FashionMNISTNet network, and
>4. update the parameters of the network $f_\theta(\cdot)$.
To ensure learning while training our ANN model, we will monitor whether the loss decreases with progressing training. Therefore, we obtain and evaluate the classification performance of the entire training dataset after each training epoch. Based on this evaluation, we can conclude on the training progress and whether the loss is converging (indicating that the model might not improve any further).
The following elements of the network training code below should be given particular attention:
>- `loss.backward()` computes the gradients based on the magnitude of the reconstruction loss,
>- `optimizer.step()` updates the network parameters based on the gradient.
```
# init collection of training epoch losses
train_epoch_losses = []
# set the model in training mode
model.train()
# train the MNISTNet model
for epoch in range(num_epochs):
# init collection of mini-batch losses
train_mini_batch_losses = []
# iterate over all-mini batches
for i, (images, labels) in enumerate(fashion_mnist_train_dataloader):
# push mini-batch data to computation device
images = images.to(device)
labels = labels.to(device)
# run forward pass through the network
output = model(images)
# reset graph gradients
model.zero_grad()
# determine classification loss
loss = nll_loss(output, labels)
# run backward pass
loss.backward()
# update network paramaters
optimizer.step()
# collect mini-batch reconstruction loss
train_mini_batch_losses.append(loss.data.item())
# determine mean min-batch loss of epoch
train_epoch_loss = np.mean(train_mini_batch_losses)
# print epoch loss
now = datetime.utcnow().strftime("%Y%m%d-%H:%M:%S")
print('[LOG {}] epoch: {} train-loss: {}'.format(str(now), str(epoch), str(train_epoch_loss)))
# set filename of actual model
model_name = 'fashion_mnist_model_epoch_{}.pth'.format(str(epoch))
# save current model to GDrive models directory
torch.save(model.state_dict(), os.path.join(models_directory, model_name))
# determine mean min-batch loss of epoch
train_epoch_losses.append(train_epoch_loss)
```
Upon successfull training let's visualize and inspect the training loss per epoch:
```
# prepare plot
fig = plt.figure()
ax = fig.add_subplot(111)
# add grid
ax.grid(linestyle='dotted')
# plot the training epochs vs. the epochs' classification error
ax.plot(np.array(range(1, len(train_epoch_losses)+1)), train_epoch_losses, label='epoch loss (blue)')
# add axis legends
ax.set_xlabel("[training epoch $e_i$]", fontsize=10)
ax.set_ylabel("[Classification Error $\mathcal{L}^{NLL}$]", fontsize=10)
# set plot legend
plt.legend(loc="upper right", numpoints=1, fancybox=True)
# add plot title
plt.title('Training Epochs $e_i$ vs. Classification Error $L^{NLL}$', fontsize=10);
```
Ok, fantastic. The training error is nicely going down. We could train the network a couple more epochs until the error converges. But let's stay with the 20 training epochs for now and continue with evaluating our trained model.
## 6. Neural Network Model Evaluation
Before evaluating our model let's load the best performing model. Remember, that we stored a snapshot of the model after each training epoch to our local model directory. We will now load the last snapshot saved.
```
### load state_dict from some url
# # restore pre-trained model snapshot
# best_model_name = 'https://raw.githubusercontent.com/HSG-AIML-Teaching/ML2022-Lab/main/lab_02/models/fashion_mnist_model_epoch_19.pth'
# # read stored model from the remote location
# model_bytes = urllib.request.urlopen(best_model_name)
# # load model tensor from io.BytesIO object
# model_buffer = io.BytesIO(model_bytes.read())
# # init pre-trained model class
# best_model = FashionMNISTNet()
# # load pre-trained models
# best_model.load_state_dict(torch.load(model_buffer, map_location=torch.device('cpu')))
## load state_dict from local path
# restore pre-trained model snapshot
best_model_name = models_directory +'/fashion_mnist_model_epoch_19.pth'
# load state_dict from path
state_dict_best = torch.load(best_model_name)
# init pre-trained model class
best_model = FashionMNISTNet()
# load pre-trained state_dict to model
best_model.load_state_dict(state_dict_best)
```
Let's inspect if the model was loaded successfully:
```
# set model in evaluation mode
best_model.eval()
```
To evaluate our trained model, we need to feed the FashionMNIST images reserved for evaluation (the images that we didn't use as part of the training process) through the model. Therefore, let's again define a corresponding PyTorch data loader that feeds the image tensors to our neural network:
```
fashion_mnist_eval_dataloader = torch.utils.data.DataLoader(fashion_mnist_eval_data, batch_size=10000, shuffle=True)
```
We will now evaluate the trained model using the same mini-batch approach as we did throughout the network training and derive the mean negative log-likelihood loss of the mini-batches:
```
# init collection of mini-batch losses
eval_mini_batch_losses = []
# iterate over all-mini batches
for i, (images, labels) in enumerate(fashion_mnist_eval_dataloader):
# run forward pass through the network
output = best_model(images)
# determine classification loss
loss = nll_loss(output, labels)
# collect mini-batch reconstruction loss
eval_mini_batch_losses.append(loss.data.item())
# determine mean min-batch loss of epoch
eval_loss = np.mean(eval_mini_batch_losses)
# print epoch loss
now = datetime.utcnow().strftime("%Y%m%d-%H:%M:%S")
print('[LOG {}] eval-loss: {}'.format(str(now), str(eval_loss)))
```
Ok, great. The evaluation loss looks in-line with our training loss. Let's now inspect a few sample predictions to get an impression of the model quality. Therefore, we will again pick a random image of our evaluation dataset and retrieve its PyTorch tensor as well as the corresponding label:
```
# set (random) image id
image_id = 2000
# retrieve image exhibiting the image id
fashion_mnist_eval_image, fashion_mnist_eval_label = fashion_mnist_eval_data[image_id]
```
Let's now inspect the true class of the image we selected:
```
fashion_classes[fashion_mnist_eval_label]
```
Ok, the randomly selected image should contain a bag. Let's inspect the image accordingly:
```
# define tensor to image transformation
trans = torchvision.transforms.ToPILImage()
# set image plot title
plt.title('Example: {}, Label: {}'.format(str(image_id), fashion_classes[fashion_mnist_eval_label]))
# plot mnist handwritten digit sample
plt.imshow(trans(fashion_mnist_eval_image), cmap='gray')
```
Let's compare the true label with the prediction of our model:
```
best_model(fashion_mnist_eval_image)
```
We can even determine the likelihood of the most probable class:
```
most_probable = torch.argmax(best_model(fashion_mnist_eval_image), dim=1).item()
print('Most probable class: {}'.format(most_probable))
print('This class represents the following fashion article: {}'.format(fashion_classes[most_probable]))
```
Let's now obtain the predictions for all the fashion item images of the evaluation data:
```
predictions = torch.argmax(best_model(fashion_mnist_eval_data.data.float()), dim=1)
```
Furthermore, let's obtain the overall classifcation accuracy:
```
metrics.accuracy_score(fashion_mnist_eval_data.targets, predictions.detach())
```
Let's also inspect the confusion matrix to determine major sources of misclassification:
```
# determine classification matrix of the predicted and target classes
mat = confusion_matrix(fashion_mnist_eval_data.targets, predictions.detach())
# initialize the plot and define size
plt.figure(figsize=(8, 8))
# plot corresponding confusion matrix
sns.heatmap(mat.T, square=True, annot=True, fmt='d', cbar=False, cmap='YlOrRd_r', xticklabels=fashion_classes.values(), yticklabels=fashion_classes.values())
plt.tick_params(axis='both', which='major', labelsize=8, labelbottom = False, bottom=False, top = False, left = False, labeltop=True)
# set plot title
plt.title('Fashion MNIST classification matrix')
# set axis labels
plt.xlabel('[true label]')
plt.ylabel('[predicted label]');
```
Ok, we can easily see that our current model confuses sandals with either sneakers or ankle boots. However, the inverse does not really hold. The model sometimes confuses sneakers with ankle boots, and only very rarely with sandals. The same holds ankle boots. Our model also has issues distinguishing shirts from coats (and, to a lesser degree, from T-shirts and pullovers).
These mistakes are not very surprising, as these items exhibit a high similarity.
## 7. Lab Summary:
In this lab, a step by step introduction into the **design, implementation, training and evaluation** of neural networks to classify images of fashion items is presented. The code and exercises presented in this lab may serves as a starting point for developing more complex, more deep and tailored **neural networks**.
|
github_jupyter
|
##### Copyright 2019 The TensorFlow Authors.
```
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
```
# Premade Estimators
<table class="tfo-notebook-buttons" align="left">
<td>
<a target="_blank" href="https://www.tensorflow.org/tutorials/estimator/premade"><img src="https://www.tensorflow.org/images/tf_logo_32px.png" />View on TensorFlow.org</a>
</td>
<td>
<a target="_blank" href="https://colab.research.google.com/github/tensorflow/docs/blob/master/site/en/tutorials/estimator/premade.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
</td>
<td>
<a target="_blank" href="https://github.com/tensorflow/docs/blob/master/site/en/tutorials/estimator/premade.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View source on GitHub</a>
</td>
<td>
<a href="https://storage.googleapis.com/tensorflow_docs/docs/site/en/tutorials/estimator/premade.ipynb"><img src="https://www.tensorflow.org/images/download_logo_32px.png" />Download notebook</a>
</td>
</table>
This tutorial shows you
how to solve the Iris classification problem in TensorFlow using Estimators. An Estimator is TensorFlow's high-level representation of a complete model, and it has been designed for easy scaling and asynchronous training. For more details see
[Estimators](https://www.tensorflow.org/guide/estimator).
Note that in TensorFlow 2.0, the [Keras API](https://www.tensorflow.org/guide/keras) can accomplish many of these same tasks, and is believed to be an easier API to learn. If you are starting fresh, we would recommend you start with Keras. For more information about the available high level APIs in TensorFlow 2.0, see [Standardizing on Keras](https://medium.com/tensorflow/standardizing-on-keras-guidance-on-high-level-apis-in-tensorflow-2-0-bad2b04c819a).
## First things first
In order to get started, you will first import TensorFlow and a number of libraries you will need.
```
import tensorflow as tf
import pandas as pd
```
## The data set
The sample program in this document builds and tests a model that
classifies Iris flowers into three different species based on the size of their
[sepals](https://en.wikipedia.org/wiki/Sepal) and
[petals](https://en.wikipedia.org/wiki/Petal).
You will train a model using the Iris data set. The Iris data set contains four features and one
[label](https://developers.google.com/machine-learning/glossary/#label).
The four features identify the following botanical characteristics of
individual Iris flowers:
* sepal length
* sepal width
* petal length
* petal width
Based on this information, you can define a few helpful constants for parsing the data:
```
CSV_COLUMN_NAMES = ['SepalLength', 'SepalWidth', 'PetalLength', 'PetalWidth', 'Species']
SPECIES = ['Setosa', 'Versicolor', 'Virginica']
```
Next, download and parse the Iris data set using Keras and Pandas. Note that you keep distinct datasets for training and testing.
```
train_path = tf.keras.utils.get_file(
"iris_training.csv", "https://storage.googleapis.com/download.tensorflow.org/data/iris_training.csv")
test_path = tf.keras.utils.get_file(
"iris_test.csv", "https://storage.googleapis.com/download.tensorflow.org/data/iris_test.csv")
train = pd.read_csv(train_path, names=CSV_COLUMN_NAMES, header=0)
test = pd.read_csv(test_path, names=CSV_COLUMN_NAMES, header=0)
```
You can inspect your data to see that you have four float feature columns and one int32 label.
```
train.head()
```
For each of the datasets, split out the labels, which the model will be trained to predict.
```
train_y = train.pop('Species')
test_y = test.pop('Species')
# The label column has now been removed from the features.
train.head()
```
## Overview of programming with Estimators
Now that you have the data set up, you can define a model using a TensorFlow Estimator. An Estimator is any class derived from `tf.estimator.Estimator`. TensorFlow
provides a collection of
`tf.estimator`
(for example, `LinearRegressor`) to implement common ML algorithms. Beyond
those, you may write your own
[custom Estimators](https://www.tensorflow.org/guide/custom_estimators).
We recommend using pre-made Estimators when just getting started.
To write a TensorFlow program based on pre-made Estimators, you must perform the
following tasks:
* Create one or more input functions.
* Define the model's feature columns.
* Instantiate an Estimator, specifying the feature columns and various
hyperparameters.
* Call one or more methods on the Estimator object, passing the appropriate
input function as the source of the data.
Let's see how those tasks are implemented for Iris classification.
## Create input functions
You must create input functions to supply data for training,
evaluating, and prediction.
An **input function** is a function that returns a `tf.data.Dataset` object
which outputs the following two-element tuple:
* [`features`](https://developers.google.com/machine-learning/glossary/#feature) - A Python dictionary in which:
* Each key is the name of a feature.
* Each value is an array containing all of that feature's values.
* `label` - An array containing the values of the
[label](https://developers.google.com/machine-learning/glossary/#label) for
every example.
Just to demonstrate the format of the input function, here's a simple
implementation:
```
def input_evaluation_set():
features = {'SepalLength': np.array([6.4, 5.0]),
'SepalWidth': np.array([2.8, 2.3]),
'PetalLength': np.array([5.6, 3.3]),
'PetalWidth': np.array([2.2, 1.0])}
labels = np.array([2, 1])
return features, labels
```
Your input function may generate the `features` dictionary and `label` list any
way you like. However, we recommend using TensorFlow's [Dataset API](https://www.tensorflow.org/guide/datasets), which can
parse all sorts of data.
The Dataset API can handle a lot of common cases for you. For example,
using the Dataset API, you can easily read in records from a large collection
of files in parallel and join them into a single stream.
To keep things simple in this example you are going to load the data with
[pandas](https://pandas.pydata.org/), and build an input pipeline from this
in-memory data:
```
def input_fn(features, labels, training=True, batch_size=256):
"""An input function for training or evaluating"""
# Convert the inputs to a Dataset.
dataset = tf.data.Dataset.from_tensor_slices((dict(features), labels))
# Shuffle and repeat if you are in training mode.
if training:
dataset = dataset.shuffle(1000).repeat()
return dataset.batch(batch_size)
```
## Define the feature columns
A [**feature column**](https://developers.google.com/machine-learning/glossary/#feature_columns)
is an object describing how the model should use raw input data from the
features dictionary. When you build an Estimator model, you pass it a list of
feature columns that describes each of the features you want the model to use.
The `tf.feature_column` module provides many options for representing data
to the model.
For Iris, the 4 raw features are numeric values, so we'll build a list of
feature columns to tell the Estimator model to represent each of the four
features as 32-bit floating-point values. Therefore, the code to create the
feature column is:
```
# Feature columns describe how to use the input.
my_feature_columns = []
for key in train.keys():
my_feature_columns.append(tf.feature_column.numeric_column(key=key))
```
Feature columns can be far more sophisticated than those we're showing here. You can read more about Feature Columns in [this guide](https://www.tensorflow.org/guide/feature_columns).
Now that you have the description of how you want the model to represent the raw
features, you can build the estimator.
## Instantiate an estimator
The Iris problem is a classic classification problem. Fortunately, TensorFlow
provides several pre-made classifier Estimators, including:
* `tf.estimator.DNNClassifier` for deep models that perform multi-class
classification.
* `tf.estimator.DNNLinearCombinedClassifier` for wide & deep models.
* `tf.estimator.LinearClassifier` for classifiers based on linear models.
For the Iris problem, `tf.estimator.DNNClassifier` seems like the best choice.
Here's how you instantiated this Estimator:
```
# Build a DNN with 2 hidden layers with 30 and 10 hidden nodes each.
classifier = tf.estimator.DNNClassifier(
feature_columns=my_feature_columns,
# Two hidden layers of 30 and 10 nodes respectively.
hidden_units=[30, 10],
# The model must choose between 3 classes.
n_classes=3)
```
## Train, Evaluate, and Predict
Now that you have an Estimator object, you can call methods to do the following:
* Train the model.
* Evaluate the trained model.
* Use the trained model to make predictions.
### Train the model
Train the model by calling the Estimator's `train` method as follows:
```
# Train the Model.
classifier.train(
input_fn=lambda: input_fn(train, train_y, training=True),
steps=5000)
```
Note that you wrap up your `input_fn` call in a
[`lambda`](https://docs.python.org/3/tutorial/controlflow.html)
to capture the arguments while providing an input function that takes no
arguments, as expected by the Estimator. The `steps` argument tells the method
to stop training after a number of training steps.
### Evaluate the trained model
Now that the model has been trained, you can get some statistics on its
performance. The following code block evaluates the accuracy of the trained
model on the test data:
```
eval_result = classifier.evaluate(
input_fn=lambda: input_fn(test, test_y, training=False))
print('\nTest set accuracy: {accuracy:0.3f}\n'.format(**eval_result))
```
Unlike the call to the `train` method, you did not pass the `steps`
argument to evaluate. The `input_fn` for eval only yields a single
[epoch](https://developers.google.com/machine-learning/glossary/#epoch) of data.
The `eval_result` dictionary also contains the `average_loss` (mean loss per sample), the `loss` (mean loss per mini-batch) and the value of the estimator's `global_step` (the number of training iterations it underwent).
### Making predictions (inferring) from the trained model
You now have a trained model that produces good evaluation results.
You can now use the trained model to predict the species of an Iris flower
based on some unlabeled measurements. As with training and evaluation, you make
predictions using a single function call:
```
# Generate predictions from the model
expected = ['Setosa', 'Versicolor', 'Virginica']
predict_x = {
'SepalLength': [5.1, 5.9, 6.9],
'SepalWidth': [3.3, 3.0, 3.1],
'PetalLength': [1.7, 4.2, 5.4],
'PetalWidth': [0.5, 1.5, 2.1],
}
def input_fn(features, batch_size=256):
"""An input function for prediction."""
# Convert the inputs to a Dataset without labels.
return tf.data.Dataset.from_tensor_slices(dict(features)).batch(batch_size)
predictions = classifier.predict(
input_fn=lambda: input_fn(predict_x))
```
The `predict` method returns a Python iterable, yielding a dictionary of
prediction results for each example. The following code prints a few
predictions and their probabilities:
```
for pred_dict, expec in zip(predictions, expected):
class_id = pred_dict['class_ids'][0]
probability = pred_dict['probabilities'][class_id]
print('Prediction is "{}" ({:.1f}%), expected "{}"'.format(
SPECIES[class_id], 100 * probability, expec))
```
|
github_jupyter
|
# SVR with Scale & Quantile Transformer
This Code template is for regression analysis using the SVR Regressor where rescaling method used is Scale and feature transformation is done via Quantile Transformer.
### Required Packages
```
import warnings
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as se
from sklearn.model_selection import train_test_split
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import QuantileTransformer, scale
from sklearn.svm import SVR
from sklearn.metrics import r2_score, mean_absolute_error, mean_squared_error
warnings.filterwarnings('ignore')
```
### Initialization
Filepath of CSV file
```
#filepath
file_path= ""
```
List of features which are required for model training.
```
#x_values
features=[]
```
Target feature for prediction.
```
#y_value
target=''
```
### Data Fetching
Pandas is an open-source, BSD-licensed library providing high-performance, easy-to-use data manipulation and data analysis tools.
We will use panda's library to read the CSV file using its storage path.And we use the head function to display the initial row or entry.
```
df=pd.read_csv(file_path)
df.head()
```
### Feature Selections
It is the process of reducing the number of input variables when developing a predictive model. Used to reduce the number of input variables to both reduce the computational cost of modelling and, in some cases, to improve the performance of the model.
We will assign all the required input features to X and target/outcome to Y.
```
X=df[features]
Y=df[target]
```
### Data Preprocessing
Since the majority of the machine learning models in the Sklearn library doesn't handle string category data and Null value, we have to explicitly remove or replace null values. The below snippet have functions, which removes the null value if any exists. And convert the string classes data in the datasets by encoding them to integer classes.
```
def NullClearner(df):
if(isinstance(df, pd.Series) and (df.dtype in ["float64","int64"])):
df.fillna(df.mean(),inplace=True)
return df
elif(isinstance(df, pd.Series)):
df.fillna(df.mode()[0],inplace=True)
return df
else:return df
def EncodeX(df):
return pd.get_dummies(df)
```
Calling preprocessing functions on the feature and target set.
```
x=X.columns.to_list()
for i in x:
X[i]=NullClearner(X[i])
X=EncodeX(X)
Y=NullClearner(Y)
X.head()
```
#### Correlation Map
In order to check the correlation between the features, we will plot a correlation matrix. It is effective in summarizing a large amount of data where the goal is to see patterns.
```
f,ax = plt.subplots(figsize=(18, 18))
matrix = np.triu(X.corr())
se.heatmap(X.corr(), annot=True, linewidths=.5, fmt= '.1f',ax=ax, mask=matrix)
plt.show()
```
### Data Splitting
The train-test split is a procedure for evaluating the performance of an algorithm. The procedure involves taking a dataset and dividing it into two subsets. The first subset is utilized to fit/train the model. The second subset is used for prediction. The main motive is to estimate the performance of the model on new data.
```
x_train, x_test, y_train, y_test = train_test_split(X, Y, test_size=0.2, random_state=123)
```
###Data Rescaling
####Scale
It is a step of Data Pre Processing which is applied to independent variables or features of data. It basically helps to normalise the data within a particular range. Sometimes, it also helps in speeding up the calculations in an algorithm.
```
x_train =scale(x_train)
x_test = scale(x_test)
```
### Quantile Transformer
This method transforms the features to follow a uniform or a normal distribution. Therefore, for a given feature, this transformation tends to spread out the most frequent values. It also reduces the impact of (marginal) outliers: this is therefore a robust preprocessing scheme.
Transform features using quantiles information.
####Epsilon-Support Vector Regression.
Support vector machines (SVMs) are a set of supervised learning methods used for classification, regression and outliers detection.
A Support Vector Machine is a discriminative classifier formally defined by a separating hyperplane. In other terms, for a given known/labelled data points, the SVM outputs an appropriate hyperplane that classifies the inputted new cases based on the hyperplane. In 2-Dimensional space, this hyperplane is a line separating a plane into two segments where each class or group occupied on either side.
Here we will use SVR, the svr implementation is based on libsvm. The fit time scales at least quadratically with the number of samples and maybe impractical beyond tens of thousands of samples.
#### Parameters:
**kernel: {‘linear’, ‘poly’, ‘rbf’, ‘sigmoid’, ‘precomputed’}, default=’rbf’** ->
Specifies the kernel type to be used in the algorithm. It must be one of ‘linear’, ‘poly’, ‘rbf’, ‘sigmoid’, ‘precomputed’ or a callable. If none is given, ‘rbf’ will be used. If a callable is given it is used to precompute the kernel matrix.
**degree: int, default=3** ->
Degree of the polynomial kernel function (‘poly’). Ignored by all other kernels.
**gamma: {‘scale’, ‘auto’} or float, default=’scale’** ->
Kernel coefficient for ‘rbf’, ‘poly’ and ‘sigmoid’.
**coef0: float, default=0.0** ->
Independent term in kernel function. It is only significant in ‘poly’ and ‘sigmoid’.
**tol: float, default=1e-3** ->
Tolerance for stopping criterion.
**C: float, default=1.0** ->
Regularization parameter. The strength of the regularization is inversely proportional to C. Must be strictly positive. The penalty is a squared l2 penalty.
**epsilon: float, default=0.1** ->
Epsilon in the epsilon-SVR model. It specifies the epsilon-tube within which no penalty is associated in the training loss function with points predicted within a distance epsilon from the actual value.
**shrinking: bool, default=True** ->
Whether to use the shrinking heuristic. See the User Guide.
**cache_size: float, default=200** ->
Specify the size of the kernel cache (in MB).
**verbose: bool, default=False** ->
Enable verbose output. Note that this setting takes advantage of a per-process runtime setting in libsvm that, if enabled, may not work properly in a multithreaded context.
**max_iter: int, default=-1** ->
Hard limit on iterations within solver, or -1 for no limit.
```
model=make_pipeline(QuantileTransformer(), SVR(kernel='poly', degree=13))
model.fit(x_train, y_train)
```
#### Model Accuracy
We will use the trained model to make a prediction on the test set.Then use the predicted value for measuring the accuracy of our model.
score: The score function returns the coefficient of determination R2 of the prediction.
```
print("Accuracy score {:.2f} %\n".format(model.score(x_test,y_test)*100))
```
> **r2_score**: The **r2_score** function computes the percentage variablility explained by our model, either the fraction or the count of correct predictions.
> **mae**: The **mean abosolute error** function calculates the amount of total error(absolute average distance between the real data and the predicted data) by our model.
> **mse**: The **mean squared error** function squares the error(penalizes the model for large errors) by our model.
```
y_pred=model.predict(x_test)
print("R2 Score: {:.2f} %".format(r2_score(y_test,y_pred)*100))
print("Mean Absolute Error {:.2f}".format(mean_absolute_error(y_test,y_pred)))
print("Mean Squared Error {:.2f}".format(mean_squared_error(y_test,y_pred)))
```
#### Prediction Plot
First, we make use of a plot to plot the actual observations, with x_train on the x-axis and y_train on the y-axis.
For the regression line, we will use x_train on the x-axis and then the predictions of the x_train observations on the y-axis.
```
n=len(x_test) if len(x_test)<20 else 20
plt.figure(figsize=(14,10))
plt.plot(range(n),y_test[0:n], color = "green")
plt.plot(range(n),model.predict(x_test[0:n]), color = "red")
plt.legend(["Actual","prediction"])
plt.title("Predicted vs True Value")
plt.xlabel("Record number")
plt.ylabel(target)
plt.show()
```
#### Creator: Ayush Gupta , Github: [Profile](https://github.com/guptayush179)
|
github_jupyter
|
```
%matplotlib inline
from matplotlib import style
style.use('fivethirtyeight')
import matplotlib.pyplot as plt
from datetime import datetime
import numpy as np
import pandas as pd
import datetime as dt
```
# Reflect Tables into SQLAlchemy ORM
```
# Python SQL toolkit and Object Relational Mapper
import sqlalchemy
from sqlalchemy.ext.automap import automap_base
from sqlalchemy.orm import Session
from sqlalchemy import create_engine, func, MetaData, Table, Column, ForeignKey, Integer, String, Float, DateTime, inspect, distinct, desc, and_
# Create Database Connection
engine = create_engine("sqlite:///Resources/hawaii.sqlite")
Base.metadata.create_all(engine)
# reflect an existing database into a new model
Base=automap_base()
# reflect the tables
Base.prepare(engine, reflect=True)
# save refernece to the table
Measurement = Base.classes.measurement
Station = Base.classes.station
session = Session(engine)
# We can view all of the classes that automap found
Base.classes.keys()
# Save references to each table
Measurement = Base.classes.measurement
Station = Base.classes.station
# Create our session (link) from Python to the DB
session = Session(bind=engine)
inspector = inspect(engine)
columns = inspector.get_columns('measurement')
for c in columns:
print(c['name'], c["type"])
engine.execute('SELECT * FROM measurement LIMIT 5').fetchall()
columns = inspector.get_columns('station')
for c in columns:
print(c['name'], c["type"])
engine.execute('SELECT * FROM station LIMIT 5').fetchall()
```
# Exploratory Climate Analysis
```
# Design a query to retrieve the last 12 months of precipitation data and plot the results
# Calculate the date 1 year ago from the last data point in the database
end_date, = session.query(Measurement.date).order_by(Measurement.date.desc()).first()
begin_date=dt.datetime.strptime(end_date, '%Y-%m-%d')-dt.timedelta(days=365)
end_date = dt.datetime.strptime(end_date, '%Y-%m-%d')
print(end_date,begin_date)
# Perform a query to retrieve the data and precipitation scores
# data = session.query(Measurement.id,Measurement.station,Measurement.date, Measurement.prcp, Measurement.tobs)\
# .filter(and_(Measurement.date>=begin_date, Measurement.date<=end_date)).all()
data = session.query(Measurement.id,Measurement.station,Measurement.date, Measurement.prcp, Measurement.tobs)\
.filter(Measurement.date>=begin_date).filter(Measurement.date<=end_date).all()
# Save the query results as a Pandas DataFrame and set the index to the date column
# Sort the dataframe by date
prcp_data = pd.DataFrame(data).set_index('date').sort_values(by='date', ascending=False)
# Use Pandas Plotting with Matplotlib to plot the data
prcp_data
# Use Pandas to calcualte the summary statistics for the precipitation data
prcp_data["prcp"].agg(["mean","median", "sum", "count", "max", "min", "std", "var"])
# Design a query to show how many stations are available in this dataset.
stations_lastyr = prcp_data.station.nunique()
stations, = session.query(func.count(distinct(Measurement.station))).order_by
(f'There are {stations_lastyr} unique weather stations with measurments taken in the last year of data. There are {stations} unique weather stations in the entire dataset.')
# What are the most active stations? (i.e. what stations have the most rows)?
# List the stations and the counts in descending order.
active_all = session.query(Measurement.station, func.count(Measurement.station)).group_by(Measurement.station) \
.order_by(desc(func.count(Measurement.station))).all()
active = prcp_data["station"].value_counts() #Returns descending by default
active = pd.DataFrame(active)
# prcp_data["station"].value_counts(normalize=True) #returns percentages of whole instead of count!
print('This is the dataset filtered for the last year of data.')
active
print('This is the whole dataset.')
active_all = [[ i for i, j in active_all ],
[ j for i, j in active_all ]]
active_all
# Using the station id from the previous query, calculate the lowest temperature recorded,
# highest temperature recorded, and average temperature of the most active station?
most_active = active.index[0]
active_agg = prcp_data.loc[prcp_data["station"] == most_active]
active_agg["tobs"].agg(["mean", "max", "min"])
most_active_all =
# Choose the station with the highest number of temperature observations.
# Query the last 12 months of temperature observation data for this station and plot the results as a histogram
```
## Bonus Challenge Assignment
```
# This function called `calc_temps` will accept start date and end date in the format '%Y-%m-%d'
# and return the minimum, average, and maximum temperatures for that range of dates
def calc_temps(start_date, end_date):
"""TMIN, TAVG, and TMAX for a list of dates.
Args:
start_date (string): A date string in the format %Y-%m-%d
end_date (string): A date string in the format %Y-%m-%d
Returns:
TMIN, TAVE, and TMAX
"""
return session.query(func.min(Measurement.tobs), func.avg(Measurement.tobs), func.max(Measurement.tobs)).\
filter(Measurement.date >= start_date).filter(Measurement.date <= end_date).all()
# function usage example
print(calc_temps('2012-02-28', '2012-03-05'))
# Use your previous function `calc_temps` to calculate the tmin, tavg, and tmax
# for your trip using the previous year's data for those same dates.
# Plot the results from your previous query as a bar chart.
# Use "Trip Avg Temp" as your Title
# Use the average temperature for the y value
# Use the peak-to-peak (tmax-tmin) value as the y error bar (yerr)
# Calculate the total amount of rainfall per weather station for your trip dates using the previous year's matching dates.
# Sort this in descending order by precipitation amount and list the station, name, latitude, longitude, and elevation
# Create a query that will calculate the daily normals
# (i.e. the averages for tmin, tmax, and tavg for all historic data matching a specific month and day)
def daily_normals(date):
"""Daily Normals.
Args:
date (str): A date string in the format '%m-%d'
Returns:
A list of tuples containing the daily normals, tmin, tavg, and tmax
"""
sel = [func.min(Measurement.tobs), func.avg(Measurement.tobs), func.max(Measurement.tobs)]
return session.query(*sel).filter(func.strftime("%m-%d", Measurement.date) == date).all()
daily_normals("01-01")
# calculate the daily normals for your trip
# push each tuple of calculations into a list called `normals`
# Set the start and end date of the trip
# Use the start and end date to create a range of dates
# Stip off the year and save a list of %m-%d strings
# Loop through the list of %m-%d strings and calculate the normals for each date
# Load the previous query results into a Pandas DataFrame and add the `trip_dates` range as the `date` index
# Plot the daily normals as an area plot with `stacked=False`
# class Measurement_two(Base):
# __tablename__= "measurement"
# id = Column(Integer, primary_key=True)
# station = Column(String(200))
# date = Column(DateTime)
# prcp = Column(Float)
# tobs = Column(Float)
# class Station_two(Base):
# __tablename__= "station"
# id = Column(Integer, primary_key=True)
# station = Column(String(200))
# name = Column(String(200))
# latitude = Column(Float)
# longitude = Column(Float)
# elevation = Column(Float)
```
|
github_jupyter
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.