text
stringlengths 2.5k
6.39M
| kind
stringclasses 3
values |
|---|---|
```
import sys
sys.path.append("/Users/msachde1/Downloads/Research/Development/mgwr/")
import warnings
warnings.filterwarnings("ignore")
from mgwr.gwr import GWR
import pandas as pd
import numpy as np
from spglm.family import Gaussian, Binomial, Poisson
from mgwr.gwr import MGWR
from mgwr.sel_bw import Sel_BW
import multiprocessing as mp
pool = mp.Pool()
from scipy import linalg
import numpy.linalg as la
from scipy import sparse as sp
from scipy.sparse import linalg as spla
from spreg.utils import spdot, spmultiply
from scipy import special
import libpysal as ps
import seaborn as sns
import matplotlib.pyplot as plt
import numpy as np
from copy import deepcopy
import copy
from collections import namedtuple
```
<img src="image.png">
### IWLS convergence loop
```
data_p = pd.read_csv("C:/Users/msachde1/Downloads/logistic_mgwr_data/landslides.csv")
coords = list(zip(data_p['X'],data_p['Y']))
y = np.array(data_p['Landslid']).reshape((-1,1))
elev = np.array(data_p['Elev']).reshape((-1,1))
slope = np.array(data_p['Slope']).reshape((-1,1))
SinAspct = np.array(data_p['SinAspct']).reshape(-1,1)
CosAspct = np.array(data_p['CosAspct']).reshape(-1,1)
X = np.hstack([elev,slope,SinAspct,CosAspct])
x = CosAspct
X_std = (X-X.mean(axis=0))/X.std(axis=0)
x_std = (x-x.mean(axis=0))/x.std(axis=0)
y_std = (y-y.mean(axis=0))/y.std(axis=0)
```
### Initialization with GWPR
```
sel=Sel_BW(coords,y,x,family=Binomial(),constant=False)
bw_in=sel.search()
def gwr_func(y,X,bw):
return GWR(coords,y,X,bw,family=Binomial(),fixed=False,kernel='bisquare',constant=False).fit()
optim_model = gwr_func(y=y,X=x,bw=bw_in)
om_p=optim_model.params
bw_in
```
### Starting values
```
n_iter=0
n=x.shape[0]
diff = 1.0e+06
tol = 1.0e-06
max_iter=200
betas=om_p
XB =np.sum( np.multiply(optim_model.params,optim_model.X),axis=1)
mu = 1 / ( 1 + np.exp (-1 * XB))
ni_old = np.log((mu)/(1-mu))
while diff> tol and n_iter < max_iter:
n_iter +=1
w = mu*(1-mu)
z = (ni_old + ((optim_model.y - mu)/mu*(1-mu))).reshape(-1,1)
wx = spmultiply(x.reshape(-1),w.reshape(-1),array_out=False)
x_std=((wx-wx.mean(axis=0))/wx.std(axis=0)).reshape(-1,1)
print(x_std.shape)
selector=Sel_BW(coords,z,x_std,multi=True,constant=False)
selector.search(pool=pool)
print(selector.bw[0])
mgwr_model=MGWR(coords,z,x_std,selector,family=Gaussian(),constant=False).fit()
n_betas=mgwr_model.params
XB =np.sum( np.multiply(n_betas,mgwr_model.X),axis=1)
mu = 1 / ( 1 + np.exp (-1 * XB))
ni_old = np.log((mu)/(1-mu))
diff=min(min(abs(betas-n_betas).reshape(1,-1).tolist()))
print("diff = "+str(diff))
betas = n_betas
#print (betas, w, z, n_iter)
bw=Sel_BW(coords,y,x_std,family=Binomial(),constant=False)
bw=bw.search()
bw
gwr_mod = GWR(coords,y,x_std,bw,family=Binomial(),constant=False).fit()
gwr_mod.aic
sns.distplot(z)
sns.distplot(x_std)
mgwr_model.aic
optim_model.aic
```
|
github_jupyter
|
# Hidden Markov Models
### Problem Statement
The following problem is from the Udacity course on Artificial Intelligence (Thrun and Norvig), chapter 11 (HMMs and filters). It involves a simple scenario where a person's current emotional state is determined by the weather on that particular day. The task is to find the underlying hidden sequence of states (in this case, the weather), given only a set of observations (moods) and information about state/observation changes.
```
#import required libraries
import numpy as np
import warnings
from pprint import pprint
```
$P(\;Rainy\;) = P(R_{0}) = 0.5$ (initial probabilites)
$P(\;Sunny\;) = P(S_{0}) = 0.5$
The chances of weather changing are given as follows:
For rainy weather, $P(S_{tomorrow}|R_{today}) = 0.4$, and $P(R_{tomorrow}|R_{today}) = 0.6$
For sunny weather, $P(R_{tomorrow}|S_{today}) = 0.2$, therefore $P(S_{tomorrow}| S_{today}) = 0.8$
For the purpose of formulating an HMM, we call the above ***Transition Probabilities.***
The corresponding mood changes, given the weather are :
$P(H|R) = 0.4$, therefore $P(G|R) = 0.6$
$P(H|S) = 0.9$, and $P(G|S) = 0.1$
We call these ***Emission Probabilities***
```
S = np.array([0, 1]) # 0 Rainy, 1 Sunny
S_names = ('Rainy', 'Sunny')
pi = np.array([0.5, 0.5]) # Initial Probabilities
O = np.array(['Happy', 'Grumpy']) # Set of observations
A = np.array([[0.6, 0.4], [0.2, 0.8]]) # {R:{R, S}, S:{R, S}} Transition Matrix
B = np.array([[0.4, 0.6], [0.9, 0.1]]) # {R: {H, G}, S: {H, G}} Emission Matrix
Y = np.array([0, 0, 1]) # 0 Happy, 1 Grumpy -- Observation sequence
```
### Hidden Markov Models
[HMMs](https://en.wikipedia.org/wiki/Hidden_Markov_model) are a class of probabilistic graphical models that can predict the sequence of states, given a sequence of observations that are dependent on those states, and when the states themselves are unobservable. HMMs have seen widespread success in a variety of applications, from Speech processing and Robotics to DNA Sequencing. An HMM operates according to a set of assumptions, which are :
1. ** Markov Assumption **
Current state is dependent on only the previous state.
2. ** Stationarity Assumption **
Transition probabilities are independent of time of transition.
3. ** Independence Assumption **
Each observation depends solely on the current underlying state (which in turn depends on the previous one), and is independent of other observations.
An HMM is a **Generative model**, in that it attempts to find the probability of a set of observations being produced or *generated* by a class. The parameters that we pass to the HMM class, defined below, are:
*O* = a set of observations
*S* = a set of states
*A* = transition probabilities, represented as a matrix
*B* = emission probabilities, represented as a matrix
*pi* = initial state probabilties
*Y* = sequence observed
### Viterbi Algorithm
The Viterbi algorithm is a Dynamic Programming algorithm for decoding the observation sequence to uncover the most probable state sequence. Given the required parameters, it starts from the initial state and uses the transition/emission information to calculate probabilities of subsequent states. Information from the previous step is passed along to the next, similar to a belief propagation mechanism (such as one used in the Forward-Backward algorithm explained later).
We store the results of each step in a table or matrix of size $k * t$, where k is the number of possible states, and t is the length of the observation sequence. The idea here is to find the path through possible states that has the maximum probability. Since initially we do not have a transition from state to state, we multiply the initial probabilities (from pi) and $P(\;observation\;|\;state\;)$ (from emission matrix B).
Eg. For the first day, we have the observation as Happy, so :
$P(R_{1}) = P(R_{0}) * P(H|R_{1}) = 0.5 * 0.4 = 0.2$
$P(S_{1}) = P(S_{0}) * P(H|S_{1}) \;= 0.5 * 0.9 = 0.45$
We log both these results in the table, since we are starting from an initial state. For the following observations, however, each state has only its maximum probability of moving to the next state logged.
#### On Day 2 : (observation - Happy) :
If current state = Rainy:
$P(R_{1}) * P(R_{2}|R_{1}) = 0.20 * 0.6 = 0.12$ (given Rainy was previous state)
$P(S_{1}) * P(R_{2}|S_{1}) = 0.45 * 0.2 = 0.09$ (Given Sunny was previous state)
Since $0.12>0.09$, We choose $P(R_{2}|H)$ as the most probable transition from $R_{1}$, and update the table with
$P(R_{2}|H) = P(R_{1}) * P(R_{2}|R_{1}) * P(H|R_{2}) = 0.12 * 0.4 = 0.048$
If current state = Sunny:
$P(R_{1}) * P(S_{2}|R_{1}) = 0.20 * 0.4 = 0.08$ (given Rainy was previous state)
$P(S_{1}) * P(S_{2}|S_{1}) = 0.45 * 0.8 = 0.36$ (given Sunny was previous state)
Here too, we choose $P(S_{2}|H)$ as the most probable transition from $S_{1}$, and add it to the table.
$P(S_{2}|H) = P(S_{1}) * P(S_{2}|S_{1}) * P(H|S_{2}) = 0.36 * 0.9 = 0.324$
#### On Day 3: (observation - Grumpy) :
If current state = Rainy:
$P(R_{2}) * P(R_{3}|R_{2}) = 0.048 * 0.6 = 0.0288$ (given Rainy was previous state)
$P(S_{2}) * P(R_{3}|S_{2}) = 0.324 * 0.2 = 0.0648$ (given Sunny was previous state)
As $0.0648>0.0288$, We choose $P(R_{3}|G)$ as the most probable transition from $R_{2}$, and update the table with
$P(R_{3}|G) = P(R_{2}) * P(R_{3}|R_{2}) * P(G|R_{3}) = 0.0648 * 0.6 = 0.03888$
If current state = Sunny:
$P(R_{2}) * P(S_{3}|R_{2}) = 0.048 * 0.4 = 0.0192$ (given Rainy was previous state)
$P(S_{2}) * P(S_{3}|S_{2}) = 0.324 * 0.8 = 0.2592$ (given Sunny was previous state)
Here too, we choose $P(S_{3}|G)$ as the most probable transition from $S_{1}$, and add it to the table.
$P(S_{3}|G) = P(S_{2}) * P(S_{3}|S_{2}) * P(G|S_{3}) = 0.2592 * 0.1 = 0.02592$
Since now the table is completely filled, we work in reverse from probability of the last observation and its inferred state (in this case, $0.0388$ i.e Rainy) finding which state had the maximum probability upto that point. In this way, we find the most probable sequence of states corresponding to our observations!
```
class HMM:
def __init__(self, observations, states, start_probs, trans_probs, emm_probs, obs_sequence):
self.O = observations
self.S = states
self.state_names = None
self.pi = start_probs
self.A = trans_probs
self.B = emm_probs
self.Y = obs_sequence
self.k = np.array(self.S).shape[0]
self.t = self.Y.shape[0]
self.table_1 = np.zeros((self.k, self.t))
self.output_sequence = np.zeros((self.t,))
self.fwds = None
self.bwds = None
self.smoothened = None
def viterbi(self):
# loop through states, but only for first observation
print "Day 1 : Observation was", self.Y[0], "i.e", self.O[self.Y[0]]
for i in range(self.k):
self.table_1[i, 0] = self.pi[i] * self.B[i, self.Y[0]]
print "Probability of state", i, "-->", self.table_1[i, 0]
print "-------------------------------------------"
print "========================================="
# loop through second to last observation
for i in range(1, self.t):
print "Day", i + 1, ": Observation was", self.Y[i], "i.e", self.O[self.Y[i]]
for j in range(self.k): # loop through states
print "If current state", j, "i.e", self.state_names[j]
max_t1_A = 0.0
for d in range(self.k): # loop through states*states
print "probability of the previous state i.e", d, "-->", self.table_1[d, i - 1]
val = self.table_1[d, i - 1] * self.A[d, j]
print "State", d, "to State", j, "-->", self.A[d, j]
print self.table_1[d, i - 1], "*", self.A[d, j], "=", val
if val > max_t1_A:
max_t1_A = val
else:
continue
self.table_1[j, i] = max_t1_A
tmp = self.table_1[j, i]
self.table_1[j, i] = self.table_1[j, i] * self.B[j, self.Y[i]]
print "Probability of next state given previous state, transition and observation :"
print tmp, "*", self.B[j, self.Y[i]], "=", self.table_1[j, i]
print "-------------------------------------------"
print "==========================================="
print ""
# work backwards from the last day, comparing probabilities
# from observations and transitions up to that day.
for i in range(self.t - 1, -1, -1):
max_at_i = 0.0
max_j = 0.0
for j in range(self.k):
if self.table_1[j][i] > max_at_i:
max_at_i = self.table_1[j][i]
max_j = j
else:
continue
self.output_sequence[i] = j
print "State", self.state_names[int(self.output_sequence[i])], "was most likely on day", i+1
print ""
return self.output_sequence
def get_obs(self, obs_val, emm_prob):
ob_mat = np.zeros((self.k, self.k))
for i in self.S:
for j in self.S:
if i == j:
ob_mat[i, j] = emm_prob[i, obs_val]
return ob_mat
def get_diagonal(self, mat_A, mat_B):
x = np.transpose(mat_A).shape[1]
mat_C = np.dot(mat_A, np.transpose(mat_B))
mat_D = np.zeros((self.k, 1))
for i in range(x):
for j in range(x):
if i == j:
mat_D[i][0] = mat_C[i][j]
return mat_D
def forward_backward(self):
self.m = self.O.shape[0]
# print self.m
obs_mats = [None for i in range(self.t)]
for i in range(self.t):
obs_mats[i] = self.get_obs(self.Y[i], self.B)
print "Observation matrices :"
pprint(obs_mats)
print ""
# forward probability calculation
f = [[] for i in range(self.t + 1)]
f[0] = self.pi.reshape(self.k, 1)
csum = 0.0
for j in f[0]:
csum += j
for j in range(f[0].shape[0]):
f[0][j] = f[0][j] / csum
for i in range(1, self.t + 1):
# print "obs", obs_mats[i-1]
# print "prev f", f[i-1]
f[i] = np.dot(np.dot(obs_mats[i - 1], self.A),
f[i - 1]).reshape(self.k, 1)
# scaling done here
csum = 0.0
for j in f[i]:
csum += j
for j in range(f[i].shape[0]):
f[i][j] = f[i][j] / csum
# print "new f", f[i]
f = np.array(f)
print "Forward probabilities :"
pprint(f)
print ""
# backward probability calculation
b = [[] for i in range(self.t + 1)]
b[-1] = np.array([[1.0] for i in range(self.k)])
for i in range(self.t - 1, -1, -1):
b[i] = np.dot(np.dot(self.A, obs_mats[i]),
b[i + 1]).reshape(self.k, 1)
# scaling done here
csum = 0.0
for j in b[i]:
csum += j
for j in range(b[i].shape[0]):
b[i][j] = b[i][j] / csum
b = np.array(b)
print "Backward probabilities :"
pprint(b)
print ""
# smoothed values
smooth = [[] for i in range(self.t + 1)]
for i in range(self.t + 1):
smooth[i] = self.get_diagonal(f[i], b[i])
csum = 0.0
for j in smooth[i]:
csum += j
for j in range(smooth[i].shape[0]):
smooth[i][j] = smooth[i][j] / csum
smooth = np.array(smooth)
print "Smoothed probabilities :"
pprint(smooth)
self.fwds = f
self.bwds = b
self.smoothened = smooth
for i in range(1, smooth.shape[0]):
max_prob = max(smooth[i].tolist())
print "Day", i, "probability was max for state", smooth[i].tolist().index(max_prob), "-->", max_prob[0]
self.output_sequence[i - 1] = smooth[i].tolist().index(max_prob)
return self.output_sequence
weather_hmm = HMM(O, S, pi, A, B, Y)
weather_hmm.state_names = S_names
obs_states = [O[i] for i in Y]
print "Observations :"
print obs_states, "\n"
with warnings.catch_warnings():
warnings.simplefilter("ignore")
print "Using Viterbi Algorithm:\n"
op1 = weather_hmm.viterbi()
print "Table of state probabilities :"
for i in weather_hmm.table_1:
print "----------------------------"
print "|",
for j in i:
print "{0:.4f} |".format(j),
print ""
print "----------------------------\n"
op_states1 = [S_names[int(i)] for i in op1]
print op_states1
```
### Forward-Backward Algorithm
Explanation : **TO-DO**
```
#reset output sequence values to zero
weather_hmm.output_sequence = np.zeros((weather_hmm.t,))
print "Using Forward-Backward Algorithm:"
op2 = weather_hmm.forward_backward()
op_states2 = [S_names[int(i)] for i in op2]
print op_states2
```
|
github_jupyter
|
## Finding entity classes in embeddings
In this notebook we're going to use embeddings to find entity classes and how they correlate with other things
```
%matplotlib inline
from sklearn import svm
from keras.utils import get_file
import os
import gensim
import numpy as np
import random
import requests
import geopandas as gpd
from IPython.core.pylabtools import figsize
figsize(12, 8)
import pycountry
import csv
```
as before, let's load up the model
```
MODEL = 'GoogleNews-vectors-negative300.bin'
path = get_file(MODEL + '.gz', 'https://s3.amazonaws.com/dl4j-distribution/%s.gz' % MODEL)
unzipped = os.path.join('generated', MODEL)
if not os.path.isfile(unzipped):
with open(unzipped, 'wb') as fout:
zcat = subprocess.Popen(['zcat'],
stdin=open(path),
stdout=fout
)
zcat.wait()
```
Most similar to a bunch of countries are some other countries!
```
model = gensim.models.KeyedVectors.load_word2vec_format(unzipped, binary=True)
model.most_similar(positive=['Germany'])
model.most_similar(positive=['Annita_Kirsten'])
```
No we'll create a training set with countries and non countries and get a support vector machine to learn the difference.
```
countries = list(csv.DictReader(open('data/countries.csv')))
countries[:10]
positive = [x['name'] for x in random.sample(countries, 40)]
negative = random.sample(model.vocab.keys(), 5000)
negative[:4]
labelled = [(p, 1) for p in positive] + [(n, 0) for n in negative]
random.shuffle(labelled)
X = np.asarray([model[w] for w, l in labelled])
y = np.asarray([l for w, l in labelled])
X.shape, y.shape
TRAINING_FRACTION = 0.3
cut_off = int(TRAINING_FRACTION * len(labelled))
clf = svm.SVC(kernel='linear')
clf.fit(X[:cut_off], y[:cut_off])
```
We did alright, 99.9% precision:
```
res = clf.predict(X[cut_off:])
missed = [country for (pred, truth, country) in
zip(res, y[cut_off:], labelled[cut_off:]) if pred != truth]
100 - 100 * float(len(missed)) / len(res), missed
all_predictions = clf.predict(model.syn0)
res = []
for word, pred in zip(model.index2word, all_predictions):
if pred:
res.append(word)
if len(res) == 150:
break
random.sample(res, 10)
country_to_idx = {country['name']: idx for idx, country in enumerate(countries)}
country_vecs = np.asarray([model[c['name']] for c in countries])
country_vecs.shape
```
Quick sanity check to see what is similar to Canada:
```
dists = np.dot(country_vecs, country_vecs[country_to_idx['Canada']])
for idx in reversed(np.argsort(dists)[-10:]):
print(countries[idx]['name'], dists[idx])
```
Ranking countries for a specific term:
```
def rank_countries(term, topn=10, field='name'):
if not term in model:
return []
vec = model[term]
dists = np.dot(country_vecs, vec)
return [(countries[idx][field], float(dists[idx]))
for idx in reversed(np.argsort(dists)[-topn:])]
rank_countries('cricket')
```
Now let's visualize this on a world map:
```
world = gpd.read_file(gpd.datasets.get_path('naturalearth_lowres'))
world.head()
```
We can now plot some maps!
```
def map_term(term):
d = {k.upper(): v for k, v in rank_countries(term, topn=0, field='cc3')}
world[term] = world['iso_a3'].map(d)
world[term] /= world[term].max()
world.dropna().plot(term, cmap='OrRd')
map_term('coffee')
map_term('cricket')
map_term('China')
```
|
github_jupyter
|
##### Copyright 2019 The TensorFlow Authors.
```
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
```
# Masking and padding in Keras
<table class="tfo-notebook-buttons" align="left">
<td>
<a target="_blank" href="https://www.tensorflow.org/beta/guide/keras/masking_and_padding">
<img src="https://www.tensorflow.org/images/tf_logo_32px.png" />
View on TensorFlow.org</a>
</td>
<td>
<a target="_blank" href="https://colab.research.google.com/github/tensorflow/docs/blob/master/site/en/r2/guide/keras/masking_and_padding.ipynb">
<img src="https://www.tensorflow.org/images/colab_logo_32px.png" />
Run in Google Colab</a>
</td>
<td>
<a target="_blank" href="https://github.com/tensorflow/docs/blob/master/site/en/r2/guide/keras/masking_and_padding.ipynb">
<img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />
View source on GitHub</a>
</td>
<td>
<a target="_blank" href="https://storage.googleapis.com/tensorflow_docs/docs/site/en/r2/guide/keras/masking_and_padding.ipynb">
<img src="https://www.tensorflow.org/images/download_logo_32px.png" />
Download notebook</a>
</td>
</table>
## Setup
```
from __future__ import absolute_import, division, print_function, unicode_literals
import numpy as np
try:
# %tensorflow_version only exists in Colab.
%tensorflow_version 2.x
except Exception:
pass
import tensorflow as tf
from tensorflow.keras import layers
```
## Padding sequence data
When processing sequence data, it is very common for individual samples to have different lengths. Consider the following example (text tokenized as words):
```
[
["The", "weather", "will", "be", "nice", "tomorrow"],
["How", "are", "you", "doing", "today"],
["Hello", "world", "!"]
]
```
After vocabulary lookup, the data might be vectorized as integers, e.g.:
```
[
[83, 91, 1, 645, 1253, 927],
[73, 8, 3215, 55, 927],
[71, 1331, 4231]
]
```
The data is a 2D list where individual samples have length 6, 5, and 3 respectively. Since the input data for a deep learning model must be a single tensor (of shape e.g. `(batch_size, 6, vocab_size)` in this case), samples that are shorter than the longest item need to be padded with some placeholder value (alternatively, one might also truncate long samples before padding short samples).
Keras provides an API to easily truncate and pad sequences to a common length: `tf.keras.preprocessing.sequence.pad_sequences`.
```
raw_inputs = [
[83, 91, 1, 645, 1253, 927],
[73, 8, 3215, 55, 927],
[711, 632, 71]
]
# By default, this will pad using 0s; it is configurable via the
# "value" parameter.
# Note that you could "pre" padding (at the beginning) or
# "post" padding (at the end).
# We recommend using "post" padding when working with RNN layers
# (in order to be able to use the
# CuDNN implementation of the layers).
padded_inputs = tf.keras.preprocessing.sequence.pad_sequences(raw_inputs,
padding='post')
print(padded_inputs)
```
## Masking
Now that all samples have a uniform length, the model must be informed that some part of the data is actually padding and should be ignored. That mechanism is <b>masking</b>.
There are three ways to introduce input masks in Keras models:
- Add a `keras.layers.Masking` layer.
- Configure a `keras.layers.Embedding` layer with `mask_zero=True`.
- Pass a `mask` argument manually when calling layers that support this argument (e.g. RNN layers).
## Mask-generating layers: `Embedding` and `Masking`
Under the hood, these layers will create a mask tensor (2D tensor with shape `(batch, sequence_length)`), and attach it to the tensor output returned by the `Masking` or `Embedding` layer.
```
embedding = layers.Embedding(input_dim=5000, output_dim=16, mask_zero=True)
masked_output = embedding(padded_inputs)
print(masked_output._keras_mask)
masking_layer = layers.Masking()
# Simulate the embedding lookup by expanding the 2D input to 3D,
# with embedding dimension of 10.
unmasked_embedding = tf.cast(
tf.tile(tf.expand_dims(padded_inputs, axis=-1), [1, 1, 10]),
tf.float32)
masked_embedding = masking_layer(unmasked_embedding)
print(masked_embedding._keras_mask)
```
As you can see from the printed result, the mask is a 2D boolean tensor with shape `(batch_size, sequence_length)`, where each individual `False` entry indicates that the corresponding timestep should be ignored during processing.
## Mask propagation in the Functional API and Sequential API
When using the Functional API or the Sequential API, a mask generated by an `Embedding` or `Masking` layer will be propagated through the network for any layer that is capable of using them (for example, RNN layers). Keras will automatically fetch the mask corresponding to an input and pass it to any layer that knows how to use it.
Note that in the `call` method of a subclassed model or layer, masks aren't automatically propagated, so you will need to manually pass a `mask` argument to any layer that needs one. See the section below for details.
For instance, in the following Sequential model, the `LSTM` layer will automatically receive a mask, which means it will ignore padded values:
```
model = tf.keras.Sequential([
layers.Embedding(input_dim=5000, output_dim=16, mask_zero=True),
layers.LSTM(32),
])
```
This is also the case for the following Functional API model:
```
inputs = tf.keras.Input(shape=(None,), dtype='int32')
x = layers.Embedding(input_dim=5000, output_dim=16, mask_zero=True)(inputs)
outputs = layers.LSTM(32)(x)
model = tf.keras.Model(inputs, outputs)
```
## Passing mask tensors directly to layers
Layers that can handle masks (such as the `LSTM` layer) have a `mask` argument in their `__call__` method.
Meanwhile, layers that produce a mask (e.g. `Embedding`) expose a `compute_mask(input, previous_mask)` method which you can call.
Thus, you can do something like this:
```
class MyLayer(layers.Layer):
def __init__(self, **kwargs):
super(MyLayer, self).__init__(**kwargs)
self.embedding = layers.Embedding(input_dim=5000, output_dim=16, mask_zero=True)
self.lstm = layers.LSTM(32)
def call(self, inputs):
x = self.embedding(inputs)
# Note that you could also prepare a `mask` tensor manually.
# It only needs to be a boolean tensor
# with the right shape, i.e. (batch_size, timesteps).
mask = self.embedding.compute_mask(inputs)
output = self.lstm(x, mask=mask) # The layer will ignore the masked values
return output
layer = MyLayer()
x = np.random.random((32, 10)) * 100
x = x.astype('int32')
layer(x)
```
## Supporting masking in your custom layers
Sometimes you may need to write layers that generate a mask (like `Embedding`), or layers that need to modify the current mask.
For instance, any layer that produces a tensor with a different time dimension than its input, such as a `Concatenate` layer that concatenates on the time dimension, will need to modify the current mask so that downstream layers will be able to properly take masked timesteps into account.
To do this, your layer should implement the `layer.compute_mask()` method, which produces a new mask given the input and the current mask.
Most layers don't modify the time dimension, so don't need to worry about masking. The default behavior of `compute_mask()` is just pass the current mask through in such cases.
Here is an example of a `TemporalSplit` layer that needs to modify the current mask.
```
class TemporalSplit(tf.keras.layers.Layer):
"""Split the input tensor into 2 tensors along the time dimension."""
def call(self, inputs):
# Expect the input to be 3D and mask to be 2D, split the input tensor into 2
# subtensors along the time axis (axis 1).
return tf.split(inputs, 2, axis=1)
def compute_mask(self, inputs, mask=None):
# Also split the mask into 2 if it presents.
if mask is None:
return None
return tf.split(mask, 2, axis=1)
first_half, second_half = TemporalSplit()(masked_embedding)
print(first_half._keras_mask)
print(second_half._keras_mask)
```
Here is another example of a `CustomEmbedding` layer that is capable of generating a mask from input values:
```
class CustomEmbedding(tf.keras.layers.Layer):
def __init__(self, input_dim, output_dim, mask_zero=False, **kwargs):
super(CustomEmbedding, self).__init__(**kwargs)
self.input_dim = input_dim
self.output_dim = output_dim
self.mask_zero = mask_zero
def build(self, input_shape):
self.embeddings = self.add_weight(
shape=(self.input_dim, self.output_dim),
initializer='random_normal',
dtype='float32')
def call(self, inputs):
return tf.nn.embedding_lookup(self.embeddings, inputs)
def compute_mask(self, inputs, mask=None):
if not self.mask_zero:
return None
return tf.not_equal(inputs, 0)
layer = CustomEmbedding(10, 32, mask_zero=True)
x = np.random.random((3, 10)) * 9
x = x.astype('int32')
y = layer(x)
mask = layer.compute_mask(x)
print(mask)
```
## Writing layers that need mask information
Some layers are mask *consumers*: they accept a `mask` argument in `call` and use it to dertermine whether to skip certain time steps.
To write such a layer, you can simply add a `mask=None` argument in your `call` signature. The mask associated with the inputs will be passed to your layer whenever it is available.
```python
class MaskConsumer(tf.keras.layers.Layer):
def call(self, inputs, mask=None):
...
```
## Recap
That is all you need to know about masking in Keras. To recap:
- "Masking" is how layers are able to know when to skip / ignore certain timesteps in sequence inputs.
- Some layers are mask-generators: `Embedding` can generate a mask from input values (if `mask_zero=True`), and so can the `Masking` layer.
- Some layers are mask-consumers: they expose a `mask` argument in their `__call__` method. This is the case for RNN layers.
- In the Functional API and Sequential API, mask information is propagated automatically.
- When writing subclassed models or when using layers in a standalone way, pass the `mask` arguments to layers manually.
- You can easily write layers that modify the current mask, that generate a new mask, or that consume the mask associated with the inputs.
|
github_jupyter
|
```
# Install TensorFlow
!pip install tensorflow-gpu
try:
%tensorflow_version 2.x # Colab only.
except Exception:
pass
import tensorflow as tf
print(tf.__version__)
print(tf.test.gpu_device_name())
print("Num GPUs Available: ", len(tf.config.experimental.list_physical_devices('GPU')))
#imports some required libraries
import numpy as np
import matplotlib.pyplot as plt
from tensorflow.keras.layers import Input, Conv2D, Dense, Flatten, Dropout, MaxPooling2D
from tensorflow.keras.models import Model
# Load in the data
fashion_mnist = tf.keras.datasets.fashion_mnist
(x_train, y_train), (x_test, y_test) = fashion_mnist.load_data()
x_train, x_test = x_train / 255.0, x_test / 255.0
print("x_train.shape:", x_train.shape)
# the data is only 2D!
# convolution expects height x width x color
x_train = np.expand_dims(x_train, -1)
x_test = np.expand_dims(x_test, -1)
print(x_train.shape)
# number of classes
K = len(set(y_train))
print("number of classes:", K)
# Build the model using the functional API
i = Input(shape=x_train[0].shape)
x = Conv2D(128, (3, 3), strides=2, activation='relu', padding='same')(i)
x = Conv2D(256, (3, 3), strides=2, activation='relu', padding='same')(x)
x = MaxPooling2D((3, 3))(x)
x = Conv2D(512, (3, 3), strides=2, activation='relu', padding='same')(x)
x = Flatten()(x)
x = Dropout(0.2)(x)
x = Dense(1024, activation='relu')(x)
x = Dropout(0.2)(x)
x = Dense(512, activation='relu')(x)
x = Dropout(0.2)(x)
x = Dense(K, activation='softmax')(x)
model = Model(i, x)
# Compile and fit
# Note: make sure you are using the GPU for this!
model.compile(optimizer='adam',
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
history = model.fit(x_train, y_train, validation_data=(x_test, y_test), epochs=25)
# Plot loss per iteration
import matplotlib.pyplot as plt
plt.plot(history.history['loss'], label='loss')
plt.plot(history.history['val_loss'], label='val_loss')
plt.legend()
# Plot accuracy per iteration
plt.plot(history.history['accuracy'], label='acc')
plt.plot(history.history['val_accuracy'], label='val_acc')
plt.legend()
# Plot confusion matrix
from sklearn.metrics import confusion_matrix
import itertools
def plot_confusion_matrix(cm, classes,
normalize=False,
title='Confusion matrix',
cmap=plt.cm.Blues):
"""
This function prints and plots the confusion matrix.
Normalization can be applied by setting `normalize=True`.
"""
if normalize:
cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
print("Normalized confusion matrix")
else:
print('Confusion matrix, without normalization')
print(cm)
plt.imshow(cm, interpolation='nearest', cmap=cmap)
plt.title(title)
plt.colorbar()
tick_marks = np.arange(len(classes))
plt.xticks(tick_marks, classes, rotation=45)
plt.yticks(tick_marks, classes)
fmt = '.2f' if normalize else 'd'
thresh = cm.max() / 2.
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i, format(cm[i, j], fmt),
horizontalalignment="center",
color="white" if cm[i, j] > thresh else "black")
plt.tight_layout()
plt.ylabel('True label')
plt.xlabel('Predicted label')
plt.show()
p_test = model.predict(x_test).argmax(axis=1)
cm = confusion_matrix(y_test, p_test)
plot_confusion_matrix(cm, list(range(10)))
# Label mapping
labels = '''T-shirt/top
Trouser
Pullover
Dress
Coat
Sandal
Shirt
Sneaker
Bag
Ankle boot'''.split("\n")
# Show some misclassified examples
misclassified_idx = np.where(p_test != y_test)[0]
i = np.random.choice(misclassified_idx)
plt.imshow(x_test[i].reshape(28,28), cmap='gray')
plt.title("True label: %s Predicted: %s" % (labels[y_test[i]], labels[p_test[i]]));
```
|
github_jupyter
|
```
print("hello world")
1 + (3 * 4) + 5
(1 + 3) * (4 + 5)
2**4
temperature = 72.5
print("temperature")
print(temperature)
type(temperature)
day_of_week = 3
type(day_of_week)
day = "tuesday"
type(day)
print(day)
whos
day_of_week + 1
print(day)
print(temperature)
day_of_week
day_of_week + 1
day_of_week = 4
day_of_week
day_of_week = day_of_week + 1
day_of_week
day_of_week = day_of_week + 10
day_of_week
day
day + 10
"20" + 30
"20" + str(30)
int("20") + 30 + " " + 40
# exercise
# create a humidity (humidity = 0.6)
# create a temperature = 75
# create a day "saturday"
# try printing out humidity + temperature
# try printing out day plus temperature
# try printing day plus temperature plus humidity (with spaces between)
# takes you through
# creating variables
# converting variables
# adding them
# printing
# take 5 min (til 10:07 now)
humidity = 0.6
temperature = 75
day = "saturday"
print(humidity + temperature)
print(day + " " + str(humidity) + " " + str(temperature))
print(day, humidity, temperature)
# built in functions and help
max(1, 5, 2, 6)
min(1, 5, 2, 6)
#cos(3.14)
import math
math.cos(3.14)
#alias
import math as m
m.cos(3.14)
from math import cos
cos(3.14)
m.pi
m.e
cos(m.pi)
help(math)
# exercise
# calculate the sin of two times pi
# try another method or two from the math library
# (maybe calculate the natural log of euler's constant)
# take 5 min (til 10:28)
m.sin(round(2 * m.pi, 2))
m.log(m.e)
m.log10(10)
# reconvene at 10:42
# lists, loops, and conditionals
temperatures = [76, 73, 71, 68, 72, 65, 75]
temperatures[0]
temperatures[1]
temperatures[6]
temperatures[-1]
temperatures[-2]
temperatures[0:4]
temperatures[4:7]
len(temperatures)
temperatures[2:len(temperatures)]
temperatures[:4]
# exercise
# create a new list called humidities
# values [.6, .65, .7, .75, .65, .6, .55]
# print the full list
# print the length of the list
# print from index 2 through 5
# take til 11:00am
humidities = [.6, .65, .7, .75, .65, .6, .55]
print(humidities)
len(humidities)
humidities[2:6]
# enumerator
print(temperatures)
for t in temperatures:
t = t + 10
print(t)
print("all done!")
# exercise - take the code in cell 110, and replace temperatures with humidities
# move various print calls (either print(h) or print("all done") in and out of the loop
# take 5 min to do this, resume at 11:18
# try out tuples vs lists if you have extra time
# tuples
humidities_tuple = (.5, .6, 7, .8)
for h in humidities_tuple:
print(h)
humidities_tuple[2]
my_list = [1, 2, 3, 4]
my_tuple = (1, 2, 3, 4)
my_list[2] = 10
my_list
temperatures
# enumerator
for t in temperatures:
print(t)
# iterator
for i in range(len(temperatures)):
print(i, temperatures[i])
# a couple of common errors in loop processing, using iterator syntax with enumerator values
#for t in temperatures:
# print(t)
# print(temperatures[t])
#for h in humidities:
# print(h)
# print(humidities[h])
for i in range(len(temperatures)):
print(i, temperatures[i], humidities[i])
# exercise
# days of the week
# days = ['sunday', 'monday', ...]
# add days[i] to the loop above
# take 5 min, back at 11:38
days = ['sunday', 'monday', 'tuesday', 'wednesday', 'thursday', 'friday', 'saturday']
for i in range(len(days)):
print(i, days[i], temperatures[i], humidities[i])
for i in range(len(day)):
if temperatures[i] > 72:
print("it's hot", temperatures[i])
elif temperatures[i] > 70 or humidities[i] > .6:
print("it's warm", temperatures[i])
else:
print("it's cold", temperatures[i])
# as an exercise on your own, I'd recommend doing this with humidities or a combination of temp and humidity
day
day[2]
temperature = 75
temperature[1]
for d in day:
print(d)
day[3]
day[3] = 'w'
day
days
len(day)
```
|
github_jupyter
|
# Cross Validation
Splitting our datasetes into train/test sets allows us to test our model on unseen examples. However, it might be the case that we got a lucky (or unlucky) split that doesn't represent the model's actual performance. To solve this problem, we'll use a technique called cross-validation, where we use the entire dataset for training and for testing and evaluate the model accordingly.
There are several ways of performing cross-validation, and there are several corresponding iterators defined in scikit-learn. Each defines a `split` method, which will generate arrays of indices from the data set, each array indicating the instances to go into the training or testing set.
```
import pandas as pd
import numpy as np
from sklearn import datasets, svm, metrics, model_selection
x, y = datasets.load_breast_cancer(return_X_y=True)
# Define a function to split our dataset into train/test splits using indices
def kfold_train_test_split(x, y, train_indices, test_indices):
return x[train_indices], x[test_indices], y[train_indices], y[test_indices]
```
### `KFold`
`KFold` is arguably the simplest. It partitions the data into $k$ folds. It does not attempt to keep the proportions of classes.
```
k_fold = model_selection.KFold(n_splits=10) # splits the data into 10 splits, using 9 for training and 1 for testing in each iteration
# Empty array to store the scores
scores = []
for train_indices, test_indices in k_fold.split(x):
# Split data using our predefined function
x_train, x_test, y_train, y_test = kfold_train_test_split(x, y, train_indices, test_indices)
# Train model
svc = svm.SVC()
svc.fit(x_train, y_train)
# Predict using test set
y_pred = svc.predict(x_test)
# Calculate scores
accuracy = metrics.accuracy_score(y_test, y_pred)
precision = metrics.precision_score(y_test, y_pred)
recall = metrics.recall_score(y_test, y_pred)
# Create scores dictionary
scores_dict = {"accuracy": accuracy, "precision": precision, "recall": recall}
# Append to scores array
scores.append(scores_dict)
# Conver scores array to dataframe
scores_df = pd.DataFrame(scores)
scores_df
# Calculate the mean of the scores
scores_df.mean()
```
### `StratifiedKFold`
`StratifiedKFold` ensures that the proportion of classes are preserved in each training/testing set.
```
stratified_k_fold = model_selection.StratifiedKFold(n_splits=10) # splits the data into 10 splits, using 9 for training and 1 for testing in each iteration
# Empty array to store the scores
scores = []
for train_indices, test_indices in stratified_k_fold.split(x, y): # y is needed here for stratification, similar to stratify = y.
# Split data using our predefined function
x_train, x_test, y_train, y_test = kfold_train_test_split(x, y, train_indices, test_indices)
# Train model
svc = svm.SVC()
svc.fit(x_train, y_train)
# Predict using test set
y_pred = svc.predict(x_test)
# Calculate scores
accuracy = metrics.accuracy_score(y_test, y_pred)
precision = metrics.precision_score(y_test, y_pred)
recall = metrics.recall_score(y_test, y_pred)
# Create scores dictionary
scores_dict = {"accuracy": accuracy, "precision": precision, "recall": recall}
# Append to scores array
scores.append(scores_dict)
# Conver scores array to dataframe
scores_df = pd.DataFrame(scores)
scores_df
# Calculate the mean of the scores
scores_df.mean()
```
### `ShuffleSplit`
`ShuffleSplit` will generate indepedent pairs of randomly shuffled training and testing sets.
```
shuffle_k_fold = model_selection.ShuffleSplit(n_splits=10, random_state=42) # splits the data into 10 splits, using 9 for training and 1 for testing in each iteration
# Empty array to store the scores
scores = []
for train_indices, test_indices in shuffle_k_fold.split(x):
# Split data using our predefined function
x_train, x_test, y_train, y_test = kfold_train_test_split(x, y, train_indices, test_indices)
# Train model
svc = svm.SVC()
svc.fit(x_train, y_train)
# Predict using test set
y_pred = svc.predict(x_test)
# Calculate scores
accuracy = metrics.accuracy_score(y_test, y_pred)
precision = metrics.precision_score(y_test, y_pred)
recall = metrics.recall_score(y_test, y_pred)
# Create scores dictionary
scores_dict = {"accuracy": accuracy, "precision": precision, "recall": recall}
# Append to scores array
scores.append(scores_dict)
# Conver scores array to dataframe
scores_df = pd.DataFrame(scores)
scores_df
# Calculate the mean of the scores
scores_df.mean()
```
### `StratifiedShuffleSplit`
`StratifiedShuffleSplit` will generate indepedent pairs of shuffled training and testing sets. Here, however, it will ensure the training and test sets are stratified.
```
stratified_shuffled_k_fold = model_selection.StratifiedShuffleSplit(n_splits=10) # splits the data into 10 splits, using 9 for training and 1 for testing in each iteration
# Empty array to store the scores
scores = []
for train_indices, test_indices in stratified_shuffled_k_fold.split(x, y): # y is needed here for stratification, similar to stratify = y.
# Split data using our predefined function
x_train, x_test, y_train, y_test = kfold_train_test_split(x, y, train_indices, test_indices)
# Train model
svc = svm.SVC()
svc.fit(x_train, y_train)
# Predict using test set
y_pred = svc.predict(x_test)
# Calculate scores
accuracy = metrics.accuracy_score(y_test, y_pred)
precision = metrics.precision_score(y_test, y_pred)
recall = metrics.recall_score(y_test, y_pred)
# Create scores dictionary
scores_dict = {"accuracy": accuracy, "precision": precision, "recall": recall}
# Append to scores array
scores.append(scores_dict)
# Conver scores array to dataframe
scores_df = pd.DataFrame(scores)
scores_df
# Calculate the mean of the scores
scores_df.mean()
```
|
github_jupyter
|
# FloPy
### A quick demo of how to control the ASCII format of numeric arrays written by FloPy
load and run the Freyberg model
```
import sys
import os
import platform
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
# run installed version of flopy or add local path
try:
import flopy
except:
fpth = os.path.abspath(os.path.join('..', '..'))
sys.path.append(fpth)
import flopy
#Set name of MODFLOW exe
# assumes executable is in users path statement
version = 'mf2005'
exe_name = 'mf2005'
if platform.system() == 'Windows':
exe_name = 'mf2005.exe'
mfexe = exe_name
#Set the paths
loadpth = os.path.join('..', 'data', 'freyberg')
modelpth = os.path.join('data')
#make sure modelpth directory exists
if not os.path.exists(modelpth):
os.makedirs(modelpth)
print(sys.version)
print('numpy version: {}'.format(np.__version__))
print('matplotlib version: {}'.format(mpl.__version__))
print('flopy version: {}'.format(flopy.__version__))
ml = flopy.modflow.Modflow.load('freyberg.nam', model_ws=loadpth,
exe_name=exe_name, version=version)
ml.model_ws = modelpth
ml.write_input()
success, buff = ml.run_model()
if not success:
print ('Something bad happened.')
files = ['freyberg.hds', 'freyberg.cbc']
for f in files:
if os.path.isfile(os.path.join(modelpth, f)):
msg = 'Output file located: {}'.format(f)
print (msg)
else:
errmsg = 'Error. Output file cannot be found: {}'.format(f)
print (errmsg)
```
Each ``Util2d`` instance now has a ```.format``` attribute, which is an ```ArrayFormat``` instance:
```
print(ml.lpf.hk[0].format)
```
The ```ArrayFormat``` class exposes each of the attributes seen in the ```ArrayFormat.___str___()``` call. ```ArrayFormat``` also exposes ``.fortran``, ``.py`` and ``.numpy`` atrributes, which are the respective format descriptors:
```
print(ml.dis.botm[0].format.fortran)
print(ml.dis.botm[0].format.py)
print(ml.dis.botm[0].format.numpy)
```
#### (re)-setting ```.format```
We can reset the format using a standard fortran type format descriptor
```
ml.dis.botm[0].format.fortran = "(6f10.4)"
print(ml.dis.botm[0].format.fortran)
print(ml.dis.botm[0].format.py)
print(ml.dis.botm[0].format.numpy)
ml.write_input()
success, buff = ml.run_model()
```
Let's load the model we just wrote and check that the desired ```botm[0].format``` was used:
```
ml1 = flopy.modflow.Modflow.load("freyberg.nam",model_ws=modelpth)
print(ml1.dis.botm[0].format)
```
We can also reset individual format components (we can also generate some warnings):
```
ml.dis.botm[0].format.width = 9
ml.dis.botm[0].format.decimal = 1
print(ml1.dis.botm[0].format)
```
We can also select ``free`` format. Note that setting to free format resets the format attributes to the default, max precision:
```
ml.dis.botm[0].format.free = True
print(ml1.dis.botm[0].format)
ml.write_input()
success, buff = ml.run_model()
ml1 = flopy.modflow.Modflow.load("freyberg.nam",model_ws=modelpth)
print(ml1.dis.botm[0].format)
```
|
github_jupyter
|
### Simple Residual model in Keras
This notebook is simply for testing a resnet-50 inspired model built in Keras on a numerical signs dataset.
```
import keras
import numpy as np
import matplotlib.pyplot as plt
from keras import layers
from keras.layers import Input, Dense, Activation, ZeroPadding2D, BatchNormalization, Flatten, Conv2D,ZeroPadding1D, Conv1D, Add
from keras.layers import MaxPooling2D, Dropout, AveragePooling2D
from keras.models import Model
from sklearn.model_selection import train_test_split
from sklearn.utils import shuffle
import warnings
warnings.filterwarnings('ignore')
# Using a signs dataset, with images of numerical signs from 0-9
X = np.load("../data/sign-digits/X.npy")
y = np.load("../data/sign-digits/y.npy")
X.shape = (2062, 64, 64, 1)
X = shuffle(X,random_state=0)
y = shuffle(y,random_state=0)
print(X.shape)
print(y.shape)
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.1)
print(X_train.shape)
print(X_test.shape)
# Block corresponding with no change in size
def identity(X, f, filters):
"""
filters: filters for each of the conv2D
f: size of filter to use in mid block
"""
F1,F2,F3 = filters
X_earlier = X
# Block 1
X = Conv2D(F1, kernel_size=(1,1), strides=(1,1),padding="valid",kernel_initializer=keras.initializers.glorot_normal())(X)
X = BatchNormalization(axis=3)(X)
X = Activation("relu")(X)
# Block 2
X = Conv2D(F2, kernel_size=(f,f), strides=(1,1),padding="same",kernel_initializer=keras.initializers.glorot_normal())(X)
X = BatchNormalization(axis=3)(X)
X = Activation("relu")(X)
# Block 3
X = Conv2D(F3, kernel_size=(1,1), strides=(1,1),padding="valid",kernel_initializer=keras.initializers.glorot_normal())(X)
X = BatchNormalization(axis=3)(X)
X = Add()([X,X_earlier]) # Add earlier activation
X = Activation("relu")(X)
return X
# Block corresponding with a change in size
def conv_resid(X, f, filters,s):
"""
filters: filters for each of the conv2D
s: stride size to resize the output
"""
F1,F2,F3 = filters
X_earlier = X
# Block 1
X = Conv2D(F1, kernel_size=(1,1), strides=(s,s),padding="valid",kernel_initializer=keras.initializers.glorot_normal())(X)
X = BatchNormalization(axis=3)(X)
X = Activation("relu")(X)
# Block 2
X = Conv2D(F2, kernel_size=(f,f), strides=(1,1),padding="same",kernel_initializer=keras.initializers.glorot_normal())(X)
X = BatchNormalization(axis=3)(X)
X = Activation("relu")(X)
# Block 3
X = Conv2D(F3, kernel_size=(1,1), strides=(1,1),padding="valid",kernel_initializer=keras.initializers.glorot_normal())(X)
X = BatchNormalization(axis=3)(X)
# Resize earlier activation (X_earlier)
X_earlier = Conv2D(F3, kernel_size=(1,1), strides=(s,s),padding="valid",kernel_initializer=keras.initializers.glorot_normal())(X_earlier)
X_earlier = BatchNormalization(axis=3)(X_earlier)
# Add earlier activation
X = Add()([X,X_earlier])
X = Activation("relu")(X)
return X
# The Input shape for this model will be 64x64x1
def model(input_shape):
X_input = Input(input_shape)
X = ZeroPadding2D(padding=(3,3))(X_input)
X = Conv2D(64,kernel_size=(7,7),padding="valid",kernel_initializer=keras.initializers.glorot_uniform())(X)
X = BatchNormalization(axis=3)(X)
X = Activation(("relu"))(X)
X = MaxPooling2D((3,3),strides=(2,2))(X)
# indentity block 1
X = conv_resid(X, 3, [64,64,256], 1)
X = identity(X, 3, [64,64,256])
X = identity(X, 3, [64,64,256])
# Identity block 2
X = conv_resid(X, 3, [128,128,512], 2)
X = identity(X, 3, [128,128,512])
X = identity(X, 3, [128,128,512])
X = identity(X, 3, [128,128,512])
# Identity block 3
X = conv_resid(X, 3, [256, 256, 1024], 2)
X = identity(X, 3, [256, 256, 1024])
X = identity(X, 3, [256, 256, 1024])
X = identity(X, 3, [256, 256, 1024])
X = identity(X, 3, [256, 256, 1024])
X = identity(X, 3, [256, 256, 1024])
# Identity block 4
X = conv_resid(X, 3, [512, 512, 2048], 2)
X = identity(X, 3, [512, 512, 2048])
X = identity(X, 3, [512, 512, 2048])
X = AveragePooling2D((2,2), name="avg_pool")(X)
# Flatten final layer
X = Flatten()(X)
X = Dense(10, activation="softmax",name="dense02",kernel_initializer = keras.initializers.glorot_normal())(X)
model = Model(inputs=X_input, outputs=X, name="resnet")
return model
resid_classi = model(X_train[0].shape)
resid_classi.compile(optimizer="adam", loss="categorical_crossentropy", metrics=['accuracy'])
resid_classi.fit(X_train, y_train,epochs=10,batch_size=10, validation_data=[X_test,y_test])
```
|
github_jupyter
|
# UCI Metro dataset
```
import pandas as pd
import os
from pathlib import Path
from config import data_raw_folder, data_processed_folder
from timeeval import Datasets
import matplotlib.pyplot as plt
%matplotlib inline
plt.rcParams['figure.figsize'] = (20, 10)
dataset_collection_name = "Metro"
source_folder = Path(data_raw_folder) / "UCI ML Repository/Metro"
target_folder = Path(data_processed_folder)
from pathlib import Path
print(f"Looking for source datasets in {source_folder.absolute()} and\nsaving processed datasets in {target_folder.absolute()}")
```
## Dataset transformation and pre-processing
```
train_type = "unsupervised"
train_is_normal = False
input_type = "multivariate"
datetime_index = True
dataset_type = "real"
# create target directory
dataset_subfolder = os.path.join(input_type, dataset_collection_name)
target_subfolder = os.path.join(target_folder, dataset_subfolder)
try:
os.makedirs(target_subfolder)
print(f"Created directories {target_subfolder}")
except FileExistsError:
print(f"Directories {target_subfolder} already exist")
pass
dm = Datasets(target_folder)
# get target filenames
dataset_name = "metro-traffic-volume"
filename = f"{dataset_name}.test.csv"
source_file = source_folder / "Metro_Interstate_Traffic_Volume.csv"
path = os.path.join(dataset_subfolder, filename)
target_filepath = os.path.join(target_subfolder, filename)
# transform file
df = pd.read_csv(source_file)
df = df[["date_time", "traffic_volume", "temp", "rain_1h", "snow_1h", "clouds_all", "holiday"]].copy()
df.insert(0, "timestamp", pd.to_datetime(df["date_time"]))
df.loc[df["holiday"] == "None", "is_anomaly"] = 0
df.loc[~(df["holiday"] == "None"), "is_anomaly"] = 1
df["is_anomaly"] = df["is_anomaly"].astype(int)
df = df.drop(columns=["date_time", "holiday"])
df.to_csv(target_filepath, index=False)
print(f"Processed source dataset {source_file} -> {target_filepath}")
dataset_length = len(df)
# save metadata
dm.add_dataset((dataset_collection_name, dataset_name),
train_path = None,
test_path = path,
dataset_type = dataset_type,
datetime_index = datetime_index,
split_at = None,
train_type = train_type,
train_is_normal = train_is_normal,
input_type = input_type,
dataset_length = dataset_length
)
dm.save()
dm.refresh()
dm._df.loc[slice(dataset_collection_name, dataset_collection_name)]
```
## Experimentation
```
source_file = source_folder / "Metro_Interstate_Traffic_Volume.csv"
df = pd.read_csv(source_file)
df
df1 = df[["date_time", "traffic_volume", "temp", "rain_1h", "snow_1h", "clouds_all", "holiday"]].copy()
df1.insert(0, "timestamp", pd.to_datetime(df1["date_time"]))
df1.loc[df1["holiday"] == "None", "is_anomaly"] = 0
df1.loc[~(df1["holiday"] == "None"), "is_anomaly"] = 1
df1["is_anomaly"] = df1["is_anomaly"].astype(int)
df1 = df1.drop(columns=["date_time", "holiday"])
df1
df1[["traffic_volume", "temp", "rain_1h", "snow_1h", "clouds_all"]].plot()
df1["is_anomaly"].plot(secondary_y=True)
plt.show()
```
|
github_jupyter
|
## Practice: Dealing with Word Embeddings
Today we gonna play with word embeddings: train our own little embedding, load one from gensim model zoo and use it to visualize text corpora.
This whole thing is gonna happen on top of embedding dataset.
__Requirements:__ `pip install --upgrade nltk gensim bokeh umap-learn` , but only if you're running locally.
```
import itertools
import string
import numpy as np
import umap
from nltk.tokenize import WordPunctTokenizer
from matplotlib import pyplot as plt
from IPython.display import clear_output
# download the data:
!wget https://www.dropbox.com/s/obaitrix9jyu84r/quora.txt?dl=1 -O ./quora.txt -nc
# alternative download link: https://yadi.sk/i/BPQrUu1NaTduEw
data = list(open("./quora.txt", encoding="utf-8"))
data[50]
```
__Tokenization:__ a typical first step for an nlp task is to split raw data into words.
The text we're working with is in raw format: with all the punctuation and smiles attached to some words, so a simple str.split won't do.
Let's use __`nltk`__ - a library that handles many nlp tasks like tokenization, stemming or part-of-speech tagging.
```
tokenizer = WordPunctTokenizer()
print(tokenizer.tokenize(data[50]))
# TASK: lowercase everything and extract tokens with tokenizer.
# data_tok should be a list of lists of tokens for each line in data.
data_tok = # YOUR CODE HEER
```
Let's peek at the result:
```
' '.join(data_tok[0])
```
Small check that everything is alright
```
assert all(isinstance(row, (list, tuple)) for row in data_tok), "please convert each line into a list of tokens (strings)"
assert all(all(isinstance(tok, str) for tok in row) for row in data_tok), "please convert each line into a list of tokens (strings)"
is_latin = lambda tok: all('a' <= x.lower() <= 'z' for x in tok)
assert all(map(lambda l: not is_latin(l) or l.islower(), map(' '.join, data_tok))), "please make sure to lowercase the data"
```
__Word vectors:__ as the saying goes, there's more than one way to train word embeddings. There's Word2Vec and GloVe with different objective functions. Then there's fasttext that uses character-level models to train word embeddings.
The choice is huge, so let's start someplace small: __gensim__ is another NLP library that features many vector-based models incuding word2vec.
```
from gensim.models import Word2Vec
model = Word2Vec(data_tok,
size=32, # embedding vector size
min_count=5, # consider words that occured at least 5 times
window=5).wv # define context as a 5-word window around the target word
# now you can get word vectors !
model.get_vector('anything')
# or query similar words directly. Go play with it!
model.most_similar('bread')
```
### Using pre-trained model
Took it a while, huh? Now imagine training life-sized (100~300D) word embeddings on gigabytes of text: wikipedia articles or twitter posts.
Thankfully, nowadays you can get a pre-trained word embedding model in 2 lines of code (no sms required, promise).
```
import gensim.downloader as api
model = api.load('glove-twitter-25')
model.most_similar(positive=["coder", "money"], negative=["brain"])
```
### Visualizing word vectors
One way to see if our vectors are any good is to plot them. Thing is, those vectors are in 30D+ space and we humans are more used to 2-3D.
Luckily, we machine learners know about __dimensionality reduction__ methods.
Let's use that to plot 1000 most frequent words
```
words = sorted(model.vocab.keys(),
key=lambda word: model.vocab[word].count,
reverse=True)[:1000]
print(words[::100])
# for each word, compute it's vector with model
word_vectors = # YOUR CODE
assert isinstance(word_vectors, np.ndarray)
assert word_vectors.shape == (len(words), 25)
assert np.isfinite(word_vectors).all()
word_vectors.shape
```
#### Linear projection: PCA
The simplest linear dimensionality reduction method is __P__rincipial __C__omponent __A__nalysis.
In geometric terms, PCA tries to find axes along which most of the variance occurs. The "natural" axes, if you wish.
<img src="https://github.com/yandexdataschool/Practical_RL/raw/master/yet_another_week/_resource/pca_fish.png" style="width:30%">
Under the hood, it attempts to decompose object-feature matrix $X$ into two smaller matrices: $W$ and $\hat W$ minimizing _mean squared error_:
$$\|(X W) \hat{W} - X\|^2_2 \to_{W, \hat{W}} \min$$
- $X \in \mathbb{R}^{n \times m}$ - object matrix (**centered**);
- $W \in \mathbb{R}^{m \times d}$ - matrix of direct transformation;
- $\hat{W} \in \mathbb{R}^{d \times m}$ - matrix of reverse transformation;
- $n$ samples, $m$ original dimensions and $d$ target dimensions;
```
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
pca = PCA(2)
scaler = StandardScaler()
# map word vectors onto 2d plane with PCA. Use good old sklearn api (fit, transform)
# after that, normalize vectors to make sure they have zero mean and unit variance
word_vectors_pca = # YOUR CODE
# and maybe MORE OF YOUR CODE here :)
assert word_vectors_pca.shape == (len(word_vectors), 2), "there must be a 2d vector for each word"
assert max(abs(word_vectors_pca.mean(0))) < 1e-5, "points must be zero-centered"
assert max(abs(1.0 - word_vectors_pca.std(0))) < 1e-2, "points must have unit variance"
```
#### Let's draw it!
```
import bokeh.models as bm, bokeh.plotting as pl
from bokeh.io import output_notebook
output_notebook()
def draw_vectors(x, y, radius=10, alpha=0.25, color='blue',
width=600, height=400, show=True, **kwargs):
""" draws an interactive plot for data points with auxilirary info on hover """
if isinstance(color, str): color = [color] * len(x)
data_source = bm.ColumnDataSource({ 'x' : x, 'y' : y, 'color': color, **kwargs })
fig = pl.figure(active_scroll='wheel_zoom', width=width, height=height)
fig.scatter('x', 'y', size=radius, color='color', alpha=alpha, source=data_source)
fig.add_tools(bm.HoverTool(tooltips=[(key, "@" + key) for key in kwargs.keys()]))
if show: pl.show(fig)
return fig
draw_vectors(word_vectors_pca[:, 0], word_vectors_pca[:, 1], token=words)
# hover a mouse over there and see if you can identify the clusters
```
### Visualizing neighbors with UMAP
PCA is nice but it's strictly linear and thus only able to capture coarse high-level structure of the data.
If we instead want to focus on keeping neighboring points near, we could use UMAP, which is itself an embedding method. Here you can read __[more on UMAP (ru)](https://habr.com/ru/company/newprolab/blog/350584/)__ and on __[t-SNE](https://distill.pub/2016/misread-tsne/)__, which is also an embedding.
```
embedding = umap.UMAP(n_neighbors=5).fit_transform(word_vectors) # преобразовываем
draw_vectors(embedding[:, 0], embedding[:, 1], token=words)
# hover a mouse over there and see if you can identify the clusters
```
### Visualizing phrases
Word embeddings can also be used to represent short phrases. The simplest way is to take __an average__ of vectors for all tokens in the phrase with some weights.
This trick is useful to identify what data are you working with: find if there are any outliers, clusters or other artefacts.
Let's try this new hammer on our data!
```
def get_phrase_embedding(phrase):
"""
Convert phrase to a vector by aggregating it's word embeddings. See description above.
"""
# 1. lowercase phrase
# 2. tokenize phrase
# 3. average word vectors for all words in tokenized phrase
# skip words that are not in model's vocabulary
# if all words are missing from vocabulary, return zeros
vector = np.zeros([model.vector_size], dtype='float32')
phrase_tokenized = # YOUR CODE HERE
phrase_vectors = [model[x] for x in phrase_tokenized if x in model.vocab.keys()]
if len(phrase_vectors) != 0:
vector = np.mean(phrase_vectors, axis=0)
# YOUR CODE
return vector
get_phrase_embedding(data[402687])
vector = get_phrase_embedding("I'm very sure. This never happened to me before...")
# let's only consider ~5k phrases for a first run.
chosen_phrases = data[::len(data) // 1000]
# compute vectors for chosen phrases and turn them to numpy array
phrase_vectors = np.asarray([get_phrase_embedding(x) for x in chosen_phrases]) # YOUR CODE
assert isinstance(phrase_vectors, np.ndarray) and np.isfinite(phrase_vectors).all()
assert phrase_vectors.shape == (len(chosen_phrases), model.vector_size)
# map vectors into 2d space with pca, tsne or your other method of choice
# don't forget to normalize
phrase_vectors_2d = umap.UMAP(n_neighbors=3).fit_transform(phrase_vectors) # преобразовываем
# phrase_vectors_2d = (phrase_vectors_2d - phrase_vectors_2d.mean(axis=0)) / phrase_vectors_2d.std(axis=0)
draw_vectors(phrase_vectors_2d[:, 0], phrase_vectors_2d[:, 1],
phrase=[phrase[:50] for phrase in chosen_phrases],
radius=20,)
```
Finally, let's build a simple "similar question" engine with phrase embeddings we've built.
```
# compute vector embedding for all lines in data
data_vectors = np.vstack([get_phrase_embedding(l) for l in data])
norms = np.linalg.norm(data_vectors, axis=1)
printable_set = set(string.printable)
data_subset = [x for x in data if set(x).issubset(printable_set)]
def find_nearest(query, k=10):
"""
given text line (query), return k most similar lines from data, sorted from most to least similar
similarity should be measured as cosine between query and line embedding vectors
hint: it's okay to use global variables: data and data_vectors. see also: np.argpartition, np.argsort
"""
# YOUR CODE
query_vector = get_phrase_embedding(query)
dists = data_vectors.dot(query_vector[:, None])[:, 0] / ((norms+1e-16)*np.linalg.norm(query_vector))
nearest_elements = dists.argsort(axis=0)[-k:][::-1]
out = [data[i] for i in nearest_elements]
return out# <YOUR CODE: top-k lines starting from most similar>
results = find_nearest(query="How do i enter the matrix?", k=10)
print(''.join(results))
assert len(results) == 10 and isinstance(results[0], str)
assert results[0] == 'How do I get to the dark web?\n'
# assert results[3] == 'What can I do to save the world?\n'
find_nearest(query="How does Trump?", k=10)
find_nearest(query="Why don't i ask a question myself?", k=10)
from sklearn.cluster import DBSCAN, KMeans
kmeans = KMeans(3)
labels = kmeans.fit_predict(np.asarray(phrase_vectors))
plt.figure(figsize=(12, 10))
plt.scatter(phrase_vectors_2d[:,0], phrase_vectors_2d[:, 1], c=labels.astype(float))
```
__Now what?__
* Try running TSNE instead of UMAP (it takes a long time)
* Try running UMAP or TSNEon all data, not just 1000 phrases
* See what other embeddings are there in the model zoo: `gensim.downloader.info()`
* Take a look at [FastText](https://github.com/facebookresearch/fastText) embeddings
* Optimize find_nearest with locality-sensitive hashing: use [nearpy](https://github.com/pixelogik/NearPy) or `sklearn.neighbors`.
|
github_jupyter
|
```
import numpy as np
import cv2
import mediapipe as mp
import tensorflow as tf
import time
mp_drawing = mp.solutions.drawing_utils
mp_drawing_styles = mp.solutions.drawing_styles
mp_hands = mp.solutions.hands
# load model
tflite_save_path = 'model/model.tflite'
interpreter = tf.lite.Interpreter(model_path=tflite_save_path)
interpreter.allocate_tensors()
input_details = interpreter.get_input_details()
output_details = interpreter.get_output_details()
def gesture_preprocess(landmark):
"""
convert landmarks for trainable data
66 features
X (21): 0-20
Y (21): 21-41
Z (21): 42-62
X,Y,Z range (3): 63-65
params landmark: mediapipe landmark for 1 hand
params label: str
return: np.array (1,66)
"""
lm_x = np.array([])
lm_y = np.array([])
lm_z = np.array([])
for hlm in landmark.landmark:
lm_x = np.append(lm_x, hlm.x)
lm_y = np.append(lm_y, hlm.y)
lm_z = np.append(lm_z, hlm.z)
data_gest = [lm_x, lm_y, lm_z]
x_rng, y_rng, z_rng = lm_x.max()-lm_x.min(), lm_y.max()-lm_y.min(), lm_z.max()-lm_z.min()
data_gest = np.ravel([(k-k.min())/(k.max()-k.min()) for i, k in enumerate(data_gest)])
data_gest = np.append(data_gest, [x_rng, y_rng, z_rng])
return data_gest.astype('float32')
def gesture_inference(data):
"""
inference
param data: np.array
return: int class
"""
interpreter.set_tensor(input_details[0]['index'], np.array([data]))
interpreter.invoke()
tflite_results = interpreter.get_tensor(output_details[0]['index'])
inf_class_idx = np.argmax(np.squeeze(tflite_results))
if np.squeeze(tflite_results)[inf_class_idx] < 0.95:
return 4
return inf_class_idx
# For webcam input:
detect_time = time.time()
inf_class = {0: 'Hit', 1: 'Stand', 2: 'Split', 3: 'Reset', 4: 'None'}
inf_class_idx = 4
cap = cv2.VideoCapture(0)
with mp_hands.Hands(
max_num_hands=1,
model_complexity=1,
min_detection_confidence=0.5,
min_tracking_confidence=0.5) as hands:
while cap.isOpened():
success, image = cap.read()
if not success:
print("Ignoring empty camera frame.")
continue
# To improve performance, optionally mark the image as not writeable to
# pass by reference.
image.flags.writeable = False
image = cv2.cvtColor(image, cv2.COLOR_BGR2RGB)
results = hands.process(image)
# Draw + infer: the hand annotations on the image.
image.flags.writeable = True
image = cv2.cvtColor(image, cv2.COLOR_RGB2BGR)
if results.multi_hand_landmarks:
if (time.time() - detect_time) > 0.5:
print("detected hand")
for hand_landmarks in results.multi_hand_landmarks:
# inference
gest_data = gesture_preprocess(hand_landmarks)
inf_class_idx = gesture_inference(gest_data)
# draw
mp_drawing.draw_landmarks(
image,
hand_landmarks,
mp_hands.HAND_CONNECTIONS,
mp_drawing_styles.get_default_hand_landmarks_style(),
mp_drawing_styles.get_default_hand_connections_style())
else:
detect_time = time.time()
image_height, image_width, _ = image.shape
cv2.putText(image, f"{inf_class[inf_class_idx]}", (0, 25), cv2.FONT_HERSHEY_SIMPLEX, 0.9, (36,255,12), 2)
cv2.imshow('MediaPipe Hands', image)
if cv2.waitKey(5) & 0xFF == 27:
break
cap.release()
cv2.destroyAllWindows()
```
|
github_jupyter
|
# Rule Scorer Example
The Rule Scorer is used to generate scores for a set of rules based on a labelled dataset.
## Requirements
To run, you'll need the following:
* A rule set (specifically the binary columns of the rules as applied to a dataset).
* The binary target column associated with the above dataset.
----
## Import packages
```
from iguanas.rule_scoring import RuleScorer, PerformanceScorer, ConstantScaler
from iguanas.metrics.classification import Precision
import pandas as pd
```
## Read in data
Let's read in some dummy rules (stored as binary columns) and the target column.
```
X_rules_train = pd.read_csv(
'dummy_data/X_rules_train.csv',
index_col='eid'
)
y_train = pd.read_csv(
'dummy_data/y_train.csv',
index_col='eid'
).squeeze()
X_rules_test = pd.read_csv(
'dummy_data/X_rules_test.csv',
index_col='eid'
)
y_test = pd.read_csv(
'dummy_data//y_test.csv',
index_col='eid'
).squeeze()
```
----
## Generate scores
### Set up class parameters
Now we can set our class parameters for the Rule Scorer. Here we pass an instantiated scoring class (which generates the raw scores) and an instantiated scaling class (which scales the scores to be more readable - **this is optional**). The scoring classes are located in the `rule_scoring_methods` module; the scaling classes are located in the `rule_score_scalers` module. **See the class docstrings for more information on each type of scoring/scaling class.**
In this example, we'll use the `PerformanceScorer` class for scoring the rules (based on the precision score) and the `ConstantScaler` class for scaling. **Note that we're using the *Precision* class from the *metrics.classification* module rather than Sklearn's *precision_score* function, as the former is ~100 times faster on larger datasets.**
**Please see the class docstring for more information on each parameter.**
```
precision_score = Precision()
params = {
'scoring_class': PerformanceScorer(metric=precision_score.fit),
'scaling_class': ConstantScaler(limit=-100)
}
```
### Instantiate class and run fit method
Once the parameters have been set, we can run the `fit` method to generate scores.
```
rs = RuleScorer(**params)
rs.fit(
X_rules=X_rules_train,
y=y_train
)
```
### Outputs
The `fit` method does not return anything. See the `Attributes` section in the class docstring for a description of each attribute generated:
```
rs.rule_scores.head()
```
----
## Apply rules to a separate dataset
Use the `transform` method to apply the generated rules to another dataset.
```
X_scores_test = rs.transform(X_rules=X_rules_test)
```
### Outputs
The `transform` method returns a dataframe giving the scores of the rules as applied to the dataset.
```
X_scores_test.head()
```
----
## Generate rule score and apply them to the training set (in one step)
You can also use the `fit_transform` method to generate scores and apply them to the training set.
```
X_scores_train = rs.fit_transform(
X_rules=X_rules_train,
y=y_train
)
```
### Outputs
The `transform` method returns a dataframe giving the scores of the rules as applied to the dataset. See the `Attributes` section in the class docstring for a description of each attribute generated:
```
rs.rule_scores.head()
X_scores_train.head()
```
----
|
github_jupyter
|
Importando as Dependências
```
import os
import copy
# os.chdir('corpora')
from scripts.anntools import Collection
from pathlib import Path
import nltk
nltk.download('punkt')
```
Leitura de Arquivo
```
c = Collection()
for fname in Path("original/training/").rglob("*.txt"):
c.load(fname)
```
Acesso a uma instância anotada
```
c.sentences[0]
```
Acesso ao texto de uma instância
```
c.sentences[0].text
```
Acesso às entidades nomeadas de uma instância
```
c.sentences[0].keyphrases
```
Acesso às relações anotadas de uma instância
```
c.sentences[0].relations
```
Pré-processando os Dados
```
def extract_keyphrases(keyphrases, text):
tags = {}
for keyphrase in sorted(keyphrases, key=lambda x: len(x.text)):
ktext = keyphrase.text
ktokens = [text[s[0]:s[1]] for s in keyphrase.spans]
# casos contínuos
idxs, ponteiro = [], 0
for i, token in enumerate(tokens):
if token == ktokens[ponteiro]:
idxs.append(i)
ponteiro += 1
else:
idxs, ponteiro = [], 0
if ponteiro == len(ktokens):
break
if len(ktokens) != len(idxs):
idxs, ponteiro = [], 0
for i, token in enumerate(tokens):
if token == ktokens[ponteiro]:
idxs.append(i)
ponteiro += 1
if ponteiro == len(ktokens):
break
error = False
if len(ktokens) != len(idxs):
error = True
tags[keyphrase.id] = {
'text': ktext,
'idxs': idxs,
'tokens': [text[s[0]:s[1]] for s in keyphrase.spans],
'attributes': [attr.__repr__() for attr in keyphrase.attributes],
'spans': keyphrase.spans,
'label': keyphrase.label,
'id': keyphrase.id,
'error': error
}
return tags
data = []
for instance in c.sentences:
text = instance.text
tokens = nltk.word_tokenize(text.replace('–', ' – '), language='spanish')
keyphrases = extract_keyphrases(instance.keyphrases, text)
relations = []
for relation in instance.relations:
relations.append({
'arg1': relation.origin,
'arg2': relation.destination,
'label': relation.label
})
data.append({
'text': text,
'tokens': tokens,
'keyphrases': keyphrases,
'relations': relations
})
```
Separando dados e salvando
```
from random import shuffle
shuffle(data)
size = int(len(data)*0.2)
trainset, _set = data[size:], data[:size]
size = int(len(_set)*0.5)
devset, testset = _set[size:], _set[:size]
import json
if not os.path.exists('preprocessed'):
os.mkdir('preprocessed')
json.dump(trainset, open('preprocessed/trainset.json', 'w'), sort_keys=True, indent=4, separators=(',', ':'))
json.dump(devset, open('preprocessed/devset.json', 'w'), sort_keys=True, indent=4, separators=(',', ':'))
json.dump(testset, open('preprocessed/testset.json', 'w'), sort_keys=True, indent=4, separators=(',', ':'))
for row in trainset:
keyphrases = row['keyphrases']
for kid in keyphrases:
keyphrase = keyphrases[kid]
for i, idx in enumerate(keyphrase['idxs']):
if i > 0:
if keyphrase['idxs'][i-1]+1 != idx:
print(keyphrase)
print(row['tokens'])
print()
break
```
|
github_jupyter
|
# SU Deep Learning with Tensorflow: Python & NumPy Tutorial
Python 3 and NumPy will be used extensively throughout this course, so it's important to be familiar with them.
One can also check the website's tutorial for further preparation:
https://deep-learning-su.github.io/python-numpy-tutorial/
## Python 3
If you're unfamiliar with Python 3, here are some of the most common changes from Python 2 to look out for.
### Print is a function
```
print("Hello!")
```
Without parentheses, printing will not work.
```
print "Hello!"
```
### Floating point division by default
```
5 / 2
```
To do integer division, we use two backslashes:
```
5 // 2
```
### No xrange
The xrange from Python 2 is now merged into "range" for Python 3 and there is no xrange in Python 3. In Python 3, range(3) does not create a list of 3 elements as it would in Python 2, rather just creates a more memory efficient iterator.
Hence,
xrange in Python 3: Does not exist
range in Python 3: Has very similar behavior to Python 2's xrange
```
for i in range(3):
print(i)
range(3)
# If need be, can use the following to get a similar behavior to Python 2's range:
print(list(range(3)))
```
# NumPy
"NumPy is the fundamental package for scientific computing in Python. It is a Python library that provides a multidimensional array object, various derived objects (such as masked arrays and matrices), and an assortment of routines for fast operations on arrays, including mathematical, logical, shape manipulation, sorting, selecting, I/O, discrete Fourier transforms, basic linear algebra, basic statistical operations, random simulation and much more"
-https://docs.scipy.org/doc/numpy-1.10.1/user/whatisnumpy.html.
```
import numpy as np
```
Let's run through an example showing how powerful NumPy is. Suppose we have two lists a and b, consisting of the first 100,000 non-negative numbers, and we want to create a new list c whose *i*th element is a[i] + 2 * b[i].
Without NumPy:
```
%%time
a = [i for i in range(100000)]
b = [i for i in range(100000)]
%%time
c = []
for i in range(len(a)):
c.append(a[i] + 2 * b[i])
```
With NumPy:
```
%%time
a = np.arange(100000)
b = np.arange(100000)
%%time
c = a + 2 * b
```
The result is 10 to 15 times faster, and we could do it in fewer lines of code (and the code itself is more intuitive)!
Regular Python is much slower due to type checking and other overhead of needing to interpret code and support Python's abstractions.
For example, if we are doing some addition in a loop, constantly type checking in a loop will lead to many more instructions than just performing a regular addition operation. NumPy, using optimized pre-compiled C code, is able to avoid a lot of the overhead introduced.
The process we used above is **vectorization**. Vectorization refers to applying operations to arrays instead of just individual elements (i.e. no loops).
Why vectorize?
1. Much faster
2. Easier to read and fewer lines of code
3. More closely assembles mathematical notation
Vectorization is one of the main reasons why NumPy is so powerful.
## ndarray
ndarrays, n-dimensional arrays of homogenous data type, are the fundamental datatype used in NumPy. As these arrays are of the same type and are fixed size at creation, they offer less flexibility than Python lists, but can be substantially more efficient runtime and memory-wise. (Python lists are arrays of pointers to objects, adding a layer of indirection.)
The number of dimensions is the rank of the array; the shape of an array is a tuple of integers giving the size of the array along each dimension.
```
# Can initialize ndarrays with Python lists, for example:
a = np.array([1, 2, 3]) # Create a rank 1 array
print(type(a)) # Prints "<class 'numpy.ndarray'>"
print(a.shape) # Prints "(3,)"
print(a[0], a[1], a[2]) # Prints "1 2 3"
a[0] = 5 # Change an element of the array
print(a) # Prints "[5, 2, 3]"
b = np.array([[1, 2, 3],
[4, 5, 6]]) # Create a rank 2 array
print(b.shape) # Prints "(2, 3)"
print(b[0, 0], b[0, 1], b[1, 0]) # Prints "1 2 4"
```
There are many other initializations that NumPy provides:
```
a = np.zeros((2, 2)) # Create an array of all zeros
print(a) # Prints "[[ 0. 0.]
# [ 0. 0.]]"
b = np.full((2, 2), 7) # Create a constant array
print(b) # Prints "[[ 7. 7.]
# [ 7. 7.]]"
c = np.eye(2) # Create a 2 x 2 identity matrix
print(c) # Prints "[[ 1. 0.]
# [ 0. 1.]]"
d = np.random.random((2, 2)) # Create an array filled with random values
print(d) # Might print "[[ 0.91940167 0.08143941]
# [ 0.68744134 0.87236687]]"
```
How do we create a 2 by 2 matrix of ones?
```
a = np.ones((2, 2)) # Create an array of all ones
print(a) # Prints "[[ 1. 1.]
# [ 1. 1.]]"
```
Useful to keep track of shape; helpful for debugging and knowing dimensions will be very useful when computing gradients, among other reasons.
```
nums = np.arange(8)
print(nums)
print(nums.shape)
nums = nums.reshape((2, 4))
print('Reshaped:\n', nums)
print(nums.shape)
# The -1 in reshape corresponds to an unknown dimension that numpy will figure out,
# based on all other dimensions and the array size.
# Can only specify one unknown dimension.
# For example, sometimes we might have an unknown number of data points, and
# so we can use -1 instead without worrying about the true number.
nums = nums.reshape((4, -1))
print('Reshaped with -1:\n', nums)
print(nums.shape)
```
NumPy supports an object-oriented paradigm, such that ndarray has a number of methods and attributes, with functions similar to ones in the outermost NumPy namespace. For example, we can do both:
```
nums = np.arange(8)
print(nums.min()) # Prints 0
print(np.min(nums)) # Prints 0
```
## Array Operations/Math
NumPy supports many elementwise operations:
```
x = np.array([[1, 2],
[3, 4]], dtype=np.float64)
y = np.array([[5, 6],
[7, 8]], dtype=np.float64)
# Elementwise sum; both produce the array
# [[ 6.0 8.0]
# [10.0 12.0]]
print(x + y)
print(np.add(x, y))
# Elementwise difference; both produce the array
# [[-4.0 -4.0]
# [-4.0 -4.0]]
print(x - y)
print(np.subtract(x, y))
# Elementwise product; both produce the array
# [[ 5.0 12.0]
# [21.0 32.0]]
print(x * y)
print(np.multiply(x, y))
# Elementwise square root; produces the array
# [[ 1. 1.41421356]
# [ 1.73205081 2. ]]
print(np.sqrt(x))
```
How do we elementwise divide between two arrays?
```
x = np.array([[1, 2], [3, 4]], dtype=np.float64)
y = np.array([[5, 6], [7, 8]], dtype=np.float64)
# Elementwise division; both produce the array
# [[ 0.2 0.33333333]
# [ 0.42857143 0.5 ]]
print(x / y)
print(np.divide(x, y))
```
Note * is elementwise multiplication, not matrix multiplication. We instead use the dot function to compute inner products of vectors, to multiply a vector by a matrix, and to multiply matrices. dot is available both as a function in the numpy module and as an instance method of array objects:
```
x = np.array([[1, 2], [3, 4]])
y = np.array([[5, 6], [7, 8]])
v = np.array([9, 10])
w = np.array([11, 12])
# Inner product of vectors; both produce 219
print(v.dot(w))
print(np.dot(v, w))
# Matrix / vector product; both produce the rank 1 array [29 67]
print(x.dot(v))
print(np.dot(x, v))
# Matrix / matrix product; both produce the rank 2 array
# [[19 22]
# [43 50]]
print(x.dot(y))
print(np.dot(x, y))
```
There are many useful functions built into NumPy, and often we're able to express them across specific axes of the ndarray:
```
x = np.array([[1, 2, 3],
[4, 5, 6]])
print(np.sum(x)) # Compute sum of all elements; prints "21"
print(np.sum(x, axis=0)) # Compute sum of each column; prints "[5 7 9]"
print(np.sum(x, axis=1)) # Compute sum of each row; prints "[6 15]"
print(np.max(x, axis=1)) # Compute max of each row; prints "[3 6]"
```
How can we compute the index of the max value of each row? Useful, to say, find the class that corresponds to the maximum score for an input image.
```
x = np.array([[1, 2, 3],
[4, 5, 6]])
print(np.argmax(x, axis=1)) # Compute index of max of each row; prints "[2 2]"
```
Note the axis you apply the operation will have its dimension removed from the shape.
This is useful to keep in mind when you're trying to figure out what axis corresponds
to what.
For example:
```
x = np.array([[1, 2, 3],
[4, 5, 6]])
print(x.shape) # Has shape (2, 3)
print((x.max(axis=0)).shape) # Taking the max over axis 0 has shape (3,)
# corresponding to the 3 columns.
# An array with rank 3
x = np.array([[[1, 2, 3],
[4, 5, 6]],
[[10, 23, 33],
[43, 52, 16]]
])
print(x)
print(x.shape) # Has shape (2, 2, 3)
print((x.max(axis=1)).shape) # Taking the max over axis 1 has shape (2, 3)
print((x.max(axis=(1, 2)))) # Can take max over multiple axes; prints [6 52]
print((x.max(axis=(1, 2))).shape) # Taking the max over axes 1, 2 has shape (2,)
```
## Indexing
NumPy also provides powerful indexing schemes.
```
# Create the following rank 2 array with shape (3, 4)
# [[ 1 2 3 4]
# [ 5 6 7 8]
# [ 9 10 11 12]]
a = np.array([[1, 2, 3, 4],
[5, 6, 7, 8],
[9, 10, 11, 12]])
print('Original:\n', a)
# Can select an element as you would in a 2 dimensional Python list
print('Element (0, 0) (a[0][0]):\n', a[0][0]) # Prints 1
# or as follows
print('Element (0, 0) (a[0, 0]) :\n', a[0, 0]) # Prints 1
# Use slicing to pull out the subarray consisting of the first 2 rows
# and columns 1 and 2; b is the following array of shape (2, 2):
# [[2 3]
# [6 7]]
b = a[:2, 1:3]
print('Sliced (a[:2, 1:3]):\n', b)
# Steps are also supported in indexing. The following reverses the first row:
print('Reversing the first row (a[0, ::-1]) :\n', a[0, ::-1]) # Prints [4 3 2 1]
```
Often, it's useful to select or modify one element from each row of a matrix. The following example employs **fancy indexing**, where we index into our array using an array of indices (say an array of integers or booleans):
```
# Create a new array from which we will select elements
a = np.array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9],
[10, 11, 12]])
print(a) # prints "array([[ 1, 2, 3],
# [ 4, 5, 6],
# [ 7, 8, 9],
# [10, 11, 12]])"
# Create an array of indices
b = np.array([0, 2, 0, 1])
# Select one element from each row of a using the indices in b
print(a[np.arange(4), b]) # Prints "[ 1 6 7 11]"
# Mutate one element from each row of a using the indices in b
a[np.arange(4), b] += 10
print(a) # prints "array([[11, 2, 3],
# [ 4, 5, 16],
# [17, 8, 9],
# [10, 21, 12]])
```
We can also use boolean indexing/masks. Suppose we want to set all elements greater than MAX to MAX:
```
MAX = 5
nums = np.array([1, 4, 10, -1, 15, 0, 5])
print(nums > MAX) # Prints [False, False, True, False, True, False, False]
nums[nums > MAX] = MAX
print(nums) # Prints [1, 4, 5, -1, 5, 0, 5]
```
Finally, note that the indices in fancy indexing can appear in any order and even multiple times:
```
nums = np.array([1, 4, 10, -1, 15, 0, 5])
print(nums[[1, 2, 3, 1, 0]]) # Prints [4 10 -1 4 1]
```
## Broadcasting
Many of the operations we've looked at above involved arrays of the same rank.
However, many times we might have a smaller array and use that multiple times to update an array of a larger rank.
For example, consider the below example of shifting the mean of each column from the elements of the corresponding column:
```
x = np.array([[1, 2, 3],
[3, 5, 7]])
print(x.shape) # Prints (2, 3)
col_means = x.mean(axis=0)
print(col_means) # Prints [2. 3.5 5.]
print(col_means.shape) # Prints (3,)
# Has a smaller rank than x!
mean_shifted = x - col_means
print('\n', mean_shifted)
print(mean_shifted.shape) # Prints (2, 3)
```
Or even just multiplying a matrix by 2:
```
x = np.array([[1, 2, 3],
[3, 5, 7]])
print(x * 2) # Prints [[ 2 4 6]
# [ 6 10 14]]
```
Broadcasting two arrays together follows these rules:
1. If the arrays do not have the same rank, prepend the shape of the lower rank array with 1s until both shapes have the same length.
2. The two arrays are said to be compatible in a dimension if they have the same size in the dimension, or if one of the arrays has size 1 in that dimension.
3. The arrays can be broadcast together if they are compatible in all dimensions.
4. After broadcasting, each array behaves as if it had shape equal to the elementwise maximum of shapes of the two input arrays.
5. In any dimension where one array had size 1 and the other array had size greater than 1, the first array behaves as if it were copied along that dimension.
For example, when subtracting the columns above, we had arrays of shape (2, 3) and (3,).
1. These arrays do not have same rank, so we prepend the shape of the lower rank one to make it (1, 3).
2. (2, 3) and (1, 3) are compatible (have the same size in the dimension, or if one of the arrays has size 1 in that dimension).
3. Can be broadcast together!
4. After broadcasting, each array behaves as if it had shape equal to (2, 3).
5. The smaller array will behave as if it were copied along dimension 0.
Let's try to subtract the mean of each row!
```
x = np.array([[1, 2, 3],
[3, 5, 7]])
row_means = x.mean(axis=1)
print(row_means) # Prints [2. 5.]
mean_shifted = x - row_means
```
To figure out what's wrong, we print some shapes:
```
x = np.array([[1, 2, 3],
[3, 5, 7]])
print(x.shape) # Prints (2, 3)
row_means = x.mean(axis=1)
print(row_means) # Prints [2. 5.]
print(row_means.shape) # Prints (2,)
# Results in the following error: ValueError: operands could not be broadcast together with shapes (2,3) (2,)
mean_shifted = x - row_means
```
What happened?
Answer: If we following broadcasting rule 1, then we'd prepend a 1 to the smaller rank array ot get (1, 2). However, the last dimensions don't match now between (2, 3) and (1, 2), and so we can't broadcast.
Take 2, reshaping the row means to get the desired behavior:
```
x = np.array([[1, 2, 3],
[3, 5, 7]])
print(x.shape) # Prints (2, 3)
row_means = x.mean(axis=1).reshape((-1, 1))
print(row_means) # Prints [[2.], [5.]]
print(row_means.shape) # Prints (2, 1)
mean_shifted = x - row_means
print(mean_shifted)
print(mean_shifted.shape) # Prints (2, 3)
```
More broadcasting examples!
```
# Compute outer product of vectors
v = np.array([1, 2, 3]) # v has shape (3,)
w = np.array([4, 5]) # w has shape (2,)
# To compute an outer product, we first reshape v to be a column
# vector of shape (3, 1); we can then broadcast it against w to yield
# an output of shape (3, 2), which is the outer product of v and w:
# [[ 4 5]
# [ 8 10]
# [12 15]]
print(np.reshape(v, (3, 1)) * w)
# Add a vector to each row of a matrix
x = np.array([[1, 2, 3], [4, 5, 6]])
# x has shape (2, 3) and v has shape (3,) so they broadcast to (2, 3),
# giving the following matrix:
# [[2 4 6]
# [5 7 9]]
print(x + v)
# Add a vector to each column of a matrix
# x has shape (2, 3) and w has shape (2,).
# If we transpose x then it has shape (3, 2) and can be broadcast
# against w to yield a result of shape (3, 2); transposing this result
# yields the final result of shape (2, 3) which is the matrix x with
# the vector w added to each column. Gives the following matrix:
# [[ 5 6 7]
# [ 9 10 11]]
print((x.T + w).T)
# Another solution is to reshape w to be a column vector of shape (2, 1);
# we can then broadcast it directly against x to produce the same
# output.
print(x + np.reshape(w, (2, 1)))
```
## Views vs. Copies
Unlike a copy, in a **view** of an array, the data is shared between the view and the array. Sometimes, our results are copies of arrays, but other times they can be views. Understanding when each is generated is important to avoid any unforeseen issues.
Views can be created from a slice of an array, changing the dtype of the same data area (using arr.view(dtype), not the result of arr.astype(dtype)), or even both.
```
x = np.arange(5)
print('Original:\n', x) # Prints [0 1 2 3 4]
# Modifying the view will modify the array
view = x[1:3]
view[1] = -1
print('Array After Modified View:\n', x) # Prints [0 1 -1 3 4]
x = np.arange(5)
view = x[1:3]
view[1] = -1
# Modifying the array will modify the view
print('View Before Array Modification:\n', view) # Prints [1 -1]
x[2] = 10
print('Array After Modifications:\n', x) # Prints [0 1 10 3 4]
print('View After Array Modification:\n', view) # Prints [1 10]
```
However, if we use fancy indexing, the result will actually be a copy and not a view:
```
x = np.arange(5)
print('Original:\n', x) # Prints [0 1 2 3 4]
# Modifying the result of the selection due to fancy indexing
# will not modify the original array.
copy = x[[1, 2]]
copy[1] = -1
print('Copy:\n', copy) # Prints [1 -1]
print('Array After Modified Copy:\n', x) # Prints [0 1 2 3 4]
# Another example involving fancy indexing
x = np.arange(5)
print('Original:\n', x) # Prints [0 1 2 3 4]
copy = x[x >= 2]
print('Copy:\n', copy) # Prints [2 3 4]
x[3] = 10
print('Modified Array:\n', x) # Prints [0 1 2 10 4]
print('Copy After Modified Array:\n', copy) # Prints [2 3 4]
```
## Summary
1. NumPy is an incredibly powerful library for computation providing both massive efficiency gains and convenience.
2. Vectorize! Orders of magnitude faster.
3. Keeping track of the shape of your arrays is often useful.
4. Many useful math functions and operations built into NumPy.
5. Select and manipulate arbitrary pieces of data with powerful indexing schemes.
6. Broadcasting allows for computation across arrays of different shapes.
7. Watch out for views vs. copies.
|
github_jupyter
|
# How do I create my own dataset?
So Caffe2 uses a binary DB format to store the data that we would like to train models on. A Caffe2 DB is a glorified name of a key-value storage where the keys are usually randomized so that the batches are approximately i.i.d. The values are the real stuff here: they contain the serialized strings of the specific data formats that you would like your training algorithm to ingest. So, the stored DB would look (semantically) like this:
key1 value1
key2 value2
key3 value3
...
To a DB, it treats the keys and values as strings, but you probably want structured contents. One way to do this is to use a TensorProtos protocol buffer: it essentially wraps Tensors, aka multi-dimensional arrays, together with the tensor data type and shape information. Then, one can use the TensorProtosDBInput operator to load the data into an SGD training fashion.
Here, we will show you one example of how to create your own dataset. To this end, we will use the UCI Iris dataset - which was a very popular classical dataset for classifying Iris flowers. It contains 4 real-valued features representing the dimensions of the flower, and classifies things into 3 types of Iris flowers. The dataset can be downloaded [here](https://archive.ics.uci.edu/ml/datasets/Iris).
```
# First let's import a few things needed.
%matplotlib inline
import urllib2 # for downloading the dataset from the web.
import numpy as np
from matplotlib import pyplot
from StringIO import StringIO
from caffe2.python import core, utils, workspace
from caffe2.proto import caffe2_pb2
f = urllib2.urlopen('https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data')
raw_data = f.read()
print('Raw data looks like this:')
print(raw_data[:100] + '...')
# load the features to a feature matrix.
features = np.loadtxt(StringIO(raw_data), dtype=np.float32, delimiter=',', usecols=(0, 1, 2, 3))
# load the labels to a feature matrix
label_converter = lambda s : {'Iris-setosa':0, 'Iris-versicolor':1, 'Iris-virginica':2}[s]
labels = np.loadtxt(StringIO(raw_data), dtype=np.int, delimiter=',', usecols=(4,), converters={4: label_converter})
```
Before we do training, one thing that is often beneficial is to separate the dataset into training and testing. In this case, let's randomly shuffle the data, use the first 100 data points to do training, and the remaining 50 to do testing. For more sophisticated approaches, you can use e.g. cross validation to separate your dataset into multiple training and testing splits. Read more about cross validation [here](http://scikit-learn.org/stable/modules/cross_validation.html).
```
random_index = np.random.permutation(150)
features = features[random_index]
labels = labels[random_index]
train_features = features[:100]
train_labels = labels[:100]
test_features = features[100:]
test_labels = labels[100:]
# Let's plot the first two features together with the label.
# Remember, while we are plotting the testing feature distribution
# here too, you might not be supposed to do so in real research,
# because one should not peek into the testing data.
legend = ['rx', 'b+', 'go']
pyplot.title("Training data distribution, feature 0 and 1")
for i in range(3):
pyplot.plot(train_features[train_labels==i, 0], train_features[train_labels==i, 1], legend[i])
pyplot.figure()
pyplot.title("Testing data distribution, feature 0 and 1")
for i in range(3):
pyplot.plot(test_features[test_labels==i, 0], test_features[test_labels==i, 1], legend[i])
```
Now, as promised, let's put things into a Caffe2 DB. In this DB, what would happen is that we will use "train_xxx" as the key, and use a TensorProtos object to store two tensors for each data point: one as the feature and one as the label. We will use Caffe2 python's DB interface to do so.
```
# First, let's see how one can construct a TensorProtos protocol buffer from numpy arrays.
feature_and_label = caffe2_pb2.TensorProtos()
feature_and_label.protos.extend([
utils.NumpyArrayToCaffe2Tensor(features[0]),
utils.NumpyArrayToCaffe2Tensor(labels[0])])
print('This is what the tensor proto looks like for a feature and its label:')
print(str(feature_and_label))
print('This is the compact string that gets written into the db:')
print(feature_and_label.SerializeToString())
# Now, actually write the db.
def write_db(db_type, db_name, features, labels):
db = core.C.create_db(db_type, db_name, core.C.Mode.write)
transaction = db.new_transaction()
for i in range(features.shape[0]):
feature_and_label = caffe2_pb2.TensorProtos()
feature_and_label.protos.extend([
utils.NumpyArrayToCaffe2Tensor(features[i]),
utils.NumpyArrayToCaffe2Tensor(labels[i])])
transaction.put(
'train_%03d'.format(i),
feature_and_label.SerializeToString())
# Close the transaction, and then close the db.
del transaction
del db
write_db("minidb", "iris_train.minidb", train_features, train_labels)
write_db("minidb", "iris_test.minidb", test_features, test_labels)
```
Now, let's create a very simple network that only consists of one single TensorProtosDBInput operator, to showcase how we load data from the DB that we created. For training, you might want to do something more complex: creating a network, train it, get the model, and run the prediction service. To this end you can look at the MNIST tutorial for details.
```
net_proto = core.Net("example_reader")
dbreader = net_proto.CreateDB([], "dbreader", db="iris_train.minidb", db_type="minidb")
net_proto.TensorProtosDBInput([dbreader], ["X", "Y"], batch_size=16)
print("The net looks like this:")
print(str(net_proto.Proto()))
workspace.CreateNet(net_proto)
# Let's run it to get batches of features.
workspace.RunNet(net_proto.Proto().name)
print("The first batch of feature is:")
print(workspace.FetchBlob("X"))
print("The first batch of label is:")
print(workspace.FetchBlob("Y"))
# Let's run again.
workspace.RunNet(net_proto.Proto().name)
print("The second batch of feature is:")
print(workspace.FetchBlob("X"))
print("The second batch of label is:")
print(workspace.FetchBlob("Y"))
```
|
github_jupyter
|
# Significance Tests with PyTerrier
```
import pyterrier as pt
import pandas as pd
RUN_DIR='/mnt/ceph/storage/data-in-progress/data-teaching/theses/wstud-thesis-probst/retrievalExperiments/runs-ecir22/'
RUN_DIR_MARCO_V2='/mnt/ceph/storage/data-in-progress/data-teaching/theses/wstud-thesis-probst/retrievalExperiments/runs-marco-v2-ecir22/'
QREL_DIR = '/mnt/ceph/storage/data-tmp/2021/kibi9872/thesis-probst/Data/navigational-topics-and-qrels-ms-marco-'
if not pt.started():
pt.init()
def pt_qrels(ret):
from trectools import TrecQrel
ret = TrecQrel(QREL_DIR + ret).qrels_data
ret = ret.copy()
del ret['q0']
ret = ret.rename(columns={'query': 'qid','docid': 'docno', 'rel': 'label'})
ret['qid'] = ret['qid'].astype(str)
ret['label'] = ret['label'].astype(int)
return ret
def pt_topics(ret):
from trectools import TrecQrel
qids = TrecQrel(QREL_DIR + ret).qrels_data['query'].unique()
ret = []
for qid in qids:
ret += [{'qid': str(qid), 'query': 'Unused, only for significance tests for qid: ' + str(qid)}]
return pd.DataFrame(ret)
def trec_run(run_name):
from pyterrier.transformer import get_transformer
return get_transformer(pt.io.read_results(run_name))
QRELS = {
'v1-popular': pt_qrels('v1/qrels.msmarco-entrypage-popular.txt'),
'v1-random': pt_qrels('v1/qrels.msmarco-entrypage-random.txt'),
'v2-popular': pt_qrels('v2/qrels.msmarco-v2-entrypage-popular.txt'),
'v2-random': pt_qrels('v2/qrels.msmarco-v2-entrypage-random.txt'),
}
TOPICS = {
'v1-popular': pt_topics('v1/qrels.msmarco-entrypage-popular.txt'),
'v1-random': pt_topics('v1/qrels.msmarco-entrypage-random.txt'),
'v2-popular': pt_topics('v2/qrels.msmarco-v2-entrypage-popular.txt'),
'v2-random': pt_topics('v2/qrels.msmarco-v2-entrypage-random.txt'),
}
APPROACH_TO_MARCO_V1_RUN_FILE={
'BM25@2016-07': 'run.cc-16-07-anchortext.bm25-default.txt',
'BM25@2017-04': 'run.cc-17-04-anchortext.bm25-default.txt',
'BM25@2018-13': 'run.cc-18-13-anchortext.bm25-default.txt',
'BM25@2019-47': 'run.cc-19-47-anchortext.bm25-default.txt',
'BM25@2020-05': 'run.cc-20-05-anchortext.bm25-default.txt',
'BM25@2021-04': 'run.cc-21-04-anchortext.bm25-default.txt',
'BM25@16--21': 'run.cc-combined-anchortext.bm25-default.txt',
'BM25@Content': 'run.ms-marco-content.bm25-default.txt',
'BM25@Title': 'run.msmarco-document-v1-title-only.pos+docvectors+raw.bm25-default.txt',
'BM25@Orcas': 'run.orcas.bm25-default.txt',
'DeepCT@Anchor': 'run.ms-marco-deepct-v1-anserini-docs-cc-2019-47-sampled-test-overlap-removed-389979.bm25-default.txt',
'DeepCT@Orcas': 'run.ms-marco-deepct-v1-anserini-docs-orcas-sampled-test-overlap-removed-390009.bm25-default.txt',
'DeepCT@Train':'run.ms-marco-deepct-v1-anserini-docs-ms-marco-training-set-test-overlap-removed-389973.bm25-default.txt',
'MonoT5': 'run.ms-marco-content.bm25-mono-t5-maxp.txt',
'MonoBERT': 'run.ms-marco-content.bm25-mono-bert-maxp.txt',
'LambdaMART@CTA':'run.ms-marco.lambda-mart-cta-trees-1000.txt',
'LambdaMART@CTOA':'run.ms-marco.lambda-mart-ctoa-trees-1000.txt',
'LambdaMART@CTO':'run.ms-marco.lambda-mart-cto-trees-1000.txt',
'LambdaMART@CT':'run.ms-marco.lambda-mart-ct-trees-1000.txt',
}
APPROACH_TO_MARCO_V2_RUN_FILE={
'BM25@Content': 'run.msmarco-doc-v2.bm25-default.txt',
'BM25@Orcas': 'run.orcas-ms-marco-v2.bm25-default.txt',
'BM25@2016-07': 'run.cc-16-07-anchortext.bm25-default.txt',
'BM25@2017-04': 'run.cc-17-04-anchortext.bm25-default.txt',
'BM25@2018-13': 'run.cc-18-13-anchortext.bm25-default.txt',
'BM25@2019-47': 'run.cc-19-47-anchortext-v2.bm25-default.txt',
'BM25@2020-05': 'run.cc-20-05-anchortext.bm25-default.txt',
'BM25@2021-04': 'run.cc-21-04-anchortext.bm25-default.txt',
'BM25@16--21': 'run.cc-union-16-to-21-anchortext-1000.bm25-default.txt',
'DeepCT@Anchor': 'run.ms-marco-deepct-v2-anserini-docs-cc-2019-47-sampled-test-overlap-removed-389979.bm25-default.txt',
'DeepCT@Orcas': 'run.ms-marco-deepct-v2-anserini-docs-orcas-sampled-test-overlap-removed-390009.bm25-default.txt',
'DeepCT@Train':'run.ms-marco-deepct-v2-anserini-docs-ms-marco-training-set-test-overlap-removed-389973.bm25-default.txt',
'MonoT5': 'run.ms-marco-content.bm25-mono-t5-maxp.txt',
'MonoBERT': 'run.ms-marco-content.bm25-mono-bert-maxp.txt',
'LambdaMART@CTA':'run.ms-marco.lambda-mart-cta-trees-1000.txt',
'LambdaMART@CTOA':'run.ms-marco.lambda-mart-ctoa-trees-1000.txt',
'LambdaMART@CTO':'run.ms-marco.lambda-mart-cto-trees-1000.txt',
'LambdaMART@CT':'run.ms-marco.lambda-mart-ct-trees-1000.txt',
}
```
### Comparison of MRR for Anchor Text approaches to DeepCT
```
runs = ['DeepCT@Anchor', 'BM25@2016-07', 'BM25@2017-04', 'BM25@2018-13', 'BM25@2019-47', 'BM25@2020-05', 'BM25@2021-04', 'BM25@16--21']
runs = [(i, trec_run(RUN_DIR + '/entrypage-random/' + APPROACH_TO_MARCO_V1_RUN_FILE[i])) for i in runs]
pt.Experiment(
[i for _, i in runs],
TOPICS['v1-random'],
QRELS['v1-random'],
['recip_rank'],
[i for i, _ in runs],
baseline = 0,
test='t',
correction='b'
)
```
Result: From xy above we see....
### Comparison of MRR for BM25 on Content with DeepCT trained on anchor text, DeepCT, MonoT5, MonoBERT, and LambdaMART
```
runs = ['BM25@Content', 'DeepCT@Orcas', 'DeepCT@Anchor', 'DeepCT@Train', 'MonoT5', 'MonoBERT', 'LambdaMART@CTA', 'LambdaMART@CTOA', 'LambdaMART@CTO', 'LambdaMART@CT']
runs = [(i, trec_run(RUN_DIR + '/entrypage-random/' + APPROACH_TO_MARCO_V1_RUN_FILE[i])) for i in runs]
pt.Experiment(
[i for _, i in runs],
TOPICS['v1-random'],
QRELS['v1-random'],
['recip_rank'],
[i for i, _ in runs],
baseline = 0,
test='t',
correction='b'
)
```
Result:
DeepCT trained on anchor text, DeepCT trained on the ORCAS query log, MonoT5, MonoBERT, and three of the LambdaMART models improve statistically significant upon the MRR of 0.21 achieved by the BM25 retrieval on the content.
### Comparison of BM25 on Orcas with other Content-Only Models
```
runs = ['BM25@Orcas', 'BM25@Content', 'DeepCT@Orcas', 'DeepCT@Anchor', 'DeepCT@Train', 'MonoT5', 'MonoBERT']
runs = [(i, trec_run(RUN_DIR + '/entrypage-random/' + APPROACH_TO_MARCO_V1_RUN_FILE[i])) for i in runs]
pt.Experiment(
[i for _, i in runs],
TOPICS['v1-random'],
QRELS['v1-random'],
['recip_rank'],
[i for i, _ in runs],
baseline = 0,
test='t',
correction='b'
)
```
Result:
BM25 on ORCAS improves statistically significantly upon all content-only models.
### Comparison of all Anchor-Text Models with all other approaches
```
runs = ['BM25@2016-07', 'BM25@Content', 'DeepCT@Anchor', 'DeepCT@Orcas', 'DeepCT@Train', 'MonoT5', 'MonoBERT', 'BM25@Orcas', 'LambdaMART@CTOA', 'LambdaMART@CTO', 'LambdaMART@CTA', 'LambdaMART@CT']
runs = [(i, trec_run(RUN_DIR + '/entrypage-popular/' + APPROACH_TO_MARCO_V1_RUN_FILE[i])) for i in runs]
pt.Experiment(
[i for _, i in runs],
TOPICS['v1-popular'],
QRELS['v1-popular'],
['recip_rank'],
[i for i, _ in runs],
baseline = 0,
test='t',
correction='b'
)
runs = ['BM25@2017-04', 'BM25@Content', 'DeepCT@Anchor', 'DeepCT@Orcas', 'DeepCT@Train', 'MonoT5', 'MonoBERT', 'BM25@Orcas', 'LambdaMART@CTOA', 'LambdaMART@CTO', 'LambdaMART@CTA', 'LambdaMART@CT']
runs = [(i, trec_run(RUN_DIR + '/entrypage-popular/' + APPROACH_TO_MARCO_V1_RUN_FILE[i])) for i in runs]
pt.Experiment(
[i for _, i in runs],
TOPICS['v1-popular'],
QRELS['v1-popular'],
['recip_rank'],
[i for i, _ in runs],
baseline = 0,
test='t',
correction='b'
)
runs = ['BM25@2018-13', 'BM25@Content', 'DeepCT@Anchor', 'DeepCT@Orcas', 'DeepCT@Train', 'MonoT5', 'MonoBERT', 'BM25@Orcas', 'LambdaMART@CTOA', 'LambdaMART@CTO', 'LambdaMART@CTA', 'LambdaMART@CT']
runs = [(i, trec_run(RUN_DIR + '/entrypage-popular/' + APPROACH_TO_MARCO_V1_RUN_FILE[i])) for i in runs]
pt.Experiment(
[i for _, i in runs],
TOPICS['v1-popular'],
QRELS['v1-popular'],
['recip_rank'],
[i for i, _ in runs],
baseline = 0,
test='t',
correction='b'
)
runs = ['BM25@2019-47', 'BM25@Content', 'DeepCT@Anchor', 'DeepCT@Orcas', 'DeepCT@Train', 'MonoT5', 'MonoBERT', 'BM25@Orcas', 'LambdaMART@CTOA', 'LambdaMART@CTO', 'LambdaMART@CTA', 'LambdaMART@CT']
runs = [(i, trec_run(RUN_DIR + '/entrypage-popular/' + APPROACH_TO_MARCO_V1_RUN_FILE[i])) for i in runs]
pt.Experiment(
[i for _, i in runs],
TOPICS['v1-popular'],
QRELS['v1-popular'],
['recip_rank'],
[i for i, _ in runs],
baseline = 0,
test='t',
correction='b'
)
runs = ['BM25@2020-05', 'BM25@Content', 'DeepCT@Anchor', 'DeepCT@Orcas', 'DeepCT@Train', 'MonoT5', 'MonoBERT', 'BM25@Orcas', 'LambdaMART@CTOA', 'LambdaMART@CTO', 'LambdaMART@CTA', 'LambdaMART@CT']
runs = [(i, trec_run(RUN_DIR + '/entrypage-popular/' + APPROACH_TO_MARCO_V1_RUN_FILE[i])) for i in runs]
pt.Experiment(
[i for _, i in runs],
TOPICS['v1-popular'],
QRELS['v1-popular'],
['recip_rank'],
[i for i, _ in runs],
baseline = 0,
test='t',
correction='b'
)
runs = ['BM25@2021-04', 'BM25@Content', 'DeepCT@Anchor', 'DeepCT@Orcas', 'DeepCT@Train', 'MonoT5', 'MonoBERT', 'BM25@Orcas', 'LambdaMART@CTOA', 'LambdaMART@CTO', 'LambdaMART@CTA', 'LambdaMART@CT']
runs = [(i, trec_run(RUN_DIR + '/entrypage-popular/' + APPROACH_TO_MARCO_V1_RUN_FILE[i])) for i in runs]
pt.Experiment(
[i for _, i in runs],
TOPICS['v1-popular'],
QRELS['v1-popular'],
['recip_rank'],
[i for i, _ in runs],
baseline = 0,
test='t',
correction='b'
)
runs = ['BM25@16--21', 'BM25@Content', 'DeepCT@Anchor', 'DeepCT@Orcas', 'DeepCT@Train', 'MonoT5', 'MonoBERT', 'BM25@Orcas', 'LambdaMART@CTOA', 'LambdaMART@CTO', 'LambdaMART@CTA', 'LambdaMART@CT']
runs = [(i, trec_run(RUN_DIR + '/entrypage-popular/' + APPROACH_TO_MARCO_V1_RUN_FILE[i])) for i in runs]
pt.Experiment(
[i for _, i in runs],
TOPICS['v1-popular'],
QRELS['v1-popular'],
['recip_rank'],
[i for i, _ in runs],
baseline = 0,
test='t',
correction='b'
)
```
Result:
For queries pointing to popular entry pages, all BM25 models retrieving on anchor text outperform all other retrieval models statistically significant
### Compare BM25 on ORCAS for popular topics with all other non-anchor-approaches
```
runs = ['BM25@Orcas', 'BM25@Content', 'DeepCT@Anchor', 'DeepCT@Orcas', 'DeepCT@Train', 'MonoT5', 'MonoBERT', 'LambdaMART@CTOA', 'LambdaMART@CTO', 'LambdaMART@CTA', 'LambdaMART@CT']
runs = [(i, trec_run(RUN_DIR + '/entrypage-popular/' + APPROACH_TO_MARCO_V1_RUN_FILE[i])) for i in runs]
pt.Experiment(
[i for _, i in runs],
TOPICS['v1-popular'],
QRELS['v1-popular'],
['recip_rank'],
[i for i, _ in runs],
baseline = 0,
test='t',
correction='b'
)
```
# Evaluations Recall@3 and Recall@10
### Comparison of Recall for Anchor Text approaches to DeepCT
```
runs = ['DeepCT@Anchor', 'BM25@2016-07', 'BM25@2017-04', 'BM25@2018-13', 'BM25@2019-47', 'BM25@2020-05', 'BM25@2021-04', 'BM25@16--21']
runs = [(i, trec_run(RUN_DIR + '/entrypage-random/' + APPROACH_TO_MARCO_V1_RUN_FILE[i])) for i in runs]
pt.Experiment(
[i for _, i in runs],
TOPICS['v1-random'],
QRELS['v1-random'],
['recall.3', 'recall.10'],
[i for i, _ in runs],
baseline = 0,
test='t',
correction='b'
)
```
### Comparison of Recall for BM25 on Content with DeepCT trained on anchor text, DeepCT, MonoT5, MonoBERT, and LambdaMART
```
runs = ['BM25@Content', 'DeepCT@Orcas', 'DeepCT@Anchor', 'DeepCT@Train', 'MonoT5', 'MonoBERT', 'LambdaMART@CTA', 'LambdaMART@CTOA', 'LambdaMART@CTO', 'LambdaMART@CT']
runs = [(i, trec_run(RUN_DIR + '/entrypage-random/' + APPROACH_TO_MARCO_V1_RUN_FILE[i])) for i in runs]
pt.Experiment(
[i for _, i in runs],
TOPICS['v1-random'],
QRELS['v1-random'],
['recall.3', 'recall.10'],
[i for i, _ in runs],
baseline = 0,
test='t',
correction='b'
)
```
### Comparison of BM25 on Orcas with other Content-Only Models
```
runs = ['BM25@Orcas', 'BM25@Content', 'DeepCT@Orcas', 'DeepCT@Anchor', 'DeepCT@Train', 'MonoT5', 'MonoBERT']
runs = [(i, trec_run(RUN_DIR + '/entrypage-random/' + APPROACH_TO_MARCO_V1_RUN_FILE[i])) for i in runs]
pt.Experiment(
[i for _, i in runs],
TOPICS['v1-random'],
QRELS['v1-random'],
['recall.3', 'recall.10'],
[i for i, _ in runs],
baseline = 0,
test='t',
correction='b'
)
```
Result:
BM25 on ORCAS does not statisticall improve upon DeepCT@Anchor (for Recall@3) and DeepCT@Anchor, DeepCT@Orcas, and MonoT5 (Recall@10)
### Comparison of all Anchor-Text Models with all other approaches
```
runs = ['BM25@2016-07', 'BM25@Content', 'DeepCT@Anchor', 'DeepCT@Orcas', 'DeepCT@Train', 'MonoT5', 'MonoBERT', 'BM25@Orcas', 'LambdaMART@CTOA', 'LambdaMART@CTO', 'LambdaMART@CTA', 'LambdaMART@CT']
runs = [(i, trec_run(RUN_DIR + '/entrypage-popular/' + APPROACH_TO_MARCO_V1_RUN_FILE[i])) for i in runs]
pt.Experiment(
[i for _, i in runs],
TOPICS['v1-popular'],
QRELS['v1-popular'],
['recall.3', 'recall.10'],
[i for i, _ in runs],
baseline = 0,
test='t',
correction='b'
)
runs = ['BM25@2017-04', 'BM25@Content', 'DeepCT@Anchor', 'DeepCT@Orcas', 'DeepCT@Train', 'MonoT5', 'MonoBERT', 'BM25@Orcas', 'LambdaMART@CTOA', 'LambdaMART@CTO', 'LambdaMART@CTA', 'LambdaMART@CT']
runs = [(i, trec_run(RUN_DIR + '/entrypage-popular/' + APPROACH_TO_MARCO_V1_RUN_FILE[i])) for i in runs]
pt.Experiment(
[i for _, i in runs],
TOPICS['v1-popular'],
QRELS['v1-popular'],
['recall.3', 'recall.10'],
[i for i, _ in runs],
baseline = 0,
test='t',
correction='b'
)
runs = ['BM25@2018-13', 'BM25@Content', 'DeepCT@Anchor', 'DeepCT@Orcas', 'DeepCT@Train', 'MonoT5', 'MonoBERT', 'BM25@Orcas', 'LambdaMART@CTOA', 'LambdaMART@CTO', 'LambdaMART@CTA', 'LambdaMART@CT']
runs = [(i, trec_run(RUN_DIR + '/entrypage-popular/' + APPROACH_TO_MARCO_V1_RUN_FILE[i])) for i in runs]
pt.Experiment(
[i for _, i in runs],
TOPICS['v1-popular'],
QRELS['v1-popular'],
['recall.3', 'recall.10'],
[i for i, _ in runs],
baseline = 0,
test='t',
correction='b'
)
runs = ['BM25@2019-47', 'BM25@Content', 'DeepCT@Anchor', 'DeepCT@Orcas', 'DeepCT@Train', 'MonoT5', 'MonoBERT', 'BM25@Orcas', 'LambdaMART@CTOA', 'LambdaMART@CTO', 'LambdaMART@CTA', 'LambdaMART@CT']
runs = [(i, trec_run(RUN_DIR + '/entrypage-popular/' + APPROACH_TO_MARCO_V1_RUN_FILE[i])) for i in runs]
pt.Experiment(
[i for _, i in runs],
TOPICS['v1-popular'],
QRELS['v1-popular'],
['recall.3', 'recall.10'],
[i for i, _ in runs],
baseline = 0,
test='t',
correction='b'
)
runs = ['BM25@2020-05', 'BM25@Content', 'DeepCT@Anchor', 'DeepCT@Orcas', 'DeepCT@Train', 'MonoT5', 'MonoBERT', 'BM25@Orcas', 'LambdaMART@CTOA', 'LambdaMART@CTO', 'LambdaMART@CTA', 'LambdaMART@CT']
runs = [(i, trec_run(RUN_DIR + '/entrypage-popular/' + APPROACH_TO_MARCO_V1_RUN_FILE[i])) for i in runs]
pt.Experiment(
[i for _, i in runs],
TOPICS['v1-popular'],
QRELS['v1-popular'],
['recall.3', 'recall.10'],
[i for i, _ in runs],
baseline = 0,
test='t',
correction='b'
)
runs = ['BM25@2021-04', 'BM25@Content', 'DeepCT@Anchor', 'DeepCT@Orcas', 'DeepCT@Train', 'MonoT5', 'MonoBERT', 'BM25@Orcas', 'LambdaMART@CTOA', 'LambdaMART@CTO', 'LambdaMART@CTA', 'LambdaMART@CT']
runs = [(i, trec_run(RUN_DIR + '/entrypage-popular/' + APPROACH_TO_MARCO_V1_RUN_FILE[i])) for i in runs]
pt.Experiment(
[i for _, i in runs],
TOPICS['v1-popular'],
QRELS['v1-popular'],
['recall.3', 'recall.10'],
[i for i, _ in runs],
baseline = 0,
test='t',
correction='b'
)
runs = ['BM25@16--21', 'BM25@Content', 'DeepCT@Anchor', 'DeepCT@Orcas', 'DeepCT@Train', 'MonoT5', 'MonoBERT', 'BM25@Orcas', 'LambdaMART@CTOA', 'LambdaMART@CTO', 'LambdaMART@CTA', 'LambdaMART@CT']
runs = [(i, trec_run(RUN_DIR + '/entrypage-popular/' + APPROACH_TO_MARCO_V1_RUN_FILE[i])) for i in runs]
pt.Experiment(
[i for _, i in runs],
TOPICS['v1-popular'],
QRELS['v1-popular'],
['recall.3', 'recall.10'],
[i for i, _ in runs],
baseline = 0,
test='t',
correction='b'
)
```
Result: We see exactly the same relevance results as for MRR.
### Compare BM25 on ORCAS for popular topics with all other non-anchor-approaches
```
runs = ['BM25@Orcas', 'BM25@Content', 'DeepCT@Anchor', 'DeepCT@Orcas', 'DeepCT@Train', 'MonoT5', 'MonoBERT', 'LambdaMART@CTOA', 'LambdaMART@CTO', 'LambdaMART@CTA', 'LambdaMART@CT']
runs = [(i, trec_run(RUN_DIR + '/entrypage-popular/' + APPROACH_TO_MARCO_V1_RUN_FILE[i])) for i in runs]
pt.Experiment(
[i for _, i in runs],
TOPICS['v1-popular'],
QRELS['v1-popular'],
['recall.3', 'recall.10'],
[i for i, _ in runs],
baseline = 0,
test='t',
correction='b'
)
```
|
github_jupyter
|
# 5 minutes intro to IPython for ROOT users
In this notebook we show how to use inside IPython __ROOT__ (C++ library, de-facto standard in High Energy Physics).
This notebook is aimed to help __ROOT__ users.
Working using ROOT-way loops is very slow in python and in most cases useless.
You're proposed to use `root_numpy` — a very convenient python library to operate with ROOT (`root_numpy` is included in REP docker image, but it is installed quite easily).
### Allowing inline plots
```
%matplotlib inline
```
## Creating ROOT file using root_numpy
There are two libraries to work with ROOT files
* rootpy http://www.rootpy.org - direct wrapper to ROOT methods.
* root_numpy http://rootpy.github.io/root_numpy/ - new-style, efficient and simple library to deal with ROOT files from python
Let's show how to use the second library.
```
import numpy
import root_numpy
# generating random data
data = numpy.random.normal(size=[10000, 2])
# adding names of columns
data = data.view([('first', float), ('second', float)])
# saving to file
root_numpy.array2root(data, filename='./toy_datasets/random.root', treename='tree', mode='recreate')
!ls ./toy_datasets
```
## Add column to the ROOT file using root_numpy
```
from rootpy.io import root_open
with root_open('./toy_datasets/random.root', mode='a') as myfile:
new_column = numpy.array(numpy.ones([10000, 1]) , dtype=[('new', 'f8')])
root_numpy.array2tree(new_column, tree=myfile.tree)
myfile.write()
root_numpy.root2array('./toy_datasets/random.root', treename='tree')
```
# Plot function using ROOT
pay attention that `canvas` is on the last line. This is an output value of cell.
When IPython cell return canvas, it is automatically drawn
```
import ROOT
from rep.plotting import canvas
canvas = canvas('my_canvas')
function1 = ROOT.TF1( 'fun1', 'abs(sin(x)/x)', 0, 10)
canvas.SetGridx()
canvas.SetGridy()
function1.Draw()
# Drawing output (last line is considered as output of cell)
canvas
```
# Plot histogram using ROOT for branch in root file
```
File = ROOT.TFile("toy_datasets/random.root")
Tree = File.Get("tree")
Tree.Draw("first")
canvas
```
## use histogram settings
```
# we need to keep histogram in any variable, otherwise it will be deleted automatically
h1 = ROOT.TH1F("h1","hist from tree",50, -0.25, 0.25)
Tree.Draw("first>>h1")
canvas
```
# root_numpy + ipython way
But IPython provides it's own plotting / data manipulation techniques. Brief demostration below.
Pay attention that there is column-expression which is evaluated on-the-fly.
```
data = root_numpy.root2array("toy_datasets/random.root",
treename='tree',
branches=['first', 'second', 'sin(first) * exp(second)'],
selection='first > 0')
```
__in the example above__ we selected three branches (one of which is an expression and was computed on-the-fly) and selections
```
# taking, i.e. first 10 elements using python slicing:
data2 = data[:10]
```
### Convert to pandas
pandas allows easy manipulations with data.
```
import pandas
dataframe = pandas.DataFrame(data)
# looking at first elements
dataframe.head()
# taking elements, that satisfy some condition, again showing only first
dataframe[dataframe['second'] > 0].head()
# adding new column as result of some operation
dataframe['third'] = dataframe['first'] + dataframe['second']
dataframe.head()
```
## Histograms in python
Default library for plotting in python is matplotlib.
```
import matplotlib.pyplot as plt
plt.figure(figsize=(9, 7))
plt.hist(data['first'], bins=50)
plt.xlabel('first')
plt.figure(figsize=(9, 7))
plt.hist(data['second'], bins=50)
plt.xlabel('second')
```
## Summary
- you can work in standard way with ROOT (by using rootpy), but it is slow
- you can benefit serously from python tools (those are fast and very flexible):
- matplotlib for plotting
- numpy / pandas for manipating arrays/dataframes
- to deal with ROOT files, you can use `root_numpy` as a very nice bridge between two worlds.
|
github_jupyter
|
# High-level Chainer Example
```
import os
os.environ['CHAINER_TYPE_CHECK'] = '0'
import sys
import numpy as np
import math
import chainer
import chainer.functions as F
import chainer.links as L
from chainer import optimizers
from chainer import cuda
from common.params import *
from common.utils import *
cuda.set_max_workspace_size(512 * 1024 * 1024)
chainer.global_config.autotune = True
print("OS: ", sys.platform)
print("Python: ", sys.version)
print("Chainer: ", chainer.__version__)
print("CuPy: ", chainer.cuda.cupy.__version__)
print("Numpy: ", np.__version__)
print("GPU: ", get_gpu_name())
class SymbolModule(chainer.Chain):
def __init__(self):
super(SymbolModule, self).__init__()
with self.init_scope():
self.conv1 = L.Convolution2D(3, 50, ksize=3, pad=1)
self.conv2 = L.Convolution2D(50, 50, ksize=3, pad=1)
self.conv3 = L.Convolution2D(50, 100, ksize=3, pad=1)
self.conv4 = L.Convolution2D(100, 100, ksize=3, pad=1)
# feature map size is 8*8 by pooling
self.fc1 = L.Linear(100*8*8, 512)
self.fc2 = L.Linear(512, N_CLASSES)
def __call__(self, x):
h = F.relu(self.conv2(F.relu(self.conv1(x))))
h = F.max_pooling_2d(h, ksize=2, stride=2)
h = F.dropout(h, 0.25)
h = F.relu(self.conv4(F.relu(self.conv3(h))))
h = F.max_pooling_2d(h, ksize=2, stride=2)
h = F.dropout(h, 0.25)
h = F.dropout(F.relu(self.fc1(h)), 0.5)
return self.fc2(h)
def init_model(m):
optimizer = optimizers.MomentumSGD(lr=LR, momentum=MOMENTUM)
optimizer.setup(m)
return optimizer
%%time
# Data into format for library
#x_train, x_test, y_train, y_test = mnist_for_library(channel_first=True)
x_train, x_test, y_train, y_test = cifar_for_library(channel_first=True)
print(x_train.shape, x_test.shape, y_train.shape, y_test.shape)
print(x_train.dtype, x_test.dtype, y_train.dtype, y_test.dtype)
%%time
# Create symbol
sym = SymbolModule()
if GPU:
chainer.cuda.get_device(0).use() # Make a specified GPU current
sym.to_gpu() # Copy the model to the GPU
%%time
optimizer = init_model(sym)
%%time
# 162s
for j in range(EPOCHS):
for data, target in yield_mb(x_train, y_train, BATCHSIZE, shuffle=True):
# Get samples
data = cuda.to_gpu(data)
target = cuda.to_gpu(target)
output = sym(data)
loss = F.softmax_cross_entropy(output, target)
sym.cleargrads()
loss.backward()
optimizer.update()
# Log
print(j)
%%time
n_samples = (y_test.shape[0]//BATCHSIZE)*BATCHSIZE
y_guess = np.zeros(n_samples, dtype=np.int)
y_truth = y_test[:n_samples]
c = 0
with chainer.using_config('train', False), chainer.using_config('enable_backprop', False):
for data, target in yield_mb(x_test, y_test, BATCHSIZE):
# Forwards
pred = cuda.to_cpu(sym(cuda.to_gpu(data)).data.argmax(-1))
# Collect results
y_guess[c*BATCHSIZE:(c+1)*BATCHSIZE] = pred
c += 1
print("Accuracy: ", sum(y_guess == y_truth)/len(y_guess))
```
|
github_jupyter
|
# Gases: Perfect and Semiperfect Models
In this Notebook we will use `PerfectIdealGas` and `SemiperfectIdealGas` classes from **pyTurb**, to access the thermodynamic properties with a Perfect Ideal Gas or a Semiperfect Ideal Gas approach. Both classes acquire the thermodynamic properties of different species from the *NASA Glenn coefficients* in `thermo_properties.py`.
Note that `PerfectIdealGas` and `SemiperfectIdealGas` classes are two different approaches for an *Ideal Gas*.
The `gas_models` functions and classes can be found in the following folders:
- pyturb
- gas_models
- thermo_prop
- PerfectIdealGas
- SemiperfectIdealGas
- GasMixture
```python
from pyturb.gas_models import ThermoProperties
from pyturb.gas_models import PerfectIdealGas
from pyturb.gas_models import SemiperfectIdealGas
from pyturb.gas_models import GasMixture
```
For an example about how to declae and use a Gas Mixture in **pyTurb**, go the "Gas Mixtures.ipynb" Notebook.
### Ideal Gas
While an Ideal Gas is characterized by a compressibility factor of 1:
$$Z=1=\frac{pv}{R_gT}$$
Which means that the *Ideal Gas Equation of State* is available: ($pv=R_gT$). It also means that the Mayer Equation is applicable: $R_g=c_p-c_v$.
### Perfect and Semiperfect approaches
A Perfect Gas or a Semiperfect Ideal Gas approach means:
- If the gas is perfect: $c_v, c_p, \gamma_g \equiv constant$
- If the gas is Semiperfect: $c_v(T), c_p(T), \gamma_g(T) \equiv f(T)$
By definition, the model used in `ThermoProperties` provide a 7 coefficients polynomial for the heat capacity at constant pressure ($c_p$):
$$ \frac{c_p}{R_g} = a_1T^{-2}+a_2T^{-1} + a_3 + a_4T + a_5T^2 a_6T^3 + a_7T^4$$
With the $c_p$, the Mayer Equation (valid for $Z=1$) and the heat capacity ratio we can obtain $c_v \left(T\right)$ and $\gamma \left(T\right)$:
$$ R_g =c_p\left(T\right)-c_v \left(T\right) $$
$$\gamma_g\left(T\right) = \frac{c_p\left(T\right)}{c_v\left(T\right)}$$
> In practice, the `PerfectIdealGas` object is a `SemiperfectIdealGas` where the temperature is set to $25ºC$.
### Perfect and Semiperfect content
Both `PerfectIdealGas` and `SemiPerfectIdealGas` classes have the following content:
- **Gas properties:** Ru, Rg, Mg, cp, cp_molar, cv, cv_molar, gamma
- **Gas enthalpies, moles and mass:** h0, h0_molar, mg, Ng
- **Chemical properties:** gas_species, thermo_prop
### Other dependencies:
We will import `numpy` and `pyplot` as well, to make some graphical examples.
---
### Check Gas Species availability:
```
from pyturb.gas_models import ThermoProperties
tp = ThermoProperties()
print(tp.species_list[850:875])
tp.is_available('Air')
```
---
### Import Perfect and Semiperfect Ideal Gas classes:
Examples with Air:
```
from pyturb.gas_models import PerfectIdealGas
from pyturb.gas_models import SemiperfectIdealGas
# Air as perfect gas:
perfect_air = PerfectIdealGas('Air')
# Air as semiperfect gas:
semiperfect_air = SemiperfectIdealGas('Air')
```
---
##### To retrieve the thermodynamic properties you can `print` the `thermo_prop` from the gas:
Including:
- Chemical formula
- Heat of formation
- Molecular mass
- cp coefficients
```
print(perfect_air.thermo_prop)
```
---
You can get the thermodynamic properties directly from the gas object. Note that all units are International System of Units (SI):
```
print(perfect_air.Rg)
print(perfect_air.Mg)
print(perfect_air.cp())
print(perfect_air.cp_molar())
print(perfect_air.cv())
print(perfect_air.cv_molar())
print(perfect_air.gamma())
```
---
##### Use the docstrings for more info about the content of a PerfectIdealGas or a SemiperfectIdealGas:
```
perfect_air?
```
---
##### Compare both models:
Note that *Perfect Ideal Air*, with constant $c_p$, $c_v$ and $\gamma$, yields the same properties than a semiperfect gas model at 25ºC (reference temperature):
```
T = 288.15 #K
cp_perf = perfect_air.cp()
cp_sp = semiperfect_air.cp(T)
print('At T={0:8.2f}K, cp_perfect={1:8.2f}J/kg/K'.format(T, cp_perf))
print('At T={0:8.2f}K, cp_semipft={1:8.2f}J/kg/K'.format(T, cp_sp))
T = 1500 #K
cp_perf = perfect_air.cp()
cp_sp = semiperfect_air.cp(T)
print('At T={0:8.2f}K, cp_perfect={1:8.2f}J/kg/K'.format(T, cp_perf))
print('At T={0:8.2f}K, cp_semipft={1:8.2f}J/kg/K'.format(T, cp_sp))
```
---
##### $c_p$, $c_v$ and $\gamma$ versus temperature:
```
import numpy as np
from matplotlib import pyplot as plt
T = np.linspace(200, 2000, 50)
cp = np.zeros_like(T)
cv = np.zeros_like(T)
gamma = np.zeros_like(T)
for ii, temperature in enumerate(T):
cp[ii] = semiperfect_air.cp(temperature)
cv[ii] = semiperfect_air.cv(temperature)
gamma[ii] = semiperfect_air.gamma(temperature)
fig, (ax1, ax2) = plt.subplots(2)
fig.suptitle('Air properties')
ax1.plot(T, cp)
ax1.plot(T, cv)
ax2.plot(T, gamma)
ax1.set(xlabel="Temperature [K]", ylabel="cp, cv [J/kg/K]")
ax2.set(xlabel="Temperature [K]", ylabel="gamma [-]")
ax1.grid()
ax2.grid()
plt.show()
```
|
github_jupyter
|
# General parameters
```
import files
import utils
import os
import models
import numpy as np
from tqdm.autonotebook import tqdm
import pandas as pd
from sklearn.preprocessing import OneHotEncoder
import datetime
import seaborn as sns
import matplotlib as mpl
from matplotlib.backends.backend_pgf import FigureCanvasPgf
mpl.backend_bases.register_backend('pdf', FigureCanvasPgf)
from mpl_toolkits.axes_grid1.inset_locator import zoomed_inset_axes, mark_inset,inset_axes
size=19
mpl.rcParams.update({
"pgf.texsystem": "pdflatex",
'font.family': 'serif',
'font.serif': 'Times',
'text.usetex': True,
'pgf.rcfonts': False,
'font.size': size,
'axes.labelsize':size,
'axes.titlesize':size,
'figure.titlesize':size,
'xtick.labelsize':size,
'ytick.labelsize':size,
'legend.fontsize':size,
})
import matplotlib.pyplot as plt
import matplotlib.lines as mlines
#########################################################
# Global random forests parameters
#########################################################
# the number of trees in the forest
n_estimators = 1000
# the minimum number of samples required to be at a leaf node
# (default skgarden's parameter)
min_samples_leaf = 1
# the number of features to consider when looking for the best split
# (default skgarden's parameter)
max_features = 6
params_basemodel = {'n_estimators':n_estimators, 'min_samples_leaf':min_samples_leaf, 'max_features':max_features,
'cores':1}
```
# Data import
```
# load the dataset
data = pd.read_csv("data_prices/Prices_2016_2019_extract.csv")
data.shape
# the first week (24*7 rows) has been removed because of the lagged variables.
date_plot = pd.to_datetime(data.Date)
plt_1 = plt.figure(figsize=(10, 5))
plt.plot(date_plot, data.Spot, color='black', linewidth=0.6)
locs, labels = plt.xticks()
plt.xticks(locs[0:len(locs):2], labels=['2016','2017','2018','2019','2020'])
plt.xlabel('Date')
plt.ylabel('Spot price (\u20AC/MWh)')
plt.show()
limit = datetime.datetime(2019, 1, 1, tzinfo=datetime.timezone.utc)
id_train = data.index[pd.to_datetime(data['Date'], utc=True) < limit].tolist()
data_train = data.iloc[id_train,:]
sub_data_train = data_train.loc[:,['hour','dow_0','dow_1','dow_2','dow_3','dow_4','dow_5','dow_6'] +
['lag_24_%d'%i for i in range(24)] +
['lag_168_%d'%i for i in range(24)] + ['conso']]
all_x_train = [np.array(sub_data_train.loc[sub_data_train.hour == h]) for h in range(24)]
train_size = all_x_train[0].shape[0]
sub_data = data.loc[:,['hour','dow_0','dow_1','dow_2','dow_3','dow_4','dow_5','dow_6'] +
['lag_24_%d'%i for i in range(24)] +
['lag_168_%d'%i for i in range(24)] + ['conso']]
all_x = [np.array(sub_data.loc[sub_data.hour == h]) for h in range(24)]
all_y = [np.array(data.loc[data.hour == h, 'Spot']) for h in range(24)]
all_x_train[0].shape
```
# CP methods
```
alpha = 0.1
for h in tqdm(range(24)):
X = all_x[h]
Y = all_y[h]
data_dict = {'X': np.transpose(X), 'Y': Y}
dataset = 'Spot_France_Hour_'+str(h)+'_train_'+str(limit)[:10]
methods = ['CP', 'EnbPI']
params_methods = {'B': 30}
results, methods_ran = models.run_experiments_real_data(data_dict, alpha, methods, params_methods, 'RF', params_basemodel,
train_size, dataset, erase=False)
for method in methods_ran:
name_dir, name_method = files.get_name_results(method, dataset=dataset)
results_method = results[method]
files.write_file('results/'+name_dir, name_method, 'pkl', results_method)
# Mean EnbPI
params_methods = {'B': 30, 'mean': True}
results, methods_ran = models.run_experiments_real_data(data_dict, alpha, methods, params_methods, 'RF', params_basemodel,
train_size, dataset, erase=False)
for method in methods_ran:
name_dir, name_method = files.get_name_results(method, dataset=dataset)
results_method = results[method]
files.write_file('results/'+name_dir, name_method, 'pkl', results_method)
# Offline
methods = ['CP']
params_methods = {'online': False}
results, methods_ran = models.run_experiments_real_data(data_dict, alpha, methods, params_methods, 'RF', params_basemodel,
train_size, dataset, erase=False)
for method in methods_ran:
name_dir, name_method = files.get_name_results(method, online=False, dataset=dataset)
results_method = results[method]
files.write_file('results/'+name_dir, name_method, 'pkl', results_method)
tab_gamma = [0,
0.000005,
0.00005,
0.0001,0.0002,0.0003,0.0004,0.0005,0.0006,0.0007,0.0008,0.0009,
0.001,0.002,0.003,0.004,0.005,0.006,0.007,0.008,0.009,
0.01,0.02,0.03,0.04,0.05,0.06,0.07,0.08,0.09]
for h in tqdm(range(24)):
X = all_x[h]
Y = all_y[h]
data_dict = {'X': np.transpose(X), 'Y': Y}
dataset = 'Spot_France_Hour_'+str(h)+'_train_'+str(limit)[:10]
results, methods_ran = models.run_multiple_gamma_ACP_real_data(data_dict, alpha, tab_gamma, 'RF',
params_basemodel, train_size, dataset,
erase=False)
online = True
for method in methods_ran:
name_dir, name_method = files.get_name_results(method, dataset=dataset)
results_method = results[method]
files.write_file('results/'+name_dir, name_method, 'pkl', results_method)
```
## Results concatenated
Be careful that the aggregation algorithm (AgACI) must be run in R separately from this notebook before running the following cells (if you use a new data set or if you erased the supplied results).
```
id_test = data.index[pd.to_datetime(data['Date'], utc=True) >= limit].tolist()
data_test = data.iloc[id_test,:]
methods = ['CP','EnbPI','EnbPI_Mean']+['ACP_'+str(gamma) for gamma in tab_gamma]+['Aggregation_EWA_Gradient','Aggregation_EWA',
'Aggregation_MLpol_Gradient','Aggregation_MLpol',
'Aggregation_BOA_Gradient','Aggregation_BOA']
for method in methods:
y_upper = [None]*data_test.shape[0]
y_lower = [None]*data_test.shape[0]
for i in range(24):
dataset = 'Spot_France_Hour_'+str(i)+'_train_'+str(limit)[:10]
name_dir, name_method = files.get_name_results(method, dataset=dataset)
results = files.load_file('results/'+name_dir, name_method, 'pkl')
y_upper[i::24] = list(results['Y_sup'].reshape(1,-1)[0])
y_lower[i::24] = list(results['Y_inf'].reshape(1,-1)[0])
y_upper = np.array(y_upper)
y_lower = np.array(y_lower)
results_method = {'Y_inf': y_lower, 'Y_sup':y_upper}
dataset = 'Spot_France_ByHour_train_'+str(limit)[:10]
name_dir, name_method = files.get_name_results(method, dataset=dataset)
if not os.path.isdir('results/'+name_dir):
os.mkdir('results/'+name_dir)
files.write_file('results/'+name_dir, name_method, 'pkl', results_method)
if method == 'CP':
y_upper = [None]*data_test.shape[0]
y_lower = [None]*data_test.shape[0]
for i in range(24):
dataset = 'Spot_France_Hour_'+str(i)+'_train_'+str(limit)[:10]
name_dir, name_method = files.get_name_results(method, online=False, dataset=dataset)
results = files.load_file('results/'+name_dir, name_method, 'pkl')
y_upper[i::24] = list(results['Y_sup'].reshape(1,-1)[0])
y_lower[i::24] = list(results['Y_inf'].reshape(1,-1)[0])
y_upper = np.array(y_upper)
y_lower = np.array(y_lower)
results_method = {'Y_inf': y_lower, 'Y_sup':y_upper}
dataset = 'Spot_France_ByHour_train_'+str(limit)[:10]
name_dir, name_method = files.get_name_results(method, online=False, dataset=dataset)
if not os.path.isdir('results/'+name_dir):
os.mkdir('results/'+name_dir)
files.write_file('results/'+name_dir, name_method, 'pkl', results_method)
dataset = 'Spot_France_ByHour_train_'+str(limit)[:10]
Y = data_test['Spot'].values
```
### Visualisation
```
colors_blindness = sns.color_palette("colorblind")
method = 'Aggregation_BOA_Gradient'
name_dir, name_method = files.get_name_results(method, dataset=dataset)
results = files.load_file('results/'+name_dir, name_method, 'pkl')
contains = (Y <= results['Y_sup']) & (Y >= results['Y_inf'])
lengths = results['Y_sup'] - results['Y_inf']
y_pred = (results['Y_sup'] + results['Y_inf'])/2
d = 20
plt.plot(pd.to_datetime(data_test['Date'])[24*d:(24*(d+4)+1)],data_test['Spot'][24*d:(24*(d+4)+1)], color='black',
label='Observed price')
plt.plot(pd.to_datetime(data_test['Date'])[24*(d+4):24*(d+5)],data_test['Spot'][24*(d+4):24*(d+5)],
color='black',alpha=.5)
plt.plot(pd.to_datetime(data_test['Date'])[24*(d+4):24*(d+5)],y_pred[24*(d+4):24*(d+5)],'--',
color=(230/255,120/255,20/255), label='Predicted price')
plt.ylabel("Spot price (€/MWh)")
plt.xticks(rotation=45)
plt.legend()
#plt.savefig('plots/prices/spot_last.png', bbox_inches='tight',dpi=300)
plt.show()
plt.plot(pd.to_datetime(data_test['Date'])[24*d:(24*(d+4)+1)],data_test['Spot'][24*d:(24*(d+4)+1)], color='black',
label='Observed price')
plt.plot(pd.to_datetime(data_test['Date'])[24*(d+4):24*(d+5)],data_test['Spot'][24*(d+4):24*(d+5)],
color='black', alpha=.5)
plt.plot(pd.to_datetime(data_test['Date'])[24*(d+4):24*(d+5)],results['Y_sup'][24*(d+4):24*(d+5)],
color=colors_blindness[9])
plt.plot(pd.to_datetime(data_test['Date'])[24*(d+4):24*(d+5)],results['Y_inf'][24*(d+4):24*(d+5)],
color=colors_blindness[9])
plt.fill_between(pd.to_datetime(data_test['Date'])[24*(d+4):24*(d+5)],results['Y_sup'][24*(d+4):24*(d+5)],
results['Y_inf'][24*(d+4):24*(d+5)],
alpha=.3, fc=colors_blindness[9], ec='None', label='Predicted interval')
plt.plot(pd.to_datetime(data_test['Date'])[24*(d+4):24*(d+5)],y_pred[24*(d+4):24*(d+5)],'--',
color=colors_blindness[1], label='Predicted price')
plt.ylabel("Spot price (€/MWh)")
plt.xticks(rotation=45)
plt.legend()
#plt.savefig('plots/prices/ex_int_'+method+'.pdf', bbox_inches='tight',dpi=300)
plt.show()
date_plot = pd.to_datetime(data.Date)
fig,ax = plt.subplots(1,1,figsize=(10, 5))
axins = inset_axes(ax,4.3,2.1,loc='upper right')
ax.plot(date_plot, data.Spot, color='black', linewidth=0.6)
locs = ax.get_xticks()
ax.set_xticks(locs[0:len(locs):2])
ax.set_xticklabels(['2016','2017','2018','2019','2020'])
ax.set_xlabel('Date')
ax.set_ylabel('Spot price (\u20AC/MWh)')
axins.plot(pd.to_datetime(data_test['Date'])[24*d:(24*(d+4)+1)],data_test['Spot'][24*d:(24*(d+4)+1)], color='black',
label='Observed price')
axins.plot(pd.to_datetime(data_test['Date'])[24*(d+4):24*(d+5)],data_test['Spot'][24*(d+4):24*(d+5)],
color='black', alpha=.5)
axins.plot(pd.to_datetime(data_test['Date'])[24*(d+4):24*(d+5)],results['Y_sup'][24*(d+4):24*(d+5)],
color=colors_blindness[9])
axins.plot(pd.to_datetime(data_test['Date'])[24*(d+4):24*(d+5)],results['Y_inf'][24*(d+4):24*(d+5)],
color=colors_blindness[9])
axins.fill_between(pd.to_datetime(data_test['Date'])[24*(d+4):24*(d+5)],results['Y_sup'][24*(d+4):24*(d+5)],
results['Y_inf'][24*(d+4):24*(d+5)],
alpha=.3, fc=colors_blindness[9], ec='None', label='Predicted interval')
axins.plot(pd.to_datetime(data_test['Date'])[24*(d+4):24*(d+5)],y_pred[24*(d+4):24*(d+5)],'--',
color=colors_blindness[1], label='Predicted price')
axins.legend(prop={'size': 14})
axins.set_yticks([50,75,100,125])
axins.set_yticklabels([50,75,100,125])
locs = axins.get_xticks()
axins.set_xticks(locs[:len(locs)-1])
axins.set_xticklabels(['21/01','22/01','23/01','24/01','25/01'])
axins.tick_params(axis='x', rotation=20)
mark_inset(ax, axins, loc1=3, loc2=4, fc="none", ec="0.7")
#plt.savefig('plots/prices/spot_and_ex_int_'+method+'.pdf', bbox_inches='tight',dpi=300)
plt.show()
```
### Marginal validity and efficiency comparison
```
lines = False
add_offline = True
methods = ['CP', 'EnbPI_Mean', 'ACP_0','ACP_0.01', 'ACP_0.05', 'Aggregation_BOA_Gradient']
marker_size = 80
fig, (ax1) = plt.subplots(1, 1, figsize=(10,5), sharex=True, sharey=True)
markers = {'Gaussian': "o", 'CP': "s", 'ACP':'D','ACP_0.05':'D', 'ACP_0.01': "d", 'ACP_0': "^", 'Aggregation_BOA_Gradient':'*',
'QR': "v", 'CQR': "D", 'CQR_CV': "d", 'EnbPI': 'x','EnbPI_Mean': '+'}
methods_display = {'Gaussian': 'Gaussian', 'CP': 'OSSCP', # (adapted from Lei et al., 2018)
'EnbPI': 'EnbPI (Xu \& Xie, 2021)','EnbPI_Mean': 'EnbPI V2',
'ACP': 'ACI '+r'$\gamma = 0.05$',#(Gibbs \& Candès, 2021)
'ACP_0.05': 'ACI '+r'$\gamma = 0.05$',#(Gibbs \& Candès, 2021)
'ACP_0.01': 'ACI '+r'$\gamma = 0.01$',# (Gibbs \& Candès, 2021),
'ACP_0': 'ACI '+r'$\gamma = 0$',# (Gibbs \& Candès, 2021),
'Aggregation_BOA_Gradient':'AgACI'}
for method in methods:
name_dir, name_method = files.get_name_results(method, dataset=dataset)
results = files.load_file('results/'+name_dir, name_method, 'pkl')
contains = (Y <= results['Y_sup']) & (Y >= results['Y_inf'])
lengths = results['Y_sup'] - results['Y_inf']
if method not in ["ACP","ACP_0.01","ACP_QCP_0.05",'EnbPI_Mean', 'Aggregation_BOA_Gradient']:
ax1.scatter(np.mean(contains),np.median(lengths),
marker=markers[method], color='black',s=marker_size)
elif method in ["ACP","ACP_0.01","ACP_QCP_0.05"]:
ax1.scatter(np.mean(contains),np.median(lengths),
marker=markers[method], color='black',s=marker_size)
elif method in ['EnbPI_Mean','Aggregation_BOA_Gradient']:
ax1.scatter(np.mean(contains),np.median(lengths),
marker=markers[method], color='black',s=marker_size+30)
if add_offline and method in ['Gaussian','CP','CQR','CQR_CV']:
name_dir, name_method = files.get_name_results(method, online=False, dataset=dataset)
results = files.load_file('results/'+name_dir, name_method, 'pkl')
contains = (Y <= results['Y_sup']) & (Y >= results['Y_inf'])
lengths = results['Y_sup'] - results['Y_inf']
ax1.scatter(np.mean(contains),np.median(lengths),
marker=markers[method], color='black', facecolors='none',s=marker_size)
ax1.axvline(x=1-alpha, color='black', ls=':')
ax1.set_xlabel("Coverage")
ax1.set_ylabel("Median length")
# Methods legend
handles = []
names = []
names_wo_offline = list( map(methods_display.get, methods) )
if add_offline:
names = np.append(names,names_wo_offline[0])
names = np.append(names,names_wo_offline)
names[1] = 'Offline SSCP'# (adapted from Lei et al., 2018)
else:
names = names_wo_offlines
for marker in list( map(markers.get, methods) ):
handles.append(mlines.Line2D([], [], color='black', marker=marker, linestyle='None'))
if add_offline and marker == 's':
handles.append(mlines.Line2D([], [], color='black', marker=marker, linestyle='None', markerfacecolor='none'))
fig.legend(handles, names, bbox_to_anchor=(0,0.95,1,0.2), loc='upper center', ncol=3)
if lines:
name_plot = 'plots/prices/'+dataset+'_lines'
else:
name_plot = 'plots/prices/'+dataset+'_median'
if add_offline :
name_plot = name_plot + '_offline'
#plt.savefig(name_plot+'.pdf', bbox_inches='tight',dpi=300)
plt.show()
lines = False
add_offline = True
methods = ['CP', 'EnbPI_Mean', 'ACP_0','ACP_0.01', 'ACP_0.05', 'Aggregation_BOA_Gradient']
marker_size = 80
fig, (ax1) = plt.subplots(1, 1, figsize=(10,5), sharex=True, sharey=True)
markers = {'Gaussian': "o", 'CP': "s", 'ACP':'D','ACP_0.05':'D', 'ACP_0.01': "d", 'ACP_0': "^", 'Aggregation_BOA_Gradient':'*',
'QR': "v", 'CQR': "D", 'CQR_CV': "d", 'EnbPI': 'x','EnbPI_Mean': '+'}
methods_display = {'Gaussian': 'Gaussian', 'CP': 'OSSCP', # (adapted from Lei et al., 2018)
'EnbPI': 'EnbPI (Xu \& Xie, 2021)','EnbPI_Mean': 'EnbPI V2',
'ACP': 'ACI '+r'$\gamma = 0.05$',#(Gibbs \& Candès, 2021)
'ACP_0.05': 'ACI '+r'$\gamma = 0.05$',#(Gibbs \& Candès, 2021)
'ACP_0.01': 'ACI '+r'$\gamma = 0.01$',# (Gibbs \& Candès, 2021),
'ACP_0': 'ACI '+r'$\gamma = 0$',# (Gibbs \& Candès, 2021),
'Aggregation_BOA_Gradient':'AgACI',
'ACP_QCP_0.05': 'ACI (Gibbs \& Candès, 2021) with corrected quantile',
'QR': 'QR (Koenker \& Bassett)', 'CQR': 'CQR (Romano et al., 2019)',
'CQR_CV': 'CQR with CV (Romano et al., 2019)'}
# Get values for imputation
name_dir, name_method = files.get_name_results('ACP_0', dataset=dataset)
results = files.load_file('results/'+name_dir, name_method, 'pkl')
borne_sup = results['Y_sup']
borne_inf = results['Y_inf']
y_chap = (borne_sup+borne_inf)/2
abs_res = np.abs(Y - y_chap)
max_eps = np.max(abs_res)
val_max = y_chap+max_eps
val_min = y_chap-max_eps
for method in methods:
name_dir, name_method = files.get_name_results(method, dataset=dataset)
results = files.load_file('results/'+name_dir, name_method, 'pkl')
contains = (Y <= results['Y_sup']) & (Y >= results['Y_inf'])
lengths = results['Y_sup']-results['Y_inf']
if method[:3] in ['ACP','Agg']:
borne_sup = results['Y_sup']
borne_inf = results['Y_inf']
borne_sup[np.isinf(borne_sup)] = val_max[np.isinf(borne_sup)]
borne_inf[np.isinf(borne_inf)] = val_min[np.isinf(borne_inf)]
borne_sup[borne_sup > val_max] = val_max[borne_sup > val_max]
borne_inf[borne_inf < val_min] = val_min[borne_inf < val_min]
lengths = borne_sup-borne_inf
if method not in ["ACP","ACP_0.01","ACP_QCP_0.05",'EnbPI_Mean', 'Aggregation_BOA_Gradient']:
ax1.scatter(np.mean(contains),np.mean(lengths),
marker=markers[method], color='black',s=marker_size)
elif method in ["ACP","ACP_0.01","ACP_QCP_0.05"]:
ax1.scatter(np.mean(contains),np.mean(lengths),
marker=markers[method], color='black',s=marker_size)
elif method in ['EnbPI_Mean','Aggregation_BOA_Gradient']:
ax1.scatter(np.mean(contains),np.mean(lengths),
marker=markers[method], color='black',s=marker_size+30)
if add_offline and method in ['Gaussian','CP','CQR','CQR_CV']:
name_dir, name_method = files.get_name_results(method, online=False, dataset=dataset)
results = files.load_file('results/'+name_dir, name_method, 'pkl')
contains = (Y <= results['Y_sup']) & (Y >= results['Y_inf'])
lengths = results['Y_sup'] - results['Y_inf']
ax1.scatter(np.mean(contains),np.mean(lengths),
marker=markers[method], color='black', facecolors='none',s=marker_size)
ax1.axvline(x=1-alpha, color='black', ls=':')
ax1.set_xlabel("Coverage")
ax1.set_ylabel("Average length")
# Methods legend
handles = []
names = []
names_wo_offline = list( map(methods_display.get, methods) )
if add_offline:
names = np.append(names,names_wo_offline[0])
names = np.append(names,names_wo_offline)
names[1] = 'Offline SSCP'# (adapted from Lei et al., 2018)
else:
names = names_wo_offlines
for marker in list( map(markers.get, methods) ):
handles.append(mlines.Line2D([], [], color='black', marker=marker, linestyle='None'))
if add_offline and marker == 's':
handles.append(mlines.Line2D([], [], color='black', marker=marker, linestyle='None', markerfacecolor='none'))
fig.legend(handles, names, bbox_to_anchor=(0,0.95,1,0.2), loc='upper center', ncol=3)
if lines:
name_plot = 'plots/prices/'+dataset+'imputed_lines'
else:
name_plot = 'plots/prices/'+dataset+'imputed_mean'
if add_offline :
name_plot = name_plot + '_offline'
#plt.savefig(name_plot+'.pdf', bbox_inches='tight',dpi=300)
plt.show()
```
|
github_jupyter
|
<a href="https://colab.research.google.com/github/lionelsamrat10/machine-learning-a-to-z/blob/main/Deep%20Learning/Convolutional%20Neural%20Networks%20(CNN)/convolutional_neural_network_samrat_with_10_epochs.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Convolutional Neural Network
### Importing the libraries
```
import tensorflow as tf
from keras.preprocessing.image import ImageDataGenerator
import numpy as np
tf.__version__
```
## Part 1 - Data Preprocessing
### Preprocessing the Training set
```
# Transforming the Image
# Rescale applies Feature Scaling to each pixels in our images
# We are doing this to avoid Overfitting
train_datagen = ImageDataGenerator(rescale = 1./255,
shear_range = 0.2,
zoom_range = 0.2,
horizontal_flip = True)
# Only 32 images will run in one batch
training_set = train_datagen.flow_from_directory('dataset/training_set',
target_size = (64, 64),
batch_size = 32,
class_mode = 'binary')
```
### Preprocessing the Test set
```
test_datagen = ImageDataGenerator(rescale = 1./255)
test_set = test_datagen.flow_from_directory('dataset/test_set',
target_size = (64, 64),
batch_size = 32,
class_mode = 'binary')
```
## Part 2 - Building the CNN
### Initialising the CNN
```
cnn = tf.keras.models.Sequential();
```
### Step 1 - Convolution
```
cnn.add(tf.keras.layers.Conv2D(filters=32, kernel_size=3, activation='relu', input_shape=[64, 64, 3]))
# Kernel Size is same as the number of rows in the Feature Detector
# The images are resized as 64px X 64px and 3 denotes 3D R, G, B
```
### Step 2 - Pooling
```
cnn.add(tf.keras.layers.MaxPool2D(pool_size=2, strides=2))
```
### Adding a second convolutional layer
```
cnn.add(tf.keras.layers.Conv2D(filters=32, kernel_size=3, activation='relu'))
cnn.add(tf.keras.layers.MaxPool2D(pool_size=2, strides=2))
```
### Step 3 - Flattening
```
cnn.add(tf.keras.layers.Flatten()) #Flattens the 2D array into an 1D array
```
### Step 4 - Full Connection
```
cnn.add(tf.keras.layers.Dense(units=128, activation='relu')) # Units mean the number of neurons in the hidden layer
```
### Step 5 - Output Layer
```
cnn.add(tf.keras.layers.Dense(units=1, activation='sigmoid'))
```
## Part 3 - Training the CNN
### Compiling the CNN
```
cnn.compile(optimizer = 'adam', loss = 'binary_crossentropy', metrics = ['accuracy'])
```
### Training the CNN on the Training set and evaluating it on the Test set
```
cnn.fit(x = training_set, validation_data = test_set, epochs = 10)
```
## Part 4 - Making a single prediction
```
from keras.preprocessing import image
test_image = image.load_img('dataset/single_prediction/cat_or_dog_1.jpg', target_size = (64, 64)) # Creates a PIL image
test_image = image.img_to_array(test_image) # Converts the PIL image to a NumPy Array
test_image = np.expand_dims(test_image, axis = 0) # Cobtain the image into a Batch
result = cnn.predict(test_image)
training_set.class_indices
if result[0][0] == 1:
prediction = 'dog'
else:
prediction = 'cat'
print(prediction) # cat_or_dog_1.jpg originally is an image of a dog
```
|
github_jupyter
|
<div align="Right"><font size="1">https://github.com/mrola/jupyter_themes_preview<br>Ola Söderström - 2018</font></div>
-----
<p align="center"><font size="6">Jupyter notebook for testing out different themes</font></p>
-----
# import libs
```
%matplotlib inline
import os
import sys
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib as mpl
import matplotlib.pyplot as plt
from IPython.core.display import display, HTML
from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = "all"
```
## Display version info
```
try:
%load_ext version_information
%version_information wget, pandas, numpy
except ModuleNotFoundError:
print("Module \"version_information\" not found, install using \"pip install version_information\"")
pass
```
## Check requirements
```
if not (sys.version_info.major > 2 and sys.version_info.minor > 2):
print("Notebook requires Python 3.2 or higher")
```
# Try new style css
## Fetch css and store as new profile
```
def mynewstyle(new_style_url, profilename="newcoolprofile"):
'''Creates directory and custom.css for new notebook style.
Run HTML command displayed at the end of execution to apply new style.
<style> tags will be inserted if missing.
To revert to default style, comment out HTML command using "#".
Parameters:
new_style_url : URL to css file to download
profilename : Name of new profile (arbitrary)
'''
use_new_style = True
print("Will use {}".format(os.path.basename(new_style_url)))
m = !ipython locate profile
print("{:35} {}".format("Default profile location:", m[0]))
!ipython profile create $profilename
m1 = !ipython locate profile $profilename
print("{:35} {}".format("New profile directory created", m1[0]))
p=!ipython locate profile $profilename
p = p[0] + '/static/custom/'
if os.path.exists(p) is True:
print("{:35} {}".format("Directory already exists:", p))
else:
print("Creating {}".format(p))
os.makedirs(p, exist_ok=True)
ccss = p + 'custom.css'
print()
!wget $new_style_url -nv -O $ccss
styletag = False
with open(ccss, 'r+') as f:
for line in f.readlines():
if 'DOCTYPE' in line:
print("This appears to be a html document, need standalone css.")
return
elif '<style>' in line:
styletag = True
break
if styletag is False:
# print("\nHTML <style> tags appears to be missing in custom.css, will add...")
!sed -i '1s/^/\<style\>/' $ccss
!echo "<\style>" >> $ccss
html_line = 'HTML(open(\'{}\', \'r\').read())'.format(ccss)
print("\nNow you need to execute the follwing line in single cell: \n {}".format(html_line))
```
### Set URL
Just some random themes I picked up for testing.
```
#new_style_url='https://raw.githubusercontent.com/dunovank/jupyter-themes/master/jupyterthemes/styles/compiled/monokai.css'
new_style_url='https://raw.githubusercontent.com/neilpanchal/spinzero-jupyter-theme/master/custom.css'
print("Will be using css from {}".format(new_style_url))
```
### Run script
```
mynewstyle(new_style_url, profilename="newprofile_34")
```
## Activate new style
```
HTML(open('/home/ola/.ipython/profile_newprofile_34/static/custom/custom.css', 'r').read())
```
# Check style on some random stuff
```
df = pd.DataFrame(np.random.randint(low=0, high=10, size=(5, 5)),columns=['a', 'b', 'c', 'd', 'e'])
df.loc[0, 'a'] = "This is some text"
df
```
## This is heading 2
### This is heading 3
This is markdown text.
# Viz
```
def sinplot(flip=1):
x = np.linspace(0, 14, 100)
for i in range(1, 7):
plt.plot(x, np.sin(x + i * .5) * (7 - i) * flip)
sinplot()
sns.set_style("ticks")
sns.despine(offset=10, trim=True)
```
# Setting individual styles using display(HTML)
```
display(HTML("<style>.cell { font-size: 12px; width:900px }</style>"))
display(HTML("<style>.input { margin-top:2em, margin-bottom:2em }</style>"))
#display(HTML("<style>.div.output_wrapper { margin-top:2em, margin-bottom:2em }</style>"))
#display(HTML("<style>.rendered_html { background-color: white; }</style>"))
#display(HTML("<style>.text_cell_render { font-size: 15px; }</style>"))
#display(HTML("<style>.text_cell { font-size: 15px; }</style>"))
#display(HTML("<style>.cell { font-size: 12px; max-width:000px }</style>"))
#display(HTML("<style>.CodeMirror { background-color: #2b303b; }</style>"))
#display(HTML("<style>.cell { background-color: #2b303b; }</style>"))
```
|
github_jupyter
|
# Linear regression from scratch
Powerful ML libraries can eliminate repetitive work, but if you rely too much on abstractions, you might never learn how neural networks really work under the hood. So for this first example, let's get our hands dirty and build everything from scratch, relying only on autograd and NDArray. First, we'll import the same dependencies as in the [autograd chapter](../chapter01_crashcourse/autograd.ipynb). We'll also import the powerful `gluon` package but in this chapter, we'll only be using it for data loading.
```
from __future__ import print_function
import mxnet as mx
from mxnet import nd, autograd, gluon
mx.random.seed(1)
```
## Set the context
We'll also want to specify the contexts where computation should happen. This tutorial is so simple that you could probably run it on a calculator watch. But, to develop good habits we're going to specify two contexts: one for data and one for our models.
```
data_ctx = mx.cpu()
model_ctx = mx.cpu()
```
## Linear regression
To get our feet wet, we'll start off by looking at the problem of regression.
This is the task of predicting a *real valued target* $y$ given a data point $x$.
In linear regression, the simplest and still perhaps the most useful approach,
we assume that prediction can be expressed as a *linear* combination of the input features
(thus giving the name *linear* regression):
$$\hat{y} = w_1 \cdot x_1 + ... + w_d \cdot x_d + b$$
Given a collection of data points $X$, and corresponding target values $\boldsymbol{y}$,
we'll try to find the *weight* vector $\boldsymbol{w}$ and bias term $b$
(also called an *offset* or *intercept*)
that approximately associate data points $\boldsymbol{x}_i$ with their corresponding labels ``y_i``.
Using slightly more advanced math notation, we can express the predictions $\boldsymbol{\hat{y}}$
corresponding to a collection of datapoints $X$ via the matrix-vector product:
$$\boldsymbol{\hat{y}} = X \boldsymbol{w} + b$$
Before we can get going, we will need two more things
* Some way to measure the quality of the current model
* Some way to manipulate the model to improve its quality
### Square loss
In order to say whether we've done a good job,
we need some way to measure the quality of a model.
Generally, we will define a *loss function*
that says *how far* are our predictions from the correct answers.
For the classical case of linear regression,
we usually focus on the squared error.
Specifically, our loss will be the sum, over all examples, of the squared error $(y_i-\hat{y})^2)$ on each:
$$\ell(y, \hat{y}) = \sum_{i=1}^n (\hat{y}_i-y_i)^2.$$
For one-dimensional data, we can easily visualize the relationship between our single feature and the target variable. It's also easy to visualize a linear predictor and it's error on each example.
Note that squared loss *heavily penalizes outliers*. For the visualized predictor below, the lone outlier would contribute most of the loss.

### Manipulating the model
For us to minimize the error,
we need some mechanism to alter the model.
We do this by choosing values of the *parameters*
$\boldsymbol{w}$ and $b$.
This is the only job of the learning algorithm.
Take training data ($X$, $y$) and the functional form of the model $\hat{y} = X\boldsymbol{w} + b$.
Learning then consists of choosing the best possible $\boldsymbol{w}$ and $b$ based on the available evidence.
### Historical note
You might reasonably point out that linear regression is a classical statistical model.
[According to Wikipedia](https://en.wikipedia.org/wiki/Regression_analysis#History),
Legendre first developed the method of least squares regression in 1805,
which was shortly thereafter rediscovered by Gauss in 1809.
Presumably, Legendre, who had Tweeted about the paper several times,
was peeved that Gauss failed to cite his arXiv preprint.

Matters of provenance aside, you might wonder - if Legendre and Gauss
worked on linear regression, does that mean there were the original deep learning researchers?
And if linear regression doesn't wholly belong to deep learning,
then why are we presenting a linear model
as the first example in a tutorial series on neural networks?
Well it turns out that we can express linear regression
as the simplest possible (useful) neural network.
A neural network is just a collection of nodes (aka neurons) connected by directed edges.
In most networks, we arrange the nodes into layers with each feeding its output into the layer above.
To calculate the value of any node, we first perform a weighted sum of the inputs (according to weights ``w``)
and then apply an *activation function*.
For linear regression, we only have two layers, one corresponding to the input (depicted in orange)
and a one-node layer (depicted in green) correspnding to the ouput.
For the output node the activation function is just the identity function.

While you certainly don't have to view linear regression through the lens of deep learning,
you can (and we will!).
To ground the concepts that we just discussed in code,
let's actually code up a neural network for linear regression from scratch.
To get going, we will generate a simple synthetic dataset by sampling random data points ``X[i]`` and corresponding labels ``y[i]`` in the following manner. Out inputs will each be sampled from a random normal distribution with mean $0$ and variance $1$. Our features will be independent. Another way of saying this is that they will have diagonal covariance. The labels will be generated accoding to the *true* labeling function `y[i] = 2 * X[i][0]- 3.4 * X[i][1] + 4.2 + noise` where the noise is drawn from a random gaussian with mean ``0`` and variance ``.01``. We could express the labeling function in mathematical notation as:
$$y = X \cdot w + b + \eta, \quad \text{for } \eta \sim \mathcal{N}(0,\sigma^2)$$
```
num_inputs = 2
num_outputs = 1
num_examples = 10000
def real_fn(X):
return 2 * X[:, 0] - 3.4 * X[:, 1] + 4.2
X = nd.random_normal(shape=(num_examples, num_inputs), ctx=data_ctx)
noise = .1 * nd.random_normal(shape=(num_examples,), ctx=data_ctx)
y = real_fn(X) + noise
```
Notice that each row in ``X`` consists of a 2-dimensional data point and that each row in ``Y`` consists of a 1-dimensional target value.
```
print(X[0])
print(y[0])
```
Note that because our synthetic features `X` live on `data_ctx` and because our noise also lives on `data_ctx`, the labels `y`, produced by combining `X` and `noise` in `real_fn` also live on `data_ctx`.
We can confirm that for any randomly chosen point,
a linear combination with the (known) optimal parameters
produces a prediction that is indeed close to the target value
```
print(2 * X[0, 0] - 3.4 * X[0, 1] + 4.2)
```
We can visualize the correspondence between our second feature (``X[:, 1]``) and the target values ``Y`` by generating a scatter plot with the Python plotting package ``matplotlib``. Make sure that ``matplotlib`` is installed. Otherwise, you may install it by running ``pip2 install matplotlib`` (for Python 2) or ``pip3 install matplotlib`` (for Python 3) on your command line.
In order to plot with ``matplotlib`` we'll just need to convert ``X`` and ``y`` into NumPy arrays by using the `.asnumpy()` function.
```
import matplotlib.pyplot as plt
plt.scatter(X[:, 1].asnumpy(),y.asnumpy())
plt.show()
```
## Data iterators
Once we start working with neural networks, we're going to need to iterate through our data points quickly. We'll also want to be able to grab batches of ``k`` data points at a time, to shuffle our data. In MXNet, data iterators give us a nice set of utilities for fetching and manipulating data. In particular, we'll work with the simple ``DataLoader`` class, that provides an intuitive way to use an ``ArrayDataset`` for training models.
We can load `X` and `y` into an ArrayDataset, by calling `gluon.data.ArrayDataset(X, y)`. It's ok for `X` to be a multi-dimensional input array (say, of images) and `y` to be just a one-dimensional array of labels. The one requirement is that they have equal lengths along the first axis, i.e., `len(X) == len(y)`.
Given an `ArrayDataset`, we can create a DataLoader which will grab random batches of data from an `ArrayDataset`. We'll want to specify two arguments. First, we'll need to say the `batch_size`, i.e., how many examples we want to grab at a time. Second, we'll want to specify whether or not to shuffle the data between iterations through the dataset.
```
batch_size = 4
train_data = gluon.data.DataLoader(gluon.data.ArrayDataset(X, y),
batch_size=batch_size, shuffle=True)
```
Once we've initialized our DataLoader (``train_data``), we can easily fetch batches by iterating over `train_data` just as if it were a Python list. You can use your favorite iterating techniques like foreach loops: `for data, label in train_data` or enumerations: `for i, (data, label) in enumerate(train_data)`.
First, let's just grab one batch and break out of the loop.
```
for i, (data, label) in enumerate(train_data):
print(data, label)
break
```
If we run that same code again you'll notice that we get a different batch. That's because we instructed the `DataLoader` that `shuffle=True`.
```
for i, (data, label) in enumerate(train_data):
print(data, label)
break
```
Finally, if we actually pass over the entire dataset, and count the number of batches, we'll find that there are 2500 batches. We expect this because our dataset has 10,000 examples and we configured the `DataLoader` with a batch size of 4.
```
counter = 0
for i, (data, label) in enumerate(train_data):
pass
print(i+1)
```
## Model parameters
Now let's allocate some memory for our parameters and set their initial values. We'll want to initialize these parameters on the `model_ctx`.
```
w = nd.random_normal(shape=(num_inputs, num_outputs), ctx=model_ctx)
b = nd.random_normal(shape=num_outputs, ctx=model_ctx)
params = [w, b]
```
In the succeeding cells, we're going to update these parameters to better fit our data. This will involve taking the gradient (a multi-dimensional derivative) of some *loss function* with respect to the parameters. We'll update each parameter in the direction that reduces the loss. But first, let's just allocate some memory for each gradient.
```
for param in params:
param.attach_grad()
```
## Neural networks
Next we'll want to define our model. In this case, we'll be working with linear models, the simplest possible *useful* neural network. To calculate the output of the linear model, we simply multiply a given input with the model's weights (``w``), and add the offset ``b``.
```
def net(X):
return mx.nd.dot(X, w) + b
```
Ok, that was easy.
## Loss function
Train a model means making it better and better over the course of a period of training. But in order for this goal to make any sense at all, we first need to define what *better* means in the first place. In this case, we'll use the squared distance between our prediction and the true value.
```
def square_loss(yhat, y):
return nd.mean((yhat - y) ** 2)
```
## Optimizer
It turns out that linear regression actually has a closed-form solution. However, most interesting models that we'll care about cannot be solved analytically. So we'll solve this problem by stochastic gradient descent. At each step, we'll estimate the gradient of the loss with respect to our weights, using one batch randomly drawn from our dataset. Then, we'll update our parameters a small amount in the direction that reduces the loss. The size of the step is determined by the *learning rate* ``lr``.
```
def SGD(params, lr):
for param in params:
param[:] = param - lr * param.grad
```
## Execute training loop
Now that we have all the pieces, we just need to wire them together by writing a training loop.
First we'll define ``epochs``, the number of passes to make over the dataset. Then for each pass, we'll iterate through ``train_data``, grabbing batches of examples and their corresponding labels.
For each batch, we'll go through the following ritual:
* Generate predictions (``yhat``) and the loss (``loss``) by executing a forward pass through the network.
* Calculate gradients by making a backwards pass through the network (``loss.backward()``).
* Update the model parameters by invoking our SGD optimizer.
```
epochs = 10
learning_rate = .0001
num_batches = num_examples/batch_size
for e in range(epochs):
cumulative_loss = 0
# inner loop
for i, (data, label) in enumerate(train_data):
data = data.as_in_context(model_ctx)
label = label.as_in_context(model_ctx).reshape((-1, 1))
with autograd.record():
output = net(data)
loss = square_loss(output, label)
loss.backward()
SGD(params, learning_rate)
cumulative_loss += loss.asscalar()
print(cumulative_loss / num_batches)
```
## Visualizing our training progess
In the succeeding chapters, we'll introduce more realistic data, fancier models, more complicated loss functions, and more. But the core ideas are the same and the training loop will look remarkably familiar. Because these tutorials are self-contained, you'll get to know this ritual quite well. In addition to updating out model, we'll often want to do some bookkeeping. Among other things, we might want to keep track of training progress and visualize it graphically. We demonstrate one slighly more sophisticated training loop below.
```
############################################
# Re-initialize parameters because they
# were already trained in the first loop
############################################
w[:] = nd.random_normal(shape=(num_inputs, num_outputs), ctx=model_ctx)
b[:] = nd.random_normal(shape=num_outputs, ctx=model_ctx)
############################################
# Script to plot the losses over time
############################################
def plot(losses, X, sample_size=100):
xs = list(range(len(losses)))
f, (fg1, fg2) = plt.subplots(1, 2)
fg1.set_title('Loss during training')
fg1.plot(xs, losses, '-r')
fg2.set_title('Estimated vs real function')
fg2.plot(X[:sample_size, 1].asnumpy(),
net(X[:sample_size, :]).asnumpy(), 'or', label='Estimated')
fg2.plot(X[:sample_size, 1].asnumpy(),
real_fn(X[:sample_size, :]).asnumpy(), '*g', label='Real')
fg2.legend()
plt.show()
learning_rate = .0001
losses = []
plot(losses, X)
for e in range(epochs):
cumulative_loss = 0
for i, (data, label) in enumerate(train_data):
data = data.as_in_context(model_ctx)
label = label.as_in_context(model_ctx).reshape((-1, 1))
with autograd.record():
output = net(data)
loss = square_loss(output, label)
loss.backward()
SGD(params, learning_rate)
cumulative_loss += loss.asscalar()
print("Epoch %s, batch %s. Mean loss: %s" % (e, i, cumulative_loss/num_batches))
losses.append(cumulative_loss/num_batches)
plot(losses, X)
```
## Conclusion
You've seen that using just mxnet.ndarray and mxnet.autograd, we can build statistical models from scratch. In the following tutorials, we'll build on this foundation, introducing the basic ideas behind modern neural networks and demonstrating the powerful abstractions in MXNet's `gluon` package for building complex models with little code.
## Next
[Linear regression with gluon](../chapter02_supervised-learning/linear-regression-gluon.ipynb)
For whinges or inquiries, [open an issue on GitHub.](https://github.com/zackchase/mxnet-the-straight-dope)
|
github_jupyter
|
... ***CURRENTLY UNDER DEVELOPMENT*** ...
## Simulate Monthly Mean Sea Level using a multivariate-linear regression model based on the annual SST PCs
inputs required:
* WaterLevel historical data from a tide gauge at the study site
* Historical and simulated Annual PCs (*from Notebook 01*)
in this notebook:
* Obtain monthly mean sea level anomalies (MMSLA) from the tidal gauge record
* Perform linear regression between MMSLA and annual PCs
* Obtain predicted timeseries of MMSLA based on simulated timeseries of annual PCs
### Workflow:
<div>
<img src="resources/nb01_02.png" width="300px">
</div>
Monthly sea level variability is typically due to processes occurring at longer timescales than the daily weather. Slowly varying seasonality and anomalies due to ENSO are retained in the climate emulator via the principle components (APC) used to develop the AWT. A multivariate regression model containing a mean plus annual and seasonal cycles at 12-month and 6-month periods for each APC covariate was fit to the MMSLA. This simple model explains ~75% of the variance without any specific information regarding local conditions (i.e., local anomalies due to coastal shelf dynamics, or local SSTAs) and slightly underpredicts extreme monthly sea level anomalies by ~10 cm. While this component of the approach is a subject of ongoing research, the regression model produces an additional ~0.35 m of regional SWL variability about mean sea level, which was deemed sufficient for the purposes of demonstrating the development of the stochastic climate emulator.
```
#!/usr/bin/env python
# -*- coding: utf-8 -*-
# basic import
import os
import os.path as op
from collections import OrderedDict
# python libs
import numpy as np
from numpy.random import multivariate_normal
import xarray as xr
from scipy.stats import linregress
from scipy.optimize import least_squares, curve_fit
from datetime import datetime, timedelta
# DEV: override installed teslakit
import sys
sys.path.insert(0, op.join(os.path.abspath(''), '..', '..', '..'))
# teslakit
from teslakit.database import Database
from teslakit.tides import Calculate_MMSL
from teslakit.statistical import runmean
from teslakit.util.time_operations import date2yearfrac as d2yf
from teslakit.plotting.tides import Plot_Tide_SLR, Plot_Tide_RUNM, Plot_Tide_MMSL, \
Plot_Validate_MMSL_tseries, Plot_Validate_MMSL_scatter, Plot_MMSL_Prediction, \
Plot_MMSL_Histogram
```
## Database and Site parameters
```
# --------------------------------------
# Teslakit database
p_data = r'/media/administrador/HD/Dropbox/Guam/teslakit/data'
db = Database(p_data)
# set site
db.SetSite('GUAM')
# --------------------------------------
# load data and set parameters
WL_split = db.Load_TIDE_hist_astro() # water level historical data (tide gauge)
WL = WL_split.WaterLevels
SST_KMA = db.Load_SST_KMA() # SST Anual Weather Types PCs
SST_PCs_sim_m = db.Load_SST_PCs_sim_m() # simulated SST PCs (monthly)
# parameters for mmsl calculation
mmsl_year_ini = 1947
mmsl_year_end = 2018
```
## Monthly Mean Sea Level
```
# --------------------------------------
# Calculate SLR using linear regression
time = WL.time.values[:]
wl = WL.values[:] * 1000 # (m to mm)
lr_time = np.array(range(len(time))) # for linregress
mask = ~np.isnan(wl) # remove nans with mask
slope, intercept, r_value, p_value, std_err = linregress(lr_time[mask], wl[mask])
slr = intercept + slope * lr_time
# Plot tide with SLR
Plot_Tide_SLR(time, wl, slr);
# --------------------------------------
# remove SLR and runmean from tide
tide_noslr = wl - slr
# calculate tide running mean
time_window = 365*24*3
runm = runmean(tide_noslr, time_window, 'mean')
# remove running mean
tide_noslr_norunm = tide_noslr - runm
# store data
TNSR = xr.DataArray(tide_noslr_norunm, dims=('time'), coords={'time':time})
# Plot tide without SLR and runm
Plot_Tide_RUNM(time, tide_noslr, runm);
# --------------------------------------
# calculate Monthly Mean Sea Level (mmsl)
MMSL = Calculate_MMSL(TNSR, mmsl_year_ini, mmsl_year_end)
# fill nans with interpolated values
p_nan = np.isnan(MMSL.mmsl)
MMSL.mmsl[p_nan]= np.interp(MMSL.time[p_nan], MMSL.time[~p_nan], MMSL.mmsl[~p_nan])
mmsl_time = MMSL.time.values[:]
mmsl_vals = MMSL.mmsl.values[:]
# Plot tide and mmsl
Plot_Tide_MMSL(TNSR.time, TNSR.values, mmsl_time, mmsl_vals);
# store historical mmsl
db.Save_TIDE_hist_mmsl(MMSL)
```
## Monthly Mean Sea Level - Principal Components
The annual PCs are passed to a monthly resolution
```
# --------------------------------------
# SST Anual Weather Types PCs
PCs = np.array(SST_KMA.PCs.values)
PC1, PC2, PC3 = PCs[:,0], PCs[:,1], PCs[:,2]
PCs_years = [int(str(t).split('-')[0]) for t in SST_KMA.time.values[:]]
# MMSL PCs calculations: cut and pad it to monthly resolution
ntrs_m_mean = np.array([])
ntrs_time = []
MMSL_PC1 = np.array([])
MMSL_PC2 = np.array([])
MMSL_PC3 = np.array([])
for c, y in enumerate(PCs_years):
pos = np.where(
(mmsl_time >= np.datetime64('{0}-06-01'.format(y))) &
(mmsl_time <= np.datetime64('{0}-05-29'.format(y+1)))
)
if pos[0].size:
ntrs_m_mean = np.concatenate((ntrs_m_mean, mmsl_vals[pos]),axis=0)
# TODO check for 0s and nans in ntrs_m_mean?
ntrs_time.append(mmsl_time[pos])
MMSL_PC1 = np.concatenate((MMSL_PC1, np.ones(pos[0].size)*PC1[c]),axis=0)
MMSL_PC2 = np.concatenate((MMSL_PC2, np.ones(pos[0].size)*PC2[c]),axis=0)
MMSL_PC3 = np.concatenate((MMSL_PC3, np.ones(pos[0].size)*PC3[c]),axis=0)
ntrs_time = np.concatenate(ntrs_time)
# Parse time to year fraction for linear-regression seasonality
frac_year = np.array([d2yf(x) for x in ntrs_time])
```
## Monthly Mean Sea Level - Multivariate-linear Regression Model
```
# --------------------------------------
# Fit linear regression model
def modelfun(data, *x):
pc1, pc2, pc3, t = data
return x[0] + x[1]*pc1 + x[2]*pc2 + x[3]*pc3 + \
np.array([x[4] + x[5]*pc1 + x[6]*pc2 + x[7]*pc3]).flatten() * np.cos(2*np.pi*t) + \
np.array([x[8] + x[9]*pc1 + x[10]*pc2 + x[11]*pc3]).flatten() * np.sin(2*np.pi*t) + \
np.array([x[12] + x[13]*pc1 + x[14]*pc2 + x[15]*pc3]).flatten() * np.cos(4*np.pi*t) + \
np.array([x[16] + x[17]*pc1 + x[18]*pc2 + x[19]*pc3]).flatten() * np.sin(4*np.pi*t)
# use non-linear least squares to fit our model
split = 160 # train / validation split index
x0 = np.ones(20)
sigma = np.ones(split)
# select data for scipy.optimize.curve_fit
x_train = ([MMSL_PC1[:split], MMSL_PC2[:split], MMSL_PC3[:split], frac_year[:split]])
y_train = ntrs_m_mean[:split]
res_lsq, res_cov = curve_fit(modelfun, x_train, y_train, x0, sigma)
# print optimal parameters and covariance
#print('optimal parameters (minimized sum of squares residual)\n{0}\n'.format(res_lsq))
#print('optimal parameters covariance\n{0}\n'.format(res_cov))
```
## Train and test model
```
# Check model at fitting period
yp_train = modelfun(x_train, *res_lsq)
Plot_Validate_MMSL_tseries(ntrs_time[:split], ntrs_m_mean[:split], yp_train);
Plot_Validate_MMSL_scatter(ntrs_m_mean[:split], yp_train);
# Check model at validation period
x_val = ([MMSL_PC1[split:], MMSL_PC2[split:], MMSL_PC3[split:], frac_year[split:]])
yp_val = modelfun(x_val, *res_lsq)
Plot_Validate_MMSL_tseries(ntrs_time[split:], ntrs_m_mean[split:], yp_val);
Plot_Validate_MMSL_scatter(ntrs_m_mean[split:], yp_val);
# Parameter sampling (generate sample of params based on covariance matrix)
n_sims = 10
theta_gen = res_lsq
theta_sim = multivariate_normal(theta_gen, res_cov, n_sims)
# Check model at validation period
yp_valp = np.ndarray((n_sims, len(ntrs_time[split:]))) * np.nan
for i in range(n_sims):
yp_valp[i, :] = modelfun(x_val, *theta_sim[i,:])
# 95% percentile
yp_val_quant = np.percentile(yp_valp, [2.275, 97.275], axis=0)
Plot_Validate_MMSL_tseries(ntrs_time[split:], ntrs_m_mean[split:], yp_val, mmsl_pred_quantiles=yp_val_quant);
# Fit model using entire dataset
sigma = np.ones(len(frac_year))
x_fit = ([MMSL_PC1, MMSL_PC2, MMSL_PC3, frac_year])
y_fit = ntrs_m_mean
res_lsq, res_cov = curve_fit(modelfun, x_fit, y_fit, x0, sigma)
# obtain model output
yp = modelfun(x_fit, *res_lsq)
# Generate 1000 simulations of the parameters
n_sims = 1000
theta_gen = res_lsq
param_sim = multivariate_normal(theta_gen, res_cov, n_sims)
# Check model
yp_p = np.ndarray((n_sims, len(ntrs_time))) * np.nan
for i in range(n_sims):
yp_p[i, :] = modelfun(x_fit, *param_sim[i,:])
# 95% percentile
yp_quant = np.percentile(yp_p, [2.275, 97.275], axis=0)
Plot_Validate_MMSL_tseries(ntrs_time, ntrs_m_mean, yp, mmsl_pred_quantiles=yp_quant);
# Save model parameters to use in climate change
model_coefs = xr.Dataset({'sim_params' : (('n_sims','n_params'), param_sim)})
db.Save_TIDE_mmsl_params(model_coefs)
```
## Monthly Mean Sea Level - Prediction
```
# --------------------------------------
# Predict 1000 years using simulated PCs (monthly time resolution)
# get simulation time as year fractions
PCs_sim_time = SST_PCs_sim_m.time.values[:]
frac_year_sim = np.array([d2yf(x) for x in PCs_sim_time])
# solve each PCs simulation
y_sim_n = np.ndarray((len(SST_PCs_sim_m.n_sim), len(frac_year_sim))) * np.nan
for s in SST_PCs_sim_m.n_sim:
PCs_s_m = SST_PCs_sim_m.sel(n_sim=s)
MMSL_PC1_sim = PCs_s_m.PC1.values[:]
MMSL_PC2_sim = PCs_s_m.PC2.values[:]
MMSL_PC3_sim = PCs_s_m.PC3.values[:]
# use linear-regression model
x_sim = ([MMSL_PC1_sim, MMSL_PC2_sim, MMSL_PC3_sim, frac_year_sim])
y_sim_n[s, :] = modelfun(x_sim, *param_sim[s,:])
# join output and store it
MMSL_sim = xr.Dataset(
{
'mmsl' : (('n_sim','time'), y_sim_n / 1000), # mm to m
},
{'time' : PCs_sim_time}
)
print(MMSL_sim)
db.Save_TIDE_sim_mmsl(MMSL_sim)
# Plot mmsl simulation
plot_sim = 0
y_sim = MMSL_sim.sel(n_sim=plot_sim).mmsl.values[:] * 1000 # m to mm
t_sim = MMSL_sim.sel(n_sim=plot_sim).time.values[:]
# Plot mmsl prediction
Plot_MMSL_Prediction(t_sim, y_sim);
# compare model histograms
Plot_MMSL_Histogram(ntrs_m_mean, y_sim);
# compare model histograms for all simulations
y_sim = MMSL_sim.mmsl.values[:].flatten() * 1000 # m to mm
Plot_MMSL_Histogram(ntrs_m_mean, y_sim);
```
|
github_jupyter
|
# Exact GP Regression with Multiple GPUs and Kernel Partitioning
In this notebook, we'll demonstrate training exact GPs on large datasets using two key features from the paper https://arxiv.org/abs/1903.08114:
1. The ability to distribute the kernel matrix across multiple GPUs, for additional parallelism.
2. Partitioning the kernel into chunks computed on-the-fly when performing each MVM to reduce memory usage.
We'll be using the `protein` dataset, which has about 37000 training examples. The techniques in this notebook can be applied to much larger datasets, but the training time required will depend on the computational resources you have available: both the number of GPUs available and the amount of memory they have (which determines the partition size) have a significant effect on training time.
```
import math
import torch
import gpytorch
import sys
from matplotlib import pyplot as plt
sys.path.append('../')
from LBFGS import FullBatchLBFGS
%matplotlib inline
%load_ext autoreload
%autoreload 2
```
## Downloading Data
We will be using the Protein UCI dataset which contains a total of 40000+ data points. The next cell will download this dataset from a Google drive and load it.
```
import os
import urllib.request
from scipy.io import loadmat
dataset = 'protein'
if not os.path.isfile(f'{dataset}.mat'):
print(f'Downloading \'{dataset}\' UCI dataset...')
urllib.request.urlretrieve('https://drive.google.com/uc?export=download&id=1nRb8e7qooozXkNghC5eQS0JeywSXGX2S',
f'{dataset}.mat')
data = torch.Tensor(loadmat(f'{dataset}.mat')['data'])
```
## Normalization and train/test Splits
In the next cell, we split the data 80/20 as train and test, and do some basic z-score feature normalization.
```
import numpy as np
N = data.shape[0]
# make train/val/test
n_train = int(0.8 * N)
train_x, train_y = data[:n_train, :-1], data[:n_train, -1]
test_x, test_y = data[n_train:, :-1], data[n_train:, -1]
# normalize features
mean = train_x.mean(dim=-2, keepdim=True)
std = train_x.std(dim=-2, keepdim=True) + 1e-6 # prevent dividing by 0
train_x = (train_x - mean) / std
test_x = (test_x - mean) / std
# normalize labels
mean, std = train_y.mean(),train_y.std()
train_y = (train_y - mean) / std
test_y = (test_y - mean) / std
# make continguous
train_x, train_y = train_x.contiguous(), train_y.contiguous()
test_x, test_y = test_x.contiguous(), test_y.contiguous()
output_device = torch.device('cuda:0')
train_x, train_y = train_x.to(output_device), train_y.to(output_device)
test_x, test_y = test_x.to(output_device), test_y.to(output_device)
```
## How many GPUs do you want to use?
In the next cell, specify the `n_devices` variable to be the number of GPUs you'd like to use. By default, we will use all devices available to us.
```
n_devices = torch.cuda.device_count()
print('Planning to run on {} GPUs.'.format(n_devices))
```
## GP Model + Training Code
In the next cell we define our GP model and training code. For this notebook, the only thing different from the Simple GP tutorials is the use of the `MultiDeviceKernel` to wrap the base covariance module. This allows for the use of multiple GPUs behind the scenes.
```
class ExactGPModel(gpytorch.models.ExactGP):
def __init__(self, train_x, train_y, likelihood, n_devices):
super(ExactGPModel, self).__init__(train_x, train_y, likelihood)
self.mean_module = gpytorch.means.ConstantMean()
base_covar_module = gpytorch.kernels.ScaleKernel(gpytorch.kernels.RBFKernel())
self.covar_module = gpytorch.kernels.MultiDeviceKernel(
base_covar_module, device_ids=range(n_devices),
output_device=output_device
)
def forward(self, x):
mean_x = self.mean_module(x)
covar_x = self.covar_module(x)
return gpytorch.distributions.MultivariateNormal(mean_x, covar_x)
def train(train_x,
train_y,
n_devices,
output_device,
checkpoint_size,
preconditioner_size,
n_training_iter,
):
likelihood = gpytorch.likelihoods.GaussianLikelihood().to(output_device)
model = ExactGPModel(train_x, train_y, likelihood, n_devices).to(output_device)
model.train()
likelihood.train()
optimizer = FullBatchLBFGS(model.parameters(), lr=0.1)
# "Loss" for GPs - the marginal log likelihood
mll = gpytorch.mlls.ExactMarginalLogLikelihood(likelihood, model)
with gpytorch.beta_features.checkpoint_kernel(checkpoint_size), \
gpytorch.settings.max_preconditioner_size(preconditioner_size):
def closure():
optimizer.zero_grad()
output = model(train_x)
loss = -mll(output, train_y)
return loss
loss = closure()
loss.backward()
for i in range(n_training_iter):
options = {'closure': closure, 'current_loss': loss, 'max_ls': 10}
loss, _, _, _, _, _, _, fail = optimizer.step(options)
print('Iter %d/%d - Loss: %.3f lengthscale: %.3f noise: %.3f' % (
i + 1, n_training_iter, loss.item(),
model.covar_module.module.base_kernel.lengthscale.item(),
model.likelihood.noise.item()
))
if fail:
print('Convergence reached!')
break
print(f"Finished training on {train_x.size(0)} data points using {n_devices} GPUs.")
return model, likelihood
```
## Automatically determining GPU Settings
In the next cell, we automatically determine a roughly reasonable partition or *checkpoint* size that will allow us to train without using more memory than the GPUs available have. Not that this is a coarse estimate of the largest possible checkpoint size, and may be off by as much as a factor of 2. A smarter search here could make up to a 2x performance improvement.
```
import gc
def find_best_gpu_setting(train_x,
train_y,
n_devices,
output_device,
preconditioner_size
):
N = train_x.size(0)
# Find the optimum partition/checkpoint size by decreasing in powers of 2
# Start with no partitioning (size = 0)
settings = [0] + [int(n) for n in np.ceil(N / 2**np.arange(1, np.floor(np.log2(N))))]
for checkpoint_size in settings:
print('Number of devices: {} -- Kernel partition size: {}'.format(n_devices, checkpoint_size))
try:
# Try a full forward and backward pass with this setting to check memory usage
_, _ = train(train_x, train_y,
n_devices=n_devices, output_device=output_device,
checkpoint_size=checkpoint_size,
preconditioner_size=preconditioner_size, n_training_iter=1)
# when successful, break out of for-loop and jump to finally block
break
except RuntimeError as e:
print('RuntimeError: {}'.format(e))
except AttributeError as e:
print('AttributeError: {}'.format(e))
finally:
# handle CUDA OOM error
gc.collect()
torch.cuda.empty_cache()
return checkpoint_size
# Set a large enough preconditioner size to reduce the number of CG iterations run
preconditioner_size = 100
checkpoint_size = find_best_gpu_setting(train_x, train_y,
n_devices=n_devices,
output_device=output_device,
preconditioner_size=preconditioner_size)
```
# Training
```
model, likelihood = train(train_x, train_y,
n_devices=n_devices, output_device=output_device,
checkpoint_size=checkpoint_size,
preconditioner_size=preconditioner_size,
n_training_iter=20)
```
# Testing: Computing test time caches
```
# Get into evaluation (predictive posterior) mode
model.eval()
likelihood.eval()
with torch.no_grad(), gpytorch.settings.fast_pred_var():
latent_pred = model(test_x)
```
# Testing: Computing predictions
```
with torch.no_grad(), gpytorch.settings.fast_pred_var():
%time latent_pred = model(test_x)
test_rmse = torch.sqrt(torch.mean(torch.pow(latent_pred.mean - test_y, 2)))
print(f"Test RMSE: {test_rmse.item()}")
```
|
github_jupyter
|
## Purpose: Try different models-- Part5.
### Penalized_SVM.
```
# import dependencies.
import pandas as pd
import numpy as np
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import classification_report
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.svm import SVC
```
#### STEP1: Read in dataset. Remove data from 2016-2019.
- data from 2016-2018 will be used to bs test the model.
- data from 2019 will be used to predict the winners of the 2019 WS.
```
# read in the data.
team_data = pd.read_csv("../../Resources/clean_data_1905.csv")
del team_data["Unnamed: 0"]
team_data.head()
# remove data from 2016 through 2019.
team_data_new = team_data.loc[team_data["year"] < 2016]
team_data_new.head()
target = team_data_new["winners"]
features = team_data_new.drop({"team", "year", "winners"}, axis=1)
feature_columns = list(features.columns)
print (target.shape)
print (features.shape)
print (feature_columns)
```
#### STEP2: Split and scale the data.
```
# split data.
X_train, X_test, y_train, y_test = train_test_split(features, target, random_state=42)
# scale data.
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.fit_transform(X_test)
```
#### STEP3: Try the SVC model.
```
# generate the model.
model = SVC(kernel="rbf",
class_weight="balanced",
probability=True)
# fit the model.
model.fit(X_train_scaled, y_train)
# predict.
prediction = model.predict(X_test_scaled)
print ((classification_report(y_test, prediction, target_names=["0", "1"])))
```
#### STEP4: Predict the winner 2016-2018.
```
def predict_the_winner(model, year, team_data, X_train):
'''
INPUT:
-X_train = scaled X train data.
-model = the saved model.
-team_data = complete dataframe with all data.
-year = the year want to look at.
OUTPUT:
-printed prediction.
DESCRIPTION:
-data from year of interest is isolated.
-the data are scaled.
-the prediction is made.
-print out the resulting probability and the name of the team.
'''
# grab the data.
team_data = team_data.loc[team_data["year"] == year].reset_index()
# set features (no team, year, winners).
# set target (winners).
features = team_data[feature_columns]
# scale.
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
features = scaler.fit_transform(features)
# fit the model.
probabilities = model.predict_proba(features)
# convert predictions to datafram.e
WS_predictions = pd.DataFrame(probabilities[:,1])
# Sort the DataFrame (descending)
WS_predictions = WS_predictions.sort_values(0, ascending=False)
WS_predictions['Probability'] = WS_predictions[0]
# Print 50 highest probability HoF inductees from still eligible players
for i, row in WS_predictions.head(50).iterrows():
prob = ' '.join(('WS Probability =', str(row['Probability'])))
print('')
print(prob)
print(team_data.iloc[i,1:27]["team"])
# predict for 2018.
predict_the_winner(model, 2018, team_data, X_train_scaled)
# predict for 2017.
predict_the_winner(model, 2017, team_data, X_train_scaled)
```
Ok. This didn't work. Let's try this penalized model with a grid search.
```
def grid_search_svc(X_train, X_test, y_train, y_test):
'''
INPUT:
-X_train = scaled X train data.
-X_test = scaled X test data.
-y_train = y train data.
-y_test = y test data.
OUTPUT:
-classification report (has F1 score, precision and recall).
-grid = saved model for prediction.
DESCRIPTION:
-the scaled and split data is put through a grid search with svc.
-the model is trained.
-a prediction is made.
-print out the classification report and give the model.
'''
# set up svc model.
model = SVC(kernel="rbf",
class_weight="balanced",
probability=True)
# create gridsearch estimator.
param_grid = {"C": [0.0001, 0.001, 0.01, 0.1, 1, 10, 100],
"gamma": [0.0001, 0.001, 0.01, 0.1]}
grid = GridSearchCV(model, param_grid, verbose=3)
# fit the model.
grid.fit(X_train, y_train)
# predict.
prediction = grid.predict(X_test)
# print out the basic information about the grid search.
print (grid.best_params_)
print (grid.best_score_)
print (grid.best_estimator_)
grid = grid.best_estimator_
predictions = grid.predict(X_test)
print (classification_report(y_test, prediction, target_names=["0", "1"]))
return grid
model_grid = grid_search_svc(X_train, X_test, y_train, y_test)
```
Nope. This is terrible. Lots of no.
|
github_jupyter
|
### 当涉及圆形子数组时,有两种情况。
1、情况1:没有交叉边界的最大子数组总和
2、情况2:具有交叉边界的最大子数组总和
写下一些小写的案例,并考虑案例2的一般模式。
记住为输入数组中的所有元素都为负数做一个角点案例句柄。
<img src='https://assets.leetcode.com/users/brianchiang_tw/image_1589539736.png'>
```
class Solution:
def maxSubarraySumCircular(self, A) -> int:
array_sum = 0
local_min_sum, global_min_sum = 0, float('inf')
local_max_sum, global_max_sum = 0, float('-inf')
for num in A:
local_min_sum = min(local_min_sum + num, num)
global_min_sum = min(global_min_sum, local_min_sum)
local_max_sum = max(local_max_sum + num, num)
global_max_sum = max(global_max_sum, local_max_sum)
array_sum += num
if global_max_sum > 0:
return max(array_sum - global_min_sum, global_max_sum)
return global_max_sum
class Solution:
def maxSubarraySumCircular(self, A) -> int:
min_sum = min_glo_sum = max_sum = max_glo_sum = A[0]
for a in A[1:]:
min_sum = min(a, a + min_sum)
min_glo_sum = min(min_sum, min_glo_sum)
max_sum = max(a, a + max_sum)
max_glo_sum = max(max_sum, max_glo_sum)
if sum(A) == min_glo_sum:
return max_glo_sum
return max(max_glo_sum, sum(A) - min_glo_sum)
class Solution:
def maxSubarraySumCircular(self, A) -> int:
array_sum = 0
local_min_sum, global_min_sum = 0, float('inf')
local_max_sum, global_max_sum = 0, float('-inf')
for number in A:
local_min_sum = min( local_min_sum + number, number )
global_min_sum = min( global_min_sum, local_min_sum )
local_max_sum = max( local_max_sum + number, number )
global_max_sum = max( global_max_sum, local_max_sum )
array_sum += number
# global_max_sum denotes the maximum subarray sum without crossing boundary
# arry_sum - global_min_sum denotes the maximum subarray sum with crossing boundary
if global_max_sum > 0:
return max( array_sum - global_min_sum, global_max_sum )
else:
# corner case handle for all number are negative
return global_max_sum
solution = Solution()
solution.maxSubarraySumCircular([3,1,3,2,6])
# 时间复杂度较高
class Solution:
def maxSubarraySumCircular(self, A) -> int:
res = -float('inf')
for i in range(len(A)):
temp_sum = A[i]
temp_max = A[i]
for j in range(i+1, len(A) * 2):
j %= len(A)
if j == i:
break
temp_sum += A[j]
temp_max = max(temp_max, temp_sum)
res = max(temp_max, res, A[i])
return res
from collections import Counter
# 时间复杂度较高
class Solution:
def maxSubarraySumCircular(self, A) -> int:
h = Counter(A)
solution = Solution()
solution.maxSubarraySumCircular([3,1,3,2,6])
```
|
github_jupyter
|
```
import tensorflow as tf
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib import rc
from IPython import display
import os
rc('font',**{'family':'sans-serif','sans-serif':['Helvetica']})
rc('text', usetex=True)
path = "rt-polaritydata/rt-polaritydata/"
pos_path = os.path.join(path, 'rt-polarity.pos')
neg_path = os.path.join(path, 'rt-polarity.neg')
def load_review(path, is_pos=True):
with open(path, encoding='latin-1') as f:
review = pd.DataFrame({'review':f.read().splitlines()})
review['sentiment'] = 1 if is_pos else 0
return review
pos_review = load_review(pos_path, is_pos=True)
neg_review = load_review(neg_path, is_pos=False)
# display.display(pos_review.head(), neg_review.head())
all_reviews = pd.concat([pos_review, neg_review])
all_reviews.head()
plt.hist(all_reviews.sentiment)
plt.show()
all_reviews["review_splitted"] = all_reviews.review.apply(lambda review: tf.keras.preprocessing.text.text_to_word_sequence(review))
import functools
import operator
def get_all_characters(df):
chars = []
for review in df.review_splitted:
for word in review:
chars.append(word)
chars = functools.reduce(operator.iconcat, chars, [])
return list(set(chars))
chars = get_all_characters(all_reviews)
NUM_CHARS = len(chars)
print('Total number of characters: {}\n{}'.format(NUM_CHARS, chars))
char_to_num = {chars[i]: i for i in range(NUM_CHARS)}
num_to_char = {i: chars[i] for i in range(NUM_CHARS)}
```
Find the maximum length of review -- padding
```
def get_max_len(df):
all_lenghts = []
for review in df.review:
all_lenghts.append(len(list(review)))
return max(all_lenghts)
MAX_LEN_POS = get_max_len(pos_review)
MAX_LEN_NEG = get_max_len(neg_review)
MAX_LEN_POS, MAX_LEN_NEG
MAX_LEN = get_max_len(all_reviews)
print('Maximum length of review: {} (in characters)'.format(MAX_LEN))
from stop_words import get_stop_words
def review_to_one_hot(char):
one_hot = [0] * NUM_CHARS
pos = char_to_num[char]
one_hot[pos] = 1
return one_hot
def process_review(review, pad=True, max_len=MAX_LEN):
review = tf.keras.preprocessing.text.text_to_word_sequence(review)
review = [word for word in review if word not in get_stop_words('english')]
review = [list(s) for s in review] # to characters
review = functools.reduce(operator.iconcat, review, [])
review_one_hot = [review_to_one_hot(char) for char in review]
if pad:
# append 0 value padding
while len(review_one_hot) < max_len:
review_one_hot.append([0] * NUM_CHARS)
review_one_hot = review_one_hot[:max_len] # trucate to max length
return review_one_hot
def get_len_review(review):
review = tf.keras.preprocessing.text.text_to_word_sequence(review)
review = [word for word in review if word not in get_stop_words('english')]
review = [list(s) for s in review] # to characters
review = functools.reduce(operator.iconcat, review, [])
return len(review)
reviews_len = all_reviews.review.apply(get_len_review)
np.median(reviews_len)
plt.hist(reviews_len, bins=20, color=(2/255, 0, 247/255, 0.5))
plt.vlines(np.median(reviews_len), 0, 1500)
# plt.vlines(np.quantile(reviews_len, q=0.75), 0, 1500, color='red')
plt.ylim([0, 1300])
plt.xlabel('# characters')
plt.ylabel('Count')
plt.savefig('figures/cnn_character_matrix.pdf', bbox_inches='tight')
# plt.show()
plt.figure(figsize=(6, 5))
plt.subplot(1, 2, 1)
position = 180
title = plt.title(neg_review.review.iloc[position])
plt.setp(title, color='blue')
plt.imshow([p for p in process_review(neg_review.review.iloc[position], max_len=100)], cmap='gray')
plt.axis('off')
plt.subplot(1, 2, 2)
t1 = pos_review.review.iloc[position]
t2 = 'a droll , well-acted , character-driven \ncomedy with unexpected deposits of feeling . '
title = plt.title(t2, y=-0.15)
plt.setp(title, color='red')
plt.imshow([p for p in process_review(pos_review.review.iloc[position], max_len=100)], cmap='gray')
plt.axis('off')
# plt.savefig('cnn_character_example.pdf', bbox_inches='tight')
# plt.show()
MAX_LEN_SEQ = 66 # 66 - median -- in characters
processed_review = all_reviews.review.apply(lambda review: process_review(review, max_len=MAX_LEN_SEQ))
X = processed_review.to_numpy().tolist()
y = all_reviews.sentiment.values
from tensorflow.keras import backend as K
def f1(y_true, y_pred):
"""
Create F1 metric for Keras
From: https://stackoverflow.com/a/45305384/9511702
"""
def recall(y_true, y_pred):
tp = K.sum(K.round(K.clip(y_true * y_pred, 0, 1)))
possible_positives = K.sum(K.round(K.clip(y_true, 0, 1)))
recall = tp / (possible_positives + K.epsilon())
return recall
def precision(y_true, y_pred):
tp = K.sum(K.round(K.clip(y_true * y_pred, 0, 1)))
predicted_positives = K.sum(K.round(K.clip(y_pred, 0, 1)))
precision = tp / (predicted_positives + K.epsilon())
return precision
precision = precision(y_true, y_pred)
recall = recall(y_true, y_pred)
return 2 * ((precision * recall) / (precision + recall + K.epsilon()))
def build_model():
model = tf.keras.Sequential([
tf.keras.layers.Conv2D(32, (3, 3), activation='relu', input_shape=(MAX_LEN_SEQ, NUM_CHARS, 1)),
tf.keras.layers.MaxPool2D((2, 2)),
tf.keras.layers.Dropout(0.25),
tf.keras.layers.Conv2D(64, (3, 3), activation='relu'),
tf.keras.layers.MaxPool2D((2, 2)),
tf.keras.layers.Dropout(0.25),
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(128, activation='relu'),
tf.keras.layers.Dropout(0.25),
tf.keras.layers.Dense(10, activation='relu'),
tf.keras.layers.Dense(1, activation='sigmoid')
])
metrics = ['accuracy', tf.keras.metrics.AUC(), f1]
optimizer = tf.keras.optimizers.RMSprop(lr=0.001, rho=0.9, epsilon=1e-08, decay=0.0)
model.compile(optimizer=optimizer, loss='binary_crossentropy', metrics=metrics)
return model
early_stopping = tf.keras.callbacks.EarlyStopping(monitor='val_accuracy', patience=8)
learning_rate_reduction = tf.keras.callbacks.ReduceLROnPlateau(monitor='val_accuracy',
patience=4,
verbose=1,
factor=0.5,
min_lr=0.00001)
def train(X_train, y_train, X_test, y_test, epochs=30, batch_size=64):
model = build_model()
history = model.fit(X_train,
y_train,
epochs=epochs,
batch_size=batch_size,
validation_data=(X_test, y_test),
callbacks=[early_stopping, learning_rate_reduction],
verbose=0)
test_results = model.evaluate(X_test, y_test, batch_size)
return history.history, model, test_results
from sklearn.model_selection import StratifiedKFold
def X_transform(X):
X = tf.convert_to_tensor(X)
X = tf.reshape(X, [X.shape[0], X.shape[1], X.shape[2], 1]) # one channel (black or white)
return X
def y_transform(y):
return tf.convert_to_tensor(y)
def cross_validate(X, y, split_size=3):
results = []
models = []
test_results = []
kf = StratifiedKFold(n_splits=split_size)
for train_idx, val_idx in kf.split(X, y):
X_train = X_transform(X[train_idx])
y_train = y_transform(y[train_idx])
X_test = X_transform(X[val_idx])
y_test = y_transform(y[val_idx])
result, model, test_result = train(X_train, y_train, X_test, y_test)
results.append(result)
models.append(model)
test_results.append(test_result)
return results, models, test_results
X_new = np.array(X)
y_new = np.array(y)
results, models, test_results = cross_validate(X_new, y_new)
test_results
def predict(model, review, max_len=MAX_LEN_SEQ, shape=(MAX_LEN_SEQ, NUM_CHARS, 1)):
input_ = [p for p in process_review(review, max_len=max_len)]
input_ = tf.cast(input_, tf.float32)
input_ = tf.reshape(input_, shape)
input_ = input_[np.newaxis, ...]
prediction = model.predict(input_)[0][0]
print(prediction)
if prediction > 0.5:
print('Positive review with probability: {:.2f}%'.format(prediction * 100))
else:
print('Negative review with probability: {:.2f}%'.format(100 - prediction * 100))
shape = (MAX_LEN_SEQ, NUM_CHARS, 1)
predict(models[2], "I really like this film, one of the best I've ever seen", shape=shape)
predict(models[2], 'I like this film and recommend to everyone.', shape=shape)
predict(models[2], "The movie was terrible, not worth watching once again", shape=shape)
for i, model in enumerate(models):
print(f"\nModel {i}: \n")
predict(model, "I really like this film, one of the best I've ever seen", shape=shape)
predict(model, 'I like this film and recommend to everyone.', shape=shape)
predict(model, 'Sometimes boring with a simple plot twist.', shape=shape)
predict(model, "The movie was terrible, not worth watching once again", shape=shape)
def plot_result(i, result):
plt.figure(figsize=(20, 4))
plt.subplot(1, 4, 1)
plt.plot(result['loss'], label='train')
plt.plot(result['val_loss'], label='test')
plt.xlabel('epoch', fontsize=14)
plt.ylabel('loss', fontsize=14)
plt.suptitle(f'Model {i+1}', fontsize=15)
plt.legend(fontsize=13)
#plt.tick_params(labelsize=14)
auc_metrics = []
for key, value in result.items():
if 'auc' in key:
auc_metrics.append(key)
plt.subplot(1, 4, 2)
plt.plot(result[auc_metrics[0]], label='train')
plt.plot(result[auc_metrics[1]], label='test')
plt.xlabel('epoch', fontsize=14)
plt.ylabel('AUC', fontsize=14)
plt.legend(fontsize=13)
plt.subplot(1, 4, 3)
plt.plot(result['f1'], label='train')
plt.plot(result['val_f1'], label='test')
plt.xlabel('epoch', fontsize=14)
plt.ylabel(r'$F_1$', fontsize=14)
plt.legend(fontsize=13)
plt.subplot(1, 4, 4)
plt.plot(result['accuracy'], label='train')
plt.plot(result['val_accuracy'], label='test')
plt.xlabel('epoch', fontsize=14)
plt.ylabel('accuracy', fontsize=14)
plt.legend(fontsize=13)
plt.savefig(f'figures/cnn_character_training_{i+1}.pdf', bbox_inches='tight')
#plt.show()
for i, r in enumerate(results):
plot_result(i, r)
from tensorflow.keras.utils import model_to_dot
def save_model_architecture(filename):
dot_model = model_to_dot(build_model(), show_shapes=True, show_layer_names=False)
dot_model.write_pdf(filename)
save_model_architecture('figures/cnn_characters_model.pdf')
```
|
github_jupyter
|
```
import pandas as pd
from sklearn.metrics import classification_report
!ls
train = pd.read_csv('../Post Processing/data/postproc_train.csv')
val = pd.read_csv('../Post Processing/data/postproc_val.csv')
test = pd.read_csv('../Post Processing/data/postproc_test.csv')
test_gt = pd.read_csv('../../data/english_test_with_labels.csv')
val_gt = pd.read_csv('../../data/Constraint_Val.csv')
def post_proc(row):
if (row['domain_real']>row['domain_fake']) & (row['domain_real']>0.88):
return 0
elif (row['domain_real']<row['domain_fake']) & (row['domain_fake']>0.88):
return 1
else:
# if (row['username_real']>row['username_fake']) & (row['username_real']>0.88):
# return 0
# elif (row['username_real']<row['username_fake']) & (row['username_fake']>0.88):
# return 1
# else:
if row['class1_pred']>row['class0_pred']:
return 1
elif row['class1_pred']<row['class0_pred']:
return 0
def post_proc1(row):
if row['class1_pred']>row['class0_pred']:
return 1
elif row['class1_pred']<row['class0_pred']:
return 0
train['final_pred'] = train.apply(lambda x: post_proc(x), 1)
print(classification_report(train['label'], train['final_pred']))
val['final_pred'] = val.apply(lambda x: post_proc(x), 1)
print(classification_report(val['label'], val['final_pred']))
from sklearn.metrics import f1_score,accuracy_score,precision_score,recall_score
print('f1_score : ',f1_score(val['label'], val['final_pred'],average='micro'))
print('precision_score : ',precision_score(val['label'], val['final_pred'],average='micro'))
print('recall_score : ',recall_score(val['label'], val['final_pred'],average='micro'))
test['final_pred'] = test.apply(lambda x: post_proc(x), 1)
print(classification_report(test['label'], test['final_pred']))
from sklearn.metrics import f1_score,accuracy_score,precision_score,recall_score
print('f1_score : ',f1_score(test['label'], test['final_pred'],average='micro'))
print('precision_score : ',precision_score(test['label'], test['final_pred'],average='micro'))
print('recall_score : ',recall_score(test['label'], test['final_pred'],average='micro'))
```
## Get False Pred samples
```
val_false_pred = val[val.final_pred!=val.label]
pd.merge(val_false_pred, val_gt, left_index=True, right_index=True)
pd.merge(val_false_pred, val_gt, left_index=True, right_index=True).to_csv('../Post Processing/results/val_false_pred_var_1.csv')
test_false_pred = test[test.final_pred!=test.label]
pd.merge(test_false_pred, test_gt, left_index=True, right_index=True)
pd.merge(test_false_pred, test_gt, left_index=True, right_index=True).to_csv('../Post Processing/results/test_false_pred_var_1.csv')
```
|
github_jupyter
|
# Visualizing CNN Layers
---
In this notebook, we load a trained CNN (from a solution to FashionMNIST) and implement several feature visualization techniques to see what features this network has learned to extract.
### Load the [data](http://pytorch.org/docs/stable/torchvision/datasets.html)
In this cell, we load in just the **test** dataset from the FashionMNIST class.
```
# our basic libraries
import torch
import torchvision
# data loading and transforming
from torchvision.datasets import FashionMNIST
from torch.utils.data import DataLoader
from torchvision import transforms
# The output of torchvision datasets are PILImage images of range [0, 1].
# We transform them to Tensors for input into a CNN
## Define a transform to read the data in as a tensor
data_transform = transforms.ToTensor()
test_data = FashionMNIST(root='./data', train=False,
download=True, transform=data_transform)
# Print out some stats about the test data
print('Test data, number of images: ', len(test_data))
# prepare data loaders, set the batch_size
## TODO: you can try changing the batch_size to be larger or smaller
## when you get to training your network, see how batch_size affects the loss
batch_size = 32
test_loader = DataLoader(test_data, batch_size=batch_size, shuffle=True)
# specify the image classes
classes = ['T-shirt/top', 'Trouser', 'Pullover', 'Dress', 'Coat',
'Sandal', 'Shirt', 'Sneaker', 'Bag', 'Ankle boot']
```
### Visualize some test data
This cell iterates over the training dataset, loading a random batch of image/label data, using `dataiter.next()`. It then plots the batch of images and labels in a `2 x batch_size/2` grid.
```
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
# obtain one batch of training images
dataiter = iter(test_loader)
images, labels = dataiter.next()
images = images.numpy()
print(images.shape)
# plot the images in the batch, along with the corresponding labels
fig = plt.figure(figsize=(25, 4))
for idx in np.arange(batch_size):
ax = fig.add_subplot(2, batch_size/2, idx+1, xticks=[], yticks=[])
ax.imshow(np.squeeze(images[idx]), cmap='gray')
ax.set_title(classes[labels[idx]])
```
### Define the network architecture
The various layers that make up any neural network are documented, [here](http://pytorch.org/docs/stable/nn.html). For a convolutional neural network, we'll use a simple series of layers:
* Convolutional layers
* Maxpooling layers
* Fully-connected (linear) layers
```
import torch.nn as nn
import torch.nn.functional as F
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
# 1 input image channel (grayscale), 10 output channels/feature maps
# 3x3 square convolution kernel
## output size = (W-F)/S +1 = (28-3)/1 +1 = 26
# the output Tensor for one image, will have the dimensions: (10, 26, 26)
# after one pool layer, this becomes (10, 13, 13)
self.conv1 = nn.Conv2d(1, 10, 3)
# maxpool layer
# pool with kernel_size=2, stride=2
self.pool = nn.MaxPool2d(2, 2)
# second conv layer: 10 inputs, 20 outputs, 3x3 conv
## output size = (W-F)/S +1 = (13-3)/1 +1 = 11
# the output tensor will have dimensions: (20, 11, 11)
# after another pool layer this becomes (20, 5, 5); 5.5 is rounded down
self.conv2 = nn.Conv2d(10, 20, 3)
# 20 outputs * the 5*5 filtered/pooled map size
self.fc1 = nn.Linear(20*5*5, 50)
# dropout with p=0.4
self.fc1_drop = nn.Dropout(p=0.4)
# finally, create 10 output channels (for the 10 classes)
self.fc2 = nn.Linear(50, 10)
# define the feedforward behavior
def forward(self, x):
# two conv/relu + pool layers
x = self.pool(F.relu(self.conv1(x)))
x = self.pool(F.relu(self.conv2(x)))
# prep for linear layer
# this line of code is the equivalent of Flatten in Keras
x = x.view(x.size(0), -1)
# two linear layers with dropout in between
x = F.relu(self.fc1(x))
x = self.fc1_drop(x)
x = self.fc2(x)
# final output
return x
```
### Load in our trained net
This notebook needs to know the network architecture, as defined above, and once it knows what the "Net" class looks like, we can instantiate a model and load in an already trained network.
The architecture above is taken from the example solution code, which was trained and saved in the directory `saved_models/`.
```
# instantiate your Net
net = Net()
# load the net parameters by name
net.load_state_dict(torch.load('saved_models/fashion_net_ex.pt'))
print(net)
```
## Feature Visualization
Sometimes, neural networks are thought of as a black box, given some input, they learn to produce some output. CNN's are actually learning to recognize a variety of spatial patterns and you can visualize what each convolutional layer has been trained to recognize by looking at the weights that make up each convolutional kernel and applying those one at a time to a sample image. These techniques are called feature visualization and they are useful for understanding the inner workings of a CNN.
In the cell below, you'll see how to extract and visualize the filter weights for all of the filters in the first convolutional layer.
Note the patterns of light and dark pixels and see if you can tell what a particular filter is detecting. For example, the filter pictured in the example below has dark pixels on either side and light pixels in the middle column, and so it may be detecting vertical edges.
<img src='edge_filter_ex.png' width= 30% height=30%/>
```
# Get the weights in the first conv layer
weights = net.conv1.weight.data
w = weights.numpy()
# for 10 filters
fig=plt.figure(figsize=(20, 8))
columns = 5
rows = 2
for i in range(0, columns*rows):
fig.add_subplot(rows, columns, i+1)
plt.imshow(w[i][0], cmap='gray')
print('First convolutional layer')
plt.show()
weights = net.conv2.weight.data
w = weights.numpy()
```
### Activation Maps
Next, you'll see how to use OpenCV's `filter2D` function to apply these filters to a sample test image and produce a series of **activation maps** as a result. We'll do this for the first and second convolutional layers and these activation maps whould really give you a sense for what features each filter learns to extract.
```
# obtain one batch of testing images
dataiter = iter(test_loader)
images, labels = dataiter.next()
images = images.numpy()
# select an image by index
idx = 3
img = np.squeeze(images[idx])
# Use OpenCV's filter2D function
# apply a specific set of filter weights (like the one's displayed above) to the test image
import cv2
plt.imshow(img, cmap='gray')
weights = net.conv1.weight.data
w = weights.numpy()
# 1. first conv layer
# for 10 filters
fig=plt.figure(figsize=(30, 10))
columns = 5*2
rows = 2
for i in range(0, columns*rows):
fig.add_subplot(rows, columns, i+1)
if ((i%2)==0):
plt.imshow(w[int(i/2)][0], cmap='gray')
else:
c = cv2.filter2D(img, -1, w[int((i-1)/2)][0])
plt.imshow(c, cmap='gray')
plt.show()
# Same process but for the second conv layer (20, 3x3 filters):
plt.imshow(img, cmap='gray')
# second conv layer, conv2
weights = net.conv2.weight.data
w = weights.numpy()
# 1. first conv layer
# for 20 filters
fig=plt.figure(figsize=(30, 10))
columns = 5*2
rows = 2*2
for i in range(0, columns*rows):
fig.add_subplot(rows, columns, i+1)
if ((i%2)==0):
plt.imshow(w[int(i/2)][0], cmap='gray')
else:
c = cv2.filter2D(img, -1, w[int((i-1)/2)][0])
plt.imshow(c, cmap='gray')
plt.show()
```
### Question: Choose a filter from one of your trained convolutional layers; looking at these activations, what purpose do you think it plays? What kind of feature do you think it detects?
**Answer**: In the first convolutional layer (conv1), the very first filter, pictured in the top-left grid corner, appears to detect horizontal edges. It has a negatively-weighted top row and positively weighted middel/bottom rows and seems to detect the horizontal edges of sleeves in a pullover.
In the second convolutional layer (conv2) the first filter looks like it may be dtecting the background color (since that is the brightest area in the filtered image) and the more vertical edges of a pullover.
|
github_jupyter
|
# "Text Classification with Roberta - Does a Twitter post actually announce a diasater?"
- toc:true
- branch: master
- badges: true
- comments: true
- author: Peiyi Hung
- categories: [category, project]
- image: "images/tweet-class.png"
```
import numpy as np
import pandas as pd
from fastai.text.all import *
import re
```
# Import the data and clean it
```
dir_path = "/kaggle/input/nlp-getting-started/"
train_df = pd.read_csv(dir_path + "train.csv")
test_df = pd.read_csv(dir_path + "test.csv")
train_df
train_df = train_df.drop(columns=["id", "keyword", "location"])
train_df["target"].value_counts()
def remove_URL(text):
url = re.compile(r'https?://\S+|www\.\S+')
return url.sub(r'',text)
train_df["text"] = train_df["text"].apply(remove_URL)
test_df["text"] = test_df["text"].apply(remove_URL)
def remove_html(text):
html=re.compile(r'<.*?>')
return html.sub(r'',text)
train_df["text"] = train_df["text"].apply(remove_html)
test_df["text"] = test_df["text"].apply(remove_html)
def remove_emoji(text):
emoji_pattern = re.compile("["
u"\U0001F600-\U0001F64F" # emoticons
u"\U0001F300-\U0001F5FF" # symbols & pictographs
u"\U0001F680-\U0001F6FF" # transport & map symbols
u"\U0001F1E0-\U0001F1FF" # flags (iOS)
u"\U00002702-\U000027B0"
u"\U000024C2-\U0001F251"
"]+", flags=re.UNICODE)
return emoji_pattern.sub(r'', text)
train_df["text"] = train_df["text"].apply(remove_emoji)
test_df["text"] = test_df["text"].apply(remove_emoji)
train_df
train_df["text"].apply(lambda x:len(x.split())).plot(kind="hist");
```
# Get tokens for the transformer
```
from transformers import AutoTokenizer, AutoModelForSequenceClassification
tokenizer = AutoTokenizer.from_pretrained("roberta-large")
```
From the graph above, we can know that the longest tweet has 30 words, so I set the `max_length` to 30.
```
train_tensor = tokenizer(list(train_df["text"]), padding="max_length",
truncation=True, max_length=30,
return_tensors="pt")["input_ids"]
```
# Preparing datasets and dataloaders
```
class TweetDataset:
def __init__(self, tensors, targ, ids):
self.text = tensors[ids, :]
self.targ = targ[ids].reset_index(drop=True)
def __len__(self):
return len(self.text)
def __getitem__(self, idx):
t = self.text[idx]
y = self.targ[idx]
return t, tensor(y)
train_ids, valid_ids = RandomSplitter()(train_df)
target = train_df["target"]
train_ds = TweetDataset(train_tensor, target, train_ids)
valid_ds = TweetDataset(train_tensor, target, valid_ids)
train_dl = DataLoader(train_ds, bs=64)
valid_dl = DataLoader(valid_ds, bs=512)
dls = DataLoaders(train_dl, valid_dl).to("cuda")
```
# Get the model
```
bert = AutoModelForSequenceClassification.from_pretrained("roberta-large", num_labels=2).train().to("cuda")
class BertClassifier(Module):
def __init__(self, bert):
self.bert = bert
def forward(self, x):
return self.bert(x).logits
model = BertClassifier(bert)
```
# Start training
```
learn = Learner(dls, model, metrics=[accuracy, F1Score()]).to_fp16()
learn.lr_find()
learn.fit_one_cycle(3, lr_max=1e-5)
```
# Find the best threshold for f1 score
```
from sklearn.metrics import f1_score
preds, targs = learn.get_preds()
min_threshold = None
max_f1 = -float("inf")
thresholds = np.linspace(0.3, 0.7, 50)
for threshold in thresholds:
f1 = f1_score(targs, F.softmax(preds, dim=1)[:, 1]>threshold)
if f1 > max_f1:
min_threshold = threshold
min_f1 = f1
print(f"threshold:{threshold:.4f} - f1:{f1:.4f}")
```
# Make prediction on the test set and submit the prediction
```
test_tensor = tokenizer(list(test_df["text"]),
padding="max_length",
truncation=True,
max_length=30,
return_tensors="pt")["input_ids"]
class TestDS:
def __init__(self, tensors):
self.tensors = tensors
def __len__(self):
return len(self.tensors)
def __getitem__(self, idx):
t = self.tensors[idx]
return t, tensor(0)
test_dl = DataLoader(TestDS(test_tensor), bs=128)
test_preds = learn.get_preds(dl=test_dl)
sub = pd.read_csv(dir_path + "sample_submission.csv")
prediction = (F.softmax(test_preds[0], dim=1)[:, 1]>min_threshold).int()
sub = pd.read_csv(dir_path + "sample_submission.csv")
sub["target"] = prediction
sub.to_csv("submission.csv", index=False)
```
|
github_jupyter
|
<a href="https://colab.research.google.com/github/google/jax-md/blob/main/notebooks/talk_demo.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
#@title Import & Util
!pip install -q git+https://www.github.com/google/jax
!pip install -q git+https://www.github.com/google/jax-md
!pip install dm-haiku
!pip install optax
import jax.numpy as np
from jax import device_put
from jax.config import config
# TODO: Uncomment this and enable warnings when XLA bug is fixed.
import warnings; warnings.simplefilter('ignore')
# config.update('jax_enable_x64', True)
from IPython.display import set_matplotlib_formats
set_matplotlib_formats('pdf', 'svg')
import matplotlib.pyplot as plt
import seaborn as sns
import pickle
import warnings
warnings.simplefilter("ignore")
sns.set_style(style='white')
background_color = [56 / 256] * 3
def plot(x, y, *args):
plt.plot(x, y, *args, linewidth=3)
plt.gca().set_facecolor([1, 1, 1])
def draw(R, **kwargs):
if 'c' not in kwargs:
kwargs['color'] = [1, 1, 0.9]
ax = plt.axes(xlim=(0, float(np.max(R[:, 0]))),
ylim=(0, float(np.max(R[:, 1]))))
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
ax.set_facecolor(background_color)
plt.scatter(R[:, 0], R[:, 1], marker='o', s=1024, **kwargs)
plt.gcf().patch.set_facecolor(background_color)
plt.gcf().set_size_inches(6, 6)
plt.tight_layout()
def draw_big(R, **kwargs):
if 'c' not in kwargs:
kwargs['color'] = [1, 1, 0.9]
fig = plt.figure(dpi=128)
ax = plt.axes(xlim=(0, float(np.max(R[:, 0]))),
ylim=(0, float(np.max(R[:, 1]))))
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
ax.set_facecolor(background_color)
s = plt.scatter(R[:, 0], R[:, 1], marker='o', s=0.5, **kwargs)
s.set_rasterized(True)
plt.gcf().patch.set_facecolor(background_color)
plt.gcf().set_size_inches(10, 10)
plt.tight_layout()
def draw_displacement(R, dR):
plt.quiver(R[:, 0], R[:, 1], dR[:, 0], dR[:, 1], color=[1, 0.5, 0.5])
# Progress Bars
from IPython.display import HTML, display
import time
def ProgressIter(iter_fun, iter_len=0):
if not iter_len:
iter_len = len(iter_fun)
out = display(progress(0, iter_len), display_id=True)
for i, it in enumerate(iter_fun):
yield it
out.update(progress(i + 1, iter_len))
def progress(value, max):
return HTML("""
<progress
value='{value}'
max='{max}',
style='width: 45%'
>
{value}
</progress>
""".format(value=value, max=max))
# Data Loading
!wget -O silica_train.npz https://www.dropbox.com/s/3dojk4u4di774ve/silica_train.npz?dl=0
!wget https://raw.githubusercontent.com/google/jax-md/main/examples/models/si_gnn.pickle
import numpy as onp
with open('silica_train.npz', 'rb') as f:
files = onp.load(f)
Rs, Es, Fs = [device_put(x) for x in (files['arr_0'], files['arr_1'], files['arr_2'])]
Rs = Rs[:10]
Es = Es[:10]
Fs = Fs[:10]
test_Rs, test_Es, test_Fs = [device_put(x) for x in (files['arr_3'], files['arr_4'], files['arr_5'])]
test_Rs = test_Rs[:200]
test_Es = test_Es[:200]
test_Fs = test_Fs[:200]
def tile(box_size, positions, tiles):
pos = positions
for dx in range(tiles):
for dy in range(tiles):
for dz in range(tiles):
if dx == 0 and dy == 0 and dz == 0:
continue
pos = np.concatenate((pos, positions + box_size * np.array([[dx, dy, dz]])))
return box_size * tiles, pos
```
## Demo
www.github.com/google/jax-md -> notebooks -> talk_demo.ipynb
### Energy and Automatic Differentiation
$u(r) = \begin{cases}\frac13(1 - r)^3 & \text{if $r < 1$} \\ 0 & \text{otherwise} \end{cases}$
```
import jax.numpy as np
def soft_sphere(r):
return np.where(r < 1,
1/3 * (1 - r) ** 3,
0.)
print(soft_sphere(0.5))
r = np.linspace(0, 2., 200)
plot(r, soft_sphere(r))
```
We can compute its derivative automatically
```
from jax import grad
du_dr = grad(soft_sphere)
print(du_dr(0.5))
```
We can vectorize the derivative computation over many radii
```
from jax import vmap
du_dr_v = vmap(du_dr)
plot(r, soft_sphere(r))
plot(r, -du_dr_v(r))
```
### Randomly Initialize a System
```
from jax import random
key = random.PRNGKey(0)
particle_count = 128
dim = 2
from jax_md.quantity import box_size_at_number_density
# number_density = N / V
box_size = box_size_at_number_density(particle_count = particle_count,
number_density = 1.0,
spatial_dimension = dim)
R = random.uniform(key, (particle_count, dim), maxval=box_size)
draw(R)
```
### Displacements and Distances
```
from jax_md import space
displacement, shift = space.periodic(box_size)
print(displacement(R[0], R[1]))
metric = space.metric(displacement)
print(metric(R[0], R[1]))
```
Compute distances between pairs of points
```
displacement = space.map_product(displacement)
metric = space.map_product(metric)
print(metric(R[:3], R[:3]))
```
### Total energy of a system
```
def energy(R):
dr = metric(R, R)
return 0.5 * np.sum(soft_sphere(dr))
print(energy(R))
print(grad(energy)(R).shape)
```
### Minimization
```
from jax_md.minimize import fire_descent
init_fn, apply_fn = fire_descent(energy, shift)
state = init_fn(R)
trajectory = []
while np.max(np.abs(state.force)) > 1e-3:
state = apply_fn(state)
trajectory += [state.position]
from jax_md.colab_tools import renderer
trajectory = np.stack(trajectory)
renderer.render(box_size,
{'particles': renderer.Disk(trajectory)},
resolution=(512, 512))
cond_fn = lambda state: np.max(np.abs(state.force)) > 1e-3
```
### Making it Fast
```
def minimize(R):
init, apply = fire_descent(energy, shift)
state = init(R)
for _ in range(20):
state = apply(state)
return energy(state.position)
%%timeit
minimize(R).block_until_ready()
from jax import jit
# Just-In-Time compile to GPU
minimize = jit(minimize)
# The first call incurs a compilation cost
minimize(R)
%%timeit
minimize(R).block_until_ready()
from jax.lax import while_loop
def minimize(R):
init_fn, apply_fn = fire_descent(energy, shift)
state = init_fn(R)
# Using a JAX loop reduces compilation cost
state = while_loop(cond_fun=cond_fn,
body_fun=apply_fn,
init_val=state)
return state.position
from jax import jit
minimize = jit(minimize)
R_is = minimize(R)
%%timeit
minimize(R).block_until_ready()
```
### Elastic Moduli
```
displacement, shift = space.periodic_general(box_size,
fractional_coordinates=False)
from jax_md import energy
soft_sphere = energy.soft_sphere_pair(displacement, alpha=3)
print(soft_sphere(R_is))
strain_energy = lambda strain, R: soft_sphere(R, new_box=box_size * strain)
from jax import hessian
elastic_constants = hessian(strain_energy)(np.eye(2), R_is)
elastic_constants.shape
from jax_md.quantity import bulk_modulus
B = bulk_modulus(elastic_constants)
print(B)
from functools import partial
@jit
def elastic_moduli(number_density, key):
# Randomly initialize particles.
box_size = box_size_at_number_density(particle_count = particle_count,
number_density = number_density,
spatial_dimension = dim)
R = random.uniform(key, (particle_count, dim), maxval=box_size)
# Create the space and energy function.
displacement, shift = space.periodic_general(box_size,
fractional_coordinates=False)
soft_sphere = energy.soft_sphere_pair(displacement, alpha=3)
# Minimize at no strain.
init_fn, apply_fn = fire_descent(soft_sphere, shift)
state = init_fn(R)
state = while_loop(cond_fn, apply_fn, state)
# Compute the bulk modulus.
strain_energy = lambda strain, R: soft_sphere(R, new_box=box_size * strain)
elastic_constants = hessian(strain_energy)(np.eye(2), state.position)
return bulk_modulus(elastic_constants)
number_densities = np.linspace(1.0, 1.6, 40)
elastic_moduli = vmap(elastic_moduli, in_axes=(0, None))
B = elastic_moduli(number_densities, key)
plot(number_densities, B)
keys = random.split(key, 10)
elastic_moduli = vmap(elastic_moduli, in_axes=(None, 0))
B_ensemble = elastic_moduli(number_densities, keys)
for B in B_ensemble:
plt.plot(number_densities, B)
plot(number_densities, np.mean(B_ensemble, axis=0), 'k')
```
### Going Big
```
key = random.PRNGKey(0)
particle_count = 128000
box_size = box_size_at_number_density(particle_count = particle_count,
number_density = 1.0,
spatial_dimension = dim)
R = random.uniform(key, (particle_count, dim)) * box_size
displacement, shift = space.periodic(box_size)
renderer.render(box_size,
{'particles': renderer.Disk(R)},
resolution=(512, 512))
from jax_md.energy import soft_sphere_neighbor_list
neighbor_fn, energy_fn = soft_sphere_neighbor_list(displacement, box_size)
init_fn, apply_fn = fire_descent(energy_fn, shift)
nbrs = neighbor_fn(R)
print(nbrs.idx.shape)
state = init_fn(R, neighbor=nbrs)
def cond_fn(state_and_nbrs):
state, _ = state_and_nbrs
return np.any(np.abs(state.force) > 1e-3)
def step_fn(state_and_nbrs):
state, nbrs = state_and_nbrs
nbrs = neighbor_fn(state.position, nbrs)
state = apply_fn(state, neighbor=nbrs)
return state, nbrs
state, nbrs = while_loop(cond_fn,
step_fn,
(state, nbrs))
renderer.render(box_size,
{'particles': renderer.Disk(state.position)},
resolution=(700, 700))
nbrs = neighbor_fn(state.position)
nbrs.idx.shape
```
## Neural Network Potentials
Here is some data we loaded of a 64-atom Silicon system computed using DFT.
```
print(Rs.shape) # Positions
print(Es.shape) # Energies
print(Fs.shape) # Forces
E_mean = np.mean(Es)
E_std = np.std(Es)
print(f'E_mean = {E_mean}, E_std = {E_std}')
plt.hist(Es)
```
Setup the system and a Graph Neural Network energy function
```
box_size = 10.862
displacement, shift = space.periodic(box_size)
from jax_md.energy import graph_network
init_fn, energy_fn = graph_network(displacement, r_cutoff=3.0)
params = init_fn(key, test_Rs[0])
energy_fn(params, test_Rs[0])
vectorized_energy_fn = vmap(energy_fn, (None, 0))
predicted_Es = vectorized_energy_fn(params, test_Rs)
plt.plot(test_Es, predicted_Es, 'o')
```
Define a loss function.
```
def energy_loss_fn(params):
return np.mean((vectorized_energy_fn(params, Rs) - Es) ** 2)
def force_loss_fn(params):
# We want the gradient with respect to the position, not the parameters.
grad_fn = vmap(grad(energy_fn, argnums=1), (None, 0))
return np.mean((grad_fn(params, Rs) + Fs) ** 2)
@jit
def loss_fn(params):
return energy_loss_fn(params) + force_loss_fn(params)
```
Take a few steps of gradient descent.
```
import optax
opt = optax.chain(optax.clip_by_global_norm(0.01),
optax.adam(1e-4))
opt_state = opt.init(params)
@jit
def update(params, opt_state):
updates, opt_state = opt.update(grad(loss_fn)(params), opt_state)
return optax.apply_updates(params, updates), opt_state
for i in ProgressIter(range(100)):
params, opt_state = update(params, opt_state)
if i % 10 == 0:
print(f'Loss at step {i} is {loss_fn(params)}')
predicted_Es = vectorized_energy_fn(params, test_Rs)
plt.plot(test_Es, predicted_Es, 'o')
```
Now load a pretrained model.
```
with open('si_gnn.pickle', 'rb') as f:
params = pickle.load(f)
from functools import partial
energy_fn = partial(energy_fn, params)
predicted_Es = vmap(energy_fn)(test_Rs)
plt.plot(test_Es, predicted_Es, 'o')
from jax_md.quantity import force
force_fn = force(energy_fn)
predicted_Fs = force_fn(test_Rs[1])
plt.plot(test_Fs[1].reshape((-1,)), predicted_Fs.reshape((-1,)), 'o')
```
This energy can be used in a simulation
```
from jax_md.simulate import nvt_nose_hoover
from jax_md.quantity import temperature
K_B = 8.617e-5
dt = 1e-3
kT = K_B * 300
Si_mass = 2.91086E-3
init_fn, apply_fn = nvt_nose_hoover(energy_fn, shift, dt, kT)
apply_fn = jit(apply_fn)
from jax.lax import fori_loop
state = init_fn(key, Rs[0], Si_mass, T_initial=300 * K_B)
@jit
def take_steps(state):
return fori_loop(0, 100, lambda i, state: apply_fn(state), state)
times = np.arange(100) * dt
temperatures = []
trajectory = []
for _ in ProgressIter(times):
state = take_steps(state)
temperatures += [temperature(state.velocity, Si_mass) / K_B]
trajectory += [state.position]
plot(times, temperatures)
trajectory = np.stack(trajectory)
renderer.render(box_size,
{'atoms': renderer.Sphere(trajectory)},
resolution=(512,512))
box_size, R = tile(box_size, Rs[0], 3)
displacement, shift = space.periodic(box_size)
neighbor_fn, _, energy_fn = energy.graph_network_neighbor_list(displacement,
box_size,
r_cutoff=3.0,
dr_threshold=0.5)
energy_fn = partial(energy_fn, params)
init_fn, apply_fn = nvt_nose_hoover(energy_fn, shift, dt, kT)
apply_fn = jit(apply_fn)
nbrs = neighbor_fn(R)
state = init_fn(key, R, Si_mass, T_initial=300 * K_B, neighbor=nbrs)
def step_fn(i, state_and_nbrs):
state, nbrs = state_and_nbrs
nbrs = neighbor_fn(state.position, nbrs)
state = apply_fn(state, neighbor=nbrs)
return state, nbrs
times = np.arange(100) * dt
temperatures = []
trajectory = []
for _ in ProgressIter(times):
state, nbrs = fori_loop(0, 100, step_fn, (state, nbrs))
temperatures += [temperature(state.velocity, Si_mass) / K_B]
trajectory += [state.position]
trajectory = np.stack(trajectory)
renderer.render(box_size,
{
'atoms': renderer.Sphere(trajectory,
color=np.array([0, 0, 1])),
'bonds': renderer.Bond('atoms', nbrs.idx,
color=np.array([1, 0, 0]))
},
resolution=(512,512))
```
|
github_jupyter
|
# IBM Cloud Pak for Data - Multi-Cloud Virtualization Hands-on Lab
## Introduction
Welcome to the IBM Cloud Pak for Data Multi-Cloud Virtualization Hands on Lab.
In this lab you analyze data from multiple data sources, from across multiple Clouds, without copying data into a warehouse.
This hands-on lab uses live databases, were data is “virtually” available through the IBM Cloud Pak for Data Virtualization Service. This makes it easy to analyze data from across your multi-cloud enterprise using tools like, Jupyter Notebooks, Watson Studio or your favorite reporting tool like Cognos.
### Where to find this sample online
You can find a copy of this notebook on GITHUB at https://github.com/Db2-DTE-POC/CPDDVLAB.
### The business problem and the landscape
The Acme Company needs timely analysis of stock trading data from multiple source systems.
Their data science and development teams needs access to:
* Customer data
* Account data
* Trading data
* Stock history and Symbol data
<img src="https://raw.githubusercontent.com/Db2-DTE-POC/CPDDVLAB/master/media/CPDDVLandscape.png">
The data sources are running on premises and on the cloud. In this example many of the databases are also running on OpenShift but they could be managed, virtual or bare-metal cloud installations. IBM Cloud Pak for Data doesn't care. Enterprise DB (Postgres) is also running in the Cloud. Mongo and Informix are running on premises. Finally, we also have a VSAM file on zOS leveraging the Data Virtualization Manager for zOS.
To simplify access for Data Scientists and Developers the Acme team wants to make all their data look like it is coming from a single database. They also want to combine data to create simple to use tables.
In the past, Acme built a dedicated data warehouse, and then created ETL (Export, Transform and Load) job to move data from each data source into the warehouse were it could be combined. Now they can just virtualize your data without moving it.
### In this lab you learn how to:
* Sign into IBM Cloud Pak for Data using your own Data Engineer and Data Scientist (User) userids
* Connect to different data sources, on premises and across a multi-vendor Cloud
* Make remote data from across your multi-vendor enterprise look and act like local tables in a single database
* Make combining complex data and queries simple even for basic users
* Capture complex SQL in easy to consume VIEWs that act just like simple tables
* Ensure that users can securely access even complex data across multiple sources
* Use roles and priviledges to ensure that only the right user may see the right data
* Make development easy by connecting to your virtualized data using Analytic tools and Application from outside of IBM Cloud Pak for Data.
## Getting Started
### Using Jupyter notebooks
You are now officially using a Jupyter notebook! If this is your first time using a Jupyter notebook you might want to go through the [An Introduction to Jupyter Notebooks](http://localhost:8888/notebooks/An_Introduction_to_Jupyter_Notebooks.ipynb). The introduction shows you some of the basics of using a notebook, including how to create the cells, run code, and save files for future use.
Jupyter notebooks are based on IPython which started in development in the 2006/7 timeframe. The existing Python interpreter was limited in functionality and work was started to create a richer development environment. By 2011 the development efforts resulted in IPython being released (http://blog.fperez.org/2012/01/ipython-notebook-historical.html).
Jupyter notebooks were a spinoff (2014) from the original IPython project. IPython continues to be the kernel that Jupyter runs on, but the notebooks are now a project on their own.
Jupyter notebooks run in a browser and communicate to the backend IPython server which renders this content. These notebooks are used extensively by data scientists and anyone wanting to document, plot, and execute their code in an interactive environment. The beauty of Jupyter notebooks is that you document what you do as you go along.
### Connecting to IBM Cloud Pak for Data
For this lab you will be assigned two IBM Cloud Pak for Data User IDs: A Data Engineer userid and and end-user userid. Check with the lab coordinator which userid and passwords you should use.
* **Engineer:**
* ID: LABDATAENGINEERx
* PASSWORD: xxx
* **User:**
* ID: LABUSERx
* PASSWORD: xxx
To get started, sign in using you Engineer id:
1. Right-click the following link and select **open link in new window** to open the IBM Cloud Pak for Data Console: https://services-uscentral.skytap.com:9152/
1. Organize your screen so that you can see both this notebook as well as the IBM Cloud Pak for Data Console at the same time. This will make it much easier for you to complete the lab without switch back and forth between screens.
2. Sign in using your Engineer userid and password
3. Click the icon at the very top right of the webpage. It will look something like this:
<img src="https://raw.githubusercontent.com/Db2-DTE-POC/CPDDVLAB/master/media/11.06.10 EngineerUserIcon.png">
4. Click **Profile and settings**
5. Click **Permissions** and review the user permissions for this user
6. Click the **three bar menu** at the very top left of the console webpage
<img src="https://raw.githubusercontent.com/Db2-DTE-POC/CPDDVLAB/master/media/2.42.03 Three Bar.png">
7. Click **Collect** if the Collect menu isn't already open
7. Click **Data Virtualization**. The Data Virtualization user interface is displayed
<img src="https://raw.githubusercontent.com/Db2-DTE-POC/CPDDVLAB/master/media/11.06.12 CollectDataVirtualization.png">
8. Click the carrot symbol beside **Menu** below the Data Virtualization title
<img src="https://raw.githubusercontent.com/Db2-DTE-POC/CPDDVLAB/master/media/3.07.47 Menu Carrot.png">
This displays the actions available to your user. Different user have access to more or fewer menu options depending on their role in Data Virtualization.
As a Data Engineer you can:
* Add and modify Data sources. Each source is a connection to a single database, either inside or outside of IBM Cloud Pak for Data.
* Virtualize data. This makes tables in other data sources look and act like tables that are local to the Data Virtualization database
* Work with the data you have virtualized.
* Write SQL to access and join data that you have virtualized
* See detailed information on how to connect external analytic tools and applications to your virtualized data
<img src="https://raw.githubusercontent.com/Db2-DTE-POC/CPDDVLAB/master/media/11.12.54 Menu Data sources.png">
As a User you can only:
* Work with data that has been virtualized for you
* Write SQL to work with that data
* See detailed connection information
As an Administrator (only available to the course instructor) you can also:
* Manage IBM Cloud Pak for Data User Access and Roles
* Create and Manage Data Caches to accelerate performance
* Change key service setttings
## Basic Data Virtualiation
### Exploring Data Source Connections
Let's start by looking at the the Data Source Connections that are already available.
1. Click the Data Virtualization menu and select **Data Sources**.
<img src="https://raw.githubusercontent.com/Db2-DTE-POC/CPDDVLAB/master/media/11.12.54 Menu Data sources.png">
2. Click the **icon below the menu with a circle with three connected dots**.
<img src="https://raw.githubusercontent.com/Db2-DTE-POC/CPDDVLAB/master/media/11.14.50 Connections Icons Spider.png">
3. A spider diagram of the connected data sources opens.
<img src="https://raw.githubusercontent.com/Db2-DTE-POC/CPDDVLAB/master/media/11.15.31 Data Sources Spider.png">
This displays the Data Source Graph with 8 active data sources:
* 4 Db2 Family Databases hosted on premises, IBM Cloud, Azure and AWS
* 1 EDB Postgres Database on Azure
* 1 zOS VSAM file
* 1 Informix Database running on premises
**We are not going to add a new data source** but just go through the steps so you can see how to add additional data sources.
1. Click **+ Add** at the right of the console screen
2. Select **Add data source** from the menu
You can see a history of other data source connection information that was used before. This history is maintain to make reconnecting to data sources easier and faster.
3. Click **Add connection**
4. Click the field below **Connection type**
5. Scroll through all the **available data sources** to see the available connection types
6. Select **different data connection types** from the list to see the information required to connect to a new data source.
At a minumum you typically need the host URL and port address, database name, userid and password. You can also connect using an SSL certificate that can be dragged and dropped directly into the console interface.
7. Click **Cancel** to return to the previous list of connections to add
8. Click **Cancel** again to return to the list of currently connected data sources
### Exploring the available data
Now that you understand how to connect to data sources you can start virtualizing data. Much of the work has already been done for you. IBM Cloud Pak for Data searches through the available data sources and compiles a single large inventory of all the tables and data available to virtualize in IBM Cloud Pak for Data.
1. Click the Data Virtualization menu and select **Virtualize**
<img src="https://raw.githubusercontent.com/Db2-DTE-POC/CPDDVLAB/master/media/11.13.07 Menu Virtualize.png">
2. Check the total number of available tables at the top of the list. There should be well over 500 available.
<img src="https://raw.githubusercontent.com/Db2-DTE-POC/CPDDVLAB/master/media/11.15.50 Available Tables.png">
3. Enter "STOCK" into the search field and hit **Enter**. Any tables with the string
**STOCK** in the table name, the table schema or with a colunn name that includes **STOCK** appears in the search results.
<img src="https://raw.githubusercontent.com/Db2-DTE-POC/CPDDVLAB/master/media/11.39.43 Find STOCK.png">
4. Hover your mouse pointer to the far right side to the search results table. An **eye** icon will appear on each row as you move your mouse.
5. Click the **eye** icon beside one table. This displays a preview of the data in the selected table.
<img src="https://raw.githubusercontent.com/Db2-DTE-POC/CPDDVLAB/master/media/3.26.54 Eye.png">
6. Click **X** at the top right of the dialog box to return to the search results.
### Creating New Tables
So that each user in this lab can have their own data to virtualize you will create your own table in a remote database.
In this part of the lab you will use this Jupyter notebook and Python code to connect to a source database, create a simple table and populate it with data.
IBM Cloud Pak for Data will automatically detect the change in the source database and make the new table available for virtualization.
In this example, you connect to the Db2 Warehouse database running in IBM Cloud Pak for Data but the database can be anywhere. All you need is the connection information and authorized credentials.
<img src="https://raw.githubusercontent.com/Db2-DTE-POC/CPDDVLAB/master/media/Db2CPDDatabase.png">
The first step is to connect to one of our remote data sources directly as if we were part of the team builing a new business application. Since each lab user will create their own table in their own schema the first thing you need to do is update and run the cell below with your engineer name.
1. In this Juypyter notebook, click on the cell below
2. Update the lab number in the cell below to your assigned user and lab number
3. Click **Run** from the Jupyter notebook menu above
```
# Setting your userID
labnumber = 0
engineer = 'DATAENGINEER' + str(labnumber)
print('variable engineer set to = ' + str(engineer))
```
The next part of the lab relies on a Jupyter notebook extension, commonly refer to as a "magic" command, to connect to a Db2 database. To use the commands you load load the extension by running another notebook call db2 that contains all the required code
<pre>
%run db2.ipynb
</pre>
The cell below loads the Db2 extension directly from GITHUB. Note that it will take a few seconds for the extension to load, so you should generally wait until the "Db2 Extensions Loaded" message is displayed in your notebook.
1. Click the cell below
2. Click **Run**. When the cell is finished running, In[*] will change to In[2]
```
# !wget https://raw.githubusercontent.com/IBM/db2-jupyter/master/db2.ipynb
!wget -O db2.ipynb https://raw.githubusercontent.com/Db2-DTE-POC/CPDDVLAB/master/db2.ipynb
%run db2.ipynb
print('db2.ipynb loaded')
```
#### Connecting to Db2
Before any SQL commands can be issued, a connection needs to be made to the Db2 database that you will be using.
The Db2 magic command tracks whether or not a connection has occured in the past and saves this information between notebooks and sessions. When you start up a notebook and issue a command, the program will reconnect to the database using your credentials from the last session. In the event that you have not connected before, the system will prompt you for all the information it needs to connect. This information includes:
- Database name
- Hostname
- PORT
- Userid
- Password
Run the next cell.
#### Connecting to Db2
```
# Connect to the Db2 Warehouse on IBM Cloud Pak for Data Database from inside of IBM Cloud Pak for Data
database = 'bludb'
user = 'user999'
password = 't1cz?K9-X1_Y-2Wi'
host = 'openshift-skytap-nfs-woker-5.ibm.com'
port = '31928'
%sql CONNECT TO {database} USER {user} USING {password} HOST {host} PORT {port}
```
To check that the connection is working. Run the following cell. It lists the tables in the database in the **DVDEMO** schema. Only the first 5 tables are listed.
```
%sql select TABNAME, OWNER from syscat.tables where TABSCHEMA = 'DVDEMO'
```
Now that you can successfully connect to the database, you are going to create two tables with the same name and column across two different schemas. In following steps of the lab you are going to virtualize these tables in IBM Cloud Paks for Data and fold them together into a single table.
The next cell sets the default schema to your engineer name followed by 'A'. Notice how you can set a python variable and substitute it into the SQL Statement in the cell. The **-e** option echos the command.
Run the next cell.
```
schema_name = engineer+'A'
table_name = 'DISCOVER_'+str(labnumber)
print("")
print("Lab #: "+str(labnumber))
print("Schema name: " + str(schema_name))
print("Table name: " + str(table_name))
%sql -e SET CURRENT SCHEMA {schema}
```
Run next cell to create a table with a single INTEGER column containing values from 1 to 10. The **-q** flag in the %sql command supresses any warning message if the table already exists.
```
sqlin = f'''
DROP TABLE {table_name};
CREATE TABLE {table_name} (A INT);
INSERT INTO {table_name} VALUES 1,2,3,4,5,6,7,8,9,10;
SELECT * FROM {table_name};
'''
%sql -q {sqlin}
```
Run the next two cells to create the same table in a schema ending in **B**. It is populated with values from 11 to 20.
```
schema_name = engineer+'B'
print("")
print("Lab #: "+str(labnumber))
print("Schema name: " + str(schema_name))
print("Table name: " + str(table_name))
%sql -e SET CURRENT SCHEMA {schema_name}
sqlin = f'''
DROP TABLE {table_name};
CREATE TABLE {table_name} (A INT);
INSERT INTO {table_name} VALUES 11,12,13,14,15,16,17,18,19,20;
SELECT * FROM {table_name};
'''
%sql -q {sqlin}
```
Run the next cell to see all the tables in the database you just created.
```
%sql SELECT TABSCHEMA, TABNAME FROM SYSCAT.TABLES WHERE TABNAME = '{table_name}'
```
Run the next cell to see all the tables in the database that are like **DISCOVER**. You may see tables created by other people running the lab.
```
%sql SELECT TABSCHEMA, TABNAME FROM SYSCAT.TABLES WHERE TABNAME LIKE 'DISCOVER%'
```
### Virtualizing your new Tables
Now that you have created two new tables you can virtualize that data and make it look like a single table in your database.
1. Return to the IBM Cloud Pak for Data Console
2. Click **Virtualize** in the Data Virtualization menu if you are not still in the Virtualize page
<img src="https://raw.githubusercontent.com/Db2-DTE-POC/CPDDVLAB/master/media/11.13.07 Menu Virtualize.png">
3. Enter your current userid, i.e. DATAENGINEER1 in the search bar and hit **Enter**. Now you can see that your new tables have automatically been discovered by IBM Cloud Pak for Data.
<img src="https://raw.githubusercontent.com/Db2-DTE-POC/CPDDVLAB/master/media/11.31.01 Available Discover Tables.png">
4. Select the two tables you just created by clicking the **check box** beside each table. Make sure you only select those for your LABDATAENGINEER schema.
5. Click **Add to Cart**. Notice that the number of items in your cart is now **2**.
<img src="https://raw.githubusercontent.com/Db2-DTE-POC/CPDDVLAB/master/media/11.33.11 Available ENGINEER Tables.png">
6. Click **View Cart**
<img src="https://raw.githubusercontent.com/Db2-DTE-POC/CPDDVLAB/master/media/11.33.31 View Cart(2).png">
7. Change the name of your two tables from DISCOVER to **DISCOVERA** and **DISCOVERB**. These are the new names that you will be able to use to find your tables in the Data Virtualization database. Don't change the Schema name. It is unique to your current userid.
<img src="https://raw.githubusercontent.com/Db2-DTE-POC/CPDDVLAB/master/media/11.34.21 Assign to Project.png">
9. Click the **back arrow** beside **Review cart and virtualize tables**. We are going to add one more thing to your cart.
<img src="https://raw.githubusercontent.com/Db2-DTE-POC/CPDDVLAB/master/media/11.34.30 Back Arrow Icon.png">
10. Click the checkbox beside **Automatically group tables**. Notice how all the tables called **DISCOVER** have been grouped together into a single entry.
<img src="https://raw.githubusercontent.com/Db2-DTE-POC/CPDDVLAB/master/media/11.35.18 Automatically Group Available Tables.png">
11. Select the row were all the DISCOVER tables have been grouped together
12. Click **Add to cart**.
13. Click **View cart**
<img src="https://raw.githubusercontent.com/Db2-DTE-POC/CPDDVLAB/master/media/11.35.28 View cart(3).png">
You should now see three items in your cart.
<img src="https://raw.githubusercontent.com/Db2-DTE-POC/CPDDVLAB/master/media/11.35.57 Cart with Fold.png">
14. Hover over the elipsis icon at the right side of the list for the **DISCOVER** table
<img src="https://raw.githubusercontent.com/Db2-DTE-POC/CPDDVLAB/master/media/11.34.44 Elipsis.png">
15. Select **Edit grouped tables**
<img src="https://raw.githubusercontent.com/Db2-DTE-POC/CPDDVLAB/master/media/11.36.11 Cart Elipsis Menu.png">
16. Deselect all the tables except for those in one of the schemas you created. You should now have two tables selected.
17. Click **Apply**
17. Change the name of the new combined table to **DISCOVERFOLD**
18. Select the **Data Virtualization Hands in Lab** project from the drop down list.
20. Click **Virtualize**. You see that three new virtual tables have been created.
<img src="https://raw.githubusercontent.com/Db2-DTE-POC/CPDDVLAB/master/media/11.36.49 Virtualize.png">
The Virtual tables created dialog box opens.
<img src="https://raw.githubusercontent.com/Db2-DTE-POC/CPDDVLAB/master/media/11.37.24 Virtual tables created.png">
21. Click **View my virtualized data**. You return to the My virtualized data page.
### Working with your new tables
1. Enter DISCOVER_# where # is your lab number
<img src="https://raw.githubusercontent.com/Db2-DTE-POC/CPDDVLAB/master/media/11.37.55 Find DISCOVER.png">
You should see the three virtual tables you just created. Notice that you do not see tables that other users have created. By default, Data Engineers only see virtualized tables they have virtualized or virtual tables where they have been given access by other users.
2. Click the elipsis (...) beside your **DISCOVERFOLD_#** table and select **Preview** to confirm that it contains 20 rows.
<img src="https://raw.githubusercontent.com/Db2-DTE-POC/CPDDVLAB/master/media/4.32.01 Elipsis Fold.png">
3. Click **SQL Editor** from the Data Virtualization menu
<img src="https://raw.githubusercontent.com/Db2-DTE-POC/CPDDVLAB/master/media/11.13.33 Menu SQL editor.png">
4. Click **Blank** to create a new blank SQL Script
<img src="https://raw.githubusercontent.com/Db2-DTE-POC/CPDDVLAB/master/media/11.38.24 + Blank.png">
4. Enter **SELECT * FROM DISCOVERFOLD_#;** into the SQL Editor
<img src="https://raw.githubusercontent.com/Db2-DTE-POC/CPDDVLAB/master/media/11.38.44 SELECT*.png">
5. Click **Run All** at the bottom left of the SQL Editor window. You should see 20 rows returned in the result.
<img src="https://raw.githubusercontent.com/Db2-DTE-POC/CPDDVLAB/master/media/11.38.52 Run all.png">
Notice that you didn't have to specify the schema for your new virtual tables. The SQL Editor automatically uses the schema associated with your userid that was used when you created your new tables.
Now you can:
* Create connection to a remote data source
* Make a new or existing table in that remote data source look and act like a local table
* Fold data from different tables in the same data source or access data sources by folding it together into a single virtual table
## Gaining Insight from Virtualized Data
Now that you understand the basics of Data Virtualization you can explore how easy it is to gain insight across multiple data sources without moving data.
In the next set of steps you connect to virtualized data from this notebook using your LABDATAENGINEER userid. You can use the same techniques to connect to virtualized data from applications and analytic tools from outside of IBM Cloud Pak for Data.
<img src="https://raw.githubusercontent.com/Db2-DTE-POC/CPDDVLAB/master/media/ConnectingTotheAnalyticsDatabase.png">
Connecting to all your virtualized data is just like connecting to a single database. All the complexity of a dozens of tables across multiple databases on different on premises and cloud providers is now as simple as connecting to a single database and querying a table.
We are going to connect to the IBM Cloud Pak for Data Virtualization database in exactly the same way we connected to a Db2 database earlier in this lab. However we need to change the detailed connection information.
1. Click **Connection Details** in the Data Virtualization menu
<img src="https://raw.githubusercontent.com/Db2-DTE-POC/CPDDVLAB/master/media/11.13.44 Menu connection details.png">
2. Click **Without SSL**
<img src="https://raw.githubusercontent.com/Db2-DTE-POC/CPDDVLAB/master/media/11.14.29 Connection details.png">
3. Copy the **User ID** by highlighting it with your mouse, right click and select **Copy**
4. Paste the **User ID** in to the next cell in this notebook where **user=** (see below) between the quotation marks
<img src="https://raw.githubusercontent.com/Db2-DTE-POC/CPDDVLAB/master/media/11.54.27 Notebook Login.png">
5. Click **Service Settings** in the Data Virtualization menu
<img src="https://raw.githubusercontent.com/Db2-DTE-POC/CPDDVLAB/master/media/11.14.05 Menu Service settings.png">
6. Look for the Access Information section of the page
<img src="https://raw.githubusercontent.com/Db2-DTE-POC/CPDDVLAB/master/media/11.14.15 Access information.png">
6. Click **Show** to see the password. Highlight the password and copy using the right-click menu
7. Paste the **password** into the cell below between the quotation marks using the righ click paste.
8. Run the cell below to connect to the Data Virtualization database.
#### Connecting to Data Virtualization SQL Engine
```
# Connect to the IBM Cloud Pak for Data Virtualization Database from inside CPD
database = 'bigsql'
user = 'userxxxx'
password = 'xxxxxxxxxxxxxx'
host = 'openshift-skytap-nfs-lb.ibm.com'
port = '32080'
%sql CONNECT TO {database} USER {user} USING {password} HOST {host} PORT {port}
```
### Stock Symbol Table
#### Get information about the stocks that are in the database
**System Z - VSAM**
This table comes from a VSAM file on zOS. IBM Cloud Pak for Data Virtualization works together with Data Virtualization Manager for zOS to make this looks like a local database table. For the following examples you can substitute any of the symbols below.
```
%sql -a select * from DVDEMO.STOCK_SYMBOLS
```
### Stock History Table
#### Get Price of a Stock over the Year
Set the Stock Symbol in the line below and run the cell. This information is folded together with data coming from two identical tables, one on Db2 database and on on and Informix database. Run the next two cells. Then pick a new stock symbol from the list above, enter it into the cell below and run both cells again.
**CP4D - Db2, Skytap - Informix**
```
stock = 'AXP'
print('variable stock set to = ' + str(stock))
%%sql -pl
SELECT WEEK(TX_DATE) AS WEEK, OPEN FROM FOLDING.STOCK_HISTORY
WHERE SYMBOL = :stock AND TX_DATE != '2017-12-01'
ORDER BY WEEK(TX_DATE) ASC
```
#### Trend of Three Stocks
This chart shows three stock prices over the course of a year. It uses the same folded stock history information.
**CP4D - Db2, Skytap - Informix**
```
stocks = ['INTC','MSFT','AAPL']
%%sql -pl
SELECT SYMBOL, WEEK(TX_DATE), OPEN FROM FOLDING.STOCK_HISTORY
WHERE SYMBOL IN (:stocks) AND TX_DATE != '2017-12-01'
ORDER BY WEEK(TX_DATE) ASC
```
#### 30 Day Moving Average of a Stock
Enter the Stock Symbol below to see the 30 day moving average of a single stock.
**CP4D - Db2, Skytap - Informix**
```
stock = 'AAPL'
sqlin = \
"""
SELECT WEEK(TX_DATE) AS WEEK, OPEN,
AVG(OPEN) OVER (
ORDER BY TX_DATE
ROWS BETWEEN 15 PRECEDING AND 15 FOLLOWING) AS MOVING_AVG
FROM FOLDING.STOCK_HISTORY
WHERE SYMBOL = :stock
ORDER BY WEEK(TX_DATE)
"""
df = %sql {sqlin}
txdate= df['WEEK']
sales = df['OPEN']
avg = df['MOVING_AVG']
plt.xlabel("Day", fontsize=12);
plt.ylabel("Opening Price", fontsize=12);
plt.suptitle("Opening Price and Moving Average of " + stock, fontsize=20);
plt.plot(txdate, sales, 'r');
plt.plot(txdate, avg, 'b');
plt.show();
```
#### Trading volume of INTC versus MSFT and AAPL in first week of November
**CP4D - Db2, Skytap - Informix**
```
stocks = ['INTC','MSFT','AAPL']
%%sql -pb
SELECT SYMBOL, DAY(TX_DATE), VOLUME/1000000 FROM FOLDING.STOCK_HISTORY
WHERE SYMBOL IN (:stocks) AND WEEK(TX_DATE) = 45
ORDER BY DAY(TX_DATE) ASC
```
#### Show Stocks that Represent at least 3% of the Total Purchases during Week 45
**CP4D - Db2, Skytap - Informix**
```
%%sql -pie
WITH WEEK45(SYMBOL, PURCHASES) AS (
SELECT SYMBOL, SUM(VOLUME * CLOSE) FROM FOLDING.STOCK_HISTORY
WHERE WEEK(TX_DATE) = 45 AND SYMBOL <> 'DJIA'
GROUP BY SYMBOL
),
ALL45(TOTAL) AS (
SELECT SUM(PURCHASES) * .03 FROM WEEK45
)
SELECT SYMBOL, PURCHASES FROM WEEK45, ALL45
WHERE PURCHASES > TOTAL
ORDER BY SYMBOL, PURCHASES
```
### Stock Transaction Table
#### Show Transactions by Customer
This next two examples uses data folded together from three different data sources representing three different trading organizations to create a combined of a single customer's stock trades.
**AWS - Db2, Azure - EDB (Postgres), Azure - Db2**
```
%%sql -a
SELECT * FROM FOLDING.STOCK_TRANSACTIONS_DV
WHERE CUSTID = '107196'
FETCH FIRST 10 ROWS ONLY
```
#### Bought/Sold Amounts of Top 5 stocks
**AWS - Db2, Azure - EDB (Postgres), Azure - Db2**
```
%%sql -a
WITH BOUGHT(SYMBOL, AMOUNT) AS
(
SELECT SYMBOL, SUM(QUANTITY) FROM FOLDING.STOCK_TRANSACTIONS_DV
WHERE QUANTITY > 0
GROUP BY SYMBOL
),
SOLD(SYMBOL, AMOUNT) AS
(
SELECT SYMBOL, -SUM(QUANTITY) FROM FOLDING.STOCK_TRANSACTIONS_Dv
WHERE QUANTITY < 0
GROUP BY SYMBOL
)
SELECT B.SYMBOL, B.AMOUNT AS BOUGHT, S.AMOUNT AS SOLD
FROM BOUGHT B, SOLD S
WHERE B.SYMBOL = S.SYMBOL
ORDER BY B.AMOUNT DESC
FETCH FIRST 5 ROWS ONLY
```
### Customer Accounts
#### Show Top 5 Customer Balance
These next two examples use data folded from systems running on AWS and Azure.
**AWS - Db2, Azure - EDB (Postgres), Azure - Db2**
```
%%sql -a
SELECT CUSTID, BALANCE FROM FOLDING.ACCOUNTS_DV
ORDER BY BALANCE DESC
FETCH FIRST 5 ROWS ONLY
```
#### Show Bottom 5 Customer Balance
**AWS - Db2, Azure - EDB (Postgres), Azure - Db2**
```
%%sql -a
SELECT CUSTID, BALANCE FROM FOLDING.ACCOUNTS_DV
ORDER BY BALANCE ASC
FETCH FIRST 5 ROWS ONLY
```
### Selecting Customer Information from MongoDB
The MongoDB database (running on premises) has customer information in a document format. In order to materialize the document data as relational tables, a total of four virtual tables are generated. The following query shows the tables that are generated for the Customer document collection.
```
%sql LIST TABLES FOR SCHEMA MONGO_ONPREM
```
The tables are all connected through the CUSTOMERID field, which is based on the generated _id of the main CUSTOMER colllection. In order to reassemble these tables into a document, we must join them using this unique identifier. An example of the contents of the CUSTOMER_CONTACT table is shown below.
```
%sql -a SELECT * FROM MONGO_ONPREM.CUSTOMER_CONTACT FETCH FIRST 5 ROWS ONLY
```
A full document record is shown in the following SQL statement which joins all of the tables together.
```
%%sql -a
SELECT C.CUSTOMERID AS CUSTID,
CI.FIRSTNAME, CI.LASTNAME, CI.BIRTHDATE,
CC.CITY, CC.ZIPCODE, CC.EMAIL, CC.PHONE, CC.STREET, CC.STATE,
CP.CARD_TYPE, CP.CARD_NO
FROM MONGO_ONPREM.CUSTOMER C, MONGO_ONPREM.CUSTOMER_CONTACT CC,
MONGO_ONPREM.CUSTOMER_IDENTITY CI, MONGO_ONPREM.CUSTOMER_PAYMENT CP
WHERE CC.CUSTOMER_ID = C."_ID" AND
CI.CUSTOMER_ID = C."_ID" AND
CP.CUSTOMER_ID = C."_ID"
FETCH FIRST 3 ROWS ONLY
```
### Querying All Virtualized Data
In this final example we use data from each data source to answer a complex business question. "What are the names of the customers in Ohio, who bought the most during the highest trading day of the year (based on the Dow Jones Industrial Index)?"
**AWS Db2, Azure EDB, Azure Db2, Skytap MongoDB, CP4D Db2Wh, Skytap Informix**
```
%%sql
WITH MAX_VOLUME(AMOUNT) AS (
SELECT MAX(VOLUME) FROM FOLDING.STOCK_HISTORY
WHERE SYMBOL = 'DJIA'
),
HIGHDATE(TX_DATE) AS (
SELECT TX_DATE FROM FOLDING.STOCK_HISTORY, MAX_VOLUME M
WHERE SYMBOL = 'DJIA' AND VOLUME = M.AMOUNT
),
CUSTOMERS_IN_OHIO(CUSTID) AS (
SELECT C.CUSTID FROM TRADING.CUSTOMERS C
WHERE C.STATE = 'OH'
),
TOTAL_BUY(CUSTID,TOTAL) AS (
SELECT C.CUSTID, SUM(SH.QUANTITY * SH.PRICE)
FROM CUSTOMERS_IN_OHIO C, FOLDING.STOCK_TRANSACTIONS_DV SH, HIGHDATE HD
WHERE SH.CUSTID = C.CUSTID AND
SH.TX_DATE = HD.TX_DATE AND
QUANTITY > 0
GROUP BY C.CUSTID
)
SELECT LASTNAME, T.TOTAL
FROM MONGO_ONPREM.CUSTOMER_IDENTITY CI, MONGO_ONPREM.CUSTOMER C, TOTAL_BUY T
WHERE CI.CUSTOMER_ID = C."_ID" AND C.CUSTOMERID = CUSTID
ORDER BY TOTAL DESC
```
### Seeing where your Virtualized Data is coming from
You may eventually work with a complex Data Virtualization system. As an administrator or a Data Scientist you may need to understand where data is coming from.
Fortunately, the Data Virtualization engine is based on Db2. It includes the same catalog of information as does Db2 with some additional features. If you want to work backwards and understand where each of your virtualized tables comes from, the information is included in the **SYSCAT.TABOPTIONS** catalog table.
```
%%sql
SELECT TABSCHEMA, TABNAME, SETTING
FROM SYSCAT.TABOPTIONS
WHERE OPTION = 'SOURCELIST'
AND TABSCHEMA <> 'QPLEXSYS';
%%sql
SELECT * from SYSCAT.TABOPTIONS;
```
The table includes more information than you need to answer the question of where is my data coming from. The query below only shows the rows that contain the information of the source of the data ('SOURCELIST'). Notice that tables that have been folded together from several tables includes each of the data source information seperated by a semi-colon.
```
%%sql
SELECT TABSCHEMA, TABNAME, SETTING
FROM SYSCAT.TABOPTIONS
WHERE OPTION = 'SOURCELIST'
AND TABSCHEMA <> 'QPLEXSYS';
%%sql
SELECT TABSCHEMA, TABNAME, SETTING
FROM SYSCAT.TABOPTIONS
WHERE TABSCHEMA = 'DVDEMO';
```
In this last example, you can search for any virtualized data coming from a Postgres database by searching for **SETTING LIKE '%POST%'**.
```
%%sql
SELECT TABSCHEMA, TABNAME, SETTING
FROM SYSCAT.TABOPTIONS
WHERE OPTION = 'SOURCELIST'
AND SETTING LIKE '%POST%'
AND TABSCHEMA <> 'QPLEXSYS';
```
What is missing is additional detail for each connection. For example all we can see in the table above is a connection. You can find that detail in another table: **QPLEXSYS.LISTRDBC**. In the last cell, you can see that CID DB210113 is included in the STOCK_TRANSACTIONS virtual table. You can find the details on that copy of Db2 by running the next cell.
```
%%sql
SELECT CID, USR, SRCTYPE, SRCHOSTNAME, SRCPORT, DBNAME, IS_DOCKER FROM QPLEXSYS.LISTRDBC;
```
## Advanced Data Virtualization
Now that you have seen how powerful and easy it is to gain insight from your existing virtualized data, you can learn more about how to do advanced data virtualization. You will learn how to join different remote tables together to create a new virtual table and how to capture complex SQL into VIEWs.
### Joining Tables Together
The virtualized tables below come from different data sources on different systems. We can combine them into a single virtual table.
* Select **My virtualized data** from the Data Virtualization menu
<img src="https://raw.githubusercontent.com/Db2-DTE-POC/CPDDVLAB/master/media/11.13.20 Menu My virtual data.png">
* Enter **Stock** in the find field and hit enter
<img src="https://raw.githubusercontent.com/Db2-DTE-POC/CPDDVLAB/master/media/11.39.43 Find STOCK.png">
* Select table **STOCK_TRANSACTIONS** in the **FOLDING** schema
* Select table **STOCK_SYMBOLS** in the **DVDEMO** schema
<img src="https://raw.githubusercontent.com/Db2-DTE-POC/CPDDVLAB/master/media/11.40.18 Two STOCK seleted.png">
* Click **Join View**
* In table STOCK_SYMBOLS: deselect **SYMBOL**
* In table STOCK_TRANSACTIONS: deselect **TX_NO**
* Click **STOCK_TRANSACTION.SYMBOL** and drag to **STOCK_SYMBOLS.SYMBOL**
<img src="https://raw.githubusercontent.com/Db2-DTE-POC/CPDDVLAB/master/media/11.41.07 Joining Tables.png">
* Click **Preview** to check that your join is working. Each row shoud now contain the stock symbol and the long stock name.
<img src="https://raw.githubusercontent.com/Db2-DTE-POC/CPDDVLAB/master/media/11.41.55 New Join Preview.png">
* Click **X** to close the preview window
* Click **JOIN**
<img src="https://raw.githubusercontent.com/Db2-DTE-POC/CPDDVLAB/master/media/11.42.20 Join.png">
* Type view name **TRANSACTIONS_FULLNAME**
* Don't change the default schema. This corresponds to your LABENGINEER user id.
<img src="https://raw.githubusercontent.com/Db2-DTE-POC/CPDDVLAB/master/media/11.43.10 View Name.png">
* Click **NEXT**
<img src="https://raw.githubusercontent.com/Db2-DTE-POC/CPDDVLAB/master/media/11.43.30 Next.png">
* Select the **Data Virtualization Hands on Lab** project.
<img src="https://raw.githubusercontent.com/Db2-DTE-POC/CPDDVLAB/master/media/11.43.58 Assign to Project.png">
* Click **CREATE VIEW**.
<img src="https://raw.githubusercontent.com/Db2-DTE-POC/CPDDVLAB/master/media/11.44.06 Create view.png">
You see the successful Join View window.
<img src="https://raw.githubusercontent.com/Db2-DTE-POC/CPDDVLAB/master/media/11.44.23 Join view created.png">
* Click **View my virtualized data**
* Click the elipsis menu beside **TRANSACTIONS_FULLNAME**
* Click **Preview**
You can now join virtualize tables together to combine them into new virtualized tables. Now that you know how to perform simple table joins you can learn how to combine multiple data sources and virtual tables using the powerful SQL query engine that is part of the IBM Cloud Pak for Data - Virtualization.
### Using Queries to Answer Complex Business Questions
The IBM Cloud Pak for Data Virtualization Administrator has set up more complex data from multiple source for the next steps. The administrator has also given you access to this virtualized data. You may have noticed this in previous steps.
1. Select **My virtualized data** from the Data Virtualiztion menu. All of these virtualized tables look and act like normal Db2 tables.
<img src="https://raw.githubusercontent.com/Db2-DTE-POC/CPDDVLAB/master/media/11.13.20 Menu My virtual data.png">
2. Click **Preview** for any of the tables to see what they contain.
The virtualized tables in the **FOLDING** schema have all been created by combining the same tables from different data sources. Folding isn't something that is restricted to the same data source in the simple example you just completed.
The virtualized tables in the **TRADING** schema are a view of complex queries that were use to combine data from multiple data sources to answer specific business questions.
3. Select **SQL Editor** from the Data Virtualization menu.
<img src="https://raw.githubusercontent.com/Db2-DTE-POC/CPDDVLAB/master/media/11.13.33 Menu SQL editor.png">
4. Select **Script Library**
<img src="https://raw.githubusercontent.com/Db2-DTE-POC/CPDDVLAB/master/media/11.45.02 Script Library.png">
5. Search for **OHIO**
6. Select and expand the **OHIO Customer** query
<img src="https://raw.githubusercontent.com/Db2-DTE-POC/CPDDVLAB/master/media/11.45.47 Ohio Script.png">
7. Click the **Open a script to edit** icon to open the script in the SQL Editor. **Note** that if you cannot open the script then you may have to refresh your browser or contract and expand the script details section before the icon is active.
<img src="https://raw.githubusercontent.com/Db2-DTE-POC/CPDDVLAB/master/media/11.45.54 Open Script.png">
8. Click **Run All**
<img src="https://raw.githubusercontent.com/Db2-DTE-POC/CPDDVLAB/master/media/11.46.21 Run Ohio Script.png">
This script is a complex SQL join query that uses data from all the virtualize data sources you explored in the first steps of this lab. While the SQL looks complex the author of the query did not have be aware that the data was coming from multiple sources. Everything used in this query looks like it comes from a single database, not eight different data sources across eight different systems on premises or in the Cloud.
### Making Complex SQL Simple to Consume
You can easily make this complex query easy for a user to consume. Instead of sharing this query with other users, you can wrap the query into a view that looks and acts like a simple table.
1. Enter **CREATE VIEW MYOHIOQUERY AS** in the SQL Editor at the first line below the comment and before the **WITH** clause
<img src="https://raw.githubusercontent.com/Db2-DTE-POC/CPDDVLAB/master/media/11.46.54 Add CREATE VIEW.png">
2. Click **Run all**
3. Click **+** to **Add a new script**
<img src="https://raw.githubusercontent.com/Db2-DTE-POC/CPDDVLAB/master/media/11.48.28 Add to script.png">
4. Click **Blank**
4. Enter **SELECT * FROM MYOHIOQUERY;**
5. Click **Run all**
<img src="https://raw.githubusercontent.com/Db2-DTE-POC/CPDDVLAB/master/media/11.48.57 Run Ohio View.png">
Now you have a very simple virtualized table that is pulling data from eight different data sources, combining the data together to resolve a complex business problem. In the next step you will share your new virtualized data with a user.
### Sharing Virtualized Tables
1. Select **My virtualized data** from the Data Virtualization Menu.
<img src="https://raw.githubusercontent.com/Db2-DTE-POC/CPDDVLAB/master/media/11.13.20 Menu My virtual data.png">
2. Click the elipsis (...) menu to the right of the **MYOHIOQUERY** virtualized table
<img src="https://raw.githubusercontent.com/Db2-DTE-POC/CPDDVLAB/master/media/11.49.30 Select MYOHIOQUERY.png">
3. Select **Manage Access** from the elipsis menu
<img src="https://raw.githubusercontent.com/Db2-DTE-POC/CPDDVLAB/master/media/11.49.46 Virtualized Data Menu.png">
3. Click **Grant access**
<img src="https://raw.githubusercontent.com/Db2-DTE-POC/CPDDVLAB/master/media/11.50.07 Grant access.png">
4. Select the **LABUSERx** id associated with your lab. For example, if you are LABDATAENGINEER5, then select LABUSER5.
<img src="https://raw.githubusercontent.com/Db2-DTE-POC/CPDDVLAB/master/media/11.52.42 Grant access to specific user.png">
5. Click **Add**
<img src="https://raw.githubusercontent.com/Db2-DTE-POC/CPDDVLAB/master/media/11.50.28 Add.png">
You should now see that your **LABUSER** id has view-only access to the new virtualized table. Next switch to your LABUSERx id to check that you can see the data you have just granted access for.
6. Click the user icon at the very top right of the console
7. Click **Log out**
8. Sign in using the LABUSER id specified by your lab instructor
9. Click the three bar menu at the top left of the IBM Cloud Pak for Data console
10. Select **Data Virtualization**
You should see the **MYOHIOQUERY** with the schema from your engineer userid in the list of virtualized data.
11. Make a note of the schema of the MYOHIOQUERY in your list of virtualized tables. It starts with **USER**.
12. Select the **SQL Editor** from the Data virtualization menu
13. Click **Blank** to open a new SQL Editor window
14. Enter **SELECT * FROM USERxxxx.MYOHIOQUERY** where xxxx is the user number of your engineer user. The view created by your engineer user was created in their default schema.
15. Click **Run all**
16. Add the following to your query: **WHERE TOTAL > 3000 ORDER BY TOTAL**
17. Click **</>** to format the query so it is easiler to read
18. Click **Run all**
You can see how you have just make a very complex data set extremely easy to consume by a data user. They don't have to know how to connect to multiple data sources or how to combine the data using complex SQL. You can hide that complexity while ensuring only the right user has access to the right data.
In the next steps you will learn how to access virtualized data from outside of IBM Cloud Pak for Data.
### Allowing User to Access Virtualized Data with Analytic Tools
In the next set of steps you connect to virtualized data from this notebook using your **LABUSER** userid.
Just like you connected to IBM Cloud Pak for Data Virtualized Data using your LABDATAENGINEER you can connect using your LABUSER.
We are going to connect to the IBM Cloud Pak for Data Virtualization database in exactly the same way we connected using you LABENGINEER. However you need to change the detailed connection information. Each user has their own unique userid and password to connect to the service. This ensures that no matter what tool you use to connect to virtualized data you are always in control over who can access specifical virtualized data.
2. Click the user icon at the top right of the IBM Cloud Pak for data console to confirm that you are using your **LABUSER** id
1. Click **Connection Details** in the Data Virtualization menu
2. Click **Without SSL**
3. Copy the **User ID** by highlighting it with your mouse, right click and select **Copy**
4. Paste the **User ID** in to the cell below were **user =** between the quotation marks
5. Click **Service Settings** in the Data Virtualization menu
6. Show the password. Highlight the password and copy using the right click menu
7. Paste the **password** into the cell below between the quotation marks using the righ click paste.
8. Run the cell below to connect to the Data Virtualization database.
#### Connecting a USER to Data Virtualization SQL Engine
```
# Connect to the IBM Cloud Pak for Data Virtualization Database from inside CPD
database = 'bigsql'
user = 'userxxxx'
password = 'xxxxxxxxxxxxxxxxxx'
host = 'openshift-skytap-nfs-lb.ibm.com'
port = '32080'
%sql CONNECT TO {database} USER {user} USING {password} HOST {host} PORT {port}
```
Now you can try out the view that was created by the LABDATAENGINEER userid.
Substitute the **xxxx** for the schema used by your ***LABDATAENGINEERx*** user in the next two cells before you run them.
```
%sql SELECT * FROM USERxxxx.MYOHIOQUERY WHERE TOTAL > 3000 ORDER BY TOTAL;
```
Only LABENGINEER virtualized tables that have been authorized for the LABUSER to see are available. Try running the next cell. You should receive an error that the current user does not have the required authorization or privlege to perform the operation.
```
%sql SELECT * FROM USERxxxx.DISCOVERFOLD;
```
### Next Steps:
Now you can use IBM Cloud Pak for Data to make even complex data and queries from different data sources, on premises and across a multi-vendor Cloud look like simple tables in a single database. You are ready for some more advanced labs.
1. Use Db2 SQL and Jupyter Notebooks to Analyze Virtualized Data
* Build simple to complex queries to answer important business questions using the virtualized data available to you in IBM Cloud Pak for Data
* See how you can transform the queries into simple tables available to all your users
2. Use Open RESTful Services to connect to the IBM Cloud Pak for Data Virtualization
* Everything you can do in the IBM Cloud Pak for Data User Interface is accessible through Open RESTful APIs
* Learn how to automate and script your managment of Data Virtualization using RESTful API
* Learn how to accelerate appliation development by accessing virtaulied data through RESTful APIs
## Automating Data Virtualization Setup and Management through REST
The IBM Cloud Pak for Data Console is only one way you can interact with the Virtualization service. IBM Cloud Pak for Data is built on a set of microservices that communicate with each other and the Console user interface using RESTful APIs. You can use these services to automate anything you can do throught the user interface.
This Jupyter Notebook contains examples of how to use the Open APIs to retrieve information from the virtualization service, how to run SQL statements directly against the service through REST and how to provide authoritization to objects. This provides a way write your own script to automate the setup and configuration of the virtualization service.
The next part of the lab relies on a set of base classes to help you interact with the RESTful Services API for IBM Cloud Pak for Data Virtualization. You can access this library on GITHUT. The commands below download the library and run them as part of this notebook.
<pre>
%run CPDDVRestClass.ipynb
</pre>
The cell below loads the RESTful Service Classes and methods directly from GITHUB. Note that it will take a few seconds for the extension to load, so you should generally wait until the "Db2 Extensions Loaded" message is displayed in your notebook.
1. Click the cell below
2. Click **Run**
```
!wget -O CPDDVRestClass.ipynb https://raw.githubusercontent.com/Db2-DTE-POC/CPDDVLAB/master/CPDDVRestClass.ipynb
%run CPDDVRestClass.ipynb
```
### The Db2 Class
The CPDDVRestClass.ipynb notebook includes a Python class called Db2 that encapsulates the Rest API calls used to connect to the IBM Cloud Pak for Data Virtualization service.
To access the service you need to first authenticate with the service and create a reusable token that we can use for each call to the service. This ensures that we don't have to provide a userID and password each time we run a command. The token makes sure this is secure.
Each request is constructed of several parts. First, the URL and the API identify how to connect to the service. Second the REST service request that identifies the request and the options. For example '/metrics/applications/connections/current/list'. And finally some complex requests also include a JSON payload. For example running SQL includes a JSON object that identifies the script, statement delimiters, the maximum number of rows in the results set as well as what do if a statement fails.
You can find this class and use it for your own notebooks in GITHUB. Have a look at how the class encapsulated the API calls by clicking on the following link: https://github.com/Db2-DTE-POC/CPDDVLAB/blob/master/CPDDVRestClass.ipynb
### Example Connections
To connect to the Data Virtualization service you need to provide the URL, the service name (v1) and profile the console user name and password. For this lab we are assuming that the following values are used for the connection:
* Userid: LABDATAENGINEERx
* Password: password
Substitute your assigned LABDATAENGINEER userid below along with your password and run the cell. It will generate a breaer token that is used in the following steps to authenticate your use of the API.
#### Connecting to Data Virtualization API Service
```
# Set the service URL to connect from inside the ICPD Cluster
Console = 'https://openshift-skytap-nfs-lb.ibm.com'
# Connect to the Db2 Data Management Console service
user = 'labdataengineerx'
password = 'password'
# Set up the required connection
databaseAPI = Db2(Console)
api = '/v1'
databaseAPI.authenticate(api, user, password)
database = Console
```
#### Data Sources
The following call (getDataSources) uses an SQL call in the DB2 class to run the same SQL statement you saw earlier in the lab.
```
# Display the Available Data Sources already configured
json = databaseAPI.getDataSources()
databaseAPI.displayResults(json)
```
#### Virtualized Data
This call retrieves all of the virtualized data available to the role of Data Engineer. It uses a direct RESTful service call and does not use SQL. The service returns a JSON result set that is converted into a Python Pandas dataframe. Dataframes are very useful in being able to manipulate tables of data in Python. If there is a problem with the call, the error code is displayed.
```
# Display the Virtualized Assets Avalable to Engineers
roles = ['DV_ENGINEER']
for role in roles:
r = databaseAPI.getRole(role)
if (databaseAPI.getStatusCode(r)==200):
json = databaseAPI.getJSON(r)
df = pd.DataFrame(json_normalize(json['objects']))
display(df)
else:
print(databaseAPI.getStatusCode(r))
```
#### Virtualized Tables and Views
This call retrieves all the virtualized tables and view available to the userid that you use to connect to the service. In this example the whole call is included in the DB2 class library and returned as a complete Dataframe ready for display or to be used for analysis or administration.
```
### Display Virtualized Tables and Views
display(databaseAPI.getVirtualizedTablesDF())
display(databaseAPI.getVirtualizedViewsDF())
```
#### Get a list of the IBM Cloud Pak for Data Users
This example returns a list of all the users of the IBM Cloud Pak for Data system. It only displays three colunns in the Dataframe, but the list of all the available columns is als printed out. Try changing the code to display other columns.
```
# Get the list of CPD Users
r = databaseAPI.getUsers()
if (databaseAPI.getStatusCode(r)==200):
json = databaseAPI.getJSON(r)
df = pd.DataFrame(json_normalize(json))
print(', '.join(list(df))) # List available column names
display(df[['uid','username','displayName']])
else:
print(databaseAPI.getStatusCode(r))
```
#### Get the list of available schemas in the DV Database
Do not forget that the Data Virtualization engine supports the same function as a regular Db2 database. So you can also look at standard Db2 objects like schemas.
```
# Get the list of available schemas in the DV Database
r = databaseAPI.getSchemas()
if (databaseAPI.getStatusCode(r)==200):
json = databaseAPI.getJSON(r)
df = pd.DataFrame(json_normalize(json['resources']))
print(', '.join(list(df)))
display(df[['name']].head(10))
else:
print(databaseAPI.getStatusCode(r))
```
#### Object Search
Fuzzy object search is also available. The call is a bit more complex. If you look at the routine in the DB2 class it posts a RESTful service call that includes a JSON payload. The payload includes the details of the search request.
```
# Search for tables across all schemas that match simple search critera
# Display the first 100
# Switch between searching tables or views
object = 'view'
# object = 'table'
r = databaseAPI.postSearchObjects(object,"TRADING",10,'false','false')
if (databaseAPI.getStatusCode(r)==200):
json = databaseAPI.getJSON(r)
df = pd.DataFrame(json_normalize(json))
print('Columns:')
print(', '.join(list(df)))
display(df[[object+'_name']].head(100))
else:
print("RC: "+str(databaseAPI.getStatusCode(r)))
```
#### Run SQL through the SQL Editor Service
You can also use the SQL Editor service to run your own SQL. Statements are submitted to the editor. Your code then needs to poll the editor service until the script is complete. Fortunately you can use the DB2 class included in this lab so that it becomes a very simple Python call. The **runScript** routine runs the SQL and the **displayResults** routine formats the returned JSON.
```
sqlText = \
'''
WITH MAX_VOLUME(AMOUNT) AS (
SELECT MAX(VOLUME) FROM FOLDING.STOCK_HISTORY
WHERE SYMBOL = 'DJIA'
),
HIGHDATE(TX_DATE) AS (
SELECT TX_DATE FROM FOLDING.STOCK_HISTORY, MAX_VOLUME M
WHERE SYMBOL = 'DJIA' AND VOLUME = M.AMOUNT
),
CUSTOMERS_IN_OHIO(CUSTID) AS (
SELECT C.CUSTID FROM TRADING.CUSTOMERS C
WHERE C.STATE = 'OH'
),
TOTAL_BUY(CUSTID,TOTAL) AS (
SELECT C.CUSTID, SUM(SH.QUANTITY * SH.PRICE)
FROM CUSTOMERS_IN_OHIO C, FOLDING.STOCK_TRANSACTIONS SH, HIGHDATE HD
WHERE SH.CUSTID = C.CUSTID AND
SH.TX_DATE = HD.TX_DATE AND
QUANTITY > 0
GROUP BY C.CUSTID
)
SELECT LASTNAME, T.TOTAL
FROM MONGO_ONPREM.CUSTOMER_IDENTITY CI, MONGO_ONPREM.CUSTOMER C, TOTAL_BUY T
WHERE CI.CUSTOMER_ID = C."_ID" AND C.CUSTOMERID = CUSTID
ORDER BY TOTAL DESC
FETCH FIRST 5 ROWS ONLY;
'''
databaseAPI.displayResults(databaseAPI.runScript(sqlText))
```
#### Run scripts of SQL Statements repeatedly through the SQL Editor Service
The runScript routine can contain more than one statement. The next example runs a scipt with eight SQL statements multple times.
```
repeat = 3
sqlText = \
'''
SELECT * FROM TRADING.MOVING_AVERAGE;
SELECT * FROM TRADING.VOLUME;
SELECT * FROM TRADING.THREEPERCENT;
SELECT * FROM TRADING.TRANSBYCUSTOMER;
SELECT * FROM TRADING.TOPBOUGHTSOLD;
SELECT * FROM TRADING.TOPFIVE;
SELECT * FROM TRADING.BOTTOMFIVE;
SELECT * FROM TRADING.OHIO;
'''
for x in range(0, repeat):
print('Repetition number: '+str(x))
databaseAPI.displayResults(databaseAPI.runScript(sqlText))
print('done')
```
### What's next
if you are inteested in finding out more about using RESTful services to work with Db2, check out this DZone article: https://dzone.com/articles/db2-dte-pocdb2dmc. The article also includes a link to a complete hands-on lab for Db2 and the Db2 Data Management Console. In it you can find out more about using REST and Db2 together.
#### Credits: IBM 2019, Peter Kohlmann [[email protected]]
|
github_jupyter
|
```
import pandas as pd
d = pd.read_csv("YouTube-Spam-Collection-v1/Youtube01-Psy.csv")
d.tail()
len(d.query('CLASS == 1'))
len(d.query('CLASS == 0'))
len(d)
from sklearn.feature_extraction.text import CountVectorizer
vectorizer = CountVectorizer()
dvec = vectorizer.fit_transform(d['CONTENT'])
dvec
analyze = vectorizer.build_analyzer()
print(d['CONTENT'][349])
analyze(d['CONTENT'][349])
vectorizer.get_feature_names()
dshuf = d.sample(frac=1)
d_train = dshuf[:300]
d_test = dshuf[300:]
d_train_att = vectorizer.fit_transform(d_train['CONTENT']) # fit bag-of-words on training set
d_test_att = vectorizer.transform(d_test['CONTENT']) # reuse on testing set
d_train_label = d_train['CLASS']
d_test_label = d_test['CLASS']
d_train_att
d_test_att
from sklearn.ensemble import RandomForestClassifier
clf = RandomForestClassifier(n_estimators=80)
clf.fit(d_train_att, d_train_label)
clf.score(d_test_att, d_test_label)
from sklearn.metrics import confusion_matrix
pred_labels = clf.predict(d_test_att)
confusion_matrix(d_test_label, pred_labels)
from sklearn.model_selection import cross_val_score
scores = cross_val_score(clf, d_train_att, d_train_label, cv=5)
# show average score and +/- two standard deviations away (covering 95% of scores)
print("Accuracy: %0.2f (+/- %0.2f)" % (scores.mean(), scores.std() * 2))
# load all datasets and combine them
d = pd.concat([pd.read_csv("YouTube-Spam-Collection-v1/Youtube01-Psy.csv"),
pd.read_csv("YouTube-Spam-Collection-v1/Youtube02-KatyPerry.csv"),
pd.read_csv("YouTube-Spam-Collection-v1/Youtube03-LMFAO.csv"),
pd.read_csv("YouTube-Spam-Collection-v1/Youtube04-Eminem.csv"),
pd.read_csv("YouTube-Spam-Collection-v1/Youtube05-Shakira.csv")])
len(d)
len(d.query('CLASS == 1'))
len(d.query('CLASS == 0'))
dshuf = d.sample(frac=1)
d_content = dshuf['CONTENT']
d_label = dshuf['CLASS']
# set up a pipeline
from sklearn.pipeline import Pipeline, make_pipeline
pipeline = Pipeline([
('bag-of-words', CountVectorizer()),
('random forest', RandomForestClassifier()),
])
pipeline
# or: pipeline = make_pipeline(CountVectorizer(), RandomForestClassifier())
make_pipeline(CountVectorizer(), RandomForestClassifier())
pipeline.fit(d_content[:1500],d_label[:1500])
pipeline.score(d_content[1500:], d_label[1500:])
pipeline.predict(["what a neat video!"])
pipeline.predict(["plz subscribe to my channel"])
scores = cross_val_score(pipeline, d_content, d_label, cv=5)
print("Accuracy: %0.2f (+/- %0.2f)" % (scores.mean(), scores.std() * 2))
# add tfidf
from sklearn.feature_extraction.text import TfidfTransformer
pipeline2 = make_pipeline(CountVectorizer(),
TfidfTransformer(norm=None),
RandomForestClassifier())
scores = cross_val_score(pipeline2, d_content, d_label, cv=5)
print("Accuracy: %0.2f (+/- %0.2f)" % (scores.mean(), scores.std() * 2))
pipeline2.steps
# parameter search
parameters = {
'countvectorizer__max_features': (None, 1000, 2000),
'countvectorizer__ngram_range': ((1, 1), (1, 2)), # unigrams or bigrams
'countvectorizer__stop_words': ('english', None),
'tfidftransformer__use_idf': (True, False), # effectively turn on/off tfidf
'randomforestclassifier__n_estimators': (20, 50, 100)
}
from sklearn.model_selection import GridSearchCV
grid_search = GridSearchCV(pipeline2, parameters, n_jobs=-1, verbose=1)
grid_search.fit(d_content, d_label)
print("Best score: %0.3f" % grid_search.best_score_)
print("Best parameters set:")
best_parameters = grid_search.best_estimator_.get_params()
for param_name in sorted(parameters.keys()):
print("\t%s: %r" % (param_name, best_parameters[param_name]))
```
|
github_jupyter
|
# Jupyter-Specific Functionality
While GAP does provide a lot of useful functionality by itself on the command line, it is enhanced greatly by the numerous features that Jupyter notebooks have to offer. This notebook attempts to provide some insight into how Jupyter notebooks can improve the workflow of a user who is already well-versed in GAP.
## The Basics
In Jupyter, code is split into a number of cells. While these cells may look independent from one another, and can be run independently, there is some interconnectedness between them. One major example of this is that variables defined in one cell are accessible from cells that are run **after** the cell containing the variable. The value of the variable will be taken from the **most recent** assignment to that variable:
```
a := 3; b := 5;
a + b;
a := 7;
a + b;
```
To run a cell, users can either use the toolbar at the top and clicking the play button, or use the handy keyboard shortcut `Shift + Enter`. Using this shortcut will also create a new cell so users can continue their work while the cell runs. Using `Enter` by itself will allow users to add lines to a cell, should they so desire. The `Cell` option in the top menu also provides some other commands to run all cells.
Additionally, cells can also support a multitude of different inputs. One useful example of this is markdown. In order to use markdown syntax within a cell, it must be converted to a markdown cell. This conversion can be done by either using the dropdown menu at the top which allows users to change the type of the cell (it will be `Code` by default). Alternatively, users can press the `Esc` key while in the cell, which allows them to access "Command Mode" for the cell. While in this mode, the `M` key can be pressed to convert the cell to a Markdown cell. While in Markdown cells, all the typical markdown syntax is supported.
Furthermore, while in "Command Mode", users can use the key sequence `D` `D` to delete cells as they wish. The key `H` can be pressed to look at other useful key shortcuts while in this mode.
## Cell Magic
While the main purpose of most users will be GAP-orientated, Jupyter can also render and run some other code fragments. For example, the code magic `%%html` allows Jupyter to render the contents of a code cell as html:
## Visualisation
Another neat feature about Jupyter is the ability to visualise items right after running cells.
## Notebook Conversion
Since Jupyter Notebooks are simply JSON, they can be easily converted to other formats. For example, to convert to HTML one would run:
jupyter nbconvert --to html notebook.ipynb
from their terminal.
|
github_jupyter
|
# Kurulum ve Gerekli Modullerin Yuklenmesi
```
from google.colab import drive
drive.mount('/content/gdrive')
import sys
import os
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import nltk
import os
from nltk import sent_tokenize, word_tokenize
from nltk.stem.snowball import SnowballStemmer
from nltk.stem.wordnet import WordNetLemmatizer
import nltk
nltk.download('stopwords')
import matplotlib.pyplot as plt
import pandas as pd
nltk.download('punkt')
import string
from nltk.corpus import stopwords
import pandas as pd
import numpy as np
import re
```
# Incelenecek konu basligindaki tweetlerin yuklenmesi
Burada ornek olarak ulkeler konu basligi gosteriliyor gosteriliyor
```
os.chdir("/content/gdrive/My Drive/css/dezenformasyon_before")
df3 = pd.read_csv("/content/gdrive/My Drive/css/dezenformasyon_before/dezenformasyon_before_nodublication.csv", engine = 'python')
df3['tweet'] = df3['tweet'].astype(str)
```
Data pre-processing (on temizlemesi):
1. kucuk harfe cevirme
2. turkce karakter uyumlarini duzeltme
3. ozel karakterleri, noktalamalari temizleme
```
df3.tweet = df3.tweet.apply(lambda x: re.sub(r"İ", "i",x)) #harika calisiyor
df3.tweet = df3.tweet.apply(lambda x: x.lower())
df3.loc[:,"tweet"] = df3.tweet.apply(lambda x : " ".join(re.findall('[\w]+',x)))
```
# Tokenize islemi, stop wordlerin atilmasi ve kelime frequencylerini (kullanim sayilarini) ileride gelecek gorsellestirme icin kaydetme
```
top_N = 10
txt = df3.tweet.str.lower().str.replace(r'\|', ' ').str.cat(sep=' ')
words = nltk.tokenize.word_tokenize(txt)
word_dist = nltk.FreqDist(words)
user_defined_stop_words = ['ekonomi', '1', 'ye', 'nin' ,'nın', 'koronavirüs', 'olsun', 'karşı' , 'covid_19', 'artık', '3', 'sayısı' , 'olarak', 'oldu', 'olan', '2' , 'nedeniyle','bile' , 'sonra' ,'sen','virüs', 'ben', 'vaka' , 'son', 'yeni', 'sayi', 'sayisi','virüsü','bir','com','twitter', 'kadar', 'dan' , 'değil' ,'pic' , 'http', 'https' , 'www' , 'status' , 'var', 'bi', 'mi','yok', 'bu' , 've', 'korona' ,'corona' ,'19' ,'kovid', 'covid']
i = nltk.corpus.stopwords.words('turkish')
j = list(string.punctuation) + user_defined_stop_words
stopwords = set(i).union(j)
words_except_stop_dist = nltk.FreqDist(w for w in words if w not in stopwords)
print('All frequencies, including STOPWORDS:')
print('=' * 60)
rslt3 = pd.DataFrame(word_dist.most_common(top_N),
columns=['Word', 'Frequency'])
print(rslt3)
print('=' * 60)
rslt3 = pd.DataFrame(words_except_stop_dist.most_common(top_N),
columns=['Word', 'Frequency']).set_index('Word')
```
# TR deki ilk vakan onceki tweetlerin incelenmek icin yuklenmesi
```
df2 = pd.read_csv("/content/gdrive/My Drive/css/dezenformasyon_after/dezenformasyon_after_nodublication.csv", engine = 'python')
df2['tweet'] = df2['tweet'].astype(str)
df2['tweet'] = df2['tweet'].astype(str)
df2.tweet = df2.tweet.apply(lambda x: re.sub(r"İ", "i",x)) #harika calisiyor
df2.tweet = df2.tweet.apply(lambda x: x.lower())
df2.loc[:,"tweet"] = df2.tweet.apply(lambda x : " ".join(re.findall('[\w]+',x)))
top_N = 10
txt = df2.tweet.str.lower().str.replace(r'\|', ' ').str.cat(sep=' ')
words = nltk.tokenize.word_tokenize(txt)
word_dist = nltk.FreqDist(words)
user_defined_stop_words = ['ekonomi', '1', 'ye', 'nin' ,'nın', 'koronavirüs', 'olsun', 'karşı' , 'covid_19', 'artık', '3', 'sayısı' , 'olarak', 'oldu', 'olan', '2' , 'nedeniyle','bile' , 'sonra' ,'sen','virüs', 'ben', 'vaka' , 'son', 'yeni', 'sayi', 'sayisi','virüsü','bir','com','twitter', 'kadar', 'dan' , 'değil' ,'pic' , 'http', 'https' , 'www' , 'status' , 'var', 'bi', 'mi','yok', 'bu' , 've', 'korona' ,'corona' ,'19' ,'kovid', 'covid']
i = nltk.corpus.stopwords.words('turkish')
j = list(string.punctuation) + user_defined_stop_words
stopwords = set(i).union(j)
words_except_stop_dist = nltk.FreqDist(w for w in words if w not in stopwords)
print('All frequencies, including STOPWORDS:')
print('=' * 60)
rslt = pd.DataFrame(word_dist.most_common(top_N),
columns=['Word', 'Frequency'])
print(rslt)
print('=' * 60)
rslt = pd.DataFrame(words_except_stop_dist.most_common(top_N),
columns=['Word', 'Frequency']).set_index('Word')
```
# Karsilastirmali gorsellestirme (Ayni konu basliklarinin 11 marttan oncesi ve sonrasi )
```
fig, (ax1, ax2) = plt.subplots(1,2, sharex=False, sharey= True, figsize=(24,5))
rslt3.plot.bar(rot=0, ax =ax1 , title = "Dezenformasyon_Once" )
rslt.plot.bar(rot=0, ax =ax2 , title = "Dezenformasyon_Sonra" )
plt.savefig('Disinfo_comparison.png',dpi=300)
```
|
github_jupyter
|
## <small>
Copyright (c) 2017-21 Andrew Glassner
Permission is hereby granted, free of charge, to any person obtaining a copy of this software and associated documentation files (the "Software"), to deal in the Software without restriction, including without limitation the rights to use, copy, modify, merge, publish, distribute, sublicense, and/or sell copies of the Software, and to permit persons to whom the Software is furnished to do so, subject to the following conditions:
The above copyright notice and this permission notice shall be included in all copies or substantial portions of the Software.
THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE SOFTWARE.
</small>
# Deep Learning: A Visual Approach
## by Andrew Glassner, https://glassner.com
### Order: https://nostarch.com/deep-learning-visual-approach
### GitHub: https://github.com/blueberrymusic
------
### What's in this notebook
This notebook is provided as a “behind-the-scenes” look at code used to make some of the figures in this chapter. It is cleaned up a bit from the original code that I hacked together, and is only lightly commented. I wrote the code to be easy to interpret and understand, even for those who are new to Python. I tried never to be clever or even more efficient at the cost of being harder to understand. The code is in Python3, using the versions of libraries as of April 2021.
This notebook may contain additional code to create models and images not in the book. That material is included here to demonstrate additional techniques.
Note that I've included the output cells in this saved notebook, but Jupyter doesn't save the variables or data that were used to generate them. To recreate any cell's output, evaluate all the cells from the start up to that cell. A convenient way to experiment is to first choose "Restart & Run All" from the Kernel menu, so that everything's been defined and is up to date. Then you can experiment using the variables, data, functions, and other stuff defined in this notebook.
## Chapter 11: Classifers, Notebook 1: kNN
Figures demonstrating k nearest neighbors (kNN)
```
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets.samples_generator import make_blobs
from sklearn.neighbors import KNeighborsClassifier
import math
import seaborn as sns; sns.set()
# Make a File_Helper for saving and loading files.
save_files = False
import os, sys, inspect
current_dir = os.path.dirname(os.path.abspath(inspect.getfile(inspect.currentframe())))
sys.path.insert(0, os.path.dirname(current_dir)) # path to parent dir
from DLBasics_Utilities import File_Helper
file_helper = File_Helper(save_files)
# create a custom color map with nice colors
from matplotlib.colors import LinearSegmentedColormap
dot_clr_0 = np.array((79, 135, 219))/255. # blue
dot_clr_1 = np.array((255, 141, 54))/255. # orange
dot_cmap = LinearSegmentedColormap.from_list('dot_map', [dot_clr_0, dot_clr_1], N=100)
# Show a scatter plot with blue/orange colors and no ticks
def show_Xy(X, y, filename):
plt.scatter(X[:,0], X[:,1], c=y, s=50, cmap=dot_cmap)
plt.xticks([],[])
plt.yticks([],[])
file_helper.save_figure(filename)
plt.show()
# Create the "smile" dataset. A curve for the smile with a circle at each end.
# All the magic values were picked by hand.
def make_smile(num_samples = 20, thickness=0.3, noise=0.0):
np.random.seed(42)
X = []
y = []
for i in range(num_samples):
px = np.random.uniform(-1.5, 1.5)
py = np.random.uniform(-1, 1)
c = 0
if (px - -0.8)**2 + (py-.4)**2 < thickness**2:
c = 1
if (px - 0.8)**2 + (py-.4)**2 < thickness**2:
c = 1
theta = np.arctan2(py-.4, px)
r = math.sqrt((px**2)+((py-.4)**2))
if (theta < 0) and (r > .8-thickness) and (r < .8+thickness):
c = 1
px += np.random.uniform(-noise, noise)
py += np.random.uniform(-noise, noise)
X.append([px,py])
y.append(c)
return (np.array(X),y)
# Create the "happy face" dataset by adding some eyes to the smile.
# All the magic values were picked by hand.
def make_happy_face(num_samples = 20, thickness=0.3, noise=0.0):
np.random.seed(42)
X = []
y = []
eye_x = .5
eye_y = 1.5
for i in range(num_samples):
px = np.random.uniform(-1.5, 1.5)
py = np.random.uniform(-1, 2.0)
c = 0
if (px - eye_x)**2 + (py-eye_y)**2 < thickness**2:
c = 1
if (px - -eye_x)**2 + (py-eye_y)**2 < thickness**2:
c = 1
if (px - -0.8)**2 + (py-.4)**2 < thickness**2:
c = 1
if (px - 0.8)**2 + (py-.4)**2 < thickness**2:
c = 1
theta = np.arctan2(py-.4, px)
r = math.sqrt((px**2)+((py-.4)**2))
if (theta < 0) and (r > .8-thickness) and (r < .8+thickness):
c = 1
px += np.random.uniform(-noise, noise)
py += np.random.uniform(-noise, noise)
X.append([px,py])
y.append(c)
return (np.array(X),y)
# Show the clean smile
X_clean, y_clean = make_smile(1000, .3, 0)
show_Xy(X_clean, y_clean, 'KNN-smile-data-clean')
# Show the noisy smile
X_noisy, y_noisy = make_smile(1000, .3, .25)
show_Xy(X_noisy, y_noisy, 'KNN-smile-data-noisy')
# Show a grid of k-nearest-neighbors (kNN) results for different values of k.
# For large values of k, this can take a little while.
def show_fit_grid(X, y, data_version):
k_list = [1, 2, 3, 4, 5, 6, 10, 20, 50]
plt.figure(figsize=(8,6))
resolution = 500
xmin = np.min(X[:,0]) - .1
xmax = np.max(X[:,0]) + .1
ymin = np.min(X[:,1]) - .1
ymax = np.max(X[:,1]) + .1
xx, yy = np.meshgrid(np.linspace(xmin, xmax, resolution), np.linspace(ymin, ymax, resolution))
zin = np.array([xx.ravel(), yy.ravel()]).T
for i in range(9):
plt.subplot(3, 3, i+1)
num_neighbors = k_list[i]
knn = KNeighborsClassifier(n_neighbors=num_neighbors)
knn.fit(X,y)
Z = knn.predict(zin)
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, cmap=dot_cmap)
#plt.scatter(X[:,0], X[:,1], c=y, s=5, alpha=0.3, cmap='cool')
plt.xticks([],[])
plt.yticks([],[])
plt.title('k='+str(num_neighbors))
plt.tight_layout()
file_helper.save_figure('KNN-smile-grid-'+data_version)
plt.show()
# Show the grid for the clean smile dataset
show_fit_grid(X_clean, y_clean, 'clean')
# Show the grid for the noisy smile dataset
show_fit_grid(X_noisy, y_noisy, 'noisy')
# Show the clean face dataset
X_clean_face, y_clean_face = make_happy_face(1000, .3, 0)
show_Xy(X_clean_face, y_clean_face, 'KNN-face-data-clean')
# Show the grid for the clean face dataset
show_fit_grid(X_clean_face, y_clean_face, 'clean-face')
# Show the noisy face dataset
X_noisy_face, y_noisy_face = make_happy_face(1000, .3, .25)
show_Xy(X_noisy_face, y_noisy_face, 'KNN-face-data-noisy')
# Show the grid for the noisy face dataset
show_fit_grid(X_noisy_face, y_noisy_face, 'noisy-face')
```
|
github_jupyter
|
# PyTorch Basics
```
import torch
import numpy as np
torch.manual_seed(1234)
```
## Tensors
* Scalar is a single number.
* Vector is an array of numbers.
* Matrix is a 2-D array of numbers.
* Tensors are N-D arrays of numbers.
#### Creating Tensors
You can create tensors by specifying the shape as arguments. Here is a tensor with 5 rows and 3 columns
```
def describe(x):
print("Type: {}".format(x.type()))
print("Shape/size: {}".format(x.shape))
print("Values: \n{}".format(x))
describe(torch.Tensor(2, 3))
describe(torch.randn(2, 3))
```
It's common in prototyping to create a tensor with random numbers of a specific shape.
```
x = torch.rand(2, 3)
describe(x)
```
You can also initialize tensors of ones or zeros.
```
describe(torch.zeros(2, 3))
x = torch.ones(2, 3)
describe(x)
x.fill_(5)
describe(x)
```
Tensors can be initialized and then filled in place.
Note: operations that end in an underscore (`_`) are in place operations.
```
x = torch.Tensor(3,4).fill_(5)
print(x.type())
print(x.shape)
print(x)
```
Tensors can be initialized from a list of lists
```
x = torch.Tensor([[1, 2,],
[2, 4,]])
describe(x)
```
Tensors can be initialized from numpy matrices
```
npy = np.random.rand(2, 3)
describe(torch.from_numpy(npy))
print(npy.dtype)
```
#### Tensor Types
The FloatTensor has been the default tensor that we have been creating all along
```
import torch
x = torch.arange(6).view(2, 3)
describe(x)
x = torch.FloatTensor([[1, 2, 3],
[4, 5, 6]])
describe(x)
x = x.long()
describe(x)
x = torch.tensor([[1, 2, 3],
[4, 5, 6]], dtype=torch.int64)
describe(x)
x = x.float()
describe(x)
x = torch.randn(2, 3)
describe(x)
describe(torch.add(x, x))
describe(x + x)
x = torch.arange(6)
describe(x)
x = x.view(2, 3)
describe(x)
describe(torch.sum(x, dim=0))
describe(torch.sum(x, dim=1))
describe(torch.transpose(x, 0, 1))
import torch
x = torch.arange(6).view(2, 3)
describe(x)
describe(x[:1, :2])
describe(x[0, 1])
indices = torch.LongTensor([0, 2])
describe(torch.index_select(x, dim=1, index=indices))
indices = torch.LongTensor([0, 0])
describe(torch.index_select(x, dim=0, index=indices))
row_indices = torch.arange(2).long()
col_indices = torch.LongTensor([0, 1])
describe(x[row_indices, col_indices])
```
Long Tensors are used for indexing operations and mirror the `int64` numpy type
```
x = torch.LongTensor([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
describe(x)
print(x.dtype)
print(x.numpy().dtype)
```
You can convert a FloatTensor to a LongTensor
```
x = torch.FloatTensor([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
x = x.long()
describe(x)
```
### Special Tensor initializations
We can create a vector of incremental numbers
```
x = torch.arange(0, 10)
print(x)
```
Sometimes it's useful to have an integer-based arange for indexing
```
x = torch.arange(0, 10).long()
print(x)
```
## Operations
Using the tensors to do linear algebra is a foundation of modern Deep Learning practices
Reshaping allows you to move the numbers in a tensor around. One can be sure that the order is preserved. In PyTorch, reshaping is called `view`
```
x = torch.arange(0, 20)
print(x.view(1, 20))
print(x.view(2, 10))
print(x.view(4, 5))
print(x.view(5, 4))
print(x.view(10, 2))
print(x.view(20, 1))
```
We can use view to add size-1 dimensions, which can be useful for combining with other tensors. This is called broadcasting.
```
x = torch.arange(12).view(3, 4)
y = torch.arange(4).view(1, 4)
z = torch.arange(3).view(3, 1)
print(x)
print(y)
print(z)
print(x + y)
print(x + z)
```
Unsqueeze and squeeze will add and remove 1-dimensions.
```
x = torch.arange(12).view(3, 4)
print(x.shape)
x = x.unsqueeze(dim=1)
print(x.shape)
x = x.squeeze()
print(x.shape)
```
all of the standard mathematics operations apply (such as `add` below)
```
x = torch.rand(3,4)
print("x: \n", x)
print("--")
print("torch.add(x, x): \n", torch.add(x, x))
print("--")
print("x+x: \n", x + x)
```
The convention of `_` indicating in-place operations continues:
```
x = torch.arange(12).reshape(3, 4)
print(x)
print(x.add_(x))
```
There are many operations for which reduce a dimension. Such as sum:
```
x = torch.arange(12).reshape(3, 4)
print("x: \n", x)
print("---")
print("Summing across rows (dim=0): \n", x.sum(dim=0))
print("---")
print("Summing across columns (dim=1): \n", x.sum(dim=1))
```
#### Indexing, Slicing, Joining and Mutating
```
x = torch.arange(6).view(2, 3)
print("x: \n", x)
print("---")
print("x[:2, :2]: \n", x[:2, :2])
print("---")
print("x[0][1]: \n", x[0][1])
print("---")
print("Setting [0][1] to be 8")
x[0][1] = 8
print(x)
```
We can select a subset of a tensor using the `index_select`
```
x = torch.arange(9).view(3,3)
print(x)
print("---")
indices = torch.LongTensor([0, 2])
print(torch.index_select(x, dim=0, index=indices))
print("---")
indices = torch.LongTensor([0, 2])
print(torch.index_select(x, dim=1, index=indices))
```
We can also use numpy-style advanced indexing:
```
x = torch.arange(9).view(3,3)
indices = torch.LongTensor([0, 2])
print(x[indices])
print("---")
print(x[indices, :])
print("---")
print(x[:, indices])
```
We can combine tensors by concatenating them. First, concatenating on the rows
```
x = torch.arange(6).view(2,3)
describe(x)
describe(torch.cat([x, x], dim=0))
describe(torch.cat([x, x], dim=1))
describe(torch.stack([x, x]))
```
We can concentate along the first dimension.. the columns.
```
x = torch.arange(9).view(3,3)
print(x)
print("---")
new_x = torch.cat([x, x, x], dim=1)
print(new_x.shape)
print(new_x)
```
We can also concatenate on a new 0th dimension to "stack" the tensors:
```
x = torch.arange(9).view(3,3)
print(x)
print("---")
new_x = torch.stack([x, x, x])
print(new_x.shape)
print(new_x)
```
#### Linear Algebra Tensor Functions
Transposing allows you to switch the dimensions to be on different axis. So we can make it so all the rows are columsn and vice versa.
```
x = torch.arange(0, 12).view(3,4)
print("x: \n", x)
print("---")
print("x.tranpose(1, 0): \n", x.transpose(1, 0))
```
A three dimensional tensor would represent a batch of sequences, where each sequence item has a feature vector. It is common to switch the batch and sequence dimensions so that we can more easily index the sequence in a sequence model.
Note: Transpose will only let you swap 2 axes. Permute (in the next cell) allows for multiple
```
batch_size = 3
seq_size = 4
feature_size = 5
x = torch.arange(batch_size * seq_size * feature_size).view(batch_size, seq_size, feature_size)
print("x.shape: \n", x.shape)
print("x: \n", x)
print("-----")
print("x.transpose(1, 0).shape: \n", x.transpose(1, 0).shape)
print("x.transpose(1, 0): \n", x.transpose(1, 0))
```
Permute is a more general version of tranpose:
```
batch_size = 3
seq_size = 4
feature_size = 5
x = torch.arange(batch_size * seq_size * feature_size).view(batch_size, seq_size, feature_size)
print("x.shape: \n", x.shape)
print("x: \n", x)
print("-----")
print("x.permute(1, 0, 2).shape: \n", x.permute(1, 0, 2).shape)
print("x.permute(1, 0, 2): \n", x.permute(1, 0, 2))
```
Matrix multiplication is `mm`:
```
torch.randn(2, 3, requires_grad=True)
x1 = torch.arange(6).view(2, 3).float()
describe(x1)
x2 = torch.ones(3, 2)
x2[:, 1] += 1
describe(x2)
describe(torch.mm(x1, x2))
x = torch.arange(0, 12).view(3,4).float()
print(x)
x2 = torch.ones(4, 2)
x2[:, 1] += 1
print(x2)
print(x.mm(x2))
```
See the [PyTorch Math Operations Documentation](https://pytorch.org/docs/stable/torch.html#math-operations) for more!
## Computing Gradients
```
x = torch.tensor([[2.0, 3.0]], requires_grad=True)
z = 3 * x
print(z)
```
In this small snippet, you can see the gradient computations at work. We create a tensor and multiply it by 3. Then, we create a scalar output using `sum()`. A Scalar output is needed as the the loss variable. Then, called backward on the loss means it computes its rate of change with respect to the inputs. Since the scalar was created with sum, each position in z and x are independent with respect to the loss scalar.
The rate of change of x with respect to the output is just the constant 3 that we multiplied x by.
```
x = torch.tensor([[2.0, 3.0]], requires_grad=True)
print("x: \n", x)
print("---")
z = 3 * x
print("z = 3*x: \n", z)
print("---")
loss = z.sum()
print("loss = z.sum(): \n", loss)
print("---")
loss.backward()
print("after loss.backward(), x.grad: \n", x.grad)
```
### Example: Computing a conditional gradient
$$ \text{ Find the gradient of f(x) at x=1 } $$
$$ {} $$
$$ f(x)=\left\{
\begin{array}{ll}
sin(x) \text{ if } x>0 \\
cos(x) \text{ otherwise } \\
\end{array}
\right.$$
```
def f(x):
if (x.data > 0).all():
return torch.sin(x)
else:
return torch.cos(x)
x = torch.tensor([1.0], requires_grad=True)
y = f(x)
y.backward()
print(x.grad)
```
We could apply this to a larger vector too, but we need to make sure the output is a scalar:
```
x = torch.tensor([1.0, 0.5], requires_grad=True)
y = f(x)
# this is meant to break!
y.backward()
print(x.grad)
```
Making the output a scalar:
```
x = torch.tensor([1.0, 0.5], requires_grad=True)
y = f(x)
y.sum().backward()
print(x.grad)
```
but there was an issue.. this isn't right for this edge case:
```
x = torch.tensor([1.0, -1], requires_grad=True)
y = f(x)
y.sum().backward()
print(x.grad)
x = torch.tensor([-0.5, -1], requires_grad=True)
y = f(x)
y.sum().backward()
print(x.grad)
```
This is because we aren't doing the boolean computation and subsequent application of cos and sin on an elementwise basis. So, to solve this, it is common to use masking:
```
def f2(x):
mask = torch.gt(x, 0).float()
return mask * torch.sin(x) + (1 - mask) * torch.cos(x)
x = torch.tensor([1.0, -1], requires_grad=True)
y = f2(x)
y.sum().backward()
print(x.grad)
def describe_grad(x):
if x.grad is None:
print("No gradient information")
else:
print("Gradient: \n{}".format(x.grad))
print("Gradient Function: {}".format(x.grad_fn))
import torch
x = torch.ones(2, 2, requires_grad=True)
describe(x)
describe_grad(x)
print("--------")
y = (x + 2) * (x + 5) + 3
describe(y)
z = y.mean()
describe(z)
describe_grad(x)
print("--------")
z.backward(create_graph=True, retain_graph=True)
describe_grad(x)
print("--------")
x = torch.ones(2, 2, requires_grad=True)
y = x + 2
y.grad_fn
```
### CUDA Tensors
PyTorch's operations can seamlessly be used on the GPU or on the CPU. There are a couple basic operations for interacting in this way.
```
print(torch.cuda.is_available())
x = torch.rand(3,3)
describe(x)
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
print(device)
x = torch.rand(3, 3).to(device)
describe(x)
print(x.device)
cpu_device = torch.device("cpu")
# this will break!
y = torch.rand(3, 3)
x + y
y = y.to(cpu_device)
x = x.to(cpu_device)
x + y
if torch.cuda.is_available(): # only is GPU is available
a = torch.rand(3,3).to(device='cuda:0') # CUDA Tensor
print(a)
b = torch.rand(3,3).cuda()
print(b)
print(a + b)
a = a.cpu() # Error expected
print(a + b)
```
### Exercises
Some of these exercises require operations not covered in the notebook. You will have to look at [the documentation](https://pytorch.org/docs/) (on purpose!)
(Answers are at the bottom)
#### Exercise 1
Create a 2D tensor and then add a dimension of size 1 inserted at the 0th axis.
#### Exercise 2
Remove the extra dimension you just added to the previous tensor.
#### Exercise 3
Create a random tensor of shape 5x3 in the interval [3, 7)
#### Exercise 4
Create a tensor with values from a normal distribution (mean=0, std=1).
#### Exercise 5
Retrieve the indexes of all the non zero elements in the tensor torch.Tensor([1, 1, 1, 0, 1]).
#### Exercise 6
Create a random tensor of size (3,1) and then horizonally stack 4 copies together.
#### Exercise 7
Return the batch matrix-matrix product of two 3 dimensional matrices (a=torch.rand(3,4,5), b=torch.rand(3,5,4)).
#### Exercise 8
Return the batch matrix-matrix product of a 3D matrix and a 2D matrix (a=torch.rand(3,4,5), b=torch.rand(5,4)).
Answers below
Answers still below.. Keep Going
#### Exercise 1
Create a 2D tensor and then add a dimension of size 1 inserted at the 0th axis.
```
a = torch.rand(3,3)
a = a.unsqueeze(0)
print(a)
print(a.shape)
```
#### Exercise 2
Remove the extra dimension you just added to the previous tensor.
```
a = a.squeeze(0)
print(a.shape)
```
#### Exercise 3
Create a random tensor of shape 5x3 in the interval [3, 7)
```
3 + torch.rand(5, 3) * 4
```
#### Exercise 4
Create a tensor with values from a normal distribution (mean=0, std=1).
```
a = torch.rand(3,3)
a.normal_(mean=0, std=1)
```
#### Exercise 5
Retrieve the indexes of all the non zero elements in the tensor torch.Tensor([1, 1, 1, 0, 1]).
```
a = torch.Tensor([1, 1, 1, 0, 1])
torch.nonzero(a)
```
#### Exercise 6
Create a random tensor of size (3,1) and then horizonally stack 4 copies together.
```
a = torch.rand(3,1)
a.expand(3,4)
```
#### Exercise 7
Return the batch matrix-matrix product of two 3 dimensional matrices (a=torch.rand(3,4,5), b=torch.rand(3,5,4)).
```
a = torch.rand(3,4,5)
b = torch.rand(3,5,4)
torch.bmm(a, b)
```
#### Exercise 8
Return the batch matrix-matrix product of a 3D matrix and a 2D matrix (a=torch.rand(3,4,5), b=torch.rand(5,4)).
```
a = torch.rand(3,4,5)
b = torch.rand(5,4)
torch.bmm(a, b.unsqueeze(0).expand(a.size(0), *b.size()))
```
### END
|
github_jupyter
|
# Support Vector Machines
Let's create the same fake income / age clustered data that we used for our K-Means clustering example:
```
import numpy as np
#Create fake income/age clusters for N people in k clusters
def createClusteredData(N, k):
np.random.seed(1234)
pointsPerCluster = float(N)/k
X = []
y = []
for i in range (k):
incomeCentroid = np.random.uniform(20000.0, 200000.0)
ageCentroid = np.random.uniform(20.0, 70.0)
for j in range(int(pointsPerCluster)):
X.append([np.random.normal(incomeCentroid, 10000.0), np.random.normal(ageCentroid, 2.0)])
y.append(i)
X = np.array(X)
y = np.array(y)
return X, y
%matplotlib inline
from pylab import *
from sklearn.preprocessing import MinMaxScaler
(X, y) = createClusteredData(100, 5)
plt.figure(figsize=(8, 6))
plt.scatter(X[:,0], X[:,1], c=y.astype(np.float))
plt.show()
scaling = MinMaxScaler(feature_range=(-1,1)).fit(X)
X = scaling.transform(X)
plt.figure(figsize=(8, 6))
plt.scatter(X[:,0], X[:,1], c=y.astype(np.float))
plt.show()
```
Now we'll use linear SVC to partition our graph into clusters:
```
from sklearn import svm, datasets
C = 1.0
svc = svm.SVC(kernel='linear', C=C).fit(X, y)
```
By setting up a dense mesh of points in the grid and classifying all of them, we can render the regions of each cluster as distinct colors:
```
def plotPredictions(clf):
# Create a dense grid of points to sample
xx, yy = np.meshgrid(np.arange(-1, 1, .001),
np.arange(-1, 1, .001))
# Convert to Numpy arrays
npx = xx.ravel()
npy = yy.ravel()
# Convert to a list of 2D (income, age) points
samplePoints = np.c_[npx, npy]
# Generate predicted labels (cluster numbers) for each point
Z = clf.predict(samplePoints)
plt.figure(figsize=(8, 6))
Z = Z.reshape(xx.shape) #Reshape results to match xx dimension
plt.contourf(xx, yy, Z, cmap=plt.cm.Paired, alpha=0.8) # Draw the contour
plt.scatter(X[:,0], X[:,1], c=y.astype(np.float)) # Draw the points
plt.show()
plotPredictions(svc)
```
Or just use predict for a given point:
```
print(svc.predict(scaling.transform([[200000, 40]])))
print(svc.predict(scaling.transform([[50000, 65]])))
```
## Activity
"Linear" is one of many kernels scikit-learn supports on SVC. Look up the documentation for scikit-learn online to find out what the other possible kernel options are. Do any of them work well for this data set?
|
github_jupyter
|
```
from google.colab import drive
drive.mount('/content/drive')
import tensorflow as tf
# run on training variation of powerlaw:
# path for fine tuning: !python3 "/content/drive/MyDrive/PhD work/Projects/parameter estimation/Window method Supervised autoencoder with fine tuning/script.py"
# path for stage 1: !python3 "/content/drive/MyDrive/PhD work/Projects/parameter estimation/Window_method_Supervised_autoencoder/script.py"
# path for stage 2: !python3 "/content/drive/MyDrive/PhD work/Projects/parameter estimation/stage 2 - window method/script.py"
2+3
#
# run trivial test results:----------------------------------
# trivial 0 : !python3 "/content/drive/MyDrive/PhD work/Projects/parameter estimation/trivial tests/trivial 0/script.py"
# trivial 1: !python3 "/content/drive/MyDrive/PhD work/Projects/parameter estimation/trivial tests/trivial 1/script.py"
# train on just observed: !python3 "/content/drive/MyDrive/PhD work/Projects/parameter estimation/trivial tests/train on only observed entries/script.py"
# run codes for train bombing network:
# stage 0: !python3 "/content/drive/MyDrive/PhD work/Projects/parameter estimation/codes for Rasika/stage 1/script.py"
# stage 1:
# stage 2:
!python3 "/content/drive/MyDrive/PhD work/Projects/parameter estimation/trivial tests/trivial 1/script.py"
-------------- Calculating error only for unobserved entries--------------------
72.93460370607394 2.691420013784058 1.194878183344078 1.194878183344078
Fraction-------------------------------- 40
-------------- Calculating error only for unobserved entries--------------------
72.95451892710567 2.6908033993328098 1.1939517644297712 1.1939517644297712
Fraction-------------------------------- 20
inside main_code
-------------- Calculating error only for unobserved entries--------------------
72.92523846562295 2.6921294640853106 1.1942552286744916 1.1942552286744916
Fraction-------------------------------- 99
inside main_code
-------------- Calculating error only for unobserved entries--------------------
72.92569927908839 2.692057610346308 1.1943441352077104 1.1943441352077104
Fraction-------------------------------- 90
inside main_code
-------------- Calculating error only for unobserved entries--------------------
72.92596729008994 2.69190896794981 1.194432209824622 1.194432209824622
Fraction-------------------------------- 80
inside main_code
-------------- Calculating error only for unobserved entries--------------------
72.93001407568013 2.6919051981735547 1.194144671184917 1.194144671184917
Fraction-------------------------------- 60
inside main_code
# run protein network
# try collaboration network
cost3 = [158.96724, 98.78402, 74.9231, 64.00145, 58.63235, 55.861347, 54.366524, 53.519352, 53.006138, 52.66433, 52.408646, 52.192135, 51.986546, 51.774937, 51.549442, 51.309853, 51.061428, 50.811607, 50.565613, 50.329323, 58.723026, 58.361225, 58.161457, 58.010284, 57.86779, 57.714756, 57.539577, 57.335247, 57.09924, 56.833363, 56.542717, 56.234505, 55.917282, 55.598743, 55.28897, 54.9952, 54.72235, 54.47319, 54.24661, 54.041183, 61.436134, 60.774326, 60.399055, 60.09885, 59.79915, 59.45637, 59.046936, 58.57618, 58.07581, 57.58582, 57.134533, 56.730938, 56.37296, 56.049274, 55.762352, 55.497215, 55.25945, 55.037453, 54.838146, 54.65893]
cost2 = [158.96724, 98.78402, 74.9231, 64.00145, 58.63235, 55.861347, 54.366524, 53.519352, 53.006138, 52.66433, 52.408646, 52.192135, 51.986546, 51.774937, 51.549442, 51.309853, 51.061428, 50.811607, 50.565613, 50.329323, 58.723026, 58.361225, 58.161457, 58.010284, 57.86779, 57.714756, 57.539577, 57.335247, 57.09924, 56.833363, 56.542717, 56.234505, 55.917282, 55.598743, 55.28897, 54.9952, 54.72235, 54.47319, 54.24661, 54.041183]
cost1 = [158.96724, 98.78402, 74.9231, 64.00145, 58.63235, 55.861347, 54.366524, 53.519352, 53.006138, 52.66433, 52.408646, 52.192135, 51.986546, 51.774937, 51.549442, 51.309853, 51.061428, 50.811607, 50.565613, 50.329323]
import matplotlib.pyplot as plt
plt.plot(cost1, label = 'nw1')
# plt.plot(cost2, label = 'nw2')
# plt.plot(cost3, label = 'nw3')
plt.xlabel('number of iterations')
plt.ylabel('cost')
plt.title('Cost value vs Iterations for various training sessions')
plt.legend()
plt.show()
# run for facebook:
!python3 "/content/drive/MyDrive/PhD work/Projects/parameter estimation/codes for Rasika/stage 1/script.py"
```
|
github_jupyter
|
# Getting Started
In this tutorial, you will know how to
- use the models in **ConvLab-2** to build a dialog agent.
- build a simulator to chat with the agent and evaluate the performance.
- try different module combinations.
- use analysis tool to diagnose your system.
Let's get started!
## Environment setup
Run the command below to install ConvLab-2. Then restart the notebook and skip this commend.
```
# first install ConvLab-2 and restart the notebook
! git clone https://github.com/thu-coai/ConvLab-2.git && cd ConvLab-2 && pip install -e .
# installing en_core_web_sm for spacy to resolve error in BERTNLU
!python -m spacy download en_core_web_sm
```
## build an agent
We use the models adapted on [Multiwoz](https://www.aclweb.org/anthology/D18-1547) dataset to build our agent. This pipeline agent consists of NLU, DST, Policy and NLG modules.
First, import some models:
```
# common import: convlab2.$module.$model.$dataset
from convlab2.nlu.jointBERT.multiwoz import BERTNLU
from convlab2.nlu.milu.multiwoz import MILU
from convlab2.dst.rule.multiwoz import RuleDST
from convlab2.policy.rule.multiwoz import RulePolicy
from convlab2.nlg.template.multiwoz import TemplateNLG
from convlab2.dialog_agent import PipelineAgent, BiSession
from convlab2.evaluator.multiwoz_eval import MultiWozEvaluator
from pprint import pprint
import random
import numpy as np
import torch
```
Then, create the models and build an agent:
```
# go to README.md of each model for more information
# BERT nlu
sys_nlu = BERTNLU()
# simple rule DST
sys_dst = RuleDST()
# rule policy
sys_policy = RulePolicy()
# template NLG
sys_nlg = TemplateNLG(is_user=False)
# assemble
sys_agent = PipelineAgent(sys_nlu, sys_dst, sys_policy, sys_nlg, name='sys')
```
That's all! Let's chat with the agent using its response function:
```
sys_agent.response("I want to find a moderate hotel")
sys_agent.response("Which type of hotel is it ?")
sys_agent.response("OK , where is its address ?")
sys_agent.response("Thank you !")
sys_agent.response("Try to find me a Chinese restaurant in south area .")
sys_agent.response("Which kind of food it provides ?")
sys_agent.response("Book a table for 5 , this Sunday .")
```
## Build a simulator to chat with the agent and evaluate
In many one-to-one task-oriented dialog system, a simulator is essential to train an RL agent. In our framework, we doesn't distinguish user or system. All speakers are **agents**. The simulator is also an agent, with specific policy inside for accomplishing the user goal.
We use `Agenda` policy for the simulator, this policy requires dialog act input, which means we should set DST argument of `PipelineAgent` to None. Then the `PipelineAgent` will pass dialog act to policy directly. Refer to `PipelineAgent` doc for more details.
```
# MILU
user_nlu = MILU()
# not use dst
user_dst = None
# rule policy
user_policy = RulePolicy(character='usr')
# template NLG
user_nlg = TemplateNLG(is_user=True)
# assemble
user_agent = PipelineAgent(user_nlu, user_dst, user_policy, user_nlg, name='user')
```
Now we have a simulator and an agent. we will use an existed simple one-to-one conversation controller BiSession, you can also define your own Session class for your special need.
We add `MultiWozEvaluator` to evaluate the performance. It uses the parsed dialog act input and policy output dialog act to calculate **inform f1**, **book rate**, and whether the task is **success**.
```
evaluator = MultiWozEvaluator()
sess = BiSession(sys_agent=sys_agent, user_agent=user_agent, kb_query=None, evaluator=evaluator)
```
Let's make this two agents chat! The key is `next_turn` method of `BiSession` class.
```
def set_seed(r_seed):
random.seed(r_seed)
np.random.seed(r_seed)
torch.manual_seed(r_seed)
set_seed(20200131)
sys_response = ''
sess.init_session()
print('init goal:')
pprint(sess.evaluator.goal)
print('-'*50)
for i in range(20):
sys_response, user_response, session_over, reward = sess.next_turn(sys_response)
print('user:', user_response)
print('sys:', sys_response)
print()
if session_over is True:
break
print('task success:', sess.evaluator.task_success())
print('book rate:', sess.evaluator.book_rate())
print('inform precision/recall/f1:', sess.evaluator.inform_F1())
print('-'*50)
print('final goal:')
pprint(sess.evaluator.goal)
print('='*100)
```
## Try different module combinations
The combination modes of pipeline agent modules are flexible. We support joint models such as TRADE, SUMBT for word-DST and MDRG, HDSA, LaRL for word-Policy, once the input and output are matched with previous and next module. We also support End2End models such as Sequicity.
Available models:
- NLU: BERTNLU, MILU, SVMNLU
- DST: RuleDST
- Word-DST: SUMBT, TRADE (set `sys_nlu` to `None`)
- Policy: RulePolicy, Imitation, REINFORCE, PPO, GDPL
- Word-Policy: MDRG, HDSA, LaRL (set `sys_nlg` to `None`)
- NLG: Template, SCLSTM
- End2End: Sequicity, DAMD, RNN_rollout (directly used as `sys_agent`)
- Simulator policy: Agenda, VHUS (for `user_policy`)
```
# available NLU models
from convlab2.nlu.svm.multiwoz import SVMNLU
from convlab2.nlu.jointBERT.multiwoz import BERTNLU
from convlab2.nlu.milu.multiwoz import MILU
# available DST models
from convlab2.dst.rule.multiwoz import RuleDST
from convlab2.dst.sumbt.multiwoz import SUMBT
from convlab2.dst.trade.multiwoz import TRADE
# available Policy models
from convlab2.policy.rule.multiwoz import RulePolicy
from convlab2.policy.ppo.multiwoz import PPOPolicy
from convlab2.policy.pg.multiwoz import PGPolicy
from convlab2.policy.mle.multiwoz import MLEPolicy
from convlab2.policy.gdpl.multiwoz import GDPLPolicy
from convlab2.policy.vhus.multiwoz import UserPolicyVHUS
from convlab2.policy.mdrg.multiwoz import MDRGWordPolicy
from convlab2.policy.hdsa.multiwoz import HDSA
from convlab2.policy.larl.multiwoz import LaRL
# available NLG models
from convlab2.nlg.template.multiwoz import TemplateNLG
from convlab2.nlg.sclstm.multiwoz import SCLSTM
# available E2E models
from convlab2.e2e.sequicity.multiwoz import Sequicity
from convlab2.e2e.damd.multiwoz import Damd
```
NLU+RuleDST or Word-DST:
```
# NLU+RuleDST:
sys_nlu = BERTNLU()
# sys_nlu = MILU()
# sys_nlu = SVMNLU()
sys_dst = RuleDST()
# or Word-DST:
# sys_nlu = None
# sys_dst = SUMBT()
# sys_dst = TRADE()
```
Policy+NLG or Word-Policy:
```
# Policy+NLG:
sys_policy = RulePolicy()
# sys_policy = PPOPolicy()
# sys_policy = PGPolicy()
# sys_policy = MLEPolicy()
# sys_policy = GDPLPolicy()
sys_nlg = TemplateNLG(is_user=False)
# sys_nlg = SCLSTM(is_user=False)
# or Word-Policy:
# sys_policy = LaRL()
# sys_policy = HDSA()
# sys_policy = MDRGWordPolicy()
# sys_nlg = None
```
Assemble the Pipeline system agent:
```
sys_agent = PipelineAgent(sys_nlu, sys_dst, sys_policy, sys_nlg, 'sys')
```
Or Directly use an end-to-end model:
```
# sys_agent = Sequicity()
# sys_agent = Damd()
```
Config an user agent similarly:
```
user_nlu = BERTNLU()
# user_nlu = MILU()
# user_nlu = SVMNLU()
user_dst = None
user_policy = RulePolicy(character='usr')
# user_policy = UserPolicyVHUS(load_from_zip=True)
user_nlg = TemplateNLG(is_user=True)
# user_nlg = SCLSTM(is_user=True)
user_agent = PipelineAgent(user_nlu, user_dst, user_policy, user_nlg, name='user')
```
## Use analysis tool to diagnose the system
We provide an analysis tool presents rich statistics and summarizes common mistakes from simulated dialogues, which facilitates error analysis and
system improvement. The analyzer will generate an HTML report which contains
rich statistics of simulated dialogues. For more information, please refer to `convlab2/util/analysis_tool`.
```
from convlab2.util.analysis_tool.analyzer import Analyzer
# if sys_nlu!=None, set use_nlu=True to collect more information
analyzer = Analyzer(user_agent=user_agent, dataset='multiwoz')
set_seed(20200131)
analyzer.comprehensive_analyze(sys_agent=sys_agent, model_name='sys_agent', total_dialog=100)
```
To compare several models:
```
set_seed(20200131)
analyzer.compare_models(agent_list=[sys_agent1, sys_agent2], model_name=['sys_agent1', 'sys_agent2'], total_dialog=100)
```
|
github_jupyter
|
# Jetsoncar Rosey V2
Tensorflow 2.0, all in notebook, optimized with RT
```
import tensorflow as tf
print(tf.__version__)
tf.config.experimental.list_physical_devices('GPU') # If device does not show and using conda env with tensorflow-gpu then try restarting computer
# verify the image data directory
import os
data_directory = "/media/michael/BigMemory/datasets/jetsoncar/training_data/data/dataset"
os.listdir(data_directory)[:10]
import matplotlib.pyplot as plt
img = plt.imread(os.path.join(data_directory + "/color_images", os.listdir(data_directory + "/color_images")[0]))
print(img.shape)
plt.imshow(img)
```
## Create the datagenerator and augmentation framework
```
# Include the custom utils.py and perform tests
import importlib
utils = importlib.import_module('utils')
import numpy as np
print(utils.INPUT_SHAPE)
img = utils.load_image(os.path.join(data_directory, 'color_images'),os.listdir(data_directory + "/color_images")[0])
print(img.shape)
fig = plt.figure(figsize=(20,20))
fig.add_subplot(1, 3, 1)
plt.imshow(img)
img, _ = utils.preprocess_data(last_color_image=img)
print(img.shape)
fig.add_subplot(1, 3, 2)
plt.imshow(np.squeeze(img))
plt.show()
# Load the steering angles and image paths from labels.csv
import csv, random
import seaborn as sns
# these will be 2D arrays where each row represents a dataset
x = [] # images
y = [] # steering
z = [] # speed
with open(os.path.join(data_directory, "tags.csv")) as csvfile:
reader = csv.DictReader(csvfile)
for row in reader:
# print(row['Time_stamp'] + ".jpg", row['Steering_angle'])
if not float(row['raw_speed']) == 0:
x.append(row['time_stamp'] + ".jpg",) # get image path
y.append(float(row['raw_steering']),) # get steering value
z.append(float(row['raw_speed']))
print("Number of data samples is " + str(len(y)))
data = list(zip(x,y))
random.shuffle(data)
x,y = zip(*data)
# plot of steering angle distribution without correction
sns.distplot(y)
# plot of speed distribution
sns.distplot(z)
# Split the training data
validation_split = 0.2
train_x = x[0:int(len(x)*(1.0-validation_split))]
train_y = y[0:int(len(y)*(1.0-validation_split))]
print("Training data shape: " + str(len(train_x)))
test_x = x[int(len(x)*(1.0-validation_split)):]
test_y = y[int(len(y)*(1.0-validation_split)):]
print("Validation data shape: " + str(len(test_x)) + "\n")
# Define and test batch generator
def batch_generator(data_dir, image_paths, steering_angles, batch_size, is_training):
"""
Generate training image give image paths and associated steering angles
"""
images = np.empty([batch_size, utils.IMAGE_HEIGHT, utils.IMAGE_WIDTH, utils.IMAGE_CHANNELS], dtype=np.float32)
steers = np.empty(batch_size)
while True:
i = 0
for index in np.random.permutation(len(image_paths)):
img = image_paths[index]
steering_angle = steering_angles[index]
# argumentation
if is_training and np.random.rand() < 0.8:
image, steering_angle = utils.augument(data_dir, os.path.join("color_images",img), steering_angle)
else:
image, _ = utils.preprocess_data(utils.load_image(data_dir, os.path.join("color_images",img)))
# add the image and steering angle to the batch
images[i] = image
steers[i] = steering_angle
i += 1
if i == batch_size:
break
yield images, steers
train_generator = batch_generator(data_directory, train_x, train_y, 32, True)
validation_generator = batch_generator(data_directory, test_x, test_y, 32, False)
train_image = next(train_generator) # returns tuple with steering and throttle
print(train_image[0].shape)
print(train_image[1][0])
plt.imshow(train_image[0][0])
```
## Define the model and start training
```
model = tf.keras.models.Sequential([
tf.keras.Input((utils.IMAGE_HEIGHT, utils.IMAGE_WIDTH, utils.IMAGE_CHANNELS)),
tf.keras.layers.Conv2D(32, (11,11), padding='same', kernel_initializer='lecun_uniform'),
tf.keras.layers.BatchNormalization(),
tf.keras.layers.ELU(),
tf.keras.layers.MaxPool2D((2,2)),
tf.keras.layers.Conv2D(32, (7,7), padding='same', kernel_initializer='lecun_uniform'),
tf.keras.layers.BatchNormalization(),
tf.keras.layers.ELU(),
tf.keras.layers.MaxPool2D((2,2)),
tf.keras.layers.Conv2D(64, (5,5), padding='same', kernel_initializer='lecun_uniform'),
tf.keras.layers.BatchNormalization(),
tf.keras.layers.ELU(),
tf.keras.layers.MaxPool2D((2,2)),
tf.keras.layers.Conv2D(64, (3,3), padding='same', kernel_initializer='lecun_uniform'),
tf.keras.layers.BatchNormalization(),
tf.keras.layers.ELU(),
tf.keras.layers.MaxPool2D((2,2)),
tf.keras.layers.Conv2D(32, (3,3), padding='same', kernel_initializer='lecun_uniform'),
tf.keras.layers.BatchNormalization(),
tf.keras.layers.ELU(),
tf.keras.layers.MaxPool2D((2,3)),
tf.keras.layers.Conv2D(16, (3,3), padding='same', kernel_initializer='lecun_uniform'),
tf.keras.layers.BatchNormalization(),
tf.keras.layers.ELU(),
tf.keras.layers.MaxPool2D((2,3)),
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(10, activation='elu'),
tf.keras.layers.Dense(1, activation='linear')
])
model.summary()
model.compile(loss='mean_squared_error', optimizer='adam')
import datetime
log_dir="logs/fit/" + datetime.datetime.now().strftime("%Y%m%d-%H%M%S")
tensorboard_callback = tf.keras.callbacks.TensorBoard(log_dir=log_dir)
print("To view tensorboard please run `tensorboard --logdir logs/fit` in the code directory from the terminal with deeplearning env active")
checkpoint = tf.keras.callbacks.ModelCheckpoint('rosey_v2.{epoch:03d}-{val_loss:.2f}.h5', # filepath = working directory/
monitor='val_loss',
verbose=0,
save_best_only=True,
mode='auto')
model.fit_generator(train_generator,
steps_per_epoch=100,
epochs=20,
validation_data=validation_generator,
validation_steps=1,
callbacks=[tensorboard_callback, checkpoint])
# Test the model
image, steering = next(train_generator)
print(steering)
print(model.predict(image))
print("")
image, steering = next(validation_generator)
print(steering)
print(model.predict(image))
```
## Save the model as tensor RT and export to Jetson format
```
# Load the model that you would like converted to RT
model_path = 'model.h5'
export_path = "/home/michael/Desktop/model"
import shutil
if not os.path.isdir(export_path):
os.mkdir(export_path)
else:
response = input("Do you want to delete existing export_path directory? y/n")
if response == 'y':
shutil.rmtree(export_path)
os.mkdir(export_path)
loaded_model = tf.keras.models.load_model(model_path)
shutil.copy("./utils.py", os.path.join(export_path, "utils.py"))
shutil.copy("./__init__.py", os.path.join(export_path, "__init__.py"))
shutil.copy("./notes.txt", os.path.join(export_path, "notes.txt"))
shutil.copy("./config.yaml", os.path.join(export_path, "config.yaml"))
# Save as tf saved_model (faster than h5)
tf.saved_model.save(loaded_model, export_path)
from tensorflow.python.compiler.tensorrt import trt_convert as trt
conversion_params = trt.DEFAULT_TRT_CONVERSION_PARAMS
conversion_params = conversion_params._replace(max_workspace_size_bytes=(1 << 32))
conversion_params = conversion_params._replace(precision_mode="INT8")
conversion_params = conversion_params._replace(maximum_cached_engines=100)
conversion_params = conversion_params._replace(use_calibration=True)
def my_calibration_input_fn():
for i in range(20):
image, _ = utils.preprocess_data(utils.load_image(data_directory, os.path.join("color_images",x[i])))
yield image.astype(np.float32),
converter = tf.experimental.tensorrt.Converter(input_saved_model_dir=export_path,conversion_params=conversion_params)
gen = my_calibration_input_fn()
converter.convert(calibration_input_fn=my_calibration_input_fn)
converter.build(my_calibration_input_fn)
if not os.path.isdir(os.path.join(export_path, "rt")):
os.mkdir(os.path.join(export_path, "rt"))
converter.save(os.path.join(export_path, "rt"))
# Test normal saved model
saved_model = tf.saved_model.load(export_path) # normal saved model
image, _ = next(validation_generator)
import time
output = saved_model(image.astype(np.float32)) # load once to get more accurate representation of speed
start = time.time()
output = saved_model(image.astype(np.float32))
stop = time.time()
print("inference time: " + str(stop - start))
print("Output: %.20f"%output[8,0])
# Test TRT optimized saved model
saved_model = tf.saved_model.load(os.path.join(export_path, "rt")) # normal saved model
image, _ = next(validation_generator)
import time
output = saved_model(image) # load once to get more accurate representation of speed
start = time.time()
output = saved_model(image)
stop = time.time()
print("inference time: " + str(stop - start))
print("Output: %.20f"%output[8,0])
# Run many samples through and save distribution
validation_generator = batch_generator(data_directory, test_x, test_y, 32, False)
test = []
for i in range(50):
img, _ = next(validation_generator)
test.append(saved_model(img.astype(np.float32))[0][0])
print(str(i), end="\r")
sns.distplot(test)
```
|
github_jupyter
|
# Transfer learning & fine-tuning
**Author:** [fchollet](https://twitter.com/fchollet)<br>
**Date created:** 2020/04/15<br>
**Last modified:** 2020/05/12<br>
**Description:** Complete guide to transfer learning & fine-tuning in Keras.
## Setup
```
import numpy as np
import tensorflow as tf
from tensorflow import keras
```
## Introduction
**Transfer learning** consists of taking features learned on one problem, and
leveraging them on a new, similar problem. For instance, features from a model that has
learned to identify racoons may be useful to kick-start a model meant to identify
tanukis.
Transfer learning is usually done for tasks where your dataset has too little data to
train a full-scale model from scratch.
The most common incarnation of transfer learning in the context of deep learning is the
following workflow:
1. Take layers from a previously trained model.
2. Freeze them, so as to avoid destroying any of the information they contain during
future training rounds.
3. Add some new, trainable layers on top of the frozen layers. They will learn to turn
the old features into predictions on a new dataset.
4. Train the new layers on your dataset.
A last, optional step, is **fine-tuning**, which consists of unfreezing the entire
model you obtained above (or part of it), and re-training it on the new data with a
very low learning rate. This can potentially achieve meaningful improvements, by
incrementally adapting the pretrained features to the new data.
First, we will go over the Keras `trainable` API in detail, which underlies most
transfer learning & fine-tuning workflows.
Then, we'll demonstrate the typical workflow by taking a model pretrained on the
ImageNet dataset, and retraining it on the Kaggle "cats vs dogs" classification
dataset.
This is adapted from
[Deep Learning with Python](https://www.manning.com/books/deep-learning-with-python)
and the 2016 blog post
["building powerful image classification models using very little
data"](https://blog.keras.io/building-powerful-image-classification-models-using-very-little-data.html).
## Freezing layers: understanding the `trainable` attribute
Layers & models have three weight attributes:
- `weights` is the list of all weights variables of the layer.
- `trainable_weights` is the list of those that are meant to be updated (via gradient
descent) to minimize the loss during training.
- `non_trainable_weights` is the list of those that aren't meant to be trained.
Typically they are updated by the model during the forward pass.
**Example: the `Dense` layer has 2 trainable weights (kernel & bias)**
```
layer = keras.layers.Dense(3)
layer.build((None, 4)) # Create the weights
print("weights:", len(layer.weights))
print("trainable_weights:", len(layer.trainable_weights))
print("non_trainable_weights:", len(layer.non_trainable_weights))
```
In general, all weights are trainable weights. The only built-in layer that has
non-trainable weights is the `BatchNormalization` layer. It uses non-trainable weights
to keep track of the mean and variance of its inputs during training.
To learn how to use non-trainable weights in your own custom layers, see the
[guide to writing new layers from scratch](https://keras.io/guides/making_new_layers_and_models_via_subclassing/).
**Example: the `BatchNormalization` layer has 2 trainable weights and 2 non-trainable
weights**
```
layer = keras.layers.BatchNormalization()
layer.build((None, 4)) # Create the weights
print("weights:", len(layer.weights))
print("trainable_weights:", len(layer.trainable_weights))
print("non_trainable_weights:", len(layer.non_trainable_weights))
```
Layers & models also feature a boolean attribute `trainable`. Its value can be changed.
Setting `layer.trainable` to `False` moves all the layer's weights from trainable to
non-trainable. This is called "freezing" the layer: the state of a frozen layer won't
be updated during training (either when training with `fit()` or when training with
any custom loop that relies on `trainable_weights` to apply gradient updates).
**Example: setting `trainable` to `False`**
```
layer = keras.layers.Dense(3)
layer.build((None, 4)) # Create the weights
layer.trainable = False # Freeze the layer
print("weights:", len(layer.weights))
print("trainable_weights:", len(layer.trainable_weights))
print("non_trainable_weights:", len(layer.non_trainable_weights))
```
When a trainable weight becomes non-trainable, its value is no longer updated during
training.
```
# Make a model with 2 layers
layer1 = keras.layers.Dense(3, activation="relu")
layer2 = keras.layers.Dense(3, activation="sigmoid")
model = keras.Sequential([keras.Input(shape=(3,)), layer1, layer2])
# Freeze the first layer
layer1.trainable = False
# Keep a copy of the weights of layer1 for later reference
initial_layer1_weights_values = layer1.get_weights()
# Train the model
model.compile(optimizer="adam", loss="mse")
model.fit(np.random.random((2, 3)), np.random.random((2, 3)))
# Check that the weights of layer1 have not changed during training
final_layer1_weights_values = layer1.get_weights()
np.testing.assert_allclose(
initial_layer1_weights_values[0], final_layer1_weights_values[0]
)
np.testing.assert_allclose(
initial_layer1_weights_values[1], final_layer1_weights_values[1]
)
```
Do not confuse the `layer.trainable` attribute with the argument `training` in
`layer.__call__()` (which controls whether the layer should run its forward pass in
inference mode or training mode). For more information, see the
[Keras FAQ](
https://keras.io/getting_started/faq/#whats-the-difference-between-the-training-argument-in-call-and-the-trainable-attribute).
## Recursive setting of the `trainable` attribute
If you set `trainable = False` on a model or on any layer that has sublayers,
all children layers become non-trainable as well.
**Example:**
```
inner_model = keras.Sequential(
[
keras.Input(shape=(3,)),
keras.layers.Dense(3, activation="relu"),
keras.layers.Dense(3, activation="relu"),
]
)
model = keras.Sequential(
[keras.Input(shape=(3,)), inner_model, keras.layers.Dense(3, activation="sigmoid"),]
)
model.trainable = False # Freeze the outer model
assert inner_model.trainable == False # All layers in `model` are now frozen
assert inner_model.layers[0].trainable == False # `trainable` is propagated recursively
```
## The typical transfer-learning workflow
This leads us to how a typical transfer learning workflow can be implemented in Keras:
1. Instantiate a base model and load pre-trained weights into it.
2. Freeze all layers in the base model by setting `trainable = False`.
3. Create a new model on top of the output of one (or several) layers from the base
model.
4. Train your new model on your new dataset.
Note that an alternative, more lightweight workflow could also be:
1. Instantiate a base model and load pre-trained weights into it.
2. Run your new dataset through it and record the output of one (or several) layers
from the base model. This is called **feature extraction**.
3. Use that output as input data for a new, smaller model.
A key advantage of that second workflow is that you only run the base model once on
your data, rather than once per epoch of training. So it's a lot faster & cheaper.
An issue with that second workflow, though, is that it doesn't allow you to dynamically
modify the input data of your new model during training, which is required when doing
data augmentation, for instance. Transfer learning is typically used for tasks when
your new dataset has too little data to train a full-scale model from scratch, and in
such scenarios data augmentation is very important. So in what follows, we will focus
on the first workflow.
Here's what the first workflow looks like in Keras:
First, instantiate a base model with pre-trained weights.
```python
base_model = keras.applications.Xception(
weights='imagenet', # Load weights pre-trained on ImageNet.
input_shape=(150, 150, 3),
include_top=False) # Do not include the ImageNet classifier at the top.
```
Then, freeze the base model.
```python
base_model.trainable = False
```
Create a new model on top.
```python
inputs = keras.Input(shape=(150, 150, 3))
# We make sure that the base_model is running in inference mode here,
# by passing `training=False`. This is important for fine-tuning, as you will
# learn in a few paragraphs.
x = base_model(inputs, training=False)
# Convert features of shape `base_model.output_shape[1:]` to vectors
x = keras.layers.GlobalAveragePooling2D()(x)
# A Dense classifier with a single unit (binary classification)
outputs = keras.layers.Dense(1)(x)
model = keras.Model(inputs, outputs)
```
Train the model on new data.
```python
model.compile(optimizer=keras.optimizers.Adam(),
loss=keras.losses.BinaryCrossentropy(from_logits=True),
metrics=[keras.metrics.BinaryAccuracy()])
model.fit(new_dataset, epochs=20, callbacks=..., validation_data=...)
```
## Fine-tuning
Once your model has converged on the new data, you can try to unfreeze all or part of
the base model and retrain the whole model end-to-end with a very low learning rate.
This is an optional last step that can potentially give you incremental improvements.
It could also potentially lead to quick overfitting -- keep that in mind.
It is critical to only do this step *after* the model with frozen layers has been
trained to convergence. If you mix randomly-initialized trainable layers with
trainable layers that hold pre-trained features, the randomly-initialized layers will
cause very large gradient updates during training, which will destroy your pre-trained
features.
It's also critical to use a very low learning rate at this stage, because
you are training a much larger model than in the first round of training, on a dataset
that is typically very small.
As a result, you are at risk of overfitting very quickly if you apply large weight
updates. Here, you only want to readapt the pretrained weights in an incremental way.
This is how to implement fine-tuning of the whole base model:
```python
# Unfreeze the base model
base_model.trainable = True
# It's important to recompile your model after you make any changes
# to the `trainable` attribute of any inner layer, so that your changes
# are take into account
model.compile(optimizer=keras.optimizers.Adam(1e-5), # Very low learning rate
loss=keras.losses.BinaryCrossentropy(from_logits=True),
metrics=[keras.metrics.BinaryAccuracy()])
# Train end-to-end. Be careful to stop before you overfit!
model.fit(new_dataset, epochs=10, callbacks=..., validation_data=...)
```
**Important note about `compile()` and `trainable`**
Calling `compile()` on a model is meant to "freeze" the behavior of that model. This
implies that the `trainable`
attribute values at the time the model is compiled should be preserved throughout the
lifetime of that model,
until `compile` is called again. Hence, if you change any `trainable` value, make sure
to call `compile()` again on your
model for your changes to be taken into account.
**Important notes about `BatchNormalization` layer**
Many image models contain `BatchNormalization` layers. That layer is a special case on
every imaginable count. Here are a few things to keep in mind.
- `BatchNormalization` contains 2 non-trainable weights that get updated during
training. These are the variables tracking the mean and variance of the inputs.
- When you set `bn_layer.trainable = False`, the `BatchNormalization` layer will
run in inference mode, and will not update its mean & variance statistics. This is not
the case for other layers in general, as
[weight trainability & inference/training modes are two orthogonal concepts](
https://keras.io/getting_started/faq/#whats-the-difference-between-the-training-argument-in-call-and-the-trainable-attribute).
But the two are tied in the case of the `BatchNormalization` layer.
- When you unfreeze a model that contains `BatchNormalization` layers in order to do
fine-tuning, you should keep the `BatchNormalization` layers in inference mode by
passing `training=False` when calling the base model.
Otherwise the updates applied to the non-trainable weights will suddenly destroy
what the model has learned.
You'll see this pattern in action in the end-to-end example at the end of this guide.
## Transfer learning & fine-tuning with a custom training loop
If instead of `fit()`, you are using your own low-level training loop, the workflow
stays essentially the same. You should be careful to only take into account the list
`model.trainable_weights` when applying gradient updates:
```python
# Create base model
base_model = keras.applications.Xception(
weights='imagenet',
input_shape=(150, 150, 3),
include_top=False)
# Freeze base model
base_model.trainable = False
# Create new model on top.
inputs = keras.Input(shape=(150, 150, 3))
x = base_model(inputs, training=False)
x = keras.layers.GlobalAveragePooling2D()(x)
outputs = keras.layers.Dense(1)(x)
model = keras.Model(inputs, outputs)
loss_fn = keras.losses.BinaryCrossentropy(from_logits=True)
optimizer = keras.optimizers.Adam()
# Iterate over the batches of a dataset.
for inputs, targets in new_dataset:
# Open a GradientTape.
with tf.GradientTape() as tape:
# Forward pass.
predictions = model(inputs)
# Compute the loss value for this batch.
loss_value = loss_fn(targets, predictions)
# Get gradients of loss wrt the *trainable* weights.
gradients = tape.gradient(loss_value, model.trainable_weights)
# Update the weights of the model.
optimizer.apply_gradients(zip(gradients, model.trainable_weights))
```
Likewise for fine-tuning.
## An end-to-end example: fine-tuning an image classification model on a cats vs. dogs dataset
To solidify these concepts, let's walk you through a concrete end-to-end transfer
learning & fine-tuning example. We will load the Xception model, pre-trained on
ImageNet, and use it on the Kaggle "cats vs. dogs" classification dataset.
### Getting the data
First, let's fetch the cats vs. dogs dataset using TFDS. If you have your own dataset,
you'll probably want to use the utility
`tf.keras.preprocessing.image_dataset_from_directory` to generate similar labeled
dataset objects from a set of images on disk filed into class-specific folders.
Transfer learning is most useful when working with very small datasets. To keep our
dataset small, we will use 40% of the original training data (25,000 images) for
training, 10% for validation, and 10% for testing.
```
import tensorflow_datasets as tfds
tfds.disable_progress_bar()
train_ds, validation_ds, test_ds = tfds.load(
"cats_vs_dogs",
# Reserve 10% for validation and 10% for test
split=["train[:40%]", "train[40%:50%]", "train[50%:60%]"],
as_supervised=True, # Include labels
)
print("Number of training samples: %d" % tf.data.experimental.cardinality(train_ds))
print(
"Number of validation samples: %d" % tf.data.experimental.cardinality(validation_ds)
)
print("Number of test samples: %d" % tf.data.experimental.cardinality(test_ds))
```
These are the first 9 images in the training dataset -- as you can see, they're all
different sizes.
```
import matplotlib.pyplot as plt
plt.figure(figsize=(10, 10))
for i, (image, label) in enumerate(train_ds.take(9)):
ax = plt.subplot(3, 3, i + 1)
plt.imshow(image)
plt.title(int(label))
plt.axis("off")
```
We can also see that label 1 is "dog" and label 0 is "cat".
### Standardizing the data
Our raw images have a variety of sizes. In addition, each pixel consists of 3 integer
values between 0 and 255 (RGB level values). This isn't a great fit for feeding a
neural network. We need to do 2 things:
- Standardize to a fixed image size. We pick 150x150.
- Normalize pixel values between -1 and 1. We'll do this using a `Normalization` layer as
part of the model itself.
In general, it's a good practice to develop models that take raw data as input, as
opposed to models that take already-preprocessed data. The reason being that, if your
model expects preprocessed data, any time you export your model to use it elsewhere
(in a web browser, in a mobile app), you'll need to reimplement the exact same
preprocessing pipeline. This gets very tricky very quickly. So we should do the least
possible amount of preprocessing before hitting the model.
Here, we'll do image resizing in the data pipeline (because a deep neural network can
only process contiguous batches of data), and we'll do the input value scaling as part
of the model, when we create it.
Let's resize images to 150x150:
```
size = (150, 150)
train_ds = train_ds.map(lambda x, y: (tf.image.resize(x, size), y))
validation_ds = validation_ds.map(lambda x, y: (tf.image.resize(x, size), y))
test_ds = test_ds.map(lambda x, y: (tf.image.resize(x, size), y))
```
Besides, let's batch the data and use caching & prefetching to optimize loading speed.
```
batch_size = 32
train_ds = train_ds.cache().batch(batch_size).prefetch(buffer_size=10)
validation_ds = validation_ds.cache().batch(batch_size).prefetch(buffer_size=10)
test_ds = test_ds.cache().batch(batch_size).prefetch(buffer_size=10)
```
### Using random data augmentation
When you don't have a large image dataset, it's a good practice to artificially
introduce sample diversity by applying random yet realistic transformations to
the training images, such as random horizontal flipping or small random rotations. This
helps expose the model to different aspects of the training data while slowing down
overfitting.
```
from tensorflow import keras
from tensorflow.keras import layers
data_augmentation = keras.Sequential(
[layers.RandomFlip("horizontal"), layers.RandomRotation(0.1),]
)
```
Let's visualize what the first image of the first batch looks like after various random
transformations:
```
import numpy as np
for images, labels in train_ds.take(1):
plt.figure(figsize=(10, 10))
first_image = images[0]
for i in range(9):
ax = plt.subplot(3, 3, i + 1)
augmented_image = data_augmentation(
tf.expand_dims(first_image, 0), training=True
)
plt.imshow(augmented_image[0].numpy().astype("int32"))
plt.title(int(labels[0]))
plt.axis("off")
```
## Build a model
Now let's built a model that follows the blueprint we've explained earlier.
Note that:
- We add a `Rescaling` layer to scale input values (initially in the `[0, 255]`
range) to the `[-1, 1]` range.
- We add a `Dropout` layer before the classification layer, for regularization.
- We make sure to pass `training=False` when calling the base model, so that
it runs in inference mode, so that batchnorm statistics don't get updated
even after we unfreeze the base model for fine-tuning.
```
base_model = keras.applications.Xception(
weights="imagenet", # Load weights pre-trained on ImageNet.
input_shape=(150, 150, 3),
include_top=False,
) # Do not include the ImageNet classifier at the top.
# Freeze the base_model
base_model.trainable = False
# Create new model on top
inputs = keras.Input(shape=(150, 150, 3))
x = data_augmentation(inputs) # Apply random data augmentation
# Pre-trained Xception weights requires that input be scaled
# from (0, 255) to a range of (-1., +1.), the rescaling layer
# outputs: `(inputs * scale) + offset`
scale_layer = keras.layers.Rescaling(scale=1 / 127.5, offset=-1)
x = scale_layer(x)
# The base model contains batchnorm layers. We want to keep them in inference mode
# when we unfreeze the base model for fine-tuning, so we make sure that the
# base_model is running in inference mode here.
x = base_model(x, training=False)
x = keras.layers.GlobalAveragePooling2D()(x)
x = keras.layers.Dropout(0.2)(x) # Regularize with dropout
outputs = keras.layers.Dense(1)(x)
model = keras.Model(inputs, outputs)
model.summary()
```
## Train the top layer
```
model.compile(
optimizer=keras.optimizers.Adam(),
loss=keras.losses.BinaryCrossentropy(from_logits=True),
metrics=[keras.metrics.BinaryAccuracy()],
)
epochs = 20
model.fit(train_ds, epochs=epochs, validation_data=validation_ds)
```
## Do a round of fine-tuning of the entire model
Finally, let's unfreeze the base model and train the entire model end-to-end with a low
learning rate.
Importantly, although the base model becomes trainable, it is still running in
inference mode since we passed `training=False` when calling it when we built the
model. This means that the batch normalization layers inside won't update their batch
statistics. If they did, they would wreck havoc on the representations learned by the
model so far.
```
# Unfreeze the base_model. Note that it keeps running in inference mode
# since we passed `training=False` when calling it. This means that
# the batchnorm layers will not update their batch statistics.
# This prevents the batchnorm layers from undoing all the training
# we've done so far.
base_model.trainable = True
model.summary()
model.compile(
optimizer=keras.optimizers.Adam(1e-5), # Low learning rate
loss=keras.losses.BinaryCrossentropy(from_logits=True),
metrics=[keras.metrics.BinaryAccuracy()],
)
epochs = 10
model.fit(train_ds, epochs=epochs, validation_data=validation_ds)
```
After 10 epochs, fine-tuning gains us a nice improvement here.
|
github_jupyter
|
<h1>Table of Contents<span class="tocSkip"></span></h1>
<div class="toc"><ul class="toc-item"><li><span><a href="#Sandford+-2020,-Section-3:-Methods" data-toc-modified-id="Sandford+-2020,-Section-3:-Methods-1"><span class="toc-item-num">1 </span>Sandford+ 2020, Section 3: Methods</a></span><ul class="toc-item"><li><span><a href="#Imports" data-toc-modified-id="Imports-1.1"><span class="toc-item-num">1.1 </span>Imports</a></span></li><li><span><a href="#Plotting-Configs" data-toc-modified-id="Plotting-Configs-1.2"><span class="toc-item-num">1.2 </span>Plotting Configs</a></span></li><li><span><a href="#Figure-2:-HR-&-Kiel-Diagrams" data-toc-modified-id="Figure-2:-HR-&-Kiel-Diagrams-1.3"><span class="toc-item-num">1.3 </span>Figure 2: HR & Kiel Diagrams</a></span></li></ul></li></ul></div>
# Sandford+ 2020, Section 3: Methods
## Imports
```
import numpy as np
import pandas as pd
import matplotlib as mpl
import matplotlib.pyplot as plt
from matplotlib.gridspec import GridSpec
%matplotlib inline
```
## Plotting Configs
```
output_dir = './figures/'
mpl.rc('axes', grid=True, lw=2)
mpl.rc('ytick', direction='in', labelsize=14)
mpl.rc('ytick.major', size=5, width=1)
mpl.rc('xtick', direction='in', labelsize=14)
mpl.rc('xtick.major', size=5, width=1)
mpl.rc('ytick', direction='in', labelsize=14)
mpl.rc('ytick.major', size=5, width=1)
mpl.rc('grid', lw=0)
mpl.rc('figure', dpi=300)
```
## Figure 2: HR & Kiel Diagrams
```
log_age = 10 # Select 10 Gyr old isochrones
metallicities = [-0.5, -1.0, -1.5, -2.0, -2.5] # Select isochrone metallicities
c = plt.cm.get_cmap('plasma', len(metallicities) + 1)
# Initialize figure
fig = plt.figure(figsize=(5, 9))
gs = GridSpec(2, 1, hspace=0)
ax1 = plt.subplot(gs[0, 0])
ax2 = plt.subplot(gs[1, 0])
# Loop through metallicities
for i, feh in enumerate(metallicities):
iso = pd.read_hdf('./isochrones.h5', f'{feh:1.1f}') # Load isochrone
iso = iso[(iso['log10_isochrone_age_yr'] == log_age) & (10**iso['log_Teff'] >= 3500)] # Select on age and effective temperature
rgb_idx = (np.abs(iso['Bessell_V'] + 0.5)).idxmin() # Find RGB star w/ M_V = -0.5
# Plot Isochrones
ax1.plot(10**iso['log_Teff'], iso['Bessell_V'], c=c(i), lw=2, zorder=-1, label=r'$\log(Z)=$'+f'{feh:1.1f}')
ax2.plot(10**iso['log_Teff'], iso['log_g'], c=c(i), lw=2, zorder=-1, label=r'$\log(Z)=$'+f'{feh:1.1f}')
# Plot Reference Stars
ax1.scatter(10**iso['log_Teff'][rgb_idx], iso['Bessell_V'][rgb_idx],
marker='*', c=[c(i)], edgecolor='k', lw=0.5, s=150)
ax2.scatter(10**iso['log_Teff'][rgb_idx], iso['log_g'][rgb_idx],
marker='*', c=[c(i)], edgecolor='k', lw=0.5, s=150)
if feh == -1.5:
trgb_idx = (np.abs(iso['Bessell_V'] + 2.5)).idxmin() # Find TRGB star w/ M_V = -2.5
msto_idx = (np.abs(iso['Bessell_V'] - 3.5)).idxmin() # Find MSTO star w/ M_V = +3.5
ax1.scatter(10**iso['log_Teff'][trgb_idx], iso['Bessell_V'][trgb_idx],
marker='o', c=[c(2)], edgecolor='k', lw=0.5, s=100, label=f'TRGB')
ax2.scatter(10**iso['log_Teff'][trgb_idx], iso['log_g'][trgb_idx],
marker='o', c=[c(2)], edgecolor='k', lw=0.5, s=100, label=f'TRGB')
ax1.scatter(10**iso['log_Teff'][rgb_idx], iso['Bessell_V'][rgb_idx],
marker='*', c=[c(2)], edgecolor='k', lw=0.5, s=150, label=f'RGB')
ax2.scatter(10**iso['log_Teff'][rgb_idx], iso['log_g'][rgb_idx],
marker='*', c=[c(2)], edgecolor='k', lw=0.5, s=150, label=f'RGB')
ax1.scatter(10**iso['log_Teff'][msto_idx], iso['Bessell_V'][msto_idx],
marker='s', c=[c(2)], edgecolor='k', lw=0.5, s=100, label=f'MSTO')
ax2.scatter(10**iso['log_Teff'][msto_idx], iso['log_g'][msto_idx],
marker='s', c=[c(2)], edgecolor='k', lw=0.5, s=100, label=f'MSTO')
# Axes
ax1.set_ylabel(r'$M_V$', size=24)
ax2.set_ylabel(r'$\log(g)$', size=24)
ax2.set_xlabel(r'$T_{eff}$', size=24)
ax1.set_ylim(-3.5, 7)
ax1.invert_xaxis()
ax1.invert_yaxis()
ax2.invert_xaxis()
ax2.invert_yaxis()
# Legend
ax1.legend(fontsize=10, loc='upper left')
plt.tight_layout()
fig.savefig('./figures/hr_kiel.png')
plt.show()
```
|
github_jupyter
|
<img style="float: center;" src="images/CI_horizontal.png" width="600">
<center>
<span style="font-size: 1.5em;">
<a href='https://www.coleridgeinitiative.org'>Website</a>
</span>
</center>
Ghani, Rayid, Frauke Kreuter, Julia Lane, Adrianne Bradford, Alex Engler, Nicolas Guetta Jeanrenaud, Graham Henke, Daniela Hochfellner, Clayton Hunter, Brian Kim, Avishek Kumar, Jonathan Morgan, and Benjamin Feder.
_source to be updated when notebook added to GitHub_
# Table of Contents
JupyterLab contains a dynamic Table of Contents that can be accessed by clicking the last of the six icons on the left-hand sidebar.
# Dataset Preparation
----------
In this notebook, we will walk through preparing our data for machine learning. In practice, the data preparation should take some time as you will need to think deeply about the question at the heart of your project.
## The Machine Learning Process
The Machine Learning Process is as follows:
- [**Understand the problem and goal.**](#problem-formulation) *This sounds obvious but is often nontrivial.* Problems typically start as vague
descriptions of a goal - improving health outcomes, increasing graduation rates, understanding the effect of a
variable *X* on an outcome *Y*, etc. It is really important to work with people who understand the domain being
studied to dig deeper and define the problem more concretely. What is the analytical formulation of the metric
that you are trying to optimize?
- [**Formulate it as a machine learning problem.**](#problem-formulation) Is it a classification problem or a regression problem? Is the
goal to build a model that generates a ranked list prioritized by risk, or is it to detect anomalies as new data
come in? Knowing what kinds of tasks machine learning can solve will allow you to map the problem you are working on
to one or more machine learning settings and give you access to a suite of methods.
- **Data exploration and preparation.** Next, you need to carefully explore the data you have. What additional data
do you need or have access to? What variable will you use to match records for integrating different data sources?
What variables exist in the data set? Are they continuous or categorical? What about missing values? Can you use the
variables in their original form, or do you need to alter them in some way?
- [**Feature engineering.**](#feature-generation) In machine learning language, what you might know as independent variables or predictors
or factors or covariates are called "features." Creating good features is probably the most important step in the
machine learning process. This involves doing transformations, creating interaction terms, or aggregating over data
points or over time and space.
- **Method selection.** Having formulated the problem and created your features, you now have a suite of methods to
choose from. It would be great if there were a single method that always worked best for a specific type of problem. Typically, in machine learning, you take a variety of methods and try them, empirically validating which one is the best approach to your problem.
- [**Evaluation.**](#evaluation) As you build a large number of possible models, you need a way choose the best among them. We'll cover methodology to validate models on historical data and discuss a variety of evaluation metrics. The next step is to validate using a field trial or experiment.
- [**Deployment.**](#deployment) Once you have selected the best model and validated it using historical data as well as a field
trial, you are ready to put the model into practice. You still have to keep in mind that new data will be coming in,
and the model might change over time.
Here, to reiterate, we will work through all the steps we can accomplish querying directly from our Athena database, and then in the following notebook, we will bring our table we created in this notebook into python and complete the machine learning process.
## Problem Formulation
First, you need to turn something into a real objective function. What do you care about? Do you have data on that thing? What action can you take based on your findings? Do you risk introducing any bias based on the way you model something?
### Four Main Types of ML Tasks for Policy Problems
- **Description**: [How can we identify and respond to the most urgent online government petitions?](https://dssg.uchicago.edu/project/improving-government-response-to-citizen-requests-online/)
- **Prediction**: [Which students will struggle academically by third grade?](https://dssg.uchicago.edu/project/predicting-students-that-will-struggle-academically-by-third-grade/)
- **Detection**: [Which police officers are likely to have an adverse interaction with the public?](https://dssg.uchicago.edu/project/expanding-our-early-intervention-system-for-adverse-police-interactions/)
- **Behavior Change**: [How can we prevent juveniles from interacting with the criminal justice system?](https://dssg.uchicago.edu/project/preventing-juvenile-interactions-with-the-criminal-justice-system/)
### Our Machine Learning Problem
> Out of low-income households, can we predict which ones did not purchase a 100% whole wheat product in a year's time? If so, what are the most important household features?
This is an example of a *binary prediction classification problem*.
Note the time windows are completely arbitrary. You could use an outcome window of 5, 3, 1 years or 1 day. The outcome window will depend on how often you receive new data, how accurate your predictions are for a given time period, or on what time-scale you can use the output of the data.
> By low-income households, we're referring to only those who are WIC participants or WIC-eligible.
## Access the Data
As always, we will bring in the python libraries that we need to use, as well as set up our connection to the database.
```
# pandas-related imports
import pandas as pd
# database interaction imports
from pyathenajdbc import connect
conn = connect(s3_staging_dir = 's3://usda-iri-2019-queryresults/',
region_name = 'us-gov-west-1',
LogLevel = '0',
workgroup = 'workgroup-iri_usda')
```
## Define our Cohort
Since the machine learning problem focuses on finding the features most important in predicting if a low-income household will not purchase 100% whole wheat product at least once in a year, we will focus just on households that were either WIC-eligible or participants in a given year. Here, we will train our models on data from low-income households in 2014 and their presence of 100% whole wheat purchases in 2015 and test on low-income households in 2015 buying 100% whole wheat product(s) in 2016.
Let's first see how many of these households we will have in our testing and training datasets.
> We already created our 2014 and 2015 household tables, `init_train` and `init_test` in the `iri_usda_2019_db` database, by changing the years from the code used to create `project_q2_cohort` in the [Second Data Exploration](02_02_Data_Exploration_Popular_Foods.ipynb) notebook. We also subsetted the `panid` to only include households who had static purchasing data (`projection61k` > 0) the year we're predicting on and the year prior (i.e. 2014 and 2015 for our training set). `init_train` and `init_test` contain the exact same variables as the `demo_all` table in the `iri_usda` Athena database.
```
# get count for 2014 low-income households
qry = '''
select count(*) as num_2014
from iri_usda_2019_db.init_train
'''
pd.read_sql(qry, conn)
# get count for 2015 low-income households
qry = '''
select count(*) as num_2015
from iri_usda_2019_db.init_test
'''
pd.read_sql(qry, conn)
```
## Create Foundation for Training and Testing Datasets
Now that we have defined our cohorts for our testing and training datasets, we need to combine our available datasets so that each low-income household is a row containing demographic data from the previous year, if they purchased a 100% whole wheat proudct in the following calendar year, and aggregate purchasing data from the prior year. For the purchasing data, we want to aggregate the amount the household spent and their total amount of trips.
To do this, we will first find all households that purchased any 100% whole wheat product in our given prediction years (2015 and 2016), and then we will join it to our low-income household datasets from the previous year. Because we will be relying on the table of households who purchased any 100% whole wheat product to create our desired table in Athena, we will save it as a permanent table. Then, we will join this table with our low-income cohort and one containing aggregate purchasing data for the prior year for these households.
> Note: It is possible to do this process in one step. However, for your understanding and ease in reproducibility, we broke it down into multiple steps to avoid a larger subquerying process.
```
# see existing table list
table_list = pd.read_sql('show tables IN iri_usda_2019_db;', conn)
print(table_list)
# get a series of tab_name values
s = pd.Series(list(table_list['tab_name']))
# create table to find households that bought 100% whole wheat products in 2015 or 2016
if('ml_aggregate' not in s.unique()):
print('creating table')
qry = '''
create table iri_usda_2019_db.ml_aggregate
with(
format = 'Parquet',
parquet_compression = 'SNAPPY'
)
as
select t.panid, t.year, sum(t.dollarspaid) as dollarspaid
from iri_usda.pd_pos_all p, iri_usda.trip_all t
where p.upc = t.upc and (t.year = '2016' or t.year = '2015') and p.upcdesc like '%100% WHOLE WHEAT%' and
p.year = t.year
group by t.panid, t.year
;
'''
with conn.cursor() as cursor:
cursor.execute(qry)
else:
print('table already exists')
```
<font color = red><h2> Checkpoint 1: What question are we asking?</h2> </font>
Above, we are creating an aggregated table of all purchases in which a product with "100% Whole Wheat" in the description was purchased. However, we might want to broaden the definition to include other whole grains. For example, you might want to include corn tortillas or oatmeal, to make sure you're catching as many of the different types of whole grains that people may purchase. How would you include these other whole grain items in your table?
## Creating Train and Test Sets
Now that we've created the aggregated table for households that purchased any 100% whole wheat products, we can combine that with `init_train` and `init_test` to get demographic data and define our label. Let's first take a look at the `ml_aggregate` table to see how it looks. Remember, this is a table that contains each household that purchased a 100% whole wheat product along with the total dollars paid in that year for 100% whole wheat products.
```
# view ml_aggregate
qry = '''
select *
from iri_usda_2019_db.ml_aggregate
limit 10
'''
pd.read_sql(qry, conn)
```
We can now join `ml_aggregate` with `init_train` and `init_test` to grab the demographic data. Since we would like to match households that purchased 100% whole wheat products in either 2015 or 2016 to low-income households in `init_train` and `init_test` (those with no 100% whole wheat product purchases the following year will have NAs), we will left join `ml_aggregate` to `init_train` and `init_test`. Also, we will add our dependent variable, `label`, using a `case when` statement that is `yes` when the household purchased 100% whole wheat products in the following calendar year.
```
# match ml_aggregate with demographic data for just our training cohort
# left join so that we maintain all low-income households who didn't buy any 100% whole wheat products
if('ml_combined_train' not in s.unique()):
qry = '''
create table iri_usda_2019_db.ml_combined_train
with(
format = 'Parquet',
parquet_compression = 'SNAPPY'
)
as
select c.panid, c.hhsize, c.hhinc, c.race, c.hisp, c.ac, c.fed, c.femp, c.med,
c.memp, c.mocc, c.marital, c.rentown, c.cats, c.dogs, c.hhtype, c.region, c.wic_june, c.snap_june,
c.projection61k,
case when a.dollarspaid > 0 then 0
else 1
end as label
from iri_usda_2019_db.init_train c
left join (
select *
from iri_usda_2019_db.ml_aggregate a
where year = '2015'
) a
on c.panid = a.panid
'''
with conn.cursor() as cursor:
cursor.execute(qry)
else:
print('table already exists')
# match ml_aggregate with demographic data for just our testing cohort
# left join so that we maintain all low-income households who didn't buy any 100% whole wheat products
if('ml_combined_test' not in s.unique()):
qry = '''
create table iri_usda_2019_db.ml_combined_test
with(
format = 'Parquet',
parquet_compression = 'SNAPPY'
)
as
select c.panid, c.hhsize, c.hhinc, c.race, c.hisp, c.ac, c.fed, c.femp, c.med,
c.memp, c.mocc, c.marital, c.rentown, c.cats, c.dogs, c.hhtype, c.region, c.wic_june, c.snap_june,
c.projection61k,
case when a.dollarspaid > 0 then 0
else 1
end as label
from iri_usda_2019_db.init_test c
left join (
select *
from iri_usda_2019_db.ml_aggregate a
where year = '2016'
) a
on c.panid = a.panid
'''
with conn.cursor() as cursor:
cursor.execute(qry)
else:
print('table already exists')
# verify ml_combined_train is what we want
qry = '''
select *
from iri_usda_2019_db.ml_combined_train
limit 5
'''
pd.read_sql(qry, conn)
# verify ml_combined_test is what we want
qry = '''
select *
from iri_usda_2019_db.ml_combined_test
limit 5
'''
pd.read_sql(qry, conn)
```
Finally, we want to add in the amount spent and number of trips in 2014 or 2015 for these households in the IRI database. We will first confirm that we can find the amount spent and number of trips a household took according to the `trip_all` table in either 2014 or 2015 for households in `ml_combined_train` and `ml_combined_test`.
> Recall that to calculate the amount spent, you can subtract `coupon` from `dollarspaid`. The number of trips per household is the distinct value of `tripnumber` and `purdate`.
```
# find aggregate purchasing information by households in 2014 and 2015
qry = '''
select panid, year, round(sum(dollarspaid) - sum(coupon),2) as total,
count(distinct(purdate, tripnumber)) as num_trips
from iri_usda.trip_all
where year in ('2014', '2015') and panid in
(
select distinct panid
from iri_usda_2019_db.ml_combined
)
group by year, panid
limit 5
'''
pd.read_sql(qry, conn)
```
Now that we can find aggregate purchasing data in 2014 and 2015 for households in `ml_combined_train` and `ml_combined_test`, we can perform another left join using this query. We just need to make sure that we are matching based on `panid`, and making sure that we are selecting the purchasing data from the year prior for each row in `ml_combined_train` and `ml_combined_test`.
This will be our final table we create before moving onto the [Machine Learning](04_02_Machine_Learning.ipynb) notebook.
```
if('ml_model_train' not in s.unique()):
qry = '''
create table iri_usda_2019_db.ml_model_train
with(
format = 'Parquet',
parquet_compression = 'SNAPPY'
)
as
select a.*, b.total, b.num_trips
from iri_usda_2019_db.ml_combined_train a
left join
(select panid, round(sum(dollarspaid) - sum(coupon),2) as total,
count(distinct(purdate, tripnumber)) as num_trips
from iri_usda.trip_all
where year in ('2014') and panid in
(
select distinct panid
from iri_usda_2019_db.ml_combined_train
)
group by panid
) b
on a.panid = b.panid
'''
with conn.cursor() as cursor:
cursor.execute(qry)
else:
print('table already exists')
if('ml_model_test' not in s.unique()):
qry = '''
create table iri_usda_2019_db.ml_model_test
with(
format = 'Parquet',
parquet_compression = 'SNAPPY'
)
as
select a.*, b.total, b.num_trips
from iri_usda_2019_db.ml_combined_test a
left join
(select panid, round(sum(dollarspaid) - sum(coupon),2) as total,
count(distinct(purdate, tripnumber)) as num_trips
from iri_usda.trip_all
where year in ('2015') and panid in
(
select distinct panid
from iri_usda_2019_db.ml_combined_test
)
group by panid
) b
on a.panid = b.panid
'''
with conn.cursor() as cursor:
cursor.execute(qry)
else:
print('table already exists')
# verify ml_model_train is what we want
qry = '''
select *
from iri_usda_2019_db.ml_model_train
limit 5
'''
pd.read_sql(qry, conn)
# verify ml_model_test is what we want
qry = '''
select *
from iri_usda_2019_db.ml_model_test
limit 5
'''
pd.read_sql(qry, conn)
# and that tables have unique PANID values, ie a row is a household in the given year
qry = '''
select count(*) recs, count(distinct panid)
from iri_usda_2019_db.ml_model_train
'''
pd.read_sql(qry, conn)
# same for test set
qry = '''
select count(*) recs, count(distinct panid)
from iri_usda_2019_db.ml_model_test
'''
pd.read_sql(qry, conn)
```
Now we should have everything we need from our Athena data tables to run some machine learning models to tackle our guiding question.
|
github_jupyter
|
```
from datetime import datetime
import backtrader as bt
import pandas as pd
import numpy as np
import vectorbt as vbt
df = pd.DataFrame(index=[datetime(2020, 1, i + 1) for i in range(9)])
df['open'] = [1, 1, 2, 3, 4, 5, 6, 7, 8]
df['high'] = df['open'] + 0.5
df['low'] = df['open'] - 0.5
df['close'] = df['open']
data = bt.feeds.PandasData(dataname=df)
size = np.array([5, 5, -5, -5, -5, -5, 5, 5, 0])
class CommInfoFloat(bt.CommInfoBase):
"""Commission schema that keeps size as float."""
params = (
('stocklike', True),
('commtype', bt.CommInfoBase.COMM_PERC),
('percabs', True),
)
def getsize(self, price, cash):
if not self._stocklike:
return self.p.leverage * (cash / self.get_margin(price))
return self.p.leverage * (cash / price)
class CashValueAnalyzer(bt.analyzers.Analyzer):
"""Analyzer to extract cash and value."""
def create_analysis(self):
self.rets = {}
def notify_cashvalue(self, cash, value):
self.rets[self.strategy.datetime.datetime()] = (cash, value)
def get_analysis(self):
return self.rets
class TestStrategy(bt.Strategy):
def __init__(self):
self.i = 0
def log(self, txt, dt=None):
dt = dt or self.data.datetime[0]
dt = bt.num2date(dt)
print('%s, %s' % (dt.isoformat(), txt))
def notify_order(self, order):
if order.status in [bt.Order.Submitted, bt.Order.Accepted]:
return # Await further notifications
if order.status == order.Completed:
if order.isbuy():
buytxt = 'BUY COMPLETE {}, size = {:.2f}, price = {:.2f}'.format(
order.data._name, order.executed.size, order.executed.price)
self.log(buytxt, order.executed.dt)
else:
selltxt = 'SELL COMPLETE {}, size = {:.2f}, price = {:.2f}'.format(
order.data._name, order.executed.size, order.executed.price)
self.log(selltxt, order.executed.dt)
elif order.status in [order.Expired, order.Canceled, order.Margin]:
self.log('%s ,' % order.Status[order.status])
pass # Simply log
# Allow new orders
self.orderid = None
def next(self):
if size[self.i] > 0:
self.buy(size=size[self.i])
elif size[self.i] < 0:
self.sell(size=-size[self.i])
self.i += 1
def bt_simulate(shortcash):
cerebro = bt.Cerebro()
comminfo = CommInfoFloat(commission=0.01)
cerebro.broker.addcommissioninfo(comminfo)
cerebro.addstrategy(TestStrategy)
cerebro.addanalyzer(CashValueAnalyzer)
cerebro.broker.setcash(100.)
cerebro.broker.set_checksubmit(False)
cerebro.broker.set_shortcash(shortcash)
cerebro.adddata(data)
return cerebro.run()[0]
strategy = bt_simulate(True)
strategy.analyzers.cashvalueanalyzer.get_analysis()
portfolio = vbt.Portfolio.from_orders(df.close, [np.nan] + size[:-1].tolist(), fees=0.01)
print(portfolio.cash(free=False))
print(portfolio.value())
strategy = bt_simulate(False)
strategy.analyzers.cashvalueanalyzer.get_analysis()
print(portfolio.cash(free=True))
print(portfolio.value())
```
|
github_jupyter
|
# Gaussian mixture model
The model in prototyped with TensorFlow Probability and inferecne is performed with variational Bayes by stochastic gradient descent.
Details on [Wikipedia](https://en.wikipedia.org/wiki/Mixture_model#Gaussian_mixture_model).
Some codes are borrowed from
[Brendan Hasz](https://brendanhasz.github.io/2019/06/12/tfp-gmm.html) and
[TensorFlow Probability examples](https://www.tensorflow.org/probability/overview)
Author: Yuanhua Huang
Date: 29/01/2020
#### Definition of likelihood
Below is the definition of likelihood by introducing the latent variable Z for sample assignment identity, namely, Z is a Categorical distribution (a sepcial case of multinomial with total_counts=1), and the prior $P(z_i=k)$ can be specified per data point or shared by whole data set:
$$ \mathcal{L} = P(X | \mu, \sigma, Z) = \prod_{i=1}^N \prod_{j=1}^D \prod_{k=1}^K P(z_i=k) \{ \mathcal{N}(x_{ij}|\mu_{k,j}, \sigma_{k,j}) \}^{z_i=k}$$
The evidence lower bound (ELBO) can be written as
$$\mathtt{L}=\mathtt{KL}(q(Y)||p(Y)) - \int{q(Y)\log{p(X|Y)}dY}$$
where $Y$ denotes the set of all unknown variables and $X$ denotes the observed data points. The derivations can be found in page 463 in [Bishop, PRML 2006](https://www.springer.com/gp/book/9780387310732).
**Note**, this implementation is mainly for tutorial example, and hasn't been optimised, for example introducing multiple initialization to avoid local optimal caused by poor initialization.
**Also**, the assignment variable $z$ can be marginalised and the impelementation can be found in
[GaussianMixture_VB.ipynb](https://github.com/huangyh09/TensorFlow-Bayes/blob/master/examples/GaussianMixture_VB.ipynb).
```
import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
import tensorflow_probability as tfp
from tensorflow_probability import distributions as tfd
# Random seed
np.random.seed(1)
tf.random.set_seed(1)
```
## Generate data
```
# Generate some data
np.random.seed(0)
N = 3000
X = np.random.randn(N, 2).astype('float32')
X[:1000, :] += [2, 0]
X[1000:2000, :] -= [2, 4]
X[2000:, :] += [-2, 4]
# Plot the data
plt.plot(X[:, 0], X[:, 1], '.')
plt.axis('equal')
plt.show()
```
## Define model
```
from TFBayes.mixture.Gaussian_MM_full import GaussianMixture
model = GaussianMixture(3, 2, 3000)
# model.set_prior(theta_prior = tfd.Dirichlet(5 * tf.ones((3, ))))
model.KLsum
# model.alpha, model.beta, model.gamma
# losses = model.fit(X, sampling=False, learn_rate=0.03, num_steps=500)
losses = model.fit(X, sampling=True, learn_rate=0.02, num_steps=500, n_sample=10)
plt.plot(losses)
plt.show()
# Compute log likelihood at each point on a grid
Np = 100 #number of grid points
Xp, Yp = np.meshgrid(np.linspace(-6,6,Np), np.linspace(-6,6,Np))
Pp = np.column_stack([Xp.flatten(), Yp.flatten()])
Z = model.logLik(Pp.astype('float32'), sampling=False, use_ident=False)
Z = np.reshape(Z, (Np, Np))
# Show the fit mixture density
plt.imshow(np.exp(Z),
extent=(-6, 6, -6, 6),
origin='lower')
cbar = plt.colorbar()
cbar.ax.set_ylabel('Likelihood')
```
## Model
The codes below is also included in [TFBayes.mixture.Gaussian_MM_full.py](https://github.com/huangyh09/TensorFlow-Bayes/blob/master/TFBayes/mixture/Gaussian_MM_full.py).
```
class GaussianMixture():
"""A Bayesian Gaussian mixture model.
Assumes Gaussians' variances in each dimension are independent.
Parameters
----------
Nc : int > 0
Number of mixture components.
Nd : int > 0
Number of dimensions.
Ns : int > 0
Number of data points.
"""
def __init__(self, Nc, Nd, Ns=0):
# Initialize
self.Nc = Nc
self.Nd = Nd
self.Ns = Ns
# Variational distribution variables for means
self.locs = tf.Variable(tf.random.normal((Nc, Nd)))
self.scales = tf.Variable(tf.pow(tf.random.gamma((Nc, Nd), 5, 5), -0.5))
# Variational distribution variables for standard deviations
self.alpha = tf.Variable(tf.random.uniform((Nc, Nd), 4., 6.))
self.beta = tf.Variable(tf.random.uniform((Nc, Nd), 4., 6.))
# Variational distribution variables for assignment logit
self.gamma = tf.Variable(tf.random.uniform((Ns, Nc), -2, 2))
self.set_prior()
def set_prior(self, mu_prior=None, sigma_prior=None, ident_prior=None):
"""Set prior ditributions
"""
# Prior distributions for the means
if mu_prior is None:
self.mu_prior = tfd.Normal(tf.zeros((self.Nc, self.Nd)),
tf.ones((self.Nc, self.Nd)))
else:
self.mu_prior = self.mu_prior
# Prior distributions for the standard deviations
if sigma_prior is None:
self.sigma_prior = tfd.Gamma(2 * tf.ones((self.Nc, self.Nd)),
2 * tf.ones((self.Nc, self.Nd)))
else:
self.sigma_prior = sigma_prior
# Prior distributions for sample assignment
if ident_prior is None:
self.ident_prior = tfd.Multinomial(total_count=1,
probs=tf.ones((self.Ns, self.Nc))/self.Nc)
else:
self.ident_prior = ident_prior
@property
def mu(self):
"""Variational posterior for distribution mean"""
return tfd.Normal(self.locs, self.scales)
@property
def sigma(self):
"""Variational posterior for distribution variance"""
return tfd.Gamma(self.alpha, self.beta)
# return tfd.Gamma(tf.math.exp(self.alpha), tf.math.exp(self.beta))
@property
def ident(self):
return tfd.Multinomial(total_count=1,
probs=tf.math.softmax(self.gamma))
@property
def KLsum(self):
"""
Sum of KL divergences between posteriors and priors
The KL divergence for multinomial distribution is defined manually
"""
kl_mu = tf.reduce_sum(tfd.kl_divergence(self.mu, self.mu_prior))
kl_sigma = tf.reduce_sum(tfd.kl_divergence(self.sigma, self.sigma_prior))
kl_ident = tf.reduce_sum(self.ident.mean() *
tf.math.log(self.ident.mean() /
self.ident_prior.mean())) # axis=0
return kl_mu + kl_sigma + kl_ident
def logLik(self, x, sampling=False, n_sample=10, use_ident=True):
"""Compute log likelihood given a batch of data.
Parameters
----------
x : tf.Tensor, (n_sample, n_dimention)
A batch of data
sampling : bool
Whether to sample from the variational posterior
distributions (if True, the default), or just use the
mean of the variational distributions (if False).
n_sample : int
The number of samples to generate
use_ident : bool
Setting True for fitting the model and False for testing logLik
Returns
-------
log_likelihoods : tf.Tensor
Log likelihood for each sample
"""
#TODO: sampling doesn't converge well in the example data set
Nb, Nd = x.shape
x = tf.reshape(x, (1, Nb, 1, Nd)) # (n_sample, Ns, Nc, Nd)
# Sample from the variational distributions
if sampling:
_mu = self.mu.sample((n_sample, 1))
_sigma = tf.pow(self.sigma.sample((n_sample, 1)), -0.5)
else:
_mu = tf.reshape(self.mu.mean(), (1, 1, self.Nc, self.Nd))
_sigma = tf.pow(tf.reshape(self.sigma.mean(),
(1, 1, self.Nc, self.Nd)), -0.5)
# Calculate the probability density
_model = tfd.Normal(_mu, _sigma)
_log_lik_mix = _model.log_prob(x)
if use_ident:
_ident = tf.reshape(self.ident.mean(), (1, self.Ns, self.Nc, 1))
_log_lik_mix = _log_lik_mix * _ident
log_likelihoods = tf.reduce_sum(_log_lik_mix, axis=[0, 2, 3])
else:
_fract = tf.reshape(tf.reduce_mean(self.ident.mean(), axis=0),
(1, 1, self.Nc, 1))
_log_lik_mix = _log_lik_mix + tf.math.log(_fract)
log_likelihoods = tf.reduce_mean(tf.math.reduce_logsumexp(
tf.reduce_sum(_log_lik_mix, axis=3), axis=2), axis=0)
return log_likelihoods
def fit(self, x, num_steps=200,
optimizer=None, learn_rate=0.05, **kwargs):
"""Fit the model's parameters"""
if optimizer is None:
optimizer = tf.optimizers.Adam(learning_rate=learn_rate)
loss_fn = lambda: (self.KLsum -
tf.reduce_sum(self.logLik(x, **kwargs)))
losses = tfp.math.minimize(loss_fn,
num_steps=num_steps,
optimizer=optimizer)
return losses
```
|
github_jupyter
|
# Direct optimal control of a pendulum
We want to control an inverted pendulum and stabilize it in the upright position. The equations in Hamiltonian form describing an inverted pendulum with a torsional spring are as following:
$$\begin{equation}
\begin{bmatrix} \dot{q}\\ \dot{p}\\ \end{bmatrix} =
\begin{bmatrix}
0& 1/m \\
-k& -\beta/m\\
\end{bmatrix}
\begin{bmatrix} q\\ p\\ \end{bmatrix} -
\begin{bmatrix}
0\\
mgl \sin{q}\\
\end{bmatrix}+
\begin{bmatrix}
0\\
1\\
\end{bmatrix} u
\end{equation}$$
```
import sys; sys.path.append(2*'../') # go n dirs back
import matplotlib.pyplot as plt
import torch
from torchdyn.numerics.odeint import odeint
from torchcontrol.systems.classic_control import Pendulum
from torchcontrol.cost import IntegralCost
from torchcontrol.controllers import *
%load_ext autoreload
%autoreload 2
# Change device according to your configuration
device = torch.device('cuda:0') if torch.cuda.is_available() else torch.device('cpu') # feel free to change :)
device = torch.device('cpu') # override
```
## Optimal control problem
In order to control the pendulum, we have to define a proper _integral cost function_ which will be our loss to be minimized during training. In a general form, it can be defined as:
$$\begin{equation}
\min_{u_\theta} J = (x(t_f) - x^\star)^\top\mathbf{P} (x(t_f) - x^\star)) + \int_{t_0}^{t_f} \left[ (x(t) - x^\star)^\top \mathbf{Q} (x(t) - x^\star) + (u_\theta(t) - u^\star)^\top \mathbf{R} (u_\theta(t) - u^\star) \right] dt
\end{equation}$$
where $ x $ is the state and $u_\theta$ is the controller; $x^\star$ and $u^\star$ are the desired position and zero-cost controller; matrices $\mathbf{P},~\mathbf{Q}, ~ \mathbf{R}$ are weights for tweaking the performance.
```
# Declaring the cost function
x_star = torch.Tensor([0, 0]).to(device)
u_star = 0.
cost = IntegralCost(x_star=x_star, u_star=u_star, P=0, Q=1, R=0)
```
## Initial conditions
Now we can see how the system behaves with no control input in time. Let's declare some initial variables:
```
from math import pi as π
# Time span
dt = 0.05 # step size
t0, tf = 0, 3 # initial and final time
steps = int((tf - t0)/dt) + 1
t_span = torch.linspace(t0, tf, steps).to(device)
# Initial distribution
x_0 = π # limit of the state distribution (in rads and rads/second)
init_dist = torch.distributions.Uniform(torch.Tensor([-x_0, -x_0]), torch.Tensor([x_0, x_0]))
```
## Box-constrained controller
We want to give a limited control input. We consider the box-constrained neural controller (parameters $\theta$ of $u_\theta$ belong to a feed-forward neural network):
```
?? BoxConstrainedController
# Controller
output_scaling = torch.Tensor([-5, 5]).to(device) # controller limits
u = BoxConstrainedController(2, 1, constrained=True, output_scaling=output_scaling).to(device)
# Initialize pendulum with given controller
pendulum = Pendulum(u, solver='euler')
```
## Optimization loop
Here we run the optimization: in particular, we use stochastic gradient descent with `Adam` to optimize the parameters
```
from tqdm import trange
# Hyperparameters
lr = 1e-3
epochs = 300
bs = 1024
opt = torch.optim.Adam(u.parameters(), lr=lr)
# Training loop
losses=[]
with trange(0, epochs, desc="Epochs") as eps:
for epoch in eps:
x0 = init_dist.sample((bs,)).to(device)
trajectory = pendulum(x0, t_span)
loss = cost(trajectory); losses.append(loss.detach().cpu().item())
loss.backward(); opt.step(); opt.zero_grad()
eps.set_postfix(loss=(loss.detach().cpu().item()))
fig, ax = plt.subplots(1, 1, figsize=(8,4))
ax.plot(losses)
ax.set_title('Losses')
ax.set_xlabel('Epochs')
ax.set_yscale('log')
```
## Plot results
```
# Change the solver to 'dopri5' (adaptive step size, more accurate than Euler)
pendulum.solver = 'dopri5'
# Forward propagate some trajectories
x0 = init_dist.sample((100,)).to(device)*0.8
# Prolong time span
dt = 0.05 # step size
t0, tf = 0, 5 # initial and final time
steps = int((tf - t0)/dt) + 1
t_span = torch.linspace(t0, tf, steps).to(device)
traj = pendulum(x0, t_span)
def plot_pendulum_trajs():
fig, axs = plt.subplots(1, 2, figsize=(12,4))
for i in range(len(x0)):
axs[0].plot(t_span.cpu(), traj[:,i,0].detach().cpu(), 'tab:red', alpha=.3)
axs[1].plot(t_span.cpu(), traj[:,i,1].detach().cpu(), 'tab:blue', alpha=.3)
axs[0].set_xlabel(r'Time [s]'); axs[1].set_xlabel(r'Time [s]')
axs[0].set_ylabel(r'p'); axs[1].set_ylabel(r'q')
axs[0].set_title(r'Positions'); axs[1].set_title(r'Momenta')
plot_pendulum_trajs()
# Plot learned vector field and trajectories in phase space
n_grid = 50
graph_lim = π
def plot_phase_space():
fig, ax = plt.subplots(1, 1, figsize=(6,6))
x = torch.linspace(-graph_lim, graph_lim, n_grid).to(device)
Q, P = torch.meshgrid(x, x) ; z = torch.cat([Q.reshape(-1, 1), P.reshape(-1, 1)], 1)
f = pendulum.dynamics(0, z).detach().cpu()
Fq, Fp = f[:,0].reshape(n_grid, n_grid), f[:,1].reshape(n_grid, n_grid)
val = pendulum.u(0, z).detach().cpu()
U = val.reshape(n_grid, n_grid)
ax.streamplot(Q.T.detach().cpu().numpy(), P.T.detach().cpu().numpy(),
Fq.T.detach().cpu().numpy(), Fp.T.detach().cpu().numpy(), color='black', density=0.6, linewidth=0.5)
ax.set_xlim([-graph_lim, graph_lim]) ; ax.set_ylim([-graph_lim, graph_lim])
traj = pendulum(x0, t_span).detach().cpu()
for j in range(traj.shape[1]):
ax.plot(traj[:,j,0], traj[:,j,1], color='tab:purple', alpha=.4)
ax.set_title('Phase Space')
ax.set_xlabel(r'p')
ax.set_ylabel(r'q')
plot_phase_space()
```
Nice! The controller manages to stabilize the pendulum in our desired $x^\star$ 🎉
|
github_jupyter
|
```
import seaborn as sns
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
from IPython.display import display
```
## Exercise 1
You've just been hired at a real estate investment firm and they would like you to build a model for pricing houses. You are given a dataset that contains data for house prices and a few features like number of bedrooms, size in square feet and age of the house. Let's see if you can build a model that is able to predict the price. In this exercise we extend what we have learned about linear regression to a dataset with more than one feature. Here are the steps to complete it:
1. Load the dataset ../data/housing-data.csv
- plot the histograms for each feature
- create 2 variables called X and y: X shall be a matrix with 3 columns (sqft,bdrms,age) and y shall be a vector with 1 column (price)
- create a linear regression model in Keras with the appropriate number of inputs and output
- split the data into train and test with a 20% test size
- train the model on the training set and check its accuracy on training and test set
- how's your model doing? Is the loss growing smaller?
- try to improve your model with these experiments:
- normalize the input features with one of the rescaling techniques mentioned above
- use a different value for the learning rate of your model
- use a different optimizer
- once you're satisfied with training, check the R2score on the test set
```
df = pd.read_csv('housing-data.csv')
display(df.info())
display(df.head())
display(df.describe().round(2))
# plot the histograms for each feature
plt.figure(figsize=(15, 5))
for i, feature in enumerate(df.columns):
plt.subplot(1, 4, i+1)
df[feature].plot(kind='hist', title=feature)
plt.xlabel(feature)
```
#### Feature Engineering
```
df['sqft1000'] = df['sqft']/1000.0
df['age10'] = df['age']/10.0
df['price100k'] = df['price']/1e5
display(df.describe().round(2))
```
#### Train/Test split
```
X = df[['sqft1000', 'bdrms', 'age10']].values
y = df['price100k'].values
display(X.shape)
display(y.shape)
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.2)
```
#### model
```
from keras.models import Sequential
from keras.layers import Dense
from keras.optimizers import Adam, SGD
model = Sequential()
model.add(Dense(1, input_shape=(3,)))
model.compile(Adam(lr=0.1), 'mean_squared_error')
model.summary()
# Train
history = model.fit(
X_train, y_train,
epochs=40, verbose=0)
historydf = pd.DataFrame(history.history, index=history.epoch)
historydf.plot();
```
#### Evaluate
```
y_train_pred = model.predict(X_train)
y_test_pred = model.predict(X_test)
from sklearn.metrics import mean_squared_error as mse
print("The Mean Squared Error on the Train set is:\t{:0.5f}".format(mse(y_train, y_train_pred)))
print("The Mean Squared Error on the Test set is:\t{:0.5f}".format(mse(y_test, y_test_pred)))
from sklearn.metrics import r2_score
print("The R2 score on the Train set is:\t{:0.3f}".format(r2_score(y_train, y_train_pred)))
print("The R2 score on the Test set is:\t{:0.3f}".format(r2_score(y_test, y_test_pred)))
```
## Exercise 2
Your boss was extremely happy with your work on the housing price prediction model and decided to entrust you with a more challenging task. They've seen a lot of people leave the company recently and they would like to understand why that's happening. They have collected historical data on employees and they would like you to build a model that is able to predict which employee will leave next. The would like a model that is better than random guessing. They also prefer false negatives than false positives, in this first phase. Fields in the dataset include:
- Employee satisfaction level
- Last evaluation
- Number of projects
- Average monthly hours
- Time spent at the company
- Whether they have had a work accident
- Whether they have had a promotion in the last 5 years
- Department
- Salary
- Whether the employee has left
Your goal is to predict the binary outcome variable `left` using the rest of the data. Since the outcome is binary, this is a classification problem. Here are some things you may want to try out:
1. load the dataset at ../data/HR_comma_sep.csv, inspect it with `.head()`, `.info()` and `.describe()`.
- Establish a benchmark: what would be your accuracy score if you predicted everyone stay?
- Check if any feature needs rescaling. You may plot a histogram of the feature to decide which rescaling method is more appropriate.
- convert the categorical features into binary dummy columns. You will then have to combine them with the numerical features using `pd.concat`.
- do the usual train/test split with a 20% test size
- play around with learning rate and optimizer
- check the confusion matrix, precision and recall
- check if you still get the same results if you use a 5-Fold cross validation on all the data
- Is the model good enough for your boss?
As you will see in this exercise, the a logistic regression model is not good enough to help your boss. In the next chapter we will learn how to go beyond linear models.
This dataset comes from https://www.kaggle.com/ludobenistant/hr-analytics/ and is released under [CC BY-SA 4.0 License](https://creativecommons.org/licenses/by-sa/4.0/).
```
df = pd.read_csv('HR_comma_sep.csv')
display(df.info())
display(df.head())
display(df.describe().round(2))
display(df['left'].value_counts())
```
#### Baseline model
Establish a benchmark: what would be your accuracy score if you predicted everyone stay?
```
df.left.value_counts() / len(df)
```
--> Predict all 0 accuracy = 76.19%
--> Accuracy must >> 76%
#### Feature Engineering
```
df['average_montly_hours_100'] = df['average_montly_hours']/100.0
cat_features = pd.get_dummies(df[['sales', 'salary']])
```
#### Train/Test split
```
display(df.columns)
display(cat_features.columns)
X = pd.concat([df[['satisfaction_level', 'last_evaluation', 'number_project',
'time_spend_company', 'Work_accident',
'promotion_last_5years', 'average_montly_hours_100']],
cat_features], axis=1).values
y = df['left'].values
display(X.shape)
display(y.shape)
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.2)
```
#### Model
```
from keras.models import Sequential
from keras.layers import Dense
from keras.optimizers import Adam, SGD
model = Sequential()
model.add(Dense(1, input_shape=(20,), activation='sigmoid'))
model.compile(Adam(lr=0.5), 'binary_crossentropy', metrics=['accuracy'])
model.summary()
# Train
history = model.fit(
X_train, y_train,
epochs=40, verbose=0)
historydf = pd.DataFrame(history.history, index=history.epoch)
historydf.plot();
```
#### Evaluate
```
y_test_pred = model.predict_classes(X_test)
# Confusion matrix
from sklearn.metrics import confusion_matrix
def pretty_confusion_matrix(y_true, y_pred, labels=["False", "True"]):
cm = confusion_matrix(y_true, y_pred)
pred_labels = ['Predicted '+ l for l in labels]
df = pd.DataFrame(cm, index=labels, columns=pred_labels)
return df
pretty_confusion_matrix(y_test, y_test_pred, labels=['Stay', 'Leave'])
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score
print("The test Accuracy score is {:0.3f}".format(accuracy_score(y_test, y_test_pred)))
print("The test Precision score is {:0.3f}".format(precision_score(y_test, y_test_pred)))
print("The test Recall score is {:0.3f}".format(recall_score(y_test, y_test_pred)))
print("The test F1 score is {:0.3f}".format(f1_score(y_test, y_test_pred)))
# Report
from sklearn.metrics import classification_report
print(classification_report(y_test, y_test_pred))
```
--> the model is not good enough since it performs no better than the benchmark.
#### Cross Validation Trainning
```
from keras.wrappers.scikit_learn import KerasClassifier
def build_logistic_regression_model():
model = Sequential()
model.add(Dense(1, input_dim=20, activation='sigmoid'))
model.compile(Adam(lr=0.5), 'binary_crossentropy', metrics=['accuracy'])
return model
model = KerasClassifier(
build_fn=build_logistic_regression_model,
epochs=25, verbose=0)
from sklearn.model_selection import KFold, cross_val_score
scores = cross_val_score(
model,
X, y,
cv=KFold(5, shuffle=True))
display(scores)
print("The cross validation accuracy is {:0.4f} ± {:0.4f}".format(scores.mean(), scores.std()))
```
--> the model is not good enough since it performs no better than the benchmark.
|
github_jupyter
|
# Knowledge Graph Triplet
Generate MS text -> EN Knowledge Graph Triplet.
<div class="alert alert-info">
This tutorial is available as an IPython notebook at [Malaya/example/knowledge-graph-triplet](https://github.com/huseinzol05/Malaya/tree/master/example/knowledge-graph-triplet).
</div>
<div class="alert alert-warning">
This module only trained on standard language structure, so it is not save to use it for local language structure.
</div>
```
%%time
import malaya
```
### List available Transformer model
```
malaya.knowledge_graph.available_transformer()
```
### Load Transformer model
```python
def transformer(model: str = 'base', quantized: bool = False, **kwargs):
"""
Load transformer to generate knowledge graphs in triplet format from texts,
MS text -> EN triplet format.
Parameters
----------
model : str, optional (default='base')
Model architecture supported. Allowed values:
* ``'base'`` - Transformer BASE parameters.
* ``'large'`` - Transformer LARGE parameters.
quantized : bool, optional (default=False)
if True, will load 8-bit quantized model.
Quantized model not necessary faster, totally depends on the machine.
Returns
-------
result: malaya.model.tf.KnowledgeGraph class
"""
```
```
model = malaya.knowledge_graph.transformer()
```
### Load Quantized model
To load 8-bit quantized model, simply pass `quantized = True`, default is `False`.
We can expect slightly accuracy drop from quantized model, and not necessary faster than normal 32-bit float model, totally depends on machine.
```
quantized_model = malaya.knowledge_graph.transformer(quantized = True)
string1 = "Yang Berhormat Dato Sri Haji Mohammad Najib bin Tun Haji Abdul Razak ialah ahli politik Malaysia dan merupakan bekas Perdana Menteri Malaysia ke-6 yang mana beliau menjawat jawatan dari 3 April 2009 hingga 9 Mei 2018. Beliau juga pernah berkhidmat sebagai bekas Menteri Kewangan dan merupakan Ahli Parlimen Pekan Pahang"
string2 = "Pahang ialah negeri yang ketiga terbesar di Malaysia Terletak di lembangan Sungai Pahang yang amat luas negeri Pahang bersempadan dengan Kelantan di utara Perak Selangor serta Negeri Sembilan di barat Johor di selatan dan Terengganu dan Laut China Selatan di timur."
```
These models heavily trained on neutral texts, if you give political or news texts, the results returned not really good.
#### Predict using greedy decoder
```python
def greedy_decoder(self, strings: List[str], get_networkx: bool = True):
"""
Generate triples knowledge graph using greedy decoder.
Example, "Joseph Enanga juga bermain untuk Union Douala." -> "Joseph Enanga member of sports team Union Douala"
Parameters
----------
strings : List[str]
get_networkx: bool, optional (default=True)
If True, will generate networkx.MultiDiGraph.
Returns
-------
result: List[Dict]
"""
```
```
r = model.greedy_decoder([string1, string2])
r[0]
import matplotlib.pyplot as plt
import networkx as nx
g = r[0]['G']
plt.figure(figsize=(6, 6))
pos = nx.spring_layout(g)
nx.draw(g, with_labels=True, node_color='skyblue', edge_cmap=plt.cm.Blues, pos = pos)
nx.draw_networkx_edge_labels(g, pos=pos)
plt.show()
g = r[1]['G']
plt.figure(figsize=(6, 6))
pos = nx.spring_layout(g)
nx.draw(g, with_labels=True, node_color='skyblue', edge_cmap=plt.cm.Blues, pos = pos)
nx.draw_networkx_edge_labels(g, pos=pos)
plt.show()
```
#### Predict using beam decoder
```python
def beam_decoder(self, strings: List[str], get_networkx: bool = True):
"""
Generate triples knowledge graph using beam decoder.
Example, "Joseph Enanga juga bermain untuk Union Douala." -> "Joseph Enanga member of sports team Union Douala"
Parameters
----------
strings : List[str]
get_networkx: bool, optional (default=True)
If True, will generate networkx.MultiDiGraph.
Returns
-------
result: List[Dict]
"""
```
```
r = model.beam_decoder([string1, string2])
g = r[0]['G']
plt.figure(figsize=(6, 6))
pos = nx.spring_layout(g)
nx.draw(g, with_labels=True, node_color='skyblue', edge_cmap=plt.cm.Blues, pos = pos)
nx.draw_networkx_edge_labels(g, pos=pos)
plt.show()
# https://ms.wikipedia.org/wiki/Malaysia
string = """
Malaysia secara rasminya Persekutuan Malaysia ialah sebuah negara raja berperlembagaan persekutuan di Asia Tenggara yang terdiri daripada tiga belas negeri dan tiga wilayah persekutuan, yang menduduki bumi berkeluasan 330,803 kilometer persegi (127,720 bt2). Malaysia terbahagi kepada dua kawasan yang mengapit Laut China Selatan, iaitu Semenanjung Malaysia dan Borneo Malaysia (juga Malaysia Barat dan Timur). Malaysia berkongsi sempadan darat dengan Thailand, Indonesia, dan Brunei dan juga sempadan laut dengan Singapura dan Filipina. Ibu negara Malaysia ialah Kuala Lumpur, manakala Putrajaya merupakan pusat kerajaan persekutuan. Pada tahun 2009, Malaysia diduduki oleh 28 juta penduduk dan pada tahun 2017 dianggarkan telah mencecah lebih 30 juta orang yang menduduki di Malaysia.
Malaysia berakar-umbikan Kerajaan-kerajaan Melayu yang wujud di wilayahnya dan menjadi taklukan Empayar British sejak abad ke-18. Wilayah British pertama di sini dikenali sebagai Negeri-Negeri Selat. Semenanjung Malaysia yang ketika itu dikenali sebagai Tanah Melayu atau Malaya, mula-mula disatukan di bawah komanwel pada tahun 1946, sebelum menjadi Persekutuan Tanah Melayu pada tahun 1948. Pada tahun 1957 Semenanjung Malaysia mencapai Kemerdekaan dan bebas daripada penjajah dan sekali gus menjadi catatan sejarah terpenting bagi Malaysia. Pada tahun 1963, Tanah Melayu bersatu bersama dengan negara Sabah, Sarawak, dan Singapura bagi membentuk Malaysia. Pada tahun 1965, Singapura keluar dari persekutuan untuk menjadi negara kota yang bebas. Semenjak itu, Malaysia menikmati antara ekonomi yang terbaik di Asia, dengan purata pertumbuhan keluaran dalam negara kasarnya (KDNK) kira-kira 6.5% selama 50 tahun pertama kemerdekaannya.
Ekonomi negara yang selama ini dijana oleh sumber alamnya kini juga berkembang dalam sektor-sektor ukur tanah, sains, kejuruteraan, pendidikan, pelancongan, perkapalan, perdagangan dan perubatan.
Ketua negara Malaysia ialah Yang di-Pertuan Agong, iaitu raja elektif yang terpilih dan diundi dari kalangan sembilan raja negeri Melayu. Ketua kerajaannya pula ialah Perdana Menteri. Sistem kerajaan Malaysia banyak berdasarkan sistem parlimen Westminster, dan sistem perundangannya juga berasaskan undang-undang am Inggeris.
Malaysia terletak berdekatan dengan khatulistiwa dan beriklim tropika, serta mempunyai kepelbagaian flora dan fauna, sehingga diiktiraf menjadi salah satu daripada 17 negara megadiversiti. Di Malaysia terletaknya Tanjung Piai, titik paling selatan di seluruh tanah besar Eurasia. Malaysia ialah sebuah negara perintis Persatuan Negara-Negara Asia Tenggara dan Pertubuhan Persidangan Islam, dan juga anggota Kerjasama Ekonomi Asia-Pasifik, Negara-Negara Komanwel, dan Pergerakan Negara-Negara Berkecuali.
"""
def simple_cleaning(string):
return ''.join([s for s in string if s not in ',.\'";'])
string = malaya.text.function.split_into_sentences(string)
string = [simple_cleaning(s) for s in string if len(s) > 50]
string
r = model.greedy_decoder(string)
g = r[0]['G']
for i in range(1, len(r), 1):
g.update(r[i]['G'])
plt.figure(figsize=(17, 17))
pos = nx.spring_layout(g)
nx.draw(g, with_labels=True, node_color='skyblue', edge_cmap=plt.cm.Blues, pos = pos)
nx.draw_networkx_edge_labels(g, pos=pos)
plt.show()
```
|
github_jupyter
|
```
import os
mingw_path = 'C:\\Users\\a1\\mingw\\mingw64\\bin'
os.environ['PATH'] = mingw_path + ';' + os.environ['PATH']
import xgboost as xgb
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline
train = pd.read_csv('new_train_mean_cl.csv')
test = pd.read_csv('new_test_mean_cl.csv')
del test['Unnamed: 0']
del train['Unnamed: 0']
test = test.drop_duplicates(subset='id').set_index(keys='id').sort_index()
test = test[[u'Semana', u'Producto_ID', u'Cliente_ID', u'lag1', u'lag2', u'lag3', u'Agencia_ID', u'Canal_ID', u'Ruta_SAK',
u'Cliente_ID_town_count', u'price', u'weight', u'pieces', u'cluster_nombre', u'drink', u'w_per_piece', u'OXXO',
u'ARTELI', u'ALSUPER', u'BODEGA', u'CALIMAX', u'XICANS', u'ABARROTES', u'CARNICERIA', u'FRUTERIA',
u'DISTRIBUIDORA', u'ELEVEN', u'HOTEL', u'HOSPITAL', u'CAFE', u'FARMACIA', u'CREME', u'SUPER', u'COMOD',
u'MODELOR', u'UNKN']]
def RMSLE_score(pred, true):
score = np.power(pred-true, 2)
return np.sqrt(np.mean(score))
from sklearn import cross_validation
from sklearn.preprocessing import LabelEncoder
from xgboost.sklearn import XGBRegressor
from sklearn import grid_search
X = train
y = train['Demanda_uni_equil_log0'].copy()
del train['Demanda_uni_equil_log0']
del X['drink']
del X['DISTRIBUIDORA']
del X['ARTELI']
del X['CALIMAX']
del X['MODELOR']
del X['HOSPITAL']
del X['HOTEL']
del test['drink']
del test['DISTRIBUIDORA']
del test['ARTELI']
del test['CALIMAX']
del test['MODELOR']
del test['HOSPITAL']
del test['HOTEL']
mean_submission = pd.read_csv('submit_mean.csv').set_index(keys='id').sort_index()
for w in [6, 7]:
train_index = (train['Semana'] == w)
test_index = ~(train['Semana'] == w)
X_train, X_test = X[train_index], X[test_index]
y_train, y_test = y[train_index], y[test_index]
xgbr = XGBRegressor(colsample_bytree=0.8,learning_rate=0.05, max_depth=15, n_estimators=100, reg_lambda=0.01, subsample=0.8)
xgbr.fit(X_train, y_train)
preds = xgbr.predict(X_test)
preds[preds<0] = 0
print RMSLE_score(preds, y_test)
subms = xgbr.predict(test)
mean_submission['xgb_demanda'+str(w)] = np.expm1(subms)
mean_submission.to_csv('subm_xgb_mean6.csv')
subms = xgbr.predict(test)
pd.Series(np.expm1(subms)).to_csv('subm_xgb.csv')
mean_submission = pd.read_csv('submit_mean.csv').set_index(keys='id').sort_index()
mean_submission['xgb_demanda'] = np.expm1(subms)
mean_submission['subm'] = 0.3*mean_submission['xgb_demanda6']+0.7*(0.3*mean_submission['xgb_demanda6']+0.3*mean_submission['xgb_demanda7']+
0.2*mean_submission['xgb_demanda8']+0.2*mean_submission['xgb_demanda9'])
mean_submission['subm'].to_csv('subm_xgb.csv')
mean_submission
test.head()
```
|
github_jupyter
|
# Access and mosaic Planet NICFI monthly basemaps
> A guide for accessing monthly Planet NICFI basemaps, selecting data by a defined AOI and mosaicing to produce a single image.
You will need a configuration file named `planet_api.cfg` (simple text file with `.cfg` extension will do) to run this notebook. It should be located in your `My Drive` folder.
The contents of the file should reflect the template below, swapping in the API access key that you should have receieved once you signed up for and subscribed to the Planet NICFI program. Please visit https://www.planet.com/nicfi/ to sign up if you have not already.
```
[credentials]
api_key = xxxxxxxxxxxxxxxxx
```
## Setup Notebook
```{admonition} **Version control**
Colab updates without warning to users, which can cause notebooks to break. Therefore, we are pinning library versions.
```
```
!pip install -q rasterio==1.2.10
!pip install -q geopandas==0.10.2
!pip install -q shapely==1.8.0
!pip install -q radiant_mlhub # for dataset access, see: https://mlhub.earth/
# import required libraries
import os, glob, functools, fnmatch, requests, io, shutil, tarfile, json
from pathlib import Path
from zipfile import ZipFile
from itertools import product
from configparser import ConfigParser
import urllib.request
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
mpl.rcParams['axes.grid'] = False
mpl.rcParams['figure.figsize'] = (12,12)
import rasterio
from rasterio.merge import merge
from rasterio.plot import show
import geopandas as gpd
from folium import Map, GeoJson, Figure
from shapely.geometry import box
from IPython.display import clear_output
from radiant_mlhub import Dataset, client, get_session, Collection
# configure Radiant Earth MLHub access
!mlhub configure
# set your root directory and tiled data folders
if 'google.colab' in str(get_ipython()):
# mount google drive
from google.colab import drive
drive.mount('/content/gdrive')
root_dir = '/content/gdrive/My Drive/tf-eo-devseed/'
workshop_dir = '/content/gdrive/My Drive/tf-eo-devseed-workshop'
dirs = [root_dir, workshop_dir]
for d in dirs:
if not os.path.exists(d):
os.makedirs(d)
print('Running on Colab')
else:
root_dir = os.path.abspath("./data/tf-eo-devseed")
workshop_dir = os.path.abspath('./tf-eo-devseed-workshop')
print(f'Not running on Colab, data needs to be downloaded locally at {os.path.abspath(root_dir)}')
# Go to root folder
%cd $root_dir
```
```{admonition} **GCS note!**
We won't be using Google Cloud Storage to download data, but here is a code snippet to show how to practically do so with the a placeholder "aoi" vector file. This code works if you have access to the a project on GCP.
```
```python
#authenticate Google Cloud Storage
from google.colab import auth
auth.authenticate_user()
print("Authenticated Google Gloud access.")
# Imports the Google Cloud client library
from google.cloud import storage
# Instantiates a client
project = 'tf-eo-training-project'
storage_client = storage.Client(project=project)
# The name for the new bucket
bucket_name = "dev-seed-workshop"
data_dir = os.path.join(workshop_dir,'data/')
gcs_to_local_dir = os.path.join(data_dir,'gcs/')
prefix = 'data/'
local_dir = os.path.join(gcs_to_local_dir, prefix)
dirs = [data_dir, gcs_to_local_dir, local_dir]
for dir in dirs:
if not os.path.exists(dir):
os.makedirs(dir)
bucket_name = "dev-seed-workshop"
bucket = storage_client.get_bucket(bucket_name)
blobs = bucket.list_blobs(prefix=prefix) # Get list of files
for blob in blobs:
print(blob)
filename = blob.name.replace('/', '_')
filename_split = os.path.splitext(filename)
filename_zero, fileext = filename_split
basename = os.path.basename(filename_zero)
filename = 'aoi'
blob.download_to_filename(os.path.join(local_dir, "%s%s" % (basename, fileext))) # Download
print(blob, "%s%s" % (basename, fileext))
```
### Get search parameters
- Read the AOI from a [Radiant Earth MLHub dataset](https://mlhub.earth/data/ref_african_crops_kenya_01) that overlaps with NICFI coverage into a Geopandas dataframe.
- Get AOI bounds and centroid.
- Authenticate with Planet NICFI API key.
- Choose mosaic based on month/year of interest.
```
collections = [
'ref_african_crops_kenya_01_labels'
]
def download(collection_id):
print(f'Downloading {collection_id}...')
collection = Collection.fetch(collection_id)
path = collection.download('.')
tar = tarfile.open(path, "r:gz")
tar.extractall()
tar.close()
os.remove(path)
def resolve_path(base, path):
return Path(os.path.join(base, path)).resolve()
def load_df(collection_id):
collection = json.load(open(f'{collection_id}/collection.json', 'r'))
rows = []
item_links = []
for link in collection['links']:
if link['rel'] != 'item':
continue
item_links.append(link['href'])
for item_link in item_links:
item_path = f'{collection_id}/{item_link}'
current_path = os.path.dirname(item_path)
item = json.load(open(item_path, 'r'))
tile_id = item['id'].split('_')[-1]
for asset_key, asset in item['assets'].items():
rows.append([
tile_id,
None,
None,
asset_key,
str(resolve_path(current_path, asset['href']))
])
for link in item['links']:
if link['rel'] != 'source':
continue
link_path = resolve_path(current_path, link['href'])
source_path = os.path.dirname(link_path)
try:
source_item = json.load(open(link_path, 'r'))
except FileNotFoundError:
continue
datetime = source_item['properties']['datetime']
satellite_platform = source_item['collection'].split('_')[-1]
for asset_key, asset in source_item['assets'].items():
rows.append([
tile_id,
datetime,
satellite_platform,
asset_key,
str(resolve_path(source_path, asset['href']))
])
return pd.DataFrame(rows, columns=['tile_id', 'datetime', 'satellite_platform', 'asset', 'file_path'])
for c in collections:
download(c)
# Load the shapefile into a geopandas dataframe (for more info see: https://geopandas.org/en/stable/)
gdf = gpd.read_file(os.path.join(root_dir, 'ref_african_crops_kenya_01_labels/ref_african_crops_kenya_01_labels_00/labels.geojson'))
gdf = gdf.to_crs("EPSG:4326")
# Get AOI bounds
bbox_aoi = gdf.geometry.total_bounds
# Get AOI centroid for plotting with folium
centroid_aoi = [box(*bbox_aoi).centroid.x, box(*bbox_aoi).centroid.y]
# authenticate with Planet NICFI API KEY
config = ConfigParser()
configFilePath = '/content/gdrive/My Drive/planet_api.cfg'
with open(configFilePath) as f:
config.read_file(f)
API_KEY = config.get('credentials', 'api_key')
PLANET_API_KEY = API_KEY # <= insert API key here
#setup Planet base URL
API_URL = "https://api.planet.com/basemaps/v1/mosaics"
#setup session
session = requests.Session()
#authenticate
session.auth = (PLANET_API_KEY, "") #<= change to match variable for API Key if needed
```
```{important}
In the following cell, the **name__is** parameter is the basemap name. It is only differentiable by the time range in the name.
E.g. `planet_medres_normalized_analytic_2021-06_mosaic` is for June, 2021.
```
```
#set params for search using name of mosaic
parameters = {
"name__is" :"planet_medres_normalized_analytic_2021-06_mosaic" # <= customized to month/year of interest
}
#make get request to access mosaic from basemaps API
res = session.get(API_URL, params = parameters)
#response status code
print(res.status_code)
#print metadata for mosaic
mosaic = res.json()
#print("mosaic metadata (this will expose your API key so be careful about if/where you uncomment this line): ", json.dumps(mosaic, indent=2))
#get id
mosaic_id = mosaic['mosaics'][0]['id']
#get bbox for entire mosaic
mosaic_bbox = mosaic['mosaics'][0]['bbox']
print("mosaic_bbox: ", mosaic_bbox)
print("bbox_aoi: ", bbox_aoi)
#converting bbox to string for search params
string_bbox = ','.join(map(str, bbox_aoi))
print('Mosaic id: ', mosaic_id)
```
#### Plot the gridded AOI.
```
m = Map(tiles="Stamen Terrain",
control_scale=True,
location = [centroid_aoi[1], centroid_aoi[0]],
zoom_start = 10,
max_zoom = 20,
min_zoom =6,
width = '100%',
height = '100%',
zoom_control=False )
GeoJson(gdf).add_to(m)
Figure(width=500, height=300).add_child(m)
```
### Request the quad tiles fitting the search parameters
```
#search for mosaic quad using AOI
search_parameters = {
'bbox': string_bbox,
'minimal': True
}
#accessing quads using metadata from mosaic
quads_url = "{}/{}/quads".format(API_URL, mosaic_id)
res = session.get(quads_url, params=search_parameters, stream=True)
print(res.status_code)
quads = res.json()
quads = res.json()
items = quads['items']
#printing an example of quad metadata
#print("quad tiles metadata (this will expose your API key so be careful about if/where you uncomment this line): ", json.dumps(items[0], indent=2))
```
#### Plot the requested quad tiles.
```
for item, i in zip(items, range(len(items))):
quad_box = item["bbox"]
GeoJson(box(*quad_box)).add_to(m)
Figure(width=500, height=300).add_child(m)
# Set directory for downloading the quad tiles to
nicfi_dir = os.path.join(root_dir,'062021_basemap_nicfi_aoi/')
quads_dir = os.path.join(nicfi_dir,'quads/')
dirs = [nicfi_dir, quads_dir]
for dir in dirs:
if not os.path.exists(dir):
os.makedirs(dir)
#iterate over quad download links and saving to folder by id
for i in items:
link = i['_links']['download']
name = i['id']
name = name + '.tiff'
DIR = quads_dir
filename = os.path.join(DIR, name)
#print(filename)
#checks if file already exists before s
if not os.path.isfile(filename):
urllib.request.urlretrieve(link, filename)
```
### Mosaic the quad tiles
```
# File and folder paths
out_mosaic = os.path.join(nicfi_dir,'062021_basemap_nicfi_aoi_Mosaic.tif')
# Make a search criteria to select the quad tile files
search_criteria = "*.tiff"
q = os.path.join(nicfi_dir,'quads', search_criteria)
print(q)
# Get all of the quad tiles
quad_files = glob.glob(q)
quad_files
src_files_to_mosaic = []
for f in quad_files:
src = rasterio.open(f)
src_files_to_mosaic.append(src)
# Create the mosaic
mosaic, out_trans = merge(src_files_to_mosaic)
out_meta = src.meta.copy()
out_meta.update({"driver": "GTiff",
"height": mosaic.shape[1],
"width": mosaic.shape[2],
"transform": out_trans
}
)
# Write the mosaic to raster file
with rasterio.open(out_mosaic, "w", **out_meta) as dest:
dest.write(mosaic)
# Write true color (RGB).
rgb_out_mosaic = os.path.join(nicfi_dir,'062021_basemap_nicfi_aoi_rgb_Mosaic.tif')
out_meta.update({"count": 3})
print(out_meta)
rgb = np.dstack([mosaic[2], mosaic[1], mosaic[0]])
rgb = rgb.transpose(2,0,1)
with rasterio.open(rgb_out_mosaic, "w", **out_meta) as dest:
dest.write(rgb)
```
#### Plot the mosaic
```
src = rasterio.open(rgb_out_mosaic)
show(src)
```
|
github_jupyter
|
<table class="ee-notebook-buttons" align="left">
<td><a target="_blank" href="https://github.com/giswqs/earthengine-py-notebooks/tree/master/Array/spectral_unmixing.ipynb"><img width=32px src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" /> View source on GitHub</a></td>
<td><a target="_blank" href="https://nbviewer.jupyter.org/github/giswqs/earthengine-py-notebooks/blob/master/Array/spectral_unmixing.ipynb"><img width=26px src="https://upload.wikimedia.org/wikipedia/commons/thumb/3/38/Jupyter_logo.svg/883px-Jupyter_logo.svg.png" />Notebook Viewer</a></td>
<td><a target="_blank" href="https://mybinder.org/v2/gh/giswqs/earthengine-py-notebooks/master?filepath=Array/spectral_unmixing.ipynb"><img width=58px src="https://mybinder.org/static/images/logo_social.png" />Run in binder</a></td>
<td><a target="_blank" href="https://colab.research.google.com/github/giswqs/earthengine-py-notebooks/blob/master/Array/spectral_unmixing.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" /> Run in Google Colab</a></td>
</table>
## Install Earth Engine API and geemap
Install the [Earth Engine Python API](https://developers.google.com/earth-engine/python_install) and [geemap](https://github.com/giswqs/geemap). The **geemap** Python package is built upon the [ipyleaflet](https://github.com/jupyter-widgets/ipyleaflet) and [folium](https://github.com/python-visualization/folium) packages and implements several methods for interacting with Earth Engine data layers, such as `Map.addLayer()`, `Map.setCenter()`, and `Map.centerObject()`.
The following script checks if the geemap package has been installed. If not, it will install geemap, which automatically installs its [dependencies](https://github.com/giswqs/geemap#dependencies), including earthengine-api, folium, and ipyleaflet.
**Important note**: A key difference between folium and ipyleaflet is that ipyleaflet is built upon ipywidgets and allows bidirectional communication between the front-end and the backend enabling the use of the map to capture user input, while folium is meant for displaying static data only ([source](https://blog.jupyter.org/interactive-gis-in-jupyter-with-ipyleaflet-52f9657fa7a)). Note that [Google Colab](https://colab.research.google.com/) currently does not support ipyleaflet ([source](https://github.com/googlecolab/colabtools/issues/60#issuecomment-596225619)). Therefore, if you are using geemap with Google Colab, you should use [`import geemap.eefolium`](https://github.com/giswqs/geemap/blob/master/geemap/eefolium.py). If you are using geemap with [binder](https://mybinder.org/) or a local Jupyter notebook server, you can use [`import geemap`](https://github.com/giswqs/geemap/blob/master/geemap/geemap.py), which provides more functionalities for capturing user input (e.g., mouse-clicking and moving).
```
# Installs geemap package
import subprocess
try:
import geemap
except ImportError:
print('geemap package not installed. Installing ...')
subprocess.check_call(["python", '-m', 'pip', 'install', 'geemap'])
# Checks whether this notebook is running on Google Colab
try:
import google.colab
import geemap.eefolium as emap
except:
import geemap as emap
# Authenticates and initializes Earth Engine
import ee
try:
ee.Initialize()
except Exception as e:
ee.Authenticate()
ee.Initialize()
```
## Create an interactive map
The default basemap is `Google Satellite`. [Additional basemaps](https://github.com/giswqs/geemap/blob/master/geemap/geemap.py#L13) can be added using the `Map.add_basemap()` function.
```
Map = emap.Map(center=[40,-100], zoom=4)
Map.add_basemap('ROADMAP') # Add Google Map
Map
```
## Add Earth Engine Python script
```
# Add Earth Engine dataset
# Array-based spectral unmixing.
# Create a mosaic of Landsat 5 images from June through September, 2007.
allBandMosaic = ee.ImageCollection('LANDSAT/LT05/C01/T1') \
.filterDate('2007-06-01', '2007-09-30') \
.select('B[0-7]') \
.median()
# Create some representative endmembers computed previously by sampling
# the Landsat 5 mosaic.
urbanEndmember = [88, 42, 48, 38, 86, 115, 59]
vegEndmember = [50, 21, 20, 35, 50, 110, 23]
waterEndmember = [51, 20, 14, 9, 7, 116, 4]
# Compute the 3x7 pseudo inverse.
endmembers = ee.Array([urbanEndmember, vegEndmember, waterEndmember])
inverse = ee.Image(endmembers.matrixPseudoInverse().transpose())
# Convert the bands to a 2D 7x1 array. The toArray() call concatenates
# pixels from each band along the default axis 0 into a 1D vector per
# pixel, and the toArray(1) call concatenates each band (in this case
# just the one band of 1D vectors) along axis 1, forming a 2D array.
inputValues = allBandMosaic.toArray().toArray(1)
# Matrix multiply the pseudo inverse of the endmembers by the pixels to
# get a 3x1 set of endmembers fractions from 0 to 1.
unmixed = inverse.matrixMultiply(inputValues)
# Create and show a colored image of the endmember fractions. Since we know
# the result has size 3x1, project down to 1D vectors at each pixel (since the
# second axis is pointless now), and then flatten back to a regular scalar
# image.
colored = unmixed \
.arrayProject([0]) \
.arrayFlatten([['urban', 'veg', 'water']])
Map.setCenter(-98.4, 19, 11)
# Load a hillshade to use as a backdrop.
Map.addLayer(ee.Algorithms.Terrain(ee.Image('CGIAR/SRTM90_V4')).select('hillshade'))
Map.addLayer(colored, {'min': 0, 'max': 1},
'Unmixed (red=urban, green=veg, blue=water)')
```
## Display Earth Engine data layers
```
Map.addLayerControl() # This line is not needed for ipyleaflet-based Map.
Map
```
|
github_jupyter
|
# Lists
Data Structure:
A data structure is a collection of data elements (such as numbers or characters—or even other data structures) that is structured in some way, for example, by numbering the elements. The most basic data structure in Python is the "sequence".
-> List is one of the Sequence Data structure
-> Lists are collection of items (Strings, integers or even other lists)
-> Lists are enclosed in [ ]
-> Each item in the list has an assigned index value.
-> Each item in a list is separated by a comma
-> Lists are mutable, which means they can be changed.
# List Creation
```
emptyList = []
lst = ['one', 'two', 'three', 'four'] # list of strings
lst2 = [1, 2, 3, 4] #list of integers
lst3 = [[1, 2], [3, 4]] # list of lists
lst4 = [1, 'ramu', 24, 1.24] # list of different datatypes
print(lst4)
```
# List Length
```
lst = ['one', 'two', 'three', 'four']
#find length of a list
print(len(lst))
```
# List Append
```
lst = ['one', 'two', 'three', 'four']
lst.append('five') # append will add the item at the end
print(lst)
```
# List Insert
```
#syntax: lst.insert(x, y)
lst = ['one', 'two', 'four']
lst.insert(2, "three") # will add element y at location x
print(lst)
```
# List Remove
```
#syntax: lst.remove(x)
lst = ['one', 'two', 'three', 'four', 'two']
lst.remove('two') #it will remove first occurence of 'two' in a given list
print(lst)
```
# List Append & Extend
```
lst = ['one', 'two', 'three', 'four']
lst2 = ['five', 'six']
#append
lst.append(lst2)
print(lst)
lst = ['one', 'two', 'three', 'four']
lst2 = ['five', 'six']
#extend will join the list with list1
lst.extend(lst2)
print(lst)
```
# List Delete
```
#del to remove item based on index position
lst = ['one', 'two', 'three', 'four', 'five']
del lst[1]
print(lst)
#or we can use pop() method
a = lst.pop(1)
print(a)
print(lst)
lst = ['one', 'two', 'three', 'four']
#remove an item from list
lst.remove('three')
print(lst)
```
# List realted keywords in Python
```
#keyword 'in' is used to test if an item is in a list
lst = ['one', 'two', 'three', 'four']
if 'two' in lst:
print('AI')
#keyword 'not' can combined with 'in'
if 'six' not in lst:
print('ML')
```
# List Reverse
```
#reverse is reverses the entire list
lst = ['one', 'two', 'three', 'four']
lst.reverse()
print(lst)
```
# List Sorting
The easiest way to sort a List is with the sorted(list) function.
That takes a list and returns a new list with those elements in sorted order.
The original list is not changed.
The sorted() optional argument reverse=True, e.g. sorted(list, reverse=True),
makes it sort backwards.
```
#create a list with numbers
numbers = [3, 1, 6, 2, 8]
sorted_lst = sorted(numbers)
print("Sorted list :", sorted_lst)
#original list remain unchanged
print("Original list: ", numbers)
#print a list in reverse sorted order
print("Reverse sorted list :", sorted(numbers, reverse=True))
#orginal list remain unchanged
print("Original list :", numbers)
lst = [1, 20, 5, 5, 4.2]
#sort the list and stored in itself
lst.sort()
# add element 'a' to the list to show an error
print("Sorted list: ", lst)
lst = [1, 20, 'b', 5, 'a']
print(lst.sort()) # sort list with element of different datatypes.
```
# List Having Multiple References
```
lst = [1, 2, 3, 4, 5]
abc = lst
abc.append(6)
#print original list
print("Original list: ", lst)
```
# String Split to create a list
```
#let's take a string
s = "one,two,three,four,five"
slst = s.split(',')
print(slst)
s = "This is applied AI Course"
split_lst = s.split() # default split is white-character: space or tab
print(split_lst)
```
# List Indexing
Each item in the list has an assigned index value starting from 0.
Accessing elements in a list is called indexing.
```
lst = [1, 2, 3, 4]
print(lst[1]) #print second element
#print last element using negative index
print(lst[-2])
```
# List Slicing
Accessing parts of segments is called slicing.
The key point to remember is that the :end value represents the first value that
is not in the selected slice.
```
numbers = [10, 20, 30, 40, 50,60,70,80]
#print all numbers
print(numbers[:])
#print from index 0 to index 3
print(numbers[0:4])
print (numbers)
#print alternate elements in a list
print(numbers[::2])
#print elemnts start from 0 through rest of the list
print(numbers[2::2])
```
# List extend using "+"
```
lst1 = [1, 2, 3, 4]
lst2 = ['varma', 'naveen', 'murali', 'brahma']
new_lst = lst1 + lst2
print(new_lst)
```
# List Count
```
numbers = [1, 2, 3, 1, 3, 4, 2, 5]
#frequency of 1 in a list
print(numbers.count(1))
#frequency of 3 in a list
print(numbers.count(3))
```
# List Looping
```
#loop through a list
lst = ['one', 'two', 'three', 'four']
for ele in lst:
print(ele)
```
# List Comprehensions
List comprehensions provide a concise way to create lists.
Common applications are to make new lists where each element is the result of some operations applied to each member of another sequence or iterable, or to create a subsequence of those elements that satisfy a certain condition.
```
# without list comprehension
squares = []
for i in range(10):
squares.append(i**2) #list append
print(squares)
#using list comprehension
squares = [i**2 for i in range(10)]
print(squares)
#example
lst = [-10, -20, 10, 20, 50]
#create a new list with values doubled
new_lst = [i*2 for i in lst]
print(new_lst)
#filter the list to exclude negative numbers
new_lst = [i for i in lst if i >= 0]
print(new_lst)
#create a list of tuples like (number, square_of_number)
new_lst = [(i, i**2) for i in range(10)]
print(new_lst)
```
# Nested List Comprehensions
```
#let's suppose we have a matrix
matrix = [
[1, 2, 3, 4],
[5, 6, 7, 8],
[9, 10, 11, 12]
]
#transpose of a matrix without list comprehension
transposed = []
for i in range(4):
lst = []
for row in matrix:
lst.append(row[i])
transposed.append(lst)
print(transposed)
#with list comprehension
transposed = [[row[i] for row in matrix] for i in range(4)]
print(transposed)
```
|
github_jupyter
|
<div align="right"><a href="https://github.com/lucasliano/Medidas1">Link Github</a></div>
<img src="logo.jpg" width="400"></img>
<div align="center">
<h1>Resúmen Teórico de Medidas Electrónicas 1</h1>
<h2>Incertidumbre</h2>
<h3>Liaño, Lucas</h3>
</div>
# Contenidos
- **Introducción**
- **Marco Teórico**
- Conceptos Básicos Metrología
- ¿Qué es la incertidumbre?
- Modelo matemático de una medición ($Y$)
- Evaluación incertidumbre Tipo A
- Evaluación incertidumbre Tipo B
- Incertidumbre Conjunta
- Grado de Confianza
- Caso de análisis: $u_{i}(x_{i}) \gg u_{j}(X_{i})$
- Caso de análisis: $u_{i}(x_{i}) \ll u_{j}(X_{i})$
- Correlación
- **Experimentación**
- Caso General
- Caso Incertidumbre tipo A dominante
- Caso Incertidumbre tipo B dominante
- Ejemplo Correlación
- **Bibliografía**
***
# Introducción
El objetivo del presente documento es de resumir, al mismo tiempo que simular, los contenidos teóricos correspondientes a la unidad N°1 de la materia medidas 1. Para ello, utilizaremos los recursos disponibles en el drive de la materia.
<div class="alert alert-success">
<strong>Link:</strong> <a href="https://drive.google.com/folderview?id=1p1eVB4UoS0C-5gyienup-XiewKsTpcNc">https://drive.google.com/folderview?id=1p1eVB4UoS0C-5gyienup-XiewKsTpcNc</a>
</div>
***
# Marco Teórico
## Conceptos Básicos Metrología
La de medición de una magnitud física, atributo de un cuerpo mensurable, consiste en el proceso mediante el cual se da a conocer el valor de dicha magnitud. A lo largo de la historia se han desarrollado diversos modelos de medición, todos ellos consisten en la comparación de la magnitud contra un patrón.
A su vez, a medida que se fueron confeccionando mejores métodos de medición, se empezó a tener en consideración el error en la medida. Este error consiste en una indicación cuantitativa de la calidad del resultado. Valor que demuestra la confiabilidad del proceso.
Actualmente, definimos al **resultado de una medición** como al conjunto de valores de una magnitud, atribuidos a un mensurando. Se puede definir a partir de una función distribución densidad de probabilidad (también denomidada _pdf_, de la sígla inglesa _probability density function_). El resultado de una medición está caracterizado por la media de la muestra, la incertidumbre y el grado de confianza de la medida.
Denominaremos **incertidumbre de una medición** al parámetro asociado con el resultado de la medición que caracteríza la dispersión de los valores atribuidos a un mensurando. Mientras que el **error de medida** será la diferencia entre el valor medido con un valor de referencia. [[1]](http://depa.fquim.unam.mx/amyd/archivero/CALCULODEINCERTIDUMBRESDR.JAVIERMIRANDA_26197.pdf)
#### Tipos de errores
Existen dos tipos:
> **Error sistemático:** Componente del error que en repetidas mediciones permanece constante.
> **Error aleatorio:** Componente del error que en repetidas mediciones varía de manera impredecible.
***
## ¿Qué es la incertidumbre?
Como bien definimos anteriormente, la incertidumbre es un parámetro que caracteríza la dispersión de los valores atribuidos a un mensurando. Esto significa que, considerando al resultado de la medición como una función distribución densidad de probabilidad, la incertidumbre representa el desvío estándar de la misma. Se suele denominar **incertidumbre estándar** a dicha expresión de la incertidumbre.
#### Componentes de la incertidumbre
> **Tipo A:** Componente de la incertidumbre descripta únicamente a partir del estudio estadístico de las muestras.
> **Tipo B:** Componente de la incertidumbre descripta a partir de las hojas de datos previstas por los fabricantes de los instrumentos de medición, junto con datos de calibración.
En las próximas secciones se describe en detalle como son los test efectuados para determinar cada una de las componentes. [[2]](https://es.wikipedia.org/wiki/Propagaci%C3%B3n_de_errores)
***
## Modelo matemático de una medición ($Y$)
Supongamos una magnitud a mensurar ($Y$), la cual se va a estimar de forma indirecta a partir de una relación fundamental con otras $N$ magnitudes mensurables, de manera que se cumple:
\begin{equation}
Y = f(x_{1},x_{2},...,x_{N})
\end{equation}
Como definimos previamente, las variables $x_{i}$ son funciones distribución densidad de probabilidad por ser resultados de mediciones. Cada una de estas mediciones viene determinada, idealmente, por el valor de su media ($\mu_{X_{i}}$), su desvío estándar ($\sigma_{x_{i}}$) y el grado de confianza de la medición. Dado que en la vida real no es posible conseguir una estimación lo suficientemente buena de estos parámetros, se utilizarán sus estimadores en su lugar.
Por tanto, si se tomaron $M$ muestras de cada una de estas variables, podemos utilizar la **media poblacional ($\bar{Y}$)** como estimador de la media ($\mu_{Y}$) de la distribución densidad de probabilidad de la medición como:
\begin{equation}
\hat{Y} = \bar{Y} = \frac{1}{M} \sum_{k=0}^{M} f_{k}(x_{1},x_{2},...,x_{N}) = f(\bar{X_{1}},\bar{X_{2}},...,\bar{X_{N}})
\end{equation}
<div class="alert alert-danger">
<strong>Verificar que esto este bien.</strong> Sospecho que no porque estamos suponiendo que podes aplicar linealidad adentro de la función. Estoy leyendo el ejemplo del calculo de resistencia y hacemos "resistencia= (media_V/media_I)" en la línea 39 del documento compartido en el canal general de Slack.
</div>
Asimismo, para determinar el otro parámetro fundamental de la medición (la incertidumbre) utilizaremos como estimador a la **incertidumbre combinada ($u_{c}$)** definida a partir de la siguiente ecuación,
\begin{equation}
u_{c}^{2}(Y) = \sum_{i=1}^{N} (\dfrac{\partial f}{\partial x_{i}})^{2} \cdot u_{c}^{2}(x_{i}) + 2 \sum_{i=1}^{N-1} \sum_{j = i+1}^{N} \dfrac{\partial f}{\partial x_{i}} \dfrac{\partial f}{\partial x_{j}} u(x_{i},x_{j})
\end{equation}
donde $u(x_{i},x_{j})$ es la expresión de la covariancia entre las pdf de las $x_{i}$.
Esta expresión, para permitir el uso de funciones $f_{k}$ no lineales, es la aproximación por serie de Taylor de primer orden de la expresión original para funciones que cumplen linealidad. [[2]](https://es.wikipedia.org/wiki/Propagaci%C3%B3n_de_errores)
A su vez, a partir de la **ley de propagación de incertidumbres**, podemos decir que para la determinación de una variable unitaria mediante medición directa es posible reducir la expresión anterior a la siguiente:
\begin{equation}
u_{c}^{2}(x_{i}) = u_{i}^{2}(x_{i}) + u_{j}^{2}(x_{i})
\end{equation}
donde denominaremos $u_{i}(x_{i})$ a la incertidumbre tipo A, y $u_{j}(x_{i})$ a la incertidumbre tipo B.
***
## Evaluación incertidumbre Tipo A
La incertidumbre tipo A, recordando que se trata de una medida de dispersión y al ser tipo A se relaciona con la estadística de las muestras, se puede estimar con el desvío estándar experimental de la media ($S(\bar{X_{i}})$). Para ello hace falta recordar algunos conceptos de estadística.
Suponiendo que se toman $N$ muestras:
> **Estimador media poblacional:**
>> $\hat{x_{i}}=\bar{X_{i}}=\dfrac{1}{N} \sum_{k=1}^{N}x_{i,k}$
> **Grados de libertad:**
>> $\nu = N-1$
> **Varianza experimental de las observaciones:**
>> $\hat{\sigma^{2}(X_{i})}=S^{2}(X_{i})=\dfrac{1}{\nu} \sum_{k=1}^{N}(X_{i,k} - \bar{X_{i}})^{2}$
> **Varianza experimental de la media:**
>> $\hat{\sigma^{2}(\bar{X_{i}})}=S^{2}(\bar{X_{i}})=\dfrac{S^{2}(x_{i})}{N}$
<div class="alert alert-success">
<strong>Por ende, la componente de la incertidumbre tipo A nos queda:</strong>
\begin{equation}
u_{i}(x_{i}) = \sqrt{S^{2}(\bar{X_{i}})}
\end{equation}
</div>
<div class="alert alert-info">
<strong>Nota:</strong> Para calcular el std con un divisor de $\nu = N-1$ es necesario modificar un argumento en la función de python. El comando correctamente utilizado es: 'myVars.std(ddof=1)'.
</div>
***
## Evaluación incertidumbre Tipo B
La incertidumbre tipo B viene determinada por la información que proveen los fabricantes de los instrumentos de medición, asi como también por los datos resultantes por la calibración de los mismos.
En estos instrumentos de medición la incertidumbre viene descripta en forma de distribuciones densidad de probabilidad, no en forma estadística. Para ello utilizamos los siguientes estadísticos que caracterízan a las variables aleatorias, en caso de que su dominio fuera continuo:
> **Esperanza:**
>> $E(x)=\int x.f(x)dx$
> **Varianza:**
>> $V(x)=\int x^{2}.f(x)dx$
<div class="alert alert-success">
<strong>Por tanto, si la incertidumbre es un parámetro de dispersión, la misma vendrá descripta por la expresión:</strong>
\begin{equation}
u_{j}(x_{i}) = \sqrt{V(x)}
\end{equation}
</div>
Por simplicidad a la hora de trabajar, a continuación se presenta una tabla con los valores típicos del desvío estándar para el caso de distintas distribuciones. Se demuestra el caso de distribución uniforme.

Suponiendo que la distribución esta centrada en $\bar{X_{i}}$, nos quedaría que $a = \bar{X_{i}} - \Delta X$ y $b = \bar{X_{i}} - \Delta X$.
Por tanto si la expresión de la varianza es $V(x_{i}) = \frac{(b-a)^{2}}{12}$, finalmente quedaría:
\begin{equation}
V(x_{i}) = \frac{(b-a)^{2}}{12} = \frac{(2 \Delta X)^{2}}{12} = \frac{4 \Delta X^{2}}{12} = \frac{\Delta X^{2}}{3}
\end{equation}
\begin{equation}
\sigma_{x_{i}} = \frac{\Delta X}{\sqrt{3}}
\end{equation}
Finalmente la tabla queda,
| Distribution | $u_{j}(x_{i}) = \sigma_{x_{i}}$|
| :----: | :----: |
| Uniforme | $\frac{\Delta X}{\sqrt{3}}$ |
| Normal | $\Delta X $ |
| Normal ($K=2$) | $\frac{\Delta X}{2} $ |
| Triangular | $\frac{\Delta X}{\sqrt{6}}$ |
| U | $\frac{\Delta X}{\sqrt{2}}$ |
<div class="alert alert-danger">
<strong>Verificar que esto este bien.</strong> Me genera dudas el término $\Delta X$. Esto no creo que deba ser así porque en el caso de la distribución normal $\sigma_{x_{i}} = \sigma$. No creo que deba aparecer ningun error absoluto ahí.
</div>
***
## Incertidumbre Conjunta
Como definimos anteriormente, la incertidumbre conjunta queda definida como:
\begin{equation}
u_{c}^{2}(x_{i}) = u_{i}^{2}(x_{i}) + u_{j}^{2}(x_{i})
\end{equation}
#### ¿Qué función distribución densidad de probabilidad tiene $u_{c}$?
Si se conocen $x_{1},x_{2},...,x_{N}$ y $Y$ es una combinación lineal de $x_{i}$ (o en su defecto una aproximación lineal, como en el caso del polinomio de taylor de primer grado de la función), podemos conocer la función distribución densidad de probabilidad a partir de la convolución de las $x_{i}$, al igual que se hace para SLIT. [[3]](https://es.wikipedia.org/wiki/Convoluci%C3%B3n)
Dado que habitualmente no se conoce con precisión la función distribución densidad de probabilidad de $u_{i}(x_{i})$, se suele utilizar el **teorema central del límite** para conocer $u_{c}(x_{i})$. El mismo plantea que cuantas más funciones $x_{i}$ con función distribución densidad de probabilidad deconocida sumemos, más va a tender su resultado a una distribución normal.
***
## Grado de Confianza
Finalmente, el último parámetro que nos interesa conocer para determinar el resultado de la medición es el grado de confianza.
> **Grado de confianza:** Es la probabilidad de que al evaluar nuevamente la media poblacional ($\bar{y}$) nos encontremos con un valor dentro del intervalo $[\bar{Y} - K.\sigma_{Y}(\bar{Y}) \le \mu_{Y} \le \bar{Y} - K.\sigma_{Y}(\bar{Y})]$ para el caso de una distribución que cumpla el teorema central del límite, donde $K$ es el factor de cobertura.
Otra forma de verlo es:

donde el grado de confianza viene representado por $(1-\alpha)$. Recomiendo ver el ejemplo [[4]](https://es.wikipedia.org/wiki/Intervalo_de_confianza#Ejemplo_pr%C3%A1ctico) en caso de no entender lo que representa.
De esta forma, el factor de cobertura ($K$) nos permite modificar el grado de confianza. Agrandar $K$ aumentará el área bajo la curva de la gaussiana, lo que representará un mayor grado de confianza.
Se definirá **incertidumbre expandida** a $U(x_{i}) = K \cdot u_{c}(x_{i})$ si $u_{c}(x_{i})$ es la incertidumbre que nos proveé un grado de confianza de aproximadamente $ 68\% $.
Para una función que distribuye como normal podemos estimar el grado de confianza mediante la siguiente tabla,
| Factor de cobertura | Grado de confianza|
| :----: | :----: |
| $K=1$ | $68.26\% $ |
| $K=2$ | $95.44\% $ |
| $K=3$ | $99.74\% $ |
#### ¿Qué sucede si $u_{c}$ no distribuye normalmente?
En este caso también se podrá utilizar la ecuación $U(x_{i}) = K \cdot u_{c}(x_{i})$, pero el método mediante el cual obtendremos a $K$ será distinto.
***
## Caso de análisis: $u_{i}(x_{i}) \gg u_{j}(X_{i})$
Cuando sucede que la incertidumbre que proveé la evaluación tipo A es muy significativa frente a la tipo B, esto querrá decir que no tenemos suficientes grados de libertad para que $u_{c}(x_{i})$ se aproxime a una gaussiana. En otras palabras, la muestra obtenida no es significativa.
En estos casos vamos a suponer que $u_{c}(x_{i})$ distribuye como t-Student. La distribución t-Student surge justamente del problema de estimar la media de una población normalmente distribuida cuando el tamaño de la muestra es pequeño.
Como la distribución de t-Student tiene como parámetro los grados de libertad efectivos, debemos calcularlos. Para ello utilizaremos la fórmula de Welch-Satterthwaite:
\begin{equation}
\nu_{eff} = \dfrac{u_{c}^{4}(y)}{\sum_{i=1}^{N} \dfrac{ c_{i}^{4} u^{4}(x_{i})} {\nu_{i}} }
\end{equation}
donde $c_i = \dfrac{\partial f}{\partial x_{i}}$ y $u_{i}(x_{i})$ es la incertidumbre tipo A.

Para obtener el factor de cobertura que nos asegure un factor de cobertura del $95/%$ debemos recurrir a la tabla del t-Student. Para ello existe una función dentro del módulo _scipy.stats_ que nos integra la función hasta lograr un área del $95.4%$.
A continuación presentamos la función que utilizaremos con dicho fin,
~~~
def get_factor_Tstudent(V_eff, porcentaje_confianza_objetivo=95.4):
"""
Funcion de calculo de factor de expansión por T-student
input:
V_eff: Grados de libertad (float)
porcentaje_confianza_objetivo: porcentaje_confianza_objetivo (float)
returns:
Factor de expansión (float)
"""
return np.abs( -(stats.t.ppf((1.0+(porcentaje_confianza_objetivo/100))/2.0,V_eff)) )
~~~
***
## Caso de análisis: $u_{i}(x_{i}) \ll u_{j}(X_{i})~$
Para el caso en el que la incertidumbre del muestreo es muy inferior a la incertidumbre tipo B, nos encontramos frente al caso de incertidumbre B dominante. Esta situación es equivalente a tener la convolución entre una delta de dirac con una función de distribución cualquiera.

Como observamos en la imagen, la función distribución densidad de probabilidad resultate se asemeja más a la distribución uniforme del tipo B. En este caso para encontrar el factor de cobertura utilizaremos otra tabla distinta. En esta tabla el parámetro de entrada es el cociente $\dfrac{u_{i}}{u_{j}}$.
A continuación presentamos la función que utilizaremos con dicho fin,
~~~
def tabla_B(arg):
tabla_tipoB = np.array([
[0.0, 1.65],
[0.1, 1.66],
[0.15, 1.68],
[0.20, 1.70],
[0.25, 1.72],
[0.30, 1.75],
[0.35, 1.77],
[0.40, 1.79],
[0.45, 1.82],
[0.50, 1.84],
[0.55, 1.85],
[0.60, 1.87],
[0.65, 1.89],
[0.70, 1.90],
[0.75, 1.91],
[0.80, 1.92],
[0.85, 1.93],
[0.90, 1.94],
[0.95, 1.95],
[1.00, 1.95],
[1.10, 1.96],
[1.20, 1.97],
[1.40, 1.98],
[1.80, 1.99],
[1.90, 1.99]])
if arg >= 2.0:
K = 2.0
else:
pos_min = np.argmin(np.abs(tabla_tipoB[:,0]-arg))
K = tabla_tipoB[pos_min,1]
return K
~~~
***
## Correlación
Finalmente nos encontramos con el caso mas general. En esta situación las variables se encuentran correlacionadas, por lo que la expresión de $u_{c}(Y)$ debe utilizarse en su totalidad.
Por simplicidad de computo vamos a definir al coeficiente correlación como,
\begin{equation}
r(q,w) = \dfrac{ u(q,w) }{ u(q)u(w) }
\end{equation}
De esta forma podemos expresar a $u_{c}$ como:
\begin{equation}
u_{c}^{2}(Y) = \sum_{i=1}^{N} (\dfrac{\partial f}{\partial x_{i}})^{2} \cdot u_{c}^{2}(x_{i}) + 2 \sum_{i=1}^{N-1} \sum_{j = i+1}^{N} \dfrac{\partial f}{\partial x_{i}} \dfrac{\partial f}{\partial x_{j}} r(x_{i},x_{j})u(x_{i})u(x_{j})
\end{equation}
Esta expresión debe utilizarse cada vez que $r(x_{i},x_{j}) \ne 0$.
# Experimentación
**Comenzamos inicializando los módulos necesarios**
```
# módulos genericos
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
from scipy import signal
# Módulos para Jupyter (mejores graficos!)
import warnings
warnings.filterwarnings('ignore')
plt.rcParams['figure.figsize'] = [12, 4]
plt.rcParams['figure.dpi'] = 150 # 200 e.g. is really fine, but slower
from pandas import DataFrame
from IPython.display import HTML
```
**Definimos las funciones previamente mencionadas**
```
# Tabla para el caso A dominante
def get_factor_Tstudent(V_eff, porcentaje_confianza_objetivo=95.4):
"""
Funcion de calculo de factor de expansión por T-student
input:
V_eff: Grados de libertad (float)
porcentaje_confianza_objetivo: porcentaje_confianza_objetivo (float)
returns: .libertad efectivosdenoted
Factor de expansión (float)
"""
return np.abs( -(stats.t.ppf((1.0+(porcentaje_confianza_objetivo/100))/2.0,V_eff)) )
# Tabla para el caso B dominante
def tabla_B(arg):
tabla_tipoB = np.array([
[0.0, 1.65],
[0.1, 1.66],
[0.15, 1.68],
[0.20, 1.70],
[0.25, 1.72],
[0.30, 1.75],
[0.35, 1.77],
[0.40, 1.79],
[0.45, 1.82],
[0.50, 1.84],
[0.55, 1.85],
[0.60, 1.87],
[0.65, 1.89],
[0.70, 1.90],
[0.75, 1.91],
[0.80, 1.92],
[0.85, 1.93],
[0.90, 1.94],
[0.95, 1.95],
[1.00, 1.95],
[1.10, 1.96],
[1.20, 1.97],
[1.40, 1.98],
[1.80, 1.99],
[1.90, 1.99]])
if arg >= 2.0:
K = 2.0
else:
pos_min = np.argmin(np.abs(tabla_tipoB[:,0]-arg))
K = tabla_tipoB[pos_min,1]
return K
```
## Caso general
**Definimos las constantes necesarias**
```
# Constantes del instrumento
CONST_ERROR_PORCENTUAL = 0.5 # Error porcentual del instrumento de medición
CONST_ERROR_CUENTA = 3 # Error en cuentas del instrumento de medición
CONST_DECIMALES = 2 # Cantidad de decimales que representa el instrumento
# Constantes del muestro
N = 10 # Cantidad de muestras tomadas
# Señal a muestrear idealizada
mu = 100 # Valor medio de la distribución normal de la población ideal
std = 2 # Desvío estándar de la distribución normal de la población ideal
# Muestreo mi señal ideal (Normal)
muestra = np.random.randn(N) * std + mu
```
**Ahora solamente genero un gráfico que compare el histograma con la distribución normal de fondo**
```
num_bins = 50
fig, ax = plt.subplots()
# the histogram of the 1.1data
n, bins, patches = ax.hist(muestra, num_bins, density=True)
# add a 'best fit' line
y = ((1 / (np.sqrt(2 * np.pi) * std)) *
np.exp(-0.5 * (1 / std * (bins - mu))**2))
ax.plot(bins, y, '--')
ax.set_xlabel('Smarts')
ax.set_ylabel('Probability density')
ax.set_title('Histogram of IQ: $\mu=$'+ str(mu) + ', $\sigma=$' + str(std))
# Tweak spacing to prevent clipping of ylabel
fig.tight_layout()
plt.show()
media = np.round(muestra.mean(), CONST_DECIMALES) # Redondeamos los decimales a los valores que puede ver el tester
desvio = muestra.std(ddof=1)
print("Mean:",media )
print("STD:" ,desvio)
```
**Calculamos el desvío estándar experimental de la media como:**
\begin{equation}
u_{i}(x_{i}) = \sqrt{S^{2}(\bar{X_{i}})}
\end{equation}
```
#Incertidumbre Tipo A
ui = desvio/np.sqrt(N)
ui
```
**Calculamos el error porcentual total del dispositivo de medición como:**
\begin{equation}
e_{\%T} = e_{\%} + \dfrac{e_{cuenta}\cdot 100\%}{\bar{X_{i}}(10^{cte_{Decimales}})}
\end{equation}
```
#Incertidumbre Tipo B
ERROR_PORCENTUAL_CUENTA = (CONST_ERROR_CUENTA*100)/(media * (10**CONST_DECIMALES ))
ERROR_PORCENTUAL_TOTAL = CONST_ERROR_PORCENTUAL + ERROR_PORCENTUAL_CUENTA
ERROR_PORCENTUAL_CUENTA
```
**Por tanto el error absoluto se representa como:**
\begin{equation}
\Delta X = e_{\%T} \dfrac{\bar{X_{i}}}{100\%}
\end{equation}
```
deltaX = ERROR_PORCENTUAL_TOTAL * media/100
deltaX
```
**Finalmente la incertidumbre tipo B queda:**
\begin{equation}
u_{j}(x_{i}) = \sqrt{Var(x_{i})} = \dfrac{\Delta X}{\sqrt{3}}
\end{equation}
donde recordamos que, al suponer una distribución uniforme en el dispositivo de medición, la varianza nos queda $Var(X_{uniforme}) = \dfrac {(b-a)^{2}}{12}$.
```
uj = deltaX / np.sqrt(3)
uj
```
**Calculamos la incertidumbre conjunta**
Como este es el caso de una medición directa de una sola variable, la expresión apropiada es:
\begin{equation}
u_{c}^{2}(x_{i}) = u_{i}^{2}(x_{i}) + u_{j}^{2}(x_{i})
\end{equation}
```
#incertidumbre combinada
uc = np.sqrt(ui**2 + uj**2)
uc
```
**Ahora debemos evaluar frente a que caso nos encontramos**
En primera instancia evaluamos que componente de la incertidumbre es mayoritaria y en que proporción.
Entonces tenemos tres situaciones posibles:
1. **Caso B dominante** $\Rightarrow \dfrac{u_{i}(x_{i})}{u_{j}(x_{i})} \lt 1 \Rightarrow$ Se utiliza la tabla de B dominante.
1. **Caso Normal** $\Rightarrow \dfrac{u_{i}(x_{i})}{u_{j}(x_{i})} \gt 1$ y $V_{eff} \gt 30 \Rightarrow$ Se toma $K=2$.
1. **Caso A dominante** $\Rightarrow \dfrac{u_{i}(x_{i})}{u_{j}(x_{i})} \gt 1$ y $V_{eff} \lt 30 \Rightarrow$ Se utiliza t-Student con los grados de libertad efectivos.
```
def evaluacion(uc,ui,uj,N):
cte_prop = ui/uj
print("Constante de proporcionalidad", cte_prop)
if cte_prop > 1:
# Calculo los grados de libertad efectivos
veff = int ((uc**4)/((ui**4)/(N-1)))
print("Grados efectivos: ", veff)
if veff > 30:
# Caso Normal
k = 2
else:
# Caso t-Student
k = get_factor_Tstudent(veff)
else:
# Caso B Dominante
k = tabla_B(cte_prop)
print("Constante de expansión: ",k)
return k
```
<div class="alert alert-warning">
<strong>Nota:</strong> La contribución de $u_{j}(x_{i})$ no se tiene en cuenta dado que, al ser una distribución continua, tiene infinitos grados de libertad.
\begin{equation}
\nu_{eff} = \dfrac{u_{c}^{4}(y)}{\sum_{i=1}^{N} \dfrac{ c_{i}^{4} u^{4}(x_{i})} {\nu_{i}} }
\end{equation}
</div>
```
k = evaluacion(uc,ui,uj,N)
```
**Análisis y presentación del resultado**
Como el cociente $\dfrac{u_{i}(x_{i})}{u_{j}(x_{i})} \gt 2$, entonces suponemos que nos encontramos frente al caso de distribución normal o distribución t-Student. Para ello utilizamos el criterio de los grados de libertad efectivos.
En este caso los grado de libertad efectivos $V_{eff} \gt 30$, por lo que suponemos distribución normal.
Finalmente presentamos el resultado con 1 dígito significativo.
```
U = uc*k
print("Resultado de la medición: (",np.round(media,1),"+-",np.round(U,1),")V con un grado de confianza del 95%")
```
# Bibliografía
_Nota: Las citas **no** respetan el formato APA._
1. [Evaluación de la Incertidumbre en Datos Experimentales, Javier Miranda Martín del Campo](http://depa.fquim.unam.mx/amyd/archivero/CALCULODEINCERTIDUMBRESDR.JAVIERMIRANDA_26197.pdf)
1. [Propagación de erroes, Wikipedia](https://es.wikipedia.org/wiki/Propagaci%C3%B3n_de_errores)
1. [Convolución, Wikipedia](https://es.wikipedia.org/wiki/Convoluci%C3%B3n)
1. [Intervalo de Confianza, Wikipedia](https://es.wikipedia.org/wiki/Intervalo_de_confianza#Ejemplo_pr%C3%A1ctico)
|
github_jupyter
|
### Analyze Auto sales trend and verify if RCF detects abrupt shift in sales
#### Years: 2005 to 2020. This period covers recession due to housing crisis in 2008, followed by recovery and economic impact due to Covid
### Data Source: Monthly New Vehicle Sales for the United States Automotive Market
### https://www.goodcarbadcar.net/usa-auto-industry-total-sales-figures/
### Raw data: http://www.bea.gov/
```
import sys
import pandas as pd
import numpy as np
%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
matplotlib.rcParams['figure.dpi'] = 100
import boto3
import botocore
import sagemaker
from sagemaker import RandomCutForest
bucket = sagemaker.Session().default_bucket() # Feel free to change to another bucket you have access to
prefix = 'sagemaker/autosales'
execution_role = sagemaker.get_execution_role()
# check if the bucket exists
try:
boto3.Session().client('s3').head_bucket(Bucket=bucket)
except botocore.exceptions.ParamValidationError as e:
print('Hey! You either forgot to specify your S3 bucket'
' or you gave your bucket an invalid name!')
except botocore.exceptions.ClientError as e:
if e.response['Error']['Code'] == '403':
print("Hey! You don't have permission to access the bucket, {}.".format(bucket))
elif e.response['Error']['Code'] == '404':
print("Hey! Your bucket, {}, doesn't exist!".format(bucket))
else:
raise
else:
print('Training input/output will be stored in: s3://{}/{}'.format(bucket, prefix))
%%time
data_filename = 'auto_sales_year_month.csv'
df = pd.read_csv(data_filename)
df.shape
df
plt.plot(df['value'])
plt.ylabel('Sales')
plt.title('Monthly Auto Sales - USA')
plt.show()
```
### Big increase in autosales Feb-2012
https://www.theautochannel.com/news/2012/03/02/027504-february-2012-u-s-auto-sales-highest-4-years.html
```
df[75:90]
```
### U.S. Auto Sales Hit Record Low In April 2020
#### Coronavirus Chaos Also Drives Zero-Interest Deals to Record Highs
https://www.edmunds.com/car-news/us-auto-sales-hit-record-low-in-april.html
```
df[175:]
```
# Training
***
Next, we configure a SageMaker training job to train the Random Cut Forest (RCF) algorithm on the taxi cab data.
## Hyperparameters
Particular to a SageMaker RCF training job are the following hyperparameters:
* **`num_samples_per_tree`** - the number randomly sampled data points sent to each tree. As a general rule, `1/num_samples_per_tree` should approximate the the estimated ratio of anomalies to normal points in the dataset.
* **`num_trees`** - the number of trees to create in the forest. Each tree learns a separate model from different samples of data. The full forest model uses the mean predicted anomaly score from each constituent tree.
* **`feature_dim`** - the dimension of each data point.
In addition to these RCF model hyperparameters, we provide additional parameters defining things like the EC2 instance type on which training will run, the S3 bucket containing the data, and the AWS access role. Note that,
* Recommended instance type: `ml.m4`, `ml.c4`, or `ml.c5`
* Current limitations:
* The RCF algorithm does not take advantage of GPU hardware.
```
# Use Spot Instance - Save up to 90% of training cost by using spot instances when compared to on-demand instances
# Reference: https://github.com/aws-samples/amazon-sagemaker-managed-spot-training/blob/main/xgboost_built_in_managed_spot_training_checkpointing/xgboost_built_in_managed_spot_training_checkpointing.ipynb
# if you are still on two-month free-tier you can use the on-demand instance by setting:
# use_spot_instances = False
# We will use spot for training
use_spot_instances = True
max_run = 3600 # in seconds
max_wait = 3600 if use_spot_instances else None # in seconds
job_name = 'rcf-autosales-1yr'
checkpoint_s3_uri = None
if use_spot_instances:
checkpoint_s3_uri = f's3://{bucket}/{prefix}/checkpoints/{job_name}'
print (f'Checkpoint uri: {checkpoint_s3_uri}')
# SDK 2.0
session = sagemaker.Session()
# specify general training job information
# 48 samples = 48 Months of data
rcf = RandomCutForest(role=execution_role,
instance_count=1,
instance_type='ml.m4.xlarge',
data_location='s3://{}/{}/'.format(bucket, prefix),
output_path='s3://{}/{}/output'.format(bucket, prefix),
num_samples_per_tree=48,
num_trees=50,
base_job_name = job_name,
use_spot_instances=use_spot_instances,
max_run=max_run,
max_wait=max_wait,
checkpoint_s3_uri=checkpoint_s3_uri)
# automatically upload the training data to S3 and run the training job
rcf.fit(rcf.record_set(df.value.to_numpy().reshape(-1,1)))
rcf.hyperparameters()
print('Training job name: {}'.format(rcf.latest_training_job.job_name))
```
# Inference
***
A trained Random Cut Forest model does nothing on its own. We now want to use the model we computed to perform inference on data. In this case, it means computing anomaly scores from input time series data points.
We create an inference endpoint using the SageMaker Python SDK `deploy()` function from the job we defined above. We specify the instance type where inference is computed as well as an initial number of instances to spin up. We recommend using the `ml.c5` instance type as it provides the fastest inference time at the lowest cost.
```
rcf_inference = rcf.deploy(
initial_instance_count=1,
instance_type='ml.m5.xlarge',
endpoint_name = job_name)
```
Congratulations! You now have a functioning SageMaker RCF inference endpoint. You can confirm the endpoint configuration and status by navigating to the "Endpoints" tab in the AWS SageMaker console and selecting the endpoint matching the endpoint name, below:
```
print('Endpoint name: {}'.format(rcf_inference.endpoint_name))
```
## Data Serialization/Deserialization
We can pass data in a variety of formats to our inference endpoint. In this example we will demonstrate passing CSV-formatted data. Other available formats are JSON-formatted and RecordIO Protobuf. We make use of the SageMaker Python SDK utilities `csv_serializer` and `json_deserializer` when configuring the inference endpoint.
```
# SDK 2.0 serializers
from sagemaker.serializers import CSVSerializer
from sagemaker.deserializers import JSONDeserializer
rcf_inference.serializer = CSVSerializer()
rcf_inference.deserializer = JSONDeserializer()
```
Let's pass the training dataset, in CSV format, to the inference endpoint so we can automatically detect the anomalies we saw with our eyes in the plots, above. Note that the serializer and deserializer will automatically take care of the datatype conversion from Numpy NDArrays.
For starters, let's only pass in the first six datapoints so we can see what the output looks like.
```
df_numpy = df.value.to_numpy().reshape(-1,1)
print(df_numpy[:6])
results = rcf_inference.predict(df_numpy[:6])
print(results)
```
## Computing Anomaly Scores
Now, let's compute and plot the anomaly scores from the entire taxi dataset.
```
results = rcf_inference.predict(df_numpy)
scores = [datum['score'] for datum in results['scores']]
# add scores to taxi data frame and print first few values
df['score'] = pd.Series(scores, index=df.index)
df.head()
fig, ax1 = plt.subplots()
ax2 = ax1.twinx()
#
# *Try this out* - change `start` and `end` to zoom in on the
# anomaly found earlier in this notebook
#
start, end = 0, len(df)
df_subset = df[start:end]
ax1.plot(df_subset['value'], color='C0', alpha=0.8)
ax2.plot(df_subset['score'], color='C1')
ax1.grid(which='major', axis='both')
ax1.set_ylabel('Auto Sales', color='C0')
ax2.set_ylabel('Anomaly Score', color='C1')
ax1.tick_params('y', colors='C0')
ax2.tick_params('y', colors='C1')
ax2.set_ylim(min(scores), 1.4*max(scores))
fig.set_figwidth(10)
```
Note that the anomaly score spikes where our eyeball-norm method suggests there is an anomalous data point as well as in some places where our eyeballs are not as accurate.
Below we print and plot any data points with scores greater than 3 standard deviations (approx 99.9th percentile) from the mean score.
```
score_mean = df['score'].mean()
score_std = df['score'].std()
score_cutoff = score_mean + 3*score_std
anomalies = df_subset[df_subset['score'] > score_cutoff]
anomalies
score_mean, score_std, score_cutoff
ax2.plot(anomalies.index, anomalies.score, 'ko')
fig
```
With the current hyperparameter choices we see that the three-standard-deviation threshold, while able to capture the known anomalies as well as the ones apparent in the ridership plot, is rather sensitive to fine-grained peruturbations and anomalous behavior. Adding trees to the SageMaker RCF model could smooth out the results as well as using a larger data set.
## Stop and Delete the Endpoint
Finally, we should delete the endpoint before we close the notebook.
To do so execute the cell below. Alternately, you can navigate to the "Endpoints" tab in the SageMaker console, select the endpoint with the name stored in the variable `endpoint_name`, and select "Delete" from the "Actions" dropdown menu.
```
# SDK 2.0
rcf_inference.delete_endpoint()
```
# Epilogue
---
We used Amazon SageMaker Random Cut Forest to detect anomalous datapoints in a taxi ridership dataset. In these data the anomalies occurred when ridership was uncharacteristically high or low. However, the RCF algorithm is also capable of detecting when, for example, data breaks periodicity or uncharacteristically changes global behavior.
Depending on the kind of data you have there are several ways to improve algorithm performance. One method, for example, is to use an appropriate training set. If you know that a particular set of data is characteristic of "normal" behavior then training on said set of data will more accurately characterize "abnormal" data.
Another improvement is make use of a windowing technique called "shingling". This is especially useful when working with periodic data with known period, such as the NYC taxi dataset used above. The idea is to treat a period of $P$ datapoints as a single datapoint of feature length $P$ and then run the RCF algorithm on these feature vectors. That is, if our original data consists of points $x_1, x_2, \ldots, x_N \in \mathbb{R}$ then we perform the transformation,
```
data = [[x_1], shingled_data = [[x_1, x_2, ..., x_{P}],
[x_2], ---> [x_2, x_3, ..., x_{P+1}],
... ...
[x_N]] [x_{N-P}, ..., x_{N}]]
```
```
df.head()
import numpy as np
# made a minor correction. increased size by 1 as the original code was missing last shingle
def shingle(data, shingle_size):
num_data = len(data)
# +1
shingled_data = np.zeros((num_data-shingle_size+1, shingle_size))
# +1
for n in range(num_data - shingle_size+1):
shingled_data[n] = data[n:(n+shingle_size)]
return shingled_data
# single data with shingle size=12 (1 year - 12 months)
# let's try one year auto sales
# let's try 1 year window
shingle_size = 12
prefix_shingled = 'sagemaker/randomcutforest_shingled_1year'
auto_data_shingled = shingle(df.values[:,1], shingle_size)
job_name = 'rcf-autosales-shingled-1year'
checkpoint_s3_uri = None
if use_spot_instances:
checkpoint_s3_uri = f's3://{bucket}/{prefix_shingled}/checkpoints/{job_name}'
print (f'Checkpoint uri: {checkpoint_s3_uri}')
df.values[:24,1]
shingle(df.values[:24,1],12)
auto_data_shingled[:5]
auto_data_shingled[-5:]
auto_data_shingled.shape
```
We create a new training job and and inference endpoint. (Note that we cannot re-use the endpoint created above because it was trained with one-dimensional data.)
```
# SDK 2.0
session = sagemaker.Session()
# specify general training job information
rcf = RandomCutForest(role=execution_role,
instance_count=1,
instance_type='ml.m5.xlarge',
data_location='s3://{}/{}/'.format(bucket, prefix_shingled),
output_path='s3://{}/{}/output'.format(bucket, prefix_shingled),
num_samples_per_tree=48,
num_trees=50,
base_job_name = job_name,
use_spot_instances=use_spot_instances,
max_run=max_run,
max_wait=max_wait,
checkpoint_s3_uri=checkpoint_s3_uri)
# automatically upload the training data to S3 and run the training job
rcf.fit(rcf.record_set(auto_data_shingled))
rcf.hyperparameters()
# SDK 2.0 serializers
from sagemaker.serializers import CSVSerializer
from sagemaker.deserializers import JSONDeserializer
rcf_inference = rcf.deploy(
initial_instance_count=1,
instance_type='ml.m5.xlarge',
endpoint_name = job_name
)
rcf_inference.serializer = CSVSerializer()
rcf_inference.deserializer = JSONDeserializer()
```
Using the above inference endpoint we compute the anomaly scores associated with the shingled data.
```
# Score the shingled datapoints
results = rcf_inference.predict(auto_data_shingled)
scores = np.array([datum['score'] for datum in results['scores']])
# Save the scores
np.savetxt("scores_shingle_annual.csv",
np.asarray(scores),
delimiter=",",
fmt='%10.5f')
# compute the shingled score distribution and cutoff and determine anomalous scores
score_mean = scores.mean()
score_std = scores.std()
score_cutoff = score_mean + 1.5*score_std
anomalies = scores[scores > score_cutoff]
anomaly_indices = np.arange(len(scores))[scores > score_cutoff]
print(anomalies)
score_mean, score_std, score_cutoff
anomalies.size
```
Finally, we plot the scores from the shingled data on top of the original dataset and mark the score lying above the anomaly score threshold.
```
fig, ax1 = plt.subplots()
ax2 = ax1.twinx()
#
# *Try this out* - change `start` and `end` to zoom in on the
# anomaly found earlier in this notebook
#
start, end = 0, len(df)
taxi_data_subset = df[start:end]
ax1.plot(df['value'], color='C0', alpha=0.8)
ax2.plot(scores, color='C1')
ax2.scatter(anomaly_indices, anomalies, color='k')
ax1.grid(which='major', axis='both')
ax1.set_ylabel('Auto Sales', color='C0')
ax2.set_ylabel('Anomaly Score', color='C1')
ax1.tick_params('y', colors='C0')
ax2.tick_params('y', colors='C1')
ax2.set_ylim(min(scores), 1.4*max(scores))
fig.set_figwidth(10)
```
We see that with this particular shingle size, hyperparameter selection, and anomaly cutoff threshold that the shingled approach more clearly captures the major anomalous events: the spike at around t=6000 and the dips at around t=9000 and t=10000. In general, the number of trees, sample size, and anomaly score cutoff are all parameters that a data scientist may need experiment with in order to achieve desired results. The use of a labeled test dataset allows the used to obtain common accuracy metrics for anomaly detection algorithms. For more information about Amazon SageMaker Random Cut Forest see the [AWS Documentation](https://docs.aws.amazon.com/sagemaker/latest/dg/randomcutforest.html).
```
# compute the shingled score distribution and cutoff and determine anomalous scores
score_mean = scores.mean()
score_std = scores.std()
score_cutoff = score_mean + 2.0*score_std
anomalies = scores[scores > score_cutoff]
anomaly_indices = np.arange(len(scores))[scores > score_cutoff]
print(anomalies)
fig, ax1 = plt.subplots()
ax2 = ax1.twinx()
#
# *Try this out* - change `start` and `end` to zoom in on the
# anomaly found earlier in this notebook
#
start, end = 0, len(df)
taxi_data_subset = df[start:end]
ax1.plot(df['value'], color='C0', alpha=0.8)
ax2.plot(scores, color='C1')
ax2.scatter(anomaly_indices, anomalies, color='k')
ax1.grid(which='major', axis='both')
ax1.set_ylabel('Auto Sales', color='C0')
ax2.set_ylabel('Anomaly Score', color='C1')
ax1.tick_params('y', colors='C0')
ax2.tick_params('y', colors='C1')
ax2.set_ylim(min(scores), 1.4*max(scores))
fig.set_figwidth(10)
# SDK 2.0
rcf_inference.delete_endpoint()
```
|
github_jupyter
|
```
import glob
import os
import warnings
import geopandas
import matplotlib
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import matplotlib.colors
import pandas
import seaborn
from cartopy import crs as ccrs
from mpl_toolkits.axes_grid1 import make_axes_locatable
# from geopandas/geoseries.py:358, when using geopandas.clip:
#
# UserWarning: GeoSeries.notna() previously returned False for both missing (None) and empty geometries.
# Now, it only returns False for missing values. Since the calling GeoSeries contains empty geometries,
# the result has changed compared to previous versions of GeoPandas.
#
# Given a GeoSeries 's', you can use '~s.is_empty & s.notna()' to get back the old behaviour.
#
# To further ignore this warning, you can do:
warnings.filterwarnings('ignore', 'GeoSeries.notna', UserWarning)
# default to larger figures
plt.rcParams['figure.figsize'] = 10, 10
```
# Postprocessing and plotting EEH analysis
Scenarios
- [x] Colour coded map showing the percentage changes in EEH population by LAD
- [x] Total EEH population compared with ONS projection
- [x] Total housing growth per LAD, 2015-2020, 2020-2030, 2030-2040, 2040-2050 (may be better as cumulative chart with LADs)
Pathways
- [x] Proportion of engine types for each Pathway 2015-2050
- [x] Annual CO2 emission * 5 Pathways 2015, 2020, 2030, 2040, 2050
- [x] Colour coded map showing Vehicle km in 2050 for each LAD * 5 Pathways
- [x] Annual electricity consumption for car trips * 5 Pathways, 2015, 2020, 2030, 2040, 2050
- [x] Congestion/capacity utilisation in 2050 for each LAD * 5 Pathways (map/chart)
```
all_zones = geopandas.read_file('../preparation/Local_Authority_Districts__December_2019__Boundaries_UK_BUC-shp/Local_Authority_Districts__December_2019__Boundaries_UK_BUC.shp')
zone_codes = pandas.read_csv('lads-codes-eeh.csv').lad19cd
eeh_zones = all_zones \
[all_zones.lad19cd.isin(zone_codes)] \
[['lad19cd', 'lad19nm', 'st_areasha', 'geometry']]
eeh_zones.plot()
scenarios = [os.path.basename(d) for d in sorted(glob.glob('eeh/0*'))]
scenarios
timesteps = [os.path.basename(d) for d in sorted(glob.glob('eeh/01-BaU/*'))]
timesteps
```
## Population scenario
```
def read_pop(fname):
pop = pandas.read_csv(fname)
pop = pop \
[pop.year.isin([2015, 2050])] \
.melt(id_vars='year', var_name='lad19cd', value_name='population')
pop = pop[pop.lad19cd.isin(zone_codes)] \
.pivot(index='lad19cd', columns='year')
pop.columns = ['pop2015', 'pop2050']
pop['perc_change'] = (pop.pop2050 - pop.pop2015) / pop.pop2015
pop.perc_change *= 100
return pop
eehpop = read_pop('../preparation/data/csvfiles/eehPopulation.csv')
arcpop = read_pop('../preparation/data/csvfiles/eehArcPopulationBaseline.csv')
eehpop.sort_values(by='perc_change').tail()
def plot_pop(eeh_zones, pop):
df = eeh_zones.merge(pop, on='lad19cd', validate='one_to_one')
fig, ax = plt.subplots(1, 1)
ax.xaxis.set_visible(False)
ax.yaxis.set_visible(False)
divider = make_axes_locatable(ax)
cax = divider.append_axes("right", size="5%", pad=0.1)
df.plot(column='perc_change', ax=ax, legend=True, cax=cax, cmap='coolwarm_r', vmax=95, vmin=-95)
cax.yaxis.set_label_text('Population (% change 2015-2050)')
cax.yaxis.get_label().set_visible(True)
return fig
eehpop.to_csv('eehPopulationChange.csv')
fig = plot_pop(eeh_zones, eehpop)
plt.savefig("eehPopulationChange.png")
plt.savefig("eehPopulationChange.svg")
fig = plot_pop(eeh_zones, arcpop)
plt.savefig("snppPopulationChange.png")
plt.savefig("snppPopulationChange.svg")
```
## Results
```
def read_result(fname, scenarios, timesteps):
dfs = []
for s in scenarios:
for t in timesteps:
path = os.path.join('eeh', s, t, fname)
_, ext = os.path.splitext(fname)
if ext == '.csv':
df = pandas.read_csv(path)
elif ext in ('.shp', '.gpkg', '.geojson'):
df = geopandas.read_file(path)
else:
raise Exception(f"Don't know how to read files of type '{ext}'")
df['year'] = t
df['scenario'] = s
dfs.append(df)
return pandas.concat(dfs)
```
## CO2 Emissions
```
zone_vehicle_emissions = read_result('totalCO2EmissionsZonalPerVehicleType.csv', scenarios, timesteps)
zone_vehicle_emissions.head(2)
annual_eeh_emissions = zone_vehicle_emissions[zone_vehicle_emissions.zone.isin(zone_codes)] \
.groupby(['scenario', 'year']) \
.sum()
annual_eeh_emissions['TOTAL'] = annual_eeh_emissions.sum(axis=1)
annual_eeh_emissions.to_csv('eehCO2Emissions.csv')
annual_eeh_emissions.head(10)
```
## Vehicle km per LAD
```
vkm_a = read_result('vehicleKilometresWithAccessEgress.csv', scenarios, timesteps)
eeh_vkm_a = vkm_a[vkm_a.zone.isin(zone_codes)] \
.set_index(['scenario', 'year', 'zone'])
eeh_vkm_a['TOTAL'] = eeh_vkm_a.sum(axis=1)
eeh_vkm_a.to_csv('eehVehicleKilometresWithAccessEgress.csv')
eeh_vkm_a.head()
vkm = read_result('vehicleKilometres.csv', scenarios, timesteps)
eeh_vkm = vkm[vkm.zone.isin(zone_codes)] \
.set_index(['scenario', 'year', 'zone'])
eeh_vkm['TOTAL'] = eeh_vkm.sum(axis=1)
eeh_vkm.to_csv('eehVehicleKilometres.csv')
eeh_vkm.head()
eeh_vkm.describe()
df = eeh_vkm.reset_index().drop(columns='zone').groupby(['scenario', 'year']).sum()[['TOTAL']].reset_index()
seaborn.catplot(
x = "year",
y = "TOTAL",
hue = "scenario",
data = df,
kind = "bar")
def plot_vkm(eeh_zones, eeh_vkm, scenario, year):
vmax = eeh_vkm.TOTAL.max()
df = eeh_vkm[['TOTAL']].reset_index() \
.rename(columns={'TOTAL': 'vkm'})
df = df[(df.scenario == scenario) & (df.year == year)] \
.drop(columns=['scenario', 'year'])
df = geopandas.GeoDataFrame(df.merge(eeh_zones, left_on='zone', right_on='lad19cd', validate='one_to_one'))
fig, ax = plt.subplots(1, 1)
ax.xaxis.set_visible(False)
ax.yaxis.set_visible(False)
divider = make_axes_locatable(ax)
cax = divider.append_axes("right", size="5%", pad=0.1)
df.plot(column='vkm', ax=ax, legend=True, cax=cax, cmap='inferno', vmax=vmax)
cax.yaxis.set_label_text('Vehicle kilometres (km)')
cax.yaxis.get_label().set_visible(True)
return fig
fig = plot_vkm(eeh_zones, eeh_vkm, scenarios[0], "2015")
plt.savefig("eehVehicleKilometres2015.png")
plt.savefig("eehVehicleKilometres2015.svg")
for s in scenarios:
fig = plot_vkm(eeh_zones, eeh_vkm, s, "2050")
plt.savefig(f"eehVehicleKilometres2050_{s}.png")
plt.savefig(f"eehVehicleKilometres2050_{s}.svg")
```
## Electricity consumption for car trips
```
car_elec = read_result('zonalTemporalElectricityCAR.csv', scenarios, timesteps)
car_elec = car_elec[car_elec.zone.isin(zone_codes)] \
.set_index(['scenario', 'year', 'zone'])
car_elec['TOTAL'] = car_elec.sum(axis=1)
car_elec.to_csv('eehZonalTemporalElectricityCAR.csv')
car_elec.head(2)
car_energy = read_result('energyConsumptionsZonalCar.csv', scenarios, timesteps)
car_energy = car_energy[car_energy.zone.isin(zone_codes)] \
.set_index(['scenario', 'year', 'zone'])
car_energy.to_csv('eehEnergyConsumptionsZonalCar.csv')
car_energy.head(2)
```
## Congestion/capacity utilisation
```
zb = eeh_zones.bounds
extent = (zb.minx.min(), zb.maxx.max(), zb.miny.min(), zb.maxy.max())
extent
network_base = read_result('outputNetwork.shp', [scenarios[0]], ["2015"])
eeh_nb = network_base.cx[extent[0]:extent[1], extent[2]:extent[3]].copy()
eeh_nbc = geopandas.clip(eeh_nb, eeh_zones)
eeh_nb.head(1)
eeh_nb.drop(columns=['SRefE','SRefN','IsFerry', 'iDir', 'Anode', 'Bnode', 'CP', 'year', 'CapUtil', 'scenario']).to_file('eehNetwork.gpkg', driver='GPKG')
def plot_cap(zones, network, network_clipped):
fig, ax = plt.subplots(1, 1)
ax.xaxis.set_visible(False)
ax.yaxis.set_visible(False)
divider = make_axes_locatable(ax)
cax = divider.append_axes("right", size="5%", pad=0.1)
zones.plot(ax=ax, color='#eeeeee', edgecolor='white')
network.plot(ax=ax, color='#eeeeee')
network_clipped.plot(column='CapUtil', ax=ax, legend=True, cax=cax, cmap='inferno', vmax=200)
cax.yaxis.set_label_text('Capacity Utilisation (%)')
cax.yaxis.get_label().set_visible(True)
return fig
fig = plot_cap(eeh_zones, eeh_nb, eeh_nbc)
plt.savefig('eehCapacity2015.png')
plt.savefig('eehCapacity2015.svg')
for s in scenarios:
network = read_result('outputNetwork.shp', [s], ["2050"])
eeh_nb = network.cx[extent[0]:extent[1], extent[2]:extent[3]].copy()
eeh_nbc = geopandas.clip(eeh_nb, eeh_zones)
fig = plot_cap(eeh_zones, eeh_nb, eeh_nbc)
plt.savefig(f'eehCapacity2050_{s}.png')
plt.savefig(f'eehCapacity2050_{s}.svg')
dfs = []
df = read_result('outputNetwork.shp', [scenarios[0]], ["2015"])
df = geopandas.clip(df, eeh_zones) \
[['EdgeID', 'Anode', 'Bnode', 'CP', 'RoadNumber', 'iDir', 'SRefE',
'SRefN', 'Distance', 'FFspeed', 'FFtime', 'IsFerry', 'Lanes', 'CapUtil',
'year', 'scenario']]
dfs.append(df)
for s in scenarios:
df = read_result('outputNetwork.shp', [s], ["2050"])
df = geopandas.clip(df, eeh_zones) \
[['EdgeID', 'Anode', 'Bnode', 'CP', 'RoadNumber', 'iDir', 'SRefE',
'SRefN', 'Distance', 'FFspeed', 'FFtime', 'IsFerry', 'Lanes', 'CapUtil',
'year', 'scenario']]
dfs.append(df)
link_capacity = pandas.concat(dfs) \
.set_index(['scenario', 'year'])
link_capacity.head(2)
link_to_lad = geopandas.sjoin(eeh_nbc, eeh_zones, how="left", op='intersects') \
[['EdgeID','lad19cd','lad19nm']] \
.drop_duplicates(subset=['EdgeID'])
link_to_lad
link_capacity
link_capacity_with_lad = link_capacity \
.reset_index() \
.merge(link_to_lad, on='EdgeID', how='left') \
.set_index(['scenario', 'year', 'EdgeID'])
link_capacity_with_lad
link_capacity_with_lad.to_csv('eehLinkCapUtil.csv')
mean_cap = link_capacity_with_lad[['CapUtil', 'lad19cd','lad19nm']] \
.reset_index() \
.drop(columns='EdgeID') \
.groupby(['scenario', 'year', 'lad19cd', 'lad19nm']) \
.mean()
mean_cap.to_csv('eehLADAverageCapUtil.csv')
mean_cap
df = mean_cap.reset_index()
print(len(df.scenario.unique()))
print(len(df.year.unique()))
print(len(df.lad19cd.unique()))
print(6 * 37)
```
## Link travel times/speeds
```
link_times = read_result('linkTravelTimes.csv', scenarios, timesteps)
link_times.head(1)
eeh_nbc
eeh_lt = link_times[link_times.edgeID.isin(eeh_nbc.EdgeID)]
eeh_lt.to_csv('eehLinkTravelTimes.csv', index=False)
KM_TO_MILES = 0.6213712
hours = [
'MIDNIGHT', 'ONEAM', 'TWOAM', 'THREEAM', 'FOURAM', 'FIVEAM',
'SIXAM', 'SEVENAM', 'EIGHTAM', 'NINEAM', 'TENAM', 'ELEVENAM',
'NOON', 'ONEPM', 'TWOPM', 'THREEPM', 'FOURPM', 'FIVEPM',
'SIXPM', 'SEVENPM', 'EIGHTPM', 'NINEPM', 'TENPM', 'ELEVENPM'
]
def merge_times_to_network(network_clipped, link_times, hours):
# nbc is clipped network
# lt is link times
# hours is list of hour names
# merge link times (by hour of day) onto network
df = network_clipped \
.drop(columns=['scenario', 'year']) \
.rename(columns={'EdgeID': 'edgeID'}) \
.merge(
link_times,
on="edgeID"
) \
[[
'edgeID', 'RoadNumber', 'iDir', 'Lanes', 'Distance', 'FFspeed',
'MIDNIGHT', 'ONEAM', 'TWOAM', 'THREEAM', 'FOURAM', 'FIVEAM',
'SIXAM', 'SEVENAM', 'EIGHTAM', 'NINEAM', 'TENAM', 'ELEVENAM',
'NOON', 'ONEPM', 'TWOPM', 'THREEPM', 'FOURPM', 'FIVEPM',
'SIXPM', 'SEVENPM', 'EIGHTPM', 'NINEPM', 'TENPM', 'ELEVENPM',
'geometry'
]]
# calculate flow speeds from distance / time * 60 [to get back to km/h] * 0.6213712 [to miles/h]
for hour in hours:
df[hour] = (df.Distance / df[hour]) * 60 * KM_TO_MILES
df.FFspeed *= KM_TO_MILES
return df
eeh_ltb = merge_times_to_network(
eeh_nbc,
eeh_lt[(eeh_lt.scenario == '01-BaU') & (eeh_lt.year == "2015")],
hours)
eeh_ltb
eeh_ltb.columns
def plot_speed(zones, network, network_clipped, col, label=None):
fig, ax = plt.subplots(1, 1)
ax.xaxis.set_visible(False)
ax.yaxis.set_visible(False)
divider = make_axes_locatable(ax)
cax = divider.append_axes("right", size="5%", pad=0.1)
zones.plot(ax=ax, color='#eeeeee', edgecolor='white')
network.plot(ax=ax, color='#eeeeee')
network_clipped.plot(column=col, ax=ax, legend=True, cax=cax, cmap='inferno', vmax=75, vmin=0)
if label is not None:
# place a text box in upper left in axes coords
props = props = dict(boxstyle='round', facecolor='white', alpha=0.5)
ax.text(0.05, 0.95, label, transform=ax.transAxes, fontsize=14,
verticalalignment='top', bbox=props)
cax.yaxis.set_label_text('Speed (km/h)')
cax.yaxis.get_label().set_visible(True)
return fig
fig = plot_speed(eeh_zones, eeh_nb, eeh_ltb, 'EIGHTAM', "Morning peak")
fname = f"speed2015_peakam.png"
plt.savefig(fname)
plt.close(fig)
fig = plot_speed(eeh_zones, eeh_nb, eeh_ltb, 'FFspeed', "Free flow")
fname = f"speed2015_free.png"
plt.savefig(fname)
plt.close(fig)
for i, hour in enumerate(hours):
fig = plot_speed(eeh_zones, eeh_nb, eeh_ltb, hour, f"{str(i).zfill(2)}:00")
fname = f"speed2015_{str(i).zfill(3)}.png"
print(fname, end=" ")
plt.savefig(fname)
plt.close(fig)
```
### Convert to GIF
Using imagemagick, needs installing, next line runs in the shell
```
! convert -delay 20 -loop 0 speed2015_0*.png speed2015.gif
```
### Each scenario peak speeds in 2050
```
for scenario in scenarios:
ltb = merge_times_to_network(
eeh_nbc,
eeh_lt[(eeh_lt.scenario == scenario) & (eeh_lt.year == "2050")],
hours)
fig = plot_speed(eeh_zones, eeh_nb, ltb, 'EIGHTAM', "Morning peak")
fname = f"speed2050_{scenario}_peakam.png"
print(fname, end=" ")
plt.savefig(fname)
plt.close(fig)
```
## Rank links per-scenario for peak speed in 2050
```
eeh_flow = eeh_lt[eeh_lt.year == "2050"] \
[["scenario", "edgeID", "EIGHTAM", "freeFlow"]] \
.rename(columns={'EIGHTAM': 'peakFlow'})
eeh_flow['flowRatio'] = eeh_flow.freeFlow / eeh_flow.peakFlow
eeh_flow.drop(columns=['peakFlow', 'freeFlow'], inplace=True)
eeh_flow = eeh_flow.pivot_table(columns='scenario', index='edgeID', values='flowRatio')
eeh_flow.columns.name = None
eeh_flow['bestScenarioAtPeak'] = eeh_flow.idxmax(axis=1)
eeh_flow.head(2)
eeh_flow.groupby('bestScenarioAtPeak').count()[["01-BaU"]]
eeh_flowg = eeh_nbc \
[["EdgeID", "RoadNumber", "iDir", "Distance", "Lanes", "geometry"]] \
.rename(columns={'EdgeID': 'edgeID'}) \
.merge(
eeh_flow,
on="edgeID"
)
lu = {
# '01-BaU': '1:Business as Usual',
# '02-HighlyConnected': '2:Highly Connected',
# '03-AdaptedFleet': '3:Adapted Fleet',
# '04-BehavShiftPolicy': '4:Behaviour Shift (policy-led)',
# '05-BehavShiftResults': '5:Behaviour Shift (results-led)',
'01-BaU': '01 BaU',
'02-HighlyConnected': '02 HC',
'03-AdaptedFleet': '03 AF',
'04-BehavShiftPolicy': '04 BSp',
'05-BehavShiftResults': '05 BSr',
}
eeh_flowg.bestScenarioAtPeak = eeh_flowg.bestScenarioAtPeak \
.apply(lambda s: lu[s])
eeh_flowg.head(1)
eehcm = matplotlib.colors.ListedColormap(
[(74/255, 120/255, 199/255),
(238/255, 131/255, 54/255),
(170/255, 170/255, 170/255),
(255/255, 196/255, 0/255),
(84/255, 130/255, 53/255)],
name='eeh')
fig, ax = plt.subplots(1, 1)
ax.xaxis.set_visible(False)
ax.yaxis.set_visible(False)
eeh_zones.plot(ax=ax, color='#f2f2f2', edgecolor='white')
eeh_nb.plot(ax=ax, color='#eeeeee')
eeh_flowg.plot(column='bestScenarioAtPeak', ax=ax, legend=True, cmap=eehcm)
plt.savefig("bestScenarioPeakFlowRatio.png")
plt.savefig("bestScenarioPeakFlowRatio.svg")
```
## Link travel times direct
|
github_jupyter
|
```
#@title Copyright 2021 Google LLC. { display-mode: "form" }
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
```
<table class="ee-notebook-buttons" align="left"><td>
<a target="_blank" href="http://colab.research.google.com/github/google/earthengine-api/blob/master/python/examples/ipynb/Earth_Engine_TensorFlow_AI_Platform.ipynb">
<img src="https://www.tensorflow.org/images/colab_logo_32px.png" /> Run in Google Colab</a>
</td><td>
<a target="_blank" href="https://github.com/google/earthengine-api/blob/master/python/examples/ipynb/Earth_Engine_TensorFlow_AI_Platform.ipynb"><img width=32px src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" /> View source on GitHub</a></td></table>
# Introduction
This is an Earth Engine <> TensorFlow demonstration notebook. This demonstrates a per-pixel neural network implemented in a way that allows the trained model to be hosted on [Google AI Platform](https://cloud.google.com/ai-platform) and used in Earth Engine for interactive prediction from an `ee.Model.fromAIPlatformPredictor`. See [this example notebook](http://colab.research.google.com/github/google/earthengine-api/blob/master/python/examples/ipynb/TF_demo1_keras.ipynb) for background on the dense model.
**Running this demo may incur charges to your Google Cloud Account!**
# Setup software libraries
Import software libraries and/or authenticate as necessary.
## Authenticate to Colab and Cloud
To read/write from a Google Cloud Storage bucket to which you have access, it's necessary to authenticate (as yourself). *This should be the same account you use to login to Earth Engine*. When you run the code below, it will display a link in the output to an authentication page in your browser. Follow the link to a page that will let you grant permission to the Cloud SDK to access your resources. Copy the code from the permissions page back into this notebook and press return to complete the process.
(You may need to run this again if you get a credentials error later.)
```
from google.colab import auth
auth.authenticate_user()
```
## Upgrade Earth Engine and Authenticate
Update Earth Engine to ensure you have the latest version. Authenticate to Earth Engine the same way you did to the Colab notebook. Specifically, run the code to display a link to a permissions page. This gives you access to your Earth Engine account. *This should be the same account you used to login to Cloud previously*. Copy the code from the Earth Engine permissions page back into the notebook and press return to complete the process.
```
!pip install -U earthengine-api --no-deps
import ee
ee.Authenticate()
ee.Initialize()
```
## Test the TensorFlow installation
Import TensorFlow and check the version.
```
import tensorflow as tf
print(tf.__version__)
```
## Test the Folium installation
We will use the Folium library for visualization. Import the library and check the version.
```
import folium
print(folium.__version__)
```
# Define variables
The training data are land cover labels with a single vector of Landsat 8 pixel values (`BANDS`) as predictors. See [this example notebook](http://colab.research.google.com/github/google/earthengine-api/blob/master/python/examples/ipynb/TF_demo1_keras.ipynb) for details on how to generate these training data.
```
# REPLACE WITH YOUR CLOUD PROJECT!
PROJECT = 'your-project'
# Cloud Storage bucket with training and testing datasets.
DATA_BUCKET = 'ee-docs-demos'
# Output bucket for trained models. You must be able to write into this bucket.
OUTPUT_BUCKET = 'your-bucket'
# This is a good region for hosting AI models.
REGION = 'us-central1'
# Training and testing dataset file names in the Cloud Storage bucket.
TRAIN_FILE_PREFIX = 'Training_demo'
TEST_FILE_PREFIX = 'Testing_demo'
file_extension = '.tfrecord.gz'
TRAIN_FILE_PATH = 'gs://' + DATA_BUCKET + '/' + TRAIN_FILE_PREFIX + file_extension
TEST_FILE_PATH = 'gs://' + DATA_BUCKET + '/' + TEST_FILE_PREFIX + file_extension
# The labels, consecutive integer indices starting from zero, are stored in
# this property, set on each point.
LABEL = 'landcover'
# Number of label values, i.e. number of classes in the classification.
N_CLASSES = 3
# Use Landsat 8 surface reflectance data for predictors.
L8SR = ee.ImageCollection('LANDSAT/LC08/C01/T1_SR')
# Use these bands for prediction.
BANDS = ['B2', 'B3', 'B4', 'B5', 'B6', 'B7']
# These names are used to specify properties in the export of
# training/testing data and to define the mapping between names and data
# when reading into TensorFlow datasets.
FEATURE_NAMES = list(BANDS)
FEATURE_NAMES.append(LABEL)
# List of fixed-length features, all of which are float32.
columns = [
tf.io.FixedLenFeature(shape=[1], dtype=tf.float32) for k in FEATURE_NAMES
]
# Dictionary with feature names as keys, fixed-length features as values.
FEATURES_DICT = dict(zip(FEATURE_NAMES, columns))
```
# Read data
### Check existence of the data files
Check that you have permission to read the files in the output Cloud Storage bucket.
```
print('Found training file.' if tf.io.gfile.exists(TRAIN_FILE_PATH)
else 'No training file found.')
print('Found testing file.' if tf.io.gfile.exists(TEST_FILE_PATH)
else 'No testing file found.')
```
## Read into a `tf.data.Dataset`
Here we are going to read a file in Cloud Storage into a `tf.data.Dataset`. ([these TensorFlow docs](https://www.tensorflow.org/guide/data) explain more about reading data into a `tf.data.Dataset`). Check that you can read examples from the file. The purpose here is to ensure that we can read from the file without an error. The actual content is not necessarily human readable. Note that we will use all data for training.
```
# Create a dataset from the TFRecord file in Cloud Storage.
train_dataset = tf.data.TFRecordDataset([TRAIN_FILE_PATH, TEST_FILE_PATH],
compression_type='GZIP')
# Print the first record to check.
print(iter(train_dataset).next())
```
## Parse the dataset
Now we need to make a parsing function for the data in the TFRecord files. The data comes in flattened 2D arrays per record and we want to use the first part of the array for input to the model and the last element of the array as the class label. The parsing function reads data from a serialized `Example` proto (i.e. [`example.proto`](https://github.com/tensorflow/tensorflow/blob/r1.12/tensorflow/core/example/example.proto)) into a dictionary in which the keys are the feature names and the values are the tensors storing the value of the features for that example. ([Learn more about parsing `Example` protocol buffer messages](https://www.tensorflow.org/programmers_guide/datasets#parsing_tfexample_protocol_buffer_messages)).
```
def parse_tfrecord(example_proto):
"""The parsing function.
Read a serialized example into the structure defined by FEATURES_DICT.
Args:
example_proto: a serialized Example.
Returns:
A tuple of the predictors dictionary and the LABEL, cast to an `int32`.
"""
parsed_features = tf.io.parse_single_example(example_proto, FEATURES_DICT)
labels = parsed_features.pop(LABEL)
return parsed_features, tf.cast(labels, tf.int32)
# Map the function over the dataset.
parsed_dataset = train_dataset.map(parse_tfrecord, num_parallel_calls=4)
from pprint import pprint
# Print the first parsed record to check.
pprint(iter(parsed_dataset).next())
```
Note that each record of the parsed dataset contains a tuple. The first element of the tuple is a dictionary with bands names for keys and tensors storing the pixel data for values. The second element of the tuple is tensor storing the class label.
## Adjust dimension and shape
Turn the dictionary of *{name: tensor,...}* into a 1x1xP array of values, where P is the number of predictors. Turn the label into a 1x1x`N_CLASSES` array of indicators (i.e. one-hot vector), in order to use a categorical crossentropy-loss function. Return a tuple of (predictors, indicators where each is a three dimensional array; the first two dimensions are spatial x, y (i.e. 1x1 kernel).
```
# Inputs as a tuple. Make predictors 1x1xP and labels 1x1xN_CLASSES.
def to_tuple(inputs, label):
return (tf.expand_dims(tf.transpose(list(inputs.values())), 1),
tf.expand_dims(tf.one_hot(indices=label, depth=N_CLASSES), 1))
input_dataset = parsed_dataset.map(to_tuple)
# Check the first one.
pprint(iter(input_dataset).next())
input_dataset = input_dataset.shuffle(128).batch(8)
```
# Model setup
Make a densely-connected convolutional model, where the convolution occurs in a 1x1 kernel. This is exactly analogous to the model generated in [this example notebook](http://colab.research.google.com/github/google/earthengine-api/blob/master/python/examples/ipynb/TF_demo1_keras.ipynb), but operates in a convolutional manner in a 1x1 kernel. This allows Earth Engine to apply the model spatially, as demonstrated below.
Note that the model used here is purely for demonstration purposes and hasn't gone through any performance tuning.
## Create the Keras model
Before we create the model, there's still a wee bit of pre-processing to get the data into the right input shape and a format that can be used with cross-entropy loss. Specifically, Keras expects a list of inputs and a one-hot vector for the class. (See [the Keras loss function docs](https://keras.io/losses/), [the TensorFlow categorical identity docs](https://www.tensorflow.org/guide/feature_columns#categorical_identity_column) and [the `tf.one_hot` docs](https://www.tensorflow.org/api_docs/python/tf/one_hot) for details).
Here we will use a simple neural network model with a 64 node hidden layer. Once the dataset has been prepared, define the model, compile it, fit it to the training data. See [the Keras `Sequential` model guide](https://keras.io/getting-started/sequential-model-guide/) for more details.
```
from tensorflow import keras
# Define the layers in the model. Note the 1x1 kernels.
model = tf.keras.models.Sequential([
tf.keras.layers.Input((None, None, len(BANDS),)),
tf.keras.layers.Conv2D(64, (1,1), activation=tf.nn.relu),
tf.keras.layers.Dropout(0.1),
tf.keras.layers.Conv2D(N_CLASSES, (1,1), activation=tf.nn.softmax)
])
# Compile the model with the specified loss and optimizer functions.
model.compile(optimizer=tf.keras.optimizers.Adam(),
loss='categorical_crossentropy',
metrics=['accuracy'])
# Fit the model to the training data. Lucky number 7.
model.fit(x=input_dataset, epochs=7)
```
## Save the trained model
Export the trained model to TensorFlow `SavedModel` format in your cloud storage bucket. The [Cloud Platform storage browser](https://console.cloud.google.com/storage/browser) is useful for checking on these saved models.
```
MODEL_DIR = 'gs://' + OUTPUT_BUCKET + '/demo_pixel_model'
model.save(MODEL_DIR, save_format='tf')
```
# EEification
EEIfication prepares the model for hosting on [Google AI Platform](https://cloud.google.com/ai-platform). Learn more about EEification from [this doc](https://developers.google.com/earth-engine/tensorflow#interacting-with-models-hosted-on-ai-platform). First, get (and SET) input and output names of the nodes. **CHANGE THE OUTPUT NAME TO SOMETHING THAT MAKES SENSE FOR YOUR MODEL!** Keep the input name of 'array', which is how you'll pass data into the model (as an array image).
```
from tensorflow.python.tools import saved_model_utils
meta_graph_def = saved_model_utils.get_meta_graph_def(MODEL_DIR, 'serve')
inputs = meta_graph_def.signature_def['serving_default'].inputs
outputs = meta_graph_def.signature_def['serving_default'].outputs
# Just get the first thing(s) from the serving signature def. i.e. this
# model only has a single input and a single output.
input_name = None
for k,v in inputs.items():
input_name = v.name
break
output_name = None
for k,v in outputs.items():
output_name = v.name
break
# Make a dictionary that maps Earth Engine outputs and inputs to
# AI Platform inputs and outputs, respectively.
import json
input_dict = "'" + json.dumps({input_name: "array"}) + "'"
output_dict = "'" + json.dumps({output_name: "output"}) + "'"
print(input_dict)
print(output_dict)
```
## Run the EEifier
The actual EEification is handled by the `earthengine model prepare` command. Note that you will need to set your Cloud Project prior to running the command.
```
# Put the EEified model next to the trained model directory.
EEIFIED_DIR = 'gs://' + OUTPUT_BUCKET + '/eeified_pixel_model'
# You need to set the project before using the model prepare command.
!earthengine set_project {PROJECT}
!earthengine model prepare --source_dir {MODEL_DIR} --dest_dir {EEIFIED_DIR} --input {input_dict} --output {output_dict}
```
# Deploy and host the EEified model on AI Platform
Now there is another TensorFlow `SavedModel` stored in `EEIFIED_DIR` ready for hosting by AI Platform. Do that from the `gcloud` command line tool, installed in the Colab runtime by default. Be sure to specify a regional model with the `REGION` parameter. Note that the `MODEL_NAME` must be unique. If you already have a model by that name, either name a new model or a new version of the old model. The [Cloud Console AI Platform models page](https://console.cloud.google.com/ai-platform/models) is useful for monitoring your models.
**If you change anything about the trained model, you'll need to re-EEify it and create a new version!**
```
MODEL_NAME = 'pixel_demo_model'
VERSION_NAME = 'v0'
!gcloud ai-platform models create {MODEL_NAME} \
--project {PROJECT} \
--region {REGION}
!gcloud ai-platform versions create {VERSION_NAME} \
--project {PROJECT} \
--region {REGION} \
--model {MODEL_NAME} \
--origin {EEIFIED_DIR} \
--framework "TENSORFLOW" \
--runtime-version=2.3 \
--python-version=3.7
```
# Connect to the hosted model from Earth Engine
1. Generate the input imagery. This should be done in exactly the same way as the training data were generated. See [this example notebook](http://colab.research.google.com/github/google/earthengine-api/blob/master/python/examples/ipynb/TF_demo1_keras.ipynb) for details.
2. Connect to the hosted model.
3. Use the model to make predictions.
4. Display the results.
Note that it takes the model a couple minutes to spin up and make predictions.
```
# Cloud masking function.
def maskL8sr(image):
cloudShadowBitMask = ee.Number(2).pow(3).int()
cloudsBitMask = ee.Number(2).pow(5).int()
qa = image.select('pixel_qa')
mask = qa.bitwiseAnd(cloudShadowBitMask).eq(0).And(
qa.bitwiseAnd(cloudsBitMask).eq(0))
return image.updateMask(mask).select(BANDS).divide(10000)
# The image input data is a 2018 cloud-masked median composite.
image = L8SR.filterDate('2018-01-01', '2018-12-31').map(maskL8sr).median()
# Get a map ID for display in folium.
rgb_vis = {'bands': ['B4', 'B3', 'B2'], 'min': 0, 'max': 0.3, 'format': 'png'}
mapid = image.getMapId(rgb_vis)
# Turn into an array image for input to the model.
array_image = image.float().toArray()
# Point to the model hosted on AI Platform. If you specified a region other
# than the default (us-central1) at model creation, specify it here.
model = ee.Model.fromAiPlatformPredictor(
projectName=PROJECT,
modelName=MODEL_NAME,
version=VERSION_NAME,
# Can be anything, but don't make it too big.
inputTileSize=[8, 8],
# Keep this the same as your training data.
proj=ee.Projection('EPSG:4326').atScale(30),
fixInputProj=True,
# Note the names here need to match what you specified in the
# output dictionary you passed to the EEifier.
outputBands={'output': {
'type': ee.PixelType.float(),
'dimensions': 1
}
},
)
# model.predictImage outputs a one dimensional array image that
# packs the output nodes of your model into an array. These
# are class probabilities that you need to unpack into a
# multiband image with arrayFlatten(). If you want class
# labels, use arrayArgmax() as follows.
predictions = model.predictImage(array_image)
probabilities = predictions.arrayFlatten([['bare', 'veg', 'water']])
label = predictions.arrayArgmax().arrayGet([0]).rename('label')
# Get map IDs for display in folium.
probability_vis = {
'bands': ['bare', 'veg', 'water'], 'max': 0.5, 'format': 'png'
}
label_vis = {
'palette': ['red', 'green', 'blue'], 'min': 0, 'max': 2, 'format': 'png'
}
probability_mapid = probabilities.getMapId(probability_vis)
label_mapid = label.getMapId(label_vis)
# Visualize the input imagery and the predictions.
map = folium.Map(location=[37.6413, -122.2582], zoom_start=11)
folium.TileLayer(
tiles=mapid['tile_fetcher'].url_format,
attr='Map Data © <a href="https://earthengine.google.com/">Google Earth Engine</a>',
overlay=True,
name='median composite',
).add_to(map)
folium.TileLayer(
tiles=label_mapid['tile_fetcher'].url_format,
attr='Map Data © <a href="https://earthengine.google.com/">Google Earth Engine</a>',
overlay=True,
name='predicted label',
).add_to(map)
folium.TileLayer(
tiles=probability_mapid['tile_fetcher'].url_format,
attr='Map Data © <a href="https://earthengine.google.com/">Google Earth Engine</a>',
overlay=True,
name='probability',
).add_to(map)
map.add_child(folium.LayerControl())
map
```
|
github_jupyter
|
# Prominent paths originating from epilepsy to a Compound
```
import math
import pandas
from neo4j import GraphDatabase
from tqdm.notebook import tqdm
import hetnetpy.readwrite
import hetnetpy.neo4j
from src.database_utils import get_db_connection
epilepsy_id = 'DOID:1826'
# Get top ten most important metapaths for Compound-epilepsy
query = f'''\
SELECT
outer_pc.dwpc as dwpc,
outer_pc.p_value as p_value,
outer_pc.metapath_id as metapath_id,
top_ids.source_name as source_name,
top_ids.target_name as target_name
FROM (
SELECT dwpc, p_value, metapath_id, source_id, target_id, n1.name AS source_name, n2.name AS target_name
FROM dj_hetmech_app_pathcount pc
JOIN dj_hetmech_app_node join_node
ON pc.target_id=join_node.id OR pc.source_id=join_node.id
JOIN dj_hetmech_app_node n1
ON pc.source_id = n1.id
JOIN dj_hetmech_app_node n2
ON pc.target_id = n2.id
WHERE join_node.identifier='{epilepsy_id}' AND (n1.metanode_id = 'Compound' OR n2.metanode_id = 'Compound')
ORDER BY pc.p_value
) AS top_ids
JOIN dj_hetmech_app_pathcount outer_pc
ON (top_ids.source_id = outer_pc.source_id AND
top_ids.target_id = outer_pc.target_id) OR
(top_ids.source_id = outer_pc.target_id AND
top_ids.target_id = outer_pc.source_id)
ORDER BY outer_pc.p_value;
'''
with get_db_connection() as connection:
top_metapaths = pandas.read_sql(query, connection)
top_metapaths = top_metapaths.sort_values(by=['source_name', 'metapath_id'])
# Ensure that you only have one copy of each (source_name, metapath_id) pair
top_metapaths = top_metapaths.drop_duplicates(subset=['source_name', 'metapath_id'])
top_metapaths = top_metapaths.sort_values(by='p_value')
# Remove any rows with NaN values
top_metapaths = top_metapaths.dropna()
min_p_value = top_metapaths[top_metapaths.p_value != 0].p_value.min()
top_metapaths.loc[top_metapaths.p_value == 0, 'p_value'] = min_p_value
print(top_metapaths.p_value.min())
top_metapaths['neg_log_p_value'] = top_metapaths.p_value.apply(lambda x: -math.log10(x))
top_metapaths.head()
url = 'https://github.com/hetio/hetionet/raw/76550e6c93fbe92124edc71725e8c7dd4ca8b1f5/hetnet/json/hetionet-v1.0-metagraph.json'
metagraph = hetnetpy.readwrite.read_metagraph(url)
def get_paths_for_metapath(metagraph, row):
'''
Return a list of dictionaries containing the information for all paths with a given source, target, and metapath
Parameters
----------
metagraph : a hetnetpy.hetnet.Metagraph instance to interpret metapath abbreviations
row : a row from a pandas dataframe with information about the given metapath, source, and target
'''
damping_exponent = .5
metapath_data = metagraph.metapath_from_abbrev(row['metapath_id'])
query = hetnetpy.neo4j.construct_pdp_query(metapath_data, path_style='string', property='name')
driver = GraphDatabase.driver("bolt://neo4j.het.io")
params = {
'source': row['source_name'],
'target': row['target_name'],
'w': damping_exponent
}
with driver.session() as session:
metapath_result = session.run(query, params)
metapath_result = metapath_result.data()
for path in metapath_result:
path['metapath'] = row['metapath_id']
path['metapath_importance'] = row['neg_log_p_value']
path['path_importance'] = path['metapath_importance'] * path['percent_of_DWPC']
path['source'] = row['source_name']
metapath_df = pandas.DataFrame(metapath_result)
return metapath_df
%%time
# For row in top_metapaths
result_list = []
for index, row in tqdm(top_metapaths.iterrows(), total=len(top_metapaths.index)):
metapath_df = get_paths_for_metapath(metagraph, row)
result_list.append(metapath_df)
result_df = pandas.concat(result_list, ignore_index=True)
result_df = result_df.sort_values(by=['source', 'path_importance', 'metapath'], ascending=[True, False, True])
result_df.head()
result_df.to_csv('data/epilepsy_paths.tsv.xz', index=False, sep='\t', float_format="%.5g")
```
|
github_jupyter
|
```
from hyperneat.spatial_node import SpatialNode, SpatialNodeType
from hyperneat.substrate import Substrate
from hyperneat.evolution import Hyperneat
from neat.genes import ConnectionGene, NodeGene, NodeType
from neat.genome import Genome
from neat.activation_functions import ActivationFunction
from neat.neural_network import NeuralNetwork
import numpy as np
import matplotlib.pyplot as plt
import os
import sys
# Genome
genome = Genome(num_layers=15, weights_range=[-3.0, 3.0])
genome.create_genome_by_size(8, 3)
net = genome.build_phenotype()
# Substrate setting
# Init substrate set
substrate_set = []
for i in range(2):
s = Substrate()
s.activation_function = ActivationFunction().get('TANH')
# Must create new objects or deep copies
s.input_nodes = [SpatialNode(0, SpatialNodeType.INPUT, [0.0, -0.5], ActivationFunction().get('TANH'), 0)]
s.output_nodes = [SpatialNode(1, SpatialNodeType.OUTPUT, [-0.5, 0.5], ActivationFunction().get('TANH'), 2),
SpatialNode(2, SpatialNodeType.OUTPUT, [0.5, 0.5], ActivationFunction().get('TANH'), 2)]
s.hidden_nodes = [SpatialNode(3, SpatialNodeType.HIDDEN, [-0.5, 0.0], ActivationFunction().get('TANH'), 1),
SpatialNode(4, SpatialNodeType.HIDDEN, [0.5, 0.0], ActivationFunction().get('TANH'), 1)]
s.input_count = 1
s.output_count = 2
s.hidden_count = 2
s.extend_nodes_list()
substrate_set.append(s)
substrate_set[0].coordinates = (-0.5, 0.5)
substrate_set[1].coordinates = (0.5, 0.5)
intra_substrate_conn = [[0, 1], [0, 2], [0, 3], [0, 4], [3, 1], [3, 2], [3, 4], [4, 1], [4, 2], [4, 3]]
inter_substrate_conn = [[0, 4, 1, 3], [1, 3, 0, 4]]
ea = Hyperneat()
ea.connection_threshold = 0.05
ea.max_connection_weight = 0.5
ea.max_bias = 0.06
ea.max_delay = 0.2
net = ea.build_modular_substrate(genome, substrate_set, intra_substrate_conn, inter_substrate_conn)
net.reset_values()
time = np.linspace(0, 20, 20 / 0.05)
signal_1 = np.sin(time)
signal_2 = np.cos(time)
output_signal = np.zeros([4, time.shape[0]])
out_id = net.out_neurons
for t, _ in enumerate(time):
net.input([signal_1[t], signal_2[t]])
net.activate_net(0.05)
for o, oid in enumerate(out_id):
output_signal[o, t] = net.neurons[oid].output
fig, ax = plt.subplots(2, 2)
ax[0, 0].plot(output_signal[0])
ax[0, 1].plot(output_signal[1])
ax[1, 0].plot(output_signal[2])
ax[1, 1].plot(output_signal[3])
plt.tight_layout()
np.linspace(0, 1, int(6 / 0.05), endpoint=False).shape[0]
inter_substrate_conn = [[0, 1], [0, 2], [0, 3], [0, 4], [3, 1], [3, 2], [3, 4], [4, 1], [4, 2], [4, 3]]
inter_substrate_conn = inter_substrate_conn * 4, [[1, 0], [2, 0], [3, 0], [4, 0]]
inter_substrate_conn[0]
arr = []
for _ in range(4):
arr.append(inter_substrate_conn)
arr.append([[1, 0], [2, 0], [3, 0], [4, 0]])
arr
for item in arr[0]:
print(item)
```
|
github_jupyter
|
### Task Video :
#### Dataset Link:
Dataset can be found at " /data/videos/ " in the respective challenge's repo.
#### Description:
Video series is just a sequence of images arranged in a specific order. Images of that sequence are called frames. Therefore, in video intelligence tasks, we take advantage of the temporal nature of video and semantic content in consecutive frames.
#### Objective:
How to read video data and convert it into useable format for machine learning
#### Tasks:
- Load dataset from provided link. Videos are in “.mp4” format.
- Extract frames from video at fps=10 (opencv’s VideoCapture Class)
- Plot 4th frame of 'VID_2.mp4' (matplotlib or Pillow library)
- Print dimensions of any single frame of 'VID_6.mp4'
- Print all pixel values of 10th frame of 'VID_14.mp4'
- Perform sanity check for each video whether all frames have same dimensions or not
#### Further fun (will not be evaluated):
_Prerequisites: CNN and image processing_
- We will perform video classification for fun on this sample dataset. You can download labels here: _(Link to be added soon or self-annotation for small dataset is also possible)_
- Train image classifier on all frames extracted at fps=10 from all videos.
- The naive approach to do video classification would be to classify each frame and save results in sequential format, and that is it !! Obviously there are much better ways of doing video classification taking advantage of the temporal nature of data.
#### Helpful Links:
- Detailed description of how to process video frames: https://www.youtube.com/watch?v=tQetgoLy70s
- Nice tutorial on video classification: https://www.analyticsvidhya.com/blog/2018/09/deep-learning-video-classification-python/
- Used .avi format but the idea is same: https://www.analyticsvidhya.com/blog/2019/09/step-by-step-deep-learning-tutorial-video-classification-python/
- Line-by-Line explanation of video classification code: https://www.pyimagesearch.com/2019/07/15/video-classification-with-keras-and-deep-learning/
```
import cv2 # For handling videos
import matplotlib.pyplot as plt # For plotting images, you can use pillow library as well
import numpy as np # For mathematical operations
# Capture the video from a file
videoFile = 'data/videos/VID_2.mp4'
cap = cv2.VideoCapture(videoFile)
# Get frame rate of video
frameRate = cap.get(5)
print("Frame rate of video:", frameRate)
# Get time length of video
total_frames = cap.get(7)
print("Total frames:", total_frames)
print("Length of video: %.2f seconds" % (total_frames/frameRate))
# https://docs.opencv.org/2.4/modules/highgui/doc/reading_and_writing_images_and_video.html#videocapture-get
# Get frame width and height
width = cap.get(3)
height = cap.get(4)
print("(width, height) = ", (width,height))
# Defining desired fps
desired_fps = 10
frame_skipping_rate = int(np.ceil(frameRate / desired_fps))
print("Frame skipping rate:", frame_skipping_rate, "frames")
# Store frames
frames = []
# Start extracting frames till we reach the end of the loop
while(cap.isOpened()):
# Get the current frame number
frameId = cap.get(1)
# Reads the next incoming frame
ret, frame = cap.read()
# If we reached the end of the video, then ret returns true
if (ret != True):
break
if (frameId % frame_skipping_rate == 0):
frames.append(frame)
cap.release()
print ("Done!")
# NHWC
single_video = np.array(frames)
print("NHWC format:", single_video.shape)
print("Plotted 4th frame of 2nd video")
plt.imshow(single_video[3,:,:,:])
plt.show()
print("Dimensions of 5th frame of 6th video")
single_video[4,:,:,:].shape
single_video[13,:,:,:]
```
### Here's the solution now
```
import glob
filenames = glob.glob('data/videos/*.mp4')
print(filenames)
videos = {}
for file in filenames:
cap = cv2.VideoCapture(file)
frameRate = cap.get(5)
desired_fps = 10
frame_skipping_rate = int(np.ceil(frameRate / desired_fps))
# Store frames
frames = []
# Start extracting frames till we reach the end of the loop
while(cap.isOpened()):
# Get the current frame number
frameId = cap.get(1)
# Reads the next incoming frame
ret, frame = cap.read()
# If we reached the end of the video, then ret returns true
if (ret != True):
break
if (frameId % frame_skipping_rate == 0):
frames.append(frame)
cap.release()
frames = np.array(frames)
videos[file] = frames
print("Number of videos:", len(videos))
plt.imshow(videos["data/videos\\VID_2.mp4"][3,:,:,:])
plt.show()
videos["data/videos\\VID_6.mp4"][4,:,:,:].shape
videos["data/videos\\VID_14.mp4"][13,:,:,:]
sanity_check = True
dim_set = set()
for video in videos.values():
dim_set.add(video[0].shape) # Get dimensions of first frame and add it in set
if len(dim_set)>1:
sanity_check = False
print("Sanity check:", sanity_check)
```
|
github_jupyter
|
# *Data Visualization and Statistics*
Gallery of Matplotlib examples: [https://matplotlib.org/gallery.html](https://matplotlib.org/gallery.html)
```
## First, let's import some packages.
import os
from pprint import pprint
from textblob import TextBlob
import numpy as np
from scipy import stats
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
# The line above tells Jupyter to display Matplotlib graphics within the notebook.
## Download sample text corpora from GitHub, then unzip.
os.chdir('/sharedfolder/')
!wget -N https://github.com/pcda17/pcda17.github.io/blob/master/week/8/Sample_corpora.zip?raw=true -O Sample_corpora.zip
!unzip -o Sample_corpora.zip
os.chdir('/sharedfolder/Sample_corpora')
os.listdir('./')
!ls Jane_Austen
!ls Herman_Melville
## Loading a Melville novel as a TextBlob object
melville_path = 'Herman_Melville/Moby_Dick.txt'
melville_blob = TextBlob(open(melville_path).read().replace('\n', ' '))
## Loading an Austen novel as a TextBlob object
austen_path = 'Jane_Austen/Pride_and_Prejudice.txt'
austen_blob = TextBlob(open(austen_path).read().replace('\n', ' '))
## Recall that 'some_textblob_object.words' is a WordList object ...
melville_blob.words[5100:5140]
# ... which we can cast to an ordinary list.
list(melville_blob.words[5100:5140])
## And 'some_textblob_object.sentences' is a list of Sentence objects ...
austen_blob.sentences[100:105]
# ... which we can convert to a list of strings using a list comprehension.
[str(item) for item in austen_blob.sentences[100:105]]
## For reference, here's another example of a list comprehension:
word_list = ['Call', 'me', 'Ishmael.']
uppercase_list = [word.upper() for word in word_list]
uppercase_list
## And one more for good measure:
string_nums = [str(i) for i in range(12)]
string_nums
```
### ▷ Sentiment analysis with TextBlob
Details on the training data that NLTK (via TextBlob) uses to measure polarity:
[http://www.cs.cornell.edu/people/pabo/movie-review-data/](http://www.cs.cornell.edu/people/pabo/movie-review-data/)
```
## Negative sentiment polarity example
# (result between -1 and +1)
from textblob import TextBlob
text = "This is a very mean and nasty sentence."
blob = TextBlob(text)
sentiment_score = blob.sentiment.polarity
print(sentiment_score)
## Positive sentiment polarity example
# (result between -1 and +1)
text = "This is a very nice and positive sentence."
blob = TextBlob(text)
sentiment_score = blob.sentiment.polarity
print(sentiment_score)
## Neutral polarity / not enough information
text = "What is this?"
blob = TextBlob(text)
sentiment_score = blob.sentiment.polarity
print(sentiment_score)
## High subjectivity example
# result between 0 and 1
text="This is a very mean and nasty sentence."
blob = TextBlob(text)
sentiment_score = blob.sentiment.subjectivity
print(sentiment_score)
## Low subjectivity example
# result between 0 and 1
text="This sentence states a fact, with an apparently objective adjective."
blob = TextBlob(text)
sentiment_score=blob.sentiment.subjectivity
print(sentiment_score)
```
### ▷ Plotting Sentiment Values
Let's map sentiment polarity values across the course of a full novel.
```
## Viewing Pyplot style templates
pprint(plt.style.available)
## Selecting a Pyplot style
plt.style.use('ggplot')
# The 'ggplot' style imitates the R graphing package 'ggplot2.' (http://ggplot2.org)
austen_sentiments = [item.sentiment.polarity for item in austen_blob.sentences]
austen_sentiments[:15]
## Austen sentiment values for first 60 sentences
plt.figure(figsize=(18,8))
plt.plot(austen_sentiments[:60])
austen_blob.sentences[30]
austen_blob.sentences[37]
## Plotting 'Pride and Prejudice' sentence sentiment values over full novel
plt.figure(figsize=(18,8))
plt.plot(austen_sentiments)
plt.show()
## Finding the most 'positive' sentences in 'Pride and Prejudice' and printing them
max_sentiment = max(austen_sentiments)
print(max_sentiment) # max sentiment polarity value
print()
for sentence in austen_blob.sentences:
if sentence.sentiment.polarity == max_sentiment:
print(sentence)
print()
## Finding the most 'negative' sentences in 'Pride and Prejudice' and printing them
min_sentiment = min(austen_sentiments)
print(min_sentiment) # max sentiment polarity value
print()
for sentence in austen_blob.sentences:
if sentence.sentiment.polarity == min_sentiment:
print(sentence)
print()
## Example: smoothing a list of numbers using the 'pandas' package
some_values = [5, 4, 5, 6, 6, 7, 6, 19, 4, 4, 3, 3, 3, 1, 5, 5, 6, 7, 0]
pandas_series = pd.Series(some_values)
list(pandas_series.rolling(window=4).mean())
## Smoothing our data before plotting
austen_sentiments_pd = pd.Series(austen_sentiments)
austen_sentiments_smooth = austen_sentiments_pd.rolling(window=200).mean()
print(austen_sentiments_smooth[190:220])
## Plotting smoothed sentiment polarity values for each sentence in 'Pride and Prejudice'
plt.figure(figsize=(18,8))
plt.plot(austen_sentiments_smooth)
plt.show()
## Comparing 'Moby Dick' sentiment values
melville_sentiments = [item.sentiment.polarity for item in melville_blob.sentences]
melville_sentiments_pd = pd.Series(melville_sentiments)
melville_sentiments_smooth = melville_sentiments_pd.rolling(window=200).mean()
plt.figure(figsize=(18,8))
plt.plot(melville_sentiments_smooth)
plt.show()
## Finding and printing the most 'negative' sentence in a list of smoothed sentiment values
min_sentiment = min(melville_sentiments_smooth[199:])
print(min_sentiment) # min sentiment polarity value
print()
min_sentiment_index = list(melville_sentiments_smooth).index(min_sentiment) # index position of the 'min_sentiment' value
print(melville_blob.sentences[min_sentiment_index])
## Finding and printing the most 'positive' sentence in a list of smoothed sentiment values
max_sentiment = max(melville_sentiments_smooth[199:])
print(max_sentiment) # max sentiment polarity value
print()
max_sentiment_index = list(melville_sentiments_smooth).index(max_sentiment) # index position of the 'min_sentiment' value
print(melville_blob.sentences[max_sentiment_index])
## Finding and printing the most 'positive' sentence in a list of smoothed sentiment values
max_sentiment = max(austen_sentiments_smooth[199:])
print(max_sentiment) # max sentiment polarity value
print()
max_sentiment_index = list(austen_sentiments_smooth).index(max_sentiment) # index position of the 'max_sentiment' value
print(austen_blob.sentences[max_sentiment_index])
## Finding and printing the most 'negative' sentence in a list of smoothed sentiment values
min_sentiment = min(austen_sentiments_smooth[199:])
print(min_sentiment) # min sentiment polarity value
print()
min_sent_index=list(austen_sentiments_smooth).index(min_sentiment) # index position of the 'min_sentiment' value
print(austen_blob.sentences[min_sent_index])
## Creating functions to expedite the steps we put together above process
# This function accepts an optional second argument for smoothing window size. The default is 200 windows.
def plot_polarity(text_path, window=200):
text_in = open(text_path).read().replace('\n', ' ')
blob = TextBlob(text_in)
sentiments = [sentence.sentiment.polarity for sentence in blob.sentences]
sentiments_pd = pd.Series(sentiments)
sentiments_smooth = sentiments_pd.rolling(window).mean()
plt.figure(figsize = (18,8))
plt.plot(sentiments_smooth)
plt.show()
!find ./
plot_polarity('George_Eliot/Silas_Marner.txt')
plot_polarity('Joseph_Conrad/Heart_of_Darkness.txt')
```
### ▷ Plotting smoothed random data (for comparison)
```
## Plotting completely random data
random_vals = np.random.rand(4000)
vals_pd = pd.Series(random_vals)
vals_smooth = vals_pd.rolling(window=200).mean()
plt.figure(figsize=(18,8))
plt.plot(vals_smooth)
```
### ▷ Working with multiple files
```
!ls *
os.chdir('/sharedfolder/Sample_corpora/Inaugural_Speeches/')
sorted(os.listdir('./'))
inaugural_filenames = sorted(os.listdir('./'))
inaugural_sentiment_values = []
for filename in inaugural_filenames:
inaugural_text = open(filename).read()
sentiment_polarity_value = TextBlob(inaugural_text).sentiment.polarity
inaugural_sentiment_values.append(sentiment_polarity_value)
print(inaugural_sentiment_values)
## Creating nicely formatted labels for the sentiment values above
inaugural_labels = [item.replace('.txt','').replace('_', ' ').title() for item in inaugural_filenames]
inaugural_labels
## Plotting presidential inaugural address sentiment values over time
plt.figure(figsize = (20,8))
plt.xticks(range(len(inaugural_sentiment_values)), inaugural_labels) # two arguments: tick positions, tick display list
plt.xticks(rotation=-85)
plt.ylabel('Sentiment Polarity Value')
plt.plot(inaugural_sentiment_values)
plt.show()
```
## ▷ Assignment
For each author in our set of corpora, which is their most 'positive' novel? Their most 'negative'?
## ▷ Sentiment Histograms
```
os.chdir('/sharedfolder/Sample_corpora/')
text_in = open('Jane_Austen/Pride_and_Prejudice.txt').read().replace('\n', ' ')
blob = TextBlob(text_in)
sentiments = [sentence.sentiment.polarity for sentence in blob.sentences]
plt.figure(figsize=(20,10))
plt.hist(sentiments, bins=25)
plt.show()
text_in = open('Jane_Austen/Pride_and_Prejudice.txt').read().replace('\n', ' ')
blob = TextBlob(text_in)
sentiments = [sentence.sentiment.subjectivity for sentence in blob.sentences]
plt.figure(figsize=(20,10))
plt.hist(sentiments, bins=25)
plt.show()
```
## ▷ Cleaning sentiment values
```
text_in = open('Jane_Austen/Pride_and_Prejudice.txt').read().replace('\n', ' ')
blob = TextBlob(text_in)
sentiments = [sentence.sentiment.polarity for sentence in blob.sentences]
sentiments_cleaned = [value for value in sentiments if value!=0]
plt.figure(figsize=(20,10))
plt.hist(sentiments_cleaned, bins=25)
plt.show()
def polarity_histogram_cleaned(text_path):
text_in = open(text_path).read().replace('\n', ' ')
blob = TextBlob(text_in)
sentiments = [sentence.sentiment.polarity for sentence in blob.sentences]
sentiments_cleaned = [value for value in sentiments if value!=0]
plt.figure(figsize=(20,10))
plt.hist(sentiments_cleaned, bins=25)
plt.show()
!find ./
polarity_histogram_cleaned('./Joseph_Conrad/The_Secret_Agent.txt')
```
## ▷ Comparing Sentiment Distributions
```
melville_blob = TextBlob(open('Herman_Melville/Moby_Dick.txt').read().replace('\n', ' '))
austen_blob = TextBlob(open('Jane_Austen/Pride_and_Prejudice.txt').read().replace('\n', ' '))
melville_sentiments = [sentence.sentiment.polarity for sentence in melville_blob.sentences]
melville_sentiments_cleaned = [value for value in melville_sentiments if value!=0.0]
austen_sentiments = [sentence.sentiment.polarity for sentence in austen_blob.sentences]
austen_sentiments_cleaned = [value for value in austen_sentiments if value!=0.0]
plt.figure(figsize=(15,8))
plt.hist(melville_sentiments_cleaned, bins=25, alpha=0.5, label='Moby Dick')
plt.hist(austen_sentiments_cleaned, bins=25, alpha=0.5, label='Pride and Prejudice')
plt.legend(loc='upper right')
plt.show()
print(np.mean(melville_sentiments_cleaned))
print(np.mean(austen_sentiments_cleaned))
```
## ▷ Statistical Tests
```
## t-test of independent values
# (used to determine whether two *normally distributed* sets of values are significantly different)
from scipy import stats
stats.ttest_ind(melville_sentiments_cleaned, austen_sentiments_cleaned)
## Mann-Whitney U test
# (used to test two sets of *non-normally distributed* values are significantly different)
stats.mannwhitneyu(melville_sentiments, austen_sentiments)
```
## ▷ Assignment
Is George Eliot significantly more subjective than Jane Austen?
Is Herman Melville significantly more 'positive' than Joseph Conrad?
## ▷ Assignment
Write a function that takes two texts' paths as arguments and
(a) plots a histogram comparing their sentences' sentiment distributions
(b) tests whether their sentiment values are significantly different
|
github_jupyter
|
### Introduction
This is a `View` Notebook to show an `IntSlider` widget either in an interactive Notebook or in a `Voila` Dashboard mode that will then print the [Fibonnaci sequence](https://en.wikipedia.org/wiki/Fibonacci_number) answer for that number. It will also show how long it takes each handler to calculate the number, which should demonstrate what kind of overhead is involved with `refactored code`, `PythonModel`, and `KernelModel`.
```
import ipywidgets as widgets
grid = widgets.GridspecLayout(4, 3)
# top row
input_label = widgets.Label("User Input")
user_input = widgets.IntText(value=1, description='Fibonnaci n:')
grid[0, 0] = input_label
grid[0, 1:] = user_input
# refactored code row
label1 = widgets.Label('Refactored code')
output1 = widgets.Text(disabled=True, description='Result:')
debug1 = widgets.Text(disabled=True, description='Debug:')
grid[1, 0] = label1
grid[1, 1] = output1
grid[1, 2] = debug1
# PythonModel row
label2 = widgets.Label('PythonModel')
output2 = widgets.Text(disabled=True, description='Result:')
debug2 = widgets.Text(disabled=True, description='Debug:')
grid[2, 0] = label2
grid[2, 1] = output2
grid[2, 2] = debug2
# KernelModel row
label3 = widgets.Label('KernelModel')
output3 = widgets.Text(disabled=True, description='Result:')
debug3 = widgets.Text(disabled=True, description='Debug:')
grid[3, 0] = label3
grid[3, 1] = output3
grid[3, 2] = debug3
grid
import time
### Refactored code handler
def fibonacci_generator():
"A generator that yields the last number in the sequence plus the number before that"
a, b = 0, 1
while True:
yield a
tmp_value = b
b = a + b
a = tmp_value
def handler1(ev):
start = time.time()
gen = fibonacci_generator()
n = user_input.value
for i in range(n+1):
answer = next(gen)
output1.value = str(answer)
debug1.value = 'took %.4f seconds' % (time.time() - start)
user_input.observe(handler1, names='value')
### Create PythonModel and KernelModel objects
import notebook_restified
pm = notebook_restified.PythonModel('model.ipynb')
km = notebook_restified.KernelModel('model.ipynb')
### PythonModel handler
def handler2(ev):
start = time.time()
params = {'n' : user_input.value}
result = pm.execute(params)
output2.value = str(result)
debug2.value = 'took %.4f seconds' % (time.time() - start)
user_input.observe(handler2, names='value')
### KernelModel handler
def handler3(ev):
start = time.time()
params = {'n' : user_input.value}
result = km.execute(params)
output3.value = str(result)
debug3.value = 'took %.4f seconds' % (time.time() - start)
user_input.observe(handler3, names='value')
```
|
github_jupyter
|
## 1. Meet Dr. Ignaz Semmelweis
<p><img style="float: left;margin:5px 20px 5px 1px" src="https://s3.amazonaws.com/assets.datacamp.com/production/project_20/img/ignaz_semmelweis_1860.jpeg"></p>
<!--
<img style="float: left;margin:5px 20px 5px 1px" src="https://s3.amazonaws.com/assets.datacamp.com/production/project_20/datasets/ignaz_semmelweis_1860.jpeg">
-->
<p>This is Dr. Ignaz Semmelweis, a Hungarian physician born in 1818 and active at the Vienna General Hospital. If Dr. Semmelweis looks troubled it's probably because he's thinking about <em>childbed fever</em>: A deadly disease affecting women that just have given birth. He is thinking about it because in the early 1840s at the Vienna General Hospital as many as 10% of the women giving birth die from it. He is thinking about it because he knows the cause of childbed fever: It's the contaminated hands of the doctors delivering the babies. And they won't listen to him and <em>wash their hands</em>!</p>
<p>In this notebook, we're going to reanalyze the data that made Semmelweis discover the importance of <em>handwashing</em>. Let's start by looking at the data that made Semmelweis realize that something was wrong with the procedures at Vienna General Hospital.</p>
```
# importing modules
import pandas as pd
# Read datasets/yearly_deaths_by_clinic.csv into yearly
yearly = pd.read_csv('datasets/yearly_deaths_by_clinic.csv')
# Print out yearly
print(yearly)
```
## 2. The alarming number of deaths
<p>The table above shows the number of women giving birth at the two clinics at the Vienna General Hospital for the years 1841 to 1846. You'll notice that giving birth was very dangerous; an <em>alarming</em> number of women died as the result of childbirth, most of them from childbed fever.</p>
<p>We see this more clearly if we look at the <em>proportion of deaths</em> out of the number of women giving birth. Let's zoom in on the proportion of deaths at Clinic 1.</p>
```
# Calculate proportion of deaths per no. births
yearly["proportion_deaths"]=yearly['deaths']/yearly['births']
# Extract clinic 1 data into yearly1 and clinic 2 data into yearly2
yearly1 = yearly[yearly["clinic"] == "clinic 1"]
yearly2 = yearly[yearly["clinic"] == "clinic 2"]
# Print out yearly1
print(yearly1)
```
## 3. Death at the clinics
<p>If we now plot the proportion of deaths at both clinic 1 and clinic 2 we'll see a curious pattern...</p>
```
# This makes plots appear in the notebook
%matplotlib inline
import matplotlib.pyplot as plt
# Plot yearly proportion of deaths at the two clinics
ax = yearly1.plot(x="year",
y="proportion_deaths",
label="Clinic 1")
yearly2.plot(x="year", y="proportion_deaths",
label="Clinic 2", ax=ax)
ax.set_ylabel("Proportion deaths")
```
## 4. The handwashing begins
<p>Why is the proportion of deaths constantly so much higher in Clinic 1? Semmelweis saw the same pattern and was puzzled and distressed. The only difference between the clinics was that many medical students served at Clinic 1, while mostly midwife students served at Clinic 2. While the midwives only tended to the women giving birth, the medical students also spent time in the autopsy rooms examining corpses. </p>
<p>Semmelweis started to suspect that something on the corpses, spread from the hands of the medical students, caused childbed fever. So in a desperate attempt to stop the high mortality rates, he decreed: <em>Wash your hands!</em> This was an unorthodox and controversial request, nobody in Vienna knew about bacteria at this point in time. </p>
<p>Let's load in monthly data from Clinic 1 to see if the handwashing had any effect.</p>
```
# Read datasets/monthly_deaths.csv into monthly
monthly = pd.read_csv("datasets/monthly_deaths.csv", parse_dates=["date"])
# Calculate proportion of deaths per no. births
monthly["proportion_deaths"] = monthly['deaths']/ monthly['births']
# Print out the first rows in monthly
monthly.head()
```
## 5. The effect of handwashing
<p>With the data loaded we can now look at the proportion of deaths over time. In the plot below we haven't marked where obligatory handwashing started, but it reduced the proportion of deaths to such a degree that you should be able to spot it!</p>
```
# Plot monthly proportion of deaths
ax = monthly.plot(x="date", y="proportion_deaths")
ax.set_ylabel("Proportion deaths")
```
## 6. The effect of handwashing highlighted
<p>Starting from the summer of 1847 the proportion of deaths is drastically reduced and, yes, this was when Semmelweis made handwashing obligatory. </p>
<p>The effect of handwashing is made even more clear if we highlight this in the graph.</p>
```
# Date when handwashing was made mandatory
import pandas as pd
handwashing_start = pd.to_datetime('1847-06-01')
# Split monthly into before and after handwashing_start
before_washing = monthly[monthly["date"] < handwashing_start]
after_washing = monthly[monthly["date"] >= handwashing_start]
# Plot monthly proportion of deaths before and after handwashing
ax = before_washing.plot(x="date", y="proportion_deaths",
label="Before handwashing")
after_washing.plot(x="date", y="proportion_deaths",
label="After handwashing", ax=ax)
ax.set_ylabel("Proportion deaths")
```
## 7. More handwashing, fewer deaths?
<p>Again, the graph shows that handwashing had a huge effect. How much did it reduce the monthly proportion of deaths on average?</p>
```
# Difference in mean monthly proportion of deaths due to handwashing
before_proportion = before_washing["proportion_deaths"]
after_proportion = after_washing["proportion_deaths"]
mean_diff = after_proportion.mean() - before_proportion.mean()
mean_diff
```
## 8. A Bootstrap analysis of Semmelweis handwashing data
<p>It reduced the proportion of deaths by around 8 percentage points! From 10% on average to just 2% (which is still a high number by modern standards). </p>
<p>To get a feeling for the uncertainty around how much handwashing reduces mortalities we could look at a confidence interval (here calculated using the bootstrap method).</p>
```
# A bootstrap analysis of the reduction of deaths due to handwashing
boot_mean_diff = []
for i in range(3000):
boot_before = before_proportion.sample(frac=1, replace=True)
boot_after = after_proportion.sample(frac=1, replace=True)
boot_mean_diff.append( boot_after.mean() - boot_before.mean() )
# Calculating a 95% confidence interval from boot_mean_diff
confidence_interval = pd.Series(boot_mean_diff).quantile([0.025, 0.975])
confidence_interval
```
## 9. The fate of Dr. Semmelweis
<p>So handwashing reduced the proportion of deaths by between 6.7 and 10 percentage points, according to a 95% confidence interval. All in all, it would seem that Semmelweis had solid evidence that handwashing was a simple but highly effective procedure that could save many lives.</p>
<p>The tragedy is that, despite the evidence, Semmelweis' theory — that childbed fever was caused by some "substance" (what we today know as <em>bacteria</em>) from autopsy room corpses — was ridiculed by contemporary scientists. The medical community largely rejected his discovery and in 1849 he was forced to leave the Vienna General Hospital for good.</p>
<p>One reason for this was that statistics and statistical arguments were uncommon in medical science in the 1800s. Semmelweis only published his data as long tables of raw data, but he didn't show any graphs nor confidence intervals. If he would have had access to the analysis we've just put together he might have been more successful in getting the Viennese doctors to wash their hands.</p>
```
# The data Semmelweis collected points to that:
doctors_should_wash_their_hands = True
```
|
github_jupyter
|
# Time-energy fit
3ML allows the possibility to model a time-varying source by explicitly fitting the time-dependent part of the model. Let's see this with an example.
First we import what we need:
```
from threeML import *
import matplotlib.pyplot as plt
from jupyterthemes import jtplot
%matplotlib inline
jtplot.style(context="talk", fscale=1, ticks=True, grid=False)
plt.style.use("mike")
```
## Generating the datasets
Then we generate a simulated dataset for a source with a cutoff powerlaw spectrum with a constant photon index and cutoff but with a normalization that changes with time following a powerlaw:
```
def generate_one(K, ax):
# Let's generate some data with y = Powerlaw(x)
gen_function = Cutoff_powerlaw()
gen_function.K = K
# Generate a dataset using the power law, and a
# constant 30% error
x = np.logspace(0, 2, 50)
xyl_generator = XYLike.from_function(
"sim_data", function=gen_function, x=x, yerr=0.3 * gen_function(x)
)
y = xyl_generator.y
y_err = xyl_generator.yerr
ax.loglog(x, gen_function(x))
return x, y, y_err
```
These are the times at which the simulated spectra have been observed
```
time_tags = np.array([1.0, 2.0, 5.0, 10.0])
```
This describes the time-varying normalization. If everything works as it should, we should recover from the fit a normalization of 0.23 and a index of -1.2 for the time law.
```
normalizations = 0.23 * time_tags ** (-3.5)
```
Now that we have a simple function to create the datasets, let's build them.
```
fig, ax = plt.subplots()
datasets = [generate_one(k, ax) for k in normalizations]
ax.set_xlabel("Energy")
ax.set_ylabel("Flux")
```
## Setup the model
Now set up the fit and fit it. First we need to tell 3ML that we are going to fit using an independent variable (time in this case). We init it to 1.0 and set the unit to seconds.
```
time = IndependentVariable("time", 1.0, u.s)
```
Then we load the data that we have generated, tagging them with their time of observation.
```
plugins = []
for i, dataset in enumerate(datasets):
x, y, y_err = dataset
xyl = XYLike("data%i" % i, x, y, y_err)
# This is the important part: we need to tag the instance of the
# plugin so that 3ML will know that this instance corresponds to the
# given tag (a time coordinate in this case). If instead of giving
# one time coordinate we give two time coordinates, then 3ML will
# take the average of the model between the two time coordinates
# (computed as the integral of the model between t1 and t2 divided
# by t2-t1)
xyl.tag = (time, time_tags[i])
# To access the tag we have just set we can use:
independent_variable, start, end = xyl.tag
# NOTE: xyl.tag will return 3 things: the independent variable, the start and the
# end. If like in this case you do not specify an end when assigning the tag, end
# will be None
plugins.append(xyl)
```
Generate the datalist as usual
```
data = DataList(*plugins)
```
Now let's generate the spectral model, in this case a point source with a cutoff powerlaw spectrum.
```
spectrum = Cutoff_powerlaw()
src = PointSource("test", ra=0.0, dec=0.0, spectral_shape=spectrum)
model = Model(src)
```
Now we need to tell 3ML that we are going to use the time coordinate to specify a time dependence for some of the parameters of the model.
```
model.add_independent_variable(time)
```
Now let's specify the time-dependence (a powerlaw) for the normalization of the powerlaw spectrum.
```
time_po = Powerlaw()
time_po.K.bounds = (0.01, 1000)
```
Link the normalization of the cutoff powerlaw spectrum with time through the time law we have just generated.
```
model.link(spectrum.K, time, time_po)
model
```
## Performing the fit
```
jl = JointLikelihood(model, data)
best_fit_parameters, likelihood_values = jl.fit()
for p in plugins:
p.plot(x_scale='log', y_scale='log');
```
|
github_jupyter
|
<a name="top"></a>
<div style="width:1000 px">
<div style="float:right; width:98 px; height:98px;">
<img src="https://raw.githubusercontent.com/Unidata/MetPy/master/metpy/plots/_static/unidata_150x150.png" alt="Unidata Logo" style="height: 98px;">
</div>
<h1>Hodographs</h1>
<h3>Unidata Python Workshop</h3>
<div style="clear:both"></div>
</div>
<hr style="height:2px;">
<div style="float:right; width:250 px"><img src="https://unidata.github.io/MetPy/latest/_images/sphx_glr_Advanced_Sounding_001.png" alt="Example Skew-T" style="height: 500px;"></div>
### Questions
1. What is a hodograph?
1. How can MetPy plot hodographs?
1. How can the style of the hodographs be modified to encode other information?
### Objectives
1. <a href="#upperairdata">Obtain upper air data</a>
1. <a href="#simpleplot">Make a simple hodograph</a>
1. <a href="#annotate">Annotate the hodograph with wind vectors</a>
1. <a href="#continuous">Color the plot (continuous)</a>
1. <a href="#segmented">Color the plot (segmented)</a>
<a name="upperairdata"></a>
## Obtain upper air data
Just as we learned in the siphon basics and upper air and skew-T notebook, we need to obtain upperair data to plot. We are going to stick with September 10, 2017 at 00Z for Key West, Fl. If you need a review on obtaining upper air data, please review those lessons.
```
from datetime import datetime
from metpy.units import pandas_dataframe_to_unit_arrays
from siphon.simplewebservice.wyoming import WyomingUpperAir
df = WyomingUpperAir.request_data(datetime(1998, 10, 4, 0), 'OUN')
data = pandas_dataframe_to_unit_arrays(df)
```
<a href="#top">Top</a>
<hr style="height:2px;">
<a name="simpleplot"></a>
## Make a Simple Hodograph
The hodograph is a plot of the wind shear in the sounding. It is constructed by drawing the winds as vectors from the origin and connecting the heads of those vectors. MetPy makes this simple!
```
import matplotlib.pyplot as plt
from metpy.plots import Hodograph
%matplotlib inline
fig = plt.figure(figsize=(6, 6))
ax = fig.add_subplot(1, 1, 1)
h = Hodograph(ax, component_range=60.)
h.add_grid(increment=20)
h.plot(data['u_wind'], data['v_wind'], color='tab:red')
```
It's relatively common to not want or need to display the entire sounding on a hodograph. Let's limit these data to the lowest 10km and plot it again.
```
import metpy.calc as mpcalc
from metpy.units import units
_, u_trimmed, v_trimmed, speed_trimmed, height_trimmed = mpcalc.get_layer(data['pressure'], data['u_wind'],
data['v_wind'], data['speed'], data['height'],
heights=data['height'], depth=10 * units.km)
fig = plt.figure(figsize=(6, 6))
ax = fig.add_subplot(1, 1, 1)
h = Hodograph(ax, component_range=30.)
h.add_grid(increment=10)
h.plot(u_trimmed, v_trimmed, color='tab:red')
```
<a name="annotate"></a>
## Annotate the hodograph with wind vectors
It may be useful when introducing hodographs to actually show the wind vectors on the plot. The `wind_vectors` method does exactly this. It is often necessary to decimate the wind vectors for the plot to be intelligible.
```
h.wind_vectors(u_trimmed[::3], v_trimmed[::3])
fig
```
We can also set the limits to be asymmetric to beter utilize the plot space.
```
ax.set_xlim(-10, 30)
ax.set_ylim(-10, 20)
fig
```
<a name="continuous"></a>
## Color the plot (continuous)
We can color the line on the hodograph by another variable as well. In the simplest case it will be "continuously" colored, changing with the value of the variable such as windspeed.
```
fig = plt.figure(figsize=(6, 6))
ax = fig.add_subplot(1, 1, 1)
h = Hodograph(ax, component_range=30.)
h.add_grid(increment=10)
h.plot_colormapped(u_trimmed, v_trimmed, speed_trimmed)
from metpy.plots import colortables
import numpy as np
fig = plt.figure(figsize=(6, 6))
ax = fig.add_subplot(1, 1, 1)
norm, cmap = colortables.get_with_range('Carbone42', np.min(speed_trimmed), np.max(speed_trimmed))
h = Hodograph(ax, component_range=30.)
h.add_grid(increment=10)
h.plot_colormapped(u_trimmed, v_trimmed, speed_trimmed, cmap=cmap, norm=norm)
```
<a name="segmented"></a>
## Color the plot (segmented)
It may be useful when introducing hodographs to actually show the wind vectors on the plot. The `wind_vectors` method does exactly this. It is often necessary to decimate the wind vectors for the plot to be intelligible.
We can also color the hodograph based on another variable - either continuously or in a segmented way. Here we'll color the hodograph by height above ground level.
```
fig = plt.figure(figsize=(6, 6))
ax = fig.add_subplot(1, 1, 1)
boundaries = np.array([0, 1, 3, 5, 8]) * units.km
colors = ['tab:red', 'tab:green', 'tab:blue', 'tab:olive']
# Since we want to do things in terms of AGL, we need to make AGL heights
agl = height_trimmed - height_trimmed[0]
h = Hodograph(ax, component_range=30.)
h.add_grid(increment=10)
h.plot_colormapped(u_trimmed, v_trimmed, agl, bounds=boundaries, colors=colors)
```
<a href="#top">Top</a>
<hr style="height:2px;">
|
github_jupyter
|
```
import holoviews as hv
hv.extension('bokeh')
hv.opts.defaults(hv.opts.Curve(width=500),
hv.opts.Image(width=500, colorbar=True, cmap='Viridis'))
import numpy as np
import scipy.signal
import scipy.fft
from IPython.display import Audio
```
# Diseño de sistemas y filtros IIR
Un filtro FIR de buena calidad puede requerir una gran cantidad de coeficientes
Es posible implementar filtros más eficientes usando **recursividad**. Esta es la base de los filtros de respuesta al impulso infinita o IIR que veremos en esta lección
## Definición de un sistema IIR
Generalizando el sistema FIR para incluir versiones pasadas de la salida y asumiendo $a[0] = 1$ llegamos a
$$
\begin{align}
y[n] &= b[0] x[n] + b[1] x[n-1] + b[2] x[n-2] + \ldots + b[L] x[n-L] \nonumber \\
& - a[1] y[n-1] - a[2] y[n-2] - \ldots - a[M] y[n-M] \nonumber \\
&= \sum_{l=0}^{L} b[l] x[n-l] - \sum_{m=1}^{M} a[m] y[n-m] \nonumber \\
\sum_{m=0}^{M} a[m] y[n-m] &= \sum_{l=0}^{L} b[l] x[n-l] \nonumber \\
(a * y)[n] &= (b * x)[n], \nonumber
\end{align}
$$
es decir dos convoluciones discretas que definen una **ecuación de diferencias**
Este tipo de sistema se conoce como
- sistema *infinite impulse response* (IIR)
- sistema *auto-regresive moving average* (ARMA)
- autoregresivo de orden M: incluye valores pasados de la salida
- media movil de orden L+1: pondera el valor presente y pasados de la entrada
Podemos ver el sistema IIR como una generalización del sistema FIR. El caso particular del sistema FIR se recupera si
$a[m] = 0$ para $m=[1, \ldots, M]$
### Respuesta en frecuencia del sistema IIR
Aplicando la transformada de Fourier convertimos las convoluciones en multiplicaciones y encontramos la respuesta en frecuencia como
$$
\begin{align}
\text{DFT}_N[(a * y)[n]] &= \text{DFT}_N[(b * x)[n]] \nonumber \\
A[k] Y[k] &= B[k] X[k] \nonumber \\
H[k] = \frac{Y[k]}{X[k]} &= \frac{B[k]}{A[k]} = \frac{ \sum_{l=0}^L b[l]e^{-j \frac{2\pi}{N} nl} }{ \sum_{m=0}^M a[m]e^{-j \frac{2\pi}{N} mk}} \nonumber
\end{align}
$$
que existe siempre que $A[k] \neq 0$.
La respuesta en frecuencia también suele expresarse como
$$
H[k] = K \frac{ \prod_{l=1}^L (e^{j \frac{2\pi}{N} k}- \beta[l]) }{ \prod_{m=1}^M (e^{j \frac{2\pi}{N} k}- \alpha[m])}
$$
donde
- $K$ se llama **ganancia**
- las raices del polinomio del numerador $\alpha$ se llaman conjuntamente **ceros**
- las raices del polinomio del denominador $\beta$ se llaman conjuntamente **polos**
### Ejemplo de respuesta al impulso de un sistema IIR
Consideremos el siguiente sistema IIR
$$
\begin{align}
y[n] &= (1-\gamma) x[n] + \gamma y[n-1] \nonumber \\
y[n] - \gamma y[n-1] &= (1-\gamma) x[n] \nonumber
\end{align}
$$
Los coeficientes del sistema son
$a[0] = 1$, $a[1] = -\gamma$ y $b[0] = (1-\gamma)$
Es decir que es AR de orden 1 y MA de orden 1
¿Cúal es su respuesta al impulso? Asumiendo $y[n]=0, n<0$, tenemos que
$$
\begin{matrix}
n & \delta[n] & y[n] \\
-2 & 0 & 0 \\
-1 & 0 & 0 \\
0 & 1 & (1-\gamma) \\
1 & 0 & \gamma(1-\gamma) \\
2 & 0 & \gamma^2(1-\gamma) \\
3 & 0 & \gamma^3(1-\gamma) \\
4 & 0 & \gamma^4(1-\gamma) \\
\end{matrix}
$$
¿Cómo cambia la respuesta al impulso con distintos valores de $\gamma$? ¿Qué pasa si $\gamma \geq 1$?
Respondamos estas preguntas visualizando la respuesta al impulso de este sistema con la función `scipy.signal.dimpulse`
```
# Valores de gamma que probaremos:
gamma = [-1.5, -1, -0.5, 0.5, 1., 1.5]
p = []
for g in gamma:
t, y = scipy.signal.dimpulse(([1-g, 0], [1,-g], 1), x0=0, n=30)
p.append(hv.Curve((t, y[0][:, 0]), label=f"gamma={g}"))
hv.Layout(p).cols(3).opts(hv.opts.Curve(width=250, height=200, axiswise=True))
```
De las figuras podemos ver que:
- Para $\gamma < 0$ (primera fila) los coeficientes del sistema son alternantes en signo
- Para $|\gamma| < 1$ los coeficientes del sistema tienden a cero
- Para $|\gamma| > 1$ los coeficientes del sistema divergen y tienen a infinito
:::{warning}
A diferencia de un sistema FIR, el sistema IIR puede tener configuraciones inestables en que los coeficientes crecen o decrecen infinitamente
:::
Por otro lado consideremos el sistema anterior y asumamos que $|\gamma|<1$, desenrollando tenemos que
$$
\begin{align}
y[0] &= (1-\gamma) x[0] \nonumber \\
y[1] &= (1-\gamma) (x[1] + \gamma x[0]) \nonumber \\
y[2] &= (1-\gamma) (x[2] + \gamma x[1] + \gamma^2 x[0]) \nonumber \\
y[3] &= (1-\gamma) (x[3] + \gamma x[2] + \gamma^2 x[1] + \gamma^3 x[0]) \nonumber \\
y[4] &= (1-\gamma) (x[4] + \gamma x[3] + \gamma^2 x[2] + \gamma^3 x[1] + \gamma^4 x[0]) \nonumber \\
y[5] &= \ldots \nonumber
\end{align}
$$
:::{note}
Con un sistema IIR de pocos coeficientes podemos representar un sistema FIR considerablemente más grande
:::
En el ejemplo anterior, si escogemos $\gamma$ tal que $\gamma^{20 }\approx 0$ entonces aproximamos un sistema FIR de orden 20 con tan sólo 3 coeficientes
### Ejemplo de respuesta en frecuencia de un sistema IIR
Para el sistema del ejemplo anterior su respuesta en frecuencia es
$$
\begin{align}
Y[k] &= (1-\gamma) X[k] + \gamma Y[k] e^{-j \frac{2\pi}{N} k} \nonumber \\
H[k] = \frac{Y[k]}{X[k]} &= \frac{1-\gamma}{1 - \gamma e^{-j \frac{2\pi}{N} k} } \nonumber
\end{align}
$$
que en notación de polos y ceros se escribe como
$$
H[k] = (1-\gamma)\frac{e^{j \frac{2\pi}{N} k} - 0}{e^{j \frac{2\pi}{N} k} - \gamma }
$$
es decir que tiene un cero en $0$, un polo en $\gamma$ y una ganancia de $(1-\gamma)$
Para entender mejor este sistema estudiemos la magnitud de $|H[k]|$ para $\gamma < 1$
$$
\begin{align}
| H[k]| &= \frac{|1-\gamma|}{|1 - \gamma e^{-j \frac{2\pi}{N} k}|} \nonumber \\
&= \frac{1-\gamma}{\sqrt{1 - 2\gamma \cos(\frac{2\pi}{N} k) + \gamma^2}} \nonumber
\end{align}
$$
¿Cómo se ve $|H[k]|$? ¿Qué función cumple este sistema?
```
k = np.arange(-24, 25)/50
Hk = lambda gamma, k : (1-gamma)/np.sqrt(1 - 2*gamma*np.cos(2.0*np.pi*k) + gamma**2)
p = []
for gamma in [0.25, 0.5, 0.75]:
p.append(hv.Curve((k, Hk(gamma, k)), 'Frecuencia', 'Respuesta', label=f'gamma={gamma}'))
hv.Overlay(p)
```
:::{note}
Este sistema atenua las frecuencias altas, es decir que actua como un filtro pasa bajos
:::
## Diseño de filtros IIR simples
Los filtros IIR más simples son los de un polo y un cero, es decir filtros de primer orden
$$
H[k] = \frac{b[0] + b[1] e^{-j \frac{2\pi}{N} k}}{1 + a[1] e^{-j \frac{2\pi}{N} k}} = K\frac{e^{j \frac{2\pi}{N} k} - \beta}{e^{j \frac{2\pi}{N} k} - \alpha }
$$
donde podemos reconocer
- $b[0]=K$
- $\beta = - b[1] \cdot K$
- $\alpha=-a[1]$
Definimos la frecuencia de corte $f_c$ como aquella frecuencia en la que el filtro alcanza una atenuación de 0.7 (-3 dB). Haciendo la equivalencia con el ejemplo anterior tenemos que $\gamma = e^{-2\pi f_c}$
### Receta para un filtro pasa bajo IIR con frecuencia de corte $f_c$
Asignamos
- $b[0] = 1 - e^{-2\pi f_c}$
- $b[1] = 0$
- $a[1] = -e^{-2\pi f_c}$
Lo que resulta en la siguiente respuesta en frecuencia
$$
H[k] = \frac{1-e^{-2\pi f_c}}{1 - e^{-2\pi f_c} e^{-j \frac{2\pi}{N} k}} = (1-e^{-2\pi f_c}) \frac{(e^{j \frac{2\pi}{N} k}- 0)}{(e^{j \frac{2\pi}{N} k} - e^{-2\pi f_c} )}
$$
Es decir un cero en $0$, un polo en $e^{-2\pi f_c}$ y ganancia $1-e^{-2\pi f_c}$
### Receta para un filtro pasa alto IIR con frecuencia de corte $f_c$
Asignamos
- $b[0] = (1 + e^{-2\pi f_c})/2$
- $b[1] = -(1 + e^{-2\pi f_c})/2$
- $a[1] = -e^{-2\pi f_c}$
Lo que resulta en la siguiente respuesta en frecuencia
$$
H[k] = \frac{1+e^{-2\pi f_c}}{2} \frac{(e^{j \frac{2\pi}{N} k} - 1)}{(e^{j \frac{2\pi}{N} k} - e^{-2\pi f_c})}
$$
Es decir un cero en $1$, un polo en $e^{-2\pi f_c}$ y ganancia $\frac{1+e^{-2\pi f_c}}{2}$
### Aplicar un filtro a una señal con scipy
Para filtrar una señal unidimensional con un filtro IIR (sin variar la fase de la señal) podemos utilizar la función
```python
scipy.signal.filtfilt(b, # Coeficientes del numerador
a, # Coeficientes del denominador
x, # Señal a filtrar
...
)
```
Los siguientes ejemplos muestran un señal de tipo pulso rectangular filtrada con sistemas IIR de primer orden pasa bajo y pasa-alto diseñados con las recetas mostradas anteriormente
```
n = np.arange(0, 500)
x = 0.5 + 0.5*scipy.signal.square((n)/(2.*np.pi*5), duty=0.3)
def iir_low_pass(signal, fc):
gamma = np.exp(-2*np.pi*(fc))
b, a = [(1-gamma), 0], [1, -gamma]
return scipy.signal.filtfilt(b, a, signal)
y = {}
for fc in [0.05, 0.02, 0.01]:
y[fc] = iir_low_pass(x, fc)
px = hv.Curve((n, x))
py = []
for fc, y_ in y.items():
py.append(hv.Curve((n, y_), label=f'fc={fc}'))
hv.Layout([px, hv.Overlay(py)]).cols(1).opts(hv.opts.Curve(height=200))
def iir_high_pass(signal, fc):
gamma = np.exp(-2*np.pi*(fc))
b, a = [(1+gamma)/2, -(1+gamma)/2], [1, -gamma]
return scipy.signal.filtfilt(b, a, signal)
y = {}
for fc in [0.01, 0.02, 0.05]:
y[fc] = iir_high_pass(x, fc)
px = hv.Curve((n, x))
py = []
for fc, y_ in y.items():
py.append(hv.Curve((n, y_), label=f'fc={fc}'))
hv.Layout([px, hv.Overlay(py)]).cols(1).opts(hv.opts.Curve(height=200))
```
:::{note}
El filtro pasa-bajos suaviza los cambios de los pulsos rectangulares. El filtro pasa-altos elimina las zonas constantes y resalta los cambios de la señal.
:::
## Diseño de filtros IIR de segundo orden
Los filtros IIR de segundo orden o **biquad** tienen dos polos y dos ceros.
Su respuesta en frecuencia es
$$
H[k] = \frac{b[0] + b[1] W_N^k + b[2] W_N^{2k}}{1 + a[1] W_N^k + a[2] W_N^{2k}} = K \frac{(W_N^{-k} - \beta_1) (W_N^{-k} - \beta_2)}{(W_N^{-k} - \alpha_1)(W_N^{-k} - \alpha_2)},
$$
donde $W_N = e^{-j \frac{2 \pi}{N}}$ y la relación entreo coeficientes y polos/ceros es:
$$
b[0] = K, \quad b[1] = -K (\beta_1 + \beta_2), \quad b[2]= K \beta_1\beta_2
$$
$$
a[1] = - (\alpha_1 + \alpha_2), \quad a[2]=\alpha_1 \alpha_2
$$
Con arquitecturas de segundo orden se pueden crear filtros pasabanda y rechaza banda
## Diseño de filtros IIR de orden mayor
Para crear los coeficientes de filtro IIR de orden mayor podemos usar la función
```python
scipy.signal.iirfilter(N, # Orden del filtro
Wn, # Frecuencias de corte (normalizadas en [0,1])
fs, # Frecuencia de muestreo
btype='bandpass', # Tipo de filtro: 'bandpass', 'lowpass', 'highpass', 'bandstop'
ftype='butter', # Familia del filtro: 'butter', 'ellip', 'cheby1', 'cheby2', 'bessel'
output='ba', # Retornar coeficientes
...
)
```
El filtro Butterworth es óptimo en el sentido de tener la banda de paso lo más plana posible.
Otros filtros se diseñaron con otras consideraciones.
Los filtros IIR digitales están basados en los filtros IIR analógicos.
Observe como al aumentar el orden el filtro pasabajo IIR comienza a cortar de forma más abrupta
```
Hk = {}
for order in [1, 2, 5, 20]:
b, a = scipy.signal.iirfilter(N=order, Wn=0.2, fs=1,
ftype='butter', btype='lowpass', output='ba')
freq, response = scipy.signal.freqz(b, a, fs=1)
Hk[order] = np.abs(response)
p = []
for order, response in Hk.items():
p.append(hv.Curve((freq, response), 'Frecuencia', 'Respuesta', label=f'orden={order}'))
hv.Overlay(p)
```
## Comparación de la respuesta en frecuencia de filtros FIR e IIR del orden equivalente
Comparemos la respuesta en frecuencia de un filtro IIR y otro FIR ambos pasa-bajo con 20 coeficientes
```
Fs = 1
fc = 0.25
h = scipy.signal.firwin(numtaps=20, cutoff=fc, pass_zero=True, window='hann', fs=Fs)
b, a = scipy.signal.iirfilter(N=9, Wn=fc, fs=Fs, ftype='butter', btype='lowpass')
display(len(h), len(b)+len(a))
freq_fir, response_fir = scipy.signal.freqz(h, 1, fs=Fs)
freq_iir, response_iir = scipy.signal.freqz(b, a, fs=Fs)
p1 = hv.Curve((freq_fir, np.abs(response_fir)), 'Frecuencia', 'Respuesta', label='FIR')
p2 = hv.Curve((freq_iir, np.abs(response_iir)), 'Frecuencia', 'Respuesta', label='IIR')
hv.Overlay([p1, p2])*hv.VLine(fc).opts(color='k', alpha=0.5)
```
La linea negra marca la ubicación de la frecuencia de corte
:::{note}
El filtro IIR es mucho más abrupto, es decir filtra mejor, que el filtro FIR equivalente
:::
Una desventaja del filtro IIR es que por definición introduce una desfase no constante en la señal de salida
```
freq_fir, delay_fir = scipy.signal.group_delay(system=(h, 1), fs=Fs)
freq_iir, delay_iir = scipy.signal.group_delay(system=(b, a), fs=Fs)
p1 = hv.Curve((freq_fir, delay_fir), 'Frecuencia', 'Desfase', label='FIR')
p2 = hv.Curve((freq_iir, delay_iir), 'Frecuencia', 'Desfase', label='IIR')
hv.Overlay([p1, p2])*hv.VLine(fc).opts(color='k', alpha=0.5)
```
¿Cómo se ve una señal filtrada donde se preserva la fase versus una donde no se preserva la fase?
Consideremos la señal rectangular anterior y apliquemos un filtro pasa-bajo IIR de orden 1
Esta vez compararemos el filtro con la función `scipy.signal.lfilter` y la función `scipy.signal.filtfilt`. La primera no preserva la fase mientras que la segunda si lo hace
```
Fs = 1
fc = 0.01
n = np.arange(0, 500)
x = 0.5 + 0.5*scipy.signal.square((n)/(2.*np.pi*5), duty=0.3)
b, a = scipy.signal.iirfilter(N=1, Wn=fc, fs=Fs, ftype='butter', btype='lowpass')
# No se preserva la fase
y_lfilter = scipy.signal.lfilter(b, a, x)
# Se preserva la fase
y_filtfilt = scipy.signal.filtfilt(b, a, x)
px = hv.Curve((n, x), 'Tiempo', 'Entrada')
py = []
py.append(hv.Curve((n, y_filtfilt), 'Tiempo', 'Salida', label=f'Fase constante'))
py.append(hv.Curve((n, y_lfilter), 'Tiempo', 'Salida', label=f'Fase no constante'))
hv.Layout([px, hv.Overlay(py)]).cols(1).opts(hv.opts.Curve(height=200))
```
:::{note}
En el caso donde no se preserva la fase podemos notar que la señal de salida está desplazada con respecto a la original. Además los cambios tienen una transición asimétrica
:::
La función `scipy.signal.filtfilt` "arregla" el problema del desfase filtrando la señal dos veces. La primera vez se filtra hacia adelante en el tiempo y la segunda vez hacia atrás. Por ende no se puede aplicar en un escenario de tipo *streaming* donde los datos van llegando de forma causal.
En una aplicación causal donde se necesite preservar la fase debemos usar un filtro FIR.
## Apéndice: Efectos de audio con filtros IIR
El siguiente ejemplo muestra como implementar el conocido filtro <a href="https://en.wikipedia.org/wiki/Wah-wah_(music)">Wah-wah</a> usando un sistema IIR
Este es un filtro pasabanda modulado con ancho de pasada fijo $f_b$ [Hz] y una frecuencia central variable $f_c$ [Hz], donde La frecuencia central se modula con una onda lenta
Se modela como el siguiente sistema **IIR**
$$
H[k] = \frac{(1+c)W_N^{2k} -(1+c) }{W_N^{2k} + d(1-c)W_N^k -c}
$$
donde
$$
d=-\cos(2\pi f_c/f_s)
$$
y
$$
c = \frac{\tan(\pi f_b/f_s) -1}{\tan(2\pi f_b /f_s)+1}
$$
Veamos como modifica este filtro una señal de audio
```
import librosa
data, fs = librosa.load("../../data/DPSAU.ogg")
Audio(data, rate=fs)
data_wah = []
zi = np.zeros(shape=(2,))
# Parámetros fijos del filtro
fb, Nw = 200, 5
c = (np.tan(np.pi*fb/fs) - 1.)/(np.tan(2*np.pi*fb/fs) +1)
# Filtramos una ventana de la señal moviendo lentamente fc
for k in range(len(data)//Nw):
# Cálculo de la frecuencia central
fc = 500 + 2000*(np.cos(2.0*np.pi*k*30./fs) +1)/2
d = -np.cos(2*np.pi*fc/fs)
# Coeficientes del filtro
b, a = [(1+c), 0, -(1+c)], [1, d*(1-c), -c]
# Filtramos, usando el filtrado anterior como borde (zi)
data2, zi = scipy.signal.lfilter(b, a, data[k*Nw:(k+1)*Nw], zi=zi)
# Guardamos
data_wah.append(data2)
Audio(np.hstack(data_wah), rate=int(fs))
```
Si quieres profundizar en el tema de los filtros IIR aplicados a efectos de audio recomiendo: https://www.ee.columbia.edu/~ronw/adst-spring2010/lectures/lecture2.pdf
|
github_jupyter
|
# The Schrödinger equation
#### Let's have some serious fun!
We'll look at the solutions of the Schrödinger equation for a harmonic potential.
```
from __future__ import absolute_import
from __future__ import division
from __future__ import print_function
import numpy as np
import math
from math import pi as Pi
import matplotlib.pyplot as plt
from scipy import (inf, integrate)
import seaborn as sns
sns.set()
```
### Prelude: Hermite's Polynomials
Hermite's Polynomials are a subset of polynomials that will help us construct solutions of the Schrödinger equation.
#### Modelling polynomials
Some object-oriented Python programming with polynomials. We represent an arbitrary polynomial
$$
P(x) = \sum_{n=0}^{N} p_n \cdot x^n
$$
unambiguously by its coefficients $p_n$, i.e. an array of real numbers of length $N+1$. Apart from the algebraic operators we also define the multiplication with x as ```mulx()``` and the differentiation as ```d_dx()```.
```
class Polynomial():
"""
A class representing a polynomial by its coefficients
"""
def __init__(self, array=[0]):
self.p = np.array(array)
def mulx(self):
return Polynomial(np.insert(self.p, 0, 0))
def d_dx(self):
return Polynomial([i*self.p[i] for i in range(1, len(self.p))])
def __eq__(self, other):
return np.equal(self.p, other.p).all()
def __rmul__(self, number):
return Polynomial(number * self.p)
def __sub__(self, other):
l=max(len(self.p), len(other.p))
return Polynomial(Polynomial.pad(self.p,l) - Polynomial.pad(other.p,l))
def __add__(self, other):
l=max(len(self.p), len(other.p))
return Polynomial(Polynomial.pad(self.p,l) + Polynomial.pad(other.p,l))
def __call__(self, x):
return np.sum([self.p[i] * x**i for i in range(len(self.p))], axis=0)
@staticmethod
def pad(array, l):
if len(array) == l:
return array
if len(array) > l:
raise ValueError("can't pad to lower dimension")
return np.append(array, np.zeros(l-len(array)))
@staticmethod
def mono_repr(c, i):
if c==0:
return ''
if i==0:
return str(int(c))
elif i==1:
return "{}x".format(int(c))
else:
if c==1:
return "x^{}".format(i)
else:
return "{}x^{}".format(int(c),i)
def __repr__(self):
return " + ".join(
np.flipud([Polynomial.mono_repr(self.p[i],i)
for i in range(len(self.p)) if self.p[i] != 0] ))
```
#### The Hermite Polynomial generator
Now, Hermite's polynomials are a special subset of all polynomials, defined e.g. by a recursion relation:
From [Wikipedia](https://en.wikipedia.org/wiki/Hermite_polynomials) (if not good memories), we know that
$$
H_n(x) = (2x-\frac{d}{dx})^n \cdot 1
$$
generates the *physicist's* Hermite polynomials. We define our python generator in a recursive fashion returning Polynomial instances
$$
H_n(x) = (2x-\frac{d}{dx}) \cdot H_{n-1}
$$
```
def H(n):
if n<0:
raise ValueError("Not defined for negativ n")
if n==0:
return Polynomial([1])
p = H(n-1)
return 2 * p.mulx() - p.d_dx()
```
Note that we can evaluate the polynomial at any (even complex) x.
```
H_3 = H(3)
H_3, H_3(1), H_3(1+2j)
```
The Hermite polynomials have the special properties:
$$
x \cdot H_\nu(x) = \frac{1}{2} H_{\nu+1}(x) + \nu \cdot H_{\nu-1}(x)
$$
$$
\frac{d}{dx}H_\nu(x) = 2 \nu \cdot H_{\nu-1}(x)
$$
which we can verify using our implementation for the first 10 polynomials ($\nu = {1..9}$):
```
[H(nu).mulx() == .5 * H(nu+1) + nu*H(nu-1) for nu in range(1,10)]
[H(nu).d_dx() == 2 * nu * H(nu - 1) for nu in range(1,10)]
```
---
### The time-dependent Schrödinger equation
$$
i\hbar \frac{\partial \Psi(x,t)}{\partial t} =
\mathcal{H}\Psi(x,t) =
E\Psi(x,t)
$$
This is the Schrödinger equation. Now, with the time-independent Hamilton operator $\mathcal{H}$ for a particle with mass m and the harmonic potential given by $ V(x)=\frac{1}{2}m\omega^2 x^2$ looks like
$$
\mathcal{H} = -\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2} + \frac{1}{2}m\omega^2 x^2
$$
we can separate the variables $x$ and $t$ like so:
$$
\Psi(x, t) = \psi(x) \cdot \varphi(t)
$$
and solve both
$$
i\hbar \frac{\partial \varphi(t)}{\partial t} = E \cdot \varphi(t)
$$
and
$$
[-\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2} + \frac{1}{2}m\omega^2 x^2] \cdot \psi(x) = E \psi(x)
$$
separately.
A neat trick to get rid of the physical constants is rescaling:
$$\xi = \frac{m \omega}{\hbar} \cdot x$$
with which you can easily check by yourself that the Schrödinger equation becomes:
$$
[ -\frac{\partial^2}{\partial \xi^2} + \xi^2 - \frac{2E}{\hbar \omega}] \cdot \psi(\xi) = 0
$$
where we postulate the boundary conditions for a constrained particle as
$$
\psi(-\infty) = \psi(\infty) = 0
$$
The so-called stationary solutions of the equation in $x$ form an ortho-normal eigenbasis of the Hilbert space of bounded functions $\psi_{\nu}(\xi)$ with eigenvalues $E_{\nu}=\hbar \omega (\nu + \frac{1}{2})$. And although we're not interested in the boring (yawn!) stationary solutions, we'll use this eigenbasis to construct an analytical function that obeys the time-dependent Schrödinger equation.
With the above eigenvalues we finally arrive at the following concise representation of the time-independent Schrödinger equation.
$$
[ -\frac{\partial^2}{\partial \xi^2} + \xi^2 - (2\nu+1)] \cdot \psi(\xi) = 0
$$
### Functions as eigenvectors
The solutions of this equation span a vector space, a so-called Hilbert space. That means we can define addition, multiplication by a number and even an inner product on these functions. When we look at functions as vectors in a Hilbert space, then the Schrödinger equation can as well be considered an eigenvalue problem. We'll provide the solutions without proof.
The eigenfunctions are composed of the Hermite polynomials and a gaussian:
$$
\psi_\nu(\xi) = \frac{1}{\sqrt{2^\nu \cdot \nu! \cdot \sqrt{\pi}}} \cdot H_\nu(\xi) \cdot
e^{-\frac{\xi^2}{2}}
$$
$$
\varphi_\nu(t) = e^{-i (\nu+\frac{1}{2}) t}
$$
Thus arriving at the full solution of the time-dependent Schrödinger equation as
$$
\psi_\nu(\xi, t) = \frac{1}{\sqrt{2^\nu \cdot \nu! \cdot \sqrt{\pi}}} \cdot H_\nu(\xi) \cdot
e^{-\frac{\xi^2}{2}-i(\nu+\frac{1}{2}) t}
$$
These solutions are called stationary because they rotate in the complex plane keeping their shape. That means that for every x the value of $\psi_\nu(x)$ rotates in the complex plane with exactly the same *frequency* as any other. Please note that we have clandestinely scaled the time t such that it *swallowed* the physical constants. For our purpose, namely visualizing the non-stationary solutions of the Schrödinger equation, this does not make a difference.
---
Defining the normalization factor $A_\nu$ as
$$
A_\nu = \frac{1}{\sqrt{2^\nu \cdot \nu! \cdot \sqrt{\pi}}}
$$
we visualize these stationary solutions such that we get an idea what they look like:
```
def A(nu):
return 1/math.sqrt(2**nu * math.factorial(nu) * math.sqrt(math.pi))
def psi(nu):
def _psi(x):
return A(nu) * H(nu)(x) * np.exp(-x*x/2)
return _psi
N_points=200
x_ = np.linspace(-6, 6, N_points)
plt.plot(x_, psi(0)(x_))
plt.plot(x_, psi(1)(x_))
plt.plot(x_, psi(2)(x_))
plt.plot(x_, psi(3)(x_));
```
---
#### Ortho-normal basis
Let's verify that our $\psi_\nu(\xi)$ form an ortho-normal basis with the inner product $\langle \psi_\mu | \psi_\nu \rangle$, $\mathbb{H} \times \mathbb{H} \rightarrow \mathbb{R}$ defined by
$$
\int_{-\infty}^{\infty} \bar{\psi}_\nu(\xi) \cdot \psi_\mu(\xi) d\xi= \delta^{\mu\nu}
$$
$\bar{\psi}_\nu(\xi)$ being the complex conjugate of $\psi_\nu(\xi)$
```
[[round(integrate.quad(lambda x: psi(mu)(x)*psi(nu)(x), -inf, +inf)[0], 6) for mu in range(5)] for nu in range(5)]
```
You can see that all inner products of two basis functions are zero, apart from the product with itself, which is what the *Kronecker* delta $\delta^{\mu \nu}$ demands.
---
### The fun part: coherent solutions
Now, let's have some fun. As we have just verified, the eigenstates of the Schrödinger equation form an ortho-normal basis of the Hilbert space of functions in one dimension. We expect that one can approximate any other bounded function as a linear combination of the first $N$ eigenfunctions. We'll do that for the following shifted gaussian. Note that is is centered around $x=-3$, so it's not equal to the first basis function.
```
x0=-3
fun=lambda x: psi(0)(x-x0)
#sns.set_style("ticks", {"xtick.major.size": 2, "ytick.major.size": .1})
sns.set()
plt.plot(x_, fun(x_));
```
We compute it's coordinates in the Schrödinger eigenbases simply by projecting it to the first $N$ eigenfunctions like this
```
N = 15
coords = [integrate.quad(lambda x: psi(mu)(x)*fun(x), -inf, +inf)[0] for mu in range(N)]
coords
```
Calling those coordinates $c_\nu$, we compute
$$
\psi_0(x-x_0) \approx \big[\sum_{\nu=0}^9 c_\nu \cdot A_\nu H_\nu(x)\big] \cdot e^{-\frac{-x^2}{2}}
$$
```
pol = Polynomial([0])
for nu in range(N):
pol = pol + coords[nu] * A(nu) * H(nu)
projection = lambda x: pol(x) * np.exp(-x*x/2)
plt.plot(x_, projection(x_));
```
What you see is that the 15-dimensional projection of our shifted function into the Schrödinger eigenbasis is a formidable approximation.
It's actually much more than an approximation. You can interpret this function as the wave function of a particle resting (the momentum is zero) at $x=x_0$. Remember there's still the harmonic potential. Thus, in the limit of classical mechanics, we would expect that our particle will slowly accelerate to the right until it *feels* the potential there. Then it would reflect and move all the way back. Lacking friction, we indeed expect that this oscillation continues until eternity.
---
#### Let the clock tick...
Because now we have this function as a linear combination of Schrödinger solutions, we can switch on time and see ourselves. Under the influence of the time-dependent Schrödinger equation, the the fifteen eigenvectors each rotate at their own frequency determined by the eigenvalue $2\nu+1$
The time-dependent solutions
$$
\psi_\nu(\xi, t) = \frac{1}{\sqrt{2^\nu \cdot \nu! \cdot \sqrt{\pi}}} \cdot H_\nu(\xi) \cdot
e^{-\frac{\xi^2}{2}-i(\nu+\frac{1}{2}) t}
$$
Note that now this function is complex-valued!
```
def psit(nu):
def _psi(x, t):
return A(nu) * H(nu)(x) * np.exp(-x*x/2) * np.exp(-1j*(nu+.5)*t)
return _psi
psit(3)(1, .3)
```
---
#### 3-D data
To appreciate the dynamics of a wave function in time we display both the real part and the imaginary part of the complex value of $\psi$.
- The figure's y-axis is our space coordinate $x$
- its z-axis spans the real part of the wave function
- and its x-axis spans the wave function's imaginary part
```
import mpl_toolkits.mplot3d.axes3d as p3
```
We display $\psi_2(x, t) $ at $t=0.5$
```
x_ = np.linspace(-6,6, N_points)
f = psit(2)(x_, 0.5)
r_f = [c.real for c in f]
i_f = [c.imag for c in f]
fig=plt.figure(figsize=(12,8))
ax = fig.gca(projection='3d')
ax.view_init(30, -15)
ax.set_xlim(-1, 1)
ax.set_zlim(-1, 1)
ax.set_xlabel('Imag')
ax.set_ylabel('X')
ax.set_zlabel('Real')
ax.plot(i_f, x_, r_f)
plt.show()
```
As you can see, the function is tilted in the complex plan due to the complex phase $e^{-\frac{5}{2}it}$
---
#### Time-dependent wave functions
Here, we'll create an analytical time-dependent wave function from our set of coordinates in Hilbert space that represent the resting particle at $x_0=-3$
```
def WF(sc):
return lambda x,t: sum([sc[nu] * np.exp(-1j*(nu+.5)*t) * A(nu) * H(nu)(x) * np.exp(-x*x/2)
# ============================== ==================================
# ^ ^
# time dependent coefficient Basis function
for nu in range(len(sc))])
particle = WF(coords)
particle(-3, 0) # a particle resting at x=-3 at time t=0
```
### Animating a Schrödinger particle!
```
%autosave 3600
N_frames=100
N_Points=200
XL, XR = -6, 6
def snapshot(N, f, t):
x = np.linspace(XL,XR, N)
f=f(x, t)
r_f = np.array([c.real for c in f])
i_f = np.array([c.imag for c in f])
return np.array([i_f, x, r_f])
def update(num, n_points, n_frames, wave_function, line):
data= snapshot(n_points, wave_function, num*4.0/n_frames*math.pi)
line.set_data(data[0], data[1])
line.set_3d_properties(data[2])
return line
```
Recording the animation will take a couple of seconds. Be patient. It's worth waiting for!
```
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
from IPython.display import HTML
fig=plt.figure(figsize=(12,8))
ax = p3.Axes3D(fig)
initial_data = snapshot(N_points, particle, 0.0)
line = ax.plot(initial_data[0], initial_data[1], initial_data[2])[0]
ax.set_xlim(-1, 1)
ax.set_zlim(-1, 1)
ax.set_ylim(XL, XR)
ax.set_xlabel('Imag')
ax.set_ylabel('X')
ax.set_zlabel('Real')
ax.set_title('Schroedinger particle in action!')
ax.view_init(10, -10)
line_ani = animation.FuncAnimation(
fig, update, N_frames,
fargs=(N_Points, N_frames, particle, line),
interval=200, blit=False)
jshtml = line_ani.to_jshtml()
#Uncomment and run this cell the see the movie. The cell will be so large that the notebook refuses to save. Thus I always comment it out before saving.
#HTML(data=jshtml)
# Uncomment to save your file and serve it elsewhere
#with open("Schroedinger.html", "w") as file:
# file.write(jshtml)
```
---
### Measuring location and momentum
Measurements in the real world are represented by computing expectation values of the operator associated with the given observable.
#### Angle notation
In the following, we denote eigenfunctions of the Schrödinger equation in angle notation
$$
|\nu \rangle \equiv \psi_\nu(x,t)
$$
In our unit-free notation, and introducing a more concise notation for the partial derivative, the momentum operator $\hat{p}$ is defined by
$$
\hat{p} = -i \partial_x
$$
Operators in our Hilbert space will be written in *hat* notation. You have seen $\hat{p}$ already. The Hamilton operator becomes:
$$
\hat{H} = \hat{p}^2 + \hat{x}^2
$$
Note that we're back to using $x$, but what we really mean is the unit-less $\xi$.
The Schrödinger equation in its eigenbasis looks like
$$
\hat{H} |\nu\rangle = 2(\nu+1)|\nu\rangle
$$
The inner product of any two wave functions (not necessarily basisvectors) as defined by the integral over the product of both functions has a neat short notation:
$$
\langle \psi_1 | \psi_2 \rangle
\equiv
\int_{-\infty}^{\infty} \bar{\psi_1}(\xi) \cdot \psi_2(\xi) d\xi
$$
The expectation value of an observable represented by an Operator like e.g. $\hat{p}$, given a particular wave function $\psi$ is defined by
$$
\langle \psi | \hat{p} | \psi \rangle
\equiv
\int_{-\infty}^{\infty} \bar{\psi}(\xi) \cdot (-i\partial_x) \psi(\xi) d\xi
$$
---
#### Dirac's ladder operators
Let us introduce the two *ladder* operators $a$ and $a^\dagger$ as
$$
a \equiv \frac{1}{\sqrt 2} (\hat{x} + i\hat{p})
$$
$$
a^\dagger \equiv \frac{1}{\sqrt 2} (\hat{x} - i\hat{p})
$$
using which we can express $\hat{p}$ and $\hat{x}$ like so:
$$
\hat{p} = \frac{i}{\sqrt 2}(a^\dagger - a)
$$
$$
\hat{x} = \frac{1}{\sqrt 2}(a^\dagger + a)
$$
Then you can convince yourself easily using the properties of the Hermite polynomials:
$$
x \cdot H_\nu(x) = \frac{1}{2} H_{\nu+1}(x) + \nu \cdot H_{\nu-1}(x)
$$
$$
\frac{d}{dx}H_\nu(x) = 2 \nu \cdot H_{\nu-1}(x)
$$
and our solutions of the Schrödinger equations
$$
\psi_\nu(x) = A_\nu \cdot H_\nu(x) \cdot
e^{-\frac{x^2}{2}}
$$
that
$$ a|\nu\rangle = \sqrt{\nu} |\nu-1 \rangle $$
and
$$ a^\dagger|\nu\rangle = \sqrt{\nu+1} |\nu+1 \rangle $$
It should be obvious by now why these operators are called *ladder* operators. They map each basis vector on the next resp. previous basis vector. And this neat property leads to a surprisingly simple method of applying $\hat{p}$ or $\hat{x}$ to arbitrary wave functions.
---
#### Matrix representation
We can compute a matrix representation easily by projecting the the result of every
$a|\nu\rangle$ resp. $a^\dagger|\nu\rangle$ onto every eigenvector.
$$
\langle \mu|a|\nu\rangle = \sqrt{\nu}\cdot\langle \mu | \nu-1\rangle = \sqrt{\nu} \cdot \delta^{\mu,\nu-1}
$$
and
$$
\langle \mu|a^\dagger|\nu\rangle = \sqrt{\nu+1}\cdot\langle \mu | \nu+1\rangle = \sqrt{\nu+1} \cdot \delta^{\mu,\nu+1}
$$
In this matrix representation, the ladder operators populate the positions right above or below the diagonal, respectively.
$$
a = \left[
\begin{array}{c c c c c c}
0 & 1 & 0 & 0 & 0 & 0 & \dots \\
0 & 0 & \sqrt{2} & 0 & 0 & 0 & \dots\\
0 & 0 & 0 & \sqrt{3} & 0 & 0 & \dots\\
0 & 0 & 0 & 0 & \sqrt{4} & 0 & \dots\\
0 & 0 & 0 & 0 & 0 & \sqrt{5} & \dots\\
0 & 0 & 0 & 0 & 0 & 0 & \dots \\
\dots
\end{array}
\right]
$$
$$
a^\dagger =
\left[
\begin{array}{c c c c c c}
0 & 0 & 0 & 0 & 0 & 0 & \dots\\
1 & 0 & 0 & 0 & 0 & 0 & \dots\\
0 & \sqrt{2} & 0 & 0 & 0 & 0 & \dots\\
0 & 0 & \sqrt{3} & 0 & 0 & 0 & \dots\\
0 & 0 & 0 & \sqrt{4} & 0 & 0 & \dots\\
0 & 0 & 0 & 0 & \sqrt{5} & 0 & \dots\\
\dots
\end{array}
\right]
$$
which leads to
$$
\hat{p} = \frac{1}{\sqrt{2}} \cdot \left[
\begin{array}{c c c c c c}
0 & 1 & 0 & 0 & 0 & 0 & \dots\\
i & 0 & \sqrt{2} & 0 & 0 & 0 & \dots\\
0 & i\sqrt{2} & 0 & \sqrt{3} & 0 & 0 & \dots\\
0 & 0 & i\sqrt{3} & 0 & \sqrt{4} & 0 & \dots\\
0 & 0 & 0 & i\sqrt{4} & 0 & \sqrt{5} & \dots\\
0 & 0 & 0 & 0 & i\sqrt{5} & 0 & \dots\\
\dots
\end{array}
\right]
$$
$$
\hat{x} = \frac{1}{\sqrt{2}} \cdot \left[
\begin{array}{c c c c c c}
0 & i & 0 & 0 & 0 & 0 & \dots\\
1 & 0 & i\sqrt{2} & 0 & 0 & 0 & \dots\\
0 & \sqrt{2} & 0 & i\sqrt{3} & 0 & 0 & \dots\\
0 & 0 & \sqrt{3} & 0 & i\sqrt{4} & 0 & \dots\\
0 & 0 & 0 & \sqrt{4} & 0 & i\sqrt{5} & \dots\\
0 & 0 & 0 & 0 & \sqrt{5} & 0 & \dots\\
\dots
\end{array}
\right]
$$
---
With these matrices we can do all our calculations just like highschool algebra! Let's verify that
$$ a|2\rangle = \sqrt{2} \cdot |1\rangle $$
and
$$ a^\dagger |2\rangle = \sqrt{3} \cdot |3\rangle $$
```
N=4 # just so that displaying the matrices doesn't clutter the notebook
```
The ladder operators as numpy arrays:
```
a=np.array([[math.sqrt(nu) if mu==nu-1 else 0.0 for nu in range(N)] for mu in range(N)])
a
a_d=np.array([[math.sqrt(nu+1) if mu==nu+1 else 0.0 for nu in range(N)] for mu in range(N)])
a_d
nu2 = np.array([0, 0, 1, 0])
np.matmul(a, nu2), np.matmul(a_d, nu2)
```
Convinced?
---
#### Expectation values
We can do even more exciting stuff with these matrices. Remember our initial wave function from the movie? It was a gaussian located a x=-3, and I claimed that it was at rest. It's about time to prove both.
The expectation value of the location $x$ is defined by
$$
\langle \psi | \hat{x} | \psi \rangle
\equiv
\int_{-\infty}^{\infty} \bar{\psi}(x) \cdot x \cdot \psi(x) dx
$$
```
# Using the 15-dimensional coordinates of our initial wave function in the Hilbert space spun by the
# solutions of the Schrödinger equation with harmonic potential
c = coords
N = len(coords)
a=np.array([[math.sqrt(nu) if mu==nu-1 else 0.0 for nu in range(N)] for mu in range(N)])
a_d=np.array([[math.sqrt(nu+1) if mu==nu+1 else 0.0 for nu in range(N)] for mu in range(N)])
```
Below we calculate
$$
\langle \psi | \hat{x} | \psi \rangle =
\frac{1}{\sqrt{2}} \cdot (\langle \psi | \hat{a} \psi \rangle + \langle \psi | \hat{a}^\dagger \psi \rangle)
= \frac{1}{\sqrt{2}} \cdot (\psi^T \cdot \mathbb{M} \cdot \psi + \psi^T \cdot \mathbb{M}^\dagger \cdot \psi)
$$
where $\psi^T$ is the transposed vector and $\mathbb{M}, \mathbb{M}^\dagger$ are the matrix representations of the ladder operators $a, a^\dagger$.
```
psi=np.array(coords)
1/math.sqrt(2) * (np.matmul(np.matmul(psi.T, a), psi) + np.matmul(np.matmul(psi.T, a_d), psi))
# Transposing is just for visual clarity.
# Actually, Python would understand the matmul operation correctly, anyway.
```
Convinced? That's almost exactly what we expected.
Btw. we could have been smarter by computing the $\hat{x}$ operator first and then compute the expectation value of it: Let's do that also for $\hat{p}$
$\hat{p} = \frac{i}{\sqrt 2}(a^\dagger - a)$ ;
$\hat{x} = \frac{1}{\sqrt 2}(a^\dagger + a)$:
```
p_hat = 1j/math.sqrt(2) * ( a_d - a )
x_hat = 1/math.sqrt(2) * ( a_d + a )
```
$\langle \psi | \hat{p} | \psi \rangle$:
```
np.matmul(np.matmul(psi.T, p_hat), psi)
```
That's almost zero. C'mon, now you are convinced, right?
---
#### Observing location and momentum over time
```
def psi_t(sc, t):
return np.array([sc[nu] * np.exp(-1j*(nu+.5)*t) for nu in range(N)])
psi_07 = psi_t(psi, 0.7)
psi_07
```
Please note that for complex coefficients we must compute $\langle \psi | $ as the complex conjugate of $| \psi \rangle$
```
np.matmul(np.matmul(np.conj(psi_07).T, p_hat), psi_07)
def p_exp (sc, t):
psit = psi_t(sc, t)
return np.matmul(np.matmul(np.conj(psit).T, p_hat), psit).real
p_exp(psi, .7)
def x_exp (sc, t):
psit = psi_t(sc, t)
return np.matmul(np.matmul(np.conj(psit).T, x_hat), psit).real
x_exp(psi, np.array(0.7))
t_ = np.linspace(0, 2*math.pi, 100)
xt_ = [x_exp(psi, t) for t in t_]
pt_ = [p_exp(psi, t) for t in t_]
plt.plot(xt_, pt_);
```
Just like in classical mechanics, the expectation values of location and momentum form an elipse (in our case even a perfect circle) in the phase space spun by values of $p$ and $x$.
|
github_jupyter
|
```
import pandas as pd
# movies dataset
movies = pd.read_pickle('./dataset/movies/movies.p')
print(movies.shape)
movies.head()
#taglines dataset
taglines = pd.read_pickle('./dataset/movies/taglines.p')
print(taglines.shape)
taglines.head()
```
## Filter joins
- semi join
- anti join
Mutation join vs filter join
- mutation is commbining data from two tables based on matching obsevation in both tables
- filtering observation from table is based on weather or not they match an observation in another table
### 1. semi joins
- return the intersection, similar to an inner join
- return only column from left table and **not** the rigth
- No duplicated
<img src='./media/semi_join.png' width=700 height=800>
- step 1 --> simple inner join for semi join
- step 2 --> making a filter of semi join
- step 3 --> filtering data
```
#step1 -->simple inner join for semi join
movies_tag = movies.merge(taglines, on='id')
movies_tag.head()
#step 2 --> making a filter of semi join
movies['id'].isin(movies_tag['id'])
# step 3 --> filtering data
tagged_movies = movies[movies['id'].isin(movies_tag['id'])]
tagged_movies.head()
#semi join in one
movies_tag = movies.merge(taglines, on='id')
tagged_movies = movies[movies['id'].isin(movies_tag['id'])]
tagged_movies.head()
```
### 2. anti join
- opposite to semi join
- return the left table, **excluding the intersaction**
- return only column from the left **not** from the right
<img src='./media/anti join.png' width= 700 height=800>
- step 1 --> simple left join for anti join
- step 2 --> making a filter of anti join
```
# step 1 --> simple left join for anti join
movies_tag = movies.merge(taglines, on='id', how='left', indicator=True)
print(movies_tag.shape)
movies_tag.head()
# step 2 --> making a filter for anti join
id_list = movies_tag.loc[movies_tag['_merge']=='left_only', 'id']
pd.DataFrame(id_list).head()
# step 3 --> applying filter
movies_tag = movies.merge(taglines, on='id', how='left', indicator=True)
id_list = movies_tag.loc[movies_tag['_merge']=='left_only', 'id']
non_tagged_movies = movies_tag[movies_tag['id'].isin(id_list)]
non_tagged_movies.head()
```
## Concatenate DataFrames together vertically
- pandas **.concat()** can concatenate both vertically and horizentally
- **axis=0** for vertical
<img src='./media/verticaal_concatenation.png' width= 400 height= 500>
```
jan_movies = movies.iloc[1:5]
jan_movies
feb_movies = movies.iloc[11:15]
feb_movies
march_movies = movies.iloc[21:25]
march_movies
#basic concatenation
pd.concat([jan_movies,feb_movies,march_movies])
# Ignoring the index
pd.concat([jan_movies,feb_movies,march_movies], ignore_index=True)
# Setting labels to original tables
pd.concat([jan_movies,feb_movies,march_movies], ignore_index=False, keys=['jan', 'feb', 'mar'])
jan_tags = taglines.iloc[1:5]
jan_tags
# Concatenate tables with different column names
pd.concat([jan_movies,jan_tags], sort=True) #<-- sorting column name
pd.concat([jan_movies,jan_tags], sort=False) #<-- without sorting column names bydefault False
# Concatenate tables with different column names
pd.concat([jan_movies, jan_tags],join='inner')#<-- applying inner join on columns by default outer
```
### Using append method
**.append()**
- Simplified version of **.concat()**
- suppor : **sort_index** and **sort**
- Not support : **keys** and **join** i:e. always **join == outer**
```
jan_movies.append([feb_movies,march_movies], ignore_index=True, sort=True)
```
## Verifying integrity
<img src= './media/verfying_integrity.png'>
## Validating merges
**.merge(validate=None)**
- check if merge is not specified type
- 'one to one'
- 'one to many'
- 'many to one'
- 'many to many'
```
# lets check it on movies and taglines
print(movies.merge(taglines , on='id', validate='one_to_one').shape)
movies.merge(taglines , on='id', validate='one_to_one').head()
```
if one possible we'll get below error
**Traceback (most recent call last):<br>
MergeError: Merge keys are not unique in right dataset; not a one-to-one merge**
## Verifying concatenations
**.concat(verify_integrity=False)** :
- Check whether the new concatenated index contains duplicates
- Default value is **False**
```
pd.concat([jan_movies,feb_movies], verify_integrity=False)
duplicate_jan_movies = movies.iloc[1:5]
duplicate_feb_movies = movies.iloc[4:5]
pd.concat([duplicate_jan_movies,duplicate_feb_movies], verify_integrity=False)
#<-- Give Error because integrity is true to chk duplicated
pd.concat([duplicate_jan_movies,duplicate_feb_movies], verify_integrity=True)
```
# Practice
### Task1
#### Required datasets
```
employees = pd.read_csv('./employees.csv')
employees.head()
top_cust = pd.read_csv('./top_cust.csv')
top_cust.head()
```
#### requirements
- Merge employees and top_cust with a left join, setting indicator argument to True. Save the result to empl_cust.
- Select the srid column of empl_cust and the rows where _merge is 'left_only'. Save the result to srid_list.
- Subset the employees table and select those rows where the srid is in the variable srid_list and print the results.
```
# Merge employees and top_cust
empl_cust = employees.merge(top_cust, on='srid',
how='left', indicator=True)
# Select the srid column where _merge is left_only
srid_list = empl_cust.loc[empl_cust['_merge'] == 'left_only', 'srid']
# Get employees not working with top customers
employees[employees['srid'].isin(srid_list)]
```
### Task2
#### The required datasets
```
non_mus_tcks = pd.read_csv('./non_musk_tcks.csv')
non_mus_tcks.head()
top_invoices = pd.read_csv('./top_invoices.csv')
top_invoices.head()
genres = pd.read_csv('./genres.csv')
genres.head()
```
#### The required tasks
- Merge non_mus_tcks and top_invoices on tid using an inner join. Save the result as tracks_invoices.
- Use .isin() to subset the rows of non_mus_tck where tid is in the tid column of tracks_invoices. Save the result as top_tracks.
- Group top_tracks by gid and count the tid rows. Save the result to cnt_by_gid.
- Merge cnt_by_gid with the genres table on gid and print the result.
```
non_mus_tcks.info()
top_invoices.info()
def numbers(x):
try:
x = str(x)
return "".join([i for i in x if str.isnumeric(i)])
except:
return 0
non_mus_tcks.tid.apply(numbers).head()
import numpy as np
non_mus_tcks['tid'] = non_mus_tcks['tid'].apply(numbers)
non_mus_tcks['tid'] = non_mus_tcks['tid'].apply(np.int64)
# Merge the non_mus_tck and top_invoices tables on tid
tracks_invoices = non_mus_tcks.merge(top_invoices, on='tid')
# Use .isin() to subset non_mus_tcsk to rows with tid in tracks_invoices
top_tracks = non_mus_tcks[non_mus_tcks['tid'].isin(tracks_invoices['tid'])]
# Group the top_tracks by gid and count the tid rows
cnt_by_gid = top_tracks.groupby(['gid'], as_index=False).agg({'tid':'count'})
# Merge the genres table to cnt_by_gid on gid and print
cnt_by_gid.merge(genres, on='gid')
```
### Task3
#### required datasets
```
tracks_master = pd.read_csv('./tracks_master.csv')
tracks_master.head()
tracks_ride = pd.read_csv('./tracks_ride.csv')
tracks_ride.head()
tracks_st = pd.read_csv('./tracks_st.csv')
tracks_st.head()
```
#### required tasks
- Concatenate tracks_master, tracks_ride, and tracks_st, in that order, setting sort to True.
- Concatenate tracks_master, tracks_ride, and tracks_st, where the index goes from 0 to n-1.
- Concatenate tracks_master, tracks_ride, and tracks_st, showing only columns that are in all tables.
```
# Concatenate the tracks
tracks_from_albums = pd.concat([tracks_master,tracks_ride,tracks_st],
sort=True)
tracks_from_albums.head()
# Concatenate the tracks so the index goes from 0 to n-1
tracks_from_albums = pd.concat([tracks_master, tracks_ride, tracks_st],
ignore_index = True,
sort=True)
tracks_from_albums.head()
# Concatenate the tracks, show only columns names that are in all tables
tracks_from_albums = pd.concat([tracks_master, tracks_ride, tracks_st],join= 'inner', sort=True)
tracks_from_albums.head()
```
### Task4
#### required datasets
```
inv_jul = pd.read_csv('./inv_jul.csv')
inv_jul.head()
inv_aug = pd.read_csv('./inv_aug.csv')
inv_aug.head()
inv_sep = pd.read_csv('./inv_sep.csv')
inv_sep.head()
```
- Concatenate the three tables together vertically in order with the oldest month first, adding '7Jul', '8Aug', and '9Sep' as keys for their respective months, and save to variable avg_inv_by_month.
- Use the .agg() method to find the average of the total column from the grouped invoices.
- Create a bar chart of avg_inv_by_month.
```
# Concatenate the tables and add keys
inv_jul_thr_sep = pd.concat([inv_jul, inv_aug, inv_sep],
keys=['7Jul', '8Aug', '9Sep'])
inv_jul_thr_sep
# inv_jul_thr_sep['total']=inv_jul_thr_sep['total'].astype(float)
inv_jul_thr_sep['total'] = inv_jul_thr_sep['total'].apply(numbers)
inv_jul_thr_sep['total'] = inv_jul_thr_sep['total'].apply(np.int64)
# Group the invoices by the index keys and find avg of the total column
avg_inv_by_month = inv_jul_thr_sep.groupby(level=0).agg({'total':'mean'})
# Bar plot of avg_inv_by_month
avg_inv_by_month.plot(kind='bar')
plt.show()
```
### Task5
#### Required tables
```
artists = pd.read_csv('./artist.csv')
artists.head()
albums = pd.read_csv('./album.csv')
albums.head()
```
- You have been given 2 tables, artists, and albums. Use the console to merge them using artists.merge(albums, on='artid').head(). Adjust the validate argument to answer which statement is False.
1- You can use 'many_to_many' without an error, since there is a duplicate key in one of the tables.
2- You can use 'one_to_many' without error, since there is a duplicate key in the right table.
3- You can use 'many_to_one' without an error, since there is a duplicate key in the left table.
```
# artists.merge(albums, on='artid').head()
# artists.merge(albums, on='artid', validate = 'one_to_many').head()
```
### Task6
#### required file
```
classic_18 = pd.read_csv('./classic_18.csv')
classic_18.head()
classic_19 = pd.read_csv('./classic_19.csv')
classic_19.head()
pop_18 = pd.read_csv('./pop_18.csv')
pop_18.head()
pop_19 = pd.read_csv('./pop_19.csv')
pop_19.head()
```
- Concatenate the classic_18 and classic_19 tables vertically where the index goes from 0 to n-1, and save to classic_18_19.
- Concatenate the pop_18 and pop_19 tables vertically where the index goes from 0 to n-1, and save to pop_18_19.
- With classic_18_19 on the left, merge it with pop_18_19 on tid using an inner join.
- Use .isin() to filter classic_18_19 where tid is in classic_pop.
```
# Concatenate the classic tables vertically
classic_18_19 = pd.concat([classic_18, classic_19], ignore_index=True)
# Concatenate the pop tables vertically
pop_18_19 = pd.concat([pop_18, pop_19], ignore_index=True)
# Merge classic_18_19 with pop_18_19
classic_pop = classic_18_19.merge(pop_18_19, on='tid')
# Using .isin(), filter classic_18_19 rows where tid is in classic_pop
popular_classic = classic_18_19[classic_18_19['tid'].isin(classic_pop['tid'])]
# Print popular chart
print(popular_classic)
```
|
github_jupyter
|
```
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets
from sklearn.decomposition import PCA
```
### Generate a dataset
```
xy = np.random.multivariate_normal([0,0], [[10,7],[7,10]],1000)
plt.plot(xy[:,0],xy[:,1],"o")
plt.show()
```
### Create a Principle Component Analysis (PCA) object
What is `n_components`?
```
pca = PCA(n_components=2)
```
`num_components` is the number of axes on which you spread the data out. You can only have as many components as you have axes (2 in this case).
### Fit the axes
What does the following code do?
```
xy_pca = pca.fit(xy)
```
Does the PCA, finding the primary axes of variation.
```
plt.plot(xy[:,0],xy[:,1],"o")
scalar = xy_pca.explained_variance_[0]
plt.plot([0,xy_pca.components_[0,0]*scalar/2],[0,xy_pca.components_[0,1]*scalar/2],color="red")
plt.plot([0,-xy_pca.components_[0,0]*scalar/2],[0,-xy_pca.components_[0,1]*scalar/2],color="red")
scalar = xy_pca.explained_variance_[1]
plt.plot([0,xy_pca.components_[1,0]*scalar/2],[0,xy_pca.components_[1,1]*scalar/2],color="yellow")
plt.plot([0,-xy_pca.components_[1,0]*scalar/2],[0,-xy_pca.components_[1,1]*scalar/2],color="yellow")
```
### What does the following do?
```
xy_trans = xy_pca.transform(xy)
```
Transforms `x` and `y` onto the PCA axes.
```
fig, ax = plt.subplots(1,2,figsize=(10,5))
ax[0].plot(xy[:,0],xy[:,1],"o")
ax[0].set_xlabel("x")
ax[0].set_ylabel("y")
ax[0].set_xlim((-15,15)); ax[0].set_ylim((-15,15))
ax[1].plot(xy_trans[:,0],xy_trans[:,1],"o")
ax[1].set_xlabel("PCA1")
ax[1].set_ylabel("PCA2")
ax[1].set_xlim((-15,15)); ax[1].set_ylim((-15,15))
plt.show()
```
### What does the following do?
```
print("Variation explained:")
print("First component: {:.3f}".format(xy_pca.explained_variance_ratio_[0]))
print("Second component: {:.3f}".format(xy_pca.explained_variance_ratio_[1]))
```
Describes how much variation each PCA axis captures.
Informally: if you only included the first component in a predictive model, the $R^{2}$ between you prediction and reality would be 0.85.
### Some helper code, which takes an xy_pair and does all of the steps above.
```
def pca_wrapper(xy_pairs):
"""
Take an array of x/y data and perform a principle component analysis.
"""
fig, ax = plt.subplots(1,2,figsize=(10,5))
ax[0].plot(xy_pairs[:,0],xy_pairs[:,1],"o")
ax[0].set_xlim((-18,18))
ax[0].set_ylim((-18,18))
ax[0].set_title("raw x,y data")
ax[0].set_xlabel("x")
ax[0].set_ylabel("y")
# Perform the PCA fit
pca = PCA(n_components=2)
z = pca.fit(xy_pairs)
# Transforom the data onto the new PCA axes
new_xy_pairs = z.transform(xy_pairs)
# Plot the PCA data
ax[1].plot(new_xy_pairs[:,0],new_xy_pairs[:,1],"o")
ax[1].set_title("PCA transformed data")
ax[1].set_xlim((-18,18))
ax[1].set_ylim((-18,18))
ax[1].set_xlabel("PCA1")
ax[1].set_ylabel("PCA2")
print("Variation explained:")
print("First component: {:.3f}".format(pca.explained_variance_ratio_[0]))
print("Second component: {:.3f}".format(pca.explained_variance_ratio_[1]))
```
### How does fraction variation relate to skew in the data?
```
d1 = np.random.multivariate_normal([0,0], [[10,1],[1,10]],1000)
pca_wrapper(d1)
d2 = np.random.multivariate_normal([0,0], [[10,5],[5,10]],1000)
pca_wrapper(d2)
d3 = np.random.multivariate_normal([0,0], [[10,9],[9,10]],1000)
pca_wrapper(d3)
```
The stronger the covariation between parameters, the more readily the PCA can reduce dimensionality.
### Using PCA to try to classify things
### The "Iris" dataset
<img style="margin:auto" align="center" src="https://www.math.umd.edu/~petersd/666/html/iris_with_labels.jpg" />
+ Three species of iris
+ Four properties measured for many representatives from each species
+ Properties are: sepal length, sepal width, petal length, petal width
### Load in the data
```
iris = datasets.load_iris()
obs = iris.data
species = iris.target
mean = obs.mean(axis=0)
std = obs.std(axis=0)
obs = (obs - mean)/std
```
The mean, standard deviation business normalizes the data so the values are all on the same scale.
```
def plot_slice(obs_r,axis_i,axis_j):
"""
Define a helper function.
"""
plt.plot(obs_r[species == 0,axis_i],obs_r[species == 0,axis_j],"o",color='navy')
plt.plot(obs_r[species == 1,axis_i],obs_r[species == 1,axis_j],"o",color='turquoise')
plt.plot(obs_r[species == 2,axis_i],obs_r[species == 2,axis_j],"o",color='darkorange')
plt.xlabel(axis_i)
plt.ylabel(axis_j)
plt.show()
```
### Species separate on some axes, but not all axes
```
plot_slice(obs,axis_i=0,axis_j=1)
```
### Do PCA
```
pca = PCA(n_components=4)
obs_pca = pca.fit(obs)
obs_trans = obs_pca.transform(obs)
```
### What is different about PCA axes?
```
plot_slice(obs_trans,axis_i=0,axis_j=1)
```
All of that separating power is jammed into the first axis.
### Quantify this with explained varience ratio:
```
for r in obs_pca.explained_variance_ratio_:
print("{:.3f}".format(r))
```
### Summary
+ PCA is a way to spread data out on "natural" axes
+ Clusters in PCA space can be used to classify things
+ Axes may be hard to interpret directly
|
github_jupyter
|
```
%matplotlib inline
import numpy as np
import pylab as plt
import ccgpack as ccg
from itertools import product
from matplotlib.colors import LogNorm
cl = np.load('../data/cl_planck_lensed.npy')
sfs = ccg.StochasticFieldSimulator(cl)
nside = 1024
size = 30
ms = []
for i in range(4):
ms.append(sfs.simulate(nside,size))
fig,((ax1,ax2),(ax3,ax4)) = plt.subplots(ncols=2
,nrows=2,figsize=(6 ,6))
ax1.imshow(ms[0])
ax2.imshow(ms[1])
ax3.imshow(ms[2])
ax4.imshow(ms[3])
# ll0 = cl[:600,0]
# dl0 = cl[:600,1]*(ll0[:600]*(ll0[:600]+1)/(2*np.pi))
# ll,p1 = ccg.power_spectrum(ms[0],size=15)
# plt.plot(ll0,dl0,'k--')
# plt.plot(ll[:600],p1[:600],'b')
# plt.xscale('log')
# plt.yscale('log')
# plt.xlim(2,600)
# # plt.ylim(5e-8,5e4)
cor,ecor = ccg.correlarion_fucntion(ms[0],n_p=1e6)
plt.plot(cor)
ksi = ccg.ppcf(ms[0],2,1e6,700)
plt.plot(ksi)
def N1(d,num=100,gt=True):
nu = np.linspace(d.min(),d.max(),num)
n1 = []
for i in nu:
if gt:
n1.append(np.mean(d>i))
else:
n1.append(np.mean(d<i))
n1 = np.array(n1)
return nu,n1
def exterma(arr,peak=True):
dim = len(arr.shape) # number of dimensions
offsets = [0, -1, 1] # offsets, 0 first so the original entry is first
filt = np.ones(arr.shape,dtype=np.int8)
for shift in product(offsets, repeat=dim):
if np.all(np.array(shift)==0):
continue
# print(shift)
# print(np.roll(b, shift, np.arange(dim)))
rolled = np.roll(arr, shift, np.arange(dim))
if peak:
filt = filt*(arr>rolled)
else:
filt = filt*(arr<rolled)
return filt
ms[0] = ms[0]-ms[0].mean()
ms[0] = ms[0]/ms[0].std()
nu,n1_gt = N1(ms[0],num=100,gt=True)
plt.plot(nu,n1_gt)
ms[0] = ms[0]-ms[0].mean()
ms[0] = ms[0]/ms[0].std()
nu,n1_lt = N1(ms[0],num=100,gt=False)
plt.plot(nu,n1_lt)
plt.plot(nu[:-1],np.diff(n1_gt))
plt.plot(nu[:-1],np.diff(n1_lt))
th = 0
mcopy = ms[0]+0
peaks = exterma(mcopy ,peak=True)
mcopy[np.logical_not(peaks.astype(bool))] = 0
mcopy[mcopy<th] = 0
nf1 = np.argwhere(mcopy).T
nnn = 5*nf1.shape[1]
rlist = np.random.randint(0,1024,(2,nnn))
ksi1 = ccg.ffcf_no_random(fl1=nf1, fl2=nf1, rlist=rlist, rmax=700)
# plt.plot(ksi1)
fig,(ax1,ax2) = plt.subplots(1,2,figsize=(16,8))
ax1.imshow(mcopy,cmap='gray')
rimg = np.zeros(mcopy.shape)
rows, cols = zip(*rlist.T)
rimg[rows, cols] = 1
ax2.imshow(rimg,cmap='gray')
mask = np.zeros(ms[0].shape)+1
mask[700:1000,100:400] = 0
mask[100:300,700:900] = 0
mask[100:300,200:400] = 0
mask[700:800,700:890] = 0
mcopy = ms[0]*mask+0
peaks = exterma(mcopy ,peak=True)
mcopy[np.logical_not(peaks.astype(bool))] = 0
mcopy[mcopy<th] = 0
nf1 = np.argwhere(mcopy).T
nnn = 5*nf1.shape[1]
rlist = np.random.randint(0,1024,(nnn,2))
rimg = np.zeros(mcopy.shape)
rows, cols = zip(*rlist)
rimg[rows, cols] = 1
rimg = rimg*mask
rlist = np.argwhere(rimg).T
ksi2 = ccg.ffcf_no_random(fl1=nf1, fl2=nf1, rlist=rlist, rmax=700)
fig,(ax1,ax2) = plt.subplots(1,2,figsize=(16,8))
ax1.imshow(mcopy,cmap='gray')
ax2.imshow(rimg,cmap='gray')
rlist = np.random.randint(0,1024,(2,nnn))
ksi3 = ccg.ffcf_no_random(fl1=nf1, fl2=nf1, rlist=rlist, rmax=700)
ksi4 = eval_ksi(ms[0],mask,thresholds=[0],peak=True)[0]
# plt.plot(ksi)
plt.plot(ksi1,'r',label='normal')
plt.plot(ksi2,'b',label='both_masked')
plt.plot(ksi4,'k',label='func')
plt.plot(ksi3,'g',label='peak_masked')
plt.legend()
plt.savefig('tpcf.jpg',dpi=150)
# thresholds = [-2,-1,0,1,2]
# ksis = eval_ksi(ms[0],mask,thresholds,peak=True,rmax=700,crand=5)
for i in range(len(ksis)):
plt.plot(ksis[i],label=str(thresholds[i]))
plt.xlim(-1,100)
plt.legend()
thresholds = [-2,-1,0,1,2]
ksis = eval_ksi(ms[0],mask,thresholds,peak=False,rmax=700,crand=5)
for i in range(len(ksis)):
plt.plot(ksis[i],label=str(thresholds[i]))
plt.xlim(-1,100)
plt.legend()
def eval_ksi(m,mask,thresholds,peak=True,rmax=700,crand=5):
ksis = []
mc1 = m*mask
nside = mc1.shape[0]
peaks = exterma(mc1 ,peak=peak)
mc1[np.logical_not(peaks.astype(bool))] = 0
for th in thresholds:
mc2 = mc1+0
if peak:
mc2[mc2<th] = 0
else:
mc2[mc2>th] = 0
nf1 = np.argwhere(mc2).T
nnn = crand*nf1.shape[1]
rlist = np.random.randint(0,nside,(nnn,2))
rimg = np.zeros(mc2.shape)
rows, cols = zip(*rlist)
rimg[rows, cols] = 1
rimg = rimg*mask
rlist = np.argwhere(rimg).T
ksis.append(ccg.ffcf_no_random(fl1=nf1, fl2=nf1, rlist=rlist, rmax=rmax))
return ksis
# def bias(m,ths,kmin,kmax):
# if not isinstance(ths, list):
# ths = [ths]
# bs = []
# for th in ths:
# ksi = ccg.ppcf(m,th,1e6,700)
# biask = np.sqrt(np.absolute(ksi[:700]/cor[:700]))
# bs.append(np.mean(biask[kmin:kmax]))
# return bs
# ths = [0.5,1.0,1.5,2.0,2.5]
# kmin = 10
# kmax = 50
# bs = bias(ms[0],ths,kmin,kmax)
# bsth = np.array(ths)
# plt.plot(ths,bsth,'r--')
# plt.plot(ths,bs,'bo')
# plt.xlabel(r'$\nu$',fontsize=15)
# plt.ylabel(r'$b(\nu)$',fontsize=15)
```
|
github_jupyter
|
# Counterfactual explanations with ordinally encoded categorical variables
This example notebook illustrates how to obtain [counterfactual explanations](https://docs.seldon.io/projects/alibi/en/latest/methods/CFProto.html) for instances with a mixture of ordinally encoded categorical and numerical variables. A more elaborate notebook highlighting additional functionality can be found [here](./cfproto_cat_adult_ohe.ipynb). We generate counterfactuals for instances in the *adult* dataset where we predict whether a person's income is above or below $50k.
```
import tensorflow as tf
tf.get_logger().setLevel(40) # suppress deprecation messages
tf.compat.v1.disable_v2_behavior() # disable TF2 behaviour as alibi code still relies on TF1 constructs
from tensorflow.keras.layers import Dense, Input, Embedding, Concatenate, Reshape, Dropout, Lambda
from tensorflow.keras.models import Model
from tensorflow.keras.utils import to_categorical
%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import os
from sklearn.preprocessing import OneHotEncoder
from time import time
from alibi.datasets import fetch_adult
from alibi.explainers import CounterfactualProto
print('TF version: ', tf.__version__)
print('Eager execution enabled: ', tf.executing_eagerly()) # False
```
## Load adult dataset
The `fetch_adult` function returns a `Bunch` object containing the features, the targets, the feature names and a mapping of the categories in each categorical variable.
```
adult = fetch_adult()
data = adult.data
target = adult.target
feature_names = adult.feature_names
category_map_tmp = adult.category_map
target_names = adult.target_names
```
Define shuffled training and test set:
```
def set_seed(s=0):
np.random.seed(s)
tf.random.set_seed(s)
set_seed()
data_perm = np.random.permutation(np.c_[data, target])
X = data_perm[:,:-1]
y = data_perm[:,-1]
idx = 30000
y_train, y_test = y[:idx], y[idx+1:]
```
Reorganize data so categorical features come first:
```
X = np.c_[X[:, 1:8], X[:, 11], X[:, 0], X[:, 8:11]]
```
Adjust `feature_names` and `category_map` as well:
```
feature_names = feature_names[1:8] + feature_names[11:12] + feature_names[0:1] + feature_names[8:11]
print(feature_names)
category_map = {}
for i, (_, v) in enumerate(category_map_tmp.items()):
category_map[i] = v
```
Create a dictionary with as keys the categorical columns and values the number of categories for each variable in the dataset. This dictionary will later be used in the counterfactual explanation.
```
cat_vars_ord = {}
n_categories = len(list(category_map.keys()))
for i in range(n_categories):
cat_vars_ord[i] = len(np.unique(X[:, i]))
print(cat_vars_ord)
```
## Preprocess data
Scale numerical features between -1 and 1:
```
X_num = X[:, -4:].astype(np.float32, copy=False)
xmin, xmax = X_num.min(axis=0), X_num.max(axis=0)
rng = (-1., 1.)
X_num_scaled = (X_num - xmin) / (xmax - xmin) * (rng[1] - rng[0]) + rng[0]
X_num_scaled_train = X_num_scaled[:idx, :]
X_num_scaled_test = X_num_scaled[idx+1:, :]
```
Combine numerical and categorical data:
```
X = np.c_[X[:, :-4], X_num_scaled].astype(np.float32, copy=False)
X_train, X_test = X[:idx, :], X[idx+1:, :]
print(X_train.shape, X_test.shape)
```
## Train a neural net
The neural net will use entity embeddings for the categorical variables.
```
def nn_ord():
x_in = Input(shape=(12,))
layers_in = []
# embedding layers
for i, (_, v) in enumerate(cat_vars_ord.items()):
emb_in = Lambda(lambda x: x[:, i:i+1])(x_in)
emb_dim = int(max(min(np.ceil(.5 * v), 50), 2))
emb_layer = Embedding(input_dim=v+1, output_dim=emb_dim, input_length=1)(emb_in)
emb_layer = Reshape(target_shape=(emb_dim,))(emb_layer)
layers_in.append(emb_layer)
# numerical layers
num_in = Lambda(lambda x: x[:, -4:])(x_in)
num_layer = Dense(16)(num_in)
layers_in.append(num_layer)
# combine
x = Concatenate()(layers_in)
x = Dense(60, activation='relu')(x)
x = Dropout(.2)(x)
x = Dense(60, activation='relu')(x)
x = Dropout(.2)(x)
x = Dense(60, activation='relu')(x)
x = Dropout(.2)(x)
x_out = Dense(2, activation='softmax')(x)
nn = Model(inputs=x_in, outputs=x_out)
nn.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
return nn
set_seed()
nn = nn_ord()
nn.summary()
nn.fit(X_train, to_categorical(y_train), batch_size=128, epochs=30, verbose=0)
```
## Generate counterfactual
Original instance:
```
X = X_test[0].reshape((1,) + X_test[0].shape)
```
Initialize counterfactual parameters:
```
shape = X.shape
beta = .01
c_init = 1.
c_steps = 5
max_iterations = 500
rng = (-1., 1.) # scale features between -1 and 1
rng_shape = (1,) + data.shape[1:]
feature_range = ((np.ones(rng_shape) * rng[0]).astype(np.float32),
(np.ones(rng_shape) * rng[1]).astype(np.float32))
```
Initialize explainer. Since the `Embedding` layers in `tf.keras` do not let gradients propagate through, we will only make use of the model's predict function, treat it as a black box and perform numerical gradient calculations.
```
set_seed()
# define predict function
predict_fn = lambda x: nn.predict(x)
cf = CounterfactualProto(predict_fn,
shape,
beta=beta,
cat_vars=cat_vars_ord,
max_iterations=max_iterations,
feature_range=feature_range,
c_init=c_init,
c_steps=c_steps,
eps=(.01, .01) # perturbation size for numerical gradients
)
```
Fit explainer. Please check the [documentation](https://docs.seldon.io/projects/alibi/en/latest/methods/CFProto.html) for more info about the optional arguments.
```
cf.fit(X_train, d_type='abdm', disc_perc=[25, 50, 75]);
```
Explain instance:
```
set_seed()
explanation = cf.explain(X)
```
Helper function to more clearly describe explanations:
```
def describe_instance(X, explanation, eps=1e-2):
print('Original instance: {} -- proba: {}'.format(target_names[explanation.orig_class],
explanation.orig_proba[0]))
print('Counterfactual instance: {} -- proba: {}'.format(target_names[explanation.cf['class']],
explanation.cf['proba'][0]))
print('\nCounterfactual perturbations...')
print('\nCategorical:')
X_orig_ord = X
X_cf_ord = explanation.cf['X']
delta_cat = {}
for i, (_, v) in enumerate(category_map.items()):
cat_orig = v[int(X_orig_ord[0, i])]
cat_cf = v[int(X_cf_ord[0, i])]
if cat_orig != cat_cf:
delta_cat[feature_names[i]] = [cat_orig, cat_cf]
if delta_cat:
for k, v in delta_cat.items():
print('{}: {} --> {}'.format(k, v[0], v[1]))
print('\nNumerical:')
delta_num = X_cf_ord[0, -4:] - X_orig_ord[0, -4:]
n_keys = len(list(cat_vars_ord.keys()))
for i in range(delta_num.shape[0]):
if np.abs(delta_num[i]) > eps:
print('{}: {:.2f} --> {:.2f}'.format(feature_names[i+n_keys],
X_orig_ord[0,i+n_keys],
X_cf_ord[0,i+n_keys]))
describe_instance(X, explanation)
```
The person's incomce is predicted to be above $50k by increasing his or her capital gain.
|
github_jupyter
|
# Batch correction
What is batch correction? A "Batch" is when experiments have been performed at different times and there's some obvious difference between them. Single-cell experiments are often inherently "batchy" because you can only perform so many single cell captures at once, and you do multiple captures, over different days, with different samples. How do you correct for the technical noise without deleting the true biological signal?
## Avoiding batch effects
First things first, it's best to design your experiments to minimize batch effects. For example, if you can mix your samples such that there are multiple representations of samples per single-cell capture, then this will help because you will have representations of both biological and technical variance across batches, rather than BOTH biological and technical variance.

[Hicks et al, preprint](http://biorxiv.org/content/early/2015/12/27/025528)
### Bad: Technical variance is the same as biological variance

Here, when you try to correct for batch effects between captures, it's impossible to know whether you're removing the technical noise of the different captures, or the biological signal of the data.
### Good: Technical variance is different from biological variance
The idea here is that you would ahead of time, mix the cells from your samples in equal proportions and then perform cell capture on the mixed samples, so you would get different technical batches, but they wouldn't be counfounded by the biological signals.

Here, when you correct for batch effects, the technical batches and biological signals are separate.
### If it's completely impossible to do multiple biological samples in the same technical replicate...
For example, if you have to harvest your cells at parcticular timepoints, here are some ways that you can try to mitigate the batch effects:
* Repeat the timepoint
* Save an aliquot of cells from each timepoint and run another experiment with the mixed aliquots
## Correcting batch effects
Okay so say your data are such that you couldn't have mixed your biological samples ahead of time. What do you do?
There's two main ways to approach batch correction: using groups of samples or groups of features (genes).
### Sample-batchy
This is when you have groups of samples that may have some biological difference between them, but also have technical differences between them. Say, you performed single-cell capture on several different days from different mice, of somewhat overlapping ages. You know that you have the biological signal from the different mice and the different ages, but you *also* have the technical signal from the different batches. BUT there's no getting around that you had to sacrifice the mice and collect their cells in one batch
### Feature-batchy
This is when you think particular groups of genes are contributing to the batch effects.
How to find these features:
* Numerical feature (e.g. RIN) associated with each sample
* Cell cycle genes (??Buetttner 2015?)
* (RUVseq) - Use an external dataset (e.g. bulk samples) to find non-differentially expressed genes and use them to correct between groups
```
from __future__ import print_function
# Interactive Python (IPython - now Jupyter) widgets for interactive exploration
import ipywidgets
# Numerical python library
import numpy as np
# PLotting library
import matplotlib.pyplot as plt
# Dataframes in python
import pandas as pd
# Linear model correction
import patsy
# Even better plotting
import seaborn as sns
# Batch effect correction
# This import statement only works because there's a folder called "combat_py" here, not that there's a module installed
from combat_py.combat import combat
# Use the styles and colors that I like
sns.set(style='white', context='talk', palette='Set2')
%matplotlib inline
```
### Feature-batchy
```
np.random.seed(2016)
n_samples = 10
n_genes = 20
half_genes = int(n_genes/2)
half_samples = int(n_samples/2)
size = n_samples * n_genes
genes = ['Gene_{}'.format(str(i+1).zfill(2)) for i in range(n_genes)]
samples = ['Sample_{}'.format(str(i+1).zfill(2)) for i in range(n_samples)]
data = pd.DataFrame(np.random.randn(size).reshape(n_samples, n_genes), index=samples, columns=genes)
# Add biological variance
data.iloc[:half_samples, :half_genes] += 1
data.iloc[:half_samples, half_genes:] += -1
data.iloc[half_samples:, half_genes:] += 1
data.iloc[half_samples:, :half_genes] += -1
# Biological samples
mouse_groups = pd.Series(dict(zip(data.index, (['Mouse_01'] * int(n_samples/2)) + (['Mouse_02'] * int(n_samples/2)))),
name="Mouse")
mouse_to_color = dict(zip(['Mouse_01', 'Mouse_02'], ['lightgrey', 'black']))
mouse_colors = [mouse_to_color[mouse_groups[x]] for x in samples]
# Gene colors
gene_colors = sns.color_palette('husl', n_colors=n_genes)
```
### Plot original biological variance data
```
g = sns.clustermap(data, row_colors=mouse_colors, col_cluster=False, row_cluster=False, linewidth=0.5,
col_colors=gene_colors,
cbar_kws=dict(label='Normalized Expression'))
plt.setp(g.ax_heatmap.get_yticklabels(), rotation=0);
def make_tidy(data, sample_groups):
tidy = data.unstack()
tidy = tidy.reset_index()
tidy = tidy.rename(columns={'level_0': 'Gene', 'level_1': "Sample", 0: "Normalized Expression"})
tidy = tidy.join(sample_groups, on='Sample')
return tidy
tidy = make_tidy(data, mouse_groups)
fig, ax = plt.subplots()
sns.boxplot(hue='Gene', y='Normalized Expression', data=tidy, x='Mouse')
ax.legend_.set_visible(False)
```
### Add technical noise
```
# Choose odd-numbered samples to be in batch1 and even numbered samples to be in batch 2
batch1_samples = samples[::2]
batch2_samples = data.index.difference(batch1_samples)
batches = pd.Series(dict((x, 'Batch_01') if x in batch1_samples else (x, "Batch_02") for x in samples), name="Batch")
# Add random noise for all genes except the last two in each batch
noisy_data = data.copy()
noisy_data.ix[batch1_samples, :-2] += np.random.normal(size=n_genes-2, scale=2)
noisy_data.ix[batch2_samples, :-2] += np.random.normal(size=n_genes-2, scale=2)
# Assign colors for batches
batch_to_color = dict(zip(["Batch_01", "Batch_02"], sns.color_palette()))
batch_colors = [batch_to_color[batches[x]] for x in samples]
row_colors = [mouse_colors, batch_colors]
g = sns.clustermap(noisy_data, row_colors=row_colors, col_cluster=False, row_cluster=False, linewidth=0.5,
col_colors=gene_colors, cbar_kws=dict(label='Normalized Expression'))
plt.setp(g.ax_heatmap.get_yticklabels(), rotation=0);
```
We can see that there's some batch effect - for batch1 (light grey), `Gene_15` is in general lower, and `Gene_01` is in general higher. And for batch2 (black), `Gene_16` is in general higher.
But, Gene_19 and Gene_20 are unaffected.
```
tidy_noisy = make_tidy(noisy_data, mouse_groups)
tidy_noisy = tidy_noisy.join(batches, on='Sample')
tidy_noisy.head()
```
Lets plot the boxplots of data the same way, with the x-axis as the mouse they came from and the y-axis ad the genes
```
fig, ax = plt.subplots()
sns.boxplot(hue='Gene', y='Normalized Expression', data=tidy_noisy, x='Mouse')
ax.legend_.set_visible(False)
```
We can see that compared to before, where we had clear differences in gene expression from genes 1-10 and 11-19 in the two mice, we don't see it as much with the noisy data.
Now let's plot the data a different way, with the x-axis as the *batch*
```
fig, ax = plt.subplots()
sns.boxplot(hue='Gene', y='Normalized Expression', data=tidy_noisy, x='Batch')
ax.legend_.set_visible(False)
```
## How to quantify the batch effect?
```
fig, ax = plt.subplots()
sns.pointplot(hue='Batch', x='Normalized Expression', data=tidy_noisy, y='Gene', orient='horizontal',
scale=0.5, palette=batch_colors)
fig, ax = plt.subplots()
sns.pointplot(hue='Batch', x='Normalized Expression', data=tidy_noisy, y='Gene', orient='horizontal', scale=0.5)
sns.pointplot(x='Normalized Expression', data=tidy_noisy, y='Gene', orient='horizontal', scale=0.75, color='k',
linestyle=None)
```
## How to get rid of the batch effect?
### COMBAT
We will use "COMBAT" to get rid of the batch effect. What combat does is basically what we just did with our eyes and intuition - find genes whose gene expression varies greatly between batches, and adjust the expression of the gene so it's closer to the mean total expression across batches.
(may need to whiteboard here)
Create metadata matrix
```
metadata = pd.concat([batches, mouse_groups], axis=1)
metadata
def remove_batch_effects_with_combat(batch, keep_constant=None, cluster_on_correlations=False):
if keep_constant is not None or keep_constant in metadata:
# We'll use patsy (statistical models in python) to create a "Design matrix" which encodes the batch as
# a boolean (0 or 1) value so the computer cna understand it.
model = patsy.dmatrix('~ {}'.format(keep_constant), metadata, return_type="dataframe")
elif keep_constant == 'null' or keep_constant is None:
model = None
# --- Correct for batch effects --- #
corrected_data = combat(noisy_data.T, metadata[batch], model)
# Transpose so samples are the rows and the features are the columns
corrected_data = corrected_data.T
# --- Plot the heatmap --- #
if cluster_on_correlations:
g = sns.clustermap(corrected_data.T.corr(), row_colors=row_colors, col_cluster=True, row_cluster=True, linewidth=0.5,
vmin=-1, vmax=1, col_colors=row_colors, cbar_kws=dict(label='Pearson R'))
plt.setp(g.ax_heatmap.get_yticklabels(), rotation=0);
else:
g = sns.clustermap(corrected_data, row_colors=row_colors, col_cluster=False, row_cluster=False, linewidth=0.5,
col_colors=gene_colors, cbar_kws=dict(label='Normalized Expression'))
plt.setp(g.ax_heatmap.get_yticklabels(), rotation=0);
# Uncomment the line below to save the batch corrected heatmap
# g.savefig('combat_batch_corrected_clustermap.pdf')
# --- Quantification of the batch effect correction --- #
# Create a "tidy" version of the dataframe for plotting
tidy_corrected = make_tidy(corrected_data, mouse_groups)
tidy_corrected = tidy_corrected.join(batches, on='Sample')
tidy_corrected.head()
# Set up the figure
# 4 columns of figure panels
figure_columns = 4
width = 4.5 * figure_columns
height = 4
fig, axes = plt.subplots(ncols=figure_columns, figsize=(width, height))
# PLot original data vs the corrected data
ax = axes[0]
ax.plot(data.values.flat, corrected_data.values.flat, 'o',
# Everything in the next line is my personal preference so it looks nice
alpha=0.5, markeredgecolor='k', markeredgewidth=0.5)
ax.set(xlabel='Original (Batchy) data', ylabel='COMBAT corrected data')
# PLot the mean gene expression within batch in colors, and the mean gene expression across both batches in black
ax = axes[1]
sns.pointplot(hue='Batch', x='Normalized Expression', data=tidy_corrected, y='Gene', orient='horizontal', scale=.5, ax=ax)
sns.pointplot(x='Normalized Expression', data=tidy_corrected, y='Gene', orient='horizontal',
scale=0.75, color='k', linestyle=None, ax=ax)
# PLot the gene epxression distribution per mouse
ax = axes[2]
sns.boxplot(hue='Gene', y='Normalized Expression', data=tidy_corrected, x='Mouse', ax=ax,
# Adjusting linewidth for my personal preference
linewidth=1)
# Don't show legend because it's too big
ax.legend_.set_visible(False)
# --- Plot boxplots of average difference between gene expression in batches --- #
# Gete mean gene expression within batch for the original noisy data
mean_batch_expression = noisy_data.groupby(batches).mean()
noisy_batch_diff = (mean_batch_expression.loc['Batch_01'] - mean_batch_expression.loc['Batch_02']).abs()
noisy_batch_diff.name = 'mean(|batch1 - batch2|)'
noisy_batch_diff = noisy_batch_diff.reset_index()
noisy_batch_diff['Data type'] = 'Noisy'
# Get mean gene expression within batch for the corrected data
mean_corrected_batch_expression = corrected_data.groupby(batches).mean()
corrected_batch_diff = (mean_corrected_batch_expression.loc['Batch_01'] - mean_corrected_batch_expression.loc['Batch_02']).abs()
corrected_batch_diff.name = 'mean(|batch1 - batch2|)'
corrected_batch_diff = corrected_batch_diff.reset_index()
corrected_batch_diff['Data type'] = 'Corrected'
# Compile the two tables into one (concatenate)
batch_differences = pd.concat([noisy_batch_diff, corrected_batch_diff])
batch_differences.head()
sns.boxplot(x='Data type', y='mean(|batch1 - batch2|)', data=batch_differences, ax=axes[3])
# Remove right and top axes lines so it looks nicer
sns.despine()
# Magically adjust the figure panels (axes) so they fit nicely
fig.tight_layout()
# Uncomment the line below to save the figure of three panels
# fig.savefig('combat_batch_corrected_panels.pdf')
ipywidgets.interact(
remove_batch_effects_with_combat,
batch=ipywidgets.Dropdown(options=['Mouse', 'Batch'], value="Batch", description='Batch to correct for'),
keep_constant=ipywidgets.Dropdown(value=None, options=[None, 'Mouse', 'Batch', 'Mouse + Batch'],
description='Variable of interest'),
cluster_on_correlations=ipywidgets.Checkbox(value=False, description="Cluster on (Pearson) correlations between samples"));
```
Try doing these and see how they compare. Do you see similar trends to the original data? Do any of these create errors? Why would that be?
1. Batch to correct for = Batch, Variable of interest = Mouse
2. Batch to correct for = Mouse, Variable of interest = Batch
3. Batch to correct for = Batch, Variable of interest = Mouse + Batch
4. ... your own combinations!
With each of these try turning "Cluster on (Pearson) correlations between samples" on and off.
This is a nice way that we can visualize the improvement in reducing the batch-dependent signal.
## Feature-batchy
What if there are specific genes or features that are contributing to the batches?
This is the idea behind correcting for cell-cycle genes or some other feature that you know is associated with the data, e.g. the RNA Integrity Number (RIN).
Let's add some feature-batchy noise to our original data
```
metadata['RIN'] = np.arange( len(samples)) + 0.5
metadata
```
Add noise and plot it. Use first and last genes as controls that dno't have any noise
```
# rin_noise = metadata['RIN'].apply(lambda x: pd.Series(np.random.normal(loc=x, size=n_genes), index=genes))
rin_noise = metadata['RIN'].apply(lambda x: pd.Series(np.ones(n_genes-2)*x, index=genes[1:-1]))
rin_noise = rin_noise.reindex(columns=genes)
rin_noise = rin_noise.fillna(0)
g = sns.clustermap(rin_noise, row_colors=mouse_colors, col_cluster=False, row_cluster=False, linewidth=0.5,
col_colors=gene_colors, cbar_kws=dict(label='RIN Noise'))
plt.setp(g.ax_heatmap.get_yticklabels(), rotation=0);
```
Add the noise to the data and re-center so that each gene's mean is approximately zero.
```
rin_batchy_data = data + rin_noise
rin_batchy_data
# Renormalize the data so genes are 0-centered
rin_batchy_data = (rin_batchy_data - rin_batchy_data.mean())/rin_batchy_data.std()
g = sns.clustermap(rin_batchy_data, row_colors=mouse_colors, col_cluster=False, row_cluster=False, linewidth=0.5,
col_colors=gene_colors, cbar_kws=dict(label='Normalized Expression'))
plt.setp(g.ax_heatmap.get_yticklabels(), rotation=0);
```
If we plot the RIN vs the RIN-batchy gene expression, we'll see that from this one variable, we see an increase in expression! Of course, we could also have created a variable that linearly decreases expression.
```
tidy_rin_batchy = make_tidy(rin_batchy_data, mouse_groups)
tidy_rin_batchy = tidy_rin_batchy.join(metadata['RIN'], on='Sample')
g = sns.FacetGrid(tidy_rin_batchy, hue='Gene')
g.map(plt.plot, 'RIN', 'Normalized Expression', alpha=0.5)
```
### Use RIN to predict gene expression
We will use linear regression to use RIN as our dependent variable and predict gene expression from there. Then we'll create a new, corrected matrix, with the influence of RIN removed
```
from __future__ import print_function
import six
from sklearn import linear_model
regressor = linear_model.LinearRegression()
regressor
# Use RIN as the "X" - the "dependent" variable, the one you expect your gene expression to vary with.
regressor.fit(metadata['RIN'].to_frame(), rin_batchy_data)
# Use RIN to predict gene expression
rin_dependent_data = pd.DataFrame(regressor.predict(metadata['RIN'].to_frame()), columns=genes, index=samples)
rin_dependent_data
from sklearn.metrics import r2_score
# explained_variance = r2_score(rin_batchy_data, rin_dependent_data)
# six.print_("Explained variance by RIN:", explained_variance)
rin_corrected_data = rin_batchy_data - rin_dependent_data
rin_corrected_data
# Somewhat contrived, but try to predict the newly corrected data with RIN
r2_score(rin_corrected_data, rin_dependent_data)
tidy_rin_corrected = make_tidy(rin_corrected_data, mouse_groups)
tidy_rin_corrected = tidy_rin_corrected.join(metadata['RIN'], on="Sample")
tidy_rin_corrected.head()
g = sns.FacetGrid(tidy_rin_corrected, hue='Gene')
g.map(plt.plot, 'RIN', 'Normalized Expression', alpha=0.5)
g = sns.clustermap(rin_corrected_data, row_colors=mouse_colors, col_cluster=False, row_cluster=False, linewidth=0.5,
col_colors=gene_colors, cbar_kws=dict(label='Normalized Expression'))
plt.setp(g.ax_heatmap.get_yticklabels(), rotation=0);
sns.clustermap(rin_corrected_data.T.corr(), row_colors=mouse_colors,linewidth=0.5,
col_colors=mouse_colors, cbar_kws=dict(label='Pearson R'))
plt.setp(g.ax_heatmap.get_yticklabels(), rotation=0);
```
Now the data dcoens't vary by RIN! But.... now we over-corrected and removed the biological signal as well.
### Other options to talk about
As you have seen, dealing with batch effects in single-cell data is supremely difficult and the best thing you can do for yourself is design your experiment nicely so you don't have to.
* [SVA](http://www.biostat.jhsph.edu/~jleek/papers/sva.pdf)
* Can specify that you want to correct for something (like RIN) but don't correct for what you're interested in. But... often in single cell data you're trying to find new populations so you don't know *a prior* what you want to not be corrected for
* [RUVseq](http://www.nature.com/nbt/journal/v32/n9/full/nbt.2931.html)
* "RUV" = "Remove unwanted variation"
* With the "RUVg" version can specify a set of control genes that you know aren't supposed to change between groups (maybe from a bulk experiment) but they say in their manual not to use the normalized counts for differential expression, only for exploration, because you may have corrected for something you actually *DID* want but didn't know
* [scLVM](https://github.com/PMBio/scLVM)
* This method claims to account for differences in cell cycle stage and help to put all cells onto the same scale, so you can then do pseudotime ordering and clustering and all that jazz.
|
github_jupyter
|
```
import numpy as np
import cv2
import tensorflow as tf
face_cascade = cv2.CascadeClassifier('haarcascade_frontalface_default.xml')
model = tf.keras.models.load_model("/home/d3adsh0t/Tunex/8")
# EMOTIONS = ["angry" ,"disgust","scared", "happy", "sad", "surprised","neutral"]
# EMOTIONS=["angry",
# "disgust",
# "happy",
# "neutral",
# "sad",
# "surprise"]
EMOTIONS = ["afraid","angry","disgust","happy","neutral","sad","surprised"]
def prepare(ima):
IMG_SIZE = 48 # image size
img_array = cv2.cvtColor(ima,cv2.COLOR_BGR2GRAY)
img_array=img_array/255.0
new_array = cv2.resize(img_array, (IMG_SIZE, IMG_SIZE)) # resize image to match model's expected sizing
return new_array.reshape(-1,IMG_SIZE, IMG_SIZE,1)
```
# Static Test
```
image=cv2.imread("afraid.jpeg")
# faces = face_cascade.detectMultiScale(image, 1.3, 5)
# faces = sorted(faces, reverse=True, key = lambda x: (x[2]-x[0]) *(x[3]-x[1]))[0]
# (x,y,w,h)=faces
# roi = image[y-40:y+h+40, x:x+w]
prediction = model.predict([prepare(image)])
preds = prediction[0]
label = EMOTIONS[preds.argmax()]
print(label)
# image = cv2.rectangle(image,(x,y-40),(x+w,y+h+40),(255,0,0),2)
cv2.imshow("image",image)
cv2.waitKey(0)
cv2.destroyAllWindows()
```
# Live Test
```
# cap=cv2.VideoCapture("test3.mp4")
cap=cv2.VideoCapture(0)
# result = cv2.VideoWriter('1testface.avi',cv2.VideoWriter_fourcc(*'MJPG'), 30, (540, 960))
while True:
ret, img=cap.read()
# print(img.shape)
# img = cv2.resize(img, (540, 960))
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
faces = face_cascade.detectMultiScale(gray, 1.1, 5)
canvas = np.zeros((256,256,3), dtype="uint8")
frameclone=img
try:
faces = sorted(faces, reverse=True, key = lambda x: (x[2]-x[0]) *(x[3]-x[1]))[0]
(x,y,w,h)=faces
img = cv2.rectangle(img,(x,y),(x+w,y+h),(255,0,0),2)
roi = img[y:y+h, x:x+w]
cv2.imshow('img2',roi)
prediction = (model.predict([prepare(roi)]))
preds = prediction[0]
label = EMOTIONS[preds.argmax()]
for (i, (emotion, prob)) in enumerate(zip(EMOTIONS, preds)):
text = "{}: {:.2f}%".format(emotion, prob*100)
w = int(prob*300)
cv2.rectangle(canvas, (7, (i*35)+5), (w, (i*35)+35),(0,0,255), -1)
cv2.putText(canvas, text, (10, (i*35) +23), cv2.FONT_HERSHEY_SIMPLEX, 0.45, (255,255,255), 2)
cv2.imshow("Probabilities", canvas)
cv2.putText(img,label, (x, y-10), cv2.FONT_HERSHEY_SIMPLEX, 0.45, (0, 0, 255), 2)
result.write(img)
except:
pass
cv2.imshow('img',img)
cv2.waitKey(1)
if cv2.waitKey(1) & cv2.waitKey(1) == ord('q'):
break
cap.release()
cv2.destroyAllWindows()
```
# Test on static Validation data
```
for j in range(0,7):
right_count=0
wrong_count=0
for i in range(1,50):
# try:
img=cv2.imread("/home/arjun/DM/Face/validation/"+str(j)+"/"+str(i)+".jpg")
# cv2.imshow("image",img)
# cv2.waitKey(0)
# cv2.destroyAllWindows()
# faces = face_cascade.detectMultiScale(img, 1.3, 5)
# print(faces)
# faces = sorted(faces, reverse=True, key = lambda x: (x[2]-x[0]) *(x[3]-x[1]))[0]
# (x,y,w,h)=faces
# roi = image[y-20:y+h, x:x+w]
pr=model.predict([prepare(img)])
preds=pr[0]
label = EMOTIONS[preds.argmax()]
if(label==EMOTIONS[j]):
right_count+=1
else:
wrong_count+=1
# except:
# pass
print(EMOTIONS[j])
print("Right "+str(right_count)+" Wrong "+str(wrong_count))
```
```
angry
Right 20 Wrong 29
disgust
Right 30 Wrong 19
fear
Right 23 Wrong 26
happy
Right 40 Wrong 9
neutral
Right 26 Wrong 23
sad
Right 32 Wrong 17
surprise
Right 34 Wrong 15
```
|
github_jupyter
|
# Chapter 7: n-step Bootstrapping
## 1. n-step TD Prediction
- Generalize one-step TD(0) method
- Temporal difference extends over n-steps

- Want to update estimated value $v_\pi(S_t)$ of state $S_t$ from:
$$S_t,R_{t+1},S_{t+1},R_{t+1},...,R_T,S_T$$
- for *MC*, target is complete return
$$G_t = R_{t+1}+\gamma R_{t+3}+\gamma^2R_{t+3}+...+\gamma^{T-t-1}R_T$$
- for *TD*, one-step method
$$G_{t:t+1} = R_{t+1}+\gamma V_t(S_{t+1})$$
- for *two-step TD*, one-step method
$$G_{t:t+2} = R_{t+1}+\gamma R_{t+2}+\gamma^2V_{t+1}(S_{t+2})$$
- for *n-step TD*, one-step method with $n\ge 1, 0\le t<T-n$
$$
\begin{cases}
G_{t:t+n} &= R_{t+1}+\gamma R_{t+2}+...+\gamma^{n-1}R_{t+n}+\gamma^nV_{t+n-1}(S_{t+n})
\\G_{t:t+n} &= G_t ~~~,\text{if } t+n\ge T
\end{cases}
$$
- Wait for $R_{t+n}, V_{t+n-1}$, until time $t+n$, then update estimate values:
$$V_{t+n}(S_t) = V_{t+n-1}(S_t)+\alpha\big[G_{t:t+n}-V_{t+n-1}(S_t)\big] ~~~, 0\le t<T$$
- all other states remain unchanged: $V_{t+n}(s)=V_{t+n-1}(s), \forall s\neq S_t$

- **Error Reduction Property** of n-step returns:
$$\max_s\big| E_\pi[G_{t:t+n} | S_t=s]-v_\pi(s)\big| \le \gamma^n\max_s\big| V_{t+n-1}(s)-v_\pi(s)\big|, \forall n\ge 1$$
- Can show formally that n-step TD methods converge to the correct predictions
## 2. n-step Sarsa
- Switch states for actions (state-action pairs) and then use an ε-greedy policy

- n-step returns for action-value:
$$G_{t:t+n}=R_{t+1}+\gamma R_{t+2}+...+\gamma^{n-1}R_{t+n}+\gamma^nQ_{t+n-1}(S_{t+n},A_{t+n})~~~, n\ge 1, 0\le t<T-n$$
with $G_{t:t+n}=G_t \text{ if }t+n\ge T$
- **n-step Sarsa**:
$$Q_{t+n}(S_t,A_t)=Q_{t+n-1}(S_t,A_t)+\alpha\big[G_{t:t+n}-Q_{t+n-1}(S_t,A_t)\big]~~~,0\le t<T$$
- **n-step Expected Sarsa**:
$$G_{t:t+n}=R_{t+1}+\gamma R_{t+2}+...+\gamma^{n-1}R_{t+n}+\gamma^n\overline V_{t+n-1}(S_{t+n},A_{t+n})~~~, t+n<T$$
- where, *expected approximate value* of state $s$:
$$\overline V_t(s)=\sum_a\pi(a | s)Q_t(s,a) ~~~, \forall s\in\mathcal S$$
- if $s$ is terminal, then $\overline V(s)=0$

## 3. n-step Off-policy Learning
- Use relative probability of just n actions:
$$\rho_{t:h}=\prod_{k=t}^{\min(h,T-1)}\frac{\pi(A_k | S_k)}{b(A_k | S_k)}$$
- n-step TD:
$$V_{t+n}(S_t)=V_{t+n-1}(S_t)+\alpha\color{blue}{\rho_{t:t+n-1}}\big[G_{t:t+n}-V_{t+n-1}(S_t)\big]~~~,0\le t<T$$
- n-step Sarsa:
$$Q_{t+n}(S_t,A_t)=V_{t+n-1}(S_t,A_t)+\alpha\color{blue}{\rho_{t+1:t+n}}\big[G_{t:t+n}-Q_{t+n-1}(S_t,A_1)\big]~~~,0\le t<T$$
- n-step Expected Sarsa:
$$Q_{t+n}(S_t,A_t)=V_{t+n-1}(S_t,A_t)+\alpha\color{blue}{\rho_{t+1:t+n-1}}\big[G_{t:t+n}-Q_{t+n-1}(S_t,A_1)\big]~~~,0\le t<T$$

## 4. Per-decision Methods with Control Variates
- add *control variate* to **off-policy** of n-step return to reduce variance
$$G_{t:h}=\rho_t(R_{t+1}+\gamma G_{t+1:h})+(1-\rho_t)V_{h-1}(S_t) ~~~,t<h<T$$
where, $G_{h:h}=V_{h-1}(S_h)$
- if $\rho_t=0$, then the target does not change
- Includes on-policy when $\rho_t=1$
- for action values, the first action does not play a role in the importance sampling
$$
\begin{aligned}
G_{t:h} &= R_{t+1}+\gamma\big(\rho_{t+1}G_{t+1:h}+\overline V_{h-1}(S_{t+1})-\rho_{t+1}Q_{h-1}(S_{t+1},A_{t+1})\big)
\\ &= R_{t+1}+\gamma\rho_{t+1}\big(G_{t+1:h}-Q_{h-1}(S_{t+1},A_{t+1})\big)+\gamma\overline V_{h-1}(S_{t+1})
\end{aligned}
$$
where, $t<h\le T$, if $h<T$, then $G_{h:h}=Q_{h-1}(S_h,A_h)$, else $G_{T-1:h}=R_T$
## 5. Off-policy Learning Without Importance Sampling: The n-step Tree Backup Algorithm
- Use **left nodes** to estimate action-values

- one-step return is them same as Expected Sarsa for $t<T-1$:
$$G_{t:t+1}=R_{t+1}+\gamma\sum_a\pi(a | S_{t+1})Q_t(S_{t+1},a)$$
- two-step tree-backup for $t<T-2$:
$$
\begin{aligned}
G_{t:t+1} &= R_{t+1}+\gamma\sum_{a\neq A_{t+1}}\pi(a | S_{t+1})Q_{t+1}(S_{t+1},a)
\\ & ~~~ +\gamma\pi(A_{t+1} | S_{t+1})\big(R_{t+1:t+2}\gamma\sum_{a\neq A_{t+1}}\pi(a | S_{t+2})Q_{t+1}(S_{t+2},a)\big)
\\ &= R_{t+1}+\gamma\sum_{a\neq A_{t+1}}\pi(a | S_{t+1})Q_{t+1}(S_{t+1},a)+\gamma\pi(A_{t+1} | S_{t+1})Q_{t+1:t+2}
\end{aligned}
$$
- n-step tree-backup for $t<T-1,n\ge 2$:
$$G_{t:t+1} = R_{t+1}+\gamma\sum_{a\neq A_{t+1}}\pi(a | S_{t+1})Q_{t+1}(S_{t+1},a)+\gamma\pi(A_{t+1} | S_{t+1})Q_{t+1:t+n}$$
- action-value update rule as usual from n-step Sarsa:
$$Q_{t+n}(S_t,A_t)=Q_{t+n-1}(S_t,A_t)+\alpha[G_{t:t+n}-Q_{t+n-1}(S_t,A_t)]$$
for, $0\le t < T$

## 6. A Unifying Algorithm: n-step Q(σ)

- $\sigma_t\in[0,1]$ denote the degree of sampling on step $t$
- $\sigma=0$ for full sampling
- $\sigma=1$ for pure expection
- Rewrite the n-step back-up tree as:
$$
\begin{aligned}
G_{t:h} &= R_{t+1}+\gamma\sum_{a\neq A_{t+1}}\pi(a | S_{t+1})Q_{h-1}(S_{t+1},a)+\gamma\pi(A_{t+1} | S_{t+1})G_{t+1:h}
\\ &= R_{t+1}+\gamma\overline V_{h-1}(S_{t+1})-\gamma\pi(A_{t+1} | S_{t+1})Q_{h-1}(S_{t+1},A_{t+1})+\gamma\pi(A_{t+1} | S_{t+1})G_{t+1:h}
\\ &= R_{t+1}+\gamma\pi(A_{t+1} | S_{t+1})\big(G_{t+1:h}-Q_{h-1}(S_{t+1},A_{t+1})\big)+\gamma\overline V_{h-1}(S_{t+1})
\end{aligned}
$$
- n-step $Q(\sigma)$:
$$G_{t:h}=R_{t+1}+\gamma\big(\sigma_{t+1}\rho_{t+1}+(1-\sigma_{t+1})\pi(A_{t+1} | S_{t+1})\big)\big(G_{t+1:h}-Q_{h-1}(S_{t+1},A_{t+1})\big)+\gamma\overline V_{h-1}(S_{t+1})$$
where, $t<h\le T$
- if $h<T$, then $G_{h:h}=Q_{h-1}(S_h,A_h)$
- if $h=T$, then $G_{T-1:T}=R_T$

|
github_jupyter
|
This script takes the notebook with RNA and DNA BSID's and collects information for the corresponding samples from fusion summary files, breakpoint density files, GISTIC CNA broad_values file and FPKM files
```
import argparse
import pandas as pd
import numpy as np
import zipfile
import statistics
import scipy
from scipy import stats
# Reading all the input files
zip=zipfile.ZipFile("/Users/kogantit/Documents/OpenPBTA/OpenPBTA-analysis/data/pbta-cnv-cnvkit-gistic.zip")
CNA=pd.read_csv(zip.open("2019-12-10-gistic-results-cnvkit/broad_values_by_arm.txt"), sep="\t")
CNA = CNA.set_index("Chromosome Arm")
gsva = pd.read_csv("/Users/kogantit/Documents/OpenPBTA/OpenPBTA-analysis/analyses/gene-set-enrichment-analysis/results/gsva_scores_stranded.tsv", sep="\t")
gsva_NFKB = gsva.loc[gsva['hallmark_name'] == "HALLMARK_TNFA_SIGNALING_VIA_NFKB"]
gsva_NFKB = gsva_NFKB.set_index("Kids_First_Biospecimen_ID")
fpkm_df = pd.read_csv("/Users/kogantit/Documents/OpenPBTA/OpenPBTA-analysis/analyses/molecular-subtyping-EPN/epn-subset/epn-pbta-gene-expression-rsem-fpkm-collapsed.stranded.tsv.gz", sep = "\t")
fpkm_df = fpkm_df.set_index("GENE")
zscore_fpkm_df = fpkm_df.apply(scipy.stats.zscore)
fusion = pd.read_csv("/Users/kogantit/Documents/OpenPBTA/OpenPBTA-analysis/analyses/fusion-summary/results/fusion_summary_ependymoma_foi.tsv", sep="\t")
fusion = fusion.set_index("Kids_First_Biospecimen_ID")
breakpoint_density = pd.read_csv("/Users/kogantit/Documents/OpenPBTA/OpenPBTA-analysis/analyses/chromosomal-instability/breakpoint-data/union_of_breaks_densities.tsv", sep="\t")
breakpoint_density = breakpoint_density.set_index("samples")
EPN_notebook = pd.read_csv("/Users/kogantit/Documents/OpenPBTA/OpenPBTA-analysis/analyses/molecular-subtyping-EPN/results/EPN_molecular_subtype.tsv", sep="\t")
# This function takes in a GISTIC broad_values
# and a string (loss/gain) and returns 0/1 accordingly
def DNA_samples_fill_df(CNA_value, loss_gain):
if CNA_value<0 and loss_gain=="loss":
return(1)
elif loss_gain=="gain" and CNA_value>0:
return(1)
else:
return(0)
# Function to generate Z-scores column for every gene
def fill_df_with_fpkm_zscores(df,fpkmdf, column_name, gene_name):
zscore_list = scipy.stats.zscore(np.array(df.apply(lambda x: fpkmdf.loc[gene_name, x["Kids_First_Biospecimen_ID_RNA"]], axis=1)))
df[column_name] = pd.Series(zscore_list)
return(df)
# Input notebook before adding columns
EPN_notebook.head()
# Input. CNA file
CNA.head()
#Adding columns to EPN_notebook based on values from CNA file (boolean value)
# Matching based on DNA BSID (row names in CNA file and column names in EPN_notebook) -> Look at row 4 below
EPN_notebook["1q_loss"] = EPN_notebook.apply(lambda x: DNA_samples_fill_df(CNA.loc["1q", x["Kids_First_Biospecimen_ID_DNA"]], "loss")
if x["Kids_First_Biospecimen_ID_DNA"] is not np.nan else 0,axis=1)
EPN_notebook.head()
#. Similar to the above, adding more columns to EPN_notebook
EPN_notebook["9p_loss"] = EPN_notebook.apply(lambda x: DNA_samples_fill_df(CNA.loc["9p", x["Kids_First_Biospecimen_ID_DNA"]], "loss")
if x["Kids_First_Biospecimen_ID_DNA"] is not np.nan else 0,axis=1)
EPN_notebook["9q_loss"] = EPN_notebook.apply(lambda x: DNA_samples_fill_df(CNA.loc["9q", x["Kids_First_Biospecimen_ID_DNA"]], "loss")
if x["Kids_First_Biospecimen_ID_DNA"] is not np.nan else 0,axis=1)
EPN_notebook["6p_loss"] = EPN_notebook.apply(lambda x: DNA_samples_fill_df(CNA.loc["6p", x["Kids_First_Biospecimen_ID_DNA"]], "loss")
if x["Kids_First_Biospecimen_ID_DNA"] is not np.nan else 0,axis=1)
EPN_notebook["6q_loss"] = EPN_notebook.apply(lambda x: DNA_samples_fill_df(CNA.loc["6q", x["Kids_First_Biospecimen_ID_DNA"]], "loss")
if x["Kids_First_Biospecimen_ID_DNA"] is not np.nan else 0,axis=1)
EPN_notebook["11q_loss"] = EPN_notebook.apply(lambda x: DNA_samples_fill_df(CNA.loc["11q", x["Kids_First_Biospecimen_ID_DNA"]], "loss")
if x["Kids_First_Biospecimen_ID_DNA"] is not np.nan else 0,axis=1)
EPN_notebook["11q_gain"] = EPN_notebook.apply(lambda x: DNA_samples_fill_df(CNA.loc["11q", x["Kids_First_Biospecimen_ID_DNA"]], "gain")
if x["Kids_First_Biospecimen_ID_DNA"] is not np.nan else 0,axis=1)
EPN_notebook.head(4)
gsva_NFKB.head(3)
# GSVA. score for NFKB score
# Adding column for NFKB GSEA_score to EPN_notebook
# If DNA sample BSID not found, then fill with "NA"
EPN_notebook["breaks_density-chromosomal_instability"] = EPN_notebook.apply(lambda x: breakpoint_density.loc[x["Kids_First_Biospecimen_ID_DNA"], "breaks_density"]
if x["Kids_First_Biospecimen_ID_DNA"] is not np.nan else "NA", axis=1)
EPN_notebook.head(3)
# Printing. FPKM dataframe
fpkm_df.head(2)
# Adding FPKM for different genes to EPN_notebook using function fill_df_with_fpkm_zscores
EPN_notebook = fill_df_with_fpkm_zscores(EPN_notebook, fpkm_df, "RELA_expr_Z-scores", "RELA")
EPN_notebook = fill_df_with_fpkm_zscores(EPN_notebook, fpkm_df, "L1CAM_expr_Zscore", "L1CAM")
EPN_notebook = fill_df_with_fpkm_zscores(EPN_notebook, fpkm_df, "ARL4D_expr_Zscore", "ARL4D")
EPN_notebook = fill_df_with_fpkm_zscores(EPN_notebook, fpkm_df, "CLDN1_expr_zscore", "CLDN1")
EPN_notebook = fill_df_with_fpkm_zscores(EPN_notebook, fpkm_df, "CXorf67_expr_zscore", "CXorf67")
EPN_notebook = fill_df_with_fpkm_zscores(EPN_notebook, fpkm_df, "TKTL1_expr_zscore", "TKTL1")
EPN_notebook = fill_df_with_fpkm_zscores(EPN_notebook, fpkm_df, "GPBP1_expr_zscore", "GPBP1")
EPN_notebook = fill_df_with_fpkm_zscores(EPN_notebook, fpkm_df, "IFT46_expr_zscore", "IFT46")
EPN_notebook.head(4)
# Finally print out the dataframe to an output file
```
|
github_jupyter
|
```
# importing libraries
import h5py
import scipy.io as io
import PIL.Image as Image
import numpy as np
import os
import glob
from matplotlib import pyplot as plt
from scipy.ndimage.filters import gaussian_filter
import scipy
from scipy import spatial
import json
from matplotlib import cm as CM
from image import *
from model import CSRNet
import torch
from tqdm import tqdm
%matplotlib inline
# function to create density maps for images
def gaussian_filter_density(gt):
print (gt.shape)
density = np.zeros(gt.shape, dtype=np.float32)
gt_count = np.count_nonzero(gt)
if gt_count == 0:
return density
pts = np.array(list(zip(np.nonzero(gt)[1], np.nonzero(gt)[0])))
leafsize = 2048
# build kdtree
tree = scipy.spatial.KDTree(pts.copy(), leafsize=leafsize)
# query kdtree
distances, locations = tree.query(pts, k=4)
print ('generate density...')
for i, pt in enumerate(pts):
pt2d = np.zeros(gt.shape, dtype=np.float32)
pt2d[pt[1],pt[0]] = 1.
if gt_count > 1:
sigma = (distances[i][1]+distances[i][2]+distances[i][3])*0.1
else:
sigma = np.average(np.array(gt.shape))/2./2. #case: 1 point
density += scipy.ndimage.filters.gaussian_filter(pt2d, sigma, mode='constant')
print ('done.')
return density
#setting the root to the Shanghai dataset you have downloaded
# change the root path as per your location of dataset
root = '../ShanghaiTech/'
part_A_train = os.path.join(root,'part_A/train_data','images')
part_A_test = os.path.join(root,'part_A/test_data','images')
part_B_train = os.path.join(root,'part_B/train_data','images')
part_B_test = os.path.join(root,'part_B/test_data','images')
path_sets = [part_A_train,part_A_test]
img_paths = []
for path in path_sets:
for img_path in glob.glob(os.path.join(path, '*.jpg')):
img_paths.append(img_path)
for img_path in img_paths:
print (img_path)
mat = io.loadmat(img_path.replace('.jpg','.mat').replace('images','ground-truth').replace('IMG_','GT_IMG_'))
img= plt.imread(img_path)
k = np.zeros((img.shape[0],img.shape[1]))
gt = mat["image_info"][0,0][0,0][0]
for i in range(0,len(gt)):
if int(gt[i][1])<img.shape[0] and int(gt[i][0])<img.shape[1]:
k[int(gt[i][1]),int(gt[i][0])]=1
k = gaussian_filter_density(k)
with h5py.File(img_path.replace('.jpg','.h5').replace('images','ground-truth'), 'w') as hf:
hf['density'] = k
plt.imshow(Image.open(img_paths[0]))
gt_file = h5py.File(img_paths[0].replace('.jpg','.h5').replace('images','ground-truth'),'r')
groundtruth = np.asarray(gt_file['density'])
plt.imshow(groundtruth,cmap=CM.jet)
np.sum(groundtruth)
path_sets = [part_B_train,part_B_test]
img_paths = []
for path in path_sets:
for img_path in glob.glob(os.path.join(path, '*.jpg')):
img_paths.append(img_path)
# creating density map for part_b images
for img_path in img_paths:
print (img_path)
mat = io.loadmat(img_path.replace('.jpg','.mat').replace('images','ground-truth').replace('IMG_','GT_IMG_'))
img= plt.imread(img_path)
k = np.zeros((img.shape[0],img.shape[1]))
gt = mat["image_info"][0,0][0,0][0]
for i in range(0,len(gt)):
if int(gt[i][1])<img.shape[0] and int(gt[i][0])<img.shape[1]:
k[int(gt[i][1]),int(gt[i][0])]=1
k = gaussian_filter_density(k)
with h5py.File(img_path.replace('.jpg','.h5').replace('images','ground-truth'), 'w') as hf:
hf['density'] = k
```
|
github_jupyter
|
<a href="https://colab.research.google.com/github/arjunparmar/VIRTUON/blob/main/Harshit/SwapNet_Experimentation.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
from google.colab import drive
drive.mount('/content/drive')
## Imports
import os
import sys
import random
import numpy as np
import cv2
import matplotlib.pyplot as plt
from glob import glob
import tensorflow
from tensorflow import keras
from tensorflow.python.keras import backend as K
from tensorflow.python.keras.preprocessing import image
from tensorflow.python.keras.preprocessing.image import ImageDataGenerator
from tensorflow.python.keras.layers import concatenate, Concatenate
## Seeding
seed = 2019
random.seed = seed
np.random.seed = seed
tensorflow.seed = seed
def load_image(img_path, show=False):
img = cv2.imread(img_path)
img = cv2.resize(img, (128,128))
img_tensor = image.img_to_array(img) # (height, width, channels)
#|img_tensor = np.expand_dims(img_tensor, axis=0) # (1, height, width, channels), add a dimension because the model expects this shape: (batch_size, height, width, channels) # imshow expects values in the range [0, 1]
return img_tensor
!mkdir seg_train
!cp -r /content/drive/Shareddrives/Virtuon/Clothing\ Coparsing/dataset/seg_train/* /content/seg_train/
!mkdir seg_test
!cp -r /content/drive/Shareddrives/Virtuon/Clothing\ Coparsing/dataset/seg_test/* /content/seg_test/
!mkdir pos_train
!cp -r /content/drive/Shareddrives/Virtuon/Clothing\ Coparsing/dataset/pose_train/* /content/pos_train/
!mkdir pos_test
!cp -r /content/drive/Shareddrives/Virtuon/Clothing\ Coparsing/dataset/pose_test/* /content/pos_test/
x = []
y = []
def get_image(path):
data =[]
for subdir, dirs, files in os.walk(path):
for f in files:
path = os.path.join(subdir, f)
img = load_image(path)
# print(img.shape)
data.append(img)
return data
x_1 = get_image(r'/content/pos_train') #BS
x_2 = get_image(r'/content/seg_train') #CS
y = get_image(r'/content/seg_train')
x_1 = np.asarray(x_1)
x_2 = np.asarray(x_2)
y = np.asarray(y)
print(x_1.shape)
print(x_2.shape)
print(y.shape)
def down_block(x, filters, kernel_size=(3, 3), padding="same", strides=1):
c = keras.layers.Conv2D(filters, kernel_size, padding=padding, strides=strides, activation="relu")(x)
c = keras.layers.Conv2D(filters, kernel_size, padding=padding, strides=strides, activation="relu")(c)
c = keras.layers.Conv2D(filters, kernel_size, padding=padding, strides=strides, activation="relu")(c)
c = keras.layers.Conv2D(filters, kernel_size, padding=padding, strides=strides, activation="relu")(c)
p = keras.layers.MaxPool2D((2, 2), (2, 2))(c)
return c, p
def up_block(x, skip, filters, kernel_size=(3, 3), padding="same", strides=1):
us = keras.layers.UpSampling2D((2, 2))(x)
concat = keras.layers.Concatenate()([us, skip])
c = keras.layers.Conv2D(filters, kernel_size, padding=padding, strides=strides, activation="relu")(concat)
c = keras.layers.Conv2D(filters, kernel_size, padding=padding, strides=strides, activation="relu")(c)
c = keras.layers.Conv2D(filters, kernel_size, padding=padding, strides=strides, activation="relu")(c)
return c
def bottleneck(x, filters, kernel_size=(3, 3), padding="same", strides=1):
c = keras.layers.Conv2D(filters, kernel_size, padding=padding, strides=strides, activation="relu")(x)
c = keras.layers.Conv2D(filters, kernel_size, padding=padding, strides=strides, activation="relu")(c)
c = keras.layers.Conv2D(filters, kernel_size, padding=padding, strides=strides, activation="relu")(c)
return c
def res_block(u3):
c1 = keras.layers.Conv2D(64, kernel_size= (3,3), padding="same", strides=1, activation="relu")(u3)
c2 = keras.layers.Conv2D(32, kernel_size= (3,3), padding="same", strides=1, activation="relu")(c1)
c3 = keras.layers.Conv2D(32, kernel_size= (3,3), padding="same", strides=1, activation="relu")(c2)
c3 = keras.layers.Concatenate()([u3, c3])
c4 = keras.layers.Conv2D(64, kernel_size= (3,3), padding="same", strides=1, activation="relu")(c3)
c5 = keras.layers.Conv2D(32, kernel_size= (3,3), padding="same", strides=1, activation="relu")(c4)
c6 = keras.layers.Conv2D(32, kernel_size= (3,3), padding="same", strides=1, activation="relu")(c5)
c6 = keras.layers.Concatenate()([u3, c3, c6])
c7 = keras.layers.Conv2D(64, kernel_size= (3,3), padding="same", strides=1, activation="relu")(c6)
c8 = keras.layers.Conv2D(32, kernel_size= (3,3), padding="same", strides=1, activation="relu")(c7)
c9 = keras.layers.Conv2D(16, kernel_size= (3,3), padding="same", strides=1, activation="relu")(c8)
return c9
K.clear_session()
def UNet():
f = [16, 32, 64, 128, 256]
inputs1 = keras.layers.Input((128,128, 3))
inputs2 = keras.layers.Input((128,128, 3))
p0 = inputs1
c1, p1 = down_block(p0, f[0]) #128 -> 64
c2, p2 = down_block(p1, f[1]) #64 -> 32
c3, p3 = down_block(p2, f[2]) #32 -> 16
bn1 = bottleneck(p3, f[3])
print(bn1.shape)
inputs2 = keras.layers.Input((128,128, 3))
np0 = inputs2
nc1, np1 = down_block(np0, f[0]) #128 -> 64
nc2, np2 = down_block(np1, f[1]) #64 -> 32
nc3, np3 = down_block(np2, f[2]) #32 -> 16
bn2 = bottleneck(np3, f[3])
print(bn2.shape)
bn = keras.layers.Concatenate()([bn1, bn2])
print(bn.shape)
u1 = up_block(bn, nc3, f[2]) #16 -> 32
u2 = up_block(u1, nc2, f[1]) #32 -> 64
u3 = up_block(u2, nc1, f[0]) #64 -> 128
print(u3.shape)
#apply resblocks
res = res_block(u3)
outputs = keras.layers.Conv2D(3, (1, 1), padding="same", activation="sigmoid")(res)
model = keras.models.Model([inputs1, inputs2], outputs)
return model
model = UNet()
model.compile(optimizer="adam", loss="categorical_crossentropy", metrics=["acc"])
model.summary()
#Data augmentation to generate new data from the given data at the time of each batch
# construct the training image generator for data augmentation
batch_size = 32
aug = ImageDataGenerator(rotation_range=20)
# train the network
model.fit_generator(aug.flow([x_1, x_2], y, batch_size=batch_size), steps_per_epoch=len(x_1) // batch_size, epochs=100)
def plot(img):
plt.imshow(img)
plt.axis('off')
plt.show()
p1 = r'/content/pos_test/0.jpg'
img1= cv2.imread(p1)
plot(img1)
p2 = r'/content/seg_test/0.jpg'
img2= cv2.imread(p2)
plot(img2)
img1 = load_image(p1)
img2 = load_image(p2)
print(img1.shape)
print(img2.shape)
img1 = np.expand_dims(img1, axis = 0)
img2 = np.expand_dims(img2, axis = 0)
result = model.predict([img1, img2])
# result = np.resize(result, (128,128,3))
result.shape
result = np.squeeze(result)
plt.imshow(result)
```
|
github_jupyter
|
<table style="float:left; border:none">
<tr style="border:none">
<td style="border:none">
<a href="https://bokeh.org/">
<img
src="assets/bokeh-transparent.png"
style="width:50px"
>
</a>
</td>
<td style="border:none">
<h1>Bokeh Tutorial</h1>
</td>
</tr>
</table>
<div style="float:right;"><h2>08. Graph and Network Plots</h2></div>
This chapter will cover how to plot network node/link graphs in Bokeh using NetworkX. For information on creating graph renderers from a low level, see [Visualizing Network Graphs](https://docs.bokeh.org/en/latest/docs/user_guide/graph.html)
```
from bokeh.io import show, output_notebook
from bokeh.plotting import figure
output_notebook()
```
## Plotting from NetworkX
The easiest way to plot network graphs with Bokeh is to use the `from_networkx` function. This function accepts any NetworkX graph and returns a Bokeh `GraphRenderer` that can be added to a plot. The `GraphRenderer` has `node_renderer` and `edge_renderer` properties that contain the Bokeh renderers that draw the nodes and edges, respectively.
The example below shows a Bokeh plot of `nx.desargues_graph()`, setting some of the node and edge properties.
```
import networkx as nx
from bokeh.models import Range1d, Plot
from bokeh.plotting import from_networkx
G = nx.desargues_graph()
# We could use figure here but don't want all the axes and titles
plot = Plot(x_range=Range1d(-2, 2), y_range=Range1d(-2, 2))
# Create a Bokeh graph from the NetworkX input using nx.spring_layout
graph = from_networkx(G, nx.spring_layout, scale=1.8, center=(0,0))
plot.renderers.append(graph)
# Set some of the default node glyph (Circle) properties
graph.node_renderer.glyph.update(size=20, fill_color="orange")
# Set some edge properties too
graph.edge_renderer.glyph.line_dash = [2,2]
show(plot)
# Exercise: try a different NetworkX layout, and set some properies on `graph.edge_renderer.glyph`
# and `graph.node_renderer.glyph`
```
## Adding Extra Data Columns.
The `node_renderer` and `edge_renderer` properties of the graph renderer each have a `data_source` that is a standard `ColumnDataSource` that you can add new data to, e.g. to drive a hover tool, or to specify colors for the renderer. The example below demonstates both.
```
from bokeh.models import HoverTool
from bokeh.palettes import Category20_20
G = nx.desargues_graph() # always 20 nodes
# We could use figure here but don't want all the axes and titles
plot = Plot(x_range=Range1d(-2, 2), y_range=Range1d(-2, 2))
# Create a Bokeh graph from the NetworkX input using nx.spring_layout
graph = from_networkx(G, nx.spring_layout, scale=1.8, center=(0,0))
plot.renderers.append(graph)
# Add some new columns to the node renderer data source
graph.node_renderer.data_source.data['index'] = list(range(len(G)))
graph.node_renderer.data_source.data['colors'] = Category20_20
graph.node_renderer.glyph.update(size=20, fill_color="colors")
plot.add_tools(HoverTool(tooltips="index: @index"))
show(plot)
# Exercise: Add your own columns for other node or edge properties e.g. fill_alpha or line_color,
# or to show other fields in a tooltoip
```
## Inspection and Selection Policies
Bokeh graph renderers have `inspection_policy` and `selection_policy` properties. These can be used to control how hover inspections highlight the graph, or how selection tools make selections. These properties may be set to any of the inpection policies in `bokeh.graphs`. For instance, if a user hovers over a node, you may wish to highlight all the associated edges as well. This can be accomplished by setting the inspection policy:
graph.inspection_policy = NodesAndLinkedEdges()
as the example below demonstrates.
```
from bokeh.models.graphs import NodesAndLinkedEdges
from bokeh.models import Circle, HoverTool, MultiLine
G = nx.gnm_random_graph(15, 30)
# We could use figure here but don't want all the axes and titles
plot = Plot(x_range=Range1d(-2, 2), y_range=Range1d(-2 ,2))
# Create a Bokeh graph from the NetworkX input using nx.spring_layout
graph = from_networkx(G, nx.spring_layout, scale=1.8, center=(0,0))
plot.renderers.append(graph)
# Blue circles for nodes, and light grey lines for edges
graph.node_renderer.glyph = Circle(size=25, fill_color='#2b83ba')
graph.edge_renderer.glyph = MultiLine(line_color="#cccccc", line_alpha=0.8, line_width=2)
# green hover for both nodes and edges
graph.node_renderer.hover_glyph = Circle(size=25, fill_color='#abdda4')
graph.edge_renderer.hover_glyph = MultiLine(line_color='#abdda4', line_width=4)
# When we hover over nodes, highlight adjecent edges too
graph.inspection_policy = NodesAndLinkedEdges()
plot.add_tools(HoverTool(tooltips=None))
show(plot)
# Exercise: try a different inspection (or selection) policy like NodesOnly or EdgesAndLinkedNodes
```
# Next Section
Click on this link to go to the next notebook: [09 - Geographic Plots](09%20-%20Geographic%20Plots.ipynb).
To go back to the overview, click [here](00%20-%20Introduction%20and%20Setup.ipynb).
|
github_jupyter
|
```
from pathlib import Path
import os
import shlex
import shutil
import subprocess
import pandas as pd
names_rows_stability = [
['dg', 1], # totalEnergy
['backbone_hbond', 2],
['sidechain_hbond', 3],
['van_der_waals', 4],
['electrostatics', 5],
['solvation_polar', 6],
['solvation_hydrophobic', 7],
['van_der_waals_clashes', 8],
['entropy_sidechain', 9],
['entropy_mainchain', 10],
['sloop_entropy', 11],
['mloop_entropy', 12],
['cis_bond', 13],
['torsional_clash', 14],
['backbone_clash', 15],
['helix_dipole', 16],
['water_bridge', 17],
['disulfide', 18],
['electrostatic_kon', 19],
['partial_covalent_bonds', 20],
['energy_ionisation', 21],
['entropy_complex', 22],
['number_of_residues', 23],
['interface_residues', 24],
['interface_residues_clashing', 25],
['interface_residues_vdw_clashing', 26],
['interface_residues_bb_clashing', 27]
]
names_rows_stability_complex = ([
['intraclashes_energy_1', 3],
['intraclashes_energy_2', 4],
] + [[x[0], x[1] + 4] for x in names_rows_stability])
names_stability_complex = list(next(zip(*names_rows_stability_complex)))
names_stability_complex_wt = [name + '_wt'
for name in names_stability_complex[:-5]] + \
['number_of_residues', 'interface_residues_wt', 'interface_residues_clashing_wt',
'interface_residues_vdw_clashing_wt', 'interface_residues_bb_clashing_wt']
names_stability_complex_mut = [name + '_mut'
for name in names_stability_complex[:-5]] + \
['number_of_residues', 'interface_residues_mut', 'interface_residues_clashing_mut',
'interface_residues_vdw_clashing_mut', 'interface_residues_bb_clashing_mut']
def _export_foldxpath(path_to_export):
# export PATH=$PATH:/path/to/folder
if str(path_to_export) not in os.environ["PATH"]:
os.environ["PATH"] += ":" + str(path_to_export)
print("foldx path exported")
else:
print("foldx bin folder already in PATH")
def _rotabase_symlink(rotabase_path):
# rotabase symlink
sym_rotabase = Path("rotabase.txt")
if not sym_rotabase.is_symlink():
sym_rotabase.symlink_to(rotabase_path)
print("Symlink to rotabase.txt create on working dir")
else:
print("rotabase.txt symlink already exist on working dir")
def read_analyse_complex(output_file):
df = pd.read_csv(output_file, sep='\t', index_col=False, skiprows=8)
# Format dataframe
df = df.rename(columns=lambda s: s.lower().replace(' ', '_'))
#logger.debug(df.head())
assert df.shape[0] == 1
result = df.drop(pd.Index(['pdb', 'group1', 'group2']), axis=1).iloc[0].tolist()
return result
def convert_features_to_differences(df, keep_mut=False):
"""Convert `_wt` and `_mut` columns into `_wt` and `_change` columns.
Create a new set of features (ending in `_change`) that describe the difference between values
of the wildtype (features ending in `_wt`) and mutant (features ending in `_mut`) features.
If `keep_mut` is `False`, removes all mutant features (features ending in `_mut`).
"""
column_list = []
for column_name, column in df.iteritems():
if ('_mut' in column_name and column_name.replace('_mut', '_wt') in df.columns and
df[column_name].dtype != object):
if keep_mut:
column_list.append(column)
new_column = column - df[column_name.replace('_mut', '_wt')]
if 'secondary_structure' in column_name:
new_column = new_column.apply(lambda x: 1 if x else 0)
new_column.name = column_name.replace('_mut', '_change')
column_list.append(new_column)
else:
column_list.append(column)
new_df = pd.concat(column_list, axis=1)
return new_df
foldx_exe = "/mnt/d/Python_projects/AbPred/libs/foldx5Linux64/"
class FoldX:
def __init__(self, foldx_dir=None, verbose=True):
self._tempdir = Path(foldx_exe)
_export_foldxpath(self._tempdir)
#self.verbose = verbose
self.pdbfile = None
def _run(self, cmd, **options):
""" ********************************************
*** ***
*** FoldX 4 (c) ***
*** ***
*** code by the FoldX Consortium ***
*** ***
*** Jesper Borg, Frederic Rousseau ***
*** Joost Schymkowitz, Luis Serrano ***
*** Peter Vanhee, Erik Verschueren ***
*** Lies Baeten, Javier Delgado ***
*** and Francois Stricher ***
*** and any other of the 9! permutations ***
*** based on an original concept by ***
*** Raphael Guerois and Luis Serrano ***
********************************************
FoldX program options:
Basic OPTIONS:
-v [ --version ] arg (=Version beta 4)
print version string
-h [ --help ] produce help message
-c [ --command ] arg Choose your FoldX Command:
AlaScan
AnalyseComplex
BuildModel
CrystalWaters
Dihedrals
DNAContact
DNAScan
LoopReconstruction
MetalBinding
Optimize
PDBFile
PepX
PositionScan
PrintNetworks
Pssm
QualityAssessment
ReconstructSideChains
RepairPDB
Rmsd
SequenceDetail
SequenceOnly
Stability
-f [ --config ] arg config file location
-d [ --debug ] arg Debug, produces more output
Generic OPTIONS:
--pdb arg (="")
--pdb-list arg (="") File with a list of PDB files
--pdb-dir arg (="./") PDB directory
--output-dir arg (="./") OutPut directory
--output-file arg (="") OutPut file
--queue arg cluster queue: fast, normal, infinity,
highmem, all.q
--clean-mode arg (=0) FoldX clean mode: none, all, output or
pdb
--max-nr-retries arg (=1) Maximum number of retries of a FoldX
command if not finished successfully.
Especially important to set at least to
two when working on a cluster and file
transfers often fail.
--skip-build arg (=0) Skip the build step in the algorithm
FoldX OPTIONS:
input:
--fixSideChains arg allows FoldX to complete missing
sidechains at read-time, defaults to
true
--rotabaseLocation arg set the location of the rotabase,
defaults to rotabase.txt
--noCterm arg set whether the last residue in a list
of peptides (ex:ABC) shouldn't be
considered as the C-terminal (i.e.,
have an OXT), defaults to none
--noNterm arg set whether the first residue in a list
peptides (ex: ABC) shouldn't be
considered as the N-Terminal (i.e.,
have a third proton on the N), defaults
to none
output:
--screen arg (=1) sets screen output, defaults to true
--overwriteBatch arg (=1) set to overwrite or not the specific
name given as the first value in a
command, defaults to true
--noHeader arg (=0) remove standard FoldX Header from
outputs, defaults to false
PDB output:
--out-pdb arg (=1) set to output PDBs when doing
mutations, defaults to true
--pdbHydrogens arg (=0) output the hydrogens we place in the
generated pdbs, defaults to false
--pdbWaters arg (=0) output the predicted water bridges in
the generated pdbs, defaults to false
--pdbIons arg (=0) output the predicted metal ions in the
generated pdbs, defaults to false
--pdbDummys arg (=0) output the the dummy atoms we use (for
N and C caps of helixes as well as the
free orbitals) in the generated pdbs,
defaults to false
--pdbIsoforms arg (=0) output the isoforms of the His in the
generated pdbs, defaults to false
physico chemical parameters:
--temperature arg set the temperature (in K) of the
calculations, defaults to 298 K
--pH arg set the pH of the calculations,
defaults to 7
--ionStrength arg set the ionic strength of the
calculations, defaults to 0.05
force-field:
--vdwDesign arg set VdWDesign of the experiment,
defaults to 2 ( 0 very soft, 1 medium
soft, 2 strong used for design )
--clashCapDesign arg set maximun penalty per atom of the van
der waals' clashes, defaults set to 5.0
--backBoneAtoms arg consider only backbone atoms for all
energy calculations, defaults to false
--dipoles arg set to consider helices dipoles,
defaults to true
--complexClashes arg set the threshold (in kcal/mol) for
counting clashing aminoacids at the
interface, defaults to 1.
entropy calculations:
--fullMainEntropy arg set to maximally penalize the main
chain of ligand and protein (usefull
when comparing peptide data with
poly-Alanine backbones), defaults to
false
water and ion evaluations:
--water arg set how FoldX considers waters:
-CRYSTAL (read the pdb waters) -PREDICT
(predict water bridges from sratch)
-IGNORE (don't consider waters)
-COMPARE, defaults to -IGNORE
complex options:
--complexWithDNA arg set to consider only two groups in a
protein-DNA complex, DNA + protein,
defaults to false
algorithm specific parameters:
--moveNeighbours arg set to move neighbours when we mutate,
defaults to true
--numberOfRuns arg set the number of runs done in
BuidModel, defaults to 1
--fitAtoms arg set atoms involved in the RMSD command
BB(backbone atoms), CA(Calpha),
CA_CB(both Calpha and Cbeta),
N_CA_O(N,Calpha and O), defaults to BB
--rmsdPDB arg print out the rotated target of the
RMSD command, defaults to true
--repair_Interface arg set to limit RepairPDB when applying to
a complex: ALL(repair all residues
including interface), ONLY(repair only
the interface), NONE(no repair of the
interface), defaults to ALL
--burialLimit arg set a burial limit under which a
residue is not repaired, defaults to 1.
(inactive)
--bFactorLimit arg set a relative bFactor limit above
which a residue is not repaired,
defaults to 0. (inactive)"""
if options:
for key, value in options.items():
cmd.extend(["--" + key, value])
p = subprocess.Popen(shlex.split(cmd), universal_newlines=True, shell=False, stdout=subprocess.PIPE)
while True:
out = p.stdout.readline()
if not out and p.poll() is not None:
break
if self.verbose and out:
print(out.splitlines()[0])
def _run(self,cmd):
# call external program on `filename`
fout = open("stdout_{}.txt".format(self.pdbfile[:-4]),"w")
subprocess.check_call(shlex.split(cmd),stdout=fout)
fout.close()
def repair_pdb(self, pdbfile):
"""Run FoldX ``RepairPDB`` """
pdb = Path(pdbfile).absolute()
self.pdbfile = pdb.name
command = ("foldx --command=RepairPDB --pdb={}".format(self.pdbfile))
self._run(command)
def analyse_complex(self, pdb_file, partners):
"""Run FoldX ``AnalyseComplex``."""
pdb = Path(pdb_file).absolute()
pdb_name = pdb.name[:-4]
partner1 = partners.split('_')[0]
partner2 = partners.split('_')[1]
command = ("foldx --command=AnalyseComplex --pdb={} ".format(pdb.name) +
"--analyseComplexChains={},{} ".format(partner1, partner2))
self._run(command)
output_file = pdb.parent.joinpath('Interaction_%s_AC.fxout' % pdb_name)
result = read_analyse_complex(output_file)
return result
def point_mutations(self, pdb_file, partners, to_mutate, mutations):
"""Run FoldX ``Pssm``.
Parameters
----------
to_mutate:
Mutation specified in the following format:
{mutation.residue_wt}{chain_id}{residue_id}
mutations:
Mutant residues
"""
pdb = Path(pdb_file).absolute()
pdb_mutation = pdb.name[:-4]+'_'+to_mutate+mutations
partner1 = partners.split('_')[0]
partner2 = partners.split('_')[1]
command = ("foldx --command=Pssm --pdb={} ".format(pdb.name) +
"--analyseComplexChains={},{} ".format(partner1, partner2) +
"--positions={}a ".format(to_mutate) + "--aminoacids={} ".format(mutations) +
'--output-file={}'.format(pdb_mutation))
self._run(command)
# Copy foldX result to mantain local copy
wt_result = Path('WT_{}_1.pdb'.format(pdb.name[:-4]))
mut_result = Path('{}_1.pdb'.format(pdb.name[:-4]))
wt_rename = Path('{}-{}-wt.pdb'.format(pdb.name[:-4], to_mutate+mutations))
mut_rename = Path('{}-{}-mut.pdb'.format(pdb.name[:-4], to_mutate+mutations))
shutil.copy(wt_result, wt_rename)
shutil.copy(mut_result, mut_rename)
def build_model(self, pdb_file, foldx_mutation):
pdb = Path(pdb_file).absolute()
mutation_file = self._get_mutation_file(pdb_file, foldx_mutation)
command = ("foldx --command=BuildModel --pdb='{}' ".format(pdb.name) +
"--mutant-file='{}'".format(mutation_file))
self._run(command)
# Copy foldX result to mantain local copy
wt_result = Path('WT_{}_1.pdb'.format(pdb.name[:-4]))
mut_result = Path('{}_1.pdb'.format(pdb.name[:-4]))
wt_rename = Path('{}-{}-wt.pdb'.format(pdb.name[:-4], foldx_mutation))
mut_rename = Path('{}-{}-mut.pdb'.format(pdb.name[:-4], foldx_mutation))
shutil.copy(wt_result, wt_rename)
shutil.copy(mut_result, mut_rename)
def _get_mutation_file(self, pdb_file, foldx_mutation):
"""
Parameters
----------
foldx_mutation:
Mutation specified in the following format:
{mutation.residue_wt}{chain_id}{residue_id}{mutation.residue_mut}
"""
pdb = Path(pdb_file).absolute()
mutation_file = Path('individual_list_{}_{}.txt'.format(pdb.name[:-4], foldx_mutation))
mutation_file.write_text('{};\n'.format(foldx_mutation))
return mutation_file
```
```
PDBS_DIR = Path("out_models/")
pdbs_paths = list(PDBS_DIR.glob("*mut.pdb"))
subprocess.DEVNULL?
### form 1
procs = []
for p in range(2):
pdb = Path("VRC01.pdb").absolute()
command = ("foldx --command=RepairPDB --pdb={}".format(pdb.name))
fout = open("stdout_%d.txt" % p,'w')
p = subprocess.Popen(shlex.split(command), stdout=fout)
fout.close()
procs.append(p)
for p in procs:
p.wait()
f.name
# form 2
import os
import concurrent.futures
def run(command):
... # call external program on `filename`
command = shlex.split(command)
fout = open("stdout_{}.txt".format(f.name),"w")
subprocess.check_call(command,stdout=fout)
fout.close()
def repair_pdb(pdbfile):
pdb = Path(pdbfile).absolute()
command = ("foldx --command=RepairPDB --pdb={}".format(pdb.name))
run(command)
# populate files
pdbs_paths = list(PDBS_DIR.glob("*mut.pdb"))[:10]
CWD = os.getcwd()
try:
os.chdir(PDBS_DIR)
# start threads
with concurrent.futures.ProcessPoolExecutor(max_workers=3) as executor:
future_to_file = dict((executor.submit(repair_pdb, f), f) for f in pdbs_paths)
for future in concurrent.futures.as_completed(future_to_file):
f = future_to_file[future]
if future.exception() is not None:
print('%r generated an exception: %s' % (f, future.exception()))
# run() doesn't return anything so `future.result()` is always `None`
finally:
os.chdir(CWD)
foldx.
# form 2 with foldx class
pdbs_paths = list(PDBS_DIR.glob("*mut.pdb"))[:10]
CWD = os.getcwd()
try:
os.chdir(PDBS_DIR)
# start threads
foldx = FoldX()
with concurrent.futures.ProcessPoolExecutor(max_workers=3) as executor:
future_to_file = dict((executor.submit(foldx.repair_pdb, f), f) for f in pdbs_paths)
for future in concurrent.futures.as_completed(future_to_file):
f = future_to_file[future]
if future.exception() is not None:
print('%r generated an exception: %s' % (f, future.exception()))
# run() doesn't return anything so `future.result()` is always `None`
finally:
os.chdir(CWD)
concurrent.futures.as_completed?
```
# Testing foldx class
```
foldx = FoldX(verbose=True)
foldx.repair_pdb(pdb_file="VRC01.pdb")
pdbs_to_repair = PDBS_DIR.glob("*.pdb")
try:
os.chdir(PDBS_DIR)
#create symlink to rotabase.txt
rotabase_symlink(ROTABASE)
(PDBS_DIR.glob("*.pdb"))
for pdb in pdbs_to_repair:
options = {"command":"RepairPDB","repair_Interface":"ONLY","pdb":str(pdb.name)}
FoldX(exe="foldx",verbose=True,**options).run()
finally:
os.chdir(CWD)
subprocess.Popen?
```
|
github_jupyter
|
# Classifying OUV using NGram features and MLP
## Imports
```
import sys
sys.executable
from argparse import Namespace
from collections import Counter
import json
import os
import re
import string
import random
import numpy as np
import pandas as pd
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torch.utils.data import Dataset, DataLoader
from tqdm.notebook import tqdm
from sklearn.feature_extraction.text import TfidfTransformer
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.pipeline import Pipeline
from sklearn.metrics import confusion_matrix
from scipy.special import softmax
import pickle
import matplotlib.pyplot as plt
import torch.autograd.profiler as profiler
import torchtext
from torchtext.data import get_tokenizer
tokenizer = get_tokenizer('spacy')
print("PyTorch version {}".format(torch.__version__))
print("GPU-enabled installation? {}".format(torch.cuda.is_available()))
device = torch.device("cuda:0") if torch.cuda.is_available() else torch.device("cpu")
print(device)
```
## Data Vectorization Classes
### The Vocabulary
```
class Vocabulary(object):
"""Class to process text and extract vocabulary for mapping"""
def __init__(self, token_to_idx=None, add_unk=True, unk_token="<UNK>"):
"""
Args:
token_to_idx (dict): a pre-existing map of tokens to indices
add_unk (bool): a flag that indicates whether to add the UNK token
unk_token (str): the UNK token to add into the Vocabulary
"""
if token_to_idx is None:
token_to_idx = {}
self._token_to_idx = token_to_idx
self._idx_to_token = {idx: token
for token, idx in self._token_to_idx.items()}
self._add_unk = add_unk
self._unk_token = unk_token
self.unk_index = -1
if add_unk:
self.unk_index = self.add_token(unk_token)
def to_serializable(self):
""" returns a dictionary that can be serialized """
return {'token_to_idx': self._token_to_idx,
'add_unk': self._add_unk,
'unk_token': self._unk_token}
@classmethod
def from_serializable(cls, contents):
""" instantiates the Vocabulary from a serialized dictionary """
return cls(**contents)
def add_token(self, token):
"""Update mapping dicts based on the token.
Args:
token (str): the item to add into the Vocabulary
Returns:
index (int): the integer corresponding to the token
"""
if token in self._token_to_idx:
index = self._token_to_idx[token]
else:
index = len(self._token_to_idx)
self._token_to_idx[token] = index
self._idx_to_token[index] = token
return index
def add_many(self, tokens):
"""Add a list of tokens into the Vocabulary
Args:
tokens (list): a list of string tokens
Returns:
indices (list): a list of indices corresponding to the tokens
"""
return [self.add_token(token) for token in tokens]
def lookup_token(self, token):
"""Retrieve the index associated with the token
or the UNK index if token isn't present.
Args:
token (str): the token to look up
Returns:
index (int): the index corresponding to the token
Notes:
`unk_index` needs to be >=0 (having been added into the Vocabulary)
for the UNK functionality
"""
if self.unk_index >= 0:
return self._token_to_idx.get(token, self.unk_index)
else:
return self._token_to_idx[token]
def lookup_index(self, index):
"""Return the token associated with the index
Args:
index (int): the index to look up
Returns:
token (str): the token corresponding to the index
Raises:
KeyError: if the index is not in the Vocabulary
"""
if index not in self._idx_to_token:
raise KeyError("the index (%d) is not in the Vocabulary" % index)
return self._idx_to_token[index]
def __str__(self):
return "<Vocabulary(size=%d)>" % len(self)
def __len__(self):
return len(self._token_to_idx)
"""### The Vectorizer"""
def sparse_to_tensor(M):
"""
input: M is Scipy sparse matrix
output: pytorch sparse tensor in GPU
"""
M = M.tocoo().astype(np.float32)
indices = torch.from_numpy(np.vstack((M.row, M.col))).long()
values = torch.from_numpy(M.data)
shape = torch.Size(M.shape)
Ms = torch.sparse.FloatTensor(indices, values, shape)
return Ms.to_dense().to(args.device)
```
### The Vectorizer
```
def ngrams_iterator(token_list, ngrams):
"""Return an iterator that yields the given tokens and their ngrams.
Arguments:
token_list: A list of tokens
ngrams: the number of ngrams.
Examples:
>>> token_list = ['here', 'we', 'are']
>>> list(ngrams_iterator(token_list, 2))
>>> ['here', 'here we', 'we', 'we are', 'are']
"""
def _get_ngrams(n):
return zip(*[token_list[i:] for i in range(n)])
for x in token_list:
yield x
for n in range(2, ngrams + 1):
for x in _get_ngrams(n):
yield ' '.join(x)
# Vectorization parameters
# Range (inclusive) of n-gram sizes for tokenizing text.
NGRAM_RANGE = (1, 2)
# Limit on the number of features. We use the top 20K features.
TOP_K = 20000
# Whether text should be split into word or character n-grams.
# One of 'word', 'char'.
TOKEN_MODE = 'word'
# Minimum document/corpus frequency below which a token will be discarded.
MIN_DOCUMENT_FREQUENCY = 2
def sparse_to_tensor(M):
"""
input: M is Scipy sparse matrix
output: pytorch sparse tensor in GPU
"""
M = M.tocoo().astype(np.float32)
indices = torch.from_numpy(np.vstack((M.row, M.col))).long()
values = torch.from_numpy(M.data)
shape = torch.Size(M.shape)
Ms = torch.sparse.FloatTensor(indices, values, shape)
return Ms.to_dense().to(args.device)
class OuvVectorizer(object):
""" The Vectorizer which coordinates the Vocabularies and puts them to use"""
def __init__(self, ouv_vocab, ngrams, vectorizer):
"""
Args:
review_vocab (Vocabulary): maps words to integers
"""
self.ouv_vocab = ouv_vocab
self.ngrams = ngrams
self.vectorizer = vectorizer
def vectorize(self, data):
"""Create a tf_idf vector for the ouv data
Args:
data (str): the ouv description data
ngrams (int): the maximum ngram value
Returns:
tf_idf (np.ndarray): the tf-idf encoding
"""
data = [data]
tf_idf = self.vectorizer.transform(data)
return sparse_to_tensor(tf_idf)[0]
@classmethod
def from_dataframe(cls, ouv_df, ngrams, cutoff=5):
"""Instantiate the vectorizer from the dataset dataframe
Args:
ouv_df (pandas.DataFrame): the ouv dataset
cutoff (int): the parameter for frequency-based filtering
ngrams (int): the maximum ngram value
Returns:
an instance of the OuvVectorizer
"""
ouv_vocab = Vocabulary(add_unk=True)
corpus=[]
# Add top words if count > provided count
word_counts = Counter()
for data in ouv_df.data:
corpus.append(data)
for word in ngrams_iterator(data.split(' '),ngrams=ngrams):
if word not in string.punctuation:
word_counts[word] += 1
for word, count in word_counts.items():
if count > cutoff:
ouv_vocab.add_token(word)
# Create keyword arguments to pass to the 'tf-idf' vectorizer.
kwargs = {
'ngram_range': NGRAM_RANGE, # Use 1-grams + 2-grams.
'dtype': 'int32',
'strip_accents': 'unicode',
'decode_error': 'replace',
'analyzer': TOKEN_MODE, # Split text into word tokens.
'min_df': MIN_DOCUMENT_FREQUENCY,
}
vectorizer = TfidfVectorizer(**kwargs)
# Learn vocabulary from training texts and vectorize training texts.
vectorizer.fit_transform(corpus).astype('float32')
return cls(ouv_vocab, ngrams, vectorizer)
@classmethod
def from_serializable(cls, contents, ngrams, vectorizer):
"""Instantiate a OuvVectorizer from a serializable dictionary
Args:
contents (dict): the serializable dictionary
Returns:
an instance of the OuvVectorizer class
"""
ouv_vocab = Vocabulary.from_serializable(contents['ouv_vocab'])
return cls(ouv_vocab=ouv_vocab, ngrams=ngrams, vectorizer = vectorizer)
def to_serializable(self):
"""Create the serializable dictionary for caching
Returns:
contents (dict): the serializable dictionary
"""
return {'ouv_vocab': self.ouv_vocab.to_serializable()}
```
### The Dataset
```
class OuvDataset(Dataset):
def __init__(self, ouv_df, vectorizer):
"""
Args:
ouv_df (pandas.DataFrame): the dataset
vectorizer (ReviewVectorizer): vectorizer instantiated from dataset
"""
self.ouv_df = ouv_df
self._vectorizer = vectorizer
self.train_df = self.ouv_df[self.ouv_df.split=='train']
self.train_size = len(self.train_df)
self.val_df = self.ouv_df[self.ouv_df.split=='dev']
self.validation_size = len(self.val_df)
self.test_df = self.ouv_df[self.ouv_df.split=='test']
self.test_size = len(self.test_df)
self._lookup_dict = {'train': (self.train_df, self.train_size),
'val': (self.val_df, self.validation_size),
'test': (self.test_df, self.test_size)}
self.set_split('train')
@classmethod
def load_dataset_and_make_vectorizer(cls, ouv_csv, ngrams, cutoff):
"""Load dataset and make a new vectorizer from scratch
Args:
ouv_csv (str): location of the dataset
Returns:
an instance of OuvDataset
"""
ouv_df = pd.read_csv(ouv_csv)
train_ouv_df = ouv_df[ouv_df.split=='train']
return cls(ouv_df, OuvVectorizer.from_dataframe(train_ouv_df,ngrams=ngrams, cutoff=cutoff))
@classmethod
def load_dataset_and_load_vectorizer(cls, ouv_csv, vectorizer_filepath, ngrams, vectorizer):
"""Load dataset and the corresponding vectorizer.
Used in the case in the vectorizer has been cached for re-use
Args:
ouv_csv (str): location of the dataset
vectorizer_filepath (str): location of the saved vectorizer
Returns:
an instance of OuvDataset
"""
ouv_df = pd.read_csv(ouv_csv)
vectorizer = cls.load_vectorizer_only(vectorizer_filepath, ngrams=ngrams, vectorizer=vectorizer)
return cls(ouv_df, vectorizer)
@staticmethod
def load_vectorizer_only(vectorizer_filepath,ngrams, vectorizer):
"""a static method for loading the vectorizer from file
Args:
vectorizer_filepath (str): the location of the serialized vectorizer
Returns:
an instance of ReviewVectorizer
"""
with open(vectorizer_filepath) as fp:
return OuvVectorizer.from_serializable(json.load(fp),ngrams=ngrams, vectorizer=vectorizer)
def save_vectorizer(self, vectorizer_filepath):
"""saves the vectorizer to disk using json
Args:
vectorizer_filepath (str): the location to save the vectorizer
"""
with open(vectorizer_filepath, "w") as fp:
json.dump(self._vectorizer.to_serializable(), fp)
def get_vectorizer(self):
""" returns the vectorizer """
return self._vectorizer
def set_split(self, split="train"):
""" selects the splits in the dataset using a column in the dataframe
Args:
split (str): one of "train", "val", or "test"
"""
self._target_split = split
self._target_df, self._target_size = self._lookup_dict[split]
def __len__(self):
return self._target_size
def __getitem__(self, index):
"""the primary entry point method for PyTorch datasets
Args:
index (int): the index to the data point
Returns:
a dictionary holding the data point's features (x_data) and component for labels (y_target and y_fuzzy)
"""
row = self._target_df.iloc[index]
ouv_vector = \
self._vectorizer.vectorize(row.data)
true_label = \
np.fromstring(row.true[1:-1],dtype=float, sep=' ')
if len(true_label)==10:
true_label = np.append(true_label,0.0)
fuzzy_label = \
np.fromstring(row.fuzzy[1:-1],dtype=float, sep=' ')
return {'x_data': ouv_vector,
'y_target': true_label,
'y_fuzzy': fuzzy_label
}
def get_num_batches(self, batch_size):
"""Given a batch size, return the number of batches in the dataset
Args:
batch_size (int)
Returns:
number of batches in the dataset
"""
return len(self) // batch_size
def generate_batches(dataset, batch_size, shuffle=True,
drop_last=True, device="cpu"):
"""
A generator function which wraps the PyTorch DataLoader. It will
ensure each tensor is on the write device location.
"""
dataloader = DataLoader(dataset=dataset, batch_size=batch_size,
shuffle=shuffle, drop_last=drop_last)
for data_dict in dataloader:
out_data_dict = {}
for name, tensor in data_dict.items():
out_data_dict[name] = data_dict[name].to(device)
yield out_data_dict
```
## The Model: Naive_Bayers_Classifier
```
class MLPClassifier(nn.Module):
def __init__(self, embedding_size, hidden_dim, num_classes, dropout_p,
pretrained_embeddings=None, padding_idx=0):
"""
Args:
embedding_size (int): size of the embedding vectors
num_embeddings (int): number of embedding vectors
hidden_dim (int): the size of the hidden dimension
num_classes (int): the number of classes in classification
dropout_p (float): a dropout parameter
pretrained_embeddings (numpy.array): previously trained word embeddings
default is None. If provided,
padding_idx (int): an index representing a null position
"""
super(MLPClassifier, self).__init__()
self._dropout_p = dropout_p
self.dropout = nn.Dropout(dropout_p)
self.fc1 = nn.Linear(embedding_size, hidden_dim)
self.fc2 = nn.Linear(hidden_dim, num_classes)
def forward(self, x_in, apply_softmax=False):
"""The forward pass of the classifier
Args:
x_in (torch.Tensor): an input data tensor.
x_in.shape should be (batch, dataset._max_seq_length)
apply_softmax (bool): a flag for the softmax activation
should be false if used with the Cross Entropy losses
Returns:
the resulting tensor. tensor.shape should be (batch, num_classes)
"""
intermediate_vector = F.relu(self.dropout(self.fc1(x_in)))
prediction_vector = self.fc2(intermediate_vector)
if apply_softmax:
prediction_vector = F.softmax(prediction_vector, dim=1)
return prediction_vector
```
## Training Routine
### Helper Functions
```
def make_train_state(args):
return {'stop_early': False,
'early_stopping_step': 0,
'early_stopping_best_k_acc_val': 0,
'learning_rate': args.learning_rate,
'epoch_index': 0,
'train_loss': [],
'train_1_acc': [],
'train_k_acc': [],
'train_k_jac': [],
'val_loss': [],
'val_1_acc': [],
'val_k_acc': [],
'val_k_jac': [],
'test_loss': -1,
'test_1_acc': -1,
'test_k_acc':-1,
'test_k_jac':-1,
'model_filename': args.model_state_file}
def update_train_state(args, model, train_state):
"""Handle the training state updates.
Components:
- Early Stopping: Prevent overfitting.
- Model Checkpoint: Model is saved if the model is better
:param args: main arguments
:param model: model to train
:param train_state: a dictionary representing the training state values
:returns:
a new train_state
"""
# Save one model at least
if train_state['epoch_index'] == 0:
torch.save(model.state_dict(), train_state['model_filename'])
train_state['stop_early'] = False
# Save model if performance improved
elif train_state['epoch_index'] >= 1:
acc_tm1, acc_t = train_state['val_k_acc'][-2:]
# If accuracy worsened
if acc_t <= train_state['early_stopping_best_k_acc_val']:
# Update step
train_state['early_stopping_step'] += 1
# Loss decreased
else:
# Save the best model from sklearn
if acc_t > train_state['early_stopping_best_k_acc_val']:
train_state['early_stopping_best_k_acc_val'] = acc_t
torch.save(model.state_dict(), train_state['model_filename'])
# Reset early stopping step
train_state['early_stopping_step'] = 0
# Stop early ?
train_state['stop_early'] = \
train_state['early_stopping_step'] >= args.early_stopping_criteria
return train_state
```
### Evaluation Metrics
```
def compute_cross_entropy(y_pred, y_target):
y_target = y_target.cpu().float()
y_pred = y_pred.cpu().float()
criterion = nn.BCEWithLogitsLoss()
return criterion(y_target, y_pred)
def compute_1_accuracy(y_pred, y_target):
y_target_indices = y_target.max(dim=1)[1]
y_pred_indices = y_pred.max(dim=1)[1]
n_correct = torch.eq(y_pred_indices, y_target_indices).sum().item()
return n_correct / len(y_pred_indices) * 100
def compute_k_accuracy(y_pred, y_target, k=3):
y_pred_indices = y_pred.topk(k, dim=1)[1]
y_target_indices = y_target.max(dim=1)[1]
n_correct = torch.tensor([y_pred_indices[i] in y_target_indices[i] for i in range(len(y_pred))]).sum().item()
return n_correct / len(y_pred_indices) * 100
def compute_k_jaccard_index(y_pred, y_target, k=3):
y_target_indices = y_target.topk(k, dim=1)[1]
y_pred_indices = y_pred.max(dim=1)[1]
jaccard = torch.tensor([len(np.intersect1d(y_target_indices[i], y_pred_indices[i]))/
len(np.union1d(y_target_indices[i], y_pred_indices[i]))
for i in range(len(y_pred))]).sum().item()
return jaccard / len(y_pred_indices)
def compute_jaccard_index(y_pred, y_target, k=3, multilabel=False):
threshold = 1.0/(k+1)
threshold_2 = 0.5
if multilabel:
y_pred_indices = y_pred.gt(threshold_2)
else:
y_pred_indices = y_pred.gt(threshold)
y_target_indices = y_target.gt(threshold)
jaccard = ((y_target_indices*y_pred_indices).sum(axis=1)/((y_target_indices+y_pred_indices).sum(axis=1)+1e-8)).sum().item()
return jaccard / len(y_pred_indices)
def softmax_sensitive(T):
T = np.exp(T) - np.exp(0) + 1e-9
if len(T.shape)==1:
return T/T.sum()
return T/(T.sum(axis=1).unsqueeze(1))
def cross_entropy(pred, soft_targets):
logsoftmax = nn.LogSoftmax(dim=1)
return torch.mean(torch.sum(- soft_targets * logsoftmax(pred), 1))
# convert a df to tensor to be used in pytorch
def df_to_tensor(df):
device = args.device
return torch.from_numpy(df.values).float().to(device)
def get_prior():
prior = pd.read_csv(args.prior_csv,sep=';',names=classes[:-1], skiprows=1)
prior['Others'] = 1
prior = prior.T
prior['Others'] = 1
prior = df_to_tensor(prior)
return prior
def compute_fuzzy_label(y_target, y_fuzzy, fuzzy=False, how='uni', lbd=0):
'''
Using two sets of prediction labels and fuzziness parameters to compute the fuzzy label in the form as
a distribution over classes
Args:
y_target (torch.Tensor) of shape (n_batch, n_classes): the true label of the ouv description
y_fuzzy (torch.Tensor) of shape (n_batch, n_classes): the fuzzy label of the ouv description
fuzzy (bool): whether or not to turn on the fuzziness option
how (string): the way fuzziness weights are used, one of the options in {'uni', 'prior'}
lbd (float): the scaler applied to the fuzziness of the label
Returns:
A pytorch Tensor of shape (n_batch, n_classes): The processed label in the form of distribution that add to 1
'''
assert y_target.shape == y_fuzzy.shape, 'target labels must have the same size'
assert how in {'uni', 'prior', 'origin'}, '''how must be one of the two options in {'uni', 'prior', 'origin'}'''
if not fuzzy:
return softmax_sensitive(y_target)
if how == 'uni':
y_label = y_target + lbd * y_fuzzy
return softmax_sensitive(y_label)
### TO DO ###
elif how == 'prior':
prior = get_prior()
y_inter = torch.matmul(y_target.float(),prior)
y_inter = y_inter/(y_inter.max(dim=1, keepdim=True)[0])
y_label = y_target + lbd * y_fuzzy * y_inter
return softmax_sensitive(y_label)
else:
y_label = y_target + lbd
return softmax_sensitive(y_label)
def sparse_to_tensor(M):
"""
input: M is Scipy sparse matrix
output: pytorch sparse tensor in GPU
"""
M = M.tocoo().astype(np.float32)
indices = torch.from_numpy(np.vstack((M.row, M.col))).long()
values = torch.from_numpy(M.data)
shape = torch.Size(M.shape)
Ms = torch.sparse.FloatTensor(indices, values, shape, device=args.device)
return Ms.to_dense()
```
### General Utilities
```
def set_seed_everywhere(seed, cuda):
np.random.seed(seed)
random.seed(seed)
torch.manual_seed(seed)
if cuda:
torch.cuda.manual_seed_all(seed)
def handle_dirs(dirpath):
if not os.path.exists(dirpath):
os.makedirs(dirpath)
```
### Settings and Some Prep Work
```
args = Namespace(
# Data and Path information
frequency_cutoff=1,
model_state_file='model.pth',
ouv_csv='Data/ouv_with_splits_full.csv',
#ouv_csv='Data/all_with_splits_full.csv',
prior_csv = 'Data/Coappearance_matrix.csv',
save_dir='model_storage/ngram/',
vectorizer_file='vectorizer.json',
# Model hyper parameters
ngrams=2,
hidden_dim=200,
# Training hyper parameters
batch_size=128,
early_stopping_criteria=5,
learning_rate=0.0002,
l2 = 1e-5,
dropout_p=0.5,
k = 3,
fuzzy = True,
fuzzy_how = 'uni',
fuzzy_lambda = 0.1,
num_epochs=100,
seed=1337,
# Runtime options
catch_keyboard_interrupt=True,
cuda=True,
expand_filepaths_to_save_dir=True,
reload_from_files=False,
)
classes = ['Criteria i', 'Criteria ii', 'Criteria iii', 'Criteria iv', 'Criteria v', 'Criteria vi',
'Criteria vii', 'Criteria viii', 'Criteria ix', 'Criteria x', 'Others']
if args.expand_filepaths_to_save_dir:
args.vectorizer_file = os.path.join(args.save_dir,
args.vectorizer_file)
args.model_state_file = os.path.join(args.save_dir,
args.model_state_file)
print("Expanded filepaths: ")
print("\t{}".format(args.vectorizer_file))
print("\t{}".format(args.model_state_file))
# Check CUDA
if not torch.cuda.is_available():
args.cuda = False
print("Using CUDA: {}".format(args.cuda))
args.device = torch.device("cuda" if args.cuda else "cpu")
# Set seed for reproducibility
set_seed_everywhere(args.seed, args.cuda)
# handle dirs
handle_dirs(args.save_dir)
```
## Initialization
```
set_seed_everywhere(args.seed, args.cuda)
if args.reload_from_files:
# training from a checkpoint
dataset = OuvDataset.load_dataset_and_load_vectorizer(args.ouv_csv, args.vectorizer_file)
else:
# create dataset and vectorizer
dataset = OuvDataset.load_dataset_and_make_vectorizer(args.ouv_csv,
cutoff=args.frequency_cutoff, ngrams=args.ngrams)
dataset.save_vectorizer(args.vectorizer_file)
vectorizer = dataset.get_vectorizer()
embedding_size = len(vectorizer.vectorizer.vocabulary_)
classifier = MLPClassifier(embedding_size=embedding_size,
hidden_dim=args.hidden_dim,
num_classes=len(classes),
dropout_p=args.dropout_p)
embedding_size
```
### Training Loop
```
with profiler.profile(record_shapes=True) as prof:
with profiler.record_function("model_inference"):
classifier(X)
print(prof.key_averages().table(sort_by="cpu_time_total", row_limit=10))
```
## Loading Trained Models
### Option 1 LS Model
```
with open(args.save_dir+'hyperdict_fuzzy.p', 'rb') as fp:
hyperdict_fuzzy = pickle.load(fp)
train_state = hyperdict_fuzzy[('uni',0.1)]
classifier.load_state_dict(torch.load(args.save_dir+'1337/model.pth',map_location=torch.device('cpu')))
classifier.eval()
```
### Option 2 Baseline w/o LS
```
with open(args.save_dir+'hyperdict_fuzzy.p', 'rb') as fp:
hyperdict_fuzzy = pickle.load(fp)
train_state = hyperdict_fuzzy[('uni',0)]
classifier.load_state_dict(torch.load(args.save_dir+'baseline/model.pth',map_location=torch.device('cpu')))
classifier.eval()
def count_parameters(model):
return sum(p.numel() for p in model.parameters() if p.requires_grad)
count_parameters(classifier)
# compute the loss & accuracy on the test set using the best available model
loss_func = cross_entropy
set_seed_everywhere(args.seed, args.cuda)
dataset.set_split('test')
batch_generator = generate_batches(dataset,
batch_size=args.batch_size,
device=args.device)
running_loss = 0.
running_1_acc = 0.
running_k_acc = 0.
running_k_jac = 0.
classifier.eval()
for batch_index, batch_dict in enumerate(batch_generator):
# get the data compute fuzzy labels
X = batch_dict['x_data']
y_target = batch_dict['y_target']
y_fuzzy = batch_dict['y_fuzzy']
Y = compute_fuzzy_label(y_target, y_fuzzy, fuzzy= args.fuzzy,
how=args.fuzzy_how, lbd = args.fuzzy_lambda)
# compute the output
with torch.no_grad():
y_pred = classifier(X)
# compute the loss
loss = loss_func(y_pred, Y)
loss_t = loss.item()
running_loss += (loss_t - running_loss) / (batch_index + 1)
# compute the accuracy
acc_1_t = compute_1_accuracy(y_pred, y_target)
acc_k_t = compute_k_accuracy(y_pred, y_target, args.k)
jac_k_t = compute_jaccard_index(y_pred, y_target, args.k)
running_1_acc += (acc_1_t - running_1_acc) / (batch_index + 1)
running_k_acc += (acc_k_t - running_k_acc) / (batch_index + 1)
running_k_jac += (jac_k_t - running_k_jac) / (batch_index + 1)
train_state['test_loss'] = running_loss
train_state['test_1_acc'] = running_1_acc
train_state['test_k_acc'] = running_k_acc
train_state['test_k_jac'] = running_k_jac
# Result of LS Model
train_state
# Result of Baseline
train_state
```
## Inference
```
def preprocess_text(text):
text = text.lower()
text = re.sub(r"([.,!?])", r" \1 ", text)
text = re.sub(r"[^a-zA-Z.,!?]+", r" ", text)
return text
def predict_rating(text, classifier, vectorizer, classes, k=1):
"""Predict the rating of a review
Args:
text (str): the text of the description
classifier (ReviewClassifier): the trained model
vectorizer (ReviewVectorizer): the corresponding vectorizer
classes (list of str): The name of the ouv classes
k (int): show the largest k prediction, default to 1
"""
classifier.eval()
ouv = preprocess_text(text)
vectorized_ouv = vectorizer.vectorize(ouv)
X = vectorized_ouv.view(1,-1)
with torch.no_grad():
result = classifier(vectorized_ouv.unsqueeze(0), apply_softmax=True)
if k==1:
pred_id = result.argmax().item()
return (classes[pred_id], result[0][pred_id])
else:
pred_indices = [i.item() for i in result.topk(k)[1][0]]
output = []
for pred_id in pred_indices:
output.append((classes[pred_id],result[0][pred_id].item()))
return output
test_ouv = 'this is a very old building dating back to 13th century'
prediction = predict_rating(test_ouv,classifier,vectorizer,classes)
print('{} -> {} with a probability of {:0.2f}'.format(test_ouv, prediction[0],prediction[1]))
test_ouv = 'this is a very old building dating back to 13th century'
k=3
predictions = predict_rating(test_ouv,classifier,vectorizer,classes,k)
print("Top {} predictions:".format(k))
print("===================")
for prediction in predictions:
print('{} -> {} with a probability of {:0.2f}'.format(test_ouv, prediction[0],prediction[1]))
test_ouv = 'The particular layout of the complex is unique to this site'
k=3
predictions = predict_rating(test_ouv,classifier,vectorizer,classes,k)
print("Top {} predictions:".format(k))
print("===================")
for prediction in predictions:
print('{} -> {} with a probability of {:0.2f}'.format(test_ouv, prediction[0],prediction[1]))
test_ouv = '''the lagoon of venice also has one of the highest concentrations of masterpieces in the world from
torcellos cathedral to the church of santa maria della salute . the years of the republics extraordinary golden
age are represented by monuments of incomparable beauty'''
k=3
predictions = predict_rating(test_ouv,classifier,vectorizer,classes,k)
print("Top {} predictions:".format(k))
print("===================")
for prediction in predictions:
print('{} -> {} with a probability of {:0.2f}'.format(test_ouv, prediction[0],prediction[1]))
test_ouv = '''the lagoon of venice also has one of the highest concentrations of masterpieces in the world'''
k=3
predictions = predict_rating(test_ouv,classifier,vectorizer,classes,k)
print("Top {} predictions:".format(k))
print("===================")
for prediction in predictions:
print('{} -> {} with a probability of {:0.2f}'.format(test_ouv, prediction[0],prediction[1]))
test_ouv = '''from torcellos cathedral to the church of santa maria della salute'''
k=3
predictions = predict_rating(test_ouv,classifier,vectorizer,classes,k)
print("Top {} predictions:".format(k))
print("===================")
for prediction in predictions:
print('{} -> {} with a probability of {:0.2f}'.format(test_ouv, prediction[0],prediction[1]))
test_ouv = '''the years of the republics extraordinary golden age are represented by monuments of incomparable beauty'''
k=3
predictions = predict_rating(test_ouv,classifier,vectorizer,classes,k)
print("Top {} predictions:".format(k))
print("===================")
for prediction in predictions:
print('{} -> {} with a probability of {:0.2f}'.format(test_ouv, prediction[0],prediction[1]))
import time
class Timer(object):
def __init__(self, name=None):
self.name = name
def __enter__(self):
self.tstart = time.time()
def __exit__(self, type, value, traceback):
if self.name:
print('[%s]' % self.name,)
print('Elapsed: %s' % (time.time() - self.tstart))
set_seed_everywhere(args.seed, args.cuda)
test_ouv = 'The particular layout of the complex is unique to this site'
k=3
with Timer():
predictions = predict_rating(test_ouv,classifier,vectorizer,classes,k=k)
```
## Interpretability
```
def infer_tokens_importance(vocab, classifier, vectorizer, classes, k=50):
"""Predict the rating of a review
Args:
vocab (list of str): the whole vocabulary
classifier (ReviewClassifier): the trained model
vectorizer (ReviewVectorizer): the corresponding vectorizer
classes (list of str): The name of the ouv classes
k (int): show the largest k prediction, default to 1
"""
classifier.eval()
X = sparse_to_tensor(vectorizer.vectorizer.transform(list(vocab.keys())))
with torch.no_grad():
result = classifier(X, apply_softmax=True)
vocab_id = result[1:].topk(k, dim=0)[1]
vocab_weight = result[1:].topk(k, dim=0)[0]
return vocab_id, vocab_weight
vocab = vectorizer.vectorizer.vocabulary_
len(vocab)
all_k = infer_tokens_importance(vocab, classifier, vectorizer, classes, k=50)[0]
all_k.shape
id_vocab = {vocab[token]:token for token in vocab.keys()}
def make_top_k_DataFrame(vocab, classifier, vectorizer, classes, k=10):
vocab_id = infer_tokens_importance(vocab, classifier, vectorizer, classes, k)[0]
df = pd.DataFrame(columns = classes)
for i in range(len(classes)):
indices = vocab_id[:,i].tolist()
words = pd.Series([id_vocab[j] for j in indices])
df[classes[i]] = words
return df
make_top_k_DataFrame(vocab, classifier, vectorizer, classes, k=20)
make_top_k_DataFrame(vocab, classifier, vectorizer, classes, k=50).to_csv(args.save_dir+'top_words.csv')
```
## Confusion Matrix
```
dataset.set_split('test')
set_seed_everywhere(args.seed, args.cuda)
batch_generator = generate_batches(dataset,
batch_size=args.batch_size,
device=args.device)
conf_mat_test = np.zeros((len(classes)-1,len(classes)-1))
for batch_index, batch_dict in enumerate(batch_generator):
# get the data compute fuzzy labels
X = batch_dict['x_data']
y_target = batch_dict['y_target']
y_fuzzy = batch_dict['y_fuzzy']
Y = compute_fuzzy_label(y_target, y_fuzzy, fuzzy= args.fuzzy,
how=args.fuzzy_how, lbd = args.fuzzy_lambda)
# compute the output
y_pred = classifier(X)
conf_mat_test = np.add(conf_mat_test,confusion_matrix(y_target.argmax(axis=1), y_pred.argmax(axis=1),
labels=range(len(classes)-1)))
conf_mat_test
dataset.set_split('val')
set_seed_everywhere(args.seed, args.cuda)
batch_generator = generate_batches(dataset,
batch_size=args.batch_size,
device=args.device)
conf_mat_val = np.zeros((len(classes)-1,len(classes)-1))
for batch_index, batch_dict in enumerate(batch_generator):
# get the data compute fuzzy labels
X = batch_dict['x_data']
y_target = batch_dict['y_target']
y_fuzzy = batch_dict['y_fuzzy']
Y = compute_fuzzy_label(y_target, y_fuzzy, fuzzy= args.fuzzy,
how=args.fuzzy_how, lbd = args.fuzzy_lambda)
# compute the output
y_pred = classifier(X)
conf_mat_val = np.add(conf_mat_val,confusion_matrix(y_target.argmax(axis=1), y_pred.argmax(axis=1),labels=range(len(classes)-1)))
conf_mat_val
dataset.set_split('train')
set_seed_everywhere(args.seed, args.cuda)
batch_generator = generate_batches(dataset,
batch_size=args.batch_size,
device=args.device)
conf_mat_train = np.zeros((len(classes)-1,len(classes)-1))
for batch_index, batch_dict in enumerate(batch_generator):
# get the data compute fuzzy labels
X = batch_dict['x_data']
y_target = batch_dict['y_target']
y_fuzzy = batch_dict['y_fuzzy']
Y = compute_fuzzy_label(y_target, y_fuzzy, fuzzy= args.fuzzy,
how=args.fuzzy_how, lbd = args.fuzzy_lambda)
# compute the output
y_pred = classifier(X)
conf_mat_train = np.add(conf_mat_train,confusion_matrix(y_target.argmax(axis=1), y_pred.argmax(axis=1),labels=range(len(classes)-1)))
conf_mat_train
pd.concat([pd.DataFrame(conf_mat_test),pd.DataFrame(conf_mat_val),pd.DataFrame(conf_mat_train)],axis=1).to_csv(args.save_dir+'confusion_matrix.csv')
pd.concat([pd.DataFrame(conf_mat_test),pd.DataFrame(conf_mat_val),pd.DataFrame(conf_mat_train)],axis=1).to_csv(args.save_dir+'baseline_confusion_matrix.csv')
def per_class_metrics(confusion_matrix, classes):
'''
Compute the per class precision, recall, and F1 for all the classes
Args:
confusion_matrix (np.ndarry) with shape of (n_classes,n_classes): a confusion matrix of interest
classes (list of str) with shape (n_classes,): The names of classes
Returns:
metrics_dict (dictionary): a dictionary that records the per class metrics
'''
num_class = confusion_matrix.shape[0]
metrics_dict = {}
for i in range(num_class):
key = classes[i]
temp_dict = {}
row = confusion_matrix[i,:]
col = confusion_matrix[:,i]
val = confusion_matrix[i,i]
precision = val/row.sum()
recall = val/col.sum()
F1 = 2*(precision*recall)/(precision+recall)
temp_dict['precision'] = precision
temp_dict['recall'] = recall
temp_dict['F1'] = F1
metrics_dict[key] = temp_dict
return metrics_dict
metrics_dict = {}
metrics_dict['test'] = per_class_metrics(conf_mat_test, classes[:-1])
metrics_dict['val'] = per_class_metrics(conf_mat_val, classes[:-1])
metrics_dict['train'] = per_class_metrics(conf_mat_train, classes[:-1])
metrics_df = pd.DataFrame.from_dict({(i,j): metrics_dict[i][j]
for i in metrics_dict.keys()
for j in metrics_dict[i].keys()},
orient='index')
metrics_df.to_csv(args.save_dir+'per_class_metrics.csv')
metrics_df.to_csv(args.save_dir+'baseline_per_class_metrics.csv')
```
## Try on totally Unseen Data
```
#ouv_csv='Data/ouv_with_splits_full.csv',
new_ouv_csv='Data/sd_full.csv'
def compute_jac_k_accuracy(y_pred, y_target, k=3, multilabel=False):
y_pred_indices = y_pred.topk(k, dim=1)[1]
y_target_indices = y_target.topk(k, dim=1)[1]
n_correct = torch.tensor([torch.tensor([y_pred_indices[j][i] in y_target_indices[j] for i in range(k)]).sum()>0
for j in range(len(y_pred))]).sum().item()
return n_correct / len(y_pred_indices) * 100
def compute_jac_1_accuracy(y_pred, y_target, k=3, multilabel=False):
y_pred_indices = y_pred.topk(1, dim=1)[1]
y_target_indices = y_target.topk(k, dim=1)[1]
n_correct = torch.tensor([torch.tensor([y_pred_indices[j] in y_target_indices[j] for i in range(k)]).sum()>0
for j in range(len(y_pred))]).sum().item()
return n_correct / len(y_pred_indices) * 100
with Timer():
loss_func = cross_entropy
set_seed_everywhere(args.seed, args.cuda)
train_state = make_train_state(args)
dataset = OuvDataset.load_dataset_and_load_vectorizer(new_ouv_csv, args.vectorizer_file,
ngrams=args.ngrams, vectorizer=vectorizer.vectorizer)
dataset.set_split('val')
verbose=False
try:
# Iterate over training dataset
# setup: batch generator, set loss and acc to 0, set train mode on
dataset.set_split('val')
batch_generator = generate_batches(dataset,
batch_size=args.batch_size,
device=args.device)
running_loss = 0.0
running_1_acc = 0.0
running_k_acc = 0.0
running_k_jac = 0.0
classifier.eval()
for batch_index, batch_dict in enumerate(batch_generator):
# step 2. get the data compute fuzzy labels
X = batch_dict['x_data']
y_target = batch_dict['y_target']
y_fuzzy = batch_dict['y_fuzzy']
Y = compute_fuzzy_label(y_target, y_fuzzy, fuzzy= args.fuzzy,
how=args.fuzzy_how, lbd = args.fuzzy_lambda)
# step 3. compute the output
with torch.no_grad():
y_pred = classifier(X)
# step 4. compute the loss
loss = loss_func(y_pred, Y)
loss_t = loss.item()
running_loss += (loss_t - running_loss) / (batch_index + 1)
# -----------------------------------------
# compute the accuracies
acc_1_t = compute_jac_1_accuracy(y_pred, y_target)
acc_k_t = compute_jac_k_accuracy(y_pred, y_target, args.k)
jac_k_t = compute_jaccard_index(y_pred, y_target, len(classes))
running_1_acc += (acc_1_t - running_1_acc) / (batch_index + 1)
running_k_acc += (acc_k_t - running_k_acc) / (batch_index + 1)
running_k_jac += (jac_k_t - running_k_jac) / (batch_index + 1)
# update bar
if verbose:
val_bar.set_postfix(loss=running_loss,
acc_1=running_1_acc,
acc_k=running_k_acc,
jac_k=running_k_jac,
epoch=epoch_index)
val_bar.update()
train_state['val_loss'].append(running_loss)
train_state['val_1_acc'].append(running_1_acc)
train_state['val_k_acc'].append(running_k_acc)
train_state['val_k_jac'].append(running_k_jac)
except KeyboardInterrupt:
print("Exiting loop")
pass
# LS Model
train_state
# Baseline
train_state
```
## END
|
github_jupyter
|
# Overlap matrices
This notebook will look at different ways of plotting overlap matrices and making them visually appealing.
One way to guarantee right color choices for color blind poeple is using this tool: https://davidmathlogic.com/colorblind
```
%pylab inline
import pandas as pd
import seaborn as sbn
sbn.set_style("ticks")
sbn.set_context("notebook", font_scale = 1.5)
data = np.loadtxt('raw_matrices_review.dat')
good = (data[:9][:])
bad = data[-9:][:]
ugly = data[9:18][:]
# Your Standard plot
fig =figsize(8,8)
ax = sbn.heatmap(bad,annot=True, fmt='.2f', linewidths=.3, annot_kws={"size": 14},square=True,robust=True,cmap=sbn.light_palette((210, 90, 60), input="husl") )
ax.set_xlabel(r'$\lambda$ index')
ax.set_ylabel(r'$\lambda$ index')
# Changing the colour map
from matplotlib import colors
from matplotlib.colors import LogNorm
#cmap = colors.ListedColormap(['#FBE8EB','#88CCEE','#78C592', '#117733'])
cmap = colors.ListedColormap(['#117733','#88CCEE', '#FBE8EB'])
bounds=[0.0, 0.025, 0.1, 0.8]
norm = colors.BoundaryNorm(bounds, cmap.N, clip=False)
cbar_kws=dict(ticks=[0.2, 0.4, 0.6, 0.8 ,1.0])
#ax = sbn.heatmap(ugly,annot=True, fmt='.2f', linewidths=.3, annot_kws={"size": 14},square=True,robust=True,cmap=cmap, norm=norm,cbar_kws=cbar_kws )
ax = sbn.heatmap(ugly,annot=True, fmt='.2f', linewidths=0, linecolor='white', annot_kws={"size": 14},square=True,robust=True,cmap='bone_r', vmin=0, vmax=1 )
ax.xaxis.tick_top()
ax.xaxis.set_label_position('top')
ax.set_xlabel(r'$\lambda$ index')
ax.set_ylabel(r'$\lambda$ index')
for _, spine in ax.spines.items():
spine.set_visible(True)
show_annot_array = ugly >= 0.0001
for text, show_annot in zip(ax.texts, (element for row in show_annot_array for element in row)):
text.set_visible(show_annot)
# Changing the colour map
from matplotlib import colors
from matplotlib.colors import LogNorm
#cmap = colors.ListedColormap(['#FBE8EB','#88CCEE','#78C592', '#117733'])
cmap = colors.ListedColormap(['#117733','#88CCEE', '#FBE8EB'])
bounds=[0.0, 0.025, 0.1, 0.8]
norm = colors.BoundaryNorm(bounds, cmap.N, clip=False)
cbar_kws=dict(ticks=[0.2, 0.4, 0.6, 0.8 ,1.0])
#ax = sbn.heatmap(ugly,annot=True, fmt='.2f', linewidths=.3, annot_kws={"size": 14},square=True,robust=True,cmap=cmap, norm=norm,cbar_kws=cbar_kws )
ax = sbn.heatmap(good,annot=True, fmt='.2f', linewidths=0, linecolor='black', annot_kws={"size": 14},square=True,robust=True,cmap='bone_r',vmin=0, vmax=1 )
ax.xaxis.tick_top()
ax.xaxis.set_label_position('top')
ax.set_xlabel(r'$\lambda$ index')
ax.set_ylabel(r'$\lambda$ index')
for _, spine in ax.spines.items():
spine.set_visible(True)
show_annot_array = good >= 0.001
for text, show_annot in zip(ax.texts, (element for row in show_annot_array for element in row)):
text.set_visible(show_annot)
# Changing the colour map
from matplotlib import colors
from matplotlib.colors import LogNorm
#cmap = colors.ListedColormap(['#FBE8EB','#88CCEE','#78C592', '#117733'])
cmap = colors.ListedColormap(['#117733','#88CCEE', '#FBE8EB'])
bounds=[0.0, 0.025, 0.1, 0.8]
norm = colors.BoundaryNorm(bounds, cmap.N, clip=False)
cbar_kws=dict(ticks=[0.2, 0.4, 0.6, 0.8 ,1.0])
#ax = sbn.heatmap(ugly,annot=True, fmt='.2f', linewidths=.3, annot_kws={"size": 14},square=True,robust=True,cmap=cmap, norm=norm,cbar_kws=cbar_kws )
ax = sbn.heatmap(bad,annot=True, fmt='.2f', linewidths=0, linecolor='black', annot_kws={"size": 14},square=True,robust=True,cmap='bone_r',vmin=0, vmax=1 )
ax.xaxis.tick_top()
ax.xaxis.set_label_position('top')
ax.set_xlabel(r'$\lambda$ index')
ax.set_ylabel(r'$\lambda$ index')
for _, spine in ax.spines.items():
spine.set_visible(True)
show_annot_array = bad >= 0.01
for text, show_annot in zip(ax.texts, (element for row in show_annot_array for element in row)):
text.set_visible(show_annot)
# Changing the colour map
from matplotlib import colors
#cmap = colors.ListedColormap(['#FBE8EB','#88CCEE','#78C592', '#117733'])
cmap = colors.ListedColormap(['#FBE8EB','#88CCEE','#78C592', '#117733'])
bounds=[0.0, 0.025, 0.1, 0.3,0.8]
norm = colors.BoundaryNorm(bounds, cmap.N, clip=False)
cbar_kws=dict(ticks=[.025, .1, .3,0.8])
ax = sbn.heatmap(ugly,annot=True, fmt='.2f', linewidths=.3, annot_kws={"size": 14},square=True,robust=True,cmap=cmap, norm=norm,cbar_kws=cbar_kws )
ax.xaxis.tick_top()
ax.xaxis.set_label_position('top')
ax.set_xlabel(r'$\lambda$ index')
ax.set_ylabel(r'$\lambda$ index')
cmap = colors.ListedColormap(['#FBE8EB','#88CCEE','#78C592', '#117733'])
bounds=[0.0, 0.025, 0.1, 0.3,0.8]
norm = colors.BoundaryNorm(bounds, cmap.N, clip=False)
cbar_kws=dict(ticks=[.025, .1, .3,0.8])
ax = sbn.heatmap(bad,annot=True, fmt='.2f', linewidths=.3, annot_kws={"size": 14},square=True,robust=True,cmap=cmap, norm=norm, cbar_kws=cbar_kws )
ax.set_xlabel(r'$\lambda$ index')
ax.set_ylabel(r'$\lambda$ index')
ax.xaxis.tick_top()
ax.xaxis.set_label_position('top')
ax.set_xlabel(r'$\lambda$ index')
ax.set_ylabel(r'$\lambda$ index')
cmap = colors.ListedColormap(['#FBE8EB','#88CCEE','#78C592', '#117733'])
bounds=[0.0, 0.025, 0.1, 0.3,0.8]
norm = colors.BoundaryNorm(bounds, cmap.N, clip=False)
cbar_kws=dict(ticks=[.025, .1, .3,0.8])
ax = sbn.heatmap(good,annot=True, fmt='.2f', linewidths=.3, annot_kws={"size": 14},square=True,robust=True, cmap=cmap, norm=norm,vmin=0,vmax=1,cbar_kws=cbar_kws )
ax.set_xlabel(r'$\lambda$ index')
ax.set_ylabel(r'$\lambda$ index')
ax.xaxis.tick_top()
ax.xaxis.set_label_position('top')
ax.set_xlabel(r'$\lambda$ index')
ax.set_ylabel(r'$\lambda$ index')
cbar_kws={'ticks': '[0.0, 0.2, 0.4, 0.6, 0.8, 1.0]'}
# Playing with pandas and getting more exotic
df = pd.DataFrame(bad, columns=["1","2","3","4","5","6","7","8","9"])
#https://towardsdatascience.com/better-heatmaps-and-correlation-matrix-plots-in-python-41445d0f2bec
def heatmap(x, y, x1,y1, **kwargs):
if 'color' in kwargs:
color = kwargs['color']
else:
color = [1]*len(x)
if 'palette' in kwargs:
palette = kwargs['palette']
n_colors = len(palette)
else:
n_colors = 256 # Use 256 colors for the diverging color palette
palette = sbn.color_palette("Blues", n_colors)
if 'color_range' in kwargs:
color_min, color_max = kwargs['color_range']
else:
color_min, color_max = min(color), max(color) # Range of values that will be mapped to the palette, i.e. min and max possible correlation
def value_to_color(val):
if color_min == color_max:
return palette[-1]
else:
val_position = float((val - color_min)) / (color_max - color_min) # position of value in the input range, relative to the length of the input range
val_position = min(max(val_position, 0), 1) # bound the position betwen 0 and 1
ind = int(val_position * (n_colors - 1)) # target index in the color palette
return palette[ind]
if 'size' in kwargs:
size = kwargs['size']
else:
size = [1]*len(x)
if 'size_range' in kwargs:
size_min, size_max = kwargs['size_range'][0], kwargs['size_range'][1]
else:
size_min, size_max = min(size), max(size)
size_scale = kwargs.get('size_scale', 500)
def value_to_size(val):
if size_min == size_max:
return 1 * size_scale
else:
val_position = (val - size_min) * 0.99 / (size_max - size_min) + 0.01 # position of value in the input range, relative to the length of the input range
val_position = min(max(val_position, 0), 1) # bound the position betwen 0 and 1
return val_position * size_scale
if 'x_order' in kwargs:
x_names = [t for t in kwargs['x_order']]
else:
x_names = [t for t in sorted(set([v for v in x]))]
x_to_num = {p[1]:p[0] for p in enumerate(x_names)}
if 'y_order' in kwargs:
y_names = [t for t in kwargs['y_order']]
else:
y_names = [t for t in sorted(set([v for v in y]))]
y_to_num = {p[1]:p[0] for p in enumerate(y_names)}
plot_grid = plt.GridSpec(1, 15, hspace=0.2, wspace=0.1) # Setup a 1x10 grid
ax = plt.subplot(plot_grid[:,:-1]) # Use the left 14/15ths of the grid for the main plot
marker = kwargs.get('marker', 's')
kwargs_pass_on = {k:v for k,v in kwargs.items() if k not in [
'color', 'palette', 'color_range', 'size', 'size_range', 'size_scale', 'marker', 'x_order', 'y_order'
]}
print(x_names)
print(y_names)
print('here------------')
ax.scatter(
x=x1,
y=y1,
marker=marker,
s=[value_to_size(v) for v in size],
c=[value_to_color(v) for v in color],
**kwargs_pass_on
)
ax.set_xticks([v for k,v in x_to_num.items()])
ax.set_xticklabels([k for k in x_to_num], rotation=45, horizontalalignment='right')
ax.set_yticks([v for k,v in y_to_num.items()])
ax.set_yticklabels([k for k in y_to_num])
ax.grid(False, 'major')
ax.grid(True, 'minor')
ax.set_xticks([t + 0.5 for t in ax.get_xticks()], minor=True)
ax.set_yticks([t + 0.5 for t in ax.get_yticks()], minor=True)
ax.set_xlim([-0.5, max([v for v in x_to_num.values()]) + 0.5])
ax.set_ylim([-0.5, max([v for v in y_to_num.values()]) + 0.5])
ax.set_facecolor('#F1F1F1')
# Add color legend on the right side of the plot
if color_min < color_max:
ax = plt.subplot(plot_grid[:,-1]) # Use the rightmost column of the plot
col_x = [0]*len(palette) # Fixed x coordinate for the bars
bar_y=np.linspace(color_min, color_max, n_colors) # y coordinates for each of the n_colors bars
bar_height = bar_y[1] - bar_y[0]
ax.barh(
y=bar_y,
width=[5]*len(palette), # Make bars 5 units wide
left=col_x, # Make bars start at 0
height=bar_height,
color=palette,
linewidth=0
)
ax.set_xlim(1, 2) # Bars are going from 0 to 5, so lets crop the plot somewhere in the middle
ax.grid(False) # Hide grid
ax.set_facecolor('white') # Make background white
ax.set_xticks([]) # Remove horizontal ticks
ax.set_yticks(np.linspace(min(bar_y), max(bar_y), 3)) # Show vertical ticks for min, middle and max
ax.yaxis.tick_right() # Show vertical ticks on the right
def corrplot(data, size_scale=500, marker='s'):
corr = pd.melt(data.reset_index(), id_vars='index')
print(corr)
corr.columns = ['index', 'variable', 'value']
x_names = [t for t in sorted(set([v for v in corr['index']]))]
x_to_num = {p[1]:p[0] for p in enumerate(x_names)}
x=[x_to_num[v] for v in corr['index']]
y_names = [t for t in sorted(set([v for v in corr['index']]))]
y_to_num = {p[1]:p[0] for p in enumerate(y_names)}
y=[y_to_num[v] for v in corr['index']]
heatmap(
corr['index'], corr['value'],x1,y1,
color=corr['value'], color_range=[0, 1],
palette=sbn.diverging_palette(20, 220, n=256),
size=corr['value'].abs(), size_range=[0,1],
marker=marker,
x_order=data.columns,
y_order=data.columns[::-1],
size_scale=size_scale
)
corrplot(df)
corr = pd.melt(df.reset_index(), id_vars='index')
print(corr)
x_names = [t for t in sorted(set([v for v in corr['index']]))]
x_to_num = {p[1]:p[0] for p in enumerate(x_names)}
x1=[x_to_num[v] for v in corr['index']]
y_names = [t for t in sorted(set([v for v in corr['variable']]))]
y_to_num = {p[1]:p[0] for p in enumerate(y_names)}
y1=[y_to_num[v] for v in corr['variable']]
def value_to_size(val):
if size_min == size_max:
return 1 * size_scale
else:
val_position = (val - size_min) * 0.99 / (size_max - size_min) + 0.01 # position of value in the input range, relative to the length of the input range
val_position = min(max(val_position, 0), 1) # bound the position betwen 0 and 1
return val_position * size_scale
value_names = [t for t in sorted(set([v for v in corr['value']]))]
value = []
for v in corr['value']:
value.append(v)
for v in corr['value']:
print (v)
n_colors = 256 # Use 256 colors for the diverging color palette
palette = sbn.cubehelix_palette(n_colors)
mapping = linspace(0,1,256)
c_index = np.digitize(value, mapping)
plot_colors =[]
for i in c_index:
plot_colors.append(palette[i])
s =np.array(value)*4000
fig = figsize(10,10)
plot_grid = plt.GridSpec(1, 15, hspace=0.2, wspace=0.1) # Setup a 1x10 grid
ax = plt.subplot(plot_grid[:,:-1]) # Use the left 14/15ths of the grid for the main plot
ax.scatter(x1,y1,marker='s',s=s,c=plot_colors)
sbn.despine()
ax.grid(False, 'major')
ax.grid(True, 'minor', color='white')
ax.set_xticks([t + 0.5 for t in ax.get_xticks()], minor=True)
ax.set_yticks([t + 0.5 for t in ax.get_yticks()], minor=True)
ax.set_xlim([-0.5, max([v for v in x_to_num.values()]) + 0.5])
ax.set_ylim([-0.5, max([v for v in y_to_num.values()]) + 0.5])
ax.set_facecolor((0,0,0))
plt.gca().invert_yaxis()
ax.xaxis.tick_top()
ax.xaxis.set_label_position('top')
xlabel(r'$\lambda$ index')
ylabel(r'$\lambda$ index')
def value_to_size(val, vlaue):
size_scale = 500
size = [1]*len(value)
size_min, size_max = min(size), max(size)
if size_min == size_max:
return 1 * size_scale
else:
val_position = (val - size_min) * 0.99 / (size_max - size_min) + 0.01 # position of value in the input range, relative to the length of the input range
val_position = min(max(val_position, 0), 1) # bound the position betwen 0 and 1
return val_position * size_scale
heatmap2
value_to_size(value[5], value)
from biokit.viz import corrplot
c = corrplot.Corrplot(df)
c.plot()
def plot(index, columns):
values = "bad_status"
vmax = 0.10
cellsize_vmax = 10000
g_ratio = df.pivot_table(index=index, columns=columns, values=values, aggfunc="mean")
g_size = df.pivot_table(index=index, columns=columns, values=values, aggfunc="size")
annot = np.vectorize(lambda x: "" if np.isnan(x) else "{:.1f}%".format(x * 100))(g_ratio)
# adjust visual balance
figsize = (g_ratio.shape[1] * 0.8, g_ratio.shape[0] * 0.8)
cbar_width = 0.05 * 6.0 / figsize[0]
f, ax = plt.subplots(1, 1, figsize=figsize)
cbar_ax = f.add_axes([.91, 0.1, cbar_width, 0.8])
heatmap2(g_ratio, ax=ax, cbar_ax=cbar_ax,
vmax=vmax, cmap="PuRd", annot=annot, fmt="s", annot_kws={"fontsize":"small"},
cellsize=g_size, cellsize_vmax=cellsize_vmax,
square=True, ax_kws={"title": "{} x {}".format(index, columns)})
plt.show()
"""
This script is created by modifying seaborn matrix.py
in https://github.com/mwaskom/seaborn, by Michael L. Waskom
"""
from __future__ import division
import itertools
import matplotlib as mpl
from matplotlib.collections import LineCollection
import matplotlib.pyplot as plt
from matplotlib import gridspec
import matplotlib.patheffects as patheffects
import numpy as np
import pandas as pd
from scipy.cluster import hierarchy
import seaborn as sns
from seaborn import cm
from seaborn.axisgrid import Grid
from seaborn.utils import (despine, axis_ticklabels_overlap, relative_luminance, to_utf8)
from seaborn.external.six import string_types
def _index_to_label(index):
"""Convert a pandas index or multiindex to an axis label."""
if isinstance(index, pd.MultiIndex):
return "-".join(map(to_utf8, index.names))
else:
return index.name
def _index_to_ticklabels(index):
"""Convert a pandas index or multiindex into ticklabels."""
if isinstance(index, pd.MultiIndex):
return ["-".join(map(to_utf8, i)) for i in index.values]
else:
return index.values
def _matrix_mask(data, mask):
"""Ensure that data and mask are compatabile and add missing values.
Values will be plotted for cells where ``mask`` is ``False``.
``data`` is expected to be a DataFrame; ``mask`` can be an array or
a DataFrame.
"""
if mask is None:
mask = np.zeros(data.shape, np.bool)
if isinstance(mask, np.ndarray):
# For array masks, ensure that shape matches data then convert
if mask.shape != data.shape:
raise ValueError("Mask must have the same shape as data.")
mask = pd.DataFrame(mask,
index=data.index,
columns=data.columns,
dtype=np.bool)
elif isinstance(mask, pd.DataFrame):
# For DataFrame masks, ensure that semantic labels match data
if not mask.index.equals(data.index) \
and mask.columns.equals(data.columns):
err = "Mask must have the same index and columns as data."
raise ValueError(err)
# Add any cells with missing data to the mask
# This works around an issue where `plt.pcolormesh` doesn't represent
# missing data properly
mask = mask | pd.isnull(data)
return mask
class _HeatMapper2(object):
"""Draw a heatmap plot of a matrix with nice labels and colormaps."""
def __init__(self, data, vmin, vmax, cmap, center, robust, annot, fmt,
annot_kws, cellsize, cellsize_vmax,
cbar, cbar_kws,
xticklabels=True, yticklabels=True, mask=None, ax_kws=None, rect_kws=None):
"""Initialize the plotting object."""
# We always want to have a DataFrame with semantic information
# and an ndarray to pass to matplotlib
if isinstance(data, pd.DataFrame):
plot_data = data.values
else:
plot_data = np.asarray(data)
data = pd.DataFrame(plot_data)
# Validate the mask and convet to DataFrame
mask = _matrix_mask(data, mask)
plot_data = np.ma.masked_where(np.asarray(mask), plot_data)
# Get good names for the rows and columns
xtickevery = 1
if isinstance(xticklabels, int):
xtickevery = xticklabels
xticklabels = _index_to_ticklabels(data.columns)
elif xticklabels is True:
xticklabels = _index_to_ticklabels(data.columns)
elif xticklabels is False:
xticklabels = []
ytickevery = 1
if isinstance(yticklabels, int):
ytickevery = yticklabels
yticklabels = _index_to_ticklabels(data.index)
elif yticklabels is True:
yticklabels = _index_to_ticklabels(data.index)
elif yticklabels is False:
yticklabels = []
# Get the positions and used label for the ticks
nx, ny = data.T.shape
if not len(xticklabels):
self.xticks = []
self.xticklabels = []
elif isinstance(xticklabels, string_types) and xticklabels == "auto":
self.xticks = "auto"
self.xticklabels = _index_to_ticklabels(data.columns)
else:
self.xticks, self.xticklabels = self._skip_ticks(xticklabels,
xtickevery)
if not len(yticklabels):
self.yticks = []
self.yticklabels = []
elif isinstance(yticklabels, string_types) and yticklabels == "auto":
self.yticks = "auto"
self.yticklabels = _index_to_ticklabels(data.index)
else:
self.yticks, self.yticklabels = self._skip_ticks(yticklabels,
ytickevery)
# Get good names for the axis labels
xlabel = _index_to_label(data.columns)
ylabel = _index_to_label(data.index)
self.xlabel = xlabel if xlabel is not None else ""
self.ylabel = ylabel if ylabel is not None else ""
# Determine good default values for the colormapping
self._determine_cmap_params(plot_data, vmin, vmax,
cmap, center, robust)
# Determine good default values for cell size
self._determine_cellsize_params(plot_data, cellsize, cellsize_vmax)
# Sort out the annotations
if annot is None:
annot = False
annot_data = None
elif isinstance(annot, bool):
if annot:
annot_data = plot_data
else:
annot_data = None
else:
try:
annot_data = annot.values
except AttributeError:
annot_data = annot
if annot.shape != plot_data.shape:
raise ValueError('Data supplied to "annot" must be the same '
'shape as the data to plot.')
annot = True
# Save other attributes to the object
self.data = data
self.plot_data = plot_data
self.annot = annot
self.annot_data = annot_data
self.fmt = fmt
self.annot_kws = {} if annot_kws is None else annot_kws
#self.annot_kws.setdefault('color', "black")
self.annot_kws.setdefault('ha', "center")
self.annot_kws.setdefault('va', "center")
self.cbar = cbar
self.cbar_kws = {} if cbar_kws is None else cbar_kws
self.cbar_kws.setdefault('ticks', mpl.ticker.MaxNLocator(6))
self.ax_kws = {} if ax_kws is None else ax_kws
self.rect_kws = {} if rect_kws is None else rect_kws
# self.rect_kws.setdefault('edgecolor', "black")
def _determine_cmap_params(self, plot_data, vmin, vmax,
cmap, center, robust):
"""Use some heuristics to set good defaults for colorbar and range."""
calc_data = plot_data.data[~np.isnan(plot_data.data)]
if vmin is None:
vmin = np.percentile(calc_data, 2) if robust else calc_data.min()
if vmax is None:
vmax = np.percentile(calc_data, 98) if robust else calc_data.max()
self.vmin, self.vmax = vmin, vmax
# Choose default colormaps if not provided
if cmap is None:
if center is None:
self.cmap = cm.rocket
else:
self.cmap = cm.icefire
elif isinstance(cmap, string_types):
self.cmap = mpl.cm.get_cmap(cmap)
elif isinstance(cmap, list):
self.cmap = mpl.colors.ListedColormap(cmap)
else:
self.cmap = cmap
# Recenter a divergent colormap
if center is not None:
vrange = max(vmax - center, center - vmin)
normlize = mpl.colors.Normalize(center - vrange, center + vrange)
cmin, cmax = normlize([vmin, vmax])
cc = np.linspace(cmin, cmax, 256)
self.cmap = mpl.colors.ListedColormap(self.cmap(cc))
def _determine_cellsize_params(self, plot_data, cellsize, cellsize_vmax):
if cellsize is None:
self.cellsize = np.ones(plot_data.shape)
self.cellsize_vmax = 1.0
else:
if isinstance(cellsize, pd.DataFrame):
cellsize = cellsize.values
self.cellsize = cellsize
if cellsize_vmax is None:
cellsize_vmax = cellsize.max()
self.cellsize_vmax = cellsize_vmax
def _skip_ticks(self, labels, tickevery):
"""Return ticks and labels at evenly spaced intervals."""
n = len(labels)
if tickevery == 0:
ticks, labels = [], []
elif tickevery == 1:
ticks, labels = np.arange(n) + .5, labels
else:
start, end, step = 0, n, tickevery
ticks = np.arange(start, end, step) + .5
labels = labels[start:end:step]
return ticks, labels
def _auto_ticks(self, ax, labels, axis):
"""Determine ticks and ticklabels that minimize overlap."""
transform = ax.figure.dpi_scale_trans.inverted()
bbox = ax.get_window_extent().transformed(transform)
size = [bbox.width, bbox.height][axis]
axis = [ax.xaxis, ax.yaxis][axis]
tick, = axis.set_ticks([0])
fontsize = tick.label.get_size()
max_ticks = int(size // (fontsize / 72))
if max_ticks < 1:
return [], []
tick_every = len(labels) // max_ticks + 1
tick_every = 1 if tick_every == 0 else tick_every
ticks, labels = self._skip_ticks(labels, tick_every)
return ticks, labels
def plot(self, ax, cax):
"""Draw the heatmap on the provided Axes."""
# Remove all the Axes spines
#despine(ax=ax, left=True, bottom=True)
# Draw the heatmap and annotate
height, width = self.plot_data.shape
xpos, ypos = np.meshgrid(np.arange(width) + .5, np.arange(height) + .5)
data = self.plot_data.data
cellsize = self.cellsize
mask = self.plot_data.mask
if not isinstance(mask, np.ndarray) and not mask:
mask = np.zeros(self.plot_data.shape, np.bool)
annot_data = self.annot_data
if not self.annot:
annot_data = np.zeros(self.plot_data.shape)
# Draw rectangles instead of using pcolormesh
# Might be slower than original heatmap
for x, y, m, val, s, an_val in zip(xpos.flat, ypos.flat, mask.flat, data.flat, cellsize.flat, annot_data.flat):
if not m:
vv = (val - self.vmin) / (self.vmax - self.vmin)
size = np.clip(s / self.cellsize_vmax, 0.1, 1.0)
color = self.cmap(vv)
rect = plt.Rectangle([x - size / 2, y - size / 2], size, size, facecolor=color, **self.rect_kws)
ax.add_patch(rect)
if self.annot:
annotation = ("{:" + self.fmt + "}").format(an_val)
text = ax.text(x, y, annotation, **self.annot_kws)
print(text)
# add edge to text
text_luminance = relative_luminance(text.get_color())
text_edge_color = ".15" if text_luminance > .408 else "w"
text.set_path_effects([mpl.patheffects.withStroke(linewidth=1, foreground=text_edge_color)])
# Set the axis limits
ax.set(xlim=(0, self.data.shape[1]), ylim=(0, self.data.shape[0]))
# Set other attributes
ax.set(**self.ax_kws)
if self.cbar:
norm = mpl.colors.Normalize(vmin=self.vmin, vmax=self.vmax)
scalar_mappable = mpl.cm.ScalarMappable(cmap=self.cmap, norm=norm)
scalar_mappable.set_array(self.plot_data.data)
cb = ax.figure.colorbar(scalar_mappable, cax, ax, **self.cbar_kws)
cb.outline.set_linewidth(0)
# if kws.get('rasterized', False):
# cb.solids.set_rasterized(True)
# Add row and column labels
if isinstance(self.xticks, string_types) and self.xticks == "auto":
xticks, xticklabels = self._auto_ticks(ax, self.xticklabels, 0)
else:
xticks, xticklabels = self.xticks, self.xticklabels
if isinstance(self.yticks, string_types) and self.yticks == "auto":
yticks, yticklabels = self._auto_ticks(ax, self.yticklabels, 1)
else:
yticks, yticklabels = self.yticks, self.yticklabels
ax.set(xticks=xticks, yticks=yticks)
xtl = ax.set_xticklabels(xticklabels)
ytl = ax.set_yticklabels(yticklabels, rotation="vertical")
# Possibly rotate them if they overlap
ax.figure.draw(ax.figure.canvas.get_renderer())
if axis_ticklabels_overlap(xtl):
plt.setp(xtl, rotation="vertical")
if axis_ticklabels_overlap(ytl):
plt.setp(ytl, rotation="horizontal")
# Add the axis labels
ax.set(xlabel=self.xlabel, ylabel=self.ylabel)
# Invert the y axis to show the plot in matrix form
ax.invert_yaxis()
def heatmap2(data, vmin=None, vmax=None, cmap=None, center=None, robust=False,
annot=None, fmt=".2g", annot_kws=None,
cellsize=None, cellsize_vmax=None,
cbar=True, cbar_kws=None, cbar_ax=None,
square=False, xticklabels="auto", yticklabels="auto",
mask=None, ax=None, ax_kws=None, rect_kws=None):
# Initialize the plotter object
plotter = _HeatMapper2(data, vmin, vmax, cmap, center, robust,
annot, fmt, annot_kws,
cellsize, cellsize_vmax,
cbar, cbar_kws, xticklabels,
yticklabels, mask, ax_kws, rect_kws)
# Draw the plot and return the Axes
if ax is None:
ax = plt.gca()
if square:
ax.set_aspect("equal")
# delete grid
ax.grid(False)
plotter.plot(ax, cbar_ax)
return ax
fig =figsize(10,10)
ax = heatmap2(good,annot=True, fmt='.2f',cellsize=np.array(value),cellsize_vmax=1, annot_kws={"size": 13},square=True,robust=True,cmap='PiYG' )
ax.set_xlabel(r'$\lambda$ index')
ax.set_ylabel(r'$\lambda$ index')
ax.grid(False, 'major')
ax.grid(True, 'minor', color='black', alpha=0.3)
ax.set_xticks([t + 0.5 for t in ax.get_xticks()], minor=True)
ax.set_yticks([t + 0.5 for t in ax.get_yticks()], minor=True)
ax.xaxis.tick_top()
ax.xaxis.set_label_position('top')
fig =figsize(8,8)
ax = sbn.heatmap(good,annot=True, fmt='.2f', linewidths=.3, annot_kws={"size": 14},cmap=sbn.light_palette((210, 90, 60), input="husl") )
ax.set_xlabel(r'$\lambda$ index')
ax.set_ylabel(r'$\lambda$ index')
sbn.despine()
ax.grid(False, 'major')
ax.grid(True, 'minor', color='white')
ax.set_xticks([t + 0.5 for t in ax.get_xticks()], minor=True)
ax.set_yticks([t + 0.5 for t in ax.get_yticks()], minor=True)
text = ax.text(x, y, annotation, **self.annot_kws)
# add edge to text
text_luminance = relative_luminance(text.get_color())
text_edge_color = ".15" if text_luminance > .408 else "w"
text.set_path_effects([mpl.patheffects.withStroke(linewidth=1, foreground=text_edge_color)])
ax.text()
```
|
github_jupyter
|
*Accompanying code examples of the book "Introduction to Artificial Neural Networks and Deep Learning: A Practical Guide with Applications in Python" by [Sebastian Raschka](https://sebastianraschka.com). All code examples are released under the [MIT license](https://github.com/rasbt/deep-learning-book/blob/master/LICENSE). If you find this content useful, please consider supporting the work by buying a [copy of the book](https://leanpub.com/ann-and-deeplearning).*
Other code examples and content are available on [GitHub](https://github.com/rasbt/deep-learning-book). The PDF and ebook versions of the book are available through [Leanpub](https://leanpub.com/ann-and-deeplearning).
```
%load_ext watermark
%watermark -a 'Sebastian Raschka' -v -p tensorflow
```
# Model Zoo -- Convolutional Autoencoder with Deconvolutions
A convolutional autoencoder using deconvolutional layers that compresses 768-pixel MNIST images down to a 7x7x4 (196 pixel) representation.
```
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
##########################
### DATASET
##########################
mnist = input_data.read_data_sets("./", validation_size=0)
##########################
### SETTINGS
##########################
# Hyperparameters
learning_rate = 0.001
training_epochs = 5
batch_size = 128
# Architecture
hidden_size = 16
input_size = 784
image_width = 28
# Other
print_interval = 200
random_seed = 123
##########################
### GRAPH DEFINITION
##########################
g = tf.Graph()
with g.as_default():
tf.set_random_seed(random_seed)
# Input data
tf_x = tf.placeholder(tf.float32, [None, input_size], name='inputs')
input_layer = tf.reshape(tf_x, shape=[-1, image_width, image_width, 1])
###########
# Encoder
###########
# 28x28x1 => 28x28x8
conv1 = tf.layers.conv2d(input_layer, filters=8, kernel_size=(3, 3),
strides=(1, 1), padding='same',
activation=tf.nn.relu)
# 28x28x8 => 14x14x8
maxpool1 = tf.layers.max_pooling2d(conv1, pool_size=(2, 2),
strides=(2, 2), padding='same')
# 14x14x8 => 14x14x4
conv2 = tf.layers.conv2d(maxpool1, filters=4, kernel_size=(3, 3),
strides=(1, 1), padding='same',
activation=tf.nn.relu)
# 14x14x4 => 7x7x4
encode = tf.layers.max_pooling2d(conv2, pool_size=(2, 2),
strides=(2, 2), padding='same',
name='encoding')
###########
# Decoder
###########
# 7x7x4 => 14x14x8
deconv1 = tf.layers.conv2d_transpose(encode, filters=8,
kernel_size=(3, 3), strides=(2, 2),
padding='same',
activation=tf.nn.relu)
# 14x14x8 => 28x28x8
deconv2 = tf.layers.conv2d_transpose(deconv1, filters=8,
kernel_size=(3, 3), strides=(2, 2),
padding='same',
activation=tf.nn.relu)
# 28x28x8 => 28x28x1
logits = tf.layers.conv2d(deconv2, filters=1, kernel_size=(3,3),
strides=(1, 1), padding='same',
activation=None)
decode = tf.nn.sigmoid(logits, name='decoding')
##################
# Loss & Optimizer
##################
loss = tf.nn.sigmoid_cross_entropy_with_logits(labels=input_layer,
logits=logits)
cost = tf.reduce_mean(loss, name='cost')
optimizer = tf.train.AdamOptimizer(learning_rate)
train = optimizer.minimize(cost, name='train')
# Saver to save session for reuse
saver = tf.train.Saver()
import numpy as np
##########################
### TRAINING & EVALUATION
##########################
with tf.Session(graph=g) as sess:
sess.run(tf.global_variables_initializer())
np.random.seed(random_seed) # random seed for mnist iterator
for epoch in range(training_epochs):
avg_cost = 0.
total_batch = mnist.train.num_examples // batch_size
for i in range(total_batch):
batch_x, batch_y = mnist.train.next_batch(batch_size)
_, c = sess.run(['train', 'cost:0'], feed_dict={'inputs:0': batch_x})
avg_cost += c
if not i % print_interval:
print("Minibatch: %03d | Cost: %.3f" % (i + 1, c))
print("Epoch: %03d | AvgCost: %.3f" % (epoch + 1, avg_cost / (i + 1)))
saver.save(sess, save_path='./autoencoder.ckpt')
%matplotlib inline
import matplotlib.pyplot as plt
##########################
### VISUALIZATION
##########################
n_images = 15
fig, axes = plt.subplots(nrows=2, ncols=n_images, sharex=True,
sharey=True, figsize=(20, 2.5))
test_images = mnist.test.images[:n_images]
with tf.Session(graph=g) as sess:
saver.restore(sess, save_path='./autoencoder.ckpt')
decoded = sess.run('decoding:0', feed_dict={'inputs:0': test_images})
for i in range(n_images):
for ax, img in zip(axes, [test_images, decoded]):
ax[i].imshow(img[i].reshape((image_width, image_width)), cmap='binary')
```
|
github_jupyter
|
# Object and Scene Detection using Amazon Rekognition
This notebook provides a walkthrough of [object detection API](https://docs.aws.amazon.com/rekognition/latest/dg/labels.html) in Amazon Rekognition to identify objects.
```
import boto3
from IPython.display import HTML, display, Image as IImage
from PIL import Image, ImageDraw, ImageFont
import time
import os
import sagemaker
import boto3
sagemaker_session = sagemaker.Session()
role = sagemaker.get_execution_role()
bucket = sagemaker_session.default_bucket()
region = boto3.Session().region_name
rekognition = boto3.client('rekognition')
s3 = boto3.client('s3')
!mkdir -p ./tmp
temp_folder = 'tmp/'
```
# Detect Objects in Image
```
imageName = 'content-moderation/media/cars.png'
display(IImage(url=s3.generate_presigned_url('get_object', Params={'Bucket': bucket, 'Key': imageName})))
```
# Call Rekognition to Detect Objects in the Image
https://docs.aws.amazon.com/rekognition/latest/dg/API_DetectLabels.html
```
detectLabelsResponse = rekognition.detect_labels(
Image={
'S3Object': {
'Bucket': bucket,
'Name': imageName,
}
}
)
```
# Review the Raw JSON Response from Rekognition
Show JSON response returned by Rekognition Labels API (Object Detection).
In the JSON response below, you will see Label, detected instances, confidence score and additional information.
```
display(detectLabelsResponse)
```
# Show Bounding Boxes Around Recognized Objects
```
def drawBoundingBoxes (sourceImage, boxes):
# blue, green, red, grey
colors = ((255,255,255),(255,255,255),(76,182,252),(52,194,123))
# Download image locally
imageLocation = temp_folder + os.path.basename(sourceImage)
s3.download_file(bucket, sourceImage, imageLocation)
# Draws BB on Image
bbImage = Image.open(imageLocation)
draw = ImageDraw.Draw(bbImage)
width, height = bbImage.size
col = 0
maxcol = len(colors)
line= 3
for box in boxes:
x1 = int(box[1]['Left'] * width)
y1 = int(box[1]['Top'] * height)
x2 = int(box[1]['Left'] * width + box[1]['Width'] * width)
y2 = int(box[1]['Top'] * height + box[1]['Height'] * height)
draw.text((x1,y1),box[0],colors[col])
for l in range(line):
draw.rectangle((x1-l,y1-l,x2+l,y2+l),outline=colors[col])
col = (col+1)%maxcol
imageFormat = "PNG"
ext = sourceImage.lower()
if(ext.endswith('jpg') or ext.endswith('jpeg')):
imageFormat = 'JPEG'
bbImage.save(imageLocation,format=imageFormat)
display(bbImage)
boxes = []
objects = detectLabelsResponse['Labels']
for obj in objects:
for einstance in obj["Instances"]:
boxes.append ((obj['Name'], einstance['BoundingBox']))
drawBoundingBoxes(imageName, boxes)
```
# Display List of Detected Objects
```
flaggedObjects = ["Car"]
for label in detectLabelsResponse["Labels"]:
if(label["Name"] in flaggedObjects):
print("Detected object:")
print("- {} (Confidence: {})".format(label["Name"], label["Confidence"]))
print(" - Parents: {}".format(label["Parents"]))
```
# Recognize Objects in Video
Object recognition in video is an async operation.
https://docs.aws.amazon.com/rekognition/latest/dg/API_StartLabelDetection.html.
- First we start a label detection job which returns a Job Id.
- We can then call `get_label_detection` to get the job status and after job is complete, we can get object metadata.
- In production use cases, you would usually use StepFunction or SNS topic to get notified when job is complete.
```
videoName = 'content-moderation/media/GrandTour720.mp4'
strDetail = 'Objects detected in video<br>=======================================<br>'
strOverall = 'Objects in the overall video:<br>=======================================<br>'
# Show video in a player
s3VideoUrl = s3.generate_presigned_url('get_object', Params={'Bucket': bucket, 'Key': videoName})
videoTag = "<video controls='controls' autoplay width='640' height='360' name='Video' src='{0}'></video>".format(s3VideoUrl)
videoui = "<table><tr><td style='vertical-align: top'>{}</td></tr></table>".format(videoTag)
display(HTML(videoui))
```
# Call Rekognition to Start a Job for Object Detection
### Additional (Optional) Request Attributes
ClientRequestToken:
https://docs.aws.amazon.com/rekognition/latest/dg/API_StartLabelDetection.html#rekognition-StartLabelDetection-request-ClientRequestToken
JobTag:
https://docs.aws.amazon.com/rekognition/latest/dg/API_StartLabelDetection.html#rekognition-StartLabelDetection-request-JobTag
MinConfidence:
https://docs.aws.amazon.com/rekognition/latest/dg/API_StartLabelDetection.html#rekognition-StartLabelDetection-request-MinConfidence
NotificationChannel:
https://docs.aws.amazon.com/rekognition/latest/dg/API_StartLabelDetection.html#rekognition-StartLabelDetection-request-NotificationChannel
```
# Start video label recognition job
startLabelDetection = rekognition.start_label_detection(
Video={
'S3Object': {
'Bucket': bucket,
'Name': videoName,
}
},
)
labelsJobId = startLabelDetection['JobId']
display("Job Id: {0}".format(labelsJobId))
```
# Wait for Object Detection Job to Complete
```
# Wait for object detection job to complete
# In production use cases, you would usually use StepFunction or SNS topic to get notified when job is complete.
getObjectDetection = rekognition.get_label_detection(
JobId=labelsJobId,
SortBy='TIMESTAMP'
)
while(getObjectDetection['JobStatus'] == 'IN_PROGRESS'):
time.sleep(5)
print('.', end='')
getObjectDetection = rekognition.get_label_detection(
JobId=labelsJobId,
SortBy='TIMESTAMP')
display(getObjectDetection['JobStatus'])
```
# Review Raw JSON Response from Rekognition
* Show JSON response returned by Rekognition Object Detection API.
* In the JSON response below, you will see list of detected objects and activities.
* For each detected object, you will see the `Timestamp` of the frame within the video.
```
display(getObjectDetection)
```
# Display Recognized Objects in the Video
Display timestamps and objects detected at that time.
```
flaggedObjectsInVideo = ["Car"]
theObjects = {}
# Objects detected in each frame
for obj in getObjectDetection['Labels']:
ts = obj ["Timestamp"]
cconfidence = obj['Label']["Confidence"]
oname = obj['Label']["Name"]
if(oname in flaggedObjectsInVideo):
print("Found flagged object at {} ms: {} (Confidence: {})".format(ts, oname, round(cconfidence,2)))
strDetail = strDetail + "At {} ms: {} (Confidence: {})<br>".format(ts, oname, round(cconfidence,2))
if oname in theObjects:
cojb = theObjects[oname]
theObjects[oname] = {"Name" : oname, "Count": 1+cojb["Count"]}
else:
theObjects[oname] = {"Name" : oname, "Count": 1}
# Unique objects detected in video
for theObject in theObjects:
strOverall = strOverall + "Name: {}, Count: {}<br>".format(theObject, theObjects[theObject]["Count"])
# Display results
display(HTML(strOverall))
listui = "<table><tr><td style='vertical-align: top'>{}</td></tr></table>".format(strDetail)
display(HTML(listui))
```
# Worker Safety with Amazon Rekognition
You can use Amazon Rekognition to detect if certain objects are not present in the image or video. For example you can perform worker safety audit by revieweing images/video of a construction site and detecting if there are any workers without safety hat.
```
imageName = "content-moderation/media/hat-detection.png"
display(IImage(url=s3.generate_presigned_url('get_object', Params={'Bucket': bucket, 'Key': imageName})))
```
# Call Amazon Rekognition to Detect Objects in the Image
```
detectLabelsResponse = rekognition.detect_labels(
Image={
'S3Object': {
'Bucket': bucket,
'Name': imageName,
}
}
)
```
# Display Rekognition Response
```
display(detectLabelsResponse)
```
# Show Bounding Boxes Around Recognized Objects
```
def drawBoundingBoxes (sourceImage, boxes):
# blue, green, red, grey
colors = ((255,255,255),(255,255,255),(76,182,252),(52,194,123))
# Download image locally
imageLocation = temp_folder + os.path.basename(sourceImage)
s3.download_file(bucket, sourceImage, imageLocation)
# Draws BB on Image
bbImage = Image.open(imageLocation)
draw = ImageDraw.Draw(bbImage)
width, height = bbImage.size
col = 0
maxcol = len(colors)
line= 3
for box in boxes:
x1 = int(box[1]['Left'] * width)
y1 = int(box[1]['Top'] * height)
x2 = int(box[1]['Left'] * width + box[1]['Width'] * width)
y2 = int(box[1]['Top'] * height + box[1]['Height'] * height)
draw.text((x1,y1),box[0],colors[col])
for l in range(line):
draw.rectangle((x1-l,y1-l,x2+l,y2+l),outline=colors[col])
col = (col+1)%maxcol
imageFormat = "PNG"
ext = sourceImage.lower()
if(ext.endswith('jpg') or ext.endswith('jpeg')):
imageFormat = 'JPEG'
bbImage.save(imageLocation,format=imageFormat)
display(bbImage)
boxes = []
objects = detectLabelsResponse['Labels']
for obj in objects:
for einstance in obj["Instances"]:
boxes.append ((obj['Name'], einstance['BoundingBox']))
drawBoundingBoxes(imageName, boxes)
def matchPersonsAndHats(personsList, hardhatsList):
persons = []
hardhats = []
personsWithHats = []
for person in personsList:
persons.append(person)
for hardhat in hardhatsList:
hardhats.append(hardhat)
h = 0
matched = 0
totalHats = len(hardhats)
while(h < totalHats):
hardhat = hardhats[h-matched]
totalPersons = len(persons)
p = 0
while(p < totalPersons):
person = persons[p]
if(not (hardhat['BoundingBoxCoordinates']['x2'] < person['BoundingBoxCoordinates']['x1']
or hardhat['BoundingBoxCoordinates']['x1'] > person['BoundingBoxCoordinates']['x2']
or hardhat['BoundingBoxCoordinates']['y4'] < person['BoundingBoxCoordinates']['y1']
or hardhat['BoundingBoxCoordinates']['y1'] > person['BoundingBoxCoordinates']['y4']
)):
personsWithHats.append({'Person' : person, 'Hardhat' : hardhat})
del persons[p]
del hardhats[h - matched]
matched = matched + 1
break
p = p + 1
h = h + 1
return (personsWithHats, persons, hardhats)
def getBoundingBoxCoordinates(boundingBox, imageWidth, imageHeight):
x1 = 0
y1 = 0
x2 = 0
y2 = 0
x3 = 0
y3 = 0
x4 = 0
y4 = 0
boxWidth = boundingBox['Width']*imageWidth
boxHeight = boundingBox['Height']*imageHeight
x1 = boundingBox['Left']*imageWidth
y1 = boundingBox['Top']*imageWidth
x2 = x1 + boxWidth
y2 = y1
x3 = x2
y3 = y1 + boxHeight
x4 = x1
y4 = y3
return({'x1': x1, 'y1' : y1, 'x2' : x2, 'y2' : y2, 'x3' : x3, 'y3' : y3, 'x4' : x4, 'y4' : y4})
def getPersonsAndHardhats(labelsResponse, imageWidth, imageHeight):
persons = []
hardhats = []
for label in labelsResponse['Labels']:
if label['Name'] == 'Person' and 'Instances' in label:
for person in label['Instances']:
persons.append({'BoundingBox' : person['BoundingBox'], 'BoundingBoxCoordinates' : getBoundingBoxCoordinates(person['BoundingBox'], imageWidth, imageHeight), 'Confidence' : person['Confidence']})
elif ((label['Name'] == 'Hardhat' or label['Name'] == 'Helmet') and 'Instances' in label):
for hardhat in label['Instances']:
hardhats.append({'BoundingBox' : hardhat['BoundingBox'], 'BoundingBoxCoordinates' : getBoundingBoxCoordinates(hardhat['BoundingBox'], imageWidth, imageHeight), 'Confidence' : hardhat['Confidence']})
return (persons, hardhats)
s3Resource = boto3.resource('s3')
bucket = s3Resource.Bucket(bucket)
iojb = bucket.Object(imageName)
response = iojb.get()
file_stream = response['Body']
im = Image.open(file_stream)
imageWidth, imageHeight = im.size
persons, hardhats = getPersonsAndHardhats(detectLabelsResponse, imageWidth, imageHeight)
personsWithHats, personsWithoutHats, hatsWihoutPerson = matchPersonsAndHats(persons, hardhats)
personsWithHatsCount = len(personsWithHats)
personsWithoutHatsCount = len(personsWithoutHats)
hatsWihoutPersonCount = len(hatsWihoutPerson)
outputMessage = "Person(s): {}".format(personsWithHatsCount+personsWithoutHatsCount)
outputMessage = outputMessage + "\nPerson(s) With Safety Hat: {}\nPerson(s) Without Safety Hat: {}".format(personsWithHatsCount, personsWithoutHatsCount)
print(outputMessage)
```
# Congratulations!
You have successfully used Amazon Rekognition to identify specific objects in images and videos.
# References
- https://docs.aws.amazon.com/rekognition/latest/dg/API_DetectLabels.html
- https://docs.aws.amazon.com/rekognition/latest/dg/API_StartLabelDetection.html
- https://docs.aws.amazon.com/rekognition/latest/dg/API_GetLabelDetection.html
# Release Resources
```
%%html
<p><b>Shutting down your kernel for this notebook to release resources.</b></p>
<button class="sm-command-button" data-commandlinker-command="kernelmenu:shutdown" style="display:none;">Shutdown Kernel</button>
<script>
try {
els = document.getElementsByClassName("sm-command-button");
els[0].click();
}
catch(err) {
// NoOp
}
</script>
%%javascript
try {
Jupyter.notebook.save_checkpoint();
Jupyter.notebook.session.delete();
}
catch(err) {
// NoOp
}
```
|
github_jupyter
|
# 5. Statistical Packages in Python for Mathematicians
Statisticians use the following packages in Python:
- Data creation: `random`
- Data analysis/manipulation: `pandas`, `scikit-learn`
- Statistical functions: `scipy.stats`
- Statistical data visualization: `matplotlib`, `seaborn`
- Statistical data exploration: `statsmodels`
## Table of Contents
- Random
- Scipy Statistics
- Seaborn
- Statistical Models
- Python vs. R
Next week? Choose among:
- Machine Learning 2/Deep Learning: `scikit-learn`, `keras`, `tensorflow`
- SAGE
- Other: ___________?
## 5.1 Random
The `random` package implements pseudo-random number generators for various distributions.
```
import random
```
The documentation is available here: https://docs.python.org/3/library/random.html.
```
help(random)
```
Almost all module functions depend on the basic function `random()`, which generates a random float uniformly in the semi-open range `[0.0, 1.0)`. Python uses the Mersenne Twister as the core generator. It produces 53-bit precision floats and has a period of `2**19937-1`. The underlying implementation in C is both fast and threadsafe. The Mersenne Twister is one of the most extensively tested random number generators in existence. However, being completely deterministic, it is not suitable for all purposes, and is completely unsuitable for cryptographic purposes.
```
random.uniform(0,1)
```
For integers, there is uniform selection from a range. For sequences, there is uniform selection of a random element. Let's play a simple game.
```
number = random.choice(range(1,11))
choice = 0
while number != choice:
choice = int(input('Choose a number between 1 and 10 (inclusive): '))
print('Congratulations, you have guessed the right number!')
```
If we used the following line, the number above would be equal to `3`:
```
random.seed(2) # initialize the random number generator
```
We can also use NumPy's random sampling package `numpy.random` (https://docs.scipy.org/doc/numpy-1.15.0/reference/routines.random.html):
```
import numpy as np
np.random.uniform(0,1)
# dir(np.random)
```
With this package, we could immediately create samples drawn from a specific distribution:
```
sample = np.random.normal(0,1,100000)
# sample
import matplotlib.pyplot as plt
plt.hist(sample, bins=50, density=True)
plt.show()
```
## 5.2 Scipy Statistics
This module contains a large number of probability distributions.
```
import scipy.stats
help(scipy.stats)
```
Let's plot some probability density functions of the Gaussian distribution:
```
from scipy.stats import norm
x = np.linspace(-5,5,num=200)
fig = plt.figure(figsize=(12,6))
for mu, s in zip([0.5, 0.5, 0.5], [0.2, 0.5, 0.8]):
plt.plot(x, norm.pdf(x,mu,s), lw=2,
label="$\mu={0:.1f}, s={1:.1f}$".format(mu, s))
plt.fill_between(x, norm.pdf(x, mu, s), alpha = .4)
plt.xlim([-5,5])
plt.legend(loc=0)
plt.ylabel("pdf at $x$")
plt.xlabel("$x$")
plt.show()
```
Let's create an interactive plot of the Gamma distribution:
```
%%capture
from ipywidgets import interactive
from scipy.stats import gamma
x = np.arange(0, 40, 0.005)
shape, scale = 5, 0.5
fig, ax = plt.subplots()
y = gamma.pdf(x, shape, scale=scale)
line = ax.plot(x, y)
ax.set_ylim((0,0.5))
def gamma_update(shape, scale):
y = gamma.pdf(x, shape, scale=scale)
line[0].set_ydata(y)
fig.canvas.draw()
display(fig)
interactive(gamma_update, shape=(0.1, 10.0), scale=(0.3, 3.0))
```
## 5.3 Seaborn
Seaborn is a Python data visualization library based on `matplotlib`. It is the equivalent to `R`'s package `ggplot2` and provides a high-level interface for drawing attractive and informative statistical graphics.
```
import seaborn as sns
```
We will create some basic `seaborn` plots. A gallery is alvailable here: http://seaborn.pydata.org/examples/index.html.
A scatterplot of a bivariate normal distribution:
```
import pandas as pd
mean, cov = [0, 1], [(1, .5), (.5, 1)]
data = np.random.multivariate_normal(mean, cov, 500)
df = pd.DataFrame(data, columns=["x", "y"])
sns.jointplot(x="x", y="y", data=df)
```
A scatterplot matrix:
```
df
df = sns.load_dataset("iris")
sns.pairplot(df, hue="species")
tips = sns.load_dataset("tips")
tips
```
A linear model plot:
```
sns.lmplot(x="total_bill", y="tip", data=tips, hue="smoker")
```
## 5.4 Statistical Models
Statsmodels is a Python package that allows users to explore data, estimate statistical models, and perform statistical tests. An extensive list of descriptive statistics, statistical tests, plotting functions, and result statistics are available for different types of data and each estimator. It complements SciPy's stats module.
```
import numpy as np
import statsmodels.api as sm
```
The user guide can be found here: https://www.statsmodels.org/stable/user-guide.html.
Let's explore our `iris` dataset again:
```
df
```
We would like to know whether the `sepal_length` depends on the explanatory variable `species`. Let's create a boxplot:
```
sns.boxplot(x="species", y="sepal_length", data=df)
```
It seems like this is indeed the case. However, we need to perform some statistical test to conclude this. Let's do some ANOVA (see syllabus Statistical Models, M. de Gunst):
```
lm = sm.OLS.from_formula('sepal_length ~ species', data=df)
fitted_model = lm.fit()
print(sm.stats.anova_lm(fitted_model))
```
We conclude that `species` is a significant explanatory variable for `sepal_length`. We can find the coefficients using the following code:
```
print(fitted_model.summary())
```
Now let's explore a dataset from `statsmodels`:
```
spector_data = sm.datasets.spector.load_pandas().data
spector_data
```
We will again do some ANOVA:
```
m = sm.OLS.from_formula('GRADE ~ GPA + TUCE', spector_data)
print(m.df_model, m.df_resid)
print(m.endog_names, m.exog_names)
res = m.fit()
# res.summary()
print(res.summary())
```
From this table, we conclude that `GPA` is a significant factor but `TUCE` is not. We can extract the coefficients of our fitted model as follows:
```
res.params # parameters
```
Given the values `GPA` and `TUCE`, we can get a predicted value for `GRADE`:
```
m.predict(res.params, [1, 4.0, 25])
```
We predict `GRADE = 1`.
We can also perform some _Fisher tests_ to check whether the explanatory variables are significant:
```
a = res.f_test("GPA = 0")
a.summary()
b = res.f_test("GPA = TUCE = 0")
b.summary()
```
Now let's take the full model:
```
spector_data
m = sm.OLS.from_formula('GRADE ~ GPA + TUCE + PSI', spector_data)
res1 = m.fit()
print(res1.summary())
```
As we can see, `PSI` is an important explanatory variable! We compare our models using the information criteria, or by performing some other tests:
```
res1.compare_f_test(res) # res1 better
res1.compare_lm_test(res)
res1.compare_lr_test(res)
help(sm)
```
We can also use a generalized linear model using the `sm.GLM` function or do some time series analysis using the `sm.tsa` subpackage. The investigation of this is left to the entusiastic reader. An introduction video can be found here:
```
from IPython.display import YouTubeVideo
YouTubeVideo('o7Ux5jKEbcw', width=533, height=300)
```
## 5.5 Python vs. R
There’s a lot of recurrent discussion on the right tool to use for statistics and machine learning. `R` and `Python` are often considered alternatives: they are both good for statistics and machine learning tasks. But which one is the fastest? For a benchmark, it is relatively hard to make it fair: the speed of execution may well depend on the code, or the speed of the different libraries used. We decide to do classification on the Iris dataset. It is a relatively easy Machine Learning project, which seems to make for a fair comparison. We use the commonly used libraries in both `R` and `Python`. The following steps are executed:
1. Read a csv file with the iris data.
2. Randomly split the data in 80% training data and 20% test data.
3. Fit a number of models (logistic regression, linear discriminant analysis, k-nearest neighbors, and support vector machines) on the training data using built-in grid-search and cross-validation methods
4. Evaluate each of those best models on the test data and select the best model
We get the following results:
```
# %load resources/python_vs_R.py
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.model_selection import GridSearchCV, KFold
from sklearn.neighbors import KNeighborsClassifier
from sklearn import svm
def main():
names = ["sepal_length", "sepal_width", "petal_length", "petal_width", "Name"]
iris_data = pd.read_csv("https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data", names = names)
train, test = train_test_split(iris_data, test_size=0.2)
X_train = train.drop('Name', axis=1)
y_train = train['Name']
X_test = test.drop('Name', axis=1)
y_test = test['Name']
# logistic regression
lr = LogisticRegression(solver='lbfgs', multi_class='auto', max_iter=1000)
lr.fit(X_train, y_train)
# linear discriminant analysis
lda = LinearDiscriminantAnalysis()
lda.fit(X_train,y_train)
# KNN (k-nearest neighbours)
parameters = {'n_neighbors': range(1,11)}
knn = GridSearchCV(KNeighborsClassifier(), parameters, scoring = 'accuracy', cv = KFold(n_splits=5))
knn.fit(X_train,y_train)
# SVM
parameters = {'C': range(1,11)}
svc = GridSearchCV(svm.SVC(kernel = 'linear'), parameters, scoring = 'accuracy', cv = KFold(n_splits=5))
svc.fit(X_train,y_train)
# evaluate
lr_test_acc = lr.score(X_test,y_test)
lda_test_acc = lda.score(X_test,y_test)
knn_test_acc = knn.best_estimator_.score(X_test,y_test)
svc_test_acc= svc.best_estimator_.score(X_test,y_test)
# print(lr_test_acc, lda_test_acc, knn_test_acc, svc_test_acc)
from datetime import datetime as dt
now = dt.now()
for i in range(5):
main()
print(dt.now() - now)
```
It seems that the `Python` code runs a little bit faster. However, when we make the model more complex, or use multiprocessing, the difference is even higher! If speed matters, using `Python` is the best alternative.
### 🔴 *Next Week:*
```
np.random.choice(['Machine learning 2','Something else'], p=[0.99,0.01])
```
|
github_jupyter
|
# Analysis for the floor control detection (FCD) model and competitor models
This notebook analyses the predictions of the FCD model and the competitor models discussed in the paper and show how they are compared over a few performance measurements. It also includes some stats about the dataset and the annotated floor properties, and an optimised FCD model for highest accuracy.
```
import itertools
import pathlib
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pyjags
from scipy import optimize as soptimize
import predict_fcd
import utils.annotated_floor
import utils.iteration
import utils.mcmc_plot
import utils.path
%load_ext autoreload
%autoreload 2
plt.style.use('ggplot')
plt.rcParams.update({'axes.titlesize': 'large'})
np.random.seed(1234)
FEATURES_DIR = pathlib.Path('features')
PREDICTIONS_DIR = pathlib.Path('predictions')
ANALYSIS_SAMPLE_RATE = 10
SAMPLE_RATE = {
'fcd': 50,
'optimised_fcd': 50,
'lstm': 20,
'partial_lstm': 20,
'vad': 50,
'random': ANALYSIS_SAMPLE_RATE,
}
MODELS = list(SAMPLE_RATE.keys())
DEFAULT_FCD_PARAMS = (0.35, 0.1)
OPTIMISED_FCD_PARAMS = (1.78924915, 1.06722576) # Overriden by lengthy optimisation below
CHAINS = 4
ITERATIONS = 10_000
```
# Utilities
Utility functions and generator functions that are used throughout the code and use the constants declared above. More utilities are imported from the `util` package. These are considered more generic.
### General utilities
```
def array_to_series(x, name, sample_rate):
'''
Convert a numpy array to a pandas series
with time index.
'''
x = x[::sample_rate // ANALYSIS_SAMPLE_RATE]
return pd.Series(
x,
index=np.arange(len(x)) / ANALYSIS_SAMPLE_RATE,
name=name,
)
def utterances_to_floor(utterances_df):
'''
Calculate the floor timeseries from a dataframe
of utterances (every row has start_time, end_time,
and participant).
'''
return array_to_series(
list(
utils.annotated_floor.gen(
utterances_df,
sample_rate=ANALYSIS_SAMPLE_RATE,
)
),
name='floor',
sample_rate=ANALYSIS_SAMPLE_RATE,
)
```
### Random model utilities
```
def _generate_random_model_intervals(average_floor_duration):
floor_holder = np.random.randint(2)
previous_timestamp = 0
while True:
samples = np.random.exponential(average_floor_duration, 100)
timestamps = samples.cumsum() + previous_timestamp
for timestamp in timestamps:
yield {
'start_time': previous_timestamp,
'end_time': timestamp,
'participant': floor_holder,
}
floor_holder = (floor_holder * -1) + 1
previous_timestamp = timestamp
def calculate_random_model(average_floor_duration, part_duration):
'''
Calculate a random floor array with turns duration distributin
exponentially with `average_floor_duration` as mean.
'''
gen = _generate_random_model_intervals(average_floor_duration)
gen = itertools.takewhile(lambda i: i['start_time'] < part_duration, gen)
return list(
utils.iteration.intervals_to_values_gen(
gen,
sample_rate=ANALYSIS_SAMPLE_RATE,
key='participant',
)
)
```
### Dataset stats utilities
```
def dataset_stats_gen():
'''
Calculate basic stats about the annotated floor.
'''
for part in utils.path.session_parts_gen(train_set=True, test_set=True):
utterances_df = pd.read_csv(FEATURES_DIR / 'utterances' / f'{part}.csv')
floor_intervals = list(utils.annotated_floor.utterances_to_floor_intervals_gen(utterances_df))
floor = utterances_to_floor(utterances_df)
yield {
'competition_for_floor': np.isnan(floor).mean(),
'average_floor_duration': np.mean([i['end_time'] - i['start_time'] for i in floor_intervals]),
'average_part_duration': utterances_df['end_time'].max(),
}
```
### Performance measurment generator functions
```
def accuracy(model, floor):
'''
Every 10 seconds, if defined floor (no competition nor silence)
yields 1 if the model and the floor agrees, 0 otherwise. 10 seconds
jumps are used to make sure the samples are independent.
'''
jump = 10 * ANALYSIS_SAMPLE_RATE
both = pd.concat([model, floor], axis=1)[::jump].dropna()
yield from (both.iloc[:, 0] == both.iloc[:, 1]).astype(int)
def backchannels(model, utterances_df):
'''
For each backchannel yield 1 if the model report a floor
for the partner, 0 otherwise.
'''
backchannels = utterances_df[utterances_df['backchannel']]
for _, bc in backchannels.iterrows():
bc_timestamp = bc['start_time']
prediction_at_bc = model[bc_timestamp:].values[0]
if prediction_at_bc:
yield int(prediction_at_bc != bc['participant'])
def _floor_holder_changes(array):
array = array[~np.isnan(array)]
items = utils.iteration.dedup(array)
return len(list(items)) - 1 # number of changes is number of values minus 1
def stability(model, floor):
'''
Ratio of actual floor changes vs. predicted floor changes.
'''
annotated_floor_changes = _floor_holder_changes(floor)
model_floor_changes = _floor_holder_changes(model)
yield annotated_floor_changes / model_floor_changes
def lag(model, floor):
'''
Yield positive lags in seconds.
'''
model_change = pd.Series(dict(utils.iteration.dedup(model.dropna().iteritems(), key=lambda x: x[1])))
floor_change = pd.Series(dict(utils.iteration.dedup(floor.dropna().iteritems(), key=lambda x: x[1])))
visited_timestamps = set()
for timestamp, prediction in model_change.iteritems():
previous_floors = floor_change[:timestamp]
if not previous_floors.empty:
current_floor_timestamp = previous_floors.index[-1]
current_floor_value = previous_floors.values[-1]
if (current_floor_value == prediction and current_floor_timestamp not in visited_timestamps):
yield (timestamp - current_floor_timestamp)
visited_timestamps.add(current_floor_timestamp)
```
### Models' performance (stats) collection utilities
```
def _part_models_stats_gen(part, average_floor_duration):
utterances_df = pd.read_csv(FEATURES_DIR / 'utterances' / f'{part}.csv')
floor = utterances_to_floor(utterances_df)
rms = np.load(FEATURES_DIR / 'FCD' / f'{part}.npy')
models = {
'fcd': np.load(PREDICTIONS_DIR / 'FCD' / f'{part}.npy'),
'optimised_fcd': list(predict_fcd.gen_from_rms(rms, *OPTIMISED_FCD_PARAMS)),
'lstm': np.load(PREDICTIONS_DIR / 'LSTM' / f'full-{part}.npy'),
'partial_lstm': np.load(PREDICTIONS_DIR / 'LSTM' / f'partial-{part}.npy'),
'vad': np.load(PREDICTIONS_DIR / 'VAD' / f'{part}.npy'),
'random': calculate_random_model(
average_floor_duration,
part_duration=floor.index[-1],
),
}
models_df = pd.concat(
[array_to_series(x, name=n, sample_rate=SAMPLE_RATE[n]) for n, x in models.items()],
axis=1,
)
measurement_functions_and_args = {
backchannels: utterances_df,
**{f: floor for f in [accuracy, stability, lag]},
}
for model in models:
for f, arg in measurement_functions_and_args.items():
for value in f(models_df[model], arg):
yield {
'part': part,
'model': model,
'measurement': f.__name__,
'value': value,
}
def models_stats_gen(average_floor_duration):
'''
Calculate the performance measure for each model accross the
test-set.
'''
for part in utils.path.session_parts_gen(train_set=False, test_set=True):
yield from _part_models_stats_gen(part, average_floor_duration)
```
### Bayesian analysis utilities
```
def gamma_template(mode, sd):
'''
Return a string template with shape and rate from mode and sd.
'''
rate = f'({mode} + sqrt({mode} ^ 2 + 4 * {sd} ^ 2)) / (2 * {sd} ^ 2)'
shape = f'1 + {mode} * {rate}'
return f'{shape}, {rate}'
def beta_template(mode, k):
'''
Return a string template with a and b from mode and concentration.
'''
a = f'{mode} * ({k} - 2) + 1'
b = f'(1 - {mode}) * ({k} - 2) + 1'
return f'{a}, {b}'
def run_model(code, data):
'''
Create and sample a JAGS model.
'''
model = pyjags.Model(code=code, data=data, chains=CHAINS)
return model.sample(ITERATIONS, vars=['mode'])
def mode_comparison(trace, models, diag_xlim, comp_xlim):
utils.mcmc_plot.param_comparison(
trace,
'mode',
comparison=[MODELS.index(m) for m in models],
names=models,
diag_xlim=diag_xlim,
comp_xlim=comp_xlim,
)
def compare_two(models, traces, xlim):
_, axes = plt.subplots(ncols=len(traces), figsize=(8, 2))
for ax, (measurement, trace) in zip(axes, traces.items()):
m1, m2 = [MODELS.index(m) for m in models]
ax.set(title=measurement)
ax.axvline(0, linestyle='--', c='grey')
utils.mcmc_plot.dist(
trace['mode'][m1].reshape(-1) - trace['mode'][m2].reshape(-1),
histplot_kwargs={'binrange': xlim},
ax=ax,
)
def _hdi_as_dict(model, samples):
return {
'model': model,
'hdi_start': np.percentile(samples, 2.5),
'hdi_end': np.percentile(samples, 97.5),
}
def hdi_summary(models, trace):
for m in models:
samples = trace['mode'][MODELS.index(m)].reshape(-1)
yield _hdi_as_dict(m, samples)
for m1, m2 in itertools.combinations(models, 2):
samples_m1 = trace['mode'][MODELS.index(m1)].reshape(-1)
samples_m2 = trace['mode'][MODELS.index(m2)].reshape(-1)
diff = samples_m1 - samples_m2
yield _hdi_as_dict(f'{m1} - {m2}', diff)
```
# Analysis starts here!
## Dataset stats
```
dataset_stats_df = pd.DataFrame(dataset_stats_gen())
dataset_stats_df.describe()
# Keep the average floor duration for later, for the random model
average_floor_duration = dataset_stats_df['average_floor_duration'].mean()
```
## Optimising FCD parameters for accuracy
This is done on the train set.
```
optimisation_data = []
for part in utils.path.session_parts_gen(train_set=True, test_set=False):
utterances_df = pd.read_csv(FEATURES_DIR / 'utterances' / f'{part}.csv')
floor = utterances_to_floor(utterances_df)
rms = np.load(FEATURES_DIR / 'FCD' / f'{part}.npy')
optimisation_data.append((rms, floor))
def get_negative_accuracy_from_model(params):
accuracies = []
for rms, floor in optimisation_data:
fcd_gen = predict_fcd.gen_from_rms(rms, *params)
fcd = array_to_series(list(fcd_gen), name='fcd', sample_rate=SAMPLE_RATE['fcd'])
accuracies.append(np.mean(list(accuracy(fcd, floor))))
return -np.mean(accuracies)
```
**Note!** This cell takes a while to run. It is commented out as the entire notebook can be executed without it. The default optimised parameters (declared at the top of the notebook) are used in that case.
```
# %%time
# res = soptimize.basinhopping(
# get_negative_accuracy_from_model,
# DEFAULT_FCD_PARAMS,
# seed=1234,
# )
# OPTIMISED_FCD_PARAMS = res.x
# res
```
**Example of the output of the cell above for reference**
```
CPU times: user 1h 7min 23s, sys: 24.2 s, total: 1h 7min 47s
Wall time: 1h 7min 40s
fun: -0.890908193538182
lowest_optimization_result: fun: -0.890908193538182
hess_inv: array([[1, 0],
[0, 1]])
jac: array([0., 0.])
message: 'Optimization terminated successfully.'
nfev: 3
nit: 0
njev: 1
status: 0
success: True
x: array([1.78924915, 1.06722576])
message: ['requested number of basinhopping iterations completed successfully']
minimization_failures: 0
nfev: 303
nit: 100
njev: 101
x: array([1.78924915, 1.06722576])
```
## The average of the models' performance on each measurement
```
models_stats_df = pd.DataFrame(models_stats_gen(average_floor_duration))
models_stats_df['model'] = pd.Categorical(
models_stats_df['model'],
categories=MODELS,
ordered=True,
)
for c in ['part', 'measurement']:
models_stats_df[c] = models_stats_df[c].astype('category')
(
models_stats_df
# Average within parts
.groupby(['model', 'measurement', 'part'])
.mean()
# Average accross parts
.reset_index()
.pivot_table(index='model', columns='measurement', values='value')
)
```
## Bayesian analysis of differences between the models
Here we estimate the mode of the accuracy, backchannels classification, stability, and lag, for each model. The Bayesian method provides a direct way to estimate the differences between the modes.
```
group_by_measurement = models_stats_df.groupby('measurement')
```
### Accuracy
```
hierarchical_beta_code = f"""
model {{
for (m in 1:n_models) {{
for (p in 1:n_parts) {{
correct[m, p] ~ dbin(part_mode[m, p], attempts[m, p])
part_mode[m, p] ~ dbeta({beta_template('mode[m]', 'concentration[m]')})
}}
mode[m] ~ dunif(0, 1)
concentration[m] = concentration_minus_two[m] + 2
concentration_minus_two[m] ~ dgamma({gamma_template(20, 20)})
}}
}}
"""
_df = group_by_measurement.get_group('accuracy')
accuracy_data = {
'n_parts': len(_df['part'].unique()),
'n_models': len(_df['model'].unique()),
'correct': _df.pivot_table(index='model', columns='part', values='value', aggfunc='sum'),
'attempts': _df.pivot_table(index='model', columns='part', values='value', aggfunc='count'),
}
accuracy_trace = run_model(code=hierarchical_beta_code, data=accuracy_data)
mode_comparison(accuracy_trace, ['fcd', 'lstm', 'random'], diag_xlim=(0, 1), comp_xlim=(-0.6, 0.6))
```
### Backchannels categorisation
```
_df = group_by_measurement.get_group('backchannels')
bc_data = {
'n_parts': len(_df['part'].unique()),
'n_models': len(_df['model'].unique()),
'correct': _df.pivot_table(index='model', columns='part', values='value', aggfunc='sum'),
'attempts': _df.pivot_table(index='model', columns='part', values='value', aggfunc='count'),
}
bc_trace = run_model(code=hierarchical_beta_code, data=bc_data)
mode_comparison(bc_trace, ['fcd', 'lstm', 'random'], diag_xlim=(0, 1), comp_xlim=(-0.6, 0.6))
```
### Stability
```
stability_code = f"""
model {{
for (m in 1:n_models) {{
for (p in 1:n_parts) {{
stability[m, p] ~ dgamma({gamma_template('mode[m]', 'sd[m]')})
}}
mode[m] ~ dgamma({gamma_template(1, 1)})
sd[m] ~ dgamma({gamma_template(1, 1)})
}}
}}
"""
_df = group_by_measurement.get_group('stability')
stability_data = {
'n_parts': len(_df['part'].unique()),
'n_models': len(_df['model'].unique()),
'stability': _df.pivot(index='model', columns='part', values='value'),
}
stability_trace = run_model(code=stability_code, data=stability_data)
mode_comparison(stability_trace, ['fcd', 'lstm', 'random'], diag_xlim=(0, 1.25), comp_xlim=(-1.2, 1.2))
```
### Lag
```
lag_code = f"""
model {{
for (i in 1:n_lags) {{
lag[i] ~ dexp(1 / part_mean[models[i], part[i]])
}}
for (i in 1:n_models) {{
for (j in 1:n_parts) {{
part_mean[i, j] ~ dgamma({gamma_template('mode[i]', 'sd[i]')})
}}
mode[i] ~ dgamma({gamma_template(0.5, 1)})
sd[i] ~ dgamma({gamma_template(1, 1)})
}}
}}
"""
_df = group_by_measurement.get_group('lag')
lag_data = {
'n_parts': len(_df['part'].unique()),
'n_models': len(_df['model'].unique()),
'n_lags': len(_df),
'lag': _df['value'],
'models': _df['model'].cat.codes + 1,
'part': _df['part'].cat.codes + 1,
}
lag_trace = run_model(code=lag_code, data=lag_data)
mode_comparison(lag_trace, ['fcd', 'lstm', 'random'], diag_xlim=(0, 2.1), comp_xlim=(-2.2, 2.2))
```
### FCD with default params vs. optimised FCD
```
traces = {
'accuracy': accuracy_trace,
'backchannels': bc_trace,
'stability': stability_trace,
'lag': lag_trace,
}
compare_two(['fcd', 'optimised_fcd'], traces, xlim=(-0.75, 0.75))
```
### LSTM vs. partial-LSTM
```
compare_two(['lstm', 'partial_lstm'], traces, xlim=(-0.75, 0.75))
```
### Optimised FCD vs. LSTM
This is marely to see if the lag of the optimised FCD is better.
```
compare_two(['optimised_fcd', 'lstm'], traces, xlim=(-0.75, 0.75))
```
### HDIs summary
```
models = ['fcd', 'lstm', 'random']
comp_values = [0.5, 0.5, 1, average_floor_duration / 2]
fig, axes = plt.subplots(nrows=len(traces), figsize=(8, 8), sharex=True)
for ax, (measurement, trace), comp_value in zip(axes, traces.items(), comp_values):
yticks = {}
ax.axvline(0, linestyle='--', c='grey')
if comp_value:
ax.axvline(comp_value, linestyle='dotted', c='grey')
for i, row in enumerate(hdi_summary(models, trace)):
ax.plot((row['hdi_start'], row['hdi_end']), (-i, -i), linewidth=4, c='k')
for tail, alignment in zip(['hdi_start', 'hdi_end'], ['right', 'left']):
s = format(row[tail], '.2f').replace('-0', '-').lstrip('0')
ax.text(row[tail], -i + 0.1, s, horizontalalignment=alignment)
yticks[-i] = row['model']
ax.set(title=measurement)
ax.set_yticks(list(yticks.keys()))
ax.set_yticklabels(list(yticks.values()))
fig.tight_layout()
fig.savefig('graphics/hdis.svg')
```
|
github_jupyter
|
# 3D Object Detection Evaluation Tutorial
Welcome to the 3D object detection evaluation tutorial! We'll walk through the steps to submit your detections to the competition server.
```
from av2.evaluation.detection.eval import evaluate
from av2.evaluation.detection.utils import DetectionCfg
from pathlib import Path
from av2.utils.io import read_feather, read_all_annotations
```
### Constructing the evaluation configuration
The `DetectionCfg` class stores the configuration for the 3D object detection challenge.
- During evaluation, we remove _all_ cuboids which are not within the region-of-interest (ROI) which spatially is a 5 meter dilation of the drivable area isocontour.
- **NOTE**: If you would like to _locally_ enable this behavior, you **must** pass in the directory to sensor dataset (to build the raster maps from the included vector maps).
```
dataset_dir = Path.home() / "data" / "datasets" / "av2" / "sensor" # Path to your AV2 sensor dataset directory.
competition_cfg = DetectionCfg(dataset_dir=dataset_dir) # Defaults to competition parameters.
split = "val"
gts = read_all_annotations(dataset_dir=dataset_dir, split=split) # Contains all annotations in a particular split.
display(gts)
```
## Preparing detections for submission.
The evaluation expects the following 14 fields within a `pandas.DataFrame`:
- `tx_m`: x-component of the object translation in the egovehicle reference frame.
- `ty_m`: y-component of the object translation in the egovehicle reference frame.
- `tz_m`: z-component of the object translation in the egovehicle reference frame.
- `length_m`: Object extent along the x-axis in meters.
- `width_m`: Object extent along the y-axis in meters.
- `height_m`: Object extent along the z-axis in meters.
- `qw`: Real quaternion coefficient.
- `qx`: First quaternion coefficient.
- `qy`: Second quaternion coefficient.
- `qz`: Third quaternion coefficient.
- `score`: Object confidence.
- `log_id`: Log id associated with the detection.
- `timestamp_ns`: Timestamp associated with the detection.
- `category`: Object category.
Additional details can be found in [SUBMISSION_FORMAT.md](../src/av2/evaluation/detection/SUBMISSION_FORMAT.md).
```
# If you've already aggregated your detections into one file.
dts_path = Path("detections.feather")
dts = read_feather(dts_path)
dts, gts, metrics = evaluate(dts, gts, cfg=competition_cfg) # Evaluate instances.
display(metrics)
```
Finally, if you would like to submit to the evaluation server, you just need to export your detections into a `.feather` file. This can be done by:
```python
dts.to_feather("detections.feather")
```
|
github_jupyter
|
# Synthetic seismic: wedge
We're going to make the famous wedge model, which interpreters can use to visualize the tuning effect. Then we can extend the idea to other kinds of model.
## Make a wedge earth model
```
import matplotlib.pyplot as plt
import numpy as np
length = 80 # x range
depth = 200 # z range
```
### EXERCISE
Make a NumPy array of integers with these dimensions, placing a boundary at a 'depth' of 66 and another at a depth of 133.
A plot of a vertical section through this array should look something like:
|
|
---
|
|
---
|
|
```
# YOUR CODE HERE
# We have to pass dtype=int or we get floats.
# We need ints because we're going to use for indexing later.
model = 1 + np.tri(depth, length, -depth//3, dtype=int)
plt.imshow(model)
plt.colorbar()
plt.show()
```
Now set the upper part of the model — above the wedge — to zero.
```
model[:depth//3,:] = 0
plt.imshow(model)
plt.colorbar()
plt.show()
```
Now we can make some Vp-rho pairs (rock 0, rock 1, and rock 2).
```
rocks = np.array([[2540, 2550], # <-- Upper layer
[2400, 2450], # <-- Wedge
[2650, 2800]]) # <-- Lower layer
```
Now we can use ['fancy indexing'](http://docs.scipy.org/doc/numpy/user/basics.indexing.html) to use `model`, which is an array of 0, 1, and 2, as the indices of the rock property pairs to 'grab' from `rocks`.
```
earth = rocks[model]
```
Now apply `np.prod` (product) to those Vp-rho pairs to get impedance at every sample.
```
imp = np.apply_along_axis(np.prod, arr=earth, axis=-1)
```
## Model seismic reflections
Now we have an earth model — giving us acoustic impedance everywhere in this 2D grid — we define a function to compute reflection coefficients for every trace.
### EXERCISE
Can you write a function to compute the reflection coefficients in this model?
It should implement this equation, where $Z$ is acoustic impedance and :
$$ R = \frac{Z_\mathrm{lower} - Z_\mathrm{upper}}{Z_\mathrm{lower} + Z_\mathrm{upper}} $$
The result should be a sparse 2D array of shape (199, 80). The upper interface of the wedge should be positive.
```
def make_rc(imp):
# YOUR CODE HERE
return rc
rc = make_rc(imp)
def make_rc(imp):
"""
Compute reflection coefficients.
"""
upper = imp[ :-1, :]
lower = imp[1: , :]
return (lower - upper) / (lower + upper)
rc = make_rc(imp)
```
You should be able to plot the RC series like so:
```
plt.figure(figsize=(8,4))
plt.imshow(rc, aspect='auto')
plt.colorbar()
plt.show()
```
### EXERCISE
Implement a Ricker wavelet of frequency $f$ with amplitude $A$ at time $t$ given by:
$$ \mathbf{a}(\mathbf{t}) = (1-2 \pi^2 f^2 \mathbf{t}^2) \mathrm{e}^{-\pi^2 f^2 \mathbf{t}^2} $$
```
# YOUR CODE HERE
```
There is an implementation in `scipy.signal` but it has a 'width parameter' instead of 'frequency' so it's harder to parameterize.
Instead, we'll use `bruges` to make a wavelet:
```
from bruges.filters import ricker
f = 25 # We'll use this later.
w, t = ricker(duration=0.128, dt=0.001, f=f, return_t=True)
plt.plot(t, w)
plt.show()
```
### EXERCISE
Make an RC series 200 samples long, with one positive and one negative RC. Make a corresponding time array.
Pass the RC series to `np.convolve()` along with the wavelet, then plot the resulting synthetic seismogram.
```
# YOUR CODE HERE
temp = np.zeros(200)
temp[66] = 1
temp[133] = -0.5
tr = np.convolve(temp, w, mode='same')
plt.plot(tr)
```
## Synthetic wedge
It's only a little trickier for us to apply 1D convolution to every trace in our 2D reflection coeeficient matrix. NumPy provides a function, `apply_along_axis()` to apply any function along any one axis of an n-dimensional array. I don't think it's much faster than looping, but I find it easier to think about.
```
def convolve(trace, wavelet):
return np.convolve(trace, wavelet, mode='same')
synth = np.apply_along_axis(convolve,
axis=0,
arr=rc,
wavelet=w)
plt.figure(figsize=(12,6))
plt.imshow(synth, cmap="Greys", aspect=0.2)
plt.colorbar()
plt.show()
```
### EXERCISE
Use `ipywidgets.interact` to turn this into an interactive plot, so that we can vary the frequency of the wavelet and see the effect on the synthetic.
Here's a reminder of how to use it:
from ipywidgets import interact
@interact(a=(0, 10, 1), b=(0, 100, 10))
def main(a, b):
"""Do the things!"""
print(a + b)
return
```
# YOUR CODE HERE
from ipywidgets import interact
@interact(f=(4, 100, 4))
def show(f):
w, t = ricker(duration=0.128, dt=0.001, f=f, return_t=True)
synth = np.apply_along_axis(convolve,
axis=0,
arr=rc,
wavelet=w)
plt.figure(figsize=(12,6))
plt.imshow(synth, cmap="Greys", aspect=0.2)
plt.colorbar()
plt.show()
```
<hr />
<div>
<img src="https://avatars1.githubusercontent.com/u/1692321?s=50"><p style="text-align:center">© Agile Scientific 2020</p>
</div>
|
github_jupyter
|
```
#@title Environment Setup
import glob
BASE_DIR = "gs://download.magenta.tensorflow.org/models/music_vae/colab2"
print('Installing dependencies...')
!apt-get update -qq && apt-get install -qq libfluidsynth1 fluid-soundfont-gm build-essential libasound2-dev libjack-dev
!pip install -q pyfluidsynth
!pip install -qU magenta
# Hack to allow python to pick up the newly-installed fluidsynth lib.
# This is only needed for the hosted Colab environment.
import ctypes.util
orig_ctypes_util_find_library = ctypes.util.find_library
def proxy_find_library(lib):
if lib == 'fluidsynth':
return 'libfluidsynth.so.1'
else:
return orig_ctypes_util_find_library(lib)
ctypes.util.find_library = proxy_find_library
print('Importing libraries and defining some helper functions...')
from google.colab import files
import magenta.music as mm
from magenta.models.music_vae import configs
from magenta.models.music_vae.trained_model import TrainedModel
import numpy as np
import os
import tensorflow.compat.v1 as tf
tf.disable_v2_behavior()
# Necessary until pyfluidsynth is updated (>1.2.5).
import warnings
warnings.filterwarnings("ignore", category=DeprecationWarning)
def play(note_sequence):
mm.play_sequence(note_sequence, synth=mm.fluidsynth)
def interpolate(model, start_seq, end_seq, num_steps, max_length=32,
assert_same_length=True, temperature=0.5,
individual_duration=4.0):
"""Interpolates between a start and end sequence."""
note_sequences = model.interpolate(
start_seq, end_seq,num_steps=num_steps, length=max_length,
temperature=temperature,
assert_same_length=assert_same_length)
print('Start Seq Reconstruction')
play(note_sequences[0])
print('End Seq Reconstruction')
play(note_sequences[-1])
print('Mean Sequence')
play(note_sequences[num_steps // 2])
print('Start -> End Interpolation')
interp_seq = mm.sequences_lib.concatenate_sequences(
note_sequences, [individual_duration] * len(note_sequences))
play(interp_seq)
mm.plot_sequence(interp_seq)
return interp_seq if num_steps > 3 else note_sequences[num_steps // 2]
def download(note_sequence, filename):
mm.sequence_proto_to_midi_file(note_sequence, filename)
files.download(filename)
print('Done')
#@title Drive Setup
#@markdown If your training sample is in google drive you need to connect it.
#@markdown You can also upload the data to a temporary folder but it will be
#@markdown lost when the session is closed.
from google.colab import drive
drive.mount('/content/drive')
!music_vae_generate \
--config=cat-mel_2bar_big \
--checkpoint_file=/content/drive/My\ Drive/cat-mel_2bar_big.tar \
--mode=interpolate \
--num_outputs=5 \
--input_midi_1=/2bar902_1.mid \
--input_midi_2=/2bar907_1.mid \
--output_dir=/tmp/music_vae/generated2
!convert_dir_to_note_sequences \
--input_dir=/content/drive/My\ Drive/pop909_melody_train \
--output_file=/temp/notesequences.tfrecord \
--log=INFO
!music_vae_train \
--config=cat-mel_2bar_big \
--run_dir=/temp/music_vae/ \
--mode=train \
--examples_path=/temp/notesequences.tfrecord \
--hparams=max_seq_len=32, z_size=512, free_bits=0, max_beta=0.5, beta_rate=0.99999, batch_size=512, grad_clip=1.0, clip_mode='global_norm', grad_norm_clip_to_zero=10000, learning_rate=0.01, decay_rate=0.9999, min_learning_rate=0.00001
!music_vae_generate \
--config=cat-mel_2bar_big \
--input_midi_1=/064.mid \
--input_midi_2=/058.mid \
--checkpoint_file=/temp/music_vae/train/model.ckpt-1795 \
--mode=interpolate \
--num_outputs=3 \
--output_dir=/tmp/music_vae/generated8
!music_vae_generate \
--config=cat-mel_2bar_big \
--input_midi_1=/2bar058_1.mid \
--input_midi_2=/2bar064_1.mid \
--checkpoint_file=/temp/music_vae/train/model.ckpt-1795 \
--mode=interpolate \
--num_outputs=5 \
--output_dir=/tmp/music_vae/generated9
!music_vae_generate \
--config=cat-mel_2bar_big \
--input_midi_1=/756.mid \
--input_midi_2=/746.mid \
--checkpoint_file=/temp/music_vae/train/model.ckpt-1795 \
--mode=interpolate \
--num_outputs=3 \
--output_dir=/tmp/music_vae/generated10
!music_vae_generate \
--config=cat-mel_2bar_big \
--input_midi_1=/2bar902_1.mid \
--input_midi_2=/2bar907_1.mid \
--checkpoint_file=/temp/music_vae/train/model.ckpt-1795 \
--mode=interpolate \
--num_outputs=5 \
--output_dir=/tmp/music_vae/generated13
```
|
github_jupyter
|
# Download Data
This notebook downloads the necessary data to replicate the results of our paper on Gender Inequalities on Wikipedia.
Note that we use a file named `dbpedia_config.py` where we set which language editions we will we study, as well as where to save and load data files.
By [Eduardo Graells-Garrido](http://carnby.github.io).
```
!cat dbpedia_config.py
import subprocess
import os
import dbpedia_config
target = dbpedia_config.DATA_FOLDER
languages = dbpedia_config.LANGUAGES
# Ontology
# note that previously (2014 version and earlier) this was in bzip format.
if not os.path.exists('{0}/dbpedia.owl'.format(target)):
subprocess.call(['/usr/bin/wget',
'http://downloads.dbpedia.org/2015-10/dbpedia_2015-10.owl',
'-O', '{0}/dbpedia.owl'.format(target)],
stdout=None, stderr=None)
# current version: http://wiki.dbpedia.org/Downloads2015-04
db_uri = 'http://downloads.dbpedia.org/2015-10/core-i18n'
for lang in languages:
if not os.path.exists('{0}/instance_types_{1}.ttl.bz2'.format(target, lang)):
subprocess.call(['/usr/bin/wget',
'{1}/{0}/instance_types_{0}.ttl.bz2'.format(lang, db_uri),
'-O', '{0}/instance_types_{1}.ttl.bz2'.format(target, lang)],
stdout=None, stderr=None)
if not os.path.exists('{0}/interlanguage_links_{1}.ttl.bz2'.format(target, lang)):
subprocess.call(['/usr/bin/wget',
'{1}/{0}/interlanguage_links_{0}.ttl.bz2'.format(lang, db_uri),
'-O', '{0}/interlanguage_links_{1}.ttl.bz2'.format(target, lang)],
stdout=None, stderr=None)
if not os.path.exists('{0}/labels_{1}.ttl.bz2'.format(target, lang)):
subprocess.call(['/usr/bin/wget',
'{1}/{0}/labels_{0}.ttl.bz2'.format(lang, db_uri),
'-O', '{0}/labels_{1}.ttl.bz2'.format(target, lang)],
stdout=None, stderr=None)
if not os.path.exists('{0}/mappingbased_literals_{1}.ttl.bz2'.format(target, lang)):
subprocess.call(['/usr/bin/wget',
'{1}/{0}/mappingbased_literals_{0}.ttl.bz2'.format(lang, db_uri),
'-O', '{0}/mappingbased_literals_{1}.ttl.bz2'.format(target, lang)],
stdout=None, stderr=None)
if not os.path.exists('{0}/mappingbased_objects_{1}.ttl.bz2'.format(target, lang)):
subprocess.call(['/usr/bin/wget',
'{1}/{0}/mappingbased_objects_{0}.ttl.bz2'.format(lang, db_uri),
'-O', '{0}/mappingbased_objects_{1}.ttl.bz2'.format(target, lang)],
stdout=None, stderr=None)
# http://oldwiki.dbpedia.org/Datasets/NLP#h172-7
dbpedia_gender = 'http://wifo5-04.informatik.uni-mannheim.de/downloads/datasets/genders_en.nt.bz2'
if not os.path.exists('{0}/genders_en.nt.bz2'.format(target)):
subprocess.call(['/usr/bin/wget',
dbpedia_gender,
'-O', '{0}/genders_en.nt.bz2'.format(target)],
stdout=None, stderr=None)
# http://www.davidbamman.com/?p=12
# note that, in previous versions, this was a text file. now it's a bzipped file with n-triplets.
wikipedia_gender = 'http://www.ark.cs.cmu.edu/bio/data/wiki.genders.txt'
if not os.path.exists('{0}/wiki.genders.txt'.format(target)):
subprocess.call(['/usr/bin/wget',
dbpedia_gender,
'-O', '{0}/wiki.genders.txt'.format(target)],
stdout=None, stderr=None)
if not os.path.exists('{0}/long_abstracts_{1}.nt.bz2'.format(target, dbpedia_config.MAIN_LANGUAGE)):
subprocess.call(['/usr/bin/wget',
'{1}/{0}/long_abstracts_{0}.ttl.bz2'.format(dbpedia_config.MAIN_LANGUAGE, db_uri),
'-O', '{0}/long_abstracts_{1}.ttl.bz2'.format(target, dbpedia_config.MAIN_LANGUAGE)],
stdout=None, stderr=None)
# network data for english only
if not os.path.exists('{0}/page_links_{1}.ttl.bz2'.format(target, dbpedia_config.MAIN_LANGUAGE)):
subprocess.call(['/usr/bin/wget',
'{1}/{0}/page_links_{0}.nt.bz2'.format(dbpedia_config.MAIN_LANGUAGE, db_uri),
'-O', '{0}/page_links_{1}.ttl.bz2'.format(target, dbpedia_config.MAIN_LANGUAGE)],
stdout=None, stderr=None)
```
|
github_jupyter
|
# Quantum Cryptography: Quantum Key Distribution
***
### Contributors:
A.J. Rasmusson, Richard Barney
Have you ever wanted to send a super secret message to a friend? Then you need a key to encrypt your message, and your friend needs the same key to decrypt your message. But, how do you send a super secret key to your friend without your eavesdropping enemies finding out what it is? Businesses and governments face this problem every day. People are always innovating new ways to intercept personal data or other sensitive information. Ideally, we'd like to find a way to share information that cannot be intercepted. [Quantum key distribution](https://en.wikipedia.org/wiki/Quantum_key_distribution) (QKD) was created as a solution to this problem. In this tutorial, you'll learn about and implement a version of the [BB84 QKD protocol](https://en.wikipedia.org/wiki/BB84), developed by Bennet and Brassard, to generate a secure, [one-time pad](https://en.wikipedia.org/wiki/One-time_pad) encryption key.
Quantum key distribution is all about making the right information publicly known at the right times (and keeping the secret information secret). This tutorial will take you through a quantum key distribution between you (Alice) and your friend Bob. After you get a feel for the ropes by sending your first encrypted message to Bob, we'll introduce Eve--your eavesdropping enemy. You'll learn how to detect Eve's presence and thus prevent her from intercepting your super secret key and decrypting your messages.
```
#import all the packages
# Checking the version of PYTHON
import sys
if sys.version_info < (3,5):
raise Exception('Please use Python version 3.5 or greater.')
#append to system path so qiskit and Qconfig can be found from home directory
sys.path.append('../qiskit-sdk-py/')
# Import the QuantumProgram and configuration
from qiskit import QuantumProgram
#import Qconfig
#other useful packages
import math
```
## Part 1: Encrypting and Decrypting a Message
### Pick Your Super Secret Message
The super secret message you want to send must be the same or less than the length of the super secret key.
If the key is shorter than the message, you will be forced to use parts of the key more than once. This may allow your lurking enemies to pick up a pattern in your encrypted message and possibly decrypt it. (As you'll see later on, we need to start out with a key at least double the number of characters used in your message. For now, don't worry about those details, pick your message! For this tutorial, we picked the initial key to be 3x greater--just to be safe.) Enter your message on the line below which reads "mes = ".
```
#Super secret message
mes = 'hello world'
print('Your super secret message: ',mes)
#initial size of key
n = len(mes)*3
#break up message into smaller parts if length > 10
nlist = []
for i in range(int(n/10)):
nlist.append(10)
if n%10 != 0:
nlist.append(n%10)
print('Initial key length: ',n)
```
### The Big Picture
Now that you (Alice) have the key, here's the big question: how are we going to get your key to Bob without eavesdroppers intercepting it? Quantum key distribution! Here are the steps and big picture (the effects of eavesdropping will be discussed later on):
1. You (Alice) generate a random string--the key you wish to give to Bob.
2. You (Alice) convert your string bits into corresponding qubits.
3. You (Alice) send those qubits to Bob, BUT! you randomly rotate some into a superposition. This effectively turns your key into random noise. (This is good because your lurking enemies might measure your qubits.)
4. Bob receives yours qubits AND randomly rotates some qubits in the opposite direction before measuring.
5. Alice and Bob publicly share which qubits they rotated. When they both did the same thing (either both did nothing or both rotated), they know the original key bit value made it to Bob! (Overall, you can see that only some of the bits from Alice's original key should make it.)
6. Alice and Bob create their keys. Alice modifies her original key by keeping only the bits that she knows made it to Bob. Bob does the same.
Alice and Bob now have matching keys! They can now use this key to encrypt and decrypt their messages.
<img src='QKDnoEve.png'>
Here we see Alice sending the initial key to Bob. She sends her qubits and rotates them based on her rotation string. Bob rotates the incoming qubits based on his rotation string and measures the qubits.
### Step 1: Alice Generates a Random Key
You and your friend need a super secret key so you can encrypt your message and your friend can decrypt it. Let's make a key--a pure random key.
To make a purely random string, we'll use quantum superposition. A qubit in the xy-plane of the [Bloch sphere](https://quantumexperience.ng.bluemix.net/qx/tutorial?sectionId=beginners-guide&page=004-The_Weird_and_Wonderful_World_of_the_Qubit~2F001-The_Weird_and_Wonderful_World_of_the_Qubit) is in a 50-50 [superposition](https://quantumexperience.ng.bluemix.net/qx/tutorial?sectionId=beginners-guide&page=005-Single-Qubit_Gates~2F002-Creating_superposition); 50% of the time it'll be measured as 0, and 50% of the time it'll be measured as 1. We have Alice prepare several qubits like this and measure them to generate a purely random string of 1s and 0s.
```
# Make random strings of length string_length
def randomStringGen(string_length):
#output variables used to access quantum computer results at the end of the function
output_list = []
output = ''
#start up your quantum program
qp = QuantumProgram()
backend = 'local_qasm_simulator'
circuits = ['rs']
#run circuit in batches of 10 qubits for fastest results. The results
#from each run will be appended and then clipped down to the right n size.
n = string_length
temp_n = 10
temp_output = ''
for i in range(math.ceil(n/temp_n)):
#initialize quantum registers for circuit
q = qp.create_quantum_register('q',temp_n)
c = qp.create_classical_register('c',temp_n)
rs = qp.create_circuit('rs',[q],[c])
#create temp_n number of qubits all in superpositions
for i in range(temp_n):
rs.h(q[i]) #the .h gate is the Hadamard gate that makes superpositions
rs.measure(q[i],c[i])
#execute circuit and extract 0s and 1s from key
result = qp.execute(circuits, backend, shots=1)
counts = result.get_counts('rs')
result_key = list(result.get_counts('rs').keys())
temp_output = result_key[0]
output += temp_output
#return output clipped to size of desired string length
return output[:n]
key = randomStringGen(n)
print('Initial key: ',key)
```
### Steps 2-4: Send Alice's Qubits to Bob
Alice turns her key bits into corresponding qubit states. If a bit is a 0 she will prepare a qubit on the negative z axis. If the bit is a 1 she will prepare a qubit on the positive z axis. Next, if Alice has a 1 in her rotate string, she rotates her key qubit with a [Hadamard](https://quantumexperience.ng.bluemix.net/qx/tutorial?sectionId=beginners-guide&page=005-Single-Qubit_Gates~2F002-Creating_superposition) gate. She then sends the qubit to Bob. If Bob has a 1 in his rotate string, he rotates the incoming qubit in the opposite direction with a Hadamard gate. Bob then measures the state of the qubit and records the result. The quantum circuit below executes each of these steps.
```
#generate random rotation strings for Alice and Bob
Alice_rotate = randomStringGen(n)
Bob_rotate = randomStringGen(n)
print("Alice's rotation string:",Alice_rotate)
print("Bob's rotation string: ",Bob_rotate)
#start up your quantum program
backend = 'local_qasm_simulator'
shots = 1
circuits = ['send_over']
Bob_result = ''
for ind,l in enumerate(nlist):
#define temp variables used in breaking up quantum program if message length > 10
if l < 10:
key_temp = key[10*ind:10*ind+l]
Ar_temp = Alice_rotate[10*ind:10*ind+l]
Br_temp = Bob_rotate[10*ind:10*ind+l]
else:
key_temp = key[l*ind:l*(ind+1)]
Ar_temp = Alice_rotate[l*ind:l*(ind+1)]
Br_temp = Bob_rotate[l*ind:l*(ind+1)]
#start up the rest of your quantum program
qp2 = QuantumProgram()
q = qp2.create_quantum_register('q',l)
c = qp2.create_classical_register('c',l)
send_over = qp2.create_circuit('send_over',[q],[c])
#prepare qubits based on key; add Hadamard gates based on Alice's and Bob's
#rotation strings
for i,j,k,n in zip(key_temp,Ar_temp,Br_temp,range(0,len(key_temp))):
i = int(i)
j = int(j)
k = int(k)
if i > 0:
send_over.x(q[n])
#Look at Alice's rotation string
if j > 0:
send_over.h(q[n])
#Look at Bob's rotation string
if k > 0:
send_over.h(q[n])
send_over.measure(q[n],c[n])
#execute quantum circuit
result_so = qp2.execute(circuits, backend, shots=shots)
counts_so = result_so.get_counts('send_over')
result_key_so = list(result_so.get_counts('send_over').keys())
Bob_result += result_key_so[0][::-1]
print("Bob's results: ", Bob_result)
```
### Steps 5-6: Compare Rotation Strings and Make Keys
Alice and Bob can now generate a secret quantum encryption key. First, they publicly share their rotation strings. If a bit in Alice's rotation string is the same as the corresponding bit in Bob's they know that Bob's result is the same as what Alice sent. They keep these bits to form the new key. (Alice based on her original key and Bob based on his measured results).
```
def makeKey(rotation1,rotation2,results):
key = ''
count = 0
for i,j in zip(rotation1,rotation2):
if i == j:
key += results[count]
count += 1
return key
Akey = makeKey(Bob_rotate,Alice_rotate,key)
Bkey = makeKey(Bob_rotate,Alice_rotate,Bob_result)
print("Alice's key:",Akey)
print("Bob's key: ",Bkey)
```
### Pause
We see that using only the public knowledge of Bob's and Alice's rotation strings, Alice and Bob can create the same identical key based on Alice's initial random key and Bob's results. Wow!! :D
<strong>If Alice's and Bob's key length is less than the message</strong>, the encryption is compromised. If this is the case for you, rerun all the cells above and see if you get a longer key. (We set the initial key length to 3x the message length to avoid this, but it's still possible.)
### Encrypt (and decrypt) using quantum key
We can now use our super secret key to encrypt and decrypt messages!! (of length less than the key). Note: the below "encryption" method is not powerful and should not be used for anything you want secure; it's just for fun. In real life, the super secret key you made and shared with Bob would be used in a much more sophisticated encryption algorithm.
```
#make key same length has message
shortened_Akey = Akey[:len(mes)]
encoded_m=''
#encrypt message mes using encryption key final_key
for m,k in zip(mes,shortened_Akey):
encoded_c = chr(ord(m) + 2*ord(k) % 256)
encoded_m += encoded_c
print('encoded message: ',encoded_m)
#make key same length has message
shortened_Bkey = Bkey[:len(mes)]
#decrypt message mes using encryption key final_key
result = ''
for m,k in zip(encoded_m,shortened_Bkey):
encoded_c = chr(ord(m) - 2*ord(k) % 256)
result += encoded_c
print('recovered message:',result)
```
# Part 2: Eve the Eavesdropper
What if someone is eavesdropping on Alice and Bob's line of communication? This process of random string making and rotations using quantum mechanics is only useful if it's robust against eavesdroppers.
Eve is your lurking enemy. She eavesdrops by intercepting your transmission to Bob. To be sneaky, Eve must send on the intercepted transmission--otherwise Bob will never receive anything and know that something is wrong!
Let's explain further why Eve can be detected. If Eve intercepts a qubit from Alice, she will not know if Alice rotated its state or not. Eve can only measure a 0 or 1. And she can't measure the qubit and then send the same qubit on, because her measurement will destroy the quantum state. Consequently, Eve doesn't know when or when not to rotate to recreate Alice's original qubit. She may as well send on qubits that have not been rotated, hoping to get the rotation right 50% of the time. After she sends these qubits to Bob, Alice and Bob can compare select parts of their keys to see if they have discrepancies in places they should not.
The scheme goes as follows:
1. Alice sends her qubit transmission Bob--but Eve measures the results
2. To avoid suspicion, Eve prepares qubits corresponding to the bits she measured and sends them to Bob.
3. Bob and Alice make their keys like normal
4. Alice and Bob randomly select the same parts of their keys to share publicly
5. If the selected part of the keys don't match, they know Eve was eavesdropping
6. If the selected part of the keys DO match, they can be confident Eve wasn't eavesdropping
7. They throw away the part of the key they made public and encrypt and decrypt super secret messages with the portion of the key they have left.
<img src="QKD.png">
Here we see Alice sending her qubits, rotationing them based on her rotation string, and Eve intercepting the transmittion. Eve then sending her results onto Bob who--like normal--rotates and measures the qubits.
### Step 1: Eve intercepts Alice's transmission
The code below has Alice sending her qubits and Eve intercepting them. It then displays the results of Eve's measurements.
```
#start up your quantum program
backend = 'local_qasm_simulator'
shots = 1
circuits = ['Eve']
Eve_result = ''
for ind,l in enumerate(nlist):
#define temp variables used in breaking up quantum program if message length > 10
if l < 10:
key_temp = key[10*ind:10*ind+l]
Ar_temp = Alice_rotate[10*ind:10*ind+l]
else:
key_temp = key[l*ind:l*(ind+1)]
Ar_temp = Alice_rotate[l*ind:l*(ind+1)]
#start up the rest of your quantum program
qp3 = QuantumProgram()
q = qp3.create_quantum_register('q',l)
c = qp3.create_classical_register('c',l)
Eve = qp3.create_circuit('Eve',[q],[c])
#prepare qubits based on key; add Hadamard gates based on Alice's and Bob's
#rotation strings
for i,j,n in zip(key_temp,Ar_temp,range(0,len(key_temp))):
i = int(i)
j = int(j)
if i > 0:
Eve.x(q[n])
if j > 0:
Eve.h(q[n])
Eve.measure(q[n],c[n])
#execute
result_eve = qp3.execute(circuits, backend, shots=shots)
counts_eve = result_eve.get_counts('Eve')
result_key_eve = list(result_eve.get_counts('Eve').keys())
Eve_result += result_key_eve[0][::-1]
print("Eve's results: ", Eve_result)
```
### Step 2: Eve deceives Bob
Eve sends her measured qubits on to Bob to deceive him! Since she doesn't know which of the qubits she measured were in a superposition or not, she doesn't even know whether to send the exact values she measured or opposite values. In the end, sending on the exact values is just as good a deception as mixing them up again.
```
#start up your quantum program
backend = 'local_qasm_simulator'
shots = 1
circuits = ['Eve2']
Bob_badresult = ''
for ind,l in enumerate(nlist):
#define temp variables used in breaking up quantum program if message length > 10
if l < 10:
key_temp = key[10*ind:10*ind+l]
Eve_temp = Eve_result[10*ind:10*ind+l]
Br_temp = Bob_rotate[10*ind:10*ind+l]
else:
key_temp = key[l*ind:l*(ind+1)]
Eve_temp = Eve_result[l*ind:l*(ind+1)]
Br_temp = Bob_rotate[l*ind:l*(ind+1)]
#start up the rest of your quantum program
qp4 = QuantumProgram()
q = qp4.create_quantum_register('q',l)
c = qp4.create_classical_register('c',l)
Eve2 = qp4.create_circuit('Eve2',[q],[c])
#prepare qubits
for i,j,n in zip(Eve_temp,Br_temp,range(0,len(key_temp))):
i = int(i)
j = int(j)
if i > 0:
Eve2.x(q[n])
if j > 0:
Eve2.h(q[n])
Eve2.measure(q[n],c[n])
#execute
result_eve = qp4.execute(circuits, backend, shots=shots)
counts_eve = result_eve.get_counts('Eve2')
result_key_eve = list(result_eve.get_counts('Eve2').keys())
Bob_badresult += result_key_eve[0][::-1]
print("Bob's previous results (w/o Eve):",Bob_result)
print("Bob's results from Eve:\t\t ",Bob_badresult)
```
### Step 4: Spot Check
Alice and Bob know Eve is lurking out there. They decide to pick a few random values from their individual keys and compare with each other. This requires making these subsections of their keys public (so the other can see them). If any of the values in their keys are different, they know Eve's eavesdropping messed up the superposition Alice originally created! If they find all the values are identical, they can be reasonably confident that Eve wasn't eavesdropping. Of course, making some random key values known to the public will require them to remove those values from their keys because those parts are no longer super secret. Also, Alice and Bob need to make sure they are sharing corresponding values from their respective keys.
Let's make a check key. If the randomly generated check key is a one, Alice and Bob will compare that part of their keys with each other (aka make publicly known).
```
#make keys for Alice and Bob
Akey = makeKey(Bob_rotate,Alice_rotate,key)
Bkey = makeKey(Bob_rotate,Alice_rotate,Bob_badresult)
print("Alice's key: ",Akey)
print("Bob's key: ",Bkey)
check_key = randomStringGen(len(Akey))
print('spots to check:',check_key)
```
### Steps 5-7: Compare strings and detect Eve
Alice and Bob compare the subsections of their keys. If they notice any discrepancy, they know that Eve was trying to intercept their message. They create new keys by throwing away the parts they shared publicly. It's possible that by throwing these parts away, they will not have a key long enough to encrypt the message and they will have to try again.
```
#find which values in rotation string were used to make the key
Alice_keyrotate = makeKey(Bob_rotate,Alice_rotate,Alice_rotate)
Bob_keyrotate = makeKey(Bob_rotate,Alice_rotate,Bob_rotate)
# Detect Eve's interference
#extract a subset of Alice's key
sub_Akey = ''
sub_Arotate = ''
count = 0
for i,j in zip(Alice_rotate,Akey):
if int(check_key[count]) == 1:
sub_Akey += Akey[count]
sub_Arotate += Alice_keyrotate[count]
count += 1
#extract a subset of Bob's key
sub_Bkey = ''
sub_Brotate = ''
count = 0
for i,j in zip(Bob_rotate,Bkey):
if int(check_key[count]) == 1:
sub_Bkey += Bkey[count]
sub_Brotate += Bob_keyrotate[count]
count += 1
print("subset of Alice's key:",sub_Akey)
print("subset of Bob's key: ",sub_Bkey)
#compare Alice and Bob's key subsets
secure = True
for i,j in zip(sub_Akey,sub_Bkey):
if i == j:
secure = True
else:
secure = False
break;
if not secure:
print('Eve detected!')
else:
print('Eve escaped detection!')
#sub_Akey and sub_Bkey are public knowledge now, so we remove them from Akey and Bkey
if secure:
new_Akey = ''
new_Bkey = ''
for index,i in enumerate(check_key):
if int(i) == 0:
new_Akey += Akey[index]
new_Bkey += Bkey[index]
print('new A and B keys: ',new_Akey,new_Bkey)
if(len(mes)>len(new_Akey)):
print('Your new key is not long enough.')
```
# Probability of Detecting Eve
The longer the key, the more likely you will detect Eve. In fact, the [probability](hhttps://en.wikipedia.org/wiki/Quantum_key_distribution#Intercept_and_resend) goes up as a function of $1 - (3/4)^n$ where n is the number of bits Alice and Bob compare in their spot check. So, the longer the key, the more bits you can use to compare and the more likely you will detect Eve.
```
#!!! you may need to execute this cell twice in order to see the output due to an problem with matplotlib
import matplotlib.pyplot as plt
import numpy as np
x = np.arange(0., 30.0)
y = 1-(3/4)**x
plt.plot(y)
plt.title('Probablity of detecting Eve')
plt.xlabel('# of key bits compared')
plt.ylabel('Probablity of detecting Eve')
plt.show()
```
|
github_jupyter
|
_ELMED219-2021_. Alexander S. Lundervold, 10.01.2021.
# Natural language processing and machine learning: a small case-study
This is a quick example of some techniques and ideas from natural language processing (NLP) and some modern approaches to NLP based on _deep learning_.
> Note: we'll take a close look at what deep learning is in tomorrow's lecture and lab.
> Note: If you want to run this notebook on your own computer, ask Alexander for assistance. The software requirements are different from the other ELMED219 notebooks (and also slightly more tricky to install, depending on your setup).
# Setup
We'll use the [spacy library]() for NLP and the [fastai]() library for deep learning.
```
import spacy
from fastai.text.all import *
from pprint import pprint as pp
```
# Load data
We use a data set collected in the work of Wakamiya et.al, _Tweet Classification Toward Twitter-Based Disease Surveillance: New Data, Methods, and Evaluations_, 2019: https://www.jmir.org/2019/2/e12783/

The data us supposed to represent tweets that discusses one or more of eight symptoms.
From the original paper:
<img src="assets/medweb_examples.png">
We'll only look at the English language tweets:
```
df = pd.read_csv('data/medweb/medwebdata.csv')
df.head()
pp(df['Tweet'][10])
```
From this text the goal is to determine whether the person is talking about one or more of the eight symptoms or conditions listed above:
```
list(df.columns[2:-2])
```
> **BUT:** How can a computer read??
<img src="http://2.bp.blogspot.com/_--uVHetkUIQ/TDae5jGna8I/AAAAAAAAAK0/sBSpLudWmcw/s1600/reading.gif">
# Prepare the data
For a computer, everything is numbers. We have to convert the text to a series of numbers, and then feed those to the computer.
This can be done in two widely used steps in natural language processing: **tokenization** and **numericalization**:
## Tokenization
In tokenization the text is split into single words, called tokens. A simple way to achieve this is to split according to spaces in the text. But then we, among other things, lose punctuation, and also the fact that some words are contractions of multiple words (for example _isn't_ and _don't_).
<img src="https://spacy.io/tokenization-57e618bd79d933c4ccd308b5739062d6.svg">
Here are some result after tokenization:
```
data_lm = TextDataLoaders.from_df(df, text_col='Tweet', is_lm=True, valid_pct=0.1)
data_lm.show_batch(max_n=2)
```
Tokens starting with "xx" are special. `xxbos` means the beginning of the text, `xxmaj` means that the following word is capitalized, `xxup` means that the following word is in all caps, and so on.
The tokens `xxunk` replaces words that are rare in the text corpus. We keep only words that appear at least twice (with a set maximum number of different words, 60.000 in our case). This is called our **vocabulary**.
## Numericalization
We convert tokens to numbers by making a list of all the tokens that have been used and assign them to numbers.
The above text is replaced by numbers, as in this example
```
data_lm.train_ds[0][0]
```
> **We are now in a position where the computer can compute on the text.**
# "Classical" versus deep learning-based NLP
```
#import sys
#!{sys.executable} -m spacy download en
nlp = spacy.load('en')
```
### Sentence Boundary Detection: splitting into sentences
Example sentence:
> _"Patient presents for initial evaluation of cough. Cough is reported to have developed acutely and has been present for 4 days. Symptom severity is moderate. Will return next week."_
```
sentence = "Patient presents for initial evaluation of cough. Cough is reported to have developed acutely and has been present for 4 days. Symptom severity is moderate. Will return next week."
doc = nlp(sentence)
for sent in doc.sents:
print(sent)
```
### Named Entity Recognition
```
for ent in doc.ents:
print(ent.text, ent.label_)
from spacy import displacy
displacy.render(doc, style='ent', jupyter=True)
```
### Dependency parsing
```
displacy.render(doc, style='dep', jupyter=True, options={'distance': 90})
```
> There's a lot more to natural language processing, of course! Have a look at [spaCy 101: Everything you need to know](https://spacy.io/usage/spacy-101) for some examples.
In general, data preparation and feature engineering is a huge and difficult undertaking when using machine learning to analyse text.
However, in what's called _deep learning_ (discussed in detail tomorrow) most of this work is done by the computer! That's because deep learning does feature extraction _and_ prediction in the same model.
This results in much less work and, often, _in much better models_!
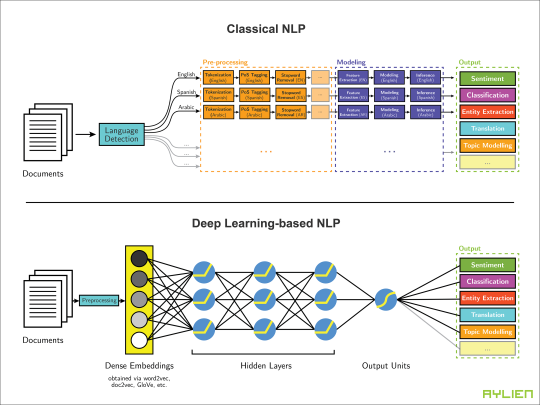
# Deep learning language model
We now come to a relatively new and very powerful idea for deep learning and NLP. An idea that created a small revolution in NLP a couple of years ago ([1](https://blog.openai.com/language-unsupervised/), [2](http://ruder.io/nlp-imagenet/))
We want to create a system that can classify text into one or more categories. This is a difficult problem as the computer must somehow implicitly learn to "read".
Idea: why not _first_ teach the computer to "read" and _then_ let it loose on the classification task?
We can teach the computer to "understand" language by training it to predict the next word of a sentence, using as much training data we can get hold of. This is called ***language modelling*** in NLP.
This is a difficult task: to guess the next word of a sentence one has to know a lot about language, and also a lot about the world.
> What word fits here? _"The light turned green and Per crossed the ___"_
Luckily, obtaining large amounts of training data for language models is simple: any text can be used. The labels are simply the next word of a subpart of the text.
We can for example use Wikipedia. After the model performs alright at predicting the next word of Wikipedia text, we can fine-tune it on text that's closer to the classification task we're after.
> This is often called ***transfer learning***.
We can use the tweet text to fine-tune a model that's already been pretrained on Wikipedia:
```
data_lm = TextDataLoaders.from_df(df, text_col='Tweet', is_lm=True, valid_pct=0.1)
data_lm.show_batch(max_n=3)
learn = language_model_learner(data_lm, AWD_LSTM, pretrained=True,
metrics=[accuracy, Perplexity()], wd=0.1).to_fp16()
```
Let's start training:
```
learn.fit_one_cycle(1, 1e-2)
learn.unfreeze()
learn.fit_one_cycle(10, 1e-3)
```
...and save the parts of the model that we can reuse for classification later:
```
learn.save_encoder('medweb_finetuned')
```
## Test the language model
We can test the language model by having it guess the next given number of words on a starting text:
```
def make_text(seed_text, nb_words):
"""
Use the trained language model to produce text.
Input:
seed_text: some text to get the model started
nb_words: number of words to produce
"""
pred = learn.predict(seed_text, nb_words, temperature=0.75)
pp(pred)
make_text("I'm not feeling too good as my", 10)
make_text("No, that's a", 40)
```
Now we have something that seems to produce text that resembles the text to be classified.
> **Note:** It's interesting to see that the model can come up with text that makes some sense (mostly thanks to training on Wikipedia), and that the text resembles the medical tweets (thanks to the fine-tuning).
> **Note** also that an accuracy of 30-40% when predicting the next word of a sentence is pretty impressive, as the number of possibilities is very large (equal to the size of the vocabulary).
> **Also note** that this is not the task we care about: it's a pretext task before the tweet classification.
# Classifier
```
medweb = DataBlock(blocks=(TextBlock.from_df(text_cols='Tweet', seq_len=12, vocab=data_lm.vocab), MultiCategoryBlock),
get_x = ColReader(cols='text'),
get_y = ColReader(cols='labels', label_delim=";"),
splitter = ColSplitter(col='is_test'))
data = medweb.dataloaders(df, bs=8)
```
Now our task is to predict the possible classes the tweets can be assigned to:
```
data.show_batch()
learn_clf = text_classifier_learner(data, AWD_LSTM, seq_len=16, pretrained=True,
drop_mult=0.5, metrics=accuracy_multi).to_fp16()
learn_clf = learn_clf.load_encoder('medweb_finetuned')
learn_clf.fine_tune(12, base_lr=1e-2)
```
## Is it a good classifier?
We can test it out on some example text:
```
learn_clf.predict("I'm feeling really bad. My head hurts. My nose is runny. I've felt like this for days.")
```
It seems to produce reasonable results. _But remember that this is a very small data set._ One cannot expect very great things when asking the model to make predictions on text outside the small material it has been trained on. This illustrates the need for "big data" in deep learning.
### How does it compare to other approaches?
From the [original article](https://www.jmir.org/2019/2/e12783/) that presented the data set:
<img src="assets/medweb_results.png">
# End notes
* This of course only skratches the surface of NLP and deep learning applied to NLP. The goal was to "lift the curtain" and show some of the ideas behind modern text analysis software.
* If you're interested in digging into deep learning for NLP you should check out `fastai` (used above) and also `Hugging Face`: https://huggingface.co.
|
github_jupyter
|
```
pip install jupyter-dash
pip install dash_daq
pip install --ignore-installed --upgrade plotly==4.5.0
```
At this point, restart the runtime environment for Colab
```
import pandas as pd
import numpy as np
import datetime
import matplotlib.pyplot as plt
import random
import scipy.stats
import plotly.express as px
from jupyter_dash import JupyterDash
import dash_core_components as dcc
import dash_daq as daq
import dash_html_components as html
from dash.dependencies import Input, Output
import plotly.graph_objects as go
import plotly.express as px
from itertools import cycle
import plotly
%load_ext autoreload
%autoreload 2
print(plotly.__version__)
df = pd.read_csv('https://raw.githubusercontent.com/wesleybeckner/ds_for_engineers/main/data/truffle_margin/margin_data.csv')
df['Width'] = df['Width'].apply(str)
df['Height'] = df['Height'].apply(str)
descriptors = df.columns[:-3]
delimiters = df.columns[:-3]
moodsdf = pd.DataFrame()
pop = list(df['EBITDA'])
# pop = np.random.choice(pop, size=int(1e5))
for delimiter in delimiters:
grouped = df.groupby(delimiter)['EBITDA']
group_with_values = grouped.apply(list)
# bootstrap population of values based on groups
# pop = np.random.choice((np.concatenate(group_with_values)),
# size=int(1e4))
for index, group in enumerate(group_with_values):
stat, p, m, table = scipy.stats.median_test(group, pop)
median = np.median(group)
mean = np.mean(group)
size = len(group)
moodsdf = pd.concat([moodsdf,
pd.DataFrame([delimiter, group_with_values.index[index],
stat, p, m, mean, median, size, table]).T])
moodsdf.columns = ['descriptor', 'group', 'pearsons_chi_square', 'p_value', 'grand_median', 'group_mean',
'group_median', 'size', 'table']
moodsdf = moodsdf.loc[moodsdf['p_value'] < 1e-3]
moodsdf = moodsdf.sort_values('group_median').reset_index(drop=True)
def make_violin_plot(sort='Worst', select=[0,5], descriptors=None):
if sort == 'Best':
local_df = moodsdf.sort_values('group_median', ascending=False)
local_df = local_df.reset_index(drop=True)
else:
local_df = moodsdf
if descriptors != None:
local_df = local_df.loc[local_df['descriptor'].isin(descriptors)]
fig = go.Figure()
for index in range(select[0],select[1]):
x = df.loc[(df[local_df.iloc[index]['descriptor']] == \
local_df.iloc[index]['group'])]['EBITDA']
y = local_df.iloc[index]['descriptor'] + ': ' + df.loc[(df[local_df\
.iloc[index]['descriptor']] == local_df.iloc[index]['group'])]\
[local_df.iloc[index]['descriptor']]
name = '€ {:.0f}'.format(x.median())
fig.add_trace(go.Violin(x=y,
y=x,
name=name,
box_visible=True,
meanline_visible=True))
fig.update_layout({
"plot_bgcolor": "#FFFFFF",
"paper_bgcolor": "#FFFFFF",
"title": 'EBITDA by Product Descriptor (Median in Legend)',
"yaxis.title": "EBITDA (€)",
"height": 325,
"font": dict(
size=10),
"margin": dict(
l=0,
r=0,
b=0,
t=30,
pad=4
),
})
return fig
def make_sunburst_plot(clickData=None, toAdd=None, col=None, val=None):
if clickData != None:
col = clickData["points"][0]['x'].split(": ")[0]
val = clickData["points"][0]['x'].split(": ")[1]
elif col == None:
col = moodsdf.iloc[-1]['descriptor']
val = moodsdf.iloc[-1]['group']
desc = list(descriptors[:-2])
if col in desc:
desc.remove(col)
if toAdd != None:
for item in toAdd:
desc.append(item)
test = df.loc[df[col] == val]
fig = px.sunburst(test, path=desc[:], color='EBITDA', title='{}: {}'.format(
col, val),
color_continuous_scale=px.colors.sequential.Viridis
)
fig.update_layout({
"plot_bgcolor": "#FFFFFF",
"title": '(Select in Violin) {}: {}'.format(col,val),
"paper_bgcolor": "#FFFFFF",
"height": 325,
"font": dict(
size=10),
"margin": dict(
l=0,
r=0,
b=0,
t=30,
pad=4
),
})
return fig
def make_ebit_plot(df, select=None, sort='Worst', descriptors=None):
families = df[df.columns[0]].unique()
colors = ['#636EFA', '#EF553B', '#00CC96', '#AB63FA', '#FFA15A', '#19D3F3',\
'#FF6692', '#B6E880', '#FF97FF', '#FECB52']
colors_cycle = cycle(colors)
color_dic = {'{}'.format(i): '{}'.format(j) for i, j in zip(families,
colors)}
fig = go.Figure()
if select == None:
for data in px.scatter(
df,
x='Product',
y='EBITDA',
color=df.columns[0],
color_discrete_map=color_dic,
opacity=1).data:
fig.add_trace(
data
)
elif select != None:
color_dic = {'{}'.format(i): '{}'.format(j) for i, j in zip(select,
colors)}
for data in px.scatter(
df,
x='Product',
y='EBITDA',
color=df.columns[0],
color_discrete_map=color_dic,
opacity=0.09).data:
fig.add_trace(
data
)
if sort == 'Best':
local_df = moodsdf.sort_values('group_median', ascending=False)
elif sort == 'Worst':
local_df = moodsdf
new_df = pd.DataFrame()
if descriptors != None:
local_df = local_df.loc[local_df['descriptor'].isin(descriptors)]
for index in select:
x = df.loc[(df[local_df.iloc[index]\
['descriptor']] == local_df.iloc[index]['group'])]
x['color'] = next(colors_cycle) # for line shapes
new_df = pd.concat([new_df, x])
new_df = new_df.reset_index(drop=True)
# for data in px.scatter(
# new_df,
# x='Product',
# y='EBITDA',
# color=df.columns[0],
# color_discrete_map=color_dic,
# opacity=1).data:
# fig.add_trace(
# data
# )
shapes=[]
for index, i in enumerate(new_df['Product']):
shapes.append({'type': 'line',
'xref': 'x',
'yref': 'y',
'x0': i,
'y0': -4e5,
'x1': i,
'y1': 4e5,
'line':dict(
dash="dot",
color=new_df['color'][index],)})
fig.update_layout(shapes=shapes)
fig.update_layout({
"plot_bgcolor": "#FFFFFF",
"paper_bgcolor": "#FFFFFF",
"title": 'Rank Order EBITDA by {}'.format(df.columns[0]),
"yaxis.title": "EBITDA (€)",
"height": 325,
"font": dict(
size=10),
"xaxis": dict(
showticklabels=False
),
"margin": dict(
l=0,
r=0,
b=0,
t=30,
pad=4
),
"xaxis.tickfont.size": 8,
})
return fig
# Build App
external_stylesheets = ['../assets/styles.css', '../assets/s1.css', 'https://codepen.io/chriddyp/pen/bWLwgP.css']
app = JupyterDash(__name__, external_stylesheets=external_stylesheets)
app.layout = html.Div([
html.Div([
html.Div([
html.P('Descriptors'),
dcc.Dropdown(id='descriptor_dropdown',
options=[{'label': i, 'value': i} for i in descriptors],
value=descriptors,
multi=True,
className="dcc_control"),
html.P('Number of Descriptors:', id='descriptor-number'),
dcc.RangeSlider(
id='select',
min=0,
max=moodsdf.shape[0],
step=1,
value=[0,10]),
html.P('Sort by:'),
dcc.RadioItems(
id='sort',
options=[{'label': i, 'value': j} for i, j in \
[['Low EBITDA', 'Worst'],
['High EBITDA', 'Best']]],
value='Best',
labelStyle={'display': 'inline-block'},
style={"margin-bottom": "10px"},),
html.P('Toggle view Violin/Descriptor Data'),
daq.BooleanSwitch(
id='daq-violin',
on=False,
style={"margin-bottom": "10px", "margin-left": "0px",
'display': 'inline-block'}),
],
className='mini_container',
id='descriptorBlock',
style={'width': '32%', 'display': 'inline-block'}
),
html.Div([
dcc.Graph(
id='ebit_plot',
figure=make_ebit_plot(df)),
],
className='mini_container',
style={'width': '65%', 'float': 'right', 'display': 'inline-block'},
id='ebit-family-block'
),
], className='row container-display',
),
html.Div([
html.Div([
dcc.Graph(
id='violin_plot',
figure=make_violin_plot()),
],
className='mini_container',
style={'width': '65%', 'display': 'inline-block'},
id='violin',
),
html.Div([
dcc.Dropdown(id='length_width_dropdown',
options=[{'label': 'Height', 'value': 'Height'},
{'label': 'Width', 'value': 'Width'}],
value=['Width'],
multi=True,
placeholder="Include in sunburst chart...",
className="dcc_control"),
dcc.Graph(
id='sunburst_plot',
figure=make_sunburst_plot()
),
],
className='mini_container',
style={'width': '32%', 'display': 'inline-block'},
id='sunburst',
),
], className='row container-display',
style={'margin-bottom': '50px'},
),
], className='pretty container'
)
@app.callback(
Output('sunburst_plot', 'figure'),
[Input('violin_plot', 'clickData'),
Input('length_width_dropdown', 'value'),
Input('sort', 'value'),
Input('select', 'value'),
Input('descriptor_dropdown', 'value')])
def display_sunburst_plot(clickData, toAdd, sort, select, descriptors):
if sort == 'Best':
local_df = moodsdf.sort_values('group_median', ascending=False)
local_df = local_df.reset_index(drop=True)
else:
local_df = moodsdf
if descriptors != None:
local_df = local_df.loc[local_df['descriptor'].isin(descriptors)]
local_df = local_df.reset_index(drop=True)
col = local_df['descriptor'][select[0]]
val = local_df['group'][select[0]]
return make_sunburst_plot(clickData, toAdd, col, val)
@app.callback(
[Output('select', 'max'),
Output('select', 'value')],
[Input('descriptor_dropdown', 'value')]
)
def update_descriptor_choices(descriptors):
max_value = moodsdf.loc[moodsdf['descriptor'].isin(descriptors)].shape[0]
value = min(5, max_value)
return max_value, [0, value]
@app.callback(
Output('descriptor-number', 'children'),
[Input('select', 'value')]
)
def display_descriptor_number(select):
return "Number of Descriptors: {}".format(select[1]-select[0])
@app.callback(
Output('violin_plot', 'figure'),
[Input('sort', 'value'),
Input('select', 'value'),
Input('descriptor_dropdown', 'value')]
)
def display_violin_plot(sort, select, descriptors):
return make_violin_plot(sort, select, descriptors)
@app.callback(
Output('ebit_plot', 'figure'),
[Input('sort', 'value'),
Input('select', 'value'),
Input('descriptor_dropdown', 'value'),
Input('daq-violin', 'on')]
)
def display_ebit_plot(sort, select, descriptors, switch):
if switch == True:
select = list(np.arange(select[0],select[1]))
return make_ebit_plot(df, select, sort=sort, descriptors=descriptors)
else:
return make_ebit_plot(df)
app.run_server(mode='external', port='8881')
```
|
github_jupyter
|
This Notebook is a short example of how to use the Ising solver implemented using the QAOA algorithm. We start by declaring the import of the ising function.
```
from grove.ising.ising_qaoa import ising
from mock import patch
```
This code finds the global minima of an Ising model with external fields of the form
$$f(x)= \Sigma_i h_i x_i + \Sigma_{i,j} J_{i,j} x_i x_j.$$
Two adjacent sites $i,j$ have an interaction equal to $J_{i,j}$. There is also an external magnetic field $h_i$ that affects each individual spin. The discrete variables take the values $x_i \in \{+1,-1\}$.
In order to assert the correctness of the code we will find the minima of the following Ising model
$$f(x)=x_0+x_1-x_2+x_3-2 x_0 x_1 +3 x_2 x_3.$$
Which corresponds to $x_{min}=[-1, -1, 1, -1]$ in numerical order, with a minimum value of $f(x_{min})=-9$.
This Ising code runs on quantum hardware, which means that we need to specify a connection to a QVM or QPU. Due to the absence of a real connection in this notebook, we will mock out the response to correspond to the expected value. In order to run this notebook on a QVM or QPU, replace cxn with a valid PyQuil connection object.
```
with patch("pyquil.api.SyncConnection") as cxn:
cxn.run_and_measure.return_value = [[1,1,0,1]]
cxn.expectation.return_value = [-0.4893891813015294, 0.8876822987380573, -0.4893891813015292, -0.9333372094534063, -0.9859245403423198, 0.9333372094534065]
```
The input for the code in the default mode corresponds simply to the parameters $h_i$ and $J_{i,j}$, that we specify as a list in numerical order and a dictionary. The code returns the bitstring of the minima, the minimum value, and the QAOA quantum circuit used to obtain that result.
```
J = {(0, 1): -2, (2, 3): 3}
h = [1, 1, -1, 1]
solution, min_energy, circuit = ising(h, J, connection=cxn)
```
It is also possible to specify the Trotterization order for the QAOA algorithm used to implement the Ising model. By default this value is equal to double the number of variables. It is also possible to change the verbosity of the function, which is True by default. There are more advanced parameters that can be specified and are not described here.
```
solution_2, min_energy_2, circuit_2 = ising(h, J, num_steps=9, verbose=False, connection=cxn)
```
For large Ising problems, or those with many and close suboptimal minima, it is possible for the code to not return the global minima. Increasing the number of steps can solve this problem.
Finally, we will check if the correct bitstring was found, corresponding to the global minima, in both runs.
```
assert solution == [-1, -1, 1, -1], "Found bitstring for first run does not correspond to global minima"
print("Energy for first run solution", min_energy)
assert solution_2 == [-1, -1, 1, -1], "Found bitstring for second run does not correspond to global minima"
print("Energy for second run solution", min_energy_2)
```
If the assertions succeeded, and the energy was equal to $-9$, we have found the correct solution for both runs.
```
```
|
github_jupyter
|
```
import matplotlib.pyplot as plt
import numpy as np
from matplotlib.colors import ListedColormap
from ml.data import create_lineal_data
from ml.visualization import decision_boundary
%matplotlib inline
```
# Función de coste y gradiente
## Generación de datos
### Entrenamiento
```
np.random.seed(0) # Para hacer más determinística la generación de datos
samples_per_class = 5
Xa = np.c_[create_lineal_data(0.75, 0.9, spread=0.2, data_size=samples_per_class)]
Xb = np.c_[create_lineal_data(0.5, 0.75, spread=0.2, data_size=samples_per_class)]
X_train = np.r_[Xa, Xb]
y_train = np.r_[np.zeros(samples_per_class), np.ones(samples_per_class)]
cmap_dots = ListedColormap(['tomato', 'dodgerblue'])
plt.scatter(X_train[:, 0], X_train[:, 1], c=y_train, cmap=cmap_dots, edgecolors='k')
plt.show()
```
### Validación
```
np.random.seed(0) # Para hacer más determinística la generación de datos
samples_per_class = 25
Xa = np.c_[create_lineal_data(0.75, 0.9, spread=0.2, data_size=samples_per_class)]
Xb = np.c_[create_lineal_data(0.5, 0.75, spread=0.2, data_size=samples_per_class)]
X_val = np.r_[Xa, Xb]
y_val = np.r_[np.zeros(samples_per_class), np.ones(samples_per_class)]
cmap_dots = ListedColormap(['tomato', 'dodgerblue'])
plt.scatter(X_val[:, 0], X_val[:, 1], c=y_val, cmap=cmap_dots, edgecolors='k')
plt.show()
```
## Regresión Logística
### Función de coste y gradiente
```
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def logloss(w, x, y):
m = y.shape[0]
y_hat = sigmoid(x.dot(w))
cost1 = np.log(y_hat).dot(y)
cost2 = np.log(1 - y_hat).dot(1 - y)
J = -(cost1 + cost2)
return J
def logloss_gradient(w, x, y):
m = y.shape[0]
y_hat = sigmoid(x.dot(w))
gradient = np.dot(x.T, y_hat - y)
return gradient
```
### Algoritmo de optimización (descenso por la gradiente)
```
def gradient_descent(w, x_train, y_train, x_val, y_va, cost_function,
cost_function_gradient, alpha=0.01, max_iter=1000):
train_costs = np.zeros(max_iter)
val_costs = np.zeros(max_iter)
for iteration in range(max_iter):
train_costs[iteration] = cost_function(w, x_train, y_train)
val_costs[iteration] = cost_function(w, x_val, y_val)
gradient = cost_function_gradient(w, x_train, y_train)
w = w - alpha * gradient
return w, train_costs, val_costs
# Agregar el vector de bias a los ejemplos (bias trick)
X_b_train = np.c_[np.ones(X_train.shape[0]), X_train]
X_b_val = np.c_[np.ones(X_val.shape[0]), X_val]
w0 = np.zeros(X_b_train.shape[1]) # Initial weights
w, train_costs, val_costs = gradient_descent(w0, X_b_train, y_train, X_b_val, y_val,
logloss, logloss_gradient, max_iter=20000)
```
### Exactitud (entrenamiento vs validación)
```
y_pred = (X_b_train.dot(w) >= 0.5).astype(np.int) # Obtenemos las predicciones (como 0 o 1)
accuracy = (y_train == y_pred).astype(np.int).sum() / y_train.shape[0] # Calcular la exactitud
print("Exactitud del algoritmo para conjunto de entrenamiento: %.2f" % accuracy)
y_pred = (X_b_val.dot(w) >= 0.5).astype(np.int) # Obtenemos las predicciones (como 0 o 1)
accuracy = (y_val == y_pred).astype(np.int).sum() / y_val.shape[0] # Calcular la exactitud
print("Exactitud del algoritmo para conjunto de validación: %.2f" % accuracy)
```
### Curva de aprendizaje (entrenamiento vs validación)
```
plt.plot(train_costs, label="Datos de entrenamiento")
plt.plot(val_costs, label="Datos de validación")
plt.xlabel("Iteraciones")
plt.ylabel("Costo")
plt.title("Curva de aprendizaje")
plt.legend()
plt.show()
```
### Frontera de decisión
```
xx, yy, Z = decision_boundary(np.r_[X_train, X_val], w)
cmap_back = ListedColormap(['lightcoral', 'skyblue'])
cmap_dots = ['tomato', 'dodgerblue', 'red', 'darkslateblue']
plt.figure(figsize=(6, 5), dpi= 80, facecolor='w', edgecolor='k')
plt.pcolormesh(xx, yy, Z, cmap=cmap_back)
for i in (0, 1):
plt.scatter(X_train[y_train==i, 0], X_train[y_train==i, 1],
color=cmap_dots[i], label='Entrenamiento clase %d' % i,
edgecolor='k', s=20)
plt.scatter(X_val[y_val==i, 0], X_val[y_val==i, 1],
color=cmap_dots[i+2], label='Validación clase %d' % i,
edgecolor='k', s=20)
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
plt.legend()
plt.show()
```
|
github_jupyter
|
# Notebook served by Voilà
#### Notebook copied from https://github.com/ChakriCherukuri/mlviz
<h2>Gradient Descent</h2>
* Given a the multi-variable function $\large {F(x)}$ differentiable in a neighborhood of a point $\large a$
* $\large F(x)$ decreases fastest if one goes from $\large a$ in the direction of the negative gradient of $\large F$ at $\large a$, $\large -\nabla{F(a)}$
<h3>Gradient Descent Algorithm:</h3>
* Choose a starting point, $\large x_0$
* Choose the sequence $\large x_0, x_1, x_2, ...$ such that
$ \large x_{n+1} = x_n - \eta \nabla(F(x_n) $
So convergence of the gradient descent depends on the starting point $\large x_0$ and the learning rate $\large \eta$
```
from time import sleep
import numpy as np
from ipywidgets import *
import bqplot.pyplot as plt
from bqplot import Toolbar
f = lambda x: np.exp(-x) * np.sin(5 * x)
df = lambda x: -np.exp(-x) * np.sin(5 * x) + 5 * np.cos(5 *x) * np.exp(-x)
x = np.linspace(0.5, 2.5, 500)
y = f(x)
def update_sol_path(x, y):
with sol_path.hold_sync():
sol_path.x = x
sol_path.y = y
with sol_points.hold_sync():
sol_points.x = x
sol_points.y = y
def gradient_descent(x0, f, df, eta=.1, tol=1e-6, num_iters=10):
x = [x0]
i = 0
while i < num_iters:
x_prev = x[-1]
grad = df(x_prev)
x_curr = x_prev - eta * grad
x.append(x_curr)
sol_lbl.value = sol_lbl_tmpl.format(x_curr)
sleep(.5)
update_sol_path(x, [f(i) for i in x])
if np.abs(x_curr - x_prev) < tol:
break
i += 1
txt_layout = Layout(width='150px')
x0_box = FloatText(description='x0', layout=txt_layout, value=2.4)
eta_box = FloatText(description='Learning Rate',
style={'description_width':'initial'},
layout=txt_layout, value=.1)
go_btn = Button(description='GO', button_style='success', layout=Layout(width='50px'))
reset_btn = Button(description='Reset', button_style='success', layout=Layout(width='100px'))
sol_lbl_tmpl = 'x = {:.4f}'
sol_lbl = Label()
# sol_lbl.layout.width = '300px'
# plot of curve and solution
fig_layout = Layout(width='720px', height='500px')
fig = plt.figure(layout=fig_layout, title='Gradient Descent', display_toolbar=True)
fig.pyplot = Toolbar(figure=fig)
curve = plt.plot(x, y, colors=['dodgerblue'], stroke_width=2)
sol_path = plt.plot([], [], colors=['#ccc'], opacities=[.7])
sol_points = plt.plot([], [], 'mo', default_size=20)
def optimize():
f.marks = [curve]
gradient_descent(x0_box.value, f, df, eta=eta_box.value)
def reset():
curve.scales['x'].min = .4
curve.scales['x'].max = 2.5
curve.scales['y'].min = -.5
curve.scales['y'].max = .4
sol_path.x = sol_path.y = []
sol_points.x = sol_points.y = []
sol_lbl.value = ''
go_btn.on_click(lambda btn: optimize())
reset_btn.on_click(lambda btn: reset())
final_fig = VBox([fig, fig.pyplot],
layout=Layout(overflow_x='hidden'))
HBox([final_fig, VBox([x0_box, eta_box, go_btn, reset_btn, sol_lbl])])
```
|
github_jupyter
|
<table class="ee-notebook-buttons" align="left">
<td><a target="_blank" href="https://github.com/giswqs/earthengine-py-notebooks/tree/master/GetStarted/02_adding_data_to_qgis.ipynb"><img width=32px src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" /> View source on GitHub</a></td>
<td><a target="_blank" href="https://nbviewer.jupyter.org/github/giswqs/earthengine-py-notebooks/blob/master/GetStarted/02_adding_data_to_qgis.ipynb"><img width=26px src="https://upload.wikimedia.org/wikipedia/commons/thumb/3/38/Jupyter_logo.svg/883px-Jupyter_logo.svg.png" />Notebook Viewer</a></td>
<td><a target="_blank" href="https://mybinder.org/v2/gh/giswqs/earthengine-py-notebooks/master?filepath=GetStarted/02_adding_data_to_qgis.ipynb"><img width=58px src="https://mybinder.org/static/images/logo_social.png" />Run in binder</a></td>
<td><a target="_blank" href="https://colab.research.google.com/github/giswqs/earthengine-py-notebooks/blob/master/GetStarted/02_adding_data_to_qgis.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" /> Run in Google Colab</a></td>
</table>
## Install Earth Engine API
Install the [Earth Engine Python API](https://developers.google.com/earth-engine/python_install) and [geehydro](https://github.com/giswqs/geehydro). The **geehydro** Python package builds on the [folium](https://github.com/python-visualization/folium) package and implements several methods for displaying Earth Engine data layers, such as `Map.addLayer()`, `Map.setCenter()`, `Map.centerObject()`, and `Map.setOptions()`.
The following script checks if the geehydro package has been installed. If not, it will install geehydro, which automatically install its dependencies, including earthengine-api and folium.
```
import subprocess
try:
import geehydro
except ImportError:
print('geehydro package not installed. Installing ...')
subprocess.check_call(["python", '-m', 'pip', 'install', 'geehydro'])
```
Import libraries
```
import ee
import folium
import geehydro
```
Authenticate and initialize Earth Engine API. You only need to authenticate the Earth Engine API once.
```
try:
ee.Initialize()
except Exception as e:
ee.Authenticate()
ee.Initialize()
```
## Create an interactive map
This step creates an interactive map using [folium](https://github.com/python-visualization/folium). The default basemap is the OpenStreetMap. Additional basemaps can be added using the `Map.setOptions()` function.
The optional basemaps can be `ROADMAP`, `SATELLITE`, `HYBRID`, `TERRAIN`, or `ESRI`.
```
Map = folium.Map(location=[40, -100], zoom_start=4)
Map.setOptions('HYBRID')
```
## Add Earth Engine Python script
```
# Load an image.
image = ee.Image('LANDSAT/LC08/C01/T1/LC08_044034_20140318')
# Center the map on the image.
Map.centerObject(image, 9)
# Display the image.
Map.addLayer(image, {}, 'Landsat 8 original image')
# Define visualization parameters in an object literal.
vizParams = {'bands': ['B5', 'B4', 'B3'],
'min': 5000, 'max': 15000, 'gamma': 1.3}
# Center the map on the image and display.
Map.centerObject(image, 9)
Map.addLayer(image, vizParams, 'Landsat 8 False color')
# Use Map.addLayer() to add features and feature collections to the map. For example,
counties = ee.FeatureCollection('TIGER/2016/Counties')
Map.addLayer(ee.Image().paint(counties, 0, 2), {}, 'counties')
```
## Display Earth Engine data layers
```
Map.setControlVisibility(layerControl=True, fullscreenControl=True, latLngPopup=True)
Map
```
|
github_jupyter
|
```
import os
import sys
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
import pickle
from tqdm.notebook import tqdm
from tqdm import trange
%matplotlib inline
def read_list_of_arrays(filename):
A = pickle.load(open(filename, 'rb'))
if len(A) == 3:
print(A[1][0], A[2][0])
A = A[0]
dim = A[0].flatten().shape[0]
B = np.zeros((len(A), dim))
for i in range(len(A)):
B[i, :] = A[i].flatten()
return B
epochs = np.arange(500, 5500, 500)
epochs
cloud_base = read_list_of_arrays('/gan-clouds/timegan_data.pickle')
clouds = []
for ep in epochs:
epo = ep
clouds.append(read_list_of_arrays('/gan-clouds/timegan_various_epochs5k/model_%d.pickle' % epo))
cloud_base.shape
for cloud in clouds:
print(cloud.shape)
```
### Compute cross-barcodes
```
import mtd
res1 = []
trials = 50
for i in trange(len(clouds)):
np.random.seed(7)
barcs = [mtd.calc_cross_barcodes(cloud_base, clouds[i], batch_size1 = 100, batch_size2 = 1000,\
cuda = 1, pdist_device = 'gpu') for _ in range(trials)]
res1.append(barcs)
res2 = []
trials = 50
for i in trange(len(clouds)):
np.random.seed(7)
barcs = [mtd.calc_cross_barcodes(clouds[i], cloud_base, batch_size1 = 100, batch_size2 = 1000,\
cuda = 1, pdist_device = 'gpu') for _ in range(trials)]
res2.append(barcs)
```
### Absolute barcodes
```
barc = mtd.calc_cross_barcodes(clouds[-1], np.zeros((0,0)), batch_size1 = 100, batch_size2 = 0)
barc = mtd.calc_cross_barcodes(cloud_base, np.zeros((0,0)), batch_size1 = 100, batch_size2 = 0)
def get_scores(res, args_dict, trials = 10):
scores = []
for i in range(len(res)):
barc_list = []
for exp_id, elem in enumerate(res[i]):
barc_list.append(mtd.get_score(elem, **args_dict))
r = sum(barc_list) / len(barc_list)
scores.append(r)
return scores
scores = get_scores(res1, {'h_idx' : 1, 'kind' : 'sum_length'})
for ep, s in zip(epochs, scores):
print(s)
scores = get_scores(res2, {'h_idx' : 1, 'kind' : 'sum_length'})
for ep, s in zip(epochs, scores):
print(s)
#pickle.dump(res1, open('res1_timegan.pickle', 'wb'))
#pickle.dump(res2, open('res2_timegan.pickle', 'wb'))
```
### PCA
```
import numpy as np
from sklearn.decomposition import PCA
%pylab inline
import matplotlib.pyplot as plt
# Create data
def plot2(data, groups = ("base", "cloud")):
colors = ("red", "green")
# Create plot
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
for data, color, group in zip(data, colors, groups):
x, y = data
ax.scatter(x, y, alpha=0.5, c=color, edgecolors='none', s=5, label=group)
#plt.title('Matplot scatter plot')
plt.legend(loc=2)
plt.show()
```
#### PCA from base+last GAN
```
all_pca = []
for i in range(len(epochs)):
pca = PCA(n_components=2)
cb = np.concatenate((cloud_base, clouds[-1]))
pca.fit(cb)
cb = cloud_base
cloud_base_pca = pca.transform(cb)
data = [(cloud_base_pca[:,0], cloud_base_pca[:,1])]
cg = clouds[i]
cloud_pca = pca.transform(cg)
data.append((cloud_pca[:,0], cloud_pca[:,1]))
all_pca.append(data)
plot2(data, groups = ("real", "generated, epoch %d" % epochs[i]))
#pickle.dump(all_pca, open('timegan_all_pca.pickle', 'wb'))
```
|
github_jupyter
|
# SP via class imbalance
Example [test scores](https://www.brookings.edu/blog/social-mobility-memos/2015/07/29/when-average-isnt-good-enough-simpsons-paradox-in-education-and-earnings/)
SImpson's paradox can also occur due to a class imbalance, where for example, over time the value of several differnt subgroups all increase, but the totla average decreases over tme. This is also am mportant tpe to catch because this can inicate a large class disparity beased on the subgrouping variable.
```
import numpy as np
import pandas as pd
import matplotlib.pylab as plt
from mlsim import sp_plot
t = np.linspace(0,50,11)
count_rate = np.asarray([1,1.5,1.4])
count_pow = np.asarray([1,1.4, 1.3])
count_0 = np.asarray([100,60,40])
count = np.asarray([count_0 + count_rate*(t_i**count_pow) for t_i in t])
share = count/np.asarray([np.sum(count, axis=1)]*3).T
score_rate = np.asarray([.2, .25, .3])
score_0 = [310,290,280]
scores_group = np.asarray([score_0 + score_rate*t_i for t_i in t])
total_score = np.sum(scores_group*share,axis=1)
total_score
plt.plot(t,scores_group)
plt.plot(t,total_score,'k', label ='average')
plt.title('score per group and averge');
plt.plot(t,count)
plt.title('count per group over time');
```
We can change the numbers a bit to see tht it still works.
```
t = np.linspace(0,50,11)
count_rate = np.asarray([.5,3,1.8])
count_pow = np.asarray([1,1,1.15]) #1.24, 1.13])
group_names = ['W','B','H']
count_0 = np.asarray([200,60,40])
count = np.asarray([np.floor(count_0 + count_rate*(t_i**count_pow)) for t_i in t])
share = count/np.asarray([np.sum(count, axis=1)]*3).T
score_rate = np.asarray([.1, .112, .25])
score_0 = [310,270,265]
scores_group = np.asarray([score_0 + score_rate*t_i for t_i in t])
total_score = np.sum(scores_group*share,axis=1)
plt.figure(figsize=(12,4))
plt.subplot(1,3,1)
plt.plot(t,scores_group)
plt.plot(t,total_score,'k', label ='average')
plt.title('score per group and averge');
plt.subplot(1,3,2)
plt.plot(t,count)
plt.title('count per group');
plt.subplot(1,3,3)
plt.plot(t,share)
plt.title('% per group');
```
The above is occuring in aggregate data, we should generate and aim to detect from the individual measurements. So we can expand the above generator. We'll use the group score and counts to draw the indivdual rows of our table.
```
dat = [[t_t,np.random.normal(loc=sg,scale=5),g ]
for sg_t, c_t,t_t in zip(scores_group,count,t)
for sg,c,g in zip(sg_t,c_t,group_names)
for i in range(int(c))]
len(dat)
df = pd.DataFrame(data=dat,columns = ['year','score','race'])
df.head()
df.groupby(['race','year']).mean().unstack()
df.groupby(['year']).mean().T
```
The overall goes down while each of the groupwise means goes up, as expected.
```
df.groupby('race').corr()
df.corr()
```
We can see this in the correlation matrices as well, so our existing detector will work, but it has an intuitively different generating mechanism.
```
sp_plot(df,'year','score','race',domain_range=[-1, 51, 225, 350])
```
Vizually, the scatter plots for this are also somewhat different, the groups are not as separable as they were in the regression-based examples we worked with initially.
# Generalizing this
instead of setting a growth rate and being completely computational, we can set the start and end and then add noise in the middle
```
# set this final value
score_t = (score_0*score_growth*N_t).T
total_t = .85*total_0
count_t = total_t*np.linalg.pinv(score_t)
count = np.linspace(count_0,count_t,N_t)
share = count/np.asarray([np.sum(count, axis=1)]*3).T
scores_group = np.asarray([score_0 + score_rate*t_i for t_i in t])
total_score = np.sum(scores_group*share,axis=1)
plt.figure(figsize=(12,5))
plt.subplot(1,2,1)
plt.plot(t,scores_group)
plt.plot(t,total_score,'k', label ='average')
plt.title('score per group and averge');
plt.subplot(1,2,2)
plt.plot(t,count)
plt.title('count per group');
N_t = 11
t = np.linspace(0,50,N_t)
group_names = ['W','B','H']
`
count_0 = np.asarray([200,60,40])
count_0
share_0 = count_0/np.asarray([np.sum(count_0)]*3).T
score_0 = np.asarray([310,270,265])
score_growth = [1.1,1.3,1.4]
total_0 = np.sum(share_0*score_0)
total_0
```
|
github_jupyter
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.