text
stringlengths 2.5k
6.39M
| kind
stringclasses 3
values |
|---|---|
```
#写函数,求n个随机整数均值的平方根,整数范围在m与k之间
import random,math
def pingfanggeng():
m = int(input('请输入一个大于0的整数,作为随机整数的下界,回车结束。'))
k = int(input('请输入一个大于0的整数,作为随机整数的上界,回车结束。'))
n = int(input('请输入随机整数的个数,回车结束。'))
i=0
total=0
while i<n:
total=total+random.randint(m,k)
i=i+1
average=total/n
number=math.sqrt(average)
print(number)
def main():
pingfanggeng()
if __name__ == '__main__':
main()
#写函数,共n个随机整数,整数范围在m与k之间,求西格玛log(随机整数)及西格玛1/log(随机整数)
import random,math
def xigema():
m = int(input('请输入一个大于0的整数,作为随机整数的下界,回车结束。'))
k = int(input('请输入一个大于0的整数,作为随机整数的上界,回车结束。'))
n = int(input('请输入随机整数的个数,回车结束。'))
i=0
total1=0
total2=0
while i<n:
total1=total1+math.log(random.randint(m,k))
total2=total2+1/(math.log(random.randint(m,k)))
i=i+1
print(total1)
print(total2)
def main():
xigema()
if __name__ == '__main__':
main()
#写函数,求s=a+aa+aaa+aaaa+aa...a的值,其中a是[1,9]之间的随机整数。例如2+22+222+2222+22222(此时共有5个数相加),几个数相加由键盘输入
import random
def sa():
n = int(input('请输入整数的个数,回车结束。'))
a=random.randint(1,9)
i=0
s=0
f=0
while i<n:
f=math.pow(10,i)*a+f
s=s+f
i=i+1
print(s)
def main():
sa()
if __name__ == '__main__':
main()
import random, math
def win():
print('Win!')
def lose():
print('Lose!')
def menu():
print('''=====游戏菜单=====
1. 游戏说明
2. 开始游戏
3. 退出游戏
4. 制作团队
=====游戏菜单=====''')
def guess_game():
n = int(input('请输入一个大于0的整数,作为神秘整数的上界,回车结束。'))
number = int(input('请输入神秘整数,回车结束。'))
max_times = math.ceil(math.log(n, 2))
guess_times = 0
while guess_times <= max_times:
guess = random.randint(1, n)
guess_times += 1
print('一共可以猜', max_times, '次')
print('你已经猜了', guess_times, '次')
if guess == number:
win()
print('神秘数字是:', guess)
print('你比标准次数少', max_times-guess_times, '次')
break
elif guess > number:
print('抱歉,你猜大了')
else:
print('抱歉,你猜小了')
else:
print('神秘数字是:', number)
lose()
# 主函数
def main():
while True:
menu()
choice = int(input('请输入你的选择'))
if choice == 1:
show_instruction()
elif choice == 2:
guess_game()
elif choice == 3:
game_over()
break
else:
show_team()
#主程序
if __name__ == '__main__':
main()
```
|
github_jupyter
|
# `pandas` Part 2: this notebook is a 2nd lesson on `pandas`
## The main objective of this tutorial is to slice up some DataFrames using `pandas`
>- Reading data into DataFrames is step 1
>- But most of the time we will want to select specific pieces of data from our datasets
# Learning Objectives
## By the end of this tutorial you will be able to:
1. Select specific data from a pandas DataFrame
2. Insert data into a DataFrame
## Files Needed for this lesson: `winemag-data-130k-v2.csv`
>- Download this csv from Canvas prior to the lesson
## The general steps to working with pandas:
1. import pandas as pd
>- Note the `as pd` is optional but is a common alias used for pandas and makes writing the code a bit easier
2. Create or load data into a pandas DataFrame or Series
>- In practice, you will likely be loading more datasets than creating but we will learn both
3. Reading data with `pd.read_`
>- Excel files: `pd.read_excel('fileName.xlsx')`
>- Csv files: `pd.read_csv('fileName.csv')`
4. After steps 1-3 you will want to check out your DataFrame
>- Use `shape` to see how many records and columns are in your DataFrame
>- Use `head()` to show the first 5-10 records in your DataFrame
5. Then you will likely want to slice up your data into smaller subset datasets
>- This step is the focus of this lesson
Narrated type-along videos are available:
- Part 1: https://youtu.be/uA96V-u8wkE
- Part 2: https://youtu.be/fsc0G77c5Kc
# First, check your working directory
# Step 1: Import pandas and give it an alias
# Step 2 Read Data Into a DataFrame
>- Knowing how to create your own data can be useful
>- However, most of the time we will read data into a DataFrame from a csv or Excel file
## File Needed: `winemag-data-130k-v2.csv`
>- Make sure you download this file from Canvas and place in your working directory
### Read the csv file with `pd.read_csv('fileName.csv`)
>- Set the index to column 0
### Check how many rows/records and columns are in the the `wine_reviews` DataFrame
>- Use `shape`
### Check a couple of rows of data
### Now we can access columns in the dataframe using syntax similar to how we access values in a dictionary
### To get a single value...
### Using the indexing operator and attribute selection like we did above should seem familiar
>- We have accessed data like this using dictionaries
>- However, pandas also has it's own selection/access operators, `loc` and `iloc`
>- For basic operations, we can use the familiar dictionary syntax
>- As we get more advanced, we should use `loc` and `iloc`
>- It might help to think of `loc` as "label based location" and `iloc` as "index based location"
### Both `loc` and `iloc` start with with the row then the column
#### Use `iloc` for index based location similar to what we have done with lists and dictionaries
#### Use `loc` for label based location. This uses the column names vs indexes to retrieve the data we want.
# First, let's look at index based selection using `iloc`
## As we work these examples, remember we specify row first then column
### Selecting the first row using `iloc`
>- For the wine reviews dataset this is our header row
### To return all the rows of a particular column with `iloc`
>- To get everything, just put a `:` for row and/or column
### To return the first three rows of the first column...
### To return the second and third rows...
### We can also pass a list for the rows to get specific values
### Can we pass lists for both rows and columns...?
### We can also go from the end of the rows just like we did with lists
>- The following gets the last 5 records for country in the dataset
### To get the last 5 records for all columns...
# Label-Based Selection with `loc`
## With `loc`, we use the names of the columns to retrieve data
### Get all the records for the following fields/columns using `loc`:
>- taster_name
>- taster_twitter_handle
>- points
# Notice we have been using the default index so far
## We can change the index with `set_index`
# Conditional Selection
>- Suppose we only want to analyze data for one country, reviewer, etc...
>- Or we want to pull the data only for points and/or prices above a certain criteria
## Which wines are from the US with 95 or greater points?
# Some notes on our previous example:
>- We just quickly took at dataset that has almost 130K rows and reduced it to one that has 993
>- This tells us that less that 1% of the wines are from the US and have ratings of 95 or higher
>- With some simple slicing using pandas we already have some decent start to an analytics project
# Q: What are all the wines from Italy or that have a rating higher than 95?
>- To return the results for an "or" question use the pipe `|` between your conditions
# Q: What are all the wines from Italy or France?
>- We can do this with an or statement or the `isin()` selector
>- Note: if you know SQL, this is the same thing as the IN () statement
>- Using `isin()` replaces multiple "or" statements and makes your code a little shorter
# Q: What are all the wines without prices?
>- Here we can use the `isnull` method to show when values are not entered for a particular column
# What are all the wines with prices?
>- Use `notnull()`
# We can also add columns/fields to our DataFrames
|
github_jupyter
|
# Exp 101 analysis
See `./informercial/Makefile` for experimental
details.
```
import os
import numpy as np
from IPython.display import Image
import matplotlib
import matplotlib.pyplot as plt
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
import seaborn as sns
sns.set_style('ticks')
matplotlib.rcParams.update({'font.size': 16})
matplotlib.rc('axes', titlesize=16)
from infomercial.exp import meta_bandit
from infomercial.exp import epsilon_bandit
from infomercial.exp import beta_bandit
from infomercial.exp import softbeta_bandit
from infomercial.local_gym import bandit
from infomercial.exp.meta_bandit import load_checkpoint
import gym
def plot_meta(env_name, result):
"""Plots!"""
# episodes, actions, scores_E, scores_R, values_E, values_R, ties, policies
episodes = result["episodes"]
actions =result["actions"]
bests =result["p_bests"]
scores_E = result["scores_E"]
scores_R = result["scores_R"]
values_R = result["values_R"]
values_E = result["values_E"]
ties = result["ties"]
policies = result["policies"]
# -
env = gym.make(env_name)
best = env.best
print(f"Best arm: {best}, last arm: {actions[-1]}")
# Plotz
fig = plt.figure(figsize=(6, 14))
grid = plt.GridSpec(6, 1, wspace=0.3, hspace=0.8)
# Arm
plt.subplot(grid[0, 0])
plt.scatter(episodes, actions, color="black", alpha=.5, s=2, label="Bandit")
plt.plot(episodes, np.repeat(best, np.max(episodes)+1),
color="red", alpha=0.8, ls='--', linewidth=2)
plt.ylim(-.1, np.max(actions)+1.1)
plt.ylabel("Arm choice")
plt.xlabel("Episode")
# Policy
policies = np.asarray(policies)
episodes = np.asarray(episodes)
plt.subplot(grid[1, 0])
m = policies == 0
plt.scatter(episodes[m], policies[m], alpha=.4, s=2, label="$\pi_E$", color="purple")
m = policies == 1
plt.scatter(episodes[m], policies[m], alpha=.4, s=2, label="$\pi_R$", color="grey")
plt.ylim(-.1, 1+.1)
plt.ylabel("Controlling\npolicy")
plt.xlabel("Episode")
plt.legend(loc='center left', bbox_to_anchor=(1, 0.5))
_ = sns.despine()
# score
plt.subplot(grid[2, 0])
plt.scatter(episodes, scores_E, color="purple", alpha=0.4, s=2, label="E")
plt.plot(episodes, scores_E, color="purple", alpha=0.4)
plt.scatter(episodes, scores_R, color="grey", alpha=0.4, s=2, label="R")
plt.plot(episodes, scores_R, color="grey", alpha=0.4)
plt.plot(episodes, np.repeat(tie_threshold, np.max(episodes)+1),
color="violet", alpha=0.8, ls='--', linewidth=2)
plt.ylabel("Score")
plt.xlabel("Episode")
# plt.semilogy()
plt.legend(loc='center left', bbox_to_anchor=(1, 0.5))
_ = sns.despine()
# Q
plt.subplot(grid[3, 0])
plt.scatter(episodes, values_E, color="purple", alpha=0.4, s=2, label="$Q_E$")
plt.scatter(episodes, values_R, color="grey", alpha=0.4, s=2, label="$Q_R$")
plt.plot(episodes, np.repeat(tie_threshold, np.max(episodes)+1),
color="violet", alpha=0.8, ls='--', linewidth=2)
plt.ylabel("Value")
plt.xlabel("Episode")
# plt.semilogy()
plt.legend(loc='center left', bbox_to_anchor=(1, 0.5))
_ = sns.despine()
# Ties
plt.subplot(grid[4, 0])
plt.scatter(episodes, bests, color="red", alpha=.5, s=2)
plt.ylabel("p(best)")
plt.xlabel("Episode")
plt.ylim(0, 1)
# Ties
plt.subplot(grid[5, 0])
plt.scatter(episodes, ties, color="black", alpha=.5, s=2, label="$\pi_{tie}$ : 1\n $\pi_\pi$ : 0")
plt.ylim(-.1, 1+.1)
plt.ylabel("Ties index")
plt.xlabel("Episode")
plt.legend(loc='center left', bbox_to_anchor=(1, 0.5))
def plot_epsilon(env_name, result):
"""Plots!"""
# episodes, actions, scores_E, scores_R, values_E, values_R, ties, policies
episodes = result["episodes"]
actions =result["actions"]
bests =result["p_bests"]
scores_R = result["scores_R"]
values_R = result["values_R"]
epsilons = result["epsilons"]
# -
env = gym.make(env_name)
best = env.best
print(f"Best arm: {best}, last arm: {actions[-1]}")
# Plotz
fig = plt.figure(figsize=(6, 14))
grid = plt.GridSpec(6, 1, wspace=0.3, hspace=0.8)
# Arm
plt.subplot(grid[0, 0])
plt.scatter(episodes, actions, color="black", alpha=.5, s=2, label="Bandit")
for b in best:
plt.plot(episodes, np.repeat(b, np.max(episodes)+1),
color="red", alpha=0.8, ls='--', linewidth=2)
plt.ylim(-.1, np.max(actions)+1.1)
plt.ylabel("Arm choice")
plt.xlabel("Episode")
# score
plt.subplot(grid[1, 0])
plt.scatter(episodes, scores_R, color="grey", alpha=0.4, s=2, label="R")
plt.ylabel("Score")
plt.xlabel("Episode")
# plt.semilogy()
plt.legend(loc='center left', bbox_to_anchor=(1, 0.5))
_ = sns.despine()
# Q
plt.subplot(grid[2, 0])
plt.scatter(episodes, values_R, color="grey", alpha=0.4, s=2, label="$Q_R$")
plt.ylabel("Value")
plt.xlabel("Episode")
# plt.semilogy()
plt.legend(loc='center left', bbox_to_anchor=(1, 0.5))
_ = sns.despine()
# best
plt.subplot(grid[3, 0])
plt.scatter(episodes, bests, color="red", alpha=.5, s=2)
plt.ylabel("p(best)")
plt.xlabel("Episode")
plt.ylim(0, 1)
# Decay
plt.subplot(grid[4, 0])
plt.scatter(episodes, epsilons, color="black", alpha=.5, s=2)
plt.ylabel("$\epsilon_R$")
plt.xlabel("Episode")
plt.legend(loc='center left', bbox_to_anchor=(1, 0.5))
def plot_critic(critic_name, env_name, result):
# -
env = gym.make(env_name)
best = env.best
# Data
critic = result[critic_name]
arms = list(critic.keys())
values = list(critic.values())
# Plotz
fig = plt.figure(figsize=(8, 3))
grid = plt.GridSpec(1, 1, wspace=0.3, hspace=0.8)
# Arm
plt.subplot(grid[0])
plt.scatter(arms, values, color="black", alpha=.5, s=30)
plt.plot([best]*10, np.linspace(min(values), max(values), 10), color="red", alpha=0.8, ls='--', linewidth=2)
plt.ylabel("Value")
plt.xlabel("Arm")
```
# Load and process data
```
data_path ="/Users/qualia/Code/infomercial/data/"
exp_name = "exp97"
sorted_params = load_checkpoint(os.path.join(data_path, f"{exp_name}_sorted.pkl"))
# print(sorted_params.keys())
best_params = sorted_params[0]
sorted_params
```
# Performance
of best parameters
```
env_name = 'BanditTwoHigh10-v0'
num_episodes = 1000
# Run w/ best params
result = epsilon_bandit(
env_name=env_name,
num_episodes=num_episodes,
lr_R=best_params["lr_R"],
epsilon=best_params["epsilon"],
seed_value=2,
)
print(best_params)
plot_epsilon(env_name, result=result)
plot_critic('critic_R', env_name, result)
```
# Sensitivity
to parameter choices
```
total_Rs = []
eps = []
lrs_R = []
lrs_E = []
trials = list(sorted_params.keys())
for t in trials:
total_Rs.append(sorted_params[t]['total_R'])
lrs_R.append(sorted_params[t]['lr_R'])
eps.append(sorted_params[t]['epsilon'])
# Init plot
fig = plt.figure(figsize=(5, 18))
grid = plt.GridSpec(6, 1, wspace=0.3, hspace=0.8)
# Do plots:
# Arm
plt.subplot(grid[0, 0])
plt.scatter(trials, total_Rs, color="black", alpha=.5, s=6, label="total R")
plt.xlabel("Sorted params")
plt.ylabel("total R")
_ = sns.despine()
plt.subplot(grid[1, 0])
plt.scatter(trials, lrs_R, color="black", alpha=.5, s=6, label="total R")
plt.xlabel("Sorted params")
plt.ylabel("lr_R")
_ = sns.despine()
plt.subplot(grid[2, 0])
plt.scatter(lrs_R, total_Rs, color="black", alpha=.5, s=6, label="total R")
plt.xlabel("lrs_R")
plt.ylabel("total_Rs")
_ = sns.despine()
plt.subplot(grid[3, 0])
plt.scatter(eps, total_Rs, color="black", alpha=.5, s=6, label="total R")
plt.xlabel("epsilon")
plt.ylabel("total_Rs")
_ = sns.despine()
```
# Parameter correlations
```
from scipy.stats import spearmanr
spearmanr(eps, lrs_R)
spearmanr(eps, total_Rs)
spearmanr(lrs_R, total_Rs)
```
# Distributions
of parameters
```
# Init plot
fig = plt.figure(figsize=(5, 6))
grid = plt.GridSpec(3, 1, wspace=0.3, hspace=0.8)
plt.subplot(grid[0, 0])
plt.hist(eps, color="black")
plt.xlabel("epsilon")
plt.ylabel("Count")
_ = sns.despine()
plt.subplot(grid[1, 0])
plt.hist(lrs_R, color="black")
plt.xlabel("lr_R")
plt.ylabel("Count")
_ = sns.despine()
```
of total reward
```
# Init plot
fig = plt.figure(figsize=(5, 2))
grid = plt.GridSpec(1, 1, wspace=0.3, hspace=0.8)
plt.subplot(grid[0, 0])
plt.hist(total_Rs, color="black", bins=50)
plt.xlabel("Total reward")
plt.ylabel("Count")
# plt.xlim(0, 10)
_ = sns.despine()
```
|
github_jupyter
|
# Creating a Linear Cellular Automaton
Let's start by creating a linear cellular automaton

> A cellular automaton is a discrete model of computation studied in automata theory.
It consists of a regular grid of cells, each in one of a finite number of states, such as on and off (in contrast to a coupled map lattice). The grid can be in any finite number of dimensions. For each cell, a set of cells called its neighborhood is defined relative to the specified cell.An initial state (time t = 0) is selected by assigning a state for each cell. A new generation is created (advancing t by 1), according to some fixed rule (generally, a mathematical function) that determines the new state of each cell in terms of the current state of the cell and the states of the cells in its neighborhood. Typically, the rule for updating the state of cells is the same for each cell and does not change over time.
## Rules
For this example, the rule for updating the state of the cells is:
> For each cell of the automaton, it will take the state of its left neighboring cell.
With this rule, the cells will move one step to the right side every generation.
## Implementing cells
To implement cells, you can extend the class `DiscreteTimeModel`, and define the abstract protected methods.
```
from typing import Dict
from gsf.dynamic_system.dynamic_systems import DiscreteEventDynamicSystem
from gsf.models.models import DiscreteTimeModel
class Cell(DiscreteTimeModel):
"""Cell of the linear cellular automaton
It has an state alive or dead. When receives an input, changes its state to that input.
Its output is the state.
Attributes:
_symbol (str): Symbol that represents the cell when it is printed in console.
"""
_symbol: str
def __init__(self, dynamic_system: DiscreteEventDynamicSystem, state: bool, symbol: str = None):
"""
Args:
dynamic_system (DiscreteEventDynamicSystem): Automaton Grid where the cell belongs.
state (bool); State that indicates whether the cell is alive (True) or dead (False).
symbol (str): Symbol that represents the cell when it is printed in console.
"""
super().__init__(dynamic_system, state=state)
self._symbol = symbol or "\u2665"
def _state_transition(self, state: bool, inputs: Dict[str, bool]) -> bool:
"""
Receives an input and changes the state of the cell.
Args:
state (bool); Current state of the cell.
inputs: A dictionary where the key is the input source cell and the value the output of that cell.
Returns:
The new state of the cell.
"""
next_state: bool = list(inputs.values())[0]
return next_state
def _output_function(self, state: bool) -> bool:
"""
Returns the state of the cell.
"""
return state
def __str__(self):
"""Prints the cell with the defined symbol"""
is_alive = self.get_state()
if is_alive:
return self._symbol
else:
return "-"
```
The `Cell` class, must receive the `DiscreteEventDynamicSystem` where the model belongs. We also include the state of the cell as a bool and a symbol that represents the cells when they will be printed.
When a generation is running, the framework will obtain the outputs of every cell defined by `_output_function`, and will inject them on the next model by `_state_transition`. The state transition member, receives a dict with the source input model and its state, and returns the new state that will take the cell.
`DiscreteTimeModels` will schedule their transitions indefinitely every so often with a constant period in between.
## Implementing the Automaton
The Automaton is a dynamic system, a discrete event dynamic system, so it extends `DiscreteEventDynamicSystem`.
```
from random import random, seed
from typing import List
from gsf.dynamic_system.dynamic_systems import DiscreteEventDynamicSystem
class LinearAutomaton(DiscreteEventDynamicSystem):
"""Linear Automaton implementation
It has a group of cells, connected between them. The output cell of each cell is its right neighbor.
Attributes:
_cells (List[Cell]): Group of cells of the linear automaton.
"""
_cells: List[Cell]
def __init__(self, cells: int = 5, random_seed: int = 42):
"""
Args:
cells (int): Number of cells of the automaton.
random_seed (int): Random seed for determinate the state of the seeds.
"""
super().__init__()
seed(random_seed)
self._create_cells(cells)
self._create_relations(cells)
def _create_cells(self, cells: int):
"""Appends the cells to the automaton.
Args:
cells (int): Number of cells of the automaton.
"""
self._cells = []
for i in range(cells):
is_alive = random() < 0.5
self._cells.append(Cell(self, is_alive))
def _create_relations(self, cells: int):
"""Creates the connections between the left cell and the right cell.
Args:
cells (int): Number of cells of the automaton.
"""
for i in range(cells):
self._cells[i-1].add(self._cells[i])
def __str__(self):
"""Changes the format to show the linear automaton when is printed"""
s = ""
for cell in self._cells:
s += str(cell)
return s
```
The `LinearAutomaton` receives the number of cells that it will have and a random seed to determine the initial random state of the cells.
First it creates the cells, setting the state as alive or dead with a probability of 0.5, and giving as `DiscreteEventDynamicSystem` the current linear automaton.
Then, it connects the models, setting as the output of the `cell[i-1]`, the `cell[i]`.
`DiscreteEventDynamicSystem`s link models, route outputs and inputs between models and execute the transitions of the models.
## Running the simulation
We defined a dynamic system, so we can simulate it. Use the class `DiscreteEventExperiment` to run 5 geneations!
```
from gsf.experiments.experiment_builders import DiscreteEventExperiment
linear_automaton = LinearAutomaton(cells=10)
experiment = DiscreteEventExperiment(linear_automaton)
print(linear_automaton)
experiment.simulation_control.start(stop_time=5)
experiment.simulation_control.wait()
print(linear_automaton)
```
Create the experiment with the linear automaton as `DiscreteEventDynamicSystem`. Then, run it during 5 generations.
As the simulation runs in a different thread, we wait for it to finish with `experiment.simulation_control.wait()`.
Try the example by your custom params and have fun.
|
github_jupyter
|
```
from molmap import model as molmodel
import molmap
import matplotlib.pyplot as plt
import pandas as pd
from tqdm import tqdm
from joblib import load, dump
tqdm.pandas(ascii=True)
import numpy as np
import tensorflow as tf
import os
os.environ["CUDA_VISIBLE_DEVICES"]="1"
np.random.seed(123)
tf.compat.v1.set_random_seed(123)
tmp_feature_dir = './tmpignore'
if not os.path.exists(tmp_feature_dir):
os.makedirs(tmp_feature_dir)
def get_attentiveFP_idx(df):
""" attentiveFP dataset"""
train, valid,test = load('./split_and_data/07_BBBP_attentiveFP.data')
print('training set: %s, valid set: %s, test set %s' % (len(train), len(valid), len(test)))
train_idx = df[df.smiles.isin(train.smiles)].index
valid_idx = df[df.smiles.isin(valid.smiles)].index
test_idx = df[df.smiles.isin(test.smiles)].index
print('training set: %s, valid set: %s, test set %s' % (len(train_idx), len(valid_idx), len(test_idx)))
return train_idx, valid_idx, test_idx
task_name = 'BBBP'
from chembench import load_data
df, _ = load_data(task_name)
train_idx, valid_idx, test_idx = get_attentiveFP_idx(df)
len(train_idx), len(valid_idx), len(test_idx)
mp1 = molmap.loadmap('../descriptor.mp')
mp2 = molmap.loadmap('../fingerprint.mp')
tmp_feature_dir = '../02_OutofTheBox_benchmark_comparison_DMPNN/tmpignore'
if not os.path.exists(tmp_feature_dir):
os.makedirs(tmp_feature_dir)
smiles_col = df.columns[0]
values_col = df.columns[1:]
Y = df[values_col].astype('float').values
Y = Y.reshape(-1, 1)
X1_name = os.path.join(tmp_feature_dir, 'X1_%s.data' % task_name)
X2_name = os.path.join(tmp_feature_dir, 'X2_%s.data' % task_name)
if not os.path.exists(X1_name):
X1 = mp1.batch_transform(df.smiles, n_jobs = 8)
dump(X1, X1_name)
else:
X1 = load(X1_name)
if not os.path.exists(X2_name):
X2 = mp2.batch_transform(df.smiles, n_jobs = 8)
dump(X2, X2_name)
else:
X2 = load(X2_name)
molmap1_size = X1.shape[1:]
molmap2_size = X2.shape[1:]
def get_pos_weights(trainY):
"""pos_weights: neg_n / pos_n """
dfY = pd.DataFrame(trainY)
pos = dfY == 1
pos_n = pos.sum(axis=0)
neg = dfY == 0
neg_n = neg.sum(axis=0)
pos_weights = (neg_n / pos_n).values
neg_weights = (pos_n / neg_n).values
return pos_weights, neg_weights
prcs_metrics = ['MUV', 'PCBA']
print(len(train_idx), len(valid_idx), len(test_idx))
trainX = (X1[train_idx], X2[train_idx])
trainY = Y[train_idx]
validX = (X1[valid_idx], X2[valid_idx])
validY = Y[valid_idx]
testX = (X1[test_idx], X2[test_idx])
testY = Y[test_idx]
epochs = 800
patience = 50 #early stopping
dense_layers = [256, 128, 32]
batch_size = 128
lr = 1e-4
weight_decay = 0
monitor = 'val_loss'
dense_avf = 'relu'
last_avf = None #sigmoid in loss
if task_name in prcs_metrics:
metric = 'PRC'
else:
metric = 'ROC'
results = []
for i, seed in enumerate([7, 77, 77]):
np.random.seed(seed)
tf.compat.v1.set_random_seed(seed)
pos_weights, neg_weights = get_pos_weights(trainY)
loss = lambda y_true, y_pred: molmodel.loss.weighted_cross_entropy(y_true,y_pred, pos_weights, MASK = -1)
model = molmodel.net.DoublePathNet(molmap1_size, molmap2_size,
n_outputs=Y.shape[-1],
dense_layers=dense_layers,
dense_avf = dense_avf,
last_avf=last_avf)
opt = tf.keras.optimizers.Adam(lr=lr, beta_1=0.9, beta_2=0.999, epsilon=1e-08, decay=0.0) #
#import tensorflow_addons as tfa
#opt = tfa.optimizers.AdamW(weight_decay = 0.1,learning_rate=0.001,beta1=0.9,beta2=0.999, epsilon=1e-08)
model.compile(optimizer = opt, loss = loss)
if i == 0:
performance = molmodel.cbks.CLA_EarlyStoppingAndPerformance((trainX, trainY),
(validX, validY),
patience = patience,
criteria = monitor,
metric = metric,
)
model.fit(trainX, trainY, batch_size=batch_size,
epochs=epochs, verbose= 0, shuffle = True,
validation_data = (validX, validY),
callbacks=[performance])
else:
model.fit(trainX, trainY, batch_size=batch_size,
epochs = performance.best_epoch + 1, verbose = 1, shuffle = True,
validation_data = (validX, validY))
performance.model.set_weights(model.get_weights())
best_epoch = performance.best_epoch
trainable_params = model.count_params()
train_aucs = performance.evaluate(trainX, trainY)
valid_aucs = performance.evaluate(validX, validY)
test_aucs = performance.evaluate(testX, testY)
final_res = {
'task_name':task_name,
'train_auc':np.nanmean(train_aucs),
'valid_auc':np.nanmean(valid_aucs),
'test_auc':np.nanmean(test_aucs),
'metric':metric,
'# trainable params': trainable_params,
'best_epoch': best_epoch,
'batch_size':batch_size,
'lr': lr,
'weight_decay':weight_decay
}
results.append(final_res)
pd.DataFrame(results).test_auc.mean()
pd.DataFrame(results).test_auc.std()
pd.DataFrame(results).to_csv('./results/%s.csv' % task_name)
```
|
github_jupyter
|
# The Discrete-Time Fourier Transform
*This Jupyter notebook is part of a [collection of notebooks](../index.ipynb) in the bachelors module Signals and Systems, Comunications Engineering, Universität Rostock. Please direct questions and suggestions to [[email protected]](mailto:[email protected]).*
## Theorems
The theorems of the discrete-time Fourier transform (DTFT) relate basic operations applied to discrete signals to their equivalents in the DTFT domain. They are of use to transform signals composed from modified [standard signals](../discrete_signals/standard_signals.ipynb), for the computation of the response of a linear time-invariant (LTI) system and to predict the consequences of modifying a signal or system by certain operations.
### Convolution Theorem
The [convolution theorem](https://en.wikipedia.org/wiki/Convolution_theorem) states that the DTFT of the linear convolution of two discrete signals $x[k]$ and $y[k]$ is equal to the scalar multiplication of their DTFTs $X(e^{j \Omega}) = \mathcal{F}_* \{ x[k] \}$ and $Y(e^{j \Omega}) = \mathcal{F}_* \{ y[k] \}$
\begin{equation}
\mathcal{F}_* \{ x[k] * y[k] \} = X(e^{j \Omega}) \cdot Y(e^{j \Omega})
\end{equation}
The theorem can be proven by introducing the [definition of the linear convolution](../discrete_systems/linear_convolution.ipynb) into the [definition of the DTFT](definition.ipynb) and changing the order of summation
\begin{align}
\mathcal{F} \{ x[k] * y[k] \} &= \sum_{k = -\infty}^{\infty} \left( \sum_{\kappa = -\infty}^{\infty} x[\kappa] \cdot y[k - \kappa] \right) e^{-j \Omega k} \\
&= \sum_{\kappa = -\infty}^{\infty} \left( \sum_{k = -\infty}^{\infty} y[k - \kappa] \, e^{-j \Omega k} \right) x[\kappa] \\
&= Y(e^{j \Omega}) \cdot \sum_{\kappa = -\infty}^{\infty} x[\kappa] \, e^{-j \Omega \kappa} \\
&= Y(e^{j \Omega}) \cdot X(e^{j \Omega})
\end{align}
The convolution theorem is very useful in the context of LTI systems. The output signal $y[k]$ of an LTI system is given as the convolution of the input signal $x[k]$ with its impulse response $h[k]$. Hence, the signals and the system can be represented equivalently in the time and frequency domain

Calculation of the system response by transforming the problem into the DTFT domain can be beneficial since this replaces the computation of the linear convolution by a scalar multiplication. The (inverse) DTFT is known for many signals or can be derived by applying the properties and theorems to standard signals and their transforms. In many cases this procedure simplifies the calculation of the system response significantly.
The convolution theorem can also be useful to derive the DTFT of a signal. The key is here to express the signal as convolution of two other signals for which the transforms are known. This is illustrated in the following example.
#### Transformation of the triangular signal
The linear convolution of two [rectangular signals](../discrete_signals/standard_signals.ipynb#Rectangular-Signal) of lengths $N$ and $M$ defines a [signal of trapezoidal shape](../discrete_systems/linear_convolution.ipynb#Finite-Length-Signals)
\begin{equation}
x[k] = \text{rect}_N[k] * \text{rect}_M[k]
\end{equation}
Application of the convolution theorem together with the [DTFT of the rectangular signal](definition.ipynb#Transformation-of-the-Rectangular-Signal) yields its DTFT as
\begin{equation}
X(e^{j \Omega}) = \mathcal{F}_* \{ \text{rect}_N[k] \} \cdot \mathcal{F}_* \{ \text{rect}_M[k] \} =
e^{-j \Omega \frac{N+M-2}{2}} \cdot \frac{\sin(\frac{N \Omega}{2}) \sin(\frac{M \Omega}{2})}{\sin^2 ( \frac{\Omega}{2} )}
\end{equation}
The transform of the triangular signal can be derived from this result. The convolution of two rectangular signals of equal length $N=M$ yields the triangular signal $\Lambda[k]$ of length $2N - 1$
\begin{equation}
\Lambda_{2N - 1}[k] = \begin{cases} k + 1 & \text{for } 0 \leq k < N \\
2N - 1 - k & \text{for } N \leq k < 2N - 1 \\
0 & \text{otherwise}
\end{cases}
\end{equation}
From above result the DTFT of the triangular signal is derived by substitution of $N$ by $M$
\begin{equation}
\mathcal{F}_* \{ \Lambda_{2N - 1}[k] \} =
e^{-j \Omega (N-1)} \cdot \frac{\sin^2(\frac{N \Omega}{2}) }{\sin^2 ( \frac{\Omega}{2} )}
\end{equation}
Both the signal and the magnitude of its DTFT are plotted for illustration
```
%matplotlib inline
import sympy as sym
import numpy as np
import matplotlib.pyplot as plt
N = 7
x = np.convolve(np.ones(N), np.ones(N), mode='full')
plt.stem(x)
plt.xlabel('$k$')
plt.ylabel('$x[k]$')
W = sym.symbols('Omega')
X = sym.exp(-sym.I*W *(N-1)) * sym.sin(N*W/2)**2 / sym.sin(W/2)**2
sym.plot(sym.Abs(X), (W, -5, 5), xlabel='$\Omega$', ylabel='$|X(e^{j \Omega})|$');
```
**Exercise**
* Change the length of the triangular signal in above example. How does its DTFT change?
* The triangular signal introduced above is of odd length $2N - 1$
* Define a triangular signal of even length by convolving two rectangular signals
* Derive its DTFT
* Compare the DTFTs of a triangular signal of odd/even length
### Shift Theorem
The [shift of a signal](../discrete_signals/operations.ipynb#Shift) $x[k]$ can be expressed by a convolution with a shifted Dirac impulse
\begin{equation}
x[k - \kappa] = x[k] * \delta[k - \kappa]
\end{equation}
for $\kappa \in \mathbb{Z}$. This follows from the sifting property of the Dirac impulse. Applying the DTFT to the left- and right-hand side and exploiting the convolution theorem yields
\begin{equation}
\mathcal{F}_* \{ x[k - \kappa] \} = X(e^{j \Omega}) \cdot e^{- j \Omega \kappa}
\end{equation}
where $X(e^{j \Omega}) = \mathcal{F}_* \{ x[k] \}$. Note that $\mathcal{F}_* \{ \delta(k - \kappa) \} = e^{- j \Omega \kappa}$ can be derived from the definition of the DTFT together with the sifting property of the Dirac impulse. Above relation is known as shift theorem of the DTFT.
Expressing the DTFT $X(e^{j \Omega}) = |X(e^{j \Omega})| \cdot e^{j \varphi(e^{j \Omega})}$ by its absolute value $|X(e^{j \Omega})|$ and phase $\varphi(e^{j \Omega})$ results in
\begin{equation}
\mathcal{F}_* \{ x[k - \kappa] \} = | X(e^{j \Omega}) | \cdot e^{j (\varphi(e^{j \Omega}) - \Omega \kappa)}
\end{equation}
Shifting of a signal does not change the absolute value of its spectrum but it subtracts the linear contribution $\Omega \kappa$ from its phase.
### Multiplication Theorem
The transform of a multiplication of two signals $x[k] \cdot y[k]$ is derived by introducing the signals into the definition of the DTFT, expressing the signal $x[k]$ by its spectrum $X(e^{j \Omega}) = \mathcal{F}_* \{ x[k] \}$ and rearranging terms
\begin{align}
\mathcal{F}_* \{ x[k] \cdot y[k] \} &= \sum_{k=-\infty}^{\infty} x[k] \cdot y[k] \, e^{-j \Omega k} \\
&= \sum_{k=-\infty}^{\infty} \left( \frac{1}{2 \pi} \int_{-\pi}^{\pi} X(e^{j \nu}) \, e^{j \nu k} \; d \nu \right) y[k] \, e^{-j \Omega k} \\
&= \frac{1}{2 \pi} \int_{-\pi}^{\pi} X(e^{j \nu}) \sum_{k=-\infty}^{\infty} y[k] \, e^{-j (\Omega - \nu) k} \; d\nu \\
&= \frac{1}{2 \pi} \int_{-\pi}^{\pi} X(e^{j \nu}) \cdot Y(e^{j (\Omega - \nu)}) d\nu
\end{align}
where $Y(e^{j \Omega}) = \mathcal{F}_* \{ y[k] \}$.
The [periodic (cyclic/circular) convolution](https://en.wikipedia.org/wiki/Circular_convolution) of two aperiodic signals $h(t)$ and $g(t)$ is defined as
\begin{equation}
h(t) \circledast_{T} g(t) = \int_{-\infty}^{\infty} h(\tau) \cdot g_\text{p}(t - \tau) \; d\tau
\end{equation}
where $T$ denotes the period of the convolution, $g_\text{p}(t) = \sum_{n=-\infty}^{\infty} g(t + n T)$ the periodic summation of $g(t)$ and $\tau \in \mathbb{R}$ an arbitrary constant. The periodic convolution is commonly abbreviated by $\circledast_{T}$. With $h_\text{p}(t)$ denoting the periodic summation of $h(t)$ the periodic convolution can be rewritten as
\begin{equation}
h(t) \circledast_{T} g(t) = \int_{\tau_0}^{\tau_0 + T} h_\text{p}(\tau) \cdot g_\text{p}(t - \tau) \; d\tau
\end{equation}
where $\tau_0 \in \mathbb{R}$ denotes an arbitrary constant. The latter definition holds also for two [periodic signals](../periodic_signals/spectrum.ipynb) $h(t)$ and $g(t)$ with period $T$.
Comparison of the DTFT of two multiplied signals with the definition of the periodic convolution reveals that the preliminary result above can be expressed as
\begin{equation}
\mathcal{F}_* \{ x[k] \cdot y[k] \} = \frac{1}{2\pi} \, X(e^{j \Omega}) \circledast_{2 \pi} Y(e^{j \Omega})
\end{equation}
The DTFT of a multiplication of two signals $x[k] \cdot y[k]$ is given by the periodic convolution of their transforms $X(e^{j \Omega})$ and $Y(e^{j \Omega})$ weighted with $\frac{1}{2 \pi}$. The periodic convolution has a period of $T = 2 \pi$. Note, the convolution is performed with respect to the normalized angular frequency $\Omega$.
Applications of the multiplication theorem include the modulation and windowing of signals. The former leads to the modulation theorem introduced later, the latter is illustrated by the following example.
**Example**
Windowing of signals is used to derive signals of finite duration from signals of infinite duration or to truncate signals to a shorter length. The signal $x[k]$ is multiplied by a weighting function $w[k]$ in order to derive the finite length signal
\begin{equation}
y[k] = w[k] \cdot x[k]
\end{equation}
Application of the multiplication theorem yields the spectrum $Y(e^{j \Omega}) = \mathcal{F}_* \{ y[k] \}$ of the windowed signal as
\begin{equation}
Y(e^{j \Omega}) = \frac{1}{2 \pi} W(e^{j \Omega}) \circledast X(e^{j \Omega})
\end{equation}
where $W(e^{j \Omega}) = \mathcal{F}_* \{ w[k] \}$ and $X(e^{j \Omega}) = \mathcal{F}_* \{ x[k] \}$. In order to illustrate the consequence of windowing, a cosine signal $x[k] = \cos(\Omega_0 k)$ is truncated to a finite length using a rectangular signal
\begin{equation}
y[k] = \text{rect}_N[k] \cdot \cos(\Omega_0 k)
\end{equation}
where $N$ denotes the length of the truncated signal and $\Omega_0$ its normalized angular frequency. Using the DTFT of the [rectangular signal](definition.ipynb#Transformation-of-the-Rectangular-Signal) and the [cosine signal](properties.ipynb#Transformation-of-the-cosine-and-sine-signal) yields
\begin{align}
Y(e^{j \Omega}) &= \frac{1}{2 \pi} e^{-j \Omega \frac{N-1}{2}} \cdot \frac{\sin \left(\frac{N \Omega}{2} \right)}{\sin \left( \frac{\Omega}{2} \right)} \circledast \frac{1}{2} \left[ {\bot \!\! \bot \!\! \bot} \left( \frac{\Omega + \Omega_0}{2 \pi} \right) + {\bot \!\! \bot \!\! \bot} \left( \frac{\Omega - \Omega_0}{2 \pi} \right) \right] \\
&= \frac{1}{2} \left[ e^{-j (\Omega+\Omega_0) \frac{N-1}{2}} \cdot \frac{\sin \left(\frac{N (\Omega+\Omega_0)}{2} \right)}{\sin \left( \frac{\Omega+\Omega_0}{2} \right)} + e^{-j (\Omega-\Omega_0) \frac{N-1}{2}} \cdot \frac{\sin \left(\frac{N (\Omega-\Omega_0)}{2} \right)}{\sin \left( \frac{\Omega-\Omega_0}{2} \right)} \right]
\end{align}
The latter identity results from the sifting property of the Dirac impulse and the periodicity of both spectra. The signal $y[k]$ and its magnitude spectrum $|Y(e^{j \Omega})|$ are plotted for specific values of $N$ and $\Omega_0$.
```
N = 20
W0 = 2*np.pi/10
k = np.arange(N)
x = np.cos(W0 * k)
plt.stem(k, x)
plt.xlabel('$k$')
plt.ylabel('$y[k]$');
W = sym.symbols('Omega')
Y = 1/2 * ((sym.exp(-sym.I*(W+W0)*(N-1)/2) * sym.sin(N*(W+W0)/2) / sym.sin((W+W0)/2)) +
(sym.exp(-sym.I*(W-W0)*(N-1)/2) * sym.sin(N*(W-W0)/2) / sym.sin((W-W0)/2)))
sym.plot(sym.Abs(Y), (W, -sym.pi, sym.pi), xlabel='$\Omega$', ylabel='$|Y(e^{j \Omega})|$');
```
**Exercise**
* Change the length $N$ of the signal by modifying the example. How does the spectrum change if you decrease or increase the length?
* What happens if you change the normalized angular frequency $\Omega_0$ of the signal?
* Assume a signal that is composed from a superposition of two finite length cosine signals with different frequencies. What qualitative condition has to hold that you can derive these frequencies from inspection of the spectrum?
### Modulation Theorem
The complex modulation of a signal $x[k]$ is defined as $e^{j \Omega_0 k} \cdot x[k]$ with $\Omega_0 \in \mathbb{R}$. The DTFT of the modulated signal is derived by applying the multiplication theorem
\begin{equation}
\mathcal{F}_* \left\{ e^{j \Omega_0 k} \cdot x[k] \right\} = \frac{1}{2 \pi} \cdot {\bot \!\! \bot \!\! \bot}\left( \frac{\Omega - \Omega_0}{2 \pi} \right) \circledast X(e^{j \Omega})
= X \big( e^{j \, (\Omega - \Omega_0)} \big)
\end{equation}
where $X(e^{j \Omega}) = \mathcal{F}_* \{ x[k] \}$. Above result states that the complex modulation of a signal leads to a shift of its spectrum. This result is known as modulation theorem.
**Example**
An example for the application of the modulation theorem is the [downsampling/decimation](https://en.wikipedia.org/wiki/Decimation_(signal_processing) of a discrete signal $x[k]$. Downsampling refers to lowering the sampling rate of a signal. The example focuses on the special case of removing every second sample, hence halving the sampling rate. The downsampling is modeled by defining a signal $x_\frac{1}{2}[k]$ where every second sample is set to zero
\begin{equation}
x_\frac{1}{2}[k] = \begin{cases}
x[k] & \text{for even } k \\
0 & \text{for odd } k
\end{cases}
\end{equation}
In order to derive the spectrum $X_\frac{1}{2}(e^{j \Omega}) = \mathcal{F}_* \{ x_\frac{1}{2}[k] \}$, the signal $u[k]$ is introduced where every second sample is zero
\begin{equation}
u[k] = \frac{1}{2} ( 1 + e^{j \pi k} ) = \begin{cases} 1 & \text{for even } k \\
0 & \text{for odd } k \end{cases}
\end{equation}
Using $u[k]$, the process of setting every second sample of $x[k]$ to zero can be expressed as
\begin{equation}
x_\frac{1}{2}[k] = u[k] \cdot x[k]
\end{equation}
Now the spectrum $X_\frac{1}{2}(e^{j \Omega})$ is derived by applying the multiplication theorem and introducing the [DTFT of the exponential signal](definition.ipynb#Transformation-of-the-Exponential-Signal). This results in
\begin{equation}
X_\frac{1}{2}(e^{j \Omega}) = \frac{1}{4 \pi} \left( {\bot \!\! \bot \!\! \bot}\left( \frac{\Omega}{2 \pi} \right) +
{\bot \!\! \bot \!\! \bot}\left( \frac{\Omega - \pi}{2 \pi} \right) \right) \circledast X(e^{j \Omega}) =
\frac{1}{2} X(e^{j \Omega}) + \frac{1}{2} X(e^{j (\Omega- \pi)})
\end{equation}
where $X(e^{j \Omega}) = \mathcal{F}_* \{ x[k] \}$. The spectrum $X_\frac{1}{2}(e^{j \Omega})$ consists of the spectrum of the original signal $X(e^{j \Omega})$ superimposed by the shifted spectrum $X(e^{j (\Omega- \pi)})$ of the original signal. This may lead to overlaps that constitute aliasing. In order to avoid aliasing, the spectrum of the signal $x[k]$ has to be band-limited to $-\frac{\pi}{2} < \Omega < \frac{\pi}{2}$ before downsampling.
### Parseval's Theorem
[Parseval's theorem](https://en.wikipedia.org/wiki/Parseval's_theorem) relates the energy of a discrete signal to its spectrum. The squared absolute value of a signal $x[k]$ represents its instantaneous power. It can be expressed as
\begin{equation}
| x[k] |^2 = x[k] \cdot x^*[k]
\end{equation}
where $x^*[k]$ denotes the complex conjugate of $x[k]$. Transformation of the right-hand side and application of the multiplication theorem results in
\begin{equation}
\mathcal{F}_* \{ x[k] \cdot x^*[k] \} = \frac{1}{2 \pi} \cdot X(e^{j \Omega}) \circledast_{2 \pi} X^*(e^{-j \Omega})
\end{equation}
Introducing the definition of the DTFT and the periodic convolution
\begin{equation}
\sum_{k = -\infty}^{\infty} x[k] \cdot x^*[k] \, e^{-j \Omega k} =
\frac{1}{2 \pi} \int_{-\pi}^{\pi} X(e^{j \nu}) \cdot X^*(e^{j (\Omega - \nu)}) \; d\nu
\end{equation}
Setting $\Omega = 0$ followed by the substitution $\nu = \Omega$ yields Parseval's theorem
\begin{equation}
\sum_{k = -\infty}^{\infty} | x[k] |^2 = \frac{1}{2 \pi} \int_{-\pi}^{\pi} | X(e^{j \Omega}) |^2 \; d\Omega
\end{equation}
The sum over the samples of the squared absolute signal is equal to the integral over its squared absolute spectrum divided by $2 \pi$. Since the left-hand side represents the energy $E$ of the signal $x[k]$, Parseval's theorem states that the energy can be computed alternatively in the spectral domain by integrating over the squared absolute value of the spectrum.
**Copyright**
The notebooks are provided as [Open Educational Resource](https://de.wikipedia.org/wiki/Open_Educational_Resources). Feel free to use the notebooks for your own educational purposes. The text is licensed under [Creative Commons Attribution 4.0](https://creativecommons.org/licenses/by/4.0/), the code of the IPython examples under the [MIT license](https://opensource.org/licenses/MIT). Please attribute the work as follows: *Lecture Notes on Signals and Systems* by Sascha Spors.
|
github_jupyter
|
# KakaoBrunch12M
KakaoBrunch12M은 [카카오 아레나에서 공개한 데이터](https://arena.kakao.com/datasets?id=2)로 [브런치 서비스](https://brunch.co.kr) 사용자를 통해 수집한 데이터입니다.
이 예제에서는 브런치 데이터에서 ALS를 활용해 특정 글과 유사한 글을 추천하는 예제와 개인화 추천 예제 두 가지를 살펴보겠습니다.
```
import buffalo.data
from buffalo.algo.als import ALS
from buffalo.algo.options import ALSOption
from buffalo.misc import aux
from buffalo.misc import log
from buffalo.data.mm import MatrixMarketOptions
log.set_log_level(1) # set log level 3 or higher to check more information
```
## 데이터 불러오기
```
# 브런치 데이터를 ./data/kakao-brunch-12m/ 아래에 위치했다고 가정하겠습니다.
data_opt = MatrixMarketOptions().get_default_option()
data_opt.input = aux.Option(
{
'main': 'data/kakao-brunch-12m/main',
'iid': 'data/kakao-brunch-12m/iid',
'uid': 'data/kakao-brunch-12m/uid'
}
)
data_opt
import os
import shutil
# KakaoBrunch12M 데이터에는 '#' 으로 시작하는 아이템과 사용자 아이디가 있는데,
# numpy에서 이런 라인은 주석으로 인식하기 때문에 다른 문자로 치환할 필요가 있습니다.
for filename in ['main', 'uid', 'iid']:
src = f'./data/kakao-brunch-12m/{filename}'
dest = f'./data/kakao-brunch-12m/{filename}.tmp'
with open(src, 'r') as fin:
with open(dest, 'w') as fout:
while True:
read = fin.read(4098)
if len(read) == 0:
break
read = read.replace('#', '$')
fout.write(read)
shutil.move(dest, src)
data = buffalo.data.load(data_opt)
data.create()
```
## 유사아이템 추천
```
# ALS 알고리즘의 기본 옵션으로 파라미터를 학습을 하겠습니다.
# 앞선 예제에 비해서는 데이터가 크기 때문에 워커 개수를 늘렸습니다.
als_opt = ALSOption().get_default_option()
als_opt.num_workers = 4
model = ALS(als_opt, data=data)
model.initialize()
model.train()
model.save('brunch.als.model')
# https://brunch.co.kr/@brunch/148 - 작가 인터뷰 - 브랜드 마케터, 정혜윤 by 브런치팀
model.load('brunch.als.model')
similar_items = model.most_similar('@brunch_148', 5)
for rank, (item, score) in enumerate(similar_items):
bid, aid = item.split('_')
print(f'{rank + 1:02d}. {score:.3f} https://brunch.co.kr/{bid}/{aid}')
```
브런치팀이 쓴 글중에서 아래와 같은 글들이 유사한 결과로 나왔습니다.
- https://brunch.co.kr/@brunch/149 : 글의 완성도를 높이는 팁, 맞춤법 검사
- https://brunch.co.kr/@brunch/147 : 크리에이터스 데이'글력' 후기
- https://brunch.co.kr/@brunch/144 : 글을 읽고 쓰는 것, 이 두 가지에만 집중하세요.
- https://brunch.co.kr/@brunch/145 : 10인의 에디터와 함께 하는, 브런치북 프로젝트 #6
- https://brunch.co.kr/@brunch/143 : 크리에이터스 스튜디오 '글쓰기 클래스' 후기
## 개인화 추천 예제
```
# 사용자에 대한 개인화 추천 결과는 topk_recommendation으로 얻을 수 있습니다.
# ALS 모델을 사용하는 가장 기본적인 방식입니다.
for rank, item in enumerate(model.topk_recommendation('$424ec49fa8423d82629c73e6d5ae9408')):
bid, aid = item.split('_')
print(f'{rank + 1:02d}. https://brunch.co.kr/{bid}/{aid}')
# get_weighted_feature를 응용하면 임의의 관심사를 가진 사용자에게
# 전달할 추천 결과를 만들 수 있습니다.
personal_feat = model.get_weighted_feature({
'@lonelyplanet_3': 1, # https://brunch.co.kr/@lonelyplanet/3
'@tube007_66': 1 # https://brunch.co.kr/@tube007/66
})
similar_items = model.most_similar(personal_feat, 10)
for rank, (item, score) in enumerate(similar_items):
bid, aid = item.split('_')
print(f'{rank + 1:02d}. {score:.3f} https://brunch.co.kr/{bid}/{aid}')
```
|
github_jupyter
|
# Análisis de la Movilidad en Bogotá
¿Cuáles son las rutas más críticas de movilidad y sus características en la ciudad de Bogotá?
Se toman los datos de la plataforma:
https://datos.movilidadbogota.gov.co
```
import pandas as pd
import os
os.chdir('../data_raw')
data_file_list = !ls
data_file_list
data_file_list[len(data_file_list)-1]
```
La adquisición de datos será de 4 meses del año 2019 con el propósito de optimizar espacio de almacenamiento y cargas de procesamiento.
```
''' Función df_builder
Recibe como parámetro de entrada una lista de archivos CSV,
hace la lectura y concatena los dataframes, siendo esta concatenación el retorno.
Los datos en los archivos CSV deben tener la misma estructura.
'''
def df_builder(data_list):
n_files = len(data_list) - 1
df_full = pd.read_csv(data_list[n_files])
for i in range(n_files):
df_i = pd.read_csv(data_list[i])
df_full = pd.concat([df_full, df_i])
return df_full
df_mov = df_builder(data_file_list)
df_mov.shape
df_mov.describe
df_mov.dtypes
## Limpieza de datos
# Verificación que todos los registros correspondan con el año de estudio: 2019
df_mov['AÑO'].value_counts()
```
Dentro de los datasets obtenidos se encuentran datos de otros años.
Vamos a eliminar los registros del año 2020.
```
df_mov.shape # Tamaño original
## Borrar los renglones cuando el AÑO es igual que 2020
df_mov = df_mov.loc[df_mov['AÑO'] == 2019]
df_mov['AÑO'].value_counts() # Verificación
df_mov.shape # Tamaño final del dataframe
```
### Columnas sin datos
Vamos a verificar las columnas que no tienen datos (Nan), posterior las eliminamos para tener un dataset más limpio.
```
df_mov['CODIGO'].value_counts()
df_mov['COEF_BRT'].value_counts()
df_mov['COEF_MIXTO'].value_counts()
df_mov['VEL_MEDIA_BRT'].value_counts()
df_mov['VEL_MEDIA_MIXTO'].value_counts()
df_mov['VEL_MEDIA_PONDERADA'].value_counts()
df_mov['VEL_PONDERADA'].value_counts()
## Borrar las columnas
df_mov = df_mov.drop(labels=['CODIGO', 'COEF_BRT', 'COEF_MIXTO', 'VEL_MEDIA_BRT',
'VEL_MEDIA_MIXTO', 'VEL_MEDIA_PONDERADA', 'VEL_PONDERADA'], axis=1)
df_mov.describe
df_mov.columns
df_mov.to_csv('../notebook/data/data_Mov_Bogota_2019.csv', index=None)
```
## Análisis Unidimensional de las Variables
```
## Conteo de la ocurrencia de una variable y un valor
# Conteo de la movilidad en cada mes
df_mov_sorted = df_mov.sort_values('MES')
df_mov_sorted['MES'].hist(bins=15, xrot=45, grid=True)
##plt.xticks(rotation=45)
df_mov['DIA_SEMANA'].value_counts(normalize=True)
df_mov['NAME_FROM'].value_counts()
df_mov['NAME_TO'].value_counts()
df_mov
```
## Análisis Multidimensional de las Variables
Velocidad promedio versus la trayectoria realizada.
La trayectoria se va a definir como la concatenación entre NAME_FROM y NAME_TO.
```
df_mov['TRAYEC'] = df_mov['NAME_FROM'] + ' - ' +df_mov['NAME_TO']
df_mov['TRAYEC'].value_counts()
```
Mediana de la velocidad promedio en cada trayecto. VEL_PROMEDIO que es más común en cada trayecto:
```
medianVel_Tray = df_mov.groupby('TRAYEC').median()['VEL_PROMEDIO']
medianVel_Tray
```
## Análisis de Texto
```
import nltk
from nltk.corpus import stopwords
print(stopwords.words('spanish'))
list_lite_NAME_TO = df_mov['NAME_TO'].value_counts().sort_values(ascending=False).index[0:10]
list_lite_NAME_TO
df_mov_filter_lite_NAME_TO = df_mov[df_mov['NAME_TO'].isin(list_lite_NAME_TO)]
df_mov_filter_lite_NAME_TO
textos_destino = ''
for row in df_mov_filter_lite_NAME_TO['NAME_TO']:
textos_destino = textos_destino + ' ' + row
## to check the ModuleNotFoundError: No module named 'wordcloud'
## install:
## /anaconda3/bin/python -m pip install wordcloud
import sys
print(sys.executable)
from wordcloud import WordCloud
import matplotlib.pyplot as plt
wc = WordCloud(background_color= 'white')
wc.generate(textos_destino)
plt.axis("off")
plt.imshow(wc, interpolation='bilinear')
plt.show()
```
|
github_jupyter
|
**Chapter 11 – Training Deep Neural Networks**
_This notebook contains all the sample code and solutions to the exercises in chapter 11._
<table align="left">
<td>
<a target="_blank" href="https://colab.research.google.com/github/ageron/handson-ml2/blob/master/11_training_deep_neural_networks.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
</td>
</table>
# Setup
First, let's import a few common modules, ensure MatplotLib plots figures inline and prepare a function to save the figures. We also check that Python 3.5 or later is installed (although Python 2.x may work, it is deprecated so we strongly recommend you use Python 3 instead), as well as Scikit-Learn ≥0.20 and TensorFlow ≥2.0.
```
# Python ≥3.5 is required
import sys
assert sys.version_info >= (3, 5)
# Scikit-Learn ≥0.20 is required
import sklearn
assert sklearn.__version__ >= "0.20"
try:
# %tensorflow_version only exists in Colab.
%tensorflow_version 2.x
except Exception:
pass
# TensorFlow ≥2.0 is required
import tensorflow as tf
from tensorflow import keras
assert tf.__version__ >= "2.0"
# Common imports
import numpy as np
import os
# to make this notebook's output stable across runs
np.random.seed(42)
# To plot pretty figures
%matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rc('axes', labelsize=14)
mpl.rc('xtick', labelsize=12)
mpl.rc('ytick', labelsize=12)
# Where to save the figures
PROJECT_ROOT_DIR = "."
CHAPTER_ID = "deep"
IMAGES_PATH = os.path.join(PROJECT_ROOT_DIR, "images", CHAPTER_ID)
os.makedirs(IMAGES_PATH, exist_ok=True)
def save_fig(fig_id, tight_layout=True, fig_extension="png", resolution=300):
path = os.path.join(IMAGES_PATH, fig_id + "." + fig_extension)
print("Saving figure", fig_id)
if tight_layout:
plt.tight_layout()
plt.savefig(path, format=fig_extension, dpi=resolution)
```
# Vanishing/Exploding Gradients Problem
```
def logit(z):
return 1 / (1 + np.exp(-z))
z = np.linspace(-5, 5, 200)
plt.plot([-5, 5], [0, 0], 'k-')
plt.plot([-5, 5], [1, 1], 'k--')
plt.plot([0, 0], [-0.2, 1.2], 'k-')
plt.plot([-5, 5], [-3/4, 7/4], 'g--')
plt.plot(z, logit(z), "b-", linewidth=2)
props = dict(facecolor='black', shrink=0.1)
plt.annotate('Saturating', xytext=(3.5, 0.7), xy=(5, 1), arrowprops=props, fontsize=14, ha="center")
plt.annotate('Saturating', xytext=(-3.5, 0.3), xy=(-5, 0), arrowprops=props, fontsize=14, ha="center")
plt.annotate('Linear', xytext=(2, 0.2), xy=(0, 0.5), arrowprops=props, fontsize=14, ha="center")
plt.grid(True)
plt.title("Sigmoid activation function", fontsize=14)
plt.axis([-5, 5, -0.2, 1.2])
save_fig("sigmoid_saturation_plot")
plt.show()
```
## Xavier and He Initialization
```
[name for name in dir(keras.initializers) if not name.startswith("_")]
keras.layers.Dense(10, activation="relu", kernel_initializer="he_normal")
init = keras.initializers.VarianceScaling(scale=2., mode='fan_avg',
distribution='uniform')
keras.layers.Dense(10, activation="relu", kernel_initializer=init)
```
## Nonsaturating Activation Functions
### Leaky ReLU
```
def leaky_relu(z, alpha=0.01):
return np.maximum(alpha*z, z)
plt.plot(z, leaky_relu(z, 0.05), "b-", linewidth=2)
plt.plot([-5, 5], [0, 0], 'k-')
plt.plot([0, 0], [-0.5, 4.2], 'k-')
plt.grid(True)
props = dict(facecolor='black', shrink=0.1)
plt.annotate('Leak', xytext=(-3.5, 0.5), xy=(-5, -0.2), arrowprops=props, fontsize=14, ha="center")
plt.title("Leaky ReLU activation function", fontsize=14)
plt.axis([-5, 5, -0.5, 4.2])
save_fig("leaky_relu_plot")
plt.show()
[m for m in dir(keras.activations) if not m.startswith("_")]
[m for m in dir(keras.layers) if "relu" in m.lower()]
```
Let's train a neural network on Fashion MNIST using the Leaky ReLU:
```
(X_train_full, y_train_full), (X_test, y_test) = keras.datasets.fashion_mnist.load_data()
X_train_full = X_train_full / 255.0
X_test = X_test / 255.0
X_valid, X_train = X_train_full[:5000], X_train_full[5000:]
y_valid, y_train = y_train_full[:5000], y_train_full[5000:]
tf.random.set_seed(42)
np.random.seed(42)
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.Dense(300, kernel_initializer="he_normal"),
keras.layers.LeakyReLU(),
keras.layers.Dense(100, kernel_initializer="he_normal"),
keras.layers.LeakyReLU(),
keras.layers.Dense(10, activation="softmax")
])
model.compile(loss="sparse_categorical_crossentropy",
optimizer=keras.optimizers.SGD(lr=1e-3),
metrics=["accuracy"])
history = model.fit(X_train, y_train, epochs=10,
validation_data=(X_valid, y_valid))
```
Now let's try PReLU:
```
tf.random.set_seed(42)
np.random.seed(42)
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.Dense(300, kernel_initializer="he_normal"),
keras.layers.PReLU(),
keras.layers.Dense(100, kernel_initializer="he_normal"),
keras.layers.PReLU(),
keras.layers.Dense(10, activation="softmax")
])
model.compile(loss="sparse_categorical_crossentropy",
optimizer=keras.optimizers.SGD(lr=1e-3),
metrics=["accuracy"])
history = model.fit(X_train, y_train, epochs=10,
validation_data=(X_valid, y_valid))
```
### ELU
```
def elu(z, alpha=1):
return np.where(z < 0, alpha * (np.exp(z) - 1), z)
plt.plot(z, elu(z), "b-", linewidth=2)
plt.plot([-5, 5], [0, 0], 'k-')
plt.plot([-5, 5], [-1, -1], 'k--')
plt.plot([0, 0], [-2.2, 3.2], 'k-')
plt.grid(True)
plt.title(r"ELU activation function ($\alpha=1$)", fontsize=14)
plt.axis([-5, 5, -2.2, 3.2])
save_fig("elu_plot")
plt.show()
```
Implementing ELU in TensorFlow is trivial, just specify the activation function when building each layer:
```
keras.layers.Dense(10, activation="elu")
```
### SELU
This activation function was proposed in this [great paper](https://arxiv.org/pdf/1706.02515.pdf) by Günter Klambauer, Thomas Unterthiner and Andreas Mayr, published in June 2017. During training, a neural network composed exclusively of a stack of dense layers using the SELU activation function and LeCun initialization will self-normalize: the output of each layer will tend to preserve the same mean and variance during training, which solves the vanishing/exploding gradients problem. As a result, this activation function outperforms the other activation functions very significantly for such neural nets, so you should really try it out. Unfortunately, the self-normalizing property of the SELU activation function is easily broken: you cannot use ℓ<sub>1</sub> or ℓ<sub>2</sub> regularization, regular dropout, max-norm, skip connections or other non-sequential topologies (so recurrent neural networks won't self-normalize). However, in practice it works quite well with sequential CNNs. If you break self-normalization, SELU will not necessarily outperform other activation functions.
```
from scipy.special import erfc
# alpha and scale to self normalize with mean 0 and standard deviation 1
# (see equation 14 in the paper):
alpha_0_1 = -np.sqrt(2 / np.pi) / (erfc(1/np.sqrt(2)) * np.exp(1/2) - 1)
scale_0_1 = (1 - erfc(1 / np.sqrt(2)) * np.sqrt(np.e)) * np.sqrt(2 * np.pi) * (2 * erfc(np.sqrt(2))*np.e**2 + np.pi*erfc(1/np.sqrt(2))**2*np.e - 2*(2+np.pi)*erfc(1/np.sqrt(2))*np.sqrt(np.e)+np.pi+2)**(-1/2)
def selu(z, scale=scale_0_1, alpha=alpha_0_1):
return scale * elu(z, alpha)
plt.plot(z, selu(z), "b-", linewidth=2)
plt.plot([-5, 5], [0, 0], 'k-')
plt.plot([-5, 5], [-1.758, -1.758], 'k--')
plt.plot([0, 0], [-2.2, 3.2], 'k-')
plt.grid(True)
plt.title("SELU activation function", fontsize=14)
plt.axis([-5, 5, -2.2, 3.2])
save_fig("selu_plot")
plt.show()
```
By default, the SELU hyperparameters (`scale` and `alpha`) are tuned in such a way that the mean output of each neuron remains close to 0, and the standard deviation remains close to 1 (assuming the inputs are standardized with mean 0 and standard deviation 1 too). Using this activation function, even a 1,000 layer deep neural network preserves roughly mean 0 and standard deviation 1 across all layers, avoiding the exploding/vanishing gradients problem:
```
np.random.seed(42)
Z = np.random.normal(size=(500, 100)) # standardized inputs
for layer in range(1000):
W = np.random.normal(size=(100, 100), scale=np.sqrt(1 / 100)) # LeCun initialization
Z = selu(np.dot(Z, W))
means = np.mean(Z, axis=0).mean()
stds = np.std(Z, axis=0).mean()
if layer % 100 == 0:
print("Layer {}: mean {:.2f}, std deviation {:.2f}".format(layer, means, stds))
```
Using SELU is easy:
```
keras.layers.Dense(10, activation="selu",
kernel_initializer="lecun_normal")
```
Let's create a neural net for Fashion MNIST with 100 hidden layers, using the SELU activation function:
```
np.random.seed(42)
tf.random.set_seed(42)
model = keras.models.Sequential()
model.add(keras.layers.Flatten(input_shape=[28, 28]))
model.add(keras.layers.Dense(300, activation="selu",
kernel_initializer="lecun_normal"))
for layer in range(99):
model.add(keras.layers.Dense(100, activation="selu",
kernel_initializer="lecun_normal"))
model.add(keras.layers.Dense(10, activation="softmax"))
model.compile(loss="sparse_categorical_crossentropy",
optimizer=keras.optimizers.SGD(lr=1e-3),
metrics=["accuracy"])
```
Now let's train it. Do not forget to scale the inputs to mean 0 and standard deviation 1:
```
pixel_means = X_train.mean(axis=0, keepdims=True)
pixel_stds = X_train.std(axis=0, keepdims=True)
X_train_scaled = (X_train - pixel_means) / pixel_stds
X_valid_scaled = (X_valid - pixel_means) / pixel_stds
X_test_scaled = (X_test - pixel_means) / pixel_stds
history = model.fit(X_train_scaled, y_train, epochs=5,
validation_data=(X_valid_scaled, y_valid))
```
Now look at what happens if we try to use the ReLU activation function instead:
```
np.random.seed(42)
tf.random.set_seed(42)
model = keras.models.Sequential()
model.add(keras.layers.Flatten(input_shape=[28, 28]))
model.add(keras.layers.Dense(300, activation="relu", kernel_initializer="he_normal"))
for layer in range(99):
model.add(keras.layers.Dense(100, activation="relu", kernel_initializer="he_normal"))
model.add(keras.layers.Dense(10, activation="softmax"))
model.compile(loss="sparse_categorical_crossentropy",
optimizer=keras.optimizers.SGD(lr=1e-3),
metrics=["accuracy"])
history = model.fit(X_train_scaled, y_train, epochs=5,
validation_data=(X_valid_scaled, y_valid))
```
Not great at all, we suffered from the vanishing/exploding gradients problem.
# Batch Normalization
```
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.BatchNormalization(),
keras.layers.Dense(300, activation="relu"),
keras.layers.BatchNormalization(),
keras.layers.Dense(100, activation="relu"),
keras.layers.BatchNormalization(),
keras.layers.Dense(10, activation="softmax")
])
model.summary()
bn1 = model.layers[1]
[(var.name, var.trainable) for var in bn1.variables]
bn1.updates
model.compile(loss="sparse_categorical_crossentropy",
optimizer=keras.optimizers.SGD(lr=1e-3),
metrics=["accuracy"])
history = model.fit(X_train, y_train, epochs=10,
validation_data=(X_valid, y_valid))
```
Sometimes applying BN before the activation function works better (there's a debate on this topic). Moreover, the layer before a `BatchNormalization` layer does not need to have bias terms, since the `BatchNormalization` layer some as well, it would be a waste of parameters, so you can set `use_bias=False` when creating those layers:
```
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.BatchNormalization(),
keras.layers.Dense(300, use_bias=False),
keras.layers.BatchNormalization(),
keras.layers.Activation("relu"),
keras.layers.Dense(100, use_bias=False),
keras.layers.Activation("relu"),
keras.layers.BatchNormalization(),
keras.layers.Dense(10, activation="softmax")
])
model.compile(loss="sparse_categorical_crossentropy",
optimizer=keras.optimizers.SGD(lr=1e-3),
metrics=["accuracy"])
history = model.fit(X_train, y_train, epochs=10,
validation_data=(X_valid, y_valid))
```
## Gradient Clipping
All Keras optimizers accept `clipnorm` or `clipvalue` arguments:
```
optimizer = keras.optimizers.SGD(clipvalue=1.0)
optimizer = keras.optimizers.SGD(clipnorm=1.0)
```
## Reusing Pretrained Layers
### Reusing a Keras model
Let's split the fashion MNIST training set in two:
* `X_train_A`: all images of all items except for sandals and shirts (classes 5 and 6).
* `X_train_B`: a much smaller training set of just the first 200 images of sandals or shirts.
The validation set and the test set are also split this way, but without restricting the number of images.
We will train a model on set A (classification task with 8 classes), and try to reuse it to tackle set B (binary classification). We hope to transfer a little bit of knowledge from task A to task B, since classes in set A (sneakers, ankle boots, coats, t-shirts, etc.) are somewhat similar to classes in set B (sandals and shirts). However, since we are using `Dense` layers, only patterns that occur at the same location can be reused (in contrast, convolutional layers will transfer much better, since learned patterns can be detected anywhere on the image, as we will see in the CNN chapter).
```
def split_dataset(X, y):
y_5_or_6 = (y == 5) | (y == 6) # sandals or shirts
y_A = y[~y_5_or_6]
y_A[y_A > 6] -= 2 # class indices 7, 8, 9 should be moved to 5, 6, 7
y_B = (y[y_5_or_6] == 6).astype(np.float32) # binary classification task: is it a shirt (class 6)?
return ((X[~y_5_or_6], y_A),
(X[y_5_or_6], y_B))
(X_train_A, y_train_A), (X_train_B, y_train_B) = split_dataset(X_train, y_train)
(X_valid_A, y_valid_A), (X_valid_B, y_valid_B) = split_dataset(X_valid, y_valid)
(X_test_A, y_test_A), (X_test_B, y_test_B) = split_dataset(X_test, y_test)
X_train_B = X_train_B[:200]
y_train_B = y_train_B[:200]
X_train_A.shape
X_train_B.shape
y_train_A[:30]
y_train_B[:30]
tf.random.set_seed(42)
np.random.seed(42)
model_A = keras.models.Sequential()
model_A.add(keras.layers.Flatten(input_shape=[28, 28]))
for n_hidden in (300, 100, 50, 50, 50):
model_A.add(keras.layers.Dense(n_hidden, activation="selu"))
model_A.add(keras.layers.Dense(8, activation="softmax"))
model_A.compile(loss="sparse_categorical_crossentropy",
optimizer=keras.optimizers.SGD(lr=1e-3),
metrics=["accuracy"])
history = model_A.fit(X_train_A, y_train_A, epochs=20,
validation_data=(X_valid_A, y_valid_A))
model_A.save("my_model_A.h5")
model_B = keras.models.Sequential()
model_B.add(keras.layers.Flatten(input_shape=[28, 28]))
for n_hidden in (300, 100, 50, 50, 50):
model_B.add(keras.layers.Dense(n_hidden, activation="selu"))
model_B.add(keras.layers.Dense(1, activation="sigmoid"))
model_B.compile(loss="binary_crossentropy",
optimizer=keras.optimizers.SGD(lr=1e-3),
metrics=["accuracy"])
history = model_B.fit(X_train_B, y_train_B, epochs=20,
validation_data=(X_valid_B, y_valid_B))
model.summary()
model_A = keras.models.load_model("my_model_A.h5")
model_B_on_A = keras.models.Sequential(model_A.layers[:-1])
model_B_on_A.add(keras.layers.Dense(1, activation="sigmoid"))
model_A_clone = keras.models.clone_model(model_A)
model_A_clone.set_weights(model_A.get_weights())
for layer in model_B_on_A.layers[:-1]:
layer.trainable = False
model_B_on_A.compile(loss="binary_crossentropy",
optimizer=keras.optimizers.SGD(lr=1e-3),
metrics=["accuracy"])
history = model_B_on_A.fit(X_train_B, y_train_B, epochs=4,
validation_data=(X_valid_B, y_valid_B))
for layer in model_B_on_A.layers[:-1]:
layer.trainable = True
model_B_on_A.compile(loss="binary_crossentropy",
optimizer=keras.optimizers.SGD(lr=1e-3),
metrics=["accuracy"])
history = model_B_on_A.fit(X_train_B, y_train_B, epochs=16,
validation_data=(X_valid_B, y_valid_B))
```
So, what's the final verdict?
```
model_B.evaluate(X_test_B, y_test_B)
model_B_on_A.evaluate(X_test_B, y_test_B)
```
Great! We got quite a bit of transfer: the error rate dropped by a factor of almost 4!
```
(100 - 97.05) / (100 - 99.25)
```
# Faster Optimizers
## Momentum optimization
```
optimizer = keras.optimizers.SGD(lr=0.001, momentum=0.9)
```
## Nesterov Accelerated Gradient
```
optimizer = keras.optimizers.SGD(lr=0.001, momentum=0.9, nesterov=True)
```
## AdaGrad
```
optimizer = keras.optimizers.Adagrad(lr=0.001)
```
## RMSProp
```
optimizer = keras.optimizers.RMSprop(lr=0.001, rho=0.9)
```
## Adam Optimization
```
optimizer = keras.optimizers.Adam(lr=0.001, beta_1=0.9, beta_2=0.999)
```
## Adamax Optimization
```
optimizer = keras.optimizers.Adamax(lr=0.001, beta_1=0.9, beta_2=0.999)
```
## Nadam Optimization
```
optimizer = keras.optimizers.Nadam(lr=0.001, beta_1=0.9, beta_2=0.999)
```
## Learning Rate Scheduling
### Power Scheduling
```lr = lr0 / (1 + steps / s)**c```
* Keras uses `c=1` and `s = 1 / decay`
```
optimizer = keras.optimizers.SGD(lr=0.01, decay=1e-4)
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.Dense(300, activation="selu", kernel_initializer="lecun_normal"),
keras.layers.Dense(100, activation="selu", kernel_initializer="lecun_normal"),
keras.layers.Dense(10, activation="softmax")
])
model.compile(loss="sparse_categorical_crossentropy", optimizer=optimizer, metrics=["accuracy"])
n_epochs = 25
history = model.fit(X_train_scaled, y_train, epochs=n_epochs,
validation_data=(X_valid_scaled, y_valid))
learning_rate = 0.01
decay = 1e-4
batch_size = 32
n_steps_per_epoch = len(X_train) // batch_size
epochs = np.arange(n_epochs)
lrs = learning_rate / (1 + decay * epochs * n_steps_per_epoch)
plt.plot(epochs, lrs, "o-")
plt.axis([0, n_epochs - 1, 0, 0.01])
plt.xlabel("Epoch")
plt.ylabel("Learning Rate")
plt.title("Power Scheduling", fontsize=14)
plt.grid(True)
plt.show()
```
### Exponential Scheduling
```lr = lr0 * 0.1**(epoch / s)```
```
def exponential_decay_fn(epoch):
return 0.01 * 0.1**(epoch / 20)
def exponential_decay(lr0, s):
def exponential_decay_fn(epoch):
return lr0 * 0.1**(epoch / s)
return exponential_decay_fn
exponential_decay_fn = exponential_decay(lr0=0.01, s=20)
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.Dense(300, activation="selu", kernel_initializer="lecun_normal"),
keras.layers.Dense(100, activation="selu", kernel_initializer="lecun_normal"),
keras.layers.Dense(10, activation="softmax")
])
model.compile(loss="sparse_categorical_crossentropy", optimizer="nadam", metrics=["accuracy"])
n_epochs = 25
lr_scheduler = keras.callbacks.LearningRateScheduler(exponential_decay_fn)
history = model.fit(X_train_scaled, y_train, epochs=n_epochs,
validation_data=(X_valid_scaled, y_valid),
callbacks=[lr_scheduler])
plt.plot(history.epoch, history.history["lr"], "o-")
plt.axis([0, n_epochs - 1, 0, 0.011])
plt.xlabel("Epoch")
plt.ylabel("Learning Rate")
plt.title("Exponential Scheduling", fontsize=14)
plt.grid(True)
plt.show()
```
The schedule function can take the current learning rate as a second argument:
```
def exponential_decay_fn(epoch, lr):
return lr * 0.1**(1 / 20)
```
If you want to update the learning rate at each iteration rather than at each epoch, you must write your own callback class:
```
K = keras.backend
class ExponentialDecay(keras.callbacks.Callback):
def __init__(self, s=40000):
super().__init__()
self.s = s
def on_batch_begin(self, batch, logs=None):
# Note: the `batch` argument is reset at each epoch
lr = K.get_value(self.model.optimizer.lr)
K.set_value(self.model.optimizer.lr, lr * 0.1**(1 / s))
def on_epoch_end(self, epoch, logs=None):
logs = logs or {}
logs['lr'] = K.get_value(self.model.optimizer.lr)
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.Dense(300, activation="selu", kernel_initializer="lecun_normal"),
keras.layers.Dense(100, activation="selu", kernel_initializer="lecun_normal"),
keras.layers.Dense(10, activation="softmax")
])
lr0 = 0.01
optimizer = keras.optimizers.Nadam(lr=lr0)
model.compile(loss="sparse_categorical_crossentropy", optimizer=optimizer, metrics=["accuracy"])
n_epochs = 25
s = 20 * len(X_train) // 32 # number of steps in 20 epochs (batch size = 32)
exp_decay = ExponentialDecay(s)
history = model.fit(X_train_scaled, y_train, epochs=n_epochs,
validation_data=(X_valid_scaled, y_valid),
callbacks=[exp_decay])
n_steps = n_epochs * len(X_train) // 32
steps = np.arange(n_steps)
lrs = lr0 * 0.1**(steps / s)
plt.plot(steps, lrs, "-", linewidth=2)
plt.axis([0, n_steps - 1, 0, lr0 * 1.1])
plt.xlabel("Batch")
plt.ylabel("Learning Rate")
plt.title("Exponential Scheduling (per batch)", fontsize=14)
plt.grid(True)
plt.show()
```
### Piecewise Constant Scheduling
```
def piecewise_constant_fn(epoch):
if epoch < 5:
return 0.01
elif epoch < 15:
return 0.005
else:
return 0.001
def piecewise_constant(boundaries, values):
boundaries = np.array([0] + boundaries)
values = np.array(values)
def piecewise_constant_fn(epoch):
return values[np.argmax(boundaries > epoch) - 1]
return piecewise_constant_fn
piecewise_constant_fn = piecewise_constant([5, 15], [0.01, 0.005, 0.001])
lr_scheduler = keras.callbacks.LearningRateScheduler(piecewise_constant_fn)
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.Dense(300, activation="selu", kernel_initializer="lecun_normal"),
keras.layers.Dense(100, activation="selu", kernel_initializer="lecun_normal"),
keras.layers.Dense(10, activation="softmax")
])
model.compile(loss="sparse_categorical_crossentropy", optimizer="nadam", metrics=["accuracy"])
n_epochs = 25
history = model.fit(X_train_scaled, y_train, epochs=n_epochs,
validation_data=(X_valid_scaled, y_valid),
callbacks=[lr_scheduler])
plt.plot(history.epoch, [piecewise_constant_fn(epoch) for epoch in history.epoch], "o-")
plt.axis([0, n_epochs - 1, 0, 0.011])
plt.xlabel("Epoch")
plt.ylabel("Learning Rate")
plt.title("Piecewise Constant Scheduling", fontsize=14)
plt.grid(True)
plt.show()
```
### Performance Scheduling
```
tf.random.set_seed(42)
np.random.seed(42)
lr_scheduler = keras.callbacks.ReduceLROnPlateau(factor=0.5, patience=5)
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.Dense(300, activation="selu", kernel_initializer="lecun_normal"),
keras.layers.Dense(100, activation="selu", kernel_initializer="lecun_normal"),
keras.layers.Dense(10, activation="softmax")
])
optimizer = keras.optimizers.SGD(lr=0.02, momentum=0.9)
model.compile(loss="sparse_categorical_crossentropy", optimizer=optimizer, metrics=["accuracy"])
n_epochs = 25
history = model.fit(X_train_scaled, y_train, epochs=n_epochs,
validation_data=(X_valid_scaled, y_valid),
callbacks=[lr_scheduler])
plt.plot(history.epoch, history.history["lr"], "bo-")
plt.xlabel("Epoch")
plt.ylabel("Learning Rate", color='b')
plt.tick_params('y', colors='b')
plt.gca().set_xlim(0, n_epochs - 1)
plt.grid(True)
ax2 = plt.gca().twinx()
ax2.plot(history.epoch, history.history["val_loss"], "r^-")
ax2.set_ylabel('Validation Loss', color='r')
ax2.tick_params('y', colors='r')
plt.title("Reduce LR on Plateau", fontsize=14)
plt.show()
```
### tf.keras schedulers
```
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.Dense(300, activation="selu", kernel_initializer="lecun_normal"),
keras.layers.Dense(100, activation="selu", kernel_initializer="lecun_normal"),
keras.layers.Dense(10, activation="softmax")
])
s = 20 * len(X_train) // 32 # number of steps in 20 epochs (batch size = 32)
learning_rate = keras.optimizers.schedules.ExponentialDecay(0.01, s, 0.1)
optimizer = keras.optimizers.SGD(learning_rate)
model.compile(loss="sparse_categorical_crossentropy", optimizer=optimizer, metrics=["accuracy"])
n_epochs = 25
history = model.fit(X_train_scaled, y_train, epochs=n_epochs,
validation_data=(X_valid_scaled, y_valid))
```
For piecewise constant scheduling, try this:
```
learning_rate = keras.optimizers.schedules.PiecewiseConstantDecay(
boundaries=[5. * n_steps_per_epoch, 15. * n_steps_per_epoch],
values=[0.01, 0.005, 0.001])
```
### 1Cycle scheduling
```
K = keras.backend
class ExponentialLearningRate(keras.callbacks.Callback):
def __init__(self, factor):
self.factor = factor
self.rates = []
self.losses = []
def on_batch_end(self, batch, logs):
self.rates.append(K.get_value(self.model.optimizer.lr))
self.losses.append(logs["loss"])
K.set_value(self.model.optimizer.lr, self.model.optimizer.lr * self.factor)
def find_learning_rate(model, X, y, epochs=1, batch_size=32, min_rate=10**-5, max_rate=10):
init_weights = model.get_weights()
iterations = len(X) // batch_size * epochs
factor = np.exp(np.log(max_rate / min_rate) / iterations)
init_lr = K.get_value(model.optimizer.lr)
K.set_value(model.optimizer.lr, min_rate)
exp_lr = ExponentialLearningRate(factor)
history = model.fit(X, y, epochs=epochs, batch_size=batch_size,
callbacks=[exp_lr])
K.set_value(model.optimizer.lr, init_lr)
model.set_weights(init_weights)
return exp_lr.rates, exp_lr.losses
def plot_lr_vs_loss(rates, losses):
plt.plot(rates, losses)
plt.gca().set_xscale('log')
plt.hlines(min(losses), min(rates), max(rates))
plt.axis([min(rates), max(rates), min(losses), (losses[0] + min(losses)) / 2])
plt.xlabel("Learning rate")
plt.ylabel("Loss")
tf.random.set_seed(42)
np.random.seed(42)
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.Dense(300, activation="selu", kernel_initializer="lecun_normal"),
keras.layers.Dense(100, activation="selu", kernel_initializer="lecun_normal"),
keras.layers.Dense(10, activation="softmax")
])
model.compile(loss="sparse_categorical_crossentropy",
optimizer=keras.optimizers.SGD(lr=1e-3),
metrics=["accuracy"])
batch_size = 128
rates, losses = find_learning_rate(model, X_train_scaled, y_train, epochs=1, batch_size=batch_size)
plot_lr_vs_loss(rates, losses)
class OneCycleScheduler(keras.callbacks.Callback):
def __init__(self, iterations, max_rate, start_rate=None,
last_iterations=None, last_rate=None):
self.iterations = iterations
self.max_rate = max_rate
self.start_rate = start_rate or max_rate / 10
self.last_iterations = last_iterations or iterations // 10 + 1
self.half_iteration = (iterations - self.last_iterations) // 2
self.last_rate = last_rate or self.start_rate / 1000
self.iteration = 0
def _interpolate(self, iter1, iter2, rate1, rate2):
return ((rate2 - rate1) * (self.iteration - iter1)
/ (iter2 - iter1) + rate1)
def on_batch_begin(self, batch, logs):
if self.iteration < self.half_iteration:
rate = self._interpolate(0, self.half_iteration, self.start_rate, self.max_rate)
elif self.iteration < 2 * self.half_iteration:
rate = self._interpolate(self.half_iteration, 2 * self.half_iteration,
self.max_rate, self.start_rate)
else:
rate = self._interpolate(2 * self.half_iteration, self.iterations,
self.start_rate, self.last_rate)
rate = max(rate, self.last_rate)
self.iteration += 1
K.set_value(self.model.optimizer.lr, rate)
n_epochs = 25
onecycle = OneCycleScheduler(len(X_train) // batch_size * n_epochs, max_rate=0.05)
history = model.fit(X_train_scaled, y_train, epochs=n_epochs, batch_size=batch_size,
validation_data=(X_valid_scaled, y_valid),
callbacks=[onecycle])
```
# Avoiding Overfitting Through Regularization
## $\ell_1$ and $\ell_2$ regularization
```
layer = keras.layers.Dense(100, activation="elu",
kernel_initializer="he_normal",
kernel_regularizer=keras.regularizers.l2(0.01))
# or l1(0.1) for ℓ1 regularization with a factor or 0.1
# or l1_l2(0.1, 0.01) for both ℓ1 and ℓ2 regularization, with factors 0.1 and 0.01 respectively
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.Dense(300, activation="elu",
kernel_initializer="he_normal",
kernel_regularizer=keras.regularizers.l2(0.01)),
keras.layers.Dense(100, activation="elu",
kernel_initializer="he_normal",
kernel_regularizer=keras.regularizers.l2(0.01)),
keras.layers.Dense(10, activation="softmax",
kernel_regularizer=keras.regularizers.l2(0.01))
])
model.compile(loss="sparse_categorical_crossentropy", optimizer="nadam", metrics=["accuracy"])
n_epochs = 2
history = model.fit(X_train_scaled, y_train, epochs=n_epochs,
validation_data=(X_valid_scaled, y_valid))
from functools import partial
RegularizedDense = partial(keras.layers.Dense,
activation="elu",
kernel_initializer="he_normal",
kernel_regularizer=keras.regularizers.l2(0.01))
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
RegularizedDense(300),
RegularizedDense(100),
RegularizedDense(10, activation="softmax")
])
model.compile(loss="sparse_categorical_crossentropy", optimizer="nadam", metrics=["accuracy"])
n_epochs = 2
history = model.fit(X_train_scaled, y_train, epochs=n_epochs,
validation_data=(X_valid_scaled, y_valid))
```
## Dropout
```
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.Dropout(rate=0.2),
keras.layers.Dense(300, activation="elu", kernel_initializer="he_normal"),
keras.layers.Dropout(rate=0.2),
keras.layers.Dense(100, activation="elu", kernel_initializer="he_normal"),
keras.layers.Dropout(rate=0.2),
keras.layers.Dense(10, activation="softmax")
])
model.compile(loss="sparse_categorical_crossentropy", optimizer="nadam", metrics=["accuracy"])
n_epochs = 2
history = model.fit(X_train_scaled, y_train, epochs=n_epochs,
validation_data=(X_valid_scaled, y_valid))
```
## Alpha Dropout
```
tf.random.set_seed(42)
np.random.seed(42)
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.AlphaDropout(rate=0.2),
keras.layers.Dense(300, activation="selu", kernel_initializer="lecun_normal"),
keras.layers.AlphaDropout(rate=0.2),
keras.layers.Dense(100, activation="selu", kernel_initializer="lecun_normal"),
keras.layers.AlphaDropout(rate=0.2),
keras.layers.Dense(10, activation="softmax")
])
optimizer = keras.optimizers.SGD(lr=0.01, momentum=0.9, nesterov=True)
model.compile(loss="sparse_categorical_crossentropy", optimizer=optimizer, metrics=["accuracy"])
n_epochs = 20
history = model.fit(X_train_scaled, y_train, epochs=n_epochs,
validation_data=(X_valid_scaled, y_valid))
model.evaluate(X_test_scaled, y_test)
model.evaluate(X_train_scaled, y_train)
history = model.fit(X_train_scaled, y_train)
```
## MC Dropout
```
tf.random.set_seed(42)
np.random.seed(42)
y_probas = np.stack([model(X_test_scaled, training=True)
for sample in range(100)])
y_proba = y_probas.mean(axis=0)
y_std = y_probas.std(axis=0)
np.round(model.predict(X_test_scaled[:1]), 2)
np.round(y_probas[:, :1], 2)
np.round(y_proba[:1], 2)
y_std = y_probas.std(axis=0)
np.round(y_std[:1], 2)
y_pred = np.argmax(y_proba, axis=1)
accuracy = np.sum(y_pred == y_test) / len(y_test)
accuracy
class MCDropout(keras.layers.Dropout):
def call(self, inputs):
return super().call(inputs, training=True)
class MCAlphaDropout(keras.layers.AlphaDropout):
def call(self, inputs):
return super().call(inputs, training=True)
tf.random.set_seed(42)
np.random.seed(42)
mc_model = keras.models.Sequential([
MCAlphaDropout(layer.rate) if isinstance(layer, keras.layers.AlphaDropout) else layer
for layer in model.layers
])
mc_model.summary()
optimizer = keras.optimizers.SGD(lr=0.01, momentum=0.9, nesterov=True)
mc_model.compile(loss="sparse_categorical_crossentropy", optimizer=optimizer, metrics=["accuracy"])
mc_model.set_weights(model.get_weights())
```
Now we can use the model with MC Dropout:
```
np.round(np.mean([mc_model.predict(X_test_scaled[:1]) for sample in range(100)], axis=0), 2)
```
## Max norm
```
layer = keras.layers.Dense(100, activation="selu", kernel_initializer="lecun_normal",
kernel_constraint=keras.constraints.max_norm(1.))
MaxNormDense = partial(keras.layers.Dense,
activation="selu", kernel_initializer="lecun_normal",
kernel_constraint=keras.constraints.max_norm(1.))
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
MaxNormDense(300),
MaxNormDense(100),
keras.layers.Dense(10, activation="softmax")
])
model.compile(loss="sparse_categorical_crossentropy", optimizer="nadam", metrics=["accuracy"])
n_epochs = 2
history = model.fit(X_train_scaled, y_train, epochs=n_epochs,
validation_data=(X_valid_scaled, y_valid))
```
# Exercises
## 1. to 7.
See appendix A.
## 8. Deep Learning
### 8.1.
_Exercise: Build a DNN with five hidden layers of 100 neurons each, He initialization, and the ELU activation function._
### 8.2.
_Exercise: Using Adam optimization and early stopping, try training it on MNIST but only on digits 0 to 4, as we will use transfer learning for digits 5 to 9 in the next exercise. You will need a softmax output layer with five neurons, and as always make sure to save checkpoints at regular intervals and save the final model so you can reuse it later._
### 8.3.
_Exercise: Tune the hyperparameters using cross-validation and see what precision you can achieve._
### 8.4.
_Exercise: Now try adding Batch Normalization and compare the learning curves: is it converging faster than before? Does it produce a better model?_
### 8.5.
_Exercise: is the model overfitting the training set? Try adding dropout to every layer and try again. Does it help?_
## 9. Transfer learning
### 9.1.
_Exercise: create a new DNN that reuses all the pretrained hidden layers of the previous model, freezes them, and replaces the softmax output layer with a new one._
### 9.2.
_Exercise: train this new DNN on digits 5 to 9, using only 100 images per digit, and time how long it takes. Despite this small number of examples, can you achieve high precision?_
### 9.3.
_Exercise: try caching the frozen layers, and train the model again: how much faster is it now?_
### 9.4.
_Exercise: try again reusing just four hidden layers instead of five. Can you achieve a higher precision?_
### 9.5.
_Exercise: now unfreeze the top two hidden layers and continue training: can you get the model to perform even better?_
## 10. Pretraining on an auxiliary task
In this exercise you will build a DNN that compares two MNIST digit images and predicts whether they represent the same digit or not. Then you will reuse the lower layers of this network to train an MNIST classifier using very little training data.
### 10.1.
Exercise: _Start by building two DNNs (let's call them DNN A and B), both similar to the one you built earlier but without the output layer: each DNN should have five hidden layers of 100 neurons each, He initialization, and ELU activation. Next, add one more hidden layer with 10 units on top of both DNNs. You should use the `keras.layers.concatenate()` function to concatenate the outputs of both DNNs, then feed the result to the hidden layer. Finally, add an output layer with a single neuron using the logistic activation function._
### 10.2.
_Exercise: split the MNIST training set in two sets: split #1 should containing 55,000 images, and split #2 should contain contain 5,000 images. Create a function that generates a training batch where each instance is a pair of MNIST images picked from split #1. Half of the training instances should be pairs of images that belong to the same class, while the other half should be images from different classes. For each pair, the training label should be 0 if the images are from the same class, or 1 if they are from different classes._
### 10.3.
_Exercise: train the DNN on this training set. For each image pair, you can simultaneously feed the first image to DNN A and the second image to DNN B. The whole network will gradually learn to tell whether two images belong to the same class or not._
### 10.4.
_Exercise: now create a new DNN by reusing and freezing the hidden layers of DNN A and adding a softmax output layer on top with 10 neurons. Train this network on split #2 and see if you can achieve high performance despite having only 500 images per class._
|
github_jupyter
|
```
import os
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns
sns.set_style("whitegrid", {'axes.grid' : False})
import joblib
import catboost
import xgboost as xgb
import lightgbm as lgb
from category_encoders import BinaryEncoder
from sklearn.metrics import mean_squared_error
from sklearn.ensemble import ExtraTreesRegressor
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import FunctionTransformer
def run_lgbm(X_train, X_test, y_train, y_test, feature_names, categorical_features='auto', model_params=None, fit_params=None, seed=21):
X_train_GBM = lgb.Dataset(X_train, label=y_train, feature_name=feature_names, categorical_feature=categorical_features, free_raw_data=False)
X_test_GBM = lgb.Dataset(X_test, label=y_test, reference=X_train_GBM, feature_name=feature_names, free_raw_data=False)
if model_params is None:
model_params = {'seed': seed, 'num_threads': 16, 'objective':'root_mean_squared_error',
'metric': ['root_mean_squared_error'] }
if fit_params is None:
fit_params = {'verbose_eval': True, 'num_boost_round': 300, 'valid_sets': [X_test_GBM],
'early_stopping_rounds': 30,'categorical_feature': categorical_features, 'feature_name': feature_names}
model = lgb.train(model_params, X_train_GBM, **fit_params)
y_pred = model.predict(X_test, model.best_iteration)
return model, y_pred, mean_squared_error(y_test, y_pred)
def run_lr(X_train, X_test, y_train, y_test, model_params=None):
if model_params is None:
model_params = {'n_jobs': 16}
model = LinearRegression(**model_params)
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
return model, y_pred, mean_squared_error(y_test, y_pred)
def run_etr(X_train, X_test, y_train, y_test, model_params=None, seed=21):
if model_params is None:
model_params = {'verbose': 1, 'n_estimators': 300, 'criterion': 'mse', 'n_jobs': 16, 'random_state': seed}
model = ExtraTreesRegressor(**model_params)
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
return model, y_pred, mean_squared_error(y_test, y_pred)
def run_xgb(X_train, X_test, y_train, y_test, feature_names, model_params=None, fit_params=None, seed=21):
dtrain = xgb.DMatrix(X_train, y_train, feature_names=feature_names)
dtest = xgb.DMatrix(X_test, y_test, feature_names=feature_names)
if model_params is None:
model_params = {'booster': 'gbtree', 'nthread': 16, 'objective': 'reg:linear', 'eval_metric': 'rmse', 'seed': seed,
'verbosity': 1}
if fit_params is None:
fit_params = {'num_boost_round': 300, 'evals': [(dtest, 'eval')], 'early_stopping_rounds': 30}
model = xgb.train(model_params, dtrain, **fit_params)
y_pred = model.predict(dtest)
return model, y_pred, mean_squared_error(y_test, y_pred)
def run_catb(X_train, X_test, y_train, y_test, feature_names, cat_features=None, model_params=None, fit_params=None, predict_params=None, seed=21):
train_pool = catboost.Pool(X_train, y_train, cat_features=cat_features)
test_pool = catboost.Pool(X_test, y_test, cat_features=cat_features)
if model_params is None:
model_params = {'n_estimators': 300, 'thread_count': 16, 'loss_function': 'RMSE', 'eval_metric': 'RMSE',
'random_state': seed, 'verbose': True}
if fit_params is None:
fit_params = {'use_best_model': True, 'eval_set': test_pool}
if predict_params is None:
predict_params = {'thread_count': 16}
model = catboost.CatBoostRegressor(**model_params)
model.fit(train_pool, **fit_params)
y_pred = model.predict(test_pool, **predict_params)
return model, y_pred, mean_squared_error(y_test, y_pred)
df_train_dataset = pd.read_pickle('data/df/df_train_dataset.pkl')
df_validation_dataset = pd.read_pickle('data/df/df_validation_dataset.pkl')
continuous_features = joblib.load('data/iterables/continuous_features.joblib')
categorical_features = joblib.load('data/iterables/categorical_features.joblib')
categorical_features_encoded = joblib.load('data/iterables/categorical_features_encoded.joblib')
target_features = joblib.load('data/iterables/target_features.joblib')
target_transformer = joblib.load('models/preprocessing/target_transformer.joblib')
df_train_dataset.shape, df_validation_dataset.shape
X = df_train_dataset[categorical_features_encoded + continuous_features]
y = df_train_dataset[target_features].values.flatten()
print(X.shape, y.shape)
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.8, test_size=0.2, shuffle=True, random_state=10)
# https://github.com/scikit-learn/scikit-learn/issues/8723
X_train = X_train.copy()
X_test = X_test.copy()
print(X_train.shape, X_test.shape, y_train.shape, y_test.shape)
X_train.reset_index(inplace=True, drop=True)
X_test.reset_index(inplace=True, drop=True)
```
## Linear reg
```
reg_linear, y_pred, score = run_lr(X_train, X_test, y_train, y_test)
print('mse', score, 'rmse', score ** .5)
y_pred_val = reg_linear.predict(df_validation_dataset[categorical_features_encoded + continuous_features].values)
y_pred_val = target_transformer.inverse_transform(np.expand_dims(y_pred_val, axis=1))
```
## Xgb
```
reg_xgb, y_pred, score = run_xgb(X_train, X_test, y_train, y_test, feature_names=categorical_features_encoded + continuous_features)
print('mse', score, 'rmse', score ** .5)
d_val = xgb.DMatrix(df_validation_dataset[categorical_features_encoded + continuous_features].values, feature_names=categorical_features_encoded + continuous_features)
y_pred_val = reg_xgb.predict(d_val)
y_pred_val = target_transformer.inverse_transform(np.expand_dims(y_pred_val, axis=1))
df_validation_dataset[target_features] = y_pred_val
df_validation_dataset[['reservation_id', 'amount_spent_per_room_night_scaled']].to_csv('submission.csv', index=False)
fig, ax = plt.subplots(nrows=1, ncols=1)
fig.set_size_inches(24, 24)
xgb.plot_importance(reg_xgb, ax=ax, max_num_features=100, height=0.5);
```
## Lgbm
```
df_train_dataset = pd.read_pickle('data/df/df_train_dataset.pkl')
df_validation_dataset = pd.read_pickle('data/df/df_validation_dataset.pkl')
continuous_features = joblib.load('data/iterables/continuous_features.joblib')
categorical_features = joblib.load('data/iterables/categorical_features.joblib')
target_features = joblib.load('data/iterables/target_features.joblib')
target_transformer = joblib.load('models/preprocessing/target_transformer.joblib')
df_train_dataset.shape, df_validation_dataset.shape
X = df_train_dataset[categorical_features + continuous_features]
y = df_train_dataset[target_features].values.flatten()
print(X.shape, y.shape)
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.8, test_size=0.2, shuffle=True, random_state=10)
# https://github.com/scikit-learn/scikit-learn/issues/8723
X_train = X_train.copy()
X_test = X_test.copy()
print(X_train.shape, X_test.shape, y_train.shape, y_test.shape)
X_train.reset_index(inplace=True, drop=True)
X_test.reset_index(inplace=True, drop=True)
feature_names = categorical_features + continuous_features
reg_lgbm, y_pred, score = run_lgbm(X_train, X_test, y_train, y_test, feature_names, categorical_features)
print('mse', score, 'rmse', score ** .5)
y_pred_val = reg_lgbm.predict(df_validation_dataset[categorical_features + continuous_features].values, reg_lgbm.best_iteration)
y_pred_val = target_transformer.inverse_transform(np.expand_dims(y_pred_val, axis=1))
df_validation_dataset[target_features] = y_pred_val
df_validation_dataset[['reservation_id', 'amount_spent_per_room_night_scaled']].to_csv('submission.csv', index=False)
fig, ax = plt.subplots(nrows=1, ncols=1)
fig.set_size_inches(24, 24)
lgb.plot_importance(reg_lgbm, ax=ax, height=0.5, max_num_features=100);
```
## Catboost
```
feature_names = categorical_features + continuous_features
cat_features = [i for i, c in enumerate(feature_names) if c in categorical_features]
reg_catb, y_pred, score = run_catb(X_train, X_test, y_train, y_test, feature_names, cat_features)
print('mse', score, 'rmse', score ** .5)
feature_names = categorical_features + continuous_features
cat_features = [i for i, c in enumerate(feature_names) if c in categorical_features]
val_pool = catboost.Pool(df_validation_dataset[categorical_features + continuous_features].values, feature_names=feature_names, cat_features=cat_features)
y_pred_val = reg_catb.predict(val_pool)
y_pred_val = target_transformer.inverse_transform(np.expand_dims(y_pred_val, axis=1))
df_validation_dataset[target_features] = y_pred_val
df_validation_dataset[['reservation_id', 'amount_spent_per_room_night_scaled']].to_csv('submission.csv', index=False)
```
|
github_jupyter
|
# Session 7: The Errata Review No. 1
This session is a review of the prior six sessions and covering those pieces that were left off. Not necessarily errors, but missing pieces to complete the picture from the series. These topics answer some questions and will help complete the picture of the C# language features discussed to this point.
## Increment and Assignment operators
In session 1, we reviewed operators and interacting with numbers. We skipped the [increment](https://docs.microsoft.com/en-us/dotnet/csharp/language-reference/operators/arithmetic-operators?WT.mc_id=visualstudio-twitch-jefritz#increment-operator-) `++` and [decrement](https://docs.microsoft.com/en-us/dotnet/csharp/language-reference/operators/arithmetic-operators?WT.mc_id=visualstudio-twitch-jefritz#decrement-operator---) `--` operators. These operators allow you to increment and decrement values quickly. You can place these operators before and after the variable you would like to act on, and they will be incremented or decremented before or after being returned.
Let's take a look:
```
var counter = 1;
display(counter--); // Running ++ AFTER counter will display 1
display(counter); // and then display 2 in the next row
var counter = 1;
display(--counter); // Running ++ BEFORE counter will display 2 as it is incrementing the variable before
// displaying it
```
## Logical negation operator
Sometimes you want to invert the value of a boolean, converting from `true` to `false` and from `false` to `true`. Quite simply, just prefix your test or boolean value with the [negation operator](https://docs.microsoft.com/en-us/dotnet/csharp/language-reference/operators/boolean-logical-operators?WT.mc_id=visualstudio-twitch-jefritz#logical-negation-operator-) `!` to invert values
```
var isTrue = true;
display(!isTrue);
display(!(1 > 2))
```
## TypeOf, GetType and NameOf methods
Sometimes you need to work with the type of a variable or the name of a value. The methods `typeof`, `GetType()` and `nameof` allow you to interact with the types and pass them along for further interaction.
[typeof](https://docs.microsoft.com/en-us/dotnet/csharp/language-reference/operators/type-testing-and-cast?WT.mc_id=visualstudio-twitch-jefritz#typeof-operator) allows you to get a reference to a type for use in methods where you need to inspect the underlying type system
```
display(typeof(int));
```
Conversely, the `GetType()` method allows you to get the type information for a variable already in use. Every object in C# has the `GetType()` method available.
```
var myInt = 5;
display(myInt.GetType());
```
The [`nameof` expression](https://docs.microsoft.com/en-us/dotnet/csharp/language-reference/operators/nameof?WT.mc_id=visualstudio-twitch-jefritz) gives the name of a type or member as a string. This is particularly useful when you are generating error messages.
```
class People {
public string Name { get; set; }
public TimeSpan CalculateAge() => DateTime.Now.Subtract(new DateTime(2000,1,1));
}
var fritz = new People { Name="Fritz" };
display(nameof(People));
display(typeof(People));
display(nameof(fritz.Name));
```
## String Formatting
Formatting and working with strings or text is a fundamental building block of working with user-input. We failed to cover the various ways to interact with those strings. Let's take a look at a handful of the ways to work with text data.
## Concatenation
You may have seen notes and output that concatenates strings by using the [`+` operator](https://docs.microsoft.com/en-us/dotnet/csharp/language-reference/operators/addition-operator?WT.mc_id=visualstudio-twitch-jefritz#string-concatenation). This is the simplest form of concatenation and only works when both sides of the `+` operator are strings.
```
var greeting = "Hello";
display(greeting + " World!");
// += also works
greeting += " C# developers";
display(greeting);
```
If you have multiple strings to combine, the `+` operator gets a little unwieldy and is not as performance aware as several other techniques. We can [combine multiple strings](https://docs.microsoft.com/en-us/dotnet/csharp/how-to/concatenate-multiple-strings?WT.mc_id=visualstudio-twitch-jefritz) using the `Concat`, `Join`, `Format` and interpolation features of C#.
```
var greeting = "Good";
var time = DateTime.Now.Hour < 12 && DateTime.Now.Hour > 3 ? "Morning" : DateTime.Now.Hour < 17 ? "Afternoon" : "Evening";
var name = "Visual Studio Channel";
// Use string.concat with a comma separated list of arguments
display(string.Concat(greeting, " ", time, " ", name + "!"));
var terms = new [] {greeting, time, name};
// Use string.Join to assembly values in an array with a separator
display(string.Join(" ", terms));
// Use string.Format to configure a template string and load values into it based on position
var format = "Good {1} {0}";
display(string.Format(format, time, name));
// With C# 7 and later you can now use string interpolation to format a string.
// Simply prefix a string with a $ to allow you to insert C# expressions in { } inside
// a string
var names = new string[] {"Fritz", "Scott", "Maria", "Jayme"};
display($"Good {time} {name} {string.Join(",",names)}");
// Another technique that can be used when you don't know the exact number of strings
// to concatenate is to use the StringBuilder class.
var sb = new StringBuilder();
sb.AppendFormat("Good {0}", time);
sb.Append(" ");
sb.Append(name);
display(sb.ToString());
```
### Parsing strings with Split
You can turn a string into an array of strings using the `Split` method on a string variable. Pass the character that identifies the boundary between elements of your array to turn it into an array:
```
var phrase = "Good Morning Cleveland";
display(phrase.Split(' '));
display(phrase.Split(' ')[2]);
var fibonacci = "1,1,2,3,5,8,13,21";
display(fibonacci.Split(','));
```
## A Deeper Dive on Enums
We briefly discussed enumeration types in session 3 and touched on using the `enum` keyword to represent related values. Let's go a little further into conversions and working with the enum types.
### Conversions
[Enum types](https://docs.microsoft.com/en-us/dotnet/csharp/language-reference/builtin-types/enum?WT.mc_id=visualstudio-twitch-jefritz) are extensions on top of numeric types. By default, they wrap the `int` integer data type. While this base numeric type can be overridden, we can also convert data into and out of the enum using standard explicit conversion operators
```
enum DotNetLanguages : byte {
csharp = 100,
visual_basic = 2,
fsharp = 3
}
var myLanguage = DotNetLanguages.csharp;
display(myLanguage);
display((byte)myLanguage);
display((int)myLanguage);
// Push a numeric type INTO DotNetLanguages
myLanguage = (DotNetLanguages)2;
display(myLanguage);
```
### Working with strings using Parse and TryParse
What about the string value of the enumeration itself? We can work with that using the [`Parse`](https://docs.microsoft.com/en-us/dotnet/api/system.enum.parse?view=netcore-3.1&WT.mc_id=visualstudio-twitch-jefritz) and [`TryParse`](https://docs.microsoft.com/en-us/dotnet/api/system.enum.tryparse?view=netcore-3.1&WT.mc_id=visualstudio-twitch-jefritz) methods of the Enum object to convert a string into the Enum type
```
var thisLanguage = "csharp";
myLanguage = Enum.Parse<DotNetLanguages>(thisLanguage);
display(myLanguage);
// Use the optional boolean flag parameter to indicate if the Parse operation is case-insensitive
thisLanguage = "CSharp";
myLanguage = Enum.Parse<DotNetLanguages>(thisLanguage, true);
display(myLanguage);
// TryParse has a similar signature, but returns a boolean to indicate success
var success = Enum.TryParse<DotNetLanguages>("Visual_Basic", true, out var foo);
display(success);
display(foo);
```
### GetValues and the Enumeration's available values
The constant values of the enum type can be exposed using the [Enum.GetValues](https://docs.microsoft.com/en-us/dotnet/api/system.enum.getvalues?view=netcore-3.1&WT.mc_id=visualstudio-twitch-jefritz) method. This returns an array of the numeric values of the enum. Let's inspect our `DotNetLanguages` type:
```
var languages = Enum.GetValues(typeof(DotNetLanguages));
display(languages);
// We can convert back to the named values of the enum with a little conversion
foreach (var l in languages) {
display((DotNetLanguages)l);
}
```
## Classes vs. Structs
In the second session we introduced the `class` keyword to create reference types. There is another keyword, `struct`, that allows you to create [Structure](https://docs.microsoft.com/en-us/dotnet/csharp/language-reference/builtin-types/struct?WT.mc_id=visualstudio-twitch-jefritz) **value types** which will be allocated in memory and reclaimed more quickly than a class. While a `struct` looks like a class in syntax, there are some constraints:
- A constructor must be defined that configures all properties / fields
- The parameterless constructor is not allowed
- Instance Fields / Properties cannot be assigned in their declaration
- Finalizers are not allowed
- A struct cannot inherit from another type, but can implement interfaces
Structs are typically used to store related numeric types. Let's tinker with an example:
```
struct Rectangle {
public Rectangle(int length, int width) {
this.Length = length;
this.Width = width;
}
public static readonly int Depth = DateTime.Now.Minute;
public int Length {get;set;}
public int Width {get;set;}
public int Area { get { return Length * Width;}}
public int Perimeter { get { return Length*2 + Width*2;}}
}
var myRectangle = new Rectangle(2, 5);
display(myRectangle);
display(Rectangle.Depth);
enum CountryCode {
USA = 1
}
struct PhoneNumber {
public PhoneNumber(CountryCode countryCode, string exchange, string number) {
this.CountryCode = countryCode;
this.Exchange = exchange;
this.Number = number;
}
public CountryCode CountryCode { get; set;}
public string Exchange { get; set;}
public string Number {get; set;}
}
var jennysNumber = new PhoneNumber(CountryCode.USA, "867", "5309");
display(jennysNumber);
```
### When should I use a struct instead of a class?
This is a common question among C# developers. How do you decide? Since a `struct` is a simple value type, there are [several guidelines to help you decide](https://docs.microsoft.com/en-us/dotnet/standard/design-guidelines/choosing-between-class-and-struct?WT.mc_id=visualstudio-twitch-jefritz):
**Choose a struct INSTEAD of a class if all of these are true about the type:**
- It will be small and short-lived in memory
- It represents a single value
- It can be represented in 16 bytes or less
- It will not be changed, and is immutable
- You will not be converting it to a class (called `boxing` and `unboxing`)
## Stopping and Skipping Loops
In session four we learned about loops using `for`, `while`, and `do`. We can speed up our loop by moving to the next iteration in the loop and we can stop a loop process completely using the `continue` and `break` keywords. Let's take a look at some examples:
```
for (var i=1; i<10_000_000; i++) {
display(i);
if (i%10 == 0) break; // Stop if the value is a multiple of 10
}
// We can skip an iteration in the loop using the continue keyword
for (var i = 1; i<10_000_000; i++) {
if (i%3 == 0) continue; // Skip this iteration
display(i);
if (i%10 == 0) break;
}
```
## Initializing Collections
In the fifth session we explored Arrays, Lists, and Dictionary types. We saw that you could initialize an array with syntax like the following:
```
var fibonacci = new int[] {1,1,2,3,5,8,13};
display(fibonacci);
//var coordinates = new int[,] {{1,2}, {2,3}};
//display(coordinates);
```
We can also initialize List and Dictionary types using the curly braces notation:
```
var myList = new List<string> {
"C#",
"Visual Basic",
"F#"
};
display(myList);
var myShapes = new List<Rectangle> {
new Rectangle(2, 5),
new Rectangle(3, 4),
new Rectangle(4, 3)
};
display(myShapes);
var myDictionary = new Dictionary<int, string> {
{100, "C#"},
{200, "Visual Basic"},
{300, "F#"}
};
display(myDictionary);
```
## Dictionary Types
This question was raised on an earlier stream, and [David Fowler](https://twitter.com/davidfowl) (.NET Engineering Team Architect) wrote a series of [Tweets](https://twitter.com/davidfowl/status/1444467842418548737) about it based on discussions with [Stephen Toub](https://twitter.com/stephentoub/) (Architect for the .NET Libraries)
There are 4 built-in Dictionary types with .NET:
- [Hashtable](https://docs.microsoft.com/dotnet/api/system.collections.hashtable)
- This is the most efficient dictionary type with keys organized by the hash of their values.
- David says: "Good read speed (no lock required), sameish weight as dictionary but more expensive to mutate and no generics!"
```
var hashTbl = new Hashtable();
hashTbl.Add("key1", "value1");
hashTbl.Add("key2", "value2");
display(hashTbl);
```
- [Dictionary](https://docs.microsoft.com/dotnet/api/system.collections.generic.dictionary-2)
- A generic dictionary object that you can search easily by keys.
- David says: "Lightweight to create and 'medium' update speed. Poor read speed when used with a lock. As an immutable object it has the best read speed and heavy to update."
```
private readonly Dictionary<string,string> readonlyDictionary = new() {
{"txt", "Text Files"},
{"wav", "Sound Files"},
{"mp3", "Compressed Music Files"},
};
display(readonlyDictionary);
readonlyDictionary.Add("mp4", "Video Files");
display(newDictionary);
```
- [ConcurrentDictionary](https://docs.microsoft.com/dotnet/api/system.collections.concurrent.concurrentdictionary-2)
- A thread-safe version of Dictionary that is optimized for use by multiple threads. It is not recommended for use by a single thread due to the extra overhead allocate for multi-threaded support.
- David says: "Poorish read speed, no locking required but more allocations require to update than a dictionary."
Instead of Adding, Updating and Getting values from the ConcurrentDictionary, we TryAdd, TryUpdate, and TryGetValue. TryAdd will return false if the key already exists, and TryUpdate will return false if the key does not exist. TryGetValue will return false if the key does not exist. We can also AddOrUpdate to add a value if the key does not exist and GetOrAdd to add a value if the key does not exist.
```
using System.Collections.Concurrent;
var cd = new ConcurrentDictionary<string, string>();
cd.AddOrUpdate("key1", "value1", (key, oldValue) => "value2");
cd.AddOrUpdate("key1", "value1", (key, oldValue) => "value2");
display(cd.TryAdd("key2", "value1"));
display(cd);
```
- [ImmutableDictionary](https://docs.microsoft.com/dotnet/api/system.collections.immutable.immutabledictionary-2)
- A new type in .NET Core and .NET 5/6 that is a read-only version of Dictionary. Changes to it's contents involve creation of a new Dictionary object and copying of the contents.
- David says: "Poorish read speed, no locking required but more allocations required to update than a dictionary."
```
using System.Collections.Immutable;
var d = ImmutableDictionary.CreateBuilder<string,string>();
d.Add("key1", "value1");
d.Add("key2", "value2");
var theDict = d.ToImmutable();
//theDict = theDict.Add("key3", "value3");
display(theDict);
```
## Const and Static keywords
```
const int Five = 5;
// Five = 6;
display(Five);
class Student {
public const decimal MaxGPA = 5.0m;
}
display(Student.MaxGPA);
class Student {
public static bool InClass = false;
public string Name { get; set; }
public override string ToString() {
return Name + ": " + Student.InClass;
}
public static void GoToClass() {
Student.InClass = true;
}
public static void DitchClass() {
Student.InClass = false;
}
}
var students = new Student[] { new Student { Name="Hugo" }, new Student {Name="Fritz"}, new Student {Name="Lily"}};
foreach (var s in students) {
display(s.ToString());
}
Student.GoToClass();
foreach (var s in students) {
display(s.ToString());
}
static class DateMethods {
public static int CalculateAge(DateTime date1, DateTime date2) {
return 10;
}
}
display(DateMethods.CalculateAge(DateTime.Now, DateTime.Now))
```
|
github_jupyter
|
<a href="https://colab.research.google.com/github/jonkrohn/ML-foundations/blob/master/notebooks/2-linear-algebra-ii.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Linear Algebra II: Matrix Operations
This topic, *Linear Algebra II: Matrix Operations*, builds on the basics of linear algebra. It is essential because these intermediate-level manipulations of tensors lie at the heart of most machine learning approaches and are especially predominant in deep learning.
Through the measured exposition of theory paired with interactive examples, you’ll develop an understanding of how linear algebra is used to solve for unknown values in high-dimensional spaces as well as to reduce the dimensionality of complex spaces. The content covered in this topic is itself foundational for several other topics in the *Machine Learning Foundations* series, especially *Probability & Information Theory* and *Optimization*.
Over the course of studying this topic, you'll:
* Develop a geometric intuition of what’s going on beneath the hood of machine learning algorithms, including those used for deep learning.
* Be able to more intimately grasp the details of machine learning papers as well as all of the other subjects that underlie ML, including calculus, statistics, and optimization algorithms.
* Reduce the dimensionalty of complex spaces down to their most informative elements with techniques such as eigendecomposition, singular value decomposition, and principal components analysis.
**Note that this Jupyter notebook is not intended to stand alone. It is the companion code to a lecture or to videos from Jon Krohn's [Machine Learning Foundations](https://github.com/jonkrohn/ML-foundations) series, which offer detail on the following:**
*Review of Matrix Properties*
* Modern Linear Algebra Applications
* Tensors, Vectors, and Norms
* Matrix Multiplication
* Matrix Inversion
* Identity, Diagonal and Orthogonal Matrices
*Segment 2: Eigendecomposition*
* Eigenvectors
* Eigenvalues
* Matrix Determinants
* Matrix Decomposition
* Applications of Eigendecomposition
*Segment 3: Matrix Operations for Machine Learning*
* Singular Value Decomposition (SVD)
* The Moore-Penrose Pseudoinverse
* The Trace Operator
* Principal Component Analysis (PCA): A Simple Machine Learning Algorithm
* Resources for Further Study of Linear Algebra
## Segment 1: Review of Tensor Properties
```
import numpy as np
import torch
```
### Vector Transposition
```
x = np.array([25, 2, 5])
x
x.shape
x = np.array([[25, 2, 5]])
x
x.shape
x.T
x.T.shape
x_p = torch.tensor([25, 2, 5])
x_p
x_p.T
x_p.view(3, 1) # "view" because we're changing output but not the way x is stored in memory
```
**Return to slides here.**
## $L^2$ Norm
```
x
(25**2 + 2**2 + 5**2)**(1/2)
np.linalg.norm(x)
```
So, if units in this 3-dimensional vector space are meters, then the vector $x$ has a length of 25.6m
```
# the following line of code will fail because torch.norm() requires input to be float not integer
# torch.norm(p)
torch.norm(torch.tensor([25, 2, 5.]))
```
**Return to slides here.**
### Matrices
```
X = np.array([[25, 2], [5, 26], [3, 7]])
X
X.shape
X_p = torch.tensor([[25, 2], [5, 26], [3, 7]])
X_p
X_p.shape
```
**Return to slides here.**
### Matrix Transposition
```
X
X.T
X_p.T
```
**Return to slides here.**
### Matrix Multiplication
Scalars are applied to each element of matrix:
```
X*3
X*3+3
X_p*3
X_p*3+3
```
Using the multiplication operator on two tensors of the same size in PyTorch (or Numpy or TensorFlow) applies element-wise operations. This is the **Hadamard product** (denoted by the $\odot$ operator, e.g., $A \odot B$) *not* **matrix multiplication**:
```
A = np.array([[3, 4], [5, 6], [7, 8]])
A
X
X * A
A_p = torch.tensor([[3, 4], [5, 6], [7, 8]])
A_p
X_p * A_p
```
Matrix multiplication with a vector:
```
b = np.array([1, 2])
b
np.dot(A, b) # even though technically dot products is between 2 vectors
b_p = torch.tensor([1, 2])
b_p
torch.matmul(A_p, b_p)
```
Matrix multiplication with two matrices:
```
B = np.array([[1, 9], [2, 0]])
B
np.dot(A, B) # note first column is same as Xb
B_p = torch.tensor([[1, 9], [2, 0]])
B_p
torch.matmul(A_p, B_p)
```
### Matrix Inversion
```
X = np.array([[4, 2], [-5, -3]])
X
Xinv = np.linalg.inv(X)
Xinv
y = np.array([4, -7])
y
w = np.dot(Xinv, y)
w
```
Show that $y = Xw$:
```
np.dot(X, w)
X_p = torch.tensor([[4, 2], [-5, -3.]]) # note that torch.inverse() requires floats
X_p
Xinv_p = torch.inverse(X_p)
Xinv_p
y_p = torch.tensor([4, -7.])
y_p
w_p = torch.matmul(Xinv_p, y_p)
w_p
torch.matmul(X_p, w_p)
```
**Return to slides here.**
## Segment 2: Eigendecomposition
### Eigenvectors and Eigenvalues
Let's say we have a vector $v$:
```
v = np.array([3, 1])
v
```
Let's plot $v$ using Hadrien Jean's handy `plotVectors` function (from [this notebook](https://github.com/hadrienj/deepLearningBook-Notes/blob/master/2.7%20Eigendecomposition/2.7%20Eigendecomposition.ipynb) under [MIT license](https://github.com/hadrienj/deepLearningBook-Notes/blob/master/LICENSE)).
```
import matplotlib.pyplot as plt
def plotVectors(vecs, cols, alpha=1):
"""
Plot set of vectors.
Parameters
----------
vecs : array-like
Coordinates of the vectors to plot. Each vectors is in an array. For
instance: [[1, 3], [2, 2]] can be used to plot 2 vectors.
cols : array-like
Colors of the vectors. For instance: ['red', 'blue'] will display the
first vector in red and the second in blue.
alpha : float
Opacity of vectors
Returns:
fig : instance of matplotlib.figure.Figure
The figure of the vectors
"""
plt.figure()
plt.axvline(x=0, color='#A9A9A9', zorder=0)
plt.axhline(y=0, color='#A9A9A9', zorder=0)
for i in range(len(vecs)):
x = np.concatenate([[0,0],vecs[i]])
plt.quiver([x[0]],
[x[1]],
[x[2]],
[x[3]],
angles='xy', scale_units='xy', scale=1, color=cols[i],
alpha=alpha)
plotVectors([v], cols=['lightblue'])
_ = plt.xlim(-1, 5)
_ = plt.ylim(-1, 5)
```
"Applying" a matrix to a vector (i.e., performing matrix-vector multiplication) can linearly transform the vector, e.g, rotate it or rescale it.
The identity matrix, introduced earlier, is the exception that proves the rule: Applying an identity matrix does not transform the vector:
```
I = np.array([[1, 0], [0, 1]])
I
Iv = np.dot(I, v)
Iv
v == Iv
plotVectors([Iv], cols=['blue'])
_ = plt.xlim(-1, 5)
_ = plt.ylim(-1, 5)
```
In contrast, let's see what happens when we apply (some non-identity matrix) $A$ to the vector $v$:
```
A = np.array([[-1, 4], [2, -2]])
A
Av = np.dot(A, v)
Av
plotVectors([v, Av], ['lightblue', 'blue'])
_ = plt.xlim(-1, 5)
_ = plt.ylim(-1, 5)
# a second example:
v2 = np.array([2, 1])
plotVectors([v2, np.dot(A, v2)], ['lightgreen', 'green'])
_ = plt.xlim(-1, 5)
_ = plt.ylim(-1, 5)
```
We can concatenate several vectors together into a matrix (say, $V$), where each column is a separate vector. Then, whatever linear transformations we apply to $V$ will be independently applied to each column (vector):
```
v
# recall that we need to convert array to 2D to transpose into column, e.g.:
np.matrix(v).T
v3 = np.array([-3, -1]) # mirror image of x over both axes
v4 = np.array([-1, 1])
V = np.concatenate((np.matrix(v).T,
np.matrix(v2).T,
np.matrix(v3).T,
np.matrix(v4).T),
axis=1)
V
IV = np.dot(I, V)
IV
AV = np.dot(A, V)
AV
# function to convert column of matrix to 1D vector:
def vectorfy(mtrx, clmn):
return np.array(mtrx[:,clmn]).reshape(-1)
vectorfy(V, 0)
vectorfy(V, 0) == v
plotVectors([vectorfy(V, 0), vectorfy(V, 1), vectorfy(V, 2), vectorfy(V, 3),
vectorfy(AV, 0), vectorfy(AV, 1), vectorfy(AV, 2), vectorfy(AV, 3)],
['lightblue', 'lightgreen', 'lightgray', 'orange',
'blue', 'green', 'gray', 'red'])
_ = plt.xlim(-4, 6)
_ = plt.ylim(-5, 5)
```
Now that we can appreciate linear transformation of vectors by matrices, let's move on to working with eigenvectors and eigenvalues.
An **eigenvector** (*eigen* is German for "typical"; we could translate *eigenvector* to "characteristic vector") is a special vector $v$ such that when it is transformed by some matrix (let's say $A$), the product $Av$ has the exact same direction as $v$.
An **eigenvalue** is a scalar (traditionally represented as $\lambda$) that simply scales the eigenvector $v$ such that the following equation is satisfied:
$Av = \lambda v$
Easiest way to understand this is to work through an example:
```
A
```
Eigenvectors and eigenvalues can be derived algebraically (e.g., with the [QR algorithm](https://en.wikipedia.org/wiki/QR_algorithm), which was independent developed in the 1950s by both [Vera Kublanovskaya](https://en.wikipedia.org/wiki/Vera_Kublanovskaya) and John Francis), however this is outside scope of today's class. We'll cheat with NumPy `eig()` method, which returns a tuple of:
* a vector of eigenvalues
* a matrix of eigenvectors
```
lambdas, V = np.linalg.eig(A)
```
The matrix contains as many eigenvectors as there are columns of A:
```
V # each column is a separate eigenvector v
```
With a corresponding eigenvalue for each eigenvector:
```
lambdas
```
Let's confirm that $Av = \lambda v$ for the first eigenvector:
```
v = V[:,0]
v
lambduh = lambdas[0] # note that "lambda" is reserved term in Python
lambduh
Av = np.dot(A, v)
Av
lambduh * v
plotVectors([Av, v], ['blue', 'lightblue'])
_ = plt.xlim(-1, 2)
_ = plt.ylim(-1, 2)
```
And again for the second eigenvector of A:
```
v2 = V[:,1]
v2
lambda2 = lambdas[1]
lambda2
Av2 = np.dot(A, v2)
Av2
lambda2 * v2
plotVectors([Av, v, Av2, v2],
['blue', 'lightblue', 'green', 'lightgreen'])
_ = plt.xlim(-1, 4)
_ = plt.ylim(-3, 2)
```
Using the PyTorch `eig()` method, we can do exactly the same:
```
A
A_p = torch.tensor([[-1, 4], [2, -2.]]) # must be float for PyTorch eig()
A_p
eigens = torch.eig(A_p, eigenvectors=True)
eigens
v_p = eigens.eigenvectors[:,0]
v_p
lambda_p = eigens.eigenvalues[0][0]
lambda_p
Av_p = torch.matmul(A_p, v_p)
Av_p
lambda_p * v_p
v2_p = eigens.eigenvectors[:,1]
v2_p
lambda2_p = eigens.eigenvalues[1][0]
lambda2_p
Av2_p = torch.matmul(A_p, v2_p)
Av2_p
lambda2_p * v2_p
plotVectors([Av_p.numpy(), v_p.numpy(), Av2_p.numpy(), v2_p.numpy()],
['blue', 'lightblue', 'green', 'lightgreen'])
_ = plt.xlim(-1, 4)
_ = plt.ylim(-3, 2)
```
### Eigenvectors in >2 Dimensions
While plotting gets trickier in higher-dimensional spaces, we can nevertheless find and use eigenvectors with more than two dimensions. Here's a 3D example (there are three dimensions handled over three rows):
```
X
lambdas_X, V_X = np.linalg.eig(X)
V_X # one eigenvector per column of X
lambdas_X # a corresponding eigenvalue for each eigenvector
```
Confirm $Xv = \lambda v$ for an example vector:
```
v_X = V_X[:,0]
v_X
lambda_X = lambdas_X[0]
lambda_X
np.dot(X, v_X) # matrix multiplication
lambda_X * v_X
```
**Exercises**:
1. Use PyTorch to confirm $Xv = \lambda v$ for the first eigenvector of $X$.
2. Confirm $Xv = \lambda v$ for the remaining eigenvectors of $X$ (you can use NumPy or PyTorch, whichever you prefer).
**Return to slides here.**
### 2x2 Matrix Determinants
```
X
np.linalg.det(X)
```
**Return to slides here.**
```
N = np.array([[-4, 1], [-8, 2]])
N
np.linalg.det(N)
# Uncommenting the following line results in a "singular matrix" error
# Ninv = np.linalg.inv(N)
N = torch.tensor([[-4, 1], [-8, 2.]]) # must use float not int
torch.det(N)
```
**Return to slides here.**
### Generalizing Determinants
```
X = np.array([[1, 2, 4], [2, -1, 3], [0, 5, 1]])
X
np.linalg.det(X)
```
### Determinants & Eigenvalues
```
lambdas, V = np.linalg.eig(X)
lambdas
np.product(lambdas)
```
**Return to slides here.**
```
np.abs(np.product(lambdas))
B = np.array([[1, 0], [0, 1]])
B
plotVectors([vectorfy(B, 0), vectorfy(B, 1)],
['lightblue', 'lightgreen'])
_ = plt.xlim(-1, 3)
_ = plt.ylim(-1, 3)
N
np.linalg.det(N)
NB = np.dot(N, B)
NB
plotVectors([vectorfy(B, 0), vectorfy(B, 1), vectorfy(NB, 0), vectorfy(NB, 1)],
['lightblue', 'lightgreen', 'blue', 'green'])
_ = plt.xlim(-6, 6)
_ = plt.ylim(-9, 3)
I
np.linalg.det(I)
IB = np.dot(I, B)
IB
plotVectors([vectorfy(B, 0), vectorfy(B, 1), vectorfy(IB, 0), vectorfy(IB, 1)],
['lightblue', 'lightgreen', 'blue', 'green'])
_ = plt.xlim(-1, 3)
_ = plt.ylim(-1, 3)
J = np.array([[-0.5, 0], [0, 2]])
J
np.linalg.det(J)
np.abs(np.linalg.det(J))
JB = np.dot(J, B)
JB
plotVectors([vectorfy(B, 0), vectorfy(B, 1), vectorfy(JB, 0), vectorfy(JB, 1)],
['lightblue', 'lightgreen', 'blue', 'green'])
_ = plt.xlim(-1, 3)
_ = plt.ylim(-1, 3)
doubleI = I*2
np.linalg.det(doubleI)
doubleIB = np.dot(doubleI, B)
doubleIB
plotVectors([vectorfy(B, 0), vectorfy(B, 1), vectorfy(doubleIB, 0), vectorfy(doubleIB, 1)],
['lightblue', 'lightgreen', 'blue', 'green'])
_ = plt.xlim(-1, 3)
_ = plt.ylim(-1, 3)
```
**Return to slides here.**
### Eigendecomposition
The **eigendecomposition** of some matrix $A$ is
$A = V \Lambda V^{-1}$
Where:
* As in examples above, $V$ is the concatenation of all the eigenvectors of $A$
* $\Lambda$ (upper-case $\lambda$) is the diagonal matrix diag($\lambda$). Note that the convention is to arrange the lambda values in descending order; as a result, the first eigenvector (and its associated eigenvector) may be a primary characteristic of the matrix $A$.
```
# This was used earlier as a matrix X; it has nice clean integer eigenvalues...
A = np.array([[4, 2], [-5, -3]])
A
lambdas, V = np.linalg.eig(A)
V
Vinv = np.linalg.inv(V)
Vinv
Lambda = np.diag(lambdas)
Lambda
```
Confirm that $A = V \Lambda V^{-1}$:
```
np.dot(V, np.dot(Lambda, Vinv))
```
Eigendecomposition is not possible with all matrices. And in some cases where it is possible, the eigendecomposition involves complex numbers instead of straightforward real numbers.
In machine learning, however, we are typically working with real symmetric matrices, which can be conveniently and efficiently decomposed into real-only eigenvectors and real-only eigenvalues. If $A$ is a real symmetric matrix then...
$A = Q \Lambda Q^T$
...where $Q$ is analogous to $V$ from the previous equation except that it's special because it's an orthogonal matrix.
```
A = np.array([[2, 1], [1, 2]])
A
lambdas, Q = np.linalg.eig(A)
lambdas
Lambda = np.diag(lambdas)
Lambda
Q
```
Recalling that $Q^TQ = QQ^T = I$, can demonstrate that $Q$ is an orthogonal matrix:
```
np.dot(Q.T, Q)
np.dot(Q, Q.T)
```
Let's confirm $A = Q \Lambda Q^T$:
```
np.dot(Q, np.dot(Lambda, Q.T))
```
**Exercises**:
1. Use PyTorch to decompose the matrix $P$ (below) into its components $V$, $\Lambda$, and $V^{-1}$. Confirm that $P = V \Lambda V^{-1}$.
2. Use PyTorch to decompose the symmetric matrix $S$ (below) into its components $Q$, $\Lambda$, and $Q^T$. Confirm that $S = Q \Lambda Q^T$.
```
P = torch.tensor([[25, 2, -5], [3, -2, 1], [5, 7, 4.]])
P
S = torch.tensor([[25, 2, -5], [2, -2, 1], [-5, 1, 4.]])
S
```
**Return to slides here.**
## Segment 3: Matrix Operations for ML
### Singular Value Decomposition (SVD)
As on slides, SVD of matrix $A$ is:
$A = UDV^T$
Where:
* $U$ is an orthogonal $m \times m$ matrix; its columns are the **left-singular vectors** of $A$.
* $V$ is an orthogonal $n \times n$ matrix; its columns are the **right-singular vectors** of $A$.
* $D$ is a diagonal $m \times n$ matrix; elements along its diagonal are the **singular values** of $A$.
```
A = np.array([[-1, 2], [3, -2], [5, 7]])
A
U, d, VT = np.linalg.svd(A) # V is already transposed
U
VT
d
np.diag(d)
D = np.concatenate((np.diag(d), [[0, 0]]), axis=0)
D
np.dot(U, np.dot(D, VT))
```
SVD and eigendecomposition are closely related to each other:
* Left-singular vectors of $A$ = eigenvectors of $AA^T$.
* Right-singular vectors of $A$ = eigenvectors of $A^TA$.
* Non-zero singular values of $A$ = square roots of eigenvectors of $AA^T$ = square roots of eigenvectors of $A^TA$
**Exercise**: Using the matrix `P` from the preceding PyTorch exercises, demonstrate that these three SVD-eigendecomposition equations are true.
### Image Compression via SVD
The section features code adapted from [Frank Cleary's](https://gist.github.com/frankcleary/4d2bd178708503b556b0).
```
import time
from PIL import Image
```
Fetch photo of Oboe, a terrier, with the book *Deep Learning Illustrated*:
```
! wget https://raw.githubusercontent.com/jonkrohn/DLTFpT/master/notebooks/oboe-with-book.jpg
img = Image.open('oboe-with-book.jpg')
plt.imshow(img)
```
Convert image to grayscale so that we don't have to deal with the complexity of multiple color channels:
```
imggray = img.convert('LA')
plt.imshow(imggray)
```
Convert data into numpy matrix, which doesn't impact image data:
```
imgmat = np.array(list(imggray.getdata(band=0)), float)
imgmat.shape = (imggray.size[1], imggray.size[0])
imgmat = np.matrix(imgmat)
plt.imshow(imgmat, cmap='gray')
```
Calculate SVD of the image:
```
U, sigma, V = np.linalg.svd(imgmat)
```
As eigenvalues are arranged in descending order in diag($\lambda$) so to are singular values, by convention, arranged in descending order in $D$ (or, in this code, diag($\sigma$)). Thus, the first left-singular vector of $U$ and first right-singular vector of $V$ may represent the most prominent feature of the image:
```
reconstimg = np.matrix(U[:, :1]) * np.diag(sigma[:1]) * np.matrix(V[:1, :])
plt.imshow(reconstimg, cmap='gray')
```
Additional singular vectors improve the image quality:
```
for i in [2, 4, 8, 16, 32, 64]:
reconstimg = np.matrix(U[:, :i]) * np.diag(sigma[:i]) * np.matrix(V[:i, :])
plt.imshow(reconstimg, cmap='gray')
title = "n = %s" % i
plt.title(title)
plt.show()
```
With 64 singular vectors, the image is reconstructed quite well, however the data footprint is much smaller than the original image:
```
imgmat.shape
full_representation = 4032*3024
full_representation
svd64_rep = 64*4032 + 64 + 64*3024
svd64_rep
svd64_rep/full_representation
```
Specifically, the image represented as 64 singular vectors is 3.7% of the size of the original!
**Return to slides here.**
### The Moore-Penrose Pseudoinverse
Let's calculate the pseudoinverse $A^+$ of some matrix $A$ using the formula from the slides:
$A^+ = VD^+U^T$
```
A
```
As shown earlier, the NumPy SVD method returns $U$, $d$, and $V^T$:
```
U, d, VT = np.linalg.svd(A)
U
VT
d
```
To create $D^+$, we first invert the non-zero values of $d$:
```
D = np.diag(d)
D
1/8.669
1/4.104
```
...and then we would take the tranpose of the resulting matrix.
Because $D$ is a diagonal matrix, this can, however, be done in a single step by inverting $D$:
```
Dinv = np.linalg.inv(D)
Dinv
```
The final $D^+$ matrix needs to have a shape that can undergo matrix multiplication in the $A^+ = VD^+U^T$ equation. These dimensions can be obtained from $A$:
```
A.shape[0]
A.shape[1]
Dplus = np.zeros((3, 2)).T
Dplus
Dplus[:2, :2] = Dinv
Dplus
```
Now we have everything we need to calculate $A^+$ with $VD^+U^T$:
```
np.dot(VT.T, np.dot(Dplus, U.T))
```
Working out this derivation is helpful for understanding how Moore-Penrose pseudoinverses work, but unsurprisingly NumPy is loaded with an existing method `pinv()`:
```
np.linalg.pinv(A)
```
**Exercise**
Use the `torch.svd()` method to calculate the pseudoinverse of `A_p`, confirming that your result matches the output of `torch.pinverse(A_p)`:
```
A_p = torch.tensor([[-1, 2], [3, -2], [5, 7.]])
A_p
torch.pinverse(A_p)
```
**Return to slides here.**
For regression problems, we typically have many more cases ($n$, or rows of $X$) than features to predict ($m$, or columns of $X$). Let's solve a miniature example of such an overdetermined situation.
We have eight data points ($n$ = 8):
```
x1 = [0, 1, 2, 3, 4, 5, 6, 7.]
y = [1.86, 1.31, .62, .33, .09, -.67, -1.23, -1.37]
fig, ax = plt.subplots()
_ = ax.scatter(x1, y)
```
Although it appears there is only one predictor ($x_1$), we need a second one (let's call it $x_0$) in order to allow for a $y$-intercept (therefore, $m$ = 2). Without this second variable, the line we fit to the plot would need to pass through the origin (0, 0). The $y$-intercept is constant across all the points so we can set it equal to `1` across the board:
```
x0 = np.ones(8)
x0
```
Concatenate $x_0$ and $x_1$ into a matrix $X$:
```
X = np.concatenate((np.matrix(x0).T, np.matrix(x1).T), axis=1)
X
```
From the slides, we know that we can compute the weights $w$ using the pseudoinverse of $w = X^+y$:
```
w = np.dot(np.linalg.pinv(X), y)
w
```
The first weight corresponds to the $y$-intercept of the line, which is typically denoted as $b$:
```
b = np.asarray(w).reshape(-1)[0]
b
```
While the second weight corresponds to the slope of the line, which is typically denoted as $m$:
```
m = np.asarray(w).reshape(-1)[1]
m
```
With the weights we can plot the line to confirm it fits the points:
```
fig, ax = plt.subplots()
ax.scatter(x1, y)
x_min, x_max = ax.get_xlim()
y_min, y_max = b, b + m*(x_max-x_min)
ax.plot([x_min, x_max], [y_min, y_max])
_ = ax.set_xlim([x_min, x_max])
```
### The Trace Operator
Denoted as Tr($A$). Simply the sum of the diagonal elements of a matrix: $$\sum_i A_{i,i}$$
```
A = np.array([[25, 2], [5, 4]])
A
25 + 4
np.trace(A)
```
The trace operator has a number of useful properties that come in handy while rearranging linear algebra equations, e.g.:
* Tr($A$) = Tr($A^T$)
* Assuming the matrix shapes line up: Tr(ABC) = Tr(CAB) = Tr(BCA)
In particular, the trace operator can provide a convenient way to calculate a matrix's Frobenius norm: $$||A||_F = \sqrt{\mathrm{Tr}(AA^\mathrm{T})}$$
**Exercise**
Using the matrix `A_p`:
1. Identify the PyTorch trace method and the trace of the matrix.
2. Further, use the PyTorch Frobenius norm method (for the left-hand side of the equation) and the trace method (for the right-hand side of the equation) to demonstrate that $||A||_F = \sqrt{\mathrm{Tr}(AA^\mathrm{T})}$
```
A_p
```
**Return to slides here.**
### Principal Component Analysis
This PCA example code is adapted from [here](https://jupyter.brynmawr.edu/services/public/dblank/CS371%20Cognitive%20Science/2016-Fall/PCA.ipynb).
```
from sklearn import datasets
iris = datasets.load_iris()
iris.data.shape
iris.get("feature_names")
iris.data[0:6,:]
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
X = pca.fit_transform(iris.data)
X.shape
X[0:6,:]
plt.scatter(X[:, 0], X[:, 1])
iris.target.shape
iris.target[0:6]
unique_elements, counts_elements = np.unique(iris.target, return_counts=True)
np.asarray((unique_elements, counts_elements))
list(iris.target_names)
plt.scatter(X[:, 0], X[:, 1], c=iris.target)
```
**Return to slides here.**
|
github_jupyter
|

## Classification
Classification - predicting the discrete class ($y$) of an object from a vector of input features ($\vec x$).
Models used in this notebook include: Logistic Regression, Support Vector Machines, KNN
**Author List**: Kevin Li
**Original Sources**: http://scikit-learn.org, http://archive.ics.uci.edu/ml/datasets/Iris
**License**: Feel free to do whatever you want to with this code
## Iris Dataset
```
from sklearn import datasets
# import some data to play with
iris = datasets.load_iris()
X = iris.data
Y = iris.target
# type(iris)
print("feature vector shape=", X.shape)
print("class shape=", Y.shape)
print(iris.target_names, type(iris.target_names))
print(iris.feature_names, type(iris.feature_names))
print type (X)
print X[0:5]
print type (Y)
print Y[0:5]
print "---"
print(iris.DESCR)
# specifies that figures should be shown inline, directly in the notebook.
%pylab inline
# Learn more about thhis visualization package at http://seaborn.pydata.org/
# http://seaborn.pydata.org/tutorial/axis_grids.html
# http://seaborn.pydata.org/tutorial/aesthetics.html#aesthetics-tutorial
import seaborn as sns
import matplotlib.pyplot as plt
sns.set(style="white")
df = sns.load_dataset("iris")
print "df is a ", type(df)
g = sns.PairGrid(df, diag_sharey=False,hue="species")
g.map_lower(sns.kdeplot, cmap="Blues_d")
g.map_upper(plt.scatter)
g.map_diag(sns.kdeplot, lw=3)
# sns.load_dataset?
sns.load_dataset
```
- Logistic Regression: `linear_model.LogisticRegression`
- KNN Classification: `neighbors.KNeighborsClassifier`
- LDA / QDA: `lda.LDA` / `lda.QDA`
- Naive Bayes: `naive_bayes.GaussianNB`
- Support Vector Machines: `svm.SVC`
- Classification Trees: `tree.DecisionTreeClassifier`
- Random Forest: `ensemble.RandomForestClassifier`
- Multi-class & multi-label Classification is supported: `multiclass.OneVsRest` `multiclass.OneVsOne`
- Boosting & Ensemble Learning: xgboost, cart
## Logistic Regression
A standard logistic sigmoid function
<img src="https://upload.wikimedia.org/wikipedia/commons/thumb/8/88/Logistic-curve.svg/320px-Logistic-curve.svg.png" width="50%">
```
%matplotlib inline
import numpy as np
from sklearn import linear_model, datasets
# set_context
sns.set_context("talk")
# import some data to play with
iris = datasets.load_iris()
X = iris.data[:, 1:3] # we only take the first two features.
Y = iris.target
h = .02 # step size in the mesh
# https://en.wikipedia.org/wiki/Logistic_regression
logreg = linear_model.LogisticRegression(C=1e5)
# we create an instance of Neighbours Classifier and fit the data.
logreg.fit(X, Y)
# Plot the decision boundary. For that, we will assign a color to each
# point in the mesh [x_min, x_max]x[y_min, y_max].
x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
Z = logreg.predict(np.c_[xx.ravel(), yy.ravel()])
# numpy.ravel: Return a contiguous flattened array.
# Put the result into a color plot
Z = Z.reshape(xx.shape)
plt.figure(1, figsize=(4, 3))
plt.pcolormesh(xx, yy, Z, cmap=plt.cm.Paired)
# Plot also the training points
plt.scatter(X[:, 0], X[:, 1], c=Y, edgecolors='k', cmap=get_cmap("Spectral"))
plt.xlabel('Sepal length')
plt.ylabel('Sepal width')
#plt.xlim(xx.min(), xx.max())
#plt.ylim(yy.min(), yy.max())
#plt.xticks(())
#plt.yticks(())
plt.show()
```
## Support Vector Machines (Bell Labs, 1992)
<img src="http://docs.opencv.org/2.4/_images/optimal-hyperplane.png" width="50%">
```
# adapted from http://scikit-learn.org/0.13/auto_examples/svm/plot_iris.html#example-svm-plot-iris-py
%matplotlib inline
import numpy as np
from sklearn import svm, datasets
sns.set_context("talk")
# import some data to play with
iris = datasets.load_iris()
X = iris.data[:, 1:3] # we only take the first two features. We could
# avoid this ugly slicing by using a two-dim dataset
Y = iris.target
h = 0.02 # step size in the mesh
# we create an instance of SVM and fit out data. We do not scale our
# data since we want to plot the support vectors
C = 1.0 # SVM regularization parameter
svc = svm.SVC(kernel='linear', C=C).fit(X, Y)
rbf_svc = svm.SVC(kernel='rbf', gamma=0.7, C=C).fit(X, Y)
poly_svc = svm.SVC(kernel='poly', degree=3, C=C).fit(X, Y)
lin_svc = svm.LinearSVC(C=C).fit(X, Y)
# create a mesh to plot in
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
# title for the plots
titles = ['SVC with linear kernel',
'SVC with RBF kernel',
'SVC with polynomial (degree 3) kernel',
'LinearSVC (linear kernel)']
clfs = [svc, rbf_svc, poly_svc, lin_svc]
f,axs = plt.subplots(2,2)
for i, clf in enumerate(clfs):
# Plot the decision boundary. For that, we will assign a color to each
# point in the mesh [x_min, m_max]x[y_min, y_max].
ax = axs[i//2][i % 2]
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
# Put the result into a color plot
Z = Z.reshape(xx.shape)
ax.contourf(xx, yy, Z,cmap=get_cmap("Spectral"))
ax.axis('off')
# Plot also the training points
ax.scatter(X[:, 0], X[:, 1], c=Y,cmap=get_cmap("Spectral"))
ax.set_title(titles[i])
```
## Beyond Linear SVM
```
# SVM with polynomial kernel visualization
from IPython.display import YouTubeVideo
YouTubeVideo("3liCbRZPrZA")
```
## kNearestNeighbors (kNN)
```
# %load http://scikit-learn.org/stable/_downloads/plot_classification.py
"""
================================
Nearest Neighbors Classification
================================
Sample usage of Nearest Neighbors classification.
It will plot the decision boundaries for each class.
"""
print(__doc__)
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
from sklearn import neighbors, datasets
n_neighbors = 15
# import some data to play with
iris = datasets.load_iris()
X = iris.data[:, :2] # we only take the first two features. We could
# avoid this ugly slicing by using a two-dim dataset
y = iris.target
h = .02 # step size in the mesh
# Create color maps
cmap_light = ListedColormap(['#FFAAAA', '#AAFFAA', '#AAAAFF'])
cmap_bold = ListedColormap(['#FF0000', '#00FF00', '#0000FF'])
for weights in ['uniform', 'distance']:
# we create an instance of Neighbours Classifier and fit the data.
clf = neighbors.KNeighborsClassifier(n_neighbors, weights=weights)
clf.fit(X, y)
# Plot the decision boundary. For that, we will assign a color to each
# point in the mesh [x_min, x_max]x[y_min, y_max].
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
# Put the result into a color plot
Z = Z.reshape(xx.shape)
plt.figure()
plt.pcolormesh(xx, yy, Z, cmap=cmap_light)
# Plot also the training points
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=cmap_bold)
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
plt.title("3-Class classification (k = %i, weights = '%s')"
% (n_neighbors, weights))
plt.show()
```
##### Back to the Iris Data Set
```
iris = datasets.load_iris()
iris_X = iris.data
iris_y = iris.target
indices = np.random.permutation(len(iris_X))
iris_X_train = iris_X[indices[:-10]]
iris_y_train = iris_y[indices[:-10]]
iris_X_test = iris_X[indices[-10:]]
iris_y_test = iris_y[indices[-10:]]
# Create and fit a nearest-neighbor classifier
from sklearn.neighbors import KNeighborsClassifier
knn = KNeighborsClassifier()
knn.fit(iris_X_train, iris_y_train)
KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
metric_params=None, n_jobs=1, n_neighbors=15, p=2,
weights='uniform')
print("predicted:", knn.predict(iris_X_test))
print("actual :", iris_y_test)
```
|
github_jupyter
|
# Inference
## Imports & Args
```
import argparse
import json
import logging
import os
import random
from io import open
import numpy as np
import math
import _pickle as cPickle
from scipy.stats import spearmanr
from tensorboardX import SummaryWriter
from tqdm import tqdm
from bisect import bisect
import yaml
from easydict import EasyDict as edict
import sys
import pdb
import torch
import torch.nn.functional as F
import torch.nn as nn
from vilbert.task_utils import (
LoadDatasetEval,
LoadLosses,
ForwardModelsTrain,
ForwardModelsVal,
EvaluatingModel,
)
import vilbert.utils as utils
import torch.distributed as dist
def evaluate(
args,
task_dataloader_val,
task_stop_controller,
task_cfg,
device,
task_id,
model,
task_losses,
epochId,
default_gpu,
tbLogger,
):
model.eval()
for i, batch in enumerate(task_dataloader_val[task_id]):
loss, score, batch_size = ForwardModelsVal(
args, task_cfg, device, task_id, batch, model, task_losses
)
tbLogger.step_val(
epochId, float(loss), float(score), task_id, batch_size, "val"
)
if default_gpu:
sys.stdout.write("%d/%d\r" % (i, len(task_dataloader_val[task_id])))
sys.stdout.flush()
# update the multi-task scheduler.
task_stop_controller[task_id].step(tbLogger.getValScore(task_id))
score = tbLogger.showLossVal(task_id, task_stop_controller)
logging.basicConfig(
format="%(asctime)s - %(levelname)s - %(name)s - %(message)s",
datefmt="%m/%d/%Y %H:%M:%S",
level=logging.INFO,
)
logger = logging.getLogger(__name__)
parser = argparse.ArgumentParser()
parser.add_argument(
"--bert_model",
default="bert-base-uncased",
type=str,
help="Bert pre-trained model selected in the list: bert-base-uncased, "
"bert-large-uncased, bert-base-cased, bert-base-multilingual, bert-base-chinese.",
)
parser.add_argument(
"--from_pretrained",
default="bert-base-uncased",
type=str,
help="Bert pre-trained model selected in the list: bert-base-uncased, "
"bert-large-uncased, bert-base-cased, bert-base-multilingual, bert-base-chinese.",
)
parser.add_argument(
"--output_dir",
default="results",
type=str,
help="The output directory where the model checkpoints will be written.",
)
parser.add_argument(
"--config_file",
default="config/bert_config.json",
type=str,
help="The config file which specified the model details.",
)
parser.add_argument(
"--no_cuda", action="store_true", help="Whether not to use CUDA when available"
)
parser.add_argument(
"--do_lower_case",
default=True,
type=bool,
help="Whether to lower case the input text. True for uncased models, False for cased models.",
)
parser.add_argument(
"--local_rank",
type=int,
default=-1,
help="local_rank for distributed training on gpus",
)
parser.add_argument(
"--seed", type=int, default=42, help="random seed for initialization"
)
parser.add_argument(
"--fp16",
action="store_true",
help="Whether to use 16-bit float precision instead of 32-bit",
)
parser.add_argument(
"--loss_scale",
type=float,
default=0,
help="Loss scaling to improve fp16 numeric stability. Only used when fp16 set to True.\n"
"0 (default value): dynamic loss scaling.\n"
"Positive power of 2: static loss scaling value.\n",
)
parser.add_argument(
"--num_workers",
type=int,
default=16,
help="Number of workers in the dataloader.",
)
parser.add_argument(
"--save_name", default="", type=str, help="save name for training."
)
parser.add_argument(
"--use_chunk",
default=0,
type=float,
help="whether use chunck for parallel training.",
)
parser.add_argument(
"--batch_size", default=30, type=int, help="what is the batch size?"
)
parser.add_argument(
"--tasks", default="", type=str, help="1-2-3... training task separate by -"
)
parser.add_argument(
"--in_memory",
default=False,
type=bool,
help="whether use chunck for parallel training.",
)
parser.add_argument(
"--baseline", action="store_true", help="whether use single stream baseline."
)
parser.add_argument("--split", default="", type=str, help="which split to use.")
parser.add_argument(
"--dynamic_attention",
action="store_true",
help="whether use dynamic attention.",
)
parser.add_argument(
"--clean_train_sets",
default=True,
type=bool,
help="whether clean train sets for multitask data.",
)
parser.add_argument(
"--visual_target",
default=0,
type=int,
help="which target to use for visual branch. \
0: soft label, \
1: regress the feature, \
2: NCE loss.",
)
parser.add_argument(
"--task_specific_tokens",
action="store_true",
help="whether to use task specific tokens for the multi-task learning.",
)
```
## load the textual input
```
args = parser.parse_args(['--bert_model', 'bert-base-uncased',
'--from_pretrained', 'save/NLVR2_bert_base_6layer_6conect-finetune_from_multi_task_model-task_12/pytorch_model_19.bin',
'--config_file', 'config/bert_base_6layer_6conect.json',
'--tasks', '19',
'--split', 'trainval_dc', # this is the deep captions training split
'--save_name', 'task-19',
'--task_specific_tokens',
'--batch_size', '128'])
with open("vilbert_tasks.yml", "r") as f:
task_cfg = edict(yaml.safe_load(f))
random.seed(args.seed)
np.random.seed(args.seed)
torch.manual_seed(args.seed)
if args.baseline:
from pytorch_transformers.modeling_bert import BertConfig
from vilbert.basebert import BaseBertForVLTasks
else:
from vilbert.vilbert import BertConfig
from vilbert.vilbert import VILBertForVLTasks
task_names = []
for i, task_id in enumerate(args.tasks.split("-")):
task = "TASK" + task_id
name = task_cfg[task]["name"]
task_names.append(name)
# timeStamp = '-'.join(task_names) + '_' + args.config_file.split('/')[1].split('.')[0]
timeStamp = args.from_pretrained.split("/")[-1] + "-" + args.save_name
savePath = os.path.join(args.output_dir, timeStamp)
config = BertConfig.from_json_file(args.config_file)
if args.task_specific_tokens:
config.task_specific_tokens = True
if args.local_rank == -1 or args.no_cuda:
device = torch.device(
"cuda" if torch.cuda.is_available() and not args.no_cuda else "cpu"
)
n_gpu = torch.cuda.device_count()
else:
torch.cuda.set_device(args.local_rank)
device = torch.device("cuda", args.local_rank)
n_gpu = 1
# Initializes the distributed backend which will take care of sychronizing nodes/GPUs
torch.distributed.init_process_group(backend="nccl")
logger.info(
"device: {} n_gpu: {}, distributed training: {}, 16-bits training: {}".format(
device, n_gpu, bool(args.local_rank != -1), args.fp16
)
)
default_gpu = False
if dist.is_available() and args.local_rank != -1:
rank = dist.get_rank()
if rank == 0:
default_gpu = True
else:
default_gpu = True
if default_gpu and not os.path.exists(savePath):
os.makedirs(savePath)
task_batch_size, task_num_iters, task_ids, task_datasets_val, task_dataloader_val = LoadDatasetEval(
args, task_cfg, args.tasks.split("-")
)
tbLogger = utils.tbLogger(
timeStamp,
savePath,
task_names,
task_ids,
task_num_iters,
1,
save_logger=False,
txt_name="eval.txt",
)
# num_labels = max([dataset.num_labels for dataset in task_datasets_val.values()])
if args.dynamic_attention:
config.dynamic_attention = True
if "roberta" in args.bert_model:
config.model = "roberta"
if args.visual_target == 0:
config.v_target_size = 1601
config.visual_target = args.visual_target
else:
config.v_target_size = 2048
config.visual_target = args.visual_target
if args.task_specific_tokens:
config.task_specific_tokens = True
task_batch_size, task_num_iters, task_ids, task_datasets_val, task_dataloader_val
len(task_datasets_val['TASK19']), len(task_dataloader_val['TASK19'])
```
## load the pretrained model
```
num_labels = 0
if args.baseline:
model = BaseBertForVLTasks.from_pretrained(
args.from_pretrained,
config=config,
num_labels=num_labels,
default_gpu=default_gpu,
)
else:
model = VILBertForVLTasks.from_pretrained(
args.from_pretrained,
config=config,
num_labels=num_labels,
default_gpu=default_gpu,
)
task_losses = LoadLosses(args, task_cfg, args.tasks.split("-"))
model.to(device)
if args.local_rank != -1:
try:
from apex.parallel import DistributedDataParallel as DDP
except ImportError:
raise ImportError(
"Please install apex from https://www.github.com/nvidia/apex to use distributed and fp16 training."
)
model = DDP(model, delay_allreduce=True)
elif n_gpu > 1:
model = nn.DataParallel(model)
```
## Propagate Training Split
```
print("***** Running evaluation *****")
print(" Num Iters: ", task_num_iters)
print(" Batch size: ", task_batch_size)
pooled_output_mul_list, pooled_output_sum_list, pooled_output_t_list, pooled_output_v_list = list(), list(), list(), list()
targets_list = list()
model.eval()
# when run evaluate, we run each task sequentially.
for task_id in task_ids:
results = []
others = []
for i, batch in enumerate(task_dataloader_val[task_id]):
loss, score, batch_size, results, others, target = EvaluatingModel(
args,
task_cfg,
device,
task_id,
batch,
model,
task_dataloader_val,
task_losses,
results,
others,
)
pooled_output_mul_list.append(model.pooled_output_mul)
pooled_output_sum_list.append(model.pooled_output_sum)
pooled_output_t_list.append(model.pooled_output_t)
pooled_output_v_list.append(model.pooled_output_v)
targets_list.append(target)
tbLogger.step_val(0, float(loss), float(score), task_id, batch_size, "val")
sys.stdout.write("%d/%d\r" % (i, len(task_dataloader_val[task_id])))
sys.stdout.flush()
# save the result or evaluate the result.
ave_score = tbLogger.showLossVal(task_id)
if args.split:
json_path = os.path.join(savePath, args.split)
else:
json_path = os.path.join(savePath, task_cfg[task_id]["val_split"])
json.dump(results, open(json_path + "_result.json", "w"))
json.dump(others, open(json_path + "_others.json", "w"))
```
## save ViLBERT output
```
pooled_output_mul = torch.cat(pooled_output_mul_list, 0)
pooled_output_sum = torch.cat(pooled_output_sum_list, 0)
pooled_output_t = torch.cat(pooled_output_t_list, 0)
pooled_output_v = torch.cat(pooled_output_v_list, 0)
concat_pooled_output = torch.cat([pooled_output_t, pooled_output_v], 1)
targets = torch.cat(targets_list, 0)
targets
train_save_path = "datasets/ME/out_features/train_dc_features_nlvr2.pkl"
pooled_dict = {
"pooled_output_mul": pooled_output_mul,
"pooled_output_sum": pooled_output_sum,
"pooled_output_t": pooled_output_t,
"pooled_output_v": pooled_output_v,
"concat_pooled_output": concat_pooled_output,
"targets": targets,
}
pooled_dict.keys()
cPickle.dump(pooled_dict, open(train_save_path, 'wb'))
#cPickle.dump(val_pooled_dict, open(val_save_path, 'wb'))
```
# Training a Regressor
```
import torch
import torch.nn as nn
import torch.utils.data as Data
from torch.autograd import Variable
from statistics import mean
import matplotlib.pyplot as plt
import _pickle as cPickle
from tqdm import tqdm
from scipy.stats import spearmanr
train_save_path = "datasets/ME/out_features/train_dc_features_nlvr2.pkl"
# val_save_path = "datasets/ME/out_features/val_features.pkl"
pooled_dict = cPickle.load(open(train_save_path, 'rb'))
#val_pooled_dict = cPickle.load(open(val_save_path, 'rb'))
pooled_output_mul = pooled_dict["pooled_output_mul"]
pooled_output_sum = pooled_dict["pooled_output_sum"]
pooled_output_t = pooled_dict["pooled_output_t"]
pooled_output_v = pooled_dict["pooled_output_v"]
concat_pooled_output = pooled_dict["concat_pooled_output"]
targets = pooled_dict["targets"]
indices = {
"0": {},
"1": {},
"2": {},
"3": {},
}
import numpy as np
from sklearn.model_selection import KFold
kf = KFold(n_splits=4)
for i, (train_index, test_index) in enumerate(kf.split(pooled_output_mul)):
indices[str(i)]["train"] = train_index
indices[str(i)]["test"] = test_index
class Net(nn.Module):
def __init__(self, input_size, hidden_size_1, hidden_size_2, num_scores):
super(Net, self).__init__()
self.out = nn.Sequential(
nn.Linear(input_size, hidden_size_1),
GeLU(),
nn.Linear(hidden_size_1, hidden_size_2),
GeLU(),
nn.Linear(hidden_size_2, num_scores)
)
def forward(self, x):
return self.out(x)
class LinNet(nn.Module):
def __init__(self, input_size, hidden_size_1, num_scores):
super(LinNet, self).__init__()
self.out = nn.Sequential(
nn.Linear(input_size, hidden_size_1),
nn.Linear(hidden_size_1, num_scores),
)
def forward(self, x):
return self.out(x)
class SimpleLinNet(nn.Module):
def __init__(self, input_size, num_scores):
super(SimpleLinNet, self).__init__()
self.out = nn.Sequential(
nn.Linear(input_size, num_scores),
)
def forward(self, x):
return self.out(x)
class SigLinNet(nn.Module):
def __init__(self, input_size,
hidden_size_1,
hidden_size_2,
hidden_size_3,
num_scores):
super(SigLinNet, self).__init__()
self.out = nn.Sequential(
nn.Linear(input_size, hidden_size_1),
nn.Sigmoid(),
nn.Linear(hidden_size_1, hidden_size_2),
nn.Sigmoid(),
nn.Linear(hidden_size_2, hidden_size_3),
nn.Sigmoid(),
nn.Linear(hidden_size_3, num_scores),
)
def forward(self, x):
return self.out(x)
class ReLuLinNet(nn.Module):
def __init__(self, input_size, hidden_size_1, hidden_size_2, num_scores):
super(ReLuLinNet, self).__init__()
self.out = nn.Sequential(
nn.Linear(input_size, hidden_size_1),
nn.ReLU(),
nn.Dropout(0.1),
nn.Linear(hidden_size_1, hidden_size_2),
nn.ReLU(),
nn.Dropout(0.1),
nn.Linear(hidden_size_2, num_scores),
)
def forward(self, x):
return self.out(x)
def train_reg(inputs, targets, input_size, output_size, split, model, batch_size, epoch, lr, score, *argv):
torch.manual_seed(42)
nets = []
los = []
for i in range(len(split)):
ind = list(split[str(i)]["train"])
if score == "both":
torch_dataset = Data.TensorDataset(inputs[ind], targets[ind])
elif score == "stm":
torch_dataset = Data.TensorDataset(inputs[ind], targets[ind,0].reshape(-1,1))
elif score == "ltm":
torch_dataset = Data.TensorDataset(inputs[ind], targets[ind,1].reshape(-1,1))
loader = Data.DataLoader(
dataset=torch_dataset,
batch_size=batch_size,
shuffle=True
)
net = model(input_size, *argv, output_size)
net.cuda()
optimizer = torch.optim.Adam(net.parameters(), lr=lr, weight_decay=1e-4)
loss_func = torch.nn.MSELoss()
losses = []
net.train()
for _ in tqdm(range(epoch), desc="Split %d" % i):
errors = []
for step, (batch_in, batch_out) in enumerate(loader):
optimizer.zero_grad()
b_in = Variable(batch_in)
b_out = Variable(batch_out)
prediction = net(b_in)
loss = loss_func(prediction, b_out)
errors.append(loss.item())
loss.backward()
optimizer.step()
losses.append(mean(errors))
#if not (epoch+1) % 10:
# print('Epoch {}: train loss: {}'.format(epoch+1, mean(errors))
nets.append(net)
los.append(losses)
return nets, los
def test_reg(nets, inputs, targets, split, score):
losses = list()
rhos = {"stm": [], "ltm": []}
loss_func = torch.nn.MSELoss()
for i, net in enumerate(nets):
ind = list(split[str(i)]["test"])
if score == "both":
torch_dataset_val = Data.TensorDataset(inputs[ind], targets[ind])
elif score == "stm":
torch_dataset_val = Data.TensorDataset(inputs[ind], targets[ind,0].reshape(-1,1))
elif score == "ltm":
torch_dataset_val = Data.TensorDataset(inputs[ind], targets[ind,1].reshape(-1,1))
loader_val = Data.DataLoader(
dataset=torch_dataset_val,
batch_size=VAL_BATCH_SIZE,
shuffle=False
)
dataiter_val = iter(loader_val)
in_, out_ = dataiter_val.next()
curr_net = net
curr_net.eval()
pred_scores = curr_net(in_)
loss = loss_func(pred_scores, out_)
losses.append(loss.item())
r, _ = spearmanr(
pred_scores.cpu().detach().numpy()[:,0],
out_.cpu().detach().numpy()[:,0],
axis=0
)
rhos["stm"].append(r)
r, _ = spearmanr(
pred_scores.cpu().detach().numpy()[:,1],
out_.cpu().detach().numpy()[:,1],
axis=0
)
rhos["ltm"].append(r)
return rhos, losses
BATCH_SIZE = 128
VAL_BATCH_SIZE = 2000
EPOCH = 200
lr = 4e-4
```
## 1024-input train
```
nets, los = train_reg(
pooled_output_v,
targets,
1024, # input size
2, # output size
indices, # train and validation indices for each split
SigLinNet, # model class to be used
BATCH_SIZE,
EPOCH,
lr,
"both", # predict both scores
512, 64, 32 # sizes of hidden network layers
)
for l in los:
plt.plot(l[3:])
plt.yscale('log')
```
## 1024-input test
```
rhos, losses = test_reg(nets, pooled_output_v, targets, indices, "both")
rhos
mean(rhos["stm"]), mean(rhos["ltm"])
```
## 2048-input train
```
nets_2, los_2 = train_reg(
concat_pooled_output,
targets,
2048,
2,
indices,
SigLinNet,
BATCH_SIZE,
EPOCH,
lr,
"both",
512, 64, 32
)
for l in los_2:
plt.plot(l[3:])
plt.yscale('log')
```
## 2048-input test
```
rhos_2, losses_2 = test_reg(nets_2, concat_pooled_output, targets, indices, "both")
rhos_2
mean(rhos_2["stm"]), mean(rhos_2["ltm"])
```
|
github_jupyter
|
# Day 9 - Finding the sum, again, with a running series
* https://adventofcode.com/2020/day/9
This looks to be a variant of the [day 1, part 1 puzzle](./Day%2001.ipynb); finding the sum of two numbers in a set. Only now, we have to make sure we know what number to remove as we progres! This calls for a _sliding window_ iterator really, where we view the whole series through a slit X entries wide as it moves along the inputs.
As this puzzle is easier with a set of numbers, I create a sliding window of size `preamble + 2`, so we have access to the value to be removed and the value to be checked, at the same time; to achieve this, I created a window function that takes an *offset*, where you can take `offset` fewer items at the start, then have the window grow until it reaches the desired size:
```
from collections import deque
from itertools import islice
from typing import Iterable, Iterator, TypeVar
T = TypeVar("T")
def window(iterable: Iterable[T], n: int = 2, offset: int = 0) -> Iterator[deque[T]]:
it = iter(iterable)
queue = deque(islice(it, n - offset), maxlen=n)
yield queue
append = queue.append
for elem in it:
append(elem)
yield queue
def next_invalid(numbers: Iterable[int], preamble: int = 25) -> int:
it = window(numbers, preamble + 2, 2)
pool = set(next(it))
for win in it:
to_check = win[-1]
if len(win) == preamble + 2:
# remove the value now outside of our preamble window
pool.remove(win[0])
# validate the value can be created from a sum
for a in pool:
b = to_check - a
if b == a:
continue
if b in pool:
# number validated
break
else:
# no valid sum found
return to_check
pool.add(to_check)
test = [int(v) for v in """\
35
20
15
25
47
40
62
55
65
95
102
117
150
182
127
219
299
277
309
576
""".split()]
assert next_invalid(test, 5) == 127
import aocd
number_stream = [int(v) for v in aocd.get_data(day=9, year=2020).split()]
print("Part 1:", next_invalid(number_stream))
```
## Part 2
To solve the second part, you need a _dynamic_ window size over the input stream, and a running total. When the running total equals the value from part 1, we can then take the min and max values from the window.
- While the running total is too low, grow the window one stap and add the extra value to the total
- If the running total is too high, remove a value at the back of the window from the running total, and shrink that side of the window by one step.
With the Python `deque` (double-ended queue) already used in part one, this is a trivial task to achieve:
```
def find_weakness(numbers: Iterable[int], preamble: int = 25) -> int:
invalid = next_invalid(numbers, preamble)
it = iter(numbers)
total = next(it)
window = deque([total])
while total != invalid and window:
if total < invalid:
window.append(next(it))
total += window[-1]
else:
total -= window.popleft()
if not window:
raise ValueError("Could not find a weakness")
return min(window) + max(window)
assert find_weakness(test, 5) == 62
print("Part 2:", find_weakness(number_stream))
```
|
github_jupyter
|
# Campus SEIR Modeling
## Campus infection data
The following data consists of new infections reported since August 3, 2020, from diagnostic testing administered by the Wellness Center and University Health Services at the University of Notre Dame. The data is publically available on the [Notre Dame Covid-19 Dashboard](https://here.nd.edu/our-approach/dashboard/).
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.dates as mdates
from scipy.integrate import solve_ivp
from scipy.optimize import minimize
from datetime import timedelta
data = [
["2020-08-03", 0],
["2020-08-04", 0],
["2020-08-05", 0],
["2020-08-06", 1],
["2020-08-07", 0],
["2020-08-08", 1],
["2020-08-09", 2],
["2020-08-10", 4],
["2020-08-11", 4],
["2020-08-12", 7],
["2020-08-13", 10],
["2020-08-14", 14],
["2020-08-15", 3],
["2020-08-16", 15],
["2020-08-17", 80],
]
df = pd.DataFrame(data, columns=["date", "new cases"])
df["date"] = pd.to_datetime(df["date"])
fig, ax = plt.subplots(figsize=(8,4))
ax.bar(df["date"], df["new cases"], width=0.6)
ax.xaxis.set_major_locator(mdates.WeekdayLocator(byweekday=mdates.MO))
ax.xaxis.set_major_formatter(mdates.DateFormatter("%b %d"))
plt.title("Reported New Infections")
plt.grid()
```
## Fitting an SEIR model to campus data
Because of the limited amount of data available at the time this notebook was prepared, the model fitting has been limited to an SEIR model for infectious disease in a homogeneous population. In an SEIR model, the progression of an epidemic can be modeled by the rate processes shown in the following diagram.
$$\text{Susceptible}
\xrightarrow {\frac{\beta S I}{N}}
\text{Exposed}
\xrightarrow{\alpha E}
\text{Infectious}
\xrightarrow{\gamma I}
\text{Recovered} $$
which yeild the following model for the population of the four compartments
$$\begin{align*}
\frac{dS}{dt} &= -\beta S \frac{I}{N} \\
\frac{dE}{dt} &= \beta S \frac{I}{N} - \alpha E \\
\frac{dI}{dt} &= \alpha E - \gamma I \\
\frac{dR}{dt} &= \gamma I \\
\end{align*}$$
The recovery rate is given by $\gamma = 1/t_{recovery}$ where the average recovery time $t_{recovery}$ is estimated as 8 days.
| Parameter | Description | Estimated Value | Source |
| :-- | :-- | :-- | :-- |
| $N$ | campus population | 15,000 | estimate |
| $\alpha$ | 1/average latency period | 1/(3.0 d) |
| $\gamma$ | 1/average recovery period | 1/(8.0 d) | literature |
| $\beta$ | infection rate constant | tbd | fitted to data |
| $I_0$ | initial infectives on Aug 3, 2020 | tbd | fitted to data
| $R_0$ | reproduction number | ${\beta}/{\gamma}$ |
```
N = 15000 # estimated campus population
gamma = 1/8.0 # recovery rate = 1 / average recovery time in days
alpha = 1/3.0
def model(t, y, beta):
S, E, I, R = y
dSdt = -beta*S*I/N
dEdt = beta*S*I/N - alpha*E
dIdt = alpha*E - gamma*I
dRdt = gamma*I
return np.array([dSdt, dEdt, dIdt, dRdt])
def solve_model(t, params):
beta, I_initial = params
IC = [N - I_initial, I_initial, 0.0, 0.0]
soln = solve_ivp(lambda t, y: model(t, y, beta), np.array([t[0], t[-1]]),
IC, t_eval=t, atol=1e-6, rtol=1e-9)
S, E, I, R = soln.y
U = beta*S*I/N
return S, E, I, R, U
def residuals(df, params):
S, E, I, R, U = solve_model(df.index, params)
return np.linalg.norm(df["new cases"] - U)
def fit_model(df, params_est=[0.5, 0.5]):
return minimize(lambda params: residuals(df, params), params_est, method="Nelder-Mead").x
def plot_data(df):
plt.plot(df.index, np.array(df["new cases"]), "r.", ms=20, label="data")
plt.xlabel("days")
plt.title("new cases")
plt.legend()
def plot_model(t, params):
print("R0 =", round(beta/gamma, 1))
S, E, I, R, U = solve_model(t, params)
plt.plot(t, U, lw=3, label="model")
plt.xlabel("days")
plt.title("new cases")
plt.legend()
plot_data(df)
beta, I_initial = fit_model(df)
plot_model(df.index, [beta, I_initial])
```
## Fitted parameter values
```
from tabulate import tabulate
parameter_table = [
["N", 15000],
["I0", I_initial],
["beta", beta],
["gamma", gamma],
["R0", beta/gamma]
]
print(tabulate(parameter_table, headers=["Parameter", "Value"]))
```
## Short term predictions of newly confirmed cases
Using the fitted parameters, the following code presents a short term projection of newly diagnosed infections. Roughly speaking, the model projects a 50% increase per day in newly diagnosed cases as a result of testing sympotomatic individuals.
The number of infected but asympotomatic individuals is unknown at this time, but can be expected to be a 2x multiple of this projection.
```
# prediction horizon (days ahead)
H = 1
# retrospective lag
K = 6
fig, ax = plt.subplots(1, 1, figsize=(12, 4))
for k in range(0, K+1):
# use data up to k days ago
if k > 0:
beta, I_initial = fit_model(df[:-k])
P = max(df[:-k].index) + H
c = 'b'
a = 0.25
else:
beta, I_initial = fit_model(df)
P = max(df.index) + H
c = 'r'
a = 1.0
# simulation
t = np.linspace(0, P, P+1)
S, E, I, R, U = solve_model(t, [beta, I_initial])
# plotting
dates = [df["date"][0] + timedelta(days=t) for t in t]
ax.plot(dates, U, c, lw=3, alpha=a)
ax.plot(df["date"], df["new cases"], "r.", ms=25, label="new infections (data)")
ax.xaxis.set_major_locator(mdates.WeekdayLocator(byweekday=mdates.MO))
ax.xaxis.set_major_formatter(mdates.DateFormatter("%b %d"))
ax.grid(True)
ax.set_title(f"{H} day-ahead predictions of confirmed new cases");
```
|
github_jupyter
|
```
# dependencies
import pandas as pd
from sqlalchemy import create_engine, inspect
# read raw data csv
csv_file = "NYC_Dog_Licensing_Dataset.csv"
all_dog_data = pd.read_csv(csv_file)
all_dog_data.head(10)
# trim data frame to necessary columns
dog_data_df = all_dog_data[['AnimalName','AnimalGender','BreedName','Borough','ZipCode']]
dog_data_df.head(10)
# remove incomplete rows
dog_data_df.count()
cleaned_dog_data_df = dog_data_df.dropna(how='any')
cleaned_dog_data_df.count()
# reformat zip code as integer
cleaned_dog_data_df['ZipCode'] = cleaned_dog_data_df['ZipCode'].astype(int)
cleaned_dog_data_df.head(10)
# connect to postgres to create dog database
engine = create_engine('postgres://postgres:postgres@localhost:5432')
conn = engine.connect()
conn.execute("commit")
conn.execute("drop database if exists dog_db")
conn.execute("commit")
conn.execute("create database dog_db")
# import dataframe into database table
engine = create_engine('postgres://postgres:postgres@localhost:5432/dog_db')
conn = engine.connect()
cleaned_dog_data_df.to_sql('dog_names', con=conn, if_exists='replace', index=False)
# check for data
engine.execute('SELECT * FROM dog_names').fetchall()
# inspect table names and column names
inspector = inspect(engine)
inspector.get_table_names()
inspector = inspect(engine)
columns = inspector.get_columns('dog_names')
print(columns)
# query the table and save as dataframe for analysis
dog_table = pd.read_sql_query('select * from dog_names', con=engine)
dog_table.head(20)
dog_data = dog_table.loc[(dog_table["AnimalName"] != "UNKNOWN") & (dog_table["AnimalName"] != "NAME NOT PROVIDED"), :]
dog_data.head(20)
name_counts = pd.DataFrame(dog_data.groupby("AnimalName")["AnimalName"].count())
name_counts_df = name_counts.rename(columns={"AnimalName":"Count"})
name_counts_df.head()
top_names = name_counts_df.sort_values(["Count"], ascending=False)
top_names.head(12)
f_dog_data = dog_data.loc[dog_data["AnimalGender"] == "F", :]
f_dog_data.head()
f_name_counts = pd.DataFrame(f_dog_data.groupby("AnimalName")["AnimalName"].count())
f_name_counts_df = f_name_counts.rename(columns={"AnimalName":"Count"})
f_top_names = f_name_counts_df.sort_values(["Count"], ascending=False)
f_top_names.head(12)
m_dog_data = dog_data.loc[dog_data["AnimalGender"] == "M", :]
m_name_counts = pd.DataFrame(m_dog_data.groupby("AnimalName")["AnimalName"].count())
m_name_counts_df = m_name_counts.rename(columns={"AnimalName":"Count"})
m_top_names = m_name_counts_df.sort_values(["Count"], ascending=False)
m_top_names.head(12)
borough_counts = pd.DataFrame(dog_data.groupby("Borough")["AnimalName"].count())
borough_counts_df = borough_counts.rename(columns={"AnimalName":"Count"})
borough_dogs = borough_counts_df.sort_values(["Count"], ascending=False)
borough_dogs.head()
top_boroughs = dog_data.loc[(dog_data["Borough"] == "Manhattan") | (dog_data["Borough"] == "Brooklyn") | (dog_data["Borough"] == "Queens") | (dog_data["Borough"] == "Bronx") | (dog_data["Borough"] == "Staten Island"), :]
f_m_top_boroughs = top_boroughs.loc[(top_boroughs["AnimalGender"] == "F") | (top_boroughs["AnimalGender"] == "M"), :]
f_m_top_boroughs.head()
borough_data = f_m_top_boroughs.groupby(['Borough','AnimalGender'])["AnimalName"].count()
borough_dogs = pd.DataFrame(borough_data)
borough_dogs
mt_dog_data = dog_data.loc[dog_data["Borough"].str.contains("Manhattan", case=False), :]
mt_name_counts = pd.DataFrame(mt_dog_data.groupby("AnimalName")["AnimalName"].count())
mt_name_counts_df = mt_name_counts.rename(columns={"AnimalName":"Count"})
mt_top_names = mt_name_counts_df.sort_values(["Count"], ascending=False)
mt_top_names.head(12)
bk_dog_data = dog_data.loc[dog_data["Borough"].str.contains("Brooklyn", case=False), :]
bk_name_counts = pd.DataFrame(bk_dog_data.groupby("AnimalName")["AnimalName"].count())
bk_name_counts_df = bk_name_counts.rename(columns={"AnimalName":"Count"})
bk_top_names = bk_name_counts_df.sort_values(["Count"], ascending=False)
bk_top_names.head(12)
qn_dog_data = dog_data.loc[dog_data["Borough"].str.contains("Queens", case=False), :]
qn_name_counts = pd.DataFrame(qn_dog_data.groupby("AnimalName")["AnimalName"].count())
qn_name_counts_df = qn_name_counts.rename(columns={"AnimalName":"Count"})
qn_top_names = qn_name_counts_df.sort_values(["Count"], ascending=False)
qn_top_names.head(12)
bx_dog_data = dog_data.loc[dog_data["Borough"].str.contains("Bronx", case=False), :]
bx_name_counts = pd.DataFrame(bx_dog_data.groupby("AnimalName")["AnimalName"].count())
bx_name_counts_df = bx_name_counts.rename(columns={"AnimalName":"Count"})
bx_top_names = bx_name_counts_df.sort_values(["Count"], ascending=False)
bx_top_names.head(12)
si_dog_data = dog_data.loc[dog_data["Borough"].str.contains("Staten Island", case=False), :]
si_name_counts = pd.DataFrame(si_dog_data.groupby("AnimalName")["AnimalName"].count())
si_name_counts_df = si_name_counts.rename(columns={"AnimalName":"Count"})
si_top_names = si_name_counts_df.sort_values(["Count"], ascending=False)
si_top_names.head(12)
```
|
github_jupyter
|
# What's this PyTorch business?
You've written a lot of code in this assignment to provide a whole host of neural network functionality. Dropout, Batch Norm, and 2D convolutions are some of the workhorses of deep learning in computer vision. You've also worked hard to make your code efficient and vectorized.
For the last part of this assignment, though, we're going to leave behind your beautiful codebase and instead migrate to one of two popular deep learning frameworks: in this instance, PyTorch (or TensorFlow, if you choose to use that notebook).
### What is PyTorch?
PyTorch is a system for executing dynamic computational graphs over Tensor objects that behave similarly as numpy ndarray. It comes with a powerful automatic differentiation engine that removes the need for manual back-propagation.
### Why?
* Our code will now run on GPUs! Much faster training. When using a framework like PyTorch or TensorFlow you can harness the power of the GPU for your own custom neural network architectures without having to write CUDA code directly (which is beyond the scope of this class).
* We want you to be ready to use one of these frameworks for your project so you can experiment more efficiently than if you were writing every feature you want to use by hand.
* We want you to stand on the shoulders of giants! TensorFlow and PyTorch are both excellent frameworks that will make your lives a lot easier, and now that you understand their guts, you are free to use them :)
* We want you to be exposed to the sort of deep learning code you might run into in academia or industry.
### PyTorch versions
This notebook assumes that you are using **PyTorch version 1.4**. In some of the previous versions (e.g. before 0.4), Tensors had to be wrapped in Variable objects to be used in autograd; however Variables have now been deprecated. In addition 1.0+ versions separate a Tensor's datatype from its device, and use numpy-style factories for constructing Tensors rather than directly invoking Tensor constructors.
## How will I learn PyTorch?
Justin Johnson has made an excellent [tutorial](https://github.com/jcjohnson/pytorch-examples) for PyTorch.
You can also find the detailed [API doc](http://pytorch.org/docs/stable/index.html) here. If you have other questions that are not addressed by the API docs, the [PyTorch forum](https://discuss.pytorch.org/) is a much better place to ask than StackOverflow.
## Install PyTorch 1.4 (ONLY IF YOU ARE WORKING LOCALLY)
1. Have the latest version of Anaconda installed on your machine.
2. Create a new conda environment starting from Python 3.7. In this setup example, we'll call it `torch_env`.
3. Run the command: `conda activate torch_env`
4. Run the command: `pip install torch==1.4 torchvision==0.5.0`
# Table of Contents
This assignment has 5 parts. You will learn PyTorch on **three different levels of abstraction**, which will help you understand it better and prepare you for the final project.
1. Part I, Preparation: we will use CIFAR-10 dataset.
2. Part II, Barebones PyTorch: **Abstraction level 1**, we will work directly with the lowest-level PyTorch Tensors.
3. Part III, PyTorch Module API: **Abstraction level 2**, we will use `nn.Module` to define arbitrary neural network architecture.
4. Part IV, PyTorch Sequential API: **Abstraction level 3**, we will use `nn.Sequential` to define a linear feed-forward network very conveniently.
5. Part V, CIFAR-10 open-ended challenge: please implement your own network to get as high accuracy as possible on CIFAR-10. You can experiment with any layer, optimizer, hyperparameters or other advanced features.
Here is a table of comparison:
| API | Flexibility | Convenience |
|---------------|-------------|-------------|
| Barebone | High | Low |
| `nn.Module` | High | Medium |
| `nn.Sequential` | Low | High |
# Part I. Preparation
First, we load the CIFAR-10 dataset. This might take a couple minutes the first time you do it, but the files should stay cached after that.
In previous parts of the assignment we had to write our own code to download the CIFAR-10 dataset, preprocess it, and iterate through it in minibatches; PyTorch provides convenient tools to automate this process for us.
```
import torch
assert '.'.join(torch.__version__.split('.')[:2]) == '1.4'
import torch.nn as nn
import torch.optim as optim
from torch.utils.data import DataLoader
from torch.utils.data import sampler
import torchvision.datasets as dset
import torchvision.transforms as T
import numpy as np
NUM_TRAIN = 49000
# The torchvision.transforms package provides tools for preprocessing data
# and for performing data augmentation; here we set up a transform to
# preprocess the data by subtracting the mean RGB value and dividing by the
# standard deviation of each RGB value; we've hardcoded the mean and std.
transform = T.Compose([
T.ToTensor(),
T.Normalize((0.4914, 0.4822, 0.4465), (0.2023, 0.1994, 0.2010))
])
# We set up a Dataset object for each split (train / val / test); Datasets load
# training examples one at a time, so we wrap each Dataset in a DataLoader which
# iterates through the Dataset and forms minibatches. We divide the CIFAR-10
# training set into train and val sets by passing a Sampler object to the
# DataLoader telling how it should sample from the underlying Dataset.
cifar10_train = dset.CIFAR10('./cs231n/datasets', train=True, download=True,
transform=transform)
loader_train = DataLoader(cifar10_train, batch_size=64,
sampler=sampler.SubsetRandomSampler(range(NUM_TRAIN)))
cifar10_val = dset.CIFAR10('./cs231n/datasets', train=True, download=True,
transform=transform)
loader_val = DataLoader(cifar10_val, batch_size=64,
sampler=sampler.SubsetRandomSampler(range(NUM_TRAIN, 50000)))
cifar10_test = dset.CIFAR10('./cs231n/datasets', train=False, download=True,
transform=transform)
loader_test = DataLoader(cifar10_test, batch_size=64)
```
You have an option to **use GPU by setting the flag to True below**. It is not necessary to use GPU for this assignment. Note that if your computer does not have CUDA enabled, `torch.cuda.is_available()` will return False and this notebook will fallback to CPU mode.
The global variables `dtype` and `device` will control the data types throughout this assignment.
## Colab Users
If you are using Colab, you need to manually switch to a GPU device. You can do this by clicking `Runtime -> Change runtime type` and selecting `GPU` under `Hardware Accelerator`. Note that you have to rerun the cells from the top since the kernel gets restarted upon switching runtimes.
```
USE_GPU = True
dtype = torch.float32 # we will be using float throughout this tutorial
if USE_GPU and torch.cuda.is_available():
device = torch.device('cuda')
else:
device = torch.device('cpu')
# Constant to control how frequently we print train loss
print_every = 100
print('using device:', device)
```
# Part II. Barebones PyTorch
PyTorch ships with high-level APIs to help us define model architectures conveniently, which we will cover in Part II of this tutorial. In this section, we will start with the barebone PyTorch elements to understand the autograd engine better. After this exercise, you will come to appreciate the high-level model API more.
We will start with a simple fully-connected ReLU network with two hidden layers and no biases for CIFAR classification.
This implementation computes the forward pass using operations on PyTorch Tensors, and uses PyTorch autograd to compute gradients. It is important that you understand every line, because you will write a harder version after the example.
When we create a PyTorch Tensor with `requires_grad=True`, then operations involving that Tensor will not just compute values; they will also build up a computational graph in the background, allowing us to easily backpropagate through the graph to compute gradients of some Tensors with respect to a downstream loss. Concretely if x is a Tensor with `x.requires_grad == True` then after backpropagation `x.grad` will be another Tensor holding the gradient of x with respect to the scalar loss at the end.
### PyTorch Tensors: Flatten Function
A PyTorch Tensor is conceptionally similar to a numpy array: it is an n-dimensional grid of numbers, and like numpy PyTorch provides many functions to efficiently operate on Tensors. As a simple example, we provide a `flatten` function below which reshapes image data for use in a fully-connected neural network.
Recall that image data is typically stored in a Tensor of shape N x C x H x W, where:
* N is the number of datapoints
* C is the number of channels
* H is the height of the intermediate feature map in pixels
* W is the height of the intermediate feature map in pixels
This is the right way to represent the data when we are doing something like a 2D convolution, that needs spatial understanding of where the intermediate features are relative to each other. When we use fully connected affine layers to process the image, however, we want each datapoint to be represented by a single vector -- it's no longer useful to segregate the different channels, rows, and columns of the data. So, we use a "flatten" operation to collapse the `C x H x W` values per representation into a single long vector. The flatten function below first reads in the N, C, H, and W values from a given batch of data, and then returns a "view" of that data. "View" is analogous to numpy's "reshape" method: it reshapes x's dimensions to be N x ??, where ?? is allowed to be anything (in this case, it will be C x H x W, but we don't need to specify that explicitly).
```
def flatten(x):
N = x.shape[0] # read in N, C, H, W
return x.view(N, -1) # "flatten" the C * H * W values into a single vector per image
def test_flatten():
x = torch.arange(12).view(2, 1, 3, 2)
print('Before flattening: ', x)
print('After flattening: ', flatten(x))
test_flatten()
```
### Barebones PyTorch: Two-Layer Network
Here we define a function `two_layer_fc` which performs the forward pass of a two-layer fully-connected ReLU network on a batch of image data. After defining the forward pass we check that it doesn't crash and that it produces outputs of the right shape by running zeros through the network.
You don't have to write any code here, but it's important that you read and understand the implementation.
```
import torch.nn.functional as F # useful stateless functions
def two_layer_fc(x, params):
"""
A fully-connected neural networks; the architecture is:
NN is fully connected -> ReLU -> fully connected layer.
Note that this function only defines the forward pass;
PyTorch will take care of the backward pass for us.
The input to the network will be a minibatch of data, of shape
(N, d1, ..., dM) where d1 * ... * dM = D. The hidden layer will have H units,
and the output layer will produce scores for C classes.
Inputs:
- x: A PyTorch Tensor of shape (N, d1, ..., dM) giving a minibatch of
input data.
- params: A list [w1, w2] of PyTorch Tensors giving weights for the network;
w1 has shape (D, H) and w2 has shape (H, C).
Returns:
- scores: A PyTorch Tensor of shape (N, C) giving classification scores for
the input data x.
"""
# first we flatten the image
x = flatten(x) # shape: [batch_size, C x H x W]
w1, w2 = params
# Forward pass: compute predicted y using operations on Tensors. Since w1 and
# w2 have requires_grad=True, operations involving these Tensors will cause
# PyTorch to build a computational graph, allowing automatic computation of
# gradients. Since we are no longer implementing the backward pass by hand we
# don't need to keep references to intermediate values.
# you can also use `.clamp(min=0)`, equivalent to F.relu()
x = F.relu(x.mm(w1))
x = x.mm(w2)
return x
def two_layer_fc_test():
hidden_layer_size = 42
x = torch.zeros((64, 50), dtype=dtype) # minibatch size 64, feature dimension 50
w1 = torch.zeros((50, hidden_layer_size), dtype=dtype)
w2 = torch.zeros((hidden_layer_size, 10), dtype=dtype)
scores = two_layer_fc(x, [w1, w2])
print(scores.size()) # you should see [64, 10]
two_layer_fc_test()
```
### Barebones PyTorch: Three-Layer ConvNet
Here you will complete the implementation of the function `three_layer_convnet`, which will perform the forward pass of a three-layer convolutional network. Like above, we can immediately test our implementation by passing zeros through the network. The network should have the following architecture:
1. A convolutional layer (with bias) with `channel_1` filters, each with shape `KW1 x KH1`, and zero-padding of two
2. ReLU nonlinearity
3. A convolutional layer (with bias) with `channel_2` filters, each with shape `KW2 x KH2`, and zero-padding of one
4. ReLU nonlinearity
5. Fully-connected layer with bias, producing scores for C classes.
Note that we have **no softmax activation** here after our fully-connected layer: this is because PyTorch's cross entropy loss performs a softmax activation for you, and by bundling that step in makes computation more efficient.
**HINT**: For convolutions: http://pytorch.org/docs/stable/nn.html#torch.nn.functional.conv2d; pay attention to the shapes of convolutional filters!
```
def three_layer_convnet(x, params):
"""
Performs the forward pass of a three-layer convolutional network with the
architecture defined above.
Inputs:
- x: A PyTorch Tensor of shape (N, 3, H, W) giving a minibatch of images
- params: A list of PyTorch Tensors giving the weights and biases for the
network; should contain the following:
- conv_w1: PyTorch Tensor of shape (channel_1, 3, KH1, KW1) giving weights
for the first convolutional layer
- conv_b1: PyTorch Tensor of shape (channel_1,) giving biases for the first
convolutional layer
- conv_w2: PyTorch Tensor of shape (channel_2, channel_1, KH2, KW2) giving
weights for the second convolutional layer
- conv_b2: PyTorch Tensor of shape (channel_2,) giving biases for the second
convolutional layer
- fc_w: PyTorch Tensor giving weights for the fully-connected layer. Can you
figure out what the shape should be?
- fc_b: PyTorch Tensor giving biases for the fully-connected layer. Can you
figure out what the shape should be?
Returns:
- scores: PyTorch Tensor of shape (N, C) giving classification scores for x
"""
conv_w1, conv_b1, conv_w2, conv_b2, fc_w, fc_b = params
scores = None
################################################################################
# TODO: Implement the forward pass for the three-layer ConvNet. #
################################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
x = F.conv2d(x, conv_w1, bias=conv_b1, padding=conv_w1.size()[-1] // 2)
x = F.relu(x)
x = F.conv2d(x, conv_w2, bias=conv_b2, padding=conv_w2.size()[-1] // 2)
x = F.relu(x)
x = x.view(x.size()[0], -1)
scores = F.linear(x, fc_w.transpose(0, 1), bias=fc_b)
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
################################################################################
# END OF YOUR CODE #
################################################################################
return scores
```
After defining the forward pass of the ConvNet above, run the following cell to test your implementation.
When you run this function, scores should have shape (64, 10).
```
def three_layer_convnet_test():
x = torch.zeros((64, 3, 32, 32), dtype=dtype) # minibatch size 64, image size [3, 32, 32]
conv_w1 = torch.zeros((6, 3, 5, 5), dtype=dtype) # [out_channel, in_channel, kernel_H, kernel_W]
conv_b1 = torch.zeros((6,)) # out_channel
conv_w2 = torch.zeros((9, 6, 3, 3), dtype=dtype) # [out_channel, in_channel, kernel_H, kernel_W]
conv_b2 = torch.zeros((9,)) # out_channel
# you must calculate the shape of the tensor after two conv layers, before the fully-connected layer
fc_w = torch.zeros((9 * 32 * 32, 10))
fc_b = torch.zeros(10)
scores = three_layer_convnet(x, [conv_w1, conv_b1, conv_w2, conv_b2, fc_w, fc_b])
print(scores.size()) # you should see [64, 10]
three_layer_convnet_test()
```
### Barebones PyTorch: Initialization
Let's write a couple utility methods to initialize the weight matrices for our models.
- `random_weight(shape)` initializes a weight tensor with the Kaiming normalization method.
- `zero_weight(shape)` initializes a weight tensor with all zeros. Useful for instantiating bias parameters.
The `random_weight` function uses the Kaiming normal initialization method, described in:
He et al, *Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification*, ICCV 2015, https://arxiv.org/abs/1502.01852
```
def random_weight(shape):
"""
Create random Tensors for weights; setting requires_grad=True means that we
want to compute gradients for these Tensors during the backward pass.
We use Kaiming normalization: sqrt(2 / fan_in)
"""
if len(shape) == 2: # FC weight
fan_in = shape[0]
else:
fan_in = np.prod(shape[1:]) # conv weight [out_channel, in_channel, kH, kW]
# randn is standard normal distribution generator.
w = torch.randn(shape, device=device, dtype=dtype) * np.sqrt(2. / fan_in)
w.requires_grad = True
return w
def zero_weight(shape):
return torch.zeros(shape, device=device, dtype=dtype, requires_grad=True)
# create a weight of shape [3 x 5]
# you should see the type `torch.cuda.FloatTensor` if you use GPU.
# Otherwise it should be `torch.FloatTensor`
random_weight((3, 5))
```
### Barebones PyTorch: Check Accuracy
When training the model we will use the following function to check the accuracy of our model on the training or validation sets.
When checking accuracy we don't need to compute any gradients; as a result we don't need PyTorch to build a computational graph for us when we compute scores. To prevent a graph from being built we scope our computation under a `torch.no_grad()` context manager.
```
def check_accuracy_part2(loader, model_fn, params):
"""
Check the accuracy of a classification model.
Inputs:
- loader: A DataLoader for the data split we want to check
- model_fn: A function that performs the forward pass of the model,
with the signature scores = model_fn(x, params)
- params: List of PyTorch Tensors giving parameters of the model
Returns: Nothing, but prints the accuracy of the model
"""
split = 'val' if loader.dataset.train else 'test'
print('Checking accuracy on the %s set' % split)
num_correct, num_samples = 0, 0
with torch.no_grad():
for x, y in loader:
x = x.to(device=device, dtype=dtype) # move to device, e.g. GPU
y = y.to(device=device, dtype=torch.int64)
scores = model_fn(x, params)
_, preds = scores.max(1)
num_correct += (preds == y).sum()
num_samples += preds.size(0)
acc = float(num_correct) / num_samples
print('Got %d / %d correct (%.2f%%)' % (num_correct, num_samples, 100 * acc))
```
### BareBones PyTorch: Training Loop
We can now set up a basic training loop to train our network. We will train the model using stochastic gradient descent without momentum. We will use `torch.functional.cross_entropy` to compute the loss; you can [read about it here](http://pytorch.org/docs/stable/nn.html#cross-entropy).
The training loop takes as input the neural network function, a list of initialized parameters (`[w1, w2]` in our example), and learning rate.
```
def train_part2(model_fn, params, learning_rate):
"""
Train a model on CIFAR-10.
Inputs:
- model_fn: A Python function that performs the forward pass of the model.
It should have the signature scores = model_fn(x, params) where x is a
PyTorch Tensor of image data, params is a list of PyTorch Tensors giving
model weights, and scores is a PyTorch Tensor of shape (N, C) giving
scores for the elements in x.
- params: List of PyTorch Tensors giving weights for the model
- learning_rate: Python scalar giving the learning rate to use for SGD
Returns: Nothing
"""
for t, (x, y) in enumerate(loader_train):
# Move the data to the proper device (GPU or CPU)
x = x.to(device=device, dtype=dtype)
y = y.to(device=device, dtype=torch.long)
# Forward pass: compute scores and loss
scores = model_fn(x, params)
loss = F.cross_entropy(scores, y)
# Backward pass: PyTorch figures out which Tensors in the computational
# graph has requires_grad=True and uses backpropagation to compute the
# gradient of the loss with respect to these Tensors, and stores the
# gradients in the .grad attribute of each Tensor.
loss.backward()
# Update parameters. We don't want to backpropagate through the
# parameter updates, so we scope the updates under a torch.no_grad()
# context manager to prevent a computational graph from being built.
with torch.no_grad():
for w in params:
w -= learning_rate * w.grad
# Manually zero the gradients after running the backward pass
w.grad.zero_()
if t % print_every == 0:
print('Iteration %d, loss = %.4f' % (t, loss.item()))
check_accuracy_part2(loader_val, model_fn, params)
print()
```
### BareBones PyTorch: Train a Two-Layer Network
Now we are ready to run the training loop. We need to explicitly allocate tensors for the fully connected weights, `w1` and `w2`.
Each minibatch of CIFAR has 64 examples, so the tensor shape is `[64, 3, 32, 32]`.
After flattening, `x` shape should be `[64, 3 * 32 * 32]`. This will be the size of the first dimension of `w1`.
The second dimension of `w1` is the hidden layer size, which will also be the first dimension of `w2`.
Finally, the output of the network is a 10-dimensional vector that represents the probability distribution over 10 classes.
You don't need to tune any hyperparameters but you should see accuracies above 40% after training for one epoch.
```
hidden_layer_size = 4000
learning_rate = 1e-2
w1 = random_weight((3 * 32 * 32, hidden_layer_size))
w2 = random_weight((hidden_layer_size, 10))
train_part2(two_layer_fc, [w1, w2], learning_rate)
```
### BareBones PyTorch: Training a ConvNet
In the below you should use the functions defined above to train a three-layer convolutional network on CIFAR. The network should have the following architecture:
1. Convolutional layer (with bias) with 32 5x5 filters, with zero-padding of 2
2. ReLU
3. Convolutional layer (with bias) with 16 3x3 filters, with zero-padding of 1
4. ReLU
5. Fully-connected layer (with bias) to compute scores for 10 classes
You should initialize your weight matrices using the `random_weight` function defined above, and you should initialize your bias vectors using the `zero_weight` function above.
You don't need to tune any hyperparameters, but if everything works correctly you should achieve an accuracy above 42% after one epoch.
```
learning_rate = 3e-3
channel_1 = 32
channel_2 = 16
conv_w1 = None
conv_b1 = None
conv_w2 = None
conv_b2 = None
fc_w = None
fc_b = None
################################################################################
# TODO: Initialize the parameters of a three-layer ConvNet. #
################################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
conv_w1 = random_weight((32, 3, 5, 5))
conv_b1 = zero_weight(32)
conv_w2 = random_weight((16, 32, 3, 3))
conv_b2 = zero_weight(16)
fc_w = random_weight((16 * 32 * 32, 10))
fc_b = zero_weight(10)
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
################################################################################
# END OF YOUR CODE #
################################################################################
params = [conv_w1, conv_b1, conv_w2, conv_b2, fc_w, fc_b]
train_part2(three_layer_convnet, params, learning_rate)
```
# Part III. PyTorch Module API
Barebone PyTorch requires that we track all the parameter tensors by hand. This is fine for small networks with a few tensors, but it would be extremely inconvenient and error-prone to track tens or hundreds of tensors in larger networks.
PyTorch provides the `nn.Module` API for you to define arbitrary network architectures, while tracking every learnable parameters for you. In Part II, we implemented SGD ourselves. PyTorch also provides the `torch.optim` package that implements all the common optimizers, such as RMSProp, Adagrad, and Adam. It even supports approximate second-order methods like L-BFGS! You can refer to the [doc](http://pytorch.org/docs/master/optim.html) for the exact specifications of each optimizer.
To use the Module API, follow the steps below:
1. Subclass `nn.Module`. Give your network class an intuitive name like `TwoLayerFC`.
2. In the constructor `__init__()`, define all the layers you need as class attributes. Layer objects like `nn.Linear` and `nn.Conv2d` are themselves `nn.Module` subclasses and contain learnable parameters, so that you don't have to instantiate the raw tensors yourself. `nn.Module` will track these internal parameters for you. Refer to the [doc](http://pytorch.org/docs/master/nn.html) to learn more about the dozens of builtin layers. **Warning**: don't forget to call the `super().__init__()` first!
3. In the `forward()` method, define the *connectivity* of your network. You should use the attributes defined in `__init__` as function calls that take tensor as input and output the "transformed" tensor. Do *not* create any new layers with learnable parameters in `forward()`! All of them must be declared upfront in `__init__`.
After you define your Module subclass, you can instantiate it as an object and call it just like the NN forward function in part II.
### Module API: Two-Layer Network
Here is a concrete example of a 2-layer fully connected network:
```
class TwoLayerFC(nn.Module):
def __init__(self, input_size, hidden_size, num_classes):
super().__init__()
# assign layer objects to class attributes
self.fc1 = nn.Linear(input_size, hidden_size)
# nn.init package contains convenient initialization methods
# http://pytorch.org/docs/master/nn.html#torch-nn-init
nn.init.kaiming_normal_(self.fc1.weight)
self.fc2 = nn.Linear(hidden_size, num_classes)
nn.init.kaiming_normal_(self.fc2.weight)
def forward(self, x):
# forward always defines connectivity
x = flatten(x)
scores = self.fc2(F.relu(self.fc1(x)))
return scores
def test_TwoLayerFC():
input_size = 50
x = torch.zeros((64, input_size), dtype=dtype) # minibatch size 64, feature dimension 50
model = TwoLayerFC(input_size, 42, 10)
scores = model(x)
print(scores.size()) # you should see [64, 10]
test_TwoLayerFC()
```
### Module API: Three-Layer ConvNet
It's your turn to implement a 3-layer ConvNet followed by a fully connected layer. The network architecture should be the same as in Part II:
1. Convolutional layer with `channel_1` 5x5 filters with zero-padding of 2
2. ReLU
3. Convolutional layer with `channel_2` 3x3 filters with zero-padding of 1
4. ReLU
5. Fully-connected layer to `num_classes` classes
You should initialize the weight matrices of the model using the Kaiming normal initialization method.
**HINT**: http://pytorch.org/docs/stable/nn.html#conv2d
After you implement the three-layer ConvNet, the `test_ThreeLayerConvNet` function will run your implementation; it should print `(64, 10)` for the shape of the output scores.
```
class ThreeLayerConvNet(nn.Module):
def __init__(self, in_channel, channel_1, channel_2, num_classes):
super().__init__()
########################################################################
# TODO: Set up the layers you need for a three-layer ConvNet with the #
# architecture defined above. #
########################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
self.conv1 = nn.Conv2d(in_channel, channel_1, 5, padding=2)
self.conv2 = nn.Conv2d(channel_1, channel_2, 3, padding=1)
self.fc = nn.Linear(channel_2 * 32 * 32, num_classes)
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
########################################################################
# END OF YOUR CODE #
########################################################################
def forward(self, x):
scores = None
########################################################################
# TODO: Implement the forward function for a 3-layer ConvNet. you #
# should use the layers you defined in __init__ and specify the #
# connectivity of those layers in forward() #
########################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
scores = self.fc(F.relu(self.conv2(F.relu(self.conv1(x)))).reshape(-1, self.fc.in_features))
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
########################################################################
# END OF YOUR CODE #
########################################################################
return scores
def test_ThreeLayerConvNet():
x = torch.zeros((64, 3, 32, 32), dtype=dtype) # minibatch size 64, image size [3, 32, 32]
model = ThreeLayerConvNet(in_channel=3, channel_1=12, channel_2=8, num_classes=10)
scores = model(x)
print(scores.size()) # you should see [64, 10]
test_ThreeLayerConvNet()
```
### Module API: Check Accuracy
Given the validation or test set, we can check the classification accuracy of a neural network.
This version is slightly different from the one in part II. You don't manually pass in the parameters anymore.
```
def check_accuracy_part34(loader, model):
if loader.dataset.train:
print('Checking accuracy on validation set')
else:
print('Checking accuracy on test set')
num_correct = 0
num_samples = 0
model.eval() # set model to evaluation mode
with torch.no_grad():
for x, y in loader:
x = x.to(device=device, dtype=dtype) # move to device, e.g. GPU
y = y.to(device=device, dtype=torch.long)
scores = model(x)
_, preds = scores.max(1)
num_correct += (preds == y).sum()
num_samples += preds.size(0)
acc = float(num_correct) / num_samples
print('Got %d / %d correct (%.2f)' % (num_correct, num_samples, 100 * acc))
```
### Module API: Training Loop
We also use a slightly different training loop. Rather than updating the values of the weights ourselves, we use an Optimizer object from the `torch.optim` package, which abstract the notion of an optimization algorithm and provides implementations of most of the algorithms commonly used to optimize neural networks.
```
def train_part34(model, optimizer, epochs=1):
"""
Train a model on CIFAR-10 using the PyTorch Module API.
Inputs:
- model: A PyTorch Module giving the model to train.
- optimizer: An Optimizer object we will use to train the model
- epochs: (Optional) A Python integer giving the number of epochs to train for
Returns: Nothing, but prints model accuracies during training.
"""
model = model.to(device=device) # move the model parameters to CPU/GPU
for e in range(epochs):
for t, (x, y) in enumerate(loader_train):
model.train() # put model to training mode
x = x.to(device=device, dtype=dtype) # move to device, e.g. GPU
y = y.to(device=device, dtype=torch.long)
scores = model(x)
loss = F.cross_entropy(scores, y)
# Zero out all of the gradients for the variables which the optimizer
# will update.
optimizer.zero_grad()
# This is the backwards pass: compute the gradient of the loss with
# respect to each parameter of the model.
loss.backward()
# Actually update the parameters of the model using the gradients
# computed by the backwards pass.
optimizer.step()
if t % print_every == 0:
print('Iteration %d, loss = %.4f' % (t, loss.item()))
check_accuracy_part34(loader_val, model)
print()
```
### Module API: Train a Two-Layer Network
Now we are ready to run the training loop. In contrast to part II, we don't explicitly allocate parameter tensors anymore.
Simply pass the input size, hidden layer size, and number of classes (i.e. output size) to the constructor of `TwoLayerFC`.
You also need to define an optimizer that tracks all the learnable parameters inside `TwoLayerFC`.
You don't need to tune any hyperparameters, but you should see model accuracies above 40% after training for one epoch.
```
hidden_layer_size = 4000
learning_rate = 1e-2
model = TwoLayerFC(3 * 32 * 32, hidden_layer_size, 10)
optimizer = optim.SGD(model.parameters(), lr=learning_rate)
train_part34(model, optimizer)
```
### Module API: Train a Three-Layer ConvNet
You should now use the Module API to train a three-layer ConvNet on CIFAR. This should look very similar to training the two-layer network! You don't need to tune any hyperparameters, but you should achieve above above 45% after training for one epoch.
You should train the model using stochastic gradient descent without momentum.
```
learning_rate = 3e-3
channel_1 = 32
channel_2 = 16
model = None
optimizer = None
################################################################################
# TODO: Instantiate your ThreeLayerConvNet model and a corresponding optimizer #
################################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
model = ThreeLayerConvNet(in_channel=3, channel_1=channel_1, channel_2=channel_2, num_classes=10)
optimizer = optim.SGD(model.parameters(), lr=learning_rate)
train_part34(model, optimizer)
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
################################################################################
# END OF YOUR CODE
################################################################################
train_part34(model, optimizer)
```
# Part IV. PyTorch Sequential API
Part III introduced the PyTorch Module API, which allows you to define arbitrary learnable layers and their connectivity.
For simple models like a stack of feed forward layers, you still need to go through 3 steps: subclass `nn.Module`, assign layers to class attributes in `__init__`, and call each layer one by one in `forward()`. Is there a more convenient way?
Fortunately, PyTorch provides a container Module called `nn.Sequential`, which merges the above steps into one. It is not as flexible as `nn.Module`, because you cannot specify more complex topology than a feed-forward stack, but it's good enough for many use cases.
### Sequential API: Two-Layer Network
Let's see how to rewrite our two-layer fully connected network example with `nn.Sequential`, and train it using the training loop defined above.
Again, you don't need to tune any hyperparameters here, but you shoud achieve above 40% accuracy after one epoch of training.
```
# We need to wrap `flatten` function in a module in order to stack it
# in nn.Sequential
class Flatten(nn.Module):
def forward(self, x):
return flatten(x)
hidden_layer_size = 4000
learning_rate = 1e-2
model = nn.Sequential(
Flatten(),
nn.Linear(3 * 32 * 32, hidden_layer_size),
nn.ReLU(),
nn.Linear(hidden_layer_size, 10),
)
# you can use Nesterov momentum in optim.SGD
optimizer = optim.SGD(model.parameters(), lr=learning_rate,
momentum=0.9, nesterov=True)
train_part34(model, optimizer)
```
### Sequential API: Three-Layer ConvNet
Here you should use `nn.Sequential` to define and train a three-layer ConvNet with the same architecture we used in Part III:
1. Convolutional layer (with bias) with 32 5x5 filters, with zero-padding of 2
2. ReLU
3. Convolutional layer (with bias) with 16 3x3 filters, with zero-padding of 1
4. ReLU
5. Fully-connected layer (with bias) to compute scores for 10 classes
You should initialize your weight matrices using the `random_weight` function defined above, and you should initialize your bias vectors using the `zero_weight` function above.
You should optimize your model using stochastic gradient descent with Nesterov momentum 0.9.
Again, you don't need to tune any hyperparameters but you should see accuracy above 55% after one epoch of training.
```
channel_1 = 32
channel_2 = 16
learning_rate = 1e-2
model = None
optimizer = None
################################################################################
# TODO: Rewrite the 2-layer ConvNet with bias from Part III with the #
# Sequential API. #
################################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
model = nn.Sequential(
nn.Conv2d(3, channel_1, 5, padding=2),
nn.ReLU(),
nn.Conv2d(channel_1, channel_2, 3, padding=1),
nn.ReLU(),
Flatten(),
nn.Linear(channel_2 * 32 * 32, 10),
)
optimizer = optim.SGD(model.parameters(), lr=learning_rate,
momentum=0.9, nesterov=True)
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
################################################################################
# END OF YOUR CODE
################################################################################
train_part34(model, optimizer)
```
# Part V. CIFAR-10 open-ended challenge
In this section, you can experiment with whatever ConvNet architecture you'd like on CIFAR-10.
Now it's your job to experiment with architectures, hyperparameters, loss functions, and optimizers to train a model that achieves **at least 70%** accuracy on the CIFAR-10 **validation** set within 10 epochs. You can use the check_accuracy and train functions from above. You can use either `nn.Module` or `nn.Sequential` API.
Describe what you did at the end of this notebook.
Here are the official API documentation for each component. One note: what we call in the class "spatial batch norm" is called "BatchNorm2D" in PyTorch.
* Layers in torch.nn package: http://pytorch.org/docs/stable/nn.html
* Activations: http://pytorch.org/docs/stable/nn.html#non-linear-activations
* Loss functions: http://pytorch.org/docs/stable/nn.html#loss-functions
* Optimizers: http://pytorch.org/docs/stable/optim.html
### Things you might try:
- **Filter size**: Above we used 5x5; would smaller filters be more efficient?
- **Number of filters**: Above we used 32 filters. Do more or fewer do better?
- **Pooling vs Strided Convolution**: Do you use max pooling or just stride convolutions?
- **Batch normalization**: Try adding spatial batch normalization after convolution layers and vanilla batch normalization after affine layers. Do your networks train faster?
- **Network architecture**: The network above has two layers of trainable parameters. Can you do better with a deep network? Good architectures to try include:
- [conv-relu-pool]xN -> [affine]xM -> [softmax or SVM]
- [conv-relu-conv-relu-pool]xN -> [affine]xM -> [softmax or SVM]
- [batchnorm-relu-conv]xN -> [affine]xM -> [softmax or SVM]
- **Global Average Pooling**: Instead of flattening and then having multiple affine layers, perform convolutions until your image gets small (7x7 or so) and then perform an average pooling operation to get to a 1x1 image picture (1, 1 , Filter#), which is then reshaped into a (Filter#) vector. This is used in [Google's Inception Network](https://arxiv.org/abs/1512.00567) (See Table 1 for their architecture).
- **Regularization**: Add l2 weight regularization, or perhaps use Dropout.
### Tips for training
For each network architecture that you try, you should tune the learning rate and other hyperparameters. When doing this there are a couple important things to keep in mind:
- If the parameters are working well, you should see improvement within a few hundred iterations
- Remember the coarse-to-fine approach for hyperparameter tuning: start by testing a large range of hyperparameters for just a few training iterations to find the combinations of parameters that are working at all.
- Once you have found some sets of parameters that seem to work, search more finely around these parameters. You may need to train for more epochs.
- You should use the validation set for hyperparameter search, and save your test set for evaluating your architecture on the best parameters as selected by the validation set.
### Going above and beyond
If you are feeling adventurous there are many other features you can implement to try and improve your performance. You are **not required** to implement any of these, but don't miss the fun if you have time!
- Alternative optimizers: you can try Adam, Adagrad, RMSprop, etc.
- Alternative activation functions such as leaky ReLU, parametric ReLU, ELU, or MaxOut.
- Model ensembles
- Data augmentation
- New Architectures
- [ResNets](https://arxiv.org/abs/1512.03385) where the input from the previous layer is added to the output.
- [DenseNets](https://arxiv.org/abs/1608.06993) where inputs into previous layers are concatenated together.
- [This blog has an in-depth overview](https://chatbotslife.com/resnets-highwaynets-and-densenets-oh-my-9bb15918ee32)
### Have fun and happy training!
```
################################################################################
# TODO: #
# Experiment with any architectures, optimizers, and hyperparameters. #
# Achieve AT LEAST 70% accuracy on the *validation set* within 10 epochs. #
# #
# Note that you can use the check_accuracy function to evaluate on either #
# the test set or the validation set, by passing either loader_test or #
# loader_val as the second argument to check_accuracy. You should not touch #
# the test set until you have finished your architecture and hyperparameter #
# tuning, and only run the test set once at the end to report a final value. #
################################################################################
model = None
optimizer = None
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
model = nn.Sequential(
nn.Conv2d(3, 6, 3, padding=1),
nn.BatchNorm2d(6),
nn.ReLU(),
nn.MaxPool2d(2),
nn.Conv2d(6, 16, 3, padding=1),
nn.BatchNorm2d(16),
nn.ReLU(),
nn.MaxPool2d(2),
nn.Conv2d(16, 120, 3, padding=1),
nn.BatchNorm2d(120),
nn.ReLU(),
nn.MaxPool2d(2),
Flatten(),
nn.Linear(120 * 4 * 4, 84 * 4),
nn.Linear(84 * 4, 10)
)
optimizer = optim.Adam(model.parameters(), lr=1e-3)
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
################################################################################
# END OF YOUR CODE
################################################################################
# You should get at least 70% accuracy
train_part34(model, optimizer, epochs=10)
```
## Describe what you did
In the cell below you should write an explanation of what you did, any additional features that you implemented, and/or any graphs that you made in the process of training and evaluating your network.
TODO: Describe what you did
## Test set -- run this only once
Now that we've gotten a result we're happy with, we test our final model on the test set (which you should store in best_model). Think about how this compares to your validation set accuracy.
```
best_model = model
check_accuracy_part34(loader_test, best_model)
```
|
github_jupyter
|
# test note
* jupyterはコンテナ起動すること
* テストベッド一式起動済みであること
```
!pip install --upgrade pip
!pip install --force-reinstall ../lib/ait_sdk-0.1.7-py3-none-any.whl
from pathlib import Path
import pprint
from ait_sdk.test.hepler import Helper
import json
# settings cell
# mounted dir
root_dir = Path('/workdir/root/ait')
ait_name='eval_mnist_data_coverage'
ait_version='0.1'
ait_full_name=f'{ait_name}_{ait_version}'
ait_dir = root_dir / ait_full_name
td_name=f'{ait_name}_test'
# (dockerホスト側の)インベントリ登録用アセット格納ルートフォルダ
current_dir = %pwd
with open(f'{current_dir}/config.json', encoding='utf-8') as f:
json_ = json.load(f)
root_dir = json_['host_ait_root_dir']
is_container = json_['is_container']
invenotory_root_dir = f'{root_dir}\\ait\\{ait_full_name}\\local_qai\\inventory'
# entry point address
# コンテナ起動かどうかでポート番号が変わるため、切り替える
if is_container:
backend_entry_point = 'http://host.docker.internal:8888/qai-testbed/api/0.0.1'
ip_entry_point = 'http://host.docker.internal:8888/qai-ip/api/0.0.1'
else:
backend_entry_point = 'http://host.docker.internal:5000/qai-testbed/api/0.0.1'
ip_entry_point = 'http://host.docker.internal:6000/qai-ip/api/0.0.1'
# aitのデプロイフラグ
# 一度実施すれば、それ以降は実施しなくてOK
is_init_ait = True
#is_init_ait = False
# インベントリの登録フラグ
# 一度実施すれば、それ以降は実施しなくてOK
is_init_inventory = True
helper = Helper(backend_entry_point=backend_entry_point,
ip_entry_point=ip_entry_point,
ait_dir=ait_dir,
ait_full_name=ait_full_name)
# health check
helper.get_bk('/health-check')
helper.get_ip('/health-check')
# create ml-component
res = helper.post_ml_component(name=f'MLComponent_{ait_full_name}', description=f'Description of {ait_full_name}', problem_domain=f'ProbremDomain of {ait_full_name}')
helper.set_ml_component_id(res['MLComponentId'])
# deploy AIT
if is_init_ait:
helper.deploy_ait_non_build()
else:
print('skip deploy AIT')
res = helper.get_data_types()
model_data_type_id = [d for d in res['DataTypes'] if d['Name'] == 'model'][0]['Id']
dataset_data_type_id = [d for d in res['DataTypes'] if d['Name'] == 'dataset'][0]['Id']
res = helper.get_file_systems()
unix_file_system_id = [f for f in res['FileSystems'] if f['Name'] == 'UNIX_FILE_SYSTEM'][0]['Id']
windows_file_system_id = [f for f in res['FileSystems'] if f['Name'] == 'WINDOWS_FILE'][0]['Id']
# add inventories
if is_init_inventory:
inv1_name = helper.post_inventory('images', dataset_data_type_id, windows_file_system_id,
f'{invenotory_root_dir}\\train_images\\train-images-idx3-ubyte.gz',
'MNIST images', ['gz'])
inv2_name = helper.post_inventory('labels', dataset_data_type_id, windows_file_system_id,
f'{invenotory_root_dir}\\train_labels\\train-labels-idx1-ubyte.gz',
'MNIST labels', ['gz'])
else:
print('skip add inventories')
# get ait_json and inventory_jsons
res_json = helper.get_bk('/QualityMeasurements/RelationalOperators', is_print_json=False).json()
eq_id = int([r['Id'] for r in res_json['RelationalOperator'] if r['Expression'] == '=='][0])
nq_id = int([r['Id'] for r in res_json['RelationalOperator'] if r['Expression'] == '!='][0])
gt_id = int([r['Id'] for r in res_json['RelationalOperator'] if r['Expression'] == '>'][0])
ge_id = int([r['Id'] for r in res_json['RelationalOperator'] if r['Expression'] == '>='][0])
lt_id = int([r['Id'] for r in res_json['RelationalOperator'] if r['Expression'] == '<'][0])
le_id = int([r['Id'] for r in res_json['RelationalOperator'] if r['Expression'] == '<='][0])
res_json = helper.get_bk('/testRunners', is_print_json=False).json()
ait_json = [j for j in res_json['TestRunners'] if j['Name'] == ait_name][-1]
inv_1_json = helper.get_inventory(inv1_name)
inv_2_json = helper.get_inventory(inv2_name)
# add teast_descriptions
helper.post_td(td_name, 3,
quality_measurements=[
{"Id":ait_json['Report']['Measures'][0]['Id'], "Value":"0.75", "RelationalOperatorId":gt_id, "Enable":True},
{"Id":ait_json['Report']['Measures'][1]['Id'], "Value":"0.75", "RelationalOperatorId":gt_id, "Enable":True}
],
target_inventories=[
{"Id":1, "InventoryId": inv_1_json['Id'], "TemplateInventoryId": ait_json['TargetInventories'][0]['Id']},
{"Id":2, "InventoryId": inv_2_json['Id'], "TemplateInventoryId": ait_json['TargetInventories'][1]['Id']}
],
test_runner={
"Id":ait_json['Id'],
"Params":[
{"TestRunnerParamTemplateId":ait_json['ParamTemplates'][0]['Id'], "Value":"Area"},
{"TestRunnerParamTemplateId":ait_json['ParamTemplates'][1]['Id'], "Value":"100"},
{"TestRunnerParamTemplateId":ait_json['ParamTemplates'][2]['Id'], "Value":"800"}
]
})
# get test_description_jsons
td_1_json = helper.get_td(td_name)
# run test_descriptions
helper.post_run_and_wait(td_1_json['Id'])
res_json = helper.get_td_detail(td_1_json['Id'])
pprint.pprint(res_json)
# generate report
res = helper.post_report(td_1_json['Id'])
pprint.pprint(res)
```
|
github_jupyter
|
# HM2: Numerical Optimization for Logistic Regression.
### Name: [Your-Name?]
## 0. You will do the following:
1. Read the lecture note: [click here](https://github.com/wangshusen/DeepLearning/blob/master/LectureNotes/Logistic/paper/logistic.pdf)
2. Read, complete, and run my code.
3. **Implement mini-batch SGD** and evaluate the performance.
4. Convert the .IPYNB file to .HTML file.
* The HTML file must contain **the code** and **the output after execution**.
* Missing **the output after execution** will not be graded.
5. Upload this .HTML file to your Google Drive, Dropbox, or your Github repo. (If you submit the file to Google Drive or Dropbox, you must make the file "open-access". The delay caused by "deny of access" may result in late penalty.)
6. Submit the link to this .HTML file to Canvas.
* Example: https://github.com/wangshusen/CS583-2020S/blob/master/homework/HM2/HM2.html
## Grading criteria:
1. When computing the ```gradient``` and ```objective function value``` using a batch of samples, use **matrix-vector multiplication** rather than a FOR LOOP of **vector-vector multiplications**.
2. Plot ```objective function value``` against ```epochs```. In the plot, compare GD, SGD, and MB-SGD (with $b=8$ and $b=64$). The plot must look reasonable.
# 1. Data processing
- Download the Diabete dataset from https://www.csie.ntu.edu.tw/~cjlin/libsvmtools/datasets/binary/diabetes
- Load the data using sklearn.
- Preprocess the data.
## 1.1. Load the data
```
from sklearn import datasets
import numpy
x_sparse, y = datasets.load_svmlight_file('diabetes')
x = x_sparse.todense()
print('Shape of x: ' + str(x.shape))
print('Shape of y: ' + str(y.shape))
```
## 1.2. Partition to training and test sets
```
# partition the data to training and test sets
n = x.shape[0]
n_train = 640
n_test = n - n_train
rand_indices = numpy.random.permutation(n)
train_indices = rand_indices[0:n_train]
test_indices = rand_indices[n_train:n]
x_train = x[train_indices, :]
x_test = x[test_indices, :]
y_train = y[train_indices].reshape(n_train, 1)
y_test = y[test_indices].reshape(n_test, 1)
print('Shape of x_train: ' + str(x_train.shape))
print('Shape of x_test: ' + str(x_test.shape))
print('Shape of y_train: ' + str(y_train.shape))
print('Shape of y_test: ' + str(y_test.shape))
```
## 1.3. Feature scaling
Use the standardization to trainsform both training and test features
```
# Standardization
import numpy
# calculate mu and sig using the training set
d = x_train.shape[1]
mu = numpy.mean(x_train, axis=0).reshape(1, d)
sig = numpy.std(x_train, axis=0).reshape(1, d)
# transform the training features
x_train = (x_train - mu) / (sig + 1E-6)
# transform the test features
x_test = (x_test - mu) / (sig + 1E-6)
print('test mean = ')
print(numpy.mean(x_test, axis=0))
print('test std = ')
print(numpy.std(x_test, axis=0))
```
## 1.4. Add a dimension of all ones
```
n_train, d = x_train.shape
x_train = numpy.concatenate((x_train, numpy.ones((n_train, 1))), axis=1)
n_test, d = x_test.shape
x_test = numpy.concatenate((x_test, numpy.ones((n_test, 1))), axis=1)
print('Shape of x_train: ' + str(x_train.shape))
print('Shape of x_test: ' + str(x_test.shape))
```
# 2. Logistic regression model
The objective function is $Q (w; X, y) = \frac{1}{n} \sum_{i=1}^n \log \Big( 1 + \exp \big( - y_i x_i^T w \big) \Big) + \frac{\lambda}{2} \| w \|_2^2 $.
```
# Calculate the objective function value
# Inputs:
# w: d-by-1 matrix
# x: n-by-d matrix
# y: n-by-1 matrix
# lam: scalar, the regularization parameter
# Return:
# objective function value (scalar)
def objective(w, x, y, lam):
n, d = x.shape
yx = numpy.multiply(y, x) # n-by-d matrix
yxw = numpy.dot(yx, w) # n-by-1 matrix
vec1 = numpy.exp(-yxw) # n-by-1 matrix
vec2 = numpy.log(1 + vec1) # n-by-1 matrix
loss = numpy.mean(vec2) # scalar
reg = lam / 2 * numpy.sum(w * w) # scalar
return loss + reg
# initialize w
d = x_train.shape[1]
w = numpy.zeros((d, 1))
# evaluate the objective function value at w
lam = 1E-6
objval0 = objective(w, x_train, y_train, lam)
print('Initial objective function value = ' + str(objval0))
```
# 3. Numerical optimization
## 3.1. Gradient descent
The gradient at $w$ is $g = - \frac{1}{n} \sum_{i=1}^n \frac{y_i x_i }{1 + \exp ( y_i x_i^T w)} + \lambda w$
```
# Calculate the gradient
# Inputs:
# w: d-by-1 matrix
# x: n-by-d matrix
# y: n-by-1 matrix
# lam: scalar, the regularization parameter
# Return:
# g: g: d-by-1 matrix, full gradient
def gradient(w, x, y, lam):
n, d = x.shape
yx = numpy.multiply(y, x) # n-by-d matrix
yxw = numpy.dot(yx, w) # n-by-1 matrix
vec1 = numpy.exp(yxw) # n-by-1 matrix
vec2 = numpy.divide(yx, 1+vec1) # n-by-d matrix
vec3 = -numpy.mean(vec2, axis=0).reshape(d, 1) # d-by-1 matrix
g = vec3 + lam * w
return g
# Gradient descent for solving logistic regression
# Inputs:
# x: n-by-d matrix
# y: n-by-1 matrix
# lam: scalar, the regularization parameter
# stepsize: scalar
# max_iter: integer, the maximal iterations
# w: d-by-1 matrix, initialization of w
# Return:
# w: d-by-1 matrix, the solution
# objvals: a record of each iteration's objective value
def grad_descent(x, y, lam, stepsize, max_iter=100, w=None):
n, d = x.shape
objvals = numpy.zeros(max_iter) # store the objective values
if w is None:
w = numpy.zeros((d, 1)) # zero initialization
for t in range(max_iter):
objval = objective(w, x, y, lam)
objvals[t] = objval
print('Objective value at t=' + str(t) + ' is ' + str(objval))
g = gradient(w, x, y, lam)
w -= stepsize * g
return w, objvals
```
Run gradient descent.
```
lam = 1E-6
stepsize = 1.0
w, objvals_gd = grad_descent(x_train, y_train, lam, stepsize)
```
## 3.2. Stochastic gradient descent (SGD)
Define $Q_i (w) = \log \Big( 1 + \exp \big( - y_i x_i^T w \big) \Big) + \frac{\lambda}{2} \| w \|_2^2 $.
The stochastic gradient at $w$ is $g_i = \frac{\partial Q_i }{ \partial w} = -\frac{y_i x_i }{1 + \exp ( y_i x_i^T w)} + \lambda w$.
```
# Calculate the objective Q_i and the gradient of Q_i
# Inputs:
# w: d-by-1 matrix
# xi: 1-by-d matrix
# yi: scalar
# lam: scalar, the regularization parameter
# Return:
# obj: scalar, the objective Q_i
# g: d-by-1 matrix, gradient of Q_i
def stochastic_objective_gradient(w, xi, yi, lam):
yx = yi * xi # 1-by-d matrix
yxw = float(numpy.dot(yx, w)) # scalar
# calculate objective function Q_i
loss = numpy.log(1 + numpy.exp(-yxw)) # scalar
reg = lam / 2 * numpy.sum(w * w) # scalar
obj = loss + reg
# calculate stochastic gradient
g_loss = -yx.T / (1 + numpy.exp(yxw)) # d-by-1 matrix
g = g_loss + lam * w # d-by-1 matrix
return obj, g
# SGD for solving logistic regression
# Inputs:
# x: n-by-d matrix
# y: n-by-1 matrix
# lam: scalar, the regularization parameter
# stepsize: scalar
# max_epoch: integer, the maximal epochs
# w: d-by-1 matrix, initialization of w
# Return:
# w: the solution
# objvals: record of each iteration's objective value
def sgd(x, y, lam, stepsize, max_epoch=100, w=None):
n, d = x.shape
objvals = numpy.zeros(max_epoch) # store the objective values
if w is None:
w = numpy.zeros((d, 1)) # zero initialization
for t in range(max_epoch):
# randomly shuffle the samples
rand_indices = numpy.random.permutation(n)
x_rand = x[rand_indices, :]
y_rand = y[rand_indices, :]
objval = 0 # accumulate the objective values
for i in range(n):
xi = x_rand[i, :] # 1-by-d matrix
yi = float(y_rand[i, :]) # scalar
obj, g = stochastic_objective_gradient(w, xi, yi, lam)
objval += obj
w -= stepsize * g
stepsize *= 0.9 # decrease step size
objval /= n
objvals[t] = objval
print('Objective value at epoch t=' + str(t) + ' is ' + str(objval))
return w, objvals
```
Run SGD.
```
lam = 1E-6
stepsize = 0.1
w, objvals_sgd = sgd(x_train, y_train, lam, stepsize)
```
# 4. Compare GD with SGD
Plot objective function values against epochs.
```
import matplotlib.pyplot as plt
%matplotlib inline
fig = plt.figure(figsize=(6, 4))
epochs_gd = range(len(objvals_gd))
epochs_sgd = range(len(objvals_sgd))
line0, = plt.plot(epochs_gd, objvals_gd, '--b', LineWidth=4)
line1, = plt.plot(epochs_sgd, objvals_sgd, '-r', LineWidth=2)
plt.xlabel('Epochs', FontSize=20)
plt.ylabel('Objective Value', FontSize=20)
plt.xticks(FontSize=16)
plt.yticks(FontSize=16)
plt.legend([line0, line1], ['GD', 'SGD'], fontsize=20)
plt.tight_layout()
plt.show()
fig.savefig('compare_gd_sgd.pdf', format='pdf', dpi=1200)
```
# 5. Prediction
```
# Predict class label
# Inputs:
# w: d-by-1 matrix
# X: m-by-d matrix
# Return:
# f: m-by-1 matrix, the predictions
def predict(w, X):
xw = numpy.dot(X, w)
f = numpy.sign(xw)
return f
# evaluate training error
f_train = predict(w, x_train)
diff = numpy.abs(f_train - y_train) / 2
error_train = numpy.mean(diff)
print('Training classification error is ' + str(error_train))
# evaluate test error
f_test = predict(w, x_test)
diff = numpy.abs(f_test - y_test) / 2
error_test = numpy.mean(diff)
print('Test classification error is ' + str(error_test))
```
# 6. Mini-batch SGD (fill the code)
## 6.1. Compute the objective $Q_I$ and its gradient using a batch of samples
Define $Q_I (w) = \frac{1}{b} \sum_{i \in I} \log \Big( 1 + \exp \big( - y_i x_i^T w \big) \Big) + \frac{\lambda}{2} \| w \|_2^2 $, where $I$ is a set containing $b$ indices randomly drawn from $\{ 1, \cdots , n \}$ without replacement.
The stochastic gradient at $w$ is $g_I = \frac{\partial Q_I }{ \partial w} = \frac{1}{b} \sum_{i \in I} \frac{- y_i x_i }{1 + \exp ( y_i x_i^T w)} + \lambda w$.
```
# Calculate the objective Q_I and the gradient of Q_I
# Inputs:
# w: d-by-1 matrix
# xi: b-by-d matrix
# yi: b-by-1 matrix
# lam: scalar, the regularization parameter
# b: integer, the batch size
# Return:
# obj: scalar, the objective Q_i
# g: d-by-1 matrix, gradient of Q_i
def mb_stochastic_objective_gradient(w, xi, yi, lam, b):
# Fill the function
# Follow the implementation of stochastic_objective_gradient
# Use matrix-vector multiplication; do not use FOR LOOP of vector-vector multiplications
...
return obj, g
```
## 6.2. Implement mini-batch SGD
Hints:
1. In every epoch, randomly permute the $n$ samples (just like SGD).
2. Each epoch has $\frac{n}{b}$ iterations. In every iteration, use $b$ samples, and compute the gradient and objective using the ``mb_stochastic_objective_gradient`` function. In the next iteration, use the next $b$ samples, and so on.
```
# Mini-Batch SGD for solving logistic regression
# Inputs:
# x: n-by-d matrix
# y: n-by-1 matrix
# lam: scalar, the regularization parameter
# b: integer, the batch size
# stepsize: scalar
# max_epoch: integer, the maximal epochs
# w: d-by-1 matrix, initialization of w
# Return:
# w: the solution
# objvals: record of each iteration's objective value
def mb_sgd(x, y, lam, b, stepsize, max_epoch=100, w=None):
# Fill the function
# Follow the implementation of sgd
# Record one objective value per epoch (not per iteration!)
...
return w, objvals
```
## 6.3. Run MB-SGD
```
# MB-SGD with batch size b=8
lam = 1E-6 # do not change
b = 8 # do not change
stepsize = 0.1 # you must tune this parameter
w, objvals_mbsgd8 = mb_sgd(x_train, y_train, lam, b, stepsize)
# MB-SGD with batch size b=64
lam = 1E-6 # do not change
b = 64 # do not change
stepsize = 0.1 # you must tune this parameter
w, objvals_mbsgd64 = mb_sgd(x_train, y_train, lam, b, stepsize)
```
# 7. Plot and compare GD, SGD, and MB-SGD
You are required to compare the following algorithms:
- Gradient descent (GD)
- SGD
- MB-SGD with b=8
- MB-SGD with b=64
Follow the code in Section 4 to plot ```objective function value``` against ```epochs```. There should be four curves in the plot; each curve corresponds to one algorithm.
Hint: Logistic regression with $\ell_2$-norm regularization is a strongly convex optimization problem. All the algorithms will converge to the same solution. **In the end, the ``objective function value`` of the 4 algorithms will be the same. If not the same, your implementation must be wrong. Do NOT submit wrong code and wrong result!**
```
# plot the 4 curves:
```
|
github_jupyter
|
```
%matplotlib inline
import math
import numpy
import pandas
import seaborn
import matplotlib.pyplot as plt
import plot
def fmt_money(number):
return "${:,.0f}".format(number)
def run_pmt(market, pmt_rate):
portfolio = 1_000_000
age = 65
max_age = 100
df = pandas.DataFrame(index=range(age, max_age), columns=['withdrawal', 'portfolio'])
for i in range(age, max_age):
withdraw = -numpy.pmt(pmt_rate, max_age-i, portfolio, 0, 1)
portfolio -= withdraw
portfolio *= (1 + market)
df.loc[i] = [int(withdraw), int(portfolio)]
return df
pmt_df = run_pmt(0.03, 0.04)
pmt_df.head()
def run_smile(target):
spend = target
s = pandas.Series(index=range(66,100), dtype=int)
for age in range(66, 100):
d = (0.00008 * age * age) - (0.0125 * age) - (0.0066 * math.log(target)) + 0.546
spend *= (1 + d)
s.loc[age] = int(spend)
return s
smile_s = run_smile(pmt_df.iloc[0]['withdrawal'])
smile_s.head()
def rmse(s1, s2):
return numpy.sqrt(numpy.mean((s1-s2)**2))
rmse(pmt_df['withdrawal'][1:26], smile_s[:26])
def harness():
df = pandas.DataFrame(columns=['market', 'pmtrate', 'rmse'])
for returns in numpy.arange(0.01, 0.10+0.001, 0.001):
for pmt_rate in numpy.arange(0.01, 0.10+0.001, 0.001):
pmt_df = run_pmt(returns, pmt_rate)
iwd = pmt_df.iloc[0]['withdrawal']
smile_s = run_smile(iwd)
errors = rmse(pmt_df['withdrawal'], smile_s)
df = df.append({'market': returns, 'pmtrate': pmt_rate, 'rmse': errors}, ignore_index=True)
return df
error_df = harness()
error_df.head()
#seaborn.scatterplot(data=error_df, x='market', y='pmtrate', size='rmse')
#seaborn.scatterplot(data=error_df[0:19], x='pmtrate', y='rmse')
error_df[0:91]
slice_size = 91
n_slices = int(len(error_df) / slice_size)
print(len(error_df), n_slices, slice_size)
for i in range(n_slices):
start = i * slice_size
end = i * slice_size + slice_size
slice_df = error_df[start:end]
delta = slice_df['pmtrate'] - slice_df['market']
plot_df = pandas.DataFrame({'delta': delta, 'rmse': slice_df['rmse']})
sp = seaborn.scatterplot(data=plot_df, x='delta', y='rmse')
mkt_rate = slice_df.iloc[0]['market']
plt.xticks(numpy.arange(-0.100, +0.100, 0.005), rotation='vertical')
# plt.title(f'Market returns: {mkt_rate*100}%')
series = pandas.Series(index=range(40_000, 101_000, 5_000))
for t in range(40_000, 101_000, 5_000):
s = run_smile(t)
contingency = (t - s[0:20]).sum()
series.loc[t] = contingency
series.plot()
plt.xlabel('Targeted annual withdrawal at retirement')
plt.ylabel('Contigency fund')
xticks = plt.xticks()
plt.xticks(xticks[0], [fmt_money(x) for x in xticks[0]])
yticks = plt.yticks()
plt.yticks(yticks[0], [fmt_money(y) for y in yticks[0]])
plt.title('Contigency at age 85')
series
(series / series.index).plot()
plt.title('Ratio of contingency to expected spending')
xticks = plt.xticks()
plt.xticks(xticks[0], [fmt_money(x) for x in xticks[0]])
len(error_df)
```
|
github_jupyter
|
```
import os
import json
import boto3
import sagemaker
import numpy as np
from source.config import Config
config = Config(filename="config/config.yaml")
sage_session = sagemaker.session.Session()
s3_bucket = config.S3_BUCKET
s3_output_path = 's3://{}/'.format(s3_bucket)
print("S3 bucket path: {}".format(s3_output_path))
# run in local_mode on this machine, or as a SageMaker TrainingJob
local_mode = False
if local_mode:
instance_type = 'local'
else:
instance_type = "ml.c5.xlarge"
role = sagemaker.get_execution_role()
print("Using IAM role arn: {}".format(role))
# only run from SageMaker notebook instance
if local_mode:
!/bin/bash ./setup.sh
cpu_or_gpu = 'gpu' if instance_type.startswith('ml.p') else 'cpu'
# create a descriptive job name
job_name_prefix = 'HPO-pdm'
metric_definitions = [
{'Name': 'Epoch', 'Regex': 'Epoch: ([-+]?[0-9]*[.]?[0-9]+([eE][-+]?[0-9]+)?)'},
{'Name': 'train_loss', 'Regex': 'Train loss: ([-+]?[0-9]*[.]?[0-9]+([eE][-+]?[0-9]+)?)'},
{'Name': 'train_acc', 'Regex': 'Train acc: ([-+]?[0-9]*[.]?[0-9]+([eE][-+]?[0-9]+)?)'},
{'Name': 'train_auc', 'Regex': 'Train auc: ([-+]?[0-9]*[.]?[0-9]+([eE][-+]?[0-9]+)?)'},
{'Name': 'test_loss', 'Regex': 'Test loss: ([-+]?[0-9]*[.]?[0-9]+([eE][-+]?[0-9]+)?)'},
{'Name': 'test_acc', 'Regex': 'Test acc: ([-+]?[0-9]*[.]?[0-9]+([eE][-+]?[0-9]+)?)'},
{'Name': 'test_auc', 'Regex': 'Test auc: ([-+]?[0-9]*[.]?[0-9]+([eE][-+]?[0-9]+)?)'},
]
from sagemaker.pytorch import PyTorch
```
# Define your data
```
print("Using dataset {}".format(config.train_dataset_fn))
from sagemaker.s3 import S3Uploader
key_prefix='fpm-data'
training_data = S3Uploader.upload(config.train_dataset_fn, 's3://{}/{}'.format(s3_bucket, key_prefix))
testing_data = S3Uploader.upload(config.test_dataset_fn, 's3://{}/{}'.format(s3_bucket, key_prefix))
print("Training data: {}".format(training_data))
print("Testing data: {}".format(testing_data))
```
# HPO
```
from sagemaker.tuner import IntegerParameter, CategoricalParameter, ContinuousParameter, HyperparameterTuner
max_jobs = 20
max_parallel_jobs = 5
hyperparameter_ranges = {
'lr': ContinuousParameter(1e-5, 1e-2),
'batch_size': IntegerParameter(16, 256),
'dropout': ContinuousParameter(0.0, 0.8),
'fc_hidden_units': CategoricalParameter(["[256, 128]", "[256, 128, 128]", "[256, 256, 128]", "[256, 128, 64]"]),
'conv_channels': CategoricalParameter(["[2, 8, 2]", "[2, 16, 2]", "[2, 16, 16, 2]"]),
}
estimator = PyTorch(entry_point="train.py",
source_dir='source',
role=role,
dependencies=["source/dl_utils"],
train_instance_type=instance_type,
train_instance_count=1,
output_path=s3_output_path,
framework_version="1.5.0",
py_version='py3',
base_job_name=job_name_prefix,
metric_definitions=metric_definitions,
hyperparameters= {
'epoch': 5000,
'target_column': config.target_column,
'sensor_headers': json.dumps(config.sensor_headers),
'train_input_filename': os.path.basename(config.train_dataset_fn),
'test_input_filename': os.path.basename(config.test_dataset_fn),
}
)
if local_mode:
estimator.fit({'train': training_data, 'test': testing_data})
tuner = HyperparameterTuner(estimator,
objective_metric_name='test_auc',
objective_type='Maximize',
hyperparameter_ranges=hyperparameter_ranges,
metric_definitions=metric_definitions,
max_jobs=max_jobs,
max_parallel_jobs=max_parallel_jobs,
base_tuning_job_name=job_name_prefix)
tuner.fit({'train': training_data, 'test': testing_data})
# Save the HPO job name
hpo_job_name = tuner.describe()['HyperParameterTuningJobName']
if "hpo_job_name" in config.__dict__:
!sed -i 's/hpo_job_name: .*/hpo_job_name: \"{hpo_job_name}\"/' config/config.yaml
else:
!echo -e "\n" >> config/config.yaml
!echo "hpo_job_name: \"$hpo_job_name\"" >> config/config.yaml
```
|
github_jupyter
|
<!--BOOK_INFORMATION-->
<img align="left" style="padding-right:10px;" src="figures/PDSH-cover-small.png">
*This notebook contains an excerpt from the [Python Data Science Handbook](http://shop.oreilly.com/product/0636920034919.do) by Jake VanderPlas; the content is available [on GitHub](https://github.com/jakevdp/PythonDataScienceHandbook).*
*The text is released under the [CC-BY-NC-ND license](https://creativecommons.org/licenses/by-nc-nd/3.0/us/legalcode), and code is released under the [MIT license](https://opensource.org/licenses/MIT). If you find this content useful, please consider supporting the work by [buying the book](http://shop.oreilly.com/product/0636920034919.do)!*
<!--NAVIGATION-->
< [Keyboard Shortcuts in the IPython Shell](01.02-Shell-Keyboard-Shortcuts.ipynb) | [Contents](Index.ipynb) | [Input and Output History](01.04-Input-Output-History.ipynb) >
# IPython Magic Commands
The previous two sections showed how IPython lets you use and explore Python efficiently and interactively.
Here we'll begin discussing some of the enhancements that IPython adds on top of the normal Python syntax.
These are known in IPython as *magic commands*, and are prefixed by the ``%`` character.
These magic commands are designed to succinctly solve various common problems in standard data analysis.
Magic commands come in two flavors: *line magics*, which are denoted by a single ``%`` prefix and operate on a single line of input, and *cell magics*, which are denoted by a double ``%%`` prefix and operate on multiple lines of input.
We'll demonstrate and discuss a few brief examples here, and come back to more focused discussion of several useful magic commands later in the chapter.
## Pasting Code Blocks: ``%paste`` and ``%cpaste``
When working in the IPython interpreter, one common gotcha is that pasting multi-line code blocks can lead to unexpected errors, especially when indentation and interpreter markers are involved.
A common case is that you find some example code on a website and want to paste it into your interpreter.
Consider the following simple function:
``` python
>>> def donothing(x):
... return x
```
The code is formatted as it would appear in the Python interpreter, and if you copy and paste this directly into IPython you get an error:
```ipython
In [2]: >>> def donothing(x):
...: ... return x
...:
File "<ipython-input-20-5a66c8964687>", line 2
... return x
^
SyntaxError: invalid syntax
```
In the direct paste, the interpreter is confused by the additional prompt characters.
But never fear–IPython's ``%paste`` magic function is designed to handle this exact type of multi-line, marked-up input:
```ipython
In [3]: %paste
>>> def donothing(x):
... return x
## -- End pasted text --
```
The ``%paste`` command both enters and executes the code, so now the function is ready to be used:
```ipython
In [4]: donothing(10)
Out[4]: 10
```
A command with a similar intent is ``%cpaste``, which opens up an interactive multiline prompt in which you can paste one or more chunks of code to be executed in a batch:
```ipython
In [5]: %cpaste
Pasting code; enter '--' alone on the line to stop or use Ctrl-D.
:>>> def donothing(x):
:... return x
:--
```
These magic commands, like others we'll see, make available functionality that would be difficult or impossible in a standard Python interpreter.
## Running External Code: ``%run``
As you begin developing more extensive code, you will likely find yourself working in both IPython for interactive exploration, as well as a text editor to store code that you want to reuse.
Rather than running this code in a new window, it can be convenient to run it within your IPython session.
This can be done with the ``%run`` magic.
For example, imagine you've created a ``myscript.py`` file with the following contents:
```python
#-------------------------------------
# file: myscript.py
def square(x):
"""square a number"""
return x ** 2
for N in range(1, 4):
print(N, "squared is", square(N))
```
You can execute this from your IPython session as follows:
```ipython
In [6]: %run myscript.py
1 squared is 1
2 squared is 4
3 squared is 9
```
Note also that after you've run this script, any functions defined within it are available for use in your IPython session:
```ipython
In [7]: square(5)
Out[7]: 25
```
There are several options to fine-tune how your code is run; you can see the documentation in the normal way, by typing **``%run?``** in the IPython interpreter.
## Timing Code Execution: ``%timeit``
Another example of a useful magic function is ``%timeit``, which will automatically determine the execution time of the single-line Python statement that follows it.
For example, we may want to check the performance of a list comprehension:
```ipython
In [8]: %timeit L = [n ** 2 for n in range(1000)]
1000 loops, best of 3: 325 µs per loop
```
The benefit of ``%timeit`` is that for short commands it will automatically perform multiple runs in order to attain more robust results.
For multi line statements, adding a second ``%`` sign will turn this into a cell magic that can handle multiple lines of input.
For example, here's the equivalent construction with a ``for``-loop:
```ipython
In [9]: %%timeit
...: L = []
...: for n in range(1000):
...: L.append(n ** 2)
...:
1000 loops, best of 3: 373 µs per loop
```
We can immediately see that list comprehensions are about 10% faster than the equivalent ``for``-loop construction in this case.
We'll explore ``%timeit`` and other approaches to timing and profiling code in [Profiling and Timing Code](01.07-Timing-and-Profiling.ipynb).
## Help on Magic Functions: ``?``, ``%magic``, and ``%lsmagic``
Like normal Python functions, IPython magic functions have docstrings, and this useful
documentation can be accessed in the standard manner.
So, for example, to read the documentation of the ``%timeit`` magic simply type this:
```ipython
In [10]: %timeit?
```
Documentation for other functions can be accessed similarly.
To access a general description of available magic functions, including some examples, you can type this:
```ipython
In [11]: %magic
```
For a quick and simple list of all available magic functions, type this:
```ipython
In [12]: %lsmagic
```
Finally, I'll mention that it is quite straightforward to define your own magic functions if you wish.
We won't discuss it here, but if you are interested, see the references listed in [More IPython Resources](01.08-More-IPython-Resources.ipynb).
<!--NAVIGATION-->
< [Keyboard Shortcuts in the IPython Shell](01.02-Shell-Keyboard-Shortcuts.ipynb) | [Contents](Index.ipynb) | [Input and Output History](01.04-Input-Output-History.ipynb) >
|
github_jupyter
|
# TV Script Generation
In this project, you'll generate your own [Seinfeld](https://en.wikipedia.org/wiki/Seinfeld) TV scripts using RNNs. You'll be using part of the [Seinfeld dataset](https://www.kaggle.com/thec03u5/seinfeld-chronicles#scripts.csv) of scripts from 9 seasons. The Neural Network you'll build will generate a new ,"fake" TV script, based on patterns it recognizes in this training data.
## Get the Data
The data is already provided for you in `./data/Seinfeld_Scripts.txt` and you're encouraged to open that file and look at the text.
>* As a first step, we'll load in this data and look at some samples.
* Then, you'll be tasked with defining and training an RNN to generate a new script!
```
"""
DON'T MODIFY ANYTHING IN THIS CELL
"""
# load in data
import helper
data_dir = './data/Seinfeld_Scripts.txt'
text = helper.load_data(data_dir)
```
## Explore the Data
Play around with `view_line_range` to view different parts of the data. This will give you a sense of the data you'll be working with. You can see, for example, that it is all lowercase text, and each new line of dialogue is separated by a newline character `\n`.
```
view_line_range = (0, 10)
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
import numpy as np
print('Dataset Stats')
print('Roughly the number of unique words: {}'.format(len({word: None for word in text.split()})))
lines = text.split('\n')
print('Number of lines: {}'.format(len(lines)))
word_count_line = [len(line.split()) for line in lines]
print('Average number of words in each line: {}'.format(np.average(word_count_line)))
print()
print('The lines {} to {}:'.format(*view_line_range))
print('\n'.join(text.split('\n')[view_line_range[0]:view_line_range[1]]))
```
---
## Implement Pre-processing Functions
The first thing to do to any dataset is pre-processing. Implement the following pre-processing functions below:
- Lookup Table
- Tokenize Punctuation
### Lookup Table
To create a word embedding, you first need to transform the words to ids. In this function, create two dictionaries:
- Dictionary to go from the words to an id, we'll call `vocab_to_int`
- Dictionary to go from the id to word, we'll call `int_to_vocab`
Return these dictionaries in the following **tuple** `(vocab_to_int, int_to_vocab)`
```
import problem_unittests as tests
def create_lookup_tables(text):
"""
Create lookup tables for vocabulary
:param text: The text of tv scripts split into words
:return: A tuple of dicts (vocab_to_int, int_to_vocab)
"""
# TODO: Implement Function
int_to_vocab = {}
vocab_to_int = {}
for sent in text:
for word in sent.split():
if word not in vocab_to_int:
vocab_to_int[word] = len(vocab_to_int)
int_to_vocab = {ii : ch for ch , ii in vocab_to_int.items()}
# return tuple
return (vocab_to_int, int_to_vocab)
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
tests.test_create_lookup_tables(create_lookup_tables)
create_lookup_tables("Hi")
```
### Tokenize Punctuation
We'll be splitting the script into a word array using spaces as delimiters. However, punctuations like periods and exclamation marks can create multiple ids for the same word. For example, "bye" and "bye!" would generate two different word ids.
Implement the function `token_lookup` to return a dict that will be used to tokenize symbols like "!" into "||Exclamation_Mark||". Create a dictionary for the following symbols where the symbol is the key and value is the token:
- Period ( **.** )
- Comma ( **,** )
- Quotation Mark ( **"** )
- Semicolon ( **;** )
- Exclamation mark ( **!** )
- Question mark ( **?** )
- Left Parentheses ( **(** )
- Right Parentheses ( **)** )
- Dash ( **-** )
- Return ( **\n** )
This dictionary will be used to tokenize the symbols and add the delimiter (space) around it. This separates each symbols as its own word, making it easier for the neural network to predict the next word. Make sure you don't use a value that could be confused as a word; for example, instead of using the value "dash", try using something like "||dash||".
```
def token_lookup():
"""
Generate a dict to turn punctuation into a token.
:return: Tokenized dictionary where the key is the punctuation and the value is the token
"""
# TODO: Implement Function
punct = {'.' : '||dot||' ,
',' : '||comma||' ,
'"' : '||invcoma||',
';' : '||semicolon||',
'!' : '||exclamation_mark||' ,
'?' : '||question_mark||' ,
'(' : '||openparanthesys||' ,
')' : '||closeparanthesys||' ,
'-' : '||hyphen||' ,
'\n' : '||line_feed||'}
return punct
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
tests.test_tokenize(token_lookup)
```
## Pre-process all the data and save it
Running the code cell below will pre-process all the data and save it to file. You're encouraged to lok at the code for `preprocess_and_save_data` in the `helpers.py` file to see what it's doing in detail, but you do not need to change this code.
```
"""
DON'T MODIFY ANYTHING IN THIS CELL
"""
# pre-process training data
helper.preprocess_and_save_data(data_dir, token_lookup, create_lookup_tables)
```
# Check Point
This is your first checkpoint. If you ever decide to come back to this notebook or have to restart the notebook, you can start from here. The preprocessed data has been saved to disk.
```
"""
DON'T MODIFY ANYTHING IN THIS CELL
"""
import helper
import problem_unittests as tests
int_text, vocab_to_int, int_to_vocab, token_dict = helper.load_preprocess()
token_dict
```
## Build the Neural Network
In this section, you'll build the components necessary to build an RNN by implementing the RNN Module and forward and backpropagation functions.
### Check Access to GPU
```
"""
DON'T MODIFY ANYTHING IN THIS CELL
"""
import torch
# Check for a GPU
train_on_gpu = torch.cuda.is_available()
if not train_on_gpu:
print('No GPU found. Please use a GPU to train your neural network.')
from torch.utils.data import TensorDataset, DataLoader
def batch_data(words, sequence_length, batch_size):
"""
Batch the neural network data using DataLoader
:param words: The word ids of the TV scripts
:param sequence_length: The sequence length of each batch
:param batch_size: The size of each batch; the number of sequences in a batch
:return: DataLoader with batched data
"""
n_batches = len(words)//batch_size
words = words[:batch_size*n_batches]
x , y = [] , []
for idx in range(0 , len(words) - sequence_length):
bx = words[idx:idx+sequence_length]
by = words[idx+sequence_length]
x.append(bx)
y.append(by)
x , y = np.array(x) , np.array(y)
print("Feature Data : ",x[:20])
print("Target Data : ", y[:20])
# TODO: Implement function
dataset = TensorDataset(torch.from_numpy(x) , torch.from_numpy(y))
# return a dataloader
return DataLoader(dataset , shuffle = True , batch_size = batch_size)
# there is no test for this function, but you are encouraged to create
# print statements and tests of your own
```
### Test your dataloader
You'll have to modify this code to test a batching function, but it should look fairly similar.
Below, we're generating some test text data and defining a dataloader using the function you defined, above. Then, we are getting some sample batch of inputs `sample_x` and targets `sample_y` from our dataloader.
Your code should return something like the following (likely in a different order, if you shuffled your data):
```
torch.Size([10, 5])
tensor([[ 28, 29, 30, 31, 32],
[ 21, 22, 23, 24, 25],
[ 17, 18, 19, 20, 21],
[ 34, 35, 36, 37, 38],
[ 11, 12, 13, 14, 15],
[ 23, 24, 25, 26, 27],
[ 6, 7, 8, 9, 10],
[ 38, 39, 40, 41, 42],
[ 25, 26, 27, 28, 29],
[ 7, 8, 9, 10, 11]])
torch.Size([10])
tensor([ 33, 26, 22, 39, 16, 28, 11, 43, 30, 12])
```
### Sizes
Your sample_x should be of size `(batch_size, sequence_length)` or (10, 5) in this case and sample_y should just have one dimension: batch_size (10).
### Values
You should also notice that the targets, sample_y, are the *next* value in the ordered test_text data. So, for an input sequence `[ 28, 29, 30, 31, 32]` that ends with the value `32`, the corresponding output should be `33`.
```
# test dataloader
test_text = list(range(50))
t_loader = batch_data(test_text, sequence_length=5, batch_size=10)
data_iter = iter(t_loader)
sample_x, sample_y = data_iter.next()
print(sample_x.shape)
print(sample_x)
print()
print(sample_y.shape)
print(sample_y)
```
---
## Build the Neural Network
Implement an RNN using PyTorch's [Module class](http://pytorch.org/docs/master/nn.html#torch.nn.Module). You may choose to use a GRU or an LSTM. To complete the RNN, you'll have to implement the following functions for the class:
- `__init__` - The initialize function.
- `init_hidden` - The initialization function for an LSTM/GRU hidden state
- `forward` - Forward propagation function.
The initialize function should create the layers of the neural network and save them to the class. The forward propagation function will use these layers to run forward propagation and generate an output and a hidden state.
**The output of this model should be the *last* batch of word scores** after a complete sequence has been processed. That is, for each input sequence of words, we only want to output the word scores for a single, most likely, next word.
### Hints
1. Make sure to stack the outputs of the lstm to pass to your fully-connected layer, you can do this with `lstm_output = lstm_output.contiguous().view(-1, self.hidden_dim)`
2. You can get the last batch of word scores by shaping the output of the final, fully-connected layer like so:
```
# reshape into (batch_size, seq_length, output_size)
output = output.view(batch_size, -1, self.output_size)
# get last batch
out = output[:, -1]
```
```
import torch.nn as nn
class RNN(nn.Module):
def __init__(self, vocab_size, output_size, embedding_dim, hidden_dim, n_layers, dropout=0.5):
"""
Initialize the PyTorch RNN Module
:param vocab_size: The number of input dimensions of the neural network (the size of the vocabulary)
:param output_size: The number of output dimensions of the neural network
:param embedding_dim: The size of embeddings, should you choose to use them
:param hidden_dim: The size of the hidden layer outputs
:param dropout: dropout to add in between LSTM/GRU layers
"""
super(RNN, self).__init__()
# TODO: Implement function
# set class variables
self.vocab_size = vocab_size
self.output_size = output_size
self.embedding_dim = embedding_dim
self.hidden_dim = hidden_dim
self.n_layers = n_layers
self.dropout_prob = dropout
# define model layers
self.embed = nn.Embedding(self.vocab_size , self.embedding_dim)
self.lstm = nn.LSTM(self.embedding_dim , self.hidden_dim , self.n_layers , batch_first = True , dropout = self.dropout_prob)
self.linear = nn.Linear(self.hidden_dim , self.output_size)
def forward(self, nn_input, hidden):
"""
Forward propagation of the neural network
:param nn_input: The input to the neural network
:param hidden: The hidden state
:return: Two Tensors, the output of the neural network and the latest hidden state
"""
# TODO: Implement function
embed_out = self.embed(nn_input)
lstm_out , hidden_out = self.lstm(embed_out , hidden)
lstm_out = lstm_out.contiguous().view(-1 , self.hidden_dim)
output = self.linear(lstm_out)
output = output.view(nn_input.size(0) , -1 , self.output_size)
output = output[: , -1]
# return one batch of output word scores and the hidden state
return output, hidden
def init_hidden(self, batch_size):
'''
Initialize the hidden state of an LSTM/GRU
:param batch_size: The batch_size of the hidden state
:return: hidden state of dims (n_layers, batch_size, hidden_dim)
'''
# Implement function
weight = next(self.parameters()).data
# initialize hidden state with zero weights, and move to GPU if available
if train_on_gpu:
hidden = (weight.new(self.n_layers,batch_size,self.hidden_dim).zero_().cuda(),
weight.new(self.n_layers,batch_size,self.hidden_dim).zero_().cuda())
else:
hidden = (weight.new(self.n_layers,batch_size,self.hidden_dim).zero_(),
weight.new(self.n_layers,batch_size,self.hidden_dim).zero_())
return hidden
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
tests.test_rnn(RNN, train_on_gpu)
```
### Define forward and backpropagation
Use the RNN class you implemented to apply forward and back propagation. This function will be called, iteratively, in the training loop as follows:
```
loss = forward_back_prop(decoder, decoder_optimizer, criterion, inp, target)
```
And it should return the average loss over a batch and the hidden state returned by a call to `RNN(inp, hidden)`. Recall that you can get this loss by computing it, as usual, and calling `loss.item()`.
**If a GPU is available, you should move your data to that GPU device, here.**
```
def forward_back_prop(rnn, optimizer, criterion, inp, target, hidden):
"""
Forward and backward propagation on the neural network
:param decoder: The PyTorch Module that holds the neural network
:param decoder_optimizer: The PyTorch optimizer for the neural network
:param criterion: The PyTorch loss function
:param inp: A batch of input to the neural network
:param target: The target output for the batch of input
:return: The loss and the latest hidden state Tensor
"""
# TODO: Implement Function
# move data to GPU, if available
if train_on_gpu:
rnn.cuda()
inp = inp.cuda()
target = target.cuda()
# perform backpropagation and optimization
h = tuple([w.data for w in hidden])
optimizer.zero_grad()
out , h = rnn(inp , h)
loss = criterion(out , target)
loss.backward()
nn.utils.clip_grad_norm_(rnn.parameters() , 5)
optimizer.step()
# return the loss over a batch and the hidden state produced by our model
return loss.item(), h
# Note that these tests aren't completely extensive.
# they are here to act as general checks on the expected outputs of your functions
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
tests.test_forward_back_prop(RNN, forward_back_prop, train_on_gpu)
```
## Neural Network Training
With the structure of the network complete and data ready to be fed in the neural network, it's time to train it.
### Train Loop
The training loop is implemented for you in the `train_decoder` function. This function will train the network over all the batches for the number of epochs given. The model progress will be shown every number of batches. This number is set with the `show_every_n_batches` parameter. You'll set this parameter along with other parameters in the next section.
```
"""
DON'T MODIFY ANYTHING IN THIS CELL
"""
def train_rnn(rnn, batch_size, optimizer, criterion, n_epochs, show_every_n_batches=100):
batch_losses = []
rnn.train()
print("Training for %d epoch(s)..." % n_epochs)
for epoch_i in range(1, n_epochs + 1):
# initialize hidden state
hidden = rnn.init_hidden(batch_size)
for batch_i, (inputs, labels) in enumerate(train_loader, 1):
# make sure you iterate over completely full batches, only
n_batches = len(train_loader.dataset)//batch_size
if(batch_i > n_batches):
break
# forward, back prop
loss, hidden = forward_back_prop(rnn, optimizer, criterion, inputs, labels, hidden)
# record loss
batch_losses.append(loss)
# printing loss stats
if batch_i % show_every_n_batches == 0:
print('Epoch: {:>4}/{:<4} Loss: {}\n'.format(
epoch_i, n_epochs, np.average(batch_losses)))
batch_losses = []
# returns a trained rnn
return rnn
```
### Hyperparameters
Set and train the neural network with the following parameters:
- Set `sequence_length` to the length of a sequence.
- Set `batch_size` to the batch size.
- Set `num_epochs` to the number of epochs to train for.
- Set `learning_rate` to the learning rate for an Adam optimizer.
- Set `vocab_size` to the number of uniqe tokens in our vocabulary.
- Set `output_size` to the desired size of the output.
- Set `embedding_dim` to the embedding dimension; smaller than the vocab_size.
- Set `hidden_dim` to the hidden dimension of your RNN.
- Set `n_layers` to the number of layers/cells in your RNN.
- Set `show_every_n_batches` to the number of batches at which the neural network should print progress.
If the network isn't getting the desired results, tweak these parameters and/or the layers in the `RNN` class.
```
# Data params
# Sequence Length
sequence_length = 10 # of words in a sequence
# Batch Size
batch_size = 256
# data loader - do not change
train_loader = batch_data(int_text, sequence_length, batch_size)
# Training parameters
# Number of Epochs
num_epochs = 15
# Learning Rate
learning_rate = 3e-3
# Model parameters
# Vocab size
vocab_size = len(vocab_to_int)
# Output size
output_size = vocab_size
# Embedding Dimension
embedding_dim = 512
# Hidden Dimension
hidden_dim = 256
# Number of RNN Layers
n_layers = 3
# Show stats for every n number of batches
show_every_n_batches = 2000
```
### Train
In the next cell, you'll train the neural network on the pre-processed data. If you have a hard time getting a good loss, you may consider changing your hyperparameters. In general, you may get better results with larger hidden and n_layer dimensions, but larger models take a longer time to train.
> **You should aim for a loss less than 3.5.**
You should also experiment with different sequence lengths, which determine the size of the long range dependencies that a model can learn.
```
"""
DON'T MODIFY ANYTHING IN THIS CELL
"""
# create model and move to gpu if available
rnn = RNN(vocab_size, output_size, embedding_dim, hidden_dim, n_layers, dropout=0.5)
if train_on_gpu:
rnn.cuda()
# defining loss and optimization functions for training
optimizer = torch.optim.Adam(rnn.parameters(), lr=learning_rate)
criterion = nn.CrossEntropyLoss()
# training the model
trained_rnn = train_rnn(rnn, batch_size, optimizer, criterion, num_epochs, show_every_n_batches)
# saving the trained model
helper.save_model('./save/trained_rnn', trained_rnn)
print('Model Trained and Saved')
```
### Question: How did you decide on your model hyperparameters?
For example, did you try different sequence_lengths and find that one size made the model converge faster? What about your hidden_dim and n_layers; how did you decide on those?
**Answer:** After training I observed that if the sequence_length is too large the model convergers faster. Also, taking bigger batches is improving the model. Coming to the hidden_dim I choose it to be 256 and I decided the value taking into consideration the embedding dim that is 512. Finally the n_layers I choose it to be 3 as 2 or 3 is the usually set value.
---
# Checkpoint
After running the above training cell, your model will be saved by name, `trained_rnn`, and if you save your notebook progress, **you can pause here and come back to this code at another time**. You can resume your progress by running the next cell, which will load in our word:id dictionaries _and_ load in your saved model by name!
```
"""
DON'T MODIFY ANYTHING IN THIS CELL
"""
import torch
import helper
import problem_unittests as tests
_, vocab_to_int, int_to_vocab, token_dict = helper.load_preprocess()
trained_rnn = helper.load_model('./save/trained_rnn')
```
## Generate TV Script
With the network trained and saved, you'll use it to generate a new, "fake" Seinfeld TV script in this section.
### Generate Text
To generate the text, the network needs to start with a single word and repeat its predictions until it reaches a set length. You'll be using the `generate` function to do this. It takes a word id to start with, `prime_id`, and generates a set length of text, `predict_len`. Also note that it uses topk sampling to introduce some randomness in choosing the most likely next word, given an output set of word scores!
```
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
import torch.nn.functional as F
def generate(rnn, prime_id, int_to_vocab, token_dict, pad_value, predict_len=100):
"""
Generate text using the neural network
:param decoder: The PyTorch Module that holds the trained neural network
:param prime_id: The word id to start the first prediction
:param int_to_vocab: Dict of word id keys to word values
:param token_dict: Dict of puncuation tokens keys to puncuation values
:param pad_value: The value used to pad a sequence
:param predict_len: The length of text to generate
:return: The generated text
"""
rnn.eval()
# create a sequence (batch_size=1) with the prime_id
current_seq = np.full((1, sequence_length), pad_value)
current_seq[-1][-1] = prime_id
predicted = [int_to_vocab[prime_id]]
for _ in range(predict_len):
if train_on_gpu:
current_seq = torch.LongTensor(current_seq).cuda()
else:
current_seq = torch.LongTensor(current_seq)
# initialize the hidden state
hidden = rnn.init_hidden(current_seq.size(0))
# get the output of the rnn
output, _ = rnn(current_seq, hidden)
# get the next word probabilities
p = F.softmax(output, dim=1).data
if(train_on_gpu):
p = p.cpu() # move to cpu
# use top_k sampling to get the index of the next word
top_k = 5
p, top_i = p.topk(top_k)
top_i = top_i.numpy().squeeze()
# select the likely next word index with some element of randomness
p = p.numpy().squeeze()
word_i = np.random.choice(top_i, p=p/p.sum())
# retrieve that word from the dictionary
word = int_to_vocab[word_i]
predicted.append(word)
# the generated word becomes the next "current sequence" and the cycle can continue
current_seq = np.roll(current_seq, -1, 1)
current_seq[-1][-1] = word_i
gen_sentences = ' '.join(predicted)
# Replace punctuation tokens
for key, token in token_dict.items():
ending = ' ' if key in ['\n', '(', '"'] else ''
gen_sentences = gen_sentences.replace(' ' + token.lower(), key)
gen_sentences = gen_sentences.replace('\n ', '\n')
gen_sentences = gen_sentences.replace('( ', '(')
# return all the sentences
return gen_sentences
```
### Generate a New Script
It's time to generate the text. Set `gen_length` to the length of TV script you want to generate and set `prime_word` to one of the following to start the prediction:
- "jerry"
- "elaine"
- "george"
- "kramer"
You can set the prime word to _any word_ in our dictionary, but it's best to start with a name for generating a TV script. (You can also start with any other names you find in the original text file!)
```
# run the cell multiple times to get different results!
gen_length = 400 # modify the length to your preference
prime_word = 'jerry' # name for starting the script
"""
DON'T MODIFY ANYTHING IN THIS CELL THAT IS BELOW THIS LINE
"""
pad_word = helper.SPECIAL_WORDS['PADDING']
generated_script = generate(trained_rnn, vocab_to_int[prime_word + ':'], int_to_vocab, token_dict, vocab_to_int[pad_word], gen_length)
print(generated_script)
```
#### Save your favorite scripts
Once you have a script that you like (or find interesting), save it to a text file!
```
# save script to a text file
f = open("generated_script_1.txt","w")
f.write(generated_script)
f.close()
```
# The TV Script is Not Perfect
It's ok if the TV script doesn't make perfect sense. It should look like alternating lines of dialogue, here is one such example of a few generated lines.
### Example generated script
>jerry: what about me?
>
>jerry: i don't have to wait.
>
>kramer:(to the sales table)
>
>elaine:(to jerry) hey, look at this, i'm a good doctor.
>
>newman:(to elaine) you think i have no idea of this...
>
>elaine: oh, you better take the phone, and he was a little nervous.
>
>kramer:(to the phone) hey, hey, jerry, i don't want to be a little bit.(to kramer and jerry) you can't.
>
>jerry: oh, yeah. i don't even know, i know.
>
>jerry:(to the phone) oh, i know.
>
>kramer:(laughing) you know...(to jerry) you don't know.
You can see that there are multiple characters that say (somewhat) complete sentences, but it doesn't have to be perfect! It takes quite a while to get good results, and often, you'll have to use a smaller vocabulary (and discard uncommon words), or get more data. The Seinfeld dataset is about 3.4 MB, which is big enough for our purposes; for script generation you'll want more than 1 MB of text, generally.
# Submitting This Project
When submitting this project, make sure to run all the cells before saving the notebook. Save the notebook file as "dlnd_tv_script_generation.ipynb" and save another copy as an HTML file by clicking "File" -> "Download as.."->"html". Include the "helper.py" and "problem_unittests.py" files in your submission. Once you download these files, compress them into one zip file for submission.
|
github_jupyter
|
```
import pandas as pd
import numpy as np
from keras.models import Sequential
from keras.layers import Dense
from keras.wrappers.scikit_learn import KerasRegressor
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import KFold
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline
from sklearn.model_selection import train_test_split
from sklearn.model_selection import cross_validate, cross_val_predict
from keras import models
from keras import layers
model_data = pd.read_csv('write_data/stage_1/lr_modeling.csv')
model_data.head()
training = model_data[(model_data['Season'] < 2020) & (model_data['Target_clf'] >0)]
training.Target_clf.value_counts()
y = training['Target'].values
X = training.drop(columns=['WTeamID', 'LTeamID', 'Season', 'Target', 'Target_clf']).values
# baseline neural networks
def baseline_model():
# create model
model = Sequential()
model.add(Dense(15, input_dim=32, kernel_initializer='normal', activation='relu'))
model.add(Dense(1, kernel_initializer='normal'))
# Compile model
model.compile(loss='mean_squared_error', optimizer='adam')
return model
estimator = KerasRegressor(build_fn=baseline_model, epochs=100, batch_size=50, verbose=0)
kfold = KFold(n_splits=10)
results = cross_val_score(estimator, X, y, cv=kfold, scoring='neg_mean_squared_error')
print("Baseline: %.2f (%.2f) MSE" % (np.sqrt(-1 * results.mean()), results.std()))
estimators = []
estimators.append(('std', StandardScaler()))
estimators.append(('mlp', KerasRegressor(build_fn=baseline_model, epochs=100, batch_size=50, verbose=0)))
pipeline = Pipeline(estimators)
kfold = KFold(n_splits=10)
results = cross_val_score(pipeline, X, y, cv=kfold, scoring='neg_mean_squared_error')
print("Baseline: %.2f (%.2f) MSE" % (np.sqrt(-1 * results.mean()), np.sqrt(results.std())))
# baseline neural networks
def develop_model():
model = Sequential()
model.add(Dense(15, input_dim=32, kernel_initializer='normal', activation='relu'))
model.add(Dense(5, kernel_initializer='normal', activation='relu'))
model.add(Dense(1, kernel_initializer='normal'))
# Compile model
model.compile(loss='mean_squared_error', optimizer='adam')
return model
def eval_nn(model):
estimators = []
estimators.append(('std', StandardScaler()))
estimators.append(('mlp', KerasRegressor(build_fn=model, epochs=100, batch_size=50, verbose=0)))
pipeline = Pipeline(estimators)
kfold = KFold(n_splits=10)
pipeline.fit(X, y)
# results = cross_val_score(pipeline, X, y, cv=kfold, scoring='neg_mean_squared_error')
# mod = cross_val_predict(pipeline, X, y, cv=kfold)
# print('RMSE: ', np.round(np.sqrt(-1 * results.mean())))
return pipeline
# return [np.round(np.sqrt(-1 * results.mean())), np.round(np.sqrt(results.std()))], pipeline
# data
k = 5
num_val_samples = len(X_train) // k
num_epochs = 100
mse = []
rmse = []
X_train_ = StandardScaler().fit_transform(X_train)
# from keras.metrics import
from keras.metrics import RootMeanSquaredError
def build_model():
model = models.Sequential()
model.add(layers.Dense(15, activation='relu', input_shape=(X_train_.shape[1],)))
model.add(layers.Dense(5, activation='relu'))
model.add(layers.Dense(1))
model.compile(optimizer='adam'
, loss="mean_squared_error"
, metrics=[RootMeanSquaredError(name="root_mean_squared_error"
, dtype=None)])
return model
for i in range(k):
print('processing fold #', i)
val_data = X_train_[i * num_val_samples: (i + 1) * num_val_samples]
val_targets = y_train[i * num_val_samples: (i + 1) * num_val_samples]
partial_train_data = np.concatenate([X_train_[:i * num_val_samples]
, X_train_[(i + 1) * num_val_samples:]]
,axis=0)
partial_train_targets = np.concatenate([y_train[:i * num_val_samples]
,y_train[(i + 1) * num_val_samples:]]
, axis=0)
model = build_model()
model.fit(partial_train_data, partial_train_targets,
epochs=num_epochs, batch_size=1, verbose=0)
val_mse, val_rmse = model.evaluate(val_data, val_targets, verbose=0)
print('mse is: ', val_mse)
print('rmse is: ', val_rmse)
mse.append(val_mse)
rmse.append(val_rmse)
np.array(rmse).mean()
data_test = pd.read_csv('write_data/stage_1/submission_1.csv')
data_test = data_test.drop(columns=['WTeamID', 'LTeamID'])
data_test.head()
data_lr = data_test[['ID']].copy()
data_lr['pred_nn'] = model.predict(data_test.drop(columns=['Season', 'ID']))
data_lr.head()
df_sub = load_dataframe('write_data/stage_1/01_spread_pred.csv')
data_linear_predict = df_sub\
.withColumn('Season', split(df_sub.ID, '_').getItem(0)) \
.withColumn('WTeamID', split(df_sub.ID, '_').getItem(1)) \
.withColumn('LTeamID', split(df_sub.ID, '_').getItem(2)) \
.toPandas()
compare =data_linear_predict.join(data_lr, on='ID', how='inner')
```
|
github_jupyter
|
```
# - Decide which map to plot
# in main notebook code
#mapvarnow = 'skj' # choose: skj, bet
# - Define constant plot params
stipsizenow = 10; stipmarknow = 'o'
stipfacecolnow = 'none'
stipedgeltcolnow = 'whitesmoke'
stipewnow = 0.8 # marker edge width
eezfcnow = 'none'; eezlcnow = 'lightgray' #'silver'
eezlsnow = '-'; eezlwnow = 0.9
# - Define subplot-variable plot params
if mapvarnow=='skj':
fignamenow = 'S6_fig'
unitsnow = 8*['[metric tons/set]']
mapsnow = [skj_cp_tot_seas.sel(season='DJF'),
skj_cp_tot_seas.sel(season='DJF')-skj_cp_tot_mean,
skj_cp_tot_seas.sel(season='MAM'),
skj_cp_tot_seas.sel(season='MAM')-skj_cp_tot_mean,
skj_cp_tot_seas.sel(season='JJA'),
skj_cp_tot_seas.sel(season='JJA')-skj_cp_tot_mean,
skj_cp_tot_seas.sel(season='SON'),
skj_cp_tot_seas.sel(season='SON')-skj_cp_tot_mean]
vmaxsnow = 4*[60, 12]
vminsnow = 4*[0, -12]
pvsnow = 8*[skj_cp_tot_seas_kw_pval]
ptfsnow = 8*[skj_cp_tot_seas_kw_ptf]
titlesnow = ['SKJ CPUE - Winter','SKJ CPUE - Winter minus mean',
'SKJ CPUE - Spring','SKJ CPUE - Spring minus mean',
'SKJ CPUE - Summer','SKJ CPUE - Summer minus mean',
'SKJ CPUE - Fall','SKJ CPUE - Fall minus mean']
elif mapvarnow=='bet':
fignamenow = 'S7_fig'
unitsnow = 8*['[metric tons/set]']
mapsnow = [bet_cp_tot_seas.sel(season='DJF'),
bet_cp_tot_seas.sel(season='DJF')-bet_cp_tot_mean,
bet_cp_tot_seas.sel(season='MAM'),
bet_cp_tot_seas.sel(season='MAM')-bet_cp_tot_mean,
bet_cp_tot_seas.sel(season='JJA'),
bet_cp_tot_seas.sel(season='JJA')-bet_cp_tot_mean,
bet_cp_tot_seas.sel(season='SON'),
bet_cp_tot_seas.sel(season='SON')-bet_cp_tot_mean]
vmaxsnow = 4*[15, 4]
vminsnow = 4*[0, -4]
pvsnow = 8*[bet_cp_tot_seas_kw_pval]
ptfsnow = 8*[bet_cp_tot_seas_kw_ptf]
titlesnow = ['BET CPUE - Winter','BET CPUE - Winter minus mean',
'BET CPUE - Spring','BET CPUE - Spring minus mean',
'BET CPUE - Summer','BET CPUE - Summer minus mean',
'BET CPUE - Fall','BET CPUE - Fall minus mean']
stipltdkcosnow = 0.5*np.asarray(vmaxsnow) # light/dark stip cutoff value
stipedgedkcolsnow = 4*['lightgray', 'darkslategray', None]
signifstipsnow = 4*[0, 1, None]
ploteezsnow = 4*[1, 0, None]
cmseqnow = plt.cm.get_cmap('viridis',11)
cmdivnow = plt.cm.get_cmap('PuOr',11)
cmsnow = 4*[cmseqnow, cmdivnow]
stipltdkcosnow = 0.5*np.asarray(vmaxsnow) # light/dark stip cutoff value
stipedgedkcolsnow = 4*['lightgray', 'darkslategray']
signifstipsnow = 4*[0,1]
ploteezsnow = 4*[1,0]
# - Set proj and define axes
fig,axes = plt.subplots(nrows=4, ncols=2, figsize=(12,10),
subplot_kw={'projection': ccrs.PlateCarree(central_longitude=200)})
# - Make maps pretty + plot
isp = 0
for irow in range(4):
for icol in range(2):
ax = axes[irow][icol]
exec(open('helper_scripts/create_map_bgs.py').read())
ax.text(-0.08, 1.08, string.ascii_uppercase[isp],
transform=ax.transAxes, size=16, weight='bold')
mapsnow[isp].plot(
ax=ax, transform=ccrs.PlateCarree(), cmap=cmsnow[isp],
vmin=vminsnow[isp], vmax=vmaxsnow[isp],
cbar_kwargs={'pad': 0.02, 'label': unitsnow[isp]})
if ploteezsnow[isp]==1:
nueezs.plot(ax=ax, transform=ccrs.PlateCarree(),
color=eezfcnow, edgecolor=eezlcnow, linewidth=eezlwnow)
if signifstipsnow[isp]==1:
[ltcol_signiflonnow,ltcol_signiflatnow]=find_where_pval_small(
pvsnow[isp].where(abs(mapsnow[isp])>stipltdkcosnow[isp]),
ptfsnow[isp])
[dkcol_signiflonnow,dkcol_signiflatnow]=find_where_pval_small(
pvsnow[isp].where(abs(mapsnow[isp])<=stipltdkcosnow[isp]),
ptfsnow[isp])
ax.scatter(ltcol_signiflonnow, ltcol_signiflatnow,
marker=stipmarknow, linewidths=stipewnow,
facecolors=stipfacecolnow, edgecolors=stipedgeltcolnow,
s=stipsizenow, transform=ccrs.PlateCarree())
ax.scatter(dkcol_signiflonnow, dkcol_signiflatnow,
marker=stipmarknow, linewidths=stipewnow,
facecolors=stipfacecolnow, edgecolors=stipedgedkcolnow,
s=stipsizenow, transform=ccrs.PlateCarree())
ax.set_xlabel(''); ax.set_ylabel('')
ax.set_title(titlesnow[isp])
isp = isp + 1
# - Save fig
fig.savefig(figpath + fignamenow + '.pdf',
bbox_inches='tight', pad_inches = 0, dpi = 300)
fig.savefig(figpath + fignamenow + '.png',
bbox_inches='tight', pad_inches = 0, dpi = 300)
```
|
github_jupyter
|

# Ejemplo de simulación numérica
```
import numpy as np
from scipy.integrate import odeint
from matplotlib import rc
import matplotlib.pyplot as plt
%matplotlib inline
rc("text", usetex=True)
rc("font", size=18)
rc("figure", figsize=(6,4))
rc("axes", grid=True)
```
## Problema físico

Definimos un SR con el origen en el orificio donde el hilo atravieza el plano, la coordenada $\hat{z}$ apuntando hacia abajo. Con esto sacamos, de la segunda ley de Newton para las particulas:
$$
\begin{align}
\text{Masa 1)}\quad&\vec{F}_1 = m_1 \vec{a}_1 \\
&-T \hat{r} = m_1 \vec{a}_1 \\
&-T \hat{r} = m_1 \left\{ \left(\ddot{r} - r \dot{\theta}^2\right) \hat{r} + \left(r\ddot{\theta} + 2\dot{r}\dot{\theta}\right)\hat{\theta} \right\} \\
&\begin{cases}
\hat{r})\ - T = m_1\left( \ddot{r} - r\, \dot{\theta}^2\right)\\
\hat{\theta})\ 0 = m_1 \left(r \ddot{\theta} + 2 \dot{r}\dot{\theta}\right)\\
\end{cases}\\
\\
\text{Masa 2)}\quad&\vec{F}_2 = m_2 \vec{a}_2 \\
&-T \hat{z} + m_2 g \hat{z} = m_2 \ddot{z} \hat{z} \\
\implies & \boxed{T = m_2 \left( g - \ddot{z} \right)}\\
\end{align}
$$
Ahora reemplazando este resultado para la tension (que es igual en ambas expresiones) y entendiendo que $\ddot{z} = -\ddot{r}$ pues la soga es ideal y de largo constante, podemos rescribir las ecuaciones obtenidas para la masa 1 como:
$$
\begin{cases}
\hat{r})\quad - m_2 \left( g + \ddot{r} \right) = m_1\left( \ddot{r} - r\, \dot{\theta}^2\right)\\
\\
\hat{\theta})\quad 0 = m_1 \left(r \ddot{\theta} + 2 \dot{r}\dot{\theta}\right)
\end{cases}
\implies
\begin{cases}
\hat{r})\quad \ddot{r} = \dfrac{- m_2 g + m_1 r \dot{\theta}^2}{m_1 + m_2}\\
\\
\hat{\theta})\quad \ddot{\theta} = -2 \dfrac{\dot{r}\dot{\theta}}{r}\\
\end{cases}
$$
La gracia de estos métodos es lograr encontrar una expresión de la forma $y'(x) = f(x,t)$ donde x será la solución buscada, aca como estamos en un sistema de segundo orden en dos variables diferentes ($r$ y $\theta$) sabemos que nuestra solución va a tener que involucrar 4 componentes. Es como en el oscilador armónico, que uno tiene que definir posicion y velocidad inicial para poder conocer el sistema, solo que aca tenemos dos para $r$ y dos para $\theta$.
Se puede ver entonces que vamos a necesitar una solucion del tipo:
$$\mathbf{X} = \begin{pmatrix} r \\ \dot{r}\\ \theta \\ \dot{\theta} \end{pmatrix} $$
Y entonces
$$
\dot{\mathbf{X}} =
\begin{pmatrix} \dot{r} \\ \ddot{r}\\ \dot{\theta} \\ \ddot{\theta} \end{pmatrix} =
\begin{pmatrix} \dot{r} \\ \dfrac{-m_2 g + m_1 r \dot{\theta}^2}{m_1 + m_2} \\ \dot{\theta} \\ -2 \dfrac{\dot{r}\dot{\theta}}{r} \end{pmatrix} =
\mathbf{f}(\mathbf{X}, t)
$$
---
Si alguno quiere, tambien se puede escribir la evolucion del sistema de una forma piola, que no es otra cosa que una querida expansión de Taylor a orden lineal.
$$
\begin{align}
r(t+dt) &= r(t) + \dot{r}(t)\cdot dt \\
\dot{r}(t+dt) &= \dot{r}(t) + \ddot{r}(t)\cdot dt \\
\theta(t+dt) &= \theta(t) + \dot{\theta}(t)\cdot dt \\
\dot{\theta}(t+dt) &= \dot{\theta}(t) + \ddot{\theta}(t)\cdot dt
\end{align}
\implies
\begin{pmatrix}
r\\
\dot{r}\\
\theta\\
\ddot{\theta}
\end{pmatrix}(t + dt) =
\begin{pmatrix}
r\\
\dot{r}\\
\theta\\
\ddot{\theta}
\end{pmatrix}(t) +
\begin{pmatrix}
\dot{r}\\
\ddot{r}\\
\dot{\theta}\\
\ddot{\theta}
\end{pmatrix}(t) \cdot dt
$$
Aca tenemos que recordar que la compu no puede hacer cosas continuas, porque son infinitas cuentas, entones si o si hay que discretizar el tiempo y el paso temporal!
$$
\begin{pmatrix}
r\\
\dot{r}\\
\theta\\
\ddot{\theta}
\end{pmatrix}_{i+1} =
\begin{pmatrix}
r\\
\dot{r}\\
\theta\\
\ddot{\theta}
\end{pmatrix}_i +
\begin{pmatrix}
\dot{r}\\
\ddot{r}\\
\dot{\theta}\\
\ddot{\theta}
\end{pmatrix}_i \cdot dt
$$
Si entonces decido llamar a este vector columna $\mathbf{X}$, el sistema queda escrito como:
$$
\mathbf{X}_{i+1} = \mathbf{X}_i + \dot{\mathbf{X}}_i\ dt
$$
Donde sale denuevo que $\dot{\mathbf{X}}$ es lo que está escrito arriba.
Es decir que para encontrar cualquier valor, solo hace falta saber el vector anterior y la derivada, pero las derivadas ya las tenemos (es todo el trabajo que hicimos de fisica antes)!!
---
---
De cualquier forma que lo piensen, ojala hayan entendido que entonces con tener las condiciones iniciales y las ecuaciones diferenciales ya podemos resolver (tambien llamado *integrar*) el sistema.
```
# Constantes del problema:
M1 = 3
M2 = 3
g = 9.81
# Condiciones iniciales del problema:
r0 = 2
r_punto0 = 0
tita0 = 0
tita_punto0 = 1
C1 = (M2*g)/(M1+M2) # Defino constantes utiles
C2 = (M1)/(M1+M2)
cond_iniciales = [r0, r_punto0, tita0, tita_punto0]
def derivada(X, t, c1, c2): # esto sería la f del caso { x' = f(x,t) }
r, r_punto, tita, tita_punto = X
deriv = [0, 0, 0, 0] # es como el vector columna de arriba pero en filado
deriv[0] = r_punto # derivada de r
deriv[1] = -c1 + c2*r*(tita_punto)**2 # r dos puntos
deriv[2] = tita_punto # derivada de tita
deriv[3] = -2*r_punto*tita_punto/r
return deriv
def resuelvo_sistema(m1, m2, tmax = 20):
t0 = 0
c1 = (m2*g)/(m1+m2) # Defino constantes utiles
c2 = (m1)/(m1+m2)
t = np.arange(t0, tmax, 0.001)
# aca podemos definirnos nuestro propio algoritmo de integracion
# o bien usar el que viene a armado de scipy.
# Ojo que no es perfecto eh, a veces es mejor escribirlo uno
out = odeint(derivada, cond_iniciales, t, args = (c1, c2,))
return [t, out.T]
t, (r, rp, tita, titap) = resuelvo_sistema(M1, M2, tmax=10)
plt.figure()
plt.plot(t, r/r0, 'r')
plt.ylabel(r"$r / r_0$")
plt.xlabel(r"tiempo")
# plt.savefig("directorio/r_vs_t.pdf", dpi=300)
plt.figure()
plt.plot(t, tita-tita0, 'b')
plt.ylabel(r"$\theta - \theta_0$")
plt.xlabel(r"tiempo")
# plt.savefig("directorio/tita_vs_t.pdf", dpi=300)
plt.figure()
plt.plot(r*np.cos(tita-tita0)/r0, r*np.sin(tita-tita0)/r0, 'g')
plt.ylabel(r"$r/r_0\ \sin\left(\theta - \theta_0\right)$")
plt.xlabel(r"$r/r_0\ \cos\left(\theta - \theta_0\right)$")
# plt.savefig("directorio/trayectoria.pdf", dpi=300)
```
Todo muy lindo!!
Cómo podemos verificar si esto está andando ok igual? Porque hasta acá solo sabemos que dio razonable, pero el ojímetro no es una medida cuantitativa.
Una opción para ver que el algoritmo ande bien (y que no hay errores numéricos, y que elegimos un integrador apropiado **ojo con esto eh... te estoy mirando a vos, Runge-Kutta**), es ver si se conserva la energía.
Les recuerdo que la energía cinética del sistema es $K = \frac{1}{2} m_1 \left|\vec{v}_1 \right|^2 + \frac{1}{2} m_2 \left|\vec{v}_2 \right|^2$, cuidado con cómo se escribe cada velocidad, y que la energía potencial del sistema únicamente depende de la altura de la pelotita colgante.
Hace falta conocer la longitud $L$ de la cuerda para ver si se conserva la energía mecánica total? (Spoiler: No. Pero piensen por qué)
Les queda como ejercicio a ustedes verificar eso, y también pueden experimentar con distintos metodos de integración a ver qué pasa con cada uno, abajo les dejamos una ayudita para que prueben.
```
from scipy.integrate import solve_ivp
def resuelvo_sistema(m1, m2, tmax = 20, metodo='RK45'):
t0 = 0
c1 = (m2*g)/(m1+m2) # Defino constantes utiles
c2 = (m1)/(m1+m2)
t = np.arange(t0, tmax, 0.001)
# acá hago uso de las lambda functions, solamente para usar
# la misma funcion que definimos antes. Pero como ahora
# voy a usar otra funcion de integracion (no odeint)
# que pide otra forma de definir la funcion, en vez de pedir
# f(x,t) esta te pide f(t, x), entonces nada, hay que dar vuelta
# parametros y nada mas...
deriv_bis = lambda t, x: derivada(x, t, c1, c2)
out = solve_ivp(fun=deriv_bis, t_span=(t0, tmax), y0=cond_iniciales,\
method=metodo, t_eval=t)
return out
# Aca armo dos arrays con los metodos posibles y otro con colores
all_metodos = ['RK45', 'RK23', 'Radau', 'BDF', 'LSODA']
all_colores = ['r', 'b', 'm', 'g', 'c']
# Aca les dejo la forma piola de loopear sobre dos arrays a la par
for met, col in zip(all_metodos, all_colores):
result = resuelvo_sistema(M1, M2, tmax=30, metodo=met)
t = result.t
r, rp, tita, titap = result.y
plt.plot(t, r/r0, col, label=met)
plt.xlabel("tiempo")
plt.ylabel(r"$r / r_0$")
plt.legend(loc=3)
```
Ven cómo los distintos métodos van modificando más y más la curva de $r(t)$ a medida que van pasando los pasos de integración. Tarea para ustedes es correr el mismo código con la conservación de energía.
Cuál es mejor, por qué y cómo saberlo son preguntas que deberán hacerse e investigar si en algún momento trabajan con esto.
Por ejemplo, pueden buscar en Wikipedia "Symplectic Integrator" y ver qué onda.
### Les dejamos también abajo la simulación de la trayectoria de la pelotita
```
from matplotlib import animation
%matplotlib notebook
result = resuelvo_sistema(M1, M2, tmax=30, metodo='Radau')
t = result.t
r, rp, tita, titap = result.y
fig, ax = plt.subplots()
ax.set_xlim([-1, 1])
ax.set_ylim([-1, 1])
ax.plot(r*np.cos(tita)/r0, r*np.sin(tita)/r0, 'm', lw=0.2)
line, = ax.plot([], [], 'ko', ms=5)
N_SKIP = 50
N_FRAMES = int(len(r)/N_SKIP)
def animate(frame_no):
i = frame_no*N_SKIP
r_i = r[i]/r0
tita_i = tita[i]
line.set_data(r_i*np.cos(tita_i), r_i*np.sin(tita_i))
return line,
anim = animation.FuncAnimation(fig, animate, frames=N_FRAMES,
interval=50, blit=False)
```
Recuerden que esta animación no va a parar eh, sabemos que verla te deja en una especie de trance místico, pero recuerden pararla cuando haya transcurrido suficiente tiempo
# Animación Interactiva
Usando `ipywidgets` podemos agregar sliders a la animación, para modificar el valor de las masitas
```
from ipywidgets import interactive, interact, FloatProgress
from IPython.display import clear_output, display
%matplotlib inline
@interact(m1=(0,5,0.5), m2=(0,5,0.5), tmax=(0.01,20,0.5)) #Permite cambiar el parámetro de la ecuación
def resuelvo_sistema(m1, m2, tmax = 20):
t0 = 0
c1 = (m2*g)/(m1+m2) # Defino constantes utiles
c2 = (m1)/(m1+m2)
t = np.arange(t0, tmax, 0.05)
# out = odeint(derivada, cond_iniciales, t, args = (c1, c2,))
r, rp, tita, titap = odeint(derivada, cond_iniciales, t, args=(c1, c2,)).T
plt.xlim((-1,1))
plt.ylim((-1,1))
plt.plot(r*np.cos(tita)/r0, r*np.sin(tita)/r0,'b-')
# plt.xlabel("tiempo")
# plt.ylabel(r"$r / r_0$")
# plt.show()
```
|
github_jupyter
|
# 4 データ前処理
## 4.1 欠損データへの対処
```
from IPython.core.display import display
import pandas as pd
from io import StringIO
csv_data = '''A,B,C,D
1.0,2.0,3.0,4.0
5.0,6.0,,8.0
10.0,11.0,12.0,'''
df = pd.read_csv(StringIO(csv_data))
df
# 各特徴量の欠測値をカウント
df.isnull().sum()
df.values
```
### 4.1.1 欠測値を持つサンプル/特徴量を取り除く
```
# 欠測値を含む行を削除
df.dropna()
# 欠測値を含む列を削除
df.dropna(axis=1)
# すべての列がNaNである行だけを削除
df.dropna(how='all')
# 非NaN値が4つ未満の行を削除
df.dropna(thresh=4)
# 特定の列にNaNが含まれている行だけを削除
df.dropna(subset=['C'])
```
### 4.1.2 欠測値を補完する
```
from sklearn.preprocessing import Imputer
# 欠測値補完のインスタンスを生成(平均値補完)
# median: 中央値、most_frequent: 最頻値
imr = Imputer(missing_values='NaN', strategy='mean', axis=0)
# データを適合
imr = imr.fit(df)
# 補完を実行
imputed_data = imr.transform(df.values)
imputed_data
```
## 4.2 カテゴリデータの処理
```
import pandas as pd
# サンプルデータを生成
df = pd.DataFrame([
['green', 'M', 10.1, 'class1'],
['red', 'L', 13.5, 'class2'],
['blue', 'XL', 15.3, 'class1'],
])
# 列名を設定
df.columns = ['color', 'size', 'price', 'classlabel']
df
```
### 4.2.1 順序特徴量のマッピング
```
# Tシャツのサイズと整数を対応させるディクショナリを生成
size_mapping = {'XL': 3, 'L': 2, 'M': 1}
# Tシャツのサイズを整数に変換
df['size'] = df['size'].map(size_mapping)
df
# Tシャツのサイズを文字列に戻す辞書
inv_size_mapping = {v: k for k, v in size_mapping.items()}
inv_size_mapping
```
### 4.2.2 クラスラベルのエンコーディング
```
import numpy as np
# クラスラベルと整数を対応させる辞書
class_mapping = {label: i for i, label in enumerate(np.unique(df['classlabel']))}
class_mapping
# クラスラベルを整数に変換
df['classlabel'] = df['classlabel'].map(class_mapping)
df
inv_class_mapping = {v: k for k, v in class_mapping.items()}
# 整数からクラスラベルに変換
df['classlabel'] = df['classlabel'].map(inv_class_mapping)
df
from sklearn.preprocessing import LabelEncoder
class_le = LabelEncoder()
y = class_le.fit_transform(df['classlabel'].values)
y
class_le.inverse_transform(y)
```
### 4.2.3 名義特徴量での one-hot エンコーディング
```
# Tシャツの色、サイズ、価格を抽出
X = df[['color', 'size', 'price']].values
color_le = LabelEncoder()
X[:, 0] = color_le.fit_transform(X[:, 0])
X
from sklearn.preprocessing import OneHotEncoder
# one-hot エンコーダの生成
ohe = OneHotEncoder(categorical_features=[0])
# one-hot エンコーディングを実行
ohe.fit_transform(X).toarray()
# one-hot エンコーディングを実行
pd.get_dummies(df[['price', 'color', 'size']])
```
## 4.3 データセットをトレーニングデータセットとテストデータセットに分割する
```
# http://archive.ics.uci.edu/ml/datasets/Wine
df_wine = pd.read_csv('http://archive.ics.uci.edu/ml/machine-learning-databases/wine/wine.data', header=None)
display(df_wine.head())
# 列名を設定
df_wine.columns = ['Class label', 'Alcohol', 'Malic acid', 'Ash', 'Alcalinity of ash', 'Magnesium', 'Total phenols',
'Flavanoids', 'Nonflavanoid phenols', 'Proanthocyanins', 'Color intensity', 'Hue',
'OD280/OD315 of diluted wines', 'Proline']
display(df_wine.head())
print('Class labels', np.unique(df_wine['Class label']))
from sklearn.cross_validation import train_test_split
# 特徴量とクラスラベルを別々に抽出
X, y = df_wine.iloc[:, 1:].values, df_wine.iloc[:, 0].values
# 全体の30%をテストデータにする
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)
```
## 4.4 特徴量の尺度を揃える
```
from sklearn.preprocessing import MinMaxScaler
# min-max スケーリングのインスタンスを生成
mms = MinMaxScaler()
# トレーニングデータをスケーリング
X_train_norm = mms.fit_transform(X_train)
# テストデータをスケーリング
X_test_norm = mms.transform(X_test)
X_train, X_train_norm
from sklearn.preprocessing import StandardScaler
# 標準化のインスタンスを生成
stdsc = StandardScaler()
X_train_std = stdsc.fit_transform(X_train)
X_test_std = stdsc.transform(X_test)
X_train_std
```
## 4.5 有益な特徴量の選択
### 4.5.1 L1 正則化による疎な解
```
from sklearn.linear_model import LogisticRegression
# L1正則化ロジスティック回帰のインスタンスを生成
LogisticRegression(penalty='l1')
# L1正則化ロジスティック回帰のインスタンスを生成(逆正則化パラメータ C=0.1)
lr = LogisticRegression(penalty='l1', C=0.1)
lr.fit(X_train_std, y_train)
print('Training accuracy:', lr.score(X_train_std, y_train))
print('Test accuracy:', lr.score(X_test_std, y_test))
# 切片の表示
lr.intercept_
# 重み係数の表示
lr.coef_
import matplotlib.pyplot as plt
fig = plt.figure()
ax = plt.subplot(111)
colors = ['blue', 'green', 'red', 'cyan', 'magenta', 'yellow', 'black',
'pink', 'lightgreen', 'lightblue', 'gray', 'indigo', 'orange']
# 空のリストを生成(重み係数、逆正則化パラメータ
weights, params = [], []
# 逆正則化パラメータの値ごとに処理
for c in np.arange(-4, 6):
# print(c) # -4~5
lr = LogisticRegression(penalty='l1', C=10 ** c, random_state=0)
lr.fit(X_train_std, y_train)
weights.append(lr.coef_[1])
params.append(10 ** c)
# 重み係数をNumPy配列に変換
weights = np.array(weights)
# 各重み係数をプロット
# print(weights.shape[1]) # -> 13
for column, color in zip(range(weights.shape[1]), colors):
plt.plot(params, weights[:, column], label=df_wine.columns[column + 1], color=color)
# y=0 に黒い破線を引く
plt.axhline(0, color='black', linestyle='--', linewidth=3)
plt.xlim([10 ** (-5), 10 ** 5])
# 軸のラベルの設定
plt.ylabel('weight coefficient')
plt.xlabel('C')
# 横軸を対数スケールに設定
plt.xscale('log')
plt.legend(loc='upper left')
ax.legend(loc='upper center', bbox_to_anchor=(1.38, 1.03), ncol=1, fancybox=True)
plt.show()
```
### 4.5.2 逐次特徴選択アルゴリズム
```
from sklearn.base import clone
from itertools import combinations
import numpy as np
from sklearn.cross_validation import train_test_split
from sklearn.metrics import accuracy_score
class SBS():
"""
逐次後退選択(sequencial backward selection)を実行するクラス
"""
def __init__(self, estimator, k_features, scoring=accuracy_score,
test_size=0.25, random_state=1):
self.scoring = scoring # 特徴量を評価する指標
self.estimator = clone(estimator) # 推定器
self.k_features = k_features # 選択する特徴量の個数
self.test_size = test_size # テストデータの悪愛
self.random_state = random_state # 乱数種を固定する random_state
def fit(self, X, y):
# トレーニングデータとテストデータに分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=self.test_size,
random_state=self.random_state)
#print(len(X_train), len(X_test), len(y_train), len(y_test))
# 全ての特徴量の個数、列インデックス
dim = X_train.shape[1]
self.indices_ = tuple(range(dim))
self.subsets_ = [self.indices_]
#print(self.indices_)
# 全ての特徴量を用いてスコアを算出
score = self._calc_score(X_train, y_train, X_test, y_test, self.indices_)
# スコアを格納
self.scores_ = [score]
# 指定した特徴量の個数になるまで処理を反復
while dim > self.k_features:
# 空のリストの生成(スコア、列インデックス)
scores = []
subsets = []
# 特徴量の部分集合を表す列インデックスの組み合わせ毎に処理を反復
for p in combinations(self.indices_, r=dim - 1):
# スコアを算出して格納
score = self._calc_score(X_train, y_train, X_test, y_test, p)
scores.append(score)
# 特徴量の部分集合を表す列インデックスのリストを格納
subsets.append(p)
# 最良のスコアのインデックスを抽出
best = np.argmax(scores)
# 最良のスコアとなる列インデックスを抽出して格納
self.indices_ = subsets[best]
self.subsets_.append(self.indices_)
# 特徴量の個数を1つだけ減らして次のステップへ
dim -= 1
# スコアを格納
self.scores_.append(scores[best])
# 最後に格納したスコア
self.k_score_ = self.scores_[-1]
return self
def transform(self, X):
# 抽出した特徴量を返す
return X[:, self.indices_]
def _calc_score(self, X_train, y_train, X_test, y_test, indices):
# 指定された列番号 indices の特徴量を抽出してモデルに適合
self.estimator.fit(X_train[:, indices], y_train)
# テストデータを用いてクラスラベルを予測
y_pred = self.estimator.predict(X_test[:, indices])
# 真のクラスラベルと予測値を用いてスコアを算出
score = self.scoring(y_test, y_pred)
return score
from sklearn.neighbors import KNeighborsClassifier
import matplotlib.pyplot as plt
knn = KNeighborsClassifier(n_neighbors=2)
sbs = SBS(knn, k_features=1)
sbs.fit(X_train_std, y_train)
# 近傍点の個数のリスト
k_feat = [len(k) for k in sbs.subsets_]
display(k_feat)
# 横軸を近傍店の個数、縦軸をスコアとした折れ線グラフのプロット
plt.plot(k_feat, sbs.scores_, marker='o')
plt.ylim([0.7, 1.1])
plt.ylabel('Accuracy')
plt.xlabel('Number of features')
plt.grid()
plt.show()
k5 = list(sbs.subsets_[8])
print(k5)
print(df_wine.columns[1:][k5])
# 13個全ての特徴量を用いてモデルに適合
knn.fit(X_train_std, y_train)
# トレーニングの正解率を出力
print('Training accuracy:', knn.score(X_train_std, y_train))
# テストの正解率を出力
print('Test accuracy:', knn.score(X_test_std, y_test))
# 5個の特徴量を用いてモデルに適合
knn.fit(X_train_std[:, k5], y_train)
# トレーニングの正解率を出力
print('Training accuracy:', knn.score(X_train_std[:, k5], y_train))
# テストの正解率を出力
print('Test accuracy:', knn.score(X_test_std[:, k5], y_test))
```
## 4.6 ランダムフォレストで特徴量の重要度にアクセスする
```
from sklearn.ensemble import RandomForestClassifier
# Wine データセットの特徴量の名所
feat_labels = df_wine.columns[1:]
# ランダムフォレストオブジェクトの生成
# (木の個数=10,000、すべての怖を用いて並列計算を実行
forest = RandomForestClassifier(n_estimators=10000, random_state=0, n_jobs=-1)
# モデルに適合
forest.fit(X_train, y_train)
# 特徴量の重要度を抽出
importances = forest.feature_importances_
# 重要度の降順で特徴量のインデックスを抽出
indices = np.argsort(importances)[::-1]
# 重要度の降順で特徴量の名称、重要度を表示
for f in range(X_train.shape[1]):
print("{:2d}) {:<30} {:f}".format(f + 1, feat_labels[indices[f]], importances[indices[f]]))
plt.title('Feature Importances')
plt.bar(range(X_train.shape[1]), importances[indices], color='lightblue', align='center')
plt.xticks(range(X_train.shape[1]), feat_labels[indices], rotation=90)
plt.xlim([-1, X_train.shape[1]])
plt.tight_layout()
plt.show()
from sklearn.feature_selection import SelectFromModel
# 特徴選択オブジェクトの生成(重要度のしきい値を0.15に設定)
sfm = SelectFromModel(forest, prefit=True, threshold=0.15)
# 特徴量を抽出
X_selected = sfm.transform(X_train)
X_selected.shape
for f in range(X_selected.shape[1]):
print("{:2d}) {:<30} {:f}".format(f + 1, feat_labels[indices[f]], importances[indices[f]]))
```
|
github_jupyter
|
# CLX Asset Classification (Supervised)
## Authors
- Eli Fajardo (NVIDIA)
- Görkem Batmaz (NVIDIA)
- Bhargav Suryadevara (NVIDIA)
## Table of Contents
* Introduction
* Dataset
* Reading in the datasets
* Training and inference
* References
# Introduction
In this notebook, we will show how to predict the function of a server with Windows Event Logs using cudf, cuml and pytorch. The machines are labeled as DC, SQL, WEB, DHCP, MAIL and SAP. The dependent variable will be the type of the machine. The features are selected from Windows Event Logs which is in a tabular format. This is a first step to learn the behaviours of certain types of machines in data-centres by classifying them probabilistically. It could help to detect unusual behaviour in a data-centre. For example, some compromised computers might be acting as web/database servers but with their original tag.
This work could be expanded by using different log types or different events from the machines as features to improve accuracy. Various labels can be selected to cover different types of machines or data-centres.
## Library imports
```
from clx.analytics.asset_classification import AssetClassification
import cudf
from cuml.preprocessing import train_test_split
from cuml.preprocessing import LabelEncoder
import torch
from sklearn.metrics import accuracy_score, f1_score, confusion_matrix
import pandas as pd
from os import path
import s3fs
```
## Initialize variables
10000 is chosen as the batch size to optimise the performance for this dataset. It can be changed depending on the data loading mechanism or the setup used.
EPOCH should also be adjusted depending on convergence for a specific dataset.
label_col indicates the total number of features used plus the dependent variable. Feature names are listed below.
```
batch_size = 10000
label_col = '19'
epochs = 15
ac = AssetClassification()
```
## Read the dataset into a GPU dataframe with `cudf.read_csv()`
The original data had many other fields. Many of them were either static or mostly blank. After filtering those, there were 18 meaningful columns left. In this notebook we use a fake continuous feature to show the inclusion of continuous features too. When you are using raw data the cell below need to be uncommented
```
# win_events_gdf = cudf.read_csv("raw_features_and_labels.csv")
```
```
win_events_gdf.dtypes
eventcode int64
keywords object
privileges object
message object
sourcename object
taskcategory object
account_for_which_logon_failed_account_domain object
detailed_authentication_information_authentication_package object
detailed_authentication_information_key_length float64
detailed_authentication_information_logon_process object
detailed_authentication_information_package_name_ntlm_only object
logon_type float64
network_information_workstation_name object
new_logon_security_id object
impersonation_level object
network_information_protocol float64
network_information_direction object
filter_information_layer_name object
cont1 int64
label object
dtype: object
```
### Define categorical and continuous feature columns.
```
cat_cols = [
"eventcode",
"keywords",
"privileges",
"message",
"sourcename",
"taskcategory",
"account_for_which_logon_failed_account_domain",
"detailed_authentication_information_authentication_package",
"detailed_authentication_information_key_length",
"detailed_authentication_information_logon_process",
"detailed_authentication_information_package_name_ntlm_only",
"logon_type",
"network_information_workstation_name",
"new_logon_security_id",
"impersonation_level",
"network_information_protocol",
"network_information_direction",
"filter_information_layer_name",
"label"
]
cont_cols = [
"cont1"
]
```
The following are functions used to preprocess categorical and continuous feature columns. This can very depending on what best fits your application and data.
```
def categorize_columns(cat_gdf):
for col in cat_gdf.columns:
cat_gdf[col] = cat_gdf[col].astype('str')
cat_gdf[col] = cat_gdf[col].fillna("NA")
cat_gdf[col] = LabelEncoder().fit_transform(cat_gdf[col])
cat_gdf[col] = cat_gdf[col].astype('int16')
return cat_gdf
def normalize_conts(cont_gdf):
means, stds = (cont_gdf.mean(0), cont_gdf.std(ddof=0))
cont_gdf = (cont_gdf - means) / stds
return cont_gdf
```
Preprocessing steps below are not executed in this notebook, because we release already preprocessed data.
```
#win_events_gdf[cat_cols] = categorize_columns(win_events_gdf[cat_cols])
#win_events_gdf[cont_cols] = normalize_conts(win_events_gdf[cont_cols])
```
Read Windows Event data already preprocessed by above steps
```
S3_BASE_PATH = "rapidsai-data/cyber/clx"
WINEVT_PREPROC_CSV = "win_events_features_preproc.csv"
# Download Zeek conn log
if not path.exists(WINEVT_PREPROC_CSV):
fs = s3fs.S3FileSystem(anon=True)
fs.get(S3_BASE_PATH + "/" + WINEVT_PREPROC_CSV, WINEVT_PREPROC_CSV)
win_events_gdf = cudf.read_csv("win_events_features_preproc.csv")
win_events_gdf.head()
```
### Split the dataset into training and test sets using cuML `train_test_split` function
Column 19 contains the ground truth about each machine's function that the logs come from. i.e. DC, SQL, WEB, DHCP, MAIL and SAP. Hence it will be used as a label.
```
X_train, X_test, Y_train, Y_test = train_test_split(win_events_gdf, "label", train_size=0.9)
X_train["label"] = Y_train
X_train.head()
Y_train.unique()
```
### Print Labels
Making sure the test set contains all labels
```
Y_test.unique()
```
## Training
Asset Classification training uses the fastai tabular model. More details can be found at https://github.com/fastai/fastai/blob/master/fastai/tabular/models.py#L6
Feature columns will be embedded so that they can be used as categorical values. The limit can be changed depending on the accuracy of the dataset.
Adam is the optimizer used in the training process; it is popular because it produces good results in various tasks. In its paper, computing the first and the second moment estimates and updating the parameters are summarized as follows
$$\alpha_{t}=\alpha \cdot \sqrt{1-\beta_{2}^{t}} /\left(1-\beta_{1}^{t}\right)$$
More detailson Adam can be found at https://arxiv.org/pdf/1412.6980.pdf
We have found that the way we partition the dataframes with a 10000 batch size gives us the optimum data loading capability. The **batch_size** argument can be adjusted for different sizes of datasets.
```
cat_cols.remove("label")
ac.train_model(X_train, cat_cols, cont_cols, "label", batch_size, epochs, lr=0.01, wd=0.0)
```
## Evaluation
```
pred_results = ac.predict(X_test, cat_cols, cont_cols).to_array()
true_results = Y_test.to_array()
f1_score_ = f1_score(pred_results, true_results, average='micro')
print('micro F1 score: %s'%(f1_score_))
torch.cuda.empty_cache()
labels = ["DC","DHCP","MAIL","SAP","SQL","WEB"]
a = confusion_matrix(true_results, pred_results)
pd.DataFrame(a, index=labels, columns=labels)
```
The confusion matrix shows that some machines' function can be predicted really well, whereas some of them need more tuning or more features. This work can be improved and expanded to cover individual data-centres to create a realistic map of the network using ML by not just relying on the naming conventions. It could also help to detect more prominent scale anomalies like multiple machines, not acting per their tag.
## References:
* https://github.com/fastai/fastai/blob/master/fastai/tabular/models.py#L6
* https://jovian.ml/aakashns/04-feedforward-nn
* https://www.kaggle.com/dienhoa/reverse-tabular-module-of-fast-ai-v1
* https://github.com/fastai/fastai/blob/master/fastai/layers.py#L44
|
github_jupyter
|

# Chapter 8: Basic Data Wrangling With Pandas
<h2>Chapter Outline<span class="tocSkip"></span></h2>
<hr>
<div class="toc"><ul class="toc-item"><li><span><a href="#1.-DataFrame-Characteristics" data-toc-modified-id="1.-DataFrame-Characteristics-2">1. DataFrame Characteristics</a></span></li><li><span><a href="#2.-Basic-DataFrame-Manipulations" data-toc-modified-id="2.-Basic-DataFrame-Manipulations-3">2. Basic DataFrame Manipulations</a></span></li><li><span><a href="#3.-DataFrame-Reshaping" data-toc-modified-id="3.-DataFrame-Reshaping-4">3. DataFrame Reshaping</a></span></li><li><span><a href="#4.-Working-with-Multiple-DataFrames" data-toc-modified-id="4.-Working-with-Multiple-DataFrames-5">4. Working with Multiple DataFrames</a></span></li><li><span><a href="#5.-More-DataFrame-Operations" data-toc-modified-id="5.-More-DataFrame-Operations-6">5. More DataFrame Operations</a></span></li></ul></div>
## Chapter Learning Objectives
<hr>
- Inspect a dataframe with `df.head()`, `df.tail()`, `df.info()`, `df.describe()`.
- Obtain dataframe summaries with `df.info()` and `df.describe()`.
- Manipulate how a dataframe displays in Jupyter by modifying Pandas configuration options such as `pd.set_option("display.max_rows", n)`.
- Rename columns of a dataframe using the `df.rename()` function or by accessing the `df.columns` attribute.
- Modify the index name and index values of a dataframe using `.set_index()`, `.reset_index()` , `df.index.name`, `.index`.
- Use `df.melt()` and `df.pivot()` to reshape dataframes, specifically to make tidy dataframes.
- Combine dataframes using `df.merge()` and `pd.concat()` and know when to use these different methods.
- Apply functions to a dataframe `df.apply()` and `df.applymap()`
- Perform grouping and aggregating operations using `df.groupby()` and `df.agg()`.
- Perform aggregating methods on grouped or ungrouped objects such as finding the minimum, maximum and sum of values in a dataframe using `df.agg()`.
- Remove or fill missing values in a dataframe with `df.dropna()` and `df.fillna()`.
## 1. DataFrame Characteristics
<hr>
Last chapter we looked at how we can create dataframes. Let's now look at some helpful ways we can view our dataframe.
```
import numpy as np
import pandas as pd
```
### Head/Tail
The `.head()` and `.tail()` methods allow you to view the top/bottom *n* (default 5) rows of a dataframe. Let's load in the cycling data set from last chapter and try them out:
```
df = pd.read_csv('data/cycling_data.csv')
df.head()
```
The default return value is 5 rows, but we can pass in any number we like. For example, let's take a look at the top 10 rows:
```
df.head(10)
```
Or the bottom 5 rows:
```
df.tail()
```
### DataFrame Summaries
Three very helpful attributes/functions for getting high-level summaries of your dataframe are:
- `.shape`
- `.info()`
- `.describe()`
`.shape` is just like the ndarray attribute we've seen previously. It gives the shape (rows, cols) of your dataframe:
```
df.shape
```
`.info()` prints information about the dataframe itself, such as dtypes, memory usages, non-null values, etc:
```
df.info()
```
`.describe()` provides summary statistics of the values within a dataframe:
```
df.describe()
```
By default, `.describe()` only print summaries of numeric features. We can force it to give summaries on all features using the argument `include='all'` (although they may not make sense!):
```
df.describe(include='all')
```
### Displaying DataFrames
Displaying your dataframes effectively can be an important part of your workflow. If a dataframe has more than 60 rows, Pandas will only display the first 5 and last 5 rows:
```
pd.DataFrame(np.random.rand(100))
```
For dataframes of less than 60 rows, Pandas will print the whole dataframe:
```
df
```
I find the 60 row threshold to be a little too much, I prefer something more like 20. You can change the setting using `pd.set_option("display.max_rows", 20)` so that anything with more than 20 rows will be summarised by the first and last 5 rows as before:
```
pd.set_option("display.max_rows", 20)
df
```
There are also other display options you can change, such as how many columns are shown, how numbers are formatted, etc. See the [official documentation](https://pandas.pydata.org/pandas-docs/stable/user_guide/options.html#options-and-settings) for more.
One display option I will point out is that Pandas allows you to style your tables, for example by highlighting negative values, or adding conditional colour maps to your dataframe. Below I'll style values based on their value ranging from negative (purple) to postive (yellow) but you can see the [styling documentation](https://pandas.pydata.org/pandas-docs/stable/user_guide/style.html#Styling) for more examples.
```
test = pd.DataFrame(np.random.randn(5, 5),
index = [f"row_{_}" for _ in range(5)],
columns = [f"feature_{_}" for _ in range(5)])
test.style.background_gradient(cmap='plasma')
```
### Views vs Copies
In previous chapters we've discussed views ("looking" at a part of an existing object) and copies (making a new copy of the object in memory). These things get a little abstract with Pandas and "...it’s very hard to predict whether it will return a view or a copy" (that's a quote straight [from a dedicated section in the Pandas documentation](https://pandas.pydata.org/pandas-docs/stable/user_guide/indexing.html#returning-a-view-versus-a-copy)).
Basically, it depends on the operation you are trying to perform, your dataframe's structure and the memory layout of the underlying array. But don't worry, let me tell you all you need to know. Firstly, the most common warning you'll encounter in Pandas is the `SettingWithCopy`, Pandas raises it as a warning that you might not be doing what you think you're doing. Let's see an example. You may recall there is one outlier `Time` in our dataframe:
```
df[df['Time'] > 4000]
```
Imagine we wanted to change this to `2000`. You'd probably do the following:
```
df[df['Time'] > 4000]['Time'] = 2000
```
Ah, there's that warning. Did our dataframe get changed?
```
df[df['Time'] > 4000]
```
No it didn't, even though you probably thought it did. What happened above is that `df[df['Time'] > 4000]` was executed first and returned a copy of the dataframe, we can confirm by using `id()`:
```
print(f"The id of the original dataframe is: {id(df)}")
print(f" The id of the indexed dataframe is: {id(df[df['Time'] > 4000])}")
```
We then tried to set a value on this new object by appending `['Time'] = 2000`. Pandas is warning us that we are doing that operation on a copy of the original dataframe, which is probably not what we want. To fix this, you need to index in a single go, using `.loc[]` for example:
```
df.loc[df['Time'] > 4000, 'Time'] = 2000
```
No error this time! And let's confirm the change:
```
df[df['Time'] > 4000]
```
The second thing you need to know is that if you're ever in doubt about whether something is a view or a copy, you can just use the `.copy()` method to force a copy of a dataframe. Just like this:
```
df2 = df[df['Time'] > 4000].copy()
```
That way, your guaranteed a copy that you can modify as you wish.
## 2. Basic DataFrame Manipulations
<hr>
### Renaming Columns
We can rename columns two ways:
1. Using `.rename()` (to selectively change column names)
2. By setting the `.columns` attribute (to change all column names at once)
```
df
```
Let's give it a go:
```
df.rename(columns={"Date": "Datetime",
"Comments": "Notes"})
df
```
Wait? What happened? Nothing changed? In the code above we did actually rename columns of our dataframe but we didn't modify the dataframe inplace, we made a copy of it. There are generally two options for making permanent dataframe changes:
- 1. Use the argument `inplace=True`, e.g., `df.rename(..., inplace=True)`, available in most functions/methods
- 2. Re-assign, e.g., `df = df.rename(...)`
The Pandas team recommends **Method 2 (re-assign)**, for a [few reasons](https://www.youtube.com/watch?v=hK6o_TDXXN8&t=700) (mostly to do with how memory is allocated under the hood).
```
df = df.rename(columns={"Date": "Datetime",
"Comments": "Notes"})
df
```
If you wish to change all of the columns of a dataframe, you can do so by setting the `.columns` attribute:
```
df.columns = [f"Column {_}" for _ in range(1, 7)]
df
```
### Changing the Index
You can change the index labels of a dataframe in 3 main ways:
1. `.set_index()` to make one of the columns of the dataframe the index
2. Directly modify `df.index.name` to change the index name
3. `.reset_index()` to move the current index as a column and to reset the index with integer labels starting from 0
4. Directly modify the `.index()` attribute
```
df
```
Below I will set the index as `Column 1` and rename the index to "New Index":
```
df = df.set_index("Column 1")
df.index.name = "New Index"
df
```
I can send the index back to a column and have a default integer index using `.reset_index()`:
```
df = df.reset_index()
df
```
Like with column names, we can also modify the index directly, but I can't remember ever doing this, usually I'll use `.set_index()`:
```
df.index
df.index = range(100, 133, 1)
df
```
### Adding/Removing Columns
There are two main ways to add/remove columns of a dataframe:
1. Use `[]` to add columns
2. Use `.drop()` to drop columns
Let's re-read in a fresh copy of the cycling dataset.
```
df = pd.read_csv('data/cycling_data.csv')
df
```
We can add a new column to a dataframe by simply using `[]` with a new column name and value(s):
```
df['Rider'] = 'Tom Beuzen'
df['Avg Speed'] = df['Distance'] * 1000 / df['Time'] # avg. speed in m/s
df
df = df.drop(columns=['Rider', 'Avg Speed'])
df
```
### Adding/Removing Rows
You won't often be adding rows to a dataframe manually (you'll usually add rows through concatenating/joining - that's coming up next). You can add/remove rows of a dataframe in two ways:
1. Use `.append()` to add rows
2. Use `.drop()` to drop rows
```
df
```
Let's add a new row to the bottom of this dataframe:
```
another_row = pd.DataFrame([["12 Oct 2019, 00:10:57", "Morning Ride", "Ride",
2331, 12.67, "Washed and oiled bike last night"]],
columns = df.columns,
index = [33])
df = df.append(another_row)
df
```
We can drop all rows above index 30 using `.drop()`:
```
df.drop(index=range(30, 34))
```
## 3. DataFrame Reshaping
<hr>
[Tidy data](https://vita.had.co.nz/papers/tidy-data.pdf) is about "linking the structure of a dataset with its semantics (its meaning)". It is defined by:
1. Each variable forms a column
2. Each observation forms a row
3. Each type of observational unit forms a table
Often you'll need to reshape a dataframe to make it tidy (or for some other purpose).

Source: [r4ds](https://r4ds.had.co.nz/tidy-data.html#fig:tidy-structure)
### Melt and Pivot
Pandas `.melt()`, `.pivot()` and `.pivot_table()` can help reshape dataframes
- `.melt()`: make wide data long.
- `.pivot()`: make long data width.
- `.pivot_table()`: same as `.pivot()` but can handle multiple indexes.

Source: [Garrick Aden-Buie's GitHub](https://github.com/gadenbuie/tidyexplain#spread-and-gather)
The below data shows how many courses different instructors taught across different years. If the question you want to answer is something like: "Does the number of courses taught vary depending on year?" then the below would probably not be considered tidy because there are multiple observations of courses taught in a year per row (i.e., there is data for 2018, 2019 and 2020 in a single row):
```
df = pd.DataFrame({"Name": ["Tom", "Mike", "Tiffany", "Varada", "Joel"],
"2018": [1, 3, 4, 5, 3],
"2019": [2, 4, 3, 2, 1],
"2020": [5, 2, 4, 4, 3]})
df
```
Let's make it tidy with `.melt()`. `.melt()` takes a few arguments, most important is the `id_vars` which indicated which column should be the "identifier".
```
df_melt = df.melt(id_vars="Name",
var_name="Year",
value_name="Courses")
df_melt
```
The `value_vars` argument allows us to select which specific variables we want to "melt" (if you don't specify `value_vars`, all non-identifier columns will be used). For example, below I'm omitting the `2018` column:
```
df.melt(id_vars="Name",
value_vars=["2019", "2020"],
var_name="Year",
value_name="Courses")
```
Sometimes, you want to make long data wide, which we can do with `.pivot()`. When using `.pivot()` we need to specify the `index` to pivot on, and the `columns` that will be used to make the new columns of the wider dataframe:
```
df_pivot = df_melt.pivot(index="Name",
columns="Year",
values="Courses")
df_pivot
```
You'll notice that Pandas set our specified `index` as the index of the new dataframe and preserved the label of the columns. We can easily remove these names and reset the index to make our dataframe look like it originally did:
```
df_pivot = df_pivot.reset_index()
df_pivot.columns.name = None
df_pivot
```
`.pivot()` will often get you what you want, but it won't work if you want to:
- Use multiple indexes (next chapter), or
- Have duplicate index/column labels
In these cases you'll have to use `.pivot_table()`. I won't focus on it too much here because I'd rather you learn about `pivot()` first.
```
df = pd.DataFrame({"Name": ["Tom", "Tom", "Mike", "Mike"],
"Department": ["CS", "STATS", "CS", "STATS"],
"2018": [1, 2, 3, 1],
"2019": [2, 3, 4, 2],
"2020": [5, 1, 2, 2]}).melt(id_vars=["Name", "Department"], var_name="Year", value_name="Courses")
df
```
In the above case, we have duplicates in `Name`, so `pivot()` won't work. It will throw us a `ValueError: Index contains duplicate entries, cannot reshape`:
```
df.pivot(index="Name",
columns="Year",
values="Courses")
```
In such a case, we'd use `.pivot_table()`. It will apply an aggregation function to our duplicates, in this case, we'll `sum()` them up:
```
df.pivot_table(index="Name", columns='Year', values='Courses', aggfunc='sum')
```
If we wanted to keep the numbers per department, we could specify both `Name` and `Department` as multiple indexes:
```
df.pivot_table(index=["Name", "Department"], columns='Year', values='Courses')
```
The result above is a mutlti-index or "hierarchically indexed" dataframe (more on those next chapter). If you ever have a need to use it, you can read more about `pivot_table()` in the [documentation](https://pandas.pydata.org/pandas-docs/stable/user_guide/reshaping.html#pivot-tables).
## 4. Working with Multiple DataFrames
<hr>
Often you'll work with multiple dataframes that you want to stick together or merge. `df.merge()` and `df.concat()` are all you need to know for combining dataframes. The Pandas [documentation](https://pandas.pydata.org/pandas-docs/stable/user_guide/merging.html) is very helpful for these functions, but they are pretty easy to grasp.
```{note}
The example joins shown in this section are inspired by [Chapter 15](https://stat545.com/join-cheatsheet.html) of Jenny Bryan's STAT 545 materials.
```
### Sticking DataFrames Together with `pd.concat()`
You can use `pd.concat()` to stick dataframes together:
- Vertically: if they have the same **columns**, OR
- Horizontally: if they have the same **rows**
```
df1 = pd.DataFrame({'A': [1, 3, 5],
'B': [2, 4, 6]})
df2 = pd.DataFrame({'A': [7, 9, 11],
'B': [8, 10, 12]})
df1
df2
pd.concat((df1, df2), axis=0) # axis=0 specifies a vertical stick, i.e., on the columns
```
Notice that the indexes were simply joined together? This may or may not be what you want. To reset the index, you can specify the argument `ignore_index=True`:
```
pd.concat((df1, df2), axis=0, ignore_index=True)
```
Use `axis=1` to stick together horizontally:
```
pd.concat((df1, df2), axis=1, ignore_index=True)
```
You are not limited to just two dataframes, you can concatenate as many as you want:
```
pd.concat((df1, df2, df1, df2), axis=0, ignore_index=True)
```
### Joining DataFrames with `pd.merge()`
`pd.merge()` gives you the ability to "join" dataframes using different rules (just like with SQL if you're familiar with it). You can use `df.merge()` to join dataframes based on shared `key` columns. Methods include:
- "inner join"
- "outer join"
- "left join"
- "right join"
See this great [cheat sheet](https://pandas.pydata.org/pandas-docs/stable/getting_started/comparison/comparison_with_sql.html#compare-with-sql-join) and [these great animations](https://github.com/gadenbuie/tidyexplain) for more insights.
```
df1 = pd.DataFrame({"name": ['Magneto', 'Storm', 'Mystique', 'Batman', 'Joker', 'Catwoman', 'Hellboy'],
'alignment': ['bad', 'good', 'bad', 'good', 'bad', 'bad', 'good'],
'gender': ['male', 'female', 'female', 'male', 'male', 'female', 'male'],
'publisher': ['Marvel', 'Marvel', 'Marvel', 'DC', 'DC', 'DC', 'Dark Horse Comics']})
df2 = pd.DataFrame({'publisher': ['DC', 'Marvel', 'Image'],
'year_founded': [1934, 1939, 1992]})
```

An "inner" join will return all rows of `df1` where matching values for "publisher" are found in `df2`:
```
pd.merge(df1, df2, how="inner", on="publisher")
```

An "outer" join will return all rows of `df1` and `df2`, placing NaNs where information is unavailable:
```
pd.merge(df1, df2, how="outer", on="publisher")
```

Return all rows from `df1` and all columns of `df1` and `df2`, populated where matches occur:
```
pd.merge(df1, df2, how="left", on="publisher")
```

```
pd.merge(df1, df2, how="right", on="publisher")
```
There are many ways to specify the `key` to join dataframes on, you can join on index values, different, column names, etc. Another helpful argument is the `indicator` argument which will add a column to the result telling you where matches were found in the dataframes:
```
pd.merge(df1, df2, how="outer", on="publisher", indicator=True)
```
By the way, you can use `pd.concat()` to do a simple "inner" or "outer" join on multiple datadrames at once. It's less flexible than merge, but can be useful sometimes.
## 5. More DataFrame Operations
<hr>
### Applying Custom Functions
There will be times when you want to apply a function that is not built-in to Pandas. For this, we also have methods:
- `df.apply()`, applies a function column-wise or row-wise across a dataframe (the function must be able to accept/return an array)
- `df.applymap()`, applies a function element-wise (for functions that accept/return single values at a time)
- `series.apply()`/`series.map()`, same as above but for Pandas series
For example, say you want to use a numpy function on a column in your dataframe:
```
df = pd.read_csv('data/cycling_data.csv')
df[['Time', 'Distance']].apply(np.sin)
```
Or you may want to apply your own custom function:
```
def seconds_to_hours(x):
return x / 3600
df[['Time']].apply(seconds_to_hours)
```
This may have been better as a lambda function...
```
df[['Time']].apply(lambda x: x / 3600)
```
You can even use functions that require additional arguments. Just specify the arguments in `.apply()`:
```
def convert_seconds(x, to="hours"):
if to == "hours":
return x / 3600
elif to == "minutes":
return x / 60
df[['Time']].apply(convert_seconds, to="minutes")
```
Some functions only accept/return a scalar:
```
int(3.141)
float([3.141, 10.345])
```
For these, we need `.applymap()`:
```
df[['Time']].applymap(int)
```
However, there are often "vectorized" versions of common functions like this already available, which are much faster. In the case above, we can use `.astype()` to change the dtype of a whole column quickly:
```
time_applymap = %timeit -q -o -r 3 df[['Time']].applymap(float)
time_builtin = %timeit -q -o -r 3 df[['Time']].astype(float)
print(f"'astype' is {time_applymap.average / time_builtin.average:.2f} faster than 'applymap'!")
```
### Grouping
Often we are interested in examining specific groups in our data. `df.groupby()` allows us to group our data based on a variable(s).
```
df = pd.read_csv('data/cycling_data.csv')
df
```
Let's group this dataframe on the column `Name`:
```
dfg = df.groupby(by='Name')
dfg
```
What is a `DataFrameGroupBy` object? It contains information about the groups of the dataframe:

The groupby object is really just a dictionary of index-mappings, which we could look at if we wanted to:
```
dfg.groups
```
We can also access a group using the `.get_group()` method:
```
dfg.get_group('Afternoon Ride')
```
The usual thing to do however, is to apply aggregate functions to the groupby object:

```
dfg.mean()
```
We can apply multiple functions using `.aggregate()`:
```
dfg.aggregate(['mean', 'sum', 'count'])
```
And even apply different functions to different columns:
```
def num_range(x):
return x.max() - x.min()
dfg.aggregate({"Time": ['max', 'min', 'mean', num_range],
"Distance": ['sum']})
```
By the way, you can use aggregate for non-grouped dataframes too. This is pretty much what `df.describe` does under-the-hood:
```
df.agg(['mean', 'min', 'count', num_range])
```
### Dealing with Missing Values
Missing values are typically denoted with `NaN`. We can use `df.isnull()` to find missing values in a dataframe. It returns a boolean for each element in the dataframe:
```
df.isnull()
```
But it's usually more helpful to get this information by row or by column using the `.any()` or `.info()` method:
```
df.info()
df[df.isnull().any(axis=1)]
```
When you have missing values, we usually either drop them or impute them.You can drop missing values with `df.dropna()`:
```
df.dropna()
```
Or you can impute ("fill") them using `.fillna()`. This method has various options for filling, you can use a fixed value, the mean of the column, the previous non-nan value, etc:
```
df = pd.DataFrame([[np.nan, 2, np.nan, 0],
[3, 4, np.nan, 1],
[np.nan, np.nan, np.nan, 5],
[np.nan, 3, np.nan, 4]],
columns=list('ABCD'))
df
df.fillna(0) # fill with 0
df.fillna(df.mean()) # fill with the mean
df.fillna(method='bfill') # backward (upwards) fill from non-nan values
df.fillna(method='ffill') # forward (downward) fill from non-nan values
```
Finally, sometimes I use visualizations to help identify (patterns in) missing values. One thing I often do is print a heatmap of my dataframe to get a feel for where my missing values are. If you want to run this code, you may need to install `seaborn`:
```sh
conda install seaborn
```
```
import seaborn as sns
sns.set(rc={'figure.figsize':(7, 7)})
df
sns.heatmap(df.isnull(), cmap='viridis', cbar=False);
# Generate a larger synthetic dataset for demonstration
np.random.seed(2020)
npx = np.zeros((100,20))
mask = np.random.choice([True, False], npx.shape, p=[.1, .9])
npx[mask] = np.nan
sns.heatmap(pd.DataFrame(npx).isnull(), cmap='viridis', cbar=False);
```
|
github_jupyter
|
```
#hide
from qbism import *
```
# Tutorial
> "Chauncey Wright, a nearly forgotten philosopher of real merit, taught me when young that I must not say necessary about the universe, that we don’t know whether anything is necessary or not. So I describe myself as a bettabilitarian. I believe that we can bet on the behavior of the universe in its contact with us." (Oliver Wendell Holmes, Jr.)
QBism, as I understand it, consists of two interlocking components, one part philosophical and one part mathematical. We'll deal with the mathematical part first.
## The Math
A Von Neumann measurement consists in a choice of observable represented by a Hermitian operator $H$. Such an operator will have real eigenvalues and orthogonal eigenvectors. For example, $H$ could be the energy operator. Then the eigenvectors would represent possible energy states, and the eigenvalues would represent possible values of the energy. According to textbook quantum mechanics, which state the system ends up in after a measurement will in general be random, and quantum mechanics allows you to calculate the probabilities.
A Hermitian observable provides what is known as a "projection valued measure." Suppose our system were represented by a density matrix $\rho$. We could form the projectors $P_{i} = \mid v_{i} \rangle \langle v_{i} \mid$, where $\mid v_{i} \rangle$ is the $i^{th}$ eigenvector. Then the probability for the $i^{th}$ outcome would be given by $Pr(i) = tr(P_{i}\rho)$, and the state after measurement would be given by $\frac{P_{i} \rho P_{i}}{tr(P_{i}\rho)}$. Moreover, the expectation value of the observable $\langle H \rangle$ would be given by $tr(H\rho)$, and it amounts to a sum over the eigenvalues weighted by the corresponding probabilities.
```
import numpy as np
import qutip as qt
d = 2
rho = qt.rand_dm(d)
H = qt.rand_herm(d)
L, V = H.eigenstates()
P = [v*v.dag() for v in V]
p = [(proj*rho).tr() for proj in P]
print("probabilities: %s" % p)
print("expectation value: %.3f" % (H*rho).tr())
print("expectation value again: %.3f" % (sum([L[i]*p[i] for i in range(d)])))
```
<hr>
But there is a more general notion of measurement: a POVM (a positive operator valued measure). A POVM consists in a set of positive semidefinite operators that sum to the identity, i.e., a set $\{E_{i}\}$ such that $\sum_{i} E_{i} = I$. Positive semidefinite just means that the eigenvalues must be non-negative, so that $\langle \psi \mid E \mid \psi \rangle$ is always positive or zero for any $\mid \psi \rangle$. Indeed, keep in mind that density matrices are defined by Hermitian, positive semi-definite operators with trace $1$.
For a POVM, each *operator* corresponds to a possible outcome of the experiment, and whereas for a Von Neumann measurement, assuming no degeneracies, there would be $d$ possible outcomes, corresponding to the dimension of the Hilbert space, there can be *any* number of outcomes to a POVM measurement, as long as all the associated operators sum to the identity. The probability of an outcome, however, is similarly given by $Pr(i) = tr(E_{i}\rho)$.
If we write each $E_{i}$ as a product of so-called Kraus operators $E_{i} = A_{i}^{\dagger}A_{i}$, then the state after measurement will be: $\frac{A_{i}\rho A_{i}^{\dagger}}{tr(E_{i}\rho)}$. The Kraus operators, however, aren't uniquely defined by the POVM, and so the state after measurement will depend on its implementation: to implement POVM's, you couple your system to an auxilliary system and make a standard measurement on the latter. We'll show how to do that in a little bit!
In the case we'll be considering, however, the $\{E_{i}\}$ will be rank-1, and so the state after measurement will be $\frac{\Pi_{i}\rho \Pi_{i}}{tr(\Pi_{i}\rho)}$ as before, where $\Pi_{i}$ are normalized projectors associated to each element of the POVM (details to follow).
(For a reference, recall that spin coherent states form an "overcomplete" basis, or frame, for spin states of a given $j$ value. This can be viewed as a POVM. In this case, the POVM would have an infinite number of elements, one for each point on the sphere: and the integral over the sphere gives $1$.)
<hr>
A very special kind of POVM is a so-called SIC-POVM: a symmetric informationally complete positive operator valued measure. They've been conjectured to exist in all dimensions, and numerical evidence suggests this is indeed the case. For a given Hilbert space of dimension $d$, a SIC is a set of $d^2$ rank-one projection operators $\Pi_{i} = \mid \psi_{i} \rangle \langle \psi_{i} \mid$ such that:
$$tr(\Pi_{k}\Pi_{l}) = \frac{d\delta_{k,l} + 1}{d+1} $$
Such a set of projectors will be linearly independent, and if you rescale they to $\frac{1}{d}\Pi_{i}$, they form a POVM: $\sum_{i} \frac{1}{d} \Pi_{i} = I$.
The key point is that for any quantum state $\rho$, a SIC specifies a measurement *for which the probabilities of outcomes $p(i)$ specify $\rho$ itself*. Normally, say, in the case of a qubit, we'd have to measure the separate expectation values $(\langle X \rangle, \langle Y \rangle, \langle Z \rangle)$ to nail down the state: in other words, we'd have to repeat many times three *different* measurements. But for a SIC-POVM, the probabilities on each of the elements of the POVM fully determine the state: we're talking here about a *single* type of measurement.
<hr>
Thanks to Chris Fuchs & Co., we have a repository of SIC-POVM's in a variety of dimensions. One can download them [here](http://www.physics.umb.edu/Research/QBism/solutions.html). You'll get a zip of text files, one for each dimension: and in each text file will be a single complex vector: the "fiducial" vector. From this vector, the SIC can be derived.
In order to do this, we first define (with Sylvester) the unitary clock and shift matrices for a given dimension $d$:
$$
X = \begin{pmatrix}
0 & 0 & 0 & \cdots & 0 & 1\\
1 & 0 & 0 & \cdots & 0 & 0\\
0 & 1 & 0 & \cdots & 0 & 0\\
0 & 0 & 1 & \cdots & 0 & 0\\
\vdots & \vdots & \vdots & \ddots &\vdots &\vdots\\
0 & 0 & 0 & \cdots & 1 & 0\\
\end{pmatrix}
$$
$$
Z = \begin{pmatrix}
1 & 0 & 0 & \cdots & 0\\
0 & \omega & 0 & \cdots & 0\\
0 & 0 & \omega^2 & \cdots & 0\\
\vdots & \vdots & \vdots & \ddots & \vdots\\
0 & 0 & 0 & \cdots & \omega^{d-1}
\end{pmatrix}
$$
Where $\omega = e^{\frac{2\pi i}{d}}$.
Note that when $d=2$, this amounts to Pauli $X$ and $Z$.
```
def shift(d):
return sum([qt.basis(d, i+1)*qt.basis(d, i).dag()\
if i != d-1 else qt.basis(d, 0)*qt.basis(d, i).dag()\
for i in range(d) for j in range(d)])/d
def clock(d):
w = np.exp(2*np.pi*1j/d)
return qt.Qobj(np.diag([w**i for i in range(d)]))
```
We can then define displacement operators:
$$D_{a,b} = (-e^{\frac{i\pi}{d}})^{ab}X^{b}Z^{a} $$
For $a, b$ each from $0$ to $d$.
```
def displace(d, a, b):
Z, X = clock(d), shift(d)
return (-np.exp(1j*np.pi/d))**(a*b)*X**b*Z**a
def displacement_operators(d):
return dict([((a, b), displace(d, a, b)) for b in range(d) for a in range(d)])
```
Finally, if we act on the fiducial vector with each of the displacement operators, we obtain the $d^2$ pure states, whose projectors, weighted by $\frac{1}{d}$, form the SIC-POVM.
```
def sic_states(d):
fiducial = load_fiducial(d)
return [D*fiducial for index, D in displacement_operators(d).items()]
```
Cf. `load_fiducial`.
By the way, this construction works because these SIC-POVM's are covariant under the Weyl-Heisenberg group. This means is that if you apply one of those displacement operators to all the SIC states, you get the same set of SIC states back! They just switch places among themselves. (It's also worth considering the action of elements of the "Clifford group", since these operators leave the Weyl-Heisenberg group invariant or, in other words, "normalize" it.)
```
sic = sic_states(2)
D = displacement_operators(2)
print(sic)
print()
print([D[(1,1)]*state for state in sic])
```
As far as anyone knows, the construction seems to work for SIC's in all dimensions. It's worth noting, however, the exceptional case of $d=8$, where there is *also another* SIC-POVM covariant under the tensor product of three copies of the Pauli group ($d=2$). Cf. `hoggar_fiducial`.
We can test that a given SIC has the property:
$$tr(\Pi_{k}\Pi_{l}) = \frac{d\delta_{k,l} + 1}{d+1} $$
```
def test_sic_states(states):
d = int(np.sqrt(len(states)))
for i, s in enumerate(states):
for j, t in enumerate(states):
should_be = 1 if i == j else 1/(d+1)
print("(%d, %d): %.4f | should be: %.4f" % (i, j, np.abs(s.overlap(t)**2), should_be))
states = sic_states(2)
test_sic_states(states)
```
In the case of a two dimensional Hilbert space, the SIC-POVM states will form a regular tetrahedron in the Bloch sphere:
```
pts = np.array([[qt.expect(qt.sigmax(), state),\
qt.expect(qt.sigmay(), state),\
qt.expect(qt.sigmaz(), state)] for state in states])
sphere = qt.Bloch()
sphere.point_size = [300]
sphere.add_points(pts.T)
sphere.add_vectors(pts)
sphere.make_sphere()
```
In general, in higher dimensions, the study of SIC's is a very interesting geometry problem involving the study of "maximal sets of complex equiangular lines," which has implications in various domains of mathematics.
```
def sic_povm(d):
return [(1/d)*state*state.dag() for state in sic_states(d)]
d = 2
ref_povm = sic_povm(d)
print("elements sum to identity? %s" % np.allclose(sum(ref_povm), qt.identity(d)))
```
Given a density matrix $\rho$, we can expand it in terms of the SIC-POVM elements via $tr(E_{i}\rho)$:
```
def dm_probs(dm, ref_povm):
return np.array([(e*dm).tr() for e in ref_povm]).real
rho = qt.rand_dm(d)
p = dm_probs(rho, ref_povm)
print("probabilities: %s" % p)
print("sum to 1? %s" % np.isclose(sum(p), 1))
```
From these probabilities, we can uniquely reconstruct the density matrix via:
$$ \rho = \sum_{i} ((d+1)p(i) - \frac{1}{d})\Pi_{i} $$
Where $\Pi_{i}$ are the projectors onto the SIC states: $E_{i} = \frac{1}{d}\Pi_{i}$.
Or given the fact that $\sum_{i} \frac{1}{d} \Pi_{i} = I$:
$$\rho = (d+1) \sum_{i} p(i)\Pi_{i} - I $$
```
def probs_dm_sic(p, ref_povm):
d = int(np.sqrt(len(p)))
return sum([((d+1)*p[i] - 1/d)*(e/e.tr()) for i, e in enumerate(ref_povm)])
def probs_dm_sic2(p, ref_povm):
d = int(np.sqrt(len(p)))
return (d+1)*sum([p[i]*e/e.tr() for i, e in enumerate(ref_povm)]) - qt.identity(d)
rho2 = probs_dm_sic(p, ref_povm)
rho3 = probs_dm_sic2(p, ref_povm)
print("recovered? %s" % (np.allclose(rho, rho2, rtol=1e-02, atol=1e-04) and np.allclose(rho, rho3, rtol=1e-02, atol=1e-04)))
```
<hr>
Now suppose we have the following situation. We first make a SIC-POVM measurement, and then we make a standard Von Neumann (PVM) measurement on a given system. Following the vivid imagery of Fuchs, we'll refer to the SIC-POVM as being "up in the sky" and the Von Neumann measurement as being "down on the ground".
So given our state $\rho$, above we've calculated the probabilities $p(i)$ for each outcome of the POVM. Now we'd like to assign probabilities for the outcomes of the Von Neumann measurement. What we need are the conditional probabilities $r(j|i)$, the probability of Von Neumann outcome $j$ given that the SIC-POVM returned $i$. Then:
$s(j) = \sum_{i}^{d^2} p(i)r(j|i)$
This is just standard probability theory: the law of total probability. The probability for an outcome $j$ of the Von Neumann measurement is the sum over all the conditional probabilities for $j$, given some outcome $i$ of the SIC-POVM, multiplied by the probability that $i$ occured.
The standard way of thinking about this would be that after the SIC-POVM measurement:
$\rho^{\prime} = \sum_{i} p(i)\Pi_{i}$
In other words, after the first measurement, $\rho$ becomes a mixture of outcome states weighted by the probabilities of them occuring. In this simple case, where we aren't considering a subsystem of larger system, and we're sticking with SIC-POVM's whose elements, we recall, are rank-1, we can just use the projectors $\Pi_{i}$ for the SIC-POVM outcome states. Then the probabilities for the Von Neumann measurement are:
$s(j) = tr(\tilde{\Pi}_{j}\rho^{\prime})$
Where $\tilde{\Pi}_{j}$ is the projector for the $j^{th}$ Von Neumann outcome.
```
von_neumann = qt.rand_herm(d)
vn_projectors = [v*v.dag() for v in von_neumann.eigenstates()[1]]
vn_rho = sum([prob*ref_povm[i]/ref_povm[i].tr() for i, prob in enumerate(p)])
vn_s = np.array([(proj*vn_rho).tr() for proj in vn_projectors]).real
print("vn probabilities after sic: %s" % vn_s)
```
Alternatively, however, we could form conditional probabilities directly:
$r(j|i) = tr(\tilde{\Pi}_{j}\Pi_{i})$
Where $\Pi_{i}$ is the projector for the $i^{th}$ POVM outcome (in the sky), and $\tilde{\Pi}_{j}$ is the projector for the $j^{th}$ Von Neumann outcome (on the ground).
Then we can use the formula:
$s(j) = \sum_{i}^{d^2} p(i)r(j|i)$
```
def vn_conditional_probs(von_neumann, ref_povm):
d = von_neumann.shape[0]
vn_projectors = [v*v.dag() for v in von_neumann.eigenstates()[1]]
return np.array([[(vn_projectors[j]*(e/e.tr())).tr() for i, e in enumerate(ref_povm)] for j in range(d)]).real
def vn_posterior(dm, von_neumann, ref_povm):
d = dm.shape[0]
p = dm_probs(rho, ref_povm)
r = vn_conditional_probs(von_neumann, ref_povm)
return np.array([sum([p[i]*r[j][i] for i in range(d**2)]) for j in range(d)])
print("vn probabilities after sic: %s" % vn_posterior(rho, von_neumann, ref_povm))
```
Indeed, $r(j|i)$ is a valid conditional probability matrix: its columns all sum to 1.
```
np.sum(vn_conditional_probs(von_neumann, ref_povm), axis=0)
```
Incidentally, there's no need to confine ourselves to the case of Von Neumann measurements. Suppose the "measurement on the ground" is given by another POVM. In fact, we can get one by just rotating our SIC-POVM by some random unitary. We'll obtain another SIC-POVM $\{F_{j}\}$.
In this case, we'd form $\rho^{\prime} = \sum_{i} p(i)\Pi_{i}$ just as before, and then take $s(j) = tr(F_{j}\rho^{\prime})$.
```
U = qt.rand_unitary(d)
ground_povm = [U*e*U.dag() for e in ref_povm]
povm_rho = sum([prob*ref_povm[i]/ref_povm[i].tr() for i, prob in enumerate(p)])
povm_s = np.array([(e*povm_rho).tr() for e in ground_povm]).real
print("povm probabilities after sic: %s" % povm_s)
```
And alternatively, we could work with the conditional probabilities:
$r(j|i) = tr(F_{j}\Pi_{i})$
And then apply:
$s(j) = \sum_{i}^{d^2} p(i)r(j|i)$
Where now $j$ will range from $0$ to $d^2$.
```
def povm_conditional_probs(povm, ref_povm):
d = int(np.sqrt(len(ref_povm)))
return np.array([[(a*(b/b.tr())).tr() for i, b in enumerate(ref_povm)] for j, a in enumerate(povm)]).real
def povm_posterior(dm, povm, ref_povm):
d = dm.shape[0]
p = dm_probs(dm, ref_povm)
r = povm_conditional_probs(povm, ref_povm)
return np.array([sum([p[i]*r[j][i] for i in range(d**2)]) for j in range(d**2)])
print("povm probabilities after sic: %s" % povm_posterior(rho, ground_povm, ref_povm))
```
<hr>
Okay, now we get to the punch line. Let's consider the case of the Von Neumann measurement. Suppose we *didn't* make the SIC-POVM measurement first. What would the probabilities be? Well, we all know:
$q(j) = tr(\tilde{\Pi}_{i}\rho)$
```
vn_p = np.array([(proj*rho).tr() for proj in vn_projectors]).real
print("vn probabilities (no sic in the sky): %s" % vn_p)
```
Now it turns out that we can get these same probabilities in a different way:
$q(j) = (d+1)[\sum_{i}^{d^2} p(i)r(j|i)] - 1$
```
def vn_born(dm, von_neumann, ref_povm):
d = dm.shape[0]
p = dm_probs(dm, ref_povm)
r = vn_conditional_probs(von_neumann, ref_povm)
return np.array([(d+1)*sum([p[i]*r[j][i] for i in range(d**2)]) - 1 for j in range(d)]).real
print("vn probabilities (no sic in the sky): %s" % vn_born(rho, von_neumann, ref_povm))
```
In other words, we can express the usual quantum probabilities in the case that we go directly to the Von Neumann measurement in a way that looks *ridiculously* close to our formula from before, involving probabilities for the SIC-POVM outcomes and conditional probabilities for Von Neumann outcomes given SIC-POVM outcomes! We sum over *hypothetical* outcomes of the SIC-POVM, multiplying the probability of each outcome, given our state $\rho$, by the conditional probability for the Von Neumann measurement giving the $j^{th}$ outcome, given that the SIC-POVM outcome was $i$. Except the formula is somewhat deformed by the the $(d+1)$ and the $-1$.
Clearly, this is equivalent to the usual Born Rule: but it's expressed *entirely* in terms of probabilities and conditional probabilities. It makes sense, in the end, that you can do this, given that the probabilities for the SIC-POVM measurement completely nail down the state. The upshot is that we can just work with the probabilities instead! Indeed, we could just pick some SIC-POVM to be our "reference apparatus", and describe any quantum state we're ever interested in terms of probabilities with reference to it, and any measurement in terms of conditional probabilities.
Operationally, what *is* difference between:
$s(j) = \sum_{i}^{d^2} p(i)r(j|i)$
and
$q(j) = (d+1)[\sum_{i}^{d^2} p(i)r(j|i)] - 1$
The difference is precisely *whether the SIC-POVM measurement has actually been performed*. If it has, then we lose quantum coherence. If it hasn't, we maintain it. In other words, the difference between classical and quantum is summed up in the minor difference between these two formulas.
In slogan form, due to Asher Peres, "unperformed measurements have no results." We'll get to the philosophy of this later, but the point is that classically speaking, we should be able to use the law of total probability *whether or not we actually do the measurement in the sky*: but quantum mechanically, if we don't actually do the measurement, we can't. But we have something just as good: the Born Rule.
<hr>
If we want to consider a more general measurement "on the ground," in particular, another SIC-POVM measurement, then our formula becomes:
$q(j) = (d+1)[\sum_{i}^{d^2} p(i)r(j|i)] - \frac{1}{d}[\sum_{i}^{d^2} r(j|i) ]$
Where now $i$ ranges to $d^2$.
```
print("povm probabilities (no sic in the sky): %s" % dm_probs(rho, ground_povm))
def povm_born(dm, povm, ref_povm):
d = dm.shape[0]
p = dm_probs(dm, ref_povm)
r = povm_conditional_probs(povm, ref_povm)
return np.array([(d+1)*sum([p[i]*r[j][i] for i in range(d**2)]) - (1/d)*sum([r[j][i] for i in range(d**2)]) for j in range(d**2)]).real
print("povm probabilities (no sic in the sky): %s" % povm_born(rho, ground_povm, ref_povm))
```
We can write these rules in much more compact matrix form.
Define $\Phi = (d+1)I_{d^2} - \frac{1}{d}J_{d^2}$
Where $I_{d^2}$ is the $d^2 \times d^2$ identity, and $J_{d^2}$ is the $d^2 \times d^2$ matrix all full of $1$'s.
If $R$ is the matrix of conditional probabilities, and $p$ is the vector of probabilities for the reference POVM in the sky, then the vector of values for $q(i)$ is:
$\vec{q} = R \Phi p$
```
def vn_born_matrix(dm, von_neumann, ref_povm):
d = rho.shape[0]
p = dm_probs(dm, ref_povm)
r = vn_conditional_probs(von_neumann, ref_povm)
phi = (d+1)*np.eye(d**2) - (1/d)*np.ones((d**2,d**2))
return r @ phi @ p
print("vn probabilities (no sic in the sky): %s" % vn_born_matrix(rho, von_neumann, ref_povm))
def povm_born_matrix(dm, povm, ref_povm):
d = dm.shape[0]
p = dm_probs(dm, ref_povm)
r = povm_conditional_probs(povm, ref_povm)
phi = (d+1)*np.eye(d**2) - (1/d)*np.ones((d**2,d**2))
return r @ phi @ p
print("povm probabilities (no sic in the sky): %s" % povm_born_matrix(rho, ground_povm, ref_povm))
```
And for that matter, we can calculate the "classical" probabilities from before in the same vectorized way: we just leave out $\Phi$!
```
print("vn probabilities after sic: %s" % (vn_conditional_probs(von_neumann, ref_povm) @ dm_probs(rho, ref_povm)))
print("povm probabilities after sic: %s" % (povm_conditional_probs(ground_povm, ref_povm) @ dm_probs(rho, ref_povm)))
```
In fact, this this is how qbist operators are implemented in this library behind the scenes. It allows one to easily handle the general case of IC-POVM's (informationally complete POVM's) which aren't SIC's: in that case, the matrix $\Phi$ will be different. Cf. `povm_phi`.
<hr>
Let's consider time evolution in this picture. We evolve our $\rho$ by some unitary:
$\rho_{t} = U \rho U^{\dagger}$
Naturally, we can calculate the new probabilities with reference to our SIC-POVM:
```
U = qt.rand_unitary(d)
rhot = U*rho*U.dag()
pt = dm_probs(rhot, ref_povm)
print("time evolved probabilities: %s" % pt)
```
But we could also express this in terms of conditional probabilities:
$u(j|i) = \frac{1}{d}tr(\Pi_{j}U\Pi_{i}U^{\dagger})$
As:
$p_{t}(j) = \sum_{i}^{d^2} ((d+1)p(i) - \frac{1}{d})u(j|i)$
```
def temporal_conditional_probs(U, ref_povm):
d = U.shape[0]
return np.array([[(1/d)*((a/a.tr())*U*(b/b.tr())*U.dag()).tr() for i, b in enumerate(ref_povm)] for j, a in enumerate(ref_povm)]).real
u = temporal_conditional_probs(U, ref_povm)
pt2 = np.array([sum([((d+1)*p[i] - 1/d)*u[j][i] for i in range(d**2)]) for j in range(d**2)]).real
print("time evolved probabilities: %s" % pt2)
```
We can compare this to the standard rule for stochastic evolution:
$p_{t}(j) = \sum_{i} p(i)u(j|i)$
We can see how the expression is deformed in exactly the same way. Indeed $u(j|i)$ is a doubly stochastic matrix: its rows and colums all sum to 1. And we can describe the time evolution of the quantum system in terms of it.
```
print(np.sum(u, axis=0))
print(np.sum(u, axis=1))
```
For more on the subleties of time evolution, consider the notes on `conditional_probs`.
<hr>
You can express the inner product between states in terms of SIC-POVM probability vectors via:
$tr(\rho \sigma) = d(d+1)[\vec{p} \cdot \vec{s}] - 1$
```
d = 3
ref_povm = sic_povm(d)
rho = qt.rand_dm(d)
sigma = qt.rand_dm(d)
p = dm_probs(rho, ref_povm)
s = dm_probs(sigma, ref_povm)
def quantum_inner_product_sic(p, s):
d = int(np.sqrt(len(p)))
return d*(d+1)*np.dot(p, s) - 1
print("inner product of rho and sigma: %.3f" % (rho*sigma).tr().real)
print("inner product of rho and sigma: %.3f" % quantum_inner_product_sic(p, s))
```
This brings up an important point.
You might wonder: Suppose we have a SIC-POVM with $d^2$ elements which provides $d^2$ probabilities which completely nail down the quantum state, given as a $d \times d$ density matrix. But what if we just start off with any old random vector of $d^2$ probabilities? Will we always get a valid density matrix? In other words, we've seen how we can start with quantum states, and then proceed to do quantum mechanics entirely in terms of probabilities and conditional probabilities. But now we're considering going in reverse. Does *any* assignment of probabilities to SIC-POVM outcomes specify a valid quantum state?
Well: any probability assignment will give us a $\rho$ which is Hermitian and has trace 1, which is great--BUT: this $\rho$ may not be positive-semidefinite (which is a requirement for density matrices). Like: if you assigned any old probabilites to the SIC-POVM outcomes, and then constructed a correponding $\rho$, it might end up having negative eigenvalues. Since the eigenvalues of $\rho$ are supposed to be probabilities (positive, summing to 1, etc), this is a problem.
In fact, you can't even have probability vectors that are too sharply peaked at any one value!
```
d = 3
povm = sic_povm(d)
vec = np.zeros(d**2)
vec[np.random.randint(d**2)] = 1
print("probs: %s" % vec)
print(probs_dm(vec, povm))
```
Note the negative entries. Furthermore, even if we start off in a SIC-POVM state, that doesn't mean we'll get that state with certainty after the measurement--indeed, unlike with projective measurements, repeated measurements don't always give the same results.
```
d = 3
povm = sic_povm(d)
print(dm_probs(povm[0]/povm[0].tr(), povm))
```
Above we see the probabilities for SIC-POVM outcomes given that we start off in the first SIC-POVM state. We see that indeed, the first SIC-POVM state has the highest probability, but all the other elements have non-zero probability (and for SIC's this is the same probability: not true for general IC-POVM's).
Indeed, it's a theorem that no such probability vector can have an element which exceeds $\frac{1}{d}$, and that the number of $0$ entries is bounded above by $\frac{d(d-1)}{2}$.
So we need another constraint. In other words, the quantum state space is a *proper subset* of the probability simplex over $d^2$ outcomes. There's some very interesting work exploring the geometric aspects of this constraint.
For example, insofar as pure states are those Hermitian matrices satisfying $tr(\rho^2) = tr(\rho^3) = 1$, we can evidently finagle this into two conditions:
$\sum_{i}^{d^2} p(i)^2 = \frac{2}{d(d+1)}$
and
$\sum_{i,j,k} c_{i, j, k}p(i)p(j)p(k) = \frac{d+7}{(d+1)^3}$
Where $c_{i, j, k} = \Re{[tr(\Pi_{i}\Pi_{j}\Pi_{k})]}$, which is a real-valued, completely symmetric three index tensor. The quantum state space is the <a href="https://en.wikipedia.org/wiki/Convex_hull">convex hull</a> of probability distributions satisfying these two equations.
On this same note, considering our expression for the inner product, since we know that the inner product between two quantum states $\rho$ and $\sigma$ is bounded between $0$ and $1$, we must have:
$\frac{1}{d(d+1)} \leq \vec{p} \cdot \vec{s} \leq \frac{2}{d(d+1)}$
The upper bound corresponds to our first condition. Call two vectors $\vec{p}$ and $\vec{s}$ "consistent" if their inner product obeys both inequalities. If we have a subset of the probability simplex for which every pair of vectors satisfies the inequalities, call it a "germ." If adding one more vector to a germ makes the set inconsistent, call the germ "maximal." And finally, call a maximal germ a "qplex." The space of quantum states in the SIC representation form a qplex, but not all qplexes correspond to quantum state spaces. The geometry of the qplexes are explored in <a href="https://arxiv.org/abs/1612.03234">Introducing the Qplex: A Novel Arena for Quantum Theory</a>. The conclusion?
"\[Turning\] to the problem of identifying the “missing assumption” which will serve to pick out quantum state space uniquely from the set of all qplexes... Of course, as is usual in such cases, there is more than one possibility. We identify one such assumption: the requirement that the symmetry group contain a subgroup isomorphic to the projective unitary group. This is a useful result because it means that we have a complete characterization of quantum state space in probabilistic terms. It also has an important corollary: That SIC existence in dimension d is equivalent to the existence of a certain kind of subgroup of the real orthogonal group in dimension $d^2 − 1$."
<hr>
Here's one final thing, for flavor. Having specified a SIC-POVM with $n$ elements and then an additional measurement (Von Neumann or POVM), we can construct the matrix $r(j|i)$.
```
d = 2
ref_povm = sic_povm(d)
von_neumann = qt.rand_herm(d)
n = len(ref_povm)
r = vn_conditional_probs(von_neumann, ref_povm)
r
```
We can then consider its rows, and extract a set of vectors $s_{j}$, each of which sums to 1:
$r(j|i) = n\gamma_{j} s_{j}(i)$
```
s = np.array([row/sum(row) for row in r])
gammas = [sum(row)/n for row in r]
np.array([n*gammas[i]*row for i, row in enumerate(s)])
```
We'll call these vectors $s_{j}$ "measurement vectors."
Suppose we're completely indifferent to the outcomes of the POVM in the sky. We could represent this by: $p(i) = \frac{1}{n}$. In other words, equal probability for each outcome.
The probabilities for outcomes to the later Von Neumann measurement would be:
$q(j) = \frac{1}{n}\sum_{i}r(j|i)$
```
p = [1/n for i in range(n)]
vn_probs = np.array([sum([p[i]*r[j][i] for i in range(n)]) for j in range(d)])
vn_probs
```
We could describe this by assigning to $\rho$ the maximally mixed state.
```
max_mixed = qt.identity(d)/d
vn_born(max_mixed, von_neumann, ref_povm)
```
But we could also rewrite $q(j)$ as:
$q(j) = \frac{1}{n} \sum_{i} n\gamma_{j} s_{j}(i) = \gamma_{j} \sum_{i} s_{j}(i)$
And since the $s_{j}(i)$ sum to 1:
$q(j) = \gamma_{j}$
```
np.array([gammas[j]*sum([s[j][i] for i in range(n)]) for j in range(d)])
gammas
```
Thus you can interpret the $\gamma_{j}$'s as: the probabilities of obtaining the $j^{th}$ outcome on the ground when you're completely indifferent to the potential outcomes in the sky.
Now let's rewrite:
$r(j|i) = n\gamma_{j} s_{j}(i)$
as
$s_{j}(i) = \frac{\frac{1}{n}r(j|i)}{\gamma_{j}}$
We know that $\gamma_{j}$ is the probability of obtaining $j$ on the ground, given complete ignorance about the potential outcomes of the sky experiment. We also know that $\frac{1}{n}$ is the probability assigned to each outcome of the sky experiment from complete indifference.
So write $Pr_{CI}(i)= \frac{1}{n}$ and $Pr_{CI}(j) = \gamma_{i}$, where $CI$ stands for complete ignorance/indifference. And we could apply the same notation: $Pr_{CI}(j|i) = r(j|i)$:
$s_{j}(i) = \frac{Pr_{CI}(i)Pr_{CI}(j|i)}{Pr_{CI}(j)}$
But this is just the Baysian formula for inverting conditional probabilities:
$Pr_{CI}(i|j) = \frac{Pr_{CI}(i)Pr_{CI}(j|i)}{Pr_{CI}(j)}$
In a similar vein:
<img src="img/fuchs.png">
<hr>
## Interlude: Implementing POVM's
It's worth mentioning how POVM's are actually implemented in practice. Here's the simplest way of thinking about it. Suppose we have a system with Hilbert space dimension $d$, and we have a POVM with $n$ elements. (In the case of our SIC-POVM's, we'd have $d^2$ elements.) We then adjoin an auxilliary system with Hilbert space dimension $n$: as many dimensions as POVM elements. So now we're working with $\mathcal{H}_{d} \otimes \mathcal{H}_{n}$.
Let's define projectors onto the basis states of the auxilliary system: $\Xi_{i} = I_{d} \otimes \mid i \rangle \langle i \mid$. If we denote the elements of the POVM by $\{ E_{i} \}$, then we can construct an isometry:
$V = \sum_{i}^{n} \sqrt{E_{i}} \otimes \mid i \rangle$
Such that any element of the POVM can be written:
$E_{i} = V^{\dagger}\Xi_{i}V $
```
d = 3
my_povm = sic_povm(d)
n = len(my_povm)
aux_projectors = [qt.tensor(qt.identity(d), qt.basis(n, i)*qt.basis(n, i).dag()) for i in range(n)]
V = sum([qt.tensor(my_povm[i].sqrtm(), qt.basis(n, i)) for i in range(n)])
povm_elements = [V.dag()*aux_projectors[i]*V for i in range(n)]
print("recovered povm elements? %s" % np.all([np.allclose(my_povm[i], povm_elements[i]) for i in range(n)]))
```
So this isometry $V$ takes us from $\mathcal{H}_{d}$ to $\mathcal{H}_{d} \otimes \mathcal{H}_{n}$.
We can extend this to a unitary $U$ (that takes $\mathcal{H}_{d} \otimes \mathcal{H}_{n}$ to $\mathcal{H}_{d} \otimes \mathcal{H}_{n}$) using the QR decomposition. In essence, we use the Gram-Schmidt procedure to fill out the rectangular matrix to a square matrix with extra orthogonal columns. (And then we have to rearrange the columns so that the columns of $V$ appear every $n^{th}$ column, in order to take into account the tensor product structure.)
```
Q, R = np.linalg.qr(V, mode="complete")
for i in range(d):
Q.T[[i,n*i]] = Q.T[[n*i,i]]
Q[:,n*i] = V[:,i].T
U = qt.Qobj(Q)
U.dims = [[d, n],[d, n]]
```
We can check our work. It should be the case that:
$V = U(I_{d} \otimes \mid 0 \rangle)$
```
print("recovered V?: %s" % np.allclose(V, U*qt.tensor(qt.identity(d), qt.basis(n, 0))))
```
Now for the finale. We know how to calculate the probabilities for each of the POVM outcomes. It's just:
$Pr(i) = tr(E_{i}\rho)$
To actually implement this, we start off with our auxilliary system in the $\mid 0 \rangle$ state, so that the overall density matrix is: $\rho \otimes \mid 0 \rangle \langle 0 \mid$. We then evolve the system and the auxilliary with our unitary $U$:
$$U [\rho \otimes \mid 0 \rangle \langle 0 \mid] U^{\dagger} $$
Finally, we perform a standard Von Neumann measurement on the auxilliary system (whose outcomes correspond to the basis states we've been using). Recalling that we defined the projectors onto the auxilliary basis states as $\Xi_{i} = I_{d} \otimes \mid i \rangle \langle i \mid$, we can then write probabilities for each outcome:
$Pr(i) = tr(\Xi_{i} U [\rho \otimes \mid 0 \rangle \langle 0 \mid] U^{\dagger} )$
These are the same probabilities as above.
```
rho = qt.rand_dm(d)
povm_probs = np.array([(my_povm[i]*rho).tr() for i in range(n)]).real
system_aux_probs = np.array([(aux_projectors[i]*\
U*qt.tensor(rho, qt.basis(n,0)*qt.basis(n,0).dag())*U.dag()).tr()\
for i in range(n)]).real
print("povm probs:\n%s" % povm_probs)
print("system and aux probs:\n%s" % system_aux_probs)
```
Moreover, we can see that the states after measurement correspond to the SIC-POVM projectors:
```
states = [(aux_projectors[i]*(U*qt.tensor(rho, qt.basis(n,0)*qt.basis(n,0).dag())*U.dag())).ptrace(0) for i in range(n)]
print(states[0].unit())
print(d*my_povm[0])
```
Indeed, whether you buy the philosophy that we're about to go into, SIC-POVM's have deep practical value in terms of quantum tomography and quantum information theory generally.
Cf. `implement_povm`.
<hr>
## The Philosophy
So in some sense the difference between classical and quantum is summed up in the difference between these two formulas:
$s(j) = \sum_{i}^{d^2} p(i)r(j|i)$
and
$q(j) = (d+1)[\sum_{i}^{d^2} p(i)r(j|i)] - 1$
In the first case, I make a SIC-POVM measurement in the sky, and then make a Von Neumann measurement on the ground. I can calculate the probabilities for the outcomes of the latter measurement using the law of total probability. Given the probabilities for the sky outcomes, and the conditional probabilities that relate ground outcomes to sky outcomes, I can calculate the probabilities for ground outcomes. Classically speaking, and this is the crucial point, I could use the first formula *whether or not I actually did the sky measurement*.
In other words, insofar as classically we've identified the relevant "degrees of freedom," and the assignment of sky probabilities uniquely characterizes the state, then it's a matter of mathematical convenience if we express $s(j)$ as a sum over those degrees of freedom $\sum_{i}^{d^2} p(i)r(j|i)$: by the nature of the formula, by the law of total probability, all the $i$'s drop out, and we're left with the value for $j$. We could actually perform the sky measurement or not: either way, we'd use the same formula to calculate the ground probabilities.
This is precisely what changes with quantum mechanics: it makes a difference *whether you actually do the sky measurement or not*. If you do, then you use the classical formula. If you don't, then you use the quantum formula.
One way of interpreting the moral of this is that, to quote Asher Peres again, "Unperformed measurements have no results." In contrast, classically, you *can* always regard unperformed measurements as having results: indeed, classical objectivity consists in, as it were, everything wearing its outcomes on its sleeve. In other words, outcomes aren't a special category: one can just speak of the properties of things. And this is just another way of saying you can use the law of total probability whether or not you actually do an intermediate measurement. But this is exactly what you can't rely on in quantum mechanics.
But remarkably, all you need to do to update your probability calculus is to use the quantum formula, which is ultimately the Born Rule in disguise. In other words, in a world where unperformed measurements have no results, when we consider different kinds of sequences of measurements, we need a (minor) addition to probability theory so that our probability assignments are coherent/consistent/no one can make a buck off of us.
Moreover, Blake Stacey makes the nice point, considering the realtionship between SIC-POVM's and Von Neumann measurements:
"Two orthogonal quantum states are perfectly distinguishable with respect to some experiment, yet in terms of the reference \[SIC-POVM\] measurement, they are inevitably overlapping probability distributions. The idea that any two valid probability distributions for the reference measurement must overlap, and that the minimal overlap in fact corresponds to distinguishability with respect to some other test, expresses the fact that quantum probability is not about hidden variables" (Stacey 2020).
<hr>
de Finetti famously advocated a subjectivist, personalist view of classical probability theory, and he and his theorems have proved to be an inspiration for QBists like Christopher Fuchs and others. In this view, probabilities don't "exist" out in the world: they are mathematical representations of personal beliefs which you are free to update in the face of new evidence. There isn't ever "one objective probability distribution" for things: rather, there's a constant personal process of convergence towards better beliefs. If you don't want to make bad bets, there are some basic consistency criteria that your probabilities have to satisfy. And that's what probability theory as such amounts to. The rest is just "priors."
"Statisticians for years had been speaking of how statistical sampling can reveal the 'unknown probability distribution'. But from de Finetti’s point of view, this makes as little sense as the unknown quantum state made for us. What de Finetti’s representation theorem established was that all this talk of an unknown probability was just that, talk. Instead, one could show that there was a way of thinking of the resultant of statistical sampling purely in terms of a transition from prior subjective probabilities (for the sampler himself) to posterior subjective probabilities (for the sampler himself). That is, every bit of statistical sampling from beginning to end wasn’t about revealing a true state of affairs (the “unknown probability”), but about the statistician’s own states of information about a set of “exchangeable” trials, full stop. The quantum de Finetti theorem does the same sort of thing, but for quantum states" (Fuchs 2018).
Indeed, QBists advocate a similar epistemic interpretation of the quantum state. The quantum state does not represent a quantum system. It represents *your beliefs about that quantum system*. In other words, interpretations that assign ontological roles to quantum states miss the mark. Quantum states are just packages of probabilities, indeed, probabilities personal to you. (In this sense, one can see a close relation to relational interpretations of quantum mechanics, where the quantum state is always defined not objectively, but to one system relative to another system.) Similarly, all the superstructure of quantum mechanics, operators, time evolution, etc-- are all just a matter of making subjective probabilities consistent with each other, given the *objective fact* that you should use the quantum formula when you haven't done an intermediate measurement, and the classical formula if you have. (And one should also mention that the formulas above imply that the *dimension* of the Hilbert space is, in fact, objective.)
On the other hand, QBists also hold that the very outcomes of measurements themselves are subjective--not in the sense of being vacuously open to intepretation, but in the sense that they are *experiences*; and it is precisely these subjective experiences that are being gambled upon. In other words, quantum mechanics is not a theory of the objective physical world as such, but is instead a first person theory by which one may predict the future consequences of one's own actions in experience.
This is how they deal with the dilemma of Wigner's friend. Fuchs: "...for the QBist, the real world, the one both agents are embedded in—with its objects and events—is taken for granted. What is not taken for granted is each agent's access to the parts of it he has not touched. Wigner holds two thoughts in his head: a) that his friend interacted with a quantum system, eliciting some consequences of the interaction for himself, and b) after the specified time, for any of Wigner's own future interactions with his friend or the system or both, he ought to gamble upon their consequences according to $U(\rho \otimes \mid \psi \rangle \langle \psi \mid) U^{\dagger}$. One statement refers to the friend's potential experiences, and one refers to Wigner's own. So long as it is explicit that $U(\rho \otimes \mid \psi \rangle \langle \psi \mid) U^{\dagger}$ refers to the latter--i.e., how Wigner should gamble upon the things that might happen to him--making no statement whatsoever about the former, there is no conflict. The world is filled with all the same things it was before quantum theory came along, like each of our experiences, that rock and that tree, and all the other things under the sun; it is just that quantum theory provides a calculus for gambling on each agent's experiences--it doesn't give anything other than that. It certainly doesn't give one agent the ability to conceptually pierce the other agent's personal experience. It is true that with enough effort Wigner \[could apply the reverse unitary, disentangling the friend and the spin\], causing him to predict that his friend will have amnesia to any future questions on his old measurement results. But we always knew Wigner could do that--a mallet to the head would have been good enough" (Fuchs, Stacey 2019).
Most assuredly, this is not a solipsistic theory: indeed, the actual results of measurement are precisely not within one's control. The way they imagine it is that whenever you set up an experiment, you divide the world into subject and object: the subject has the autonomy to set up the experiment, and the object has the autonomy to respond to the experiment. But the act of measurement itself is a kind of creation, a mutual experience which transcends the very distinction between subject and object itself, a linkage between oneself and the other. "QBism says that when an agent reaches out and touches a quantum system—when he performs a quantum measurement—this process gives rise to birth in a nearly literal sense" (Fuchs, Stacey 2019).
The only conflict here is with a notion that the only valid physical theories are those that attempt to directly represent the universe "in its totality as a pre-existing static system; an unchanging, monistic something that just *is*." Moreover, a theory like QBism clears a space for "real particularity and 'interiority' in the world." For Wigner, considering his friend and the system, with his back turned, "that phenomenon has an inside, a vitality that he takes no part in until he again interacts with one or both relevant pieces of it."
Often in the interpretation of quantum mechanics, one tries to achieve objectivity by focusing on the big bulky apparatuses we use and the "objective" record of outcomes left behind by these machines. The QBists take a different track: Bohr himself considers the analogy of a blind man seeing with a stick. He's not actively, rationally thinking about the stick and how it's skittering off this or that: rather, for him, it becomes an extension of his body: he *sees with the stick*. And thus one can understand Fuchs's three tenants of QBism:
1. Quantum Theory Is Normative, Not Descriptive
2. My Probabilities Cannot Tell Nature What To Do
3. A Measuring Device Is Literally an Extension of the Agent
<hr>
<img width=600 src="img/qbism_assumptions1.png">
<img width=600 src="img/qbism_assumptions2.png">
<hr>
Indeed, one might wonder about entanglement in this picture. In line with the discussion of Wigner's friend, we can interpret entanglement and the use of tensor product itself as relating to the objective fact that we require a way of representing correlations while being completely agnostic about what is correlated insofar as we haven't yet reached out and "touched" the thing.
Moreover, in this sense, one can look at QBism as a completely "local" theory. An experimenter has one half of an entangled pair of spins, and makes a measurement, and has an experience. In the textbook way of thinking it, this causes the state of the other spin to immedietely collapse. QBism takes a different approach. They say: quantum theory allows the experimenter to predict that if they go over and measure the other spin in the same direction, they will have another experience, of the answers of the two particles being correlated. But just because quantum theory licenses the experimenter to assign a probability 1 for the latter outcome after they do the first measurement doesn't mean that the latter particle *really is now $\uparrow$, say, as a property*. If the experimenter never actually goes to check out the other particle, it's yet another unperformed measurement: and it has no outcome yet. To paraphrase William James, if it isn't experienced, it isn't real. And in order to "cash out" on entanglement, one actually has to traverse the distance between the two particles and compare the results.
With regard to quantum teleportation, in this view, it's not about getting "things" from one place to another, but about making one's information cease referring to this part of the universe and start referring instead to another part of the universe, without referring to anything else in between. "The only nontrivial thing transferred in the process of teleportation is *reference*" (Fuchs, Stacey 2019).
<hr>
One of the things that makes QBism so interesting is its attempt to give nature as much latitude as possible. Usually in science, we're mentally trying to constraint nature, applying concepts, laws, systems, to it, etc. QBism instead proposes that we live in a unfinished world, whose creation is ongoing and ceaseless, and that this profound openendedness is the real meaning behind "quantum indeterminism." In itself, the universe is not governed by immutable laws and initial conditions fixed from the beginning: instead, new situations are coming into being all the time. Of course, regularities arise by evolution, the laws of large numbers, symmetries and so forth. But they take seriously John Wheeler's idea of the "participatory universe," that we and everything else are constantly engaged bringing the universe into being, together.
Wheeler writes:
"How did the universe come into being? Is that some strange, far-off process beyond hope of analysis? Or is the mechanism that comes into play one which all the time shows itself? Of all the signs that testify to 'quantum phenomenon' as being the elementary act and building block of existence, none is more striking than its utter absence of internal structure and its untouchability. For a process of creation that can and does operate anywhere, that is more basic than particles or fields or spacetime geometry themselves, a process that reveals and yet hides itself, what could one have dreamed up out of pure imagination more magic and more fitting than this?"
"'Law without law': It is difficult to see what else than that can be the “plan” for physics. It is preposterous to think of the laws of physics as installed by a Swiss watchmaker to endure from everlasting to everlasting when we know that the universe began with a big bang. The laws must have come into being. Therefore they could not have been always a hundred percent accurate. That means that they are derivative, not primary. Also derivative, also not primary is the statistical law of distribution of the molecules of a dilute gas between two intersecting portions of a total volume. This law is always violated and yet always upheld. The individual molecules laugh at it; yet as they laugh they find themselves obeying it. ... Are the laws of physics of a similar statistical character? And if so, statistics of what? Of billions and billions of acts of observer-participancy which individually defy all law? . . . \[Might\] the entirety of existence, rather than \[be\] built on particles or fields or multidimensional geometry, \[be\] built on billions upon billions of elementary quantum phenomena, those elementary acts of observer-participancy?"
<img src="img/wheeler.png">
<hr>
In such world, to quote William James, "Theories thus become instruments, not answers to enigmas, in which we can rest. We don’t lie back upon them, we move forward, and, on occasion, make nature over again by their aid." Moreover, in relegating quantum states to the observers who use them for predictions, one clears some ontological space for the quantum systems themselves to be "made of" who knows what qualitative, experiential stuff.
"\[QBism\] means that reality differs from one agent to another. This is not as strange as it may sound. What is real for an agent rests entirely on what that agent experiences, and different agents have different experiences. An agent-dependent reality is constrained by the fact that different agents can communicate their experience to each other, limited only by the extent that personal experience can be expressed in ordinary language. Bob’s verbal representation of his own experience can enter Alice’s, and vice-versa. In this way a common body of reality can be constructed, limited only by the inability of language to represent the full flavor — the “qualia” — of personal experience" (Fuchs, Mermin, Schack 2013).
Indeed, the QBists reach back in time and draw on the work of the old American pragmatists: James, John Dewey, Charles Sanders Peirce, and others. It's interesting to read their works particularly as many of them date from the pre-quantum era, so that even in the very face of classical physics, they were advocating a radically indeterministic, experience-first view of the world.
For example, James writes:
"Chance] is a purely negative and relative term, giving us no information about that of which it is predicated, except that it happens to be disconnected with something else—not controlled, secured, or necessitated by other things in advance of its own actual presence... What I say is that it tells us nothing about what a thing may be in itself to call it “chance.” ... All you mean by calling it “chance” is that this is not guaranteed, that it may also fall out otherwise. For the system of other things has no positive hold on the chance-thing. Its origin is in a certain fashion negative: it escapes, and says, Hands off! coming, when it comes, as a free gift, or not at all."
"This negativeness, however, and this opacity of the chance-thing when thus considered ab extra, or from the point of view of previous things or distant things, do not preclude its having any amount of positiveness and luminosity from within, and at its own place and moment. All that its chance-character asserts about it is that there is something in it really of its own, something that is not the unconditional property of the whole. If the whole wants this property, the whole must wait till it can get it, if it be a matter of chance. That the universe may actually be a sort of joint-stock society of this sort, in which the sharers have both limited liabilities and limited powers, is of course a simple and conceivable notion."
<hr>
"Why may not the world be a sort of republican banquet of this sort, where all the qualities of being respect one another’s personal sacredness, yet sit at the common table of space and time?
To me this view seems deeply probable. Things cohere, but the act of cohesion itself implies but few conditions, and leaves the rest of their qualifications indeterminate. As the first three notes of a tune comport many endings, all melodious, but the tune is not named till a particular ending has actually come,—so the parts actually known of the universe may comport many ideally possible complements. But as the facts are not the complements, so the knowledge of the one is not the knowledge of the other in anything but the few necessary elements of which all must partake in order to be together at all. Why, if one act of knowledge could from one point take in the total perspective, with all mere possibilities abolished, should there ever have been anything more than that act? Why duplicate it by the tedious unrolling, inch by inch, of the foredone reality? No answer seems possible. On the other hand, if we stipulate only a partial community of partially independent powers, we see perfectly why no one part controls the whole view, but each detail must come and be actually given, before, in any special sense, it can be said to be determined at all. This is the moral view, the view that gives to other powers the same freedom it would have itself."
<hr>
"Does our act then create the world’s salvation so far as it makes room for itself, so far as it leaps into the gap? Does it create, not the whole world’s salvation of course, but just so much of this as itself covers of the world’s extent? Here I take the bull by the horns, and in spite of the whole crew of rationalists and monists, of whatever brand they be, I ask why not? Our acts, our turning-places, where we seem to ourselves to make ourselves and grow, are the parts of the world to which we are closest, the parts of which our knowledge is the most intimate and complete. Why should we not take them at their facevalue? Why may they not be the actual turning-places and growing-places which they seem to be, of the world—why not the workshop of being, where we catch fact in the making, so that nowhere may the world grow in any other kind of way than this?"
"Irrational! we are told. How can new being come in local spots and patches which add themselves or stay away at random, independently of the rest? There must be a reason for our acts, and where in the last resort can any reason be looked for save in the material pressure or the logical compulsion of the total nature of the world? There can be but one real agent of growth, or seeming growth, anywhere, and that agent is the integral world itself. It may grow all-over, if growth there be, but that single parts should grow per se is irrational."
"But if one talks of rationality—and of reasons for things, and insists that they can’t just come in spots, what kind of a reason can there ultimately be why anything should come at all?"
<hr>
"What does determinism profess? It professes that those parts of the universe already laid down absolutely appoint and decree what the other parts shall be. The future has no ambiguous possibilities hidden in its womb; the part we call the present is compatible with only one totality. Any other future complement than the one fixed from eternity is impossible. The whole is in each and every part, and welds it with the rest into an absolute unity, an iron block, in which there can be no equivocation or shadow of turning."
"Indeterminism, on the contrary, says that the parts have a certain amount of loose play on one another, so that the laying down of one of them does not necessarily determine what the others shall be. It admits that possibilities may be in excess of actualities, and that things not yet revealed to our knowledge may really in themselves be ambiguous. Of two alternative futures which we conceive, both may now be really possible; and the one become impossible only at the very moment when the other excludes it by becoming real itself. Indeterminism thus denies the world to be one unbending unit of fact. It says there is a certain ultimate pluralism in it."
<hr>
"The import of the difference between pragmatism and rationalism is now in sight throughout its whole extent. The essential contrast is that for rationalism reality is ready-made and complete from all eternity, while for pragmatism it is still in the making, and awaits part of its complexion from the future. On the one side the universe is absolutely secure, on the other it is still pursuing its adventures..."
"The humanist view of 'reality,' as something resisting, yet malleable, which controls our thinking as an energy that must be taken 'account' of incessantly is evidently a difficult one to introduce to novices...
The alternative between pragmatism and rationalism, in the shape in which we now have it before us, is no longer a question in the theory of knowledge, it concerns the structure of the universe itself."
"On the pragmatist side we have only one edition of the universe, unfinished, growing in all sorts of places, especially in the places where thinking beings are at work. On the rationalist side we have a universe in many editions, one real one, the infinite folio, or ́edition de luxe, eternally complete; and then the various finite editions, full of false readings, distorted and mutilated each in its own way."
<hr>
And yet, we know that quantum mechanics presents many faces, Bohmian deterministic faces, the many faces of Many Worlds, and so forth. It's beautiful, in a way: there's something for everybody. One is reminded of another passage from James:
"The history of philosophy is to a great extent that of a certain clash of human temperaments. Undignified as such a treatment may seem to some of my colleagues, I shall have to take account of this clash and explain a good many of the divergencies of philosophies by it. Of whatever temperament a professional philosopher is, he tries, when philosophizing, to sink the fact of his temperament. Temperament is no conventionally recognized reason, so he urges impersonal reasons only for his conclusions. Yet his temperament really gives him a stronger bias than any of his more strictly objective premises. It loads the evidence for him one way or the other ... just as this fact or that principle would. He trusts his temperament. Wanting a universe that suits it, he believes in any representation of the universe that does suit it."
"Why does Clifford fearlessly proclaim his belief in the conscious-automaton theory, although the ‘proofs’ before him are the same which make Mr. Lewes reject it? Why does he believe in primordial units of ‘mind-stuff’ on evidence which would seem quite worthless to Professor Bain? Simply because, like every human being of the slightest mental originality, he is peculiarly sensitive to evidence that bears in some one direction. It is utterly hopeless to try to exorcise such sensitiveness by calling it the disturbing subjective factor, and branding it as the root of all evil. ‘Subjective’ be it called! and ‘disturbing’ to those whom it foils! But if it helps those who, as Cicero says, “vim naturae magis sentiunt” \[feel the force of nature more\], it is good and not evil. Pretend what we may, the whole man within us is at work when we form our philosophical opinions. Intellect, will, taste, and passion co-operate just as they do in practical affairs...\[I\]n the forum \[one\] can make no claim, on the bare ground of his temperament, to superior discernment or authority. There arises thus a certain insincerity in our philosophic discussions: the potentest of all our premises is never mentioned. I am sure it would contribute to clearness if in these lectures we should break this rule and mention it, and I accordingly feel free to do so."
Indeed, for James, the value of a philosophy lies not so much in its proofs, but in the total vision that it expresses. As I say, perhaps the universe itself has something for everyone, whatever their temperament.
<hr>
As a final word, it seems to me that QBism has taught us something genuinely new about quantum theory and its relationship to probability theory. On the other hand, it also pretends to be a theory of "experience": and yet, I'm not sure that I've learned anything new about experience. If QBism is to really prove itself, it will have to make novel predictions not just on the quantum side, but also on the side of our everyday perceptions.
"The burning question for the QBist is how to model in Hilbert-space terms the common sorts of measurements we perform just by opening our eyes, cupping our ears, and extending our fingers" (Fuchs, Stacey 2019).
## Bibliography
<a href="https://arxiv.org/abs/1612.07308">QBism: Quantum Theory as a Hero’s Handbook</a>
<a href="https://arxiv.org/abs/1612.03234">Introducing the Qplex: A Novel Arena for Quantum Theory</a>
<a href="https://arxiv.org/abs/1311.5253">An Introduction to QBism with an Application to the Locality of Quantum Mechanics</a>
<a href="https://arxiv.org/abs/1003.5209">QBism, the Perimeter of Quantum Bayesianism</a>
<a href="https://arxiv.org/abs/1301.3274">Quantum-Bayesian Coherence: The No-Nonsense Version</a>
<a href="https://arxiv.org/abs/1401.7254">Some Negative Remarks on Operational Approaches to Quantum Theory</a>
<a href="https://arxiv.org/abs/1405.2390">My Struggles with the Block Universe</a>
<a href="https://arxiv.org/abs/1412.4209">Quantum Measurement and the Paulian Idea</a>
<a href="https://arxiv.org/abs/quant-ph/0105039">Notes on a Paulian Idea</a>
<a href="https://arxiv.org/abs/1601.04360">On Participatory Realism</a>
<a href="https://arxiv.org/abs/0906.1968">Delirium Quantum</a>
<a href="https://arxiv.org/abs/1703.07901">The SIC Question: History and State of Play</a>
<a href="https://arxiv.org/abs/1705.03483">Notwithstanding Bohr, the Reasons for QBism</a>
<a href="https://arxiv.org/abs/2012.14397">The Born Rule as Dutch-Book Coherence (and only a little more)</a>
<a href="https://arxiv.org/abs/quant-ph/0205039">Quantum Mechanics as Quantum Information (and only a little more)</a>
<a href="https://arxiv.org/abs/1907.02432">Quantum Theory as Symmetry Broken by Vitality</a>
https://en.wikipedia.org/wiki/POVM
https://en.wikipedia.org/wiki/SIC-POVM
<a href="refs/wheeler_law_without_law.pdf">Law without Law</a>
<a href="http://www.gutenberg.org/ebooks/11984">A Pluralistic Universe</a>
<a href="http://www.gutenberg.org/ebooks/32547">Essays in Radical Empiricism</a>
|
github_jupyter
|
# 5장
```
import matplotlib
matplotlib.rc('font', family="NanumBarunGothicOTF")
%matplotlib inline
```
# 5.2 아이리스 데이터셋
```
import pandas as pd
from matplotlib import pyplot as plt
import sklearn.datasets
def get_iris_df():
ds = sklearn.datasets.load_iris()
df = pd.DataFrame(ds['data'], columns=ds['feature_names'])
code_species_map = dict(zip(
range(3), ds['target_names']))
df['species'] = [code_species_map[c] for c in ds['target']]
return df
df = get_iris_df()
df_iris = df
```
# 5.3 원형 차트
```
sums_by_species = df.groupby('species').sum()
var = 'sepal width (cm)'
sums_by_species[var].plot(kind='pie', fontsize=20)
plt.ylabel(var, horizontalalignment='left')
plt.title('꽃받침 너비로 분류한 붓꽃', fontsize=25)
# plt.savefig('iris_pie_for_one_variable.png')
# plt.close()
sums_by_species = df.groupby('species').sum()
sums_by_species.plot(kind='pie', subplots=True,
layout=(2,2), legend=False)
plt.title('종에 따른 전체 측정값Total Measurements, by Species')
# plt.savefig('iris_pie_for_each_variable.png')
# plt.close()
```
# 5.4 막대그래프
```
sums_by_species = df.groupby('species').sum()
var = 'sepal width (cm)'
sums_by_species[var].plot(kind='bar', fontsize=15, rot=30)
plt.title('꽃받침 너비(cm)로 분류한 붓꽃', fontsize=20)
# plt.savefig('iris_bar_for_one_variable.png')
# plt.close()
sums_by_species = df.groupby('species').sum()
sums_by_species.plot(
kind='bar', subplots=True, fontsize=12)
plt.suptitle('종에 따른 전체 측정값')
# plt.savefig('iris_bar_for_each_variable.png')
# plt.close()
```
# 5.5 히스토그램
```
df.plot(kind='hist', subplots=True, layout=(2,2))
plt.suptitle('붓꽃 히스토그램', fontsize=20)
# plt.show()
for spec in df['species'].unique():
forspec = df[df['species']==spec]
forspec['petal length (cm)'].plot(kind='hist', alpha=0.4, label=spec)
plt.legend(loc='upper right')
plt.suptitle('종에 따른 꽃잎 길이')
# plt.savefig('iris_hist_by_spec.png')
```
# 5.6 평균, 표준편차, 중간값, 백분위
```
col = df['petal length (cm)']
average = col.mean()
std = col.std()
median = col.quantile(0.5)
percentile25 = col.quantile(0.25)
percentile75 = col.quantile(0.75)
print(average, std, median, percentile25, percentile75)
```
### 아웃라이어 걸러내기
```
col = df['petal length (cm)']
perc25 = col.quantile(0.25)
perc75 = col.quantile(0.75)
clean_avg = col[(col>perc25)&(col<perc75)].mean()
print(clean_avg)
```
# 5.7 상자그림
```
col = 'sepal length (cm)'
df['ind'] = pd.Series(df.index).apply(lambda i: i% 50)
df.pivot('ind','species')[col].plot(kind='box')
# plt.show()
```
# 5.8 산포도
```
df.plot(kind="scatter",
x="sepal length (cm)", y="sepal width (cm)")
plt.title("Length vs Width")
# plt.show()
colors = ["r", "g", "b"]
markers= [".", "*", "^"]
fig, ax = plt.subplots(1, 1)
for i, spec in enumerate(df['species'].unique() ):
ddf = df[df['species']==spec]
ddf.plot(kind="scatter",
x="sepal width (cm)", y="sepal length (cm)",
alpha=0.5, s=10*(i+1), ax=ax,
color=colors[i], marker=markers[i], label=spec)
plt.legend()
plt.show()
import pandas as pd
import sklearn.datasets as ds
import matplotlib.pyplot as plt
# 팬다스 데이터프레임 생성
bs = ds.load_boston()
df = pd.DataFrame(bs.data, columns=bs.feature_names)
df['MEDV'] = bs.target
# 일반적인 산포도
df.plot(x='CRIM',y='MEDV',kind='scatter')
plt.title('일반축에 나타낸 범죄 발생률')
# plt.show()
```
## 로그를 적용
```
df.plot(x='CRIM',y='MEDV',kind='scatter',logx=True)
plt.title('Crime rate on logarithmic axis')
plt.show()
```
# 5.10 산포 행렬
```
from pandas.tools.plotting import scatter_matrix
scatter_matrix(df_iris)
plt.show()
```
# 5.11 히트맵
```
df_iris.plot(kind="hexbin", x="sepal width (cm)", y="sepal length (cm)")
plt.show()
```
# 5.12 상관관계
```
df["sepal width (cm)"].corr(df["sepal length (cm)"]) # Pearson corr
df["sepal width (cm)"].corr(df["sepal length (cm)"], method="pearson")
df["sepal width (cm)"].corr(df["sepal length (cm)"], method="spearman")
df["sepal width (cm)"].corr(df["sepal length (cm)"], method="spearman")
```
# 5.12 시계열 데이터
```
# $ pip install statsmodels
import statsmodels.api as sm
dta = sm.datasets.co2.load_pandas().data
dta.plot()
plt.title("이산화탄소 농도")
plt.ylabel("PPM")
plt.show()
```
## 구글 주가 불러오는 코드는 야후 API가 작동하지 않아서 생략합니다.
|
github_jupyter
|
In this notebook you can define your own configuration and run the model based on your custom configuration.
## Dataset
`dataset_name` is the name of the dataset which will be used in the model. In case of using KITTI, `dataset_path` shows the path to `data_paths` directory that contains every image and its pair path, and for Cityscape it is the path to the directory that contains `leftImg8bit` and `rightImg8bit` folders. The `resize` value selects the width, and the height dimensions that each image will be resized to.
```
dataset_name: 'KITTI'
dataset_path = '.'
resize = [128, 256]
```
## Model
`baseline_model` selects the compression model. The accepted models for this parameter are bmshj18 for [Variational image compression with a scale hyperprior](https://arxiv.org/abs/1802.01436) and bls17 for [End-to-end Optimized Image Compression](https://arxiv.org/abs/1611.01704). If `use_side_info` is set as `True`, then the baseline model is modified using our proposed method for using side information for compressing.
If `load_weight` is `True`, then in model initialization, the weight saved in `weight_path` is loaded to the model. You can also specify the experiment name in `experiment_name`.
```
baseline_model = 'bls17' # can be bmshj18 for Variational image compression with a scale hyperprior by Ballé, et al.
# or bls17 for End-to-end Optimized Image Compression by Ballé, et al.
use_side_info = True # if True then the modified version of baseline model for distributed compression is used.
num_filters = 192 # number of filters used in the baseline model network
cuda = True
load_weight = False
weight_path = './pretrained_weights/ours+balle17_MS-SSIM_lambda3e-05.pt' # weight path for loading the weight
# note that we provide some pretrained weights, accessible from the anonymous link provided in README.md
```
## Training
For training set `train` to be `True`. `lambda` shows the lambda value in the rate-distortion equation and `alpha` and `beta` correspond to the handles on the reconstruction of the correlated image and amount of common information extracted from the decoder-only side information, respectively. `distortion_loss` selects the distortion evaluating method. Its accepted values are MS-SSIM for the ms-ssim method or MSE for mean squared error.
`verbose_period: 50` indicates that every 50 epochs print the results of the validation dataset.
```
train = True
epochs = 50000
train_batch_size = 1
lr = 0.0001
lmbda = 0.00003 # the lambda value in rate-distortion equation
alpha = 1
beta = 1
distortion_loss = 'MS-SSIM' # can be MS-SSIM or MSE. selects the method by which the distortion is calculated during training
verbose_period = 50 # non-positive value indicates no verbose
```
## Weights and Results parameters
If you wish to save the model weights after training set `save_weights` `True`. `save_output_path` shows the directory path where the model weights are saved.
For the weights, in `save_output_path` a `weight` folder will be created, and the weights will be saved there with the name according to `experiment_name`.
```
save_weights = True
save_output_path = './outputs' # path where results and weights will be saved
experiment_name = 'bls17_with_side_info_MS-SSIM_lambda:3e-05'
```
## Test
If you wish to test the model and save the results set `test` to `True`. If `save_image` is set to `True` then a `results` folder will be created, and the reconstructed images will be saved in `save_output_path/results` during testing, with the results named according to `experiment_name`.
```
test = True
save_image = True
```
## Inference
In order to (only) carry out inference, please open `configs/config.yaml` and change the relevant lines as follows:
```
resize = [128, 256] # we used this crop size for our inference
dataset_path = '.'
train = False
load_weight = True
test = True
save_output_path = './inference'
save_image = True
```
Download the desired weights and put them in `pretrained_weights` folder and put the dataset folder in the root .
Based on the weight you chose, specify the weight name, and the experiment name in `configs/config.yaml`:
```
weight_path: './pretrained_weights/...' # load a specified pre-trained weight
experiment_name: '...' # a handle for the saved results of the inference
```
Also, change `baseline_model` and `use_side_info` parameters in `configs/config.yaml` accordingly.
For example, for the `balle2017+ours` weights, these parameters should be:
```
baseline_model: 'bls17'
use_side_info: True
```
After running the code using the commands in below section, the results will be saved in `inference` folder.
## Saving Custom Configuration
By running this piece of code you can save your configuration as a yaml file file in the configs folder. You can set your configuration file name by changing `config_name` variable.
```
import yaml
config = {
"dataset_name": dataset_name,
"dataset_path": dataset_path,
"resize": resize,
"baseline_model": baseline_model,
"use_side_info": use_side_info,
"num_filters": num_filters,
"cuda": cuda,
"load_weight": load_weight,
"weight_path": weight_path,
"experiment_name": experiment_name,
"train": train,
"epochs": epochs,
"train_batch_size": train_batch_size,
"lr": lr,
"lambda": lmbda,
"distortion_loss": distortion_loss,
"verbose_period": verbose_period,
"save_weights": save_weights,
"save_output_path": save_output_path,
"test": test,
"save_image": save_image
}
config_name = "CUSTOM_CONFIG_FILE_NAME.yaml"
with open('configs/' + config_name) + config_name, 'w') as outfile:
yaml.dump(config, outfile, default_flow_style=None, sort_keys=False)
```
## Running the Model
```
!python main.py --config=configs/$config_name
```
|
github_jupyter
|
# <font color=green> PYTHON PARA DATA SCIENCE - PANDAS
---
# <font color=green> 1. INTRODUÇÃO AO PYTHON
---
# 1.1 Introdução
> Python é uma linguagem de programação de alto nível com suporte a múltiplos paradigmas de programação. É um projeto *open source* e desde seu surgimento, em 1991, vem se tornando uma das linguagens de programação interpretadas mais populares.
>
> Nos últimos anos Python desenvolveu uma comunidade ativa de processamento científico e análise de dados e vem se destacando como uma das linguagens mais relevantes quando o assundo é ciência de dados e machine learning, tanto no ambiente acadêmico como também no mercado.
# 1.2 Instalação e ambiente de desenvolvimento
### Instalação Local
### https://www.python.org/downloads/
### ou
### https://www.anaconda.com/distribution/
### Google Colaboratory
### https://colab.research.google.com
### Verificando versão
```
!python -V
```
# 1.3 Trabalhando com dados
```
import pandas as pd
pd.set_option('display.max_rows', 10)
pd.set_option('display.max_columns', 10)
dataset = pd.read_csv('db.csv', sep = ';')
dataset
dataset.dtypes
dataset[['Quilometragem', 'Valor']].describe()
dataset.info()
```
# <font color=green> 2. TRABALHANDO COM TUPLAS
---
# 2.1 Criando tuplas
Tuplas são sequências imutáveis que são utilizadas para armazenar coleções de itens, geralmente heterogêneos. Podem ser construídas de várias formas:
```
- Utilizando um par de parênteses: ( )
- Utilizando uma vírgula à direita: x,
- Utilizando um par de parênteses com itens separados por vírgulas: ( x, y, z )
- Utilizando: tuple() ou tuple(iterador)
```
```
()
1,2,3
nome = "Teste"
valor = 1
(nome,valor)
nomes_carros = tuple(['Jetta Variant', 'Passat', 'Crossfox', 'DS5'])
nomes_carros
type(nomes_carros)
```
# 2.2 Seleções em tuplas
```
nomes_carros = tuple(['Jetta Variant', 'Passat', 'Crossfox', 'DS5'])
nomes_carros
nomes_carros[0]
nomes_carros[1]
nomes_carros[-1]
nomes_carros[1:3]
nomes_carros = ('Jetta Variant', 'Passat', 'Crossfox', 'DS5', ('Fusca', 'Gol', 'C4'))
nomes_carros
nomes_carros[-1]
nomes_carros[-1][1]
```
# 2.3 Iterando em tuplas
```
nomes_carros = ('Jetta Variant', 'Passat', 'Crossfox', 'DS5')
nomes_carros
for item in nomes_carros:
print(item)
```
### Desempacotamento de tuplas
```
nomes_carros = ('Jetta Variant', 'Passat', 'Crossfox', 'DS5')
nomes_carros
carro_1, carro_2, carro_3, carro_4 = nomes_carros
carro_1
carro_2
carro_3
carro_4
_, A, _, B = nomes_carros
A
B
_, C, *_ = nomes_carros
C
```
## *zip()*
https://docs.python.org/3.6/library/functions.html#zip
```
carros = ['Jetta Variant', 'Passat', 'Crossfox', 'DS5']
carros
valores = [88078.64, 106161.94, 72832.16, 124549.07]
valores
zip(carros, valores)
list(zip(carros, valores))
for carro, valor in zip(carros, valores):
print(carro, valor)
```
# <font color=green> 3. TRABALHANDO COM DICIONÁRIOS
---
# 3.1 Criando dicionários
Listas são coleções sequenciais, isto é, os itens destas sequências estão ordenados e utilizam índices (números inteiros) para acessar os valores.
Os dicionários são coleções um pouco diferentes. São estruturas de dados que representam um tipo de mapeamento. Mapeamentos são coleções de associações entre pares de valores onde o primeiro elemento do par é conhecido como chave (*key*) e o segundo como valor (*value*).
```
dicionario = {key_1: value_1, key_2: value_2, ..., key_n: value_n}
```
https://docs.python.org/3.6/library/stdtypes.html#typesmapping
```
carros = ['Jetta Variant', 'Passat', 'Crossfox']
carros
valores = [88078.64, 106161.94, 72832.16]
valores
carros.index("Passat")
valores[carros.index("Passat")]
valores_carros = {"Jetta Variant": 88078.64, "Passat": 106161.94, "Crossfox": 72832.16}
valores_carros
type(valores_carros)
```
### Criando dicionários com *zip()*
```
list(zip(carros, valores))
valores_carros = dict(zip(carros, valores))
valores_carros
```
# 3.2 Operações com dicionários
```
valores_carros = dict(zip(carros, valores))
valores_carros
```
## *dict[ key ]*
Retorna o valor correspondente à chave (*key*) no dicionário.
```
valores_carros["Passat"]
```
## *key in dict*
Retorna **True** se a chave (*key*) for encontrada no dicionário.
```
import termcolor
from termcolor import colored
is_it = colored('tá lá', 'green') if "Passat" in valores_carros else colored('tá não','red')
print(f'Tá lá? \n R: {is_it}')
is_it = colored('tá lá', 'green') if "Fusqueta" in valores_carros else colored('tá não','red')
print(f'Tá lá? \n R: {is_it}')
is_it = colored('tá não','red') if "Passat" not in valores_carros else colored('tá lá', 'green')
print(f'Tá lá? \n R: {is_it}')
```
## *len(dict)*
Retorna o número de itens do dicionário.
```
len(valores_carros)
```
## *dict[ key ] = value*
Inclui um item ao dicionário.
```
valores_carros["DS5"] = 124549.07
valores_carros
```
## *del dict[ key ]*
Remove o item de chave (*key*) do dicionário.
```
del valores_carros["DS5"]
valores_carros
```
# 3.3 Métodos de dicionários
## *dict.update()*
Atualiza o dicionário.
```
valores_carros
valores_carros.update({'DS5': 124549.07})
valores_carros
valores_carros.update({'DS5': 124549.10, 'Fusca': 75000})
valores_carros
```
## *dict.copy()*
Cria uma cópia do dicionário.
```
copia = valores_carros.copy()
copia
del copia['Fusca']
copia
valores_carros
```
## *dict.pop(key[, default ])*
Se a chave for encontrada no dicionário, o item é removido e seu valor é retornado. Caso contrário, o valor especificado como *default* é retornado. Se o valor *default* não for fornecido e a chave não for encontrada no dicionário um erro será gerado.
```
copia
copia.pop('Passat')
copia
# copia.pop('Passat')
copia.pop('Passat', 'Chave não encontrada')
copia.pop('DS5', 'Chave não encontrada')
copia
```
## *dict.clear()*
Remove todos os itens do dicionário.
```
copia.clear()
copia
```
# 3.4 Iterando em dicionários
## *dict.keys()*
Retorna uma lista contendo as chaves (*keys*) do dicionário.
```
valores_carros.keys()
for key in valores_carros.keys():
print(valores_carros[key])
```
## *dict.values()*
Retorna uma lista com todos os valores (*values*) do dicionário.
```
valores_carros.values()
```
## *dict.items()*
Retorna uma lista contendo uma tupla para cada par chave-valor (*key-value*) do dicionário.
```
valores_carros.items()
for item in valores_carros.items():
print(item)
for key,value in valores_carros.items():
print(key,value)
for key,value in valores_carros.items():
if(value >= 100000):
print(key,value)
dados = {
'Crossfox': {'valor': 72000, 'ano': 2005},
'DS5': {'valor': 125000, 'ano': 2015},
'Fusca': {'valor': 150000, 'ano': 1976},
'Jetta': {'valor': 88000, 'ano': 2010},
'Passat': {'valor': 106000, 'ano': 1998}
}
for item in dados.items():
if(item[1]['ano'] >= 2000):
print(item[0])
```
# <font color=green> 4. FUNÇÕES E PACOTES
---
Funções são unidades de código reutilizáveis que realizam uma tarefa específica, podem receber alguma entrada e também podem retornar alguma resultado.
# 4.1 Built-in function
A linguagem Python possui várias funções integradas que estão sempre acessíveis. Algumas já utilizamos em nosso treinamento: type(), print(), zip(), len(), set() etc.
https://docs.python.org/3.6/library/functions.html
```
dados = {'Jetta Variant': 88078.64, 'Passat': 106161.94, 'Crossfox': 72832.16}
dados
valores = []
for valor in dados.values():
valores.append(valor)
valores
soma = 0
for valor in dados.values():
soma += valor
soma
list(dados.values())
sum(dados.values())
help(print)
print?
```
# 4.2 Definindo funções sem e com parâmetros
### Funções sem parâmetros
#### Formato padrão
```
def <nome>():
<instruções>
```
```
def mean():
valor = (1+2+3)/3
return valor
mean()
```
### Funções com parâmetros
#### Formato padrão
```
def <nome>(<param_1>, <param_2>, ..., <param_n>):
<instruções>
```
```
def mean(lista):
mean = sum(lista)/len(lista)
return mean
media = mean([1,2,3])
print(f'A média é: {media}')
media = mean([65665656,96565454,4565545])
print(f'A média é: {media}')
dados = {
'Crossfox': {'km': 35000, 'ano': 2005},
'DS5': {'km': 17000, 'ano': 2015},
'Fusca': {'km': 130000, 'ano': 1979},
'Jetta': {'km': 56000, 'ano': 2011},
'Passat': {'km': 62000, 'ano': 1999}
}
def km_media(dataset, ano_atual):
for item in dataset.items():
result = item[1]['km'] / (ano_atual - item[1]['ano'])
print(result)
km_media(dados,2019)
```
# 4.3 Definindo funções que retornam valores
### Funções que retornam um valor
#### Formato padrão
```
def <nome>(<param_1>, <param_2>, ..., <param_n>):
<instruções>
return <resultado>
```
```
def mean(lista):
mean = sum(lista)/len(lista)
return mean
result = mean([1,2,3])
result
```
### Funções que retornam mais de um valor
#### Formato padrão
```
def <nome>(<param_1>, <param_2>, ..., <param_n>):
<instruções>
return (<resultado_1>, <resultado_2>, ..., <resultado_n>)
```
```
def mean(lista):
mean = sum(lista)/len(lista)
return (mean,len(lista))
result = mean([1,2,3])
result
result, length = mean([1,2,3])
print(f'{result}, {length}')
dados = {
'Crossfox': {'km': 35000, 'ano': 2005},
'DS5': {'km': 17000, 'ano': 2015},
'Fusca': {'km': 130000, 'ano': 1979},
'Jetta': {'km': 56000, 'ano': 2011},
'Passat': {'km': 62000, 'ano': 1999}
}
def km_media(dataset, ano_atual):
result = {}
for item in dataset.items():
media = item[1]['km'] / (ano_atual - item[1]['ano'])
item[1].update({ 'km_media': media })
result.update({ item[0]: item[1] })
return result
km_media(dados, 2019)
```
# <font color=green> 5. PANDAS BÁSICO
---
**versão: 0.25.2**
Pandas é uma ferramenta de manipulação de dados de alto nível, construída com base no pacote Numpy. O pacote pandas possui estruturas de dados bastante interessantes para manipulação de dados e por isso é muito utilizado por cientistas de dados.
## Estruturas de Dados
### Series
Series são arrays unidimensionais rotulados capazes de armazenar qualquer tipo de dado. Os rótulos das linhas são chamados de **index**. A forma básica de criação de uma Series é a seguinte:
```
s = pd.Series(dados, index = index)
```
O argumento *dados* pode ser um dicionário, uma lista, um array Numpy ou uma constante.
### DataFrames
DataFrame é uma estrutura de dados tabular bidimensional com rótulos nas linha e colunas. Como a Series, os DataFrames são capazes de armazenar qualquer tipo de dados.
```
df = pd.DataFrame(dados, index = index, columns = columns)
```
O argumento *dados* pode ser um dicionário, uma lista, um array Numpy, uma Series e outro DataFrame.
**Documentação:** https://pandas.pydata.org/pandas-docs/version/0.25/
# 5.1 Estruturas de dados
```
import pandas as pd
```
### Criando uma Series a partir de uma lista
```
carros: {'Jetta Variant', 'Passat', 'Crossfox'}
carros
pd.Series(carros)
```
### Criando um DataFrame a partir de uma lista de dicionários
```
dados = [
{'Nome': 'Jetta Variant', 'Motor': 'Motor 4.0 Turbo', 'Ano': 2003, 'Quilometragem': 44410.0, 'Zero_km': False, 'Valor': 88078.64},
{'Nome': 'Passat', 'Motor': 'Motor Diesel', 'Ano': 1991, 'Quilometragem': 5712.0, 'Zero_km': False, 'Valor': 106161.94},
{'Nome': 'Crossfox', 'Motor': 'Motor Diesel V8', 'Ano': 1990, 'Quilometragem': 37123.0, 'Zero_km': False, 'Valor': 72832.16}
]
dataset = pd.DataFrame(dados)
dataset
dataset[['Motor','Valor','Ano', 'Nome', 'Quilometragem', 'Zero_km']]
```
### Criando um DataFrame a partir de um dicionário
```
dados = {
'Nome': ['Jetta Variant', 'Passat', 'Crossfox'],
'Motor': ['Motor 4.0 Turbo', 'Motor Diesel', 'Motor Diesel V8'],
'Ano': [2003, 1991, 1990],
'Quilometragem': [44410.0, 5712.0, 37123.0],
'Zero_km': [False, False, False],
'Valor': [88078.64, 106161.94, 72832.16]
}
dataset = pd.DataFrame(dados)
dataset
```
### Criando um DataFrame a partir de uma arquivo externo
```
dataset = pd.read_csv('db.csv', sep=';', index_col =0)
dataset
dados = {
'Crossfox': {'km': 35000, 'ano': 2005},
'DS5': {'km': 17000, 'ano': 2015},
'Fusca': {'km': 130000, 'ano': 1979},
'Jetta': {'km': 56000, 'ano': 2011},
'Passat': {'km': 62000, 'ano': 1999}
}
def km_media(dataset, ano_atual):
result = {}
for item in dataset.items():
media = item[1]['km'] / (ano_atual - item[1]['ano'])
item[1].update({ 'km_media': media })
result.update({ item[0]: item[1] })
return result
km_media(dados, 2019)
import pandas as pd
carros = pd.DataFrame(km_media(dados, 2019)).T
carros
```
# 5.2 Seleções com DataFrames
### Selecionando colunas
```
dataset.head()
dataset['Valor']
type(dataset['Valor'])
dataset[['Valor']]
type(dataset[['Valor']])
```
### Selecionando linhas - [ i : j ]
<font color=red>**Observação:**</font> A indexação tem origem no zero e nos fatiamentos (*slices*) a linha com índice i é **incluída** e a linha com índice j **não é incluída** no resultado.
```
dataset[0:3]
```
### Utilizando .loc para seleções
<font color=red>**Observação:**</font> Seleciona um grupo de linhas e colunas segundo os rótulos ou uma matriz booleana.
```
dataset.loc[['Passat', 'DS5']]
dataset.loc[['Passat', 'DS5'], ['Motor', 'Ano']]
dataset.loc[:, ['Motor', 'Ano']]
```
### Utilizando .iloc para seleções
<font color=red>**Observação:**</font> Seleciona com base nos índices, ou seja, se baseia na posição das informações.
```
dataset.head()
dataset.iloc[1]
dataset.iloc[[1]]
dataset.iloc[1:4]
dataset.iloc[1:4, [0, 5, 2]]
dataset.iloc[[1,42,22], [0, 5, 2]]
dataset.iloc[:, [0, 5, 2]]
import pandas as pd
dados = {
'Nome': ['Jetta', 'Passat', 'Crossfox', 'DS5', 'Fusca'],
'Motor': ['Motor 4.0 Turbo', 'Motor Diesel', 'Motor Diesel V8', 'Motor 2.0', 'Motor 1.6'],
'Ano': [2019, 2003, 1991, 2019, 1990],
'Quilometragem': [0.0, 5712.0, 37123.0, 0.0, 120000.0],
'Zero_km': [True, False, False, True, False],
'Valor': [88000.0, 106000.0, 72000.0, 89000.0, 32000.0]
}
dataset = pd.DataFrame(dados)
dataset[['Nome', 'Ano', 'Quilometragem', 'Valor']][1:3]
import pandas as pd
dados = {
'Motor': ['Motor 4.0 Turbo', 'Motor Diesel', 'Motor Diesel V8', 'Motor 2.0', 'Motor 1.6'],
'Ano': [2019, 2003, 1991, 2019, 1990],
'Quilometragem': [0.0, 5712.0, 37123.0, 0.0, 120000.0],
'Zero_km': [True, False, False, True, False],
'Valor': [88000.0, 106000.0, 72000.0, 89000.0, 32000.0]
}
dataset = pd.DataFrame(dados, index = ['Jetta', 'Passat', 'Crossfox', 'DS5', 'Fusca'])
dataset.loc[['Passat', 'DS5'], ['Motor', 'Valor']]
dataset.iloc[[1,3], [0,-1]]
```
# 5.3 Queries com DataFrames
```
dataset.head()
dataset.Motor
select = dataset.Motor == 'Motor Diesel'
type(select)
dataset[select]
dataset[(select) & (dataset.Zero_km == True)]
(select) & (dataset.Zero_km == True)
```
### Utilizando o método query
```
dataset.query('Motor == "Motor Diesel" and Zero_km == True')
import pandas as pd
dados = {
'Motor': ['Motor 4.0 Turbo', 'Motor Diesel', 'Motor Diesel V8', 'Motor Diesel', 'Motor 1.6'],
'Ano': [2019, 2003, 1991, 2019, 1990],
'Quilometragem': [0.0, 5712.0, 37123.0, 0.0, 120000.0],
'Zero_km': [True, False, False, True, False],
'Valor': [88000.0, 106000.0, 72000.0, 89000.0, 32000.0]
}
dataset = pd.DataFrame(dados, index = ['Jetta', 'Passat', 'Crossfox', 'DS5', 'Fusca'])
dataset.query('Motor == "Motor Diesel" or Zero_km == True')
dataset.query('Motor == "Motor Diesel" | Zero_km == True')
```
# 5.4 Iterando com DataFrames
```
dataset.head()
for index, row in dataset.iterrows():
if (2019 - row['Ano'] != 0):
dataset.loc[index, "km_media"] = row['Quilometragem'] / 2019 - row['Ano']
else:
dataset.loc[index, "km_media"] = 0
dataset
```
# 5.5 Tratamento de dados
```
dataset.head()
dataset.info()
dataset.Quilometragem.isna()
dataset[dataset.Quilometragem.isna()]
dataset.fillna(0, inplace = True)
dataset
dataset.query('Zero_km == True')
dataset = pd.read_csv('db.csv', sep=';')
dataset.dropna(subset = ['Quilometragem'], inplace = True)
dataset
```
|
github_jupyter
|
<a href="https://colab.research.google.com/github/google/applied-machine-learning-intensive/blob/master/content/03_regression/04_polynomial_regression/colab.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
#### Copyright 2020 Google LLC.
```
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
```
# Polynomial Regression and Overfitting
So far in this course, we have dealt exclusively with linear models. These have all been "straight-line" models where we attempt to draw a straight line that fits a regression.
Today we will start building curved-lined models based on [polynomial equations](https://en.wikipedia.org/wiki/Polynomial).
## Generating Sample Data
Let's start by generating some data based on a second degree polynomial.
```
import numpy as np
import matplotlib.pyplot as plt
num_items = 100
np.random.seed(seed=420)
X = np.random.randn(num_items, 1)
# These coefficients are chosen arbitrarily.
y = 0.6*(X**2) - 0.4*X + 1.3
plt.plot(X, y, 'b.')
plt.show()
```
Let's add some randomness to create a more realistic dataset and re-plot the randomized data points and the fit line.
```
import numpy as np
import matplotlib.pyplot as plt
num_items = 100
np.random.seed(seed=420)
X = np.random.randn(num_items, 1)
# Create some randomness.
randomness = np.random.randn(num_items, 1) / 2
# This is the same equation as the plot above, with added randomness.
y = 0.6*(X**2) - 0.4*X + 1.3 + randomness
X_line = np.linspace(X.min(), X.max(), num=num_items)
y_line = 0.6*(X_line**2) - 0.4*X_line + 1.3
plt.plot(X, y, 'b.')
plt.plot(X_line, y_line, 'r-')
plt.show()
```
That looks much better! Now we can see that a 2-degree polynomial function fits this data reasonably well.
## Polynomial Fitting
We can now see a pretty obvious 2-degree polynomial that fits the scatter plot.
Scikit-learn offers a `PolynomialFeatures` class that handles polynomial combinations for a linear model. In this case, we know that a 2-degree polynomial is a good fit since the data was generated from a polynomial curve. Let's see if the model works.
We begin by creating a `PolynomialFeatures` instance of degree 2.
```
from sklearn.preprocessing import PolynomialFeatures
pf = PolynomialFeatures(degree=2)
X_poly = pf.fit_transform(X)
X.shape, X_poly.shape
```
You might be wondering what the `include_bias` parameter is. By default, it is `True`, in which case it forces the first exponent to be 0.
This adds a constant bias term to the equation. When we ask for no bias we start our exponents at 1 instead of 0.
This preprocessor generates a new feature matrix consisting of all polynomial combinations of the features. Notice that the input shape of `(100, 1)` becomes `(100, 2)` after transformation.
In this simple case, we doubled the number of features since we asked for a 2-degree polynomial and had one input feature. The number of generated features grows exponentially as the number of features and polynomial degrees increases.
## Model Fitting
We can now fit the model by passing our polynomial preprocessing data to the linear regressor.
How close did the intercept and coefficient match the values in the function we used to generate our data?
```
from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(X_poly, y)
lin_reg.intercept_, lin_reg.coef_
```
## Visualization
We can plot our fitted line against the equation we used to generate the data. The fitted line is green, and the actual curve is red.
```
np.random.seed(seed=420)
# Create 100 even-spaced x-values.
X_line_fitted = np.linspace(X.min(), X.max(), num=100)
# Start our equation with the intercept.
y_line_fitted = lin_reg.intercept_
# For each exponent, raise the X value to that exponent and multiply it by the
# appropriate coefficient
for i in range(len(pf.powers_)):
exponent = pf.powers_[i][0]
y_line_fitted = y_line_fitted + \
lin_reg.coef_[0][i] * (X_line_fitted**exponent)
plt.plot(X_line_fitted, y_line_fitted, 'g-')
plt.plot(X_line, y_line, 'r-')
plt.plot(X, y, 'b.')
plt.show()
```
# Overfitting
When using polynomial regression, it can be easy to *overfit* the data so that it performs well on the training data but doesn't perform well in the real world.
To understand overfitting we will create a fake dataset generated off of a linear equation, but we will use a polynomial regression as the model.
```
np.random.seed(seed=420)
# Create 50 points from a linear dataset with randomness.
num_items = 50
X = 6 * np.random.rand(num_items, 1)
y = X + 2 + np.random.randn(num_items, 1)
X_line = np.array([X.min(), X.max()])
y_line = X_line + 2
plt.plot(X_line, y_line, 'r-')
plt.plot(X, y, 'b.')
plt.show()
```
Let's now create a 10 degree polynomial to fit the linear data and fit the model.
```
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
np.random.seed(seed=420)
poly_features = PolynomialFeatures(degree=10, include_bias=False)
X_poly = poly_features.fit_transform(X)
regression = LinearRegression()
regression.fit(X_poly, y)
```
## Visualization
Let's draw the polynomial line that we fit to the data. To draw the line, we need to execute the 10 degree polynomial equation.
$$
y = k_0 + k_1x^1 + k_2x^2 + k_3x^3 + ... + k_9x^9 + k_{10}x^{10}
$$
Coding the above equation by hand is tedious and error-prone. It also makes it difficult to change the degree of the polynomial we are fitting.
Let's see if there is a way to write the code more dynamically, using the `PolynomialFeatures` and `LinearRegression` functions.
The `PolynomialFeatures` class provides us with a list of exponents that we can use for each portion of the polynomial equation.
```
poly_features.powers_
```
The `LinearRegression` class provides us with a list of coefficients that correspond to the powers provided by `PolynomialFeatures`.
```
regression.coef_
```
It also provides an intercept.
```
regression.intercept_
```
Having this information, we can take a set of $X$ values (in the code below we use 100), then run our equation on those values.
```
np.random.seed(seed=420)
# Create 100 even-spaced x-values.
X_line_fitted = np.linspace(X.min(), X.max(), num=100)
# Start our equation with the intercept.
y_line_fitted = regression.intercept_
# For each exponent, raise the X value to that exponent and multiply it by the
# appropriate coefficient
for i in range(len(poly_features.powers_)):
exponent = poly_features.powers_[i][0]
y_line_fitted = y_line_fitted + \
regression.coef_[0][i] * (X_line_fitted**exponent)
```
We can now plot the data points, the actual line used to generate them, and our fitted model.
```
plt.plot(X_line, y_line, 'r-')
plt.plot(X_line_fitted, y_line_fitted, 'g-')
plt.plot(X, y, 'b.')
plt.show()
```
Notice how our line is very wavy, and it spikes up and down to pass through specific data points. (This is especially true for the lowest and highest $x$-values, where the curve passes through them exactly.) This is a sign of overfitting. The line fits the training data reasonably well, but it may not be as useful on new data.
## Using a Simpler Model
The most obvious way to prevent overfitting in this example is to simply reduce the degree of the polynomial.
The code below uses a 2-degree polynomial and seems to fit the data much better. A linear model would work well too.
```
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
poly_features = PolynomialFeatures(degree=2, include_bias=False)
X_poly = poly_features.fit_transform(X)
regression = LinearRegression()
regression.fit(X_poly, y)
X_line_fitted = np.linspace(X.min(), X.max(), num=100)
y_line_fitted = regression.intercept_
for i in range(len(poly_features.powers_)):
exponent = poly_features.powers_[i][0]
y_line_fitted = y_line_fitted + \
regression.coef_[0][i] * (X_line_fitted**exponent)
plt.plot(X_line, y_line, 'r-')
plt.plot(X_line_fitted, y_line_fitted, 'g-')
plt.plot(X, y, 'b.')
plt.show()
```
## Lasso Regularization
It is not always so clear what the "simpler" model choice is. Often, you will have to rely on regularization methods. A **regularization** is a method that penalizes large coefficients, with the aim of shrinking unnecessary coefficients to zero.
Least Absolute Shrinkage and Selection Operator (Lasso) regularization, also called L1 regularization, is a regularization method that adds the sum of the absolute values of the coefficients as a penalty in a cost function.
In scikit-learn, we can use the [Lasso](https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.Lasso.html) model, which performs a linear regression with an L1 regression penalty.
In the resultant graph, you can see that the regression smooths out our polynomial curve quite a bit despite the polynomial being a degree 10 polynomial. Note that Lasso regression can make the impact of less important features completely disappear.
```
from sklearn.linear_model import Lasso
poly_features = PolynomialFeatures(degree=10, include_bias=False)
X_poly = poly_features.fit_transform(X)
lasso_reg = Lasso(alpha=5.0)
lasso_reg.fit(X_poly, y)
X_line_fitted = np.linspace(X.min(), X.max(), num=100)
y_line_fitted = lasso_reg.intercept_
for i in range(len(poly_features.powers_)):
exponent = poly_features.powers_[i][0]
y_line_fitted = y_line_fitted + lasso_reg.coef_[i] * (X_line_fitted**exponent)
plt.plot(X_line, y_line, 'r-')
plt.plot(X_line_fitted, y_line_fitted, 'g-')
plt.plot(X, y, 'b.')
plt.show()
```
## Ridge Regularization
Similar to Lasso regularization, [Ridge](https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.Ridge.html) regularization adds a penalty to the cost function of a model. In the case of Ridge, also called L2 regularization, the penalty is the sum of squares of the coefficients.
Again, we can see that the regression smooths out the curve of our 10-degree polynomial.
```
from sklearn.linear_model import Ridge
poly_features = PolynomialFeatures(degree=10, include_bias=False)
X_poly = poly_features.fit_transform(X)
ridge_reg = Ridge(alpha=0.5)
ridge_reg.fit(X_poly, y)
X_line_fitted = np.linspace(X.min(), X.max(), num=100)
y_line_fitted = ridge_reg.intercept_
for i in range(len(poly_features.powers_)):
exponent = poly_features.powers_[i][0]
y_line_fitted = y_line_fitted + ridge_reg.coef_[0][i] * (X_line_fitted**exponent)
plt.plot(X_line, y_line, 'r-')
plt.plot(X_line_fitted, y_line_fitted, 'g-')
plt.plot(X, y, 'b.')
plt.show()
```
## ElasticNet Regularization
Another common form of regularization is [ElasticNet](https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.ElasticNet.html) regularization. This regularization method combines the concepts of L1 and L2 regularization by applying a penalty containing both a squared value and an absolute value.
```
from sklearn.linear_model import ElasticNet
poly_features = PolynomialFeatures(degree=10, include_bias=False)
X_poly = poly_features.fit_transform(X)
elastic_reg = ElasticNet(alpha=2.0, l1_ratio=0.5)
elastic_reg.fit(X_poly, y)
X_line_fitted = np.linspace(X.min(), X.max(), num=100)
y_line_fitted = elastic_reg.intercept_
for i in range(len(poly_features.powers_)):
exponent = poly_features.powers_[i][0]
y_line_fitted = y_line_fitted + \
elastic_reg.coef_[i] * (X_line_fitted**exponent)
plt.plot(X_line, y_line, 'r-')
plt.plot(X_line_fitted, y_line_fitted, 'g-')
plt.plot(X, y, 'b.')
plt.show()
```
## Other Strategies
Aside from regularization, there are other strategies that can be used to prevent overfitting. These include:
* [Early stopping](https://en.wikipedia.org/wiki/Early_stopping)
* [Cross-validation](https://en.wikipedia.org/wiki/Cross-validation_(statistics)
* [Ensemble methods](https://en.wikipedia.org/wiki/Ensemble_learning)
* Simplifying your model
* Removing features
# Exercises
For these exercises we will work with the [diabetes dataset](https://scikit-learn.org/stable/datasets/index.html#diabetes-dataset) that comes with scikit-learn. The data contains the following features:
1. age
1. sex
1. body mass index (bmi)
1. average blood pressure (bp)
It also contains six measures of blood serum, `s1` through `s6`. The target is a numeric assessment of the progression of the disease over the course of a year.
The data has been standardized.
```
from sklearn.datasets import load_diabetes
import numpy as np
import pandas as pd
data = load_diabetes()
df = pd.DataFrame(data.data, columns=data.feature_names)
df['progression'] = data.target
df.describe()
```
Let's plot how body mass index relates to blood pressure.
```
import matplotlib.pyplot as plt
plt.plot(df['bmi'], df['bp'], 'b.')
plt.show()
```
## Exercise 1: Polynomial Regression
Let's create a model to see if we can map body mass index to blood pressure.
1. Create a 10-degree polynomial preprocessor for our regression
1. Create a linear regression model
1. Fit and transform the `bmi` values with the polynomial features preprocessor
1. Fit the transformed data using the linear regression
1. Plot the fitted line over a scatter plot of the data points
**Student Solution**
```
# Your code goes here
```
---
## Exercise 2: Regularization
Your model from exercise one likely looked like it overfit. Experiment with the Lasso, Ridge, and/or ElasticNet classes in the place of the `LinearRegression`. Adjust the parameters for whichever regularization class you use until you create a line that doesn't look to be under- or over-fitted.
**Student Solution**
```
# Your code goes here
```
---
## Exercise 3: Other Models
Experiment with the [BayesianRidge](https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.BayesianRidge.html). Does its fit line look better or worse than your other models?
**Student Solution**
```
# Your code goes here.
```
Does your fit line look better or worse than your other models?
> *Your Answer Goes Here*
---
|
github_jupyter
|
# Portfolio Variance
```
import sys
!{sys.executable} -m pip install -r requirements.txt
import numpy as np
import pandas as pd
import time
import os
import quiz_helper
import matplotlib.pyplot as plt
%matplotlib inline
plt.style.use('ggplot')
plt.rcParams['figure.figsize'] = (14, 8)
```
### data bundle
```
import os
import quiz_helper
from zipline.data import bundles
os.environ['ZIPLINE_ROOT'] = os.path.join(os.getcwd(), '..', '..','data','module_4_quizzes_eod')
ingest_func = bundles.csvdir.csvdir_equities(['daily'], quiz_helper.EOD_BUNDLE_NAME)
bundles.register(quiz_helper.EOD_BUNDLE_NAME, ingest_func)
print('Data Registered')
```
### Build pipeline engine
```
from zipline.pipeline import Pipeline
from zipline.pipeline.factors import AverageDollarVolume
from zipline.utils.calendars import get_calendar
universe = AverageDollarVolume(window_length=120).top(500)
trading_calendar = get_calendar('NYSE')
bundle_data = bundles.load(quiz_helper.EOD_BUNDLE_NAME)
engine = quiz_helper.build_pipeline_engine(bundle_data, trading_calendar)
```
### View Data¶
With the pipeline engine built, let's get the stocks at the end of the period in the universe we're using. We'll use these tickers to generate the returns data for the our risk model.
```
universe_end_date = pd.Timestamp('2016-01-05', tz='UTC')
universe_tickers = engine\
.run_pipeline(
Pipeline(screen=universe),
universe_end_date,
universe_end_date)\
.index.get_level_values(1)\
.values.tolist()
universe_tickers
len(universe_tickers)
from zipline.data.data_portal import DataPortal
data_portal = DataPortal(
bundle_data.asset_finder,
trading_calendar=trading_calendar,
first_trading_day=bundle_data.equity_daily_bar_reader.first_trading_day,
equity_minute_reader=None,
equity_daily_reader=bundle_data.equity_daily_bar_reader,
adjustment_reader=bundle_data.adjustment_reader)
```
## Get pricing data helper function
```
from quiz_helper import get_pricing
```
## get pricing data into a dataframe
```
returns_df = \
get_pricing(
data_portal,
trading_calendar,
universe_tickers,
universe_end_date - pd.DateOffset(years=5),
universe_end_date)\
.pct_change()[1:].fillna(0) #convert prices into returns
returns_df
```
## Let's look at a two stock portfolio
Let's pretend we have a portfolio of two stocks. We'll pick Apple and Microsoft in this example.
```
aapl_col = returns_df.columns[3]
msft_col = returns_df.columns[312]
asset_return_1 = returns_df[aapl_col].rename('asset_return_aapl')
asset_return_2 = returns_df[msft_col].rename('asset_return_msft')
asset_return_df = pd.concat([asset_return_1,asset_return_2],axis=1)
asset_return_df.head(2)
```
## Factor returns
Let's make up a "factor" by taking an average of all stocks in our list. You can think of this as an equal weighted index of the 490 stocks, kind of like a measure of the "market". We'll also make another factor by calculating the median of all the stocks. These are mainly intended to help us generate some data to work with. We'll go into how some common risk factors are generated later in the lessons.
Also note that we're setting axis=1 so that we calculate a value for each time period (row) instead of one value for each column (assets).
```
factor_return_1 = returns_df.mean(axis=1)
factor_return_2 = returns_df.median(axis=1)
factor_return_l = [factor_return_1, factor_return_2]
```
## Factor exposures
Factor exposures refer to how "exposed" a stock is to each factor. We'll get into this more later. For now, just think of this as one number for each stock, for each of the factors.
```
from sklearn.linear_model import LinearRegression
"""
For now, just assume that we're calculating a number for each
stock, for each factor, which represents how "exposed" each stock is
to each factor.
We'll discuss how factor exposure is calculated later in the lessons.
"""
def get_factor_exposures(factor_return_l, asset_return):
lr = LinearRegression()
X = np.array(factor_return_l).T
y = np.array(asset_return.values)
lr.fit(X,y)
return lr.coef_
factor_exposure_l = []
for i in range(len(asset_return_df.columns)):
factor_exposure_l.append(
get_factor_exposures(factor_return_l,
asset_return_df[asset_return_df.columns[i]]
))
factor_exposure_a = np.array(factor_exposure_l)
print(f"factor_exposures for asset 1 {factor_exposure_a[0]}")
print(f"factor_exposures for asset 2 {factor_exposure_a[1]}")
```
## Variance of stock 1
Calculate the variance of stock 1.
$\textrm{Var}(r_{1}) = \beta_{1,1}^2 \textrm{Var}(f_{1}) + \beta_{1,2}^2 \textrm{Var}(f_{2}) + 2\beta_{1,1}\beta_{1,2}\textrm{Cov}(f_{1},f_{2}) + \textrm{Var}(s_{1})$
```
factor_exposure_1_1 = factor_exposure_a[0][0]
factor_exposure_1_2 = factor_exposure_a[0][1]
common_return_1 = factor_exposure_1_1 * factor_return_1 + factor_exposure_1_2 * factor_return_2
specific_return_1 = asset_return_1 - common_return_1
covm_f1_f2 = np.cov(factor_return_1,factor_return_2,ddof=1) #this calculates a covariance matrix
# get the variance of each factor, and covariances from the covariance matrix covm_f1_f2
var_f1 = covm_f1_f2[0,0]
var_f2 = covm_f1_f2[1,1]
cov_f1_f2 = covm_f1_f2[0][1]
# calculate the specific variance.
var_s_1 = np.var(specific_return_1,ddof=1)
# calculate the variance of asset 1 in terms of the factors and specific variance
var_asset_1 = (factor_exposure_1_1**2 * var_f1) + \
(factor_exposure_1_2**2 * var_f2) + \
2 * (factor_exposure_1_1 * factor_exposure_1_2 * cov_f1_f2) + \
var_s_1
print(f"variance of asset 1: {var_asset_1:.8f}")
```
## Variance of stock 2
Calculate the variance of stock 2.
$\textrm{Var}(r_{2}) = \beta_{2,1}^2 \textrm{Var}(f_{1}) + \beta_{2,2}^2 \textrm{Var}(f_{2}) + 2\beta_{2,1}\beta_{2,2}\textrm{Cov}(f_{1},f_{2}) + \textrm{Var}(s_{2})$
```
factor_exposure_2_1 = factor_exposure_a[1][0]
factor_exposure_2_2 = factor_exposure_a[1][1]
common_return_2 = factor_exposure_2_1 * factor_return_1 + factor_exposure_2_2 * factor_return_2
specific_return_2 = asset_return_2 - common_return_2
# Notice we already calculated the variance and covariances of the factors
# calculate the specific variance of asset 2
var_s_2 = np.var(specific_return_2,ddof=1)
# calcualte the variance of asset 2 in terms of the factors and specific variance
var_asset_2 = (factor_exposure_2_1**2 * var_f1) + \
(factor_exposure_2_2**2 * var_f2) + \
(2 * factor_exposure_2_1 * factor_exposure_2_2 * cov_f1_f2) + \
var_s_2
print(f"variance of asset 2: {var_asset_2:.8f}")
```
## Covariance of stocks 1 and 2
Calculate the covariance of stock 1 and 2.
$\textrm{Cov}(r_{1},r_{2}) = \beta_{1,1}\beta_{2,1}\textrm{Var}(f_{1}) + \beta_{1,1}\beta_{2,2}\textrm{Cov}(f_{1},f_{2}) + \beta_{1,2}\beta_{2,1}\textrm{Cov}(f_{1},f_{2}) + \beta_{1,2}\beta_{2,2}\textrm{Var}(f_{2})$
```
# TODO: calculate the covariance of assets 1 and 2 in terms of the factors
cov_asset_1_2 = (factor_exposure_1_1 * factor_exposure_2_1 * var_f1) + \
(factor_exposure_1_1 * factor_exposure_2_2 * cov_f1_f2) + \
(factor_exposure_1_2 * factor_exposure_2_1 * cov_f1_f2) + \
(factor_exposure_1_2 * factor_exposure_2_2 * var_f2)
print(f"covariance of assets 1 and 2: {cov_asset_1_2:.8f}")
```
## Quiz 1: calculate portfolio variance
We'll choose stock weights for now (in a later lesson, you'll learn how to use portfolio optimization that uses alpha factors and a risk factor model to choose stock weights).
$\textrm{Var}(r_p) = x_{1}^{2} \textrm{Var}(r_1) + x_{2}^{2} \textrm{Var}(r_2) + 2x_{1}x_{2}\textrm{Cov}(r_{1},r_{2})$
```
weight_1 = 0.60
weight_2 = 0.40
# TODO: calculate portfolio variance
var_portfolio = # ...
print(f"variance of portfolio is {var_portfolio:.8f}")
```
## Quiz 2: Do it with Matrices!
Create matrices $\mathbf{F}$, $\mathbf{B}$ and $\mathbf{S}$, where
$\mathbf{F}= \begin{pmatrix}
\textrm{Var}(f_1) & \textrm{Cov}(f_1,f_2) \\
\textrm{Cov}(f_2,f_1) & \textrm{Var}(f_2)
\end{pmatrix}$
is the covariance matrix of factors,
$\mathbf{B} = \begin{pmatrix}
\beta_{1,1}, \beta_{1,2}\\
\beta_{2,1}, \beta_{2,2}
\end{pmatrix}$
is the matrix of factor exposures, and
$\mathbf{S} = \begin{pmatrix}
\textrm{Var}(s_i) & 0\\
0 & \textrm{Var}(s_j)
\end{pmatrix}$
is the matrix of specific variances.
$\mathbf{X} = \begin{pmatrix}
x_{1} \\
x_{2}
\end{pmatrix}$
### Concept Question
What are the dimensions of the $\textrm{Var}(r_p)$ portfolio variance? Given this, when choosing whether to multiply a row vector or a column vector on the left and right sides of the $\mathbf{BFB}^T$, which choice helps you get the dimensions of the portfolio variance term?
In other words:
Given that $\mathbf{X}$ is a column vector, which makes more sense?
$\mathbf{X}^T(\mathbf{BFB}^T + \mathbf{S})\mathbf{X}$ ?
or
$\mathbf{X}(\mathbf{BFB}^T + \mathbf{S})\mathbf{X}^T$ ?
## Answer 2 here:
## Quiz 3: Calculate portfolio variance using matrices
```
# TODO: covariance matrix of factors
F = # ...
F
# TODO: matrix of factor exposures
B = # ...
B
# TODO: matrix of specific variances
S = # ...
S
```
#### Hint for column vectors
Try using [reshape](https://docs.scipy.org/doc/numpy-1.15.1/reference/generated/numpy.reshape.html)
```
# TODO: make a column vector for stock weights matrix X
X = # ...
X
# TODO: covariance matrix of assets
var_portfolio = # ...
print(f"portfolio variance is \n{var_portfolio[0][0]:.8f}")
```
## Solution
[Solution notebook is here](portfolio_variance_solution.ipynb)
|
github_jupyter
|
# Exploring Weather Trends
### by Phone Thiri Yadana
In this project, we will analyze Gobal vs Singapore weather data across 10 Years Moving Average.
[<img src="./new24397338.png"/>](https://www.vectorstock.com/royalty-free-vector/kawaii-world-and-thermometer-cartoon-vector-24397338)
-------------
```
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
#load data
global_df = pd.read_csv("Data/global_data.csv")
city_df = pd.read_csv("Data/city_data.csv")
city_list_df = pd.read_csv("Data/city_list.csv")
```
## Check info, duplicate or missing data
```
global_df.head()
global_df.tail()
global_df.shape
sum(global_df.duplicated())
global_df.info()
city_df.head()
city_df.shape
city_df.info()
sum(city_df.duplicated())
city_list_df.head()
city_list_df.shape
city_list_df.info()
sum(city_list_df.duplicated())
```
## Calculate Moving Average
### Global Temperature
```
#yearly plot
plt.plot(global_df["year"], global_df["avg_temp"])
# 10 years Moving Avearge
global_df["10 Years MA"] = global_df["avg_temp"].rolling(window=10).mean()
global_df.iloc[8:18, :]
#10 years Moving Average
plt.plot(global_df["year"], global_df["10 Years MA"])
```
### Specific City Temperature (Singapore)
```
city_df.head()
singapore_df = city_df[city_df["country"] == "Singapore"]
singapore_df.head()
singapore_df.tail()
#check which rows are missing values
singapore_df[singapore_df["avg_temp"].isnull()]
```
As singapore data are missing from 1826 till 1862, so it won't make sense to compare temperature during those period.
```
singapore_df = singapore_df[singapore_df["year"] >= 1863]
# to make sure, check again for null values
singapore_df.info()
singapore_df.head()
# calculate 10 years moving average
singapore_df["10 Years MA"] = singapore_df["avg_temp"].rolling(window=10).mean()
singapore_df.iloc[8:18, :]
plt.plot(singapore_df["year"], singapore_df["10 Years MA"])
```
## Compare with Global Data (10 Years Moving Average)
```
years = global_df.query('year >= 1872 & year <= 2013')[["year"]]
global_ma = global_df.query('year >= 1872 & year <= 2013')[["10 Years MA"]]
singapore_ma = singapore_df.query('year >= 1872 & year <= 2013')["10 Years MA"]
plt.figure(figsize=[10,5])
plt.grid(True)
plt.plot(years, global_ma, label = "Global")
plt.plot(years,singapore_ma, label = "Singapore")
plt.xlabel("Year")
plt.ylabel("Temperature (C)")
plt.title("Temperature in Singapore vs Global (10 Years Moving Average)")
plt.legend()
plt.show()
global_ma.describe()
singapore_ma.describe()
```
----------------------
# Observations:
- As per the findings, we can see in the plot that both Global and Specific City (In this case: Singapore) temperature are rising over the years.
- There are certain ups and downs before 1920 and since then Temperatures have been steadily increasing.
|
github_jupyter
|
[0: NumPy and the ndarray](gridded_data_tutorial_0.ipynb) | **1: Introduction to xarray** | [2: Daymet data access](gridded_data_tutorial_2.ipynb) | [3: Investigating SWE at Mt. Rainier with Daymet](gridded_data_tutorial_3.ipynb)
# Notebook 1: Introduction to xarray
Waterhackweek 2020 | Steven Pestana ([email protected])
**By the end of this notebook you will be able to:**
* Create xarray DataArrays and Datasets
* Index and slice DataArrays and Datasets
* Make plots using xarray objects
* Export xarray Datasets as NetCDF or CSV files
---
#### What do we mean by "gridded data"?
Broadly speaking, this can mean any data with a corresponding location in one or more dimensions. Typically, our dimensions represent points on the Earth's surface in two or three dimensions (latitude, longitude, and elevation), and often include time as an additional dimension. You may also hear the term "raster" data, which also means data points on some grid. These multi-dimensional datasets can be thought of as 2-D images, stacks of 2-D images, or data "cubes" in 3 or more dimensions.
Examples of gridded data:
* Satellite images of Earth's surface, where each pixel represents reflection or emission at some wavelength
* Climate model output, where the model is evaluated at discrete nodes or grid cells
Examples of raster/gridded data formats that combine multi-dimensional data along with metadata in a single file:
* [NetCDF](https://www.unidata.ucar.edu/software/netcdf/docs/) (Network Common Data Form) for model data, satellite imagery, and more
* [GeoTIFF](https://trac.osgeo.org/geotiff/) for georeferenced raster imagery (satellite images, digital elevation models, maps, and more)
* [HDF-EOS](https://earthdata.nasa.gov/esdis/eso/standards-and-references/hdf-eos5) (Hierarchical Data Format - Earth Observing Systems)
* [GRIB](https://en.wikipedia.org/wiki/GRIB) (GRIdded Binary) for meteorological data
**How can we easily work with these types of data in python?**
Some python packages for working with gridded data:
* [rasterio](https://rasterio.readthedocs.io/en/latest/)
* [xarray](https://xarray.pydata.org/en/stable/)
* [rioxarray](https://corteva.github.io/rioxarray/stable/)
* [cartopy](https://scitools.org.uk/cartopy/docs/latest/)
**Today we'll be using xarray!**
---
# xarray
The [xarray](https://xarray.pydata.org/) library allows us to read, manipulate, and create **labeled** multi-dimensional arrays and datasets, such as [NetCDF](https://www.unidata.ucar.edu/software/netcdf/) files.
In the image below, we can imagine having two "data cubes" (3-dimensional data arrays) of temperature and precipitation values, each of which corresponds to a particular x and y spatial coordinate, and t time step.
<img src="https://xarray.pydata.org/en/stable/_images/dataset-diagram.png" width=700>
Let's import xarray and start to explore its features...
```
# import the package, and give it the alias "xr"
import xarray as xr
# we will also be using numpy and pandas, import both of these
import numpy as np
import pandas as pd
# for plotting, import matplotlib.pyplot
import matplotlib.pyplot as plt
# tell jupyter to display plots "inline" in the notebook
%matplotlib inline
```
---
# DataArrays
Similar to the `numpy.ndarray` object, the `xarray.DataArray` is a multi-dimensional array, with the addition of labeled dimensions, coordinates, and other metadata. A [DataArray](https://xarray.pydata.org/en/stable/generated/xarray.DataArray.html) contains the following:
* `values` which store the actual data values in a `numpy.ndarray`
* `dims` are the names for each dimension of the `values` array
* `coords` are arrays of labels for each point
* `attrs` is a [dictionary](https://docs.python.org/3/tutorial/datastructures.html#dictionaries) that can contain additional metadata
**Let's create some fake air temperature data to see how these different parts work together to form a DataArray.**
Our goal here is to have 100 years of annual maximum air temperature data for a 10 by 10 grid in a DataArray. (Our data will have a shape of 100 x 10 x 10)
I'm going to use a numpy function to generate some random numbers that are [normally distributed](https://numpy.org/devdocs/reference/random/generated/numpy.random.normal.html) (`np.random.normal()`).
```
# randomly generated annual maximum air temperature data for a 10 by 10 grid
# choose a mean and standard deviation for our random data
mean = 20
standard_deviation = 5
# specify that we want to generate 100 x 10 x 10 random samples
samples = (100, 10, 10)
# generate the random samples
air_temperature_max = np.random.normal(mean, standard_deviation, samples)
# look at this ndarray we just made
air_temperature_max
# look at the shape of this ndarray
air_temperature_max.shape
```
`air_temperature` will be the `values` within the DataArray. It is a three-dimensional array, and we've given it a shape of 100x10x10.
The three dimensions will need names (`dims`) and labels (`coords`)
**Make the `coords` that will be our 100 years**
```
# Make a sequence of 100 years to be our time dimension
years = pd.date_range('1920', periods=100, freq ='1Y')
```
**Make the `coords` that will be our longitudes and latitudes**
```
# Make a sequence of linearly spaced longitude and latitude values
lon = np.linspace(-119, -110, 10)
lat = np.linspace(30, 39, 10)
```
**Make the `dims` names**
```
# We can call our dimensions time, lat, and lon corresponding to the dimensions with lengths 100 (years) and 10 (lat and lon) respectively
dimensions = ['time', 'lat', 'lon']
```
**Finally we can create a metadata dictionary which will be included in the DataArray**
```
metadata = {'units': 'C',
'description': 'maximum annual air temperature'}
```
**Now that we have all the individual components of an xarray DataArray, we can create it**
```
tair_max = xr.DataArray(air_temperature_max,
coords=[years, lat, lon],
dims=dimensions,
name='tair_max',
attrs=metadata)
```
**Inspect the DataArray we just created**
```
tair_max
# Get the DataArray dimensions (labels for coordinates)
tair_max.dims
# Get the DataArray coordinates
tair_max.coords
# Look at our attributes
tair_max.attrs
# Take a look at the data values
tair_max.values
```
---
## DataArray indexing/slicing methods
DataArrays can be [indexed or sliced](https://xarray.pydata.org/en/stable/indexing.html) much like ndarrays, but with the addition of using labels.
| Dimension lookup | Index lookup | DataArray syntax |
| --- | --- | --- |
| positional | by integer | `da[:,0]` |
| positional | by label | `da.loc[:,'east_watershed']` |
| by name | by integer | `da.isel(watershed=0)` |
| by name | by label | `da.sel(watershed='east_watershed')` |
Let's select by name and by label, air temperature for just one year, and plot it. (Conveniently, x-array will add axes labels and a title by default.)
```
tair_max.sel(time='2019').plot()
```
Similarly we can select by longitude and latitude to plot a timeseries. (We made this easy on ourselves here by choosing whole number integers for our longitude and latitude)
```
tair_max.sel(lat=34, lon=-114).plot()
```
Now let's select a shorter time range using a `slice()` to plot data for this location.
```
tair_max.sel(lat=34, lon=-114, time=slice('2000','2020')).plot()
```
And if we try to plot the whole DataArray, xarray gives us a histogram!
```
tair_max.plot()
```
---
# Datasets
Similar to the `pandas.dataframe`, the `xarray.Dataset` contains one or more labeled `xarray.DataArray` objects.
We can create a [Dataset](https://xarray.pydata.org/en/stable/data-structures.html#dataset) with our simulated data here.
**First, create a two more DataArrays with annual miminum air temperatures, and annual cumulative precipitation**
```
# randomly generated annual minimum air temperature data for a 10 by 10 grid
air_temperature_min = np.random.normal(-10, 10, (100, 10, 10))
# randomly generated annualcumulative precipitation data for a 10 by 10 grid
cumulative_precip = np.random.normal(100, 25, (100, 10, 10))
```
Make the DataArrays (note that we're using the same `coords` and `dims` as our first maximum air temperature DataArray)
```
tair_min = xr.DataArray(air_temperature_min,
coords=[years, lat, lon],
dims=dimensions,
name='tair_min',
attrs={'units':'C',
'description': 'minimum annual air temperature'})
precip = xr.DataArray(cumulative_precip,
coords=[years, lat, lon],
dims=dimensions,
name='cumulative_precip',
attrs={'units':'cm',
'description': 'annual cumulative precipitation'})
```
**Now merge our two DataArrays and create a Dataset.**
```
my_data = xr.merge([tair_max, tair_min, precip])
# inspect the Dataset
my_data
```
## Dataset indexing/slicing methods
Datasets can also be [indexed or sliced](https://xarray.pydata.org/en/stable/indexing.html) using the `.isel()` or `.sel()` methods.
| Dimension lookup | Index lookup | Dataset syntax |
| --- | --- | --- |
| positional | by integer | *n/a* |
| positional | by label | *n/a* |
| by name | by integer | `ds.isel(location=0)` |
| by name | by label | `ds.sel(location='stream_gage_1')` |
**Select with `.sel()` temperatures and precipitation for just one grid cell**
```
# by name, by label
my_data.sel(lon='-114', lat='35')
```
**Select with `.isel()` temperatures and precipitation for just one year**
```
# by name, by integer
my_data.isel(time=0)
```
---
## Make some plots:
Using our indexing/slicing methods, create some plots showing 1) a timseries of all three variables at a single point, then 2) plot some maps of each variable for two points in time.
```
# 1) create a timeseries for the two temperature variables for a single location
# create a figure with 2 rows and 1 column of subplots
fig, ax = plt.subplots(nrows=2, ncols=1, figsize=(10,7), tight_layout=True)
# pick a longitude and latitude in our dataset
my_lon=-114
my_lat=35
# first subplot
# Plot tair_max
my_data.sel(lon=my_lon, lat=my_lat).tair_max.plot(ax=ax[0], color='r', linestyle='-', label='Tair_max')
# Plot tair_min
my_data.sel(lon=my_lon, lat=my_lat).tair_min.plot(ax=ax[0], color='b', linestyle='--', label='Tair_max')
# Add a title
ax[0].set_title('Annual maximum and minimum air temperatures at {}, {}'.format(my_lon,my_lat))
# Add a legend
ax[0].legend(loc='lower left')
# second subplot
# Plot precip
my_data.sel(lon=my_lon, lat=my_lat).cumulative_precip.plot(ax=ax[1], color='black', linestyle='-', label='Cumulative Precip.')
# Add a title
ax[1].set_title('Annualcumulative precipitation at {}, {}'.format(my_lon,my_lat))
# Add a legend
ax[1].legend(loc='lower left')
# Save the figure
plt.savefig('my_data_plot_timeseries.jpg')
# 2) plot maps of temperature and precipitation for two years
# create a figure with 2 rows and 3 columns of subplots
fig, ax = plt.subplots(nrows=2, ncols=3, figsize=(15,7), tight_layout=True)
# The two years we want to plot
year1 = '1980'
year2 = '2019'
# Plot tair_max for the year 1980
my_data.sel(time=year1).tair_max.plot(ax=ax[0,0], cmap='RdBu_r', vmin=-20, vmax=40)
# set a title for this subplot
ax[0,0].set_title('Tair_max {}'.format(year1));
# Plot tair_max for the year 1980
my_data.sel(time=year1).tair_min.plot(ax=ax[0,1], cmap='RdBu_r', vmin=-20, vmax=40)
# set a title for this subplot
ax[0,1].set_title('Tair_min {}'.format(year1));
# Plot tair_max for the year 1980
my_data.sel(time=year1).cumulative_precip.plot(ax=ax[0,2], cmap='Blues')
# set a title for this subplot
ax[0,2].set_title('Precip {}'.format(year1));
# Plot tair_max for the year 2019
my_data.sel(time=year2).tair_max.plot(ax=ax[1,0], cmap='RdBu_r', vmin=-20, vmax=40)
# set a title for this subplot
ax[1,0].set_title('Tair_max {}'.format(year2));
# Plot tair_max for the year 2019
my_data.sel(time=year2).tair_min.plot(ax=ax[1,1], cmap='RdBu_r', vmin=-20, vmax=40)
# set a title for this subplot
ax[1,1].set_title('Tair_min {}'.format(year2));
# Plot tair_max for the year 2019
my_data.sel(time=year2).cumulative_precip.plot(ax=ax[1,2], cmap='Blues')
# set a title for this subplot
ax[1,2].set_title('Precip {}'.format(year2));
# save the figure as a jpg image
plt.savefig('my_data_plot_rasters.jpg')
```
---
## Save our data to a file:
**As a NetCDF file:**
```
my_data.to_netcdf('my_data.nc')
```
**We can also convert a Dataset or DataArray to a pandas dataframe**
```
my_data.to_dataframe()
```
**Via a pandas dataframe, save our data to a csv file**
```
my_data.to_dataframe().to_csv('my_data.csv')
```
|
github_jupyter
|
# Big Query Connector - Quick Start
The BigQuery connector enables you to read/write data within BigQuery with ease and integrate it with YData's platform.
Reading a dataset from BigQuery directly into a YData's `Dataset` allows its usage for Data Quality, Data Synthetisation and Preprocessing blocks.
## Storage and Performance Notes
BigQuery is not intended to hold large volumes of data as a pure data storage service. Its main advantages are based on the ability to execute SQL-like queries on existing tables which can efficiently aggregate data into new views. As such, for storage purposes we advise the use of Google Cloud Storage and provide the method `write_query_to_gcs`, available from the `BigQueryConnector`, that allows the user to export a given query to a Google Cloud Storage object.
```
from ydata.connectors import BigQueryConnector
from ydata.utils.formats import read_json
# Load your credentials from a file\n",
token = read_json('{insert-path-to-credentials}')
# Instantiate the Connector
connector = BigQueryConnector(project_id='{insert-project-id}', keyfile_dict=token)
# Load a dataset
data = connector.query(
"SELECT * FROM {insert-dataset}.{insert-table}"
)
# Load a sample of a dataset
small_data = connector.query(
"SELECT * FROM {insert-dataset}.{insert-table}"
n_sample=10_000
)
# Check the available datasets
connector.datasets
# Check the available tables for a given dataset
connector.list_tables('{insert-dataset}')
connector.table_schema(dataset='{insert-dataset}', table='{insert-table}')
```
## Advanced
With `BigQueryConnector`, you can access useful properties and methods directly from the main class.
```
# List the datasets of a given project
connector.datasets
# Access the BigQuery Client
connector.client
# Create a new dataset
connector.get_or_create_dataset(dataset='{insert-dataset}')
# Delete a dataset. WARNING: POTENTIAL LOSS OF DATA
# connector.delete_table_if_exists(dataset='{insert-dataset}', table='{insert-table}')
# Delete a dataset. WARNING: POTENTIAL LOSS OF DATA
# connector.delete_dataset_if_exists(dataset='{insert-dataset}')
```
### Example #1 - Execute Pandas transformations and store to BigQuery
```
# export data to pandas
# small_df = small_data.to_pandas()
#
# DO TRANSFORMATIONS
# (...)
#
# Write results to BigQuery table
# connector.write_table_from_data(data=small_df, dataset='{insert-dataset}', table='{insert-table}')
```
### Example #2 - Write a BigQuery results to Google Cloud Storage
```
# Run a query in BigQuery and store it in Google Cloud Storage
# connector.write_query_to_gcs(query="{insert-query}",
# path="gs://{insert-bucket}/{insert-filepath}")
```
|
github_jupyter
|
# Developing a Pretrained Alexnet model using ManufacturingNet
###### To know more about the manufacturingnet please visit: http://manufacturingnet.io/
```
import ManufacturingNet
import numpy as np
```
First we import manufacturingnet. Using manufacturingnet we can create deep learning models with greater ease.
It is important to note that all the dependencies of the package must also be installed in your environment
##### Now we first need to download the data. You can use our dataset class where we have curated different types of datasets and you just need to run two lines of code to download the data :)
```
from ManufacturingNet import datasets
datasets.CastingData()
```
##### Alright! Now please check your working directory. The data should be present inside it. That was super easy !!
The Casting dataset is an image dataset with 2 classes. The task that we need to perform using Pretrained Alexnet is classification. ManufacturingNet has also provided different datasets in the package which the user can choose depending on type of application
Pretrained models use Imagefolder dataset from pytorch and image size is (224,224,channels). The pretrained model needs the root folder path of train and test images(Imagefolder format). Manufacturing pretrained models have image resizing feature.
```
#paths of root folder
train_data_address='casting_data/train/'
val_data_address='casting_data/test/'
```
#### Now all we got to do is import the pretrained model class and answer a few simple questions and we will be all set. The manufacturingnet has been designed in a way to make things easy for user and provide them the tools to implement complex used
```
from ManufacturingNet.models import AlexNet
# from ManufacturingNet.models import ResNet
# from ManufacturingNet.models import DenseNet
# from ManufacturingNet.models import MobileNet
# from ManufacturingNet.models import GoogleNet
# from ManufacturingNet.models import VGG
```
###### We import the pretrained Alexnet model (AlexNet) from package and answer a few simple questions
```
model=AlexNet(train_data_address,val_data_address)
# model=ResNet(train_data_address,val_data_address)
# model=DenseNet(train_data_address,val_data_address)
# model=MobileNet(train_data_address,val_data_address)
# model=GoogleNet(train_data_address,val_data_address)
# model=VGG(train_data_address,val_data_address)
```
Alright! Its done you have built your pretrained AlexNet using the manufacturingnet package. Just by answering a few simple questions. It is really easy
The Casting dataset contains more 7000 images including training and testing. The results produced above are just for introducing ManufacturingNet. Hence, only 3 epochs were performed. Better results can be obtained by running more epochs.
A few pointers about developing the pretrained models. These models require image size to be (224,224,channels) as the input size of the image. The number of classes for classification can be varied and is handled by the package. User can use only the architecture without using the pretrained weights.
The loss functions, optimizer, epochs, scheduler should be chosen by the user. The model summary, training accuracy, validation accuracy, confusion matrix, Loss vs epoch are also provided by the package.
ManufacturingNet provides many pretrained models with similar scripts. ManufacturingNet offer ResNet(different variants), AlexNet, GoogleNet, VGG(different variants) and DenseNet(different variants).
Users can follow a similar tutorial on pretrained ResNet(different variants).
|
github_jupyter
|
```
# reload packages
%load_ext autoreload
%autoreload 2
```
### Choose GPU (this may not be needed on your computer)
```
%env CUDA_DEVICE_ORDER=PCI_BUS_ID
%env CUDA_VISIBLE_DEVICES=''
```
### load packages
```
from tfumap.umap import tfUMAP
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
from tqdm.autonotebook import tqdm
import umap
import pandas as pd
```
### Load dataset
```
from sklearn.datasets import make_moons
X_train, Y_train = make_moons(1000, random_state=0, noise=0.1)
X_test, Y_test = make_moons(1000, random_state=1, noise=0.1)
X_valid, Y_valid = make_moons(1000, random_state=2, noise=0.1)
def norm(x):
return (x - np.min(x)) / (np.max(x) - np.min(x))
X_train = norm(X_train)
X_valid = norm(X_valid)
X_test = norm(X_test)
X_train_flat = X_train
X_test_flat = X_test
plt.scatter(X_test[:,0], X_test[:,1], c=Y_test)
```
### Create model and train
### define networks
```
dims = (2)
n_components = 2
from tfumap.vae import VAE, Sampling
encoder_inputs = tf.keras.Input(shape=dims)
x = tf.keras.layers.Flatten()(encoder_inputs)
x = tf.keras.layers.Dense(units=100, activation="relu")(x)
x = tf.keras.layers.Dense(units=100, activation="relu")(x)
x = tf.keras.layers.Dense(units=100, activation="relu")(x)
z_mean = tf.keras.layers.Dense(n_components, name="z_mean")(x)
z_log_var = tf.keras.layers.Dense(n_components, name="z_log_var")(x)
z = Sampling()([z_mean, z_log_var])
encoder = tf.keras.Model(encoder_inputs, [z_mean, z_log_var, z], name="encoder")
encoder.summary()
latent_inputs = tf.keras.Input(shape=(n_components,))
x = tf.keras.layers.Dense(units=100, activation="relu")(latent_inputs)
x = tf.keras.layers.Dense(units=100, activation="relu")(x)
x = tf.keras.layers.Dense(units=100, activation="relu")(x)
decoder_outputs = tf.keras.layers.Dense(units=2, activation="sigmoid")(x)
decoder = tf.keras.Model(latent_inputs, decoder_outputs, name="decoder")
decoder.summary()
```
### Create model and train
```
X_train.shape
vae = VAE(encoder, decoder)
vae.compile(optimizer=tf.keras.optimizers.Adam())
vae.fit(X_train, epochs=500, batch_size=128)
z = vae.encoder.predict(X_train)[0]
```
### Plot model output
```
fig, ax = plt.subplots( figsize=(8, 8))
sc = ax.scatter(
z[:, 0],
z[:, 1],
c=Y_train.astype(int)[:len(z)].flatten(),
cmap="tab10",
s=0.1,
alpha=0.5,
rasterized=True,
)
ax.axis('equal')
ax.set_title("UMAP in Tensorflow embedding", fontsize=20)
plt.colorbar(sc, ax=ax);
z_recon = decoder.predict(z)
fig, ax = plt.subplots()
ax.scatter(z_recon[:,0], z_recon[:,1], s = 1, c = z_recon[:,0], alpha = 1)
ax.axis('equal')
```
### Save output
```
from tfumap.paths import ensure_dir, MODEL_DIR
dataset = 'moons'
output_dir = MODEL_DIR/'projections'/ dataset / 'vae'
ensure_dir(output_dir)
encoder.save(output_dir / 'encoder')
decoder.save(output_dir / 'encoder')
#loss_df.to_pickle(output_dir / 'loss_df.pickle')
np.save(output_dir / 'z.npy', z)
```
|
github_jupyter
|
# Power Production Project for *Fundamentals of Data Analysis* at GMIT
by Radek Wojtczak G00352936<br>
**Instructions:**
>In this project you must perform and explain simple linear regression using Python
on the powerproduction dataset. The goal is to accurately predict wind turbine power output from wind speed values using the data set as a basis.
Your submission must be in the form of a git repository containing, at a minimum, the
following items:
>1. Jupyter notebook that performs simple linear regression on the data set.
>2. In that notebook, an explanation of your regression and an analysis of its accuracy.
>3. Standard items in a git repository such as a README.
>To enhance your submission, you might consider comparing simple linear regression to
other types of regression on this data set.
# Wind power
**How does a wind turbine work?**
Wind turbines can turn the power of wind into the electricity we all use to power our homes and businesses. They can be stand-alone, supplying just one or a very small number of homes or businesses, or they can be clustered to form part of a wind farm.
The visible parts of the wind farm that we’re all used to seeing – those towering white or pale grey turbines. Each of these turbines consists of a set of blades, a box beside them called a nacelle and a shaft. The wind – and this can be just a gentle breeze – makes the blades spin, creating kinetic energy. The blades rotating in this way then also make the shaft in the nacelle turn and a generator in the nacelle converts this kinetic energy into electrical energy.

**What happens to the wind-turbine generated electricity next?**
To connect to the national grid, the electrical energy is then passed through a transformer on the site that increases the voltage to that used by the national electricity system. It’s at this stage that the electricity usually moves onto the National Grid transmission network, ready to then be passed on so that, eventually, it can be used in homes and businesses. Alternatively, a wind farm or a single wind turbine can generate electricity that is used privately by an individual or small set of homes or businesses.
**How strong does the wind need to be for a wind turbine to work?**
Wind turbines can operate in anything from very light to very strong wind speeds. They generate around 80% of the time, but not always at full capacity. In really high winds they shut down to prevent damage.

**Where are wind farms located?**
Wind farms tend to be located in the windiest places possible, to maximise the energy they can create – this is why you’ll be more likely to see them on hillsides or at the coast. Wind farms that are in the sea are called offshore wind farms, whereas those on dry land are termed onshore wind farms.
**Wind energy in Ireland**
Wind energy is currently the largest contributing resource of renewable energy in Ireland. It is both Ireland’s largest and cheapest renewable electricity resource. In 2018 Wind provided 85% of Ireland’s renewable electricity and 30% of our total electricity demand. It is the second greatest source of electricity generation in Ireland after natural gas. Ireland is one of the leading countries in its use of wind energy and 3rd place worldwide in 2018, after Denmark and Uruguay.

### Exploring dataset:
```
# importing all necessary packages
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model as lm
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
import seaborn as sns
from sklearn import metrics
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import r2_score
from sklearn.preprocessing import LabelEncoder
from sklearn.preprocessing import PolynomialFeatures
from matplotlib import pyplot
# loading our dataset, seting columns names and changing index to start from 1 instead of 0
df = pd.read_csv('dataset/powerproduction.txt', sep=",", header=None)
df.columns = ["speed", "power"]
df = df[1:]
df
# checking for nan values
count_nan = len(df) - df.count()
count_nan
# Converting Strings to Floats
df = df.astype(float)
# showing first 20 results
df.head(20)
# basic statistic of speed column
df['speed'].describe()
# basic statistic of power column
df['power'].describe()
# histogram of 'speed' data
sns.set_style('darkgrid')
sns.distplot(df['speed'])
plt.show()
```
We can clearly see normal distribution in above 'speed' column data.
```
# histogram od 'power' data
sns.set_style('darkgrid')
sns.distplot(df['power'])
plt.show()
```
As we can see above this distribution look like bimodal distribution.
```
# scatter plot of our dataset
plt.xlabel('wind speed',fontsize = 16)
plt.ylabel('power',fontsize = 16)
plt.scatter(df['speed'],df['power'])
plt.show()
df
```
## Regression
Regression analysis is a set of statistical methods used for the estimation of relationships between a dependent variable and one or more independent variables. It can be utilized to assess the strength of the relationship between variables and for modeling the future relationship between them.
The term regression is used when you try to find the relationship between variables.
In Machine Learning, and in statistical modeling, that relationship is used to predict the outcome of future events.
## Linear Regression
The term “linearity” in algebra refers to a linear relationship between two or more variables. If we draw this relationship in a two-dimensional space (between two variables), we get a straight line.
Simple linear regression is useful for finding relationship between two continuous variables. One is predictor or independent variable and other is response or dependent variable. It looks for statistical relationship but not deterministic relationship. Relationship between two variables is said to be deterministic if one variable can be accurately expressed by the other. For example, using temperature in degree Celsius it is possible to accurately predict Fahrenheit. Statistical relationship is not accurate in determining relationship between two variables. For example, relationship between height and weight.
The core idea is to obtain a line that best fits the data. The best fit line is the one for which total prediction error (all data points) are as small as possible. Error is the distance between the point to the regression line.
```
# divide data to x = speed and y = power
x = df['speed']
y = df['power']
# model of Linear regression
model = LinearRegression(fit_intercept=True)
# fiting the model
model.fit(x[:, np.newaxis], y)
# making predyctions
xfit = np.linspace(0, 25, 100)
yfit = model.predict(xfit[:, np.newaxis])
# creating plot
plt.xlabel('wind speed',fontsize = 16)
plt.ylabel('power',fontsize = 16)
plt.scatter(x, y)
plt.plot(xfit, yfit, color="red");
# slope and intercept parameters
print("Parameters:", model.coef_, model.intercept_)
print("Model slope: ", model.coef_[0])
print("Model intercept:", model.intercept_)
```
**Different approach: Simple linear regression model**
Fiting line helps to determine, if our model is predicting well on test dataset.
With help of a line we can calculate the error of each datapoint from a line on basis of how fare it is from the line.
Error could be +ve or -ve, and on basis of that we can calculate the cost function.
I have used Fitted Line Plot to display the relationship between one continuous predictor and a response. A fitted line plot shows a scatterplot of the data with a regression line representing the regression equation.
A best fitted line can be roughly determined using an eyeball method by drawing a straight line on a scatter plot so that the number of points above the line and below the line is about equal (and the line passes through as many points as possible).As we can see below our data,are a little bit sinusoidal and in this case best fitted line is trying to cover most of points that are on diagonal, but also it has to cover other data points so its little bit tweaked due to overestimation and underestimation.
I divided data into training and testing samples at ratio of 70-30%. After that I will apply different models to compare the accuracy scores of all models.
```
# training our main model
x_train,x_test,y_train,y_test = train_test_split(df[['speed']],df.power,test_size = 0.3)
```
Simple linear regression model
```
reg_simple = lm.LinearRegression()
reg_simple.fit(x_train,y_train)
```
Best fit line on test dataset with simple linear regression
```
plt.xlabel('wind speed',fontsize = 16)
plt.ylabel('power',fontsize = 16)
plt.scatter(x_test,y_test, color='blue')
plt.plot(x_test,reg_simple.predict(x_test),color = 'r')
plt.show()
```
Slope, y-intercept and score of our predictions.
```
reg_simple.coef_ #slope
reg_simple.intercept_ #y-intercept
reg_simple.score(x_test,y_test)
```
## Ridge regression and classification
Ridge regression is an extension of linear regression where the loss function is modified to minimize the complexity of the model. This modification is done by adding a penalty parameter that is equivalent to the square of the magnitude of the coefficients.
Ridge Regression is a technique for analyzing multiple regression data that suffer from multicollinearity. When
multicollinearity occurs, least squares estimates are unbiased, but their variances are large so they may be far from
the true value. By adding a degree of bias to the regression estimates, ridge regression reduces the standard errors.
It is hoped that the net effect will be to give estimates that are more reliable
```
reg_ridge = lm.Ridge(alpha=.5)
reg_ridge.fit(x_train,y_train)
plt.xlabel('wind speed',fontsize = 16)
plt.ylabel('power',fontsize = 16)
plt.scatter(x_test,y_test, color='blue')
plt.plot(x_test,reg_ridge.predict(x_test),color = 'r')
plt.show()
```
Slope, y-intercept and score of our predictions.
```
reg_ridge.coef_ #slope
reg_ridge.intercept_ #y-intercept
reg_ridge.score(x_test,y_test)
```
**With regularization parameter.**
```
reg_ridgecv = lm.RidgeCV(alphas=np.logspace(-6, 6, 13))
reg_ridgecv.fit(x_train,y_train)
plt.xlabel('wind speed',fontsize = 16)
plt.ylabel('power',fontsize = 16)
plt.scatter(x_test,y_test, color='blue')
plt.plot(x_test,reg_ridgecv.predict(x_test),color = 'r')
plt.show()
```
Slope, y-intercept and score of our predictions.
```
reg_ridgecv.coef_ #slope
reg_ridgecv.intercept_ #y-intercept
reg_ridgecv.score(x_test,y_test)
```
# Lasso
Lasso regression is a type of linear regression that uses shrinkage. Shrinkage is where data values are shrunk towards a central point, like the mean. The lasso procedure encourages simple, sparse models (i.e. models with fewer parameters). This particular type of regression is well-suited for models showing high levels of muticollinearity or when you want to automate certain parts of model selection, like variable selection/parameter elimination.
The acronym “LASSO” stands for Least Absolute Shrinkage and Selection Operator.
```
reg_lasso = lm.Lasso(alpha=0.1)
reg_lasso.fit(x_train,y_train)
plt.xlabel('wind speed',fontsize = 16)
plt.ylabel('power',fontsize = 16)
plt.scatter(x_test,y_test, color='blue')
plt.plot(x_test,reg_lasso.predict(x_test),color = 'r')
plt.show()
```
Slope, y-intercept and score of our predictions.
```
reg_lasso.coef_ #slope
reg_lasso.intercept_ #y-intercept
reg_lasso.score(x_test,y_test)
```
# LARS Lasso
In statistics, least-angle regression (LARS) is an algorithm for fitting linear regression models to high-dimensional data, developed by Bradley Efron, Trevor Hastie, Iain Johnstone and Robert Tibshirani.[1]
Suppose we expect a response variable to be determined by a linear combination of a subset of potential covariates. Then the LARS algorithm provides a means of producing an estimate of which variables to include, as well as their coefficients.
Instead of giving a vector result, the LARS solution consists of a curve denoting the solution for each value of the L1 norm of the parameter vector. The algorithm is similar to forward stepwise regression, but instead of including variables at each step, the estimated parameters are increased in a direction equiangular to each one's correlations with the residual.
```
reg_lars = lm.Lars(n_nonzero_coefs=1)
reg_lars.fit(x_train,y_train)
plt.xlabel('wind speed',fontsize = 16)
plt.ylabel('power',fontsize = 16)
plt.scatter(x_test,y_test, color='blue')
plt.plot(x_test,reg_lars.predict(x_test),color = 'r')
plt.show()
```
Slope, y-intercept and score of our predictions.
```
reg_lars.coef_ #slope
reg_lars.intercept_ #y-intercept
reg_lars.score(x_test,y_test)
```
**Accuracy** of all models are almost 78% and model having accuracy between 70% to 80% are considered as a good models.<br>
If score value is between 80% and 90%, then model is cosidered as excellent model. If score value is between 90% and 100%, it's a probably an overfitting case.
<img src="img/img2.png">
Above image explains over and under **estimation** of data, We can see in below image that how
datapoints are overestimating and underestimating at some points
<img src="img/img_exp.png">
## Logistic Regression
Logistic regression is a statistical method for predicting binary classes. The outcome or target variable is dichotomous in nature. Dichotomous means there are only two possible classes. For example, it can be used for cancer detection problems. It computes the probability of an event occurrence.
It is a special case of linear regression where the target variable is categorical in nature. It uses a log of odds as the dependent variable. Logistic Regression predicts the probability of occurrence of a binary event utilizing a logit function.
**Linear Regression Vs. Logistic Regression**
Linear regression gives you a continuous output, but logistic regression provides a constant output. An example of the continuous output is house price and stock price. Example's of the discrete output is predicting whether a patient has cancer or not, predicting whether the customer will churn. Linear regression is estimated using Ordinary Least Squares (OLS) while logistic regression is estimated using Maximum Likelihood Estimation (MLE) approach.
<img src="img/linlog.png">
```
# Logistic regression model
logistic_regression = LogisticRegression(max_iter=5000)
# importing necessary packages
from sklearn import preprocessing
from sklearn import utils
# encoding data to be able to proceed with Logistic regression
lab_enc = preprocessing.LabelEncoder()
y_train_encoded = lab_enc.fit_transform(y_train)
print(y_train_encoded)
print(utils.multiclass.type_of_target(y_train))
print(utils.multiclass.type_of_target(y_train.astype('int')))
print(utils.multiclass.type_of_target(y_train_encoded))
# training model
logistic_regression.fit(x_train, y_train_encoded)
logistic_regression.fit(x_train, y_train_encoded)
# predicting "y"
y_pred = logistic_regression.predict(x_test)
# creating plot
plt.xlabel('wind speed',fontsize = 16)
plt.ylabel('power',fontsize = 16)
plt.scatter(x_test,y_test, color='blue')
plt.plot(x_test,logistic_regression.predict_proba(x_test)[:,1],color = 'r')
plt.show()
```
Slope, y-intercept and score of our predictions.
```
logistic_regression.coef_.mean() #slope
logistic_regression.intercept_ .mean()#y-intercept
test_enc = preprocessing.LabelEncoder()
y_test_encoded = test_enc.fit_transform(y_test)
logistic_regression.score(x_test,y_test_encoded)
# trying to get rid of outliers
filter = df["power"]==0.0
filter
# using enumerate() + list comprehension
# to return true indices.
res = [i for i, val in enumerate(filter) if val]
# printing result
print ("The list indices having True values are : " + str(res))
# updating list by dropping "0" power not including first few data points
update = df.drop(df.index[[15, 16, 24, 26, 31, 35, 37, 39, 42, 43, 44, 47, 60, 65, 67, 70, 73, 74, 75, 83, 89, 105, 110, 111, 114, 133, 135, 136, 140, 149, 208, 340, 404, 456, 490, 491, 492, 493, 494, 495, 496, 497, 498, 499]])
update
# training updated data
x_train,x_test,y_train,y_test = train_test_split(update[['speed']],update.power,test_size = 0.3)
# updated model
log = LogisticRegression(max_iter=5000)
# encoding data again
lab_enc = preprocessing.LabelEncoder()
y_train_encoded = lab_enc.fit_transform(y_train)
print(y_train_encoded)
print(utils.multiclass.type_of_target(y_train))
print(utils.multiclass.type_of_target(y_train.astype('int')))
print(utils.multiclass.type_of_target(y_train_encoded))
# fitting data
log.fit(x_train, y_train_encoded)
"predicting "y"
y_pred = log.predict_proba(x_test)[:,1]
# creating plot
plt.xlabel('wind speed',fontsize = 16)
plt.ylabel('power',fontsize = 16)
plt.scatter(x_test,y_test, color='blue')
plt.plot(x_test,log.predict_proba(x_test)[:,300],color = 'r')
plt.show()
```
**Logistic regression** is not able to handle a large number of categorical features/variables. It is vulnerable to overfitting. Also, can't solve the non-linear problem with the logistic regression that is why it requires a transformation of non-linear features. Logistic regression will not perform well with independent variables that are not correlated to the target variable and are very similar or correlated to each other.
It was very bad on our data with score below 0.05, even when I have tried to cut outliners.
## Polynomial regression
is a special case of linear regression where we fit a polynomial equation on the data with a curvilinear relationship between the target variable and the independent variables.
In a curvilinear relationship, the value of the target variable changes in a non-uniform manner with respect to the predictor (s).
The number of higher-order terms increases with the increasing value of n, and hence the equation becomes more complicated.
While there might be a temptation to fit a higher degree polynomial to get lower error, this can result in over-fitting. Always plot the relationships to see the fit and focus on making sure that the curve fits the nature of the problem. Here is an example of how plotting can help:
<img src="img/fitting.png">
Especially look out for curve towards the ends and see whether those shapes and trends make sense. Higher polynomials can end up producing wierd results on extrapolation.
```
# Training Polynomial Regression Model
poly_reg = PolynomialFeatures(degree = 4)
x_poly = poly_reg.fit_transform(x_train)
poly_reg.fit(x_poly, y_train)
lin_reg = LinearRegression()
lin_reg.fit(x_poly, y_train)
# Predict Result with Polynomial Regression
poly = lin_reg.predict(poly_reg.fit_transform(x_test))
poly
# Change into array
x = np.array(df['speed'])
y = np.array(df['power'])
# Changing the shape of array
x = x.reshape(-1,1)
y = y.reshape(-1,1)
# Visualise the Results of Polynomial Regression
plt.scatter(x_train, y_train, color = 'blue')
plt.plot(x, lin_reg.predict(poly_reg.fit_transform(x)), color = 'red')
plt.title('Polynomial Regression')
plt.xlabel('Wind speed')
plt.ylabel('Power')
plt.show()
```
Slope, y-intercept and score of our predictions.
```
lin_reg.coef_.mean() #slope
lin_reg.intercept_#y-intercept
model.score(x_test, y_test) #score
```
## Spearman’s Rank Correlation
This statistical method quantifies the degree to which ranked variables are associated by a monotonic function, meaning an increasing or decreasing relationship. As a statistical hypothesis test, the method assumes that the samples are uncorrelated (fail to reject H0).
>The Spearman rank-order correlation is a statistical procedure that is designed to measure the relationship between two variables on an ordinal scale of measurement.
>— Nonparametric Statistics for Non-Statisticians: A Step-by-Step Approach, 2009.
The intuition for the Spearman’s rank correlation is that it calculates a Pearson’s correlation (e.g. a parametric measure of correlation) using the rank values instead of the real values. Where the Pearson’s correlation is the calculation of the covariance (or expected difference of observations from the mean) between the two variables normalized by the variance or spread of both variables.
Spearman’s rank correlation can be calculated in Python using the spearmanr() SciPy function.
The function takes two real-valued samples as arguments and returns both the correlation coefficient in the range between -1 and 1 and the p-value for interpreting the significance of the coefficient.
```
# importing sperman correlation
from scipy.stats import spearmanr
# prepare data
x = df['speed']
y = df['power']
# calculate spearman's correlation
coef, p = spearmanr(x, y)
print('Spearmans correlation coefficient: %.3f' % coef)
# interpret the significance
alpha = 0.05
if p > alpha:
print('Samples are uncorrelated (fail to reject H0) p=%.3f' % p)
else:
print('Samples are correlated (reject H0) p=%.3f' % p)
```
The statistical test reports a strong positive correlation with a value of 0.819. The p-value is close to zero, which means that the likelihood of observing the data given that the samples are uncorrelated is very unlikely (e.g. 95% confidence) and that we can reject the null hypothesis that the samples are uncorrelated.
## Kendall’s Rank Correlation
The intuition for the test is that it calculates a normalized score for the number of matching or concordant rankings between the two samples. As such, the test is also referred to as Kendall’s concordance test.
The Kendall’s rank correlation coefficient can be calculated in Python using the kendalltau() SciPy function. The test takes the two data samples as arguments and returns the correlation coefficient and the p-value. As a statistical hypothesis test, the method assumes (H0) that there is no association between the two samples.
```
# importing kendall correaltion
from scipy.stats import kendalltau
# calculate kendall's correlation
coef, p = kendalltau(x, y)
print('Kendall correlation coefficient: %.3f' % coef)
# interpret the significance
alpha = 0.05
if p > alpha:
print('Samples are uncorrelated (fail to reject H0) p=%.3f' % p)
else:
print('Samples are correlated (reject H0) p=%.3f' % p)
```
Running the example calculates the Kendall’s correlation coefficient as 0.728, which is highly correlated.
The p-value is close to zero (and printed as zero), as with the Spearman’s test, meaning that we can confidently reject the null hypothesis that the samples are uncorrelated.
## Conclusion
Spearman’s & Kendall’s Rank Correlation shows us that our data are strongly correlated. After trying Linear, Ridge, Lasso and LARS Lasso regressions all of them are equally effective, so the best choice would be to stick with Linear Regression to simplify.
As I wanted to find the better way I tried Logistic regression and I found out it is pretty useless for our dataset even when I get rid of outliers.
Next in line was Polynomial regression and it was great success with nearly 90% score. Seeing results best approach for our dataset would Polynomial regression with Linear regression for our second choice if we would like to keep it simple.
**References:**
- https://www.goodenergy.co.uk/media/1775/howawindturbineworks.jpg?width=640&height=¢er=0.5,0.5&mode=crop
- https://www.nationalgrid.com/stories/energy-explained/how-does-wind-turbine-work
- https://www.pluralsight.com/guides/linear-lasso-ridge-regression-scikit-learn
- https://www.seai.ie/technologies/wind-energy/
- https://towardsdatascience.com/ridge-regression-python-example-f015345d936b
- https://towardsdatascience.com/ridge-and-lasso-regression-a-complete-guide-with-python-scikit-learn-e20e34bcbf0b
- https://realpython.com/linear-regression-in-python/
- https://en.wikipedia.org/wiki/Least-angle_regression
- https://towardsdatascience.com/simple-and-multiple-linear-regression-in-python-c928425168f9
- https://jakevdp.github.io/PythonDataScienceHandbook/05.06-linear-regression.html
- https://www.statisticshowto.com/lasso-regression/
- https://saskeli.github.io/data-analysis-with-python-summer-2019/linear_regression.html
- https://www.w3schools.com/python/python_ml_linear_regression.asp
- https://www.geeksforgeeks.org/linear-regression-python-implementation/
- https://www.kdnuggets.com/2019/03/beginners-guide-linear-regression-python-scikit-learn.html
- https://towardsdatascience.com/an-introduction-to-linear-regression-for-data-science-9056bbcdf675
- https://www.kaggle.com/ankitjha/comparing-regression-models
- https://machinelearningmastery.com/compare-machine-learning-algorithms-python-scikit-learn/
- https://www.datacamp.com/community/tutorials/understanding-logistic-regression-python
- https://www.researchgate.net/post/Is_there_a_test_which_can_compare_which_of_two_regression_models_is_best_explains_more_variance
- https://heartbeat.fritz.ai/logistic-regression-in-python-using-scikit-learn-d34e882eebb1
- https://www.analyticsvidhya.com/blog/2015/08/comprehensive-guide-regression/
- https://towardsdatascience.com/machine-learning-polynomial-regression-with-python-5328e4e8a386
- https://www.w3schools.com/python/python_ml_polynomial_regression.asp
- https://www.dailysmarty.com/posts/polynomial-regression
- https://www.analyticsvidhya.com/blog/2015/08/comprehensive-guide-regression/
- https://machinelearningmastery.com/how-to-calculate-nonparametric-rank-correlation-in-python/
|
github_jupyter
|
```
import random
import torch.nn as nn
import torch
import pickle
import pandas as pd
from pandas import Series, DataFrame
from pandarallel import pandarallel
pandarallel.initialize(progress_bar=False)
from sklearn.metrics import roc_auc_score, roc_curve, accuracy_score, matthews_corrcoef, f1_score, precision_score, recall_score
import numpy as np
import torch.optim as optim
folder = "/data/AIpep-clean/"
import matplotlib.pyplot as plt
from vocabulary import Vocabulary
from datasethem import Dataset
from datasethem import collate_fn_no_activity as collate_fn
from models import Generator
from tqdm.autonotebook import trange, tqdm
import os
from collections import defaultdict
```
# Load data
```
df = pd.read_pickle(folder + "pickles/DAASP_RNN_dataset_with_hemolysis.plk")
df_training = df.query("Set == 'training' and (baumannii == True or aeruginosa == True) and isNotHemolytic==1")
df_test = df.query("Set == 'test' and (baumannii == True or aeruginosa == True) and isNotHemolytic==1")
if torch.cuda.is_available():
device = "cuda"
else:
device = "cpu"
print("Against A. baumannii or P. aeruginosa:\nactive training "+ str(len(df_training[df_training["activity"]==1])) \
+ "\nactive test " + str(len(df_test[df_test["activity"]==1])) \
+ "\ninactive training "+ str(len(df_training[df_training["activity"]==0])) \
+ "\ninactive test " + str(len(df_test[df_test["activity"]==0])))
```
# Define helper functions
```
def randomChoice(l):
return l[random.randint(0, len(l) - 1)]
def categoryFromOutput(output):
top_n, top_i = output.topk(1)
category_i = top_i[0].item()
return category_i
def nan_equal(a,b):
try:
np.testing.assert_equal(a,b)
except AssertionError:
return False
return True
def models_are_equal(model1, model2):
model1.vocabulary == model2.vocabulary
model1.hidden_size == model2.hidden_size
for a,b in zip(model1.model.parameters(), model2.model.parameters()):
if nan_equal(a.detach().numpy(), b.detach().numpy()) == True:
print("true")
```
# Define hyper parameters
```
n_embedding = 100
n_hidden = 400
n_layers = 2
n_epoch = 200
learning_rate = 0.00001
momentum = 0.9
batch_size = 10
epoch = 22
```
# Loading and Training
```
if not os.path.exists(folder+"pickles/generator_TL_gramneg_results_hem.pkl"):
model = Generator.load_from_file(folder+"models/RNN-generator/ep{}.pkl".format(epoch))
model.to(device)
vocabulary = model.vocabulary
df_training_active = df_training.query("activity == 1")
df_test_active = df_test.query("activity == 1")
df_training_inactive = df_training.query("activity == 0")
df_test_inactive = df_test.query("activity == 0")
training_dataset_active = Dataset(df_training_active, vocabulary, with_activity=False)
test_dataset_active = Dataset(df_test_active, vocabulary, with_activity=False)
training_dataset_inactive = Dataset(df_training_inactive, vocabulary, with_activity=False)
test_dataset_inactive = Dataset(df_test_inactive, vocabulary, with_activity=False)
optimizer = optim.SGD(model.model.parameters(), lr = learning_rate, momentum=momentum)
# the only one used for training
training_dataloader_active = torch.utils.data.DataLoader(training_dataset_active, batch_size=batch_size, shuffle=True, collate_fn = collate_fn, drop_last=True, pin_memory=True, num_workers=4)
# used for evaluation
test_dataloader_active = torch.utils.data.DataLoader(test_dataset_active, batch_size=batch_size, shuffle=False, collate_fn = collate_fn, drop_last=False, pin_memory=True, num_workers=4)
training_dataloader_inactive = torch.utils.data.DataLoader(training_dataset_inactive, batch_size=batch_size, shuffle=False, collate_fn = collate_fn, drop_last=False, pin_memory=True, num_workers=4)
test_dataloader_inactive = torch.utils.data.DataLoader(test_dataset_inactive, batch_size=batch_size, shuffle=False, collate_fn = collate_fn, drop_last=False, pin_memory=True, num_workers=4)
training_dataloader_active_eval = torch.utils.data.DataLoader(training_dataset_active, batch_size=batch_size, shuffle=False, collate_fn = collate_fn, drop_last=False, pin_memory=True, num_workers=4)
training_dictionary = {}
for e in trange(1, n_epoch + 1):
print("Epoch {}".format(e))
for i_batch, sample_batched in tqdm(enumerate(training_dataloader_active), total=len(training_dataloader_active) ):
seq_batched = sample_batched[0].to(model.device, non_blocking=True)
seq_lengths = sample_batched[1].to(model.device, non_blocking=True)
nll = model.likelihood(seq_batched, seq_lengths)
loss = nll.mean()
optimizer.zero_grad()
loss.backward()
torch.nn.utils.clip_grad_value_(model.model.parameters(), 2)
optimizer.step()
model.save(folder+"models/RNN-generator-TL-hem/gramneg_ep{}.pkl".format(e))
print("\tExample Sequences")
sampled_seq = model.sample(5)
for s in sampled_seq:
print("\t\t{}".format(model.vocabulary.tensor_to_seq(s, debug=True)))
nll_training = []
with torch.no_grad():
for i_batch, sample_batched in enumerate(training_dataloader_active_eval):
seq_batched = sample_batched[0].to(model.device, non_blocking=True)
seq_lengths = sample_batched[1].to(model.device, non_blocking=True)
nll_training += model.likelihood(seq_batched, seq_lengths)
nll_training_active_mean = torch.stack(nll_training).mean().item()
print("\tNLL Train Active: {}".format(nll_training_active_mean))
del nll_training
nll_test = []
with torch.no_grad():
for i_batch, sample_batched in enumerate(test_dataloader_active):
seq_batched = sample_batched[0].to(model.device, non_blocking=True)
seq_lengths = sample_batched[1].to(model.device, non_blocking=True)
nll_test += model.likelihood(seq_batched, seq_lengths)
nll_test_active_mean = torch.stack(nll_test).mean().item()
print("\tNLL Test Active: {}".format(nll_test_active_mean))
del nll_test
nll_training = []
with torch.no_grad():
for i_batch, sample_batched in enumerate(training_dataloader_inactive):
seq_batched = sample_batched[0].to(model.device, non_blocking=True)
seq_lengths = sample_batched[1].to(model.device, non_blocking=True)
nll_training += model.likelihood(seq_batched, seq_lengths)
nll_training_inactive_mean = torch.stack(nll_training).mean().item()
print("\tNLL Train Inactive: {}".format(nll_training_inactive_mean))
del nll_training
nll_test = []
with torch.no_grad():
for i_batch, sample_batched in enumerate(test_dataloader_inactive):
seq_batched = sample_batched[0].to(model.device, non_blocking=True)
seq_lengths = sample_batched[1].to(model.device, non_blocking=True)
nll_test += model.likelihood(seq_batched, seq_lengths)
nll_test_inactive_mean = torch.stack(nll_test).mean().item()
print("\tNLL Test Inactive: {}".format(nll_test_inactive_mean))
del nll_test
print()
training_dictionary[e]=[nll_training_active_mean, nll_test_active_mean, nll_training_inactive_mean, nll_test_inactive_mean]
with open(folder+"pickles/generator_TL_gramneg_results_hem.pkl",'wb') as fd:
pickle.dump(training_dictionary, fd)
else:
with open(folder+"pickles/generator_TL_gramneg_results_hem.pkl",'rb') as fd:
training_dictionary = pickle.load(fd)
min_nll_test_active = float("inf")
for epoch, training_values in training_dictionary.items():
nll_test_active = training_values[1]
if nll_test_active < min_nll_test_active:
best_epoch = epoch
min_nll_test_active = nll_test_active
```
# Sampling evaluation
```
print(best_epoch)
model = Generator.load_from_file(folder+"models/RNN-generator-TL-hem/gramneg_ep{}.pkl".format(best_epoch))
```
199
```
training_seq = df_training.Sequence.values.tolist()
def _sample(model, n):
sampled_seq = model.sample(n)
sequences = []
for s in sampled_seq:
sequences.append(model.vocabulary.tensor_to_seq(s))
return sequences
def novelty(seqs, list_):
novel_seq = []
for s in seqs:
if s not in list_:
novel_seq.append(s)
return novel_seq, (len(novel_seq)/len(seqs))*100
def is_in_training(seq, list_ = training_seq):
if seq not in list_:
return False
else:
return True
def uniqueness(seqs):
unique_seqs = defaultdict(int)
for s in seqs:
unique_seqs[s] += 1
return unique_seqs, (len(unique_seqs)/len(seqs))*100
# sample
seqs = _sample(model, 50000)
unique_seqs, perc_uniqueness = uniqueness(seqs)
notintraining_seqs, perc_novelty = novelty(unique_seqs, training_seq)
# create dataframe
df_generated = pd.DataFrame(list(unique_seqs.keys()), columns =['Sequence'])
df_generated["Repetition"] = df_generated["Sequence"].map(lambda x: unique_seqs[x])
df_generated["inTraining"] = df_generated["Sequence"].map(is_in_training)
df_generated["Set"] = "generated-TL-GN-hem"
# save
df_generated.to_pickle(folder+"pickles/Generated-TL-gramneg-hem.pkl")
print(perc_uniqueness, perc_novelty)
```
82.89999999999999 99.61158021712907
|
github_jupyter
|
# Tigergraph<>Graphistry Fraud Demo: Raw REST
Accesses Tigergraph's fraud demo directly via manual REST calls
```
#!pip install graphistry
import pandas as pd
import graphistry
import requests
#graphistry.register(key='MY_API_KEY', server='labs.graphistry.com', api=2)
TIGER = "http://MY_TIGER_SERVER:9000"
#curl -X GET "http://MY_TIGER_SERVER:9000/query/circleDetection?srcId=111"
# string -> dict
def query_raw(query_string):
url = TIGER + "/query/" + query_string
r = requests.get(url)
return r.json()
def flatten (lst_of_lst):
try:
if type(lst_of_lst[0]) == list:
return [item for sublist in lst_of_lst for item in sublist]
else:
return lst_of_lst
except:
print('fail', lst_of_lst)
return lst_of_lst
#str * dict -> dict
def named_edge_to_record(name, edge):
record = {k: edge[k] for k in edge.keys() if not (type(edge[k]) == dict) }
record['type'] = name
nested = [k for k in edge.keys() if type(edge[k]) == dict]
if len(nested) == 1:
for k in edge[nested[0]].keys():
record[k] = edge[nested[0]][k]
else:
for prefix in nested:
for k in edge[nested[prefix]].keys():
record[prefix + "_" + k] = edge[nested[prefix]][k]
return record
def query(query_string):
results = query_raw(query_string)['results']
out = {}
for o in results:
for k in o.keys():
if type(o[k]) == list:
out[k] = flatten(o[k])
out = flatten([[named_edge_to_record(k,v) for v in out[k]] for k in out.keys()])
print('# results', len(out))
return pd.DataFrame(out)
def plot_edges(edges):
return graphistry.bind(source='from_id', destination='to_id').edges(edges).plot()
```
# 1. Fraud
## 1.a circleDetection
```
circle = query("circleDetection?srcId=10")
circle.sample(3)
plot_edges(circle)
```
## 1.b fraudConnectivity
```
connectivity = query("fraudConnectivity?inputUser=111&trustScore=0.1")
connectivity.sample(3)
plot_edges(connectivity)
```
## Combined
```
circle['provenance'] = 'circle'
connectivity['provenance'] = 'connectivity'
plot_edges(pd.concat([circle, connectivity]))
```
## Color by type
```
edges = pd.concat([circle, connectivity])
froms = edges.rename(columns={'from_id': 'id', 'from_type': 'node_type'})[['id', 'node_type']]
tos = edges.rename(columns={'to_id': 'id', 'to_type': 'node_type'})[['id', 'node_type']]
nodes = pd.concat([froms, tos], ignore_index=True).drop_duplicates().dropna()
nodes.sample(3)
nodes['node_type'].unique()
#https://labs.graphistry.com/docs/docs/palette.html
type2color = {
'User': 0,
'Transaction': 1,
'Payment_Instrument': 2,
'Device_Token': 3
}
nodes['color'] = nodes['node_type'].apply(lambda type_str: type2color[type_str])
nodes.sample(3)
graphistry.bind(source='from_id', destination='to_id', node='id', point_color='color').edges(edges).nodes(nodes).plot()
```
|
github_jupyter
|
# Project 1
- **Team Members**: Chika Ozodiegwu, Kelsey Wyatt, Libardo Lambrano, Kurt Pessa

### Data set used:
* https://open-fdoh.hub.arcgis.com/datasets/florida-covid19-case-line-data
```
import requests
import pandas as pd
import io
import datetime as dt
import numpy as np
import matplotlib.pyplot as plt
from IPython.display import JSON
df = pd.read_csv("Resources/Florida_COVID19_Case_Line_Data_new.csv")
df.head(3)
#Clean dataframe
new_csv_data_df = df[['ObjectId', "County",'Age',"Age_group", "Gender", "Jurisdiction", "Travel_related", "Hospitalized","Case1"]]
new_csv_data_df.head()
#Create new csv
new_csv_data_df.to_csv ("new_covid_dataframe.csv")
```
# There is no change in hospitalizations since reopening
### Research Question to Answer:
* “There is no change in hospitalizations since reopening.”
### Part 1: Six (6) Steps for Hypothesis Testing
<details><summary> click to expand </summary>
#### 1. Identify
- **Populations** (divide Hospitalization data in two groups of data):
1. Prior to opening
2. After opening
* Decide on the **date**:
* May 4th - restaurants opening to 25% capacity
* June (Miami opening beaches)
- Distribution:
* Distribution
#### 2. State the hypotheses
- **H0**: There is no change in hospitalizations after Florida has reopened
- **H1**: There is a change in hospitalizations after Florida has reopened
#### 3. Characteristics of the comparison distribution
- Population means, standard deviations
#### 4. Critical values
- p = 0.05
- Our hypothesis is nondirectional so our hypothesis test is **two-tailed**
#### 5. Calculate
#### 6. Decide!
</details>
### Part 2: Visualization
```
#Calculate total number of cases
Total_covid_cases = new_csv_data_df["ObjectId"].nunique()
Total_covid_cases = pd.DataFrame({"Total Number of Cases": [Total_covid_cases]})
Total_covid_cases
#Total number of cases per county
total_cases_county = new_csv_data_df.groupby(by="County").count().reset_index().loc[:,["County","Case1"]]
total_cases_county.rename(columns={"County": "County", "Case1": "Total Cases"})
#Total number of cases per county sorted
total_cases_county = total_cases_county.sort_values('Case1',ascending=False)
total_cases_county.head(20)
#Create bar chart for total cases per county
total_cases_county.plot(kind='bar',x='County',y='Case1', title ="Total Cases per County", figsize=(15, 10), color="blue")
plt.title("Total Cases per County")
plt.xlabel("County")
plt.ylabel("Number of Cases")
plt.legend(["Number of Cases"])
plt.show()
#Calculate top 10 counties with total cases
top10_county_cases = total_cases_county.sort_values(by="Case1",ascending=False).head(10)
top10_county_cases["Rank"] = np.arange(1,11)
top10_county_cases.set_index("Rank").style.format({"Case1":"{:,}"})
#Create bar chart for total cases for top 10 counties
top10_county_cases.plot(kind='bar',x='County',y='Case1', title ="Total Cases for Top 10 Counties", figsize=(15, 10), color="blue")
plt.title("Total Hospitalizations for Top 10 Counties")
plt.xlabel("County")
plt.ylabel("Number of Cases")
plt.legend(["Number of Cases"])
plt.show()
#Total number of cases by gender
total_cases_gender = new_csv_data_df.groupby(by="Gender").count().reset_index().loc[:,["Gender","Case1"]]
total_cases_gender.rename(columns={"Gender": "Gender", "Case1": "Total Cases"})
#Create pie chart for total number of cases by gender
total_cases_gender = new_csv_data_df["Gender"].value_counts()
colors=["pink", "blue", "green"]
explode=[0.1,0.1,0.1]
total_cases_gender.plot.pie(explode=explode,colors=colors, autopct="%1.1f%%", shadow=True, subplots=True, startangle=120);
plt.title("Total Number of Cases in Males vs. Females")
#Filter data to show only cases that include hospitalization
filt = new_csv_data_df["Hospitalized"] == "YES"
df = new_csv_data_df[filt]
df
#Calculate total number of hospitalizations
pd.DataFrame({
"Total Hospitalizations (Florida)" : [df.shape[0]]
}).style.format("{:,}")
#Total number of hospitalization for all counties
hospitalizations_county = df.groupby(by="County").count().reset_index().loc[:,["County","Hospitalized"]]
hospitalizations_county
#Total number of hospitalization for all counties sorted
hospitalizations_county = hospitalizations_county.sort_values('Hospitalized',ascending=False)
hospitalizations_county.head(10)
#Create bar chart for total hospitalizations per county
hospitalizations_county.plot(kind='bar',x='County',y='Hospitalized', title ="Total Hospitalizations per County", figsize=(15, 10), color="blue")
plt.title("Total Hospitalizations per County")
plt.xlabel("County")
plt.ylabel("Number of Hospitalizations")
plt.show()
#Calculate top 10 counties with hospitalizations
top10_county = hospitalizations_county.sort_values(by="Hospitalized",ascending=False).head(10)
top10_county["Rank"] = np.arange(1,11)
top10_county.set_index("Rank").style.format({"Hospitalized":"{:,}"})
#Create a bar chart for the top 10 counties with hospitalizations
top10_county.plot(kind='bar',x='County',y='Hospitalized', title ="Total Hospitalizations for the Top 10 Counties", figsize=(15, 10), color="blue")
plt.title("Total Hospitalizations for the Top 10 Counties")
plt.xlabel("County")
plt.ylabel("Number of Hospitalizations")
plt.show()
#Average number of hospitalization by county (Not done yet) (Kelsey)
average = hospitalizations_county["Hospitalized"].mean()
average
#Filter data to show only cases that include hospitalization
filt = new_csv_data_df["Hospitalized"] == "YES"
df = new_csv_data_df[filt]
df
#Percentage of hospitalization by gender # Create Visualization (Libardo)
#code on starter_notebook.ipynb
new_csv_data_df
import seaborn as sns
new_csv_data_df['Count']=np.where(new_csv_data_df['Hospitalized']=='YES', 1,0)
new_csv_data_df.head()
new_csv_data_df['Count2']=1
new_csv_data_df['Case1']=pd.to_datetime(new_csv_data_df['Case1'])
case_plot_df=pd.DataFrame(new_csv_data_df.groupby(['Hospitalized', pd.Grouper(key='Case1', freq='W')])['Count2'].count())
case_plot_df.reset_index(inplace=True)
plt.subplots(figsize=[15,7])
sns.lineplot(x='Case1', y='Count2', data=case_plot_df, hue='Hospitalized')
plt.xticks(rotation=45)
#Percentage of hospitalization by age group (Chika) #Create visualization
#Hospitalization by case date/month (needs more) (Libardo)
#Compare travel-related hospitalization to non-travelrelated cases (Not done yet) (Chika)
#Divide hospitalization data in two groups of data prior to reopening and create new dataframe (Kurt) consider total (Chika)
#Divide hospitalization data in two groups of data after reopening and create new dataframe (Kurt) condider total (Chika)
#Percentage of hospitalization before shut down (Not done yet) (Rephrase) (Chika)
#Percentage of hospitalization during shut down (backburner)
#Percentage of hospitalization after reopening(Not done yet) (Rephrase) (Chika)
#Statistical testing between before and after reopening
```
|
github_jupyter
|
# Benchmark NumPyro in large dataset
This notebook uses `numpyro` and replicates experiments in references [1] which evaluates the performance of NUTS on various frameworks. The benchmark is run with CUDA 10.1 on a NVIDIA RTX 2070.
```
import time
import numpy as np
import jax.numpy as jnp
from jax import random
import numpyro
import numpyro.distributions as dist
from numpyro.examples.datasets import COVTYPE, load_dataset
from numpyro.infer import HMC, MCMC, NUTS
assert numpyro.__version__.startswith('0.3.0')
# NB: replace gpu by cpu to run this notebook in cpu
numpyro.set_platform("gpu")
```
We do preprocessing steps as in [source code](https://github.com/google-research/google-research/blob/master/simple_probabilistic_programming/no_u_turn_sampler/logistic_regression.py) of reference [1]:
```
_, fetch = load_dataset(COVTYPE, shuffle=False)
features, labels = fetch()
# normalize features and add intercept
features = (features - features.mean(0)) / features.std(0)
features = jnp.hstack([features, jnp.ones((features.shape[0], 1))])
# make binary feature
_, counts = np.unique(labels, return_counts=True)
specific_category = jnp.argmax(counts)
labels = (labels == specific_category)
N, dim = features.shape
print("Data shape:", features.shape)
print("Label distribution: {} has label 1, {} has label 0"
.format(labels.sum(), N - labels.sum()))
```
Now, we construct the model:
```
def model(data, labels):
coefs = numpyro.sample('coefs', dist.Normal(jnp.zeros(dim), jnp.ones(dim)))
logits = jnp.dot(data, coefs)
return numpyro.sample('obs', dist.Bernoulli(logits=logits), obs=labels)
```
## Benchmark HMC
```
step_size = jnp.sqrt(0.5 / N)
kernel = HMC(model, step_size=step_size, trajectory_length=(10 * step_size), adapt_step_size=False)
mcmc = MCMC(kernel, num_warmup=500, num_samples=500, progress_bar=False)
mcmc.warmup(random.PRNGKey(2019), features, labels, extra_fields=('num_steps',))
mcmc.get_extra_fields()['num_steps'].sum().copy()
tic = time.time()
mcmc.run(random.PRNGKey(2020), features, labels, extra_fields=['num_steps'])
num_leapfrogs = mcmc.get_extra_fields()['num_steps'].sum().copy()
toc = time.time()
print("number of leapfrog steps:", num_leapfrogs)
print("avg. time for each step :", (toc - tic) / num_leapfrogs)
mcmc.print_summary()
```
In CPU, we get `avg. time for each step : 0.02782863507270813`.
## Benchmark NUTS
```
mcmc = MCMC(NUTS(model), num_warmup=50, num_samples=50, progress_bar=False)
mcmc.warmup(random.PRNGKey(2019), features, labels, extra_fields=('num_steps',))
mcmc.get_extra_fields()['num_steps'].sum().copy()
tic = time.time()
mcmc.run(random.PRNGKey(2020), features, labels, extra_fields=['num_steps'])
num_leapfrogs = mcmc.get_extra_fields()['num_steps'].sum().copy()
toc = time.time()
print("number of leapfrog steps:", num_leapfrogs)
print("avg. time for each step :", (toc - tic) / num_leapfrogs)
mcmc.print_summary()
```
In CPU, we get `avg. time for each step : 0.028006251705287415`.
## Compare to other frameworks
| | HMC | NUTS |
| ------------- |----------:|----------:|
| Edward2 (CPU) | | 56.1 ms |
| Edward2 (GPU) | | 9.4 ms |
| Pyro (CPU) | 35.4 ms | 35.3 ms |
| Pyro (GPU) | 3.5 ms | 4.2 ms |
| NumPyro (CPU) | 27.8 ms | 28.0 ms |
| NumPyro (GPU) | 1.6 ms | 2.2 ms |
Note that in some situtation, HMC is slower than NUTS. The reason is the number of leapfrog steps in each HMC trajectory is fixed to $10$, while it is not fixed in NUTS.
**Some takeaways:**
+ The overhead of iterative NUTS is pretty small. So most of computation time is indeed spent for evaluating potential function and its gradient.
+ GPU outperforms CPU by a large margin. The data is large, so evaluating potential function in GPU is clearly faster than doing so in CPU.
## References
1. `Simple, Distributed, and Accelerated Probabilistic Programming,` [arxiv](https://arxiv.org/abs/1811.02091)<br>
Dustin Tran, Matthew D. Hoffman, Dave Moore, Christopher Suter, Srinivas Vasudevan, Alexey Radul, Matthew Johnson, Rif A. Saurous
|
github_jupyter
|
```
import pandas as pd
df = pd.read_csv(r'C:\Users\rohit\Documents\Flight Delay\flightdata.csv')
df.head()
df.shape
df.isnull().values.any()
df.isnull().sum()
df = df.drop('Unnamed: 25', axis=1)
df.isnull().sum()
df = pd.read_csv(r'C:\Users\rohit\Documents\Flight Delay\flightdata.csv')
df = df[["MONTH", "DAY_OF_MONTH", "DAY_OF_WEEK", "ORIGIN", "DEST", "CRS_DEP_TIME", "DEP_DEL15", "CRS_ARR_TIME", "ARR_DEL15"]]
df.isnull().sum()
df[df.isnull().values.any(axis=1)].head()
df = df.fillna({'ARR_DEL15': 1})
df = df.fillna({'DEP_DEL15': 1})
df.iloc[177:185]
df.head()
import math
for index, row in df.iterrows():
df.loc[index, 'CRS_DEP_TIME'] = math.floor(row['CRS_DEP_TIME'] / 100)
df.loc[index, 'CRS_ARR_TIME'] = math.floor(row['CRS_ARR_TIME'] / 100)
df.head()
df = pd.get_dummies(df, columns=['ORIGIN', 'DEST'])
df.head()
from sklearn.model_selection import train_test_split
train_x, test_x, train_y, test_y = train_test_split(df.drop(['ARR_DEL15','DEP_DEL15'], axis=1), df[['ARR_DEL15','DEP_DEL15']], test_size=0.2, random_state=42)
train_x.shape
test_x.shape
train_y.shape
test_y.shape
from sklearn.ensemble import RandomForestClassifier
model = RandomForestClassifier(random_state=13)
model.fit(train_x, train_y)
predicted = model.predict(test_x)
model.score(test_x, test_y)
from sklearn.metrics import roc_auc_score
probabilities = model.predict_proba(test_x)
roc_auc_score(test_y, probabilities[0])
from sklearn.metrics import multilabel_confusion_matrix
multilabel_confusion_matrix(test_y, predicted)
from sklearn.metrics import precision_score
train_predictions = model.predict(train_x)
precision_score(train_y, train_predictions, average = None)
from sklearn.metrics import recall_score
recall_score(train_y, train_predictions, average = None)
%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
from sklearn.metrics import roc_curve
fpr, tpr, _ = roc_curve(test_y, probabilities[0])
plt.plot(fpr, tpr)
plt.plot([0, 1], [0, 1], color='grey', lw=1, linestyle='--')
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
def predict_delay(departure_date_time, arrival_date_time, origin, destination):
from datetime import datetime
try:
departure_date_time_parsed = datetime.strptime(departure_date_time, '%d/%m/%Y %H:%M:%S')
arrival_date_time_parsed = datetime.strptime(departure_date_time, '%d/%m/%Y %H:%M:%S')
except ValueError as e:
return 'Error parsing date/time - {}'.format(e)
month = departure_date_time_parsed.month
day = departure_date_time_parsed.day
day_of_week = departure_date_time_parsed.isoweekday()
hour = departure_date_time_parsed.hour
origin = origin.upper()
destination = destination.upper()
input = [{'MONTH': month,
'DAY': day,
'DAY_OF_WEEK': day_of_week,
'CRS_DEP_TIME': hour,
'ORIGIN_ATL': 1 if origin == 'ATL' else 0,
'ORIGIN_DTW': 1 if origin == 'DTW' else 0,
'ORIGIN_JFK': 1 if origin == 'JFK' else 0,
'ORIGIN_MSP': 1 if origin == 'MSP' else 0,
'ORIGIN_SEA': 1 if origin == 'SEA' else 0,
'DEST_ATL': 1 if destination == 'ATL' else 0,
'DEST_DTW': 1 if destination == 'DTW' else 0,
'DEST_JFK': 1 if destination == 'JFK' else 0,
'DEST_MSP': 1 if destination == 'MSP' else 0,
'DEST_SEA': 1 if destination == 'SEA' else 0 }]
return model.predict_proba(pd.DataFrame(input))[0][0]
```
|
github_jupyter
|
# Python Dictionaries
## Dictionaries
* Collection of Key - Value pairs
* also known as associative array
* unordered
* keys unique in one dictionary
* storing, extracting
```
emptyd = {}
len(emptyd)
type(emptyd)
tel = {'jack': 4098, 'sape': 4139}
print(tel)
tel['guido'] = 4127
print(tel.keys())
print(tel.values())
# add key 'valdis' with value 4127 to our tel dictionary
tel['valdis'] = 4127
tel
#get value from key in dictionary
# very fast even in large dictionaries! O(1)
tel['jack']
tel['sape'] = 54545
# remove key value pair
del tel['sape']
tel['sape']
'valdis' in tel.keys()
'karlis' in tel.keys()
# this will be slower going through all the key:value pairs
4127 in tel.values()
type(tel.values())
dir(tel.values())
tel['irv'] = 4127
tel
list(tel.keys())
list(tel.values())
sorted([5,7,1,66], reverse=True)
?sorted
tel.keys()
sorted(tel.keys())
'guido' in tel
'Valdis' in tel
'valdis' in tel
# alternative way of creating a dictionary using tuples ()
t2=dict([('sape', 4139), ('guido', 4127), ('jack', 4098)])
print(t2)
names = ['Valdis', 'valdis', 'Antons', 'Anna', 'Kārlis', 'karlis']
names
sorted(names)
```
* `globals()` always returns the dictionary of the module namespace
* `locals()` always returns a dictionary of the current namespace
* `vars()` returns either a dictionary of the current namespace (if called with no argument) or the dictionary of the argument.
```
globals()
'print(a,b)' in globals()['In']
vars().keys()
sorted(vars().keys())
# return value of the key AND destroy the key:value
# if key does not exist, then KeyError will appear
tel.pop('valdis')
# return value of the key AND destroy the key:value
# if key does not exist, then KeyError will appear
tel.pop('valdis')
# we can store anything in dictionaries
# including other dictionaries and lists
mydict = {'mylist':[1,2,6,6,"Badac"], 55:165, 'innerd':{'a':100,'b':[1,2,6]}}
mydict
mydict.keys()
# we can use numeric keys as well!
mydict[55]
mydict['55'] = 330
mydict
mlist = mydict['mylist']
mlist
mytext = mlist[-1]
mytext
mychar = mytext[-3]
mychar
# get letter d
mydict['mylist'][-1][-3]
mydict['mylist'][-1][2]
mlist[-1][2]
mydict['real55'] = mydict[55]
del mydict[55]
mydict
sorted(mydict.keys())
mydict.get('55')
# we get None on nonexisting key instead of KeyError
mydict.get('53253242452')
# here we will get KeyError on nonexisting key
mydict['53253242452']
mydict.get("badkey") == None
k,v = mydict.popitem()
k,v
# update for updating multiple dictionary values at once
mydict.update({'a':[1,3,'valdis',5],'anotherkey':567})
mydict
mydict.setdefault('b', 3333)
mydict
# change dictionary key value pair ONLY if key does not exist
mydict.setdefault('a', 'aaaaaaaa')
mydict
# here we overwite no matter what
mydict['a'] = 'changed a value'
mydict
# and we clear our dictionary
mydict.clear()
mydict
type(mydict)
mydict = 5
type(mydict)
```
|
github_jupyter
|
# Chapter 1 - Softmax from First Principles
## Language barriers between humans and autonomous systems
If our goal is to help humans and autnomous systems communicate, we need to speak in a common language. Just as humans have verbal and written languages to communicate ideas, so have we developed mathematical languages to communicate information. Probability is one of those languages and, thankfully for us, autonomous systems are pretty good at describing probabilities, even if humans aren't. This document shows one technique for translating a human language (English) into a language known by autonomous systems (probability).
Our translator is something called the **SoftMax classifier**, which is one type of probability distribution that takes discrete labels and translates them to probabilities. We'll show you the details on how to create a softmax model, but let's get to the punchline first: we can decompose elements of human language to represent a partitioning of arbitrary state spaces.
Say, for instance, we'd like to specify the location of an object in two dimensional cartesian coordinates. Our state space is all combinations of *x* and *y*, and we'd like to translate human language into some probability that our target is at a given combination of *x* and *y*. One common tactic humans use to communicate position is range (near, far, next to, etc.) and bearing (North, South, SouthEast, etc.). This already completely partitions our *xy* space: if something is north, it's not south; if it's east, it's not west; and so on.
A softmax model that translates range and bearing into probability in a state space is shown below:
<img src="https://raw.githubusercontent.com/COHRINT/cops_and_robots/master/notebooks/softmax/img/softmax_range_bearing.png" alt="Softmax range and bearing" width=500px>
Assuming that *next to* doesn't require a range, we see seventeen different word combinations we can use to describe something's position: two ranges (*nearby* and *far*) for each cardinal and intercardinal direction (eight total), and then one extra label for *next to*. This completely partitions our entire state space $\mathbb{R}^2$.
This range and bearing language is, by its nature, inexact. If I say, "That boat is far north.", you don't have a deterministic notion of exactly where the boat is -- but you have a good sense of where it is, and where it is not. We can represent that sense probabilistically, such that the probability of a target existing at a location described by a range and bearing label is nonzero over the entire state space, but that probability is very small if not in the area most associated with that label.
What do we get from this probabilistic interpretation of the state space? We get a two-way translation between humans and autonomous systems to describe anything we'd like. If our state space is one-dimensional relative velocity (i.e. the derivative of range without bearing), I can say, "She's moving really fast!", to give the autonomous system a probability distribution over my target's velocity with an expected value of, say, 4 m/s. Alternatively, if my autnomous system knows my target's moving at 0.04352 m/s, it can tell me, "Your target is moving slowly." Our labeled partitioning of the state space (that is, our classifier) is the mechanism that translates for us.
## Softmax model construction
The [SoftMax function](http://en.wikipedia.org/wiki/Softmax_function) goes by many names: normalized exponential, multinomial logistic function, log-linear model, sigmoidal function. We use the SoftMax function to develop a classification model for our state space:
$$
\begin{equation}
P(L=i \vert \mathbf{x}) = \frac{e^{\mathbf{w}_i^T \mathbf{x} + b_i}}{\sum_{k=1}^M e^{\mathbf{w}_k^T\mathbf{x} + b_k}}
\end{equation}
$$
Where $L = i$ is our random variable of class labels instantiated as class $i$, $\mathbf{x}$ is our state vector, $\mathbf{w}_i$ is a vector of parameters (or weights) associated with our class $i$, $b_i$ is a bias term for class $i$, and $M$ is the total number of classes.
The terms *label* and *class* require some distinction: a label is a set of words associated with a class (i.e. *far northwest*) whereas a class is a probability distribution over the entire state space. They are sometimes used interchangeably, and the specific meaning should be clear from context.
Several key factors come out of the SoftMax equation:
- The probabilities of all classes for any given point $\mathbf{x}$ sum to 1.
- The probability any single class for any given point $\mathbf{x}$ is bounded by 0 and 1.
- The space can be partitioned into an arbitrary number of classes (with some restrictions about those classes - more on this later).
- The probability of one class for a given point $\mathbf{x}$ is determined by that class' weighted exponential sum of the state vector *relative* to the weighted exponential sums of *all* classes.
- Since the probability of a class is conditioned on $\mathbf{x}$, we can apply estimators such as [Maximum Likelihood](http://en.wikipedia.org/wiki/Maximum_likelihood) to learn SoftMax models.
- $P(L=i \vert \mathbf{x})$ is convex in $\mathbf{w_i}$ for any $\mathbf{x}$.
Let's try to get some intuition about this setup. For a two-dimensional case with state $\mathbf{x} = \begin{bmatrix}x & y\end{bmatrix}^T$, each class $i$ has weights $\mathbf{w}_i = \begin{bmatrix}w_{i,x} & w_{i,y}\end{bmatrix}^T$. Along with the constant bias term $b_i$, we have one weighted linear function of $x$ and one weighted linear function of $y$. Each class's probability is normalized with respect to the sum of all other classes, so the weights can be seen as a relative scaling of one class over another in any given state. The bias weight increases a class's probability in all cases, the $x$ weight increases the class's probability for greater values of $x$ (and positive weights), and the $y$ weight, naturally, increases the class's probability for greater values of $y$ (and positive weights).
We can get fancy with our state space, having states of the form $\mathbf{x} = \begin{bmatrix}x & y & x^2 & y^2 & 2xy\end{bmatrix}^T$, but we'll build up to states like that. Let's look at some simpler concepts first.
## Class boundaries
For any two classes, we can take the ratio of their probabilities to determine the **odds** of one class instead of the other:
$$
L(i,j) =\frac{P(L=i \vert \mathbf{x})}{P(L=j \vert \mathbf{x})} =
\frac{\frac{e^{\mathbf{w}_i^T \mathbf{x} + b_i}}{\sum_{k=i}^M e^{\mathbf{w}_k^T\mathbf{x} + b_k}}}{\frac{e^{\mathbf{w}_j^T \mathbf{x} + b_{j}}}{\sum_{k=i}^M e^{\mathbf{w}_k^T\mathbf{x} + b_k}}} = \frac{e^{\mathbf{w}_i^T \mathbf{x} + b_i}}{e^{\mathbf{w}_j^T\mathbf{x} + b_j}}
$$
When $L(i,j)=1$, the two classes have equal probability. This doesn't give us a whole lot of insight until we take the **log-odds** (the logarithm of the odds):
$$
\begin{align}
L_{log}(i,j) &=
\log{\frac{P(L=i \vert \mathbf{x})}{P(L=j \vert \mathbf{x})}}
= \log{\frac{e^{\mathbf{w}_i^T \mathbf{x} + b_j}}{e^{\mathbf{w}_j^T\mathbf{x} + b_j}}}
= (\mathbf{w}_i^T\mathbf{x} + b_i)- (\mathbf{w}_j^T\mathbf{x} + b_j) \\
&= (\mathbf{w}_i - \mathbf{w}_j)^T\mathbf{x} + (b_i - b_j)
\end{align}
$$
When $L_{log}(i,j) = \log{L(i,j)} = \log{1} = 0$, we have equal probability between the two classes, and we've also stumbled upon the equation for an n-dimensional affine hyperplane dividing the two classes:
$$
\begin{align}
0 &= (\mathbf{w}_i - \mathbf{w}_j)^T\mathbf{x} + (b_i - b_j) \\
&= (w_{i,x_1} - w_{j,x_1})x_1 + (w_{i,x_2} - w_{j,x_2})x_2 + \dots + (w_{i,x_n} - w_{j,x_n})x_n + (b_i - b_j)
\end{align}
$$
This follows from the general definition of an <a href="http://en.wikipedia.org/wiki/Plane_(geometry)#Point-normal_form_and_general_form_of_the_equation_of_a_plane">Affine Hyperplane</a> (that is, an n-dimensional flat plane):
$$
a_1x_1 + a_2x_2 + \dots + a_nx_n + b = 0
$$
Where $a_1 = w_{i,x_1} - w_{j,x_1}$, $a_2 = w_{i,x_2} - w_{j,x_2}$, and so on. This gives us a general formula for the division of class boundaries -- that is, we can specify the class boundaries directly, rather than specifying the weights leading to those class boundaries.
### Example
Let's take a step back and look at an example. Suppose I'm playing Pac-Man, and I want to warn our eponymous hero of a ghost approaching him. Let's restrict my language to the four intercardinal directions: NE, SE, SW and NW. My state space is $\mathbf{x} = \begin{bmatrix}x & y\end{bmatrix}^T$ (one term for each cartesian direction in $\mathbb{R}^2$).
<img src="https://raw.githubusercontent.com/COHRINT/cops_and_robots/master/notebooks/softmax/img/pacman.png" alt="Pacman with intercardinal bearings" width="500px">
In this simple problem, we can expect our weights to be something along the lines of:
$$
\begin{align}
\mathbf{w}_{SW} &= \begin{bmatrix}-1 & -1 \end{bmatrix}^T \\
\mathbf{w}_{NW} &= \begin{bmatrix}-1 & 1 \end{bmatrix}^T \\
\mathbf{w}_{SE} &= \begin{bmatrix}1 & -1 \end{bmatrix}^T \\
\mathbf{w}_{NE} &= \begin{bmatrix}1 & 1 \end{bmatrix}^T \\
\end{align}
$$
If we run these weights in our SoftMax model, we get the following results:
```
# See source at: https://github.com/COHRINT/cops_and_robots/blob/master/src/cops_and_robots/robo_tools/fusion/softmax.py
import numpy as np
from cops_and_robots.robo_tools.fusion.softmax import SoftMax
%matplotlib inline
labels = ['SW', 'NW', 'SE',' NE']
weights = np.array([[-1, -1],
[-1, 1],
[1, -1],
[1, 1],
])
pacman = SoftMax(weights, class_labels=labels)
pacman.plot(title='Unshifted Pac-Man Bearing Model')
```
Which is along the right path, but needs to be shifted down to Pac-Man's location. Say Pac-Man is approximately one quarter of the map south from the center point, we can bias our model accordingly (assuming a $10m \times 10m$ space):
$$
\begin{align}
b_{SW} &= -2.5\\
b_{NW} &= 2.5\\
b_{SE} &= -2.5\\
b_{NE} &= 2.5\\
\end{align}
$$
```
biases = np.array([-2.5, 2.5, -2.5, 2.5,])
pacman = SoftMax(weights, biases, class_labels=labels)
pacman.plot(title='Y-Shifted Pac-Man Bearing Model')
```
Looking good! Note that we'd get the same answer had we used the following weights:
$$
\begin{align}
b_{SW} &= -5\\
b_{NW} &= 0\\
b_{SE} &= -5\\
b_{NE} &= 0\\
\end{align}
$$
Because the class boundaries and probability distributions are defined by the *relative differences*.
But this simply shifts the weights in the $y$ direction. How do we go about shifting weights in any state dimension?
Remember that our biases will essentially scale an entire class, so, what we did was scale up the two classes that have a positive scaling for negative $y$ values. If we want to place the center of the four classes in the top-left, for instance, we'll want to bias the NW class less than the other classes.
Let's think of what happens if we use another coordinate system:
$$
\mathbf{x}' = \mathbf{x} + \mathbf{b}
$$
Where $\mathbf{x}'$ is our new state vector and $\mathbf{b}$ are offsets to each state in our original coordinate frame (assume the new coordinate system is unbiased). For example, something like:
$$
\mathbf{x}' = \begin{bmatrix}x & y\end{bmatrix}^T + \begin{bmatrix}2 & -3\end{bmatrix}^T = \begin{bmatrix}x + 2 & y -3\end{bmatrix}^T
$$
Can we represent this shift simply by adjusting our biases, instead of having to redefine our state vector? Assuming we're just shifting the distributions, the probabilities, and thus, the hyperplanes, will simply be shifted as well, so we have:
$$
0 = (\mathbf{w}_i - \mathbf{w}_j)^T \mathbf{x}' = (\mathbf{w}_i - \mathbf{w}_j)^T \mathbf{x} + (\mathbf{w}_i - \mathbf{w}_j)^T \mathbf{b}
$$
Which retains our original state and shifts only our biases. If we distribute the offset $\mathbf{b}$, we can define each class's bias term:
$$
\begin{align}
b_i - b_j &= (\mathbf{w}_i - \mathbf{w}_j)^T \mathbf{b} \\
&= \mathbf{w}_i^T \mathbf{b} - \mathbf{w}_j^T \mathbf{b}
\end{align}
$$
Our bias for each class $i$ in our original coordinate frame is simply $\mathbf{w}_i^T \mathbf{b}$.
Let's try this out with $\mathbf{b} = \begin{bmatrix}2 & -3\end{bmatrix}^T$ (remembering that this will push the shifted origin negatively along the x-axis and positively along the y-axis):
$$
\begin{align}
b_{SW} &= \begin{bmatrix}-1 & -1 \end{bmatrix} \begin{bmatrix}2 \\ -3\end{bmatrix} = 1\\
b_{NW} &= \begin{bmatrix}-1 & 1 \end{bmatrix} \begin{bmatrix}2 \\ -3\end{bmatrix} =-5 \\
b_{SE} &= \begin{bmatrix}1 & -1 \end{bmatrix} \begin{bmatrix}2 \\ -3\end{bmatrix} = 5\\
b_{NE} &= \begin{bmatrix}1 & 1 \end{bmatrix} \begin{bmatrix}2 \\ -3\end{bmatrix} = -1 \\
\end{align}
$$
```
biases = np.array([1, -5, 5, -1,])
pacman = SoftMax(weights, biases, class_labels=labels)
pacman.plot(title='Shifted Pac-Man Bearing Model')
```
One other thing we can illustrate with this example: how would the SoftMax model change if we multiplied all our weights and biases by 10?
We get:
```
weights = np.array([[-10, -10],
[-10, 10],
[10, -10],
[10, 10],
])
biases = np.array([10, -50, 50, -10,])
pacman = SoftMax(weights, biases, class_labels=labels)
pacman.plot(title='Steep Pac-Man Bearing Model')
```
Why does this increase in slope happen? Let's investigate.
## SoftMax slope for linear states
The [gradient](http://en.wikipedia.org/wiki/Gradient) of $P(L=i \vert \mathbf{x})$ will give us a function for the slope of our SoftMax model of class $i$. For a linear state space, such as our go-to $\mathbf{x} = \begin{bmatrix}x & y\end{bmatrix}$, our gradient is defined as:
$$
\nabla P(L=i \vert \mathbf{x}) = \nabla \frac{e^{\mathbf{w}_i^T \mathbf{x} + b_i}}{\sum_{k=1}^M e^{\mathbf{w}_k^T\mathbf{x} + b_k}} =
\frac{\partial}{\partial x} \frac{e^{\mathbf{w}_i^T \mathbf{x}}}{\sum_{k=1}^M e^{\mathbf{w}_k^T\mathbf{x}}} \mathbf{\hat{i}} +
\frac{\partial}{\partial y} \frac{e^{\mathbf{w}_i^T \mathbf{x}}}{\sum_{k=1}^M e^{\mathbf{w}_k^T\mathbf{x}}} \mathbf{\hat{j}}
$$
Where $\mathbf{\hat{i}}$ and $\mathbf{\hat{j}}$ are unit vectors in the $x$ and $y$ dimensions, respectively. Given the structure of our equation, the form of either partial derivative will be the same as the other, so let's look at the partial with respect to $x$, using some abused notation:
$$
\begin{align}
\frac{\partial P(L = i \vert \mathbf{x})} {\partial x} &= \frac{d P(L = i \vert x)} {dx} =
\frac{\partial}{\partial x} \frac{e^{w_{i,x}x}}{\sum_{k=1}^M e^{w_{k,x}x}} \\
&= \frac{w_{i,x}e^{w_{i,x}x}\sum_{k=1}^M e^{w_{k,x}x} - e^{w_{i,x}x}(\sum_{k=1}^M w_{k,x}e^{w_{k,x}x})}{(\sum_{k=1}^M e^{w_{k,x}x})^2} \\
&= \frac{w_{i,x}e^{w_{i,x}x}\sum_{k=1}^M e^{w_{k,x}x}}{(\sum_{k=1}^M e^{w_{k,x}x})^2} -
\frac{e^{w_{i,x}x}(\sum_{k=1}^M w_{k,x}e^{w_{k,x}x})}{(\sum_{k=1}^M e^{w_{k,x}x})^2}\\
&= w_{i,x} \left( \frac{e^{w_{i,x}x}}{\sum_{k=1}^M e^{w_{k,x}x}}\right) -
\left( \frac{e^{w_{i,x}x}}{\sum_{k=1}^M e^{w_{k,x}x}}\right)\frac{\sum_{k=1}^M w_{k,x}e^{w_{k,x}x}}{\sum_{k=1}^M e^{w_{k,x}x}}\\
& = P(L = i \vert x) \left(w_{i,x} - \frac{\sum_{k=1}^M w_{k,x}e^{w_{k,x}x}}{\sum_{k=1}^M e^{w_{k,x}x}}\right) \\
& = P(L = i \vert x) \left(w_{i,x} - \sum_{k=1}^M w_{k,x}P(L = k \vert x) \right) \\
\end{align}
$$
Where line 2 was found using the quotient rule. This is still hard to interpret, so let's break it down into multiple cases:
If $P(L = i \vert x) \approx 1$, the remaining probabilities are near zero, thus reducing the impact of their weights, leaving:
$$
\frac{\partial P(L = i \vert \mathbf{x})} {\partial x}
\approx P(L = i \vert x) \left(w_{i,x} - w_{i,x}P(L = i \vert x) \right)
= 0
$$
This makes sense: a dominating probability will be flat.
If $P(L = i \vert x) \approx 0$, we get:
$$
\frac{\partial P(L = i \vert \mathbf{x})} {\partial x}
\approx 0 \left(w_{i,x} - w_{i,x}P(L = i \vert x) \right)
= 0
$$
This also makes sense: a diminished probability will be flat.
We can expect the greatest slope of a [logistic function](http://en.wikipedia.org/wiki/Logistic_function) (which is simply a univariate SoftMax function) to appear at its midpoint $P(L = i \vert x) = 0.5$. Our maximum slope, then, is:
$$
\frac{\partial P(L = i \vert \mathbf{x})} {\partial x}
= 0.5 \left(w_{i,x} - \sum_{k=1}^M w_{k,x}P(L = k \vert x) \right) \\
= 0.5 \left(w_{i,x} - \sum^M _{\substack{k = 1, \\ k \neq i}} w_{k,x}P(L = k \vert x) - 0.5w_{i,x}\right) \\
= 0.25w_{i,x} - 0.5\sum^M _{\substack{k = 1, \\ k \neq i}} w_{k,x}P(L = k \vert x) \\
$$
NOTE: This section feels really rough, and possibly unnecessary. I need to work on it some more.
## Rotations
Just as we were able to shift our SoftMax distributions to a new coordinate origin, we can apply a [rotation](http://en.wikipedia.org/wiki/Rotation_matrix) to our weights and biases. Let's once again update our weights and biases through a new, rotated, coordinate scheme:
$$
R(\theta)\mathbf{x}' = R(\theta)(\mathbf{x} + \mathbf{b})
$$
As before, we examine the case at the linear hyperplane boundaries:
$$
0 = (\mathbf{w}_i - \mathbf{w}_j)^T \mathbf{x}' = (\mathbf{w}_i - \mathbf{w}_j)^T R(\theta)\mathbf{x} + (\mathbf{w}_i - \mathbf{w}_j)^T R(\theta) \mathbf{b}
$$
Our weights are already defined, so we simply need to multiply them by $R(\theta)$ to find our rotated weights. Let's find our biases:
$$
\begin{align}
b_i - b_j &= (\mathbf{w}_i - \mathbf{w}_j)^T R(\theta) \mathbf{b} \\
&= \mathbf{w}_i^T R(\theta) \mathbf{b} - \mathbf{w}_j^T R(\theta) \mathbf{b}
\end{align}
$$
So, under rotation, $b_i = \mathbf{w}_i^T R(\theta) \mathbf{b}$.
Let's try this with a two-dimensional rotation matrix using $\theta = \frac{\pi}{4} rad$ and $\mathbf{b} = \begin{bmatrix}2 & -3\end{bmatrix}^T$:
$$
\begin{align}
b_{SW} &= \begin{bmatrix}-1 & -1 \end{bmatrix}
\begin{bmatrix}\frac{\sqrt{2}}{2} & -\frac{\sqrt{2}}{2}\\ \frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2}\end{bmatrix}
\begin{bmatrix}2 \\ -3\end{bmatrix} = -2\sqrt{2} \\
b_{NW} &= \begin{bmatrix}-1 & 1 \end{bmatrix}
\begin{bmatrix}\frac{\sqrt{2}}{2} & -\frac{\sqrt{2}}{2}\\ \frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2}\end{bmatrix}
\begin{bmatrix}2 \\ -3\end{bmatrix} = -3\sqrt{2} \\
b_{SE} &= \begin{bmatrix}1 & -1 \end{bmatrix}
\begin{bmatrix}\frac{\sqrt{2}}{2} & -\frac{\sqrt{2}}{2}\\ \frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2}\end{bmatrix}
\begin{bmatrix}2 \\ -3\end{bmatrix} = 3\sqrt{2} \\
b_{NE} &= \begin{bmatrix}1 & 1 \end{bmatrix}\begin{bmatrix}\frac{\sqrt{2}}{2} & -\frac{\sqrt{2}}{2}\\ \frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2}\end{bmatrix}
\begin{bmatrix}2 \\ -3\end{bmatrix} = 2\sqrt{2} \\
\end{align}
$$
```
# Define rotation matrix
theta = np.pi/4
R = np.array([[np.cos(theta), -np.sin(theta)],
[np.sin(theta), np.cos(theta)]])
# Rotate weights
weights = np.array([[-1, -1],
[-1, 1],
[1, -1],
[1, 1],
])
weights = np.dot(weights,R)
# Apply rotated biases
biases = np.array([-2 * np.sqrt(2),
-3 * np.sqrt(2),
3 * np.sqrt(2),
2 * np.sqrt(2),])
pacman = SoftMax(weights, biases, class_labels=labels)
pacman.plot(title='Rotated and Shifted Pac-Man Bearing Model')
```
##Summary
That should be a basic introduction to the SoftMax model. We've only barely scraped the surface of why you might want to use SoftMax models as a tool for aspects of HRI.
Let's move on to [Chapter 2](02_from_normals.ipynb) where we examine a more practical way of constructing SoftMax distributions.
```
from IPython.core.display import HTML
# Borrowed style from Probabilistic Programming and Bayesian Methods for Hackers
def css_styling():
styles = open("../styles/custom.css", "r").read()
return HTML(styles)
css_styling()
```
|
github_jupyter
|
---
_You are currently looking at **version 1.1** of this notebook. To download notebooks and datafiles, as well as get help on Jupyter notebooks in the Coursera platform, visit the [Jupyter Notebook FAQ](https://www.coursera.org/learn/python-text-mining/resources/d9pwm) course resource._
---
# Assignment 1
In this assignment, you'll be working with messy medical data and using regex to extract relevant infromation from the data.
Each line of the `dates.txt` file corresponds to a medical note. Each note has a date that needs to be extracted, but each date is encoded in one of many formats.
The goal of this assignment is to correctly identify all of the different date variants encoded in this dataset and to properly normalize and sort the dates.
Here is a list of some of the variants you might encounter in this dataset:
* 04/20/2009; 04/20/09; 4/20/09; 4/3/09
* Mar-20-2009; Mar 20, 2009; March 20, 2009; Mar. 20, 2009; Mar 20 2009;
* 20 Mar 2009; 20 March 2009; 20 Mar. 2009; 20 March, 2009
* Mar 20th, 2009; Mar 21st, 2009; Mar 22nd, 2009
* Feb 2009; Sep 2009; Oct 2010
* 6/2008; 12/2009
* 2009; 2010
Once you have extracted these date patterns from the text, the next step is to sort them in ascending chronological order accoring to the following rules:
* Assume all dates in xx/xx/xx format are mm/dd/yy
* Assume all dates where year is encoded in only two digits are years from the 1900's (e.g. 1/5/89 is January 5th, 1989)
* If the day is missing (e.g. 9/2009), assume it is the first day of the month (e.g. September 1, 2009).
* If the month is missing (e.g. 2010), assume it is the first of January of that year (e.g. January 1, 2010).
* Watch out for potential typos as this is a raw, real-life derived dataset.
With these rules in mind, find the correct date in each note and return a pandas Series in chronological order of the original Series' indices.
For example if the original series was this:
0 1999
1 2010
2 1978
3 2015
4 1985
Your function should return this:
0 2
1 4
2 0
3 1
4 3
Your score will be calculated using [Kendall's tau](https://en.wikipedia.org/wiki/Kendall_rank_correlation_coefficient), a correlation measure for ordinal data.
*This function should return a Series of length 500 and dtype int.*
```
# Load the data
# Reference: https://necromuralist.github.io/data_science/posts/extracting-dates-from-medical-data/
import pandas
doc = []
with open('dates.txt') as file:
for line in file:
doc.append(line)
data = pandas.Series(doc)
data.head(10)
data.describe()
# 4 The Grammar
# 4.1 Cardinality
ZERO_OR_MORE = '*'
ONE_OR_MORE = "+"
ZERO_OR_ONE = '?'
EXACTLY_TWO = "{2}"
ONE_OR_TWO = "{1,2}"
EXACTLY_ONE = '{1}'
# 4.2 Groups and Classes
GROUP = r"({})"
NAMED = r"(?P<{}>{})"
CLASS = "[{}]"
NEGATIVE_LOOKAHEAD = "(?!{})"
NEGATIVE_LOOKBEHIND = "(?<!{})"
POSITIVE_LOOKAHEAD = "(?={})"
POSITIVE_LOOKBEHIND = "(?<={})"
ESCAPE = "\{}"
# 4.3 Numbers
DIGIT = r"\d"
ONE_DIGIT = DIGIT + EXACTLY_ONE
ONE_OR_TWO_DIGITS = DIGIT + ONE_OR_TWO
NON_DIGIT = NEGATIVE_LOOKAHEAD.format(DIGIT)
TWO_DIGITS = DIGIT + EXACTLY_TWO
THREE_DIGITS = DIGIT + "{3}"
EXACTLY_TWO_DIGITS = DIGIT + EXACTLY_TWO + NON_DIGIT
FOUR_DIGITS = DIGIT + r"{4}" + NON_DIGIT
# 4.4 String Literals
SLASH = r"/"
OR = r'|'
LOWER_CASE = "a-z"
SPACE = "\s"
DOT = "."
DASH = "-"
COMMA = ","
PUNCTUATION = CLASS.format(DOT + COMMA + DASH)
EMPTY_STRING = ""
# 4.5 Dates
# These are parts to build up the date-expressions.
MONTH_SUFFIX = (CLASS.format(LOWER_CASE) + ZERO_OR_MORE
+ CLASS.format(SPACE + DOT + COMMA + DASH) + ONE_OR_TWO)
MONTH_PREFIXES = "Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec".split()
MONTHS = [month + MONTH_SUFFIX for month in MONTH_PREFIXES]
MONTHS = GROUP.format(OR.join(MONTHS))
DAY_SUFFIX = CLASS.format(DASH + COMMA + SPACE) + ONE_OR_TWO
DAYS = ONE_OR_TWO_DIGITS + DAY_SUFFIX
YEAR = FOUR_DIGITS
# This is for dates like Mar 21st, 2009, those with suffixes on the days.
CONTRACTED = (ONE_OR_TWO_DIGITS
+ LOWER_CASE
+ EXACTLY_TWO
)
CONTRACTION = NAMED.format("contraction",
MONTHS
+ CONTRACTED
+ DAY_SUFFIX
+ YEAR)
# This is for dates that have no days in them, like May 2009.
NO_DAY_BEHIND = NEGATIVE_LOOKBEHIND.format(DIGIT + SPACE)
NO_DAY = NAMED.format("no_day", NO_DAY_BEHIND + MONTHS + YEAR)
# This is for the most common form (that I use) - May 21, 2017.
WORDS = NAMED.format("words", MONTHS + DAYS + YEAR)
BACKWARDS = NAMED.format("backwards", ONE_OR_TWO_DIGITS + SPACE + MONTHS + YEAR)
slashed = SLASH.join([ONE_OR_TWO_DIGITS,
ONE_OR_TWO_DIGITS,
EXACTLY_TWO_DIGITS])
dashed = DASH.join([ONE_OR_TWO_DIGITS,
ONE_OR_TWO_DIGITS,
EXACTLY_TWO_DIGITS])
TWENTIETH_CENTURY = NAMED.format("twentieth",
OR.join([slashed, dashed]))
NUMERIC = NAMED.format("numeric",
SLASH.join([ONE_OR_TWO_DIGITS,
ONE_OR_TWO_DIGITS,
FOUR_DIGITS]))
NO_PRECEDING_SLASH = NEGATIVE_LOOKBEHIND.format(SLASH)
NO_PRECEDING_SLASH_DIGIT = NEGATIVE_LOOKBEHIND.format(CLASS.format(SLASH + DIGIT))
NO_ONE_DAY = (NO_PRECEDING_SLASH_DIGIT
+ ONE_DIGIT
+ SLASH
+ FOUR_DIGITS)
NO_TWO_DAYS = (NO_PRECEDING_SLASH
+ TWO_DIGITS
+ SLASH
+ FOUR_DIGITS)
NO_DAY_NUMERIC = NAMED.format("no_day_numeric",
NO_ONE_DAY
+ OR
+ NO_TWO_DAYS
)
CENTURY = GROUP.format('19' + OR + "20") + TWO_DIGITS
DIGIT_SLASH = DIGIT + SLASH
DIGIT_DASH = DIGIT + DASH
DIGIT_SPACE = DIGIT + SPACE
LETTER_SPACE = CLASS.format(LOWER_CASE) + SPACE
COMMA_SPACE = COMMA + SPACE
YEAR_PREFIX = NEGATIVE_LOOKBEHIND.format(OR.join([
DIGIT_SLASH,
DIGIT_DASH,
DIGIT_SPACE,
LETTER_SPACE,
COMMA_SPACE,
]))
YEAR_ONLY = NAMED.format("year_only",
YEAR_PREFIX + CENTURY
)
IN_PREFIX = POSITIVE_LOOKBEHIND.format(CLASS.format('iI') + 'n' + SPACE) + CENTURY
SINCE_PREFIX = POSITIVE_LOOKBEHIND.format(CLASS.format("Ss") + 'ince' + SPACE) + CENTURY
AGE = POSITIVE_LOOKBEHIND.format("Age" + SPACE + TWO_DIGITS + COMMA + SPACE) + CENTURY
AGE_COMMA = POSITIVE_LOOKBEHIND.format("Age" + COMMA + SPACE + TWO_DIGITS + COMMA + SPACE) + CENTURY
OTHERS = ['delivery', "quit", "attempt", "nephrectomy", THREE_DIGITS]
OTHERS = [POSITIVE_LOOKBEHIND.format(label + SPACE) + CENTURY for label in OTHERS]
OTHERS = OR.join(OTHERS)
LEFTOVERS_PREFIX = OR.join([IN_PREFIX, SINCE_PREFIX, AGE, AGE_COMMA]) + OR + OTHERS
LEFTOVERS = NAMED.format("leftovers", LEFTOVERS_PREFIX)
DATE = NAMED.format("date", OR.join([NUMERIC,
TWENTIETH_CENTURY,
WORDS,
BACKWARDS,
CONTRACTION,
NO_DAY,
NO_DAY_NUMERIC,
YEAR_ONLY,
LEFTOVERS]))
def twentieth_century(date):
"""adds a 19 to the year
Args:
date (re.Regex): Extracted date
"""
month, day, year = date.group(1).split(SLASH)
year = "19{}".format(year)
return SLASH.join([month, day, year])
def take_two(line):
match = re.search(TWENTIETH_CENTURY, line)
if match:
return twentieth_century(match)
return line
def extract_and_count(expression, data, name):
"""extract all matches and report the count
Args:
expression (str): regular expression to match
data (pandas.Series): data with dates to extratc
name (str): name of the group for the expression
Returns:
tuple (pandas.Series, int): extracted dates, count
"""
extracted = data.str.extractall(expression)[name]
count = len(extracted)
print("'{}' matched {} rows".format(name, count))
return extracted, count
numeric, numeric_count = extract_and_count(NUMERIC, data, 'numeric')
# 'numeric' matched 25 rows
twentieth, twentieth_count = extract_and_count(TWENTIETH_CENTURY, data, 'twentieth')
# 'twentieth' matched 100 rows
words, words_count = extract_and_count(WORDS, data, 'words')
# 'words' matched 34 rows
backwards, backwards_count = extract_and_count(BACKWARDS, data, 'backwards')
# 'backwards' matched 69 rows
contraction_data, contraction = extract_and_count(CONTRACTION, data, 'contraction')
# 'contraction' matched 0 rows
no_day, no_day_count = extract_and_count(NO_DAY, data, 'no_day')
# 'no_day' matched 115 rows
no_day_numeric, no_day_numeric_count = extract_and_count(NO_DAY_NUMERIC, data,
"no_day_numeric")
# 'no_day_numeric' matched 112 rows
year_only, year_only_count = extract_and_count(YEAR_ONLY, data, "year_only")
# 'year_only' matched 15 rows
leftovers, leftovers_count = extract_and_count(LEFTOVERS, data, "leftovers")
# 'leftovers' matched 30 rows
found = data.str.extractall(DATE)
total_found = len(found.date)
print("Total Found: {}".format(total_found))
print("Remaining: {}".format(len(data) - total_found))
print("Discrepancy: {}".format(total_found - (numeric_count
+ twentieth_count
+ words_count
+ backwards_count
+ contraction
+ no_day_count
+ no_day_numeric_count
+ year_only_count
+ leftovers_count)))
# Total Found: 500
# Remaining: 0
# Discrepancy: 0
missing = [label for label in data.index if label not in found.index.levels[0]]
try:
print(missing[0], data.loc[missing[0]])
except IndexError:
print("all rows matched")
# all rows matched
def clean(source, expression, replacement, sample=5):
"""applies the replacement to the source
as a side-effect shows sample rows before and after
Args:
source (pandas.Series): source of the strings
expression (str): regular expression to match what to replace
replacement: function or expression to replace the matching expression
sample (int): number of randomly chosen examples to show
Returns:
pandas.Series: the source with the replacement applied to it
"""
print("Random Sample Before:")
print(source.sample(sample))
cleaned = source.str.replace(expression, replacement)
print("\nRandom Sample After:")
print(cleaned.sample(sample))
print("\nCount of cleaned: {}".format(len(cleaned)))
assert len(source) == len(cleaned)
return cleaned
def clean_punctuation(source, sample=5):
"""removes punctuation
Args:
source (pandas.Series): data to clean
sample (int): size of sample to show
Returns:
pandas.Series: source with punctuation removed
"""
print("Cleaning Punctuation")
if any(source.str.contains(PUNCTUATION)):
source = clean(source, PUNCTUATION, EMPTY_STRING)
return source
LONG_TO_SHORT = dict(January="Jan",
February="Feb",
March="Mar",
April="Apr",
May="May",
June="Jun",
July="Jul",
August="Aug",
September="Sep",
October="Oct",
November="Nov",
December="Dec")
# it turns out there are spelling errors in the data so this has to be fuzzy
LONG_TO_SHORT_EXPRESSION = OR.join([GROUP.format(month)
+ CLASS.format(LOWER_CASE)
+ ZERO_OR_MORE
for month in LONG_TO_SHORT.values()])
def long_month_to_short(match):
"""convert long month to short
Args:
match (re.Match): object matching a long month
Returns:
str: shortened version of the month
"""
return match.group(match.lastindex)
def convert_long_months_to_short(source, sample=5):
"""convert long month names to short
Args:
source (pandas.Series): data with months
sample (int): size of sample to show
Returns:
pandas.Series: data with short months
"""
return clean(source,
LONG_TO_SHORT_EXPRESSION,
long_month_to_short)
def add_month_date(match):
"""adds 01/01 to years
Args:
match (re.Match): object that only matched a 4-digit year
Returns:
str: 01/01/YYYY
"""
return "01/01/" + match.group()
def add_january_one(source):
"""adds /01/01/ to year-only dates
Args:
source (pandas.Series): data with the dates
Returns:
pandas.Series: years in source with /01/01/ added
"""
return clean(source, YEAR_ONLY, add_month_date)
two_digit_expression = GROUP.format(ONE_OR_TWO_DIGITS) + POSITIVE_LOOKAHEAD.format(SLASH)
def two_digits(match):
"""add a leading zero if needed
Args:
match (re.Match): match with one or two digits
Returns:
str: the matched string with leading zero if needed
"""
# for some reason the string-formatting raises an error if it's a string
# so cast it to an int
return "{:02}".format(int(match.group()))
def clean_two_digits(source, sample=5):
"""makes sure source has two-digits
Args:
source (pandas.Series): data with digit followed by slash
sample (int): number of samples to show
Returns:
pandas.Series: source with digits coerced to two digits
"""
return clean(source, two_digit_expression, two_digits, sample)
def clean_two_digits_isolated(source, sample=5):
"""cleans two digits that are standalone
Args:
source (pandas.Series): source of the data
sample (int): number of samples to show
Returns:
pandas.Series: converted data
"""
return clean(source, ONE_OR_TWO_DIGITS, two_digits, sample)
digits = ("{:02}".format(month) for month in range(1, 13))
MONTH_TO_DIGITS = dict(zip(MONTH_PREFIXES, digits))
SHORT_MONTHS_EXPRESSION = OR.join((GROUP.format(month) for month in MONTH_TO_DIGITS))
def month_to_digits(match):
"""converts short month to digits
Args:
match (re.Match): object with short-month
Returns:
str: month as two-digit number (e.g. Jan -> 01)
"""
return MONTH_TO_DIGITS[match.group()]
def convert_short_month_to_digits(source, sample=5):
"""converts three-letter months to two-digits
Args:
source (pandas.Series): data with three-letter months
sample (int): number of samples to show
Returns:
pandas.Series: source with short-months coverted to digits
"""
return clean(source,
SHORT_MONTHS_EXPRESSION,
month_to_digits,
sample)
def clean_months(source, sample=5):
"""clean up months (which start as words)
Args:
source (pandas.Series): source of the months
sample (int): number of random samples to show
"""
cleaned = clean_punctuation(source)
print("Converting long months to short")
cleaned = clean(cleaned,
LONG_TO_SHORT_EXPRESSION,
long_month_to_short, sample)
print("Converting short months to digits")
cleaned = clean(cleaned,
SHORT_MONTHS_EXPRESSION,
month_to_digits, sample)
return cleaned
def frame_to_series(frame, index_source, samples=5):
"""re-combines data-frame into a series
Args:
frame (pandas.DataFrame): frame with month, day, year columns
index_source (pandas.series): source to copy index from
samples (index): number of random entries to print when done
Returns:
pandas.Series: series with dates as month/day/year
"""
combined = frame.month + SLASH + frame.day + SLASH + frame.year
combined.index = index_source.index
print(combined.sample(samples))
return combined
year_only_cleaned = add_january_one(year_only)
# Random Sample Before:
# match
# 472 0 2010
# 495 0 1979
# 497 0 2008
# 481 0 1974
# 486 0 1973
# Name: year_only, dtype: object
# Random Sample After:
# match
# 495 0 01/01/1979
# 470 0 01/01/1983
# 462 0 01/01/1988
# 481 0 01/01/1974
# 480 0 01/01/2013
# Name: year_only, dtype: object
# Count of cleaned: 15
leftovers_cleaned = add_january_one(leftovers)
# Random Sample Before:
# match
# 487 0 1992
# 477 0 1994
# 498 0 2005
# 488 0 1977
# 484 0 2004
# Name: leftovers, dtype: object
# Random Sample After:
# match
# 464 0 01/01/2016
# 455 0 01/01/1984
# 465 0 01/01/1976
# 475 0 01/01/2015
# 498 0 01/01/2005
# Name: leftovers, dtype: object
# Count of cleaned: 30
cleaned = pandas.concat([year_only_cleaned, leftovers_cleaned])
print(len(cleaned))
no_day_numeric_cleaned = clean_two_digits(no_day_numeric)
no_day_numeric_cleaned = clean(no_day_numeric_cleaned,
SLASH,
lambda m: "/01/")
original = len(cleaned)
cleaned = pandas.concat([cleaned, no_day_numeric_cleaned])
assert len(cleaned) == no_day_numeric_count + original
print(len(cleaned))
no_day_cleaned = clean_months(no_day)
no_day_cleaned = clean(no_day_cleaned,
SPACE + ONE_OR_MORE,
lambda match: "/01/")
original = len(cleaned)
cleaned = pandas.concat([cleaned, no_day_cleaned])
print(len(cleaned))
assert len(cleaned) == no_day_count + original
frame = pandas.DataFrame(backwards.str.split().tolist(),
columns="day month year".split())
frame.head()
frame.day = clean_two_digits(frame.day)
frame.month = clean_months(frame.month)
backwards_cleaned = frame_to_series(frame, backwards)
original = len(cleaned)
cleaned = pandas.concat([cleaned, backwards_cleaned])
assert len(cleaned) == original + backwards_count
print(len(cleaned))
frame = pandas.DataFrame(words.str.split().tolist(), columns="month day year".split())
print(frame.head())
frame.month = clean_months(frame.month)
frame.day = clean_punctuation(frame.day)
frame.head()
words_cleaned = frame_to_series(frame, words)
original = len(cleaned)
cleaned = pandas.concat([cleaned, words_cleaned])
assert len(cleaned) == original + words_count
print(len(cleaned))
print(twentieth.iloc[21])
twentieth_cleaned = twentieth.str.replace(DASH, SLASH)
print(cleaned.iloc[21])
frame = pandas.DataFrame(twentieth_cleaned.str.split(SLASH).tolist(),
columns=["month", "day", "year"])
print(frame.head())
frame.month = clean_two_digits_isolated(frame.month)
frame.day = clean_two_digits_isolated(frame.day)
frame.head()
frame.year = clean(frame.year, TWO_DIGITS, lambda match: "19" + match.group())
twentieth_cleaned = frame_to_series(frame, twentieth)
original = len(cleaned)
cleaned = pandas.concat([cleaned, twentieth_cleaned])
assert len(cleaned) == original + twentieth_count
print(numeric.head())
has_dashes = numeric.str.contains(DASH)
print(numeric[has_dashes])
frame = pandas.DataFrame(numeric.str.split(SLASH).tolist(),
columns="month day year".split())
print(frame.head())
frame.month = clean_two_digits_isolated(frame.month)
frame.day = clean_two_digits_isolated(frame.day)
numeric_cleaned = frame_to_series(frame, numeric)
original = len(cleaned)
cleaned = pandas.concat([cleaned, numeric_cleaned])
assert len(cleaned) == original + numeric_count
print(len(cleaned))
cleaned = pandas.concat([numeric_cleaned,
twentieth_cleaned,
words_cleaned,
backwards_cleaned,
no_day_cleaned,
no_day_numeric_cleaned,
year_only_cleaned,
leftovers_cleaned,
])
print(len(cleaned))
print(cleaned.head())
assert len(cleaned) == len(data)
print(cleaned.head())
datetimes = pandas.to_datetime(cleaned, format="%m/%d/%Y")
print(datetimes.head())
sorted_dates = datetimes.sort_values()
print(sorted_dates.head())
print(sorted_dates.tail())
answer = pandas.Series(sorted_dates.index.labels[0])
print(answer.head())
def date_sorter():
return answer
```
|
github_jupyter
|
# Imports
```
import torch
from torch.autograd import Variable
from torch.utils.data import DataLoader
import matplotlib.pyplot as plt
import numpy as np
import sys
sys.path.insert(0, "lib/")
from utils.preprocess_sample import preprocess_sample
from utils.collate_custom import collate_custom
from utils.utils import to_cuda_variable
from utils.json_dataset_evaluator import evaluate_boxes,evaluate_masks
from model.detector import detector
import utils.result_utils as result_utils
import utils.vis as vis_utils
import skimage.io as io
from utils.blob import prep_im_for_blob
import utils.dummy_datasets as dummy_datasets
from utils.selective_search import selective_search # needed for proposal extraction in Fast RCNN
from PIL import Image
torch_ver = torch.__version__[:3]
```
# Parameters
```
# Pretrained model
arch='resnet50'
# COCO minival2014 dataset path
coco_ann_file='datasets/data/coco/annotations/instances_minival2014.json'
img_dir='datasets/data/coco/val2014'
# model type
model_type='mask' # change here
if model_type=='mask':
# https://s3-us-west-2.amazonaws.com/detectron/35858828/12_2017_baselines/e2e_mask_rcnn_R-50-C4_2x.yaml.01_46_47.HBThTerB/output/train/coco_2014_train%3Acoco_2014_valminusminival/generalized_rcnn/model_final.pkl
pretrained_model_file = 'files/trained_models/mask/model_final.pkl'
use_rpn_head = True
use_mask_head = True
elif model_type=='faster':
# https://s3-us-west-2.amazonaws.com/detectron/35857281/12_2017_baselines/e2e_faster_rcnn_R-50-C4_2x.yaml.01_34_56.ScPH0Z4r/output/train/coco_2014_train%3Acoco_2014_valminusminival/generalized_rcnn/model_final.pkl
pretrained_model_file = 'files/trained_models/faster/model_final.pkl'
use_rpn_head = True
use_mask_head = False
elif model_type=='fast':
# https://s3-us-west-2.amazonaws.com/detectron/36224046/12_2017_baselines/fast_rcnn_R-50-C4_2x.yaml.08_22_57.XFxNqEnL/output/train/coco_2014_train%3Acoco_2014_valminusminival/generalized_rcnn/model_final.pkl
pretrained_model_file = 'files/trained_models/fast/model_final.pkl'
use_rpn_head = False
use_mask_head = False
```
# Load image
```
image_fn = 'demo/33823288584_1d21cf0a26_k.jpg'
# Load image
image = io.imread(image_fn)
if len(image.shape) == 2: # convert grayscale to RGB
image = np.repeat(np.expand_dims(image,2), 3, axis=2)
orig_im_size = image.shape
# Preprocess image
im_list, im_scales = prep_im_for_blob(image)
# Build sample
sample = {}
sample['image'] = torch.FloatTensor(im_list[0]).permute(2,0,1).unsqueeze(0)
sample['scaling_factors'] = torch.FloatTensor([im_scales[0]])
sample['original_im_size'] = torch.FloatTensor(orig_im_size)
# Extract proposals
if model_type=='fast':
# extract proposals using selective search (xmin,ymin,xmax,ymax format)
rects = selective_search(pil_image=Image.fromarray(image),quality='f')
sample['proposal_coords']=torch.FloatTensor(preprocess_sample().remove_dup_prop(rects)[0])*im_scales[0]
else:
sample['proposal_coords']=torch.FloatTensor([-1]) # dummy value
# Convert to cuda variable
sample = to_cuda_variable(sample)
```
# Create detector model
```
model = detector(arch=arch,
detector_pkl_file=pretrained_model_file,
use_rpn_head = use_rpn_head,
use_mask_head = use_mask_head)
model = model.cuda()
```
# Evaluate
```
def eval_model(sample):
class_scores,bbox_deltas,rois,img_features=model(sample['image'],
sample['proposal_coords'],
scaling_factor=sample['scaling_factors'].cpu().data.numpy().item())
return class_scores,bbox_deltas,rois,img_features
if torch_ver=="0.4":
with torch.no_grad():
class_scores,bbox_deltas,rois,img_features=eval_model(sample)
else:
class_scores,bbox_deltas,rois,img_features=eval_model(sample)
# postprocess output:
# - convert coordinates back to original image size,
# - treshold proposals based on score,
# - do NMS.
scores_final, boxes_final, boxes_per_class = result_utils.postprocess_output(rois,
sample['scaling_factors'],
sample['original_im_size'],
class_scores,
bbox_deltas)
if model_type=='mask':
# compute masks
boxes_final_th = Variable(torch.cuda.FloatTensor(boxes_final))*sample['scaling_factors']
masks=model.mask_head(img_features,boxes_final_th)
# postprocess mask output:
h_orig = int(sample['original_im_size'].squeeze()[0].data.cpu().numpy().item())
w_orig = int(sample['original_im_size'].squeeze()[1].data.cpu().numpy().item())
cls_segms = result_utils.segm_results(boxes_per_class, masks.cpu().data.numpy(), boxes_final, h_orig, w_orig)
else:
cls_segms = None
print('Done!')
```
# Visualize
```
output_dir = 'demo/output/'
vis_utils.vis_one_image(
image, # BGR -> RGB for visualization
image_fn,
output_dir,
boxes_per_class,
cls_segms,
None,
dataset=dummy_datasets.get_coco_dataset(),
box_alpha=0.3,
show_class=True,
thresh=0.7,
kp_thresh=2,
show=True
)
```
|
github_jupyter
|
<h1>Table of Contents<span class="tocSkip"></span></h1>
<div class="toc" style="margin-top: 1em;"><ul class="toc-item"><li><span><a href="#Queries" data-toc-modified-id="Queries-1"><span class="toc-item-num">1 </span>Queries</a></span><ul class="toc-item"><li><span><a href="#All-Videos" data-toc-modified-id="All-Videos-1.1"><span class="toc-item-num">1.1 </span>All Videos</a></span></li><li><span><a href="#Videos-by-Channel" data-toc-modified-id="Videos-by-Channel-1.2"><span class="toc-item-num">1.2 </span>Videos by Channel</a></span></li><li><span><a href="#Videos-by-Show" data-toc-modified-id="Videos-by-Show-1.3"><span class="toc-item-num">1.3 </span>Videos by Show</a></span></li><li><span><a href="#Videos-by-Canonical-Show" data-toc-modified-id="Videos-by-Canonical-Show-1.4"><span class="toc-item-num">1.4 </span>Videos by Canonical Show</a></span></li><li><span><a href="#Videos-by-time-of-day" data-toc-modified-id="Videos-by-time-of-day-1.5"><span class="toc-item-num">1.5 </span>Videos by time of day</a></span></li></ul></li><li><span><a href="#Shots" data-toc-modified-id="Shots-2"><span class="toc-item-num">2 </span>Shots</a></span><ul class="toc-item"><li><span><a href="#Shot-Validation" data-toc-modified-id="Shot-Validation-2.1"><span class="toc-item-num">2.1 </span>Shot Validation</a></span></li><li><span><a href="#All-Shots" data-toc-modified-id="All-Shots-2.2"><span class="toc-item-num">2.2 </span>All Shots</a></span></li><li><span><a href="#Shots-by-Channel" data-toc-modified-id="Shots-by-Channel-2.3"><span class="toc-item-num">2.3 </span>Shots by Channel</a></span></li><li><span><a href="#Shots-by-Show" data-toc-modified-id="Shots-by-Show-2.4"><span class="toc-item-num">2.4 </span>Shots by Show</a></span></li><li><span><a href="#Shots-by-Canonical-Show" data-toc-modified-id="Shots-by-Canonical-Show-2.5"><span class="toc-item-num">2.5 </span>Shots by Canonical Show</a></span></li><li><span><a href="#Shots-by-Time-of-Day" data-toc-modified-id="Shots-by-Time-of-Day-2.6"><span class="toc-item-num">2.6 </span>Shots by Time of Day</a></span></li></ul></li><li><span><a href="#Commercials" data-toc-modified-id="Commercials-3"><span class="toc-item-num">3 </span>Commercials</a></span><ul class="toc-item"><li><span><a href="#All-Commercials" data-toc-modified-id="All-Commercials-3.1"><span class="toc-item-num">3.1 </span>All Commercials</a></span></li><li><span><a href="#Commercials-by-Channel" data-toc-modified-id="Commercials-by-Channel-3.2"><span class="toc-item-num">3.2 </span>Commercials by Channel</a></span></li><li><span><a href="#Commercials-by-Show" data-toc-modified-id="Commercials-by-Show-3.3"><span class="toc-item-num">3.3 </span>Commercials by Show</a></span></li><li><span><a href="#Commercials-by-Canonical-Show" data-toc-modified-id="Commercials-by-Canonical-Show-3.4"><span class="toc-item-num">3.4 </span>Commercials by Canonical Show</a></span></li><li><span><a href="#Commercials-by-Time-of-Day" data-toc-modified-id="Commercials-by-Time-of-Day-3.5"><span class="toc-item-num">3.5 </span>Commercials by Time of Day</a></span></li></ul></li><li><span><a href="#Faces" data-toc-modified-id="Faces-4"><span class="toc-item-num">4 </span>Faces</a></span><ul class="toc-item"><li><span><a href="#Face-Validation" data-toc-modified-id="Face-Validation-4.1"><span class="toc-item-num">4.1 </span>Face Validation</a></span></li><li><span><a href="#All-Faces" data-toc-modified-id="All-Faces-4.2"><span class="toc-item-num">4.2 </span>All Faces</a></span></li></ul></li><li><span><a href="#Genders" data-toc-modified-id="Genders-5"><span class="toc-item-num">5 </span>Genders</a></span><ul class="toc-item"><li><span><a href="#All-Gender" data-toc-modified-id="All-Gender-5.1"><span class="toc-item-num">5.1 </span>All Gender</a></span><ul class="toc-item"><li><span><a href="#Persist-for-Report" data-toc-modified-id="Persist-for-Report-5.1.1"><span class="toc-item-num">5.1.1 </span>Persist for Report</a></span></li></ul></li><li><span><a href="#Gender-by-Channel" data-toc-modified-id="Gender-by-Channel-5.2"><span class="toc-item-num">5.2 </span>Gender by Channel</a></span></li><li><span><a href="#Gender-by-Show" data-toc-modified-id="Gender-by-Show-5.3"><span class="toc-item-num">5.3 </span>Gender by Show</a></span><ul class="toc-item"><li><span><a href="#Persist-for-Report" data-toc-modified-id="Persist-for-Report-5.3.1"><span class="toc-item-num">5.3.1 </span>Persist for Report</a></span></li></ul></li><li><span><a href="#Gender-by-Canonical-Show" data-toc-modified-id="Gender-by-Canonical-Show-5.4"><span class="toc-item-num">5.4 </span>Gender by Canonical Show</a></span><ul class="toc-item"><li><span><a href="#Persist-for-Report" data-toc-modified-id="Persist-for-Report-5.4.1"><span class="toc-item-num">5.4.1 </span>Persist for Report</a></span></li></ul></li><li><span><a href="#Gender-by-time-of-day" data-toc-modified-id="Gender-by-time-of-day-5.5"><span class="toc-item-num">5.5 </span>Gender by time of day</a></span></li><li><span><a href="#Gender-by-Day-of-the-Week" data-toc-modified-id="Gender-by-Day-of-the-Week-5.6"><span class="toc-item-num">5.6 </span>Gender by Day of the Week</a></span></li><li><span><a href="#Gender-by-topic" data-toc-modified-id="Gender-by-topic-5.7"><span class="toc-item-num">5.7 </span>Gender by topic</a></span></li><li><span><a href="#Male-vs.-female-faces-in-panels" data-toc-modified-id="Male-vs.-female-faces-in-panels-5.8"><span class="toc-item-num">5.8 </span>Male vs. female faces in panels</a></span></li></ul></li><li><span><a href="#Pose" data-toc-modified-id="Pose-6"><span class="toc-item-num">6 </span>Pose</a></span></li><li><span><a href="#Topics" data-toc-modified-id="Topics-7"><span class="toc-item-num">7 </span>Topics</a></span></li></ul></div>
```
%matplotlib inline
from esper.stdlib import *
from esper.prelude import *
from esper.spark_util import *
from esper.validation import *
import IPython
import shutil
shows = get_shows()
print('Schema:', shows)
print('Count:', shows.count())
videos = get_videos()
print('Schema:', videos)
print('Count:', videos.count())
shots = get_shots()
print('Schema:', shots)
print('Count:', shots.count())
speakers = get_speakers()
print('Schema:', speakers)
print('Count:', speakers.count())
# speakers.where(speakers.in_commercial == True).show()
# speakers.where(speakers.in_commercial == False).show()
segments = get_segments()
print('Schema:', segments)
print('Count:', segments.count())
# segments.where(segments.in_commercial == True).show()
# segments.where(segments.in_commercial == False).show()
faces = get_faces()
print('Schema:', faces)
print('Count:', faces.count())
face_genders = get_face_genders()
print('Schema:', face_genders)
print('Count:', face_genders.count())
face_identities = get_face_identities()
print('Schema:', face_identities)
print('Count:', face_identities.count())
commercials = get_commercials()
print('Schema:', commercials)
print('Count:', commercials.count())
```
# Queries
```
def format_time(seconds, padding=4):
return '{{:0{}d}}:{{:02d}}:{{:02d}}'.format(padding).format(
int(seconds/3600), int(seconds/60 % 60), int(seconds % 60))
def format_number(n):
def fmt(n):
suffixes = {
6: 'thousand',
9: 'million',
12: 'billion',
15: 'trillion'
}
log = math.log10(n)
suffix = None
key = None
for k in sorted(suffixes.keys()):
if log < k:
suffix = suffixes[k]
key = k
break
return '{:.2f} {}'.format(n / float(10**(key-3)), suffix)
if isinstance(n, list):
return map(fmt, n)
else:
return fmt(n)
def show_df(table, ordering, clear=True):
if clear:
IPython.display.clear_output()
return pd.DataFrame(table)[ordering]
def format_hour(h):
if h <= 12:
return '{} AM'.format(h)
else:
return '{} PM'.format(h-12)
def video_stats(key, labels):
if key is not None:
rows = videos.groupBy(key).agg(
videos[key],
func.count('duration'),
func.avg('duration'),
func.sum('duration'),
func.stddev_pop('duration')
).collect()
else:
rows = videos.agg(
func.count('duration'),
func.avg('duration'),
func.sum('duration'),
func.stddev_pop('duration')
).collect()
rmap = {(0 if key is None else r[key]): r for r in rows}
return [{
'label': label['name'],
'count': rmap[label['id']]['count(duration)'],
'duration': format_time(int(rmap[label['id']]['sum(duration)'])),
'avg_duration': '{} (σ = {})'.format(
format_time(int(rmap[label['id']]['avg(duration)'])),
format_time(int(rmap[label['id']]['stddev_pop(duration)']), padding=0))
} for label in labels if not key or label['id'] in rmap]
video_ordering = ['label', 'count', 'duration', 'avg_duration']
hours = [
r['hour'] for r in
Video.objects.annotate(
hour=Extract('time', 'hour')
).distinct('hour').order_by('hour').values('hour')
]
```
## All Videos
```
show_df(
video_stats(None, [{'id': 0, 'name': 'whole dataset'}]),
video_ordering)
```
## Videos by Channel
```
show_df(
video_stats('channel_id', list(Channel.objects.all().values('id', 'name'))),
video_ordering)
```
## Videos by Show
"Situation Room with Wolf Blitzer" and "Special Report with Bret Baier" were ingested as 60 10-minute segments each, whereas the other shows have 10 ≥1 hour segments.
```
show_df(
video_stats('show_id', list(Show.objects.all().values('id', 'name'))),
video_ordering)
```
## Videos by Canonical Show
```
show_df(
video_stats('canonical_show_id', list(CanonicalShow.objects.all().values('id', 'name'))),
video_ordering)
```
## Videos by time of day
Initial selection of videos was only prime-time, so between 4pm-11pm.
```
show_df(
video_stats('hour', [{'id': hour, 'name': format_hour(hour)} for hour in hours]),
video_ordering)
```
# Shots
```
med_withcom = shots.approxQuantile('duration', [0.5], 0.01)[0]
print('Median shot length with commercials: {:0.2f}s'.format(med_withcom))
med_nocom = shots.where(
shots.in_commercial == False
).approxQuantile('duration', [0.5], 0.01)[0]
print('Median shot length w/o commercials: {:0.2f}s'.format(med_nocom))
med_channels = {
c.name: shots.where(
shots.channel_id == c.id
).approxQuantile('duration', [0.5], 0.01)[0]
for c in Channel.objects.all()
}
print('Median shot length by_channel:')
for c, v in med_channels.items():
print(' {}: {:0.2f}s'.format(c, v))
pickle.dump({
'withcom': med_withcom,
'nocom': med_nocom,
'channels': med_channels
}, open('/app/data/shot_medians.pkl', 'wb'))
all_shot_durations = np.array(
[r['duration'] for r in shots.select('duration').collect()]
)
hist, edges = np.histogram(all_shot_durations, bins=list(range(0, 3600)) + [10000000])
pickle.dump(hist, open('/app/data/shot_histogram.pkl', 'wb'))
```
## Shot Validation
```
# TODO: what is this hack?
shot_precision = 0.97
shot_recall = 0.97
def shot_error_interval(n):
return [n * shot_precision, n * (2 - shot_recall)]
def shot_stats(key, labels, shots=shots):
if key is not None:
df = shots.groupBy(key)
rows = df.agg(shots[key], func.count('duration'), func.avg('duration'), func.sum('duration'), func.stddev_pop('duration')).collect()
else:
df = shots
rows = df.agg(func.count('duration'), func.avg('duration'), func.sum('duration'), func.stddev_pop('duration')).collect()
rmap = {(0 if key is None else r[key]): r for r in rows}
out_rows = []
for label in labels:
try:
out_rows.append({
'label': label['name'],
'count': rmap[label['id']]['count(duration)'], #format_number(shot_error_interval(rmap[label['id']]['count(duration)'])),
'duration': format_time(int(rmap[label['id']]['sum(duration)'])),
'avg_duration': '{:06.2f}s (σ = {:06.2f})'.format(
rmap[label['id']]['avg(duration)'],
rmap[label['id']]['stddev_pop(duration)'])
})
except KeyError:
pass
return out_rows
shot_ordering = ['label', 'count', 'duration', 'avg_duration']
```
## All Shots
```
show_df(
shot_stats(None, [{'id': 0, 'name': 'whole dataset'}]),
shot_ordering)
```
## Shots by Channel
```
show_df(
shot_stats('channel_id', list(Channel.objects.all().values('id', 'name'))),
shot_ordering)
```
## Shots by Show
```
show_df(
shot_stats('show_id', list(Show.objects.all().values('id', 'name'))),
shot_ordering)
```
## Shots by Canonical Show
```
show_df(
shot_stats('canonical_show_id', list(CanonicalShow.objects.all().values('id', 'name'))),
shot_ordering)
```
## Shots by Time of Day
```
show_df(
shot_stats('hour', [{'id': hour, 'name': format_hour(hour)} for hour in hours]),
shot_ordering)
```
# Commercials
```
def commercial_stats(key, labels):
if key is not None:
rows = commercials.groupBy(key).agg(
commercials[key],
func.count('duration'),
func.avg('duration'),
func.sum('duration')
).collect()
else:
rows = commercials.agg(
func.count('duration'),
func.avg('duration'),
func.sum('duration')
).collect()
rmap = {(0 if key is None else r[key]): r for r in rows}
out_rows = []
for label in labels:
try:
out_rows.append({
'label': label['name'],
'count': format_number(rmap[label['id']]['count(duration)']),
'duration': format_time(int(rmap[label['id']]['sum(duration)'])),
'avg_duration': '{:06.2f}s'.format(rmap[label['id']]['avg(duration)'])
})
except KeyError:
pass
return out_rows
commercial_ordering = ['label', 'count', 'duration', 'avg_duration']
```
## All Commercials
```
show_df(
commercial_stats(None, [{'id': 0, 'name': 'whole dataset'}]),
commercial_ordering)
print('Average # of commercials per video: {:0.2f}'.format(
commercials.groupBy('video_id').count().agg(
func.avg(func.col('count'))
).collect()[0]['avg(count)']
))
```
## Commercials by Channel
```
show_df(
commercial_stats('channel_id', list(Channel.objects.all().values('id', 'name'))),
commercial_ordering)
```
## Commercials by Show
```
show_df(
commercial_stats('show_id', list(Show.objects.all().values('id', 'name'))),
commercial_ordering)
```
## Commercials by Canonical Show
```
show_df(
commercial_stats('canonical_show_id', list(CanonicalShow.objects.all().values('id', 'name'))),
commercial_ordering)
```
## Commercials by Time of Day
```
show_df(
commercial_stats('hour', [{'id': hour, 'name': format_hour(hour)} for hour in hours]),
commercial_ordering)
```
# Faces
## Face Validation
```
base_face_stats = face_validation('All faces', lambda x: x)
big_face_stats = face_validation(
'Faces height > 0.2', lambda qs: qs.annotate(height=F('bbox_y2') - F('bbox_y1')).filter(height__gte=0.2))
shot_precision = 0.97
shot_recall = 0.97
def face_error_interval(n, face_stats):
(face_precision, face_recall, _) = face_stats
return [n * shot_precision * face_precision, n * (2 - shot_recall) * (2 - face_recall)]
```
## All Faces
```
print('Total faces: {}'.format(
format_number(face_error_interval(faces.count(), base_face_stats[2]))))
total_duration = videos.agg(func.sum('duration')).collect()[0]['sum(duration)'] - \
commercials.agg(func.sum('duration')).collect()[0]['sum(duration)']
face_duration = faces.groupBy('shot_id') \
.agg(
func.first('duration').alias('duration')
).agg(func.sum('duration')).collect()[0]['sum(duration)']
print('% of time a face is on screen: {:0.2f}'.format(100.0 * face_duration / total_duration))
```
# Genders
These queries analyze the distribution of men vs. women across a number of axes. We use faces detected by [MTCNN](https://github.com/kpzhang93/MTCNN_face_detection_alignment/) and gender detected by [rude-carnie](https://github.com/dpressel/rude-carnie). We only consider faces with a height > 20% of the frame to eliminate people in the background.
Time for a given gender is the amount of time during which at least one person of that gender was on screen. Percentages are (gender screen time) / (total time any person was on screen).
```
_, Cm = gender_validation('Gender w/ face height > 0.2', big_face_stats)
def P(y, yhat):
d = {'M': 0, 'F': 1, 'U': 2}
return float(Cm[d[y]][d[yhat]]) / sum([Cm[i][d[yhat]] for i in d.values()])
# TODO: remove a host -- use face features to identify and remove rachel maddow from computation
# TODO: more discrete time zones ("sunday mornings", "prime time", "daytime", "late evening")
# TODO: by year
# TODO: specific dates, e.g. during the RNC
MALE = Gender.objects.get(name='M')
FEMALE = Gender.objects.get(name='F')
UNKNOWN = Gender.objects.get(name='U')
gender_names = {g.id: g.name for g in Gender.objects.all()}
def gender_singlecount_stats(key, labels, min_dur=None):
if key == 'topic':
# TODO: Fix this
df1 = face_genders.join(segment_links, face_genders.segment_id == segment_links.segment_id)
df2 = df1.join(things, segment_links.thing_id == things.id)
topic_type = ThingType.objects.get(name='topic').id
df3 = df2.where(things.type_id == topic_type).select(
*(['duration', 'channel_id', 'show_id', 'hour', 'week_day', 'gender_id'] + \
[things.id.alias('topic'), 'shot_id']))
full_df = df3
else:
full_df = face_genders
keys = ['duration', 'channel_id', 'show_id', 'hour', 'week_day']
aggs = [func.count('gender_id')] + [func.first(full_df[k]).alias(k) for k in keys] + \
([full_df.topic] if key == 'topic' else [])
groups = ([key] if key is not None else []) + ['gender_id']
counts = full_df.groupBy(
# this is very brittle, need to add joined fields like 'canonical_show_id' here
*(['shot_id', 'gender_id', 'canonical_show_id'] + (['topic'] if key == 'topic' else []))
).agg(*aggs)
rows = counts.where(
counts['count(gender_id)'] > 0
).groupBy(
*groups
).agg(
func.sum('duration')
).collect()
if key is not None:
base_counts = full_df.groupBy(
['shot_id', key]
).agg(full_df[key], func.first('duration').alias('duration')) \
.groupBy(key).agg(full_df[key], func.sum('duration')).collect()
else:
base_counts = full_df.groupBy(
'shot_id'
).agg(
func.first('duration').alias('duration')
).agg(func.sum('duration')).collect()
base_map = {
(row[key] if key is not None else 0): row['sum(duration)']
for row in base_counts
}
out_rows = []
for label in labels:
label_rows = {
row.gender_id: row for row in rows if key is None or row[key] == label['id']
}
if len(label_rows) < 3:
continue
base_dur = int(base_map[label['id']])
if min_dur != None and base_dur < min_dur:
continue
durs = {
g.id: int(label_rows[g.id]['sum(duration)'])
for g in [MALE, FEMALE, UNKNOWN]
}
def adjust(g):
return int(
reduce(lambda a, b:
a + b, [durs[g2] * P(gender_names[g], gender_names[g2])
for g2 in durs]))
adj_durs = {
g: adjust(g)
for g in durs
}
out_rows.append({
key: label['name'],
'M': format_time(durs[MALE.id]),
'F': format_time(durs[FEMALE.id]),
'U': format_time(durs[UNKNOWN.id]),
'base': format_time(base_dur),
'M%': int(100.0 * durs[MALE.id] / base_dur),
'F%': int(100.0 * durs[FEMALE.id] / base_dur),
'U%': int(100.0 * durs[UNKNOWN.id] / base_dur),
# 'M-Adj': format_time(adj_durs[MALE.id]),
# 'F-Adj': format_time(adj_durs[FEMALE.id]),
# 'U-Adj': format_time(adj_durs[UNKNOWN.id]),
# 'M-Adj%': int(100.0 * adj_durs[MALE.id] / base_dur),
# 'F-Adj%': int(100.0 * adj_durs[FEMALE.id] / base_dur),
# 'U-Adj%': int(100.0 * adj_durs[UNKNOWN.id] / base_dur),
#'Overlap': int(100.0 * float(male_dur + female_dur) / base_dur) - 100
})
return out_rows
gender_ordering = ['M', 'M%', 'F', 'F%', 'U', 'U%']
#gender_ordering = ['M', 'M%', 'M-Adj', 'M-Adj%', 'F', 'F%', 'F-Adj', 'F-Adj%', 'U', 'U%', 'U-Adj', 'U-Adj%']
def gender_multicount_stats(key, labels, min_dur=None, no_host=False, just_host=False):
df0 = face_genders
if no_host:
df0 = df0.where(df0.is_host == False)
if just_host:
df0 = df0.where(df0.is_host == True)
if key == 'topic':
df1 = df0.join(segment_links, df0.segment_id == segment_links.segment_id)
df2 = df1.join(things, segment_links.thing_id == things.id)
topic_type = ThingType.objects.get(name='topic').id
df3 = df2.where(things.type_id == topic_type).select(
*(['duration', 'channel_id', 'show_id', 'hour', 'week_day', 'gender_id'] + \
[things.id.alias('topic'), 'shot_id']))
full_df = df3
else:
full_df = df0
groups = ([key] if key is not None else []) + ['gender_id']
rows = full_df.groupBy(*groups).agg(func.sum('duration')).collect()
out_rows = []
for label in labels:
label_rows = {row.gender_id: row for row in rows if key is None or row[key] == label['id']}
if len(label_rows) < 3: continue
male_dur = int(label_rows[MALE.id]['sum(duration)'])
female_dur = int(label_rows[FEMALE.id]['sum(duration)'])
unknown_dur = int(label_rows[UNKNOWN.id]['sum(duration)'])
base_dur = male_dur + female_dur
if min_dur != None and base_dur < min_dur:
continue
out_rows.append({
key: label['name'],
'M': format_time(male_dur),
'F': format_time(female_dur),
'U': format_time(unknown_dur),
'base': format_time(base_dur),
'M%': int(100.0 * male_dur / base_dur),
'F%': int(100.0 * female_dur / base_dur),
'U%': int(100.0 * unknown_dur / (base_dur + unknown_dur)),
'Overlap': 0,
})
return out_rows
def gender_speaker_stats(key, labels, min_dur=None, no_host=False):
keys = ['duration', 'channel_id', 'show_id', 'hour', 'week_day']
df0 = speakers
if no_host:
df0 = df0.where(df0.has_host == False)
if key == 'topic':
df1 = df0.join(segment_links, speakers.segment_id == segment_links.segment_id)
df2 = df1.join(things, segment_links.thing_id == things.id)
topic_type = ThingType.objects.get(name='topic').id
df3 = df2.where(things.type_id == topic_type).select(
*(keys + ['gender_id', things.id.alias('topic')]))
full_df = df3
else:
full_df = df0
aggs = [func.count('gender_id')] + [func.first(full_df[k]).alias(k) for k in keys] + \
([full_df.topic] if key == 'topic' else [])
groups = ([key] if key is not None else []) + ['gender_id'] + (['topic'] if key == 'topic' else [])
rows = full_df.groupBy(*groups).agg(func.sum('duration')).collect()
if key is not None:
base_counts = full_df.groupBy(key).agg(full_df[key], func.sum('duration')).collect()
else:
base_counts = full_df.agg(func.sum('duration')).collect()
base_map = {
(row[key] if key is not None else 0): row['sum(duration)']
for row in base_counts
}
out_rows = []
for label in labels:
label_rows = {row.gender_id: row for row in rows if key is None or row[key] == label['id']}
if len(label_rows) < 2: continue
male_dur = int(label_rows[MALE.id]['sum(duration)'])
female_dur = int(label_rows[FEMALE.id]['sum(duration)'])
base_dur = int(base_map[label['id']])
if min_dur != None and base_dur < min_dur:
continue
out_rows.append({
key: label['name'],
'M': format_time(male_dur),
'F': format_time(female_dur),
'base': format_time(base_dur),
'M%': int(100.0 * male_dur / base_dur),
'F%': int(100.0 * female_dur / base_dur),
})
return out_rows
gender_speaker_ordering = ['M', 'M%', 'F', 'F%']
```
## All Gender
```
print('Singlecount')
show_df(gender_singlecount_stats(None, [{'id': 0, 'name': 'whole dataset'}]),
gender_ordering)
print('Multicount')
gender_screen_all = gender_multicount_stats(None, [{'id': 0, 'name': 'whole dataset'}])
gender_screen_all_nh = gender_multicount_stats(None, [{'id': 0, 'name': 'whole dataset'}],
no_host=True)
show_df(gender_screen_all, gender_ordering)
show_df(gender_screen_all_nh, gender_ordering)
print('Speaking time')
gender_speaking_all = gender_speaker_stats(None, [{'id': 0, 'name': 'whole dataset'}])
gender_speaking_all_nh = gender_speaker_stats(
None, [{'id': 0, 'name': 'whole dataset'}],
no_host=True)
show_df(gender_speaking_all, gender_speaker_ordering)
show_df(gender_speaking_all_nh, gender_speaker_ordering)
```
### Persist for Report
```
pd.DataFrame(gender_screen_all).to_csv('/app/data/screen_all.csv')
pd.DataFrame(gender_screen_all_nh).to_csv('/app/data/screen_all_nh.csv')
pd.DataFrame(gender_speaking_all).to_csv('/app/data/speaking_all.csv')
```
## Gender by Channel
```
print('Singlecount')
show_df(
gender_singlecount_stats('channel_id', list(Channel.objects.values('id', 'name'))),
['channel_id'] + gender_ordering)
print('Multicount')
show_df(
gender_multicount_stats('channel_id', list(Channel.objects.values('id', 'name'))),
['channel_id'] + gender_ordering)
print('Speaking time')
show_df(
gender_speaker_stats('channel_id', list(Channel.objects.values('id', 'name'))),
['channel_id'] + gender_speaker_ordering)
```
## Gender by Show
```
print('Singlecount')
show_df(
gender_singlecount_stats('show_id', list(Show.objects.values('id', 'name')), min_dur=3600*500),
['show_id'] + gender_ordering)
print('Multicount')
gender_screen_show = gender_multicount_stats('show_id', list(Show.objects.values('id', 'name')), min_dur=3600*250)
gender_screen_show_nh = gender_multicount_stats('show_id', list(Show.objects.values('id', 'name')), min_dur=3600*250, no_host=True)
gender_screen_show_jh = gender_multicount_stats('show_id', list(Show.objects.values('id', 'name')), min_dur=3600*50, just_host=True)
show_df(gender_screen_show, ['show_id'] + gender_ordering)
gshow = face_genders.groupBy('video_id', 'gender_id').agg(func.sum('duration').alias('screen_sum'), func.first('show_id').alias('show_id'))
gspeak = speakers.groupBy('video_id', 'gender_id').agg(func.sum('duration').alias('speak_sum'))
rows = gshow.join(gspeak, ['video_id', 'gender_id']).toPandas()
# TODO: this is really sketchy and clobbers some variables such as videos
# show = Show.objects.get(name='Fox and Friends First')
# rows2 = rows[rows.show_id == show.id]
# videos = collect([r for _, r in rows2.iterrows()], lambda r: int(r.video_id))
# bs = []
# vkeys = []
# for vid, vrows in videos.iteritems():
# vgender = {int(r.gender_id): r for r in vrows}
# def balance(key):
# return vgender[1][key] / float(vgender[1][key] + vgender[2][key])
# try:
# bs.append(balance('screen_sum') / balance('speak_sum'))
# except KeyError:
# bs.append(0)
# vkeys.append(vid)
# idx = np.argsort(bs)[-20:]
# print(np.array(vkeys)[idx].tolist(), np.array(bs)[idx].tolist())
show_df(gender_screen_show_nh, ['show_id'] + gender_ordering)
print('Speaking time')
gender_speaking_show = gender_speaker_stats('show_id', list(Show.objects.values('id', 'name')), min_dur=3600*3)
gender_speaking_show_nh = gender_speaker_stats('show_id', list(Show.objects.values('id', 'name')), min_dur=3600*3, no_host=True)
show_df(
gender_speaking_show,
['show_id'] + gender_speaker_ordering)
show_df(
gender_speaking_show_nh,
['show_id'] + gender_speaker_ordering)
```
### Persist for Report
```
pd.DataFrame(gender_screen_show).to_csv('/app/data/screen_show.csv')
pd.DataFrame(gender_screen_show_nh).to_csv('/app/data/screen_show_nh.csv')
pd.DataFrame(gender_screen_show_jh).to_csv('/app/data/screen_show_jh.csv')
pd.DataFrame(gender_speaking_show).to_csv('/app/data/speaking_show.csv')
pd.DataFrame(gender_speaking_show_nh).to_csv('/app/data/speaking_show_nh.csv')
```
## Gender by Canonical Show
```
print('Singlecount')
show_df(
gender_singlecount_stats(
'canonical_show_id',
list(CanonicalShow.objects.values('id', 'name')),
min_dur=3600*500
),
['canonical_show_id'] + gender_ordering
)
print('Multicount')
gender_screen_canonical_show = gender_multicount_stats(
'canonical_show_id',
list(CanonicalShow.objects.values('id', 'name')),
min_dur=3600*250
)
gender_screen_canonical_show_nh = gender_multicount_stats(
'canonical_show_id',
list(CanonicalShow.objects.values('id', 'name')),
min_dur=3600*250,
no_host=True
)
gender_screen_canonical_show_jh = gender_multicount_stats(
'canonical_show_id',
list(CanonicalShow.objects.values('id', 'name')),
min_dur=3600*50,
just_host=True
)
show_df(gender_screen_canonical_show, ['canonical_show_id'] + gender_ordering)
print('Speaking time')
gender_speaking_canonical_show = gender_speaker_stats(
'canonical_show_id',
list(CanonicalShow.objects.values('id', 'name')),
min_dur=3600*3
)
gender_speaking_canonical_show_nh = gender_speaker_stats(
'canonical_show_id',
list(CanonicalShow.objects.values('id', 'name')),
min_dur=3600*3,
no_host=True
)
show_df(
gender_speaking_canonical_show,
['canonical_show_id'] + gender_speaker_ordering)
show_df(
gender_speaking_canonical_show_nh,
['canonical_show_id'] + gender_speaker_ordering)
```
### Persist for Report
```
pd.DataFrame(gender_screen_canonical_show).to_csv('/app/data/screen_canonical_show.csv')
pd.DataFrame(gender_screen_canonical_show_nh).to_csv('/app/data/screen_canonical_show_nh.csv')
pd.DataFrame(gender_screen_canonical_show_jh).to_csv('/app/data/screen_canonical_show_jh.csv')
pd.DataFrame(gender_speaking_canonical_show).to_csv('/app/data/speaking_canonical_show.csv')
pd.DataFrame(gender_speaking_canonical_show_nh).to_csv('/app/data/speaking_canonical_show_nh.csv')
```
## Gender by time of day
```
print('Singlecount')
show_df(
gender_singlecount_stats('hour', [{'id': hour, 'name': format_hour(hour)} for hour in hours]),
['hour'] + gender_ordering)
print('Multicount')
gender_screen_tod = gender_multicount_stats('hour', [{'id': hour, 'name': format_hour(hour)} for hour in hours])
show_df(gender_screen_tod, ['hour'] + gender_ordering)
print('Speaking time')
gender_speaking_tod = gender_speaker_stats('hour', [{'id': hour, 'name': format_hour(hour)} for hour in hours])
show_df(gender_speaking_tod, ['hour'] + gender_speaker_ordering)
```
## Gender by Day of the Week
```
dotw = ['Monday', 'Tuesday', 'Wednesday', 'Thursday', 'Friday', 'Saturday', 'Sunday']
print('Singlecount')
show_df(
gender_singlecount_stats('week_day', [{'id': i + 1, 'name': d} for i, d in enumerate(dotw)]),
['week_day'] + gender_ordering)
print('Multicount')
show_df(
gender_multicount_stats('week_day', [{'id': i + 1, 'name': d} for i, d in enumerate(dotw)]),
['week_day'] + gender_ordering)
print('Speaking time')
show_df(
gender_speaker_stats('week_day', [{'id': i + 1, 'name': d} for i, d in enumerate(dotw)]),
['week_day'] + gender_speaker_ordering)
```
## Gender by topic
```
# TODO: FIX ME
# THOUGHTS:
# - Try topic analysis just on a "serious" news show.
# - Generate a panel from multiple clips, e.g. endless panel of people on a topic
# - Produce an endless stream of men talking about, e.g. birth control
# print('Singlecount')
# show_df(
# gender_singlecount_stats(
# 'topic', [{'id': t.id, 'name': t.name} for t in Thing.objects.filter(type__name='topic')],
# min_dur=3600*5),
# ['topic'] + gender_ordering)
# check this
# M% is the pecent of time that men are on screen when this topic is being discussed
# print('Multicount')
# gender_screen_topic = gender_multicount_stats(
# 'topic', [{'id': t.id, 'name': t.name} for t in Thing.objects.filter(type__name='topic')],
# min_dur=3600*300)
# gender_screen_topic_nh = gender_multicount_stats(
# 'topic', [{'id': t.id, 'name': t.name} for t in Thing.objects.filter(type__name='topic')],
# min_dur=3600*300, no_host=True)
# show_df(gender_screen_topic, ['topic'] + gender_ordering)
# print('Speaking time')
# gender_speaking_topic = gender_speaker_stats(
# 'topic', [{'id': t.id, 'name': t.name} for t in Thing.objects.filter(type__name='topic')],
# min_dur=3600*100)
# gender_speaking_topic_nh = gender_speaker_stats(
# 'topic', [{'id': t.id, 'name': t.name} for t in Thing.objects.filter(type__name='topic')],
# min_dur=3600*100, no_host=True)
# show_df(gender_speaking_topic, ['topic'] + gender_speaker_ordering)
```
## Male vs. female faces in panels
* Smaller percentage of women in panels relative to overall dataset.
```
# # TODO: female-domainated situations?
# # TODO: slice this on # of people in the panel
# # TODO: small visualization that shows sample of segments
# # TODO: panels w/ majority male vs. majority female
# print('Computing panels')
# panels = queries.panels()
# print('Computing gender stats')
# frame_ids = [frame.id for (frame, _) in panels]
# counts = filter_gender(lambda qs: qs.filter(face__person__frame__id__in=frame_ids), lambda qs: qs)
# show_df([counts], ordering)
```
# Pose
* Animatedness of people (specifically hosts)
* e.g. Rachel Maddow vs. others
* Pick 3-4 hours of a few specific hosts, compute dense poses and tracks
* Devise acceleration metric
* More gesturing on heated exchanges?
* Sitting vs. standing
* Repeated gestures (debates vs. state of the union)
* Head/eye orientation (are people looking at each other?)
* Camera orientation (looking at someone from above/below)
* How much are the hosts facing each other
* Quantify aggressive body language
# Topics
```
df = pd.DataFrame(gender_screen_tod)
ax = df.plot('hour', 'M%')
pd.DataFrame(gender_speaking_tod).plot('hour', 'M%', ax=ax)
ax.set_ylim(0, 100)
ax.set_xticks(range(len(df)))
ax.set_xticklabels(df.hour)
ax.axhline(50, color='r', linestyle='--')
ax.legend(['Screen time', 'Speaking time', '50%'])
# pd.DataFrame(gender_screen_topic).to_csv('/app/data/screen_topic.csv')
# pd.DataFrame(gender_screen_topic_nh).to_csv('/app/data/screen_topic_nh.csv')
# pd.DataFrame(gender_speaking_topic).to_csv('/app/data/speaking_topic.csv')
# pd.DataFrame(gender_speaking_topic_nh).to_csv('/app/data/speaking_topic_nh.csv')
```
|
github_jupyter
|
# Check Cell Count
## Libraries
```
import pandas
import MySQLdb
import numpy as np
import pickle
import os
```
## Functions and definitions
```
# - - - - - - - - - - - - - - - - - - - -
# Define Experiment
table = 'IsabelCLOUPAC_Per_Image'
# - - - - - - - - - - - - - - - - - - - -
def ensure_dir(file_path):
'''
Function to ensure a file path exists, else creates the path
:param file_path:
:return:
'''
directory = os.path.dirname(file_path)
if not os.path.exists(directory):
os.makedirs(directory)
```
## Main Functions
```
def create_Single_CellCounts(db_table):
db = MySQLdb.connect("menchelabdb.int.cemm.at", "root", "cqsr4h", "ImageAnalysisDDI")
string = "select Image_Metadata_ID_A from "+db_table+" group by Image_Metadata_ID_A;"
data = pandas.read_sql(string, con=db)['Image_Metadata_ID_A']
#with open('../results/FeatureVectors/SingleVectors_' + str(min(plates)) + '_to_' + str(
# max(plates)) + '_NoCutoff_' + str(cast_int) + '.pickle', 'rb') as handle:
# single_Vectors = pickle.load(handle)
singles = list(data)
singles.sort()
if 'PosCon' in singles:
singles.remove('PosCon')
if 'DMSO' in singles:
singles.remove('DMSO')
# Define Database to check for missing Images
string = "select SUM(Image_Count_Cytoplasm), Image_Metadata_Well, Image_Metadata_ID_A,Image_Metadata_Conc_A,Image_Metadata_Plate from " + db_table + " where Image_Metadata_ID_A not like 'DMSO' and Image_Metadata_Transfer_A like 'YES' and Image_Metadata_Transfer_A like 'YES' group by Image_Metadata_ID_A,Image_Metadata_Plate,Image_Metadata_Well;"
data = pandas.read_sql(string,con=db)
ensure_dir('../results/'+table+'/CellCount/SinglesCellCount.csv')
fp_out = open('../results/'+table+'/CellCount/SinglesCellCount.csv','w')
fp_out.write('Drug,Conc,AVG_CellCount\n')
for drug in singles:
drug_values = data.loc[data['Image_Metadata_ID_A'] == drug][['SUM(Image_Count_Cytoplasm)','Image_Metadata_Conc_A']]
concentrations = list(set(drug_values['Image_Metadata_Conc_A'].values))
concentrations.sort()
for conc in concentrations:
if len(drug_values.loc[drug_values['Image_Metadata_Conc_A'] == conc]['SUM(Image_Count_Cytoplasm)'].values) > 0:
cellcount = np.mean(drug_values.loc[drug_values['Image_Metadata_Conc_A'] == conc]['SUM(Image_Count_Cytoplasm)'].values)
cellcount = int(cellcount)
else:
cellcount = 'nan'
fp_out.write(drug+','+str(conc)+','+str(cellcount) +'\n')
fp_out.close()
def create_Single_CellCounts_individualReplicates(db_table):
db = MySQLdb.connect("menchelabdb.int.cemm.at", "root", "cqsr4h", "ImageAnalysisDDI")
string = "select Image_Metadata_ID_A from "+db_table+" group by Image_Metadata_ID_A;"
data = pandas.read_sql(string, con=db)['Image_Metadata_ID_A']
#with open('../results/FeatureVectors/SingleVectors_' + str(min(plates)) + '_to_' + str(
# max(plates)) + '_NoCutoff_' + str(cast_int) + '.pickle', 'rb') as handle:
# single_Vectors = pickle.load(handle)
singles = list(data)
singles.sort()
if 'PosCon' in singles:
singles.remove('PosCon')
if 'DMSO' in singles:
singles.remove('DMSO')
#plates = range(1315001, 1315124, 10)
#string = "select SUM(Image_Count_Cytoplasm), Image_Metadata_Well, Image_Metadata_ID_A,Image_Metadata_ID_B,Image_Metadata_Plate from " + db_table + " where Image_Metadata_ID_B like 'DMSO' and Image_Metadata_Transfer_A like 'YES' and Image_Metadata_Transfer_B like 'YES' group by Image_Metadata_ID_A,Image_Metadata_Plate,Image_Metadata_Well;"
string = "select SUM(Image_Count_Cytoplasm), Image_Metadata_Well, Image_Metadata_ID_A,Image_Metadata_Conc_A,Image_Metadata_Plate from " + db_table + " where Image_Metadata_ID_A not like 'DMSO' and Image_Metadata_Transfer_A like 'YES' and Image_Metadata_Transfer_A like 'YES' group by Image_Metadata_ID_A,Image_Metadata_Plate,Image_Metadata_Well;"
data = pandas.read_sql(string,con=db)
ensure_dir('../results/' + table + '/CellCount/SinglesCellCount_AllReplicates.csv')
fp_out = open('../results/' + table + '/CellCount/SinglesCellCount_AllReplicates.csv','w')
#fp_out.write('Drug,CellCounts\n')
fp_out.write('Drug,Conc,Replicate1,Replicate2\n')
for drug in singles:
drug_values = data.loc[data['Image_Metadata_ID_A'] == drug][['SUM(Image_Count_Cytoplasm)','Image_Metadata_Conc_A']]
concentrations = list(set(drug_values['Image_Metadata_Conc_A'].values))
concentrations.sort()
for conc in concentrations:
if len(drug_values.loc[drug_values['Image_Metadata_Conc_A'] == conc]['SUM(Image_Count_Cytoplasm)'].values) > 0:
cellcounts = drug_values.loc[drug_values['Image_Metadata_Conc_A'] == conc]['SUM(Image_Count_Cytoplasm)'].values
fp_out.write(drug + ',' +str(conc)+','+ ','.join([str(x) for x in cellcounts]) + '\n')
fp_out.close()
def getDMSO_Untreated_CellCount(db_table):
# Define Database to check for missing Images
db = MySQLdb.connect("menchelabdb.int.cemm.at", "root", "cqsr4h", "ImageAnalysisDDI")
string = "select SUM(Image_Count_Cytoplasm), Image_Metadata_Well, Image_Metadata_Plate from " + db_table + " where Image_Metadata_ID_A like 'DMSO' and Image_Metadata_Transfer_A like 'YES' group by Image_Metadata_Well,Image_Metadata_Plate;"
data = pandas.read_sql(string,con=db)
mean = np.mean(data['SUM(Image_Count_Cytoplasm)'])
std = np.std(data['SUM(Image_Count_Cytoplasm)'])
max_val = np.percentile(data['SUM(Image_Count_Cytoplasm)'],98)
ensure_dir('../results/' + table + '/CellCount/DMSO_Overview.csv')
fp_out = open('../results/' + table + '/CellCount/DMSO_Overview.csv', 'w')
fp_out.write('Mean,Std,Max\n%f,%f,%f' %(mean,std,max_val))
fp_out.close()
fp_out = open('../results/' + table + '/CellCount/DMSO_Replicates.csv', 'w')
fp_out.write('Plate,Well,CellCount\n')
for row in data.iterrows():
fp_out.write(str(row[1][2])+','+row[1][1]+','+str(row[1][0])+'\n')
fp_out.close()
def get_CellCount_perWell(db_table):
# Define Database to check for missing Images
db = MySQLdb.connect("menchelabdb.int.cemm.at", "root", "cqsr4h", "ImageAnalysisDDI")
string = "select SUM(Image_Count_Cytoplasm),Image_Metadata_ID_A, Image_Metadata_Well, Image_Metadata_Plate,Image_Metadata_Transfer_A from " + db_table + " group by Image_Metadata_Well,Image_Metadata_Plate;"
data = pandas.read_sql(string,con=db)
data.sort_values(by=['Image_Metadata_Plate','Image_Metadata_Well'])
ensure_dir('../results/' + db_table + '/CellCount/Individual_Well_Results.csv')
fp_out = open('../results/' + db_table + '/CellCount/Individual_Well_Results.csv', 'w')
fp_out.write('ID_A,ID_B,Plate,Well,CellCount,TransferOK\n')
for row in data.iterrows():
ID_A = row[1][1]
Trans_A = row[1][4]
if ID_A == 'DMSO' or ID_A == 'PosCon':
if Trans_A == 'YES':
worked = 'TRUE'
else:
worked = 'FALSE'
else:
if Trans_A == 'YES':
worked = 'TRUE'
else:
worked = 'FALSE'
fp_out.write(ID_A+','+str(row[1][3])+','+row[1][2]+','+str(row[1][0])+','+worked+'\n')
fp_out.close()
def PlotResult_file(table,all=False):
from matplotlib import pylab as plt
drug_values = {}
dmso_values = []
fp = open('../results/' + table + '/CellCount/Individual_Well_Results.csv')
fp.next()
for line in fp:
tmp = line.strip().split(',')
if tmp[4] == 'TRUE':
if tmp[0] != 'DMSO':
if drug_values.has_key(tmp[0]):
drug_values[tmp[0]].append(float(tmp[3]))
else:
drug_values[tmp[0]] = [float(tmp[3])]
if tmp[0] == 'DMSO':
dmso_values.append(float(tmp[3]))
max_val = np.mean(dmso_values) + 0.5 * np.std(dmso_values)
#max_val = np.mean([np.mean(x) for x in drug_values.values()]) + 1.2 * np.std([np.mean(x) for x in drug_values.values()])
effect = 0
normalized = []
for drug in drug_values:
scaled = (np.mean(drug_values[drug]) - 0) / max_val
if scaled <= 1:
normalized.append(scaled)
else:
normalized.append(1)
if scaled < 0.5:
effect +=1
print 'Number of drugs with more than 50%% cytotoxicity: %d' %effect
print 'Number of drugs with les than 50%% cytotoxicity: %d' %(len(drug_values) - effect)
plt.hist(normalized,bins='auto', color = '#40B9D4')
#plt.show()
plt.xlabel('Viability')
plt.ylabel('Frequency')
plt.savefig('../results/' + table + '/CellCount/CellCountHistogram.pdf')
plt.close()
#create_Single_CellCounts(table)
#create_Single_CellCounts_individualReplicates(table)
#getDMSO_Untreated_CellCount(table)
#get_CellCount_perWell(table)
PlotResult_file(table)
```
|
github_jupyter
|
```
# Binary Tree Basic Implimentations
# For harder questions and answers, refer to:
# https://github.com/volkansonmez/Algorithms-and-Data-Structures-1/blob/master/Binary_Tree_All_Methods.ipynb
import numpy as np
np.random.seed(0)
class BST():
def __init__(self, root = None):
self.root = root
def add_node(self, value):
if self.root == None:
self.root = Node(value)
else:
self._add_node(self.root, value)
def _add_node(self, key_node, value):
if key_node == None: return
if value < key_node.cargo: # go left
if key_node.left == None:
key_node.left = Node(value)
key_node.left.parent = key_node
else:
self._add_node(key_node.left, value)
elif value > key_node.cargo: # go right
if key_node.right == None:
key_node.right = Node(value)
key_node.right.parent = key_node
else:
self._add_node(key_node.right, value)
else: # if the value already exists
return
def add_random_nodes(self):
numbers = np.arange(0,20)
self.random_numbers = np.random.permutation(numbers)
for i in self.random_numbers:
self.add_node(i)
def find_node(self, value): # find if the value exists in the tree
if self.root == None: return None
if self.root.cargo == value:
return self.root
else:
return self._find_node(self.root, value)
def _find_node(self, key_node, value):
if key_node == None: return None
if key_node.cargo == value: return key_node
if value < key_node.cargo: # go left
key_node = key_node.left
return self._find_node(key_node, value)
else:
key_node = key_node.right
return self._find_node(key_node, value)
def print_in_order(self): # do a dfs, print from left leaf to the right leaf
if self.root == None: return
key_node = self.root
self._print_in_order(key_node)
def _print_in_order(self, key_node):
if key_node == None: return
self._print_in_order(key_node.left)
print(key_node.cargo, end = ' ')
self._print_in_order(key_node.right)
def print_leaf_nodes_by_stacking(self):
all_nodes = [] # append the node objects
leaf_nodes = [] # append the cargos of the leaf nodes
if self.root == None: return None
all_nodes.append(self.root)
while len(all_nodes) > 0:
curr_node = all_nodes.pop() # pop the last item, last in first out
if curr_node.left != None:
all_nodes.append(curr_node.left)
if curr_node.right != None:
all_nodes.append(curr_node.right)
elif curr_node.left == None and curr_node.right == None:
leaf_nodes.append(curr_node.cargo)
return leaf_nodes
def print_bfs(self, todo = None):
if todo == None: todo = []
if self.root == None: return
todo.append(self.root)
while len(todo) > 0:
curr_node = todo.pop()
if curr_node.left != None:
todo.append(curr_node.left)
if curr_node.right != None:
todo.append(curr_node.right)
print(curr_node.cargo, end = ' ')
def find_height(self):
if self.root == None: return 0
else:
return self._find_height(self.root, left = 0, right = 0)
def _find_height(self, key_node, left, right):
if key_node == None: return max(left, right)
return self._find_height(key_node.left, left + 1, right)
return self._find_height(key_node.right, left, right +1)
def is_valid(self):
if self.root == None: return True
key_node = self.root
return self._is_valid(self.root, -np.inf, np.inf)
def _is_valid(self, key_node, min_value , max_value):
if key_node == None: return True
if key_node.cargo > max_value or key_node.cargo < min_value: return False
left_valid = True
right_valid = True
if key_node != None and key_node.left != None:
left_valid = self._is_valid(key_node.left, min_value, key_node.cargo)
if key_node != None and key_node.right != None:
right_valid = self._is_valid(key_node.right, key_node.cargo, max_value)
return left_valid and right_valid
def zig_zag_printing_top_to_bottom(self):
if self.root == None: return
even_stack = [] # stack the nodes in levels that are in even numbers
odd_stack = [] # stack the nodes in levels that are in odd numbers
print_nodes = [] # append the items' cargos in zigzag order
even_stack.append(self.root)
while len(even_stack) > 0 or len(odd_stack) > 0:
while len(even_stack) > 0:
tmp = even_stack.pop()
print_nodes.append(tmp.cargo)
if tmp.right != None:
odd_stack.append(tmp.right)
if tmp.left != None:
odd_stack.append(tmp.left)
while len(odd_stack) > 0:
tmp = odd_stack.pop()
print_nodes.append(tmp.cargo)
if tmp.left != None:
even_stack.append(tmp.left)
if tmp.right != None:
even_stack.append(tmp.right)
return print_nodes
def lowest_common_ancestor(self, node1, node2): # takes two cargos and prints the lca node of them
if self.root == None: return
node1_confirm = self.find_node(node1)
if node1_confirm == None: return
node2_confirm = self.find_node(node2)
if node2_confirm == None: return
key_node = self.root
print('nodes are in the tree')
return self._lowest_common_ancestor(key_node, node1, node2)
def _lowest_common_ancestor(self, key_node, node1, node2):
if key_node == None: return
if node1 < key_node.cargo and node2 < key_node.cargo:
key_node = key_node.left
return self._lowest_common_ancestor(key_node, node1, node2)
elif node1 > key_node.cargo and node2 > key_node.cargo:
key_node = key_node.right
return self._lowest_common_ancestor(key_node, node1, node2)
else:
return key_node , key_node.cargo
def maximum_path_sum(self): # function to find the maximum path sum
if self.root == None: return
max_value = -np.inf
return self._maximum_path_sum(self.root, max_value)
def _maximum_path_sum(self, key_node, max_value): # recursive function to search and return the max path sum
if key_node == None: return 0
left = self._maximum_path_sum(key_node.left, max_value)
right = self._maximum_path_sum(key_node.right, max_value)
max_value = max(max_value, key_node.cargo + left + right)
return max(left, right) + self.root.cargo
class Node():
def __init__(self, cargo = None, parent = None, left = None, right = None):
self.cargo = cargo
self.parent = parent
self.left = left
self.right = right
test_bst = BST()
test_bst.add_random_nodes()
#print(test_bst.print_in_order())
#test_bst.find_node(11)
#test_bst.print_leaf_nodes_by_stacking()
#test_bst.print_bfs()
#test_bst.find_height()
#test_bst.is_valid()
test_bst.zig_zag_printing_top_to_bottom()
#test_bst.lowest_common_ancestor(8, 0)
#test_bst.maximum_path_sum()
```
|
github_jupyter
|
```
import os
os.environ['CUDA_VISIBLE_DEVICES'] = '0' # specify GPUs locally
package_paths = [
'./input/pytorch-image-models/pytorch-image-models-master', #'../input/efficientnet-pytorch-07/efficientnet_pytorch-0.7.0'
'./input/pytorch-gradual-warmup-lr-master'
]
import sys;
for pth in package_paths:
sys.path.append(pth)
from glob import glob
from sklearn.model_selection import GroupKFold, StratifiedKFold
import cv2
from skimage import io
import torch
from torch import nn
import os
from datetime import datetime
import time
import random
import cv2
import torchvision
from torchvision import transforms
import pandas as pd
import numpy as np
from tqdm import tqdm
import matplotlib.pyplot as plt
from torch.utils.data import Dataset,DataLoader
from torch.utils.data.sampler import SequentialSampler, RandomSampler
from torch.cuda.amp import autocast, GradScaler
from torch.nn.modules.loss import _WeightedLoss
import torch.nn.functional as F
import timm
import sklearn
import warnings
import joblib
from sklearn.metrics import roc_auc_score, log_loss
from sklearn import metrics
import warnings
import cv2
#from efficientnet_pytorch import EfficientNet
from scipy.ndimage.interpolation import zoom
from adamp import AdamP
CFG = {
'fold_num': 5,
'seed': 719,
'model_arch': 'regnety_040',
'model_path' : 'regnety_040_bs24_epoch20_reset_swalr_step',
'img_size': 512,
'epochs': 20,
'train_bs': 24,
'valid_bs': 8,
'T_0': 10,
'lr': 1e-4,
'min_lr': 1e-6,
'weight_decay':1e-6,
'num_workers': 4,
'accum_iter': 1, # suppoprt to do batch accumulation for backprop with effectively larger batch size
'verbose_step': 1,
'device': 'cuda:0',
'target_size' : 5,
'smoothing' : 0.2
}
if not os.path.isdir(CFG['model_path']):
os.mkdir(CFG['model_path'])
train = pd.read_csv('./input/cassava-leaf-disease-classification/merged.csv')
# delete_id
## 2019 : 이미지의 한 변이 500보다 작거나 1000보다 큰 경우
## 2020 : 중복되는 3개 이미지
delete_id = ['train-cbb-1.jpg', 'train-cbb-12.jpg', 'train-cbb-126.jpg', 'train-cbb-134.jpg', 'train-cbb-198.jpg',
'train-cbb-244.jpg', 'train-cbb-245.jpg', 'train-cbb-30.jpg', 'train-cbb-350.jpg', 'train-cbb-369.jpg',
'train-cbb-65.jpg', 'train-cbb-68.jpg', 'train-cbb-77.jpg', 'train-cbsd-1354.jpg', 'train-cbsd-501.jpg',
'train-cgm-418.jpg', 'train-cmd-1145.jpg', 'train-cmd-2080.jpg', 'train-cmd-2096.jpg', 'train-cmd-332.jpg',
'train-cmd-494.jpg', 'train-cmd-745.jpg', 'train-cmd-896.jpg', 'train-cmd-902.jpg', 'train-healthy-118.jpg',
'train-healthy-181.jpg', 'train-healthy-5.jpg','train-cbb-69.jpg', 'train-cbsd-463.jpg', 'train-cgm-547.jpg',
'train-cgm-626.jpg', 'train-cgm-66.jpg', 'train-cgm-768.jpg', 'train-cgm-98.jpg', 'train-cmd-110.jpg',
'train-cmd-1208.jpg', 'train-cmd-1566.jpg', 'train-cmd-1633.jpg', 'train-cmd-1703.jpg', 'train-cmd-1917.jpg',
'train-cmd-2197.jpg', 'train-cmd-2289.jpg', 'train-cmd-2304.jpg', 'train-cmd-2405.jpg', 'train-cmd-2490.jpg',
'train-cmd-412.jpg', 'train-cmd-587.jpg', 'train-cmd-678.jpg', 'train-healthy-250.jpg']
delete_id += ['2947932468.jpg', '2252529694.jpg', '2278017076.jpg']
train = train[~train['image_id'].isin(delete_id)].reset_index(drop=True)
print(train.shape)
submission = pd.read_csv('./input/cassava-leaf-disease-classification/sample_submission.csv')
submission.head()
def seed_everything(seed):
random.seed(seed)
os.environ['PYTHONHASHSEED'] = str(seed)
np.random.seed(seed)
torch.manual_seed(seed)
torch.cuda.manual_seed(seed)
torch.backends.cudnn.deterministic = True
torch.backends.cudnn.benchmark = False
def get_img(path):
im_bgr = cv2.imread(path)
im_rgb = im_bgr[:, :, ::-1]
#print(im_rgb)
return im_rgb
def rand_bbox(size, lam):
W = size[0]
H = size[1]
cut_rat = np.sqrt(1. - lam)
cut_w = np.int(W * cut_rat)
cut_h = np.int(H * cut_rat)
# uniform
cx = np.random.randint(W)
cy = np.random.randint(H)
bbx1 = np.clip(cx - cut_w // 2, 0, W)
bby1 = np.clip(cy - cut_h // 2, 0, H)
bbx2 = np.clip(cx + cut_w // 2, 0, W)
bby2 = np.clip(cy + cut_h // 2, 0, H)
return bbx1, bby1, bbx2, bby2
class CassavaDataset(Dataset):
def __init__(self, df, data_root,
transforms=None,
output_label=True,
):
super().__init__()
self.df = df.reset_index(drop=True).copy()
self.transforms = transforms
self.data_root = data_root
self.output_label = output_label
self.labels = self.df['label'].values
def __len__(self):
return self.df.shape[0]
def __getitem__(self, index: int):
# get labels
if self.output_label:
target = self.labels[index]
img = get_img("{}/{}".format(self.data_root, self.df.loc[index]['image_id']))
if self.transforms:
img = self.transforms(image=img)['image']
if self.output_label == True:
return img, target
else:
return img
from albumentations.core.transforms_interface import DualTransform
from albumentations.augmentations import functional as F
class GridMask(DualTransform):
"""GridMask augmentation for image classification and object detection.
Author: Qishen Ha
Email: [email protected]
2020/01/29
Args:
num_grid (int): number of grid in a row or column.
fill_value (int, float, lisf of int, list of float): value for dropped pixels.
rotate ((int, int) or int): range from which a random angle is picked. If rotate is a single int
an angle is picked from (-rotate, rotate). Default: (-90, 90)
mode (int):
0 - cropout a quarter of the square of each grid (left top)
1 - reserve a quarter of the square of each grid (left top)
2 - cropout 2 quarter of the square of each grid (left top & right bottom)
Targets:
image, mask
Image types:
uint8, float32
Reference:
| https://arxiv.org/abs/2001.04086
| https://github.com/akuxcw/GridMask
"""
def __init__(self, num_grid=3, fill_value=0, rotate=0, mode=0, always_apply=False, p=0.5):
super(GridMask, self).__init__(always_apply, p)
if isinstance(num_grid, int):
num_grid = (num_grid, num_grid)
if isinstance(rotate, int):
rotate = (-rotate, rotate)
self.num_grid = num_grid
self.fill_value = fill_value
self.rotate = rotate
self.mode = mode
self.masks = None
self.rand_h_max = []
self.rand_w_max = []
def init_masks(self, height, width):
if self.masks is None:
self.masks = []
n_masks = self.num_grid[1] - self.num_grid[0] + 1
for n, n_g in enumerate(range(self.num_grid[0], self.num_grid[1] + 1, 1)):
grid_h = height / n_g
grid_w = width / n_g
this_mask = np.ones((int((n_g + 1) * grid_h), int((n_g + 1) * grid_w))).astype(np.uint8)
for i in range(n_g + 1):
for j in range(n_g + 1):
this_mask[
int(i * grid_h) : int(i * grid_h + grid_h / 2),
int(j * grid_w) : int(j * grid_w + grid_w / 2)
] = self.fill_value
if self.mode == 2:
this_mask[
int(i * grid_h + grid_h / 2) : int(i * grid_h + grid_h),
int(j * grid_w + grid_w / 2) : int(j * grid_w + grid_w)
] = self.fill_value
if self.mode == 1:
this_mask = 1 - this_mask
self.masks.append(this_mask)
self.rand_h_max.append(grid_h)
self.rand_w_max.append(grid_w)
def apply(self, image, mask, rand_h, rand_w, angle, **params):
h, w = image.shape[:2]
mask = F.rotate(mask, angle) if self.rotate[1] > 0 else mask
mask = mask[:,:,np.newaxis] if image.ndim == 3 else mask
image *= mask[rand_h:rand_h+h, rand_w:rand_w+w].astype(image.dtype)
return image
def get_params_dependent_on_targets(self, params):
img = params['image']
height, width = img.shape[:2]
self.init_masks(height, width)
mid = np.random.randint(len(self.masks))
mask = self.masks[mid]
rand_h = np.random.randint(self.rand_h_max[mid])
rand_w = np.random.randint(self.rand_w_max[mid])
angle = np.random.randint(self.rotate[0], self.rotate[1]) if self.rotate[1] > 0 else 0
return {'mask': mask, 'rand_h': rand_h, 'rand_w': rand_w, 'angle': angle}
@property
def targets_as_params(self):
return ['image']
def get_transform_init_args_names(self):
return ('num_grid', 'fill_value', 'rotate', 'mode')
from albumentations import (
HorizontalFlip, VerticalFlip, IAAPerspective, ShiftScaleRotate, CLAHE, RandomRotate90,
Transpose, ShiftScaleRotate, Blur, OpticalDistortion, GridDistortion, HueSaturationValue,
IAAAdditiveGaussianNoise, GaussNoise, MotionBlur, MedianBlur, IAAPiecewiseAffine, RandomResizedCrop,
IAASharpen, IAAEmboss, RandomBrightnessContrast, Flip, OneOf, Compose, Normalize, Cutout, CoarseDropout, ShiftScaleRotate, CenterCrop, Resize
)
from albumentations.pytorch import ToTensorV2
def get_train_transforms():
return Compose([
Resize(600, 800),
RandomResizedCrop(CFG['img_size'], CFG['img_size']),
Transpose(p=0.5),
HorizontalFlip(p=0.5),
VerticalFlip(p=0.5),
ShiftScaleRotate(p=0.5),
HueSaturationValue(hue_shift_limit=0.2, sat_shift_limit=0.2, val_shift_limit=0.2, p=0.5),
RandomBrightnessContrast(brightness_limit=(-0.1,0.1), contrast_limit=(-0.1, 0.1), p=0.5),
Normalize(mean=[0.485, 0.456, 0.406], std=[0.229, 0.224, 0.225], max_pixel_value=255.0, p=1.0),
CoarseDropout(p=0.5),
GridMask(num_grid=3, p=0.5),
ToTensorV2(p=1.0),
], p=1.)
def get_valid_transforms():
return Compose([
Resize(600, 800),
CenterCrop(CFG['img_size'], CFG['img_size'], p=1.),
Resize(CFG['img_size'], CFG['img_size']),
Normalize(mean=[0.485, 0.456, 0.406], std=[0.229, 0.224, 0.225], max_pixel_value=255.0, p=1.0),
ToTensorV2(p=1.0),
], p=1.)
def get_inference_transforms():
return Compose([
Resize(600, 800),
OneOf([
Resize(CFG['img_size'], CFG['img_size'], p=1.),
CenterCrop(CFG['img_size'], CFG['img_size'], p=1.),
RandomResizedCrop(CFG['img_size'], CFG['img_size'], p=1.)
], p=1.),
Transpose(p=0.5),
HorizontalFlip(p=0.5),
#VerticalFlip(p=0.5),
Resize(CFG['img_size'], CFG['img_size']),
Normalize(mean=[0.485, 0.456, 0.406], std=[0.229, 0.224, 0.225], max_pixel_value=255.0, p=1.0),
ToTensorV2(p=1.0),
], p=1.)
class CassvaImgClassifier(nn.Module):
def __init__(self, model_arch, n_class, pretrained=False):
super().__init__()
self.model = timm.create_model(model_arch, pretrained=pretrained)
if model_arch == 'regnety_040':
self.model.head = nn.Sequential(
nn.AdaptiveAvgPool2d((1,1)),
nn.Flatten(),
nn.Linear(1088, n_class)
)
elif model_arch == 'regnety_320':
self.model.head = nn.Sequential(
nn.AdaptiveAvgPool2d((1,1)),
nn.Flatten(),
nn.Linear(3712, n_class)
)
elif model_arch == 'regnety_080':
self.model.head = nn.Sequential(
nn.AdaptiveAvgPool2d((1,1)),
nn.Flatten(),
nn.Linear(2016, n_class)
)
elif model_arch == 'regnety_160':
self.model.head = nn.Sequential(
nn.AdaptiveAvgPool2d((1,1)),
nn.Flatten(),
nn.Linear(3024, n_class)
)
else:
n_features = self.model.classifier.in_features
self.model.classifier = nn.Linear(n_features, n_class)
def forward(self, x):
x = self.model(x)
return x
def prepare_dataloader(df, trn_idx, val_idx, data_root='./input/cassava-leaf-disease-classification/train_images/'):
# from catalyst.data.sampler import BalanceClassSampler
train_ = df.loc[trn_idx,:].reset_index(drop=True)
valid_ = df.loc[val_idx,:].reset_index(drop=True)
train_ds = CassavaDataset(train_, data_root, transforms=get_train_transforms(), output_label=True)
valid_ds = CassavaDataset(valid_, data_root, transforms=get_valid_transforms(), output_label=True)
train_loader = torch.utils.data.DataLoader(
train_ds,
batch_size=CFG['train_bs'],
pin_memory=False,
drop_last=False,
shuffle=True,
num_workers=CFG['num_workers'],
#sampler=BalanceClassSampler(labels=train_['label'].values, mode="downsampling")
)
val_loader = torch.utils.data.DataLoader(
valid_ds,
batch_size=CFG['valid_bs'],
num_workers=CFG['num_workers'],
shuffle=False,
pin_memory=False,
)
return train_loader, val_loader
def train_one_epoch(epoch, model, loss_fn, optimizer, train_loader, device, scheduler=None, schd_batch_update=False):
model.train()
t = time.time()
running_loss = None
# pbar = tqdm(enumerate(train_loader), total=len(train_loader))
for step, (imgs, image_labels) in enumerate(train_loader):
imgs = imgs.to(device).float()
image_labels = image_labels.to(device).long()
with autocast():
image_preds = model(imgs) #output = model(input)
loss = loss_fn(image_preds, image_labels)
scaler.scale(loss).backward()
if running_loss is None:
running_loss = loss.item()
else:
running_loss = running_loss * .99 + loss.item() * .01
if ((step + 1) % CFG['accum_iter'] == 0) or ((step + 1) == len(train_loader)):
scaler.step(optimizer)
scaler.update()
optimizer.zero_grad()
if scheduler is not None and schd_batch_update:
scheduler.step()
if scheduler is not None and not schd_batch_update:
scheduler.step()
def valid_one_epoch(epoch, model, loss_fn, val_loader, device, scheduler=None, schd_loss_update=False):
model.eval()
t = time.time()
loss_sum = 0
sample_num = 0
image_preds_all = []
image_targets_all = []
# pbar = tqdm(enumerate(val_loader), total=len(val_loader))
for step, (imgs, image_labels) in enumerate(val_loader):
imgs = imgs.to(device).float()
image_labels = image_labels.to(device).long()
image_preds = model(imgs) #output = model(input)
image_preds_all += [torch.argmax(image_preds, 1).detach().cpu().numpy()]
image_targets_all += [image_labels.detach().cpu().numpy()]
loss = loss_fn(image_preds, image_labels)
loss_sum += loss.item()*image_labels.shape[0]
sample_num += image_labels.shape[0]
# if ((step + 1) % CFG['verbose_step'] == 0) or ((step + 1) == len(val_loader)):
# description = f'epoch {epoch} loss: {loss_sum/sample_num:.4f}'
# pbar.set_description(description)
image_preds_all = np.concatenate(image_preds_all)
image_targets_all = np.concatenate(image_targets_all)
print('epoch = {}'.format(epoch+1), 'validation multi-class accuracy = {:.4f}'.format((image_preds_all==image_targets_all).mean()))
if scheduler is not None:
if schd_loss_update:
scheduler.step(loss_sum/sample_num)
else:
scheduler.step()
def inference_one_epoch(model, data_loader, device):
model.eval()
image_preds_all = []
# pbar = tqdm(enumerate(data_loader), total=len(data_loader))
with torch.no_grad():
for step, (imgs, _labels) in enumerate(data_loader):
imgs = imgs.to(device).float()
image_preds = model(imgs) #output = model(input)
image_preds_all += [torch.softmax(image_preds, 1).detach().cpu().numpy()]
image_preds_all = np.concatenate(image_preds_all, axis=0)
return image_preds_all
# reference: https://www.kaggle.com/c/siim-isic-melanoma-classification/discussion/173733
class MyCrossEntropyLoss(_WeightedLoss):
def __init__(self, weight=None, reduction='mean'):
super().__init__(weight=weight, reduction=reduction)
self.weight = weight
self.reduction = reduction
def forward(self, inputs, targets):
lsm = F.log_softmax(inputs, -1)
if self.weight is not None:
lsm = lsm * self.weight.unsqueeze(0)
loss = -(targets * lsm).sum(-1)
if self.reduction == 'sum':
loss = loss.sum()
elif self.reduction == 'mean':
loss = loss.mean()
return loss
# ====================================================
# Label Smoothing
# ====================================================
class LabelSmoothingLoss(nn.Module):
def __init__(self, classes, smoothing=0.0, dim=-1):
super(LabelSmoothingLoss, self).__init__()
self.confidence = 1.0 - smoothing
self.smoothing = smoothing
self.cls = classes
self.dim = dim
def forward(self, pred, target):
pred = pred.log_softmax(dim=self.dim)
with torch.no_grad():
true_dist = torch.zeros_like(pred)
true_dist.fill_(self.smoothing / (self.cls - 1))
true_dist.scatter_(1, target.data.unsqueeze(1), self.confidence)
return torch.mean(torch.sum(-true_dist * pred, dim=self.dim))
from torchcontrib.optim import SWA
from sklearn.metrics import accuracy_score
for c in range(5):
train[c] = 0
folds = StratifiedKFold(n_splits=CFG['fold_num'], shuffle=True, random_state=CFG['seed']).split(np.arange(train.shape[0]), train.label.values)
for fold, (trn_idx, val_idx) in enumerate(folds):
print('Training with {} started'.format(fold))
print(len(trn_idx), len(val_idx))
train_loader, val_loader = prepare_dataloader(train, trn_idx, val_idx, data_root='./input/cassava-leaf-disease-classification/train/')
device = torch.device(CFG['device'])
model = CassvaImgClassifier(CFG['model_arch'], train.label.nunique(), pretrained=True).to(device)
scaler = GradScaler()
base_opt = AdamP(model.parameters(), lr=CFG['lr'], weight_decay=CFG['weight_decay'])
# base_opt = torch.optim.Adam(model.parameters(), lr=CFG['lr'], weight_decay=CFG['weight_decay'])
optimizer = SWA(base_opt, swa_start=2*len(trn_idx)//CFG['train_bs'], swa_freq=len(trn_idx)//CFG['train_bs'])
scheduler = torch.optim.lr_scheduler.CosineAnnealingWarmRestarts(optimizer, T_0=CFG['T_0'], T_mult=1, eta_min=CFG['min_lr'], last_epoch=-1)
loss_tr = LabelSmoothingLoss(classes=CFG['target_size'], smoothing=CFG['smoothing']).to(device)
loss_fn = nn.CrossEntropyLoss().to(device)
for epoch in range(CFG['epochs']):
train_one_epoch(epoch, model, loss_tr, optimizer, train_loader, device, scheduler=scheduler, schd_batch_update=False)
with torch.no_grad():
valid_one_epoch(epoch, model, loss_fn, val_loader, device, scheduler=None, schd_loss_update=False)
optimizer.swap_swa_sgd()
optimizer.bn_update(train_loader, model, device)
with torch.no_grad():
valid_one_epoch(epoch, model, loss_fn, val_loader, device, scheduler=None, schd_loss_update=False)
torch.save(model.state_dict(),'./{}/swa_{}_fold_{}_{}'.format(CFG['model_path'],CFG['model_arch'], fold, epoch))
tst_preds = []
for tta in range(5):
tst_preds += [inference_one_epoch(model, val_loader, device)]
train.loc[val_idx, [0, 1, 2, 3, 4]] = np.mean(tst_preds, axis=0)
del model, optimizer, train_loader, val_loader, scaler, scheduler
torch.cuda.empty_cache()
train['pred'] = np.array(train[[0, 1, 2, 3, 4]]).argmax(axis=1)
print(accuracy_score(train['label'].values, train['pred'].values))
```
|
github_jupyter
|
<a href="https://colab.research.google.com/github/temiafeye/Colab-Projects/blob/master/Fraud_Detection_Algorithm(Using_SOMs).ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
!pip install numpy
#Build Hybrid Deep Learning Model
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
#Importing The Dataset
from google.colab import files
uploaded = files.upload()
dataset = pd.read_csv(io.BytesIO(uploaded['Credit_Card_Applications.csv']))
X = dataset.iloc[:, :-1].values
y = dataset.iloc[:, -1].values
# Feature Scaling
from sklearn.preprocessing import MinMaxScaler
sc = MinMaxScaler(feature_range = (0, 1))
X = sc.fit_transform(X)
#Importing the SOM
from google.colab import files
uploaded = files.upload()
# Training the SOM
from minisom import MiniSom
som = MiniSom(x = 10, y = 10, input_len = 15, sigma = 1.0, learning_rate = 0.5)
som.random_weights_init(X)
som.train_random(data = X, num_iteration = 100)
#Visualizing the results
from pylab import bone, pcolor, colorbar, plot, show
bone()
pcolor(som.distance_map().T)
colorbar()
markers = ['o', 's']
colors = ['r', 'g']
for i, x in enumerate(X):
w = som.winner(x)
plot(w[0] + 0.5,
w[1] + 0.5,
markers[y[i]],
markeredgecolor = colors[y[i]],
markerfacecolor = 'None',
markersize = 10,
markeredgewidth = 2)
show()
# Finding the frauds
mappings = som.win_map(X)
frauds = np.concatenate((mappings[(2,4)], mappings[(8,8)]), axis = 0)
frauds = sc.inverse_transform(frauds)
#Part 2 - Create a supervised deep learning model
#Creates a matrix of features
customers = dataset.iloc[:, 1:].values
#Create the dependent variable
is_fraud = np.zeros(len(dataset)) #creates an array of zeroes, scanning through dataset
#initiate a loop, to append values of 1 if fraud data found in dataset
for i in range(len(dataset)):
if dataset.iloc[i,0] in frauds:
is_fraud[i] = 1
#train artificial neural network
# Feature Scaling
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
customers = sc.fit_transform(customers)
from keras.models import Sequential
from keras.layers import Dense
# Initialising the ANN
classifier = Sequential()
# Adding the input layer and the first hidden layer
classifier.add(Dense(units = 2, kernel_initializer = 'uniform', activation = 'relu', input_dim = 15))
# Adding the output layer
classifier.add(Dense(units = 1, kernel_initializer = 'uniform', activation = 'sigmoid'))
# Compiling the ANN
classifier.compile(optimizer = 'adam', loss = 'binary_crossentropy', metrics = ['accuracy'])
# Fitting the ANN to the Training set
classifier.fit(customers, is_fraud, batch_size = 1, epochs = 2)
# Part 3 - Making predictions and evaluating the model
# Predicting the probabilities of fraud
y_pred= classifier.predict(customers)
y_pred = np.concatenate((dataset.iloc[:,0:1].values, y_pred), axis = 1)
#Sorts numpy array in one colum
y_pred = y_pred[y_pred[:,1].argsort()]
y_pred.shape
```
```
```
|
github_jupyter
|
```
# THIS SCRIPT IS TO GENERATE AGGREGATIONS OF EXPLANATIONS for interesting FINDINGS
%load_ext autoreload
%autoreload 2
import os
import json
import numpy as np
from matplotlib.colors import LinearSegmentedColormap
import torch.nn.functional as F
import torchvision
from torchvision import models
from torchvision import transforms
import torch
import torchvision
torch.set_num_threads(1)
torch.manual_seed(0)
np.random.seed(0)
from torchvision.models import *
from visualisation.core.utils import device, image_net_postprocessing
from torch import nn
from operator import itemgetter
from visualisation.core.utils import imshow
from IPython.core.debugger import Tracer
NN_flag = True
layer = 4
if NN_flag:
feature_extractor = nn.Sequential(*list(resnet34(pretrained=True).children())[:layer-6]).to(device)
model = resnet34(pretrained=True).to(device)
model.eval()
# %matplotlib notebook
import glob
import matplotlib.pyplot as plt
import numpy as np
import torch
from utils import *
from PIL import Image
plt.rcParams["figure.figsize"]= 16,8
def make_dir(path):
if os.path.isdir(path) == False:
os.mkdir(path)
import glob
import matplotlib.pyplot as plt
import numpy as np
from matplotlib.pyplot import imshow
from visualisation.core.utils import device
from PIL import Image
from torchvision.transforms import ToTensor, Resize, Compose, ToPILImage
from visualisation.core import *
from visualisation.core.utils import image_net_preprocessing
size = 224
# Pre-process the image and convert into a tensor
transform = torchvision.transforms.Compose([
torchvision.transforms.Resize(256),
torchvision.transforms.CenterCrop(224),
torchvision.transforms.ToTensor(),
torchvision.transforms.Normalize(mean=[0.485, 0.456, 0.406],
std=[0.229, 0.224, 0.225]),
])
img_num = 50
# methods = ['Conf', 'GradCAM', 'EP', 'SHAP', 'NNs', 'PoolNet', 'AIonly']
methods = ['Conf', 'GradCAM', 'EP', 'NNs', 'PoolNet', 'AIonly']
task = 'Natural'
# Adversarial_Nat
# Added for loading ImageNet classes
def load_imagenet_label_map():
"""
Load ImageNet label dictionary.
return:
"""
input_f = open("input_txt_files/imagenet_classes.txt")
label_map = {}
for line in input_f:
parts = line.strip().split(": ")
(num, label) = (int(parts[0]), parts[1].replace('"', ""))
label_map[num] = label
input_f.close()
return label_map
# Added for loading ImageNet classes
def load_imagenet_id_map():
"""
Load ImageNet ID dictionary.
return;
"""
input_f = open("input_txt_files/synset_words.txt")
label_map = {}
for line in input_f:
parts = line.strip().split(" ")
(num, label) = (parts[0], ' '.join(parts[1:]))
label_map[num] = label
input_f.close()
return label_map
def convert_imagenet_label_to_id(label_map, key_list, val_list, prediction_class):
"""
Convert imagenet label to ID: for example - 245 -> "French bulldog" -> n02108915
:param label_map:
:param key_list:
:param val_list:
:param prediction_class:
:return:
"""
class_to_label = label_map[prediction_class]
prediction_id = key_list[val_list.index(class_to_label)]
return prediction_id
# gt_dict = load_imagenet_validation_gt()
id_map = load_imagenet_id_map()
label_map = load_imagenet_label_map()
key_list = list(id_map.keys())
val_list = list(id_map.values())
def convert_imagenet_id_to_label(label_map, key_list, val_list, class_id):
"""
Convert imagenet label to ID: for example - n02108915 -> "French bulldog" -> 245
:param label_map:
:param key_list:
:param val_list:
:param prediction_class:
:return:
"""
return key_list.index(str(class_id))
from torchray.attribution.extremal_perturbation import extremal_perturbation, contrastive_reward
from torchray.attribution.grad_cam import grad_cam
import PIL.Image
def get_EP_saliency_maps(model, path):
img_index = (path.split('.jpeg')[0]).split('images/')[1]
img = PIL.Image.open(path)
x = transform(img).unsqueeze(0).to(device)
out = model(x)
p = torch.nn.functional.softmax(out, dim=1)
score, index = torch.topk(p, 1)
category_id_1 = index[0][0].item()
gt_label_id = img_index.split('val_')[1][9:18]
input_prediction_id = convert_imagenet_label_to_id(label_map, key_list, val_list, category_id_1)
masks, energy = extremal_perturbation(
model, x, category_id_1,
areas=[0.025, 0.05, 0.1, 0.2],
num_levels=8,
step=7,
sigma=7 * 3,
max_iter=800,
debug=False,
jitter=True,
smooth=0.09,
perturbation='blur'
)
saliency = masks.sum(dim=0, keepdim=True)
saliency = saliency.detach()
return saliency[0].to('cpu')
# import os
import os.path
from visualisation.core.utils import tensor2cam
postprocessing_t = image_net_postprocessing
import cv2 as cv
import sys
imagenet_train_path = '/home/dexter/Downloads/train'
## Creating colormap
cMap = 'Reds'
id_list= list()
conf_dict = {}
eps=1e-5
cnt = 0
K = 3 # Change to your expected number of nearest neighbors
import csv
reader = csv.reader(open('csv_files/definition.csv'))
definition_dict = dict()
for row in reader:
key = row[0][:9]
definition = row[0][12:]
definition_dict[key] = definition
# Added for loading ImageNet classes
def load_imagenet_id_map():
"""
Load ImageNet ID dictionary.
return;
"""
input_f = open("input_txt_files/synset_words.txt")
label_map = {}
for line in input_f:
parts = line.strip().split(" ")
(num, label) = (parts[0], ' '.join(parts[1:]))
label_map[num] = label
input_f.close()
return label_map
id_map = load_imagenet_id_map()
Q1_path = '/home/dexter/Downloads/A-journey-into-Convolutional-Neural-Network-visualization-/Finding_explanations/SOD_wrong_dogs_aggregate'
Q2_path = '/home/dexter/Downloads/A-journey-into-Convolutional-Neural-Network-visualization-/Finding_explanations/NNs_hard_imagenet_aggregate'
Q3_path = '/home/dexter/Downloads/A-journey-into-Convolutional-Neural-Network-visualization-/Finding_explanations/NNs_adversarial_imagenet_aggregate'
Q4_path = '/home/dexter/Downloads/A-journey-into-Convolutional-Neural-Network-visualization-/Finding_explanations/Conf_adversarial_dog_aggregate'
Q5_path = '/home/dexter/Downloads/A-journey-into-Convolutional-Neural-Network-visualization-/Finding_explanations/GradCAM_norm_imagenet_aggregate'
Q6_path = '/home/dexter/Downloads/A-journey-into-Convolutional-Neural-Network-visualization-/Finding_explanations/NNs_easy_imagenet_aggregate'
Q_datapath = ['/home/dexter/Downloads/Human_experiments/Dataset/Dog/mixed_images',
'/home/dexter/Downloads/Human_experiments/Dataset/Natural/mixed_images',
'/home/dexter/Downloads/Human_experiments/Dataset/Adversarial_Nat/mixed_images',
'/home/dexter/Downloads/Human_experiments/Dataset/Adversarial_Dog/mixed_images',
'/home/dexter/Downloads/Human_experiments/Dataset/Natural/mixed_images',
'/home/dexter/Downloads/Human_experiments/Dataset/Natural/mixed_images']
for idx, question_path in enumerate([Q1_path, Q2_path, Q3_path, Q4_path, Q5_path, Q6_path]):
representatives = glob.glob(question_path + '/*.*')
# Tracer()()
if idx != 1:
continue
for representative in representatives:
if '21805' not in representative:
continue
sample_idx = representative.split('aggregate/')[1]
image_path = os.path.join(Q_datapath[idx], sample_idx)
# image_path = os.path.join('/home/dexter/Downloads/val', sample_folder, sample_idx)
# if '6952' not in image_path:
# continue
distance_dict = dict()
neighbors = list()
categories_confidences = list()
confidences= list ()
img = Image.open(image_path)
if NN_flag:
embedding = feature_extractor(transform(img).unsqueeze(0).to(device)).flatten(start_dim=1)
input_image = img.resize((size,size), Image.ANTIALIAS)
# Get the ground truth of the input image
gt_label_id = image_path.split('val_')[1][9:18]
gt_label = id_map.get(gt_label_id)
id = key_list.index(gt_label_id)
gt_label = gt_label.split(',')[0]
# Get the prediction for the input image
img = Image.open(image_path)
x = transform(img).unsqueeze(0).to(device)
out = model(x)
p = torch.nn.functional.softmax(out, dim=1)
score, index = torch.topk(p, 1)
input_category_id = index[0][0].item()
predicted_confidence = score[0][0].item()
predicted_confidence = ("%.2f") %(predicted_confidence)
input_prediction_id = convert_imagenet_label_to_id(label_map, key_list, val_list, input_category_id)
predicted_label = id_map.get(input_prediction_id).split(',')[0]
predicted_label = predicted_label[0].lower() + predicted_label[1:]
print(predicted_label)
print(predicted_confidence)
# Original image
plt.gca().set_axis_off()
plt.subplots_adjust(top = 1, bottom = 0, right = 1, left = 0,
hspace = 0, wspace = 0)
plt.margins(0,0)
plt.gca().xaxis.set_major_locator(plt.NullLocator())
plt.gca().yaxis.set_major_locator(plt.NullLocator())
fig = plt.figure()
# plt.figure(figsize=(6.0,4.5), dpi=300)
plt.axis('off')
#predicted_label = 'african hunting dog'
plt.title('{}: {}'.format(predicted_label, predicted_confidence), fontsize=30)
plt.imshow(input_image)
plt.savefig('tmp/original.jpeg', figsize=(6.0,4.5), dpi=300, bbox_inches='tight', pad_inches=0)
plt.close()
cmd = 'convert tmp/original.jpeg -resize 630x600\! tmp/original.jpeg'
os.system(cmd)
# Edge image
img = cv.resize(cv.imread(image_path,0),((size,size)))
edges = cv.Canny(img,100,200)
edges = edges - 255
fig = plt.figure()
# plt.figure(figsize=(6.0,4.5), dpi=300)
plt.axis('off')
plt.title(' ', fontsize=60)
plt.imshow(edges, cmap = 'gray')
plt.savefig('tmp/Edge.jpeg', figsize=(6.0,4.5), dpi=300, bbox_inches='tight', pad_inches=0)
plt.close()
# GradCAM
saliency = grad_cam(
model, x, input_category_id,
saliency_layer='layer4',
resize=True
)
saliency *= 1.0/saliency.max()
GradCAM = saliency[0][0].cpu().detach().numpy()
fig = plt.figure()
# plt.figure(figsize=(6.0,4.5), dpi=300)
plt.axis('off')
plt.title('GradCAM', fontsize=30)
mlb = plt.imshow(GradCAM, cmap=cMap, vmin=0, vmax=1)
# plt.colorbar(orientation='vertical')
plt.savefig('tmp/heatmap.jpeg', figsize=(6.0,4.5), dpi=300, bbox_inches='tight', pad_inches=0)
# plt.close()
myCmd = 'composite -blend 10 tmp/Edge.jpeg -gravity SouthWest tmp/heatmap.jpeg tmp/GradCAM.jpeg'
os.system(myCmd)
cmd = 'convert tmp/GradCAM.jpeg -resize 600x600\! tmp/GradCAM.jpeg'
os.system(cmd)
# draw a new figure and replot the colorbar there
fig,ax = plt.subplots()
cbar = plt.colorbar(mlb,ax=ax)
cbar.ax.tick_params(labelsize=20)
ax.remove()
# save the same figure with some approximate autocropping
plt.title(' ', fontsize=30)
plt.savefig('tmp/color_bar.jpeg', dpi=300, bbox_inches='tight')
cmd = 'convert tmp/color_bar.jpeg -resize 100x600\! tmp/color_bar.jpeg'
os.system(cmd)
# Extremal Perturbation
saliency = get_EP_saliency_maps(model, image_path)
ep_saliency_map = tensor2img(saliency)
ep_saliency_map *= 1.0/ep_saliency_map.max()
fig = plt.figure()
# plt.figure(figsize=(6.0,4.5), dpi=300)
plt.axis('off')
plt.title('EP', fontsize=30)
plt.imshow(ep_saliency_map, cmap=cMap, vmin=0, vmax=1)
# plt.colorbar(orientation='vertical')
plt.savefig('tmp/heatmap.jpeg', figsize=(6.0,4.5), dpi=300, bbox_inches='tight', pad_inches=0)
plt.close()
# Get overlay version
myCmd = 'composite -blend 10 tmp/Edge.jpeg -gravity SouthWest tmp/heatmap.jpeg tmp/EP.jpeg'
os.system(myCmd)
cmd = 'convert tmp/EP.jpeg -resize 600x600\! tmp/EP.jpeg'
os.system(cmd)
# Salient Object Detection
from shutil import copyfile, rmtree
def rm_and_mkdir(path):
if os.path.isdir(path) == True:
rmtree(path)
os.mkdir(path)
# Prepare dataset
rm_and_mkdir('/home/dexter/Downloads/run-0/run-0-sal-p/')
rm_and_mkdir('/home/dexter/Downloads/PoolNet-master/data/PASCALS/Imgs/')
if os.path.isdir('/home/dexter/Downloads/PoolNet-master/data/PASCALS/test.lst'):
os.remove('/home/dexter/Downloads/PoolNet-master/data/PASCALS/test.lst')
src_paths = [image_path]
for src_path in src_paths:
dst_path = '/home/dexter/Downloads/PoolNet-master/data/PASCALS/Imgs/' + src_path.split('images/')[1]
copyfile(src_path, dst_path)
cmd = 'ls /home/dexter/Downloads/PoolNet-master/data/PASCALS/Imgs/ > /home/dexter/Downloads/PoolNet-master/data/PASCALS/test.lst'
os.system(cmd)
cmd = 'python /home/dexter/Downloads/PoolNet-master/main.py --mode=\'test\' --model=\'/home/dexter/Downloads/run-0/run-0/models/final.pth\' --test_fold=\'/home/dexter/Downloads/run-0/run-0-sal-p/\' --sal_mode=\'p\''
os.system(cmd)
npy_file_paths = glob.glob('/home/dexter/Downloads/run-0/run-0-sal-p/*.*')
npy_file = np.load(npy_file_paths[0])
fig = plt.figure()
# plt.figure(figsize=(6.0,4.5), dpi=300)
plt.axis('off')
plt.title('SOD', fontsize=30)
plt.imshow(npy_file, cmap=cMap, vmin=0, vmax=1)
# plt.colorbar(orientation='vertical')
plt.savefig('tmp/heatmap.jpeg', figsize=(6.0,4.5), dpi=300, bbox_inches='tight', pad_inches=0)
plt.close()
# Get overlay version
myCmd = 'composite -blend 10 tmp/Edge.jpeg -gravity SouthWest tmp/heatmap.jpeg tmp/SOD.jpeg'
os.system(myCmd)
cmd = 'convert tmp/SOD.jpeg -resize 600x600\! tmp/SOD.jpeg'
os.system(cmd)
# Nearest Neighbors
imagenet_train_path = '/home/dexter/Downloads/train'
if NN_flag:
from utils import *
## Nearest Neighbors
predicted_set_path = os.path.join(imagenet_train_path, input_prediction_id)
predicted_set_img_paths = glob.glob(predicted_set_path + '/*.*')
predicted_set_color_images= list()
embedding = embedding.detach()
embedding.to(device)
# Build search space for nearest neighbors
for i, path in enumerate(predicted_set_img_paths):
img = Image.open(path)
if img.mode != 'RGB':
img.close()
del img
continue
x = transform(img).unsqueeze(0).to(device)
out = model(x)
p = torch.nn.functional.softmax(out, dim=1)
del out
score, index = torch.topk(p, 1)
del p
category_id = index[0][0].item()
del score, index
# This is to avoid the confusion from crane 134 and crane 517 and to make NNs work :)
# Because in Imagenet, annotators mislabeled 134 and 517
if input_category_id != 134 and input_category_id != 517 and category_id != 134 and category_id != 517:
if input_category_id != category_id:
continue
f = feature_extractor(x)
feature_vector = f.flatten(start_dim=1).to(device)
feature_vector = feature_vector.detach()
del f
distance_dict[path] = torch.dist(embedding, feature_vector)
del feature_vector
torch.cuda.empty_cache()
img.close()
del img
predicted_set_color_images.append(path)
# Get K most similar images
res = dict(sorted(distance_dict.items(), key = itemgetter(1))[:K])
print("Before...")
print(res)
# Tracer()()
while distance_dict[list(res.keys())[0]] < 100:
del distance_dict[list(res.keys())[0]]
res = dict(sorted(distance_dict.items(), key = itemgetter(1))[:K])
print("After...")
print(res)
# del distance_dict
del embedding
similar_images = list(res.keys())
for similar_image in similar_images:
img = Image.open(similar_image)
neighbors.append(img.resize((size,size), Image.ANTIALIAS))
x = transform(img).unsqueeze(0).to(device)
out = model(x)
p = torch.nn.functional.softmax(out, dim=1)
score, index = torch.topk(p, 1) # Get 1 most probable classes
category_id = index[0][0].item()
confidence = score[0][0].item()
label = label_map.get(category_id).split(',')[0].replace("\"", "")
label = label[0].lower() + label[1:]
print(label + ": %.2f" %(confidence))
categories_confidences.append((label + ": %.2f" %(confidence)))
confidences.append(confidence)
img.close()
for index, neighbor in enumerate(neighbors):
fig = plt.figure()
# plt.figure(figsize=(6.0,4.5), dpi=300)
plt.axis('off')
if index == 1: # Make title for the middle image (2nd image) to annotate the 3 NNs
plt.title('3-NN'.format(predicted_label), fontsize=30)
else:
plt.title(' ', fontsize=30)
plt.imshow(neighbor)
plt.savefig('tmp/{}.jpeg'.format(index), figsize=(6.0,4.5), dpi=300, bbox_inches='tight', pad_inches=0)
plt.close()
cmd = 'convert tmp/{}.jpeg -resize 600x600\! tmp/{}.jpeg'.format(index, index)
os.system(cmd)
myCmd = 'montage tmp/[0-2].jpeg -tile 3x1 -geometry +0+0 tmp/NN.jpeg'
os.system(myCmd)
# Sample images and definition
print(image_path)
gt_label = image_path.split('images/')[1][34:43]
print(image_path)
print(gt_label)
sample_path = '/home/dexter/Downloads/A-journey-into-Convolutional-Neural-Network-visualization-/sample_images'
predicted_sample_path = os.path.join(sample_path, gt_label + '.jpeg')
textual_label = id_map.get(gt_label).split(',')[0]
textual_label = textual_label[0].lower() + textual_label[1:]
definition = '{}: {}'.format(textual_label, definition_dict[gt_label])
definition = definition.replace("'s", "")
print(definition)
# definition = 'any sluggish bottom-dwelling ray of the order Torpediniformes having a rounded body and electric organs on each side of the head capable of emitting strong electric discharges'
# Responsive annotation of imagemagick (only caption has responsive functions)
cmd = 'convert {} -resize 2400x600\! tmp/sample_def.jpeg'.format(predicted_sample_path)
os.system(cmd)
cmd = 'convert tmp/sample_def.jpeg -background White -size 2395x \
-pointsize 50 -gravity Center \
caption:\'{}\' \
+swap -gravity Center -append tmp/sample_def.jpeg'.format(definition)
os.system(cmd)
# Top-k predictions
img = Image.open(image_path)
x = transform(img).unsqueeze(0).to(device)
out = model(x)
p = torch.nn.functional.softmax(out, dim=1)
score, index = torch.topk(p, 5)
# Tracer()()
predicted_labels = []
predicted_confidences = []
colors = []
for i in range(5):
input_prediction_id = convert_imagenet_label_to_id(label_map, key_list, val_list, index[0][i].item())
if input_prediction_id == gt_label:
colors.append('lightcoral')
else:
colors.append('mediumslateblue')
predicted_label = id_map.get(input_prediction_id).split(',')[0]
predicted_label = predicted_label[0].lower() + predicted_label[1:]
predicted_labels.append(predicted_label)
predicted_confidences.append(score[0][i].item())
# plt.rcdefaults()
fig, ax = plt.subplots()
y_pos = np.arange(len(predicted_labels))
ax.tick_params(axis='y', direction='in',pad=-100)
ax.tick_params(axis = "x", which = "both", bottom = False, top = False) # turn off xtick
ax.barh(predicted_labels, predicted_confidences, align='center', color=colors, height=1.0)
ax.set_xlim(0,1)
ax.set_yticklabels(predicted_labels, horizontalalignment = "left", fontsize=64, weight='bold')
ax.invert_yaxis() # labels read top-to-bottom
ax.set_title(textual_label, fontsize=60, weight='bold') #1
# remove the x and y ticks
ax.set_xticks([])
plt.savefig('tmp/top5.jpeg', figsize=(6.0,4.5), dpi=300, bbox_inches='tight', pad_inches=0)
plt.close()
#cmd = 'convert tmp/top5.jpeg -resize 570x400\! tmp/top5.jpeg'
cmd = 'convert tmp/top5.jpeg -resize 580x400\! tmp/top5.jpeg'
os.system(cmd)
cmd = 'convert tmp/top5.jpeg -gravity North -background white -extent 100x150% tmp/top5.jpeg'
os.system(cmd)
# cmd = 'montage original.jpeg GradCAM.jpeg EP.jpeg SOD.jpeg color_bar.jpeg -tile 5x1 -geometry 600x600+0+0 agg1.jpeg'
cmd = 'convert tmp/original.jpeg tmp/GradCAM.jpeg tmp/EP.jpeg tmp/SOD.jpeg tmp/color_bar.jpeg -gravity center +append tmp/agg1.jpeg'
os.system(cmd)
# cmd = 'montage top5.jpeg NN.jpeg -tile 2x1 -geometry +0+0 agg2.jpeg'
# cmd = 'montage top5.jpeg [0-2].jpeg -tile 4x1 -geometry 600x600+0+0 agg2.jpeg'
cmd = 'convert tmp/top5.jpeg tmp/[0-2].jpeg -gravity center +append tmp/agg2.jpeg'
os.system(cmd)
cmd = 'convert tmp/agg2.jpeg -gravity West -background white -extent 101.5x100% tmp/agg2.jpeg'
os.system(cmd)
cmd = 'convert tmp/agg1.jpeg tmp/agg2.jpeg tmp/sample_def.jpeg -gravity center -append {}'.format(representative)
print(cmd)
os.system(cmd)
```
|
github_jupyter
|
# Ejercicios de agua subterránea
```
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
%matplotlib inline
plt.style.use('dark_background')
#plt.style.use('seaborn-whitegrid')
```
## <font color=steelblue>Ejercicio 1 - Infiltración. Método de Green-Ampt
<font color=steelblue>Usando el modelo de Green-Ampt, calcula la __infiltración acumulada__, la __tasa de infiltración__ y la __profundidad del frente de mojado__ durante una precipitación constante de 5 cm/h que dure 2 h en un _loam_ limoso típico con un contenido de agua inicial de 0,45.
Las propiedades típicas del _loam_ limoso son: <br>
$\phi=0.485$ <br>
$K_{s}=2.59 cm/h$ <br>
$|\Psi_{ae}|=78.6 cm$ <br>
$b=5.3$ <br>
```
# datos del enunciado
phi = 0.485 # -
theta_o = 0.45 # -
Ks = 2.59 # cm/h
psi_ae = 78.6 # cm
b = 5.3 # -
ho = 0 # cm
i = 5 # cm/h
tc = 2 # h
epsilon = 0.001 # cm
```
### Modelo de infiltración de Green-Ampt
Hipótesis:
* Suelo encharcado con una lámina de altura $h_o$ desde el inicio.
* Frente de avance de la humedad plano (frente pistón).
* Suelo profundo y homogéneo ($\theta_o$, $\theta_s$, $K_s$ constantes).
Tasa de infiltración, $f \left[ \frac{L}{T} \right]$:
$$f = K_s \left( 1 + \frac{\Psi_f · \Delta\theta}{F} \right) \qquad \textrm{(1)}$$
Infiltración acumulada, $f \left[ L \right]$:
$$F = K_s · t + \Psi_f · \Delta\theta · \ln \left(1 + \frac{F}{\Psi_f · \Delta\theta} \right) \qquad \textrm{(2)}$$
Es una ecuación implícita. Para resolverla, se puede utilizar, por ejemplo, el método de Picard. Se establece un valor inicial de ($F_o=K_s·t$) y se itera el siguiente cálculo hasta converger ($F_{m+1}-F_m<\varepsilon$):
$$F_{m+1} = K_s · t + \Psi_f · \Delta\theta · \ln \left(1 + \frac{F_m}{\Psi_f · \Delta\theta} \right) \qquad \textrm{(3)}$$
##### Suelo no encharcado al inicio
Si no se cumple la hipótesis de encharcamiento desde el inicio, se debe calcular el tiempo de encharcamiento ($t_p$) y la cantidad de agua infiltrada hata ese momento ($F_p$):
$$t_p = \frac{K_s · \Psi_f · \Delta\theta}{i \left( i - K_s \right)} \qquad \textrm{(4)}$$
$$F_p = i · t_p = \frac{K_s · \Psi_f · \Delta\theta}{i - K_s} \qquad \textrm{(5)}$$
Conocidos $t_p$ y $F_p$, se ha de resolver la ecuación (1) sobre una nueva variable tiempo $t_p'=t_p-t_o$, con lo que se llega a la siguiente ecuación emplícita:
$$F_{m+1} = K_s · (t - t_o) + \Psi_f · \Delta\theta · \ln \left(1 + \frac{F_m}{\Psi_f · \Delta\theta} \right) \qquad \textrm{(6)}$$
donde $t_o$ es:<br>
$$t_o = t_p - \frac{F_p - \Psi_f · \Delta\theta · \ln \left(1 + \frac{F_p}{\Psi_f · \Delta\theta} \right)}{K_s} \qquad \textrm{(7)}$$
```
# calcular variables auxiliares
Atheta = phi - theta_o # incremento de la humedad del suelo
psi_f = (2 * b + 3) / (2 * b + 6) * psi_ae # tensión en el frente húmedo
# tiempo hasta el encharcamiento
tp = psi_f * Atheta * Ks / (i * (i - Ks))
# infiltración acumulada cuando ocurre el encharcamiento
Fp = tp * i
# tiempo de inicio de la curva de infiltración
to = tp - (Fp - psi_f * Atheta * np.log(1 + Fp / (psi_f * Atheta))) / Ks
# infiltración acumulada en el tiempo de cálculo
Fo = Ks * (tc - to)
Fi = Ks * (tc - to) + psi_f * Atheta * np.log(1 + Fo / (psi_f * Atheta))
while (Fi - Fo) > epsilon:
Fo = Fi
Fi = Ks * (tc - to) + psi_f * Atheta * np.log(1 + Fo / (psi_f * Atheta))
print(Fo, Fi)
Fc = Fi
print()
print('Fc = {0:.3f} cm'.format(Fc))
# tasa de infiltración en el tiempo de cálculo
fc = Ks * (1 + psi_f * Atheta / Fc)
print('fc = {0:.3f} cm/h'.format(fc))
# profundidad del frente de húmedo
L = Fc / Atheta
print('L = {0:.3f} cm'.format(L))
def GreenAmpt(i, tc, ho, phi, theta_o, Ks, psi_ae, b=5.3, epsilon=0.001):
"""Se calcula la infiltración en un suelo para una precipitación constante mediante el método de Green-Ampt.
Entradas:
---------
i: float. Intensidad de precipitación (cm/h)
tc: float. Tiempo de cálculo (h)
ho: float. Altura de la lámina de agua del encharcamiento en el inicio (cm)
phi: float. Porosidad (-)
theta_o: float. Humedad del suelo en el inicio (-)
Ks: float. Conductividad saturada (cm/h)
psi_ae: float. Tensión del suelo para el punto de entrada de aire (cm)
b: float. Coeficiente para el cálculo de la tensión en el frente húmedo (cm)
epsilo: float. Error tolerable en el cálculo (cm)
Salidas:
--------
Fc: float. Infiltración acumulada en el tiempo de cálculo (cm)
fc: float. Tasa de infiltración en el tiempo de cálculo (cm/h)
L: float. Profundidad del frente húmedo en el tiempo de cálculo (cm)"""
# calcular variables auxiliares
Atheta = phi - theta_o # incremento de la humedad del suelo
psi_f = (2 * b + 3) / (2 * b + 6) * psi_ae # tensión en el frente húmedo
if ho > 0: # encharcamiento inicial
tp = 0
to = 0
elif ho == 0: # NO hay encharcamiento inicial
# tiempo hasta el encharcamiento
tp = psi_f * Atheta * Ks / (i * (i - Ks))
# infiltración acumulada cuando ocurre el encharcamiento
Fp = tp * i
# tiempo de inicio de la curva de infiltración
to = tp - (Fp - psi_f * Atheta * np.log(1 + Fp / (psi_f * Atheta))) / Ks
# infiltración acumulada en el tiempo de cálculo
if tc <= tp:
Fc = i * tc
elif tc > tp:
Fo = Ks * (tc - to)
Fi = Ks * (tc - to) + psi_f * Atheta * np.log(1 + Fo / (psi_f * Atheta))
while (Fi - Fo) > epsilon:
Fo = Fi
Fi = Ks * (tc - to) + psi_f * Atheta * np.log(1 + Fo / (psi_f * Atheta))
Fc = Fi
# tasa de infiltración en el tiempo de cálculo
fc = Ks * (1 + psi_f * Atheta / Fc)
# profundidad del frente de húmedo
L = Fc / Atheta
return Fc, fc, L
Fc, fc, L = GreenAmpt(i, tc, ho, phi, theta_o, Ks, psi_ae, b, epsilon)
print('Fc = {0:.3f} cm'.format(Fc))
print('fc = {0:.3f} cm/h'.format(fc))
print('L = {0:.3f} cm'.format(L))
# Guardar resultados
results = pd.DataFrame([Fc, fc, L], index=['Fc (cm)', 'fc (cm/h)', 'L (cm)']).transpose()
results.to_csv('../output/Ej1_resultados.csv', index=False, float_format='%.3f')
```
|
github_jupyter
|
```
%matplotlib inline
```
Training a Classifier
=====================
This is it. You have seen how to define neural networks, compute loss and make
updates to the weights of the network.
Now you might be thinking,
What about data?
----------------
Generally, when you have to deal with image, text, audio or video data,
you can use standard python packages that load data into a numpy array.
Then you can convert this array into a ``torch.*Tensor``.
- For images, packages such as Pillow, OpenCV are useful
- For audio, packages such as scipy and librosa
- For text, either raw Python or Cython based loading, or NLTK and
SpaCy are useful
Specifically for vision, we have created a package called
``torchvision``, that has data loaders for common datasets such as
Imagenet, CIFAR10, MNIST, etc. and data transformers for images, viz.,
``torchvision.datasets`` and ``torch.utils.data.DataLoader``.
This provides a huge convenience and avoids writing boilerplate code.
For this tutorial, we will use the CIFAR10 dataset.
It has the classes: ‘airplane’, ‘automobile’, ‘bird’, ‘cat’, ‘deer’,
‘dog’, ‘frog’, ‘horse’, ‘ship’, ‘truck’. The images in CIFAR-10 are of
size 3x32x32, i.e. 3-channel color images of 32x32 pixels in size.
.. figure:: /_static/img/cifar10.png
:alt: cifar10
cifar10
Training an image classifier
----------------------------
We will do the following steps in order:
1. Load and normalizing the CIFAR10 training and test datasets using
``torchvision``
2. Define a Convolution Neural Network
3. Define a loss function
4. Train the network on the training data
5. Test the network on the test data
1. Loading and normalizing CIFAR10
^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
Using ``torchvision``, it’s extremely easy to load CIFAR10.
```
import torch
import torchvision
import torchvision.transforms as transforms
```
The output of torchvision datasets are PILImage images of range [0, 1].
We transform them to Tensors of normalized range [-1, 1].
```
transform = transforms.Compose(
[transforms.ToTensor(),
transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))])
trainset = torchvision.datasets.CIFAR10(root='./data', train=True,
download=True, transform=transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=4,
shuffle=True, num_workers=2)
testset = torchvision.datasets.CIFAR10(root='./data', train=False,
download=True, transform=transform)
testloader = torch.utils.data.DataLoader(testset, batch_size=4,
shuffle=False, num_workers=2)
classes = ('plane', 'car', 'bird', 'cat',
'deer', 'dog', 'frog', 'horse', 'ship', 'truck')
```
Let us show some of the training images, for fun.
```
import matplotlib.pyplot as plt
import numpy as np
# functions to show an image
def imshow(img):
img = img / 2 + 0.5 # unnormalize
npimg = img.numpy()
plt.imshow(np.transpose(npimg, (1, 2, 0)))
# get some random training images
dataiter = iter(trainloader)
images, labels = dataiter.next()
# show images
imshow(torchvision.utils.make_grid(images))
# print labels
print(' '.join('%5s' % classes[labels[j]] for j in range(4)))
```
2. Define a Convolution Neural Network
^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
Copy the neural network from the Neural Networks section before and modify it to
take 3-channel images (instead of 1-channel images as it was defined).
```
import torch.nn as nn
import torch.nn.functional as F
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.conv1 = nn.Conv2d(3, 6, 5)
self.pool = nn.MaxPool2d(2, 2)
self.conv2 = nn.Conv2d(6, 16, 5)
self.fc1 = nn.Linear(16 * 5 * 5, 120)
self.fc2 = nn.Linear(120, 84)
self.fc3 = nn.Linear(84, 10)
def forward(self, x):
x = self.pool(F.relu(self.conv1(x)))
x = self.pool(F.relu(self.conv2(x)))
x = x.view(-1, 16 * 5 * 5)
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = self.fc3(x)
return x
net = Net()
```
3. Define a Loss function and optimizer
^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
Let's use a Classification Cross-Entropy loss and SGD with momentum.
```
import torch.optim as optim
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(net.parameters(), lr=0.001, momentum=0.9)
```
4. Train the network
^^^^^^^^^^^^^^^^^^^^
This is when things start to get interesting.
We simply have to loop over our data iterator, and feed the inputs to the
network and optimize.
```
for epoch in range(2): # loop over the dataset multiple times
running_loss = 0.0
for i, data in enumerate(trainloader, 0):
# get the inputs
inputs, labels = data
# zero the parameter gradients
optimizer.zero_grad()
# forward + backward + optimize
outputs = net(inputs)
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
# print statistics
running_loss += loss.item()
if i % 2000 == 1999: # print every 2000 mini-batches
print('[%d, %5d] loss: %.3f' %
(epoch + 1, i + 1, running_loss / 2000))
running_loss = 0.0
print('Finished Training')
```
5. Test the network on the test data
^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
We have trained the network for 2 passes over the training dataset.
But we need to check if the network has learnt anything at all.
We will check this by predicting the class label that the neural network
outputs, and checking it against the ground-truth. If the prediction is
correct, we add the sample to the list of correct predictions.
Okay, first step. Let us display an image from the test set to get familiar.
```
dataiter = iter(testloader)
images, labels = dataiter.next()
# print images
imshow(torchvision.utils.make_grid(images))
print('GroundTruth: ', ' '.join('%5s' % classes[labels[j]] for j in range(4)))
```
Okay, now let us see what the neural network thinks these examples above are:
```
outputs = net(images)
```
The outputs are energies for the 10 classes.
Higher the energy for a class, the more the network
thinks that the image is of the particular class.
So, let's get the index of the highest energy:
```
_, predicted = torch.max(outputs, 1)
print('Predicted: ', ' '.join('%5s' % classes[predicted[j]]
for j in range(4)))
```
The results seem pretty good.
Let us look at how the network performs on the whole dataset.
```
correct = 0
total = 0
with torch.no_grad():
for data in testloader:
images, labels = data
outputs = net(images)
_, predicted = torch.max(outputs.data, 1)
total += labels.size(0)
correct += (predicted == labels).sum().item()
print('Accuracy of the network on the 10000 test images: %d %%' % (
100 * correct / total))
```
That looks waaay better than chance, which is 10% accuracy (randomly picking
a class out of 10 classes).
Seems like the network learnt something.
Hmmm, what are the classes that performed well, and the classes that did
not perform well:
```
class_correct = list(0. for i in range(10))
class_total = list(0. for i in range(10))
with torch.no_grad():
for data in testloader:
images, labels = data
outputs = net(images)
_, predicted = torch.max(outputs, 1)
c = (predicted == labels).squeeze()
for i in range(4):
label = labels[i]
class_correct[label] += c[i].item()
class_total[label] += 1
for i in range(10):
print('Accuracy of %5s : %2d %%' % (
classes[i], 100 * class_correct[i] / class_total[i]))
```
Okay, so what next?
How do we run these neural networks on the GPU?
Training on GPU
----------------
Just like how you transfer a Tensor on to the GPU, you transfer the neural
net onto the GPU.
Let's first define our device as the first visible cuda device if we have
CUDA available:
```
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
# Assume that we are on a CUDA machine, then this should print a CUDA device:
print(device)
net.to(device)
for epoch in range(2): # loop over the dataset multiple times
running_loss = 0.0
for i, data in enumerate(trainloader, 0):
# get the inputs
inputs, labels = data
inputs, labels = inputs.to(device), labels.to(device)
# zero the parameter gradients
optimizer.zero_grad()
# forward + backward + optimize
outputs = net(inputs).to(device)
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
# print statistics
running_loss += loss.item()
if i % 2000 == 1999: # print every 2000 mini-batches
print('[%d, %5d] loss: %.3f' %
(epoch + 1, i + 1, running_loss / 2000))
running_loss = 0.0
print('Finished Training')
```
The rest of this section assumes that `device` is a CUDA device.
Then these methods will recursively go over all modules and convert their
parameters and buffers to CUDA tensors:
.. code:: python
net.to(device)
Remember that you will have to send the inputs and targets at every step
to the GPU too:
.. code:: python
inputs, labels = inputs.to(device), labels.to(device)
Why dont I notice MASSIVE speedup compared to CPU? Because your network
is realllly small.
**Exercise:** Try increasing the width of your network (argument 2 of
the first ``nn.Conv2d``, and argument 1 of the second ``nn.Conv2d`` –
they need to be the same number), see what kind of speedup you get.
**Goals achieved**:
- Understanding PyTorch's Tensor library and neural networks at a high level.
- Train a small neural network to classify images
Training on multiple GPUs
-------------------------
If you want to see even more MASSIVE speedup using all of your GPUs,
please check out :doc:`data_parallel_tutorial`.
Where do I go next?
-------------------
- :doc:`Train neural nets to play video games </intermediate/reinforcement_q_learning>`
- `Train a state-of-the-art ResNet network on imagenet`_
- `Train a face generator using Generative Adversarial Networks`_
- `Train a word-level language model using Recurrent LSTM networks`_
- `More examples`_
- `More tutorials`_
- `Discuss PyTorch on the Forums`_
- `Chat with other users on Slack`_
|
github_jupyter
|
```
#from nbdev import *
%load_ext autoreload
%autoreload 2
#%nbdev_hide
#import sys
#sys.path.append("..")
```
# Examples
> Examples of the PCT library in use.
```
import gym
render=False
runs=1
#gui
render=True
runs=2000
```
## Cartpole
Cartpole is an Open AI gym environment for the inverted pendulum problem. The goal is to keep the pole balanced, by moving the cart left or right.
The environment provides observations (perceptions) for the state of the cart and pole.
0 - Cart Position
1 - Cart Velocity
2 - Pole Angle
3 - Pole Angular Velocity
It takes one value, of 0 or 1, for applying a force to the left or right, respectively.
The PCT solution is a four-level hierarchy for controlling the perceptions at goal values. Only one goal reference is manually set, the highest level which is the pole angle of 0.
This example shows how a perceptual control hierarchy can be implemented with this library.
```
import matplotlib.pyplot as plt
import numpy as np
from pct.hierarchy import PCTHierarchy
from pct.putils import FunctionsList
from pct.environments import CartPoleV1
from pct.functions import IndexedParameter
from pct.functions import Integration
from pct.functions import GreaterThan
from pct.functions import PassOn
```
Create a hierarchy of 4 levels each with one node.
```
cartpole_hierarchy = PCTHierarchy(levels=4, cols=1, name="cartpoleh", build=False)
namespace=cartpole_hierarchy.namespace
cartpole_hierarchy.get_node(0, 0).name = 'cart_velocity_node'
cartpole_hierarchy.get_node(1, 0).name = 'cart_position_node'
cartpole_hierarchy.get_node(2, 0).name = 'pole_velocity_node'
cartpole_hierarchy.get_node(3, 0).name = 'pole_angle_node'
#FunctionsList.getInstance().report()
#cartpole_hierarchy.summary(build=True)
```
Create the Cartpole gym environment function. This will apply the "action" output from the hierarchy and provide the new observations.
```
cartpole = CartPoleV1(name="CartPole-v1", render=render, namespace=namespace)
```
Create functions for each of the observation parameters of the Cartpole environment. Insert them into the hierarchy at the desired places.
```
cartpole_hierarchy.insert_function(level=0, col=0, collection="perception", function=IndexedParameter(index=1, name="cart_velocity", links=[cartpole], namespace=namespace))
cartpole_hierarchy.insert_function(level=1, col=0, collection="perception", function=IndexedParameter(index=0, name="cart_position", links=[cartpole], namespace=namespace))
cartpole_hierarchy.insert_function(level=2, col=0, collection="perception", function=IndexedParameter(index=3, name="pole_velocity", links=[cartpole], namespace=namespace))
cartpole_hierarchy.insert_function(level=3, col=0, collection="perception", function=IndexedParameter(index=2, name="pole_angle", links=[cartpole], namespace=namespace))
```
Link the references to the outputs of the level up.
```
cartpole_hierarchy.insert_function(level=0, col=0, collection="reference", function=PassOn(name="cart_velocity_reference", links=['proportional1'], namespace=namespace))
cartpole_hierarchy.insert_function(level=1, col=0, collection="reference", function=PassOn(name="cart_position_reference", links=['proportional2'], namespace=namespace))
cartpole_hierarchy.insert_function(level=2, col=0, collection="reference", function=PassOn(name="pole_velocity_reference", links=['proportional3'], namespace=namespace))
```
Set the highest level reference.
```
top = cartpole_hierarchy.get_function(level=3, col=0, collection="reference")
top.set_name("pole_angle_reference")
top.set_value(0)
```
Link the output of the hierarchy back to the Cartpole environment.
```
cartpole_hierarchy.summary(build=True)
cartpole_hierarchy.insert_function(level=0, col=0, collection="output", function=Integration(gain=-0.05, slow=4, name="force", links='subtract', namespace=namespace))
```
Set the names and gains of the output functions. This also shows another way of getting a function, by name.
```
FunctionsList.getInstance().get_function(namespace=namespace, name="proportional3").set_name("pole_angle_output")
FunctionsList.getInstance().get_function(namespace=namespace, name="pole_angle_output").set_property('gain', 3.5)
FunctionsList.getInstance().get_function(namespace=namespace, name="proportional2").set_name("pole_velocity_output")
FunctionsList.getInstance().get_function(namespace=namespace, name="pole_velocity_output").set_property('gain', 0.5)
FunctionsList.getInstance().get_function(namespace=namespace, name="proportional1").set_name("cart_position_output")
FunctionsList.getInstance().get_function(namespace=namespace, name="cart_position_output").set_property('gain', 2)
```
Add a post function to convert the output to 1 or 0 as required by the Cartpole environment.
```
greaterthan = GreaterThan(threshold=0, upper=1, lower=0, links='force', namespace=namespace)
cartpole_hierarchy.add_postprocessor(greaterthan)
```
Add the cartpole function as one that is executed before the actual hierarchy.
```
cartpole_hierarchy.add_preprocessor(cartpole)
```
Set the output of the hierachy as the action input to the Cartpole environment.
```
#link = cartpole_hierarchy.get_output_function()
cartpole.add_link(greaterthan)
```
Sit back and observe the brilliance of your efforts.
```
cartpole_hierarchy.set_order("Down")
cartpole_hierarchy.summary()
#gui
cartpole_hierarchy.draw(font_size=10, figsize=(8,12), move={'CartPole-v1': [-0.075, 0]}, node_size=1000, node_color='red')
cartpole_hierarchy.save("cartpole.json")
import networkx as nx
gr = cartpole_hierarchy.graph()
print(nx.info(gr))
print(gr.nodes())
```
Run the hierarchy for 500 steps.
```
cartpole_hierarchy.run(1,verbose=False)
cartpole_hierarchy.run(runs,verbose=False)
cartpole.close()
```
|
github_jupyter
|
# Getting Started with NumPy
<h1>Table of Contents<span class="tocSkip"></span></h1>
<div class="toc"><ul class="toc-item"><li><span><a href="#Getting-Started-with-NumPy" data-toc-modified-id="Getting-Started-with-NumPy-1"><span class="toc-item-num">1 </span>Getting Started with NumPy</a></span><ul class="toc-item"><li><span><a href="#Learning-Objectives" data-toc-modified-id="Learning-Objectives-1.1"><span class="toc-item-num">1.1 </span>Learning Objectives</a></span></li><li><span><a href="#What-is-NumPy?" data-toc-modified-id="What-is-NumPy?-1.2"><span class="toc-item-num">1.2 </span>What is NumPy?</a></span></li><li><span><a href="#The-NumPy-Array-Object" data-toc-modified-id="The-NumPy-Array-Object-1.3"><span class="toc-item-num">1.3 </span>The NumPy Array Object</a></span></li><li><span><a href="#Data-types" data-toc-modified-id="Data-types-1.4"><span class="toc-item-num">1.4 </span>Data types</a></span><ul class="toc-item"><li><span><a href="#Basic-Numerical-Data-Types-Available-in-NumPy" data-toc-modified-id="Basic-Numerical-Data-Types-Available-in-NumPy-1.4.1"><span class="toc-item-num">1.4.1 </span>Basic Numerical Data Types Available in NumPy</a></span></li><li><span><a href="#Data-Type-Promotion" data-toc-modified-id="Data-Type-Promotion-1.4.2"><span class="toc-item-num">1.4.2 </span>Data Type Promotion</a></span></li></ul></li><li><span><a href="#Going-Further" data-toc-modified-id="Going-Further-1.5"><span class="toc-item-num">1.5 </span>Going Further</a></span></li></ul></li></ul></div>
## Learning Objectives
- Understand NumPy Array Object
## What is NumPy?
- NumPy provides the numerical backend for nearly every scientific or technical library for Python. In fact, NumPy is the foundation library for scientific computing in Python since it provides data structures and high-performing functions that the basic Python standard library cannot provide. Therefore, knowledge of this library is essential in terms of numerical calculations since its correct use can greatly influence the performance of your computations.
- NumPy provides the following additional features:
- `Ndarray`: A multidimensional array much faster and more efficient
than those provided by the basic package of Python. The core of NumPy is implemented in C and provides efficient functions for manipulating and processing arrays.
- `Element-wise computation`: A set of functions for performing this type of calculation with arrays and mathematical operations between arrays.
- `Integration with other languages such as C, C++, and FORTRAN`: A
set of tools to integrate code developed with these programming
languages.
- At a first glance, NumPy arrays bear some resemblance to Python’s list data structure. But an important difference is that while Python lists are generic containers of objects:
- NumPy arrays are homogenous and typed arrays of fixed size.
- Homogenous means that all elements in the array have the same data type.
- Fixed size means that an array cannot be resized (without creating a new array).
## The NumPy Array Object
- The core of the NumPy Library is one main object: `ndarray` (which stands for N-dimensional array)
- This object is a multi-dimensional homogeneous array with a predetermined number of items
- In addition to the data stored in the array, this data structure also contains important metadata about the array, such as its shape, size, data type, and other attributes.
**Basic Attributes of the ndarray Class**
| Attribute | Description |
|-----------|----------------------------------------------------------------------------------------------------------|
| shape | A tuple that contains the number of elements (i.e., the length) for each dimension (axis) of the array. |
| size | The total number elements in the array. |
| ndim | Number of dimensions (axes). |
| nbytes | Number of bytes used to store the data. |
| dtype | The data type of the elements in the array. |
| itemsize | Defines teh size in bytes of each item in the array. |
| data | A buffer containing the actual elements of the array. |
In order to use the NumPy library, we need to import it in our program. By convention,
the numPy module imported under the alias np, like so:
```
import numpy as np
```
After this, we can access functions and classes in the numpy module using the np
namespace. Throughout this notebook, we assume that the NumPy module is imported in
this way.
```
data = np.array([[10, 2], [5, 8], [1, 1]])
data
```
Here the ndarray instance data is created from a nested Python list using the
function `np.array`. More ways to create ndarray instances from data and from rules of
various kinds are introduced later in this tutorial.
```
type(data)
data.ndim
data.size
data.dtype
data.nbytes
data.itemsize
data.data
```
## Data types
- `dtype` attribute of the `ndarray` describes the data type of each element in the array.
- Since NumPy arrays are homogeneous, all elements have the same data type.
### Basic Numerical Data Types Available in NumPy
| dtype | Variants | Description |
|---------|-------------------------------------|---------------------------------------|
| int | int8, int16, int32, int64 | Integers |
| uint | uint8, uint16, uint32, uint64 | Unsigned (non-negative) integers |
| bool | Bool | Boolean (True or False) |
| float | float16, float32, float64, float128 | Floating-point numbers |
| complex | complex64, complex128, complex256 | Complex-valued floating-point numbers |
Once a NumPy array is created, its `dtype` cannot be changed, other than by creating a new copy with type-casted array values
```
data = np.array([5, 9, 87], dtype=np.float32)
data
data = np.array(data, dtype=np.int32) # use np.array function for type-casting
data
data = np.array([5, 9, 87], dtype=np.float32)
data
data = data.astype(np.int32) # Use astype method of the ndarray class for type-casting
data
```
### Data Type Promotion
When working with NumPy arrays, the data type might get promoted from one type to another, if required by the operation.
For instance, adding float-value and integer-valued arrays, the resulting array is a float-valued array:
```
arr1 = np.array([0, 2, 3], dtype=float)
arr1
arr2 = np.array([10, 20, 30], dtype=int)
arr2
res = arr1 + arr2
res
res.dtype
```
<div class="alert alert-block alert-info">
In some cases, depending on the application and its requirements, it is essential to create arrays with data type appropriately set to right data type. The default data type is `float`:
<div>
```
np.sqrt(np.array([0, -1, 2]))
np.sqrt(np.array([0, -1, 2], dtype=complex))
```
Here, using the `np.sqrt` function to compute the square root of each element in
an array gives different results depending on the data type of the array. Only when the data type of the array is complex is the square root of `–1` resulting in the imaginary unit (denoted as `1j` in Python).
## Going Further
The NumPy library is the topic of several books, including the Guide to NumPy, by the creator of the NumPy T. Oliphant, available for free online at http://web.mit.edu/dvp/Public/numpybook.pdf, and *Numerical Python (2019)*, and *Python for Data Analysis (2017)*.
- [NumPy Reference Documentation](https://docs.scipy.org/doc/numpy/reference/)
- Robert Johansson, Numerical Python 2nd.Urayasu-shi, Apress, 2019.
- McKinney, Wes. Python for Data Analysis 2nd. Sebastopol: O’Reilly, 2017.
<div class="alert alert-block alert-success">
<p>Next: <a href="02_memory_layout.ipynb">Memory Layout</a></p>
</div>
|
github_jupyter
|
RMedian : Phase 3 / Clean Up Phase
```
import math
import random
import statistics
```
Testfälle :
```
# User input
testcase = 3
# Automatic
X = [i for i in range(101)]
cnt = [0 for _ in range(101)]
# ------------------------------------------------------------
# Testcase 1 : Det - max(sumL, sumR) > n/2
# Unlabanced
if testcase == 1:
X = [i for i in range(101)]
L = [[i, i+1] for i in reversed(range(0, 21, 2))]
C = [i for i in range(21, 28)]
R = [[i, i+1] for i in range(28, 100, 2)]
# ------------------------------------------------------------
# Testcase 2 : AKS - |C| < log(n)
elif testcase == 2:
X = [i for i in range(101)]
L = [[i, i+1] for i in reversed(range(0, 48, 2))]
C = [i for i in range(48, 53)]
R = [[i, i+1] for i in range(53, 100, 2)]
# ------------------------------------------------------------
# Testcase 3 : Rek - Neither
elif testcase == 3:
L = [[i, i+1] for i in reversed(range(0, 30, 2))]
C = [i for i in range(30, 71)]
R = [[i, i+1] for i in range(71, 110, 2)]
# ------------------------------------------------------------
lc = len(C)
# ------------------------------------------------------------
# Show Testcase
print('L :', L)
print('C :', C)
print('R :', R)
```
Algorithmus : Phase 3
```
def phase3(X, L, C, R, cnt):
res = 'error'
n = len(X)
sumL, sumR = 0, 0
for l in L:
sumL += len(l)
for r in R:
sumR += len(r)
s = sumL - sumR
# Det Median
if max(sumL, sumR) > n/2:
res = 'DET'
if len(X) % 2 == 0:
return (X[int(len(X)/2 - 1)] + X[int(len(X)/2)]) / 2, cnt, res, s
else:
return X[int(len(X) / 2 - 0.5)], cnt, res, s
# AKS
if len(C) < math.log(n) / math.log(2):
res = 'AKS'
C.sort()
if len(C) % 2 == 0:
return (C[int(len(C)/2 - 1)] + C[int(len(C)/2)]) / 2, cnt, res, s
else:
return C[int(len(C) / 2 - 0.5)], cnt, res, s
print(sumR)
# Expand
if s < 0:
rs = []
for r in R:
rs += r
random.shuffle(rs)
for i in range(-s):
C.append(rs[i])
for r in R:
if rs[i] in r:
r.remove(rs[i])
else:
ls = []
for l in L:
ls += l
random.shuffle(ls)
for i in range(s):
C.append(ls[i])
for l in L:
if ls[i] in l:
l.remove(ls[i])
res = 'Expand'
return -1, cnt, res, s
# Testfall
med, cnt, res, s = phase3(X, L, C, R, cnt)
```
Resultat :
```
def test(X, L, C, R, lc, med, cnt, res, s):
n, l, c, r, sumL, sumR, mx = len(X), len(L), len(C), len(R), 0, 0, max(cnt)
m = statistics.median(X)
for i in range(len(L)):
sumL += len(L[i])
sumR += len(R[i])
print('')
print('Testfall:')
print('=======================================')
print('|X| / |L| / |C| / |R| :', n, '/', sumL, '/', c, '/', sumR)
print('=======================================')
print('Case :', res)
print('SumL - SumR :', s)
print('|C| / |C_new| :', lc, '/', len(C))
print('---------------------------------------')
print('Algo / Median :', med, '/', m)
print('=======================================')
print('max(cnt) :', mx)
print('=======================================')
return
# Testfall
test(X, L, C, R, lc, med, cnt, res, s)
```
|
github_jupyter
|
# CS229: Problem Set 1
## Problem 3: Gaussian Discriminant Analysis
**C. Combier**
This iPython Notebook provides solutions to Stanford's CS229 (Machine Learning, Fall 2017) graduate course problem set 1, taught by Andrew Ng.
The problem set can be found here: [./ps1.pdf](ps1.pdf)
I chose to write the solutions to the coding questions in Python, whereas the Stanford class is taught with Matlab/Octave.
## Notation
- $x^i$ is the $i^{th}$ feature vector
- $y^i$ is the expected outcome for the $i^{th}$ training example
- $m$ is the number of training examples
- $n$ is the number of features
### Question 3.a)
The gist of the solution is simply to apply Bayes rule, and simplify the exponential terms in the denominator which gives us the sigmoid function. The calculations are somewhat heavy:
$$
\begin{align*}
p(y=1 \mid x) & = \frac{p(x \mid y=1)p(y=1)}{p(x)} \\
& = \frac{p(x \mid y=1)p(y=1)}{p(x \mid y=1)p(y=1)+ p(x \mid y=-1)p(y=-1)} \\
& = \frac{\frac{1}{(2\pi)^{\frac{n}{2}} \lvert \Sigma \rvert^{\frac{1}{2}}} \exp \left(-\frac{1}{2} \left(x-\mu_{1} \right)^T\Sigma^{-1} \left(x-\mu_{1} \right) \right) \phi }{ \frac{1}{(2\pi)^{\frac{n}{2}} \lvert \Sigma \rvert^{\frac{1}{2}}} \exp \left(-\frac{1}{2} \left(x-\mu_{1} \right)^T\Sigma^{-1} \left(x-\mu_{1} \right) \right) \phi + \frac{1}{(2\pi)^{\frac{n}{2}} \lvert \Sigma \rvert^{\frac{1}{2}}} \exp \left(-\frac{1}{2} \left(x-\mu_{-1} \right)^T\Sigma^{-1} \left(x-\mu_{-1} \right) \right)\left(1-\phi \right)} \\
& = \frac{\phi \exp \left(-\frac{1}{2} \left(x-\mu_{1} \right)^T\Sigma^{-1} \left(x-\mu_{1} \right) \right) }{\phi \exp \left(-\frac{1}{2} \left(x-\mu_{1} \right)^T\Sigma^{-1} \left(x-\mu_{1} \right) \right) + \left(1-\phi \right) \exp \left(-\frac{1}{2} \left(x-\mu_{-1} \right)^T\Sigma^{-1} \left(x-\mu_{-1} \right) \right)} \\
& = \frac{1}{1+ \exp \left(\log\left(\frac{\left(1-\phi \right)}{\phi}\right) -\frac{1}{2} \left(x-\mu_{-1} \right)^T\Sigma^{-1} \left(x-\mu_{-1} \right) + \frac{1}{2} \left(x-\mu_{1} \right)^T\Sigma^{-1} \left(x-\mu_{1} \right) \right)} \\
& = \frac{1}{1+\exp \left(\log \left(\frac{1-\phi}{\phi}\right) -\frac{1}{2} \left(x^T \Sigma^{-1}x -2x^T \Sigma^{-1}\mu_{-1}+ \mu_{-1}^T \Sigma^{-1} \mu_{-1}\right) + \frac{1}{2} \left(x^T \Sigma^{-1}x -2x^T \Sigma^{-1}\mu_{1}+ \mu_{1}^T \Sigma^{-1} \mu_{1} \right)\right)} \\
& = \frac{1}{1+\exp \left(\log \left(\frac{1-\phi}{\phi}\right) + x^T \Sigma^{-1} \mu_{-1} - x^T \Sigma^{-1} \mu_1 - \frac{1}{2} \mu_{-1}^T \Sigma^{-1} \mu_{-1} + \frac{1}{2} \mu_1^T\Sigma^{-1}\mu_1 \right)} \\
& = \frac{1}{1+ \exp\left(\log\left(\frac{1-\phi}{\phi}\right) + x^T \Sigma^{-1} \left(\mu_{-1}-\mu_1 \right) - \frac{1}{2}\mu_{-1}^T\Sigma^{-1}\mu_{-1} + \mu_1^T \Sigma^{-1} \mu_1 \right)} \\
\\
\end{align*}
$$
With:
- $\theta_0 = \frac{1}{2}\left(\mu_{-1}^T \Sigma^{-1} \mu_{-1}- \mu_1^T \Sigma^{-1}\mu_1 \right)-\log\frac{1-\phi}{\phi} $
- $\theta = \Sigma^{-1}\left(\mu_{1}-\mu_{-1} \right)$
we have:
$$
p(y=1 \mid x) = \frac{1}{1+\exp \left(-y(\theta^Tx + \theta_0) \right)}
$$
### Questions 3.b) and 3.c)
Question 3.b) is the special case where $n=1$. Let us prove the general case directly, as required in 3.c):
$$
\begin{align*}
\ell \left(\phi, \mu_{-1}, \mu_1, \Sigma \right) & = \log \prod_{i=1}^m p(x^{i}\mid y^i; \phi, \mu_{-1}, \mu_1, \Sigma)p(y^{i};\phi) \\
& = \sum_{i=1}^m \log p(x^{i}\mid y^{i}; \phi, \mu_{-1}, \mu_1, \Sigma) + \sum_{i=1}^m \log p(y^{i};\phi) \\
& = \sum_{i=1}^m \left[\log \frac{1}{\left(2 \pi \right)^{\frac{n}{2}} \lvert \Sigma \rvert^{\frac{1}{2}}} - \frac{1}{2} \left(x^{i} - \mu_{y^{i}} \right)^T \Sigma^{-1} \left(x^{i} - \mu_{y^{i}} \right) + \log \phi^{y^{i}} + \log \left(1- \phi \right)^{\left(1-y^{i} \right)} \right] \\
& \simeq \sum_{i=1}^m \left[- \frac{1}{2} \log \lvert \Sigma \rvert - \frac{1}{2} \left(x^{i} - \mu_{y^{i}} \right)^T \Sigma^{-1} \left(x^{i} - \mu_{y^{i}} \right) + y^{i} \log \phi + \left(1-y^{i} \right) \log \left(1- \phi \right) \right] \\
\end{align*}
$$
Now we calculate the maximum likelihood be calculating the gradient of the log-likelihood with respect to the parameters and setting it to $0$:
$$
\begin{align*}
\frac{\partial \ell}{\partial \phi} &= \sum_{i=1}^{m}( \frac{y^i}{\phi} - \frac{1-y^i}{1-\phi}) \\
&= \sum_{i=1}^{m}\frac{1(y^i = 1)}{\phi} + \frac{m-\sum_{i=1}^{m}1(y^i = 1)}{1-\phi}
\end{align*}
$$
Therefore, $\phi = \frac{1}{m} \sum_{i=1}^m 1(y^i =1 )$, i.e. the percentage of the training examples such that $y^i = 1$
Now for $\mu_{-1}:$
$$
\begin{align*}
\nabla_{\mu_{-1}} \ell & = - \frac{1}{2} \sum_{i : y^{i}=-1} \nabla_{\mu_{-1}} \left[ -2 \mu_{-1}^T \Sigma^{-1} x^{(i)} + \mu_{-1}^T \Sigma^{-1} \mu_{-1} \right] \\
& = - \frac{1}{2} \sum_{i : y^{i}=-1} \left[-2 \Sigma^{-1}x^{(i)} + 2 \Sigma^{-1} \mu_{-1} \right]
\end{align*}
$$
Again, we set the gradient to $0$:
$$
\begin{align*}
\sum_{i:y^i=-1} \left[\Sigma^{-1}x^{i}-\Sigma^{-1} \mu_{-1} \right] &= 0 \\
\sum_{i=1}^m 1 \left\{y^{i}=-1\right\} \Sigma^{-1} x^{(i)} - \sum_{i=1}^m 1 \left\{y^{i}=-1 \right\} \Sigma^{-1} \mu_{-1} &=0 \\
\end{align*}
$$
This yields:
$$
\Sigma^{-1} \mu_{-1} \sum_{i=1}^m 1 \left\{y^{i}=-1 \right\} = \Sigma^{-1} \sum_{i=1}^m 1 \left\{y^{(i)}=-1\right\} x^{i}
$$
Allowing us to finally write:
$$\mu_{-1} = \frac{\sum_{i=1}^m 1 \left\{y^{i}=-1\right\} x^{i}}{\sum_{i=1}^m 1 \left\{y^{(i)}=-1 \right\}}$$
The calculations are similar for $\mu_1$, and we obtain:
$$\mu_{1} = \frac{\sum_{i=1}^m 1 \left\{y^{i}=1\right\} x^{i}}{\sum_{i=1}^m 1 \left\{y^{i}=1 \right\}}$$
The last step is to calculate the gradient with respect to $\Sigma$. To simplify calculations, let us calculate the gradient for $S = \frac{1}{\Sigma}$.
$$
\begin{align*}
\nabla_{S} \ell & = - \frac{1}{2}\sum_{i=1}^m \nabla_{\Sigma} \left[-\log \lvert S \rvert + \left(x^{i}- \mu_{y^{i}} \right)^T S \left(x^{i}- \mu_{y^{i}} \right) \right] \\
& = - \frac{1}{2}\sum_{i=1}^m \left[-S^{-1} + \left(x^{i}- \mu_{y^{i}} \right)\left(x^{i}- \mu_{y^{i}} \right)^T \right] \\
& = \sum_{i=1}^m \frac{1}{2} \Sigma - \frac{1}{2} \sum_{i=1}^m \left(x^{i}- \mu_{y^{i}} \right)\left(x^{i}- \mu_{y^{i}} \right)^T\\
\end{align*}
$$
Again, we set the gradient to $0$, allowing us to write:
$$
\frac{1}{2} m \Sigma = \frac{1}{2} \sum_{i=1}^m \left(x^{i}- \mu_{y^{i}} \right)\left(x^{i}- \mu_{y^{i}} \right)^T \\
$$
Finally, we obtain the maximum likelihood estimate for $\Sigma$:
$$
\Sigma = \frac{1}{m}\sum_{i=1}^m \left(x^{i}- \mu_{y^{i}} \right)\left(x^{i}- \mu_{y^{i}} \right)^T
$$
|
github_jupyter
|
# Variable Distribution Type Tests (Gaussian)
- Shapiro-Wilk Test
- D’Agostino’s K^2 Test
- Anderson-Darling Test
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
sns.set(font_scale=2, palette= "viridis")
from scipy import stats
data = pd.read_csv('../data/pulse_data.csv')
data.head()
```
## Visual Normality Check
```
data.Height.describe()
data.skew()
data.kurtosis()
plt.figure(figsize=(10,8))
sns.histplot(data=data, x='Height')
plt.show()
plt.figure(figsize=(10,8))
sns.histplot(data=data, x='Age', kde=True)
plt.show()
# Checking for normality by Q-Q plot graph
plt.figure(figsize=(12, 8))
stats.probplot(data['Age'], plot=plt, dist='norm')
plt.show()
```
__the data should be on the red line. If there are data points that are far off of it, it’s an indication that there are some deviations from normality.__
```
# Checking for normality by Q-Q plot graph
plt.figure(figsize=(12, 8))
stats.probplot(data['Height'], plot=plt, dist='norm')
plt.show()
```
__the data should be on the red line. If there are data points that are far off of it, it’s an indication that there are some deviations from normality.__
## Shapiro-Wilk Test
Tests whether a data sample has a Gaussian distribution/normal distribution.
### Assumptions
Observations in each sample are independent and identically distributed (iid).
### Interpretation
- H0: The sample has a Gaussian/normal distribution.
- Ha: The sample does not have a Gaussian/normal distribution.
```
stats.shapiro(data['Age'])
stat, p_value = stats.shapiro(data['Age'])
print(f'statistic = {stat}, p-value = {p_value}')
alpha = 0.05
if p_value > alpha:
print("The sample has normal distribution(Fail to reject the null hypothesis, the result is not significant)")
else:
print("The sample does not have a normal distribution(Reject the null hypothesis, the result is significant)")
```
## D’Agostino’s K^2 Test
Tests whether a data sample has a Gaussian distribution/normal distribution.
### Assumptions
Observations in each sample are independent and identically distributed (iid).
### Interpretation
- H0: The sample has a Gaussian/normal distribution.
- Ha: The sample does not have a Gaussian/normal distribution.
```
stats.normaltest(data['Age'])
stat, p_value = stats.normaltest(data['Age'])
print(f'statistic = {stat}, p-value = {p_value}')
alpha = 0.05
if p_value > alpha:
print("The sample has normal distribution(Fail to reject the null hypothesis, the result is not significant)")
else:
print("The sample does not have a normal distribution(Reject the null hypothesis, the result is significant)")
```
__Remember__
- If Data Is Gaussian:
- Use Parametric Statistical Methods
- Else:
- Use Nonparametric Statistical Methods
|
github_jupyter
|
# Collaboration and Competition
---
In this notebook, you will learn how to use the Unity ML-Agents environment for the third project of the [Deep Reinforcement Learning Nanodegree](https://www.udacity.com/course/deep-reinforcement-learning-nanodegree--nd893) program.
### 1. Start the Environment
We begin by importing the necessary packages. If the code cell below returns an error, please revisit the project instructions to double-check that you have installed [Unity ML-Agents](https://github.com/Unity-Technologies/ml-agents/blob/master/docs/Installation.md) and [NumPy](http://www.numpy.org/).
```
from unityagents import UnityEnvironment
import numpy as np
import copy
from collections import namedtuple, deque
import random
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
import matplotlib.pyplot as plt
%matplotlib inline
```
Next, we will start the environment! **_Before running the code cell below_**, change the `file_name` parameter to match the location of the Unity environment that you downloaded.
- **Mac**: `"path/to/Tennis.app"`
- **Windows** (x86): `"path/to/Tennis_Windows_x86/Tennis.exe"`
- **Windows** (x86_64): `"path/to/Tennis_Windows_x86_64/Tennis.exe"`
- **Linux** (x86): `"path/to/Tennis_Linux/Tennis.x86"`
- **Linux** (x86_64): `"path/to/Tennis_Linux/Tennis.x86_64"`
- **Linux** (x86, headless): `"path/to/Tennis_Linux_NoVis/Tennis.x86"`
- **Linux** (x86_64, headless): `"path/to/Tennis_Linux_NoVis/Tennis.x86_64"`
For instance, if you are using a Mac, then you downloaded `Tennis.app`. If this file is in the same folder as the notebook, then the line below should appear as follows:
```
env = UnityEnvironment(file_name="Tennis.app")
```
```
env = UnityEnvironment(file_name="Tennis_Linux_NoVis/Tennis.x86_64")
```
Environments contain **_brains_** which are responsible for deciding the actions of their associated agents. Here we check for the first brain available, and set it as the default brain we will be controlling from Python.
```
# get the default brain
brain_name = env.brain_names[0]
brain = env.brains[brain_name]
```
### 2. Examine the State and Action Spaces
In this environment, two agents control rackets to bounce a ball over a net. If an agent hits the ball over the net, it receives a reward of +0.1. If an agent lets a ball hit the ground or hits the ball out of bounds, it receives a reward of -0.01. Thus, the goal of each agent is to keep the ball in play.
The observation space consists of 8 variables corresponding to the position and velocity of the ball and racket. Two continuous actions are available, corresponding to movement toward (or away from) the net, and jumping.
Run the code cell below to print some information about the environment.
```
# reset the environment
env_info = env.reset(train_mode=True)[brain_name]
# number of agents
num_agents = len(env_info.agents)
print('Number of agents:', num_agents)
# size of each action
action_size = brain.vector_action_space_size
print('Size of each action:', action_size)
# examine the state space
states = env_info.vector_observations
state_size = states.shape[1]
print('There are {} agents. Each observes a state with length: {}'.format(states.shape[0], state_size))
print('The state for the first agent looks like:', states[0])
```
### 3. Take Random Actions in the Environment
In the next code cell, you will learn how to use the Python API to control the agents and receive feedback from the environment.
Once this cell is executed, you will watch the agents' performance, if they select actions at random with each time step. A window should pop up that allows you to observe the agents.
Of course, as part of the project, you'll have to change the code so that the agents are able to use their experiences to gradually choose better actions when interacting with the environment!
```
for i in range(1, 6): # play game for 5 episodes
env_info = env.reset(train_mode=False)[brain_name] # reset the environment
states = env_info.vector_observations # get the current state (for each agent)
scores = np.zeros(num_agents) # initialize the score (for each agent)
while True:
actions = np.random.randn(num_agents, action_size) # select an action (for each agent)
actions = np.clip(actions, -1, 1) # all actions between -1 and 1
env_info = env.step(actions)[brain_name] # send all actions to tne environment
next_states = env_info.vector_observations # get next state (for each agent)
rewards = env_info.rewards # get reward (for each agent)
dones = env_info.local_done # see if episode finished
scores += env_info.rewards # update the score (for each agent)
states = next_states # roll over states to next time step
if np.any(dones): # exit loop if episode finished
break
print('Score (max over agents) from episode {}: {}'.format(i, np.max(scores)))
```
When finished, you can close the environment.
```
# env.close()
```
### 4. It's Your Turn!
Now it's your turn to train your own agent to solve the environment! When training the environment, set `train_mode=True`, so that the line for resetting the environment looks like the following:
```python
env_info = env.reset(train_mode=True)[brain_name]
```
### 5. My Multi DDPG
```
from ddpg.multi_ddpg_agent import Agent
agent_0 = Agent(state_size, action_size, num_agents=1, random_seed=0)
agent_1 = Agent(state_size, action_size, num_agents=1, random_seed=0)
def get_actions(states, add_noise):
'''gets actions for each agent and then combines them into one array'''
action_0 = agent_0.act(states, add_noise) # agent 0 chooses an action
action_1 = agent_1.act(states, add_noise) # agent 1 chooses an action
return np.concatenate((action_0, action_1), axis=0).flatten()
SOLVED_SCORE = 0.5
CONSEC_EPISODES = 100
PRINT_EVERY = 10
ADD_NOISE = True
def run_multi_ddpg(n_episodes=2000, max_t=1000, train_mode=True):
"""Multi-Agent Deep Deterministic Policy Gradient (MADDPG)
Params
======
n_episodes (int) : maximum number of training episodes
max_t (int) : maximum number of timesteps per episode
train_mode (bool) : if 'True' set environment to training mode
"""
scores_window = deque(maxlen=CONSEC_EPISODES)
scores_all = []
moving_average = []
best_score = -np.inf
best_episode = 0
already_solved = False
for i_episode in range(1, n_episodes+1):
env_info = env.reset(train_mode=train_mode)[brain_name] # reset the environment
states = np.reshape(env_info.vector_observations, (1,48)) # get states and combine them
agent_0.reset()
agent_1.reset()
scores = np.zeros(num_agents)
while True:
actions = get_actions(states, ADD_NOISE) # choose agent actions and combine them
env_info = env.step(actions)[brain_name] # send both agents' actions together to the environment
next_states = np.reshape(env_info.vector_observations, (1, 48)) # combine the agent next states
rewards = env_info.rewards # get reward
done = env_info.local_done # see if episode finished
agent_0.step(states, actions, rewards[0], next_states, done, 0) # agent 1 learns
agent_1.step(states, actions, rewards[1], next_states, done, 1) # agent 2 learns
scores += np.max(rewards) # update the score for each agent
states = next_states # roll over states to next time step
if np.any(done): # exit loop if episode finished
break
ep_best_score = np.max(scores)
scores_window.append(ep_best_score)
scores_all.append(ep_best_score)
moving_average.append(np.mean(scores_window))
# save best score
if ep_best_score > best_score:
best_score = ep_best_score
best_episode = i_episode
# print results
if i_episode % PRINT_EVERY == 0:
print(f'Episodes {i_episode}\tMax Reward: {np.max(scores_all[-PRINT_EVERY:]):.3f}\tMoving Average: {moving_average[-1]:.3f}')
# determine if environment is solved and keep best performing models
if moving_average[-1] >= SOLVED_SCORE:
if not already_solved:
print(f'Solved in {i_episode-CONSEC_EPISODES} episodes! \
\n<-- Moving Average: {moving_average[-1]:.3f} over past {CONSEC_EPISODES} episodes')
already_solved = True
torch.save(agent_0.actor_local.state_dict(), 'checkpoint_actor_0.pth')
torch.save(agent_0.critic_local.state_dict(), 'checkpoint_critic_0.pth')
torch.save(agent_1.actor_local.state_dict(), 'checkpoint_actor_1.pth')
torch.save(agent_1.critic_local.state_dict(), 'checkpoint_critic_1.pth')
elif ep_best_score >= best_score:
print(f'Best episode {i_episode}\tMax Reward: {ep_best_score:.3f}\tMoving Average: {moving_average[-1]:.3f}')
torch.save(agent_0.actor_local.state_dict(), 'checkpoint_actor_0.pth')
torch.save(agent_0.critic_local.state_dict(), 'checkpoint_critic_0.pth')
torch.save(agent_1.actor_local.state_dict(), 'checkpoint_actor_1.pth')
torch.save(agent_1.critic_local.state_dict(), 'checkpoint_critic_1.pth')
elif (i_episode-best_episode) >= 200:
# stop training if model stops converging
print('Done')
break
else:
continue
return scores_all, moving_average
scores, avgs = run_multi_ddpg()
plt.plot(np.arange(1, len(scores)+1), scores, label='Score')
plt.plot(np.arange(len(scores)), avgs, c='r', label='100 Average')
plt.legend(loc=0)
plt.ylabel('Score')
plt.xlabel('Episode #')
plt.title('Udacity Project3 Solution by Bongsang')
plt.savefig('result.png')
plt.show()
env.close()
```
|
github_jupyter
|
# K-Nearest Neighbours
Let’s build a K-Nearest Neighbours model from scratch.
First, we will define some generic `KNN` object. In the constructor, we pass three parameters:
- The number of neighbours being used to make predictions
- The distance measure we want to use
- Whether or not we want to use weighted distances
```
import sys
sys.path.append("D:/source/skratch/source")
from collections import Counter
import numpy as np
from utils.distances import euclidean
class KNN:
def __init__(self, k, distance=euclidean, weighted=False):
self.k = k
self.weighted = weighted # Whether or not to use weighted distances
self.distance = distance
```
Now we will define the fit function, which is the function which describes how to train a model. For a K-Nearest Neighbours model, the training is rather simplistic. Indeed, all there needs to be done is to store the training instances as the model’s parameters.
```
def fit(self, X, y):
self.X_ = X
self.y_ = y
return self
```
Similarly, we can build an update function which will update the state of the model as more data points are provided for training. Training a model by feeding it data in a stream-like fashion is often referred to as online learning. Not all models allow for computationally efficient online learning, but K-Nearest Neighbours does.
```
def update(self, X, y):
self.X_ = np.concatenate((self.X_, X))
self.y_ = np.concatenate((self.y_, y))
return self
```
In order to make predictions, we also need to create a predict function. For a K-Nearest Neighbours model, a prediction is made in two steps:
- Find the K-nearest neighbours by computing their distances to the data point we want to predict
- Given these neighbours and their distances, compute the predicted output
```
def predict(self, X):
predictions = []
for x in X:
neighbours, distances = self._get_neighbours(x)
prediction = self._vote(neighbours, distances)
predictions.append(prediction)
return np.array(predictions)
```
Retrieving the neighbours can be done by calculating all pairwise distances between the data point and the data stored inside the state of the model. Once these distances are known, the K instances that have the shortest distance to the example are returned.
```
def _get_neighbours(self, x):
distances = np.array([self._distance(x, x_) for x_ in self.X_])
indices = np.argsort(distances)[:self.k]
return self.y_[indices], distances[indices]
```
In case we would like to use weighted distances, we need to compute the weights. By default, these weights are all set to 1 to make all instances equal. To weigh the instances, neighbours that are closer are typically favoured by given them a weight equal to 1 divided by their distance.
>If neighbours have distance 0, since we can’t divide by zero, their weight is set to 1, and all other weights are set to 0. This is also how scikit-learn deals with this problem according to their source code.
```
def _get_weights(self, distances):
weights = np.ones_like(distances, dtype=float)
if self.weighted:
if any(distances == 0):
weights[distances != 0] = 0
else:
weights /= distances
return weights
```
The only function that we have yet to define is the vote function that is called in the predict function. Depending on the implementation of that function, K-Nearest Neighbours can be used for regression, classification, or even as a meta-learner.
## KNN for Regression
In order to use K-Nearest Neighbour for regression, the vote function is defined as the average of the neighbours. In case weighting is used, the vote function returns the weighted average, favouring closer instances.
```
class KNN_Regressor(KNN):
def _vote(self, targets, distances):
weights = self._get_weights(distances)
return np.sum(weights * targets) / np.sum(weights)
```
## KNN for Classification
In the classification case, the vote function uses a majority voting scheme. If weighting is used, each neighbour has a different impact on the prediction.
```
class KNN_Classifier(KNN):
def _vote(self, classes, distances):
weights = self._get_weights(distances)
prediction = None
max_weighted_frequency = 0
for c in classes:
weighted_frequency = np.sum(weights[classes == c])
if weighted_frequency > max_weighted_frequency:
prediction = c
max_weighted_frequency = weighted_frequency
return prediction
```
|
github_jupyter
|
```
import pandas as pd
import numpy as np
import json
from cold_start import get_cold_start_rating
import pyspark
spark = pyspark.sql.SparkSession.builder.getOrCreate()
sc = spark.sparkContext
ratings_df = spark.read.json('data/ratings.json').toPandas()
metadata = pd.read_csv('data/movies_metadata.csv')
request_df = spark.read.json('data/requests.json').toPandas()
ratings_df['user_id'].nunique()
ratings_df['rating'].value_counts()
ratings_df.isna().sum()
len(metadata), metadata['tagline'].isna().sum()
metadata.loc[0]['genres']
len(requests_df)
users = []
for line in open('data/users.dat', 'r'):
item = line.split('\n')
users.append(item[0].split("::"))
user_df = pd.read_csv('data/users.dat', sep='::', header=None, names=['id', 'gender', 'age', 'occupation', 'zip'])
movie_info_df = pd.read_csv('data/movies.dat', sep='::', header=None, names=['id', 'name', 'genres'])
user_df[20:53]
movie_info_df.head()
movie_info_df['genres'] = movie_info_df['genres'].apply(lambda x: x.split('|'))
movie_info_df.head()
all_genres = set([item for movie in movie_info_df['genres'] for item in movie])
all_genres
user_df = user_df.drop('zip', axis=1)
user_df.head()
from sklearn.preprocessing import OneHotEncoder
from sklearn.model_selection import train_test_split
from sklearn.cluster import KMeans
def ohe_columns(series, name):
ohe = OneHotEncoder(categories='auto')
ohe.fit(series)
cols = ohe.get_feature_names(name)
ohe = ohe.transform(series)
final_df = pd.DataFrame(ohe.toarray(), columns=cols)
return final_df
# OHE the user cols
my_cols = ['gender', 'age', 'occupation']
ohe_multi = OneHotEncoder(categories='auto')
ohe_multi.fit(user_df[my_cols])
ohe_mat = ohe_multi.transform(user_df[my_cols])
# Then KMeans cluster
k_clusters = KMeans(n_clusters=8, random_state=42)
k_clusters.fit(ohe_mat)
preds = k_clusters.predict(ohe_mat)
preds
preds.shape
def add_clusters_to_users(n_clusters=8):
"""
parameters:number of clusters
return: user dataframe
"""
# Get the user data
user_df = pd.read_csv('data/users.dat', sep='::', header=None
, names=['id', 'gender', 'age', 'occupation', 'zip'])
# OHE for clustering
my_cols = ['gender', 'age', 'occupation']
ohe_multi = OneHotEncoder(categories='auto')
ohe_multi.fit(user_df[my_cols])
ohe_mat = ohe_multi.transform(user_df[my_cols])
# Then KMeans cluster
k_clusters = KMeans(n_clusters=8, random_state=42)
k_clusters.fit(ohe_mat)
preds = k_clusters.predict(ohe_mat)
# Add clusters to user df
user_df['cluster'] = preds
return user_df
test_df = add_clusters_to_users()
test_df.to_csv('data/u_info.csv')
temp_ohe = ohe_2.get_feature_names(['age'])
gender_df = pd.DataFrame(gender_ohe.toarray(), columns=['F', 'M'])
gender_df.head()
ohe.fit(user_df[['gender']])
gender_ohe = ohe.transform(user_df[['gender']])
gender_df = pd.DataFrame(gender_ohe.toarray(), columns=['F', 'M'])
gender_df.head()
ohe_2.fit(user_df[['age']])
temp_ohe = ohe_2.get_feature_names(['age'])
age_ohe = ohe_2.transform(user_df[['age']])
age_df = pd.DataFrame(age_ohe.toarray(), columns=temp_ohe)
age_df.head()
ohe_3.fit(user_df[['occupation']])
cols = ohe_3.get_feature_names(['occupation'])
occ_ohe = ohe_3.transform(user_df[['occupation']])
occ_df = pd.DataFrame(occ_ohe.toarray(), columns=cols)
occ_df.head()
all_cat = pd.concat([gender_df, age_df, occ_df], axis=1)
all_cat.head()
k_clusters = KMeans(n_clusters=8, random_state=42)
k_clusters.fit(all_cat)
preds = k_clusters.predict(all_cat)
preds
user_df['cluster'] = preds
user_df[user_df['id'] == 6040]
cluster_dict = {}
for k, v in zip(user_df['id'].tolist(), user_df['cluster'].tolist()):
cluster_dict[k] = v
ratings_df['cluster'] = ratings_df['user_id'].apply(lambda x: cluster_dict[x])
def add_cluster_to_ratings(user_df):
"""
given user_df with clusters, add clusters to ratings data
parameters
---------
user_df: df with user data
returns
-------
ratings_df: ratings_df with cluster column
"""
# Read in ratings file
#Get ratings file
ratings_df = spark.read.json('data/ratings.json').toPandas()
# Set up clusters
cluster_dict = {}
for k, v in zip(user_df['id'].tolist(), user_df['cluster'].tolist()):
cluster_dict[k] = v
# Add cluster to ratings
ratings_df['cluster'] = ratings_df['user_id'].apply(lambda x: cluster_dict[x])
return ratings_df
all_df = add_cluster_to_ratings(user_df)
all_df.to_csv('data/user_cluster.csv')
movie_by_cluster = all_df.groupby(by=['cluster', 'movie_id']).agg({'rating': 'mean'}).reset_index()
movie_by_cluster.head()
movie_by_cluster = pd.read_csv('data/u_info.csv', index_col=0)
movie_by_cluster.head()
ratings_df.head()
request_df.head()
def cluster_rating(df, movie_id, cluster):
cluster_rating = df[(df['movie_id'] == movie_id) & (df['cluster'] == cluster)]
return cluster_rating['rating'].mean()
def user_bias(df, user_id):
return df.loc[df['user_id'] == user_id, 'rating'].mean() - df['rating'].mean()
def item_bias(df, movie_id):
return df.loc[df['movie_id'] == movie_id, 'rating'].mean() - df['rating'].mean()
avg = cluster_rating(df=ratings_df, movie_id=1617, cluster=1)
u = user_bias(ratings_df, 6040)
i = item_bias(ratings_df, 2019)
avg + u + i
movie_info_df[movie_info_df['id'] == 1617]
def get_cold_start_rating(user_id, movie_id):
"""
Given user_id and movie_id, return a predicted rating
parameters
----------
user_id, movie_id
returns
-------
movie rating (float)
"""
# Get user df with clusters
user_df = pd.read_csv('data/user_cluster.csv', index_col=0)
u_clusters = pd.read_csv('data/u_info.csv', index_col=0)
# Get ratings data, with clusters
ratings_df = pd.read_csv('data/movie_cluster_avg.csv', index_col=0)
# User Cluster
user_cluster = u_clusters.loc[u_clusters['id'] == user_id]['cluster'].tolist()[0]
# Get score components
avg = ratings_df.loc[ratings_df['user_id'] == movie_id]['rating'].tolist()[0]
u = user_bias(user_df, user_id)
i = item_bias(user_df, movie_id)
pred_rating = avg + u + i
return pred_rating
blah = get_cold_start_rating(user_id=53, movie_id=9999)
blah
df = pd.read_csv('data/user_cluster.csv', index_col=0)
ratings_df = pd.read_csv('data/movie_cluster_avg.csv', index_col=0)
ratings_df.head()
```
|
github_jupyter
|
```
import os
import sys
import numpy as np
import pandas as pd
import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
from torchsummary import summary
sys.path.append('../')
sys.path.append('../src/')
from src import utils
from src import generators
import imp
os.environ['CUDA_VISIBLE_DEVICES'] = "0"
```
# Inference
```
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
model_LoadWeights = '../data/trainings/train_UNETA_class/vgg_5.pkl'
mvcnn = torch.load(model_LoadWeights)
test_patient_information = utils.get_PatientInfo('/home/alex/Dataset3/', test=True)
sep = generators.SEPGenerator(base_DatabasePath='/home/alex/Dataset3/',
channels=1,
resize=296,
normalization='min-max')
test_generator = sep.generator(test_patient_information, dataset='test')
final = []
with torch.no_grad():
for v_m, v_item in enumerate(test_generator):
image_3D, p_id = torch.tensor(v_item[0], device=device).float(), v_item[1]
if image_3D.shape[0] == 0:
print(p_id)
continue
output = mvcnn(image_3D, batch_size=1, mvcnn=True)
print(output, p_id)
final.append((p_id, output.to('cpu').detach().numpy()))
if v_m == len(test_patient_information) - 1:
break
keys = {0: 0.0,
1: 1.0,
2: 1.5,
3: 2.0,
4: 2.5,
5: 3.0,
6: 3.5,
7: 4.0,
8: 4.5,
9: 5.0,
10: 5.5,
11: 6.0,
12: 6.5,
13: 7.0,
14: 7.5,
15: 8.0,
16: 8.5,
17: 9.0}
list(map(lambda a : [[int(a[0])], [keys[np.argmax(a[1])]]], (final)))
final[1][1]
import csv
csvData = [["Sequence_id"],["EDSS"]] + list(map(lambda a : [int(a[0]), keys[np.argmax(a[1])]], (final)))
with open('AZmed_Unet.csv', 'w') as csvFile:
writer = csv.writer(csvFile)
writer.writerows(csvData)
csvFile.close()
csvData
database_path =
train_patient_information, valid_patient_information = get_PatientInfo(database_path)
# Create train and valid generators
sep = SEPGenerator(database_path,
channels=channels,
resize=resize,
normalization=normalization)
train_generator = sep.generator(train_patient_information)
valid_generator = sep.generator(valid_patient_information, train=False)
train_patient_information, valid_patient_information = get_PatientInfo(database_path)
# Create train and valid generators
sep = SEPGenerator(database_path,
channels=channels,
resize=resize,
normalization=normalization)
train_generator = sep.generator(train_patient_information)
valid_generator = sep.generator(valid_patient_information, train=False)
with torch.no_grad():
for v_m, v_item in enumerate(valid_generator):
image_3D, label = torch.tensor(v_item[0], device=device).float(), torch.tensor(v_item[1], device=device).float()
if image_3D.shape[0] == 0:
continue
output = mvcnn(image_3D, batch_size, use_mvcnn)
total_ValidLoss += criterion(output, label)
```
# Models
## Base Mode - CNN_1
```
class VGG(nn.Module):
def __init__(self):
super(VGG,self).__init__()
pad = 1
self.cnn = nn.Sequential(nn.BatchNorm2d(1),
nn.Conv2d(1,32,3,padding=pad),
nn.ReLU(),
nn.BatchNorm2d(32),
nn.Conv2d(32,32,3,padding=pad),
nn.ReLU(),
nn.MaxPool2d(2,2),
nn.BatchNorm2d(32),
nn.Conv2d(32,64,3,padding=pad),
nn.ReLU(),
nn.BatchNorm2d(64),
nn.Conv2d(64,64,3,padding=pad),
nn.ReLU(),
nn.MaxPool2d(2,2),
nn.BatchNorm2d(64),
nn.Conv2d(64,128,3,padding=pad),
nn.ReLU(),
nn.BatchNorm2d(128),
nn.Conv2d(128,128,3,padding=pad),
nn.ReLU(),
nn.MaxPool2d(2,2),
nn.BatchNorm2d(128),
nn.Conv2d(128,256,3,padding=pad),
nn.ReLU(),
nn.BatchNorm2d(256),
nn.Conv2d(256,256,3,padding=pad),
nn.ReLU(),
nn.MaxPool2d(2,2),
nn.BatchNorm2d(256),
nn.Conv2d(256,256,3,padding=pad),
nn.ReLU(),
nn.BatchNorm2d(256),
nn.Conv2d(256,256,3,padding=pad),
nn.ReLU(),
nn.MaxPool2d(2,2),
nn.BatchNorm2d(256),
nn.Conv2d(256,512,3,padding=pad),
nn.ReLU(),
nn.BatchNorm2d(512),
nn.Conv2d(512,512,3,padding=pad),
nn.ReLU(),
nn.MaxPool2d(2,2))
self.fc1 = nn.Sequential(nn.Linear(8192, 1096),
nn.ReLU(),
nn.Dropout(0.8),
nn.Linear(1096, 96),
nn.ReLU(),
nn.Dropout(0.9),
nn.Linear(96, 1))
# self.fc2 = nn.Sequential(nn.Linear(8192, 4096),
# nn.ReLU(),
# nn.Dropout(0.8),
# nn.Linear(4096, 4096),
# nn.ReLU(),
# nn.Dropout(0.9),
# nn.Linear(4096, 1))
def forward(self, x, batch_size=1, mvcnn=False):
if mvcnn:
view_pool = []
# Assuming x has shape (x, 1, 299, 299)
for n, v in enumerate(x):
v = v.unsqueeze(0)
v = self.cnn(v)
v = v.view(v.size(0), 512 * 4 * 4)
view_pool.append(v)
pooled_view = view_pool[0]
for i in range(1, len(view_pool)):
pooled_view = torch.max(pooled_view, view_pool[i])
output = self.fc1(pooled_view)
else:
x = self.cnn(x)
x = x.view(-1, 512 * 4* 4)
x = self.fc1(x)
output = F.sigmoid(x)
return output
device = torch.device("cuda" if torch.cuda.is_available() else "cpu") # PyTorch v0.4.0
model = VGG().to(device)
summary(model, (1, 299, 299))
```
Since patients have varying images, create single images where the channels occupy the slices of the patient
```
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
mvcnn = MVCNN().to(device)
criterion = nn.MSELoss()
optimizer = optim.Adam(mvcnn.parameters(), lr=0.0003)
file_path = '/home/alex/Dataset 1/Dataset - 1.xlsx'
df = pd.read_excel(file_path, sheet_name='Feuil1')
edss = df['EDSS'].tolist()
p_id = df['Sequence_id'].tolist()
channels = 1
resize = 299
normalization = 'min-max'
patient_information = [(p_id[i], edss[i]) for i in range(df.shape[0])]
train_patient_information = patient_information[:int(0.9*len(patient_information))]
valid_patient_information = patient_information[int(0.9*len(patient_information)):]
base_DatabasePath = '/home/alex/Dataset 1'
generator_inst = generators.SEPGenerator(base_DatabasePath,
channels=channels,
resize=resize,
normalization=normalization)
train_generator = generator_inst.generator(train_patient_information)
valid_generator = generator_inst.generator(valid_patient_information)
#dataloader = torch.utils.data.DataLoader(train_generator, batch_size=1, shuffle=True)
valid_iterations
total_loss = 0
train_iterations = 100
valid_iterations = len(valid_patient_information)
epochs = 5
for epoch in range(epochs):
total_TrainLoss = 0
for t_m, t_item in enumerate(train_generator):
image_3D, label = torch.tensor(t_item[0], device=device).float(), torch.tensor(t_item[1], device=device).float()
output = mvcnn(image_3D, 1)
loss = criterion(output, label)
loss.backward()
optimizer.step()
total_TrainLoss += loss
if not (t_m+1)%50:
print("On_Going_Epoch : {} \t | Iteration : {} \t | Training Loss : {}".format(epoch+1, t_m+1, total_TrainLoss/(t_m+1)))
if (t_m+1) == train_iterations:
total_ValidLoss = 0
with torch.no_grad():
for v_m, v_item in enumerate(valid_generator):
image_3D, label = torch.tensor(v_item[0], device=device).float(), torch.tensor(v_item[1], device=device).float()
output = mvcnn(image_3D, 1)
total_ValidLoss += criterion(output, label)
print(total_ValidLoss)
if (v_m + 1) == valid_iterations:
break
print("Epoch : {} \t | Training Loss : {} \t | Validation Loss : {} ".format(epoch+1, total_TrainLoss/(t_m+1), total_ValidLoss/(v_m+1)) )
torch.save(mvcnn, './' + 'vgg_' + str(epoch) + '.pkl')
break
total_ValidLoss
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
c = torch.randn(90, 512, 4, 4).to(device)
#torch.randn(90, 1, 299, 299)
for n,v in enumerate(c):
v = v.view(1, 512*4*4).to(device)
print(n)
if n:
pooled_view = torch.max(pooled_view, v).to(device)
else:
pooled_view = v.to(device)
```
# Augmenter
```
def generate_images(image, transformation='original', angle=30):
"""
Function to generate images based on the requested transfomations
Args:
- image (nd.array) : input image array
- transformation (str) : image transformation to be effectuated
- angle (int) : rotation angle if transformation is a rotation
Returns:
- trans_image (nd.array) : transformed image array
"""
def rotateImage(image, angle):
"""
Function to rotate an image at its center
"""
image_center = tuple(np.array(image.shape[1::-1]) / 2)
rot_mat = cv2.getRotationMatrix2D(image_center, angle, 1.0)
result = cv2.warpAffine(image, rot_mat, image.shape[1::-1], flags=cv2.INTER_LINEAR)
return result
# Image transformations
if transformation == 'original':
trans_image = image
elif transformation == 'flip_v':
trans_image = cv2.flip(image, 0)
elif transformation == 'flip_h':
trans_image = cv2.flip(image, 1)
elif transformation == 'flip_vh':
trans_image = cv2.flip(image, -1)
elif transformation == 'rot_c':
trans_image = rotateImage(image, -angle)
elif transformation == 'rot_ac':
trans_image = rotateImage(image, angle)
else:
raise ValueError("In valid transformation value passed : {}".format(transformation))
return trans_image
"""
The agumenter ought to be able to do the following:
- Get list of patient paths and their respective scores (make sure to do the validation and test splits before)
- Select a random augmentation (flag='test')
- Select a patient path and his/her corresponding score
- With each .dcm file do following:
- read image
- normalized image
- resize image
- get percentage of white matter (%, n) and append to list
- transform image
- store in an array
- yield image_3D (top 70 images with white matter), label
"""
def SEP_generator(object):
def __init__(self,
resize,
normalization,
transformations)
import imgaug as ia
from imgaug import augmenters as iaa
import imgaug as ia
from imgaug import augmenters as iaa
class ImageBaseAug(object):
def __init__(self):
sometimes = lambda aug: iaa.Sometimes(0.5, aug)
self.seq = iaa.Sequential(
[
# Blur each image with varying strength using
# gaussian blur (sigma between 0 and 3.0),
# average/uniform blur (kernel size between 2x2 and 7x7)
# median blur (kernel size between 3x3 and 11x11).
iaa.OneOf([
iaa.GaussianBlur((0, 3.0)),
iaa.AverageBlur(k=(2, 7)),
iaa.MedianBlur(k=(3, 11)),
]),
# Sharpen each image, overlay the result with the original
# image using an alpha between 0 (no sharpening) and 1
# (full sharpening effect).
sometimes(iaa.Sharpen(alpha=(0, 0.5), lightness=(0.75, 1.5))),
# Add gaussian noise to some images.
sometimes(iaa.AdditiveGaussianNoise(loc=0, scale=(0.0, 0.05*255), per_channel=0.5)),
# Add a value of -5 to 5 to each pixel.
sometimes(iaa.Add((-5, 5), per_channel=0.5)),
# Change brightness of images (80-120% of original value).
sometimes(iaa.Multiply((0.8, 1.2), per_channel=0.5)),
# Improve or worsen the contrast of images.
sometimes(iaa.ContrastNormalization((0.5, 2.0), per_channel=0.5)),
],
# do all of the above augmentations in random order
random_order=True
)
def __call__(self, sample):
seq_det = self.seq.to_deterministic()
image, label = sample['image'], sample['label']
image = seq_det.augment_images([image])[0]
return {'image': image, 'label': label}
```
# UNET
```
def double_conv(in_channels, out_channels):
return nn.Sequential(
nn.Conv2d(in_channels, out_channels, 3, padding=1),
nn.ReLU(inplace=True),
nn.Conv2d(out_channels, out_channels, 3, padding=1),
nn.ReLU(inplace=True)
)
class UNet(nn.Module):
def __init__(self, n_class=1):
super().__init__()
self.dconv_down1 = double_conv(1, 32)
self.dconv_down2 = double_conv(32, 64)
self.dconv_down3 = double_conv(64, 128)
self.dconv_down4 = double_conv(128, 256)
self.maxpool = nn.MaxPool2d(2)
self.upsample = nn.Upsample(scale_factor=2, mode='bilinear', align_corners=True)
self.dconv_up3 = double_conv(128 + 256, 128)
self.dconv_up2 = double_conv(64 + 128, 64)
self.dconv_up1 = double_conv(32 + 64, 32)
self.conv_last = nn.Sequential(nn.BatchNorm2d(32),
nn.MaxPool2d(2,2))
def forward(self, x):
conv1 = self.dconv_down1(x)
x = self.maxpool(conv1)
conv2 = self.dconv_down2(x)
x = self.maxpool(conv2)
conv3 = self.dconv_down3(x)
x = self.maxpool(conv3)
x = self.dconv_down4(x)
x = self.upsample(x)
x = torch.cat([x, conv3], dim=1)
x = self.dconv_up3(x)
x = self.upsample(x)
x = torch.cat([x, conv2], dim=1)
x = self.dconv_up2(x)
x = self.upsample(x)
x = torch.cat([x, conv1], dim=1)
x = self.dconv_up1(x)
out = self.conv_last(x)
return out
import torch
import torch.nn as nn
def attention_block():
return nn.Sequential(
nn.ReLU(),
nn.Conv2d(1, 1, 1, padding=0),
nn.BatchNorm2d(1),
nn.Sigmoid()
)
def double_conv(in_channels, out_channels):
return nn.Sequential(
nn.BatchNorm2d(in_channels),
nn.Conv2d(in_channels, out_channels, 3, padding=1),
nn.ReLU(inplace=True),
nn.BatchNorm2d(out_channels),
nn.Conv2d(out_channels, out_channels, 3, padding=1),
nn.ReLU(inplace=True))
def one_conv(in_channels, padding=0):
return nn.Sequential(
nn.BatchNorm2d(in_channels),
nn.Conv2d(in_channels, 1, 1, padding=padding))
class UNet(nn.Module):
def __init__(self, n_class):
super().__init__()
self.dconv_down1 = double_conv(1, 32)
self.dconv_down2 = double_conv(32, 64)
self.dconv_down3 = double_conv(64, 128)
self.dconv_down4 = double_conv(128, 256)
self.maxpool = nn.MaxPool2d(2)
self.upsample = nn.Upsample(scale_factor=2, mode='bilinear', align_corners=True)
self.oneconv = one_conv
self.attention = attention_block()
self.oneconvx3 = one_conv(128)
self.oneconvg3 = one_conv(256)
self.dconv_up3 = double_conv(128 + 256, 128)
self.oneconvx2 = one_conv(64)
self.oneconvg2 = one_conv(128)
self.dconv_up2 = double_conv(64 + 128, 64)
self.conv_last = nn.Sequential(nn.BatchNorm2d(64),
nn.Conv2d(64,32,3,padding=0),
nn.ReLU(),
nn.MaxPool2d(2,2),
nn.BatchNorm2d(32),
nn.Conv2d(32,8,3,padding=0),
nn.ReLU(),
nn.MaxPool2d(2,2))
self.fc1 = nn.Sequential(nn.Linear(9800, 1096),
nn.ReLU(),
nn.Dropout(0.8),
nn.Linear(1096, 96),
nn.ReLU(),
nn.Dropout(0.9),
nn.Linear(96, 1))
def forward(self, x):
conv1 = self.dconv_down1(x) # 1 -> 32 filters
x = self.maxpool(conv1)
conv2 = self.dconv_down2(x) # 32 -> 64 filters
x = self.maxpool(conv2)
conv3 = self.dconv_down3(x) # 64 -> 128 filters
x = self.maxpool(conv3)
x = self.dconv_down4(x) # 128 -> 256 filters
x = self.upsample(x)
_g = self.oneconvg3(x)
_x = self.oneconvx3(conv3)
_xg = _g + _x
psi = self.attention(_xg)
conv3 = conv3*psi
x = torch.cat([x, conv3], dim=1)
x = self.dconv_up3(x) # 128 + 256 -> 128 filters
x = self.upsample(x)
_g = self.oneconvg2(x)
_x = self.oneconvx2(conv2)
_xg = _g + _x
psi = self.attention(_xg)
conv2 = conv2*psi
x = torch.cat([x, conv2], dim=1)
x = self.dconv_up2(x)
# x = self.upsample(x)
# _g = self.oneconvg1(x)
# _x = self.oneconvx1(conv1)
# _xg = _g + _x
# psi = self.attention(_xg)
# conv1 = conv1*psi
# x = torch.cat([x, conv1], dim=1)
# x = self.dconv_up1(x)
x = self.conv_last(x)
x = x.view(-1, 35*35*8)
x = self.fc1(x)
return x
net = UNet(1)
device = torch.device("cuda" if torch.cuda.is_available() else "cpu") # PyTorch v0.4.0
model = UNet(1).to(device)
summary(model, (1, 296, 296))
transform = transforms.Compose(
[transforms.ToTensor(),
transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))])
trainset = torchvision.datasets.CIFAR10(root='./data', train=True,
download=True, transform=transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=4,
shuffle=True, num_workers=2)
testset = torchvision.datasets.CIFAR10(root='./data', train=False,
download=True, transform=transform)
testloader = torch.utils.data.DataLoader(testset, batch_size=4,
shuffle=False, num_workers=2)
```
# Trails (Pytorch)
```
import os
import torch
import numpy as np
os.environ['CUDA_VISIBLE_DEVICES'] = "2"
## TENSORS
# create an 'un-initialized' matrix
x = torch.empty(5, 3)
print(x)
# construct a randomly 'initialized' matrix
x = torch.rand(5, 3)
print(x)
# construct a matrix filled with zeros an dtype=long
x = torch.zeros(5, 3, dtype=torch.long)
print(x)
# construct a tensor from data
x = torch.tensor([[5.5, 3]])
print(x)
# Create a tensor based on existing tensor
x = x.new_ones(5, 3, dtype=torch.double)
print(x)
x = torch.randn_like(x, dtype=torch.float)
print(x)
## OPERATIONS
# Addition syntax 1
y = torch.rand(5, 3)
print(x + y)
# Addition syntax 2
print(torch.add(x, y))
# Addtion output towards a tensor
result = torch.empty(5,3)
torch.add(x, y, out=result)
print(result)
# Addition in place
y.add(x)
print(y)
# Any operation that mutates a tensor in-place is post-fixed with an _.
x.copy_(y)
x.t_()
# Resizing tensors
x = torch.randn(4, 4)
y = x.view(16)
z = x.view(-1,8)
print(x.size(), y.size(), z.size())
# Use get value off a one element tensor
x = torch.randn(1)
print(x)
print(x.item())
## NUMPY BRIDGE
# Torch tensor to numpy array
a = torch.ones(5)
b = a.numpy()
print(a)
print(b)
a.add_(1)
print(a)
print(b)
# Numpy array to torch tensor
a = np.ones(5)
b = torch.from_numpy(a)
np.add(a, 1, out=a)
print(a)
print(b)
## USING CUDA
if torch.cuda.is_available():
device = torch.device("cuda") # Cuda device object
y = torch.ones_like(x, device=device) # Directly creates a tensor on GPU
x = x.to(device) #
z = x + y
print(z)
print(z.to("cpu", torch.double))
"""
AUTO-GRAD
- The autograd package provides automatic differntation for all
opeations on tensors.
- A define-by-run framework i.e backprop defined by how code
is run and every single iteration can be different.
TENSOR
- torch.tensor is the central class of the 'torch' package.
- If one sets attribute '.requires_grad()' as 'True', all
operations on it are tracked.
- When computations are finished one can call'backward()'
and have all the gradients computed.
- Gradient of a tensor is accumulated into '.grad' attribute.
- To stop tensor from tracking history, call '.detach()' to detach
it from computation history and prevent future computation
from being tracked
- To prevent tacking histroy and using memory, wrap the code
block in 'with torch.no_grad()'. Helpful when evaluating a model
cause model has trainable parameters with 'requires_grad=True'
- 'Function' class is very important for autograd implementation
- 'Tensor' and 'Function' are interconnected and buid up an acyclic
graph that encodes a complete history of computation.
- Each tensor has a '.grad_fn' attribute that references a 'Function'
that has created the 'Tensor' (except for tensors created by user)
- To compute derivates, '.backward()' is called on a Tensor. If
tensor is a scalar, no arguments ought to be passed to '.backward()'
if not, a 'gradient' argument ought to be specified.
"""
## TENSORS
# Create tenor to track all operations
x = torch.ones(2,2, requires_grad=True)
print(x)
y = x + 2
print(y)
z = y * y * 3
out = z.mean()
print(z, out)
## GRADIENTS
# Peforming backprop on 'out'
out.backward()
print(x.grad)
# An example of vector-Jacobian product
x = torch.randn(3, requires_grad=True)
y = x * 2
while y.data.norm() < 1000:
y = y * 2
print(y)
v = torch.tensor([0.1, 1.0, 0.0001], dtype=torch.float)
y.backward(v)
print(x.grad)
# Stop autograd from tracking history on Tensors
# with .requires_grad=True
print(x.requires_grad)
print((x ** 2).requires_grad)
with torch.no_grad():
print((x**2).requires_grad)
image.requires_grad_(True)
image
"""
## NEURAL NETWORKS
- Can be constructed using 'torch.nn' package
- 'nn' depends on 'autograd' to define models and differentiate
them.
- 'nn.Module' contains layers and a method forward(input) that
returns the 'output'.
- Training procedure:
- Define neural network that has some learnable parameter
- Iterate over a dataset of inputs
- Process input through the network
- Compute loss
- Propagate gradients back into the network's parameters
- Update weights
"""
import torch.nn as nn
import torch.nn.functional as F
class Net(nn.Module):
def __init__(self):
super().__init__()
# Convolutional Layers
self.conv1 = nn.Conv2d(1, 6, 3)
self.conv2 = nn.Conv2d(6, 16, 3)
# An affine operation
self.fc1 = nn.Linear(16*6*6, 128)
self.fc2 = nn.Linear(128, 84)
self.fc3 = nn.Linear(84, 10)
def forward(self, x):
x = F.max_pool2d(F.relu(self.conv1(x)), (2, 2))
x = F.max_pool2d(F.relu(self.conv2(x)), 2)
x = x.view(-1, self.num_flat_features(x))
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = self.fc3(x)
return x
def num_flat_features(self, x):
size = x.size()[1:]
num_features = 1
for s in size:
num_features *= s
return num_features
net = Net()
print(net)
```
|
github_jupyter
|
Corrigir versao de scipy para Inception
```
pip install scipy==1.3.3
```
Importar bibliotecas
```
from __future__ import division, print_function
from torchvision import datasets, models, transforms
import copy
import matplotlib.pyplot as plt
import numpy as np
import os
import shutil
import time
import torch
import torch.nn as nn
import torch.optim as optim
import torchvision
import zipfile
```
Montar Google Drive
```
from google.colab import drive
drive.mount('/content/drive')
```
Definir constantes
```
DEVICE = torch.device('cuda:0' if torch.cuda.is_available() else 'cpu')
ZIP_FILE_PATH = './dataset.zip'
DATASET_PATH = './dataset'
INCEPTION = 'inception'
VGG19 = 'vgg-19'
MODEL = INCEPTION # Define o tipo de modelo a ser usado.
IMG_SIZE = {
INCEPTION: 299,
VGG19: 224,
}[MODEL]
NORMALIZE_MEAN = [0.485, 0.456, 0.406]
NORMALIZE_STD = [0.229, 0.224, 0.225]
BATCH_SIZE = 4
NUM_WORKERS = 4
TRAIN = 'train'
VAL = 'val'
TEST = 'test'
PHASES = {
TRAIN: 'train',
VAL: 'val',
TEST: 'test',
}
print(DEVICE)
```
Limpar diretorio do dataset
```
shutil.rmtree(DATASET_PATH)
```
Extrair dataset
```
zip_file = zipfile.ZipFile(ZIP_FILE_PATH)
zip_file.extractall()
zip_file.close()
```
Carregar dataset
```
# Augmentacao de dados para treinamento,
# apenas normalizacao para validacao e teste.
data_transforms = {
TRAIN: transforms.Compose([
transforms.Resize(IMG_SIZE),
transforms.RandomHorizontalFlip(),
transforms.RandomRotation(15),
transforms.ToTensor(),
transforms.Normalize(NORMALIZE_MEAN, NORMALIZE_STD),
]),
VAL: transforms.Compose([
transforms.Resize(IMG_SIZE),
transforms.ToTensor(),
transforms.Normalize(NORMALIZE_MEAN, NORMALIZE_STD),
]),
TEST: transforms.Compose([
transforms.Resize(IMG_SIZE),
transforms.ToTensor(),
transforms.Normalize(NORMALIZE_MEAN, NORMALIZE_STD),
]),
}
data_sets = {
phase: datasets.ImageFolder(
os.path.join(DATASET_PATH, PHASES[phase]),
data_transforms[phase],
) for phase in PHASES
}
data_loaders = {
phase: torch.utils.data.DataLoader(
data_sets[phase],
batch_size = BATCH_SIZE,
shuffle = True,
num_workers = NUM_WORKERS,
) for phase in PHASES
}
data_sizes = {
phase: len(data_sets[phase]) for phase in PHASES
}
class_names = data_sets[TRAIN].classes
print(data_sets)
print(data_loaders)
print(data_sizes)
print(class_names)
```
Helper functions
```
# Exibe uma imagem a partir de um Tensor.
def imshow(data):
mean = np.array(NORMALIZE_MEAN)
std = np.array(NORMALIZE_STD)
image = data.numpy().transpose((1, 2, 0))
image = std * image + mean
image = np.clip(image, 0, 1)
plt.imshow(image)
# Treina o modelo e retorna o modelo treinado.
def train_model(model_type, model, optimizer, criterion, num_epochs = 25):
start_time = time.time()
num_epochs_without_improvement = 0
best_acc = 0.0
best_model = copy.deepcopy(model.state_dict())
torch.save(best_model, 'model.pth')
for epoch in range(num_epochs):
print('Epoch {}/{} ...'.format(epoch + 1, num_epochs))
for phase in PHASES:
if phase == TRAIN:
model.train()
elif phase == VAL:
model.eval()
else:
continue
running_loss = 0.0
running_corrects = 0
for data, labels in data_loaders[phase]:
data = data.to(DEVICE)
labels = labels.to(DEVICE)
optimizer.zero_grad()
with torch.set_grad_enabled(phase == TRAIN):
outputs = model(data)
if phase == TRAIN and model_type == INCEPTION:
outputs = outputs.logits
_, preds = torch.max(outputs, 1)
loss = criterion(outputs, labels)
if phase == TRAIN:
loss.backward()
optimizer.step()
running_loss += loss.item() * data.size(0)
running_corrects += torch.sum(preds == labels.data)
epoch_loss = running_loss / data_sizes[phase]
epoch_acc = running_corrects.double() / data_sizes[phase]
print('{} => Loss: {:.4f}, Acc: {:.4f}'.format(phase, epoch_loss, epoch_acc))
if phase == VAL:
if epoch_acc > best_acc:
num_epochs_without_improvement = 0
best_acc = epoch_acc
best_model = copy.deepcopy(model.state_dict())
torch.save(best_model, 'model.pth')
else:
num_epochs_without_improvement += 1
if num_epochs_without_improvement == 50:
print('Exiting early...')
break
elapsed_time = time.time() - start_time
print('Took {:.0f}m {:.0f}s'.format(elapsed_time // 60, elapsed_time % 60))
print('Best Acc: {:4f}'.format(best_acc))
model.load_state_dict(best_model)
return model
# Visualiza algumas predicoes do modelo.
def visualize_model(model, num_images = 6):
was_training = model.training
model.eval()
fig = plt.figure()
images_so_far = 0
with torch.no_grad():
for i, (data, labels) in enumerate(data_loaders[TEST]):
data = data.to(DEVICE)
labels = labels.to(DEVICE)
outputs = model(data)
_, preds = torch.max(outputs, 1)
for j in range(data.size()[0]):
images_so_far += 1
ax = plt.subplot(num_images // 2, 2, images_so_far)
ax.axis('off')
ax.set_title('Predicted: {}'.format(class_names[preds[j]]))
imshow(data.cpu().data[j])
if images_so_far == num_images:
model.train(mode = was_training)
return
model.train(mode = was_training)
# Testa o modelo.
def test_model(model, criterion):
was_training = model.training
model.eval()
running_loss = 0.0
running_corrects = 0
with torch.no_grad():
for data, labels in data_loaders[TEST]:
data = data.to(DEVICE)
labels = labels.to(DEVICE)
outputs = model(data)
_, preds = torch.max(outputs, 1)
loss = criterion(outputs, labels)
running_loss += loss.item() * data.size(0)
running_corrects += torch.sum(preds == labels.data)
loss = running_loss / data_sizes[TEST]
acc = running_corrects.double() / data_sizes[TEST]
print('Loss: {:4f}, Acc: {:4f}'.format(loss, acc))
model.train(mode = was_training)
```
Exibir amostra do dataset
```
data, labels = next(iter(data_loaders[TRAIN]))
grid = torchvision.utils.make_grid(data)
imshow(grid)
```
Definir modelo
```
if MODEL == INCEPTION:
model = models.inception_v3(pretrained = True, progress = True)
print(model.fc)
for param in model.parameters():
param.requires_grad = False
num_features = model.fc.in_features
model.fc = nn.Linear(num_features, len(class_names))
model = model.to(DEVICE)
optimizer = optim.SGD(model.fc.parameters(), lr = 0.001, momentum = 0.9)
elif MODEL == VGG19:
model = models.vgg19(pretrained = True, progress = True)
print(model.classifier[6])
for param in model.parameters():
param.requires_grad = False
num_features = model.classifier[6].in_features
model.classifier[6] = nn.Linear(num_features, len(class_names))
model = model.to(DEVICE)
optimizer = optim.SGD(model.classifier[6].parameters(), lr = 0.001, momentum = 0.9)
else:
print('ERRO: Nenhum tipo de modelo definido!')
criterion = nn.CrossEntropyLoss()
print(model)
```
Treinar modelo
```
model = train_model(MODEL, model, optimizer, criterion)
```
Visualizar modelo
```
visualize_model(model)
```
Testar modelo
```
model.load_state_dict(torch.load('model.pth'))
test_model(model, criterion)
```
Salvar modelo para CPU
```
model = model.cpu()
torch.save(model.state_dict(), 'model-cpu.pth')
```
Salvar no Google Drive
```
torch.save(model.state_dict(), '/content/drive/My Drive/model-inception.pth')
```
|
github_jupyter
|
<a href="https://colab.research.google.com/github/flych3r/IA025_2022S1/blob/main/ex04/matheus_xavier/IA025_A04.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Regressão Softmax com dados do MNIST utilizando gradiente descendente estocástico por minibatches
Este exercicío consiste em treinar um modelo de uma única camada linear no MNIST **sem** usar as seguintes funções do pytorch:
- torch.nn.Linear
- torch.nn.CrossEntropyLoss
- torch.nn.NLLLoss
- torch.nn.LogSoftmax
- torch.optim.SGD
- torch.utils.data.Dataloader
## Importação das bibliotecas
```
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
import random
import torch
import torchvision
from torchvision.datasets import MNIST
```
## Fixando as seeds
```
random.seed(123)
np.random.seed(123)
torch.manual_seed(123)
```
## Dataset e dataloader
### Definição do tamanho do minibatch
```
batch_size = 50
```
### Carregamento, criação dataset e do dataloader
```
dataset_dir = '../data/'
dataset_train_full = MNIST(
dataset_dir, train=True, download=True,
transform=torchvision.transforms.ToTensor()
)
print(dataset_train_full.data.shape)
print(dataset_train_full.targets.shape)
```
### Usando apenas 1000 amostras do MNIST
Neste exercício utilizaremos 1000 amostras de treinamento.
```
indices = torch.randperm(len(dataset_train_full))[:1000]
dataset_train = torch.utils.data.Subset(dataset_train_full, indices)
# Escreva aqui o equivalente do código abaixo:
# loader_train = torch.utils.data.DataLoader(dataset_train, batch_size=batch_size, shuffle=False)
import math
class DataLoader:
def __init__(self, dataset: torch.utils.data.Dataset, batch_size: int = 1, shuffle: bool = True):
self.dataset = dataset
self.batch_size = batch_size
self.shuffle = shuffle
self.idx = 0
self.indexes = np.arange(len(dataset))
self._size = math.ceil(len(dataset) / self.batch_size)
def __iter__(self):
self.idx = 0
return self
def __next__(self):
if self.idx < len(self):
if self.idx == 0 and self.shuffle:
np.random.shuffle(self.indexes)
batch = self.indexes[self.idx * self.batch_size: (self.idx + 1) * self.batch_size]
self.idx += 1
x_batch, y_batch = [], []
for b in batch:
x, y = self.dataset[b]
x_batch.append(x)
y_batch.append(y)
return torch.stack(x_batch), torch.tensor(y_batch)
raise StopIteration
def __len__(self):
return self._size
loader_train = DataLoader(dataset_train, batch_size=batch_size, shuffle=False)
print('Número de minibatches de trenamento:', len(loader_train))
x_train, y_train = next(iter(loader_train))
print("\nDimensões dos dados de um minibatch:", x_train.size())
print("Valores mínimo e máximo dos pixels: ", torch.min(x_train), torch.max(x_train))
print("Tipo dos dados das imagens: ", type(x_train))
print("Tipo das classes das imagens: ", type(y_train))
```
## Modelo
```
# Escreva aqui o codigo para criar um modelo cujo o equivalente é:
# model = torch.nn.Linear(28*28, 10)
# model.load_state_dict(dict(weight=torch.zeros(model.weight.shape), bias=torch.zeros(model.bias.shape)))
class Model:
def __init__(self, in_features: int, out_features: int):
self.weight = torch.zeros(out_features, in_features, requires_grad=True)
self.bias = torch.zeros(out_features, requires_grad=True)
def __call__(self, x: torch.Tensor) -> torch.Tensor:
y_pred = x.mm(torch.t(self.weight)) + self.bias.unsqueeze(0)
return y_pred
def parameters(self):
return self.weight, self.bias
model = Model(28*28, 10)
```
## Treinamento
### Inicialização dos parâmetros
```
n_epochs = 50
lr = 0.1
```
## Definição da Loss
```
# Escreva aqui o equivalente de:
# criterion = torch.nn.CrossEntropyLoss()
class CrossEntropyLoss:
def __init__(self):
self.loss = 0
def __call__(self, inputs: torch.Tensor, targets: torch.Tensor):
log_sum_exp = torch.log(torch.sum(torch.exp(inputs), dim=1, keepdim=True))
logits = inputs.gather(dim=1, index=targets.unsqueeze(dim=1))
return torch.mean(-logits + log_sum_exp)
criterion = CrossEntropyLoss()
```
# Definição do Optimizer
```
# Escreva aqui o equivalente de:
# optimizer = torch.optim.SGD(model.parameters(), lr)
from typing import Iterable
class SGD:
def __init__(self, parameters: Iterable[torch.Tensor], learning_rate: float):
self.parameters = parameters
self.learning_rate = learning_rate
def step(self):
for p in self.parameters:
p.data -= self.learning_rate * p.grad
def zero_grad(self):
for p in self.parameters:
p.grad = torch.zeros_like(p.data)
optimizer = SGD(model.parameters(), lr)
```
### Laço de treinamento dos parâmetros
```
epochs = []
loss_history = []
loss_epoch_end = []
total_trained_samples = 0
for i in range(n_epochs):
# Substitua aqui o loader_train de acordo com sua implementação do dataloader.
for x_train, y_train in loader_train:
# Transforma a entrada para uma dimensão
inputs = x_train.view(-1, 28 * 28)
# predict da rede
outputs = model(inputs)
# calcula a perda
loss = criterion(outputs, y_train)
# zero, backpropagation, ajusta parâmetros pelo gradiente descendente
# Escreva aqui o código cujo o resultado é equivalente às 3 linhas abaixo:
optimizer.zero_grad()
loss.backward()
optimizer.step()
total_trained_samples += x_train.size(0)
epochs.append(total_trained_samples / len(dataset_train))
loss_history.append(loss.item())
loss_epoch_end.append(loss.item())
print(f'Epoch: {i:d}/{n_epochs - 1:d} Loss: {loss.item()}')
```
### Visualizando gráfico de perda durante o treinamento
```
plt.plot(epochs, loss_history)
plt.xlabel('época')
```
### Visualização usual da perda, somente no final de cada minibatch
```
n_batches_train = len(loader_train)
plt.plot(epochs[::n_batches_train], loss_history[::n_batches_train])
plt.xlabel('época')
# Assert do histórico de losses
target_loss_epoch_end = np.array([
1.1979684829711914,
0.867622971534729,
0.7226786613464355,
0.6381281018257141,
0.5809749960899353,
0.5387411713600159,
0.5056464076042175,
0.4786270558834076,
0.4558936357498169,
0.4363219141960144,
0.4191650450229645,
0.4039044976234436,
0.3901679515838623,
0.3776799440383911,
0.3662314713001251,
0.35566139221191406,
0.34584277868270874,
0.33667415380477905,
0.32807353138923645,
0.31997355818748474,
0.312318354845047,
0.3050611615180969,
0.29816246032714844,
0.29158851504325867,
0.28531041741371155,
0.2793029546737671,
0.273544579744339,
0.2680158317089081,
0.26270008087158203,
0.2575823664665222,
0.25264936685562134,
0.24788929522037506,
0.24329163134098053,
0.23884665966033936,
0.23454584181308746,
0.23038141429424286,
0.22634628415107727,
0.22243399918079376,
0.2186385989189148,
0.21495483815670013,
0.21137762069702148,
0.20790249109268188,
0.20452524721622467,
0.20124195516109467,
0.19804897904396057,
0.1949428766965866,
0.19192075729370117,
0.188979372382164,
0.18611609935760498,
0.1833282858133316])
assert np.allclose(np.array(loss_epoch_end), target_loss_epoch_end, atol=1e-6)
```
## Exercício
Escreva um código que responda às seguintes perguntas:
Qual é a amostra classificada corretamente, com maior probabilidade?
Qual é a amostra classificada erradamente, com maior probabilidade?
Qual é a amostra classificada corretamente, com menor probabilidade?
Qual é a amostra classificada erradamente, com menor probabilidade?
```
# Escreva o código aqui:
loader_eval = DataLoader(dataset_train, batch_size=len(dataset_train), shuffle=False)
x, y = next(loader_eval)
logits = model(x.view(-1, 28 * 28))
exp_logits = torch.exp(logits)
sum_exp_logits = torch.sum(exp_logits, dim=1, keepdim=True)
softmax = (exp_logits / sum_exp_logits).detach()
y_pred = torch.argmax(softmax, dim=1)
y_proba = softmax.gather(-1, y_pred.view(-1, 1)).ravel()
corret_preditions = (y == y_pred)
wrong_predictions = (y != y_pred)
def plot_image_and_proba(images, probas, idx, title):
plt.figure(figsize=(16, 8))
x_labels = list(range(10))
plt.subplot(121)
plt.imshow(images[idx][0])
plt.subplot(122)
plt.bar(x_labels, probas[idx])
plt.xticks(x_labels)
plt.suptitle(title)
plt.show()
# Qual é a amostra classificada corretamente, com maior probabilidade?
mask = corret_preditions
idx = torch.argmax(y_proba[mask])
title = 'Predita: {} | Probabilidate: {:.4f} | Correta: {}'.format(
y_pred[mask][idx],
y_proba[mask][idx],
y[mask][idx],
)
plot_image_and_proba(x[mask], softmax[mask], idx, title)
# Qual é a amostra classificada erradamente, com maior probabilidade?
mask = wrong_predictions
idx = torch.argmax(y_proba[mask])
title = 'Predita: {} | Probabilidate: {:.4f} | Correta: {}'.format(
y_pred[mask][idx],
y_proba[mask][idx],
y[mask][idx],
)
plot_image_and_proba(x[mask], softmax[mask], idx, title)
# Qual é a amostra classificada corretamente, com menor probabilidade?
mask = corret_preditions
idx = torch.argmin(y_proba[mask])
title = 'Predita: {} | Probabilidate: {:.4f} | Correta: {}'.format(
y_pred[mask][idx],
y_proba[mask][idx],
y[mask][idx],
)
plot_image_and_proba(x[mask], softmax[mask], idx, title)
# Qual é a amostra classificada erradamente, com menor probabilidade?
mask = wrong_predictions
idx = torch.argmin(y_proba[mask])
title = 'Predita: {} | Probabilidate: {:.4f} | Correta: {}'.format(
y_pred[mask][idx],
y_proba[mask][idx],
y[mask][idx],
)
plot_image_and_proba(x[mask], softmax[mask], idx, title)
```
## Exercício Bonus
Implemente um dataloader que aceite como parâmetro de entrada a distribuição probabilidade das classes que deverão compor um batch.
Por exemplo, se a distribuição de probabilidade passada como entrada for:
`[0.01, 0.01, 0.72, 0.2, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01]`
Em média, 72% dos exemplos do batch deverão ser da classe 2, 20% deverão ser da classe 3, e os demais deverão ser das outras classes.
Mostre também que sua implementação está correta.
|
github_jupyter
|
# Science User Case - Inspecting a Candidate List
Ogle et al. (2016) mined the NASA/IPAC Extragalactic Database (NED) to identify a new type of galaxy: Superluminous Spiral Galaxies. Here's the paper:
Here's the paper: https://ui.adsabs.harvard.edu//#abs/2016ApJ...817..109O/abstract
Table 1 lists the positions of these Super Spirals. Based on those positions, let's create multiwavelength cutouts for each super spiral to see what is unique about this new class of objects.
## 1. Import the Python modules we'll be using.
```
# Suppress unimportant warnings.
import warnings
warnings.filterwarnings("ignore", module="astropy.io.votable.*")
warnings.filterwarnings("ignore", module="pyvo.utils.xml.*")
warnings.filterwarnings('ignore', '.*RADECSYS=*', append=True)
import matplotlib.pyplot as plt
import numpy as np
from astropy.coordinates import SkyCoord
from astropy.io import fits
from astropy.nddata import Cutout2D
import astropy.visualization as vis
from astropy.wcs import WCS
from astroquery.ned import Ned
import pyvo as vo
```
## 2. Search NED for objects in this paper.
Consult QuickReference.md to figure out how to use astroquery to search NED for all objects in a paper, based on the refcode of the paper. Inspect the resulting astropy table.
## 3. Filter the NED results.
The results from NED will include galaxies, but also other kinds of objects. Print the 'Type' column to see the full range of classifications. Next, print the 'Type' of just the first source in the table, in order to determine its data type (since Python 3 distinguishes between strings and byte strings). Finally, use the data type information to filter the results so that we only keep the galaxies in the list.
## 4. Search the NAVO Registry for image resources.
The paper selected super spirals using WISE, SDSS, and GALEX images. Search the NAVO registry for all image resources, using the 'service_type' search parameter. How many image resources are currently available?
## 5. Search the NAVO Registry for image resources that will allow you to search for AllWISE images.
There are hundreds of image resources...too many to quickly read through. Try adding the 'keyword' search parameter to your registry search, and find the image resource you would need to search the AllWISE images. Remember from the Known Issues that 'keywords' must be a list.
## 6. Select the AllWISE image service that you are interested in.
Hint: there should be only one service after searching with ['allwise']
## 7. Make a SkyCoord from the first galaxy in the NED list.
```
ra = galaxies['RA'][0]
dec = galaxies['DEC'][0]
pos = SkyCoord(ra, dec, unit = 'deg')
```
## 8. Search for a list of AllWISE images that cover this galaxy.
How many images are returned? Which are you most interested in?
## 9. Use the .to_table() method to view the results as an Astropy table.
## 10. From the result in 8., select the first record for an image taken in WISE band W1 (3.6 micron)
Hints:
* Loop over records and test on the `.bandpass_id` attribute of each record
* Print the `.title` and `.bandpass_id` of the record you find, to verify it is the right one.
## 11. Visualize this AllWISE image.
```
allwise_w1_image = fits.open(allwise_image_record.getdataurl())
fig = plt.figure()
wcs = WCS(allwise_w1_image[0].header)
ax = fig.add_subplot(1, 1, 1, projection=wcs)
ax.imshow(allwise_w1_image[0].data, cmap='gray_r', origin='lower', vmax = 10)
ax.scatter(ra, dec, transform=ax.get_transform('fk5'), s=500, edgecolor='red', facecolor='none')
```
## 12. Plot a cutout of the AllWISE image, centered on your position.
Try a 60 arcsecond cutout. Use `Cutout2D` that we imported earlier.
## 13. Try visualizing a cutout of a GALEX image that covers your position.
Repeat steps 4, 5, 6, 8 through 12 for GALEX.
## 14. Try visualizing a cutout of an SDSS image that covers your position.
Hints:
* Search the registry using `keywords=['sloan']
* Find the service with a `short_name` of `b'SDSS SIAP'`
* From Known Issues, recall that an empty string must be specified to the `format` parameter dues to a bug in the service.
* After obtaining your search results, select r-band images using the `.title` attribute of the records that are returned, since `.bandpass_id` is not populated.
## 15. Try looping over the first few positions and plotting multiwavelength cutouts.
|
github_jupyter
|

<font size=3 color="midnightblue" face="arial">
<h1 align="center">Escuela de Ciencias Básicas, Tecnología e Ingeniería</h1>
</font>
<font size=3 color="navy" face="arial">
<h1 align="center">ECBTI</h1>
</font>
<font size=2 color="darkorange" face="arial">
<h1 align="center">Curso:</h1>
</font>
<font size=2 color="navy" face="arial">
<h1 align="center">Introducción al lenguaje de programación Python</h1>
</font>
<font size=1 color="darkorange" face="arial">
<h1 align="center">Febrero de 2020</h1>
</font>
<h2 align="center">Sesión 11 - Ecosistema Python - Pandas</h2>
## Instructor:
> <strong> *Carlos Alberto Álvarez Henao, I.C. Ph.D.* </strong>
## *Pandas*
Es un módulo (biblioteca) en *Python* de código abierto (open source) que proporciona estructuras de datos flexibles y permite trabajar con la información de forma eficiente (gran parte de Pandas está implementado usando `C/Cython` para obtener un buen rendimiento).
Desde [este enlace](http://pandas.pydata.org "Pandas") podrás acceder a la página oficial de Pandas.
Antes de *Pandas*, *Python* se utilizó principalmente para la manipulación y preparación de datos. Tenía muy poca contribución al análisis de datos. *Pandas* resolvió este problema. Usando *Pandas*, podemos lograr cinco pasos típicos en el procesamiento y análisis de datos, independientemente del origen de los datos:
- cargar,
- preparar,
- manipular,
- modelar, y
- analizar.
## Principales características de *Pandas*
- Objeto tipo DataFrame rápido y eficiente con indexación predeterminada y personalizada.
- Herramientas para cargar datos en objetos de datos en memoria desde diferentes formatos de archivo.
- Alineación de datos y manejo integrado de datos faltantes.
- Remodelación y pivoteo de conjuntos de datos.
- Etiquetado de corte, indexación y subconjunto de grandes conjuntos de datos.
- Las columnas de una estructura de datos se pueden eliminar o insertar.
- Agrupamiento por datos para agregación y transformaciones.
- Alto rendimiento de fusión y unión de datos.
- Funcionalidad de series de tiempo
### Configuración de *Pandas*
La distribución estándar del no incluye el módulo de `pandas`. Es necesario realizar el procedimiento de instalacion y difiere del ambiente o el sistema operativo empleados.
Si usa el ambiente *[Anaconda](https://anaconda.org/)*, la alternativa más simple es usar el comando:
o empleando *conda*:
### Estructuras de datos en *Pandas*
Ofrece varias estructuras de datos que nos resultarán de mucha utilidad y que vamos a ir viendo poco a poco. Todas las posibles estructuras de datos que ofrece a día de hoy son:
- **`Series`:** Son arrays unidimensionales con indexación (arrays con índice o etiquetados), similar a los diccionarios. Pueden generarse a partir de diccionarios o de listas.
- **`DataFrame`:** Similares a las tablas de bases de datos relacionales como `SQL`.
- **`Panel`, `Panel4D` y `PanelND`:** Permiten trabajar con más de dos dimensiones. Dado que es algo complejo y poco utilizado trabajar con arrays de más de dos dimensiones no trataremos los paneles en estos tutoriales de introducción a Pandas.
## Dimensionado y Descripción
La mejor manera para pensar sobre estas estructuras de datos es que la estructura de dato de dimension mayor contiene a la estructura de datos de menor dimensión.
`DataFrame` contiene a las `Series`, `Panel` contiene al `DataFrame`
| Data Structure | Dimension | Descripción |
|----------------|:---------:|-------------|
|`Series` | 1 | Arreglo 1-Dimensional homogéneo de tamaño inmutable |
|`DataFrames` | 2 | Estructura tabular 2-Dimensional, tamaño mutable con columnas heterogéneas|
|`Panel` | 3 | Arreglo general 3-Dimensional, tamaño variable|
La construcción y el manejo de dos o más matrices dimensionales es una tarea tediosa, se le impone una carga al usuario para considerar la orientación del conjunto de datos cuando se escriben las funciones. Pero al usar las estructuras de datos de *Pandas*, se reduce el esfuerzo mental del usuario.
- Por ejemplo, con datos tabulares (`DataFrame`), es más útil semánticamente pensar en el índice (las filas) y las columnas, en lugar del eje 0 y el eje 1.
### Mutabilidad
Las estructuras en *Pandas* son de valor mutable (se pueden cambiar), y excepto las `Series`, todas son de tamaño mutables. Los `DataFrames` son los más usados, los `Panel` no se usan tanto.
## Cargando el módulo *Pandas*
```
import pandas as pd
import numpy as np
```
## `Series`:
Las series se definen de la siguiente manera:
donde:
- `data` es el vector de datos
- `index` (opcional) es el vector de índices que usará la serie. Si los índices son datos de fechas directamente se creará una instancia de una `TimeSeries` en lugar de una instancia de `Series`. Si se omite, por defecto es: `np.arrange(n)`
- `dtype`, tipo de dato. Si se omite, el tipo de dato se infiere.
- `copy`, copia datos, por defecto es `False`.
Veamos un ejemplo de como crear este tipo de contenedor de datos. Primero vamos a crear una `Series` y `Pandas` nos creará índices automáticamente:
#### Creando una `Series` sin datos (vacía, `empty`)
```
s = pd.Series()
print(s)
```
#### Creando una *Serie* con datos
Si los datos provienen de un `ndarray`, el índice pasado debe ser de la misma longitud. Si no se pasa ningún índice, el índice predeterminado será `range(n)` donde `n` es la longitud del arreglo, es decir, $[0,1,2, \ldots rango(len(array))-1]$.
```
data = np.array(['a','b','c','d'])
s = pd.Series(data)
print(s)
```
- Obsérvese que no se pasó ningún índice, por lo que, de forma predeterminada, se asignaron los índices que van de `0` a `len(datos) - 1`, es decir, de `0` a `3`.
```
data = np.array(['a','b','c','d'])
s = pd.Series(data,index=[150,1,"can?",10])
print(s)
```
- Aquí pasamos los valores del índice. Ahora podemos ver los valores indexados de forma personalizada en la salida.
#### Creando una `Series` desde un diccionario
```
data = {'a' : 0., 'b' : 1.,True : 2.}
s = pd.Series(data)
print(s)
```
- La `clave` del diccionario es usada para construir el índice.
```
data = {'a' : 0., 'b' : 1., 'c' : 2.}
s = pd.Series(data,index=['b','c','d','a'])
print(s)
```
- El orden del índice se conserva y el elemento faltante se llena con `NaN` (*Not a Number*).
#### Creando una *Serie* desde un escalar
```
s = pd.Series(5, index=[0, 1, 2, 3])
print(s)
```
#### Accesando a los datos desde la `Series` con la posición
Los datos en una `Series` se pueden acceder de forma similar a un `ndarray`
```
s = pd.Series([1,2,3,4,5],index = ['a','b','c','d','e'])
print(s['c']) # recupera el primer elemento
```
Ahora, recuperemos los tres primeros elementos en la `Series`. Si se inserta `a:` delante, se extraerán todos los elementos de ese índice en adelante. Si se usan dos parámetros (con `:` entre ellos), se extraerán los elementos entre los dos índices (sin incluir el índice de detención).
```
print(s[:3]) # recupera los tres primeros elementos
```
Recupere los tres últimos elementos
```
print(s[-3:])
```
#### Recuperando los datos usando indexación
Recupere un único elemento usando el valor del índice
```
print(s['a'])
```
Recupere múltiples elementos usando una lista de valores de los índices
```
print(s[['a','c','d']])
```
Si una etiqueta no está contenida, se emitirá un mensaje de excepción (error)
```
print(s['f'])
```
* Vamos a crear una serie con índices generados aleatoriamente (de forma automática)
```
# serie con índices automáticos
serie = pd.Series(np.random.random(10))
print('Serie con índices automáticos'.format())
print('{}'.format(serie))
print(type(serie))
```
* Ahora vamos a crear una serie donde nosotros le vamos a decir los índices que queremos usar (definidos por el usuario)
```
serie = pd.Series(np.random.randn(4),
index = ['itzi','kikolas','dieguete','nicolasete'])
print('Serie con índices definidos')
print('{}'.format(serie))
print(type(serie))
```
* Por último, vamos a crear una serie temporal usando índices que son fechas.
```
# serie(serie temporal) con índices que son fechas
n = 60
serie = pd.Series(np.random.randn(n),
index = pd.date_range('2001/01/01', periods = n))
print('Serie temporal con índices de fechas')
print('{}'.format(serie))
print(type(serie))
pd.
```
En los ejemplos anteriores hemos creado las series a partir de un `numpy array` pero las podemos crear a partir de muchas otras cosas: listas, diccionarios, numpy arrays,... Veamos ejemplos:
```
serie_lista = pd.Series([i*i for i in range(10)])
print('Serie a partir de una lista')
print('{}'.format(serie_lista))
```
Serie a partir de un diccionario
```
dicc = {'cuadrado de {}'.format(i) : i*i for i in range(10)}
serie_dicc = pd.Series(dicc)
print('Serie a partir de un diccionario ')
print('{}'.format(serie_dicc))
```
Serie a partir de valores de otra serie...
```
serie_serie = pd.Series(serie_dicc.values)
print('Serie a partir de los valores de otra (pandas) serie')
print('{}'.format(serie_serie))
```
Serie a partir de un valor constante ...
```
serie_cte = pd.Series(-999, index = np.arange(10))
print('Serie a partir de un valor constante')
print('{}'.format(serie_cte))
```
Una serie (`Series` o `TimeSeries`) se puede manejar igual que si tuviéramos un `numpy array` de una dimensión o igual que si tuviéramos un diccionario. Vemos ejemplos de esto:
```
serie = pd.Series(np.random.randn(10),
index = ['a','b','c','d','e','f','g','h','i','j'])
print('Serie que vamos a usar en este ejemplo:')
print('{}'.format(serie))
```
Ejemplos de comportamiento como `numpy array`
```
print('serie.max() {}'.format(serie.max()))
print('serie.sum() {}'.format(serie.sum()))
print('serie.abs()')
print('{}'.format(serie.abs()))
print('serie[serie > 0]')
print('{}'.format(serie[serie > 0]))
#...
print('\n')
```
Ejemplos de comportamiento como diccionario
```
print("Se comporta como un diccionario:")
print("================================")
print("serie['a'] \n {}".format(serie['a']))
print("'a' en la serie \n {}".format('a' in serie))
print("'z' en la serie \n {}".format('z' in serie))
```
Las operaciones están 'vectorizadas' y se hacen elemento a elemento con los elementos alineados en función del índice.
- Si se hace, por ejemplo, una suma de dos series, si en una de las dos series no existe un elemento, i.e. el índice no existe en la serie, el resultado para ese índice será `NAN`.
- En resumen, estamos haciendo una unión de los índices y funciona diferente a los `numpy arrays`.
Se puede ver el esquema en el siguiente ejemplo:
```
s1 = serie[1:]
s2 = serie[:-1]
suma = s1 + s2
print(' s1 s2 s1 + s2')
print('------------------ ------------------ ------------------')
for clave in sorted(set(list(s1.keys()) + list(s2.keys()))):
print('{0:1} {1:20} + {0:1} {2:20} = {0:1} {3:20}'.format(clave,
s1.get(clave),
s2.get(clave),
suma.get(clave)))
```
En la anterior línea de código se usa el método `get` para no obtener un `KeyError`, como sí obtendría si se usa, p.e., `s1['a']`
## `DataFrame`
Un `DataFrame` es una estructura 2-Dimensional, es decir, los datos se alinean en forma tabular por filas y columnas.
### Características del`DataFrame`
- Las columnas pueden ser de diferente tipo.
- Tamaño cambiable.
- Ejes etiquetados (filas y columnas).
- Se pueden desarrollar operaciones aritméticas en filas y columnas.
### `pandas.DataFrame`
una estructura de `DataFrame` puede crearse usando el siguiente constructor:
Los parámetros de este constructor son los siguientes:
- **`data`:** Pueden ser de diferentes formas como `ndarray`, `Series`, `map`, `lists`, `dict`, constantes o también otro `DataFrame`.
- **`index`:** para las etiquetas de fila, el índice que se utilizará para la trama resultante es dado de forma opcional por defecto por `np.arange(n)`, si no se especifica ningún índice.
- **`columns`:** para las etiquetas de columnas, la sintaxis por defecto es `np.arange(n)`. Esto es así si no se especifíca ningún índice.
- **`dtype`:** tipo de dato para cada columna
- **`copy`:*** Es usado para copiar los datos. Por defecto es `False`.
#### Creando un `DataFrame`
Un `DataFrame` en Pandas se puede crear usando diferentes entradas, como: `listas`, `diccionarios`, `Series`, `ndarrays`, otros `DataFrame`.
#### Creando un `DataFrame`
vacío
```
df = pd.DataFrame()
print(df)
```
#### Creando un `DataFrame` desde listas
```
data = [1,2,3,4,5]
df = pd.DataFrame(data)
print(df)
data = [['Alex',10],['Bob',12],['Clarke',13]]
df = pd.DataFrame(data,columns=['Name','Age'])
print(df)
df = pd.DataFrame(data,columns=['Name','Age'],dtype=float)
print(df)
```
#### Creando un `DataFrame` desde diccionarios de `ndarrays`/`lists`
Todos los `ndarrays` deben ser de la misma longitud. Si se pasa el índice, entonces la longitud del índice debe ser igual a la longitud de las matrices.
Si no se pasa ningún índice, de manera predeterminada, el índice será `range(n)`, donde `n` es la longitud del arreglo.
```
data = {'Name':['Tom', 'Jack', 'Steve', 'Ricky'],'Age':[28,34,29,42]}
df = pd.DataFrame(data)
print(df)
```
- Observe los valores $0,1,2,3$. Son el índice predeterminado asignado a cada uno usando la función `range(n)`.
Ahora crearemos un `DataFrame` indexado usando `arrays`
```
df = pd.DataFrame(data, index=['rank1','rank2','rank3','rank4'])
print(df)
```
#### Creando un `DataFrame` desde listas de diccionarios
Se puede pasar una lista de diccionarios como datos de entrada para crear un `DataFrame`. Las `claves` serán usadas por defecto como los nombres de las columnas.
```
data = [{'a': 1, 'b': 2},{'a': 5, 'b': 10, 'c': 20}]
df = pd.DataFrame(data)
print(df)
```
- un `NaN` aparece en donde no hay datos.
El siguiente ejemplo muestra como se crea un `DataFrame` pasando una lista de diccionarios y los índices de las filas:
```
df = pd.DataFrame(data, index=['first', 'second'])
print(df)
```
El siguiente ejemplo muestra como se crea un `DataFrame` pasando una lista de diccionarios, y los índices de las filas y columnas:
```
# Con dos índices de columnas, los valores son iguales que las claves del diccionario
df1 = pd.DataFrame(data, index=['first', 'second'], columns=['a', 'b'])
# Con dos índices de columna y con un índice con otro nombre
df2 = pd.DataFrame(data, index=['first', 'second'], columns=['a', 'b1'])
print(df1)
print(df2)
```
- Observe que el `DataFrame` `df2` se crea con un índice de columna que no es la clave del diccionario; por lo tanto, se generan los `NaN` en su lugar. Mientras que, `df1` se crea con índices de columnas iguales a las claves del diccionario, por lo que no se agrega `NaN`.
#### Creando un `DataFrame` desde un diccionario de `Series`
Se puede pasar una Serie de diccionarios para formar un `DataFrame`. El índice resultante es la unión de todos los índices de serie pasados.
```
d = {'one' : pd.Series([1, 2, 3], index=['a', 'b', 'c']),
'two' : pd.Series([1, 2, 3, 4], index=['a', 'b', 'c', 'd'])}
df = pd.DataFrame(d)
print(df)
```
- para la serie `one`, no hay una etiqueta `'d'` pasada, pero en el resultado, para la etiqueta `d`, se agrega `NaN`.
Ahora vamos a entender la selección, adición y eliminación de columnas a través de ejemplos.
#### Selección de columna
```
df = pd.DataFrame(d)
print(df['one'])
```
#### Adición de columna
```
df = pd.DataFrame(d)
# Adding a new column to an existing DataFrame object with column label by passing new series
print ("Adicionando una nueva columna pasando como Serie:, \n")
df['three']=pd.Series([10,20,30],index=['a','b','c'])
print(df,'\n')
print ("Adicionando una nueva columna usando las columnas existentes en el DataFrame:\n")
df['four']=df['one']+df['three']
print(df)
```
#### Borrado de columna
```
d = {'one' : pd.Series([1, 2, 3], index=['a', 'b', 'c']),
'two' : pd.Series([1, 2, 3, 4], index=['a', 'b', 'c', 'd']),
'three' : pd.Series([10,20,30], index=['a','b','c'])}
df = pd.DataFrame(d)
print ("Our dataframe is:\n")
print(df, '\n')
# using del function
print ("Deleting the first column using DEL function:\n")
del df['one']
print(df,'\n')
# using pop function
print ("Deleting another column using POP function:\n")
df.pop('two')
print(df)
```
### Selección, Adición y Borrado de fila
#### Selección por etiqueta
Las filas se pueden seleccionar pasando la etiqueta de fila por la función `loc`
```
d = {'one' : pd.Series([1, 2, 3], index=['a', 'b', 'c']),
'two' : pd.Series([1, 2, 3, 4], index=['a', 'b', 'c', 'd'])}
df = pd.DataFrame(d)
print(df)
print(df.loc['b'])
```
- El resultado es una serie con etiquetas como nombres de columna del `DataFrame`. Y, el Nombre de la serie es la etiqueta con la que se recupera.
#### Selección por ubicación entera
Las filas se pueden seleccionar pasando la ubicación entera a una función `iloc`.
```
df = pd.DataFrame(d)
print(df.iloc[2])
```
#### Porcion de fila
Múltiples filas se pueden seleccionar usando el operador `:`
```
df = pd.DataFrame(d)
print(df[2:4])
```
#### Adición de filas
Adicionar nuevas filas al `DataFrame` usando la función `append`. Esta función adiciona las filas al final.
```
df = pd.DataFrame([[1, 2], [3, 4]])
df2 = pd.DataFrame([[5, 6], [7, 8]])
print(df)
df = df.append(df2)
print(df)
```
#### Borrado de filas
Use la etiqueta de índice para eliminar o cortar filas de un `DataFrame`. Si la etiqueta está duplicada, se eliminarán varias filas.
Si observa, en el ejemplo anterior, las etiquetas están duplicadas. Cortemos una etiqueta y veamos cuántas filas se descartarán.
```
df = pd.DataFrame([[1, 2], [3, 4]], columns = ['a','b'])
df2 = pd.DataFrame([[5, 6], [7, 8]], columns = ['a','b'])
df = df.append(df2)
print(df)
# Drop rows with label 0
df = df.drop(1)
print(df)
```
- En el ejemplo anterior se quitaron dos filas porque éstas dos contenían la misma etiqueta `0`.
### Lectura / Escritura en Pandas
Una de las grandes capacidades de *`Pandas`* es la potencia que aporta a lo hora de leer y/o escribir archivos de datos.
- Pandas es capaz de leer datos de archivos `csv`, `excel`, `HDF5`, `sql`, `json`, `html`,...
Si se emplean datos de terceros, que pueden provenir de muy diversas fuentes, una de las partes más tediosas del trabajo será tener los datos listos para empezar a trabajar: Limpiar huecos, poner fechas en formato usable, saltarse cabeceros,...
Sin duda, una de las funciones que más se usarán será `read_csv()` que permite una gran flexibilidad a la hora de leer un archivo de texto plano.
```
help(pd.read_csv)
```
En [este enlace](http://pandas.pydata.org/pandas-docs/stable/io.html "pandas docs") se pueden encontrar todos los posibles formatos con los que Pandas trabaja:
Cada uno de estos métodos de lectura de determinados formatos (`read_NombreFormato`) tiene infinidad de parámetros que se pueden ver en la documentación y que no vamos a explicar por lo extensísima que seria esta explicación.
Para la mayoría de los casos que nos vamos a encontrar los parámetros serían los siguientes:
Básicamente hay que pasarle el archivo a leer, cual es su separador, si la primera linea del archivo contiene el nombre de las columnas y en el caso de que no las tenga pasarle en `names` el nombre de las columnas.
Veamos un ejemplo de un dataset del cómo leeriamos el archivo con los datos de los usuarios, siendo el contenido de las 10 primeras lineas el siguiente:
```
# Load users info
userHeader = ['ID', 'Sexo', 'Edad', 'Ocupacion', 'PBOX']
users = pd.read_csv('Datasets/users.txt', engine='python', sep='::', header=None, names=userHeader)
# print 5 first users
print ('# 10 primeros usuarios: \n%s' % users[:100])
```
Para escribir un `DataFrame` en un archivo de texto se pueden utilizar los [método de escritura](http://pandas.pydata.org/pandas-docs/stable/io.html) para escribirlos en el formato que se quiera.
- Por ejemplo si utilizamos el método `to_csv()` nos escribirá el `DataFrame` en este formato estandar que separa los campos por comas; pero por ejemplo, podemos decirle al método que en vez de que utilice como separador una coma, que utilice por ejemplo un guión.
Si queremos escribir en un archivo el `DataFrame` `users` con estas características lo podemos hacer de la siguiente manera:
```
users.to_csv('Datasets/MyUsers3.txt', sep='-')
```
### Merge
Una funcionalidad muy potente que ofrece Pandas es la de poder juntar, `merge` (en bases de datos sería hacer un `JOIN`) datos siempre y cuando este sea posible.
En el ejemplo que estamos haciendo con el dataset podemos ver esta funcionalidad de forma muy intuitiva, ya que los datos de este data set se han obtenido a partir de una bases de datos relacional.
Veamos a continuación como hacer un `JOIN` o un `merge` de los archivos `users.txt` y `ratings.txt` a partir del `user_id`:
```
# Load users info
userHeader = ['user_id', 'gender', 'age', 'ocupation', 'zip']
users = pd.read_csv('Datasets/users.txt', engine='python', sep='::', header=None, names=userHeader)
# Load ratings
ratingHeader = ['user_id', 'movie_id', 'rating', 'timestamp']
ratings = pd.read_csv('Datasets/ratings.txt', engine='python', sep='::', header=None, names=ratingHeader)
# Merge tables users + ratings by user_id field
merger_ratings_users = pd.merge(users, ratings)
print('%s' % merger_ratings_users[:10])
```
De la misma forma que hemos hecho el `JOIN` de los usuarios y los votos, podemos hacer lo mismo añadiendo también los datos relativos a las películas:
```
userHeader = ['user_id', 'gender', 'age', 'ocupation', 'zip']
users = pd.read_csv('Datasets/users.txt', engine='python', sep='::', header=None, names=userHeader)
movieHeader = ['movie_id', 'title', 'genders']
movies = pd.read_csv('Datasets/movies.txt', engine='python', sep='::', header=None, names=movieHeader)
ratingHeader = ['user_id', 'movie_id', 'rating', 'timestamp']
ratings = pd.read_csv('Datasets/ratings.txt', engine='python', sep='::', header=None, names=ratingHeader)
# Merge data
#mergeRatings = pd.merge(pd.merge(users, ratings), movies)
mergeRatings = pd.merge(merger_ratings_users, movies)
```
Si quisiésemos ver por ejemplo un elemento de este nuevo `JOIN` creado (por ejemplo la posición 1000), lo podríamos hacer de la siguiente forma:
```
info1000 = mergeRatings.loc[1000]
print('Info of 1000 position of the table: \n%s' % info1000[:1000])
```
### Trabajando con Datos, Indexación, Selección
¿Cómo podemos seleccionar, añadir, eliminar, mover,..., columnas, filas,...?
- Para seleccionar una columna solo hay que usar el nombre de la columna y pasarlo como si fuera un diccionario (o un atributo).
- Para añadir una columna simplemente hay que usar un nombre de columna no existente y pasarle los valores para esa columna.
- Para eliminar una columna podemos usar `del` o el método `pop` del `DataFrame`.
- Para mover una columna podemos usar una combinación de las metodologías anteriores.
Como ejemplo, vamos crear un `DataFrame`con datos aleatorios y a seleccionar los valores de una columna:
```
df = pd.DataFrame(np.random.randn(5,3),
index = ['primero','segundo','tercero','cuarto','quinto'],
columns = ['velocidad', 'temperatura','presion'])
print(df)
print(df['velocidad'])
print(df.velocidad)
```
Para acceder a la columna `velocidad` lo podemos hacer de dos formas.
- O bien usando el nombre de la columna como si fuera una clave de un diccionario
- O bien usando el nombre de la columna como si fuera un atributo.
En el caso de que los nombres de las columnas sean números, la segunda opción no podríais usarla...
Vamos a añadir una columna nueva al `DataFrame`. Es algo tan sencillo como usar un nombre de columna no existente y pasarle los datos:
```
df['velocidad_maxima'] = np.random.randn(df.shape[0])
print(df)
```
Pero qué pasa si quiero añadir la columna en un lugar específico. Para ello podemos usar el método `insert` (y de paso vemos como podemos borrar una columna):
**Forma 1:**
- Borramos la columna 'velocidad_maxima' que está al final del df usando `del`
- Colocamos la columna eliminada en la posición que especifiquemos
```
print(df)
columna = df['velocidad_maxima']
del df['velocidad_maxima']
df.insert(1, 'velocidad_maxima', columna)
print(df)
```
**Forma 2:** Usando el método `pop`: borramos usando el método `pop` y añadimos la columna borrada en la última posición de nuevo.
```
print(df)
columna = df.pop('velocidad_maxima')
print(df)
#print(columna)
df.insert(3, 'velocidad_maxima', columna)
print(df)
```
Para seleccionar datos concretos de un `DataFrame` podemos usar el índice, una rebanada (*slicing*), valores booleanos, la columna,...
- Seleccionamos la columna de velocidades:
```
print(df.velocidad)
```
- Seleccionamos todas las columnas cuyo índice es igual a tercero:
```
print(df.xs('tercero'))
```
- Seleccionamos todas las columnas cuyo índice está entre tercero y quinto (en este caso los índices son inclusivos)
```
print(df.loc['tercero':'quinto'])
```
- Seleccionamos todos los valores de velocidad donde la temperatura > 0
```
print(df['velocidad'][df['temperatura']>0])
```
Seleccionamos todos los valores de una columna por índice usando una rebanada (`slice`) de enteros.
- En este caso el límite superior de la rebanada no se incluye (Python tradicional)
```
print(df.iloc[1:3])
```
- Seleccionamos filas y columnas
```
print(df.iloc[1:3, ['velocidad', 'presion']])
help(df.ix)
```
|
github_jupyter
|
Copyright (c) Microsoft Corporation. All rights reserved.
Licensed under the MIT License.
# Deploying a web service to Azure Kubernetes Service (AKS)
This notebook shows the steps for deploying a service: registering a model, creating an image, provisioning a cluster (one time action), and deploying a service to it.
We then test and delete the service, image and model.
```
from azureml.core import Workspace
from azureml.core.compute import AksCompute, ComputeTarget
from azureml.core.webservice import Webservice, AksWebservice
from azureml.core.image import Image
from azureml.core.model import Model
import azureml.core
print(azureml.core.VERSION)
```
# Get workspace
Load existing workspace from the config file info.
```
from azureml.core.workspace import Workspace
ws = Workspace.from_config()
print(ws.name, ws.resource_group, ws.location, ws.subscription_id, sep = '\n')
```
# Register the model
Register an existing trained model, add descirption and tags.
```
#Register the model
from azureml.core.model import Model
model = Model.register(model_path = "sklearn_regression_model.pkl", # this points to a local file
model_name = "sklearn_regression_model.pkl", # this is the name the model is registered as
tags = {'area': "diabetes", 'type': "regression"},
description = "Ridge regression model to predict diabetes",
workspace = ws)
print(model.name, model.description, model.version)
```
# Create an image
Create an image using the registered model the script that will load and run the model.
```
%%writefile score.py
import pickle
import json
import numpy
from sklearn.externals import joblib
from sklearn.linear_model import Ridge
from azureml.core.model import Model
def init():
global model
# note here "sklearn_regression_model.pkl" is the name of the model registered under
# this is a different behavior than before when the code is run locally, even though the code is the same.
model_path = Model.get_model_path('sklearn_regression_model.pkl')
# deserialize the model file back into a sklearn model
model = joblib.load(model_path)
# note you can pass in multiple rows for scoring
def run(raw_data):
try:
data = json.loads(raw_data)['data']
data = numpy.array(data)
result = model.predict(data)
# you can return any data type as long as it is JSON-serializable
return result.tolist()
except Exception as e:
error = str(e)
return error
from azureml.core.conda_dependencies import CondaDependencies
myenv = CondaDependencies.create(conda_packages=['numpy','scikit-learn'])
with open("myenv.yml","w") as f:
f.write(myenv.serialize_to_string())
from azureml.core.image import ContainerImage
image_config = ContainerImage.image_configuration(execution_script = "score.py",
runtime = "python",
conda_file = "myenv.yml",
description = "Image with ridge regression model",
tags = {'area': "diabetes", 'type': "regression"}
)
image = ContainerImage.create(name = "myimage1",
# this is the model object
models = [model],
image_config = image_config,
workspace = ws)
image.wait_for_creation(show_output = True)
```
# Provision the AKS Cluster
This is a one time setup. You can reuse this cluster for multiple deployments after it has been created. If you delete the cluster or the resource group that contains it, then you would have to recreate it.
```
# Use the default configuration (can also provide parameters to customize)
prov_config = AksCompute.provisioning_configuration()
aks_name = 'my-aks-9'
# Create the cluster
aks_target = ComputeTarget.create(workspace = ws,
name = aks_name,
provisioning_configuration = prov_config)
%%time
aks_target.wait_for_completion(show_output = True)
print(aks_target.provisioning_state)
print(aks_target.provisioning_errors)
```
## Optional step: Attach existing AKS cluster
If you have existing AKS cluster in your Azure subscription, you can attach it to the Workspace.
```
'''
# Use the default configuration (can also provide parameters to customize)
resource_id = '/subscriptions/92c76a2f-0e1c-4216-b65e-abf7a3f34c1e/resourcegroups/raymondsdk0604/providers/Microsoft.ContainerService/managedClusters/my-aks-0605d37425356b7d01'
create_name='my-existing-aks'
# Create the cluster
aks_target = AksCompute.attach(workspace=ws, name=create_name, resource_id=resource_id)
# Wait for the operation to complete
aks_target.wait_for_completion(True)
'''
```
# Deploy web service to AKS
```
#Set the web service configuration (using default here)
aks_config = AksWebservice.deploy_configuration()
%%time
aks_service_name ='aks-service-1'
aks_service = Webservice.deploy_from_image(workspace = ws,
name = aks_service_name,
image = image,
deployment_config = aks_config,
deployment_target = aks_target)
aks_service.wait_for_deployment(show_output = True)
print(aks_service.state)
```
# Test the web service
We test the web sevice by passing data.
```
%%time
import json
test_sample = json.dumps({'data': [
[1,2,3,4,5,6,7,8,9,10],
[10,9,8,7,6,5,4,3,2,1]
]})
test_sample = bytes(test_sample,encoding = 'utf8')
prediction = aks_service.run(input_data = test_sample)
print(prediction)
```
# Clean up
Delete the service, image and model.
```
%%time
aks_service.delete()
image.delete()
model.delete()
```
|
github_jupyter
|
##### Copyright 2020 The TensorFlow Authors.
```
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
```
# TF Lattice Custom Estimators
<table class="tfo-notebook-buttons" align="left">
<td>
<a target="_blank" href="https://www.tensorflow.org/lattice/tutorials/custom_estimators"><img src="https://www.tensorflow.org/images/tf_logo_32px.png" />View on TensorFlow.org</a>
</td>
<td>
<a target="_blank" href="https://colab.research.google.com/github/tensorflow/lattice/blob/master/docs/tutorials/custom_estimators.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
</td>
<td>
<a target="_blank" href="https://github.com/tensorflow/lattice/blob/master/docs/tutorials/custom_estimators.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View source on GitHub</a>
</td>
<td>
<a href="https://storage.googleapis.com/tensorflow_docs/lattice/docs/tutorials/custom_estimators.ipynb"><img src="https://www.tensorflow.org/images/download_logo_32px.png" />Download notebook</a>
</td>
</table>
## Overview
You can use custom estimators to create arbitrarily monotonic models using TFL layers. This guide outlines the steps needed to create such estimators.
## Setup
Installing TF Lattice package:
```
#@test {"skip": true}
!pip install tensorflow-lattice
```
Importing required packages:
```
import tensorflow as tf
import logging
import numpy as np
import pandas as pd
import sys
import tensorflow_lattice as tfl
from tensorflow import feature_column as fc
from tensorflow_estimator.python.estimator.canned import optimizers
from tensorflow_estimator.python.estimator.head import binary_class_head
logging.disable(sys.maxsize)
```
Downloading the UCI Statlog (Heart) dataset:
```
csv_file = tf.keras.utils.get_file(
'heart.csv', 'http://storage.googleapis.com/download.tensorflow.org/data/heart.csv')
df = pd.read_csv(csv_file)
target = df.pop('target')
train_size = int(len(df) * 0.8)
train_x = df[:train_size]
train_y = target[:train_size]
test_x = df[train_size:]
test_y = target[train_size:]
df.head()
```
Setting the default values used for training in this guide:
```
LEARNING_RATE = 0.1
BATCH_SIZE = 128
NUM_EPOCHS = 1000
```
## Feature Columns
As for any other TF estimator, data needs to be passed to the estimator, which is typically via an input_fn and parsed using [FeatureColumns](https://www.tensorflow.org/guide/feature_columns).
```
# Feature columns.
# - age
# - sex
# - ca number of major vessels (0-3) colored by flourosopy
# - thal 3 = normal; 6 = fixed defect; 7 = reversable defect
feature_columns = [
fc.numeric_column('age', default_value=-1),
fc.categorical_column_with_vocabulary_list('sex', [0, 1]),
fc.numeric_column('ca'),
fc.categorical_column_with_vocabulary_list(
'thal', ['normal', 'fixed', 'reversible']),
]
```
Note that categorical features do not need to be wrapped by a dense feature column, since `tfl.laysers.CategoricalCalibration` layer can directly consume category indices.
## Creating input_fn
As for any other estimator, you can use input_fn to feed data to the model for training and evaluation.
```
train_input_fn = tf.compat.v1.estimator.inputs.pandas_input_fn(
x=train_x,
y=train_y,
shuffle=True,
batch_size=BATCH_SIZE,
num_epochs=NUM_EPOCHS,
num_threads=1)
test_input_fn = tf.compat.v1.estimator.inputs.pandas_input_fn(
x=test_x,
y=test_y,
shuffle=False,
batch_size=BATCH_SIZE,
num_epochs=1,
num_threads=1)
```
## Creating model_fn
There are several ways to create a custom estimator. Here we will construct a `model_fn` that calls a Keras model on the parsed input tensors. To parse the input features, you can use `tf.feature_column.input_layer`, `tf.keras.layers.DenseFeatures`, or `tfl.estimators.transform_features`. If you use the latter, you will not need to wrap categorical features with dense feature columns, and the resulting tensors will not be concatenated, which makes it easier to use the features in the calibration layers.
To construct a model, you can mix and match TFL layers or any other Keras layers. Here we create a calibrated lattice Keras model out of TFL layers and impose several monotonicity constraints. We then use the Keras model to create the custom estimator.
```
def model_fn(features, labels, mode, config):
"""model_fn for the custom estimator."""
del config
input_tensors = tfl.estimators.transform_features(features, feature_columns)
inputs = {
key: tf.keras.layers.Input(shape=(1,), name=key) for key in input_tensors
}
lattice_sizes = [3, 2, 2, 2]
lattice_monotonicities = ['increasing', 'none', 'increasing', 'increasing']
lattice_input = tf.keras.layers.Concatenate(axis=1)([
tfl.layers.PWLCalibration(
input_keypoints=np.linspace(10, 100, num=8, dtype=np.float32),
# The output range of the calibrator should be the input range of
# the following lattice dimension.
output_min=0.0,
output_max=lattice_sizes[0] - 1.0,
monotonicity='increasing',
)(inputs['age']),
tfl.layers.CategoricalCalibration(
# Number of categories including any missing/default category.
num_buckets=2,
output_min=0.0,
output_max=lattice_sizes[1] - 1.0,
)(inputs['sex']),
tfl.layers.PWLCalibration(
input_keypoints=[0.0, 1.0, 2.0, 3.0],
output_min=0.0,
output_max=lattice_sizes[0] - 1.0,
# You can specify TFL regularizers as tuple
# ('regularizer name', l1, l2).
kernel_regularizer=('hessian', 0.0, 1e-4),
monotonicity='increasing',
)(inputs['ca']),
tfl.layers.CategoricalCalibration(
num_buckets=3,
output_min=0.0,
output_max=lattice_sizes[1] - 1.0,
# Categorical monotonicity can be partial order.
# (i, j) indicates that we must have output(i) <= output(j).
# Make sure to set the lattice monotonicity to 'increasing' for this
# dimension.
monotonicities=[(0, 1), (0, 2)],
)(inputs['thal']),
])
output = tfl.layers.Lattice(
lattice_sizes=lattice_sizes, monotonicities=lattice_monotonicities)(
lattice_input)
training = (mode == tf.estimator.ModeKeys.TRAIN)
model = tf.keras.Model(inputs=inputs, outputs=output)
logits = model(input_tensors, training=training)
if training:
optimizer = optimizers.get_optimizer_instance_v2('Adagrad', LEARNING_RATE)
else:
optimizer = None
head = binary_class_head.BinaryClassHead()
return head.create_estimator_spec(
features=features,
mode=mode,
labels=labels,
optimizer=optimizer,
logits=logits,
trainable_variables=model.trainable_variables,
update_ops=model.updates)
```
## Training and Estimator
Using the `model_fn` we can create and train the estimator.
```
estimator = tf.estimator.Estimator(model_fn=model_fn)
estimator.train(input_fn=train_input_fn)
results = estimator.evaluate(input_fn=test_input_fn)
print('AUC: {}'.format(results['auc']))
```
|
github_jupyter
|
# Analyzing Street Trees: Diversity Indices and the 10/20/30 Rule
This notebook analyzes the diversity indices of the street trees inside and outside the city center you've selected, and then check the tree inventory according to the 10/20/30 rule, discussed below.
```
# library import
import pandas as pd
import geopandas as gpd
import numpy as np
import matplotlib.pyplot as plt
import descartes
import treeParsing as tP
```
# Import Tree Inventory and City Center Boundary
Import your tree data and city center boundary data below. These data may use any geospatial data format (SHP, Geojson, Geopackage) and should be in the same coordinate projection.
Your tree data will need the following columns:
* Point geographic location
* Diameter at breast height (DBH)
* Tree Scientific Name
* Tree Genus Name
* Tree Family Name
Your city center geography simply needs to be a single, dissolved geometry representing your city center area.
```
### Enter the path to your data below ###
tree_data_path = 'example_data/trees_paris.gpkg'
tree_data = gpd.read_file(tree_data_path)
tree_data.plot()
### Enter the path to your data below ###
city_center_boundary_path = 'example_data/paris.gpkg'
city_center = gpd.read_file(city_center_boundary_path)
city_center.plot()
```
# Clean Data and Calculate Basal Area
To start, we need to remove features missing data and remove the top quantile of data. Removing any missing data and the top quantile helps remove erroneous entries that are too large or too small than what we would expect. If your data has already been cleaned, feel free to skip the second cell below.
```
### Enter your column names here ###
scientific_name_column = 'Scientific'
genus_name_column = 'genus'
family_name_column = 'family'
diameter_breast_height_column = 'DBH'
### Ignore if data is already cleaned ###
# Exclude Data Missing DBH
tree_data = tree_data[tree_data[diameter_breast_height_column]>0]
# Exclude data larger than the 99th quantile (often erroneously large)
tree_data = tree_data[tree_data[diameter_breast_height_column]<=tree_data.quantile(0.99).DBH]
# Calculate Basal Area
basal_area_column = 'BA'
tree_data[basal_area_column] = tree_data[diameter_breast_height_column]**2 * 0.00007854
```
# Calculating Simpson and Shannon Diversity Indices
The following cells spatially join your city center geometry to your tree inventory data, and then calculates the simpson and shannon diversity indices for the city center, area outside the city center -- based on area and tree count.
```
# Add dummy column to city center geometry
city_center['inside'] = True
city_center = city_center[['geometry','inside']]
# Spatial Join -- this may take a while
sjoin_tree_data = gpd.sjoin(tree_data, city_center, how="left")
def GenerateIndices(label, df, scientific_name_column, genus_name_column, family_name_column, basal_area_column):
# Derive counts, areas, for species, genus, and family
species_count = df[[scientific_name_column, basal_area_column]].groupby(scientific_name_column).count().reset_index()
species_area = df[[scientific_name_column, basal_area_column]].groupby(scientific_name_column).sum().reset_index()
genus_count = df[[genus_name_column, basal_area_column]].groupby(genus_name_column).count().reset_index()
genus_area = df[[genus_name_column, basal_area_column]].groupby(genus_name_column).sum().reset_index()
family_count = df[[family_name_column, basal_area_column]].groupby(family_name_column).count().reset_index()
family_area = df[[family_name_column, basal_area_column]].groupby(family_name_column).sum().reset_index()
# Calculate Percentages by count and area
species_count["Pct"] = species_count[basal_area_column]/sum(species_count[basal_area_column])
species_area["Pct"] = species_area[basal_area_column]/sum(species_area[basal_area_column])
genus_count["Pct"] = genus_count[basal_area_column]/sum(genus_count[basal_area_column])
genus_area["Pct"] = genus_area[basal_area_column]/sum(genus_area[basal_area_column])
family_count["Pct"] = family_count[basal_area_column]/sum(family_count[basal_area_column])
family_area["Pct"] = family_area[basal_area_column]/sum(family_area[basal_area_column])
# Calculate Shannon Indices
species_shannon_count = tP.ShannonEntropy(list(species_count["Pct"]))
species_shannon_area = tP.ShannonEntropy(list(species_area["Pct"]))
genus_shannon_count = tP.ShannonEntropy(list(genus_count["Pct"]))
genus_shannon_area = tP.ShannonEntropy(list(genus_area["Pct"]))
family_shannon_count = tP.ShannonEntropy(list(family_count["Pct"]))
family_shannon_area = tP.ShannonEntropy(list(family_area["Pct"]))
# Calculate Simpson Indices
species_simpson_count = tP.simpson_di(list(species_count[scientific_name_column]), list(species_count[basal_area_column]))
species_simpson_area = tP.simpson_di(list(species_area[scientific_name_column]),list(species_area[basal_area_column]))
genus_simpson_count = tP.simpson_di(list(genus_count[genus_name_column]), list(genus_count[basal_area_column]))
genus_simpson_area = tP.simpson_di(list(genus_area[genus_name_column]), list(genus_area[basal_area_column]))
family_simpson_count = tP.simpson_di(list(family_count[family_name_column]), list(family_count[basal_area_column]))
family_simpson_area = tP.simpson_di(list(family_area[family_name_column]), list(family_area[basal_area_column]))
return {
'Geography':label,
'species_simpson_count': species_simpson_count,
'species_simpson_area': species_simpson_area,
'genus_simpson_count': genus_simpson_count,
'genus_simpson_area': genus_simpson_area,
'family_simpson_count': family_simpson_count,
'family_simpson_area': family_simpson_area,
'species_shannon_count': species_shannon_count,
'species_shannon_area': species_shannon_area,
'genus_shannon_count': genus_shannon_count,
'genus_shannon_area': genus_shannon_area,
'family_shannon_count': family_shannon_count,
'family_shannon_area': family_shannon_area
}
# Generate results and load into dataframe
temp_results = []
city_center_data = sjoin_tree_data[sjoin_tree_data.inside == True]
outside_center_data = sjoin_tree_data[sjoin_tree_data.inside != True]
temp_results.append(
GenerateIndices(
'Inside City Center',
city_center_data,
scientific_name_column,
genus_name_column,
family_name_column,
basal_area_column
)
)
temp_results.append(
GenerateIndices(
'Outside City Center',
outside_center_data,
scientific_name_column,
genus_name_column,
family_name_column,
basal_area_column
)
)
results = pd.DataFrame(temp_results)
results.head()
# Split up results for plotting
shannon_area = results.round(4)[['species_shannon_area','genus_shannon_area','family_shannon_area']].values
shannon_count = results.round(4)[['species_shannon_count','genus_shannon_count','family_shannon_count']].values
simpson_area = results.round(4)[['species_simpson_area','genus_simpson_area','family_simpson_area']].values
simpson_count = results.round(4)[['species_simpson_count','genus_simpson_count','family_simpson_count']].values
def autolabel(rects, axis):
"""Attach a text label above each bar in *rects*, displaying its height."""
for rect in rects:
height = rect.get_height()
axis.annotate('{}'.format(height),
xy=(rect.get_x() + rect.get_width() / 2, height),
xytext=(0, 3), # 3 points vertical offset
textcoords="offset points",
ha='center', va='bottom')
labels = ['Species', 'Genus', 'Family']
plt.rcParams["figure.figsize"] = [14, 7]
x = np.arange(len(labels)) # the label locations
width = 0.35 # the width of the bars
fig, axs = plt.subplots(2, 2)
rects1 = [axs[0,0].bar(x - width/2, shannon_area[0], width, color="lightsteelblue", label='City Center'), axs[0,0].bar(x + width/2, shannon_area[1], width, color="darkgreen", label='Outside City Center')]
rects2 = [axs[0,1].bar(x - width/2, shannon_count[0], width, color="lightsteelblue", label='City Center'), axs[0,1].bar(x + width/2, shannon_count[1], width, color="darkgreen", label='Outside City Center')]
rects3 = [axs[1,0].bar(x - width/2, simpson_area[0], width, color="lightsteelblue", label='City Center'), axs[1,0].bar(x + width/2, simpson_area[1], width, color="darkgreen", label='Outside City Center')]
rects4 = [axs[1,1].bar(x - width/2, simpson_count[0], width, color="lightsteelblue", label='City Center'), axs[1,1].bar(x + width/2, simpson_count[1], width, color="darkgreen", label='Outside City Center')]
axs[0,0].set_ylabel('Diversity Index')
axs[0,0].set_title('Shannon Diversity by Basal Area')
axs[0,0].set_xticks(x)
axs[0,0].set_xticklabels(labels)
axs[0,0].legend()
axs[0,1].set_ylabel('Diversity Index')
axs[0,1].set_title('Shannon Diversity by Count')
axs[0,1].set_xticks(x)
axs[0,1].set_xticklabels(labels)
axs[0,1].legend()
axs[1,0].set_ylabel('Diversity Index')
axs[1,0].set_title('Simpson Diversity by Basal Area')
axs[1,0].set_xticks(x)
axs[1,0].set_xticklabels(labels)
axs[1,0].legend()
axs[1,1].set_ylabel('Diversity Index')
axs[1,1].set_title('Simpson Diversity by Count')
axs[1,1].set_xticks(x)
axs[1,1].set_xticklabels(labels)
axs[1,1].legend()
autolabel(rects1[0], axs[0,0])
autolabel(rects1[1], axs[0,0])
autolabel(rects2[0], axs[0,1])
autolabel(rects2[1], axs[0,1])
autolabel(rects3[0], axs[1,0])
autolabel(rects3[1], axs[1,0])
autolabel(rects4[0], axs[1,1])
autolabel(rects4[1], axs[1,1])
axs[0,0].set_ylim([0,max(shannon_count.max(), shannon_area.max())+0.5])
axs[0,1].set_ylim([0,max(shannon_count.max(), shannon_area.max())+0.5])
axs[1,0].set_ylim([0,1])
axs[1,1].set_ylim([0,1])
fig.tight_layout()
plt.show()
```
# Interpreting these Results
For both indices, a higher score represents a more diverse body of street trees. If your city follows our general findings, the city center tends to be less diverse. The results provide some context on the evenness of the diversity in the city center and outside areas. The cells below calculate how well your street trees adhere to the 10/20/30 standard.
____
# 10/20/30 Standard
The 10/20/30 rule suggests that urban forests should be made up of no more than 10% from one species, 20% from one genus, or 30% from one family. A more optimistic version, the 5/10/15 rule, argues that those values should be halved.
Below, we'll calculate how well your tree inventory data adheres to these rules and then chart the results.
```
def GetPctRule(df, column, basal_area_column, predicate, location):
if predicate == 'area':
tempData = df[[basal_area_column,column]].groupby(column).sum().sort_values(basal_area_column, ascending=False).reset_index()
else:
tempData = df[[basal_area_column,column]].groupby(column).count().sort_values(basal_area_column, ascending=False).reset_index()
total = tempData[basal_area_column].sum()
return {
'name':column,
'location': location,
'predicate':predicate,
'most common': tempData.iloc[0][column],
'amount': tempData.iloc[0][basal_area_column],
'percent': round(tempData.iloc[0][basal_area_column]/total*100,2),
'total': total,
}
temp_results = []
for location in ['City Center', 'Outside City Center']:
for column in [scientific_name_column, genus_name_column, family_name_column]:
for predicate in ['area', 'count']:
if location == 'City Center':
df = city_center_data
else:
df = outside_center_data
temp_results.append(GetPctRule(df, column, basal_area_column, predicate, location))
results = pd.DataFrame(temp_results)
results.head()
results[results.name=='Scientific']
fig, axs = plt.subplots(3,2)
columns = [scientific_name_column, genus_name_column, family_name_column]
predicates=['area', 'count']
max_value = results.percent.max() * 1.2
for row in [0,1,2]:
temp_data = results[results.name==columns[row]]
for col in [0,1]:
temp_col_data = temp_data[temp_data.predicate==predicates[col]]
if row == 0:
x_value = 10
text="Species Benchmark"
elif row == 1:
x_value = 20
text="Genus Benchmark"
else:
x_value = 30
text="Family Benchmark"
if col == 0:
title = text + ' (Area)'
else:
title = text + ' (Count)'
axs[row,col].set_xlabel('Percent of Tree Inventory')
axs[row,col].set_xlim([0,max_value])
axs[row,col].set_ylim([-0.1,0.1])
axs[row,col].get_yaxis().set_visible(False)
axs[row,col].plot([0,max_value], [0,0], c='darkgray')
axs[row,col].scatter(x=x_value, y=0, marker='|', s=1000, c='darkgray')
axs[row,col].text(x=x_value+1, y=0.02, linespacing=2, s=text, c='black')
axs[row,col].set_title(title)
axs[row,col].scatter(x=float(temp_col_data[temp_col_data.location=='City Center'].percent), y=0, s=100, c='lightsteelblue', label='City Center')
axs[row,col].scatter(x=float(temp_col_data[temp_col_data.location=='Outside City Center'].percent), y=0, s=100, c='darkgreen', label='Outside City Center')
axs[row,col].legend()
plt.tight_layout()
plt.show()
```
# Interpreting these Results
The closer the green dots are to the vertical benchmark line, the closer the tree inventory is to meeting the benchmark. Ideally, each dot should be at or to the left of that taxonomy level's benchmark (10, 20, or 30%). The charts on the left reflect tree species diversity by area, which may better reflect the street trees scaled to their mass, and the right column tracks the count of trees, which is more widely used in urban forestry.
These charts do not define the success of the street tree inventory you are exploring, but they do highlight whether or not the data adheres to suggested urban forestry standards.
___
Want to share you results? Contact us at ***[email protected]***, we'd love to hear how you used this notebook!
|
github_jupyter
|
# Linear Regression
---
- Author: Diego Inácio
- GitHub: [github.com/diegoinacio](https://github.com/diegoinacio)
- Notebook: [regression_linear.ipynb](https://github.com/diegoinacio/machine-learning-notebooks/blob/master/Machine-Learning-Fundamentals/regression_linear.ipynb)
---
Overview and implementation of *Linear Regression* analysis.
```
%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
from regression__utils import *
# Synthetic data 1
x, yA, yB, yC, yD = synthData1()
```

## 1. Simple
---
$$ \large
y_i=mx_i+b
$$
Where **m** describes the angular coefficient (or line slope) and **b** the linear coefficient (or line y-intersept).
$$ \large
m=\frac{\sum_i^n (x_i-\overline{x})(y_i-\overline{y})}{\sum_i^n (x_i-\overline{x})^2}
$$
$$ \large
b=\overline{y}-m\overline{x}
$$
```
class linearRegression_simple(object):
def __init__(self):
self._m = 0
self._b = 0
def fit(self, X, y):
X = np.array(X)
y = np.array(y)
X_ = X.mean()
y_ = y.mean()
num = ((X - X_)*(y - y_)).sum()
den = ((X - X_)**2).sum()
self._m = num/den
self._b = y_ - self._m*X_
def pred(self, x):
x = np.array(x)
return self._m*x + self._b
lrs = linearRegression_simple()
%%time
lrs.fit(x, yA)
yA_ = lrs.pred(x)
lrs.fit(x, yB)
yB_ = lrs.pred(x)
lrs.fit(x, yC)
yC_ = lrs.pred(x)
lrs.fit(x, yD)
yD_ = lrs.pred(x)
```

$$ \large
MSE=\frac{1}{n} \sum_i^n (Y_i- \hat{Y}_i)^2
$$

## 2. Multiple
---
$$ \large
y=m_1x_1+m_2x_2+...+m_nx_n+b
$$
```
class linearRegression_multiple(object):
def __init__(self):
self._m = 0
self._b = 0
def fit(self, X, y):
X = np.array(X).T
y = np.array(y).reshape(-1, 1)
X_ = X.mean(axis = 0)
y_ = y.mean(axis = 0)
num = ((X - X_)*(y - y_)).sum(axis = 0)
den = ((X - X_)**2).sum(axis = 0)
self._m = num/den
self._b = y_ - (self._m*X_).sum()
def pred(self, x):
x = np.array(x).T
return (self._m*x).sum(axis = 1) + self._b
lrm = linearRegression_multiple()
%%time
# Synthetic data 2
M = 10
s, t, x1, x2, y = synthData2(M)
# Prediction
lrm.fit([x1, x2], y)
y_ = lrm.pred([x1, x2])
```


## 3. Gradient Descent
---
$$ \large
e_{m,b}=\frac{1}{n} \sum_i^n (y_i-(mx_i+b))^2
$$
To perform the gradient descent as a function of the error, it is necessary to calculate the gradient vector $\nabla$ of the function, described by:
$$ \large
\nabla e_{m,b}=\Big\langle\frac{\partial e}{\partial m},\frac{\partial e}{\partial b}\Big\rangle
$$
where:
$$ \large
\begin{aligned}
\frac{\partial e}{\partial m}&=\frac{2}{n} \sum_{i}^{n}-x_i(y_i-(mx_i+b)), \\
\frac{\partial e}{\partial b}&=\frac{2}{n} \sum_{i}^{n}-(y_i-(mx_i+b))
\end{aligned}
$$
```
class linearRegression_GD(object):
def __init__(self,
mo = 0,
bo = 0,
rate = 0.001):
self._m = mo
self._b = bo
self.rate = rate
def fit_step(self, X, y):
X = np.array(X)
y = np.array(y)
n = X.size
dm = (2/n)*np.sum(-x*(y - (self._m*x + self._b)))
db = (2/n)*np.sum(-(y - (self._m*x + self._b)))
self._m -= dm*self.rate
self._b -= db*self.rate
def pred(self, x):
x = np.array(x)
return self._m*x + self._b
%%time
lrgd = linearRegression_GD(rate=0.01)
# Synthetic data 3
x, x_, y = synthData3()
iterations = 3072
for i in range(iterations):
lrgd.fit_step(x, y)
y_ = lrgd.pred(x)
```

## 4. Non-linear analysis
---
```
# Synthetic data 4
# Anscombe's quartet
x1, y1, x2, y2, x3, y3, x4, y4 = synthData4()
%%time
lrs.fit(x1, y1)
y1_ = lrs.pred(x1)
lrs.fit(x2, y2)
y2_ = lrs.pred(x2)
lrs.fit(x3, y3)
y3_ = lrs.pred(x3)
lrs.fit(x4, y4)
y4_ = lrs.pred(x4)
```


|
github_jupyter
|
```
import sys
sys.path.append('../src')
import csv
import yaml
import tqdm
import math
import pickle
import numpy as np
import pandas as pd
import itertools
import operator
from operator import concat, itemgetter
from pickle_wrapper import unpickle, pickle_it
import matplotlib.pyplot as plt
import dask
from dask.distributed import Client
from pathlib import Path
from collections import defaultdict
from functools import reduce
from operator import concat, itemgetter
import ast
from pickle_wrapper import unpickle, pickle_it
from mcmc_norm_learning.algorithm_1_v4 import to_tuple
from mcmc_norm_learning.algorithm_1_v4 import create_data
from mcmc_norm_learning.rules_4 import get_prob, get_log_prob
from mcmc_norm_learning.environment import position,plot_env
from mcmc_norm_learning.robot_task_new import task, robot, plot_task
from mcmc_norm_learning.algorithm_1_v4 import algorithm_1, over_dispersed_starting_points
from mcmc_norm_learning.mcmc_convergence import prepare_sequences, calculate_R
from mcmc_norm_learning.rules_4 import q_dict, rule_dict, get_log_prob
from algorithm_2_utilities import Likelihood
from mcmc_norm_learning.mcmc_performance import performance
from collections import Counter
with open("../params_nc.yaml", 'r') as fd:
params = yaml.safe_load(fd)
```
### Step 1: Default Environment and params
```
##Get default env
env = unpickle('../data/env.pickle')
##Get default task
true_norm_exp = params['true_norm']['exp']
num_observations = params['num_observations']
obs_data_set = params['obs_data_set']
w_nc=params["w_nc"]
n = params['n']
m = params['m']
rf = params['rf']
rhat_step_size = params['rhat_step_size']
top_n = params["top_norms_n"]
colour_specific = params['colour_specific']
shape_specific = params['shape_specific']
target_area_parts = params['target_area'].replace(' ','').split(';')
target_area_part0 = position(*map(float, target_area_parts[0].split(',')))
target_area_part1 = position(*map(float, target_area_parts[1].split(',')))
target_area = (target_area_part0, target_area_part1)
print(target_area_part0.coordinates())
print(target_area_part1.coordinates())
the_task = task(colour_specific, shape_specific,target_area)
fig,axs=plt.subplots(1,2,figsize=(9,4),dpi=100);
plot_task(env,axs[0],"Initial Task State",the_task,True)
axs[1].text(0,0.5,"\n".join([str(x) for x in true_norm_exp]),wrap=True)
axs[1].axis("off")
```
### Step 2: Non Compliant Obs
```
obs = nc_obs= create_data(true_norm_exp,env,name=None,task=the_task,random_task=False,
num_actionable=np.nan,num_repeat=num_observations,w_nc=w_nc,verbose=False)
true_norm_prior = get_prob("NORMS",true_norm_exp)
true_norm_log_prior = get_log_prob("NORMS",true_norm_exp)
if not Path('../data_nc/observations_ad_0.1.pickle').exists():
pickle_it(obs, '../data_nc/observations_ad_0.1.pickle')
```
### Step 3: MCMC chains
```
%%time
%%capture
num_chains = math.ceil(m/2)
starts, info = over_dispersed_starting_points(num_chains,obs,env,\
the_task,time_threshold=math.inf,w_normative=(1-w_nc))
with open('../metrics/starts_info_nc_parallel.txt', 'w') as chain_info:
chain_info.write(info)
@dask.delayed
def delayed_alg1(obs,env,the_task,q_dict,rule_dict,start,rf,max_iters,w_nc):
exp_seq,log_likelihoods = algorithm_1(obs,env,the_task,q_dict,rule_dict,
"dummy value",start = start,relevance_factor=rf,\
max_iterations=max_iters,w_normative=1-w_nc,verbose=False)
log_posteriors = [None]*len(exp_seq)
for i in range(len(exp_seq)):
exp = exp_seq[i]
ll = log_likelihoods[i]
log_prior = get_log_prob("NORMS",exp) # Note: this imports the rules dict from rules_4.py
log_posteriors[i] = log_prior + ll
return {'chain': exp_seq, 'log_posteriors': log_posteriors}
%%time
%%capture
chains_and_log_posteriors=[]
for i in tqdm.tqdm(range(num_chains),desc="Loop for Individual Chains"):
chains_and_log_posteriors.append(
delayed_alg1(obs,env,the_task,q_dict,rule_dict,starts[i],rf,4*n,w_nc).compute())
from joblib import Parallel, delayed
def delayed_alg1_joblib(start_i):
alg1_result=delayed_alg1(obs=obs,env=env,the_task=the_task,q_dict=q_dict,\
rule_dict=rule_dict,start=start_i,rf=rf,\
max_iters=4*n,w_nc=w_nc).compute()
return (alg1_result)
%%time
%%capture
chains_and_log_posteriors=[]
chains_and_log_posteriors=Parallel(verbose = 2,n_jobs = -1\
)(delayed( delayed_alg1_joblib )(starts[run])\
for run in tqdm.tqdm(range(num_chains),desc="Loop for Individual Chains"))
pickle_it(chains_and_log_posteriors, '../data_nc/chains_and_log_posteriors.pickle')
```
### Step 4: Pass to analyse chains
```
with open('../metrics/chain_posteriors_nc.csv', 'w', newline='') as csvfile, \
open('../metrics/chain_info.txt', 'w') as chain_info:
chain_info.write(f'Number of chains: {len(chains_and_log_posteriors)}\n')
chain_info.write(f'Length of each chain: {len(chains_and_log_posteriors[0]["chain"])}\n')
csv_writer = csv.writer(csvfile)
csv_writer.writerow(('chain_number', 'chain_pos', 'expression', 'log_posterior'))
exps_in_chains = [None]*len(chains_and_log_posteriors)
for i,chain_data in enumerate(chains_and_log_posteriors): # Consider skipping first few entries
chain = chain_data['chain']
log_posteriors = chain_data['log_posteriors']
exp_lp_pairs = list(zip(chain,log_posteriors))
exps_in_chains[i] = set(map(to_tuple, chain))
#print(sorted(log_posteriors, reverse=True))
lps_to_exps = defaultdict(set)
for exp,lp in exp_lp_pairs:
lps_to_exps[lp].add(to_tuple(exp))
num_exps_in_chain = len(exps_in_chains[i])
print(lps_to_exps.keys())
print('\n')
chain_info.write(f'Num. expressions in chain {i}: {num_exps_in_chain}\n')
decreasing_lps = sorted(lps_to_exps.keys(), reverse=True)
chain_info.write("Expressions by decreasing log posterior\n")
for lp in decreasing_lps:
chain_info.write(f'lp = {lp} [{len(lps_to_exps[lp])} exps]:\n')
for exp in lps_to_exps[lp]:
chain_info.write(f' {exp}\n')
chain_info.write('\n')
chain_info.write('\n')
changed_exp_indices = [i for i in range(1,len(chain)) if chain[i] != chain[i-1]]
print(f'Writing {len(exp_lp_pairs)} rows to CSV file\n')
csv_writer.writerows(((i,j,chain_lp_pair[0],chain_lp_pair[1]) for j,chain_lp_pair in enumerate(exp_lp_pairs)))
all_exps = set(itertools.chain(*exps_in_chains))
chain_info.write(f'Total num. distinct exps across all chains (including warm-up): {len(all_exps)}\n')
true_norm_exp = params['true_norm']['exp']
true_norm_tuple = to_tuple(true_norm_exp)
chain_info.write(f'True norm in some chain(s): {true_norm_tuple in all_exps}\n')
num_chains_in_to_exps = defaultdict(set)
for exp in all_exps:
num_chains_in = operator.countOf(map(operator.contains,
exps_in_chains,
(exp for _ in range(len(exps_in_chains)))
),
True)
num_chains_in_to_exps[num_chains_in].add(exp)
for num in sorted(num_chains_in_to_exps.keys(), reverse=True):
chain_info.write(f'Out of {len(exps_in_chains)} chains ...\n')
chain_info.write(f'{len(num_chains_in_to_exps[num])} exps are in {num} chains.\n')
csvfile.close()
chain_info.close()
result=pd.read_csv("../metrics/chain_posteriors_nc.csv")
log_post_no_norm=Likelihood(["Norms",["No-Norm"]],the_task,obs,env,w_normative=1-w_nc)
log_post_true_norm=Likelihood(true_norm_exp,the_task,obs,env,w_normative=1-w_nc)
print(log_post_no_norm,log_post_true_norm)
result.groupby("chain_number")[["log_posterior"]].agg(['min','max','mean','std'])
hist_plot=result['log_posterior'].hist(by=result['chain_number'],bins=10)
plt.savefig("../data_nc/nc_hist.jpg")
grouped = result.groupby('chain_number')[["log_posterior"]]
ncols=2
nrows = int(np.ceil(grouped.ngroups/ncols))
fig, axes = plt.subplots(nrows=nrows, ncols=ncols, figsize=(14,5), sharey=False)
for (key, ax) in zip(grouped.groups.keys(), axes.flatten()):
grouped.get_group(key).plot(ax=ax)
ax.axhline(y=log_post_no_norm,label="No Norm",c='r')
ax.axhline(y=log_post_true_norm,label="True Norm",c='g')
ax.title.set_text("For chain={}".format(key))
ax.legend()
plt.show()
plt.savefig("../plots/nc_movement.jpg")
```
### Step 5: Convergence Tests
```
def conv_test(chains):
convergence_result, split_data = calculate_R(chains, rhat_step_size)
with open('../metrics/conv_test_nc.txt', 'w') as f:
f.write(convergence_result.to_string())
return reduce(concat, split_data)
chains = list(map(itemgetter('chain'), chains_and_log_posteriors))
posterior_sample = conv_test(prepare_sequences(chains, warmup=True))
pickle_it(posterior_sample, '../data_nc/posterior_nc.pickle')
```
### Step 6: Extract Top Norms
```
learned_expressions=Counter(map(to_tuple, posterior_sample))
top_norms_with_freq = learned_expressions.most_common(top_n)
top_norms = list(map(operator.itemgetter(0), top_norms_with_freq))
exp_posterior_df = pd.read_csv('../metrics/chain_posteriors_nc.csv', usecols=['expression','log_posterior'])
exp_posterior_df = exp_posterior_df.drop_duplicates()
exp_posterior_df['post_rank'] = exp_posterior_df['log_posterior'].rank(method='dense',ascending=False)
exp_posterior_df.sort_values('post_rank', inplace=True)
exp_posterior_df['expression'] = exp_posterior_df['expression'].transform(ast.literal_eval)
exp_posterior_df['expression'] = exp_posterior_df['expression'].transform(to_tuple)
exp_posterior_df
def log_posterior(exp, exp_lp_df):
return exp_lp_df.loc[exp_lp_df['expression'] == exp]['log_posterior'].iloc[0]
with open('../metrics/precision_recall_nc.txt', 'w') as f:
f.write(f"Number of unique Norms in sequence={len(learned_expressions)}\n")
f.write(f"Top {top_norms} norms:\n")
for expression,freq in top_norms_with_freq:
f.write(f"Freq. {freq}, lp {log_posterior(expression, exp_posterior_df)}: ")
f.write(f"{expression}\n")
f.write("\n")
pr_result=performance(the_task,env,true_norm_exp,learned_expressions,
folder_name="temp",file_name="top_norm",
top_n=n,beta=1,repeat=100000,verbose=False)
top_norms[3]
true_norm_exp
```
|
github_jupyter
|
# Clusters as Knowledge Areas of Annotators
```
# import required packages
import sys
sys.path.append("../..")
import warnings
warnings.filterwarnings('ignore')
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
from annotlib import ClusterBasedAnnot
from sklearn.datasets import make_classification
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import accuracy_score
from sklearn.cluster import KMeans
from sklearn.metrics import accuracy_score
```
A popular approach to simulate annotators is to use clustering methods.
By using clustering methods, we can emulate areas of knowledge.
The assumption is that the knowledge of an annotator is not constant for a whole classification problem, but there are areas where the annotator has a wider knowledge compared to areas of sparse knowledge.
As the samples lie in a feature space, we can model the area of knowledge as an area in the feature space.
The simulation of annotators by means of clustering is implemented by the class [ClusterBasedAnnot](../annotlib.cluster_based.rst).
To create such annotators, you have to provide the samples `X`, their corresponding true class labels `y_true` and the cluster labels `y_cluster`.
In this section, we introduce the following simulation options:
- class labels as clustering,
- clustering algorithms to find clustering,
- and feature space as a single cluster.
The code below generates a two-dimensional (`n_features=2`) artificial data set with `n_samples=500` samples and `n_classes=4` classes.
```
X, y_true = make_classification(n_samples=500, n_features=2,
n_informative=2, n_redundant=0,
n_repeated=0, n_classes=4,
n_clusters_per_class=1,
flip_y=0.1, random_state=4)
plt.figure(figsize=(5, 3), dpi=150)
plt.scatter(X[:, 0], X[:, 1], marker='o', c=y_true, s=10)
plt.title('artificial data set: samples with class labels', fontsize=7)
plt.xticks(fontsize=7)
plt.yticks(fontsize=7)
plt.show()
```
## 1. Class Labels as Clustering
If you do not provide any cluster labels `y_cluster`, the true class labels `y_true` are assumed to be a representive clustering.
As a result the class labels and cluster labels are equivalent `y_cluster = y_true` and define the knowledge areas of the simulated annotators.
To simulate annotators on this dataset, we create an instance of the [ClusterBasedAnnot](../annotlib.cluster_based.rst) class by providing the samples `X` with the true labels `y_true` as input.
```
# simulate annotators where the clusters are defined by the class labels
clust_annot_cls = ClusterBasedAnnot(X=X, y_true=y_true, random_state=42)
```
The above simulated annotators have knowledge areas defined by the class label distribution.
As a result, there are four knowledge areas respectively clusters.
In the default setting, the number of annotators is equal to the number of defined clusters.
Correspondingly, there are four simulated annotators in our example.
☝🏽An important aspect is the simulation of the labelling performances of the annotators on the different clusters.
By default, each annotator is assumed to be an expert on a single cluster.
Since we have four clusters and four annotators, each cluster has only one annotator as expert.
Being an expert means that an annotator has a higher probability for providing the correct class label for a sample than in the clusters of low expertise.
Let the number of clusters be $K$ (`n_clusters`) and the number of annotators be $A$ (`n_annotators`).
For the case $K=A$, an annotator $a_i$ is expert on cluster $c_i$ with $i \in \{0,\dots,A-1\}$, the probability of providing the correct class label $y^{\text{true}}_\mathbf{x}$ for sample $\mathbf{x} \in c_i$ is defined by
$$p(y^{\text{true}}_\mathbf{x} \mid \mathbf{x}, a_i, c_i) = U(0.8, 1.0)$$
where $U(a,b)$ means that a value is uniformly drawn from the interval $[0.8, 1.0]$.
In contrast for the clusters of low expertise, the default probability for providing a correct class label is defined by
$$p(y^{\text{true}}_\mathbf{x} \mid \mathbf{x}, a_i, c_j) = U\left(\frac{1}{C}, \text{min}(\frac{1}{C}+0.1,1)\right),$$
where $j=0,\dots,A-1$, $j\neq i$ and $C$ denotes the number of classes (`n_classes`).
These properties apply only for the default settings.
The actual labelling accuracies per cluster are exemplary plotted for annotator $a_0$ below.
```
acc_cluster = clust_annot_cls.labelling_performance_per_cluster(accuracy_score)
x = np.arange(len(np.unique(clust_annot_cls.y_cluster_)))
plt.figure(figsize=(4, 2), dpi=150)
plt.bar(x, acc_cluster[0])
plt.xticks(x, ('cluster $c_0$', 'cluster $c_1$', 'cluster $c_2$',
'cluster $c_3$'), fontsize=7)
plt.ylabel('labelling accuracy', fontsize=7)
plt.title('labelling accuracy of annotator $a_0$',
fontsize=7)
plt.show()
```
The above figure matches the description of the default behaviour.
We can see that the accuracy of annotator $a_0$ is high in cluster $c_0$, whereas the labelling accuracy on the remaining clusters is comparable to randomly guessing of class labels.
You can also manually define properties of the annotators.
This may be interesting when you want to evaluate the performance of a developed method coping with multiple uncertain annotators.
Let's see how the ranges of uniform distributions for correct class labels on the clusters can be defined manually. For the default setting, we observe the following ranges:
```
print('ranges of uniform distributions for correct'
+' class labels on the clusters:')
for a in range(clust_annot_cls.n_annotators()):
print('annotator a_' + str(a) + ':\n'
+ str(clust_annot_cls.cluster_labelling_acc_[a]))
```
The attribute `cluster_labelling_acc_` is an array with the shape `(n_annotators, n_clusters, 2)` and can be defined by means of the parameter `cluster_labelling_acc`.
This parameter may be either a `str` or array-like.
By default, `cluster_labelling_acc='one_hot'` is valid, which indicates that each annotator is expert on one cluster.
Another option is `cluster_labelling_acc='equidistant'` and is explained in one of the following examples.
The entry `cluster_labelling_acc_[i, j , 0]` indicates the lower limit of the uniform distribution for correct class labels of annotator $a_i$ on cluster $c_j$. Analogous, the entry `cluster_labelling_acc_[i, j ,1]` represents the upper limit.
The sampled probabilities for correct class labels are also the confidence scores of the annotators.
An illustration of the annotators $a_0$ and $a_1$ simulated with default values on the predefined data set is given in the following plots.
The confidence scores correspond to the size of the crosses and dots.
```
clust_annot_cls.plot_class_labels(X=X, y_true=y_true, annotator_ids=[0, 1],
plot_confidences=True)
print('The confidence scores correspond to the size of the crosses and dots.')
plt.tight_layout()
plt.show()
```
☝🏽To sum up, by using the true class labels `y_true` as proxy of a clustering and specifying the input parameter `cluster_labelling_acc`, annotators being experts on different classes can be simulated.
## 2. Clustering Algorithms to Find Clustering
There are several algorithms available for perfoming clustering on a data set. The framework *scikit-learn* provides many clustering algorithms, e.g.
- `sklearn.cluster.KMeans`,
- `sklearn.cluster.DBSCAN`,
- `sklearn.cluster.AgglomerativeClustering`,
- `sklearn.cluster.bicluster.SpectralBiclusterin`,
- `sklearn.mixture.BayesianGaussianMixture`,
- and `sklearn.mixture.GaussianMixture`.
We examplary apply the `KMeans` algorithm being a very popular clustering algorithm.
For this purpose, you have to specify the number of clusters.
By doing so, you determine the number of different knowledge areas in the feature space with reference to the simulation of annotators.
We set `n_clusters = 3` as number of clusters.
The clusters found by `KMeans` on the previously defined data set are given in the following:
```
# standardize features of samples
X_z = StandardScaler().fit_transform(X)
# apply k-means algorithm
y_cluster_k_means = KMeans(n_clusters=3).fit_predict(X_z)
# plot found clustering
plt.figure(figsize=(5, 3), dpi=150)
plt.scatter(X[:, 0], X[:, 1], c=y_cluster_k_means, s=10)
plt.title('samples with cluster labels of k-means algorithm', fontsize=7)
plt.xticks(fontsize=7)
plt.yticks(fontsize=7)
plt.show()
```
The clusters are found on the standardised data set, so that the mean of each feature is 0 and the variance is 1.
The computed cluster labels `y_cluster` are used as input parameter to simulate two annotators, where the annotator $a_0$ is expert on two clusters and the annotator $a_1$ is expert on one cluster.
```
# define labelling accuracy ranges on four clusters for three annotators
clu_label_acc_km = np.array([[[0.8, 1], [0.8, 1], [0.3, 0.5]],
[[0.3, 0.5], [0.3, 0.5], [0.8, 1]]])
# simulate annotators
cluster_annot_kmeans = ClusterBasedAnnot(X=X, y_true=y_true,
y_cluster=y_cluster_k_means,
n_annotators=2,
cluster_labelling_acc=clu_label_acc_km)
# scatter plots of annotators
cluster_annot_kmeans.plot_class_labels(X=X, y_true=y_true,
plot_confidences=True,
annotator_ids=[0, 1])
plt.tight_layout()
plt.show()
```
☝🏽The employment of different clustering allows to define almost arbitrarily knowledge areas and offers a huge flexibiility.
However, the clusters should reflect the actual regions within a feature space.
## 3. Feature Space as a Single Cluster
Finally, you can simulate annotators whose knowledge does not depend on clusters.
Hence, their knowledge level is constant over the whole feature space.
To emulate such a behaviour, you create a clustering array `y_cluster_const`, in which all samples in the feature space are assigned to the same cluster.
```
y_cluster_const = np.zeros(len(X), dtype=int)
cluster_annot_const = ClusterBasedAnnot(X=X, y_true=y_true,
y_cluster=y_cluster_const,
n_annotators=5,
cluster_labelling_acc='equidistant')
# plot labelling accuracies
cluster_annot_const.plot_labelling_accuracy(X=X, y_true=y_true,
figsize=(4, 2), fontsize=6)
plt.show()
# print predefined labelling accuracies
print('ranges of uniform distributions for correct class '
+ 'labels on the clusters:')
for a in range(cluster_annot_const.n_annotators()):
print('annotator a_' + str(a) + ': '
+ str(cluster_annot_const.cluster_labelling_acc_[a]))
```
Five annotators are simulated whose labelling accuracy intervals are increasing with the index number of the annotator.
☝🏽The input parameter `cluster_labelling_acc='equidistant'` means that the lower bounds of the labelling accuracy intervals between two annotators have always the same distance.
In general, the interval of the correct labelling probability for annotator $a_i$ is computed by
$$d = \frac{1 - \frac{1}{C}}{A+1},$$
$$p(y^{(\text{true})}_\mathbf{x} \mid \mathbf{x}, a_i, c_j) \in U(\frac{1}{C} + i \cdot d, \frac{1}{C} + 2 \cdot i \cdot d),$$
where $i=0,\dots,A-1$ and $j=0,\dots,K-1$ with $K$.
This procedure ensures that the intervals of the correct labelling probabilities are overlapping.
|
github_jupyter
|
**This notebook is an exercise in the [Introduction to Machine Learning](https://www.kaggle.com/learn/intro-to-machine-learning) course. You can reference the tutorial at [this link](https://www.kaggle.com/dansbecker/your-first-machine-learning-model).**
---
## Recap
So far, you have loaded your data and reviewed it with the following code. Run this cell to set up your coding environment where the previous step left off.
```
# Code you have previously used to load data
import pandas as pd
# Path of the file to read
iowa_file_path = '../input/home-data-for-ml-course/train.csv'
home_data = pd.read_csv(iowa_file_path)
# Set up code checking
from learntools.core import binder
binder.bind(globals())
from learntools.machine_learning.ex3 import *
print("Setup Complete")
```
# Exercises
## Step 1: Specify Prediction Target
Select the target variable, which corresponds to the sales price. Save this to a new variable called `y`. You'll need to print a list of the columns to find the name of the column you need.
```
# print the list of columns in the dataset to find the name of the prediction target
home_data.columns
y = home_data.SalePrice
# Check your answer
step_1.check()
# The lines below will show you a hint or the solution.
# step_1.hint()
# step_1.solution()
```
## Step 2: Create X
Now you will create a DataFrame called `X` holding the predictive features.
Since you want only some columns from the original data, you'll first create a list with the names of the columns you want in `X`.
You'll use just the following columns in the list (you can copy and paste the whole list to save some typing, though you'll still need to add quotes):
* LotArea
* YearBuilt
* 1stFlrSF
* 2ndFlrSF
* FullBath
* BedroomAbvGr
* TotRmsAbvGrd
After you've created that list of features, use it to create the DataFrame that you'll use to fit the model.
```
# Create the list of features below
feature_names = ['LotArea', 'YearBuilt', '1stFlrSF', '2ndFlrSF', 'FullBath', 'BedroomAbvGr', 'TotRmsAbvGrd']
# Select data corresponding to features in feature_names
X = home_data[feature_names]
# Check your answer
step_2.check()
# step_2.hint()
# step_2.solution()
```
## Review Data
Before building a model, take a quick look at **X** to verify it looks sensible
```
# Review data
# print description or statistics from X
X.describe()
# print the top few lines
X.head()
```
## Step 3: Specify and Fit Model
Create a `DecisionTreeRegressor` and save it iowa_model. Ensure you've done the relevant import from sklearn to run this command.
Then fit the model you just created using the data in `X` and `y` that you saved above.
```
from sklearn.tree import DecisionTreeRegressor
#specify the model.
#For model reproducibility, set a numeric value for random_state when specifying the model
iowa_model = DecisionTreeRegressor(random_state=2021)
# Fit the model
iowa_model.fit(X, y)
# Check your answer
step_3.check()
# step_3.hint()
# step_3.solution()
```
## Step 4: Make Predictions
Make predictions with the model's `predict` command using `X` as the data. Save the results to a variable called `predictions`.
```
predictions = iowa_model.predict(X)
print(predictions)
# Check your answer
step_4.check()
# step_4.hint()
# step_4.solution()
```
## Think About Your Results
Use the `head` method to compare the top few predictions to the actual home values (in `y`) for those same homes. Anything surprising?
```
# You can write code in this cell
y.head()
```
It's natural to ask how accurate the model's predictions will be and how you can improve that. That will be you're next step.
# Keep Going
You are ready for **[Model Validation](https://www.kaggle.com/dansbecker/model-validation).**
---
*Have questions or comments? Visit the [Learn Discussion forum](https://www.kaggle.com/learn-forum/161285) to chat with other Learners.*
|
github_jupyter
|
# Meet in the Middle Attack
- Given prime `p`
- then `Zp* = {1, 2, 3, ..., p-1}`
- let `g` and `h` be elements in `Zp*` such that
- such that `h mod p = g^x mod p` where ` 0 < x < 2^40`
- find `x` given `h`, `g`, and `p`
# Idea
- let `B = 2^20` then `B^2 = 2^40`
- then `x= xo * B + x1` where `xo` and `x1` are in `{0, 1, ..., B-1}`
- Then smallest x is `x = 0 * B + O = 0`
- Largest x is `x = B * (B-1) + B - 1 = B^2 - B + B -1 = B^2 - 1 = 2^40 - 1`
- Then:
```
h = g^x
h = g^(xo * B + x1)
h = g^(xo * B) * g^(x1)
h / g^(x1) = g^(xo *B)
```
- Find `xo` and `x1` given `g`, `h`, `B`
# Strategy
- Build a hash table key: `h / g^(x1)`, with value `x1` for `x1` in `{ 0, 1, 2, .., 2^20 - 1}`
- For each value `x0` in `{0, 1, 2, ... 20^20 -1}` check if `(g^B)^(x0) mod P` is in hashtable. If it is then you've found `x0` and `x1`
- Return `x = xo * B + x1`
### Modulo Division
```
(x mod p) / ( y mod p) = ((x mod p) * (y_inverse mod p)) mod p
```
### Definition of inverse
```
Definition of modular inverse in Zp
y_inverse * y mod P = 1
```
### Inverse of `x` in `Zp*`
```
Given p is prime,
then for every element x in set Zp* = {1, ..., p - 1}
the element x is invertible (there exist an x_inverse such that:
x_inverse * x mod p = 1
The following is true (according to Fermat's 1640)
> x^(p - 1) mod = 1
> x ^ (p - 2) * x mod p = 1
> x_inverse = x^(p-2)
```
# Notes
- Work is `2^20` multiplications and `2^20` lookups in the worst case
- If we brute forced it, we would do `2^40` multiplications
- So the work is squareroot of brute force
# Test Numbers
```
p = 134078079299425970995740249982058461274793658205923933\
77723561443721764030073546976801874298166903427690031\
858186486050853753882811946569946433649006084171
g = 11717829880366207009516117596335367088558084999998952205\
59997945906392949973658374667057217647146031292859482967\
5428279466566527115212748467589894601965568
h = 323947510405045044356526437872806578864909752095244\
952783479245297198197614329255807385693795855318053\
2878928001494706097394108577585732452307673444020333
```
# Library used
- https://gmpy2.readthedocs.io/en/latest/mpz.html
```
from gmpy2 import mpz
from gmpy2 import t_mod, invert, powmod, add, mul, is_prime
def build_table(h, g, p, B):
table, z = {}, h
g_inverse = invert(g, p)
table[h] = 0
for x1 in range(1, B):
z = t_mod(mul(z, g_inverse), p)
table[z] = x1
return table
def lookup(table, g, p, B):
gB, z = powmod(g, B, p), 1
for x0 in range(B):
if z in table:
x1 = table[z]
return x0, x1
z = t_mod(mul(z, gB), p)
return None, None
def find_x(h, g, p, B):
table = build_table(h, g, p, B)
x0, x1 = lookup(table, g, p, B)
# assert x0 != None and x1 != None
Bx0 = mul(x0, B)
x = add(Bx0, x1)
print(x0, x1)
return x
p_string = '13407807929942597099574024998205846127479365820592393377723561443721764030073546976801874298166903427690031858186486050853753882811946569946433649006084171'
g_string = '11717829880366207009516117596335367088558084999998952205599979459063929499736583746670572176471460312928594829675428279466566527115212748467589894601965568'
h_string = '3239475104050450443565264378728065788649097520952449527834792452971981976143292558073856937958553180532878928001494706097394108577585732452307673444020333'
p = mpz(p_string)
g = mpz(g_string)
h = mpz(h_string)
B = mpz(2) ** mpz(20)
assert is_prime(p)
assert g < p
assert h < p
x = find_x(h, g, p, B)
print(x)
assert h == powmod(g, x, p)
```
|
github_jupyter
|
# Vega, Ibis, and OmniSci Performance
In this notebook we will show two charts. The first generally works, albeit is a bit slow. The second is basically inoperable because of performance issues.
I believe these performance issues are primarily due to two limitations in Vega currently:
1. Each transform in the dataflow graph is executed syncronously. Ideally, we should be able to parallilize the database queries launched by each transform.
2. The UI blocks while waiting for an async transform to complete. This isn't noticeable normally in Vega, but when running all the transforms takes multiple seconds, it makes scrolling and panning basically inoperable.
We will use Jaeger / OpenTracing to look at the timing of the various events to understand the performance.
## Setup
Before launching these, first open the "Jager UI" in a new window, so traces will be collected. You can do this by going to `./jaeger` instead of `./lab` or by clicking the `Jaeger` button in the JupyterLab launcher.
## Time Series Chart
1. Run these cells to create a chart
```
import altair as alt
import ibis_vega_transform
import warnings
try:
from ibis.backends import omniscidb as ibis_omniscidb
except ImportError as msg:
warnings.warn(str(msg))
from ibis import omniscidb as ibis_omniscidb
conn = ibis_omniscidb.connect(
host='metis.mapd.com', user='demouser', password='HyperInteractive',
port=443, database='mapd', protocol= 'https'
)
t = conn.table("flights_donotmodify")
states = alt.selection_multi(fields=['origin_state'])
airlines = alt.selection_multi(fields=['carrier_name'])
# Copy default from
# https://github.com/vega/vega-lite/blob/8936751a75c3d3713b97a85b918fb30c35262faf/src/selection.ts#L281
# but add debounce
# https://vega.github.io/vega/docs/event-streams/#basic-selectors
DEBOUNCE_MS = 400
dates = alt.selection_interval(
fields=['dep_timestamp'],
encodings=['x'],
on=f'[mousedown, window:mouseup] > window:mousemove!{{0, {DEBOUNCE_MS}}}',
translate=f'[mousedown, window:mouseup] > window:mousemove!{{0, {DEBOUNCE_MS}}}',
zoom=False
)
HEIGHT = 800
WIDTH = 1000
count_filter = alt.Chart(
t[t.dep_timestamp, t.depdelay, t.origin_state, t.carrier_name],
title="Selected Rows"
).transform_filter(
airlines
).transform_filter(
dates
).transform_filter(
states
).mark_text().encode(
text='count()'
)
count_total = alt.Chart(
t,
title="Total Rows"
).mark_text().encode(
text='count()'
)
flights_by_state = alt.Chart(
t[t.origin_state, t.carrier_name, t.dep_timestamp],
title="Total Number of Flights by State"
).transform_filter(
airlines
).transform_filter(
dates
).mark_bar().encode(
x='count()',
y=alt.Y('origin_state', sort=alt.Sort(encoding='x', order='descending')),
color=alt.condition(states, alt.ColorValue("steelblue"), alt.ColorValue("grey"))
).add_selection(
states
).properties(
height= 2 * HEIGHT / 3,
width=WIDTH / 2
) + alt.Chart(
t[t.origin_state, t.carrier_name, t.dep_timestamp],
).transform_filter(
airlines
).transform_filter(
dates
).mark_text(dx=20).encode(
x='count()',
y=alt.Y('origin_state', sort=alt.Sort(encoding='x', order='descending')),
text='count()'
).properties(
height= 2 * HEIGHT / 3,
width=WIDTH / 2
)
carrier_delay = alt.Chart(
t[t.depdelay, t.arrdelay, t.carrier_name, t.origin_state, t.dep_timestamp],
title="Carrier Departure Delay by Arrival Delay (Minutes)"
).transform_filter(
states
).transform_filter(
dates
).transform_aggregate(
depdelay='mean(depdelay)',
arrdelay='mean(arrdelay)',
groupby=["carrier_name"]
).mark_point(filled=True, size=200).encode(
x='depdelay',
y='arrdelay',
color=alt.condition(airlines, alt.ColorValue("steelblue"), alt.ColorValue("grey")),
tooltip=['carrier_name', 'depdelay', 'arrdelay']
).add_selection(
airlines
).properties(
height=2 * HEIGHT / 3,
width=WIDTH / 2
) + alt.Chart(
t[t.depdelay, t.arrdelay, t.carrier_name, t.origin_state, t.dep_timestamp],
).transform_filter(
states
).transform_filter(
dates
).transform_aggregate(
depdelay='mean(depdelay)',
arrdelay='mean(arrdelay)',
groupby=["carrier_name"]
).mark_text().encode(
x='depdelay',
y='arrdelay',
text='carrier_name',
).properties(
height=2 * HEIGHT / 3,
width=WIDTH / 2
)
time = alt.Chart(
t[t.dep_timestamp, t.depdelay, t.origin_state, t.carrier_name],
title='Number of Flights by Departure Time'
).transform_filter(
'datum.dep_timestamp != null'
).transform_filter(
airlines
).transform_filter(
states
).mark_line().encode(
alt.X(
'yearmonthdate(dep_timestamp):T',
),
alt.Y(
'count():Q',
scale=alt.Scale(zero=False)
)
).add_selection(
dates
).properties(
height=HEIGHT / 3,
width=WIDTH + 50
)
(
(count_filter | count_total) &
(flights_by_state | carrier_delay) &
time
).configure_axis(
grid=False
).configure_view(
strokeOpacity=0
)
```
1. Wait for it to render
2. Reload the Jaeger UI page
3. Select the "kernel" service
4. Select "Find Traces"
5. Select the first trace.
6. Now you should be able to see that each transform happens syncronously.
7. If you click on each trace, you should also be able to see logs, including the original Vega Lite spec, the original Vega Spec, and the transformed Vega spec.
If filter based on the top charts, things seem to work OK, even though the UI is a bit slow.
However, if you try to filter based on the bottom chart, by clicking and dragging, you will see it does work, but the UI is not ideal, because you can't see your selection until it finishes getting the data. Ideally, it would show your current time selectiona show some sort of loading UI in the other sections.
## Geospatial Chart
Now we will try to render a geospatial chart, by binning by pixel:
```
t2 = conn.table("tweets_nov_feb")
x, y = t2.goog_x, t2.goog_y
WIDTH = 385
HEIGHT = 564
X_DOMAIN = [
-3650484.1235206556,
7413325.514451755
]
Y_DOMAIN = [
-5778161.9183506705,
10471808.487466192
]
scales = alt.selection_interval(bind='scales')
alt.Chart(t2[x, y], width=WIDTH, height=HEIGHT).mark_rect().encode(
alt.X(
'bin_x:Q',
bin=alt.Bin(binned=True),
title='goog_x',
scale=alt.Scale(domain=X_DOMAIN)
),
alt.X2('bin_x_end'),
alt.Y(
'bin_y:Q',
bin=alt.Bin(binned=True),
title='goog_y',
scale=alt.Scale(domain=Y_DOMAIN)
),
alt.Y2('bin_y_end'),
tooltip='count()',
color=alt.Color(
'count()',
scale=alt.Scale(type='log')
)
).add_selection(
scales
).transform_filter(
scales
).transform_bin(
'bin_x',
'goog_x',
bin=alt.Bin(maxbins=WIDTH)
).transform_bin(
'bin_y',
'goog_y',
bin=alt.Bin(maxbins=HEIGHT)
)
```
Now try to drag this to pan around.
You will notice a few things. First, it actually will does work, but it takes so long to move that it's hard to control. Second, It seems like the initial bin is different than the later bins.
|
github_jupyter
|
# Cross-Validation
Cross-validation is a step where we take our training sample and further divide it in many folds, as in the illustration here:
```{image} ./img/feature_5_fold_cv.jpg
:alt: 5-fold
:width: 400px
:align: center
```
As we talked about in the last chapter, cross-validation allows us to test our models outside the training data more often. This trick reduces the likelihood of overfitting and improves generalization: It _should_ improve our model's performance when we apply it outside the training data.
```{warning}
I say "_should_" because the exact manner in which you create the folds matters.
```
- **If your data has groups** (i.e. repeated observations for a given firm), you should use [group-wise cross-validation](https://scikit-learn.org/stable/modules/cross_validation.html#group-cv), like `GroupKFold` to make sure no group is in the training and validation partitions of the fold
- **If your data and/or task is time dependent**, like predicting stock returns, you should use a [time-wise cross-validation](https://scikit-learn.org/stable/modules/cross_validation.html#timeseries-cv), like `TimeSeriesSplit` to ensure that the validation partitions are subsequent to the training sample
```{margin}
Illustration: If you emulate the simple folding method as depicted in the above graphic for stock return data, some folds will end up testing your model on data from _before_ the periods where the model was estimated!
```
---
## CV in practice
Like before, let's load the data. Notice I consolidated the import lines at the top.
```
import pandas as pd
import numpy as np
from sklearn.linear_model import Ridge
from sklearn.model_selection import train_test_split
url = 'https://github.com/LeDataSciFi/ledatascifi-2021/blob/main/data/Fannie_Mae_Plus_Data.gzip?raw=true'
fannie_mae = pd.read_csv(url,compression='gzip').dropna()
y = fannie_mae.Original_Interest_Rate
fannie_mae = (fannie_mae
.assign(l_credscore = np.log(fannie_mae['Borrower_Credit_Score_at_Origination']),
l_LTV = np.log(fannie_mae['Original_LTV_(OLTV)']),
)
.iloc[:,-11:] # limit to these vars for the sake of this example
)
```
### **STEP 1:** Set up your test and train split samples
```
rng = np.random.RandomState(0) # this helps us control the randomness so we can reproduce results exactly
X_train, X_test, y_train, y_test = train_test_split(fannie_mae, y, random_state=rng)
```
---
**An important digression:** Now that we've introduced some of the conceptual issues with how you create folds for CV, let's revisit this `test_train_split` code above. [This page](https://scikit-learn.org/stable/modules/cross_validation.html#using-cross-validation-iterators-to-split-train-and-test) says `train_test_split` uses [ShuffleSplit](https://scikit-learn.org/stable/modules/cross_validation.html#random-permutations-cross-validation-a-k-a-shuffle-split). This method does not divide by time or any group type.
```{dropdown} Q: Does this data need special attention to how we divide it up?
A question to ponder, in class perhaps...
```
If you want to use any other CV iterators to divide up your sample, you can:
```python
# Just replace "GroupShuffleSplit" with your CV of choice,
# and update the contents of split() as needed
train_idx, test_idx = next(
GroupShuffleSplit(random_state=7).split(X, y, groups)
)
X_train, X_test, y_train, y_test = X[train_idx], X[train_idx], y[test_idx], y[test_idx]
```
---
Back to our regularly scheduled "CV in Practice" programming.
### **STEP 2:** Set up the CV
SK-learn makes cross-validation pretty easy. The `cross_validate("estimator",X_train,y_train,cv,scoring,...)` function ([documentation here](https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.cross_validate.html)) will
1. Create folds in X_train and y_train using the method you put in the `cv` parameter. For each fold, it will create a smaller "training partition" and "testing partition" like in the figure at the top of this page.
1. For each fold,
1. It will fit your "estimator" (as if you ran `estimator.fit(X_trainingpartition,y_trainingpartition)`) on the smaller training partition it creates. **Your estimator will be a "pipeline" object** ([covered in detail on the next page](04e_pipelines)) that tells sklearn to apply a series of steps to the data (preprocessing, etc.), culminating in a model.
1. Use that fitted estimator on the testing partition (as if you ran `estimator.predict(X_testingpartition)` will apply all of the data transformations in the pipeline and use the estimated model on it)
1. Score those predictions with the function(s) you put in `scoring`
1. Output a dictionary object with performance data
You can even give it multiple scoring metrics to evaluate.
So, you need to set up
1. Your preferred folding method (and number of folds)
1. Your estimator
1. Your scoring method (you can specify this inside the cross_validate function)
```
from sklearn.model_selection import KFold, cross_validate
cv = KFold(5) # set up fold method
ridge = Ridge(alpha=1.0) # set up model/estimator
cross_validate(ridge,X_train,y_train,
cv=cv, scoring='r2') # tell it the scoring method here
```
```{note}
Wow, that was easy! Just 3 lines of code (and an import)
```
And we can output test score statistics like:
```
scores = cross_validate(ridge,X_train,y_train,cv=cv, scoring='r2')
print(scores['test_score'].mean()) # scores is just a dictionary
print(scores['test_score'].std())
```
## Next step: Pipelines
The model above
- Only uses a few continuous variables: what if we want to include other variable types (like categorical)?
- Uses the variables as given: ML algorithms often need you to transform your variables
- Doesn't deal with any data problems (e.g. missing values or outliers)
- Doesn't create any interaction terms or polynomial transformations
- Uses every variable I give it: But if your input data had 400 variables, you'd be in danger of overfitting!
At this point, you are capable of solving all of these problems. (For example, you could clean the data in pandas.)
But for our models to be robust to evil monsters like "data leakage", we need the fixes to be done within pipelines.
|
github_jupyter
|
# Project Euler in R
## Number letter counts
If the numbers 1 to 5 are written out in words: one, two, three, four, five, then there are 3 + 3 + 5 + 4 + 4 = 19 letters used in total.
If all the numbers from 1 to 1000 (one thousand) inclusive were written out in words, how many letters would be used?
**NOTE:** Do not count spaces or hyphens. For example, 342 (three hundred and forty-two) contains 23 letters and 115 (one hundred and fifteen) contains 20 letters. The use of "and" when writing out numbers is in compliance with British usage.
```
ones = c('one', 'two', 'three', 'four', 'five', 'six', 'seven', 'eight', 'nine')
tens_ones = c('eleven', 'twelve', 'thirteen', 'fourteen', 'fifteen', 'sixteen', 'seventeen', 'eighteen', 'nineteen')
tens = c('ten', 'twenty', 'thirty', 'forty', 'fifty', 'sixty', 'seventy', 'eighty', 'ninety')
hundreds = c('hundred')
split_number = function(x) {
hundreds = (x - x %% 100) / 100
tens = (x - x %% 10) / 10 - hundreds * 10
ones = (x %% 10)
return (c(hundreds, tens, ones))
}
split_number(543)
spell_number = function(x) {
word = ""
if (x[1] > 0) {
word = paste(if(x[1] == 1) 'a' else ones[x[1]], "hundred")
}
if(x[1] > 0 && x[2] > 0) {
word = paste(word, 'and')
}
if(x[2] == 1) {
word = paste(word, tens_ones[x[3]])
}
if(x[2] > 1) {
word = paste(word, tens[x[2]])
if(x[3] > 0) {
word = paste(word, "-", sep="")
}
}
if(x[3] > 0 && x[2] != 1) {
if(x[1] > 0 && x[2] == 0 && x[3] != 0) {
word = paste(word, 'and')
}
word = paste(word, ones[x[3]], sep=if(x[1] > 0 && x[2] == 0) " " else "")
}
if(x[2] == 1 && x[3] == 0) {
word = paste(word, 'ten', sep='')
}
return (word)
}
split_number(10)
spell_number(split_number(10))
spell_number(split_number(119))
count_words = function(x) lengths(gregexpr('[a-z]', x))
n = 1:1000
samples = sample(1000, 50, replace=TRUE)
total = 0
for (s in 100:999) {
word = spell_number(split_number(s))
count = count_words(word)
total = total + count
print(paste(s, word, 'letter_count:', count_words(word)))
}
print(paste('Total letters:', total))
20913 + count_words('a thousand')
has_letters = function(x) {
split = split_number(x)
word = spell_number(split)
count = count_words(word)
print(paste(x, word, count))
return (count)
}
has_letters(115)
count_words('a thousand')
```
Fuck this shit.
|
github_jupyter
|
# Module 5: Research Dissemination (30 minutes)
From "[Piled Higher and Deeper](http://phdcomics.com/comics/archive.php?comicid=1174)" by Jorge Cham
<img src="http://www.phdcomics.com/comics/archive/phd051809s.gif" />
## Take a moment to read these University policies
### Openness in Research
In Section 2.2 of the [Research Handbook](http://osp.utah.edu/policies/handbook/conduct-standards/openness.php)
### Ownership of Copyrightable Works and Related Works
In [Policy 7-003](http://regulations.utah.edu/research/7-003.php)
### Copyright and Creative Commons Licensing
<center><img src="https://upload.wikimedia.org/wikipedia/commons/thumb/e/e1/Creative_commons_license_spectrum.svg/600px-Creative_commons_license_spectrum.svg.png" width="500px" /></center>
### Exercise: Reading publisher contracts
* [PLOS ONE](http://journals.plos.org/plosone/s/licenses-and-copyright)
* [New England Journal of Medicine](http://www.nejm.org/page/author-center/manuscript-submission)
* [Journal of Biomedical Informatics](https://www.elsevier.com/journals/journal-of-biomedical-informatics/1532-0464/guide-for-authors)
* Find copyright information for a journal you're planning to publish in.
### Author Rights
* [SPARC Author Addendum](https://sparcopen.org/our-work/author-rights/)
## Reporting Guidelines and Writing Support
<table>
<tr>
<td><a href="http://www.icmje.org/recommendations/browse/manuscript-preparation/preparing-for-submission.html"><img src="http://www.icmje.org/images/icmje_logo.gif" width="450px" /></a></td>
<td><a href="http://www.equator-network.org/"><img src="http://www.equator-network.org/wp-content/themes/equator/images/equator_logo.png" width="300px" /></a></td>
</tr>
</table>
### At The University
* [University Writing Center](http://writingcenter.utah.edu/)
* [Dissertation Writing Boot Camp](http://gradschool.utah.edu/thesis/dissertation-writing-boot-camps/)
## Peer Review
<table>
<tr>
<td><a href="https://peerreviewweek.wordpress.com/"><img src="https://peerreviewweek.files.wordpress.com/2018/05/peerreviewweek_logo_2018_v1.jpg" width="300px" /></a></td>
<td><a href="https://publons.com/"><img src="https://static1.squarespace.com/static/576fcda2e4fcb5ab5152b4d8/58404af86a496371af54f1b2/58404b30b3db2b7f14442eed/1480608562794/light_blue_alt.png?format=300w" /></a></td>
</tr>
</table>
* single-blind
* double-blind
* open
* post-publication
Read more about it [here](http://www.editage.com/insights/what-are-the-types-of-peer-review).
## Choosing a journal
* [Ulrichsweb](http://ulrichsweb.serialssolutions.com/)
* [Directory of Open Access Journals](http://www.doaj.org/)
* [Questions to evaluate a journal](http://thinkchecksubmit.org/check/)
### Based on certain factors
* [Journal Citation Reports](https://login.ezproxy.lib.utah.edu/login?url=http://jcr.incites.thomsonreuters.com)
* [Scopus Compare Journals](https://login.ezproxy.lib.utah.edu/login?url=http://www.scopus.com/source/eval.url)
* [Cofactor Journal Selector](http://cofactorscience.com/journal-selector)
### Based on your abstract
* [Journal/Author Name Estimator](http://jane.biosemantics.org/)
## Publishing Models: Traditional vs Open Access
More information about open access at <a href="http://www.openaccessweek.org/">OpenAccessWeek.org</a>
<img src="http://api.ning.com/files/j2M1I3T7jzmpxqaCOjCDmPPu-MUwscmeVKPZjQGk6mqdKfYeq3rZzvgZJ6AcltgJTWQwtgnOUxbTMKzHsh3syLN-7pXZlVeY/OpenAccessWeek_logo.jpg" />
```
from IPython.display import YouTubeVideo
YouTubeVideo("L5rVH1KGBCY", width=600, height=350)
```
### How Open Is It?
From [SPARC](https://sparcopen.org/our-work/howopenisit/)
<img src="https://sparcopen.org/wp-content/uploads/2015/12/HowOpenIsIt_English_001.png" width="1200px" />
### Green Open Access
From CSU Fullerton's [Open Access guide](http://libraryguides.fullerton.edu/open-access/GreenOAPolicy)
<img src="https://s3.amazonaws.com/libapps/customers/114/images/green-access-infographic-web.png" width="500px" />
## How does "public access" fit in?
<table>
<tr>
<td><a href="https://www.nsf.gov/pubs/2017/nsf17060/nsf17060.jsp"><img src="https://www.nsf.gov/images/nsf_logo.png" width="400px" /></a></td>
<td><a href="https://publicaccess.nih.gov/"><img src="https://www.nih.gov/sites/all/themes/nih/images/nih-logo-color.png" width="400px" /></a></td>
</tr>
</table>
## Archiving your paper (aka practicing green open access)
### Does your publisher allow you to post a preprint/postprint?
* [SHERPA/RoMEO](http://www.sherpa.ac.uk/romeo/index.php)
### Where can you post it?
* [PubMed Central](https://www.ncbi.nlm.nih.gov/pmc/)
* [bioRxiv](http://www.biorxiv.org/)
* [OSF Preprints](https://cos.io/our-products/osf-preprints/)
* [OpenDOAR](http://www.opendoar.org/)
* [USpace](http://www.lib.utah.edu/digital-scholarship/uspace-uscholar.php)
* Your own website (but consider discoverability)
### Finding a "free" copy of a paper (legally)
* [Unpaywall](http://unpaywall.org/)
* Unpaywall which is a plug in for your browser just recieved an 850,000 dollar grant from he Arcadia Fund, to build a website where *everyone* can find, read, and understand the research literature. Sign up now for early access [unpaywall](http://gettheresearch.org)
* [Open Access Button](https://openaccessbutton.org/)
* Author's personal or academic social networking website (ResearchGate, Academia.edu)
## Other publication types/models
* [The Journal of Irreproducible Results](http://www.jir.com/)
* [MedEdPortal](https://www.mededportal.org)
* [Data journals](http://campusguides.lib.utah.edu/c.php?g=160788&p=1051837)
* [Protocols.io](https://www.protocols.io/welcome)
* [Registered Reports](https://osf.io/8mpji/wiki/home/)
## Tracking research impact
### Citation counts & h-index
* [Scopus](http://ezproxy.lib.utah.edu/login?url=http://www.scopus.com/home.url)
* [Web of Science](https://login.ezproxy.lib.utah.edu/login?url=http://www.webofknowledge.com/)
* [Google Scholar](http://scholar.google.com/)
### Altmetrics
<table>
<tr>
<td><img src="http://www.springersource.com/wp-content/uploads/2015/08/Altmetric-Donut1.png" width="600px" /></td>
</tr>
</table>
**Resources**
* [Altmetric](https://www.altmetric.com/) and the [bookmarklet](https://www.altmetric.com/products/free-tools/bookmarklet/)
### Scholarly impact
<table>
<tr>
<td><img src="https://orcid.org/sites/all/themes/orcidResponsiveNoto/img/orcid-logo.png" width="300px" /></td>
<td><img src="https://profiles.impactstory.org/static/img/impactstory-logo-sideways.png" width="300px" /></td>
</tr>
</table>
### Exercise
Set up your [ORCID](https://orcid.org/) and sign up for [Impact Story](https://profiles.impactstory.org/).
### Impact Story examples
* [Vicky Steeves](https://profiles.impactstory.org/u/0000-0003-4298-168X)
* [Wendy Chapman](https://profiles.impactstory.org/u/0000-0001-8702-4483)
* Of note, Dr. Chapman's impact story was autogenerated and might be missing data
|
github_jupyter
|
## Introduction
This notebook demostrates the core functionality of pymatgen, including the core objects representing Elements, Species, Lattices, and Structures.
By convention, we import pymatgen as mg.
```
import pymatgen as mg
```
## Basic Element, Specie and Composition objects
Pymatgen contains a set of core classes to represent an Element, Specie and Composition. These objects contains useful properties such as atomic mass, ionic radii, etc. These core classes are loaded by default with pymatgen. An Element can be created as follows:
```
si = mg.Element("Si")
print("Atomic mass of Si is {}".format(si.atomic_mass))
print("Si has a melting point of {}".format(si.melting_point))
print("Ionic radii for Si: {}".format(si.ionic_radii))
```
You can see that units are printed for atomic masses and ionic radii. Pymatgen comes with a complete system of managing units in pymatgen.core.unit. A Unit is a subclass of float that attaches units and handles conversions. For example,
```
print("Atomic mass of Si in kg: {}".format(si.atomic_mass.to("kg")))
```
Please refer to the Units example for more information on units. Species are like Elements, except they have an explicit oxidation state. They can be used wherever Element is used for the most part.
```
fe2 = mg.Specie("Fe", 2)
print(fe2.atomic_mass)
print(fe2.ionic_radius)
```
A Composition is essentially an **immutable** mapping of Elements/Species with amounts, and useful properties like molecular weight, get_atomic_fraction, etc. Note that you can conveniently either use an Element/Specie object or a string as keys (this is a feature).
```
comp = mg.Composition("Fe2O3")
print("Weight of Fe2O3 is {}".format(comp.weight))
print("Amount of Fe in Fe2O3 is {}".format(comp["Fe"]))
print("Atomic fraction of Fe is {}".format(comp.get_atomic_fraction("Fe")))
print("Weight fraction of Fe is {}".format(comp.get_wt_fraction("Fe")))
```
## Lattice & Structure objects
A Lattice represents a Bravais lattice. Convenience static functions are provided for the creation of common lattice types from a minimum number of arguments.
```
# Creates cubic Lattice with lattice parameter 4.2
lattice = mg.Lattice.cubic(4.2)
print(lattice.lengths_and_angles)
```
A Structure object represents a crystal structure (lattice + basis). A Structure is essentially a list of PeriodicSites with the same Lattice. Let us now create a CsCl structure.
```
structure = mg.Structure(lattice, ["Cs", "Cl"], [[0, 0, 0], [0.5, 0.5, 0.5]])
print("Unit cell vol = {}".format(structure.volume))
print("First site of the structure is {}".format(structure[0]))
```
The Structure object contains many useful manipulation functions. Since Structure is essentially a list, it contains a simple pythonic API for manipulation its sites. Some examples are given below. Please note that there is an immutable version of Structure known as IStructure, for the use case where you really need to enforce that the structure does not change. Conversion between these forms of Structure can be performed using from_sites().
```
structure.make_supercell([2, 2, 1]) #Make a 3 x 2 x 1 supercell of the structure
del structure[0] #Remove the first site
structure.append("Na", [0,0,0]) #Append a Na atom.
structure[-1] = "Li" #Change the last added atom to Li.
structure[0] = "Cs", [0.01, 0.5, 0] #Shift the first atom by 0.01 in fractional coordinates in the x-direction.
immutable_structure = mg.IStructure.from_sites(structure) #Create an immutable structure (cannot be modified).
print(immutable_structure)
```
## Basic analyses
Pymatgen provides many analyses functions for Structures. Some common ones are given below.
```
#Determining the symmetry
from pymatgen.symmetry.analyzer import SpacegroupAnalyzer
finder = SpacegroupAnalyzer(structure)
print("The spacegroup is {}".format(finder.get_spacegroup_symbol()))
```
We also have an extremely powerful structure matching tool.
```
from pymatgen.analysis.structure_matcher import StructureMatcher
#Let's create two structures which are the same topologically, but with different elements, and one lattice is larger.
s1 = mg.Structure(lattice, ["Cs", "Cl"], [[0, 0, 0], [0.5, 0.5, 0.5]])
s2 = mg.Structure(mg.Lattice.cubic(5), ["Rb", "F"], [[0, 0, 0], [0.5, 0.5, 0.5]])
m = StructureMatcher()
print(m.fit_anonymous(s1, s2)) #Returns a mapping which maps s1 and s2 onto each other. Strict element fitting is also available.
```
## Input/output
Pymatgen also provides IO support for various file formats in the pymatgen.io package. A convenient set of read_structure and write_structure functions are also provided which auto-detects several well-known formats.
```
#Convenient IO to various formats. Format is intelligently determined from file name and extension.
structure.to(filename="POSCAR")
structure.to(filename="CsCl.cif")
#Or if you just supply fmt, you simply get a string.
print(structure.to(fmt="poscar"))
print(structure.to(fmt="cif"))
#Reading a structure from a file.
structure = mg.Structure.from_file("POSCAR")
```
The vaspio_set module provides a means o obtain a complete set of VASP input files for performing calculations. Several useful presets based on the parameters used in the Materials Project are provided.
```
from pymatgen.io.vaspio_set import MPVaspInputSet
v = MPVaspInputSet()
v.write_input(structure, "MyInputFiles") #Writes a complete set of input files for structure to the directory MyInputFiles
```
### This concludes this pymatgen tutorial. Please explore the usage pages on pymatgen.org for more information.
|
github_jupyter
|
# Stock Price Prediction From Employee / Job Market Information
## Modelling: Linear Model
Objective utilise the Thinknum LinkedIn and Job Postings datasets, along with the Quandl WIKI prices dataset to investigate the effect of hiring practices on stock price. In this notebook I'll begin exploring the increase in predictive power from historic employment data.
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from pathlib import Path
from glob import glob
# Utilities
from utils import *
%matplotlib inline
PATH = Path('D:\data\jobs')
%%capture #ignore output warnings for now
link, companies, stocks = data_load(PATH)
```
Let's start with some of the series that had the most promising cross correlations.
```
filtered = companies.sort_values('max_corr',ascending=False)[['dataset_id', 'company_name','MarketCap', 'Sector', 'Symbol',
'max_corr', 'best_lag']]
filtered = filtered.query('(max_corr > 0.95) & (best_lag < -50)')
filtered.head()
```
Modelling for the top stock here USA Truck Inc.
```
USAK = stocks.USAK
USAK_link = link[link['dataset_id']==929840]['employees_on_platform']
start = min(USAK_link.index)
end = max(USAK_link.index)
fig, ax = plt.subplots(figsize=(12,8))
ax.set_xlim(start,end)
ax.plot(USAK.index,USAK, label='Adjusted Close Price (USAK)')
ax.set_ylabel('Adjusted close stock price')
ax1=ax.twinx()
ax1.set_ylabel('LinkedIn employee count')
ax1.plot(USAK_link.index, USAK_link,color='r',label='LinkedIn employee data')
plt.legend();
# Error in this code leading to slightly different train time ranges
def build_t_feats(stock,employ,n, include_employ=True):
if include_employ:
X = pd.concat([stock,employ],axis=1)
X.columns = ['close','emps']
else:
X = pd.DataFrame(stock)
X.columns = ['close']
y=None
start = max(pd.datetime(2016,7,1),min(stock.dropna().index)) - pd.Timedelta(1, unit='d')
end = max(stock.dropna().index)
X = X.loc[start:end]
# Normalize
X = (X-X.mean())/X.std()
# Fill gaps
X = X.interpolate()
# Daily returns
X = X.diff()
# Create target variable
X['y'] = X.close.shift(-1)
# Create time shifted features
for t in range(n):
X['c'+str(t+1)] = X.close.shift(t+1)
if include_employ: X['e'+str(t+1)] = X.emps.shift(t+1)
X = X.dropna()
y = X.y
X.drop('y',axis=1,inplace=True)
return X,y
X, y = build_t_feats(USAK,USAK_link,180)
```
## Linear Model
Start with a basic linear model, so we can easily interpret the model outputs.
```
from sklearn.model_selection import TimeSeriesSplit, cross_val_score
from sklearn.linear_model import Ridge, LinearRegression
from sklearn.metrics import mean_absolute_error
reg = Ridge()
def fit_predict(reg, X, y, plot=True):
cv = TimeSeriesSplit(n_splits=10)
scores = cross_val_score(reg, X, y, cv=cv, scoring='neg_mean_absolute_error')
if plot: print('Mean absolute error: ', np.mean(-scores), '\nSplit scores: ',-scores)
cut = int(X.shape[0]*0.9)
X_train, y_train = X[:cut], y[:cut].values.reshape(-1,1)
X_dev, y_dev = X[cut:], y[cut:].values.reshape(-1,1)
reg.fit(X_train,y_train)
pred_dev = reg.predict(X_dev)
pred_train = reg.predict(X_train)
if plot:
f,ax = plt.subplots(nrows=1,ncols=2,figsize=(25,8))
ax[0].plot(y_train,pred_train,marker='.',linestyle='None',alpha=0.6,label='train')
ax[0].plot(y_dev,pred_dev,marker='.',linestyle='None',color='r',alpha=0.6,label='dev')
ax[0].set_title('Predicted v actual daily changes')
ax[0].legend()
ax[1].plot(X[cut:].index,y_dev,alpha=0.6,label='actual',marker='.')
ax[1].plot(X[cut:].index,pred_dev,color='r',alpha=0.6,label='predict',marker='.')
ax[1].set_title('Development set, predicted v actual daily changes')
ax[1].legend();
return reg, np.mean(-scores)
reg, _ = fit_predict(reg, X, y)
```
Using MAE (Mean Absolute Error) as the evaluation metric here. Around 0.05 MAE seems acceptable at predicting the daily changes.
```
coefs = reg.coef_.ravel()
idx = coefs.argsort()[-40:]
x = np.arange(len(coefs[idx]))
fig,ax = plt.subplots(figsize=(20,5))
plt.bar(x,coefs[idx])
plt.xticks(x,X.columns.values[idx])
plt.title('Importance of shifted feature in model')
plt.show();
```
Looks like most of the top features are time lagged versions of the daily price change rather than the employment data.
## Same model excluding employment data
I'll now rerun the same analysis but exluced the employment data.
```
X, y = build_t_feats(USAK,USAK_link,180,include_employ=False)
reg = Ridge()
reg, _ = fit_predict(reg, X, y)
coefs = reg.coef_.ravel()
idx = coefs.argsort()[-40:]
x = np.arange(len(coefs[idx]))
fig,ax = plt.subplots(figsize=(20,5))
plt.bar(x,coefs[idx])
plt.xticks(x,X.columns.values[idx])
plt.title('Importance of shifted feature in model')
plt.show();
```
Over a similar time period it looks like our model performed better using employment data.
## Rerun analysis for all top stocks
```
%%capture
def run_for_all(filtered):
MAEs = np.full((len(filtered),2),np.nan)
for i,ID in enumerate(filtered.dataset_id.values):
print(i, ID, filtered.set_index('dataset_id').loc[ID].company_name)
try:
sym = filtered.set_index('dataset_id').loc[ID].Symbol
tick = stocks[sym]
emp = link[link['dataset_id']==ID]['employees_on_platform']
except:
print('Symbol Error, Skipping')
# Including employee data
X, y = build_t_feats(tick,emp,180,True)
reg = Ridge()
reg, MAE = fit_predict(reg, X, y, plot=False)
MAEs[i][0] = MAE
# Excluding employee data
X, y = build_t_feats(tick,emp,180,False)
reg = Ridge()
reg, MAE = fit_predict(reg, X, y, plot=False)
MAEs[i][1] = MAE
# Create columns with mean absolute errors added
filtered['MAE_w_emp'] = MAEs[:,0]
filtered['MAE_wo_emp'] = MAEs[:,1]
return filtered
filtered = filtered[filtered.dataset_id != 868877].copy()
filtered = run_for_all(filtered)
from bokeh.plotting import figure, show, output_notebook
from bokeh.models import HoverTool
output_notebook()
def plot_predicts(filtered):
TOOLS="hover,save"
p1 = figure(plot_width=600, plot_height=600, title="Prediction score with and without LinkedIn data",tools=TOOLS)
p1.xgrid.grid_line_color = None
p1.circle(x='MAE_wo_emp', y='MAE_w_emp', size=12, alpha=0.5, source=filtered)
p1.line(x=np.arange(0,0.25,0.01),y=np.arange(0,0.25,0.01))
p1.xaxis.axis_label = 'MAE with employee data in model'
p1.yaxis.axis_label = 'MAE without employee data in model'
hover = p1.select(dict(type=HoverTool))
hover.tooltips = [
("Name", "@company_name"),
("Correlation", "@max_corr"),
("Optimal Lag", "@best_lag"),
]
show(p1)
plot_predicts(filtered)
```
The vast majority of points fall below the line, suggesting the predictions generated with a simple linear model were improved when Employee data was included in the model.
**However** upon further review of my methodology it looks like I'm using comparing prediction accuracy on slightly different time ranges. I'll re-run the code below this time fixing identical time ranges.
```
# Updated code for processing data
def build_t_feats(stock,employ,n, include_employ=True, norm_diff=True):
X = pd.concat([stock,employ],axis=1)
X.columns = ['close','emps']
y=None
#start = max(pd.datetime(2016,7,1),min(stock.dropna().index)) - pd.Timedelta(1, unit='d')
start = min(employ.dropna().index) - pd.Timedelta(1, unit='d')
end = max(stock.dropna().index)
#print(start,end)
X = X.loc[start:end]
if norm_diff:
# Normalize
X = (X-X.mean())/X.std()
# Fill gaps
X = X.interpolate()
if norm_diff:
# Daily returns
X = X.diff()
# Create target variable
X['y'] = X.close.shift(-1)
# Create time shifted features
for t in range(n):
X['c'+str(t+1)] = X.close.shift(t+1)
if include_employ: X['e'+str(t+1)] = X.emps.shift(t+1)
X = X.dropna()
if not include_employ: X = X.drop('emps',axis=1)
y = X.y
X.drop('y',axis=1,inplace=True)
return X,y
```
### With employment data
```
X, y = build_t_feats(USAK,USAK_link,180)
reg = Ridge()
reg, _ = fit_predict(reg, X, y)
```
### Without Employment Data
```
X, y = build_t_feats(USAK,USAK_link,180,include_employ=False)
reg = Ridge()
reg, _ = fit_predict(reg, X, y)
```
As you can see the results are a lot less clear here. It looks as if there is no improved predictive power from including employment data.
## Rerun on all stocks
```
%%capture
filtered = companies.sort_values('max_corr',ascending=False)[['dataset_id', 'company_name','MarketCap', 'Sector', 'Symbol',
'max_corr', 'best_lag']]
filtered = filtered.query('(max_corr > 0.95) & (best_lag < -50)')
filtered = filtered[filtered.dataset_id != 868877].copy()
filtered = run_for_all(filtered)
plot_predicts(filtered)
```
As you can see except for some noise most stocks fall along the line **suggesting that there is no improvement in prediction accuracy when including LinkedIn data**.
|
github_jupyter
|
```
from IPython.core.display import display, HTML
display(HTML("<style>.container { width:75% !important; }</style>"))
import numpy as np
import torch
import time
from carle.env import CARLE
from carle.mcl import CornerBonus, SpeedDetector, PufferDetector, AE2D, RND2D
from game_of_carle.agents.harli import HARLI
from game_of_carle.agents.carla import CARLA
from game_of_carle.agents.grnn import ConvGRNN
from game_of_carle.agents.toggle import Toggle
import bokeh
import bokeh.io as bio
from bokeh.io import output_notebook, show
from bokeh.plotting import figure
from bokeh.layouts import column, row
from bokeh.models import TextInput, Button, Paragraph
from bokeh.models import ColumnDataSource
from bokeh.events import DoubleTap, Tap
import matplotlib.pyplot as plt
my_cmap = plt.get_cmap("magma")
output_notebook()
"""
Trained with the SpeedDetector and RND2D bonus wrappers with the B358/S245 Morely rules,
some of these agents learned that they could game that reward system by exploiting a chaotic boundary with
essentially random actions. This is something of a specification gaming/reward hacking strategy, as it is
unlikely for agents to learn more interesting strategies when they already get a high reward from cells near
the border transiently becoming active. One way to improve this would be to restrict agent activity to the center
of the action space (like with the Toggle agent), which yields a buffer between what the agent modifies and
what the speed reward wrapper uses to calculate center of mass. Likewise the reward wrapper could be modified to
include a 'frontier zone' itself.
Occasionally agents exhibit a 'wave' strategy, where toggling all the cells at the action space boundary
creates a diminishing line of active cells that propagates toward the CA grid edges. For CARLA agents, this
strategy mostly if not only is used immediately after resetting the environment/agent.
"""
agent = CARLA()
params_list = [\
"../policies/CARLA_42_glider_rnd2d_experiment1622466808best_params_gen31.npy",\
"../policies/CARLA_43110_glider_rnd2d_experiment1622503099best_params_gen31.npy"]
# choose parameters to load
params_index = 0
agent.set_params(np.load(params_list[params_index]))
env = CARLE(height=128, width=128)
env = SpeedDetector(env)
my_rules = "B368/S245"
env.rules_from_string(my_rules)
"""
The Toggle agent parameters become the actions at step 0, after which the agent does nothing until `agent.reset`
is called. In other words you can use the Toggle agent to optimize an initial pattern directly.
Using CMA-ES with this strategy and SpeedDetector + RND2D reward wrappers pretty reliably finds patterns than
coalesce into a moving machine, although so far the pattern always turns into either a jellyfish glider or
the common puffer.
"""
agent = Toggle()
#my_params = np.load("../policies/Toggle_13_glider_rnd2d_experiment1622420340best_params_gen31.npy") # glider
#my_params = np.load("../policies/Toggle_1337_glider_rnd2d_experiment1622437453best_params_gen31.npy") # glider
#my_params = np.load("../policies/Toggle_42_glider_rnd2d_experiment1622455453best_params_gen31.npy") # glider
#my_params = np.load("../policies/Toggle_12345_glider_rnd2d_experiment1622474002best_params_gen31.npy") # puffer
#my_params = np.load("../policies/Toggle_43110_glider_rnd2d_experiment1622491637best_params_gen31.npy") # puffer
params_list = ["../policies/Toggle_13_glider_rnd2d_experiment1622420340best_params_gen31.npy", \
"../policies/Toggle_1337_glider_rnd2d_experiment1622437453best_params_gen31.npy",\
"../policies/Toggle_42_glider_rnd2d_experiment1622455453best_params_gen31.npy",\
"../policies/Toggle_12345_glider_rnd2d_experiment1622474002best_params_gen31.npy",\
"../policies/Toggle_43110_glider_rnd2d_experiment1622491637best_params_gen31.npy"]
params_index = 0
agent.set_params(np.load(params_list[params_index]))
env = CARLE(height=128, width=128)
env = SpeedDetector(env)
my_rules = "B368/S245"
env.rules_from_string(my_rules)
"""
Trained with the SpeedDetector and RND2D bonus wrappers with the B358/S245 Morely rules,
some of these agents learned that they could game that reward system by exploiting a chaotic boundary with
essentially random actions. This is something of a specification gaming/reward hacking strategy, as it is
unlikely for agents to learn more interesting strategies when they already get a high reward from cells near
the border transiently becoming active. One way to improve this would be to restrict agent activity to the center
of the action space (like with the Toggle agent), which yields a buffer between what the agent modifies and
what the speed reward wrapper uses to calculate center of mass. Likewise the reward wrapper could be modified to
include a 'frontier zone' itself.
There is an interesting reward hack that is sometimes exhibited by HARLI agents trained with SpeedDetector.
CARLE instances can be reset if the agent toggles every cell in the action space simultaneously, and this can generate
high rewards in one of two ways. The first is that if there are many live cells outside the action space these will
be zeroed out when the environment is reset, making for an large change in the center of mass of all live cells as
is used by SpeedDetector to calculate rewards. The second is that this sets up the environment perfectly for a
highly rewarding "wave" strategy, where a line of active cells at the action space boundary sets up conditions for
a fast moving line of live cells to propagate toward the grid edge. When both those mechanisms are combined,
the rewards can be quite high, although we probably would have preferred agents that come up with or rediscover
interesting glider and spaceship patterns.
"""
agent = HARLI()
params_list = ["../policies/HARLI_13_glider_rnd2d_experiment1622423202best_params_gen31.npy", \
"../policies/HARLI_42_glider_rnd2d_experiment1622458272best_params_gen31.npy",\
"../policies/HARLI_1337_glider_rnd2d_experiment1622440720best_params_gen31.npy",\
"../policies/HARLI_12345_glider_rnd2d_experiment1622477110best_params_gen31.npy",\
"../policies/HARLI_43110_glider_rnd2d_experiment1622494528best_params_gen31.npy"]
# choose parameters to load
params_index = 0
agent.set_params(np.load(params_list[params_index]))
env = CARLE(height=128, width=128)
env = SpeedDetector(env)
#env = AE2D(env)
my_rules = "B368/S245"
env.rules_from_string(my_rules)
def modify_doc(doc):
#agent = SubmissionAgent()
#agent.toggle_rate = 0.48
global obs
obs = env.reset()
p = figure(plot_width=3*256, plot_height=3*256, title="CA Universe")
p_plot = figure(plot_width=int(2.5*256), plot_height=int(2.5*256), title="'Reward'")
global my_period
global number_agents
global agent_number
agent_number = 0
number_agents = len(params_list)
my_period = 512
source = ColumnDataSource(data=dict(my_image=[obs.squeeze().cpu().numpy()]))
source_plot = ColumnDataSource(data=dict(x=np.arange(1), y=np.arange(1)*0))
img = p.image(image='my_image',x=0, y=0, dw=256, dh=256, palette="Magma256", source=source)
line_plot = p_plot.line(line_width=3, color="firebrick", source=source_plot)
button_go = Button(sizing_mode="stretch_width", label="Run >")
button_slower = Button(sizing_mode="stretch_width",label="<< Slower")
button_faster = Button(sizing_mode="stretch_width",label="Faster >>")
button_reset = Button(sizing_mode="stretch_width",label="Reset")
button_reset_prev_agent = Button(sizing_mode="stretch_width",label="Reset w/ Prev. Agent")
button_reset_this_agent = Button(sizing_mode="stretch_width",label="Reset w/ This Agent")
button_reset_next_agent = Button(sizing_mode="stretch_width",label="Reset w/ Next Agent")
input_birth = TextInput(value="B")
input_survive = TextInput(value="S")
button_birth = Button(sizing_mode="stretch_width", label="Update Birth Rules")
button_survive = Button(sizing_mode="stretch_width", label="Update Survive Rules")
button_agent_switch = Button(sizing_mode="stretch_width", label="Turn Agent Off")
message = Paragraph()
def update():
global obs
global stretch_pixel
global action
global agent_on
global my_step
global rewards
obs, r, d, i = env.step(action)
rewards = np.append(rewards, r.cpu().numpy().item())
if agent_on:
action = agent(obs) #1.0 * (torch.rand(env.instances,1,env.action_height,env.action_width) < 0.05)
else:
action = torch.zeros_like(action)
#padded_action = stretch_pixel/2 + env.action_padding(action).squeeze()
padded_action = stretch_pixel/2 + env.inner_env.action_padding(action).squeeze()
my_img = (padded_action*2 + obs.squeeze()).cpu().numpy()
my_img[my_img > 3.0] = 3.0
(padded_action*2 + obs.squeeze()).cpu().numpy()
new_data = dict(my_image=[my_img])
#new_line = dict(x=np.arange(my_step+2), y=rewards)
new_line = dict(x=[my_step], y=[r.cpu().numpy().item()])
source.stream(new_data, rollover=1)
source_plot.stream(new_line, rollover=2000)
my_step += 1
message.text = f"agent {agent_number}, step {my_step}, reward: {r.item()} \n"\
f"{params_list[agent_number]}"
def go():
if button_go.label == "Run >":
my_callback = doc.add_periodic_callback(update, my_period)
button_go.label = "Pause"
#doc.remove_periodic_callback(my_callback)
else:
doc.remove_periodic_callback(doc.session_callbacks[0])
button_go.label = "Run >"
def faster():
global my_period
my_period = max([my_period * 0.5, 1])
go()
go()
def slower():
global my_period
my_period = min([my_period * 2, 8192])
go()
go()
def reset():
global obs
global stretch_pixel
global my_step
global rewards
my_step = 0
obs = env.reset()
agent.reset()
stretch_pixel = torch.zeros_like(obs).squeeze()
stretch_pixel[0,0] = 3
new_data = dict(my_image=[(stretch_pixel + obs.squeeze()).cpu().numpy()])
rewards = np.array([0])
new_line = dict(x=[my_step], y=[0])
source_plot.stream(new_line, rollover=1)
source.stream(new_data, rollover=8)
def reset_this_agent():
global obs
global stretch_pixel
global my_step
global rewards
global agent_number
global number_agents
my_step = 0
obs = env.reset()
agent.reset()
stretch_pixel = torch.zeros_like(obs).squeeze()
stretch_pixel[0,0] = 3
new_data = dict(my_image=[(stretch_pixel + obs.squeeze()).cpu().numpy()])
rewards = np.array([0])
new_line = dict(x=[my_step], y=[0])
source_plot.stream(new_line, rollover=1)
source.stream(new_data, rollover=8)
def reset_next_agent():
global obs
global stretch_pixel
global my_step
global rewards
global agent_number
global number_agents
my_step = 0
obs = env.reset()
stretch_pixel = torch.zeros_like(obs).squeeze()
stretch_pixel[0,0] = 3
new_data = dict(my_image=[(stretch_pixel + obs.squeeze()).cpu().numpy()])
rewards = np.array([0])
new_line = dict(x=[my_step], y=[0])
source_plot.stream(new_line, rollover=1)
source.stream(new_data, rollover=8)
agent_number = (agent_number + 1) % number_agents
agent.set_params(np.load(params_list[agent_number]))
agent.reset()
message.text = f"reset with agent {agent_number}"
def reset_prev_agent():
global obs
global stretch_pixel
global my_step
global rewards
global agent_number
global number_agents
my_step = 0
obs = env.reset()
stretch_pixel = torch.zeros_like(obs).squeeze()
stretch_pixel[0,0] = 3
new_data = dict(my_image=[(stretch_pixel + obs.squeeze()).cpu().numpy()])
rewards = np.array([0])
new_line = dict(x=[my_step], y=[0])
source_plot.stream(new_line, rollover=1)
source.stream(new_data, rollover=8)
agent_number = (agent_number - 1) % number_agents
agent.set_params(np.load(params_list[agent_number]))
agent.reset()
message.text = f"reset with agent {agent_number}"
def set_birth_rules():
env.birth_rule_from_string(input_birth.value)
my_message = "Rules updated to B"
for elem in env.birth:
my_message += str(elem)
my_message += "/S"
for elem in env.survive:
my_message += str(elem)
message.text = my_message
time.sleep(0.1)
def set_survive_rules():
env.survive_rule_from_string(input_survive.value)
my_message = "Rules updated to B"
for elem in env.birth:
my_message += str(elem)
my_message += "/S"
for elem in env.survive:
my_message += str(elem)
message.text = my_message
time.sleep(0.1)
def human_toggle(event):
global action
coords = [np.round(env.height*event.y/256-0.5), np.round(env.width*event.x/256-0.5)]
offset_x = (env.height - env.action_height) / 2
offset_y = (env.width - env.action_width) / 2
coords[0] = coords[0] - offset_x
coords[1] = coords[1] - offset_y
coords[0] = np.uint8(np.clip(coords[0], 0, env.action_height-1))
coords[1] = np.uint8(np.clip(coords[1], 0, env.action_height-1))
action[:, :, coords[0], coords[1]] = 1.0 * (not(action[:, :, coords[0], coords[1]]))
padded_action = stretch_pixel/2 + env.inner_env.action_padding(action).squeeze()
my_img = (padded_action*2 + obs.squeeze()).cpu().numpy()
my_img[my_img > 3.0] = 3.0
(padded_action*2 + obs.squeeze()).cpu().numpy()
new_data = dict(my_image=[my_img])
source.stream(new_data, rollover=8)
def clear_toggles():
global action
if button_go.label == "Pause":
action *= 0
doc.remove_periodic_callback(doc.session_callbacks[0])
button_go.label = "Run >"
padded_action = stretch_pixel/2 + env.inner_env.action_padding(action).squeeze()
my_img = (padded_action*2 + obs.squeeze()).cpu().numpy()
my_img[my_img > 3.0] = 3.0
(padded_action*2 + obs.squeeze()).cpu().numpy()
new_data = dict(my_image=[my_img])
source.stream(new_data, rollover=8)
else:
doc.add_periodic_callback(update, my_period)
button_go.label = "Pause"
def agent_on_off():
global agent_on
if button_agent_switch.label == "Turn Agent Off":
agent_on = False
button_agent_switch.label = "Turn Agent On"
else:
agent_on = True
button_agent_switch.label = "Turn Agent Off"
global agent_on
agent_on = True
global action
action = torch.zeros(1, 1, env.action_height, env.action_width)
reset()
p.on_event(Tap, human_toggle)
p.on_event(DoubleTap, clear_toggles)
button_reset_prev_agent.on_click(reset_prev_agent)
button_reset_this_agent.on_click(reset_this_agent)
button_reset_next_agent.on_click(reset_next_agent)
button_birth.on_click(set_birth_rules)
button_survive.on_click(set_survive_rules)
button_go.on_click(go)
button_faster.on_click(faster)
button_slower.on_click(slower)
button_reset.on_click(reset)
button_agent_switch.on_click(agent_on_off)
control_layout = row(button_slower, button_go, button_faster, button_reset)
policy_change_layout = row(button_reset_prev_agent, button_reset_this_agent, button_reset_next_agent)
rule_layout = row(input_birth, button_birth, input_survive, button_survive)
agent_toggle_layout = row(button_agent_switch)
display_layout = row(p, p_plot)
message_layout = row(message)
doc.add_root(display_layout)
doc.add_root(control_layout)
doc.add_root(policy_change_layout)
doc.add_root(rule_layout)
doc.add_root(message_layout)
doc.add_root(agent_toggle_layout)
show(modify_doc)
```
|
github_jupyter
|
# Network Visualization (TensorFlow)
In this notebook we will explore the use of *image gradients* for generating new images.
When training a model, we define a loss function which measures our current unhappiness with the model's performance; we then use backpropagation to compute the gradient of the loss with respect to the model parameters, and perform gradient descent on the model parameters to minimize the loss.
Here we will do something slightly different. We will start from a convolutional neural network model which has been pretrained to perform image classification on the ImageNet dataset. We will use this model to define a loss function which quantifies our current unhappiness with our image, then use backpropagation to compute the gradient of this loss with respect to the pixels of the image. We will then keep the model fixed, and perform gradient descent *on the image* to synthesize a new image which minimizes the loss.
In this notebook we will explore three techniques for image generation:
1. **Saliency Maps**: Saliency maps are a quick way to tell which part of the image influenced the classification decision made by the network.
2. **Fooling Images**: We can perturb an input image so that it appears the same to humans, but will be misclassified by the pretrained network.
3. **Class Visualization**: We can synthesize an image to maximize the classification score of a particular class; this can give us some sense of what the network is looking for when it classifies images of that class.
This notebook uses **TensorFlow**; we have provided another notebook which explores the same concepts in PyTorch. You only need to complete one of these two notebooks.
```
# As usual, a bit of setup
import time, os, json
import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
from cs231n.classifiers.squeezenet import SqueezeNet
from cs231n.data_utils import load_tiny_imagenet
from cs231n.image_utils import preprocess_image, deprocess_image
from cs231n.image_utils import SQUEEZENET_MEAN, SQUEEZENET_STD
%matplotlib inline
plt.rcParams['figure.figsize'] = (10.0, 8.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'
def get_session():
"""Create a session that dynamically allocates memory."""
# See: https://www.tensorflow.org/tutorials/using_gpu#allowing_gpu_memory_growth
config = tf.ConfigProto()
config.gpu_options.allow_growth = True
session = tf.Session(config=config)
return session
# for auto-reloading external modules
# see http://stackoverflow.com/questions/1907993/autoreload-of-modules-in-ipython
%load_ext autoreload
%autoreload 2
```
# Pretrained Model
For all of our image generation experiments, we will start with a convolutional neural network which was pretrained to perform image classification on ImageNet. We can use any model here, but for the purposes of this assignment we will use SqueezeNet [1], which achieves accuracies comparable to AlexNet but with a significantly reduced parameter count and computational complexity.
Using SqueezeNet rather than AlexNet or VGG or ResNet means that we can easily perform all image generation experiments on CPU.
We have ported the PyTorch SqueezeNet model to TensorFlow; see: `cs231n/classifiers/squeezenet.py` for the model architecture.
To use SqueezeNet, you will need to first **download the weights** by descending into the `cs231n/datasets` directory and running `get_squeezenet_tf.sh`. Note that if you ran `get_assignment3_data.sh` then SqueezeNet will already be downloaded.
Once you've downloaded the Squeezenet model, we can load it into a new TensorFlow session:
[1] Iandola et al, "SqueezeNet: AlexNet-level accuracy with 50x fewer parameters and < 0.5MB model size", arXiv 2016
```
tf.reset_default_graph()
sess = get_session()
SAVE_PATH = 'cs231n/datasets/squeezenet.ckpt'
if not os.path.exists(SAVE_PATH + ".index"):
raise ValueError("You need to download SqueezeNet!")
model = SqueezeNet(save_path=SAVE_PATH, sess=sess)
```
## Load some ImageNet images
We have provided a few example images from the validation set of the ImageNet ILSVRC 2012 Classification dataset. To download these images, descend into `cs231n/datasets/` and run `get_imagenet_val.sh`.
Since they come from the validation set, our pretrained model did not see these images during training.
Run the following cell to visualize some of these images, along with their ground-truth labels.
```
from cs231n.data_utils import load_imagenet_val
X_raw, y, class_names = load_imagenet_val(num=5)
plt.figure(figsize=(12, 6))
for i in range(5):
plt.subplot(1, 5, i + 1)
plt.imshow(X_raw[i])
plt.title(class_names[y[i]])
plt.axis('off')
plt.gcf().tight_layout()
```
## Preprocess images
The input to the pretrained model is expected to be normalized, so we first preprocess the images by subtracting the pixelwise mean and dividing by the pixelwise standard deviation.
```
X = np.array([preprocess_image(img) for img in X_raw])
```
# Saliency Maps
Using this pretrained model, we will compute class saliency maps as described in Section 3.1 of [2].
A **saliency map** tells us the degree to which each pixel in the image affects the classification score for that image. To compute it, we compute the gradient of the unnormalized score corresponding to the correct class (which is a scalar) with respect to the pixels of the image. If the image has shape `(H, W, 3)` then this gradient will also have shape `(H, W, 3)`; for each pixel in the image, this gradient tells us the amount by which the classification score will change if the pixel changes by a small amount. To compute the saliency map, we take the absolute value of this gradient, then take the maximum value over the 3 input channels; the final saliency map thus has shape `(H, W)` and all entries are nonnegative.
You will need to use the `model.scores` Tensor containing the scores for each input, and will need to feed in values for the `model.image` and `model.labels` placeholder when evaluating the gradient. Open the file `cs231n/classifiers/squeezenet.py` and read the documentation to make sure you understand how to use the model. For example usage, you can see the `loss` attribute.
[2] Karen Simonyan, Andrea Vedaldi, and Andrew Zisserman. "Deep Inside Convolutional Networks: Visualising
Image Classification Models and Saliency Maps", ICLR Workshop 2014.
```
def compute_saliency_maps(X, y, model):
"""
Compute a class saliency map using the model for images X and labels y.
Input:
- X: Input images, numpy array of shape (N, H, W, 3)
- y: Labels for X, numpy of shape (N,)
- model: A SqueezeNet model that will be used to compute the saliency map.
Returns:
- saliency: A numpy array of shape (N, H, W) giving the saliency maps for the
input images.
"""
saliency = None
# Compute the score of the correct class for each example.
# This gives a Tensor with shape [N], the number of examples.
#
# Note: this is equivalent to scores[np.arange(N), y] we used in NumPy
# for computing vectorized losses.
correct_scores = tf.gather_nd(model.scores,
tf.stack((tf.range(X.shape[0]), model.labels), axis=1))
###############################################################################
# TODO: Produce the saliency maps over a batch of images. #
# #
# 1) Compute the “loss” using the correct scores tensor provided for you. #
# (We'll combine losses across a batch by summing) #
# 2) Use tf.gradients to compute the gradient of the loss with respect #
# to the image (accessible via model.image). #
# 3) Compute the actual value of the gradient by a call to sess.run(). #
# You will need to feed in values for the placeholders model.image and #
# model.labels. #
# 4) Finally, process the returned gradient to compute the saliency map. #
###############################################################################
pass
##############################################################################
# END OF YOUR CODE #
##############################################################################
return saliency
```
Once you have completed the implementation in the cell above, run the following to visualize some class saliency maps on our example images from the ImageNet validation set:
```
def show_saliency_maps(X, y, mask):
mask = np.asarray(mask)
Xm = X[mask]
ym = y[mask]
saliency = compute_saliency_maps(Xm, ym, model)
for i in range(mask.size):
plt.subplot(2, mask.size, i + 1)
plt.imshow(deprocess_image(Xm[i]))
plt.axis('off')
plt.title(class_names[ym[i]])
plt.subplot(2, mask.size, mask.size + i + 1)
plt.title(mask[i])
plt.imshow(saliency[i], cmap=plt.cm.hot)
plt.axis('off')
plt.gcf().set_size_inches(10, 4)
plt.show()
mask = np.arange(5)
show_saliency_maps(X, y, mask)
```
# INLINE QUESTION
A friend of yours suggests that in order to find an image that maximizes the correct score, we can perform gradient ascent on the input image, but instead of the gradient we can actually use the saliency map in each step to update the image. Is this assertion true? Why or why not?
# Fooling Images
We can also use image gradients to generate "fooling images" as discussed in [3]. Given an image and a target class, we can perform gradient **ascent** over the image to maximize the target class, stopping when the network classifies the image as the target class. Implement the following function to generate fooling images.
[3] Szegedy et al, "Intriguing properties of neural networks", ICLR 2014
```
def make_fooling_image(X, target_y, model):
"""
Generate a fooling image that is close to X, but that the model classifies
as target_y.
Inputs:
- X: Input image, a numpy array of shape (1, 224, 224, 3)
- target_y: An integer in the range [0, 1000)
- model: Pretrained SqueezeNet model
Returns:
- X_fooling: An image that is close to X, but that is classifed as target_y
by the model.
"""
# Make a copy of the input that we will modify
X_fooling = X.copy()
# Step size for the update
learning_rate = 1
##############################################################################
# TODO: Generate a fooling image X_fooling that the model will classify as #
# the class target_y. Use gradient *ascent* on the target class score, using #
# the model.scores Tensor to get the class scores for the model.image. #
# When computing an update step, first normalize the gradient: #
# dX = learning_rate * g / ||g||_2 #
# #
# You should write a training loop, where in each iteration, you make an #
# update to the input image X_fooling (don't modify X). The loop should #
# stop when the predicted class for the input is the same as target_y. #
# #
# HINT: It's good practice to define your TensorFlow graph operations #
# outside the loop, and then just make sess.run() calls in each iteration. #
# #
# HINT 2: For most examples, you should be able to generate a fooling image #
# in fewer than 100 iterations of gradient ascent. You can print your #
# progress over iterations to check your algorithm. #
##############################################################################
pass
##############################################################################
# END OF YOUR CODE #
##############################################################################
return X_fooling
```
Run the following to generate a fooling image. You should ideally see at first glance no major difference between the original and fooling images, and the network should now make an incorrect prediction on the fooling one. However you should see a bit of random noise if you look at the 10x magnified difference between the original and fooling images. Feel free to change the `idx` variable to explore other images.
```
idx = 0
Xi = X[idx][None]
target_y = 6
X_fooling = make_fooling_image(Xi, target_y, model)
# Make sure that X_fooling is classified as y_target
scores = sess.run(model.scores, {model.image: X_fooling})
assert scores[0].argmax() == target_y, 'The network is not fooled!'
# Show original image, fooling image, and difference
orig_img = deprocess_image(Xi[0])
fool_img = deprocess_image(X_fooling[0])
# Rescale
plt.subplot(1, 4, 1)
plt.imshow(orig_img)
plt.axis('off')
plt.title(class_names[y[idx]])
plt.subplot(1, 4, 2)
plt.imshow(fool_img)
plt.title(class_names[target_y])
plt.axis('off')
plt.subplot(1, 4, 3)
plt.title('Difference')
plt.imshow(deprocess_image((Xi-X_fooling)[0]))
plt.axis('off')
plt.subplot(1, 4, 4)
plt.title('Magnified difference (10x)')
plt.imshow(deprocess_image(10 * (Xi-X_fooling)[0]))
plt.axis('off')
plt.gcf().tight_layout()
```
# Class visualization
By starting with a random noise image and performing gradient ascent on a target class, we can generate an image that the network will recognize as the target class. This idea was first presented in [2]; [3] extended this idea by suggesting several regularization techniques that can improve the quality of the generated image.
Concretely, let $I$ be an image and let $y$ be a target class. Let $s_y(I)$ be the score that a convolutional network assigns to the image $I$ for class $y$; note that these are raw unnormalized scores, not class probabilities. We wish to generate an image $I^*$ that achieves a high score for the class $y$ by solving the problem
$$
I^* = {\arg\max}_I (s_y(I) - R(I))
$$
where $R$ is a (possibly implicit) regularizer (note the sign of $R(I)$ in the argmax: we want to minimize this regularization term). We can solve this optimization problem using gradient ascent, computing gradients with respect to the generated image. We will use (explicit) L2 regularization of the form
$$
R(I) = \lambda \|I\|_2^2
$$
**and** implicit regularization as suggested by [3] by periodically blurring the generated image. We can solve this problem using gradient ascent on the generated image.
In the cell below, complete the implementation of the `create_class_visualization` function.
[2] Karen Simonyan, Andrea Vedaldi, and Andrew Zisserman. "Deep Inside Convolutional Networks: Visualising
Image Classification Models and Saliency Maps", ICLR Workshop 2014.
[3] Yosinski et al, "Understanding Neural Networks Through Deep Visualization", ICML 2015 Deep Learning Workshop
```
from scipy.ndimage.filters import gaussian_filter1d
def blur_image(X, sigma=1):
X = gaussian_filter1d(X, sigma, axis=1)
X = gaussian_filter1d(X, sigma, axis=2)
return X
def create_class_visualization(target_y, model, **kwargs):
"""
Generate an image to maximize the score of target_y under a pretrained model.
Inputs:
- target_y: Integer in the range [0, 1000) giving the index of the class
- model: A pretrained CNN that will be used to generate the image
Keyword arguments:
- l2_reg: Strength of L2 regularization on the image
- learning_rate: How big of a step to take
- num_iterations: How many iterations to use
- blur_every: How often to blur the image as an implicit regularizer
- max_jitter: How much to gjitter the image as an implicit regularizer
- show_every: How often to show the intermediate result
"""
l2_reg = kwargs.pop('l2_reg', 1e-3)
learning_rate = kwargs.pop('learning_rate', 25)
num_iterations = kwargs.pop('num_iterations', 100)
blur_every = kwargs.pop('blur_every', 10)
max_jitter = kwargs.pop('max_jitter', 16)
show_every = kwargs.pop('show_every', 25)
# We use a single image of random noise as a starting point
X = 255 * np.random.rand(224, 224, 3)
X = preprocess_image(X)[None]
########################################################################
# TODO: Compute the loss and the gradient of the loss with respect to #
# the input image, model.image. We compute these outside the loop so #
# that we don't have to recompute the gradient graph at each iteration #
# #
# Note: loss and grad should be TensorFlow Tensors, not numpy arrays! #
# #
# The loss is the score for the target label, target_y. You should #
# use model.scores to get the scores, and tf.gradients to compute #
# gradients. Don't forget the (subtracted) L2 regularization term! #
########################################################################
loss = None # scalar loss
grad = None # gradient of loss with respect to model.image, same size as model.image
pass
############################################################################
# END OF YOUR CODE #
############################################################################
for t in range(num_iterations):
# Randomly jitter the image a bit; this gives slightly nicer results
ox, oy = np.random.randint(-max_jitter, max_jitter+1, 2)
X = np.roll(np.roll(X, ox, 1), oy, 2)
########################################################################
# TODO: Use sess to compute the value of the gradient of the score for #
# class target_y with respect to the pixels of the image, and make a #
# gradient step on the image using the learning rate. You should use #
# the grad variable you defined above. #
# #
# Be very careful about the signs of elements in your code. #
########################################################################
pass
############################################################################
# END OF YOUR CODE #
############################################################################
# Undo the jitter
X = np.roll(np.roll(X, -ox, 1), -oy, 2)
# As a regularizer, clip and periodically blur
X = np.clip(X, -SQUEEZENET_MEAN/SQUEEZENET_STD, (1.0 - SQUEEZENET_MEAN)/SQUEEZENET_STD)
if t % blur_every == 0:
X = blur_image(X, sigma=0.5)
# Periodically show the image
if t == 0 or (t + 1) % show_every == 0 or t == num_iterations - 1:
plt.imshow(deprocess_image(X[0]))
class_name = class_names[target_y]
plt.title('%s\nIteration %d / %d' % (class_name, t + 1, num_iterations))
plt.gcf().set_size_inches(4, 4)
plt.axis('off')
plt.show()
return X
```
Once you have completed the implementation in the cell above, run the following cell to generate an image of Tarantula:
```
target_y = 76 # Tarantula
out = create_class_visualization(target_y, model)
```
Try out your class visualization on other classes! You should also feel free to play with various hyperparameters to try and improve the quality of the generated image, but this is not required.
```
target_y = np.random.randint(1000)
# target_y = 78 # Tick
# target_y = 187 # Yorkshire Terrier
# target_y = 683 # Oboe
# target_y = 366 # Gorilla
# target_y = 604 # Hourglass
print(class_names[target_y])
X = create_class_visualization(target_y, model)
```
|
github_jupyter
|
# LassoRegresion with Scale & Power Transformer
This Code template is for the regression analysis using Lasso Regression, the feature transformation technique Power Transformer and rescaling technique Scale in a pipeline. Lasso stands for Least Absolute Shrinkage and Selection Operator is a type of linear regression that uses shrinkage.
### Required Packages
```
import warnings
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as se
from sklearn.linear_model import Lasso
from sklearn.model_selection import train_test_split
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import PowerTransformer
from sklearn.preprocessing import scale
from sklearn.metrics import r2_score, mean_absolute_error, mean_squared_error
warnings.filterwarnings('ignore')
```
### Initialization
Filepath of CSV file
```
#filepath
file_path = ""
```
List of features which are required for model training .
```
#x_values
features = []
```
Target feature for prediction.
```
#y_value
target = ''
```
### Data Fetching
Pandas is an open-source, BSD-licensed library providing high-performance, easy-to-use data manipulation and data analysis tools.
We will use panda's library to read the CSV file using its storage path.And we use the head function to display the initial row or entry.
```
df=pd.read_csv(file_path)
df.head()
```
### Feature Selections
It is the process of reducing the number of input variables when developing a predictive model. Used to reduce the number of input variables to both reduce the computational cost of modelling and, in some cases, to improve the performance of the model.
We will assign all the required input features to X and target/outcome to Y.
```
X=df[features]
Y=df[target]
```
### Data Preprocessing
Since the majority of the machine learning models in the Sklearn library doesn't handle string category data and Null value, we have to explicitly remove or replace null values. The below snippet have functions, which removes the null value if any exists. And convert the string classes data in the datasets by encoding them to integer classes.
```
def NullClearner(df):
if(isinstance(df, pd.Series) and (df.dtype in ["float64","int64"])):
df.fillna(df.mean(),inplace=True)
return df
elif(isinstance(df, pd.Series)):
df.fillna(df.mode()[0],inplace=True)
return df
else:return df
def EncodeX(df):
return pd.get_dummies(df)
```
Calling preprocessing functions on the feature and target set.
```
x=X.columns.to_list()
for i in x:
X[i]=NullClearner(X[i])
X=EncodeX(X)
Y=NullClearner(Y)
X.head()
```
#### Correlation Map
In order to check the correlation between the features, we will plot a correlation matrix. It is effective in summarizing a large amount of data where the goal is to see patterns.
```
f,ax = plt.subplots(figsize=(18, 18))
matrix = np.triu(X.corr())
se.heatmap(X.corr(), annot=True, linewidths=.5, fmt= '.1f',ax=ax, mask=matrix)
plt.show()
```
### Data Splitting
The train-test split is a procedure for evaluating the performance of an algorithm. The procedure involves taking a dataset and dividing it into two subsets. The first subset is utilized to fit/train the model. The second subset is used for prediction. The main motive is to estimate the performance of the model on new data.
```
x_train,x_test,y_train,y_test=train_test_split(X,Y,test_size=0.2,random_state=123)
```
## Data Rescaling
### Scale:
Standardize a dataset along any axis.
Center to the mean and component wise scale to unit variance.
for more... [click here](https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.scale.html)
```
x_train = scale(x_train)
x_test = scale(x_test)
```
### Model
Linear Model trained with L1 prior as regularizer (aka the Lasso)
The Lasso is a linear model that estimates sparse coefficients. It is useful in some contexts due to its tendency to prefer solutions with fewer non-zero coefficients, effectively reducing the number of features upon which the given solution is dependent. For this reason Lasso and its variants are fundamental to the field of compressed sensing.
#### Model Tuning Parameter
> **alpha** -> Constant that multiplies the L1 term. Defaults to 1.0. alpha = 0 is equivalent to an ordinary least square, solved by the LinearRegression object. For numerical reasons, using alpha = 0 with the Lasso object is not advised.
> **selection** -> If set to ‘random’, a random coefficient is updated every iteration rather than looping over features sequentially by default. This (setting to ‘random’) often leads to significantly faster convergence especially when tol is higher than 1e-4.
> **tol** -> The tolerance for the optimization: if the updates are smaller than tol, the optimization code checks the dual gap for optimality and continues until it is smaller than tol.
> **max_iter** -> The maximum number of iterations.
#### Feature Transformation
Power Transformers are a family of parametric, monotonic transformations that are applied to make data more Gaussian-like. This is useful for modeling issues related to heteroscedasticity (non-constant variance), or other situations where normality is desired
[More on PowerTransformer module and parameters](https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.PowerTransformer.html)
```
model=make_pipeline(PowerTransformer(),Lasso(random_state=123))
model.fit(x_train,y_train)
```
#### Model Accuracy
We will use the trained model to make a prediction on the test set.Then use the predicted value for measuring the accuracy of our model.
> **score**: The **score** function returns the coefficient of determination <code>R<sup>2</sup></code> of the prediction.
```
print("Accuracy score {:.2f} %\n".format(model.score(x_test,y_test)*100))
```
> **r2_score**: The **r2_score** function computes the percentage variablility explained by our model, either the fraction or the count of correct predictions.
> **mae**: The **mean abosolute error** function calculates the amount of total error(absolute average distance between the real data and the predicted data) by our model.
> **mse**: The **mean squared error** function squares the error(penalizes the model for large errors) by our model.
```
y_pred=model.predict(x_test)
print("R2 Score: {:.2f} %".format(r2_score(y_test,y_pred)*100))
print("Mean Absolute Error {:.2f}".format(mean_absolute_error(y_test,y_pred)))
print("Mean Squared Error {:.2f}".format(mean_squared_error(y_test,y_pred)))
```
#### Prediction Plot
First, we make use of a plot to plot the actual observations, with x_train on the x-axis and y_train on the y-axis.
For the regression line, we will use x_train on the x-axis and then the predictions of the x_train observations on the y-axis.
```
plt.figure(figsize=(14,10))
plt.plot(range(20),y_test[0:20], color = "green")
plt.plot(range(20),model.predict(x_test[0:20]), color = "red")
plt.legend(["Actual","prediction"])
plt.title("Predicted vs True Value")
plt.xlabel("Record number")
plt.ylabel(target)
plt.show()
```
##### Creator - Vikas Mishra, Github: [Profile](https://github.com/Vikaas08)
|
github_jupyter
|
```
#http://colah.github.io/posts/2015-08-Understanding-LSTMs/
from collections import Counter
import json
import nltk
from nltk.corpus import stopwords
WORD_FREQUENCY_FILE_FULL_PATH = "analysis.vocab"
class MyVocabulary:
def __init__(self, vocabulary, wordFrequencyFilePath):
self.vocabulary = vocabulary
self.WORD_FREQUENCY_FILE_FULL_PATH = wordFrequencyFilePath
self.input_word_index = {}
self.reverse_input_word_index = {}
self.input_word_index["START"] = 1
self.input_word_index["UNKOWN"] = -1
self.MaxSentenceLength = None
def PrepareVocabulary(self,reviews):
self._prepare_Word_Frequency_Count_File(reviews)
self._create_Vocab_Indexes()
self.MaxSentenceLength = max([len(txt.split(" ")) for txt in reviews])
def Get_Top_Words(self, number_words = None):
if number_words == None:
number_words = self.vocabulary
chars = json.loads(open(self.WORD_FREQUENCY_FILE_FULL_PATH).read())
counter = Counter(chars)
most_popular_words = {key for key, _value in counter.most_common(number_words)}
return most_popular_words
def _prepare_Word_Frequency_Count_File(self,reviews):
counter = Counter()
for s in reviews:
counter.update(s.split(" "))
with open(self.WORD_FREQUENCY_FILE_FULL_PATH, 'w') as output_file:
output_file.write(json.dumps(counter))
def _create_Vocab_Indexes(self):
INPUT_WORDS = self.Get_Top_Words(self.vocabulary)
#word to int
#self.input_word_index = dict(
# [(word, i) for i, word in enumerate(INPUT_WORDS)])
for i, word in enumerate(INPUT_WORDS):
self.input_word_index[word] = i
#int to word
#self.reverse_input_word_index = dict(
# (i, word) for word, i in self.input_word_index.items())
for word, i in self.input_word_index.items():
self.reverse_input_word_index[i] = word
#self.input_word_index = input_word_index
#self.reverse_input_word_index = reverse_input_word_index
#seralize.dump(config.DATA_FOLDER_PATH+"input_word_index.p",input_word_index)
#seralize.dump(config.DATA_FOLDER_PATH+"reverse_input_word_index.p",reverse_input_word_index)
def TransformSentencesToId(self, sentences):
vectors = []
for r in sentences:
words = r.split(" ")
vector = np.zeros(len(words))
for t, word in enumerate(words):
if word in self.input_word_index:
vector[t] = self.input_word_index[word]
else:
pass
#vector[t] = 2 #unk
vectors.append(vector)
return vectors
def ReverseTransformSentencesToId(self, sentences):
vectors = []
for r in sentences:
words = r.split(" ")
vector = np.zeros(len(words))
for t, word in enumerate(words):
if word in self.input_word_index:
vector[t] = self.input_word_index[word]
else:
pass
#vector[t] = 2 #unk
vectors.append(vector)
return vectors
#Download DataSet
#http://ai.stanford.edu/~amaas/data/sentiment/
#https://www.liip.ch/en/blog/sentiment-detection-with-keras-word-embeddings-and-lstm-deep-learning-networks
import os
def GetTextFilePathsInDirectory(directory):
files = []
for file in os.listdir(directory):
if file.endswith(".txt"):
filePath = os.path.join(directory, file)
files.append(filePath)
return files
def GetLinesFromTextFile(filePath):
with open(filePath,"r", encoding="utf-8") as f:
lines = [line.strip() for line in f]
return lines
def RemoveStopWords(line, stopwords):
words = []
for word in line.split(" "):
word = word.strip()
if word not in stopwords and word != "" and word != "&":
words.append(word)
return " ".join(words)
import re
REPLACE_NO_SPACE = re.compile("(\.)|(\;)|(\:)|(\!)|(\')|(\?)|(\,)|(\")|(\()|(\))|(\[)|(\])")
REPLACE_WITH_SPACE = re.compile("(<br\s*/><br\s*/>)|(\-)|(\/)")
#https://gist.github.com/aaronkub/257a1bd9215da3a7221148600d849450#file-clean_movie_reviews-py
def preprocess_reviews(reviews):
default_stop_words = nltk.corpus.stopwords.words('english')
stopwords = set(default_stop_words)
reviews = [REPLACE_NO_SPACE.sub("", line.lower()) for line in reviews]
reviews = [REPLACE_WITH_SPACE.sub(" ", line) for line in reviews]
reviews = [RemoveStopWords(line,stopwords) for line in reviews]
return reviews
default_stop_words = nltk.corpus.stopwords.words('english')
stopwords = set(default_stop_words)
RemoveStopWords("this is a very large test",stopwords)
```
<h2>Prepare Data</h2>
```
positive_files = GetTextFilePathsInDirectory("aclImdb/train/pos/")
negative_files = GetTextFilePathsInDirectory("aclImdb/train/neg/")
reviews_positive = []
for i in range(0,500):
reviews_positive.extend(GetLinesFromTextFile(positive_files[i]))
reviews_negative = []
for i in range(0,500):
reviews_negative.extend(GetLinesFromTextFile(negative_files[i]))
print("Positive Review---> {0}".format(reviews_positive[5]))
print()
print("Negative Review---> {0}".format(reviews_negative[5]))
print()
reviews_positive = preprocess_reviews(reviews_positive)
print("Processed Positive Review---> {0}".format(reviews_positive[5]))
reviews_negative = preprocess_reviews(reviews_negative)
print("Processed Negative Review---> {0}".format(reviews_negative[5]))
```
<h2>Labeled DataSet</h2>
```
Reviews_Labeled = list(zip(reviews_positive, np.ones(len(reviews_positive))))
Reviews_Labeled.extend(list(zip(reviews_negative, np.zeros(len(reviews_negative)))))
Reviews_Labeled[10]
```
<h3>Prepare Vocabulary</h3>
```
TOP_WORDS = 500
vocab = MyVocabulary(TOP_WORDS,"analysis.vocab")
reviews_text = [line[0] for line in Reviews_Labeled]
vocab.PrepareVocabulary(reviews_text)
#vocab.Get_Top_Words(10)
vocab.input_word_index["START"]
#vocab.input_word_index["UNKOWN"]
#vocab.input_word_index
```
<h2>Integer Encode Words</h2>
```
reviews,labels=zip(*Reviews_Labeled)
reviews_int = vocab.TransformSentencesToId(reviews)
Reviews_Labeled_Int = list(zip(reviews_int,labels))
#print(len(Reviews_Labeled_Int))
print(Reviews_Labeled_Int[5])
```
<h2>Split Train and Test </h2>
```
from sklearn.model_selection import train_test_split
train, test = train_test_split(Reviews_Labeled_Int, test_size=0.2)
```
<h3>Pad Sentences</h3>
```
X_train, y_train = list(zip(*train))
X_test, y_test = list(zip(*test))
y_train = np.array(y_train)
y_test = np.array(y_test)
#max_review_length = vocab.MaxSentenceLength
max_review_length = 500
# Truncate and pad the review sequences
from keras.preprocessing import sequence
max_review_length = 500
X_train = sequence.pad_sequences(X_train, maxlen=max_review_length)
X_test = sequence.pad_sequences(X_test, maxlen=max_review_length)
print(type(X_train))
print(type(X_test))
print(X_train.shape)
print(X_test.shape)
print(type(y_train))
print(type(y_test))
print(y_train.shape)
print(y_test.shape)
```
<h2>Model</h2>
```
from keras.models import Sequential
from keras.layers import Dense, Activation, Embedding, LSTM
import keras
# create the model
embedding_vecor_length = 32
model = Sequential()
model.add(Embedding(TOP_WORDS, embedding_vecor_length, input_length=max_review_length))
model.add(LSTM(100))
model.add(Dense(1, activation='sigmoid'))
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
print(model.summary())
model.fit(X_train, y_train, validation_data=(X_test, y_test), epochs=3, batch_size=64)
TOP_WORDS
w = ["a","b","c"]
for i,w in enumerate(w):
print(i+2)
```
|
github_jupyter
|
##### Copyright 2018 The TensorFlow Authors.
```
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
#@title MIT License
#
# Copyright (c) 2017 François Chollet
#
# Permission is hereby granted, free of charge, to any person obtaining a
# copy of this software and associated documentation files (the "Software"),
# to deal in the Software without restriction, including without limitation
# the rights to use, copy, modify, merge, publish, distribute, sublicense,
# and/or sell copies of the Software, and to permit persons to whom the
# Software is furnished to do so, subject to the following conditions:
#
# The above copyright notice and this permission notice shall be included in
# all copies or substantial portions of the Software.
#
# THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
# IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
# FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL
# THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
# LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING
# FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER
# DEALINGS IN THE SOFTWARE.
```
# Basic classification: Classify images of clothing
<table class="tfo-notebook-buttons" align="left">
<td>
<a target="_blank" href="https://www.tensorflow.org/tutorials/keras/classification"><img src="https://www.tensorflow.org/images/tf_logo_32px.png" />View on TensorFlow.org</a>
</td>
<td>
<a target="_blank" href="https://colab.research.google.com/github/tensorflow/docs/blob/master/site/en/tutorials/keras/classification.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
</td>
<td>
<a target="_blank" href="https://github.com/tensorflow/docs/blob/master/site/en/tutorials/keras/classification.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View source on GitHub</a>
</td>
<td>
<a href="https://storage.googleapis.com/tensorflow_docs/docs/site/en/tutorials/keras/classification.ipynb"><img src="https://www.tensorflow.org/images/download_logo_32px.png" />Download notebook</a>
</td>
</table>
This guide trains a neural network model to classify images of clothing, like sneakers and shirts. It's okay if you don't understand all the details; this is a fast-paced overview of a complete TensorFlow program with the details explained as you go.
This guide uses [tf.keras](https://www.tensorflow.org/guide/keras), a high-level API to build and train models in TensorFlow.
```
try:
# %tensorflow_version only exists in Colab.
%tensorflow_version 2.x
except Exception:
pass
from __future__ import absolute_import, division, print_function, unicode_literals
# TensorFlow and tf.keras
import tensorflow as tf
from tensorflow import keras
# Helper libraries
import numpy as np
import matplotlib.pyplot as plt
print(tf.__version__)
```
## Import the Fashion MNIST dataset
This guide uses the [Fashion MNIST](https://github.com/zalandoresearch/fashion-mnist) dataset which contains 70,000 grayscale images in 10 categories. The images show individual articles of clothing at low resolution (28 by 28 pixels), as seen here:
<table>
<tr><td>
<img src="https://tensorflow.org/images/fashion-mnist-sprite.png"
alt="Fashion MNIST sprite" width="600">
</td></tr>
<tr><td align="center">
<b>Figure 1.</b> <a href="https://github.com/zalandoresearch/fashion-mnist">Fashion-MNIST samples</a> (by Zalando, MIT License).<br/>
</td></tr>
</table>
Fashion MNIST is intended as a drop-in replacement for the classic [MNIST](http://yann.lecun.com/exdb/mnist/) dataset—often used as the "Hello, World" of machine learning programs for computer vision. The MNIST dataset contains images of handwritten digits (0, 1, 2, etc.) in a format identical to that of the articles of clothing you'll use here.
This guide uses Fashion MNIST for variety, and because it's a slightly more challenging problem than regular MNIST. Both datasets are relatively small and are used to verify that an algorithm works as expected. They're good starting points to test and debug code.
Here, 60,000 images are used to train the network and 10,000 images to evaluate how accurately the network learned to classify images. You can access the Fashion MNIST directly from TensorFlow. Import and load the Fashion MNIST data directly from TensorFlow:
```
fashion_mnist = keras.datasets.fashion_mnist
(train_images, train_labels), (test_images, test_labels) = fashion_mnist.load_data()
```
Loading the dataset returns four NumPy arrays:
* The `train_images` and `train_labels` arrays are the *training set*—the data the model uses to learn.
* The model is tested against the *test set*, the `test_images`, and `test_labels` arrays.
The images are 28x28 NumPy arrays, with pixel values ranging from 0 to 255. The *labels* are an array of integers, ranging from 0 to 9. These correspond to the *class* of clothing the image represents:
<table>
<tr>
<th>Label</th>
<th>Class</th>
</tr>
<tr>
<td>0</td>
<td>T-shirt/top</td>
</tr>
<tr>
<td>1</td>
<td>Trouser</td>
</tr>
<tr>
<td>2</td>
<td>Pullover</td>
</tr>
<tr>
<td>3</td>
<td>Dress</td>
</tr>
<tr>
<td>4</td>
<td>Coat</td>
</tr>
<tr>
<td>5</td>
<td>Sandal</td>
</tr>
<tr>
<td>6</td>
<td>Shirt</td>
</tr>
<tr>
<td>7</td>
<td>Sneaker</td>
</tr>
<tr>
<td>8</td>
<td>Bag</td>
</tr>
<tr>
<td>9</td>
<td>Ankle boot</td>
</tr>
</table>
Each image is mapped to a single label. Since the *class names* are not included with the dataset, store them here to use later when plotting the images:
```
class_names = ['T-shirt/top', 'Trouser', 'Pullover', 'Dress', 'Coat',
'Sandal', 'Shirt', 'Sneaker', 'Bag', 'Ankle boot']
```
## Explore the data
Let's explore the format of the dataset before training the model. The following shows there are 60,000 images in the training set, with each image represented as 28 x 28 pixels:
```
train_images.shape
```
Likewise, there are 60,000 labels in the training set:
```
len(train_labels)
```
Each label is an integer between 0 and 9:
```
train_labels
```
There are 10,000 images in the test set. Again, each image is represented as 28 x 28 pixels:
```
test_images.shape
```
And the test set contains 10,000 images labels:
```
len(test_labels)
```
## Preprocess the data
The data must be preprocessed before training the network. If you inspect the first image in the training set, you will see that the pixel values fall in the range of 0 to 255:
```
plt.figure()
plt.imshow(train_images[0])
plt.colorbar()
plt.grid(False)
plt.show()
```
Scale these values to a range of 0 to 1 before feeding them to the neural network model. To do so, divide the values by 255. It's important that the *training set* and the *testing set* be preprocessed in the same way:
```
train_images = train_images / 255.0
test_images = test_images / 255.0
```
To verify that the data is in the correct format and that you're ready to build and train the network, let's display the first 25 images from the *training set* and display the class name below each image.
```
plt.figure(figsize=(10,10))
for i in range(25):
plt.subplot(5,5,i+1)
plt.xticks([])
plt.yticks([])
plt.grid(False)
plt.imshow(train_images[i], cmap=plt.cm.binary)
plt.xlabel(class_names[train_labels[i]])
plt.show()
```
## Build the model
Building the neural network requires configuring the layers of the model, then compiling the model.
### Set up the layers
The basic building block of a neural network is the *layer*. Layers extract representations from the data fed into them. Hopefully, these representations are meaningful for the problem at hand.
Most of deep learning consists of chaining together simple layers. Most layers, such as `tf.keras.layers.Dense`, have parameters that are learned during training.
```
model = keras.Sequential([
keras.layers.Flatten(input_shape=(28, 28)),
keras.layers.Dense(128, activation='relu'),
keras.layers.Dense(10)
])
```
The first layer in this network, `tf.keras.layers.Flatten`, transforms the format of the images from a two-dimensional array (of 28 by 28 pixels) to a one-dimensional array (of 28 * 28 = 784 pixels). Think of this layer as unstacking rows of pixels in the image and lining them up. This layer has no parameters to learn; it only reformats the data.
After the pixels are flattened, the network consists of a sequence of two `tf.keras.layers.Dense` layers. These are densely connected, or fully connected, neural layers. The first `Dense` layer has 128 nodes (or neurons). The second (and last) layer is a 10-node *softmax* layer that returns an array of 10 probability scores that sum to 1. Each node contains a score that indicates the probability that the current image belongs to one of the 10 classes.
### Compile the model
Before the model is ready for training, it needs a few more settings. These are added during the model's *compile* step:
* *Loss function* —This measures how accurate the model is during training. You want to minimize this function to "steer" the model in the right direction.
* *Optimizer* —This is how the model is updated based on the data it sees and its loss function.
* *Metrics* —Used to monitor the training and testing steps. The following example uses *accuracy*, the fraction of the images that are correctly classified.
```
model.compile(optimizer='adam',
loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True),
metrics=['accuracy'])
```
## Train the model
Training the neural network model requires the following steps:
1. Feed the training data to the model. In this example, the training data is in the `train_images` and `train_labels` arrays.
2. The model learns to associate images and labels.
3. You ask the model to make predictions about a test set—in this example, the `test_images` array.
4. Verify that the predictions match the labels from the `test_labels` array.
### Feed the model
To start training, call the `model.fit` method—so called because it "fits" the model to the training data:
```
model.fit(train_images, train_labels, epochs=10)
```
As the model trains, the loss and accuracy metrics are displayed. This model reaches an accuracy of about 0.91 (or 91%) on the training data.
### Evaluate accuracy
Next, compare how the model performs on the test dataset:
```
test_loss, test_acc = model.evaluate(test_images, test_labels, verbose=2)
print('\nTest accuracy:', test_acc)
```
It turns out that the accuracy on the test dataset is a little less than the accuracy on the training dataset. This gap between training accuracy and test accuracy represents *overfitting*. Overfitting is when a machine learning model performs worse on new, previously unseen inputs than on the training data. An overfitted model "memorizes" the training data—with less accuracy on testing data. For more information, see the following:
* [Demonstrate overfitting](https://www.tensorflow.org/tutorials/keras/overfit_and_underfit#demonstrate_overfitting)
* [Strategies to prevent overfitting](https://www.tensorflow.org/tutorials/keras/overfit_and_underfit#strategies_to_prevent_overfitting)
### Make predictions
With the model trained, you can use it to make predictions about some images.
```
predictions = model.predict(test_images)
```
Here, the model has predicted the label for each image in the testing set. Let's take a look at the first prediction:
```
predictions[0]
```
A prediction is an array of 10 numbers. They represent the model's "confidence" that the image corresponds to each of the 10 different articles of clothing. You can see which label has the highest confidence value:
```
np.argmax(predictions[0])
```
So, the model is most confident that this image is an ankle boot, or `class_names[9]`. Examining the test label shows that this classification is correct:
```
test_labels[0]
```
Graph this to look at the full set of 10 class predictions.
```
def plot_image(i, predictions_array, true_label, img):
predictions_array, true_label, img = predictions_array, true_label[i], img[i]
plt.grid(False)
plt.xticks([])
plt.yticks([])
plt.imshow(img, cmap=plt.cm.binary)
predicted_label = np.argmax(predictions_array)
if predicted_label == true_label:
color = 'blue'
else:
color = 'red'
plt.xlabel("{} {:2.0f}% ({})".format(class_names[predicted_label],
100*np.max(predictions_array),
class_names[true_label]),
color=color)
def plot_value_array(i, predictions_array, true_label):
predictions_array, true_label = predictions_array, true_label[i]
plt.grid(False)
plt.xticks(range(10))
plt.yticks([])
thisplot = plt.bar(range(10), predictions_array, color="#777777")
plt.ylim([0, 1])
predicted_label = np.argmax(predictions_array)
thisplot[predicted_label].set_color('red')
thisplot[true_label].set_color('blue')
```
### Verify predictions
With the model trained, you can use it to make predictions about some images.
Let's look at the 0th image, predictions, and prediction array. Correct prediction labels are blue and incorrect prediction labels are red. The number gives the percentage (out of 100) for the predicted label.
```
i = 0
plt.figure(figsize=(6,3))
plt.subplot(1,2,1)
plot_image(i, predictions[i], test_labels, test_images)
plt.subplot(1,2,2)
plot_value_array(i, predictions[i], test_labels)
plt.show()
i = 12
plt.figure(figsize=(6,3))
plt.subplot(1,2,1)
plot_image(i, predictions[i], test_labels, test_images)
plt.subplot(1,2,2)
plot_value_array(i, predictions[i], test_labels)
plt.show()
```
Let's plot several images with their predictions. Note that the model can be wrong even when very confident.
```
# Plot the first X test images, their predicted labels, and the true labels.
# Color correct predictions in blue and incorrect predictions in red.
num_rows = 5
num_cols = 3
num_images = num_rows*num_cols
plt.figure(figsize=(2*2*num_cols, 2*num_rows))
for i in range(num_images):
plt.subplot(num_rows, 2*num_cols, 2*i+1)
plot_image(i, predictions[i], test_labels, test_images)
plt.subplot(num_rows, 2*num_cols, 2*i+2)
plot_value_array(i, predictions[i], test_labels)
plt.tight_layout()
plt.show()
```
## Use the trained model
Finally, use the trained model to make a prediction about a single image.
```
# Grab an image from the test dataset.
img = test_images[1]
print(img.shape)
```
`tf.keras` models are optimized to make predictions on a *batch*, or collection, of examples at once. Accordingly, even though you're using a single image, you need to add it to a list:
```
# Add the image to a batch where it's the only member.
img = (np.expand_dims(img,0))
print(img.shape)
```
Now predict the correct label for this image:
```
predictions_single = model.predict(img)
print(predictions_single)
plot_value_array(1, predictions_single[0], test_labels)
_ = plt.xticks(range(10), class_names, rotation=45)
```
`model.predict` returns a list of lists—one list for each image in the batch of data. Grab the predictions for our (only) image in the batch:
```
np.argmax(predictions_single[0])
```
And the model predicts a label as expected.
|
github_jupyter
|
# Le Bloc Note pour ajouter du style
Dans un notebook jupyter on peut rédiger des commentaires en langage naturel, intégrer des liens hypertextes, des images et des vidéos en langage HTML dans des cellules de type **`Markdown`**.
C'est ce que décrit le bloc-note [HTML](HTML-Le_BN_pour_multimedier.ipynb) - Un bloc-note pour créer un document Web multimédia en HTML dans un jupyter notebook.
Cependant, l'affichage se fait avec le rendu définit dans le style par défaut de l'environnement jupyter notebook qui est utilisé pour lire le document.
Nous allons voir qu'il est possible de modifier cet affichage en apportant du code CSS et cela à différents niveaux...
***
> Ce document est un notebook jupyter, pour bien vous familiariser avec cet environnement regardez cette rapide [Introduction](Introduction-Le_BN_pour_explorer.ipynb).
***
**CSS**, pour [Cascading Style Sheets](https://fr.wikipedia.org/wiki/Feuilles_de_style_en_cascade), est un langage qui décrit au navigateur le style dans lequel le contenu d'une page HTML doit être affichée.
Il s'agit de déclarer des propriétés CSS et leur valeur, soit directement dans la balise du code HTML à "styler", ou par l'intermédiaire d'un sélecteur qui pointe vers l'élément HTML visé.
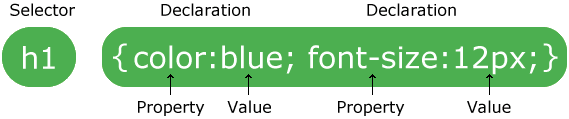
La suite n'utilise que quelques propriétés de CSS afin de montrer comment les appliquer dans un jupyter notebook.
Pour bien comprendre et vous initiez au langage CSS vous pouvez, par exemple, faire ce tutoriel de la [Khanacademy](https://fr.khanacademy.org/computing/computer-programming/html-css/intro-to-css/pt/css-basics) et pour le découvrir de façon plus complète et détaillée rendez-vous sur ce site de référence https://www.w3schools.com/css/...
## Déclaration CSS en ligne :
La façon la plus simple d'apporter un peu de style dans une cellule de type Markdown d'un jupyter notebook est d'écrire la déclaration CSS directement dans la balise HTML concernée :
> <h3 class='fa fa-cogs' style="color: darkorange"> A faire vous-même </h3>
>
> Pour voir le résultat du code **CSS** associé au **HTML** copier/coller les deux codes suivants dans deux cellules de type **`Markdown`**, puis appuyer sur les touches **`<Maj+Entree>`** ou sur le bouton <button class='fa fa-step-forward icon-step-forward btn btn-xs btn-default'></button>.
****
````html
<h1 style="color:purple;text-shadow: 3px 2px darkorange;text-align:center; font-size:5vw;font-variant: small-caps;">
Un résultat stylé !
</h1>
<h1>
Le résultat par défaut.
</h1>
````
****
````html
<center><br>
<img src="https://ericecmorlaix.github.io/img/Jupyter_logo.svg" style = "display:inline-block">
<img src="https://ericecmorlaix.github.io/img/Jupyter_logo.svg" style = "display:inline-block">
<img src="https://ericecmorlaix.github.io/img/Jupyter_logo.svg" style = "display:inline-block">
<img src="https://ericecmorlaix.github.io/img/Jupyter_logo.svg">
<img src="https://ericecmorlaix.github.io/img/Jupyter_logo.svg">
<img src="https://ericecmorlaix.github.io/img/Jupyter_logo.svg">
</center>
````
****
```
# Tester votre code ici
# Tester votre code ici
```
> L'attribut style ajouté en ligne dans une balise HTML permet de surcharger le CSS pour forcer un style d'affichage différent du style par défaut. Les trois premières images s'affichent donc ici en ligne, l'une à coté de l'autre, et non pas comme par défaut, en bloc, l'une sous l'autre : https://www.w3schools.com/css/css_inline-block.asp.
## Déclaration CSS en interne :
La déclaration du CSS en ligne est limitée car elle ne s'applique qu'à une seule balise. Si on souhaite appliquer le même style à plusieurs balises, il nous faut le réécrire à chaque fois...
Si on écrit toutes les déclaration de CSS entre deux balises `<styles>...</style>` dans un code HTML, il s'appliquera potentiellement à tout le contenu de ce code. Et alors, pour distinguer à quelle balise le style doit s'appliquer spécifiquement, on utilise des sélecteurs : https://www.w3schools.com/css/css_selectors.asp
Celà devient très pertinent lorsque l'on souhaite faire une simple modification dans le style car il suffit de la faire à un seul endroit pour qu'elle s'étende sur l'ensemble du code concerné.
> <h3 class='fa fa-cogs' style="color: darkorange"> A faire vous-même </h3>
>
> Pour voir le résultat du code **CSS** sur le **HTML** visé copier/coller tout le code suivant dans une cellule de type **`Markdown`**, puis appuyer sur les touches **`<Maj+Entree>`** ou sur le bouton <button class='fa fa-step-forward icon-step-forward btn btn-xs btn-default'></button>.
****
````html
<style>
h1 {
color:purple;
text-shadow: 3px 2px darkorange;
text-align:center;
font-style: oblique;
font-variant: small-caps;
}
</style>
<h1 style="font-size:5vw">Un résultat sur-stylé !</h1>
<h1>Le nouveau résultat par défaut.</h1>
````
****
```
# Tester votre code ici
```
On observe que le style définit entre deux balises `<styles>...</style>` dans un code HTML, ne s'applique pas dans une cellule de type Markdown.
Pour celà il nous faut recourrir à la fonction "magic" `%%html` de IPython dans une cellule de type **`Code`** :
```
%%HTML
<style>
h1 {
color:purple;
text-shadow: 3px 2px darkorange;
text-align:center;
font-style: oblique;
font-variant: small-caps;
}
</style>
<h1 style="font-size:5vw">Un résultat sur-stylé !</h1>
<h1>Le nouveau résultat par défaut.</h1>
```
***Super !*** Notre style c'est maintenant bien appliqué aux balises `<h1>` ciblés et on peut toujours surcharger une balise en particulier avec du style en ligne...
***Problème !*** Notre style c'est aussi appliqué à toutes les balises `<h1>` précédentes de ce notebook et même au titre de niveau 1 codé en Markdown tout en haut de cette page, comme il s'appliquera au code suivant s'il est copier/coller dans une cellule de type **`Markdown`** :
****
````markdown
# Mon titre de niveau 1 codé en markdown est stylé !
````
****
```
# Tester votre code ici
```
On vient de définir un style qui s'applique à tout ce jupyter notebook. C'est intéressant...
Pour annuler son effet il faut Redémarrer le Noyau & Effacer toutes les sorties (``Kernel > Restart & Clear Output``).
Mais si on souhaite que ce style ne s'applique qu'à certaines balises, il nous faut être plus précis avec nos sélecteurs CSS, par exemple, en utilisant une sélection par classe :
```
%%HTML
<style>
.maClasse {
color:purple;
text-shadow: 3px 2px darkorange;
text-align:center;
font-style: oblique;
font-variant: small-caps;
}
</style>
<h1 class = "maClasse" style="font-size:5vw">Un résultat sur-stylé !</h1>
<h1 class = "maClasse">Le nouveau résultat stylé.</h1>
```
Et on peut maintenant le réutiliser n'importe où dans ce jupyter notebook dans une simple cellule Markdown
```
<p class = "maClasse">Super ! Mon style s'applique où je le souhaite...</p>
```
### Exemple d'application :
Ainsi si on utilise un [générateur de tableau HTML](https://www.tablesgenerator.com/html_tables#) et que l'on souhaite que le style CSS soit pris en compte, on peut copier/coller le code du style CSS dans une cellule de ``Code`` et celui du contenu HTML dans une cellule ``Markdown``:
```
%%html
<style type="text/css">
.tg {border-collapse:collapse;border-spacing:0;border-color:#aabcfe;margin:0px auto;}
.tg td{font-family:Arial, sans-serif;font-size:14px;padding:12px 12px;border-style:solid;border-width:1px;overflow:hidden;word-break:normal;border-color:#aabcfe;color:#669;background-color:#e8edff;}
.tg th{font-family:Arial, sans-serif;font-size:14px;font-weight:normal;padding:12px 12px;border-style:solid;border-width:1px;overflow:hidden;word-break:normal;border-color:#aabcfe;color:#039;background-color:#b9c9fe;}
.tg .tg-c9kt{font-size:16px;font-family:"Comic Sans MS", cursive, sans-serif !important;;text-align:left;vertical-align:middle}
.tg .tg-sd90{font-weight:bold;font-size:16px;font-family:"Comic Sans MS", cursive, sans-serif !important;;text-align:left;vertical-align:middle}
.tg .tg-nyir{background-color:#D2E4FC;font-size:16px;font-family:"Comic Sans MS", cursive, sans-serif !important;;text-align:left;vertical-align:middle}
</style>
```
> <h3 class='fa fa-cogs' style="color: darkorange"> A faire vous-même </h3>
>
> Pour voir le résultat du code **CSS** sur le **HTML** visé, copier/coller le code suivant dans une cellule de type **`Markdown`**, puis appuyer sur les touches **`<Maj+Entree>`** ou sur le bouton <button class='fa fa-step-forward icon-step-forward btn btn-xs btn-default'></button>.
****
````html
<center>
<table class="tg">
<tr>
<th class="tg-sd90">A</th>
<th class="tg-sd90">B</th>
<th class="tg-sd90">C</th>
</tr>
<tr>
<td class="tg-nyir">a1</td>
<td class="tg-nyir">b1</td>
<td class="tg-nyir">c1</td>
</tr>
<tr>
<td class="tg-c9kt">a2</td>
<td class="tg-c9kt">b2</td>
<td class="tg-c9kt">c2</td>
</tr>
<tr>
<td class="tg-nyir">a3</td>
<td class="tg-nyir">b3</td>
<td class="tg-nyir">c3</td>
</tr>
</table>
</center>
````
****
```
# Tester votre code ici
```
<h2 class="maClasse">On peut alors réutiliser le style pour d'autres tableaux :</h2>
<br>
<center>
<table class="tg">
<tr>
<th class="tg-sd90">Décimal</th>
<th class="tg-sd90">Binaire</th>
<th class="tg-sd90">Hexadécimal</th>
<th class="tg-sd90">Décimal</th>
<th class="tg-sd90">Binaire</th>
<th class="tg-sd90">Hexadécimal</th>
</tr>
<tr>
<td class="tg-nyir">0</td>
<td class="tg-nyir">0b0000</td>
<td class="tg-nyir">0x0</td>
<td class="tg-nyir">8</td>
<td class="tg-nyir">0b1000</td>
<td class="tg-nyir">0x8</td>
</tr>
<tr>
<td class="tg-c9kt">1</td>
<td class="tg-c9kt">0b0001</td>
<td class="tg-c9kt">0x1</td>
<td class="tg-c9kt">9</td>
<td class="tg-c9kt">0b1001</td>
<td class="tg-c9kt">0x9</td>
</tr>
<tr>
<td class="tg-nyir">2</td>
<td class="tg-nyir">0b0010</td>
<td class="tg-nyir">0x2</td>
<td class="tg-nyir">10</td>
<td class="tg-nyir">0b1010</td>
<td class="tg-nyir">0xA</td>
</tr>
<tr>
<td class="tg-c9kt">3</td>
<td class="tg-c9kt">0b0011</td>
<td class="tg-c9kt">0x3</td>
<td class="tg-c9kt">11</td>
<td class="tg-c9kt">0b1011</td>
<td class="tg-c9kt">0xB</td>
</tr>
<tr>
<td class="tg-nyir">4</td>
<td class="tg-nyir">0b0100</td>
<td class="tg-nyir">0x4</td>
<td class="tg-nyir">12</td>
<td class="tg-nyir">0b1100</td>
<td class="tg-nyir">0xC</td>
</tr>
<tr>
<td class="tg-c9kt">5</td>
<td class="tg-c9kt">0b0101</td>
<td class="tg-c9kt">0x5</td>
<td class="tg-c9kt">13</td>
<td class="tg-c9kt">0b1101</td>
<td class="tg-c9kt">0xD</td>
</tr>
<tr>
<td class="tg-nyir">6</td>
<td class="tg-nyir">0b0110</td>
<td class="tg-nyir">0x6</td>
<td class="tg-nyir">14</td>
<td class="tg-nyir">0b1110</td>
<td class="tg-nyir">0xE</td>
</tr>
<tr>
<td class="tg-c9kt">7</td>
<td class="tg-c9kt">0b0111</td>
<td class="tg-c9kt">0x7</td>
<td class="tg-c9kt">15</td>
<td class="tg-c9kt">0b1111</td>
<td class="tg-c9kt">0xF</td>
</tr>
</table>
</center>
## Déclaration CSS en externe :
Le défaut de la déclaration du CSS en interne est qu'il ne s'applique que sur la page dans laquelle il est défini.
Il serait intéressant de pouvoir définir une feuille de style CSS commune à plusieurs carnets jupyter...
Ici aussi, lorsque l'on souhaitera faire une simple modification dans le style, il suffira de la faire à un seul endroit pour qu'elle s'étende sur l'ensemble des bloc-notes qui s'y réfèrent.
De plus on peut définir plusieurs feuilles de style différentes et choisir, au gré de nos envies, laquelle appliquée en ne changeant qu'une ligne de code...
On va créer un fichier externe nommé ``monStyle.css`` qui contiendra notre déclaration de style telle que :
```css
h1 {
color: red;
}
h2 {
color: green;
}
p {
color: blue;
}
```
Puis l'enregistrer dans le même dossier que ce notebook.
Par ailleurs, nous allons utiliser deux autres feuilles de style disponibles sur le web :
- https://ericecmorlaix.github.io/monStyle.css ;
- https://ericecmorlaix.github.io/monAutreStyle.css.
Pour appliquer le résultat du code **CSS** sur le **HTML** basculer le type de la cellule ci-dessous de **`Code`** en **`Markdown`**, et appuyer sur les touches **`<Maj+Entree>`** ou sur le bouton <button class='fa fa-step-forward icon-step-forward btn btn-xs btn-default'></button>.
Enfin exécuter successivement les trois cellules de codes suivantes...
```
<h1>Mon titre de niveau 1 :</h1>
<h2>Mon titre de niveau 2 :</h2>
<p>Mon paragraphe.</p>
%%html
<link rel="stylesheet" type="text/css" href="monStyle.css">
%%html
<link rel="stylesheet" type="text/css" href="https://ericecmorlaix.github.io/monStyle.css">
%%html
<link rel="stylesheet" type="text/css" href="https://ericecmorlaix.github.io/monAutreStyle.css">
```
> <h3 class='fa fa-cogs' style="color: darkorange"> A faire vous-même </h3>
>
> Jouer avec les flèches <button class='fa fa-arrow-up icon-arrow-up btn btn-xs btn-default'></button> <button class='fa fa-arrow-down icon-arrow-down btn btn-xs btn-default'></button> pour modifier l'ordre des cellules de code.
> On observe que c'est toujours le style de la cellule la plus basse qui s'applique...
> Rappel : pour revenir au style par défaut de l'environnement jupyter, il faut Redémarrer le Noyau & Effacer toutes les sorties (``Kernel > Restart & Clear Output``).
## Complément avec la fonction HTML() de IPython.display :
La fonction HTML() du module IPython.display permet d'afficher directement une chaine de caractères écrite en langage HTML. Cette chaine générée par un script Python peut inclure du CSS.
```
from IPython.display import HTML
enLigne = '<img src="https://ericecmorlaix.github.io/img/Jupyter_logo.svg" style = "display:inline-block">'
enBloc = '<img src="https://ericecmorlaix.github.io/img/Jupyter_logo.svg">'
chaine = '<center><br>' + enLigne * 8 + enBloc * 3 + '</center>'
HTML(chaine)
from IPython.display import HTML
from random import randint
couleur=['red','blue','green', 'yellow', 'purple', 'pink', 'orange', 'cyan', 'magenta', 'nany', 'yellowgreen', 'lightcoral']
chaine = ''
for i in range(1,7) :
chaine = chaine + f'<h{i} style = "color:{couleur[randint(0, len(couleur) - 1)]}; text-align:center;">Mon titre de niveau {i}</h{i}>'
HTML(chaine)
```
## Ressources :
* Pour aller plus loin en HTML/CSS : http://api.si.lycee.ecmorlaix.fr/APprentissageHtmlCss/
* Un site de référence pour le CSS : https://www.w3schools.com/css/default.asp
* On peut très avantageusement utiliser un [générateur de feuille de style CSS](https://www.megaptery.com/2012/05/21-outils-generateurs-css-developpeurs-web.html)
## A vous de jouer :
> <h3 class='fa fa-cogs' style="color: darkorange"> A faire vous-même </h3>
>
***
> **Félicitations !** Vous êtes parvenu au bout des activités de ce bloc note.
> Vous êtes maintenant capable d'imposer votre style en **CSS** dans l'environnement interactif jupyter notebook.
> Pour explorer plus avant d'autres fonctionnalités de jupyter notebook repassez par le [Sommaire](index.ipynb).
***
<a rel="license" href="http://creativecommons.org/licenses/by-sa/4.0/"><img alt="Licence Creative Commons" style="border-width:0" src="https://i.creativecommons.org/l/by-sa/4.0/88x31.png" /></a><br />Ce document est mis à disposition selon les termes de la <a rel="license" href="http://creativecommons.org/licenses/by-sa/4.0/">Licence Creative Commons Attribution - Partage dans les Mêmes Conditions 4.0 International</a>.
Pour toute question, suggestion ou commentaire : <a href="mailto:[email protected]">[email protected]</a>
|
github_jupyter
|
```
%cd ../..
%run cryptolytic/notebooks/init.ipynb
import pandas as pd
import cryptolytic.util.core as util
import cryptolytic.start as start
import cryptolytic.viz.plot as plot
import cryptolytic.data.sql as sql
import cryptolytic.data.historical as h
import cryptolytic.model as m
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
from matplotlib.pylab import rcParams
from IPython.core.display import HTML
from pandas.plotting import register_matplotlib_converters # to stop a warning message
ohclv = ['open', 'high', 'close', 'low', 'volume']
plt.style.use('ggplot')
rcParams['figure.figsize'] = 20,7
start.init()
register_matplotlib_converters()
# Make math readable
HTML("""
<style>
.MathJax {
font-size: 2rem;
}
</style>""")
df = sql.get_some_candles(
info={'start':1574368000, 'end':1579046400, 'exchange_id':'hitbtc',
'trading_pair':'btc_usd', 'period':300}, n=5e4)
df2 = df.copy() # mutable copy
train_test_pivot = int(len(df)*0.8)
df['diff'] = df['high'] - df['low']
```
# Considerations for time series
- Understanding temporal behavior of data: seasonality, stationarity
- Identifying underlying distributions and nature of temporal process producing data
- Estimation of past, present, and future values
- filtering vs forecasting
- Classification of time series (for example, arrhythmia in heart data)
- Anomaly detection of outlier points within time series
```
from scipy.stats import pearsonr
#a = m.get_by_time(df, '2019-11-22', '2019-11-26')
#b = m.get_by_time(df, '2019-11-26', '2019-11-28')
train = df
params = {
'level' : 'smooth trend',
'cycle' : False,
'seasonal' : None
}
import statsmodels as sm
util.bdir(sm.tsa)
util.bdir(sm.tsa.tsatools)
util.bdir(sm.tsa.stattools)
# statsmodels.api
import statsmodels.api as sm
import statsmodels as sm
candles_in_day = int(1440 / 5)
candles_in_day
```
# Hidden Markov Models (HMMs)
Type of state space model: Observations are an indicator of underlying state
Markov process: past doesn't matter if preset status is known
Parameter estimation: Baum-Welch Algorithm
Smootheing/state labeling: Viterbi algorithm
There is an unobservable state that is affecting the output, along with the input
$x_{t-1} -> x_{t} -> x_{t+1}$
$y_{t-1} -> y_{t} -> y_{t+1}$
# Baum-Welch Algorithm for Determining Parameters
- Expectation maximization parameter estimation:
- - Initialize parameters (with informative priors or randomly)
- - Em iterations
- - - Compute the expectation of the log likelihood given the data
- - Exit when desired convergence is reached
- - - Choose the parameters that maximize the log likelihood expectation
- Guarantee that the likelihood increases with each iteration (Forward-Backward Expectation Maximization Algorithm)
- - Figure out your likelihood expectation is given the data, that's the expectation step and the maximization step
- is to update the estimates of your parameters to maximize that likelihood given that expression of that likelihood,
and then repeat
- BUT
- - converges to a local maximum not a global maximum
- - can overfit the data
Problem
A : Transition Matrix probability, how likely x to transition to another state at that timestep. Gives a matrix, saying how likely for example to go from state i to state k, etc.
B : What is the probability of seeing a value at y, given a particular x.
$\theta = (A,B,\pi)$
Forward Step
$\pi$ : Priors, telling how likely you are to begin in a particular state
$\alpha_i(t) = P(Y_1 = y_1,...,Y_t = y_t, X_t = i |\theta) \\
\alpha_i(1) = \pi_ib_i(y_1)\\
\alpha_i(t+1) = b_i(y_{t+1})\sum_{j=1}^N\alpha_j(t)\alpha_{ji}
$
Backward Step
How probable is it, being conditionod on being in state i at time t, how probable is it to see the sequence from t+1 to T.
$
\beta_i(t) = P(Y_{t+1}=y_{t+1},...,Y_T=y_T|X_t=i,\theta)\\
\beta_i(T) = 1\\
\beta_i(t)=\sum_{j=1}^N\beta_j(t+1)a_{ij}b_j(y_{t+1}
$
Then there are $\gamma_i$ the probabliity of being in state i at time t given all the observed data and parameters $\theta$
$\gamma_i(t) = P(X_t=i|Y,\theta)=\frac{P(X_t=i|Y,\theta)}{P(Y|\theta)}=\frac{\alpha_i(t)\beta_i(t)}{\sum_{j=1}^N\alpha_j(t)\beta_j(t)}$
$\xi_{ij}(t)=P(X_t=i,X_{t+1}=j|Y,\theta)$
- Prior, how likely at the beginning of a sequennce to be at any given starting state
$$\pi_i^*=\gamma_i(1)$$
- How likely to transition from state i to state j at a particular timestep
$$\alpha_{ij}^*\frac{\sum_{t=1}^{T-1}\xi_ij(t)}{\sum_{t=1}^{T-1}\gamma_i(t)}$$
- How likely to see a observed value, given being in state i
$$b_i^*(v_k) = \frac{ \sum_{t=1}^T1_{y_t=v_k}\gamma_i(t) }{\sum_{t=1}^T\gamma_i(t)}$$
```
import matplotlib.pyplot as plt
plt.plot(df.index, df.close)
!pip -q install hmmlearn
df_sub = df.iloc[:int(len(df)/4)]
from hmmlearn import hmm
# HMM Learn
vals = np.expand_dims(df_sub.close.values, 1) # requires two dimensions for the input
n_states = 2
model = hmm.GaussianHMM(n_components=n_states, n_iter=100, random_state=100).fit(vals)
hidden_states = model.predict(vals)
# Predicts two different states for the thing to be in. Kind of mirrors how
hidden_states
np.unique(hidden_states)
# There should be 2 distinct states, a Low flow state, high flow state
plt.plot(df_sub.index, df_sub.close)
_min = df_sub.close.min()
_max = df_sub.close.max()
h_min = hidden_states.min()
h_max = hidden_states.max()
plt.title('2 State HMM')
plt.plot(df_sub.index,[np.interp(x,[h_min,h_max], [_min,_max]) for x in hidden_states])
def fitHMM(vals, n_states):
vals = np.reshape(vals, [len(vals), 1])
# Fit Gaussian HMM to 0
model = hmm.GaussianHMM(n_components=n_states, n_iter=100).fit(vals)
# classify each observation as state 0 or 1
hidden_states = model.predict(vals)
# fit HMM parameters
mus = np.squeeze(model.means_)
sigmas = np.squeeze(np.sqrt(model.covars_))
# Transition matrix which describes how likely you are to go from state i to state j
transmat = np.array(model.transmat_)
print(mus)
print(sigmas)
# reorder parameters in ascending order of mean of underlying distributions
idx = np.argsort(mus)
mus = mus[idx]
sigmas = sigmas[idx]
transmat = transmat[idx, :][:, idx]
state_dict = {}
states = [i for i in range(n_states)]
for i in idx:
state_dict[i] = states[idx[i]]
relabeled_states = [state_dict[h] for h in hidden_states]
return (relabeled_states, mus, sigmas, transmat, model)
hidden_states, mus, sigmas, transmat, model = fitHMM(df.close.values, 3)
hidden_states
np.unique(hidden_states, return_counts=True)
rcParams['figure.figsize'] = 20,7
def plot_states(ts_vals, states, time_vals):
fig, ax1 = plt.subplots()
color = 'tab:red'
ax1.set_ylabel('Data', color=color)
ax1.plot(time_vals, ts_vals, color=color)
ax1.tick_params(axis='y', labelcolor=color)
ax2 = ax1.twinx()
color = 'tab:blue'
ax2.set_ylabel('Hidden state', color=color)
ax2.plot(time_vals,states, color=color)
ax2.tick_params(axis='y', labelcolor=color)
plt.title(f'{len(np.unique(states))} State Model')
fig.tight_layout()
plt.show()
plot_states(df.close, hidden_states, df.index)
x = np.array([hidden_states]).T
m = np.array([mus])
print(np.shape(x), np.shape(m))
print(np.shape(m.T), np.shape(x.T))
z = np.matmul(x, m)
```
# Comparing the states
```
# The averages for the three states
mus
# In the high state, variance is highest, and it's lowest in the middle transitioning state.
sigmas
# Transmat gives teh probability of one state transition to another.
# The values are very low because the number of data points is large.
rcParams['figure.figsize'] = 9, 5
import seaborn as sns
sns.heatmap(transmat)
# Can see from here though that the probability of transitioning
# from the state 1 to state 3 and vice versa is low, they are more
# likely to transition to the in-between state instead.
transmat
rcParams['figure.figsize'] = 20, 7
len(z[:, 0]), len(z[0])
```
# Time series feature generation
Time series features: catch22 canonical set
https://arxiv.org/pdf/1901.10200.pdf
xgboost
Good at time series analysis
Clustering
```
df
```
|
github_jupyter
|
# 0. Setup
```
# Imports
import arviz as az
import io
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pymc3 as pm
import scipy
import scipy.stats as st
import theano.tensor as tt
# Helper functions
def plot_golf_data(data, ax=None):
"""Utility function to standardize a pretty plotting of the golf data."""
if ax is None:
_, ax = plt.subplots(figsize=(10, 6))
bg_color = ax.get_facecolor()
ax.vlines(
data["distance"],
ymin=data["p_hat"] - data["se"],
ymax=data["p_hat"] + data["se"],
label=None,
)
ax.plot(data["distance"], data["p_hat"], 'o', mfc=bg_color, label=None)
ax.set_xlabel("Distance from hole")
ax.set_ylabel("Proportion of putts made")
ax.set_ylim(bottom=0, top=1)
ax.set_xlim(left=0)
ax.grid(True, axis='y', alpha=0.7)
return ax
```
# 1. Introduction
The following example is based on a study by [Gelman and Nolan (2002)](http://www.stat.columbia.edu/~gelman/research/published/golf.pdf), where they use Bayesian methods to estimate the accuracy of pro golfers with respect to putting.
The data comes from Don Berry's textbook *Statistics: A Bayesian Perspective* (1995) and describes the number of tries and successes of golf putting from a range of distances.
This example is also featured in the case studies sections of the [Stan](https://mc-stan.org/users/documentation/case-studies/golf.html) and [PyMC3](https://docs.pymc.io/notebooks/putting_workflow.html) documentation. This notebook is based heavily on these two sources.
## 1.1 Data
```
# Putting data from Berry (1995)
data = pd.read_csv("golf_1995.csv", sep=",")
data["p_hat"] = data["successes"] / data["tries"]
data
```
The authors start by estimating the standard error of the estimated probability of success for each distance in order to get a sense of how closely the model should be expected to fit the data, given by
$SE(\hat{p}_i) = \sqrt{\dfrac{\hat{p}_i(1 - \hat{p}_i)}{n}}$
```
def se(data):
"""Calculate standard error of estimator."""
p_hat = data["p_hat"]
n = data["tries"]
return np.sqrt(p_hat * (1 - p_hat) / n)
data["se"] = se(data)
ax = plot_golf_data(data)
ax.set_title("Overview of data from Berry (1995)")
plt.show()
```
# 2. Baseline: Logit model
As a baseline model, we fit a simple logistic regression to the data, where the probability is give as a function of the distance $x_j$ from the hole. The data generating process for $y_j$ is assumed to be a [binomial distribution](https://en.wikipedia.org/wiki/Binomial_distribution):
$$y_j \sim \text{Binomial}(n_j, p_j),\\
p_j = \dfrac{1}{1 + e^{-(a + bx_j)}}, \quad \text{for} j = 1 \ldots J,\\
a, b \sim \text{Normal}(0, 1)$$
```
def logit_model(data):
"""Logistic regression model."""
with pm.Model() as logit_binomial:
# Priors
a = pm.Normal('a', mu=0, tau=1)
b = pm.Normal('b', mu=0, tau=1)
# Logit link
link = pm.math.invlogit(a + b*data["distance"])
# Likelihood
success = pm.Binomial(
'success',
n=data["tries"],
p=link,
observed=data["successes"]
)
return logit_binomial
# Visualise model as graph
pm.model_to_graphviz(logit_model(data))
# Sampling from posterior
with logit_model(data):
logit_trace = pm.sample(10000, tune=1000)
# Retrieving summaries from models
pm.summary(logit_trace)
# Plotting posterior distributions of a, b
pm.plot_posterior(logit_trace)
plt.show()
```
Our estimates seem to make sense. As the distance $x_j \rightarrow 0$, it seems intuitive that the probability of success is high. Conversely, if $x_j \rightarrow \infty$, the probability of success should be close to zero.
```
p_test = lambda x: scipy.special.expit(2.224 - 0.255*x)
print(f" x = 0 --> p = {p_test(0)}")
print(f" x = really big --> p = {p_test(10**5)}")
```
## 2.1 Baseline: Posterior predictive samples
We plot the our probability model by drawing 50 samples from the posterior distribution of $a$ and $b$ and calculating the inverse logit (expit) for each sample:
```
# Plotting
ax = plot_golf_data(data)
distances = np.linspace(0, data["distance"].max(), 200)
# Plotting individual predicted sigmoids for 50 random draws of (a, b)
for idx in np.random.randint(0, len(logit_trace), 50):
post_logit = scipy.special.expit(logit_trace["a"][idx] + logit_trace["b"][idx] * distances)
ax.plot(
distances,
post_logit,
lw=1,
color="tab:orange",
alpha=.7,
)
# Plotting average prediction over all sampled (a, b)
logit_average = scipy.special.expit(
logit_trace["a"].reshape(-1, 1) + logit_trace["b"].reshape(-1, 1) * distances,
).mean(axis=0)
ax.plot(
distances,
logit_average,
label = "Inverse logit mean",
color="k",
linestyle="--",
)
ax.set_title("Fitted logistic regression")
ax.legend()
plt.show()
```
We see that:
* The posterior uncertainty is relatively low.
* The fit is OK, but we tend to overestimate the difficulty of making short putts and underestimate the probability of making long puts.
# 3. Modelling from first principles
Not satisfied with the logistic regression, we contact a golf pro who also happens to have a background in mathematics. She suggests that as an alternative, we could build a model from first principles and fit it to the data.
She provides us with the following sketch (from the [Stan case study](https://mc-stan.org/users/documentation/case-studies/golf.html)):
> The graph below shows a simplified sketch of a golf shot. The dotted line represents the angle within which the ball of radius r must be hit so that it falls within the hole of radius R. This threshold angle is $sin^{−1}\Bigg(\dfrac{R−r}{x}\Bigg)$. The graph, which is not to scale, is intended to illustrate the geometry of the ball needing to go into the hole.

If the angle is less (in absolute value) than the threshold, the show will go in the cup. The mathematically inclined golf pro suggests that we can assume that the putter will attempt to shoot perfectly straight, but that external factors will interfere with this goal. She suggests modelling this uncertainty using a normal distribution centered at 0 (i.e. assume that shots don't deviate systematically to the right or left) with some variance in angle (in radians) given by $\sigma_{\text{angle}}$.
Since our golf expert is also a expert mathematician, she provides us with an expression for the probability that the ball goes in the cup (which is the probability that the angle is less than the threshold):
$$p\Bigg(\vert\text{angle}\vert < sin^{−1}\Bigg(\dfrac{R−r}{x}\Bigg)\Bigg) = 2\Theta\Bigg(\dfrac{1}{\sigma_{\text{angle}}}sin^{−1}\Bigg(\dfrac{R−r}{x}\Bigg)\Bigg) - 1,$$
where $\Theta$ is the cumulative normal distribution function.
The full model is then given by
$$y_j \sim \text{Binomial}(n_j, p_j)\\
p_j = 2\Theta\Bigg(\dfrac{1}{\sigma_{\text{angle}}}sin^{−1}\Bigg(\dfrac{R−r}{x}\Bigg)\Bigg) - 1, \quad \text{for} j = 1 \ldots J.$$
Prior to fitting the model, our expert provides us with the appropriate measurements for the golf ball and cup radii. We also plot the probabilities given by the above expression for different values of $\sigma_{\text{angle}}$ to get a feel for the model:
```
def forward_angle_model(variance_of_shot, distance):
"""Geometry-based probabilities."""
BALL_RADIUS = (1.68 / 2) / 12
CUP_RADIUS = (4.25 / 2) / 12
return 2 * st.norm(0, variance_of_shot).cdf(np.arcsin((CUP_RADIUS - BALL_RADIUS) / distance)) - 1
# Plotting
variance_of_shot = (0.01, 0.02, 0.05, 0.1, 0.2, 1)
distances = np.linspace(0, data["distance"].max(), 200)
ax = plot_golf_data(data)
for sigma in variance_of_shot:
ax.plot(distances, forward_angle_model(sigma, distances), label=f"$\sigma$ = {sigma}")
ax.set_title("Model prediction for selected amounts of variance")
ax.legend()
plt.show()
def phi(x):
"""Calculates the standard normal CDF."""
return 0.5 + 0.5 * tt.erf(x / tt.sqrt(2.))
def angle_model(data):
"""Geometry-based model."""
BALL_RADIUS = (1.68 / 2) / 12
CUP_RADIUS = (4.25 / 2) / 12
with pm.Model() as angle_model:
variance_of_shot = pm.HalfNormal('variance_of_shot')
prob = 2 * phi(tt.arcsin((CUP_RADIUS - BALL_RADIUS) / data["distance"]) / variance_of_shot) - 1
prob_success = pm.Deterministic('prob_success', prob)
success = pm.Binomial('success', n=data["tries"], p=prob_success, observed=data["successes"])
return angle_model
# Plotting model as graph
pm.model_to_graphviz(angle_model(data))
```
## 3.1 Geometry-based model: Prior predictive checks
```
# Drawing 500 samples from the prior predictive distribution
with angle_model(data):
angle_prior = pm.sample_prior_predictive(500)
# Use these variances to sample an equivalent amount of random angles from a normal distribution
angle_of_shot = np.random.normal(0, angle_prior['variance_of_shot'])
distance = 20
# Calculate possible end positions
end_positions = np.array([
distance * np.cos(angle_of_shot),
distance * np.sin(angle_of_shot)
])
# Plotting
fig, ax = plt.subplots(figsize=(10, 6))
for endx, endy in end_positions.T:
ax.plot([0, endx], [0, endy], 'k-o', lw=1, mfc='w', alpha=0.1);
ax.plot(0, 0, 'o', color="tab:blue", label='Start', ms=10)
ax.plot(distance, 0, 'o', color="tab:orange", label='Goal', ms=10)
ax.set_title(f"Prior distribution of putts from {distance}ft away")
ax.legend()
plt.show()
```
## 3.2 Fitting model
```
# Draw samples from posterior distribution
with angle_model(data):
angle_trace = pm.sample(10000, tune=1000)
pm.summary(angle_trace)
# Plotting posterior distribution of angle variance
pm.plot_posterior(angle_trace["variance_of_shot"])
pm.forestplot(angle_trace)
plt.show()
```
## 3.3 Logistic regression vs. geometry-based model
```
# Plot model
ax = plot_golf_data(data)
distances = np.linspace(0, data["distance"].max(), 200)
for idx in np.random.randint(0, len(angle_trace), 50):
ax.plot(
distances,
forward_angle_model(angle_trace['variance_of_shot'][idx], distances),
lw=1,
color="tab:orange",
alpha=0.7,
)
# Average of angle model
ax.plot(
distances,
forward_angle_model(angle_trace['variance_of_shot'].mean(), distances),
label='Geometry-based model',
color="tab:blue",
)
# Compare with average of logit model
ax.plot(distances, logit_average, color="tab:green", label='Logit-binomial model (avg.)')
ax.set_title("Comparing the fit of geometry-based and logit-binomial model")
ax.set_ylim([0, 1.05])
ax.legend()
plt.show()
# Comparing models using WAIC (Watanabe-Akaike Information Criterion)
models = {
"logit": logit_trace,
"geometry": angle_trace,
}
pm.compare(models)
```
## 3.4 Geometry-based model: Posterior predictive check
```
# Randomly sample a sigma from the posterior distribution
variances = np.random.choice(angle_trace['variance_of_shot'].flatten())
# Randomly sample 500 angles based on sample from posterior
angle_of_shot = np.random.normal(0, variances, 500) # radians
distance = 20
# Calculate end positions
end_positions = np.array([
distance * np.cos(angle_of_shot),
distance * np.sin(angle_of_shot)
])
# Plotting
fig, ax = plt.subplots(figsize=(10, 6))
for endx, endy in end_positions.T:
ax.plot([0, endx], [0, endy], '-o', color="gray", lw=1, mfc='w', alpha=0.05);
ax.plot(0, 0, 'o', color="tab:blue", label='Start', ms=10)
ax.plot(distance, 0, 'o', color="tab:orange", label='Goal', ms=10)
ax.set_xlim(-21, 21)
ax.set_ylim(-21, 21)
ax.set_title(f"Posterior distribution of putts from {distance}ft.")
ax.legend()
plt.show()
```
# 4. Further work
The [official](https://docs.pymc.io/notebooks/putting_workflow.html) [docs](https://mc-stan.org/users/documentation/case-studies/golf.html) further extend the angle model by accounting for distance and distance plus dispersion. Furthermore, the [PyMC3 docs](https://docs.pymc.io/notebooks/putting_workflow.html) show how you can model the final position of the putt, given starting distance from the cup, e.g.:


The authors show how this information can be leveraged to
> [...] work out how many putts a player may need to take from a given distance. This can influence strategic decisions like trying to reach the green in fewer shots, which may lead to a longer first putt, vs. a more conservative approach. We do this by simulating putts until they have all gone in.

|
github_jupyter
|
# RoadMap 16 - Classification 3 - Training & Validating [Custom CNN, Custom Dataset]
```
import torch
import torchvision
import torchvision.transforms as transforms
import torch.optim as optim
import matplotlib.pyplot as plt
import numpy as np
from torchvision import datasets
```
# [NOTE: - The network, transformation and training parameters are not suited for the dataset. Hence, the training does not converge]
# Steps to take
1. Create a network
- Arrange layers
- Visualize layers
- Creating loss function module
- Creating optimizer module [Set learning rates here]
2. Data prepraration
- Creating a data transformer
- Downloading and storing dataset
- Applying transformation
- Understanding dataset
- Loading the transformed dataset [Set batch size and number of parallel processors here]
3. Setting up data - plotters
4. Training
- Set Epoch
- Train model
5. Validating
- Overall-accuracy validation
- Class-wise accuracy validation
```
# 1.1 Creating a custom neural network
import torch.nn as nn
import torch.nn.functional as F
'''
Network arrangement
Input -> Conv1 -> Relu -> Pool -> Conv2 -> Relu -> Pool -> FC1 -> Relu -> FC2 -> Relu -> FC3 -> Output
'''
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.conv1 = nn.Conv2d(in_channels=3, out_channels=6, kernel_size=5)
self.pool = nn.MaxPool2d(kernel_size=2, stride=2)
self.relu = nn.ReLU() # Activation function
self.conv2 = nn.Conv2d(in_channels=6, out_channels=16, kernel_size=5)
self.fc1 = nn.Linear(16 * 53 * 53, 120) # In-channels, Out-Channels
self.fc2 = nn.Linear(120, 84) # In-channels, Out-Channels
self.fc3 = nn.Linear(84, 2) # In-channels, Out-Channels
def forward(self, x):
x = self.relu(self.conv1(x))
x = self.pool(x)
x = self.relu(self.conv2(x))
x = self.pool(x)
x = x.view(-1, 16 * 53 * 53) #Reshaping - Like flatten in caffe
x = self.fc1(x)
x = self.fc2(x)
x = self.fc3(x)
return x
net = Net()
net.cuda()
# 1.2 Visualizing network
from torchsummary import summary
print("Network - ")
summary(net, (3, 224, 224))
# 1.3. Creating loss function module
cross_entropy_loss = nn.CrossEntropyLoss()
# 1.4. Creating optimizer module
optimizer = optim.SGD(net.parameters(), lr=0.001, momentum=0.9)
# 2.1. Creating data trasnformer
data_transform = transforms.Compose([
transforms.RandomResizedCrop(224),
transforms.RandomHorizontalFlip(),
transforms.ToTensor(),
transforms.Normalize(mean=[0.485, 0.456, 0.406],
std=[0.229, 0.224, 0.225])
])
```
### 2.2 Storing downloaded dataset
Data storage directory
[NOTE: Directory and File names can be anything]
Parent Directory [cat_dog]
|
|----Train
| |
| |----Class1 [cat]
| | |----img1.png
| | |----img2.png
| |----Class2 [dog]
| | |----img1.png
| |----img2.png
|-----Val
| |
| |----Class1 [cat]
| | |----img1.png
| | |----img2.png
| |----Class2 [dog]
| | |----img1.png
| | |----img2.png
```
# 2.2. Applying transformations simultaneously
trainset = datasets.ImageFolder(root='cat_dog/train',
transform=data_transform)
valset = datasets.ImageFolder(root='cat_dog/val',
transform=data_transform)
print(dir(trainset))
# 2.3. - Understanding dataset
print("Number of training images - ", len(trainset.imgs))
print("Number of testing images - ", len(valset.imgs))
print("Classes - ", trainset.classes)
# 2.4. - Loading the transformed dataset
batch = 4
parallel_processors = 3
trainloader = torch.utils.data.DataLoader(trainset, batch_size=batch,
shuffle=True, num_workers=parallel_processors)
valloader = torch.utils.data.DataLoader(valset, batch_size=batch,
shuffle=False, num_workers=parallel_processors)
# Class list
classes = tuple(trainset.classes)
# 3. Setting up data plotters
def imshow(inp, title=None):
"""Imshow for Tensor."""
inp = inp.numpy().transpose((1, 2, 0))
mean = np.array([0.485, 0.456, 0.406])
std = np.array([0.229, 0.224, 0.225])
inp = std * inp + mean
inp = np.clip(inp, 0, 1)
plt.imshow(inp)
if title is not None:
plt.title(title)
plt.pause(0.001) # pause a bit so that plots are updated
# Get a batch of training data
inputs, labels = next(iter(trainloader))
# Make a grid from batch
out = torchvision.utils.make_grid(inputs)
imshow(out, title=[classes[x] for x in labels])
from tqdm.notebook import tqdm
# 4. Training
num_epochs = 2
for epoch in range(num_epochs): # loop over the dataset multiple times
running_loss = 0.0
pbar = tqdm(total=len(trainloader))
for i, data in enumerate(trainloader):
pbar.update();
# get the inputs
inputs, labels = data
inputs = inputs.cuda()
labels = labels.cuda()
# zero the parameter gradients
optimizer.zero_grad()
# forward + backward + optimize
outputs = net(inputs)
loss = cross_entropy_loss(outputs, labels)
loss.backward()
optimizer.step()
# print statistics
running_loss += loss.item()
if i % 10 == 9: # print every 2000 mini-batches
print('[%d, %5d] loss: %.3f' %
(epoch + 1, i + 1, running_loss / 2000))
running_loss = 0.0
print('Finished Training')
# 5.1 Overall-accuracy Validation
correct = 0
total = 0
with torch.no_grad():
for data in valloader:
images, labels = data
images = images.cuda()
labels = labels.cuda()
outputs = net(images)
_, predicted = torch.max(outputs.data, 1)
total += labels.size(0)
correct += (predicted == labels).sum().item()
print('Accuracy of the network on the 10000 test images: %d %%' % (
100 * correct / total))
# 5.2 Classwise-accuracy Validation
class_correct = list(0. for i in range(2))
class_total = list(0. for i in range(2))
with torch.no_grad():
for data in valloader:
images, labels = data
images = images.cuda()
labels = labels.cuda()
outputs = net(images)
_, predicted = torch.max(outputs, 1)
c = (predicted == labels).squeeze()
for i in range(len(c)):
label = labels[i]
class_correct[label] += c[i].item()
class_total[label] += 1
for i in range(2):
print('Accuracy of %5s : %2d %%' % (
classes[i], 100 * class_correct[i] / class_total[i]))
```
## Author - Tessellate Imaging - https://www.tessellateimaging.com/
## Monk Library - https://github.com/Tessellate-Imaging/monk_v1
Monk is an opensource low-code tool for computer vision and deep learning
### Monk features
- low-code
- unified wrapper over major deep learning framework - keras, pytorch, gluoncv
- syntax invariant wrapper
### Enables
- to create, manage and version control deep learning experiments
- to compare experiments across training metrics
- to quickly find best hyper-parameters
### At present it only supports transfer learning, but we are working each day to incorporate
- GUI based custom model creation
- various object detection and segmentation algorithms
- deployment pipelines to cloud and local platforms
- acceleration libraries such as TensorRT
- preprocessing and post processing libraries
## To contribute to Monk AI or Pytorch RoadMap repository raise an issue in the git-repo or dm us on linkedin
- Abhishek - https://www.linkedin.com/in/abhishek-kumar-annamraju/
- Akash - https://www.linkedin.com/in/akashdeepsingh01/
|
github_jupyter
|
```
%reload_ext autoreload
%autoreload 2
import warnings
warnings.filterwarnings('ignore')
import os.path as op
from collections import Counter
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# from tabulate import tabulate
from rdkit.Chem import AllChem as Chem
from rdkit.Chem import Draw
from rdkit.Chem.Draw import IPythonConsole
Draw.DrawingOptions.atomLabelFontFace = "DejaVu Sans"
Draw.DrawingOptions.atomLabelFontSize = 18
from misc_tools import nb_tools as nbt # , html_templates as html, apl_tools as apt
from rdkit_ipynb_tools import tools # , bokeh_tools as bt, pipeline as p, clustering as cl
from cellpainting import processing as cpp, tools as cpt
import ipywidgets as ipyw
from IPython.core.display import HTML, display, clear_output #, Javascript, display_png, clear_output, display
COMAS = "/home/pahl/comas/share/export_data_b64.tsv.gz"
```
# Prepare References
Generate the references file.
```
REF_DIR = "/home/pahl/comas/projects/painting/references"
PLATE_NAMES = ["S0195", "S0198", "S0203"] # "S0195", "S0198", "S0203"
DATES = {"S0195": "170523", "S0198": "170516", "S0203": "170512"}
keep = ["Compound_Id", "Container_Id", "Producer", "Conc_uM", "Activity", "Rel_Cell_Count", "Pure_Flag", "Toxic",
'Trivial_Name', 'Known_Act', 'Act_Profile', "Metadata_Well", "Plate", 'Smiles']
data_keep = ["Compound_Id", "Container_Id", "Producer", "Conc_uM", "Pure_Flag", "Activity", "Rel_Cell_Count", "Toxic",
'Act_Profile', "Metadata_Well", "Plate", 'Smiles']
ds_list = []
pb = nbt.ProgressbarJS()
num_steps = 4 * len(PLATE_NAMES)
step = 0
for plate in PLATE_NAMES:
for idx in range(1, 5):
step += 1
pb.update(100 * step / num_steps)
path = op.join(REF_DIR, "{}-{}".format(plate, idx))
print("\nProcessing plate {}-{} ...".format(plate, idx))
ds_plate = cpp.load(op.join(path, "Results.tsv"))
ds_plate = ds_plate.group_on_well()
ds_plate = ds_plate.remove_skipped_echo_direct_transfer(op.join(path, "*_print.xml"))
ds_plate = ds_plate.well_type_from_position()
ds_plate = ds_plate.flag_toxic()
ds_plate = ds_plate.activity_profile()
ds_plate = ds_plate.join_layout_1536(plate, idx)
ds_plate.data["Plate"] = "{}-{}-{}".format(DATES[plate], plate, idx)
ds_list.append(ds_plate.data)
pb.done()
# *** ds_all <- concat(ds_list) ***
ds_all = cpp.DataSet()
ds_all.data = pd.concat(ds_list)
ds_all.print_log("concat data")
del ds_list
ds_all.write_pkl("170630_references.pkl")
# ds_all = cpp.load_pkl("170630_references.pkl")
# *** ds_profile <- ds_all ***
ds_profile = ds_all.join_smiles()
# *** ds_ref <- ds_profile ***
ds_ref, _ = ds_profile.remove_impure()
ds_ref, _ = ds_ref.remove_toxic()
ds_ref = ds_ref[ds_ref["Activity"] >= 2.5]
ds_ref = ds_ref.join_annotations()
ds_ref.update_similar_refs(mode="ref")
ds_ref = ds_ref[keep]
ds_ref.write_csv("references_act_prof.tsv")
# *** update DATASTORE ***
ds_profile.update_datastore(mode="ref")
```
|
github_jupyter
|
## Some fundamental elements of programming III
### Understanding and creating correlated datasets and how to create functions
As we said before, the core of data science is computer programming.
To really explore data, we need to be able to write code to
(1) wrangle or even generate data that has the properties needed for analysis and
(2) do actual data analysis and visualization.
If data science didn't involve programming – if it only involved clicking buttons in a statistics program like SPSS – it wouldn't be called data *science*. In fact, it wouldn't even be a "thing" at all.
Learning goals:
- Understand how to generate correlated variables.
- More indexing
- More experiments with loops
#### Generate correlated datasets
In thispart of the tutorial we will learn how generate datasets that are 'related.' While doing that we will practice a few things learned recently in previous tutorials:
- Plotting with matplotlib
- generating numpy arrays
- indexing into arrays
- using `while` loops
First thing first, we will import the basic libraries we need.
```
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
```
After that we will create a few datasets. More specifically, we will create `n` datasets each called `x` (say 5 datasets, where `n=5`). Each dataset will have the length of `m` (where for example, `m` could be 100), this means for example that each dataset will have the shape of (m,1) or in our example (100,1).
After that, we will create another group of `n` datasets called `y` of the same shape of `x`. Each one of the `y` datasets will have a corresponding `x` dataset that it will be correlated with.
This means that for each dataset in `x` there will be a dataset in `y` that is correlated with it.
Let's get started with a hands on method. Forst we will make the example of a single dataset `x` and a correlated dataset `y`.
```
# We first build the dataset `x`,
# we will use our standard method
# based on randn
m = 1000
mu = 5
sd = 1
x = mu + sd*np.random.randn(m,1)
# let take a look at it
plt.hist(x, 60)
```
OK. After generating the first dataset we will generate a second dataset, let's call it `y`. This second dataset will be correlated to the first.
To generate a dataset correlated to `x` we will indeed use `x` as our base for the data and add on top of `x` a small amount of noise, let's call it `noise`. `noise` represents the small (or larger) difference between `x` and `y`.
```
err = np.random.randn(m,1)
y = x + err
plt.hist(y,60)
```
OK. The two histograms seem similar (similar range and height), but it is difficult to judge if `x` and `y` are indeed correlated. To do that we need to make a scatter plot.
`matplotlib` has a convenient function for scatter plots, `plt.scatter()`, we will use that function to take a look at whether the two datasets are correlated.
```
plt.scatter(x,y)
```
Great, the symbols should be aligned along the major diagonal. This means that they are indeed correlated. To get to understand more what we did above, let's think about `err`.
Imagine, if there were no error, e.g., no `err`. That would mean that there would be no difference between `x` and `y`. Literally, the two datasets would be identical.
We can do that with the code above by setting `err` to `0`.
```
err = 0
y = x + err
plt.scatter(x,y)
```
The symbols should all lay on the major diagonal. So, `err` effectively controls the level of correlation between `x` and `y`. So if we set it to something small, in other words if we add only a small amount of error then the two arrays (`x` and `y`) would be very similar. For example, let's try setting it up to 10% of the original `err`.
```
err = np.random.randn(m,1);
err = err*0.1 # 0.1 -> scaling factor
y = x + err
plt.scatter(x,y)
```
OK. It should have worked. The error added is not large, the symbols should lay almost on the diagonal, but not quite.
As we increase the `err` the symbols should move away from the diagonal.
```
err = np.random.randn(m,1);
scaling_factor = 0.9
err = err*scaling_factor
y = x + err
plt.scatter(x,y)
```
One way to think about the scaling factor and `err` is that they are related to correlation. Indeed, they are not directly related to correlation (not a one-to-one relationship, but a proxy).
The scaling factor is inversely related to correlation because as the scaling factor increases the correlation decreases. Furthermore, they are not directly related to correlation because they both depend on a couple of variables, for example, the variance of the distributions (both `err` and `x` will affect the relationship between the correlation and the scaling factor).
Python has a method to generate couples of correlated arrays. We will now briefly explore it, but leave a deeper dive on each function to you. You are suggested to further explore the code below and its implications. It might come helpful to us later down the road, you never know!
#### A more principled way to make correlated datasets
NumPy has a function called `multivariate_normal` that generates pairs of correlated datasets. The correlation values can be specified conveniently. A little bit of thinking is required, though. The function uses the covariance matrix. The covariance matrix is composed of 4 numbers. Two of the numbers describe the variances of the two datasamples we want to generate. The other two values describe the correlation between the samples and are generally called `covariances` (co-variations or co-relations).
```
from numpy.random import multivariate_normal # we import the function
x_mu = 0; # we set up the mean of the first set of data points
y_mu = 0; # we set up the mean of the second sample
x_var = 1; # the variance of the first sample
y_var = 1; # the variance of the second sample
cov = 0.9; # this is the covariance (can be thought of as correlation)
# the function multivariate_normal will need a matrix to control
# the relation between the samples, this matrix is called covariance matrix
cov_m = [[x_var, cov],
[cov, y_var]]
# we now create the two data sets by setting the the proper
# means and passing the covariance matrix, we also pass the
# requested size of the sample
data = multivariate_normal([x_mu, y_mu], cov_m, size=1000)
# We can plot the two data sets
x, y = data[:,0], data[:,1]
plt.scatter(x, y)
```
#### Creating many correlated datasets
Imagine now if we were asked to create a series of correlated datasets. Not one, nottwo, more than that.
Once the basic code used to build one is known. The rest of the datasets can be generated reusing the same code and putting the code inside a loop. Below we will show how to create 5 datasets using a `while` loop.
```
counter = 0;
n_datasets = 5;
siz_datasets = 1000;
x_mu = 1; # mean of the first dataset
y_mu = 1; # mean of the second dataset
x_var = 2; # the variance of the first dataset
y_var = 2; # the variance of the second dataset
cov = 0.85; # this is the covariance (can be thought of as correlation)
# covariance matrix
cov_m = [[x_var, cov],
[cov, y_var]]
while counter < n_datasets :
data = multivariate_normal([x_mu, y_mu],
cov_m,
size=siz_datasets)
x, y = data[:,0], data[:,1]
counter = counter + 1
# Make a plot, show it, wait some time
print("Plotting dataset: ", counter)
plt.scatter(x, y);
plt.show() ;
plt.pause(0.05)
else:
print("DONE Plotting datasets!")
```
|
github_jupyter
|
## Prep notebook
```
import bz2
import json
import os
import random
import re
import string
import mwparserfromhell
import numpy as np
import pandas as pd
import requests
import findspark
findspark.init('/usr/lib/spark2')
from pyspark.sql import SparkSession
!which python
spark = (
SparkSession.builder
.appName('Pyspark notebook (isaacj -- wikitext)')
.master('yarn')
.config(
'spark.driver.extraJavaOptions',
' '.join('-D{}={}'.format(k, v) for k, v in {
'http.proxyHost': 'webproxy.eqiad.wmnet',
'http.proxyPort': '8080',
'https.proxyHost': 'webproxy.eqiad.wmnet',
'https.proxyPort': '8080',
}.items()))
# .config('spark.jars.packages', 'graphframes:graphframes:0.6.0-spark2.3-s_2.11')
.config("spark.driver.memory", "2g")
.config('spark.dynamicAllocation.maxExecutors', 64)
.config("spark.executor.memory", "8g")
.config("spark.executor.cores", 4)
.config("spark.sql.shuffle.partitions", 256)
.getOrCreate()
)
spark
```
## Parameters / Utilities
```
snapshot = '2020-12' # data will be current to this date -- e.g., 2020-05 means data is up to 30 April 2020 (at least)
wd_snapshot = '2020-12-07' # closest Wikidata item-page-link to data snapshot
def getCleanedText(wikitext):
"""Clean/preprocess wikitext for fastText modeling.
Should work ok for any space-delimited language. Might need to update punctuation / category names.
What it does:
* Lowercase
* Removes wiki markup -- e.g., brackets
* Removes categories (this is mainly to prevent WikiProject categories from bleeding labels into data)
* Removes extraneous white-space + punctuation
What it returns:
* Cleaned, space-delimited tokens as a string
"""
try:
wt = mwparserfromhell.parse(wikitext).strip_code().lower()
return ' '.join([w for w in re.sub('["\'.,?(){}]','', wt).split() if not w.startswith('category:')])
except Exception:
return None
spark.udf.register('getCleanedText', getCleanedText, 'String')
```
## Gather wikitext data and write to TSV
```
print_for_hive = False
do_execute = True
query = f"""
WITH wikidata_ids AS (
SELECT page_id,
item_id
FROM wmf.wikidata_item_page_link wd
WHERE wd.snapshot = '{wd_snapshot}'
AND wd.page_namespace = 0
AND wiki_db = 'enwiki'
)
SELECT item_id,
getCleanedText(revision_text) as cleaned_wikitext
FROM wmf.mediawiki_wikitext_current wt
INNER JOIN wikidata_ids wd
ON (wt.page_id = wd.page_id)
WHERE snapshot = '{snapshot}'
AND wiki_db = 'enwiki'
AND page_namespace = 0
"""
if print_for_hive:
print(re.sub(' +', ' ', re.sub('\n', ' ', query)).strip())
else:
print(query)
if do_execute:
result = spark.sql(query)
result.write.csv(path="/user/isaacj/enwiki-cleaned-wikitext", compression="bzip2", header=True, sep="\t")
```
## Pull from HDFS to local
```
file_parts_dir = './text_file_parts/'
!rm -R {file_parts_dir}
!mkdir {file_parts_dir}
!hdfs dfs -copyToLocal enwiki-cleaned-wikitext/part* {file_parts_dir}
```
## Add labels and train/test split
```
base_fasttext_fn = './fasttext/wt_2020_12.txt'
groundtruth_data = 'labeled_enwiki_with_topics_metadata.json.bz2'
train_prop = 0.9
val_prop = 0.02
test_prop = 0.08
assert train_prop + val_prop + test_prop == 1
train_fn = base_fasttext_fn.replace('.txt', '_train.txt')
train_metadata_fn = base_fasttext_fn.replace('.txt', '_train_metadata.txt')
val_fn = base_fasttext_fn.replace('.txt', '_val.txt')
val_metadata_fn = base_fasttext_fn.replace('.txt', '_val_metadata.txt')
test_fn = base_fasttext_fn.replace('.txt', '_test.txt')
test_metadata_fn = base_fasttext_fn.replace('.txt', '_test_metadata.txt')
nogroundtruth_fn = base_fasttext_fn.replace('.txt', '_nogt.txt')
nogroundtruth_metadata_fn = base_fasttext_fn.replace('.txt', '_nogt_metadata.txt')
def fasttextify(topic):
"""Translate articletopic labels into fastText format (prefixed with __label__ and no spaces)."""
return '__label__{0}'.format(topic.replace(' ', '_'))
# load in groundtruth
qid_topics = {}
with bz2.open(groundtruth_data, 'rt') as fin:
for line in fin:
line = json.loads(line)
qid = line.get('qid')
topics = line.get('topics')
if qid and topics:
qid_topics[qid] = topics
print("{0} QIDs with topics.".format(len(qid_topics)))
train_written = 0
val_written = 0
test_written = 0
nogt_written = 0
i = 0
qids_to_split = {}
input_header = ['item_id', 'cleaned_wikitext']
fns = [fn for fn in os.listdir(file_parts_dir) if fn.endswith('.csv.bz2')]
with open(train_fn, 'w') as train_fout:
with open(train_metadata_fn, 'w') as train_metadata_fout:
with open(val_fn, 'w') as val_fout:
with open(val_metadata_fn, 'w') as val_metadata_fout:
with open(test_fn, 'w') as test_fout:
with open(test_metadata_fn, 'w') as test_metadata_fout:
with open(nogroundtruth_fn, 'w') as nogt_fout:
with open(nogroundtruth_metadata_fn, 'w') as nogt_metadata_fout:
for fidx, fn in enumerate(fns, start=1):
with bz2.open(os.path.join(file_parts_dir, fn), 'rt') as fin:
header = next(fin).strip().split('\t')
assert header == input_header
for i, line_str in enumerate(fin, start=1):
line = line_str.strip().split('\t')
assert len(line) == len(input_header)
qid = line[0]
wikitext = line[1]
if not wikitext or not qid:
continue
topics = qid_topics.get(qid)
if topics:
if qid in qids_to_split:
r = qids_to_split[qid]
else:
r = random.random()
qids_to_split[qid] = r
if r <= train_prop:
data_fout = train_fout
metadata_fout = train_metadata_fout
train_written += 1
elif r <= train_prop + val_prop:
data_fout = val_fout
metadata_fout = val_metadata_fout
val_written += 1
else:
data_fout = test_fout
metadata_fout = test_metadata_fout
test_written += 1
else:
topics = []
data_fout = nogt_fout
metadata_fout = nogt_metadata_fout
nogt_written += 1
data_fout.write('{0} {1}\n'.format(' '.join([fasttextify(t) for t in topics]), wikitext))
metadata_fout.write('{0}\n'.format(qid))
print("{0} of {1} processed: {2} train. {3} val. {4} test. {5} no groundtruth.".format(fidx, len(fns),
train_written,
val_written,
test_written,
nogt_written))
!ls -lht /home/isaacj/fasttext/
```
|
github_jupyter
|
### Demonstration of Quantum Key Distribution with the Ekert 91 Protocol
Algorithm -
1. First generate the a maximally entangled qubit pair |psi+> = 1/root(2) * (|01> + |10>)
2. Send one qubit to Alice and one qubit to Bob
3. Both Alice and Bob perform their measurement and make the measurement bases public.
4. According to the new information obtained, a sifted key is created, which can be used for secure communication
Modification to this Algorithm (because we get only 1 quantum computer) -
1. First generate the a maximally entangled qubit pair |psi+> = 1/root(2) * (|01> + |10>)
2. Take the measurement bases from Alice and Bob
3. Perform measurement, and send the measurement results to Alice and Bob respectively
4. Note that Alice and Bob do not have each other's measurement outcomes, they have only theirs
5. The measurement bases are made public, and the sifted key is obtained
```
import os
from qiskit import execute
from qiskit.circuit import QuantumRegister, ClassicalRegister, QuantumCircuit
from quantuminspire.credentials import get_authentication, save_account
from quantuminspire.qiskit import QI
from apikey import token
QI_URL = os.getenv('API_URL', 'https://api.quantum-inspire.com/')
import re
import numpy as np
import random
print("Process Complete!")
```
<a id="layout"></a>
# 1. Quantum Key Distribution Activity layout
In project, we are going to implement the E91 protocol. Steps of the protocol:
1. The serves creates a singlet state where one pair corresponds to Alice and other to Bob.
2. Alice randomly selects a sequence of measurement basis from Z,X,V and sends it to server
3. Bob randomly selects a sequence of measurement basis from W,V,X and sends it to server
4. `Intermediate interface function 1`: a MUX that creates a circuit based on Alice and Bob's selection of bases
5. `Intermediate interface function 2`: execute the measurement on Quantum Inspire
6. `Intermediate interface function 3`: check the basis and create the key and send it to Alice and Bob
These 6 steps allow a key to be distributed between Alice and Bob securely, now the two can send secure and encrypted messages through an insecure channel.
In this lab, we will not worry about an eavesdropper, but focus on the code for the basic protocol. Therefore, Alice and Bob don't need to run an analysis step. We can further extend it this to try implementing code for Eve.
```
# Parameters
N_en_pairs = 10
alice_seq = [random.randint(1, 3) for i in range(N_en_pairs)]
bob_seq = [random.randint(1, 3) for i in range(N_en_pairs)]
print("Process Complete!")
```
<a id="layout"></a>
## 1. Create entangled states and encode measurement sequence
```
Quantum_Circuit = [] # list for storing the quantum circuit for each bit
for i in range(N_en_pairs):
Alice_Reg = QuantumRegister(1, name="alice")
Bob_Reg = QuantumRegister(1, name="bob")
cr = ClassicalRegister(2, name="cr")
qc = QuantumCircuit(Alice_Reg, Bob_Reg, cr)
# Create an entangled pair for Alice and Bob in each loop
qc.x(Alice_Reg)
qc.x(Bob_Reg)
qc.h(Alice_Reg)
qc.cx(Alice_Reg, Bob_Reg)
# Cicuit Measurement for different bases
if alice_seq[i]== 1: #If Alice's random sequence is 1, Alice measures in the Z basis
qc.measure(Alice_Reg,cr[0])
elif alice_seq[i] == 2: #If Alice's random sequence is 2, Alice measures in the X basis
qc.h(Alice_Reg)
qc.measure(Alice_Reg,cr[0])
elif alice_seq==3: #If Alice's random sequence is 3, Alice measures in the V basis (-1/sqrt(2), 0, 1/sqrt(2))
qc.s(Alice_Reg)
qc.h(Alice_Reg)
qc.tdg(Alice_Reg)
qc.h(Alice_Reg)
qc.measure(Alice_Reg, cr[0])
if bob_seq[i]==1: #If Bob's random sequence is 1, Bob measures in the -W basis
qc.s(Bob_Reg)
qc.h(Bob_Reg)
qc.t(Bob_Reg)
qc.h(Bob_Reg)
qc.measure(Bob_Reg, cr[1])
elif bob_seq[i] == 2: #If Bob's random sequence is 2, Bob measures in the V basis
qc.s(Bob_Reg)
qc.h(Bob_Reg)
qc.tdg(Bob_Reg)
qc.h(Bob_Reg)
qc.measure(Bob_Reg, cr[1])
elif bob_seq[i] == 3: #If Bob's random sequence is 3, Bob measures in the X basis
qc.h(Bob_Reg)
qc.measure(Bob_Reg, cr[1])
Quantum_Circuit.append(qc)
print("Process Complete!")
Quantum_Circuit[0].draw(output='mpl')
print("Process Complete!")
```
## To QI
```
save_account(token)
project_name = 'E91_test_hardware'
authentication = get_authentication()
QI.set_authentication()
# Create an interface between Qiskit and Quantum Inpsire to execute the circuit
# qi_backend = QI.get_backend('Starmon-5')
qi_backend = QI.get_backend('QX single-node simulator')
job = execute(Quantum_Circuit, qi_backend, shots = 1)
print("Process Complete!")
results = job.result()
counts = results.get_counts()
print("Process Complete!")
abPatterns = [
re.compile('00'), # search for the '..00' output (Alice obtained -1 and Bob obtained -1)
re.compile('01'), # search for the '..01' output
re.compile('10'), # search for the '..10' output (Alice obtained -1 and Bob obtained 1)
re.compile('11') # search for the '..11' output
]
print("Process Complete!")
```
### Alices and Bobs measurement result
```
aliceResults = [] # Alice's results (string a)
bobResults = [] # Bob's results (string a')
for i in range(N_en_pairs):
res = list(counts[i].keys())[0] # extract the key from the dict and transform it to str; execution result of the i-th circuit
if abPatterns[0].search(res): # check if the key is '..00' (if the measurement results are -1,-1)
aliceResults.append(-1) # Alice got the result -1
bobResults.append(-1) # Bob got the result -1
if abPatterns[1].search(res):
aliceResults.append(1)
bobResults.append(-1)
if abPatterns[2].search(res): # check if the key is '..10' (if the measurement results are -1,1)
aliceResults.append(-1) # Alice got the result -1
bobResults.append(1) # Bob got the result 1
if abPatterns[3].search(res):
aliceResults.append(1)
bobResults.append(1)
print("Process Complete!")
```
### Key Generation
```
aliceKey = [] # Alice's key string k
bobKey = [] # Bob's key string k'
# comparing the strings with measurement choices
for i in range(N_en_pairs):
# if Alice and Bob have measured the spin projections onto the a_2/b_3 or a_3/b_2 directions
if (alice_seq[i] == 2 and bob_seq[i] == 3) or (alice_seq[i] == 3 and bob_seq[i] == 2):
aliceKey.append(aliceResults[i-1]) # record the i-th result obtained by Alice as the bit of the secret key k
bobKey.append(- bobResults[i-1]) # record the multiplied by -1 i-th result obtained Bob as the bit of the secret key k'
keyLength = len(aliceKey) # length of the secret key
print(aliceKey)
print("Process Complete!")
abKeyMismatches = 0 # number of mismatching bits in Alice's and Bob's keys
for j in range(keyLength):
if aliceKey[j] != bobKey[j]:
abKeyMismatches += 1
print(abKeyMismatches)
print("Process Complete!")
```
Thus, Quantum Key Distribution has been demonstrated!
|
github_jupyter
|
# Modules
Python has a way to put definitions in a file so they can easily be reused.
Such files are called a modules. You can define your own module (for instance see [here](https://docs.python.org/3/tutorial/modules.html)) how to do this but in this course we will only discuss how to use
existing modules as they come with python as the [python standard library](https://docs.python.org/3.9/tutorial/stdlib.html?highlight=library) or as third party libraries as they for instance are distributed
through [anaconda](https://www.anaconda.com/) or your Linux distribution or you can install trough `pip` or from source.
Definitions from a module can be imported into your jupyter notebook, your python script, and into other modules.
The module is imported using the import statement. Here we import the mathematics library from the python standard library:
```
import math
```
You can find a list of the available functions, variables and classes using the `dir` method:
```
dir(math)
```
A particular function (or class or constant) can be called in the form `<module name>.<function name>`:
```
math.exp(1)
```
Documentation of a function (or class or constant) can be obtained using the `help` function (if the developer has written it):
```
help(math.exp)
```
You can also import a specific function (or a set of functions) so you can directly use them without a prefix:
```
from cmath import exp
exp(1j)
```
In python terminology that means that - in this case - the `exp` function is imported into the main *name space*.
This needs to be applied with care as existing functions (or class definition) with identical names are overwritten.
For instance the `math` and the `cmath` module have a function `exp`. Importing both will create a problem
in the main name space.
If you are conficdent in what you are doing you can import all functions and class definitions into the main name space:
```
from cmath import *
cos(1.)
```
Modules can contain submodules. The functions are then
accessed `<module name>.<sub-module name>.<function name>`:
```
import os
os.path.exists('FileHandling.ipynb')
```
In these cases it can be useful to use an alias to make the code easier to read:
```
import os.path as pth
pth.exists('FileHandling.ipynb')
```
# More on printing
Python provides a powerful way of formatting output using formatted string.
Basicly the ideas is that in a formatted string marked by a leading 'f' variable
names are replaced by the corresponding variable values. Here comes an example:
```
x, y = 2.124, 3
f"the value of x is {x} and of y is {y}."
```
python makes guesses on how to format the value of the variable but you can also be specific if values should be shown in a specific way. here we want to show `x` as a floating point numbers with a scientific number representation indicated by `e` and `y` to be shown as an integer indicated by `d`:
```
f"x={x} x={x:10f} x={x:e} y={y:d}"
```
More details on [Formatted string literals](https://docs.python.org/3.7/reference/lexical_analysis.html#index-24)
Formatted strings are used to prettify output when printing:
```
print(f"x={x:10f}")
print(f"y={y:10d}")
```
An alternative way of formatting is the `format` method of a string. You can use the
positional arguments:
```
guest='John'
'Hi {0}, welcome to {1}!"'.format(guest, 'Brisbane')
```
Or keyword arguments:
```
'Hi {guest}, welcome to {place}!'.format(guest='Mike', place='Brisbane')
```
and a combination of positional arguments and keyword arguments:
```
'Hi {guest}, welcome to {1}! Enjoy your stay for {0} days.'.format(10, 'Brisbane', guest="Bob")
```
You can also introduce some formatting on how values are represented:
```
'Hi {guest}, welcome to {0}! Enjoy your stay for {1:+10d} days.'.format('Brisbane', 10, guest="Bob")
```
More details in particular for formating numbers are found [here](https://docs.python.org/3.9/library/string.html).
# Writing and Reading files
To open a file for reading or writing use the `open` function. `open()`
returns a file object, and is most commonly used with two arguments: open(filename, mode).
```
outfile=open("myRicker.csv", 'wt')
```
It is commonly used with two arguments: `open(filename, mode)` where the `mode` takes the values:
- `w` open for writing. An existing file with the same name will be erased.
- `a` opens the file for appending; any data written to the file is automatically added to the end.
- `r` opens the file for both reading only.
By default text mode `t` is used that means, you read and write strings from and to the file, which are encoded in a specific encoding. `b` appended to the mode opens the file in binary mode: now the data is read and written in the form of bytes objects.
We want to write some code that writes the `Ricker` wavelet of a period of
`length` and given frequency `f` to the files `myRicker.csv` in the comma-separated-value (CSV) format. The time is incremented by `dt`.
```
length=0.128
f=25
dt=0.001
def ricker(t, f):
"""
return the value of the Ricker wavelet at time t for peak frequency f
"""
r = (1.0 - 2.0*(math.pi**2)*(f**2)*(t**2)) * math.exp(-(math.pi**2)*(f**2)*(t**2))
return r
t=-length/2
n=0
while t < length/2:
outfile.write("{0}, {1}\n".format(t, ricker(t, f)))
t+=dt
n+=1
print("{} records writen to {}.".format(n, outfile.name))
```
You can download/open the file ['myRicker.csv'](myRicker.csv).
** Notice ** There is an extra new line character `\n` at the of string in the `write` statement. This makes sure that separate rows can be identified in the file.
Don't forget to close the file at the end:
```
outfile.close()
```
Now we want to read this back. First we need to open the file for reading:
```
infile=open("myRicker.csv", 'r')
```
We then can read the entire file as a string:
```
content=infile.read()
content[0:100]
```
In some cases it is more easier to read the file row-by-row. First we need to move back to the beginning of the file:
```
infile.seek(0)
```
Now we read the file line by line. Each line is split into the time and wavelet value which are
collected as floats in two lists `times` and `ricker`:
```
infile.seek(0)
line=infile.readline()
times=[]
ricker=[]
n=0
while len(line)>0:
a, b=line.split(',')
times.append(float(a))
ricker.append(float(b))
line=infile.readline()
n+=1
print("{} records read from {}.".format(n, infile.name))
```
Notice that the end of file is reached when the read line is empty (len(line)=0). Then the loop is exited.
```
time[:10]
```
# JSON Files
JSON files (JavaScript Object Notation) is an open-standard file format that uses human-readable text to transmit data objects consisting of dictionaries and lists. It is a very common data format, with a diverse range of applications in particular when exchanging data between web browsers and web services.
A typical structure that is saved in JSON files are combinations of lists and dictionaries
with string, integer and float entries. For instance
```
course = [ { "name": "John", "age": 30, "id" : 232483948} ,
{ "name": "Tim", "age": 45, "id" : 3246284632} ]
course
```
The `json` module provides the necessary functionality to write `course` into file, here `course.json`:
```
import json
json.dump(course, open("course.json", 'w'), indent=4)
```
You can access the [course.json](course.json). Depending on your web browser the file is identified as JSON file
and presented accordingly.
We can easily read the file back using the `load` method:
```
newcourse=json.load(open("course.json", 'r'))
```
This recovers the original list+dictionary structure:
```
newcourse
```
We can recover the names of the persons in the course:
```
[ p['name'] for p in newcourse ]
```
We can add new person to `newcourse`:
```
newcourse.append({'age': 29, 'name': 'Jane', 'studentid': 2643746328})
newcourse
```
# Visualization
We would like to plot the Ricker wavelet.
The `matplotlib` library provides a convenient, flexible and powerful tool for visualization at least for 2D data sets. Here we can give only a very brief introduction with more functionality being presented as the course evolves.
For a comprehensive documentation and list of examples we refer to the [matplotlib web page](https://matplotlib.org).
Here we use the `matplotlib.pyplot` library which is a collection of command style functions but there
is also a more general API which gives a reacher functionality:
```
#%matplotlib notebook
import matplotlib.pyplot as plt
```
It is very easy to plot data point we have read:
```
plt.figure(figsize=(8,5))
plt.scatter(times, ricker)
```
We can also plot this as a function rather than just data point:
```
plt.figure(figsize=(8,5))
plt.plot(times, ricker)
```
Let's use proper labeling of the horizontal axis:
```
plt.xlabel('time [sec]')
```
and for the vertical axis:
```
plt.ylabel('aplitude')
```
And maybe a title:
```
plt.title('Ricker wavelet for frequency f = 25 hz')
```
We can also change the line style, eg. red doted line:
```
plt.figure(figsize=(8,5))
plt.plot(times, ricker, 'r:')
plt.xlabel('time [sec]')
plt.ylabel('aplitude')
```
We can put different data sets or representations into the plot:
```
plt.figure(figsize=(8,5))
plt.plot(times, ricker, 'r:', label="function")
plt.scatter(times, ricker, c='b', s=10, label="data")
plt.xlabel('time [sec]')
plt.ylabel('aplitude')
plt.legend()
```
You can also add grid line to make the plot easier to read:
```
plt.grid(True)
```
Save the plot to a file:
```
plt.savefig("ricker.png")
```
see [ricker.png](ricker.png) for the file.
|
github_jupyter
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.