text
stringlengths 2.5k
6.39M
| kind
stringclasses 3
values |
|---|---|
### Introduction
The `Lines` object provides the following features:
1. Ability to plot a single set or multiple sets of y-values as a function of a set or multiple sets of x-values
2. Ability to style the line object in different ways, by setting different attributes such as the `colors`, `line_style`, `stroke_width` etc.
3. Ability to specify a marker at each point passed to the line. The marker can be a shape which is at the data points between which the line is interpolated and can be set through the `markers` attribute
The `Lines` object has the following attributes
| Attribute | Description | Default Value |
|:-:|---|:-:|
| `colors` | Sets the color of each line, takes as input a list of any RGB, HEX, or HTML color name | `CATEGORY10` |
| `opacities` | Controls the opacity of each line, takes as input a real number between 0 and 1 | `1.0` |
| `stroke_width` | Real number which sets the width of all paths | `2.0` |
| `line_style` | Specifies whether a line is solid, dashed, dotted or both dashed and dotted | `'solid'` |
| `interpolation` | Sets the type of interpolation between two points | `'linear'` |
| `marker` | Specifies the shape of the marker inserted at each data point | `None` |
| `marker_size` | Controls the size of the marker, takes as input a non-negative integer | `64` |
|`close_path`| Controls whether to close the paths or not | `False` |
|`fill`| Specifies in which way the paths are filled. Can be set to one of `{'none', 'bottom', 'top', 'inside'}`| `None` |
|`fill_colors`| `List` that specifies the `fill` colors of each path | `[]` |
| **Data Attribute** | **Description** | **Default Value** |
|`x` |abscissas of the data points | `array([])` |
|`y` |ordinates of the data points | `array([])` |
|`color` | Data according to which the `Lines` will be colored. Setting it to `None` defaults the choice of colors to the `colors` attribute | `None` |
## pyplot's plot method can be used to plot lines with meaningful defaults
```
import numpy as np
from pandas import date_range
import bqplot.pyplot as plt
from bqplot import *
security_1 = np.cumsum(np.random.randn(150)) + 100.
security_2 = np.cumsum(np.random.randn(150)) + 100.
```
## Basic Line Chart
```
fig = plt.figure(title='Security 1')
axes_options = {'x': {'label': 'Index'}, 'y': {'label': 'Price'}}
# x values default to range of values when not specified
line = plt.plot(security_1, axes_options=axes_options)
fig
```
**We can explore the different attributes by changing each of them for the plot above:**
```
line.colors = ['DarkOrange']
```
In a similar way, we can also change any attribute after the plot has been displayed to change the plot. Run each of the cells below, and try changing the attributes to explore the different features and how they affect the plot.
```
# The opacity allows us to display the Line while featuring other Marks that may be on the Figure
line.opacities = [.5]
line.stroke_width = 2.5
```
To switch to an area chart, set the `fill` attribute, and control the look with `fill_opacities` and `fill_colors`.
```
line.fill = 'bottom'
line.fill_opacities = [0.2]
line.line_style = 'dashed'
line.interpolation = 'basis'
```
While a `Lines` plot allows the user to extract the general shape of the data being plotted, there may be a need to visualize discrete data points along with this shape. This is where the `markers` attribute comes in.
```
line.marker = 'triangle-down'
```
The `marker` attributes accepts the values `square`, `circle`, `cross`, `diamond`, `square`, `triangle-down`, `triangle-up`, `arrow`, `rectangle`, `ellipse`. Try changing the string above and re-running the cell to see how each `marker` type looks.
## Plotting a Time-Series
The `DateScale` allows us to plot time series as a `Lines` plot conveniently with most `date` formats.
```
# Here we define the dates we would like to use
dates = date_range(start='01-01-2007', periods=150)
fig = plt.figure(title='Time Series')
axes_options = {'x': {'label': 'Date'}, 'y': {'label': 'Security 1'}}
time_series = plt.plot(dates, security_1,
axes_options=axes_options)
fig
```
## Plotting multiples sets of data
The `Lines` mark allows the user to plot multiple `y`-values for a single `x`-value. This can be done by passing an `ndarray` or a list of the different `y`-values as the y-attribute of the `Lines` as shown below.
```
dates_new = date_range(start='06-01-2007', periods=150)
```
We pass each data set as an element of a `list`
```
fig = plt.figure()
axes_options = {'x': {'label': 'Date'}, 'y': {'label': 'Price'}}
line = plt.plot(dates, [security_1, security_2],
labels=['Security 1', 'Security 2'],
axes_options=axes_options,
display_legend=True)
fig
```
Similarly, we can also pass multiple `x`-values for multiple sets of `y`-values
```
line.x, line.y = [dates, dates_new], [security_1, security_2]
```
### Coloring Lines according to data
The `color` attribute of a `Lines` mark can also be used to encode one more dimension of data. Suppose we have a portfolio of securities and we would like to color them based on whether we have bought or sold them. We can use the `color` attribute to encode this information.
```
fig = plt.figure()
axes_options = {'x': {'label': 'Date'},
'y': {'label': 'Security 1'},
'color' : {'visible': False}}
# add a custom color scale to color the lines
plt.scales(scales={'color': ColorScale(colors=['Red', 'Green'])})
dates_color = date_range(start='06-01-2007', periods=150)
securities = 100. + np.cumsum(np.random.randn(150, 10), axis=0)
# we generate 10 random price series and 10 random positions
positions = np.random.randint(0, 2, size=10)
# We pass the color scale and the color data to the plot method
line = plt.plot(dates_color, securities.T, color=positions,
axes_options=axes_options)
fig
```
We can also reset the colors of the Line to their defaults by setting the `color` attribute to `None`.
```
line.color = None
```
## Patches
The `fill` attribute of the `Lines` mark allows us to fill a path in different ways, while the `fill_colors` attribute lets us control the color of the `fill`
```
fig = plt.figure(animation_duration=1000)
patch = plt.plot([],[],
fill_colors=['orange', 'blue', 'red'],
fill='inside',
axes_options={'x': {'visible': False}, 'y': {'visible': False}},
stroke_width=10,
close_path=True,
display_legend=True)
patch.x = [[0, 2, 1.2, np.nan, np.nan, np.nan, np.nan], [0.5, 2.5, 1.7 , np.nan, np.nan, np.nan, np.nan], [4, 5, 6, 6, 5, 4, 3]],
patch.y = [[0, 0, 1 , np.nan, np.nan, np.nan, np.nan], [0.5, 0.5, -0.5, np.nan, np.nan, np.nan, np.nan], [1, 1.1, 1.2, 2.3, 2.2, 2.7, 1.0]]
fig
patch.opacities = [0.1, 0.2]
patch.x = [[2, 3, 3.2, np.nan, np.nan, np.nan, np.nan], [0.5, 2.5, 1.7, np.nan, np.nan, np.nan, np.nan], [4,5,6, 6, 5, 4, 3]]
patch.close_path = False
```
|
github_jupyter
|
# Clean-Label Feature Collision Attacks on a Keras Classifier
In this notebook, we will learn how to use ART to run a clean-label feature collision poisoning attack on a neural network trained with Keras. We will be training our data on a subset of the CIFAR-10 dataset. The methods described are derived from [this paper](https://arxiv.org/abs/1804.00792) by Shafahi, Huang, et. al. 2018.
```
import os, sys
from os.path import abspath
module_path = os.path.abspath(os.path.join('..'))
if module_path not in sys.path:
sys.path.append(module_path)
import warnings
warnings.filterwarnings('ignore')
from keras.models import load_model
from art import config
from art.utils import load_dataset, get_file
from art.estimators.classification import KerasClassifier
from art.attacks.poisoning import FeatureCollisionAttack
import numpy as np
%matplotlib inline
import matplotlib.pyplot as plt
np.random.seed(301)
(x_train, y_train), (x_test, y_test), min_, max_ = load_dataset('cifar10')
num_samples_train = 1000
num_samples_test = 1000
x_train = x_train[0:num_samples_train]
y_train = y_train[0:num_samples_train]
x_test = x_test[0:num_samples_test]
y_test = y_test[0:num_samples_test]
class_descr = ['airplane', 'automobile', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck']
```
## Load Model to be Attacked
In this example, we using a RESNET50 model pretrained on the CIFAR dataset.
```
path = get_file('cifar_alexnet.h5',extract=False, path=config.ART_DATA_PATH,
url='https://www.dropbox.com/s/ta75pl4krya5djj/cifar_alexnet.h5?dl=1')
classifier_model = load_model(path)
classifier = KerasClassifier(clip_values=(min_, max_), model=classifier_model, use_logits=False,
preprocessing=(0.5, 1))
```
## Choose Target Image from Test Set
```
target_class = "bird" # one of ['airplane', 'automobile', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck']
target_label = np.zeros(len(class_descr))
target_label[class_descr.index(target_class)] = 1
target_instance = np.expand_dims(x_test[np.argmax(y_test, axis=1) == class_descr.index(target_class)][3], axis=0)
fig = plt.imshow(target_instance[0])
print('true_class: ' + target_class)
print('predicted_class: ' + class_descr[np.argmax(classifier.predict(target_instance), axis=1)[0]])
feature_layer = classifier.layer_names[-2]
```
## Poison Training Images to Misclassify Test
The attacker wants to make it such that whenever a prediction is made on this particular cat the output will be a horse.
```
base_class = "frog" # one of ['airplane', 'automobile', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck']
base_idxs = np.argmax(y_test, axis=1) == class_descr.index(base_class)
base_instances = np.copy(x_test[base_idxs][:10])
base_labels = y_test[base_idxs][:10]
x_test_pred = np.argmax(classifier.predict(base_instances), axis=1)
nb_correct_pred = np.sum(x_test_pred == np.argmax(base_labels, axis=1))
print("New test data to be poisoned (10 images):")
print("Correctly classified: {}".format(nb_correct_pred))
print("Incorrectly classified: {}".format(10-nb_correct_pred))
plt.figure(figsize=(10,10))
for i in range(0, 9):
pred_label, true_label = class_descr[x_test_pred[i]], class_descr[np.argmax(base_labels[i])]
plt.subplot(330 + 1 + i)
fig=plt.imshow(base_instances[i])
fig.axes.get_xaxis().set_visible(False)
fig.axes.get_yaxis().set_visible(False)
fig.axes.text(0.5, -0.1, pred_label + " (" + true_label + ")", fontsize=12, transform=fig.axes.transAxes,
horizontalalignment='center')
```
The captions on the images can be read: `predicted label (true label)`
## Creating Poison Frogs
```
attack = FeatureCollisionAttack(classifier, target_instance, feature_layer, max_iter=10, similarity_coeff=256, watermark=0.3)
poison, poison_labels = attack.poison(base_instances)
poison_pred = np.argmax(classifier.predict(poison), axis=1)
plt.figure(figsize=(10,10))
for i in range(0, 9):
pred_label, true_label = class_descr[poison_pred[i]], class_descr[np.argmax(poison_labels[i])]
plt.subplot(330 + 1 + i)
fig=plt.imshow(poison[i])
fig.axes.get_xaxis().set_visible(False)
fig.axes.get_yaxis().set_visible(False)
fig.axes.text(0.5, -0.1, pred_label + " (" + true_label + ")", fontsize=12, transform=fig.axes.transAxes,
horizontalalignment='center')
```
Notice how the network classifies most of theses poison examples as frogs, and it's not incorrect to do so. The examples look mostly froggy. A slight watermark of the target instance is also added to push the poisons closer to the target class in feature space.
## Training with Poison Images
```
classifier.set_learning_phase(True)
print(x_train.shape)
print(base_instances.shape)
adv_train = np.vstack([x_train, poison])
adv_labels = np.vstack([y_train, poison_labels])
classifier.fit(adv_train, adv_labels, nb_epochs=5, batch_size=4)
```
## Fooled Network Misclassifies Bird
```
fig = plt.imshow(target_instance[0])
print('true_class: ' + target_class)
print('predicted_class: ' + class_descr[np.argmax(classifier.predict(target_instance), axis=1)[0]])
```
These attacks allow adversaries who can poison your dataset the ability to mislabel any particular target instance of their choosing without manipulating labels.
|
github_jupyter
|
# Lecture 12: Canonical Economic Models
[Download on GitHub](https://github.com/NumEconCopenhagen/lectures-2022)
[<img src="https://mybinder.org/badge_logo.svg">](https://mybinder.org/v2/gh/NumEconCopenhagen/lectures-2022/master?urlpath=lab/tree/12/Canonical_economic_models.ipynb)
1. [OverLapping Generations (OLG) model](#OverLapping-Generations-(OLG)-model)
2. [Ramsey model](#Ramsey-model)
3. [Further perspectives](#Further-perspectives)
You will learn how to solve **two canonical economic models**:
1. The **overlapping generations (OLG) model**
2. The **Ramsey model**
**Main take-away:** Hopefully inspiration to analyze such models on your own.
```
%load_ext autoreload
%autoreload 2
import numpy as np
from scipy import optimize
# plotting
import matplotlib.pyplot as plt
plt.style.use('seaborn-whitegrid')
plt.rcParams.update({'font.size': 12})
# models
from OLGModel import OLGModelClass
from RamseyModel import RamseyModelClass
```
<a id="OverLapping-Generations-(OLG)-model"></a>
# 1. OverLapping Generations (OLG) model
## 1.1 Model description
**Time:** Discrete and indexed by $t\in\{0,1,\dots\}$.
**Demographics:** Population is constant. A life consists of
two periods, *young* and *old*.
**Households:** As young a household supplies labor exogenously, $L_{t}=1$, and earns a after tax wage $(1-\tau_w)w_{t}$. Consumption as young and old
are denoted by $C_{1t}$ and $C_{2t+1}$. The after-tax return on saving is $(1-\tau_{r})r_{t+1}$. Utility is
$$
\begin{aligned}
U & =\max_{s_{t}\in[0,1]}\frac{C_{1t}^{1-\sigma}}{1-\sigma}+\beta\frac{C_{1t+1}^{1-\sigma}}{1-\sigma},\,\,\,\beta > -1, \sigma > 0\\
& \text{s.t.}\\
& S_{t}=s_{t}(1-\tau_{w})w_{t}\\
& C_{1t}=(1-s_{t})(1-\tau_{w})w_{t}\\
& C_{2t+1}=(1+(1-\tau_{r})r_{t+1})S_{t}
\end{aligned}
$$
The problem is formulated in terms of the saving rate $s_t\in[0,1]$.
**Firms:** Firms rent capital $K_{t-1}$ at the rental rate $r_{t}^{K}$,
and hires labor $E_{t}$ at the wage rate $w_{t}$. Firms have access
to the production function
$$
\begin{aligned}
Y_{t}=F(K_{t-1},E_{t})=(\alpha K_{t-1}^{-\theta}+(1-\alpha)E_{t}^{-\theta})^{\frac{1}{-\theta}},\,\,\,\theta>-1,\alpha\in(0,1)
\end{aligned}
$$
Profits are
$$
\begin{aligned}
\Pi_{t}=Y_{t}-w_{t}E_{t}-r_{t}^{K}K_{t-1}
\end{aligned}
$$
**Government:** Choose public consumption, $G_{t}$, and tax rates $\tau_w \in [0,1]$ and $\tau_r \in [0,1]$. Total tax revenue is
$$
\begin{aligned}
T_{t} &=\tau_r r_{t} (K_{t-1}+B_{t-1})+\tau_w w_{t}
\end{aligned}
$$
Government debt accumulates according to
$$
\begin{aligned}
B_{t} &=(1+r^b_{t})B_{t-1}-T_{t}+G_{t}
\end{aligned}
$$
A *balanced budget* implies $G_{t}=T_{t}-r_{t}B_{t-1}$.
**Capital:** Depreciates with a rate of $\delta \in [0,1]$.
**Equilibrium:**
1. Households maximize utility
2. Firms maximize profits
3. No-arbitrage between bonds and capital
$$
r_{t}=r_{t}^{K}-\delta=r_{t}^{b}
$$
4. Labor market clears: $E_{t}=L_{t}=1$
5. Goods market clears: $Y_{t}=C_{1t}+C_{2t}+G_{t}+I_{t}$
6. Asset market clears: $S_{t}=K_{t}+B_{t}$
7. Capital follows its law of motion: $K_{t}=(1-\delta)K_{t-1}+I_{t}$
**For more details on the OLG model:** See chapter 3-4 [here](https://web.econ.ku.dk/okocg/VM/VM-general/Material/Chapters-VM.htm).
## 1.2 Solution and simulation
**Implication of profit maximization:** From FOCs
$$
\begin{aligned}
r_{t}^{k} & =F_{K}(K_{t-1},E_{t})=\alpha K_{t-1}^{-\theta-1}Y_{t}^{1+\theta}\\
w_{t} & =F_{E}(K_{t-1},E_{t})=(1-\alpha)E_{t}^{-\theta-1}Y_{t}^{1+\theta}
\end{aligned}
$$
**Implication of utility maximization:** From FOC
$$
\begin{aligned}
C_{1t}^{-\sigma}=\beta (1+(1-\tau_r)r_{t+1})C_{2t+1}^{-\sigma}
\end{aligned}
$$
**Simulation algorithm:** At the beginning of period $t$, the
economy can be summarized in the state variables $K_{t-1}$ and $B_{t-1}$. *Before* $s_t$ is known, we can calculate:
$$
\begin{aligned}
Y_{t} & =F(K_{t-1},1)\\
r_{t}^{k} & =F_{K}(K_{t-1},1)\\
w_{t} & =F_{E}(K_{t-1},1)\\
r_{t} & =r^k_{t}-\delta\\
r_{t}^{b} & =r_{t}\\
\tilde{r}_{t} & =(1-\tau_{r})r_{t}\\
C_{2t} & =(1+\tilde{r}_{t})(K_{t-1}+B_{t-1})\\
T_{t} & =\tau_{r}r_{t}(K_{t-1}+B_{t-1})+\tau_{w}w_{t}\\
B_{t} & =(1+r^b_{t})B_{t-1}+T_{t}-G_{t}\\
\end{aligned}
$$
*After* $s_t$ is known we can calculate:
$$
\begin{aligned}
C_{1t} & = (1-s_{t})(1-\tau_{w})w_{t}\\
I_{t} & =Y_{t}-C_{1t}-C_{2t}-G_{t}\\
K_{t} & =(1-\delta)K_{t-1} + I_t
\end{aligned}
$$
**Solution algorithm:** Simulate forward choosing $s_{t}$ so
that we always have
$$
\begin{aligned}
C_{1t}^{-\sigma}=\beta(1+\tilde{r}_{t+1})C_{2t+1}^{-\sigma}
\end{aligned}
$$
**Implementation:**
1. Use a bisection root-finder to determine $s_t$
2. Low $s_t$: A lot of consumption today. Low marginal utility. LHS < RHS.
3. High $s_t$: Little consumption today. High marginal utility. LHS > RHS.
4. Problem: Too low $s_t$ might not be feasible if $B_t > 0$.
**Note:** Never errors in the Euler-equation due to *perfect foresight*.
**Question:** Are all the requirements for the equilibrium satisfied?
## 1.3 Test case
1. Production is Cobb-Douglas ($\theta = 0$)
2. Utility is logarithmic ($\sigma = 1$)
3. The government is not doing anything ($\tau_w=\tau_r=0$, $T_t = G_t = 0$ and $B_t = 0$)
**Analytical steady state:** It can be proven
$$ \lim_{t\rightarrow\infty} K_t = \left(\frac{1-\alpha}{1+1/\beta}\right)^{\frac{1}{1-\alpha}} $$
**Setup:**
```
model = OLGModelClass()
par = model.par # SimpeNamespace
sim = model.sim # SimpeNamespace
# a. production
par.production_function = 'cobb-douglas'
par.theta = 0.0
# b. households
par.sigma = 1.0
# c. government
par.tau_w = 0.0
par.tau_r = 0.0
sim.balanced_budget[:] = True # G changes to achieve this
# d. initial values
K_ss = ((1-par.alpha)/((1+1.0/par.beta)))**(1/(1-par.alpha))
par.K_lag_ini = 0.1*K_ss
```
### Simulate first period manually
```
from OLGModel import simulate_before_s, simulate_after_s, find_s_bracket, calc_euler_error
```
**Make a guess:**
```
s_guess = 0.41
```
**Evaluate first period:**
```
# a. initialize
sim.K_lag[0] = par.K_lag_ini
sim.B_lag[0] = par.B_lag_ini
simulate_before_s(par,sim,t=0)
print(f'{sim.C2[0] = : .4f}')
simulate_after_s(par,sim,s=s_guess,t=0)
print(f'{sim.C1[0] = : .4f}')
simulate_before_s(par,sim,t=1)
print(f'{sim.C2[1] = : .4f}')
print(f'{sim.rt[1] = : .4f}')
LHS_Euler = sim.C1[0]**(-par.sigma)
RHS_Euler = (1+sim.rt[1])*par.beta * sim.C2[1]**(-par.sigma)
print(f'euler-error = {LHS_Euler-RHS_Euler:.8f}')
```
**Implemented as function:**
```
euler_error = calc_euler_error(s_guess,par,sim,t=0)
print(f'euler-error = {euler_error:.8f}')
```
**Find bracket to search in:**
```
s_min,s_max = find_s_bracket(par,sim,t=0,do_print=True);
```
**Call root-finder:**
```
obj = lambda s: calc_euler_error(s,par,sim,t=0)
result = optimize.root_scalar(obj,bracket=(s_min,s_max),method='bisect')
print(result)
```
**Check result:**
```
euler_error = calc_euler_error(result.root,par,sim,t=0)
print(f'euler-error = {euler_error:.8f}')
```
### Full simulation
```
model.simulate()
```
**Check euler-errors:**
```
for t in range(5):
LHS_Euler = sim.C1[t]**(-par.sigma)
RHS_Euler = (1+sim.rt[t+1])*par.beta * sim.C2[t+1]**(-par.sigma)
print(f't = {t:2d}: euler-error = {LHS_Euler-RHS_Euler:.8f}')
```
**Plot and check with analytical solution:**
```
fig = plt.figure(figsize=(6,6/1.5))
ax = fig.add_subplot(1,1,1)
ax.plot(model.sim.K_lag,label=r'$K_{t-1}$')
ax.axhline(K_ss,ls='--',color='black',label='analytical steady state')
ax.legend(frameon=True)
fig.tight_layout()
K_lag_old = model.sim.K_lag.copy()
```
**Task:** Test if the starting point matters?
**Additional check:** Not much should change with only small parameter changes.
```
# a. production (close to cobb-douglas)
par.production_function = 'ces'
par.theta = 0.001
# b. household (close to logarithmic)
par.sigma = 1.1
# c. goverment (weakly active)
par.tau_w = 0.001
par.tau_r = 0.001
# d. simulate
model.simulate()
fig = plt.figure(figsize=(6,6/1.5))
ax = fig.add_subplot(1,1,1)
ax.plot(model.sim.K_lag,label=r'$K_{t-1}$')
ax.plot(K_lag_old,label=r'$K_{t-1}$ ($\theta = 0.0, \sigma = 1.0$, inactive government)')
ax.axhline(K_ss,ls='--',color='black',label='analytical steady state (wrong)')
ax.legend(frameon=True)
fig.tight_layout()
```
## 1.4 Active government
```
model = OLGModelClass()
par = model.par
sim = model.sim
```
**Baseline:**
```
model.simulate()
fig = plt.figure(figsize=(6,6/1.5))
ax = fig.add_subplot(1,1,1)
ax.plot(sim.K_lag/(sim.Y),label=r'$\frac{K_{t-1}}{Y_t}$')
ax.plot(sim.B_lag/(sim.Y),label=r'$\frac{B_{t-1}}{Y_t}$')
ax.legend(frameon=True)
fig.tight_layout()
```
**Remember steady state:**
```
K_ss = sim.K_lag[-1]
B_ss = sim.B_lag[-1]
G_ss = sim.G[-1]
```
**Spending spree of 5% in $T=3$ periods:**
```
# a. start from steady state
par.K_lag_ini = K_ss
par.B_lag_ini = B_ss
# b. spending spree
T0 = 0
dT = 3
sim.G[T0:T0+dT] = 1.05*G_ss
sim.balanced_budget[:T0] = True #G adjusts
sim.balanced_budget[T0:T0+dT] = False # B adjusts
sim.balanced_budget[T0+dT:] = True # G adjusts
```
**Simulate:**
```
model.simulate()
```
**Crowding-out of capital:**
```
fig = plt.figure(figsize=(6,6/1.5))
ax = fig.add_subplot(1,1,1)
ax.plot(sim.K/(sim.Y),label=r'$\frac{K_{t-1}}{Y_t}$')
ax.plot(sim.B/(sim.Y),label=r'$\frac{B_{t-1}}{Y_t}$')
ax.legend(frameon=True)
fig.tight_layout()
```
**Question:** Would the households react today if the spending spree is say 10 periods in the future?
## 1.5 Getting an overview
1. Spend 3 minutes looking at `OLGModel.py`
2. Write one question at [https://b.socrative.com/login/student/](https://b.socrative.com/login/student/) with `ROOM=NUMECON`
## 1.6 Potential analysis and extension
**Potential analysis:**
1. Over-accumulation of capital relative to golden rule?
2. Calibration to actual data
3. Generational inequality
4. Multiple equilibria
**Extensions:**
1. Add population and technology growth
2. More detailed tax and transfer system
3. Utility and productive effect of government consumption/investment
4. Endogenous labor supply
5. Bequest motive
6. Uncertain returns on capital
7. Additional assets (e.g. housing)
8. More than two periods in the life-cycle (life-cycle)
9. More than one dynasty (cross-sectional inequality dynamics)
<a id="Ramsey-model"></a>
# 2. Ramsey model
... also called the Ramsey-Cass-Koopman model.
## 2.1 Model descripton
**Time:** Discrete and indexed by $t\in\{0,1,\dots\}$.
**Demographics::** Population is constant. Everybody lives forever.
**Household:** Households supply labor exogenously, $L_{t}=1$, and earns a wage $w_{t}$. The return on saving is $r_{t+1}$. Utility is
$$
\begin{aligned}
U & =\max_{\{C_{t}\}_{t=0}^{\infty}}\sum_{t=0}^{\infty}\beta^{t}\frac{C_{t}^{1-\sigma}}{1-\sigma},\beta\in(0,1),\sigma>0\\
& \text{s.t.}\\
& M_{t}=(1+r_{t})N_{t-1}+w_{t}\\
& N_{t}=M_{t}-C_{t}
\end{aligned}
$$
where $M_{t}$ is cash-on-hand and $N_{t}$ is end-of-period assets.
**Firms:** Firms rent capital $K_{t-1}$ at the rental rate $r_{t}^{K}$
and hires labor $E_{t}$ at the wage rate $w_{t}$. Firms have access
to the production function
$$
\begin{aligned}
Y_{t}= F(K_{t-1},E_{t})=A_t(\alpha K_{t-1}^{-\theta}+(1-\alpha)E_{t}^{-\theta})^{\frac{1}{-\theta}},\,\,\,\theta>-1,\alpha\in(0,1),A_t>0
\end{aligned}
$$
Profits are
$$
\begin{aligned}
\Pi_{t}=Y_{t}-w_{t}E_{t}-r_{t}^{K}K_{t-1}
\end{aligned}
$$
**Equilibrium:**
1. Households maximize utility
2. Firms maximize profits
3. Labor market clear: $E_{t}=L_{t}=1$
4. Goods market clear: $Y_{t}=C_{t}+I_{t}$
5. Asset market clear: $N_{t}=K_{t}$ and $r_{t}=r_{t}^{k}-\delta$
6. Capital follows its law of motion: $K_{t}=(1-\delta)K_{t-1}+I_{t}$
**Implication of profit maximization:** From FOCs
$$
\begin{aligned}
r_{t}^{k} & = F_{K}(K_{t-1},E_{t})=A_t \alpha K_{t-1}^{-\theta-1}Y_{t}^{-1}\\
w_{t} & = F_{E}(K_{t-1},E_{t})=A_t (1-\alpha)E_{t}^{-\theta-1}Y_{t}^{-1}
\end{aligned}
$$
**Implication of utility maximization:** From FOCs
$$
\begin{aligned}
C_{t}^{-\sigma}=\beta(1+r_{t+1})C_{t+1}^{-\sigma}
\end{aligned}
$$
**Solution algorithm:**
We can summarize the model in the **non-linear equation system**
$$
\begin{aligned}
\boldsymbol{H}(\boldsymbol{K},\boldsymbol{C},K_{-1})=\left[\begin{array}{c}
H_{0}\\
H_{1}\\
\begin{array}{c}
\vdots\end{array}
\end{array}\right]=\left[\begin{array}{c}
0\\
0\\
\begin{array}{c}
\vdots\end{array}
\end{array}\right]
\end{aligned}
$$
where $\boldsymbol{K} = [K_0,K_1\dots]$, $\boldsymbol{C} = [C_0,C_1\dots]$, and
$$
\begin{aligned}
H_{t}
=\left[\begin{array}{c}
C_{t}^{-\sigma}-\beta(1+r_{t+1})C_{t+1}^{-\sigma}\\
K_{t}-[(1-\delta)K_{t-1}+Y_t-C_{t}]
\end{array}\right]
=\left[\begin{array}{c}
C_{t}^{-\sigma}-\beta(1+F_{K}(K_{t},1))C_{t+1}^{-\sigma}\\
K_{t}-[(1-\delta)K_{t-1} + F(K_{t-1},1)-C_{t}])
\end{array}\right]
\end{aligned}
$$
**Path:** We refer to $\boldsymbol{K}$ and $\boldsymbol{C}$ as *transition paths*.
**Implementation:** We solve this equation system in **two steps**:
1. Assume all variables are in steady state after some **truncation horizon**.
1. Calculate the numerical **jacobian** of $\boldsymbol{H}$ wrt. $\boldsymbol{K}$
and $\boldsymbol{C}$ around the steady state
2. Solve the equation system using a **hand-written Broyden-solver**
**Note:** The equation system can also be solved directly using `scipy.optimize.root`.
**Remember:** The jacobian is just a gradient. I.e. the matrix of what the implied errors are in $\boldsymbol{H}$ when a *single* $K_t$ or $C_t$ change.
## 2.2 Solution
```
model = RamseyModelClass()
par = model.par
ss = model.ss
path = model.path
```
**Find steady state:**
1. Target steady-state capital-output ratio, $K_{ss}/Y_{ss}$ of 4.0.
2. Force steady-state output $Y_{ss} = 1$.
3. Adjust $\beta$ and $A_{ss}$ to achieve this.
```
model.find_steady_state(KY_ss=4.0)
```
**Test that errors and the path are 0:**
```
# a. set initial value
par.K_lag_ini = ss.K
# b. set path
path.A[:] = ss.A
path.C[:] = ss.C
path.K[:] = ss.K
# c. check errors
errors_ss = model.evaluate_path_errors()
assert np.allclose(errors_ss,0.0)
model.calculate_jacobian()
```
**Solve:**
```
par.K_lag_ini = 0.50*ss.K # start away from steady state
model.solve() # find transition path
fig = plt.figure(figsize=(6,6/1.5))
ax = fig.add_subplot(1,1,1)
ax.plot(path.K_lag,label=r'$K_{t-1}$')
ax.legend(frameon=True)
fig.tight_layout()
```
## 2.3 Comparison with scipy solution
**Note:** scipy computes the jacobian internally
```
model_scipy = RamseyModelClass()
model_scipy.par.solver = 'scipy'
model_scipy.find_steady_state(KY_ss=4.0)
model_scipy.par.K_lag_ini = 0.50*model_scipy.ss.K
model_scipy.path.A[:] = model_scipy.ss.A
model_scipy.solve()
fig = plt.figure(figsize=(6,6/1.5))
ax = fig.add_subplot(1,1,1)
ax.plot(path.K_lag,label=r'$K_{t-1}$, broyden')
ax.plot(model_scipy.path.K_lag,ls='--',label=r'$K_{t-1}$, scipy')
ax.legend(frameon=True)
fig.tight_layout()
```
## 2.4 Persistent technology shock
**Shock:**
```
par.K_lag_ini = ss.K # start from steady state
path.A[:] = 0.95**np.arange(par.Tpath)*0.1*ss.A + ss.A # shock path
```
**Terminology:** This is called an MIT-shock. Households do not expect shocks. Know the full path of the shock when it arrives. Continue to believe no future shocks will happen.
**Solve:**
```
model.solve()
fig = plt.figure(figsize=(2*6,6/1.5))
ax = fig.add_subplot(1,2,1)
ax.set_title('Capital, $K_{t-1}$')
ax.plot(path.K_lag)
ax = fig.add_subplot(1,2,2)
ax.plot(path.A)
ax.set_title('Technology, $A_t$')
fig.tight_layout()
```
**Question:** Could a much more persistent shock be problematic?
## 2.5 Future persistent technology shock
**Shock happing after period $H$:**
```
par.K_lag_ini = ss.K # start from steady state
# shock
H = 50
path.A[:] = ss.A
path.A[H:] = 0.95**np.arange(par.Tpath-H)*0.1*ss.A + ss.A
```
**Solve:**
```
model.solve()
fig = plt.figure(figsize=(2*6,6/1.5))
ax = fig.add_subplot(1,2,1)
ax.set_title('Capital, $K_{t-1}$')
ax.plot(path.K_lag)
ax = fig.add_subplot(1,2,2)
ax.plot(path.A)
ax.set_title('Technology, $A_t$')
fig.tight_layout()
par.K_lag_ini = path.K[30]
path.A[:] = ss.A
model.solve()
```
**Take-away:** Households are forward looking and responds before the shock hits.
## 2.6 Getting an overview
1. Spend 3 minutes looking at `RamseyModel.py`
2. Write one question at [https://b.socrative.com/login/student/](https://b.socrative.com/login/student/) with `ROOM=NUMECON`
## 2.7 Potential analysis and extension
**Potential analysis:**
1. Different shocks (e.g. discount factor)
2. Multiple shocks
3. Permanent shocks ($\rightarrow$ convergence to new steady state)
4. Transition speed
**Extensions:**
1. Add a government and taxation
2. Endogenous labor supply
3. Additional assets (e.g. housing)
4. Add nominal rigidities (New Keynesian)
<a id="Further-perspectives"></a>
# 3. Further perspectives
**The next steps beyond this course:**
1. The **Bewley-Huggett-Aiyagari** model. A multi-period OLG model or Ramsey model with households making decisions *under uncertainty and borrowing constraints* as in lecture 11 under "dynamic optimization". Such heterogenous agent models are used in state-of-the-art research, see [Quantitative Macroeconomics with Heterogeneous Households](https://www.annualreviews.org/doi/abs/10.1146/annurev.economics.050708.142922).
2. Further adding nominal rigidities this is called a **Heterogenous Agent New Keynesian (HANK)** model. See [Macroeconomics with HANK models](https://drive.google.com/file/d/16Qq7NJ_AZh5NmjPFSrLI42mfT7EsCUeH/view).
3. This extends the **Representative Agent New Keynesian (RANK)** model, which itself is a Ramsey model extended with nominal rigidities.
4. The final frontier is including **aggregate risk**, which either requires linearization or using a **Krussell-Smith method**. Solving the model in *sequence-space* as we did with the Ramsey model is a frontier method (see [here](https://github.com/shade-econ/sequence-jacobian/#sequence-space-jacobian)).
**Next lecture:** Agent Based Models
|
github_jupyter
|
```
##### Copyright 2020 Google LLC.
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
```
# We are using NitroML on Kubeflow:
This notebook allows users to analyze NitroML benchmark results.
```
# This notebook assumes you have followed the following steps to setup port-forwarding:
# Step 1: Configure your cluster with gcloud
# `gcloud container clusters get-credentials <cluster_name> --zone <cluster-zone> --project <project-id>
# Step 2: Get the port where the gRPC service is running on the cluster
# `kubectl get configmap metadata-grpc-configmap -o jsonpath={.data}`
# Use `METADATA_GRPC_SERVICE_PORT` in the next step. The default port used is 8080.
# Step 3: Port forwarding
# `kubectl port-forward deployment/metadata-grpc-deployment 9898:<METADATA_GRPC_SERVICE_PORT>`
# Troubleshooting
# If getting error related to Metadata (For examples, Transaction already open). Try restarting the metadata-grpc-service using:
# `kubectl rollout restart deployment metadata-grpc-deployment`
import sys, os
PROJECT_DIR=os.path.join(sys.path[0], '..')
%cd {PROJECT_DIR}
from ml_metadata.proto import metadata_store_pb2
from ml_metadata.metadata_store import metadata_store
from nitroml.benchmark import results
```
## Connect to the ML Metadata (MLMD) database
First we need to connect to our MLMD database which stores the results of our
benchmark runs.
```
connection_config = metadata_store_pb2.MetadataStoreClientConfig()
connection_config.host = 'localhost'
connection_config.port = 9898
store = metadata_store.MetadataStore(connection_config)
```
## Display benchmark results
Next we load and visualize `pd.DataFrame` containing our benchmark results.
These results contain contextual features such as the pipeline ID, and
benchmark metrics as computed by the downstream Evaluators. If your
benchmark included an `EstimatorTrainer` component, its hyperparameters may also
display in the table below.
```
#@markdown ### Choose how to aggregate metrics:
mean = False #@param { type: "boolean" }
stdev = False #@param { type: "boolean" }
min_and_max = False #@param { type: "boolean" }
agg = []
if mean:
agg.append("mean")
if stdev:
agg.append("std")
if min_and_max:
agg += ["min", "max"]
df = results.overview(store, metric_aggregators=agg)
df.head()
```
### We can display an interactive table using qgrid
Please follow the latest instructions on downloading qqgrid package from here: https://github.com/quantopian/qgrid
```
import qgrid
qgid_wdget = qgrid.show_grid(df, show_toolbar=True)
qgid_wdget
```
|
github_jupyter
|
# Group Metrics
The `fairlearn` package contains algorithms which enable machine learning models to minimise disparity between groups. The `metrics` portion of the package provides the means required to verify that the mitigation algorithms are succeeding.
```
import numpy as np
import pandas as pd
import sklearn.metrics as skm
```
## Ungrouped Metrics
At their simplest, metrics take a set of 'true' values $Y_{true}$ (from the input data) and predicted values $Y_{pred}$ (by applying the model to the input data), and use these to compute a measure. For example, the _recall_ or _true positive rate_ is given by
\begin{equation}
P( Y_{pred}=1 | Y_{true}=1 )
\end{equation}
That is, a measure of whether the model finds all the positive cases in the input data. The `scikit-learn` package implements this in [sklearn.metrics.recall_score](https://scikit-learn.org/stable/modules/generated/sklearn.metrics.recall_score.html).
Suppose we have the following data:
```
Y_true = [0, 1, 1, 1, 1, 0, 1, 0, 1, 0, 0, 0, 1, 1, 1, 1]
Y_pred = [0, 0, 1, 0, 1, 1, 1, 0, 0, 1, 1, 1, 1, 0, 0, 1]
```
we can see that the prediction is 1 in five of the ten cases where the true value is 1, so we expect the recall to be 0.0.5:
```
skm.recall_score(Y_true, Y_pred)
```
## Metrics with Grouping
When considering fairness, each row of input data will have an associated group label $g \in G$, and we will want to know how the metric behaves for each $g$. To help with this, Fairlearn provides wrappers, which take an existing (ungrouped) metric function, and apply it to each group within a set of data.
Suppose in addition to the $Y_{true}$ and $Y_{pred}$ above, we had the following set of labels:
```
group_membership_data = ['d', 'a', 'c', 'b', 'b', 'c', 'c', 'c', 'b', 'd', 'c', 'a', 'b', 'd', 'c', 'c']
df = pd.DataFrame({ 'Y_true': Y_true, 'Y_pred': Y_pred, 'group_membership_data': group_membership_data})
df
```
```
import fairlearn.metrics as flm
group_metrics = flm.group_summary(skm.recall_score, Y_true, Y_pred, sensitive_features=group_membership_data, sample_weight=None)
print("Overall recall = ", group_metrics.overall)
print("recall by groups = ", group_metrics.by_group)
```
Note that the overall recall is the same as that calculated above in the Ungrouped Metric section, while the `by_group` dictionary matches the values we calculated by inspection from the table above.
In addition to these basic scores, `fairlearn.metrics` also provides convenience functions to recover the maximum and minimum values of the metric across groups and also the difference and ratio between the maximum and minimum:
```
print("min recall over groups = ", flm.group_min_from_summary(group_metrics))
print("max recall over groups = ", flm.group_max_from_summary(group_metrics))
print("difference in recall = ", flm.difference_from_summary(group_metrics))
print("ratio in recall = ", flm.ratio_from_summary(group_metrics))
```
## Supported Ungrouped Metrics
To be used by `group_summary`, the supplied Python function must take arguments of `y_true` and `y_pred`:
```python
my_metric_func(y_true, y_pred)
```
An additional argument of `sample_weight` is also supported:
```python
my_metric_with_weight(y_true, y_pred, sample_weight=None)
```
The `sample_weight` argument is always invoked by name, and _only_ if the user supplies a `sample_weight` argument.
## Convenience Wrapper
Rather than require a call to `group_summary` each time, we also provide a function which turns an ungrouped metric into a grouped one. This is called `make_metric_group_summary`:
```
recall_score_group_summary = flm.make_metric_group_summary(skm.recall_score)
results = recall_score_group_summary(Y_true, Y_pred, sensitive_features=group_membership_data)
print("Overall recall = ", results.overall)
print("recall by groups = ", results.by_group)
```
|
github_jupyter
|
# The importance of space
Agent based models are useful when the aggregate system behavior emerges out of local interactions amongst the agents. In the model of the evolution of cooperation, we created a set of agents and let all agents play against all other agents. Basically, we pretended as if all our agents were perfectly mixed. In practice, however, it is much more common that agents only interact with some, but not all, other agents. For example, in models of epidemiology, social interactions are a key factors. Thus, interactions are dependend on your social network. In other situations, our behavior might be based on what we see around us. Phenomena like fashion are at least partly driven by seeing what others are doing and mimicking this behavior. The same is true for many animals. Flocking dynamics as exhibited by starling, or shoaling behavior in fish, can be explained by the animal looking at its neirest neighbors and staying within a given distance of them. In agent based models, anything that structures the interaction amongst agents is typically called a space. This space can be a 2d or 3d space with euclidian distances (as in models of flocking and shoaling), it can also be a grid structure (as we will show below), or it can be a network structure.
MESA comes with several spaces that we can readily use. These are
* **SingleGrid;** an 'excel-like' space with each agent occopying a single grid cell
* **MultiGrid;** like grid, but with more than one agent per grid cell
* **HexGrid;** like grid, but on a hexagonal grid (*e.g.*, the board game Catan) thus changing who your neighbours are
* **ConinuousSpace;** a 2d continous space were agents can occupy any coordinate
* **NetworkGrid;** a network structure were one or more agents occupy a given node.
A key concern when using a none-networked space, is to think carefull about what happens at the edges of the space. In a basic implementation, agents in for example the top left corner has only 2 neighbors, while an agent in the middle has four neighbors. This can give rise to artifacts in the results. Basically, the dynamics at the edges are different from the behavior further away from the edges. It is therefore quite common to use a torus, or donut, shape for the space. In this way, there is no longer any edge and artifacts are thus removed.
# The emergence of cooperation in space
The documentation of MESA on the different spaces is quite limited. Therefore, this assignment is largely a tutorial continuing on the evolution of cooperation.
We make the following changes to the model
* Each agent gets a position, which is an x,y coordinate indicating the grid cell the agent occupies.
* The model has a grid, with an agent of random class. We initialize the model with equal probabilities for each type of class.
* All agents play against their neighbors. On a grid, neighborhood can be defined in various ways. For example, a Von Neumann neighborhood contains the four cells that share a border with the central cell. A Moore neighborhood with distance one contains 8 cells by also considering the diagonal. Below, we use a neighborhood distance of 1, and we do include diagonal neighbors. So we set Moore to True. Feel free to experiment with this model by setting it to False,
* The evolutionary dynamic, after all agents having played, is that each agent compares its scores to its neighbors. It will adopt whichever strategy within its neighborhood performed best.
* Next to using a SingleGrid from MESA, we also use a DataCollector to handle collecting statistics.
Below, I discuss in more detail the code containing the most important modifications.
```
from collections import deque, Counter, defaultdict
from enum import Enum
from itertools import combinations
from math import floor
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from mesa import Model, Agent
from mesa.space import SingleGrid
from mesa.datacollection import DataCollector
class Move(Enum):
COOPERATE = 1
DEFECT = 2
class AxelrodAgent(Agent):
"""An Abstract class from which all strategies have to be derived
Attributes
----------
points : int
pos : tuple
"""
def __init__(self, unique_id, pos, model):
super().__init__(unique_id, model)
self.points = 0
self.pos = pos
def step(self):
'''
This function defines the move and any logic for deciding
on the move goes here.
Returns
-------
Move.COOPERATE or Move.DEFECT
'''
raise NotImplemetedError
def receive_payoff(self, payoff, my_move, opponent_move):
'''receive payoff and the two moves resulting in this payoff
Parameters
----------
payoff : int
my_move : {Move.COOPERATE, Move.DEFECT}
opponements_move : {Move.COOPERATE, Move.DEFECT}
'''
self.points += payoff
def reset(self):
'''
This function is called after playing N iterations against
another player.
'''
raise NotImplementedError
class TitForTat(AxelrodAgent):
"""This class defines the following strategy: play nice, unless,
in the previous move, the other player betrayed you."""
def __init__(self, unique_id, pos, model):
super().__init__(unique_id, pos, model)
self.opponent_last_move = Move.COOPERATE
def step(self):
return self.opponent_last_move
def receive_payoff(self, payoff, my_move, opponent_move):
super().receive_payoff(payoff, my_move, opponent_move)
self.opponent_last_move = opponent_move
def reset(self):
self.opponent_last_move = Move.COOPERATE
class ContriteTitForTat(AxelrodAgent):
"""This class defines the following strategy: play nice, unless,
in the previous two moves, the other player betrayed you."""
def __init__(self, unique_id, pos, model):
super().__init__(unique_id, pos, model)
self.opponent_last_two_moves = deque([Move.COOPERATE, Move.COOPERATE], maxlen=2)
def step(self):
if (self.opponent_last_two_moves[0] == Move.DEFECT) and\
(self.opponent_last_two_moves[1] == Move.DEFECT):
return Move.DEFECT
else:
return Move.COOPERATE
def receive_payoff(self, payoff, my_move, opponent_move):
super().receive_payoff(payoff, my_move, opponent_move)
self.opponent_last_two_moves.append(opponent_move)
def reset(self):
self.opponent_last_two_moves = deque([Move.COOPERATE, Move.COOPERATE], maxlen=2)
class NoisySpatialEvolutionaryAxelrodModel(Model):
def __init__(self, N, noise_level=0.01, seed=None,
height=20, width=20,):
super().__init__(seed=seed)
self.noise_level = noise_level
self.num_iterations = N
self.agents = set()
self.payoff_matrix = {}
self.payoff_matrix[(Move.COOPERATE, Move.COOPERATE)] = (2, 2)
self.payoff_matrix[(Move.COOPERATE, Move.DEFECT)] = (0, 3)
self.payoff_matrix[(Move.DEFECT, Move.COOPERATE)] = (3, 0)
self.payoff_matrix[(Move.DEFECT, Move.DEFECT)] = (1, 1)
self.grid = SingleGrid(width, height, torus=True)
strategies = AxelrodAgent.__subclasses__()
num_strategies = len(strategies)
self.agent_id = 0
for cell in self.grid.coord_iter():
_, x, y = cell
pos = (x, y)
self.agent_id += 1
strategy_index = int(floor(self.random.random()*num_strategies))
agent = strategies[strategy_index](self.agent_id, pos, self)
self.grid.position_agent(agent, (x, y))
self.agents.add(agent)
self.datacollector = DataCollector(model_reporters={klass.__name__:klass.__name__
for klass in strategies})
def count_agent_types(self):
counter = Counter()
for agent in self.agents:
counter[agent.__class__.__name__] += 1
for k,v in counter.items():
setattr(self, k, v)
def step(self):
'''Advance the model by one step.'''
self.count_agent_types()
self.datacollector.collect(self)
for (agent_a, x, y) in self.grid.coord_iter():
for agent_b in self.grid.neighbor_iter((x,y), moore=True):
for _ in range(self.num_iterations):
move_a = agent_a.step()
move_b = agent_b.step()
#insert noise in movement
if self.random.random() < self.noise_level:
if move_a == Move.COOPERATE:
move_a = Move.DEFECT
else:
move_a = Move.COOPERATE
if self.random.random() < self.noise_level:
if move_b == Move.COOPERATE:
move_b = Move.DEFECT
else:
move_b = Move.COOPERATE
payoff_a, payoff_b = self.payoff_matrix[(move_a, move_b)]
agent_a.receive_payoff(payoff_a, move_a, move_b)
agent_b.receive_payoff(payoff_b, move_b, move_a)
agent_a.reset()
agent_b.reset()
# evolution
# tricky, we need to determine for each grid cell
# is a change needed, if so, log position, agent, and type to change to
agents_to_change = []
for agent_a in self.agents:
neighborhood = self.grid.iter_neighbors(agent_a.pos, moore=True,
include_center=True)
neighborhood = ([n for n in neighborhood])
neighborhood.sort(key=lambda x:x.points, reverse=True)
best_strategy = neighborhood[0].__class__
# if best type of strategy in neighborhood is
# different from strategy type of agent, we need
# to change our strategy
if not isinstance(agent_a, best_strategy):
agents_to_change.append((agent_a, best_strategy))
for entry in agents_to_change:
agent, klass = entry
self.agents.remove(agent)
self.grid.remove_agent(agent)
pos = agent.pos
self.agent_id += 1
new_agent = klass(self.agent_id, pos, self)
self.grid.position_agent(new_agent, pos)
self.agents.add(new_agent)
```
In the `__init__`, we now instantiate a SingleGrid, with a specified width and height. We set the kwarg torus to True indicating we are using a donut shape grid to avoid edge effects. Next, we fill this grid with random agents of the different types. This can be implemented in various ways. What I do here is using a list with the different classes (*i.e.*, types of strategies). By drawing a random number from a unit interval, multiplying it with the lenght of the list of classes and flooring the resulting number to an integer, I now have a random index into this list with the different classes. Next, I can get the class from the list and instantiate the agent object.
Some minor points with instantiating the agents. First, we give the agent a position, called pos, this is a default attribute assumed by MESA. We also still need a unique ID for the agent, we do this with a simple counter (`self.agent_id`). `self.grid.coord_iter` is a method on the grid. It returns an iterator over the cells in the grid. This iterator returns the agent occupying the cell and the x and y coordinate. Since the first item is `null` because we are filling the grid, we can ignore this. We do this by using the underscore variable name (`_`). This is a python convention.
Once we have instantiated the agent, we place the agent in the grid and add it to our collection of agents. If you look in more detail at the model class, you will see that I use a set for agents, rather than a list. The reason for this is that we are going to remove agents in the evolutionary phase. Removing agents from a list is memory and compute intensive, while it is computationally easy and cheap when we have a set.
```python
self.grid = SingleGrid(width, height, torus=True)
strategies = AxelrodAgent.__subclasses__()
num_strategies = len(strategies)
self.agent_id = 0
for cell in self.grid.coord_iter():
_, x, y = cell
pos = (x, y)
self.agent_id += 1
strategy_index = int(floor(self.random.random()*num_strategies))
agent = strategies[strategy_index](self.agent_id, pos, self)
self.grid.position_agent(agent, (x, y))
self.agents.add(agent)
```
We also use a DataCollector. This is a default class provided by MESA that can be used for keeping track of relevant statistics. It can store both model level variables as well as agent level variables. Here we are only using model level variables (i.e. attributes of the model). Specifically, we are going to have an attribute on the model for each type of agent strategy (i.e. classes). This attribute is the current count of agents in the grid of the specific type. To implement this, we need to do several things.
1. initialize a data collector instance
2. at every step update the current count of agents of each strategy
3. collect the current counts with the data collector.
For step 1, we set a DataCollector as an attribute. This datacollector needs to know the names of the attributes on the model it needs to collect. So we pass a dict as kwarg to model_reporters. This dict has as key the name by which the variable will be known in the DataCollector. As value, I pass the name of the attribute on the model, but it can also be a function or method which returns a number. Note th at the ``klass`` misspelling is deliberate. The word ``class`` is protected in Python, so you cannot use it as a variable name. It is common practice to use ``klass`` instead in the rare cases were you are having variable refering to a specific class.
```python
self.datacollector = DataCollector(model_reporters={klass.__name__:klass.__name__
for klass in strategies})
```
For step 2, we need to count at every step the number of agents per strategy type. To help keep track of this, we define a new method, `count_agent_types`. The main magic is the use of `setattr` which is a standard python function for setting attributes to a particular value on a given object. This reason for writing our code this way is that we automatically adapt our attributes to the classes of agents we have, rather than hardcoding the agent classes as attributes on our model. If we now add new classes of agents, we don't need to change the model code itself. There is also a ``getattr`` function, which is used by for example the DataCollector to get the values for the specified attribute names.
```python
def count_agent_types(self):
counter = Counter()
for agent in self.agents:
counter[agent.__class__.__name__] += 1
for k,v in counter.items():
setattr(self, k, v)
```
For step 3, we modify the first part of the ``step`` method. We first count the types of agents and next collect this data with the datacollector.
```python
self.count_agent_types()
self.datacollector.collect(self)
```
The remainder of the ``step`` method has also been changed quite substantially. First, We have to change against whom each agent is playing. We do this by iterating over all agents in the model. Next, we use the grid to give us the neighbors of a given agent. By setting the kwarg ``moore`` to ``True``, we indicate that we include also our diagonal neighbors. Next, we play as we did before in the noisy version of the Axelrod model.
```python
for agent_a in self.agents:
for agent_b in self.grid.neighbor_iter(agent_a.pos, moore=True):
for _ in range(self.num_iterations):
```
Second, we have to add the evolutionary dynamic. This is a bit tricky. First, we loop again over all agents in the model. We check its neighbors and see which strategy performed best. If this is of a different type (``not isinstance(agent_a, best_strategy)``, we add it to a list of agents that needs to be changed and the type of agent to which it needs to be changed. Once we know all agents that need to be changed, we can make this change.
Making the change is quite straighforward. We remove the agent from the set of agents (`self.agents`) and from the grid. Next we get the position of the agent, we increment our unique ID counter, and create a new agent. This new agent is than added to the grid and to the set of agents.
```python
# evolution
agents_to_change = []
for agent_a in self.agents:
neighborhood = self.grid.iter_neighbors(agent_a.pos, moore=True,
include_center=True)
neighborhood = ([n for n in neighborhood])
neighborhood.sort(key=lambda x:x.points, reverse=True)
best_strategy = neighborhood[0].__class__
# if best type of strategy in neighborhood is
# different from strategy type of agent, we need
# to change our strategy
if not isinstance(agent_a, best_strategy):
agents_to_change.append((agent_a, best_strategy))
for entry in agents_to_change:
agent, klass = entry
self.agents.remove(agent)
self.grid.remove_agent(agent)
pos = agent.pos
self.agent_id += 1
new_agent = klass(self.agent_id, pos, self)
self.grid.position_agent(new_agent, pos)
self.agents.add(new_agent)
```
## Assignment 1
Can you explain why we need to first loop over all agents before we are changing a given agent to a different strategy?
## Assignment 2
Add all agents classes (i.e., strategie) from the previous assignment to this model. Note that you might have to update the ``__init__`` method to reflect the new pos keyword argument and attribute.
## Assignment 3
Run the model for 50 steps, and with 200 rounds of the iterated game. Use the defaults for all other keyword arguments.
Plot the results.
*hint: the DataCollector can return the statistics it has collected as a dataframe, which in turn you can plot directly.*
This new model is quite a bit noisier than previously. We have a random initialization of the grid and depending on the initial neighborhood, different evolutionary dynamics can happen. On top, we have the noise in game play, and the random agent.
## Assignment 4
Let's explore the model for 10 replications. Run the model 10 times, with 200 rounds of the iterated prisoners dilemma. Run each model for fifty steps. Plot the results for each run.
1. Can you say anything generalizable about the behavioral dynamics of the model?
2. What do you find striking in the results and why?
3. If you compare the results for this spatially explicit version of the Emergence of Cooperation with the none spatially explicit version, what are the most important differences in dynamics. Can you explain why adding local interactions results in these changes?
|
github_jupyter
|
## Getting Data
```
#import os
#import requests
#DATASET = (
# "https://archive.ics.uci.edu/ml/machine-learning-databases/abalone/abalone.data",
# "https://archive.ics.uci.edu/ml/machine-learning-databases/abalone/abalone.names"
#)
#def download_data(path='data', urls=DATASET):
# if not os.path.exists(path):
# os.mkdir(path)
#
# for url in urls:
# response = requests.get(url)
# name = os.path.basename(url)
# with open(os.path.join(path, name), 'wb') as f:
# f.write(response.content)
#download_data()
#DOWNLOAD AND LOAD IN DATA FROM URL!!!!!!!!!!!!!!!!!!!
#import requests
#import io
#data = io.BytesIO(requests.get('URL HERE'))
#whitedata = pd.read_csv(data.content)
#whitedata.head()
```
## Load Data
```
import pandas as pd
import yellowbrick
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
import io
import sklearn
columns = [
"fixed acidity",
"volatile acidity",
"citric acid",
"residual sugar",
"chlorides",
"free sulfur dioxide",
"total sulfur dioxide",
"density",
"pH",
"sulphates",
"alcohol",
"quality"
]
reddata = pd.read_csv('data/winequality-red.csv', sep=";")
whitedata = pd.read_csv('data/winequality-white.csv', sep=";")
```
## Check it out
```
whitedata.head(10)
whitedata.describe()
whitedata.info()
whitedata.pH.describe()
whitedata['poor'] = np.where(whitedata['quality'] < 5, 1, 0)
whitedata['poor'].value_counts()
whitedata['expected'] = np.where(whitedata['quality'] > 4, 1, 0)
whitedata['expected'].value_counts()
whitedata['expected'].describe()
whitedata.head()
#set up the figure size
%matplotlib inline
plt.rcParams['figure.figsize'] = (30, 30)
#make the subplot
fig, axes = plt.subplots(nrows = 6, ncols = 2)
#specify the features of intersest
num_features = ['pH', 'alcohol', 'citric acid', 'chlorides', 'residual sugar', 'free sulfur dioxide', 'total sulfur dioxide', 'density', 'sulphates']
xaxes = num_features
yaxes = ['Counts', 'Counts', 'Counts', 'Counts', 'Counts', 'Counts', 'Counts', 'Counts', 'Counts']
#draw the histogram
axes = axes.ravel()
for idx, ax in enumerate(axes):
ax.hist(whitedata[num_features[idx]].dropna(), bins = 30)
ax.set_xlabel(xaxes[idx], fontsize = 20)
ax.set_ylabel(yaxes[idx], fontsize = 20)
ax.tick_params(axis = 'both', labelsize = 20)
features = ['pH', 'alcohol', 'citric acid', 'residual sugar', 'chlorides', 'free sulfur dioxide', 'total sulfur dioxide', 'density', 'sulphates']
classes = ['unexpected', 'expected']
X = whitedata[features].as_matrix()
y = whitedata['quality'].as_matrix()
from sklearn.naive_bayes import GaussianNB
viz = GaussianNB()
viz.fit(X, y)
viz.score(X, y)
from sklearn.naive_bayes import MultinomialNB
viz = MultinomialNB()
viz.fit(X, y)
viz.score(X, y)
from sklearn.naive_bayes import BernoulliNB
viz = BernoulliNB()
viz.fit(X, y)
viz.score(X, y)
```
## Features and Targets
```
y = whitedata["quality"]
y
X = whitedata.iloc[:,1:-1]
X
from sklearn.ensemble import RandomForestClassifier as rfc
estimator = rfc(n_estimators=7)
estimator.fit(X,y)
y_hat = estimator.predict(X)
print(y_hat)
%matplotlib notebook
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import cross_val_score
data = pd.read_csv(".../data/occupency.csv")
data.head()
X = data(['temperature', 'relative humidity', 'light', 'CO2', 'humidity'])
y = data('occupency')
def n_estimators_tuning(X, y, min_estimator=1, max_estimator=50, ax=None, save=None):
if ax is None:
_, ax = plt.subplots()
mean = []
stds = []
n_estimators = np.arrange(min_estimators, mx_estimators+1)
for n in n_estimators:
model = RandomForestClassifier(n_estimators=n)
scores = cross_val_score(model, X, y, cv=cv)
means.append(scores.mean())
stds.append(scores.std())
means = np.array(means)
stds = np.array(stds)
ax.plot(n_estimatrors, scores, label='CV+{} scores'.forest(cv))
ax.fill_between(n_estimators, means-stds, means+stds, alpha=0.3)
max_score = means.max()
max_score_idx = np.where(means==max_score)[0]
ax.hline#???????????????
ax.set_xlim(min_estimators, max_estimators)
ax.set_xlabel("n_estimators")
ax.set_ylabel("F1 Score")
ax.set_title("Random Forest Hyperparameter Tuning")
ax.legend(loc='best')
if save:
plt.savefig(save)
return ax
#print(scores)
n_estimators_tuning(X, y)
whitedata[winecolor] = 0
reddata[winecolor] = 1
df3 = [whitedata, reddata]
df = pd.concat(df3)
df.reset_index(drop = True, inplace = True)
df.isnull().sum()
whitedata.head()
reddata.head()
df = df.drop(columns=['poor', 'expected'])
df.isnull().sum()
df.head()
df.describe()
df['recommended'] = np.where(df['quality'] < 6, 0, 1)
df.head(50)
df["quality"].value_counts().sort_values(ascending = False)
df["recommended"].value_counts().sort_values(ascending = False)
df['recommended'] = np.where(df['quality'] < 6, 0, 1)
df["recommended"].value_counts().sort_values(ascending = False)
from pandas.plotting import radviz
plt.figure(figsize=(8,8))
radviz(df, 'recommended', color=['blue', 'red'])
plt.show()
features = ['pH', 'alcohol', 'citric acid', 'residual sugar', 'chlorides', 'free sulfur dioxide', 'total sulfur dioxide', 'density', 'sulphates']
#classes = ['unexpected', 'expected']
X = df[features].as_matrix()
y = df['recommended'].as_matrix()
viz = GaussianNB()
viz.fit(X, y)
viz.score(X, y)
viz = MultinomialNB()
viz.fit(X, y)
viz.score(X, y)
viz = BernoulliNB()
viz.fit(X, y)
viz.score(X, y)
from sklearn.ensemble import RandomForestClassifier
viz = RandomForestClassifier()
viz.fit(X, y)
viz.score(X, y)
from sklearn.metrics import (auc, roc_curve, recall_score, accuracy_score, confusion_matrix, classification_report, f1_score, precision_score)
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=11)
predicted = viz.predict(X_test)
cm = confusion_matrix(y_test, predicted)
fig = plt.figure(figsize=(7, 5))
ax = plt.subplot()
cm1 = (cm.astype(np.float64) / cm.sum(axis=1, keepdims=1))
cmap = sns.cubehelix_palette(light=1, as_cmap=True)
sns.heatmap(cm1, annot=True, ax = ax, cmap=cmap); #annot=True to annotate cells
# labels, title and ticks
ax.set_xlabel('Features');
ax.set_ylabel('Recommended');
ax.set_title('Normalized confusion matrix');
ax.xaxis.set_ticklabels(['Good', 'Bad']);
ax.yaxis.set_ticklabels(['Good', 'Bad']);
print(cm)
# Recursive Feature Elimination (RFE)
from sklearn.feature_selection import (chi2, RFE)
model = RandomForestClassifier()
rfe = RFE(model, 38)
fit = rfe.fit(X, y)
print("Num Features: ", fit.n_features_)
print("Selected Features: ", fit.support_)
print("Feature Ranking: ", fit.ranking_)
from sklearn.model_selection import StratifiedKFold
from sklearn.datasets import make_classification
from yellowbrick.features import RFECV
sns.set(font_scale=3)
cv = StratifiedKFold(5)
oz = RFECV(RandomForestClassifier(), cv=cv, scoring='f1')
oz.fit(X, y)
oz.poof()
# Ridge
# Create a new figure
#mpl.rcParams['axes.prop_cycle'] = cycler('color', ['red'])
from yellowbrick.features.importances import FeatureImportances
from sklearn.linear_model import (LogisticRegression, LogisticRegressionCV, RidgeClassifier, Ridge, Lasso, ElasticNet)
fig = plt.gcf()
fig.set_size_inches(10,10)
ax = plt.subplot(311)
labels = features
viz = FeatureImportances(Ridge(alpha=0.5), ax=ax, labels=labels, relative=False)
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.grid(False) # Fit and display
viz.fit(X, y)
viz.poof()
estimator = RandomForestClassifier(class_weight='balanced')
y_pred_proba = RandomForestClassifier(X_test)
#y_pred_proba[:5]
def plot_roc_curve(y_test, y_pred_proba):
fpr, tpr, thresholds = roc_curve(y_test, y_pred_proba[:, 1])
roc_auc = auc(fpr, tpr)
plt.plot(fpr, tpr, label='ROC curve (area = %0.3f)' % roc_auc, color='darkblue')
plt.plot([0, 1], [0, 1], 'k--') # random predictions curve
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.0])
plt.xlabel('False Positive Rate or (1 - Specifity)')
plt.ylabel('True Positive Rate or (Sensitivity)')
plt.title('Receiver Operating Characteristic')
plt.legend(loc="lower right")
plt.grid(False)
plot_roc_curve(y_test, y_pred_proba)
```
|
github_jupyter
|
# Draw an isochrone map with OSMnx
How far can you travel on foot in 15 minutes?
- [Overview of OSMnx](http://geoffboeing.com/2016/11/osmnx-python-street-networks/)
- [GitHub repo](https://github.com/gboeing/osmnx)
- [Examples, demos, tutorials](https://github.com/gboeing/osmnx-examples)
- [Documentation](https://osmnx.readthedocs.io/en/stable/)
- [Journal article/citation](http://geoffboeing.com/publications/osmnx-complex-street-networks/)
```
import geopandas as gpd
import matplotlib.pyplot as plt
import networkx as nx
import osmnx as ox
from descartes import PolygonPatch
from shapely.geometry import Point, LineString, Polygon
ox.config(log_console=True, use_cache=True)
ox.__version__
# configure the place, network type, trip times, and travel speed
place = 'Berkeley, CA, USA'
network_type = 'walk'
trip_times = [5, 10, 15, 20, 25] #in minutes
travel_speed = 4.5 #walking speed in km/hour
```
## Download and prep the street network
```
# download the street network
G = ox.graph_from_place(place, network_type=network_type)
# find the centermost node and then project the graph to UTM
gdf_nodes = ox.graph_to_gdfs(G, edges=False)
x, y = gdf_nodes['geometry'].unary_union.centroid.xy
center_node = ox.get_nearest_node(G, (y[0], x[0]))
G = ox.project_graph(G)
# add an edge attribute for time in minutes required to traverse each edge
meters_per_minute = travel_speed * 1000 / 60 #km per hour to m per minute
for u, v, k, data in G.edges(data=True, keys=True):
data['time'] = data['length'] / meters_per_minute
```
## Plots nodes you can reach on foot within each time
How far can you walk in 5, 10, 15, 20, and 25 minutes from the origin node? We'll use NetworkX to induce a subgraph of G within each distance, based on trip time and travel speed.
```
# get one color for each isochrone
iso_colors = ox.get_colors(n=len(trip_times), cmap='Reds', start=0.3, return_hex=True)
# color the nodes according to isochrone then plot the street network
node_colors = {}
for trip_time, color in zip(sorted(trip_times, reverse=True), iso_colors):
subgraph = nx.ego_graph(G, center_node, radius=trip_time, distance='time')
for node in subgraph.nodes():
node_colors[node] = color
nc = [node_colors[node] if node in node_colors else 'none' for node in G.nodes()]
ns = [20 if node in node_colors else 0 for node in G.nodes()]
fig, ax = ox.plot_graph(G, fig_height=8, node_color=nc, node_size=ns, node_alpha=0.8, node_zorder=2)
```
## Plot the time-distances as isochrones
How far can you walk in 5, 10, 15, 20, and 25 minutes from the origin node? We'll use a convex hull, which isn't perfectly accurate. A concave hull would be better, but shapely doesn't offer that.
```
# make the isochrone polygons
isochrone_polys = []
for trip_time in sorted(trip_times, reverse=True):
subgraph = nx.ego_graph(G, center_node, radius=trip_time, distance='time')
node_points = [Point((data['x'], data['y'])) for node, data in subgraph.nodes(data=True)]
bounding_poly = gpd.GeoSeries(node_points).unary_union.convex_hull
isochrone_polys.append(bounding_poly)
# plot the network then add isochrones as colored descartes polygon patches
fig, ax = ox.plot_graph(G, fig_height=8, show=False, close=False, edge_color='k', edge_alpha=0.2, node_color='none')
for polygon, fc in zip(isochrone_polys, iso_colors):
patch = PolygonPatch(polygon, fc=fc, ec='none', alpha=0.6, zorder=-1)
ax.add_patch(patch)
plt.show()
```
## Or, plot isochrones as buffers to get more faithful isochrones than convex hulls can offer
in the style of http://kuanbutts.com/2017/12/16/osmnx-isochrones/
```
def make_iso_polys(G, edge_buff=25, node_buff=50, infill=False):
isochrone_polys = []
for trip_time in sorted(trip_times, reverse=True):
subgraph = nx.ego_graph(G, center_node, radius=trip_time, distance='time')
node_points = [Point((data['x'], data['y'])) for node, data in subgraph.nodes(data=True)]
nodes_gdf = gpd.GeoDataFrame({'id': subgraph.nodes()}, geometry=node_points)
nodes_gdf = nodes_gdf.set_index('id')
edge_lines = []
for n_fr, n_to in subgraph.edges():
f = nodes_gdf.loc[n_fr].geometry
t = nodes_gdf.loc[n_to].geometry
edge_lines.append(LineString([f,t]))
n = nodes_gdf.buffer(node_buff).geometry
e = gpd.GeoSeries(edge_lines).buffer(edge_buff).geometry
all_gs = list(n) + list(e)
new_iso = gpd.GeoSeries(all_gs).unary_union
# try to fill in surrounded areas so shapes will appear solid and blocks without white space inside them
if infill:
new_iso = Polygon(new_iso.exterior)
isochrone_polys.append(new_iso)
return isochrone_polys
isochrone_polys = make_iso_polys(G, edge_buff=25, node_buff=0, infill=True)
fig, ax = ox.plot_graph(G, fig_height=8, show=False, close=False, edge_color='k', edge_alpha=0.2, node_color='none')
for polygon, fc in zip(isochrone_polys, iso_colors):
patch = PolygonPatch(polygon, fc=fc, ec='none', alpha=0.6, zorder=-1)
ax.add_patch(patch)
plt.show()
```
|
github_jupyter
|
# Raven annotations
Raven Sound Analysis Software enables users to inspect spectrograms, draw time and frequency boxes around sounds of interest, and label these boxes with species identities. OpenSoundscape contains functionality to prepare and use these annotations for machine learning.
## Download annotated data
We published an example Raven-annotated dataset here: https://doi.org/10.1002/ecy.3329
```
from opensoundscape.commands import run_command
from pathlib import Path
```
Download the zipped data here:
```
link = "https://esajournals.onlinelibrary.wiley.com/action/downloadSupplement?doi=10.1002%2Fecy.3329&file=ecy3329-sup-0001-DataS1.zip"
name = 'powdermill_data.zip'
out = run_command(f"wget -O powdermill_data.zip {link}")
```
Unzip the files to a new directory, `powdermill_data/`
```
out = run_command("unzip powdermill_data.zip -d powdermill_data")
```
Keep track of the files we have now so we can delete them later.
```
files_to_delete = [Path("powdermill_data"), Path("powdermill_data.zip")]
```
## Preprocess Raven data
The `opensoundscape.raven` module contains preprocessing functions for Raven data, including:
* `annotation_check` - for all the selections files, make sure they all contain labels
* `lowercase_annotations` - lowercase all of the annotations
* `generate_class_corrections` - create a CSV to see whether there are any weird names
* Modify the CSV as needed. If you need to look up files you can use `query_annotations`
* Can be used in `SplitterDataset`
* `apply_class_corrections` - replace incorrect labels with correct labels
* `query_annotations` - look for files that contain a particular species or a typo
```
import pandas as pd
import opensoundscape.raven as raven
import opensoundscape.audio as audio
raven_files_raw = Path("./powdermill_data/Annotation_Files/")
```
### Check Raven files have labels
Check that all selections files contain labels under one column name. In this dataset the labels column is named `"species"`.
```
raven.annotation_check(directory=raven_files_raw, col='species')
```
### Create lowercase files
Convert all the text in the files to lowercase to standardize them. Save these to a new directory. They will be saved with the same filename but with ".lower" appended.
```
raven_directory = Path('./powdermill_data/Annotation_Files_Standardized')
if not raven_directory.exists(): raven_directory.mkdir()
raven.lowercase_annotations(directory=raven_files_raw, out_dir=raven_directory)
```
Check that the outputs are saved as expected.
```
list(raven_directory.glob("*.lower"))[:5]
```
### Generate class corrections
This function generates a table that can be modified by hand to correct labels with typos in them. It identifies the unique labels in the provided column (here `"species"`) in all of the lowercase files in the directory `raven_directory`.
For instance, the generated table could be something like the following:
```
raw,corrected
sparrow,sparrow
sparow,sparow
goose,goose
```
```
print(raven.generate_class_corrections(directory=raven_directory, col='species'))
```
The released dataset has no need for class corrections, but if it did, we could save the return text to a CSV and use the CSV to apply corrections to future dataframes.
### Query annotations
This function can be used to print all annotations of a particular class, e.g. "amro" (American Robin)
```
output = raven.query_annotations(directory=raven_directory, cls='amro', col='species', print_out=True)
```
## Split Raven annotations and audio files
The Raven module's `raven_audio_split_and_save` function enables splitting of both audio data and associated annotations. It requires that the annotation and audio filenames are unique, and that corresponding annotation and audiofilenames are named the same filenames as each other.
```
audio_directory = Path('./powdermill_data/Recordings/')
destination = Path('./powdermill_data/Split_Recordings')
out = raven.raven_audio_split_and_save(
# Where to look for Raven files
raven_directory = raven_directory,
# Where to look for audio files
audio_directory = audio_directory,
# The destination to save clips and the labels CSV to
destination = destination,
# The column name of the labels
col = 'species',
# Desired audio sample rate
sample_rate = 22050,
# Desired duration of clips
clip_duration = 5,
# Verbose (uncomment the next line to see progress--this cell takes a while to run)
#verbose=True,
)
```
The results of the splitting are saved in the destination folder under the name `labels.csv`.
```
labels = pd.read_csv(destination.joinpath("labels.csv"), index_col='filename')
labels.head()
```
The `raven_audio_split_and_save` function contains several options. Notable options are:
* `clip_duration`: the length of the clips
* `clip_overlap`: the overlap, in seconds, between clips
* `final_clip`: what to do with the final clip if it is not exactly `clip_duration` in length (see API docs for more details)
* `labeled_clips_only`: whether to only save labeled clips
* `min_label_length`: minimum length, in seconds, of an annotation for a clip to be considered labeled. For instance, if an annotation only overlaps 0.1s with a 5s clip, you might want to exclude it with `min_label_length=0.2`.
* `species`: a subset of species to search for labels of (by default, finds all species labels in dataset)
* `dry_run`: if `True`, produces print statements and returns dataframe of labels, but does not save files.
* `verbose`: if `True`, prints more information, e.g. clip-by-clip progress.
For instance, let's extract labels for one species, American Redstart (AMRE) only saving clips that contain at least 0.5s of label for that species. The "verbose" flag causes the function to print progress splitting each clip.
```
btnw_split_dir = Path('./powdermill_data/btnw_recordings')
out = raven.raven_audio_split_and_save(
raven_directory = raven_directory,
audio_directory = audio_directory,
destination = btnw_split_dir,
col = 'species',
sample_rate = 22050,
clip_duration = 5,
clip_overlap = 0,
verbose=True,
species='amre',
labeled_clips_only=True,
min_label_len=1
)
```
The labels CSV only has a column for the species of interest:
```
btnw_labels = pd.read_csv(btnw_split_dir.joinpath("labels.csv"), index_col='filename')
btnw_labels.head()
```
The split files and associated labels csv can now be used to train machine learning models (see additional tutorials).
The command below cleans up after the tutorial is done -- only run it if you want to delete all of the files.
```
from shutil import rmtree
for file in files_to_delete:
if file.is_dir():
rmtree(file)
else:
file.unlink()
```
|
github_jupyter
|
# CER043 - Install signed Master certificates
This notebook installs into the Big Data Cluster the certificates signed
using:
- [CER033 - Sign Master certificates with generated
CA](../cert-management/cer033-sign-master-generated-certs.ipynb)
## Steps
### Parameters
```
app_name = "master"
scaledset_name = "master"
container_name = "mssql-server"
common_name = "master-svc"
user = "mssql"
group = "mssql"
mode = "550"
prefix_keyfile_name = "sql"
certificate_names = {"master-0" : "master-0-certificate.pem", "master-1" : "master-1-certificate.pem", "master-2" : "master-2-certificate.pem"}
key_names = {"master-0" : "master-0-privatekey.pem", "master-1" : "master-1-privatekey.pem", "master-2" : "master-2-privatekey.pem"}
test_cert_store_root = "/var/opt/secrets/test-certificates"
timeout = 600 # amount of time to wait before cluster is healthy: default to 10 minutes
check_interval = 10 # amount of time between health checks - default 10 seconds
min_pod_count = 10 # minimum number of healthy pods required to assert health
```
### Common functions
Define helper functions used in this notebook.
```
# Define `run` function for transient fault handling, suggestions on error, and scrolling updates on Windows
import sys
import os
import re
import platform
import shlex
import shutil
import datetime
from subprocess import Popen, PIPE
from IPython.display import Markdown
retry_hints = {} # Output in stderr known to be transient, therefore automatically retry
error_hints = {} # Output in stderr where a known SOP/TSG exists which will be HINTed for further help
install_hint = {} # The SOP to help install the executable if it cannot be found
def run(cmd, return_output=False, no_output=False, retry_count=0, base64_decode=False, return_as_json=False):
"""Run shell command, stream stdout, print stderr and optionally return output
NOTES:
1. Commands that need this kind of ' quoting on Windows e.g.:
kubectl get nodes -o jsonpath={.items[?(@.metadata.annotations.pv-candidate=='data-pool')].metadata.name}
Need to actually pass in as '"':
kubectl get nodes -o jsonpath={.items[?(@.metadata.annotations.pv-candidate=='"'data-pool'"')].metadata.name}
The ' quote approach, although correct when pasting into Windows cmd, will hang at the line:
`iter(p.stdout.readline, b'')`
The shlex.split call does the right thing for each platform, just use the '"' pattern for a '
"""
MAX_RETRIES = 5
output = ""
retry = False
# When running `azdata sql query` on Windows, replace any \n in """ strings, with " ", otherwise we see:
#
# ('HY090', '[HY090] [Microsoft][ODBC Driver Manager] Invalid string or buffer length (0) (SQLExecDirectW)')
#
if platform.system() == "Windows" and cmd.startswith("azdata sql query"):
cmd = cmd.replace("\n", " ")
# shlex.split is required on bash and for Windows paths with spaces
#
cmd_actual = shlex.split(cmd)
# Store this (i.e. kubectl, python etc.) to support binary context aware error_hints and retries
#
user_provided_exe_name = cmd_actual[0].lower()
# When running python, use the python in the ADS sandbox ({sys.executable})
#
if cmd.startswith("python "):
cmd_actual[0] = cmd_actual[0].replace("python", sys.executable)
# On Mac, when ADS is not launched from terminal, LC_ALL may not be set, which causes pip installs to fail
# with:
#
# UnicodeDecodeError: 'ascii' codec can't decode byte 0xc5 in position 4969: ordinal not in range(128)
#
# Setting it to a default value of "en_US.UTF-8" enables pip install to complete
#
if platform.system() == "Darwin" and "LC_ALL" not in os.environ:
os.environ["LC_ALL"] = "en_US.UTF-8"
# When running `kubectl`, if AZDATA_OPENSHIFT is set, use `oc`
#
if cmd.startswith("kubectl ") and "AZDATA_OPENSHIFT" in os.environ:
cmd_actual[0] = cmd_actual[0].replace("kubectl", "oc")
# To aid supportability, determine which binary file will actually be executed on the machine
#
which_binary = None
# Special case for CURL on Windows. The version of CURL in Windows System32 does not work to
# get JWT tokens, it returns "(56) Failure when receiving data from the peer". If another instance
# of CURL exists on the machine use that one. (Unfortunately the curl.exe in System32 is almost
# always the first curl.exe in the path, and it can't be uninstalled from System32, so here we
# look for the 2nd installation of CURL in the path)
if platform.system() == "Windows" and cmd.startswith("curl "):
path = os.getenv('PATH')
for p in path.split(os.path.pathsep):
p = os.path.join(p, "curl.exe")
if os.path.exists(p) and os.access(p, os.X_OK):
if p.lower().find("system32") == -1:
cmd_actual[0] = p
which_binary = p
break
# Find the path based location (shutil.which) of the executable that will be run (and display it to aid supportability), this
# seems to be required for .msi installs of azdata.cmd/az.cmd. (otherwise Popen returns FileNotFound)
#
# NOTE: Bash needs cmd to be the list of the space separated values hence shlex.split.
#
if which_binary == None:
which_binary = shutil.which(cmd_actual[0])
# Display an install HINT, so the user can click on a SOP to install the missing binary
#
if which_binary == None:
print(f"The path used to search for '{cmd_actual[0]}' was:")
print(sys.path)
if user_provided_exe_name in install_hint and install_hint[user_provided_exe_name] is not None:
display(Markdown(f'HINT: Use [{install_hint[user_provided_exe_name][0]}]({install_hint[user_provided_exe_name][1]}) to resolve this issue.'))
raise FileNotFoundError(f"Executable '{cmd_actual[0]}' not found in path (where/which)")
else:
cmd_actual[0] = which_binary
start_time = datetime.datetime.now().replace(microsecond=0)
print(f"START: {cmd} @ {start_time} ({datetime.datetime.utcnow().replace(microsecond=0)} UTC)")
print(f" using: {which_binary} ({platform.system()} {platform.release()} on {platform.machine()})")
print(f" cwd: {os.getcwd()}")
# Command-line tools such as CURL and AZDATA HDFS commands output
# scrolling progress bars, which causes Jupyter to hang forever, to
# workaround this, use no_output=True
#
# Work around a infinite hang when a notebook generates a non-zero return code, break out, and do not wait
#
wait = True
try:
if no_output:
p = Popen(cmd_actual)
else:
p = Popen(cmd_actual, stdout=PIPE, stderr=PIPE, bufsize=1)
with p.stdout:
for line in iter(p.stdout.readline, b''):
line = line.decode()
if return_output:
output = output + line
else:
if cmd.startswith("azdata notebook run"): # Hyperlink the .ipynb file
regex = re.compile(' "(.*)"\: "(.*)"')
match = regex.match(line)
if match:
if match.group(1).find("HTML") != -1:
display(Markdown(f' - "{match.group(1)}": "{match.group(2)}"'))
else:
display(Markdown(f' - "{match.group(1)}": "[{match.group(2)}]({match.group(2)})"'))
wait = False
break # otherwise infinite hang, have not worked out why yet.
else:
print(line, end='')
if wait:
p.wait()
except FileNotFoundError as e:
if install_hint is not None:
display(Markdown(f'HINT: Use {install_hint} to resolve this issue.'))
raise FileNotFoundError(f"Executable '{cmd_actual[0]}' not found in path (where/which)") from e
exit_code_workaround = 0 # WORKAROUND: azdata hangs on exception from notebook on p.wait()
if not no_output:
for line in iter(p.stderr.readline, b''):
try:
line_decoded = line.decode()
except UnicodeDecodeError:
# NOTE: Sometimes we get characters back that cannot be decoded(), e.g.
#
# \xa0
#
# For example see this in the response from `az group create`:
#
# ERROR: Get Token request returned http error: 400 and server
# response: {"error":"invalid_grant",# "error_description":"AADSTS700082:
# The refresh token has expired due to inactivity.\xa0The token was
# issued on 2018-10-25T23:35:11.9832872Z
#
# which generates the exception:
#
# UnicodeDecodeError: 'utf-8' codec can't decode byte 0xa0 in position 179: invalid start byte
#
print("WARNING: Unable to decode stderr line, printing raw bytes:")
print(line)
line_decoded = ""
pass
else:
# azdata emits a single empty line to stderr when doing an hdfs cp, don't
# print this empty "ERR:" as it confuses.
#
if line_decoded == "":
continue
print(f"STDERR: {line_decoded}", end='')
if line_decoded.startswith("An exception has occurred") or line_decoded.startswith("ERROR: An error occurred while executing the following cell"):
exit_code_workaround = 1
# inject HINTs to next TSG/SOP based on output in stderr
#
if user_provided_exe_name in error_hints:
for error_hint in error_hints[user_provided_exe_name]:
if line_decoded.find(error_hint[0]) != -1:
display(Markdown(f'HINT: Use [{error_hint[1]}]({error_hint[2]}) to resolve this issue.'))
# Verify if a transient error, if so automatically retry (recursive)
#
if user_provided_exe_name in retry_hints:
for retry_hint in retry_hints[user_provided_exe_name]:
if line_decoded.find(retry_hint) != -1:
if retry_count < MAX_RETRIES:
print(f"RETRY: {retry_count} (due to: {retry_hint})")
retry_count = retry_count + 1
output = run(cmd, return_output=return_output, retry_count=retry_count)
if return_output:
if base64_decode:
import base64
return base64.b64decode(output).decode('utf-8')
else:
return output
elapsed = datetime.datetime.now().replace(microsecond=0) - start_time
# WORKAROUND: We avoid infinite hang above in the `azdata notebook run` failure case, by inferring success (from stdout output), so
# don't wait here, if success known above
#
if wait:
if p.returncode != 0:
raise SystemExit(f'Shell command:\n\n\t{cmd} ({elapsed}s elapsed)\n\nreturned non-zero exit code: {str(p.returncode)}.\n')
else:
if exit_code_workaround !=0 :
raise SystemExit(f'Shell command:\n\n\t{cmd} ({elapsed}s elapsed)\n\nreturned non-zero exit code: {str(exit_code_workaround)}.\n')
print(f'\nSUCCESS: {elapsed}s elapsed.\n')
if return_output:
if base64_decode:
import base64
return base64.b64decode(output).decode('utf-8')
else:
return output
# Hints for tool retry (on transient fault), known errors and install guide
#
retry_hints = {'azdata': ['Endpoint sql-server-master does not exist', 'Endpoint livy does not exist', 'Failed to get state for cluster', 'Endpoint webhdfs does not exist', 'Adaptive Server is unavailable or does not exist', 'Error: Address already in use', 'Login timeout expired (0) (SQLDriverConnect)', 'SSPI Provider: No Kerberos credentials available', ], 'kubectl': ['A connection attempt failed because the connected party did not properly respond after a period of time, or established connection failed because connected host has failed to respond', ], 'python': [ ], }
error_hints = {'azdata': [['Please run \'azdata login\' to first authenticate', 'SOP028 - azdata login', '../common/sop028-azdata-login.ipynb'], ['The token is expired', 'SOP028 - azdata login', '../common/sop028-azdata-login.ipynb'], ['Reason: Unauthorized', 'SOP028 - azdata login', '../common/sop028-azdata-login.ipynb'], ['Max retries exceeded with url: /api/v1/bdc/endpoints', 'SOP028 - azdata login', '../common/sop028-azdata-login.ipynb'], ['Look at the controller logs for more details', 'TSG027 - Observe cluster deployment', '../diagnose/tsg027-observe-bdc-create.ipynb'], ['provided port is already allocated', 'TSG062 - Get tail of all previous container logs for pods in BDC namespace', '../log-files/tsg062-tail-bdc-previous-container-logs.ipynb'], ['Create cluster failed since the existing namespace', 'SOP061 - Delete a big data cluster', '../install/sop061-delete-bdc.ipynb'], ['Failed to complete kube config setup', 'TSG067 - Failed to complete kube config setup', '../repair/tsg067-failed-to-complete-kube-config-setup.ipynb'], ['Data source name not found and no default driver specified', 'SOP069 - Install ODBC for SQL Server', '../install/sop069-install-odbc-driver-for-sql-server.ipynb'], ['Can\'t open lib \'ODBC Driver 17 for SQL Server', 'SOP069 - Install ODBC for SQL Server', '../install/sop069-install-odbc-driver-for-sql-server.ipynb'], ['Control plane upgrade failed. Failed to upgrade controller.', 'TSG108 - View the controller upgrade config map', '../diagnose/tsg108-controller-failed-to-upgrade.ipynb'], ['NameError: name \'azdata_login_secret_name\' is not defined', 'SOP013 - Create secret for azdata login (inside cluster)', '../common/sop013-create-secret-for-azdata-login.ipynb'], ['ERROR: No credentials were supplied, or the credentials were unavailable or inaccessible.', 'TSG124 - \'No credentials were supplied\' error from azdata login', '../repair/tsg124-no-credentials-were-supplied.ipynb'], ['Please accept the license terms to use this product through', 'TSG126 - azdata fails with \'accept the license terms to use this product\'', '../repair/tsg126-accept-license-terms.ipynb'], ], 'kubectl': [['no such host', 'TSG010 - Get configuration contexts', '../monitor-k8s/tsg010-get-kubernetes-contexts.ipynb'], ['No connection could be made because the target machine actively refused it', 'TSG056 - Kubectl fails with No connection could be made because the target machine actively refused it', '../repair/tsg056-kubectl-no-connection-could-be-made.ipynb'], ], 'python': [['Library not loaded: /usr/local/opt/unixodbc', 'SOP012 - Install unixodbc for Mac', '../install/sop012-brew-install-odbc-for-sql-server.ipynb'], ['WARNING: You are using pip version', 'SOP040 - Upgrade pip in ADS Python sandbox', '../install/sop040-upgrade-pip.ipynb'], ], }
install_hint = {'azdata': [ 'SOP063 - Install azdata CLI (using package manager)', '../install/sop063-packman-install-azdata.ipynb' ], 'kubectl': [ 'SOP036 - Install kubectl command line interface', '../install/sop036-install-kubectl.ipynb' ], }
print('Common functions defined successfully.')
```
### Get the Kubernetes namespace for the big data cluster
Get the namespace of the Big Data Cluster use the kubectl command line
interface .
**NOTE:**
If there is more than one Big Data Cluster in the target Kubernetes
cluster, then either:
- set \[0\] to the correct value for the big data cluster.
- set the environment variable AZDATA_NAMESPACE, before starting Azure
Data Studio.
```
# Place Kubernetes namespace name for BDC into 'namespace' variable
if "AZDATA_NAMESPACE" in os.environ:
namespace = os.environ["AZDATA_NAMESPACE"]
else:
try:
namespace = run(f'kubectl get namespace --selector=MSSQL_CLUSTER -o jsonpath={{.items[0].metadata.name}}', return_output=True)
except:
from IPython.display import Markdown
print(f"ERROR: Unable to find a Kubernetes namespace with label 'MSSQL_CLUSTER'. SQL Server Big Data Cluster Kubernetes namespaces contain the label 'MSSQL_CLUSTER'.")
display(Markdown(f'HINT: Use [TSG081 - Get namespaces (Kubernetes)](../monitor-k8s/tsg081-get-kubernetes-namespaces.ipynb) to resolve this issue.'))
display(Markdown(f'HINT: Use [TSG010 - Get configuration contexts](../monitor-k8s/tsg010-get-kubernetes-contexts.ipynb) to resolve this issue.'))
display(Markdown(f'HINT: Use [SOP011 - Set kubernetes configuration context](../common/sop011-set-kubernetes-context.ipynb) to resolve this issue.'))
raise
print(f'The SQL Server Big Data Cluster Kubernetes namespace is: {namespace}')
```
### Create a temporary directory to stage files
```
# Create a temporary directory to hold configuration files
import tempfile
temp_dir = tempfile.mkdtemp()
print(f"Temporary directory created: {temp_dir}")
```
### Helper function to save configuration files to disk
```
# Define helper function 'save_file' to save configuration files to the temporary directory created above
import os
import io
def save_file(filename, contents):
with io.open(os.path.join(temp_dir, filename), "w", encoding='utf8', newline='\n') as text_file:
text_file.write(contents)
print("File saved: " + os.path.join(temp_dir, filename))
print("Function `save_file` defined successfully.")
```
### Instantiate Kubernetes client
```
# Instantiate the Python Kubernetes client into 'api' variable
import os
from IPython.display import Markdown
try:
from kubernetes import client, config
from kubernetes.stream import stream
except ImportError:
# Install the Kubernetes module
import sys
!{sys.executable} -m pip install kubernetes
try:
from kubernetes import client, config
from kubernetes.stream import stream
except ImportError:
display(Markdown(f'HINT: Use [SOP059 - Install Kubernetes Python module](../install/sop059-install-kubernetes-module.ipynb) to resolve this issue.'))
raise
if "KUBERNETES_SERVICE_PORT" in os.environ and "KUBERNETES_SERVICE_HOST" in os.environ:
config.load_incluster_config()
else:
try:
config.load_kube_config()
except:
display(Markdown(f'HINT: Use [TSG118 - Configure Kubernetes config](../repair/tsg118-configure-kube-config.ipynb) to resolve this issue.'))
raise
api = client.CoreV1Api()
print('Kubernetes client instantiated')
```
### Helper functions for waiting for the cluster to become healthy
```
import threading
import time
import sys
import os
from IPython.display import Markdown
isRunning = True
def all_containers_ready(pod):
"""helper method returns true if all the containers within the given pod are ready
Arguments:
pod {v1Pod} -- Metadata retrieved from the api call to.
"""
return all(map(lambda c: c.ready is True, pod.status.container_statuses))
def pod_is_ready(pod):
"""tests that the pod, and all containers are ready
Arguments:
pod {v1Pod} -- Metadata retrieved from api call.
"""
return "job-name" in pod.metadata.labels or (pod.status.phase == "Running" and all_containers_ready(pod))
def waitReady():
"""Waits for all pods, and containers to become ready.
"""
while isRunning:
try:
time.sleep(check_interval)
pods = get_pods()
allReady = len(pods.items) >= min_pod_count and all(map(pod_is_ready, pods.items))
if allReady:
return True
else:
display(Markdown(get_pod_failures(pods)))
display(Markdown(f"cluster not healthy, rechecking in {check_interval} seconds."))
except Exception as ex:
last_error_message = str(ex)
display(Markdown(last_error_message))
time.sleep(check_interval)
def get_pod_failures(pods=None):
"""Returns a status message for any pods that are not ready.
"""
results = ""
if not pods:
pods = get_pods()
for pod in pods.items:
if "job-name" not in pod.metadata.labels:
if pod.status and pod.status.container_statuses:
for container in filter(lambda c: c.ready is False, pod.status.container_statuses):
results = results + "Container {0} in Pod {1} is not ready. Reported status: {2} <br/>".format(container.name, pod.metadata.name, container.state)
else:
results = results + "Pod {0} is not ready. <br/>".format(pod.metadata.name)
return results
def get_pods():
"""Returns a list of pods by namespace, or all namespaces if no namespace is specified
"""
pods = None
if namespace is not None:
display(Markdown(f'Checking namespace {namespace}'))
pods = api.list_namespaced_pod(namespace, _request_timeout=30)
else:
display(Markdown('Checking all namespaces'))
pods = api.list_pod_for_all_namespaces(_request_timeout=30)
return pods
def wait_for_cluster_healthy():
isRunning = True
mt = threading.Thread(target=waitReady)
mt.start()
mt.join(timeout=timeout)
if mt.is_alive():
raise SystemExit("Timeout waiting for all cluster to be healthy.")
isRunning = False
```
### Get name of the ‘Running’ `controller` `pod`
```
# Place the name of the 'Running' controller pod in variable `controller`
controller = run(f'kubectl get pod --selector=app=controller -n {namespace} -o jsonpath={{.items[0].metadata.name}} --field-selector=status.phase=Running', return_output=True)
print(f"Controller pod name: {controller}")
```
### Get the name of the `master` `pods`
```
# Place the name of the master pods in variable `pods`
podNames = run(f'kubectl get pod --selector=app=master -n {namespace} -o jsonpath={{.items[*].metadata.name}}', return_output=True)
pods = podNames.split(" ")
print(f"Master pod names: {pods}")
```
### Validate certificate common name and alt names
```
import json
from urllib.parse import urlparse
kubernetes_default_record_name = 'kubernetes.default'
kubernetes_default_svc_prefix = 'kubernetes.default.svc'
default_dns_suffix = 'svc.cluster.local'
dns_suffix = ''
nslookup_output=run(f'kubectl exec {controller} -c controller -n {namespace} -- bash -c "nslookup {kubernetes_default_record_name} > /tmp/nslookup.out; cat /tmp/nslookup.out; rm /tmp/nslookup.out" ', return_output=True)
name = re.findall('Name:\s+(.[^,|^\s|^\n]+)', nslookup_output)
if not name or kubernetes_default_svc_prefix not in name[0]:
dns_suffix = default_dns_suffix
else:
dns_suffix = 'svc' + name[0].replace(kubernetes_default_svc_prefix, '')
pods.sort()
for pod_name in pods:
alt_names = ""
bdc_fqdn = ""
alt_names += f"DNS.1 = {common_name}\n"
alt_names += f"DNS.2 = {common_name}.{namespace}.{dns_suffix} \n"
hdfs_vault_svc = "hdfsvault-svc"
bdc_config = run("azdata bdc config show", return_output=True)
bdc_config = json.loads(bdc_config)
dns_counter = 3 # DNS.1 and DNS.2 are already in the certificate template
# Stateful set related DNS names
#
if app_name == "gateway" or app_name == "master":
alt_names += f'DNS.{str(dns_counter)} = {pod_name}.{common_name}\n'
dns_counter = dns_counter + 1
alt_names += f'DNS.{str(dns_counter)} = {pod_name}.{common_name}.{namespace}.{dns_suffix}\n'
dns_counter = dns_counter + 1
# AD related DNS names
#
if "security" in bdc_config["spec"] and "activeDirectory" in bdc_config["spec"]["security"]:
domain_dns_name = bdc_config["spec"]["security"]["activeDirectory"]["domainDnsName"]
subdomain_name = bdc_config["spec"]["security"]["activeDirectory"]["subdomain"]
if subdomain_name:
bdc_fqdn = f"{subdomain_name}.{domain_dns_name}"
else:
bdc_fqdn = f"{namespace}.{domain_dns_name}"
alt_names += f"DNS.{str(dns_counter)} = {common_name}.{bdc_fqdn}\n"
dns_counter = dns_counter + 1
if app_name == "gateway" or app_name == "master":
alt_names += f'DNS.{str(dns_counter)} = {pod_name}.{bdc_fqdn}\n'
dns_counter = dns_counter + 1
# Endpoint DNS names for bdc certificates
#
if app_name in bdc_config["spec"]["resources"]:
app_name_endpoints = bdc_config["spec"]["resources"][app_name]["spec"]["endpoints"]
for endpoint in app_name_endpoints:
if "dnsName" in endpoint:
alt_names += f'DNS.{str(dns_counter)} = {endpoint["dnsName"]}\n'
dns_counter = dns_counter + 1
# Endpoint DNS names for control plane certificates
#
if app_name == "controller" or app_name == "mgmtproxy":
bdc_endpoint_list = run("azdata bdc endpoint list", return_output=True)
bdc_endpoint_list = json.loads(bdc_endpoint_list)
# Parse the DNS host name from:
#
# "endpoint": "https://monitor.aris.local:30777"
#
for endpoint in bdc_endpoint_list:
if endpoint["name"] == app_name:
url = urlparse(endpoint["endpoint"])
alt_names += f"DNS.{str(dns_counter)} = {url.hostname}\n"
dns_counter = dns_counter + 1
# Special case for the controller certificate
#
if app_name == "controller":
alt_names += f"DNS.{str(dns_counter)} = localhost\n"
dns_counter = dns_counter + 1
# Add hdfsvault-svc host for key management calls.
#
alt_names += f"DNS.{str(dns_counter)} = {hdfs_vault_svc}\n"
dns_counter = dns_counter + 1
# Add hdfsvault-svc FQDN for key management calls.
#
if bdc_fqdn:
alt_names += f"DNS.{str(dns_counter)} = {hdfs_vault_svc}.{bdc_fqdn}\n"
dns_counter = dns_counter + 1
required_dns_names = re.findall('DNS\.[0-9] = ([^,|^\s|^\n]+)', alt_names)
# Get certificate common name and DNS names
# use nameopt compat, to generate CN= format on all versions of openssl
#
cert = run(f'kubectl exec {controller} -c controller -n {namespace} -- openssl x509 -nameopt compat -in {test_cert_store_root}/{app_name}/{certificate_names[pod_name]} -text -noout', return_output=True)
subject = re.findall('Subject:(.+)', cert)[0]
certficate_common_name = re.findall('CN=(.[^,|^\s|^\n]+)', subject)[0]
certficate_dns_names = re.findall('DNS:(.[^,|^\s|^\n]+)', cert)
# Validate the common name
#
if (common_name != certficate_common_name):
run(f'kubectl exec {controller} -c controller -n {namespace} -- bash -c "rm -rf {test_cert_store_root}/{app_name}"')
raise SystemExit(f'Certficate common name does not match the expected one: {common_name}')
# Validate the DNS names
#
if not all(dns_name in certficate_dns_names for dns_name in required_dns_names):
run(f'kubectl exec {controller} -c controller -n {namespace} -- bash -c "rm -rf {test_cert_store_root}/{app_name}"')
raise SystemExit(f'Certficate does not have all required DNS names: {required_dns_names}')
```
### Copy certifcate files from `controller` to local machine
```
import os
cwd = os.getcwd()
os.chdir(temp_dir) # Use chdir to workaround kubectl bug on Windows, which incorrectly processes 'c:\' on kubectl cp cmd line
for pod_name in pods:
run(f'kubectl cp {controller}:{test_cert_store_root}/{app_name}/{certificate_names[pod_name]} {certificate_names[pod_name]} -c controller -n {namespace}')
run(f'kubectl cp {controller}:{test_cert_store_root}/{app_name}/{key_names[pod_name]} {key_names[pod_name]} -c controller -n {namespace}')
os.chdir(cwd)
```
### Copy certifcate files from local machine to `controldb`
```
import os
cwd = os.getcwd()
os.chdir(temp_dir) # Workaround kubectl bug on Windows, can't put c:\ on kubectl cp cmd line
for pod_name in pods:
run(f'kubectl cp {certificate_names[pod_name]} controldb-0:/var/opt/mssql/{certificate_names[pod_name]} -c mssql-server -n {namespace}')
run(f'kubectl cp {key_names[pod_name]} controldb-0:/var/opt/mssql/{key_names[pod_name]} -c mssql-server -n {namespace}')
os.chdir(cwd)
```
### Get the `controller-db-rw-secret` secret
Get the controller SQL symmetric key password for decryption.
```
import base64
controller_db_rw_secret = run(f'kubectl get secret/controller-db-rw-secret -n {namespace} -o jsonpath={{.data.encryptionPassword}}', return_output=True)
controller_db_rw_secret = base64.b64decode(controller_db_rw_secret).decode('utf-8')
print("controller_db_rw_secret retrieved")
```
### Update the files table with the certificates through opened SQL connection
```
import os
sql = f"""
OPEN SYMMETRIC KEY ControllerDbSymmetricKey DECRYPTION BY PASSWORD = '{controller_db_rw_secret}'
DECLARE @FileData VARBINARY(MAX), @Key uniqueidentifier;
SELECT @Key = KEY_GUID('ControllerDbSymmetricKey');
"""
for pod_name in pods:
insert = f"""
SELECT TOP 1 @FileData = doc.BulkColumn FROM OPENROWSET(BULK N'/var/opt/mssql/{certificate_names[pod_name]}', SINGLE_BLOB) AS doc;
EXEC [dbo].[sp_set_file_data_encrypted] @FilePath = '/config/scaledsets/{scaledset_name}/pods/{pod_name}/containers/{container_name}/files/{prefix_keyfile_name}-certificate.pem',
@Data = @FileData,
@KeyGuid = @Key,
@Version = '0',
@User = '{user}',
@Group = '{group}',
@Mode = '{mode}';
SELECT TOP 1 @FileData = doc.BulkColumn FROM OPENROWSET(BULK N'/var/opt/mssql/{key_names[pod_name]}', SINGLE_BLOB) AS doc;
EXEC [dbo].[sp_set_file_data_encrypted] @FilePath = '/config/scaledsets/{scaledset_name}/pods/{pod_name}/containers/{container_name}/files/{prefix_keyfile_name}-privatekey.pem',
@Data = @FileData,
@KeyGuid = @Key,
@Version = '0',
@User = '{user}',
@Group = '{group}',
@Mode = '{mode}';
"""
sql += insert
save_file("insert_certificates.sql", sql)
cwd = os.getcwd()
os.chdir(temp_dir) # Workaround kubectl bug on Windows, can't put c:\ on kubectl cp cmd line
run(f'kubectl cp insert_certificates.sql controldb-0:/var/opt/mssql/insert_certificates.sql -c mssql-server -n {namespace}')
run(f"""kubectl exec controldb-0 -c mssql-server -n {namespace} -- bash -c "SQLCMDPASSWORD=`cat /var/run/secrets/credentials/mssql-sa-password/password` /opt/mssql-tools/bin/sqlcmd -b -U sa -d controller -i /var/opt/mssql/insert_certificates.sql" """)
# Clean up
run(f"""kubectl exec controldb-0 -c mssql-server -n {namespace} -- bash -c "rm /var/opt/mssql/insert_certificates.sql" """)
for pod_name in pods:
run(f"""kubectl exec controldb-0 -c mssql-server -n {namespace} -- bash -c "rm /var/opt/mssql/{certificate_names[pod_name]}" """)
run(f"""kubectl exec controldb-0 -c mssql-server -n {namespace} -- bash -c "rm /var/opt/mssql/{key_names[pod_name]}" """)
os.chdir(cwd)
```
### Clear out the controller_db_rw_secret variable
```
controller_db_rw_secret= ""
```
### Get the name of the `master` `pods`
```
# Place the name of the master pods in variable `pods`
podNames = run(f'kubectl get pod --selector=app=master -n {namespace} -o jsonpath={{.items[*].metadata.name}}', return_output=True)
pods = podNames.split(" ")
print(f"Master pod names: {pods}")
```
### Restart Pods
```
import threading
import time
if len(pods) == 1:
# One master pod indicates non-HA environment, just delete it
run(f'kubectl delete pod {pods[0]} -n {namespace}')
wait_for_cluster_healthy()
else:
# HA setup, delete secondaries before primary
timeout_s = 300
check_interval_s = 20
master_primary_svc_ip = run(f'kubectl get service master-p-svc -n {namespace} -o jsonpath={{.spec.clusterIP}}', return_output=True)
master_password = run(f'kubectl exec master-0 -c mssql-server -n {namespace} -- cat /var/run/secrets/credentials/pool/mssql-system-password', return_output=True)
def get_number_of_unsynchronized_replicas(result):
cmd = 'select count(*) from sys.dm_hadr_database_replica_states where synchronization_state <> 2'
res = run(f"kubectl exec controldb-0 -c mssql-server -n {namespace} -- /opt/mssql-tools/bin/sqlcmd -S {master_primary_svc_ip} -U system -P {master_password} -h -1 -q \"SET NOCOUNT ON; {cmd}\" ", return_output=True)
rows = res.strip().split("\n")
result[0] = int(rows[0])
return True
def get_primary_replica():
cmd = 'select distinct replica_server_name from sys.dm_hadr_database_replica_states s join sys.availability_replicas r on s.replica_id = r.replica_id where is_primary_replica = 1'
res = run(f"kubectl exec controldb-0 -c mssql-server -n {namespace} -- /opt/mssql-tools/bin/sqlcmd -S {master_primary_svc_ip} -U system -P {master_password} -h -1 -q \"SET NOCOUNT ON; {cmd}\" ", return_output=True)
rows = res.strip().split("\n")
return rows[0]
def get_secondary_replicas():
cmd = 'select distinct replica_server_name from sys.dm_hadr_database_replica_states s join sys.availability_replicas r on s.replica_id = r.replica_id where is_primary_replica = 0'
res = run(f"kubectl exec controldb-0 -c mssql-server -n {namespace} -- /opt/mssql-tools/bin/sqlcmd -S {master_primary_svc_ip} -U system -P {master_password} -h -1 -q \"SET NOCOUNT ON; {cmd}\" ", return_output=True)
rows = res.strip().split("\n")
res = []
for row in rows:
if (row != "" and "Sqlcmd: Warning" not in row):
res.append(row.strip())
return res
def all_replicas_syncrhonized():
while True:
unsynchronized_replicas_cnt = len(pods)
rows = [None]
time.sleep(check_interval_s)
getNumberOfReplicasThread = threading.Thread(target=get_number_of_unsynchronized_replicas, args=(rows,) )
getNumberOfReplicasThread.start()
getNumberOfReplicasThread.join(timeout=timeout_s)
if getNumberOfReplicasThread.is_alive():
raise SystemExit("Timeout getting the number of unsynchronized replicas.")
unsynchronized_replicas_cnt = rows[0]
if (unsynchronized_replicas_cnt == 0):
return True
def wait_for_replicas_to_synchronize():
waitForReplicasToSynchronizeThread = threading.Thread(target=all_replicas_syncrhonized)
waitForReplicasToSynchronizeThread.start()
waitForReplicasToSynchronizeThread.join(timeout=timeout_s)
if waitForReplicasToSynchronizeThread.is_alive():
raise SystemExit("Timeout waiting for all replicas to be synchronized.")
secondary_replicas = get_secondary_replicas()
for replica in secondary_replicas:
wait_for_replicas_to_synchronize()
run(f'kubectl delete pod {replica} -n {namespace}')
primary_replica = get_primary_replica()
wait_for_replicas_to_synchronize()
key = "/var/run/secrets/certificates/sqlha/mssql-ha-operator-controller-client/mssql-ha-operator-controller-client-privatekey.pem"
cert = "/var/run/secrets/certificates/sqlha/mssql-ha-operator-controller-client/mssql-ha-operator-controller-client-certificate.pem"
content_type_header = "Content-Type: application/json"
authorization_header = "Authorization: Certificate"
data = f'{{"TargetReplicaName":"{secondary_replicas[0]}","ForceFailover":"false"}}'
request_url = f'https://controller-svc:443/internal/api/v1/bdc/services/sql/resources/master/availabilitygroups/containedag/failover'
manual_failover_api_command = f"curl -sS --key {key} --cert {cert} -X POST --header '{content_type_header}' --header '{authorization_header}' --data '{data}' {request_url}"
operator_pod = run(f'kubectl get pod --selector=app=mssql-operator -n {namespace} -o jsonpath={{.items[0].metadata.name}}', return_output=True)
run(f'kubectl exec {operator_pod} -c mssql-ha-operator -n {namespace} -- {manual_failover_api_command}')
wait_for_replicas_to_synchronize()
run(f'kubectl delete pod {primary_replica} -n {namespace}')
wait_for_replicas_to_synchronize()
```
### Clean up certificate staging area
Remove the certificate files generated on disk (they have now been
placed in the controller database).
```
cmd = f"rm -r {test_cert_store_root}/{app_name}"
run(f'kubectl exec {controller} -c controller -n {namespace} -- bash -c "{cmd}"')
```
### Clean up temporary directory for staging configuration files
```
# Delete the temporary directory used to hold configuration files
import shutil
shutil.rmtree(temp_dir)
print(f'Temporary directory deleted: {temp_dir}')
print("Notebook execution is complete.")
```
Related
-------
- [CER023 - Create Master certificates](../cert-management/cer023-create-master-certs.ipynb)
- [CER033 - Sign Master certificates with generated CA](../cert-management/cer033-sign-master-generated-certs.ipynb)
- [CER044 - Install signed Controller certificate](../cert-management/cer044-install-controller-cert.ipynb)
|
github_jupyter
|
```
from ei_net import *
from ce_net import *
import matplotlib.pyplot as plt
import datetime as dt
%matplotlib inline
##########################################
############ PLOTTING SETUP ##############
EI_cmap = "Greys"
where_to_save_pngs = "../figs/pngs/"
where_to_save_pdfs = "../figs/pdfs/"
save = True
plt.rc('axes', axisbelow=True)
##########################################
##########################################
```
# The emergence of informative higher scales in complex networks
# Chapter 06 - Causal Emergence and the Emergence of Scale
## Network Macroscales
First we must introduce how to recast a network, $G$, at a higher scale. This is represented by a new network, $G_M$. Within $G_M$, a micro-node is a node that was present in the original $G$, whereas a macro-node is defined as a node, $v_M$, that represents a subgraph, $S_i$, from the original $G$ (replacing the subgraph within the network). Since the original network has been dimensionally reduced by grouping nodes together, $G_M$ will always have fewer nodes than $G$.
A macro-node $\mu$ is defined by some $W^{out}_{\mu}$, derived from the edge weights of the various nodes within the subgraph it represents. One can think of a macro-node as being a summary statistic of the underlying subgraph's behavior, a statistic that takes the form of a single node. Ultimately there are many ways of representing a subgraph, that is, building a macro-node, and some ways are more accurate than others in capturing the subgraph's behavior, depending on the connectivity. To decide whether or not a macro-node is an accurate summary of its underlying subgraph, we check whether random walkers behave identically on $G$ and $G_M$. We do this because many important analyses and algorithms---such as using PageRank for determining a node's centrality or InfoMap for community discovery---are based on random walking.
Specifically, we define the *inaccuracy* of a macroscale as the Kullback-Leibler divergence between the expected distribution of random walkers on $G$ vs. $G_M$, given some identical initial distribution on each. The expected distribution over $G$ at some future time $t$ is $P_m(t)$, while the distribution over $G_M$ at some future time $t$ is $P_M(t)$. To compare the two, the distribution $P_m(t)$ is summed over the same nodes in the macroscale $G_M$, resulting in the distribution $P_{M|m}(t)$ (the microscale given the macroscale). We can then define the macroscale inaccuracy over some series of time steps $T$ as:
$$ \text{inaccuracy} = \sum_{t=0}^T \text{D}_{_{KL}}[P_{M}(t) || P_{M|m}(t)] $$
This measure addresses the extent to which a random dynamical process on the microscale topology will be recapitulated on a dimensionally-reduced topology.
What constitutes an accurate macroscale depends on the connectivity of the subgraph that gets grouped into a macro-node. The $W^{out}_{\mu}$ can be constructed based on the collective $W^{out}$ of the subgraph. For instance, in some cases one could just coarse-grain a subgraph by using its average $W^{out}$ as the $W^{out}_{\mu}$ of some new macro-node $\mu$. However, it may be that the subgraph has dependencies not captured by such a coarse-grain. Indeed, this is similar to the recent discovery that when constructing networks from data it is often necessary to explicitly model higher-order dependencies by using higher-order nodes so that the dynamics of random walks to stay true to the original data. We therefore introduce *higher-order macro-nodes* (HOMs), which draw on similar techniques to accurately represent subgraphs as single nodes.
____________
<img src="../figs/pngs/CoarseGraining.png" width=800>
- Top: The original network, $G$ along with its adjacency matrix (left). The shaded oval indicates that subgraph $S$ member nodes $v_B$ and $v_C$ will be grouped together, forming a macro-node, ${\mu}$. All macro-nodes are some transformation of the original adjacency matrix via recasting it as a new adjacency matrix (right). The manner of this recasting depends on the type of macro-node.
- Bottom left: The simplest form of a macro-node is when $W^{out}_{\mu}$ is an average of the $W^{out}_{i}$ of each node in the subgraph.
- Bottom center left: A macro-node that represents some path-dependency, such as input from $A$. Here, in averaging to create the $W^{out}_{\mu}$ the out-weights of nodes $v_B$ and $v_C$ are weighted by their input from $v_A$.
- Bottom center right: A macro-node that represents the subgraph's output over the network's stationary dynamics. Each node has some associated ${\pi}_{i}$, which is the probability of ${v}_{i}$ in the stationary distribution of the network. The $W^{out}_{\mu}$ of a $\mu | \pi$ macro-node is created by weighting each $W^{out}_{i}$ of the micro-nodes in the subgraph $S$ by $\frac{{\pi}_{i}}{\sum_{k \in S} {\pi}_{k}}$.
- Bottom right: A macro-node with a single timestep delay between input $\mu | j$ and its output $\mu | \pi$, each constructed using the same techniques as its components. However, $\mu | j$ always deterministically outputs to $\mu | \pi$.
Different subgraph connectivities require different types of HOMs to accurately represent. For instance, HOMs can be based on the input weights to the macro-node, which take the form $\mu | j$. In these cases the $W^{out}_{\mu|j}$ is a weighted average of each node's $W^{out}$ in the subgraph, where the weight is based on the input weight to each node in the subgraph. Another type of HOM that generally leads to accurate macro-nodes over time is when the $W^{out}_{\mu}$ is based on the stationary output from the subgraph to the rest of the network, which we represent as $\mu | \pi$. These types of HOMs may sometimes have minor inaccuracies given some initial state, but will almost always trend toward perfect accuracy as the network approaches its stationary dynamics.
Subgraphs with complex internal dynamics can require a more complex type of HOM in order to preserve the network's accuracy. For instance, in cases where subgraphs have a delay between their inputs and outputs, this can be represented by a combination of $\mu | j$ and $\mu | \pi$, which when combined captures that delay. In these cases the macro-node $\mu$ has two components, one of which acts as a buffer over a timestep. This means that macro-nodes can possess memory even when constructed from networks that are at the microscale memoryless, and in fact this type of HOM is sometimes necessary to accurately capture the microscale dynamics.
We present these types of macro-nodes not as an exhaustive list of all possible HOMs, but rather as examples of how to construct higher scales in a network by representing subgraphs as nodes, and also sometimes using higher-order dependencies to ensure those nodes are accurate. This approach offers a complete generalization of previous work on coarse-grains and also black boxes, while simultaneously solving the previously unresolved issue of macroscale accuracy by using higher-order dependencies. The types of macro-nodes formed by subgraphs also provides substantive information about the network, such as whether the macroscale of a network possesses memory or path-dependency.
## Causal emergence reveals the scale of networks
Causal emergence occurs when a recast network, $G_M$ (a macroscale), has more $EI$ than the original network, $G$ (the microscale). In general, networks with lower effectiveness (low $EI$ given their size) have a higher potential for causal emergence, since they can be recast to reduce their uncertainty. Searching across groupings allows the identification or approximation of a macroscale that maximizes the $EI$.
Checking all possible groupings is computationally intractable for all but the smallest networks. Therefore, in order to find macro-nodes which increase the $EI$, we use a greedy algorithm that groups nodes together and checks if the $EI$ increases. By choosing a node and then pairing it iteratively with its surrounding nodes we can grow macro-nodes until pairings no longer increase the $EI$, and then move on to a new node.
By generating undirected preferential attachment networks and varying the degree of preferential attachment, $\alpha$, we observe a crucial relationship between preferential attachment and causal emergence. One of the central results in network science has been the identification of "scale-free" networks. Our results show that networks that are not "scale-free" can be further separated into micro-, meso-, and macroscales depending on their connectivity. This scale can be identified based on their degree of causal emergence. In cases of sublinear preferential attachment ($\alpha < 1.0$) networks lack higher scales. Linear preferential attachment ($\alpha=1.0$) produces networks that are scale-free, which is the zone of preferential attachment right before the network develops higher scales. Such higher scales only exist in cases of superlinear preferential attachment ($\alpha > 1.0$). And past $\alpha > 3.0$ the network begins to converge to a macroscale where almost all the nodes are grouped into a single macro-node. The greatest degree of causal emergence is found in mesoscale networks, which is when $\alpha$ is between 1.5 and 3.0, when networks possess a rich array of macro-nodes.
Correspondingly the size of $G_M$ decreases as $\alpha$ increases and the network develops an informative higher scale, which can be seen in the ratio of macroscale network size, $N_M$, to the original network size, $N$. As discussed in previous sections, on the upper end of the spectrum of $\alpha$ the resulting network will approximate a hub-and-spoke, star-like network. Star-like networks have higher degeneracy and thus less $EI$, and because of this, we expect that there are more opportunities to increase the network's $EI$ through grouping nodes into macro-nodes. Indeed, the ideal grouping of a star network is when $N_M=2$ and $EI$ is 1 bit. This result is similar to recent advances in spectral coarse-graining that also observe that the ideal coarse-graining of a star network is to collapse it into a two-node network, grouping all the spokes into a single macro-node, which is what happens to star networks that are recast as macroscales.
Our results offer a principled and general approach to such community detection by asking when there is an informational gain from replacing a subgraph with a single node. Therefore we can define *causal communities* as being when a cluster of nodes, or some subgraph, forms a viable macro-node. Fundamentally causal communities represent noise at the microscale. The closer a subgraph is to complete noise, the greater the gain in $EI$ by replacing it with a macro-node. Minimizing the noise in a given network also identifies the optimal scale to represent that network. However, there must be some structure that can be revealed by noise minimization in the first place. In cases of random networks that form a single large component which lacks any such structure, causal emergence does not occur.
____________
## 6.1 Causal Emergence in Preferential Attachment Networks
```
def preferential_attachment_network(N, alpha=1.0, m=1):
"""
Generates a network based off of a preferential attachment
growth rule. Under this growth rule, new nodes place their
$m$ edges to nodes already present in the graph, G, with
a probability proportional to $k^\alpha$.
Params
------
N (int): the desired number of nodes in the final network
alpha (float): the exponent of preferential attachment.
When alpha is less than 1.0, we describe it
as sublinear preferential attachment. At
alpha > 1.0, it is superlinear preferential
attachment. And at alpha=1.0, the network
was grown under linear preferential attachment,
as in the case of Barabasi-Albert networks.
m (int): the number of new links that each new node joins
the network with.
Returns
-------
G (nx.Graph): a graph grown under preferential attachment.
"""
G = nx.Graph()
G = nx.complete_graph(m+1)
for node_i in range(m+1,N):
degrees = np.array(list(dict(G.degree()).values()))
probs = (degrees**alpha) / sum(degrees**alpha)
eijs = np.random.choice(G.number_of_nodes(),
size=(m,), replace=False, p=probs)
for node_j in eijs:
G.add_edge(node_i, node_j)
return G
Nvals = sorted([30,60,90,120,150])
alphas= np.linspace(-1,5,25)
Niter = 2
m = 1
pa_ce = {'alpha' :[],
'N_micro':[],
'N_macro':[],
'EI_micro':[],
'EI_macro':[],
'CE' :[],
'N_frac' :[],
'runtime' :[]}
```
### Note: the following cell was run on a super-computing cluster. It is included as an example computation.
```
for N in Nvals:
for alpha in alphas:
for _ in range(Niter):
G = preferential_attachment_network(N,alpha,m)
startT = dt.datetime.now()
CE = causal_emergence(G, printt=False)
finisH = dt.datetime.now()
diff = finisH-startT
diff = diff.total_seconds()
pa_ce['alpha'].append(alpha)
pa_ce['N_micro'].append(N)
pa_ce['N_macro'].append(CE['G_macro'].number_of_nodes())
pa_ce['EI_micro'].append(CE['EI_micro'])
pa_ce['EI_macro'].append(CE['EI_macro'])
pa_ce['CE'].append(CE['EI_macro']-CE['EI_micro'])
pa_ce['N_frac'].append(CE['G_macro'].number_of_nodes()/N)
pa_ce['runtime'].append(diff)
NCE = pa_ce.copy()
# import cmocean as cmo
# colorz = cmo.cm.amp(np.linspace(0.2,0.9,len(Nvals)))
colorz = plt.cm.viridis(np.linspace(0,0.9,len(Nvals)))
mult=0.95
fig,ax=plt.subplots(1,1,figsize=(5.0*mult,4.5*mult))
plt.subplots_adjust(wspace=0.24, hspace=0.11)
ymax_so_far = 0
xmin_so_far = 0
xmax_so_far = 0
for i,Nn in enumerate(Nvals):
col = colorz[i]
means = [np.mean(NCE[Nn][i]['CE']) for i in NCE[Nn].keys()]
stdvs = [np.std(NCE[Nn][i]['CE']) for i in NCE[Nn].keys()]
alphs = list(NCE[Nn].keys())
alphs = np.array([(alphs[i]+alphs[i+1])/2
for i in range(0,len(alphs)-1,2)])
means = np.array([(means[i]+means[i+1])/2
for i in range(0,len(means)-1,2)])
stdvs = np.array([(stdvs[i]+stdvs[i+1])/2
for i in range(0,len(stdvs)-1,2)])
xmin_so_far = min([xmin_so_far, min(alphs)])
xmax_so_far = max([xmax_so_far, max(alphs)])
ymax_so_far = max([ymax_so_far, max(means+stdvs)])
ax.plot(alphs, means,
markeredgecolor=col, color=col,
markerfacecolor='w',
markeredgewidth=1.5,markersize=5.0,
linestyle='-',marker='o',linewidth=2.2,label='N = %i'%Nn)
ax.fill_between(alphs, means-stdvs, means+stdvs,
facecolor=col, alpha=0.2,
edgecolors='w', linewidth=1)
cols = ["#a7d6ca","#dbb9d1","#d6cdae","#a5c9e3"]
ax.fill_between([-2,0.90],[-1,-1],[3,3],
facecolor=cols[0],alpha=0.3,edgecolors='w',linewidth=0)
ax.fill_between([0.90,1.1],[-1,-1],[3,3],
facecolor=cols[1],alpha=0.7,edgecolors='w',linewidth=0)
ax.fill_between([1.1,3.0],[-1,-1],[3,3],
facecolor=cols[2],alpha=0.3,edgecolors='w',linewidth=0)
ax.fill_between([3.0,6],[-1,-1],[3,3],
facecolor=cols[3],alpha=0.3,edgecolors='w',linewidth=0)
ax.text(-0.500, 2.65, '|', fontsize=14)
ax.text(0.9425, 2.65, '|', fontsize=14)
ax.text(0.9425, 2.72, '|', fontsize=14)
ax.text(0.9425, 2.79, '|', fontsize=14)
ax.text(2.4000, 2.65, '|', fontsize=14)
ax.text(4.2500, 2.65, '|', fontsize=14)
ax.text(-1.1, 2.81,'microscale',fontsize=12)
ax.text(0.35, 2.95,'scale-free',fontsize=12)
ax.text(1.70, 2.81,'mesoscale',fontsize=12)
ax.text(3.45, 2.81,'macroscale',fontsize=12)
ax.set_ylim(-0.025*ymax_so_far,ymax_so_far*1.05)
ax.set_xlim(-1.075,5*1.01)
ax.set_xlabel(r'$\alpha$',fontsize=14)
ax.set_ylabel('Causal emergence',fontsize=14, labelpad=10)
ax.legend(loc=6,framealpha=0.99)
ax.set_xticks(np.linspace(-1,5,7))
ax.set_xticklabels(["%i"%i for i in np.linspace(-1,5,7)])
ax.grid(linestyle='-', linewidth=2.0, color='#999999', alpha=0.3)
if save:
plt.savefig(
where_to_save_pngs+\
'CE_pa_alpha_labs.png',
dpi=425, bbox_inches='tight')
plt.savefig(
where_to_save_pdfs+\
'CE_pa_alpha_labs.pdf',
dpi=425, bbox_inches='tight')
plt.show()
mult=0.95
fig,ax=plt.subplots(1,1,figsize=(5.0*mult,4.5*mult))
plt.subplots_adjust(wspace=0.24, hspace=0.11)
ymax_so_far = 0
xmin_so_far = 0
xmax_so_far = 0
for i,Nn in enumerate(Nvals):
col = colorz[i]
means = [np.mean(NCE[Nn][i]['N_frac']) for i in NCE[Nn].keys()]
stdvs = [np.std(NCE[Nn][i]['N_frac']) for i in NCE[Nn].keys()]
alphs = list(NCE[Nn].keys())
alphs = np.array([(alphs[i]+alphs[i+1])/2
for i in range(0,len(alphs)-1,2)])
means = np.array([(means[i]+means[i+1])/2
for i in range(0,len(means)-1,2)])
stdvs = np.array([(stdvs[i]+stdvs[i+1])/2
for i in range(0,len(stdvs)-1,2)])
xmin_so_far = min([xmin_so_far, min(alphs)])
xmax_so_far = max([xmax_so_far, max(alphs)])
ymax_so_far = max([ymax_so_far, max(means+stdvs)])
ax.semilogy(alphs, means, markeredgecolor=col,
color=col,markerfacecolor='w',
markeredgewidth=1.5, markersize=5.0,
linestyle='-',marker='o',linewidth=2.0,
alpha=0.99,label='N = %i'%Nn)
ax.fill_between(alphs, means-stdvs, means+stdvs,
facecolor=col,alpha=0.2,
edgecolors='w',linewidth=1)
cols = ["#a7d6ca","#dbb9d1","#d6cdae","#a5c9e3"]
ax.fill_between([-2,0.9],[-1,-1],[3,3],
facecolor=cols[0],alpha=0.3,edgecolors='w',linewidth=0)
ax.fill_between([0.9,1.1],[-1,-1],[3,3],
facecolor=cols[1],alpha=0.7,edgecolors='w',linewidth=0)
ax.fill_between([1.1,3.0],[-1,-1],[3,3],
facecolor=cols[2],alpha=0.3,edgecolors='w',linewidth=0)
ax.fill_between([3.0,6],[-1,-1],[3,3],
facecolor=cols[3],alpha=0.3,edgecolors='w',linewidth=0)
ax.text(-0.50, 1.036,'|', fontsize=14)
ax.text(0.935, 1.036,'|', fontsize=14)
ax.text(0.935, 1.170,'|', fontsize=14)
ax.text(0.935, 1.320,'|', fontsize=14)
ax.text(2.400, 1.036,'|', fontsize=14)
ax.text(4.250, 1.036,'|', fontsize=14)
ax.text(-1.1, 1.368, 'microscale', fontsize=12)
ax.text(0.35, 1.750, 'scale-free', fontsize=12)
ax.text(1.70, 1.368, 'mesoscale', fontsize=12)
ax.text(3.45, 1.368, 'macroscale', fontsize=12)
ax.set_ylim(0.009*ymax_so_far,ymax_so_far*1.075)
ax.set_xlim(-1.075,5*1.01)
ax.set_xlabel(r'$\alpha$',fontsize=14)
ax.set_ylabel('Size ratio: macro to micro',
fontsize=14, labelpad=2)
ax.legend(loc=6,framealpha=0.99)
ax.set_xticks(np.linspace(-1,5,7))
ax.set_xticklabels(["%i"%i for i in np.linspace(-1,5,7)])
ax.grid(linestyle='-', linewidth=2.0, color='#999999', alpha=0.3)
if save:
plt.savefig(
where_to_save_pngs+\
'Nfrac_pa_alpha_labs.png',
dpi=425, bbox_inches='tight')
plt.savefig(
where_to_save_pdfs+\
'Nfrac_pa_alpha_labs.pdf',
dpi=425, bbox_inches='tight')
plt.show()
```
_______________
## 6.2 Causal Emergence of Random Networks
```
Ns = [20,30,40,50]
ps = np.round(np.logspace(-3.25,-0.4,31),5)
Niter = 40
er_ce = {'p' :[],
'N_micro':[],
'N_macro':[],
'EI_micro':[],
'EI_macro':[],
'CE_mean' :[],
'CE_stdv' :[],
'N_frac' :[],
'runtime' :[]}
ER_CE = {N:er_ce for N in Ns}
```
### Note: the following cell was run on a super-computing cluster. It is included as an example computation.
```
for N in Ns:
print(N, dt.datetime.now())
er_ce = {'p' :[],
'N_micro':[],
'N_macro':[],
'EI_micro':[],
'EI_macro':[],
'CE_mean' :[],
'CE_stdv' :[],
'N_frac' :[],
'runtime' :[]}
for p in ps:
print('\t',p)
cee = []
for rr in range(Niter):
G = nx.erdos_renyi_graph(N,p)
startT = dt.datetime.now()
CE = causal_emergence(G,printt=False)
finisH = dt.datetime.now()
diff = finisH-startT
diff = diff.total_seconds()
ce = CE['EI_macro']-CE['EI_micro']
cee.append(ce)
er_ce['p'].append(p)
er_ce['N_micro'].append(N)
er_ce['N_macro'].append(CE['G_macro'].number_of_nodes())
er_ce['EI_micro'].append(CE['EI_micro'])
er_ce['EI_macro'].append(CE['EI_macro'])
er_ce['CE_mean'].append(np.mean(cee))
er_ce['CE_stdv'].append(np.std( cee))
er_ce['runtime'].append(diff)
ER_CE[N] = er_ce.copy()
# import cmocean as cmo
# colors = cmo.cm.thermal(np.linspace(0.1,0.95,len(Ns)))
colors = plt.cm.viridis(np.linspace(0.0,1,len(Ns)))
i = 0
ymax = 0
plt.vlines(100, -1, 1,
label=r'$\langle k \rangle=1$', linestyle='--',
color="#333333", linewidth=3.5, alpha=0.99)
for N in Ns:
CE1 = np.array(ER_CE1[N]['CE_mean'].copy())
CE2 = np.array(ER_CE2[N]['CE_mean'].copy())
CE3 = np.array(ER_CE3[N]['CE_mean'].copy())
CE4 = np.array(ER_CE4[N]['CE_mean'].copy())
CE5 = np.array(ER_CE5[N]['CE_mean'].copy())
CE6 = np.array(ER_CE6[N]['CE_mean'].copy())
CEs = (CE1 + CE2 + CE3 + CE4 + CE5 + CE6)/6
CEs = list(CEs)
CEs = [(CEs[i] + CEs[i+1])/2 for i in range(0,len(CEs)-1)]
CEs = [0] + CEs
CEs.append(0)
x1 = np.array(ER_CE1[N]['p'].copy())
x2 = np.array(ER_CE2[N]['p'].copy())
x3 = np.array(ER_CE3[N]['p'].copy())
x4 = np.array(ER_CE4[N]['p'].copy())
x5 = np.array(ER_CE5[N]['p'].copy())
x6 = np.array(ER_CE6[N]['p'].copy())
xx = (x1 + x2 + x3 + x4 + x5 + x6)/6
xx = list(xx)
xx = [(xx[i] + xx[i+1])/2 for i in range(0,len(xx)-1)]
xx = [1e-4] + xx
xx.append(1)
std1 = np.array(ER_CE1[N]['CE_stdv'].copy())
std2 = np.array(ER_CE2[N]['CE_stdv'].copy())
std3 = np.array(ER_CE3[N]['CE_stdv'].copy())
std4 = np.array(ER_CE4[N]['CE_stdv'].copy())
std5 = np.array(ER_CE5[N]['CE_stdv'].copy())
std6 = np.array(ER_CE6[N]['CE_stdv'].copy())
stds = (std1 + std2 + std3 + std4 + std5 + std6)/6
stds = list(stds)
stds = [(stds[i] + stds[i+1])/2 for i in range(0,len(stds)-1)]
stds = [0] + stds
stds.append(0)
ytop = np.array(CEs) + np.array(stds)
ybot = np.array(CEs) - np.array(stds)
ybot[ybot<0] = 0
ymax = max([ymax, max(ytop)])
plt.semilogx(xx, CEs, label='N=%i'%N,
color=colors[i], linewidth=4.0, alpha=0.95)
plt.vlines(1/(N-1), -1, 1, linestyle='--',
color=colors[i], linewidth=3.5, alpha=0.95)
i += 1
plt.xlim(2.5e-4,max(xx))
plt.ylim(-0.0015, ymax*0.6)
plt.grid(linestyle='-', linewidth=2.5, alpha=0.3, color='#999999')
plt.ylabel('Causal emergence', fontsize=14)
plt.xlabel(r'$p$', fontsize=14)
plt.legend(fontsize=12)
if save:
plt.savefig(
where_to_save_pngs+\
'CE_ER_p_N.png', dpi=425, bbox_inches='tight')
plt.savefig(
where_to_save_pdfs+\
'CE_ER_p_N.pdf', dpi=425, bbox_inches='tight')
plt.show()
# import cmocean as cmo
# colors = cmo.cm.thermal(np.linspace(0.1,0.95,len(Ns)))
colors = plt.cm.viridis(np.linspace(0.0,1,len(Ns)))
i = 0
ymax = 0
plt.vlines(100, -1, 1, label=r'$\langle k \rangle=1$', linestyle='--',
color="#333333", linewidth=3.5, alpha=0.99)
for N in Ns:
CE1 = np.array(ER_CE1[N]['CE_mean'].copy())
CE2 = np.array(ER_CE2[N]['CE_mean'].copy())
CE3 = np.array(ER_CE3[N]['CE_mean'].copy())
CE4 = np.array(ER_CE4[N]['CE_mean'].copy())
CE5 = np.array(ER_CE5[N]['CE_mean'].copy())
CE6 = np.array(ER_CE6[N]['CE_mean'].copy())
CEs = (CE1 + CE2 + CE3 + CE4 + CE5 + CE6)/6
CEs = list(CEs)
CEs = [(CEs[i] + CEs[i+1])/2 for i in range(0,len(CEs)-1)]
CEs = [0] + CEs
CEs.append(0)
x1 = np.array(ER_CE1[N]['p'].copy())
x2 = np.array(ER_CE2[N]['p'].copy())
x3 = np.array(ER_CE3[N]['p'].copy())
x4 = np.array(ER_CE4[N]['p'].copy())
x5 = np.array(ER_CE5[N]['p'].copy())
x6 = np.array(ER_CE6[N]['p'].copy())
xx = (x1 + x2 + x3 + x4 + x5 + x6)/6
xx = list(xx)
xx = [(xx[i] + xx[i+1])/2 for i in range(0,len(xx)-1)]
xx = [1e-4] + xx
xx.append(1)
std1 = np.array(ER_CE1[N]['CE_stdv'].copy())
std2 = np.array(ER_CE2[N]['CE_stdv'].copy())
std3 = np.array(ER_CE3[N]['CE_stdv'].copy())
std4 = np.array(ER_CE4[N]['CE_stdv'].copy())
std5 = np.array(ER_CE5[N]['CE_stdv'].copy())
std6 = np.array(ER_CE6[N]['CE_stdv'].copy())
stds = (std1 + std2 + std3 + std4 + std5 + std6)/6
stds = list(stds)
stds = [(stds[i] + stds[i+1])/2 for i in range(0,len(stds)-1)]
stds = [0] + stds
stds.append(0)
ytop = np.array(CEs) + np.array(stds)
ybot = np.array(CEs) - np.array(stds)
ybot[ybot<0] = 0
ymax = max([ymax, max(ytop)])
plt.semilogx(xx, CEs, label='N=%i'%N, color=colors[i],
linewidth=4.0, alpha=0.95)
plt.fill_between(xx, ytop, ybot, facecolor=colors[i],
linewidth=2.0, alpha=0.35, edgecolor='w')
plt.vlines(1/(N-1), -1, 1, linestyle='--',
color=colors[i], linewidth=3.5, alpha=0.95)
i += 1
plt.xlim(2.5e-4,max(xx))
plt.ylim(-0.0015, ymax)
plt.grid(linestyle='-', linewidth=2.5,
alpha=0.3, color='#999999')
plt.ylabel('Causal emergence', fontsize=14)
plt.xlabel(r'$p$', fontsize=14)
plt.legend(fontsize=12)
if save:
plt.savefig(
where_to_save_pngs+\
'CE_ER_p_N0.png', dpi=425, bbox_inches='tight')
plt.savefig(
where_to_save_pdfs+\
'CE_ER_p_N0.pdf', dpi=425, bbox_inches='tight')
plt.show()
for n in ER_CE1.keys():
ER_CE1[n]['k'] = np.array(ER_CE1[n]['p'])*n
for n in ER_CE2.keys():
ER_CE2[n]['k'] = np.array(ER_CE2[n]['p'])*n
for n in ER_CE3.keys():
ER_CE3[n]['k'] = np.array(ER_CE3[n]['p'])*n
for n in ER_CE4.keys():
ER_CE4[n]['k'] = np.array(ER_CE4[n]['p'])*n
for n in ER_CE5.keys():
ER_CE5[n]['k'] = np.array(ER_CE5[n]['p'])*n
for n in ER_CE6.keys():
ER_CE6[n]['k'] = np.array(ER_CE6[n]['p'])*n
# import cmocean as cmo
# colors = cmo.cm.thermal(np.linspace(0.1,0.95,len(Ns)))
colors = plt.cm.viridis(np.linspace(0.0,1,len(Ns)))
i = 0
ymax = 0
for N in Ns:
CE1 = np.array(ER_CE1[N]['CE_mean'].copy())
CE2 = np.array(ER_CE2[N]['CE_mean'].copy())
CE3 = np.array(ER_CE3[N]['CE_mean'].copy())
CE4 = np.array(ER_CE4[N]['CE_mean'].copy())
CE5 = np.array(ER_CE5[N]['CE_mean'].copy())
CE6 = np.array(ER_CE6[N]['CE_mean'].copy())
CEs = (CE1 + CE2 + CE3 + CE4 + CE5 + CE6)/6
CEs = list(CEs)
CEs = [(CEs[i] + CEs[i+1])/2 for i in range(0,len(CEs)-1)]
CEs = [0] + CEs
x1 = np.array(ER_CE1[N]['k'].copy())
x2 = np.array(ER_CE2[N]['k'].copy())
x3 = np.array(ER_CE3[N]['k'].copy())
x4 = np.array(ER_CE4[N]['k'].copy())
x5 = np.array(ER_CE5[N]['k'].copy())
x6 = np.array(ER_CE6[N]['k'].copy())
xx = (x1 + x2 + x3 + x4 + x5 + x6)/6
xx = list(xx)
xx = [(xx[i] + xx[i+1])/2 for i in range(0,len(xx)-1)]
xx = [1e-4] + xx
std1 = np.array(ER_CE1[N]['CE_stdv'].copy())
std2 = np.array(ER_CE2[N]['CE_stdv'].copy())
std3 = np.array(ER_CE3[N]['CE_stdv'].copy())
std4 = np.array(ER_CE4[N]['CE_stdv'].copy())
std5 = np.array(ER_CE5[N]['CE_stdv'].copy())
std6 = np.array(ER_CE6[N]['CE_stdv'].copy())
stds = (std1 + std2 + std3 + std4 + std5 + std6)/6
stds = list(stds)
stds = [(stds[i] + stds[i+1])/2 for i in range(0,len(stds)-1)]
stds = [0] + stds
ytop = np.array(CEs) + np.array(stds)
ybot = np.array(CEs) - np.array(stds)
ybot[ybot<0] = 0
ymax = max([ymax, max(ytop)])
plt.semilogx(xx, CEs, label='N=%i'%N,
color=colors[i], linewidth=4.0, alpha=0.95)
plt.fill_between(xx, ytop, ybot,
facecolor=colors[i],
linewidth=2.0, alpha=0.3, edgecolor='w')
i += 1
plt.vlines(1, -1, 1, linestyle='--',label=r'$\langle k \rangle=1$',
color='k', linewidth=3.0, alpha=0.95)
plt.xlim(1.0e-2,max(xx))
plt.ylim(-0.0015, ymax*1.01)
plt.grid(linestyle='-', linewidth=2.5, alpha=0.3, color='#999999')
plt.ylabel('Causal emergence', fontsize=14)
plt.xlabel(r'$\langle k \rangle$', fontsize=14)
plt.legend(fontsize=12)
if save:
plt.savefig(
where_to_save_pngs+\
'CE_ER_k_N0.png', dpi=425, bbox_inches='tight')
plt.savefig(
where_to_save_pdfs+\
'CE_ER_k_N0.pdf', dpi=425, bbox_inches='tight')
plt.show()
# import cmocean as cmo
# colors = cmo.cm.thermal(np.linspace(0.1,0.95,len(Ns)))
colors = plt.cm.viridis(np.linspace(0.0,1,len(Ns)))
i = 0
ymax = 0
for N in Ns:
CE1 = np.array(ER_CE1[N]['CE_mean'].copy())
CE2 = np.array(ER_CE2[N]['CE_mean'].copy())
CE3 = np.array(ER_CE3[N]['CE_mean'].copy())
CE4 = np.array(ER_CE4[N]['CE_mean'].copy())
CE5 = np.array(ER_CE5[N]['CE_mean'].copy())
CE6 = np.array(ER_CE6[N]['CE_mean'].copy())
CEs = (CE1 + CE2 + CE3 + CE4 + CE5 + CE6)/6
CEs = list(CEs)
CEs = [(CEs[i] + CEs[i+1])/2 for i in range(0,len(CEs)-1)]
CEs = [0] + CEs
x1 = np.array(ER_CE1[N]['k'].copy())
x2 = np.array(ER_CE2[N]['k'].copy())
x3 = np.array(ER_CE3[N]['k'].copy())
x4 = np.array(ER_CE4[N]['k'].copy())
x5 = np.array(ER_CE5[N]['k'].copy())
x6 = np.array(ER_CE6[N]['k'].copy())
xx = (x1 + x2 + x3 + x4 + x5 + x6)/6
xx = list(xx)
xx = [(xx[i] + xx[i+1])/2 for i in range(0,len(xx)-1)]
xx = [1e-4] + xx
std1 = np.array(ER_CE1[N]['CE_stdv'].copy())
std2 = np.array(ER_CE2[N]['CE_stdv'].copy())
std3 = np.array(ER_CE3[N]['CE_stdv'].copy())
std4 = np.array(ER_CE4[N]['CE_stdv'].copy())
std5 = np.array(ER_CE5[N]['CE_stdv'].copy())
std6 = np.array(ER_CE6[N]['CE_stdv'].copy())
stds = (std1 + std2 + std3 + std4 + std5 + std6)/6
stds = list(stds)
stds = [(stds[i] + stds[i+1])/2 for i in range(0,len(stds)-1)]
stds = [0] + stds
ytop = np.array(CEs) + np.array(stds)
ybot = np.array(CEs) - np.array(stds)
ybot[ybot<0] = 0
ymax = max([ymax, max(ytop)])
plt.semilogx(xx, CEs, label='N=%i'%N,
color=colors[i],
linewidth=4.0, alpha=0.95)
i += 1
plt.vlines(1, -1, 1, linestyle='--',
label=r'$\langle k \rangle=1$',
color='k', linewidth=3.0, alpha=0.95)
plt.xlim(1.0e-2,max(xx))
plt.ylim(-0.0015, ymax*0.6)
plt.grid(linestyle='-', linewidth=2.5,
alpha=0.3, color='#999999')
plt.ylabel('Causal emergence', fontsize=14)
plt.xlabel(r'$\langle k \rangle$', fontsize=14)
plt.legend(fontsize=12)
if save:
plt.savefig(
where_to_save_pngs+'CE_ER_k.png',
dpi=425, bbox_inches='tight')
plt.savefig(
where_to_save_pdfs+'CE_ER_k.pdf',
dpi=425, bbox_inches='tight')
plt.show()
```
## End of Chapter 06. In [Chapter 07](https://nbviewer.jupyter.org/github/jkbren/einet/blob/master/code/Chapter%2007%20-%20Estimating%20Causal%20Emergence%20in%20Real%20Networks.ipynb) we'll estimate causal emergence in real networks.
_______________
|
github_jupyter
|
```
import os
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.ticker import PercentFormatter
from glob import glob
%matplotlib inline
```
# Instructions for Use
The "Main Functions" section contains functions which return the success rate to be plotted as well as lower and upper bounds for uncertainty plotting.
To plot a given log, simply copy the code below two cells and replace `log_dir` with the path of the logs you wish to plot.
```
window = 1000
max_iter = None # Can set to an integer
log_dir = 'LOG_DIR'
title = 'Stack 4 Blocks, Training'
plot_it(log_dir, title, window=window, max_iter=max_iter)
```
# Main Functions
```
def get_grasp_success_rate(actions, rewards=None, window=200, reward_threshold=0.5):
"""Evaluate moving window of grasp success rate
actions: Nx4 array of actions giving [id, rotation, i, j]
"""
grasps = actions[:, 0] == 1
if rewards is None:
places = actions[:, 0] == 2
success_rate = np.zeros(actions.shape[0] - 1)
lower = np.zeros_like(success_rate)
upper = np.zeros_like(success_rate)
for i in range(success_rate.shape[0]):
start = max(i - window, 0)
if rewards is None:
successes = places[start+1: i+2][grasps[start:i+1]]
else:
successes = (rewards[start: i+1] > reward_threshold)[grasps[start:i+1]]
success_rate[i] = successes.mean()
var = np.sqrt(success_rate[i] * (1 - success_rate[i]) / successes.shape[0])
lower[i] = success_rate[i] + 3*var
upper[i] = success_rate[i] - 3*var
lower = np.clip(lower, 0, 1)
upper = np.clip(upper, 0, 1)
return success_rate, lower, upper
def get_place_success_rate(stack_height, actions, include_push=False, window=200, hot_fix=False, max_height=4):
"""
stack_heights: length N array of integer stack heights
actions: Nx4 array of actions giving [id, rotation, i, j]
hot_fix: fix the stack_height bug, where the trial didn't end on successful pushes, which reached a stack of 4.
where id=0 is a push, id=1 is grasp, and id=2 is place.
"""
if hot_fix:
indices = np.logical_or(stack_height < 4, np.array([True] + list(stack_height[:-1] < 4)))
actions = actions[:stack_height.shape[0]][indices]
stack_height = stack_height[indices]
if include_push:
success_possible = actions[:, 0] == 2
else:
success_possible = np.logical_or(actions[:, 0] == 0, actions[:, 0] == 2)
stack_height_increased = np.zeros_like(stack_height, np.bool)
stack_height_increased[0] = False
stack_height_increased[1:] = stack_height[1:] > stack_height[:-1]
success_rate = np.zeros_like(stack_height)
lower = np.zeros_like(success_rate)
upper = np.zeros_like(success_rate)
for i in range(stack_height.shape[0]):
start = max(i - window, 0)
successes = stack_height_increased[start:i+1][success_possible[start:i+1]]
success_rate[i] = successes.mean()
success_rate[np.isnan(success_rate)] = 0
var = np.sqrt(success_rate[i] * (1 - success_rate[i]) / successes.shape[0])
lower[i] = success_rate[i] + 3*var
upper[i] = success_rate[i] - 3*var
lower = np.clip(lower, 0, 1)
upper = np.clip(upper, 0, 1)
return success_rate, lower, upper
def get_action_efficiency(stack_height, window=200, ideal_actions_per_trial=6, max_height=4):
"""Calculate the running action efficiency from successful trials.
trials: array giving the number of trials up to iteration i (TODO: unused?)
min_actions: ideal number of actions per trial
Formula: successful_trial_count * ideal_actions_per_trial / window_size
"""
success = stack_height == max_height
efficiency = np.zeros_like(stack_height, np.float64)
lower = np.zeros_like(efficiency)
upper = np.zeros_like(efficiency)
for i in range(1, efficiency.shape[0]):
start = max(i - window, 1)
window_size = min(i, window)
num_trials = success[start:i+1].sum()
efficiency[i] = num_trials * ideal_actions_per_trial / window_size
var = efficiency[i] / np.sqrt(window_size)
lower[i] = efficiency[i] + 3*var
upper[i] = efficiency[i] - 3*var
lower = np.clip(lower, 0, 1)
upper = np.clip(upper, 0, 1)
return efficiency, lower, upper
def get_grasp_action_efficiency(actions, rewards, reward_threshold=0.5, window=200, ideal_actions_per_trial=3):
"""Get grasp efficiency from when the trial count increases.
"""
grasps = actions[:, 0] == 1
efficiency = np.zeros_like(rewards, np.float64)
lower = np.zeros_like(efficiency)
upper = np.zeros_like(efficiency)
for i in range(efficiency.shape[0]):
start = max(i - window, 0)
window_size = min(i+1, window)
successful = rewards[start: i+1] > reward_threshold
successful_grasps = successful[grasps[start:start+successful.shape[0]]].sum()
efficiency[i] = successful_grasps / window_size
var = efficiency[i] / np.sqrt(window_size)
lower[i] = efficiency[i] + 3*var
upper[i] = efficiency[i] - 3*var
lower = np.clip(lower, 0, 1)
upper = np.clip(upper, 0, 1)
return efficiency, lower, upper
def plot_it(log_dir, title, window=1000, colors=['tab:blue', 'tab:green', 'tab:orange'], alpha=0.35, mult=100, max_iter=None, place=False):
if place:
heights = np.loadtxt(os.path.join(log_dir, 'transitions', 'stack-height.log.txt'))
rewards = None
else:
rewards = np.loadtxt(os.path.join(log_dir, 'transitions', 'reward-value.log.txt'))
actions = np.loadtxt(os.path.join(log_dir, 'transitions', 'executed-action.log.txt'))
trials = np.loadtxt(os.path.join(log_dir, 'transitions', 'trial.log.txt'))
if max_iter is not None:
if place:
heights = heights[:max_iter]
else:
rewards = rewards[:max_iter]
actions = actions[:max_iter]
trials = trials[:max_iter]
grasp_rate, grasp_lower, grasp_upper = get_grasp_success_rate(actions, rewards=rewards, window=window)
if place:
if 'row' in log_dir or 'row' in title.lower():
place_rate, place_lower, place_upper = get_place_success_rate(heights, actions, include_push=True, hot_fix=True, window=window)
else:
place_rate, place_lower, place_upper = get_place_success_rate(heights, actions, window=window)
eff, eff_lower, eff_upper = get_action_efficiency(heights, window=window)
else:
eff, eff_lower, eff_upper = get_grasp_action_efficiency(actions, rewards, window=window)
plt.plot(mult*grasp_rate, color=colors[0], label='Grasp Success Rate')
if place:
plt.plot(mult*place_rate, color=colors[1], label='Place Success Rate')
plt.plot(mult*eff, color=colors[2], label='Action Efficiency')
plt.fill_between(np.arange(1, grasp_rate.shape[0]+1),
mult*grasp_lower, mult*grasp_upper,
color=colors[0], alpha=alpha)
if place:
plt.fill_between(np.arange(1, place_rate.shape[0]+1),
mult*place_lower, mult*place_upper,
color=colors[1], alpha=alpha)
plt.fill_between(np.arange(1, eff.shape[0]+1),
mult*eff_lower, mult*eff_upper,
color=colors[2], alpha=alpha)
ax = plt.gca()
plt.xlabel('Iteration')
plt.ylabel('Running Mean')
plt.title(title)
plt.legend()
ax.yaxis.set_major_formatter(PercentFormatter())
plt.savefig(log_dir + '_success_plot.pdf')
```
# Any-object Stacking
```
window = 1000
max_iter = None
log_dir = 'any-stack-v2-steps-37k'
title = 'Stack 4 Blocks, Training'
plot_it(log_dir, title, window=window, max_iter=max_iter)
```
# Arranging Rows
```
window = 1000
max_iter = None
log_dir = '../logs/2019-09-13.19-55-21-train-rows-no-images-16.5k'
title = 'Arrange 4 Blocks in Rows'
plot_it(log_dir, title, window=window, max_iter=max_iter)
```
# Push + Grasp
```
window = 200
max_iter = 5000
log_dir = 'train-grasp-place-split-efficientnet-21k-acc'
title = 'Push + Grasp Training'
plot_it(log_dir, title, window=window, max_iter=max_iter, place=False)
```
|
github_jupyter
|
```
# import necessary packages
import json
import requests
import pandas as pd
import polyline
import geopandas as gpd
from shapely.geometry import LineString, Point
import numpy as np
from itertools import product
from haversine import haversine, Unit
from shapely.ops import nearest_points
import os
from matplotlib import pyplot as plt
%matplotlib inline
def create_pt_grid(minx, miny, maxx, maxy):
"""creates a grid of points (lat/longs) in the range specified. lat longs
are rounded to hundredth place
Args:
minx: minimum longitude
miny: minimum latitude
maxx: maximum longitude
maxy: maximum latitude
Returns: DataFrame of all lat/long combinations in region
"""
lats = range(int(miny*1000), int(maxy*1000 +1))
longs = range(int(minx*1000), int(maxx*1000 +1))
ll_df = pd.DataFrame(product(lats, longs),
columns=['lat1000', 'long1000'])
ll_df['geometry'] = [Point(x, y) for x, y in zip(ll_df['long1000'],
ll_df['lat1000'])]
return ll_df
def get_pts_near_path(line, distance):
"""returns all lat/longs within specified distance of line that are in
manhattan
Args:
line: shapely linestring of route
distance: maximum distance from path for returned points
Returns:
pandas dataframe of all points within distance from line
"""
# get line bounds
(minx, miny, maxx, maxy) = line.bounds
# extract max/min values with buffer area
minx = round(minx, 3) -0.002
miny = round(miny, 3) -0.002
maxx = round(maxx, 3) + 0.002
maxy = round(maxy, 3) + 0.002
# load manhattan lat_longs
manhattan_pts = pd.read_csv('models/man_lat_longs.csv')
# brute force fix for floating point error
manhattan_pts['latitude'] = manhattan_pts['lat1000']/1000
manhattan_pts['longitdue'] = manhattan_pts['long1000']/1000
manhattan_pts = manhattan_pts.loc[:, ['latitude', 'longitude']]
# create a df of all lat, longs w/in bounds
all_pts = create_pt_grid(minx, miny, maxx, maxy)
# remove pts not in manhattan
all_pts = pd.merge(all_pts, manhattan_pts,
on=['latitude', 'longitude'],
how='inner')
# flag points in the grid in manhattan as on/within distance of path
all_pts['on_path'] = get_on_path(all_pts['geometry'], distance, line)
return pd.DataFrame(all_pts.loc[(all_pts['on_path']==True)])
practice_grid = create_pt_grid(-74.000, 40.750, -73.960183, 40.7800)
practice_grid_gdf = gpd.GeoDataFrame(practice_grid)
fig, ax = plt.subplots(figsize=(20,20))
practice_grid_gdf.plot(ax=ax)
manhattan_pts = pd.read_csv('/Users/allisonhonold/ds0805/walk_proj/walk_risk_engine/data/csv/man_lat_longs.csv')
manhattan_pts.head()
fig5, ax5 = plt.subplots(figsize=(20,20))
ax5.scatter(manhattan_pts['long1000'], manhattan_pts['lat1000'], alpha=.3)
all_pts = pd.merge(practice_grid_gdf, manhattan_pts.loc[:,['lat1000', 'long1000']],
on=['lat1000', 'long1000'],
how='inner')
all_pts.head()
fig2, ax2 = plt.subplots(figsize=(20,20))
all_pts.plot(ax=ax2)
manhattan_pts.shape
practice_grid_gdf.shape
practice_grid_gdf.head()
man_gdf = gpd.GeoDataFrame(manhattan_pts, geometry=[Point(x, y) for x, y in zip(manhattan_pts['long1000'],
manhattan_pts['lat1000'])])
fig3, ax3 = plt.subplots(figsize=(20,20))
man_gdf.plot(ax=ax3, markersize=2, alpha=.5)
```
|
github_jupyter
|
## 1. Regression discontinuity: banking recovery
<p>After a debt has been legally declared "uncollectable" by a bank, the account is considered "charged-off." But that doesn't mean the bank <strong><em>walks away</em></strong> from the debt. They still want to collect some of the money they are owed. The bank will score the account to assess the expected recovery amount, that is, the expected amount that the bank may be able to receive from the customer in the future. This amount is a function of the probability of the customer paying, the total debt, and other factors that impact the ability and willingness to pay.</p>
<p>The bank has implemented different recovery strategies at different thresholds (\$1000, \$2000, etc.) where the greater the expected recovery amount, the more effort the bank puts into contacting the customer. For low recovery amounts (Level 0), the bank just adds the customer's contact information to their automatic dialer and emailing system. For higher recovery strategies, the bank incurs more costs as they leverage human resources in more efforts to obtain payments. Each additional level of recovery strategy requires an additional \$50 per customer so that customers in the Recovery Strategy Level 1 cost the company \$50 more than those in Level 0. Customers in Level 2 cost \$50 more than those in Level 1, etc. </p>
<p><strong>The big question</strong>: does the extra amount that is recovered at the higher strategy level exceed the extra \$50 in costs? In other words, was there a jump (also called a "discontinuity") of more than \$50 in the amount recovered at the higher strategy level? We'll find out in this notebook.</p>
<p>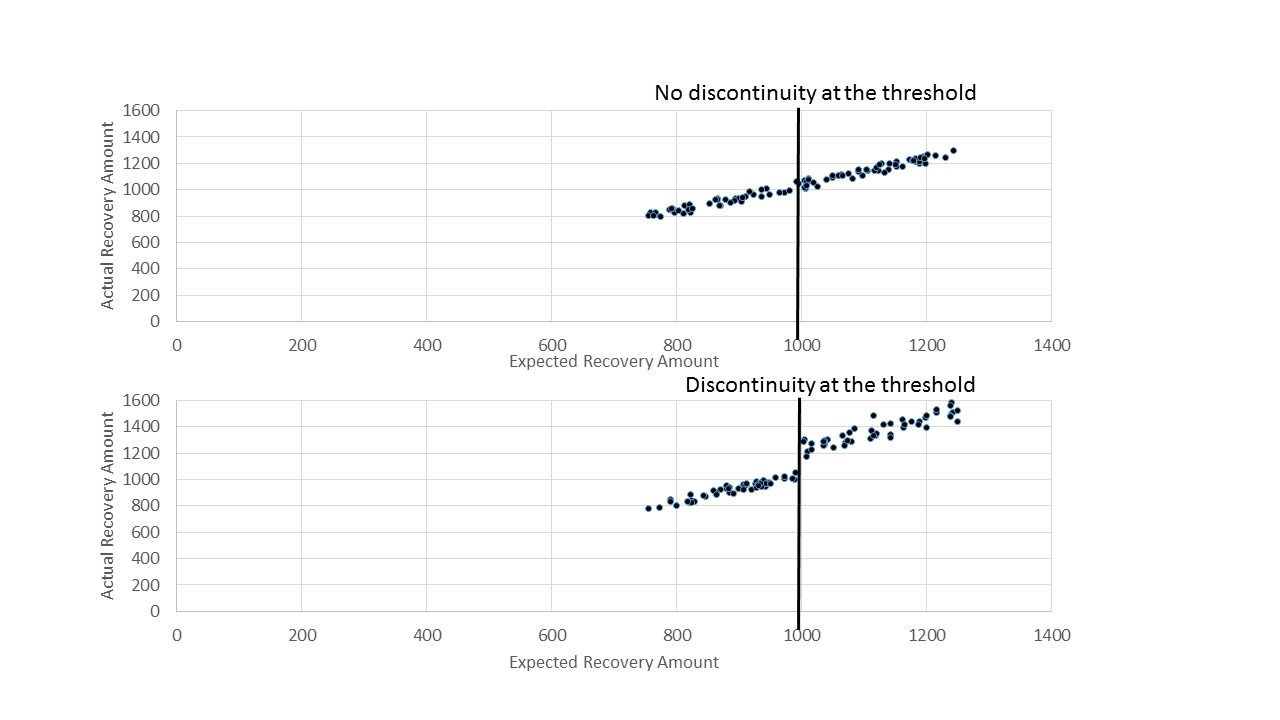</p>
<p>First, we'll load the banking dataset and look at the first few rows of data. This lets us understand the dataset itself and begin thinking about how to analyze the data.</p>
```
# Import modules
import pandas as pd
import numpy as np
# Read in dataset
df = pd.read_csv("datasets/bank_data.csv")
# Print the first few rows of the DataFrame
df.head()
```
## 2. Graphical exploratory data analysis
<p>The bank has implemented different recovery strategies at different thresholds (\$1000, \$2000, \$3000 and \$5000) where the greater the Expected Recovery Amount, the more effort the bank puts into contacting the customer. Zeroing in on the first transition (between Level 0 and Level 1) means we are focused on the population with Expected Recovery Amounts between \$0 and \$2000 where the transition between Levels occurred at \$1000. We know that the customers in Level 1 (expected recovery amounts between \$1001 and \$2000) received more attention from the bank and, by definition, they had higher Expected Recovery Amounts than the customers in Level 0 (between \$1 and \$1000).</p>
<p>Here's a quick summary of the Levels and thresholds again:</p>
<ul>
<li>Level 0: Expected recovery amounts >\$0 and <=\$1000</li>
<li>Level 1: Expected recovery amounts >\$1000 and <=\$2000</li>
<li>The threshold of \$1000 separates Level 0 from Level 1</li>
</ul>
<p>A key question is whether there are other factors besides Expected Recovery Amount that also varied systematically across the \$1000 threshold. For example, does the customer age show a jump (discontinuity) at the \$1000 threshold or does that age vary smoothly? We can examine this by first making a scatter plot of the age as a function of Expected Recovery Amount for a small window of Expected Recovery Amount, \$0 to \$2000. This range covers Levels 0 and 1.</p>
```
# Scatter plot of Age vs. Expected Recovery Amount
from matplotlib import pyplot as plt
%matplotlib inline
plt.scatter(x=df['expected_recovery_amount'], y=df['age'], c="g", s=2)
plt.xlim(0, 2000)
plt.ylim(0, 60)
plt.xlabel("Expected Recovery Amount")
plt.ylabel("Age")
plt.legend(loc=2)
plt.show()
```
## 3. Statistical test: age vs. expected recovery amount
<p>We want to convince ourselves that variables such as age and sex are similar above and below the \$1000 Expected Recovery Amount threshold. This is important because we want to be able to conclude that differences in the actual recovery amount are due to the higher Recovery Strategy and not due to some other difference like age or sex.</p>
<p>The scatter plot of age versus Expected Recovery Amount did not show an obvious jump around \$1000. We will now do statistical analysis examining the average age of the customers just above and just below the threshold. We can start by exploring the range from \$900 to \$1100.</p>
<p>For determining if there is a difference in the ages just above and just below the threshold, we will use the Kruskal-Wallis test, a statistical test that makes no distributional assumptions.</p>
```
# Import stats module
from scipy import stats
# Compute average age just below and above the threshold
era_900_1100 = df.loc[(df['expected_recovery_amount']<1100) &
(df['expected_recovery_amount']>=900)]
by_recovery_strategy = era_900_1100.groupby(['recovery_strategy'])
by_recovery_strategy['age'].describe().unstack()
# Perform Kruskal-Wallis test
Level_0_age = era_900_1100.loc[df['recovery_strategy']=="Level 0 Recovery"]['age']
Level_1_age = era_900_1100.loc[df['recovery_strategy']=="Level 1 Recovery"]['age']
stats.kruskal(Level_0_age,Level_1_age)
```
## 4. Statistical test: sex vs. expected recovery amount
<p>We have seen that there is no major jump in the average customer age just above and just
below the \$1000 threshold by doing a statistical test as well as exploring it graphically with a scatter plot. </p>
<p>We want to also test that the percentage of customers that are male does not jump across the \$1000 threshold. We can start by exploring the range of \$900 to \$1100 and later adjust this range.</p>
<p>We can examine this question statistically by developing cross-tabs as well as doing chi-square tests of the percentage of customers that are male vs. female.</p>
```
# Number of customers in each category
crosstab = pd.crosstab(df.loc[(df['expected_recovery_amount']<1100) &
(df['expected_recovery_amount']>=900)]['recovery_strategy'],
df['sex'])
print(crosstab)
# Chi-square test
chi2_stat, p_val, dof, ex = stats.chi2_contingency(crosstab)
print(p_val)
```
## 5. Exploratory graphical analysis: recovery amount
<p>We are now reasonably confident that customers just above and just below the \$1000 threshold are, on average, similar in their average age and the percentage that are male. </p>
<p>It is now time to focus on the key outcome of interest, the actual recovery amount.</p>
<p>A first step in examining the relationship between the actual recovery amount and the expected recovery amount is to develop a scatter plot where we want to focus our attention at the range just below and just above the threshold. Specifically, we will develop a scatter plot of Expected Recovery Amount (X) versus Actual Recovery Amount (Y) for Expected Recovery Amounts between \$900 to \$1100. This range covers Levels 0 and 1. A key question is whether or not we see a discontinuity (jump) around the \$1000 threshold.</p>
```
# Scatter plot of Actual Recovery Amount vs. Expected Recovery Amount
plt.scatter(x=df['expected_recovery_amount'], y=df['actual_recovery_amount'], c="g", s=2)
plt.xlim(900, 1100)
plt.ylim(0, 2000)
plt.xlabel("Expected Recovery Amount")
plt.ylabel("Actual Recovery Amount")
plt.legend(loc=2)
# ... YOUR CODE FOR TASK 5 ...
```
## 6. Statistical analysis: recovery amount
<p>As we did with age, we can perform statistical tests to see if the actual recovery amount has a discontinuity above the \$1000 threshold. We are going to do this for two different windows of the expected recovery amount \$900 to \$1100 and for a narrow range of \$950 to \$1050 to see if our results are consistent.</p>
<p>Again, we will use the Kruskal-Wallis test.</p>
<p>We will first compute the average actual recovery amount for those customers just below and just above the threshold using a range from \$900 to \$1100. Then we will perform a Kruskal-Wallis test to see if the actual recovery amounts are different just above and just below the threshold. Once we do that, we will repeat these steps for a smaller window of \$950 to \$1050.</p>
```
# Compute average actual recovery amount just below and above the threshold
by_recovery_strategy['actual_recovery_amount'].describe().unstack()
# Perform Kruskal-Wallis test
Level_0_actual = era_900_1100.loc[df['recovery_strategy']=='Level 0 Recovery']['actual_recovery_amount']
Level_1_actual = era_900_1100.loc[df['recovery_strategy']=='Level 1 Recovery']['actual_recovery_amount']
stats.kruskal(Level_0_actual,Level_1_actual)
# Repeat for a smaller range of $950 to $1050
era_950_1050 = df.loc[(df['expected_recovery_amount']<1050) &
(df['expected_recovery_amount']>=950)]
Level_0_actual = era_950_1050.loc[df['recovery_strategy']=='Level 0 Recovery']['actual_recovery_amount']
Level_1_actual = era_950_1050.loc[df['recovery_strategy']=='Level 1 Recovery']['actual_recovery_amount']
stats.kruskal(Level_0_actual,Level_1_actual)
```
## 7. Regression modeling: no threshold
<p>We now want to take a regression-based approach to estimate the program impact at the \$1000 threshold using data that is just above and below the threshold. </p>
<p>We will build two models. The first model does not have a threshold while the second will include a threshold.</p>
<p>The first model predicts the actual recovery amount (dependent variable) as a function of the expected recovery amount (independent variable). We expect that there will be a strong positive relationship between these two variables. </p>
<p>We will examine the adjusted R-squared to see the percent of variance explained by the model. In this model, we are not representing the threshold but simply seeing how the variable used for assigning the customers (expected recovery amount) relates to the outcome variable (actual recovery amount).</p>
```
# Import statsmodels
import statsmodels.api as sm
# Define X and y
X = era_900_1100['expected_recovery_amount']
y = era_900_1100['actual_recovery_amount']
X = sm.add_constant(X)
# Build linear regression model
model = sm.OLS(y, X).fit()
predictions = model.predict(X)
# Print out the model summary statistics
model.summary()
```
## 8. Regression modeling: adding true threshold
<p>From the first model, we see that the expected recovery amount's regression coefficient is statistically significant. </p>
<p>The second model adds an indicator of the true threshold to the model (in this case at \$1000). </p>
<p>We will create an indicator variable (either a 0 or a 1) that represents whether or not the expected recovery amount was greater than \$1000. When we add the true threshold to the model, the regression coefficient for the true threshold represents the additional amount recovered due to the higher recovery strategy. That is to say, the regression coefficient for the true threshold measures the size of the discontinuity for customers just above and just below the threshold.</p>
<p>If the higher recovery strategy helped recovery more money, then the regression coefficient of the true threshold will be greater than zero. If the higher recovery strategy did not help recovery more money, then the regression coefficient will not be statistically significant.</p>
```
#Create indicator (0 or 1) for expected recovery amount >= $1000
df['indicator_1000'] = np.where(df['expected_recovery_amount']<1000, 0, 1)
era_900_1100 = df.loc[(df['expected_recovery_amount']<1100) &
(df['expected_recovery_amount']>=900)]
# Define X and y
X = era_900_1100[['expected_recovery_amount','indicator_1000']]
y = era_900_1100['actual_recovery_amount']
X = sm.add_constant(X)
# Build linear regression model
model = sm.OLS(y,X).fit()
# Print the model summary
model.summary()
```
## 9. Regression modeling: adjusting the window
<p>The regression coefficient for the true threshold was statistically significant with an estimated impact of around \$278. This is much larger than the \$50 per customer needed to run this higher recovery strategy. </p>
<p>Before showing this to our manager, we want to convince ourselves that this result wasn't due to choosing an expected recovery amount window of \$900 to \$1100. Let's repeat this analysis for the window from \$950 to \$1050 to see if we get similar results.</p>
<p>The answer? Whether we use a wide (\$900 to \$1100) or narrower window (\$950 to \$1050), the incremental recovery amount at the higher recovery strategy is much greater than the \$50 per customer it costs for the higher recovery strategy. So we conclude that the higher recovery strategy is worth the extra cost of \$50 per customer.</p>
```
# Redefine era_950_1050 so the indicator variable is included
era_950_1050 = df.loc[(df['expected_recovery_amount']<1050) &
(df['expected_recovery_amount']>=950)]
# Define X and y
X = era_950_1050[['expected_recovery_amount','indicator_1000']]
y = era_950_1050['actual_recovery_amount']
X = sm.add_constant(X)
# Build linear regression model
model = sm.OLS(y,X).fit()
# Print the model summary
model.summary()
```
|
github_jupyter
|
# Cruise collocation with gridded data
Authors
* [Dr Chelle Gentemann](mailto:[email protected]) - Earth and Space Research, USA
* [Dr Marisol Garcia-Reyes](mailto:[email protected]) - Farallon Institute, USA
-------------
# Structure of this tutorial
1. Opening data
1. Collocating satellite data with a cruise dataset
-------------------
## Import python packages
You are going to want numpy, pandas, matplotlib.pyplot and xarray
```
import warnings
warnings.simplefilter('ignore') # filter some warning messages
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import xarray as xr
import cartopy.crs as ccrs
```
## A nice cartopy tutorial is [here](http://earthpy.org/tag/visualization.html)
# Collocating Saildrone cruise data with satellite SSTs
* read in the Saildrone data
## The NCEI trajectory format uses 'obs' as the coordinate. This is an example of an 'older' style of data formatting that doesn't really mesh well with modern software capabilities.
* So, let's change that by using [.swap_dims](http://xarray.pydata.org/en/stable/generated/xarray.DataArray.swap_dims.html) to change the coordinate from `obs` to `time`
* Another thing, `latitude` and `longitude` are just long and annoying, lets [.rename](http://xarray.pydata.org/en/stable/generated/xarray.Dataset.rename.html) them to `lat` and `lon`
* Finally, the first and last part of the cruise the USV is being towed, so let's only include data from `2018-04-12T02` to `2018-06-10T18`
```
#use first url if not online
#url = '../data/saildrone-gen_4-baja_2018-sd1002-20180411T180000-20180611T055959-1_minutes-v1.nc'
url = 'https://podaac-opendap.jpl.nasa.gov/opendap/hyrax/allData/insitu/L2/saildrone/Baja/saildrone-gen_4-baja_2018-sd1002-20180411T180000-20180611T055959-1_minutes-v1.nc'
ds_usv =
ds_usv2 = ds_usv.isel(trajectory=0)\
.swap_dims({'obs':'time'})\
.rename({'longitude':'lon','latitude':'lat'})
ds_usv_subset = ds_usv2.sel(time=slice('2018-04-12T02','2018-06-10T18'))
start_time = pd.to_datetime(str(ds_usv_subset.time.min().data)).strftime('%Y-%m-%dT%H:%m:%SZ')
end_time = pd.to_datetime(str(ds_usv_subset.time.max().data)).strftime('%Y-%m-%dT%H:%m:%SZ')
print('start: ',start_time,'end: ',end_time)
```
## Let's open 2 months of 0.2 km AVHRR OI SST data
`xarray`can open multiple files at once using string pattern matching. `xr.open_mfdataset()`
## Now open multiple files (lazy) using [.open_mfdataset](http://xarray.pydata.org/en/stable/generated/xarray.open_mfdataset.html#xarray.open_mfdataset)
* use the option `coords = 'minimal'`
```
files = '../data/avhrr_oi/*.nc'
ds_sst = xr.open_mfdataset(files,coords = 'minimal')
```
# Let's see what one day looks like
* add coastlines `ax.coastlines()`
* add gridlines `ax.gridlines()`
```
sst = ds_sst.sst[0,:,:]
ax = plt.axes(projection=ccrs.Orthographic(-80, 35))
sst.plot(ax=ax, transform=ccrs.PlateCarree())
```
# Change the figure
* colormap `cmap='jet'
* colorscale `vmin=-1,vmax=34`
* add land `ax.stock_imag()
```
ax = plt.axes(projection=ccrs.Orthographic(-80, 35))
sst.plot(ax=ax, transform=ccrs.PlateCarree())
```
# Look at the sst data and notice the longitude range
## Again with the 0-360 vs -180-180. Change it up below!
* `ds_sst.coords['lon'] = np.mod(ds_sst.coords['lon'] + 180,360) - 180`
* remember to sort by lon, `.sortby(ds_sst.lon)`
* Also, look at the coordinates, there is an extra one `zlev`. Drop it using .isel
```
ds_sst.coords['lon'] = #change lon -180to180
ds_sst = ds_sst # sort lon
ds_sst = ds_sst #isel zlev
ds_sst
```
`open_mfdataset` even puts them in the right order for you.
```
ds_sst.time
```
How big is all this data uncompressed? Will it fit into memory?
Use `.nbytes` / 1e9 to convert it into gigabytes
```
print('file size (GB):', ds_sst.nbytes / 1e9)
```
# Xarray interpolation won't run on chunked dimensions.
1. First let's subset the data to make it smaller to deal with by using the cruise lat/lons
* Find the max/min of the lat/lon using `.lon.min().data`
1. Now load the data into memory (de-Dask-ify) it using `.load()`
```
#Step 1 from above
lon_min,lon_max = ds_usv_subset.lon.min().data,ds_usv_subset.lon.max().data
lat_min,lat_max = ds_usv_subset.lat.min().data,ds_usv_subset.lat.max().data
subset = ds_sst.sel(lon=slice(lon_min,lon_max),
lat=slice(lat_min,lat_max))
print('file size (GB):', subset.nbytes / 1e9)
#Step 2 from above
subset.load()
```
# Collocate USV data with SST data
There are different options when you interpolate. First, let's just do a linear interpolation using [.interp()](http://xarray.pydata.org/en/stable/generated/xarray.Dataset.interp.html#xarray.Dataset.interp)
`Dataset.interp(coords=None, method='linear', assume_sorted=False, kwargs={}, **coords_kwargs))`
```
ds_collocated = subset.interp(lat=ds_usv_subset.lat,lon=ds_usv_subset.lon,time=ds_usv_subset.time,method='linear')
```
# Collocate USV data with SST data
There are different options when you interpolate. First, let's just do a nearest point rather than interpolate the data
`method = 'nearest'`
```
ds_collocated_nearest = subset.interp(lat=ds_usv_subset.lat,lon=ds_usv_subset.lon,time=ds_usv_subset.time,method='nearest')
```
## Now, calculate the different in SSTs and print the [.mean()](http://xarray.pydata.org/en/stable/generated/xarray.DataArray.mean.html#xarray.DataArray.mean) and [.std()](http://xarray.pydata.org/en/stable/generated/xarray.DataArray.std.html#xarray.DataArray.std)
For the satellite data we need to use `sst` and for the USV data we need to use `TEMP_CTD_MEAN`
```
dif = ds_collocated_nearest.sst-ds_usv_subset.TEMP_CTD_MEAN
print('mean difference = ',dif.mean().data)
print('STD = ',dif.std().data)
```
# xarray can do more!
* concatentaion
* open network located files with openDAP
* import and export Pandas DataFrames
* .nc dump to
* groupby_bins
* resampling and reduction
For more details, read this blog post: http://continuum.io/blog/xray-dask
```
#ds_collocated_nearest.to_netcdf('./data/new file.nc')
```
## Where can I find more info?
### For more information about xarray
- Read the [online documentation](http://xarray.pydata.org/)
- Ask questions on [StackOverflow](http://stackoverflow.com/questions/tagged/python-xarray)
- View the source code and file bug reports on [GitHub](http://github.com/pydata/xarray/)
### For more doing data analysis with Python:
- Thomas Wiecki, [A modern guide to getting started with Data Science and Python](http://twiecki.github.io/blog/2014/11/18/python-for-data-science/)
- Wes McKinney, [Python for Data Analysis](http://shop.oreilly.com/product/0636920023784.do) (book)
### Packages building on xarray for the geophysical sciences
For analyzing GCM output:
- [xgcm](https://github.com/xgcm/xgcm) by Ryan Abernathey
- [oogcm](https://github.com/lesommer/oocgcm) by Julien Le Sommer
- [MPAS xarray](https://github.com/pwolfram/mpas_xarray) by Phil Wolfram
- [marc_analysis](https://github.com/darothen/marc_analysis) by Daniel Rothenberg
Other tools:
- [windspharm](https://github.com/ajdawson/windspharm): wind spherical harmonics by Andrew Dawson
- [eofs](https://github.com/ajdawson/eofs): empirical orthogonal functions by Andrew Dawson
- [infinite-diff](https://github.com/spencerahill/infinite-diff) by Spencer Hill
- [aospy](https://github.com/spencerahill/aospy) by Spencer Hill and Spencer Clark
- [regionmask](https://github.com/mathause/regionmask) by Mathias Hauser
- [salem](https://github.com/fmaussion/salem) by Fabien Maussion
Resources for teaching and learning xarray in geosciences:
- [Fabien's teaching repo](https://github.com/fmaussion/teaching): courses that combine teaching climatology and xarray
|
github_jupyter
|
```
from nltk.classify import NaiveBayesClassifier
from nltk.corpus import stopwords
stopset = list(set(stopwords.words('english')))
import re
import csv
import nltk.classify
def replaceTwoOrMore(s):
pattern = re.compile(r"(.)\1{1,}", re.DOTALL)
return pattern.sub(r"\1\1", s)
def processTweet(tweet):
tweet = tweet.lower()
tweet = re.sub('((www\.[^\s]+)|(https?://[^\s]+))', 'URL', tweet)
tweet = re.sub('@[^\s]+', 'AT_USER', tweet)
tweet = re.sub('[\s]+', ' ', tweet)
tweet = re.sub(r'#([^\s]+)', r'\1', tweet)
tweet = tweet.strip('\'"')
return tweet
def getStopWordList(stopWordListFileName):
stopWords = []
stopWords.append('AT_USER')
stopWords.append('URL')
fp = open(stopWordListFileName, 'r')
line = fp.readline()
while line:
word = line.strip()
stopWords.append(word)
line = fp.readline()
fp.close()
return stopWords
def getFeatureVector(tweet, stopWords):
featureVector = []
words = tweet.split()
for w in words:
w = replaceTwoOrMore(w)
w = w.strip('\'"?,.')
val = re.search(r"^[a-zA-Z][a-zA-Z0-9]*[a-zA-Z]+[a-zA-Z0-9]*$", w)
if (w in stopWords or val is None):
continue
else:
featureVector.append(w.lower())
return featureVector
def extract_features(tweet):
tweet_words = set(tweet)
features = {}
for word in featureList:
features['contains(%s)' % word] = (word in tweet_words)
return features
inpTweets = csv.reader(open('data/training.csv', 'r'), delimiter=',', quotechar='|')
stopWords = getStopWordList('data/stopwordsID.txt')
count = 0;
featureList = []
tweets = []
for row in inpTweets:
sentiment = row[0]
tweet = row[1]
processedTweet = processTweet(tweet) # preprocessing
featureVector = getFeatureVector(processedTweet, stopWords) # get feature vector
featureList.extend(featureVector)
tweets.append((featureVector, sentiment));
featureList = list(set(featureList))
training_set = nltk.classify.util.apply_features(extract_features, tweets)
NBClassifier = nltk.NaiveBayesClassifier.train(training_set)
testTweet = 'pantai di lombok bersih bersih. pasirnya juga indah'
processedTestTweet = processTweet(testTweet)
sentiment = NBClassifier.classify(extract_features(getFeatureVector(processedTestTweet, stopWords)))
print("Test Tweets = %s, Sentiment = %s\n" % (testTweet, sentiment))
# print("Show Most Informative Features", NBClassifier.show_most_informative_features(32))
# print()
# print("Extract Features", extract_features(testTweet.split()))
print("Akurasi Hasil Klasifikasi :", (nltk.classify.accuracy(processedTestTweet, NBClassifier)) * 100)
# print("Akurasi Hasil Klasifikasi :", accuracy_score(testTweet, sentiment))
# kal = getFeatureVector(processTweet(testTweet), stopWords)
# kal = " ".join(str(x) for x in kal)
# print(kal)
# d = {}
# for word in kal.split():
# word = int(word) if word.isdigit() else word
# if word in d:
# d[word] += 1
# else:
# d[word] = 1
# print(d)
```
|
github_jupyter
|
##### Copyright 2018 The TensorFlow Authors.
```
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
```
# Ragged Tensors
<table class="tfo-notebook-buttons" align="left">
<td>
<a target="_blank" href="https://www.tensorflow.org/beta/guide/ragged_tensors"><img src="https://www.tensorflow.org/images/tf_logo_32px.png" />View on TensorFlow.org</a>
</td>
<td>
<a target="_blank" href="https://colab.research.google.com/github/tensorflow/docs/blob/master/site/en/r2/guide/ragged_tensors.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
</td>
<td>
<a target="_blank" href="https://github.com/tensorflow/docs/blob/master/site/en/r2/guide/ragged_tensors.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View source on GitHub</a>
</td>
<td>
<a href="https://storage.googleapis.com/tensorflow_docs/docs/site/en/r2/guide/ragged_tensors.ipynb"><img src="https://www.tensorflow.org/images/download_logo_32px.png" />Download notebook</a>
</td>
</table>
## Setup
```
from __future__ import absolute_import, division, print_function, unicode_literals
import math
try:
%tensorflow_version 2.x # Colab only.
except Exception:
pass
import tensorflow as tf
```
## Overview
Your data comes in many shapes; your tensors should too.
*Ragged tensors* are the TensorFlow equivalent of nested variable-length
lists. They make it easy to store and process data with non-uniform shapes,
including:
* Variable-length features, such as the set of actors in a movie.
* Batches of variable-length sequential inputs, such as sentences or video
clips.
* Hierarchical inputs, such as text documents that are subdivided into
sections, paragraphs, sentences, and words.
* Individual fields in structured inputs, such as protocol buffers.
### What you can do with a ragged tensor
Ragged tensors are supported by more than a hundred TensorFlow operations,
including math operations (such as `tf.add` and `tf.reduce_mean`), array operations
(such as `tf.concat` and `tf.tile`), string manipulation ops (such as
`tf.substr`), and many others:
```
digits = tf.ragged.constant([[3, 1, 4, 1], [], [5, 9, 2], [6], []])
words = tf.ragged.constant([["So", "long"], ["thanks", "for", "all", "the", "fish"]])
print(tf.add(digits, 3))
print(tf.reduce_mean(digits, axis=1))
print(tf.concat([digits, [[5, 3]]], axis=0))
print(tf.tile(digits, [1, 2]))
print(tf.strings.substr(words, 0, 2))
```
There are also a number of methods and operations that are
specific to ragged tensors, including factory methods, conversion methods,
and value-mapping operations.
For a list of supported ops, see the `tf.ragged` package
documentation.
As with normal tensors, you can use Python-style indexing to access specific
slices of a ragged tensor. For more information, see the section on
**Indexing** below.
```
print(digits[0]) # First row
print(digits[:, :2]) # First two values in each row.
print(digits[:, -2:]) # Last two values in each row.
```
And just like normal tensors, you can use Python arithmetic and comparison
operators to perform elementwise operations. For more information, see the section on
**Overloaded Operators** below.
```
print(digits + 3)
print(digits + tf.ragged.constant([[1, 2, 3, 4], [], [5, 6, 7], [8], []]))
```
If you need to perform an elementwise transformation to the values of a `RaggedTensor`, you can use `tf.ragged.map_flat_values`, which takes a function plus one or more arguments, and applies the function to transform the `RaggedTensor`'s values.
```
times_two_plus_one = lambda x: x * 2 + 1
print(tf.ragged.map_flat_values(times_two_plus_one, digits))
```
### Constructing a ragged tensor
The simplest way to construct a ragged tensor is using
`tf.ragged.constant`, which builds the
`RaggedTensor` corresponding to a given nested Python `list`:
```
sentences = tf.ragged.constant([
["Let's", "build", "some", "ragged", "tensors", "!"],
["We", "can", "use", "tf.ragged.constant", "."]])
print(sentences)
paragraphs = tf.ragged.constant([
[['I', 'have', 'a', 'cat'], ['His', 'name', 'is', 'Mat']],
[['Do', 'you', 'want', 'to', 'come', 'visit'], ["I'm", 'free', 'tomorrow']],
])
print(paragraphs)
```
Ragged tensors can also be constructed by pairing flat *values* tensors with
*row-partitioning* tensors indicating how those values should be divided into
rows, using factory classmethods such as `tf.RaggedTensor.from_value_rowids`,
`tf.RaggedTensor.from_row_lengths`, and
`tf.RaggedTensor.from_row_splits`.
#### `tf.RaggedTensor.from_value_rowids`
If you know which row each value belongs in, then you can build a `RaggedTensor` using a `value_rowids` row-partitioning tensor:
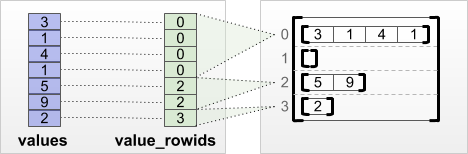
```
print(tf.RaggedTensor.from_value_rowids(
values=[3, 1, 4, 1, 5, 9, 2, 6],
value_rowids=[0, 0, 0, 0, 2, 2, 2, 3]))
```
#### `tf.RaggedTensor.from_row_lengths`
If you know how long each row is, then you can use a `row_lengths` row-partitioning tensor:
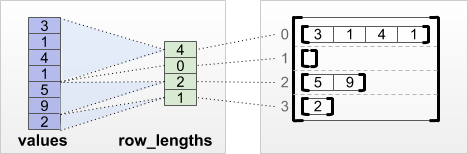
```
print(tf.RaggedTensor.from_row_lengths(
values=[3, 1, 4, 1, 5, 9, 2, 6],
row_lengths=[4, 0, 3, 1]))
```
#### `tf.RaggedTensor.from_row_splits`
If you know the index where each row starts and ends, then you can use a `row_splits` row-partitioning tensor:
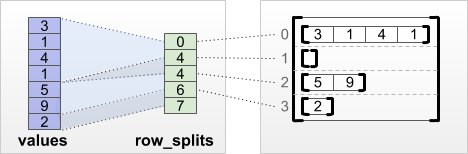
```
print(tf.RaggedTensor.from_row_splits(
values=[3, 1, 4, 1, 5, 9, 2, 6],
row_splits=[0, 4, 4, 7, 8]))
```
See the `tf.RaggedTensor` class documentation for a full list of factory methods.
### What you can store in a ragged tensor
As with normal `Tensor`s, the values in a `RaggedTensor` must all have the same
type; and the values must all be at the same nesting depth (the *rank* of the
tensor):
```
print(tf.ragged.constant([["Hi"], ["How", "are", "you"]])) # ok: type=string, rank=2
print(tf.ragged.constant([[[1, 2], [3]], [[4, 5]]])) # ok: type=int32, rank=3
try:
tf.ragged.constant([["one", "two"], [3, 4]]) # bad: multiple types
except ValueError as exception:
print(exception)
try:
tf.ragged.constant(["A", ["B", "C"]]) # bad: multiple nesting depths
except ValueError as exception:
print(exception)
```
### Example use case
The following example demonstrates how `RaggedTensor`s can be used to construct
and combine unigram and bigram embeddings for a batch of variable-length
queries, using special markers for the beginning and end of each sentence.
For more details on the ops used in this example, see the `tf.ragged` package documentation.
```
queries = tf.ragged.constant([['Who', 'is', 'Dan', 'Smith'],
['Pause'],
['Will', 'it', 'rain', 'later', 'today']])
# Create an embedding table.
num_buckets = 1024
embedding_size = 4
embedding_table = tf.Variable(
tf.random.truncated_normal([num_buckets, embedding_size],
stddev=1.0 / math.sqrt(embedding_size)))
# Look up the embedding for each word.
word_buckets = tf.strings.to_hash_bucket_fast(queries, num_buckets)
word_embeddings = tf.ragged.map_flat_values(
tf.nn.embedding_lookup, embedding_table, word_buckets) # ①
# Add markers to the beginning and end of each sentence.
marker = tf.fill([queries.nrows(), 1], '#')
padded = tf.concat([marker, queries, marker], axis=1) # ②
# Build word bigrams & look up embeddings.
bigrams = tf.strings.join([padded[:, :-1],
padded[:, 1:]],
separator='+') # ③
bigram_buckets = tf.strings.to_hash_bucket_fast(bigrams, num_buckets)
bigram_embeddings = tf.ragged.map_flat_values(
tf.nn.embedding_lookup, embedding_table, bigram_buckets) # ④
# Find the average embedding for each sentence
all_embeddings = tf.concat([word_embeddings, bigram_embeddings], axis=1) # ⑤
avg_embedding = tf.reduce_mean(all_embeddings, axis=1) # ⑥
print(avg_embedding)
```
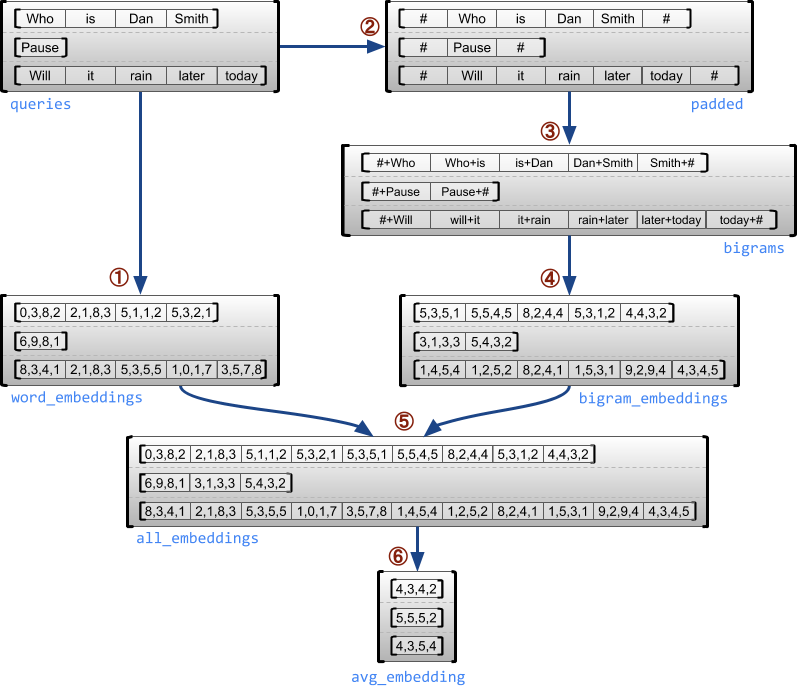
## Ragged tensors: definitions
### Ragged and uniform dimensions
A *ragged tensor* is a tensor with one or more *ragged dimensions*,
which are dimensions whose slices may have different lengths. For example, the
inner (column) dimension of `rt=[[3, 1, 4, 1], [], [5, 9, 2], [6], []]` is
ragged, since the column slices (`rt[0, :]`, ..., `rt[4, :]`) have different
lengths. Dimensions whose slices all have the same length are called *uniform
dimensions*.
The outermost dimension of a ragged tensor is always uniform, since it consists
of a single slice (and so there is no possibility for differing slice lengths).
In addition to the uniform outermost dimension, ragged tensors may also have
uniform inner dimensions. For example, we might store the word embeddings for
each word in a batch of sentences using a ragged tensor with shape
`[num_sentences, (num_words), embedding_size]`, where the parentheses around
`(num_words)` indicate that the dimension is ragged.
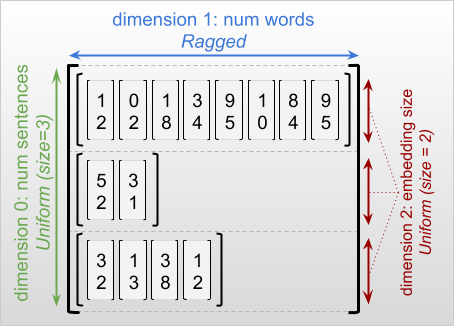
Ragged tensors may have multiple ragged dimensions. For example, we could store
a batch of structured text documents using a tensor with shape `[num_documents,
(num_paragraphs), (num_sentences), (num_words)]` (where again parentheses are
used to indicate ragged dimensions).
#### Ragged tensor shape restrictions
The shape of a ragged tensor is currently restricted to have the following form:
* A single uniform dimension
* Followed by one or more ragged dimensions
* Followed by zero or more uniform dimensions.
Note: These restrictions are a consequence of the current implementation, and we
may relax them in the future.
### Rank and ragged rank
The total number of dimensions in a ragged tensor is called its ***rank***, and
the number of ragged dimensions in a ragged tensor is called its ***ragged
rank***. In graph execution mode (i.e., non-eager mode), a tensor's ragged rank
is fixed at creation time: it can't depend
on runtime values, and can't vary dynamically for different session runs.
A ***potentially ragged tensor*** is a value that might be
either a `tf.Tensor` or a `tf.RaggedTensor`. The
ragged rank of a `tf.Tensor` is defined to be zero.
### RaggedTensor shapes
When describing the shape of a RaggedTensor, ragged dimensions are indicated by
enclosing them in parentheses. For example, as we saw above, the shape of a 3-D
RaggedTensor that stores word embeddings for each word in a batch of sentences
can be written as `[num_sentences, (num_words), embedding_size]`.
The `RaggedTensor.shape` attribute returns a `tf.TensorShape` for a
ragged tensor, where ragged dimensions have size `None`:
```
tf.ragged.constant([["Hi"], ["How", "are", "you"]]).shape
```
The method `tf.RaggedTensor.bounding_shape` can be used to find a tight
bounding shape for a given `RaggedTensor`:
```
print(tf.ragged.constant([["Hi"], ["How", "are", "you"]]).bounding_shape())
```
## Ragged vs sparse tensors
A ragged tensor should *not* be thought of as a type of sparse tensor, but
rather as a dense tensor with an irregular shape.
As an illustrative example, consider how array operations such as `concat`,
`stack`, and `tile` are defined for ragged vs. sparse tensors. Concatenating
ragged tensors joins each row to form a single row with the combined length:

```
ragged_x = tf.ragged.constant([["John"], ["a", "big", "dog"], ["my", "cat"]])
ragged_y = tf.ragged.constant([["fell", "asleep"], ["barked"], ["is", "fuzzy"]])
print(tf.concat([ragged_x, ragged_y], axis=1))
```
But concatenating sparse tensors is equivalent to concatenating the corresponding dense tensors,
as illustrated by the following example (where Ø indicates missing values):
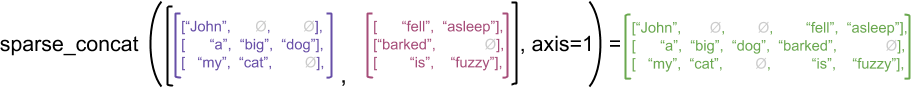
```
sparse_x = ragged_x.to_sparse()
sparse_y = ragged_y.to_sparse()
sparse_result = tf.sparse.concat(sp_inputs=[sparse_x, sparse_y], axis=1)
print(tf.sparse.to_dense(sparse_result, ''))
```
For another example of why this distinction is important, consider the
definition of “the mean value of each row” for an op such as `tf.reduce_mean`.
For a ragged tensor, the mean value for a row is the sum of the
row’s values divided by the row’s width.
But for a sparse tensor, the mean value for a row is the sum of the
row’s values divided by the sparse tensor’s overall width (which is
greater than or equal to the width of the longest row).
## Overloaded operators
The `RaggedTensor` class overloads the standard Python arithmetic and comparison
operators, making it easy to perform basic elementwise math:
```
x = tf.ragged.constant([[1, 2], [3], [4, 5, 6]])
y = tf.ragged.constant([[1, 1], [2], [3, 3, 3]])
print(x + y)
```
Since the overloaded operators perform elementwise computations, the inputs to
all binary operations must have the same shape, or be broadcastable to the same
shape. In the simplest broadcasting case, a single scalar is combined
elementwise with each value in a ragged tensor:
```
x = tf.ragged.constant([[1, 2], [3], [4, 5, 6]])
print(x + 3)
```
For a discussion of more advanced cases, see the section on
**Broadcasting**.
Ragged tensors overload the same set of operators as normal `Tensor`s: the unary
operators `-`, `~`, and `abs()`; and the binary operators `+`, `-`, `*`, `/`,
`//`, `%`, `**`, `&`, `|`, `^`, `<`, `<=`, `>`, and `>=`. Note that, as with
standard `Tensor`s, binary `==` is not overloaded; you can use
`tf.equal()` to check elementwise equality.
## Indexing
Ragged tensors support Python-style indexing, including multidimensional
indexing and slicing. The following examples demonstrate ragged tensor indexing
with a 2-D and a 3-D ragged tensor.
### Indexing a 2-D ragged tensor with 1 ragged dimension
```
queries = tf.ragged.constant(
[['Who', 'is', 'George', 'Washington'],
['What', 'is', 'the', 'weather', 'tomorrow'],
['Goodnight']])
print(queries[1])
print(queries[1, 2]) # A single word
print(queries[1:]) # Everything but the first row
print(queries[:, :3]) # The first 3 words of each query
print(queries[:, -2:]) # The last 2 words of each query
```
### Indexing a 3-D ragged tensor with 2 ragged dimensions
```
rt = tf.ragged.constant([[[1, 2, 3], [4]],
[[5], [], [6]],
[[7]],
[[8, 9], [10]]])
print(rt[1]) # Second row (2-D RaggedTensor)
print(rt[3, 0]) # First element of fourth row (1-D Tensor)
print(rt[:, 1:3]) # Items 1-3 of each row (3-D RaggedTensor)
print(rt[:, -1:]) # Last item of each row (3-D RaggedTensor)
```
`RaggedTensor`s supports multidimensional indexing and slicing, with one
restriction: indexing into a ragged dimension is not allowed. This case is
problematic because the indicated value may exist in some rows but not others.
In such cases, it's not obvious whether we should (1) raise an `IndexError`; (2)
use a default value; or (3) skip that value and return a tensor with fewer rows
than we started with. Following the
[guiding principles of Python](https://www.python.org/dev/peps/pep-0020/)
("In the face
of ambiguity, refuse the temptation to guess" ), we currently disallow this
operation.
## Tensor Type Conversion
The `RaggedTensor` class defines methods that can be used to convert
between `RaggedTensor`s and `tf.Tensor`s or `tf.SparseTensors`:
```
ragged_sentences = tf.ragged.constant([
['Hi'], ['Welcome', 'to', 'the', 'fair'], ['Have', 'fun']])
print(ragged_sentences.to_tensor(default_value=''))
print(ragged_sentences.to_sparse())
x = [[1, 3, -1, -1], [2, -1, -1, -1], [4, 5, 8, 9]]
print(tf.RaggedTensor.from_tensor(x, padding=-1))
st = tf.SparseTensor(indices=[[0, 0], [2, 0], [2, 1]],
values=['a', 'b', 'c'],
dense_shape=[3, 3])
print(tf.RaggedTensor.from_sparse(st))
```
## Evaluating ragged tensors
### Eager execution
In eager execution mode, ragged tensors are evaluated immediately. To access the
values they contain, you can:
* Use the
`tf.RaggedTensor.to_list()`
method, which converts the ragged tensor to a Python `list`.
```
rt = tf.ragged.constant([[1, 2], [3, 4, 5], [6], [], [7]])
print(rt.to_list())
```
* Use Python indexing. If the tensor piece you select contains no ragged
dimensions, then it will be returned as an `EagerTensor`. You can then use
the `numpy()` method to access the value directly.
```
print(rt[1].numpy())
```
* Decompose the ragged tensor into its components, using the
`tf.RaggedTensor.values`
and
`tf.RaggedTensor.row_splits`
properties, or row-paritioning methods such as `tf.RaggedTensor.row_lengths()`
and `tf.RaggedTensor.value_rowids()`.
```
print(rt.values)
print(rt.row_splits)
```
### Broadcasting
Broadcasting is the process of making tensors with different shapes have
compatible shapes for elementwise operations. For more background on
broadcasting, see:
* [Numpy: Broadcasting](https://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
* `tf.broadcast_dynamic_shape`
* `tf.broadcast_to`
The basic steps for broadcasting two inputs `x` and `y` to have compatible
shapes are:
1. If `x` and `y` do not have the same number of dimensions, then add outer
dimensions (with size 1) until they do.
2. For each dimension where `x` and `y` have different sizes:
* If `x` or `y` have size `1` in dimension `d`, then repeat its values
across dimension `d` to match the other input's size.
* Otherwise, raise an exception (`x` and `y` are not broadcast
compatible).
Where the size of a tensor in a uniform dimension is a single number (the size
of slices across that dimension); and the size of a tensor in a ragged dimension
is a list of slice lengths (for all slices across that dimension).
#### Broadcasting examples
```
# x (2D ragged): 2 x (num_rows)
# y (scalar)
# result (2D ragged): 2 x (num_rows)
x = tf.ragged.constant([[1, 2], [3]])
y = 3
print(x + y)
# x (2d ragged): 3 x (num_rows)
# y (2d tensor): 3 x 1
# Result (2d ragged): 3 x (num_rows)
x = tf.ragged.constant(
[[10, 87, 12],
[19, 53],
[12, 32]])
y = [[1000], [2000], [3000]]
print(x + y)
# x (3d ragged): 2 x (r1) x 2
# y (2d ragged): 1 x 1
# Result (3d ragged): 2 x (r1) x 2
x = tf.ragged.constant(
[[[1, 2], [3, 4], [5, 6]],
[[7, 8]]],
ragged_rank=1)
y = tf.constant([[10]])
print(x + y)
# x (3d ragged): 2 x (r1) x (r2) x 1
# y (1d tensor): 3
# Result (3d ragged): 2 x (r1) x (r2) x 3
x = tf.ragged.constant(
[
[
[[1], [2]],
[],
[[3]],
[[4]],
],
[
[[5], [6]],
[[7]]
]
],
ragged_rank=2)
y = tf.constant([10, 20, 30])
print(x + y)
```
Here are some examples of shapes that do not broadcast:
```
# x (2d ragged): 3 x (r1)
# y (2d tensor): 3 x 4 # trailing dimensions do not match
x = tf.ragged.constant([[1, 2], [3, 4, 5, 6], [7]])
y = tf.constant([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])
try:
x + y
except tf.errors.InvalidArgumentError as exception:
print(exception)
# x (2d ragged): 3 x (r1)
# y (2d ragged): 3 x (r2) # ragged dimensions do not match.
x = tf.ragged.constant([[1, 2, 3], [4], [5, 6]])
y = tf.ragged.constant([[10, 20], [30, 40], [50]])
try:
x + y
except tf.errors.InvalidArgumentError as exception:
print(exception)
# x (3d ragged): 3 x (r1) x 2
# y (3d ragged): 3 x (r1) x 3 # trailing dimensions do not match
x = tf.ragged.constant([[[1, 2], [3, 4], [5, 6]],
[[7, 8], [9, 10]]])
y = tf.ragged.constant([[[1, 2, 0], [3, 4, 0], [5, 6, 0]],
[[7, 8, 0], [9, 10, 0]]])
try:
x + y
except tf.errors.InvalidArgumentError as exception:
print(exception)
```
## RaggedTensor encoding
Ragged tensors are encoded using the `RaggedTensor` class. Internally, each
`RaggedTensor` consists of:
* A `values` tensor, which concatenates the variable-length rows into a
flattened list.
* A `row_splits` vector, which indicates how those flattened values are
divided into rows. In particular, the values for row `rt[i]` are stored in
the slice `rt.values[rt.row_splits[i]:rt.row_splits[i+1]]`.

```
rt = tf.RaggedTensor.from_row_splits(
values=[3, 1, 4, 1, 5, 9, 2],
row_splits=[0, 4, 4, 6, 7])
print(rt)
```
### Multiple ragged dimensions
A ragged tensor with multiple ragged dimensions is encoded by using a nested
`RaggedTensor` for the `values` tensor. Each nested `RaggedTensor` adds a single
ragged dimension.
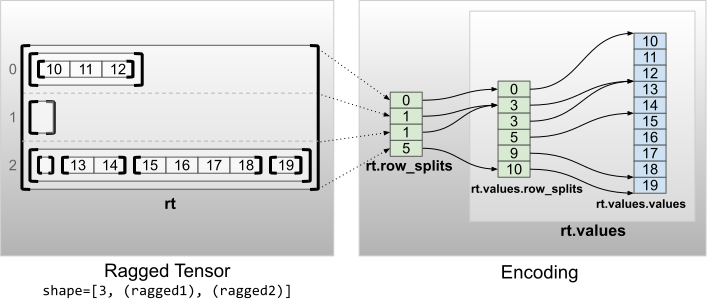
```
rt = tf.RaggedTensor.from_row_splits(
values=tf.RaggedTensor.from_row_splits(
values=[10, 11, 12, 13, 14, 15, 16, 17, 18, 19],
row_splits=[0, 3, 3, 5, 9, 10]),
row_splits=[0, 1, 1, 5])
print(rt)
print("Shape: {}".format(rt.shape))
print("Number of ragged dimensions: {}".format(rt.ragged_rank))
```
The factory function `tf.RaggedTensor.from_nested_row_splits` may be used to construct a
RaggedTensor with multiple ragged dimensions directly, by providing a list of
`row_splits` tensors:
```
rt = tf.RaggedTensor.from_nested_row_splits(
flat_values=[10, 11, 12, 13, 14, 15, 16, 17, 18, 19],
nested_row_splits=([0, 1, 1, 5], [0, 3, 3, 5, 9, 10]))
print(rt)
```
### Uniform Inner Dimensions
Ragged tensors with uniform inner dimensions are encoded by using a
multidimensional `tf.Tensor` for `values`.
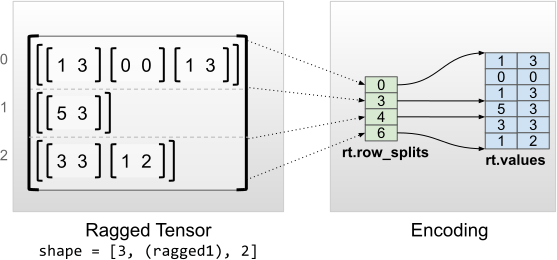
```
rt = tf.RaggedTensor.from_row_splits(
values=[[1, 3], [0, 0], [1, 3], [5, 3], [3, 3], [1, 2]],
row_splits=[0, 3, 4, 6])
print(rt)
print("Shape: {}".format(rt.shape))
print("Number of ragged dimensions: {}".format(rt.ragged_rank))
```
### Alternative row-partitioning schemes
The `RaggedTensor` class uses `row_splits` as the primary mechanism to store
information about how the values are partitioned into rows. However,
`RaggedTensor` also provides support for four alternative row-partitioning
schemes, which can be more convenient to use depending on how your data is
formatted. Internally, `RaggedTensor` uses these additional schemes to improve
efficiency in some contexts.
<dl>
<dt>Row lengths</dt>
<dd>`row_lengths` is a vector with shape `[nrows]`, which specifies the
length of each row.</dd>
<dt>Row starts</dt>
<dd>`row_starts` is a vector with shape `[nrows]`, which specifies the start
offset of each row. Equivalent to `row_splits[:-1]`.</dd>
<dt>Row limits</dt>
<dd>`row_limits` is a vector with shape `[nrows]`, which specifies the stop
offset of each row. Equivalent to `row_splits[1:]`.</dd>
<dt>Row indices and number of rows</dt>
<dd>`value_rowids` is a vector with shape `[nvals]`, corresponding
one-to-one with values, which specifies each value's row index. In
particular, the row `rt[row]` consists of the values `rt.values[j]` where
`value_rowids[j]==row`. \
`nrows` is an integer that specifies the number of rows in the
`RaggedTensor`. In particular, `nrows` is used to indicate trailing empty
rows.</dd>
</dl>
For example, the following ragged tensors are equivalent:
```
values = [3, 1, 4, 1, 5, 9, 2, 6]
print(tf.RaggedTensor.from_row_splits(values, row_splits=[0, 4, 4, 7, 8, 8]))
print(tf.RaggedTensor.from_row_lengths(values, row_lengths=[4, 0, 3, 1, 0]))
print(tf.RaggedTensor.from_row_starts(values, row_starts=[0, 4, 4, 7, 8]))
print(tf.RaggedTensor.from_row_limits(values, row_limits=[4, 4, 7, 8, 8]))
print(tf.RaggedTensor.from_value_rowids(
values, value_rowids=[0, 0, 0, 0, 2, 2, 2, 3], nrows=5))
```
The RaggedTensor class defines methods which can be used to construct
each of these row-partitioning tensors.
```
rt = tf.ragged.constant([[3, 1, 4, 1], [], [5, 9, 2], [6], []])
print(" values: {}".format(rt.values))
print(" row_splits: {}".format(rt.row_splits))
print(" row_lengths: {}".format(rt.row_lengths()))
print(" row_starts: {}".format(rt.row_starts()))
print(" row_limits: {}".format(rt.row_limits()))
print("value_rowids: {}".format(rt.value_rowids()))
```
(Note that `tf.RaggedTensor.values` and `tf.RaggedTensors.row_splits` are properties, while the remaining row-partitioning accessors are all methods. This reflects the fact that the `row_splits` are the primary underlying representation, and the other row-partitioning tensors must be computed.)
Some of the advantages and disadvantages of the different row-partitioning
schemes are:
+ **Efficient indexing**:
The `row_splits`, `row_starts`, and `row_limits` schemes all enable
constant-time indexing into ragged tensors. The `value_rowids` and
`row_lengths` schemes do not.
+ **Small encoding size**:
The `value_rowids` scheme is more efficient when storing ragged tensors that
have a large number of empty rows, since the size of the tensor depends only
on the total number of values. On the other hand, the other four encodings
are more efficient when storing ragged tensors with longer rows, since they
require only one scalar value for each row.
+ **Efficient concatenation**:
The `row_lengths` scheme is more efficient when concatenating ragged
tensors, since row lengths do not change when two tensors are concatenated
together (but row splits and row indices do).
+ **Compatibility**:
The `value_rowids` scheme matches the
[segmentation](../api_guides/python/math_ops.md#Segmentation)
format used by operations such as `tf.segment_sum`. The `row_limits` scheme
matches the format used by ops such as `tf.sequence_mask`.
```
```
|
github_jupyter
|
# LeetCode Algorithm Test Case 551
## (学生出勤记录 I)[https://leetcode-cn.com/problems/student-attendance-record-i/]
[TOC]
给你一个字符串 s 表示一个学生的出勤记录,其中的每个字符用来标记当天的出勤情况(缺勤、迟到、到场)。记录中只含下面三种字符:
1. 'A':Absent,缺勤
2. 'L':Late,迟到
3. 'P':Present,到场
如果学生能够 同时 满足下面两个条件,则可以获得出勤奖励:
1. 按 总出勤 计,学生缺勤('A')严格 少于两天。
2. 学生 不会 存在 连续 3 天或 3 天以上的迟到('L')记录。
如果学生可以获得出勤奖励,返回 true ;否则,返回 false 。
> 示例 1:
> 输入: s = "PPALLP"
> 输出: true
> 解释: 学生缺勤次数少于 2 次,且不存在 3 天或以上的连续迟到记录。
> 示例 2:
> 输入: s = "PPALLL"
> 输出: false
> 解释: 学生最后三天连续迟到,所以不满足出勤奖励的条件。
> 提示:
> - `1 <= s.length <= 1000`
> - `s[i]` 为 `A`、`L` 或 `P`
### Type A: Violent Enumeration Solution - Scheme I
> 2021/08/17 Kevin Tang
```
from typing import List
def checkRecord_TypeA_Scheme_A(s: str) -> bool:
"""
:param nums:
:param target:
:return:
>>> ic(checkRecord_TypeA_Scheme_A(s="PPALLP"))
True
>>> ic(checkRecord_TypeA_Scheme_A(s="PPALLL"))
False
>>> ic(checkRecord_TypeA_Scheme_A(s="AA"))
False
"""
absent, late, present = 0, 0, 0
lateContinuousCount = 0
for i in s:
if i == 'L':
late += 1
lateContinuousCount += 1
elif i == 'A':
absent += 1
lateContinuousCount = 0
elif i == 'P':
present += 1
lateContinuousCount = 0
if absent >= 2 or lateContinuousCount >= 3:
return False
return True
```
### Type A: Violent Enumeration Solution - Scheme II
> 2021/08/17 Kevin Tang
```
from typing import List
def checkRecord_TypeA_Scheme_B(s: str) -> bool:
"""
:param nums:
:param target:
:return:
>>> ic(checkRecord_TypeA_Scheme_B(s="PPALLP"))
True
>>> ic(checkRecord_TypeA_Scheme_B(s="PPALLL"))
False
>>> ic(checkRecord_TypeA_Scheme_B(s="AA"))
False
"""
absent: int = 0
lateContinuousCount = 0
for i in s:
if i == 'A':
absent += 1
if absent >= 2:
return False
if i == 'L':
lateContinuousCount += 1
if lateContinuousCount >= 3:
return False
else:
lateContinuousCount = 0
return True
```
### Type B: Built in Function Solution - Scheme I
> 2021/08/19 Kevin Tang
```
from typing import List
def checkRecord_TypeB_Scheme_A(s: str) -> bool:
"""
:param nums:
:param target:
:return:
>>> ic(checkRecord_TypeB_Scheme_A(s="PPALLP"))
True
>>> ic(checkRecord_TypeB_Scheme_A(s="PPALLL"))
False
>>> ic(checkRecord_TypeB_Scheme_A(s="AA"))
False
>>> ic(checkRecord_TypeB_Scheme_A(s="LPLPLPLPLPL"))
True
"""
return (s.find('A') == s.rfind('A')) and ('LLL' not in s)
```
### Test Script
```
import doctest
from icecream import ic
ic(doctest.testmod())
```
|
github_jupyter
|
# Supplemental Information
This notebook is intended to serve as a supplement to the manuscript "High-throughput workflows for determining adsorption energies on solid surfaces." It outlines basic use of the code and workflow software that has been developed for processing surface slabs and placing adsorbates according to symmetrically distinct sites on surface facets.
## Installation
To use this notebook, we recommend installing python via [Anaconda](https://www.continuum.io/downloads), which includes jupyter and the associated iPython notebook software.
The code used in this project primarily makes use of two packages, pymatgen and atomate, which are installable via pip or the matsci channel on conda (e. g. `conda install -c matsci pymatgen atomate`). Development versions with editable code may be installed by cloning the repositories and using `python setup.py develop`.
## Example 1: AdsorbateSiteFinder (pymatgen)
An example using the the AdsorbateSiteFinder class in pymatgen is shown below. We begin with an import statement for the necessay modules. To use the MP RESTful interface, you must provide your own API key either in the MPRester call i.e. ```mpr=MPRester("YOUR_API_KEY")``` or provide in in your .pmgrc.yaml configuration file. API keys can be accessed at materialsproject.org under your "Dashboard."
```
# Import statements
from pymatgen import Structure, Lattice, MPRester, Molecule
from pymatgen.analysis.adsorption import *
from pymatgen.core.surface import generate_all_slabs
from pymatgen.symmetry.analyzer import SpacegroupAnalyzer
from matplotlib import pyplot as plt
%matplotlib inline
# Note that you must provide your own API Key, which can
# be accessed via the Dashboard at materialsproject.org
mpr = MPRester()
```
We create a simple fcc structure, generate it's distinct slabs, and select the slab with a miller index of (1, 1, 1).
```
fcc_ni = Structure.from_spacegroup("Fm-3m", Lattice.cubic(3.5), ["Ni"], [[0, 0, 0]])
slabs = generate_all_slabs(fcc_ni, max_index=1, min_slab_size=8.0,
min_vacuum_size=10.0)
ni_111 = [slab for slab in slabs if slab.miller_index==(1,1,1)][0]
```
We make an instance of the AdsorbateSiteFinder and use it to find the relevant adsorption sites.
```
asf_ni_111 = AdsorbateSiteFinder(ni_111)
ads_sites = asf_ni_111.find_adsorption_sites()
print(ads_sites)
assert len(ads_sites) == 4
```
We visualize the sites using a tool from pymatgen.
```
fig = plt.figure()
ax = fig.add_subplot(111)
plot_slab(ni_111, ax, adsorption_sites=True)
```
Use the `AdsorbateSiteFinder.generate_adsorption_structures` method to generate structures of adsorbates.
```
fig = plt.figure()
ax = fig.add_subplot(111)
adsorbate = Molecule("H", [[0, 0, 0]])
ads_structs = asf_ni_111.generate_adsorption_structures(adsorbate,
repeat=[1, 1, 1])
plot_slab(ads_structs[0], ax, adsorption_sites=False, decay=0.09)
```
## Example 2: AdsorbateSiteFinder for various surfaces
In this example, the AdsorbateSiteFinder is used to find adsorption sites on different structures and miller indices.
```
fig = plt.figure()
axes = [fig.add_subplot(2, 3, i) for i in range(1, 7)]
mats = {"mp-23":(1, 0, 0), # FCC Ni
"mp-2":(1, 1, 0), # FCC Au
"mp-13":(1, 1, 0), # BCC Fe
"mp-33":(0, 0, 1), # HCP Ru
"mp-30": (2, 1, 1),
"mp-5229":(1, 0, 0),
} # Cubic SrTiO3
#"mp-2133":(0, 1, 1)} # Wurtzite ZnO
for n, (mp_id, m_index) in enumerate(mats.items()):
struct = mpr.get_structure_by_material_id(mp_id)
struct = SpacegroupAnalyzer(struct).get_conventional_standard_structure()
slabs = generate_all_slabs(struct, 1, 5.0, 2.0, center_slab=True)
slab_dict = {slab.miller_index:slab for slab in slabs}
asf = AdsorbateSiteFinder.from_bulk_and_miller(struct, m_index, undercoord_threshold=0.10)
plot_slab(asf.slab, axes[n])
ads_sites = asf.find_adsorption_sites()
sop = get_rot(asf.slab)
ads_sites = [sop.operate(ads_site)[:2].tolist()
for ads_site in ads_sites["all"]]
axes[n].plot(*zip(*ads_sites), color='k', marker='x',
markersize=10, mew=1, linestyle='', zorder=10000)
mi_string = "".join([str(i) for i in m_index])
axes[n].set_title("{}({})".format(struct.composition.reduced_formula, mi_string))
axes[n].set_xticks([])
axes[n].set_yticks([])
axes[4].set_xlim(-2, 5)
axes[4].set_ylim(-2, 5)
fig.savefig('slabs.png', dpi=200)
!open slabs.png
```
## Example 3: Generating a workflow from atomate
In this example, we demonstrate how MatMethods may be used to generate a full workflow for the determination of DFT-energies from which adsorption energies may be calculated. Note that this requires a working instance of [FireWorks](https://pythonhosted.org/FireWorks/index.html) and its dependency, [MongoDB](https://www.mongodb.com/). Note that MongoDB can be installed via [Anaconda](https://anaconda.org/anaconda/mongodb).
```
from fireworks import LaunchPad
lpad = LaunchPad()
lpad.reset('', require_password=False)
```
Import the necessary workflow-generating function from atomate:
```
from atomate.vasp.workflows.base.adsorption import get_wf_surface, get_wf_surface_all_slabs
```
Adsorption configurations take the form of a dictionary with the miller index as a string key and a list of pymatgen Molecule instances as the values.
```
co = Molecule("CO", [[0, 0, 0], [0, 0, 1.23]])
h = Molecule("H", [[0, 0, 0]])
```
Workflows are generated using the a slab a list of molecules.
```
struct = mpr.get_structure_by_material_id("mp-23") # fcc Ni
struct = SpacegroupAnalyzer(struct).get_conventional_standard_structure()
slabs = generate_all_slabs(struct, 1, 5.0, 2.0, center_slab=True)
slab_dict = {slab.miller_index:slab for slab in slabs}
ni_slab_111 = slab_dict[(1, 1, 1)]
wf = get_wf_surface([ni_slab_111], molecules=[co, h])
lpad.add_wf(wf)
```
The workflow may be inspected as below. Note that there are 9 optimization tasks correponding the slab, and 4 distinct adsorption configurations for each of the 2 adsorbates. Details on running FireWorks, including [singleshot launching](https://pythonhosted.org/FireWorks/worker_tutorial.html#launch-a-rocket-on-a-worker-machine-fireworker), [queue submission](https://pythonhosted.org/FireWorks/queue_tutorial.html#), [workflow management](https://pythonhosted.org/FireWorks/defuse_tutorial.html), and more can be found in the [FireWorks documentation](https://pythonhosted.org/FireWorks/index.html).
```
lpad.get_wf_summary_dict(1)
```
Note also that running FireWorks via atomate may require system specific tuning (e. g. for VASP parameters). More information is available in the [atomate documentation](http://pythonhosted.org/atomate/).
## Example 4 - Screening of oxygen evolution electrocatalysts on binary oxides
This final example is intended to demonstrate how to use the MP API and the adsorption workflow to do an initial high-throughput study of oxygen evolution electrocatalysis on binary oxides of transition metals.
```
from pymatgen.core.periodic_table import *
from pymatgen.core.surface import get_symmetrically_distinct_miller_indices
import tqdm
lpad.reset('', require_password=False)
```
For oxygen evolution, a common metric for the catalytic activity of a given catalyst is the theoretical overpotential corresponding to the mechanism that proceeds through OH\*, O\*, and OOH\*. So we can define our adsorbates:
```
OH = Molecule("OH", [[0, 0, 0], [-0.793, 0.384, 0.422]])
O = Molecule("O", [[0, 0, 0]])
OOH = Molecule("OOH", [[0, 0, 0], [-1.067, -0.403, 0.796],
[-0.696, -0.272, 1.706]])
adsorbates = [OH, O, OOH]
```
Then we can retrieve the structures using the MP rest interface, and write a simple for loop which creates all of the workflows corresponding to every slab and every adsorption site for each material. The code below will take ~15 minutes. This could be parallelized to be more efficient, but is not for simplicity in this case.
```
elements = [Element.from_Z(i) for i in range(1, 103)]
trans_metals = [el for el in elements if el.is_transition_metal]
# tqdm adds a progress bar so we can see the progress of the for loop
for metal in tqdm.tqdm_notebook(trans_metals):
# Get relatively stable structures with small unit cells
data = mpr.get_data("{}-O".format(metal.symbol))
data = [datum for datum in data if datum["e_above_hull"] < 0.05]
data = sorted(data, key = lambda x: x["nsites"])
struct = Structure.from_str(data[0]["cif"], fmt='cif')
# Put in conventional cell settings
struct = SpacegroupAnalyzer(struct).get_conventional_standard_structure()
# Get distinct miller indices for low-index facets
wf = get_wf_surface_all_slabs(struct, adsorbates)
lpad.add_wf(wf)
print("Processed: {}".format(struct.formula))
```
Ultimately, running this code produces workflows that contain many (tens of thousands) of calculations, all of which can be managed using FireWorks and queued on supercomputing resources. Limitations on those resources might necessitate a more selective approach towards choosing surface facets or representative materials. Nevertheless, this approach represents a way to provide for a complete and structurally accurate way of screening materials for adsorption properties than can be managed using fireworks.
|
github_jupyter
|
# Decoding specified ISS tile(s)
This notebook provides an exampe how to decode an ISS tile from the mouse brain dataset used in the PoSTcode paper that is stored at local directory ``postcode/example-iss-tile-data/``.
```
import numpy as np
import pandas as pd
from pandas import read_csv
import matplotlib.pyplot as plt
import pickle
import os
from postcode.decoding_functions import *
from postcode.spot_detection_functions import *
from postcode.reading_data_functions import *
%load_ext autoreload
%autoreload 2
```
* Specify directory location ``data_path`` with channel_info.csv and taglist.csv
```
dataset_name = 'NT_ISS_KR0018'
data_path = os.path.dirname(os.getcwd()) + '/example-iss-tile-data/' + dataset_name + '/'
```
* Read channel_info.csv and taglist.csv files
```
barcodes_01, K, R, C, gene_names, channels_info = read_taglist_and_channel_info(data_path)
```
## Spot detection
* Input parameters for spot detection via trackpy should be specified in dictionary ``spots_params``, which has to contain value for key ``'trackpy_spot_diam'`` indicating spot diameter in pixels.
```
spots_params = {'trackpy_spot_diam':5} #parameters for spot detection: spot diameter must to be specified
spots_params['trackpy_prc'] = 0 #by default this parameter is set to 64, decrease it to select more spots
spots_params['trackpy_sep'] = 2 #by default this paramerer is set to 'trackpy_spot_diam'+1
tifs_path = data_path + 'selected-tiles/'
tile_names = read_csv(data_path + 'tile_names.csv')
x_min, x_max, y_min, y_max = find_xy_range_of_tile_names(tile_names['selected_tile_names'])
tiles_info = {'tile_size':1000, 'y_max_size':1000, 'x_max_size':1000, 'filename_prefix':'out_opt_flow_registered_', 'y_max':y_max, 'x_max':x_max}
tiles_to_load = {'y_start':1, 'y_end':1, 'x_start':12, 'x_end':12} #tile(s) to load (only 'X12_Y1' tile of size 1000x1000 is stored locally)
spots_out = load_tiles_to_extract_spots(tifs_path, channels_info, C, R, tile_names, tiles_info, tiles_to_load, spots_params,
anchors_cy_ind_for_spot_detect=0, compute_also_without_tophat=False, return_anchors=True)
print('In total {} spots were detected.'.format(spots_out['spots'].shape[0]))
```
## Spot decoding
* Estimate model parameters and compute class probabilities
```
out = decoding_function(spots_out['spots'], barcodes_01, print_training_progress=True)
```
* Create a data frame from the decoding output
```
df_class_names = np.concatenate((gene_names,['infeasible','background','nan']))
df_class_codes = np.concatenate((channels_info['barcodes_AGCT'],['inf','0000','NA']))
decoded_spots_df = decoding_output_to_dataframe(out, df_class_names, df_class_codes)
decoded_df = pd.concat([decoded_spots_df, spots_out['spots_loc']], axis=1)
```
## Visualizing decoding results
* Plot loss, estimated activation parameters and covariance: loss should decrease, $\hat\alpha+\hat\beta$ shoud be separated from $\hat\alpha$, covariance matrix should have a checkerboard pattern
```
fig, (ax1, ax2, ax3) = plt.subplots(1, 3, gridspec_kw={'width_ratios': [1, 3, 1]}, figsize=(14, 2.5), dpi=100, facecolor='w', edgecolor='k')
channel_base = np.array(channels_info['channel_base'])[np.where(np.array(channels_info['coding_chs']) == True)[0]]
activation = (out['params']['codes_tr_v_star']+out['params']['codes_tr_consts_v_star'])[0,:].numpy() #corresponding to the channel activation (code=1)
no_activation = out['params']['codes_tr_consts_v_star'][0,:].numpy() # (code=0)
channel_activation=np.stack((no_activation,activation))
ax1.plot(np.arange(0,len(out['params']['losses'])),(1/out['class_probs'].shape[0]*np.asarray(out['params']['losses'])))
ax1.annotate(np.round(1/out['class_probs'].shape[0]*out['params']['losses'][-1],4),(-2+len(out['params']['losses']),0.2+1/out['class_probs'].shape[0]*out['params']['losses'][-1]),size=6)
ax1.set_title('Loss over iterations')
ax2.scatter(np.arange(1,1+R*C),activation,c='green',label=r'$\hat{\alpha}+\hat{\beta}$ (channel active)')
ax2.scatter(np.arange(1,1+R*C),no_activation,c='orange',label=r'$\hat{\alpha}$ (channel not active)')
ax2.legend(loc=9)
ax2.vlines(np.arange(0.5,R*C+.8,C), out['params']['codes_tr_consts_v_star'].min(), (out['params']['codes_tr_v_star']+out['params']['codes_tr_consts_v_star']).max(), linestyles='dashed')
ax2.set_xticks(np.arange(1,1+R*C))
ax2.set_xticklabels(np.tile(channel_base,R))
ax2.set_title('Parameters of the barcode transformation as activation / no activation')
covim = ax3.imshow(out['params']['sigma_star'])
ax3.set_xticks(np.arange(0,R*C))
ax3.set_xticklabels(np.tile(channel_base,R))
ax3.set_yticks(np.arange(0,R*C))
ax3.set_yticklabels(np.tile(channel_base,R))
ax3.set_title('Estimated covariance')
plt.colorbar(covim, ax=ax3, fraction=0.02)
plt.show()
```
* Plot histogram of barcode assignments
```
thr=0.7
df = pd.concat([decoded_df.Name[decoded_df.Probability>thr].value_counts(), decoded_df.Name[decoded_df.Probability <=thr].replace(np.unique(decoded_df.Name),'thr').value_counts()]).sort_index(axis=0)#.sort_values(ascending=False)
fig, ax = plt.subplots(1, 1, figsize=(14,3), dpi=100, facecolor='w', edgecolor='k')
df.plot(kind='bar',width=0.7,rot=90,logy=True,fontsize=6,ax=ax)
num_decoded_barcodes = sum((decoded_df.Name!='background')&(decoded_df.Name!='infeasible')&(decoded_df.Name!='NaN')&(decoded_df.Probability>thr))
for p in ax.patches:
ax.annotate(str(p.get_height()), (p.get_x() * 1.005, p.get_height() * 1.005),size=6)
plt.title('Histogram of decoded barcodes afther thresholding with {}: \n in total {} spots detected while {} spots decoded ({:.02f}%)'.format(thr,decoded_df.shape[0], num_decoded_barcodes, 100*num_decoded_barcodes/decoded_df.shape[0]), fontsize=10)
plt.show()
```
* Plot spatial patterns of a few selected barcodes over the whole tile
```
names = ['Cux2','Rorb','Grin3a','infeasible','background']
log_scale = True
fig, ax = plt.subplots(1, len(names), figsize=(3*len(names), 3), dpi=100, facecolor='w', edgecolor='k')
for i in range(len(names)):
im = heatmap_pattern(decoded_df, names[i], grid=10, thr=0.7, plot_probs=True)
if log_scale:
ims = ax[i].imshow(np.log2(1+im),cmap='jet')
else:
ims = ax[i].imshow(im)
ax[i].axis('off')
plt.colorbar(ims, ax=ax[i], fraction=0.02)
ax[i].set_title('{} (barcode: {})'.format(names[i],df_class_codes[df_class_names==names[i]][0]),fontsize=8)
fig.suptitle('Spatial patterns in logaritmic scale')
plt.show()
```
* Plot all detected / decoded spots and a selected barcode over a zoom of the anchor channel
```
x00 = 600; y00 = 350 #coordinates of the zoom (between 0--1000)
delta = 200 #size of the zoom in each axis (up to 1000)
anchor_zoom = spots_out['anchors'][y00:y00+delta,x00:x00+delta] #anchor of the last loaded tile
#in case multiple tiles were used, find coordinates corresponding to the last one loaded
y00 = y00+(int(decoded_df.Tile.iloc[-1][-2:].replace('Y',''))-tiles_to_load['y_start'])*tiles_info['tile_size']
x00 = x00+(int(decoded_df.Tile.iloc[-1][1:3].replace('_',''))-tiles_to_load['x_start'])*tiles_info['tile_size']
plt.figure(num=None, figsize=(12, 4), dpi=100, facecolor='w', edgecolor='k')
plt.subplot(1,3,1)
plt.imshow(np.log(0.06+anchor_zoom/anchor_zoom.max()),cmap='gray')
y0 = np.around(decoded_df.Y.to_numpy()).astype(np.int32)-y00; x0 = np.around(decoded_df.X.to_numpy()).astype(np.int32)-x00
y = y0[(y0>=0)&(y0<delta)&(x0>=0)&(x0<delta)]; x = x0[(y0>=0)&(y0<delta)&(x0>=0)&(x0<delta)]
plt.scatter(x,y,s=13,marker='.',c='orange')
plt.title('Detected spots',fontsize=10)
plt.axis('off')
from matplotlib import cm
from matplotlib.lines import Line2D
markers = list(Line2D.markers.keys()); markersL = markers[1:20]*(int(K/20)+1)
hsv_cols = cm.get_cmap('hsv', K+1); colL=hsv_cols(range(2*K)); colL=np.concatenate((colL[::2,],colL[1::2,]))
plt.subplot(1,3,2)
plt.imshow(np.log(0.06+anchor_zoom/anchor_zoom.max()),cmap='gray')
for name in gene_names:
col = colL[np.where(gene_names==name)[0][0],:]; mar = markersL[np.where(gene_names==name)[0][0]]
x0 = np.around(decoded_df.X[(decoded_df.Name == name) & (decoded_df.Probability >thr)].to_numpy()).astype(np.int32)-x00
y0 = np.around(decoded_df.Y[(decoded_df.Name == name) & (decoded_df.Probability >thr)].to_numpy()).astype(np.int32)-y00
y = y0[(y0>=0)&(y0<delta)&(x0>=0)&(x0<delta)]; x = x0[(y0>=0)&(y0<delta)&(x0>=0)&(x0<delta)]
plt.scatter(x,y,s=13,marker=mar,c=np.repeat(col.reshape((1,4)),x.shape[0],axis=0))
plt.title('Decoded barcodes',fontsize=10)
plt.axis('off')
plt.subplot(1,3,3)
plt.imshow(np.log(0.06+anchor_zoom/anchor_zoom.max()),cmap='gray')
name = 'Cux2'; thr=0.7
x0 = np.around(decoded_df.X[(decoded_df.Name == name) & (decoded_df.Probability >thr)].to_numpy()).astype(np.int32)-x00
y0 = np.around(decoded_df.Y[(decoded_df.Name == name) & (decoded_df.Probability >thr)].to_numpy()).astype(np.int32)-y00
y = y0[(y0>=0)&(y0<delta)&(x0>=0)&(x0<delta)]; x = x0[(y0>=0)&(y0<delta)&(x0>=0)&(x0<delta)]
plt.scatter(x,y,s=13,marker='.',c='cyan')
plt.title('{} ({})'.format(name,decoded_df.Code[decoded_df.Name==name].to_numpy()[0]),fontsize=10)
plt.axis('off')
plt.suptitle('Zoomed section of the anchor channel used for spot detection')
plt.show()
```
|
github_jupyter
|
# Self DCGAN
<table class="tfo-notebook-buttons" align="left" >
<td>
<a target="_blank" href="https://colab.research.google.com/github/HighCWu/SelfGAN/blob/master/implementations/dcgan/self_dcgan.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
</td>
<td>
<a target="_blank" href="https://github.com/HighCWu/SelfGAN/blob/master/implementations/dcgan/self_dcgan.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View source on GitHub</a>
</td>
</table>
## Datasets
```
import glob
import random
import os
import numpy as np
from torch.utils.data import Dataset
from PIL import Image
import torchvision.transforms as transforms
class ImageDataset(Dataset):
def __init__(self, root, transforms_=None):
self.transform = transforms.Compose(transforms_)
self.files = sorted(glob.glob(root + '/**/*.*', recursive=True))
def __getitem__(self, index):
img = Image.open(self.files[index % len(self.files)]).convert('RGB')
w, h = img.size
img = self.transform(img)
return img
def __len__(self):
return len(self.files)
```
## Prepare
```
import argparse
import os
import sys
import numpy as np
import math
import torchvision.transforms as transforms
from torchvision.utils import save_image
from torch.utils.data import DataLoader
from torchvision import datasets
from torch.autograd import Variable
import torch.nn as nn
import torch.nn.functional as F
import torch
os.makedirs('images', exist_ok=True)
os.makedirs('images_normal', exist_ok=True)
parser = argparse.ArgumentParser()
parser.add_argument('--n_epochs', type=int, default=200, help='number of epochs of training')
parser.add_argument('--batch_size', type=int, default=64, help='size of the batches')
parser.add_argument('--lr', type=float, default=2e-4, help='adam: learning rate')
parser.add_argument('--b1', type=float, default=0.5, help='adam: decay of first order momentum of gradient')
parser.add_argument('--b2', type=float, default=0.999, help='adam: decay of first order momentum of gradient')
parser.add_argument('--n_cpu', type=int, default=8, help='number of cpu threads to use during batch generation')
parser.add_argument('--latent_dim', type=int, default=100, help='dimensionality of the latent space')
parser.add_argument('--img_size', type=int, default=64, help='size of each image dimension')
parser.add_argument('--channels', type=int, default=3, help='number of image channels')
parser.add_argument('--sample_interval', type=int, default=200, help='interval betwen image samples')
parser.add_argument('--data_use', type=str, default='bedroom', help='datasets:[mnist]/[bedroom]')
opt, _ = parser.parse_known_args()
if opt.data_use == 'mnist':
opt.img_size = 32
opt.channels = 1
print(opt)
import os, zipfile
from google.colab import files
if opt.data_use == 'bedroom':
os.makedirs('data/bedroom', exist_ok=True)
print('Please upload your kaggle api json.')
files.upload()
! mkdir /root/.kaggle
! mv ./kaggle.json /root/.kaggle
! chmod 600 /root/.kaggle/kaggle.json
! kaggle datasets download -d jhoward/lsun_bedroom
out_fname = 'lsun_bedroom.zip'
zip_ref = zipfile.ZipFile(out_fname)
zip_ref.extractall('./')
zip_ref.close()
os.remove(out_fname)
out_fname = 'sample.zip'
zip_ref = zipfile.ZipFile(out_fname)
zip_ref.extractall('data/bedroom/')
zip_ref.close()
os.remove(out_fname)
else:
os.makedirs('data/mnist', exist_ok=True)
img_shape = (opt.channels, opt.img_size, opt.img_size)
cuda = True if torch.cuda.is_available() else False
def weights_init_normal(m):
classname = m.__class__.__name__
if classname.find('Conv') != -1:
torch.nn.init.normal_(m.weight.data, 0.0, 0.02)
elif classname.find('BatchNorm2d') != -1:
torch.nn.init.normal_(m.weight.data, 1.0, 0.02)
torch.nn.init.constant_(m.bias.data, 0.0)
class Generator(nn.Module):
def __init__(self):
super(Generator, self).__init__()
self.init_size = opt.img_size // 4
self.l1 = nn.Sequential(nn.Linear(opt.latent_dim, 128*self.init_size**2))
self.conv_blocks = nn.Sequential(
nn.BatchNorm2d(128),
nn.Upsample(scale_factor=2),
nn.Conv2d(128, 128, 3, stride=1, padding=1),
nn.BatchNorm2d(128, 0.8),
nn.LeakyReLU(0.2, inplace=True),
nn.Upsample(scale_factor=2),
nn.Conv2d(128, 64, 3, stride=1, padding=1),
nn.BatchNorm2d(64, 0.8),
nn.LeakyReLU(0.2, inplace=True),
nn.Conv2d(64, opt.channels, 3, stride=1, padding=1),
nn.Tanh()
)
def forward(self, z):
out = self.l1(z)
out = out.view(out.shape[0], 128, self.init_size, self.init_size)
img = self.conv_blocks(out)
return img
class Discriminator(nn.Module):
def __init__(self):
super(Discriminator, self).__init__()
def discriminator_block(in_filters, out_filters, bn=True):
block = [ nn.Conv2d(in_filters, out_filters, 3, 2, 1),
nn.LeakyReLU(0.2, inplace=True),
nn.Dropout2d(0.25)]
if bn:
block.append(nn.BatchNorm2d(out_filters, 0.8))
return block
self.model = nn.Sequential(
*discriminator_block(opt.channels, 16, bn=False),
*discriminator_block(16, 32),
*discriminator_block(32, 64),
*discriminator_block(64, 128),
)
# The height and width of downsampled image
ds_size = opt.img_size // 2**4
self.adv_layer = nn.Sequential( nn.Linear(128*ds_size**2, 1),
nn.Sigmoid())
def forward(self, img):
out = self.model(img)
out = out.view(out.shape[0], -1)
validity = self.adv_layer(out)
return validity
class SelfGAN(nn.Module):
def __init__(self):
super(SelfGAN, self).__init__()
# Initialize generator and discriminator
self.generator = Generator()
self.discriminator = Discriminator()
def forward(self, z, real_img, fake_img):
gen_img = self.generator(z)
validity_gen = self.discriminator(gen_img)
validity_real = self.discriminator(real_img)
validity_fake = self.discriminator(fake_img)
return gen_img, validity_gen, validity_real, validity_fake
```
## SelfGAN Part
```
# Loss function
adversarial_loss = torch.nn.BCELoss()
shard_adversarial_loss = torch.nn.BCELoss(reduction='none')
# Initialize SelfGAN model
self_gan = SelfGAN()
if cuda:
self_gan.cuda()
adversarial_loss.cuda()
shard_adversarial_loss.cuda()
# Initialize weights
self_gan.apply(weights_init_normal)
# Configure data loader
dataloader = torch.utils.data.DataLoader(
ImageDataset('data/bedroom',
transforms_=[
transforms.Resize((opt.img_size, opt.img_size)),
transforms.ToTensor(),
transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))
]) if opt.data_use == 'bedroom' else
datasets.MNIST('data/mnist', train=True, download=True,
transform=transforms.Compose([
transforms.Resize(opt.img_size),
transforms.ToTensor(),
transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))
])),
batch_size=opt.batch_size, shuffle=True, drop_last=True)
# Optimizers
optimizer = torch.optim.Adam(self_gan.parameters(), lr=opt.lr, betas=(opt.b1, opt.b2))
Tensor = torch.cuda.FloatTensor if cuda else torch.FloatTensor
last_imgs = Tensor(opt.batch_size, *img_shape)*0.0
```
### Standard performance on the GPU
```
# ----------
# Training
# ----------
for epoch in range(opt.n_epochs):
for i, imgs in enumerate(dataloader):
if opt.data_use != 'bedroom':
imgs = imgs[0]
# Adversarial ground truths
valid = Variable(Tensor(imgs.size(0), 1).fill_(1.0), requires_grad=False)
fake = Variable(Tensor(imgs.size(0), 1).fill_(0.0), requires_grad=False)
# Configure input
real_imgs = Variable(imgs.type(Tensor))
# -----------------
# Train SelfGAN
# -----------------
optimizer.zero_grad()
# Sample noise as generator input
z = Variable(Tensor(np.random.normal(0, 1, (imgs.shape[0], opt.latent_dim))))
# Generate a batch of images
gen_imgs, validity_gen, validity_real, validity_fake = self_gan(z, real_imgs, last_imgs)
# Loss measures generator's ability to fool the discriminator and measure discriminator's ability to classify real from generated samples at the same time
gen_loss = adversarial_loss(validity_gen, valid)
real_loss = adversarial_loss(validity_real, valid)
fake_loss = adversarial_loss(validity_fake, fake)
v_g = 1 - torch.mean(validity_gen)
v_f = torch.mean(validity_fake)
s_loss = (real_loss + v_g*gen_loss*0.1 + v_f*fake_loss*0.9) / 2
s_loss.backward()
optimizer.step()
last_imgs = gen_imgs.detach()
sys.stdout.flush()
print ("\r[Epoch %d/%d] [Batch %d/%d] [S loss: %f R loss: %f F loss: %f G loss: %f]" % (epoch, opt.n_epochs, i, len(dataloader),
s_loss.item(), real_loss.item(), fake_loss.item(), gen_loss.item()),
end='')
batches_done = epoch * len(dataloader) + i
if batches_done % opt.sample_interval == 0:
save_image(gen_imgs.data[:25], 'images/%d.png' % batches_done, nrow=5, normalize=True)
```
### Running on the GPU with similar performance of running on the TPU (Maybe)
```
# ----------
# Training
# ----------
for epoch in range(opt.n_epochs):
for i, imgs in enumerate(dataloader):
if opt.data_use != 'bedroom':
imgs = imgs[0]
# Adversarial ground truths
valid = Variable(Tensor(imgs.size(0), 1).fill_(1.0), requires_grad=False)
fake = Variable(Tensor(imgs.size(0), 1).fill_(0.0), requires_grad=False)
# Configure input
real_imgs = Variable(imgs.type(Tensor))
# -----------------
# Train SelfGAN
# -----------------
optimizer.zero_grad()
# Sample noise as generator input
z = Variable(Tensor(np.random.normal(0, 1, (imgs.shape[0], opt.latent_dim))))
s = opt.batch_size//8
for k in range(8):
# Generate a batch of images
gen_imgs, validity_gen, validity_real, validity_fake = self_gan(z[k*s:k*s+s], real_imgs[k*s:k*s+s], last_imgs[k*s:k*s+s])
# Loss measures generator's ability to fool the discriminator and measure discriminator's ability to classify real from generated samples at the same time
gen_loss = shard_adversarial_loss(validity_gen, valid[k*s:k*s+s])
real_loss = shard_adversarial_loss(validity_real, valid[k*s:k*s+s])
fake_loss = shard_adversarial_loss(validity_fake, fake[k*s:k*s+s])
v_g = 1 - torch.mean(validity_gen)
v_r = 1 - torch.mean(validity_real)
v_f = torch.mean(validity_fake)
v_sum = v_g + v_r + v_f
s_loss = v_r*real_loss/v_sum + v_g*gen_loss/v_sum + v_f*fake_loss/v_sum
gen_loss = torch.mean(gen_loss)
real_loss = torch.mean(real_loss)
fake_loss = torch.mean(fake_loss)
s_loss = torch.mean(s_loss)
s_loss.backward()
last_imgs[k*s:k*s+s] = gen_imgs.detach()
optimizer.step()
sys.stdout.flush()
print ("\r[Epoch %d/%d] [Batch %d/%d] [S loss: %f R loss: %f F loss: %f G loss: %f]" % (epoch, opt.n_epochs, i, len(dataloader),
s_loss.item(), real_loss.item(), fake_loss.item(), gen_loss.item()),
end='')
batches_done = epoch * len(dataloader) + i
if batches_done % opt.sample_interval == 0:
save_image(last_imgs.data[:25], 'images/%d.png' % batches_done, nrow=5, normalize=True)
```
## Normal GAN Part
```
# Loss function
adversarial_loss = torch.nn.BCELoss()
# Initialize generator and discriminator
generator = Generator()
discriminator = Discriminator()
if cuda:
generator.cuda()
discriminator.cuda()
adversarial_loss.cuda()
# Initialize weights
generator.apply(weights_init_normal)
discriminator.apply(weights_init_normal)
# Configure data loader
dataloader = torch.utils.data.DataLoader(
ImageDataset('data/bedroom',
transforms_=[
transforms.Resize((opt.img_size, opt.img_size)),
transforms.ToTensor(),
transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))
]) if opt.data_use == 'bedroom' else
datasets.MNIST('data/mnist', train=True, download=True,
transform=transforms.Compose([
transforms.Resize(opt.img_size),
transforms.ToTensor(),
transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))
])),
batch_size=opt.batch_size, shuffle=True)
# Optimizers
optimizer_G = torch.optim.Adam(generator.parameters(), lr=opt.lr, betas=(opt.b1, opt.b2))
optimizer_D = torch.optim.Adam(discriminator.parameters(), lr=opt.lr, betas=(opt.b1, opt.b2))
Tensor = torch.cuda.FloatTensor if cuda else torch.FloatTensor
# ----------
# Training
# ----------
for epoch in range(opt.n_epochs):
for i, imgs in enumerate(dataloader):
if opt.data_use != 'bedroom':
imgs = imgs[0]
# Adversarial ground truths
valid = Variable(Tensor(imgs.size(0), 1).fill_(1.0), requires_grad=False)
fake = Variable(Tensor(imgs.size(0), 1).fill_(0.0), requires_grad=False)
# Configure input
real_imgs = Variable(imgs.type(Tensor))
# -----------------
# Train Generator
# -----------------
optimizer_G.zero_grad()
# Sample noise as generator input
z = Variable(Tensor(np.random.normal(0, 1, (imgs.shape[0], opt.latent_dim))))
# Generate a batch of images
gen_imgs = generator(z)
# Loss measures generator's ability to fool the discriminator
g_loss = adversarial_loss(discriminator(gen_imgs), valid)
g_loss.backward()
optimizer_G.step()
# ---------------------
# Train Discriminator
# ---------------------
optimizer_D.zero_grad()
# Measure discriminator's ability to classify real from generated samples
real_loss = adversarial_loss(discriminator(real_imgs), valid)
fake_loss = adversarial_loss(discriminator(gen_imgs.detach()), fake)
d_loss = (real_loss + fake_loss) / 2
d_loss.backward()
optimizer_D.step()
sys.stdout.flush()
print ("\r[Epoch %d/%d] [Batch %d/%d] [D loss: %f] [G loss: %f]" % (epoch, opt.n_epochs, i, len(dataloader),
d_loss.item(), g_loss.item()),
end='')
batches_done = epoch * len(dataloader) + i
if batches_done % opt.sample_interval == 0:
save_image(gen_imgs.data[:25], 'images_normal/%d.png' % batches_done, nrow=5, normalize=True)
```
|
github_jupyter
|
# Standard Normal N(0,1)
Generate a total of 2000 i.i.d. standard normals N(0,1) using each method. Test the normality of the standard normals obtained from each method, using the Anderson-Darling test. Which data set is closer to the normal distribution? (Consult the paper by Stephens - filename 2008 Stephens.pdf on Canvas - to find the appropriate critical points for the Anderson-Darling statistic. Clearly identify those percentiles in your soultion.)
```
# imports
import random
import math
import numpy
import matplotlib.pyplot as plt
from scipy.stats import anderson
from mpl_toolkits.mplot3d import axes3d
%matplotlib notebook
# project imports
import rand
import halton
import bfs
import box_muller
import beasley_springer_moro
```
### Generate a total of 2000 i.i.d. standard normals N (0, 1) using Box Muller
```
# generate 1000 2-dim vectors, then flatten to create 2000 standard normals
N = 1000
s = 2
seq = rand.rand_seq
seq = halton.halton_seq
#seq = bfs.bfs_seq
l = box_muller.box_muller_seq(s, N, seq=seq)
# print the first 20
print(l[:10])
# flatten the sequence into 1 dimension
flattened = [item for sublist in l for item in sublist]
nums = flattened
print(nums[:20])
```
### Sort the sequence
```
nums = numpy.array(nums)
nums = sorted(nums)
print(nums[:20])
```
### Compute the sample mean and standard deviation
```
nums = numpy.array(nums)
mean = numpy.mean(nums)
var = numpy.var(nums)
std = numpy.std(nums)
print('mean = {}'.format(mean))
print('variance = {}'.format(var))
print('standard deviation = {}'.format(std))
# plot the histogram
plt.hist(nums, density=True, bins=30)
plt.ylabel('Standard Normal - Box Muller');
```
### Anderson Darling Test
reference:
https://en.wikipedia.org/wiki/Anderson%E2%80%93Darling_test#Test_for_normality
reference:
2008 Stephens.pdf pg. 4, "1.3 Modificatons for a test for normality, u, and sigma^2 unknown"
```
# normality test using scipy.stats
result = anderson(nums)
print('Statistic: %.3f' % result.statistic)
p = 0
for i in range(len(result.critical_values)):
sl, cv = result.significance_level[i], result.critical_values[i]
if result.statistic < result.critical_values[i]:
print('%.3f: %.3f, data looks normal (fail to reject H0)' % (sl, cv))
else:
print('%.3f: %.3f, data does not look normal (reject H0)' % (sl, cv))
```
### Generate a total of 2000 i.i.d. standard normals N (0, 1) using Beasley-Springer-Moro
```
N=2000
s=1
l = beasley_springer_moro.beasley_springer_moro_seq(s=s, N=N, seq=seq)
# print the first 20
print(l[:20])
# flatten the sequence into 1 dimension
flattened = [item for sublist in l for item in sublist]
nums = flattened
print(nums[:20])
```
### Sort the sequence
```
nums = numpy.array(nums)
nums = sorted(nums)
print(nums[:20])
```
### Compute the sample mean and standard deviation
```
nums = numpy.array(nums)
mean = numpy.mean(nums)
var = numpy.var(nums)
std = numpy.std(nums)
print('mean = {}'.format(mean))
print('variance = {}'.format(var))
print('standard deviation = {}'.format(std))
# plot the histogram
fig = plt.figure()
ax = fig.add_subplot(111)
ax.hist(nums, density=True, bins=30)
ax.set_ylabel('Standard Normal - Beasley-Springer-Moro');
# normality test using scipy.stats
result = anderson(nums)
print('Statistic: %.3f' % result.statistic)
p = 0
for i in range(len(result.critical_values)):
sl, cv = result.significance_level[i], result.critical_values[i]
if result.statistic < result.critical_values[i]:
print('%.3f: %.3f, data looks normal (fail to reject H0)' % (sl, cv))
else:
print('%.3f: %.3f, data does not look normal (reject H0)' % (sl, cv))
```
|
github_jupyter
|
##### Copyright 2020 The TensorFlow Authors.
```
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
```
# Post-training integer quantization with int16 activations
<table class="tfo-notebook-buttons" align="left">
<td>
<a target="_blank" href="https://www.tensorflow.org/lite/performance/post_training_quant_16x8"><img src="https://www.tensorflow.org/images/tf_logo_32px.png" />View on TensorFlow.org</a>
</td>
<td>
<a target="_blank" href="https://colab.research.google.com/github/tensorflow/tensorflow/blob/master/tensorflow/lite/g3doc/performance/post_training_quant_16x8.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
</td>
<td>
<a target="_blank" href="https://github.com/tensorflow/tensorflow/blob/master/tensorflow/lite/g3doc/performance/post_training_quant_16x8.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View source on GitHub</a>
</td>
<td>
<a href="https://storage.googleapis.com/tensorflow_docs/tensorflow/lite/g3doc/performance/post_training_quant_16x8.ipynb"><img src="https://www.tensorflow.org/images/download_logo_32px.png" />Download notebook</a>
</td>
</table>
## Overview
[TensorFlow Lite](https://www.tensorflow.org/lite/) now supports
converting activations to 16-bit integer values and weights to 8-bit integer values during model conversion from TensorFlow to TensorFlow Lite's flat buffer format. We refer to this mode as the "16x8 quantization mode". This mode can improve accuracy of the quantized model significantly, when activations are sensitive to the quantization, while still achieving almost 3-4x reduction in model size. Moreover, this fully quantized model can be consumed by integer-only hardware accelerators.
Some examples of models that benefit from this mode of the post-training quantization include:
* super-resolution,
* audio signal processing such
as noise cancelling and beamforming,
* image de-noising,
* HDR reconstruction
from a single image
In this tutorial, you train an MNIST model from scratch, check its accuracy in TensorFlow, and then convert the model into a Tensorflow Lite flatbuffer using this mode. At the end you check the accuracy of the converted model and compare it to the original float32 model. Note that this example demonstrates the usage of this mode and doesn't show benefits over other available quantization techniques in TensorFlow Lite.
## Build an MNIST model
### Setup
```
import logging
logging.getLogger("tensorflow").setLevel(logging.DEBUG)
import tensorflow as tf
from tensorflow import keras
import numpy as np
import pathlib
```
Check that the 16x8 quantization mode is available
```
tf.lite.OpsSet.EXPERIMENTAL_TFLITE_BUILTINS_ACTIVATIONS_INT16_WEIGHTS_INT8
```
### Train and export the model
```
# Load MNIST dataset
mnist = keras.datasets.mnist
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()
# Normalize the input image so that each pixel value is between 0 to 1.
train_images = train_images / 255.0
test_images = test_images / 255.0
# Define the model architecture
model = keras.Sequential([
keras.layers.InputLayer(input_shape=(28, 28)),
keras.layers.Reshape(target_shape=(28, 28, 1)),
keras.layers.Conv2D(filters=12, kernel_size=(3, 3), activation=tf.nn.relu),
keras.layers.MaxPooling2D(pool_size=(2, 2)),
keras.layers.Flatten(),
keras.layers.Dense(10)
])
# Train the digit classification model
model.compile(optimizer='adam',
loss=keras.losses.SparseCategoricalCrossentropy(from_logits=True),
metrics=['accuracy'])
model.fit(
train_images,
train_labels,
epochs=1,
validation_data=(test_images, test_labels)
)
```
For the example, you trained the model for just a single epoch, so it only trains to ~96% accuracy.
### Convert to a TensorFlow Lite model
Using the Python [TFLiteConverter](https://www.tensorflow.org/lite/convert/python_api), you can now convert the trained model into a TensorFlow Lite model.
Now, convert the model using `TFliteConverter` into default float32 format:
```
converter = tf.lite.TFLiteConverter.from_keras_model(model)
tflite_model = converter.convert()
```
Write it out to a `.tflite` file:
```
tflite_models_dir = pathlib.Path("/tmp/mnist_tflite_models/")
tflite_models_dir.mkdir(exist_ok=True, parents=True)
tflite_model_file = tflite_models_dir/"mnist_model.tflite"
tflite_model_file.write_bytes(tflite_model)
```
To instead quantize the model to 16x8 quantization mode, first set the `optimizations` flag to use default optimizations. Then specify that 16x8 quantization mode is the required supported operation in the target specification:
```
converter.optimizations = [tf.lite.Optimize.DEFAULT]
converter.target_spec.supported_ops = [tf.lite.OpsSet.EXPERIMENTAL_TFLITE_BUILTINS_ACTIVATIONS_INT16_WEIGHTS_INT8]
```
As in the case of int8 post-training quantization, it is possible to produce a fully integer quantized model by setting converter options `inference_input(output)_type` to tf.int16.
Set the calibration data:
```
mnist_train, _ = tf.keras.datasets.mnist.load_data()
images = tf.cast(mnist_train[0], tf.float32) / 255.0
mnist_ds = tf.data.Dataset.from_tensor_slices((images)).batch(1)
def representative_data_gen():
for input_value in mnist_ds.take(100):
# Model has only one input so each data point has one element.
yield [input_value]
converter.representative_dataset = representative_data_gen
```
Finally, convert the model as usual. Note, by default the converted model will still use float input and outputs for invocation convenience.
```
tflite_16x8_model = converter.convert()
tflite_model_16x8_file = tflite_models_dir/"mnist_model_quant_16x8.tflite"
tflite_model_16x8_file.write_bytes(tflite_16x8_model)
```
Note how the resulting file is approximately `1/3` the size.
```
!ls -lh {tflite_models_dir}
```
## Run the TensorFlow Lite models
Run the TensorFlow Lite model using the Python TensorFlow Lite Interpreter.
### Load the model into the interpreters
```
interpreter = tf.lite.Interpreter(model_path=str(tflite_model_file))
interpreter.allocate_tensors()
interpreter_16x8 = tf.lite.Interpreter(model_path=str(tflite_model_16x8_file))
interpreter_16x8.allocate_tensors()
```
### Test the models on one image
```
test_image = np.expand_dims(test_images[0], axis=0).astype(np.float32)
input_index = interpreter.get_input_details()[0]["index"]
output_index = interpreter.get_output_details()[0]["index"]
interpreter.set_tensor(input_index, test_image)
interpreter.invoke()
predictions = interpreter.get_tensor(output_index)
import matplotlib.pylab as plt
plt.imshow(test_images[0])
template = "True:{true}, predicted:{predict}"
_ = plt.title(template.format(true= str(test_labels[0]),
predict=str(np.argmax(predictions[0]))))
plt.grid(False)
test_image = np.expand_dims(test_images[0], axis=0).astype(np.float32)
input_index = interpreter_16x8.get_input_details()[0]["index"]
output_index = interpreter_16x8.get_output_details()[0]["index"]
interpreter_16x8.set_tensor(input_index, test_image)
interpreter_16x8.invoke()
predictions = interpreter_16x8.get_tensor(output_index)
plt.imshow(test_images[0])
template = "True:{true}, predicted:{predict}"
_ = plt.title(template.format(true= str(test_labels[0]),
predict=str(np.argmax(predictions[0]))))
plt.grid(False)
```
### Evaluate the models
```
# A helper function to evaluate the TF Lite model using "test" dataset.
def evaluate_model(interpreter):
input_index = interpreter.get_input_details()[0]["index"]
output_index = interpreter.get_output_details()[0]["index"]
# Run predictions on every image in the "test" dataset.
prediction_digits = []
for test_image in test_images:
# Pre-processing: add batch dimension and convert to float32 to match with
# the model's input data format.
test_image = np.expand_dims(test_image, axis=0).astype(np.float32)
interpreter.set_tensor(input_index, test_image)
# Run inference.
interpreter.invoke()
# Post-processing: remove batch dimension and find the digit with highest
# probability.
output = interpreter.tensor(output_index)
digit = np.argmax(output()[0])
prediction_digits.append(digit)
# Compare prediction results with ground truth labels to calculate accuracy.
accurate_count = 0
for index in range(len(prediction_digits)):
if prediction_digits[index] == test_labels[index]:
accurate_count += 1
accuracy = accurate_count * 1.0 / len(prediction_digits)
return accuracy
print(evaluate_model(interpreter))
```
Repeat the evaluation on the 16x8 quantized model:
```
# NOTE: This quantization mode is an experimental post-training mode,
# it does not have any optimized kernels implementations or
# specialized machine learning hardware accelerators. Therefore,
# it could be slower than the float interpreter.
print(evaluate_model(interpreter_16x8))
```
In this example, you have quantized a model to 16x8 with no difference in the accuracy, but with the 3x reduced size.
|
github_jupyter
|
# Diagramas de Cortante e Momento em Vigas
Exemplo disponível em https://youtu.be/MNW1-rB46Ig
<img src="viga1.jpg">
```
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.font_manager as font_manager
from matplotlib import rc
# Set the font dictionaries (for plot title and axis titles)
rc('font', **{'family': 'serif', 'serif': ['Computer Modern'],'size': '18'})
rc('text', usetex=True)
q = 10
L = 1
N=10
# Reações de Apoio
VA=3*q*L/4
VB=q*L/4
print("Reação de Apoio em A (kN) =",VA)
print("Reação de Apoio em B (kN) =",VB)
```
Cálculo da Cortante pela integração do carregamento usando a Regra do Trapézio
```
def Cortante(q,x,V0):
# Entro com o carregamento, comprimento do trecho e cortante em x[0]
V = np.zeros(len(x)) # inicializa
dx=x[1] # passo
V[0]=V0 # Valor inicial da cortante
for i in range(1,N):
V[i]=V[i-1]+dx*(q[i-1]+q[i])/2
return np.array(V)
```
Cálculo do Momento Fletor pela integração do carregamento usando a Regra do Trapézio
```
def Momento(V,x,M0):
# Entro com a cortante, comprimento do trecho e momento em x[0]
M = np.zeros(len(x)) # inicializa
dx=x[1] # passo
M[0]=M0 # Valor inicial da cortante
for i in range(1,N):
M[i]=M0+M[i-1]+dx*(V[i-1]+V[i])/2
return np.array(M)
carregamento1 = q*np.ones(N)
carregamento2 =0*np.ones(N)
x1=np.linspace(0,L,N)
x2=np.linspace(L,2*L,N)
# Carregamento
plt.figure(figsize=(15,5))
plt.plot(x1,carregamento1,color='r',linewidth=2)
plt.fill_between(x1,carregamento1, facecolor='b', alpha=0.5)
plt.plot(x2,carregamento2,color='r',linewidth=2)
plt.fill_between(x2,carregamento2, facecolor='b', alpha=0.5)
plt.xlabel("Comprimento (m)")
plt.ylabel("Carregamento (kN/m)")
plt.grid(which='major', axis='both')
plt.title("Carregamento")
plt.show()
# Trecho I - 0<x<L
V1=-q*x1+VA # Cortante Teórica
M1=VA*x1-q*(x1*x1)/2 # Momento Teórico
# por integração numérica
V1int = Cortante(-carregamento1,x1,VA)
M1int = Momento(V1int,x1,0)
# Trecho II - L<x<2L
V2=VA-q*np.ones(N)*L # Cortante Teórico
M2=VA*x2-q*L*(x2-L/2) # Momento Teórico
# por integração numérica
V2int=Cortante(-carregamento2,x2,V1int[N-1])
M2int=Momento(V2int,x2,M1int[N-1])
# Cortante
plt.figure(figsize=(15,5))
plt.plot(x1,V1,color='r',linewidth=2)
plt.fill_between(x1, V1, facecolor='b', alpha=0.5)
plt.plot(x2,V2,color='r',linewidth=2,label="Método das Seções")
plt.fill_between(x2, V2, facecolor='b', alpha=0.5)
plt.plot(x1,V1int,color='k',linestyle = 'dotted', linewidth=5,label="Integração")
plt.plot(x2,V2int,color='k',linestyle = 'dotted', linewidth=5)
plt.legend(loc ="upper right")
plt.xlabel("Comprimento (m)")
plt.ylabel("Cortante (kN)")
plt.grid(which='major', axis='both')
plt.title("Diagrama de Cortante")
plt.show()
# Momento Fletor
plt.figure(figsize=(15,5))
plt.plot(x1,M1,color='r',linewidth=2)
plt.fill_between(x1, M1, facecolor='b', alpha=0.5)
plt.plot(x2,M2,color='r',linewidth=2,label="Método das Seções")
plt.fill_between(x2, M2, facecolor='b', alpha=0.5)
plt.plot(x1,M1int,color='k',linestyle = 'dotted', linewidth=5,label="Integração")
plt.plot(x2,M2int,color='k',linestyle = 'dotted', linewidth=5)
plt.legend(loc ="upper right")
plt.xlabel("Comprimento (m)")
plt.ylabel("Momento (kN.m)")
plt.grid(which='major', axis='both')
plt.title("Diagrama de Momento Fletor")
plt.show()
```
|
github_jupyter
|
# EventVestor: Shareholder Meetings
In this notebook, we'll take a look at EventVestor's *Shareholder Meetings* dataset, available on the [Quantopian Store](https://www.quantopian.com/store). This dataset spans January 01, 2007 through the current day, and documents companies' annual and special shareholder meetings calendars.
### Blaze
Before we dig into the data, we want to tell you about how you generally access Quantopian Store data sets. These datasets are available through an API service known as [Blaze](http://blaze.pydata.org). Blaze provides the Quantopian user with a convenient interface to access very large datasets.
Blaze provides an important function for accessing these datasets. Some of these sets are many millions of records. Bringing that data directly into Quantopian Research directly just is not viable. So Blaze allows us to provide a simple querying interface and shift the burden over to the server side.
It is common to use Blaze to reduce your dataset in size, convert it over to Pandas and then to use Pandas for further computation, manipulation and visualization.
Helpful links:
* [Query building for Blaze](http://blaze.pydata.org/en/latest/queries.html)
* [Pandas-to-Blaze dictionary](http://blaze.pydata.org/en/latest/rosetta-pandas.html)
* [SQL-to-Blaze dictionary](http://blaze.pydata.org/en/latest/rosetta-sql.html).
Once you've limited the size of your Blaze object, you can convert it to a Pandas DataFrames using:
> `from odo import odo`
> `odo(expr, pandas.DataFrame)`
### Free samples and limits
One other key caveat: we limit the number of results returned from any given expression to 10,000 to protect against runaway memory usage. To be clear, you have access to all the data server side. We are limiting the size of the responses back from Blaze.
There is a *free* version of this dataset as well as a paid one. The free one includes about three years of historical data, though not up to the current day.
With preamble in place, let's get started:
```
# import the dataset
from quantopian.interactive.data.eventvestor import shareholder_meetings
# or if you want to import the free dataset, use:
# from quantopian.data.eventvestor import shareholder_meetings_free
# import data operations
from odo import odo
# import other libraries we will use
import pandas as pd
# Let's use blaze to understand the data a bit using Blaze dshape()
shareholder_meetings.dshape
# And how many rows are there?
# N.B. we're using a Blaze function to do this, not len()
shareholder_meetings.count()
# Let's see what the data looks like. We'll grab the first three rows.
shareholder_meetings[:3]
```
Let's go over the columns:
- **event_id**: the unique identifier for this event.
- **asof_date**: EventVestor's timestamp of event capture.
- **symbol**: stock ticker symbol of the affected company.
- **event_headline**: a brief description of the event
- **meeting_type**: types include *annual meeting, special meeting, proxy contest*.
- **record_date**: record date to be eligible for proxy vote
- **meeting_date**: shareholder meeting date
- **timestamp**: this is our timestamp on when we registered the data.
- **sid**: the equity's unique identifier. Use this instead of the symbol.
We've done much of the data processing for you. Fields like `timestamp` and `sid` are standardized across all our Store Datasets, so the datasets are easy to combine. We have standardized the `sid` across all our equity databases.
We can select columns and rows with ease. Below, we'll fetch Tesla's 2013 and 2014 meetings.
```
# get tesla's sid first
tesla_sid = symbols('TSLA').sid
meetings = shareholder_meetings[('2012-12-31' < shareholder_meetings['asof_date']) &
(shareholder_meetings['asof_date'] <'2015-01-01') &
(shareholder_meetings.sid == tesla_sid)]
# When displaying a Blaze Data Object, the printout is automatically truncated to ten rows.
meetings.sort('asof_date')
```
Now suppose we want a DataFrame of the Blaze Data Object above, but only want the `record_date, meeting_date`, and `sid`.
```
df = odo(meetings, pd.DataFrame)
df = df[['record_date','meeting_date','sid']]
df
```
|
github_jupyter
|
```
import mxnet as mx
import numpy as np
import random
import bisect
# set up logging
import logging
reload(logging)
logging.basicConfig(format='%(asctime)s %(levelname)s:%(message)s', level=logging.DEBUG, datefmt='%I:%M:%S')
```
# A Glance of LSTM structure and embedding layer
We will build a LSTM network to learn from char only. At each time, input is a char. We will see this LSTM is able to learn words and grammers from sequence of chars.
The following figure is showing an unrolled LSTM network, and how we generate embedding of a char. The one-hot to embedding operation is a special case of fully connected network.
<img src="http://data.dmlc.ml/mxnet/data/char-rnn_1.png">
<img src="http://data.dmlc.ml/mxnet/data/char-rnn_2.png">
```
from lstm import lstm_unroll, lstm_inference_symbol
from bucket_io import BucketSentenceIter
from rnn_model import LSTMInferenceModel
# Read from doc
def read_content(path):
with open(path) as ins:
content = ins.read()
return content
# Build a vocabulary of what char we have in the content
def build_vocab(path):
content = read_content(path)
content = list(content)
idx = 1 # 0 is left for zero-padding
the_vocab = {}
for word in content:
if len(word) == 0:
continue
if not word in the_vocab:
the_vocab[word] = idx
idx += 1
return the_vocab
# We will assign each char with a special numerical id
def text2id(sentence, the_vocab):
words = list(sentence)
words = [the_vocab[w] for w in words if len(w) > 0]
return words
# Evaluation
def Perplexity(label, pred):
label = label.T.reshape((-1,))
loss = 0.
for i in range(pred.shape[0]):
loss += -np.log(max(1e-10, pred[i][int(label[i])]))
return np.exp(loss / label.size)
```
# Get Data
```
import os
data_url = "http://data.dmlc.ml/mxnet/data/lab_data.zip"
os.system("wget %s" % data_url)
os.system("unzip -o lab_data.zip")
```
Sample training data:
```
all to Renewal Keynote Address Call to Renewal Pt 1Call to Renewal Part 2 TOPIC: Our Past, Our Future & Vision for America June
28, 2006 Call to Renewal' Keynote Address Complete Text Good morning. I appreciate the opportunity to speak here at the Call to R
enewal's Building a Covenant for a New America conference. I've had the opportunity to take a look at your Covenant for a New Ame
rica. It is filled with outstanding policies and prescriptions for much of what ails this country. So I'd like to congratulate yo
u all on the thoughtful presentations you've given so far about poverty and justice in America, and for putting fire under the fe
et of the political leadership here in Washington.But today I'd like to talk about the connection between religion and politics a
nd perhaps offer some thoughts about how we can sort through some of the often bitter arguments that we've been seeing over the l
ast several years.I do so because, as you all know, we can affirm the importance of poverty in the Bible; and we can raise up and
pass out this Covenant for a New America. We can talk to the press, and we can discuss the religious call to address poverty and
environmental stewardship all we want, but it won't have an impact unless we tackle head-on the mutual suspicion that sometimes
```
# LSTM Hyperparameters
```
# The batch size for training
batch_size = 32
# We can support various length input
# For this problem, we cut each input sentence to length of 129
# So we only need fix length bucket
buckets = [129]
# hidden unit in LSTM cell
num_hidden = 512
# embedding dimension, which is, map a char to a 256 dim vector
num_embed = 256
# number of lstm layer
num_lstm_layer = 3
# we will show a quick demo in 2 epoch
# and we will see result by training 75 epoch
num_epoch = 2
# learning rate
learning_rate = 0.01
# we will use pure sgd without momentum
momentum = 0.0
# we can select multi-gpu for training
# for this demo we only use one
devs = [mx.context.gpu(i) for i in range(1)]
# build char vocabluary from input
vocab = build_vocab("./obama.txt")
# generate symbol for a length
def sym_gen(seq_len):
return lstm_unroll(num_lstm_layer, seq_len, len(vocab) + 1,
num_hidden=num_hidden, num_embed=num_embed,
num_label=len(vocab) + 1, dropout=0.2)
# initalize states for LSTM
init_c = [('l%d_init_c'%l, (batch_size, num_hidden)) for l in range(num_lstm_layer)]
init_h = [('l%d_init_h'%l, (batch_size, num_hidden)) for l in range(num_lstm_layer)]
init_states = init_c + init_h
# we can build an iterator for text
data_train = BucketSentenceIter("./obama.txt", vocab, buckets, batch_size,
init_states, seperate_char='\n',
text2id=text2id, read_content=read_content)
# the network symbol
symbol = sym_gen(buckets[0])
```
# Train model
```
# Train a LSTM network as simple as feedforward network
model = mx.model.FeedForward(ctx=devs,
symbol=symbol,
num_epoch=num_epoch,
learning_rate=learning_rate,
momentum=momentum,
wd=0.0001,
initializer=mx.init.Xavier(factor_type="in", magnitude=2.34))
# Fit it
model.fit(X=data_train,
eval_metric = mx.metric.np(Perplexity),
batch_end_callback=mx.callback.Speedometer(batch_size, 50),
epoch_end_callback=mx.callback.do_checkpoint("obama"))
```
# Inference from model
```
# helper strcuture for prediction
def MakeRevertVocab(vocab):
dic = {}
for k, v in vocab.items():
dic[v] = k
return dic
# make input from char
def MakeInput(char, vocab, arr):
idx = vocab[char]
tmp = np.zeros((1,))
tmp[0] = idx
arr[:] = tmp
# helper function for random sample
def _cdf(weights):
total = sum(weights)
result = []
cumsum = 0
for w in weights:
cumsum += w
result.append(cumsum / total)
return result
def _choice(population, weights):
assert len(population) == len(weights)
cdf_vals = _cdf(weights)
x = random.random()
idx = bisect.bisect(cdf_vals, x)
return population[idx]
# we can use random output or fixed output by choosing largest probability
def MakeOutput(prob, vocab, sample=False, temperature=1.):
if sample == False:
idx = np.argmax(prob, axis=1)[0]
else:
fix_dict = [""] + [vocab[i] for i in range(1, len(vocab) + 1)]
scale_prob = np.clip(prob, 1e-6, 1 - 1e-6)
rescale = np.exp(np.log(scale_prob) / temperature)
rescale[:] /= rescale.sum()
return _choice(fix_dict, rescale[0, :])
try:
char = vocab[idx]
except:
char = ''
return char
# load from check-point
_, arg_params, __ = mx.model.load_checkpoint("obama", 75)
# build an inference model
model = LSTMInferenceModel(num_lstm_layer, len(vocab) + 1,
num_hidden=num_hidden, num_embed=num_embed,
num_label=len(vocab) + 1, arg_params=arg_params, ctx=mx.gpu(), dropout=0.2)
# generate a sequence of 1200 chars
seq_length = 1200
input_ndarray = mx.nd.zeros((1,))
revert_vocab = MakeRevertVocab(vocab)
# Feel free to change the starter sentence
output ='The joke'
random_sample = True
new_sentence = True
ignore_length = len(output)
for i in range(seq_length):
if i <= ignore_length - 1:
MakeInput(output[i], vocab, input_ndarray)
else:
MakeInput(output[-1], vocab, input_ndarray)
prob = model.forward(input_ndarray, new_sentence)
new_sentence = False
next_char = MakeOutput(prob, revert_vocab, random_sample)
if next_char == '':
new_sentence = True
if i >= ignore_length - 1:
output += next_char
# Let's see what we can learned from char in Obama's speech.
print(output)
```
|
github_jupyter
|
# p-Hacking and Multiple Comparisons Bias
By Delaney Mackenzie and Maxwell Margenot.
Part of the Quantopian Lecture Series:
* [www.quantopian.com/lectures](https://www.quantopian.com/lectures)
* [github.com/quantopian/research_public](https://github.com/quantopian/research_public)
Notebook released under the Creative Commons Attribution 4.0 License.
---
Multiple comparisons bias is a pervasive problem in statistics, data science, and in general forecasting/predictions. The short explanation is that the more tests you run, the more likely you are to get an outcome that you want/expect. If you ignore the multitude of tests that failed, you are clearly setting yourself up for failure by misinterpreting what's going on in your data.
A particularly common example of this is when looking for relationships in large data sets comprising of many indepedent series or variables. In this case you run a test each time you evaluate whether a relationship exists between a set of variables.
## Statistics Merely Illuminates This Issue
Most folks also fall prey to multiple comparisons bias in real life. Any time you make a decision you are effectively taking an action based on an hypothesis. That hypothesis is often tested. You can end up unknowingly making many tests in your daily life.
An example might be deciding which medicine is helping cure a cold you have. Many people will take multiple medicines at once to try and get rid of symptoms. You may think that a certain medicine worked, when in reality none did and the cold just happened to start getting better at some point.
The point here is that this problem doesn't stem from statistical testing and p-values. Rather, these techniques give us much more information about the problem and when it might be occuring.
```
import numpy as np
import pandas as pd
import scipy.stats as stats
import matplotlib.pyplot as plt
```
### Refresher: Spearman Rank Correlation
Please refer to [this lecture](https://www.quantopian.com/lectures/spearman-rank-correlation) for more full info, but here is a very brief refresher on Spearman Rank Correlation.
It's a variation of correlation that takes into account the ranks of the data. This can help with weird distributions or outliers that would confuse other measures. The test also returns a p-value, which is key here.
A higher coefficient means a stronger estimated relationship.
```
X = pd.Series(np.random.normal(0, 1, 100))
Y = X
r_s = stats.spearmanr(Y, X)
print 'Spearman Rank Coefficient: ', r_s[0]
print 'p-value: ', r_s[1]
```
If we add some noise our coefficient will drop.
```
X = pd.Series(np.random.normal(0, 1, 100))
Y = X + np.random.normal(0, 1, 100)
r_s = stats.spearmanr(Y, X)
print 'Spearman Rank Coefficient: ', r_s[0]
print 'p-value: ', r_s[1]
```
### p-value Refresher
For more info on p-values see [this lecture](https://www.quantopian.com/lectures/hypothesis-testing). What's important to remember is they're used to test a hypothesis given some data. Here we are testing the hypothesis that a relationship exists between two series given the series values.
####IMPORTANT: p-values must be treated as binary.
A common mistake is that p-values are treated as more or less significant. This is bad practice as it allows for what's known as [p-hacking](https://en.wikipedia.org/wiki/Data_dredging) and will result in more false positives than you expect. Effectively, you will be too likely to convince yourself that relationships exist in your data.
To treat p-values as binary, a cutoff must be set in advance. Then the p-value must be compared with the cutoff and treated as significant/not signficant. Here we'll show this.
### The Cutoff is our Significance Level
We can refer to the cutoff as our significance level because a lower cutoff means that results which pass it are significant at a higher level of confidence. So if you have a cutoff of 0.05, then even on random data 5% of tests will pass based on chance. A cutoff of 0.01 reduces this to 1%, which is a more stringent test. We can therefore have more confidence in our results.
```
# Setting a cutoff of 5% means that there is a 5% chance
# of us getting a significant p-value given no relationship
# in our data (false positive).
# NOTE: This is only true if the test's assumptions have been
# satisfied and the test is therefore properly calibrated.
# All tests have different assumptions.
cutoff = 0.05
X = pd.Series(np.random.normal(0, 1, 100))
Y = X + np.random.normal(0, 1, 100)
r_s = stats.spearmanr(Y, X)
print 'Spearman Rank Coefficient: ', r_s[0]
if r_s[1] < cutoff:
print 'There is significant evidence of a relationship.'
else:
print 'There is not significant evidence of a relationship.'
```
## Experiment - Running Many Tests
We'll start by defining a data frame.
```
df = pd.DataFrame()
```
Now we'll populate it by adding `N` randomly generated timeseries of length `T`.
```
N = 20
T = 100
for i in range(N):
X = np.random.normal(0, 1, T)
X = pd.Series(X)
name = 'X%s' % i
df[name] = X
df.head()
```
Now we'll run a test on all pairs within our data looking for instances where our p-value is below our defined cutoff of 5%.
```
cutoff = 0.05
significant_pairs = []
for i in range(N):
for j in range(i+1, N):
Xi = df.iloc[:, i]
Xj = df.iloc[:, j]
results = stats.spearmanr(Xi, Xj)
pvalue = results[1]
if pvalue < cutoff:
significant_pairs.append((i, j))
```
Before we check how many significant results we got, let's run out some math to check how many we'd expect. The formula for the number of pairs given N series is
$$\frac{N(N-1)}{2}$$
There are no relationships in our data as it's all randomly generated. If our test is properly calibrated we should expect a false positive rate of 5% given our 5% cutoff. Therefore we should expect the following number of pairs that achieved significance based on pure random chance.
```
(N * (N-1) / 2) * 0.05
```
Now let's compare to how many we actually found.
```
len(significant_pairs)
```
We shouldn't expect the numbers to match too closely here on a consistent basis as we've only run one experiment. If we run many of these experiments we should see a convergence to what we'd expect.
### Repeating the Experiment
```
def do_experiment(N, T, cutoff=0.05):
df = pd.DataFrame()
# Make random data
for i in range(N):
X = np.random.normal(0, 1, T)
X = pd.Series(X)
name = 'X%s' % i
df[name] = X
significant_pairs = []
# Look for relationships
for i in range(N):
for j in range(i+1, N):
Xi = df.iloc[:, i]
Xj = df.iloc[:, j]
results = stats.spearmanr(Xi, Xj)
pvalue = results[1]
if pvalue < cutoff:
significant_pairs.append((i, j))
return significant_pairs
num_experiments = 100
results = np.zeros((num_experiments,))
for i in range(num_experiments):
# Run a single experiment
result = do_experiment(20, 100, cutoff=0.05)
# Count how many pairs
n = len(result)
# Add to array
results[i] = n
```
The average over many experiments should be closer.
```
np.mean(results)
```
## Visualizing What's Going On
What's happening here is that p-values should be uniformly distributed, given no signal in the underlying data. Basically, they carry no information whatsoever and will be equally likely to be 0.01 as 0.99. Because they're popping out randomly, you will expect a certain percentage of p-values to be underneath any threshold you choose. The lower the threshold the fewer will pass your test.
Let's visualize this by making a modified function that returns p-values.
```
def get_pvalues_from_experiment(N, T):
df = pd.DataFrame()
# Make random data
for i in range(N):
X = np.random.normal(0, 1, T)
X = pd.Series(X)
name = 'X%s' % i
df[name] = X
pvalues = []
# Look for relationships
for i in range(N):
for j in range(i+1, N):
Xi = df.iloc[:, i]
Xj = df.iloc[:, j]
results = stats.spearmanr(Xi, Xj)
pvalue = results[1]
pvalues.append(pvalue)
return pvalues
```
We'll now collect a bunch of pvalues. As in any case we'll want to collect quite a number of p-values to start getting a sense of how the underlying distribution looks. If we only collect few, it will be noisy like this:
```
pvalues = get_pvalues_from_experiment(10, 100)
plt.hist(pvalues)
plt.ylabel('Frequency')
plt.title('Observed p-value');
```
Let's dial up our `N` parameter to get a better sense. Keep in mind that the number of p-values will increase at a rate of
$$\frac{N (N-1)}{2}$$
or approximately quadratically. Therefore we don't need to increase `N` by much.
```
pvalues = get_pvalues_from_experiment(50, 100)
plt.hist(pvalues)
plt.ylabel('Frequency')
plt.title('Observed p-value');
```
Starting to look pretty flat, as we expected. Lastly, just to visualize the process of drawing a cutoff, we'll draw two artificial lines.
```
pvalues = get_pvalues_from_experiment(50, 100)
plt.vlines(0.01, 0, 150, colors='r', linestyle='--', label='0.01 Cutoff')
plt.vlines(0.05, 0, 150, colors='r', label='0.05 Cutoff')
plt.hist(pvalues, label='P-Value Distribution')
plt.legend()
plt.ylabel('Frequency')
plt.title('Observed p-value');
```
We can see that with a lower cutoff we should expect to get fewer false positives. Let's check that with our above experiment.
```
num_experiments = 100
results = np.zeros((num_experiments,))
for i in range(num_experiments):
# Run a single experiment
result = do_experiment(20, 100, cutoff=0.01)
# Count how many pairs
n = len(result)
# Add to array
results[i] = n
np.mean(results)
```
And finally compare it to what we expected.
```
(N * (N-1) / 2) * 0.01
```
## Sensitivity / Specificity Tradeoff
As with any adjustment of p-value cutoff, we have a tradeoff. A lower cutoff decreases the rate of false positives, but also decreases the chance we find a real relationship (true positive). So you can't just decrease your cutoff to solve this problem.
https://en.wikipedia.org/wiki/Sensitivity_and_specificity
## Reducing Multiple Comparisons Bias
You can't really eliminate multiple comparisons bias, but you can reduce how much it impacts you. To do so we have two options.
### Option 1: Run fewer tests.
This is often the best option. Rather than just sweeping around hoping you hit an interesting signal, use your expert knowledge of the system to develop a great hypothesis and test that. This process of exploring the data, coming up with a hypothesis, then gathering more data and testing the hypothesis on the new data is considered the gold standard in statistical and scientific research. It's crucial that the data set on which you develop your hypothesis is not the one on which you test it. Because you found the effect while exploring, the test will likely pass and not really tell you anything. What you want to know is how consistent the effect is. Moving to new data and testing there will not only mean you only run one test, but will be an 'unbiased estimator' of whether your hypothesis is true. We discuss this a lot in other lectures.
### Option 2: Adjustment Factors and Bon Ferroni Correction
#### WARNING: This section gets a little technical. Unless you're comfortable with significance levels, we recommend looking at the code examples first and maybe reading the linked articles before fully diving into the text.
If you must run many tests, try to correct your p-values. This means applying a correction factor to the cutoff you desire to obtain the one actually used when determining whether p-values are significant. The most conservative and common correction factor is Bon Ferroni.
### Example: Bon Ferroni Correction
The concept behind Bon Ferroni is quite simple. It just says that if we run $m$ tests, and we have a significance level/cutoff of $a$, then we should use $a/m$ as our new cutoff when determining significance. The math works out because of the following.
Let's say we run $m$ tests. We should expect to see $ma$ false positives based on random chance that pass out cutoff. If we instead use $a/m$ as our cutoff, then we should expect to see $ma/m = a$ tests that pass our cutoff. Therefore we are back to our desired false positive rate of $a$.
Let's try it on our experiment above.
```
num_experiments = 100
results = np.zeros((num_experiments,))
N = 20
T = 100
desired_level = 0.05
num_tests = N * (N - 1) / 2
new_cutoff = desired_level / num_tests
for i in range(num_experiments):
# Run a single experiment
result = do_experiment(20, 100, cutoff=new_cutoff)
# Count how many pairs
n = len(result)
# Add to array
results[i] = n
np.mean(results)
```
As you can see, our number of significant results is now far lower on average. Which is good because the data was random to begin with.
### These are Often Overly Conservative
Because Bon Ferroni is so stringent, you can often end up passing over real relationships. There is a good example in the following article
https://en.wikipedia.org/wiki/Multiple_comparisons_problem
Effectively, it assumes that all the tests you are running are independent, and doesn't take into account any structure in your data. You may be able to design a more finely tuned correction factor, but this is adding a layer of complexity and therefore a point of failure to your research. In general any time you relax your stringency, you need to be very careful not to make a mistake.
Because of the over-zealousness of Bon Ferroni, often running fewer tests is the better option. Or, if you must run many tests, reserve multiple sets of data so your candidate signals can undergo an out-of-sample round of testing. For example, you might have the following flow:
* Let's say there are 100,000 possible relationships.
* Run a test on each possible relationship, and pick those that passed the test.
* With these candidates, run a test on a new out-of-sample set of data. Because you have many fewer candidates, you can now apply a Bon Ferroni correction to these p-values, or if necessary repeat another round of out-of-sample testing.
# What is p-Hacking?
p-hacking is just intentional or accidental abuse of multiple comparisons bias. It is surprisingly common, even in academic literature. The excellent statistical news website FiveThirtyEight has a great visualization here:
https://fivethirtyeight.com/features/science-isnt-broken/
Wikipedia's article is also informative:
https://en.wikipedia.org/wiki/Data_dredging
In general, the concept is simple. By running many tests or experiments and then focusing only on the ones that worked, you can present false positives as real results. Keep in mind that this also applies to running many different models or different types of experiments and on different data sets. Imagine that you spend a summer researching a new model to forecast corn future prices. You try 50 different models until finally one succeeds. Is this just luck at this point? Certainly you would want to be more careful about validating that model and testing it out-of-sample on new data before believing that it works.
# Final Notes
## You can never eliminate, only reduce risk.
In general you can never completely eliminate multiple comparisons bias, you can only reduce the risk of false positives using techniques we described above. At the end of the day most ideas tried in research don't work, so you'll end up testing many different hypotheses over time. Just try to be careful and use common sense about whether there is sufficient evidence that a hypothesis is true, or that you just happened to get lucky on this iteration.
## Use Out-of-Sample Testing
As mentioned above, out-of-sample testing is one of the best ways to reduce your risk. You should always use it, no matter the circumstances. Often one of the ways that false positives make it through your workflow is a lack of an out-of-sample test at the end.
####Sources
* https://en.wikipedia.org/wiki/Multiple_comparisons_problem
* https://en.wikipedia.org/wiki/Sensitivity_and_specificity
* https://en.wikipedia.org/wiki/Bonferroni_correction
* https://fivethirtyeight.com/features/science-isnt-broken/
*This presentation is for informational purposes only and does not constitute an offer to sell, a solicitation to buy, or a recommendation for any security; nor does it constitute an offer to provide investment advisory or other services by Quantopian, Inc. ("Quantopian"). Nothing contained herein constitutes investment advice or offers any opinion with respect to the suitability of any security, and any views expressed herein should not be taken as advice to buy, sell, or hold any security or as an endorsement of any security or company. In preparing the information contained herein, Quantopian, Inc. has not taken into account the investment needs, objectives, and financial circumstances of any particular investor. Any views expressed and data illustrated herein were prepared based upon information, believed to be reliable, available to Quantopian, Inc. at the time of publication. Quantopian makes no guarantees as to their accuracy or completeness. All information is subject to change and may quickly become unreliable for various reasons, including changes in market conditions or economic circumstances.*
|
github_jupyter
|
# Simple Quantum Implementation using Qiskit Aqua for Boolean satisfiability problems
This Jupyter notebook demonstrates how easy it is to use quantum algorithms from [Qiskit Aqua](https://qiskit.org/aqua) to solve Boolean satisfiability problems [(SAT)](https://en.wikipedia.org/wiki/Boolean_satisfiability_problem).
It is based on the Qiskit tutorial [Using Grover search for 3-SAT problems](https://github.com/Qiskit/qiskit-tutorials/blob/master/community/aqua/optimization/grover.ipynb) by [Jay Gambetta](https://github.com/jaygambetta) and [Richard Chen](https://github.com/chunfuchen) and a hands-on workshop by David Mesterhazy.
Implemented by [Jan-R. Lahmann](http://twitter.com/JanLahmann) using Qiskit, binder and RISE.
## Boolean Satisfiabilty problems (SAT)
The Boolean satisfiability problem [(SAT)](https://en.wikipedia.org/wiki/Boolean_satisfiability_problem) considers a Boolean expression with N boolean variables involving negation (NOT, $\neg$), conjunction (AND, $\wedge$) and disjunction (OR, $\vee$), as in the following (simple) example:
$$ f(x_1, x_2) = (x_1 \vee x_2) \wedge (x_1 \vee \neg x_2) . $$
The problem is to determine whether there is any assignment of values (TRUE, FALSE) to the Boolean variables which makes the formula true.
It's something like trying to flip a bunch of switches to find the setting that makes a light bulb turn on.
SAT is of central importance in many areas of computer science, including complexity theory, algorithmics, cryptography, artificial intelligence, circuit design, and automatic theorem proving.
SAT was the first problem proven to be NP-complete.
This means that all problems in the [complexity class NP](https://en.wikipedia.org/wiki/NP_(complexity)) are at most as difficult to solve as SAT.
There is no known classical algorithm that efficiently solves each SAT problem, and it is generally believed that no such algorithm exists.
Whether Boolean satisfiability problems have a classical algorithm that is polynomial in time is equivalent to the [P vs. NP problem](https://en.wikipedia.org/wiki/P_versus_NP_problem).
While [Grover's quantum search algorithm](https://en.wikipedia.org/wiki/Grover's_algorithm) does not provide exponential speed-up to this problem, it may nevertheless provide some speed-up in contrast to classical black-box search strategies.
### Basic definitions and terminology
A *literal* is either a variable, or the negation of a variable.
A *clause* is a disjunction (OR, $\vee$) of literals, or a single literal.
A formula is in *conjunctive normal form* [(CNF)](https://en.wikipedia.org/wiki/Conjunctive_normal_form) if it is a conjunction (AND, $\wedge$) of clauses, or a single clause.
A problem in conjunctive normal form is called *3-SAT* if each clause is limited to at most three literals.
3-SAT is also NP-complete.
Example for 3-SAT: $ (x_1 ∨ ¬x_2) ∧ (¬x_1 ∨ x_2 ∨ x_3) ∧ ¬x_1 $.
## Solving 3-SAT using Qiskit Aqua
We will show how to solve a 3-SAT problem using quantum algorithms from [Qiskit Aqua](https://qiskit.org/aqua).
Let us consider three Boolean variables $x_1, x_2, x_3$ and a Boolean function $f$ given by:
\begin{align*}
f(x_1, x_2, x_3) \;= &\;\;\;\;
\;(\neg x_1 \vee \neg x_2 \vee \neg x_3) \\
&\;\; \wedge \; ( x_1 \vee \neg x_2 \vee x_3) \\
&\;\; \wedge \;( x_1 \vee x_2 \vee \neg x_3) \\
&\;\; \wedge \;( x_1 \vee \neg x_2 \vee \neg x_3) \\
&\;\; \wedge \;(\neg x_1 \vee x_2 \vee x_3)
\end{align*}
It is common, to state 3-SAT problems in [DIMACS CNF format](https://people.sc.fsu.edu/~jburkardt/data/cnf/cnf.html):
1. The file may begin with comment lines.
* The "problem" line begins with "p", followed by the problem type "cnf", the number of variables and the number of clauses.
* The remainder of the file contains lines defining the clauses.
* A clause is defined by listing the index of each positive literal, and the negative index of each negative literal.
```
# import the problem in DIMACS CNF format
import os
import wget
if not '3sat3-5.cnf' in os.listdir():
wget.download('https://raw.githubusercontent.com/Qiskit/qiskit-tutorials/master/community/aqua/optimization/3sat3-5.cnf')
with open('3sat3-5.cnf', 'r') as f:
sat_cnf = f.read()
print(sat_cnf)
```
To apply a quantum algorithm from Qiskit Aqua to this problem, we simply need to import the Qiskit libraries and run the algorithm with the appropriate parameters.
```
# import Qiskit quantum libraries
from qiskit import BasicAer
from qiskit.visualization import plot_histogram
from qiskit.aqua import QuantumInstance
from qiskit.aqua.algorithms import Grover
from qiskit.aqua.components.oracles import LogicalExpressionOracle, TruthTableOracle
oracle = LogicalExpressionOracle(sat_cnf)
grover = Grover(oracle)
backend = BasicAer.get_backend('qasm_simulator')
quantum_instance = QuantumInstance(backend, shots=200)
result = grover.run(quantum_instance)
plot_histogram(result['measurement'])
```
The result shows that the assignments $000, 101, 110$ for $x_1 x_2 x_3$ are potential solutions to the problem.
Whether or not these are correct solutions to the problem can be verified efficiently, as 3-SAT is in NP.
Note that the variables in the histogram are in reverse order: $x_3, x_2, x_1$ instead of $x_1, x_2, x_3$.
## Classical brute force algorithm
The solutions to the problem can also be derived with a classical (non-quantum) algorithm by simply trying every possible combination of input values $x_1, x_2, x_3$of $f$.
We find again, that the solutions for the given 3-SAT problem are the assignments $000, 101, 110$ for $x_1 x_2 x_3$.
```
from IPython.display import HTML, display
import tabulate
nbr = 3 # number of Boolean variables in Boolean function
table = []
for i in range(2**nbr):
x1, x2, x3 = [int(x) for x in '{0:03b}'.format(i)] # Boolean variables
# define clauses
c1 = [not x1, not x2, not x3] # -1 -2 -3
c2 = [ x1, not x2, x3] # 1 -2 3
c3 = [ x1, x2, not x3] # 1 2 -3
c4 = [ x1, not x2, not x3] # 1 -2 -3
c5 = [not x1, x2, x3] # -1 2 3
f = all([any(c1), any(c2), any(c3), any(c4), any(c5)]) # Boolean function
table.append([x1, x2, x3, f])
display(HTML(tabulate.tabulate(table, tablefmt = 'html',
headers = ['$x_1$', '$x_2$', '$x_3$', '$f$'])))
```
Remark: this is obviously not the most efficient classical algorithm that exists. Heuristic SAT-algorithms are able to solve problem instances involving tens of thousands of variables and formulas consisting of millions of symbols, which is sufficient for many practical SAT problems.
|
github_jupyter
|
Copyright 2020 Google LLC
Licensed under the Apache License, Version 2.0 (the "License");
you may not use this file except in compliance with the License.
You may obtain a copy of the License at
https://www.apache.org/licenses/LICENSE-2.0
Unless required by applicable law or agreed to in writing, software
distributed under the License is distributed on an "AS IS" BASIS,
WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
See the License for the specific language governing permissions and
limitations under the License.
```
# Let us explicitly ask for TensorFlow2.
# This installs a lot of stuff - and will take a while.
!pip3 install tensorflow==2.0.1
import base64
import collections
import dataclasses
import hashlib
import itertools
import math
import numpy
import pprint
import scipy.optimize
import sys
import tensorflow as tf
print('TF version is:', tf.__version__)
print('NumPy version is:', numpy.__version__)
@dataclasses.dataclass(frozen=True)
class Solution(object):
potential: float
stationarity: float
pos: numpy.ndarray
def np_esum(spec, *arrays, optimize='greedy'):
"""Numpy einsum with default greedy optimization."""
return numpy.einsum(spec, *arrays, optimize=optimize)
def get_onb_transform(k_ab):
if not numpy.allclose(k_ab, k_ab.real) or not numpy.allclose(k_ab, k_ab.T):
raise ValueError('Bad Gramian.')
eigvals, eigvecsT = numpy.linalg.eigh(k_ab)
if not all(v * eigvals[0] > 0 for v in eigvals):
raise ValueError('Non-definite Gramian.')
onb_transform = numpy.einsum('a,na->an', eigvals**(-.5), eigvecsT)
g = np_esum('ab,Aa,Bb->AB', k_ab, onb_transform, onb_transform)
assert numpy.allclose(
g, numpy.eye(g.shape[0]) * ((-1, 1)[int(eigvals[0] > 0)])
), 'Bad ONB-transform.'
return onb_transform, numpy.linalg.inv(onb_transform)
def numpy_signature(a, digits=3):
"""Produces a signature-fingerprint of a numpy array."""
# Hack to ensure that -0.0 gets consistently shown as 0.0.
minus_zero_hack = 1e-100+1e-100j
return base64.b64encode(
hashlib.sha256(
str((a.shape,
','.join(repr(x)
for x in numpy.round(a + minus_zero_hack, digits).flat))
).encode('utf-8')
).digest()).decode('utf-8').strip('\n=')
def tformat(array,
name=None,
elem_filter=lambda x: abs(x) > 1e-8,
fmt='%s',
max_rows=numpy.inf,
cols=120):
"""Formats a numpy-array in human readable table form."""
# Leading row will be replaced if caller asked for a name-row.
dim_widths = [
max(1, int(math.ceil(math.log(dim + 1e-100, 10))))
for dim in array.shape]
format_str = '%s: %s' % (' '.join('%%%dd' % w for w in dim_widths), fmt)
rows = []
for indices in itertools.product(*[range(dim) for dim in array.shape]):
v = array[indices]
if elem_filter(v):
rows.append(format_str % (indices + (v, )))
num_entries = len(rows)
if num_entries > max_rows:
rows = rows[:max_rows]
if cols is not None:
width = max(map(len, rows))
num_cols = max(1, cols // (3 + width))
num_xrows = int(math.ceil(len(rows) / num_cols))
padded = [('%%-%ds' % width) % s
for s in rows + [''] * (num_cols * num_xrows - len(rows))]
table = numpy.array(padded, dtype=object).reshape(num_cols, num_xrows).T
xrows = [' | '.join(row) for row in table]
else:
xrows = rows
if name is not None:
return '\n'.join(
['=== %s, shape=%r, %d%s / %d non-small entries ===' % (
name, array.shape,
num_entries,
'' if num_entries == len(rows) else '(%d shown)' % num_entries,
array.size)] +
[r.strip() for r in xrows])
return '\n'.join(xrows)
def tprint(array, sep=' ', end='\n', file=sys.stdout, **tformat_kwargs):
"""Prints a numpy array in human readable table form."""
print(tformat(array, **tformat_kwargs), sep=sep, end=end, file=file)
### Lie Algebra definitions for Spin(8), SU(8), E7.
def permutation_sign(p):
q = [x for x in p] # Copy to list.
parity = 1
for n in range(len(p)):
while n != q[n]:
qn = q[n]
q[n], q[qn] = q[qn], q[n] # Swap to make q[qn] = qn.
parity = -parity
return parity
def asymm2(a, einsum_spec):
"""Antisymmetrizes."""
return 0.5 * (a - numpy.einsum(einsum_spec, a))
class Spin8(object):
"""Container class for Spin(8) tensor invariants."""
def __init__(self):
r8 = range(8)
self.gamma_vsc = gamma_vsc = self._get_gamma_vsc()
#
# The gamma^{ab}_{alpha beta} tensor that translates between antisymmetric
# matrices over vectors [ij] and antisymmetric matrices over spinors [sS].
self.gamma_vvss = asymm2(
numpy.einsum('isc,jSc->ijsS', gamma_vsc, gamma_vsc), 'ijsS->jisS')
# The gamma^{ab}_{alpha* beta*} tensor that translates between antisymmetric
# matrices over vectors [ij] and antisymmetric matrices over cospinors [cC].
self.gamma_vvcc = asymm2(
numpy.einsum('isc,jsC->ijcC', gamma_vsc, gamma_vsc), 'ijcC->jicC')
#
# The gamma^{ijkl}_{alpha beta} tensor that translates between antisymmetric
# 4-forms [ijkl] and symmetric traceless matrices over the spinors (sS).
g_ijsS = numpy.einsum('isc,jSc->ijsS', self.gamma_vsc, self.gamma_vsc)
g_ijcC = numpy.einsum('isc,jsC->ijcC', self.gamma_vsc, self.gamma_vsc)
g_ijklsS = numpy.einsum('ijst,kltS->ijklsS', g_ijsS, g_ijsS)
g_ijklcC = numpy.einsum('ijcd,kldC->ijklcC', g_ijcC, g_ijcC)
gamma_vvvvss = numpy.zeros([8] * 6)
gamma_vvvvcc = numpy.zeros([8] * 6)
for perm in itertools.permutations(range(4)):
perm_ijkl = ''.join('ijkl'[p] for p in perm)
sign = permutation_sign(perm)
gamma_vvvvss += sign * numpy.einsum(perm_ijkl + 'sS->ijklsS', g_ijklsS)
gamma_vvvvcc += sign * numpy.einsum(perm_ijkl + 'cC->ijklcC', g_ijklcC)
self.gamma_vvvvss = gamma_vvvvss / 24.0
self.gamma_vvvvcc = gamma_vvvvcc / 24.0
def _get_gamma_vsc(self):
"""Computes SO(8) gamma-matrices."""
# Conventions match Green, Schwarz, Witten's, but with index-counting
# starting at zero.
entries = (
"007+ 016- 025- 034+ 043- 052+ 061+ 070- "
"101+ 110- 123- 132+ 145+ 154- 167- 176+ "
"204+ 215- 226+ 237- 240- 251+ 262- 273+ "
"302+ 313+ 320- 331- 346- 357- 364+ 375+ "
"403+ 412- 421+ 430- 447+ 456- 465+ 474- "
"505+ 514+ 527+ 536+ 541- 550- 563- 572- "
"606+ 617+ 624- 635- 642+ 653+ 660- 671- "
"700+ 711+ 722+ 733+ 744+ 755+ 766+ 777+")
ret = numpy.zeros([8, 8, 8])
for ijkc in entries.split():
ijk = tuple(map(int, ijkc[:-1]))
ret[ijk] = +1 if ijkc[-1] == '+' else -1
return ret
class SU8(object):
"""Container class for su(8) tensor invariants."""
def __init__(self):
# Tensor that translates between adjoint indices 'a' and
# (vector) x (vector) indices 'ij'
ij_map = [(i, j) for i in range(8) for j in range(8) if i < j]
#
# We also need the mapping between 8 x 8 and 35 representations, using
# common conventions for a basis of the 35-representation, and likewise
# for 8 x 8 and 28.
m_35_8_8 = numpy.zeros([35, 8, 8], dtype=numpy.complex128)
m_28_8_8 = numpy.zeros([28, 8, 8], dtype=numpy.complex128)
for n in range(7):
m_35_8_8[n, n, n] = +1.0
m_35_8_8[n, n + 1, n + 1] = -1.0
for a, (m, n) in enumerate(ij_map):
m_35_8_8[a + 7, m, n] = m_35_8_8[a + 7, n, m] = 1.0
m_28_8_8[a, m, n] = 1.0
m_28_8_8[a, n, m] = -1.0
#
# The su8 'Generator Matrices'.
t_aij = numpy.zeros([63, 8, 8], dtype=numpy.complex128)
t_aij[:35, :, :] = 1.0j * m_35_8_8
for a, (i, j) in enumerate(ij_map):
t_aij[a + 35, i, j] = -1.0
t_aij[a + 35, j, i] = 1.0
self.ij_map = ij_map
self.m_35_8_8 = m_35_8_8
self.m_28_8_8 = m_28_8_8
self.t_aij = t_aij
class E7(object):
"""Container class for e7 tensor invariants."""
def __init__(self, spin8, su8):
self._spin8 = spin8
self._su8 = su8
ij_map = su8.ij_map
t_a_ij_kl = numpy.zeros([133, 56, 56], dtype=numpy.complex128)
t_a_ij_kl[:35, 28:, :28] = (1 / 8.0) * (
np_esum('ijklsS,qsS,Iij,Kkl->qIK',
spin8.gamma_vvvvss, su8.m_35_8_8, su8.m_28_8_8, su8.m_28_8_8))
t_a_ij_kl[:35, :28, 28:] = t_a_ij_kl[:35, 28:, :28]
t_a_ij_kl[35:70, 28:, :28] = (1.0j / 8.0) * (
np_esum('ijklcC,qcC,Iij,Kkl->qIK',
spin8.gamma_vvvvcc, su8.m_35_8_8, su8.m_28_8_8, su8.m_28_8_8))
t_a_ij_kl[35:70, :28, 28:] = -t_a_ij_kl[35:70, 28:, :28]
#
# We need to find the action of the su(8) algebra on the
# 28-representation.
su8_28 = 2 * np_esum('aij,mn,Iim,Jjn->aIJ',
su8.t_aij,
numpy.eye(8, dtype=numpy.complex128),
su8.m_28_8_8, su8.m_28_8_8)
t_a_ij_kl[70:, :28, :28] = su8_28
t_a_ij_kl[70:, 28:, 28:] = su8_28.conjugate()
self.t_a_ij_kl = t_a_ij_kl
#
self.k_ab = numpy.einsum('aMN,bNM->ab', t_a_ij_kl, t_a_ij_kl)
self.v70_as_sc8x8 = numpy.einsum('sc,xab->sxcab',
numpy.eye(2),
su8.m_35_8_8).reshape(70, 2, 8, 8)
# For e7, there actually is a better orthonormal basis:
# the sd/asd 4-forms. The approach used here however readily generalizes
# to all other groups.
self.v70_onb_onbinv = get_onb_transform(self.k_ab[:70, :70])
def get_proj_35_8888(want_selfdual=True):
"""Computes the (35, 8, 8, 8, 8)-projector to the (anti)self-dual 4-forms."""
# We first need some basis for the 35 self-dual 4-forms.
# Our convention is that we lexicographically list those 8-choose-4
# combinations that contain the index 0.
sign_selfdual = 1 if want_selfdual else -1
ret = numpy.zeros([35, 8, 8, 8, 8], dtype=numpy.float64)
#
def get_selfdual(ijkl):
mnpq = tuple(n for n in range(8) if n not in ijkl)
return (sign_selfdual * permutation_sign(ijkl + mnpq),
ijkl, mnpq)
selfduals = [get_selfdual(ijkl)
for ijkl in itertools.combinations(range(8), 4)
if 0 in ijkl]
for num_sd, (sign_sd, ijkl, mnpq) in enumerate(selfduals):
for abcd in itertools.permutations(range(4)):
sign_abcd = permutation_sign(abcd)
ret[num_sd,
ijkl[abcd[0]],
ijkl[abcd[1]],
ijkl[abcd[2]],
ijkl[abcd[3]]] = sign_abcd
ret[num_sd,
mnpq[abcd[0]],
mnpq[abcd[1]],
mnpq[abcd[2]],
mnpq[abcd[3]]] = sign_abcd * sign_sd
return ret / 24.0
spin8 = Spin8()
su8 = SU8()
e7 = E7(spin8, su8)
assert (numpy_signature(e7.t_a_ij_kl) ==
'MMExYjC6Qr6gunZIYfRLLgM2PDtwUDYujBNzAIukAVY'), 'Bad E7(7) definitions.'
### SO(p, 8-p) gaugings
def get_so_pq_E(p=8):
if p == 8 or p == 0:
return numpy.eye(56, dtype=complex)
q = 8 - p
pq_ratio = p / q
x88 = numpy.diag([-1.0] * p + [1.0 * pq_ratio] * q)
t = 0.25j * numpy.pi / (1 + pq_ratio)
k_ab = numpy.einsum('aij,bij->ab', su8.m_35_8_8, su8.m_35_8_8)
v35 = numpy.einsum('mab,ab,mM->M', su8.m_35_8_8, x88, numpy.linalg.inv(k_ab))
gen_E = numpy.einsum(
'aMN,a->NM',
e7.t_a_ij_kl,
numpy.pad(v35, [(0, 133 - 35)], 'constant'))
return scipy.linalg.expm(-t * gen_E)
### Supergravity.
@dataclasses.dataclass(frozen=True)
class SUGRATensors(object):
v70: tf.Tensor
vielbein: tf.Tensor
tee_tensor: tf.Tensor
a1: tf.Tensor
a2: tf.Tensor
potential: tf.Tensor
def get_tf_stationarity(fn_potential, **fn_potential_kwargs):
"""Returns a @tf.function that computes |grad potential|^2."""
@tf.function
def stationarity(pos):
tape = tf.GradientTape()
with tape:
tape.watch(pos)
potential = fn_potential(pos, **fn_potential_kwargs)
grad_potential = tape.gradient(potential, pos)
return tf.reduce_sum(grad_potential * grad_potential)
return stationarity
@tf.function
def dwn_stationarity(t_a1, t_a2):
"""Computes the de Wit-Nicolai stationarity-condition tensor."""
# See: https://arxiv.org/pdf/1302.6219.pdf, text after (3.2).
t_x0 = (
+4.0 * tf.einsum('mi,mjkl->ijkl', t_a1, t_a2)
-3.0 * tf.einsum('mnij,nklm->ijkl', t_a2, t_a2))
t_x0_real = tf.math.real(t_x0)
t_x0_imag = tf.math.imag(t_x0)
tc_sd = tf.constant(get_proj_35_8888(True))
tc_asd = tf.constant(get_proj_35_8888(False))
t_x_real_sd = tf.einsum('aijkl,ijkl->a', tc_sd, t_x0_real)
t_x_imag_asd = tf.einsum('aijkl,ijkl->a', tc_asd, t_x0_imag)
return (tf.einsum('a,a->', t_x_real_sd, t_x_real_sd) +
tf.einsum('a,a->', t_x_imag_asd, t_x_imag_asd))
def tf_sugra_tensors(t_v70, compute_masses, t_lhs_vielbein, t_rhs_E):
"""Returns key tensors for D=4 supergravity."""
tc_28_8_8 = tf.constant(su8.m_28_8_8)
t_e7_generator_v70 = tf.einsum(
'v,vIJ->JI',
tf.complex(t_v70, tf.constant([0.0] * 70, dtype=tf.float64)),
tf.constant(e7.t_a_ij_kl[:70, :, :], dtype=tf.complex128))
t_complex_vielbein0 = tf.linalg.expm(t_e7_generator_v70) @ t_rhs_E
if compute_masses:
t_complex_vielbein = t_lhs_vielbein @ t_complex_vielbein0
else:
t_complex_vielbein = t_complex_vielbein0
@tf.function
def expand_ijkl(t_ab):
return 0.5 * tf.einsum(
'ijB,BIJ->ijIJ',
tf.einsum('AB,Aij->ijB', t_ab, tc_28_8_8),
tc_28_8_8)
#
t_u_ijIJ = expand_ijkl(t_complex_vielbein[:28, :28])
t_u_klKL = expand_ijkl(t_complex_vielbein[28:, 28:])
t_v_ijKL = expand_ijkl(t_complex_vielbein[:28, 28:])
t_v_klIJ = expand_ijkl(t_complex_vielbein[28:, :28])
#
t_uv = t_u_klKL + t_v_klIJ
t_uuvv = (tf.einsum('lmJK,kmKI->lkIJ', t_u_ijIJ, t_u_klKL) -
tf.einsum('lmJK,kmKI->lkIJ', t_v_ijKL, t_v_klIJ))
t_T = tf.einsum('ijIJ,lkIJ->lkij', t_uv, t_uuvv)
t_A1 = (-4.0 / 21.0) * tf.linalg.trace(tf.einsum('mijn->ijmn', t_T))
t_A2 = (-4.0 / (3 * 3)) * (
# Antisymmetrize in last 3 indices, taking into account antisymmetry
# in last two indices.
t_T
+ tf.einsum('lijk->ljki', t_T)
+ tf.einsum('lijk->lkij', t_T))
t_A1_real = tf.math.real(t_A1)
t_A1_imag = tf.math.imag(t_A1)
t_A2_real = tf.math.real(t_A2)
t_A2_imag = tf.math.imag(t_A2)
t_A1_potential = (-3.0 / 4) * (
tf.einsum('ij,ij->', t_A1_real, t_A1_real) +
tf.einsum('ij,ij->', t_A1_imag, t_A1_imag))
t_A2_potential = (1.0 / 24) * (
tf.einsum('ijkl,ijkl->', t_A2_real, t_A2_real) +
tf.einsum('ijkl,ijkl->', t_A2_imag, t_A2_imag))
t_potential = t_A1_potential + t_A2_potential
#
return t_v70, t_complex_vielbein, t_T, t_A1, t_A2, t_potential
def so8_sugra_tensors(t_v70, tc_rhs_E):
t_v70, t_complex_vielbein, t_T, t_A1, t_A2, t_potential = (
tf_sugra_tensors(t_v70, False, 0.0, tc_rhs_E))
return SUGRATensors(
v70=t_v70,
vielbein=t_complex_vielbein,
tee_tensor=t_T,
a1=t_A1,
a2=t_A2,
potential=t_potential)
def so8_sugra_scalar_masses(v70, so_pq_p):
# Note: In some situations, small deviations in the input give quite
# noticeable deviations in the scalar mass-spectrum.
# Getting reliable numbers here really requires satisfying
# the stationarity-condition to high accuracy.
tc_rhs_E = tf.constant(get_so_pq_E(so_pq_p), dtype=tf.complex128)
tc_e7_onb = tf.constant(e7.v70_onb_onbinv[0], dtype=tf.complex128)
tc_e7_taMN = tf.constant(e7.t_a_ij_kl[:70, :, :], dtype=tf.complex128)
t_v70 = tf.constant(v70, dtype=tf.float64)
#
def tf_grad_potential_lhs_onb(t_d_v70_onb):
tape = tf.GradientTape()
with tape:
tape.watch(t_d_v70_onb)
t_d_gen_e7 = tf.einsum(
'a,aMN->NM',
tf.einsum('Aa,A->a',
tc_e7_onb,
tf.complex(t_d_v70_onb, tf.zeros_like(t_d_v70_onb))),
tc_e7_taMN)
t_lhs_vielbein = (tf.eye(56, dtype=tf.complex128) +
t_d_gen_e7 + 0.5 * t_d_gen_e7 @ t_d_gen_e7)
t_potential = (
tf_sugra_tensors(t_v70,
tf.constant(True),
t_lhs_vielbein,
tc_rhs_E))[-1]
return tape.gradient(t_potential, t_d_v70_onb)
#
t_d_v70_onb = tf.Variable(numpy.zeros(70), dtype=tf.float64)
tape = tf.GradientTape(persistent=True)
with tape:
tape.watch(t_d_v70_onb)
grad_potential = tf.unstack(tf_grad_potential_lhs_onb(t_d_v70_onb))
t_mm = tf.stack([tape.gradient(grad_potential[k], t_d_v70_onb)
for k in range(70)], axis=1)
stensors = so8_sugra_tensors(t_v70, tc_rhs_E)
return (t_mm * (36.0 / tf.abs(stensors.potential))).numpy()
### Scanning
def scanner(
use_dwn_stationarity=True,
so_pq_p=8,
seed=1,
scale=0.15,
stationarity_threshold=1e-4,
relu_coordinate_threshold=3.0,
gtol=1e-4,
f_squashed=tf.math.asinh):
"""Scans for critical points in the scalar potential.
Args:
use_dwn_stationarity: Whether to use the explicit stationarity condition
from `dwn_stationarity`.
so_pq_p: SO(p, 8-p) non-compact form of the gauge group to use.
seed: Random number generator seed for generating starting points.
scale: Scale for normal-distributed search starting point coordinates.
stationarity_threshold: Upper bound on permissible post-optimization
stationarity for a solution to be considered good.
relu_coordinate_threshold: Threshold for any coordinate-value at which
a ReLU-term kicks in, in order to move coordinates back to near zero.
(This is relevant for noncompact gaugings with flat directions,
where solutions can move 'very far out'.)
gtol: `gtol` parameter for scipy.optimize.fmin_bfgs.
f_squashed: Squashing-function for stationarity.
Should be approximately linear near zero, monotonic, and not growing
faster than logarithmic.
Yields:
`Solution` numerical solutions.
"""
# Use a seeded random number generator for better reproducibility
# (but note that scipy's optimizers may themselves use independent
# and not-easily-controllable random state).
rng = numpy.random.RandomState(seed=seed)
def get_x0():
return rng.normal(scale=scale, size=70)
#
tc_rhs_E = tf.constant(get_so_pq_E(so_pq_p), dtype=tf.complex128)
def f_potential(scalars):
return so8_sugra_tensors(tf.constant(scalars), tc_rhs_E).potential.numpy()
#
f_grad_pot_sq_stationarity = (
None if use_dwn_stationarity
else get_tf_stationarity(
lambda t_pos: so8_sugra_tensors(t_pos, tc_rhs_E).potential))
#
def f_t_stationarity(t_pos):
if use_dwn_stationarity:
stensors = so8_sugra_tensors(t_pos, tc_rhs_E)
stationarity = dwn_stationarity(stensors.a1, stensors.a2)
else:
stationarity = f_grad_pot_sq_stationarity(t_pos)
eff_stationarity = stationarity + tf.reduce_sum(
tf.nn.relu(abs(t_pos) - relu_coordinate_threshold))
return eff_stationarity
#
def f_opt(pos):
t_pos = tf.constant(pos)
t_stationarity = f_squashed(f_t_stationarity(t_pos))
return t_stationarity.numpy()
#
def fprime_opt(pos):
t_pos = tf.constant(pos)
tape = tf.GradientTape()
with tape:
tape.watch(t_pos)
t_stationarity = f_squashed(f_t_stationarity(t_pos))
t_grad_opt = tape.gradient(t_stationarity, t_pos)
return t_grad_opt.numpy()
#
while True:
opt = scipy.optimize.fmin_bfgs(
f_opt, get_x0(), fprime=fprime_opt, gtol=gtol, maxiter=10**4, disp=0)
opt_pot = f_potential(opt)
opt_stat = f_opt(opt)
if numpy.isnan(opt_pot) or not opt_stat < stationarity_threshold:
continue # Optimization ran into a bad solution.
solution = Solution(potential=opt_pot,
stationarity=opt_stat,
pos=opt)
yield solution
### Demo.
def demo(seed=0,
scale=0.2,
use_dwn_stationarity=True,
so_pq_p=8,
num_solutions=5,
f_squashed=tf.math.asinh):
solutions_iter = scanner(scale=scale, seed=seed,
use_dwn_stationarity=use_dwn_stationarity,
so_pq_p=so_pq_p, f_squashed=f_squashed)
for num_solution in range(num_solutions):
sol = next(solutions_iter)
print('=== Solution ===')
pprint.pprint(sol)
mm0 = so8_sugra_scalar_masses(sol.pos, so_pq_p)
print('\nScalar Masses for: V/g^2=%s:' % sol.potential)
print(sorted(collections.Counter(
numpy.round(numpy.linalg.eigh(mm0)[0], 3)).items()))
demo()
```
|
github_jupyter
|
Copyright (c) Microsoft Corporation. All rights reserved.
Licensed under the MIT License.

# Deploy models to Azure Kubernetes Service (AKS) using controlled roll out
This notebook will show you how to deploy mulitple AKS webservices with the same scoring endpoint and how to roll out your models in a controlled manner by configuring % of scoring traffic going to each webservice. If you are using a Notebook VM, you are all set. Otherwise, go through the [configuration notebook](../../../configuration.ipynb) to install the Azure Machine Learning Python SDK and create an Azure ML Workspace.
```
# Check for latest version
import azureml.core
print(azureml.core.VERSION)
```
## Initialize workspace
Create a [Workspace](https://docs.microsoft.com/python/api/azureml-core/azureml.core.workspace%28class%29?view=azure-ml-py) object from your persisted configuration.
```
from azureml.core.workspace import Workspace
ws = Workspace.from_config()
print(ws.name, ws.resource_group, ws.location, ws.subscription_id, sep = '\n')
```
## Register the model
Register a file or folder as a model by calling [Model.register()](https://docs.microsoft.com/python/api/azureml-core/azureml.core.model.model?view=azure-ml-py#register-workspace--model-path--model-name--tags-none--properties-none--description-none--datasets-none--model-framework-none--model-framework-version-none--child-paths-none-).
In addition to the content of the model file itself, your registered model will also store model metadata -- model description, tags, and framework information -- that will be useful when managing and deploying models in your workspace. Using tags, for instance, you can categorize your models and apply filters when listing models in your workspace.
```
from azureml.core import Model
model = Model.register(workspace=ws,
model_name='sklearn_regression_model.pkl', # Name of the registered model in your workspace.
model_path='./sklearn_regression_model.pkl', # Local file to upload and register as a model.
model_framework=Model.Framework.SCIKITLEARN, # Framework used to create the model.
model_framework_version='0.19.1', # Version of scikit-learn used to create the model.
description='Ridge regression model to predict diabetes progression.',
tags={'area': 'diabetes', 'type': 'regression'})
print('Name:', model.name)
print('Version:', model.version)
```
## Register an environment (for all models)
If you control over how your model is run, or if it has special runtime requirements, you can specify your own environment and scoring method.
Specify the model's runtime environment by creating an [Environment](https://docs.microsoft.com/python/api/azureml-core/azureml.core.environment%28class%29?view=azure-ml-py) object and providing the [CondaDependencies](https://docs.microsoft.com/python/api/azureml-core/azureml.core.conda_dependencies.condadependencies?view=azure-ml-py) needed by your model.
```
from azureml.core import Environment
from azureml.core.conda_dependencies import CondaDependencies
environment=Environment('my-sklearn-environment')
environment.python.conda_dependencies = CondaDependencies.create(pip_packages=[
'azureml-defaults',
'inference-schema[numpy-support]',
'numpy',
'scikit-learn==0.19.1',
'scipy'
])
```
When using a custom environment, you must also provide Python code for initializing and running your model. An example script is included with this notebook.
```
with open('score.py') as f:
print(f.read())
```
## Create the InferenceConfig
Create the inference configuration to reference your environment and entry script during deployment
```
from azureml.core.model import InferenceConfig
inference_config = InferenceConfig(entry_script='score.py',
source_directory='.',
environment=environment)
```
## Provision the AKS Cluster
If you already have an AKS cluster attached to this workspace, skip the step below and provide the name of the cluster.
```
from azureml.core.compute import AksCompute
from azureml.core.compute import ComputeTarget
# Use the default configuration (can also provide parameters to customize)
prov_config = AksCompute.provisioning_configuration()
aks_name = 'my-aks'
# Create the cluster
aks_target = ComputeTarget.create(workspace = ws,
name = aks_name,
provisioning_configuration = prov_config)
aks_target.wait_for_completion(show_output=True)
```
## Create an Endpoint and add a version (AKS service)
This creates a new endpoint and adds a version behind it. By default the first version added is the default version. You can specify the traffic percentile a version takes behind an endpoint.
```
# deploying the model and create a new endpoint
from azureml.core.webservice import AksEndpoint
# from azureml.core.compute import ComputeTarget
#select a created compute
compute = ComputeTarget(ws, 'my-aks')
namespace_name="endpointnamespace"
# define the endpoint name
endpoint_name = "myendpoint2"
# define the service name
version_name= "versiona"
endpoint_deployment_config = AksEndpoint.deploy_configuration(tags = {'modelVersion':'firstversion', 'department':'finance'},
description = "my first version", namespace = namespace_name,
version_name = version_name, traffic_percentile = 40)
endpoint = Model.deploy(ws, endpoint_name, [model], inference_config, endpoint_deployment_config, compute)
endpoint.wait_for_deployment(True)
endpoint.get_logs()
```
## Add another version of the service to an existing endpoint
This adds another version behind an existing endpoint. You can specify the traffic percentile the new version takes. If no traffic_percentile is specified then it defaults to 0. All the unspecified traffic percentile (in this example 50) across all versions goes to default version.
```
# Adding a new version to an existing Endpoint.
version_name_add="versionb"
endpoint.create_version(version_name = version_name_add, inference_config=inference_config, models=[model], tags = {'modelVersion':'secondversion', 'department':'finance'},
description = "my second version", traffic_percentile = 50)
endpoint.wait_for_deployment(True)
```
## Update an existing version in an endpoint
There are two types of versions: control and treatment. An endpoint contains one or more treatment versions but only one control version. This categorization helps compare the different versions against the defined control version.
```
endpoint.update_version(version_name=endpoint.versions[version_name_add].name, description="my second version update", traffic_percentile=40, is_default=True, is_control_version_type=True)
endpoint.wait_for_deployment(True)
```
## Test the web service using run method
Test the web sevice by passing in data. Run() method retrieves API keys behind the scenes to make sure that call is authenticated.
```
# Scoring on endpoint
import json
test_sample = json.dumps({'data': [
[1,2,3,4,5,6,7,8,9,10],
[10,9,8,7,6,5,4,3,2,1]
]})
test_sample_encoded = bytes(test_sample, encoding='utf8')
prediction = endpoint.run(input_data=test_sample_encoded)
print(prediction)
```
## Delete Resources
```
# deleting a version in an endpoint
endpoint.delete_version(version_name=version_name)
endpoint.wait_for_deployment(True)
# deleting an endpoint, this will delete all versions in the endpoint and the endpoint itself
#endpoint.delete()
```
|
github_jupyter
|
# Examining Racial Discrimination in the US Job Market
### Background
Racial discrimination continues to be pervasive in cultures throughout the world. Researchers examined the level of racial discrimination in the United States labor market by randomly assigning identical résumés to black-sounding or white-sounding names and observing the impact on requests for interviews from employers.
### Data
In the dataset provided, each row represents a resume. The 'race' column has two values, 'b' and 'w', indicating black-sounding and white-sounding. The column 'call' has two values, 1 and 0, indicating whether the resume received a call from employers or not.
Note that the 'b' and 'w' values in race are assigned randomly to the resumes when presented to the employer.
<div class="span5 alert alert-info">
### Exercises
You will perform a statistical analysis to establish whether race has a significant impact on the rate of callbacks for resumes.
Answer the following questions **in this notebook below and submit to your Github account**.
1. What test is appropriate for this problem? Does CLT apply?
2. What are the null and alternate hypotheses?
3. Compute margin of error, confidence interval, and p-value.
4. Write a story describing the statistical significance in the context or the original problem.
5. Does your analysis mean that race/name is the most important factor in callback success? Why or why not? If not, how would you amend your analysis?
You can include written notes in notebook cells using Markdown:
- In the control panel at the top, choose Cell > Cell Type > Markdown
- Markdown syntax: http://nestacms.com/docs/creating-content/markdown-cheat-sheet
#### Resources
+ Experiment information and data source: http://www.povertyactionlab.org/evaluation/discrimination-job-market-united-states
+ Scipy statistical methods: http://docs.scipy.org/doc/scipy/reference/stats.html
+ Markdown syntax: http://nestacms.com/docs/creating-content/markdown-cheat-sheet
</div>
****
```
%matplotlib inline
import pandas as pd
import numpy as np
from scipy import stats
import seaborn as sns
import matplotlib.pyplot as plt
from statsmodels.stats.proportion import proportions_ztest
# read the data
data = pd.io.stata.read_stata('data/us_job_market_discrimination.dta')
# split data into black and nonblack sounding names
dfblack = data[data.race=='b']
dfnonblack = data[data.race!='b']
# display some basic statistics
data.describe()
# count the number of blacks and nonblack sounding names and calls / noncalls
black_call=sum(dfblack.call)
black_nocall=len(dfblack)-black_call
nonblack_call=sum(dfnonblack.call)
nonblack_nocall=len(dfnonblack)-nonblack_call
# number of callbacks for black and non black-sounding names
print("callbacks for black-sounding names", black_call)
print("noncallbacks for black-sounding names", black_nocall)
print("callbacks for non black-sounding names", nonblack_call)
print("noncallbacks for non black-sounding names", nonblack_nocall)
#
# create bar chart
#
call = (black_call, nonblack_call)
noncall = (black_nocall, nonblack_nocall)
fig, ax = plt.subplots()
index = np.arange(2)
bar_width = 0.35
opacity = 0.4
error_config = {'ecolor': '0.3'}
rects1 = plt.bar(index, call, bar_width,
alpha=opacity,
color='b',
error_kw=error_config,
label='call')
rects2 = plt.bar(index + bar_width, noncall, bar_width,
alpha=opacity,
color='r',
error_kw=error_config,
label='noncall')
# put labels to bar chart
plt.xlabel('Race')
plt.ylabel('Calls')
plt.title('Number of calls by race')
plt.xticks(index + bar_width / 2, ('black sounding name', 'nonblack sounding name'))
plt.legend()
plt.tight_layout()
#
# create pie chart
#
labels = 'Black sounding name', 'nonBlack sounding name'
sizes = [black_call, nonblack_call]
fig1, ax1 = plt.subplots()
ax1.pie(sizes, labels=labels, autopct='%1.0f%%')
ax1.axis('equal')
plt.show()
# measure the proportions
n1 = len(dfblack)
n2 = len(dfnonblack)
p1 = black_call / n1
p2 = nonblack_call / n2
count_call = np.array([black_call, nonblack_call])
nobs_array = np.array([n1, n2])
ls = .05
stat, pval = proportions_ztest(count=count_call, nobs=nobs_array, value=ls)
# standard error and confidence interval (CI)
se = np.sqrt(p1*(1-p1)/n1 + p1*(1-p2)/n2)
print('margin of error=', se)
print('conf interval=', (p1-p2-1.96*se, p1-p2+1.96*se))
print('p-value=', pval)
# print chi-square test
chi_value = stats.chi2_contingency(np.array([[black_call, black_nocall],[nonblack_call, nonblack_nocall]]))
print('chi_sq p-value=', chi_value[1])
#t-test on education, ofjobs and yearsexp and occupspecific and occupbroad
print('education p-value=', stats.ttest_ind(dfblack['education'], dfnonblack['education'], equal_var = False)[1])
print('ofjobs p-value=', stats.ttest_ind(dfblack['ofjobs'], dfnonblack['ofjobs'], equal_var = False)[1])
print('yearsexp p-value=', stats.ttest_ind(dfblack['yearsexp'], dfnonblack['yearsexp'], equal_var = False)[1])
print('occupspecific p-value=', stats.ttest_ind(dfblack['occupspecific'], dfnonblack['occupspecific'], equal_var = False)[1])
print('occupbroad p-value=', stats.ttest_ind(dfblack['occupbroad'], dfnonblack['occupbroad'], equal_var = False)[1])
#proportion test on honors volunteer military empholes and workinschool
print('honors p-value=', proportions_ztest(count=np.array([sum(dfblack.honors), \
sum(dfnonblack.honors)]),nobs=np.array([n1, n2]), value=ls)[1])
print('volunteer p-value=', proportions_ztest(count=np.array([sum(dfblack.volunteer), \
sum(dfnonblack.volunteer)]),nobs=np.array([n1, n2]), value=ls)[1])
print('military p-value=', proportions_ztest(count=np.array([sum(dfblack.military), \
sum(dfnonblack.military)]),nobs=np.array([n1, n2]), value=ls)[1])
print('empholes p-value=', proportions_ztest(count=np.array([sum(dfblack.empholes), \
sum(dfnonblack.empholes)]),nobs=np.array([n1, n2]), value=ls)[1])
print('workinschool p-value=', proportions_ztest(count=np.array([sum(dfblack.workinschool), \
sum(dfnonblack.workinschool)]),nobs=np.array([n1, n2]), value=ls)[1])
print('computerskills p-value=', proportions_ztest(count=np.array([sum(dfblack.computerskills), \
sum(dfnonblack.computerskills)]),nobs=np.array([n1, n2]), value=ls)[1])
corrmat = data.corr()
# Set up the matplotlib figure
f, ax = plt.subplots(figsize=(12, 9))
# Draw the heatmap using seaborn
sns.heatmap(corrmat, vmax=.8, square=True)
f.tight_layout()
```
<div class="span5 alert alert-info">
### ANSWERS:
1. What test is appropriate for this problem? <b> Comparison of two proportions </b>
Does CLT apply? <b> Yes, since np and n(1-p) where n is number of samples and p is the probability that an applicant is called, is more than 10, it can approximate the normal distribution.</b>
2. What are the null and alternate hypotheses? <b> H<sub>o</sub>= the call back for black and non-blacks are the same while H<sub>a</sub>= the call back for black and non-blacks are not the same </b>
3. Compute margin of error, confidence interval, and p-value. <b> margin of error= 0.00697820016119
conf interval= (-0.045710126525379105, -0.018355581893512069)
p-value= 2.36721263361e-25 </b>
4. Write a story describing the statistical significance in the context or the original problem.
<h3> Discrimination in Job Market on Black sounding names </h3>
> Black sounding names have 2% to 4% average less callbacks compared to non-black sounding names.
> Education, years experience and number of previous jobs have no significant difference.
> However, differences are found in honors achieved, military and volunteer work, employment holes, work in school and computer skills.
There is a discrimination in the job market for black sounding names. A study of 4870 job applicants in 2000 to 2002 shows that there is a difference between the number of callbacks for black sounding names compared to non-black sounding names. The study also shows that education, years experience and number of previous jobs are the same between the two groups. Meanwhile, there is a difference shown in honors achieved, military and volunteer work, employment holes, work in school and computer skills.
5. Does your analysis mean that race/name is the most important factor in callback success? Why or why not? If not, how would you amend your analysis?
<b> Race is not the most important factor in callback success. In fact there are differences between black and nonblack sounding names in terms of honors achieved, military and volunteer work, employment holes, work in school and computer skills. These are the reasons why there is a difference on the callbacks between the two groups</b>
#### Resources
+ Experiment information and data source: http://www.povertyactionlab.org/evaluation/discrimination-job-market-united-states
+ Scipy statistical methods: http://docs.scipy.org/doc/scipy/reference/stats.html
</div>
****
|
github_jupyter
|
```
import pandas as pd
import cv2
import numpy as np
import matplotlib.pyplot as plt
expression_df=pd.read_csv("C:/Users/user/Desktop/New folder/icml_face_data.csv")
expression_df.head()
expression_df[' Usage'].unique()
expression_df['emotion'].unique()
import collections
collections.Counter(np.array(expression_df['emotion']))
expression_df[' pixels'][0]
img=expression_df[' pixels'][920]
img=np.array(img.split(' ')).reshape(48,48,1).astype('float32')
img.shape
plt.imshow(img.squeeze(),cmap='gray')
images_list=np.zeros((len(expression_df),48,48,1))
images_list.shape
images_label=pd.get_dummies(expression_df['emotion'])
images_label
for idx in range(len(expression_df)):
single_pic=np.array(expression_df[' pixels'][idx].split(' ')).reshape(48,48,1)
images_list[idx]=single_pic
images_list.shape
images_list[35886].shape
expression_df['emotion'].value_counts()
expression_df['emotion'].value_counts().index
import seaborn as sns
sns.barplot(x=expression_df['emotion'].value_counts().index,y=expression_df['emotion'].value_counts())
plt.title('Number of images per emotion')
from sklearn.model_selection import train_test_split
X_train,X_Test,y_train,y_Test=train_test_split(images_list,images_label,test_size=0.20,shuffle=True)
X_val,X_Test,y_val,y_Test=train_test_split(X_Test,y_Test,test_size=0.5, shuffle=True)
X_train.shape
X_Test.shape
X_val.shape
X_train
```
# Normalizing
```
X_train=X_train/255
X_val=X_val/255
X_Test=X_Test/255
from keras.preprocessing.image import ImageDataGenerator
datagen=ImageDataGenerator(
featurewise_center=False,
samplewise_std_normalization=False,
zca_whitening=False,
featurewise_std_normalization=True,
rotation_range=30,
width_shift_range=0.1,
height_shift_range=0.1,
zoom_range=0.2)
datagen.fit(X_train)
input_reshape=(48,48,1)
epochs=10
batch_size=128
hidden_num_units=256
output_num_units=7
pool_size=(2,2)
import tensorflow.keras as keras
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Activation, Dropout,Convolution2D,Flatten,MaxPooling2D, Reshape,InputLayer
from keras.layers.normalization import BatchNormalization
from tensorflow.keras.preprocessing.image import load_img
model=Sequential([
Convolution2D(32,(3,3),activation='relu',input_shape=input_reshape),
Convolution2D(64,(3,3),activation='relu'),
MaxPooling2D((2,2)),
Convolution2D(64,(3,3),activation='relu'),
MaxPooling2D((2,2)),
Convolution2D(64,(3,3),activation='relu'),
Flatten(),
Dense(64,'relu'),
Dense(7,'softmax')
])
model.compile(loss='categorical_crossentropy',optimizer='adam',metrics=['accuracy'])
trained_model_cov=model.fit(X_train,y_train, epochs=epochs,batch_size=batch_size, validation_data=(X_val,y_val))
model.predict_classes(X_Test[1000].reshape(1,48,48,1))
plt.imshow(images_list[1000].squeeze(),cmap='gray')
```
|
github_jupyter
|
This notebook is designed to run in a IBM Watson Studio default runtime (NOT the Watson Studio Apache Spark Runtime as the default runtime with 1 vCPU is free of charge). Therefore, we install Apache Spark in local mode for test purposes only. Please don't use it in production.
In case you are facing issues, please read the following two documents first:
https://github.com/IBM/skillsnetwork/wiki/Environment-Setup
https://github.com/IBM/skillsnetwork/wiki/FAQ
Then, please feel free to ask:
https://coursera.org/learn/machine-learning-big-data-apache-spark/discussions/all
Please make sure to follow the guidelines before asking a question:
https://github.com/IBM/skillsnetwork/wiki/FAQ#im-feeling-lost-and-confused-please-help-me
If running outside Watson Studio, this should work as well. In case you are running in an Apache Spark context outside Watson Studio, please remove the Apache Spark setup in the first notebook cells.
```
from IPython.display import Markdown, display
def printmd(string):
display(Markdown('# <span style="color:red">'+string+'</span>'))
if ('sc' in locals() or 'sc' in globals()):
printmd('<<<<<!!!!! It seems that you are running in a IBM Watson Studio Apache Spark Notebook. Please run it in an IBM Watson Studio Default Runtime (without Apache Spark) !!!!!>>>>>')
!pip install pyspark==2.4.5
try:
from pyspark import SparkContext, SparkConf
from pyspark.sql import SparkSession
except ImportError as e:
printmd('<<<<<!!!!! Please restart your kernel after installing Apache Spark !!!!!>>>>>')
sc = SparkContext.getOrCreate(SparkConf().setMaster("local[*]"))
spark = SparkSession \
.builder \
.getOrCreate()
```
# Exercise 3.2
Welcome to the last exercise of this course. This is also the most advanced one because it somehow glues everything together you've learned.
These are the steps you will do:
- load a data frame from cloudant/ApacheCouchDB
- perform feature transformation by calculating minimal and maximal values of different properties on time windows (we'll explain what a time windows is later in here)
- reduce these now twelve dimensions to three using the PCA (Principal Component Analysis) algorithm of SparkML (Spark Machine Learning) => We'll actually make use of SparkML a lot more in the next course
- plot the dimensionality reduced data set
Now it is time to grab a PARQUET file and create a dataframe out of it. Using SparkSQL you can handle it like a database.
```
!wget https://github.com/IBM/coursera/blob/master/coursera_ds/washing.parquet?raw=true
!mv washing.parquet?raw=true washing.parquet
df = spark.read.parquet('washing.parquet')
df.createOrReplaceTempView('washing')
df.show()
```
This is the feature transformation part of this exercise. Since our table is mixing schemas from different sensor data sources we are creating new features. In other word we use existing columns to calculate new ones. We only use min and max for now, but using more advanced aggregations as we've learned in week three may improve the results. We are calculating those aggregations over a sliding window "w". This window is defined in the SQL statement and basically reads the table by a one by one stride in direction of increasing timestamp. Whenever a row leaves the window a new one is included. Therefore this window is called sliding window (in contrast to tubling, time or count windows). More on this can be found here: https://flink.apache.org/news/2015/12/04/Introducing-windows.html
```
result = spark.sql("""
SELECT * from (
SELECT
min(temperature) over w as min_temperature,
max(temperature) over w as max_temperature,
min(voltage) over w as min_voltage,
max(voltage) over w as max_voltage,
min(flowrate) over w as min_flowrate,
max(flowrate) over w as max_flowrate,
min(frequency) over w as min_frequency,
max(frequency) over w as max_frequency,
min(hardness) over w as min_hardness,
max(hardness) over w as max_hardness,
min(speed) over w as min_speed,
max(speed) over w as max_speed
FROM washing
WINDOW w AS (ORDER BY ts ROWS BETWEEN CURRENT ROW AND 10 FOLLOWING)
)
WHERE min_temperature is not null
AND max_temperature is not null
AND min_voltage is not null
AND max_voltage is not null
AND min_flowrate is not null
AND max_flowrate is not null
AND min_frequency is not null
AND max_frequency is not null
AND min_hardness is not null
AND min_speed is not null
AND max_speed is not null
""")
```
Since this table contains null values also our window might contain them. In case for a certain feature all values in that window are null we obtain also null. As we can see here (in my dataset) this is the case for 9 rows.
```
df.count()-result.count()
```
Now we import some classes from SparkML. PCA for the actual algorithm. Vectors for the data structure expected by PCA and VectorAssembler to transform data into these vector structures.
```
from pyspark.ml.feature import PCA
from pyspark.ml.linalg import Vectors
from pyspark.ml.feature import VectorAssembler
```
Let's define a vector transformation helper class which takes all our input features (result.columns) and created one additional column called "features" which contains all our input features as one single column wrapped in "DenseVector" objects
```
assembler = VectorAssembler(inputCols=result.columns, outputCol="features") ###columns of n features into a column of n_d row vector
```
Now we actually transform the data, note that this is highly optimized code and runs really fast in contrast if we had implemented it.
```
features = assembler.transform(result)
```
Let's have a look at how this new additional column "features" looks like:
```
features.rdd.map(lambda r : r.features).take(10)
```
Since the source data set has been prepared as a list of DenseVectors we can now apply PCA. Note that the first line again only prepares the algorithm by finding the transformation matrices (fit method)
```
pca = PCA(k=3, inputCol="features", outputCol="pcaFeatures") ###computes the transformation matrix
model = pca.fit(features)
```
Now we can actually transform the data. Let's have a look at the first 20 rows
```
result_pca = model.transform(features).select("pcaFeatures") ###performs the transformation
result_pca.show(truncate=False)
```
So we obtained three completely new columns which we can plot now. Let run a final check if the number of rows is the same.
```
result_pca.count()
```
Cool, this works as expected. Now we obtain a sample and read each of the three columns into a python list
```
rdd = result_pca.rdd.sample(False,0.8)
x = rdd.map(lambda a : a.pcaFeatures).map(lambda a : a[0]).collect()
y = rdd.map(lambda a : a.pcaFeatures).map(lambda a : a[1]).collect()
z = rdd.map(lambda a : a.pcaFeatures).map(lambda a : a[2]).collect()
```
Finally we plot the three lists and name each of them as dimension 1-3 in the plot
```
%matplotlib inline
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(x,y,z, c='r', marker='o')
ax.set_xlabel('dimension1')
ax.set_ylabel('dimension2')
ax.set_zlabel('dimension3')
plt.show()
```
Congratulations, we are done! We can see two clusters in the data set. We can also see a third cluster which either can be outliers or a real cluster. In the next course we will actually learn how to compute clusters automatically. For now we know that the data indicates that there are two semi-stable states of the machine and sometime we see some anomalies since those data points don't fit into one of the two clusters.
|
github_jupyter
|
```
from IPython.display import YouTubeVideo
YouTubeVideo('FPgo-hI7OiE')
```
# 如何使用和开发微信聊天机器人的系列教程
# A workshop to develop & use an intelligent and interactive chat-bot in WeChat
### WeChat is a popular social media app, which has more than 800 million monthly active users.
<img src='http://www.kudosdata.com/wp-content/uploads/2016/11/cropped-KudosLogo1.png' width=30% style="float: right;">
<img src='reference/WeChat_SamGu_QR.png' width=10% style="float: right;">
### http://www.KudosData.com
by: [email protected]
May 2017 ========== Scan the QR code to become trainer's friend in WeChat ========>>
### 第二课:图像识别和处理
### Lesson 2: Image Recognition & Processing
* 识别图片消息中的物体名字 (Recognize objects in image)
[1] 物体名 (General Object)
[2] 地标名 (Landmark Object)
[3] 商标名 (Logo Object)
* 识别图片消息中的文字 (OCR: Extract text from image)
包含简单文本翻译 (Call text translation API)
* 识别人脸 (Recognize human face)
基于人脸的表情来识别喜怒哀乐等情绪 (Identify sentiment and emotion from human face)
* 不良内容识别 (Explicit Content Detection)
### Using Google Cloud Platform's Machine Learning APIs
From the same API console, choose "Dashboard" on the left-hand menu and "Enable API".
Enable the following APIs for your project (search for them) if they are not already enabled:
<ol>
<li> Google Translate API </li>
<li> Google Cloud Vision API </li>
<li> Google Natural Language API </li>
<li> Google Cloud Speech API </li>
</ol>
Finally, because we are calling the APIs from Python (clients in many other languages are available), let's install the Python package (it's not installed by default on Datalab)
```
# Copyright 2016 Google Inc.
# Licensed under the Apache License, Version 2.0 (the "License");
# !pip install --upgrade google-api-python-client
```
### 导入需要用到的一些功能程序库:
```
import io, os, subprocess, sys, time, datetime, requests, itchat
from itchat.content import *
from googleapiclient.discovery import build
```
### Using Google Cloud Platform's Machine Learning APIs
First, visit <a href="http://console.cloud.google.com/apis">API console</a>, choose "Credentials" on the left-hand menu. Choose "Create Credentials" and generate an API key for your application. You should probably restrict it by IP address to prevent abuse, but for now, just leave that field blank and delete the API key after trying out this demo.
Copy-paste your API Key here:
```
# Here I read in my own API_KEY from a file, which is not shared in Github repository:
# with io.open('../../API_KEY.txt') as fp:
# for line in fp: APIKEY = line
# You need to un-comment below line and replace 'APIKEY' variable with your own GCP API key:
APIKEY='AIzaSyCvxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx'
# Below is for GCP Language Tranlation API
service = build('translate', 'v2', developerKey=APIKEY)
```
### 图片二进制base64码转换 (Define image pre-processing functions)
```
# Import the base64 encoding library.
import base64
# Pass the image data to an encoding function.
def encode_image(image_file):
with open(image_file, "rb") as image_file:
image_content = image_file.read()
return base64.b64encode(image_content)
```
### 机器智能API接口控制参数 (Define control parameters for API)
```
# control parameter for Image API:
parm_image_maxResults = 10 # max objects or faces to be extracted from image analysis
# control parameter for Language Translation API:
parm_translation_origin_language = '' # original language in text: to be overwriten by TEXT_DETECTION
parm_translation_target_language = 'zh' # target language for translation: Chinese
```
### * 识别图片消息中的物体名字 (Recognize objects in image)
[1] 物体名 (General Object)
```
# Running Vision API
# 'LABEL_DETECTION'
def KudosData_LABEL_DETECTION(image_base64, API_type, maxResults):
vservice = build('vision', 'v1', developerKey=APIKEY)
request = vservice.images().annotate(body={
'requests': [{
'image': {
# 'source': {
# 'gcs_image_uri': IMAGE
# }
"content": image_base64
},
'features': [{
'type': API_type,
'maxResults': maxResults,
}]
}],
})
responses = request.execute(num_retries=3)
image_analysis_reply = u'\n[ ' + API_type + u' 物体识别 ]\n'
# 'LABEL_DETECTION'
if responses['responses'][0] != {}:
for i in range(len(responses['responses'][0]['labelAnnotations'])):
image_analysis_reply += responses['responses'][0]['labelAnnotations'][i]['description'] \
+ '\n( confidence ' + str(responses['responses'][0]['labelAnnotations'][i]['score']) + ' )\n'
else:
image_analysis_reply += u'[ Nill 无结果 ]\n'
return image_analysis_reply
```
### * 识别图片消息中的物体名字 (Recognize objects in image)
[2] 地标名 (Landmark Object)
```
# Running Vision API
# 'LANDMARK_DETECTION'
def KudosData_LANDMARK_DETECTION(image_base64, API_type, maxResults):
vservice = build('vision', 'v1', developerKey=APIKEY)
request = vservice.images().annotate(body={
'requests': [{
'image': {
# 'source': {
# 'gcs_image_uri': IMAGE
# }
"content": image_base64
},
'features': [{
'type': API_type,
'maxResults': maxResults,
}]
}],
})
responses = request.execute(num_retries=3)
image_analysis_reply = u'\n[ ' + API_type + u' 地标识别 ]\n'
# 'LANDMARK_DETECTION'
if responses['responses'][0] != {}:
for i in range(len(responses['responses'][0]['landmarkAnnotations'])):
image_analysis_reply += responses['responses'][0]['landmarkAnnotations'][i]['description'] \
+ '\n( confidence ' + str(responses['responses'][0]['landmarkAnnotations'][i]['score']) + ' )\n'
else:
image_analysis_reply += u'[ Nill 无结果 ]\n'
return image_analysis_reply
```
### * 识别图片消息中的物体名字 (Recognize objects in image)
[3] 商标名 (Logo Object)
```
# Running Vision API
# 'LOGO_DETECTION'
def KudosData_LOGO_DETECTION(image_base64, API_type, maxResults):
vservice = build('vision', 'v1', developerKey=APIKEY)
request = vservice.images().annotate(body={
'requests': [{
'image': {
# 'source': {
# 'gcs_image_uri': IMAGE
# }
"content": image_base64
},
'features': [{
'type': API_type,
'maxResults': maxResults,
}]
}],
})
responses = request.execute(num_retries=3)
image_analysis_reply = u'\n[ ' + API_type + u' 商标识别 ]\n'
# 'LOGO_DETECTION'
if responses['responses'][0] != {}:
for i in range(len(responses['responses'][0]['logoAnnotations'])):
image_analysis_reply += responses['responses'][0]['logoAnnotations'][i]['description'] \
+ '\n( confidence ' + str(responses['responses'][0]['logoAnnotations'][i]['score']) + ' )\n'
else:
image_analysis_reply += u'[ Nill 无结果 ]\n'
return image_analysis_reply
```
### * 识别图片消息中的文字 (OCR: Extract text from image)
```
# Running Vision API
# 'TEXT_DETECTION'
def KudosData_TEXT_DETECTION(image_base64, API_type, maxResults):
vservice = build('vision', 'v1', developerKey=APIKEY)
request = vservice.images().annotate(body={
'requests': [{
'image': {
# 'source': {
# 'gcs_image_uri': IMAGE
# }
"content": image_base64
},
'features': [{
'type': API_type,
'maxResults': maxResults,
}]
}],
})
responses = request.execute(num_retries=3)
image_analysis_reply = u'\n[ ' + API_type + u' 文字提取 ]\n'
# 'TEXT_DETECTION'
if responses['responses'][0] != {}:
image_analysis_reply += u'----- Start Original Text -----\n'
image_analysis_reply += u'( Original Language 原文: ' + responses['responses'][0]['textAnnotations'][0]['locale'] \
+ ' )\n'
image_analysis_reply += responses['responses'][0]['textAnnotations'][0]['description'] + '----- End Original Text -----\n'
##############################################################################################################
# translation of detected text #
##############################################################################################################
parm_translation_origin_language = responses['responses'][0]['textAnnotations'][0]['locale']
# Call translation if parm_translation_origin_language is not parm_translation_target_language
if parm_translation_origin_language != parm_translation_target_language:
inputs=[responses['responses'][0]['textAnnotations'][0]['description']] # TEXT_DETECTION OCR results only
outputs = service.translations().list(source=parm_translation_origin_language,
target=parm_translation_target_language, q=inputs).execute()
image_analysis_reply += u'\n----- Start Translation -----\n'
image_analysis_reply += u'( Target Language 译文: ' + parm_translation_target_language + ' )\n'
image_analysis_reply += outputs['translations'][0]['translatedText'] + '\n' + '----- End Translation -----\n'
print('Compeleted: Translation API ...')
##############################################################################################################
else:
image_analysis_reply += u'[ Nill 无结果 ]\n'
return image_analysis_reply
```
### * 识别人脸 (Recognize human face)
### * 基于人脸的表情来识别喜怒哀乐等情绪 (Identify sentiment and emotion from human face)
```
# Running Vision API
# 'FACE_DETECTION'
def KudosData_FACE_DETECTION(image_base64, API_type, maxResults):
vservice = build('vision', 'v1', developerKey=APIKEY)
request = vservice.images().annotate(body={
'requests': [{
'image': {
# 'source': {
# 'gcs_image_uri': IMAGE
# }
"content": image_base64
},
'features': [{
'type': API_type,
'maxResults': maxResults,
}]
}],
})
responses = request.execute(num_retries=3)
image_analysis_reply = u'\n[ ' + API_type + u' 面部表情 ]\n'
# 'FACE_DETECTION'
if responses['responses'][0] != {}:
for i in range(len(responses['responses'][0]['faceAnnotations'])):
image_analysis_reply += u'----- No.' + str(i+1) + ' Face -----\n'
image_analysis_reply += u'>>> Joy 喜悦: \n' \
+ responses['responses'][0]['faceAnnotations'][i][u'joyLikelihood'] + '\n'
image_analysis_reply += u'>>> Anger 愤怒: \n' \
+ responses['responses'][0]['faceAnnotations'][i][u'angerLikelihood'] + '\n'
image_analysis_reply += u'>>> Sorrow 悲伤: \n' \
+ responses['responses'][0]['faceAnnotations'][i][u'sorrowLikelihood'] + '\n'
image_analysis_reply += u'>>> Surprise 惊奇: \n' \
+ responses['responses'][0]['faceAnnotations'][i][u'surpriseLikelihood'] + '\n'
image_analysis_reply += u'>>> Headwear 头饰: \n' \
+ responses['responses'][0]['faceAnnotations'][i][u'headwearLikelihood'] + '\n'
image_analysis_reply += u'>>> Blurred 模糊: \n' \
+ responses['responses'][0]['faceAnnotations'][i][u'blurredLikelihood'] + '\n'
image_analysis_reply += u'>>> UnderExposed 欠曝光: \n' \
+ responses['responses'][0]['faceAnnotations'][i][u'underExposedLikelihood'] + '\n'
else:
image_analysis_reply += u'[ Nill 无结果 ]\n'
return image_analysis_reply
```
### * 不良内容识别 (Explicit Content Detection)
Detect explicit content like adult content or violent content within an image.
```
# Running Vision API
# 'SAFE_SEARCH_DETECTION'
def KudosData_SAFE_SEARCH_DETECTION(image_base64, API_type, maxResults):
vservice = build('vision', 'v1', developerKey=APIKEY)
request = vservice.images().annotate(body={
'requests': [{
'image': {
# 'source': {
# 'gcs_image_uri': IMAGE
# }
"content": image_base64
},
'features': [{
'type': API_type,
'maxResults': maxResults,
}]
}],
})
responses = request.execute(num_retries=3)
image_analysis_reply = u'\n[ ' + API_type + u' 不良内容 ]\n'
# 'SAFE_SEARCH_DETECTION'
if responses['responses'][0] != {}:
image_analysis_reply += u'>>> Adult 成人: \n' + responses['responses'][0]['safeSearchAnnotation'][u'adult'] + '\n'
image_analysis_reply += u'>>> Violence 暴力: \n' + responses['responses'][0]['safeSearchAnnotation'][u'violence'] + '\n'
image_analysis_reply += u'>>> Spoof 欺骗: \n' + responses['responses'][0]['safeSearchAnnotation'][u'spoof'] + '\n'
image_analysis_reply += u'>>> Medical 医疗: \n' + responses['responses'][0]['safeSearchAnnotation'][u'medical'] + '\n'
else:
image_analysis_reply += u'[ Nill 无结果 ]\n'
return image_analysis_reply
```
### 用微信App扫QR码图片来自动登录
```
itchat.auto_login(hotReload=True) # hotReload=True: 退出程序后暂存登陆状态。即使程序关闭,一定时间内重新开启也可以不用重新扫码。
# itchat.auto_login(enableCmdQR=-2) # enableCmdQR=-2: 命令行显示QR图片
# @itchat.msg_register([PICTURE], isGroupChat=True)
@itchat.msg_register([PICTURE])
def download_files(msg):
parm_translation_origin_language = 'zh' # will be overwriten by TEXT_DETECTION
msg.download(msg.fileName)
print('\nDownloaded image file name is: %s' % msg['FileName'])
image_base64 = encode_image(msg['FileName'])
##############################################################################################################
# call image analysis APIs #
##############################################################################################################
image_analysis_reply = u'[ Image Analysis 图像分析结果 ]\n'
# 1. LABEL_DETECTION:
image_analysis_reply += KudosData_LABEL_DETECTION(image_base64, 'LABEL_DETECTION', parm_image_maxResults)
# 2. LANDMARK_DETECTION:
image_analysis_reply += KudosData_LANDMARK_DETECTION(image_base64, 'LANDMARK_DETECTION', parm_image_maxResults)
# 3. LOGO_DETECTION:
image_analysis_reply += KudosData_LOGO_DETECTION(image_base64, 'LOGO_DETECTION', parm_image_maxResults)
# 4. TEXT_DETECTION:
image_analysis_reply += KudosData_TEXT_DETECTION(image_base64, 'TEXT_DETECTION', parm_image_maxResults)
# 5. FACE_DETECTION:
image_analysis_reply += KudosData_FACE_DETECTION(image_base64, 'FACE_DETECTION', parm_image_maxResults)
# 6. SAFE_SEARCH_DETECTION:
image_analysis_reply += KudosData_SAFE_SEARCH_DETECTION(image_base64, 'SAFE_SEARCH_DETECTION', parm_image_maxResults)
print('Compeleted: Image Analysis API ...')
return image_analysis_reply
itchat.run()
# interupt kernel, then logout
itchat.logout() # 安全退出
```
### 恭喜您!已经完成了:
### 第二课:图像识别和处理
### Lesson 2: Image Recognition & Processing
* 识别图片消息中的物体名字 (Recognize objects in image)
[1] 物体名 (General Object)
[2] 地标名 (Landmark Object)
[3] 商标名 (Logo Object)
* 识别图片消息中的文字 (OCR: Extract text from image)
包含简单文本翻译 (Call text translation API)
* 识别人脸 (Recognize human face)
基于人脸的表情来识别喜怒哀乐等情绪 (Identify sentiment and emotion from human face)
* 不良内容识别 (Explicit Content Detection)
### 下一课是:
### 第三课:自然语言处理:语音合成和识别
### Lesson 3: Natural Language Processing 1
* 消息文字转成语音 (Speech synthesis: text to voice)
* 语音转换成消息文字 (Speech recognition: voice to text)
* 消息文字的多语言互译 (Text based language translation)
<img src='http://www.kudosdata.com/wp-content/uploads/2016/11/cropped-KudosLogo1.png' width=30% style="float: right;">
<img src='reference/WeChat_SamGu_QR.png' width=10% style="float: left;">
|
github_jupyter
|
```
import pandas as pd
import json
import numpy as np
megye={'Fehér':'ALBA', 'Arad':'ARAD', 'Bukarest':'B', 'Bákó':'BACAU', 'Bihar':'BIHOR', 'Beszterce-Naszód':'BISTRITA-NASAUD',
'Brassó':'BRASOV', 'Kolozs':'CLUJ', 'Kovászna':'COVASNA', 'Krassó-Szörény':'CARAS-SEVERIN', 'Hunyad':'HUNEDOARA',
'Hargita':'HARGHITA', 'Máramaros':'MARAMURES', 'Maros':'MURES', 'Szeben':'SIBIU', 'Szatmár':'SATU MARE', 'Szilágy':'SALAJ',
'Temes':'TIMIS'}
ro={'Ă':'A','Ş':'S','Â':'A','Ș':'S','Ț':'T','Â':'A','Î':'I','Ă':'A','Ţ':'T','-':' ','SC.GEN.':'','I VIII':''}
def roman(s):
return replacer(s,ro)
```
Load processed geocoded db
```
data=pd.read_excel('data/clean/erdely6.xlsx').drop('Unnamed: 0',axis=1)
data['guess_scores']=abs(data['guess_scores']).replace(0,50)
data.index=data['Denumire'].astype(str)+' '+data['Localitate'].astype(str)+', '+data['Localitate superioară'].astype(str)+', '+\
data['Stradă'].astype(str)+' nr. '+data['Număr'].astype(str)+', '+data['Cod poștal'].astype(str).str[:-2]+', '+\
data['Judet'].astype(str)+', ROMANIA'
geo=pd.read_excel('data/clean/geo.xlsx').drop('Unnamed: 0',axis=1).set_index('index')
geo['telepules_g']=geo['telepules']
geo=geo.drop('telepules',axis=1)
data=data.join(geo)
hun_city={i:i for i in np.sort(list(data['varos'].unique()))}
open('data/geo/hun_city.json','w',encoding='utf8').write(json.dumps(hun_city,ensure_ascii=False))
pd.DataFrame(data['varos'].unique()).to_excel('data/geo/geo.xlsx')
# pd.DataFrame(data['varos'].unique()).to_excel('data/geo/geo_manual.xlsx')
```
Manually edit and fix, then load back
```
geom=list(pd.read_excel('data/geo/geo_manual.xlsx').drop('Unnamed: 0',axis=1)[0].unique())
geom=data[['telepules','varos']].set_index('varos').loc[geom].reset_index().set_index('telepules')
geom.columns=['varos_geo']
#can't join, no judet
```
Geocode from Szekelydata DB
```
hun=json.loads(open('data/geo/hun2.json','r').read())
hdf=pd.DataFrame(hun).stack().reset_index().set_index('level_1').join(pd.DataFrame(megye,index=['level_1']).T.reset_index().reset_index().set_index('level_1').drop('level_0',axis=1))
hdf.columns=['telepules','telepules_hun','Megye']
hdf.index=hdf['Megye']+'+'+hdf['telepules']
data.index=data['Megye']+'+'+data['telepules']
data=data.join(hdf['telepules_hun'])
data['telepules_hun']=data[['varos','telepules_hun']].T.ffill().T['telepules_hun']
gata=data[['ID','Év','Megye', 'telepules','telepules_hun','guessed_names2', 'guess_scores','Név','Típus', 'Profil',
'Óvodás csoportok összesen',
'Óvodások összesen', 'Kiscsoportok száma', 'Kiscsoportosok',
'Középcsoportok száma', 'Középcsoportosok', 'Nagycsoportok száma',
'Nagycsoportosok', 'Vegyes csoportok száma', 'Vegyescsoportosok',
'Tanítók összesen', 'Képzett tanítók', 'Képzetlen tanítók',
'Elemi osztályok összesen', 'Elemisek összesen',
'Előkészítő osztályok száma', 'Előkészítő osztályosok',
'1. osztályok száma', '1. osztályosok', '2. osztályok száma',
'2. osztályosok', '3. osztályok száma', '3. osztályosok',
'4. osztályok száma', '4. osztályosok', 'Általános osztályok összesen',
'Általánososok összesen', '5. osztályok száma', '5. osztályosok',
'6. osztályok száma', '6. osztályosok', '7. osztályok száma',
'7. osztályosok', '8. osztályok száma', '8. osztályosok',
'Középiskolai osztályok összesen', 'Középiskolások összesen',
'9. osztályok száma', '9. osztályosok', '10. osztályok száma',
'10. osztályosok', '11. osztályok száma', '11. osztályosok',
'12. osztályok száma', '12. osztályosok', '13. osztályok száma',
'13. osztályosok', '14. osztályok száma', '14. osztályosok','Továbbtanulás', 'Iskolabusz',
'Cod SIIIR', 'Cod SIRUES', 'Denumire scurtă', 'Denumire', 'Localitate',
'Localitate superioară', 'Stradă', 'Număr', 'Cod poștal', 'Statut',
'Tip unitate', 'Unitate PJ', 'Mod funcționare', 'Formă de finanțare',
'Formă de proprietate', 'Cod fiscal', 'Judet', 'Data modificării',
'Data acreditării', 'Data intrării în vigoare', 'Data închiderii',
'Telefon', 'Fax', 'Adresa email', 'nev', 'telepules_g','varos','cim', 'koordinata', 'telefon', 'web', 'maps', 'kep',
]]
gata.columns=['ID','Év','Megye', 'Település (eredeti)','Település (magyar VÁZLAT)','Név (normalizált)', 'Adatok megbízhatósága',
'Név (eredeti)','Típus (VÁZLAT)', 'Profil (VÁZLAT)',
'Óvodás csoportok összesen',
'Óvodások összesen', 'Kiscsoportok száma', 'Kiscsoportosok',
'Középcsoportok száma', 'Középcsoportosok', 'Nagycsoportok száma',
'Nagycsoportosok', 'Vegyes csoportok száma', 'Vegyescsoportosok',
'Tanítók összesen', 'Képzett tanítók', 'Képzetlen tanítók',
'Elemi osztályok összesen', 'Elemisek összesen',
'Előkészítő osztályok száma', 'Előkészítő osztályosok',
'1. osztályok száma', '1. osztályosok', '2. osztályok száma',
'2. osztályosok', '3. osztályok száma', '3. osztályosok',
'4. osztályok száma', '4. osztályosok', 'Általános osztályok összesen',
'Általánososok összesen', '5. osztályok száma', '5. osztályosok',
'6. osztályok száma', '6. osztályosok', '7. osztályok száma',
'7. osztályosok', '8. osztályok száma', '8. osztályosok',
'Középiskolai osztályok összesen', 'Középiskolások összesen',
'9. osztályok száma', '9. osztályosok', '10. osztályok száma',
'10. osztályosok', '11. osztályok száma', '11. osztályosok',
'12. osztályok száma', '12. osztályosok', '13. osztályok száma',
'13. osztályosok', '14. osztályok száma', '14. osztályosok','Továbbtanulás (VÁZLAT)', 'Iskolabusz (VÁZLAT)',
'RSH SIIIR kód', 'RSH SIRUES kód', 'RSH Rövid név', 'RSH Név', 'RSH Település',
'RSH Község', 'RSH Cím/Utca', 'RSH Cím/Szám', 'RSH Cím/Irányítószám', 'RSH Jogi forma',
'RSH Egység típusa', 'RSH Anyaintézmény', 'RSH Működési forma', 'RSH Finanszírozás',
'RSH Tulajdonviszony', 'RSH Adószám', 'RSH Megye', 'RSH Módosítva',
'RSH Akkreditálva', 'RSH Működés kezdete', 'RSH Bezárás ideje',
'RSH Telefon', 'RSH Fax', 'RSH Email', 'GOOGLE Név', 'GOOGLE Település', 'GOOGLE Község', 'GOOGLE Cím',
'GOOGLE koordináta', 'GOOGLE Telefon', 'GOOGLE weboldal', 'GOOGLE térkép', 'GOOGLE fénykép',
]
gata['Név (normalizált)']=gata['Név (normalizált)']\
.str.replace('SGMZ','ÁLTALÁNOS ISKOLA')\
.str.replace('SPRM','ELEMI ISKOLA')\
.str.replace('SPSTL','POSZTLÍCEUM')\
.str.replace('LICTEH','SZAKLÍCEUM')\
.str.replace('LISPRT','SPORTISKOLA')\
.str.replace('CLBCOP','GYEREK-KLUB')\
.str.replace('LITEOR','ELMÉLETI LÍCEUM')\
.str.replace('LIPDGA','TANÍTÓKÉPZŐ')\
.str.replace('LITOLX','TEOLÓGIAI LÍCEUM')\
.str.replace('LIARTE','MŰVÉSZETI LÍCEUM')\
.str.replace('COLGNAT','NEMZETI KOLLÉGIUM')\
.str.replace('GRDNRM','ÓVODA')\
.str.replace('GRDPLG','NAPKÖZI-OTTHON')\
.str.replace('INSPSCJ','TANFELÜGYELŐSÉG')\
.str.replace('SCSPC','SPECIÁLIS ISKOLA')
hata=gata.set_index('ID').sort_values(['Év','Megye','Település (eredeti)','Név (normalizált)'])
hata.to_excel('data/output/Erdely_draft_output.xlsx')
```
DEPRECATED - google cant translate place names
Finish up the rest with `googletrans`
```
# !pip install googletrans
from googletrans import Translator
translator = Translator()
t=translator.translate('scoala',src='ro',dest='hu')
to_translate=list((data['telepules']+', judetul '+data['Judet']+', ROMANIA').unique())[:20]
to_translate=list((data['Denumire'].astype(str)+' '+data['Localitate'].astype(str)+', '+data['Localitate superioară'].astype(str)+', '+\
data['Stradă'].astype(str)+' nr. '+data['Număr'].astype(str)+', '+data['Cod poștal'].astype(str).str[:-2]+', '+\
data['Judet'].astype(str)+', ROMANIA').unique())[:10]
translated={}
translations = translator.translate(to_translate, src='ro', dest='hu')
for translation in translations:
translated[translation.origin]=translation.text
translated
```
|
github_jupyter
|
## RIHAD VARIAWA, Data Scientist - Who has fun LEARNING, EXPLORING & GROWING
<h1 align="center"><font size="5">COLLABORATIVE FILTERING</font></h1>
Recommendation systems are a collection of algorithms used to recommend items to users based on information taken from the user. These systems have become ubiquitous can be commonly seen in online stores, movies databases and job finders. In this notebook, we will explore recommendation systems based on Collaborative Filtering and implement simple version of one using Python and the Pandas library.
<h1>Table of contents</h1>
<div class="alert alert-block alert-info" style="margin-top: 20px">
<ol>
<li><a href="#ref1">Acquiring the Data</a></li>
<li><a href="#ref2">Preprocessing</a></li>
<li><a href="#ref3">Collaborative Filtering</a></li>
</ol>
</div>
<br>
<hr>
<a id="ref1"></a>
# Acquiring the Data
To acquire and extract the data, simply run the following Bash scripts:
Dataset acquired from [GroupLens](http://grouplens.org/datasets/movielens/). Lets download the dataset. To download the data, we will use **`!wget`** to download it from IBM Object Storage.
__Did you know?__ When it comes to Machine Learning, you will likely be working with large datasets. As a business, where can you host your data? IBM is offering a unique opportunity for businesses, with 10 Tb of IBM Cloud Object Storage: [Sign up now for free](http://cocl.us/ML0101EN-IBM-Offer-CC)
```
!wget -O moviedataset.zip https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/ML0101ENv3/labs/moviedataset.zip
print('unziping ...')
!unzip -o -j moviedataset.zip
```
Now you're ready to start working with the data!
<hr>
<a id="ref2"></a>
# Preprocessing
First, let's get all of the imports out of the way:
```
#Dataframe manipulation library
import pandas as pd
#Math functions, we'll only need the sqrt function so let's import only that
from math import sqrt
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
```
Now let's read each file into their Dataframes:
```
#Storing the movie information into a pandas dataframe
movies_df = pd.read_csv('_datasets/movies.csv')
#Storing the user information into a pandas dataframe
ratings_df = pd.read_csv('_datasets/ratings.csv')
```
Let's also take a peek at how each of them are organized:
```
#Head is a function that gets the first N rows of a dataframe. N's default is 5.
movies_df.head()
```
So each movie has a unique ID, a title with its release year along with it (Which may contain unicode characters) and several different genres in the same field. Let's remove the year from the title column and place it into its own one by using the handy [extract](http://pandas.pydata.org/pandas-docs/stable/generated/pandas.Series.str.extract.html#pandas.Series.str.extract) function that Pandas has.
Let's remove the year from the __title__ column by using pandas' replace function and store in a new __year__ column.
```
#Using regular expressions to find a year stored between parentheses
#We specify the parantheses so we don't conflict with movies that have years in their titles
movies_df['year'] = movies_df.title.str.extract('(\(\d\d\d\d\))',expand=False)
#Removing the parentheses
movies_df['year'] = movies_df.year.str.extract('(\d\d\d\d)',expand=False)
#Removing the years from the 'title' column
movies_df['title'] = movies_df.title.str.replace('(\(\d\d\d\d\))', '')
#Applying the strip function to get rid of any ending whitespace characters that may have appeared
movies_df['title'] = movies_df['title'].apply(lambda x: x.strip())
```
Let's look at the result!
```
movies_df.head()
```
With that, let's also drop the genres column since we won't need it for this particular recommendation system.
```
#Dropping the genres column
movies_df = movies_df.drop('genres', 1)
```
Here's the final movies dataframe:
```
movies_df.head()
```
<br>
Next, let's look at the ratings dataframe.
```
ratings_df.head()
```
Every row in the ratings dataframe has a user id associated with at least one movie, a rating and a timestamp showing when they reviewed it. We won't be needing the timestamp column, so let's drop it to save on memory.
```
#Drop removes a specified row or column from a dataframe
ratings_df = ratings_df.drop('timestamp', 1)
```
Here's how the final ratings Dataframe looks like:
```
ratings_df.head()
```
<hr>
<a id="ref3"></a>
# Collaborative Filtering
Now, time to start our work on recommendation systems.
The first technique we're going to take a look at is called __Collaborative Filtering__, which is also known as __User-User Filtering__. As hinted by its alternate name, this technique uses other users to recommend items to the input user. It attempts to find users that have similar preferences and opinions as the input and then recommends items that they have liked to the input. There are several methods of finding similar users (Even some making use of Machine Learning), and the one we will be using here is going to be based on the __Pearson Correlation Function__.
<img src="https://ibm.box.com/shared/static/1ql8cbwhtkmbr6nge5e706ikzm5mua5w.png" width=800px>
The process for creating a User Based recommendation system is as follows:
- Select a user with the movies the user has watched
- Based on his rating to movies, find the top X neighbours
- Get the watched movie record of the user for each neighbour.
- Calculate a similarity score using some formula
- Recommend the items with the highest score
Let's begin by creating an input user to recommend movies to:
Notice: To add more movies, simply increase the amount of elements in the userInput. Feel free to add more in! Just be sure to write it in with capital letters and if a movie starts with a "The", like "The Matrix" then write it in like this: 'Matrix, The' .
```
userInput = [
{'title':'Breakfast Club, The', 'rating':5},
{'title':'Toy Story', 'rating':3.5},
{'title':'Jumanji', 'rating':2},
{'title':"Pulp Fiction", 'rating':5},
{'title':'Akira', 'rating':4.5}
]
inputMovies = pd.DataFrame(userInput)
inputMovies
```
#### Add movieId to input user
With the input complete, let's extract the input movies's ID's from the movies dataframe and add them into it.
We can achieve this by first filtering out the rows that contain the input movies' title and then merging this subset with the input dataframe. We also drop unnecessary columns for the input to save memory space.
```
#Filtering out the movies by title
inputId = movies_df[movies_df['title'].isin(inputMovies['title'].tolist())]
#Then merging it so we can get the movieId. It's implicitly merging it by title.
inputMovies = pd.merge(inputId, inputMovies)
#Dropping information we won't use from the input dataframe
inputMovies = inputMovies.drop('year', 1)
#Final input dataframe
#If a movie you added in above isn't here, then it might not be in the original
#dataframe or it might spelled differently, please check capitalisation.
inputMovies
```
#### The users who has seen the same movies
Now with the movie ID's in our input, we can now get the subset of users that have watched and reviewed the movies in our input.
```
#Filtering out users that have watched movies that the input has watched and storing it
userSubset = ratings_df[ratings_df['movieId'].isin(inputMovies['movieId'].tolist())]
userSubset.head()
```
We now group up the rows by user ID.
```
#Groupby creates several sub dataframes where they all have the same value in the column specified as the parameter
userSubsetGroup = userSubset.groupby(['userId'])
```
lets look at one of the users, e.g. the one with userID=1130
```
userSubsetGroup.get_group(1130)
```
Let's also sort these groups so the users that share the most movies in common with the input have higher priority. This provides a richer recommendation since we won't go through every single user.
```
#Sorting it so users with movie most in common with the input will have priority
userSubsetGroup = sorted(userSubsetGroup, key=lambda x: len(x[1]), reverse=True)
```
Now lets look at the first user
```
userSubsetGroup[0:3]
```
#### Similarity of users to input user
Next, we are going to compare all users (not really all !!!) to our specified user and find the one that is most similar.
we're going to find out how similar each user is to the input through the __Pearson Correlation Coefficient__. It is used to measure the strength of a linear association between two variables. The formula for finding this coefficient between sets X and Y with N values can be seen in the image below.
Why Pearson Correlation?
Pearson correlation is invariant to scaling, i.e. multiplying all elements by a nonzero constant or adding any constant to all elements. For example, if you have two vectors X and Y,then, pearson(X, Y) == pearson(X, 2 * Y + 3). This is a pretty important property in recommendation systems because for example two users might rate two series of items totally different in terms of absolute rates, but they would be similar users (i.e. with similar ideas) with similar rates in various scales .

The values given by the formula vary from r = -1 to r = 1, where 1 forms a direct correlation between the two entities (it means a perfect positive correlation) and -1 forms a perfect negative correlation.
In our case, a 1 means that the two users have similar tastes while a -1 means the opposite.
We will select a subset of users to iterate through. This limit is imposed because we don't want to waste too much time going through every single user.
```
userSubsetGroup = userSubsetGroup[0:100]
```
Now, we calculate the Pearson Correlation between input user and subset group, and store it in a dictionary, where the key is the user Id and the value is the coefficient
```
#Store the Pearson Correlation in a dictionary, where the key is the user Id and the value is the coefficient
pearsonCorrelationDict = {}
#For every user group in our subset
for name, group in userSubsetGroup:
#Let's start by sorting the input and current user group so the values aren't mixed up later on
group = group.sort_values(by='movieId')
inputMovies = inputMovies.sort_values(by='movieId')
#Get the N for the formula
nRatings = len(group)
#Get the review scores for the movies that they both have in common
temp_df = inputMovies[inputMovies['movieId'].isin(group['movieId'].tolist())]
#And then store them in a temporary buffer variable in a list format to facilitate future calculations
tempRatingList = temp_df['rating'].tolist()
#Let's also put the current user group reviews in a list format
tempGroupList = group['rating'].tolist()
#Now let's calculate the pearson correlation between two users, so called, x and y
Sxx = sum([i**2 for i in tempRatingList]) - pow(sum(tempRatingList),2)/float(nRatings)
Syy = sum([i**2 for i in tempGroupList]) - pow(sum(tempGroupList),2)/float(nRatings)
Sxy = sum( i*j for i, j in zip(tempRatingList, tempGroupList)) - sum(tempRatingList)*sum(tempGroupList)/float(nRatings)
#If the denominator is different than zero, then divide, else, 0 correlation.
if Sxx != 0 and Syy != 0:
pearsonCorrelationDict[name] = Sxy/sqrt(Sxx*Syy)
else:
pearsonCorrelationDict[name] = 0
pearsonCorrelationDict.items()
pearsonDF = pd.DataFrame.from_dict(pearsonCorrelationDict, orient='index')
pearsonDF.columns = ['similarityIndex']
pearsonDF['userId'] = pearsonDF.index
pearsonDF.index = range(len(pearsonDF))
pearsonDF.head()
```
#### The top x similar users to input user
Now let's get the top 50 users that are most similar to the input.
```
topUsers=pearsonDF.sort_values(by='similarityIndex', ascending=False)[0:50]
topUsers.head()
```
Now, let's start recommending movies to the input user.
#### Rating of selected users to all movies
We're going to do this by taking the weighted average of the ratings of the movies using the Pearson Correlation as the weight. But to do this, we first need to get the movies watched by the users in our __pearsonDF__ from the ratings dataframe and then store their correlation in a new column called _similarityIndex". This is achieved below by merging of these two tables.
```
topUsersRating=topUsers.merge(ratings_df, left_on='userId', right_on='userId', how='inner')
topUsersRating.head()
```
Now all we need to do is simply multiply the movie rating by its weight (The similarity index), then sum up the new ratings and divide it by the sum of the weights.
We can easily do this by simply multiplying two columns, then grouping up the dataframe by movieId and then dividing two columns:
It shows the idea of all similar users to candidate movies for the input user:
```
#Multiplies the similarity by the user's ratings
topUsersRating['weightedRating'] = topUsersRating['similarityIndex']*topUsersRating['rating']
topUsersRating.head()
#Applies a sum to the topUsers after grouping it up by userId
tempTopUsersRating = topUsersRating.groupby('movieId').sum()[['similarityIndex','weightedRating']]
tempTopUsersRating.columns = ['sum_similarityIndex','sum_weightedRating']
tempTopUsersRating.head()
#Creates an empty dataframe
recommendation_df = pd.DataFrame()
#Now we take the weighted average
recommendation_df['weighted average recommendation score'] = tempTopUsersRating['sum_weightedRating']/tempTopUsersRating['sum_similarityIndex']
recommendation_df['movieId'] = tempTopUsersRating.index
recommendation_df.head()
```
Now let's sort it and see the top 20 movies that the algorithm recommended!
```
recommendation_df = recommendation_df.sort_values(by='weighted average recommendation score', ascending=False)
recommendation_df.head(10)
movies_df.loc[movies_df['movieId'].isin(recommendation_df.head(10)['movieId'].tolist())]
```
### Advantages and Disadvantages of Collaborative Filtering
##### Advantages
* Takes other user's ratings into consideration
* Doesn't need to study or extract information from the recommended item
* Adapts to the user's interests which might change over time
##### Disadvantages
* Approximation function can be slow
* There might be a low of amount of users to approximate
* Privacy issues when trying to learn the user's preferences
<h2>Want to learn more?</h2>
IBM SPSS Modeler is a comprehensive analytics platform that has many machine learning algorithms. It has been designed to bring predictive intelligence to decisions made by individuals, by groups, by systems – by your enterprise as a whole. A free trial is available through this course, available here: <a href="http://cocl.us/ML0101EN-SPSSModeler">SPSS Modeler</a>
Also, you can use Watson Studio to run these notebooks faster with bigger datasets. Watson Studio is IBM's leading cloud solution for data scientists, built by data scientists. With Jupyter notebooks, RStudio, Apache Spark and popular libraries pre-packaged in the cloud, Watson Studio enables data scientists to collaborate on their projects without having to install anything. Join the fast-growing community of Watson Studio users today with a free account at <a href="https://cocl.us/ML0101EN_DSX">Watson Studio</a>
<h3>Thanks for completing this lesson!</h3>
<h4>Author: <a href="https://ca.linkedin.com/in/saeedaghabozorgi">Saeed Aghabozorgi</a></h4>
<p><a href="https://ca.linkedin.com/in/saeedaghabozorgi">Saeed Aghabozorgi</a>, PhD is a Data Scientist in IBM with a track record of developing enterprise level applications that substantially increases clients’ ability to turn data into actionable knowledge. He is a researcher in data mining field and expert in developing advanced analytic methods like machine learning and statistical modelling on large datasets.</p>
<hr>
<p>Copyright © 2018 <a href="https://cocl.us/DX0108EN_CC">Cognitive Class</a>. This notebook and its source code are released under the terms of the <a href="https://bigdatauniversity.com/mit-license/">MIT License</a>.</p>
|
github_jupyter
|
# Let's apply the GP-based optimizer to our small Hubbard model.
Make sure your jupyter path is the same as your virtual environment that you used to install all your packages.
If nopt, do something like this in your terminal:
`$ ipython kernel install --user --name TUTORIAL --display-name "Python 3.9"`
```
# check your python
from platform import python_version
print(python_version())
```
Gaussian Process (GP) models were introduced in the __[Gaussian Process Models](optimization.ipynb)__ notebook. The GP-based optimizer uses these techniques as implemented in the included __[opti_by_gp.py](opti_by_gp.py)__ module, which also provides helpers for plotting results. Note that this module uses the ImFil optimizer underneath, a choice that can not currently be changed.
As a first step, create once more a __[Hubbard Model](hubbard_model_intro.ipynb)__ setup.
```
import hubbard as hb
import logging
import noise_model as noise
import numpy as np
import opti_by_gp as obg
from IPython.display import Image
logging.getLogger('hubbard').setLevel(logging.INFO)
# Select a model appropriate for the machine used:
# laptop -> use small model
# server -> use medium model
MODEL = hb.small_model
#MODEL = hb.medium_model
# Hubbard model for fermions (Fermi-Hubbard) required parameters
xdim, ydim, t, U, chem, magf, periodic, spinless = MODEL()
# Number of electrons to add to the system
n_electrons_up = 1
n_electrons_down = 1
n_electrons = n_electrons_up + n_electrons_down
# Total number of "sites", with each qubit representing occupied or not
spinfactor = spinless and 1 or 2
n_qubits = n_sites = xdim * ydim * spinfactor
# Create the Hubbard Model for use with Qiskit
hubbard_op = hb.hamiltonian_qiskit(
x_dimension = xdim,
y_dimension = ydim,
tunneling = t,
coulomb = U,
chemical_potential = chem,
magnetic_field = magf,
periodic = periodic,
spinless = spinless)
```
The GP modeling needs persistent access to the evaluated points, so tell the objective to save them. Otherwise, the objective is the same as before. Choose the maximum number of objective evaluations, the initial and set the bounds. Then run the optimization using GP (as mentioned before, this uses ImFil underneath).
```
# noise-free objective with enough Trotter steps to get an accurate result
objective = hb.EnergyObjective(hubbard_op, n_electrons_up, n_electrons_down,
trotter_steps=3, save_evals=True)
# initial and bounds (set good=True to get tighter bounds)
initial_amplitudes, bounds = MODEL.initial(
n_electrons_up, n_electrons_down, objective.npar(), good=False)
# max number of allowed function evals
maxevals = 100
result = obg.opti_by_gp(objective.npar(), bounds, objective, maxevals)
print('Results with GP:')
print("Estimated energy: %.5f" % result[1])
print("Parameters: ", result[0])
print("Number of iters: ", result[2])
```
Now let's analyze the results be looking at the sample evaluations and convergence plot.
```
Image(filename='samples.png')
```
The left plot shows:
1) the points sampled with GP (pink squares): you can see that we have some points everywhere in the space, but a denser pink square cloud where the function has its minimum
2) yellow circles (5) -- these are the points from which the local search with ImFil starts: we choose the best point found by the GP, and another 4 points based on their function value and distance to already selected start points. 5 is a parameter, if you want to do only one local search, you can just start from the best point found by the GP iterations. Also: not all 5 points will necessarily be used for ImFil, the optimization stops when the maximum number of allowed evaluations has been reached.
3) the green squares are the points ImFil decided to sample -- you can see that they cover most of the space. Wouldn't it be nice to force ImFil to search only a smaller radius?!
4) the red dot indicates the best point found during optimization
5) the contours are created by using a GP model and all sample information that we collected - so this is not the true contours, but the best guess of what the true contours may look like
The right plot shows the GP approximation of the energy surface - again, not the true surface, just our best guess based on training a GP on all input-output pairs
```
Image(filename='progress.png')
```
This plot shows the progress we are making with respect to improving the energy versus the number of function evaluations.
We show the best energy value found so far, thus, the graph is monotonically decreasing and has a step-like shape. whenever the graph is flat, it means that during these iterations no energy improvements were found. If you were to plot simply the energy at each function evaluation, the graph would go up and down because we use sampling based algorithms and not gradient-based algorithms. Thus, not in every iteration we find an improvement.
There is a large down-step in the beginning - this is due to our random space filling sampling initially. We can also see that ImFil does not make much progress here. The GP-based sampling is used until 30 evaluations.
Note that the GP based optimizer has parameters, including the size of the initial experimental design, the number of iterations that we want to apply the GP (here 30), the maximum number of local searches with ImFil after the GP is done, .... see the __[opti_by_gp.py](opti_by_gp.py)__ module (or run the cell below to load).
```
%load 'opti_by_gp.py'
```
**Exercise:** redo the above analysis using a noisy objective. If time is limited, consider only using sampling noise, e.g. by setting `shots=8192` (see the notebook on __[noise](hubbard_vqe_noise.ipynb)__ for more examples), and using tight bounds.
**Optional Exercise:** for comparison purposes, follow-up with an optimization run that does not use GP and try in particular what happens when using only few function evaluations (20, say, if using tight bounds). Try different optimizers (but consider that some, such as SPSA, will take more evalations per iteration; and consider that optimizers that do not respect bounds are at a severe disadvantage).
```
# Pull in a couple of optimizers to play with
from qiskit.algorithms.optimizers import COBYLA, SPSA
try:
from qiskit.algorithms.optimizers import IMFIL, SNOBFIT
except ImportError:
print("install scikit-quant to use IMFIL and SNOBFIT")
```
|
github_jupyter
|
# Introduction to Data Science
# Lecture 25: Neural Networks II
*COMP 5360 / MATH 4100, University of Utah, http://datasciencecourse.net/*
In this lecture, we'll continue discussing Neural Networks.
Recommended Reading:
* A. Géron, [Hands-On Machine Learning with Scikit-Learn & TensorFlow](http://proquest.safaribooksonline.com/book/programming/9781491962282) (2017)
* I. Goodfellow, Y. Bengio, and A. Courville, [Deep Learning](http://www.deeplearningbook.org/) (2016)
* Y. LeCun, Y. Bengio, and G. Hinton, [Deep learning](https://www.nature.com/articles/nature14539), Nature (2015)
## Recap: Neural Networks
Last time, we introduced *Neural Networks* and discussed how they can be used for classification and regression.
There are many different *network architectures* for Neural Networks, but our focus is on **Multi-layer Perceptrons**. Here, there is an *input layer*, typically drawn on the left hand side and an *output layer*, typically drawn on the right hand side. The middle layers are called *hidden layers*.
<img src="Colored_neural_network.svg" title="https://en.wikipedia.org/wiki/Artificial_neural_network#/media/File:Colored_neural_network.svg"
width="300">
Given a set of features $X = x^0 = \{x_1, x_2, ..., x_n\}$ and a target $y$, a neural network works as follows.
Each layer applies an affine transformation and an [activation function](https://en.wikipedia.org/wiki/Activation_function) (e.g., ReLU, hyperbolic tangent, or logistic) to the output of the previous layer:
$$
x^{j} = f ( A^{j} x^{j-1} + b^j ).
$$
At the $j$-th hidden layer, the input is represented as the composition of $j$ such mappings. An additional function, *e.g.* [softmax](https://en.wikipedia.org/wiki/Softmax_function), is applied to the output layer to give the prediction, $\hat y$, for classification or regression.
<img src="activationFct.png"
title="see Géron, Ch. 10"
width="700">
## Softmax function for classificaton
The *softmax function*, $\sigma:\mathbb{R}^K \to (0,1)^K$ is defined by
$$
\sigma(\mathbf{z})_j = \frac{e^{z_j}}{\sum_{k=1}^K e^{z_k}}
\qquad \qquad \textrm{for } j=1, \ldots, K.
$$
Note that each component is in the range $(0,1)$ and the values sum to 1. We interpret $\sigma(\mathbf{z})_j$ as the probability that $\mathbf{z}$ is a member of class $j$.
## Training a neural network
Neural networks uses a loss function of the form
$$
Loss(\hat{y},y,W) = \frac{1}{2} \sum_{i=1}^n g(\hat{y}_i(W),y_i) + \frac{\alpha}{2} \|W\|_2^2
$$
Here,
+ $y_i$ is the label for the $i$-th example,
+ $\hat{y}_i(W)$ is the predicted label for the $i$-th example,
+ $g$ is a function that measures the error, typically $L^2$ difference for regression or cross-entropy for classification, and
+ $\alpha$ is a regularization parameter.
Starting from initial random weights, the loss function is minimized by repeatedly updating these weights. Various **optimization methods** can be used, *e.g.*,
+ gradient descent method
+ quasi-Newton method,
+ stochastic gradient descent, or
+ ADAM.
There are various parameters associated with each method that must be tuned.
**Back propagation** is a way of using the chain rule from calculus to compute the gradient of the $Loss$ function for optimization.
## Neural Networks in scikit-learn
In the previous lecture, we used Neural Network implementations in scikit-learn to do both classification and regression:
+ [multi-layer perceptron (MLP) classifier](http://scikit-learn.org/stable/modules/generated/sklearn.neural_network.MLPClassifier.html)
+ [multi-layer perceptron (MLP) regressor](http://scikit-learn.org/stable/modules/generated/sklearn.neural_network.MLPRegressor.html)
However, there are several limitations to the scikit-learn implementation:
- no GPU support
- limited network architectures
## Neural networks with TensorFlow
Today, we'll use [TensorFlow](https://github.com/tensorflow/tensorflow) to train a Neural Network.
TensorFlow is an open-source library designed for large-scale machine learning.
### Installing TensorFlow
Instructions for installing TensorFlow are available at [the tensorflow install page](https://www.tensorflow.org/install).
It is recommended that you use the command:
```
pip install tensorflow
```
```
import tensorflow as tf
print(tf.__version__)
# to make this notebook's output stable across runs
def reset_graph(seed=42):
tf.reset_default_graph()
tf.set_random_seed(seed)
np.random.seed(seed)
```
TensorFlow represents computations by connecting op (operation) nodes into a computation graph.
<img src="graph.png"
title="An example of computational graph"
width="400">
A TensorFlow program usually has two components:
+ In the *construction phase*, a computational graph is built. During this phase, no computations are performed and the variables are not yet initialized.
+ In the *execution phase*, the graph is evaluated, typically many times. In this phase, the each operation is given to a CPU or GPU, variables are initialized, and functions can be evaluted.
```
# construction phase
x = tf.Variable(3)
y = tf.Variable(4)
f = x*x*y + y + 2
# execution phase
with tf.Session() as sess: # initializes a "session"
x.initializer.run()
y.initializer.run()
print(f.eval())
# alternatively all variables cab be initialized as follows
init = tf.global_variables_initializer()
with tf.Session() as sess: # initializes a "session"
init.run() # initializes all the variables
print(f.eval())
```
### Autodiff
TensorFlow can automatically compute the derivative of functions using [```gradients```](https://www.tensorflow.org/api_docs/python/tf/gradients).
```
# construction phase
x = tf.Variable(3.0)
y = tf.Variable(4.0)
f = x + 2*y*y + 2
grads = tf.gradients(f,[x,y])
# execution phase
with tf.Session() as sess:
sess.run(tf.global_variables_initializer()) # initializes all variables
print([g.eval() for g in grads])
```
This is enormously helpful since training a NN requires the derivate of the loss function with respect to the parameters (and there are a lot of parameters). This is computed using backpropagation (chain rule) and TensorFlow does this work for you.
**Exercise:** Use TensorFlow to compute the derivative of $f(x) = e^x$ at $x=2$.
```
# your code here
```
### Optimization methods
Tensorflow also has several built-in optimization methods.
Other optimization methods in TensorFlow:
+ [```tf.train.Optimizer```](https://www.tensorflow.org/api_docs/python/tf/compat/v1/train/Optimizer)
+ [```tf.train.GradientDescentOptimizer```](https://www.tensorflow.org/api_docs/python/tf/compat/v1/train/GradientDescentOptimizer)
+ [```tf.train.AdadeltaOptimizer```](https://www.tensorflow.org/api_docs/python/tf/compat/v1/train/AdadeltaOptimizer)
+ [```tf.train.AdagradOptimizer```](https://www.tensorflow.org/api_docs/python/tf/compat/v1/train/AdagradOptimizer)
+ [```tf.train.AdagradDAOptimizer```](https://www.tensorflow.org/api_docs/python/tf/compat/v1/train/AdagradDAOptimizer)
+ [```tf.train.MomentumOptimizer```](https://www.tensorflow.org/api_docs/python/tf/compat/v1/train/MomentumOptimizer)
+ [```tf.train.AdamOptimizer```](https://www.tensorflow.org/api_docs/python/tf/compat/v1/train/AdamOptimizer)
+ [```tf.train.FtrlOptimizer```](https://www.tensorflow.org/api_docs/python/tf/compat/v1/train/FtrlOptimizer)
+ [```tf.train.ProximalGradientDescentOptimizer```](https://www.tensorflow.org/api_docs/python/tf/compat/v1/train/ProximalGradientDescentOptimizer)
+ [```tf.train.ProximalAdagradOptimizer```](https://www.tensorflow.org/api_docs/python/tf/compat/v1/train/ProximalAdagradOptimizer)
+ [```tf.train.RMSPropOptimizer```](https://www.tensorflow.org/api_docs/python/tf/compat/v1/train/RMSPropOptimizer)
For more information, see the [TensorFlow training webpage](https://www.tensorflow.org/api_guides/python/train).
Let's see how to use the [```GradientDescentOptimizer```](https://www.tensorflow.org/api_docs/python/tf/compat/v1/train/GradientDescentOptimizer).
```
x = tf.Variable(3.0, trainable=True)
y = tf.Variable(2.0, trainable=True)
f = x*x + 100*y*y
opt = tf.train.GradientDescentOptimizer(learning_rate=5e-3).minimize(f)
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for i in range(1000):
if i%100 == 0: print(sess.run([x,y,f]))
sess.run(opt)
```
Using another optimizer, such as the [```MomentumOptimizer```](https://www.tensorflow.org/api_docs/python/tf/compat/v1/train/MomentumOptimizer),
has similiar syntax.
```
x = tf.Variable(3.0, trainable=True)
y = tf.Variable(2.0, trainable=True)
f = x*x + 100*y*y
opt = tf.train.MomentumOptimizer(learning_rate=1e-2,momentum=.5).minimize(f)
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for i in range(1000):
if i%100 == 0: print(sess.run([x,y,f]))
sess.run(opt)
```
**Exercise:** Use TensorFlow to find the minimum of the [Rosenbrock function](https://en.wikipedia.org/wiki/Rosenbrock_function):
$$
f(x,y) = (x-1)^2 + 100*(y-x^2)^2.
$$
```
# your code here
```
## Classifying the MNIST handwritten digit dataset
We now use TensorFlow to classify the handwritten digits in the MNIST dataset.
### Using plain TensorFlow
We'll first follow [Géron, Ch. 10](https://github.com/ageron/handson-ml/blob/master/10_introduction_to_artificial_neural_networks.ipynb) to build a NN using plain TensorFlow.
#### Construction phase
+ We specify the number of inputs and outputs and the size of each layer. Here the images are 28x28 and there are 10 classes (each corresponding to a digit). We'll choose 2 hidden layers, with 300 and 100 neurons respectively.
+ Placeholder nodes are used to represent the training data and targets. We use the ```None``` keyword to leave the shape (of the training batch) unspecified.
+ We add layers to the NN using the ```layers.dense()``` function. In each case, we specify the input, and the size of the layer. We also specify the activation function used in each layer. Here, we choose the ReLU function.
+ We specify that the output of the NN will be a softmax function. The loss function is cross entropy.
+ We then specify that we'll use the [GradientDescentOptimizer](https://www.tensorflow.org/api_docs/python/tf/train/GradientDescentOptimizer)
with a learning rate of 0.01.
+ Finally, we specify how the model will be evaluated. The [```in_top_k```](https://www.tensorflow.org/api_docs/python/tf/nn/in_top_k) function checks to see if the targets are in the top k predictions.
We then initialize all of the variables and create an object to save the model using the [```saver()```](https://www.tensorflow.org/programmers_guide/saved_model) function.
#### Execution phase
At each *epoch*, the code breaks the training batch into mini-batches of size 50. Cycling through the mini-batches, it uses gradient descent to train the NN. The accuracy for both the training and test datasets are evaluated.
```
import tensorflow as tf
import numpy as np
from sklearn.metrics import confusion_matrix
# to make this notebook's output stable across runs
def reset_graph(seed=42):
tf.reset_default_graph()
tf.set_random_seed(seed)
np.random.seed(seed)
# load the data
(X_train, y_train), (X_test, y_test) = tf.keras.datasets.mnist.load_data()
X_train = X_train.astype(np.float32).reshape(-1, 28*28) / 255.0
X_test = X_test.astype(np.float32).reshape(-1, 28*28) / 255.0
y_train = y_train.astype(np.int32)
y_test = y_test.astype(np.int32)
# helper code
def shuffle_batch(X, y, batch_size):
rnd_idx = np.random.permutation(len(X))
n_batches = len(X) // batch_size
for batch_idx in np.array_split(rnd_idx, n_batches):
X_batch, y_batch = X[batch_idx], y[batch_idx]
yield X_batch, y_batch
# construction phase
n_inputs = 28*28 # MNIST
n_hidden1 = 300
n_hidden2 = 100
n_outputs = 10
reset_graph()
X = tf.placeholder(tf.float32, shape=(None, n_inputs), name="X")
y = tf.placeholder(tf.int32, shape=(None), name="y")
with tf.name_scope("dnn"):
hidden1 = tf.layers.dense(X, n_hidden1, name="hidden1",activation=tf.nn.relu)
hidden2 = tf.layers.dense(hidden1, n_hidden2, name="hidden2",activation=tf.nn.relu)
logits = tf.layers.dense(hidden2, n_outputs, name="outputs")
#y_proba = tf.nn.softmax(logits)
with tf.name_scope("loss"):
xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y, logits=logits)
loss = tf.reduce_mean(xentropy, name="loss")
learning_rate = 0.01
with tf.name_scope("train"):
optimizer = tf.train.GradientDescentOptimizer(learning_rate)
training_op = optimizer.minimize(loss)
with tf.name_scope("eval"):
correct = tf.nn.in_top_k(logits, y, 1)
accuracy = tf.reduce_mean(tf.cast(correct, tf.float32))
# execution phase
init = tf.global_variables_initializer()
saver = tf.train.Saver()
n_epochs = 10
#n_batches = 50
batch_size = 50
with tf.Session() as sess:
init.run()
for epoch in range(n_epochs):
for X_batch, y_batch in shuffle_batch(X_train, y_train, batch_size):
sess.run(training_op, feed_dict={X: X_batch, y: y_batch})
acc_batch = accuracy.eval(feed_dict={X: X_batch, y: y_batch})
acc_valid = accuracy.eval(feed_dict={X: X_test, y: y_test})
print(epoch, "Batch accuracy:", acc_batch, "Validation accuracy:", acc_valid)
save_path = saver.save(sess, "./my_model_final.ckpt")
```
Since the NN has been saved, we can use it for classification using the [```saver.restore```](https://www.tensorflow.org/programmers_guide/saved_model) function.
We can also print the confusion matrix using [```confusion_matrix```](https://www.tensorflow.org/api_docs/python/tf/confusion_matrix).
```
with tf.Session() as sess:
saver.restore(sess, save_path)
Z = logits.eval(feed_dict={X: X_test})
y_pred = np.argmax(Z, axis=1)
print(confusion_matrix(y_test,y_pred))
```
### Using TensorFlow's Keras API
Next, we'll use TensorFlow's Keras API to build a NN for the MNIST dataset.
[Keras](https://keras.io/) is a high-level neural networks API, written in Python and capable of running on top of TensorFlow, CNTK, or Theano. We'll use it with TensorFlow.
```
import tensorflow as tf
import numpy as np
from sklearn.metrics import confusion_matrix
(X_train, y_train),(X_test, y_test) = tf.keras.datasets.mnist.load_data()
X_train, X_test = X_train / 255.0, X_test / 255.0
# set the model
model = tf.keras.models.Sequential([
tf.keras.layers.Flatten(input_shape=(28, 28)),
tf.keras.layers.Dense(512, activation=tf.nn.relu),
tf.keras.layers.Dropout(rate=0.2),
tf.keras.layers.Dense(10, activation=tf.nn.softmax)
])
# specifiy optimizer
model.compile(optimizer='adam',
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
# train the model
model.fit(X_train, y_train, epochs=5)
score = model.evaluate(X_test, y_test)
names = model.metrics_names
for ii in np.arange(len(names)):
print(names[ii],score[ii])
model.summary()
y_pred = np.argmax(model.predict(X_test), axis=1)
print(confusion_matrix(y_test,y_pred))
```
## Using a pre-trained network
There are many examples of pre-trained NN that can be accessed [here](https://www.tensorflow.org/api_docs/python/tf/keras/applications).
These NN are very large, having been trained on giant computers using massive datasets.
It can be very useful to initialize a NN using one of these. This is called [transfer learning](https://en.wikipedia.org/wiki/Transfer_learning).
We'll use a NN that was pretrained for image recognition. This NN was trained on the [ImageNet](http://www.image-net.org/) project, which contains > 14 million images belonging to > 20,000 classes (synsets).
```
import tensorflow as tf
import numpy as np
from tensorflow.keras.preprocessing import image
from tensorflow.keras.applications import vgg16
vgg_model = tf.keras.applications.VGG16(weights='imagenet',include_top=True)
vgg_model.summary()
img_path = 'images/scout1.jpeg'
img = image.load_img(img_path, target_size=(224, 224))
x = image.img_to_array(img)
x = np.expand_dims(x, axis=0)
x = vgg16.preprocess_input(x)
preds = vgg_model.predict(x)
print('Predicted:', vgg16.decode_predictions(preds, top=5)[0])
```
**Exercise:** Repeat the above steps for an image of your own.
**Exercise:** There are several [other pre-trained networks in Keras](https://github.com/keras-team/keras-applications). Try these!
```
# your code here
```
## Some NN topics that we didn't discuss
+ Recurrent neural networks (RNN) for time series
+ How NN can be used for unsupervised learning problems and [Reinforcement learning problems](https://en.wikipedia.org/wiki/Reinforcement_learning)
+ Special layers in NN for image processing
+ Using Tensorflow on a GPU
+ ...
## CPU vs. GPU
[CPUs (Central processing units)](https://en.wikipedia.org/wiki/Central_processing_unit) have just a few cores. The number of processes that a CPU can do in parallel is limited. However, each cores is very fast and is good for sequential tasks.
[GPUs (Graphics processing units)](https://en.wikipedia.org/wiki/Graphics_processing_unit) have thousands of cores, so can do many processes in parallel. GPU cores are typically slower and are more limited than CPU cores. However, for the right kind of computations (think matrix multiplication), GPUs are very fast. GPUs also have their own memory and caching systems, which further improves the speed of some computations, but also makes GPUs more difficult to program. (You have to use something like [CUDA](https://en.wikipedia.org/wiki/CUDA)).
TensorFlow can use GPUs to significantly speed up the training NN. See the programmer's guide [here](https://www.tensorflow.org/programmers_guide/using_gpu).
|
github_jupyter
|
<table class="ee-notebook-buttons" align="left">
<td><a target="_blank" href="https://github.com/giswqs/earthengine-py-notebooks/tree/master/Datasets/Terrain/us_ned_physio_diversity.ipynb"><img width=32px src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" /> View source on GitHub</a></td>
<td><a target="_blank" href="https://nbviewer.jupyter.org/github/giswqs/earthengine-py-notebooks/blob/master/Datasets/Terrain/us_ned_physio_diversity.ipynb"><img width=26px src="https://upload.wikimedia.org/wikipedia/commons/thumb/3/38/Jupyter_logo.svg/883px-Jupyter_logo.svg.png" />Notebook Viewer</a></td>
<td><a target="_blank" href="https://mybinder.org/v2/gh/giswqs/earthengine-py-notebooks/master?filepath=Datasets/Terrain/us_ned_physio_diversity.ipynb"><img width=58px src="https://mybinder.org/static/images/logo_social.png" />Run in binder</a></td>
<td><a target="_blank" href="https://colab.research.google.com/github/giswqs/earthengine-py-notebooks/blob/master/Datasets/Terrain/us_ned_physio_diversity.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" /> Run in Google Colab</a></td>
</table>
## Install Earth Engine API
Install the [Earth Engine Python API](https://developers.google.com/earth-engine/python_install) and [geehydro](https://github.com/giswqs/geehydro). The **geehydro** Python package builds on the [folium](https://github.com/python-visualization/folium) package and implements several methods for displaying Earth Engine data layers, such as `Map.addLayer()`, `Map.setCenter()`, `Map.centerObject()`, and `Map.setOptions()`.
The magic command `%%capture` can be used to hide output from a specific cell.
```
# %%capture
# !pip install earthengine-api
# !pip install geehydro
```
Import libraries
```
import ee
import folium
import geehydro
```
Authenticate and initialize Earth Engine API. You only need to authenticate the Earth Engine API once. Uncomment the line `ee.Authenticate()`
if you are running this notebook for this first time or if you are getting an authentication error.
```
# ee.Authenticate()
ee.Initialize()
```
## Create an interactive map
This step creates an interactive map using [folium](https://github.com/python-visualization/folium). The default basemap is the OpenStreetMap. Additional basemaps can be added using the `Map.setOptions()` function.
The optional basemaps can be `ROADMAP`, `SATELLITE`, `HYBRID`, `TERRAIN`, or `ESRI`.
```
Map = folium.Map(location=[40, -100], zoom_start=4)
Map.setOptions('HYBRID')
```
## Add Earth Engine Python script
```
dataset = ee.Image('CSP/ERGo/1_0/US/physioDiversity')
physiographicDiversity = dataset.select('b1')
physiographicDiversityVis = {
'min': 0.0,
'max': 1.0,
}
Map.setCenter(-94.625, 39.825, 7)
Map.addLayer(
physiographicDiversity, physiographicDiversityVis,
'Physiographic Diversity')
```
## Display Earth Engine data layers
```
Map.setControlVisibility(layerControl=True, fullscreenControl=True, latLngPopup=True)
Map
```
|
github_jupyter
|
```
import sys
import pickle
import numpy as np
import matplotlib.pyplot as plt
sys.path.append("../..")
import gradient_analyze as ga
import hp_file
filename = './results.pickle'
with open(filename, "rb") as file:
results = pickle.load(file)
hess_exact = np.array([[ 0.794, 0.055, 0.109, -0.145, 0. ],
[ 0.055, 0.794, -0.042, 0.056, -0. ],
[ 0.109, -0.042, 0.794, 0.11 , 0. ],
[-0.145, 0.056, 0.11 , 0.794, 0. ],
[ 0. , -0. , 0. , 0. , -0. ]])
corr = lambda x: np.array(2 * x, dtype="float64") - np.diag(np.diag(np.array(x, dtype="float64")))
ga.calculate_new_quantity(['hess_ps'], 'hess_ps_corr', corr, results, hp_file)
ga.calculate_new_quantity(['hess_fd'], 'hess_fd_corr', corr, results, hp_file)
f = lambda x: np.sum((x - hess_exact) ** 2)
ga.calculate_new_quantity(['hess_ps_corr'], 'hess_ps_err', f, results, hp_file)
ga.calculate_new_quantity(['hess_fd_corr'], 'hess_fd_err', f, results, hp_file)
results_processed = ga.avg_quantities(['hess_ps_err', 'hess_fd_err'], results, hp_file)
results_processed_accessed = ga.access_quantities(['hess_ps_err', 'hess_fd_err'], results, hp_file)
n_shots = [10, 20, 41, 84, 119, 242, 492, 1000, 2031,
4125, 8192, 11938, 24245, 49239, 100000]
n_shots = n_shots[7]
n_shots
cols = plt.rcParams['axes.prop_cycle'].by_key()['color']
results_slice = ga.calculate_slice({"n_shots": n_shots}, results_processed)
results_slice_acc = ga.calculate_slice({"n_shots": n_shots}, results_processed_accessed)
x, y_fd = ga.make_numpy(results_slice, "h", "hess_fd_err")
x, y_ps = ga.make_numpy(results_slice, "h", "hess_ps_err")
stds_fd = []
stds_ps = []
for h in x:
errors = list(ga.calculate_slice({"h": h}, results_slice_acc).values())[0]
errors_fd = errors["hess_fd_err"]
errors_ps = errors["hess_ps_err"]
stds_fd.append(np.std(errors_fd))
stds_ps.append(np.std(errors_ps))
stds_fd = np.array(stds_fd)
stds_ps = np.array(stds_ps)
plt.fill_between(x, y_fd - stds_fd, y_fd + stds_fd, color=cols[0], alpha=0.2)
plt.fill_between(x, y_ps - stds_ps, y_ps + stds_ps, color=cols[1], alpha=0.2)
plt.plot(x, y_fd, label="finite-difference", c=cols[0])
plt.plot(x, y_ps, label="parameter-shift", c=cols[1])
# plt.axvline(np.pi / 2, c="black", alpha=0.4, linestyle=":")
plt.xlabel('step size', fontsize=20)
plt.ylabel('MSE', fontsize=20)
plt.xscale("log")
plt.tick_params(labelsize=15)
plt.legend()
# plt.savefig("tradeoff_1.pdf")
plt.yscale("log")
# plt.ylim(10**-5.25, 10**(-0.95))
plt.tick_params(labelsize=15)
plt.legend(fontsize=12)
# plt.title("(A)", loc="left", fontsize=15)
plt.tight_layout()
plt.savefig("ps_vs_fd_hess.pdf")
max_point = 8
y_fit_low = np.log(y_fd[:max_point])
x_fit_low = np.log(x[:max_point])
p = np.polyfit(x_fit_low, y_fit_low, 1)
print(p[0])
y_fit_low = p[0] * np.log(x) + p[1]
y_fit_low = np.exp(y_fit_low)
min_point = 40
max_point = 50
y_fit_high_ = np.log(y_fd[min_point:max_point])
x_fit_high_ = np.log(x[min_point:max_point])
ppp = np.polyfit(x_fit_high_, y_fit_high_, 1)
print(ppp[0])
y_fit_high_ = ppp[0] * np.log(x) + ppp[1]
y_fit_high_ = np.exp(y_fit_high_)
min_point = 80
max_point = 99
y_fit_high = np.log(y_fd[min_point:max_point])
x_fit_high = np.log(x[min_point:max_point])
pp = np.polyfit(x_fit_high, y_fit_high, 1)
print(pp[0])
y_fit_high = pp[0] * np.log(x) + pp[1]
y_fit_high = np.exp(y_fit_high)
plt.plot(x, y_fd, '--bo', label="Finite difference")
plt.plot(x, y_fit_low, label="Power law fit with p={:.4f}".format(p[0]))
# plt.plot(x, y_fit_high, label="Power law fit with p={:.4f}".format(pp[0]))
plt.plot(x, y_fit_high_, label="Power law fit with p={:.4f}".format(ppp[0]))
plt.xlabel('Finite difference step size', fontsize=20)
plt.ylabel('Mean squared error', fontsize=20)
plt.xscale("log")
plt.tick_params(labelsize=15)
plt.legend()
plt.tight_layout()
plt.savefig("tradeoff_1.pdf")
plt.yscale("log")
plt.ylim(10**-4, 0)
n_shots_list = [10, 20, 41, 84, 119, 242, 492, 1000, 2031,
4125, 8192, 11938, 24245, 49239, 100000]
errs = []
err_fds = []
errs_vars = []
for n_shots in n_shots_list:
results_slice = ga.calculate_slice({"n_shots": n_shots}, results_processed)
results_slice_acc = ga.calculate_slice({"n_shots": n_shots}, results_processed_accessed)
x, y_fd = ga.make_numpy(results_slice, "h", "hess_fd_err")
x, y_ps = ga.make_numpy(results_slice, "h", "hess_ps_err")
opt_arg = np.argmin(np.abs(x - np.pi / 2))
opt_x = x[opt_arg]
err = np.min(y_ps)
opt_x = x[np.argmin(y_ps)]
results_slice_acc_h = ga.calculate_slice({"h": opt_x}, results_slice_acc)
results_slice_acc_h = list(results_slice_acc_h.values())[0]["hess_ps_err"]
errs.append(err)
err_fd = np.min(y_fd)
err_fds.append(err_fd)
errs_vars.append(np.std(results_slice_acc_h))
errs = np.array(errs)
errs_vars = np.array(errs_vars)
min_point = 0
max_point = -1
y_fit_high = np.log(errs[min_point:max_point])
x_fit_high = np.log(n_shots_list[min_point:max_point])
pp = np.polyfit(x_fit_high, y_fit_high, 1)
print(pp[0])
y_fit_high = pp[0] * np.log(x) + pp[1]
y_fit_high = np.exp(y_fit_high)
# plt.fill_between(n_shots_list, errs - errs_vars, errs + errs_vars, color=cols[0], alpha=0.2)
plt.plot(n_shots_list, err_fds, label="finite-difference")
plt.plot(n_shots_list, errs, label="paramter-shift")
plt.xlabel('N', fontsize=20)
plt.ylabel('MSE', fontsize=20)
plt.tick_params(labelsize=15)
plt.tight_layout()
plt.yscale("log")
plt.xscale("log")
plt.tick_params(labelsize=15)
plt.legend(fontsize=12)
# plt.title("(B)", loc="left", fontsize=15)
plt.tight_layout()
plt.savefig("ps_vs_fd_N.pdf")
# # plt.ylim(10**-5.25, 10**(-0.95))
min_point = 0
max_point = -1
y_fit_high = np.log(errs[min_point:max_point])
x_fit_high = np.log(n_shots_list[min_point:max_point])
pp = np.polyfit(x_fit_high, y_fit_high, 1)
print(pp[0])
y_fit_high = pp[0] * np.log(x) + pp[1]
y_fit_high = np.exp(y_fit_high)
min_point = 10
max_point = -1
y_fit_high = np.log(err_fds[min_point:max_point])
x_fit_high = np.log(n_shots_list[min_point:max_point])
pp = np.polyfit(x_fit_high, y_fit_high, 1)
print(pp[0])
y_fit_high = pp[0] * np.log(x) + pp[1]
y_fit_high = np.exp(y_fit_high)
```
|
github_jupyter
|
# Dowloading data
We'll use a shell command to download the zipped data, unzip it into are working directory (folder).
```
!wget "https://docs.google.com/uc?export=download&id=1h3YjfecYS8vJ4yXKE3oBwg3Am64kN4-x" -O temp.zip && unzip -o temp.zip && rm temp.zip
```
# Importing and Cleaning the Data
```
import pandas as pd # aliasing for convenience
```
## Importing data one file at a time
### Importing 2015 data
```
df = pd.read_csv('happiness_report/2015.csv') # loading the data to a variable called "df"
df.head(3) # looking at the first 3 rows
df.tail(2) # looking at the last 2 rows
```
#### adding a year column
To add a column we can use the syntax:
`df['new_col_name'] = values`
**note**: if there was a column with the same name, it would be overwritten
```
df['year'] = 2015 # adding a column
df
```
### Importing 2016 data
```
df_2016 = pd.read_csv('happiness_report/2016.csv')
df_2016['year'] = 2016
```
### merging (stacking vertically) the two dataframes
**note** if a column exists in one dataframe but not in the other, the values for the latter will be set to NaN (empty value)
```
list_of_df_to_merge = [df, df_2016]
df_merged = pd.concat(list_of_df_to_merge)
df_merged
```
## Interaction with the filesystem
```
# python library for OperatingSystem interaction
import os
# list of files under the speficied folder
os.listdir('happiness_report')
# getting the full path given the folder and file
os.path.join('happiness_report','2019.csv')
```
## Loading and combining data from all files
We will:
- initialise an empty list of dataframes
- loop over the content of the `happiness_report` folder
- get the filepath from the filename and folder name
- load the data from the filepath
- add a column to the dataframe so we can keep track of which file the data belongs to
- add the dataframe to the list
- merge all the dataframes (vertically)
```
fld_name = 'happiness_report'
df_list = []
for filename in os.listdir(fld_name):
filepath = os.path.join(fld_name, filename)
df = pd.read_csv(filepath)
print(filename, ':', df.columns) # printing the column name for the file
df['filename'] = filename
df_list.append(df)
df_merged = pd.concat(df_list)
```
## Data cleaning
Because of inconsistency over the years of reporting, we need to do some data cleaning:
- we want a `year` column which we can get from the filename
- there are different naming for the Happiness score over the years: `Happiness Score`, `Happiness.Score`, `Score`. We want to unify them into one column.
- the country column has the same issue: `Country`, `Country or region`
```
# `filename` column is a text (string) column, so we can use string methods to edit it
column_of_string_pairs = df_merged['filename'].str.split('.') # '2015.csv' is now ['2015', 'csv']
# selecting only the fist element for each list
column_year_string = column_of_string_pairs.str[0] # ['2015', 'csv'] is now '2015'
# converting the string to an integer (number)
column_of_years = (column_year_string).astype(int) # '2015' (string) is now 2015 (number)
df_merged['year'] = column_of_years
```
To fix the issue of change in naming, we can use:
`colA.fillna(colB)`
which checks if there are any empty valus in `colA` and fills them with the values in `colB` for the same row.
```
# checks if there are any empty valus in colA and fills them with the values in colB for the same row
df_merged['Happiness Score'] = df_merged['Happiness Score'].fillna(df_merged['Happiness.Score']).fillna(df_merged['Score'])
df_merged['Country'] = df_merged['Country or region'].fillna(df_merged['Country'])
```
## Data Reshaping and Plotting
### Trends of Happiness and Generosity over the years
We'll:
- select only the columns we care about
- group the data by `year` and take the mean
- plot the Happiness and Generosity (in separate plots)
```
df_subset = df_merged[['year', 'Happiness Score', 'Generosity']]
mean_by_year = df_subset.groupby('year').mean()
mean_by_year
mean_by_year.plot(subplots=True, grid=True)
# `subplots=True` will plot the two columns in two separate charts
# `grid=True` will add the axis grid in the background
```
### Average Generosity and Happiness by year AND Country
We'll:
- select only the columns we care about
- group the data by `Country` and `year`
- take the mean
```
df = df_merged[['year', 'Happiness Score', 'Generosity', 'Country']]
mean_by_country_and_year = df.groupby(['Country', 'year']).mean()
mean_by_country_and_year
```
#### Finding the countries and years with highest and lowest Happiness
```
mean_by_country_and_year['Happiness Score'].idxmax() # highest
mean_by_country_and_year['Happiness Score'].idxmin() # lowest
```
#### Happiness by Country and Year
```
happiness_column = mean_by_country_and_year['Happiness Score']
# turning the single column with 2d-index into a table by moving the inner index to columns
happiness_table = happiness_column.unstack()
happiness_table
# for each year, plotting the values in each country
happiness_table.plot(figsize=(20,5),grid=True)
```
# (FYI) Interactive Chart
You can also create interactive charts by using a different library (bokeh).
for more examples: https://colab.research.google.com/notebooks/charts.ipynb
```
uk_happiness = happiness_column['United Kingdom']
from bokeh.plotting import figure, output_notebook, show
output_notebook()
x = uk_happiness.index
y = uk_happiness.values
fig = figure(title="UK Happiness", x_axis_label='x', y_axis_label='y')
fig.line(x, y, legend_label="UK", line_width=2)
show(fig)
```
|
github_jupyter
|
```
%load_ext autoreload
%autoreload 2
%matplotlib inline
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.cluster import KMeans
from sklearn.svm import SVC
from sklearn.metrics import roc_auc_score, roc_curve
from mlxtend.plotting import plot_decision_regions
from sklearn import preprocessing
from sklearn.linear_model import LogisticRegression
import warnings
import numpy as np
from collections import OrderedDict
from lob_data_utils import lob, db_result, overview
from lob_data_utils.svm_calculation import lob_svm
sns.set_style('whitegrid')
warnings.filterwarnings('ignore')
data_length = 10000
stock = '11869'
df, df_cv, df_test = lob.load_prepared_data(
stock, data_dir='../queue_imbalance/data/prepared', cv=True, length=data_length)
```
## Logistic
```
log_clf = lob.logistic_regression(df, 0, len(df))
pred_train = log_clf.predict(df['queue_imbalance'].values.reshape(-1, 1))
pred_test = log_clf.predict(df_test['queue_imbalance'].values.reshape(-1, 1))
df['pred_log'] = pred_train
df_test['pred_log'] = pred_test
lob.plot_roc(df, log_clf, stock=int(stock), label='train')
lob.plot_roc(df_test, log_clf, stock=int(stock), label='test')
plt.figure(figsize=(16,2))
plt.scatter(df['queue_imbalance'], np.zeros(len(df)), c=df['mid_price_indicator'])
print(len(df[df['mid_price_indicator'] ==1]), len(df))
lob.plot_learning_curve(log_clf, df['queue_imbalance'].values.reshape(-1, 1), df['mid_price_indicator'])
```
### Let's look inside
```
df_test[df_test['pred_log'] != df_test['mid_price_indicator']][['pred_log', 'mid_price_indicator']].plot(kind='kde')
print(len(df_test[df_test['pred_log'] != df_test['mid_price_indicator']]), len(df_test))
df_test[df_test['pred_log'] != df_test['mid_price_indicator']][['pred_log', 'mid_price_indicator', 'queue_imbalance']].head()
pivot = min(df[df['pred_log'] == 1]['queue_imbalance'])
pivot
print('Amount of positive samples below the pivot and negative above the pivot for training data:')
print(len(df[df['queue_imbalance'] < pivot][df['pred_log'] == 1]),
len(df[df['queue_imbalance'] >= pivot][df['pred_log'] == 0]))
print('Amount of positive samples below the pivot and negative above the pivot for testing data:')
print(len(df_test[df_test['queue_imbalance'] < pivot][df_test['pred_log'] == 1]),
len(df_test[df_test['queue_imbalance'] >= pivot][df_test['pred_log'] == 0]))
```
So this classifier just finds a pivot. But why this particular one is choosen? Let's check what amount of data is below and above the pivot.
```
len(df[df['queue_imbalance'] < pivot]), len(df[df['queue_imbalance'] >= pivot])
df[df['queue_imbalance'] < pivot]['queue_imbalance'].plot(kind='kde')
df[df['queue_imbalance'] >= pivot]['queue_imbalance'].plot(kind='kde')
df['queue_imbalance'].plot(kind='kde')
```
## SVM
```
overview_data = overview.Overview(stock, data_length)
gammas = [0.0005, 0.005, 1, 5, 50, 500, 5000]
cs = [0.0005, 0.005, 1, 5.0, 50, 500, 1000]
coef0s = [0, 0.0005, 0.005, 1, 5, 50, 500, 5000]
df_svm_res = overview_data.write_svm_results(df, df_cv, gammas=gammas, cs=cs, coef0s=coef0s)
unnamed_columns = [c for c in df_svm_res.columns if 'Unnamed' in c]
df_svm_res.drop(columns=unnamed_columns, inplace=True)
df_svm_res.sort_values(by='roc_cv_score').head()
df_svm_res[df_svm_res['svm'] == 'linear'].sort_values(by='roc_cv_score', ascending=False).head()
df_svm_res.sort_values(by='roc_cv_score', ascending=False).head()
```
## Different kernels visualization
```
X = df[['queue_imbalance']].values
y = df['mid_price_indicator'].values.astype(np.integer)
clf = SVC(kernel='sigmoid', C=0.005, gamma=500, coef0=5.0)
clf.fit(df[['queue_imbalance']], df['mid_price_indicator'])
df['pred'] = clf.predict(df[['queue_imbalance']])
plt.figure(figsize=(16,2))
plot_decision_regions(X, y, clf=clf, legend='data')
plt.xlabel('')
plt.xlim(-1, 1)
plt.title('Sigmoid Kernel')
plt.legend()
min(df[df['pred'] == 1]['queue_imbalance']), max(df[df['pred'] == 0]['queue_imbalance']), clf.score(X, y)
X = df[['queue_imbalance']].values
y = df['mid_price_indicator'].values.astype(np.integer)
clf = SVC(kernel='rbf', C=0.005, gamma=50)
clf.fit(df[['queue_imbalance']], df['mid_price_indicator'])
df['pred'] = clf.predict(df[['queue_imbalance']])
plt.figure(figsize=(16,2))
plot_decision_regions(X, y, clf=clf, legend='data')
plt.xlim(-1, 1)
plt.xlabel('')
plt.title('Rbf')
plt.legend()
min(df[df['pred'] == 1]['queue_imbalance']), max(df[df['pred'] == 0]['queue_imbalance']), clf.score(X, y)
X = df[['queue_imbalance']].values
y = df['mid_price_indicator'].values.astype(np.integer)
clf = SVC(kernel='linear', C=0.005)
clf.fit(df[['queue_imbalance']], df['mid_price_indicator'])
df['pred'] = clf.predict(df[['queue_imbalance']])
plt.figure(figsize=(16,2))
plot_decision_regions(X, y, clf=clf, legend='data')
plt.xlabel('')
plt.xlim(-1, 1)
plt.title('Linear')
plt.legend()
min(df[df['pred'] == 1]['queue_imbalance']), max(df[df['pred'] == 0]['queue_imbalance']), clf.score(X, y)
## Some plotly visualizations
import plotly.offline as py
import plotly.figure_factory as ff
import plotly.graph_objs as go
from plotly import tools
from itertools import product
py.init_notebook_mode(connected=True)
titles=['s']
clf1 = SVC(kernel='rbf')
clf1.fit(X, y)
fig = tools.make_subplots(rows=1, cols=1,
print_grid=False,
subplot_titles=titles)
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.1),
np.arange(y_min, y_max, 0.1))
y_ = np.arange(y_min, y_max, 0.1)
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
trace1 = go.Contour(x=xx[0], y=y_,
z=Z,
colorscale=[[0, 'purple'],
[0.5, 'cyan'],
[1, 'pink']],
opacity=0.5,
showscale=False)
trace2 = go.Scatter(x=X[:, 0], y=X[:, 1],
showlegend=False,
mode='markers',
marker=dict(
color=y,
line=dict(color='black', width=1)))
fig.append_trace(trace1, 1, 1)
fig.append_trace(trace2, 1, 1)
fig['layout'].update(hovermode='closest')
fig['layout'][x].update(showgrid=False, zeroline=False)
#fig['layout'][y].update(showgrid=False, zeroline=False)
py.iplot(fig)
py.init_notebook_mode(connected=True)
from ipywidgets import interact, interactive, fixed, interact_manual, widgets
@interact(C=[1,2,3], gamma=[1,2,3], coef0=[1,2,3])
def _plot_lob(C, gamma, coef0):
py_config = {'displayModeBar': False, 'showLink': False, 'editable': False}
titles=['s']
clf1 = SVC(kernel='rbf', C=C, gamma=gamma)
clf1.fit(X, y)
fig = tools.make_subplots(rows=1, cols=1,
print_grid=False,
subplot_titles=titles)
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.1),
np.arange(y_min, y_max, 0.1))
y_ = np.arange(y_min, y_max, 0.1)
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
trace1 = go.Contour(x=xx[0], y=y_,
z=Z,
colorscale=[[0, 'purple'],
[0.5, 'cyan'],
[1, 'pink']],
opacity=0.5,
showscale=False)
trace2 = go.Scatter(x=X[:, 0], y=X[:, 1],
showlegend=False,
mode='markers',
marker=dict(
color=y,
line=dict(color='black', width=1)))
fig.append_trace(trace1, 1, 1)
fig.append_trace(trace2, 1, 1)
fig['layout'].update(hovermode='closest')
fig['layout'][x].update(showgrid=False, zeroline=False)
#fig['layout'][y].update(showgrid=False, zeroline=False)
py.iplot(fig)
```
|
github_jupyter
|
# Rejection Sampling
Rejection sampling, or "accept-reject Monte Carlo" is a Monte Carlo method used to generate obsrvations from distributions. As it is a Monte Carlo it can also be used for numerical integration.
## Monte Carlo Integration
### Example: Approximation of $\pi$
Enclose a quadrant of a circle of radius $1$ in a square of side length $1$. Then uniformly sample points inside the bounds of the square in Cartesian coordinates. If the point lies inside the circle quadrant record this information. At the ends of many throws the ratio of points inside the circle to all points thrown will approximate the ratio of the area of the cricle quadrant to the area of the square
$$
\frac{\text{points inside circle}}{\text{all points thrown}} \approx \frac{\text{area of circle quadrant}}{\text{area of square}} = \frac{\pi r^2}{4\, l^2} = \frac{\pi}{4},
$$
thus, an approximation of $\pi$ can be found to be
$$
\pi \approx 4 \cdot \frac{\text{points inside circle}}{\text{all points thrown}}.
$$
```
import numpy as np
import matplotlib.pyplot as plt
def approximate_pi(n_throws=10000, draw=True):
n_circle_points = 0
x_coord = np.random.uniform(0, 1, n_throws)
y_coord = np.random.uniform(0, 1, n_throws)
circle_x = []
circle_y = []
outside_x = []
outside_y = []
for x, y in zip(x_coord, y_coord):
radius = np.sqrt(x ** 2 + y ** 2)
if 1 > radius:
n_circle_points += 1
circle_x.append(x)
circle_y.append(y)
else:
outside_x.append(x)
outside_y.append(y)
approx_pi = 4 * (n_circle_points / n_throws)
print(f"The approximation of pi after {n_throws} throws is: {approx_pi}")
if draw:
plt.plot(circle_x, circle_y, "ro")
plt.plot(outside_x, outside_y, "bo")
plt.xlabel(r"$x$")
plt.ylabel(r"$y$")
plt.show()
approximate_pi()
```
## Sampling Distributions
To approximate a statistical distribution one can also use accept-reject Monte Carlo to approximate the distribution.
### Example: Approximation of Gaussian Distribution
```
import scipy.stats as stats
```
The Gaussian has a known analytic form
$$
f\left(\vec{x}\,\middle|\,\mu, \sigma\right) = \frac{1}{\sqrt{2\pi}\, \sigma} e^{-\left(x-\mu\right)^2/2\sigma^2}
$$
```
x = np.linspace(-5.0, 5.0, num=10000)
plt.plot(x, stats.norm.pdf(x, 0, 1), linewidth=2, color="black")
# Axes
# plt.title('Plot of $f(x;\mu,\sigma)$')
plt.xlabel(r"$x$")
plt.ylabel(r"$f(\vec{x}|\mu,\sigma)$")
# dist_window_w = sigma * 2
plt.xlim([-5, 5])
plt.show()
```
Given this it is seen that the Gaussian's maximum is at its mean. For the standard Gaussian this is at $\mu = 0$, and so it has a maximum at $1/\sqrt{2\pi}\,\sigma \approx 0.39$. Thus, this can be the maximum height of a rectangle that we need to throw our points in.
```
def approximate_Guassian(n_throws=10000, x_range=[-5, 5], draw=True):
n_accept = 0
x_coord = np.random.uniform(x_range[0], x_range[1], n_throws)
y_coord = np.random.uniform(0, stats.norm.pdf(0, 0, 1), n_throws)
# Use Freedman–Diaconis rule
# https://en.wikipedia.org/wiki/Freedman%E2%80%93Diaconis_rule
h = 2 * stats.iqr(x_coord) / np.cbrt([n_throws])
n_bins = int((x_range[1] - x_range[0]) / h)
accept_x = []
accept_y = []
reject_x = []
reject_y = []
for x, y in zip(x_coord, y_coord):
if stats.norm.pdf(x, 0, 1) > y:
n_accept += 1
accept_x.append(x)
accept_y.append(y)
else:
reject_x.append(x)
reject_y.append(y)
if draw:
fig, axes = plt.subplots(nrows=1, ncols=2, figsize=(1.2 * 14, 1.2 * 4.5))
x_space = np.linspace(x_range[0], x_range[1], num=10000)
axes[0].plot(accept_x, accept_y, "ro")
axes[0].plot(reject_x, reject_y, "bo")
axes[0].plot(x_space, stats.norm.pdf(x_space, 0, 1), linewidth=2, color="black")
axes[0].set_xlabel(r"$x$")
axes[0].set_ylabel(r"$y$")
axes[0].set_title(r"Sampled space of $f(\vec{x}|\mu,\sigma)$")
hist_count, bins, _ = axes[1].hist(accept_x, n_bins, density=True)
axes[1].set_xlabel(r"$x$")
axes[1].set_ylabel("Arbitrary normalized units")
axes[1].set_title(r"Normalized binned distribution of accepted toys")
plt.xlim(x_range)
plt.show()
approximate_Guassian()
```
This exercise is trivial but for more complex functional forms with more difficult integrals it can be a powerful numerical technique.
|
github_jupyter
|
# Ways to visualize top count with atoti
Given different categories of items, we will explore how to achieve the following with atoti:
- Visualize top 10 apps with the highest rating in table
- Visualize top 10 categories with most number of apps rated 5 in Pie chart
- Visualize top 10 apps for each category in subplots
See [pandas.ipynb](pandas.ipynb) to see how we can achieve the similar top count with Pandas.
__Note on data:__
We are using the [Google Play Store Apps data](https://www.kaggle.com/lava18/google-play-store-apps) from Kaggle. Data has been processed to convert strings with millions and thousands abbreviations into numeric data.
## Top count with atoti
```
import atoti as tt
from atoti.config import create_config
config = create_config(metadata_db="./metadata.db")
session = tt.create_session(config=config)
playstore = session.read_csv(
"s3://data.atoti.io/notebooks/topcount/googleplaystore_cleaned.csv",
store_name="playstore",
keys=["App", "Category", "Genres", "Current Ver"],
sampling_mode=tt.sampling.FULL,
types={"Reviews": tt.types.FLOAT, "Installs": tt.types.FLOAT},
)
playstore.head()
cube = session.create_cube(playstore, "Google Playstore")
cube.schema
```
### Top 10 apps with highest rating across categories
Use the content editor to apply a top count filter on the pivot table.
```
cube.visualize("Top 10 apps with highest rating across categories")
```
### Top 10 categories with the most number of apps rated 5
```
h = cube.hierarchies
l = cube.levels
m = cube.measures
m
```
#### Number of apps rated 5
Create a measure that counts the number of apps rated 5 within categories and at levels below the category.
```
m["Count with rating 5"] = tt.agg.sum(
tt.where(m["Rating.MEAN"] == 5, m["contributors.COUNT"], 0),
scope=tt.scope.origin(l["Category"], l["App"]),
)
```
We can drill down to different levels from category and the count is computed on the fly.
```
cube.visualize("Categories with apps rated 5")
```
Apply top count filter from **atoti editor** on the category by the `Count with rating 5` measure. The atoti editor is the atoti's Jupyterlab extension on the right with the <img src="https://data.atoti.io/notebooks/topcount/atoti_editor.png" alt="a." width="50"> icon.
```
cube.visualize("Top 10 categories with most number of apps rated 5")
```
### Top 10 apps for each category
Since we are performing top 10 apps filtering for each category, it's only right that we classify `App` under `Category`.
In this case, we create a multi-level hierarchy such as the following:
```
h["App Categories"] = [l["Category"], l["App"]]
h
```
This structure allows us to select at which level we want to apply the top count on from the atoti editor.
<img src="https://data.atoti.io/notebooks/topcount/filter_by_level.png" alt="Filter by level" width="30%">
```
cube.visualize("Top 10 apps with highest rating for each category")
```
#### Creating subplot to visualize top count per category
Again, go to the atoti's Jupyterlab extension and click on the ellipsis to show the subplot controls.
You should be able to add `Category` level to the subplot section sliced by `Apps`. Apply filter on `App` level of the `App Categories`
```
cube.visualize("Top 10 apps within each categories")
```
You can use the filter to select the categories that you want to view.
Alternative, use `session.url` to access the web application to build an interactive dashboard with quick filters. Check out the link below.
```
session.url + "/#/dashboard/767"
```
|
github_jupyter
|
<a href="https://colab.research.google.com/github/NeuromatchAcademy/course-content/blob/master/tutorials/W3D5_DeepLearning2/W3D5_Tutorial2.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Neuromatch Academy: Week 3, Day 5, Tutorial 2
# Deep Learning 2: Autoencoder extensions
__Content creators:__ Marco Brigham and the [CCNSS](https://www.ccnss.org/) team (2014-2018)
__Content reviewers:__ Itzel Olivos, Karen Schroeder, Karolina Stosio, Kshitij Dwivedi, Spiros Chavlis, Michael Waskom
---
# Tutorial Objectives
## Architecture
How can we improve the internal representation of shallow autoencoder with 2D bottleneck layer?
We may try the following architecture changes:
* Introducing additional hidden layers
* Wrapping latent space as a sphere

Adding hidden layers increases the number of learnable parameters to better use non-linear operations in encoding/decoding. Spherical geometry of latent space forces the network to use these additional degrees of freedom more efficiently.
Let's dive deeper into the technical aspects of autoencoders and improve their internal representations to reach the levels required for the *MNIST cognitive task*.
In this tutorial, you will:
- Increase the capacity of the network by introducing additional hidden layers
- Understand the effect of constraints in the geometry of latent space
```
# @title Video 1: Extensions
from IPython.display import YouTubeVideo
video = YouTubeVideo(id="pgkrU9UqXiU", width=854, height=480, fs=1)
print("Video available at https://youtube.com/watch?v=" + video.id)
video
```
---
# Setup
Please execute the cell(s) below to initialize the notebook environment.
```
# Imports
import numpy as np
import matplotlib.pyplot as plt
import torch
from torch import nn, optim
from sklearn.datasets import fetch_openml
# @title Figure settings
!pip install plotly --quiet
import plotly.graph_objects as go
from plotly.colors import qualitative
%config InlineBackend.figure_format = 'retina'
plt.style.use("https://raw.githubusercontent.com/NeuromatchAcademy/course-content/master/nma.mplstyle")
# @title Helper functions
def downloadMNIST():
"""
Download MNIST dataset and transform it to torch.Tensor
Args:
None
Returns:
x_train : training images (torch.Tensor) (60000, 28, 28)
x_test : test images (torch.Tensor) (10000, 28, 28)
y_train : training labels (torch.Tensor) (60000, )
y_train : test labels (torch.Tensor) (10000, )
"""
X, y = fetch_openml('mnist_784', version=1, return_X_y=True)
# Trunk the data
n_train = 60000
n_test = 10000
train_idx = np.arange(0, n_train)
test_idx = np.arange(n_train, n_train + n_test)
x_train, y_train = X[train_idx], y[train_idx]
x_test, y_test = X[test_idx], y[test_idx]
# Transform np.ndarrays to torch.Tensor
x_train = torch.from_numpy(np.reshape(x_train,
(len(x_train),
28, 28)).astype(np.float32))
x_test = torch.from_numpy(np.reshape(x_test,
(len(x_test),
28, 28)).astype(np.float32))
y_train = torch.from_numpy(y_train.astype(int))
y_test = torch.from_numpy(y_test.astype(int))
return (x_train, y_train, x_test, y_test)
def init_weights_kaiming_uniform(layer):
"""
Initializes weights from linear PyTorch layer
with kaiming uniform distribution.
Args:
layer (torch.Module)
Pytorch layer
Returns:
Nothing.
"""
# check for linear PyTorch layer
if isinstance(layer, nn.Linear):
# initialize weights with kaiming uniform distribution
nn.init.kaiming_uniform_(layer.weight.data)
def init_weights_kaiming_normal(layer):
"""
Initializes weights from linear PyTorch layer
with kaiming normal distribution.
Args:
layer (torch.Module)
Pytorch layer
Returns:
Nothing.
"""
# check for linear PyTorch layer
if isinstance(layer, nn.Linear):
# initialize weights with kaiming normal distribution
nn.init.kaiming_normal_(layer.weight.data)
def get_layer_weights(layer):
"""
Retrieves learnable parameters from PyTorch layer.
Args:
layer (torch.Module)
Pytorch layer
Returns:
list with learnable parameters
"""
# initialize output list
weights = []
# check whether layer has learnable parameters
if layer.parameters():
# copy numpy array representation of each set of learnable parameters
for item in layer.parameters():
weights.append(item.detach().numpy())
return weights
def print_parameter_count(net):
"""
Prints count of learnable parameters per layer from PyTorch network.
Args:
net (torch.Sequential)
Pytorch network
Returns:
Nothing.
"""
params_n = 0
# loop all layers in network
for layer_idx, layer in enumerate(net):
# retrieve learnable parameters
weights = get_layer_weights(layer)
params_layer_n = 0
# loop list of learnable parameters and count them
for params in weights:
params_layer_n += params.size
params_n += params_layer_n
print(f'{layer_idx}\t {params_layer_n}\t {layer}')
print(f'\nTotal:\t {params_n}')
def eval_mse(y_pred, y_true):
"""
Evaluates mean square error (MSE) between y_pred and y_true
Args:
y_pred (torch.Tensor)
prediction samples
v (numpy array of floats)
ground truth samples
Returns:
MSE(y_pred, y_true)
"""
with torch.no_grad():
criterion = nn.MSELoss()
loss = criterion(y_pred, y_true)
return float(loss)
def eval_bce(y_pred, y_true):
"""
Evaluates binary cross-entropy (BCE) between y_pred and y_true
Args:
y_pred (torch.Tensor)
prediction samples
v (numpy array of floats)
ground truth samples
Returns:
BCE(y_pred, y_true)
"""
with torch.no_grad():
criterion = nn.BCELoss()
loss = criterion(y_pred, y_true)
return float(loss)
def plot_row(images, show_n=10, image_shape=None):
"""
Plots rows of images from list of iterables (iterables: list, numpy array
or torch.Tensor). Also accepts single iterable.
Randomly selects images in each list element if item count > show_n.
Args:
images (iterable or list of iterables)
single iterable with images, or list of iterables
show_n (integer)
maximum number of images per row
image_shape (tuple or list)
original shape of image if vectorized form
Returns:
Nothing.
"""
if not isinstance(images, (list, tuple)):
images = [images]
for items_idx, items in enumerate(images):
items = np.array(items)
if items.ndim == 1:
items = np.expand_dims(items, axis=0)
if len(items) > show_n:
selected = np.random.choice(len(items), show_n, replace=False)
items = items[selected]
if image_shape is not None:
items = items.reshape([-1]+list(image_shape))
plt.figure(figsize=(len(items) * 1.5, 2))
for image_idx, image in enumerate(items):
plt.subplot(1, len(items), image_idx + 1)
plt.imshow(image, cmap='gray', vmin=image.min(), vmax=image.max())
plt.axis('off')
plt.tight_layout()
def to_s2(u):
"""
Projects 3D coordinates to spherical coordinates (theta, phi) surface of
unit sphere S2.
theta: [0, pi]
phi: [-pi, pi]
Args:
u (list, numpy array or torch.Tensor of floats)
3D coordinates
Returns:
Sperical coordinates (theta, phi) on surface of unit sphere S2.
"""
x, y, z = (u[:, 0], u[:, 1], u[:, 2])
r = np.sqrt(x**2 + y**2 + z**2)
theta = np.arccos(z / r)
phi = np.arctan2(x, y)
return np.array([theta, phi]).T
def to_u3(s):
"""
Converts from 2D coordinates on surface of unit sphere S2 to 3D coordinates
(on surface of S2), i.e. (theta, phi) ---> (1, theta, phi).
Args:
s (list, numpy array or torch.Tensor of floats)
2D coordinates on unit sphere S_2
Returns:
3D coordinates on surface of unit sphere S_2
"""
theta, phi = (s[:, 0], s[:, 1])
x = np.sin(theta) * np.sin(phi)
y = np.sin(theta) * np.cos(phi)
z = np.cos(theta)
return np.array([x, y, z]).T
def xy_lim(x):
"""
Return arguments for plt.xlim and plt.ylim calculated from minimum
and maximum of x.
Args:
x (list, numpy array or torch.Tensor of floats)
data to be plotted
Returns:
Nothing.
"""
x_min = np.min(x, axis=0)
x_max = np.max(x, axis=0)
x_min = x_min - np.abs(x_max - x_min) * 0.05 - np.finfo(float).eps
x_max = x_max + np.abs(x_max - x_min) * 0.05 + np.finfo(float).eps
return [x_min[0], x_max[0]], [x_min[1], x_max[1]]
def plot_generative(x, decoder_fn, image_shape, n_row=16, s2=False):
"""
Plots images reconstructed by decoder_fn from a 2D grid in
latent space that is determined by minimum and maximum values in x.
Args:
x (list, numpy array or torch.Tensor of floats)
2D or 3D coordinates in latent space
decoder_fn (integer)
function returning vectorized images from 2D latent space coordinates
image_shape (tuple or list)
original shape of image
n_row (integer)
number of rows in grid
s2 (boolean)
convert 3D coordinates (x, y, z) to spherical coordinates (theta, phi)
Returns:
Nothing.
"""
if s2:
x = to_s2(np.array(x))
xlim, ylim = xy_lim(np.array(x))
dx = (xlim[1] - xlim[0]) / n_row
grid = [np.linspace(ylim[0] + dx / 2, ylim[1] - dx / 2, n_row),
np.linspace(xlim[0] + dx / 2, xlim[1] - dx / 2, n_row)]
canvas = np.zeros((image_shape[0] * n_row, image_shape[1] * n_row))
cmap = plt.get_cmap('gray')
for j, latent_y in enumerate(grid[0][::-1]):
for i, latent_x in enumerate(grid[1]):
latent = np.array([[latent_x, latent_y]], dtype=np.float32)
if s2:
latent = to_u3(latent)
with torch.no_grad():
x_decoded = decoder_fn(torch.from_numpy(latent))
x_decoded = x_decoded.reshape(image_shape)
canvas[j * image_shape[0]: (j + 1) * image_shape[0],
i * image_shape[1]: (i + 1) * image_shape[1]] = x_decoded
plt.imshow(canvas, cmap=cmap, vmin=canvas.min(), vmax=canvas.max())
plt.axis('off')
def plot_latent(x, y, show_n=500, s2=False, fontdict=None, xy_labels=None):
"""
Plots digit class of each sample in 2D latent space coordinates.
Args:
x (list, numpy array or torch.Tensor of floats)
2D coordinates in latent space
y (list, numpy array or torch.Tensor of floats)
digit class of each sample
n_row (integer)
number of samples
s2 (boolean)
convert 3D coordinates (x, y, z) to spherical coordinates (theta, phi)
fontdict (dictionary)
style option for plt.text
xy_labels (list)
optional list with [xlabel, ylabel]
Returns:
Nothing.
"""
if fontdict is None:
fontdict = {'weight': 'bold', 'size': 12}
if s2:
x = to_s2(np.array(x))
cmap = plt.get_cmap('tab10')
if len(x) > show_n:
selected = np.random.choice(len(x), show_n, replace=False)
x = x[selected]
y = y[selected]
for my_x, my_y in zip(x, y):
plt.text(my_x[0], my_x[1], str(int(my_y)),
color=cmap(int(my_y) / 10.),
fontdict=fontdict,
horizontalalignment='center',
verticalalignment='center',
alpha=0.8)
xlim, ylim = xy_lim(np.array(x))
plt.xlim(xlim)
plt.ylim(ylim)
if s2:
if xy_labels is None:
xy_labels = [r'$\varphi$', r'$\theta$']
plt.xticks(np.arange(0, np.pi + np.pi / 6, np.pi / 6),
['0', '$\pi/6$', '$\pi/3$', '$\pi/2$',
'$2\pi/3$', '$5\pi/6$', '$\pi$'])
plt.yticks(np.arange(-np.pi, np.pi + np.pi / 3, np.pi / 3),
['$-\pi$', '$-2\pi/3$', '$-\pi/3$', '0',
'$\pi/3$', '$2\pi/3$', '$\pi$'])
if xy_labels is None:
xy_labels = ['$Z_1$', '$Z_2$']
plt.xlabel(xy_labels[0])
plt.ylabel(xy_labels[1])
def plot_latent_generative(x, y, decoder_fn, image_shape, s2=False,
title=None, xy_labels=None):
"""
Two horizontal subplots generated with encoder map and decoder grid.
Args:
x (list, numpy array or torch.Tensor of floats)
2D coordinates in latent space
y (list, numpy array or torch.Tensor of floats)
digit class of each sample
decoder_fn (integer)
function returning vectorized images from 2D latent space coordinates
image_shape (tuple or list)
original shape of image
s2 (boolean)
convert 3D coordinates (x, y, z) to spherical coordinates (theta, phi)
title (string)
plot title
xy_labels (list)
optional list with [xlabel, ylabel]
Returns:
Nothing.
"""
fig = plt.figure(figsize=(12, 6))
if title is not None:
fig.suptitle(title, y=1.05)
ax = fig.add_subplot(121)
ax.set_title('Encoder map', y=1.05)
plot_latent(x, y, s2=s2, xy_labels=xy_labels)
ax = fig.add_subplot(122)
ax.set_title('Decoder grid', y=1.05)
plot_generative(x, decoder_fn, image_shape, s2=s2)
plt.tight_layout()
plt.show()
def plot_latent_3d(my_x, my_y, show_text=True, show_n=500):
"""
Plot digit class or marker in 3D latent space coordinates.
Args:
my_x (list, numpy array or torch.Tensor of floats)
2D coordinates in latent space
my_y (list, numpy array or torch.Tensor of floats)
digit class of each sample
show_text (boolean)
whether to show text
image_shape (tuple or list)
original shape of image
s2 (boolean)
convert 3D coordinates (x, y, z) to spherical coordinates (theta, phi)
title (string)
plot title
Returns:
Nothing.
"""
layout = {'margin': {'l': 0, 'r': 0, 'b': 0, 't': 0},
'scene': {'xaxis': {'showspikes': False,
'title': 'z1'},
'yaxis': {'showspikes': False,
'title': 'z2'},
'zaxis': {'showspikes': False,
'title': 'z3'}}
}
selected_idx = np.random.choice(len(my_x), show_n, replace=False)
colors = [qualitative.T10[idx] for idx in my_y[selected_idx]]
x = my_x[selected_idx, 0]
y = my_x[selected_idx, 1]
z = my_x[selected_idx, 2]
text = my_y[selected_idx]
if show_text:
trace = go.Scatter3d(x=x, y=y, z=z, text=text,
mode='text',
textfont={'color': colors, 'size': 12}
)
layout['hovermode'] = False
else:
trace = go.Scatter3d(x=x, y=y, z=z, text=text,
hoverinfo='text', mode='markers',
marker={'size': 5, 'color': colors, 'opacity': 0.8}
)
fig = go.Figure(data=trace, layout=layout)
fig.show()
def runSGD(net, input_train, input_test, criterion='bce',
n_epochs=10, batch_size=32, verbose=False):
"""
Trains autoencoder network with stochastic gradient descent with Adam
optimizer and loss criterion. Train samples are shuffled, and loss is
displayed at the end of each opoch for both MSE and BCE. Plots training loss
at each minibatch (maximum of 500 randomly selected values).
Args:
net (torch network)
ANN object (nn.Module)
input_train (torch.Tensor)
vectorized input images from train set
input_test (torch.Tensor)
vectorized input images from test set
criterion (string)
train loss: 'bce' or 'mse'
n_epochs (boolean)
number of full iterations of training data
batch_size (integer)
number of element in mini-batches
verbose (boolean)
print final loss
Returns:
Nothing.
"""
# Initialize loss function
if criterion == 'mse':
loss_fn = nn.MSELoss()
elif criterion == 'bce':
loss_fn = nn.BCELoss()
else:
print('Please specify either "mse" or "bce" for loss criterion')
# Initialize SGD optimizer
optimizer = optim.Adam(net.parameters())
# Placeholder for loss
track_loss = []
print('Epoch', '\t', 'Loss train', '\t', 'Loss test')
for i in range(n_epochs):
shuffle_idx = np.random.permutation(len(input_train))
batches = torch.split(input_train[shuffle_idx], batch_size)
for batch in batches:
output_train = net(batch)
loss = loss_fn(output_train, batch)
optimizer.zero_grad()
loss.backward()
optimizer.step()
# Keep track of loss at each epoch
track_loss += [float(loss)]
loss_epoch = f'{i+1}/{n_epochs}'
with torch.no_grad():
output_train = net(input_train)
loss_train = loss_fn(output_train, input_train)
loss_epoch += f'\t {loss_train:.4f}'
output_test = net(input_test)
loss_test = loss_fn(output_test, input_test)
loss_epoch += f'\t\t {loss_test:.4f}'
print(loss_epoch)
if verbose:
# Print loss
loss_mse = f'\nMSE\t {eval_mse(output_train, input_train):0.4f}'
loss_mse += f'\t\t {eval_mse(output_test, input_test):0.4f}'
print(loss_mse)
loss_bce = f'BCE\t {eval_bce(output_train, input_train):0.4f}'
loss_bce += f'\t\t {eval_bce(output_test, input_test):0.4f}'
print(loss_bce)
# Plot loss
step = int(np.ceil(len(track_loss) / 500))
x_range = np.arange(0, len(track_loss), step)
plt.figure()
plt.plot(x_range, track_loss[::step], 'C0')
plt.xlabel('Iterations')
plt.ylabel('Loss')
plt.xlim([0, None])
plt.ylim([0, None])
plt.show()
class NormalizeLayer(nn.Module):
"""
pyTorch layer (nn.Module) that normalizes activations by their L2 norm.
Args:
None.
Returns:
Object inherited from nn.Module class.
"""
def __init__(self):
super().__init__()
def forward(self, x):
return nn.functional.normalize(x, p=2, dim=1)
```
---
# Section 1: Download and prepare MNIST dataset
We use the helper function `downloadMNIST` to download the dataset and transform it into `torch.Tensor` and assign train and test sets to (`x_train`, `y_train`) and (`x_test`, `y_test`).
The variable `input_size` stores the length of *vectorized* versions of the images `input_train` and `input_test` for training and test images.
**Instructions:**
* Please execute the cell below
```
# Download MNIST
x_train, y_train, x_test, y_test = downloadMNIST()
x_train = x_train / 255
x_test = x_test / 255
image_shape = x_train.shape[1:]
input_size = np.prod(image_shape)
input_train = x_train.reshape([-1, input_size])
input_test = x_test.reshape([-1, input_size])
test_selected_idx = np.random.choice(len(x_test), 10, replace=False)
train_selected_idx = np.random.choice(len(x_train), 10, replace=False)
print(f'shape image \t \t {image_shape}')
print(f'shape input_train \t {input_train.shape}')
print(f'shape input_test \t {input_test.shape}')
```
---
# Section 2: Deeper autoencoder (2D)
The internal representation of shallow autoencoder with 2D latent space is similar to PCA, which shows that the autoencoder is not fully leveraging non-linear capabilities to model data. Adding capacity in terms of learnable parameters takes advantage of non-linear operations in encoding/decoding to capture non-linear patterns in data.
Adding hidden layers enables us to introduce additional parameters, either layerwise or depthwise. The same amount $N$ of additional parameters can be added in a single layer or distributed among several layers. Adding several hidden layers reduces the compression/decompression ratio of each layer.
## Exercise 1: Build deeper autoencoder (2D)
Implement this deeper version of the ANN autoencoder by adding four hidden layers. The number of units per layer in the encoder is the following:
```
784 -> 392 -> 64 -> 2
```
The shallow autoencoder has a compression ratio of **784:2 = 392:1**. The first additional hidden layer has a compression ratio of **2:1**, followed by a hidden layer that sets the bottleneck compression ratio of **32:1**.
The choice of hidden layer size aims to reduce the compression rate in the bottleneck layer while increasing the count of trainable parameters. For example, if the compression rate of the first hidden layer doubles from **2:1** to **4:1**, the count of trainable parameters halves from 667K to 333K.
This deep autoencoder's performance may be further improved by adding additional hidden layers and by increasing the count of trainable parameters in each layer. These improvements have a diminishing return due to challenges associated with training under high parameter count and depth. One option explored in the *Bonus* section is to add a first hidden layer with 2x - 3x the input size. This size increase results in millions of parameters at the cost of longer training time.
Weight initialization is particularly important in deep networks. The availability of large datasets and weight initialization likely drove the deep learning revolution of 2010. We'll implement Kaiming normal as follows:
```
model[:-2].apply(init_weights_kaiming_normal)
```
**Instructions:**
* Add four additional layers and activation functions to the network
* Adjust the definitions of `encoder` and `decoder`
* Check learnable parameter count for this autoencoder by executing the last cell
```
encoding_size = 2
model = nn.Sequential(
nn.Linear(input_size, int(input_size / 2)),
nn.PReLU(),
nn.Linear(int(input_size / 2), encoding_size * 32),
#################################################
## TODO for students: add layers to build deeper autoencoder
#################################################
# Add activation function
# ...,
# Add another layer
# nn.Linear(..., ...),
# Add activation function
# ...,
# Add another layer
# nn.Linear(..., ...),
# Add activation function
# ...,
# Add another layer
# nn.Linear(..., ...),
# Add activation function
# ...,
# Add another layer
# nn.Linear(..., ...),
# Add activation function
# ....
)
model[:-2].apply(init_weights_kaiming_normal)
print(f'Autoencoder \n\n {model}\n')
# Adjust the value n_l to split your model correctly
# n_l = ...
# uncomment when you fill the code
# encoder = model[:n_l]
# decoder = model[n_l:]
# print(f'Encoder \n\n {encoder}\n')
# print(f'Decoder \n\n {decoder}')
# to_remove solution
encoding_size = 2
model = nn.Sequential(
nn.Linear(input_size, int(input_size / 2)),
nn.PReLU(),
nn.Linear(int(input_size / 2), encoding_size * 32),
# Add activation function
nn.PReLU(),
# Add another layer
nn.Linear(encoding_size * 32, encoding_size),
# Add activation function
nn.PReLU(),
# Add another layer
nn.Linear(encoding_size, encoding_size * 32),
# Add activation function
nn.PReLU(),
# Add another layer
nn.Linear(encoding_size * 32, int(input_size / 2)),
# Add activation function
nn.PReLU(),
# Add another layer
nn.Linear(int(input_size / 2), input_size),
# Add activation function
nn.Sigmoid()
)
model[:-2].apply(init_weights_kaiming_normal)
print(f'Autoencoder \n\n {model}\n')
# Adjust the value n_l to split your model correctly
n_l = 6
# uncomment when you fill the code
encoder = model[:n_l]
decoder = model[n_l:]
print(f'Encoder \n\n {encoder}\n')
print(f'Decoder \n\n {decoder}')
```
**Helper function:** `print_parameter_count`
Please uncomment the line below to inspect this function.
```
# help(print_parameter_count)
```
## Train the autoencoder
Train the network for `n_epochs=10` epochs with `batch_size=128`, and observe how the internal representation successfully captures additional digit classes.
The encoder map shows well-separated clusters that correspond to the associated digits in the decoder grid. The decoder grid also shows that the network is robust to digit skewness, i.e., digits leaning to the left or the right are recognized in the same digit class.
**Instructions:**
* Please execute the cells below
```
n_epochs = 10
batch_size = 128
runSGD(model, input_train, input_test, n_epochs=n_epochs,
batch_size=batch_size)
with torch.no_grad():
output_test = model(input_test)
latent_test = encoder(input_test)
plot_row([input_test[test_selected_idx], output_test[test_selected_idx]],
image_shape=image_shape)
plot_latent_generative(latent_test, y_test, decoder, image_shape=image_shape)
```
---
# Section 3: Spherical latent space
The previous architecture generates representations that typically spread in different directions from coordinate $(z_1, z_2)=(0,0)$. This effect is due to the initialization of weights distributed randomly around `0`.
Adding a third unit to the bottleneck layer defines a coordinate $(z_1, z_2, z_3)$ in 3D space. The latent space from such a network will still spread out from $(z_1, z_2, z_3)=(0, 0, 0)$.
Collapsing the latent space on the surface of a sphere removes the possibility of spreading indefinitely from the origin $(0, 0, 0)$ in any direction since this will eventually lead back to the origin. This constraint generates a representation that fills the surface of the sphere.

Projecting to the surface of the sphere is implemented by dividing the coordinates $(z_1, z_2, z_3)$ by their $L_2$ norm.
$(z_1, z_2, z_3)\longmapsto (s_1, s_2, s_3)=(z_1, z_2, z_3)/\|(z_1, z_2, z_3)\|_2=(z_1, z_2, z_3)/ \sqrt{z_1^2+z_2^2+z_3^2}$
This mapping projects to the surface of the [$S_2$ sphere](https://en.wikipedia.org/wiki/N-sphere) with unit radius. (Why?)
## Section 3.1: Build and train autoencoder (3D)
We start by adding one unit to the bottleneck layer and visualize the latent space in 3D.
Please execute the cell below.
```
encoding_size = 3
model = nn.Sequential(
nn.Linear(input_size, int(input_size / 2)),
nn.PReLU(),
nn.Linear(int(input_size / 2), encoding_size * 32),
nn.PReLU(),
nn.Linear(encoding_size * 32, encoding_size),
nn.PReLU(),
nn.Linear(encoding_size, encoding_size * 32),
nn.PReLU(),
nn.Linear(encoding_size * 32, int(input_size / 2)),
nn.PReLU(),
nn.Linear(int(input_size / 2), input_size),
nn.Sigmoid()
)
model[:-2].apply(init_weights_kaiming_normal)
encoder = model[:6]
decoder = model[6:]
print(f'Autoencoder \n\n {model}')
```
## Section 3.2: Train the autoencoder
Train the network for `n_epochs=10` epochs with `batch_size=128`. Observe how the internal representation spreads from the origin and reaches much lower loss due to the additional degree of freedom in the bottleneck layer.
**Instructions:**
* Please execute the cell below
```
n_epochs = 10
batch_size = 128
runSGD(model, input_train, input_test, n_epochs=n_epochs,
batch_size=batch_size)
```
## Section 3.3: Visualize the latent space in 3D
**Helper function**: `plot_latent_3d`
Please uncomment the line below to inspect this function.
```
# help(plot_latent_3d)
with torch.no_grad():
latent_test = encoder(input_test)
plot_latent_3d(latent_test, y_test)
```
### Exercise 2: Build deep autoencoder (2D) with latent spherical space
We now constrain the latent space to the surface of a sphere $S_2$.
**Instructions:**
* Add the custom layer `NormalizeLayer` after the bottleneck layer
* Adjust the definitions of `encoder` and `decoder`
* Experiment with keyword `show_text=False` for `plot_latent_3d`
**Helper function**: `NormalizeLayer`
Please uncomment the line below to inspect this function.
```
# help(NormalizeLayer)
encoding_size = 3
model = nn.Sequential(
nn.Linear(input_size, int(input_size / 2)),
nn.PReLU(),
nn.Linear(int(input_size / 2), encoding_size * 32),
nn.PReLU(),
nn.Linear(encoding_size * 32, encoding_size),
nn.PReLU(),
#################################################
## TODO for students: add custom normalize layer
#################################################
# add the normalization layer
# ...,
nn.Linear(encoding_size, encoding_size * 32),
nn.PReLU(),
nn.Linear(encoding_size * 32, int(input_size / 2)),
nn.PReLU(),
nn.Linear(int(input_size / 2), input_size),
nn.Sigmoid()
)
model[:-2].apply(init_weights_kaiming_normal)
print(f'Autoencoder \n\n {model}\n')
# Adjust the value n_l to split your model correctly
# n_l = ...
# uncomment when you fill the code
# encoder = model[:n_l]
# decoder = model[n_l:]
# print(f'Encoder \n\n {encoder}\n')
# print(f'Decoder \n\n {decoder}')
# to_remove solution
encoding_size = 3
model = nn.Sequential(
nn.Linear(input_size, int(input_size / 2)),
nn.PReLU(),
nn.Linear(int(input_size / 2), encoding_size * 32),
nn.PReLU(),
nn.Linear(encoding_size * 32, encoding_size),
nn.PReLU(),
# add the normalization layer
NormalizeLayer(),
nn.Linear(encoding_size, encoding_size * 32),
nn.PReLU(),
nn.Linear(encoding_size * 32, int(input_size / 2)),
nn.PReLU(),
nn.Linear(int(input_size / 2), input_size),
nn.Sigmoid()
)
model[:-2].apply(init_weights_kaiming_normal)
print(f'Autoencoder \n\n {model}\n')
# Adjust the value n_l to split your model correctly
n_l = 7
# uncomment when you fill the code
encoder = model[:n_l]
decoder = model[n_l:]
print(f'Encoder \n\n {encoder}\n')
print(f'Decoder \n\n {decoder}')
```
## Section 3.4: Train the autoencoder
Train the network for `n_epochs=10` epochs with `batch_size=128` and observe how loss raises again and is comparable to the model with 2D latent space.
**Instructions:**
* Please execute the cell below
```
n_epochs = 10
batch_size = 128
runSGD(model, input_train, input_test, n_epochs=n_epochs,
batch_size=batch_size)
with torch.no_grad():
latent_test = encoder(input_test)
plot_latent_3d(latent_test, y_test)
```
## Section 3.5: Visualize latent space on surface of $S_2$
The 3D coordinates $(s_1, s_2, s_3)$ on the surface of the unit sphere $S_2$ can be mapped to [spherical coordinates](https://en.wikipedia.org/wiki/Spherical_coordinate_system) $(r, \theta, \phi)$, as follows:
$$
\begin{aligned}
r &= \sqrt{s_1^2 + s_2^2 + s_3^2} \\
\phi &= \arctan \frac{s_2}{s_1} \\
\theta &= \arccos\frac{s_3}{r}
\end{aligned}
$$

What is the domain (numerical range) spanned by ($\theta, \phi)$?
We return to a 2D representation since the angles $(\theta, \phi)$ are the only degrees of freedom on the surface of the sphere. Add the keyword `s2=True` to `plot_latent_generative` to un-wrap the sphere's surface similar to a world map.
Task: Check the numerical range of the plot axis to help identify $\theta$ and $\phi$, and visualize the unfolding of the 3D plot from the previous exercise.
**Instructions:**
* Please execute the cells below
```
with torch.no_grad():
output_test = model(input_test)
plot_row([input_test[test_selected_idx], output_test[test_selected_idx]],
image_shape=image_shape)
plot_latent_generative(latent_test, y_test, decoder,
image_shape=image_shape, s2=True)
```
---
# Summary
We learned two techniques to improve representation capacity: adding a few hidden layers and projecting latent space on the sphere $S_2$.
The expressive power of autoencoder improves with additional hidden layers. Projecting latent space on the surface of $S_2$ spreads out digits classes in a more visually pleasing way but may not always produce a lower loss.
**Deep autoencoder architectures have rich internal representations to deal with sophisticated tasks such as the MNIST cognitive task.**
We now have powerful tools to explore how simple algorithms build robust models of the world by capturing relevant data patterns.
```
# @title Video 2: Wrap-up
from IPython.display import YouTubeVideo
video = YouTubeVideo(id="GnkmzCqEK3E", width=854, height=480, fs=1)
print("Video available at https://youtube.com/watch?v=" + video.id)
video
```
---
# Bonus
## Deep and thick autoencoder
In this exercise, we first expand the first hidden layer to double the input size, followed by compression to half the input size leading to 3.8M parameters. Please **do not train this network during tutorial** due to long training time.
**Instructions:**
* Please uncomment and execute the cells below
```
# encoding_size = 3
# model = nn.Sequential(
# nn.Linear(input_size, int(input_size * 2)),
# nn.PReLU(),
# nn.Linear(int(input_size * 2), int(input_size / 2)),
# nn.PReLU(),
# nn.Linear(int(input_size / 2), encoding_size * 32),
# nn.PReLU(),
# nn.Linear(encoding_size * 32, encoding_size),
# nn.PReLU(),
# NormalizeLayer(),
# nn.Linear(encoding_size, encoding_size * 32),
# nn.PReLU(),
# nn.Linear(encoding_size * 32, int(input_size / 2)),
# nn.PReLU(),
# nn.Linear(int(input_size / 2), int(input_size * 2)),
# nn.PReLU(),
# nn.Linear(int(input_size * 2), input_size),
# nn.Sigmoid()
# )
# model[:-2].apply(init_weights_kaiming_normal)
# encoder = model[:9]
# decoder = model[9:]
# print_parameter_count(model)
# n_epochs = 5
# batch_size = 128
# runSGD(model, input_train, input_test, n_epochs=n_epochs,
# batch_size=batch_size)
# Visualization
# with torch.no_grad():
# output_test = model(input_test)
# plot_row([input_test[test_selected_idx], output_test[test_selected_idx]],
# image_shape=image_shape)
# plot_latent_generative(latent_test, y_test, decoder,
# image_shape=image_shape, s2=True)
```
|
github_jupyter
|
# Author : Vedanti Ekre
# Email: [email protected]
## Task 1 : Prediction using Supervised Machine Learning
___
## GRIP @ The Sparks Foundation
____
# Role : Data Science and Business Analytics [Batch May-2021]
## TABLE OF CONTENTS:
1. [Introduction](#intro)
2. [Importing the dependencies](#libs)
3. [Loading the Data](#DL)
4. [Understanding data](#UD)
5. [Spliting data in Test and Train](#split)
6. [Use Simple Linear Regression Model to do prediction](#LR)
7. [Task](#PT)
8. [Evaluate the model using MAE and MSE metrics](#Eval)
9. [Conslusion](#conclu)
## **Introduction**<a class="anchor" id="intro"></a>
● We have given Student dataset,which have only two features Hours and scores.<br>
● Predict the percentage of an student based on the no. of study hours.<br>
● This is a simple linear regression task as it involves just 2 variables.<br>
● You can use R, Python, SAS Enterprise Miner or any other tool<br>
● Data can be found at http://bit.ly/w-data
## Importing dependencies<a class="anchor" id="libs"></a>
```
#importing packages
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
%matplotlib inline
```
## **Loading the Data**<a class="anchor" id="DL"></a>
```
#importing datasets
url = "http://bit.ly/w-data"
data = pd.read_csv(url)
```
## **Understanding data**<a class="anchor" id="UD"></a>
```
display(data.head(3),data.tail(3))
print(type(data))
print('-'*45)
print('The data set has {} rows and {} columns'.format(data.shape[0],data.shape[1]))
print('-'*45)
print('Data types :')
print(data.dtypes.value_counts())
#print('Total : ',data.dtypes.value_counts().sum())
print('-'*45)
data.info()
# Checking for the missing values
data.isnull().sum()
```
### Observation :<br>
- ```There is no missing or null value & hence we don't need to do data preprocessing```
## **Data Visualization**
```
x = data.iloc[:,:-1].values #spliting data in X & Y
y = data.iloc[:,-1].values
print(x[:5])
print(y[:5])
plt.xlabel('hours')
plt.ylabel('scores')
plt.scatter(x,y,color='red',marker='+')
plt.grid()
plt.show()
```
### Observation :
- ```From the graph we can safely assume a positive linear relation between the number of hours studied and percentage of score```
## **Spliting data in x_train , x_test and y_train , y_test** <a class="anchor" id="split"></a>
```
from sklearn.model_selection import train_test_split #spliting data in x_train , x_test & y_train,y_test
x_train,x_test,y_train,y_test = train_test_split(x,y,test_size = 0.25, random_state = 0)
```
## **Apply Linear Regression on train data**
```
from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(x_train,y_train)
plt.xlabel('hours')
plt.ylabel('scores')
plt.scatter(x_train,y_train,color='purple',marker='+',label='scatter plot')
plt.plot(x_train,lin_reg.predict(x_train),color='green',label='reg_line')
plt.legend()
plt.grid()
plt.show()
```
## **Apply Linear Regression on test data** <a class="anchor" id="LR"></a>
```
plt.xlabel('hours')
plt.ylabel('scores')
plt.scatter(x_test,y_test,color='blue',marker='+',label='scatter plot')
plt.plot(x_train,lin_reg.predict(x_train),color='purple',label='reg_line')
plt.legend()
plt.grid()
plt.show()
```
### **Coefficents and y-intercept**
```
print('coefficents : ',lin_reg.coef_)
print('y-intercept : ',lin_reg.intercept_)
y_pred = lin_reg.predict(x_test)
y_pred
```
## Comparing Actual value with Predicted value
```
result = pd.DataFrame({'Actual values':y_test,'Predicted values':y_pred})
result
# Plotting the Bar graph to depict the difference between the actual and predicted value
result.plot(kind='bar',figsize=(9,9))
plt.grid(which='major', linewidth='0.5', color='red')
plt.grid(which='minor', linewidth='0.5', color='blue')
plt.show()
diff = np.array(np.abs(y_test-y_pred))
diff
```
## Displot distribution of Actual value with Predicted value
```
sns.set_style('whitegrid')
sns.kdeplot(diff,shade=True)
plt.show()
```
# **Task** <a class="anchor" id="PT"></a>
## - What will be predicted score if a student studies for 9.25 hrs/ day?
```
import math
# y = mx + c
res = lin_reg.intercept_+9.25*lin_reg.coef_
hr= 9.25
print("If student study for {} hrs/day student will get {}% score in exam".format(hr,math.floor(res[0])))
print('-'*80)
```
# Model Evaluation <a class="anchor" id="Eval"></a>
## MAE :
- MAE measures the differences between prediction and actual observation.<br>
Formula is :<br>

```
from sklearn import metrics
print('Mean Absolute Error:',
metrics.mean_absolute_error(y_test, y_pred))
```
## MSE :
- MSE simply refers to the mean of the squared difference between the predicted value and the observed value.<br>
Formula : <br>
```
from sklearn import metrics
print('Mean Squared Error:',
metrics.mean_squared_error(y_test, y_pred))
```
## **R-Square** :
- R-squared is measure of how close the data are to the fitted regression line.<br>
Formula : <br>
```
from sklearn.metrics import r2_score
r2_score(y_test,y_pred)
```
# **Conclusion :**<br><a class="anchor" id="conclu"></a>
- We have successfully created a Simple linear Regression model to predict score of the student given number of hours one studies.
- By the MAE and MSE , we are not getting much difference in actual or predicted value , means error is less.
- The Score of R-Square **0.93** quite close to **1**.
|
github_jupyter
|
```
import run_info_utils
df = run_info_utils.get_df_run_info()
df.head()
# print(list(df.columns))
experiment_name = 'jordan_cp9_add_sub_maxstep'
df = df.loc[df['experiment_name'] == experiment_name]
cols = ['run_id', 'operator', 'rnn_type', 'confidence_prob', 'operand_bits', 'hidden_activation', 'max_steps',
'dev/last_carry-0_mean_correct_answer_step',
'dev/last_carry-1_mean_correct_answer_step',
'dev/last_carry-2_mean_correct_answer_step',
'dev/last_carry-3_mean_correct_answer_step',
'dev/last_carry-4_mean_correct_answer_step',
'dev/last_mean_correct_answer_step', 'dev/last_accuracy']
df = df[cols]
df = df.loc[df['dev/last_accuracy'] == 1.0]
df.shape
df_add_jordan_9_relu_maxstep10 = df.query('operator == "add"').query('rnn_type == "jordan"').query('confidence_prob == 0.9').query('hidden_activation == "relu"').query('max_steps == 10')
df_sub_jordan_9_relu_maxstep10 = df.query('operator == "subtract"').query('rnn_type == "jordan"').query('confidence_prob == 0.9').query('hidden_activation == "relu"').query('max_steps == 10')
df_add_jordan_9_relu_maxstep20 = df.query('operator == "add"').query('rnn_type == "jordan"').query('confidence_prob == 0.9').query('hidden_activation == "relu"').query('max_steps == 20')
df_sub_jordan_9_relu_maxstep20 = df.query('operator == "subtract"').query('rnn_type == "jordan"').query('confidence_prob == 0.9').query('hidden_activation == "relu"').query('max_steps == 20')
df_add_jordan_9_relu_maxstep30 = df.query('operator == "add"').query('rnn_type == "jordan"').query('confidence_prob == 0.9').query('hidden_activation == "relu"').query('max_steps == 30')
df_sub_jordan_9_relu_maxstep30 = df.query('operator == "subtract"').query('rnn_type == "jordan"').query('confidence_prob == 0.9').query('hidden_activation == "relu"').query('max_steps == 30')
df_add_jordan_9_relu_maxstep40 = df.query('operator == "add"').query('rnn_type == "jordan"').query('confidence_prob == 0.9').query('hidden_activation == "relu"').query('max_steps == 40')
df_sub_jordan_9_relu_maxstep40 = df.query('operator == "subtract"').query('rnn_type == "jordan"').query('confidence_prob == 0.9').query('hidden_activation == "relu"').query('max_steps == 40')
df_add_jordan_9_relu_maxstep50 = df.query('operator == "add"').query('rnn_type == "jordan"').query('confidence_prob == 0.9').query('hidden_activation == "relu"').query('max_steps == 50')
df_sub_jordan_9_relu_maxstep50 = df.query('operator == "subtract"').query('rnn_type == "jordan"').query('confidence_prob == 0.9').query('hidden_activation == "relu"').query('max_steps == 50')
df_add_jordan_9_relu_maxstep60 = df.query('operator == "add"').query('rnn_type == "jordan"').query('confidence_prob == 0.9').query('hidden_activation == "relu"').query('max_steps == 60')
df_sub_jordan_9_relu_maxstep60 = df.query('operator == "subtract"').query('rnn_type == "jordan"').query('confidence_prob == 0.9').query('hidden_activation == "relu"').query('max_steps == 60')
df_add_jordan_9_relu_maxstep90 = df.query('operator == "add"').query('rnn_type == "jordan"').query('confidence_prob == 0.9').query('hidden_activation == "relu"').query('max_steps == 90')
df_add_jordan_9_tanh_maxstep10 = df.query('operator == "add"').query('rnn_type == "jordan"').query('confidence_prob == 0.9').query('hidden_activation == "tanh"').query('max_steps == 10')
df_sub_jordan_9_tanh_maxstep10 = df.query('operator == "subtract"').query('rnn_type == "jordan"').query('confidence_prob == 0.9').query('hidden_activation == "tanh"').query('max_steps == 10')
df_add_jordan_9_tanh_maxstep20 = df.query('operator == "add"').query('rnn_type == "jordan"').query('confidence_prob == 0.9').query('hidden_activation == "tanh"').query('max_steps == 20')
df_sub_jordan_9_tanh_maxstep20 = df.query('operator == "subtract"').query('rnn_type == "jordan"').query('confidence_prob == 0.9').query('hidden_activation == "tanh"').query('max_steps == 20')
df_add_jordan_9_tanh_maxstep30 = df.query('operator == "add"').query('rnn_type == "jordan"').query('confidence_prob == 0.9').query('hidden_activation == "tanh"').query('max_steps == 30')
df_sub_jordan_9_tanh_maxstep30 = df.query('operator == "subtract"').query('rnn_type == "jordan"').query('confidence_prob == 0.9').query('hidden_activation == "tanh"').query('max_steps == 30')
df_add_jordan_9_tanh_maxstep40 = df.query('operator == "add"').query('rnn_type == "jordan"').query('confidence_prob == 0.9').query('hidden_activation == "tanh"').query('max_steps == 40')
df_sub_jordan_9_tanh_maxstep40 = df.query('operator == "subtract"').query('rnn_type == "jordan"').query('confidence_prob == 0.9').query('hidden_activation == "tanh"').query('max_steps == 40')
df_add_jordan_9_tanh_maxstep50 = df.query('operator == "add"').query('rnn_type == "jordan"').query('confidence_prob == 0.9').query('hidden_activation == "tanh"').query('max_steps == 50')
df_sub_jordan_9_tanh_maxstep50 = df.query('operator == "subtract"').query('rnn_type == "jordan"').query('confidence_prob == 0.9').query('hidden_activation == "tanh"').query('max_steps == 50')
df_add_jordan_9_tanh_maxstep60 = df.query('operator == "add"').query('rnn_type == "jordan"').query('confidence_prob == 0.9').query('hidden_activation == "tanh"').query('max_steps == 60')
df_sub_jordan_9_tanh_maxstep60 = df.query('operator == "subtract"').query('rnn_type == "jordan"').query('confidence_prob == 0.9').query('hidden_activation == "tanh"').query('max_steps == 60')
print(df_add_jordan_9_relu_maxstep10.shape)
print(df_sub_jordan_9_relu_maxstep10.shape)
print(df_add_jordan_9_relu_maxstep20.shape)
print(df_sub_jordan_9_relu_maxstep20.shape)
print(df_add_jordan_9_relu_maxstep30.shape)
print(df_sub_jordan_9_relu_maxstep30.shape)
print(df_add_jordan_9_relu_maxstep40.shape)
print(df_sub_jordan_9_relu_maxstep40.shape)
print(df_add_jordan_9_relu_maxstep50.shape)
print(df_sub_jordan_9_relu_maxstep50.shape)
print(df_add_jordan_9_relu_maxstep60.shape)
print(df_sub_jordan_9_relu_maxstep60.shape)
print(df_add_jordan_9_relu_maxstep90.shape)
print(df_add_jordan_9_tanh_maxstep10.shape)
print(df_sub_jordan_9_tanh_maxstep10.shape)
print(df_add_jordan_9_tanh_maxstep20.shape)
print(df_sub_jordan_9_tanh_maxstep20.shape)
print(df_add_jordan_9_tanh_maxstep30.shape)
print(df_sub_jordan_9_tanh_maxstep30.shape)
print(df_add_jordan_9_tanh_maxstep40.shape)
print(df_sub_jordan_9_tanh_maxstep40.shape)
print(df_add_jordan_9_tanh_maxstep50.shape)
print(df_sub_jordan_9_tanh_maxstep50.shape)
print(df_add_jordan_9_tanh_maxstep60.shape)
print(df_sub_jordan_9_tanh_maxstep60.shape)
```
# Result
```
df_add_jordan_9_relu_maxstep40.describe()
df_sub_jordan_9_relu_maxstep40.describe()
```
# Export as CSV
## Functionalize
```
import pandas as pd
import numpy as np
import data_utils
from utils import create_dir
from os.path import join
def get_csv_df(df, filename, experiment_name):
# Get configurations
n_rows = df.shape[0]
operator = df['operator'].iloc[0]
operand_digits = df['operand_bits'].iloc[0]
carry_list = list(data_utils.import_carry_datasets(operand_digits, operator).keys())
# Gather for each
csv_df_list = list()
for carries in carry_list:
col = 'dev/last_carry-{}_mean_correct_answer_step'.format(carries)
csv_df = pd.DataFrame(data={'mean_anwer_steps':df[col], 'carries':np.full((n_rows), carries)})
csv_df_list.append(csv_df)
csv_df = pd.concat(csv_df_list, ignore_index=True)
# Change the order of columns
csv_df = csv_df[['mean_anwer_steps', 'carries']]
# Create dir
dir_to_save = join('result_statistics', experiment_name)
create_dir(dir_to_save)
# Save the dataframe to a CSV file.
csv_df.to_csv(join(dir_to_save, filename), index=False)
experiment_name = 'jordan_cp9_add_sub_maxstep'
get_csv_df(df_add_jordan_9_relu_maxstep10, 'df_add_jordan_9_relu_maxstep10.csv', experiment_name)
get_csv_df(df_sub_jordan_9_relu_maxstep10, 'df_sub_jordan_9_relu_maxstep10.csv', experiment_name)
get_csv_df(df_add_jordan_9_relu_maxstep20, 'df_add_jordan_9_relu_maxstep20.csv', experiment_name)
get_csv_df(df_sub_jordan_9_relu_maxstep20, 'df_sub_jordan_9_relu_maxstep20.csv', experiment_name)
get_csv_df(df_add_jordan_9_relu_maxstep30, 'df_add_jordan_9_relu_maxstep30.csv', experiment_name)
get_csv_df(df_sub_jordan_9_relu_maxstep30, 'df_sub_jordan_9_relu_maxstep30.csv', experiment_name)
get_csv_df(df_add_jordan_9_relu_maxstep40, 'df_add_jordan_9_relu_maxstep40.csv', experiment_name)
get_csv_df(df_sub_jordan_9_relu_maxstep40, 'df_sub_jordan_9_relu_maxstep40.csv', experiment_name)
get_csv_df(df_add_jordan_9_relu_maxstep50, 'df_add_jordan_9_relu_maxstep50.csv', experiment_name)
get_csv_df(df_sub_jordan_9_relu_maxstep50, 'df_sub_jordan_9_relu_maxstep50.csv', experiment_name)
get_csv_df(df_add_jordan_9_relu_maxstep60, 'df_add_jordan_9_relu_maxstep60.csv', experiment_name)
get_csv_df(df_sub_jordan_9_relu_maxstep60, 'df_sub_jordan_9_relu_maxstep60.csv', experiment_name)
get_csv_df(df_add_jordan_9_relu_maxstep90, 'df_add_jordan_9_relu_maxstep90.csv', experiment_name)
get_csv_df(df_add_jordan_9_tanh_maxstep10, 'df_add_jordan_9_tanh_maxstep10.csv', experiment_name)
get_csv_df(df_sub_jordan_9_tanh_maxstep10, 'df_sub_jordan_9_tanh_maxstep10.csv', experiment_name)
get_csv_df(df_add_jordan_9_tanh_maxstep20, 'df_add_jordan_9_tanh_maxstep20.csv', experiment_name)
get_csv_df(df_sub_jordan_9_tanh_maxstep20, 'df_sub_jordan_9_tanh_maxstep20.csv', experiment_name)
get_csv_df(df_add_jordan_9_tanh_maxstep30, 'df_add_jordan_9_tanh_maxstep30.csv', experiment_name)
get_csv_df(df_sub_jordan_9_tanh_maxstep30, 'df_sub_jordan_9_tanh_maxstep30.csv', experiment_name)
get_csv_df(df_add_jordan_9_tanh_maxstep40, 'df_add_jordan_9_tanh_maxstep40.csv', experiment_name)
get_csv_df(df_sub_jordan_9_tanh_maxstep40, 'df_sub_jordan_9_tanh_maxstep40.csv', experiment_name)
get_csv_df(df_add_jordan_9_tanh_maxstep50, 'df_add_jordan_9_tanh_maxstep50.csv', experiment_name)
get_csv_df(df_sub_jordan_9_tanh_maxstep50, 'df_sub_jordan_9_tanh_maxstep50.csv', experiment_name)
get_csv_df(df_add_jordan_9_tanh_maxstep60, 'df_add_jordan_9_tanh_maxstep60.csv', experiment_name)
get_csv_df(df_sub_jordan_9_tanh_maxstep60, 'df_sub_jordan_9_tanh_maxstep60.csv', experiment_name)
```
|
github_jupyter
|
# What you will learn
- What is a CSV file
- Reading and writting on a csv file
### CSV = Comma seperated values
Chances are you have worked with .csv files before. There are simply values sperated by commas ...
#### Note
- All files used or created will be stored under week 3 in a folder called "data"
Here is some exampe output:
If this kinda looks like data in excel that is because excel spread-sheets can be exported as .csv files.
Above each column for a given row has a distinction. The first row shown above are the column headers - i.e. the name of each column. We'll show how to work with this data but first the basics:
## Reading a CSV file
```
import csv
import os
def run():
with open("./data/example1.csv", "r") as csvFile: # the "r" means read
fileReader = csv.reader(csvFile)
i = 0
for row in fileReader:
print(row)
i += 1
if i == 10:
break
if __name__=="__main__":
run()
```
#### Note
- The "if i == 10" break is just so all 5001 rows are not printed
- the "r" tells the file to be opened for reading only
### What is the "with open"
To operate (meaning to read or to write) on a file that file has to be accessed. This involves opening the file. But what happens when you are done? That file needs to be closed. This is where "with" comes in. It is a context manager meaning that when you fall out of the with indentation the file will automatically be closed.
You cannot write to a file that another program is using - this is like two people trying to use the remote at the same time; chaoas and confusion will result. Context mangers allow clean closing of files without having to explicitly state that the file closes.
We could write the above code as seen below - but THIS IS BAD FORM!
```
# this is bad code
csvFile = open("./data/example1.csv")
fileReader = csv.reader(csvFile)
i = 0
for row in fileReader:
print(row)
i += 1
if i == 10:
break
csvFile.close()
```
## Writing to a CSV file
Above we used "r" to read from a file. Well now that becomes "w" to write.
#### Important
If you write to a file that already exists then the file will be overwritten. There will be no warning as with many office tools saying you are about to overwrite something.
If you with to add something to a csv file we will cover that below.
```
import csv
import os
import time
import random
HEADERS = ['data', 'timeStamp', 'dataType']
def makeRow(): # random data to put in csv
return [random.randint(0,101), time.time(), "random Float"]
def makeFile(): # makes a csv
with open("./data/example2.csv", "w") as csvFile: # the "w" means write
fileWriter = csv.writer(csvFile)
fileWriter.writerow(HEADERS)
for i in range(10):
fileWriter.writerow(makeRow())
def readFile(): # read from the csv you created to see it!
with open("./data/example2.csv", "r") as csvFile:
fileReader = csv.reader(csvFile)
for row in fileReader:
print(row)
if __name__=="__main__":
makeFile()
readFile()
```
#### Note
- If you re-run the above bit of code you will notice that the all the values change
- This is, again, because the "w" mode will overwrite your files!
- Please don't accedently overwrite the results of an experiment have to redo it ...
## From csv to list of dics
Often it is good to organize data in a csv to a list of dics. This is easier to later operate on
```
# we'll take the values that you just created in the above code and turn them into the list of dics!
def csvToDict(csvData):
headers = next(csvData) # next will push the iterable object one forword
data = list(map(lambda row: dict(zip(headers, row)) , csvData))
return data
def run(): # read from the csv you created to see it!
with open("./data/example2.csv", "r") as csvFile:
fileReader = csv.reader(csvFile)
listOfDics = csvToDict(fileReader)
print(listOfDics)
if __name__=="__main__":
run()
```
## Appending a csv file
Let's take the csv file you created above and append it with 10 more rows
```
import csv
import os
import time
import random
HEADERS = ['data', 'timeStamp', 'dataType']
def makeRow(): # random data to put in csv
return [random.randint(0,101), time.time(), "random Float"]
def makeFile(): # makes a csv
with open("./data/example2.csv", "a") as csvFile: # the "a" means append
fileWriter = csv.writer(csvFile)
for i in range(10):
fileWriter.writerow(makeRow())
def readFile(): # read from the csv you created to see it!
with open("./data/example2.csv", "r") as csvFile:
fileReader = csv.reader(csvFile)
for row in fileReader:
print(row)
if __name__=="__main__":
makeFile()
readFile()
```
#### Note
- Yep, it is that simple to append. Just change "w" to "a"
- If you try to append a file that does not exist then that file will be created for you
#### Note
- There are some other options besides "r", "w", "a" but those three should work for now. Just know ther are a few more.
- See here for details: https://docs.python.org/3/library/functions.html#open
# What you need to do
- Read in the csv file from example1.csv
- Turn it into a list of dicts
- Replace all timeStamps with their equivalent time since epoch value
- Find the mean of the timeStamps
- Discard all data points that have timeStamps lower thean the that mean
- Write all data points that have a sensorType of "BME280" to a .csv file called "BME280" that is in the "data folder"
- Write all data points that have a sensorType of "ADC1115_Pyra" to a .csv file called "ADC1115_Pyra" that is in the "data folder"
|
github_jupyter
|
# Simple training tutorial
The objective of this tutorial is to show you the basics of the library and how it can be used to simplify the audio processing pipeline.
This page is generated from the corresponding jupyter notebook, that can be found on [this folder](https://github.com/fastaudio/fastaudio/tree/master/docs)
To install the library, uncomment and run this cell:
```
# !pip install git+https://github.com/fastaudio/fastaudio.git
```
**COLAB USERS: Before you continue and import the lib, go to the `Runtime` menu and select `Restart Runtime`.**
```
from fastai.vision.all import *
from fastaudio.core.all import *
from fastaudio.augment.all import *
```
# ESC-50: Dataset for Environmental Sound Classification
```
#The first time this will download a dataset that is ~650mb
path = untar_data(URLs.ESC50, dest="ESC50")
```
The audio files are inside a subfolder `audio/`
```
(path/"audio").ls()
```
And there's another folder `meta/` with some metadata about all the files and the labels
```
(path/"meta").ls()
```
Opening the metadata file
```
df = pd.read_csv(path/"meta"/"esc50.csv")
df.head()
```
## Datablock and Basic End to End Training
```
# Helper function to split the data
def CrossValidationSplitter(col='fold', fold=1):
"Split `items` (supposed to be a dataframe) by fold in `col`"
def _inner(o):
assert isinstance(o, pd.DataFrame), "ColSplitter only works when your items are a pandas DataFrame"
col_values = o.iloc[:,col] if isinstance(col, int) else o[col]
valid_idx = (col_values == fold).values.astype('bool')
return IndexSplitter(mask2idxs(valid_idx))(o)
return _inner
```
Creating the Audio to Spectrogram transform from a predefined config.
```
cfg = AudioConfig.BasicMelSpectrogram(n_fft=512)
a2s = AudioToSpec.from_cfg(cfg)
```
Creating the Datablock
```
auds = DataBlock(blocks=(AudioBlock, CategoryBlock),
get_x=ColReader("filename", pref=path/"audio"),
splitter=CrossValidationSplitter(fold=1),
batch_tfms = [a2s],
get_y=ColReader("category"))
dbunch = auds.dataloaders(df, bs=64)
```
Visualizing one batch of data. Notice that the title of each Spectrogram is the corresponding label.
```
dbunch.show_batch(figsize=(10, 5))
```
# Learner and Training
While creating the learner, we need to pass a special cnn_config to indicate that our input spectrograms only have one channel. Besides that, it's the usual vision learner.
```
learn = cnn_learner(dbunch,
resnet18,
config={"n_in":1}, #<- Only audio specific modification here
loss_func=CrossEntropyLossFlat(),
metrics=[accuracy])
from fastaudio.ci import skip_if_ci
@skip_if_ci
def learn():
learn.fine_tune(10)
```
|
github_jupyter
|
# Table of Contents
<p><div class="lev1"><a href="#Dependent-Things"><span class="toc-item-num">1 </span>Dependent Things</a></div><div class="lev1"><a href="#Cancer-Example"><span class="toc-item-num">2 </span>Cancer Example</a></div><div class="lev2"><a href="#Question-1"><span class="toc-item-num">2.1 </span>Question 1</a></div><div class="lev2"><a href="#Question-2"><span class="toc-item-num">2.2 </span>Question 2</a></div><div class="lev2"><a href="#Question-3"><span class="toc-item-num">2.3 </span>Question 3</a></div><div class="lev2"><a href="#Question-4"><span class="toc-item-num">2.4 </span>Question 4</a></div><div class="lev2"><a href="#Question-5"><span class="toc-item-num">2.5 </span>Question 5</a></div><div class="lev2"><a href="#Question-6"><span class="toc-item-num">2.6 </span>Question 6</a></div><div class="lev2"><a href="#Question-7"><span class="toc-item-num">2.7 </span>Question 7</a></div><div class="lev1"><a href="#Total-Probability"><span class="toc-item-num">3 </span>Total Probability</a></div><div class="lev1"><a href="#Two-Coins"><span class="toc-item-num">4 </span>Two Coins</a></div><div class="lev2"><a href="#Question-1"><span class="toc-item-num">4.1 </span>Question 1</a></div><div class="lev2"><a href="#Question-2"><span class="toc-item-num">4.2 </span>Question 2</a></div><div class="lev2"><a href="#Question-3"><span class="toc-item-num">4.3 </span>Question 3</a></div><div class="lev2"><a href="#Question-4"><span class="toc-item-num">4.4 </span>Question 4</a></div><div class="lev1"><a href="#Summary"><span class="toc-item-num">5 </span>Summary</a></div>
# Dependent Things
In real life, things depend on each other.
Say you can be born smart or dumb and for the sake of simplicity, let's assume whether you're smart or dumb is just nature's flip of a coin. Now whether you become a professor at Standford is non-entirely independent. I would argue becoming a professor in Standford is generally not very likely, so probability might be 0.001 but it also depends on whether you're born smart or dumb. If you are born smart the probability might be larger, whereas if you're born dumb, the probability might be marked more smaller.
Now this just is an example, but if you can think of the most two consecutive coin flips. The first is whether you are born smart or dumb. The second is whether you get a job on a certain time. And now if we take them in these two coin flips, they are not independent anymore. So whereas in our last unit, we assumed that the coin flips were independent, that is, the outcome of the first didn't affect the outcome of the second. From now on, we're going to study the more interesting cases where the outcome of the first does impact the outcome of the second, and to do so you need to use more variables to express these cases.
<img src="images/Screen Shot 2016-04-27 at 8.49.53 AM.png"/>
# Cancer Example
## Question 1
To do so, let's study a medical example--supposed there's a patient in the hospital who might suffer from a medical condition like cancer. Let's say the probability of having this cancer is 0.1. That means you can tell me what's the probability of being cancer free.
**Answer**
- The answer is 0.9 with just 1 minus the cancer.
<img src="images/Screen Shot 2016-04-27 at 8.52.39 AM.png"/>
## Question 2
Of course, in reality, we don't know whether a person suffers cancer, but we can run a test like a blood test. The outcome of it blood test may be positive or negative, but like any good test, it tells me something about the thing I really care about--whether the person has cancer or not.
Let's say, if the person has the cancer, the test comes up positive with the probability of 0.9, and that implies if the person has cancer, the negative outcome will have 0.1 probability and that's because these two things have to add to 1.
I've just given you a fairly complicated notation that says the outcome of the test depends on whether the person has cancer or not. We call this thing over here a conditional probability, and the way to understand this is a very funny notation. There's a bar in the middle, and the bar says what's the probability of the stuff on the left given that we assume the stuff on the right is actually the case.
Now, in reality, we don't know whether the person has cancer or not, and in a later unit, we're going to reason about whether the person has cancer given a certain data set, but for now, we assume we have god-like capabilities. We can tell with absolute certainty that the person has cancer, and we can determine what the outcome of the test is. This is a test that isn't exactly deterministic--it makes mistakes, but it only makes a mistake in 10% of the cases, as illustrated by the 0.1 down here.
Now, it turns out, I haven't fully specified the test. The same test might also be applied to a situation where the person does not have cancer. So this little thing over here is my shortcut of not having cancer. And now, let me say the probability of the test giving me a positive results--a false positive result when there's no cancer is 0.2. You can now tell me what's the probability of a negative outcome in case we know for a fact the person doesn't have cancer, so please tell me.
**Answer**
And the answer is 0.8. As I'm sure you noticed in the case where there is cancer, the possible test outcomes add up to 1. In the where there isn't cancer, the possible test outcomes add up to 1. So 1 - 0.2 = 0.8.
<img src="images/Screen Shot 2016-04-28 at 7.24.34 AM.png"/>
*Screenshot taken from [Udacity](https://classroom.udacity.com/courses/st101/lessons/48729372/concepts/487236390923)*
<!--TEASER_END-->
## Question 3
Look at this, this is very nontrivial but armed with this, we can now build up the truth table for all the cases of the two different variables, cancer and non-cancer and positive and negative tests outcome.
So, let me write down cancer and test and let me go through different possibilities. We could have cancer or not, and the test may come up positive or negative. So, please give me the probability of the combination of those for the very first one, and as a hint, it's kind of the same as before where we multiply two things, but you have to find the right things to multiple in this table over here.
**Answer**
And the answer is probability of cancer is 0.1, probability of test being positive given that he has cancer is the one over here--0.9, multiplying those two together gives us 0.09.
<img src="images/Screen Shot 2016-04-28 at 7.31.47 AM.png"/>
*Screenshot taken from [Udacity](https://classroom.udacity.com/courses/st101/lessons/48729372/concepts/486789140923)*
<!--TEASER_END-->
## Question 4
Moving to the next case--what do you think the probability is that the person does have cancer but the test comes back negative? What's the combined probability of these two cases?
**Answer**
And once again, we'd like to refer the corresponding numbers over here on the right side 0.1 for the cancer times the probability of getting a negative result conditioned on having cancer and that is 0.1 0.1, which is 0.01.
<img src="images/Screen Shot 2016-04-28 at 7.34.42 AM.png"/>
*Screenshot taken from [Udacity](https://classroom.udacity.com/courses/st101/lessons/48729372/concepts/486977510923)*
<!--TEASER_END-->
## Question 5
Moving on to the next two, we have:
**Answer**:
- **Cancer (N) - Test (P)**: Here the answer is 0.18 by multiplying the probability of not having cancer, which is 0.9, with the probability of getting a positive test result for a non-cancer patient 0.2. Multiplying 0.9 with 0.2 gives me 0.18.
- **Cancer (N) - Test (N)**: Here you get 0.72, which is the product of not having cancer in the first place 0.9 and the probability of getting a negative test result under the condition of not having cancer.
<img src="images/Screen Shot 2016-04-28 at 7.39.14 AM.png"/>
*Screenshot taken from [Udacity](https://classroom.udacity.com/courses/st101/lessons/48729372/concepts/486987400923)*
<!--TEASER_END-->
## Question 6
Now quickly add all of those probabilities up.
**Answer**
And as usual, the answer is 1. That is, we study in the truth table all possible cases. and when we add up the probabilities, you should always get the answer of 1.
<img src="images/Screen Shot 2016-04-28 at 7.41.53 AM.png"/>
*Screenshot taken from [Udacity](https://classroom.udacity.com/courses/st101/lessons/48729372/concepts/487214940923)*
<!--TEASER_END-->
## Question 7
Now let me ask you a really tricky question. What is the probability of a positive test result? Can you sum or determine, irrespective of whether there's cancer or not, what is the probability you get a positive test result?
** Answer**
And the result, once again, is found in the truth table, which is why this table is so powerful. Let's look at where in the truth table we get a positive test result. I would say it is right here, right here. If you take corresponding probabilities of 0.09 and 0.18, and add them up, we get 0.27.
<img src="images/Screen Shot 2016-04-28 at 7.44.52 AM.png"/>
*Screenshot taken from [Udacity](https://classroom.udacity.com/courses/st101/lessons/48729372/concepts/486987410923)*
<!--TEASER_END-->
# Total Probability
Putting all of this into mathematical notation we've given the probability of having cancer and from there, it follows the probability of not having cancer. And they give me 2 conditional probability that are the test being positive.
If we have have cancer, from which we can now predict the probability of the test being negative of having cancer. And the probability of the test being positive can be cancer free which can complete the probability of a negative test result in the cancer-free case. So these things are just easily inferred by the 1 minus rule.
Then when we read this, you complete the probability of a positive test result as the sum of a positive test result given cancer times the probability of cancer, which is our truth table entry for the combination of P and C plus the same given we don't have of cancer.
Now this notation is confusing and complicated if we ever dive deep into probability, that's called total probability, but it's useful to know that this is very, very intuitive and to further develop intuition let me just give you another exercise of exactly the same type.
<img src="images/Screen Shot 2016-04-28 at 7.50.03 AM.png"/>
*Screenshot taken from [Udacity](https://classroom.udacity.com/courses/st101/lessons/48729372/concepts/487202500923)*
<!--TEASER_END-->
# Two Coins
## Question 1
This time around, we have a bag, and in the bag are 2 coins,coin 1 and coin 2. And in advance, we know that coin 1 is fair. So P of coin 1 of coming up heads is 0.5 whereas coin 2 is loaded, that is, P of coin 2 coming up heads is 0.9. Quickly, give me the following numbers of the probability of coming up tails for coin 1 and for coin 2.
**Answer**
And the answer is 0.5 for coin 1and 0.1 for coin 2, because these things have to add up to 1 for each of the coins.
<img src="images/Screen Shot 2016-04-28 at 7.57.29 AM.png"/>
*Screenshot taken from [Udacity](https://classroom.udacity.com/courses/st101/lessons/48729372/concepts/487236400923)*
<!--TEASER_END-->
## Question 2
So now what happens is, I'm going to remove one of the coins from this bag, and each coin, coin 1 or coin 2, is being picked with equal probability. Let me now flip that coin once, and I want you to tell me, what's the probability that this coin which could be 50% chance fair coin 1and 50% chance a loaded coin. What's the probability that this coin comes up heads? Again, this is an exercise in conditional probability.
**Answer**
And let’s do the truth table. You have a pick event followed by a flip event
- We can pick coin 1 or coin 2. There is a 0.5 chance for each of the coins. Then we can flip and get heads or tails for the coin we've chosen. Now what are the probabilities?
- I'd argue picking 1 at 0.5 and once I pick the fair coin, I know that the probability of heads is, once again, 0.5 which makes it 0.25 The same is true for picking the fair coin and expecting tails
- But as we pick the unfair coin with a 0.5 chance we get a 0.9 chance of heads So 0.5 times 0.95 gives you 0.45 whereas the unfair coin, the probability of tails is 0.1 multiply by the probability of picking it at 0.5 gives us
- Now when they ask you, what's the probability of heads we'll find that 2 of those cases indeed come up with heads so if you add 0.25 and 0.45 and we get 0.7. So this example is a 0.7 chance that we might generate heads.
<img src="images/Screen Shot 2016-04-28 at 8.03.35 AM.png"/>
*Screenshot taken from [Udacity](https://classroom.udacity.com/courses/st101/lessons/48729372/concepts/486938400923)*
<!--TEASER_END-->
## Question 3
Now let me up the ante by flipping this coin twice. Once again, I'm drawing a coin from this bag, and I pick one at 50% chance. I don't know which one I have picked. It might be fair or loaded. And in flipping it twice, I get first heads, and then tails. What's the probability that if I do the following, I draw a coin at random with the probabilities shown, and then I flip it twice, that same coin. I just draw it once and then flip it twice. What's the probability of seeing heads first and then tails? Again, you might derive this using truth tables.
**Answer**
This is a non-trivial question, and the right way to do this is to go through the truth table, which I've drawn over here. There's 3 different things happening. We've taken initial pick of the coin, which can take coin 1 or coin 2 with equal probability, and then you go flip it for the first time, and there's heads or tails outcomes, and we flip it for the second time with the second outcome. So these different cases summarize my truth table.
I now need to observe just the cases where head is followed by tail. This one right here and over here. Then we compute the probability for those 2 cases.
- The probability of picking coin 1 is 0.5. For the fair coin, we get 0.5 for heads, followed by 0.5 for tails. They're together is 0.125.
- Let's do it with the second case. There's a 0.5 chance of taking coin 2. Now that one comes up with heads at 0.9. It comes up with tails at 0.1. So multiply these together, gives us 0.045, a smaller number than up here.
- Adding these 2 things together results in 0.17, which is the right answer to the question over here.
<img src="images/Screen Shot 2016-04-28 at 8.09.25 AM.png"/>
*Screenshot taken from [Udacity](https://classroom.udacity.com/courses/st101/lessons/48729372/concepts/486957990923)*
<!--TEASER_END-->
## Question 4
Let me do this once again. There are 2 coins in the bag, coin 1 and coin 2. And as before, taking coin 1 at 0.5 probability. But now I'm telling you that coin 1 is loaded, so give you heads with probability of 1. Think of it as a coin that only has heads. And coin 2 is also loaded. It gives you heads with 0.6 probability. Now work out for me into this experiment, what's the probability of seeing tails twice?
**Answer**
And the answer is depressing. If you, once again, draw the truth table, you find, for the different combinations, that if you've drawn coin 1, you'd never see tails. So this case over here, which indeed has tails, tails. We have 0 probability.
- We can work this out probability of drawing the first coin at 0.5, but the probability of tails given the first coin must be 0, because the probability of heads is 1, so 0.5 times 0 times 0, that is 0.
- So the only case where you might see tails/tails is when you actually drew coin 2, and this has a probability of 0.5 times the probability of tails given that we drew the second coin, which is 0.4 times 0.4 again, and that's the same as 0.08 would have been the correct answer.
<img src="images/Screen Shot 2016-04-28 at 8.34.08 AM.png"/>
*Screenshot taken from [Udacity](https://classroom.udacity.com/courses/st101/lessons/48729372/concepts/487015560923)*
<!--TEASER_END-->
# Summary
So there're important lessons in what we just learned, the key thing is we talked about conditional probabilities. We said that the outcome in a variable, like a test is actually not like the random coin flip but it depends on something else, like a disease.
When we looked at this, we were able to predict what's the probability of a test outcome even if we don't know whether the person has a disease or not. And we did this using the truth table, and in the truth table, we summarized multiple lines.
- For example, we multiplied the probability of a test outcome condition on this unknown variable, whether the person is diseased multiplied by the probability of the disease being present. Then we added a second row of the truth table, where our unobserved disease variable took the opposite value of not diseased.
- Written this way, it looks really clumsy, but that's effectively what we did when we went to the truth table. So we now understand that certain coin flips are dependent on other coin flips, so if god, for example, flips the coin of us having a disease or not, then the medical test again has a random outcome, but its probability really depends on whether we have the disease or not. We have to consider this when we do probabilistic inference. In the next unit, we're going to ask the real question. Say we really care about whether we have a disease like cancer or not. What do you think the probability is, given that our doctor just gave us a positive test result?
And I can tell you, you will be in for a surprise.
<img src="images/Screen Shot 2016-04-28 at 8.44.56 AM.png"/>
*Screenshot taken from [Udacity](https://classroom.udacity.com/courses/st101/lessons/48729372/concepts/487015560923)*
<!--TEASER_END-->
|
github_jupyter
|
<h3 align=center> Combining Datasets: Merge and Join</h3>
One essential feature offered by Pandas is its high-performance, in-memory join and merge operations.
If you have ever worked with databases, you should be familiar with this type of data interaction.
The main interface for this is the ``pd.merge`` function, and we'll see few examples of how this can work in practice.
For convenience, we will start by redefining the ``display()`` functionality from the previous section:
```
import pandas as pd
import numpy as np
class display(object):
"""Display HTML representation of multiple objects"""
template = """<div style="float: left; padding: 10px;">
<p style='font-family:"Courier New", Courier, monospace'>{0}</p>{1}
</div>"""
def __init__(self, *args):
self.args = args
def _repr_html_(self):
return '\n'.join(self.template.format(a, eval(a)._repr_html_())
for a in self.args)
def __repr__(self):
return '\n\n'.join(a + '\n' + repr(eval(a))
for a in self.args)
```
## Relational Algebra
The behavior implemented in ``pd.merge()`` is a subset of what is known as *relational algebra*, which is a formal set of rules for manipulating relational data, and forms the conceptual foundation of operations available in most databases.
The strength of the relational algebra approach is that it proposes several primitive operations, which become the building blocks of more complicated operations on any dataset.
With this lexicon of fundamental operations implemented efficiently in a database or other program, a wide range of fairly complicated composite operations can be performed.
Pandas implements several of these fundamental building-blocks in the ``pd.merge()`` function and the related ``join()`` method of ``Series`` and ``Dataframe``s.
As we will see, these let you efficiently link data from different sources.
## Categories of Joins
The ``pd.merge()`` function implements a number of types of joins: the
1. *one-to-one*,
2. *many-to-one*, and
3. *many-to-many* joins.
All three types of joins are accessed via an identical call to the ``pd.merge()`` interface; the type of join performed depends on the form of the input data.
Here we will show simple examples of the three types of merges, and discuss detailed options further below.
### One-to-one joins
Perhaps the simplest type of merge expresion is the one-to-one join, which is in many ways very similar to the column-wise concatenation seen in [Combining Datasets: Concat & Append](03.06-Concat-And-Append.ipynb).
As a concrete example, consider the following two ``DataFrames`` which contain information on several employees in a company:
```
df1 = pd.DataFrame({'employee': ['Raju', 'Rani', 'Ramesh', 'Ram'],
'group': ['Accounting', 'Engineering', 'Engineering', 'HR']})
df2 = pd.DataFrame({'employee': ['Raju', 'Rani', 'Ramesh', 'Ram'],
'hire_date': [2004, 2008, 2012, 2014]})
display('df1', 'df2','pd.merge(df1, df2)')
```
To combine this information into a single ``DataFrame``, we can use the ``pd.merge()`` function:
```
df3 = pd.merge(df1, df2)
df3
```
The ``pd.merge()`` function recognizes that each ``DataFrame`` has an "employee" column, and automatically joins using this column as a key.
The result of the merge is a new ``DataFrame`` that combines the information from the two inputs.
Notice that the order of entries in each column is not necessarily maintained: in this case, the order of the "employee" column differs between ``df1`` and ``df2``, and the ``pd.merge()`` function correctly accounts for this.
Additionally, keep in mind that the merge in general discards the index, except in the special case of merges by index (see the ``left_index`` and ``right_index`` keywords, discussed momentarily).
### Many-to-one joins
Many-to-one joins are joins in which one of the two key columns contains duplicate entries.
For the many-to-one case, the resulting ``DataFrame`` will preserve those duplicate entries as appropriate.
Consider the following example of a many-to-one join:
```
df4 = pd.DataFrame({'group': ['Accounting', 'Engineering', 'HR'],
'supervisor': ['Carly', 'Guido', 'Steve']})
df4
pd.merge(df3, df4)
display('df3', 'df4', 'pd.merge(df3, df4)')
```
The resulting ``DataFrame`` has an aditional column with the "supervisor" information, where the information is repeated in one or more locations as required by the inputs.
### Many-to-many joins
Many-to-many joins are a bit confusing conceptually, but are nevertheless well defined.
If the key column in both the left and right array contains duplicates, then the result is a many-to-many merge.
This will be perhaps most clear with a concrete example.
Consider the following, where we have a ``DataFrame`` showing one or more skills associated with a particular group.
By performing a many-to-many join, we can recover the skills associated with any individual person:
```
df5 = pd.DataFrame({'group': ['Accounting', 'Accounting',
'Engineering', 'Engineering', 'HR', 'Hdf4'],
'skills': ['math', 'spreadsheets', 'coding', 'linux',
'spreadsheets', 'organization']})
df5
display('df1', 'df5', "pd.merge(df1, df5)")
pd.merge(df1, df5)
```
These three types of joins can be used with other Pandas tools to implement a wide array of functionality.
But in practice, datasets are rarely as clean as the one we're working with here.
In the following section we'll consider some of the options provided by ``pd.merge()`` that enable you to tune how the join operations work.
## Specification of the Merge Key
We've already seen the default behavior of ``pd.merge()``: it looks for one or more matching column names between the two inputs, and uses this as the key.
However, often the column names will not match so nicely, and ``pd.merge()`` provides a variety of options for handling this.
### The ``on`` keyword
Most simply, you can explicitly specify the name of the key column using the ``on`` keyword, which takes a column name or a list of column names:
```
display('df1', 'df2', "pd.merge(df1, df2, on='employee')")
pd.merge(df1, df2, on='employee')
```
This option works only if both the left and right ``DataFrame``s have the specified column name.
### The ``left_on`` and ``right_on`` keywords
At times you may wish to merge two datasets with different column names; for example, we may have a dataset in which the employee name is labeled as "name" rather than "employee".
In this case, we can use the ``left_on`` and ``right_on`` keywords to specify the two column names:
```
df3 = pd.DataFrame({'name': ['Raju', 'Rani', 'Ramesh', 'Ram'],
'salary': [70000, 80000, 120000, 90000]})
display('df1', 'df3', 'pd.merge(df1, df3, left_on="employee", right_on="name")')
```
The result has a redundant column that we can drop if desired–for example, by using the ``drop()`` method of ``DataFrame``s:
```
pd.merge(df1, df3, left_on="employee", right_on="name").drop('name', axis=1) #Duplicat Col
```
### The ``left_index`` and ``right_index`` keywords
Sometimes, rather than merging on a column, you would instead like to merge on an index.
For example, your data might look like this:
```
df1a = df1.set_index('employee')
df2a = df2.set_index('employee')
display('df1a', 'df2a')
```
You can use the index as the key for merging by specifying the ``left_index`` and/or ``right_index`` flags in ``pd.merge()``:
```
display('df1a', 'df2a',
"pd.merge(df1a, df2a, left_index=True, right_index=True)")
pd.merge(df1a, df2a, left_index=True, right_index=True)
```
For convenience, ``DataFrame``s implement the ``join()`` method, which performs a merge that defaults to joining on indices:
```
display('df1a', 'df2a', 'df1a.join(df2a)')
```
If you'd like to mix indices and columns, you can combine ``left_index`` with ``right_on`` or ``left_on`` with ``right_index`` to get the desired behavior:
```
display('df1a', 'df3', "pd.merge(df1a, df3, left_index=True, right_on='name')")
```
All of these options also work with multiple indices and/or multiple columns; the interface for this behavior is very intuitive.
For more information on this, see the ["Merge, Join, and Concatenate" section](http://pandas.pydata.org/pandas-docs/stable/merging.html) of the Pandas documentation.
## Specifying Set Arithmetic for Joins
In all the preceding examples we have glossed over one important consideration in performing a join: the type of set arithmetic used in the join.
This comes up when a value appears in one key column but not the other. Consider this example:
```
df6 = pd.DataFrame({'name': ['Peter', 'Paul', 'Mary'],
'food': ['fish', 'beans', 'bread']},
columns=['name', 'food'])
df7 = pd.DataFrame({'name': ['Mary', 'Joseph','Paul'],
'drink': ['wine', 'beer','Water']},
columns=['name', 'drink'])
display('df6', 'df7', 'pd.merge(df6, df7)')
```
Here we have merged two datasets that have only a single "name" entry in common: Mary.
By default, the result contains the *intersection* of the two sets of inputs; this is what is known as an *inner join*.
We can specify this explicitly using the ``how`` keyword, which defaults to ``"inner"``:
```
pd.merge(df6, df7, how='inner') # by Defautl inner to join the data
pd.merge(df6, df7, how='outer')
```
Other options for the ``how`` keyword are ``'outer'``, ``'left'``, and ``'right'``.
An *outer join* returns a join over the union of the input columns, and fills in all missing values with NAs:
```
display('df6', 'df7', "pd.merge(df6, df7, how='outer')")
```
The *left join* and *right join* return joins over the left entries and right entries, respectively.
For example:
```
display('df6', 'df7', "pd.merge(df6, df7, how='left')")
display('df6', 'df7', "pd.merge(df6, df7, how='right')")
```
The output rows now correspond to the entries in the left input. Using
``how='right'`` works in a similar manner.
All of these options can be applied straightforwardly to any of the preceding join types.
## Overlapping Column Names: The ``suffixes`` Keyword
Finally, you may end up in a case where your two input ``DataFrame``s have conflicting column names.
Consider this example:
```
df8 = pd.DataFrame({'name': ['Bob', 'Jake', 'Lisa', 'Sue'],
'rank': [1, 2, 3, 4]})
df9 = pd.DataFrame({'name': ['Bob', 'Jake', 'Lisa', 'Sue'],
'rank': [3, 1, 4, 2]})
display('df8', 'df9', 'pd.merge(df8, df9, on="name")')
```
Because the output would have two conflicting column names, the merge function automatically appends a suffix ``_x`` or ``_y`` to make the output columns unique.
If these defaults are inappropriate, it is possible to specify a custom suffix using the ``suffixes`` keyword:
```
display('df8', 'df9', 'pd.merge(df8, df9, on="name", suffixes=["_L", "_R"])')
```
These suffixes work in any of the possible join patterns, and work also if there are multiple overlapping columns.
For more information on these patterns, see [Aggregation and Grouping](03.08-Aggregation-and-Grouping.ipynb) where we dive a bit deeper into relational algebra.
Also see the [Pandas "Merge, Join and Concatenate" documentation](http://pandas.pydata.org/pandas-docs/stable/merging.html) for further discussion of these topics.
## Example: US States Data
Merge and join operations come up most often when combining data from different sources.
Here we will consider an example of some data about US states and their populations.
The data files can be found at [DataSet](https://github.com/reddyprasade/Data-Sets-For-Machine-Learnig-and-Data-Science/tree/master/DataSets)
Let's take a look at the three datasets, using the Pandas ``read_csv()`` function:
```
pop = pd.read_csv('data/state-population.csv')
areas = pd.read_csv('data/state-areas.csv')
abbrevs = pd.read_csv('data/state-abbrevs.csv')
display('pop.head()', 'areas.head()', 'abbrevs.head()')
pop.shape,areas.shape,abbrevs.shape
pop.isna().sum()
areas.isna().sum()
abbrevs.isna().sum()
```
Given this information, say we want to compute a relatively straightforward result: rank US states and territories by their 2010 population density.
We clearly have the data here to find this result, but we'll have to combine the datasets to find the result.
We'll start with a many-to-one merge that will give us the full state name within the population ``DataFrame``.
We want to merge based on the ``state/region`` column of ``pop``, and the ``abbreviation`` column of ``abbrevs``.
We'll use ``how='outer'`` to make sure no data is thrown away due to mismatched labels.
```
merged = pd.merge(pop, abbrevs, how='outer',
left_on='state/region', right_on='abbreviation')
merged.head()
merged.isna().sum()
merged.tail()
merged = merged.drop('abbreviation', 1) # drop duplicate info
merged.head()
```
Let's double-check whether there were any mismatches here, which we can do by looking for rows with nulls:
```
merged.isnull().any()
merged.isnull().sum()
```
Some of the ``population`` info is null; let's figure out which these are!
```
merged['population'].isnull().sum()
merged['state'].isnull().sum()
merged[merged['population'].isnull()]
merged[merged['state'].isnull()]
```
It appears that all the null population values are from Puerto Rico prior to the year 2000; this is likely due to this data not being available from the original source.
More importantly, we see also that some of the new ``state`` entries are also null, which means that there was no corresponding entry in the ``abbrevs`` key!
Let's figure out which regions lack this match:
```
merged.loc[merged['state'].isnull(), 'state/region'].unique()
```
We can quickly infer the issue: our population data includes entries for Puerto Rico (PR) and the United States as a whole (USA), while these entries do not appear in the state abbreviation key.
We can fix these quickly by filling in appropriate entries:
```
merged.loc[merged['state/region'] == 'PR', 'state'] = 'Puerto Rico'
merged.loc[merged['state/region'] == 'USA', 'state'] = 'United States'
merged.isnull().any()
merged.isnull().sum()
```
No more nulls in the ``state`` column: we're all set!
Now we can merge the result with the area data using a similar procedure.
Examining our results, we will want to join on the ``state`` column in both:
```
final = pd.merge(merged, areas, on='state', how='left')
final.head()
```
Again, let's check for nulls to see if there were any mismatches:
```
final.isnull().any()
final.isna().sum()
```
There are nulls in the ``area`` column; we can take a look to see which regions were ignored here:
```
final['state'][final['area (sq. mi)'].isnull()].unique()
```
We see that our ``areas`` ``DataFrame`` does not contain the area of the United States as a whole.
We could insert the appropriate value (using the sum of all state areas, for instance), but in this case we'll just drop the null values because the population density of the entire United States is not relevant to our current discussion:
```
final.dropna(inplace=True)
final.head()
final.shape
final.isnull().info()
final.isna().sum()
```
Now we have all the data we need. To answer the question of interest, let's first select the portion of the data corresponding with the year 2000, and the total population.
We'll use the ``query()`` function to do this quickly (this requires the ``numexpr`` package to be installed; see [High-Performance Pandas: ``eval()`` and ``query()``](03.12-Performance-Eval-and-Query.ipynb)):
```
data2010 = final.query("year == 2010 & ages == 'total'") # SQL Select Stastement
data2010.head()
```
Now let's compute the population density and display it in order.
We'll start by re-indexing our data on the state, and then compute the result:
```
data2010.set_index('state', inplace=True)
data2010
density = data2010['population'] / data2010['area (sq. mi)']
density.head()
density.sort_values(ascending=True, inplace=True)
density.head()
```
The result is a ranking of US states plus Washington, DC, and Puerto Rico in order of their 2010 population density, in residents per square mile.
We can see that by far the densest region in this dataset is Washington, DC (i.e., the District of Columbia); among states, the densest is New Jersey.
We can also check the end of the list:
```
density.tail()
final.isnull().describe()
```
Converting the Data Frame into Pickle File Formate
```
Data = pd.to_pickle(final,'Data/US_States_Data.plk')# Save the Data in the from of Pickled
final.to_csv('Data/US_States_Data.csv')# Save the Data Csv
unpickled_df = pd.read_pickle("Data/US_States_Data.plk")
unpickled_df
```
We see that the least dense state, by far, is Alaska, averaging slightly over one resident per square mile.
This type of messy data merging is a common task when trying to answer questions using real-world data sources.
I hope that this example has given you an idea of the ways you can combine tools we've covered in order to gain insight from your data!
|
github_jupyter
|
```
%reload_ext autoreload
%autoreload 2
%matplotlib inline
import os
os.chdir('../../')
from musicautobot.numpy_encode import *
from musicautobot.utils.file_processing import process_all, process_file
from musicautobot.config import *
from musicautobot.music_transformer import *
from musicautobot.multitask_transformer import *
from musicautobot.utils.stacked_dataloader import StackedDataBunch
from fastai.text import *
```
## MultitaskTransformer Training
Multitask Training is an extension of [MusicTransformer](../music_transformer/Train.ipynb).
Instead a basic language model that predicts the next word...
We train on multiple tasks
* [Next Word](../music_transformer/Train.ipynb)
* [Bert Mask](https://arxiv.org/abs/1810.04805)
* [Sequence to Sequence Translation](http://jalammar.github.io/illustrated-transformer/)
This gives a more generalized model and also let's you do some really cool [predictions](Generate.ipynb)
## End to end training pipeline
1. Create and encode dataset
2. Initialize Transformer MOdel
3. Train
4. Predict
```
# Location of your midi files
midi_path = Path('data/midi/examples')
midi_path.mkdir(parents=True, exist_ok=True)
# Location to save dataset
data_path = Path('data/numpy')
data_path.mkdir(parents=True, exist_ok=True)
data_save_name = 'musicitem_data_save.pkl'
s2s_data_save_name = 'multiitem_data_save.pkl'
```
## 1. Gather midi dataset
Make sure all your midi data is in `musicautobot/data/midi` directory
Here's a pretty good dataset with lots of midi data:
https://www.reddit.com/r/datasets/comments/3akhxy/the_largest_midi_collection_on_the_internet/
Download the folder and unzip it to `data/midi`
## 2. Create dataset from MIDI files
```
midi_files = get_files(midi_path, '.mid', recurse=True); len(midi_files)
```
### 2a. Create NextWord/Mask Dataset
```
processors = [Midi2ItemProcessor()]
data = MusicDataBunch.from_files(midi_files, data_path, processors=processors,
encode_position=True, dl_tfms=mask_lm_tfm_pitchdur,
bptt=5, bs=2)
data.save(data_save_name)
xb, yb = data.one_batch(); xb
```
Key:
* 'msk' = masked input
* 'lm' = next word input
* 'pos' = timestepped postional encoding. This is in addition to relative positional encoding
Note: MultitaskTransformer trains on both the masked input ('msk') and next word input ('lm') at the same time.
The encoder is trained on the 'msk' data, while the decoder is trained on 'lm' data.
### 2b. Create sequence to sequence dataset
```
processors = [Midi2MultitrackProcessor()]
s2s_data = MusicDataBunch.from_files(midi_files, data_path, processors=processors,
preloader_cls=S2SPreloader, list_cls=S2SItemList,
dl_tfms=melody_chord_tfm,
bptt=5, bs=2)
s2s_data.save(s2s_data_save_name)
```
Structure
```
xb, yb = s2s_data.one_batch(); xb
```
Key:
* 'c2m' = chord2melody translation
* enc = chord
* dec = melody
* 'm2c' = next word input
* enc = melody
* dec = chord
* 'pos' = timestepped postional encoding. Gives the model a better reference when translating
Note: MultitaskTransformer trains both translations ('m2c' and 'c2m') at the same time.
## 3. Initialize Model
```
# Load Data
batch_size = 2
bptt = 128
lm_data = load_data(data_path, data_save_name,
bs=batch_size, bptt=bptt, encode_position=True,
dl_tfms=mask_lm_tfm_pitchdur)
s2s_data = load_data(data_path, s2s_data_save_name,
bs=batch_size//2, bptt=bptt,
preloader_cls=S2SPreloader, dl_tfms=melody_chord_tfm)
# Combine both dataloaders so we can train multiple tasks at the same time
data = StackedDataBunch([lm_data, s2s_data])
# Create Model
config = multitask_config(); config
learn = multitask_model_learner(data, config.copy())
# learn.to_fp16(dynamic=True) # Enable for mixed precision
learn.model
```
# 4. Train
```
learn.fit_one_cycle(4)
learn.save('example')
```
## Predict
---
See [Generate.ipynb](Generate.ipynb) to use a pretrained model and generate better predictions
---
```
# midi_files = get_files(midi_path, '.mid', recurse=True)
midi_file = Path('data/midi/notebook_examples/single_bar_example.mid'); midi_file
next_word = nw_predict_from_midi(learn, midi_file, n_words=20, seed_len=8); next_word.show()
pred_melody = s2s_predict_from_midi(learn, midi_file, n_words=20, seed_len=4, pred_melody=True); pred_melody.show()
pred_notes = mask_predict_from_midi(learn, midi_file, predict_notes=True); pred_notes.show()
```
|
github_jupyter
|
```
import matplotlib
from matplotlib.axes import Axes
from matplotlib.patches import Polygon
from matplotlib.path import Path
from matplotlib.ticker import NullLocator, Formatter, FixedLocator
from matplotlib.transforms import Affine2D, BboxTransformTo, IdentityTransform
from matplotlib.projections import register_projection
import matplotlib.spines as mspines
import matplotlib.axis as maxis
import matplotlib.pyplot as plt
import numpy as np
class TriangularAxes(Axes):
"""
A custom class for triangular projections.
"""
name = 'triangular'
def __init__(self, *args, **kwargs):
Axes.__init__(self, *args, **kwargs)
self.set_aspect(1, adjustable='box', anchor='SW')
self.cla()
def _init_axis(self):
self.xaxis = maxis.XAxis(self)
self.yaxis = maxis.YAxis(self)
self._update_transScale()
def cla(self):
"""
Override to set up some reasonable defaults.
"""
# Don't forget to call the base class
Axes.cla(self)
x_min = 0
y_min = 0
x_max = 1
y_max = 1
x_spacing = 0.1
y_spacing = 0.1
self.xaxis.set_minor_locator(NullLocator())
self.yaxis.set_minor_locator(NullLocator())
self.xaxis.set_ticks_position('bottom')
self.yaxis.set_ticks_position('left')
Axes.set_xlim(self, x_min, x_max)
Axes.set_ylim(self, y_min, y_max)
self.xaxis.set_ticks(np.arange(x_min, x_max+x_spacing, x_spacing))
self.yaxis.set_ticks(np.arange(y_min, y_max+y_spacing, y_spacing))
def _set_lim_and_transforms(self):
"""
This is called once when the plot is created to set up all the
transforms for the data, text and grids.
"""
# There are three important coordinate spaces going on here:
#
# 1. Data space: The space of the data itself
#
# 2. Axes space: The unit rectangle (0, 0) to (1, 1)
# covering the entire plot area.
#
# 3. Display space: The coordinates of the resulting image,
# often in pixels or dpi/inch.
# This function makes heavy use of the Transform classes in
# ``lib/matplotlib/transforms.py.`` For more information, see
# the inline documentation there.
# The goal of the first two transformations is to get from the
# data space (in this case longitude and latitude) to axes
# space. It is separated into a non-affine and affine part so
# that the non-affine part does not have to be recomputed when
# a simple affine change to the figure has been made (such as
# resizing the window or changing the dpi).
# 1) The core transformation from data space into
# rectilinear space defined in the HammerTransform class.
self.transProjection = IdentityTransform()
# 2) The above has an output range that is not in the unit
# rectangle, so scale and translate it so it fits correctly
# within the axes. The peculiar calculations of xscale and
# yscale are specific to a Aitoff-Hammer projection, so don't
# worry about them too much.
self.transAffine = Affine2D.from_values(
1., 0, 0.5, np.sqrt(3)/2., 0, 0)
self.transAffinedep = Affine2D.from_values(
1., 0, -0.5, np.sqrt(3)/2., 0, 0)
#self.transAffine = IdentityTransform()
# 3) This is the transformation from axes space to display
# space.
self.transAxes = BboxTransformTo(self.bbox)
# Now put these 3 transforms together -- from data all the way
# to display coordinates. Using the '+' operator, these
# transforms will be applied "in order". The transforms are
# automatically simplified, if possible, by the underlying
# transformation framework.
self.transData = \
self.transProjection + \
self.transAffine + \
self.transAxes
# The main data transformation is set up. Now deal with
# gridlines and tick labels.
# Longitude gridlines and ticklabels. The input to these
# transforms are in display space in x and axes space in y.
# Therefore, the input values will be in range (-xmin, 0),
# (xmax, 1). The goal of these transforms is to go from that
# space to display space. The tick labels will be offset 4
# pixels from the equator.
self._xaxis_pretransform = IdentityTransform()
self._xaxis_transform = \
self._xaxis_pretransform + \
self.transData
self._xaxis_text1_transform = \
Affine2D().scale(1.0, 0.0) + \
self.transData + \
Affine2D().translate(0.0, -20.0)
self._xaxis_text2_transform = \
Affine2D().scale(1.0, 0.0) + \
self.transData + \
Affine2D().translate(0.0, -4.0)
# Now set up the transforms for the latitude ticks. The input to
# these transforms are in axes space in x and display space in
# y. Therefore, the input values will be in range (0, -ymin),
# (1, ymax). The goal of these transforms is to go from that
# space to display space. The tick labels will be offset 4
# pixels from the edge of the axes ellipse.
self._yaxis_transform = self.transData
yaxis_text_base = \
self.transProjection + \
(self.transAffine + \
self.transAxes)
self._yaxis_text1_transform = \
yaxis_text_base + \
Affine2D().translate(-8.0, 0.0)
self._yaxis_text2_transform = \
yaxis_text_base + \
Affine2D().translate(8.0, 0.0)
def get_xaxis_transform(self,which='grid'):
assert which in ['tick1','tick2','grid']
return self._xaxis_transform
def get_xaxis_text1_transform(self, pad):
return self._xaxis_text1_transform, 'bottom', 'center'
def get_xaxis_text2_transform(self, pad):
return self._xaxis_text2_transform, 'top', 'center'
def get_yaxis_transform(self,which='grid'):
assert which in ['tick1','tick2','grid']
return self._yaxis_transform
def get_yaxis_text1_transform(self, pad):
return self._yaxis_text1_transform, 'center', 'right'
def get_yaxis_text2_transform(self, pad):
return self._yaxis_text2_transform, 'center', 'left'
def _gen_axes_spines(self):
dep_spine = mspines.Spine.linear_spine(self,
'right')
# Fix dependent axis to be transformed the correct way
dep_spine.set_transform(self.transAffinedep + self.transAxes)
return {'left':mspines.Spine.linear_spine(self,
'left'),
'bottom':mspines.Spine.linear_spine(self,
'bottom'),
'right':dep_spine}
def _gen_axes_patch(self):
"""
Override this method to define the shape that is used for the
background of the plot. It should be a subclass of Patch.
Any data and gridlines will be clipped to this shape.
"""
return Polygon([[0,0], [0.5,np.sqrt(3)/2], [1,0]], closed=True)
# Interactive panning and zooming is not supported with this projection,
# so we override all of the following methods to disable it.
def can_zoom(self):
"""
Return True if this axes support the zoom box
"""
return False
def start_pan(self, x, y, button):
pass
def end_pan(self):
pass
def drag_pan(self, button, key, x, y):
pass
# Now register the projection with matplotlib so the user can select
# it.
register_projection(TriangularAxes)
import pycalphad.io.tdb_keywords
pycalphad.io.tdb_keywords.TDB_PARAM_TYPES.extend(['EM', 'BULK', 'SHEAR', 'C11', 'C12', 'C44'])
from pycalphad import Database, Model, calculate, equilibrium
import numpy as np
import pycalphad.variables as v
import sympy
from tinydb import where
class ElasticModel(Model):
def build_phase(self, dbe, phase_name, symbols, param_search):
phase = dbe.phases[phase_name]
self.models['ref'] = self.reference_energy(phase, param_search)
self.models['idmix'] = self.ideal_mixing_energy(phase, param_search)
self.models['xsmix'] = self.excess_mixing_energy(phase, param_search)
self.models['mag'] = self.magnetic_energy(phase, param_search)
# Here is where we add our custom contribution
# EM, BULK, SHEAR, C11, C12, C44
for prop in ['EM', 'BULK', 'SHEAR', 'C11', 'C12', 'C44']:
prop_param_query = (
(where('phase_name') == phase.name) & \
(where('parameter_type') == prop) & \
(where('constituent_array').test(self._array_validity))
)
prop_val = self.redlich_kister_sum(phase, param_search, prop_param_query)
setattr(self, prop, prop_val)
# Extra code necessary for compatibility with order-disorder model
ordered_phase_name = None
disordered_phase_name = None
try:
ordered_phase_name = phase.model_hints['ordered_phase']
disordered_phase_name = phase.model_hints['disordered_phase']
except KeyError:
pass
if ordered_phase_name == phase_name:
self.models['ord'] = self.atomic_ordering_energy(dbe,
disordered_phase_name,
ordered_phase_name)
dbf = Database('ElasticTi.tdb')
mod = ElasticModel(dbf, ['TI', 'MO', 'NB', 'VA'], 'BCC_A2')
symbols = dict([(sympy.Symbol(s), val) for s, val in dbf.symbols.items()])
mod.EM = mod.EM.xreplace(symbols)
x1 = np.linspace(0,1, num=100)
x2 = np.linspace(0,1, num=100)
mesh = np.meshgrid(x1, x2)
X = mesh[0]
Y = mesh[1]
mesh_arr = np.array(mesh)
mesh_arr = np.moveaxis(mesh_arr, 0, 2)
dep_col = 1 - np.sum(mesh_arr, axis=-1, keepdims=True)
mesh_arr = np.concatenate((mesh_arr, dep_col), axis=-1)
mesh_arr = np.concatenate((mesh_arr, np.ones(mesh_arr.shape[:-1] + (1,))), axis=-1)
orig_shape = tuple(mesh_arr.shape[:-1])
mesh_arr = mesh_arr.reshape(-1, mesh_arr.shape[-1])
mesh_arr[np.any(mesh_arr < 0, axis=-1), :] = np.nan
res = calculate(dbf, ['TI', 'MO', 'NB', 'VA'], 'BCC_A2', T=300, P=101325,
model=mod, output='EM', points=mesh_arr)
res_EM = res.EM.values.reshape(orig_shape)
%matplotlib inline
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(12,12))
ax = fig.gca(projection='triangular')
CS = ax.contour(X, Y, res_EM, levels=list(range(-10, 310, 10)), linewidths=4, cmap='cool')
ax.clabel(CS, inline=1, fontsize=13, fmt='%1.0f')
#PCM=ax.get_children()[0] #get the mappable, the 1st and the 2nd are the x and y axes
#plt.colorbar(PCM, ax=ax)
ax.set_xlabel('Mole Fraction Mo', fontsize=18)
ax.set_ylabel('Mole Fraction Nb', fontsize=18, rotation=60, labelpad=-180)
ax.tick_params(axis='both', which='major', labelsize=18)
ax.tick_params(axis='both', which='minor', labelsize=18)
fig.savefig('TiMoNb-EM.pdf')
```
|
github_jupyter
|
# Set-up
```
# libraries
import re
import numpy as np
import pandas as pd
from pymongo import MongoClient
# let's connect to the localhost
client = MongoClient()
# let's create a database
db = client.moma
# collection
artworks = db.artworks
# print connection
print("""
Database
==========
{}
Collection
==========
{}
""".format(db, artworks), flush=True
)
```
## Data

```
df = pd.read_csv('https://media.githubusercontent.com/media/MuseumofModernArt/collection/master/Artworks.csv')
df.info()
```
# Loading
```
%%time
# slow loading of data
d = {}
for i in df.index:
d = {
"_id": str(df.loc[i, "Cataloged"]) + str(df.loc[i, "ObjectID"]),
"Title": df.loc[i, "Title"],
"Date": df.loc[i, "Date"],
"Artist": {
"Name": df.loc[i, "Artist"],
"Bio": df.loc[i, "ArtistBio"],
"Nationality": df.loc[i, "Nationality"],
"Birth": df.loc[i, "BeginDate"],
"Death": df.loc[i, "EndDate"],
"Gender": df.loc[i, "Gender"]
},
"Characteristics":{
"Medium": df.loc[i,'Medium'],
"Dimensions": df.loc[i,'Dimensions'],
"Circumference": df.loc[i,'Circumference (cm)'],
"Depth": df.loc[i,'Depth (cm)'],
"Diameter": df.loc[i,'Diameter (cm)'],
"Height": df.loc[i,'Height (cm)'],
"Length": df.loc[i,'Length (cm)'],
"Weight": df.loc[i,'Weight (kg)'],
"Width": df.loc[i,'Width (cm)'],
"Seat Height": df.loc[i,'Seat Height (cm)'],
"Duration": df.loc[i,'Duration (sec.)']
},
"Acquisition": {
"Date": df.loc[i, "DateAcquired"],
"CreditLine": df.loc[i, "CreditLine"],
"Number": df.loc[i, "AccessionNumber"]
},
"Classification": df.loc[i, "Classification"],
"Department": df.loc[i, "Department"],
"URL": df.loc[i, "URL"],
"ThumbnailURL": df.loc[i, "ThumbnailURL"]
}
artworks.insert_one(d)
# for further reference https://docs.mongodb.com/manual/reference/command/collStats/
stats = db.command("collstats", "artworks")
s0 = stats.get('size')/10**6
print("""
Namespace: {}
Document Count: {}
Size: {}
""".format(stats.get('ns'), stats.get('count'), s0), flush=True)
```
## Cleaning
```
# get key names
l = []
for i in d.keys():
try:
for b in d.get(str(i)).keys():
l.append(str(i) + '.' + str(b))
except:
l.append(i)
# unset NaN fields
for i in l:
update = artworks.update_many({str(i):np.nan},{"$unset": {str(i):""}})
print("""
Key: {}
Matched: {}
Modified: {}
------------
""".format(i, update.matched_count, update.modified_count), flush=True)
# for further reference https://docs.mongodb.com/manual/reference/command/collStats/
stats = db.command("collstats", "artworks")
s1 = stats.get('size')/10**6
print("""
Namespace: {}
Document Count: {}
Size: {}
Var. Size: {}
""".format(stats.get('ns'), stats.get('count'), s1, round(s0-s1, 2)), flush=True)
```
## Further Cleaning
```
# change data type
update = artworks.update_many({"Date":{"$regex": '^[0-9]*$'}}, [{ "$set": { "Date": { "$toInt": "$Date" } } }])
print("""
Key: {}
Matched: {}
Modified: {}
------------
""".format("Date", update.matched_count, update.modified_count), flush=True)
# create an array field to store ranges
for i in artworks.find({"Date":{"$regex": '^[0-9]{4}-[0-9]{4}$'}}):
date = i.get('Date').split('-')
a = int(date[0])
b = int(date[1])
id = i.get('_id')
update = artworks.update_one({"_id": str(id)},{"$set": {"Date": [a, b]}})
print(update.matched_count, update.modified_count)
for i in artworks.find({"Date":{"$regex": '^[0-9]{4}–[0-9]{4}$'}}):
date = i.get('Date').split('–')
a = int(date[0])
b = int(date[1])
id = i.get('_id')
update = artworks.update_one({"_id": str(id)},{"$set": {"Date": [a, b]}})
print(update.matched_count, update.modified_count)
for i in artworks.find({"Date": {"$regex": '^[0-9]{4}-[0-9]{2}$'}}, {"Date": 1}):
date = i.get('Date').split('-')
a = int(date[0])
b = int(date[0][0] + date[0][1] + date[1])
id = i.get('_id')
update = artworks.update_one({"_id": str(id)},{"$set": {"Date": [a, b]}})
print(update.matched_count, update.modified_count)
for i in artworks.find({"Date": {"$regex": '^[0-9]{4}–[0-9]{2}$'}}, {"Date": 1}):
date = i.get('Date').split('–')
a = int(date[0])
b = int(date[0][0] + date[0][1]+ date[1])
id = i.get('_id')
update = artworks.update_one({"_id": str(id)},{"$set": {"Date": [a, b]}})
print(update.matched_count, update.modified_count)
# perform some further cleaning
for i in artworks.find({"Date":{"$regex": '^c. [0-9]{4}$'}}):
date = i.get('Date').split(' ')
b = int(date[1])
id = i.get('_id')
update = artworks.update_one({"_id": str(id)},{"$set": {"Date": b}})
print(update.matched_count, update.modified_count)
# remove Unknown or n.d.
update = artworks.update_many({"Date": {"$in": ["n.d.", "Unknown", "unknown"]}}, {"$unset": {"Date": ""}})
print("""
Matched: {}
Modified: {}
""".format(update.matched_count, update.modified_count), flush=True)
for i in artworks.find({"Date": {"$type": "string"}}, {"Date":1}):
print(i)
```
# Aggregation and loading
```
# collection
artw = db.artw
# print connection
print("""
Database
==========
{}
Collection
==========
{}
""".format(db, artw), flush=True
)
# df to dict
df.rename(columns={'Duration (sec.)': 'Duration (sec)'}, inplace=True)
dd = df.to_dict('records')
dd[0]
%%time
# insert array
insert = artw.insert_many(dd)
# define the pipeline
pipeline = [
{"$project":
{
"_id": {"$concat": ["$Cataloged", {"$toString": "$ObjectID"}]},
"Title": "$Title",
"Date": "$Date",
"Artist": {
"Name": "$Artist",
'Bio': "$ArtistBio",
'Nationality': "$Nationality",
"Birth": "$BeginDate",
"Death": "$EndDate",
"Gender": "$Gender",
},
"Characteristics":{
"Medium": '$Medium',
"Dimensions": '$Dimensions',
"Circumference": '$Circumference (cm)',
"Depth": '$Depth (cm)',
"Diameter": '$Diameter (cm)',
"Height": '$Height (cm)',
"Length": '$Length (cm)',
"Weight": '$Weight (kg)',
"Width": '$Width (cm)',
"Seat Height": '$Seat Height (cm)',
"Duration": '$Duration (sec)'
},
"Acquisition": {
"Date": "$DateAcquired",
"CreditLine": "$CreditLine",
"Number": "$AccessionNumber"
},
"Classification": "$Classification",
"Department": "$Department",
"URL": "$URL",
"ThumbnailURL": "$ThumbnailURL"
}
},
{ "$out" : "artw" }
]
# perform the aggregation
agr = artw.aggregate(pipeline)
# unset field with null values
[artw.update_many({str(i):np.nan},{"$unset": {str(i):""}}) for i in l]
```
|
github_jupyter
|
# Gaussian Process (GP) smoothing
This example deals with the case when we want to **smooth** the observed data points $(x_i, y_i)$ of some 1-dimensional function $y=f(x)$, by finding the new values $(x_i, y'_i)$ such that the new data is more "smooth" (see more on the definition of smoothness through allocation of variance in the model description below) when moving along the $x$ axis.
It is important to note that we are **not** dealing with the problem of interpolating the function $y=f(x)$ at the unknown values of $x$. Such problem would be called "regression" not "smoothing", and will be considered in other examples.
If we assume the functional dependency between $x$ and $y$ is **linear** then, by making the independence and normality assumptions about the noise, we can infer a straight line that approximates the dependency between the variables, i.e. perform a linear regression. We can also fit more complex functional dependencies (like quadratic, cubic, etc), if we know the functional form of the dependency in advance.
However, the **functional form** of $y=f(x)$ is **not always known in advance**, and it might be hard to choose which one to fit, given the data. For example, you wouldn't necessarily know which function to use, given the following observed data. Assume you haven't seen the formula that generated it:
```
%pylab inline
figsize(12, 6);
import numpy as np
import scipy.stats as stats
x = np.linspace(0, 50, 100)
y = (np.exp(1.0 + np.power(x, 0.5) - np.exp(x/15.0)) +
np.random.normal(scale=1.0, size=x.shape))
plot(x, y);
xlabel("x");
ylabel("y");
title("Observed Data");
```
### Let's try a linear regression first
As humans, we see that there is a non-linear dependency with some noise, and we would like to capture that dependency. If we perform a linear regression, we see that the "smoothed" data is less than satisfactory:
```
plot(x, y);
xlabel("x");
ylabel("y");
lin = stats.linregress(x, y)
plot(x, lin.intercept + lin.slope * x);
title("Linear Smoothing");
```
### Linear regression model recap
The linear regression assumes there is a linear dependency between the input $x$ and output $y$, sprinkled with some noise around it so that for each observed data point we have:
$$ y_i = a + b\, x_i + \epsilon_i $$
where the observation errors at each data point satisfy:
$$ \epsilon_i \sim N(0, \sigma^2) $$
with the same $\sigma$, and the errors are independent:
$$ cov(\epsilon_i, \epsilon_j) = 0 \: \text{ for } i \neq j $$
The parameters of this model are $a$, $b$, and $\sigma$. It turns out that, under these assumptions, the maximum likelihood estimates of $a$ and $b$ don't depend on $\sigma$. Then $\sigma$ can be estimated separately, after finding the most likely values for $a$ and $b$.
### Gaussian Process smoothing model
This model allows departure from the linear dependency by assuming that the dependency between $x$ and $y$ is a Brownian motion over the domain of $x$. This doesn't go as far as assuming a particular functional dependency between the variables. Instead, by **controlling the standard deviation of the unobserved Brownian motion** we can achieve different levels of smoothness of the recovered functional dependency at the original data points.
The particular model we are going to discuss assumes that the observed data points are **evenly spaced** across the domain of $x$, and therefore can be indexed by $i=1,\dots,N$ without the loss of generality. The model is described as follows:
\begin{equation}
\begin{aligned}
z_i & \sim \mathcal{N}(z_{i-1} + \mu, (1 - \alpha)\cdot\sigma^2) \: \text{ for } i=2,\dots,N \\
z_1 & \sim ImproperFlat(-\infty,\infty) \\
y_i & \sim \mathcal{N}(z_i, \alpha\cdot\sigma^2)
\end{aligned}
\end{equation}
where $z$ is the hidden Brownian motion, $y$ is the observed data, and the total variance $\sigma^2$ of each ovservation is split between the hidden Brownian motion and the noise in proportions of $1 - \alpha$ and $\alpha$ respectively, with parameter $0 < \alpha < 1$ specifying the degree of smoothing.
When we estimate the maximum likelihood values of the hidden process $z_i$ at each of the data points, $i=1,\dots,N$, these values provide an approximation of the functional dependency $y=f(x)$ as $\mathrm{E}\,[f(x_i)] = z_i$ at the original data points $x_i$ only. Therefore, again, the method is called smoothing and not regression.
### Let's describe the above GP-smoothing model in PyMC3
```
import pymc3 as pm
from theano import shared
from pymc3.distributions.timeseries import GaussianRandomWalk
from scipy import optimize
```
Let's create a model with a shared parameter for specifying different levels of smoothing. We use very wide priors for the "mu" and "tau" parameters of the hidden Brownian motion, which you can adjust according to your application.
```
LARGE_NUMBER = 1e5
model = pm.Model()
with model:
smoothing_param = shared(0.9)
mu = pm.Normal("mu", sigma=LARGE_NUMBER)
tau = pm.Exponential("tau", 1.0/LARGE_NUMBER)
z = GaussianRandomWalk("z",
mu=mu,
tau=tau / (1.0 - smoothing_param),
shape=y.shape)
obs = pm.Normal("obs",
mu=z,
tau=tau / smoothing_param,
observed=y)
```
Let's also make a helper function for inferring the most likely values of $z$:
```
def infer_z(smoothing):
with model:
smoothing_param.set_value(smoothing)
res = pm.find_MAP(vars=[z], fmin=optimize.fmin_l_bfgs_b)
return res['z']
```
Please note that in this example, we are only looking at the MAP estimate of the unobserved variables. We are not really interested in inferring the posterior distributions. Instead, we have a control parameter $\alpha$ which lets us allocate the variance between the hidden Brownian motion and the noise. Other goals and/or different models may require sampling to obtain the posterior distributions, but for our goal a MAP estimate will suffice.
### Exploring different levels of smoothing
Let's try to allocate 50% variance to the noise, and see if the result matches our expectations.
```
smoothing = 0.5
z_val = infer_z(smoothing)
plot(x, y);
plot(x, z_val);
title("Smoothing={}".format(smoothing));
```
It appears that the variance is split evenly between the noise and the hidden process, as expected.
Let's try gradually increasing the smoothness parameter to see if we can obtain smoother data:
```
smoothing = 0.9
z_val = infer_z(smoothing)
plot(x, y);
plot(x, z_val);
title("Smoothing={}".format(smoothing));
```
### Smoothing "to the limits"
By increading the smoothing parameter, we can gradually make the inferred values of the hidden Brownian motion approach the average value of the data. This is because as we increase the smoothing parameter, we allow less and less of the variance to be allocated to the Brownian motion, so eventually it aproaches the process which almost doesn't change over the domain of $x$:
```
fig, axes = subplots(2, 2)
for ax, smoothing in zip(axes.ravel(), [0.95, 0.99, 0.999, 0.9999]):
z_val = infer_z(smoothing)
ax.plot(x, y)
ax.plot(x, z_val)
ax.set_title('Smoothing={:05.4f}'.format(smoothing))
```
This example originally contributed by: Andrey Kuzmenko, http://github.com/akuz
|
github_jupyter
|
```
# %load /Users/facai/Study/book_notes/preconfig.py
%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns
from IPython.display import SVG
```
逻辑回归在scikit-learn中的实现简介
==============================
分析用的代码版本信息:
```bash
~/W/g/scikit-learn ❯❯❯ git log -n 1
commit d161bfaa1a42da75f4940464f7f1c524ef53484f
Author: John B Nelson <[email protected]>
Date: Thu May 26 18:36:37 2016 -0400
Add missing double quote (#6831)
```
### 0. 总纲
下面是sklearn中逻辑回归的构成情况:
```
SVG("./res/sklearn_lr.svg")
```
如[逻辑回归在spark中的实现简介](./spark_ml_lr.ipynb)中分析一样,主要把精力定位到算法代码上,即寻优算子和损失函数。
### 1. 寻优算子
sklearn支持liblinear, sag, lbfgs和newton-cg四种寻优算子,其中lbfgs属于scipy包,liblinear属于LibLinear库,剩下两种由sklearn自己实现。代码很好定位,逻辑也很明了,不多说:
```python
704 if solver == 'lbfgs':
705 try:
706 w0, loss, info = optimize.fmin_l_bfgs_b(
707 func, w0, fprime=None,
708 args=(X, target, 1. / C, sample_weight),
709 iprint=(verbose > 0) - 1, pgtol=tol, maxiter=max_iter)
710 except TypeError:
711 # old scipy doesn't have maxiter
712 w0, loss, info = optimize.fmin_l_bfgs_b(
713 func, w0, fprime=None,
714 args=(X, target, 1. / C, sample_weight),
715 iprint=(verbose > 0) - 1, pgtol=tol)
716 if info["warnflag"] == 1 and verbose > 0:
717 warnings.warn("lbfgs failed to converge. Increase the number "
718 "of iterations.")
719 try:
720 n_iter_i = info['nit'] - 1
721 except:
722 n_iter_i = info['funcalls'] - 1
723 elif solver == 'newton-cg':
724 args = (X, target, 1. / C, sample_weight)
725 w0, n_iter_i = newton_cg(hess, func, grad, w0, args=args,
726 maxiter=max_iter, tol=tol)
727 elif solver == 'liblinear':
728 coef_, intercept_, n_iter_i, = _fit_liblinear(
729 X, target, C, fit_intercept, intercept_scaling, None,
730 penalty, dual, verbose, max_iter, tol, random_state,
731 sample_weight=sample_weight)
732 if fit_intercept:
733 w0 = np.concatenate([coef_.ravel(), intercept_])
734 else:
735 w0 = coef_.ravel()
736
737 elif solver == 'sag':
738 if multi_class == 'multinomial':
739 target = target.astype(np.float64)
740 loss = 'multinomial'
741 else:
742 loss = 'log'
743
744 w0, n_iter_i, warm_start_sag = sag_solver(
745 X, target, sample_weight, loss, 1. / C, max_iter, tol,
746 verbose, random_state, False, max_squared_sum, warm_start_sag)
```
### 2. 损失函数
#### 2.1 二分类
二分类的损失函数和导数由`_logistic_loss_and_grad`实现,运算逻辑和[逻辑回归算法简介和Python实现](./demo.ipynb)是相同的,不多说。
#### 2.2 多分类
sklearn的多分类支持ovr (one vs rest,一对多)和multinominal两种方式。
##### 2.2.0 ovr
默认是ovr,它会对毎个标签训练一个二分类的分类器,即总共$K$个。训练代码在
```python
1230 fold_coefs_ = Parallel(n_jobs=self.n_jobs, verbose=self.verbose,
1231 backend=backend)(
1232 path_func(X, y, pos_class=class_, Cs=[self.C],
1233 fit_intercept=self.fit_intercept, tol=self.tol,
1234 verbose=self.verbose, solver=self.solver, copy=False,
1235 multi_class=self.multi_class, max_iter=self.max_iter,
1236 class_weight=self.class_weight, check_input=False,
1237 random_state=self.random_state, coef=warm_start_coef_,
1238 max_squared_sum=max_squared_sum,
1239 sample_weight=sample_weight)
1240 for (class_, warm_start_coef_) in zip(classes_, warm_start_coef))
```
注意,1240L的`for class_ in classes`配合1232L的`pos_class=class`,就是逐个取标签来训练的逻辑。
##### 2.2.1 multinominal
前面讲到ovr会遍历标签,逐个训练。为了兼容这段逻辑,真正的二分类问题需要做变化:
```python
1201 if len(self.classes_) == 2:
1202 n_classes = 1
1203 classes_ = classes_[1:]
```
同样地,multinominal需要一次对全部标签做处理,也需要做变化:
```python
1217 # Hack so that we iterate only once for the multinomial case.
1218 if self.multi_class == 'multinomial':
1219 classes_ = [None]
1220 warm_start_coef = [warm_start_coef]
```
好,接下来,我们看multinoinal的损失函数和导数计算代码,它是`_multinomial_loss_grad`这个函数。
sklearn里多分类的代码使用的公式和[逻辑回归算法简介和Python实现](./demo.ipynb)里一致,即:
\begin{align}
L(\beta) &= \log(\sum_i e^{\beta_{i0} + \beta_i x)}) - (\beta_{k0} + \beta_k x) \\
\frac{\partial L}{\partial \beta} &= x \left ( \frac{e^{\beta_{k0} + \beta_k x}}{\sum_i e^{\beta_{i0} + \beta_i x}} - I(y = k) \right ) \\
\end{align}
具体到损失函数:
```python
244 def _multinomial_loss(w, X, Y, alpha, sample_weight):
245 #+-- 37 lines: """Computes multinomial loss and class probabilities.---
282 n_classes = Y.shape[1]
283 n_features = X.shape[1]
284 fit_intercept = w.size == (n_classes * (n_features + 1))
285 w = w.reshape(n_classes, -1)
286 sample_weight = sample_weight[:, np.newaxis]
287 if fit_intercept:
288 intercept = w[:, -1]
289 w = w[:, :-1]
290 else:
291 intercept = 0
292 p = safe_sparse_dot(X, w.T)
293 p += intercept
294 p -= logsumexp(p, axis=1)[:, np.newaxis]
295 loss = -(sample_weight * Y * p).sum()
296 loss += 0.5 * alpha * squared_norm(w)
297 p = np.exp(p, p)
298 return loss, p, w
```
+ 292L-293L是计算$\beta_{i0} + \beta_i x$。
+ 294L是计算 $L(\beta)$。注意,这里防止计算溢出,是在`logsumexp`函数里作的,原理和[逻辑回归在spark中的实现简介](./spark_ml_lr.ipynb)一样。
+ 295L是加总(注意,$Y$毎列是单位向量,所以起了选标签对应$k$的作用)。
+ 296L加上L2正则。
+ 注意,297L是p变回了$\frac{e^{\beta_{k0} + \beta_k x}}{\sum_i e^{\beta_{i0} + \beta_i x}}$,为了计算导数时直接用。
好,再看导数的计算:
```python
301 def _multinomial_loss_grad(w, X, Y, alpha, sample_weight):
302 #+-- 37 lines: """Computes the multinomial loss, gradient and class probabilities.---
339 n_classes = Y.shape[1]
340 n_features = X.shape[1]
341 fit_intercept = (w.size == n_classes * (n_features + 1))
342 grad = np.zeros((n_classes, n_features + bool(fit_intercept)))
343 loss, p, w = _multinomial_loss(w, X, Y, alpha, sample_weight)
344 sample_weight = sample_weight[:, np.newaxis]
345 diff = sample_weight * (p - Y)
346 grad[:, :n_features] = safe_sparse_dot(diff.T, X)
347 grad[:, :n_features] += alpha * w
348 if fit_intercept:
349 grad[:, -1] = diff.sum(axis=0)
350 return loss, grad.ravel(), p
```
+ 345L-346L,对应了导数的计算式;
+ 347L是加上L2的导数;
+ 348L-349L,是对intercept的计算。
#### 2.3 Hessian
注意,sklearn支持牛顿法,需要用到Hessian阵,定义见维基[Hessian matrix](https://en.wikipedia.org/wiki/Hessian_matrix),
\begin{equation}
{\mathbf H}={\begin{bmatrix}{\dfrac {\partial ^{2}f}{\partial x_{1}^{2}}}&{\dfrac {\partial ^{2}f}{\partial x_{1}\,\partial x_{2}}}&\cdots &{\dfrac {\partial ^{2}f}{\partial x_{1}\,\partial x_{n}}}\\[2.2ex]{\dfrac {\partial ^{2}f}{\partial x_{2}\,\partial x_{1}}}&{\dfrac {\partial ^{2}f}{\partial x_{2}^{2}}}&\cdots &{\dfrac {\partial ^{2}f}{\partial x_{2}\,\partial x_{n}}}\\[2.2ex]\vdots &\vdots &\ddots &\vdots \\[2.2ex]{\dfrac {\partial ^{2}f}{\partial x_{n}\,\partial x_{1}}}&{\dfrac {\partial ^{2}f}{\partial x_{n}\,\partial x_{2}}}&\cdots &{\dfrac {\partial ^{2}f}{\partial x_{n}^{2}}}\end{bmatrix}}.
\end{equation}
其实就是各点位的二阶偏导。具体推导就不写了,感兴趣可以看[Logistic Regression - Jia Li](http://sites.stat.psu.edu/~jiali/course/stat597e/notes2/logit.pdf)或[Logistic regression: a simple ANN Nando de Freitas](https://www.cs.ox.ac.uk/people/nando.defreitas/machinelearning/lecture6.pdf)。
基本公式是$\mathbf{H} = \mathbf{X}^T \operatorname{diag}(\pi_i (1 - \pi_i)) \mathbf{X}$,其中$\pi_i = \operatorname{sigm}(x_i \beta)$。
```python
167 def _logistic_grad_hess(w, X, y, alpha, sample_weight=None):
168 #+-- 33 lines: """Computes the gradient and the Hessian, in the case of a logistic loss.
201 w, c, yz = _intercept_dot(w, X, y)
202 #+-- 4 lines: if sample_weight is None:---------
206 z = expit(yz)
207 #+-- 8 lines: z0 = sample_weight * (z - 1) * y---
215 # The mat-vec product of the Hessian
216 d = sample_weight * z * (1 - z)
217 if sparse.issparse(X):
218 dX = safe_sparse_dot(sparse.dia_matrix((d, 0),
219 shape=(n_samples, n_samples)), X)
220 else:
221 # Precompute as much as possible
222 dX = d[:, np.newaxis] * X
223
224 if fit_intercept:
225 # Calculate the double derivative with respect to intercept
226 # In the case of sparse matrices this returns a matrix object.
227 dd_intercept = np.squeeze(np.array(dX.sum(axis=0)))
228
229 def Hs(s):
230 ret = np.empty_like(s)
231 ret[:n_features] = X.T.dot(dX.dot(s[:n_features]))
232 ret[:n_features] += alpha * s[:n_features]
233
234 # For the fit intercept case.
235 if fit_intercept:
236 ret[:n_features] += s[-1] * dd_intercept
237 ret[-1] = dd_intercept.dot(s[:n_features])
238 ret[-1] += d.sum() * s[-1]
239 return ret
240
241 return grad, Hs
```
+ 201L, 206L, 和216L是计算中间的$\pi_i (1 - \pi_i)$。
+ 217L-222L,对中间参数变为对角阵后,预算公式后半部份,配合231L就是整个式子了。
这里我也只知其然,以后有时间再深挖下吧。
### 3. 小结
本文简单介绍了sklearn中逻辑回归的实现,包括二分类和多分类的具体代码和公式对应。
|
github_jupyter
|
# Basic functionality tests.
If the notebook cells complete with no exception the tests have passed.
The tests must be run in the full `jupyter notebook` or `jupyter lab` environment.
*Note:* I couldn't figure out to make the validation tests run correctly
at top level cell evaluation using `Run all`
because the widgets initialize after later cells have executed, causing spurious
failures. Consequently the automated validation steps involve an extra round trip using
a widget at the bottom of the notebook which is guaranteed to render last.
```
# Some test artifacts used below:
import jp_proxy_widget
from jp_proxy_widget import notebook_test_helpers
validators = notebook_test_helpers.ValidationSuite()
import time
class PythonClass:
class_attribute = "initial class attribute value"
def __init__(self):
self.set_instance_attribute("initial instance attribute value")
def set_instance_attribute(self, value):
self.instance_attribute = value
@classmethod
def set_class_attribute(cls, value):
cls.class_attribute = value
notebook_test_helpers
jp_proxy_widget
python_instance = PythonClass()
def python_function(value1, value2):
python_instance.new_attribute = "value1=%s and value2=%s" % (value1, value2)
```
# pong: test that a proxy widget can call back to Python
```
import jp_proxy_widget
pong = jp_proxy_widget.JSProxyWidget()
def validate_pong():
# check that the Python callbacks were called.
assert python_instance.instance_attribute == "instance"
assert PythonClass.class_attribute == "class"
assert python_instance.new_attribute == 'value1=1 and value2=3'
assert pong.error_msg == 'No error'
print ("pong says", pong.error_msg)
print ("Pong callback test succeeded!")
pong.js_init("""
//debugger;
instance_method("instance");
class_method("class");
python_function(1, 3);
element.html("<b>Callback test widget: nothing interesting to see here</b>")
//validate()
""",
instance_method=python_instance.set_instance_attribute,
class_method=PythonClass.set_class_attribute,
python_function=python_function,
#validate=validate_pong
)
#widget_validator_list.append([pong, validate_pong])
validators.add_validation(pong, validate_pong)
#pong.debugging_display()
pong
# set the mainloop check to True if running cells one at a time
mainloop_check = False
if mainloop_check:
# At this time this fails on "run all"
validate_pong()
```
# pingpong: test that Python can call in to a widget
... use a widget callback to pass the value back
```
pingpong_list = "just some strings".split()
def pingpong_python_fn(argument1, argument2):
print("called pingpong_python_fn") # this print goes nowhere?
pingpong_list[:] = [argument1, argument2]
def validate_pingpong():
# check that the callback got the right values
assert pingpong_list == ["testing", 123]
print ("ping pong test callback got ", pingpong_list)
print ("ping pong test succeeded!")
pingpong = jp_proxy_widget.JSProxyWidget()
pingpong.js_init("""
element.html("<em>Ping pong test -- no call yet.</em>")
element.call_in_to_the_widget = function (argument1, argument2) {
element.html("<b> Call in sent " + argument1 + " and " + argument2 + "</b>")
call_back_to_python(argument1, argument2);
}
element.validate = validate;
""", call_back_to_python=pingpong_python_fn, validate=validate_pingpong)
#widget_validator_list.append([pingpong, validate_pingpong])
validators.add_validation(pingpong, validate_pingpong)
#pingpong.debugging_display()
pingpong
# call in to javascript
pingpong.element.call_in_to_the_widget("testing", 123)
# call in to javascript and back to python to validate
pingpong.element.validate()
if mainloop_check:
validate_pingpong()
```
# roundtrip: datatype round trip
Test that values can be passed in to the proxy widget and back out again.
```
binary = bytearray(b"\x12\xff binary bytes")
string_value = "just a string"
int_value = -123
float_value = 45.6
json_dictionary = {"keys": None, "must": 321, "be": [6, 12], "strings": "values", "can": ["be", "any json"]}
list_value = [9, string_value, json_dictionary]
roundtrip_got_values = []
from jp_proxy_widget import hex_codec
from pprint import pprint
def get_values_back(binary, string_value, int_value, float_value, json_dictionary, list_value):
# NOTE: binary values must be converted explicitly from hex string encoding!
binary = hex_codec.hex_to_bytearray(binary)
roundtrip_got_values[:] = [binary, string_value, int_value, float_value, json_dictionary, list_value]
print ("GOT VALUES BACK")
pprint(roundtrip_got_values)
roundtrip_names = "binary string_value int_value float_value json_dictionary list_value".split()
def validate_roundtrip():
#assert roundtrip_got_values == [string_value, int_value, float_value, json_dictionary, list_value]
expected_values = [binary, string_value, int_value, float_value, json_dictionary, list_value]
if len(expected_values) != len(roundtrip_got_values):
print ("bad lengths", len(expected_values), len(roundtrip_got_values))
pprint(expected_values)
pprint(roundtrip_got_values)
assert len(expected_values) == len(roundtrip_got_values)
for (name, got, expected) in zip(roundtrip_names, roundtrip_got_values, expected_values):
if (got != expected):
print(name, "BAD MATCH got")
pprint(got)
print(" ... expected")
pprint(expected)
assert got == expected, "values don't match: " + repr((name, got, expected))
print ("roundtrip values match!")
roundtrip = jp_proxy_widget.JSProxyWidget()
roundtrip.js_init(r"""
element.all_values = [binary, string_value, int_value, float_value, json_dictionary, list_value];
html = ["<pre> Binary values sent as bytearrays appear in Javascript as Uint8Arrays"]
for (var i=0; i<names.length; i++) {
html.push(names[i]);
var v = element.all_values[i];
if (v instanceof Uint8Array) {
html.push(" Uint8Array")
} else {
html.push(" type: " + (typeof v))
}
html.push(" value: " + v);
}
html.push("</pre>");
element.html(html.join("\n"));
// send the values back
callback(binary, string_value, int_value, float_value, json_dictionary, list_value);
""",
binary=binary,
string_value=string_value,
int_value=int_value,
float_value=float_value,
json_dictionary=json_dictionary,
list_value=list_value,
names=roundtrip_names,
callback=get_values_back,
# NOTE: must up the callable level!
callable_level=4
)
roundtrip.debugging_display()
validators.add_validation(roundtrip, validate_roundtrip)
if mainloop_check:
validate_roundtrip()
#validate_roundtrip()
```
# loadCSS -- test load of simple CSS file.
We want to load this css file
```
from jp_proxy_widget import js_context
style_fn="js/simple.css"
print(js_context.get_text_from_file_name(style_fn))
loadCSS = jp_proxy_widget.JSProxyWidget()
# load the file
loadCSS.load_css(style_fn)
# callback for storing the styled element color
loadCSSstyle = {}
def color_callback(color):
loadCSSstyle["color"] = color
# initialize the element using the style and callback to report the color.
loadCSS.js_init("""
element.html('<div><em class="random-style-for-testing" id="loadCSSelement">Styled widget element.</em></div>')
var e = document.getElementById("loadCSSelement");
var style = window.getComputedStyle(e);
color_callback(style["color"]);
""", color_callback=color_callback)
def validate_loadCSS():
expect = 'rgb(216, 50, 61)'
assert expect == loadCSSstyle["color"], repr((expect, loadCSSstyle))
print ("Loaded CSS color is correct!")
loadCSS
validators.add_validation(loadCSS, validate_loadCSS)
if mainloop_check:
validate_loadCSS()
```
# loadJS -- load a javascript file (once only per interpreter)
We want to load this javascript file:
```
js_fn="js/simple.js"
print(js_context.get_text_from_file_name(js_fn))
loadJS = jp_proxy_widget.JSProxyWidget()
# load the file
loadJS.load_js_files([js_fn], force=True)
# callback for storing the styled element color
loadJSinfo = {}
def answer_callback(answer):
loadJSinfo["answer"] = answer
loadJS.js_init("""
element.html('<b>The answer is ' + window.the_answer + '</b>')
answer_callback(window.the_answer);
""", answer_callback=answer_callback, js_fn=js_fn)
def validate_loadJS():
expect = 42
assert expect == loadJSinfo["answer"], repr((expect, loadJSinfo))
print ("Loaded JS value is correct!")
loadJS
validators.add_validation(loadJS, validate_loadJS)
if mainloop_check:
validate_loadJS()
loadJS.print_status()
delay_ms = 1000
validators.run_all_in_widget(delay_ms=delay_ms)
```
|
github_jupyter
|
# MNLI Diagnostic Example
## Setup
#### Install dependencies
```
%%capture
!git clone https://github.com/jiant-dev/jiant.git
%%capture
# This Colab notebook already has its CUDA-runtime compatible versions of torch and torchvision installed
!sed -e /"torch==1.5.0"/d -i jiant/requirements.txt
!sed -e /"torchvision==0.6.0"/d -i jiant/requirements.txt
!pip install -r jiant/requirements.txt
```
#### Download data
```
%%capture
# Download/preprocess MNLI and RTE data
!wget https://raw.githubusercontent.com/huggingface/transformers/master/utils/download_glue_data.py
!python download_glue_data.py \
--data_dir ./raw_data \
--tasks "MNLI,diagnostic"
!PYTHONPATH=/content/jiant python jiant/jiant/scripts/preproc/export_glue_data.py \
--input_base_path=./raw_data \
--output_base_path=./tasks/ \
--task_name_ls "mnli,glue_diagnostic"
```
## `jiant` Pipeline
```
import sys
sys.path.insert(0, "/content/jiant")
import jiant.proj.main.tokenize_and_cache as tokenize_and_cache
import jiant.proj.main.export_model as export_model
import jiant.proj.main.scripts.configurator as configurator
import jiant.proj.main.runscript as main_runscript
import jiant.shared.caching as caching
import jiant.utils.python.io as py_io
import jiant.utils.display as display
import os
import torch
```
#### Task config
```
# Write MNLI task config
py_io.write_json({
"task": "mnli",
"name": "mnli",
"paths": {
"train": "/content/tasks/data/mnli/train.jsonl",
"val": "/content/tasks/data/mnli/val.jsonl",
},
}, path="./tasks/configs/mnli_config.json")
# Write MNLI-mismatched task config
py_io.write_json({
"task": "mnli",
"name": "mnli_mismatched",
"paths": {
"val": "/content/tasks/data/mnli/val_mismatched.jsonl",
},
}, path="./tasks/configs/mnli_mismatched_config.json")
# Write GLUE diagnostic task config
py_io.write_json({
"task": "glue_diagnostics",
"name": "glue_diagnostics",
"paths": {
"test": "/content/tasks/data/glue_diagnostics/test.jsonl",
},
}, path="./tasks/configs/glue_diagnostics_config.json")
```
#### Download model
```
export_model.lookup_and_export_model(
model_type="roberta-base",
output_base_path="./models/roberta-base",
)
```
#### Tokenize and cache
```
# Tokenize and cache each task
tokenize_and_cache.main(tokenize_and_cache.RunConfiguration(
task_config_path=f"./tasks/configs/mnli_config.json",
model_type="roberta-base",
model_tokenizer_path="./models/roberta-base/tokenizer",
output_dir=f"./cache/mnli",
phases=["train", "val"],
))
tokenize_and_cache.main(tokenize_and_cache.RunConfiguration(
task_config_path=f"./tasks/configs/mnli_mismatched_config.json",
model_type="roberta-base",
model_tokenizer_path="./models/roberta-base/tokenizer",
output_dir=f"./cache/mnli_mismatched",
phases=["val"],
))
tokenize_and_cache.main(tokenize_and_cache.RunConfiguration(
task_config_path=f"./tasks/configs/glue_diagnostics_config.json",
model_type="roberta-base",
model_tokenizer_path="./models/roberta-base/tokenizer",
output_dir=f"./cache/glue_diagnostics",
phases=["test"],
))
row = caching.ChunkedFilesDataCache("./cache/mnli/train").load_chunk(0)[0]["data_row"]
print(row.input_ids)
print(row.tokens)
row = caching.ChunkedFilesDataCache("./cache/mnli_mismatched/val").load_chunk(0)[0]["data_row"]
print(row.input_ids)
print(row.tokens)
row = caching.ChunkedFilesDataCache("./cache/glue_diagnostics/test").load_chunk(0)[0]["data_row"]
print(row.input_ids)
print(row.tokens)
```
#### Writing a run config
```
jiant_run_config = configurator.SimpleAPIMultiTaskConfigurator(
task_config_base_path="./tasks/configs",
task_cache_base_path="./cache",
train_task_name_list=["mnli"],
val_task_name_list=["mnli", "mnli_mismatched"],
test_task_name_list=["glue_diagnostics"],
train_batch_size=8,
eval_batch_size=16,
epochs=0.1,
num_gpus=1,
).create_config()
display.show_json(jiant_run_config)
```
Configure all three tasks to use an `mnli` head.
```
jiant_run_config["taskmodels_config"]["task_to_taskmodel_map"] = {
"mnli": "mnli",
"mnli_mismatched": "mnli",
"glue_diagnostics": "glue_diagnostics",
}
os.makedirs("./run_configs/", exist_ok=True)
py_io.write_json(jiant_run_config, "./run_configs/jiant_run_config.json")
```
#### Start training
```
run_args = main_runscript.RunConfiguration(
jiant_task_container_config_path="./run_configs/jiant_run_config.json",
output_dir="./runs/run1",
model_type="roberta-base",
model_path="./models/roberta-base/model/roberta-base.p",
model_config_path="./models/roberta-base/model/roberta-base.json",
model_tokenizer_path="./models/roberta-base/tokenizer",
learning_rate=1e-5,
eval_every_steps=500,
do_train=True,
do_val=True,
do_save=True,
write_test_preds=True,
force_overwrite=True,
)
main_runscript.run_loop(run_args)
test_preds = torch.load("./runs/run1/test_preds.p")
test_preds["glue_diagnostics"]
```
|
github_jupyter
|
## 範例重點
* 學習如何在 keras 中加入 EarlyStop
* 知道如何設定監控目標
* 比較有無 earlystopping 對 validation 的影響
```
import os
from tensorflow import keras
# 本範例不需使用 GPU, 將 GPU 設定為 "無"
os.environ["CUDA_VISIBLE_DEVICES"] = "0"
train, test = keras.datasets.cifar10.load_data()
## 資料前處理
def preproc_x(x, flatten=True):
x = x / 255.
if flatten:
x = x.reshape((len(x), -1))
return x
def preproc_y(y, num_classes=10):
if y.shape[-1] == 1:
y = keras.utils.to_categorical(y, num_classes)
return y
x_train, y_train = train
x_test, y_test = test
# 資料前處理 - X 標準化
x_train = preproc_x(x_train)
x_test = preproc_x(x_test)
# 資料前處理 -Y 轉成 onehot
y_train = preproc_y(y_train)
y_test = preproc_y(y_test)
from tensorflow.keras.layers import BatchNormalization
"""
建立神經網路,並加入 BN layer
"""
def build_mlp(input_shape, output_units=10, num_neurons=[256, 128, 64]):
input_layer = keras.layers.Input(input_shape)
for i, n_units in enumerate(num_neurons):
if i == 0:
x = keras.layers.Dense(units=n_units,
activation="relu",
name="hidden_layer"+str(i+1))(input_layer)
x = BatchNormalization()(x)
else:
x = keras.layers.Dense(units=n_units,
activation="relu",
name="hidden_layer"+str(i+1))(x)
x = BatchNormalization()(x)
out = keras.layers.Dense(units=output_units, activation="softmax", name="output")(x)
model = keras.models.Model(inputs=[input_layer], outputs=[out])
return model
## 超參數設定
LEARNING_RATE = 1e-3
EPOCHS = 50
BATCH_SIZE = 1024
MOMENTUM = 0.95
"""
# 載入 Callbacks, 並將 monitor 設定為監控 validation loss
"""
from tensorflow.keras.callbacks import EarlyStopping
earlystop = EarlyStopping(monitor="val_loss",
patience=5,
verbose=1
)
model = build_mlp(input_shape=x_train.shape[1:])
model.summary()
optimizer = keras.optimizers.SGD(lr=LEARNING_RATE, nesterov=True, momentum=MOMENTUM)
model.compile(loss="categorical_crossentropy", metrics=["accuracy"], optimizer=optimizer)
model.fit(x_train, y_train,
epochs=EPOCHS,
batch_size=BATCH_SIZE,
validation_data=(x_test, y_test),
shuffle=True,
callbacks=[earlystop]
)
# Collect results
train_loss = model.history.history["loss"]
valid_loss = model.history.history["val_loss"]
train_acc = model.history.history["accuracy"]
valid_acc = model.history.history["val_accuracy"]
import matplotlib.pyplot as plt
%matplotlib inline
plt.plot(range(len(train_loss)), train_loss, label="train loss")
plt.plot(range(len(valid_loss)), valid_loss, label="valid loss")
plt.legend()
plt.title("Loss")
plt.show()
plt.plot(range(len(train_acc)), train_acc, label="train accuracy")
plt.plot(range(len(valid_acc)), valid_acc, label="valid accuracy")
plt.legend()
plt.title("Accuracy")
plt.show()
```
## Work
1. 試改變 monitor "Validation Accuracy" 並比較結果
2. 調整 earlystop 的等待次數至 10, 25 並比較結果
|
github_jupyter
|
# Binary Classifier on Single records
### Most basic example.
This notebook will show how to set-up learning features (i.e. fields we want to use for modeling) and read them from a CSV file. Then create a very simple feed-forward Neural Net to classify fraud vs. non-fraud, train the model and test it.
Throughout these notebooks we will not explain how Neural Nets work, which loss functions exists, how NN's are optimized, what stochastic gradient decent is etc... There are some excellent resources online which do this in great detail.
#### The math
One thing we will quickly do is recap what a FeedForward (aka Linear Layer) is, just to build some intuition and to contrast this with other layers which will be explained later.
Linear Layers are often presented as shown below on the left, basically as weights that connect one layer to the next. Each node in the second layer is a weighted sum of the input values to which a bias term is added. So for nodes $h_j$ for h=1->3; $h_j= (\sum_{i=1}^4 x_i*w_{ij})+\beta_{j}$.
If we look more in detail what happens on the right hand size we see that for a single node we effectively take the weighted sum, add a bias and then perform an activation function. The activation is needed so the model can learn non-linearity. If all NN's did was stacking linear operations, the end-result would be a linear combination of the input, ideally we would want models to learn more complex relations, non-linear activations enable that. In most DeepLearning cases the `ReLU` function is used for activation.
Taking the weighted sum on a large scale for multiple nodes in one go, is nothing more or less than taking matrix dot-product. Same for adding the bias, that is just a matrix element wise addition. Another way of looking at this is considering the input __I__ to be a vector of size (1,4) and the hidden layer __H__ a vector of size (1,3), if we set-up a weight matrix __W__ of size (4,3), and a bias vector __$\beta$__ of size (1,3) then $H = act(I \odot W + \beta)$. The dot product of the input array with the weight matrix plus a bias vector which is then 'activated'
The hidden layer would typically be connected to a next layer, and a next and a next... until we get to an output layer. The formula for the output $O$ would thus be something like; $O = act(act(act(I \odot W_1 + \beta_1) \odot W_2 + \beta_2) \odot W_3 + \beta_3)$ if we had 3 hidden layers.

#### The Intuition
We can think of the __dot products and weights__ as taking bit of each input and combining that into a __hidden__ 'feature'. For instance if $X_1$ indicates 'age' category *elder* and $X_4$ indicates 'gender' *male*. If the inputs are 0 and 1 for yes/no, then using a positive weight $w_1$ and $w_4$ and 0 for the other weights, then we'd have a feature which 'activates' for an elder male customer.
We can think of the __bias__ as setting a minimal barrier or a reinforcement of the feature. For instance in above feature if we wanted our *elder male* hidden feature to only activate as it reaches .7 we could add a -.7 bias. If we wanted the feature to activate easier, we could add a positive bias.
Our Neural Nets will learn which weights and biases work best in order to solve a specific task. In Feedforward NN's they are the *'learnable'* parameters
---
#### Note on the data set
The data set used here is not particularly complex and/or big. It's not really all that challenging to find the fraud. In an ideal world we'd be using more complex data sets to show the real power of Deep Learning. There are a bunch of PCA'ed data sets available, but the PCA obfuscates some of the elements that are useful.
*These examples are meant to show the possibilities, it's not so useful to interpret their performance on this data set*
## Imports
```
import torch
import numpy as np
import gc
import d373c7.features as ft
import d373c7.engines as en
import d373c7.pytorch as pt
import d373c7.pytorch.models as pm
import d373c7.plot as pl
```
## Set a random seed for Numpy and Torch
> Will make sure we always sample in the same way. Makes it easier to compare results. At some point it should been removed to test the model stability.
```
# Numpy
np.random.seed(42)
# Torch
torch.manual_seed(42)
torch.backends.cudnn.deterministic = True
torch.backends.cudnn.benchmark = False
```
## Define base feature and read the File
The base features are features found in the input file.
Below code snipped follows a structure we'll see a lot.
- First we define features, these are fields we'll want to use. In this case we're defining 'Source' features, features that are in the data source, here the file. As parameters we provide the name as found in the first row of the file and a type.
- Then we bundle them in a `TensorDefinition`, this is essentially a group of features. We give it a name and list of features as input.
- Lastly we set up and engine of type `EnginePandasNumpy` and call the `from_csv` method with the TensorDefinition and the `file` name. This `from_csv` method will read the file and return a Pandas DataFrame object. The `inference` parameter specifies that we are in training mode, so any stats the feature needs to use will be gathered.
All this will return a Pandas DataFrame with __594643 rows__ (the number of transactions) and __6 columns__ (the number of features we defined), it can be use to perform basic data analysis.
```
# Change this to read from another location
file = '../../../../data/bs140513_032310.csv'
age = ft.FeatureSource('age', ft.FEATURE_TYPE_CATEGORICAL)
gender = ft.FeatureSource('gender', ft.FEATURE_TYPE_CATEGORICAL)
merchant = ft.FeatureSource('merchant', ft.FEATURE_TYPE_CATEGORICAL)
category = ft.FeatureSource('category', ft.FEATURE_TYPE_CATEGORICAL)
amount = ft.FeatureSource('amount', ft.FEATURE_TYPE_FLOAT)
fraud = ft.FeatureSource('fraud', ft.FEATURE_TYPE_INT_8)
base_features = ft.TensorDefinition(
'base',
[
age,
gender,
merchant,
category,
amount,
fraud
])
with en.EnginePandasNumpy() as e:
df = e.from_csv(base_features, file, inference=False)
df
```
## Define some derived features
After we've defined and read the source features, we can define some __derived__ features. Derived features apply a form of transformation to the source features, depending on the type of feature.
In this example 3 transformations are used;
- `FeatureNormalizeScale` The amount is scaled between 0 and 1.
- `FeatureOneHot` The categorical features are turned into one-hot encoded fields.
- `FeatureLabelBinary` The Fraud field is marked as Label. This is not really a transformation, it's just so the model knows which label to use.
We apply above transformations because Neural Nets prefer data that is in Binary ranges 0->1 or normally distributed
This will create a total of 78 features we can use in the model. We create a second list with the label.
```
amount_scale = ft.FeatureNormalizeScale('amount_scale', ft.FEATURE_TYPE_FLOAT_32, amount)
age_oh = ft.FeatureOneHot('age_one_hot', ft.FEATURE_TYPE_INT_8, age)
gender_oh = ft.FeatureOneHot('gender_one_hot', ft.FEATURE_TYPE_INT_8, gender)
merchant_oh = ft.FeatureOneHot('merchant_one_hot', ft.FEATURE_TYPE_INT_8, merchant)
category_oh = ft.FeatureOneHot('category_one_hot', ft.FEATURE_TYPE_INT_8, category)
fraud_label = ft.FeatureLabelBinary('fraud_label', ft.FEATURE_TYPE_INT_8, fraud)
features = ft.TensorDefinition(
'features',
[
age_oh,
gender_oh,
merchant_oh,
category_oh,
amount_scale,
])
label = ft.TensorDefinition('label', [fraud_label])
model_features = ft.TensorDefinitionMulti([features, label])
with en.EnginePandasNumpy() as e:
ft = e.from_csv(features, file, inference=False)
lb = e.from_csv(label, file, inference=False)
ft
lb
```
## Convert to Numpy
Now we convert the panda DataFrame to a list of Numpy arrays (which can be used for training). The `NumpyList` will have an entry for each of the Learning types. It will split out the *Binary*, *Continuous*, *Categorical* and *Label* Learning type __features__. Each Learning type will have a list entry in the `NumpyList` object
This step is needed so the models understand how to use the various features in the learning and testing processes.
In this case we have a first list with 77 binary (one-hot-endoded) features, the second is a list with 1 continuous feature (the amount) and the last list is the label (Fraud or Non-Fraud).
```
with en.EnginePandasNumpy() as e:
ft_np = e.to_numpy_list(features, ft)
lb_np = e.to_numpy_list(label, lb)
data_list = en.NumpyList(ft_np.lists + lb_np.lists)
print(data_list.shapes)
print(data_list.dtype_names)
```
## Wrangle the data
Time to split the data. For time series data it is very important to keep the order of the data. Below split will start from the end and work it's way to the front of the data. Doing so the training, validation and test data are nicely colocated in time. You almost *never* want to plain shuffle time based data.
> 1. Split out a test-set of size `test_records`. This is used for model testing.
> 2. Split out a validation-set of size `validation_records`. It will be used to monitor overfitting during training
> 3. All the rest is considered training data.
__Important__; please make sure the data is ordered in ascending fashion on a date(time) field. The split function does not order the data, it assumes the data is in the correct order.

```
test_records = 100000
val_records = 30000
train_data, val_data, test_data = data_list.split_time(val_records, test_records)
print(f'Training Data shapes {train_data.shapes}')
print(f'Validation Data shapes {val_data.shapes}')
print(f'Test Data shapes {test_data.shapes}')
del ft, lb
del ft_np, lb_np
del data_list
gc.collect()
print('Done')
```
## Set-up devices
```
device, cpu = pt.init_devices()
```
# Define Model
The training data set has to be balanced for Neural Nets. A balanced data set has a more or less equal amount of each class of the label. In our case fraud vs. non-fraud classes. Failing to balance the data can have dramatic results, Neural Nets are lazy, in extreme cases they might just plain always predict the majority class.
Fraud data-sets always have more non-fraud than fraud records. In this example the fraud class will be aggressively upsampled in the training phase by a custom `ClassSampler`. It oversamples the minority label until it matches the majority label in quantity. This may not be a good idea for a really large data sets.
> 1. First set-up a NumpyListDataSet for both the training data-set and validation data-set. A NumpyListDataSet is a specialized `Pytorch Dataset` which keeps the data as numpy arrays in memory and converts on the fly to `Pytorch Tensors`
> 2. Set-up a sampler for the training set only. The sampler will over-sample the '1'/fraud class. Note that this means the training and validation sets are balanced *differently*. This is important when interpreting the plots.
> 3. Wrap the dataset in a Pytorch Dataloader. `Dataloaders` allow the training loop to iterate over `Datasets`
> 4. Create a model. Here the most basic __GeneratedClassifier__ is used. __The GeneratedClassifier__ will create a model using the information it has about the features. *We are defining it to have 1 hidden layer of size 16*.
```
# Setup Pytorch Datasets for the training and validation
batch_size = 128
train_ds = pt.NumpyListDataSetMulti(model_features, train_data)
val_ds = pt.NumpyListDataSetMulti(model_features, val_data)
train_sampler = pt.ClassSamplerMulti(model_features, train_data).over_sampler()
# Wrap them in a Pytorch Dataloader
train_dl = train_ds.data_loader(cpu, batch_size, num_workers=2, sampler=train_sampler)
val_dl = val_ds.data_loader(cpu, batch_size, num_workers=2)
# Create a Model
m = pm.GeneratedClassifier(model_features, linear_layers=[16])
print(m)
```
The generated model consists of one stream -as there is one TensorDefinition containing modeling features-. That stream has a later of type __TensorDefinitionHead__ which will in this case just concatenate our *Binary* (77 one hot) and our Continuous (amount) features into a 78 shape tensor.
Which is consequently processed through the __Tail__. As we have a binary label, the tail is binary, it will process using the requested 16 size hidden layer and then output a final output layer of size 1. The output will be a score, ranging from 0 to 1 (because of the sigmoid), indicating the likelyhood of Fraud. The higher, the more certain the model is it bad.
Grapically this network looks like below (Some of the layers have been omitted for simplicity)

# Start Training
### First find a decent Learning Rate.
> Create a trainer and run the find_lr function and plot. This function iterates over the batches, gradually increasing the learning rate from a minimum to a maximum learning rate. It tends to show where we can find a good learning rate. In this case at around __3e-3__ we start a very steep decent. The model does not learn at lower than __1e-3__ learning rates. Beyond __1e-2__ it flattens out, stops learning at around __2e-2__ and explodes later. This exloding can be validate by running with a higher number of iteration and higher upper bound. A good learning rate is a location where the curve has a steep descent, but not too far down the curve. In this case around __5e-3__
```
t = pt.Trainer(m, device, train_dl, val_dl)
r = t.find_lr(1e-4, 1e-1, 200)
pl.TrainPlot().plot_lr(r)
```
## Start Training and plot the results
In our examples we will use a one_cycle logic. This is a training logic which starts at a learning rate lower than the specified learning rate, over the course of training works its way up to the specified learning rate and decreases again towards the end of the learning cycle. Proposed by [Leslie N. Smith, A DISCIPLINED APPROACH TO NEURAL NETWORK HYPER-PARAMETERS](https://arxiv.org/pdf/1803.09820.pdf)
> We train for __10 epochs__ and __learning rate 5e-3__. That means we run over the total training data set a total of 10 times/epochs where the model learns, after each epoch we use the trained model and perform a test run on the validation set.
> The result graph plots the accuracy and loss evolution at each Epoch for both the training and the validation set. We see the model behaves fairly well during training. The loss goes up slightly in the middle of the training. This is the one_cycle logic which is reaching the max learning rate.
```
t = pt.Trainer(m, device, train_dl, val_dl)
h = t.train_one_cycle(10, 5e-3)
pl.TrainPlot().plot_history(h, fig_size=(10,10))
```
## Test the model on the test data
> Test the model on the test set, it is data that was not seen during training and allows us to validate model results. This model behaves fairly OK. It is really good at catching the fraud. It has a fairly low False Negative rate. (Lower left corner of the Confusion Matrix). But it also has a fairly large False Positive rate (Upper right corner of the Confusion Matrix).
Some research would be needed but this is likely at least partially due to the oversampling. The model saw much more fraud during the training, so it might not be surprising it gets relatively good at predicting it.
```
test_ds = pt.NumpyListDataSetMulti(model_features, test_data)
test_dl = test_ds.data_loader(cpu, 128, num_workers=2)
ts = pt.Tester(m, device, test_dl)
pr = ts.test_plot()
tp = pl.TestPlot()
tp.print_classification_report(pr)
tp.plot_confusion_matrix(pr, fig_size=(6,6))
tp.plot_roc_curve(pr, fig_size=(6,6))
tp.plot_precision_recall_curve(pr, fig_size=(6,6))
```
# Conslusion
This is a first example that showed how we can read a file, set-up some features (fields), test and train a really simple Feed-Forward Neural Net model.
|
github_jupyter
|
```
%matplotlib inline
import os.path
import pprint
import pandas as pd
from gmprocess.io.asdf.stream_workspace import StreamWorkspace
from gmprocess.io.test_utils import read_data_dir
from gmprocess.io.read import read_data
from gmprocess.streamcollection import StreamCollection
from gmprocess.processing import process_streams
from gmprocess.event import get_event_object
from gmprocess.logging import setup_logger
# Only log errors; this suppresses many warnings that are
# distracting and not important.
setup_logger(level='error')
```
## Reading Data
We currently have a few different ways of reading in data. Here we use the `read_data_dir` helper function to quickly read streams and event (i.e., origin) information from the testing data in this repository.
```
datafiles, origin = read_data_dir('geonet', 'us1000778i', '*.V1A')
```
The read_data below finds the appropriate data reader for the format supplied.
```
tstreams = []
for dfile in datafiles:
tstreams += read_data(dfile)
```
Note that `tstreams` is just a list of StationStream objects:
```
print(type(tstreams))
print(type(tstreams[0]))
```
## gmprocess Subclasses of Obspy Classes
The `StationStream` class is a subclass of ObsPy's `Stream` class, which is effectively a list of `StationTrace` objects. The `StationTrace` class is, in turn, a subclass of ObsPy's `Trace` class. The motivation for these subclasses is primarily to enforce certain required metadata in the Trace stats dictionary (that ObsPy would generally store in their `Inventory` object).
We also have a `StreamCollection` class taht is effectively a list of `StationStream` objects, and enforces some rules that are required later for processing, such forcing all `StationTraces` in a `StationStream` be from the same network/station. The basic constructor for the StreamCollection class takes a list of streams:
```
sc = StreamCollection(tstreams)
```
The StreamCollection print method gives the number of StationStreams and the number that have passed/failed processing checks. Since we have not done any processing, all StationStreams should pass checks.
```
print(sc)
```
More detailed information about the StreamCollection is given by the `describe` method:
```
sc.describe()
```
## Processing
Note that processing options can be controlled in a config file that is installed in the user's home directory (`~/.gmprocess/config.yml`) and that event/origin information is required for processing:
```
pprint.pprint(origin)
sc_processed = process_streams(sc, origin)
print(sc_processed)
```
Note that all checks have passed. When a stream does not pass a check, it is not deleted, but marked as failed and subsequent processing is aborted.
Processing steps are recorded according to the SEIS-PROV standard for each StationTrace. We log this information as a list of dictionaries, where each dictionary has keys `prov_id` and `prov_attributes`. This can be retrieved from each traces with the `getAllProvenance` method:
```
pprint.pprint(sc_processed[0][0].getAllProvenance())
```
## Workspace
We use the ASDF format as a 'workspace' for saving data and metadata at all stages of processing/analysis.
```
outfile = os.path.join(os.path.expanduser('~'), 'geonet_test.hdf')
if os.path.isfile(outfile):
os.remove(outfile)
workspace = StreamWorkspace(outfile)
# create an ObsPy event object from our dictionary
event = get_event_object(origin)
# add the "raw" (GEONET actually pre-converts to gals) data
workspace.addStreams(event, sc, label='rawgeonet')
eventid = origin['id']
workspace.addStreams(event, sc_processed, label='processed')
```
## Creating and Retrieving Stream Metrics
Computation of metrics requires specifying a list of requested intensity measure types (IMTs) and intensity measure components (IMCs). Not all IMT-IMC combinations are currently supported and in those cases the code returns NaNs.
For real uses (not just demonstration) it is probably more convenient to specify these values through the config file, which allows for specifying response spectral periods and Fourier amplitude spectra periods as linear or logspaced arrays.
```
imclist = [
'greater_of_two_horizontals',
'channels',
'rotd50',
'rotd100'
]
imtlist = [
'sa1.0',
'PGA',
'pgv',
'fas2.0',
'arias'
]
workspace.setStreamMetrics(
eventid,
labels=['processed'],
imclist=imclist,
imtlist=imtlist
)
df = workspace.getMetricsTable(
eventid,
labels=['processed']
)
```
There are a lot of columns here, so we'll show them in sections:
```
pd.set_option('display.width', 1000)
print('ARIAS:')
print(df['ARIAS'])
print('\nSpectral Acceleration (1 second)')
print(df['SA(1.0)'])
print('\nFourier Amplitude Spectra (2 second)')
print(df['FAS(2.0)'])
print('\nPGA')
print(df['PGA'])
print('\nPGV')
print(df['PGV'])
print('\nStation Information:')
print(df[['STATION', 'NAME', 'LAT', 'LON', 'SOURCE', 'NETID']])
```
## Retrieving Streams
```
raw_hses = workspace.getStreams(
eventid,
stations=['hses'],
labels=['rawgeonet'])[0]
processed_hses = workspace.getStreams(
eventid,
stations=['hses'],
labels=['processed'])[0]
raw_hses.plot()
processed_hses.plot()
```
|
github_jupyter
|
# GMNS to AequilibraE example
## Inputs
1. Nodes as a .csv flat file in GMNS format
2. Links as a .csv flat file in GMNS format
3. Trips as a .csv flat file, with the following columns: orig_node, dest_node, trips
4. Sqlite database used by AequilibraE
## Steps
1. Read the GMNS nodes
- Place in SQLite database, then translate to AequilibraE nodes
- Generate the dictionary of zones for the omx trip table (uses node_type = centroid)
2. Read the GMNS links
- Place in SQLite database, then translate to AequilibraE links
3. Read the trips
- Translate into .omx file
A separate Jupyter notebook, Route, performs the following steps
4. Run AequilibraE shortest path and routing
5. Generate detail and summary outputs
```
#!/usr/bin/env python
# coding: utf-8
import os
import numpy as np
import pandas as pd
import sqlite3
#import shutil # needed?
import openmatrix as omx
import math
#run_folder = 'C:/Users/Scott.Smith/GMNS/Lima'
run_folder = 'C:/Users/Scott/Documents/Work/AE/Lima' #Change to match your local environment
#highest_centroid_node_number = 500 #we are now finding this from the nodes dataframe
```
## Read the nodes, and set up the dictionary of centroids
The dictionary of centroids is used later in setting up the omx trip table
```
#Read the nodes
node_csvfile = os.path.join(run_folder, 'GMNS_node.csv')
df_node = pd.read_csv(node_csvfile) #data already has headers
print(df_node.head()) #debugging
df_size = df_node.shape[0]
print(df_size)
# Set up the dictionary of centroids
# Assumption: the node_type = 'centroid' for centroid nodes
# The centroid nodes are the lowest numbered nodes, at the beginning of the list of nodes,
# but node numbers need not be consecutive
tazdictrow = {}
for index in df_node.index:
if df_node['node_type'][index]=='centroid':
#DEBUG print(index, df_node['node_id'][index], df_node['node_type'][index])
tazdictrow[df_node['node_id'][index]]=index
#tazdictrow = {1:0,2:1,3:2,4:3,...,492:447,493:448}
taz_list = list(tazdictrow.keys())
matrix_size = len(tazdictrow) #Matches the number of nodes flagged as centroids
print(matrix_size) #DEBUG
highest_centroid_node_number = max(tazdictrow, key=tazdictrow.get) #for future use
print(highest_centroid_node_number) #DEBUG
```
## Read the links
```
# Read the links
link_csvfile = os.path.join(run_folder, 'GMNS_link.csv')
df_link = pd.read_csv(link_csvfile) #data already has headers
#print(df_node.head()) #debugging
#df_size = df_link.shape[0]
print(df_link.shape[0]) #debug
```
## Put nodes and links into SQLite. Then translate to AequilibraE 0.6.5 format
1. Nodes are pushed into a table named GMNS_node
2. node table used by AequilibraE is truncated, then filled with values from GMNS_node
3. Centroid nodes are assumed to be the lowest numbered nodes, limited by the highest_centroid_node_number
- Number of centroid nodes must equal matrix_size, the size of the trip OMX Matrix
3. Links are pushed into a table named GMNS_link
4. link table used by AequilibraE is truncated, then filled with values from GMNS_link
### Some notes
1. All the nodes whole id is <= highest_centroid_node_number are set as centroids
2. GMNS capacity is in veh/hr/lane, AequilibraE is in veh/hr; hence, capacity * lanes in the insert statement
3. free_flow_time (minutes) is assumed to be 60 (minutes/hr) * length (miles) / free_speed (miles/hr)
```
#Open the Sqlite database, and insert the nodes and links
network_db = os.path.join(run_folder,'1_project','Lima.sqlite')
with sqlite3.connect(network_db) as db_con:
#nodes
df_node.to_sql('GMNS_node',db_con, if_exists='replace',index=False)
db_cur = db_con.cursor()
sql0 = "delete from nodes;"
db_cur.execute(sql0)
sql1 = ("insert into nodes(ogc_fid, node_id, x, y, is_centroid)" +
" SELECT node_id, node_id, x_coord,y_coord,0 from " +
" GMNS_node")
db_cur.execute(sql1)
sql2 = ("update nodes set is_centroid = 1 where ogc_fid <= " + str(highest_centroid_node_number))
db_cur.execute(sql2)
with sqlite3.connect(network_db) as db_con:
df_link.to_sql('GMNS_link',db_con, if_exists='replace',index=False)
db_cur = db_con.cursor()
sql0 = "delete from links;"
db_cur.execute(sql0)
sql1 = ("insert into links(ogc_fid, link_id, a_node, b_node, direction, distance, modes," +
" link_type, capacity_ab, speed_ab, free_flow_time) " +
" SELECT link_id, link_id, from_node_id, to_node_id, directed, length, allowed_uses," +
" facility_type, capacity*lanes, free_speed, 60*length / free_speed" +
" FROM GMNS_link where GMNS_link.capacity > 0")
db_cur.execute(sql1)
sql2 = ("update links set capacity_ba = 0, speed_ba = 0, b=0.15, power=4")
db_cur.execute(sql2)
```
Next step is to update the links with the parameters for the volume-delay function. This step is AequilibraE-specific and makes use of the link_types Sqlite table. This table is taken from v 0.7.1 of AequilibraE, to ease future compatibility. The link_types table expects at least one row with link_type = "default" to use for default values. The user may add other rows with the real link_types.
Its CREATE statement is as follows
```
CREATE TABLE 'link_types' (link_type VARCHAR UNIQUE NOT NULL PRIMARY KEY,
link_type_id VARCHAR UNIQUE NOT NULL,
description VARCHAR,
lanes NUMERIC,
lane_capacity NUMERIC,
alpha NUMERIC,
beta NUMERIC,
gamma NUMERIC,
delta NUMERIC,
epsilon NUMERIC,
zeta NUMERIC,
iota NUMERIC,
sigma NUMERIC,
phi NUMERIC,
tau NUMERIC)
```
| link_type | link_type_id | description | lanes | lane_capacity | alpha | beta | other fields not used |
| ----- | ----- | ----- | ----- | ----- |----- |----- |----- |
| default | 99 | Default general link type | 2 | 900 | 0.15 | 4 | |
```
with sqlite3.connect(network_db) as db_con:
db_cur = db_con.cursor()
sql1 = "update links set b = (select alpha from link_types where link_type = links.link_type)"
db_cur.execute(sql1)
sql2 = ("update links set b = (select alpha from link_types where link_type = 'default') where b is NULL")
db_cur.execute(sql2)
sql3 = "update links set power = (select beta from link_types where link_type = links.link_type)"
db_cur.execute(sql3)
sql4 = ("update links set power = (select beta from link_types where link_type = 'default') where power is NULL")
db_cur.execute(sql4)
```
## Read the trips, and translate to omx file
```
#Read a flat file trip table into pandas dataframe
trip_csvfile = os.path.join(run_folder, 'demand.csv')
df_trip = pd.read_csv(trip_csvfile) #data already has headers
print(df_trip.head()) #debugging
df_size = df_trip.shape[0]
print(df_size)
#print(df.iloc[50]['o_zone_id'])
#stuff for debugging
print(df_trip['total'].sum()) #for debugging: total number of trips
#for k in range(df_size): #at most matrix_size*matrix_size
# i = tazdictrow[df_trip.iloc[k]['orig_taz']]
# j = tazdictrow[df_trip.iloc[k]['dest_taz']]
# if k == 4: print(k," i=",i," j=",j) #debugging
#Write the dataframe to an omx file
# This makes use of tazdictrow and matrix_size, that was established earlier.
# The rows are also written to a file that is used only for debugging
outfile = os.path.join(run_folder, '0_tntp_data' ,'demand.omx')
outdebugfile = open(os.path.join(run_folder,'debug_demand.txt'),"w")
output_demand = np.zeros((matrix_size,matrix_size))
f_output = omx.open_file(outfile,'w')
f_output.create_mapping('taz',taz_list)
#write the data
for k in range(df_size): #at most matrix_size*matrix_size
i = tazdictrow[df_trip.iloc[k]['orig_taz']]
j = tazdictrow[df_trip.iloc[k]['dest_taz']]
output_demand[i][j] = df_trip.iloc[k]['total']
print('Row: ',df_trip.iloc[k]['orig_taz'],i," Col: ",df_trip.iloc[k]['dest_taz'],j," Output",output_demand[i][j],file=outdebugfile)
f_output['matrix'] = output_demand #puts the output_demand array into the omx matrix
f_output.close()
outdebugfile.close()
#You may stop here
# Not needed except for debugging
#Read the input omx trip table
infile = os.path.join(run_folder, '0_tntp_data' ,'demand.omx')
f_input = omx.open_file(infile)
m1 = f_input['matrix']
input_demand = np.array(m1)
print('Shape:',f_input.shape())
print('Number of tables',len(f_input))
print('Table names:',f_input.list_matrices())
print('attributes:',f_input.list_all_attributes())
print('sum of trips',np.sum(m1))
f_input.close()
```
|
github_jupyter
|
# Performance analysis of a uniform linear array
We compare the MSE of MUSIC with the CRB for a uniform linear array (ULA).
```
import numpy as np
import doatools.model as model
import doatools.estimation as estimation
import doatools.performance as perf
import matplotlib.pyplot as plt
%matplotlib inline
wavelength = 1.0 # normalized
d0 = wavelength / 2
# Create a 12-element ULA.
ula = model.UniformLinearArray(12, d0)
# Place 8 sources uniformly within (-pi/3, pi/4)
sources = model.FarField1DSourcePlacement(
np.linspace(-np.pi/3, np.pi/4, 8)
)
# All sources share the same power.
power_source = 1 # Normalized
source_signal = model.ComplexStochasticSignal(sources.size, power_source)
# 200 snapshots.
n_snapshots = 200
# We use root-MUSIC.
estimator = estimation.RootMUSIC1D(wavelength)
```
We vary the SNR from -20 dB to 20 dB. Here the SNR is defined as:
\begin{equation}
\mathrm{SNR} = 10\log_{10}\frac{\min_i p_i}{\sigma^2_{\mathrm{n}}},
\end{equation}
where $p_i$ is the power of the $i$-th source, and $\sigma^2_{\mathrm{n}}$ is the noise power.
```
snrs = np.linspace(-20, 10, 20)
# 300 Monte Carlo runs for each SNR
n_repeats = 300
mses = np.zeros((len(snrs),))
crbs_sto = np.zeros((len(snrs),))
crbs_det = np.zeros((len(snrs),))
crbs_stouc = np.zeros((len(snrs),))
for i, snr in enumerate(snrs):
power_noise = power_source / (10**(snr / 10))
noise_signal = model.ComplexStochasticSignal(ula.size, power_noise)
# The squared errors and the deterministic CRB varies
# for each run. We need to compute the average.
cur_mse = 0.0
cur_crb_det = 0.0
for r in range(n_repeats):
# Stochastic signal model.
A = ula.steering_matrix(sources, wavelength)
S = source_signal.emit(n_snapshots)
N = noise_signal.emit(n_snapshots)
Y = A @ S + N
Rs = (S @ S.conj().T) / n_snapshots
Ry = (Y @ Y.conj().T) / n_snapshots
resolved, estimates = estimator.estimate(Ry, sources.size, d0)
# In practice, you should check if `resolved` is true.
# We skip the check here.
cur_mse += np.mean((estimates.locations - sources.locations)**2)
B_det = perf.ecov_music_1d(ula, sources, wavelength, Rs, power_noise,
n_snapshots)
cur_crb_det += np.mean(np.diag(B_det))
# Update the results.
B_sto = perf.crb_sto_farfield_1d(ula, sources, wavelength, power_source,
power_noise, n_snapshots)
B_stouc = perf.crb_stouc_farfield_1d(ula, sources, wavelength, power_source,
power_noise, n_snapshots)
mses[i] = cur_mse / n_repeats
crbs_sto[i] = np.mean(np.diag(B_sto))
crbs_det[i] = cur_crb_det / n_repeats
crbs_stouc[i] = np.mean(np.diag(B_stouc))
print('Completed SNR = {0:.2f} dB'.format(snr))
```
We plot the results below.
* The MSE should approach the stochastic CRBs in high SNR regions.
* The stochastic CRB should be tighter than the deterministic CRB.
* With the additional assumption of uncorrelated sources, we expect a even lower CRB.
* All three CRBs should converge together as the SNR approaches infinity.
```
plt.figure(figsize=(8, 6))
plt.semilogy(
snrs, mses, '-x',
snrs, crbs_sto, '--',
snrs, crbs_det, '--',
snrs, crbs_stouc, '--'
)
plt.xlabel('SNR (dB)')
plt.ylabel(r'MSE / $\mathrm{rad}^2$')
plt.grid(True)
plt.legend(['MSE', 'Stochastic CRB', 'Deterministic CRB',
'Stochastic CRB (Uncorrelated)'])
plt.title('MSE vs. CRB')
plt.margins(x=0)
plt.show()
```
|
github_jupyter
|
##### Copyright 2018 The TensorFlow Authors.
```
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
```
# Customization basics: tensors and operations
<table class="tfo-notebook-buttons" align="left">
<td>
<a target="_blank" href="https://www.tensorflow.org/tutorials/customization/basics"><img src="https://www.tensorflow.org/images/tf_logo_32px.png" />View on TensorFlow.org</a>
</td>
<td>
<a target="_blank" href="https://colab.research.google.com/github/tensorflow/docs/blob/master/site/en/tutorials/customization/basics.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
</td>
<td>
<a target="_blank" href="https://github.com/tensorflow/docs/blob/master/site/en/tutorials/customization/basics.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View source on GitHub</a>
</td>
<td>
<a href="https://storage.googleapis.com/tensorflow_docs/docs/site/en/tutorials/customization/basics.ipynb"><img src="https://www.tensorflow.org/images/download_logo_32px.png" />Download notebook</a>
</td>
</table>
This is an introductory TensorFlow tutorial that shows how to:
* Import the required package
* Create and use tensors
* Use GPU acceleration
* Demonstrate `tf.data.Dataset`
```
from __future__ import absolute_import, division, print_function, unicode_literals
try:
# %tensorflow_version only exists in Colab.
%tensorflow_version 2.x
except Exception:
pass
```
## Import TensorFlow
To get started, import the `tensorflow` module. As of TensorFlow 2, eager execution is turned on by default. This enables a more interactive frontend to TensorFlow, the details of which we will discuss much later.
```
import tensorflow as tf
```
## Tensors
A Tensor is a multi-dimensional array. Similar to NumPy `ndarray` objects, `tf.Tensor` objects have a data type and a shape. Additionally, `tf.Tensor`s can reside in accelerator memory (like a GPU). TensorFlow offers a rich library of operations ([tf.add](https://www.tensorflow.org/api_docs/python/tf/add), [tf.matmul](https://www.tensorflow.org/api_docs/python/tf/matmul), [tf.linalg.inv](https://www.tensorflow.org/api_docs/python/tf/linalg/inv) etc.) that consume and produce `tf.Tensor`s. These operations automatically convert native Python types, for example:
```
print(tf.add(1, 2))
print(tf.add([1, 2], [3, 4]))
print(tf.square(5))
print(tf.reduce_sum([1, 2, 3]))
# Operator overloading is also supported
print(tf.square(2) + tf.square(3))
```
Each `tf.Tensor` has a shape and a datatype:
```
x = tf.matmul([[1]], [[2, 3]])
print(x)
print(x.shape)
print(x.dtype)
```
The most obvious differences between NumPy arrays and `tf.Tensor`s are:
1. Tensors can be backed by accelerator memory (like GPU, TPU).
2. Tensors are immutable.
### NumPy Compatibility
Converting between a TensorFlow `tf.Tensor`s and a NumPy `ndarray` is easy:
* TensorFlow operations automatically convert NumPy ndarrays to Tensors.
* NumPy operations automatically convert Tensors to NumPy ndarrays.
Tensors are explicitly converted to NumPy ndarrays using their `.numpy()` method. These conversions are typically cheap since the array and `tf.Tensor` share the underlying memory representation, if possible. However, sharing the underlying representation isn't always possible since the `tf.Tensor` may be hosted in GPU memory while NumPy arrays are always backed by host memory, and the conversion involves a copy from GPU to host memory.
```
import numpy as np
ndarray = np.ones([3, 3])
print("TensorFlow operations convert numpy arrays to Tensors automatically")
tensor = tf.multiply(ndarray, 42)
print(tensor)
print("And NumPy operations convert Tensors to numpy arrays automatically")
print(np.add(tensor, 1))
print("The .numpy() method explicitly converts a Tensor to a numpy array")
print(tensor.numpy())
```
## GPU acceleration
Many TensorFlow operations are accelerated using the GPU for computation. Without any annotations, TensorFlow automatically decides whether to use the GPU or CPU for an operation—copying the tensor between CPU and GPU memory, if necessary. Tensors produced by an operation are typically backed by the memory of the device on which the operation executed, for example:
```
x = tf.random.uniform([3, 3])
print("Is there a GPU available: "),
print(tf.config.experimental.list_physical_devices("GPU"))
print("Is the Tensor on GPU #0: "),
print(x.device.endswith('GPU:0'))
```
### Device Names
The `Tensor.device` property provides a fully qualified string name of the device hosting the contents of the tensor. This name encodes many details, such as an identifier of the network address of the host on which this program is executing and the device within that host. This is required for distributed execution of a TensorFlow program. The string ends with `GPU:<N>` if the tensor is placed on the `N`-th GPU on the host.
### Explicit Device Placement
In TensorFlow, *placement* refers to how individual operations are assigned (placed on) a device for execution. As mentioned, when there is no explicit guidance provided, TensorFlow automatically decides which device to execute an operation and copies tensors to that device, if needed. However, TensorFlow operations can be explicitly placed on specific devices using the `tf.device` context manager, for example:
```
import time
def time_matmul(x):
start = time.time()
for loop in range(10):
tf.matmul(x, x)
result = time.time()-start
print("10 loops: {:0.2f}ms".format(1000*result))
# Force execution on CPU
print("On CPU:")
with tf.device("CPU:0"):
x = tf.random.uniform([1000, 1000])
assert x.device.endswith("CPU:0")
time_matmul(x)
# Force execution on GPU #0 if available
if tf.config.experimental.list_physical_devices("GPU"):
print("On GPU:")
with tf.device("GPU:0"): # Or GPU:1 for the 2nd GPU, GPU:2 for the 3rd etc.
x = tf.random.uniform([1000, 1000])
assert x.device.endswith("GPU:0")
time_matmul(x)
```
## Datasets
This section uses the [`tf.data.Dataset` API](https://www.tensorflow.org/guide/datasets) to build a pipeline for feeding data to your model. The `tf.data.Dataset` API is used to build performant, complex input pipelines from simple, re-usable pieces that will feed your model's training or evaluation loops.
### Create a source `Dataset`
Create a *source* dataset using one of the factory functions like [`Dataset.from_tensors`](https://www.tensorflow.org/api_docs/python/tf/data/Dataset#from_tensors), [`Dataset.from_tensor_slices`](https://www.tensorflow.org/api_docs/python/tf/data/Dataset#from_tensor_slices), or using objects that read from files like [`TextLineDataset`](https://www.tensorflow.org/api_docs/python/tf/data/TextLineDataset) or [`TFRecordDataset`](https://www.tensorflow.org/api_docs/python/tf/data/TFRecordDataset). See the [TensorFlow Dataset guide](https://www.tensorflow.org/guide/datasets#reading_input_data) for more information.
```
ds_tensors = tf.data.Dataset.from_tensor_slices([1, 2, 3, 4, 5, 6])
# Create a CSV file
import tempfile
_, filename = tempfile.mkstemp()
with open(filename, 'w') as f:
f.write("""Line 1
Line 2
Line 3
""")
ds_file = tf.data.TextLineDataset(filename)
```
### Apply transformations
Use the transformations functions like [`map`](https://www.tensorflow.org/api_docs/python/tf/data/Dataset#map), [`batch`](https://www.tensorflow.org/api_docs/python/tf/data/Dataset#batch), and [`shuffle`](https://www.tensorflow.org/api_docs/python/tf/data/Dataset#shuffle) to apply transformations to dataset records.
```
ds_tensors = ds_tensors.map(tf.square).shuffle(2).batch(2)
ds_file = ds_file.batch(2)
```
### Iterate
`tf.data.Dataset` objects support iteration to loop over records:
```
print('Elements of ds_tensors:')
for x in ds_tensors:
print(x)
print('\nElements in ds_file:')
for x in ds_file:
print(x)
```
|
github_jupyter
|
# Fast Bernoulli: Benchmark Python
In this notebooks we will measure performance of generating sequencies of Bernoulli-distributed random varibales in Python without and within LLVM JIT compiler. The baseline generator is based on top of expression `random.uniform() < p`.
```
import numpy as np
import matplotlib.pyplot as plt
from random import random
from typing import List
from bernoulli import LLVMBernoulliGenerator, PyBernoulliGenerator
from tqdm import tqdm
```
## Benchmarking
As it was mentioned above, the baseline generator is just thresholding a uniform-distributed random variable.
```
class BaselineBernoulliGenerator:
def __init__(self, probability: float, tolerance: float = float('nan'), seed: int = None):
self.prob = probability
def __call__(self, nobits: int = 32):
return [int(random() <= self.prob) for _ in range(nobits)]
```
Here we define some routines for benchmarking.
```
def benchmark(cls, nobits_list: List[int], probs: List[float], tol: float = 1e-6) -> np.ndarray:
timings = np.empty((len(probs), len(nobits_list)))
with tqdm(total=timings.size, unit='bench') as progress:
for i, prob in enumerate(probs):
generator = cls(prob, tol)
for j, nobits in enumerate(nobits_list):
try:
timing = %timeit -q -o generator(nobits)
timings[i, j] = timing.average
except Exception as e:
# Here we catch the case when number of bits is not enough
# to obtain desirable precision.
timings[i, j] = float('nan')
progress.update()
return timings
```
The proposed Bernoulli generator has two parameters. The first one is well-known that is probability of success $p$. The second one is precision of quantization.
```
NOBITS = [1, 2, 4, 8, 16, 32]
PROBAS = [1 / 2 ** n for n in range(1, 8)]
```
Now, start benchmarking!
```
baseline = benchmark(BaselineBernoulliGenerator, NOBITS, PROBAS)
py = benchmark(PyBernoulliGenerator, NOBITS, PROBAS)
llvm = benchmark(LLVMBernoulliGenerator, NOBITS, PROBAS)
```
Multiplication by factor $10^6$ corresponds to changing units from seconds to microseconds.
```
baseline *= 1e6
py *= 1e6
llvm *= 1e6
```
Save timings for the future.
```
np.save('../data/benchmark-data-baseline.npy', baseline)
np.save('../data/benchmark-data-py.npy', py)
np.save('../data/benchmark-data-llvm.npy', llvm)
```
## Visualization
On the figures below we depics how timings (or bitrate) depends on algorithm parameters.
```
fig = plt.figure(figsize=(14, 6))
ax = fig.add_subplot(1, 1, 1)
ax.grid()
for i, proba in enumerate(PROBAS):
ax.loglog(NOBITS, baseline[i, :], '-x',label=f'baseline p={proba}')
ax.loglog(NOBITS, py[i, :], '-+',label=f'python p={proba}')
ax.loglog(NOBITS, llvm[i, :], '-o',label=f'llvm p={proba}')
ax.legend(loc='center left', bbox_to_anchor=(1, 0.5))
ax.set_xlabel('Sequence length, bit')
ax.set_ylabel('Click time, $\mu s$')
plt.show()
fig = plt.figure(figsize=(14, 6))
ax = fig.add_subplot(1, 1, 1)
ax.grid()
for i, proba in enumerate(PROBAS):
ax.loglog(NOBITS, NOBITS / baseline[i, :], '-x',label=f'baseline p={proba}')
ax.loglog(NOBITS, NOBITS / py[i, :], '-+',label=f'python p={proba}')
ax.loglog(NOBITS, NOBITS / llvm[i, :], '-o',label=f'llvm p={proba}')
ax.legend(loc='center left', bbox_to_anchor=(1, 0.5))
ax.set_xlabel('Sequence length, bit')
ax.set_ylabel('Bit rate, Mbit per s')
plt.show()
fig = plt.figure(figsize=(14, 6))
ax = fig.add_subplot(1, 1, 1)
ax.grid()
for j, nobits in enumerate(NOBITS):
ax.loglog(PROBAS, nobits / baseline[:, j], '-x',label=f'baseline block={nobits}')
ax.loglog(PROBAS, nobits / py[:, j], '-+',label=f'python block={nobits}')
ax.loglog(PROBAS, nobits / llvm[:, j], '-o',label=f'llvm block={nobits}')
ax.legend(loc='center left', bbox_to_anchor=(1, 0.5))
ax.set_xlabel('Bernoulli parameter')
ax.set_ylabel('Bitrate, Mbit / sec')
plt.show()
```
## Comments and Discussions
On the figures above one can see that direct implementation of the algorithm does not improve bitrate. Also, we can see that the statement is true for implementaion with LLVM as well as without LLVM. This means that overhead is too large.
Nevertheless, the third figure is worth to note that bitrate scales note very well for baseline generator. The bitrate of baseline drops dramatically while the bitrates of the others decrease much lesser.
Such benchmarking like this has unaccounted effects like different implementation levels (IR and Python), expansion of bit block to list of bits, overhead of Python object system.
|
github_jupyter
|
# Install dependencies
```
!pip install pretrainedmodels
!pip install albumentations==0.4.5
!pip install transformers
# install dependencies for TPU
#!curl https://raw.githubusercontent.com/pytorch/xla/master/contrib/scripts/env-setup.py -o pytorch-xla-env-setup.py
#!python pytorch-xla-env-setup.py --apt-packages libomp5 libopenblas-dev
```
# Download data
```
# https://drive.google.com/file/d/1jfkX_NXF8shxyWZCxJkzsLPDr4ebvdOP/view?usp=sharing
!pip install gdown
!gdown https://drive.google.com/uc?id=1jfkX_NXF8shxyWZCxJkzsLPDr4ebvdOP
!unzip -q plant-pathology-2020-fgvc7.zip -d /content/plant-pathology-2020-fgvc7
!rm plant-pathology-2020-fgvc7.zip
```
# Import libraries
```
# Import os
import os
# Import libraries for data manipulation
import numpy as np
import pandas as pd
# Import libries for data agumentations: albumentations
import albumentations as A
from albumentations.pytorch.transforms import ToTensor
from albumentations import Rotate
import cv2 as cv
# Import Pytorch
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
import torchvision
from torch.utils.data import Dataset, DataLoader
# Import pretrainmodels
import pretrainedmodels
# Import transformers
from transformers import get_cosine_schedule_with_warmup
from transformers import AdamW
# Import metrics for model evaluation
from sklearn.metrics import roc_auc_score
from sklearn.model_selection import StratifiedKFold
# Import libraries for data visualization
import matplotlib.pyplot as plt
# Import tqdm.notebook for loading visualization
from tqdm.notebook import tqdm
# Ignore warnings
import warnings
warnings.filterwarnings('ignore')
# Import for TPU configuration
#import torch_xla
#import torch_xla.core.xla_model as xm
```
# Settings
```
# Configuration path
# Data folder
IMAGES_PATH = '/content/plant-pathology-2020-fgvc7/images/'
# Sample submission csv
SAMPLE_SUBMISSION = '/content/plant-pathology-2020-fgvc7/sample_submission.csv'
# Train, test data path
TRAIN_DATA = '/content/plant-pathology-2020-fgvc7/train.csv'
TEST_DATA = '/content/plant-pathology-2020-fgvc7/test.csv'
# Configuration for training workflow
SEED = 1234
N_FOLDS = 5
N_EPOCHS = 20
BATCH_SIZE = 2
SIZE = 512
IMG_SHAPE = (1365, 2048, 3)
lr = 8e-4
submission_df = pd.read_csv(SAMPLE_SUBMISSION)
df_train = pd.read_csv(TRAIN_DATA)
df_test = pd.read_csv(TEST_DATA)
def get_image_path(filename):
return (IMAGES_PATH + filename + '.jpg')
#df_train['image_path'] = df_train['image_id'].apply(get_image_path)
#df_test['image_path'] = df_test['image_id'].apply(get_image_path)
#rain_labels = df_train.loc[:, 'healthy':'scab']
#train_paths = df_train.image_path
#test_paths = df_test.image_path
df_train.head()
df_test.head()
submission_df.head()
# for GPU
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
device
# for TPU
#device = xm.xla_device()
#torch.set_default_tensor_type('torch.FloatTensor')
#device
```
# Define Dataset
```
class PlantDataset(Dataset):
def __init__(self, df, transforms=None):
self.df = df
self.transforms=transforms
def __len__(self):
return self.df.shape[0]
def __getitem__(self, idx):
# Solution 01: Read from raw image
image_src = IMAGES_PATH + self.df.loc[idx, 'image_id'] + '.jpg'
# Solution 02: Read from npy file, we convert all images in images folder from .jpg to .npy
# image_src = np.load(IMAGES_PATH + self.df.loc[idx, 'image_id'] + '.npy')
# print(image_src)
image = cv.imread(image_src, cv.IMREAD_COLOR)
if image.shape != IMG_SHAPE:
image = image.transpose(1, 0, 2)
image = cv.cvtColor(image, cv.COLOR_BGR2RGB)
labels = self.df.loc[idx, ['healthy', 'multiple_diseases', 'rust', 'scab']].values
labels = torch.from_numpy(labels.astype(np.int8))
labels = labels.unsqueeze(-1)
if self.transforms:
transformed = self.transforms(image=image)
image = transformed['image']
return image, labels
```
# Data Agumentations
```
# Train transformation
transforms_train = A.Compose([
A.RandomResizedCrop(height=SIZE, width=SIZE, p=1.0),
A.OneOf([A.RandomBrightness(limit=0.1, p=1), A.RandomContrast(limit=0.1, p=1)]),
A.OneOf([A.MotionBlur(blur_limit=3), A.MedianBlur(blur_limit=3), A.GaussianBlur(blur_limit=3)], p=0.5),
A.VerticalFlip(p=0.5),
A.HorizontalFlip(p=0.5),
A.ShiftScaleRotate(
shift_limit=0.2,
scale_limit=0.2,
rotate_limit=20,
interpolation=cv.INTER_LINEAR,
border_mode=cv.BORDER_REFLECT_101,
p=1,
),
A.Normalize(mean=(0.485, 0.456, 0.406), std=(0.229, 0.224, 0.225), max_pixel_value=255.0, p=1.0),
A.pytorch.ToTensorV2(p=1.0),
], p=1.0)
# Validation transformation
transforms_valid = A.Compose([
A.Resize(height=SIZE, width=SIZE, p=1.0),
A.Normalize(mean=(0.485, 0.456, 0.406), std=(0.229, 0.224, 0.225), max_pixel_value=255.0, p=1.0),
A.pytorch.ToTensorV2(p=1.0),
])
```
# StratifiedKFold
```
# Get label from df_train
train_labels = df_train.iloc[:, 1:].values
train_y = train_labels[:, 2] + train_labels[:, 3] * 2 + train_labels[:, 1] * 3
folds = StratifiedKFold(n_splits=N_FOLDS, shuffle=True, random_state=SEED)
oof_preds = np.zeros((df_train.shape[0], 4))
```
# PretrainedModels
## Define cross entropy loss one hot
```
# define cross entropy loss one hot
class CrossEntropyLossOneHot(nn.Module):
def __init__(self):
super(CrossEntropyLossOneHot, self).__init__()
self.log_softmax = nn.LogSoftmax(dim=-1)
def forward(self, preds, labels):
return torch.mean(torch.sum(-labels * self.log_softmax(preds), -1))
```
## Define dense cross entropy
```
# define dense cross entropy
class DenseCrossEntropy(nn.Module):
def __init__(self):
super(DenseCrossEntropy, self).__init__()
def forward(self, logits, labels):
logits = logits.float()
labels = labels.float()
logprobs = F.log_softmax(logits, dim=-1)
loss = -labels * logprobs
loss = loss.sum(-1)
return loss.mean()
```
## Define plant model with ResNet34
```
# define plant model with ResNet
class PlantModel(nn.Module):
# define init function
def __init__(self, num_classes=4):
super().__init__()
self.backbone = torchvision.models.resnet34(pretrained=True)
in_features = self.backbone.fc.in_features
self.logit = nn.Linear(in_features, num_classes)
# define forward function
def forward(self, x):
batch_size, C, H, W = x.shape
x = self.backbone.conv1(x)
x = self.backbone.bn1(x)
x = self.backbone.relu(x)
x = self.backbone.maxpool(x)
x = self.backbone.layer1(x)
x = self.backbone.layer2(x)
x = self.backbone.layer3(x)
x = self.backbone.layer4(x)
x = F.adaptive_avg_pool2d(x,1).reshape(batch_size,-1)
x = F.dropout(x, 0.25, self.training)
x = self.logit(x)
return x
```
# Train for StratifiedKFold
```
def train_one_fold(i_fold, model, criterion, optimizer, lr_scheduler, dataloader_train, dataloader_valid):
train_fold_results = []
for epoch in range(N_EPOCHS):
# print information
print(' Epoch {}/{}'.format(epoch + 1, N_EPOCHS))
print(' ' + ('-' * 20))
os.system(f'echo \" Epoch {epoch}\"')
# call model
model.train()
tr_loss = 0
# looping
for step, batch in enumerate(dataloader_train):
# data preparation
images = batch[0].to(device)
labels = batch[1].to(device)
# forward pass and calculate loss
outputs = model(images)
loss = criterion(outputs, labels.squeeze(-1))
# backward pass
loss.backward()
tr_loss += loss.item()
# updates
# for TPU
#xm.optimizer_step(optimizer, barrier=True)
# for GPU
optimizer.step()
# empty gradient
optimizer.zero_grad()
# Validate
model.eval()
# init validation loss, predicted and labels
val_loss = 0
val_preds = None
val_labels = None
for step, batch in enumerate(dataloader_valid):
# data preparation
images = batch[0].to(device)
labels = batch[1].to(device)
# labels preparation
if val_labels is None:
val_labels = labels.clone().squeeze(-1)
else:
val_labels = torch.cat((val_labels, labels.squeeze(-1)), dim=0)
# disable torch grad to calculating normally
with torch.no_grad():
# calculate the output
outputs = model(batch[0].to(device))
# calculate the loss value
loss = criterion(outputs, labels.squeeze(-1))
val_loss += loss.item()
# predict with softmax activation function
preds = torch.softmax(outputs, dim=1).data.cpu()
#preds = torch.softmax(outputs, dim=1).detach().cpu().numpy()
if val_preds is None:
val_preds = preds
else:
val_preds = torch.cat((val_preds, preds), dim=0)
# if train mode
lr_scheduler.step(tr_loss)
with torch.no_grad():
train_loss = tr_loss / len(dataloader_train)
valid_loss = val_loss / len(dataloader_valid)
valid_score = roc_auc_score(val_labels.view(-1).cpu(), val_preds.view(-1).cpu(), average='macro')
# print information
if epoch % 2 == 0:
print(f'Fold {i_fold} Epoch {epoch}: train_loss={train_loss:.4f}, valid_loss={valid_loss:.4f}, acc={valid_score:.4f}')
train_fold_results.append({
'fold': i_fold,
'epoch': epoch,
'train_loss': train_loss,
'valid_loss': valid_loss,
'valid_score': valid_score,
})
return val_preds, train_fold_results
```
## Prepare submission file
```
submission_df.iloc[:, 1:] = 0
```
## Dataset test
```
dataset_test = PlantDataset(df=submission_df, transforms=transforms_valid)
dataloader_test = DataLoader(dataset_test, batch_size=BATCH_SIZE, num_workers=4, shuffle=False)
```
# Init model: EfficientNetB5
```
# EfficientNetB5
# B5 is the largest EfficientNet variant that fits in GPU memory with batch size 8.
!pip install efficientnet_pytorch
from efficientnet_pytorch import EfficientNet
model = EfficientNet.from_pretrained('efficientnet-b5')
num_ftrs = model._fc.in_features
model._fc = nn.Sequential(nn.Linear(num_ftrs,1000,bias=True),
nn.ReLU(),
nn.Dropout(p=0.5),
nn.Linear(1000,4, bias = True))
model.to(device)
model
```
# Init model: ResNet
```
"""
# Download pretrained weights.
# model = PlantModel(num_classes=4)
model = torchvision.models.resnet18(pretrained=True)
# print number of features
num_features = model.fc.in_features
print(num_features)
# custome layers
model.fc = nn.Sequential(
nn.Linear(num_features, 512),
nn.ReLU(),
nn.BatchNorm1d(512),
nn.Dropout(0.5),
nn.Linear(512, 256),
nn.ReLU(),
nn.BatchNorm1d(256),
nn.Dropout(0.5),
nn.Linear(256, 4))
# initialize weights function
def init_weights(m):
if type(m) == nn.Linear:
torch.nn.init.xavier_uniform_(m.weight)
m.bias.data.fill_(0.01)
# apply model with init weights
model.apply(init_weights)
# transfer model to device (cuda:0 mean using GPU, xla mean using TPU, otherwise using CPU)
model = model.to(device)
# Model details
model
"""
print(torch.cuda.memory_summary(device=None, abbreviated=False))
```
# Training model
```
submissions = None
train_results = []
for i_fold, (train_idx, valid_idx) in enumerate(folds.split(df_train, train_y)):
# data preparation phase
print("Fold {}/{}".format(i_fold + 1, N_FOLDS))
valid = df_train.iloc[valid_idx]
valid.reset_index(drop=True, inplace=True)
train = df_train.iloc[train_idx]
train.reset_index(drop=True, inplace=True)
# data transformation phase
dataset_train = PlantDataset(df=train, transforms=transforms_train)
dataset_valid = PlantDataset(df=valid, transforms=transforms_valid)
# data loader phase
dataloader_train = DataLoader(dataset_train, batch_size=BATCH_SIZE, num_workers=4, shuffle=True, pin_memory=True, drop_last=True)
dataloader_valid = DataLoader(dataset_valid, batch_size=BATCH_SIZE, num_workers=4, shuffle=False, pin_memory=True, drop_last=False)
# device = torch.device("cuda:0")
model = model.to(device)
# optimization phase
criterion = DenseCrossEntropy()
# optimizer = optim.Adam(model.parameters(), lr=0.001)
optimizer = AdamW(model.parameters(), lr = lr, weight_decay = 1e-3)
# lr_scheduler = optim.lr_scheduler.MultiStepLR(optimizer=optimizer, milestones=[int(N_EPOCHS * 0.5), int(N_EPOCHS * 0.75)], gamma=0.1, last_epoch=-1)
num_train_steps = int(len(dataset_train) / BATCH_SIZE * N_EPOCHS)
lr_scheduler = get_cosine_schedule_with_warmup(optimizer, num_warmup_steps=len(dataset_train)/BATCH_SIZE*5, num_training_steps=num_train_steps)
# training in one fold
val_preds, train_fold_results = train_one_fold(i_fold, model, criterion, optimizer, lr_scheduler, dataloader_train, dataloader_valid)
oof_preds[valid_idx, :] = val_preds
# calculate the results phase
train_results = train_results + train_fold_results
# model evaluation phase
model.eval()
test_preds = None
# looping test dataloader
for step, batch in enumerate(dataloader_test):
images = batch[0].to(device, dtype=torch.float)
# empty torch gradient
with torch.no_grad():
outputs = model(images)
if test_preds is None:
test_preds = outputs.data.cpu()
else:
test_preds = torch.cat((test_preds, outputs.data.cpu()), dim=0)
# Save predictions per fold
submission_df[['healthy', 'multiple_diseases', 'rust', 'scab']] = torch.softmax(test_preds, dim=1)
submission_df.to_csv('submission_fold_{}.csv'.format(i_fold), index=False)
# logits avg
if submissions is None:
submissions = test_preds / N_FOLDS
else:
submissions += test_preds / N_FOLDS
print("5-Folds CV score: {:.4f}".format(roc_auc_score(train_labels, oof_preds, average='macro')))
torch.save(model.state_dict(), '5-folds_rnn34.pth')
```
# Generate training results
```
train_results = pd.DataFrame(train_results)
train_results.head(10)
train_results.to_csv('train_result.csv')
```
# Plotting results
## Training loss
```
def show_training_loss(train_result):
plt.figure(figsize=(15,10))
plt.subplot(3,1,1)
train_loss = train_result['train_loss']
plt.plot(train_loss.index, train_loss, label = 'train_loss')
plt.legend()
val_loss = train_result['valid_loss']
plt.plot(val_loss.index, val_loss, label = 'val_loss')
plt.legend()
show_training_loss(train_results)
```
## Validation score
```
def show_valid_score(train_result):
plt.figure(figsize=(15,10))
plt.subplot(3,1,1)
valid_score = train_result['valid_score']
plt.plot(valid_score.index, valid_score, label = 'valid_score')
plt.legend()
show_valid_score(train_results)
submission_df[['healthy', 'multiple_diseases', 'rust', 'scab']] = torch.softmax(submissions, dim=1)
submission_df.to_csv('submission.csv', index=False)
submission_df.head()
```
|
github_jupyter
|
# CS229: Problem Set 3
## Problem 1: A Simple Neural Network
**C. Combier**
This iPython Notebook provides solutions to Stanford's CS229 (Machine Learning, Fall 2017) graduate course problem set 3, taught by Andrew Ng.
The problem set can be found here: [./ps3.pdf](ps3.pdf)
I chose to write the solutions to the coding questions in Python, whereas the Stanford class is taught with Matlab/Octave.
## Notation
- $x^i$ is the $i^{th}$ feature vector
- $y^i$ is the expected outcome for the $i^{th}$ training example
- $m$ is the number of training examples
- $n$ is the number of features
### Question 1.b)

It seems that a triangle can separate the data.
We can construct a weight matrix by using a combination of linear classifiers, where each side of the triangle represents a decision boundary.
Each side of the triangle can be represented by an equation of the form $w_0 +w_1 x_1 + w_2 x_2 = 0$. If we transform this equality into an inequality, then the output represents on which side of the decision boundary a given data point $(x_1,x_2)$ belongs. The intersection of the outputs for each of these decision boundaries tells us whether $(x_1,x_2)$ lies within the triangle, in which case we will classify it $0$, and if not as $1$.
The first weight matrix can be written as:
$$
W^{[1]} = \left ( \begin{array}{ccc}
-1 & 4 & 0 \\
-1 & 0 & 4 \\
4.5 & -1 & -1
\end{array} \right )
$$
The input vector is:
$$
X = (\begin{array}{ccc}
1 & x_1 & x_2
\end{array})^T
$$
- The first line of $W^{[1]}$ is the equation for the vertical side of the triangle, $x_1 = 0.25$
- The second line of $W^{[1]}$ is the equation for the horizontal side of the triangle, $x_2 = 0.25$
- The third line of $W^{[1]}$ is the equation for the oblique side of the triangle, $x_2 = -x_1 + 4.5$
Consequently, with the given activation function, if the training example given by ($x_1$, $x_2$) lies within the triangle, then:
$$
f(W^{[1]}X) = (\begin{array}{ccc}
1 & 1 & 1
\end{array})^T
$$
In all other cases, at least one element of the output vector $f(W^{[1]}X)$ is not equal to $1$.
We can use this observation to find weights for the ouput layer. We take the sum of the components of $f(W^{[1]}X)$, and compare the value to 2.5 to check if all elements are equal to $1$ or not. This gives the weight matrix:
$$
W^{[2]} =(\begin{array}{cccc}
2.5 & -1 & -1 & -1
\end{array})
$$
The additional term 2.5 is the zero intercept. With this weight matrix, the ouput of the final layer will be $0$ if the training example is within the triangle, and $1$ if it is outside of the triangle.
The
### Question 1.c)
A linear activation function does not work, because the problem is not linearly separable, i.e. there is no hyperplane that perfectly separates the data.
|
github_jupyter
|
# Summarizing Data
> What we have is a data glut.
>
> \- Vernor Vinge, Professor Emeritus of Mathematics, San Diego State University
## Applied Review
### Dictionaries
* The `dict` structure is used to represent **key-value pairs**
* Like a real dictionary, you look up a word (**key**) and get its definition (**value**)
* Below is an example:
```python
ethan = {
'first_name': 'Ethan',
'last_name': 'Swan',
'alma_mater': 'Notre Dame',
'employer': '84.51˚',
'zip_code': 45208
}
```
### DataFrame Structure
* We will start by importing the `flights` data set as a DataFrame:
```
import pandas as pd
flights_df = pd.read_csv('../data/flights.csv')
```
* Each DataFrame variable is a **Series** and can be accessed with bracket subsetting notation: `DataFrame['SeriesName']`
* The DataFrame has an **Index** that is visible the far left side and can be used to slide the DataFrame
### Methods
* Methods are *operations* that are specific to Python classes
* These operations end in parentheses and *make something happen*
* An example of a method is `DataFrame.head()`
## General Model
### Window Operations
Yesterday we learned how to manipulate data across one or more variables within the row(s):

Note that we return the same number of elements that we started with. This is known as a **window function**, but you can also think of it as summarizing at the row-level.
We could achieve this result with the following code:
```python
DataFrame['A'] + DataFrame['B']
```
We subset the two Series and then add them together using the `+` operator to achieve the sum.
Note that we could also use some other operation on `DataFrame['B']` as long as it returns the same number of elements.
### Summary Operations
However, sometimes we want to work with data across rows within a variable -- that is, aggregate/summarize values rowwise rather than columnwise.
<img src="images/aggregate-series.png" alt="aggregate-series.png" width="500" height="500">
Note that we return a single value representing some aggregation of the elements we started with. This is known as a **summary function**, but you can think of it as summarizing across rows.
This is what we are going to talk about next.
## Summarizing a Series
### Summary Methods
The easiest way to summarize a specific series is by using bracket subsetting notation and the built-in Series methods:
```
flights_df['distance'].sum()
```
Note that a *single value* was returned because this is a **summary operation** -- we are summing the `distance` variable across all rows.
There are other summary methods with a series:
```
flights_df['distance'].mean()
flights_df['distance'].median()
flights_df['distance'].mode()
```
All of the above methods work on quantitative variables, but we also have methods for character variables:
```
flights_df['carrier'].value_counts()
```
While the above isn't *technically* returning a single value, it's still a useful Series method summarizing our data.
<font class="your_turn">
Your Turn
</font>
1\. What is the difference between a window operation and a summary operation?
2\. Fill in the blanks in the following code to calculate the mean delay in departure:
```python
flights_df['_____']._____()
```
3\. Find the distinct number of carriers. Hint: look for a method to find the number of unique values in a Series.
### Describe Method
There is also a method `describe()` that provides a lot of this information -- this is especially useful in exploratory data analysis.
```
flights_df['distance'].describe()
```
Note that `describe()` will return different results depending on the `type` of the Series:
```
flights_df['carrier'].describe()
```
## Summarizing a DataFrame
The above methods and operations are nice, but sometimes we want to work with multiple variables rather than just one.
### Extending Summary Methods to DataFrames
Recall how we select variables from a DataFrame:
* Single-bracket subset notation
* Pass a list of quoted variable names into the list
```python
flights_df[['sched_dep_time', 'dep_time']]
```
We can use *the same summary methods from the Series on the DataFrame* to summarize data:
```
flights_df[['sched_dep_time', 'dep_time']].mean()
flights_df[['sched_dep_time', 'dep_time']].median()
```
<font class="question">
<strong>Question</strong>:<br><em>What is the class of <code>flights_df[['sched_dep_time', 'dep_time']].median()</code>?</em>
</font>
This returns a `pandas.core.series.Series` object -- the Index is the variable name and the values are the summarieze values.
### The Aggregation Method
While summary methods can be convenient, there are a few drawbacks to using them on DataFrames:
1. You have to lookup or remember the method names each time
2. You can only apply one summary method at a time
3. You have to apply the same summary method to all variables
4. A Series is returned rather than a DataFrame -- this makes it difficult to use the values in our analysis later
In order to get around these problems, the DataFrame has a powerful method `agg()`:
```
flights_df.agg({
'sched_dep_time': ['mean']
})
```
There are a few things to notice about the `agg()` method:
1. A `dict` is passed to the method with variable names as keys and a list of quoted summaries as values
2. *A DataFrame is returned* with variable names as variables and summaries as rows
We can extend this to multiple variables by adding elements to the `dict`:
```
flights_df.agg({
'sched_dep_time': ['mean'],
'dep_time': ['mean']
})
```
And because the values of the `dict` are lists, we can do additional aggregations at the same time:
```
flights_df.agg({
'sched_dep_time': ['mean', 'median'],
'dep_time': ['mean', 'min']
})
```
And notice that not all variables have to have the same list of summaries.
<font class="your_turn">
Your Turn
</font>
1\. What class of object is the returned by the below code?
```python
flights_df[['air_time', 'distance']].mean()
```
2\. What class of object is returned by the below code?
```python
flights_df.agg({
'air_time': ['mean'],
'distance': ['mean']
})
```
3\. Fill in the blanks in the below code to calculate the minimum and maximum distances traveled and the mean and median arrival delay:
```python
flights_df.agg({
'_____': ['min', '_____'],
'_____': ['_____', 'median']
})
```
### Describe Method
While `agg()` is a powerful method, the `describe()` method -- similar to the Series `describe()` method -- is a great choice during exploratory data analysis:
```
flights_df.describe()
```
<font class="question">
<strong>Question</strong>:<br><em>What is missing from the above result?</em>
</font>
The string variables are missing!
We can make `describe()` compute on all variable types using the `include` parameter and passing a list of data types to include:
```
flights_df.describe(include = ['int', 'float', 'object'])
```
## Questions
Are there any questions before we move on?
|
github_jupyter
|
This material has been adapted by @dcapurro from the Jupyter Notebook developed by:
Author: [Yury Kashnitsky](https://yorko.github.io). Translated and edited by [Christina Butsko](https://www.linkedin.com/in/christinabutsko/), [Yuanyuan Pao](https://www.linkedin.com/in/yuanyuanpao/), [Anastasia Manokhina](https://www.linkedin.com/in/anastasiamanokhina), Sergey Isaev and [Artem Trunov](https://www.linkedin.com/in/datamove/). This material is subject to the terms and conditions of the [Creative Commons CC BY-NC-SA 4.0](https://creativecommons.org/licenses/by-nc-sa/4.0/) license. Free use is permitted for any non-commercial purpose.
## 1. Demonstration of main Pandas methods
Well... There are dozens of cool tutorials on Pandas and visual data analysis. This one will guide us through the basic tasks when you are exploring your data (how deos the data look like?)
**[Pandas](http://pandas.pydata.org)** is a Python library that provides extensive means for data analysis. Data scientists often work with data stored in table formats like `.csv`, `.tsv`, or `.xlsx`. Pandas makes it very convenient to load, process, and analyze such tabular data using SQL-like queries. In conjunction with `Matplotlib` and `Seaborn`, `Pandas` provides a wide range of opportunities for visual analysis of tabular data.
The main data structures in `Pandas` are implemented with **Series** and **DataFrame** classes. The former is a one-dimensional indexed array of some fixed data type. The latter is a two-dimensional data structure - a table - where each column contains data of the same type. You can see it as a dictionary of `Series` instances. `DataFrames` are great for representing real data: rows correspond to instances (examples, observations, etc.), and columns correspond to features of these instances.
```
import numpy as np
import pandas as pd
pd.set_option("display.precision", 2)
```
We'll demonstrate the main methods in action by analyzing a dataset that is an extract of the MIMIC III Database.
Let's read the data (using `read_csv`), and take a look at the first 5 lines using the `head` method:
```
df = pd.read_csv('/home/shared/icu_2012.txt')
df.head()
```
<details>
<summary>About printing DataFrames in Jupyter notebooks</summary>
<p>
In Jupyter notebooks, Pandas DataFrames are printed as these pretty tables seen above while `print(df.head())` is less nicely formatted.
By default, Pandas displays 20 columns and 60 rows, so, if your DataFrame is bigger, use the `set_option` function as shown in the example below:
```python
pd.set_option('display.max_columns', 100)
pd.set_option('display.max_rows', 100)
```
</p>
</details>
Recall that each row corresponds to one patient, an **instance**, and columns are **features** of this instance.
Let’s have a look at data dimensionality, feature names, and feature types.
```
print(df.shape)
```
From the output, we can see that the table contains 4000 rows and 79 columns.
Now let's try printing out column names using `columns`:
```
print(df.columns)
```
We can use the `info()` method to output some general information about the dataframe:
```
print(df.info())
```
`bool`, `int64`, `float64` and `object` are the data types of our features. We see that one feature is logical (`bool`), 3 features are of type `object`, and 16 features are numeric. With this same method, we can easily see if there are any missing values. Here, we can see that there are columns with missing variables because some columns contain less than the 4000 number of instances (or rows) we saw before with `shape`.
The `describe` method shows basic statistical characteristics of each numerical feature (`int64` and `float64` types): number of non-missing values, mean, standard deviation, range, median, 0.25 and 0.75 quartiles.
```
df.describe()
```
The `describe` methods only gives us information about numerical variables. Some of these don't really make sense, like the `subject_id` or `gender` but since they are numbers, we are getting summary statistics anyways.
In order to see statistics on non-numerical features, one has to explicitly indicate data types of interest in the `include` parameter. We would use `df.describe(include=['object', 'bool'])` but in this case, the dataset only has variables of type `int` and `float`.
For categorical (type `object`) and boolean (type `bool`) features we can use the `value_counts` method. This also woeks for variables that have been encoded into integers like Gender. Let's have a look at the distribution of `Gender`:
```
df['Gender'].value_counts()
```
Since Gender is encoded in the following way: (0: female, or 1: male)
2246 intances are male patients
### Sorting
A DataFrame can be sorted by the value of one of the variables (i.e columns). For example, we can sort by *Age* (use `ascending=False` to sort in descending order):
```
pd.set_option('display.max_columns', 100)
pd.set_option('display.max_rows', 100)
df.sort_values(by='Age', ascending=False).head()
```
We can also sort by multiple columns:
```
df.sort_values(by=['Age', 'Height'],
ascending=[False, False]).head()
```
### Indexing and retrieving data
A DataFrame can be indexed in a few different ways.
To get a single column, you can use a `DataFrame['Name']` construction. Let's use this to answer a question about that column alone: **what is the average maximum heart rate of admitted patients in our dataframe?**
```
df['HR_max'].mean()
```
106 bpm is slightly elevated, but it seems reasonable for an ICU population
**Boolean indexing** with one column is also very convenient. The syntax is `df[P(df['Name'])]`, where `P` is some logical condition that is checked for each element of the `Name` column. The result of such indexing is the DataFrame consisting only of rows that satisfy the `P` condition on the `Name` column.
Let's use it to answer the question:
**What are average values of numerical features for male patients?**
```
df[df['Gender'] == 1].mean()
```
**What is the average Max Creatinine for patients female patients?**
```
df[df['Gender'] == 0]['Creatinine_max'].mean()
```
DataFrames can be indexed by column name (label) or row name (index) or by the serial number of a row. The `loc` method is used for **indexing by name**, while `iloc()` is used for **indexing by number**.
In the first case below, we say *"give us the values of the rows with index from 0 to 5 (inclusive) and columns labeled from State to Area code (inclusive)"*. In the second case, we say *"give us the values of the first five rows in the first three columns"* (as in a typical Python slice: the maximal value is not included).
```
df.loc[0:5, 'RecordID':'ICUType']
df.iloc[0:5, 0:3]
```
If we need the first or the last line of the data frame, we can use the `df[:1]` or `df[-1:]` construct:
```
df[-1:]
```
### Applying Functions to Cells, Columns and Rows
**To apply functions to each column, use `apply()`:**
In this example, we will obtain the max value for each feature.
```
df.apply(np.max)
```
The `map` method can be used to **replace values in a column** by passing a dictionary of the form `{old_value: new_value}` as its argument. Let's change the values of female and male for the corresponding `strings`
```
d = {0 : 'Female', 1 : 'Male'}
df['Gender'] = df['Gender'].map(d)
df.head()
```
The same thing can be done with the `replace` method:
```
d2 = {1: 'Coronary Care Unit', 2: 'Cardiac Surgery Recovery Unit', 3: 'Medical ICU', 4: 'Surgical ICU'}
df = df.replace({'ICUType': d2})
df.head()
```
We can also replace missing values when it is necessary. For that we use the `filna()` methohd. In this case, we will replace them in the Mechanical Ventilation column.
```
df['MechVent_min'].fillna(0, inplace=True)
df.head()
```
### Histograms
Histograms are an important tool to understand the distribution of your variables. It can help you detect errors in the data, like extreme or unplausible values.
```
df['Age'].hist()
```
We can quickly see that the distribution of age is not normal. Let's look at Na
```
df['Na_max'].hist()
```
Not a lot of resolution here. Let's increase the number of bins to 30
```
df['Na_max'].hist(bins=30)
```
Much better! It is easy to see that this is approximately a normal distribution.
### Grouping
In general, grouping data in Pandas works as follows:
```python
df.groupby(by=grouping_columns)[columns_to_show].function()
```
1. First, the `groupby` method divides the `grouping_columns` by their values. They become a new index in the resulting dataframe.
2. Then, columns of interest are selected (`columns_to_show`). If `columns_to_show` is not included, all non groupby clauses will be included.
3. Finally, one or several functions are applied to the obtained groups per selected columns.
Here is an example where we group the data according to `Gender` variable and display statistics of three columns in each group:
```
columns_to_show = ['Na_max', 'K_max',
'HCO3_max']
df.groupby(['Gender'])[columns_to_show].describe(percentiles=[])
```
Let’s do the same thing, but slightly differently by passing a list of functions to `agg()`:
```
columns_to_show = ['Na_max', 'K_max',
'HCO3_max']
df.groupby(['Gender'])[columns_to_show].agg([np.mean, np.std, np.min,
np.max])
```
### Summary tables
Suppose we want to see how the observations in our sample are distributed in the context of two variables - `Gender` and `ICUType`. To do so, we can build a **contingency table** using the `crosstab` method:
```
pd.crosstab(df['Gender'], df['ICUType'])
```
This will resemble **pivot tables** to those familiar with Excel. And, of course, pivot tables are implemented in Pandas: the `pivot_table` method takes the following parameters:
* `values` – a list of variables to calculate statistics for,
* `index` – a list of variables to group data by,
* `aggfunc` – what statistics we need to calculate for groups, ex. sum, mean, maximum, minimum or something else.
Let's take a look at the average number of day, evening, and night calls by area code:
```
df.pivot_table(['TroponinI_max', 'TroponinT_max'],
['ICUType'], aggfunc='mean')
```
Nothing surprising here, patients in the coronary/cardiac units have higher values of Troponins.
### DataFrame transformations
Like many other things in Pandas, adding columns to a DataFrame is doable in many ways.
For example, if we want to calculate the change in creatinine, let's create the `Delta_creatinine` Series and paste it into the DataFrame:
```
Delta_creatinine = df['Creatinine_max'] - df['Creatinine_min']
df.insert(loc=len(df.columns), column='Delta_creatinine', value=Delta_creatinine)
# loc parameter is the number of columns after which to insert the Series object
# we set it to len(df.columns) to paste it at the very end of the dataframe
df.head()
```
It is possible to add a column more easily without creating an intermediate Series instance:
```
df['Delta_BUN'] = df['BUN_max'] - df['BUN_min']
df.head()
```
To delete columns or rows, use the `drop` method, passing the required indexes and the `axis` parameter (`1` if you delete columns, and nothing or `0` if you delete rows). The `inplace` argument tells whether to change the original DataFrame. With `inplace=False`, the `drop` method doesn't change the existing DataFrame and returns a new one with dropped rows or columns. With `inplace=True`, it alters the DataFrame.
```
# get rid of just created columns
df.drop(['Delta_creatinine', 'Delta_BUN'], axis=1, inplace=True)
# and here’s how you can delete rows
df.drop([1, 2]).head()
```
## 2. Exploring some associations
Let's see how mechanical ventilation is related to Gender. We'll do this using a `crosstab` contingency table and also through visual analysis with `Seaborn`.
```
pd.crosstab(df['MechVent_min'], df['Gender'], margins=True)
# some imports to set up plotting
import matplotlib.pyplot as plt
# pip install seaborn
import seaborn as sns
# Graphics in retina format are more sharp and legible
%config InlineBackend.figure_format = 'retina'
```
Now we create the plot that will show us the counts of mechanically ventilated patients by gender.
```
sns.countplot(x='Gender', hue='MechVent_min', data=df);
```
We see that th number (and probably the proportion) of mechanically ventilated patients is greater among males.
Next, let's look at the same distribution but comparing the different ICU types: Let's also make a summary table and a picture.
```
pd.crosstab(df['ICUType'], df['MechVent_min'], margins=True)
sns.countplot(x='ICUType', hue='MechVent_min', data=df);
```
As you can see, the proportion of patients ventilated and not ventilated is very different across the different types of ICUs. That is particularly true in the cardiac surgery recovery unit. Can you think of a reason why that might be?
## 3. Some useful resources
* ["Merging DataFrames with pandas"](https://nbviewer.jupyter.org/github/Yorko/mlcourse.ai/blob/master/jupyter_english/tutorials/merging_dataframes_tutorial_max_palko.ipynb) - a tutorial by Max Plako within mlcourse.ai (full list of tutorials is [here](https://mlcourse.ai/tutorials))
* ["Handle different dataset with dask and trying a little dask ML"](https://nbviewer.jupyter.org/github/Yorko/mlcourse.ai/blob/master/jupyter_english/tutorials/dask_objects_and_little_dask_ml_tutorial_iknyazeva.ipynb) - a tutorial by Irina Knyazeva within mlcourse.ai
* Main course [site](https://mlcourse.ai), [course repo](https://github.com/Yorko/mlcourse.ai), and YouTube [channel](https://www.youtube.com/watch?v=QKTuw4PNOsU&list=PLVlY_7IJCMJeRfZ68eVfEcu-UcN9BbwiX)
* Official Pandas [documentation](http://pandas.pydata.org/pandas-docs/stable/index.html)
* Course materials as a [Kaggle Dataset](https://www.kaggle.com/kashnitsky/mlcourse)
* Medium ["story"](https://medium.com/open-machine-learning-course/open-machine-learning-course-topic-1-exploratory-data-analysis-with-pandas-de57880f1a68) based on this notebook
* If you read Russian: an [article](https://habrahabr.ru/company/ods/blog/322626/) on Habr.com with ~ the same material. And a [lecture](https://youtu.be/dEFxoyJhm3Y) on YouTube
* [10 minutes to pandas](http://pandas.pydata.org/pandas-docs/stable/10min.html)
* [Pandas cheatsheet PDF](https://github.com/pandas-dev/pandas/blob/master/doc/cheatsheet/Pandas_Cheat_Sheet.pdf)
* GitHub repos: [Pandas exercises](https://github.com/guipsamora/pandas_exercises/) and ["Effective Pandas"](https://github.com/TomAugspurger/effective-pandas)
* [scipy-lectures.org](http://www.scipy-lectures.org/index.html) — tutorials on pandas, numpy, matplotlib and scikit-learn
|
github_jupyter
|
# Example of building a MLDataSet
## Building a Features MLDataSet from a Table
```
from PrimalCore.heterogeneous_table.table import Table
from ElementsKernel.Path import getPathFromEnvVariable
ph_catalog=getPathFromEnvVariable('PrimalCore/test_table.fits','ELEMENTS_AUX_PATH')
catalog=Table.from_fits_file(ph_catalog,fits_ext=0)
catalog.keep_columns(['FLUX*','reliable_S15','STAR','AGN','MASKED','FLAG_PHOT'],regex=True)
```
First we import the classes and the functions we need
```
from PrimalCore.homogeneous_table.dataset import MLDataSet
```
```
dataset=MLDataSet.new_from_table(catalog)
print dataset.features_names
```
```
print dataset.features_original_entry_ID[1:10]
```
and in this way it **safely** can not be used as a feature.
## Building a Features MLDataSet from a FITS file
```
dataset_from_file=MLDataSet.new_from_fits_file(ph_catalog,fits_ext=0,\
use_col_names_list=['FLUX*','reliable_S15','STAR','AGN','MASKED','FLAG_PHOT'],\
regex=True)
print dataset_from_file.features_names
```
## Columns selection
### using `use_col_names_list` in the factories
```
dataset=MLDataSet.new_from_table(catalog,use_col_names_list=['FLUX*','reliable_S15','STAR','AGN','MASKED','FLAG_PHOT'],\
regex=True)
print dataset.features_names
```
### using dataset_handler fucntions
```
from PrimalCore.homogeneous_table.dataset_handler import drop_features
from PrimalCore.homogeneous_table.dataset_handler import keep_features
```
```
drop_features(dataset,['FLUX*1*'])
dataset.features_names
```
```
keep_features(dataset,['FLUX*2*'],regex=True)
print dataset.features_names
```
## Adding features
```
from PrimalCore.homogeneous_table.dataset_handler import add_features
test_feature=dataset.get_feature_by_name('FLUXERR_H_2')**2
add_features(dataset,'test',test_feature)
dataset.features_names
```
Or we can add a 2dim array of features
```
test_feature_2dim=np.zeros((dataset.features_N_rows,5))
test_feature_2dim_names=['a','b','c','d','e']
add_features(dataset,test_feature_2dim_names,test_feature_2dim)
dataset.features_names
```
We can think to a more meaningful example, i.e. we want to add flux ratios. Lets start by defining the list of
contigous bands, for the flux evaluation
```
flux_bands_list_2=['FLUX_G_2','FLUX_R_2','FLUX_I_2','FLUX_Z_2','FLUX_Y_2','FLUX_J_2','FLUX_VIS','FLUX_VIS','FLUX_VIS']
flux_bands_list_1=['FLUX_R_2','FLUX_I_2','FLUX_Z_2','FLUX_Y_2','FLUX_J_2','FLUX_H_2','FLUX_Y_2','FLUX_J_2','FLUX_H_2']
```
```
from PrimalCore.phz_tools.photometry import FluxRatio
for f1,f2 in zip(flux_bands_list_1,flux_bands_list_2):
f1_name=f1.split('_')[1]
f2_name=f2.split('_')[1]
if f1 in dataset.features_names and f2 in dataset.features_names:
f=FluxRatio('F_%s'%(f2_name+'-'+f1_name),f1,f2,features=dataset)
add_features(dataset,f.name,f.values)
```
```
dataset.features_names
```
## Operations on rows
### filtering NaN/Inf with dataset_preprocessing functions
```
from PrimalCore.preprocessing.dataset_preprocessing import drop_nan_inf
drop_nan_inf(dataset)
```
|
github_jupyter
|
<img src="images/usm.jpg" width="480" height="240" align="left"/>
# MAT281 - Laboratorio N°04
## Objetivos de la clase
* Reforzar los conceptos básicos de los módulos de pandas.
## Contenidos
* [Problema 01](#p1)
* [Problema 02](#p2)
## Problema 01
<img src="https://image.freepik.com/vector-gratis/varios-automoviles-dibujos-animados_23-2147613095.jpg" width="360" height="360" align="center"/>
EL conjunto de datos se denomina `Automobile_data.csv`, el cual contiene información tal como: compañia, precio, kilometraje, etc.
Lo primero es cargar el conjunto de datos y ver las primeras filas que lo componen:
```
import pandas as pd
import numpy as np
import os
# cargar datos
df = pd.read_csv(os.path.join("data","Automobile_data.csv")).set_index('index')
df.head()
```
El objetivo es tratar de obtener la mayor información posible de este conjunto de datos. Para cumplir este objetivo debe resolver las siguientes problemáticas:
1. Elimine los valores nulos (Nan)
```
df=df.dropna()
```
2. Encuentra el nombre de la compañía de automóviles más cara
```
df.groupby(['company']).mean()['price'].idxmax()
```
3. Imprimir todos los detalles de Toyota Cars
```
df[df['company']=='toyota']
```
4. Cuente el total de automóviles por compañía
```
comp[['company']].count()
```
5. Encuentra el coche con el precio más alto por compañía
```
df[['company','price']].groupby('company').max()
```
6. Encuentre el kilometraje promedio (**average-mileage**) de cada compañía automotriz
```
comp=df.groupby('company')
df_leng = comp.agg({'average-mileage':[np.mean]}).reset_index()
df_leng
```
7. Ordenar todos los autos por columna de precio (**price**)
```
df.sort_values(by='price')
```
## Problema 02
Siguiendo la temática de los automóviles, resuelva los siguientes problemas:
#### a) Subproblema 01
A partir de los siguientes diccionarios:
```
GermanCars = {'Company': ['Ford', 'Mercedes', 'BMV', 'Audi'],
'Price': [23845, 171995, 135925 , 71400]}
japaneseCars = {'Company': ['Toyota', 'Honda', 'Nissan', 'Mitsubishi '],
'Price': [29995, 23600, 61500 , 58900]}
```
* Cree dos dataframes (**carsDf1** y **carsDf2**) según corresponda.
* Concatene ambos dataframes (**carsDf**) y añada una llave ["Germany", "Japan"], según corresponda.
```
carsDf1=pd.DataFrame(GermanCars)
carsDf2=pd.DataFrame(japaneseCars)
carsDf= pd.concat([carsDf1,carsDf2],keys=['Germany','Japan'])
carsDf
```
#### b) Subproblema 02
A partir de los siguientes diccionarios:
```
Car_Price = {'Company': ['Toyota', 'Honda', 'BMV', 'Audi'], 'Price': [23845, 17995, 135925 , 71400]}
car_Horsepower = {'Company': ['Toyota', 'Honda', 'BMV', 'Audi'], 'horsepower': [141, 80, 182 , 160]}
```
* Cree dos dataframes (**carsDf1** y **carsDf2**) según corresponda.
* Junte ambos dataframes (**carsDf**) por la llave **Company**.
```
carsDf1=pd.DataFrame(Car_Price)
carsDf2=pd.DataFrame(car_Horsepower)
carsDf= pd.merge(carsDf1, carsDf2, on='Company')
carsDf
```
|
github_jupyter
|
# Dependencies
```
import os, warnings, shutil
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from transformers import AutoTokenizer
from sklearn.utils import shuffle
from sklearn.model_selection import StratifiedKFold
SEED = 0
warnings.filterwarnings("ignore")
```
# Parameters
```
MAX_LEN = 192
tokenizer_path = 'jplu/tf-xlm-roberta-large'
positive1 = 21384 * 2
positive2 = 112226 * 2
```
# Load data
```
train1 = pd.read_csv("/kaggle/input/jigsaw-multilingual-toxic-comment-classification/jigsaw-toxic-comment-train.csv")
train2 = pd.read_csv("/kaggle/input/jigsaw-multilingual-toxic-comment-classification/jigsaw-unintended-bias-train.csv")
train_df = pd.concat([train1[['comment_text', 'toxic']].query('toxic == 1'),
train1[['comment_text', 'toxic']].query('toxic == 0').sample(n=positive1, random_state=SEED),
train2[['comment_text', 'toxic']].query('toxic > .5'),
train2[['comment_text', 'toxic']].query('toxic <= .5').sample(n=positive2, random_state=SEED)
])
train_df = shuffle(train_df, random_state=SEED).reset_index(drop=True)
train_df['toxic_int'] = train_df['toxic'].round().astype(int)
print('Train samples %d' % len(train_df))
display(train_df.head())
```
# Tokenizer
```
tokenizer = AutoTokenizer.from_pretrained(tokenizer_path)
```
# Data generation sanity check
```
for idx in range(5):
print('\nRow %d' % idx)
max_seq_len = 22
comment_text = train_df['comment_text'].loc[idx]
enc = tokenizer.encode_plus(comment_text,
return_token_type_ids=False,
pad_to_max_length=True,
max_length=max_seq_len)
print('comment_text : "%s"' % comment_text)
print('input_ids : "%s"' % enc['input_ids'])
print('attention_mask: "%s"' % enc['attention_mask'])
assert len(enc['input_ids']) == len(enc['attention_mask']) == max_seq_len
```
# 5-Fold split
```
folds = StratifiedKFold(n_splits=5, shuffle=True, random_state=SEED)
for fold_n, (train_idx, val_idx) in enumerate(folds.split(train_df, train_df['toxic_int'])):
print('Fold: %s, Train size: %s, Validation size %s' % (fold_n+1, len(train_idx), len(val_idx)))
train_df[('fold_%s' % str(fold_n+1))] = 0
train_df[('fold_%s' % str(fold_n+1))].loc[train_idx] = 'train'
train_df[('fold_%s' % str(fold_n+1))].loc[val_idx] = 'validation'
```
# Label distribution
```
for fold_n in range(folds.n_splits):
fold_n += 1
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(18, 6))
fig.suptitle('Fold %s' % fold_n, fontsize=22)
sns.countplot(x="toxic_int", data=train_df[train_df[('fold_%s' % fold_n)] == 'train'], palette="GnBu_d", ax=ax1).set_title('Train')
sns.countplot(x="toxic_int", data=train_df[train_df[('fold_%s' % fold_n)] == 'validation'], palette="GnBu_d", ax=ax2).set_title('Validation')
sns.despine()
plt.show()
for fold_n in range(folds.n_splits):
fold_n += 1
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(18, 6))
fig.suptitle('Fold %s' % fold_n, fontsize=22)
sns.distplot(train_df[train_df[('fold_%s' % fold_n)] == 'train']['toxic'], ax=ax1).set_title('Train')
sns.distplot(train_df[train_df[('fold_%s' % fold_n)] == 'validation']['toxic'], ax=ax2).set_title('Validation')
sns.despine()
plt.show()
```
# Output 5-fold set
```
train_df.to_csv('5-fold.csv', index=False)
display(train_df.head())
for fold_n in range(folds.n_splits):
if fold_n < 1:
fold_n += 1
base_path = 'fold_%d/' % fold_n
# Create dir
os.makedirs(base_path)
x_train = tokenizer.batch_encode_plus(train_df[train_df[('fold_%s' % fold_n)] == 'train']['comment_text'].values,
return_token_type_ids=False,
pad_to_max_length=True,
max_length=MAX_LEN)
x_train = np.array([np.array(x_train['input_ids']),
np.array(x_train['attention_mask'])])
x_valid = tokenizer.batch_encode_plus(train_df[train_df[('fold_%s' % fold_n)] == 'validation']['comment_text'].values,
return_token_type_ids=False,
pad_to_max_length=True,
max_length=MAX_LEN)
x_valid = np.array([np.array(x_valid['input_ids']),
np.array(x_valid['attention_mask'])])
y_train = train_df[train_df[('fold_%s' % fold_n)] == 'train']['toxic'].values
y_valid = train_df[train_df[('fold_%s' % fold_n)] == 'validation']['toxic'].values
np.save(base_path + 'x_train', np.asarray(x_train))
np.save(base_path + 'y_train', y_train)
np.save(base_path + 'x_valid', np.asarray(x_valid))
np.save(base_path + 'y_valid', y_valid)
print('\nFOLD: %d' % (fold_n))
print('x_train shape:', x_train.shape)
print('y_train shape:', y_train.shape)
print('x_valid shape:', x_valid.shape)
print('y_valid shape:', y_valid.shape)
# Compress logs dir
!tar -cvzf fold_1.tar.gz fold_1
# !tar -cvzf fold_2.tar.gz fold_2
# !tar -cvzf fold_3.tar.gz fold_3
# !tar -cvzf fold_4.tar.gz fold_4
# !tar -cvzf fold_5.tar.gz fold_5
# Delete logs dir
shutil.rmtree('fold_1')
# shutil.rmtree('fold_2')
# shutil.rmtree('fold_3')
# shutil.rmtree('fold_4')
# shutil.rmtree('fold_5')
```
# Validation set
```
valid_df = pd.read_csv("/kaggle/input/jigsaw-multilingual-toxic-comment-classification/validation.csv", usecols=['comment_text', 'toxic', 'lang'])
display(valid_df.head())
x_valid = tokenizer.batch_encode_plus(valid_df['comment_text'].values,
return_token_type_ids=False,
pad_to_max_length=True,
max_length=MAX_LEN)
x_valid = np.array([np.array(x_valid['input_ids']),
np.array(x_valid['attention_mask'])])
y_valid = valid_df['toxic'].values
np.save('x_valid', np.asarray(x_valid))
np.save('y_valid', y_valid)
print('x_valid shape:', x_valid.shape)
print('y_valid shape:', y_valid.shape)
```
# Test set
```
test_df = pd.read_csv("/kaggle/input/jigsaw-multilingual-toxic-comment-classification/test.csv", usecols=['content'])
display(test_df.head())
x_test = tokenizer.batch_encode_plus(test_df['content'].values,
return_token_type_ids=False,
pad_to_max_length=True,
max_length=MAX_LEN)
x_test = np.array([np.array(x_test['input_ids']),
np.array(x_test['attention_mask'])])
np.save('x_test', np.asarray(x_test))
print('x_test shape:', x_test.shape)
```
|
github_jupyter
|
```
import numpy as np
import lqrpols
import matplotlib.pyplot as plt
```
Here is a link to [lqrpols.py](http://www.argmin.net/code/lqrpols.py)
```
np.random.seed(1337)
# state transition matrices for linear system:
# x(t+1) = A x (t) + B u(t)
A = np.array([[1,1],[0,1]])
B = np.array([[0],[1]])
d,p = B.shape
# LQR quadratic cost per state
Q = np.array([[1,0],[0,0]])
# initial condition for system
z0 = -1 # initial position
v0 = 0 # initial velocity
x0 = np.vstack((z0,v0))
R = np.array([[1.0]])
# number of time steps to simulate
T = 10
# amount of Gaussian noise in dynamics
eq_err = 1e-2
# N_vals = np.floor(np.linspace(1,75,num=7)).astype(int)
N_vals = [1,2,5,7,12,25,50,75]
N_trials = 10
### Bunch of matrices for storing costs
J_finite_nom = np.zeros((N_trials,len(N_vals)))
J_finite_nomK = np.zeros((N_trials,len(N_vals)))
J_finite_rs = np.zeros((N_trials,len(N_vals)))
J_finite_ur = np.zeros((N_trials,len(N_vals)))
J_finite_pg = np.zeros((N_trials,len(N_vals)))
J_inf_nom = np.zeros((N_trials,len(N_vals)))
J_inf_rs = np.zeros((N_trials,len(N_vals)))
J_inf_ur = np.zeros((N_trials,len(N_vals)))
J_inf_pg = np.zeros((N_trials,len(N_vals)))
# cost for finite time horizon, true model
J_finite_opt = lqrpols.cost_finite_model(A,B,Q,R,x0,T,A,B)
### Solve for optimal infinite time horizon LQR controller
K_opt = -lqrpols.lqr_gain(A,B,Q,R)
# cost for infinite time horizon, true model
J_inf_opt = lqrpols.cost_inf_K(A,B,Q,R,K_opt)
# cost for zero control
baseline = lqrpols.cost_finite_K(A,B,Q,R,x0,T,np.zeros((p,d)))
# model for nominal control with 1 rollout
A_nom1,B_nom1 = lqrpols.lsqr_estimator(A,B,Q,R,x0,eq_err,1,T)
print(A_nom1)
print(B_nom1)
# cost for finite time horizon, one rollout, nominal control
one_rollout_cost = lqrpols.cost_finite_model(A,B,Q,R,x0,T,A_nom1,B_nom1)
K_nom1 = -lqrpols.lqr_gain(A_nom1,B_nom1,Q,R)
one_rollout_cost_inf = lqrpols.cost_inf_K(A,B,Q,R,K_nom1)
for N in range(len(N_vals)):
for trial in range(N_trials):
# nominal model, N x 40 to match sample budget of policy gradient
A_nom,B_nom = lqrpols.lsqr_estimator(A,B,Q,R,x0,eq_err,N_vals[N]*40,T);
# finite time horizon cost with nominal model
J_finite_nom[trial,N] = lqrpols.cost_finite_model(A,B,Q,R,x0,T,A_nom,B_nom)
# Solve for infinite time horizon nominal LQR controller
K_nom = -lqrpols.lqr_gain(A_nom,B_nom,Q,R)
# cost of using the infinite time horizon solution for finite time horizon
J_finite_nomK[trial,N] = lqrpols.cost_finite_K(A,B,Q,R,x0,T,K_nom)
# infinite time horizon cost of nominal model
J_inf_nom[trial,N] = lqrpols.cost_inf_K(A,B,Q,R,K_nom)
# policy gradient, batchsize 40 per iteration
K_pg = lqrpols.policy_gradient_adam_linear_policy(A,B,Q,R,x0,eq_err,N_vals[N]*5,T)
J_finite_pg[trial,N] = lqrpols.cost_finite_K(A,B,Q,R,x0,T,K_pg)
J_inf_pg[trial,N] = lqrpols.cost_inf_K(A,B,Q,R,K_pg)
# random search, batchsize 4, so uses 8 rollouts per iteration
K_rs = lqrpols.random_search_linear_policy(A,B,Q,R,x0,eq_err,N_vals[N]*5,T)
J_finite_rs[trial,N] = lqrpols.cost_finite_K(A,B,Q,R,x0,T,K_rs)
J_inf_rs[trial,N] = lqrpols.cost_inf_K(A,B,Q,R,K_rs)
# uniformly random sampling, N x 40 to match sample budget of policy gradient
K_ur = lqrpols.uniform_random_linear_policy(A,B,Q,R,x0,eq_err,N_vals[N]*40,T)
J_finite_ur[trial,N] = lqrpols.cost_finite_K(A,B,Q,R,x0,T,K_ur)
J_inf_ur[trial,N] = lqrpols.cost_inf_K(A,B,Q,R,K_ur)
colors = [ '#2D328F', '#F15C19',"#81b13c","#ca49ac"]
label_fontsize = 18
tick_fontsize = 14
linewidth = 3
markersize = 10
tot_samples = 40*np.array(N_vals)
plt.plot(tot_samples,np.amin(J_finite_pg,axis=0),'o-',color=colors[0],linewidth=linewidth,
markersize=markersize,label='policy gradient')
plt.plot(tot_samples,np.amin(J_finite_ur,axis=0),'>-',color=colors[1],linewidth=linewidth,
markersize=markersize,label='uniform sampling')
plt.plot(tot_samples,np.amin(J_finite_rs,axis=0),'s-',color=colors[2],linewidth=linewidth,
markersize=markersize,label='random search')
plt.plot([tot_samples[0],tot_samples[-1]],[baseline, baseline],color='#000000',linewidth=linewidth,
linestyle='--',label='zero control')
plt.plot([tot_samples[0],tot_samples[-1]],[J_finite_opt, J_finite_opt],color='#000000',linewidth=linewidth,
linestyle=':',label='optimal')
plt.axis([0,2000,0,12])
plt.xlabel('rollouts',fontsize=label_fontsize)
plt.ylabel('cost',fontsize=label_fontsize)
plt.legend(fontsize=18, bbox_to_anchor=(1.0, 0.54))
plt.xticks(fontsize=tick_fontsize)
plt.yticks(fontsize=tick_fontsize)
plt.grid(True)
fig = plt.gcf()
fig.set_size_inches(9, 6)
plt.show()
plt.plot(tot_samples,np.median(J_finite_pg,axis=0),'o-',color=colors[0],linewidth=linewidth,
markersize=markersize,label='policy gradient')
plt.fill_between(tot_samples, np.amin(J_finite_pg,axis=0), np.amax(J_finite_pg,axis=0), alpha=0.25)
plt.plot(tot_samples,np.median(J_finite_ur,axis=0),'>-',color=colors[1],linewidth=linewidth,
markersize=markersize,label='uniform sampling')
plt.fill_between(tot_samples, np.amin(J_finite_ur,axis=0), np.amax(J_finite_ur,axis=0), alpha=0.25)
plt.plot(tot_samples,np.median(J_finite_rs,axis=0),'s-',color=colors[2],linewidth=linewidth,
markersize=markersize,label='random search')
plt.fill_between(tot_samples, np.amin(J_finite_rs,axis=0), np.amax(J_finite_rs,axis=0), alpha=0.25)
plt.plot([tot_samples[0],tot_samples[-1]],[baseline, baseline],color='#000000',linewidth=linewidth,
linestyle='--',label='zero control')
plt.plot([tot_samples[0],tot_samples[-1]],[J_finite_opt, J_finite_opt],color='#000000',linewidth=linewidth,
linestyle=':',label='optimal')
plt.axis([0,2000,0,12])
plt.xlabel('rollouts',fontsize=label_fontsize)
plt.ylabel('cost',fontsize=label_fontsize)
plt.legend(fontsize=18, bbox_to_anchor=(1.0, 0.54))
plt.xticks(fontsize=tick_fontsize)
plt.yticks(fontsize=tick_fontsize)
plt.grid(True)
fig = plt.gcf()
fig.set_size_inches(9, 6)
plt.show()
plt.plot(tot_samples,np.median(J_inf_pg,axis=0),'o-',color=colors[0],linewidth=linewidth,
markersize=markersize,label='policy gradient')
plt.fill_between(tot_samples, np.amin(J_inf_pg,axis=0), np.minimum(np.amax(J_inf_pg,axis=0),15), alpha=0.25)
plt.plot(tot_samples,np.median(J_inf_ur,axis=0),'>-',color=colors[1],linewidth=linewidth,
markersize=markersize,label='uniform sampling')
plt.fill_between(tot_samples, np.amin(J_inf_ur,axis=0), np.minimum(np.amax(J_inf_ur,axis=0),15), alpha=0.25)
plt.plot(tot_samples,np.median(J_inf_rs,axis=0),'s-',color=colors[2],linewidth=linewidth,
markersize=markersize,label='random search')
plt.fill_between(tot_samples, np.amin(J_inf_rs,axis=0), np.minimum(np.amax(J_inf_rs,axis=0),15), alpha=0.25)
plt.plot([tot_samples[0],tot_samples[-1]],[J_inf_opt, J_inf_opt],color='#000000',linewidth=linewidth,
linestyle=':',label='optimal')
plt.axis([0,3000,5,10])
plt.xlabel('rollouts',fontsize=label_fontsize)
plt.ylabel('cost',fontsize=label_fontsize)
plt.legend(fontsize=18, bbox_to_anchor=(1.0, 0.54))
plt.xticks(fontsize=tick_fontsize)
plt.yticks(fontsize=tick_fontsize)
plt.grid(True)
fig = plt.gcf()
fig.set_size_inches(9, 6)
plt.show()
plt.plot(tot_samples,1-np.sum(np.isinf(J_inf_pg),axis=0)/10,'o-',color=colors[0],linewidth=linewidth,
markersize=markersize,label='policy gradient')
plt.plot(tot_samples,1-np.sum(np.isinf(J_inf_ur),axis=0)/10,'>-',color=colors[1],linewidth=linewidth,
markersize=markersize,label='uniform sampling')
plt.plot(tot_samples,1-np.sum(np.isinf(J_inf_rs),axis=0)/10,'s-',color=colors[2],linewidth=linewidth,
markersize=markersize,label='random search')
plt.axis([0,3000,0,1])
plt.xlabel('rollouts',fontsize=label_fontsize)
plt.ylabel('fraction stable',fontsize=label_fontsize)
plt.legend(fontsize=18, bbox_to_anchor=(1.0, 0.54))
plt.xticks(fontsize=tick_fontsize)
plt.yticks(fontsize=tick_fontsize)
plt.grid(True)
fig = plt.gcf()
fig.set_size_inches(9, 6)
plt.show()
one_rollout_cost-J_finite_opt
one_rollout_cost_inf-J_inf_opt
```
|
github_jupyter
|
# Encoding of categorical variables
In this notebook, we will present typical ways of dealing with
**categorical variables** by encoding them, namely **ordinal encoding** and
**one-hot encoding**.
Let's first load the entire adult dataset containing both numerical and
categorical data.
```
import pandas as pd
adult_census = pd.read_csv("../datasets/adult-census.csv")
# drop the duplicated column `"education-num"` as stated in the first notebook
adult_census = adult_census.drop(columns="education-num")
target_name = "class"
target = adult_census[target_name]
data = adult_census.drop(columns=[target_name])
```
## Identify categorical variables
As we saw in the previous section, a numerical variable is a
quantity represented by a real or integer number. These variables can be
naturally handled by machine learning algorithms that are typically composed
of a sequence of arithmetic instructions such as additions and
multiplications.
In contrast, categorical variables have discrete values, typically
represented by string labels (but not only) taken from a finite list of
possible choices. For instance, the variable `native-country` in our dataset
is a categorical variable because it encodes the data using a finite list of
possible countries (along with the `?` symbol when this information is
missing):
```
data["native-country"].value_counts().sort_index()
```
How can we easily recognize categorical columns among the dataset? Part of
the answer lies in the columns' data type:
```
data.dtypes
```
If we look at the `"native-country"` column, we observe its data type is
`object`, meaning it contains string values.
## Select features based on their data type
In the previous notebook, we manually defined the numerical columns. We could
do a similar approach. Instead, we will use the scikit-learn helper function
`make_column_selector`, which allows us to select columns based on
their data type. We will illustrate how to use this helper.
```
from sklearn.compose import make_column_selector as selector
categorical_columns_selector = selector(dtype_include=object)
categorical_columns = categorical_columns_selector(data)
categorical_columns
```
Here, we created the selector by passing the data type to include; we then
passed the input dataset to the selector object, which returned a list of
column names that have the requested data type. We can now filter out the
unwanted columns:
```
data_categorical = data[categorical_columns]
data_categorical.head()
print(f"The dataset is composed of {data_categorical.shape[1]} features")
```
In the remainder of this section, we will present different strategies to
encode categorical data into numerical data which can be used by a
machine-learning algorithm.
## Strategies to encode categories
### Encoding ordinal categories
The most intuitive strategy is to encode each category with a different
number. The `OrdinalEncoder` will transform the data in such manner.
We will start by encoding a single column to understand how the encoding
works.
```
from sklearn.preprocessing import OrdinalEncoder
education_column = data_categorical[["education"]]
encoder = OrdinalEncoder()
education_encoded = encoder.fit_transform(education_column)
education_encoded
```
We see that each category in `"education"` has been replaced by a numeric
value. We could check the mapping between the categories and the numerical
values by checking the fitted attribute `categories_`.
```
encoder.categories_
```
Now, we can check the encoding applied on all categorical features.
```
data_encoded = encoder.fit_transform(data_categorical)
data_encoded[:5]
print(
f"The dataset encoded contains {data_encoded.shape[1]} features")
```
We see that the categories have been encoded for each feature (column)
independently. We also note that the number of features before and after the
encoding is the same.
However, be careful when applying this encoding strategy:
using this integer representation leads downstream predictive models
to assume that the values are ordered (0 < 1 < 2 < 3... for instance).
By default, `OrdinalEncoder` uses a lexicographical strategy to map string
category labels to integers. This strategy is arbitrary and often
meaningless. For instance, suppose the dataset has a categorical variable
named `"size"` with categories such as "S", "M", "L", "XL". We would like the
integer representation to respect the meaning of the sizes by mapping them to
increasing integers such as `0, 1, 2, 3`.
However, the lexicographical strategy used by default would map the labels
"S", "M", "L", "XL" to 2, 1, 0, 3, by following the alphabetical order.
The `OrdinalEncoder` class accepts a `categories` constructor argument to
pass categories in the expected ordering explicitly. You can find more
information in the
[scikit-learn documentation](https://scikit-learn.org/stable/modules/preprocessing.html#encoding-categorical-features)
if needed.
If a categorical variable does not carry any meaningful order information
then this encoding might be misleading to downstream statistical models and
you might consider using one-hot encoding instead (see below).
### Encoding nominal categories (without assuming any order)
`OneHotEncoder` is an alternative encoder that prevents the downstream
models to make a false assumption about the ordering of categories. For a
given feature, it will create as many new columns as there are possible
categories. For a given sample, the value of the column corresponding to the
category will be set to `1` while all the columns of the other categories
will be set to `0`.
We will start by encoding a single feature (e.g. `"education"`) to illustrate
how the encoding works.
```
from sklearn.preprocessing import OneHotEncoder
encoder = OneHotEncoder(sparse=False)
education_encoded = encoder.fit_transform(education_column)
education_encoded
```
<div class="admonition note alert alert-info">
<p class="first admonition-title" style="font-weight: bold;">Note</p>
<p><tt class="docutils literal">sparse=False</tt> is used in the <tt class="docutils literal">OneHotEncoder</tt> for didactic purposes, namely
easier visualization of the data.</p>
<p class="last">Sparse matrices are efficient data structures when most of your matrix
elements are zero. They won't be covered in detail in this course. If you
want more details about them, you can look at
<a class="reference external" href="https://scipy-lectures.org/advanced/scipy_sparse/introduction.html#why-sparse-matrices">this</a>.</p>
</div>
We see that encoding a single feature will give a NumPy array full of zeros
and ones. We can get a better understanding using the associated feature
names resulting from the transformation.
```
feature_names = encoder.get_feature_names_out(input_features=["education"])
education_encoded = pd.DataFrame(education_encoded, columns=feature_names)
education_encoded
```
As we can see, each category (unique value) became a column; the encoding
returned, for each sample, a 1 to specify which category it belongs to.
Let's apply this encoding on the full dataset.
```
print(
f"The dataset is composed of {data_categorical.shape[1]} features")
data_categorical.head()
data_encoded = encoder.fit_transform(data_categorical)
data_encoded[:5]
print(
f"The encoded dataset contains {data_encoded.shape[1]} features")
```
Let's wrap this NumPy array in a dataframe with informative column names as
provided by the encoder object:
```
columns_encoded = encoder.get_feature_names_out(data_categorical.columns)
pd.DataFrame(data_encoded, columns=columns_encoded).head()
```
Look at how the `"workclass"` variable of the 3 first records has been
encoded and compare this to the original string representation.
The number of features after the encoding is more than 10 times larger than
in the original data because some variables such as `occupation` and
`native-country` have many possible categories.
### Choosing an encoding strategy
Choosing an encoding strategy will depend on the underlying models and the
type of categories (i.e. ordinal vs. nominal).
<div class="admonition note alert alert-info">
<p class="first admonition-title" style="font-weight: bold;">Note</p>
<p class="last">In general <tt class="docutils literal">OneHotEncoder</tt> is the encoding strategy used when the
downstream models are <strong>linear models</strong> while <tt class="docutils literal">OrdinalEncoder</tt> is often a
good strategy with <strong>tree-based models</strong>.</p>
</div>
Using an `OrdinalEncoder` will output ordinal categories. This means
that there is an order in the resulting categories (e.g. `0 < 1 < 2`). The
impact of violating this ordering assumption is really dependent on the
downstream models. Linear models will be impacted by misordered categories
while tree-based models will not.
You can still use an `OrdinalEncoder` with linear models but you need to be
sure that:
- the original categories (before encoding) have an ordering;
- the encoded categories follow the same ordering than the original
categories.
The **next exercise** highlights the issue of misusing `OrdinalEncoder` with
a linear model.
One-hot encoding categorical variables with high cardinality can cause
computational inefficiency in tree-based models. Because of this, it is not recommended
to use `OneHotEncoder` in such cases even if the original categories do not
have a given order. We will show this in the **final exercise** of this sequence.
## Evaluate our predictive pipeline
We can now integrate this encoder inside a machine learning pipeline like we
did with numerical data: let's train a linear classifier on the encoded data
and check the generalization performance of this machine learning pipeline using
cross-validation.
Before we create the pipeline, we have to linger on the `native-country`.
Let's recall some statistics regarding this column.
```
data["native-country"].value_counts()
```
We see that the `Holand-Netherlands` category is occurring rarely. This will
be a problem during cross-validation: if the sample ends up in the test set
during splitting then the classifier would not have seen the category during
training and will not be able to encode it.
In scikit-learn, there are two solutions to bypass this issue:
* list all the possible categories and provide it to the encoder via the
keyword argument `categories`;
* use the parameter `handle_unknown`.
Here, we will use the latter solution for simplicity.
<div class="admonition tip alert alert-warning">
<p class="first admonition-title" style="font-weight: bold;">Tip</p>
<p class="last">Be aware the <tt class="docutils literal">OrdinalEncoder</tt> exposes as well a parameter
<tt class="docutils literal">handle_unknown</tt>. It can be set to <tt class="docutils literal">use_encoded_value</tt> and by setting
<tt class="docutils literal">unknown_value</tt> to handle rare categories. You are going to use these
parameters in the next exercise.</p>
</div>
We can now create our machine learning pipeline.
```
from sklearn.pipeline import make_pipeline
from sklearn.linear_model import LogisticRegression
model = make_pipeline(
OneHotEncoder(handle_unknown="ignore"), LogisticRegression(max_iter=500)
)
```
<div class="admonition note alert alert-info">
<p class="first admonition-title" style="font-weight: bold;">Note</p>
<p class="last">Here, we need to increase the maximum number of iterations to obtain a fully
converged <tt class="docutils literal">LogisticRegression</tt> and silence a <tt class="docutils literal">ConvergenceWarning</tt>. Contrary
to the numerical features, the one-hot encoded categorical features are all
on the same scale (values are 0 or 1), so they would not benefit from
scaling. In this case, increasing <tt class="docutils literal">max_iter</tt> is the right thing to do.</p>
</div>
Finally, we can check the model's generalization performance only using the
categorical columns.
```
from sklearn.model_selection import cross_validate
cv_results = cross_validate(model, data_categorical, target)
cv_results
scores = cv_results["test_score"]
print(f"The accuracy is: {scores.mean():.3f} +/- {scores.std():.3f}")
```
As you can see, this representation of the categorical variables is
slightly more predictive of the revenue than the numerical variables
that we used previously.
In this notebook we have:
* seen two common strategies for encoding categorical features: **ordinal
encoding** and **one-hot encoding**;
* used a **pipeline** to use a **one-hot encoder** before fitting a logistic
regression.
|
github_jupyter
|
```
%load_ext autoreload
%autoreload 2
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import torch
device = 'cuda' if torch.cuda.is_available() else 'cpu'
import os,sys
opj = os.path.join
from copy import deepcopy
import pickle as pkl
sys.path.append('../../src')
sys.path.append('../../src/dsets/cosmology')
from dset import get_dataloader
from viz import viz_im_r, cshow, viz_filters
from sim_cosmology import p, load_dataloader_and_pretrained_model
from losses import get_loss_f
from train import Trainer, Validator
# wt modules
from wavelet_transform import Wavelet_Transform, Attributer, get_2dfilts, initialize_filters
from utils import tuple_L1Loss, tuple_L2Loss, thresh_attrs, viz_list
import pywt
import warnings
from itertools import product
import numpy as np
from pywt._c99_config import _have_c99_complex
from pywt._extensions._dwt import idwt_single
from pywt._extensions._swt import swt_max_level, swt as _swt, swt_axis as _swt_axis
from pywt._extensions._pywt import Wavelet, Modes, _check_dtype
from pywt._multidim import idwt2, idwtn
from pywt._utils import _as_wavelet, _wavelets_per_axis
# get dataloader and model
(train_loader, test_loader), model = load_dataloader_and_pretrained_model(p, img_size=256)
torch.manual_seed(p.seed)
im = iter(test_loader).next()[0][0:1].numpy().squeeze()
db2 = pywt.Wavelet('db2')
start_level = 0
axes = (-2, -1)
trim_approx = False
norm = False
data = np.asarray(im)
# coefs = swtn(data, wavelet, level, start_level, axes, trim_approx, norm)
axes = [a + data.ndim if a < 0 else a for a in axes]
num_axes = len(axes)
print(axes)
wavelets = _wavelets_per_axis(db2, axes)
ret = []
level = 1
i = 0
coeffs = [('', data)]
axis = axes[0]
wavelet = wavelets[0]
new_coeffs = []
subband, x = coeffs[0]
cA, cD = _swt_axis(x, wavelet, level=1, start_level=i,
axis=axis)[0]
new_coeffs.extend([(subband + 'a', cA),
(subband + 'd', cD)])
coeffs = new_coeffs
coeffs
def swtn(data, wavelet, level, start_level=0, axes=None, trim_approx=False,
norm=False):
wavelets = _wavelets_per_axis(wavelet, axes)
if norm:
if not np.all([wav.orthogonal for wav in wavelets]):
warnings.warn(
"norm=True, but the wavelets used are not orthogonal: \n"
"\tThe conditions for energy preservation are not satisfied.")
wavelets = [_rescale_wavelet_filterbank(wav, 1/np.sqrt(2))
for wav in wavelets]
ret = []
for i in range(start_level, start_level + level):
coeffs = [('', data)]
for axis, wavelet in zip(axes, wavelets):
new_coeffs = []
for subband, x in coeffs:
cA, cD = _swt_axis(x, wavelet, level=1, start_level=i,
axis=axis)[0]
new_coeffs.extend([(subband + 'a', cA),
(subband + 'd', cD)])
coeffs = new_coeffs
coeffs = dict(coeffs)
ret.append(coeffs)
# data for the next level is the approximation coeffs from this level
data = coeffs['a' * num_axes]
if trim_approx:
coeffs.pop('a' * num_axes)
if trim_approx:
ret.append(data)
ret.reverse()
return ret
def swt2(data, wavelet, level, start_level=0, axes=(-2, -1),
trim_approx=False, norm=False):
axes = tuple(axes)
data = np.asarray(data)
if len(axes) != 2:
raise ValueError("Expected 2 axes")
if len(axes) != len(set(axes)):
raise ValueError("The axes passed to swt2 must be unique.")
if data.ndim < len(np.unique(axes)):
raise ValueError("Input array has fewer dimensions than the specified "
"axes")
coefs = swtn(data, wavelet, level, start_level, axes, trim_approx, norm)
ret = []
if trim_approx:
ret.append(coefs[0])
coefs = coefs[1:]
for c in coefs:
if trim_approx:
ret.append((c['da'], c['ad'], c['dd']))
else:
ret.append((c['aa'], (c['da'], c['ad'], c['dd'])))
return ret
```
|
github_jupyter
|
This notebook is part of the orix documentation https://orix.readthedocs.io. Links to the documentation won’t work from the notebook.
## Visualizing point groups
Point group symmetry operations are shown here in the stereographic projection.
Vectors located on the upper (`z >= 0`) hemisphere are displayed as points (`o`), whereas vectors on the lower hemisphere are reprojected onto the upper hemisphere and shown as crosses (`+`) by default. For more information about plot formatting and visualization, see [Vector3d.scatter()](reference.rst#orix.vector.Vector3d.scatter).
More explanation of these figures is provided at http://xrayweb.chem.ou.edu/notes/symmetry.html#point.
```
%matplotlib inline
from matplotlib import pyplot as plt
import numpy as np
from orix import plot
from orix.quaternion import Rotation, symmetry
from orix.vector import Vector3d
plt.rcParams.update({"font.size": 15})
```
For example, the `O (432)` point group:
```
symmetry.O.plot()
```
The stereographic projection of all point groups is shown below:
```
# fmt: off
schoenflies = [
"C1", "Ci", # triclinic,
"C2x", "C2y", "C2z", "Csx", "Csy", "Csz", "C2h", # monoclinic
"D2", "C2v", "D2h", # orthorhombic
"C4", "S4", "C4h", "D4", "C4v", "D2d", "D4h", # tetragonal
"C3", "S6", "D3x", "D3y", "D3", "C3v", "D3d", "C6", # trigonal
"C3h", "C6h", "D6", "C6v", "D3h", "D6h", # hexagonal
"T", "Th", "O", "Td", "Oh", # cubic
]
# fmt: on
assert len(symmetry._groups) == len(schoenflies)
schoenflies = [s for s in schoenflies if not (s.endswith("x") or s.endswith("y"))]
assert len(schoenflies) == 32
orientation = Rotation.from_axes_angles((-1, 8, 1), np.deg2rad(65))
fig, ax = plt.subplots(
nrows=8, ncols=4, figsize=(10, 20), subplot_kw=dict(projection="stereographic")
)
ax = ax.ravel()
for i, s in enumerate(schoenflies):
sym = getattr(symmetry, s)
ori_sym = sym.outer(orientation)
v = ori_sym * Vector3d.zvector()
# reflection in the projection plane (x-y) is performed internally in
# Symmetry.plot() or when using the `reproject=True` argument for
# Vector3d.scatter()
v_reproject = Vector3d(v.data.copy())
v_reproject.z *= -1
# the Symmetry marker formatting for vectors on the upper and lower hemisphere
# can be set using `kwargs` and `reproject_scatter_kwargs`, respectively, for
# Symmetry.plot()
# vectors on the upper hemisphere are shown as open circles
ax[i].scatter(v, marker="o", fc="None", ec="k", s=150)
# vectors on the lower hemisphere are reprojected onto the upper hemisphere and
# shown as crosses
ax[i].scatter(v_reproject, marker="+", ec="C0", s=150)
ax[i].set_title(f"${s}$ $({sym.name})$")
ax[i].set_labels("a", "b", None)
fig.tight_layout()
```
|
github_jupyter
|
## Loan EDA
```
import pandas as pd
import numpy as np
dtrain = pd.read_csv('data/train.csv')
test = pd.read_csv('data/test.csv')
```
## Data Cleaning
```
dtrain.head()
dtrain.shape
# Removing the commas form `Loan_Amount_Requested`
dtrain['Loan_Amount_Requested'] = dtrain.Loan_Amount_Requested.str.replace(',', '').astype(int)
test['Loan_Amount_Requested'] = test.Loan_Amount_Requested.str.replace(',', '').astype(int)
# Filling 0 for `Annual_Income` column
dtrain['Annual_Income'] = dtrain['Annual_Income'].fillna(0).astype(int)
test['Annual_Income'] = test['Annual_Income'].fillna(0).astype(int)
# Showing the different types of values for `Home_Owner`
dtrain['Home_Owner'] = dtrain['Home_Owner'].fillna('NA')
test['Home_Owner'] = test['Home_Owner'].fillna('NA')
print(dtrain.Home_Owner.value_counts())
```
We converted the ```NaN``` in ```Home_Owner``` into ```NA```. We are going to calculate the hash value of the string and we don't know how ```NaN``` should be replced. Now we see that there are almost **25349** rows which was NaN. Dropping these would cause loosing a lot of data. Hence we replaced these with sting "NA" and then converted these into hash values
```
# Filling 0 for missing `Months_Since_Deliquency`
dtrain['Months_Since_Deliquency'] = dtrain['Months_Since_Deliquency'].fillna(0)
test['Months_Since_Deliquency'] = test['Months_Since_Deliquency'].fillna(0)
dtrain.isnull().values.any()
dtrain['Length_Employed'] = dtrain['Length_Employed'].fillna('0 year')
test['Length_Employed'] = test['Length_Employed'].fillna('0 year')
def convert_length_employed(elem):
if elem[0] == '<':
return 0.5 # because mean of 0 to 1 is 0.5
elif str(elem[2]) == '+':
return 15.0 # because mean of 10 to 20 is 15
elif str(elem) == '0 year':
return 0.0
else:
return float(str(elem).split()[0])
dtrain['Length_Employed'] = dtrain['Length_Employed'].apply(convert_length_employed)
test['Length_Employed'] = test['Length_Employed'].apply(convert_length_employed)
dtrain['Loan_Grade'] = dtrain['Loan_Grade'].fillna('NA')
test['Loan_Grade'] = test['Loan_Grade'].fillna('NA')
dtrain.Loan_Grade.value_counts()
# dtrain[(dtrain.Annual_Income == 0) & (dtrain.Income_Verified == 'not verified')]
from sklearn.preprocessing import LabelEncoder
number = LabelEncoder()
dtrain['Loan_Grade'] = number.fit_transform(dtrain.Loan_Grade.astype('str'))
dtrain['Income_Verified'] = number.fit_transform(dtrain.Income_Verified.astype('str'))
dtrain['Area_Type'] = number.fit_transform(dtrain.Area_Type.astype('str'))
dtrain['Gender'] = number.fit_transform(dtrain.Gender.astype('str'))
test['Loan_Grade'] = number.fit_transform(test.Loan_Grade.astype('str'))
test['Income_Verified'] = number.fit_transform(test.Income_Verified.astype('str'))
test['Area_Type'] = number.fit_transform(test.Area_Type.astype('str'))
test['Gender'] = number.fit_transform(test.Gender.astype('str'))
dtrain.head()
# Converting `Purpose_Of_Loan` and `Home_Owner` into hash
import hashlib
def convert_to_hashes(elem):
return round(int(hashlib.md5(elem.encode('utf-8')).hexdigest(), 16) / 1e35, 5)
dtrain['Purpose_Of_Loan'] = dtrain['Purpose_Of_Loan'].apply(convert_to_hashes)
dtrain['Home_Owner'] = dtrain['Home_Owner'].apply(convert_to_hashes)
test['Purpose_Of_Loan'] = test['Purpose_Of_Loan'].apply(convert_to_hashes)
test['Home_Owner'] = test['Home_Owner'].apply(convert_to_hashes)
import xgboost as xgb
features = np.array(dtrain.iloc[:, 1:-1])
labels = np.array(dtrain.iloc[:, -1])
import operator
from xgboost import plot_importance
from matplotlib import pylab as plt
from collections import OrderedDict
def xgb_feature_importance(features, labels, num_rounds, fnames, plot=False):
param = {}
param['objective'] = 'multi:softmax'
param['eta'] = 0.1
param['max_depth'] = 6
param['silent'] = 1
param['num_class'] = 4
param['eval_metric'] = "merror"
param['min_child_weight'] = 1
param['subsample'] = 0.7
param['colsample_bytree'] = 0.7
param['seed'] = 42
nrounds = num_rounds
xgtrain = xgb.DMatrix(features, label=labels)
xgb_params = list(param.items())
gbdt = xgb.train(xgb_params, xgtrain, nrounds)
importance = sorted(gbdt.get_fscore().items(), key=operator.itemgetter(1), reverse=True)
if plot:
df = pd.DataFrame(importance, columns=['feature', 'fscore'])
df['fscore'] = df['fscore'] / df['fscore'].sum()
plt.figure()
df.plot(kind='bar', x='feature', y='fscore', legend=False, figsize=(8, 8))
plt.title('XGBoost Feature Importance')
plt.xlabel('relative importance')
plt.show()
else:
# fnames = dtrain.columns.values[1:-1].tolist()
imp_features = OrderedDict()
imps = dict(importance)
for each in list(imps.keys()):
index = int(each.split('f')[-1])
imp_features[fnames[index]] = imps[each]
return imp_features
xgb_feature_importance(features, labels, num_rounds=1000, fnames=dtrain.columns.values[1:-1].tolist(), plot=True)
```
## Features Scores
```python
OrderedDict([('Debt_To_Income', 29377),
('Loan_Amount_Requested', 22157),
('Annual_Income', 21378),
('Total_Accounts', 16675),
('Months_Since_Deliquency', 13287),
('Number_Open_Accounts', 13016),
('Length_Employed', 9140),
('Loan_Grade', 7906),
('Purpose_Of_Loan', 7284),
('Inquiries_Last_6Mo', 5691),
('Home_Owner', 4946),
('Income_Verified', 4434),
('Area_Type', 3755),
('Gender', 2027)])
```
## Feature Creation
### 1. RatioOfLoanAndIncome
```
dtrain['RatioOfLoanAndIncome'] = dtrain.Loan_Amount_Requested / (dtrain.Annual_Income + 1)
test['RatioOfLoanAndIncome'] = test.Loan_Amount_Requested / (test.Annual_Income + 1)
```
### 2. RatioOfOpenAccToTotalAcc
```
dtrain['RatioOfOpenAccToTotalAcc'] = dtrain.Number_Open_Accounts / (dtrain.Total_Accounts + 0.001)
test['RatioOfOpenAccToTotalAcc'] = test.Number_Open_Accounts / (test.Total_Accounts + 0.001)
dtrain.drop(['Interest_Rate', 'Loan_Amount_Requested',
'Annual_Income', 'Number_Open_Accounts', 'Total_Accounts'], inplace=True, axis=1)
dtrain['Interest_Rate'] = labels
test.drop(['Loan_Amount_Requested',
'Annual_Income', 'Number_Open_Accounts', 'Total_Accounts'], inplace=True, axis=1)
features = np.array(dtrain.iloc[:, 1:-1])
testFeatures = np.array(test.iloc[:, 1:])
xgb_feature_importance(features, labels, num_rounds=1000, fnames=dtrain.columns.values[1:-1].tolist(), plot=True)
```
## Feature Score with new features
```python
OrderedDict([('Debt_To_Income', 23402),
('RatioOfLoanAndIncome', 20254),
('RatioOfOpenAccToTotalAcc', 17868),
('Loan_Amount_Requested', 16661),
('Annual_Income', 14228),
('Total_Accounts', 11892),
('Months_Since_Deliquency', 10293),
('Number_Open_Accounts', 8553),
('Length_Employed', 7614),
('Loan_Grade', 6938),
('Purpose_Of_Loan', 6013),
('Inquiries_Last_6Mo', 4284),
('Home_Owner', 3760),
('Income_Verified', 3451),
('Area_Type', 2892),
('Gender', 1708)])
```
```
from sklearn.model_selection import train_test_split # for splitting the training and testing set
from sklearn.decomposition import PCA # For possible dimentionality reduction
from sklearn.feature_selection import SelectKBest # For feature selction
from sklearn.model_selection import StratifiedShuffleSplit # For unbalanced class cross-validation
from sklearn.preprocessing import MaxAbsScaler, StandardScaler, MinMaxScaler # Different scalars
from sklearn.pipeline import Pipeline # For putting tasks in Pipeline
from sklearn.model_selection import GridSearchCV # For fine tuning the classifiers
from sklearn.naive_bayes import BernoulliNB # For Naive Bayes
from sklearn.neighbors import NearestCentroid # From modified KNN
from sklearn.svm import SVC # For SVM Classifier
from sklearn.tree import DecisionTreeClassifier # From decision Tree Classifier
X_train, X_test, y_train, y_test = train_test_split(features, labels, test_size=0.4, random_state=42)
from sklearn.metrics import accuracy_score
```
### Naive Bayes
```
clf = BernoulliNB()
clf.fit(X_train, y_train)
predictions = clf.predict(X_test)
print(accuracy_score(y_test, predictions, normalize=True))
X_test.shape
```
### XGBoost Cassification
```
def xgb_classification(X_train, X_test, y_train, y_test, num_rounds, fnames='*'):
if fnames == '*':
# All the features are being used
pass
else:
# Feature selection is being performed
fnames.append('Interest_Rate')
dataset = dtrain[fnames]
features = np.array(dataset.iloc[:, 0:-1])
labels = np.array(dataset.iloc[:, -1])
X_train, X_test, y_train, y_test = train_test_split(features, labels,
test_size=0.4,
random_state=42)
param = {}
param['objective'] = 'multi:softmax'
param['eta'] = 0.01
param['max_depth'] = 6
param['silent'] = 1
param['num_class'] = 4
param['nthread'] = -1
param['eval_metric'] = "merror"
param['min_child_weight'] = 1
param['subsample'] = 0.8
param['colsample_bytree'] = 0.5
param['seed'] = 42
xg_train = xgb.DMatrix(X_train, label=y_train)
xg_test = xgb.DMatrix(X_test, label=y_test)
watchlist = [(xg_train, 'train'), (xg_test, 'test')]
bst = xgb.train(param, xg_train, num_rounds, watchlist)
pred = bst.predict(xg_test)
return accuracy_score(y_test, pred, normalize=True)
# 0.70447629480859353 <-- Boosting Rounds 1000
# 0.70506968535086123 <--- Boosting Rounds 862
# 0.70520662162984604 <-- Boosting Rounds 846
xgb_classification(X_train, X_test, y_train, y_test, num_rounds=1000, fnames='*')
```
## Submission
```
param = {}
param['objective'] = 'multi:softmax'
param['eta'] = 0.01
param['max_depth'] = 10
param['silent'] = 1
param['num_class'] = 4
param['nthread'] = -1
param['eval_metric'] = "merror"
param['min_child_weight'] = 1
param['subsample'] = 0.8
param['colsample_bytree'] = 0.5
param['seed'] = 42
xg_train = xgb.DMatrix(features,label=labels)
xg_test = xgb.DMatrix(testFeatures)
watchlist = [(xg_train, 'train')]
gbm = xgb.train(param,xg_train, 846, watchlist)
test_pred = gbm.predict(xg_test)
test['Interest_Rate'] = test_pred
test['Interest_Rate'] = test.Interest_Rate.astype(int)
test[['Loan_ID', 'Interest_Rate']].to_csv('submission5.csv', index=False)
pd.read_csv('submission5.csv')
# test[['Loan_ID', 'Interest_Rate']]
testFeatures.shape
features.shape
```
|
github_jupyter
|
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
base_path = './data/ML-1M/'
ratings = pd.read_csv(base_path+'ratings.csv', sep='\t',
encoding='latin-1',
usecols=['user_id', 'movie_id', 'rating'])
users = pd.read_csv(base_path+'users.csv', sep='\t',
encoding='latin-1',
usecols=['user_id', 'gender', 'zipcode',
'age_desc', 'occ_desc'])
movies = pd.read_csv(base_path+'movies.csv', sep='\t',
encoding='latin-1',
usecols=['movie_id', 'title', 'genres'])
ratings.head()
users.head()
movies.head()
```
Plot the wordcloud
```
%matplotlib inline
import wordcloud
from wordcloud import WordCloud, STOPWORDS
# Create a wordcloud of the movie titles
movies['title'] = movies['title'].fillna("").astype('str')
title_corpus = ' '.join(movies['title'])
title_wordcloud = WordCloud(stopwords=STOPWORDS, background_color='black', height=2000, width=4000).generate(title_corpus)
# Plot the wordcloud
plt.figure(figsize=(16,8))
plt.imshow(title_wordcloud)
plt.axis('off')
plt.show()
```
Genre-based recommendations
```
# Import libraries
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.metrics.pairwise import linear_kernel
# Break up the big genre string into a string array
movies['genres'] = movies['genres'].str.split('|')
# Convert genres to string value
movies['genres'] = movies['genres'].fillna("").astype('str')
# Movie feature vector
tf = TfidfVectorizer(analyzer='word', ngram_range=(1, 2), min_df=0,
stop_words='english')
tfidf_matrix = tf.fit_transform(movies['genres'])
# Movie similarity matrix
cosine_sim = linear_kernel(tfidf_matrix, tfidf_matrix)
# 1-d array of movie titles
titles = movies['title']
indices = pd.Series(movies.index, index=movies['title'])
# Function to return top-k most similar movies
def genre_recommendations(title, topk=20):
idx = indices[title]
sim_scores = list(enumerate(cosine_sim[idx]))
sim_scores = sorted(sim_scores, key=lambda x: x[1], reverse=True)
sim_scores = sim_scores[1:topk+1]
movie_indices = [i[0] for i in sim_scores]
return titles.iloc[movie_indices].reset_index(drop=True)
# Checkout the results
# genre_recommendations('Good Will Hunting (1997)')
genre_recommendations('Toy Story (1995)')
# genre_recommendations('Saving Private Ryan (1998)')
```
Simple collaborative filtering
```
from math import sqrt
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
from sklearn.metrics.pairwise import pairwise_distances
# Fill NaN values in user_id and movie_id column with 0
ratings['user_id'] = ratings['user_id'].fillna(0)
ratings['movie_id'] = ratings['movie_id'].fillna(0)
# Replace NaN values in rating column with average of all values
ratings['rating'] = ratings['rating'].fillna(ratings['rating'].mean())
# Randomly sample 1% for faster processing
small_data = ratings.sample(frac=0.01)
# Split into train and test
train_data, test_data = train_test_split(small_data, test_size=0.2)
# Create two user-item matrices, one for training and another for testing
train_data_matrix = train_data.pivot(index='user_id', columns='movie_id', values='rating').fillna(0)
test_data_matrix = test_data.pivot(index='user_id', columns='movie_id', values='rating').fillna(0)
# Create user similarity using Pearson correlation
user_correlation = 1 - pairwise_distances(train_data_matrix, metric='correlation')
user_correlation[np.isnan(user_correlation)] = 0
# Create item similarity using Pearson correlation
item_correlation = 1 - pairwise_distances(train_data_matrix.T, metric='correlation')
item_correlation[np.isnan(item_correlation)] = 0
# Function to predict ratings
def predict(ratings, similarity, type='user'):
if type == 'user':
mean_user_rating = ratings.mean(axis=1)
# Use np.newaxis so that mean_user_rating has same format as ratings
ratings_diff = (ratings - mean_user_rating.values[:, np.newaxis])
pred = mean_user_rating.values[:, np.newaxis] + similarity.dot(ratings_diff) / np.array([np.abs(similarity).sum(axis=1)]).T
elif type == 'item':
pred = ratings.dot(similarity) / np.array([np.abs(similarity).sum(axis=1)])
return pred
# Function to calculate RMSE
def rmse(pred, actual):
# Ignore nonzero terms.
pred = pd.DataFrame(pred).values
actual = actual.values
pred = pred[actual.nonzero()].flatten()
actual = actual[actual.nonzero()].flatten()
return sqrt(mean_squared_error(pred, actual))
# Predict ratings on the training data with both similarity score
user_prediction = predict(train_data_matrix, user_correlation, type='user')
item_prediction = predict(train_data_matrix, item_correlation, type='item')
# RMSE on the train data
print('User-based CF RMSE Train: ' + str(rmse(user_prediction, train_data_matrix)))
print('Item-based CF RMSE Train: ' + str(rmse(item_prediction, train_data_matrix)))
# RMSE on the test data
print('User-based CF RMSE Test: ' + str(rmse(user_prediction, test_data_matrix)))
print('Item-based CF RMSE Test: ' + str(rmse(item_prediction, test_data_matrix)))
```
SVD matrix factorization based collaborative filtering
```
!pip install surprise
from scipy.sparse.linalg import svds
# Create the interaction matrix
interactions = ratings.pivot(index='user_id', columns='movie_id', values='rating').fillna(0)
print(pd.DataFrame(interactions.values).head())
# De-normalize the data (normalize by each users mean)
user_ratings_mean = np.mean(interactions.values, axis=1)
interactions_normalized = interactions.values - user_ratings_mean.reshape(-1, 1)
print(pd.DataFrame(interactions_normalized).head())
# Calculating SVD
U, sigma, Vt = svds(interactions_normalized, k=50)
sigma = np.diag(sigma)
# Make predictions from the decomposed matrix by matrix multiply U, Σ, and VT
# back to get the rank k=50 approximation of A.
all_user_predicted_ratings = np.dot(np.dot(U, sigma), Vt) + user_ratings_mean.reshape(-1, 1)
preds = pd.DataFrame(all_user_predicted_ratings, columns=interactions.columns)
print(preds.head().values)
# Get the movie with the highest predicted rating
def recommend_movies(predictions, userID, movies, original_ratings, num_recommendations):
# Get and sort the user's predictions
user_row_number = userID - 1 # User ID starts at 1, not 0
sorted_user_predictions = preds.iloc[user_row_number].sort_values(ascending=False) # User ID starts at 1
# Get the user's data and merge in the movie information.
user_data = original_ratings[original_ratings.user_id == (userID)]
user_full = (user_data.merge(movies, how = 'left', left_on = 'movie_id', right_on = 'movie_id').
sort_values(['rating'], ascending=False)
)
print('User {0} has already rated {1} movies.'.format(userID, user_full.shape[0]))
print('Recommending highest {0} predicted ratings movies not already rated.'.format(num_recommendations))
# Recommend the highest predicted rating movies that the user hasn't seen yet.
recommendations = (movies[~movies['movie_id'].isin(user_full['movie_id'])].
merge(pd.DataFrame(sorted_user_predictions).reset_index(), how = 'left',
left_on = 'movie_id',
right_on = 'movie_id').
rename(columns = {user_row_number: 'Predictions'}).
sort_values('Predictions', ascending = False).
iloc[:num_recommendations, :-1]
)
return user_full, recommendations
# Let's try to recommend 20 movies for user with ID 1310
already_rated, predictions = recommend_movies(preds, 1310, movies, ratings, 20)
# Top 20 movies that User 1310 has rated
print(already_rated.head(20))
# Top 20 movies that User 1310 hopefully will enjoy
print(predictions)
from surprise import Reader, Dataset, SVD
from surprise.model_selection import cross_validate
# Load Reader library
reader = Reader()
# Load ratings dataset with Dataset library
data = Dataset.load_from_df(ratings[['user_id', 'movie_id', 'rating']], reader)
# Use the SVD algorithm
svd = SVD()
# Compute the RMSE of the SVD algorithm
cross_validate(svd, data, cv=5, measures=['RMSE'], verbose=True)
# Train on the dataset and arrive at predictions
trainset = data.build_full_trainset()
svd.fit(trainset)
# Let's pick again user with ID 1310 and check the ratings he has given
print(ratings[ratings['user_id'] == 1310])
# Now let's use SVD to predict the rating that 1310 will give to movie 1994
print(svd.predict(1310, 1994))
```
|
github_jupyter
|
```
# hide
from nbdev.showdoc import *
```
# Load model from Weights & Biases (wandb)
This tutorial is for people who are using [Weights & Biases (wandb)](https://wandb.ai/site) `WandbCallback` in their training pipeline and are looking for a convenient way to use saved models on W&B cloud to make predictions, evaluate and submit in a few lines of code.
Currently only Keras models (`.h5`) are supported for wandb loading in this framework. Future versions will include other formats like PyTorch support.
---------------------------------------------------------------------
## 0. Authentication
To authenticate your W&B account you are given several options:
1. Run `wandb login` in terminal and follow instructions.
2. Configure global environment variable `'WANDB_API_KEY'`.
3. Run `wandb.init(project=PROJECT_NAME, entity=ENTITY_NAME)` and pass API key from [https://wandb.ai/authorize](https://wandb.ai/authorize)
-----------------------------------------------------
## 1. Download validation data
The first thing we do is download the current validation data and example predictions to evaluate against. This can be done in a few lines of code with `NumeraiClassicDownloader`.
```
#other
import pandas as pd
from numerblox.download import NumeraiClassicDownloader
from numerblox.numerframe import create_numerframe
from numerblox.model import WandbKerasModel
from numerblox.evaluation import NumeraiClassicEvaluator
#other
downloader = NumeraiClassicDownloader("wandb_keras_test")
# Path variables
val_file = "numerai_validation_data.parquet"
val_save_path = f"{str(downloader.dir)}/{val_file}"
# Download only validation parquet file
downloader.download_single_dataset(val_file,
dest_path=val_save_path)
# Download example val preds
downloader.download_example_data()
# Initialize NumerFrame from parquet file path
dataf = create_numerframe(val_save_path)
# Add example preds to NumerFrame
example_preds = pd.read_parquet("wandb_keras_test/example_validation_predictions.parquet")
dataf['prediction_example'] = example_preds.values
```
--------------------------------------------------------------------
## 2. Predict (WandbKerasModel)
`WandbKerasModel` automatically downloads and loads in a `.h5` from a specified wandb run. The path for a run is specified in the ["Overview" tab](https://docs.wandb.ai/ref/app/pages/run-page#overview-tab) of the run.
- `file_name`: The default name for the best model in a run is `model-best.h5`. If you want to use a model you have saved under a different name specify `file_name` for `WandbKerasModel` initialization.
- `replace`: The model will be downloaded to the directory you are working in. You will be warned if this directory contains models with the same filename. If these models can be overwritten specify `replace=True`.
- `combine_preds`: Setting this to True will average all columns in case you have trained a multi-target model.
- `autoencoder_mlp:` This argument is for the case where your [model architecture includes an autoencoder](https://forum.numer.ai/t/autoencoder-and-multitask-mlp-on-new-dataset-from-kaggle-jane-street/4338) and therefore the output is a tuple of 3 tensors. `WandbKerasModel` will in this case take the third output of the tuple (target predictions).
```
#other
run_path = "crowdcent/cc-numerai-classic/h4pwuxwu"
model = WandbKerasModel(run_path=run_path,
replace=True, combine_preds=True, autoencoder_mlp=True)
```
After initialization you can generate predictions with one line. `.predict` takes a `NumerFrame` as input and outputs a `NumerFrame` with a new prediction column. The prediction column name will be of the format `prediction_{RUN_PATH}`.
```
#other
dataf = model.predict(dataf)
dataf.prediction_cols
#other
main_pred_col = f"prediction_{run_path}"
main_pred_col
```
----------------------------------------------------------------------
## 3. Evaluate
We can now use the output of the model to evaluate in 2 lines of code. Additionally, we can directly submit predictions to Numerai with this `NumerFrame`. Check out the educational notebook `submitting.ipynb` for more information on this.
```
#other
evaluator = NumeraiClassicEvaluator()
val_stats = evaluator.full_evaluation(dataf=dataf,
target_col="target",
pred_cols=[main_pred_col,
"prediction_example"],
example_col="prediction_example"
)
```
The evaluator outputs a `pd.DataFrame` with most of the main validation metrics for Numerai. We welcome new ideas and metrics for Evaluators. See `nbs/07_evaluation.ipynb` in this repository for full Evaluator source code.
```
#other
val_stats
```
After we are done, downloaded files can be removed with one call on `NumeraiClassicDownloader` (optional).
```
#other
# Clean up environment
downloader.remove_base_directory()
```
------------------------------------------------------------------
We hope this tutorial explained clearly to you how to load and predict with Weights & Biases (wandb) models.
Below you will find the full docs for `WandbKerasModel` and link to the source code:
```
# other
# hide_input
show_doc(WandbKerasModel)
```
|
github_jupyter
|
```
# Copyright 2019 Google LLC
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
```
# Idiomatic Programmer Code Labs
## Code Labs #2 - Get Familiar with Data Augmentation
## Prerequistes:
1. Familiar with Python
2. Completed Handbook 2/Part 8: Data Augmentation
## Objectives:
1. Channel Conversion
2. Flip Images
3. Roll (Shift Images)
4. Rotate without Clipping
## Setup:
Install the additional relevant packages to continuen with OpenCV, and then import them.
```
# Install the matplotlib library for plotting
!pip install matplotlib
# special iPython command --tell's matplotlib to inline (in notebook) displaying plots
%matplotlib inline
# Adrian Rosenbrock's image manipulation library
!pip install imutils
# Import matplotlib python plot module
import matplotlib.pyplot as plt
# Import OpenCV
import cv2
# Import numpy scientific module for arrays
import numpy as np
# Import imutils
import imutils
```
## Channel Conversions
OpenCV reads in the channels as BGR (Blue, Green, Read) instead of the more common convention of RGB (Red, Green Blue). Let's learn how to change the channel ordering to RGB.
You fill in the blanks (replace the ??), make sure it passes the Python interpreter.
```
# Let's read in that apple image again.
image = cv2.imread('apple.jpg', cv2.IMREAD_COLOR)
plt.imshow(image)
```
### What, it's a blue apple!
Yup. It's the same data, but since matplotlib presumes RGB, then blue is the 3rd channel, but in BGR -- that's the red channel.
Let's reorder the channels from BGR to RGB and then display again.
```
# Let's convert the channel order to RGB
# HINT: RGB should be a big giveaway.
image = cv2.cvtColor(image, cv2.COLOR_BGR2??)
plt.imshow(image)
```
## Flip Images
Let's use OpenCV to flip an image (apple) vertically and then horizontally.
```
# Flip the image horizontally (upside down)
# HINT: flip should be a big giveaway
flip = cv2.??(image, 0)
plt.imshow(flip)
# Flip the image vertically (mirrored)
# HINT: If 0 was horizontal, what number would be your first guess to be vertical?
flip = cv2.flip(image, ??)
plt.imshow(flip)
```
## Roll (Shift) Images
Let's use numpy to shift an image -- say 80 pixels to the right.
```
# Let's shift the image vertical 80 pixels to the right, where axis=1 means along the width
# HINT: another name for shift is roll
roll = np.??(image, 80, axis=1)
plt.imshow(roll)
# Let's shift the image now horizontally 80 pixels down.
# HINT: if shifting the width axis is a 1, what do you think the value is for
# shifting along the height axis?
roll = np.roll(image, 80, axis=??)
plt.imshow(roll)
```
## Randomly Rotate the Image (w/o Clipping)
Let's use imutils to randomly rotate the image without clipping it.
```
import random
# Let's get a random value between 0 and 60 degrees.
degree = random.randint(0, 60)
# Let's rotate the image now by the randomly selected degree
rot = imutils.rotate_bound(image, ??)
plt.imshow(rot)
```
## End of Code Lab
|
github_jupyter
|
# Notebook 5: Clean Up Resources
Specify "Python 3" Kernel and "Data Science" Image.
### Background
In this notebook, we will clean up the resources we provisioned during this workshop:
- SageMaker Feature Groups
- SageMaker Endpoints
- Amazon Kinesis Data Stream
- Amazon Kinesis Data Analytics application
### Imports
```
from parameter_store import ParameterStore
from utils import *
```
### Session variables
```
role = sagemaker.get_execution_role()
sagemaker_session = sagemaker.Session()
region = sagemaker_session.boto_region_name
boto_session = boto3.Session()
kinesis_client = boto_session.client(service_name='kinesis', region_name=region)
kinesis_analytics_client = boto_session.client('kinesisanalytics')
ps = ParameterStore(verbose=False)
ps.set_namespace('feature-store-workshop')
```
Load variables from previous notebooks
```
parameters = ps.read()
customers_feature_group_name = parameters['customers_feature_group_name']
products_feature_group_name = parameters['products_feature_group_name']
orders_feature_group_name = parameters['orders_feature_group_name']
click_stream_historical_feature_group_name = parameters['click_stream_historical_feature_group_name']
click_stream_feature_group_name = parameters['click_stream_feature_group_name']
cf_model_endpoint_name = parameters['cf_model_endpoint_name']
ranking_model_endpoint_name = parameters['ranking_model_endpoint_name']
kinesis_stream_name = parameters['kinesis_stream_name']
kinesis_analytics_application_name = parameters['kinesis_analytics_application_name']
```
### Delete feature groups
```
feature_group_list = [customers_feature_group_name, products_feature_group_name,
orders_feature_group_name, click_stream_historical_feature_group_name,
click_stream_feature_group_name]
for feature_group in feature_group_list:
print(f'Deleting feature group: {feature_group}')
delete_feature_group(feature_group)
```
### Delete endpoints and endpoint configurations
```
def clean_up_endpoint(endpoint_name):
response = sagemaker_session.sagemaker_client.describe_endpoint(EndpointName=endpoint_name)
endpoint_config_name = response['EndpointConfigName']
print(f'Deleting endpoint: {endpoint_name}')
print(f'Deleting endpoint configuration : {endpoint_config_name}')
sagemaker_session.sagemaker_client.delete_endpoint(EndpointName=endpoint_name)
sagemaker_session.sagemaker_client.delete_endpoint_config(EndpointConfigName=endpoint_config_name)
endpoint_list = [cf_model_endpoint_name, ranking_model_endpoint_name]
for endpoint in endpoint_list:
clean_up_endpoint(endpoint)
```
### Delete Kinesis Data Stream
```
kinesis_client.delete_stream(StreamName=kinesis_stream_name,
EnforceConsumerDeletion=True)
```
### Delete Kinesis Data Analytics application
```
response = kinesis_analytics_client.describe_application(ApplicationName=kinesis_analytics_application_name)
create_ts = response['ApplicationDetail']['CreateTimestamp']
kinesis_analytics_client.delete_application(ApplicationName=kinesis_analytics_application_name, CreateTimestamp=create_ts)
```
Go back to Workshop Studio and click on "Next".
|
github_jupyter
|
[View in Colaboratory](https://colab.research.google.com/github/tomwilde/100DaysOfMLCode/blob/master/2_numpy_linearRegression_with_CostFn.ipynb)
```
!pip install -U -q PyDrive
import numpy as np
import matplotlib.pyplot as plt
import pandas
import io
# Install the PyDrive wrapper & import libraries.
# This only needs to be done once per notebook.
!pip install -U -q PyDrive
from pydrive.auth import GoogleAuth
from pydrive.drive import GoogleDrive
from google.colab import auth
from oauth2client.client import GoogleCredentials
# Authenticate and create the PyDrive client.
# This only needs to be done once per notebook.
auth.authenticate_user()
gauth = GoogleAuth()
gauth.credentials = GoogleCredentials.get_application_default()
drive = GoogleDrive(gauth)
# from: https://ml-cheatsheet.readthedocs.io/en/latest/linear_regression.html#cost-function
#
# We need a cost fn and its derivative...
# Download a file based on its file ID.
#
# A file ID looks like: laggVyWshwcyP6kEI-y_W3P8D26sz
file_id = '1_d2opSoZgMsSeoQUjtOcRQj5l0zO-Upi'
downloaded = drive.CreateFile({'id': file_id})
#print('Downloaded content "{}"'.format(downloaded.GetContentString()))
dataset = pandas.read_csv(io.StringIO(downloaded.GetContentString())).as_matrix()
def cost_function(X, y, weight, bias):
n = len(X)
total_error = 0.0
for i in range(n):
total_error += (y[i] - (weight*X[i] + bias))**2
return total_error / n
def update_weights(X, y, weight, bias, alpha):
weight_deriv = 0
bias_deriv = 0
n = len(X)
for i in range(n):
# Calculate partial derivatives
# -2x(y - (mx + b))
weight_deriv += -2*X[i] * (y[i] - (weight * X[i] + bias))
# -2(y - (mx + b))
bias_deriv += -2*(y[i] - (weight * X[i] + bias))
# We subtract because the derivatives point in direction of steepest ascent
weight -= (weight_deriv / n) * alpha
bias -= (bias_deriv / n) * alpha
return weight, bias
def train(X, y, weight, bias, alpha, iters):
cost_history = []
for i in range(iters):
weight,bias = update_weights(X, y, weight, bias, alpha)
#Calculate cost for auditing purposes
cost = cost_function(X, y, weight, bias)
# cost_history.append(cost)
# Log Progress
if i % 10 == 0:
print "iter: "+str(i) + " weight: "+str(weight) +" bias: "+str(bias) + " cost: "+str(cost)
return weight, bias #, cost_history
# work out
y = dataset[:,4].reshape(200,1)
X = dataset[:,1].reshape(200,1)
m = 0
c = 0
alpha = 0.1
iters = 100
# normalise the data
y = y/np.linalg.norm(y, ord=np.inf, axis=0, keepdims=True)
X = X/np.linalg.norm(X, ord=np.inf, axis=0, keepdims=True)
weight, bias = train(X, y, m, c, alpha, iters)
_ = plt.plot(X,y, 'o', [0, 1], [bias, weight + bias], '-')
```
|
github_jupyter
|
# A demo of XYZ and RDKitMol
There is no easy way to convert xyz to RDKit Mol/RWMol. Here RDKitMol shows a possibility by using openbabel / method from Jensen et al. [1] as a molecule perception backend.
[1] https://github.com/jensengroup/xyz2mol.
```
import os
import sys
sys.path.append(os.path.dirname(os.path.abspath('')))
from rdmc.mol import RDKitMol
```
### 1. An example of xyz str block
```
######################################
# INPUT
xyz="""14
C -1.77596 0.55032 -0.86182
C -1.86964 0.09038 -2.31577
H -0.88733 1.17355 -0.71816
H -1.70996 -0.29898 -0.17103
O -2.90695 1.36613 -0.53334
C -0.58005 -0.57548 -2.76940
H -0.35617 -1.45641 -2.15753
H 0.26635 0.11565 -2.71288
H -0.67469 -0.92675 -3.80265
O -2.92111 -0.86791 -2.44871
H -2.10410 0.93662 -2.97107
O -3.87923 0.48257 0.09884
H -4.43402 0.34141 -0.69232
O -4.16782 -0.23433 -2.64382
"""
xyz_wo_header = """O 2.136128 0.058786 -0.999372
C -1.347448 0.039725 0.510465
C 0.116046 -0.220125 0.294405
C 0.810093 0.253091 -0.73937
H -1.530204 0.552623 1.461378
H -1.761309 0.662825 -0.286624
H -1.923334 -0.892154 0.536088
H 0.627132 -0.833978 1.035748
H 0.359144 0.869454 -1.510183
H 2.513751 -0.490247 -0.302535"""
######################################
```
### 2. Use pybel to generate a OBMol from xyz
pybel backend, `header` to indicate if the str includes lines of atom number and title.
```
rdkitmol = RDKitMol.FromXYZ(xyz, backend='openbabel', header=True)
rdkitmol
```
Please correctly use `header` arguments, otherwise molecule perception can be problematic
```
rdkitmol = RDKitMol.FromXYZ(xyz_wo_header, backend='openbabel', header=False)
rdkitmol
```
Using `jensen` backend. For most cases, Jensen's method returns the same molecule as using `pybel` backend
```
rdkitmol = RDKitMol.FromXYZ(xyz, backend='jensen', header=True)
rdkitmol
```
Here some options for Jensen et al. method are listed. The nomenclature is kept as it is in the original API.
```
rdkitmol = RDKitMol.FromXYZ(xyz, backend='jensen',
header=True,
allow_charged_fragments=False, # radical => False
use_graph=False, # accelerate for larger molecule but needs networkx as backend
use_huckel=True,
embed_chiral=True)
rdkitmol
```
### 3. Check the xyz of rdkitmol conformer
```
rdkitmol.GetConformer().GetPositions()
```
### 4. Export xyz
```
print(rdkitmol.ToXYZ(header=False))
```
|
github_jupyter
|
# Dimensionality Reduction with the Shogun Machine Learning Toolbox
#### *By Sergey Lisitsyn ([lisitsyn](https://github.com/lisitsyn)) and Fernando J. Iglesias Garcia ([iglesias](https://github.com/iglesias)).*
This notebook illustrates <a href="http://en.wikipedia.org/wiki/Unsupervised_learning">unsupervised learning</a> using the suite of dimensionality reduction algorithms available in Shogun. Shogun provides access to all these algorithms using [Tapkee](http://tapkee.lisitsyn.me/), a C++ library especialized in <a href="http://en.wikipedia.org/wiki/Dimensionality_reduction">dimensionality reduction</a>.
## Hands-on introduction to dimension reduction
First of all, let us start right away by showing what the purpose of dimensionality reduction actually is. To this end, we will begin by creating a function that provides us with some data:
```
import numpy as np
import os
SHOGUN_DATA_DIR=os.getenv('SHOGUN_DATA_DIR', '../../../data')
def generate_data(curve_type, num_points=1000):
if curve_type=='swissroll':
tt = np.array((3*np.pi/2)*(1+2*np.random.rand(num_points)))
height = np.array((np.random.rand(num_points)-0.5))
X = np.array([tt*np.cos(tt), 10*height, tt*np.sin(tt)])
return X,tt
if curve_type=='scurve':
tt = np.array((3*np.pi*(np.random.rand(num_points)-0.5)))
height = np.array((np.random.rand(num_points)-0.5))
X = np.array([np.sin(tt), 10*height, np.sign(tt)*(np.cos(tt)-1)])
return X,tt
if curve_type=='helix':
tt = np.linspace(1, num_points, num_points).T / num_points
tt = tt*2*np.pi
X = np.r_[[(2+np.cos(8*tt))*np.cos(tt)],
[(2+np.cos(8*tt))*np.sin(tt)],
[np.sin(8*tt)]]
return X,tt
```
The function above can be used to generate three-dimensional datasets with the shape of a [Swiss roll](http://en.wikipedia.org/wiki/Swiss_roll), the letter S, or an helix. These are three examples of datasets which have been extensively used to compare different dimension reduction algorithms. As an illustrative exercise of what dimensionality reduction can do, we will use a few of the algorithms available in Shogun to embed this data into a two-dimensional space. This is essentially the dimension reduction process as we reduce the number of features from 3 to 2. The question that arises is: what principle should we use to keep some important relations between datapoints? In fact, different algorithms imply different criteria to answer this question.
Just to start, lets pick some algorithm and one of the data sets, for example lets see what embedding of the Swissroll is produced by the Isomap algorithm. The Isomap algorithm is basically a slightly modified Multidimensional Scaling (MDS) algorithm which finds embedding as a solution of the following optimization problem:
$$
\min_{x'_1, x'_2, \dots} \sum_i \sum_j \| d'(x'_i, x'_j) - d(x_i, x_j)\|^2,
$$
with defined $x_1, x_2, \dots \in X~~$ and unknown variables $x_1, x_2, \dots \in X'~~$ while $\text{dim}(X') < \text{dim}(X)~~~$,
$d: X \times X \to \mathbb{R}~~$ and $d': X' \times X' \to \mathbb{R}~~$ are defined as arbitrary distance functions (for example Euclidean).
Speaking less math, the MDS algorithm finds an embedding that preserves pairwise distances between points as much as it is possible. The Isomap algorithm changes quite small detail: the distance - instead of using local pairwise relationships it takes global factor into the account with shortest path on the neighborhood graph (so-called geodesic distance). The neighborhood graph is defined as graph with datapoints as nodes and weighted edges (with weight equal to the distance between points). The edge between point $x_i~$ and $x_j~$ exists if and only if $x_j~$ is in $k~$ nearest neighbors of $x_i$. Later we will see that that 'global factor' changes the game for the swissroll dataset.
However, first we prepare a small function to plot any of the original data sets together with its embedding.
```
%matplotlib inline
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
%matplotlib inline
def plot(data, embedded_data, colors='m'):
fig = plt.figure()
fig.set_facecolor('white')
ax = fig.add_subplot(121,projection='3d')
ax.scatter(data[0],data[1],data[2],c=colors,cmap=plt.cm.Spectral)
plt.axis('tight'); plt.axis('off')
ax = fig.add_subplot(122)
ax.scatter(embedded_data[0],embedded_data[1],c=colors,cmap=plt.cm.Spectral)
plt.axis('tight'); plt.axis('off')
plt.show()
import shogun as sg
# wrap data into Shogun features
data, colors = generate_data('swissroll')
feats = sg.create_features(data)
# create instance of Isomap converter and set number of neighbours used in kNN search to 20
isomap = sg.create_transformer('Isomap', target_dim=2, k=20)
# create instance of Multidimensional Scaling converter and configure it
mds = sg.create_transformer('MultidimensionalScaling', target_dim=2)
# embed Swiss roll data
embedded_data_mds = mds.transform(feats).get('feature_matrix')
embedded_data_isomap = isomap.transform(feats).get('feature_matrix')
plot(data, embedded_data_mds, colors)
plot(data, embedded_data_isomap, colors)
```
As it can be seen from the figure above, Isomap has been able to "unroll" the data, reducing its dimension from three to two. At the same time, points with similar colours in the input space are close to points with similar colours in the output space. This is, a new representation of the data has been obtained; this new representation maintains the properties of the original data, while it reduces the amount of information required to represent it. Note that the fact the embedding of the Swiss roll looks good in two dimensions stems from the *intrinsic* dimension of the input data. Although the original data is in a three-dimensional space, its intrinsic dimension is lower, since the only degree of freedom are the polar angle and distance from the centre, or height.
Finally, we use yet another method, Stochastic Proximity Embedding (SPE) to embed the helix:
```
# wrap data into Shogun features
data, colors = generate_data('helix')
features = sg.create_features(data)
# create MDS instance
converter = sg.create_transformer('StochasticProximityEmbedding', target_dim=2)
# embed helix data
embedded_features = converter.transform(features)
embedded_data = embedded_features.get('feature_matrix')
plot(data, embedded_data, colors)
```
## References
- Lisitsyn, S., Widmer, C., Iglesias Garcia, F. J. Tapkee: An Efficient Dimension Reduction Library. ([Link to paper in JMLR](http://jmlr.org/papers/v14/lisitsyn13a.html#!).)
- Tenenbaum, J. B., de Silva, V. and Langford, J. B. A Global Geometric Framework for Nonlinear Dimensionality Reduction. ([Link to Isomap's website](http://isomap.stanford.edu/).)
|
github_jupyter
|
# Feature List View
## Usage
```
import sys, json, math
from mlvis import FeatureListView
from random import uniform, gauss
from IPython.display import display
if sys.version_info[0] < 3:
import urllib2 as url
else:
import urllib.request as url
def generate_random_steps(k):
randoms = [uniform(0, 1) / 2 for i in range(0, k)]
steps = [0] * (k - 1)
t = 0
for i in range(0, k - 1):
steps[i] = t + (1 - t) * randoms[i]
t = steps[i]
return steps + [1]
def generate_categorical_feature(states):
size = len(states)
distro_a = [uniform(0, 1) for i in range(0, size)]
distro_b = [uniform(0, 1) for i in range(0, size)]
return {
'name': 'dummy-categorical-feature',
'type': 'categorical',
'domain': list(states.values()),
'distributions': [distro_a, distro_b],
'distributionNormalized': [distro_a, distro_b],
'colors': ['#47B274', '#6F5AA7'],
'divergence': uniform(0, 1)
}
def generate_numerical_feature():
domain_size = 100
distro_a = [uniform(0, 1) for i in range(0, domain_size)]
distro_b = [uniform(0, 1) for i in range(0, domain_size)]
return {
'name': 'dummy-categorical-numerical',
'type': 'numerical',
'domain': generate_random_steps(domain_size),
'distributions': [distro_a, distro_b],
'distributionNormalized': [distro_a, distro_b],
'colors': ['#47B274', '#6F5AA7'],
'divergence': uniform(0, 1)
}
def generate_random_categorical_values(states):
k = 10000
values = [None] * k
domain = list(states.values())
size = len(states)
for i in range(0, k):
d = int(math.floor(uniform(0, 1) * size))
values[i] = domain[d]
return values
def generate_raw_categorical_feature(states):
return {
'name': 'dummy-raw-categorical-feature',
'type': 'categorical',
'values': [generate_random_categorical_values(states),
generate_random_categorical_values(states)]
}
def generate_raw_numerical_feature():
return {
'name': 'dummy-raw-numerical-feature',
'type': 'numerical',
'values': [
[gauss(2, 0.5) for i in range(0, 2500)],
[gauss(0, 1) for i in range(0, 7500)]
]
}
# load the US states data
PREFIX = 'https://d1a3f4spazzrp4.cloudfront.net/mlvis/'
response = url.urlopen(PREFIX + 'jupyter/states.json')
states = json.loads(response.read().decode())
# Randomly generate the data for the feature list view
categorical_feature = generate_categorical_feature(states)
raw_categorical_feature = generate_raw_categorical_feature(states)
numerical_feature = generate_numerical_feature()
raw_numerical_feature = generate_raw_numerical_feature()
data = [categorical_feature, raw_categorical_feature, numerical_feature, raw_numerical_feature]
feature_list_view = FeatureListView(props={"data": data, "width": 1000})
display(feature_list_view)
```
|
github_jupyter
|
```
# General purpose libraries
import boto3
import copy
import csv
import datetime
import json
import numpy as np
import pandas as pd
import s3fs
from collections import defaultdict
import time
import re
import random
from sentence_transformers import SentenceTransformer
import sentencepiece
from scipy.spatial import distance
from json import JSONEncoder
import sys
sys.path.append("/Users/dafirebanks/Projects/policy-data-analyzer/")
sys.path.append("C:/Users/jordi/Documents/GitHub/policy-data-analyzer/")
from tasks.data_loading.src.utils import *
```
### 1. Set up AWS
```
def aws_credentials_from_file(f_name):
with open(f_name, "r") as f:
creds = json.load(f)
return creds["aws"]["id"], creds["aws"]["secret"]
def aws_credentials(path, filename):
file = path + filename
with open(file, 'r') as dict:
key_dict = json.load(dict)
for key in key_dict:
KEY = key
SECRET = key_dict[key]
return KEY, SECRET
```
### 2. Optimized full loop
```
def aws_credentials(path, filename):
file = path + filename
with open(file, 'r') as dict:
key_dict = json.load(dict)
for key in key_dict:
KEY = key
SECRET = key_dict[key]
return KEY, SECRET
def aws_credentials_from_file(f_name):
with open(f_name, "r") as f:
creds = json.load(f)
return creds["aws"]["id"], creds["aws"]["secret"]
def load_all_sentences(language, s3, bucket_name, init_doc, end_doc):
policy_dict = {}
sents_folder = f"{language}_documents/sentences"
for i, obj in enumerate(s3.Bucket(bucket_name).objects.all().filter(Prefix="english_documents/sentences/")):
if not obj.key.endswith("/") and init_doc <= i < end_doc:
serializedObject = obj.get()['Body'].read()
policy_dict = {**policy_dict, **json.loads(serializedObject)}
return labeled_sentences_from_dataset(policy_dict)
def save_results_as_separate_csv(results_dictionary, queries_dictionary, init_doc, results_limit, aws_id, aws_secret):
path = "s3://wri-nlp-policy/english_documents/assisted_labeling"
col_headers = ["sentence_id", "similarity_score", "text"]
for i, query in enumerate(results_dictionary.keys()):
filename = f"{path}/query_{queries_dictionary[query]}_{i}_results_{init_doc}.csv"
pd.DataFrame(results_dictionary[query], columns=col_headers).head(results_limit).to_csv(filename, storage_options={"key": aws_id, "secret": aws_secret})
def labeled_sentences_from_dataset(dataset):
sentence_tags_dict = {}
for document in dataset.values():
sentence_tags_dict.update(document['sentences'])
return sentence_tags_dict
# Set up AWS
credentials_file = '/Users/dafirebanks/Documents/credentials.json'
aws_id, aws_secret = aws_credentials_from_file(credentials_file)
region = 'us-east-1'
s3 = boto3.resource(
service_name = 's3',
region_name = region,
aws_access_key_id = aws_id,
aws_secret_access_key = aws_secret
)
path = "C:/Users/jordi/Documents/claus/"
filename = "AWS_S3_keys_wri.json"
aws_id, aws_secret = aws_credentials(path, filename)
region = 'us-east-1'
bucket = 'wri-nlp-policy'
s3 = boto3.resource(
service_name = 's3',
region_name = region,
aws_access_key_id = aws_id,
aws_secret_access_key = aws_secret
)
# Define params
init_at_doc = 13136
end_at_doc = 14778
similarity_threshold = 0
search_results_limit = 500
language = "english"
bucket_name = 'wri-nlp-policy'
transformer_name = 'xlm-r-bert-base-nli-stsb-mean-tokens'
model = SentenceTransformer(transformer_name)
# Get all sentence documents
sentences = load_all_sentences(language, s3, bucket_name, init_at_doc, end_at_doc )
# Define queries
path = "../../input/"
filename = "English_queries.xlsx"
file = path + filename
df = pd.read_excel(file, engine='openpyxl', sheet_name = "Hoja1", usecols = "A:C")
queries = {}
for index, row in df.iterrows():
queries[row['Query sentence']] = row['Policy instrument']
# Calculate and store query embeddings
query_embeddings = dict(zip(queries, [model.encode(query.lower(), show_progress_bar=False) for query in queries]))
# For each sentence, calculate its embedding, and store the similarity
query_similarities = defaultdict(list)
i = 0
for sentence_id, sentence in sentences.items():
sentence_embedding = model.encode(sentence['text'].lower(), show_progress_bar=False)
i += 1
if i % 100 == 0:
print(i)
for query_text, query_embedding in query_embeddings.items():
score = round(1 - distance.cosine(sentence_embedding, query_embedding), 4)
if score > similarity_threshold:
query_similarities[query_text].append([sentence_id, score, sentences[sentence_id]['text']])
# Sort results by similarity score
for query in query_similarities:
query_similarities[query] = sorted(query_similarities[query], key = lambda x : x[1], reverse=True)
# Store results
save_results_as_separate_csv(query_similarities, queries, init_at_doc, search_results_limit, aws_id, aws_secret)
```
|
github_jupyter
|
# Investigating ocean models skill for sea surface height with IOOS catalog and Python
The IOOS [catalog](https://ioos.noaa.gov/data/catalog) offers access to hundreds of datasets and data access services provided by the 11 regional associations.
In the past we demonstrate how to tap into those datasets to obtain sea [surface temperature data from observations](http://ioos.github.io/notebooks_demos/notebooks/2016-12-19-exploring_csw),
[coastal velocity from high frequency radar data](http://ioos.github.io/notebooks_demos/notebooks/2017-12-15-finding_HFRadar_currents),
and a simple model vs observation visualization of temperatures for the [Boston Light Swim competition](http://ioos.github.io/notebooks_demos/notebooks/2016-12-22-boston_light_swim).
In this notebook we'll demonstrate a step-by-step workflow on how ask the catalog for a specific variable, extract only the model data, and match the nearest model grid point to an observation. The goal is to create an automated skill score for quick assessment of ocean numerical models.
The first cell is only to reduce iris' noisy output,
the notebook start on cell [2] with the definition of the parameters:
- start and end dates for the search;
- experiment name;
- a bounding of the region of interest;
- SOS variable name for the observations;
- Climate and Forecast standard names;
- the units we want conform the variables into;
- catalogs we want to search.
```
import warnings
# Suppresing warnings for a "pretty output."
warnings.simplefilter("ignore")
%%writefile config.yaml
date:
start: 2018-2-28 00:00:00
stop: 2018-3-5 00:00:00
run_name: 'latest'
region:
bbox: [-71.20, 41.40, -69.20, 43.74]
crs: 'urn:ogc:def:crs:OGC:1.3:CRS84'
sos_name: 'water_surface_height_above_reference_datum'
cf_names:
- sea_surface_height
- sea_surface_elevation
- sea_surface_height_above_geoid
- sea_surface_height_above_sea_level
- water_surface_height_above_reference_datum
- sea_surface_height_above_reference_ellipsoid
units: 'm'
catalogs:
- https://data.ioos.us/csw
```
To keep track of the information we'll setup a `config` variable and output them on the screen for bookkeeping.
```
import os
import shutil
from datetime import datetime
from ioos_tools.ioos import parse_config
config = parse_config("config.yaml")
# Saves downloaded data into a temporary directory.
save_dir = os.path.abspath(config["run_name"])
if os.path.exists(save_dir):
shutil.rmtree(save_dir)
os.makedirs(save_dir)
fmt = "{:*^64}".format
print(fmt("Saving data inside directory {}".format(save_dir)))
print(fmt(" Run information "))
print("Run date: {:%Y-%m-%d %H:%M:%S}".format(datetime.utcnow()))
print("Start: {:%Y-%m-%d %H:%M:%S}".format(config["date"]["start"]))
print("Stop: {:%Y-%m-%d %H:%M:%S}".format(config["date"]["stop"]))
print(
"Bounding box: {0:3.2f}, {1:3.2f},"
"{2:3.2f}, {3:3.2f}".format(*config["region"]["bbox"])
)
```
To interface with the IOOS catalog we will use the [Catalogue Service for the Web (CSW)](https://live.osgeo.org/en/standards/csw_overview.html) endpoint and [python's OWSLib library](https://geopython.github.io/OWSLib).
The cell below creates the [Filter Encoding Specification (FES)](http://www.opengeospatial.org/standards/filter) with configuration we specified in cell [2]. The filter is composed of:
- `or` to catch any of the standard names;
- `not` some names we do not want to show up in the results;
- `date range` and `bounding box` for the time-space domain of the search.
```
def make_filter(config):
from owslib import fes
from ioos_tools.ioos import fes_date_filter
kw = dict(
wildCard="*", escapeChar="\\", singleChar="?", propertyname="apiso:Subject"
)
or_filt = fes.Or(
[fes.PropertyIsLike(literal=("*%s*" % val), **kw) for val in config["cf_names"]]
)
not_filt = fes.Not([fes.PropertyIsLike(literal="GRIB-2", **kw)])
begin, end = fes_date_filter(config["date"]["start"], config["date"]["stop"])
bbox_crs = fes.BBox(config["region"]["bbox"], crs=config["region"]["crs"])
filter_list = [fes.And([bbox_crs, begin, end, or_filt, not_filt])]
return filter_list
filter_list = make_filter(config)
```
We need to wrap `OWSlib.csw.CatalogueServiceWeb` object with a custom function,
` get_csw_records`, to be able to paginate over the results.
In the cell below we loop over all the catalogs returns and extract the OPeNDAP endpoints.
```
from ioos_tools.ioos import get_csw_records, service_urls
from owslib.csw import CatalogueServiceWeb
dap_urls = []
print(fmt(" Catalog information "))
for endpoint in config["catalogs"]:
print("URL: {}".format(endpoint))
try:
csw = CatalogueServiceWeb(endpoint, timeout=120)
except Exception as e:
print("{}".format(e))
continue
csw = get_csw_records(csw, filter_list, esn="full")
OPeNDAP = service_urls(csw.records, identifier="OPeNDAP:OPeNDAP")
odp = service_urls(
csw.records, identifier="urn:x-esri:specification:ServiceType:odp:url"
)
dap = OPeNDAP + odp
dap_urls.extend(dap)
print("Number of datasets available: {}".format(len(csw.records.keys())))
for rec, item in csw.records.items():
print("{}".format(item.title))
if dap:
print(fmt(" DAP "))
for url in dap:
print("{}.html".format(url))
print("\n")
# Get only unique endpoints.
dap_urls = list(set(dap_urls))
```
We found 10 dataset endpoints but only 9 of them have the proper metadata for us to identify the OPeNDAP endpoint,
those that contain either `OPeNDAP:OPeNDAP` or `urn:x-esri:specification:ServiceType:odp:url` scheme.
Unfortunately we lost the `COAWST` model in the process.
The next step is to ensure there are no observations in the list of endpoints.
We want only the models for now.
```
from ioos_tools.ioos import is_station
from timeout_decorator import TimeoutError
# Filter out some station endpoints.
non_stations = []
for url in dap_urls:
try:
if not is_station(url):
non_stations.append(url)
except (IOError, OSError, RuntimeError, TimeoutError) as e:
print("Could not access URL {}.html\n{!r}".format(url, e))
dap_urls = non_stations
print(fmt(" Filtered DAP "))
for url in dap_urls:
print("{}.html".format(url))
```
Now we have a nice list of all the models available in the catalog for the domain we specified.
We still need to find the observations for the same domain.
To accomplish that we will use the `pyoos` library and search the [SOS CO-OPS](https://opendap.co-ops.nos.noaa.gov/ioos-dif-sos/) services using the virtually the same configuration options from the catalog search.
```
from pyoos.collectors.coops.coops_sos import CoopsSos
collector_coops = CoopsSos()
collector_coops.set_bbox(config["region"]["bbox"])
collector_coops.end_time = config["date"]["stop"]
collector_coops.start_time = config["date"]["start"]
collector_coops.variables = [config["sos_name"]]
ofrs = collector_coops.server.offerings
title = collector_coops.server.identification.title
print(fmt(" Collector offerings "))
print("{}: {} offerings".format(title, len(ofrs)))
```
To make it easier to work with the data we extract the time-series as pandas tables and interpolate them to a common 1-hour interval index.
```
import pandas as pd
from ioos_tools.ioos import collector2table
data = collector2table(
collector=collector_coops,
config=config,
col="water_surface_height_above_reference_datum (m)",
)
df = dict(
station_name=[s._metadata.get("station_name") for s in data],
station_code=[s._metadata.get("station_code") for s in data],
sensor=[s._metadata.get("sensor") for s in data],
lon=[s._metadata.get("lon") for s in data],
lat=[s._metadata.get("lat") for s in data],
depth=[s._metadata.get("depth") for s in data],
)
pd.DataFrame(df).set_index("station_code")
index = pd.date_range(
start=config["date"]["start"].replace(tzinfo=None),
end=config["date"]["stop"].replace(tzinfo=None),
freq="1H",
)
# Preserve metadata with `reindex`.
observations = []
for series in data:
_metadata = series._metadata
series.index = series.index.tz_localize(None)
obs = series.reindex(index=index, limit=1, method="nearest")
obs._metadata = _metadata
observations.append(obs)
```
The next cell saves those time-series as CF-compliant netCDF files on disk,
to make it easier to access them later.
```
import iris
from ioos_tools.tardis import series2cube
attr = dict(
featureType="timeSeries",
Conventions="CF-1.6",
standard_name_vocabulary="CF-1.6",
cdm_data_type="Station",
comment="Data from http://opendap.co-ops.nos.noaa.gov",
)
cubes = iris.cube.CubeList([series2cube(obs, attr=attr) for obs in observations])
outfile = os.path.join(save_dir, "OBS_DATA.nc")
iris.save(cubes, outfile)
```
We still need to read the model data from the list of endpoints we found.
The next cell takes care of that.
We use `iris`, and a set of custom functions from the `ioos_tools` library,
that downloads only the data in the domain we requested.
```
from ioos_tools.ioos import get_model_name
from ioos_tools.tardis import is_model, proc_cube, quick_load_cubes
from iris.exceptions import ConstraintMismatchError, CoordinateNotFoundError, MergeError
print(fmt(" Models "))
cubes = dict()
for k, url in enumerate(dap_urls):
print("\n[Reading url {}/{}]: {}".format(k + 1, len(dap_urls), url))
try:
cube = quick_load_cubes(url, config["cf_names"], callback=None, strict=True)
if is_model(cube):
cube = proc_cube(
cube,
bbox=config["region"]["bbox"],
time=(config["date"]["start"], config["date"]["stop"]),
units=config["units"],
)
else:
print("[Not model data]: {}".format(url))
continue
mod_name = get_model_name(url)
cubes.update({mod_name: cube})
except (
RuntimeError,
ValueError,
ConstraintMismatchError,
CoordinateNotFoundError,
IndexError,
) as e:
print("Cannot get cube for: {}\n{}".format(url, e))
```
Now we can match each observation time-series with its closest grid point (0.08 of a degree) on each model.
This is a complex and laborious task! If you are running this interactively grab a coffee and sit comfortably :-)
Note that we are also saving the model time-series to files that align with the observations we saved before.
```
import iris
from ioos_tools.tardis import (
add_station,
ensure_timeseries,
get_nearest_water,
make_tree,
)
from iris.pandas import as_series
for mod_name, cube in cubes.items():
fname = "{}.nc".format(mod_name)
fname = os.path.join(save_dir, fname)
print(fmt(" Downloading to file {} ".format(fname)))
try:
tree, lon, lat = make_tree(cube)
except CoordinateNotFoundError:
print("Cannot make KDTree for: {}".format(mod_name))
continue
# Get model series at observed locations.
raw_series = dict()
for obs in observations:
obs = obs._metadata
station = obs["station_code"]
try:
kw = dict(k=10, max_dist=0.08, min_var=0.01)
args = cube, tree, obs["lon"], obs["lat"]
try:
series, dist, idx = get_nearest_water(*args, **kw)
except RuntimeError as e:
print("Cannot download {!r}.\n{}".format(cube, e))
series = None
except ValueError:
status = "No Data"
print("[{}] {}".format(status, obs["station_name"]))
continue
if not series:
status = "Land "
else:
raw_series.update({station: series})
series = as_series(series)
status = "Water "
print("[{}] {}".format(status, obs["station_name"]))
if raw_series: # Save cube.
for station, cube in raw_series.items():
cube = add_station(cube, station)
try:
cube = iris.cube.CubeList(raw_series.values()).merge_cube()
except MergeError as e:
print(e)
ensure_timeseries(cube)
try:
iris.save(cube, fname)
except AttributeError:
# FIXME: we should patch the bad attribute instead of removing everything.
cube.attributes = {}
iris.save(cube, fname)
del cube
print("Finished processing [{}]".format(mod_name))
```
With the matched set of models and observations time-series it is relatively easy to compute skill score metrics on them. In cells [13] to [16] we apply both mean bias and root mean square errors to the time-series.
```
from ioos_tools.ioos import stations_keys
def rename_cols(df, config):
cols = stations_keys(config, key="station_name")
return df.rename(columns=cols)
from ioos_tools.ioos import load_ncs
from ioos_tools.skill_score import apply_skill, mean_bias
dfs = load_ncs(config)
df = apply_skill(dfs, mean_bias, remove_mean=False, filter_tides=False)
skill_score = dict(mean_bias=df.to_dict())
# Filter out stations with no valid comparison.
df.dropna(how="all", axis=1, inplace=True)
df = df.applymap("{:.2f}".format).replace("nan", "--")
from ioos_tools.skill_score import rmse
dfs = load_ncs(config)
df = apply_skill(dfs, rmse, remove_mean=True, filter_tides=False)
skill_score["rmse"] = df.to_dict()
# Filter out stations with no valid comparison.
df.dropna(how="all", axis=1, inplace=True)
df = df.applymap("{:.2f}".format).replace("nan", "--")
import pandas as pd
# Stringfy keys.
for key in skill_score.keys():
skill_score[key] = {str(k): v for k, v in skill_score[key].items()}
mean_bias = pd.DataFrame.from_dict(skill_score["mean_bias"])
mean_bias = mean_bias.applymap("{:.2f}".format).replace("nan", "--")
skill_score = pd.DataFrame.from_dict(skill_score["rmse"])
skill_score = skill_score.applymap("{:.2f}".format).replace("nan", "--")
```
Last but not least we can assemble a GIS map, cells [17-23],
with the time-series plot for the observations and models,
and the corresponding skill scores.
```
import folium
from ioos_tools.ioos import get_coordinates
def make_map(bbox, **kw):
line = kw.pop("line", True)
zoom_start = kw.pop("zoom_start", 5)
lon = (bbox[0] + bbox[2]) / 2
lat = (bbox[1] + bbox[3]) / 2
m = folium.Map(
width="100%", height="100%", location=[lat, lon], zoom_start=zoom_start
)
if line:
p = folium.PolyLine(
get_coordinates(bbox), color="#FF0000", weight=2, opacity=0.9,
)
p.add_to(m)
return m
bbox = config["region"]["bbox"]
m = make_map(bbox, zoom_start=8, line=True, layers=True)
all_obs = stations_keys(config)
from glob import glob
from operator import itemgetter
import iris
from folium.plugins import MarkerCluster
iris.FUTURE.netcdf_promote = True
big_list = []
for fname in glob(os.path.join(save_dir, "*.nc")):
if "OBS_DATA" in fname:
continue
cube = iris.load_cube(fname)
model = os.path.split(fname)[1].split("-")[-1].split(".")[0]
lons = cube.coord(axis="X").points
lats = cube.coord(axis="Y").points
stations = cube.coord("station_code").points
models = [model] * lons.size
lista = zip(models, lons.tolist(), lats.tolist(), stations.tolist())
big_list.extend(lista)
big_list.sort(key=itemgetter(3))
df = pd.DataFrame(big_list, columns=["name", "lon", "lat", "station"])
df.set_index("station", drop=True, inplace=True)
groups = df.groupby(df.index)
locations, popups = [], []
for station, info in groups:
sta_name = all_obs[station]
for lat, lon, name in zip(info.lat, info.lon, info.name):
locations.append([lat, lon])
popups.append("[{}]: {}".format(name, sta_name))
MarkerCluster(locations=locations, popups=popups, name="Cluster").add_to(m)
titles = {
"coawst_4_use_best": "COAWST_4",
"pacioos_hycom-global": "HYCOM",
"NECOFS_GOM3_FORECAST": "NECOFS_GOM3",
"NECOFS_FVCOM_OCEAN_MASSBAY_FORECAST": "NECOFS_MassBay",
"NECOFS_FVCOM_OCEAN_BOSTON_FORECAST": "NECOFS_Boston",
"SECOORA_NCSU_CNAPS": "SECOORA/CNAPS",
"roms_2013_da_avg-ESPRESSO_Real-Time_v2_Averages_Best": "ESPRESSO Avg",
"roms_2013_da-ESPRESSO_Real-Time_v2_History_Best": "ESPRESSO Hist",
"OBS_DATA": "Observations",
}
from itertools import cycle
from bokeh.embed import file_html
from bokeh.models import HoverTool, Legend
from bokeh.palettes import Category20
from bokeh.plotting import figure
from bokeh.resources import CDN
from folium import IFrame
# Plot defaults.
colors = Category20[20]
colorcycler = cycle(colors)
tools = "pan,box_zoom,reset"
width, height = 750, 250
def make_plot(df, station):
p = figure(
toolbar_location="above",
x_axis_type="datetime",
width=width,
height=height,
tools=tools,
title=str(station),
)
leg = []
for column, series in df.iteritems():
series.dropna(inplace=True)
if not series.empty:
if "OBS_DATA" not in column:
bias = mean_bias[str(station)][column]
skill = skill_score[str(station)][column]
line_color = next(colorcycler)
kw = dict(alpha=0.65, line_color=line_color)
else:
skill = bias = "NA"
kw = dict(alpha=1, color="crimson")
line = p.line(
x=series.index,
y=series.values,
line_width=5,
line_cap="round",
line_join="round",
**kw
)
leg.append(("{}".format(titles.get(column, column)), [line]))
p.add_tools(
HoverTool(
tooltips=[
("Name", "{}".format(titles.get(column, column))),
("Bias", bias),
("Skill", skill),
],
renderers=[line],
)
)
legend = Legend(items=leg, location=(0, 60))
legend.click_policy = "mute"
p.add_layout(legend, "right")
p.yaxis[0].axis_label = "Water Height (m)"
p.xaxis[0].axis_label = "Date/time"
return p
def make_marker(p, station):
lons = stations_keys(config, key="lon")
lats = stations_keys(config, key="lat")
lon, lat = lons[station], lats[station]
html = file_html(p, CDN, station)
iframe = IFrame(html, width=width + 40, height=height + 80)
popup = folium.Popup(iframe, max_width=2650)
icon = folium.Icon(color="green", icon="stats")
marker = folium.Marker(location=[lat, lon], popup=popup, icon=icon)
return marker
dfs = load_ncs(config)
for station in dfs:
sta_name = all_obs[station]
df = dfs[station]
if df.empty:
continue
p = make_plot(df, station)
marker = make_marker(p, station)
marker.add_to(m)
folium.LayerControl().add_to(m)
def embed_map(m):
from IPython.display import HTML
m.save("index.html")
with open("index.html") as f:
html = f.read()
iframe = '<iframe srcdoc="{srcdoc}" style="width: 100%; height: 750px; border: none"></iframe>'
srcdoc = html.replace('"', """)
return HTML(iframe.format(srcdoc=srcdoc))
embed_map(m)
```
|
github_jupyter
|
### Made by Kartikey Sharma (IIT Goa)
### GOAL
Predicting the costs of used cars given the data collected from various sources and distributed across various locations in India.
#### FEATURES:
<b>Name</b>: The brand and model of the car.<br>
<b>Location</b>: The location in which the car is being sold or is available for purchase.<br>
<b>Year</b>: The year or edition of the model.<br>
<b>Kilometers_Driven</b>: The total kilometres driven in the car by the previous owner(s) in KM.<br>
<b>Fuel_Type</b>: The type of fuel used by the car.<br>
<b>Transmission</b>: The type of transmission used by the car.<br>
<b>Owner_Type</b>: Whether the ownership is Firsthand, Second hand or other.<br>
<b>Mileage</b>: The standard mileage offered by the car company in kmpl or km/kg.<br>
<b>Engine</b>: The displacement volume of the engine in cc.<br>
<b>Power</b>: The maximum power of the engine in bhp.<br>
<b>Seats</b>: The number of seats in the car.<br>
<b>Price</b>: The price of the used car in INR Lakhs.<br>
### Process
Clean the data (missing values and categorical variables).'.
<br>Build the model and check the MAE.
<br>Try to improve the model.
<br>Brand matters too! I could select the brand name of the car and treat them as categorical data.
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import warnings
import seaborn as sns
sns.set_style('darkgrid')
warnings.filterwarnings('ignore')
#Importing datasets
df_train = pd.read_excel("Data_Train.xlsx")
df_test = pd.read_excel("Data_Test.xlsx")
df_train.head()
df_train.shape
df_train.info()
#No of duplicated values in the train set
df_train.duplicated().sum()
#Seeing the number of duplicated values
df_test.duplicated().sum()
#Number of null values
df_train.isnull().sum()
df_train.nunique()
df_train['Name'] = df_train.Name.str.split().str.get(0)
df_test['Name'] = df_test.Name.str.split().str.get(0)
df_train.head()
# all rows have been modified
df_train['Name'].value_counts().sum()
```
### Missing Values
```
# Get names of columns with missing values
cols_with_missing = [col for col in df_train.columns
if df_train[col].isnull().any()]
print("Columns with missing values:")
print(cols_with_missing)
df_train['Seats'].fillna(df_train['Seats'].mean(),inplace=True)
df_test['Seats'].fillna(df_test['Seats'].mean(),inplace=True)
# for more accurate predicitions
data = pd.concat([df_train,df_test], sort=False)
plt.figure(figsize=(20,5))
data['Mileage'].value_counts().head(100).plot.bar()
plt.show()
df_train['Mileage'] = df_train['Mileage'].fillna('17.0 kmpl')
df_test['Mileage'] = df_test['Mileage'].fillna('17.0 kmpl')
# o(zero) and null are both missing values clearly
df_train['Mileage'] = df_train['Mileage'].replace("0.0 kmpl", "17.0 kmpl")
df_test['Mileage'] = df_test['Mileage'].replace("0.0 kmpl", "17.0 kmpl")
plt.figure(figsize=(20,5))
data['Engine'].value_counts().head(100).plot.bar()
plt.show()
df_train['Engine'] = df_train['Engine'].fillna('1000 CC')
df_test['Engine'] = df_test['Engine'].fillna('1000 CC')
plt.figure(figsize=(20,5))
data['Power'].value_counts().head(100).plot.bar()
plt.show()
df_train['Power'] = df_train['Power'].fillna('74 bhp')
df_test['Power'] = df_test['Power'].fillna('74 bhp')
#null bhp created a problem during LabelEncoding
df_train['Power'] = df_train['Power'].replace("null bhp", "74 bhp")
df_test['Power'] = df_test['Power'].replace("null bhp", "74 bhp")
# Method to extract 'float' from 'object'
import re
def get_number(name):
title_search = re.search('([\d+\.+\d]+\W)', name)
if title_search:
return title_search.group(1)
return ""
df_train.isnull().sum()
df_train.info()
#Acquring float values and isolating them
df_train['Mileage'] = df_train['Mileage'].apply(get_number).astype('float')
df_train['Engine'] = df_train['Engine'].apply(get_number).astype('int')
df_train['Power'] = df_train['Power'].apply(get_number).astype('float')
df_test['Mileage'] = df_test['Mileage'].apply(get_number).astype('float')
df_test['Engine'] = df_test['Engine'].apply(get_number).astype('int')
df_test['Power'] = df_test['Power'].apply(get_number).astype('float')
df_train.info()
df_test.info()
df_train.head()
```
### Categorical Variables
```
from sklearn.model_selection import train_test_split
y = np.log1p(df_train.Price) # Made a HUGE difference. MAE went down highly
X = df_train.drop(['Price'],axis=1)
X_train, X_valid, y_train, y_valid = train_test_split(X,y,train_size=0.82,test_size=0.18,random_state=0)
from sklearn.preprocessing import LabelEncoder
label_encoder = LabelEncoder()
X_train['Name'] = label_encoder.fit_transform(X_train['Name'])
X_valid['Name'] = label_encoder.transform(X_valid['Name'])
df_test['Name'] = label_encoder.fit_transform(df_test['Name'])
X_train['Location'] = label_encoder.fit_transform(X_train['Location'])
X_valid['Location'] = label_encoder.transform(X_valid['Location'])
df_test['Location'] = label_encoder.fit_transform(df_test['Location'])
X_train['Fuel_Type'] = label_encoder.fit_transform(X_train['Fuel_Type'])
X_valid['Fuel_Type'] = label_encoder.transform(X_valid['Fuel_Type'])
df_test['Fuel_Type'] = label_encoder.fit_transform(df_test['Fuel_Type'])
X_train['Transmission'] = label_encoder.fit_transform(X_train['Transmission'])
X_valid['Transmission'] = label_encoder.transform(X_valid['Transmission'])
df_test['Transmission'] = label_encoder.fit_transform(df_test['Transmission'])
X_train['Owner_Type'] = label_encoder.fit_transform(X_train['Owner_Type'])
X_valid['Owner_Type'] = label_encoder.transform(X_valid['Owner_Type'])
df_test['Owner_Type'] = label_encoder.fit_transform(df_test['Owner_Type'])
X_train.head()
X_train.info()
```
## Model
```
from xgboost import XGBRegressor
from sklearn.metrics import mean_absolute_error,mean_squared_error,mean_squared_log_error
from math import sqrt
my_model = XGBRegressor(n_estimators=1000, learning_rate=0.05)
my_model.fit(X_train, y_train,
early_stopping_rounds=5,
eval_set=[(X_valid, y_valid)],
verbose=False)
predictions = my_model.predict(X_valid)
print("MAE: " + str(mean_absolute_error(predictions, y_valid)))
print("MSE: " + str(mean_squared_error(predictions, y_valid)))
print("MSLE: " + str(mean_squared_log_error(predictions, y_valid)))
print("RMSE: "+ str(sqrt(mean_squared_error(predictions, y_valid))))
```
## Prediciting on Test
```
preds_test = my_model.predict(df_test)
preds_test = np.exp(preds_test)-1 #converting target to original state
print(preds_test)
# The Price is in the format xx.xx So let's round off and submit.
preds_test = preds_test.round(5)
print(preds_test)
output = pd.DataFrame({'Price': preds_test})
output.to_excel('Output.xlsx', index=False)
```
#### NOTE
Treating 'Mileage' and the others as categorical variables was a mistake. Eg.: Mileage went up from 23.6 to around 338! Converting it to numbers fixed it.
LabelEncoder won't work if there are missing values.
ValueError: y contains previously unseen label 'Bentley'. Fixed it by increasing training_size in train_test_split.
Scaling all the columns made the model worse (as expected).
==============================================End of Project======================================================
```
# Code by Kartikey Sharma
# Veni.Vidi.Vici.
```
|
github_jupyter
|
```
library(dslabs)
library(HistData)
library(tidyverse)
data(heights)
data(Galton)
data(murders)
# HarvardX Data Science Course
# Module 2: Data Visualization
x <- Galton$child
x_with_error <- x
x_with_error[1] <- x_with_error[1] * 10
mean(x_with_error) - mean(x)
sd(x_with_error) - sd(x)
# Median and MAD (median absolute deviation) are robust measurements
median(x_with_error) - median(x)
mad(x_with_error) - mad(x)
# Using EDA (exploratory data analisys) to explore changes
# Returns the average of the vector x after the first entry changed to k
error_avg <- function(k) {
z <- x
z[1] = k
mean(z)
}
error_avg(10^4)
error_avg(-10^4)
# Quantile-quantile Plots
male_heights <- heights$height[heights$sex == 'Male']
p <- seq(0.05, 0.95, 0.05)
observed_quantiles <- quantile(male_heights, p)
theoretical_quantiles <- qnorm(p, mean=mean(male_heights), sd=sd(male_heights))
plot(theoretical_quantiles, observed_quantiles)
abline(0,1)
# It is better to use standard units
z <- scale(male_heights)
observed_quantiles <- quantile(z, p)
theoretical_quantiles <- qnorm(p)
plot(theoretical_quantiles, observed_quantiles)
abline(0,1)
# Porcentiles: when the value of p = 0.01...0.99
# Excercises
male <- heights$height[heights$sex == 'Male']
female <- heights$height[heights$sex == 'Female']
length(male)
length(female)
male_percentiles <- quantile(male, seq(0.1, 0.9, 0.2))
female_percentiles <- quantile(female, seq(0.1, 0.9, 0.2))
df <- data.frame(female=female_percentiles, male=male_percentiles)
df
# Excercises uing Galton data
mean(x)
median(x)
# ggplot2 basics
murders %>% ggplot(aes(population, total, label = abb)) + geom_point() + geom_label(color = 'blue')
murders_plot <- murders %>% ggplot(aes(population, total, label = abb, color = region))
murders_plot + geom_point() + geom_label()
murders_plot +
geom_point() +
geom_label() +
scale_x_log10() +
scale_y_log10() +
ggtitle('Gun Murder Data')
heights_plot <- heights %>% ggplot(aes(x = height))
heights_plot + geom_histogram(binwidth = 1, color = 'darkgrey', fill = 'darkblue')
heights %>% ggplot(aes(height)) + geom_density()
heights %>% ggplot(aes(x = height, group = sex)) + geom_density()
# When setting a color category ggplot know that it has to draw more than 1 plot so the 'group' param is inferred
heights %>% ggplot(aes(x = height, color = sex)) + geom_density()
heights_plot <- heights %>% ggplot(aes(x = height, fill = sex)) + geom_density(alpha = 0.2)
heights_plot
# These two lines achieve the same, summarize creates a second data frame with a single column "rate", .$rate reads the single value finally to the "r" object, see ?summarize
r <- sum(murders$total) / sum(murders$population) * 10^6
r <- murders %>% summarize(rate = sum(total) / sum(population) * 10^6) %>% .$rate
library(ggthemes)
library(ggrepel)
murders_plot <- murders %>% ggplot(aes(x = population / 10^6, y = total, color = region, label = abb))
murders_plot <- murders_plot +
geom_abline(intercept = log10(r), lty = 2, color = 'darkgray') +
geom_point(size = 2) +
geom_text_repel() +
scale_x_log10() +
scale_y_log10() +
ggtitle("US Gun Murders in the US, 2010") +
xlab("Population in millions (log scale)") +
ylab("Total number of murders (log scale)") +
scale_color_discrete(name = 'Region') +
theme_economist()
murders_plot
library(gridExtra)
grid.arrange(heights_plot, murders_plot, ncol = 1)
```
|
github_jupyter
|
```
import pandas as pd
df = pd.read_csv("../k2scoc/results/tables/full_table.csv")
hasflares = (df.real==1) & (df.todrop.isnull())
wassearched = (df.real==0) & (df.todrop.isnull())
df = df[hasflares & (df.cluster=="hyades") & (df.Teff_median > 3250.) & (df.Teff_median < 3500.)]
df[["EPIC"]].drop_duplicates()
```
3500K < Teff < 3750 K:
- [EPIC 247122957](http://simbad.u-strasbg.fr/simbad/sim-coo?Coord=04+36+04.172+%09%2B18+53+18.88&Radius=2&Radius.unit=arcsec&submit=submit+query)
- [EPIC 211036776](http://simbad.u-strasbg.fr/simbad/sim-id?Ident=EPIC+211036776&NbIdent=1&Radius=2&Radius.unit=arcsec&submit=submit+id) **binary or multiple**
- [EPIC 210923016](http://simbad.u-strasbg.fr/simbad/sim-coo?Coord=04+19+29.784+%09%2B21+45+13.99&Radius=2&Radius.unit=arcsec&submit=submit+query)
- [EPIC 246806983](http://simbad.u-strasbg.fr/simbad/sim-coo?Coord=05+11+09.708+%09%2B15+48+57.47&Radius=2&Radius.unit=arcsec&submit=submit+query)
- [EPIC 247289039](http://simbad.u-strasbg.fr/simbad/sim-coo?Coord=04+42+30.301+%09%2B20+27+11.43&Radius=2&Radius.unit=arcsec&submit=submit+query) **spectroscopic binary**
- [EPIC 247592661](http://simbad.u-strasbg.fr/simbad/sim-coo?Coord=04+30+38.192+%09%2B22+54+28.88&Radius=2&Radius.unit=arcsec&submit=submit+query) flare star
- [EPIC 247973705](http://simbad.u-strasbg.fr/simbad/sim-coo?Coord=04+40+06.776+%09%2B25+36+46.40&Radius=2&Radius.unit=arcsec&submit=submit+query)
- [EPIC 210317378](http://simbad.u-strasbg.fr/simbad/sim-id?Ident=EPIC+210317378&submit=submit+id)
- [EPIC 210721261](http://simbad.u-strasbg.fr/simbad/sim-coo?Coord=04+29+01.010+%09%2B18+40+25.33+%09&Radius=2&Radius.unit=arcsec&submit=submit+query) BY Dra
- [EPIC 210741091](http://simbad.u-strasbg.fr/simbad/sim-id?Ident=EPIC+210741091&submit=submit+id)
- [EPIC 247164626](http://simbad.u-strasbg.fr/simbad/sim-coo?Coord=04+40+12.713+%09%2B19+17+09.97&CooFrame=FK5&CooEpoch=2000&CooEqui=2000&CooDefinedFrames=none&Radius=2&Radius.unit=arcsec&submit=submit+query&CoordList=)
Teff < 3000 K:
- [EPIC 210563410](http://simbad.u-strasbg.fr/simbad/sim-id?Ident=%403995861&Name=%5BRSP2011%5D+75&submit=display+all+measurements#lab_meas) p=21d
- [EPIC 248018423](http://simbad.u-strasbg.fr/simbad/sim-coo?Coord=04+51+18.846+%09%2B25+56+33.36+%09&Radius=2&Radius.unit=arcsec&submit=submit+query)
- [EPIC 210371851](http://simbad.u-strasbg.fr/simbad/sim-basic?Ident=EPIC+210371851&submit=SIMBAD+search) **binary**
- [EPIC 210523892](http://simbad.u-strasbg.fr/simbad/sim-basic?Ident=EPIC+210523892&submit=SIMBAD+search) not a binary in Gizis+Reid(1995)
- [EPIC 210643507](http://simbad.u-strasbg.fr/simbad/sim-id?Ident=%403995810&Name=EPIC+210643507&submit=display+all+measurements#lab_meas) p=22d
- [EPIC 210839963](http://simbad.u-strasbg.fr/simbad/sim-id?Ident=EPIC+210839963&NbIdent=1&Radius=2&Radius.unit=arcsec&submit=submit+id) no rotation
- [EPIC 210835057](http://simbad.u-strasbg.fr/simbad/sim-id?Ident=EPIC+210835057&NbIdent=1&Radius=2&Radius.unit=arcsec&submit=submit+id)
- [EPIC 247230044](http://simbad.u-strasbg.fr/simbad/sim-id?Ident=EPIC+247230044&submit=submit+id)
- [EPIC 247254123](http://simbad.u-strasbg.fr/simbad/sim-coo?Coord=+%0904+35+13.549+%09%2B20+08+01.41+%09&Radius=2&Radius.unit=arcsec&submit=submit+query)
- [EPIC 247523445](http://simbad.u-strasbg.fr/simbad/sim-basic?Ident=EPIC+247523445&submit=SIMBAD+search)
- [EPIC 247829435](http://simbad.u-strasbg.fr/simbad/sim-coo?Coord=04+46+44.990+%09%2B24+36+40.40&CooFrame=FK5&CooEpoch=2000&CooEqui=2000&CooDefinedFrames=none&Radius=2&Radius.unit=arcsec&submit=submit+query&CoordList=)
|
github_jupyter
|
# `GiRaFFE_NRPy`: Solving the Induction Equation
## Author: Patrick Nelson
This notebook documents the function from the original `GiRaFFE` that calculates the flux for $A_i$ according to the method of Harten, Lax, von Leer, and Einfeldt (HLLE), assuming that we have calculated the values of the velocity and magnetic field on the cell faces according to the piecewise-parabolic method (PPM) of [Colella and Woodward (1984)](https://crd.lbl.gov/assets/pubs_presos/AMCS/ANAG/A141984.pdf), modified for the case of GRFFE.
**Notebook Status:** <font color=green><b> Validated </b></font>
**Validation Notes:** This code has been validated by showing that it converges to the exact answer at the expected order
### NRPy+ Source Code for this module:
* [GiRaFFE_NRPy/Afield_flux.py](../../edit/in_progress/GiRaFFE_NRPy/Afield_flux.py)
Our goal in this module is to write the code necessary to solve the induction equation
$$
\partial_t A_i = \underbrace{\epsilon_{ijk} v^j B^k}_{\rm Flux\ terms} - \underbrace{\partial_i \left(\alpha \Phi - \beta^j A_j \right)}_{\rm Gauge\ terms}.
$$
To properly handle the flux terms and avoiding problems with shocks, we cannot simply take a cross product of the velocity and magnetic field at the cell centers. Instead, we must solve the Riemann problem at the cell faces using the reconstructed values of the velocity and magnetic field on either side of the cell faces. The reconstruction is done using PPM (see [here](Tutorial-GiRaFFE_NRPy-PPM.ipynb)); in this module, we will assume that that step has already been done. Metric quantities are assumed to have been interpolated to cell faces, as is done in [this](Tutorial-GiRaFFE_NRPy-Metric_Face_Values.ipynb) tutorial.
Tóth's [paper](https://www.sciencedirect.com/science/article/pii/S0021999100965197?via%3Dihub), Eqs. 30 and 31, are one of the first implementations of such a scheme. The original GiRaFFE used a 2D version of the algorithm from [Del Zanna, et al. (2002)](https://arxiv.org/abs/astro-ph/0210618); but since we are not using staggered grids, we can greatly simplify this algorithm with respect to the version used in the original `GiRaFFE`. Instead, we will adapt the implementations of the algorithm used in [Mewes, et al. (2020)](https://arxiv.org/abs/2002.06225) and [Giacomazzo, et al. (2011)](https://arxiv.org/abs/1009.2468), Eqs. 3-11.
We first write the flux contribution to the induction equation RHS as
$$
\partial_t A_i = -E_i,
$$
where the electric field $E_i$ is given in ideal MHD (of which FFE is a subset) as
$$
-E_i = \epsilon_{ijk} v^j B^k,
$$
where $v^i$ is the drift velocity, $B^i$ is the magnetic field, and $\epsilon_{ijk} = \sqrt{\gamma} [ijk]$ is the Levi-Civita tensor.
In Cartesian coordinates,
\begin{align}
-E_x &= [F^y(B^z)]_x = -[F^z(B^y)]_x \\
-E_y &= [F^z(B^x)]_y = -[F^x(B^z)]_y \\
-E_z &= [F^x(B^y)]_z = -[F^y(B^x)]_z, \\
\end{align}
where
$$
[F^i(B^j)]_k = \sqrt{\gamma} (v^i B^j - v^j B^i).
$$
To compute the actual contribution to the RHS in some direction $i$, we average the above listed field as calculated on the $+j$, $-j$, $+k$, and $-k$ faces. That is, at some point $(i,j,k)$ on the grid,
\begin{align}
-E_x(x_i,y_j,z_k) &= \frac{1}{4} \left( [F_{\rm HLL}^y(B^z)]_{x(i,j+1/2,k)}+[F_{\rm HLL}^y(B^z)]_{x(i,j-1/2,k)}-[F_{\rm HLL}^z(B^y)]_{x(i,j,k+1/2)}-[F_{\rm HLL}^z(B^y)]_{x(i,j,k-1/2)} \right) \\
-E_y(x_i,y_j,z_k) &= \frac{1}{4} \left( [F_{\rm HLL}^z(B^x)]_{y(i,j,k+1/2)}+[F_{\rm HLL}^z(B^x)]_{y(i,j,k-1/2)}-[F_{\rm HLL}^x(B^z)]_{y(i+1/2,j,k)}-[F_{\rm HLL}^x(B^z)]_{y(i-1/2,j,k)} \right) \\
-E_z(x_i,y_j,z_k) &= \frac{1}{4} \left( [F_{\rm HLL}^x(B^y)]_{z(i+1/2,j,k)}+[F_{\rm HLL}^x(B^y)]_{z(i-1/2,j,k)}-[F_{\rm HLL}^y(B^x)]_{z(i,j+1/2,k)}-[F_{\rm HLL}^y(B^x)]_{z(i,j-1/2,k)} \right). \\
\end{align}
Note the use of $F_{\rm HLL}$ here. This change signifies that the quantity output here is from the HLLE Riemann solver. Note also the indices on the fluxes. Values of $\pm 1/2$ indicate that these are computed on cell faces using the reconstructed values of $v^i$ and $B^i$ and the interpolated values of the metric gridfunctions. So,
$$
F_{\rm HLL}^i(B^j) = \frac{c_{\rm min} F_{\rm R}^i(B^j) + c_{\rm max} F_{\rm L}^i(B^j) - c_{\rm min} c_{\rm max} (B_{\rm R}^j-B_{\rm L}^j)}{c_{\rm min} + c_{\rm max}}.
$$
The speeds $c_\min$ and $c_\max$ are characteristic speeds that waves can travel through the plasma. In GRFFE, the expressions defining them reduce a function of only the metric quantities. $c_\min$ is the negative of the minimum amongst the speeds $c_-$ and $0$ and $c_\max$ is the maximum amongst the speeds $c_+$ and $0$. The speeds $c_\pm = \left. \left(-b \pm \sqrt{b^2-4ac}\right)\middle/ \left(2a\right) \right.$ must be calculated on both the left and right faces, where
$$a = 1/\alpha^2,$$
$$b = 2 \beta^i / \alpha^2$$
and $$c = g^{ii} - (\beta^i)^2/\alpha^2.$$
An outline of a general finite-volume method is as follows, with the current step in bold:
1. The Reconstruction Step - Piecewise Parabolic Method
1. Within each cell, fit to a function that conserves the volume in that cell using information from the neighboring cells
* For PPM, we will naturally use parabolas
1. Use that fit to define the state at the left and right interface of each cell
1. Apply a slope limiter to mitigate Gibbs phenomenon
1. Interpolate the value of the metric gridfunctions on the cell faces
1. **Solving the Riemann Problem - Harten, Lax, (This notebook, $E_i$ only)**
1. **Use the left and right reconstructed states to calculate the unique state at boundary**
We will assume in this notebook that the reconstructed velocities and magnetic fields are available on cell faces as input. We will also assume that the metric gridfunctions have been interpolated on the metric faces.
Solving the Riemann problem, then, consists of two substeps: First, we compute the flux through each face of the cell. Then, we add the average of these fluxes to the right-hand side of the evolution equation for the vector potential.
<a id='toc'></a>
# Table of Contents
$$\label{toc}$$
This notebook is organized as follows
1. [Step 1](#prelim): Preliminaries
1. [Step 2](#a_i_flux): Computing the Magnetic Flux
1. [Step 2.a](#hydro_speed): GRFFE characteristic wave speeds
1. [Step 2.b](#fluxes): Compute the HLLE fluxes
1. [Step 3](#code_validation): Code Validation against `GiRaFFE_NRPy.Afield_flux` NRPy+ Module
1. [Step 4](#latex_pdf_output): Output this notebook to $\LaTeX$-formatted PDF file
<a id='prelim'></a>
# Step 1: Preliminaries \[Back to [top](#toc)\]
$$\label{prelim}$$
We begin by importing the NRPy+ core functionality. We also import the Levi-Civita symbol, the GRHD module, and the GRFFE module.
```
# Step 0: Add NRPy's directory to the path
# https://stackoverflow.com/questions/16780014/import-file-from-parent-directory
import os, sys # Standard Python modules for multiplatform OS-level functions
nrpy_dir_path = os.path.join("..")
if nrpy_dir_path not in sys.path:
sys.path.append(nrpy_dir_path)
from outputC import outCfunction, outputC # NRPy+: Core C code output module
import sympy as sp # SymPy: The Python computer algebra package upon which NRPy+ depends
import NRPy_param_funcs as par # NRPy+: Parameter interface
import grid as gri # NRPy+: Functions having to do with numerical grids
import indexedexp as ixp # NRPy+: Symbolic indexed expression (e.g., tensors, vectors, etc.) support
import cmdline_helper as cmd # NRPy+: Multi-platform Python command-line interface
thismodule = "GiRaFFE_NRPy-Afield_flux"
import GRHD.equations as GRHD
# import GRFFE.equations as GRFFE
```
<a id='a_i_flux'></a>
# Step 2: Computing the Magnetic Flux \[Back to [top](#toc)\]
$$\label{a_i_flux}$$
<a id='hydro_speed'></a>
## Step 2.a: GRFFE characteristic wave speeds \[Back to [top](#toc)\]
$$\label{hydro_speed}$$
Next, we will find the speeds at which the hydrodynamics waves propagate. We start from the speed of light (since FFE deals with very diffuse plasmas), which is $c=1.0$ in our chosen units. We then find the speeds $c_+$ and $c_-$ on each face with the function `find_cp_cm`; then, we find minimum and maximum speeds possible from among those.
Below is the source code for `find_cp_cm`, edited to work with the NRPy+ version of GiRaFFE. One edit we need to make in particular is to the term `psim4*gupii` in the definition of `c`; that was written assuming the use of the conformal metric $\tilde{g}^{ii}$. Since we are not using that here, and are instead using the ADM metric, we should not multiply by $\psi^{-4}$.
```c
static inline void find_cp_cm(REAL &cplus,REAL &cminus,const REAL v02,const REAL u0,
const REAL vi,const REAL lapse,const REAL shifti,
const REAL gammadet,const REAL gupii) {
const REAL u0_SQUARED=u0*u0;
const REAL ONE_OVER_LAPSE_SQUARED = 1.0/(lapse*lapse);
// sqrtgamma = psi6 -> psim4 = gammadet^(-1.0/3.0)
const REAL psim4 = pow(gammadet,-1.0/3.0);
//Find cplus, cminus:
const REAL a = u0_SQUARED * (1.0-v02) + v02*ONE_OVER_LAPSE_SQUARED;
const REAL b = 2.0* ( shifti*ONE_OVER_LAPSE_SQUARED * v02 - u0_SQUARED * vi * (1.0-v02) );
const REAL c = u0_SQUARED*vi*vi * (1.0-v02) - v02 * ( gupii -
shifti*shifti*ONE_OVER_LAPSE_SQUARED);
REAL detm = b*b - 4.0*a*c;
//ORIGINAL LINE OF CODE:
//if(detm < 0.0) detm = 0.0;
//New line of code (without the if() statement) has the same effect:
detm = sqrt(0.5*(detm + fabs(detm))); /* Based on very nice suggestion from Roland Haas */
cplus = 0.5*(detm-b)/a;
cminus = -0.5*(detm+b)/a;
if (cplus < cminus) {
const REAL cp = cminus;
cminus = cplus;
cplus = cp;
}
}
```
Comments documenting this have been excised for brevity, but are reproduced in $\LaTeX$ [below](#derive_speed).
We could use this code directly, but there's substantial improvement we can make by changing the code into a NRPyfied form. Note the `if` statement; NRPy+ does not know how to handle these, so we must eliminate it if we want to leverage NRPy+'s full power. (Calls to `fabs()` are also cheaper than `if` statements.) This can be done if we rewrite this, taking inspiration from the other eliminated `if` statement documented in the above code block:
```c
cp = 0.5*(detm-b)/a;
cm = -0.5*(detm+b)/a;
cplus = 0.5*(cp+cm+fabs(cp-cm));
cminus = 0.5*(cp+cm-fabs(cp-cm));
```
This can be simplified further, by substituting `cp` and `cm` into the below equations and eliminating terms as appropriate. First note that `cp+cm = -b/a` and that `cp-cm = detm/a`. Thus,
```c
cplus = 0.5*(-b/a + fabs(detm/a));
cminus = 0.5*(-b/a - fabs(detm/a));
```
This fulfills the original purpose of the `if` statement in the original code because we have guaranteed that $c_+ \geq c_-$.
This leaves us with an expression that can be much more easily NRPyfied. So, we will rewrite the following in NRPy+, making only minimal changes to be proper Python. However, it turns out that we can make this even simpler. In GRFFE, $v_0^2$ is guaranteed to be exactly one. In GRMHD, this speed was calculated as $$v_{0}^{2} = v_{\rm A}^{2} + c_{\rm s}^{2}\left(1-v_{\rm A}^{2}\right),$$ where the Alfvén speed $v_{\rm A}^{2}$ $$v_{\rm A}^{2} = \frac{b^{2}}{\rho_{b}h + b^{2}}.$$ So, we can see that when the density $\rho_b$ goes to zero, $v_{0}^{2} = v_{\rm A}^{2} = 1$. Then
\begin{align}
a &= (u^0)^2 (1-v_0^2) + v_0^2/\alpha^2 \\
&= 1/\alpha^2 \\
b &= 2 \left(\beta^i v_0^2 / \alpha^2 - (u^0)^2 v^i (1-v_0^2)\right) \\
&= 2 \beta^i / \alpha^2 \\
c &= (u^0)^2 (v^i)^2 (1-v_0^2) - v_0^2 \left(\gamma^{ii} - (\beta^i)^2/\alpha^2\right) \\
&= -\gamma^{ii} + (\beta^i)^2/\alpha^2,
\end{align}
are simplifications that should save us some time; we can see that $a \geq 0$ is guaranteed. Note that we also force `detm` to be positive. Thus, `detm/a` is guaranteed to be positive itself, rendering the calls to `nrpyAbs()` superfluous. Furthermore, we eliminate any dependence on the Valencia 3-velocity and the time compoenent of the four-velocity, $u^0$. This leaves us free to solve the quadratic in the familiar way: $$c_\pm = \frac{-b \pm \sqrt{b^2-4ac}}{2a}$$.
```
# We'll write this as a function so that we can calculate the expressions on-demand for any choice of i
def find_cp_cm(lapse,shifti,gammaUUii):
# Inputs: u0,vi,lapse,shift,gammadet,gupii
# Outputs: cplus,cminus
# a = 1/(alpha^2)
a = sp.sympify(1)/(lapse*lapse)
# b = 2 beta^i / alpha^2
b = sp.sympify(2) * shifti /(lapse*lapse)
# c = -g^{ii} + (beta^i)^2 / alpha^2
c = - gammaUUii + shifti*shifti/(lapse*lapse)
# Now, we are free to solve the quadratic equation as usual. We take care to avoid passing a
# negative value to the sqrt function.
detm = b*b - sp.sympify(4)*a*c
import Min_Max_and_Piecewise_Expressions as noif
detm = sp.sqrt(noif.max_noif(sp.sympify(0),detm))
global cplus,cminus
cplus = sp.Rational(1,2)*(-b/a + detm/a)
cminus = sp.Rational(1,2)*(-b/a - detm/a)
```
In flat spacetime, where $\alpha=1$, $\beta^i=0$, and $\gamma^{ij} = \delta^{ij}$, $c_+ > 0$ and $c_- < 0$. For the HLLE solver, we will need both `cmax` and `cmin` to be positive; we also want to choose the speed that is larger in magnitude because overestimating the characteristic speeds will help damp unwanted oscillations. (However, in GRFFE, we only get one $c_+$ and one $c_-$, so we only need to fix the signs here.) Hence, the following function.
We will now write a function in NRPy+ similar to the one used in the old `GiRaFFE`, allowing us to generate the expressions with less need to copy-and-paste code; the key difference is that this one will be in Python, and generate optimized C code integrated into the rest of the operations. Notice that since we eliminated the dependence on velocities, none of the input quantities are different on either side of the face. So, this function won't really do much besides guarantee that `cmax` and `cmin` are positive, but we'll leave the machinery here since it is likely to be a useful guide to somebody who wants to something similar. The only modifications we'll make are those necessary to eliminate calls to `fabs(0)` in the C code. We use the same technique as above to replace the `if` statements inherent to the `MAX()` and `MIN()` functions.
```
# We'll write this as a function, and call it within HLLE_solver, below.
def find_cmax_cmin(field_comp,gamma_faceDD,beta_faceU,alpha_face):
# Inputs: flux direction field_comp, Inverse metric gamma_faceUU, shift beta_faceU,
# lapse alpha_face, metric determinant gammadet_face
# Outputs: maximum and minimum characteristic speeds cmax and cmin
# First, we need to find the characteristic speeds on each face
gamma_faceUU,unusedgammaDET = ixp.generic_matrix_inverter3x3(gamma_faceDD)
# Original needed for GRMHD
# find_cp_cm(alpha_face,beta_faceU[field_comp],gamma_faceUU[field_comp][field_comp])
# cpr = cplus
# cmr = cminus
# find_cp_cm(alpha_face,beta_faceU[field_comp],gamma_faceUU[field_comp][field_comp])
# cpl = cplus
# cml = cminus
find_cp_cm(alpha_face,beta_faceU[field_comp],gamma_faceUU[field_comp][field_comp])
cp = cplus
cm = cminus
# The following algorithms have been verified with random floats:
global cmax,cmin
# Now, we need to set cmax to the larger of cpr,cpl, and 0
import Min_Max_and_Piecewise_Expressions as noif
cmax = noif.max_noif(cp,sp.sympify(0))
# And then, set cmin to the smaller of cmr,cml, and 0
cmin = -noif.min_noif(cm,sp.sympify(0))
```
<a id='fluxes'></a>
## Step 2.b: Compute the HLLE fluxes \[Back to [top](#toc)\]
$$\label{fluxes}$$
Here, we we calculate the flux and state vectors for the electric field. The flux vector is here given as
$$
[F^i(B^j)]_k = \sqrt{\gamma} (v^i B^j - v^j B^i).
$$
Here, $v^i$ is the drift velocity and $B^i$ is the magnetic field.
This can be easily handled for an input flux direction $i$ with
$$
[F^j(B^k)]_i = \epsilon_{ijk} v^j B^k,
$$
where $\epsilon_{ijk} = \sqrt{\gamma} [ijk]$ and $[ijk]$ is the Levi-Civita symbol.
The state vector is simply the magnetic field $B^j$.
```
def calculate_flux_and_state_for_Induction(field_comp,flux_dirn, gammaDD,betaU,alpha,ValenciavU,BU):
# Define Levi-Civita symbol
def define_LeviCivitaSymbol_rank3(DIM=-1):
if DIM == -1:
DIM = par.parval_from_str("DIM")
LeviCivitaSymbol = ixp.zerorank3()
for i in range(DIM):
for j in range(DIM):
for k in range(DIM):
# From https://codegolf.stackexchange.com/questions/160359/levi-civita-symbol :
LeviCivitaSymbol[i][j][k] = (i - j) * (j - k) * (k - i) * sp.Rational(1,2)
return LeviCivitaSymbol
GRHD.compute_sqrtgammaDET(gammaDD)
# Here, we import the Levi-Civita tensor and compute the tensor with lower indices
LeviCivitaDDD = define_LeviCivitaSymbol_rank3()
for i in range(3):
for j in range(3):
for k in range(3):
LeviCivitaDDD[i][j][k] *= GRHD.sqrtgammaDET
global U,F
# Flux F = \epsilon_{ijk} v^j B^k
F = sp.sympify(0)
for j in range(3):
for k in range(3):
F += LeviCivitaDDD[field_comp][j][k] * (alpha*ValenciavU[j]-betaU[j]) * BU[k]
# U = B^i
U = BU[flux_dirn]
```
Now, we write a standard HLLE solver based on eq. 3.15 in [the HLLE paper](https://epubs.siam.org/doi/pdf/10.1137/1025002),
$$
F^{\rm HLL} = \frac{c_{\rm min} F_{\rm R} + c_{\rm max} F_{\rm L} - c_{\rm min} c_{\rm max} (U_{\rm R}-U_{\rm L})}{c_{\rm min} + c_{\rm max}}
$$
```
def HLLE_solver(cmax, cmin, Fr, Fl, Ur, Ul):
# This solves the Riemann problem for the flux of E_i in one direction
# F^HLL = (c_\min f_R + c_\max f_L - c_\min c_\max ( st_j_r - st_j_l )) / (c_\min + c_\max)
return (cmin*Fr + cmax*Fl - cmin*cmax*(Ur-Ul) )/(cmax + cmin)
```
Here, we will use the function we just wrote to calculate the flux through a face. We will pass the reconstructed Valencia 3-velocity and magnetic field on either side of an interface to this function (designated as the "left" and "right" sides) along with the value of the 3-metric, shift vector, and lapse function on the interface. The parameter `flux_dirn` specifies which face through which we are calculating the flux. However, unlike when we used this method to calculate the flux term, the RHS of each component of $A_i$ does not depend on all three of the flux directions. Instead, the flux of one component of the $E_i$ field depends on flux through the faces in the other two directions. This will be handled when we generate the C function, as demonstrated in the example code after this next function.
Note that we allow the user to declare their own gridfunctions if they wish, and default to declaring basic symbols if they are not provided. The default names are chosen to imply interpolation of the metric gridfunctions and reconstruction of the primitives.
```
def calculate_E_i_flux(flux_dirn,alpha_face=None,gamma_faceDD=None,beta_faceU=None,\
Valenciav_rU=None,B_rU=None,Valenciav_lU=None,B_lU=None):
global E_fluxD
E_fluxD = ixp.zerorank1()
for field_comp in range(3):
find_cmax_cmin(field_comp,gamma_faceDD,beta_faceU,alpha_face)
calculate_flux_and_state_for_Induction(field_comp,flux_dirn, gamma_faceDD,beta_faceU,alpha_face,\
Valenciav_rU,B_rU)
Fr = F
Ur = U
calculate_flux_and_state_for_Induction(field_comp,flux_dirn, gamma_faceDD,beta_faceU,alpha_face,\
Valenciav_lU,B_lU)
Fl = F
Ul = U
E_fluxD[field_comp] += HLLE_solver(cmax, cmin, Fr, Fl, Ur, Ul)
```
Below, we will write some example code to use the above functions to generate C code for `GiRaFFE_NRPy`. We need to write our own memory reads and writes because we need to add contributions from *both* faces in a given direction, which is expressed in the code as adding contributions from adjacent gridpoints to the RHS, which is not something `FD_outputC` can handle. The `.replace()` function calls adapt these reads and writes to the different directions. Note that, for reconstructions in a given direction, the fluxes are only added to the other two components, as can be seen in the equations we are implementing.
\begin{align}
-E_x(x_i,y_j,z_k) &= \frac{1}{4} \left( [F_{\rm HLL}^y(B^z)]_{x(i,j+1/2,k)}+[F_{\rm HLL}^y(B^z)]_{x(i,j-1/2,k)}-[F_{\rm HLL}^z(B^y)]_{x(i,j,k+1/2)}-[F_{\rm HLL}^z(B^y)]_{x(i,j,k-1/2)} \right) \\
-E_y(x_i,y_j,z_k) &= \frac{1}{4} \left( [F_{\rm HLL}^z(B^x)]_{y(i,j,k+1/2)}+[F_{\rm HLL}^z(B^x)]_{y(i,j,k-1/2)}-[F_{\rm HLL}^x(B^z)]_{y(i+1/2,j,k)}-[F_{\rm HLL}^x(B^z)]_{y(i-1/2,j,k)} \right) \\
-E_z(x_i,y_j,z_k) &= \frac{1}{4} \left( [F_{\rm HLL}^x(B^y)]_{z(i+1/2,j,k)}+[F_{\rm HLL}^x(B^y)]_{z(i-1/2,j,k)}-[F_{\rm HLL}^y(B^x)]_{z(i,j+1/2,k)}-[F_{\rm HLL}^y(B^x)]_{z(i,j-1/2,k)} \right). \\
\end{align}
From this, we can see that when, for instance, we reconstruct and interpolate in the $x$-direction, we must add only to the $y$- and $z$-components of the electric field.
Recall that when we reconstructed the velocity and magnetic field, we constructed to the $i-1/2$ face, so the data at $i+1/2$ is stored at $i+1$.
```
def generate_Afield_flux_function_files(out_dir,subdir,alpha_face,gamma_faceDD,beta_faceU,\
Valenciav_rU,B_rU,Valenciav_lU,B_lU,inputs_provided=True):
if not inputs_provided:
# declare all variables
alpha_face = sp.symbols(alpha_face)
beta_faceU = ixp.declarerank1("beta_faceU")
gamma_faceDD = ixp.declarerank2("gamma_faceDD","sym01")
Valenciav_rU = ixp.declarerank1("Valenciav_rU")
B_rU = ixp.declarerank1("B_rU")
Valenciav_lU = ixp.declarerank1("Valenciav_lU")
B_lU = ixp.declarerank1("B_lU")
Memory_Read = """const double alpha_face = auxevol_gfs[IDX4S(ALPHA_FACEGF, i0,i1,i2)];
const double gamma_faceDD00 = auxevol_gfs[IDX4S(GAMMA_FACEDD00GF, i0,i1,i2)];
const double gamma_faceDD01 = auxevol_gfs[IDX4S(GAMMA_FACEDD01GF, i0,i1,i2)];
const double gamma_faceDD02 = auxevol_gfs[IDX4S(GAMMA_FACEDD02GF, i0,i1,i2)];
const double gamma_faceDD11 = auxevol_gfs[IDX4S(GAMMA_FACEDD11GF, i0,i1,i2)];
const double gamma_faceDD12 = auxevol_gfs[IDX4S(GAMMA_FACEDD12GF, i0,i1,i2)];
const double gamma_faceDD22 = auxevol_gfs[IDX4S(GAMMA_FACEDD22GF, i0,i1,i2)];
const double beta_faceU0 = auxevol_gfs[IDX4S(BETA_FACEU0GF, i0,i1,i2)];
const double beta_faceU1 = auxevol_gfs[IDX4S(BETA_FACEU1GF, i0,i1,i2)];
const double beta_faceU2 = auxevol_gfs[IDX4S(BETA_FACEU2GF, i0,i1,i2)];
const double Valenciav_rU0 = auxevol_gfs[IDX4S(VALENCIAV_RU0GF, i0,i1,i2)];
const double Valenciav_rU1 = auxevol_gfs[IDX4S(VALENCIAV_RU1GF, i0,i1,i2)];
const double Valenciav_rU2 = auxevol_gfs[IDX4S(VALENCIAV_RU2GF, i0,i1,i2)];
const double B_rU0 = auxevol_gfs[IDX4S(B_RU0GF, i0,i1,i2)];
const double B_rU1 = auxevol_gfs[IDX4S(B_RU1GF, i0,i1,i2)];
const double B_rU2 = auxevol_gfs[IDX4S(B_RU2GF, i0,i1,i2)];
const double Valenciav_lU0 = auxevol_gfs[IDX4S(VALENCIAV_LU0GF, i0,i1,i2)];
const double Valenciav_lU1 = auxevol_gfs[IDX4S(VALENCIAV_LU1GF, i0,i1,i2)];
const double Valenciav_lU2 = auxevol_gfs[IDX4S(VALENCIAV_LU2GF, i0,i1,i2)];
const double B_lU0 = auxevol_gfs[IDX4S(B_LU0GF, i0,i1,i2)];
const double B_lU1 = auxevol_gfs[IDX4S(B_LU1GF, i0,i1,i2)];
const double B_lU2 = auxevol_gfs[IDX4S(B_LU2GF, i0,i1,i2)];
REAL A_rhsD0 = 0; REAL A_rhsD1 = 0; REAL A_rhsD2 = 0;
"""
Memory_Write = """rhs_gfs[IDX4S(AD0GF,i0,i1,i2)] += A_rhsD0;
rhs_gfs[IDX4S(AD1GF,i0,i1,i2)] += A_rhsD1;
rhs_gfs[IDX4S(AD2GF,i0,i1,i2)] += A_rhsD2;
"""
indices = ["i0","i1","i2"]
indicesp1 = ["i0+1","i1+1","i2+1"]
for flux_dirn in range(3):
calculate_E_i_flux(flux_dirn,alpha_face,gamma_faceDD,beta_faceU,\
Valenciav_rU,B_rU,Valenciav_lU,B_lU)
E_field_to_print = [\
sp.Rational(1,4)*E_fluxD[(flux_dirn+1)%3],
sp.Rational(1,4)*E_fluxD[(flux_dirn+2)%3],
]
E_field_names = [\
"A_rhsD"+str((flux_dirn+1)%3),
"A_rhsD"+str((flux_dirn+2)%3),
]
desc = "Calculate the electric flux on the left face in direction " + str(flux_dirn) + "."
name = "calculate_E_field_D" + str(flux_dirn) + "_right"
outCfunction(
outfile = os.path.join(out_dir,subdir,name+".h"), desc=desc, name=name,
params ="const paramstruct *params,const REAL *auxevol_gfs,REAL *rhs_gfs",
body = Memory_Read \
+outputC(E_field_to_print,E_field_names,"returnstring",params="outCverbose=False").replace("IDX4","IDX4S")\
+Memory_Write,
loopopts ="InteriorPoints",
rel_path_for_Cparams=os.path.join("../"))
desc = "Calculate the electric flux on the left face in direction " + str(flux_dirn) + "."
name = "calculate_E_field_D" + str(flux_dirn) + "_left"
outCfunction(
outfile = os.path.join(out_dir,subdir,name+".h"), desc=desc, name=name,
params ="const paramstruct *params,const REAL *auxevol_gfs,REAL *rhs_gfs",
body = Memory_Read.replace(indices[flux_dirn],indicesp1[flux_dirn]) \
+outputC(E_field_to_print,E_field_names,"returnstring",params="outCverbose=False").replace("IDX4","IDX4S")\
+Memory_Write,
loopopts ="InteriorPoints",
rel_path_for_Cparams=os.path.join("../"))
```
<a id='code_validation'></a>
# Step 3: Code Validation against `GiRaFFE_NRPy.Induction_Equation` NRPy+ Module \[Back to [top](#toc)\]
$$\label{code_validation}$$
Here, as a code validation check, we verify agreement in the SymPy expressions for the $\texttt{GiRaFFE}$ evolution equations and auxiliary quantities we intend to use between
1. this tutorial and
2. the NRPy+ [GiRaFFE_NRPy.Induction_Equation](../../edit/in_progress/GiRaFFE_NRPy/Induction_Equation.py) module.
Below are the gridfunction registrations we will need for testing. We will pass these to the above functions to self-validate the module that corresponds with this tutorial.
```
all_passed=True
def comp_func(expr1,expr2,basename,prefixname2="C2P_P2C."):
if str(expr1-expr2)!="0":
print(basename+" - "+prefixname2+basename+" = "+ str(expr1-expr2))
all_passed=False
def gfnm(basename,idx1,idx2=None,idx3=None):
if idx2 is None:
return basename+"["+str(idx1)+"]"
if idx3 is None:
return basename+"["+str(idx1)+"]["+str(idx2)+"]"
return basename+"["+str(idx1)+"]["+str(idx2)+"]["+str(idx3)+"]"
# These are the standard gridfunctions we've used before.
#ValenciavU = ixp.register_gridfunctions_for_single_rank1("AUXEVOL","ValenciavU",DIM=3)
#gammaDD = ixp.register_gridfunctions_for_single_rank2("AUXEVOL","gammaDD","sym01")
#betaU = ixp.register_gridfunctions_for_single_rank1("AUXEVOL","betaU")
#alpha = gri.register_gridfunctions("AUXEVOL",["alpha"])
#AD = ixp.register_gridfunctions_for_single_rank1("EVOL","AD",DIM=3)
#BU = ixp.register_gridfunctions_for_single_rank1("AUXEVOL","BU",DIM=3)
# We will pass values of the gridfunction on the cell faces into the function. This requires us
# to declare them as C parameters in NRPy+. We will denote this with the _face infix/suffix.
alpha_face = gri.register_gridfunctions("AUXEVOL","alpha_face")
gamma_faceDD = ixp.register_gridfunctions_for_single_rank2("AUXEVOL","gamma_faceDD","sym01")
beta_faceU = ixp.register_gridfunctions_for_single_rank1("AUXEVOL","beta_faceU")
# We'll need some more gridfunctions, now, to represent the reconstructions of BU and ValenciavU
# on the right and left faces
Valenciav_rU = ixp.register_gridfunctions_for_single_rank1("AUXEVOL","Valenciav_rU",DIM=3)
B_rU = ixp.register_gridfunctions_for_single_rank1("AUXEVOL","B_rU",DIM=3)
Valenciav_lU = ixp.register_gridfunctions_for_single_rank1("AUXEVOL","Valenciav_lU",DIM=3)
B_lU = ixp.register_gridfunctions_for_single_rank1("AUXEVOL","B_lU",DIM=3)
import GiRaFFE_NRPy.Afield_flux as Af
expr_list = []
exprcheck_list = []
namecheck_list = []
for flux_dirn in range(3):
calculate_E_i_flux(flux_dirn,alpha_face,gamma_faceDD,beta_faceU,\
Valenciav_rU,B_rU,Valenciav_lU,B_lU)
Af.calculate_E_i_flux(flux_dirn,alpha_face,gamma_faceDD,beta_faceU,\
Valenciav_rU,B_rU,Valenciav_lU,B_lU)
namecheck_list.extend([gfnm("E_fluxD",flux_dirn)])
exprcheck_list.extend([Af.E_fluxD[flux_dirn]])
expr_list.extend([E_fluxD[flux_dirn]])
for mom_comp in range(len(expr_list)):
comp_func(expr_list[mom_comp],exprcheck_list[mom_comp],namecheck_list[mom_comp])
import sys
if all_passed:
print("ALL TESTS PASSED!")
else:
print("ERROR: AT LEAST ONE TEST DID NOT PASS")
sys.exit(1)
```
We will also check the output C code to make sure it matches what is produced by the python module.
```
import difflib
import sys
subdir = os.path.join("RHSs")
out_dir = os.path.join("GiRaFFE_standalone_Ccodes")
cmd.mkdir(out_dir)
cmd.mkdir(os.path.join(out_dir,subdir))
valdir = os.path.join("GiRaFFE_Ccodes_validation")
cmd.mkdir(valdir)
cmd.mkdir(os.path.join(valdir,subdir))
generate_Afield_flux_function_files(out_dir,subdir,alpha_face,gamma_faceDD,beta_faceU,\
Valenciav_rU,B_rU,Valenciav_lU,B_lU,inputs_provided=True)
Af.generate_Afield_flux_function_files(valdir,subdir,alpha_face,gamma_faceDD,beta_faceU,\
Valenciav_rU,B_rU,Valenciav_lU,B_lU,inputs_provided=True)
print("Printing difference between original C code and this code...")
# Open the files to compare
files = ["RHSs/calculate_E_field_D0_right.h",
"RHSs/calculate_E_field_D0_left.h",
"RHSs/calculate_E_field_D1_right.h",
"RHSs/calculate_E_field_D1_left.h",
"RHSs/calculate_E_field_D2_right.h",
"RHSs/calculate_E_field_D2_left.h"]
for file in files:
print("Checking file " + file)
with open(os.path.join(valdir,file)) as file1, open(os.path.join(out_dir,file)) as file2:
# Read the lines of each file
file1_lines = file1.readlines()
file2_lines = file2.readlines()
num_diffs = 0
for line in difflib.unified_diff(file1_lines, file2_lines, fromfile=os.path.join(valdir,file), tofile=os.path.join(out_dir,file)):
sys.stdout.writelines(line)
num_diffs = num_diffs + 1
if num_diffs == 0:
print("No difference. TEST PASSED!")
else:
print("ERROR: Disagreement found with .py file. See differences above.")
```
<a id='latex_pdf_output'></a>
# Step 4: Output this notebook to $\LaTeX$-formatted PDF file \[Back to [top](#toc)\]
$$\label{latex_pdf_output}$$
The following code cell converts this Jupyter notebook into a proper, clickable $\LaTeX$-formatted PDF file. After the cell is successfully run, the generated PDF may be found in the root NRPy+ tutorial directory, with filename
[Tutorial-GiRaFFE_NRPy-Induction_Equation.pdf](Tutorial-GiRaFFE_NRPy-Induction_Equation.pdf) (Note that clicking on this link may not work; you may need to open the PDF file through another means.)
```
import cmdline_helper as cmd # NRPy+: Multi-platform Python command-line interface
cmd.output_Jupyter_notebook_to_LaTeXed_PDF("Tutorial-GiRaFFE_NRPy-Afield_flux")
```
|
github_jupyter
|
```
import numpy as np
import matplotlib.pyplot as plt
import math
from matplotlib import style
from collections import Counter
style.use('fivethirtyeight') #Shows Grid
import pandas as pd
import random
df = pd.read_csv('Breast-Cancer.csv',na_values = ['?'])
means = df.mean().to_dict()
df.drop(['id'],1,inplace=True)
header = list(df)
df.fillna(df.mean(),inplace = True)
full_data = df.astype(float).values.tolist()
full_data
test_size1 = 0.5
train_data1 = full_data[:-int(test_size1*len(full_data))]
test_data1 = full_data[-int(test_size1*len(full_data)):]
len(test_data1)
test_size2 = 0.1
train_data2 = full_data[:-int(test_size2*len(full_data))]
test_data2 = full_data[-int(test_size2*len(full_data)):]
len(test_data2)
test_size3 = 0.3
train_data3 = full_data[:-int(test_size3*len(full_data))]
test_data3 = full_data[-int(test_size3*len(full_data)):]
len(test_data3)
def unique_vals(Data,col):
return set([row[col] for row in Data])
def class_counts(Data):
counts = {}
for row in Data:
label = row[-1]
if label not in counts:
counts[label] = 0
counts[label] += 1
return counts
class Question:
def __init__(self,column,value):
self.column = column
self.value = value
def match(self,example):
val = example[self.column]
return val == self.value
def __repr__(self):
return "Is %s %s %s?" %(
header[self.column],"==",str(self.value))
def partition(Data,question):
true_rows,false_rows = [],[]
for row in Data:
if(question.match(row)):
true_rows.append(row)
else:
false_rows.append(row)
return true_rows,false_rows
def gini(Data):
counts = class_counts(Data)
impurity = 1
for lbl in counts:
prob_of_lbl = counts[lbl]/float(len(Data))
impurity-=prob_of_lbl**2
return impurity
def info_gain(left,right,current_uncertainty):
p = float(len(left))/(len(left)+len(right))
return current_uncertainty - p*gini(left) - (1-p)*gini(right)
def find_best_split(Data):
best_gain = 0
best_question = None
current_uncertainty = gini(Data)
n_features = len(Data[0]) - 1
for col in range(n_features):
values = unique_vals(Data,col)
for val in values:
question = Question(col,val)
true_rows,false_rows = partition(Data,question)
if(len(true_rows) == 0 or len(false_rows)==0):
continue
gain = info_gain(true_rows,false_rows,current_uncertainty)
if gain>=best_gain:
best_gain, best_question = gain , question
return best_gain,best_question
class Leaf:
def __init__(self,Data):
self.predictions = class_counts(Data)
class Decision_Node:
def __init__(self, question, true_branch,false_branch):
self.question = question
self.true_branch = true_branch
self.false_branch = false_branch
#print(self.question)
def build_tree(Data,i=0):
gain, question = find_best_split(Data)
if gain == 0:
return Leaf(Data)
true_rows , false_rows = partition(Data,question)
true_branch = build_tree(true_rows,i)
false_branch = build_tree(false_rows,i)
return Decision_Node(question,true_branch,false_branch)
def print_tree(node,spacing=""):
if isinstance(node, Leaf):
print(spacing + "Predict",node.predictions)
return
print(spacing+str(node.question))
print(spacing + "--> True:")
print_tree(node.true_branch , spacing + " ")
print(spacing + "--> False:")
print_tree(node.false_branch , spacing + " ")
def print_leaf(counts):
total = sum(counts.values())*1.0
probs = {}
for lbl in counts.keys():
probs[lbl] = str(int(counts[lbl]/total * 100)) + "%"
return probs
def classify(row,node):
if isinstance(node,Leaf):
return node.predictions
if node.question.match(row):
return classify(row,node.true_branch)
else:
return classify(row,node.false_branch)
my_tree = build_tree(train_data1)
print_tree(my_tree)
def calc_accuracy(test_data, my_tree):
correct,total = 0,0
for row in test_data:
if(row[-1] in print_leaf(classify(row,my_tree)).keys()):
correct += 1
total += 1
return correct/total
for row in test_data1:
print("Actual: %s. Predicted: %s" % (row[-1],print_leaf(classify(row,my_tree))))
accuracy = calc_accuracy(test_data1,my_tree)
print(accuracy,"accuracy for 50% train data and 50% test data")
my_tree2 = build_tree(train_data2)
print_tree(my_tree2)
for row in test_data2:
print("Actual: %s. Predicted: %s" % (row[-1],print_leaf(classify(row,my_tree2))))
accuracy2 = calc_accuracy(test_data2,my_tree2)
print(accuracy2,"accuracy for 90% train data and 10% test data")
my_tree3 = build_tree(train_data3)
print_tree(my_tree3)
for row in test_data3:
print("Actual: %s. Predicted: %s" % (row[-1],print_leaf(classify(row,my_tree3))))
accuracy3 = calc_accuracy(test_data3,my_tree3)
print(accuracy3,"accuracy for 70% train data and 30% test data")
```
|
github_jupyter
|
```
import os
from collections import defaultdict, namedtuple
from copy import deepcopy
from pprint import pprint
import lxml
import lxml.html
import lxml.etree
from graphviz import Digraph
from similarity.normalized_levenshtein import NormalizedLevenshtein
normalized_levenshtein = NormalizedLevenshtein()
TAG_NAME_ATTRIB = '___tag_name___'
HIERARCHICAL = 'hierarchical'
SEQUENTIAL = 'sequential'
class DataRegion(
# todo rename n_nodes_per_region -> gnode_size
# todo rename start_child_index -> first_gnode_start_index
namedtuple("DataRegion", ["n_nodes_per_region", "start_child_index", "n_nodes_covered",])
):
def __str__(self):
return "DR({0}, {1}, {2})".format(self[0], self[1], self[2])
def extend_one_gnode(self):
return self.__class__(
self.n_nodes_per_region, self.start_child_index, self.n_nodes_covered + self.n_nodes_per_region
)
@classmethod
def binary_from_last_gnode(cls, gnode):
gnode_size = gnode.end - gnode.start
return cls(gnode_size, gnode.start - gnode_size, 2 * gnode_size)
@classmethod
def empty(cls):
return cls(None, None, 0)
return cls(0, 0, 0)
@property
def is_empty(self):
return self[0] is None
# todo use this more extensively
# Generalized Node
class GNode(
namedtuple("GNode", ["start", "end"])
):
def __str__(self):
return "GN({start}, {end})".format(start=self.start, end=self.end)
def open_doc(folder, filename):
folder = os.path.abspath(folder)
filepath = os.path.join(folder, filename)
with open(filepath, 'r') as file:
doc = lxml.html.fromstring(
lxml.etree.tostring(
lxml.html.parse(file), method='html'
)
)
return doc
def html_to_dot_sequential_name(html, with_text=False):
graph = Digraph(name='html')
tag_counts = defaultdict(int)
def add_node(html_node):
tag = html_node.tag
tag_sequential = tag_counts[tag]
tag_counts[tag] += 1
node_name = "{}-{}".format(tag, tag_sequential)
graph.node(node_name, node_name)
if len(html_node) > 0:
for child in html_node.iterchildren():
child_name = add_node(child)
graph.edge(node_name, child_name)
else:
child_name = "-".join([node_name, "txt"])
graph.node(child_name, html_node.text)
graph.edge(node_name, child_name)
return node_name
add_node(html)
return graph
def html_to_dot_hierarchical_name(html, with_text=False):
graph = Digraph(name='html')
def add_node(html_node, parent_suffix, brotherhood_index):
tag = html_node.tag
if parent_suffix is None and brotherhood_index is None:
node_suffix = ""
node_name = tag
else:
node_suffix = (
"-".join([parent_suffix, str(brotherhood_index)])
if parent_suffix else
str(brotherhood_index)
)
node_name = "{}-{}".format(tag, node_suffix)
graph.node(node_name, node_name, path=node_suffix)
if len(html_node) > 0:
for child_index, child in enumerate(html_node.iterchildren()):
child_name = add_node(child, node_suffix, child_index)
graph.edge(node_name, child_name)
else:
child_name = "-".join([node_name, "txt"])
child_path = "-".join([node_suffix, "txt"])
graph.node(child_name, html_node.text, path=child_path)
graph.edge(node_name, child_name)
return node_name
add_node(html, None, None)
return graph
def html_to_dot(html, name_option='hierarchical', with_text=False):
if name_option == SEQUENTIAL:
return html_to_dot_sequential_name(html, with_text=with_text)
elif name_option == HIERARCHICAL:
return html_to_dot_hierarchical_name(html, with_text=with_text)
else:
raise Exception('No name option `{}`'.format(name_option))
class MDR:
MINIMUM_DEPTH = 3
def __init__(self, max_tag_per_gnode, edit_distance_threshold, verbose=(False, False, False)):
self.max_tag_per_gnode = max_tag_per_gnode
self.edit_distance_threshold = edit_distance_threshold
self._verbose = verbose
self._phase = None
def _debug(self, msg, tabs=0, force=False):
if self._verbose[self._phase] or (any(self._verbose) and force):
if type(msg) == str:
print(tabs * '\t' + msg)
else:
pprint(msg)
@staticmethod
def depth(node):
d = 0
while node is not None:
d += 1
node = node.getparent()
return d
@staticmethod
def gnode_to_string(list_of_nodes):
return " ".join([
lxml.etree.tostring(child).decode('utf-8') for child in list_of_nodes
])
def __call__(self, root):
self.distances = {}
self.data_regions = {}
self.tag_counts = defaultdict(int)
self.root_copy = deepcopy(root)
self._checked_data_regions = defaultdict(set)
self._phase = 0
self._debug(
">" * 20 + " COMPUTE DISTANCES PHASE ({}) ".format(self._phase) + "<" * 20, force=True
)
self._compute_distances(root)
self._debug(
"<" * 20 + " COMPUTE DISTANCES PHASE ({}) ".format(self._phase) + ">" * 20, force=True
)
# todo remove debug variable
global DEBUG_DISTANCES
self.distances = DEBUG_DISTANCES if DEBUG_DISTANCES else self.distances
# todo change _identify_data_regions to get dist table as an input
self._debug("\n\nself.distances\n", force=True)
self._debug(self.distances, force=True)
self._debug("\n\n", force=True)
self._phase = 1
self._debug(
">" * 20 + " FIND DATA REGIONS PHASE ({}) ".format(self._phase) + "<" * 20, force=True
)
self._find_data_regions(root)
self._debug(
"<" * 20 + " FIND DATA REGIONS PHASE ({}) ".format(self._phase) + ">" * 20, force=True
)
self._phase = 2
def _compute_distances(self, node):
# each tag is named sequentially
tag = node.tag
tag_name = "{}-{}".format(tag, self.tag_counts[tag])
self.tag_counts[tag] += 1
self._debug("in _compute_distances of `{}`".format(tag_name))
# todo: stock depth in attrib???
node_depth = MDR.depth(node)
if node_depth >= MDR.MINIMUM_DEPTH:
# get all possible distances of the n-grams of children
distances = self._compare_combinations(node.getchildren())
self._debug("`{}` distances".format(tag_name))
self._debug(distances)
else:
distances = None
# !!! ATTENTION !!! this modifies the input HTML
# it is important that this comes after `compare_combinations` because
# otherwise the edit distances would change
# todo: remember, in the last phase, to clear the `TAG_NAME_ATTRIB` from all tags
node.set(TAG_NAME_ATTRIB, tag_name)
self.distances[tag_name] = distances
self._debug("\n\n")
for child in node:
self._compute_distances(child)
def _compare_combinations(self, node_list):
"""
Notation: gnode = "generalized node"
:param node_list:
:return:
"""
self._debug("in _compare_combinations")
if not node_list:
return {}
# version 1: {gnode_size: {((,), (,)): float}}
distances = defaultdict(dict)
# version 2: {gnode_size: {starting_tag: {{ ((,), (,)): float }}}}
# distances = defaultdict(lambda: defaultdict(dict))
n_nodes = len(node_list)
# for (i = 1; i <= K; i++) /* start from each node */
for starting_tag in range(1, self.max_tag_per_gnode + 1):
self._debug('starting_tag (i): {}'.format(starting_tag), 1)
# for (j = i; j <= K; j++) /* comparing different combinations */
for gnode_size in range(starting_tag, self.max_tag_per_gnode + 1): # j
self._debug('gnode_size (j): {}'.format(gnode_size), 2)
# if NodeList[i+2*j-1] exists then
if (starting_tag + 2 * gnode_size - 1) < n_nodes + 1: # +1 for pythons open set notation
self._debug(" ")
self._debug(">>> if 1 <<<", 3)
left_gnode_start = starting_tag - 1 # st
# for (k = i+j; k < Size(NodeList); k+j)
# for k in range(i + j, n, j):
for right_gnode_start in range(starting_tag + gnode_size - 1, n_nodes, gnode_size): # k
self._debug('left_gnode_start (st): {}'.format(left_gnode_start), 4)
self._debug('right_gnode_start (k): {}'.format(right_gnode_start), 4)
# if NodeList[k+j-1] exists then
if right_gnode_start + gnode_size < n_nodes + 1:
self._debug(" ")
self._debug(">>> if 2 <<<", 5)
# todo: avoid recomputing strings?
# todo: avoid recomputing edit distances?
# todo: check https://pypi.org/project/strsim/ ?
# NodeList[St..(k-1)]
left_gnode_indices = (left_gnode_start, right_gnode_start)
left_gnode = node_list[left_gnode_indices[0]:left_gnode_indices[1]]
left_gnode_str = MDR.gnode_to_string(left_gnode)
self._debug('left_gnode_indices: {}'.format(left_gnode_indices), 5)
# NodeList[St..(k-1)]
right_gnode_indices = (right_gnode_start, right_gnode_start + gnode_size)
right_gnode = node_list[right_gnode_indices[0]:right_gnode_indices[1]]
right_gnode_str = MDR.gnode_to_string(right_gnode)
self._debug('right_gnode_indices: {}'.format(right_gnode_indices), 5)
# edit distance
edit_distance = normalized_levenshtein.distance(left_gnode_str, right_gnode_str)
self._debug('edit_distance: {}'.format(edit_distance), 5)
# version 1
distances[gnode_size][(left_gnode_indices, right_gnode_indices)] = edit_distance
# version 2
# distances[gnode_size][starting_tag][
# (left_gnode_indices, right_gnode_indices)
# ] = edit_distance
left_gnode_start = right_gnode_start
else:
self._debug("skipped\n", 5)
self._debug(' ')
else:
self._debug("skipped\n", 3)
self._debug(' ')
# version 1
return dict(distances)
# version 2
# return {k: dict(v) for k, v in distances.items()}
def _find_data_regions(self, node):
tag_name = node.attrib[TAG_NAME_ATTRIB]
node_depth = MDR.depth(node)
self._debug("in _find_data_regions of `{}`".format(tag_name))
# if TreeDepth(Node) => 3 then
if node_depth >= MDR.MINIMUM_DEPTH:
# Node.DRs = IdenDRs(1, Node, K, T);
# data_regions = self._identify_data_regions(1, node) # 0 or 1???
data_regions = self._identify_data_regions(0, node)
self.data_regions[tag_name] = data_regions
# todo remove debug thing
if tag_name == "table-0":
return
# tempDRs = ∅;
temp_data_regions = set()
# for each Child ∈ Node.Children do
for child in node.getchildren():
# FindDRs(Child, K, T);
self._find_data_regions(child)
# tempDRs = tempDRs ∪ UnCoveredDRs(Node, Child);
uncovered_data_regions = self._uncovered_data_regions(node, child)
temp_data_regions = temp_data_regions | uncovered_data_regions
# Node.DRs = Node.DRs ∪ tempDRs
self.data_regions[tag_name] |= temp_data_regions
else:
for child in node.getchildren():
self._find_data_regions(child)
self._debug(" ")
def _identify_data_regions(self, start_index, node):
"""
Notation: dr = data_region
"""
tag_name = node.attrib[TAG_NAME_ATTRIB]
self._debug("in _identify_data_regions node:{}".format(tag_name))
self._debug("start_index:{}".format(start_index), 1)
# 1 maxDR = [0, 0, 0];
# max_dr = DataRegion(0, 0, 0)
# current_dr = DataRegion(0, 0, 0)
max_dr = DataRegion.empty()
current_dr = DataRegion.empty()
# 2 for (i = 1; i <= K; i++) /* compute for each i-combination */
for gnode_size in range(1, self.max_tag_per_gnode + 1):
self._debug('gnode_size (i): {}'.format(gnode_size), 2)
# 3 for (f = start; f <= start+i; f++) /* start from each node */
# for start_gnode_start_index in range(start_index, start_index + gnode_size + 1):
for first_gn_start_idx in range(start_index, start_index + gnode_size): # todo check if this covers everything
self._debug('first_gn_start_idx (f): {}'.format(first_gn_start_idx), 3)
# 4 flag = true;
dr_has_started = False
# 5 for (j = f; j < size(Node.Children); j+i)
# for left_gnode_start in range(start_node, len(node) , gnode_size):
for last_gn_start_idx in range(
# start_gnode_start_index, len(node) - gnode_size + 1, gnode_size
first_gn_start_idx + gnode_size, len(node) - gnode_size + 1, gnode_size
):
self._debug('last_gn_start_idx (j): {}'.format(last_gn_start_idx), 4)
# 6 if Distance(Node, i, j) <= T then
# todo: correct here
# from _compare_combinations
# left_gnode_indices = (left_gnode_start, right_gnode_start)
# right_gnode_indices = (right_gnode_start, right_gnode_start + gnode_size)
# left_gnode_indices = (start_gnode_start_index, start_gnode_start_index + gnode_size)
# right_gnode_indices = (end_gnode_start_index, end_gnode_start_index + gnode_size)
# gn_before_last = (last_gn_start_idx - gnode_size, last_gn_start_idx)
# gn_last = (last_gn_start_idx, last_gn_start_idx + gnode_size)
gn_before_last = GNode(last_gn_start_idx - gnode_size, last_gn_start_idx)
gn_last = GNode(last_gn_start_idx, last_gn_start_idx + gnode_size)
self._debug('gn_before_last : {}'.format(gn_before_last), 5)
self._debug('gn_last : {}'.format(gn_last), 5)
gn_pair = (gn_before_last, gn_last)
distance = self.distances[tag_name][gnode_size][gn_pair]
self._checked_data_regions[tag_name].add(gn_pair)
self._debug('dist : {}'.format(distance), 5)
if distance <= self.edit_distance_threshold:
self._debug('dist passes the threshold!'.format(distance), 6)
# 7 if flag=true then
if not dr_has_started:
self._debug('it is the first pair, init the `current_dr`...'.format(distance), 6)
# 8 curDR = [i, j, 2*i];
# current_dr = DataRegion(gnode_size, first_gn_start_idx - gnode_size, 2 * gnode_size)
# current_dr = DataRegion(gnode_size, first_gn_start_idx, 2 * gnode_size)
current_dr = DataRegion.binary_from_last_gnode(gn_last)
self._debug('current_dr: {}'.format(current_dr), 6)
# 9 flag = false;
dr_has_started = True
# 10 else curDR[3] = curDR[3] + i;
else:
self._debug('extending the DR...'.format(distance), 6)
# current_dr = DataRegion(
# current_dr[0], current_dr[1], current_dr[2] + gnode_size
# )
current_dr = current_dr.extend_one_gnode()
self._debug('current_dr: {}'.format(current_dr), 6)
# 11 elseif flag = false then Exit-inner-loop;
elif dr_has_started:
self._debug('above the threshold, breaking the loop...', 6)
# todo: keep track of all continuous regions per node...
break
self._debug(" ")
# 13 if (maxDR[3] < curDR[3]) and (maxDR[2] = 0 or (curDR[2]<= maxDR[2]) then
current_is_strictly_larger = max_dr.n_nodes_covered < current_dr.n_nodes_covered
current_starts_at_same_node_or_before = (
max_dr.is_empty or current_dr.start_child_index <= max_dr.start_child_index
)
if current_is_strictly_larger and current_starts_at_same_node_or_before:
self._debug('current DR is bigger than max! replacing...', 3)
# 14 maxDR = curDR;
self._debug('old max_dr: {}, new max_dr: {}'.format(max_dr, current_dr), 3)
max_dr = current_dr
self._debug('max_dr: {}'.format(max_dr), 2)
self._debug(" ")
self._debug("max_dr: {}\n".format(max_dr))
# 16 if ( maxDR[3] != 0 ) then
if max_dr.n_nodes_covered != 0:
# 17 if (maxDR[2]+maxDR[3]-1 != size(Node.Children)) then
last_covered_tag_index = max_dr.start_child_index + max_dr.n_nodes_covered - 1
self._debug("last_covered_tag_index: {}".format(last_covered_tag_index))
if last_covered_tag_index < len(node) - 1:
# 18 return {maxDR} ∪ IdentDRs(maxDR[2]+maxDR[3], Node, K, T)
self._debug("calling recursion! \n".format(last_covered_tag_index))
return {max_dr} | self._identify_data_regions(last_covered_tag_index + 1, node)
# 19 else return {maxDR}
else:
self._debug("returning max dr".format(last_covered_tag_index))
self._debug('max_dr: {}'.format(max_dr))
return {max_dr}
# 21 return ∅;
self._debug("returning empty set")
return set()
def _uncovered_data_regions(self, node, child):
return set()
# tests for cases in dev_6_cases
%load_ext autoreload
%autoreload 2
folder = '.'
filename = 'tables-2.html'
doc = open_doc(folder, filename)
dot = html_to_dot(doc, name_option=SEQUENTIAL)
from dev_6_cases import all_cases as cases
from dev_6_cases import DEBUG_THRESHOLD as edit_distance_threshold
cases = [
{
'body-0': None,
'html-0': None,
'table-0': case
}
for case in cases
]
DEBUG_DISTANCES = cases[2]
mdr = MDR(
max_tag_per_gnode=3,
edit_distance_threshold=edit_distance_threshold,
verbose=(False, True, False)
)
mdr(doc)
# tests for cases in dev_5_cases
# %load_ext autoreload
# %autoreload 2
#
# folder = '.'
# filename = 'tables-1.html'
# doc = open_doc(folder, filename)
# dot = html_to_dot(doc, name_option=SEQUENTIAL)
#
# from dev_5_cases import all_cases as cases
# from dev_5_cases import DEBUG_THRESHOLD as edit_distance_threshold
#
# cases = [
# {
# 'body-0': None,
# 'html-0': None,
# 'table-0': case
# }
# for case in cases
# ]
#
# DEBUG_DISTANCES = cases[6]
#
# mdr = MDR(
# max_tag_per_gnode=3,
# edit_distance_threshold=edit_distance_threshold,
# verbose=(False, True, False)
# )
# mdr(doc)
```
|
github_jupyter
|
<a href="https://colab.research.google.com/github/yukinaga/minnano_kaggle/blob/main/section_2/02_titanic_random_forest.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# タイタニック号生存者の予測
「ランダムフォレスト」という機械学習のアルゴリズムにより、タイタニック号の生存者を予測します。
訓練済みのモデルによる予測結果は、csvファイルに保存して提出します。
## データの読み込み
タイタニック号の乗客データを読み込みます。
以下のページからタイタニック号の乗客データをダウロードして、「train.csv」「test.csv」をノートブック環境にアップします。
https://www.kaggle.com/c/titanic/data
訓練データには乗客が生き残ったどうかを表す"Survived"の列がありますが、テストデータにはありません。
訓練済みのモデルに、テストデータを入力して判定した結果を提出することになります。
```
import numpy as np
import pandas as pd
train_data = pd.read_csv("train.csv") # 訓練データ
test_data = pd.read_csv("test.csv") # テストデータ
train_data.head()
```
## データの前処理
判定に使用可能なデータのみを取り出し、データの欠損に対して適切な処理を行います。
また、文字列などのカテゴリ変数に対しては、数値に変換する処理を行います。
以下のコードでは、訓練データ及びテストデータから判定に使える列のみを取り出しています。
```
test_id = test_data["PassengerId"] # 結果の提出時に使用
labels = ["Pclass","Sex","Age","SibSp","Parch","Fare","Embarked"]
train_data = train_data[labels + ["Survived"]]
test_data = test_data[labels]
train_data.head()
```
`info()`によりデータの全体像を確認することができます。
Non-Null Countにより欠損していないデータの数が確認できるので、データの欠損が存在する列を確認しておきます。
```
train_data.info()
test_data.info()
```
AgeとFare、Embarkedに欠損が存在します。
AgeとFareの欠損値には平均値を、Embarkedの欠損値には最頻値をあてがって対処します。
```
# Age
age_mean = train_data["Age"].mean() # 平均値
train_data["Age"] = train_data["Age"].fillna(age_mean)
test_data["Age"] = test_data["Age"].fillna(age_mean)
# Fare
fare_mean = train_data["Fare"].mean() # 平均値
train_data["Fare"] = train_data["Fare"].fillna(fare_mean)
test_data["Fare"] = test_data["Fare"].fillna(fare_mean)
# Embarked
embarked_mode = train_data["Embarked"].mode() # 最頻値
train_data["Embarked"] = train_data["Embarked"].fillna(embarked_mode)
test_data["Embarked"] = test_data["Embarked"].fillna(embarked_mode)
```
`get_dummies()`により、カテゴリ変数の列を0か1の値を持つ複数の列に変換します。
```
cat_labels = ["Sex", "Pclass", "Embarked"] # カテゴリ変数のラベル
train_data = pd.get_dummies(train_data, columns=cat_labels)
test_data = pd.get_dummies(test_data, columns=cat_labels)
train_data.head()
```
## モデルの訓練
入力と正解を用意します。
"Survived"の列が正解となります。
```
t_train = train_data["Survived"] # 正解
x_train = train_data.drop(labels=["Survived"], axis=1) # "Survived"の列を削除して入力に
x_test = test_data
```
ランダムフォレストは、複数の決定木を組み合わせた「アンサンブル学習」の一種です。
アンサンブル学習は複数の機械学習を組み合わせる手法で、しばしば高い性能を発揮します。
以下のコードでは、`RandomForestClassifier()`を使い、ランダムフォレストのモデルを作成して訓練します。
多数の決定木の多数決により、分類が行われることになります。
```
from sklearn.ensemble import RandomForestClassifier
# n_estimators: 決定木の数 max_depth: 決定木の深さ
model = RandomForestClassifier(n_estimators=100, max_depth=5)
model.fit(x_train, t_train)
```
## 結果の確認と提出
`feature_importances_`により各特徴量の重要度を取得し、棒グラフで表示します。
```
import matplotlib.pyplot as plt
labels = x_train.columns
importances = model.feature_importances_
plt.figure(figsize = (10,6))
plt.barh(range(len(importances)), importances)
plt.yticks(range(len(labels)), labels)
plt.show()
```
テストデータを使って予測を行います。
予測結果には、分類されるクラスを表す「Label」列と、そのクラスに含まれる確率を表す「Score」ラベルが含まれます。
形式を整えた上で提出用のcsvファイルとして保存します。
```
# 判定
y_test = model.predict(x_test)
# 形式を整える
survived_test = pd.Series(y_test, name="Survived")
subm_data = pd.concat([test_id, survived_test], axis=1)
# 提出用のcsvファイルを保存
subm_data.to_csv("submission_titanic.csv", index=False)
subm_data
```
|
github_jupyter
|
# Driven Modal Simulation and S-Parameters
## Prerequisite
You must have a working local installation of Ansys.
```
%load_ext autoreload
%autoreload 2
import qiskit_metal as metal
from qiskit_metal import designs, draw
from qiskit_metal import MetalGUI, Dict, Headings
import pyEPR as epr
```
## Create the design in Metal
Set up a design of a given dimension. Dimensions will be respected in the design rendering.
<br>
Note the chip design is centered at origin (0,0).
```
design = designs.DesignPlanar({}, True)
design.chips.main.size['size_x'] = '2mm'
design.chips.main.size['size_y'] = '2mm'
#Reference to Ansys hfss QRenderer
hfss = design.renderers.hfss
gui = MetalGUI(design)
```
Perform the necessary imports.
```
from qiskit_metal.qlibrary.couplers.coupled_line_tee import CoupledLineTee
from qiskit_metal.qlibrary.tlines.meandered import RouteMeander
from qiskit_metal.qlibrary.qubits.transmon_pocket import TransmonPocket
from qiskit_metal.qlibrary.tlines.straight_path import RouteStraight
from qiskit_metal.qlibrary.terminations.open_to_ground import OpenToGround
```
Add 2 transmons to the design.
```
options = dict(
# Some options we want to modify from the deafults
# (see below for defaults)
pad_width = '425 um',
pocket_height = '650um',
# Adding 4 connectors (see below for defaults)
connection_pads=dict(
a = dict(loc_W=+1,loc_H=+1),
b = dict(loc_W=-1,loc_H=+1, pad_height='30um'),
c = dict(loc_W=+1,loc_H=-1, pad_width='200um'),
d = dict(loc_W=-1,loc_H=-1, pad_height='50um')
)
)
## Create 2 transmons
q1 = TransmonPocket(design, 'Q1', options = dict(
pos_x='+1.4mm', pos_y='0mm', orientation = '90', **options))
q2 = TransmonPocket(design, 'Q2', options = dict(
pos_x='-0.6mm', pos_y='0mm', orientation = '90', **options))
gui.rebuild()
gui.autoscale()
```
Add 2 hangers consisting of capacitively coupled transmission lines.
```
TQ1 = CoupledLineTee(design, 'TQ1', options=dict(pos_x='1mm',
pos_y='3mm',
coupling_length='200um'))
TQ2 = CoupledLineTee(design, 'TQ2', options=dict(pos_x='-1mm',
pos_y='3mm',
coupling_length='200um'))
gui.rebuild()
gui.autoscale()
```
Add 2 meandered CPWs connecting the transmons to the hangers.
```
ops=dict(fillet='90um')
design.overwrite_enabled = True
options1 = Dict(
total_length='8mm',
hfss_wire_bonds = True,
pin_inputs=Dict(
start_pin=Dict(
component='TQ1',
pin='second_end'),
end_pin=Dict(
component='Q1',
pin='a')),
lead=Dict(
start_straight='0.1mm'),
**ops
)
options2 = Dict(
total_length='9mm',
hfss_wire_bonds = True,
pin_inputs=Dict(
start_pin=Dict(
component='TQ2',
pin='second_end'),
end_pin=Dict(
component='Q2',
pin='a')),
lead=Dict(
start_straight='0.1mm'),
**ops
)
meanderQ1 = RouteMeander(design, 'meanderQ1', options=options1)
meanderQ2 = RouteMeander(design, 'meanderQ2', options=options2)
gui.rebuild()
gui.autoscale()
```
Add 2 open to grounds at the ends of the horizontal CPW.
```
otg1 = OpenToGround(design, 'otg1', options = dict(pos_x='3mm',
pos_y='3mm'))
otg2 = OpenToGround(design, 'otg2', options = dict(pos_x = '-3mm',
pos_y='3mm',
orientation='180'))
gui.rebuild()
gui.autoscale()
```
Add 3 straight CPWs that comprise the long horizontal CPW.
```
ops_oR = Dict(hfss_wire_bonds = True,
pin_inputs=Dict(
start_pin=Dict(
component='TQ1',
pin='prime_end'),
end_pin=Dict(
component='otg1',
pin='open')))
ops_mid = Dict(hfss_wire_bonds = True,
pin_inputs=Dict(
start_pin=Dict(
component='TQ1',
pin='prime_start'),
end_pin=Dict(
component='TQ2',
pin='prime_end')))
ops_oL = Dict(hfss_wire_bonds = True,
pin_inputs=Dict(
start_pin=Dict(
component='TQ2',
pin='prime_start'),
end_pin=Dict(
component='otg2',
pin='open')))
cpw_openRight = RouteStraight(design, 'cpw_openRight', options=ops_oR)
cpw_middle = RouteStraight(design, 'cpw_middle', options=ops_mid)
cpw_openLeft = RouteStraight(design, 'cpw_openLeft', options=ops_oL)
gui.rebuild()
gui.autoscale()
```
## Render the qubit from Metal into the HangingResonators design in Ansys. <br>
Open a new Ansys window, connect to it, and add a driven modal design called HangingResonators to the currently active project.<br>
If Ansys is already open, you can skip `hfss.open_ansys()`. <br>
**Wait for Ansys to fully open before proceeding.**<br> If necessary, also close any Ansys popup windows.
```
hfss.open_ansys()
hfss.connect_ansys()
hfss.activate_drivenmodal_design("HangingResonators")
```
Set the buffer width at the edge of the design to be 0.5 mm in both directions.
```
hfss.options['x_buffer_width_mm'] = 0.5
hfss.options['y_buffer_width_mm'] = 0.5
```
Here, pin cpw_openRight_end and cpw_openLeft_end are converted into lumped ports, each with an impedance of 50 Ohms. <br>
Neither of the junctions in Q1 or Q2 are rendered. <br>
As a reminder, arguments are given as <br><br>
First parameter: List of components to render (empty list if rendering whole Metal design) <br>
Second parameter: List of pins (qcomp, pin) with open endcaps <br>
Third parameter: List of pins (qcomp, pin, impedance) to render as lumped ports <br>
Fourth parameter: List of junctions (qcomp, qgeometry_name, impedance, draw_ind) to render as lumped ports or as lumped port in parallel with a sheet inductance <br>
Fifth parameter: List of junctions (qcomp, qgeometry_name) to omit altogether during rendering
Sixth parameter: Whether to render chip via box plus buffer or fixed chip size
```
hfss.render_design([],
[],
[('cpw_openRight', 'end', 50), ('cpw_openLeft', 'end', 50)],
[],
[('Q1', 'rect_jj'), ('Q2', 'rect_jj')],
True)
hfss.save_screenshot()
hfss.add_sweep(setup_name="Setup",
name="Sweep",
start_ghz=4.0,
stop_ghz=8.0,
count=2001,
type="Interpolating")
hfss.analyze_sweep('Sweep', 'Setup')
```
Plot S, Y, and Z parameters as a function of frequency. <br>
The left and right plots display the magnitude and phase, respectively.
```
hfss.plot_params(['S11', 'S21'])
hfss.plot_params(['Y11', 'Y21'])
hfss.plot_params(['Z11', 'Z21'])
hfss.disconnect_ansys()
gui.main_window.close()
```
|
github_jupyter
|
##### Copyright 2020 The TensorFlow Authors.
```
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
```
# TensorFlow Recommenders: Quickstart
<table class="tfo-notebook-buttons" align="left">
<td>
<a target="_blank" href="https://www.tensorflow.org/recommenders/quickstart"><img src="https://www.tensorflow.org/images/tf_logo_32px.png" />View on TensorFlow.org</a>
</td>
<td>
<a target="_blank" href="https://colab.research.google.com/github/tensorflow/recommenders/blob/main/docs/examples/quickstart.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
</td>
<td>
<a target="_blank" href="https://github.com/tensorflow/recommenders/blob/main/docs/examples/quickstart.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View source on GitHub</a>
</td>
<td>
<a href="https://storage.googleapis.com/tensorflow_docs/recommenders/docs/examples/quickstart.ipynb"><img src="https://www.tensorflow.org/images/download_logo_32px.png" />Download notebook</a>
</td>
</table>
In this tutorial, we build a simple matrix factorization model using the [MovieLens 100K dataset](https://grouplens.org/datasets/movielens/100k/) with TFRS. We can use this model to recommend movies for a given user.
### Import TFRS
First, install and import TFRS:
```
!pip install -q tensorflow-recommenders
!pip install -q --upgrade tensorflow-datasets
from typing import Dict, Text
import numpy as np
import tensorflow as tf
import tensorflow_datasets as tfds
import tensorflow_recommenders as tfrs
```
### Read the data
```
# Ratings data.
ratings = tfds.load('movielens/100k-ratings', split="train")
# Features of all the available movies.
movies = tfds.load('movielens/100k-movies', split="train")
# Select the basic features.
ratings = ratings.map(lambda x: {
"movie_title": x["movie_title"],
"user_id": x["user_id"]
})
movies = movies.map(lambda x: x["movie_title"])
```
Build vocabularies to convert user ids and movie titles into integer indices for embedding layers:
```
user_ids_vocabulary = tf.keras.layers.experimental.preprocessing.StringLookup(mask_token=None)
user_ids_vocabulary.adapt(ratings.map(lambda x: x["user_id"]))
movie_titles_vocabulary = tf.keras.layers.experimental.preprocessing.StringLookup(mask_token=None)
movie_titles_vocabulary.adapt(movies)
```
### Define a model
We can define a TFRS model by inheriting from `tfrs.Model` and implementing the `compute_loss` method:
```
class MovieLensModel(tfrs.Model):
# We derive from a custom base class to help reduce boilerplate. Under the hood,
# these are still plain Keras Models.
def __init__(
self,
user_model: tf.keras.Model,
movie_model: tf.keras.Model,
task: tfrs.tasks.Retrieval):
super().__init__()
# Set up user and movie representations.
self.user_model = user_model
self.movie_model = movie_model
# Set up a retrieval task.
self.task = task
def compute_loss(self, features: Dict[Text, tf.Tensor], training=False) -> tf.Tensor:
# Define how the loss is computed.
user_embeddings = self.user_model(features["user_id"])
movie_embeddings = self.movie_model(features["movie_title"])
return self.task(user_embeddings, movie_embeddings)
```
Define the two models and the retrieval task.
```
# Define user and movie models.
user_model = tf.keras.Sequential([
user_ids_vocabulary,
tf.keras.layers.Embedding(user_ids_vocabulary.vocab_size(), 64)
])
movie_model = tf.keras.Sequential([
movie_titles_vocabulary,
tf.keras.layers.Embedding(movie_titles_vocabulary.vocab_size(), 64)
])
# Define your objectives.
task = tfrs.tasks.Retrieval(metrics=tfrs.metrics.FactorizedTopK(
movies.batch(128).map(movie_model)
)
)
```
### Fit and evaluate it.
Create the model, train it, and generate predictions:
```
# Create a retrieval model.
model = MovieLensModel(user_model, movie_model, task)
model.compile(optimizer=tf.keras.optimizers.Adagrad(0.5))
# Train for 3 epochs.
model.fit(ratings.batch(4096), epochs=3)
# Use brute-force search to set up retrieval using the trained representations.
index = tfrs.layers.factorized_top_k.BruteForce(model.user_model)
index.index(movies.batch(100).map(model.movie_model), movies)
# Get some recommendations.
_, titles = index(np.array(["42"]))
print(f"Top 3 recommendations for user 42: {titles[0, :3]}")
```
|
github_jupyter
|
```
# This Python 3 environment comes with many helpful analytics libraries installed
# It is defined by the kaggle/python docker image: https://github.com/kaggle/docker-python
# For example, here's several helpful packages to load in
import numpy as np # linear algebra
import pandas as pd # data processing, CSV file I/O (e.g. pd.read_csv)
# Input data files are available in the "../input/" directory.
# For example, running this (by clicking run or pressing Shift+Enter) will list all files under the input directory
import os
for dirname, _, filenames in os.walk('/kaggle/input'):
for filename in filenames:
print(os.path.join(dirname, filename))
# Any results you write to the current directory are saved as output.
```
### Import Data Set & Normalize
---
we have imported the famoous mnist dataset, it is a 28x28 gray-scale hand written digits dataset. we have loaded the dataset, split the dataset. we also need to normalize the dataset. The original dataset has pixel value between 0 to 255. we have normalized it to 0 to 1.
```
import keras
from keras.datasets import mnist # 28x28 image data written digits 0-9
from keras.utils import normalize
#print(keras.__version__)
#split train and test dataset
(x_train, y_train), (x_test,y_test) = mnist.load_data()
#normalize data
x_train = normalize(x_train, axis=1)
x_test = normalize(x_test, axis=1)
import matplotlib.pyplot as plt
plt.imshow(x_train[0], cmap=plt.cm.binary)
plt.show()
#print(x_train[0])
```
## Specify Architecture:
---
we have specified our model architecture. added commonly used densely-connected neural network. For the output node we specified our activation function **softmax** it is a probability distribution function.
```
from keras.models import Sequential
from keras.layers import Flatten
from keras.layers import Dense
# created model
model = Sequential()
# flatten layer so it is operable by this layer
model.add(Flatten())
# regular densely-connected NN layer.
#layer 1, 128 node
model.add(Dense(128, activation='relu'))
#layer 2, 128 node
model.add(Dense(128, activation='relu'))
#output layer, since it is probability distribution we will use 'softmax'
model.add(Dense(10, activation='softmax'))
```
### Compile
---
we have compiled the model with earlystopping callback. when we see there are no improvement on accuracy we will stop compiling.
```
from keras.callbacks import EarlyStopping
model.compile(optimizer='adam',
loss='sparse_categorical_crossentropy',
metrics = ['accuracy'])
#stop when see model not improving
early_stopping_monitor = EarlyStopping(monitor='val_loss', patience=2)
```
### Fit
---
Fit the model with train data, with epochs 10.
```
model.fit(x_train, y_train, epochs=10, callbacks=[early_stopping_monitor], validation_data=(x_test, y_test))
```
### Evaluate
---
Evaluate the accuracy of the model.
```
val_loss, val_acc = model.evaluate(x_test,y_test)
print(val_loss, val_acc)
```
### Save
---
Save the model and show summary.
```
model.save('mnist_digit.h5')
model.summary()
```
### Load
----
Load the model.
```
from keras.models import load_model
new_model = load_model('mnist_digit.h5')
```
### Predict
----
Here our model predicted the probability distribution, we have to covnert it to classifcation/label.
```
predict = new_model.predict([x_test])
#return the probability
print(predict)
print(predict[1].argmax(axis=-1))
plt.imshow(x_test[1])
plt.show()
```
|
github_jupyter
|
# Tarea 98 - Análisis del rendimiento de las aplicaciones de IA
## Ejercicio: Debes programar el problema que se plantea en la siguiente secuencia de videos en el lenguaje de programación que desees:
## Primera parte
[](https://www.youtube.com/watch?v=GD254Gotp-4 "video")
#### Reto para hacer:
Definir dos funciones, una, suma_lineal, que lleve a cabo la suma de n números del 1 a n, de una forma básica, y otra, suma_constante, que lleve a cabo la misma tarea, pero utilizando la fórmula de la suma aritmética de los números del 1 a n.
```
#Instalamos line_profiler en el único caso en que no funcione el siguiente script
#! pip install line_profiler
%load_ext line_profiler
import time
def suma_lineal(n):
pass
def suma_constante(n):
pass
cantidad = 1000000
def ejemplo(cantidad):
for i in range(4): # incrementamos 5 veces
start_time = time.time()
suma1 = suma_lineal(cantidad)
middle_time = time.time()
suma2 = suma_constante(cantidad)
stop_time = time.time()
set_time = middle_time - start_time
list_time = stop_time - middle_time
print("\tTest en lineal para la cantidad de {}:\t\t{} segundos".format(cantidad, set_time))
print("\tTest en constantepara para la cantidad de {}:\t{} segundos".format(cantidad, list_time))
cantidad *= 10 # comienza en 1000000 luego *10... hasta 10000000000
# return set_time, list_time
ejemplo(cantidad)
```
El código itera sobre la lista de entrada, extrayendo elementos de esta y acumulándolos en otra lista para cada iteración. Podemos utilizar lprun para ver cuales son las operaciones más costosas.
```
%lprun -f ejemplo ejemplo(cantidad)
```
El código tarda aproximandamente 0.003842 segundos en ejecutarse (el resultado puede variar en función de vuestra máquina). Del tiempo de ejecución, aprox. la mitad (42%) se utiliza para la función lineal) y un 55% para la suma constante) y el resto del tiempo básicamente para completar la función.
## Segunda parte
[](https://www.youtube.com/watch?v=MaY6FpP0FEU "video")
En este video hacemos una introducción a la notación asintótica, y la complejidad de los algoritmos, y resolvemos el reto que teníamos pendiente de definir dos funciones para sumar de 1 a n números enteros, mediante dos algoritmos con complejidad lineal y complejidad constante.
```
def suma_lineal(n):
suma=0
for i in range(1, n+1):
suma += i
return suma
def suma_constante(n):
return (n/2) * (n+1)
cantidad = 1000000
def ejemplo2(cantidad):
for i in range(4): # incrementamos 4 veces
start_time = time.time()
suma1 = suma_lineal(cantidad)
middle_time = time.time()
suma2 = suma_constante(cantidad)
stop_time = time.time()
set_time = middle_time - start_time
list_time = stop_time - middle_time
print("\tTest en lineal para la cantidad de {}:\t\t{} segundos".format(cantidad, set_time))
print("\tTest en constantepara para la cantidad de {}:\t{} segundos".format(cantidad, list_time))
cantidad *= 10 # comienza en 1000000 luego *10... hasta 10000000000
# return set_time, list_time
%time ejemplo2(cantidad)
ejemplo2(cantidad)
%lprun -f ejemplo2 ejemplo2(cantidad)
# Podemos utilizar lprun para ver cuales son las operaciones más costosas.
```
# Representación gŕafica según su complejidad.
```
import matplotlib.pyplot as plt
import matplotlib.colors as mcolors
def plot_funs(xs):
"""
Plot a set of predefined functions for the x values in 'xs'.
"""
ys0 = [1 for x in xs]
ys1 = [x for x in xs]
ys1_b = [x + 25 for x in xs]
ys2 = [x**2 for x in xs]
ys2_b = [x**2 + x for x in xs]
ys3 = [x**3 for x in xs]
ys3_b = [x**3 + x**2 for x in xs]
fig = plt.figure()
plt.plot(xs, ys0, '-', color='tab:brown')
plt.plot(xs, ys1, '-', color='tab:blue')
plt.plot(xs, ys1_b, ':', color='tab:blue')
plt.plot(xs, ys2, '-', color='tab:orange')
plt.plot(xs, ys2_b, ':', color='tab:orange')
plt.plot(xs, ys3, '-', color='tab:green')
plt.plot(xs, ys3_b, ':', color='tab:green')
plt.legend(["$1$", "$x$", "$x+25$", "$x^2$", "$x^2+x$", "$x^3$",
"$x^3+x^2$"])
plt.xlabel('$n$')
plt.ylabel('$f(n)$')
plt.title('Function growth')
plt.show()
plot_funs(range(10))
```
Las líneas de un mismo color representan funciones que tienen el mismo grado. Así, la línea marrón que casi no se aprecia muestra una función constante (𝑓(𝑛)=1), las líneas azules muestran funciones lineales (𝑥 y 𝑥+25), las líneas naranjas funciones cuadráticas (𝑥2 y 𝑥2+𝑥), y las líneas verdes funciones cúbicas (𝑥3 y 𝑥3+𝑥2). Para cada color, la línea continua (sólida) representa la función que contiene solo el término de mayor grado, y la línea de puntos es una función que tiene también otros términos de menor grado. Como se puede apreciar, el crecimiento de las funciones con el mismo grado es similar, sobre todo cuando crece el valor de 𝑛. Fijaos con la representación de las mismas funciones si aumentamos el valor de 𝑛 de 10 (gráfica anterior) a 100 (gráfica de la celda siguiente):
```
plot_funs(range(100))
```
|
github_jupyter
|
### Komentarze w Pythonie robimy przy użyciu # - jeśli go nie użyjemy, Python będzie to próbował zinterpretować jako kod
```
#jupyter notebook; jupyter hub
jupyter notebook; jupyter hub
10 + 5
2 - 7
4 * 6
9 / 3
8 ** 2
x = 10
x = ergbreoubhtoebeobf
x
print(x)
rocznik = 1991
rocznik
teraz = 2020
teraz - rocznik
ile_lat = teraz - rocznik
ile_lat
ile_lat + 25
#integer - liczba całkowita
type(ile_lat)
zarobki_biednego_doktoranta = 5.50
zarobki_biednego_doktoranta
#float - liczba rzeczywista
type(zarobki_biednego_doktoranta)
werdykt = "To są marne zarobki"
werdykt = 'To są marne zarobki'
type(werdykt)
zarobki_biednego_doktoranta + werdykt
10 + 5.50
# Przemnożenie ciągu liter przez np. 2 duplikuje ów ciąg
werdykt * 2
# Ciągu znaków nie można dzielić (a przynajmniej nie w taki sposób)
werdykt / 3
"swps" + "jest super"
a = "UW"
b = "jest"
c = "super"
a+b+c
a + " " + b + " " + c
print(a, b, c)
?print
print(a, b, c, sep = " nie ")
print(a, b, c, sep = "\n")
test = print(a, b, c)
"UW jest super a absolwenci tej uczelni zarabiają więcej niż 5.50 brutto na h"
info = f"{a} {b} {c} a absolwenci tej uczelni zarabiają więcej niż {zarobki_biednego_doktoranta} brutto na h"
info
ocena = 2
maksimum = 10
# Metoda - rodzaj funkcji, dedykowany tylko dla konkretnego rodzaju zmiennej
"Te warsztaty zostały ocenione na {} pkt na {} możliwych".format(ocena, maksimum)
10.format()
# backslash (\) pozawala na podzielenie długiego kodu na parę linijek
"Te warsztaty zostały ocenione \
na {} pkt \
na {} możliwych".format(ocena, maksimum)
"Te warsztaty zostały ocenione
na {} pkt
na {} możliwych".format(ocena, maksimum)
nr = "300"
nr + 100
int(nr) + 100
float(nr)
int(info)
prawda = True
falsz = False
## w R: TRUE/T ; FALSE/F
prawda
type(prawda)
prawda + prawda
True == 1
False == 0
10 > 5
10 > 20
10 < 5
20 >= 10
50 <= 5
10 != 3
[]
list()
moja_lista = ["Samsung", "Huawei", "Xiaomi"]
type(moja_lista)
aj = "Apple"
lista2 = ["Samsung", "Huawei", "Xiaomi", aj]
lista2
```
#### W Pythonie adresowanie elementów zaczynamy od zera!!!
```
lista2[1]
lista2[0]
lista2[-1]
```
#### Python nie bierze ostatniego elementu, zatem taki kod jak poniżej wybierze nam tylko elementy 0 i 1 (pierwsze dwa)
```
lista2[0:2]
lista2[:3]
lista2[0][0:3]
ruskie = 4.50
ziemniaki = 2.35
surowka = 2.15
nalesniki = 7.50
kompot = 2.00
kotlet = 8.50
pomidorowa = 2.35
wodka_spod_lady = 4.00
leniwe = 3.90
kasza = 2.25
ceny = [ruskie, ziemniaki, surowka, nalesniki, kompot, kotlet, pomidorowa, wodka_spod_lady, leniwe, kasza]
menu = ['ruskie', ruskie,
'ziemniaki', ziemniaki,
'surowka', surowka,
'nalesniki', nalesniki,
'kompot', kompot,
'kotlet', kotlet,
'pomidorowa', pomidorowa,
'wódka spod lady', wodka_spod_lady,
'leniwe', leniwe,
'kasza', kasza]
menu = [
['ruskie', ruskie],
['ziemniaki', ziemniaki],
['surowka', surowka],
['nalesniki', nalesniki],
['kompot', kompot],
['kotlet', kotlet],
['pomidorowa', pomidorowa],
['wódka spod lady', wodka_spod_lady],
['leniwe', leniwe],
['kasza', kasza]
]
menu[0]
menu[0][1]
menu[0][-1]
#ruskie, surowka, wódka spod lady
menu[0][-1] + menu[2][-1] + menu[-3][-1]
menu[-1] = ["suchy chleb", 10.50]
menu
len(menu)
?len
len("to ejst tekst")
ceny.sort()
#stack overflow
ceny
ceny2 = [4.0, 4.5, 7.5, 8.5,2.0, 2.15, 2.25]
sorted(ceny2)
ceny2
ceny2 = sorted(ceny2)
menuDict = {
'ruskie': ruskie,
'ziemniaki': ziemniaki,
'surowka': surowka,
'nalesniki': nalesniki,
'kompot': kompot,
'kotlet': kotlet,
'pomidorowa': pomidorowa,
'wódka spod lady': wodka_spod_lady,
'leniwe': leniwe,
'kasza': kasza
}
```
#### Słowniki - możemy je adresować tylko po hasłach (nie możemy po pozycji w zbiorze)
```
menuDict[0]
menuDict
menuDict["ruskie"]
menuDict.keys()
menuDict.values()
menuDict.items()
menuDict.keys()[0]
menuDict['wódka spod lady']
```
##### Krotka vs lista - działają podobnie, natomiast elementy listy można zmieniać. Krotki zmienić się nie da.
```
lista = [1,2,3,4]
krotka = (1,2,3,4)
lista
krotka
lista[0]
krotka[0]
lista[0] = 6
lista
krotka[0] = 6
type(krotka)
mini = [1,2,3,4,5]
for i in mini:
print(i)
for i in mini:
q = i ** 2
print(q)
"Liczba {} podniesiona do kwadratu daje {}".format(x, y)
f"Liczba {x} podniesiona do kwadratu daje {y}"
for i in mini:
print(f"Liczba {i} podniesiona do kwadratu daje {i**2}")
mini2 = [5, 10, 15, 20, 50]
for index, numer in enumerate(mini2):
print(index, numer)
for index, numer in enumerate(mini2):
print(f"Liczba {numer} (na pozycji {index}) podniesiona do kwadratu daje {numer**2}")
mini2
100 % 2 == 0
for index, numer in enumerate(mini2):
if numer % 2 == 0:
print(f"Liczba {numer} (na pozycji {index}) jest parzysta.")
else:
print(f"Liczba {numer} (na pozycji {index}) jest nieparzysta.")
parzyste = []
nieparzyste = []
#how to add a value to a list (in a loop) python
for index, numer in enumerate(mini2):
if numer % 2 == 0:
print(f"Liczba {numer} (na pozycji {index}) jest parzysta.")
parzyste.append(numer)
else:
print(f"Liczba {numer} (na pozycji {index}) jest nieparzysta.")
nieparzyste.append(numer)
parzyste
nieparzyste
mini3 = [5, 10, 15, 20, 50, 60, 80, 30, 100, 7]
for numer in mini3:
if numer == 50:
print("To jest zakazana liczba. Nie tykam.")
elif numer % 2 == 0:
print(f"Liczba {numer} jest parzysta.")
else:
print(f"Liczba {numer} jest nieparzysta.")
mini4 = [5, 10, 15, 20, 50, 666, 80, 30, 100, 7]
for numer in mini4:
if numer == 666:
print("To jest szatańska liczba. Koniec warsztatów.")
break
elif numer == 50:
print("To jest zakazana liczba. Nie tykam.")
elif numer % 2 == 0:
print(f"Liczba {numer} jest parzysta.")
else:
print(f"Liczba {numer} jest nieparzysta.")
menuDict
menuDict["ruskie"]
co_bralem = ["pomidorowa", "ruskie", "wódka spod lady"]
ile_place = 0
for pozycja in co_bralem:
#ile_place = ile_place + menuDict[pozycja]
ile_place += menuDict[pozycja]
ile_place
tqdm
!pip install tqdm #anaconda/colab
!pip3 intall tqdm
# w terminalu/wierszu polecen
pip install xxx
pip3 install xxx
!pip3 install tqdm
import tqdm
tqdm.tqdm
#from NAZWA_PAKIETU import NAZWA_FUNKCJI
from tqdm import tqdm
tqdm
n = 0
for i in tqdm(range(0, 100000)):
x = (i * i) / 3
n += x
n
import numpy as np
seed = np.random.RandomState(100)
wzrost_lista = list(seed.normal(loc=1.70,scale=.15,size=100000).round(2))
seed2 = np.random.RandomState(100)
waga_lista = list(seed2.normal(loc=80,scale=10,size=100000).round(2))
# bmi = waga / wzrost**2
waga_lista / wzrost_lista**2
bmi_lista = []
for index, value in tqdm(enumerate(wzrost_lista)):
bmi = waga_lista[index]/wzrost_lista[index]**2
bmi_lista.append(bmi)
bmi_lista[:20]
seed = np.random.RandomState(100)
wzrost = seed.normal(loc=1.70,scale=.15,size=100000).round(2)
seed2 = np.random.RandomState(100)
waga = seed2.normal(loc=80,scale=10,size=100000).round(2)
wzrost
len(wzrost)
mini5 = [5, 10, 30, 60, 100]
np.array(mini5)
vector = np.array([5, 10, 30, 60, 100])
mini5 * 2
vector * 2
vector / 3
vector ** 2
mini5 + 3
vector + 3
seed = np.random.RandomState(100)
wzrost = seed.normal(loc=1.70,scale=.15,size=100000).round(2)
seed2 = np.random.RandomState(100)
waga = seed2.normal(loc=80,scale=10,size=100000).round(2)
bmi = waga / wzrost ** 2
bmi
np.min(bmi)
np.max(bmi)
np.mean(bmi)
!pip3 install pandas
!pip3 install gapminder
from gapminder import gapminder as df
df
np.mean(df["lifeExp"])
df.iloc[0:10]
df.iloc[0:10]["lifeExp"]
df.iloc[0:10, -1]
df.iloc[0:20,:].loc[:,"pop"]
df["year"] == 2007
df2007 = df[df["year"] == 2007]
df2007
#matplotlib
import matplotlib.pyplot as plt
plt.style.use("ggplot")
#!pip install matplotlib
?plt.plot
df["gdpPercap"]
plt.plot(df2007["gdpPercap"], df2007['lifeExp'])
plt.scatter(df2007["gdpPercap"], df2007['lifeExp'])
plt.show()
plt.scatter(df2007["gdpPercap"], df2007['lifeExp'])
plt.xscale("log")
plt.show()
plt.hist(df2007['lifeExp'])
```
|
github_jupyter
|
(docs-contribute)=
# Contributing to the Ray Documentation
There are many ways to contribute to the Ray documentation, and we're always looking for new contributors.
Even if you just want to fix a typo or expand on a section, please feel free to do so!
This document walks you through everything you need to do to get started.
## Building the Ray documentation
If you want to contribute to the Ray documentation, you'll need a way to build it.
You don't have to build Ray itself, which is a bit more involved.
Just clone the Ray repository and change into the `ray/doc` directory.
```shell
git clone [email protected]:ray-project/ray.git
cd ray/doc
```
To install the documentation dependencies, run the following command:
```shell
pip install -r requirements-doc.txt
```
Additionally, it's best if you install the dependencies for our linters with
```shell
pip install -r ../python/requirements_linters.txt
```
so that you can make sure your changes comply with our style guide.
Building the documentation is done by running the following command:
```shell
make html
```
which will build the documentation into the `_build` directory.
After the build finishes, you can simply open the `_build/html/index.html` file in your browser.
It's considered good practice to check the output of your build to make sure everything is working as expected.
Before committing any changes, make sure you run the
[linter](https://docs.ray.io/en/latest/ray-contribute/getting-involved.html#lint-and-formatting)
with `../scripts/format.sh` from the `doc` folder,
to make sure your changes are formatted correctly.
## The basics of our build system
The Ray documentation is built using the [`sphinx`](https://www.sphinx-doc.org/) build system.
We're using the [Sphinx Book Theme](https://github.com/executablebooks/sphinx-book-theme) from the
[executable books project](https://github.com/executablebooks).
That means that you can write Ray documentation in either Sphinx's native
[reStructuredText (rST)](https://www.sphinx-doc.org/en/master/usage/restructuredtext/index.html) or in
[Markedly Structured Text (MyST)](https://myst-parser.readthedocs.io/en/latest/).
The two formats can be converted to each other, so the choice is up to you.
Having said that, it's important to know that MyST is
[common markdown compliant](https://myst-parser.readthedocs.io/en/latest/syntax/reference.html#commonmark-block-tokens).
If you intend to add a new document, we recommend starting from an `.md` file.
The Ray documentation also fully supports executable formats like [Jupyter Notebooks](https://jupyter.org/).
Many of our examples are notebooks with [MyST markdown cells](https://myst-nb.readthedocs.io/en/latest/index.html).
In fact, this very document you're reading _is_ a notebook.
You can check this for yourself by either downloading the `.ipynb` file,
or directly launching this notebook into either Binder or Google Colab in the top navigation bar.
## What to contribute?
If you take Ray Tune as an example, you can see that our documentation is made up of several types of documentation,
all of which you can contribute to:
- [a project landing page](https://docs.ray.io/en/latest/tune/index.html),
- [a getting started guide](https://docs.ray.io/en/latest/tune/getting-started.html),
- [a key concepts page](https://docs.ray.io/en/latest/tune/key-concepts.html),
- [user guides for key features](https://docs.ray.io/en/latest/tune/tutorials/overview.html),
- [practical examples](https://docs.ray.io/en/latest/tune/examples/index.html),
- [a detailed FAQ](https://docs.ray.io/en/latest/tune/faq.html),
- [and API references](https://docs.ray.io/en/latest/tune/api_docs/overview.html).
This structure is reflected in the
[Ray documentation source code](https://github.com/ray-project/ray/tree/master/doc/source/tune) as well, so you
should have no problem finding what you're looking for.
All other Ray projects share a similar structure, but depending on the project there might be minor differences.
Each type of documentation listed above has its own purpose, but at the end our documentation
comes down to _two types_ of documents:
- Markup documents, written in MyST or rST. If you don't have a lot of (executable) code to contribute or
use more complex features such as
[tabbed content blocks](https://docs.ray.io/en/latest/ray-core/walkthrough.html#starting-ray), this is the right
choice. Most of the documents in Ray Tune are written in this way, for instance the
[key concepts](https://github.com/ray-project/ray/blob/master/doc/source/tune/key-concepts.rst) or
[API documentation](https://github.com/ray-project/ray/blob/master/doc/source/tune/api_docs/overview.rst).
- Notebooks, written in `.ipynb` format. All Tune examples are written as notebooks. These notebooks render in
the browser like `.md` or `.rst` files, but have the added benefit of adding launch buttons to the top of the
document, so that users can run the code themselves in either Binder or Google Colab. A good first example to look
at is [this Tune example](https://github.com/ray-project/ray/blob/master/doc/source/tune/examples/tune-serve-integration-mnist.ipynb).
## Fixing typos and improving explanations
If you spot a typo in any document, or think that an explanation is not clear enough, please consider
opening a pull request.
In this scenario, just run the linter as described above and submit your pull request.
## Adding API references
We use [Sphinx's autodoc extension](https://www.sphinx-doc.org/en/master/usage/extensions/autodoc.html) to generate
our API documentation from our source code.
In case we're missing a reference to a function or class, please consider adding it to the respective document in question.
For example, here's how you can add a function or class reference using `autofunction` and `autoclass`:
```markdown
.. autofunction:: ray.tune.integration.docker.DockerSyncer
.. autoclass:: ray.tune.integration.keras.TuneReportCallback
```
The above snippet was taken from the
[Tune API documentation](https://github.com/ray-project/ray/blob/master/doc/source/tune/api_docs/integration.rst),
which you can look at for reference.
If you want to change the content of the API documentation, you will have to edit the respective function or class
signatures directly in the source code.
For example, in the above `autofunction` call, to change the API reference for `ray.tune.integration.docker.DockerSyncer`,
you would have to [change the following source file](https://github.com/ray-project/ray/blob/7f1bacc7dc9caf6d0ec042e39499bbf1d9a7d065/python/ray/tune/integration/docker.py#L15-L38).
## Adding code to an `.rST` or `.md` file
Modifying text in an existing documentation file is easy, but you need to be careful when it comes to adding code.
The reason is that we want to ensure every code snippet on our documentation is tested.
This requires us to have a process for including and testing code snippets in documents.
In an `.rST` or `.md` file, you can add code snippets using `literalinclude` from the Sphinx system.
For instance, here's an example from the Tune's "Key Concepts" documentation:
```markdown
.. literalinclude:: doc_code/key_concepts.py
:language: python
:start-after: __function_api_start__
:end-before: __function_api_end__
```
Note that in the whole file there's not a single literal code block, code _has to be_ imported using the `literalinclude` directive.
The code that gets added to the document by `literalinclude`, including `start-after` and `end-before` tags,
reads as follows:
```
# __function_api_start__
from ray import tune
def objective(x, a, b): # Define an objective function.
return a * (x ** 0.5) + b
def trainable(config): # Pass a "config" dictionary into your trainable.
for x in range(20): # "Train" for 20 iterations and compute intermediate scores.
score = objective(x, config["a"], config["b"])
tune.report(score=score) # Send the score to Tune.
# __function_api_end__
```
This code is imported by `literalinclude` from a file called `doc_code/key_concepts.py`.
Every Python file in the `doc_code` directory will automatically get tested by our CI system,
but make sure to run scripts that you change (or new scripts) locally first.
You do not need to run the testing framework locally.
In rare situations, when you're adding _obvious_ pseudo-code to demonstrate a concept, it is ok to add it
literally into your `.rST` or `.md` file, e.g. using a `.. code-cell:: python` directive.
But if your code is supposed to run, it needs to be tested.
## Creating a new document from scratch
Sometimes you might want to add a completely new document to the Ray documentation, like adding a new
user guide or a new example.
For this to work, you need to make sure to add the new document explicitly to the
[`_toc.yml` file](https://github.com/ray-project/ray/blob/master/doc/source/_toc.yml) that determines
the structure of the Ray documentation.
Depending on the type of document you're adding, you might also have to make changes to an existing overview
page that curates the list of documents in question.
For instance, for Ray Tune each user guide is added to the
[user guide overview page](https://docs.ray.io/en/latest/tune/tutorials/overview.html) as a panel, and the same
goes for [all Tune examples](https://docs.ray.io/en/latest/tune/examples/index.html).
Always check the structure of the Ray sub-project whose documentation you're working on to see how to integrate
it within the existing structure.
In some cases you may be required to choose an image for the panel. Images are located in
`doc/source/images`.
## Creating a notebook example
To add a new executable example to the Ray documentation, you can start from our
[MyST notebook template](https://github.com/ray-project/ray/tree/master/doc/source/_templates/template.md) or
[Jupyter notebook template](https://github.com/ray-project/ray/tree/master/doc/source/_templates/template.ipynb).
You could also simply download the document you're reading right now (click on the respective download button at the
top of this page to get the `.ipynb` file) and start modifying it.
All the example notebooks in Ray Tune get automatically tested by our CI system, provided you place them in the
[`examples` folder](https://github.com/ray-project/ray/tree/master/doc/source/tune/examples).
If you have questions about how to test your notebook when contributing to other Ray sub-projects, please make
sure to ask a question in [the Ray community Slack](https://forms.gle/9TSdDYUgxYs8SA9e8) or directly on GitHub,
when opening your pull request.
To work off of an existing example, you could also have a look at the
[Ray Tune Hyperopt example (`.ipynb`)](https://github.com/ray-project/ray/blob/master/doc/source/tune/examples/hyperopt_example.ipynb)
or the [Ray Serve guide for RLlib (`.md`)](https://github.com/ray-project/ray/blob/master/doc/source/serve/tutorials/rllib.md).
We recommend that you start with an `.md` file and convert your file to an `.ipynb` notebook at the end of the process.
We'll walk you through this process below.
What makes these notebooks different from other documents is that they combine code and text in one document,
and can be launched in the browser.
We also make sure they are tested by our CI system, before we add them to our documentation.
To make this work, notebooks need to define a _kernel specification_ to tell a notebook server how to interpret
and run the code.
For instance, here's the kernel specification of a Python notebook:
```markdown
---
jupytext:
text_representation:
extension: .md
format_name: myst
kernelspec:
display_name: Python 3
language: python
name: python3
---
```
If you write a notebook in `.md` format, you need this YAML front matter at the top of the file.
To add code to your notebook, you can use the `code-cell` directive.
Here's an example:
````markdown
```{code-cell} python3
:tags: [hide-cell]
import ray
import ray.rllib.agents.ppo as ppo
from ray import serve
def train_ppo_model():
trainer = ppo.PPOTrainer(
config={"framework": "torch", "num_workers": 0},
env="CartPole-v0",
)
# Train for one iteration
trainer.train()
trainer.save("/tmp/rllib_checkpoint")
return "/tmp/rllib_checkpoint/checkpoint_000001/checkpoint-1"
checkpoint_path = train_ppo_model()
```
````
Putting this markdown block into your document will render as follows in the browser:
```
import ray
import ray.rllib.agents.ppo as ppo
from ray import serve
def train_ppo_model():
trainer = ppo.PPOTrainer(
config={"framework": "torch", "num_workers": 0},
env="CartPole-v0",
)
# Train for one iteration
trainer.train()
trainer.save("/tmp/rllib_checkpoint")
return "/tmp/rllib_checkpoint/checkpoint_000001/checkpoint-1"
checkpoint_path = train_ppo_model()
```
As you can see, the code block is hidden, but you can expand it by click on the "+" button.
### Tags for your notebook
What makes this work is the `:tags: [hide-cell]` directive in the `code-cell`.
The reason we suggest starting with `.md` files is that it's much easier to add tags to them, as you've just seen.
You can also add tags to `.ipynb` files, but you'll need to start a notebook server for that first, which may
not want to do to contribute a piece of documentation.
Apart from `hide-cell`, you also have `hide-input` and `hide-output` tags that hide the input and output of a cell.
Also, if you need code that gets executed in the notebook, but you don't want to show it in the documentation,
you can use the `remove-cell`, `remove-input`, and `remove-output` tags in the same way.
### Testing notebooks
Removing cells can be particularly interesting for compute-intensive notebooks.
We want you to contribute notebooks that use _realistic_ values, not just toy examples.
At the same time we want our notebooks to be tested by our CI system, and running them should not take too long.
What you can do to address this is to have notebook cells with the parameters you want the users to see first:
````markdown
```{code-cell} python3
num_workers = 8
num_gpus = 2
```
````
which will render as follows in the browser:
```
num_workers = 8
num_gpus = 2
```
But then in your notebook you follow that up with a _removed_ cell that won't get rendered, but has much smaller
values and make the notebook run faster:
````markdown
```{code-cell} python3
:tags: [remove-cell]
num_workers = 0
num_gpus = 0
```
````
### Converting markdown notebooks to ipynb
Once you're finished writing your example, you can convert it to an `.ipynb` notebook using `jupytext`:
```shell
jupytext your-example.md --to ipynb
```
In the same way, you can convert `.ipynb` notebooks to `.md` notebooks with `--to myst`.
And if you want to convert your notebook to a Python file, e.g. to test if your whole script runs without errors,
you can use `--to py` instead.
## Where to go from here?
There are many other ways to contribute to Ray other than documentation.
See {ref}`our contributor guide <getting-involved>` for more information.
|
github_jupyter
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.