text
stringlengths 2.5k
6.39M
| kind
stringclasses 3
values |
|---|---|
##### Copyright 2018 The TensorFlow Authors.
```
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
#@title MIT License
#
# Copyright (c) 2017 François Chollet
#
# Permission is hereby granted, free of charge, to any person obtaining a
# copy of this software and associated documentation files (the "Software"),
# to deal in the Software without restriction, including without limitation
# the rights to use, copy, modify, merge, publish, distribute, sublicense,
# and/or sell copies of the Software, and to permit persons to whom the
# Software is furnished to do so, subject to the following conditions:
#
# The above copyright notice and this permission notice shall be included in
# all copies or substantial portions of the Software.
#
# THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
# IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
# FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL
# THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
# LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING
# FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER
# DEALINGS IN THE SOFTWARE.
```
# Basic regression: Predict fuel efficiency
<table class="tfo-notebook-buttons" align="left">
<td>
<a target="_blank" href="https://tensorflow.google.cn/tutorials/keras/regression"><img src="https://tensorflow.google.cn/images/tf_logo_32px.png" />在 tensorFlow.google.cn 上查看</a>
</td>
<td>
<a target="_blank" href="https://colab.research.google.com/github/tensorflow/docs-l10n/blob/master/site/zh-cn/tutorials/keras/regression.ipynb"><img src="https://tensorflow.google.cn/images/colab_logo_32px.png" />在 Google Colab 中运行</a>
</td>
<td>
<a target="_blank" href="https://github.com/tensorflow/docs-l10n/blob/master/site/zh-cn/tutorials/keras/regression.ipynb"><img src="https://tensorflow.google.cn/images/GitHub-Mark-32px.png" />在 GitHub 上查看源代码</a>
</td>
<td>
<a href="https://storage.googleapis.com/tensorflow_docs/docs-l10n/site/zh-cn/tutorials/keras/regression.ipynb"><img src="https://tensorflow.google.cn/images/download_logo_32px.png" />下载 notebook</a>
</td>
</table>
Note: 我们的 TensorFlow 社区翻译了这些文档。因为社区翻译是尽力而为, 所以无法保证它们是最准确的,并且反映了最新的
[官方英文文档](https://www.tensorflow.org/?hl=en)。如果您有改进此翻译的建议, 请提交 pull request 到
[tensorflow/docs](https://github.com/tensorflow/docs) GitHub 仓库。要志愿地撰写或者审核译文,请加入
[[email protected] Google Group](https://groups.google.com/a/tensorflow.org/forum/#!forum/docs-zh-cn)。
在 *回归 (regression)* 问题中,我们的目的是预测出如价格或概率这样连续值的输出。相对于*分类(classification)* 问题,*分类(classification)* 的目的是从一系列的分类出选择出一个分类 (如,给出一张包含苹果或橘子的图片,识别出图片中是哪种水果)。
本 notebook 使用经典的 [Auto MPG](https://archive.ics.uci.edu/ml/datasets/auto+mpg) 数据集,构建了一个用来预测70年代末到80年代初汽车燃油效率的模型。为了做到这一点,我们将为该模型提供许多那个时期的汽车描述。这个描述包含:气缸数,排量,马力以及重量。
本示例使用 `tf.keras` API,相关细节请参阅 [本指南](https://tensorflow.google.cn/guide/keras)。
```
# 使用 seaborn 绘制矩阵图 (pairplot)
!pip install seaborn
from __future__ import absolute_import, division, print_function, unicode_literals
import pathlib
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
try:
# %tensorflow_version only exists in Colab.
%tensorflow_version 2.x
except Exception:
pass
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
print(tf.__version__)
```
## Auto MPG 数据集
该数据集可以从 [UCI机器学习库](https://archive.ics.uci.edu/ml/) 中获取.
### 获取数据
首先下载数据集。
```
dataset_path = keras.utils.get_file("auto-mpg.data", "http://archive.ics.uci.edu/ml/machine-learning-databases/auto-mpg/auto-mpg.data")
dataset_path
```
使用 pandas 导入数据集。
```
column_names = ['MPG','Cylinders','Displacement','Horsepower','Weight',
'Acceleration', 'Model Year', 'Origin']
raw_dataset = pd.read_csv(dataset_path, names=column_names,
na_values = "?", comment='\t',
sep=" ", skipinitialspace=True)
dataset = raw_dataset.copy()
dataset.tail()
```
### 数据清洗
数据集中包括一些未知值。
```
dataset.isna().sum()
```
为了保证这个初始示例的简单性,删除这些行。
```
dataset = dataset.dropna()
```
`"Origin"` 列实际上代表分类,而不仅仅是一个数字。所以把它转换为独热码 (one-hot):
```
origin = dataset.pop('Origin')
dataset['USA'] = (origin == 1)*1.0
dataset['Europe'] = (origin == 2)*1.0
dataset['Japan'] = (origin == 3)*1.0
dataset.tail()
```
### 拆分训练数据集和测试数据集
现在需要将数据集拆分为一个训练数据集和一个测试数据集。
我们最后将使用测试数据集对模型进行评估。
```
train_dataset = dataset.sample(frac=0.8,random_state=0)
test_dataset = dataset.drop(train_dataset.index)
```
### 数据检查
快速查看训练集中几对列的联合分布。
```
sns.pairplot(train_dataset[["MPG", "Cylinders", "Displacement", "Weight"]], diag_kind="kde")
```
也可以查看总体的数据统计:
```
train_stats = train_dataset.describe()
train_stats.pop("MPG")
train_stats = train_stats.transpose()
train_stats
```
### 从标签中分离特征
将特征值从目标值或者"标签"中分离。 这个标签是你使用训练模型进行预测的值。
```
train_labels = train_dataset.pop('MPG')
test_labels = test_dataset.pop('MPG')
```
### 数据规范化
再次审视下上面的 `train_stats` 部分,并注意每个特征的范围有什么不同。
使用不同的尺度和范围对特征归一化是好的实践。尽管模型*可能* 在没有特征归一化的情况下收敛,它会使得模型训练更加复杂,并会造成生成的模型依赖输入所使用的单位选择。
注意:尽管我们仅仅从训练集中有意生成这些统计数据,但是这些统计信息也会用于归一化的测试数据集。我们需要这样做,将测试数据集放入到与已经训练过的模型相同的分布中。
```
def norm(x):
return (x - train_stats['mean']) / train_stats['std']
normed_train_data = norm(train_dataset)
normed_test_data = norm(test_dataset)
```
我们将会使用这个已经归一化的数据来训练模型。
警告: 用于归一化输入的数据统计(均值和标准差)需要反馈给模型从而应用于任何其他数据,以及我们之前所获得独热码。这些数据包含测试数据集以及生产环境中所使用的实时数据。
## 模型
### 构建模型
让我们来构建我们自己的模型。这里,我们将会使用一个“顺序”模型,其中包含两个紧密相连的隐藏层,以及返回单个、连续值得输出层。模型的构建步骤包含于一个名叫 'build_model' 的函数中,稍后我们将会创建第二个模型。 两个密集连接的隐藏层。
```
def build_model():
model = keras.Sequential([
layers.Dense(64, activation='relu', input_shape=[len(train_dataset.keys())]),
layers.Dense(64, activation='relu'),
layers.Dense(1)
])
optimizer = tf.keras.optimizers.RMSprop(0.001)
model.compile(loss='mse',
optimizer=optimizer,
metrics=['mae', 'mse'])
return model
model = build_model()
```
### 检查模型
使用 `.summary` 方法来打印该模型的简单描述。
```
model.summary()
```
现在试用下这个模型。从训练数据中批量获取‘10’条例子并对这些例子调用 `model.predict` 。
```
example_batch = normed_train_data[:10]
example_result = model.predict(example_batch)
example_result
```
它似乎在工作,并产生了预期的形状和类型的结果
### 训练模型
对模型进行1000个周期的训练,并在 `history` 对象中记录训练和验证的准确性。
```
# 通过为每个完成的时期打印一个点来显示训练进度
class PrintDot(keras.callbacks.Callback):
def on_epoch_end(self, epoch, logs):
if epoch % 100 == 0: print('')
print('.', end='')
EPOCHS = 1000
history = model.fit(
normed_train_data, train_labels,
epochs=EPOCHS, validation_split = 0.2, verbose=0,
callbacks=[PrintDot()])
```
使用 `history` 对象中存储的统计信息可视化模型的训练进度。
```
hist = pd.DataFrame(history.history)
hist['epoch'] = history.epoch
hist.tail()
def plot_history(history):
hist = pd.DataFrame(history.history)
hist['epoch'] = history.epoch
plt.figure()
plt.xlabel('Epoch')
plt.ylabel('Mean Abs Error [MPG]')
plt.plot(hist['epoch'], hist['mae'],
label='Train Error')
plt.plot(hist['epoch'], hist['val_mae'],
label = 'Val Error')
plt.ylim([0,5])
plt.legend()
plt.figure()
plt.xlabel('Epoch')
plt.ylabel('Mean Square Error [$MPG^2$]')
plt.plot(hist['epoch'], hist['mse'],
label='Train Error')
plt.plot(hist['epoch'], hist['val_mse'],
label = 'Val Error')
plt.ylim([0,20])
plt.legend()
plt.show()
plot_history(history)
```
该图表显示在约100个 epochs 之后误差非但没有改进,反而出现恶化。 让我们更新 `model.fit` 调用,当验证值没有提高上是自动停止训练。
我们将使用一个 *EarlyStopping callback* 来测试每个 epoch 的训练条件。如果经过一定数量的 epochs 后没有改进,则自动停止训练。
你可以从[这里](https://tensorflow.google.cn/versions/master/api_docs/python/tf/keras/callbacks/EarlyStopping)学习到更多的回调。
```
model = build_model()
# patience 值用来检查改进 epochs 的数量
early_stop = keras.callbacks.EarlyStopping(monitor='val_loss', patience=10)
history = model.fit(normed_train_data, train_labels, epochs=EPOCHS,
validation_split = 0.2, verbose=0, callbacks=[early_stop, PrintDot()])
plot_history(history)
```
如图所示,验证集中的平均的误差通常在 +/- 2 MPG左右。 这个结果好么? 我们将决定权留给你。
让我们看看通过使用 **测试集** 来泛化模型的效果如何,我们在训练模型时没有使用测试集。这告诉我们,当我们在现实世界中使用这个模型时,我们可以期望它预测得有多好。
```
loss, mae, mse = model.evaluate(normed_test_data, test_labels, verbose=2)
print("Testing set Mean Abs Error: {:5.2f} MPG".format(mae))
```
### 做预测
最后,使用测试集中的数据预测 MPG 值:
```
test_predictions = model.predict(normed_test_data).flatten()
plt.scatter(test_labels, test_predictions)
plt.xlabel('True Values [MPG]')
plt.ylabel('Predictions [MPG]')
plt.axis('equal')
plt.axis('square')
plt.xlim([0,plt.xlim()[1]])
plt.ylim([0,plt.ylim()[1]])
_ = plt.plot([-100, 100], [-100, 100])
```
这看起来我们的模型预测得相当好。我们来看下误差分布。
```
error = test_predictions - test_labels
plt.hist(error, bins = 25)
plt.xlabel("Prediction Error [MPG]")
_ = plt.ylabel("Count")
```
它不是完全的高斯分布,但我们可以推断出,这是因为样本的数量很小所导致的。
## 结论
本笔记本 (notebook) 介绍了一些处理回归问题的技术。
* 均方误差(MSE)是用于回归问题的常见损失函数(分类问题中使用不同的损失函数)。
* 类似的,用于回归的评估指标与分类不同。 常见的回归指标是平均绝对误差(MAE)。
* 当数字输入数据特征的值存在不同范围时,每个特征应独立缩放到相同范围。
* 如果训练数据不多,一种方法是选择隐藏层较少的小网络,以避免过度拟合。
* 早期停止是一种防止过度拟合的有效技术。
|
github_jupyter
|
# Color Detect Application
----
<div class="alert alert-box alert-info">
Please use Jupyter labs http://<board_ip_address>/lab for this notebook.
</div>
This notebook shows how to download and play with the Color Detect Application
## Aims
* Instantiate the application
* Start the application
* Play with the runtime parameters
* Stop the application
## Table of Contents
* [Download Composable Overlay](#download)
* [Start Application](#start)
* [Play with the Application](#play)
* [Stop Application](#stop)
* [Conclusion](#conclusion)
----
## Revision History
* v1.0 | 30 March 2021 | First notebook revision.
----
## Download Composable Overlay <a class="anchor" id="download"></a>
Download the Composable Overlay using the `ColorDetect` class which wraps all the functionality needed to run this application
```
from composable_pipeline import ColorDetect
app = ColorDetect("../overlay/cv_dfx_4_pr.bit")
```
## Start Application <a class="anchor" id="start"></a>
Start the application by calling the `.start()` method, this will:
1. Initialize the pipeline
1. Setup initial parameters
1. Display the implemented pipelined
1. Configure HDMI in and out
The output image should be visible on the external screen at this point
<div class="alert alert-heading alert-danger">
<h4 class="alert-heading">Warning:</h4>
Failure to connect HDMI cables to a valid video source and screen may cause the notebook to hang
</div>
```
app.start()
```
## Play with the Application <a class="anchor" id="play"></a>
The `.play` attribute exposes several runtime parameters
### Color Space
This drop-down menu allows you to select between three color spaces
* [HSV](https://en.wikipedia.org/wiki/HSL_and_HSV)
* [RGB](https://en.wikipedia.org/wiki/RGB_color_space)
$h_{0-2}$, $s_{0-2}$, $v_{0-2}$ represent the thresholding values for the three channels
### Noise reduction
This drop-down menu allows you to the disable noise reduction in the application
```
app.play
```
## Stop Application <a class="anchor" id="stop"></a>
Finally stop the application to release the resources
<div class="alert alert-heading alert-danger">
<h4 class="alert-heading">Warning:</h4>
Failure to stop the HDMI Video may hang the board
when trying to download another bitstream onto the FPGA
</div>
```
app.stop()
```
----
## Conclusion <a class="anchor" id="conclusion"></a>
This notebook has presented the Color Detect Application that leverages the Composable Overlay.
The runtime parameters of such application can be modified using drop-down and sliders from `ipywidgets`
[⬅️ Corner Detect Application](02_corner_detect_app.ipynb) | | [Filter2D Application ➡️](04_filter2d_app.ipynb)
Copyright © 2021 Xilinx, Inc
SPDX-License-Identifier: BSD-3-Clause
----
|
github_jupyter
|
```
import matplotlib.pyplot as plt # pip install matplotlib
import seaborn as sns # pip install seaborn
import plotly.graph_objects as go # pip install plotly
import imageio # pip install imageio
import grid2op
env = grid2op.make(test=True)
from grid2op.PlotGrid import PlotMatplot
plot_helper = PlotMatplot(env.observation_space)
line_ids = [int(i) for i in range(env.n_line)]
fig_layout = plot_helper.plot_layout()
obs = env.reset()
fig_obs = plot_helper.plot_obs(obs)
action = env.action_space({"set_bus": {"loads_id": [(0,2)], "lines_or_id": [(3,2)], "lines_ex_id": [(0,2)]}})
print(action)
new_obs, reward, done, info = env.step(action)
fig_obs3 = plot_helper.plot_obs(new_obs)
from grid2op.Agent import RandomAgent
class CustomRandom(RandomAgent):
def __init__(self, action_space):
RandomAgent.__init__(self, action_space)
self.i = 1
def my_act(self, transformed_observation, reward, done=False):
if (self.i % 10) != 0:
res = 0
else:
res = self.action_space.sample()
self.i += 1
return res
myagent = CustomRandom(env.action_space)
obs = env.reset()
reward = env.reward_range[0]
done = False
while not done:
env.render()
act = myagent.act(obs, reward, done)
obs, reward, done, info = env.step(act)
env.close()
from grid2op.Runner import Runner
env = grid2op.make(test=True)
my_awesome_agent = CustomRandom(env.action_space)
runner = Runner(**env.get_params_for_runner(), agentClass=None, agentInstance=my_awesome_agent)
import os
path_agents = "path_agents" # this is mandatory for grid2viz to have a directory with only agents
# that is why we have it here. It is aboslutely not mandatory for this more simple class.
max_iter = 10 # to save time we only assess performance on 30 iterations
if not os.path.exists(path_agents):
os.mkdir(path_agents)
path_awesome_agent_log = os.path.join(path_agents, "awesome_agent_logs")
res = runner.run(nb_episode=2, path_save=path_awesome_agent_log, max_iter=max_iter)
from grid2op.Episode import EpisodeReplay
gif_name = "episode"
ep_replay = EpisodeReplay(agent_path=path_awesome_agent_log)
for _, chron_name, cum_reward, nb_time_step, max_ts in res:
ep_replay.replay_episode(chron_name, # which chronic was started
gif_name=gif_name, # Name of the gif file
display=False, # dont wait before rendering each frames
fps=3.0) # limit to 3 frames per second
# make a runner for this agent
from grid2op.Agent import DoNothingAgent, TopologyGreedy
import shutil
for agentClass, agentName in zip([DoNothingAgent], # , TopologyGreedy
["DoNothingAgent"]): # , "TopologyGreedy"
path_this_agent = os.path.join(path_agents, agentName)
shutil.rmtree(os.path.abspath(path_this_agent), ignore_errors=True)
runner = Runner(**env.get_params_for_runner(),
agentClass=agentClass
)
res = runner.run(path_save=path_this_agent, nb_episode=10,
max_iter=800)
print("The results for the {} agent are:".format(agentName))
for _, chron_id, cum_reward, nb_time_step, max_ts in res:
msg_tmp = "\tFor chronics with id {}\n".format(chron_id)
msg_tmp += "\t\t - cumulative reward: {:.6f}\n".format(cum_reward)
msg_tmp += "\t\t - number of time steps completed: {:.0f} / {:.0f}".format(nb_time_step, max_ts)
print(msg_tmp)
import sys
shutil.rmtree(os.path.join(os.path.abspath(path_agents), "_cache"), ignore_errors=True)
!$sys.executable -m grid2viz.main --path=$path_agents
```
|
github_jupyter
|
<a href="https://colab.research.google.com/github/mbk-dev/okama/blob/master/examples/07%20forecasting.ipynb"><img align="left" src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open in Colab" title="Open and Execute in Google Colaboratory"></a>
```
!pip install okama
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = [12.0, 6.0]
import okama as ok
```
*okama* has several methods to forecast portfolio perfomance:
- according to historical data (without distribution models)
- according to normal distribution
- according to lognormal distribution
### Testing distribution
Before we use normal or lognormal distribution models, we should test the portfolio returns historical distribution and see if it fits.
There is a notebook dedicated to backtesting distributions.
```
ls = ['GLD.US', 'SPY.US', 'VNQ.US', 'AGG.US']
al = ok.AssetList(ls, inflation=False)
al
al.names
al.kstest(distr='norm')
al.kstest(distr='lognorm')
```
We see that at least SPY is failed zero hypothesis (didn't match 5% threshold) for both normal and lognormal distributions.
But AGG has distribution close to normal. For GLD lognormal fits slightly better.
Now we can construct the portfolio.
```
weights = [0.20, 0.10, 0.10, 0.60]
pf = ok.Portfolio(ls, ccy='USD', weights=weights, inflation=False)
pf
pf.table
pf.kstest(distr='norm')
pf.kstest(distr='lognorm')
```
As expected Kolmogorov-Smirnov test shows that normal distribution fits much better. AGG has 60% weight in the allocation.
### Forecasting
The most intuitive way to present forecasted portfolio performance is to use **plot_forecast** method to draw the accumulated return chart (historical return and forecasted data).
It is possible to use arbitrary percentiles set (10, 50, 90 is a default attribute value).
Maximum forecast period is limited with 1/2 historical data period. For example, if the historical data period is 10 years, it's possible to use forecast periods up to 5 years.
```
pf.plot_forecast(distr='norm', years=5, figsize=(12,5));
```
Another way to visualize the normally distributed random forecasted data is with Monte Carlo simulation ...
```
pf.plot_forecast_monte_carlo(distr='norm', years=5, n=20) # Generates 20 forecasted wealth indexes (for random normally distributed returns time series)
```
We can get numeric CAGR percentiles for each period with **percentile_distribution_cagr** method. To get credible forecast results high n values should be used.
```
pf.percentile_distribution_cagr(distr='norm', years=5, percentiles=[1, 20, 50, 80, 99], n=10000)
```
The same could be used to get VAR (Value at Risk):
```
pf.percentile_distribution_cagr(distr='norm', years=1, percentiles=[1], n=10000) # 1% perecentile corresponds to 99% confidence level
```
One-year VAR (99% confidence level) is equal to 8%. It's a fair value for conservative portfolio.
The probability of getting negative result in forecasted period is the percentile rank for zero CAGR value (score=0).
```
pf.percentile_inverse_cagr(distr='norm', years=1, score=0, n=10000) # one year period
```
### Lognormal distribution
Some financial assets returns have returns distribution close to lognormal.
The same calculations could be repeated for lognormal distribution by setting dist='lognorm'.
```
ln = ok.Portfolio(['EDV.US'], inflation=False)
ln
ln.names
```
We can visualize the distribution and compare it with the lognormal PDF (Probability Distribution Function).
```
ln.plot_hist_fit(distr='lognorm', bins=30)
ln.kstest(distr='norm') # Kolmogorov-Smirnov test for normal distribution
ln.kstest(distr='lognorm') # Kolmogorov-Smirnov test for lognormal distribution
```
What is more important Kolmogorov-Smirnov test shows that historical distribution is slightly closer to lognormal.
Therefore, we can use lognormal distribution to forecast.
```
ln.plot_forecast(distr='lognorm', percentiles=[30, 50, 70], years=2, n=10000);
pf.percentile_distribution_cagr(distr='lognorm', years=1, percentiles=[1, 20, 50, 80, 99], n=10000)
```
### Forecasting using historical data
If it's not possible to fit the data to normal or lognormal distributions, percentiles from the historical data could be used.
```
ht = ok.Portfolio(['SPY.US'])
ht
ht.kstest('norm')
ht.kstest('lognorm')
```
Kolmogorov-Smirnov test is not passing 5% threshold...
Big deviation in the tails could be seen in Quantile-Quantile Plot.
```
ht.plot_percentiles_fit('norm')
```
Then we can use percentiles from the historical data to forecast.
```
ht.plot_forecast(years=5, percentiles=[20, 50, 80]);
ht.percentile_wealth(distr='hist', years=5)
```
Quantitative CAGR percentiles could be obtained from **percentile_history_cagr** method:
```
ht.percentile_history_cagr(years=5)
```
We can visualize the same to see how CAGR ranges were narrowing with investment horizon.
```
ht.percentile_history_cagr(years=5).plot();
```
|
github_jupyter
|
##### Copyright 2018 The TensorFlow Authors.
```
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
```
# 神经风格迁移
<table class="tfo-notebook-buttons" align="left">
<td>
<a target="_blank" href="https://tensorflow.google.cn/tutorials/generative/style_transfer"><img src="https://tensorflow.google.cn/images/tf_logo_32px.png" />在 tensorflow.google.cn 上查看</a>
</td>
<td>
<a target="_blank" href="https://colab.research.google.com/github/tensorflow/docs-l10n/blob/master/site/zh-cn/tutorials/generative/style_transfer.ipynb"><img src="https://tensorflow.google.cn/images/colab_logo_32px.png" />在 Google Colab 上运行</a>
</td>
<td>
<a target="_blank" href="https://github.com/tensorflow/docs-l10n/blob/master/site/zh-cn/tutorials/generative/style_transfer.ipynb"><img src="https://tensorflow.google.cn/images/GitHub-Mark-32px.png" />在 GitHub 上查看源代码</a>
</td>
<td>
<a href="https://storage.googleapis.com/tensorflow_docs/docs-l10n/site/zh-cn/tutorials/generative/style_transfer.ipynb"><img src="https://tensorflow.google.cn/images/download_logo_32px.png" />下载此 notebook</a>
</td>
</table>
Note: 我们的 TensorFlow 社区翻译了这些文档。因为社区翻译是尽力而为, 所以无法保证它们是最准确的,并且反映了最新的
[官方英文文档](https://tensorflow.google.cn/?hl=en)。如果您有改进此翻译的建议, 请提交 pull request 到
[tensorflow/docs](https://github.com/tensorflow/docs) GitHub 仓库。要志愿地撰写或者审核译文,请加入
[[email protected] Google Group](https://groups.google.com/a/tensorflow.org/forum/#!forum/docs-zh-cn)。
本教程使用深度学习来用其他图像的风格创造一个图像(曾经你是否希望可以像毕加索或梵高一样绘画?)。 这被称为*神经风格迁移*,该技术概述于 <a href="https://arxiv.org/abs/1508.06576" class="external">A Neural Algorithm of Artistic Style</a> (Gatys et al.).
Note: 本教程演示了原始的风格迁移算法。它将图像内容优化为特定样式。最新的一些方法训练模型以直接生成风格化图像(类似于 [cyclegan](cyclegan.ipynb))。原始的这种方法要快得多(高达 1000 倍)。[TensorFlow Hub](https://tensorflow.google.cn/hub) 和 [TensorFlow Lite](https://tensorflow.google.cn/lite/models/style_transfer/overview) 中提供了预训练的[任意图像风格化模块](https://colab.sandbox.google.com/github/tensorflow/hub/blob/master/examples/colab/tf2_arbitrary_image_stylization.ipynb)。
神经风格迁移是一种优化技术,用于将两个图像——一个*内容*图像和一个*风格参考*图像(如著名画家的一个作品)——混合在一起,使输出的图像看起来像内容图像, 但是用了风格参考图像的风格。
这是通过优化输出图像以匹配内容图像的内容统计数据和风格参考图像的风格统计数据来实现的。 这些统计数据可以使用卷积网络从图像中提取。
例如,我们选取这张小狗的照片和 Wassily Kandinsky 的作品 7:
<img src="https://storage.googleapis.com/download.tensorflow.org/example_images/YellowLabradorLooking_new.jpg" width="500px"/>
[黄色拉布拉多犬的凝视](https://commons.wikimedia.org/wiki/File:YellowLabradorLooking_new.jpg),来自 Wikimedia Commons
<img src="https://github.com/tensorflow/docs/blob/master/site/en/tutorials/generative/images/kadinsky.jpg?raw=1" style="width: 500px;"/>
如果 Kandinsky 决定用这种风格来专门描绘这只海龟会是什么样子? 是否如下图一样?
<img src="https://tensorflow.google.cn/tutorials/generative/images/stylized-image.png" style="width: 500px;"/>
## 配置
### 导入和配置模块
```
import tensorflow as tf
import IPython.display as display
import matplotlib.pyplot as plt
import matplotlib as mpl
mpl.rcParams['figure.figsize'] = (12,12)
mpl.rcParams['axes.grid'] = False
import numpy as np
import PIL.Image
import time
import functools
def tensor_to_image(tensor):
tensor = tensor*255
tensor = np.array(tensor, dtype=np.uint8)
if np.ndim(tensor)>3:
assert tensor.shape[0] == 1
tensor = tensor[0]
return PIL.Image.fromarray(tensor)
```
下载图像并选择风格图像和内容图像:
```
content_path = tf.keras.utils.get_file('YellowLabradorLooking_new.jpg', 'https://storage.googleapis.com/download.tensorflow.org/example_images/YellowLabradorLooking_new.jpg')
# https://commons.wikimedia.org/wiki/File:Vassily_Kandinsky,_1913_-_Composition_7.jpg
style_path = tf.keras.utils.get_file('kandinsky5.jpg','https://storage.googleapis.com/download.tensorflow.org/example_images/Vassily_Kandinsky%2C_1913_-_Composition_7.jpg')
```
## 将输入可视化
定义一个加载图像的函数,并将其最大尺寸限制为 512 像素。
```
def load_img(path_to_img):
max_dim = 512
img = tf.io.read_file(path_to_img)
img = tf.image.decode_image(img, channels=3)
img = tf.image.convert_image_dtype(img, tf.float32)
shape = tf.cast(tf.shape(img)[:-1], tf.float32)
long_dim = max(shape)
scale = max_dim / long_dim
new_shape = tf.cast(shape * scale, tf.int32)
img = tf.image.resize(img, new_shape)
img = img[tf.newaxis, :]
return img
```
创建一个简单的函数来显示图像:
```
def imshow(image, title=None):
if len(image.shape) > 3:
image = tf.squeeze(image, axis=0)
plt.imshow(image)
if title:
plt.title(title)
content_image = load_img(content_path)
style_image = load_img(style_path)
plt.subplot(1, 2, 1)
imshow(content_image, 'Content Image')
plt.subplot(1, 2, 2)
imshow(style_image, 'Style Image')
```
## 使用 TF-Hub 进行快速风格迁移
本教程演示了原始的风格迁移算法。其将图像内容优化为特定风格。在进入细节之前,让我们看一下 [TensorFlow Hub](https://tensorflow.google.cn/hub) 模块如何快速风格迁移:
```
import tensorflow_hub as hub
hub_module = hub.load('https://tfhub.dev/google/magenta/arbitrary-image-stylization-v1-256/1')
stylized_image = hub_module(tf.constant(content_image), tf.constant(style_image))[0]
tensor_to_image(stylized_image)
```
## 定义内容和风格的表示
使用模型的中间层来获取图像的*内容*和*风格*表示。 从网络的输入层开始,前几个层的激励响应表示边缘和纹理等低级 feature (特征)。 随着层数加深,最后几层代表更高级的 feature (特征)——实体的部分,如*轮子*或*眼睛*。 在此教程中,我们使用的是 VGG19 网络结构,这是一个已经预训练好的图像分类网络。 这些中间层是从图像中定义内容和风格的表示所必需的。 对于一个输入图像,我们尝试匹配这些中间层的相应风格和内容目标的表示。
加载 [VGG19](https://keras.io/applications/#vgg19) 并在我们的图像上测试它以确保正常运行:
```
x = tf.keras.applications.vgg19.preprocess_input(content_image*255)
x = tf.image.resize(x, (224, 224))
vgg = tf.keras.applications.VGG19(include_top=True, weights='imagenet')
prediction_probabilities = vgg(x)
prediction_probabilities.shape
predicted_top_5 = tf.keras.applications.vgg19.decode_predictions(prediction_probabilities.numpy())[0]
[(class_name, prob) for (number, class_name, prob) in predicted_top_5]
```
现在,加载没有分类部分的 `VGG19` ,并列出各层的名称:
```
vgg = tf.keras.applications.VGG19(include_top=False, weights='imagenet')
print()
for layer in vgg.layers:
print(layer.name)
```
从网络中选择中间层的输出以表示图像的风格和内容:
```
# 内容层将提取出我们的 feature maps (特征图)
content_layers = ['block5_conv2']
# 我们感兴趣的风格层
style_layers = ['block1_conv1',
'block2_conv1',
'block3_conv1',
'block4_conv1',
'block5_conv1']
num_content_layers = len(content_layers)
num_style_layers = len(style_layers)
```
#### 用于表示风格和内容的中间层
那么,为什么我们预训练的图像分类网络中的这些中间层的输出允许我们定义风格和内容的表示?
从高层理解,为了使网络能够实现图像分类(该网络已被训练过),它必须理解图像。 这需要将原始图像作为输入像素并构建内部表示,这个内部表示将原始图像像素转换为对图像中存在的 feature (特征)的复杂理解。
这也是卷积神经网络能够很好地推广的一个原因:它们能够捕获不变性并定义类别(例如猫与狗)之间的 feature (特征),这些 feature (特征)与背景噪声和其他干扰无关。 因此,将原始图像传递到模型输入和分类标签输出之间的某处的这一过程,可以视作复杂的 feature (特征)提取器。通过这些模型的中间层,我们就可以描述输入图像的内容和风格。
## 建立模型
使用`tf.keras.applications`中的网络可以让我们非常方便的利用Keras的功能接口提取中间层的值。
在使用功能接口定义模型时,我们需要指定输入和输出:
`model = Model(inputs, outputs)`
以下函数构建了一个 VGG19 模型,该模型返回一个中间层输出的列表:
```
def vgg_layers(layer_names):
""" Creates a vgg model that returns a list of intermediate output values."""
# 加载我们的模型。 加载已经在 imagenet 数据上预训练的 VGG
vgg = tf.keras.applications.VGG19(include_top=False, weights='imagenet')
vgg.trainable = False
outputs = [vgg.get_layer(name).output for name in layer_names]
model = tf.keras.Model([vgg.input], outputs)
return model
```
然后建立模型:
```
style_extractor = vgg_layers(style_layers)
style_outputs = style_extractor(style_image*255)
#查看每层输出的统计信息
for name, output in zip(style_layers, style_outputs):
print(name)
print(" shape: ", output.numpy().shape)
print(" min: ", output.numpy().min())
print(" max: ", output.numpy().max())
print(" mean: ", output.numpy().mean())
print()
```
## 风格计算
图像的内容由中间 feature maps (特征图)的值表示。
事实证明,图像的风格可以通过不同 feature maps (特征图)上的平均值和相关性来描述。 通过在每个位置计算 feature (特征)向量的外积,并在所有位置对该外积进行平均,可以计算出包含此信息的 Gram 矩阵。 对于特定层的 Gram 矩阵,具体计算方法如下所示:
$$G^l_{cd} = \frac{\sum_{ij} F^l_{ijc}(x)F^l_{ijd}(x)}{IJ}$$
这可以使用`tf.linalg.einsum`函数来实现:
```
def gram_matrix(input_tensor):
result = tf.linalg.einsum('bijc,bijd->bcd', input_tensor, input_tensor)
input_shape = tf.shape(input_tensor)
num_locations = tf.cast(input_shape[1]*input_shape[2], tf.float32)
return result/(num_locations)
```
## 提取风格和内容
构建一个返回风格和内容张量的模型。
```
class StyleContentModel(tf.keras.models.Model):
def __init__(self, style_layers, content_layers):
super(StyleContentModel, self).__init__()
self.vgg = vgg_layers(style_layers + content_layers)
self.style_layers = style_layers
self.content_layers = content_layers
self.num_style_layers = len(style_layers)
self.vgg.trainable = False
def call(self, inputs):
"Expects float input in [0,1]"
inputs = inputs*255.0
preprocessed_input = tf.keras.applications.vgg19.preprocess_input(inputs)
outputs = self.vgg(preprocessed_input)
style_outputs, content_outputs = (outputs[:self.num_style_layers],
outputs[self.num_style_layers:])
style_outputs = [gram_matrix(style_output)
for style_output in style_outputs]
content_dict = {content_name:value
for content_name, value
in zip(self.content_layers, content_outputs)}
style_dict = {style_name:value
for style_name, value
in zip(self.style_layers, style_outputs)}
return {'content':content_dict, 'style':style_dict}
```
在图像上调用此模型,可以返回 style_layers 的 gram 矩阵(风格)和 content_layers 的内容:
```
extractor = StyleContentModel(style_layers, content_layers)
results = extractor(tf.constant(content_image))
style_results = results['style']
print('Styles:')
for name, output in sorted(results['style'].items()):
print(" ", name)
print(" shape: ", output.numpy().shape)
print(" min: ", output.numpy().min())
print(" max: ", output.numpy().max())
print(" mean: ", output.numpy().mean())
print()
print("Contents:")
for name, output in sorted(results['content'].items()):
print(" ", name)
print(" shape: ", output.numpy().shape)
print(" min: ", output.numpy().min())
print(" max: ", output.numpy().max())
print(" mean: ", output.numpy().mean())
```
## 梯度下降
使用此风格和内容提取器,我们现在可以实现风格传输算法。我们通过计算每个图像的输出和目标的均方误差来做到这一点,然后取这些损失值的加权和。
设置风格和内容的目标值:
```
style_targets = extractor(style_image)['style']
content_targets = extractor(content_image)['content']
```
定义一个 `tf.Variable` 来表示要优化的图像。 为了快速实现这一点,使用内容图像对其进行初始化( `tf.Variable` 必须与内容图像的形状相同)
```
image = tf.Variable(content_image)
```
由于这是一个浮点图像,因此我们定义一个函数来保持像素值在 0 和 1 之间:
```
def clip_0_1(image):
return tf.clip_by_value(image, clip_value_min=0.0, clip_value_max=1.0)
```
创建一个 optimizer 。 本教程推荐 LBFGS,但 `Adam` 也可以正常工作:
```
opt = tf.optimizers.Adam(learning_rate=0.02, beta_1=0.99, epsilon=1e-1)
```
为了优化它,我们使用两个损失的加权组合来获得总损失:
```
style_weight=1e-2
content_weight=1e4
def style_content_loss(outputs):
style_outputs = outputs['style']
content_outputs = outputs['content']
style_loss = tf.add_n([tf.reduce_mean((style_outputs[name]-style_targets[name])**2)
for name in style_outputs.keys()])
style_loss *= style_weight / num_style_layers
content_loss = tf.add_n([tf.reduce_mean((content_outputs[name]-content_targets[name])**2)
for name in content_outputs.keys()])
content_loss *= content_weight / num_content_layers
loss = style_loss + content_loss
return loss
```
使用 `tf.GradientTape` 来更新图像。
```
@tf.function()
def train_step(image):
with tf.GradientTape() as tape:
outputs = extractor(image)
loss = style_content_loss(outputs)
grad = tape.gradient(loss, image)
opt.apply_gradients([(grad, image)])
image.assign(clip_0_1(image))
```
现在,我们运行几个步来测试一下:
```
train_step(image)
train_step(image)
train_step(image)
tensor_to_image(image)
```
运行正常,我们来执行一个更长的优化:
```
import time
start = time.time()
epochs = 10
steps_per_epoch = 100
step = 0
for n in range(epochs):
for m in range(steps_per_epoch):
step += 1
train_step(image)
print(".", end='')
display.clear_output(wait=True)
display.display(tensor_to_image(image))
print("Train step: {}".format(step))
end = time.time()
print("Total time: {:.1f}".format(end-start))
```
## 总变分损失
此实现只是一个基础版本,它的一个缺点是它会产生大量的高频误差。 我们可以直接通过正则化图像的高频分量来减少这些高频误差。 在风格转移中,这通常被称为*总变分损失*:
```
def high_pass_x_y(image):
x_var = image[:,:,1:,:] - image[:,:,:-1,:]
y_var = image[:,1:,:,:] - image[:,:-1,:,:]
return x_var, y_var
x_deltas, y_deltas = high_pass_x_y(content_image)
plt.figure(figsize=(14,10))
plt.subplot(2,2,1)
imshow(clip_0_1(2*y_deltas+0.5), "Horizontal Deltas: Original")
plt.subplot(2,2,2)
imshow(clip_0_1(2*x_deltas+0.5), "Vertical Deltas: Original")
x_deltas, y_deltas = high_pass_x_y(image)
plt.subplot(2,2,3)
imshow(clip_0_1(2*y_deltas+0.5), "Horizontal Deltas: Styled")
plt.subplot(2,2,4)
imshow(clip_0_1(2*x_deltas+0.5), "Vertical Deltas: Styled")
```
这显示了高频分量如何增加。
而且,本质上高频分量是一个边缘检测器。 我们可以从 Sobel 边缘检测器获得类似的输出,例如:
```
plt.figure(figsize=(14,10))
sobel = tf.image.sobel_edges(content_image)
plt.subplot(1,2,1)
imshow(clip_0_1(sobel[...,0]/4+0.5), "Horizontal Sobel-edges")
plt.subplot(1,2,2)
imshow(clip_0_1(sobel[...,1]/4+0.5), "Vertical Sobel-edges")
```
与此相关的正则化损失是这些值的平方和:
```
def total_variation_loss(image):
x_deltas, y_deltas = high_pass_x_y(image)
return tf.reduce_sum(tf.abs(x_deltas)) + tf.reduce_sum(tf.abs(y_deltas))
total_variation_loss(image).numpy()
```
以上说明了总变分损失的用途。但是无需自己实现,因为 TensorFlow 包含了一个标准实现:
```
tf.image.total_variation(image).numpy()
```
## 重新进行优化
选择 `total_variation_loss` 的权重:
```
total_variation_weight=30
```
现在,将它加入 `train_step` 函数中:
```
@tf.function()
def train_step(image):
with tf.GradientTape() as tape:
outputs = extractor(image)
loss = style_content_loss(outputs)
loss += total_variation_weight*tf.image.total_variation(image)
grad = tape.gradient(loss, image)
opt.apply_gradients([(grad, image)])
image.assign(clip_0_1(image))
```
重新初始化优化的变量:
```
image = tf.Variable(content_image)
```
并进行优化:
```
import time
start = time.time()
epochs = 10
steps_per_epoch = 100
step = 0
for n in range(epochs):
for m in range(steps_per_epoch):
step += 1
train_step(image)
print(".", end='')
display.clear_output(wait=True)
display.display(tensor_to_image(image))
print("Train step: {}".format(step))
end = time.time()
print("Total time: {:.1f}".format(end-start))
```
最后,保存结果:
```
file_name = 'stylized-image.png'
tensor_to_image(image).save(file_name)
try:
from google.colab import files
except ImportError:
pass
else:
files.download(file_name)
```
|
github_jupyter
|
# Factor Operations with pyBN
It is probably rare that a user wants to directly manipulate factors unless they are developing a new algorithm, but it's still important to see how factor operations are done in pyBN. Moreover, the ease-of-use and transparency of pyBN's factor operations mean it can be a great teaching/learning tool!
In this tutorial, I will go over the main operations you can do with factors. First, let's start with actually creating a factor. So, we will read in a Bayesian Network from one of the included networks:
```
from pyBN import *
bn = read_bn('data/cmu.bn')
print bn.V
print bn.E
```
As you can see, we have a Bayesian network with 5 nodes and some edges between them. Let's create a factor now. This is easy in pyBN - just pass in the BayesNet object and the name of the variable.
```
alarm_factor = Factor(bn,'Alarm')
```
Now that we have a factor, we can explore its properties. Every factor in pyBN has the following attributes:
*self.bn* : a BayesNet object
*self.var* : a string
The random variable to which this Factor belongs
*self.scope* : a list
The RV, and its parents (the RVs involved in the
conditional probability table)
*self.card* : a dictionary, where
key = an RV in self.scope, and
val = integer cardinality of the key (i.e. how
many possible values it has)
*self.stride* : a dictionary, where
key = an RV in self.scope, and
val = integer stride (i.e. how many rows in the
CPT until the NEXT value of RV is reached)
*self.cpt* : a nested numpy array
The probability values for self.var conditioned
on its parents
```
print alarm_factor.bn
print alarm_factor.var
print alarm_factor.scope
print alarm_factor.card
print alarm_factor.stride
print alarm_factor.cpt
```
Along with those properties, there are a great number of methods (functions) at hand:
*multiply_factor*
Multiply two factors together. The factor
multiplication algorithm used here is adapted
from Koller and Friedman (PGMs) textbook.
*sumover_var* :
Sum over one *rv* by keeping it constant. Thus, you
end up with a 1-D factor whose scope is ONLY *rv*
and whose length = cardinality of rv.
*sumout_var_list* :
Remove a collection of rv's from the factor
by summing out (i.e. calling sumout_var) over
each rv.
*sumout_var* :
Remove passed-in *rv* from the factor by summing
over everything else.
*maxout_var* :
Remove *rv* from the factor by taking the maximum value
of all rv instantiations over everyting else.
*reduce_factor_by_list* :
Reduce the factor by numerous sets of
[rv,val]
*reduce_factor* :
Condition the factor by eliminating any sets of
values that don't align with a given [rv, val]
*to_log* :
Convert probabilities to log space from
normal space.
*from_log* :
Convert probabilities from log space to
normal space.
*normalize* :
Make relevant collections of probabilities sum to one.
Here is a look at Factor Multiplication:
```
import numpy as np
f1 = Factor(bn,'Alarm')
f2 = Factor(bn,'Burglary')
f1.multiply_factor(f2)
f3 = Factor(bn,'Burglary')
f4 = Factor(bn,'Alarm')
f3.multiply_factor(f4)
print np.round(f1.cpt,3)
print '\n',np.round(f3.cpt,3)
```
Here is a look at "sumover_var":
```
f = Factor(bn,'Alarm')
print f.cpt
print f.scope
print f.stride
f.sumover_var('Burglary')
print '\n',f.cpt
print f.scope
print f.stride
```
Here is a look at "sumout_var", which is essentially the opposite of "sumover_var":
```
f = Factor(bn,'Alarm')
f.sumout_var('Earthquake')
print f.stride
print f.scope
print f.card
print f.cpt
```
Additionally, you can sum over a LIST of variables with "sumover_var_list". Notice how summing over every variable in the scope except for ONE variable is equivalent to summing over that ONE variable:
```
f = Factor(bn,'Alarm')
print f.cpt
f.sumout_var_list(['Burglary','Earthquake'])
print f.scope
print f.stride
print f.cpt
f1 = Factor(bn,'Alarm')
print '\n',f1.cpt
f1.sumover_var('Alarm')
print f1.scope
print f1.stride
print f1.cpt
```
Even more, you can use "maxout_var" to take the max values over a variable in the factor. This is a fundamental operation in Max-Sum Variable Elimination for MAP inference. Notice how the variable being maxed out is removed from the scope because it is conditioned upon and thus taken as truth in a sense.
```
f = Factor(bn,'Alarm')
print f.scope
print f.cpt
f.maxout_var('Burglary')
print '\n', f.scope
print f.cpt
```
Moreover, you can also use "reduce_factor" to reduce a factor based on evidence. This is different from "sumover_var" because "reduce_factor" is not summing over anything, it is simply removing any
parent-child instantiations which are not consistent with
the evidence. Moreover, there should not be any need for
normalization because the CPT should already be normalized
over the rv-val evidence (but we do it anyways because of
rounding). This function is essential when user's pass in evidence to any inference query.
```
f = Factor(bn, 'Alarm')
print f.scope
print f.cpt
f.reduce_factor('Burglary','Yes')
print '\n', f.scope
print f.cpt
```
Another piece of functionality is the capability to convert the factor probabilities to/from log-space. This is important for MAP inference, since the sum of log-probabilities is equal the product of normal probabilities
```
f = Factor(bn,'Alarm')
print f.cpt
f.to_log()
print np.round(f.cpt,2)
f.from_log()
print f.cpt
```
Lastly, we have normalization. This function does most of its work behind the scenes because it cleans up the factor probabilities after multiplication or reduction. Still, it's an important function of which users should be aware.
```
f = Factor(bn, 'Alarm')
print f.cpt
f.cpt[0]=20
f.cpt[1]=20
f.cpt[4]=0.94
f.cpt[7]=0.15
print f.cpt
f.normalize()
print f.cpt
```
That's all for factor operations with pyBN. As you can see, there is a lot going on with factor operations. While these functions are the behind-the-scenes drivers of most inference queries, it is still useful for users to see how they operate. These operations have all been optimized to run incredibly fast so that inference queries can be as fast as possible.
|
github_jupyter
|
# Clustering
See our notes on [unsupervised learning](https://jennselby.github.io/MachineLearningCourseNotes/#unsupervised-learning), [K-means](https://jennselby.github.io/MachineLearningCourseNotes/#k-means-clustering), [DBSCAN](https://jennselby.github.io/MachineLearningCourseNotes/#dbscan-clustering), and [clustering validation](https://jennselby.github.io/MachineLearningCourseNotes/#clustering-validation).
For documentation of various clustering methods in scikit-learn, see http://scikit-learn.org/stable/modules/clustering.html
This code was based on the example at http://scikit-learn.org/stable/auto_examples/cluster/plot_cluster_iris.html
which has the following comments:
Code source: Gaël Varoquaux<br/>
Modified for documentation by Jaques Grobler<br/>
License: BSD 3 clause
## Instructions
0. If you haven't already, follow [the setup instructions here](https://jennselby.github.io/MachineLearningCourseNotes/#setting-up-python3) to get all necessary software installed.
1. Read through the code in the following sections:
* [Iris Dataset](#Iris-Dataset)
* [Visualization](#Visualization)
* [Training and Visualization](#Training-and-Visualization)
2. Complete the three-part [Exercise](#Exercise)
```
%matplotlib inline
import numpy
import matplotlib.pyplot
from mpl_toolkits.mplot3d import Axes3D
from sklearn.cluster import KMeans
from sklearn import datasets
import pandas
```
## Iris Dataset
Before you go on, if you haven't used the iris dataset in a previous assignment, make sure you understand it. Modify the cell below to examine different parts of the dataset that are contained in the iris dictionary object.
What are the features? What are we trying to classify?
```
iris = datasets.load_iris()
iris.keys()
iris_df = pandas.DataFrame(iris.data)
iris_df.columns = iris.feature_names
iris_df.head()
```
## Visualization Setup
```
# We can only plot 3 of the 4 iris features, since we only see in 3D.
# These are the ones the example code picked
X_FEATURE = 'petal width (cm)'
Y_FEATURE = 'sepal length (cm)'
Z_FEATURE = 'petal length (cm)'
# set some bounds for the figures that will display the plots of clusterings with various
# hyperparameter settings
# this allows for NUM_COLS * NUM_ROWS plots in the figure
NUM_COLS = 4
NUM_ROWS = 6
FIG_WIDTH = 4 * NUM_COLS
FIG_HEIGHT = 3 * NUM_ROWS
def add_plot(figure, subplot_num, subplot_name, data, labels):
'''Create a new subplot in the figure.'''
# create a new subplot
axis = figure.add_subplot(NUM_ROWS, NUM_COLS, subplot_num, projection='3d',
elev=48, azim=134)
# Plot three of the four features on the graph, and set the color according to the labels
axis.scatter(data[X_FEATURE], data[Y_FEATURE], data[Z_FEATURE], c=labels)
# get rid of the tick numbers. Otherwise, they all overlap and it looks horrible
for axis_obj in [axis.w_xaxis, axis.w_yaxis, axis.w_zaxis]:
axis_obj.set_ticklabels([])
# label the subplot
axis.title.set_text(subplot_name)
```
## Visualization
This is the correct labeling, based on the targets.
```
# start a new figure to hold all of the subplots
truth_figure = matplotlib.pyplot.figure(figsize=(FIG_WIDTH, FIG_HEIGHT))
# Plot the ground truth
add_plot(truth_figure, 1, "Ground Truth", iris_df, iris.target)
```
## Training and Visualization
Now let's see how k-means clusters the iris dataset, with various different numbers of clusters
```
MAX_CLUSTERS = 10
# start a new figure to hold all of the subplots
kmeans_figure = matplotlib.pyplot.figure(figsize=(FIG_WIDTH, FIG_HEIGHT))
# Plot the ground truth
add_plot(kmeans_figure, 1, "Ground Truth", iris_df, iris.target)
plot_num = 2
for num_clusters in range(2, MAX_CLUSTERS + 1):
# train the model
model = KMeans(n_clusters=num_clusters)
model.fit(iris_df)
# get the predictions of which cluster each input is in
labels = model.labels_
# plot this clustering
title = '{} Clusters'.format(num_clusters)
add_plot(kmeans_figure, plot_num, title, iris_df, labels.astype(numpy.float))
plot_num += 1
```
# Exercise
1. Add [validation](https://jennselby.github.io/MachineLearningCourseNotes/#clustering-validation) to measure how good the clustering is, with different numbers of clusters.
1. Run the iris data through DBSCAN or hierarchical clustering and validate that as well.
1. Comment on the validation results, explaining which models did best and why you think that might be.
```
# your code here
```
|
github_jupyter
|
## Hyperparameter Tuning Design Pattern
In Hyperparameter Tuning, the training loop is itself inserted into an optimization method to find the optimal set of model hyperparameters.
```
import datetime
import os
import numpy as np
import pandas as pd
import tensorflow as tf
import time
from tensorflow import keras
from sklearn.model_selection import GridSearchCV
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score, f1_score
```
### Grid search in Scikit-learn
Here we'll look at how to implement hyperparameter tuning with the grid search algorithm, using Scikit-learn's built-in `GridSearchCV`. We'll do this by training a random forest model on the UCI mushroom dataset, which predicts whether a mushroom is edible or poisonous.
```
# First, download the data
# We've made it publicly available in Google Cloud Storage
!gsutil cp gs://ml-design-patterns/mushrooms.csv .
mushroom_data = pd.read_csv('mushrooms.csv')
mushroom_data.head()
```
To keep things simple, we'll first convert the label column to numeric and then
use `pd.get_dummies()` to covert the data to numeric.
```
# 1 = edible, 0 = poisonous
mushroom_data.loc[mushroom_data['class'] == 'p', 'class'] = 0
mushroom_data.loc[mushroom_data['class'] == 'e', 'class'] = 1
labels = mushroom_data.pop('class')
dummy_data = pd.get_dummies(mushroom_data)
# Split the data
train_size = int(len(mushroom_data) * .8)
train_data = dummy_data[:train_size]
test_data = dummy_data[train_size:]
train_labels = labels[:train_size].astype(int)
test_labels = labels[train_size:].astype(int)
```
Next, we'll build our Scikit-learn model and define the hyperparameters we want to optimize using grid serach.
```
model = RandomForestClassifier()
grid_vals = {
'max_depth': [5, 10, 100],
'n_estimators': [100, 150, 200]
}
grid_search = GridSearchCV(model, param_grid=grid_vals, scoring='accuracy')
# Train the model while running hyperparameter trials
grid_search.fit(train_data.values, train_labels.values)
```
Let's see which hyperparameters resulted in the best accuracy.
```
grid_search.best_params_
```
Finally, we can generate some test predictions on our model and evaluate its accuracy.
```
grid_predict = grid_search.predict(test_data.values)
grid_acc = accuracy_score(test_labels.values, grid_predict)
grid_f = f1_score(test_labels.values, grid_predict)
print('Accuracy: ', grid_acc)
print('F1-Score: ', grid_f)
```
### Hyperparameter tuning with `keras-tuner`
To show how this works we'll train a model on the MNIST handwritten digit dataset, which is available directly in Keras. For more details, see this [Keras tuner guide](https://www.tensorflow.org/tutorials/keras/keras_tuner).
```
!pip install keras-tuner --quiet
import kerastuner as kt
# Get the mnist data
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data()
def build_model(hp):
model = keras.Sequential([
keras.layers.Flatten(input_shape=(28, 28)),
keras.layers.Dense(hp.Int('first_hidden', 128, 256, step=32), activation='relu'),
keras.layers.Dense(hp.Int('second_hidden', 16, 128, step=32), activation='relu'),
keras.layers.Dense(10, activation='softmax')
])
model.compile(
optimizer=tf.keras.optimizers.Adam(
hp.Float('learning_rate', .005, .01, sampling='log')),
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
return model
tuner = kt.BayesianOptimization(
build_model,
objective='val_accuracy',
max_trials=30
)
tuner.search(x_train, y_train, validation_split=0.1, epochs=10)
best_hps = tuner.get_best_hyperparameters(num_trials = 1)[0]
```
### Hyperparameter tuning on Cloud AI Platform
In this section we'll show you how to scale your hyperparameter optimization by running it on Google Cloud's AI Platform. You'll need a Cloud account with AI Platform Training enabled to run this section.
We'll be using PyTorch to build a regression model in this section. To train the model we'll be the BigQuery natality dataset. We've made a subset of this data available in a public Cloud Storage bucket, which we'll download from within the training job.
```
from google.colab import auth
auth.authenticate_user()
```
In the cells below, replcae `your-project-id` with the ID of your Cloud project, and `your-gcs-bucket` with the name of your Cloud Storage bucket.
```
!gcloud config set project your-project-id
BUCKET_URL = 'gs://your-gcs-bucket'
```
To run this on AI Platform, we'll need to package up our model code in Python's package format, which includes an empty `__init__.py` file and a `setup.py` to install dependencies (in this case PyTorch, Scikit-learn, and Pandas).
```
!mkdir trainer
!touch trainer/__init__.py
%%writefile setup.py
from setuptools import find_packages
from setuptools import setup
REQUIRED_PACKAGES = ['torch>=1.5', 'scikit-learn>=0.20', 'pandas>=1.0']
setup(
name='trainer',
version='0.1',
install_requires=REQUIRED_PACKAGES,
packages=find_packages(),
include_package_data=True,
description='My training application package.'
)
```
Below, we're copying our model training code to a `model.py` file in our trainer package directory. This code runs training and after training completes, reports the model's final loss to Cloud HyperTune.
```
%%writefile trainer/model.py
import argparse
import hypertune
import numpy as np
import pandas as pd
import torch
import torch.nn as nn
import torch.optim as optim
from sklearn.utils import shuffle
from sklearn.preprocessing import LabelEncoder
from sklearn.preprocessing import normalize
def get_args():
"""Argument parser.
Returns:
Dictionary of arguments.
"""
parser = argparse.ArgumentParser(description='PyTorch MNIST')
parser.add_argument('--job-dir', # handled automatically by AI Platform
help='GCS location to write checkpoints and export ' \
'models')
parser.add_argument('--lr', # Specified in the config file
type=float,
default=0.01,
help='learning rate (default: 0.01)')
parser.add_argument('--momentum', # Specified in the config file
type=float,
default=0.5,
help='SGD momentum (default: 0.5)')
parser.add_argument('--hidden-layer-size', # Specified in the config file
type=int,
default=8,
help='hidden layer size')
args = parser.parse_args()
return args
def train_model(args):
# Get the data
natality = pd.read_csv('https://storage.googleapis.com/ml-design-patterns/natality.csv')
natality = natality.dropna()
natality = shuffle(natality, random_state = 2)
natality.head()
natality_labels = natality['weight_pounds']
natality = natality.drop(columns=['weight_pounds'])
train_size = int(len(natality) * 0.8)
traindata_natality = natality[:train_size]
trainlabels_natality = natality_labels[:train_size]
testdata_natality = natality[train_size:]
testlabels_natality = natality_labels[train_size:]
# Normalize and convert to PT tensors
normalized_train = normalize(np.array(traindata_natality.values), axis=0)
normalized_test = normalize(np.array(testdata_natality.values), axis=0)
train_x = torch.Tensor(normalized_train)
train_y = torch.Tensor(np.array(trainlabels_natality))
test_x = torch.Tensor(normalized_test)
test_y = torch.Tensor(np.array(testlabels_natality))
# Define our data loaders
train_dataset = torch.utils.data.TensorDataset(train_x, train_y)
train_dataloader = torch.utils.data.DataLoader(train_dataset, batch_size=128, shuffle=True)
test_dataset = torch.utils.data.TensorDataset(test_x, test_y)
test_dataloader = torch.utils.data.DataLoader(test_dataset, batch_size=128, shuffle=False)
# Define the model, while tuning the size of our hidden layer
model = nn.Sequential(nn.Linear(len(train_x[0]), args.hidden_layer_size),
nn.ReLU(),
nn.Linear(args.hidden_layer_size, 1))
criterion = nn.MSELoss()
# Tune hyperparameters in our optimizer
optimizer = optim.SGD(model.parameters(), lr=args.lr, momentum=args.momentum)
epochs = 10
for e in range(epochs):
for batch_id, (data, label) in enumerate(train_dataloader):
optimizer.zero_grad()
y_pred = model(data)
label = label.view(-1,1)
loss = criterion(y_pred, label)
loss.backward()
optimizer.step()
val_mse = 0
num_batches = 0
# Evaluate accuracy on our test set
with torch.no_grad():
for i, (data, label) in enumerate(test_dataloader):
num_batches += 1
y_pred = model(data)
mse = criterion(y_pred, label.view(-1,1))
val_mse += mse.item()
avg_val_mse = (val_mse / num_batches)
# Report the metric we're optimizing for to AI Platform's HyperTune service
# In this example, we're mimizing loss on our test set
hpt = hypertune.HyperTune()
hpt.report_hyperparameter_tuning_metric(
hyperparameter_metric_tag='val_mse',
metric_value=avg_val_mse,
global_step=epochs
)
def main():
args = get_args()
print('in main', args)
train_model(args)
if __name__ == '__main__':
main()
%%writefile config.yaml
trainingInput:
hyperparameters:
goal: MINIMIZE
maxTrials: 10
maxParallelTrials: 5
hyperparameterMetricTag: val_mse
enableTrialEarlyStopping: TRUE
params:
- parameterName: lr
type: DOUBLE
minValue: 0.0001
maxValue: 0.1
scaleType: UNIT_LINEAR_SCALE
- parameterName: momentum
type: DOUBLE
minValue: 0.0
maxValue: 1.0
scaleType: UNIT_LINEAR_SCALE
- parameterName: hidden-layer-size
type: INTEGER
minValue: 8
maxValue: 32
scaleType: UNIT_LINEAR_SCALE
MAIN_TRAINER_MODULE = "trainer.model"
TRAIN_DIR = os.getcwd() + '/trainer'
JOB_DIR = BUCKET_URL + '/output'
REGION = "us-central1"
# Create a unique job name (run this each time you submit a job)
timestamp = str(datetime.datetime.now().time())
JOB_NAME = 'caip_training_' + str(int(time.time()))
```
The command below will submit your training job to AI Platform. To view the logs, and the results of each HyperTune trial visit your Cloud console.
```
# Configure and submit the training job
!gcloud ai-platform jobs submit training $JOB_NAME \
--scale-tier basic \
--package-path $TRAIN_DIR \
--module-name $MAIN_TRAINER_MODULE \
--job-dir $JOB_DIR \
--region $REGION \
--runtime-version 2.1 \
--python-version 3.7 \
--config config.yaml
```
Copyright 2020 Google Inc. Licensed under the Apache License, Version 2.0 (the "License"); you may not use this file except in compliance with the License. You may obtain a copy of the License at http://www.apache.org/licenses/LICENSE-2.0 Unless required by applicable law or agreed to in writing, software distributed under the License is distributed on an "AS IS" BASIS, WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied. See the License for the specific language governing permissions and limitations under the License
|
github_jupyter
|
<p align="center">
<img src="https://github.com/GeostatsGuy/GeostatsPy/blob/master/TCG_color_logo.png?raw=true" width="220" height="240" />
</p>
## Bootstrap-based Hypothesis Testing Demonstration
### Boostrap and Methods for Hypothesis Testing, Difference in Means
* we calculate the hypothesis test for different in means with boostrap and compare to the analytical expression
* **Welch's t-test**: we assume the features are Gaussian distributed and the variance are unequal
#### Michael Pyrcz, Associate Professor, University of Texas at Austin
##### [Twitter](https://twitter.com/geostatsguy) | [GitHub](https://github.com/GeostatsGuy) | [Website](http://michaelpyrcz.com) | [GoogleScholar](https://scholar.google.com/citations?user=QVZ20eQAAAAJ&hl=en&oi=ao) | [Book](https://www.amazon.com/Geostatistical-Reservoir-Modeling-Michael-Pyrcz/dp/0199731446) | [YouTube](https://www.youtube.com/channel/UCLqEr-xV-ceHdXXXrTId5ig) | [LinkedIn](https://www.linkedin.com/in/michael-pyrcz-61a648a1) | [GeostatsPy](https://github.com/GeostatsGuy/GeostatsPy)
#### Hypothesis Testing
Powerful methodology for spatial data analytics:
1. extracted sample set 1 and 2, the means look different, but are they?
2. should we suspect that the samples are in fact from 2 different populations?
Now, let's try the t-test, hypothesis test for difference in means. This test assumes that the variances are similar along with the data being Gaussian distributed (see the course notes for more on this). This is our test:
\begin{equation}
H_0: \mu_{X1} = \mu_{X2}
\end{equation}
\begin{equation}
H_1: \mu_{X1} \ne \mu_{X2}
\end{equation}
To test this we will calculate the t statistic with the bootstrap and analytical approaches.
#### The Welch's t-test for Difference in Means by Analytical and Empirical Methods
We work with the following test statistic, *t-statistic*, from the two sample sets.
\begin{equation}
\hat{t} = \frac{\overline{x}_1 - \overline{x}_2}{\sqrt{\frac{s^2_1}{n_1} + \frac{s^2_2}{n_2}}}
\end{equation}
where $\overline{x}_1$ and $\overline{x}_2$ are the sample means, $s^2_1$ and $s^2_2$ are the sample variances and $n_1$ and $n_2$ are the numer of samples from the two datasets.
The critical value, $t_{critical}$ is calculated by the analytical expression by:
\begin{equation}
t_{critical} = \left|t(\frac{\alpha}{2},\nu)\right|
\end{equation}
The degrees of freedom, $\nu$, is calculated as follows:
\begin{equation}
\nu = \frac{\left(\frac{1}{n_1} + \frac{\mu}{n_2}\right)^2}{\frac{1}{n_1^2(n_1-1)} + \frac{\mu^2}{n_2^2(n_2-1)}}
\end{equation}
Alternatively, the sampling distribution of the $t_{statistic}$ and $t_{critical}$ may be calculated empirically with bootstrap.
The workflow proceeds as:
* shift both sample sets to have the mean of the combined data set, $x_1$ → $x^*_1$, $x_2$ → $x^*_2$, this makes the null hypothesis true.
* for each bootstrap realization, $\ell=1\ldots,L$
* perform $n_1$ Monte Carlo simulations, draws with replacement, from sample set $x^*_1$
* perform $n_2$ Monte Carlo simulations, draws with replacement, from sample set $x^*_2$
* calculate the t_{statistic} realization, $\hat{t}^{\ell}$ given the resulting sample means $\overline{x}^{*,\ell}_1$ and $\overline{x}^{*,\ell}_2$ and the sample variances $s^{*,2,\ell}_1$ and $s^{*,2,\ell}_2$
* pool the results to assemble the $t_{statistic}$ sampling distribution
* calculate the cumulative probability of the observed t_{statistic}m, $\hat{t}$, from the boostrap distribution based on $\hat{t}^{\ell}$, $\ell = 1,\ldots,L$.
Here's some prerequisite information on the boostrap.
#### Bootstrap
Bootstrap is a method to assess the uncertainty in a sample statistic by repeated random sampling with replacement.
Assumptions
* sufficient, representative sampling, identical, idependent samples
Limitations
1. assumes the samples are representative
2. assumes stationarity
3. only accounts for uncertainty due to too few samples, e.g. no uncertainty due to changes away from data
4. does not account for boundary of area of interest
5. assumes the samples are independent
6. does not account for other local information sources
The Bootstrap Approach (Efron, 1982)
Statistical resampling procedure to calculate uncertainty in a calculated statistic from the data itself.
* Does this work? Prove it to yourself, for uncertainty in the mean solution is standard error:
\begin{equation}
\sigma^2_\overline{x} = \frac{\sigma^2_s}{n}
\end{equation}
Extremely powerful - could calculate uncertainty in any statistic! e.g. P13, skew etc.
* Would not be possible access general uncertainty in any statistic without bootstrap.
* Advanced forms account for spatial information and sampling strategy (game theory and Journel’s spatial bootstrap (1993).
Steps:
1. assemble a sample set, must be representative, reasonable to assume independence between samples
2. optional: build a cumulative distribution function (CDF)
* may account for declustering weights, tail extrapolation
* could use analogous data to support
3. For $\ell = 1, \ldots, L$ realizations, do the following:
* For $i = \alpha, \ldots, n$ data, do the following:
* Draw a random sample with replacement from the sample set or Monte Carlo simulate from the CDF (if available).
6. Calculate a realization of the sammary statistic of interest from the $n$ samples, e.g. $m^\ell$, $\sigma^2_{\ell}$. Return to 3 for another realization.
7. Compile and summarize the $L$ realizations of the statistic of interest.
This is a very powerful method. Let's try it out and compare the result to the analytical form of the confidence interval for the sample mean.
#### Objective
Provide an example and demonstration for:
1. interactive plotting in Jupyter Notebooks with Python packages matplotlib and ipywidgets
2. provide an intuitive hands-on example of confidence intervals and compare to statistical boostrap
#### Getting Started
Here's the steps to get setup in Python with the GeostatsPy package:
1. Install Anaconda 3 on your machine (https://www.anaconda.com/download/).
2. Open Jupyter and in the top block get started by copy and pasting the code block below from this Jupyter Notebook to start using the geostatspy functionality.
#### Load the Required Libraries
The following code loads the required libraries.
```
%matplotlib inline
from ipywidgets import interactive # widgets and interactivity
from ipywidgets import widgets
from ipywidgets import Layout
from ipywidgets import Label
from ipywidgets import VBox, HBox
import matplotlib.pyplot as plt # plotting
import numpy as np # working with arrays
import pandas as pd # working with DataFrames
from scipy import stats # statistical calculations
import random # random drawing / bootstrap realizations of the data
```
#### Make a Synthetic Dataset
This is an interactive method to:
* select a parametric distribution
* select the distribution parameters
* select the number of samples and visualize the synthetic dataset distribution
```
# interactive calculation of the sample set (control of source parametric distribution and number of samples)
l = widgets.Text(value=' Interactive Hypothesis Testing, Difference in Means, Analytical & Bootstrap Methods, Michael Pyrcz, Associate Professor, The University of Texas at Austin',layout=Layout(width='950px', height='30px'))
n1 = widgets.IntSlider(min=0, max = 100, value = 10, step = 1, description = '$n_{1}$',orientation='horizontal',layout=Layout(width='300px', height='30px'))
n1.style.handle_color = 'red'
m1 = widgets.FloatSlider(min=0, max = 50, value = 3, step = 1.0, description = '$\overline{x}_{1}$',orientation='horizontal',layout=Layout(width='300px', height='30px'))
m1.style.handle_color = 'red'
s1 = widgets.FloatSlider(min=0, max = 10, value = 3, step = 0.25, description = '$s_1$',orientation='horizontal',layout=Layout(width='300px', height='30px'))
s1.style.handle_color = 'red'
ui1 = widgets.VBox([n1,m1,s1],) # basic widget formatting
n2 = widgets.IntSlider(min=0, max = 100, value = 10, step = 1, description = '$n_{2}$',orientation='horizontal',layout=Layout(width='300px', height='30px'))
n2.style.handle_color = 'yellow'
m2 = widgets.FloatSlider(min=0, max = 50, value = 3, step = 1.0, description = '$\overline{x}_{2}$',orientation='horizontal',layout=Layout(width='300px', height='30px'))
m2.style.handle_color = 'yellow'
s2 = widgets.FloatSlider(min=0, max = 10, value = 3, step = 0.25, description = '$s_2$',orientation='horizontal',layout=Layout(width='300px', height='30px'))
s2.style.handle_color = 'yellow'
ui2 = widgets.VBox([n2,m2,s2],) # basic widget formatting
L = widgets.IntSlider(min=10, max = 1000, value = 100, step = 1, description = '$L$',orientation='horizontal',layout=Layout(width='300px', height='30px'))
L.style.handle_color = 'gray'
alpha = widgets.FloatSlider(min=0, max = 50, value = 3, step = 1.0, description = '$α$',orientation='horizontal',layout=Layout(width='300px', height='30px'))
alpha.style.handle_color = 'gray'
ui3 = widgets.VBox([L,alpha],) # basic widget formatting
ui4 = widgets.HBox([ui1,ui2,ui3],) # basic widget formatting
ui2 = widgets.VBox([l,ui4],)
def f_make(n1, m1, s1, n2, m2, s2, L, alpha): # function to take parameters, make sample and plot
np.random.seed(73073)
x1 = np.random.normal(loc=m1,scale=s1,size=n1)
np.random.seed(73074)
x2 = np.random.normal(loc=m2,scale=s2,size=n2)
mu = (s2*s2)/(s1*s1)
nu = ((1/n1 + mu/n2)*(1/n1 + mu/n2))/(1/(n1*n1*(n1-1)) + ((mu*mu)/(n2*n2*(n2-1))))
prop_values = np.linspace(-8.0,8.0,100)
analytical_distribution = stats.t.pdf(prop_values,df = nu)
analytical_tcrit = stats.t.ppf(1.0-alpha*0.005,df = nu)
# Analytical Method with SciPy
t_stat_observed, p_value_analytical = stats.ttest_ind(x1,x2,equal_var=False)
# Bootstrap Method
global_average = np.average(np.concatenate([x1,x2])) # shift the means to be equal to the globla mean
x1s = x1 - np.average(x1) + global_average
x2s = x2 - np.average(x2) + global_average
t_stat = np.zeros(L); p_value = np.zeros(L)
random.seed(73075)
for l in range(0, L): # loop over realizations
samples1 = random.choices(x1s, weights=None, cum_weights=None, k=len(x1s))
#print(samples1)
samples2 = random.choices(x2s, weights=None, cum_weights=None, k=len(x2s))
#print(samples2)
t_stat[l], p_value[l] = stats.ttest_ind(samples1,samples2,equal_var=False)
bootstrap_lower = np.percentile(t_stat,alpha * 0.5)
bootstrap_upper = np.percentile(t_stat,100.0 - alpha * 0.5)
plt.subplot(121)
#print(t_stat)
plt.hist(x1,cumulative = False, density = True, alpha=0.4,color="red",edgecolor="black", bins = np.linspace(0,50,50), label = '$x_1$')
plt.hist(x2,cumulative = False, density = True, alpha=0.4,color="yellow",edgecolor="black", bins = np.linspace(0,50,50), label = '$x_2$')
plt.ylim([0,0.4]); plt.xlim([0.0,30.0])
plt.title('Sample Distributions'); plt.xlabel('Value'); plt.ylabel('Density')
plt.legend()
#plt.hist(x2)
plt.subplot(122)
plt.ylim([0,0.6]); plt.xlim([-8.0,8.0])
plt.title('Bootstrap and Analytical $t_{statistic}$ Sampling Distributions'); plt.xlabel('$t_{statistic}$'); plt.ylabel('Density')
plt.plot([t_stat_observed,t_stat_observed],[0.0,0.6],color = 'black',label='observed $t_{statistic}$')
plt.plot([bootstrap_lower,bootstrap_lower],[0.0,0.6],color = 'blue',linestyle='dashed',label = 'bootstrap interval')
plt.plot([bootstrap_upper,bootstrap_upper],[0.0,0.6],color = 'blue',linestyle='dashed')
plt.plot(prop_values,analytical_distribution, color = 'red',label='analytical $t_{statistic}$')
plt.hist(t_stat,cumulative = False, density = True, alpha=0.2,color="blue",edgecolor="black", bins = np.linspace(-8.0,8.0,50), label = 'bootstrap $t_{statistic}$')
plt.fill_between(prop_values, 0, analytical_distribution, where = prop_values <= -1*analytical_tcrit, facecolor='red', interpolate=True, alpha = 0.2)
plt.fill_between(prop_values, 0, analytical_distribution, where = prop_values >= analytical_tcrit, facecolor='red', interpolate=True, alpha = 0.2)
ax = plt.gca()
handles,labels = ax.get_legend_handles_labels()
handles = [handles[0], handles[2], handles[3], handles[1]]
labels = [labels[0], labels[2], labels[3], labels[1]]
plt.legend(handles,labels,loc=1)
plt.subplots_adjust(left=0.0, bottom=0.0, right=2.0, top=1.2, wspace=0.2, hspace=0.2)
plt.show()
# connect the function to make the samples and plot to the widgets
interactive_plot = widgets.interactive_output(f_make, {'n1': n1, 'm1': m1, 's1': s1, 'n2': n2, 'm2': m2, 's2': s2, 'L': L, 'alpha': alpha})
interactive_plot.clear_output(wait = True) # reduce flickering by delaying plot updating
```
### Boostrap and Analytical Methods for Hypothesis Testing, Difference in Means
* including the analytical and bootstrap methods for testing the difference in means
* interactive plot demonstration with ipywidget, matplotlib packages
#### Michael Pyrcz, Associate Professor, University of Texas at Austin
##### [Twitter](https://twitter.com/geostatsguy) | [GitHub](https://github.com/GeostatsGuy) | [Website](http://michaelpyrcz.com) | [GoogleScholar](https://scholar.google.com/citations?user=QVZ20eQAAAAJ&hl=en&oi=ao) | [Book](https://www.amazon.com/Geostatistical-Reservoir-Modeling-Michael-Pyrcz/dp/0199731446) | [YouTube](https://www.youtube.com/channel/UCLqEr-xV-ceHdXXXrTId5ig) | [LinkedIn](https://www.linkedin.com/in/michael-pyrcz-61a648a1) | [GeostatsPy](https://github.com/GeostatsGuy/GeostatsPy)
### The Problem
Let's simulate bootstrap, resampling with replacement from a hat with $n_{red}$ and $n_{green}$ balls
* **$n_1$**, **$n_2$** number of samples, **$\overline{x}_1$**, **$\overline{x}_2$** means and **$s_1$**, **$s_2$** standard deviation of the 2 sample sets
* **$L$**: number of bootstrap realizations
* **$\alpha$**: alpha level
```
display(ui2, interactive_plot) # display the interactive plot
```
#### Observations
Some observations:
* lower dispersion and higher difference in means increases the absolute magnitude of the observed $t_{statistic}$
* the bootstrap distribution closely matches the analytical distribution if $L$ is large enough
* it is possible to use bootstrap to calculate the sampling distribution instead of relying on the theoretical express distribution, in this case the Student's t distribution.
#### Comments
This was a demonstration of interactive hypothesis testing for the significance in difference in means aboserved between 2 sample sets in Jupyter Notebook Python with the ipywidgets and matplotlib packages.
I have many other demonstrations on data analytics and machine learning, e.g. on the basics of working with DataFrames, ndarrays, univariate statistics, plotting data, declustering, data transformations, trend modeling and many other workflows available at https://github.com/GeostatsGuy/PythonNumericalDemos and https://github.com/GeostatsGuy/GeostatsPy.
I hope this was helpful,
*Michael*
#### The Author:
### Michael Pyrcz, Associate Professor, University of Texas at Austin
*Novel Data Analytics, Geostatistics and Machine Learning Subsurface Solutions*
With over 17 years of experience in subsurface consulting, research and development, Michael has returned to academia driven by his passion for teaching and enthusiasm for enhancing engineers' and geoscientists' impact in subsurface resource development.
For more about Michael check out these links:
#### [Twitter](https://twitter.com/geostatsguy) | [GitHub](https://github.com/GeostatsGuy) | [Website](http://michaelpyrcz.com) | [GoogleScholar](https://scholar.google.com/citations?user=QVZ20eQAAAAJ&hl=en&oi=ao) | [Book](https://www.amazon.com/Geostatistical-Reservoir-Modeling-Michael-Pyrcz/dp/0199731446) | [YouTube](https://www.youtube.com/channel/UCLqEr-xV-ceHdXXXrTId5ig) | [LinkedIn](https://www.linkedin.com/in/michael-pyrcz-61a648a1)
#### Want to Work Together?
I hope this content is helpful to those that want to learn more about subsurface modeling, data analytics and machine learning. Students and working professionals are welcome to participate.
* Want to invite me to visit your company for training, mentoring, project review, workflow design and / or consulting? I'd be happy to drop by and work with you!
* Interested in partnering, supporting my graduate student research or my Subsurface Data Analytics and Machine Learning consortium (co-PIs including Profs. Foster, Torres-Verdin and van Oort)? My research combines data analytics, stochastic modeling and machine learning theory with practice to develop novel methods and workflows to add value. We are solving challenging subsurface problems!
* I can be reached at [email protected].
I'm always happy to discuss,
*Michael*
Michael Pyrcz, Ph.D., P.Eng. Associate Professor The Hildebrand Department of Petroleum and Geosystems Engineering, Bureau of Economic Geology, The Jackson School of Geosciences, The University of Texas at Austin
#### More Resources Available at: [Twitter](https://twitter.com/geostatsguy) | [GitHub](https://github.com/GeostatsGuy) | [Website](http://michaelpyrcz.com) | [GoogleScholar](https://scholar.google.com/citations?user=QVZ20eQAAAAJ&hl=en&oi=ao) | [Book](https://www.amazon.com/Geostatistical-Reservoir-Modeling-Michael-Pyrcz/dp/0199731446) | [YouTube](https://www.youtube.com/channel/UCLqEr-xV-ceHdXXXrTId5ig) | [LinkedIn](https://www.linkedin.com/in/michael-pyrcz-61a648a1)
|
github_jupyter
|
# Individual Project
## Barber review in Gliwice
### Wojciech Pragłowski
#### Data scraped from [booksy.](https://booksy.com/pl-pl/s/barber-shop/12795_gliwice)
```
import requests
from bs4 import BeautifulSoup
booksy = requests.get("https://booksy.com/pl-pl/s/barber-shop/12795_gliwice")
soup = BeautifulSoup(booksy.content, 'html.parser')
barber = soup.find_all('h2')
text_barber = [i.get_text() for i in barber]
barber_names = [i.strip() for i in text_barber]
barber_names.pop(-1)
rate = soup.find_all('div', attrs={'data-testid':'rank-average'})
text_rate = [i.get_text() for i in rate]
barber_rate = [i.strip() for i in text_rate]
opinions = soup.find_all('div', attrs={'data-testid':'rank-label'})
text_opinions = [i.get_text() for i in opinions]
replace_opinions = [i.replace('opinii', '') for i in text_opinions]
replace_opinions2 = [i.replace('opinie', '') for i in replace_opinions]
strip_opinions = [i.strip() for i in replace_opinions2]
barber_opinions = [int(i) for i in strip_opinions]
prices = soup.find_all('div', attrs={'data-testid':'service-price'})
text_prices = [i.get_text() for i in prices]
replace_prices = [i.replace('zł', '') for i in text_prices]
replace_prices2 = [i.replace(',', '.') for i in replace_prices]
replace_prices3 = [i.replace('+', '') for i in replace_prices2]
replace_null = [i.replace('Bezpłatna', '0') for i in replace_prices3]
replace_space = [i.replace(' ', '') for i in replace_null]
strip_prices = [i.strip() for i in replace_space]
barber_prices = [float(i) for i in strip_prices]
import pandas as pd
barbers = pd.DataFrame(barber_names, columns=["Barber's name"])
barbers["Barber's rate"] = barber_rate
barbers["Barber's opinions"] = barber_opinions
barbers
```
#### I want to find those barbers who have more than 500 reviews
```
# znalezienie wiarygodnych barberów, czyli takich, którzy mają opinii > 500
best_opinions = [i for i in barber_opinions if i > 500]
best_indexes = []
for amount in barber_opinions:
if amount in best_opinions:
best_indexes.append(barber_opinions.index(amount))
best_barbers = [barber_names[i] for i in best_indexes]
best_rates = [barber_rate[i] for i in best_indexes]
```
#### On the page there are 3 basic prices for one Barber, so I'm combining them
```
# połączenie 3 cen dla jednego barbera
combined_prices = [barber_prices[i:i+3] for i in range(0, len(barber_prices), 3)]
best_prices = [combined_prices[i] for i in best_indexes]
print(best_prices)
avg = [sum(i)/len(i) for i in best_prices]
avg_price = [round(i,2) for i in avg]
avg_price
df_best_barber = pd.DataFrame(best_barbers, columns=["Barber's name"])
df_best_barber["Amount of opinions"] = best_opinions
df_best_barber["Barber's rate"] = best_rates
df_best_barber["Average Barber's prices"] = avg_price
df_best_barber
import matplotlib.pyplot as plt
plt.style.use('ggplot')
x = ['POPE', 'Matt', 'Sick', 'Freak', 'WILKOSZ', 'Wojnar', 'Trendy']
y = avg_price
x_pos = [i for i, _ in enumerate(x)]
plt.bar(x_pos, y)
plt.ylabel("Barbers' prices")
plt.title("Barbers in Gliwice & their average prices")
plt.xticks(x_pos, x)
plt.show()
import seaborn as sns
sns.relplot(x = "Average Barber's prices", y = "Amount of opinions", hue="Barber's name", data = df_best_barber)
```
|
github_jupyter
|
# Systems of Nonlinear Equations
## CH EN 2450 - Numerical Methods
**Prof. Tony Saad (<a>www.tsaad.net</a>) <br/>Department of Chemical Engineering <br/>University of Utah**
<hr/>
# Example 1
A system of nonlinear equations consists of several nonlinear functions - as many as there are unknowns. Solving a system of nonlinear equations means funding those points where the functions intersect each other. Consider for example the following system of equations
\begin{equation}
y = 4x - 0.5 x^3
\end{equation}
\begin{equation}
y = \sin(x)e^{-x}
\end{equation}
The first step is to write these in residual form
\begin{equation}
f_1 = y - 4x + 0.5 x^3,\\
f_2 = y - \sin(x)e^{-x}
\end{equation}
```
import numpy as np
from numpy import cos, sin, pi, exp
%matplotlib inline
%config InlineBackend.figure_format = 'svg'
import matplotlib.pyplot as plt
from scipy.optimize import fsolve
y1 = lambda x: 4 * x - 0.5 * x**3
y2 = lambda x: sin(x)*exp(-x)
x = np.linspace(-3.5,4,100)
plt.ylim(-8,6)
plt.plot(x,y1(x), 'k')
plt.plot(x,y2(x), 'r')
plt.grid()
plt.savefig('example1.pdf')
def F(xval):
x = xval[0] # let the first value in xval denote x
y = xval[1] # let the second value in xval denote y
f1 = y - 4.0*x + 0.5*x**3 # define f1
f2 = y - sin(x)*exp(-x) # define f2
return np.array([f1,f2]) # must return an array
def J(xval):
x = xval[0]
y = xval[1]
return np.array([[1.5*x**2 - 4.0 , 1.0 ],
[-cos(x)*exp(-x) + sin(x)*exp(-x) , 1.0]]) # Jacobian matrix J = [[df1/dx, df1/dy], [df2/dx,df2/dy]]
guess = np.array([1,3])
F(guess)
J(guess)
def newton_solver(F, J, x, tol): # x is nothing more than your initial guess
F_value = F(x)
err = np.linalg.norm(F_value, ord=2) # l2 norm of vector
# err = tol + 100
niter = 0
while abs(err) > tol and niter < 100:
J_value = J(x)
delta = np.linalg.solve(J_value, - F_value)
x = x + delta # update the solution
F_value = F(x) # compute new values for vector of residual functions
err = np.linalg.norm(F_value, ord=2) # compute error norm (absolute error)
niter += 1
# Here, either a solution is found, or too many iterations
if abs(err) > tol:
niter = -1
print('No Solution Found!!!!!!!!!')
return x, niter, err
```
Try to find the root less than [-2,-4]
```
tol = 1e-8
xguess = np.array([-3,0])
roots, n, err = newton_solver(F,J,xguess,tol)
print ('# of iterations', n, 'roots:', roots)
print ('Error Norm =',err)
F(roots)
```
Use Python's fsolve routine
```
fsolve(F,xguess)
```
# Example 2
Find the roots of the following system of equations
\begin{equation}
x^2 + y^2 = 1, \\
y = x^3 - x + 1
\end{equation}
First we assign $x_1 \equiv x$ and $x_2 \equiv y$ and rewrite the system in residual form
\begin{equation}
f_1(x_1,x_2) = x_1^2 + x_2^2 - 1, \\
f_2(x_1,x_2) = x_1^3 - x_1 - x_2 + 1
\end{equation}
```
x = np.linspace(-1,1)
y1 = lambda x: x**3 - x + 1
y2 = lambda x: np.sqrt(1 - x**2)
plt.plot(x,y1(x), 'k')
plt.plot(x,y2(x), 'r')
plt.grid()
def F(xval):
?
def J(xval):
?
tol = 1e-8
xguess = np.array([0.5,0.5])
x, n, err = newton_solver(F, J, xguess, tol)
print (n, x)
print ('Error Norm =',err)
fsolve(F,(0.5,0.5))
import urllib
import requests
from IPython.core.display import HTML
def css_styling():
styles = requests.get("https://raw.githubusercontent.com/saadtony/NumericalMethods/master/styles/custom.css")
return HTML(styles.text)
css_styling()
```
|
github_jupyter
|
(pandas_plotting)=
# Plotting
``` {index} Pandas: plotting
```
Plotting with pandas is very intuitive. We can use syntax:
df.plot.*
where * is any plot from matplotlib.pyplot supported by pandas. Full tutorial on pandas plots can be found [here](https://pandas.pydata.org/pandas-docs/stable/user_guide/visualization.html).
Alternatively, we can use other plots from matplotlib library and pass specific columns as arguments:
plt.scatter(df.col1, df.col2, c=df.col3, s=df.col4, *kwargs)
In this tutorial we will use both ways of plotting.
At first we will load New Zealand earthquake data and following date-time tutorial we will create date-time index:
```
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
nz_eqs = pd.read_csv("../../geosciences/data/nz_largest_eq_since_1970.csv")
nz_eqs.head(4)
nz_eqs["hour"] = nz_eqs["utc_time"].str.split(':').str.get(0).astype(float)
nz_eqs["minute"] = nz_eqs["utc_time"].str.split(':').str.get(1).astype(float)
nz_eqs["second"] = nz_eqs["utc_time"].str.split(':').str.get(2).astype(float)
nz_eqs["datetime"] = pd.to_datetime(nz_eqs[['year', 'month', 'day', 'hour', 'minute', 'second']])
nz_eqs.head(4)
nz_eqs = nz_eqs.set_index('datetime')
```
Let's plot magnitude data for all years and then for year 2000 only using pandas way of plotting:
```
plt.figure(figsize=(7,5))
nz_eqs['mag'].plot()
plt.xlabel('Date')
plt.ylabel('Magnitude')
plt.show()
plt.figure(figsize=(7,5))
nz_eqs['mag'].loc['2000-01':'2001-01'].plot()
plt.xlabel('Date')
plt.ylabel('Magnitude')
plt.show()
```
We can calculate how many earthquakes are within each year using:
df.resample('bintype').count()
For example, if we want to use intervals for year, month, minute and second we can use 'Y', 'M', 'T' and 'S' in the bintype argument.
Let's count our earthquakes in 4 month intervals and display it with xticks every 4 years:
```
figure, ax = plt.subplots(figsize=(7,5))
# Resample datetime index into 4 month bins
# and then count how many
nz_eqs['year'].resample("4M").count().plot(ax=ax, x_compat=True)
import matplotlib
# Change xticks to be every 4 years
ax.xaxis.set_major_locator(matplotlib.dates.YearLocator(base=4))
ax.xaxis.set_major_formatter(matplotlib.dates.DateFormatter("%Y"))
plt.xlabel('Date')
plt.ylabel('No. of earthquakes')
plt.show()
```
Suppose we would like to view the earthquake locations, places with largest earthquakes and their depths. To do that, we can use Cartopy library and create a scatter plot, passing magnitude column into size and depth column into colour.
```
import cartopy.crs as ccrs
import cartopy.feature as cfeature
from cartopy.mpl.gridliner import LONGITUDE_FORMATTER, LATITUDE_FORMATTER
import matplotlib.ticker as mticker
```
Let's plot this data passing columns into scatter plot:
```
plt.rcParams.update({'font.size': 14})
central_lon, central_lat = 170, -50
extent = [160,188,-48,-32]
fig, ax = plt.subplots(1, subplot_kw=dict(projection=ccrs.Mercator(central_lon, central_lat)), figsize=(7,7))
ax.set_extent(extent)
ax.coastlines(resolution='10m')
ax.set_title("Earthquakes in New Zealand since 1970")
# Create a scatter plot
scatplot = ax.scatter(nz_eqs.lon,nz_eqs.lat, c=nz_eqs.depth_km,
s=nz_eqs.depth_km/10, edgecolor="black",
cmap="PuRd", lw=0.1,
transform=ccrs.Geodetic())
# Create colourbar
cbar = plt.colorbar(scatplot, ax=ax, fraction=0.03, pad=0.1, label='Depth [km]')
# Sort out gridlines and their density
xticks_extent = list(np.arange(160, 180, 4)) + list(np.arange(-200,-170,4))
yticks_extent = list(np.arange(-60, -30, 2))
gl = ax.gridlines(linewidths=0.1)
gl.xlabels_top = False
gl.xlabels_bottom = True
gl.ylabels_left = True
gl.ylabels_right = False
gl.xlocator = mticker.FixedLocator(xticks_extent)
gl.ylocator = mticker.FixedLocator(yticks_extent)
gl.xformatter = LONGITUDE_FORMATTER
gl.yformatter = LATITUDE_FORMATTER
plt.show()
```
This way we can easily see that the deepest and largest earthquakes are in the North.
# References
The notebook was compiled based on:
* [Pandas official Getting Started tutorials](https://pandas.pydata.org/docs/getting_started/index.html#getting-started)
* [Kaggle tutorial](https://www.kaggle.com/learn/pandas)
|
github_jupyter
|
# Machine Learning with PyTorch and Scikit-Learn
# -- Code Examples
## Package version checks
Add folder to path in order to load from the check_packages.py script:
```
import sys
sys.path.insert(0, '..')
```
Check recommended package versions:
```
from python_environment_check import check_packages
d = {
'torch': '1.8.0',
}
check_packages(d)
```
Chapter 15: Modeling Sequential Data Using Recurrent Neural Networks (part 3/3)
========
**Outline**
- Implementing RNNs for sequence modeling in PyTorch
- [Project two -- character-level language modeling in PyTorch](#Project-two----character-level-language-modeling-in-PyTorch)
- [Preprocessing the dataset](#Preprocessing-the-dataset)
- [Evaluation phase -- generating new text passages](#Evaluation-phase----generating-new-text-passages)
- [Summary](#Summary)
Note that the optional watermark extension is a small IPython notebook plugin that I developed to make the code reproducible. You can just skip the following line(s).
```
from IPython.display import Image
%matplotlib inline
```
## Project two: character-level language modeling in PyTorch
```
Image(filename='figures/15_11.png', width=500)
```
### Preprocessing the dataset
```
import numpy as np
## Reading and processing text
with open('1268-0.txt', 'r', encoding="utf8") as fp:
text=fp.read()
start_indx = text.find('THE MYSTERIOUS ISLAND')
end_indx = text.find('End of the Project Gutenberg')
text = text[start_indx:end_indx]
char_set = set(text)
print('Total Length:', len(text))
print('Unique Characters:', len(char_set))
Image(filename='figures/15_12.png', width=500)
chars_sorted = sorted(char_set)
char2int = {ch:i for i,ch in enumerate(chars_sorted)}
char_array = np.array(chars_sorted)
text_encoded = np.array(
[char2int[ch] for ch in text],
dtype=np.int32)
print('Text encoded shape: ', text_encoded.shape)
print(text[:15], ' == Encoding ==> ', text_encoded[:15])
print(text_encoded[15:21], ' == Reverse ==> ', ''.join(char_array[text_encoded[15:21]]))
for ex in text_encoded[:5]:
print('{} -> {}'.format(ex, char_array[ex]))
Image(filename='figures/15_13.png', width=500)
Image(filename='figures/15_14.png', width=500)
seq_length = 40
chunk_size = seq_length + 1
text_chunks = [text_encoded[i:i+chunk_size]
for i in range(len(text_encoded)-chunk_size+1)]
## inspection:
for seq in text_chunks[:1]:
input_seq = seq[:seq_length]
target = seq[seq_length]
print(input_seq, ' -> ', target)
print(repr(''.join(char_array[input_seq])),
' -> ', repr(''.join(char_array[target])))
import torch
from torch.utils.data import Dataset
class TextDataset(Dataset):
def __init__(self, text_chunks):
self.text_chunks = text_chunks
def __len__(self):
return len(self.text_chunks)
def __getitem__(self, idx):
text_chunk = self.text_chunks[idx]
return text_chunk[:-1].long(), text_chunk[1:].long()
seq_dataset = TextDataset(torch.tensor(text_chunks))
for i, (seq, target) in enumerate(seq_dataset):
print(' Input (x):', repr(''.join(char_array[seq])))
print('Target (y):', repr(''.join(char_array[target])))
print()
if i == 1:
break
device = torch.device("cuda:0")
# device = 'cpu'
from torch.utils.data import DataLoader
batch_size = 64
torch.manual_seed(1)
seq_dl = DataLoader(seq_dataset, batch_size=batch_size, shuffle=True, drop_last=True)
```
### Building a character-level RNN model
```
import torch.nn as nn
class RNN(nn.Module):
def __init__(self, vocab_size, embed_dim, rnn_hidden_size):
super().__init__()
self.embedding = nn.Embedding(vocab_size, embed_dim)
self.rnn_hidden_size = rnn_hidden_size
self.rnn = nn.LSTM(embed_dim, rnn_hidden_size,
batch_first=True)
self.fc = nn.Linear(rnn_hidden_size, vocab_size)
def forward(self, x, hidden, cell):
out = self.embedding(x).unsqueeze(1)
out, (hidden, cell) = self.rnn(out, (hidden, cell))
out = self.fc(out).reshape(out.size(0), -1)
return out, hidden, cell
def init_hidden(self, batch_size):
hidden = torch.zeros(1, batch_size, self.rnn_hidden_size)
cell = torch.zeros(1, batch_size, self.rnn_hidden_size)
return hidden.to(device), cell.to(device)
vocab_size = len(char_array)
embed_dim = 256
rnn_hidden_size = 512
torch.manual_seed(1)
model = RNN(vocab_size, embed_dim, rnn_hidden_size)
model = model.to(device)
model
loss_fn = nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters(), lr=0.005)
num_epochs = 10000
torch.manual_seed(1)
for epoch in range(num_epochs):
hidden, cell = model.init_hidden(batch_size)
seq_batch, target_batch = next(iter(seq_dl))
seq_batch = seq_batch.to(device)
target_batch = target_batch.to(device)
optimizer.zero_grad()
loss = 0
for c in range(seq_length):
pred, hidden, cell = model(seq_batch[:, c], hidden, cell)
loss += loss_fn(pred, target_batch[:, c])
loss.backward()
optimizer.step()
loss = loss.item()/seq_length
if epoch % 500 == 0:
print(f'Epoch {epoch} loss: {loss:.4f}')
```
### Evaluation phase: generating new text passages
```
from torch.distributions.categorical import Categorical
torch.manual_seed(1)
logits = torch.tensor([[1.0, 1.0, 1.0]])
print('Probabilities:', nn.functional.softmax(logits, dim=1).numpy()[0])
m = Categorical(logits=logits)
samples = m.sample((10,))
print(samples.numpy())
torch.manual_seed(1)
logits = torch.tensor([[1.0, 1.0, 3.0]])
print('Probabilities:', nn.functional.softmax(logits, dim=1).numpy()[0])
m = Categorical(logits=logits)
samples = m.sample((10,))
print(samples.numpy())
def sample(model, starting_str,
len_generated_text=500,
scale_factor=1.0):
encoded_input = torch.tensor([char2int[s] for s in starting_str])
encoded_input = torch.reshape(encoded_input, (1, -1))
generated_str = starting_str
model.eval()
hidden, cell = model.init_hidden(1)
hidden = hidden.to('cpu')
cell = cell.to('cpu')
for c in range(len(starting_str)-1):
_, hidden, cell = model(encoded_input[:, c].view(1), hidden, cell)
last_char = encoded_input[:, -1]
for i in range(len_generated_text):
logits, hidden, cell = model(last_char.view(1), hidden, cell)
logits = torch.squeeze(logits, 0)
scaled_logits = logits * scale_factor
m = Categorical(logits=scaled_logits)
last_char = m.sample()
generated_str += str(char_array[last_char])
return generated_str
torch.manual_seed(1)
model.to('cpu')
print(sample(model, starting_str='The island'))
```
* **Predictability vs. randomness**
```
logits = torch.tensor([[1.0, 1.0, 3.0]])
print('Probabilities before scaling: ', nn.functional.softmax(logits, dim=1).numpy()[0])
print('Probabilities after scaling with 0.5:', nn.functional.softmax(0.5*logits, dim=1).numpy()[0])
print('Probabilities after scaling with 0.1:', nn.functional.softmax(0.1*logits, dim=1).numpy()[0])
torch.manual_seed(1)
print(sample(model, starting_str='The island',
scale_factor=2.0))
torch.manual_seed(1)
print(sample(model, starting_str='The island',
scale_factor=0.5))
```
...
# Summary
...
Readers may ignore the next cell.
```
! python ../.convert_notebook_to_script.py --input ch15_part3.ipynb --output ch15_part3.py
```
|
github_jupyter
|
# Script to plot GALAH spectra, but also save them into python dictionaries
## Author: Sven Buder (SB, MPIA) buder at mpia dot de
This script is intended to plot the 4 spectra of the arms of the HERMES spectrograph
History:
181012 - SB created
```
try:
%matplotlib inline
%config InlineBackend.figure_format='retina'
except:
pass
import numpy as np
import os
import astropy.io.fits as pyfits
import matplotlib.pyplot as plt
```
### Adjust script
### Definitions which will be executed in the last cell
```
def read_spectra(sobject_id, iraf_dr = 'dr5.3', SPECTRA = 'SPECTRA'):
"""
This function reads in the 4 individual spectra from the subdirectory working_directory/SPECTRA
INPUT:
sobject_id = identifier of spectra by date (6digits), plate (4digits), combination (2digits) and pivot number (3digits)
iraf_dr = reduction which shall be used, current version: dr5.3
SPECTRA = string to indicate sub directory where spectra are saved
OUTPUT
spectrum = dictionary
"""
spectrum = dict(sobject_id = sobject_id)
# Assess if spectrum is stacked
if str(sobject_id)[11] == '1':
# Single observations are saved in 'com'
com='com'
else:
# Stacked observations are saved in 'com2'
com='com'
# Iterate through all 4 CCDs
for each_ccd in [1,2,3,4]:
try:
fits = pyfits.open(SPECTRA+'/'+iraf_dr+'/'+str(sobject_id)[0:6]+'/standard/'+com+'/'+str(sobject_id)+str(each_ccd)+'.fits')
# Extension 0: Reduced spectrum
# Extension 1: Relative error spectrum
# Extension 4: Normalised spectrum, NB: cut for CCD4
# Extract wavelength grid for the reduced spectrum
start_wavelength = fits[0].header["CRVAL1"]
dispersion = fits[0].header["CDELT1"]
nr_pixels = fits[0].header["NAXIS1"]
reference_pixel = fits[0].header["CRPIX1"]
if reference_pixel == 0:
reference_pixel = 1
spectrum['wave_red_'+str(each_ccd)] = np.array(map(lambda x:((x-reference_pixel+1)*dispersion+start_wavelength),range(0,nr_pixels)))
try:
# Extract wavelength grid for the normalised spectrum
start_wavelength = fits[4].header["CRVAL1"]
dispersion = fits[4].header["CDELT1"]
nr_pixels = fits[4].header["NAXIS1"]
reference_pixel = fits[4].header["CRPIX1"]
if reference_pixel == 0:
reference_pixel=1
spectrum['wave_norm_'+str(each_ccd)] = np.array(map(lambda x:((x-reference_pixel+1)*dispersion+start_wavelength),range(0,nr_pixels)))
except:
spectrum['wave_norm_'+str(each_ccd)] = spectrum['wave_red_'+str(each_ccd)]
# Extract flux and flux error of reduced spectrum
spectrum['sob_red_'+str(each_ccd)] = np.array(fits[0].data)
spectrum['uob_red_'+str(each_ccd)] = np.array(fits[0].data * fits[1].data)
# Extract flux and flux error of reduced spectrum
try:
spectrum['sob_norm_'+str(each_ccd)] = np.array(fits[4].data)
except:
spectrum['sob_norm_'+str(each_ccd)] = np.ones(len(fits[0].data))
if each_ccd != 4:
try:
spectrum['uob_norm_'+str(each_ccd)] = np.array(fits[4].data * fits[1].data)
except:
spectrum['uob_norm_'+str(each_ccd)] = np.array(fits[1].data)
else:
# for normalised error of CCD4, only used appropriate parts of error spectrum
try:
spectrum['uob_norm_4'] = np.array(fits[4].data * (fits[1].data)[-len(spectrum['sob_norm_4']):])
except:
spectrum['uob_norm_4'] = np.zeros(len(fits[0].data))
fits.close()
except:
spectrum['wave_norm_'+str(each_ccd)] = np.arange(7693.50,7875.55,0.074)
spectrum['wave_red_'+str(each_ccd)] = np.arange(7693.50,7875.55,0.074)
spectrum['sob_norm_'+str(each_ccd)] = np.ones(len(spectrum['wave_red_'+str(each_ccd)]))
spectrum['sob_red_'+str(each_ccd)] = np.ones(len(spectrum['wave_red_'+str(each_ccd)]))
spectrum['uob_norm_'+str(each_ccd)] = np.zeros(len(spectrum['wave_red_'+str(each_ccd)]))
spectrum['uob_red_'+str(each_ccd)] = np.zeros(len(spectrum['wave_red_'+str(each_ccd)]))
return spectrum
def interpolate_spectrum_onto_cannon_wavelength(spectrum):
"""
This function interpolates the spectrum
onto the wavelength grid of The Cannon as used for GALAH DR2
INPUT:
spectrum dictionary
OUTPUT:
interpolated spectrum dictionary
"""
# Initialise interpolated spectrum from input spectrum
interpolated_spectrum = dict()
for each_key in spectrum.keys():
interpolated_spectrum[each_key] = spectrum[each_key]
# The Cannon wavelength grid as used for GALAH DR2
wave_cannon = dict()
wave_cannon['ccd1'] = np.arange(4715.94,4896.00,0.046) # ab lines 4716.3 - 4892.3
wave_cannon['ccd2'] = np.arange(5650.06,5868.25,0.055) # ab lines 5646.0 - 5867.8
wave_cannon['ccd3'] = np.arange(6480.52,6733.92,0.064) # ab lines 6481.6 - 6733.4
wave_cannon['ccd4'] = np.arange(7693.50,7875.55,0.074) # ab lines 7691.2 - 7838.5
for each_ccd in [1, 2, 3, 4]:
# exchange wavelength
interpolated_spectrum['wave_red_'+str(each_ccd)] = wave_cannon['ccd'+str(each_ccd)]
interpolated_spectrum['wave_norm_'+str(each_ccd)] = wave_cannon['ccd'+str(each_ccd)]
# interpolate and exchange flux
interpolated_spectrum['sob_red_'+str(each_ccd)] = np.interp(
x=wave_cannon['ccd'+str(each_ccd)],
xp=spectrum['wave_red_'+str(each_ccd)],
fp=spectrum['sob_red_'+str(each_ccd)],
)
interpolated_spectrum['sob_norm_'+str(each_ccd)] = np.interp(
wave_cannon['ccd'+str(each_ccd)],
spectrum['wave_norm_'+str(each_ccd)],
spectrum['sob_norm_'+str(each_ccd)],
)
# interpolate and exchange flux error
interpolated_spectrum['uob_red_'+str(each_ccd)] = np.interp(
wave_cannon['ccd'+str(each_ccd)],
spectrum['wave_red_'+str(each_ccd)],
spectrum['uob_red_'+str(each_ccd)],
)
interpolated_spectrum['uob_norm_'+str(each_ccd)] = np.interp(
wave_cannon['ccd'+str(each_ccd)],
spectrum['wave_norm_'+str(each_ccd)],
spectrum['uob_norm_'+str(each_ccd)],
)
return interpolated_spectrum
def plot_spectrum(spectrum, normalisation = True, lines_to_indicate = None, save_as_png = False):
"""
This function plots the spectrum in 4 subplots for each arm of the HERMES spectrograph
INPUT:
spectrum = dictionary created by read_spectra()
normalisation = True or False (either normalised or un-normalised spectra are plotted)
save_as_png = Save figure as png if True
OUTPUT:
Plot that spectrum!
"""
f, axes = plt.subplots(4, 1, figsize = (15,10))
kwargs_sob = dict(c = 'k', label='Flux', rasterized=True)
kwargs_error_spectrum = dict(color = 'grey', label='Flux error', rasterized=True)
# Adjust keyword used for dictionaries and plot labels
if normalisation==True:
red_norm = 'norm'
else:
red_norm = 'red'
for each_ccd in [1, 2, 3, 4]:
axes[each_ccd-1].fill_between(
spectrum['wave_'+red_norm+'_'+str(each_ccd)],
spectrum['sob_'+red_norm+'_'+str(each_ccd)] - spectrum['uob_'+red_norm+'_'+str(each_ccd)],
spectrum['sob_'+red_norm+'_'+str(each_ccd)] + spectrum['uob_'+red_norm+'_'+str(each_ccd)],
**kwargs_error_spectrum
)
# Overplot observed spectrum a bit thicker
axes[each_ccd-1].plot(
spectrum['wave_'+red_norm+'_'+str(each_ccd)],
spectrum['sob_'+red_norm+'_'+str(each_ccd)],
**kwargs_sob
)
# Plot important lines if committed
if lines_to_indicate != None:
for each_line in lines_to_indicate:
if (float(each_line[0]) >= spectrum['wave_'+red_norm+'_'+str(each_ccd)][0]) & (float(each_line[0]) <= spectrum['wave_'+red_norm+'_'+str(each_ccd)][-1]):
axes[each_ccd-1].axvline(float(each_line[0]), color = each_line[2], ls='dashed')
if red_norm=='norm':
axes[each_ccd-1].text(float(each_line[0]), 1.25, each_line[1], color = each_line[2], ha='left', va='top')
# Plot layout
if red_norm == 'norm':
axes[each_ccd-1].set_ylim(-0.1,1.3)
else:
axes[each_ccd-1].set_ylim(0,1.3*np.median(spectrum['sob_'+red_norm+'_'+str(each_ccd)]))
axes[each_ccd-1].set_xlabel(r'Wavelength CCD '+str(each_ccd)+' [$\mathrm{\AA}$]')
axes[each_ccd-1].set_ylabel(r'Flux ('+red_norm+') [a.u.]')
if each_ccd == 1:
axes[each_ccd-1].legend(loc='lower left')
plt.tight_layout()
if save_as_png == True:
plt.savefig(str(spectrum['sobject_id'])+'_'+red_norm+'.png', dpi=200)
return f
```
### Execute and have fun looking at spectra
```
# Adjust directory you want to work in
working_directory = '/Users/buder/trunk/GALAH/'
working_directory = '/avatar/buder/trunk/GALAH/'
os.chdir(working_directory)
# You can activate a number of lines that will be plotted in the spectra
important_lines = np.array([
[4861.35, 'H' , 'red'],
[6562.79, 'H' , 'red'],
[6708. , 'Li', 'orange'],
])
# Last but not least, declare which sobject_ids shall be plotted
sobject_ids_to_plot = [
190211002201088
]
for each_sobject_id in sobject_ids_to_plot:
# read in spectrum
spectrum = read_spectra(each_sobject_id)
# interpolate spectrum onto The Cannon wavelength grid
interpolated_spectrum = interpolate_spectrum_onto_cannon_wavelength(spectrum)
# plot input spectrum
plot_spectrum(spectrum,
normalisation = False,
lines_to_indicate = None,
save_as_png = True
)
# # plot interpolated spectrum
# plot_spectrum(
# interpolated_spectrum,
# normalisation = True,
# lines_to_indicate = None,
# save_as_png = True
# )
```
|
github_jupyter
|
<a id='Top'></a>
# MultiSurv results by cancer type<a class='tocSkip'></a>
C-index value results for each cancer type of the best MultiSurv model trained on all-cancer data.
```
%load_ext autoreload
%autoreload 2
%load_ext watermark
import sys
import os
import numpy as np
import pandas as pd
import matplotlib
import matplotlib.pyplot as plt
import torch
# Make modules in "src" dir visible
project_dir = os.path.split(os.getcwd())[0]
if project_dir not in sys.path:
sys.path.append(os.path.join(project_dir, 'src'))
import dataset
from model import Model
import utils
matplotlib.style.use('multisurv.mplstyle')
```
<h1>Table of Contents<span class="tocSkip"></span></h1>
<div class="toc"><ul class="toc-item"><li><span><a href="#Load-model" data-toc-modified-id="Load-model-1"><span class="toc-item-num">1 </span>Load model</a></span></li><li><span><a href="#Evaluate" data-toc-modified-id="Evaluate-2"><span class="toc-item-num">2 </span>Evaluate</a></span></li><li><span><a href="#Result-graph" data-toc-modified-id="Result-graph-3"><span class="toc-item-num">3 </span>Result graph</a></span><ul class="toc-item"><li><span><a href="#Save-to-files" data-toc-modified-id="Save-to-files-3.1"><span class="toc-item-num">3.1 </span>Save to files</a></span></li></ul></li><li><span><a href="#Metric-correlation-with-other-attributes" data-toc-modified-id="Metric-correlation-with-other-attributes-4"><span class="toc-item-num">4 </span>Metric correlation with other attributes</a></span><ul class="toc-item"><li><span><a href="#Collect-feature-representations" data-toc-modified-id="Collect-feature-representations-4.1"><span class="toc-item-num">4.1 </span>Collect feature representations</a></span></li><li><span><a href="#Compute-dispersion-and-add-to-selected-metric-table" data-toc-modified-id="Compute-dispersion-and-add-to-selected-metric-table-4.2"><span class="toc-item-num">4.2 </span>Compute dispersion and add to selected metric table</a></span></li><li><span><a href="#Plot" data-toc-modified-id="Plot-4.3"><span class="toc-item-num">4.3 </span>Plot</a></span></li></ul></li></ul></div>
```
DATA = utils.INPUT_DATA_DIR
MODELS = utils.TRAINED_MODEL_DIR
device = torch.device('cuda:0' if torch.cuda.is_available() else 'cpu')
```
# Load model
```
dataloaders = utils.get_dataloaders(
data_location=DATA,
labels_file='../data/labels.tsv',
modalities=['clinical', 'mRNA'],
# exclude_patients=exclude_cancers,
return_patient_id=True
)
multisurv = Model(dataloaders=dataloaders, device=device)
multisurv.load_weights(os.path.join(MODELS, 'clinical_mRNA_lr0.005_epoch43_acc0.81.pth'))
```
# Evaluate
```
def get_patients_with(cancer_type, split_group='test'):
labels = pd.read_csv('../data/labels.tsv', sep='\t')
cancer_labels = labels[labels['project_id'] == cancer_type]
group_cancer_labels = cancer_labels[cancer_labels['group'] == split_group]
return list(group_cancer_labels['submitter_id'])
%%time
results = {}
minimum_n_patients = 0
cancer_types = pd.read_csv('../data/labels.tsv', sep='\t').project_id.unique()
for i, cancer_type in enumerate(cancer_types):
print('-' * 44)
print(' ' * 17, f'{i + 1}.', cancer_type)
print('-' * 44)
patients = get_patients_with(cancer_type)
if len(patients) < minimum_n_patients:
continue
exclude_patients = [p for p in dataloaders['test'].dataset.patient_ids
if not p in patients]
data = utils.get_dataloaders(
data_location=DATA,
labels_file='../data/labels.tsv',
modalities=['clinical', 'mRNA'],
exclude_patients=exclude_patients,
return_patient_id=True
)['test'].dataset
results[cancer_type] = utils.Evaluation(model=multisurv, dataset=data, device=device)
results[cancer_type].run_bootstrap()
print()
print()
print()
%%time
data = utils.get_dataloaders(
data_location=DATA,
labels_file='../data/labels.tsv',
modalities=['clinical', 'mRNA'],
return_patient_id=True
)['test'].dataset
results['All'] = utils.Evaluation(model=multisurv, dataset=data, device=device)
results['All'].run_bootstrap()
print()
```
In order to avoid very __noisy values__, establish a __minimum threshold__ for the number of patients in each given cancer type.
```
minimum_n_patients = 20
cancer_types = pd.read_csv('../data/labels.tsv', sep='\t').project_id.unique()
selected_cancer_types = ['All']
print('-' * 40)
print(' Cancer Ctd IBS # patients')
print('-' * 40)
for cancer_type in sorted(list(cancer_types)):
patients = get_patients_with(cancer_type)
if len(patients) > minimum_n_patients:
selected_cancer_types.append(cancer_type)
ctd = str(round(results[cancer_type].c_index_td, 3))
ibs = str(round(results[cancer_type].ibs, 3))
message = ' ' + cancer_type
message += ' ' * (11 - len(message)) + ctd
message += ' ' * (20 - len(message)) + ibs
message += ' ' * (32 - len(message)) + str(len(patients))
print(message)
# print(' ' + cancer_type + ' ' * (10 - len(cancer_type)) + \
# ctd + ' ' * (10 - len(ibs)) + ibs + ' ' * (13 - len(ctd)) \
# + str(len(patients)))
def format_bootstrap_output(evaluator):
results = evaluator.format_results()
for metric in results:
results[metric] = results[metric].split(' ')
val = results[metric][0]
ci_low, ci_high = results[metric][1].split('(')[1].split(')')[0].split('-')
results[metric] = val, ci_low, ci_high
results[metric] = [float(x) for x in results[metric]]
return results
formatted_results = {}
# for cancer_type in results:
for cancer_type in sorted(selected_cancer_types):
formatted_results[cancer_type] = format_bootstrap_output(results[cancer_type])
formatted_results
```
# Result graph
Exclude cancer types with less than a chosen minimum number of patients, to avoid extremely noisy results.
```
utils.plot.show_default_colors()
PLOT_SIZE = (15, 4)
default_colors = plt.rcParams['axes.prop_cycle'].by_key()['color']
def get_metric_results(metric, data):
df = pd.DataFrame()
df['Cancer type'] = data.keys()
val, err = [], []
for cancer in formatted_results:
values = formatted_results[cancer][metric]
val.append(values[0])
err.append((values[0] - values[1], values[2] - values[0]))
df[metric] = val
err = np.swapaxes(np.array(err), 1, 0)
return df, err
def plot_results(metric, data, ci, y_lim=None, y_label=None, h_lines=[1, 0.5]):
fig = plt.figure(figsize=PLOT_SIZE)
ax = fig.add_subplot(1, 1, 1)
for y in h_lines:
ax.axhline(y, linestyle='--', color='grey')
ax.bar(df['Cancer type'][:1], df[metric][:1], yerr=err[:, :1],
align='center', ecolor=default_colors[0],
alpha=0.5, capsize=5)
ax.bar(df['Cancer type'][1:], df[metric][1:], yerr=err[:, 1:],
align='center', color=default_colors[6], ecolor=default_colors[6],
alpha=0.5, capsize=5)
if y_lim is None:
y_lim = (0, 1)
ax.set_ylim(y_lim)
ax.set_title('')
ax.set_xlabel('Cancer types')
if y_label is None:
ax.set_ylabel(metric + ' (95% CI)')
else:
ax.set_ylabel(y_label)
return fig
metric='Ctd'
df, err = get_metric_results(metric, formatted_results)
fig_ctd = plot_results(metric, df, err, y_label='$C^{td}$ (95% CI)')
metric='IBS'
df, err = get_metric_results(metric, formatted_results)
fig_ibs = plot_results(metric, df, err, y_lim=(0, 0.35), y_label=None, h_lines=[0.25])
```
## Save to files
```
%%javascript
IPython.notebook.kernel.execute('nb_name = "' + IPython.notebook.notebook_name + '"')
pdf_file = nb_name.split('.ipynb')[0] + '_Ctd'
utils.plot.save_plot_for_figure(figure=fig_ctd, file_name=pdf_file)
pdf_file = nb_name.split('.ipynb')[0] + '_IBS'
utils.plot.save_plot_for_figure(figure=fig_ibs, file_name=pdf_file)
pdf_file = nb_name.split('.ipynb')[0] + '_INBLL'
utils.plot.save_plot_for_figure(figure=fig_inbll, file_name=pdf_file)
```
# Watermark<a class='tocSkip'></a>
```
%watermark --iversions
%watermark -v
print()
%watermark -u -n
```
[Top of the page](#Top)
|
github_jupyter
|
## **Initialize the connection**
```
import sqlalchemy, os
from sqlalchemy import create_engine
import pandas as pd
import matplotlib
import matplotlib.pyplot as plt
%matplotlib inline
%reload_ext sql
%config SqlMagic.displaylimit = 5
%config SqlMagic.feedback = False
%config SqlMagic.autopandas = True
hxe_connection = 'hana://ML_USER:Welcome18@hxehost:39015';
%sql $hxe_connection
pd.options.display.max_rows = 1000
pd.options.display.max_colwidth = 1000
```
# **Lag 1 And Cycles**
## Visualize the data
```
%%sql
result <<
select
l1cnn.time, l1cnn.signal as signal , l1cwn.signal as signal_wn, l1cnn.signal - l1cwn.signal as delta
from
forecast_lag_1_and_cycles l1cnn
join forecast_lag_1_and_cycles_and_wn l1cwn
on l1cnn.time = l1cwn.time
result = %sql select \
l1cnn.time, l1cnn.signal as signal , l1cwn.signal as signal_wn, l1cnn.signal - l1cwn.signal as delta \
from \
forecast_lag_1_and_cycles l1cnn \
join forecast_lag_1_and_cycles_and_wn l1cwn \
on l1cnn.time = l1cwn.time
time = matplotlib.dates.date2num(result.time)
fig, ax = plt.subplots()
ax.plot(time, result.signal, 'ro-', markersize=2, color='blue')
ax.plot(time, result.signal_wn, 'ro-', markersize=2, color='red')
ax.bar (time, result.delta , color='green')
ax.xaxis_date()
fig.autofmt_xdate()
fig.set_size_inches(20, 12)
plt.show()
```
## **Dates & intervals**
```
%%sql
select 'max' as indicator, to_varchar(max(time)) as value
from forecast_lag_1_and_cycles union all
select 'min' , to_varchar(min(time))
from forecast_lag_1_and_cycles union all
select 'delta days' , to_varchar(days_between(min(time), max(time)))
from forecast_lag_1_and_cycles union all
select 'count' , to_varchar(count(1))
from forecast_lag_1_and_cycles
%%sql
select 'max' as indicator, to_varchar(max(time)) as value
from forecast_lag_1_and_cycles_and_wn union all
select 'min' , to_varchar(min(time))
from forecast_lag_1_and_cycles_and_wn union all
select 'delta days' , to_varchar(days_between(min(time), max(time)))
from forecast_lag_1_and_cycles_and_wn union all
select 'count' , to_varchar(count(1))
from forecast_lag_1_and_cycles_and_wn
%%sql
select interval, count(1) as count
from (
select days_between (lag(time) over (order by time asc), time) as interval
from forecast_lag_1_and_cycles
order by time asc
)
where interval is not null
group by interval;
```
## **Generic statistics**
```
%%sql
with data as (
select l1cnn.signal as value_nn, l1cwn.signal as value_wn
from forecast_lag_1_and_cycles l1cnn join forecast_lag_1_and_cycles_and_wn l1cwn on l1cnn.time = l1cwn.time
)
select 'max' as indicator , round(max(value_nn), 2) as value_nn
, round(max(value_wn), 2) as value_wn from data union all
select 'min' , round(min(value_nn), 2)
, round(min(value_wn), 2) from data union all
select 'delta min/max' , round(max(value_nn) - min(value_nn), 2)
, round(max(value_wn) - min(value_wn), 2) from data union all
select 'avg' , round(avg(value_nn), 2)
, round(avg(value_wn), 2) from data union all
select 'median' , round(median(value_nn), 2)
, round(median(value_wn), 2) from data union all
select 'stddev' , round(stddev(value_nn), 2)
, round(stddev(value_wn), 2) from data
result = %sql select row_number() over (order by signal asc) as row_num, signal from forecast_lag_1_and_cycles order by 1, 2;
result_wn = %sql select row_number() over (order by signal asc) as row_num, signal from forecast_lag_1_and_cycles_and_wn order by 1, 2;
fig, ax = plt.subplots()
ax.plot(result.row_num, result.signal, 'ro-', markersize=2, color='blue')
ax.plot(result_wn.row_num, result_wn.signal, 'ro-', markersize=2, color='red')
fig.set_size_inches(20, 12)
plt.show()
```
## **Data Distribution**
```
%%sql
with data as (
select ntile(10) over (order by signal asc) as tile, signal
from forecast_lag_1_and_cycles
where signal is not null
)
select tile
, round(max(signal), 2) as max
, round(min(signal), 2) as min
, round(max(signal) - min(signal), 2) as "delta min/max"
, round(avg(signal), 2) as avg
, round(median(signal), 2) as median
, round(abs(avg(signal) - median(signal)), 2) as "delta avg/median"
, round(stddev(signal), 2) as stddev
from data
group by tile
%%sql
with data as (
select ntile(10) over (order by signal asc) as tile, signal
from forecast_lag_1_and_cycles_and_wn
where signal is not null
)
select tile
, round(max(signal), 2) as max
, round(min(signal), 2) as min
, round(max(signal) - min(signal), 2) as "delta min/max"
, round(avg(signal), 2) as avg
, round(median(signal), 2) as median
, round(abs(avg(signal) - median(signal)), 2) as "delta avg/median"
, round(stddev(signal), 2) as stddev
from data
group by tile
%%sql
with data as (
select ntile(12) over (order by signal asc) as tile, signal
from forecast_lag_1_and_cycles
where signal is not null
)
select tile
, round(max(signal), 2) as max
, round(min(signal), 2) as min
, round(max(signal) - min(signal), 2) as "delta min/max"
, round(avg(signal), 2) as avg
, round(median(signal), 2) as median
, round(abs(avg(signal) - median(signal)), 2) as "delta avg/median"
, round(stddev(signal), 2) as stddev
from data
group by tile
```
|
github_jupyter
|
# Preprocessing for numerical features
In this notebook, we will still use only numerical features.
We will introduce these new aspects:
* an example of preprocessing, namely **scaling numerical variables**;
* using a scikit-learn **pipeline** to chain preprocessing and model
training;
* assessing the generalization performance of our model via **cross-validation**
instead of a single train-test split.
## Data preparation
First, let's load the full adult census dataset.
```
import pandas as pd
adult_census = pd.read_csv("../datasets/adult-census.csv")
# to display nice model diagram
from sklearn import set_config
set_config(display='diagram')
```
We will now drop the target from the data we will use to train our
predictive model.
```
target_name = "class"
target = adult_census[target_name]
data = adult_census.drop(columns=target_name)
```
Then, we select only the numerical columns, as seen in the previous
notebook.
```
numerical_columns = [
"age", "capital-gain", "capital-loss", "hours-per-week"]
data_numeric = data[numerical_columns]
```
Finally, we can divide our dataset into a train and test sets.
```
from sklearn.model_selection import train_test_split
data_train, data_test, target_train, target_test = train_test_split(
data_numeric, target, random_state=42)
```
## Model fitting with preprocessing
A range of preprocessing algorithms in scikit-learn allow us to transform
the input data before training a model. In our case, we will standardize the
data and then train a new logistic regression model on that new version of
the dataset.
Let's start by printing some statistics about the training data.
```
data_train.describe()
```
We see that the dataset's features span across different ranges. Some
algorithms make some assumptions regarding the feature distributions and
usually normalizing features will be helpful to address these assumptions.
<div class="admonition tip alert alert-warning">
<p class="first admonition-title" style="font-weight: bold;">Tip</p>
<p>Here are some reasons for scaling features:</p>
<ul class="last simple">
<li>Models that rely on the distance between a pair of samples, for instance
k-nearest neighbors, should be trained on normalized features to make each
feature contribute approximately equally to the distance computations.</li>
<li>Many models such as logistic regression use a numerical solver (based on
gradient descent) to find their optimal parameters. This solver converges
faster when the features are scaled.</li>
</ul>
</div>
Whether or not a machine learning model requires scaling the features depends
on the model family. Linear models such as logistic regression generally
benefit from scaling the features while other models such as decision trees
do not need such preprocessing (but will not suffer from it).
We show how to apply such normalization using a scikit-learn transformer
called `StandardScaler`. This transformer shifts and scales each feature
individually so that they all have a 0-mean and a unit standard deviation.
We will investigate different steps used in scikit-learn to achieve such a
transformation of the data.
First, one needs to call the method `fit` in order to learn the scaling from
the data.
```
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(data_train)
```
The `fit` method for transformers is similar to the `fit` method for
predictors. The main difference is that the former has a single argument (the
data matrix), whereas the latter has two arguments (the data matrix and the
target).

In this case, the algorithm needs to compute the mean and standard deviation
for each feature and store them into some NumPy arrays. Here, these
statistics are the model states.
<div class="admonition note alert alert-info">
<p class="first admonition-title" style="font-weight: bold;">Note</p>
<p class="last">The fact that the model states of this scaler are arrays of means and
standard deviations is specific to the <tt class="docutils literal">StandardScaler</tt>. Other
scikit-learn transformers will compute different statistics and store them
as model states, in the same fashion.</p>
</div>
We can inspect the computed means and standard deviations.
```
scaler.mean_
scaler.scale_
```
<div class="admonition note alert alert-info">
<p class="first admonition-title" style="font-weight: bold;">Note</p>
<p class="last">scikit-learn convention: if an attribute is learned from the data, its name
ends with an underscore (i.e. <tt class="docutils literal">_</tt>), as in <tt class="docutils literal">mean_</tt> and <tt class="docutils literal">scale_</tt> for the
<tt class="docutils literal">StandardScaler</tt>.</p>
</div>
Scaling the data is applied to each feature individually (i.e. each column in
the data matrix). For each feature, we subtract its mean and divide by its
standard deviation.
Once we have called the `fit` method, we can perform data transformation by
calling the method `transform`.
```
data_train_scaled = scaler.transform(data_train)
data_train_scaled
```
Let's illustrate the internal mechanism of the `transform` method and put it
to perspective with what we already saw with predictors.

The `transform` method for transformers is similar to the `predict` method
for predictors. It uses a predefined function, called a **transformation
function**, and uses the model states and the input data. However, instead of
outputting predictions, the job of the `transform` method is to output a
transformed version of the input data.
Finally, the method `fit_transform` is a shorthand method to call
successively `fit` and then `transform`.

```
data_train_scaled = scaler.fit_transform(data_train)
data_train_scaled
data_train_scaled = pd.DataFrame(data_train_scaled,
columns=data_train.columns)
data_train_scaled.describe()
```
We can easily combine these sequential operations with a scikit-learn
`Pipeline`, which chains together operations and is used as any other
classifier or regressor. The helper function `make_pipeline` will create a
`Pipeline`: it takes as arguments the successive transformations to perform,
followed by the classifier or regressor model.
```
import time
from sklearn.linear_model import LogisticRegression
from sklearn.pipeline import make_pipeline
model = make_pipeline(StandardScaler(), LogisticRegression())
model
```
The `make_pipeline` function did not require us to give a name to each step.
Indeed, it was automatically assigned based on the name of the classes
provided; a `StandardScaler` will be a step named `"standardscaler"` in the
resulting pipeline. We can check the name of each steps of our model:
```
model.named_steps
```
This predictive pipeline exposes the same methods as the final predictor:
`fit` and `predict` (and additionally `predict_proba`, `decision_function`,
or `score`).
```
start = time.time()
model.fit(data_train, target_train)
elapsed_time = time.time() - start
```
We can represent the internal mechanism of a pipeline when calling `fit`
by the following diagram:

When calling `model.fit`, the method `fit_transform` from each underlying
transformer (here a single transformer) in the pipeline will be called to:
- learn their internal model states
- transform the training data. Finally, the preprocessed data are provided to
train the predictor.
To predict the targets given a test set, one uses the `predict` method.
```
predicted_target = model.predict(data_test)
predicted_target[:5]
```
Let's show the underlying mechanism:

The method `transform` of each transformer (here a single transformer) is
called to preprocess the data. Note that there is no need to call the `fit`
method for these transformers because we are using the internal model states
computed when calling `model.fit`. The preprocessed data is then provided to
the predictor that will output the predicted target by calling its method
`predict`.
As a shorthand, we can check the score of the full predictive pipeline
calling the method `model.score`. Thus, let's check the computational and
generalization performance of such a predictive pipeline.
```
model_name = model.__class__.__name__
score = model.score(data_test, target_test)
print(f"The accuracy using a {model_name} is {score:.3f} "
f"with a fitting time of {elapsed_time:.3f} seconds "
f"in {model[-1].n_iter_[0]} iterations")
```
We could compare this predictive model with the predictive model used in
the previous notebook which did not scale features.
```
model = LogisticRegression()
start = time.time()
model.fit(data_train, target_train)
elapsed_time = time.time() - start
model_name = model.__class__.__name__
score = model.score(data_test, target_test)
print(f"The accuracy using a {model_name} is {score:.3f} "
f"with a fitting time of {elapsed_time:.3f} seconds "
f"in {model.n_iter_[0]} iterations")
```
We see that scaling the data before training the logistic regression was
beneficial in terms of computational performance. Indeed, the number of
iterations decreased as well as the training time. The generalization
performance did not change since both models converged.
<div class="admonition warning alert alert-danger">
<p class="first admonition-title" style="font-weight: bold;">Warning</p>
<p class="last">Working with non-scaled data will potentially force the algorithm to iterate
more as we showed in the example above. There is also the catastrophic
scenario where the number of required iterations are more than the maximum
number of iterations allowed by the predictor (controlled by the <tt class="docutils literal">max_iter</tt>)
parameter. Therefore, before increasing <tt class="docutils literal">max_iter</tt>, make sure that the data
are well scaled.</p>
</div>
## Model evaluation using cross-validation
In the previous example, we split the original data into a training set and a
testing set. The score of a model will in general depend on the way we make
such a split. One downside of doing a single split is that it does not give
any information about this variability. Another downside, in a setting where
the amount of data is small, is that the the data available for training
and testing will be even smaller after splitting.
Instead, we can use cross-validation. Cross-validation consists of repeating
the procedure such that the training and testing sets are different each
time. Generalization performance metrics are collected for each repetition and
then aggregated. As a result we can get an estimate of the variability of the
model's generalization performance.
Note that there exists several cross-validation strategies, each of them
defines how to repeat the `fit`/`score` procedure. In this section, we will
use the K-fold strategy: the entire dataset is split into `K` partitions. The
`fit`/`score` procedure is repeated `K` times where at each iteration `K - 1`
partitions are used to fit the model and `1` partition is used to score. The
figure below illustrates this K-fold strategy.

<div class="admonition note alert alert-info">
<p class="first admonition-title" style="font-weight: bold;">Note</p>
<p class="last">This figure shows the particular case of K-fold cross-validation strategy.
As mentioned earlier, there are a variety of different cross-validation
strategies. Some of these aspects will be covered in more details in future
notebooks.</p>
</div>
For each cross-validation split, the procedure trains a model on all the red
samples and evaluate the score of the model on the blue samples.
Cross-validation is therefore computationally intensive because it requires
training several models instead of one.
In scikit-learn, the function `cross_validate` allows to do cross-validation
and you need to pass it the model, the data, and the target. Since there
exists several cross-validation strategies, `cross_validate` takes a
parameter `cv` which defines the splitting strategy.
```
%%time
from sklearn.model_selection import cross_validate
model = make_pipeline(StandardScaler(), LogisticRegression())
cv_result = cross_validate(model, data_numeric, target, cv=5)
cv_result
```
The output of `cross_validate` is a Python dictionary, which by default
contains three entries: (i) the time to train the model on the training data
for each fold, (ii) the time to predict with the model on the testing data
for each fold, and (iii) the default score on the testing data for each fold.
Setting `cv=5` created 5 distinct splits to get 5 variations for the training
and testing sets. Each training set is used to fit one model which is then
scored on the matching test set. This strategy is called K-fold
cross-validation where `K` corresponds to the number of splits.
Note that by default the `cross_validate` function discards the 5 models that
were trained on the different overlapping subset of the dataset. The goal of
cross-validation is not to train a model, but rather to estimate
approximately the generalization performance of a model that would have been
trained to the full training set, along with an estimate of the variability
(uncertainty on the generalization accuracy).
You can pass additional parameters to `cross_validate` to get more
information, for instance training scores. These features will be covered in
a future notebook.
Let's extract the test scores from the `cv_result` dictionary and compute
the mean accuracy and the variation of the accuracy across folds.
```
scores = cv_result["test_score"]
print("The mean cross-validation accuracy is: "
f"{scores.mean():.3f} +/- {scores.std():.3f}")
```
Note that by computing the standard-deviation of the cross-validation scores,
we can estimate the uncertainty of our model generalization performance. This is
the main advantage of cross-validation and can be crucial in practice, for
example when comparing different models to figure out whether one is better
than the other or whether the generalization performance differences are within
the uncertainty.
In this particular case, only the first 2 decimals seem to be trustworthy. If
you go up in this notebook, you can check that the performance we get
with cross-validation is compatible with the one from a single train-test
split.
In this notebook we have:
* seen the importance of **scaling numerical variables**;
* used a **pipeline** to chain scaling and logistic regression training;
* assessed the generalization performance of our model via **cross-validation**.
|
github_jupyter
|
Notebook - análise exploratória de dados
Gabriela Caesar
29/set/2021
Pergunta a ser respondida
- Defina a sua UF e o ano no input e veja as estatísticas básicas da sua UF/ano quanto ao casamento LGBT
```
# importacao da biblioteca
import pandas as pd
# leitura do dataframe
lgbt_casamento = pd.read_csv('https://raw.githubusercontent.com/gabrielacaesar/lgbt_casamento/main/data/lgbt_casamento.csv')
lgbt_casamento.head(2)
sigla_uf = pd.read_csv('https://raw.githubusercontent.com/kelvins/Municipios-Brasileiros/main/csv/estados.csv')
sigla_uf.head(2)
sigla_uf_lgbt_casamento = lgbt_casamento.merge(sigla_uf, how = 'left', left_on = 'uf', right_on = 'nome')
len(sigla_uf_lgbt_casamento['uf_y'].unique())
sigla_uf_lgbt_casamento.head(2)
sigla_uf_lgbt_casamento = sigla_uf_lgbt_casamento.drop(['uf_x', 'codigo_uf', 'latitude', 'longitude'], axis=1)
sigla_uf_lgbt_casamento = sigla_uf_lgbt_casamento.rename(columns={'uf_y':'uf', 'nome': 'nome_uf'})
sigla_uf_lgbt_casamento.columns
sigla_uf_lgbt_casamento.head(2)
print(" --------------------------- \n Bem-vindo/a! \n ---------------------------")
ano_user = int(input("Escolha um ano de 2013 a 2019: \n"))
uf_user = input("Escolha uma UF. Por exemplo, AC, AL, SP, RJ... \n")
uf_user = uf_user.upper().strip()
#print(uf_user)
print(" --------------------------- \n Já vamos calcular! \n ---------------------------")
```
# Veja os números, por mês, no ano e na UF de escolha
Gráfico mostra o número de casamentos LGBTs, por gênero, no ano e na unidade federativa informada antes pelo usuário.
Passe o mouse em cima do gráfico para mais detalhes.
```
# filtro pela UF e pelo ano informados pelo usuário
# mais gráfico
import altair as alt
alt.Chart(sigla_uf_lgbt_casamento.query('uf == @uf_user & ano == @ano_user', engine='python')).mark_line(point=True).encode(
x = alt.X('mes', title = 'Mês', sort=['Janeiro', 'Fevereiro', 'Março']),
y = alt.Y('numero', title='Número'),
color = 'genero',
tooltip = ['mes', 'ano', 'genero', 'numero']
).properties(
title = f'{uf_user}: Casamento LGBTs em {ano_user}'
).interactive()
```
# Veja as estatísticas básicas, por ano, na sua UF de escolha
Gráfico mostra todos os anos da base de dados. A unidade federativa foi informada antes pelo usuário.
Passe o mouse em cima do gráfico para mais detalhes.
```
dados_user = sigla_uf_lgbt_casamento.query('uf == @uf_user', engine='python')
alt.Chart(dados_user).mark_boxplot(size=10).encode(
x = alt.X('ano:O', title="Ano"),
y = alt.Y('numero', title="Número"),
color = 'genero',
tooltip = ['mes', 'ano', 'genero', 'numero']
).properties(
title={
"text": [f'{uf_user}: Casamento LGBTs'],
"subtitle": [f'Mulheres vs. Homens']
},
width=600,
height=300
).interactive()
```
|
github_jupyter
|
# `model_hod` module tutorial notebook
```
%load_ext autoreload
%autoreload 2
%pylab inline
import logging
mpl_logger = logging.getLogger('matplotlib')
mpl_logger.setLevel(logging.WARNING)
pil_logger = logging.getLogger('PIL')
plt.rcParams['font.family'] = 'sans-serif'
plt.rcParams['font.size'] = 18
plt.rcParams['axes.linewidth'] = 1.5
plt.rcParams['xtick.major.size'] = 5
plt.rcParams['ytick.major.size'] = 5
plt.rcParams['xtick.minor.size'] = 3
plt.rcParams['ytick.minor.size'] = 3
plt.rcParams['xtick.top'] = True
plt.rcParams['ytick.right'] = True
plt.rcParams['xtick.minor.visible'] = True
plt.rcParams['ytick.minor.visible'] = True
plt.rcParams['xtick.direction'] = 'in'
plt.rcParams['ytick.direction'] = 'in'
plt.rcParams['figure.figsize'] = (10,6)
from dark_emulator import model_hod
hod = model_hod.darkemu_x_hod({"fft_num":8})
```
## how to set cosmology and galaxy parameters (HOD, off-centering, satellite distribution, and incompleteness)
```
cparam = np.array([0.02225,0.1198,0.6844,3.094,0.9645,-1.])
hod.set_cosmology(cparam)
gparam = {"logMmin":13.13, "sigma_sq":0.22, "logM1": 14.21, "alpha": 1.13, "kappa": 1.25, # HOD parameters
"poff": 0.2, "Roff": 0.1, # off-centering parameters p_off is the fraction of off-centered galaxies. Roff is the typical off-centered scale with respect to R200m.
"sat_dist_type": "emulator", # satellite distribution. Chosse emulator of NFW. In the case of NFW, the c-M relation by Diemer & Kravtsov (2015) is assumed.
"alpha_inc": 0.44, "logM_inc": 13.57} # incompleteness parameters. For details, see More et al. (2015)
hod.set_galaxy(gparam)
```
## how to plot g-g lensing signal in DeltaSigma(R)
```
redshift = 0.55
r = np.logspace(-1,2,100)
plt.figure(figsize=(10,6))
plt.loglog(r, hod.get_ds(r, redshift), linewidth = 2, color = "k", label = "total")
plt.loglog(r, hod.get_ds_cen(r, redshift), "--", color = "k", label = "central")
plt.loglog(r, hod.get_ds_cen_off(r, redshift), ":", color = "k", label = "central w/offset")
plt.loglog(r, hod.get_ds_sat(r, redshift), "-.", color = "k", label = "satellite")
plt.xlabel(r"$R$ [Mpc/h]")
plt.ylabel(r"$\Delta\Sigma$ [hM$_\odot$/pc$^2$]")
plt.legend()
```
## how to plot g-g lensing signal in xi
```
redshift = 0.55
r = np.logspace(-1,2,100)
plt.figure(figsize=(10,6))
plt.loglog(r, hod.get_xi_gm(r, redshift), linewidth = 2, color = "k", label = "total")
plt.loglog(r, hod.get_xi_gm_cen(r, redshift), "--", color = "k", label = "central")
plt.loglog(r, hod.get_xi_gm_cen_off(r, redshift), ":", color = "k", label = "central w/offset")
plt.loglog(r, hod.get_xi_gm_sat(r, redshift), "-.", color = "k", label = "satellite")
plt.xlabel(r"$R$ [Mpc/h]")
plt.ylabel(r"$\xi_{\rm gm}$")
plt.legend()
```
## how to plot g-g clustering signal in wp
```
redshift = 0.55
rs = np.logspace(-1,2,100)
plt.figure(figsize=(10,6))
plt.loglog(r, hod.get_wp(r, redshift), linewidth = 2, color = "k", label = "total")
plt.loglog(r, hod.get_wp_1hcs(r, redshift), "--", color = "k", label = "1-halo cen-sat")
plt.loglog(r, hod.get_wp_1hss(r, redshift), ":", color = "k", label = "1-halo sat-sat")
plt.loglog(r, hod.get_wp_2hcc(r, redshift), "-.", color = "k", label = "2-halo cen-cen")
plt.loglog(r, hod.get_wp_2hcs(r, redshift), dashes=[4,1,1,1,1,1], color = "k", label = "2-halo cen-sat")
plt.loglog(r, hod.get_wp_2hss(r, redshift), dashes=[4,1,1,1,4,1], color = "k", label = "2-halo sat-sat")
plt.xlabel(r"$R$ [Mpc/h]")
plt.ylabel(r"$w_p$ [Mpc/h]")
plt.legend()
plt.ylim(0.1, 6e3)
```
## how to plot g-g clustering signal in xi
```
redshift = 0.55
rs = np.logspace(-1,2,100)
plt.figure(figsize=(10,6))
plt.loglog(r, hod.get_xi_gg(r, redshift), linewidth = 2, color = "k", label = "total")
plt.loglog(r, hod.get_xi_gg_1hcs(r, redshift), "--", color = "k", label = "1-halo cen-sat")
plt.loglog(r, hod.get_xi_gg_1hss(r, redshift), ":", color = "k", label = "1-halo sat-sat")
plt.loglog(r, hod.get_xi_gg_2hcc(r, redshift), "-.", color = "k", label = "2-halo cen-cen")
plt.loglog(r, hod.get_xi_gg_2hcs(r, redshift), dashes=[4,1,1,1,1,1], color = "k", label = "2-halo cen-sat")
plt.loglog(r, hod.get_xi_gg_2hss(r, redshift), dashes=[4,1,1,1,4,1], color = "k", label = "2-halo sat-sat")
plt.xlabel(r"$R$ [Mpc/h]")
plt.ylabel(r"$\xi$")
plt.legend()
plt.ylim(1e-3, 6e3)
```
|
github_jupyter
|
# Premier league: How has VAR impacted the rankings?
There has been much debate about the video assistant referee (VAR) when it was introduced last year (in 2019).
The goal is to lead to fairer refereeing, but concerns are high on whether this will really be the case and the fact that it could break the rythm of the game.
We will let football analysts – or soccer analysts depending on where you are reading this notebook from – answer this question. But one thing we can look at is how has VAR impacted the league so far.
This is what we will do in this notebook, alongside some other simulations we found interesting.
<div style="text-align:center"><a href="https://www.atoti.io/?utm_source=gallery&utm_content=premier-league" target="_blank" rel="noopener noreferrer"><img src="https://data.atoti.io/notebooks/banners/discover.png" alt="atoti" /></a></div>
## Importing the data
The data we will use is composed of events. An event can be anything that happens in a game: kick-off, goal, foul, etc.
In this dataset, we only kept kick-off and goal events to build our analysis.
Note that in the goal events we also have all the goals that were later cancelled by VAR during a game.
We will first start by importing atoti and creating a session.
```
import atoti as tt
session = tt.create_session()
```
Then load the events in a store
```
events = session.read_csv(
"s3://data.atoti.io/notebooks/premier-league/events.csv",
separator=";",
table_name="events",
)
events.head()
```
### Creating a cube
We create a cube on the event store so that some matches or teams that ended with no goal will still be reflected in the pivot tables.
When creating a cube in the default auto mode, a hierarchy will be created for each non float column, and average and sum measures for each float column. This setup can later be edited, or you could also define all hierarchies/measures by yourself switching to manual mode.
```
cube = session.create_cube(events)
cube.schema
```
Let's assign measures/levels/hierarchies to shorter variables
```
m = cube.measures
lvl = cube.levels
h = cube.hierarchies
h["Day"] = [events["Day"]]
```
## Computing the rankings from the goals
Computing the first measure below to count the total goals scored for each event. At this point the total still includes the potential own goals and VAR-refused goals.
```
m["Team Goals (incl Own Goals)"] = tt.agg.sum(
tt.where(lvl["EventType"] == "Goal", tt.agg.count_distinct(events["EventId"]), 0.0),
scope=tt.scope.origin(lvl["EventType"]),
)
```
In this data format, own goals are scored by players from a Team, but those points should be attributed to the opponent. Therefore we will isolate the own goals in a separate measure.
```
m["Team Own Goals"] = tt.agg.sum(
tt.where(lvl["IsOwnGoal"] == True, m["Team Goals (incl Own Goals)"], 0.0),
scope=tt.scope.origin(lvl["IsOwnGoal"]),
)
```
And deduce the actual goals scored for the team
```
m["Team Goals"] = m["Team Goals (incl Own Goals)"] - m["Team Own Goals"]
```
At this point we can already have a look at the goals per team. By right clicking on the chart we have sorted it descending by team goals.
```
session.visualize()
```
For a particular match, the `Opponent Goals` are equal to the `Team Goals` if we switch to the data facts where Team is replaced by Opponent and Opponent by Team
```
m["Opponent Goals"] = tt.agg.sum(
tt.at(
m["Team Goals"],
{lvl["Team"]: lvl["Opponent"], lvl["Opponent"]: lvl["Team"]},
),
scope=tt.scope.origin(lvl["Team"], lvl["Opponent"]),
)
m["Opponent Own Goals"] = tt.agg.sum(
tt.at(
m["Team Own Goals"],
{lvl["Team"]: lvl["Opponent"], lvl["Opponent"]: lvl["Team"]},
),
scope=tt.scope.origin(lvl["Team"], lvl["Opponent"]),
)
```
We are now going to add two measures `Team Score` and `Opponent Score` to compute the result of a particular match.
```
m["Team Score"] = m["Team Goals"] + m["Opponent Own Goals"]
m["Opponent Score"] = m["Opponent Goals"] + m["Team Own Goals"]
```
We can now visualize the result of each match of the season
```
session.visualize()
```
We now have the team goals/score and those of the opponent for each match. However, these measures include VAR cancelled goals. Let's create new measures that takes into account VAR.
```
m["VAR team goals impact"] = m["Team Goals"] - tt.filter(
m["Team Goals"], lvl["IsCancelledAfterVAR"] == False
)
m["VAR opponent goals impact"] = m["Opponent Goals"] - tt.filter(
m["Opponent Goals"], lvl["IsCancelledAfterVAR"] == False
)
```
We can visualize that in details, there are already 4 goals cancelled by VAR on the first day of the season !
```
session.visualize()
```
Now that for any game we have the number of goals of each team, we can compute how many points teams have earned.
Following the FIFA World Cup points system, three points are awarded for a win, one for a draw and none for a loss (before, winners received two points).
We create a measure for each of this condition.
```
m["Points for victory"] = 3.0
m["Points for tie"] = 1.0
m["Points for loss"] = 0.0
m["Points"] = tt.agg.sum(
tt.where(
m["Team Score"] > m["Opponent Score"],
m["Points for victory"],
tt.where(
m["Team Score"] == m["Opponent Score"],
m["Points for tie"],
m["Points for loss"],
),
),
scope=tt.scope.origin(lvl["League"], lvl["Day"], lvl["Team"]),
)
```
The previous points were computed including VAR-refused goals.
Filtering out these goals gives the actual rankings of the teams, as you would find on any sports websites.
```
m["Actual Points"] = tt.filter(m["Points"], lvl["IsCancelledAfterVAR"] == False)
```
And here we have our ranking. We will dive into it in the next section.
## Rankings and VAR impact
Color rules were added to show teams that benefited from the VAR in green and those who lost championship points because of it in red.
```
m["Difference in points"] = m["Actual Points"] - m["Points"]
session.visualize()
```
More than half of the teams have had their points total impacted by VAR.
Though it does not impact the top teams, it definitely has an impact in the ranking of many teams, Manchester United would have lost 2 ranks and Tottenham 4 for example!
We could also visualize the difference of points in a more graphical way:
```
session.visualize()
```
Since the rankings are computed from the goal level, we can perform any kind of simulation we want using simple UI filters.
You can filter the pivot table above to see what would happen if we only keep the first half of the games? If we only keep matches played home? What if we filter out Vardy, would Leicester lose some places?
Note that if you filter out VAR-refused goals, the `Points` measures takes the same value as the `Actual Points`.
## Evolution of the rankings over time
Atoti also enables you to define cumulative sums over a hierarchy, we will use that to see how the team rankings evolved during the season.
```
m["Points cumulative sum"] = tt.agg.sum(
m["Actual Points"], scope=tt.scope.cumulative(lvl["Day"])
)
session.visualize()
```
We can notice that data is missing for the 28th match of Manchester City. This is because the game was delayed due to weather, and then never played because of the COVID-19 pandemic.
## Players most impacted by the VAR
Until now we looked at most results at team level, but since the data exists at goal level, we could have a look at which players are most impacted by the VAR.
```
m["Valid player goals"] = tt.filter(
m["Team Goals"], lvl["IsCancelledAfterVAR"] == False
)
session.visualize()
```
Unsurprisingly Mané is the most impacted player. He is also one of the top scorers with only Vardy scoring more goals (you can sort on the Team Goals column to verify).
More surprisingly, Boly has had all the goals of his season cancelled by VAR and Antonio half of them..
## Simulation of a different scoring system
Although we are all used to a scoring system giving 3 points for a victory, 1 for a tie and 0 per lost match this was not always the case. Before the 1990's many european leagues only gave 2 points per victory, reason for the change being to encourage teams to score more goals during the games.
The premier league gifts us well with plenty of goals scored (take it from someone watching the French ligue 1), but how different would the results be with the old scoring system?
atoti enables us to simulate this very easily. We simply have to create a new scenario where we replace the number of points given for a victory.
We first setup a simulation on that measure.
```
scoring_system_simulation = cube.create_parameter_simulation(
name="Scoring system simulations",
measures={"Points for victory": 3.0},
base_scenario_name="Current System",
)
```
And create a new scenario where we give it another value
```
scoring_system_simulation += ("Old system", 2.0)
```
And that's it, no need to define anything else, all the measures will be re-computed on demand with the new value in the new scenario.
Let's compare the rankings between the two scoring systems.
```
session.visualize()
session.visualize()
```
Surprisingly, having only 2 points for a win would only have made Burnley and West Ham lose 2 ranks, but no other real impact on the standings.
<div style="text-align:center"><a href="https://www.atoti.io/?utm_source=gallery&utm_content=premier-league" target="_blank" rel="noopener noreferrer"><img src="https://data.atoti.io/notebooks/banners/discover-try.png" alt="atoti" /></a></div>
|
github_jupyter
|
```
#v1
#26/10/2018
dataname="epistroma" #should match the value used to train the network, will be used to load the appropirate model
gpuid=0
patch_size=256 #should match the value used to train the network
batch_size=1 #nicer to have a single batch so that we can iterately view the output, while not consuming too much
edge_weight=1
# https://github.com/jvanvugt/pytorch-unet
#torch.multiprocessing.set_start_method("fork")
import random, sys
import cv2
import glob
import math
import matplotlib.pyplot as plt
import numpy as np
import os
import scipy.ndimage
import skimage
import time
import tables
from skimage import io, morphology
from sklearn.metrics import confusion_matrix
from tensorboardX import SummaryWriter
import torch
import torch.nn.functional as F
from torch import nn
from torch.utils.data import DataLoader
from torchvision import transforms
from unet import UNet
import PIL
print(torch.cuda.get_device_properties(gpuid))
torch.cuda.set_device(gpuid)
device = torch.device(f'cuda:{gpuid}' if torch.cuda.is_available() else 'cpu')
checkpoint = torch.load(f"{dataname}_unet_best_model.pth")
#load the model, note that the paramters are coming from the checkpoint, since the architecture of the model needs to exactly match the weights saved
model = UNet(n_classes=checkpoint["n_classes"], in_channels=checkpoint["in_channels"], padding=checkpoint["padding"],depth=checkpoint["depth"],
wf=checkpoint["wf"], up_mode=checkpoint["up_mode"], batch_norm=checkpoint["batch_norm"]).to(device)
print(f"total params: \t{sum([np.prod(p.size()) for p in model.parameters()])}")
model.load_state_dict(checkpoint["model_dict"])
#this defines our dataset class which will be used by the dataloader
class Dataset(object):
def __init__(self, fname ,img_transform=None, mask_transform = None, edge_weight= False):
#nothing special here, just internalizing the constructor parameters
self.fname=fname
self.edge_weight = edge_weight
self.img_transform=img_transform
self.mask_transform = mask_transform
self.tables=tables.open_file(self.fname)
self.numpixels=self.tables.root.numpixels[:]
self.nitems=self.tables.root.img.shape[0]
self.tables.close()
self.img = None
self.mask = None
def __getitem__(self, index):
#opening should be done in __init__ but seems to be
#an issue with multithreading so doing here
if(self.img is None): #open in thread
self.tables=tables.open_file(self.fname)
self.img=self.tables.root.img
self.mask=self.tables.root.mask
#get the requested image and mask from the pytable
img = self.img[index,:,:,:]
mask = self.mask[index,:,:]
#the original Unet paper assignes increased weights to the edges of the annotated objects
#their method is more sophistocated, but this one is faster, we simply dilate the mask and
#highlight all the pixels which were "added"
if(self.edge_weight):
weight = scipy.ndimage.morphology.binary_dilation(mask==1, iterations =2) & ~mask
else: #otherwise the edge weight is all ones and thus has no affect
weight = np.ones(mask.shape,dtype=mask.dtype)
mask = mask[:,:,None].repeat(3,axis=2) #in order to use the transformations given by torchvision
weight = weight[:,:,None].repeat(3,axis=2) #inputs need to be 3D, so here we convert from 1d to 3d by repetition
img_new = img
mask_new = mask
weight_new = weight
seed = random.randrange(sys.maxsize) #get a random seed so that we can reproducibly do the transofrmations
if self.img_transform is not None:
random.seed(seed) # apply this seed to img transforms
img_new = self.img_transform(img)
if self.mask_transform is not None:
random.seed(seed)
mask_new = self.mask_transform(mask)
mask_new = np.asarray(mask_new)[:,:,0].squeeze()
random.seed(seed)
weight_new = self.mask_transform(weight)
weight_new = np.asarray(weight_new)[:,:,0].squeeze()
return img_new, mask_new, weight_new
def __len__(self):
return self.nitems
#note that since we need the transofrmations to be reproducible for both masks and images
#we do the spatial transformations first, and afterwards do any color augmentations
#in the case of using this for output generation, we want to use the original images since they will give a better sense of the exepected
#output when used on the rest of the dataset, as a result, we disable all unnecessary augmentation.
#the only component that remains here is the randomcrop, to ensure that regardless of the size of the image
#in the database, we extract an appropriately sized patch
img_transform = transforms.Compose([
transforms.ToPILImage(),
#transforms.RandomVerticalFlip(),
#transforms.RandomHorizontalFlip(),
transforms.RandomCrop(size=(patch_size,patch_size),pad_if_needed=True), #these need to be in a reproducible order, first affine transforms and then color
#transforms.RandomResizedCrop(size=patch_size),
#transforms.RandomRotation(180),
#transforms.ColorJitter(brightness=0, contrast=0, saturation=0, hue=.5),
#transforms.RandomGrayscale(),
transforms.ToTensor()
])
mask_transform = transforms.Compose([
transforms.ToPILImage(),
#transforms.RandomVerticalFlip(),
#transforms.RandomHorizontalFlip(),
transforms.RandomCrop(size=(patch_size,patch_size),pad_if_needed=True), #these need to be in a reproducible order, first affine transforms and then color
#transforms.RandomResizedCrop(size=patch_size,interpolation=PIL.Image.NEAREST),
#transforms.RandomRotation(180),
])
phases=["val"]
dataset={}
dataLoader={}
for phase in phases:
dataset[phase]=Dataset(f"./{dataname}_{phase}.pytable", img_transform=img_transform , mask_transform = mask_transform ,edge_weight=edge_weight)
dataLoader[phase]=DataLoader(dataset[phase], batch_size=batch_size,
shuffle=True, num_workers=0, pin_memory=True) #,pin_memory=True)
%matplotlib inline
#set the model to evaluation mode, since we're only generating output and not doing any back propogation
model.eval()
for ii , (X, y, y_weight) in enumerate(dataLoader["val"]):
X = X.to(device) # [NBATCH, 3, H, W]
y = y.type('torch.LongTensor').to(device) # [NBATCH, H, W] with class indices (0, 1)
output = model(X) # [NBATCH, 2, H, W]
output=output.detach().squeeze().cpu().numpy() #get output and pull it to CPU
output=np.moveaxis(output,0,-1) #reshape moving last dimension
fig, ax = plt.subplots(1,4, figsize=(10,4)) # 1 row, 2 columns
ax[0].imshow(output[:,:,1])
ax[1].imshow(np.argmax(output,axis=2))
ax[2].imshow(y.detach().squeeze().cpu().numpy())
ax[3].imshow(np.moveaxis(X.detach().squeeze().cpu().numpy(),0,-1))
```
|
github_jupyter
|
# CirComPara Pipeline
To demonstrate Dugong ́s effectiveness to distribute and run bioinformatics tools in alternative computational environments, the CirComPara pipeline was implemented in a Dugong container and tested in different OS with the aid of virtual machines (VM) or cloud computing servers.
CirComPara is a computational pipeline to detect, quantify, and correlate expression of linear and circular RNAs from RNA-seq data. Is a highly complex pipeline, which employs a series of bioinformatics software and was originally designed to run in an Ubuntu Server 16.04 LTS (x64).
Although authors provide details regarding the expected versions of each software and their dependency requirements, several problems can still be encountered during CirComPara implementation by inexperienced users.
See documentation for CirComPara installation details: https://github.com/egaffo/CirComPara
-----------------------------------------------------------------------------------------------------------------------
## Pipeline steps
- The test data is already unpacked and available in the path: **/headless/CirComPara/test_circompara/**
- The **meta.csv** and **vars.py** files are already configured to run CirComPara, as documented: https://github.com/egaffo/CirComPara
- Defining the folder for the analysis with the CirComPara of the test data provided by the developers of the tool:
```
from functools import partial
from os import chdir
chdir('/headless/CirComPara/test_circompara/analysis')
```
- Viewing files from /headless/CirComPara/test_circompara/
```
from IPython.display import FileLinks, FileLink
FileLinks('/headless/CirComPara/test_circompara/')
```
- Viewing the contents of the configuration file: vars.py
```
!cat /headless/CirComPara/test_circompara/analysis/vars.py
```
- Viewing the contents of the configuration file: meta.csv
```
!cat /headless/CirComPara/test_circompara/analysis/meta.csv
```
- Running CirCompara with test data
```
!../../circompara
```
-----------------------------------------------------------------------------------------------------------------------
## Results:
- Viewing output files after running CirComPara:
```
from IPython.display import FileLinks, FileLink
FileLinks('/headless/CirComPara/test_circompara/analysis/')
```
- Viewing graphic files after running CirComPara:
```
from IPython.display import Image
Image("/headless/CirComPara/test_circompara/analysis/circrna_analyze/Figs/corr_density_plot-1.png")
from IPython.display import Image
Image("/headless/CirComPara/test_circompara/analysis/circrna_analyze/Figs/cumulative_expression_box-1.png")
from IPython.display import Image
Image("/headless/CirComPara/test_circompara/analysis/circrna_analyze/Figs/show_circrnas_per_method-1.png")
from IPython.display import Image
Image("/headless/CirComPara/test_circompara/analysis/circrna_analyze/Figs/plot_circrnas_per_gene-1.png")
from IPython.display import Image
Image("/headless/CirComPara/test_circompara/analysis/circrna_analyze/Figs/correlations_box-1.png")
from IPython.display import Image
Image("/headless/CirComPara/test_circompara/analysis/circrna_analyze/Figs/plot_circrnas_2reads_2methods_sample-1.png")
from IPython.display import Image
Image("/headless/CirComPara/test_circompara/analysis/circrna_analyze/Figs/plot_circ_gene_expr-1.png")
from IPython.display import Image
Image("/headless/CirComPara/test_circompara/analysis/circrna_analyze/Figs/plot_gene_expressed_by_sample-1.png")
```
-----------------------------------------------------------------------------------------------------------------------
**NOTE:** This pipeline is just an example of what you can do with Dugong. I
|
github_jupyter
|
##### Copyright 2019 The TensorFlow Authors.
```
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
```
# Carregar dados NumPy
<table class="tfo-notebook-buttons" align="left">
<td>
<a target="_blank" href="https://www.tensorflow.org/tutorials/load_data/numpy"><img src="https://www.tensorflow.org/images/tf_logo_32px.png" />Ver em TensorFlow.org</a>
</td>
<td>
<a target="_blank" href="https://colab.research.google.com/github/tensorflow/docs-l10n/blob/master/site/pt-br/tutorials/load_data/numpy.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Executar em Google Colab</a>
</td>
<td>
<a target="_blank" href="https://github.com/tensorflow/docs-l10n/blob/master/site/pt-br/tutorials/load_data/numpy.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />Ver código fonte no GitHub</a>
</td>
<td>
<a href="https://storage.googleapis.com/tensorflow_docs/docs-l10n/site/pt-br/tutorials/load_data/numpy.ipynb"><img src="https://www.tensorflow.org/images/download_logo_32px.png" />Baixar notebook</a>
</td>
</table>
Este tutorial fornece um exemplo de carregamento de dados de matrizes NumPy para um `tf.data.Dataset`.
Este exemplo carrega o conjunto de dados MNIST de um arquivo `.npz`. No entanto, a fonte das matrizes NumPy não é importante.
## Configuração
```
try:
# %tensorflow_version only exists in Colab.
%tensorflow_version 2.x
except Exception:
pass
from __future__ import absolute_import, division, print_function, unicode_literals
import numpy as np
import tensorflow as tf
```
### Carregar um arquivo `.npz`
```
DATA_URL = 'https://storage.googleapis.com/tensorflow/tf-keras-datasets/mnist.npz'
path = tf.keras.utils.get_file('mnist.npz', DATA_URL)
with np.load(path) as data:
train_examples = data['x_train']
train_labels = data['y_train']
test_examples = data['x_test']
test_labels = data['y_test']
```
## Carregar matrizes NumPy com `tf.data.Dataset`
Supondo que você tenha uma matriz de exemplos e uma matriz correspondente de rótulos, passe as duas matrizes como uma tupla para `tf.data.Dataset.from_tensor_slices` para criar um `tf.data.Dataset`.
```
train_dataset = tf.data.Dataset.from_tensor_slices((train_examples, train_labels))
test_dataset = tf.data.Dataset.from_tensor_slices((test_examples, test_labels))
```
## Usar o conjunto de dados
### Aleatório e lote dos conjuntos de dados
```
BATCH_SIZE = 64
SHUFFLE_BUFFER_SIZE = 100
train_dataset = train_dataset.shuffle(SHUFFLE_BUFFER_SIZE).batch(BATCH_SIZE)
test_dataset = test_dataset.batch(BATCH_SIZE)
```
### Construir e treinar um modelo
```
model = tf.keras.Sequential([
tf.keras.layers.Flatten(input_shape=(28, 28)),
tf.keras.layers.Dense(128, activation='relu'),
tf.keras.layers.Dense(10)
])
model.compile(optimizer=tf.keras.optimizers.RMSprop(),
loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True),
metrics=['sparse_categorical_accuracy'])
model.fit(train_dataset, epochs=10)
model.evaluate(test_dataset)
```
|
github_jupyter
|
# Generic Integration With Credo AI's Governance App
Lens is primarily a framework for comprehensive assessment of AI models. However, in addition, it is the primary way to integrate assessment analysis with Credo AI's Governance App.
In this tutorial, we will take a model created and assessed _completely independently of Lens_ and send that data to Credo AI's Governance App
### Find the code
This notebook can be found on [github](https://github.com/credo-ai/credoai_lens/blob/develop/docs/notebooks/integration_demo.ipynb).
## Create an example ML Model
```
import numpy as np
from matplotlib import pyplot as plt
from pprint import pprint
from sklearn.model_selection import train_test_split
from sklearn import datasets
from sklearn.svm import SVC
from sklearn.metrics import classification_report
from sklearn.metrics import precision_recall_curve
```
### Load data and train model
For the purpose of this demonstration, we will be classifying digits after a large amount of noise has been added to each image.
We'll create some charts and assessment metrics to reflect our work.
```
# load data
digits = datasets.load_digits()
# add noise
digits.data += np.random.rand(*digits.data.shape)*16
# split into train and test
X_train, X_test, y_train, y_test = train_test_split(digits.data, digits.target)
# create and fit model
clf = SVC(probability=True)
clf.fit(X_train, y_train)
```
### Visualize example images along with predicted label
```
examples_plot = plt.figure()
for i in range(8):
image_data = X_test[i,:]
prediction = digits.target_names[clf.predict(image_data[None,:])[0]]
label = f'Pred: "{prediction}"'
# plot
ax = plt.subplot(2,4,i+1)
ax.imshow(image_data.reshape(8,8), cmap='gray')
ax.set_title(label)
ax.tick_params(labelbottom=False, labelleft=False, length=0)
plt.suptitle('Example Images and Predictions', fontsize=16)
```
### Calculate performance metrics and visualize
As a multiclassification problem, we can calculate metrics per class, or overall. We record overall metrics, but include figures for individual class performance breakdown
```
metrics = classification_report(y_test, clf.predict(X_test), output_dict=True)
overall_metrics = metrics['macro avg']
del overall_metrics['support']
pprint(overall_metrics)
probs = clf.predict_proba(X_test)
pr_curves = plt.figure(figsize=(8,6))
# plot PR curve sper digit
for digit in digits.target_names:
y_true = y_test == digit
y_prob = probs[:,digit]
precisions, recalls, thresholds = precision_recall_curve(y_true, y_prob)
plt.plot(recalls, precisions, lw=3, label=f'Digit: {digit}')
plt.xlabel('Recall', fontsize=16)
plt.ylabel('Precision', fontsize=16)
# plot iso lines
f_scores = np.linspace(0.2, 0.8, num=4)
lines = []
labels = []
for f_score in f_scores:
label = label='ISO f1 curves' if f_score==f_scores[0] else ''
x = np.linspace(0.01, 1)
y = f_score * x / (2 * x - f_score)
l, = plt.plot(x[y >= 0], y[y >= 0], color='gray', alpha=0.2, label=label)
# final touches
plt.xlim([0.5, 1.0])
plt.ylim([0.0, 1.05])
plt.tick_params(labelsize=14)
plt.title('PR Curves per Digit', fontsize=20)
plt.legend(loc='lower left', fontsize=10)
from sklearn.metrics import plot_confusion_matrix
confusion_plot = plt.figure(figsize=(6,6))
plot_confusion_matrix(clf, X_test, y_test, \
normalize='true', ax=plt.gca(), colorbar=False)
plt.tick_params(labelsize=14)
```
## Sending assessment information to Credo AI
Now that we have completed training and assessing the model, we will demonstrate how information can be sent to the Credo AI Governance App. Metrics related to performance, fairness, or other governance considerations are the most important kind of evidence needed for governance.
In addition, figures are often produced that help communicate metrics better, understand the model, or other contextualize the AI system. Credo can ingest those as well.
**Which metrics to record?**
Ideally you will have decided on the most important metrics before building the model. We refer to this stage as `Metric Alignment`. This is the phase where your team explicitly determine how you will measure whether your model can be safely deployed. It is part of the more general `Alignment Stage`, which often requires input from multiple stakeholders outside of the team specifically involved in the development of the AI model.
Of course, you may want to record more metrics than those explicitly determined during `Metric Alignment`.
For instance, in this example let's say that during `Metric Alignment`, the _F1 Score_ is the primary metric used to evaluate model performance. However, we have decided that recall and precision would be helpful supporting. So we will send those three metrics.
To reiterate: You are always free to send more metrics - Credo AI will ingest them. It is you and your team's decision which metrics are tracked specifically for governance purposes.
```
import credoai.integration as ci
from credoai.utils import list_metrics
model_name = 'SVC'
dataset_name = 'sklearn_digits'
```
## Quick reference
Below is all the code needed to record a set of metrics and figures. We will unpack each part below.
```
# metrics
metric_records = ci.record_metrics_from_dict(overall_metrics,
model_label=model_name,
dataset_label=dataset_name)
#figures
example_figure_record = ci.Figure(examples_plot._suptitle.get_text(), examples_plot)
confusion_figure_record = ci.Figure(confusion_plot.axes[0].get_title(), confusion_plot)
pr_curve_caption="""Precision-recall curves are shown for each digit separately.
These are calculated by treating each class as a separate
binary classification problem. The grey lines are
ISO f1 curves - all points on each curve have identical
f1 scores.
"""
pr_curve_figure_record = ci.Figure(pr_curves.axes[0].get_title(),
figure=pr_curves,
caption=pr_curve_caption)
figure_records = ci.MultiRecord([example_figure_record, confusion_figure_record, pr_curve_figure_record])
# export to file
# ci.export_to_file(model_record, 'model_record.json')
```
## Metric Record
To record a metric you can either record each one manually or ingest a dictionary of metrics.
### Manually entering individual metrics
```
f1_description = """Harmonic mean of precision and recall scores.
Ranges from 0-1, with 1 being perfect performance."""
f1_record = ci.Metric(metric_type='f1',
value=overall_metrics['f1-score'],
model_label=model_name,
dataset_label=dataset_name)
precision_record = ci.Metric(metric_type='precision',
value=overall_metrics['precision'],
model_label=model_name,
dataset_label=dataset_name)
recall_record = ci.Metric(metric_type='recall',
value=overall_metrics['recall'],
model_label=model_name,
dataset_label=dataset_name)
metrics = [f1_record, precision_record, recall_record]
```
### Convenience to record multiple metrics
Multiple metrics can be recorded as long as they are described using a pandas dataframe.
```
metric_records = ci.record_metrics_from_dict(overall_metrics,
model_name=model_name,
dataset_name=dataset_name)
```
## Record figures
Credo can accept a path to an image file or a matplotlib figure. Matplotlib figures are converted to PNG images and saved.
A caption can be included for futher description. Included a caption is recommended when the image is not self-explanatory, which is most of the time!
```
example_figure_record = ci.Figure(examples_plot._suptitle.get_text(), examples_plot)
confusion_figure_record = ci.Figure(confusion_plot.axes[0].get_title(), confusion_plot)
pr_curve_caption="""Precision-recall curves are shown for each digit separately.
These are calculated by treating each class as a separate
binary classification problem. The grey lines are
ISO f1 curves - all points on each curve have identical
f1 scores.
"""
pr_curve_figure_record = ci.Figure(pr_curves.axes[0].get_title(),
figure=pr_curves,
description=pr_curve_caption)
figure_records = [example_figure_record, confusion_figure_record, pr_curve_figure_record]
```
## MultiRecords
To send all the information, we wrap the records in a MuliRecord, which wraps records of the same type.
```
metric_records = ci.MultiRecord(metric_records)
figure_records = ci.MultiRecord(figure_records)
```
## Export to Credo AI
The json object of the model record can be created by calling `MultiRecord.jsonify()`. The convenience function `export_to_file` can be called to export the json record to a file. This file can then be uploaded to Credo AI's Governance App.
```
# filename is the location to save the json object of the model record
# filename="XXX.json"
# ci.export_to_file(metric_records, filename)
```
MultiRecords can be directly uploaded to Credo AI's Governance App as well. A model (or data) ID must be known to do so. You use `export_to_credo` to accomplish this.
```
# model_id = "XXX"
# ci.export_to_credo(metric_records, model_id)
```
|
github_jupyter
|
# Supercritical Steam Cycle Example
This example uses Jupyter Lab or Jupyter notebook, and demonstrates a supercritical pulverized coal (SCPC) steam cycle model. See the ```supercritical_steam_cycle.py``` to see more information on how to assemble a power plant model flowsheet. Code comments in that file will guide you through the process.
## Model Description
The example model doesn't represent any particular power plant, but should be a reasonable approximation of a typical plant. The gross power output is about 620 MW. The process flow diagram (PFD) can be shown using the code below. The initial PFD contains spaces for model results, to be filled in later.
To get a more detailed look at the model structure, you may find it useful to review ```supercritical_steam_cycle.py``` first. Although there is no detailed boiler model, there are constraints in the model to complete the steam loop through the boiler and calculate boiler heat input to the steam cycle. The efficiency calculation for the steam cycle doesn't account for heat loss in the boiler, which would be a result of a more detailed boiler model.
```
# pkg_resources is used here to get the svg information from the
# installed IDAES package
import pkg_resources
from IPython.display import SVG, display
# Get the contents of the PFD (which is an svg file)
init_pfd = pkg_resources.resource_string(
"idaes.examples.power_generation.supercritical_steam_cycle",
"supercritical_steam_cycle.svg"
)
# Make the svg contents into an SVG object and display it.
display(SVG(init_pfd))
```
## Initialize the steam cycle flowsheet
This example is part of the ```idaes``` package, which you should have installed. To run the example, the example flowsheet is imported from the ```idaes``` package. When you write your own model, you can import and run it in whatever way is appropriate for you. The Pyomo environment is also imported as ```pyo```, providing easy access to Pyomo functions and classes.
The supercritical flowsheet example main function returns a Pyomo concrete mode (m) and a solver object (solver). The model is also initialized by the ```main()``` function.
```
import pyomo.environ as pyo
from idaes.examples.power_generation.supercritical_steam_cycle import (
main,
create_stream_table_dataframe,
pfd_result,
)
m, solver = main()
```
Inside the model, there is a subblock ```fs```. This is an IDAES flowsheet model, which contains the supercritical steam cycle model. In the flowsheet, the model called ```turb``` is a multistage turbine model. The turbine model contains an expression for total power, ```power```. In this case the model is steady-state, but all IDAES models allow for dynamic simulation, and contain time indexes. Power is indexed by time, and only the "0" time point exists. By convention, in the IDAES framework, power going into a model is positive, so power produced by the turbine is negative.
The property package used for this model uses SI (mks) units of measure, so the power is in Watts. Here a function is defined which can be used to report power output in MW.
```
# Define a function to report gross power output in MW
def gross_power_mw(model):
# pyo.value(m.fs.turb.power[0]) is the power consumed in Watts
return -pyo.value(model.fs.turb.power[0])/1e6
# Show the gross power
gross_power_mw(m)
```
## Change the model inputs
The turbine in this example simulates partial arc admission with four arcs, so there are four throttle valves. For this example, we will close one of the valves to 25% open, and observe the result.
```
m.fs.turb.throttle_valve[1].valve_opening[:].value = 0.25
```
Next, we re-solve the model using the solver created by the ```supercritical_steam_cycle.py``` script.
```
solver.solve(m, tee=True)
```
Now we can check the gross power output again.
```
gross_power_mw(m)
```
## Creating a PFD with results and a stream table
A more detailed look at the model results can be obtained by creating a stream table and putting key results on the PFD. Of course, any unit model or stream result can be obtained from the model.
```
# Create a Pandas dataframe with stream results
df = create_stream_table_dataframe(streams=m._streams, orient="index")
# Create a new PFD with simulation results
res_pfd = pfd_result(m, df, svg=init_pfd)
# Display PFD with results.
display(SVG(res_pfd))
# Display the stream table.
df
```
|
github_jupyter
|
# A canonical asset pricing job
Let's estimate, for each firm, for each year, the alpha, beta, and size and value loadings.
So we want a dataset that looks like this:
| Firm | Year | alpha | beta |
| --- | --- | --- | --- |
| GM | 2000 | 0.01 | 1.04 |
| GM | 2001 | -0.005 | 0.98 |
...but it will do this for every firm, every year!
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import pandas_datareader as pdr
import seaborn as sns
# import statsmodels.api as sm
```
Load your stock returns. Here, I'll use this dataset, but you can use anything.
The returns don't even have to be firms.
**They can be any asset.** (Portfolios, mutual funds, crypto, ...)
```
crsp = pd.read_stata('https://github.com/LeDataSciFi/ledatascifi-2021/blob/main/data/3firm_ret_1990_2020.dta?raw=true')
crsp['ret'] = crsp['ret']*100 # convert to precentage to match FF's convention on scaling (daily % rets)
```
Then grab the market returns. Here, we will use one of the Fama-French datasets.
```
ff = pdr.get_data_famafrench('F-F_Research_Data_5_Factors_2x3_daily',start=1980,end=2010)[0] # the [0] is because the imported obect is a dictionary, and key=0 is the dataframe
ff = ff.reset_index().rename(columns={"Mkt-RF":"mkt_excess", "Date":"date"})
```
Merge the market returns into the stock returns.
```
crsp_ready = pd.merge(left=ff, right=crsp, on='date', how="inner",
indicator=True, validate="one_to_many")
```
So the data's basically ready. Again, the goal is to estimate, for each firm, for each year, the alpha, beta, and size and value loadings.
You caught that right? I have a dataframe, and **for each** firm, and **for each** year, I want to \<do stuff\> (run regressions).
**Pandas + "for each" = groupby!**
So we will _basically_ run `crsp.groupby([firm,year]).runregression()`. Except there is no "runregression" function that applies to pandas groupby objects. Small workaround: `crsp.groupby([firm,year]).apply(<our own reg fcn>)`.
We just need to write a reg function that works on groupby objects.
```
import statsmodels.api as sm
def reg_in_groupby(df,formula="ret_excess ~ mkt_excess + SMB + HML"):
'''
Want to run regressions after groupby?
This will do it!
Note: This defaults to a FF3 model assuming specific variable names. If you
want to run any other regression, just specify your model.
Usage:
df.groupby(<whatever>).apply(reg_in_groupby)
df.groupby(<whatever>).apply(reg_in_groupby,formula=<whatever>)
'''
return pd.Series(sm.formula.ols(formula,data = df).fit().params)
```
Let's apply that to our returns!
```
(
crsp_ready # grab the data
# Two things before the regressions:
# 1. need a year variable (to group on)
# 2. the market returns in FF are excess returns, so
# our stock returns need to be excess as well
.assign(year = crsp_ready.date.dt.year,
ret_excess = crsp_ready.ret - crsp_ready.RF)
# ok, run the regs, so easy!
.groupby(['permno','year']).apply(reg_in_groupby)
# and clean up - with better var names
.rename(columns={'Intercept':'alpha','mkt_excess':'beta'})
.reset_index()
)
```
How cool is that!
## Summary
This is all you need to do:
1. Set up the data like you would have to no matter what:
1. Load your stock prices.
1. Merge in the market returns and any factors you want to include in your model.
1. Make sure your returns are scaled like your factors (e.g., above, I converted to percentages to match the FF convention)
1. Make sure your asset returns and market returns are both excess returns (or both are not excess returns)
1. Create any variables you want to group on (e.g. above, I created a year variable)
3. `df.groupby(<whatever>).apply(reg_in_groupby)`
Holy smokes!
|
github_jupyter
|
# NYC PLUTO Data and Noise Complaints
Investigating how PLUTO data and zoning characteristics impact spatial, temporal and types of noise complaints through out New York City. Specifically looking at noise complaints that are handled by NYC's Department of Environmental Protection (DEP).
All work performed by Zoe Martiniak.
```
import os
import pandas as pd
import numpy as np
import datetime
import urllib
import requests
from sodapy import Socrata
import matplotlib
import matplotlib.pyplot as plt
import pylab as pl
from pandas.plotting import scatter_matrix
%matplotlib inline
%pylab inline
##Geospatial
import shapely
import geopandas as gp
from geopandas import GeoDataFrame
from fiona.crs import from_epsg
from shapely.geometry import Point, MultiPoint
import io
from geopandas.tools import sjoin
from shapely.ops import nearest_points
## Statistical Modelling
import statsmodels.api as sm
import statsmodels.formula.api as smf
from statsmodels.datasets.longley import load
import sklearn.preprocessing as preprocessing
from sklearn.ensemble import RandomForestRegressor as rfr
from sklearn.cross_validation import train_test_split
from sklearn.metrics import confusion_matrix
from APPTOKEN import myToken
## Save your SOTA API Token as variable myToken in a file titled SOTAPY_APPTOKEN.py
## e.g.
## myToken = 'XXXXXXXXXXXXXXXX'
```
# DATA IMPORTING
Applying domain knowledge to only read in columns of interest to reduce computing requirements.
### PLUTO csv file
```
pluto = pd.read_csv(os.getenv('MYDATA')+'/pluto_18v2.csv', usecols=['borocode','zonedist1',
'overlay1', 'bldgclass', 'landuse',
'ownertype','lotarea', 'bldgarea', 'comarea',
'resarea', 'officearea', 'retailarea', 'garagearea', 'strgearea',
'factryarea', 'otherarea', 'numfloors',
'unitsres', 'unitstotal', 'proxcode', 'lottype','lotfront',
'lotdepth', 'bldgfront', 'bldgdepth',
'yearalter1',
'assessland', 'yearbuilt','histdist', 'landmark', 'builtfar',
'residfar', 'commfar', 'facilfar','bbl', 'xcoord','ycoord'])
```
### 2010 Census Blocks
```
census = gp.read_file('Data/2010 Census Blocks/geo_export_56edaf68-bbe6-44a7-bd7c-81a898fb6f2e.shp')
```
### Read in 311 Complaints
```
complaints = pd.read_csv('Data/311DEPcomplaints.csv', usecols=['address_type','borough','city',
'closed_date', 'community_board','created_date',
'cross_street_1', 'cross_street_2', 'descriptor', 'due_date',
'facility_type', 'incident_address', 'incident_zip',
'intersection_street_1', 'intersection_street_2', 'latitude',
'location_type', 'longitude', 'resolution_action_updated_date',
'resolution_description', 'status', 'street_name' ])
## Many missing lat/lon values in complaints file
## Is it worth it to manually fill in NaN with geopy geocded laton/long?
len(complaints[(complaints.latitude.isna()) | (complaints.longitude.isna())])/len(complaints)
```
### Mannually Filling in Missing Lat/Long from Addresses
Very time and computationally expensive, so this step should be performed on a different machine.
For our intents and purposes, I will just be dropping rows with missing lat/long
```
complaints.dropna(subset=['longitude', 'latitude'],inplace=True)
complaints['createdate'] = pd.to_datetime(complaints['created_date'])
complaints = complaints[complaints.createdate >= datetime.datetime(2018,1,1)]
complaints = complaints[complaints.createdate < datetime.datetime(2019,1,1)]
complaints['lonlat']=list(zip(complaints.longitude.astype(float), complaints.latitude.astype(float)))
complaints['geometry']=complaints[['lonlat']].applymap(lambda x:shapely.geometry.Point(x))
crs = {'init':'epsg:4326', 'no_defs': True}
complaints = gp.GeoDataFrame(complaints, crs=crs, geometry=complaints['geometry'])
```
## NYC Zoning Shapefile
```
zoning = gp.GeoDataFrame.from_file('Data/nycgiszoningfeatures_201902shp/nyzd.shp')
zoning.to_crs(epsg=4326, inplace=True)
```
# PLUTO Shapefiles
## Load in PLUTO Shapefiles by Boro
The PLUTO shapefiles are incredibly large. I used ArcMAP to separate the pluto shapefiles by borough and saved them locally.
My original plan was to perform a spatial join of the complaints to the pluto shapefiles to find the relationship between PLUTO data on the building-scale and noise complaints.
While going through this exploratory analysis, I discovered that the 311 complaints are actually all located in the street and therefore the points do not intersect with the PLUTO shapefiles. This brings up some interesting questions, such as how the lat/long coordinates are assigned by the DEP.
I am including this step to showcase that the complaints do not intersect with the shapefiles, to justify my next step of simply aggregating by zoning type with the zoning shapefiles.
```
## PLUTO SHAPEFILES BY BORO
#files = ! ls Data/PLUTO_Split | grep '.shp'
boros= ['bronx','brooklyn','man','queens','staten']
columns_to_drop = ['FID_pluto_', 'Borough','CT2010', 'CB2010',
'SchoolDist', 'Council', 'FireComp', 'PolicePrct',
'HealthCent', 'HealthArea', 'Sanitboro', 'SanitDistr', 'SanitSub',
'Address','BldgArea', 'ComArea', 'ResArea', 'OfficeArea',
'RetailArea', 'GarageArea', 'StrgeArea', 'FactryArea', 'OtherArea',
'AreaSource','LotFront', 'LotDepth', 'BldgFront', 'BldgDepth', 'Ext', 'ProxCode',
'IrrLotCode', 'BsmtCode', 'AssessLand', 'AssessTot',
'ExemptLand', 'ExemptTot','ResidFAR', 'CommFAR', 'FacilFAR',
'BoroCode','CondoNo','XCoord', 'YCoord', 'ZMCode', 'Sanborn', 'TaxMap', 'EDesigNum', 'APPBBL',
'APPDate', 'PLUTOMapID', 'FIRM07_FLA', 'PFIRM15_FL', 'Version','BoroCode_1', 'BoroName']
bx_shp = gp.GeoDataFrame.from_file('Data/PLUTO_Split/Pluto_bronx.shp')
bx_311 = complaints[complaints.borough == 'BRONX']
bx_shp.to_crs(epsg=4326, inplace=True)
bx_shp.drop(columns_to_drop, axis=1, inplace=True)
```
## Mapping
```
f, ax = plt.subplots(figsize=(15,15))
#ax.get_xaxis().set_visible(False)
#ax.get_yaxis().set_visible(False)
ax.set_xlim(-73.91, -73.9)
ax.set_ylim(40.852, 40.86)
bx_shp.plot(ax=ax, color = 'w', edgecolor='k',alpha=0.5, legend=True)
plt.title("2018 Bronx Noise Complaints", size=20)
bx_311.plot(ax=ax,marker='.', color='red')#, markersize=.4, alpha=.4)
#fname = 'Bronx2018zoomed.png'
#plt.savefig(fname)
plt.show()
```
**Fig1:** This figure shows that the complaint points are located in the street, and therefore do not intersect with a tax lot. Therefore we cannot perform a spatial join on the two shapefiles.
# Data Cleaning & Simplifying
Here we apply our domain knowledge of zoning and Pluto data to do a bit of cleaning. This includes simplifying the zoning districts to extract the first letter, which can be one of the following five options:<br />
B: Ball Field, BPC<br />
P: Public Place, Park, Playground (all public areas)<br />
C: Commercial<br />
R: Residential<br />
M: Manufacturing<br />
```
print(len(zoning.ZONEDIST.unique()))
print(len(pluto.zonedist1.unique()))
def simplifying_zone(x):
if x in ['PLAYGROUND','PARK','PUBLIC PLACE','BALL FIELD' ,'BPC']:
return 'P'
if '/' in x:
return 'O'
if x[:3] == 'R10':
return x[:3]
else:
return x[:2]
def condensed_simple(x):
if x[:2] in ['R1','R2', 'R3','R4']:
return 'R1-R4'
if x[:2] in ['R5','R6', 'R7']:
return 'R5-R7'
if x[:2] in ['R8','R9', 'R10']:
return 'R8-R10'
if x[:2] in ['C1','C2']:
return 'C1-C2'
if x[:2] in ['C5','C6']:
return 'C5-C6'
if x[:2] in ['C3','C4','C7','C8']:
return 'C'
if x[:1] =='M':
return 'M'
else:
return x[:2]
cols_to_tidy = []
notcommon = []
for c in pluto.columns:
if type(pluto[c].mode()[0]) == str:
cols_to_tidy.append(c)
for c in cols_to_tidy:
pluto[c].fillna('U',inplace=True)
pluto.fillna(0,inplace=True)
pluto['bldgclass'] = pluto['bldgclass'].map(lambda x: x[0])
pluto['overlay1'] = pluto['overlay1'].map(lambda x: x[:2])
pluto['simple_zone'] = pluto['zonedist1'].map(simplifying_zone)
pluto['condensed'] = pluto['simple_zone'].map(condensed_simple)
```
```
zoning_analysis = pluto[['lotarea', 'bldgarea', 'comarea',
'resarea', 'officearea', 'retailarea', 'garagearea', 'strgearea',
'factryarea', 'otherarea', 'areasource', 'numbldgs', 'numfloors',
'unitsres', 'unitstotal', 'lotfront', 'lotdepth', 'bldgfront',
'bldgdepth','lotfront', 'lotdepth', 'bldgfront',
'bldgdepth','yearbuilt',
'yearalter1', 'yearalter2','builtfar','simple_zone']]
zoning_analysis.dropna(inplace=True)
## Cleaning the Complaint file for easier 1-hot-encoding
def TOD_shifts(x):
if x.hour <=7:
return 'M'
if x.hour >7 and x.hour<18:
return 'D'
if x.hour >= 18:
return 'E'
def DOW_(x):
weekdays = ['mon','tues','weds','thurs','fri','sat','sun']
for i in range(7):
if x.dayofweek == i:
return weekdays[i]
def resolution_(x):
descriptions = complaints.resolution_description.unique()
for a in [2,3,4,5,11,12,14,17,20,23,25]:
if x == descriptions[a]:
return 'valid_no_vio'
continue
next
if x == descriptions[1]:
return 'violation'
next
for b in [0,6,10,16,19,21,24]:
if x == descriptions[b]:
return 'further_investigation'
continue
next
for c in [7,8,9,13,15,18,22]:
if x == descriptions[c]:
return 'access_issue'
```
#### SIMPLIFIED COMPLAINT DESCRIPTIONS
0: Did not observe violation<br/>
1: Violation issued <br/>
No violation issued yet/canceled/resolved because:<br/>
2: Duplicate<br/>
3: Not warranted<br/>
4: Complainant canceled<br/>
5: Not warranted<br/>
6: Investigate further<br/>
7: Closed becuase complainant didnt respond<br/>
8: Incorrect complainant contact info (phone)<br/>
9: Incorrect complainant contact info (address)<br/>
10: Further investigation<br/>
11: NaN<br/>
12: Status unavailable<br/>
13: Could not gain access to location<br/>
14: NYPD<br/>
15: Sent letter to complainant after calling<br/>
16: Recieved letter from dog owner<br/>
17: Resolved with complainant<br/>
18: Incorrect address<br/>
19: An inspection is warranted<br/>
20: Hydrant<br/>
21: 2nd inspection<br/>
22: No complainant info<br/>
23: Refer to other agency (not nypd)<br/>
24: Inspection is scheduled<br/>
25: Call 311 for more info<br/>
Violation: [1]
not warranted/canceled/otheragency/duplicate: [2,3,4,5,11,12,14,17,20,23,25]
Complainant/access issue: [7,8,9,13,15,18,22]
Further investigtion: [0,6,10,16,19,21,24]
```
complaints['TOD']=complaints.createdate.map(TOD_shifts)
complaints['DOW']=complaints.createdate.map(DOW_)
```
## PLUTO/Zoning Feature Analysis
```
## Obtained this line of code from datascience.stackexchange @ the following link:
## https://datascience.stackexchange.com/questions/10459/calculation-and-visualization-of-correlation-matrix-with-pandas
def drange(start, stop, step):
r = start
while r <= stop:
yield r
r += step
def correlation_matrix(df):
from matplotlib import pyplot as plt
from matplotlib import cm as cm
fig = plt.figure(figsize=(10,10))
ax1 = fig.add_subplot(111)
cmap = cm.get_cmap('jet', 30)
cax = ax1.imshow(df.corr(), interpolation="nearest", cmap=cmap)
ax1.grid(True)
plt.title('PLUTO Correlation', size=20)
labels =[x for x in zoning_analysis.columns ]
ax1.set_yticklabels(labels,fontsize=14)
ax1.set_xticklabels(labels,fontsize=14, rotation='90')
# Add colorbar, make sure to specify tick locations to match desired ticklabels
fig.colorbar(cax, ticks = list(drange(-1, 1, 0.25)))
plt.show()
correlation_matrix(zoning_analysis)
zoning_analysis.sort_values(['simple_zone'],ascending=False, inplace=True)
y = zoning_analysis.groupby('simple_zone').mean()
f, axes = plt.subplots(figsize=(8,25), nrows=6, ncols=1)
cols = ['lotarea', 'bldgarea', 'comarea', 'resarea', 'officearea', 'retailarea']
for colind in range(6):
y[cols[colind]].plot(ax = plt.subplot(6,1,colind+1), kind='bar')
plt.ylabel('Avg. {} Units'.format(cols[colind]))
plt.title(cols[colind])
zoning['simple_zone'] = zoning['ZONEDIST'].map(simplifying_zone)
zoning['condensed'] = zoning['simple_zone'].map(condensed_simple)
zoning = zoning.reset_index().rename(columns={'index':'zdid'})
```
## Perform Spatial Joins
```
## Joining Census group shapefile to PLUTO shapefile
sjoin(census, plutoshp)
## Joining the zoning shapefile to complaints
zoning_joined = sjoin(zoning, complaints).reset_index()
zoning_joined.drop('index',axis=1, inplace=True)
print(zoning.shape)
print(complaints.shape)
print(zoning_joined.shape)
zoning_joined.drop(columns=['index_right', 'address_type', 'borough',
'city', 'closed_date', 'community_board', 'created_date',
'cross_street_1', 'cross_street_2', 'due_date',
'facility_type', 'incident_address', 'incident_zip',
'intersection_street_1', 'intersection_street_2',
'location_type', 'resolution_action_updated_date',
'resolution_description', 'status', 'street_name', 'lonlat'], inplace=True)
## Joining each borough PLUTO shapefile to zoning shapefile
bx_shp['centroid_colum'] = bx_shp.centroid
bx_shp = bx_shp.set_geometry('centroid_colum')
pluto_bx = sjoin(zoning, bx_shp).reset_index()
print(zoning.shape)
print(bx_shp.shape)
print(pluto_bx.shape)
pluto_bx = pluto_bx.groupby('zdid')['LandUse', 'LotArea', 'NumBldgs', 'NumFloors', 'UnitsRes',
'UnitsTotal', 'LotType', 'YearBuilt','YearAlter1', 'YearAlter2','BuiltFAR'].mean()
pluto_bx = zoning.merge(pluto_bx, on='zdid')
```
# ANALYSIS
## Visual Analysis
```
x = zoning_joined.groupby('simple_zone')['ZONEDIST'].count().index
y = zoning_joined.groupby('simple_zone')['ZONEDIST'].count()
f, ax = plt.subplots(figsize=(12,9))
plt.bar(x, y)
plt.ylabel('Counts', size=12)
plt.title('Noise Complaints by Zoning Districts (2018)', size=15)
```
**FIg 1** This shows the total counts of complaints by Zoning district. Clearly there are more complaints in middle/high-population density residential zoning districts. There are also high complaints in commercial districts C5 & C6. These commercial districts tend to have a residential overlay.
```
y.sort_values(ascending=False, inplace=True)
x = y.index
descriptors = zoning_joined.descriptor.unique()
df = pd.DataFrame(index=x)
for d in descriptors:
df[d] = zoning_joined[zoning_joined.descriptor == d].groupby('simple_zone')['ZONEDIST'].count()
df = df.div(df.sum(axis=1), axis=0)
ax = df.plot(kind="bar", stacked=True, figsize=(18,12))
df.sum(axis=1).plot(ax=ax, color="k")
plt.title('Noise Complaints by Descriptor', size=20)
plt.xlabel('Simplified Zone District (Decreasing Total Count -->)', size=12)
plt.ylabel('%', size=12)
fname = 'Descriptorpercent.jpeg'
#plt.savefig(fname)
plt.show()
```
**FIg 2** This figure shows the breakdown of the main noise complaint types per zoning district.
```
descriptors
complaints_by_zone = pd.get_dummies(zoning_joined, columns=['TOD','DOW'])
complaints_by_zone = complaints_by_zone.rename(columns={'TOD_D':'Day','TOD_E':'Night',
'TOD_M':'Morning','DOW_fri':'Friday','DOW_mon':'Monday','DOW_sat':'Saturday',
'DOW_sun':'Sunday','DOW_thurs':'Thursday','DOW_tues':'Tuesday','DOW_weds':'Wednesday'})
complaints_by_zone.drop(columns=['descriptor', 'latitude', 'longitude','createdate'],inplace=True)
complaints_by_zone = complaints_by_zone.groupby('zdid').sum()[['Day', 'Night', 'Morning', 'Friday',
'Monday', 'Saturday', 'Sunday', 'Thursday', 'Tuesday', 'Wednesday']].reset_index()
## Creating total counts of complaints by zoning district
complaints_by_zone['Count_TOD'] = (complaints_by_zone.Day +
complaints_by_zone.Night +
complaints_by_zone.Morning)
complaints_by_zone['Count_DOW'] = (complaints_by_zone.Monday +
complaints_by_zone.Tuesday +
complaints_by_zone.Wednesday +
complaints_by_zone.Thursday +
complaints_by_zone.Friday +
complaints_by_zone.Saturday +
complaints_by_zone.Sunday)
## Verifying the counts are the same
complaints_by_zone[complaints_by_zone.Count_TOD != complaints_by_zone.Count_DOW]
print(complaints_by_zone.shape)
print(zoning.shape)
complaints_by_zone = zoning.merge(complaints_by_zone, on='zdid')
print(complaints_by_zone.shape)
f, ax = plt.subplots(1,figsize=(13,13))
ax.set_axis_off()
ax.set_title('Avg # of Complaints',size=15)
complaints_by_zone.plot(ax=ax, column='Count_TOD', cmap='gist_earth', k=3, alpha=0.7, legend=True)
fname = 'AvgComplaintsbyZD.png'
plt.savefig(fname)
plt.show()
complaints_by_zone['Norm_count'] = complaints_by_zone.Count_TOD/complaints_by_zone.Shape_Area*1000000
f, ax = plt.subplots(1,figsize=(13,13))
ax.set_axis_off()
ax.set_title('Complaints Normalized by ZD Area',size=15)
complaints_by_zone[complaints_by_zone.Norm_count < 400].plot(ax=ax, column='Norm_count', cmap='gist_earth', k=3, alpha=0.7, legend=True)
fname = 'NormComplaintsbyZD.png'
plt.savefig(fname)
plt.show()
```
**Fig 3** This figure shows the spread of noise complaint density (complaints per unit area) of each zoning district.
```
complaints_by_zone.columns
TODcols = ['Day', 'Night', 'Morning']
fig = pl.figure(figsize=(30,20))
for x in range(1,8):
fig.add_subplot(2,3,x).set_axis_off()
fig.add_subplot(2,3,x).set_title(title[x-1], size=28)
pumashp.plot(column=column[x-1],cmap='Blues', alpha=1,
edgecolor='k', ax=fig.add_subplot(2,3,x), legend=True)
DOWcols = ['Friday', 'Monday', 'Saturday', 'Sunday', 'Thursday', 'Tuesday', 'Wednesday']
fig = pl.figure(figsize=(30,20))
for x in range(1,7):
fig.add_subplot(2,3,x).set_axis_off()
fig.add_subplot(2,3,x).set_title(DOWcols[x-1], size=28)
complaints_by_zone.plot(column=DOWcols[x-1],cmap='gist_stern', alpha=1,
ax=fig.add_subplot(2,3,x), legend=True)
```
## Regression
Define lat/long coordinates of zoning centroids for regression
```
complaints_by_zone.shape
complaints_by_zone['centerlong'] = complaints_by_zone.centroid.x
complaints_by_zone['centerlat'] = complaints_by_zone.centroid.y
mod = smf.ols(formula =
'Norm_count ~ centerlat + centerlong', data=complaints_by_zone)
results1 = mod.fit()
results1.summary()
len(complaints_by_zone.ZONEDIST.unique())
mod = smf.ols(formula =
'Norm_count ~ ZONEDIST', data=complaints_by_zone)
results1 = mod.fit()
results1.summary()
len(complaints_by_zone.simple_zone.unique())
mod = smf.ols(formula =
'Norm_count ~ simple_zone', data=complaints_by_zone)
results1 = mod.fit()
results1.summary()
complaints_by_zone.condensed.unique()
mod = smf.ols(formula =
'Norm_count ~ condensed', data=complaints_by_zone)
results1 = mod.fit()
results1.summary()
```
### PLAN
- JOIN ALL ZONE DIST TO PLUTO SHAPEFILES, AGGREGATE FEATURES
- PERFORM REGRESSION
COMPLEX CLASSIFIERS
- DECISION TREE AND CLUSTERING
```
import folium
from folium.plugins import HeatMap
hmap = folium.Map()
hm_wide = HeatMap( list(zip()))
f, ax = plt.subplots(figsize=(15,15))
#ax.get_xaxis().set_visible(False)
#ax.get_yaxis().set_visible(False)
zoning.plot(column='counts',ax=ax, cmap='plasma', alpha = 0.9, legend=True)
plt.title("Complaints by Zone", size=20)
```
|
github_jupyter
|
```
import time
import pandas as pd
import requests
import json5
import matplotlib.pyplot as plt
```
# Loading national data
```
df_nat = pd.read_csv("../Data/Employment_Projections.csv").sort_values('Employment 2030',ascending=False)
```
# Loading CA data
```
df_CA = pd.read_csv("../Data/CA_Long_Term_Occupational_Employment_Projections.csv").sort_values('Projected Year Employment Estimate',ascending=False)
df_Sac = df_CA[df_CA['Area Name (County Names)']=='Sacramento--Roseville--Arden-Arcade MSA (El Dorado, Placer, Sacramento, and Yolo Counties)'].copy()
df_Cal = df_CA[df_CA['Area Name (County Names)']=='California'].copy()
```
Filtering for those occupations that make 40k a year or more and cleaning occupational code for the national table to match the california tables
```
df_Sac_40k = df_Sac[df_Sac['Median Annual Wage']>=40000].copy()
df_nat['Occupation Code']=df_nat['Occupation Code'].str.extract(r'([0-9]{2}-[0-9]{4})')
```
need to bin education levels
```
df_Sac_40k['Entry Level Education'].value_counts()
education_levels = {'No formal educational credential':'<HS',
'High school diploma or equivalent':'HS+',
"Bachelor's degree":'Associates+',
"Associate's degree":'Associates+',
'Postsecondary non-degree award':'HS+',
'Some college, no degree':'HS+'
}
df_Sac['Education bin_a'] = df_Sac['Entry Level Education'].replace(to_replace=education_levels)
df_Sac_40k['Education bin_a'] = df_Sac_40k['Entry Level Education'].replace(to_replace=education_levels)
df_Cal['Education bin_a'] = df_Cal['Entry Level Education'].replace(to_replace=education_levels)
```
Less than HS
```
less_hs = df_Sac[df_Sac['Education bin_a']=='<HS'].sort_values(by='Projected Year Employment Estimate',ascending=False)
less_hs.head().transpose()
df_Sac_40k[df_Sac_40k['Education bin_a']=='<HS'].sort_values(by='Projected Year Employment Estimate',ascending=False).head().transpose()
```
HS or some colege
```
hs_plus = df_Sac[df_Sac['Education bin_a']=='HS+'].sort_values(by='Projected Year Employment Estimate',ascending=False)
hs_plus.head().transpose()
df_Sac_40k[df_Sac_40k['Education bin_a']=='HS+'].sort_values(by='Projected Year Employment Estimate',ascending=False).head().transpose()
```
Associates plus
```
sac_degree = df_Sac[df_Sac['Education bin_a']=='Associates+'].sort_values(by='Projected Year Employment Estimate',ascending=False)
sac_degree.head().transpose()
df_Sac_40k[df_Sac_40k['Education bin_a']=='Associates+'].sort_values(by='Projected Year Employment Estimate',ascending=False).head().transpose()
```
Looking at bar charts of training needed and histograms of Median Annual Wage
```
fig,axs = plt.subplots(1,3,figsize=(12,6))
axs[0].hist(less_hs[less_hs['Median Annual Wage']>0]['Median Annual Wage'],color='g')
axs[1].hist(hs_plus[hs_plus['Median Annual Wage']>0]['Median Annual Wage'],color='c')
axs[2].hist(sac_degree[sac_degree['Median Annual Wage']>0]['Median Annual Wage'],color='m')
plt.title('Distribution of Median Annual Salaries')
```
Ok, that is ugly
```
less_hs_counts = pd.DataFrame(less_hs['Job Training'].value_counts(normalize=True,sort=True,ascending=True,dropna=False))
less_hs_counts['training needed']=less_hs_counts.index
less_hs_counts.rename(columns={'Job Training':'frequency'}, inplace=True)
plt.figure(figsize=(8,4))
plt.barh(y='training needed',width='frequency',data=less_hs_counts,color='rosybrown')
plt.title('Frequencies of training needed for occupations not requiring a high school diploma')
hs_counts = pd.DataFrame(hs_plus['Job Training'].value_counts(normalize=True,sort=True,ascending=True,dropna=False))
hs_counts['training needed']=hs_counts.index
hs_counts.rename(columns={'Job Training':'frequency'}, inplace=True)
plt.figure(figsize=(8,4))
plt.barh(y='training needed',width='frequency',data=hs_counts,color='rosybrown')
plt.title('Frequencies of training needed for occupations requiring a high school diploma')
college_counts = pd.DataFrame(sac_degree['Job Training'].value_counts(normalize=True,sort=True,ascending=True,dropna=False))
college_counts['training needed']=college_counts.index
college_counts.rename(columns={'Job Training':'frequency'}, inplace=True)
plt.figure(figsize=(8,4))
plt.barh(y='training needed',width='frequency',data=college_counts,color='rosybrown')
plt.title("Frequencies of training needed for occupations requiring an associates or bachelor's degree")
```
|
github_jupyter
|
```
"""
Overriding descriptor (a.k.a. data descriptor or enforced descriptor):
# BEGIN DESCR_KINDS_DEMO1
>>> obj = Managed() # <1>
>>> obj.over # <2>
-> Overriding.__get__(<Overriding object>, <Managed object>, <class Managed>)
>>> Managed.over # <3>
-> Overriding.__get__(<Overriding object>, None, <class Managed>)
>>> obj.over = 7 # <4>
-> Overriding.__set__(<Overriding object>, <Managed object>, 7)
>>> obj.over # <5>
-> Overriding.__get__(<Overriding object>, <Managed object>, <class Managed>)
>>> obj.__dict__['over'] = 8 # <6>
>>> vars(obj) # <7>
{'over': 8}
>>> obj.over # <8>
-> Overriding.__get__(<Overriding object>, <Managed object>, <class Managed>)
# END DESCR_KINDS_DEMO1
Overriding descriptor without ``__get__``:
(these tests are reproduced below without +ELLIPSIS directives for inclusion in the book;
look for DESCR_KINDS_DEMO2)
>>> obj.over_no_get # doctest: +ELLIPSIS
<descriptorkinds.OverridingNoGet object at 0x...>
>>> Managed.over_no_get # doctest: +ELLIPSIS
<descriptorkinds.OverridingNoGet object at 0x...>
>>> obj.over_no_get = 7
-> OverridingNoGet.__set__(<OverridingNoGet object>, <Managed object>, 7)
>>> obj.over_no_get # doctest: +ELLIPSIS
<descriptorkinds.OverridingNoGet object at 0x...>
>>> obj.__dict__['over_no_get'] = 9
>>> obj.over_no_get
9
>>> obj.over_no_get = 7
-> OverridingNoGet.__set__(<OverridingNoGet object>, <Managed object>, 7)
>>> obj.over_no_get
9
Non-overriding descriptor (a.k.a. non-data descriptor or shadowable descriptor):
# BEGIN DESCR_KINDS_DEMO3
>>> obj = Managed()
>>> obj.non_over # <1>
-> NonOverriding.__get__(<NonOverriding object>, <Managed object>, <class Managed>)
>>> obj.non_over = 7 # <2>
>>> obj.non_over # <3>
7
>>> Managed.non_over # <4>
-> NonOverriding.__get__(<NonOverriding object>, None, <class Managed>)
>>> del obj.non_over # <5>
>>> obj.non_over # <6>
-> NonOverriding.__get__(<NonOverriding object>, <Managed object>, <class Managed>)
# END DESCR_KINDS_DEMO3
No descriptor type survives being overwritten on the class itself:
# BEGIN DESCR_KINDS_DEMO4
>>> obj = Managed() # <1>
>>> Managed.over = 1 # <2>
>>> Managed.over_no_get = 2
>>> Managed.non_over = 3
>>> obj.over, obj.over_no_get, obj.non_over # <3>
(1, 2, 3)
# END DESCR_KINDS_DEMO4
Methods are non-overriding descriptors:
>>> obj.spam # doctest: +ELLIPSIS
<bound method Managed.spam of <descriptorkinds.Managed object at 0x...>>
>>> Managed.spam # doctest: +ELLIPSIS
<function Managed.spam at 0x...>
>>> obj.spam()
-> Managed.spam(<Managed object>)
>>> Managed.spam()
Traceback (most recent call last):
...
TypeError: spam() missing 1 required positional argument: 'self'
>>> Managed.spam(obj)
-> Managed.spam(<Managed object>)
>>> Managed.spam.__get__(obj) # doctest: +ELLIPSIS
<bound method Managed.spam of <descriptorkinds.Managed object at 0x...>>
>>> obj.spam.__func__ is Managed.spam
True
>>> obj.spam = 7
>>> obj.spam
7
"""
"""
NOTE: These tests are here because I can't add callouts after +ELLIPSIS
directives and if doctest runs them without +ELLIPSIS I get test failures.
# BEGIN DESCR_KINDS_DEMO2
>>> obj.over_no_get # <1>
<__main__.OverridingNoGet object at 0x665bcc>
>>> Managed.over_no_get # <2>
<__main__.OverridingNoGet object at 0x665bcc>
>>> obj.over_no_get = 7 # <3>
-> OverridingNoGet.__set__(<OverridingNoGet object>, <Managed object>, 7)
>>> obj.over_no_get # <4>
<__main__.OverridingNoGet object at 0x665bcc>
>>> obj.__dict__['over_no_get'] = 9 # <5>
>>> obj.over_no_get # <6>
9
>>> obj.over_no_get = 7 # <7>
-> OverridingNoGet.__set__(<OverridingNoGet object>, <Managed object>, 7)
>>> obj.over_no_get # <8>
9
# END DESCR_KINDS_DEMO2
Methods are non-overriding descriptors:
# BEGIN DESCR_KINDS_DEMO5
>>> obj = Managed()
>>> obj.spam # <1>
<bound method Managed.spam of <descriptorkinds.Managed object at 0x74c80c>>
>>> Managed.spam # <2>
<function Managed.spam at 0x734734>
>>> obj.spam = 7 # <3>
>>> obj.spam
7
# END DESCR_KINDS_DEMO5
"""
# BEGIN DESCR_KINDS
### auxiliary functions for display only ###
def cls_name(obj_or_cls):
cls = type(obj_or_cls)
if cls is type:
cls = obj_or_cls
return cls.__name__.split('.')[-1]
def display(obj):
cls = type(obj)
if cls is type:
return '<class {}>'.format(obj.__name__)
elif cls in [type(None), int]:
return repr(obj)
else:
return '<{} object>'.format(cls_name(obj))
def print_args(name, *args):
pseudo_args = ', '.join(display(x) for x in args)
print('-> {}.__{}__({})'.format(cls_name(args[0]), name, pseudo_args))
### essential classes for this example ###
class Overriding: # <1>
"""a.k.a. data descriptor or enforced descriptor"""
def __get__(self, instance, owner):
print_args('get', self, instance, owner) # <2>
def __set__(self, instance, value):
print_args('set', self, instance, value)
class OverridingNoGet: # <3>
"""an overriding descriptor without ``__get__``"""
def __set__(self, instance, value):
print_args('set', self, instance, value)
class NonOverriding: # <4>
"""a.k.a. non-data or shadowable descriptor"""
def __get__(self, instance, owner):
print_args('get', self, instance, owner)
class Managed: # <5>
over = Overriding()
over_no_get = OverridingNoGet()
non_over = NonOverriding()
def spam(self): # <6>
print('-> Managed.spam({})'.format(display(self)))
# END DESCR_KINDS
"""
Overriding descriptor (a.k.a. data descriptor or enforced descriptor):
>>> obj = Model()
>>> obj.over # doctest: +ELLIPSIS
Overriding.__get__() invoked with args:
self = <descriptorkinds.Overriding object at 0x...>
instance = <descriptorkinds.Model object at 0x...>
owner = <class 'descriptorkinds.Model'>
>>> Model.over # doctest: +ELLIPSIS
Overriding.__get__() invoked with args:
self = <descriptorkinds.Overriding object at 0x...>
instance = None
owner = <class 'descriptorkinds.Model'>
An overriding descriptor cannot be shadowed by assigning to an instance:
>>> obj = Model()
>>> obj.over = 7 # doctest: +ELLIPSIS
Overriding.__set__() invoked with args:
self = <descriptorkinds.Overriding object at 0x...>
instance = <descriptorkinds.Model object at 0x...>
value = 7
>>> obj.over # doctest: +ELLIPSIS
Overriding.__get__() invoked with args:
self = <descriptorkinds.Overriding object at 0x...>
instance = <descriptorkinds.Model object at 0x...>
owner = <class 'descriptorkinds.Model'>
Not even by poking the attribute into the instance ``__dict__``:
>>> obj.__dict__['over'] = 8
>>> obj.over # doctest: +ELLIPSIS
Overriding.__get__() invoked with args:
self = <descriptorkinds.Overriding object at 0x...>
instance = <descriptorkinds.Model object at 0x...>
owner = <class 'descriptorkinds.Model'>
>>> vars(obj)
{'over': 8}
Overriding descriptor without ``__get__``:
>>> obj.over_no_get # doctest: +ELLIPSIS
<descriptorkinds.OverridingNoGet object at 0x...>
>>> Model.over_no_get # doctest: +ELLIPSIS
<descriptorkinds.OverridingNoGet object at 0x...>
>>> obj.over_no_get = 7 # doctest: +ELLIPSIS
OverridingNoGet.__set__() invoked with args:
self = <descriptorkinds.OverridingNoGet object at 0x...>
instance = <descriptorkinds.Model object at 0x...>
value = 7
>>> obj.over_no_get # doctest: +ELLIPSIS
<descriptorkinds.OverridingNoGet object at 0x...>
Poking the attribute into the instance ``__dict__`` means you can read the new
value for the attribute, but setting it still triggers ``__set__``:
>>> obj.__dict__['over_no_get'] = 9
>>> obj.over_no_get
9
>>> obj.over_no_get = 7 # doctest: +ELLIPSIS
OverridingNoGet.__set__() invoked with args:
self = <descriptorkinds.OverridingNoGet object at 0x...>
instance = <descriptorkinds.Model object at 0x...>
value = 7
>>> obj.over_no_get
9
Non-overriding descriptor (a.k.a. non-data descriptor or shadowable descriptor):
>>> obj = Model()
>>> obj.non_over # doctest: +ELLIPSIS
NonOverriding.__get__() invoked with args:
self = <descriptorkinds.NonOverriding object at 0x...>
instance = <descriptorkinds.Model object at 0x...>
owner = <class 'descriptorkinds.Model'>
>>> Model.non_over # doctest: +ELLIPSIS
NonOverriding.__get__() invoked with args:
self = <descriptorkinds.NonOverriding object at 0x...>
instance = None
owner = <class 'descriptorkinds.Model'>
A non-overriding descriptor can be shadowed by assigning to an instance:
>>> obj.non_over = 7
>>> obj.non_over
7
Methods are non-over descriptors:
>>> obj.spam # doctest: +ELLIPSIS
<bound method Model.spam of <descriptorkinds.Model object at 0x...>>
>>> Model.spam # doctest: +ELLIPSIS
<function Model.spam at 0x...>
>>> obj.spam() # doctest: +ELLIPSIS
Model.spam() invoked with arg:
self = <descriptorkinds.Model object at 0x...>
>>> obj.spam = 7
>>> obj.spam
7
No descriptor type survives being overwritten on the class itself:
>>> Model.over = 1
>>> obj.over
1
>>> Model.over_no_get = 2
>>> obj.over_no_get
2
>>> Model.non_over = 3
>>> obj.non_over
7
"""
# BEGIN DESCRIPTORKINDS
def print_args(name, *args): # <1>
cls_name = args[0].__class__.__name__
arg_names = ['self', 'instance', 'owner']
if name == 'set':
arg_names[-1] = 'value'
print('{}.__{}__() invoked with args:'.format(cls_name, name))
for arg_name, value in zip(arg_names, args):
print(' {:8} = {}'.format(arg_name, value))
class Overriding: # <2>
"""a.k.a. data descriptor or enforced descriptor"""
def __get__(self, instance, owner):
print_args('get', self, instance, owner) # <3>
def __set__(self, instance, value):
print_args('set', self, instance, value)
class OverridingNoGet: # <4>
"""an overriding descriptor without ``__get__``"""
def __set__(self, instance, value):
print_args('set', self, instance, value)
class NonOverriding: # <5>
"""a.k.a. non-data or shadowable descriptor"""
def __get__(self, instance, owner):
print_args('get', self, instance, owner)
class Model: # <6>
over = Overriding()
over_no_get = OverridingNoGet()
non_over = NonOverriding()
def spam(self): # <7>
print('Model.spam() invoked with arg:')
print(' self =', self)
#END DESCRIPTORKINDS
"""
# BEGIN FUNC_DESCRIPTOR_DEMO
>>> word = Text('forward')
>>> word # <1>
Text('forward')
>>> word.reverse() # <2>
Text('drawrof')
>>> Text.reverse(Text('backward')) # <3>
Text('drawkcab')
>>> type(Text.reverse), type(word.reverse) # <4>
(<class 'function'>, <class 'method'>)
>>> list(map(Text.reverse, ['repaid', (10, 20, 30), Text('stressed')])) # <5>
['diaper', (30, 20, 10), Text('desserts')]
>>> Text.reverse.__get__(word) # <6>
<bound method Text.reverse of Text('forward')>
>>> Text.reverse.__get__(None, Text) # <7>
<function Text.reverse at 0x101244e18>
>>> word.reverse # <8>
<bound method Text.reverse of Text('forward')>
>>> word.reverse.__self__ # <9>
Text('forward')
>>> word.reverse.__func__ is Text.reverse # <10>
True
# END FUNC_DESCRIPTOR_DEMO
"""
# BEGIN FUNC_DESCRIPTOR_EX
import collections
class Text(collections.UserString):
def __repr__(self):
return 'Text({!r})'.format(self.data)
def reverse(self):
return self[::-1]
# END FUNC_DESCRIPTOR_EX
# %load ./bulkfood/bulkfood_v3.py
"""
A line item for a bulk food order has description, weight and price fields::
>>> raisins = LineItem('Golden raisins', 10, 6.95)
>>> raisins.weight, raisins.description, raisins.price
(10, 'Golden raisins', 6.95)
A ``subtotal`` method gives the total price for that line item::
>>> raisins.subtotal()
69.5
The weight of a ``LineItem`` must be greater than 0::
>>> raisins.weight = -20
Traceback (most recent call last):
...
ValueError: value must be > 0
Negative or 0 price is not acceptable either::
>>> truffle = LineItem('White truffle', 100, 0)
Traceback (most recent call last):
...
ValueError: value must be > 0
No change was made::
>>> raisins.weight
10
"""
# BEGIN LINEITEM_V3
class Quantity: # <1>
def __init__(self, storage_name):
self.storage_name = storage_name # <2>
def __set__(self, instance, value): # <3>
if value > 0:
instance.__dict__[self.storage_name] = value # <4>
else:
raise ValueError('value must be > 0')
class LineItem:
weight = Quantity('weight') # <5>
price = Quantity('price') # <6>
def __init__(self, description, weight, price): # <7>
self.description = description
self.weight = weight
self.price = price
def subtotal(self):
return self.weight * self.price
# END LINEITEM_V3
# %load ./bulkfood/bulkfood_v4.py
"""
A line item for a bulk food order has description, weight and price fields::
>>> raisins = LineItem('Golden raisins', 10, 6.95)
>>> raisins.weight, raisins.description, raisins.price
(10, 'Golden raisins', 6.95)
A ``subtotal`` method gives the total price for that line item::
>>> raisins.subtotal()
69.5
The weight of a ``LineItem`` must be greater than 0::
>>> raisins.weight = -20
Traceback (most recent call last):
...
ValueError: value must be > 0
No change was made::
>>> raisins.weight
10
The value of the attributes managed by the descriptors are stored in
alternate attributes, created by the descriptors in each ``LineItem``
instance::
>>> raisins = LineItem('Golden raisins', 10, 6.95)
>>> dir(raisins) # doctest: +ELLIPSIS +NORMALIZE_WHITESPACE
['_Quantity#0', '_Quantity#1', '__class__', ...
'description', 'price', 'subtotal', 'weight']
>>> getattr(raisins, '_Quantity#0')
10
>>> getattr(raisins, '_Quantity#1')
6.95
"""
# BEGIN LINEITEM_V4
class Quantity:
__counter = 0 # <1>
def __init__(self):
cls = self.__class__ # <2>
prefix = cls.__name__
index = cls.__counter
self.storage_name = '_{}#{}'.format(prefix, index) # <3>
cls.__counter += 1 # <4>
def __get__(self, instance, owner): # <5>
return getattr(instance, self.storage_name) # <6>
def __set__(self, instance, value):
if value > 0:
setattr(instance, self.storage_name, value) # <7>
else:
raise ValueError('value must be > 0')
class LineItem:
weight = Quantity() # <8>
price = Quantity()
def __init__(self, description, weight, price):
self.description = description
self.weight = weight
self.price = price
def subtotal(self):
return self.weight * self.price
# END LINEITEM_V4
# %load ./bulkfood/bulkfood_v4b.py
"""
A line item for a bulk food order has description, weight and price fields::
>>> raisins = LineItem('Golden raisins', 10, 6.95)
>>> raisins.weight, raisins.description, raisins.price
(10, 'Golden raisins', 6.95)
A ``subtotal`` method gives the total price for that line item::
>>> raisins.subtotal()
69.5
The weight of a ``LineItem`` must be greater than 0::
>>> raisins.weight = -20
Traceback (most recent call last):
...
ValueError: value must be > 0
No change was made::
>>> raisins.weight
10
The value of the attributes managed by the descriptors are stored in
alternate attributes, created by the descriptors in each ``LineItem``
instance::
>>> raisins = LineItem('Golden raisins', 10, 6.95)
>>> dir(raisins) # doctest: +ELLIPSIS +NORMALIZE_WHITESPACE
['_Quantity#0', '_Quantity#1', '__class__', ...
'description', 'price', 'subtotal', 'weight']
>>> getattr(raisins, '_Quantity#0')
10
>>> getattr(raisins, '_Quantity#1')
6.95
If the descriptor is accessed in the class, the descriptor object is
returned:
>>> LineItem.weight # doctest: +ELLIPSIS
<bulkfood_v4b.Quantity object at 0x...>
>>> LineItem.weight.storage_name
'_Quantity#0'
"""
# BEGIN LINEITEM_V4B
class Quantity:
__counter = 0
def __init__(self):
cls = self.__class__
prefix = cls.__name__
index = cls.__counter
self.storage_name = '_{}#{}'.format(prefix, index)
cls.__counter += 1
def __get__(self, instance, owner):
if instance is None:
return self # <1>
else:
return getattr(instance, self.storage_name) # <2>
def __set__(self, instance, value):
if value > 0:
setattr(instance, self.storage_name, value)
else:
raise ValueError('value must be > 0')
# END LINEITEM_V4B
class LineItem:
weight = Quantity()
price = Quantity()
def __init__(self, description, weight, price):
self.description = description
self.weight = weight
self.price = price
def subtotal(self):
return self.weight * self.price
# %load ./bulkfood/bulkfood_v4c.py
"""
A line item for a bulk food order has description, weight and price fields::
>>> raisins = LineItem('Golden raisins', 10, 6.95)
>>> raisins.weight, raisins.description, raisins.price
(10, 'Golden raisins', 6.95)
A ``subtotal`` method gives the total price for that line item::
>>> raisins.subtotal()
69.5
The weight of a ``LineItem`` must be greater than 0::
>>> raisins.weight = -20
Traceback (most recent call last):
...
ValueError: value must be > 0
No change was made::
>>> raisins.weight
10
The value of the attributes managed by the descriptors are stored in
alternate attributes, created by the descriptors in each ``LineItem``
instance::
>>> raisins = LineItem('Golden raisins', 10, 6.95)
>>> dir(raisins) # doctest: +ELLIPSIS +NORMALIZE_WHITESPACE
['_Quantity#0', '_Quantity#1', '__class__', ...
'description', 'price', 'subtotal', 'weight']
>>> getattr(raisins, '_Quantity#0')
10
>>> getattr(raisins, '_Quantity#1')
6.95
If the descriptor is accessed in the class, the descriptor object is
returned:
>>> LineItem.weight # doctest: +ELLIPSIS
<model_v4c.Quantity object at 0x...>
>>> LineItem.weight.storage_name
'_Quantity#0'
"""
# BEGIN LINEITEM_V4C
import model_v4c as model # <1>
class LineItem:
weight = model.Quantity() # <2>
price = model.Quantity()
def __init__(self, description, weight, price):
self.description = description
self.weight = weight
self.price = price
def subtotal(self):
return self.weight * self.price
# END LINEITEM_V4C
# %load ./bulkfood/bulkfood_v4prop.py
"""
A line item for a bulk food order has description, weight and price fields::
>>> raisins = LineItem('Golden raisins', 10, 6.95)
>>> raisins.weight, raisins.description, raisins.price
(10, 'Golden raisins', 6.95)
A ``subtotal`` method gives the total price for that line item::
>>> raisins.subtotal()
69.5
The weight of a ``LineItem`` must be greater than 0::
>>> raisins.weight = -20
Traceback (most recent call last):
...
ValueError: value must be > 0
No change was made::
>>> raisins.weight
10
The value of the attributes managed by the descriptors are stored in
alternate attributes, created by the descriptors in each ``LineItem``
instance::
>>> raisins = LineItem('Golden raisins', 10, 6.95)
>>> dir(raisins) # doctest: +ELLIPSIS +NORMALIZE_WHITESPACE
[... '_quantity:0', '_quantity:1', 'description',
'price', 'subtotal', 'weight']
>>> getattr(raisins, '_quantity:0')
10
>>> getattr(raisins, '_quantity:1')
6.95
"""
# BEGIN LINEITEM_V4_PROP
def quantity(): # <1>
try:
quantity.counter += 1 # <2>
except AttributeError:
quantity.counter = 0 # <3>
storage_name = '_{}:{}'.format('quantity', quantity.counter) # <4>
def qty_getter(instance): # <5>
return getattr(instance, storage_name)
def qty_setter(instance, value):
if value > 0:
setattr(instance, storage_name, value)
else:
raise ValueError('value must be > 0')
return property(qty_getter, qty_setter)
# END LINEITEM_V4_PROP
class LineItem:
weight = quantity()
price = quantity()
def __init__(self, description, weight, price):
self.description = description
self.weight = weight
self.price = price
def subtotal(self):
return self.weight * self.price
# %load ./bulkfood/model_v4c.py
# BEGIN MODEL_V4
class Quantity:
__counter = 0
def __init__(self):
cls = self.__class__
prefix = cls.__name__
index = cls.__counter
self.storage_name = '_{}#{}'.format(prefix, index)
cls.__counter += 1
def __get__(self, instance, owner):
if instance is None:
return self
else:
return getattr(instance, self.storage_name)
def __set__(self, instance, value):
if value > 0:
setattr(instance, self.storage_name, value)
else:
raise ValueError('value must be > 0')
# END MODEL_V4
# %load ./bulkfood/bulkfood_v5.py
"""
A line item for a bulk food order has description, weight and price fields::
>>> raisins = LineItem('Golden raisins', 10, 6.95)
>>> raisins.weight, raisins.description, raisins.price
(10, 'Golden raisins', 6.95)
A ``subtotal`` method gives the total price for that line item::
>>> raisins.subtotal()
69.5
The weight of a ``LineItem`` must be greater than 0::
>>> raisins.weight = -20
Traceback (most recent call last):
...
ValueError: value must be > 0
No change was made::
>>> raisins.weight
10
The value of the attributes managed by the descriptors are stored in
alternate attributes, created by the descriptors in each ``LineItem``
instance::
>>> raisins = LineItem('Golden raisins', 10, 6.95)
>>> dir(raisins) # doctest: +ELLIPSIS +NORMALIZE_WHITESPACE
['_NonBlank#0', '_Quantity#0', '_Quantity#1', '__class__', ...
'description', 'price', 'subtotal', 'weight']
>>> getattr(raisins, '_Quantity#0')
10
>>> getattr(raisins, '_NonBlank#0')
'Golden raisins'
If the descriptor is accessed in the class, the descriptor object is
returned:
>>> LineItem.weight # doctest: +ELLIPSIS
<model_v5.Quantity object at 0x...>
>>> LineItem.weight.storage_name
'_Quantity#0'
The `NonBlank` descriptor prevents empty or blank strings to be used
for the description:
>>> br_nuts = LineItem('Brazil Nuts', 10, 34.95)
>>> br_nuts.description = ' '
Traceback (most recent call last):
...
ValueError: value cannot be empty or blank
>>> void = LineItem('', 1, 1)
Traceback (most recent call last):
...
ValueError: value cannot be empty or blank
"""
# BEGIN LINEITEM_V5
import model_v5 as model # <1>
class LineItem:
description = model.NonBlank() # <2>
weight = model.Quantity()
price = model.Quantity()
def __init__(self, description, weight, price):
self.description = description
self.weight = weight
self.price = price
def subtotal(self):
return self.weight * self.price
# END LINEITEM_V5
```
|
github_jupyter
|
<div class="alert alert-block alert-info" style="margin-top: 20px">
<a href="https://cocl.us/PY0101EN_edx_add_top">
<img src="https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/PY0101EN/Ad/TopAd.png" width="750" align="center">
</a>
</div>
<a href="https://cognitiveclass.ai/">
<img src="https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/PY0101EN/Ad/CCLog.png" width="200" align="center">
</a>
<h1>Lists in Python</h1>
<p><strong>Welcome!</strong> This notebook will teach you about the lists in the Python Programming Language. By the end of this lab, you'll know the basics list operations in Python, including indexing, list operations and copy/clone list.</p>
<h2>Table of Contents</h2>
<div class="alert alert-block alert-info" style="margin-top: 20px">
<ul>
<li>
<a href="#dataset">About the Dataset</a>
</li>
<li>
<a href="#list">Lists</a>
<ul>
<li><a href="index">Indexing</a></li>
<li><a href="content">List Content</a></li>
<li><a href="op">List Operations</a></li>
<li><a href="co">Copy and Clone List</a></li>
</ul>
</li>
<li>
<a href="#quiz">Quiz on Lists</a>
</li>
</ul>
<p>
Estimated time needed: <strong>15 min</strong>
</p>
</div>
<hr>
<h2 id="#dataset">About the Dataset</h2>
Imagine you received album recommendations from your friends and compiled all of the recommandations into a table, with specific information about each album.
The table has one row for each movie and several columns:
- **artist** - Name of the artist
- **album** - Name of the album
- **released_year** - Year the album was released
- **length_min_sec** - Length of the album (hours,minutes,seconds)
- **genre** - Genre of the album
- **music_recording_sales_millions** - Music recording sales (millions in USD) on [SONG://DATABASE](http://www.song-database.com/)
- **claimed_sales_millions** - Album's claimed sales (millions in USD) on [SONG://DATABASE](http://www.song-database.com/)
- **date_released** - Date on which the album was released
- **soundtrack** - Indicates if the album is the movie soundtrack (Y) or (N)
- **rating_of_friends** - Indicates the rating from your friends from 1 to 10
<br>
<br>
The dataset can be seen below:
<font size="1">
<table font-size:xx-small style="width:100%">
<tr>
<th>Artist</th>
<th>Album</th>
<th>Released</th>
<th>Length</th>
<th>Genre</th>
<th>Music recording sales (millions)</th>
<th>Claimed sales (millions)</th>
<th>Released</th>
<th>Soundtrack</th>
<th>Rating (friends)</th>
</tr>
<tr>
<td>Michael Jackson</td>
<td>Thriller</td>
<td>1982</td>
<td>00:42:19</td>
<td>Pop, rock, R&B</td>
<td>46</td>
<td>65</td>
<td>30-Nov-82</td>
<td></td>
<td>10.0</td>
</tr>
<tr>
<td>AC/DC</td>
<td>Back in Black</td>
<td>1980</td>
<td>00:42:11</td>
<td>Hard rock</td>
<td>26.1</td>
<td>50</td>
<td>25-Jul-80</td>
<td></td>
<td>8.5</td>
</tr>
<tr>
<td>Pink Floyd</td>
<td>The Dark Side of the Moon</td>
<td>1973</td>
<td>00:42:49</td>
<td>Progressive rock</td>
<td>24.2</td>
<td>45</td>
<td>01-Mar-73</td>
<td></td>
<td>9.5</td>
</tr>
<tr>
<td>Whitney Houston</td>
<td>The Bodyguard</td>
<td>1992</td>
<td>00:57:44</td>
<td>Soundtrack/R&B, soul, pop</td>
<td>26.1</td>
<td>50</td>
<td>25-Jul-80</td>
<td>Y</td>
<td>7.0</td>
</tr>
<tr>
<td>Meat Loaf</td>
<td>Bat Out of Hell</td>
<td>1977</td>
<td>00:46:33</td>
<td>Hard rock, progressive rock</td>
<td>20.6</td>
<td>43</td>
<td>21-Oct-77</td>
<td></td>
<td>7.0</td>
</tr>
<tr>
<td>Eagles</td>
<td>Their Greatest Hits (1971-1975)</td>
<td>1976</td>
<td>00:43:08</td>
<td>Rock, soft rock, folk rock</td>
<td>32.2</td>
<td>42</td>
<td>17-Feb-76</td>
<td></td>
<td>9.5</td>
</tr>
<tr>
<td>Bee Gees</td>
<td>Saturday Night Fever</td>
<td>1977</td>
<td>1:15:54</td>
<td>Disco</td>
<td>20.6</td>
<td>40</td>
<td>15-Nov-77</td>
<td>Y</td>
<td>9.0</td>
</tr>
<tr>
<td>Fleetwood Mac</td>
<td>Rumours</td>
<td>1977</td>
<td>00:40:01</td>
<td>Soft rock</td>
<td>27.9</td>
<td>40</td>
<td>04-Feb-77</td>
<td></td>
<td>9.5</td>
</tr>
</table></font>
<hr>
<h2 id="list">Lists</h2>
<h3 id="index">Indexing</h3>
We are going to take a look at lists in Python. A list is a sequenced collection of different objects such as integers, strings, and other lists as well. The address of each element within a list is called an <b>index</b>. An index is used to access and refer to items within a list.
<img src="https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/PY0101EN/Chapter%202/Images/ListsIndex.png" width="1000" />
To create a list, type the list within square brackets <b>[ ]</b>, with your content inside the parenthesis and separated by commas. Let’s try it!
```
# Create a list
L = ["Michael Jackson", 10.1, 1982]
L
```
We can use negative and regular indexing with a list :
<img src="https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/PY0101EN/Chapter%202/Images/ListsNeg.png" width="1000" />
```
# Print the elements on each index
print('the same element using negative and positive indexing:\n Postive:',L[0],
'\n Negative:' , L[-3] )
print('the same element using negative and positive indexing:\n Postive:',L[1],
'\n Negative:' , L[-2] )
print('the same element using negative and positive indexing:\n Postive:',L[2],
'\n Negative:' , L[-1] )
```
<h3 id="content">List Content</h3>
Lists can contain strings, floats, and integers. We can nest other lists, and we can also nest tuples and other data structures. The same indexing conventions apply for nesting:
```
# Sample List
["Michael Jackson", 10.1, 1982, [1, 2], ("A", 1)]
```
<h3 id="op">List Operations</h3>
We can also perform slicing in lists. For example, if we want the last two elements, we use the following command:
```
# Sample List
L = ["Michael Jackson", 10.1,1982,"MJ",1]
L
```
<img src="https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/PY0101EN/Chapter%202/Images/ListsSlice.png" width="1000">
```
# List slicing
L[3:5]
```
We can use the method <code>extend</code> to add new elements to the list:
```
# Use extend to add elements to list
L = [ "Michael Jackson", 10.2]
L.extend(['pop', 10])
L
```
Another similar method is <code>append</code>. If we apply <code>append</code> instead of <code>extend</code>, we add one element to the list:
```
# Use append to add elements to list
L = [ "Michael Jackson", 10.2]
L.append(['pop', 10])
L
```
Each time we apply a method, the list changes. If we apply <code>extend</code> we add two new elements to the list. The list <code>L</code> is then modified by adding two new elements:
```
# Use extend to add elements to list
L = [ "Michael Jackson", 10.2]
L.extend(['pop', 10])
L
```
If we append the list <code>['a','b']</code> we have one new element consisting of a nested list:
```
# Use append to add elements to list
L.append(['a','b'])
L
```
As lists are mutable, we can change them. For example, we can change the first element as follows:
```
# Change the element based on the index
A = ["disco", 10, 1.2]
print('Before change:', A)
A[0] = 'hard rock'
print('After change:', A)
```
We can also delete an element of a list using the <code>del</code> command:
```
# Delete the element based on the index
print('Before change:', A)
del(A[0])
print('After change:', A)
```
We can convert a string to a list using <code>split</code>. For example, the method <code>split</code> translates every group of characters separated by a space into an element in a list:
```
# Split the string, default is by space
'hard rock'.split()
```
We can use the split function to separate strings on a specific character. We pass the character we would like to split on into the argument, which in this case is a comma. The result is a list, and each element corresponds to a set of characters that have been separated by a comma:
```
# Split the string by comma
'A,B,C,D'.split(',')
```
<h3 id="co">Copy and Clone List</h3>
When we set one variable <b>B</b> equal to <b>A</b>; both <b>A</b> and <b>B</b> are referencing the same list in memory:
```
# Copy (copy by reference) the list A
A = ["hard rock", 10, 1.2]
B = A
print('A:', A)
print('B:', B)
```
<img src="https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/PY0101EN/Chapter%202/Images/ListsRef.png" width="1000" align="center">
Initially, the value of the first element in <b>B</b> is set as hard rock. If we change the first element in <b>A</b> to <b>banana</b>, we get an unexpected side effect. As <b>A</b> and <b>B</b> are referencing the same list, if we change list <b>A</b>, then list <b>B</b> also changes. If we check the first element of <b>B</b> we get banana instead of hard rock:
```
# Examine the copy by reference
print('B[0]:', B[0])
A[0] = "banana"
print('B[0]:', B[0])
```
This is demonstrated in the following figure:
<img src = "https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/PY0101EN/Chapter%202/Images/ListsRefGif.gif" width="1000" />
You can clone list **A** by using the following syntax:
```
# Clone (clone by value) the list A
B = A[:]
B
```
Variable **B** references a new copy or clone of the original list; this is demonstrated in the following figure:
<img src="https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/PY0101EN/Chapter%202/Images/ListsVal.gif" width="1000" />
Now if you change <b>A</b>, <b>B</b> will not change:
```
print('B[0]:', B[0])
A[0] = "hard rock"
print('B[0]:', B[0])
```
<h2 id="quiz">Quiz on List</h2>
Create a list <code>a_list</code>, with the following elements <code>1</code>, <code>hello</code>, <code>[1,2,3]</code> and <code>True</code>.
```
# Write your code below and press Shift+Enter to execute
a_list=[1, 'hello', [1,2,3],True]
a_list
```
Double-click <b>here</b> for the solution.
<!-- Your answer is below:
a_list = [1, 'hello', [1, 2, 3] , True]
a_list
-->
Find the value stored at index 1 of <code>a_list</code>.
```
# Write your code below and press Shift+Enter to execute
a_list[1]
```
Double-click <b>here</b> for the solution.
<!-- Your answer is below:
a_list[1]
-->
Retrieve the elements stored at index 1, 2 and 3 of <code>a_list</code>.
```
# Write your code below and press Shift+Enter to execute
a_list[1:4]
```
Double-click <b>here</b> for the solution.
<!-- Your answer is below:
a_list[1:4]
-->
Concatenate the following lists <code>A = [1, 'a']</code> and <code>B = [2, 1, 'd']</code>:
```
# Write your code below and press Shift+Enter to execute
A = [1, 'a']
B = [2, 1, 'd']
A=A+B
A
```
Double-click <b>here</b> for the solution.
<!-- Your answer is below:
A = [1, 'a']
B = [2, 1, 'd']
A + B
-->
<hr>
<h2>The last exercise!</h2>
<p>Congratulations, you have completed your first lesson and hands-on lab in Python. However, there is one more thing you need to do. The Data Science community encourages sharing work. The best way to share and showcase your work is to share it on GitHub. By sharing your notebook on GitHub you are not only building your reputation with fellow data scientists, but you can also show it off when applying for a job. Even though this was your first piece of work, it is never too early to start building good habits. So, please read and follow <a href="https://cognitiveclass.ai/blog/data-scientists-stand-out-by-sharing-your-notebooks/" target="_blank">this article</a> to learn how to share your work.
<hr>
<div class="alert alert-block alert-info" style="margin-top: 20px">
<h2>Get IBM Watson Studio free of charge!</h2>
<p><a href="https://cocl.us/PY0101EN_edx_add_bbottom"><img src="https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/PY0101EN/Ad/BottomAd.png" width="750" align="center"></a></p>
</div>
<h3>About the Authors:</h3>
<p><a href="https://www.linkedin.com/in/joseph-s-50398b136/" target="_blank">Joseph Santarcangelo</a> is a Data Scientist at IBM, and holds a PhD in Electrical Engineering. His research focused on using Machine Learning, Signal Processing, and Computer Vision to determine how videos impact human cognition. Joseph has been working for IBM since he completed his PhD.</p>
Other contributors: <a href="www.linkedin.com/in/jiahui-mavis-zhou-a4537814a">Mavis Zhou</a>
<hr>
<p>Copyright © 2018 IBM Developer Skills Network. This notebook and its source code are released under the terms of the <a href="https://cognitiveclass.ai/mit-license/">MIT License</a>.</p>
|
github_jupyter
|
<h1>Table of Contents<span class="tocSkip"></span></h1>
<div class="toc"><ul class="toc-item"><li><span><a href="#Natural-Language-Pre-Processing" data-toc-modified-id="Natural-Language-Pre-Processing-1"><span class="toc-item-num">1 </span>Natural Language Pre-Processing</a></span></li><li><span><a href="#Objectives" data-toc-modified-id="Objectives-2"><span class="toc-item-num">2 </span>Objectives</a></span></li><li><span><a href="#Overview-of-NLP" data-toc-modified-id="Overview-of-NLP-3"><span class="toc-item-num">3 </span>Overview of NLP</a></span></li><li><span><a href="#Preprocessing-for-NLP" data-toc-modified-id="Preprocessing-for-NLP-4"><span class="toc-item-num">4 </span>Preprocessing for NLP</a></span><ul class="toc-item"><li><span><a href="#Tokenization" data-toc-modified-id="Tokenization-4.1"><span class="toc-item-num">4.1 </span>Tokenization</a></span></li></ul></li><li><span><a href="#Text-Cleaning" data-toc-modified-id="Text-Cleaning-5"><span class="toc-item-num">5 </span>Text Cleaning</a></span><ul class="toc-item"><li><span><a href="#Capitalization" data-toc-modified-id="Capitalization-5.1"><span class="toc-item-num">5.1 </span>Capitalization</a></span></li><li><span><a href="#Punctuation" data-toc-modified-id="Punctuation-5.2"><span class="toc-item-num">5.2 </span>Punctuation</a></span></li><li><span><a href="#Stopwords" data-toc-modified-id="Stopwords-5.3"><span class="toc-item-num">5.3 </span>Stopwords</a></span><ul class="toc-item"><li><ul class="toc-item"><li><span><a href="#Numerals" data-toc-modified-id="Numerals-5.3.0.1"><span class="toc-item-num">5.3.0.1 </span>Numerals</a></span></li></ul></li></ul></li></ul></li><li><span><a href="#Regex" data-toc-modified-id="Regex-6"><span class="toc-item-num">6 </span>Regex</a></span><ul class="toc-item"><li><span><a href="#RegexpTokenizer()" data-toc-modified-id="RegexpTokenizer()-6.1"><span class="toc-item-num">6.1 </span><code>RegexpTokenizer()</code></a></span></li></ul></li><li><span><a href="#Exercise:-NL-Pre-Processing" data-toc-modified-id="Exercise:-NL-Pre-Processing-7"><span class="toc-item-num">7 </span>Exercise: NL Pre-Processing</a></span></li></ul></div>
# Natural Language Pre-Processing
```
# Use this to install nltk if needed
!pip install nltk
# !conda install -c anaconda nltk
%load_ext autoreload
%autoreload 2
import os
import sys
module_path = os.path.abspath(os.path.join(os.pardir, os.pardir))
if module_path not in sys.path:
sys.path.append(module_path)
import pandas as pd
import nltk
from nltk.probability import FreqDist
from nltk.corpus import stopwords
from nltk.tokenize import regexp_tokenize, word_tokenize, RegexpTokenizer
import matplotlib.pyplot as plt
import string
import re
# Use this to download the stopwords if you haven't already - only ever needs to be run once
nltk.download("stopwords")
```
# Objectives
- Describe the basic concepts of NLP
- Use pre-processing methods for NLP
- Tokenization
- Stopwords removal
# Overview of NLP
NLP allows computers to interact with text data in a structured and sensible way. In short, we will be breaking up series of texts into individual words (or groups of words), and isolating the words with **semantic value**. We will then compare texts with similar distributions of these words, and group them together.
In this section, we will discuss some steps and approaches to common text data analytic procedures. Some of the applications of natural language processing are:
- Chatbots
- Speech recognition and audio processing
- Classifying documents
Here is an example that uses some of the tools we use in this notebook.
-[chicago_justice classifier](https://github.com/chicago-justice-project/article-tagging/blob/master/lib/notebooks/bag-of-words-count-stemmed-binary.ipynb)
We will introduce you to the preprocessing steps, feature engineering, and other steps you need to take in order to format text data for machine learning tasks.
We will also introduce you to [**NLTK**](https://www.nltk.org/) (Natural Language Toolkit), which will be our main tool for engaging with textual data.
<img src="img/nlp_process.png" style="width:1000px;">
```
#No hard rule for model, could be knn, rfc, etc.
```
# Preprocessing for NLP
```
#Curse of dimensionality
```
The goal when pre-processing text data for NLP is to remove as many unnecessary words as possible while preserving as much semantic meaning as possible. This will improve your model performance dramatically.
You can think of this sort of like dimensionality reduction. The unique words in your corpus form a **vocabulary**, and each word in your vocabulary is essentially another feature in your model. So we want to get rid of unnecessary words and consolidate words that have similar meanings.
We will be working with a dataset which includes both satirical** (The Onion) and real news (Reuters) articles. We refer to the entire set of articles as the **corpus**.
 
```
corpus = pd.read_csv('data/satire_nosatire.csv')
corpus.shape
corpus.tail()
```
Our goal is to detect satire, so our target class of 1 is associated with The Onion articles.
```
corpus.loc[10].body
corpus.loc[10].target
corpus.loc[502].body
corpus.loc[502].target
```
Each article in the corpus is refered to as a **document**.
It is a balanced dataset with 500 documents of each category.
```
corpus.target.value_counts()
```
**Discussion:** Let's think about the use cases of being able to correctly separate satirical from authentic news. What might be a real-world use case?
```
# Thoughts here
```
## Tokenization
In order to convert the texts into data suitable for machine learning, we need to break down the documents into smaller parts.
The first step in doing that is **tokenization**.
Tokenization is the process of splitting documents into units of observations. We usually represent the tokens as __n-grams__, where n represent the number of consecutive words occuring in a document that we will consider a unit. In the case of unigrams (one-word tokens), the sentence "David works here" would be tokenized into:
- "David", "works", "here";
If we want (also) to consider bigrams, we would (also) consider:
- "David works" and "works here".
Let's consider the first document in our corpus:
```
first_document = corpus.iloc[0].body
first_document
sample_document = corpus.iloc[1].body
sample_document
```
There are many ways to tokenize our document.
It is a long string, so the first way we might consider is to split it by spaces.
**Knowledge Check:** How would we split our documents into words using spaces?
<p>
</p>
<details>
<summary><b><u>Click Here for Answer Code</u></b></summary>
first_document.split(' ')
</details>
```
# code
sample_document.split()
```
But this is not ideal. We are trying to create a set of tokens with **high semantic value**. In other words, we want to isolate text which best represents the meaning in each document.
# Text Cleaning
Most NL Pre-Processing will include the following tasks:
1. Remove capitalization
2. Remove punctuation
3. Remove stopwords
4. Remove numbers
We could manually perform all of these tasks with string operations.
## Capitalization
When we create our matrix of words associated with our corpus, **capital letters** will mess things up. The semantic value of a word used at the beginning of a sentence is the same as that same word in the middle of the sentence. In the two sentences:
sentence_one = "Excessive gerrymandering in small counties suppresses turnout."
sentence_two = "Turnout is suppressed in small counties by excessive gerrymandering."
'excessive' has the same semantic value, but will be treated as different tokens because of capitals.
```
sentence_one = "Excessive gerrymandering in small counties suppresses turnout."
sentence_two = "Turnout is suppressed in small counties by excessive gerrymandering."
Excessive = sentence_one.split(' ')[0]
excessive = sentence_two.split(' ')[-2]
print(excessive, Excessive)
excessive == Excessive
manual_cleanup = [word.lower() for word in first_document.split(' ')]
print(f"Our initial token set for our first document is {len(manual_cleanup)} words long")
print(f"Our initial token set for our first document has \
{len(set(first_document.split()))} unique words")
print(f"After removing capitals, our first document has \
{len(set(manual_cleanup))} unique words")
```
## Punctuation
Like capitals, splitting on white space will create tokens which include punctuation that will muck up our semantics.
Returning to the above example, 'gerrymandering' and 'gerrymandering.' will be treated as different tokens.
```
no_punct = sentence_one.split(' ')[1]
punct = sentence_two.split(' ')[-1]
print(no_punct, punct)
no_punct == punct
## Manual removal of punctuation
string.punctuation
manual_cleanup = [s.translate(str.maketrans('', '', string.punctuation))\
for s in manual_cleanup]
print(f"After removing punctuation, our first document has \
{len(set(manual_cleanup))} unique words")
manual_cleanup[:10]
```
## Stopwords
Stopwords are the **filler** words in a language: prepositions, articles, conjunctions. They have low semantic value, and often need to be removed.
Luckily, NLTK has lists of stopwords ready for our use.
```
stopwords.words('english')[:10]
stopwords.words('greek')[:10]
```
Let's see which stopwords are present in our first document.
```
stops = [token for token in manual_cleanup if token in stopwords.words('english')]
stops[:10]
print(f'There are {len(stops)} stopwords in the first document')
print(f'That is {len(stops)/len(manual_cleanup): 0.2%} of our text')
```
Let's also use the **FreqDist** tool to look at the makeup of our text before and after removal:
```
fdist = FreqDist(manual_cleanup)
plt.figure(figsize=(10, 10))
fdist.plot(30);
manual_cleanup = [token for token in manual_cleanup if\
token not in stopwords.words('english')]
manual_cleanup[:10]
# We can also customize our stopwords list
custom_sw = stopwords.words('english')
custom_sw.extend(["i'd","say"] )
custom_sw[-10:]
manual_cleanup = [token for token in manual_cleanup if token not in custom_sw]
print(f'After removing stopwords, there are {len(set(manual_cleanup))} unique words left')
fdist = FreqDist(manual_cleanup)
plt.figure(figsize=(10, 10))
fdist.plot(30);
```
#### Numerals
Numerals also usually have low semantic value. Their removal can help improve our models.
To remove them, we will use regular expressions, a powerful tool which you may already have some familiarity with.
```
manual_cleanup = [s.translate(str.maketrans('', '', '0123456789')) \
for s in manual_cleanup]
# drop empty strings
manual_cleanup = [s for s in manual_cleanup if s != '' ]
print(f'After removing numbers, there are {len(set(manual_cleanup))} unique words left')
```
# Regex
Regex allows us to match strings based on a pattern. This pattern comes from a language of identifiers, which we can begin exploring on the cheatsheet found here:
- https://regexr.com/
A few key symbols:
- . : matches any character
- \d, \w, \s : represent digit, word, whitespace
- *, ?, +: matches 0 or more, 0 or 1, 1 or more of the preceding character
- [A-Z]: matches any capital letter
- [a-z]: matches lowercase letter
Other helpful resources:
- https://regexcrossword.com/
- https://www.regular-expressions.info/tutorial.html
We can use regex to isolate numerals:
```
first_document
pattern = '[0-9]'
number = re.findall(pattern, first_document)
number
pattern2 = '[0-9]+'
number2 = re.findall(pattern2, first_document)
number2
```
## `RegexpTokenizer()`
Sklearn and NLTK provide us with a suite of **tokenizers** for our text preprocessing convenience.
```
first_document
# Remember that the '?' indicates 0 or 1 of what follows!
re.findall(r"([a-zA-Z]+(?:'[a-z]+)?)", "I'd")
pattern = "([a-zA-Z]+(?:'[a-z]+)?)"
tokenizer = RegexpTokenizer(pattern)
first_doc = tokenizer.tokenize(first_document)
first_doc = [token.lower() for token in first_doc]
first_doc = [token for token in first_doc if token not in custom_sw]
first_document
first_doc[:10]
print(f'We are down to {len(set(first_doc))} unique words')
```
# Exercise: NL Pre-Processing
**Activity:** Use what you've learned to preprocess the second article. How does the length and number of unique words in the article change?
<p>
</p>
<details>
<summary><b><u>Click Here for Answer Code</u></b></summary>
second_document = corpus.iloc[1].body
print(f'We start with {len(second_document.split())} words')
print(f'We start with {len(set(second_document.split()))} unique words')
second_doc = tokenizer.tokenize(second_document)
second_doc = [token.lower() for token in second_doc]
second_doc = [token for token in second_doc if token not in custom_sw]
print(f'We end with {len(second_doc)} words')
print(f'We end with {len(set(second_doc))} unique words')
</details>
```
second_document
len(set(corpus.iloc[1].body.split()))
list(set(corpus.iloc[1].body.split()))
len(second_document)
list(set(second_document))
second_doc
## Your code here
second_document = corpus.iloc[1].body
second_doc = tokenizer.tokenize(second_document)
second_doc = [token.lower() for token in second_doc]
second_doc = [token for token in second_doc if token not in custom_sw]
#second_doc[:10], print(f'We are down to {len(second_doc)} words'),\
#print(f'We are down to {len(set(second_doc))} unique words')
```
|
github_jupyter
|
##### Copyright 2018 The TensorFlow Authors.
```
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
#@title MIT License
#
# Copyright (c) 2017 François Chollet
#
# Permission is hereby granted, free of charge, to any person obtaining a
# copy of this software and associated documentation files (the "Software"),
# to deal in the Software without restriction, including without limitation
# the rights to use, copy, modify, merge, publish, distribute, sublicense,
# and/or sell copies of the Software, and to permit persons to whom the
# Software is furnished to do so, subject to the following conditions:
#
# The above copyright notice and this permission notice shall be included in
# all copies or substantial portions of the Software.
#
# THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
# IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
# FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL
# THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
# LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING
# FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER
# DEALINGS IN THE SOFTWARE.
```
# Знакомимся с переобучением и недообучением
<table class="tfo-notebook-buttons" align="left">
<td>
<a target="_blank" href="https://www.tensorflow.org/tutorials/keras/overfit_and_underfit"><img src="https://www.tensorflow.org/images/tf_logo_32px.png" />Читай на TensorFlow.org</a>
</td>
<td>
<a target="_blank" href="https://colab.research.google.com/github/tensorflow/docs/blob/master/site/ru/tutorials/keras/overfit_and_underfit.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Запусти в Google Colab</a>
</td>
<td>
<a target="_blank" href="https://github.com/tensorflow/docs/blob/master/site/ru/tutorials/keras/overfit_and_underfit.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />Изучай код на GitHub</a>
</td>
</table>
Как и в предыдущий раз мы будем использовать `tf.keras` API, подробнее о котором ты можешь прочитать в нашем [руководстве по Keras](https://www.tensorflow.org/guide/keras).
В обоих предыдщих примерах с классификацией обзоров фильмов и предсказанием цен на жилье, мы увидели, что точность нашей модели на проверочных данных достигает пика после определенного количества эпох, а затем начинает снижаться.
Другими словами, наша модель учится на одних и тех же данных слишком долго - это называется *переобучение*. Очень важно знать способы как можно предотвратить это. Несмотря на то, что при помощи переобучения можно достичь более высоких показателей точности, но только на *тренировочных данных*, нашей целью всегда является обучить нейросеть обобщать их и узнавать паттерны на проверочных, новых данных.
Обратным случаем переобучения является *недообучение*: оно возникает когда все еще есть возможность улучшить показатели модели на проверочном наборе данных. Недообучение может произойти по разным причинам: например, если модель недостаточно сильная, или слишком сложная, или просто недостаточно тренировалась на данных. В любом случае это будет означать, что не были выучены основные паттерны из проверочного сета.
Если ты будешь тренировать модель слишком долго, то модель начнет обучаться шаблонам, которые свойственны *только* тренировочным данным, и не научится узнавать паттерны в новых данных. Нам нужно найти золотую середину. Понимание того как долго тренировать модель, сколько эпох выбрать - это очень полезный навык, которому мы сейчас научимся.
Чтобы избежать переобучения, наиболее оптимальным решением будет использовать больше тренировочных данных. Модели, обученные на большем количестве данных, естественным образом обобщают их лучше. Когда увеличить точность более не представляется возможным, то тогда мы начинаем использовать методы *регуляризации*. Они ограничивают количество и тип инофрмации, которые модель может хранить в себе. Если нейросеть может запомнить только небольшое количество паттернов, то тогда процесс оптимизации заставит ее сфокусироваться на самых важных, наиболее заметных шаблонах, которые будут иметь более высокий шанс обобщения.
В этом уроке мы познакомимся с двумя распространенными методами регуляризации: *регуляризация весов* и *исключение* (*dropout*). Мы используем их чтобы улучшить показатели нашей модели из урока по классификации обзоров фильмов из IMDB.
```
import tensorflow as tf
from tensorflow import keras
import numpy as np
import matplotlib.pyplot as plt
print(tf.__version__)
```
## Загружаем датасет IMDB
Вместо того, чтобы использовать *embedding* слой, как мы делали это в предыдущем уроке, здесь мы попробуем *multi-hot-encoding*. Наша модель быстро начнет переобучаться на тренировочных данных. Мы посмотрим как это произойдет и рассмотрим способы предотвращения этого.
Использование multi-hot-encoding на нашем массиве конвертирует его в векторы 0 и 1. Говоря конкретнее, это означает что например последовательность `[3, 5]` будет конвертирована в 10,000-размерный вектор, который будет состоять полностью из нулей за исключением 3 и 5, которые будут представлены в виде единиц.
```
NUM_WORDS = 10000
(train_data, train_labels), (test_data, test_labels) = keras.datasets.imdb.load_data(num_words=NUM_WORDS)
def multi_hot_sequences(sequences, dimension):
# Создаем матрицу формы (len(sequences), dimension), состоящую из нулей
results = np.zeros((len(sequences), dimension))
for i, word_indices in enumerate(sequences):
results[i, word_indices] = 1.0 # назначаем единицу на конкретные показатели results[i]
return results
train_data = multi_hot_sequences(train_data, dimension=NUM_WORDS)
test_data = multi_hot_sequences(test_data, dimension=NUM_WORDS)
```
Давай посмотрим на один из получившихся multi-hot векторов. Номера слов были отсортированы по частоте, и вполне ожидаемо, что многие значения единицы будут около нуля. Проверим это на графике:
```
plt.plot(train_data[0])
```
## Продемонстрируем переобучение
Самый простой способ предотвратить переобучение, это уменьшить размер модели, или количество обучаемых параметров, которые определяются количеством слоев и блоков на каждый слой. В глубоком обучении количество обучаемых параметров часто называют *емкостью модели*. Понятно, что модель с большим количество параметров будет иметь больший запас для обучения, и следовательно легче сможет выучить взаимосвязи между тренировочными образцами данных и целевыми проверочными. Обучение же без возможности обобщения окажется бесполезным, особенно если мы попытаемся получить предсказания на новых, ранее не виденных данных.
Всегда помни об этом: модели глубокого обучения всегда хорошо справляются с подстраиванием под тренировочные данные, но наша конечная цель - обучение обощению.
С другой стороны, если нейросеть имеет ограниченные ресурсы для запоминания шаблонов, то тогда она не сможет так же легко находить паттерны в данных. Чтобы сократить потери, такая модель будет вынуждена обучаться сжатым представлениям, которые имеют больше предсказательной силы. В то же самое время, если мы сделаем нашу модель слишком маленькой, тогда ей будет трудно подстроиться под тренировочный сет данных. Всегда нужно искать баланс между *слишком большой емкостью* и *недостаточной емкостью*.
К сожалению, не существует магической формулы, чтобы определить правильный размер или архитектуру модели, говоря о количестве слоев или размере каждого слоя. Тебе необходимо попробовать использовать разные архитектуры модели, прежде чем найти подходящую.
Чтобы найди подходящий размер модели лучше начать с относительно небольших слоев и параметров, затем начать увеличивать размер слоев или добавлять новые до тех пор, пока ты показатели не начнут ухудшаться на проверочных данных. Давай попробуем разобраться на примере нашей сети для классификации обзоров.
Для начала мы построим простую модель используя только слои ```Dense``` в качестве основы, а затем сделаем маленькую и большую версию этой модели для сравнения.
### Строим основу для модели
```
baseline_model = keras.Sequential([
# Параметр `input_shape` нужен только для того, чтобы заработал `.summary`
keras.layers.Dense(16, activation=tf.nn.relu, input_shape=(NUM_WORDS,)),
keras.layers.Dense(16, activation=tf.nn.relu),
keras.layers.Dense(1, activation=tf.nn.sigmoid)
])
baseline_model.compile(optimizer='adam',
loss='binary_crossentropy',
metrics=['accuracy', 'binary_crossentropy'])
baseline_model.summary()
baseline_history = baseline_model.fit(train_data,
train_labels,
epochs=20,
batch_size=512,
validation_data=(test_data, test_labels),
verbose=2)
```
### Создаем малый вариант
Давай построим модель с меньшим количесвом скрытых блоков и сравним ее с первой моделью:
```
smaller_model = keras.Sequential([
keras.layers.Dense(4, activation=tf.nn.relu, input_shape=(NUM_WORDS,)),
keras.layers.Dense(4, activation=tf.nn.relu),
keras.layers.Dense(1, activation=tf.nn.sigmoid)
])
smaller_model.compile(optimizer='adam',
loss='binary_crossentropy',
metrics=['accuracy', 'binary_crossentropy'])
smaller_model.summary()
```
И обучим модель используя те же данные:
```
smaller_history = smaller_model.fit(train_data,
train_labels,
epochs=20,
batch_size=512,
validation_data=(test_data, test_labels),
verbose=2)
```
### Создаем большую модель
В качестве упражнения ты можешь создать модель даже еще больше, и посмотреть как быстро она начнет переобучаться. Затем протестируем эту модель, которая будет иметь гораздо бóльшую емкость, чем требуется для решения нашей задачи:
```
bigger_model = keras.models.Sequential([
keras.layers.Dense(512, activation=tf.nn.relu, input_shape=(NUM_WORDS,)),
keras.layers.Dense(512, activation=tf.nn.relu),
keras.layers.Dense(1, activation=tf.nn.sigmoid)
])
bigger_model.compile(optimizer='adam',
loss='binary_crossentropy',
metrics=['accuracy','binary_crossentropy'])
bigger_model.summary()
```
И опять потренируем уже новую модель используя те же данные:
```
bigger_history = bigger_model.fit(train_data, train_labels,
epochs=20,
batch_size=512,
validation_data=(test_data, test_labels),
verbose=2)
```
### Построим графики потерь
<!--TODO(markdaoust): This should be a one-liner with tensorboard -->
Непрерывные линии показывают потери во время обучения, а прерывистые - во время проверки (помни - чем меньше потери на проверочных данных, тем точнее модель). В нашем случае самая маленькая модель начинает переобучаться позже, чем основная (после 6 эпох вместо 4) и ее показатели ухудшаются гораздо медленее после переобучения.
```
def plot_history(histories, key='binary_crossentropy'):
plt.figure(figsize=(16,10))
for name, history in histories:
val = plt.plot(history.epoch, history.history['val_'+key],
'--', label=name.title()+' Val')
plt.plot(history.epoch, history.history[key], color=val[0].get_color(),
label=name.title()+' Train')
plt.xlabel('Epochs')
plt.ylabel(key.replace('_',' ').title())
plt.legend()
plt.xlim([0,max(history.epoch)])
plot_history([('baseline', baseline_history),
('smaller', smaller_history),
('bigger', bigger_history)])
```
Обрати внимание, что большая сеть начинает переобучаться почти сразу же после первой эпохи, и ее метрики ухудшаются гораздо быстрее. Чем больше емкость модели, тем легче она сможет вместить тренировочный сет данных, что повлечет за собой низкие потери при обучении. Но в таком случае она будет более чувствительна к переобучению: разница в потерях между обучением и проверкой будет очень велика.
## Как решить проблему переобучения?
### Добавить регуляризацию весов
Тебе может быть знаком принцип *бритвы Оккама*: если есть 2 толкования явления, то правильным является самое "простое" - то, которое содержит меньше всего предположений. Этот принцип также применим к моделям, обучемым при помощи нейронных сетей: для одних и той же сети и данных существует несколько весовых значений, или моделей, которые могут быть обучены. Простые модели переобучиваются гораздо реже, чем сложные.
В этом контексте "простая модель" - та, в которой распределение значений параметров имеет меньшую энтропию. Другими словами, модель с меньшим количеством параметров, которую мы строили выше является простой. Таким образом, для предотвращение переобучения часто используется ограничение сложности сети путем уменьшения ее коэфицентов, что делает распределение более равномерным или *регулярным*. Этот метод называется *регуляризация весов*: к функции потерь нашей сети мы добавляем штраф (или *cost*, стоимость) за использование больших весов.
Штраф имеет 2 вида:
* Регуляризация L1 - штраф прямо пропорционален абсолютному значению коэффицентов весов (сокращенно мы называем его "норма L1")
* Регуляризация L2 - штраф добавляется пропорционально квадрату значения коэффицента весов. Норму L2 также называют *угасанием весов*. Это два одинаковых названия для одной и той же математической формулы
Чтобы осуществить регуляризацию в `tf.keras` мы добавим новый регулятор в блок со слоями как аргумент. Давай попробуем добавить L2 и посмотреть что получится:
```
l2_model = keras.models.Sequential([
keras.layers.Dense(16, kernel_regularizer=keras.regularizers.l2(0.001),
activation=tf.nn.relu, input_shape=(NUM_WORDS,)),
keras.layers.Dense(16, kernel_regularizer=keras.regularizers.l2(0.001),
activation=tf.nn.relu),
keras.layers.Dense(1, activation=tf.nn.sigmoid)
])
l2_model.compile(optimizer='adam',
loss='binary_crossentropy',
metrics=['accuracy', 'binary_crossentropy'])
l2_model_history = l2_model.fit(train_data, train_labels,
epochs=20,
batch_size=512,
validation_data=(test_data, test_labels),
verbose=2)
```
Значение ```l2(0.001)``` означает, что каждый коэффицент матрицы весов слоя будет добавлять ```0.001 * weight_coefficient_value**2``` к общей потери сети. Обрати внимание, что штраф добавляется только во время обучения, потери во время этой стадии будут гораздо выше, чем во время проверки.
Вот так выглядит влияние регуляризации L2:
```
plot_history([('Базовая модель', baseline_history),
('Регуляризация L2', l2_model_history)])
```
Как видишь, прошедшая L2 регуляризцию модель стала более устойчива к переобучению, чем наша изначальная, несмотря на то, что обе модели имели равное количество параметров.
### Добавить исключение Dropout
Метод исключения (или выпадения) *Dropout* - один из самых эффективных и часто используемых приемов регуляризации нейронных сетей. Он был разработан Джеффом Хинтоном совместно с его студентами в Университете Торонто. Применяемый к слою Dropout состоит из случайно выпадающих (или равных нулю) признаков этого слоя.
Допустим, что наш слой обычно возвращает вектор [0.2, 0.5, 1.3, 0.8, 1.1] на входной образец данных. После применения Dropout этот вектор будет случайным образом приравнивать к нулю какие-то его значения, например так - [0, 0.5, 1.3, 0, 1.1].
Ту часть признаков, которые "выпадут" или обнуляться называют *коэффицентом исключения dropout*. Обычно его устанавливают между 0.2 и 0.5. Во время проверки dropout не используется, и вместо этого все выходные значения уменьшаются на соотвествующий коэффиент (скажем, 0.5). Это поможет нам сбалансировать тот факт, что во время проверки было активировано больше блоков, чем во время обучения.
В `tf.keras` ты можешь использовать метод исключения в своей сети при помощи слоя Dropout, который применяется к выводу данных из предшествующего слоя.
Давай добавим два слоя Dropout в нашу сеть на данных IMDB и посмотрим насколько хорошо она справится с переобучением:
```
dpt_model = keras.models.Sequential([
keras.layers.Dense(16, activation=tf.nn.relu, input_shape=(NUM_WORDS,)),
keras.layers.Dropout(0.5),
keras.layers.Dense(16, activation=tf.nn.relu),
keras.layers.Dropout(0.5),
keras.layers.Dense(1, activation=tf.nn.sigmoid)
])
dpt_model.compile(optimizer='adam',
loss='binary_crossentropy',
metrics=['accuracy','binary_crossentropy'])
dpt_model_history = dpt_model.fit(train_data, train_labels,
epochs=20,
batch_size=512,
validation_data=(test_data, test_labels),
verbose=2)
plot_history([('Базовая модель', baseline_history),
('Метод Dropout', dpt_model_history)])
```
Метод Dropout имеет явные преимущества по сравнению с нашей изначальной, базовой моделью.
Подведем итоги - вот самые основные способы предотвращения переобучения нейросетей:
* Использовать больше данных для обучения
* Уменьшить емкость сети
* Использовать регуляризацию весов
* Или dropout
Также существуют еще два важных подхода, которые не были продемонстрированы в этом уроке: увеличение или *аугментация данных* и *нормализация батча*.
|
github_jupyter
|
# Make spectral libraries
```
import sys, os
sys.path.append('/Users/simon/git/vimms')
sys.path.insert(0,'/Users/simon/git/mass-spec-utils/')
from vimms.Common import save_obj
from tqdm import tqdm
%load_ext autoreload
%autoreload 2
library_cache = '/Users/simon/clms_er/library_cache'
```
## Massbank
```
from mass_spec_utils.library_matching.spec_libraries import MassBankLibrary
```
Path to the local version of the massbank repo
```
massbank_data_path = '/Users/simon/git/MassBank-Data/' # final slash is important!
mb = MassBankLibrary(mb_dir=massbank_data_path, polarity='POSITIVE')
save_obj(mb, os.path.join(library_cache, 'massbank_pos.p'))
mb = MassBankLibrary(mb_dir=massbank_data_path, polarity='NEGATIVE')
save_obj(mb, os.path.join(library_cache, 'massbank_neg.p'))
mb = MassBankLibrary(mb_dir=massbank_data_path, polarity='all')
save_obj(mb, os.path.join(library_cache, 'massbank_all.p'))
```
## GNPS
Using Florian's file, because it has inchikeys
```
json_file = '/Users/simon/Downloads/gnps_positive_ionmode_cleaned_by_matchms_and_lookups.json'
import json
with open(json_file,'r') as f:
payload = json.loads(f.read())
from mass_spec_utils.library_matching.spectrum import SpectralRecord
neg_intensities = []
def json_to_spectrum(json_dat):
precursor_mz = json_dat['precursor_mz']
original_file = json_file
spectrum_id = json_dat['spectrum_id']
inchikey = json_dat['inchikey_smiles']
peaks = json_dat['peaks_json']
metadata = {}
for k,v in json_dat.items():
if not k == 'peaks':
metadata[k] = v
mz,i = zip(*peaks)
if min(i) < 0:
neg_intensities.append(spectrum_id)
return None
else:
new_spectrum = SpectralRecord(precursor_mz, peaks, metadata, original_file, spectrum_id)
return new_spectrum
records = {}
for jd in tqdm(payload):
new_spec = json_to_spectrum(jd)
if new_spec is not None:
records[new_spec.spectrum_id] = new_spec
def filter_min_peaks(spectrum, min_n_peaks=10):
n_peaks = len(spectrum.peaks)
if n_peaks < min_n_peaks:
return None
else:
return spectrum
def filter_rel_intensity(spectrum, min_rel=0.01, max_rel=1.):
pp = spectrum.peaks
mz,i = zip(*pp)
max_i = max(i)
new_pp = []
for p in pp:
ri = p[1]/max_i
if ri <= max_rel and ri >= min_rel:
new_pp.append(p)
spectrum.peaks = new_pp
return spectrum
new_records = {}
for sid in tqdm(records.keys()):
spec = records[sid]
ss = filter_min_peaks(spec)
if ss is not None:
new_records[sid] = ss
else:
continue
ss = filter_rel_intensity(ss)
new_records[sid] = ss
for sid, ss in new_records.items():
ss.metadata['inchikey'] = ss.metadata['inchikey_smiles']
from mass_spec_utils.library_matching.spec_libraries import SpectralLibrary
sl = SpectralLibrary()
sl.records = new_records
sl.sorted_record_list = sl._dic2list()
save_obj(sl, os.path.join(library_cache,'gnps.p'))
```
|
github_jupyter
|
[Table of Contents](http://nbviewer.ipython.org/github/rlabbe/Kalman-and-Bayesian-Filters-in-Python/blob/master/table_of_contents.ipynb)
# Particle Filters
```
#format the book
%matplotlib notebook
from __future__ import division, print_function
from book_format import load_style
load_style()
```
## Motivation
Here is our problem. We have moving objects that we want to track. Maybe the objects are fighter jets and missiles, or maybe we are tracking people playing cricket in a field. It doesn't really matter. Which of the filters that we have learned can handle this problem? Unfortunately, none of them are ideal. Let's think about the characteristics of this problem.
* **multimodal**: We want to track zero, one, or more than one object simultaneously.
* **occlusions**: One object can hide another, resulting in one measurement for multiple objects.
* **nonlinear behavior**: Aircraft are buffeted by winds, balls move in parabolas, and people collide into each other.
* **nonlinear measurements**: Radar gives us the distance to an object. Converting that to an (x,y,z) coordinate requires a square root, which is nonlinear.
* **non-Gaussian noise:** as objects move across a background the computer vision can mistake part of the background for the object.
* **continuous:** the object's position and velocity (i.e. the state space) can smoothly vary over time.
* **multivariate**: we want to track several attributes, such as position, velocity, turn rates, etc.
* **unknown process model**: we may not know the process model of the system
None of the filters we have learned work well with all of these constraints.
* **Discrete Bayes filter**: This has most of the attributes. It is multimodal, can handle nonlinear measurements, and can be extended to work with nonlinear behavior. However, it is discrete and univariate.
* **Kalman filter**: The Kalman filter produces optimal estimates for unimodal linear systems with Gaussian noise. None of these are true for our problem.
* **Unscented Kalman filter**: The UKF handles nonlinear, continuous, multivariate problems. However, it is not multimodal nor does it handle occlusions. It can handle noise that is modestly non-Gaussian, but does not do well with distributions that are very non-Gaussian or problems that are very nonlinear.
* **Extended Kalman filter**: The EKF has the same strengths and limitations as the UKF, except that is it even more sensitive to strong nonlinearities and non-Gaussian noise.
## Monte Carlo Sampling
In the UKF chapter I generated a plot similar to this to illustrate the effects of nonlinear systems on Gaussians:
```
from code.book_plots import interactive_plot
import code.pf_internal as pf_internal
with interactive_plot():
pf_internal.plot_monte_carlo_ukf()
```
The left plot shows 3,000 points normally distributed based on the Gaussian
$$\mu = \begin{bmatrix}0\\0\end{bmatrix},\, \, \, \Sigma = \begin{bmatrix}32&15\\15&40\end{bmatrix}$$
The right plots shows these points passed through this set of equations:
$$\begin{aligned}x&=x+y\\
y &= 0.1x^2 + y^2\end{aligned}$$
Using a finite number of randomly sampled points to compute a result is called a [*Monte Carlo*](https://en.wikipedia.org/wiki/Monte_Carlo_method) (MC) method. The idea is simple. Generate enough points to get a representative sample of the problem, run the points through the system you are modeling, and then compute the results on the transformed points.
In a nutshell this is what particle filtering does. The Bayesian filter algorithm we have been using throughout the book is applied to thousands of particles, where each particle represents a *possible* state for the system. We extract the estimated state from the thousands of particles using weighted statistics of the particles.
## Generic Particle Filter Algorithm
1. **Randomly generate a bunch of particles**
Particles can have position, heading, and/or whatever other state variable you need to estimate. Each has a weight (probability) indicating how likely it matches the actual state of the system. Initialize each with the same weight.
2. **Predict next state of the particles**
Move the particles based on how you predict the real system is behaving.
3. **Update**
Update the weighting of the particles based on the measurement. Particles that closely match the measurements are weighted higher than particles which don't match the measurements very well.
4. **Resample**
Discard highly improbable particle and replace them with copies of the more probable particles.
5. **Compute Estimate**
Optionally, compute weighted mean and covariance of the set of particles to get a state estimate.
This naive algorithm has practical difficulties which we will need to overcome, but this is the general idea. Let's see an example. I wrote a particle filter for the robot localization problem from the UKF and EKF chapters. The robot has steering and velocity control inputs. It has sensors that measures distance to visible landmarks. Both the sensors and control mechanism have noise in them, and we need to track the robot's position.
Here I run a particle filter and plotted the positions of the particles. The plot on the left is after one iteration, and on the right is after 10. The red 'X' shows the actual position of the robot, and the large circle is the computed weighted mean position.
```
with interactive_plot():
pf_internal.show_two_pf_plots()
```
If you are viewing this in a browser, this animation shows the entire sequence:
<img src='animations/particle_filter_anim.gif'>
After the first iteration the particles are still largely randomly scattered around the map, but you can see that some have already collected near the robot's position. The computed mean is quite close to the robot's position. This is because each particle is weighted based on how closely it matches the measurement. The robot is near (1,1), so particles that are near (1, 1) will have a high weight because they closely match the measurements. Particles that are far from the robot will not match the measurements, and thus have a very low weight. The estimated position is computed as the weighted mean of positions of the particles. Particles near the robot contribute more to the computation so the estimate is quite accurate.
Several iterations later you can see that all the particles have clustered around the robot. This is due to the *resampling* step. Resampling discards particles that are very improbable (very low weight) and replaces them with particles with higher probability.
I haven't fully shown *why* this works nor fully explained the algorithms for particle weighting and resampling, but it should make intuitive sense. Make a bunch of random particles, move them so they 'kind of' follow the robot, weight them according to how well they match the measurements, only let the likely ones live. It seems like it should work, and it does.
## Probability distributions via Monte Carlo
Suppose we want to know the area under the curve $y= \mathrm{e}^{\sin(x)}$ in the interval [0, $\pi$]. The area is computed with the definite integral $\int_0^\pi \mathrm{e}^{\sin(x)}\, \mathrm{d}x$. As an exercise, go ahead and find the answer; I'll wait.
If you are wise you did not take that challenge; $\mathrm{e}^{\sin(x)}$ cannot be integrated analytically. The world is filled with equations which we cannot integrate. For example, consider calculating the luminosity of an object. An object reflects some of the light that strike it. Some of the reflected light bounces off of other objects and restrikes the original object, increasing the luminosity. This creates a *recursive integral*. Good luck with that one.
However, integrals are trivial to compute using a Monte Carlo technique. To find the area under a curve create a bounding box that contains the curve in the desired interval. Generate randomly positioned point within the box, and compute the ratio of points that fall under the curve vs the total number of points. For example, if 40% of the points are under the curve and the area of the bounding box is 1, then the area under the curve is approximately 0.4. As you tend towards infinite points you can achieve any arbitrary precision. In practice, a few thousand points will give you a fairly accurate result.
You can use this technique to numerically integrate a function of any arbitrary difficulty. this includes non-integrable and noncontinuous functions. This technique was invented by Stanley Ulam at Los Alamos National Laboratory to allow him to perform computations for nuclear reactions which were unsolvable on paper.
Let's compute $\pi$ by finding the area of a circle. We will define a circle with a radius of 1, and bound it in a square. The side of the square has length 2, so the area is 4. We generate a set of uniformly distributed random points within the box, and count how many fall inside the circle. The area of the circle is computed as the area of the box times the ratio of points inside the circle vs. the total number of points. Finally, we know that $A = \pi r^2$, so we compute $\pi = A / r^2$.
We start by creating the points.
```python
N = 20000
pts = uniform(-1, 1, (N, 2))
```
A point is inside a circle if its distance from the center of the circle is less than or equal to the radius. We compute the distance with `numpy.linalg.norm`, which computes the magnitude of a vector. Since vectors start at (0, 0) calling norm will compute the point's distance from the origin.
```python
dist = np.linalg.norm(pts, axis=1)
```
Next we compute which of this distances fit the criteria. This code returns a bool array that contains `True` if it meets the condition `dist <= 1`:
```python
in_circle = dist <= 1
```
All that is left is to count the points inside the circle, compute pi, and plot the results. I've put it all in one cell so you can experiment with alternative values for `N`, the number of points.
```
import matplotlib.pyplot as plt
import numpy as np
from numpy.random import uniform
N = 20000 # number of points
radius = 1
area = (2*radius)**2
pts = uniform(-1, 1, (N, 2))
# distance from (0,0)
dist = np.linalg.norm(pts, axis=1)
in_circle = dist <= 1
pts_in_circle = np.count_nonzero(in_circle)
pi = area * (pts_in_circle / N)
# plot results
with interactive_plot():
plt.scatter(pts[in_circle,0], pts[in_circle,1],
marker=',', edgecolor='k', s=1)
plt.scatter(pts[~in_circle,0], pts[~in_circle,1],
marker=',', edgecolor='r', s=1)
plt.axis('equal')
print('mean pi(N={})= {:.4f}'.format(N, pi))
print('err pi(N={})= {:.4f}'.format(N, np.pi-pi))
```
This insight leads us to the realization that we can use Monte Carlo to compute the probability density of any probability distribution. For example, suppose we have this Gaussian:
```
from filterpy.stats import plot_gaussian_pdf
with interactive_plot():
plot_gaussian_pdf(mean=2, variance=3);
```
The probability density function (PDF) gives the probability that the random value falls between 2 values. For example, we may want to know the probability of x being between 0 and 2 in the graph above. This is a continuous function, so we need to take the integral to find the area under the curve, as the area is equal to the probability for that range of values to occur.
$$P[a \le X \le b] = \int_a^b f_X(x) \, dx$$
It is easy to compute this integral for a Gaussian. But real life is not so easy. For example, the plot below shows a probability distribution. There is no way to analytically describe an arbitrary curve, let alone integrate it.
```
with interactive_plot():
pf_internal.plot_random_pd()
```
We can use Monte Carlo methods to compute any integral. The PDF is computed with an integral, hence we can compute the PDF of this curve using Monte Carlo.
## The Particle Filter
All of this brings us to the particle filter. Consider tracking a robot or a car in an urban environment. For consistency I will use the robot localization problem from the EKF and UKF chapters. In this problem we tracked a robot that has a sensor which measures the range and bearing to known landmarks.
Particle filters are a family of algorithms. I'm presenting a specific form of a particle filter that is intuitive to grasp and relates to the problems we have studied in this book. This will leave a few of the steps seeming a bit 'magical' since I haven't offered a full explanation. That will follow later in the chapter.
Taking insight from the discussion in the previous section we start by creating several thousand *particles*. Each particle has a position that represents a possible belief of where the robot is in the scene, and perhaps a heading and velocity. Suppose that we have no knowledge of the location of the robot. We would want to scatter the particles uniformly over the entire scene. If you think of all of the particles representing a probability distribution, locations where there are more particles represent a higher belief, and locations with fewer particles represents a lower belief. If there was a large clump of particles near a specific location that would imply that we were more certain that the robot is there.
Each particle needs a weight - ideally the probability that it represents the true position of the robot. This probability is rarely computable, so we only require it be *proportional* to that probability, which is computable. At initialization we have no reason to favor one particle over another, so we assign a weight of $1/N$, for $N$ particles. We use $1/N$ so that the sum of all probabilities equals one.
The combination of particles and weights forms the *probability distribution* for our problem. Think back to the *Discrete Bayes* chapter. In that chapter we modeled positions in a hallway as discrete and uniformly spaced. This is very similar except the particles are randomly distributed in a continuous space rather than constrained to discrete locations. In this problem the robot can move on a plane of some arbitrary dimension, with the lower right corner at (0,0).
To track our robot we need to maintain states for x, y, and heading. We will store `N` particles in a `(N, 3)` shaped array. The three columns contain x, y, and heading, in that order.
If you are passively tracking something (no control input), then you would need to include velocity in the state and use that estimate to make the prediction. More dimensions requires exponentially more particles to form a good estimate, so we always try to minimize the number of random variables in the state.
This code creates a uniform and Gaussian distribution of particles over a region:
```
from numpy.random import uniform
def create_uniform_particles(x_range, y_range, hdg_range, N):
particles = np.empty((N, 3))
particles[:, 0] = uniform(x_range[0], x_range[1], size=N)
particles[:, 1] = uniform(y_range[0], y_range[1], size=N)
particles[:, 2] = uniform(hdg_range[0], hdg_range[1], size=N)
particles[:, 2] %= 2 * np.pi
return particles
def create_gaussian_particles(mean, std, N):
particles = np.empty((N, 3))
particles[:, 0] = mean[0] + (randn(N) * std[0])
particles[:, 1] = mean[1] + (randn(N) * std[1])
particles[:, 2] = mean[2] + (randn(N) * std[2])
particles[:, 2] %= 2 * np.pi
return particles
```
For example:
```
create_uniform_particles((0,1), (0,1), (0, np.pi*2), 4)
```
### Predict Step
The predict step in the Bayes algorithm uses the process model to update the belief in the system state. How would we do that with particles? Each particle represents a possible position for the robot. Suppose we send a command to the robot to move 0.1 meters while turning by 0.007 radians. We could move each particle by this amount. If we did that we would soon run into a problem. The robot's controls are not perfect so it will not move exactly as commanded. Therefore we need to add noise to the particle's movements to have a reasonable chance of capturing the actual movement of the robot. If you do not model the uncertainty in the system the particle filter will not correctly model the probability distribution of our belief in the robot's position.
```
def predict(particles, u, std, dt=1.):
""" move according to control input u (heading change, velocity)
with noise Q (std heading change, std velocity)`"""
N = len(particles)
# update heading
particles[:, 2] += u[0] + (randn(N) * std[0])
particles[:, 2] %= 2 * np.pi
# move in the (noisy) commanded direction
dist = (u[1] * dt) + (randn(N) * std[1])
particles[:, 0] += np.cos(particles[:, 2]) * dist
particles[:, 1] += np.sin(particles[:, 2]) * dist
```
### Update Step
Next we get a set of measurements - one for each landmark currently in view. How should these measurements be used to alter our probability distribution as modeled by the particles?
Think back to the **Discrete Bayes** chapter. In that chapter we modeled positions in a hallway as discrete and uniformly spaced. We assigned a probability to each position which we called the *prior*. When a new measurement came in we multiplied the current probability of that position (the *prior*) by the *likelihood* that the measurement matched that location:
```python
def update(likelihood, prior):
posterior = prior * likelihood
return normalize(posterior)
```
which is an implementation of the equation
$$x = \| \mathcal L \bar x \|$$
which is a realization of Bayes theorem:
$$\begin{aligned}P(x \mid z) &= \frac{P(z \mid x)\, P(x)}{P(z)} \\
&= \frac{\mathtt{likelihood}\times \mathtt{prior}}{\mathtt{normalization}}\end{aligned}$$
We do the same with our particles. Each particle has a position and a weight which estimates how well it matches the measurement. Normalizing the weights so they sum to one turns them into a probability distribution. The particles those that are closest to the robot will generally have a higher weight than ones far from the robot.
```
def update(particles, weights, z, R, landmarks):
weights.fill(1.)
for i, landmark in enumerate(landmarks):
distance = np.linalg.norm(particles[:, 0:2] - landmark, axis=1)
weights *= scipy.stats.norm(distance, R).pdf(z[i])
weights += 1.e-300 # avoid round-off to zero
weights /= sum(weights) # normalize
```
In the literature this part of the algorithm is called *Sequential Importance Sampling*, or SIS. The equation for the weights is called the *importance density*. I will give these theoretical underpinnings in a following section. For now I hope that this makes intuitive sense. If we weight the particles according to how how they match the measurements they are probably a good sample for the probability distribution of the system after incorporating the measurements. Theory proves this is so. The weights are the *likelihood* in Bayes theorem. Different problems will need to tackle this step in slightly different ways but this is the general idea.
### Computing the State Estimate
In most applications you will want to know the estimated state after each update, but the filter consists of nothing but a collection of particles. Assuming that we are tracking one object (i.e. it is unimodal) we can compute the mean of the estimate as the sum of the weighted values of the particles.
$$ \mu = \frac{1}{N}\sum\limits_{i=1}^N w^ix^i$$
Here I adopt the notation $x^i$ to indicate the i$^{th}$ particle. A superscript is used because we often need to use subscripts to denote time steps the k$^{th}$ or k+1$^{th}$ particle, yielding the unwieldy $x^i_{k+1}$.
This function computes both the mean and variance of the particles:
```
def estimate(particles, weights):
"""returns mean and variance of the weighted particles"""
pos = particles[:, 0:2]
mean = np.average(pos, weights=weights, axis=0)
var = np.average((pos - mean)**2, weights=weights, axis=0)
return mean, var
```
If we create a uniform distribution of points in a 1x1 square with equal weights we get a mean position very near the center of the square at (0.5, 0.5) and a small variance.
```
particles = create_uniform_particles((0,1), (0,1), (0, 5), 1000)
weights = np.array([.25]*1000)
estimate(particles, weights)
```
### Particle Resampling
The SIS algorithm suffers from the *degeneracy problem*. It starts with uniformly distributed particles with equal weights. There may only be a handful of particles near the robot. As the algorithm runs any particle that does not match the measurements will acquire an extremely low weight. Only the particles which are near the robot will have an appreciable weight. We could have 5,000 particles with only 3 contributing meaningfully to the state estimate! We say the filter has *degenerated*.
This problem is usually solved by some form of *resampling* of the particles. Particles with very small weights do not meaningfully describe the probability distribution of the robot.
The resampling algorithm discards particles with very low probability and replaces them with new particles with higher probability. It does that by duplicating particles with relatively high probability. The duplicates are slightly dispersed by the noise added in the predict step. This results in a set of points in which a large majority of the particles accurately represent the probability distribution.
There are many resampling algorithms. For now let's look at one of the simplest, *simple random resampling*, also called *multinomial resampling*. It samples from the current particle set $N$ times, making a new set of particles from the sample. The probability of selecting any given particle should be proportional to its weight.
We accomplish this with NumPy's `cumsum` function. `cumsum` computes the cumulative sum of an array. That is, element one is the sum of elements zero and one, element two is the sum of elements zero, one and two, etc. Then we generate random numbers in the range of 0.0 to 1.0 and do a binary search to find the weight that most closely matches that number:
```
def simple_resample(particles, weights):
N = len(particles)
cumulative_sum = np.cumsum(weights)
cumulative_sum[-1] = 1. # avoid round-off error
indexes = np.searchsorted(cumulative_sum, random(N))
# resample according to indexes
particles[:] = particles[indexes]
weights[:] = weights[indexes]
weights /= np.sum(weights) # normalize
```
We don't resample at every epoch. For example, if you received no new measurements you have not received any information from which the resample can benefit. We can determine when to resample by using something called the *effective N*, which approximately measures the number of particles which meaningfully contribute to the probability distribution. The equation for this is
$$\hat{N}_\text{eff} = \frac{1}{\sum w^2}$$
and we can implement this in Python with
```
def neff(weights):
return 1. / np.sum(np.square(weights))
```
If $\hat{N}_\text{eff}$ falls below some threshold it is time to resample. A useful starting point is $N/2$, but this varies by problem. It is also possible for $\hat{N}_\text{eff} = N$, which means the particle set has collapsed to one point (each has equal weight). It may not be theoretically pure, but if that happens I create a new distribution of particles in the hopes of generating particles with more diversity. If this happens to you often, you may need to increase the number of particles, or otherwise adjust your filter. We will talk more of this later.
## SIR Filter - A Complete Example
There is more to learn, but we know enough to implement a full particle filter. We will implement the *Sampling Importance Resampling filter*, or SIR.
I need to introduce a more sophisticated resampling method than I gave above. FilterPy provides several resampling methods. I will describe them later. They take an array of weights and returns indexes to the particles that have been chosen for the resampling. We just need to write a function that performs the resampling from these indexes:
```
def resample_from_index(particles, weights, indexes):
particles[:] = particles[indexes]
weights[:] = weights[indexes]
weights /= np.sum(weights)
```
To implement the filter we need to create the particles and the landmarks. We then execute a loop, successively calling `predict`, `update`, resampling, and then computing the new state estimate with `estimate`.
```
from filterpy.monte_carlo import systematic_resample
from numpy.linalg import norm
from numpy.random import randn
import scipy.stats
def run_pf1(N, iters=18, sensor_std_err=.1,
do_plot=True, plot_particles=False,
xlim=(0, 20), ylim=(0, 20),
initial_x=None):
landmarks = np.array([[-1, 2], [5, 10], [12,14], [18,21]])
NL = len(landmarks)
plt.figure()
# create particles and weights
if initial_x is not None:
particles = create_gaussian_particles(
mean=initial_x, std=(5, 5, np.pi/4), N=N)
else:
particles = create_uniform_particles((0,20), (0,20), (0, 6.28), N)
weights = np.zeros(N)
if plot_particles:
alpha = .20
if N > 5000:
alpha *= np.sqrt(5000)/np.sqrt(N)
plt.scatter(particles[:, 0], particles[:, 1],
alpha=alpha, color='g')
xs = []
robot_pos = np.array([0., 0.])
for x in range(iters):
robot_pos += (1, 1)
# distance from robot to each landmark
zs = (norm(landmarks - robot_pos, axis=1) +
(randn(NL) * sensor_std_err))
# move diagonally forward to (x+1, x+1)
predict(particles, u=(0.00, 1.414), std=(.2, .05))
# incorporate measurements
update(particles, weights, z=zs, R=sensor_std_err,
landmarks=landmarks)
# resample if too few effective particles
if neff(weights) < N/2:
indexes = systematic_resample(weights)
resample_from_index(particles, weights, indexes)
mu, var = estimate(particles, weights)
xs.append(mu)
if plot_particles:
plt.scatter(particles[:, 0], particles[:, 1],
color='k', marker=',', s=1)
p1 = plt.scatter(robot_pos[0], robot_pos[1], marker='+',
color='k', s=180, lw=3)
p2 = plt.scatter(mu[0], mu[1], marker='s', color='r')
xs = np.array(xs)
#plt.plot(xs[:, 0], xs[:, 1])
plt.legend([p1, p2], ['Actual', 'PF'], loc=4, numpoints=1)
plt.xlim(*xlim)
plt.ylim(*ylim)
print('final position error, variance:\n\t', mu, var)
from numpy.random import seed
seed(2)
run_pf1(N=5000, plot_particles=False)
```
Most of this code is devoted to initialization and plotting. The entirety of the particle filter processing consists of these lines:
```python
# move diagonally forward to (x+1, x+1)
predict(particles, u=(0.00, 1.414), std=(.2, .05))
# incorporate measurements
update(particles, weights, z=zs, R=sensor_std_err,
landmarks=landmarks)
# resample if too few effective particles
if neff(weights) < N/2:
indexes = systematic_resample(weights)
resample_from_index(particles, weights, indexes)
mu, var = estimate(particles, weights)
```
The first line predicts the position of the particles with the assumption that the robot is moving in a straight line (`u[0] == 0`) and moving 1 unit in both the x and y axis (`u[1]==1.414`). The standard deviation for the error in the turn is 0.2, and the standard deviation for the distance is 0.05. When this call returns the particles will all have been moved forward, but the weights are no longer correct as they have not been updated.
The next line incorporates the measurement into the filter. This does not alter the particle positions, it only alters the weights. If you recall the weight of the particle is computed as the probability that it matches the Gaussian of the sensor error model. The further the particle from the measured distance the less likely it is to be a good representation.
The final two lines example the effective particle count ($\hat{N}_\text{eff})$. If it falls below $N/2$ we perform resampling to try to ensure our particles form a good representation of the actual probability distribution.
Now let's look at this with all the particles plotted. Seeing this happen interactively is much more instructive, but this format still gives us useful information. I plotted the original random distribution of points in a very pale green and large circles to help distinguish them from the subsequent iterations where the particles are plotted with black pixels. The number of particles makes it hard to see the details, so I limited the number of iterations to 8 so we can zoom in and look more closely.
```
seed(2)
run_pf1(N=5000, iters=8, plot_particles=True,
xlim=(0,8), ylim=(0,8))
```
From the plot it looks like there are only a few particles at the first two robot positions. This is not true; there are 5,000 particles, but due to resampling most are duplicates of each other. The reason for this is the Gaussian for the sensor is very narrow. This is called *sample impoverishment* and can lead to filter divergence. I'll address this in detail below. For now, looking at the second step at x=2 we can see that the particles have dispersed a bit. This dispersion is due to the motion model noise. All particles are projected forward according to the control input `u`, but noise is added to each particle proportional to the error in the control mechanism in the robot. By the third step the particles have dispersed enough to make a convincing cloud of particles around the robot.
The shape of the particle cloud is an ellipse. This is not a coincidence. The sensors and robot control are both modeled as Gaussian, so the probability distribution of the system is also a Gaussian. The particle filter is a sampling of the probability distribution, so the cloud should be an ellipse.
It is important to recognize that the particle filter algorithm *does not require* the sensors or system to be Gaussian or linear. Because we represent the probability distribution with a cloud of particles we can handle any probability distribution and strongly nonlinear problems. There can be discontinuities and hard limits in the probability model.
### Effect of Sensor Errors on the Filter
The first few iterations of the filter resulted in many duplicate particles. This happens because the model for the sensors is Gaussian, and we gave it a small standard deviation of $\sigma=0.1$. This is counterintuitive at first. The Kalman filter performs better when the noise is smaller, yet the particle filter can perform worse.
We can reason about why this is true. If $\sigma=0.1$, the robot is at (1, 1) and a particle is at (2, 2) the particle is 14 standard deviations away from the robot. This gives it a near zero probability. It contributes nothing to the estimate of the mean, and it is extremely unlikely to survive after the resampling. If $\sigma=1.4$ then the particle is only $1\sigma$ away and thus it will contribute to the estimate of the mean. During resampling it is likely to be copied one or more times.
This is *very important* to understand - a very accurate sensor can lead to poor performance of the filter because few of the particles will be a good sample of the probability distribution. There are a few fixes available to us. First, we can artificially increase the sensor noise standard deviation so the particle filter will accept more points as matching the robots probability distribution. This is non-optimal because some of those points will be a poor match. The real problem is that there aren't enough points being generated such that enough are near the robot. Increasing `N` usually fixes this problem. This decision is not cost free as increasing the number of particles significantly increase the computation time. Still, let's look at the result of using 100,000 particles.
```
seed(2)
run_pf1(N=100000, iters=8, plot_particles=True,
xlim=(0,8), ylim=(0,8))
```
There are many more particles at x=1, and we have a convincing cloud at x=2. Clearly the filter is performing better, but at the cost of large memory usage and long run times.
Another approach is to be smarter about generating the initial particle cloud. Suppose we guess that the robot is near (0, 0). This is not exact, as the simulation actually places the robot at (1, 1), but it is close. If we create a normally distributed cloud near (0, 0) there is a much greater chance of the particles matching the robot's position.
`run_pf1()` has an optional parameter `initial_x`. Use this to specify the initial position guess for the robot. The code then uses `create_gaussian_particles(mean, std, N)` to create particles distributed normally around the initial guess. We will use this in the next section.
### Filter Degeneracy From Inadequate Samples
The filter as written is far from perfect. Here is how it performs with a different random seed.
```
seed(6)
run_pf1(N=5000, plot_particles=True, ylim=(-20, 20))
```
Here the initial sample of points did not generate any points near the robot. The particle filter does not create new points during the resample operation, so it ends up duplicating points which are not a representative sample of the probability distribution. As mentioned earlier this is called *sample impoverishment*. The problem quickly spirals out of control. The particles are not a good match for the landscape measurement so they become dispersed in a highly nonlinear, curved distribution, and the particle filter diverges from reality. No particles are available near the robot, so it cannot ever converge.
Let's make use of the `create_gaussian_particles()` method to try to generate more points near the robot. We can do this by using the `initial_x` parameter to specify a location to create the particles.
```
seed(6)
run_pf1(N=5000, plot_particles=True, initial_x=(1,1, np.pi/4))
```
This works great. You should always try to create particles near the initial position if you have any way to roughly estimate it. Do not be *too* careful - if you generate all the points very near a single position the particles may not be dispersed enough to capture the nonlinearities in the system. This is a fairly linear system, so we could get away with a smaller variance in the distribution. Clearly this depends on your problem. Increasing the number of particles is always a good way to get a better sample, but the processing cost may be a higher price than you are willing to pay.
## Importance Sampling
I've hand waved a difficulty away which we must now confront. There is some probability distribution that describes the position and movement of our robot. We want to draw a sample of particles from that distribution and compute the integral using MC methods.
Our difficulty is that in many problems we don't know the distribution. For example, the tracked object might move very differently than we predicted with our state model. How can we draw a sample from a probability distribution that is unknown?
There is a theorem from statistics called [*importance sampling*](https://en.wikipedia.org/wiki/Importance_sampling)[1]. Remarkably, it gives us a way to draw samples from a different and known probability distribution and use those to compute the properties of the unknown one. It's a fantastic theorem that brings joy to my heart.
The idea is simple, and we already used it. We draw samples from the known probability distribution, but *weight the samples* according to the distribution we are interested in. We can then compute properties such as the mean and variance by computing the weighted mean and weighted variance of the samples.
For the robot localization problem we drew samples from the probability distribution that we computed from our state model prediction step. In other words, we reasoned 'the robot was there, it is perhaps moving at this direction and speed, hence it might be here'. Yet the robot might have done something completely different. It may have fell off a cliff or been hit by a mortar round. In each case the probability distribution is not correct. It seems like we are stymied, but we are not because we can use importance sampling. We drew particles from that likely incorrect probability distribution, then weighted them according to how well the particles match the measurements. That weighting is based on the true probability distribution, so according to the theory the resulting mean, variance, etc, will be correct!
How can that be true? I'll give you the math; you can safely skip this if you don't plan to go beyond the robot localization problem. However, other particle filter problems require different approaches to importance sampling, and a bit of math helps. Also, the literature and much of the content on the web uses the mathematical formulation in favor of my rather imprecise "imagine that..." exposition. If you want to understand the literature you will need to know the following equations.
We have some probability distribution $\pi(x)$ which we want to take samples from. However, we don't know what $\pi(x)$ is; instead we only know an alternative probability distribution $q(x)$. In the context of robot localization, $\pi(x)$ is the probability distribution for the robot, but we don't know it, and $q(x)$ is the probability distribution of our measurements, which we do know.
The expected value of a function $f(x)$ with probability distribution $\pi(x)$ is
$$\mathbb{E}\big[f(x)\big] = \int f(x)\pi(x)\, dx$$
We don't know $\pi(x)$ so we cannot compute this integral. We do know an alternative distribution $q(x)$ so we can add it into the integral without changing the value with
$$\mathbb{E}\big[f(x)\big] = \int f(x)\pi(x)\frac{q(x)}{q(x)}\, dx$$
Now we rearrange and group terms
$$\mathbb{E}\big[f(x)\big] = \int f(x)q(x)\, \, \cdot \, \frac{\pi(x)}{q(x)}\, dx$$
$q(x)$ is known to us, so we can compute $\int f(x)q(x)$ using MC integration. That leaves us with $\pi(x)/q(x)$. That is a ratio, and we define it as a *weight*. This gives us
$$\mathbb{E}\big[f(x)\big] = \sum\limits_{i=1}^N f(x^i)w(x^i)$$
Maybe that seems a little abstract. If we want to compute the mean of the particles we would compute
$$\mu = \sum\limits_{i=1}^N x^iw^i$$
which is the equation I gave you earlier in the chapter.
It is required that the weights be proportional to the ratio $\pi(x)/q(x)$. We normally do not know the exact value, so in practice we normalize the weights by dividing them by $\sum w(x^i)$.
When you formulate a particle filter algorithm you will have to implement this step depending on the particulars of your situation. For robot localization the best distribution to use for $q(x)$ is the particle distribution from the `predict()` step of the filter. Let's look at the code again:
```python
def update(particles, weights, z, R, landmarks):
weights.fill(1.)
for i, landmark in enumerate(landmarks):
dist = np.linalg.norm(particles[:, 0:2] - landmark, axis=1)
weights *= scipy.stats.norm(dist, R).pdf(z[i])
weights += 1.e-300 # avoid round-off to zero
weights /= sum(weights) # normalize
```
The reason for `self.weights.fill(1.)` might have confused you. In all the Bayesian filters up to this chapter we started with the probability distribution created by the `predict` step, and this appears to discard that information by setting all of the weights to 1. Well, we are discarding the weights, but we do not discard the particles. That is a direct result of applying importance sampling - we draw from the known distribution, but weight by the unknown distribution. In this case our known distribution is the uniform distribution - all are weighted equally.
Of course if you can compute the posterior probability distribution from the prior you should do so. If you cannot, then importance sampling gives you a way to solve this problem. In practice, computing the posterior is incredibly difficult. The Kalman filter became a spectacular success because it took advantage of the properties of Gaussians to find an analytic solution. Once we relax the conditions required by the Kalman filter (Markov property, Gaussian measurements and process) importance sampling and monte carlo methods make the problem tractable.
## Resampling Methods
The resampling algorithm effects the performance of the filter. For example, suppose we resampled particles by picking particles at random. This would lead us to choosing many particles with a very low weight, and the resulting set of particles would be a terrible representation of the problem's probability distribution.
Research on the topic continues, but a handful of algorithms work well in practice across a wide variety of situations. We desire an algorithm that has several properties. It should preferentially select particles that have a higher probability. It should select a representative population of the higher probability particles to avoid sample impoverishment. It should include enough lower probability particles to give the filter a chance of detecting strongly nonlinear behavior.
FilterPy implements several of the popular algorithms. FilterPy doesn't know how your particle filter is implemented, so it cannot generate the new samples. Instead, the algorithms create a `numpy.array` containing the indexes of the particles that are chosen. Your code needs to perform the resampling step. For example, I used this for the robot:
```
def resample_from_index(particles, weights, indexes):
particles[:] = particles[indexes]
weights[:] = weights[indexes]
weights /= np.sum(weights)
```
### Multinomial Resampling
Multinomial resampling is the algorithm that I used while developing the robot localization example. The idea is simple. Compute the cumulative sum of the normalized weights. This gives you an array of increasing values from 0 to 1. Here is a plot which illustrates how this spaces out the weights. The colors are meaningless, they just make the divisions easier to see.
```
from code.pf_internal import plot_cumsum
print('cumulative sume is', np.cumsum([.1, .2, .1, .6]))
plot_cumsum([.1, .2, .1, .6])
```
To select a weight we generate a random number uniformly selected between 0 and 1 and use binary search to find its position inside the cumulative sum array. Large weights occupy more space than low weights, so they will be more likely to be selected.
This is very easy to code using NumPy's [ufunc](http://docs.scipy.org/doc/numpy/reference/ufuncs.html) support. Ufuncs apply functions to every element of an array, returning an array of the results. `searchsorted` is NumPy's binary search algorithm. If you provide is with an array of search values it will return an array of answers; one answer for each search value.
```
def multinomal_resample(weights):
cumulative_sum = np.cumsum(weights)
cumulative_sum[-1] = 1. # avoid round-off errors
return np.searchsorted(cumulative_sum, random(len(weights)))
```
Here is an example:
```
from code.pf_internal import plot_multinomial_resample
plot_multinomial_resample([.1, .2, .3, .4, .2, .3, .1])
```
This is an $O(n \log(n))$ algorithm. That is not terrible, but there are $O(n)$ resampling algorithms with better properties with respect to the uniformity of the samples. I'm showing it because you can understand the other algorithms as variations on this one. There is a faster implementation of this multinomial resampling that uses the inverse of the CDF of the distribution. You can search on the internet if you are interested.
Import the function from FilterPy using
```python
from filterpy.monte_carlo import multinomal_resample
```
### Residual Resampling
Residual resampling both improves the run time of multinomial resampling, and ensures that the sampling is uniform across the population of particles. It's fairly ingenious: the normalized weights are multiplied by *N*, and then the integer value of each weight is used to define how many samples of that particle will be taken. For example, if the weight of a particle is 0.0012 and $N$=3000, the scaled weight is 3.6, so 3 samples will be taken of that particle. This ensures that all higher weight particles are chosen at least once. The running time is $O(N)$, making it faster than multinomial resampling.
However, this does not generate all *N* selections. To select the rest, we take the *residual*: the weights minus the integer part, which leaves the fractional part of the number. We then use a simpler sampling scheme such as multinomial, to select the rest of the particles based on the residual. In the example above the scaled weight was 3.6, so the residual will be 0.6 (3.6 - int(3.6)). This residual is very large so the particle will be likely to be sampled again. This is reasonable because the larger the residual the larger the error in the round off, and thus the particle was relatively under sampled in the integer step.
```
def residual_resample(weights):
N = len(weights)
indexes = np.zeros(N, 'i')
# take int(N*w) copies of each weight
num_copies = (N*np.asarray(weights)).astype(int)
k = 0
for i in range(N):
for _ in range(num_copies[i]): # make n copies
indexes[k] = i
k += 1
# use multinormial resample on the residual to fill up the rest.
residual = w - num_copies # get fractional part
residual /= sum(residual) # normalize
cumulative_sum = np.cumsum(residual)
cumulative_sum[-1] = 1. # ensures sum is exactly one
indexes[k:N] = np.searchsorted(cumulative_sum, random(N-k))
return indexes
```
You may be tempted to replace the inner for loop with a slice `indexes[k:k + num_copies[i]] = i`, but very short slices are comparatively slow, and the for loop usually runs faster.
Let's look at an example:
```
from code.pf_internal import plot_residual_resample
plot_residual_resample([.1, .2, .3, .4, .2, .3, .1])
```
You may import this from FilterPy using
```python
from filterpy.monte_carlo import residual_resample
```
### Stratified Resampling
This scheme aims to make selections relatively uniformly across the particles. It works by dividing the cumulative sum into $N$ equal sections, and then selects one particle randomly from each section. This guarantees that each sample is between 0 and $\frac{2}{N}$ apart.
The plot below illustrates this. The colored bars show the cumulative sum of the array, and the black lines show the $N$ equal subdivisions. Particles, shown as black circles, are randomly placed in each subdivision.
```
from pf_internal import plot_stratified_resample
plot_stratified_resample([.1, .2, .3, .4, .2, .3, .1])
```
The code to perform the stratification is quite straightforward.
```
def stratified_resample(weights):
N = len(weights)
# make N subdivisions, chose a random position within each one
positions = (random(N) + range(N)) / N
indexes = np.zeros(N, 'i')
cumulative_sum = np.cumsum(weights)
i, j = 0, 0
while i < N:
if positions[i] < cumulative_sum[j]:
indexes[i] = j
i += 1
else:
j += 1
return indexes
```
Import it from FilterPy with
```python
from filterpy.monte_carlo import stratified_resample
```
### Systematic Resampling
The last algorithm we will look at is systemic resampling. As with stratified resampling the space is divided into $N$ divisions. We then choose a random offset to use for all of the divisions, ensuring that each sample is exactly $\frac{1}{N}$ apart. It looks like this.
```
from pf_internal import plot_systematic_resample
plot_systematic_resample([.1, .2, .3, .4, .2, .3, .1])
```
Having seen the earlier examples the code couldn't be simpler.
```
def systematic_resample(weights):
N = len(weights)
# make N subdivisions, choose positions
# with a consistent random offset
positions = (np.arange(N) + random()) / N
indexes = np.zeros(N, 'i')
cumulative_sum = np.cumsum(weights)
i, j = 0, 0
while i < N:
if positions[i] < cumulative_sum[j]:
indexes[i] = j
i += 1
else:
j += 1
return indexes
```
Import from FilterPy with
```python
from filterpy.monte_carlo import systematic_resample
```
### Choosing a Resampling Algorithm
Let's look at the four algorithms at once so they are easier to compare.
```
a = [.1, .2, .3, .4, .2, .3, .1]
np.random.seed(4)
plot_multinomial_resample(a)
plot_residual_resample(a)
plot_systematic_resample(a)
plot_stratified_resample(a)
```
The performance of the multinomial resampling is quite bad. There is a very large weight that was not sampled at all. The largest weight only got one resample, yet the smallest weight was sample was sampled twice. Most tutorials on the net that I have read use multinomial resampling, and I am not sure why. Multinomial resampling is rarely used in the literature or for real problems. I recommend not using it unless you have a very good reason to do so.
The residual resampling algorithm does excellently at what it tries to do: ensure all the largest weights are resampled multiple times. It doesn't evenly distribute the samples across the particles - many reasonably large weights are not resampled at all.
Both systematic and stratified perform very well. Systematic sampling does an excellent job of ensuring we sample from all parts of the particle space while ensuring larger weights are proportionality resampled more often. Stratified resampling is not quite as uniform as systematic resampling, but it is a bit better at ensuring the higher weights get resampled more.
Plenty has been written on the theoretical performance of these algorithms, and feel free to read it. In practice I apply particle filters to problems that resist analytic efforts, and so I am a bit dubious about the validity of a specific analysis to these problems. In practice both the stratified and systematic algorithms perform well and similarly across a variety of problems. I say try one, and if it works stick with it. If performance of the filter is critical try both, and perhaps see if there is literature published on your specific problem that will give you better guidance.
## Summary
This chapter only touches the surface of what is a vast topic. My goal was not to teach you the field, but to expose you to practical Bayesian Monte Carlo techniques for filtering.
Particle filters are a type of *ensemble* filtering. Kalman filters represents state with a Gaussian. Measurements are applied to the Gaussian using Bayes Theorem, and the prediction is done using state-space methods. These techniques are applied to the Gaussian - the probability distribution.
In contrast, ensemble techniques represent a probability distribution using a discrete collection of points and associated probabilities. Measurements are applied to these points, not the Gaussian distribution. Likewise, the system model is applied to the points, not a Gaussian. We then compute the statistical properties of the resulting ensemble of points.
These choices have many trade-offs. The Kalman filter is very efficient, and is an optimal estimator if the assumptions of linearity and Gaussian noise are true. If the problem is nonlinear than we must linearize the problem. If the problem is multimodal (more than one object being tracked) then the Kalman filter cannot represent it. The Kalman filter requires that you know the state model. If you do not know how your system behaves the performance is poor.
In contrast, particle filters work with any arbitrary, non-analytic probability distribution. The ensemble of particles, if large enough, form an accurate approximation of the distribution. It performs wonderfully even in the presence of severe nonlinearities. Importance sampling allows us to compute probabilities even if we do not know the underlying probability distribution. Monte Carlo techniques replace the analytic integrals required by the other filters.
This power comes with a cost. The most obvious costs are the high computational and memory burdens the filter places on the computer. Less obvious is the fact that they are fickle. You have to be careful to avoid particle degeneracy and divergence. It can be very difficult to prove the correctness of your filter. If you are working with multimodal distributions you have further work to cluster the particles to determine the paths of the multiple objects. This can be very difficult when the objects are close to each other.
There are many different classes of particle filter; I only described the naive SIS algorithm, and followed that with a SIR algorithm that performs well. There are many classes of filters, and many examples of filters in each class. It would take a small book to describe them all.
When you read the literature on particle filters you will find that it is strewn with integrals. We perform computations on probability distributions using integrals, so using integrals gives the authors a powerful and compact notation. You must recognize that when you reduce these equations to code you will be representing the distributions with particles, and integrations are replaced with sums over the particles. If you keep in mind the core ideas in this chapter the material shouldn't be daunting.
## References
[1] *Importance Sampling*, Wikipedia.
https://en.wikipedia.org/wiki/Importance_sampling
|
github_jupyter
|
## Desafio Final 1
Bootcamp Analista de Machine Learning @ IGTI
**Objetivos**:
* Pré-processamento dos dados.
* Detecção de anomalias
* Processamento dos dados.
* Correlações.
* Redução da dimensionalidade.
* Algoritmos supervisionados e não supervisionados
**Análise com:**
* Redução de dimensionalidade
* Clusterização com K-means
* Classificação supervisionada
```
import pandas as pd
import numpy as np
import seaborn as sns
from google.colab import drive
drive.mount('/content/drive')
cars = pd.read_csv('/content/drive/My Drive/Data Science/Bootcamp Analista de ML/Desafio Final/cars.csv')
```
## Conhecendo o dataset
**Significado das classes:**
* mpg = miles per gallon
* cylinders = quantidade de cilindros, que é a origem da força mecânica que possibilita o deslocamento do veículo
* cubicinches = volume total de ar e combustível queimado pelos cilindros através do motor
* hp = horse power
* weightlbs = peso do carro em libras
* time-to-60 = capacidade em segundos do carro de ir de 0 a 60 milhas por horas
* year = ano de fabricação
* brand = marca, origem, etc.
1 kg = 2,20462 lbs
```
cars.head()
cars.describe()
#linhas x colunas
cars.shape
#Existem dados faltantes ?
cars.isnull().sum()
cars.info()
```
## Teste: Desafio Final
Pergunta 1 - Após a utilização da biblioteca pandas para a leitura dos dados sobre os valores lidos, é CORRETO afirmar que:
```
cars.isnull().sum()
```
**Não foram encontrados valores nulos após a leitura dos dados.**
Pergunta 2 - Realize a transformação das colunas “cubicinches” e “weightlbs” do tipo “string” para o tipo numérico utilizando o pd.to_numeric(), utilizando o parâmetro errors='coerce'. Após essa transformação, é CORRETO afirmar:
```
#Convertendo valores objects para numeric
cars['cubicinches'] = pd.to_numeric(cars['cubicinches'], errors='coerce')
cars['weightlbs'] = pd.to_numeric(cars['weightlbs'], errors='coerce')
#Verificando resultado
cars.info()
cars.isnull().sum()
```
**Essa transformação adiciona valores nulos ao nosso dataset.**
Pergunta 3 - Indique quais eram os índices dos valores presentes no dataset que “forçaram” o pandas a compreender a variável “cubicinches” como string.
```
indices_cub = [cars[cars['cubicinches'].isnull()]]
indices_cub
```
Pergunta 4 - Após a transformação das variáveis “string” para os valores numéricos, quantos valores nulos (células no dataframe) passaram a existir no dataset?
```
cars.isnull().sum()
```
Pergunta 5 - Substitua os valores nulos introduzidos no dataset, após a transformação, pelo valor médio das colunas. Qual é o novo valor médio da coluna “weightlbs”?
```
cars['cubicinches'] = cars['cubicinches'].fillna(cars['cubicinches'].mean())
cars['weightlbs'] = cars['weightlbs'].fillna(cars['weightlbs'].mean())
cars.isnull().sum()
cars['weightlbs'].mean()
```
Pergunta 6 - Após substituir os valores nulos pela média das colunas, selecione as colunas ['mpg', 'cylinders', 'cubicinches', 'hp', 'weightlbs', 'time-to-60', 'year']. Qual é o valor da mediana para a característica 'mpg'?
```
cars['mpg'].median()
```
Pergunta 7 - Qual é a afirmação CORRETA sobre o valor de 14,00 para a variável “time-to-60”?
```
cars.describe()
```
75% dos dados são maiores que o valor de 14,00.
8 - Sobre o coeficiente de correlação de Pearson entre as variáveis “cylinders” e “mpg”, é correto afirmar
```
from scipy import stats
stats.pearsonr(cars['cylinders'], cars['mpg'])
from sklearn.metrics import r2_score
r2_score(cars['cylinders'], cars['mpg'])
```
Mesmo não sendo igual a 1, é possível dizer que à medida em que a variável “cylinders” aumenta, a variável “mpg” também aumenta na mesma direção.
9 - Sobre o boxplot da variável “hp”, é correto afirmar, EXCETO:
```
sns.boxplot(cars['hp'])
```
Cada um dos quartis possui a mesma quantidade de valores para a variável “hp”.
10 - Após normalizado, utilizando a função StandardScaler(), qual é o maior valor para a variável “hp”?
```
cars.head()
cars_normalizar = cars.drop('brand', axis=1)
cars_normalizar.head()
from sklearn.preprocessing import StandardScaler
normalizar = StandardScaler() #instanciando o standart scaler
scaler = normalizar.fit(cars_normalizar.values) #fitando o dataset para normalizar
cars_normalizado = scaler.transform(cars_normalizar.values) #normalizando
cars_normalizado = pd.DataFrame(cars_normalizado, columns=cars_normalizar.columns) #transformando o array numpy em data frame do pandas
cars_normalizado['hp'].max()
```
11 - Aplicando o PCA, conforme a definição acima, qual é o valor da variância explicada com pela primeira componente principal
```
from sklearn.decomposition import PCA
pca = PCA(n_components=7)
principais = pca.fit_transform(cars_normalizado)
pca.explained_variance_ratio_
```
12 - Utilize os três primeiros componentes principais para construir o K-means com um número de 3 clusters. Sobre os clusters, é INCORRETO afirmar que
```
principais.explained_variance_ratio_
principais_componentes = pd.DataFrame(principais)
principais_componentes.head()
principais_componentes_k = principais_componentes.iloc[:, :3] #selecionando todas as linhas e as 3 primeiras colunas
principais_componentes_k.columns = ['componente 1', 'componente 2', 'componente 3']
from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters=3, random_state=42).fit(principais_componentes_k) #Parâmetros dados no desafio
principais_componentes_k['cluster'] = kmeans.labels_ #adicionando coluna do cluster em que o carro está
principais_componentes_k
principais_componentes_k['cluster'].value_counts() #Contando a quantidade de elementos dos clusters gerados
```
13 - Após todo o processamento realizado nos itens anteriores, crie uma coluna que contenha a variável de eficiência do veículo. Veículos que percorrem mais de 25 milhas com um galão (“mpg”>25) devem ser considerados eficientes. Utilize as colunas ['cylinders' ,'cubicinches' ,'hp' ,'weightlbs','time-to-60'] como entradas e como saída a coluna de eficiência criada.
Utilizando a árvore de decisão como mostrado, qual é a acurácia do modelo?
```
cars.head()
entradas = np.array(cars[['cylinders' ,'cubicinches' ,'hp' ,'weightlbs' ,'time-to-60']])
saidas = np.array(cars['mpg'] > 25).astype(int) #zero = maior, 1 = menor
entradas
saidas
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(entradas, saidas, test_size=0.30, random_state=42)
from sklearn.tree import DecisionTreeClassifier
classificador = DecisionTreeClassifier(random_state=42)
classificador.fit(x_train, y_train)
y_pred = classificador.predict(x_test)
from sklearn.metrics import accuracy_score
acuracia = accuracy_score(y_test, y_pred)
acuracia
```
14 - Sobre a matriz de confusão obtida após a aplicação da árvore de decisão, como mostrado anteriormente, é INCORRETO afirmar:
```
from sklearn.metrics import confusion_matrix
confusion_matrix(y_test, y_pred)
```
Existem duas vezes mais veículos considerados não eficientes que instâncias de veículos eficientes
15 - Utilizando a mesma divisão de dados entre treinamento e teste empregada para a análise anterior, aplique o modelo de regressão logística como mostrado na descrição do trabalho.
Comparando os resultados obtidos com o modelo de árvore de decisão, é INCORRETO afirmar que:
```
from sklearn.linear_model import LogisticRegression
logreg = LogisticRegression(random_state=42).fit(x_train, y_train)
logreg_y_pred = logreg.predict(x_test)
accuracy_score(y_test, logreg_y_pred)
```
# Fim
# Visite o meu [github](https://github.com/k3ybladewielder) <3
|
github_jupyter
|
```
import pandas as pd
import numpy as np
import os, glob
import pandas as pd
import numpy as np
%matplotlib inline
#%matplotlib notebook
import seaborn as sns
sns.reset_orig()
import matplotlib.pyplot as plt
from datetime import datetime, timedelta
import pdb
import requests
import sys
from importlib import reload
from pchipOceanSlices import PchipOceanSlices
import visualizeProfs as vp
#reload(visualizeProfs)
coord = {}
coord['lat'] = 0
coord['long'] = 59.5
shape = vp.construct_box(coord, 20, 20)
ids = ['5901721_24',
'3900105_196',
'4900595_140',
'4900593_152',
'4900883_92',
'5901898_42',
'6900453_3',
'6900453_5',
'6900453_6',
'3900495_188',
'3900495_189',
'3900495_190',
'4901139_74',
'2901211_144',
'2900784_254',
'2901709_19',
'1901218_88',
'4901787_0',
'6902566_44',
'4901787_6',
'6901002_100',
'2902100_104',
'6901002_102',
'6901541_103',
'2901703_157',
'2901765_1',
'4901750_125',
'4902382_4',
'4901285_208',
'4901285_209',
'4902107_54',
'6901448_149',
'6901740_126',
'5901884_302',
'4901466_156',
'4901462_174',
'4901798_110',
'4901798_112',
'4902391_58',
'6902661_118',
'4901824_91',
'4902457_2',
'5904485_280',
'5904485_284',]
startDate='2007-6-15'
endDate='2007-7-31'
presRange='[15,35]'
#profiles = get_selection_profiles(startDate, endDate, shape, presRange)
profiles = vp.get_profiles_by_id(str(ids).replace(' ',''), None, True)
if len(profiles) > 0:
selectionDf = vp.parse_into_df(profiles)
selectionDf.replace(-999, np.nan, inplace=True)
selectionDf.head()
pos = PchipOceanSlices()
iCol = 'temp'
xLab = 'pres'
yLab = iCol
xintp = 20
pLevelRange = [15,25]
pos = PchipOceanSlices(pLevelRange)
iDf = pos.make_interpolated_df(selectionDf, xintp, xLab, yLab)
iDf.date = pd.to_datetime(iDf.date)
print(iDf.shape)
iDf.head()
for profile_id, df in selectionDf.groupby('profile_id'):
#fig.subplots_adjust(hspace=.35, wspace=.35)
pdf = iDf[iDf['profile_id'] == profile_id]
if pdf.empty:
continue
fig, axes = plt.subplots(nrows=1, ncols=1, figsize=(6,6))
ax = vp.plot_scatter(df, profile_id, 'temp', 'pres', axes)
ax.scatter(pdf.temp.iloc[0], pdf.pres.iloc[0])
badProfiles = ['3900495_189']
for row in iDf.itertuples():
coord = {}
coord['lat'] = row.lat
coord['long'] = row.lon
startDate = datetime.strftime(row.date - timedelta(days=15), '%Y-%m-%d')
endDate = datetime.strftime(row.date + timedelta(days=15), '%Y-%m-%d')
shape = vp.construct_box(coord, 5, 5)
print(row.profile_id)
vp.build_selection_page_url(startDate, endDate, shape, presRange)
```
|
github_jupyter
|
I quote myself from the last post:
> The number of tests and the probability to obtain at least one significant result increases with the number of variables (plus interactions) included in the Anova. According to Maxwell (2004) this may be a reason for prevalence of underpowered Anova studies. Researchers target some significant result by default, instead of planning sample size that would provide enough power so that all effects can be reliably discovered.
Maxwell (2004, p. 149) writes:
> a researcher who designs a 2 $\times$ 2 study with 10 participants per cell has a 71% chance of obtaining at least
one statistically significant result if the three effects he or she tests all reflect medium effect sizes. Of course, in
reality, some effects will often be smaller and others will be larger, but the general point here is that the probability of
being able to find something statistically significant and thus potentially publishable may be adequate while at the same
time the probability associated with any specific test may be much lower. Thus, from the perspective of a researcher who
aspires to obtain at least one statistically significant result, 10 participants per cell may be sufficient, despite the fact that a methodological evaluation would declare the study to be underpowered because the power for any single hypothesis is only .35.
What motivates the researcher to keep the N small? Clearly, testing more subjects is costly. But I think that in Anova designs there is additional motivation to keep N small. If we use large N we obtain all main effects and all interactions significant. This is usually not desirable because some of the effects/interactions are not predicted by researcher's theory and non-significant main effect/interaction is taken as an evidence for a lack of this component. Then the researcher needs to find some N that balances between something significant and everything significant. In particular the prediction of significant main effects and non significant interaction is attractive because it is much easier to achieve than other patterns.
Let's look at the probability of obtaining significant main effects and interaction in Anova. I'm lazy so instead of deriving closed-form results I use simulation. Let's assume 2 $\times$ 2 Anova design where the continuous outcome is given by $y= x_1 + x_2 + x_1 x_2 +\epsilon$ with $\epsilon \sim \mathcal{N}(0,2)$ and $x_1 \in \{0,1\}$ and $x_2 \in \{0,1\}$. We give equal weight to all three terms to give them equal start. It is plausible to include all three terms, because with psychological variables everything is correlated (CRUD factor). Let's first show that the interaction requires larger sample size than the main effects.
```
%pylab inline
from scipy import stats
Ns=np.arange(20,200,4);
K=10000;
ps=np.zeros((Ns.size,3))
res=np.zeros(4)
cs=np.zeros((Ns.size,8))
i=0
for N in Ns:
for k in range(K):
x1=np.zeros(N);x1[N/2:]=1
x2=np.mod(range(N),2)
y= 42+x1+x2+x1*x2+np.random.randn(N)*2
tot=np.square(y-y.mean()).sum()
x=np.ones((N,4))
x[:,1]=x1*x2
x[:,2]=x1*(1-x2)
x[:,3]=(1-x1)*x2
res[0]=np.linalg.lstsq(x,y)[1]
x=np.ones((N,2))
x[:,1]=x1
res[1]=tot-np.linalg.lstsq(x,y)[1]
x[:,1]=x2
res[2]=tot-np.linalg.lstsq(x,y)[1]
res[3]=tot-res[0]-res[1]-res[2]
mss=res/np.float32(np.array([N-4,1,1,1]))
F=mss[1:]/mss[0]
p=1-stats.f.cdf(F,1,N-4)
p=p<0.05
ps[i,:]+=np.int32(p)
cs[i,p[0]*4+p[1]*2+p[2]]+=1
i+=1
ps/=float(K)
cs/=float(K)
for k in range(ps.shape[1]): plt.plot(Ns/4, ps[:,k])
plt.legend(['A','B','X'],loc=2)
plt.xlabel('N per cell')
plt.ylabel('expected power');
```
Now we look at the probability that the various configurations of significant and non-significant results will be obtained.
```
plt.figure(figsize=(7,6))
for k in [0,1,2,3,6,7]: plt.plot(Ns/4, cs[:,k])
plt.legend(['nothing','X','B','BX','AB','ABX'],loc=2)
plt.xlabel('N per cell')
plt.ylabel('pattern frequency');
```
To keep the figure from too much clutter I omitted A and AX which is due to symmetry identical to B and BX. By A I mean "main effect A is significant and main effect B plus the interaction are not significant". X designates the presence of a significant interaction.
To state the unsurprising results first, if we decrease the sample size we are more likely to obtain no significant result. If we increase the sample size we are more likely to obtain the true model ABX. Because interaction requires large sample size to reach significance for medium sample size AB is more likely than the true model ABX. Furthermore, funny things happen if we make main effects the exclusive focus of our hypothesis. In the cases A,B and AB we can find a small-to-medium sample size that is optimal if we want to get our hypothesis significant. All this can be (unconsciously) exploited by researchers to provide more power for their favored pattern.
It is not difficult to see the applications. We could look up the frequency of various patterns in the psychological literature. This could be done in terms of the reported findings but also in terms of the reported hypotheses. We can also ask whether the reported sample size correlates with the optimal sample size.
Note, that there is nothing wrong with Anova. The purpose of Anova is NOT to provide a test for composite hypotheses such as X, AB or ABX. Rather it helps us discover sources of variability that can then be subjected to a more focused analysis. Anova is an exploratory technique and should not be used for evaluating of hypotheses.
|
github_jupyter
|
# Fine-tuning and deploying ProtBert Model for Protein Classification using Amazon SageMaker
## Contents
1. [Motivation](#Motivation)
2. [What is ProtBert?](#What-is-ProtBert?)
3. [Notebook Overview](#Notebook-Overview)
- [Setup](#Setup)
4. [Dataset](#Dataset)
- [Download Data](#Download-Data)
5. [Data Exploration](#Data-Exploration)
- [Upload Data to S3](#Upload-Data-to-S3)
6. [Training script](#Training-script)
7. [Train on Amazon SageMaker](#Train-on-Amazon-SageMaker)
8. [Deploy the Model on Amazon SageMaker](#Deploy-the-model-on-Amazon-SageMaker)
- [Create a model object](#Create-a-model-object)
- [Deploy the model on an endpoint](#Deploy-the-model-on-an-endpoint)
9. [Predicting SubCellular Localization of Protein Sequences](#Predicting-SubCellular-Localization-of-Protein-Sequences)
10. [References](#References)
---
## Motivation
<img src="https://upload.wikimedia.org/wikipedia/commons/6/60/Myoglobin.png"
alt="Protein Sequence"
style="float: left;"
height = 100
width = 250/>
**Proteins** are the key fundamental macromolecules governing in biological bodies. The study of protein localization is important to comprehend the function of protein and has great importance for drug design and other applications. It also plays an important role in characterizing the cellular function of hypothetical and newly discovered proteins [1]. There are several research endeavours that aim to localize whole proteomes by using high-throughput approaches [2–4]. These large datasets provide important information about protein function, and more generally global cellular processes. However, they currently do not achieve 100% coverage of proteomes, and the methodology used can in some cases cause mislocalization of subsets of proteins [5,6]. Therefore, complementary methods are necessary to address these problems. In this notebook, we will leverage Natural Language Processing (NLP) techniques for protein sequence classification. The idea is to interpret protein sequences as sentences and their constituent – amino acids –
as single words [7]. More specifically we will fine tune Pytorch ProtBert model from Hugging Face library.
## What is ProtBert?
ProtBert is a pretrained model on protein sequences using a masked language modeling (MLM) objective. It is based on Bert model which is pretrained on a large corpus of protein sequences in a self-supervised fashion. This means it was pretrained on the raw protein sequences only, with no humans labelling them in any way (which is why it can use lots of publicly available data) with an automatic process to generate inputs and labels from those protein sequences [8]. For more information about ProtBert, see [`ProtTrans: Towards Cracking the Language of Life’s Code Through Self-Supervised Deep Learning and High Performance Computing`](https://www.biorxiv.org/content/10.1101/2020.07.12.199554v2.full).
---
## Notebook Overview
This example notebook focuses on fine-tuning the Pytorch ProtBert model and deploying it using Amazon SageMaker, which is the most comprehensive and fully managed machine learning service. With SageMaker, data scientists and developers can quickly and easily build and train machine learning models, and then directly deploy them into a production-ready hosted environment.
During the training, we will leverage SageMaker distributed data parallel (SDP) feature which extends SageMaker’s training capabilities on deep learning models with near-linear scaling efficiency, achieving fast time-to-train with minimal code changes.
_**Note**_: Please select the Kernel as ` Python 3 (Pytorch 1.6 Python 3.6 CPU Optimized)`.
---
### Setup
To start, we import some Python libraries and initialize a SageMaker session, S3 bucket and prefix, and IAM role.
```
!pip install --upgrade pip -q
!pip install -U boto3 sagemaker -q
!pip install seaborn -q
```
Next let us import the common libraries needed for the operations done later.
```
import re
import json
import pandas as pd
from tqdm import tqdm
import seaborn as sns
import matplotlib.pyplot as plt
import numpy as np
import time
import os
import numpy as np
import pandas as pd
import sagemaker
import torch
import seaborn as sns
import matplotlib.pyplot as plt
from torch import nn, optim
from torch.utils.data import Dataset, DataLoader
```
Next, let's verify the version, create a SageMaker session and get the execution role which is the IAM role arn used to give training and hosting access to your data.
```
import sagemaker
print(sagemaker.__version__)
sagemaker_session = sagemaker.Session()
role = sagemaker.get_execution_role()
```
Now we will specify the S3 bucket and prefix where you will store your training data and model artifacts. This should be within the same region as the Notebook Instance, training, and hosting.
```
bucket = sagemaker_session.default_bucket()
prefix = "sagemaker/DEMO-pytorch-bert"
```
As the last step of setting up the enviroment lets set a value to a random seed so that we can reproduce the same results later.
```
RANDOM_SEED = 43
np.random.seed(RANDOM_SEED)
torch.manual_seed(RANDOM_SEED)
```
---
## Dataset
We are going to use a opensource public dataset of protein sequences available [here](http://www.cbs.dtu.dk/services/DeepLoc-1.0/data.php). The dataset is a `fasta file` composed by header and protein sequence. The header is composed by the accession number from Uniprot, the annotated subcellular localization and possibly a description field indicating if the protein was part of the test set. The subcellular localization includes an additional label, where S indicates soluble, M membrane and U unknown[9].
Sample of the data is as follows :
```
>Q9SMX3 Mitochondrion-M test
MVKGPGLYTEIGKKARDLLYRDYQGDQKFSVTTYSSTGVAITTTGTNKGSLFLGDVATQVKNNNFTADVKVST
DSSLLTTLTFDEPAPGLKVIVQAKLPDHKSGKAEVQYFHDYAGISTSVGFTATPIVNFSGVVGTNGLSLGTDV
AYNTESGNFKHFNAGFNFTKDDLTASLILNDKGEKLNASYYQIVSPSTVVGAEISHNFTTKENAITVGTQHAL>
DPLTTVKARVNNAGVANALIQHEWRPKSFFTVSGEVDSKAIDKSAKVGIALALKP"
```
A sequence in FASTA format begins with a single-line description, followed by lines of sequence data. The definition line (defline) is distinguished from the sequence data by a greater-than (>) symbol at the beginning. The word following the ">" symbol is the identifier of the sequence, and the rest of the line is the description.
### Download Data
```
!wget http://www.cbs.dtu.dk/services/DeepLoc-1.0/deeploc_data.fasta -P ./data -q
```
Since the data is in fasta format, we can leverage `Bio.SeqIO.FastaIO` library to read the dataset. Let us install the Bio package.
```
!pip install Bio -q
import Bio
```
Using the Bio package we will read the data directly by filtering out the columns that are of interest. We will also add a space seperater between each character in the sequence field which will be useful during model training.
```
def read_fasta(file_path, columns) :
from Bio.SeqIO.FastaIO import SimpleFastaParser
with open('./data/deeploc_data.fasta') as fasta_file: # Will close handle cleanly
records = []
for title, sequence in SimpleFastaParser(fasta_file):
record = []
title_splits = title.split(None)
record.append(title_splits[0]) # First word is ID
sequence = " ".join(sequence)
record.append(sequence)
record.append(len(sequence))
location_splits = title_splits[1].split("-")
record.append(location_splits[0]) # Second word is Location
record.append(location_splits[1]) # Second word is Membrane
if(len(title_splits) > 2):
record.append(0)
else:
record.append(1)
records.append(record)
return pd.DataFrame(records, columns = columns)
data = read_fasta("./tmp/deeploc_data.fasta", columns=["id", "sequence", "sequence_length", "location", "membrane", "is_train"])
data.head()
```
### Data Exploration
Dataset consists of 14K sequences and 6 columns in total. We will only use the following columns during training:
* _**id**_ : Unique identifier given each sequence in the dataset.
* _**sequence**_ : Protein sequence. Each character is seperated by a "space". Will be useful for BERT tokernizer.
* _**sequence_length**_ : Character length of each protein sequence.
* _**location**_ : Classification given each sequence.
* _**is_train**_ : Indicates whether the record be used for training or test. Will be used to seperate the dataset for traning and validation.
First, let's verify if there are any missing values in the dataset.
```
data.info()
data.isnull().values.any()
```
As you can see, there are **no** missing values in this dataset.
Second, we will see the number of available classes (subcellular localization), which will be used for protein classification.
```
unique_classes = data.location.unique()
print("Number of classes: ", len(unique_classes))
unique_classes
```
We can see that there are 10 unique classes in the dataset.
Third, lets check the sequence length.
```
%matplotlib inline
%config InlineBackend.figure_format='retina'
sns.set(style='whitegrid', palette='muted', font_scale=1.2)
ax = sns.distplot(data['sequence_length'].values)
ax.set_xlim(0, 3000)
plt.title(f'sequence length distribution')
plt.grid(True)
```
This is an important observation as PROTBERT model receives a fixed length of sentence as input. Usually the maximum length of a sentence depends on the data we are working on. For sentences that are shorter than this maximum length, we will have to add paddings (empty tokens) to the sentences to make up the length.
As you can see from the above plot that most of the sequences lie under the length of around 1500, therefore, its a good idea to select the `max_length = 1536` but that will increase the training time for this sample notebook, therefore, we will use `max_length = 512`. You can experiment it with the bigger length and it does improves the accuracy as most of the subcellular localization information of protiens is stored at the end of the sequence.
Next let's factorize the protein classes.
```
categories = data.location.astype('category').cat
data['location'] = categories.codes
class_names = categories.categories
num_classes = len(class_names)
print(class_names)
```
Next, let's devide the dataset into training and test. We can leverage the `is_train` column to do the split.
```
df_train = data[data.is_train == 1]
df_train = df_train.drop(["is_train"], axis = 1)
df_train.shape[0]
df_test = data[data.is_train == 0]
df_test = df_test.drop(["is_train"], axis = 1)
df_test.shape[0]
```
We got **11231** records as training set and **2773** records as the test set which is about 75:25 data split between the train and test. Also, the composition between multiple classes remains uniform between both datasets.
### Upload Data to S3
In order to accomodate model training on SageMaker we need to upload the data to s3 location. We are going to use the `sagemaker.Session.upload_data` function to upload our datasets to an S3 location. The return value inputs identifies the location -- we will use later when we start the training job.
```
train_dataset_path = './data/deeploc_per_protein_train.csv'
test_dataset_path = './data/deeploc_per_protein_test.csv'
df_train.to_csv(train_dataset_path)
df_test.to_csv(test_dataset_path)
inputs_train = sagemaker_session.upload_data(train_dataset_path, bucket=bucket, key_prefix=prefix)
inputs_test = sagemaker_session.upload_data(test_dataset_path, bucket=bucket, key_prefix=prefix)
print("S3 location for training data: ", inputs_train )
print("S3 location for testing data: ", inputs_test )
```
## Training script
We use the [PyTorch-Transformers library](https://pytorch.org/hub/huggingface_pytorch-transformers), which contains PyTorch implementations and pre-trained model weights for many NLP models, including BERT. As mentioned above, we will use `ProtBert model` which is pre-trained on protein sequences.
Our training script should save model artifacts learned during training to a file path called `model_dir`, as stipulated by the SageMaker PyTorch image. Upon completion of training, model artifacts saved in `model_dir` will be uploaded to S3 by SageMaker and will be used for deployment.
We save this script in a file named `train.py`, and put the file in a directory named `code/`. The full training script can be viewed under `code/`.
It also has the code required for distributed data parallel (DDP) training using SMDataParallel. It is very similar to a PyTorch training script you might run outside of SageMaker, but modified to run with SMDataParallel, which is a new capability in Amazon SageMaker to train deep learning models faster and cheaper. SMDataParallel's PyTorch client provides an alternative to PyTorch's native DDP. For details about how to use SMDataParallel's DDP in your native PyTorch script, see the [Getting Started with SMDataParallel tutorials](https://docs.aws.amazon.com/sagemaker/latest/dg/distributed-training.html#distributed-training-get-started).
```
!pygmentize code/train.py
```
### Train on Amazon SageMaker
We use Amazon SageMaker to train and deploy a model using our custom PyTorch code. The Amazon SageMaker Python SDK makes it easier to run a PyTorch script in Amazon SageMaker using its PyTorch estimator. After that, we can use the SageMaker Python SDK to deploy the trained model and run predictions. For more information on how to use this SDK with PyTorch, see [the SageMaker Python SDK documentation](https://sagemaker.readthedocs.io/en/stable/using_pytorch.html).
To start, we use the `PyTorch` estimator class to train our model. When creating our estimator, we make sure to specify a few things:
* `entry_point`: the name of our PyTorch script. It contains our training script, which loads data from the input channels, configures training with hyperparameters, trains a model, and saves a model. It also contains code to load and run the model during inference.
* `source_dir`: the location of our training scripts and requirements.txt file. "requirements.txt" lists packages you want to use with your script.
* `framework_version`: the PyTorch version we want to use.
The PyTorch estimator supports both single-machine & multi-machine, distributed PyTorch training using SMDataParallel. _Our training script supports distributed training for only GPU instances_.
#### Instance types
SMDataParallel supports model training on SageMaker with the following instance types only:
- ml.p3.16xlarge
- ml.p3dn.24xlarge [Recommended]
- ml.p4d.24xlarge [Recommended]
#### Instance count
To get the best performance and the most out of SMDataParallel, you should use at least 2 instances, but you can also use 1 for testing this example.
#### Distribution strategy
Note that to use DDP mode, you update the the distribution strategy, and set it to use smdistributed dataparallel.
After creating the estimator, we then call fit(), which launches a training job. We use the Amazon S3 URIs where we uploaded the training data earlier.
```
# Training job will take around 20-25 mins to execute.
from sagemaker.pytorch import PyTorch
TRAINING_JOB_NAME="protbert-training-pytorch-{}".format(time.strftime("%m-%d-%Y-%H-%M-%S"))
print('Training job name: ', TRAINING_JOB_NAME)
estimator = PyTorch(
entry_point="train.py",
source_dir="code",
role=role,
framework_version="1.6.0",
py_version="py36",
instance_count=1, # this script support distributed training for only GPU instances.
instance_type="ml.p3.16xlarge",
distribution={'smdistributed':{
'dataparallel':{
'enabled': True
}
}
},
debugger_hook_config=False,
hyperparameters={
"epochs": 3,
"num_labels": num_classes,
"batch-size": 4,
"test-batch-size": 4,
"log-interval": 100,
"frozen_layers": 15,
},
metric_definitions=[
{'Name': 'train:loss', 'Regex': 'Training Loss: ([0-9\\.]+)'},
{'Name': 'test:accuracy', 'Regex': 'Validation Accuracy: ([0-9\\.]+)'},
{'Name': 'test:loss', 'Regex': 'Validation loss: ([0-9\\.]+)'},
]
)
estimator.fit({"training": inputs_train, "testing": inputs_test}, job_name=TRAINING_JOB_NAME)
```
With `max_length=512` and running the model for only 3 epochs we get the validation accuracy of around 65%, which is pretty decent. You can optimize it further by trying bigger sequence length, increasing the number of epochs and tuning other hyperparamters. For details you can refer to the research paper:
[`ProtTrans: Towards Cracking the Language of Life’s Code Through Self-Supervised Deep Learning and High Performance Computing`](https://arxiv.org/pdf/2007.06225.pdf).
Before, we deploy the model to an endpoint, let's first store the model to S3.
```
model_data = estimator.model_data
print("Storing {} as model_data".format(model_data))
%store model_data
%store -r model_data
# If no model was found, set it manually here.
# model_data = 's3://sagemaker-{region}-XXX/protbert-training-pytorch-XX-XX-XXXX-XX-XX-XX/output/model.tar.gz'
print("Using this model: {}".format(model_data))
```
## Deploy the model on Amazon SageMaker
After training our model, we host it on an Amazon SageMaker Endpoint. To make the endpoint load the model and serve predictions, we implement a few methods in inference.py.
- `model_fn()`: function defined to load the saved model and return a model object that can be used for model serving. The SageMaker PyTorch model server loads our model by invoking model_fn.
- `input_fn()`: deserializes and prepares the prediction input. In this example, our request body is first serialized to JSON and then sent to model serving endpoint. Therefore, in input_fn(), we first deserialize the JSON-formatted request body and return the input as a torch.tensor, as required for BERT.
- `predict_fn()`: performs the prediction and returns the result.
To deploy our endpoint, we call deploy() on our PyTorch estimator object, passing in our desired number of instances and instance type:
### Create a model object
You define the model object by using SageMaker SDK's PyTorchModel and pass in the model from the estimator and the entry_point. The function loads the model and sets it to use a GPU, if available.
```
import sagemaker
from sagemaker.pytorch import PyTorchModel
ENDPOINT_NAME = "protbert-inference-pytorch-1-{}".format(time.strftime("%m-%d-%Y-%H-%M-%S"))
print("Endpoint name: ", ENDPOINT_NAME)
model = PyTorchModel(model_data=model_data, source_dir='code',
entry_point='inference.py', role=role, framework_version='1.6.0', py_version='py3')
```
### Deploy the model on an endpoint
You create a predictor by using the model.deploy function. You can optionally change both the instance count and instance type.
```
%%time
predictor = model.deploy(initial_instance_count=1, instance_type='ml.m5.2xlarge', endpoint_name=ENDPOINT_NAME)
```
## Predicting SubCellular Localization of Protein Sequences
```
import boto3
runtime= boto3.client('runtime.sagemaker')
client = boto3.client('sagemaker')
endpoint_desc = client.describe_endpoint(EndpointName=ENDPOINT_NAME)
print(endpoint_desc)
print('---'*30)
```
We then configure the predictor to use application/json for the content type when sending requests to our endpoint:
```
predictor.serializer = sagemaker.serializers.JSONSerializer()
predictor.deserializer = sagemaker.deserializers.JSONDeserializer()
```
Finally, we use the returned predictor object to call the endpoint:
```
protein_sequence = 'M G K K D A S T T R T P V D Q Y R K Q I G R Q D Y K K N K P V L K A T R L K A E A K K A A I G I K E V I L V T I A I L V L L F A F Y A F F F L N L T K T D I Y E D S N N'
prediction = predictor.predict(protein_sequence)
print(prediction)
print(f'Protein Sequence: {protein_sequence}')
print("Sequence Localization Ground Truth is: {} - prediction is: {}".format('Endoplasmic.reticulum', class_names[prediction[0]]))
protein_sequence = 'M S M T I L P L E L I D K C I G S N L W V I M K S E R E F A G T L V G F D D Y V N I V L K D V T E Y D T V T G V T E K H S E M L L N G N G M C M L I P G G K P E'
prediction = predictor.predict(protein_sequence)
print(prediction)
print(f'Protein Sequence: {protein_sequence}')
print("Sequence Localization Ground Truth is: {} - prediction is: {}".format('Nucleus', class_names[prediction[0]]))
seq = 'M G G P T R R H Q E E G S A E C L G G P S T R A A P G P G L R D F H F T T A G P S K A D R L G D A A Q I H R E R M R P V Q C G D G S G E R V F L Q S P G S I G T L Y I R L D L N S Q R S T C C C L L N A G T K G M C'
prediction = predictor.predict(seq)
print(prediction)
print(f'Protein Sequence: {seq}')
print("Sequence Localization Ground Truth is: {} - prediction is: {}".format('Cytoplasm',class_names[prediction[0]]))
```
# Cleanup
Lastly, please remember to delete the Amazon SageMaker endpoint to avoid charges:
```
predictor.delete_endpoint()
```
## References
- [1] Refining Protein Subcellular Localization (https://www.ncbi.nlm.nih.gov/pmc/articles/PMC1289393/)
- [2] Kumar A, Agarwal S, Heyman JA, Matson S, Heidtman M, et al. Subcellular localization of the yeast proteome. Genes Dev. 2002;16:707–719. [PMC free article] [PubMed] [Google Scholar]
- [3] Huh WK, Falvo JV, Gerke LC, Carroll AS, Howson RW, et al. Global analysis of protein localization in budding yeast. Nature. 2003;425:686–691. [PubMed] [Google Scholar]
- [4] Wiemann S, Arlt D, Huber W, Wellenreuther R, Schleeger S, et al. From ORFeome to biology: A functional genomics pipeline. Genome Res. 2004;14:2136–2144. [PMC free article] [PubMed] [Google Scholar]
- [5] Davis TN. Protein localization in proteomics. Curr Opin Chem Biol. 2004;8:49–53. [PubMed] [Google Scholar]
- [6] Scott MS, Thomas DY, Hallett MT. Predicting subcellular localization via protein motif co-occurrence. Genome Res. 2004;14:1957–1966. [PMC free article] [PubMed] [Google Scholar]
- [7] ProtTrans: Towards Cracking the Language of Life's Code Through Self-Supervised Deep Learning and High Performance Computing (https://www.biorxiv.org/content/10.1101/2020.07.12.199554v2.full.pdf)
- [8] ProtBert Hugging Face (https://huggingface.co/Rostlab/prot_bert)
- [9] DeepLoc-1.0: Eukaryotic protein subcellular localization predictor (http://www.cbs.dtu.dk/services/DeepLoc-1.0/data.php)
|
github_jupyter
|
# The Autodiff Cookbook
[](https://colab.sandbox.google.com/github/google/jax/blob/master/docs/notebooks/autodiff_cookbook.ipynb)
*alexbw@, mattjj@*
JAX has a pretty general automatic differentiation system. In this notebook, we'll go through a whole bunch of neat autodiff ideas that you can cherry pick for your own work, starting with the basics.
```
import jax.numpy as jnp
from jax import grad, jit, vmap
from jax import random
key = random.PRNGKey(0)
```
## Gradients
### Starting with `grad`
You can differentiate a function with `grad`:
```
grad_tanh = grad(jnp.tanh)
print(grad_tanh(2.0))
```
`grad` takes a function and returns a function. If you have a Python function `f` that evaluates the mathematical function $f$, then `grad(f)` is a Python function that evaluates the mathematical function $\nabla f$. That means `grad(f)(x)` represents the value $\nabla f(x)$.
Since `grad` operates on functions, you can apply it to its own output to differentiate as many times as you like:
```
print(grad(grad(jnp.tanh))(2.0))
print(grad(grad(grad(jnp.tanh)))(2.0))
```
Let's look at computing gradients with `grad` in a linear logistic regression model. First, the setup:
```
def sigmoid(x):
return 0.5 * (jnp.tanh(x / 2) + 1)
# Outputs probability of a label being true.
def predict(W, b, inputs):
return sigmoid(jnp.dot(inputs, W) + b)
# Build a toy dataset.
inputs = jnp.array([[0.52, 1.12, 0.77],
[0.88, -1.08, 0.15],
[0.52, 0.06, -1.30],
[0.74, -2.49, 1.39]])
targets = jnp.array([True, True, False, True])
# Training loss is the negative log-likelihood of the training examples.
def loss(W, b):
preds = predict(W, b, inputs)
label_probs = preds * targets + (1 - preds) * (1 - targets)
return -jnp.sum(jnp.log(label_probs))
# Initialize random model coefficients
key, W_key, b_key = random.split(key, 3)
W = random.normal(W_key, (3,))
b = random.normal(b_key, ())
```
Use the `grad` function with its `argnums` argument to differentiate a function with respect to positional arguments.
```
# Differentiate `loss` with respect to the first positional argument:
W_grad = grad(loss, argnums=0)(W, b)
print('W_grad', W_grad)
# Since argnums=0 is the default, this does the same thing:
W_grad = grad(loss)(W, b)
print('W_grad', W_grad)
# But we can choose different values too, and drop the keyword:
b_grad = grad(loss, 1)(W, b)
print('b_grad', b_grad)
# Including tuple values
W_grad, b_grad = grad(loss, (0, 1))(W, b)
print('W_grad', W_grad)
print('b_grad', b_grad)
```
This `grad` API has a direct correspondence to the excellent notation in Spivak's classic *Calculus on Manifolds* (1965), also used in Sussman and Wisdom's [*Structure and Interpretation of Classical Mechanics*](http://mitpress.mit.edu/sites/default/files/titles/content/sicm_edition_2/book.html) (2015) and their [*Functional Differential Geometry*](https://mitpress.mit.edu/books/functional-differential-geometry) (2013). Both books are open-access. See in particular the "Prologue" section of *Functional Differential Geometry* for a defense of this notation.
Essentially, when using the `argnums` argument, if `f` is a Python function for evaluating the mathematical function $f$, then the Python expression `grad(f, i)` evaluates to a Python function for evaluating $\partial_i f$.
### Differentiating with respect to nested lists, tuples, and dicts
Differentiating with respect to standard Python containers just works, so use tuples, lists, and dicts (and arbitrary nesting) however you like.
```
def loss2(params_dict):
preds = predict(params_dict['W'], params_dict['b'], inputs)
label_probs = preds * targets + (1 - preds) * (1 - targets)
return -jnp.sum(jnp.log(label_probs))
print(grad(loss2)({'W': W, 'b': b}))
```
You can [register your own container types](https://github.com/google/jax/issues/446#issuecomment-467105048) to work with not just `grad` but all the JAX transformations (`jit`, `vmap`, etc.).
### Evaluate a function and its gradient using `value_and_grad`
Another convenient function is `value_and_grad` for efficiently computing both a function's value as well as its gradient's value:
```
from jax import value_and_grad
loss_value, Wb_grad = value_and_grad(loss, (0, 1))(W, b)
print('loss value', loss_value)
print('loss value', loss(W, b))
```
### Checking against numerical differences
A great thing about derivatives is that they're straightforward to check with finite differences:
```
# Set a step size for finite differences calculations
eps = 1e-4
# Check b_grad with scalar finite differences
b_grad_numerical = (loss(W, b + eps / 2.) - loss(W, b - eps / 2.)) / eps
print('b_grad_numerical', b_grad_numerical)
print('b_grad_autodiff', grad(loss, 1)(W, b))
# Check W_grad with finite differences in a random direction
key, subkey = random.split(key)
vec = random.normal(subkey, W.shape)
unitvec = vec / jnp.sqrt(jnp.vdot(vec, vec))
W_grad_numerical = (loss(W + eps / 2. * unitvec, b) - loss(W - eps / 2. * unitvec, b)) / eps
print('W_dirderiv_numerical', W_grad_numerical)
print('W_dirderiv_autodiff', jnp.vdot(grad(loss)(W, b), unitvec))
```
JAX provides a simple convenience function that does essentially the same thing, but checks up to any order of differentiation that you like:
```
from jax.test_util import check_grads
check_grads(loss, (W, b), order=2) # check up to 2nd order derivatives
```
### Hessian-vector products with `grad`-of-`grad`
One thing we can do with higher-order `grad` is build a Hessian-vector product function. (Later on we'll write an even more efficient implementation that mixes both forward- and reverse-mode, but this one will use pure reverse-mode.)
A Hessian-vector product function can be useful in a [truncated Newton Conjugate-Gradient algorithm](https://en.wikipedia.org/wiki/Truncated_Newton_method) for minimizing smooth convex functions, or for studying the curvature of neural network training objectives (e.g. [1](https://arxiv.org/abs/1406.2572), [2](https://arxiv.org/abs/1811.07062), [3](https://arxiv.org/abs/1706.04454), [4](https://arxiv.org/abs/1802.03451)).
For a scalar-valued function $f : \mathbb{R}^n \to \mathbb{R}$ with continuous second derivatives (so that the Hessian matrix is symmetric), the Hessian at a point $x \in \mathbb{R}^n$ is written as $\partial^2 f(x)$. A Hessian-vector product function is then able to evaluate
$\qquad v \mapsto \partial^2 f(x) \cdot v$
for any $v \in \mathbb{R}^n$.
The trick is not to instantiate the full Hessian matrix: if $n$ is large, perhaps in the millions or billions in the context of neural networks, then that might be impossible to store.
Luckily, `grad` already gives us a way to write an efficient Hessian-vector product function. We just have to use the identity
$\qquad \partial^2 f (x) v = \partial [x \mapsto \partial f(x) \cdot v] = \partial g(x)$,
where $g(x) = \partial f(x) \cdot v$ is a new scalar-valued function that dots the gradient of $f$ at $x$ with the vector $v$. Notice that we're only ever differentiating scalar-valued functions of vector-valued arguments, which is exactly where we know `grad` is efficient.
In JAX code, we can just write this:
```
def hvp(f, x, v):
return grad(lambda x: jnp.vdot(grad(f)(x), v))(x)
```
This example shows that you can freely use lexical closure, and JAX will never get perturbed or confused.
We'll check this implementation a few cells down, once we see how to compute dense Hessian matrices. We'll also write an even better version that uses both forward-mode and reverse-mode.
### Jacobians and Hessians using `jacfwd` and `jacrev`
You can compute full Jacobian matrices using the `jacfwd` and `jacrev` functions:
```
from jax import jacfwd, jacrev
# Isolate the function from the weight matrix to the predictions
f = lambda W: predict(W, b, inputs)
J = jacfwd(f)(W)
print("jacfwd result, with shape", J.shape)
print(J)
J = jacrev(f)(W)
print("jacrev result, with shape", J.shape)
print(J)
```
These two functions compute the same values (up to machine numerics), but differ in their implementation: `jacfwd` uses forward-mode automatic differentiation, which is more efficient for "tall" Jacobian matrices, while `jacrev` uses reverse-mode, which is more efficient for "wide" Jacobian matrices. For matrices that are near-square, `jacfwd` probably has an edge over `jacrev`.
You can also use `jacfwd` and `jacrev` with container types:
```
def predict_dict(params, inputs):
return predict(params['W'], params['b'], inputs)
J_dict = jacrev(predict_dict)({'W': W, 'b': b}, inputs)
for k, v in J_dict.items():
print("Jacobian from {} to logits is".format(k))
print(v)
```
For more details on forward- and reverse-mode, as well as how to implement `jacfwd` and `jacrev` as efficiently as possible, read on!
Using a composition of two of these functions gives us a way to compute dense Hessian matrices:
```
def hessian(f):
return jacfwd(jacrev(f))
H = hessian(f)(W)
print("hessian, with shape", H.shape)
print(H)
```
This shape makes sense: if we start with a function $f : \mathbb{R}^n \to \mathbb{R}^m$, then at a point $x \in \mathbb{R}^n$ we expect to get the shapes
* $f(x) \in \mathbb{R}^m$, the value of $f$ at $x$,
* $\partial f(x) \in \mathbb{R}^{m \times n}$, the Jacobian matrix at $x$,
* $\partial^2 f(x) \in \mathbb{R}^{m \times n \times n}$, the Hessian at $x$,
and so on.
To implement `hessian`, we could have used `jacfwd(jacrev(f))` or `jacrev(jacfwd(f))` or any other composition of the two. But forward-over-reverse is typically the most efficient. That's because in the inner Jacobian computation we're often differentiating a function wide Jacobian (maybe like a loss function $f : \mathbb{R}^n \to \mathbb{R}$), while in the outer Jacobian computation we're differentiating a function with a square Jacobian (since $\nabla f : \mathbb{R}^n \to \mathbb{R}^n$), which is where forward-mode wins out.
## How it's made: two foundational autodiff functions
### Jacobian-Vector products (JVPs, aka forward-mode autodiff)
JAX includes efficient and general implementations of both forward- and reverse-mode automatic differentiation. The familiar `grad` function is built on reverse-mode, but to explain the difference in the two modes, and when each can be useful, we need a bit of math background.
#### JVPs in math
Mathematically, given a function $f : \mathbb{R}^n \to \mathbb{R}^m$, the Jacobian of $f$ evaluated at an input point $x \in \mathbb{R}^n$, denoted $\partial f(x)$, is often thought of as a matrix in $\mathbb{R}^m \times \mathbb{R}^n$:
$\qquad \partial f(x) \in \mathbb{R}^{m \times n}$.
But we can also think of $\partial f(x)$ as a linear map, which maps the tangent space of the domain of $f$ at the point $x$ (which is just another copy of $\mathbb{R}^n$) to the tangent space of the codomain of $f$ at the point $f(x)$ (a copy of $\mathbb{R}^m$):
$\qquad \partial f(x) : \mathbb{R}^n \to \mathbb{R}^m$.
This map is called the [pushforward map](https://en.wikipedia.org/wiki/Pushforward_(differential)) of $f$ at $x$. The Jacobian matrix is just the matrix for this linear map in a standard basis.
If we don't commit to one specific input point $x$, then we can think of the function $\partial f$ as first taking an input point and returning the Jacobian linear map at that input point:
$\qquad \partial f : \mathbb{R}^n \to \mathbb{R}^n \to \mathbb{R}^m$.
In particular, we can uncurry things so that given input point $x \in \mathbb{R}^n$ and a tangent vector $v \in \mathbb{R}^n$, we get back an output tangent vector in $\mathbb{R}^m$. We call that mapping, from $(x, v)$ pairs to output tangent vectors, the *Jacobian-vector product*, and write it as
$\qquad (x, v) \mapsto \partial f(x) v$
#### JVPs in JAX code
Back in Python code, JAX's `jvp` function models this transformation. Given a Python function that evaluates $f$, JAX's `jvp` is a way to get a Python function for evaluating $(x, v) \mapsto (f(x), \partial f(x) v)$.
```
from jax import jvp
# Isolate the function from the weight matrix to the predictions
f = lambda W: predict(W, b, inputs)
key, subkey = random.split(key)
v = random.normal(subkey, W.shape)
# Push forward the vector `v` along `f` evaluated at `W`
y, u = jvp(f, (W,), (v,))
```
In terms of Haskell-like type signatures, we could write
```haskell
jvp :: (a -> b) -> a -> T a -> (b, T b)
```
where we use `T a` to denote the type of the tangent space for `a`. In words, `jvp` takes as arguments a function of type `a -> b`, a value of type `a`, and a tangent vector value of type `T a`. It gives back a pair consisting of a value of type `b` and an output tangent vector of type `T b`.
The `jvp`-transformed function is evaluated much like the original function, but paired up with each primal value of type `a` it pushes along tangent values of type `T a`. For each primitive numerical operation that the original function would have applied, the `jvp`-transformed function executes a "JVP rule" for that primitive that both evaluates the primitive on the primals and applies the primitive's JVP at those primal values.
That evaluation strategy has some immediate implications about computational complexity: since we evaluate JVPs as we go, we don't need to store anything for later, and so the memory cost is independent of the depth of the computation. In addition, the FLOP cost of the `jvp`-transformed function is about 3x the cost of just evaluating the function (one unit of work for evaluating the original function, for example `sin(x)`; one unit for linearizing, like `cos(x)`; and one unit for applying the linearized function to a vector, like `cos_x * v`). Put another way, for a fixed primal point $x$, we can evaluate $v \mapsto \partial f(x) \cdot v$ for about the same marginal cost as evaluating $f$.
That memory complexity sounds pretty compelling! So why don't we see forward-mode very often in machine learning?
To answer that, first think about how you could use a JVP to build a full Jacobian matrix. If we apply a JVP to a one-hot tangent vector, it reveals one column of the Jacobian matrix, corresponding to the nonzero entry we fed in. So we can build a full Jacobian one column at a time, and to get each column costs about the same as one function evaluation. That will be efficient for functions with "tall" Jacobians, but inefficient for "wide" Jacobians.
If you're doing gradient-based optimization in machine learning, you probably want to minimize a loss function from parameters in $\mathbb{R}^n$ to a scalar loss value in $\mathbb{R}$. That means the Jacobian of this function is a very wide matrix: $\partial f(x) \in \mathbb{R}^{1 \times n}$, which we often identify with the Gradient vector $\nabla f(x) \in \mathbb{R}^n$. Building that matrix one column at a time, with each call taking a similar number of FLOPs to evaluating the original function, sure seems inefficient! In particular, for training neural networks, where $f$ is a training loss function and $n$ can be in the millions or billions, this approach just won't scale.
To do better for functions like this, we just need to use reverse-mode.
### Vector-Jacobian products (VJPs, aka reverse-mode autodiff)
Where forward-mode gives us back a function for evaluating Jacobian-vector products, which we can then use to build Jacobian matrices one column at a time, reverse-mode is a way to get back a function for evaluating vector-Jacobian products (equivalently Jacobian-transpose-vector products), which we can use to build Jacobian matrices one row at a time.
#### VJPs in math
Let's again consider a function $f : \mathbb{R}^n \to \mathbb{R}^m$.
Starting from our notation for JVPs, the notation for VJPs is pretty simple:
$\qquad (x, v) \mapsto v \partial f(x)$,
where $v$ is an element of the cotangent space of $f$ at $x$ (isomorphic to another copy of $\mathbb{R}^m$). When being rigorous, we should think of $v$ as a linear map $v : \mathbb{R}^m \to \mathbb{R}$, and when we write $v \partial f(x)$ we mean function composition $v \circ \partial f(x)$, where the types work out because $\partial f(x) : \mathbb{R}^n \to \mathbb{R}^m$. But in the common case we can identify $v$ with a vector in $\mathbb{R}^m$ and use the two almost interchageably, just like we might sometimes flip between "column vectors" and "row vectors" without much comment.
With that identification, we can alternatively think of the linear part of a VJP as the transpose (or adjoint conjugate) of the linear part of a JVP:
$\qquad (x, v) \mapsto \partial f(x)^\mathsf{T} v$.
For a given point $x$, we can write the signature as
$\qquad \partial f(x)^\mathsf{T} : \mathbb{R}^m \to \mathbb{R}^n$.
The corresponding map on cotangent spaces is often called the [pullback](https://en.wikipedia.org/wiki/Pullback_(differential_geometry))
of $f$ at $x$. The key for our purposes is that it goes from something that looks like the output of $f$ to something that looks like the input of $f$, just like we might expect from a transposed linear function.
#### VJPs in JAX code
Switching from math back to Python, the JAX function `vjp` can take a Python function for evaluating $f$ and give us back a Python function for evaluating the VJP $(x, v) \mapsto (f(x), v^\mathsf{T} \partial f(x))$.
```
from jax import vjp
# Isolate the function from the weight matrix to the predictions
f = lambda W: predict(W, b, inputs)
y, vjp_fun = vjp(f, W)
key, subkey = random.split(key)
u = random.normal(subkey, y.shape)
# Pull back the covector `u` along `f` evaluated at `W`
v = vjp_fun(u)
```
In terms of Haskell-like type signatures, we could write
```haskell
vjp :: (a -> b) -> a -> (b, CT b -> CT a)
```
where we use `CT a` to denote the type for the cotangent space for `a`. In words, `vjp` takes as arguments a function of type `a -> b` and a point of type `a`, and gives back a pair consisting of a value of type `b` and a linear map of type `CT b -> CT a`.
This is great because it lets us build Jacobian matrices one row at a time, and the FLOP cost for evaluating $(x, v) \mapsto (f(x), v^\mathsf{T} \partial f(x))$ is only about three times the cost of evaluating $f$. In particular, if we want the gradient of a function $f : \mathbb{R}^n \to \mathbb{R}$, we can do it in just one call. That's how `grad` is efficient for gradient-based optimization, even for objectives like neural network training loss functions on millions or billions of parameters.
There's a cost, though: though the FLOPs are friendly, memory scales with the depth of the computation. Also, the implementation is traditionally more complex than that of forward-mode, though JAX has some tricks up its sleeve (that's a story for a future notebook!).
For more on how reverse-mode works, see [this tutorial video from the Deep Learning Summer School in 2017](http://videolectures.net/deeplearning2017_johnson_automatic_differentiation/).
### Vector-valued gradients with VJPs
If you're interested in taking vector-valued gradients (like `tf.gradients`):
```
from jax import vjp
def vgrad(f, x):
y, vjp_fn = vjp(f, x)
return vjp_fn(jnp.ones(y.shape))[0]
print(vgrad(lambda x: 3*x**2, jnp.ones((2, 2))))
```
### Hessian-vector products using both forward- and reverse-mode
In a previous section, we implemented a Hessian-vector product function just using reverse-mode (assuming continuous second derivatives):
```
def hvp(f, x, v):
return grad(lambda x: jnp.vdot(grad(f)(x), v))(x)
```
That's efficient, but we can do even better and save some memory by using forward-mode together with reverse-mode.
Mathematically, given a function $f : \mathbb{R}^n \to \mathbb{R}$ to differentiate, a point $x \in \mathbb{R}^n$ at which to linearize the function, and a vector $v \in \mathbb{R}^n$, the Hessian-vector product function we want is
$(x, v) \mapsto \partial^2 f(x) v$
Consider the helper function $g : \mathbb{R}^n \to \mathbb{R}^n$ defined to be the derivative (or gradient) of $f$, namely $g(x) = \partial f(x)$. All we need is its JVP, since that will give us
$(x, v) \mapsto \partial g(x) v = \partial^2 f(x) v$.
We can translate that almost directly into code:
```
from jax import jvp, grad
# forward-over-reverse
def hvp(f, primals, tangents):
return jvp(grad(f), primals, tangents)[1]
```
Even better, since we didn't have to call `jnp.dot` directly, this `hvp` function works with arrays of any shape and with arbitrary container types (like vectors stored as nested lists/dicts/tuples), and doesn't even have a dependence on `jax.numpy`.
Here's an example of how to use it:
```
def f(X):
return jnp.sum(jnp.tanh(X)**2)
key, subkey1, subkey2 = random.split(key, 3)
X = random.normal(subkey1, (30, 40))
V = random.normal(subkey2, (30, 40))
ans1 = hvp(f, (X,), (V,))
ans2 = jnp.tensordot(hessian(f)(X), V, 2)
print(jnp.allclose(ans1, ans2, 1e-4, 1e-4))
```
Another way you might consider writing this is using reverse-over-forward:
```
# reverse-over-forward
def hvp_revfwd(f, primals, tangents):
g = lambda primals: jvp(f, primals, tangents)[1]
return grad(g)(primals)
```
That's not quite as good, though, because forward-mode has less overhead than reverse-mode, and since the outer differentiation operator here has to differentiate a larger computation than the inner one, keeping forward-mode on the outside works best:
```
# reverse-over-reverse, only works for single arguments
def hvp_revrev(f, primals, tangents):
x, = primals
v, = tangents
return grad(lambda x: jnp.vdot(grad(f)(x), v))(x)
print("Forward over reverse")
%timeit -n10 -r3 hvp(f, (X,), (V,))
print("Reverse over forward")
%timeit -n10 -r3 hvp_revfwd(f, (X,), (V,))
print("Reverse over reverse")
%timeit -n10 -r3 hvp_revrev(f, (X,), (V,))
print("Naive full Hessian materialization")
%timeit -n10 -r3 jnp.tensordot(hessian(f)(X), V, 2)
```
## Composing VJPs, JVPs, and `vmap`
### Jacobian-Matrix and Matrix-Jacobian products
Now that we have `jvp` and `vjp` transformations that give us functions to push-forward or pull-back single vectors at a time, we can use JAX's `vmap` [transformation](https://github.com/google/jax#auto-vectorization-with-vmap) to push and pull entire bases at once. In particular, we can use that to write fast matrix-Jacobian and Jacobian-matrix products.
```
# Isolate the function from the weight matrix to the predictions
f = lambda W: predict(W, b, inputs)
# Pull back the covectors `m_i` along `f`, evaluated at `W`, for all `i`.
# First, use a list comprehension to loop over rows in the matrix M.
def loop_mjp(f, x, M):
y, vjp_fun = vjp(f, x)
return jnp.vstack([vjp_fun(mi) for mi in M])
# Now, use vmap to build a computation that does a single fast matrix-matrix
# multiply, rather than an outer loop over vector-matrix multiplies.
def vmap_mjp(f, x, M):
y, vjp_fun = vjp(f, x)
outs, = vmap(vjp_fun)(M)
return outs
key = random.PRNGKey(0)
num_covecs = 128
U = random.normal(key, (num_covecs,) + y.shape)
loop_vs = loop_mjp(f, W, M=U)
print('Non-vmapped Matrix-Jacobian product')
%timeit -n10 -r3 loop_mjp(f, W, M=U)
print('\nVmapped Matrix-Jacobian product')
vmap_vs = vmap_mjp(f, W, M=U)
%timeit -n10 -r3 vmap_mjp(f, W, M=U)
assert jnp.allclose(loop_vs, vmap_vs), 'Vmap and non-vmapped Matrix-Jacobian Products should be identical'
def loop_jmp(f, W, M):
# jvp immediately returns the primal and tangent values as a tuple,
# so we'll compute and select the tangents in a list comprehension
return jnp.vstack([jvp(f, (W,), (mi,))[1] for mi in M])
def vmap_jmp(f, W, M):
_jvp = lambda s: jvp(f, (W,), (s,))[1]
return vmap(_jvp)(M)
num_vecs = 128
S = random.normal(key, (num_vecs,) + W.shape)
loop_vs = loop_jmp(f, W, M=S)
print('Non-vmapped Jacobian-Matrix product')
%timeit -n10 -r3 loop_jmp(f, W, M=S)
vmap_vs = vmap_jmp(f, W, M=S)
print('\nVmapped Jacobian-Matrix product')
%timeit -n10 -r3 vmap_jmp(f, W, M=S)
assert jnp.allclose(loop_vs, vmap_vs), 'Vmap and non-vmapped Jacobian-Matrix products should be identical'
```
### The implementation of `jacfwd` and `jacrev`
Now that we've seen fast Jacobian-matrix and matrix-Jacobian products, it's not hard to guess how to write `jacfwd` and `jacrev`. We just use the same technique to push-forward or pull-back an entire standard basis (isomorphic to an identity matrix) at once.
```
from jax import jacrev as builtin_jacrev
def our_jacrev(f):
def jacfun(x):
y, vjp_fun = vjp(f, x)
# Use vmap to do a matrix-Jacobian product.
# Here, the matrix is the Euclidean basis, so we get all
# entries in the Jacobian at once.
J, = vmap(vjp_fun, in_axes=0)(jnp.eye(len(y)))
return J
return jacfun
assert jnp.allclose(builtin_jacrev(f)(W), our_jacrev(f)(W)), 'Incorrect reverse-mode Jacobian results!'
from jax import jacfwd as builtin_jacfwd
def our_jacfwd(f):
def jacfun(x):
_jvp = lambda s: jvp(f, (x,), (s,))[1]
Jt =vmap(_jvp, in_axes=1)(jnp.eye(len(x)))
return jnp.transpose(Jt)
return jacfun
assert jnp.allclose(builtin_jacfwd(f)(W), our_jacfwd(f)(W)), 'Incorrect forward-mode Jacobian results!'
```
Interestingly, [Autograd](https://github.com/hips/autograd) couldn't do this. Our [implementation](https://github.com/HIPS/autograd/blob/96a03f44da43cd7044c61ac945c483955deba957/autograd/differential_operators.py#L60) of reverse-mode `jacobian` in Autograd had to pull back one vector at a time with an outer-loop `map`. Pushing one vector at a time through the computation is much less efficient than batching it all together with `vmap`.
Another thing that Autograd couldn't do is `jit`. Interestingly, no matter how much Python dynamism you use in your function to be differentiated, we could always use `jit` on the linear part of the computation. For example:
```
def f(x):
try:
if x < 3:
return 2 * x ** 3
else:
raise ValueError
except ValueError:
return jnp.pi * x
y, f_vjp = vjp(f, 4.)
print(jit(f_vjp)(1.))
```
## Complex numbers and differentiation
JAX is great at complex numbers and differentiation. To support both [holomorphic and non-holomorphic differentiation](https://en.wikipedia.org/wiki/Holomorphic_function), it helps to think in terms of JVPs and VJPs.
Consider a complex-to-complex function $f: \mathbb{C} \to \mathbb{C}$ and identify it with a corresponding function $g: \mathbb{R}^2 \to \mathbb{R}^2$,
```
def f(z):
x, y = jnp.real(z), jnp.imag(z)
return u(x, y) + v(x, y) * 1j
def g(x, y):
return (u(x, y), v(x, y))
```
That is, we've decomposed $f(z) = u(x, y) + v(x, y) i$ where $z = x + y i$, and identified $\mathbb{C}$ with $\mathbb{R}^2$ to get $g$.
Since $g$ only involves real inputs and outputs, we already know how to write a Jacobian-vector product for it, say given a tangent vector $(c, d) \in \mathbb{R}^2$, namely
$\begin{bmatrix} \partial_0 u(x, y) & \partial_1 u(x, y) \\ \partial_0 v(x, y) & \partial_1 v(x, y) \end{bmatrix}
\begin{bmatrix} c \\ d \end{bmatrix}$.
To get a JVP for the original function $f$ applied to a tangent vector $c + di \in \mathbb{C}$, we just use the same definition and identify the result as another complex number,
$\partial f(x + y i)(c + d i) =
\begin{matrix} \begin{bmatrix} 1 & i \end{bmatrix} \\ ~ \end{matrix}
\begin{bmatrix} \partial_0 u(x, y) & \partial_1 u(x, y) \\ \partial_0 v(x, y) & \partial_1 v(x, y) \end{bmatrix}
\begin{bmatrix} c \\ d \end{bmatrix}$.
That's our definition of the JVP of a $\mathbb{C} \to \mathbb{C}$ function! Notice it doesn't matter whether or not $f$ is holomorphic: the JVP is unambiguous.
Here's a check:
```
def check(seed):
key = random.PRNGKey(seed)
# random coeffs for u and v
key, subkey = random.split(key)
a, b, c, d = random.uniform(subkey, (4,))
def fun(z):
x, y = jnp.real(z), jnp.imag(z)
return u(x, y) + v(x, y) * 1j
def u(x, y):
return a * x + b * y
def v(x, y):
return c * x + d * y
# primal point
key, subkey = random.split(key)
x, y = random.uniform(subkey, (2,))
z = x + y * 1j
# tangent vector
key, subkey = random.split(key)
c, d = random.uniform(subkey, (2,))
z_dot = c + d * 1j
# check jvp
_, ans = jvp(fun, (z,), (z_dot,))
expected = (grad(u, 0)(x, y) * c +
grad(u, 1)(x, y) * d +
grad(v, 0)(x, y) * c * 1j+
grad(v, 1)(x, y) * d * 1j)
print(jnp.allclose(ans, expected))
check(0)
check(1)
check(2)
```
What about VJPs? We do something pretty similar: for a cotangent vector $c + di \in \mathbb{C}$ we define the VJP of $f$ as
$(c + di)^* \; \partial f(x + y i) =
\begin{matrix} \begin{bmatrix} c & -d \end{bmatrix} \\ ~ \end{matrix}
\begin{bmatrix} \partial_0 u(x, y) & \partial_1 u(x, y) \\ \partial_0 v(x, y) & \partial_1 v(x, y) \end{bmatrix}
\begin{bmatrix} 1 \\ -i \end{bmatrix}$.
What's with the negatives? They're just to take care of complex conjugation, and the fact that we're working with covectors.
Here's a check of the VJP rules:
```
def check(seed):
key = random.PRNGKey(seed)
# random coeffs for u and v
key, subkey = random.split(key)
a, b, c, d = random.uniform(subkey, (4,))
def fun(z):
x, y = jnp.real(z), jnp.imag(z)
return u(x, y) + v(x, y) * 1j
def u(x, y):
return a * x + b * y
def v(x, y):
return c * x + d * y
# primal point
key, subkey = random.split(key)
x, y = random.uniform(subkey, (2,))
z = x + y * 1j
# cotangent vector
key, subkey = random.split(key)
c, d = random.uniform(subkey, (2,))
z_bar = jnp.array(c + d * 1j) # for dtype control
# check vjp
_, fun_vjp = vjp(fun, z)
ans, = fun_vjp(z_bar)
expected = (grad(u, 0)(x, y) * c +
grad(v, 0)(x, y) * (-d) +
grad(u, 1)(x, y) * c * (-1j) +
grad(v, 1)(x, y) * (-d) * (-1j))
assert jnp.allclose(ans, expected, atol=1e-5, rtol=1e-5)
check(0)
check(1)
check(2)
```
What about convenience wrappers like `grad`, `jacfwd`, and `jacrev`?
For $\mathbb{R} \to \mathbb{R}$ functions, recall we defined `grad(f)(x)` as being `vjp(f, x)[1](1.0)`, which works because applying a VJP to a `1.0` value reveals the gradient (i.e. Jacobian, or derivative). We can do the same thing for $\mathbb{C} \to \mathbb{R}$ functions: we can still use `1.0` as the cotangent vector, and we just get out a complex number result summarizing the full Jacobian:
```
def f(z):
x, y = jnp.real(z), jnp.imag(z)
return x**2 + y**2
z = 3. + 4j
grad(f)(z)
```
For geneneral $\mathbb{C} \to \mathbb{C}$ functions, the Jacobian has 4 real-valued degrees of freedom (as in the 2x2 Jacobian matrices above), so we can't hope to represent all of them with in a complex number. But we can for holomorphic functions! A holomorphic function is precisely a $\mathbb{C} \to \mathbb{C}$ function with the special property that its derivative can be represented as a single complex number. (The [Cauchy-Riemann equations](https://en.wikipedia.org/wiki/Cauchy%E2%80%93Riemann_equations) ensure that the above 2x2 Jacobians have the special form of a scale-and-rotate matrix in the complex plane, i.e. the action of a single complex number under multiplication.) And we can reveal that one complex number using a single call to `vjp` with a covector of `1.0`.
Because this only works for holomorphic functions, to use this trick we need to promise JAX that our function is holomorphic; otherwise, JAX will raise an error when `grad` is used for a complex-output function:
```
def f(z):
return jnp.sin(z)
z = 3. + 4j
grad(f, holomorphic=True)(z)
```
All the `holomorphic=True` promise does is disable the error when the output is complex-valued. We can still write `holomorphic=True` when the function isn't holomorphic, but the answer we get out won't represent the full Jacobian. Instead, it'll be the Jacobian of the function where we just discard the imaginary part of the output:
```
def f(z):
return jnp.conjugate(z)
z = 3. + 4j
grad(f, holomorphic=True)(z) # f is not actually holomorphic!
```
There are some useful upshots for how `grad` works here:
1. We can use `grad` on holomorphic $\mathbb{C} \to \mathbb{C}$ functions.
2. We can use `grad` to optimize $f : \mathbb{C} \to \mathbb{R}$ functions, like real-valued loss functions of complex parameters `x`, by taking steps in the dierction of the conjugate of `grad(f)(x)`.
3. If we have an $\mathbb{R} \to \mathbb{R}$ function that just happens to use some complex-valued operations internally (some of which must be non-holomorphic, e.g. FFTs used in covolutions) then `grad` still works and we get the same result that an implementation using only real values would have given.
In any case, JVPs and VJPs are always unambiguous. And if we wanted to compute the full Jacobian matrix of a non-holomorphic $\mathbb{C} \to \mathbb{C}$ function, we can do it with JVPs or VJPs!
You should expect complex numbers to work everywhere in JAX. Here's differentiating through a Cholesky decomposition of a complex matrix:
```
A = jnp.array([[5., 2.+3j, 5j],
[2.-3j, 7., 1.+7j],
[-5j, 1.-7j, 12.]])
def f(X):
L = jnp.linalg.cholesky(X)
return jnp.sum((L - jnp.sin(L))**2)
grad(f, holomorphic=True)(A)
```
## More advanced autodiff
In this notebook, we worked through some easy, and then progressively more complicated, applications of automatic differentiation in JAX. We hope you now feel that taking derivatives in JAX is easy and powerful.
There's a whole world of other autodiff tricks and functionality out there. Topics we didn't cover, but hope to in a "Advanced Autodiff Cookbook" include:
- Gauss-Newton Vector Products, linearizing once
- Custom VJPs and JVPs
- Efficient derivatives at fixed-points
- Estimating the trace of a Hessian using random Hessian-vector products.
- Forward-mode autodiff using only reverse-mode autodiff.
- Taking derivatives with respect to custom data types.
- Checkpointing (binomial checkpointing for efficient reverse-mode, not model snapshotting).
- Optimizing VJPs with Jacobian pre-accumulation.
|
github_jupyter
|
<a href="https://colab.research.google.com/github/airctic/icevision-gradio/blob/master/IceApp_pets.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# IceVision Deployment App Example: PETS Dataset
This example uses Faster RCNN trained weights using the [PETS dataset](https://airctic.github.io/icedata/pets/)
[IceVision](https://github.com/airctic/IceVision) features:
✔ Data curation/cleaning with auto-fix
✔ Exploratory data analysis dashboard
✔ Pluggable transforms for better model generalization
✔ Access to hundreds of neural net models (Torchvision, MMDetection, EfficientDet, Timm)
✔ Access to multiple training loop libraries (Pytorch-Lightning, Fastai)
✔ Multi-task training to efficiently combine object
detection, segmentation, and classification models
## Installing packages
```
!wget https://raw.githubusercontent.com/airctic/icevision/master/install_icevision_inference.sh
!bash install_icevision_inference.sh colab
!echo "- Installing gradio"
!pip install gradio -U -q
# Restart kernel
import IPython
IPython.Application.instance().kernel.do_shutdown(True)
```
## Imports
```
from icevision.all import *
import icedata
import PIL, requests
import torch
from torchvision import transforms
import gradio as gr
```
## Loading trained model
```
_CLASSES = sorted(
{
"Abyssinian",
"great_pyrenees",
"Bombay",
"Persian",
"samoyed",
"Maine_Coon",
"havanese",
"beagle",
"yorkshire_terrier",
"pomeranian",
"scottish_terrier",
"saint_bernard",
"Siamese",
"chihuahua",
"Birman",
"american_pit_bull_terrier",
"miniature_pinscher",
"japanese_chin",
"British_Shorthair",
"Bengal",
"Russian_Blue",
"newfoundland",
"wheaten_terrier",
"Ragdoll",
"leonberger",
"english_cocker_spaniel",
"english_setter",
"staffordshire_bull_terrier",
"german_shorthaired",
"Egyptian_Mau",
"boxer",
"shiba_inu",
"keeshond",
"pug",
"american_bulldog",
"basset_hound",
"Sphynx",
}
)
class_map = ClassMap(_CLASSES)
class_map
# Loading model from IceZoo (IceVision Hub)
model = icedata.pets.trained_models.faster_rcnn_resnet50_fpn()
# Transforms
image_size = 384
valid_tfms = tfms.A.Adapter([*tfms.A.resize_and_pad(image_size), tfms.A.Normalize()])
```
## Defining the `show_preds` method: called by `gr.Interface(fn=show_preds, ...)`
```
# Setting the model type: used in end2end_detect() method here below
model_type = models.torchvision.faster_rcnn
def show_preds(input_image, display_label, display_bbox, detection_threshold):
if detection_threshold==0: detection_threshold=0.5
img = PIL.Image.fromarray(input_image, 'RGB')
pred_dict = model_type.end2end_detect(img, valid_tfms, model, class_map=class_map, detection_threshold=detection_threshold,
display_label=display_label, display_bbox=display_bbox, return_img=True,
font_size=40, label_color="#FF59D6")
return pred_dict['img']
```
## Gradio User Interface
```
display_chkbox_label = gr.inputs.Checkbox(label="Label", default=True)
display_chkbox_box = gr.inputs.Checkbox(label="Box", default=True)
detection_threshold_slider = gr.inputs.Slider(minimum=0, maximum=1, step=0.1, default=0.5, label="Detection Threshold")
outputs = gr.outputs.Image(type="pil")
gr_interface = gr.Interface(fn=show_preds, inputs=["image", display_chkbox_label, display_chkbox_box, detection_threshold_slider], outputs=outputs, title='IceApp - PETS')
gr_interface.launch(inline=False, share=True, debug=True)
```
|
github_jupyter
|
To participate, you'll need to git clone (or download the .zip from GitHub):
https://github.com/mbeyeler/2018-neurohack-skimage
You can do that in git using:
git clone https://github.com/mbeyeler/2018-neurohack-skimage
If you have already cloned the material, please issue `git pull` now and reload the notebook to ensure that you have the latest updates.
# Tutorial 1: Image Manipulation
This tutorial was adapted from https://github.com/scikit-image/skimage-tutorials/blob/master/lectures/00_images_are_arrays.ipynb.
```
%matplotlib inline
```
## Images are NumPy arrays
Images are represented in ``scikit-image`` using standard ``numpy`` arrays. This allows maximum inter-operability with other libraries in the scientific Python ecosystem, such as ``matplotlib`` and ``scipy``.
Let's see how to build a grayscale image as a 2D array:
```
import numpy as np
from matplotlib import pyplot as plt
random_image = np.random.random([500, 500])
plt.imshow(random_image, cmap='gray')
plt.colorbar();
```
The same holds for "real-world" images:
```
from skimage import data
coins = data.coins()
print('Type:', type(coins))
print('dtype:', coins.dtype)
print('shape:', coins.shape)
plt.imshow(coins, cmap='gray');
```
A color image is a 3D array, where the last dimension has size 3 and represents the red, green, and blue channels:
```
cat = data.chelsea()
print("Shape:", cat.shape)
print("Values min/max:", cat.min(), cat.max())
plt.imshow(cat);
```
These are *just NumPy arrays*. E.g., we can make a red square by using standard array slicing and manipulation:
```
cat[10:110, 10:110, :] = [255, 0, 0] # [red, green, blue]
plt.imshow(cat);
```
Images can also include transparent regions by adding a 4th dimension, called an *alpha layer*.
### Other shapes, and their meanings
|Image type|Coordinates|
|:---|:---|
|2D grayscale|(row, column)|
|2D multichannel|(row, column, channel)|
|3D grayscale (or volumetric) |(plane, row, column)|
|3D multichannel|(plane, row, column, channel)|
### Data types and image values
In literature, one finds different conventions for representing image values:
```
0 - 255 where 0 is black, 255 is white
0 - 1 where 0 is black, 1 is white
```
``scikit-image`` supports both conventions--the choice is determined by the
data-type of the array.
E.g., here, I generate two valid images:
## Displaying images using matplotlib
```
from skimage import data
img0 = data.chelsea()
img1 = data.rocket()
import matplotlib.pyplot as plt
f, (ax0, ax1) = plt.subplots(ncols=2, figsize=(20, 10))
ax0.imshow(img0)
ax0.set_title('Cat', fontsize=18)
ax0.axis('off')
ax1.imshow(img1)
ax1.set_title('Rocket', fontsize=18)
ax1.set_xlabel(r'Launching position $\alpha=320$')
ax1.vlines([202, 450], 0, img1.shape[0], colors='white', linewidth=3, label='Side tower position')
ax1.legend();
```
## Drawing
```
from skimage import draw
# Draw a circle with radius 50 at (200, 150):
r, c = draw.circle(200, 150, 50)
# Change only the green channel:
img1[r, c, 1] = 255
plt.imshow(img1)
```
For more on plotting, see the [Matplotlib documentation](https://matplotlib.org/gallery/index.html#images-contours-and-fields) and [pyplot API](https://matplotlib.org/api/pyplot_summary.html).
## Image I/O
Mostly, we won't be using input images from the scikit-image example data sets. Those images are typically stored in JPEG or PNG format. Since scikit-image operates on NumPy arrays, *any* image reader library that provides arrays will do. Options include imageio, matplotlib, pillow, etc.
scikit-image conveniently wraps many of these in the `io` submodule, and will use whichever of the libraries mentioned above are installed:
```
from skimage import io
image = io.imread('../img/skimage-logo.png')
print(type(image))
print(image.dtype)
print(image.shape)
print(image.min(), image.max())
plt.imshow(image);
```
We also have the ability to load multiple images, or multi-layer TIFF images:
```
ic = io.ImageCollection('../img/*.jpg')
print('Type:', type(ic))
ic.files
```
# Exercise: Visualizing RGB channels
Display the different color channels of the image along (each as a gray-scale image). Start with the following template:
```
# --- read in the image ---
image = io.imread('../img/skimage-logo.png')
# --- assign each color channel to a different variable ---
r = ...
g = ...
b = ...
# --- display the image and r, g, b channels ---
f, axes = plt.subplots(1, 4, figsize=(16, 5))
for ax in axes:
ax.axis('off')
(ax_r, ax_g, ax_b, ax_color) = axes
ax_r.imshow(r, cmap='gray')
ax_r.set_title('red channel')
ax_g.imshow(g, cmap='gray')
ax_g.set_title('green channel')
ax_b.imshow(b, cmap='gray')
ax_b.set_title('blue channel')
# --- Here, we stack the R, G, and B layers again
# to form a color image ---
ax_color.imshow(np.stack([r, g, b], axis=2))
ax_color.set_title('all channels');
```
Now, take a look at the following R, G, and B channels. How would their combination look? (Write some code to confirm your intuition.)
|
github_jupyter
|
# Amazon SageMaker Multi-Model Endpoints using XGBoost
With [Amazon SageMaker multi-model endpoints](https://docs.aws.amazon.com/sagemaker/latest/dg/multi-model-endpoints.html), customers can create an endpoint that seamlessly hosts up to thousands of models. These endpoints are well suited to use cases where any one of a large number of models, which can be served from a common inference container to save inference costs, needs to be invokable on-demand and where it is acceptable for infrequently invoked models to incur some additional latency. For applications which require consistently low inference latency, an endpoint deploying a single model is still the best choice.
At a high level, Amazon SageMaker manages the loading and unloading of models for a multi-model endpoint, as they are needed. When an invocation request is made for a particular model, Amazon SageMaker routes the request to an instance assigned to that model, downloads the model artifacts from S3 onto that instance, and initiates loading of the model into the memory of the container. As soon as the loading is complete, Amazon SageMaker performs the requested invocation and returns the result. If the model is already loaded in memory on the selected instance, the downloading and loading steps are skipped and the invocation is performed immediately.
To demonstrate how multi-model endpoints are created and used, this notebook provides an example using a set of XGBoost models that each predict housing prices for a single location. This domain is used as a simple example to easily experiment with multi-model endpoints.
The Amazon SageMaker multi-model endpoint capability is designed to work across with Mxnet, PyTorch and Scikit-Learn machine learning frameworks (TensorFlow coming soon), SageMaker XGBoost, KNN, and Linear Learner algorithms.
In addition, Amazon SageMaker multi-model endpoints are also designed to work with cases where you bring your own container that integrates with the multi-model server library. An example of this can be found [here](https://github.com/awslabs/amazon-sagemaker-examples/tree/master/advanced_functionality/multi_model_bring_your_own) and documentation [here.](https://docs.aws.amazon.com/sagemaker/latest/dg/build-multi-model-build-container.html)
### Contents
1. [Generate synthetic data for housing models](#Generate-synthetic-data-for-housing-models)
1. [Train multiple house value prediction models](#Train-multiple-house-value-prediction-models)
1. [Create the Amazon SageMaker MultiDataModel entity](#Create-the-Amazon-SageMaker-MultiDataModel-entity)
1. [Create the Multi-Model Endpoint](#Create-the-multi-model-endpoint)
1. [Deploy the Multi-Model Endpoint](#deploy-the-multi-model-endpoint)
1. [Get Predictions from the endpoint](#Get-predictions-from-the-endpoint)
1. [Additional Information](#Additional-information)
1. [Clean up](#Clean-up)
# Generate synthetic data
The code below contains helper functions to generate synthetic data in the form of a `1x7` numpy array representing the features of a house.
The first entry in the array is the randomly generated price of a house. The remaining entries are the features (i.e. number of bedroom, square feet, number of bathrooms, etc.).
These functions will be used to generate synthetic data for training, validation, and testing. It will also allow us to submit synthetic payloads for inference to test our multi-model endpoint.
```
import numpy as np
import pandas as pd
import time
NUM_HOUSES_PER_LOCATION = 1000
LOCATIONS = ['NewYork_NY', 'LosAngeles_CA', 'Chicago_IL', 'Houston_TX', 'Dallas_TX',
'Phoenix_AZ', 'Philadelphia_PA', 'SanAntonio_TX', 'SanDiego_CA', 'SanFrancisco_CA']
PARALLEL_TRAINING_JOBS = 4 # len(LOCATIONS) if your account limits can handle it
MAX_YEAR = 2019
def gen_price(house):
_base_price = int(house['SQUARE_FEET'] * 150)
_price = int(_base_price + (10000 * house['NUM_BEDROOMS']) + \
(15000 * house['NUM_BATHROOMS']) + \
(15000 * house['LOT_ACRES']) + \
(15000 * house['GARAGE_SPACES']) - \
(5000 * (MAX_YEAR - house['YEAR_BUILT'])))
return _price
def gen_random_house():
_house = {'SQUARE_FEET': int(np.random.normal(3000, 750)),
'NUM_BEDROOMS': np.random.randint(2, 7),
'NUM_BATHROOMS': np.random.randint(2, 7) / 2,
'LOT_ACRES': round(np.random.normal(1.0, 0.25), 2),
'GARAGE_SPACES': np.random.randint(0, 4),
'YEAR_BUILT': min(MAX_YEAR, int(np.random.normal(1995, 10)))}
_price = gen_price(_house)
return [_price, _house['YEAR_BUILT'], _house['SQUARE_FEET'],
_house['NUM_BEDROOMS'], _house['NUM_BATHROOMS'],
_house['LOT_ACRES'], _house['GARAGE_SPACES']]
def gen_houses(num_houses):
_house_list = []
for i in range(num_houses):
_house_list.append(gen_random_house())
_df = pd.DataFrame(_house_list,
columns=['PRICE', 'YEAR_BUILT', 'SQUARE_FEET', 'NUM_BEDROOMS',
'NUM_BATHROOMS','LOT_ACRES', 'GARAGE_SPACES'])
return _df
```
# Train multiple house value prediction models
In the follow section, we are setting up the code to train a house price prediction model for each of 4 different cities.
As such, we will launch multiple training jobs asynchronously, using the XGBoost algorithm.
In this notebook, we will be using the AWS Managed XGBoost Image for both training and inference - this image provides native support for launching multi-model endpoints.
```
import sagemaker
from sagemaker import get_execution_role
from sagemaker.amazon.amazon_estimator import image_uris
import boto3
from sklearn.model_selection import train_test_split
s3 = boto3.resource('s3')
sagemaker_session = sagemaker.Session()
role = get_execution_role()
BUCKET = sagemaker_session.default_bucket()
# This is references the AWS managed XGBoost container
XGBOOST_IMAGE = image_uris.retrieve(region=boto3.Session().region_name, framework='xgboost', version='1.0-1')
DATA_PREFIX = 'XGBOOST_BOSTON_HOUSING'
MULTI_MODEL_ARTIFACTS = 'multi_model_artifacts'
TRAIN_INSTANCE_TYPE = 'ml.m4.xlarge'
ENDPOINT_INSTANCE_TYPE = 'ml.m4.xlarge'
ENDPOINT_NAME = 'mme-xgboost-housing'
MODEL_NAME = ENDPOINT_NAME
```
### Split a given dataset into train, validation, and test
The code below will generate 3 sets of data. 1 set to train, 1 set for validation and 1 for testing.
```
SEED = 7
SPLIT_RATIOS = [0.6, 0.3, 0.1]
def split_data(df):
# split data into train and test sets
seed = SEED
val_size = SPLIT_RATIOS[1]
test_size = SPLIT_RATIOS[2]
num_samples = df.shape[0]
X1 = df.values[:num_samples, 1:] # keep only the features, skip the target, all rows
Y1 = df.values[:num_samples, :1] # keep only the target, all rows
# Use split ratios to divide up into train/val/test
X_train, X_val, y_train, y_val = \
train_test_split(X1, Y1, test_size=(test_size + val_size), random_state=seed)
# Of the remaining non-training samples, give proper ratio to validation and to test
X_test, X_test, y_test, y_test = \
train_test_split(X_val, y_val, test_size=(test_size / (test_size + val_size)),
random_state=seed)
# reassemble the datasets with target in first column and features after that
_train = np.concatenate([y_train, X_train], axis=1)
_val = np.concatenate([y_val, X_val], axis=1)
_test = np.concatenate([y_test, X_test], axis=1)
return _train, _val, _test
```
### Launch a single training job for a given housing location
There is nothing specific to multi-model endpoints in terms of the models it will host. They are trained in the same way as all other SageMaker models. Here we are using the XGBoost estimator and not waiting for the job to complete.
```
def launch_training_job(location):
# clear out old versions of the data
s3_bucket = s3.Bucket(BUCKET)
full_input_prefix = f'{DATA_PREFIX}/model_prep/{location}'
s3_bucket.objects.filter(Prefix=full_input_prefix + '/').delete()
# upload the entire set of data for all three channels
local_folder = f'data/{location}'
inputs = sagemaker_session.upload_data(path=local_folder, key_prefix=full_input_prefix)
print(f'Training data uploaded: {inputs}')
_job = 'xgb-{}'.format(location.replace('_', '-'))
full_output_prefix = f'{DATA_PREFIX}/model_artifacts/{location}'
s3_output_path = f's3://{BUCKET}/{full_output_prefix}'
xgb = sagemaker.estimator.Estimator(XGBOOST_IMAGE, role,
instance_count=1, instance_type=TRAIN_INSTANCE_TYPE,
output_path=s3_output_path, base_job_name=_job,
sagemaker_session=sagemaker_session)
xgb.set_hyperparameters(max_depth=5, eta=0.2, gamma=4, min_child_weight=6, subsample=0.8, silent=0,
early_stopping_rounds=5, objective='reg:linear', num_round=25)
DISTRIBUTION_MODE = 'FullyReplicated'
train_input = sagemaker.inputs.TrainingInput(s3_data=inputs+'/train',
distribution=DISTRIBUTION_MODE, content_type='csv')
val_input = sagemaker.inputs.TrainingInput(s3_data=inputs+'/val',
distribution=DISTRIBUTION_MODE, content_type='csv')
remote_inputs = {'train': train_input, 'validation': val_input}
xgb.fit(remote_inputs, wait=False)
# Return the estimator object
return xgb
```
### Kick off a model training job for each housing location
```
def save_data_locally(location, train, val, test):
os.makedirs(f'data/{location}/train')
np.savetxt( f'data/{location}/train/{location}_train.csv', train, delimiter=',', fmt='%.2f')
os.makedirs(f'data/{location}/val')
np.savetxt(f'data/{location}/val/{location}_val.csv', val, delimiter=',', fmt='%.2f')
os.makedirs(f'data/{location}/test')
np.savetxt(f'data/{location}/test/{location}_test.csv', test, delimiter=',', fmt='%.2f')
import shutil
import os
estimators = []
shutil.rmtree('data', ignore_errors=True)
for loc in LOCATIONS[:PARALLEL_TRAINING_JOBS]:
_houses = gen_houses(NUM_HOUSES_PER_LOCATION)
_train, _val, _test = split_data(_houses)
save_data_locally(loc, _train, _val, _test)
estimator = launch_training_job(loc)
estimators.append(estimator)
print()
print(f'{len(estimators)} training jobs launched: {[x.latest_training_job.job_name for x in estimators]}')
```
### Wait for all model training to finish
```
def wait_for_training_job_to_complete(estimator):
job = estimator.latest_training_job.job_name
print(f'Waiting for job: {job}')
status = estimator.latest_training_job.describe()['TrainingJobStatus']
while status == 'InProgress':
time.sleep(45)
status = estimator.latest_training_job.describe()['TrainingJobStatus']
if status == 'InProgress':
print(f'{job} job status: {status}')
print(f'DONE. Status for {job} is {status}\n')
for est in estimators:
wait_for_training_job_to_complete(est)
```
# Create the multi-model endpoint with the SageMaker SDK
### Create a SageMaker Model from one of the Estimators
```
estimator = estimators[0]
model = estimator.create_model(role=role, image_uri=XGBOOST_IMAGE)
```
### Create the Amazon SageMaker MultiDataModel entity
We create the multi-model endpoint using the [```MultiDataModel```](https://sagemaker.readthedocs.io/en/stable/api/inference/multi_data_model.html) class.
You can create a MultiDataModel by directly passing in a `sagemaker.model.Model` object - in which case, the Endpoint will inherit information about the image to use, as well as any environmental variables, network isolation, etc., once the MultiDataModel is deployed.
In addition, a MultiDataModel can also be created without explictly passing a `sagemaker.model.Model` object. Please refer to the documentation for additional details.
```
from sagemaker.multidatamodel import MultiDataModel
# This is where our MME will read models from on S3.
model_data_prefix = f's3://{BUCKET}/{DATA_PREFIX}/{MULTI_MODEL_ARTIFACTS}/'
mme = MultiDataModel(name=MODEL_NAME,
model_data_prefix=model_data_prefix,
model=model,# passing our model - passes container image needed for the endpoint
sagemaker_session=sagemaker_session)
```
# Deploy the Multi Model Endpoint
You need to consider the appropriate instance type and number of instances for the projected prediction workload across all the models you plan to host behind your multi-model endpoint. The number and size of the individual models will also drive memory requirements.
```
predictor = mme.deploy(initial_instance_count=1,
instance_type=ENDPOINT_INSTANCE_TYPE,
endpoint_name=ENDPOINT_NAME)
```
### Our endpoint has launched! Let's look at what models are available to the endpoint!
By 'available', what we mean is, what model artfiacts are currently stored under the S3 prefix we defined when setting up the `MultiDataModel` above i.e. `model_data_prefix`.
Currently, since we have no artifacts (i.e. `tar.gz` files) stored under our defined S3 prefix, our endpoint, will have no models 'available' to serve inference requests.
We will demonstrate how to make models 'available' to our endpoint below.
```
# No models visible!
list(mme.list_models())
```
### Lets deploy model artifacts to be found by the endpoint
We are now using the `.add_model()` method of the `MultiDataModel` to copy over our model artifacts from where they were initially stored, during training, to where our endpoint will source model artifacts for inference requests.
`model_data_source` refers to the location of our model artifact (i.e. where it was deposited on S3 after training completed)
`model_data_path` is the **relative** path to the S3 prefix we specified above (i.e. `model_data_prefix`) where our endpoint will source models for inference requests.
Since this is a **relative** path, we can simply pass the name of what we wish to call the model artifact at inference time (i.e. `Chicago_IL.tar.gz`)
### Dynamically deploying additional models
It is also important to note, that we can always use the `.add_model()` method, as shown below, to dynamically deploy more models to the endpoint, to serve up inference requests as needed.
```
for est in estimators:
artifact_path = est.latest_training_job.describe()['ModelArtifacts']['S3ModelArtifacts']
model_name = artifact_path.split('/')[-4]+'.tar.gz'
# This is copying over the model artifact to the S3 location for the MME.
mme.add_model(model_data_source=artifact_path, model_data_path=model_name)
```
## We have added the 4 model artifacts from our training jobs!
We can see that the S3 prefix we specified when setting up `MultiDataModel` now has 4 model artifacts. As such, the endpoint can now serve up inference requests for these models.
```
list(mme.list_models())
```
# Get predictions from the endpoint
Recall that ```mme.deploy()``` returns a [RealTimePredictor](https://github.com/aws/sagemaker-python-sdk/blob/master/src/sagemaker/predictor.py#L35) that we saved in a variable called ```predictor```.
We will use ```predictor``` to submit requests to the endpoint.
XGBoost supports ```text/csv``` for the content type and accept type. For more information on XGBoost Input/Output Interface, please see [here.](https://docs.aws.amazon.com/sagemaker/latest/dg/xgboost.html#InputOutput-XGBoost)
Since the default RealTimePredictor does not have a serializer or deserializer set for requests, we will also set these.
This will allow us to submit a python list for inference, and get back a float response.
```
from sagemaker.serializers import CSVSerializer
from sagemaker.deserializers import JSONDeserializer
predictor.serializer = CSVSerializer()
predictor.deserializer = JSONDeserializer()
#predictor.content_type =predictor.content_type , removed as mentioned https://github.com/aws/sagemaker-python-sdk/blob/e8d16f8bc4c570f763f1129afc46ba3e0b98cdad/src/sagemaker/predictor.py#L82
#predictor.accept = "text/csv" # removed also : https://github.com/aws/sagemaker-python-sdk/blob/e8d16f8bc4c570f763f1129afc46ba3e0b98cdad/src/sagemaker/predictor.py#L83
```
### Invoking models on a multi-model endpoint
Notice the higher latencies on the first invocation of any given model. This is due to the time it takes SageMaker to download the model to the Endpoint instance and then load the model into the inference container. Subsequent invocations of the same model take advantage of the model already being loaded into the inference container.
```
start_time = time.time()
predicted_value = predictor.predict(data=gen_random_house()[1:], target_model='Chicago_IL.tar.gz')
duration = time.time() - start_time
print('${:,.2f}, took {:,d} ms\n'.format(predicted_value[0], int(duration * 1000)))
start_time = time.time()
#Invoke endpoint
predicted_value = predictor.predict(data=gen_random_house()[1:], target_model='Chicago_IL.tar.gz')
duration = time.time() - start_time
print('${:,.2f}, took {:,d} ms\n'.format(predicted_value[0], int(duration * 1000)))
start_time = time.time()
#Invoke endpoint
predicted_value = predictor.predict(data=gen_random_house()[1:], target_model='Houston_TX.tar.gz')
duration = time.time() - start_time
print('${:,.2f}, took {:,d} ms\n'.format(predicted_value[0], int(duration * 1000)))
start_time = time.time()
#Invoke endpoint
predicted_value = predictor.predict(data=gen_random_house()[1:], target_model='Houston_TX.tar.gz')
duration = time.time() - start_time
print('${:,.2f}, took {:,d} ms\n'.format(predicted_value[0], int(duration * 1000)))
```
### Updating a model
To update a model, you would follow the same approach as above and add it as a new model. For example, if you have retrained the `NewYork_NY.tar.gz` model and wanted to start invoking it, you would upload the updated model artifacts behind the S3 prefix with a new name such as `NewYork_NY_v2.tar.gz`, and then change the `target_model` field to invoke `NewYork_NY_v2.tar.gz` instead of `NewYork_NY.tar.gz`. You do not want to overwrite the model artifacts in Amazon S3, because the old version of the model might still be loaded in the containers or on the storage volume of the instances on the endpoint. Invocations to the new model could then invoke the old version of the model.
Alternatively, you could stop the endpoint and re-deploy a fresh set of models.
## Using Boto APIs to invoke the endpoint
While developing interactively within a Jupyter notebook, since `.deploy()` returns a `RealTimePredictor` it is a more seamless experience to start invoking your endpoint using the SageMaker SDK. You have more fine grained control over the serialization and deserialization protocols to shape your request and response payloads to/from the endpoint.
This is great for iterative experimentation within a notebook. Furthermore, should you have an application that has access to the SageMaker SDK, you can always import `RealTimePredictor` and attach it to an existing endpoint - this allows you to stick to using the high level SDK if preferable.
Additional documentation on `RealTimePredictor` can be found [here.](https://sagemaker.readthedocs.io/en/stable/api/inference/predictors.html?highlight=RealTimePredictor#sagemaker.predictor.RealTimePredictor)
The lower level Boto3 SDK may be preferable if you are attempting to invoke the endpoint as a part of a broader architecture.
Imagine an API gateway frontend that uses a Lambda Proxy in order to transform request payloads before hitting a SageMaker Endpoint - in this example, Lambda does not have access to the SageMaker Python SDK, and as such, Boto3 can still allow you to interact with your endpoint and serve inference requests.
Boto3 allows for quick injection of ML intelligence via SageMaker Endpoints into existing applications with minimal/no refactoring to existing code.
Boto3 will submit your requests as a binary payload, while still allowing you to supply your desired `Content-Type` and `Accept` headers with serialization being handled by the inference container in the SageMaker Endpoint.
Additional documentation on `.invoke_endpoint()` can be found [here.](https://boto3.amazonaws.com/v1/documentation/api/latest/reference/services/sagemaker-runtime.html)
```
import boto3
import json
runtime_sm_client = boto3.client(service_name='sagemaker-runtime')
def predict_one_house_value(features, model_name):
print(f'Using model {model_name} to predict price of this house: {features}')
# Notice how we alter the list into a string as the payload
body = ','.join(map(str, features)) + '\n'
start_time = time.time()
response = runtime_sm_client.invoke_endpoint(
EndpointName=ENDPOINT_NAME,
ContentType='text/csv',
TargetModel=model_name,
Body=body)
predicted_value = json.loads(response['Body'].read())[0]
duration = time.time() - start_time
print('${:,.2f}, took {:,d} ms\n'.format(predicted_value, int(duration * 1000)))
predict_one_house_value(gen_random_house()[1:], 'Chicago_IL.tar.gz')
```
## Clean up
Here, to be sure we are not billed for endpoints we are no longer using, we clean up.
```
predictor.delete_endpoint()
predictor.delete_model()
```
|
github_jupyter
|
If not explicitly mentioned otherwise we assume:
- RCP2.6 scenario or the lowest ppm concentration reported (stabilized around 400-420)
- Linear phase-out of fossil fuels from model start time (2000-2015) by 2100
- BAU scenario would lead to RCP6 or higher
- as it is widely accepcted that in order to obtain RCP2.6, emissions must at least cease or turn into removals in the geological near-term (throughout this century), therefore whenever the carbon price is given in terms of percentage reduction from current levels, a linear 100% reduction is assumed from model start time (2000-2015) by 2100
- if ranges are reported, the mean is taken
- if the model reports price in dollar per ton of carbon, it is converted to dollar per ton of carbon dioxide
```
import pandas as pd, numpy as np, matplotlib.pyplot as plt, matplotlib as mpl
%matplotlib inline
mpl.style.use('classic')
d=[]
#d.append(pd.read_csv('carbon/alberth_hope2006.csv',header=None))
#d.append(pd.read_csv('carbon/alberth_hope2006_2.csv',header=None))
d.append(pd.read_csv('carbon/bauer2012.csv',header=None))
d.append(pd.read_csv('carbon/bauer2012_2a.csv',header=None))
d.append(pd.read_csv('carbon/bauer2012_2b.csv',header=None))
d.append(pd.read_csv('carbon/bauer2012_2c.csv',header=None))
d.append(pd.read_csv('carbon/bosetti2014a.csv',header=None))
d.append(pd.read_csv('carbon/bosetti2014b.csv',header=None))
d.append(pd.read_csv('carbon/bosetti2014c.csv',header=None))
d.append(pd.read_csv('carbon/cai2015.csv',header=None))
d.append(pd.read_csv('carbon/chen2005.csv',header=None))
d.append(pd.read_csv('carbon/edmonds_GCAM1994.csv',header=None))
d.append(pd.read_csv('carbon/kriegler2015_2.csv',header=None))
#d.append(pd.read_csv('carbon/luderer_REMIND2015.csv',header=None))
d.append(pd.read_csv('carbon/manne_richels_MERGE2005.csv',header=None))
d.append(pd.read_csv('carbon/paltsev2005.csv',header=None))
d.append(pd.read_csv('carbon/russ_POLES2012.csv',header=None))
d.append(pd.read_csv('carbon/wilkerson2015.csv',header=None))
from scipy.interpolate import interp1d
kd=[]
fd=[]
for z in range(len(d)):
kd.append({})
for i in range(len(d[z][0])):
if ~np.isnan(d[z][0][i]):
kd[z][np.round(d[z][0][i],0)]=d[z][1][i]
fd.append(interp1d(sorted(kd[z].keys()),[kd[z][j] for j in sorted(kd[z].keys())]))
for z in range(len(d)):
#plt.scatter(d[z][0],d[z][1])
years=range(int(min(d[z][0]))+1,int(max(d[z][0]))+1)
plt.plot(years,fd[z](years))
labels=['Bauer, Hilaire et al.\n2012 | REMIND-R',\
'Luderer, Bosetti et al.\n2011 | IMACLIM-R',\
'Luderer, Bosetti et al.\n2011 | REMIND-R',\
'Luderer, Bosetti et al.\n2011 | WITCH',\
'Bosetti, Marangoni et al.\n2015 | GCAM',\
'Bosetti, Marangoni et al.\n2015 | MARKAL US',\
'Bosetti, Marangoni et al.\n2015 | WITCH',\
'Cai, Newth et al.\n2015 | GTEM-C',\
'Chen, 2005\nMARKAL-MACRO',\
'Edmonds, Wise, MacCracken\n1994 | GCAM',\
'Kriegler, Petermann, et al.\n2015 | multiple',\
'Manne, Richels\n2005 | MERGE',\
'Paltsev, Reilly et al.\n2005 | MIT EPPA',\
'Russ, Ciscar et al.\n2009 | POLES',\
'Wilkerson, Leibowicz et al.\n2015 | multiple'\
]
co2=[1,1,1,1,0,0,0,1,0,0,1,0,0,0,1]
z=14
plt.scatter(d[z][0],d[z][1])
years=range(int(min(d[z][0]))+1,int(max(d[z][0]))+1)
plt.plot(years,fd[z](years))
def plotter(ax,x,y,c,l,z=2,zz=2,step=2,w=-50,w2=30):
yrs=range(x[0]-40,x[len(x)-1]+10)
maxi=[0,0]
maxv=-100
#try a few initial values for maximum rsquared
i=0
for k in range(1,5):
p0 = [1., 1., x[len(x)*k/5]]
fit2 = optimize.leastsq(errfunc,p0,args=(x,y),full_output=True)
ss_err=(fit2[2]['fvec']**2).sum()
ss_tot=((y-y.mean())**2).sum()
rsquared=1-(ss_err/ss_tot)
if rsquared>maxv:
maxi=[i,k]
maxv=rsquared
i=maxi[0]
k=maxi[1]
p0 = [1., 1., x[len(x)*k/5], -1+i*0.5]
fit2 = optimize.leastsq(errfunc,p0,args=(x,y),full_output=True)
ss_err=(fit2[2]['fvec']**2).sum()
ss_tot=((y-y.mean())**2).sum()
rsquared=1-(ss_err/ss_tot)
ax.scatter(x[::step],y[::step],lw*3,color=c)
#ax.plot(yrs,logist(fit2[0],yrs),color="#006d2c",lw=lw)
ax.plot(yrs,logist(fit2[0],yrs),color="#444444",lw=lw)
#ax.plot(yrs,logist(fit2[0],yrs),color=c,lw=1)
yk=logist([fit2[0][0],fit2[0][1],fit2[0][2],fit2[0][3]],range(3000))
mint=0
maxt=3000
perc=0.1
for i in range(3000):
if yk[i]<perc: mint=i
if yk[i]<1-perc: maxt=i
if z>-1:
coord=len(x)*z/5
ax.annotate('$R^2 = '+str(np.round(rsquared,2))+'$\n'+\
'$\\alpha = '+str(np.round(fit2[0][0],2))+'$\n'+\
'$\\beta = '+str(np.round(fit2[0][1],2))+'$\n'+\
'$\\Delta t = '+str(int(maxt-mint))+'$', xy=(yrs[coord], logist(fit2[0],yrs)[coord]),\
xycoords='data',
xytext=(w, w2), textcoords='offset points', color="#444444",
arrowprops=dict(arrowstyle="->",color='#444444'))
coord=len(x)*zz/5
ax.annotate(l, xy=(yrs[coord], logist(fit2[0],yrs)[coord]),\
xycoords='data',
xytext=(w, w2), textcoords='offset points',
arrowprops=dict(arrowstyle="->"))
fig, ax = plt.subplots(1,1,subplot_kw=dict(axisbg='#EEEEEE',axisbelow=True),figsize=(10,5))
lw=2
colors=["#756bb1","#d95f0e","#444444"]
ax.grid(color='white', linestyle='solid')
ax.set_xlabel('Years')
ax.set_ylabel('Carbon tax $[\$/tonCO_2]$')
ax.set_xlim([2000,2100])
ax.set_ylim([0,5000])
#ax.set_yscale('log')
ax.set_title('Carbon price estimations from various IAM models',size=13,y=1.04)
loc=[2088,2083,2084,2080,2031,2047,2043,2088,2015,2072,2050,2075,2095,2020,2062]
lz=[(-70, 20),(-70, 20),(-20, 10),(-40, 20),(-100, 40),(-110, 20),(-130, 20),(-15, 15),\
(-70, 20),(-105, 20),(-80, 20),(-60, 12),(-120, -5),(-70, 50),(-30, 7)]
for z in range(len(d))[:15]:
#ax.scatter(d[z][0],d[z][1])
years=range(int(min(d[z][0]))+1,int(max(d[z][0]))+1)
if (co2[z]==1):k=1
else: k=44.0/12.0
ax.plot(years,fd[z](years)*k,lw=lw,color=colors[z%3])
ax.annotate(labels[z]+str(z), xy=(loc[z],fd[z]([loc[z]])*k),\
xycoords='data',
xytext=lz[z], textcoords='offset points',fontsize=9, color=colors[z%3],
arrowprops=dict(arrowstyle="->",color=colors[z%3]))
#plt.savefig('ces9.png',bbox_inches = 'tight', pad_inches = 0.1, dpi=150)
plt.show()
fig, ax = plt.subplots(1,1,subplot_kw=dict(axisbg='#EEEEEE',axisbelow=True),figsize=(10,5))
lw=2
colors=["#756bb1","#d95f0e","#444444"]
ax.grid(color='white', linestyle='solid')
ax.set_xlabel('Years')
ax.set_ylabel('$MAC$ $[\$/tonCO_2]$')
ax.set_xlim([2000,2100])
ax.set_ylim([0,5000])
#ax.set_yscale('log')
ax.set_title(u'Marginal abatement cost $(MAC)$ estimations from various IAM models',size=13,y=1.04)
loc=[2088,2070,2084,2070,2031,2047,2043,2088,2015,2072,2065,2075,2095,2019,2062]
lz=[(-60, 20),(-75, 20),(-20, 10),(-70, 20),(-100, 40),(-110, 20),(-130, 20),(-15, 15),\
(-70, 20),(-90, 20),(-70, 20),(-70, 12),(-120, -5),(-60, 50),(-30, 7)]
for z in range(len(d))[:15]:
#ax.scatter(d[z][0],d[z][1])
if z not in {0,9,14}:
years=range(int(min(d[z][0]))+1,int(max(d[z][0]))+1)
if (co2[z]==1):k=1
else: k=44.0/12.0
if z in {3,6,7,12}:
lw=3
c=colors[2]
elif z in {0,1,2,5}:
lw=1
c=colors[1]
else:
lw=1
c=colors[0]
ax.plot(years,fd[z](years)*k,lw=lw,color=c)
ax.annotate(labels[z], xy=(loc[z],fd[z]([loc[z]])*k),\
xycoords='data',
xytext=lz[z], textcoords='offset points',fontsize=9, color=c,
arrowprops=dict(arrowstyle="->",color=c))
plt.savefig('ces9b.png',bbox_inches = 'tight', pad_inches = 0.1, dpi=150)
plt.show()
for z in range(len(d))[:15]:
print labels[z]
```
|
github_jupyter
|
```
import xarray as xr
import xroms
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import cmocean.cm as cmo
import cartopy
```
# How to select data
The [load_data](load_data.ipynb) notebook demonstrates how to load in data, but now how to select out parts of it?
### Load in data
More information at in [load_data notebook](load_data.ipynb)
```
loc = 'http://barataria.tamu.edu:8080/thredds/dodsC/forecast_latest/txla2_his_f_latest.nc'
chunks = {'ocean_time':1}
ds = xr.open_dataset(loc, chunks=chunks)
# set up grid
ds, grid = xroms.roms_dataset(ds)
```
## Select
### Slices by index or keyword
#### Surface layer slice
The surface in ROMS is given by the last index in the vertical dimension. The easiest way to access this is by indexing into `s_rho`. While normally it is better to access coordinates through keywords to be human-readable, it's not easy to tell what value of `s_rho` gives the surface. In this instance, it's easier to just go by index.
```
ds.salt.isel(s_rho=-1)
```
#### x/y index slice
For a curvilinear ROMS grid, selecting by the dimensions `xi_rho` or `eta_rho` (or for whichever is the relevant grid) is not very meaningful because they are given by index. Thus the following is possible to get a slice along the index, but it cannot be used to find a slice based on the lon/lat values.
```
ds.temp.sel(xi_rho=20)
```
#### Single time
Find the forecast model output available that is closest to now. Note that the `method` keyword argument is not necessary if the desired date/time is exactly a model output time.
```
now = pd.Timestamp.today()
ds.salt.isel(s_rho=-1).sel(ocean_time=now, method='nearest')
```
#### Range of time
```
ds.salt.sel(ocean_time=slice(now,now+pd.Timedelta('2 days')))
```
### Calculate slice
#### Cross-section along a longitude value
Because the example grid is curvilinear, a slice along a grid dimension is not the same as a slice along a longitude or latitude (or projected $x$/$y$) value. This needs to be calculated and we can use the `xisoslice` function to do this. The calculation is done lazily. We calculate only part of the slice, on the continental shelf. Renaming the subsetted dataset (below, as `dss`) is convenient because this variable can be used in place of `ds` for all related function calls to be consistent and only have to subset one time.
```
# want salinity along this constant value
lon0 = -91.5
# This is the array we want projected onto the longitude value.
# Note that we are requesting multiple times at once.
dss = ds.isel(ocean_time=slice(0,10), eta_rho=slice(50,-1))
# Projecting 3rd input onto constant value lon0 in iso_array ds.lon_rho
sl = xroms.xisoslice(dss.lon_rho, lon0, dss.salt, 'xi_rho')
sl
fig, axes = plt.subplots(1, 2, figsize=(15,6))
sl.isel(ocean_time=0).plot(ax=axes[0])
sl.isel(ocean_time=-1).plot(ax=axes[1])
```
Better plot: use coordinates and one colorbar to compare.
```
# calculate z values (s_rho)
slz = xroms.xisoslice(dss.lon_rho, lon0, dss.z_rho, 'xi_rho')
# calculate latitude values (eta_rho)
sllat = xroms.xisoslice(dss.lon_rho, lon0, dss.lat_rho, 'xi_rho')
# assign these as coords to be used in plot
sl = sl.assign_coords(z=slz, lat=sllat)
# points that should be masked
slmask = xroms.xisoslice(dss.lon_rho, lon0, dss.mask_rho, 'xi_rho')
# drop masked values
sl = sl.where(slmask==1, drop=True)
# find min and max of the slice itself (without values that should be masked)
vmin = sl.min().values
vmax = sl.max().values
fig, axes = plt.subplots(1, 2, figsize=(15,6), sharey=True)
sl.isel(ocean_time=0).plot(x='lat', y='z', ax=axes[0], vmin=vmin, vmax=vmax, add_colorbar=False)
mappable = sl.isel(ocean_time=-1).plot(x='lat', y='z', ax=axes[1], vmin=vmin, vmax=vmax, add_colorbar=False)
fig.colorbar(ax=axes, mappable=mappable, orientation='horizontal').set_label('salt')
```
Verify performance of isoslice by comparing slice at surface with planview surface plot.
```
vmin = dss.salt.min().values
vmax = dss.salt.max().values
fig, ax = plt.subplots(1, 1, figsize=(15,15))
ds.salt.isel(ocean_time=0, s_rho=-1).plot(ax=ax, x='lon_rho', y='lat_rho')
ax.scatter(lon0*np.ones_like(sl.lat[::10]), sl.lat[::10], c=sl.isel(ocean_time=0, s_rho=-1)[::10],
s=100, vmin=vmin, vmax=vmax, zorder=10, edgecolor='k')
```
#### Variable at constant z value
```
# want temperature along this constant depth value
z0 = -10
# This is the array we want projected
dss = ds.isel(ocean_time=0)
# Projecting 3rd input onto constant value z0 in iso_array (1st input)
sl = xroms.xisoslice(dss.z_rho, z0, dss.temp, 's_rho')
sl
sl.plot(cmap=cmo.thermal, x='lon_rho', y='lat_rho')
```
#### Variable at constant z depth, in time
```
# want temperature along this constant depth value
z0 = -10
# Projecting 3rd input onto constant value z0 in iso_array (1st input)
sl = xroms.xisoslice(ds.z_rho, z0, ds.temp, 's_rho')
sl
```
#### zeta at constant z depth, in time
... to verify that xisoslice does act in time across zeta.
```
# want temperature along this constant depth value
z0 = -10
# Projecting 3rd input onto constant value z0 in iso_array (1st input)
zeta_s_rho = ds.zeta.expand_dims({'s_rho': ds.s_rho}).transpose('ocean_time','s_rho',...)
sl = xroms.xisoslice(ds.z_rho, z0, zeta_s_rho, 's_rho')
sl.sel(eta_rho=30,xi_rho=20).plot()
```
#### Depth of isohaline surface
Calculate the depth of a specific isohaline.
Note that in this case there are a few wonky values, so we should filter them out or control the vmin/vmax values on the plot.
```
# want the depth of this constant salinity value
S0 = 33
# This is the array we want projected
dss = ds.isel(ocean_time=0)
# Projecting 3rd input onto constant value z0 in iso_array (1st input)
sl = xroms.xisoslice(dss.salt, S0, dss.z_rho, 's_rho')
sl.plot(cmap=cmo.deep, x='lon_rho', y='lat_rho', vmin=-20, vmax=0, figsize=(10, 10))
```
### Select region
Select a boxed region by min/max lon and lat values.
```
# want model output only within the box defined by these lat/lon values
lon = np.array([-97, -96])
lat = np.array([28, 29])
# this condition defines the region of interest
box = ((lon[0] < ds.lon_rho) & (ds.lon_rho < lon[1]) & (lat[0] < ds.lat_rho) & (ds.lat_rho < lat[1])).compute()
```
Plot the model output in the box at the surface
```
dss = ds.where(box).salt.isel(s_rho=-1, ocean_time=0)
dss.plot(x='lon_rho', y='lat_rho')
```
Can calculate a metric within the box:
```
dss.mean().values
```
### Find nearest model output in two dimensions
This matters for a curvilinear grid.
Can't use `sel` because it will only search in one coordinate for the nearest value and the coordinates are indices which are not necessarily geographic distance. Instead need to use a search for distance and use that for the `where` condition from the previous example.
Find the model output at the grid node nearest the point (lon0, lat0). You can create the projection to use for the distance calculation in `sel2d` and input it into the function, or you can let it choose a default for you.
```
lon0, lat0 = -96, 27
dl = 0.05
proj = cartopy.crs.LambertConformal(central_longitude=-98, central_latitude=30)
dssub = xroms.sel2d(ds, lon0, lat0, proj)
```
Or, if you instead want the indices of the nearest grid node returned, you can call `argsel2d`:
```
ix, iy = xroms.argsel2d(ds, lon0, lat0, proj)
```
Check this function, just to be sure:
```
box = (ds.lon_rho>lon0-dl) & (ds.lon_rho<lon0+dl) & (ds.lat_rho>lat0-dl) & (ds.lat_rho<lat0+dl)
dss = ds.where(box).salt.isel(ocean_time=0, s_rho=-1)
vmin = dss.min().values
vmax = dss.max().values
dss.plot(x='lon_rho', y='lat_rho')
plt.scatter(lon0, lat0, c=dssub.salt.isel(s_rho=-1, ocean_time=0), s=200, edgecolor='k', vmin=vmin, vmax=vmax)
plt.xlim(lon0-dl,lon0+dl)
plt.ylim(lat0-dl, lat0+dl)
```
Note that the `sel2d` function returned a time series since that was input, and it worked fine. Getting the numbers take time.
```
dssub.salt.isel(s_rho=-1, ocean_time=slice(0,5)).plot()
```
|
github_jupyter
|
## Viscous Inverse Design
This notebook demonstrates the use of gradients from viiflow for fully viscous inverse design.
It defines a target pressure distribution from one airfoil and, coming from another airfoil, tries to find the shape necessary to arrive at this target pressure.
It uses virtual displacements, which do not necessitate the recalculation of the panel operator.
Instead, it uses the same model used for the effect of boundary layer thickness onto the flow for modification of the airfoil shape.
The heart of this notebook is a Gauss-Newton iteration which solves for these virtual displacements.
Instead of trying to solve the pressure distribution exactly, the iteration sovles a least-squares problem that joins the pressure difference with regularizing terms.
Fully viscous inverse design is not a straightforward problem. There are several ways an optimizer may *cheat*, for example
* The velocity is defined by the inviscid solution of the airfoil shape plus boundary layer thickness. An optimizer can therefore choose to reduce the thickness of the airfoil if for some reason a thick boundary layer leads to the target velocity distribution.
* Kinks in the desired velocity are, in the case below, due to laminar-turbulent transition. However, an optimizer can choose to model this kink by an actual kink in the airfoil.
To alleviate this, the pressure error is appended by a regularizing term that penalizes non-smooth displacements - simply by adding $ \frac{\mathrm{d}^2}{\mathrm{d}^2 s} \delta_{virtual}(s) $ at every point along the airfoil surface coordinate $s$ to the Least-Squares problem.
The parameters chosen to increrase/decrease the penalties were chosen ad-hoc by trial and error.
In addition, the nodes very close to the stagnation point are not modified.
In addition, the residual $r$ of the viiflow solver itself is added to the Least-Squares problem and scaled such that at convergence its error is sufficiently low.
Every iteration then performs for dispalcements $y$ and the viiflow variables $x$
$$
y^{k+1} = y^k - \lambda {\Delta y}^k\\
x^{k+1} = x^k - \lambda {\Delta x}^k\\
{\Delta y}^k, {\Delta x}^k = \min_{\Delta y,\Delta x} \| F(y^k,x^k) - \frac{\partial F}{\partial y}(y^k,x^k) \Delta y - \frac{\partial F}{\partial x}(y^k,x^k) \Delta x\|^2\\
\|F(y,x)\|^2 = \gamma_{cp}^2\|ue(y)-ue_{target}\|^2 + \gamma_y^2\| \frac{\mathrm{d}^2}{\mathrm{d}^2 s} y \|^2 + \gamma_r^2 \|r(y,x)\|^2
$$
This may seem like a large problem, but the effort for solving the overdetermined least-squares problem grows largely with the degrees of freedom, not the amount of equations.
Below, this procedure is used to morph the S805 airfoil into the S825 airfoil. Even with the regularizing terms, little dips that enforce the laminar-turbulent transition can still be seen when zooming in.
While this solves for an airfoil shape of a specified pressure distribution, it is probably not a very smart idea to use this for actual design. A better idea is to use first an inviscid inverse design method, e.g. conformal mapping [1, 2], and remove the discrepancies using a fully viscid iteration.
The benefit of this Gauss-Newton approach is how straightforward additional constraints can be included, e.g. only fit the suction side from .1c onwards or fit multiple target distributions at multiple angles of attack.
```
import viiflow as vf
import viiflowtools.vf_tools as vft
import viiflowtools.vf_plots as vfp
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
# Analysis Settings
RE = 1e6
ncrit =5
Mach = 0.0
alpha = 4.0
N = 300
# Read Airfoils
BASE = vft.repanel(vft.read_selig("S805.dat"),N,KAPFAC=2)
TARGET = vft.repanel(vft.read_selig("S825.dat"),N,KAPFAC=2)
# Solve target for our target cp (or more precisely edge velocity)
s = vf.setup(Re=RE,Ma=Mach,Ncrit=ncrit,Alpha=alpha)
# Internal iterations
s.Itermax = 100
# Set-up and initialize based on inviscid panel solution
[p,bl,x] = vf.init([TARGET],s)
res = None
grad = None
# Solve aerodynamic problem of target airfoil
vf.iter(x,bl,p,s,None,None)
XT0 = p.foils[0].X[0,:].copy()
UT = p.gamma_viscid[0:p.foils[0].N].copy()
# Set-up and initialize based on inviscid panel solution
[p,bl,x0] = vf.init([BASE],s)
res = None
grad = None
# Solve aerodynamic problem of current airfoil and save for later plotting
[x0,_,res,grad,_] = vf.iter(x0,bl,p,s,None,None)
XC0 = p.foils[0].X[0,:].copy()
UC = p.gamma_viscid[0:p.foils[0].N].copy()
# To interpolate from one grid to the next, suction and pressure side must have unique grid points
# That is why below a grid is created where the pressure side is appended with *-1 at the nose
XT = XT0.copy()
XC = XC0.copy()
XT[np.argmin(XT0)+1::] = 2*XT0[np.argmin(XT0)]-XT0[np.argmin(XT0)+1::]
XC[np.argmin(XC0)+1::] = 2*XC0[np.argmin(XC0)]-XC0[np.argmin(XC0)+1::]
# Interpolate target pressure onto current airfoil grid
UT = np.interp(-XC.flatten(),-XT.flatten(),np.asarray(UT[:,0]).flatten())
# Weighting factors for Gauss-Newton
facx = 500 # Penalty for smooth dioscplacement
fac_err = 5 #Weighting of cp error w.r.t. above penalties
fac_res = 1e4
s.Gradients = True
NAERO = x.shape[0]
NVD = len(XC)
# Set-up and initialize based on inviscid panel solution
[p,bl,x0] = vf.init([BASE],s)
res = None
grad = None
# Solve aerodynamic problem to convergence
[x,_,_,_,_] = vf.iter(x0,bl,p,s,None,None)
fprev = np.inf
# Find ST and do not change near there
II = np.logical_and(np.fabs(XT-XT[bl[0].sti])>0.001,p.foils[0].X[0,:].ravel()>np.amin(p.foils[0].X[0,:].ravel()))
II[0]=False
II[NVD-1]=False
iter = 0
lam = 1.0
y = np.zeros(NVD)
while True:
iter+=1
# Solve Aerodynamic problem
s.Itermax = 0
s.Silent = True
[_,_,res,grad,gradients] = vf.iter(x,bl,p,s,None,None,[y])
# Residual
RESy = fac_err*(p.gamma_viscid[0:p.foils[0].N].A1-UT)
dRESydy = fac_err*gradients.partial.gam_vd[0:NVD,:]
dRESydx = fac_err*gradients.partial.gam_x[0:NVD,:]
# Penalty for thick boundary layer
#REGdelta = bl[0].bl_fl.nodes.delta*facx
#dREGdeltady = gradients.total.delta_vd[0:NVD,:]*facx
# Penalty for smooth displacement
difforder = 2
REGdelta = np.diff(y,difforder)*facx
dREGdeltady = np.diff(np.eye(NVD),difforder,0)*facx
dREGdeltadx = np.zeros((len(REGdelta),len(x)))
# Gauss-Newton step from all terms
F = np.r_[RESy,REGdelta,res*fac_res]
fcurr = np.sqrt(F.T@F)
y0 = y
fprev = fcurr
# Find ST and do not change near there
II = np.logical_and(np.fabs(XT-XT[bl[0].sti])>0.001,p.foils[0].X[0,:].ravel()>np.amin(p.foils[0].X[0,:].ravel()))
II[0]=False
II[NVD-1]=False
dFdy = np.r_[dRESydy,dREGdeltady,gradients.partial.res_vd*fac_res]
dFdx = np.r_[dRESydx,dREGdeltadx,grad*fac_res]
dF = np.c_[dFdy[:,II],dFdx]
dX = -np.linalg.lstsq(dF,F,rcond=None)[0]
dy = dX[0:np.sum(II)]
dx = dX[np.sum(II)::]
lam = 1
# Print
resaero = np.sqrt(np.matmul(res,res.T))
# Ad-hoc Damping
for k in range(len(dy)):
lam = np.fmin(lam,0.005/abs(dy[k])) # Do not move virtual displacement more than 1mm
for k in range(len(x)):
lam = np.fmin(lam,.2/(abs(dx[k]/x[k])))
print("iter %u res p:%f resaero: %f dvd:%f lam:%f"%(iter, np.sqrt(np.matmul(F,F.T)), \
resaero,np.sqrt(np.matmul(dy,dy.T)),lam))
if np.sqrt(np.matmul(dy,dy.T))<1e-4 and resaero<1e-4:
print("Converged")
break
if iter>100:
print("Not Converged (iteration)")
break
j =0
for k in np.argwhere(II):
y[k] += lam*dy[j]
j+=1
x += lam*dx
%matplotlib inline
%config InlineBackend.figure_format = 'svg'
matplotlib.rcParams['figure.figsize'] = [11, 5.5]
fig,ax = plt.subplots(1,1)
ax.plot(p.foils[0].X[0,:],np.power(UC,2)-1,'-k')
ax.plot(p.foils[0].X[0,:],np.power(p.gamma_viscid[0:p.foils[0].N].A1,2)-1,'-',color=(0.6,0.6,0.6))
ax.plot(p.foils[0].X[0,:],np.power(UT,2)-1,'2k')
ax.legend(['Initial Pressure','Found Pressure','Target Pressure'])
xlim = ax.get_xlim()
fig,ax = plt.subplots(1,1)
lines = None
ax.plot(TARGET[0,:],TARGET[1,:],'2k')
lines = vfp.plot_geometry(ax,p,bl,lines)
ax.legend(['Target Airfoil','Initial Geometry','Found Geometry'])
ax.set_xlim(xlim)
```
[1] Selig, Michael S., and Mark D. Maughmer. *Generalized multipoint inverse airfoil design.* AIAA journal 30.11 (1992): 2618-2625.
[2] Drela, Mark. *XFOIL: An analysis and design system for low Reynolds number airfoils.* Low Reynolds number aerodynamics. Springer, Berlin, Heidelberg, 1989. 1-12.
|
github_jupyter
|
This notebook was prepared by [Donne Martin](https://github.com/donnemartin). Source and license info is on [GitHub](https://github.com/donnemartin/interactive-coding-challenges).
# Solution Notebook
## Problem: Given two 16 bit numbers, n and m, and two indices i, j, insert m into n such that m starts at bit j and ends at bit i.
* [Constraints](#Constraints)
* [Test Cases](#Test-Cases)
* [Algorithm](#Algorithm)
* [Code](#Code)
* [Unit Test](#Unit-Test)
## Constraints
* Can we assume j > i?
* Yes
* Can we assume i through j have enough space for m?
* Yes
* Can we assume the inputs are valid?
* No
* Can we assume this fits memory?
* Yes
## Test Cases
* None as an input -> Exception
* Negative index for i or j -> Exception
* General case
<pre>
i = 2, j = 6
j i
n = 0000 0100 0011 1101
m = 0000 0000 0001 0011
result = 0000 0100 0100 1101
</pre>
## Algorithm
<pre>
j i
n = 0000 0100 0011 1101
m = 0000 0000 0001 0011
lmask = 1111 1111 1111 1111 -1
lmask = 1111 1111 1000 0000 -1 << (j + 1)
rmask = 0000 0000 0000 0001 1
rmask = 0000 0000 0000 0100 1 << i
rmask = 0000 0000 0000 0011 (1 << i) -1
mask = 1111 1111 1000 0011 lmask | rmask
n = 0000 0100 0011 1101
mask = 1111 1111 1000 0011 n & mask
--------------------------------------------------
n2 = 0000 0100 0000 0001
n2 = 0000 0100 0000 0001
mask2 = 0000 0000 0100 1100 m << i
--------------------------------------------------
result = 0000 0100 0100 1101 n2 | mask2
</pre>
Complexity:
* Time: O(b), where b is the number of bits
* Space: O(b), where b is the number of bits
## Code
```
class Bits(object):
def insert_m_into_n(self, m, n, i, j):
if None in (m, n, i, j):
raise TypeError('Argument cannot be None')
if i < 0 or j < 0:
raise ValueError('Index cannot be negative')
left_mask = -1 << (j + 1)
right_mask = (1 << i) - 1
n_mask = left_mask | right_mask
# Clear bits from j to i, inclusive
n_cleared = n & n_mask
# Shift m into place before inserting it into n
m_mask = m << i
return n_cleared | m_mask
```
## Unit Test
```
%%writefile test_insert_m_into_n.py
import unittest
class TestBit(unittest.TestCase):
def test_insert_m_into_n(self):
n = int('0000010000111101', base=2)
m = int('0000000000010011', base=2)
expected = int('0000010001001101', base=2)
bits = Bits()
self.assertEqual(bits.insert_m_into_n(m, n, i=2, j=6), expected)
print('Success: test_insert_m_into_n')
def main():
test = TestBit()
test.test_insert_m_into_n()
if __name__ == '__main__':
main()
%run -i test_insert_m_into_n.py
```
|
github_jupyter
|
##### Copyright 2019 The TensorFlow Authors.
```
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
```
# 構造化されたデータの分類
<table class="tfo-notebook-buttons" align="left">
<td>
<a target="_blank" href="https://www.tensorflow.org/beta/tutorials/keras/feature_columns">
<img src="https://www.tensorflow.org/images/tf_logo_32px.png" />
View on TensorFlow.org</a>
</td>
<td>
<a target="_blank" href="https://colab.research.google.com/github/tensorflow/docs/blob/master/site/ja/beta/tutorials/keras/feature_columns.ipynb">
<img src="https://www.tensorflow.org/images/colab_logo_32px.png" />
Run in Google Colab</a>
</td>
<td>
<a target="_blank" href="https://github.com/tensorflow/docs/blob/master/site/ja/beta/tutorials/keras/feature_columns.ipynb">
<img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />
View source on GitHub</a>
</td>
</table>
Note: これらのドキュメントは私たちTensorFlowコミュニティが翻訳したものです。コミュニティによる 翻訳は**ベストエフォート**であるため、この翻訳が正確であることや[英語の公式ドキュメント](https://www.tensorflow.org/?hl=en)の 最新の状態を反映したものであることを保証することはできません。 この翻訳の品質を向上させるためのご意見をお持ちの方は、GitHubリポジトリ[tensorflow/docs](https://github.com/tensorflow/docs)にプルリクエストをお送りください。 コミュニティによる翻訳やレビューに参加していただける方は、 [[email protected] メーリングリスト](https://groups.google.com/a/tensorflow.org/forum/#!forum/docs-ja)にご連絡ください。
このチュートリアルでは、(例えばCSVファイルに保存された表形式データのような)構造化されたデータをどうやって分類するかを示します。ここでは、モデルの定義に[Keras](https://www.tensorflow.org/guide/keras)を、[feature columns](https://www.tensorflow.org/guide/feature_columns)をCSVファイルの列をモデルを訓練するための特徴量にマッピングするための橋渡し役として使用します。このチュートリアルには、下記のことを行うコードすべてが含まれています。
* [Pandas](https://pandas.pydata.org/)を使用したCSVファイルの読み込み
* [tf.data](https://www.tensorflow.org/guide/datasets)を使用して行データをシャッフルし、バッチ化するための入力パイプライン構築
* feature columnsを使ったCSVの列のモデル訓練用の特徴量へのマッピング
* Kerasを使ったモデルの構築と、訓練及び評価
## データセット
ここでは、Cleveland Clinic Foundation for Heart Diseaseが提供している小さな[データセット](https://archive.ics.uci.edu/ml/datasets/heart+Disease)を使用します。このCSVファイルには数百行が含まれています。行が患者を、列がその属性を表します。この情報を使用して、患者が心臓疾患を持っているかを予測します。このデータセットの場合には二値分類タスクとなります。
下記はこのデータセットの[說明](https://archive.ics.uci.edu/ml/machine-learning-databases/heart-disease/heart-disease.names)です。数値列とカテゴリー列があることに注目してください。
>列| 說明| 特徴量の型 | データ型
>------------|--------------------|----------------------|-----------------
>Age | 年齢 | 数値型 | 整数
>Sex | (1 = 男性; 0 = 女性) | カテゴリー型 | 整数
>CP | 胸痛のタイプ (0, 1, 2, 3, 4) | カテゴリー型 | 整数
>Trestbpd | 安静時血圧 (単位:mm Hg 入院時) | 数値型 | 整数
>Chol | 血清コレステロール 単位:mg/dl | 数値型 | 整数
>FBS | (空腹時血糖 > 120 mg/dl) (1 = 真; 0 = 偽) | カテゴリー型 | 整数
>RestECG | 安静時心電図の診断結果 (0, 1, 2) | カテゴリー型 | 整数
>Thalach | 最大心拍数 | 数値型 | 整数
>Exang | 運動誘発狭心症 (1 = はい; 0 = いいえ) | カテゴリー型 | 整数
>Oldpeak | 安静時と比較した運動時のST低下 | 数値型 | 整数
>Slope | ピーク運動STセグメントの勾配 | 数値型 | 浮動小数点数
>CA | 蛍光透視法によって着色された主要血管の数(0−3) | 数値型 | 整数
>Thal | 3 = 正常; 6 = 固定欠陥; 7 = 可逆的欠陥 | カテゴリー型 | 文字列
>Target | 心臓疾患の診断 (1 = 真; 0 = 偽) | 分類 | 整数
## TensorFlow他ライブラリのインポート
```
!pip install sklearn
from __future__ import absolute_import, division, print_function, unicode_literals
import numpy as np
import pandas as pd
try:
# Colab only
%tensorflow_version 2.x
except Exception:
pass
import tensorflow as tf
from tensorflow import feature_column
from tensorflow.keras import layers
from sklearn.model_selection import train_test_split
```
## Pandasを使ったデータフレーム作成
[Pandas](https://pandas.pydata.org/)は、構造化データの読み込みや操作のための便利なユーティリティを持つPythonのライブラリです。ここでは、Pandasを使ってURLからデータをダウンロードし、データフレームに読み込みます。
```
URL = 'https://storage.googleapis.com/applied-dl/heart.csv'
dataframe = pd.read_csv(URL)
dataframe.head()
```
## データフレームを、訓練用、検証用、テスト用に分割
ダウンロードしたデータセットは1つのCSVファイルです。これを、訓練用、検証用、テスト用のデータセットに分割します。
```
train, test = train_test_split(dataframe, test_size=0.2)
train, val = train_test_split(train, test_size=0.2)
print(len(train), 'train examples')
print(len(val), 'validation examples')
print(len(test), 'test examples')
```
## tf.dataを使った入力パイプラインの構築
次に、[tf.data](https://www.tensorflow.org/guide/datasets)を使ってデータフレームをラップします。こうすることで、feature columns をPandasデータフレームの列をモデル訓練用の特徴量へのマッピングするための橋渡し役として使うことができます。(メモリに収まらないぐらいの)非常に大きなCSVファイルを扱う場合には、tf.dataを使ってディスクから直接CSVファイルを読み込むことになります。この方法は、このチュートリアルでは扱いません。
```
# Pandasデータフレームからtf.dataデータセットを作るためのユーティリティメソッド
def df_to_dataset(dataframe, shuffle=True, batch_size=32):
dataframe = dataframe.copy()
labels = dataframe.pop('target')
ds = tf.data.Dataset.from_tensor_slices((dict(dataframe), labels))
if shuffle:
ds = ds.shuffle(buffer_size=len(dataframe))
ds = ds.batch(batch_size)
return ds
batch_size = 5 # デモ用として小さなバッチサイズを使用
train_ds = df_to_dataset(train, batch_size=batch_size)
val_ds = df_to_dataset(val, shuffle=False, batch_size=batch_size)
test_ds = df_to_dataset(test, shuffle=False, batch_size=batch_size)
```
## 入力パイプラインを理解する
入力パイプラインを構築したので、それが返すデータのフォーマットを見るために呼び出してみましょう。出力を読みやすくするためにバッチサイズを小さくしてあります。
```
for feature_batch, label_batch in train_ds.take(1):
print('Every feature:', list(feature_batch.keys()))
print('A batch of ages:', feature_batch['age'])
print('A batch of targets:', label_batch )
```
データセットが(データフレームにある)列名からなるディクショナリを返すことがわかります。列名から、データフレームの行に含まれる列の値が得られます。
## feature columnsの様々な型の例
TensorFlowにはたくさんの型のfeature columnがあります。このセクションでは、いくつかの型のfeature columnsを作り、データフレームの列をどのように変換しているかを示します。
```
# いくつかの型のfeature columnsを例示するためこのバッチを使用する
example_batch = next(iter(train_ds))[0]
# feature columnsを作りデータのバッチを変換する
# ユーティリティメソッド
def demo(feature_column):
feature_layer = layers.DenseFeatures(feature_column)
print(feature_layer(example_batch).numpy())
```
### 数値コラム
feature columnsの出力はモデルへの入力になります(上記で定義したdemo関数を使うと、データフレームの列がどのように変換されるかをつぶさに見ることができます)。[数値コラム](https://www.tensorflow.org/api_docs/python/tf/feature_column/numeric_column)は、最も単純な型のコラムです。数値コラムは実数特徴量を表現するのに使われます。このコラムを使う場合、モデルにはデータフレームの列の値がそのまま渡されます。
```
age = feature_column.numeric_column("age")
demo(age)
```
心臓疾患データセットでは、データフレームのほとんどの列が数値型です。
### バケット化コラム
数値をそのままモデルに入力するのではなく、値の範囲に基づいた異なるカテゴリーに分割したいことがあります。例えば、人の年齢を表す生データを考えてみましょう。[バケット化コラム](https://www.tensorflow.org/api_docs/python/tf/feature_column/bucketized_column)を使うと年齢を数値コラムとして表現するのではなく、年齢をいくつかのバケットに分割できます。下記のワンホット値が、各行がどの年齢範囲にあるかを表していることに注目してください。
```
age_buckets = feature_column.bucketized_column(age, boundaries=[18, 25, 30, 35, 40, 45, 50, 55, 60, 65])
demo(age_buckets)
```
### カテゴリー型コラム
このデータセットでは、Thalは('fixed'、'normal'、'reversible'のような)文字列として表現されています。文字列を直接モデルに入力することはできません。まず、文字列を数値にマッピングする必要があります。categorical vocabulary コラムを使うと、(上記で示した年齢バケットのように)文字列をワンホットベクトルとして表現することができます。カテゴリーを表す語彙(vocabulary)は[categorical_column_with_vocabulary_list](https://www.tensorflow.org/api_docs/python/tf/feature_column/categorical_column_with_vocabulary_list)を使ってリストで渡すか、[categorical_column_with_vocabulary_file](https://www.tensorflow.org/api_docs/python/tf/feature_column/categorical_column_with_vocabulary_file)を使ってファイルから読み込むことができます。
```
thal = feature_column.categorical_column_with_vocabulary_list(
'thal', ['fixed', 'normal', 'reversible'])
thal_one_hot = feature_column.indicator_column(thal)
demo(thal_one_hot)
```
より複雑なデータセットでは、たくさんの列がカテゴリー型(例えば文字列)であることでしょう。feature columns はカテゴリー型データを扱う際に最も役に立ちます。このデータセットでは、カテゴリー型コラムは1つだけですが、他のデータセットを扱う際に使用できるいくつかの重要な型のfeature columnsを紹介するために、この列を使用することにします。
### 埋め込み型コラム
数種類の候補となる文字列ではなく、カテゴリー毎に数千(あるいはそれ以上)の値があるとしましょう。カテゴリーの数が多くなってくると、様々な理由から、ワンホットエンコーディングを使ってニューラルネットワークを訓練することが難しくなります。埋込み型コラムを使うと、こうした制約を克服することが可能です。[埋込み型コラム](https://www.tensorflow.org/api_docs/python/tf/feature_column/embedding_column)は、データを多次元のワンホットベクトルとして表すのではなく、セルの値が0か1かだけではなく、どんな数値でもとれるような密な低次元ベクトルとして表現します。埋め込みのサイズ(下記の例では8)は、チューニングが必要なパラメータです。
キーポイント:カテゴリー型コラムがたくさんの選択肢を持つ場合、埋め込み型コラムを使用することが最善の方法です。ここでは例を一つ示しますので、今後様々なデータセットを扱う際には、この例を参考にしてください。
```
# この埋込み型コラムの入力は、先程作成したカテゴリ型コラムであることに注意
thal_embedding = feature_column.embedding_column(thal, dimension=8)
demo(thal_embedding)
```
### ハッシュ化特徴コラム
値の種類が多いカテゴリー型コラムを表現するもう一つの方法が、[categorical_column_with_hash_bucket](https://www.tensorflow.org/api_docs/python/tf/feature_column/categorical_column_with_hash_bucket)を使う方法です。このfeature columnは文字列をエンコードするために入力のハッシュ値を計算し、`hash_bucket_size`個のバケットの中から1つを選択します。このコラムを使用する場合には、語彙を用意する必要はありません。また、スペースの節約のために、実際のカテゴリー数に比べて極めて少ないバケット数を選択することも可能です。
キーポイント:この手法の重要な欠点の一つは、異なる文字列が同じバケットにマッピングされるというハッシュ値の衝突が起きることです。実務上は、データセットによっては、この問題を無視できることがあります。
```
thal_hashed = feature_column.categorical_column_with_hash_bucket(
'thal', hash_bucket_size=1000)
demo(feature_column.indicator_column(thal_hashed))
```
### クロスフィーチャーコラム
複数の特徴量をまとめて1つの特徴量にする、[フィーチャークロス](https://developers.google.com/machine-learning/glossary/#feature_cross)として知られている手法は、モデルが特徴量の組み合わせの一つ一つに別々の重みを学習することを可能にします。ここでは年齢とThalをクロスさせて新しい特徴量を作ってみます。交差列(`crossed_column`)が、起こりうるすべての組み合わせ全体のテーブル(これは非常に大きくなる可能性があります)を作るものではないことに注意してください。クロスフィーチャーコラムは、代わりにバックエンドとしてハッシュ化コラムを使用しているため、テーブルの大きさを選択することができます。
```
crossed_feature = feature_column.crossed_column([age_buckets, thal], hash_bucket_size=1000)
demo(feature_column.indicator_column(crossed_feature))
```
## 使用するコラムを選択する
これまで、いくつかのfeature columnの使い方を見てきました。いよいよモデルの訓練にそれらを使用することにします。このチュートリアルの目的は、feature columnsを使うのに必要な完全なコード(いわば力学)を示すことです。以下ではモデルを訓練するための列を適当に選びました。
キーポイント:正確なモデルを構築するのが目的である場合には、できるだけ大きなデータセットを使用して、どの特徴量を含めるのがもっとも意味があるのかや、それらをどう表現したらよいかを、慎重に検討してください。
```
feature_columns = []
# 数値コラム
for header in ['age', 'trestbps', 'chol', 'thalach', 'oldpeak', 'slope', 'ca']:
feature_columns.append(feature_column.numeric_column(header))
# バケット化コラム
age_buckets = feature_column.bucketized_column(age, boundaries=[18, 25, 30, 35, 40, 45, 50, 55, 60, 65])
feature_columns.append(age_buckets)
# インジケーター(カテゴリー型)コラム
thal = feature_column.categorical_column_with_vocabulary_list(
'thal', ['fixed', 'normal', 'reversible'])
thal_one_hot = feature_column.indicator_column(thal)
feature_columns.append(thal_one_hot)
# 埋め込み型コラム
thal_embedding = feature_column.embedding_column(thal, dimension=8)
feature_columns.append(thal_embedding)
# クロスフィーチャーコラム
crossed_feature = feature_column.crossed_column([age_buckets, thal], hash_bucket_size=1000)
crossed_feature = feature_column.indicator_column(crossed_feature)
feature_columns.append(crossed_feature)
```
### 特徴量層の構築
feature columnsを定義し終わったので、次に[DenseFeatures](https://www.tensorflow.org/versions/r2.0/api_docs/python/tf/keras/layers/DenseFeatures)層を使ってKerasモデルへの入力とします。
```
feature_layer = tf.keras.layers.DenseFeatures(feature_columns)
```
これまでは、feature columnsの働きを見るため、小さなバッチサイズを使ってきました。ここではもう少し大きなバッチサイズの新しい入力パイプラインを作ります。
```
batch_size = 32
train_ds = df_to_dataset(train, batch_size=batch_size)
val_ds = df_to_dataset(val, shuffle=False, batch_size=batch_size)
test_ds = df_to_dataset(test, shuffle=False, batch_size=batch_size)
```
## モデルの構築、コンパイルと訓練
```
model = tf.keras.Sequential([
feature_layer,
layers.Dense(128, activation='relu'),
layers.Dense(128, activation='relu'),
layers.Dense(1, activation='sigmoid')
])
model.compile(optimizer='adam',
loss='binary_crossentropy',
metrics=['accuracy'])
model.fit(train_ds,
validation_data=val_ds,
epochs=5)
loss, accuracy = model.evaluate(test_ds)
print("Accuracy", accuracy)
```
キーポイント:一般的に、ディープラーニングが最良の結果となるのは、もっと大きくて、もっと複雑なデータセットです。この例のように小さなデータセットを使用する際には、強固なベースラインとして、決定木やランダムフォレストを使うことをおすすめします。このチュートリアルの目的は、訓練により正確なモデルを得ることではなく、構造化データの使い方をデモすることです。今後ご自分のデータセットに取り組まれる際の出発点として、これらのコードをお使いください。
## 次のステップ
構造化データの分類について更に多くのことを学ぶためには、自分自身で試してみることです。別のデータセットを見つけ、上記と同様のコードを使って、それを分類するモデルを訓練してみてください。正解率を上げるためには、モデルにどの特徴量を含めたらよいかや、その特徴量をどのように表現すべきかをじっくり考えてください。
|
github_jupyter
|
**About this challenge**
To assess the impact of climate change on Earth's flora and fauna, it is vital to quantify how human activities such as logging, mining, and agriculture are impacting our protected natural areas. Researchers in Mexico have created the VIGIA project, which aims to build a system for autonomous surveillance of protected areas. A first step in such an effort is the ability to recognize the vegetation inside the protected areas. In this competition, you are tasked with creation of an algorithm that can identify a specific type of cactus in aerial imagery.
In this kernel we will be trying to solve this challenge using CNN through **fast.ai library**
**Loading necessary libraries**
```
from fastai.vision import *
from fastai import *
import os
import pandas as pd
import numpy as np
print(os.listdir("../input/"))
train_dir="../input/train/train"
test_dir="../input/test/test"
train = pd.read_csv('../input/train.csv')
test = pd.read_csv("../input/sample_submission.csv")
data_folder = Path("../input")
```
**Analysing the given data**
```
train.head(5)
train.describe()
```
**Getting the Data. **
[reference](https://docs.fast.ai/vision.data.html)
```
test_img = ImageList.from_df(test, path=data_folder/'test', folder='test')
# Applying Data augmentation
trfm = get_transforms(do_flip=True, flip_vert=True, max_rotate=10.0, max_zoom=1.1, max_lighting=0.2, max_warp=0.2, p_affine=0.75, p_lighting=0.75)
train_img = (ImageList.from_df(train, path=data_folder/'train', folder='train')
.split_by_rand_pct(0.01)
.label_from_df()
.add_test(test_img)
.transform(trfm, size=128)
.databunch(path='.', bs=64, device= torch.device('cuda:0'))
.normalize(imagenet_stats)
)
```
**Training the data using appropriate model. We have used [densenet](https://pytorch.org/docs/stable/torchvision/models.html) here**
```
learn = cnn_learner(train_img, models.densenet161, metrics=[error_rate, accuracy])
```
**Finding the suitable learning rate**
```
learn.lr_find()
```
**Plotting the Learning Rate**
```
learn.recorder.plot()
```
**Now training the data based on suitable learning rate**
```
lr = 1e-02
learn.fit_one_cycle(3, slice(lr))
preds,_ = learn.get_preds(ds_type=DatasetType.Test)
test.has_cactus = preds.numpy()[:, 0]
test.to_csv('submission.csv', index=False)
```
**References**
* https://docs.fast.ai/
* https://www.kaggle.com/kenseitrg/simple-fastai-exercise
* https://www.kaggle.com/shahules/getting-started-with-cnn-and-vgg16
|
github_jupyter
|
#### SageMaker Pipelines Tuning Step
This notebook illustrates how a Hyperparameter Tuning Job can be run as a step in a SageMaker Pipeline.
The steps in this pipeline include -
* Preprocessing the abalone dataset
* Running a Hyperparameter Tuning job
* Creating the 2 best models
* Evaluating the performance of the top performing model of the HPO step
* Registering the top model in the model registry using a conditional step based on evaluation metrics
```
import sys
!{sys.executable} -m pip install "sagemaker>=2.48.0"
import os
import boto3
import sagemaker
from sagemaker.estimator import Estimator
from sagemaker.inputs import TrainingInput
from sagemaker.processing import (
ProcessingInput,
ProcessingOutput,
Processor,
ScriptProcessor,
)
from sagemaker import Model
from sagemaker.xgboost import XGBoostPredictor
from sagemaker.sklearn.processing import SKLearnProcessor
from sagemaker.model_metrics import (
MetricsSource,
ModelMetrics,
)
from sagemaker.workflow.parameters import (
ParameterInteger,
ParameterString,
)
from sagemaker.workflow.pipeline import Pipeline
from sagemaker.workflow.properties import PropertyFile
from sagemaker.workflow.steps import (
ProcessingStep,
CacheConfig,
TuningStep,
)
from sagemaker.workflow.step_collections import RegisterModel, CreateModelStep
from sagemaker.workflow.conditions import ConditionLessThanOrEqualTo
from sagemaker.workflow.condition_step import ConditionStep
from sagemaker.workflow.functions import Join, JsonGet
from sagemaker.workflow.execution_variables import ExecutionVariables
from sagemaker.tuner import (
ContinuousParameter,
HyperparameterTuner,
WarmStartConfig,
WarmStartTypes,
)
# Create the SageMaker Session
region = sagemaker.Session().boto_region_name
sm_client = boto3.client("sagemaker")
boto_session = boto3.Session(region_name=region)
sagemaker_session = sagemaker.session.Session(boto_session=boto_session, sagemaker_client=sm_client)
# Define variables and parameters needed for the Pipeline steps
role = sagemaker.get_execution_role()
default_bucket = sagemaker_session.default_bucket()
base_job_prefix = "tuning-step-example"
model_package_group_name = "tuning-job-model-packages"
processing_instance_count = ParameterInteger(name="ProcessingInstanceCount", default_value=1)
processing_instance_type = ParameterString(
name="ProcessingInstanceType", default_value="ml.m5.xlarge"
)
training_instance_type = ParameterString(name="TrainingInstanceType", default_value="ml.m5.xlarge")
model_approval_status = ParameterString(
name="ModelApprovalStatus", default_value="PendingManualApproval"
)
input_data = ParameterString(
name="InputDataUrl",
default_value=f"s3://sagemaker-servicecatalog-seedcode-{region}/dataset/abalone-dataset.csv",
)
model_approval_status = ParameterString(
name="ModelApprovalStatus", default_value="PendingManualApproval"
)
# Cache Pipeline steps to reduce execution time on subsequent executions
cache_config = CacheConfig(enable_caching=True, expire_after="30d")
```
#### Data Preparation
An SKLearn processor is used to prepare the dataset for the Hyperparameter Tuning job. Using the script `preprocess.py`, the dataset is featurized and split into train, test, and validation datasets.
The output of this step is used as the input to the TuningStep
```
%%writefile preprocess.py
"""Feature engineers the abalone dataset."""
import argparse
import logging
import os
import pathlib
import requests
import tempfile
import boto3
import numpy as np
import pandas as pd
from sklearn.compose import ColumnTransformer
from sklearn.impute import SimpleImputer
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler, OneHotEncoder
logger = logging.getLogger()
logger.setLevel(logging.INFO)
logger.addHandler(logging.StreamHandler())
# Since we get a headerless CSV file we specify the column names here.
feature_columns_names = [
"sex",
"length",
"diameter",
"height",
"whole_weight",
"shucked_weight",
"viscera_weight",
"shell_weight",
]
label_column = "rings"
feature_columns_dtype = {
"sex": str,
"length": np.float64,
"diameter": np.float64,
"height": np.float64,
"whole_weight": np.float64,
"shucked_weight": np.float64,
"viscera_weight": np.float64,
"shell_weight": np.float64,
}
label_column_dtype = {"rings": np.float64}
def merge_two_dicts(x, y):
"""Merges two dicts, returning a new copy."""
z = x.copy()
z.update(y)
return z
if __name__ == "__main__":
logger.debug("Starting preprocessing.")
parser = argparse.ArgumentParser()
parser.add_argument("--input-data", type=str, required=True)
args = parser.parse_args()
base_dir = "/opt/ml/processing"
pathlib.Path(f"{base_dir}/data").mkdir(parents=True, exist_ok=True)
input_data = args.input_data
bucket = input_data.split("/")[2]
key = "/".join(input_data.split("/")[3:])
logger.info("Downloading data from bucket: %s, key: %s", bucket, key)
fn = f"{base_dir}/data/abalone-dataset.csv"
s3 = boto3.resource("s3")
s3.Bucket(bucket).download_file(key, fn)
logger.debug("Reading downloaded data.")
df = pd.read_csv(
fn,
header=None,
names=feature_columns_names + [label_column],
dtype=merge_two_dicts(feature_columns_dtype, label_column_dtype),
)
os.unlink(fn)
logger.debug("Defining transformers.")
numeric_features = list(feature_columns_names)
numeric_features.remove("sex")
numeric_transformer = Pipeline(
steps=[
("imputer", SimpleImputer(strategy="median")),
("scaler", StandardScaler()),
]
)
categorical_features = ["sex"]
categorical_transformer = Pipeline(
steps=[
("imputer", SimpleImputer(strategy="constant", fill_value="missing")),
("onehot", OneHotEncoder(handle_unknown="ignore")),
]
)
preprocess = ColumnTransformer(
transformers=[
("num", numeric_transformer, numeric_features),
("cat", categorical_transformer, categorical_features),
]
)
logger.info("Applying transforms.")
y = df.pop("rings")
X_pre = preprocess.fit_transform(df)
y_pre = y.to_numpy().reshape(len(y), 1)
X = np.concatenate((y_pre, X_pre), axis=1)
logger.info("Splitting %d rows of data into train, validation, test datasets.", len(X))
np.random.shuffle(X)
train, validation, test = np.split(X, [int(0.7 * len(X)), int(0.85 * len(X))])
logger.info("Writing out datasets to %s.", base_dir)
pd.DataFrame(train).to_csv(f"{base_dir}/train/train.csv", header=False, index=False)
pd.DataFrame(validation).to_csv(
f"{base_dir}/validation/validation.csv", header=False, index=False
)
pd.DataFrame(test).to_csv(f"{base_dir}/test/test.csv", header=False, index=False)
# Process the training data step using a python script.
# Split the training data set into train, test, and validation datasets
# When defining the ProcessingOutput destination as a dynamic value using the
# Pipeline Execution ID, caching will not be in effect as each time the step runs,
# the step definition changes resulting in new execution. If caching is required,
# the ProcessingOutput definition should be status
sklearn_processor = SKLearnProcessor(
framework_version="0.23-1",
instance_type=processing_instance_type,
instance_count=processing_instance_count,
base_job_name=f"{base_job_prefix}/sklearn-abalone-preprocess",
sagemaker_session=sagemaker_session,
role=role,
)
step_process = ProcessingStep(
name="PreprocessAbaloneDataForHPO",
processor=sklearn_processor,
outputs=[
ProcessingOutput(
output_name="train",
source="/opt/ml/processing/train",
destination=Join(
on="/",
values=[
"s3:/",
default_bucket,
base_job_prefix,
ExecutionVariables.PIPELINE_EXECUTION_ID,
"PreprocessAbaloneDataForHPO",
],
),
),
ProcessingOutput(
output_name="validation",
source="/opt/ml/processing/validation",
destination=Join(
on="/",
values=[
"s3:/",
default_bucket,
base_job_prefix,
ExecutionVariables.PIPELINE_EXECUTION_ID,
"PreprocessAbaloneDataForHPO",
],
),
),
ProcessingOutput(
output_name="test",
source="/opt/ml/processing/test",
destination=Join(
on="/",
values=[
"s3:/",
default_bucket,
base_job_prefix,
ExecutionVariables.PIPELINE_EXECUTION_ID,
"PreprocessAbaloneDataForHPO",
],
),
),
],
code="preprocess.py",
job_arguments=["--input-data", input_data],
)
```
#### Hyperparameter Tuning
Amazon SageMaker automatic model tuning, also known as hyperparameter tuning, finds the best version of a model by running many training jobs on your dataset using the algorithm and ranges of hyperparameters that you specify. It then chooses the hyperparameter values that result in a model that performs the best, as measured by a metric that you choose.
[Valid metrics](https://github.com/dmlc/xgboost/blob/master/doc/parameter.rst#learning-task-parameters) for XGBoost Tuning Job
You can learn more about [Hyperparameter Tuning](https://docs.aws.amazon.com/sagemaker/latest/dg/automatic-model-tuning-how-it-works.html) in the SageMaker docs.
```
# Define the output path for the model artifacts from the Hyperparameter Tuning Job
model_path = f"s3://{default_bucket}/{base_job_prefix}/AbaloneTrain"
image_uri = sagemaker.image_uris.retrieve(
framework="xgboost",
region=region,
version="1.0-1",
py_version="py3",
instance_type=training_instance_type,
)
xgb_train = Estimator(
image_uri=image_uri,
instance_type=training_instance_type,
instance_count=1,
output_path=model_path,
base_job_name=f"{base_job_prefix}/abalone-train",
sagemaker_session=sagemaker_session,
role=role,
)
xgb_train.set_hyperparameters(
eval_metric="rmse",
objective="reg:squarederror", # Define the object metric for the training job
num_round=50,
max_depth=5,
eta=0.2,
gamma=4,
min_child_weight=6,
subsample=0.7,
silent=0,
)
objective_metric_name = "validation:rmse"
hyperparameter_ranges = {
"alpha": ContinuousParameter(0.01, 10, scaling_type="Logarithmic"),
"lambda": ContinuousParameter(0.01, 10, scaling_type="Logarithmic"),
}
tuner_log = HyperparameterTuner(
xgb_train,
objective_metric_name,
hyperparameter_ranges,
max_jobs=3,
max_parallel_jobs=3,
strategy="Random",
objective_type="Minimize",
)
step_tuning = TuningStep(
name="HPTuning",
tuner=tuner_log,
inputs={
"train": TrainingInput(
s3_data=step_process.properties.ProcessingOutputConfig.Outputs["train"].S3Output.S3Uri,
content_type="text/csv",
),
"validation": TrainingInput(
s3_data=step_process.properties.ProcessingOutputConfig.Outputs[
"validation"
].S3Output.S3Uri,
content_type="text/csv",
),
},
cache_config=cache_config,
)
```
#### Warm start for Hyperparameter Tuning Job
Use warm start to start a hyperparameter tuning job using one or more previous tuning jobs as a starting point. The results of previous tuning jobs are used to inform which combinations of hyperparameters to search over in the new tuning job. Hyperparameter tuning uses either Bayesian or random search to choose combinations of hyperparameter values from ranges that you specify.
Find more information on [Warm Starts](https://docs.aws.amazon.com/sagemaker/latest/dg/automatic-model-tuning-warm-start.html) in the SageMaker docs.
In a training pipeline, the parent tuning job name can be provided as a pipeline parameter if there is an already complete Hyperparameter tuning job that should be used as the basis for the warm start.
This step is left out of the pipeline steps in this notebook. It can be added into the steps while defining the pipeline and the appropriate parent tuning job should be specified.
```
# This is an example to illustrate how a the name of the tuning job from the previous step can be used as the parent tuning job, in practice,
# it is unlikely to have the parent job run before the warm start job on each run. Typically the first tuning job would run and the pipeline
# would be altered to use tuning jobs with a warm start using the first job as the parent job.
parent_tuning_job_name = (
step_tuning.properties.HyperParameterTuningJobName
) # Use the parent tuning job specific to the use case
warm_start_config = WarmStartConfig(
WarmStartTypes.IDENTICAL_DATA_AND_ALGORITHM, parents={parent_tuning_job_name}
)
tuner_log_warm_start = HyperparameterTuner(
xgb_train,
objective_metric_name,
hyperparameter_ranges,
max_jobs=3,
max_parallel_jobs=3,
strategy="Random",
objective_type="Minimize",
warm_start_config=warm_start_config,
)
step_tuning_warm_start = TuningStep(
name="HPTuningWarmStart",
tuner=tuner_log_warm_start,
inputs={
"train": TrainingInput(
s3_data=step_process.properties.ProcessingOutputConfig.Outputs["train"].S3Output.S3Uri,
content_type="text/csv",
),
"validation": TrainingInput(
s3_data=step_process.properties.ProcessingOutputConfig.Outputs[
"validation"
].S3Output.S3Uri,
content_type="text/csv",
),
},
cache_config=cache_config,
)
```
#### Creating and Registering the best models
After successfully completing the Hyperparameter Tuning job. You can either create SageMaker models from the model artifacts created by the training jobs from the TuningStep or register the models into the Model Registry.
When using the model Registry, if you register multiple models from the TuningStep, they will be registered as versions within the same model package group unless unique model package groups are specified for each RegisterModelStep that is part of the pipeline.
In this example, the two best models from the TuningStep are added to the same model package group in the Model Registry as v0 and v1.
You use the `get_top_model_s3_uri` method of the TuningStep class to get the model artifact from one of the top performing model versions
```
# Creating 2 SageMaker Models
model_bucket_key = f"{default_bucket}/{base_job_prefix}/AbaloneTrain"
best_model = Model(
image_uri=image_uri,
model_data=step_tuning.get_top_model_s3_uri(top_k=0, s3_bucket=model_bucket_key),
sagemaker_session=sagemaker_session,
role=role,
predictor_cls=XGBoostPredictor,
)
step_create_first = CreateModelStep(
name="CreateTopModel",
model=best_model,
inputs=sagemaker.inputs.CreateModelInput(instance_type="ml.m4.large"),
)
second_best_model = Model(
image_uri=image_uri,
model_data=step_tuning.get_top_model_s3_uri(top_k=1, s3_bucket=model_bucket_key),
sagemaker_session=sagemaker_session,
role=role,
predictor_cls=XGBoostPredictor,
)
step_create_second = CreateModelStep(
name="CreateSecondBestModel",
model=second_best_model,
inputs=sagemaker.inputs.CreateModelInput(instance_type="ml.m4.large"),
)
```
#### Evaluate the top model
Use a processing job to evaluate the top model from the tuning step
```
%%writefile evaluate.py
"""Evaluation script for measuring mean squared error."""
import json
import logging
import pathlib
import pickle
import tarfile
import numpy as np
import pandas as pd
import xgboost
from sklearn.metrics import mean_squared_error
logger = logging.getLogger()
logger.setLevel(logging.INFO)
logger.addHandler(logging.StreamHandler())
if __name__ == "__main__":
logger.debug("Starting evaluation.")
model_path = "/opt/ml/processing/model/model.tar.gz"
with tarfile.open(model_path) as tar:
tar.extractall(path=".")
logger.debug("Loading xgboost model.")
model = pickle.load(open("xgboost-model", "rb"))
logger.debug("Reading test data.")
test_path = "/opt/ml/processing/test/test.csv"
df = pd.read_csv(test_path, header=None)
logger.debug("Reading test data.")
y_test = df.iloc[:, 0].to_numpy()
df.drop(df.columns[0], axis=1, inplace=True)
X_test = xgboost.DMatrix(df.values)
logger.info("Performing predictions against test data.")
predictions = model.predict(X_test)
logger.debug("Calculating mean squared error.")
mse = mean_squared_error(y_test, predictions)
std = np.std(y_test - predictions)
report_dict = {
"regression_metrics": {
"mse": {"value": mse, "standard_deviation": std},
},
}
output_dir = "/opt/ml/processing/evaluation"
pathlib.Path(output_dir).mkdir(parents=True, exist_ok=True)
logger.info("Writing out evaluation report with mse: %f", mse)
evaluation_path = f"{output_dir}/evaluation.json"
with open(evaluation_path, "w") as f:
f.write(json.dumps(report_dict))
# A ProcessingStep is used to evaluate the performance of a selected model from the HPO step. In this case, the top performing model
# is evaluated. Based on the results of the evaluation, the model is registered into the Model Registry using a ConditionStep.
script_eval = ScriptProcessor(
image_uri=image_uri,
command=["python3"],
instance_type=processing_instance_type,
instance_count=1,
base_job_name=f"{base_job_prefix}/script-tuning-step-eval",
sagemaker_session=sagemaker_session,
role=role,
)
evaluation_report = PropertyFile(
name="BestTuningModelEvaluationReport",
output_name="evaluation",
path="evaluation.json",
)
# This can be extended to evaluate multiple models from the HPO step
step_eval = ProcessingStep(
name="EvaluateTopModel",
processor=script_eval,
inputs=[
ProcessingInput(
source=step_tuning.get_top_model_s3_uri(top_k=0, s3_bucket=model_bucket_key),
destination="/opt/ml/processing/model",
),
ProcessingInput(
source=step_process.properties.ProcessingOutputConfig.Outputs["test"].S3Output.S3Uri,
destination="/opt/ml/processing/test",
),
],
outputs=[
ProcessingOutput(output_name="evaluation", source="/opt/ml/processing/evaluation"),
],
code="evaluate.py",
property_files=[evaluation_report],
cache_config=cache_config,
)
model_metrics = ModelMetrics(
model_statistics=MetricsSource(
s3_uri="{}/evaluation.json".format(
step_eval.arguments["ProcessingOutputConfig"]["Outputs"][0]["S3Output"]["S3Uri"]
),
content_type="application/json",
)
)
# Register the model in the Model Registry
# Multiple models can be registered into the Model Registry using multiple RegisterModel steps. These models can either be added to the
# same model package group as different versions within the group or the models can be added to different model package groups.
step_register_best = RegisterModel(
name="RegisterBestAbaloneModel",
estimator=xgb_train,
model_data=step_tuning.get_top_model_s3_uri(top_k=0, s3_bucket=model_bucket_key),
content_types=["text/csv"],
response_types=["text/csv"],
inference_instances=["ml.t2.medium", "ml.m5.large"],
transform_instances=["ml.m5.large"],
model_package_group_name=model_package_group_name,
approval_status=model_approval_status,
)
# condition step for evaluating model quality and branching execution
cond_lte = ConditionLessThanOrEqualTo(
left=JsonGet(
step_name=step_eval.name,
property_file=evaluation_report,
json_path="regression_metrics.mse.value",
),
right=6.0,
)
step_cond = ConditionStep(
name="CheckMSEAbaloneEvaluation",
conditions=[cond_lte],
if_steps=[step_register_best],
else_steps=[],
)
pipeline = Pipeline(
name="tuning-step-pipeline",
parameters=[
processing_instance_type,
processing_instance_count,
training_instance_type,
input_data,
model_approval_status,
],
steps=[
step_process,
step_tuning,
step_create_first,
step_create_second,
step_eval,
step_cond,
],
sagemaker_session=sagemaker_session,
)
```
#### Execute the Pipeline
```
import json
definition = json.loads(pipeline.definition())
definition
pipeline.upsert(role_arn=role)
pipeline.start()
```
#### Cleaning up resources
Users are responsible for cleaning up resources created when running this notebook. Specify the ModelName, ModelPackageName, and ModelPackageGroupName that need to be deleted. The model names are generated by the CreateModel step of the Pipeline and the property values are available only in the Pipeline context. To delete the models created by this pipeline, navigate to the Model Registry and Console to find the models to delete.
```
# # Create a SageMaker client
# sm_client = boto3.client("sagemaker")
# # Delete SageMaker Models
# sm_client.delete_model(ModelName="...")
# # Delete Model Packages
# sm_client.delete_model_package(ModelPackageName="...")
# # Delete the Model Package Group
# sm_client.delete_model_package_group(ModelPackageGroupName="...")
# # Delete the Pipeline
# sm_client.delete_pipeline(PipelineName="tuning-step-pipeline")
```
|
github_jupyter
|
# Ensembles
```
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.metrics import mean_absolute_error, mean_squared_error
from sklearn.linear_model import LinearRegression
from sklearn.tree import DecisionTreeRegressor
sns.set_theme()
rng = np.random.default_rng(42)
x = rng.uniform(size=(150, 1), low=0.0, high=10.0)
x_train, x_test = x[:100], x[100:]
x_plot = np.linspace(0, 10, 500).reshape(-1, 1)
def lin(x):
return 0.85 * x - 1.5
def fun(x):
return 2 * np.sin(x) + 0.1 * x ** 2 - 2
def randomize(fun, x, scale=0.5):
return fun(x) + rng.normal(size=x.shape, scale=scale)
def evaluate_non_random_regressor(reg_type, f_y, *args, **kwargs):
reg = reg_type(*args, **kwargs)
y_train = f_y(x_train).reshape(-1)
y_test = f_y(x_test).reshape(-1)
reg.fit(x_train, y_train)
y_pred = reg.predict(x_test)
x_plot = np.linspace(0, 10, 500).reshape(-1, 1)
fig, ax = plt.subplots(figsize=(20, 8))
sns.lineplot(x=x_plot[:, 0], y=reg.predict(x_plot), ax=ax)
sns.lineplot(x=x_plot[:, 0], y=f_y(x_plot[:, 0]), ax=ax)
sns.scatterplot(x=x_train[:, 0], y=y_train, ax=ax)
plt.show()
mae = mean_absolute_error(y_test, y_pred)
mse = mean_squared_error(y_test, y_pred)
rmse = np.sqrt(mean_squared_error(y_test, y_pred))
print(
"\nNo randomness: " f"MAE = {mae:.2f}, MSE = {mse:.2f}, RMSE = {rmse:.2f}"
)
return reg
def plot_graphs(f_y, reg, reg_rand, reg_chaos, y_train, y_rand_train, y_chaos_train):
x_plot = np.linspace(0, 10, 500).reshape(-1, 1)
fig, ax = plt.subplots(figsize=(20, 12))
sns.lineplot(x=x_plot[:, 0], y=reg.predict(x_plot), ax=ax)
sns.scatterplot(x=x_train[:, 0], y=y_train, ax=ax)
sns.lineplot(x=x_plot[:, 0], y=reg_rand.predict(x_plot), ax=ax)
sns.scatterplot(x=x_train[:, 0], y=y_rand_train, ax=ax)
sns.lineplot(x=x_plot[:, 0], y=reg_chaos.predict(x_plot), ax=ax)
sns.scatterplot(x=x_train[:, 0], y=y_chaos_train, ax=ax)
sns.lineplot(x=x_plot[:, 0], y=f_y(x_plot[:, 0]), ax=ax)
plt.show()
def print_evaluation(y_test, y_pred, y_rand_test, y_rand_pred, y_chaos_test, y_chaos_pred):
mae = mean_absolute_error(y_test, y_pred)
mae_rand = mean_absolute_error(y_rand_test, y_rand_pred)
mae_chaos = mean_absolute_error(y_chaos_test, y_chaos_pred)
mse = mean_squared_error(y_test, y_pred)
mse_rand = mean_squared_error(y_rand_test, y_rand_pred)
mse_chaos = mean_squared_error(y_chaos_test, y_chaos_pred)
rmse = np.sqrt(mean_squared_error(y_test, y_pred))
rmse_rand = np.sqrt(mean_squared_error(y_rand_test, y_rand_pred))
rmse_chaos = np.sqrt(mean_squared_error(y_chaos_test, y_chaos_pred))
print(
"\nNo randomness: " f"MAE = {mae:.2f}, MSE = {mse:.2f}, RMSE = {rmse:.2f}"
)
print(
"Some randomness: "
f"MAE = {mae_rand:.2f}, MSE = {mse_rand:.2f}, RMSE = {rmse_rand:.2f}"
)
print(
"Lots of randomness: "
f"MAE = {mae_chaos:.2f}, MSE = {mse_chaos:.2f}, RMSE = {rmse_chaos:.2f}"
)
def evaluate_regressor(reg_type, f_y, *args, **kwargs):
reg = reg_type(*args, **kwargs)
reg_rand = reg_type(*args, **kwargs)
reg_chaos = reg_type(*args, **kwargs)
y_train = f_y(x_train).reshape(-1)
y_test = f_y(x_test).reshape(-1)
y_pred = reg.fit(x_train, y_train).predict(x_test)
y_rand_train = randomize(f_y, x_train).reshape(-1)
y_rand_test = randomize(f_y, x_test).reshape(-1)
y_rand_pred = reg_rand.fit(x_train, y_rand_train).predict(x_test)
y_chaos_train = randomize(f_y, x_train, 1.5).reshape(-1)
y_chaos_test = randomize(f_y, x_test, 1.5).reshape(-1)
y_chaos_pred = reg_chaos.fit(x_train, y_chaos_train).predict(x_test)
plot_graphs(f_y, reg, reg_rand, reg_chaos, y_train, y_rand_train, y_chaos_train)
print_evaluation(y_test, y_pred, y_rand_test, y_rand_pred, y_chaos_test, y_chaos_pred)
```
# Ensembles, Random Forests, Gradient Boosted Trees
## Ensemble Methods
Idea: combine several estimators to improve their overal performance.
- Averaging methods:
- Independent estimators, average predictions
- Reduces variance (overfitting)
- Bagging, random forests
- Boosting methods:
- Train estimators sequentially
- Each estimator is trained to reduce the bias of its (combined) predecessors
### Bagging
- Averaging method: build several estimators of the same type, average their results
- Needs some way to introduce differences between estimators
- Otherwise variance is not reduced
- Train on random subsets of the training data
- Reduce overfitting
- Work best with strong estimators (e.g., decision trees with (moderately) large depth)
### Random Forests
- Bagging classifier/regressor using decision trees
- For each tree in the forest:
- Subset of training data
- Subset of features
- Often significant reduction in variance (overfitting)
- Sometimes increase in bias
```
from sklearn.ensemble import RandomForestRegressor
evaluate_non_random_regressor(RandomForestRegressor, lin, random_state=42);
evaluate_non_random_regressor(RandomForestRegressor, fun, random_state=42);
evaluate_non_random_regressor(
RandomForestRegressor, fun, n_estimators=25, criterion="absolute_error", random_state=42
);
evaluate_regressor(RandomForestRegressor, lin, random_state=42);
evaluate_regressor(
RandomForestRegressor, lin, n_estimators=500, max_depth=3, random_state=42
)
evaluate_regressor(
RandomForestRegressor, lin, n_estimators=500, min_samples_leaf=6, random_state=42
)
evaluate_regressor(RandomForestRegressor, fun, random_state=42)
evaluate_regressor(
RandomForestRegressor,
fun,
n_estimators=1000,
min_samples_leaf=6,
random_state=43,
n_jobs=-1,
)
```
## Gradient Boosted Trees
- Boosting method for both regression and classification
- Requires differentiable loss function
```
from sklearn.ensemble import GradientBoostingRegressor
evaluate_non_random_regressor(GradientBoostingRegressor, lin);
evaluate_non_random_regressor(GradientBoostingRegressor, fun);
evaluate_regressor(GradientBoostingRegressor, lin);
evaluate_regressor(GradientBoostingRegressor, lin, n_estimators=200, learning_rate=0.05, loss="absolute_error");
evaluate_regressor(GradientBoostingRegressor, lin, n_estimators=500, learning_rate=0.01,
loss="absolute_error", subsample=0.1, random_state=46);
evaluate_regressor(GradientBoostingRegressor, fun, n_estimators=500, learning_rate=0.01,
loss="absolute_error", subsample=0.1, random_state=44);
```
### Multiple Features
```
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
np.set_printoptions(precision=1)
x, y, coef = make_regression(n_samples=250, n_features=4, n_informative=1, coef=True, random_state=42)
x.shape, y.shape, coef
fig, axs = plt.subplots(ncols=2, nrows=2, figsize=(20, 12))
for i, ax in enumerate(axs.reshape(-1)):
sns.scatterplot(x=x[:, i], y=y, ax=ax)
x, y, coef = make_regression(n_samples=250, n_features=20, n_informative=10, coef=True, random_state=42)
x.shape, y.shape, coef
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.4)
x_train.shape, x_test.shape, y_train.shape, y_test.shape
fig, axs = plt.subplots(ncols=2, nrows=2, figsize=(20, 12))
for i in range(2):
sns.scatterplot(x=x[:, i], y=y, ax=axs[0, i]);
for i in range(2):
sns.scatterplot(x=x[:, i + 6], y=y, ax=axs[1, i]);
lr_clf = LinearRegression()
lr_clf.fit(x_train, y_train)
y_lr_pred = lr_clf.predict(x_test)
mean_absolute_error(y_test, y_lr_pred), mean_squared_error(y_test, y_lr_pred)
lr_clf.coef_.astype(np.int32), coef.astype(np.int32)
dt_clf = DecisionTreeRegressor()
dt_clf.fit(x_train, y_train)
y_dt_pred = dt_clf.predict(x_test)
mean_absolute_error(y_test, y_dt_pred), mean_squared_error(y_test, y_dt_pred)
rf_clf = RandomForestRegressor()
rf_clf.fit(x_train, y_train)
y_rf_pred = rf_clf.predict(x_test)
mean_absolute_error(y_test, y_rf_pred), mean_squared_error(y_test, y_rf_pred)
gb_clf = GradientBoostingRegressor()
gb_clf.fit(x_train, y_train)
y_gb_pred = gb_clf.predict(x_test)
mean_absolute_error(y_test, y_gb_pred), mean_squared_error(y_test, y_gb_pred)
x, y, coef = make_regression(n_samples=250, n_features=20, n_informative=10, noise=100.0, coef=True, random_state=42)
x.shape, y.shape, coef
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.4)
x_train.shape, x_test.shape, y_train.shape, y_test.shape
lr_clf = LinearRegression()
lr_clf.fit(x_train, y_train)
y_lr_pred = lr_clf.predict(x_test)
mean_absolute_error(y_test, y_lr_pred), mean_squared_error(y_test, y_lr_pred)
dt_clf = DecisionTreeRegressor()
dt_clf.fit(x_train, y_train)
y_dt_pred = dt_clf.predict(x_test)
mean_absolute_error(y_test, y_dt_pred), mean_squared_error(y_test, y_dt_pred)
rf_clf = RandomForestRegressor()
rf_clf.fit(x_train, y_train)
y_rf_pred = rf_clf.predict(x_test)
mean_absolute_error(y_test, y_rf_pred), mean_squared_error(y_test, y_rf_pred)
gb_clf = GradientBoostingRegressor()
gb_clf.fit(x_train, y_train)
y_gb_pred = gb_clf.predict(x_test)
mean_absolute_error(y_test, y_gb_pred), mean_squared_error(y_test, y_gb_pred)
x, y, coef = make_regression(n_samples=250, n_features=20, n_informative=10, noise=100.0,
coef=True, random_state=42)
y += (20 * x[:, 1]) ** 2
x.shape, y.shape, coef
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.4)
x_train.shape, x_test.shape, y_train.shape, y_test.shape
fig, axs = plt.subplots(ncols=2, nrows=2, figsize=(20, 12))
for i in range(2):
sns.scatterplot(x=x[:, i], y=y, ax=axs[0, i]);
for i in range(2):
sns.scatterplot(x=x[:, i + 6], y=y, ax=axs[1, i]);
lr_clf = LinearRegression()
lr_clf.fit(x_train, y_train)
y_lr_pred = lr_clf.predict(x_test)
mean_absolute_error(y_test, y_lr_pred), mean_squared_error(y_test, y_lr_pred)
dt_clf = DecisionTreeRegressor()
dt_clf.fit(x_train, y_train)
y_dt_pred = dt_clf.predict(x_test)
mean_absolute_error(y_test, y_dt_pred), mean_squared_error(y_test, y_dt_pred)
rf_clf = RandomForestRegressor()
rf_clf.fit(x_train, y_train)
y_rf_pred = rf_clf.predict(x_test)
mean_absolute_error(y_test, y_rf_pred), mean_squared_error(y_test, y_rf_pred)
gb_clf = GradientBoostingRegressor()
gb_clf.fit(x_train, y_train)
y_gb_pred = gb_clf.predict(x_test)
mean_absolute_error(y_test, y_gb_pred), mean_squared_error(y_test, y_gb_pred)
```
## Feature Engineering
```
x = rng.uniform(size=(150, 1), low=0.0, high=10.0)
x_train, x_test = x[:100], x[100:]
x_plot = np.linspace(0, 10, 500)
x_train[:3]
y_lin_train = lin(x_train).reshape(-1)
y_lin_test = lin(x_test).reshape(-1)
y_fun_train = fun(x_train.reshape(-1))
y_fun_test = fun(x_test).reshape(-1)
x_squares = x * x
x_squares[:3]
x_sins = np.sin(x)
x_sins[:3]
x_train_aug = np.concatenate([x_train, x_train * x_train, np.sin(x_train)], axis=1)
x_train_aug[:3]
x_test_aug = np.concatenate([x_test, x_test * x_test, np.sin(x_test)], axis=1)
# from sklearn.linear_model import Ridge
# lr_aug_lin = Ridge()
lr_aug_lin = LinearRegression()
lr_aug_lin.fit(x_train_aug, y_lin_train);
lr_aug_lin.coef_, lr_aug_lin.intercept_
y_aug_lin_pred = lr_aug_lin.predict(x_test_aug)
mean_absolute_error(y_lin_test, y_aug_lin_pred), mean_squared_error(
y_lin_test, y_aug_lin_pred
)
x_test.shape, x_plot.shape
def train_and_plot_aug(f_y, scale=0.5):
y_plot = f_y(x_plot)
f_r = lambda x: randomize(f_y, x, scale=scale)
y_train = f_r(x_train_aug[:, 0])
y_test = f_r(x_test)
lr_aug = LinearRegression() # Try with Ridge() as well...
lr_aug.fit(x_train_aug, y_train)
y_pred_test = lr_aug.predict(
np.concatenate([x_test, x_test * x_test, np.sin(x_test)], axis=1)
)
x_plot2 = x_plot.reshape(-1, 1)
y_pred_plot = lr_aug.predict(
np.concatenate([x_plot2, x_plot2 * x_plot2, np.sin(x_plot2)], axis=1)
)
fig, ax = plt.subplots(figsize=(12, 6))
sns.scatterplot(x=x_plot2[:, 0], y=y_plot, color="orange")
sns.scatterplot(x=x_plot2[:, 0], y=y_pred_plot, color="red")
sns.scatterplot(x=x_train_aug[:, 0], y=y_train, color="green")
plt.show()
mae_in = mean_absolute_error(y_test, y_pred_test)
mse_in = mean_absolute_error(y_test, y_pred_test)
rmse_in = np.sqrt(mse_in)
y_nr = f_y(x_test)
mae_true = mean_absolute_error(y_nr, y_pred_test)
mse_true = mean_absolute_error(y_nr, y_pred_test)
rmse_true = np.sqrt(mse_true)
print(f"Vs. input: MAE: {mae_in:.2f}, MSE: {mse_in:.2f}, RMSE: {rmse_in:.2f}")
print(f"True: MAE: {mae_true:.2f}, MSE: {mse_true:.2f}, RMSE: {rmse_true:.2f}")
print(f"Parameters: {lr_aug.coef_}, {lr_aug.intercept_}")
train_and_plot_aug(lin)
train_and_plot_aug(fun, scale=0.0)
train_and_plot_aug(fun, scale=0.5)
train_and_plot_aug(fun, scale=1.5)
train_and_plot_aug(fun, scale=3)
def fun2(x): return 2.8 * np.sin(x) + 0.3 * x + 0.08 * x ** 2 - 2.5
train_and_plot_aug(fun2, scale=1.5)
train_and_plot_aug(lambda x: np.select([x<=6, x>6], [-0.5, 3.5]))
```
|
github_jupyter
|
# Keras tutorial - the Happy House
Welcome to the first assignment of week 2. In this assignment, you will:
1. Learn to use Keras, a high-level neural networks API (programming framework), written in Python and capable of running on top of several lower-level frameworks including TensorFlow and CNTK.
2. See how you can in a couple of hours build a deep learning algorithm.
Why are we using Keras? Keras was developed to enable deep learning engineers to build and experiment with different models very quickly. Just as TensorFlow is a higher-level framework than Python, Keras is an even higher-level framework and provides additional abstractions. Being able to go from idea to result with the least possible delay is key to finding good models. However, Keras is more restrictive than the lower-level frameworks, so there are some very complex models that you can implement in TensorFlow but not (without more difficulty) in Keras. That being said, Keras will work fine for many common models.
In this exercise, you'll work on the "Happy House" problem, which we'll explain below. Let's load the required packages and solve the problem of the Happy House!
```
import numpy as np
from keras import layers
from keras.layers import Input, Dense, Activation, ZeroPadding2D, BatchNormalization, Flatten, Conv2D
from keras.layers import AveragePooling2D, MaxPooling2D, Dropout, GlobalMaxPooling2D, GlobalAveragePooling2D
from keras.models import Model
from keras.preprocessing import image
from keras.utils import layer_utils
from keras.utils.data_utils import get_file
from keras.applications.imagenet_utils import preprocess_input
import pydot
from IPython.display import SVG
from keras.utils.vis_utils import model_to_dot
from keras.utils import plot_model
from kt_utils import *
import keras.backend as K
K.set_image_data_format('channels_last')
import matplotlib.pyplot as plt
from matplotlib.pyplot import imshow
%matplotlib inline
```
**Note**: As you can see, we've imported a lot of functions from Keras. You can use them easily just by calling them directly in the notebook. Ex: `X = Input(...)` or `X = ZeroPadding2D(...)`.
## 1 - The Happy House
For your next vacation, you decided to spend a week with five of your friends from school. It is a very convenient house with many things to do nearby. But the most important benefit is that everybody has commited to be happy when they are in the house. So anyone wanting to enter the house must prove their current state of happiness.
<img src="images/happy-house.jpg" style="width:350px;height:270px;">
<caption><center> <u> <font color='purple'> **Figure 1** </u><font color='purple'> : **the Happy House**</center></caption>
As a deep learning expert, to make sure the "Happy" rule is strictly applied, you are going to build an algorithm which that uses pictures from the front door camera to check if the person is happy or not. The door should open only if the person is happy.
You have gathered pictures of your friends and yourself, taken by the front-door camera. The dataset is labbeled.
<img src="images/house-members.png" style="width:550px;height:250px;">
Run the following code to normalize the dataset and learn about its shapes.
```
X_train_orig, Y_train_orig, X_test_orig, Y_test_orig, classes = load_dataset()
# Normalize image vectors
X_train = X_train_orig/255.
X_test = X_test_orig/255.
# Reshape
Y_train = Y_train_orig.T
Y_test = Y_test_orig.T
print ("number of training examples = " + str(X_train.shape[0]))
print ("number of test examples = " + str(X_test.shape[0]))
print ("X_train shape: " + str(X_train.shape))
print ("Y_train shape: " + str(Y_train.shape))
print ("X_test shape: " + str(X_test.shape))
print ("Y_test shape: " + str(Y_test.shape))
```
**Details of the "Happy" dataset**:
- Images are of shape (64,64,3)
- Training: 600 pictures
- Test: 150 pictures
It is now time to solve the "Happy" Challenge.
## 2 - Building a model in Keras
Keras is very good for rapid prototyping. In just a short time you will be able to build a model that achieves outstanding results.
Here is an example of a model in Keras:
```python
def model(input_shape):
# Define the input placeholder as a tensor with shape input_shape. Think of this as your input image!
X_input = Input(input_shape)
# Zero-Padding: pads the border of X_input with zeroes
X = ZeroPadding2D((3, 3))(X_input)
# CONV -> BN -> RELU Block applied to X
X = Conv2D(32, (7, 7), strides = (1, 1), name = 'conv0')(X)
X = BatchNormalization(axis = 3, name = 'bn0')(X)
X = Activation('relu')(X)
# MAXPOOL
X = MaxPooling2D((2, 2), name='max_pool')(X)
# FLATTEN X (means convert it to a vector) + FULLYCONNECTED
X = Flatten()(X)
X = Dense(1, activation='sigmoid', name='fc')(X)
# Create model. This creates your Keras model instance, you'll use this instance to train/test the model.
model = Model(inputs = X_input, outputs = X, name='HappyModel')
return model
```
Note that Keras uses a different convention with variable names than we've previously used with numpy and TensorFlow. In particular, rather than creating and assigning a new variable on each step of forward propagation such as `X`, `Z1`, `A1`, `Z2`, `A2`, etc. for the computations for the different layers, in Keras code each line above just reassigns `X` to a new value using `X = ...`. In other words, during each step of forward propagation, we are just writing the latest value in the commputation into the same variable `X`. The only exception was `X_input`, which we kept separate and did not overwrite, since we needed it at the end to create the Keras model instance (`model = Model(inputs = X_input, ...)` above).
**Exercise**: Implement a `HappyModel()`. This assignment is more open-ended than most. We suggest that you start by implementing a model using the architecture we suggest, and run through the rest of this assignment using that as your initial model. But after that, come back and take initiative to try out other model architectures. For example, you might take inspiration from the model above, but then vary the network architecture and hyperparameters however you wish. You can also use other functions such as `AveragePooling2D()`, `GlobalMaxPooling2D()`, `Dropout()`.
**Note**: You have to be careful with your data's shapes. Use what you've learned in the videos to make sure your convolutional, pooling and fully-connected layers are adapted to the volumes you're applying it to.
```
# GRADED FUNCTION: HappyModel
def HappyModel(input_shape):
"""
Implementation of the HappyModel.
Arguments:
input_shape -- shape of the images of the dataset
Returns:
model -- a Model() instance in Keras
"""
### START CODE HERE ###
# Feel free to use the suggested outline in the text above to get started, and run through the whole
# exercise (including the later portions of this notebook) once. The come back also try out other
# network architectures as well.
X_input = Input(shape=input_shape)
X = ZeroPadding2D((3,3))(X_input)
# Conv -> BN -> ReLU
X = Conv2D(32, (7, 7), strides=(1,1), name='conv0')(X)
X = BatchNormalization(axis=3, name='bn0')(X)
X = Activation('relu')(X)
# Max-pool
X = MaxPooling2D((2,2), name='max_pool')(X)
X = Flatten()(X)
X = Dense(1, activation='sigmoid', name='fc')(X)
model = Model(X_input, X, name='HappyModel')
### END CODE HERE ###
return model
```
You have now built a function to describe your model. To train and test this model, there are four steps in Keras:
1. Create the model by calling the function above
2. Compile the model by calling `model.compile(optimizer = "...", loss = "...", metrics = ["accuracy"])`
3. Train the model on train data by calling `model.fit(x = ..., y = ..., epochs = ..., batch_size = ...)`
4. Test the model on test data by calling `model.evaluate(x = ..., y = ...)`
If you want to know more about `model.compile()`, `model.fit()`, `model.evaluate()` and their arguments, refer to the official [Keras documentation](https://keras.io/models/model/).
**Exercise**: Implement step 1, i.e. create the model.
```
### START CODE HERE ### (1 line)
happyModel = HappyModel((64,64,3))
### END CODE HERE ###
```
**Exercise**: Implement step 2, i.e. compile the model to configure the learning process. Choose the 3 arguments of `compile()` wisely. Hint: the Happy Challenge is a binary classification problem.
```
### START CODE HERE ### (1 line)
happyModel.compile(optimizer='adam',
loss='binary_crossentropy',
metrics=['accuracy'])
### END CODE HERE ###
```
**Exercise**: Implement step 3, i.e. train the model. Choose the number of epochs and the batch size.
```
### START CODE HERE ### (1 line)
happyModel.fit(X_train,
Y_train,
epochs=10,
batch_size=32)
### END CODE HERE ###
```
Note that if you run `fit()` again, the `model` will continue to train with the parameters it has already learnt instead of reinitializing them.
**Exercise**: Implement step 4, i.e. test/evaluate the model.
```
### START CODE HERE ### (1 line)
preds = happyModel.evaluate(X_test, Y_test)
### END CODE HERE ###
print()
print ("Loss = " + str(preds[0]))
print ("Test Accuracy = " + str(preds[1]))
```
If your `happyModel()` function worked, you should have observed much better than random-guessing (50%) accuracy on the train and test sets. To pass this assignment, you have to get at least 75% accuracy.
To give you a point of comparison, our model gets around **95% test accuracy in 40 epochs** (and 99% train accuracy) with a mini batch size of 16 and "adam" optimizer. But our model gets decent accuracy after just 2-5 epochs, so if you're comparing different models you can also train a variety of models on just a few epochs and see how they compare.
If you have not yet achieved 75% accuracy, here're some things you can play around with to try to achieve it:
- Try using blocks of CONV->BATCHNORM->RELU such as:
```python
X = Conv2D(32, (3, 3), strides = (1, 1), name = 'conv0')(X)
X = BatchNormalization(axis = 3, name = 'bn0')(X)
X = Activation('relu')(X)
```
until your height and width dimensions are quite low and your number of channels quite large (≈32 for example). You are encoding useful information in a volume with a lot of channels. You can then flatten the volume and use a fully-connected layer.
- You can use MAXPOOL after such blocks. It will help you lower the dimension in height and width.
- Change your optimizer. We find Adam works well.
- If the model is struggling to run and you get memory issues, lower your batch_size (12 is usually a good compromise)
- Run on more epochs, until you see the train accuracy plateauing.
Even if you have achieved 75% accuracy, please feel free to keep playing with your model to try to get even better results.
**Note**: If you perform hyperparameter tuning on your model, the test set actually becomes a dev set, and your model might end up overfitting to the test (dev) set. But just for the purpose of this assignment, we won't worry about that here.
## 3 - Conclusion
Congratulations, you have solved the Happy House challenge!
Now, you just need to link this model to the front-door camera of your house. We unfortunately won't go into the details of how to do that here.
<font color='blue'>
**What we would like you to remember from this assignment:**
- Keras is a tool we recommend for rapid prototyping. It allows you to quickly try out different model architectures. Are there any applications of deep learning to your daily life that you'd like to implement using Keras?
- Remember how to code a model in Keras and the four steps leading to the evaluation of your model on the test set. Create->Compile->Fit/Train->Evaluate/Test.
## 4 - Test with your own image (Optional)
Congratulations on finishing this assignment. You can now take a picture of your face and see if you could enter the Happy House. To do that:
1. Click on "File" in the upper bar of this notebook, then click "Open" to go on your Coursera Hub.
2. Add your image to this Jupyter Notebook's directory, in the "images" folder
3. Write your image's name in the following code
4. Run the code and check if the algorithm is right (0 is unhappy, 1 is happy)!
The training/test sets were quite similar; for example, all the pictures were taken against the same background (since a front door camera is always mounted in the same position). This makes the problem easier, but a model trained on this data may or may not work on your own data. But feel free to give it a try!
```
### START CODE HERE ###
img_path = 'images/my_image.jpg'
### END CODE HERE ###
img = image.load_img(img_path, target_size=(64, 64))
imshow(img)
x = image.img_to_array(img)
x = np.expand_dims(x, axis=0)
x = preprocess_input(x)
print(happyModel.predict(x))
```
## 5 - Other useful functions in Keras (Optional)
Two other basic features of Keras that you'll find useful are:
- `model.summary()`: prints the details of your layers in a table with the sizes of its inputs/outputs
- `plot_model()`: plots your graph in a nice layout. You can even save it as ".png" using SVG() if you'd like to share it on social media ;). It is saved in "File" then "Open..." in the upper bar of the notebook.
Run the following code.
```
happyModel.summary()
plot_model(happyModel, to_file='HappyModel.png')
SVG(model_to_dot(happyModel).create(prog='dot', format='svg'))
```
|
github_jupyter
|
```
%matplotlib inline
import lsqfit
from model_avg_paper import *
from model_avg_paper.test_tmin import test_vary_tmin_SE
p0_test_ME = {
'A0': 2.0,
'E0': 0.8,
'A1': 10.4,
'E1': 1.16,
}
Nt = 32
noise_params = {
'noise_amp': 0.3,
'noise_samples': 500,
'frac_noise': True,
'cross_val': False,
'cv_frac': 0.1,
}
obs_name='E0'
correlated_data = True
rho=0.6
# Set seed for consistency of outcome
#np.random.seed(10911) # Fig 3, subfig A; Fig 4
#np.random.seed(81890) # Fig 3, subfig B
#np.random.seed(87414) # Fig 3, subfig C
np.random.seed(77700) # Fig 3, subfig D
def ME_model(x,p):
return multi_exp_model(x,p,Nexc=2)
if correlated_data:
test_data = gen_synth_data_corr(
np.arange(0,Nt),
p0_test_ME,
ME_model,
rho=rho,
**noise_params)
else:
test_data = gen_synth_data(
np.arange(0,Nt),
p0_test_ME,
ME_model,
**noise_params)
test_res = test_vary_tmin_SE(test_data, Nt=Nt, max_tmin=26, obs_name=obs_name, IC='AIC',
cross_val=noise_params['cross_val'])
print(test_res['obs_avg'])
## Figure 3
import matplotlib.ticker as ticker
gs = plt.GridSpec(2, 1, height_ratios=[3,1])
gs.update(hspace=0.06)
ax1 = plt.subplot(gs[0])
plot_gvcorr([test_res['obs_avg']], x=np.array([1.5]), color='red', markersize=7, marker='s', open_symbol=True, label='Model avg.')
plot_gvcorr(test_res['obs'], x=test_res['tmin'], label='Individual fits')
ax1.plot(np.array([-1,34]), 0*np.array([0,0])+p0_test_ME[obs_name], linestyle='--', color='k', label='Model truth')
#ax1.set_xlabel('$N_p$')
ax1.set_ylabel('$E_0$')
ax1.legend(loc='center left', bbox_to_anchor=(1,0.5))
ax1.set_xlim(0.7,27.3)
plt.setp(ax1.get_xticklabels(), visible=False)
ax2 = plt.subplot(gs[1])
p_norm = test_res['probs'] / np.sum(test_res['probs'])
Q_norm = test_res['Qs'] / np.sum(test_res['Qs'])
plt.plot(test_res['tmin'], p_norm, color='orange', label='pr$(M|D)$')
plt.plot(test_res['tmin'], Q_norm, color='blue', linestyle='-.', label='Fit p-value') # Note: fit prob != model prob!
tick_spacing = 4
ax2.xaxis.set_major_locator(ticker.MultipleLocator(tick_spacing))
plt.yticks([0,np.max(p_norm)])
ax2.yaxis.set_major_formatter(ticker.FuncFormatter(lambda x, pos: '0' if x == 0 else '{:.2f}'.format(x)))
ax2.set_xlim(0.7,27.3)
# Put a legend to the right of the current axis
ax2.legend(loc='center left', bbox_to_anchor=(1, 0.5))
ax2.set_xlabel(r'$t_{\rm min}$')
ax2.set_ylabel('p')
# Uncomment to save figure to disk
#plt.savefig('plots/exp_avg_4.pdf', bbox_inches = "tight")
# Scaling w/number of samples
Nsamp_array = np.array([20, 40, 80, 160, 320, 640, 2040, 4096, 4096*2, 4096*4])
Nsamp_max = Nsamp_array[-1]
noise_params['noise_samples'] = Nsamp_max
if correlated_data:
scale_data = gen_synth_data_corr(
np.arange(0,Nt),
p0_test_ME,
ME_model,
rho=rho,
**noise_params)
else:
scale_data = gen_synth_data(
np.arange(0,Nt),
p0_test_ME,
ME_model,
**noise_params)
model_avg_vs_Nsamp = []
naive_avg_vs_Nsamp = []
fixed_tmin_vs_Nsamp = []
fixed_tmin_2_vs_Nsamp = []
fw_vs_Nsamp = []
fix_tmin = 14
fix_tmin_2 = 8
for Nsamp in Nsamp_array:
test_data_scale = cut_synth_data_Nsamp(scale_data, Nsamp)
test_res_scale = test_vary_tmin_SE(test_data_scale, Nt=Nt, max_tmin=Nt-4, obs_name=obs_name, IC='AIC')
test_res_scale_naive = test_vary_tmin_SE(test_data_scale, Nt=Nt, max_tmin=Nt-4, obs_name=obs_name,
IC='naive')
model_avg_vs_Nsamp.append(test_res_scale['obs_avg'])
naive_avg_vs_Nsamp.append(test_res_scale_naive['obs_avg'])
fixed_tmin_vs_Nsamp.append(test_res_scale['obs'][fix_tmin])
fixed_tmin_2_vs_Nsamp.append(test_res_scale['obs'][fix_tmin_2])
fw_vs_Nsamp.append(obs_avg_full_width(test_res_scale['obs'], test_res_scale['Qs'], test_res_scale['fits'], bf_i=None))
## Figure 4
plot_gvcorr(model_avg_vs_Nsamp, x=np.log(Nsamp_array)+0.1, label='Model avg. (AIC)')
plot_gvcorr(fixed_tmin_vs_Nsamp, x=np.log(Nsamp_array)+0.2, color='red', marker='s', markersize=6, label=r'Fixed $t_{\rm min} = 14$')
plot_gvcorr(fw_vs_Nsamp, x=np.log(Nsamp_array)+0.3, marker='X', markersize=8, color='orange', label='Full-width systematic')
plot_gvcorr(naive_avg_vs_Nsamp, x=np.log(Nsamp_array)+0.4, color='silver', marker='v', markersize=8, label=r'Model avg. (naive)')
plt.plot(np.arange(0,10), 0*np.arange(0,10)+p0_test_ME[obs_name], linestyle='--', color='k', label='Model truth')
plt.xlabel(r'$\log(N_s)$')
plt.ylabel(r'$E_0$')
plt.xlim(2.7,7.)
plt.ylim(0.78,0.82)
# Put a legend to the right of the current axis
ax = plt.subplot(111)
ax.legend(loc='center left', bbox_to_anchor=(1, 0.5))
# Uncomment to save figure to disk
#plt.savefig('plots/exp_N_scaling.pdf', bbox_inches = "tight")
```
|
github_jupyter
|
### Classes
Finally we get to classes.
I assume you already have some knowledge of classes and OOP in general, so I'll focus on the semantics of creating classes and some of the differences with Java classes.
First, the question of visibility. There is no such thing as private or public in Python. Everything is public, period. So we don't have to specify the visibility of functions and attributes in Python.
Class instantiations are done in two steps - the instance is created first, and then the instance is initialized. In general we hook into the initialization phase and leave the object creation alone. We do this by using a special method in the class called `__init__`. We'll see how large a role special methods play in Python.
The important thing to note is that by the time `__init__` is called in our class, the object (instance) has **already** been created.
We use the `class` keyword to create classes:
```
class Person:
pass
```
`pass` is something we can use in Python to indicate "do nothing" (a so called "no-op" operation). Here I use it to supply a body for the class definition, but don't actually want to specify any functionality.
So now we can actually create instances of the `Person` object at this point. They will be pretty useless since we have not implemented any functionality yet.
We create instances of classes by **calling** the class - remember how we call things in Python, we use `()`:
```
p = Person()
id(p), type(p)
```
So now we may want to add some functions to the class. Whenever we define a function in a class, we have to understand what happens when we call that function from an instance, using dot notation:
For example, if we write
```p.say_hello()```
then we are calling the `say_hello()` function from the instance, and Python will **bind** that function to the specific instance - i.e. it creates an association between the instance used to call the function, and the function.
The way it does this is by passing in the instance reference to the function as the first positional argument - in this case it would actually call `say_hello(p)`. And our `say_hello` function now has access to the instance it was called from, including any internal state.
When functions are bound to an instance, they are called **methods** of the class, and, in particular **instance methods** because they are bound to instances of the class when called. (There are other types of functions that can be bound to the class, called *class methods*, but this is beyond the scope of this primer).
Let's see how this works:
```
class Person:
def say_hello(instance, name):
return f'{instance} says hello to {name}'
```
So here, we had to make sure the first argument of our function was created to receive the instance it is being called from. After that we are free to add our own arguments as needed.
```
p = Person()
```
Let's see what `p` looks like when we print it:
```
p
```
And now let's call the `say_hello` method from the instance `p`:
```
p.say_hello('Alex')
```
You'll notice that we did not pass `p` as the first argument to `say_hello` - Python did that for us since we wrote `p.say_hello`.
By convention, that `instance` argument I wrote above, is usually named `self`, for obvious reasons. But it is just a convention, although one you should stick to.
```
class Person:
def say_hello(self, name):
return f'{self} says hello to {name}'
p = Person()
p.say_hello('Alex')
```
So now let's turn our attention to instance attributes.
Python is dynamic, so instance attributes do not have to be defined at the time the class is created. In fact we rarely do so.
Let's see how we can add an attribute to an instance after it's been created:
```
p = Person()
p.name = 'Alex'
```
That's it, `p` now has an attribute called `name`:
```
p.name
```
But this is specific to this instance, not other instances:
```
p2 = Person()
p2.name
```
So instance attributes are **specific** to the instance (hence the name).
Of course we can define attributes by calling methods in our class - let's see an example of this:
```
class Person:
def set_name(self, name):
self.name = name
def get_name(self):
return self.name
p = Person()
```
At this point `p` does **not** have a `name` attribute (it hasn't been set yet!):
```
p.get_name()
```
But we can easily set it using the `set_name` method:
```
p.set_name('Alex')
p.get_name()
```
And of course the attribute is called `name` and is easily accessible directly as well:
```
p.name
```
This is what is called a *bare* attribute - it is not hidden by getter and setter methods like we would normally do in Java (remember we do not have private variables).
You'll notice the issue we had - we would get an exception if we tried to access the attribute before it was actually created.
For this reason, best practice is to create these instance attributes (even setting them to a default value or `None`) when the class instance is being created.
The best place to do this is in the *initialization* phase of the class (remember that class instantiation has two phases - creation and initialization).
To do this we use the special method `__init__`.
This is going to be a functionm in our class, and will be bound to the instance when it is called (by that time the instance has already been created), so just like our `set_name` method, we'll need to allow for the instance to be received as the first argument:
```
class Person:
def __init__(self, name):
self.name = name
```
So the `__init__` method is basically doing the same thing as our `set_name` method - the difference is in how it is called.
When we create an instance using `Person()`, Python looks for, and if available calls, the `__init__` method (that's why it's called a *special method*).
In our case here, the first argument will receive the just created object, but we have one additional argument, `name`. So we need to pass that in when we create the instance:
```
p = Person('name')
```
The `__init__` method was actually called - let's see this:
```
class Person:
def __init__(self, name):
print(f'__init__ called for object {self}')
self.name = name
p = Person('Alex')
```
And in fact, the memory address of `p` is:
```
hex(id(p))
```
which as you can see, is excactly the same object `self` was set to when `__init__` was called.
And our instance `p` now has an attribute called `name`:
```
p.name
```
We can create another instance:
```
p2 = Person('Eric')
hex(id(p2)), p2.name
```
And that has not affected the `name` of `p` - since `name` is an instance attribute (it is specific to the instance):
```
p.name
```
|
github_jupyter
|
```
import argparse
from collections import namedtuple, OrderedDict
import itertools
import os
import numpy as np
from typing import Tuple
from typing import List
from typing import Dict
import random
from itertools import product
import copy
import re
import random
import hashlib
import pathlib
import json
import matplotlib as plt
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
os.environ['QT_QPA_PLATFORM']='offscreen'
plt.rcParams["font.family"] = "DejaVu Serif"
font = {'family' : 'DejaVu Serif',
'size' : 20}
plt.rc('font', **font)
import plotly.tools as tls
from utils import one_hot
from utils import generate_possible_object_names
from utils import numpy_array_to_image
from vocabulary import *
from object_vocabulary import *
from world import *
from grammer import *
from simulator import *
from relation_graph import *
import logging
import warnings
warnings.filterwarnings("ignore")
# Helpers.
def get_relation_statistics(command_structs):
"""
Return a dictionary, (relation, position) with counts
"""
stats = {}
for i in range(2): # at max 2!
stats[f"position-{i}"] = {}
for command in command_structs:
pos_id = 0
for k, v in command["rel_map"].items():
if v in stats[f"position-{pos_id}"].keys():
stats[f"position-{pos_id}"][v] += 1
else:
stats[f"position-{pos_id}"][v] = 1
pos_id += 1
return stats
def get_attribute_statistics(command_structs, include_keywords=["circle", "cylinder", "square", "box", "object"]):
stats = {}
# for k, v in command_structs[0]["obj_map"].items():
# stats[k] = {} # we can do it in object level!
for i in range(3): # at max 2!
stats[f"$OBJ_{i}"] = {}
for command in command_structs:
for k, v in command["obj_map"].items():
for keyword in include_keywords:
keyword_list = keyword.split(" ") # in case there are a couple!
match = True
for sub_k in keyword_list:
if sub_k not in v:
match = False
break
if match:
if keyword in stats[k].keys():
stats[k][keyword] += 1
else:
stats[k][keyword] = 1
return stats
def get_keyword_statistics(command_structs, include_keyword="adverb"):
stats = {}
for command in command_structs:
keyword = command[include_keyword]
if keyword in stats.keys():
stats[keyword] += 1
else:
stats[keyword] = 1
return stats
def flatten_dictionary(
dictionary_in
):
flat_dictionary = {}
for k, v in dictionary_in.items():
for kk, vv in v.items():
if kk not in flat_dictionary:
flat_dictionary[kk] = vv
else:
flat_dictionary[kk] += vv
return flat_dictionary
def plot_dictionary(
dictionary_in,
y_label="Frequency",
x_label="Conditions",
title="Missing Title",
save_file=None,
is_plot=False,
wandb=None,
):
group_str = [k for k, _ in dictionary_in[0].items()]
if len(group_str) > 8:
rotate=90
fontsize=10
else:
rotate=45
fontsize=13
all_stats = []
for d in dictionary_in:
group_stats = [d[k] for k in group_str]
all_stats.append(group_stats)
all_stats = np.array(all_stats)
std = np.std(all_stats, axis=0)
mean = np.mean(all_stats, axis=0)
# input data
mean_values = mean
variance = std**2
bar_labels = group_str
# plot bars
x_pos = list(range(len(bar_labels)))
fig = plt.figure(figsize=(8,6))
ax = fig.add_subplot(111)
g = ax.bar(x_pos, mean_values, yerr=variance, align='center', alpha=0.5)
plt.grid()
# set height of the y-axis
max_y = max(zip(mean_values, variance)) # returns a tuple, here: (3, 5)
plt.ylim([0, (max_y[0] + max_y[1]) * 1.1])
# set axes labels and title
plt.ylabel(y_label)
plt.xticks(x_pos, bar_labels)
plt.xticks(rotation = rotate, fontsize=fontsize)
plt.yticks(rotation = 45)
plt.title(title, fontsize=10)
if mean_values[0] > 10000:
plt.ticklabel_format(axis='y', style='sci', scilimits=(4,4))
if wandb != None:
# Let us also try to log this plot to wandb!
wandb.log({title: wandb.Image(fig)})
if save_file != None:
plt.savefig(save_file, dpi=100, bbox_inches='tight')
plt.close(fig)
else:
if is_plot:
plt.show()
def get_command_struct_statistics(
command_structs, run_name="ReaSCAN-Awesome", date="2021-05-06",
split="demo",
compositional_split=False,
n_sample=-1, n_runs=10,
output_dir="../../data-files/ReaSCAN-compositional_splits/",
save_to_disk=True,
wandb=None
):
statistics = OrderedDict({
"run_name": run_name,
"date": date,
"splits": split,
"number_of_these_examples_seen_in_training": -1 if not compositional_split else 0,
"number_of_command_structs": len(command_structs),
})
if n_sample == -1:
n_sample = len(command_structs)
# If we are downsampling, we need to do more runs as well!
random.shuffle(command_structs)
patterns = set([])
for command_s in command_structs:
patterns.add(command_s["grammer_pattern"])
statistics["command_patterns"] = list(patterns)
pattern_stats = get_keyword_statistics(command_structs, include_keyword="grammer_pattern")
statistics["pattern_stats"] = pattern_stats
# verb
verb_stats = get_keyword_statistics(command_structs, include_keyword="verb")
statistics["verb_stats"] = verb_stats
plot_dictionary(
[verb_stats],
title="Verbs",
save_file=os.path.join(output_dir, f"verb_stats-{split}.png"),
wandb=wandb,
)
# adverb
adverb_stats = get_keyword_statistics(command_structs, include_keyword="adverb")
# special handling for adverb for better readabilities
adverb_stats_rebuild = {}
for k, v in adverb_stats.items():
if k == "":
adverb_stats_rebuild["EMPTY"] = v
else:
adverb_stats_rebuild[k] = v
statistics["adverb_stats"] = adverb_stats_rebuild
plot_dictionary(
[adverb_stats_rebuild],
title="Adverbs",
save_file=os.path.join(output_dir, f"adverb_stats-{split}.png"),
wandb=wandb,
)
# relation
relation_stats = get_relation_statistics(command_structs)
if len(flatten_dictionary(relation_stats)) != 0:
statistics["relation_stats"] = relation_stats
plot_dictionary(
[flatten_dictionary(relation_stats)],
title="Relation-Types",
save_file=os.path.join(output_dir, f"relation_type_stats-{split}.png"),
wandb=wandb,
)
# attribute
nouns = ["circle", "cylinder", "square", "box", "object"]
n_stats = get_attribute_statistics(command_structs, include_keywords=nouns)
statistics["shape_stats"] = n_stats
plot_dictionary(
[flatten_dictionary(n_stats)],
title="Shapes",
save_file=os.path.join(output_dir, f"shape_stats-{split}.png"),
wandb=wandb,
)
color_adjectives = ["red", "blue", "green", "yellow"]
c_stats = get_attribute_statistics(command_structs, include_keywords=color_adjectives)
statistics["color_stats"] = c_stats
if len(flatten_dictionary(c_stats)) != 0:
plot_dictionary(
[flatten_dictionary(c_stats)],
title="Colors",
save_file=os.path.join(output_dir, f"color_stats-{split}.png"),
wandb=wandb,
)
size_adjectives = ["big", "small"]
s_stats = get_attribute_statistics(command_structs, include_keywords=size_adjectives)
if len(flatten_dictionary(s_stats)) != 0:
statistics["size_stats"] = s_stats
plot_dictionary(
[flatten_dictionary(s_stats)],
title="Sizes",
save_file=os.path.join(output_dir, f"size_stats-{split}.png"),
wandb=wandb,
)
# second order attribute
color_adjectives = ["red", "blue", "green", "yellow"]
nouns = ["circle", "cylinder", "square", "box", "object"]
c_n_p = product(color_adjectives, nouns)
include_keywords = [" ".join(c_n) for c_n in c_n_p]
c_n_stats = get_attribute_statistics(command_structs, include_keywords=include_keywords)
statistics["color_and_shape_stats"] = c_n_stats
if len(flatten_dictionary(c_n_stats)) != 0:
plot_dictionary(
[flatten_dictionary(c_n_stats)],
title="Colors-Shapes",
save_file=os.path.join(output_dir, f"color+shape_stats-{split}.png"),
wandb=wandb,
)
size_adjectives = ["big", "small"]
nouns = ["circle", "cylinder", "square", "box", "object"]
s_n_p = product(size_adjectives, nouns)
include_keywords = [" ".join(s_n) for s_n in s_n_p]
s_n_stats = get_attribute_statistics(command_structs, include_keywords=include_keywords)
statistics["size_and_shape_stats"] = s_n_stats
if len(flatten_dictionary(s_n_stats)) != 0:
plot_dictionary(
[flatten_dictionary(s_n_stats)],
title="Sizes-Shapes",
save_file=os.path.join(output_dir, f"size+shape_stats-{split}.png"),
wandb=wandb,
)
# third order attribute
size_adjectives = ["big", "small"]
color_adjectives = ["red", "blue", "green", "yellow"]
nouns = ["circle", "cylinder", "square", "box", "object"]
all_p = product(size_adjectives, color_adjectives, nouns)
include_keywords = [" ".join(a) for a in all_p]
all_stats = get_attribute_statistics(command_structs, include_keywords=include_keywords)
statistics["size_and_color_and_shape_stats"] = all_stats
if save_to_disk:
import yaml
with open(os.path.join(output_dir, f"command_struct_only_stats-{split}.yml"), 'w') as yaml_file:
yaml.dump(statistics, yaml_file, default_flow_style=False)
return statistics
def arg_parse():
# This is a single loop to generate the dataset.
n_processes = 1
mode = "all"
n_command_struct = 10000
grid_size = 6
n_object_max = 10
seed = 42
date = "2021-05-07"
per_command_world_retry_max = 200
per_command_world_target_count = 10 # for each command, we target to have 50 shapeWorld!
resumed_from_file_path = ""
is_tensorboard = False
parser = argparse.ArgumentParser(description='ReaSCAN argparse.')
# Experiment management:
parser.add_argument('--n_processes', type=int, default=1,
help='Number of process used to generate the dataset.')
parser.add_argument('--index_start', type=int, default=-1,
help='Number of command sampled from the command population.')
parser.add_argument('--index_end', type=int, default=-1,
help='Number of command sampled from the command population.')
parser.add_argument('--mode', type=str, default="all",
help='mode')
parser.add_argument('--n_command_struct', type=int, default=10000,
help='Number of command sampled from the command population.')
parser.add_argument('--grid_size', type=int, default=6,
help='Grid size of the world.')
parser.add_argument('--n_object_max', type=int, default=10,
help='Number of object at max in the shapeWorld (Note that you may still have more than this number!).')
parser.add_argument('--seed', type=int, default=42,
help='Random seed.')
parser.add_argument('--date', type=str,
help='date')
parser.add_argument('--per_command_world_retry_max', type=int, default=200,
help='How many times you can retry for each world generation.')
parser.add_argument('--per_command_world_target_count', type=int, default=50,
help='The targeted number of world to have per command.')
parser.add_argument("--is_tensorboard",
default=False,
action='store_true',
help="Whether to use tensorboard.")
parser.add_argument("--include_relation_distractor",
default=False,
action='store_true',
help="Whether to use tensorboard.")
parser.add_argument("--include_attribute_distractor",
default=False,
action='store_true',
help="Whether to use tensorboard.")
parser.add_argument("--include_isomorphism_distractor",
default=False,
action='store_true',
help="Whether to use tensorboard.")
parser.add_argument("--include_random_distractor",
default=False,
action='store_true',
help="Whether to use tensorboard.")
parser.add_argument('--full_relation_probability', type=float, default=1.0,
help='Probability of including full relation distractors.')
parser.add_argument('--save_interal', type=int, default=200,
help='Saving intervel in command count.')
parser.add_argument('--command_pattern', type=str, default="p3",
help='What pattern to use, currently, we support p1-p4.')
parser.add_argument('--resumed_from_file_path', type=str, default="",
help='Whether to resume for this file.')
parser.add_argument('--output_dir', type=str, default="../../data-files/ReaSCAN-compositional_splits/",
help='Whether to resume for this file.')
parser.set_defaults(
# Exp management:
n_processes=1,
mode="all",
n_command_struct=10000,
grid_size=6,
n_object_max=10,
seed=42,
date="2021-05-07",
per_command_world_retry_max=200,
per_command_world_target_count=50,
resumed_from_file_path="",
is_tensorboard=False,
output_dir="../../data-files/ReaSCAN-compositional_splits/",
)
try:
get_ipython().run_line_magic('matplotlib', 'inline')
args = parser.parse_args([])
except:
args = parser.parse_args()
return args
def example_classifier(
task_info,
mode="demo",
default_split_prob={
"train": 0.9,
"dev": 0.01,
"test": 0.09,
},
):
"""
This will return the split this data belongs to.
"""
if mode == "demo" or mode == "all":
if random.random() < default_split_prob["train"]:
return "train"
else:
if random.random() < 0.9:
return "test"
else:
return "dev"
else:
# We need to add here logics to determine
# compositional splits!
pass
# Some tips:
# Do not debug in this file, you can simply copy the questionable struct
# to the lightweight demo file, and you can debug there!
if __name__ == "__main__":
# Loading arguments
args = arg_parse()
try:
# get_ipython().run_line_magic('matplotlib', 'inline')
# # Experiment management:
# args.n_processes=1
# args.mode="demo"
# args.n_command_struct=20
# args.grid_size=6
# args.n_object_max=10
# args.seed=42
# args.date="2021-05-07"
# args.per_command_world_retry_max=20
# args.per_command_world_target_count=3
# args.resumed_from_file_path=""
# args.is_tensorboard=True # Let us try this!
# args.output_dir="../../data-files/ReaSCAN-demo/"
# is_jupyter = True
get_ipython().run_line_magic('matplotlib', 'inline')
# Experiment management:
args.n_processes=1
args.mode="train"
args.n_command_struct=675*5
args.grid_size=6
args.n_object_max=10
args.seed=42
args.save_interal = 200
args.date="2021-05-30"
args.per_command_world_retry_max=1000
args.per_command_world_target_count=180
args.resumed_from_file_path=""
args.is_tensorboard=True # Let us try this!
args.output_dir="../../data-files/ReaSCAN-compositional-p3-full-relation/"
is_jupyter = True
args.index_start = -1
args.index_end = -1
except:
is_jupyter = False
loading_p1 = True if args.command_pattern == "p1" else False
p1_exhaustive_verb_adverb = False
loading_p2 = True if args.command_pattern == "p2" else False
loading_p3 = True if args.command_pattern == "p3" else False
loading_p4 = True if args.command_pattern == "p4" else False
save_command_stats = False
save_at_interval = True
save_interal = args.save_interal
# TODO: add these to args.
logging_interval = 1000
# Create output directory if not exists.
pathlib.Path(args.output_dir).mkdir(parents=True, exist_ok=True)
logging.basicConfig(
level=logging.INFO,
format='%(asctime)s %(levelname)-8s %(message)s',
datefmt='%a, %d %b %Y %H:%M:%S',
filename=os.path.join(args.output_dir, "generator.log"),
)
logger = logging.getLogger(__name__)
logging.getLogger().addHandler(logging.StreamHandler(os.sys.stdout))
logger.info("Generating ReaSCAN with following parameters: ")
logger.info(args)
# This is a single loop to generate the dataset.
n_processes = args.n_processes
mode = args.mode
n_command_struct = args.n_command_struct
grid_size = args.grid_size
n_object_max = args.n_object_max
seed = args.seed
date = args.date
per_command_world_retry_max = args.per_command_world_retry_max
per_command_world_target_count = args.per_command_world_target_count # for each command, we target to have 50 shapeWorld!
resumed_from_file_path = args.resumed_from_file_path
output_dir = args.output_dir
is_tensorboard = args.is_tensorboard
if is_tensorboard:
logger.warning("Enabling wandb for tensorboard logging...")
import wandb
run = wandb.init(project="ReaSCAN", entity="wuzhengx")
run_name = wandb.run.name
wandb.config.update(args)
else:
wandb = None
random.seed(seed)
np.random.seed(seed)
# We also need something to generate generalization
# splits!
params = {
"n_processes": n_processes,
"mode": mode,
"n_command_struct": n_command_struct,
"grid_size": grid_size,
"n_object_max": n_object_max,
"seed": seed,
"per_command_world_retry_max": per_command_world_retry_max,
"per_command_world_target_count": per_command_world_target_count,
}
if mode == "all" or mode == "demo" or mode == "train":
# Meaning we are generating the random ReaSCAN train + dev + test splits!
logger.warning(f"You are generating data for {mode} splits only!")
split_percentage = {
"train": 0.9,
}
elif mode == "all,noval_1,noval_2,noval_3,noval_4":
# here we need to define how to check for noval_*
pass
elif mode == "compositional":
# Meaning we are generating the random ReaSCAN train + dev + test splits!
logger.warning("You are generating data for all compositional splits!")
elif mode == "":
pass # Not implemented!
# Using the full vocabulary.
intransitive_verbs = ["walk"]
transitive_verbs = ["push", "pull"]
adverbs = ["while zigzagging", "while spinning", "cautiously", "hesitantly"]
nouns = ["circle", "cylinder", "square", "box"]
color_adjectives = ["red", "blue", "green", "yellow"]
size_adjectives = ["big", "small"]
relative_pronouns = ["that is"]
relation_clauses = ["in the same row as",
"in the same column as",
"in the same color as",
"in the same shape as",
"in the same size as",
"inside of"]
vocabulary = Vocabulary.initialize(intransitive_verbs=intransitive_verbs,
transitive_verbs=transitive_verbs, adverbs=adverbs, nouns=nouns,
color_adjectives=color_adjectives,
size_adjectives=size_adjectives,
relative_pronouns=relative_pronouns,
relation_clauses=relation_clauses)
# test out the object vocab
min_object_size = 1
max_object_size = 4
object_vocabulary = ObjectVocabulary(shapes=vocabulary.get_semantic_shapes(),
colors=vocabulary.get_semantic_colors(),
min_size=min_object_size, max_size=max_object_size)
# Generating all the core command structs.
grammer = Grammer(vocabulary)
# Bootup our simulator.
simulator = Simulator(
object_vocabulary, vocabulary,
grid_size=grid_size,
n_object_max=n_object_max,
)
command_structs = []
logger.info("Finished loading required modules...")
# Sampling all the possible command score structs.
if loading_p4:
# Currently, we hard-code the pattern!
grammer_pattern = '$OBJ_0 ^ $OBJ_1 & $OBJ_2 & $OBJ_3'
logger.info(f"Including pattern:= {grammer_pattern}...")
# Sampling relations
relations = grammer.sample_object_relation_grammer(
'$OBJ_0',
grammer.build_dependency_graph(grammer_pattern))
for relation in relations:
obj_pattern_map = relation[0]
rel_map = relation[1]
grammer_bindings = grammer.grounding_grammer_with_vocabulary(grammer_pattern, obj_pattern_map, rel_map)
for obj_map in grammer_bindings:
# here, we also sample the verb and adverb bindings!
adverb_enhance_list = vocabulary.get_adverbs()
adverb_enhance_list += [""]
command_struct = {
"obj_pattern_map" : obj_pattern_map,
"rel_map" : rel_map,
"obj_map" : obj_map,
"grammer_pattern" : grammer_pattern,
"adverb" : random.choice(adverb_enhance_list),
"verb" : random.choice(vocabulary.get_transitive_verbs() + vocabulary.get_intransitive_verbs()),
}
command_structs += [command_struct]
if loading_p3:
# Currently, we hard-code the pattern!
grammer_pattern = '$OBJ_0 ^ $OBJ_1 & $OBJ_2'
logger.info(f"Including pattern:= {grammer_pattern}...")
# Sampling relations
relations = grammer.sample_object_relation_grammer(
'$OBJ_0',
grammer.build_dependency_graph(grammer_pattern))
for relation in relations:
obj_pattern_map = relation[0]
rel_map = relation[1]
grammer_bindings = grammer.grounding_grammer_with_vocabulary(grammer_pattern, obj_pattern_map, rel_map)
for obj_map in grammer_bindings:
# here, we also sample the verb and adverb bindings!
adverb_enhance_list = vocabulary.get_adverbs()
adverb_enhance_list += [""]
command_struct = {
"obj_pattern_map" : obj_pattern_map,
"rel_map" : rel_map,
"obj_map" : obj_map,
"grammer_pattern" : grammer_pattern,
"adverb" : random.choice(adverb_enhance_list),
"verb" : random.choice(vocabulary.get_transitive_verbs() + vocabulary.get_intransitive_verbs()),
}
command_structs += [command_struct]
if loading_p2:
grammer_pattern = '$OBJ_0 ^ $OBJ_1'
logger.info(f"Including pattern:= {grammer_pattern}...")
# Sampling relations
relations = grammer.sample_object_relation_grammer(
'$OBJ_0',
grammer.build_dependency_graph(grammer_pattern))
for relation in relations:
obj_pattern_map = relation[0]
rel_map = relation[1]
grammer_bindings = grammer.grounding_grammer_with_vocabulary(grammer_pattern, obj_pattern_map, rel_map)
for obj_map in grammer_bindings:
# here, we also sample the verb and adverb bindings!
adverb_enhance_list = vocabulary.get_adverbs()
adverb_enhance_list += [""]
command_struct = {
"obj_pattern_map" : obj_pattern_map,
"rel_map" : rel_map,
"obj_map" : obj_map,
"grammer_pattern" : grammer_pattern,
"adverb" : random.choice(adverb_enhance_list),
"verb" : random.choice(vocabulary.get_transitive_verbs() + vocabulary.get_intransitive_verbs()),
}
command_structs += [command_struct]
if loading_p1:
p1_exhaustive_verb_adverb = True
# for gSCAN command, we don't need to undersample, they are small!
grammer_pattern = '$OBJ_0'
logger.info(f"Including pattern:= {grammer_pattern}...")
# Sampling relations
relations = grammer.sample_object_relation_grammer(
'$OBJ_0',
grammer.build_dependency_graph(grammer_pattern))
for relation in relations:
obj_pattern_map = relation[0]
rel_map = relation[1]
grammer_bindings = grammer.grounding_grammer_with_vocabulary(grammer_pattern, obj_pattern_map, rel_map)
for obj_map in grammer_bindings:
if p1_exhaustive_verb_adverb:
for adverb in vocabulary.get_adverbs() + [""]:
for verb in vocabulary.get_transitive_verbs() + vocabulary.get_intransitive_verbs():
# here, we also sample the verb and adverb bindings!
command_struct = {
"obj_pattern_map" : obj_pattern_map,
"rel_map" : rel_map,
"obj_map" : obj_map,
"grammer_pattern" : grammer_pattern,
"adverb" : adverb,
"verb" : verb,
}
command_structs += [command_struct]
# We only sample these command!
"""
WARNING: beaware that not all command struct can
be sampled for world-command pair! They may or
may not fail.
"""
under_sample = True
if under_sample:
sampled_command_struct = []
random.shuffle(command_structs)
if n_command_struct != -1:
sampled_command_struct = command_structs[:n_command_struct]
if args.index_start == -1 or args.index_end == -1:
pass
else:
# we only look at one shard! this is for multiprocess
logger.info(f"WARNING: contine with sharding: start at {args.index_start}; end at {args.index_end}")
sampled_command_struct = command_structs[args.index_start:args.index_end]
logger.info(f"Sampled {len(sampled_command_struct)} from {len(command_structs)} core command structs for pattern={grammer_pattern}.")
logger.info(f"Finished sampling core command structs with total {len(sampled_command_struct)}...")
command_struct_file_path = os.path.join(args.output_dir, f"command_struct-{args.mode}.txt")
formatted_sampled_command_struct = []
for command_struct in sampled_command_struct:
formatted_command_struct = {
"obj_pattern_map" : command_struct["obj_pattern_map"],
"rel_map" : [(k, v) for k, v in command_struct["rel_map"].items()],
"obj_map" : command_struct["obj_map"],
"grammer_pattern" : command_struct["grammer_pattern"],
"adverb" : command_struct["adverb"],
"verb" : command_struct["verb"],
}
formatted_sampled_command_struct += [formatted_command_struct]
# dump to the disk.
with open(command_struct_file_path, "w") as fd:
json.dump(formatted_sampled_command_struct, fd, indent=4)
logger.info(f"Saved command struct to {command_struct_file_path} for later use...")
# print out quick stats on how many command per pattern!
per_pattern_command_count = {}
for command_struct in sampled_command_struct:
grammer_pattern = command_struct["grammer_pattern"]
if grammer_pattern in per_pattern_command_count.keys():
per_pattern_command_count[grammer_pattern] += 1
else:
per_pattern_command_count[grammer_pattern] = 1
logger.info(f"Counts per command pattern: ")
logger.info(per_pattern_command_count)
# From the struct, let us sample shape world.
"""
We just need a couple more steps beyond this point:
(1) Sample a world
(2) Making sure it is valid
(3) Construct the command, providing determiners
(4) Generate action sequences to the target
(5) Get all the action related metadata as gSCAN
(6) Save it to per command example
"""
# We need a way to index the sampled command.
sampled_command_struct_indexed = OrderedDict({})
global_command_struct_index = 0
for command_struct in sampled_command_struct:
sampled_command_struct_indexed[global_command_struct_index] = command_struct
global_command_struct_index += 1
root = "$OBJ_0"
per_command_world_counts = OrderedDict({})
if mode == "demo" or mode == "all" or mode == "train":
created_examples_by_splits = OrderedDict({
"train" : [],
})
else:
pass
shaperized_command_struct = []
per_command_world_unique_check = OrderedDict({})
# Some global control for data quality control.
global_step = 0
success_step = 0
# Distractor info logs.
d_full_relation_count = 0
d_relation_count = 0
d_attribute_count = 0
d_iso_count = 0
d_random_count = 0
logger.info(f"Started to generate the dataset...")
for command_struct_index, command_struct in sampled_command_struct_indexed.items():
logger.info(f"Generating for command struct (seed={seed}): {command_struct_index+1}/{len(sampled_command_struct_indexed)}...")
per_command_world_counts[command_struct_index] = 0 # 0 world for each command in the beginning!
per_command_world_unique_check[command_struct_index] = set([])
obj_pattern_map = command_struct["obj_pattern_map"]
rel_map = command_struct["rel_map"]
obj_map = command_struct["obj_map"]
grammer_pattern = command_struct["grammer_pattern"]
verb = command_struct["verb"]
adverb = command_struct["adverb"]
# This is the target world number generated for this command
for n_world_try in range(per_command_world_target_count):
# How many time we need to retry before we give up?
at_least_success = False
for n_retry in range(per_command_world_retry_max):
global_step += 1
if success_step == 0:
denom = 1
else:
denom = success_step
d_full_relation_ratio = 1.0*d_full_relation_count/denom
d_relation_ratio = 1.0*d_relation_count/denom
d_attribute_ratio = 1.0*d_attribute_count/denom
d_iso_ratio = 1.0*d_iso_count/denom
d_random_ratio = 1.0*d_random_count/denom
global_success_ratio = 1.0*success_step/global_step
# logging some very useful information to wandb if avaliable!
if is_tensorboard:
if (global_step%logging_interval) == 0:
wandb.log({'global_success_ratio': global_success_ratio, 'global_step': global_step})
wandb.log({'current_example_count': success_step, 'global_step': global_step})
wandb.log({'d_full_relation_ratio': d_full_relation_ratio, 'global_step': global_step})
wandb.log({'d_relation_ratio': d_relation_ratio, 'global_step': global_step})
wandb.log({'d_attribute_ratio': d_attribute_ratio, 'global_step': global_step})
wandb.log({'d_iso_ratio': d_iso_ratio, 'global_step': global_step})
wandb.log({'d_random_ratio': d_random_ratio, 'global_step': global_step})
else:
if (global_step%(logging_interval*10)) == 0:
logger.info({'global_success_ratio': global_success_ratio, 'global_step': global_step})
logger.info({'current_example_count': success_step, 'global_step': global_step})
logger.info({'d_full_relation_ratio': d_full_relation_ratio, 'global_step': global_step})
logger.info({'d_relation_ratio': d_relation_ratio, 'global_step': global_step})
logger.info({'d_attribute_ratio': d_attribute_ratio, 'global_step': global_step})
logger.info({'d_iso_ratio': d_iso_ratio, 'global_step': global_step})
logger.info({'d_random_ratio': d_random_ratio, 'global_step': global_step})
if mode == "demo":
sampled_world = simulator.sample_situations_from_grounded_grammer(
copy.deepcopy(grammer_pattern),
copy.deepcopy(obj_pattern_map),
copy.deepcopy(rel_map),
copy.deepcopy(obj_map),
is_plot=False,
include_relation_distractor=args.include_relation_distractor,
include_attribute_distractor=args.include_attribute_distractor,
include_isomorphism_distractor=args.include_isomorphism_distractor,
include_random_distractor=args.include_random_distractor,
full_relation_probability=args.full_relation_probability,
debug=False
) # This is the minimum settings! You need to turn on attribute always!
else:
# Sample a shapeWorld!
sampled_world = simulator.sample_situations_from_grounded_grammer(
copy.deepcopy(grammer_pattern),
copy.deepcopy(obj_pattern_map),
copy.deepcopy(rel_map),
copy.deepcopy(obj_map),
is_plot=False,
include_relation_distractor=args.include_relation_distractor,
include_attribute_distractor=args.include_attribute_distractor,
include_isomorphism_distractor=args.include_isomorphism_distractor,
include_random_distractor=args.include_random_distractor,
full_relation_probability=args.full_relation_probability, # ReaSCAN Special: 15 distractors!
debug=False
)
# Validate the world is valid!
graph = ReaSCANGraph(
objects=sampled_world["obj_map"],
object_patterns=sampled_world["obj_pattern_map"],
vocabulary=vocabulary,
positions=sampled_world["pos_map"],
referred_object=sampled_world["referred_obj"],
debug=False
)
pattern_graph = ReaSCANGraph(
objects=obj_map,
object_patterns=None,
vocabulary=vocabulary,
relations=rel_map,
referred_object='$OBJ_0',
debug=False
)
potential_referent_target = graph.find_referred_object_super_fast(
pattern_graph, referred_object='$OBJ_0',
debug=False
)
# Save the result if the world is valid!
# This may be to strict, but it ensures 100% correct!
if len(potential_referent_target) == 1 and '$OBJ_0' in potential_referent_target:
# A quick world repeat check!
hash_world_str = hashlib.md5(str(sampled_world["situation"].to_representation()).encode('utf-8')).hexdigest()
if hash_world_str not in per_command_world_unique_check[command_struct_index]:
per_command_world_unique_check[command_struct_index].add(hash_world_str)
else:
continue # This is highly unlikely, but just to prevent!
# Form the command with grounded determiners!
obj_determiner_map = graph.find_determiners(
pattern_graph,
referred_object='$OBJ_0',
debug=False,
)
# we don't check this for P1 and P2?
# valid_determiner = True
# for k, v in obj_determiner_map.items():
# if k != '$OBJ_0':
# if v != "a":
# valid_determiner = False
# break
# if not valid_determiner:
# continue # we should abort and resample!
at_least_success = True
success_step += 1
command_str = grammer.repre_str_command(
grammer_pattern, rel_map, obj_map,
obj_determiner_map,
verb,
adverb,
)
# Form the golden label for the action list!
is_transitive = False
if verb in simulator.vocabulary.get_transitive_verbs():
is_transitive = True
# Direct walk.
action = "walk" # this is definit!
primitive_command = simulator.vocabulary.translate_word(action)
target_position = sampled_world["situation"].target_object.position
simulator._world.go_to_position(
position=target_position, manner=adverb,
primitive_command=primitive_command
)
# Object actions.
if is_transitive:
semantic_action = simulator.vocabulary.translate_word(verb)
simulator._world.move_object_to_wall(action=semantic_action, manner=adverb)
target_commands, _ = simulator._world.get_current_observations()
has_relation_distractor = False
full_relation_distractor = True
for rel_bool in sampled_world["distractor_switch_map"]["relation"]:
if rel_bool:
has_relation_distractor = True
else:
full_relation_distractor = False
# Save all relevant information for a task.
task_struct = OrderedDict({
"command": ",".join(command_str.split(" ")),
"grammer_pattern": grammer_pattern,
"meaning": ",".join(command_str.split(" ")),
"derivation": grammer_pattern,
"situation": sampled_world["situation"].to_representation(),
"target_commands": ",".join(target_commands),
"verb_in_command": verb,
"adverb_in_command": adverb,
"referred_target": obj_map["$OBJ_0"],
"object_pattern_map": obj_pattern_map,
"relation_map": [(k, v) for k, v in rel_map.items()],
"object_expression": obj_map,
"n_object": len(sampled_world["obj_map"]),
"n_distractor": len(sampled_world["obj_map"])-len(obj_map),
"full_relation_distractor": full_relation_distractor,
"has_relation_distractor": has_relation_distractor,
"has_attribute_distractor": sampled_world["distractor_switch_map"]["attribute"],
"has_isomorphism_distractor": sampled_world["distractor_switch_map"]["isomorphism"],
"has_random_distractor": True if sampled_world["n_random_distractor"] != -1 else False,
"n_random_distractor": sampled_world["n_random_distractor"] if sampled_world["n_random_distractor"] != -1 else 0,
"relation_distractor_metadata": sampled_world["relation_distractor_metadata"],
"attribute_distractor_metadata": sampled_world["attribute_distractor_metadata"],
"isomorphism_distractor_metadata": sampled_world["isomorphism_distractor_metadata"],
"random_distractor_metadata": sampled_world["random_distractor_metadata"],
})
# Record distractor related info
if task_struct["full_relation_distractor"]:
d_full_relation_count += 1
if task_struct["has_relation_distractor"]:
d_relation_count += 1
if task_struct["has_attribute_distractor"]:
d_attribute_count += 1
if task_struct["has_isomorphism_distractor"]:
d_iso_count += 1
if task_struct["n_random_distractor"]:
d_random_count += 1
# Here, we decide which split we put the example into!
split = args.mode
created_examples_by_splits[split].append(task_struct)
per_command_world_counts[command_struct_index] += 1
break # break the retry loop!
if not at_least_success:
logger.info(f"WARNING: the success rate for this command is close to 0.0%, skipping...")
break # success rate for this comman is ~= 0.0%, let us directly skip
if save_at_interval and (command_struct_index+1)% save_interal == 0:
logger.info(f"Saving data files and statistics to {args.output_dir} for checkpoints...")
# Now, we need to save data into the folder
# along with possible statistics.
to_save_command_struct = []
per_command_count = []
for command_struct_index, count in per_command_world_counts.items():
per_command_count += [count]
if count >= 1:
to_save_command_struct.append(sampled_command_struct_indexed[command_struct_index])
if save_command_stats:
_ = get_command_struct_statistics(
to_save_command_struct, run_name=f"ReaSCAN-{mode}", date=args.date,
split=mode,
compositional_split=False,
n_sample=-1,
output_dir=args.output_dir,
save_to_disk=True if args.output_dir != "" else False,
wandb=wandb
)
# wandb.log({"per_command_world_count": wandb.Histogram(per_command_count)})
data_file_path = os.path.join(args.output_dir, f"data-{args.mode}.txt")
if mode == "demo" or mode == "all" or mode == "train":
logger.info(f"total example count={success_step}...")
dataset_representation = {
"grid_size": args.grid_size,
"type_grammar": "ReaSCAN-Grammer",
"min_object_size": 1,
"max_object_size": 4,
"percentage_train": split_percentage["train"],
"examples": created_examples_by_splits,
"intransitive_verbs": intransitive_verbs,
"transitive_verbs": transitive_verbs,
"adverbs": adverbs,
"nouns": nouns,
"color_adjectives": color_adjectives,
"size_adjectives": size_adjectives,
"relative_pronouns": relative_pronouns,
"relation_clauses": relation_clauses,
}
# dump to the disk.
with open(data_file_path, "w") as fd:
json.dump(dataset_representation, fd, indent=4)
else:
pass
# Last round of saving!
logger.info(f"Saving FINAL data files and statistics to {args.output_dir}...")
# Now, we need to save data into the folder
# along with possible statistics.
to_save_command_struct = []
per_command_count = []
for command_struct_index, count in per_command_world_counts.items():
per_command_count += [count]
if count >= 1:
to_save_command_struct.append(sampled_command_struct_indexed[command_struct_index])
if save_command_stats:
_ = get_command_struct_statistics(
to_save_command_struct, run_name=f"ReaSCAN-{mode}", date=args.date,
split=mode,
compositional_split=False,
n_sample=-1,
output_dir=args.output_dir,
save_to_disk=True if args.output_dir != "" else False,
wandb=wandb
)
# wandb.log({"per_command_world_count": wandb.Histogram(per_command_count)})
data_file_path = os.path.join(args.output_dir, f"data-{args.mode}.txt")
if mode == "demo" or mode == "all" or mode == "train":
logger.info(f"total example count={success_step}...")
dataset_representation = {
"grid_size": args.grid_size,
"type_grammar": "ReaSCAN-Grammer",
"min_object_size": 1,
"max_object_size": 4,
"percentage_train": split_percentage["train"],
"examples": created_examples_by_splits,
"intransitive_verbs": intransitive_verbs,
"transitive_verbs": transitive_verbs,
"adverbs": adverbs,
"nouns": nouns,
"color_adjectives": color_adjectives,
"size_adjectives": size_adjectives,
"relative_pronouns": relative_pronouns,
"relation_clauses": relation_clauses,
}
# dump to the disk.
with open(data_file_path, "w") as fd:
json.dump(dataset_representation, fd, indent=4)
else:
pass
logger.info("==FINISH==")
if args.is_tensorboard:
# end wandb
wandb.finish()
```
|
github_jupyter
|
```
import gym
import numpy as np
import math
```
Description:
There are four designated locations in the grid world indicated by R(ed), G(reen), Y(ellow), and B(lue). When the episode starts, the taxi starts off at a random square and the passenger is at a random location. The taxi drives to the passenger's location, picks up the passenger, drives to the passenger's destination (another one of the four specified locations), and then drops off the passenger. Once the passenger is dropped off, the episode ends.
Observations:
There are 500 discrete states since there are 25 taxi positions, 5 possible locations of the passenger (including the case when the passenger is in the taxi), and 4 destination locations.
Note that there are 400 states that can actually be reached during an episode. The missing states correspond to situations in which the passenger is at the same location as their destination, as this typically signals the end of an episode.
Four additional states can be observed right after a successful episodes, when both the passenger and the taxi are at the destination.
This gives a total of 404 reachable discrete states.
Passenger locations:
- 0: R(ed)
- 1: G(reen)
- 2: Y(ellow)
- 3: B(lue)
- 4: in taxi
Destinations:
- 0: R(ed)
- 1: G(reen)
- 2: Y(ellow)
- 3: B(lue)
Actions:
There are 6 discrete deterministic actions:
- 0: move south
- 1: move north
- 2: move east
- 3: move west
- 4: pickup passenger
- 5: drop off passenger
Rewards:
There is a default per-step reward of -1,
except for delivering the passenger, which is +20,
or executing "pickup" and "drop-off" actions illegally, which is -10.
Rendering:
- blue: passenger
- magenta: destination
- yellow: empty taxi
- green: full taxi
- other letters (R, G, Y and B): locations for passengers and destinations
```
env = gym.make("Taxi-v3")
q_table = np.zeros([env.observation_space.n, env.action_space.n])
env.render()
env.reset()
"""Training the agent"""
import random
from IPython.display import clear_output
# Hyperparameters
alpha = 0.1
gamma = 0.6
epsilon = 0.1
# For plotting metrics
all_epochs = []
all_penalties = []
for i in range(1, 100001):
state = env.reset()
epochs, penalties, reward, = 0, 0, 0
done = False
while not done:
if random.uniform(0, 1) < epsilon:
action = env.action_space.sample() # Explore action space
else:
action = np.argmax(q_table[state]) # Exploit learned values
next_state, reward, done, info = env.step(action)
old_value = q_table[state, action]
next_max = np.max(q_table[next_state])
new_value = (1 - alpha) * old_value + alpha * (reward + gamma * next_max)
q_table[state, action] = new_value
if reward == -10:
penalties += 1
state = next_state
epochs += 1
if i % 100 == 0:
clear_output(wait=True)
print(f"Episode: {i}")
print("Training finished.\n")
q_table[328]
"""Evaluate agent's performance after Q-learning"""
total_epochs, total_penalties = 0, 0
episodes = 5
for _ in range(episodes):
state = env.reset()
epochs, penalties, reward = 0, 0, 0
done = False
while not done:
action = np.argmax(q_table[state])
state, reward, done, info = env.step(action)
env.render()
if reward == -10:
penalties += 1
epochs += 1
total_penalties += penalties
total_epochs += epochs
print(f"Results after {episodes} episodes:")
print(f"Average timesteps per episode: {total_epochs / episodes}")
print(f"Average penalties per episode: {total_penalties / episodes}")
```
|
github_jupyter
|
<h1><center>DBSCAN: A macroscopic investigation in Python</center></h1><br>
Cluster analysis is an important problem in data analysis. Data scientists use clustering to identify malfunctioning servers, group genes with similar expression patterns, or various other applications.
Briefly, clustering is the task of grouping together a set of objects in a way that objects in the same cluster are more similar to each other than to objects in other clusters. Similarity is an amount that reflects the strength of a relationship between two data objects. Clustering is mainly used for exploratory data mining. Clustering has manifold usage in many fields such as machine learning, pattern recognition, image analysis, information retrieval, bio-informatics, data compression, and computer graphics.
There are many families of clustering techniques, and you may be familiar with the most popular one: K-Means (which belongs to the *family of centroid-based clustering*). As a quick refresher, K-Means determines k centroids in the data and clusters points by assigning them to the nearest centroid.
While K-Means is easy to understand and implement in practice, the algorithm does not take care of outliers, so all points are assigned to a cluster even if they do not belong in any. In the domain of anomaly detection, this causes problems as anomalous points will be assigned to the same cluster as “normal” data points. The anomalous points pull the cluster centroid towards them, making it harder to classify them as anomalous points.
This tutorial will cover another type of clustering technique known as density-based clustering specifically DBSCAN (a density-based based clustering technique). Compared to centroid-based clustering like K-Means, density-based clustering works by identifying “dense” clusters of points, allowing it to learn clusters of arbitrary shape and identify outliers in the data.
<h2>In this post you will get to know about:</h2>
* Disadvantage of centroid-based clustering technique
* General introduction to density-based clustering technique
* Inner workings of DBSCAN
* A simple case study of DBSCAN in Python
* Applications of DBSCAN
<h3>Disadvantage of centroid-based clustering technique: </h3>
Before discussing the disadvantage of centroid-based clustering, let me give a brief introduction to it. A centroid is a data point (imaginary or real) at the center of a cluster. In centroid-based clustering, clusters are represented by a central vector or a centroid. This centroid might not necessarily be a member of the dataset. Centroid-based clustering is an iterative clustering algorithm in which the notion of similarity is derived by how close a data point is to the centroid of the cluster. <br><br>
Sometimes a dataset can contain extreme values that are outside the range of what is expected and unlike the other data. These are called outliers. More formally, an outlier is an observation that lies an abnormal distance from other values in a random sample from a population.
The main fundamental of centroid-based clustering techniques is driven by distance measurements between the data points and centroids. Therefore, centroid-based clustering techniques generally fail to identify the data points that deviate from the normal distribution of the data to a great extent. Even before predictive models are prepared on data, outliers can result in misleading representations and in turn misleading interpretations of collected data. This is essentially not desirable for building efficient predictive and analytical models from data. <br><br>
You can consider the following two taller bars (than rest of the bars) as outliers in that particular data:
<center>
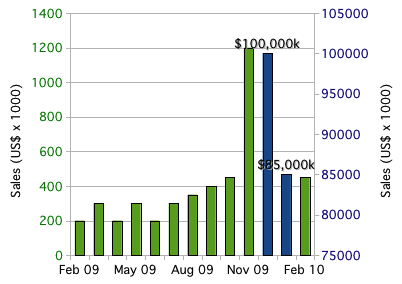
</center>
<h3>General introduction to density-based clustering technique:</h3>
Before discussing density-based clustering, you first need to cover a topic : ɛ-neighborhoods.
The general idea behind ɛ-neighborhoods is given a data point, you want to be able to reason about the data points in the space around it. Formally, for some real-valued ɛ > 0 and some point p, the ɛ-neighborhood of p is defined as the set of points that are at most distance ɛ away from p.
If you think back to geometry, the shape in which all points are equidistant from the center is the circle. In 2D space, the ɛ-neighborhood of a point p is the set of points contained in a circle of radius ɛ, centered at p. In 3D space, the ɛ-neighborhood is a sphere of radius ɛ, centered at p, and in higher dimensional space, the ɛ-neighborhood is just the [N-sphere](https://en.wikipedia.org/wiki/N-sphere) of radius ɛ, centered at p.
Let’s consider an example to make this idea more concrete.
In the image below 100 data points are scattered in the interval [1,3]X[2,4]. Let’s pick the point (3,2) to be our point p.
<center>

</center>
First, let’s consider the neighborhood of p with radius 0.5 (ɛ = 0.5), the set of points that are distance 0.5 away from p.
<center>

</center>
The opaque green oval represents our neighborhood, and there are 31 data points in this neighborhood. Since 100 data points were scattered and 31 are in the neighborhood, this means that a little under one-third of the data points are contained within the neighborhood of p with radius 0.5.
Now, let’s change our radius to 0.15 (ɛ = 0.15) and consider the resulting smaller neighborhood.
<center>

</center>
Now the neighborhood is shrunk a bit, so now only 3 data points are contained within it. By decreasing ɛ from 0.5 to 0.15 (a 70% reduction), the number of points is decreased in our neighborhood from 31 to 3 (a 90% reduction).
Now that you have a fair understanding of “neighborhood”, I will introduce the next important concept: the notion of a “density” for a neighborhood (You are proceeding towards learning “density-based clustering", after all).
In a grade-school science class, children are taught that density = mass/volume. Let’s use this idea of mass divided by volume to define density at some point p. If you consider some point p and its neighborhood of radius ɛ, you can define the mass of the neighborhood as the number of data points (or alternatively, the fraction of data points) contained within the neighborhood, and the volume of the neighborhood is volume of the resulting shape of the neighborhood. In the 2D case, the neighborhood is a circle, so the volume of the neighborhood is just the area of the resulting circle. In the 3D and higher dimensional case, the neighborhood is a sphere or n-sphere, so you can calculate the volume of this shape.
For example, let’s consider our neighborhood of p = (3,2) of radius 0.5 again.
<center>

</center>
The mass is the number of data points in the neighborhood, so mass = 31. The volume is the area of the circle, so volume = π0.5<sup>2</sup> = π/4. Therefore, our local density approximation at * p = (3,2) is calculated as density = mass/volume = 31/(π/4) = 124/π ~= 39.5.
This value is meaningless by itself, but if you calculate the local density approximation for all points in our dataset, you could cluster our points by saying that points that are nearby (contained in the same neighborhood) and have similar local density approximations belong in the same cluster. If you decrease the value of ɛ, you can construct smaller neighborhoods (less volume) that would also contain fewer data points. Ideally, you want to identify highly dense neighborhoods where most of the data points are contained in these neighborhoods, but the volume of each of these neighborhoods is relatively small.<br>
While this is not exactly what either DBSCAN or the Level Set Tree algorithm (another clustering technique belonging to the family of density-based clustering) does, it forms the general intuition behind density-based clustering.<br>
To recap, you covered the ɛ-neighborhoods and how they allow to reason about the space around a particular point. Then you learnt a notion of density at a particular point for a particular neighborhood. In the next section, you will get to know the DBSCAN algorithm where the ɛ-ball is a fundamental tool for defining clusters.
<h3>Inner workings of DBSCAN:</h3>
DBSCAN stands for Density-Based Spatial Clustering of Applications with Noise and it is hands down the most well-known density-based clustering algorithm. It was first introduced by first introduced in 1996 by [Ester et. al](http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.71.1980). Due to its importance in both theory and applications, this algorithm is one of three algorithms awarded the Test of Time Award at SIGKDD 2014.
Unlike K-Means, DBSCAN does not require the number of clusters as a parameter. Rather it infers the number of clusters based on the data, and it can discover clusters of arbitrary shape (for comparison, K-Means usually discovers spherical clusters). As you saw earlier, the ɛ-neighborhood is fundamental to DBSCAN to approximate local density, so the algorithm has two parameters:
* ɛ: The radius of our neighborhoods around a data point p.
* minPts: The minimum number of data points you want in a neighborhood to define a cluster.
Using these two parameters, DBSCAN categories the data points into three categories:
* Core Points: A data point p is a core point if Nbhd(p,ɛ) [ɛ-neighborhood of p] contains at least minPts ; |Nbhd(p,ɛ)| >= minPts.
* Border Points: A data point *q is a border point if Nbhd(q, ɛ) contains less than minPts data points, but q is reachable from some core point p.
* Outlier: A data point o is an outlier if it is neither a core point nor a border point. Essentially, this is the “other” class.
These definitions may seem abstract, so let’s cover what each one means in more detail.
<b>Core Points: </b><br>
Core Points are the foundations for our clusters are based on the density approximation I discussed in the previous section. You use the same ɛ to compute the neighborhood for each point, so the volume of all the neighborhoods is the same. However, the number of other points in each neighborhood is what differs. Recall that I said you can think of the number of data points in the neighborhood as its mass. The volume of each neighborhood is constant, and the mass of neighborhood is variable, so by putting a threshold on the minimum amount of mass needed to be core point, you are essentially setting a minimum density threshold. Therefore, core points are data points that satisfy a minimum density requirement. Our clusters are built around our core points (hence the core part), so by adjusting our minPts parameter, you can fine-tune how dense our clusters cores must be.
<b>Border Points:</b><br>
Border Points are the points in our clusters that are not core points. In the definition above for border points, I used the term density-reachable. I have not defined this term yet, but the concept is simple. To explain this concept, let’s revisit our neighborhood example with epsilon = 0.15. Consider the point r (the black dot) that is outside of the point p‘s neighborhood.
<center>

</center>
All the points inside the point p‘s neighborhood are said to be directly reachable from p. Now, let’s explore the neighborhood of point q, a point directly reachable from p. The yellow circle represents q‘s neighborhood.
<center>

</center>
Now while your target point r is not your starting point p‘s neighborhood, it is contained in the point q‘s neighborhood. This is the idea behind density-reachable: If you can get to the point r by jumping from neighborhood to neighborhood, starting at a point p, then the point r is density-reachable from the point p.
<center>

</center>
As an analogy, you can think of density-reachable points as being the “friends of a friend”. If the directly-reachable of a core point p are its “friends”, then the density-reachable points, points in neighborhood of the “friends” of p, are the “friends of its friends”. One thing that may not be clear is density-reachable points is not limited to just two adjacent neighborhood jumps. As long as you can reach the point doing “neighborhood jumps”, starting at a core point p, that point is density-reachable from p, so “friends of a friend of a friend … of a friend” are included as well. <br>
It is important to keep in mind that this idea of density-reachable is dependent on our value of ɛ. By picking larger values of ɛ, more points become density-reachable, and by choosing smaller values of ɛ, fewer points become density-reachable.
<b>Outliers:</b><br>
Finally, you get to the “other” class. Outliers are points that are neither core points nor are they close enough to a cluster to be density-reachable from a core point. Outliers are not assigned to any cluster and, depending on the context, may be considered anomalous points.
<h3>Case study of DBSCAN in Python:</h3><br>
DBSCAN is already beautifully implemented in the popular Python machine learning library *Scikit-Learn*, and because this implementation is scalable and well-tested, you will be using it to see how DBSCAN works in practice.
The steps to the DBSCAN algorithm are:
* Pick a point at random that has not been assigned to a cluster or been designated as an outlier. Compute its neighborhood to determine if it’s a core point. If yes, start a cluster around this point. If no, label the point as an outlier.
* Once we find a core point and thus a cluster, expand the cluster by adding all directly-reachable points to the cluster. Perform “neighborhood jumps” to find all density-reachable points and add them to the cluster. If an outlier is added, change that point’s status from outlier to border point.
* Repeat these two steps until all points are either assigned to a cluster or designated as an outlier.
For this case study purpose you will be using [a dataset consisting of annual customer data for a wholesale distributor](https://archive.ics.uci.edu/ml/datasets/Wholesale+customers).
So, let's get started.
```
# Let's import all your dependencies first
from sklearn.cluster import DBSCAN
from sklearn.preprocessing import StandardScaler
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
```
The dataset consists of 440 customers and has 8 attributes for each of these customers. You will use the Pandas library to import the .csv file and convert it into a DataFrame object.
Now while importing your .csv file into the , make sure you supply the accurate path of that file.
```
# Import .csv file and convert it to a DataFrame object
df = pd.read_csv("C:/Users/Sayak/data/customers.csv");
print(df.head())
```
Now before proceeding any further with applying DBSCAN, it is very important that you know the data well so as know what kind of data is in the dataset, what distribution the data follows, and which features are numerical or not.
According to the description given in the official [UCI machine learning repository of this dataset](https://archive.ics.uci.edu/ml/datasets/wholesale+customers), information about the features of the dataset is as follows:
<li>
FRESH: annual spending (m.u.) on fresh products (Continuous); </li>
<li>MILK: annual spending (m.u.) on milk products (Continuous); </li>
<li>GROCERY: annual spending (m.u.)on grocery products (Continuous); </li>
<li>FROZEN: annual spending (m.u.)on frozen products (Continuous) </li>
<li>DETERGENTS_PAPER: annual spending (m.u.) on detergents and paper products (Continuous) </li>
<li>DELICATESSEN: annual spending (m.u.)on and delicatessen products (Continuous); </li>
<li>CHANNEL: customers’ Channel - Horeca (Hotel/Restaurant/Café) or Retail channel (Nominal)
REGION
</li>
Now that you know about the features about the dataset, let's display some stats of the data.
```
print(df.info())
```
As you can see from the above output, there is no missing value in the dataset and all the data is *integer* in type. This reduces the burden of further preprocessing the data. Let's dig a bit more.
```
print(df.describe())
```
From the above output, you can derive all the necessary statistical measures like standard deviation, mean, max of each and every feature present in the dataset. You can see most of the data in this dataset is *[continuous](https://stats.stackexchange.com/questions/206/what-is-the-difference-between-discrete-data-and-continuous-data)* in nature except for two features: Channel and Region. So for easing your computations, you will drop these two:
```
df.drop(["Channel", "Region"], axis = 1, inplace = True)
# Let's get a view of the data after the drop
print(df.head())
```
So you can visualize the data, for that you are going to use two of the features:
* Groceries: The customer’s annual spending (in some monetary unit) on grocery products.
* Milk: The customer’s annual spending (in some monetary unit) on milk products.
```
# Let's plot the data now
x = df['Grocery']
y = df['Milk']
plt.scatter(x,y)
plt.xlabel("Groceries")
plt.ylabel("Milk")
plt.show()
```
Let's brief about the functions that you used for the plotting purpose:
plt.scatter() : This function actually creates the scatter plot based on the data (as parameters that you supply [*x* and *y*]).
plt.xlabel() : It helps you to put a label along the *X-axis*. (*Groceries* in this case)
plt.ylabel() : It helps you to put a label along the *Y-axis*. (*Milk* in this case)
plt.show() : After the plot is created, this function helps you to display it as the output.
You should really explore the beautiful world of *Matplotlib* for all your visualization purposes. Its [documentation](https://matplotlib.org/) is absolutely awesome.
You can easily spot the data points that are far astray. Right? Well, those are your outliers.
With DBSCAN, we want to identify this main cluster of customers, but we also want to flag customers with more unusual annual purchasing habits as outliers.
Because the values of the data are in the thousands, you are going to normalize each attribute by scaling it to 0 mean and unit variance. What is does basically is it helps to keep the inter-relationships between the features intact so that a small change in one feature would reflect in the other.
```
df = df[["Grocery", "Milk"]]
df = df.as_matrix().astype("float32", copy = False)
stscaler = StandardScaler().fit(df)
df = stscaler.transform(df)
```
You will construct a DBSCAN object that requires a minimum of 15 data points in a neighborhood of radius 0.5 to be considered a core point.
```
dbsc = DBSCAN(eps = .5, min_samples = 15).fit(df)
```
Next, we can extract our cluster labels and outliers to plot our results.
```
labels = dbsc.labels_
core_samples = np.zeros_like(labels, dtype = bool)
core_samples[dbsc.core_sample_indices_] = True
```

Lining up with the intuition, the DBSCAN algorithm was able to identify one cluster of customers who are around the mean grocery and mean milk product purchases. In addition, it was able to flag customers whose annual purchasing behavior deviated too heavily from other customers.
Because the outliers corresponded to customers with more extreme purchasing behavior, the wholesale distributor could specifically target these customers with exclusive discounts to encourage larger purchases.
<h3>Real life applications of DBSCAN:</h3>
* Suppose we have an e-commerce and we want to improve our sales by recommending relevant products to our customers. We don’t know exactly what our customers are looking for but based on a data set we can predict and recommend a relevant product to a specific customer. We can apply the DBSCAN to our data set (based on the e-commerce database) and find clusters based on the products that the users have bought. Using this clusters we can find similarities between customers, for example, if customer A has bought a pen, a book and one pair scissors, while customer B purchased a book and one pair of scissors, then you could recommend a pen to customer B.
* Before the rise of deep learning based advanced methodologies, researchers used DBSCAN in order to segregate genes from a genes dataset that had the chance of mediating cancer.
* Scientists have used DBSCAN in order to detect the stops in the trajectory data generated from mobile GPS devices. Stops represent the most meaningful and most important part of a trajectory.
<h3>Conclusion:</h3>
So, in this blogpost you got to know about the prime disadvantages of centroid-based clustering and got familiar with another family of clustering techniques i.e. density-based clustering. You also saw how they overcome the shortcomings of centroid-based clustering.
You learnt how DBSCAN works and also did a case study of it. Besides, you got a fair overview of the real life problems where DBSCAN has been incorporated for solving them. As a further reading, I would really recommend you all go through the other density-based clustering methods like *Level Set Tree clustering* and how it is different from DBSCAN.
<h4>References:</h4>
* Martin Ester, Hans-Peter Kriegel, Jörg Sander, and Xiaowei Xu. 1996. A density-based algorithm for discovering clusters a density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the Second International Conference on Knowledge Discovery and Data Mining (KDD'96), Evangelos Simoudis, Jiawei Han, and Usama Fayyad (Eds.). AAAI Press 226-231.
* https://towardsdatascience.com/how-dbscan-works-and-why-should-i-use-it-443b4a191c80
* https://www.coursera.org/learn/predictive-analytics/lecture/EVHfy/dbscan
|
github_jupyter
|
```
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from PIL import Image
from IPython.display import Image as im
%matplotlib inline
data = pd.read_csv("../data/StockX-Data-Consolidated.csv")
data['week_since_release'] = (data['Days Since Release']/7).round(1)
data.columns[21:32]
## Get brands and regions
def get_brand(row):
for brand in data.columns[4:14]:
if row[brand] == 1:
return brand
def get_region(row):
for region in data.columns[14:20]:
if row[region] == 1:
return region
def get_col(row):
for color in data.columns[21:32]:
if row[color] == 1:
return color
data['brand'] = data.apply(get_brand, axis=1)
data['region'] = data.apply(get_region, axis=1)
data['color'] = data.apply(get_col, axis=1)
timing = data[['Days Since Release',"week_since_release",'region', "brand",'color','Pct_change']]
timing = timing.rename(columns = {'Days Since Release':"days_since_release"})
np.random.seed(19680801)
N = 99956
colors = np.random.rand(N)
area = (50 * np.random.rand(N))**2
plt.scatter(x = timing['week_since_release'], y = timing['Pct_change'], c=colors, alpha=0.5)
plt.title('Price premium on Weeks since release')
plt.xlabel('weeks since release')
plt.ylabel('price premium')
plt.show()
timing.drop_duplicates(["week_since_release",'region'], inplace=True)
pivot = timing.pivot(index='region', columns='week_since_release', values='Pct_change',)
ax = sns.heatmap(pivot,annot=True,cmap = 'YlGnBu')
plt.show()
df1 = timing[["week_since_release",'region','Pct_change']]
heatmap1_data = pd.pivot_table(df1,values='Pct_change', index=['region'], columns='week_since_release')
heatmap1_data.head(n=5)
sns.heatmap(heatmap1_data, cmap="BuGn")
fig, ax = plt.subplots()
sc = ax.scatter(timing.region,timing.week_since_release, c=timing.Pct_change, cmap="YlGnBu")
fig.colorbar(sc, ax=ax)
plt.show()
fig, ax = plt.subplots()
sc = ax.scatter(timing.brand,timing.week_since_release, c=timing.Pct_change, cmap="YlGnBu")
fig.colorbar(sc, ax=ax)
plt.figure(figsize=(20, 60))
plt.show()
```
## Nike off-white days/weeks since release
```
offwhite= timing.loc[timing['brand'] != 'yeezy']
ow_nowhite = offwhite.loc[offwhite['color'] != 'White']
ow_white = offwhite.loc[offwhite['color'] == 'White']
ow_color = ow_nowhite.groupby(['color'])
img = plt.imread('../data/media/nike.jpg')
# Plot
fig, ax = plt.subplots()
ax.imshow(img, aspect='auto', extent=(-80, 800, 0, 8), zorder=-1,alpha = 0.5)
ax.yaxis.tick_left()
#ax.margins(0.05) # Optional, just adds 5% padding to the autoscaling
cmap1 = sns.color_palette("Paired")
cmap2 = sns.color_palette("Set2")
colors = [cmap1[1],cmap2[-1],cmap1[7],cmap1[4],'brown']
for i, (name, group) in enumerate(ow_color):
ax.plot(group.days_since_release, group.Pct_change, marker='o', linestyle='',
c = colors[i], ms=4, label=name, alpha = 0.2)
ax.spines['bottom'].set_color('white')
ax.xaxis.label.set_color('white')
ax.tick_params(axis='x', colors='white')
ax.spines['left'].set_color('white')
ax.yaxis.label.set_color('white')
ax.tick_params(axis='y', colors='white')
#ax.patch.set_visible(False)
plt.title('Nike: Off-White', fontsize = 'large', color = 'white' )
plt.xlabel('Days Since Release', color = 'white' )
plt.ylabel('Price Premium', color = 'white')
plt.legend()
plt.show()
offwhite['brand'].value_counts(sort=True, ascending=False, bins=None, dropna=True)
## Nike Off white Blazer
aj = offwhite.loc[offwhite['brand'] == 'airjordan']
aj_color = aj.groupby(['color'])
presto = offwhite.loc[offwhite['brand'] == 'presto']
presto_color = presto.groupby(['color'])
zoom = offwhite.loc[offwhite['brand'] == 'zoom']
zoom_color = zoom.groupby(['color'])
blazer = offwhite.loc[offwhite['brand'] == 'blazer']
blazer_color = blazer.groupby(['color'])
af = offwhite.loc[offwhite['brand'] == 'airforce']
af_color = af.groupby(['color'])
# AJ Plot
fig, ax = plt.subplots()
ax.imshow(img, aspect='auto', extent=(-20, 500, -2, 8), zorder=-1,alpha = 0.4)
ax.yaxis.tick_left()
#ax.margins(0.05) # Optional, just adds 5% padding to the autoscaling
cmap1 = sns.color_palette("Paired")
cmap2 = sns.color_palette("Set2")
colors = [cmap1[0],cmap2[-1],cmap1[7],cmap1[4],'brown']
for i, (name, group) in enumerate(aj_color):
ax.plot(group.days_since_release, group.Pct_change, marker='o', linestyle='',
c = colors[i], ms=4, label=name, alpha = 0.4)
plt.title('Nike: Off-White Air Jordan', fontsize = 'large', color = 'white')
plt.xlabel('Days Since Release', color = 'white')
plt.ylabel('Price Premium', color = 'white')
ax.spines['bottom'].set_color('white')
ax.xaxis.label.set_color('white')
ax.tick_params(axis='x', colors='white')
ax.spines['left'].set_color('white')
ax.yaxis.label.set_color('white')
ax.tick_params(axis='y', colors='white')
plt.legend()
plt.show()
# Zoom Plot
fig, ax = plt.subplots()
ax.imshow(img, aspect='auto', extent=(-20, 500, -2, 8), zorder=-1,alpha = 0.4)
ax.yaxis.tick_left()
#ax.margins(0.05) # Optional, just adds 5% padding to the autoscaling
cmap1 = sns.color_palette("Paired")
cmap2 = sns.color_palette("Set2")
colors = [cmap1[1],cmap1[7],cmap1[4],cmap1[0]]
for i, (name, group) in enumerate(zoom_color):
ax.plot(group.days_since_release, group.Pct_change, marker='o', linestyle='',
c = colors[i], ms=4, label=name, alpha = 0.3)
plt.title('Nike: Off-White Zoom', fontsize = 'large', color = 'white')
plt.xlabel('Days Since Release', color = 'white')
plt.ylabel('Price Premium', color = 'white')
ax.spines['bottom'].set_color('white')
ax.xaxis.label.set_color('white')
ax.tick_params(axis='x', colors='white')
ax.spines['left'].set_color('white')
ax.yaxis.label.set_color('white')
ax.tick_params(axis='y', colors='white')
plt.legend()
plt.show()
# Presto Plot
fig, ax = plt.subplots()
ax.imshow(img, aspect='auto', extent=(-20, 500, 0, 8), zorder=-1,alpha = 0.4)
ax.yaxis.tick_left()
#ax.margins(0.05) # Optional, just adds 5% padding to the autoscaling
cmap1 = sns.color_palette("Paired")
cmap2 = sns.color_palette("Set2")
colors = [cmap1[1],cmap1[0],cmap1[7],cmap1[4],'brown']
for i, (name, group) in enumerate(presto_color):
ax.plot(group.days_since_release, group.Pct_change, marker='o', linestyle='',
c = colors[i], ms=4, label=name, alpha = 0.3)
plt.title('Nike: Off-White Presto', fontsize = 'large', color = 'white')
plt.xlabel('Days Since Release', color = 'white')
plt.ylabel('Price Premium', color = 'white')
ax.spines['bottom'].set_color('white')
ax.xaxis.label.set_color('white')
ax.tick_params(axis='x', colors='white')
ax.spines['left'].set_color('white')
ax.yaxis.label.set_color('white')
ax.tick_params(axis='y', colors='white')
plt.legend()
plt.show()
# Blazer Plot
fig, ax = plt.subplots()
ax.imshow(img, aspect='auto', extent=(-20, 500, 0, 8), zorder=-1,alpha = 0.4)
ax.yaxis.tick_left()
#ax.margins(0.05) # Optional, just adds 5% padding to the autoscaling
cmap1 = sns.color_palette("Paired")
cmap2 = sns.color_palette("Set2")
colors = [cmap1[1],cmap1[0],cmap1[7],cmap1[0]]
for i, (name, group) in enumerate(blazer_color):
ax.plot(group.days_since_release, group.Pct_change, marker='o', linestyle='',
c = colors[i], ms=4, label=name, alpha = 0.3)
plt.title('Nike: Off-White Blazer', fontsize = 'large', color = 'white')
plt.xlabel('Days Since Release', color = 'white')
plt.ylabel('Price Premium', color = 'white')
ax.spines['bottom'].set_color('white')
ax.xaxis.label.set_color('white')
ax.tick_params(axis='x', colors='white')
ax.spines['left'].set_color('white')
ax.yaxis.label.set_color('white')
ax.tick_params(axis='y', colors='white')
plt.legend()
plt.show()
aj = offwhite.loc[offwhite['brand'] == 'airjordan']
aj_color = aj.groupby(['color'])
# Presto Plot
fig, ax = plt.subplots()
ax.imshow(img, aspect='auto', extent=(-20, 500, 0, 8), zorder=-1,alpha = 0.4)
ax.yaxis.tick_left()
#ax.margins(0.05) # Optional, just adds 5% padding to the autoscaling
cmap1 = sns.color_palette("Paired")
cmap2 = sns.color_palette("Set2")
colors = [cmap1[1],cmap1[0],cmap1[7],cmap1[4],'brown']
for i, (name, group) in enumerate(presto_color):
ax.plot(group.days_since_release, group.Pct_change, marker='o', linestyle='',
c = colors[i], ms=4, label=name, alpha = 0.2)
plt.title('Nike: Off-White Presto', fontsize = 'large')
plt.xlabel('Days Since Release')
plt.ylabel('Price Premium')
ax.spines['bottom'].set_color('white')
ax.xaxis.label.set_color('white')
ax.tick_params(axis='x', colors='white')
ax.spines['left'].set_color('white')
ax.yaxis.label.set_color('white')
ax.tick_params(axis='y', colors='white')
plt.legend()
plt.show()
aj.shape
np.random.seed(19680801)
N = 5703
colors = np.random.rand(N)
area = (50 * np.random.rand(N))**2
plt.scatter(x = aj['week_since_release'], y = aj['Pct_change'], c=colors, alpha=0.5)
plt.title('AJ: Price premium on Weeks since release')
plt.xlabel('weeks since release')
plt.ylabel('price premium')
plt.show()
np.random.seed(19680801)
N = 3622
colors = np.random.rand(N)
area = (50 * np.random.rand(N))**2
plt.scatter(x = blazer['week_since_release'], y = blazer['Pct_change'], c=colors, alpha=0.5)
plt.title('Blazer: Price premium on Weeks since release')
plt.xlabel('weeks since release')
plt.ylabel('price premium')
plt.show()
```
## Yeezy days/weeks since release
```
timing.brand.unique()
yeezy= timing.loc[timing['brand'] == 'yeezy']
img2 = plt.imread('../data/media/yeezy.jpg')
yeezy.color.unique()
yeezy_color = yeezy.groupby(['color'])
# Plot
fig, ax = plt.subplots()
ax.imshow(img2, aspect='auto', extent=(-5, 1500, -2, 12), zorder=-1,alpha = 0.5)
ax.yaxis.tick_left()
#ax.margins(0.05) # Optional, just adds 5% padding to the autoscaling
cmap1 = sns.color_palette("Paired")
cmap2 = sns.color_palette("Set2")
colors = [cmap1[1],cmap2[-1],cmap1[-1],cmap1[4],cmap1[0]]
for i, (name, group) in enumerate(yeezy_color):
ax.plot(group.days_since_release, group.Pct_change, marker='o', linestyle='',
c = colors[i], ms=4, label=name, alpha = 0.3)
plt.title('Adidas: Yeezy', fontsize = 'large')
plt.xlabel('Days Since Release')
plt.ylabel('Price Premium')
plt.legend()
plt.show()
yeezy.shape
np.random.seed(19680801)
N = 72162
colors = np.random.rand(N)
area = (50 * np.random.rand(N))**2
plt.scatter(x = yeezy['week_since_release'], y = yeezy['Pct_change'], c=colors, alpha=0.5)
plt.title('Yeezy: Price premium on Weeks since release')
plt.xlabel('weeks since release')
plt.ylabel('price premium')
plt.show()
```
|
github_jupyter
|
# EDA classification
aim: When will a project succeed?
Which features influence the success of a project?
#### assumptions
* the higher the goal, the lower the probability for success
* the longer the duration the higher the probability for success
* the longer the preparation time the higher the probability for success
* the month of launch influences the probability for success
* the country influences the probability for success
* pledged amount per backer influences the probability for success
```
# import packages
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
# read dataframe in
df = pd.read_csv('data/kickstarter_preprocess.csv')
# first summary
df.shape
df.info()
df.describe()
df.head()
# overview how many projects were successful, failed, canceled
df['state'].hist();
# make three new dataframes: one for success, one for failed and the last for canceled
df_suc = df.query('state == "successful"')
df_fai = df.query('state == "failed"')
df_can = df.query('state == "canceled"')
```
### assumption 1: the higher the goal, the lower the probability for success
```
plt.boxplot(df_suc['goal'])
plt.yscale('log');
df_suc.query('goal < 1').shape
df_suc.query('goal >= 500000').shape
# remove outlier
#df_suc.drop(df_suc[df_suc['goal'] > 100000].index, inplace=True)
df_suc1 = df_suc.query('goal <= 1500')
#plt.boxplot(df_suc1['goal'])
df_suc1.shape
df_suc2 = df_suc.query('1500 < goal < 7000')
#plt.boxplot(df_suc2['goal'])
df_suc2.shape
df_suc3 = df_suc.query('goal >= 7000')
#plt.boxplot(df_suc3['goal'])
df_suc3.shape
df_fai1 = df_fai.query('goal <= 1500')
df_fai1.shape
df_fai2 = df_fai.query('1500 < goal < 7000')
df_fai2.shape
df_fai3 = df_fai.query('goal >= 7000')
df_fai3.shape
df_can1 = df_can.query('goal <= 1500')
df_can1.shape
df_can2 = df_can.query('1500 < goal < 7000')
df_can2.shape
df_can3 = df_can.query('goal >= 7000')
df_can3.shape
# making a categorical variable for goal 0='goal <= 1500' 1='1500 < goal < 7000', 2='goal >= 7000'
#df.loc[df['goal'] <= 1500, 'goal_split'] = 0
#df.loc[(df['goal'] > 1500) & (df['goal'] < 7000), 'goal_split'] = 1
#df.loc[df['goal'] >= 7000, 'goal_split'] = 2
#sns.barplot(x='goal_split', y=None, hue="state", data=df)
# set width of bar
barWidth = 0.25
fig = plt.subplots(figsize =(12, 8))
# set height of bar
suc = [29467, 35129, 29650]
fai = [13763, 22526, 37909]
can = [1656, 2502, 4460]
# Set position of bar on X axis
br1 = np.arange(3)
br2 = [x + barWidth for x in br1]
br3 = [x + barWidth for x in br2]
p1 = plt.bar(br1, suc, color ='g', width = barWidth,
edgecolor ='grey', tick_label ='success')
p2 = plt.bar(br2, fai, color ='r', width = barWidth,
edgecolor ='grey', tick_label ='failed')
p3 = plt.bar(br3, can, color ='b', width = barWidth,
edgecolor ='grey', tick_label ='canceled')
# Adding Xticks
plt.xlabel('goal_split', fontweight ='bold')
plt.ylabel('count', fontweight ='bold')
plt.xticks([r + barWidth for r in range(3)],
['goal <= 1500', '1500 < goal < 7000', 'goal >= 7000'])
plt.legend((p1[0], p2[0], p3[0]), ('success', 'failed', 'canceled'))
plt.show()
#df1 = df.query('goal <= 1500')
#df2 = df.query('1500 < goal < 7000')
#df3 = df.query('goal >= 7000')
```
## conclucsion
the lower the goal the higher the probability for success
```
sns.violinplot(x ="state", y ="goal", data = df_suc);
var1 = 'state'
data1 = pd.concat([df_suc['goal'], df_suc[var1]], axis=1)
f, ax = plt.subplots(figsize=(8, 6))
fig1 = sns.violinplot(x=var1, y="goal", data=data1, scale="count")
fig1.axis(ymin=0, ymax=100000);
#plt.yscale('log')
df.query('goal <= 1').shape
df.query('goal >= 1000000').shape
df.query('goal >= 1000000 and state == "successful"').shape
sta_dur = df.plot(x='state',
y='duration_days',
kind='scatter')
```
### assumption 2: the longer the duration the higher the probability for success
```
plt.boxplot(df['duration_days']);
dur = [df.query('duration_days <= 20').shape, df.query('20 < duration_days <= 30').shape,
df.query('30 < duration_days <= 40').shape, df.query('duration_days > 40').shape]
dur
dur1 = [df_suc.query('duration_days <= 20').shape, df_suc.query('20 < duration_days <= 30').shape,
df_suc.query('30 < duration_days <= 40').shape, df_suc.query('duration_days > 40').shape]
dur1
dur2 = [df_fai.query('duration_days <= 20').shape, df_fai.query('20 < duration_days <= 30').shape,
df_fai.query('30 < duration_days <= 40').shape, df_fai.query('duration_days > 40').shape]
dur2
dur3 = [df_can.query('duration_days <= 20').shape, df_can.query('20 < duration_days <= 30').shape,
df_can.query('30 < duration_days <= 40').shape, df_can.query('duration_days > 40').shape]
dur3
# set width of bar
barWidth = 0.25
fig = plt.subplots(figsize =(12, 8))
# set height of bar
suc = [12052, 55097, 15513, 12116]
fai = [6150, 43036, 8119, 16893]
can = [653, 4661, 1163, 2141]
# Set position of bar on X axis
br1 = np.arange(4)
br2 = [x + barWidth for x in br1]
br3 = [x + barWidth for x in br2]
p1 = plt.bar(br1, suc, color ='g', width = barWidth,
edgecolor ='grey', tick_label ='success')
p2 = plt.bar(br2, fai, color ='r', width = barWidth,
edgecolor ='grey', tick_label ='failed')
p3 = plt.bar(br3, can, color ='b', width = barWidth,
edgecolor ='grey', tick_label ='canceled')
# Adding Xticks
plt.xlabel('goal_split', fontweight ='bold')
plt.ylabel('count', fontweight ='bold')
plt.xticks([r + barWidth for r in range(4)],
['duration_days <= 20', '20 < duration_days <= 30', '30 < duration_days <= 40', 'duration_days > 40'])
plt.legend((p1[0], p2[0], p3[0]), ('success', 'failed', 'canceled'))
plt.show()
```
### assumption 3: the longer the preparation time the higher the probability for success
### assumption 4: the month of launch influences the probability for success
```
sta_month = df.plot(x='launched_month',
y='state',
kind='scatter')
# boxplot sqft_living (small houses, big houses, bad neighborhood)
fig, axes = plt.subplots(ncols=3,sharex=True,sharey=True,figsize=(9,6))
ax1 = df_suc.boxplot(column=['duration_days'],ax=axes[0])
ax1.set_title("duration_days successful", fontsize = 10)
ax1.set_ylabel("count");
ax2 = df_fai.boxplot(column=['duration_days'],ax=axes[1])
ax2.set_title("duration_days failed", fontsize = 10);
ax3 = df_can.boxplot(column=['duration_days'],ax=axes[2]);
ax3.set_title("duration_days canceled", fontsize = 10);
df_suc['duration_days'].mean(), df_suc['duration_days'].median()
df_fai['duration_days'].mean(), df_fai['duration_days'].median()
df_can['duration_days'].mean(), df_can['duration_days'].median()
df.groupby('state').count()['successful']
```
### assumption 5: the country influences the probability for success
```
cou_suc = df_suc.groupby(['country'])['country'].count()
cou_fai = df_fai.groupby(['country'])['country'].count()
cou_can = df_can.groupby(['country'])['country'].count()
pd.merge(cou_suc, cou_fai, cou_can, on=['country'],suffixes=[' successful', ' failed', ' canceled'])
#df['country'].unique()
cou_can
fig, axes = plt.subplots(ncols=3,sharex=True,sharey=True,figsize=(15,6))
ax1 = cou_suc.hist(column=['country'],ax=axes[0])
axes[0].set_title('country successful')
axes[0].set_xlabel('country')
axes[0].set_ylabel('count')
ax2 = cou_fai.hist(column=['country'],ax=axes[1])
axes[1].set_title('country failed')
axes[1].set_xlabel('country')
axes[1].set_ylabel('count')
ax3 = cou_can.hist(column=['country'],ax=axes[2])
axes[2].set_title('country canceled')
axes[2].set_xlabel('country')
axes[2].set_ylabel('count');
cou_suc.plot(kind='bar');
cou_fai.plot(kind='bar');
cou_can.plot(kind='bar');
cou = df_suc.groupby('country')['country'].count()
cou = list(cou)
cou1 = df['country'].unique()
# Creating plot
fig = plt.figure(figsize =(10, 7))
plt.pie(cou, labels = cou1)
# show plot
plt.show()
country_suc = df_suc.groupby(df_suc['country'])
#pledged = amt_pledged.sum().sort_values(ascending=0)[0:10]
ax = country_suc.plot(kind="bar")
ax.set_title("Amount by Country")
ax.set_ylabel("Amount")
ax.set_xlabel("Country")
vals = ax.get_yticks()
```
### assumption 6: pledged amount per backer influences the probability for success
```
df.groupby('state').pledged_per_backer.mean()
df_suc.groupby('staff_pick').count()
df_fai.groupby('staff_pick').count()
df_can.groupby('staff_pick').count()
df_suc['cat_in_slug'].hist()
df_fai['cat_in_slug'].hist()
df_can['cat_in_slug'].hist()
sns.catplot(x = "cat_in_slug", kind = 'count', hue="state", data=df);
#sns.barplot(x='cat_in_slug', hue='state', data=df)
#df.groupby('cat_in_slug').plot(x='state', kind='bar')
```
|
github_jupyter
|
Copyright (c) Microsoft Corporation. All rights reserved.
Licensed under the MIT License.
# AutoML 06: Custom CV Splits and Handling Sparse Data
In this example we use the scikit-learn's [20newsgroup](http://scikit-learn.org/stable/modules/generated/sklearn.datasets.fetch_20newsgroups.html) to showcase how you can use AutoML for handling sparse data and how to specify custom cross validations splits.
Make sure you have executed the [00.configuration](00.configuration.ipynb) before running this notebook.
In this notebook you will learn how to:
1. Create an `Experiment` in an existing `Workspace`.
2. Configure AutoML using `AutoMLConfig`.
4. Train the model.
5. Explore the results.
6. Test the best fitted model.
In addition this notebook showcases the following features
- **Custom CV** splits
- Handling **sparse data** in the input
## Create an Experiment
As part of the setup you have already created an Azure ML `Workspace` object. For AutoML you will need to create an `Experiment` object, which is a named object in a `Workspace` used to run experiments.
```
import logging
import os
import random
from matplotlib import pyplot as plt
from matplotlib.pyplot import imshow
import numpy as np
import pandas as pd
from sklearn import datasets
import azureml.core
from azureml.core.experiment import Experiment
from azureml.core.workspace import Workspace
from azureml.train.automl import AutoMLConfig
from azureml.train.automl.run import AutoMLRun
ws = Workspace.from_config()
# choose a name for the experiment
experiment_name = 'automl-local-missing-data'
# project folder
project_folder = './sample_projects/automl-local-missing-data'
experiment = Experiment(ws, experiment_name)
output = {}
output['SDK version'] = azureml.core.VERSION
output['Subscription ID'] = ws.subscription_id
output['Workspace'] = ws.name
output['Resource Group'] = ws.resource_group
output['Location'] = ws.location
output['Project Directory'] = project_folder
output['Experiment Name'] = experiment.name
pd.set_option('display.max_colwidth', -1)
pd.DataFrame(data=output, index=['']).T
```
## Diagnostics
Opt-in diagnostics for better experience, quality, and security of future releases.
```
from azureml.telemetry import set_diagnostics_collection
set_diagnostics_collection(send_diagnostics = True)
```
## Creating Sparse Data
```
from sklearn.datasets import fetch_20newsgroups
from sklearn.feature_extraction.text import HashingVectorizer
from sklearn.model_selection import train_test_split
remove = ('headers', 'footers', 'quotes')
categories = [
'alt.atheism',
'talk.religion.misc',
'comp.graphics',
'sci.space',
]
data_train = fetch_20newsgroups(subset = 'train', categories = categories,
shuffle = True, random_state = 42,
remove = remove)
X_train, X_validation, y_train, y_validation = train_test_split(data_train.data, data_train.target, test_size = 0.33, random_state = 42)
vectorizer = HashingVectorizer(stop_words = 'english', alternate_sign = False,
n_features = 2**16)
X_train = vectorizer.transform(X_train)
X_validation = vectorizer.transform(X_validation)
summary_df = pd.DataFrame(index = ['No of Samples', 'No of Features'])
summary_df['Train Set'] = [X_train.shape[0], X_train.shape[1]]
summary_df['Validation Set'] = [X_validation.shape[0], X_validation.shape[1]]
summary_df
```
## Configure AutoML
Instantiate an `AutoMLConfig` object to specify the settings and data used to run the experiment.
|Property|Description|
|-|-|
|**task**|classification or regression|
|**primary_metric**|This is the metric that you want to optimize. Classification supports the following primary metrics: <br><i>accuracy</i><br><i>AUC_weighted</i><br><i>balanced_accuracy</i><br><i>average_precision_score_weighted</i><br><i>precision_score_weighted</i>|
|**max_time_sec**|Time limit in seconds for each iteration.|
|**iterations**|Number of iterations. In each iteration AutoML trains a specific pipeline with the data.|
|**preprocess**|Setting this to *True* enables AutoML to perform preprocessing on the input to handle *missing data*, and to perform some common *feature extraction*.<br>**Note:** If input data is sparse, you cannot use *True*.|
|**X**|(sparse) array-like, shape = [n_samples, n_features]|
|**y**|(sparse) array-like, shape = [n_samples, ], [n_samples, n_classes]<br>Multi-class targets. An indicator matrix turns on multilabel classification. This should be an array of integers.|
|**X_valid**|(sparse) array-like, shape = [n_samples, n_features] for the custom validation set.|
|**y_valid**|(sparse) array-like, shape = [n_samples, ], [n_samples, n_classes]<br>Multi-class targets. An indicator matrix turns on multilabel classification for the custom validation set.|
|**path**|Relative path to the project folder. AutoML stores configuration files for the experiment under this folder. You can specify a new empty folder.|
```
automl_config = AutoMLConfig(task = 'classification',
debug_log = 'automl_errors.log',
primary_metric = 'AUC_weighted',
max_time_sec = 3600,
iterations = 5,
preprocess = False,
verbosity = logging.INFO,
X = X_train,
y = y_train,
X_valid = X_validation,
y_valid = y_validation,
path = project_folder)
```
## Train the Model
Call the `submit` method on the experiment object and pass the run configuration. Execution of local runs is synchronous. Depending on the data and the number of iterations this can run for a while.
In this example, we specify `show_output = True` to print currently running iterations to the console.
```
local_run = experiment.submit(automl_config, show_output=True)
```
## Explore the Results
#### Widget for Monitoring Runs
The widget will first report a "loading" status while running the first iteration. After completing the first iteration, an auto-updating graph and table will be shown. The widget will refresh once per minute, so you should see the graph update as child runs complete.
**Note:** The widget displays a link at the bottom. Use this link to open a web interface to explore the individual run details.
```
from azureml.train.widgets import RunDetails
RunDetails(local_run).show()
```
#### Retrieve All Child Runs
You can also use SDK methods to fetch all the child runs and see individual metrics that we log.
```
children = list(local_run.get_children())
metricslist = {}
for run in children:
properties = run.get_properties()
metrics = {k: v for k, v in run.get_metrics().items() if isinstance(v, float)}
metricslist[int(properties['iteration'])] = metrics
rundata = pd.DataFrame(metricslist).sort_index(1)
rundata
```
### Retrieve the Best Model
Below we select the best pipeline from our iterations. The `get_output` method on `automl_classifier` returns the best run and the fitted model for the last invocation. Overloads on `get_output` allow you to retrieve the best run and fitted model for *any* logged metric or for a particular *iteration*.
```
best_run, fitted_model = local_run.get_output()
```
#### Best Model Based on Any Other Metric
Show the run and the model which has the smallest `accuracy` value:
```
# lookup_metric = "accuracy"
# best_run, fitted_model = local_run.get_output(metric = lookup_metric)
```
#### Model from a Specific Iteration
Show the run and the model from the third iteration:
```
# iteration = 3
# best_run, fitted_model = local_run.get_output(iteration = iteration)
```
### Register the Fitted Model for Deployment
```
description = 'AutoML Model'
tags = None
local_run.register_model(description = description, tags = tags)
local_run.model_id # Use this id to deploy the model as a web service in Azure.
```
### Testing the Fitted Model
```
# Load test data.
import sklearn
from pandas_ml import ConfusionMatrix
remove = ('headers', 'footers', 'quotes')
categories = [
'alt.atheism',
'talk.religion.misc',
'comp.graphics',
'sci.space',
]
data_test = fetch_20newsgroups(subset = 'test', categories = categories,
shuffle = True, random_state = 42,
remove = remove)
vectorizer = HashingVectorizer(stop_words = 'english', alternate_sign = False,
n_features = 2**16)
X_test = vectorizer.transform(data_test.data)
y_test = data_test.target
# Test our best pipeline.
y_pred = fitted_model.predict(X_test)
y_pred_strings = [data_test.target_names[i] for i in y_pred]
y_test_strings = [data_test.target_names[i] for i in y_test]
cm = ConfusionMatrix(y_test_strings, y_pred_strings)
print(cm)
cm.plot()
```
|
github_jupyter
|

<a href="https://hub.callysto.ca/jupyter/hub/user-redirect/git-pull?repo=https%3A%2F%2Fgithub.com%2Fcallysto%2Fcurriculum-notebooks&branch=master&subPath=Mathematics/TellingTime/telling-time.ipynb&depth=1" target="_parent"><img src="https://raw.githubusercontent.com/callysto/curriculum-notebooks/master/open-in-callysto-button.svg?sanitize=true" width="123" height="24" alt="Open in Callysto"/></a>
```
from IPython.display import HTML
from IPython.display import YouTubeVideo
import myMagics
%uiButtons
```
*Note: Run the cell above then click on the "Initialize" button to get notebook ready*
# Telling Time
Time is a concept we are all very familiar with. Seconds, minutes, hours, and days are simply part of our everyday life. Have you ever wondered about how all these units of time relate or why we use "am" and "pm" when talking about the hours of the day?
There are two important distinctions to make when thinking of time:
1. Telling the time - looking at a clock and knowing what time it is.
2. Measuring the time - using a clock or other tools to measure how long something takes.
In this notebook we will explore the relationships between all the different units of time and how to use different tools to read and keep track of time. We will also learn how to easily convert between hours, minutes and seconds.
## A Little History
When thinking of the different times of the day one thing stands out: there are two of each hour in the day; for example, 2 AM and 2 PM. Why is that?
This dates back to the Roman times. It was decided a day should be split up into two parts, one part for day time and the other for night time.
Eventually this split was made to use noon and midnight as the points where it changes from one part of the day to the other
- AM means "ante meridiem" which means "before midday"
- PM means "post meridiem" which means "after midday"
Click on the "More" button for more details
<div class="hideMe">
Initially to do this split the Romans decided to break the day up into two 12 hour blocks. As we can imagine from back in those days it would only be logical to make the 12 hours in the "day" start at sunrise and the 12 hours of the "night" start at dusk. But since the day/night cycle changes over the year (shorter days in winter for example), this caused problems.<br>
Eventually it was decided to change from sunset/dusk to midnight/midday, this is where AM and PM where born. AM means "ante meridiem" which stands for "before midday" and PM means "post meridiem" meaning, you guessed it, "after midday". When you think about it this makes sense: 3PM is 3 hours past the midday. Eventually it was decided that keeping one day split up into 24 hours instead of two blocks of 12 hours made more sense. The 24 hour clock was then introduced. The hours on this clock range from 0 to 23 (totalling 24 hours). We in North America still frequently use the AM/PM 12 hour day format but many parts of the world use the 24 hour clock.
```
%toggleMore
```
## How Well do you Know Time?
Ok so now that we have a little background on how our measurements of time came about, let's play a little game. Do you think you can guess exactly 15 seconds without using a clock? If you think you can do it, click the button below. When you think it’s been 15 seconds click it again and see how close you are. (Click again if you want to retry)
```
HTML(filename='TimeGuessWidget.html')
```
So how did you do? Not as easy as it seems eh. Most people, when trying this the first time, end up clicking much too early. You may have counted up to 15 "Mississippi’s" in your head which can help get closer to 15 seconds, but what if I asked you to guess 3 minutes? Rhythmically counting to 180 "Mississippi’s" is not particularly fun . This example shows the importance of using tools to more accurately measure time.
## Reading Time
Long ago before electricity was invented, ancient civilizations had to find other cleaver ways of reading time. Two common techniques used where:
1. Using the position of the sun to know the time of day
<img src="https://upload.wikimedia.org/wikipedia/commons/6/66/Sundial_-_Canonical_Hour.jpg" width="400" style="box-shadow: 4px 4px 12px gray;margin: 5px;">
2. Studying the position of the stars was used to know time in the night
<img src="https://c.tadst.com/gfx/750x500/tell-time-with-stars.png?1" width="400" style="box-shadow: 4px 4px 12px gray;margin: 5px;">
Now days the time is everywhere and is easily accessible. The main two ways of displaying time are using a digital clock or analog. Digital represents the time as numbers, an analog clock represents the time using clock hands going in circle.
<div class="hideMe">
These days the time is everywhere. We simply look for a clock on a wall, appliance, a watch, or our phones. This was not always the case though. Does this mean time did not exist long ago? Egyptians 1500 BC (roughly 3500 years ago) were very much aware of time and found very clever ways for measuring it. For these ancient civilizations, as for us, knowing the time and months of the year was crucial to their survival. It turns out the most important clocks of all where not found on earth but in the sky! The stars and sun have been used to measure time for thousands of years and by many civilizations. Using the position of the sun casting shadows was used during the day and the position of known constellations were used at night.
Luckily for us we have evolved far beyond using the sun and stars to tell time. Imagine trying to get to school on time on a cloudy day! Now when we get a new watch or clock we simply synchronize it to match another time piece showing the correct time. More and more, as devices are connected to the internet we don’t even have to set the time, it is done automatically!
```
%toggleMore
```
## Units of Time
So if I ask you what time it is right now you could easily look at a clock and tell me right? For example you could go as far as saying "it is 11:37:12 on Monday December 17, 2018". Now, that is probably a lot more information then was asked when asking for the time but bear with me. Let's break down all the components of that sentence:
- 1 year is made up of 365 days (366 if the year is leap)
- 1 day is made up of 24 hours
- 1 hour is made up of 60 minutes
- 1 minutes is made up of 60 seconds
- 1 second is made up of 1000 milliseconds
We could keep going but already 1 millisecond happens so fast that they are rarely used in everyday life.
Let's visualize this by using an analog clock. If you count all the ticks around the clock you will find out that there are 60 of them. This makes sense, as 1 one hour is made up of 60 minutes and 1 minute is made up of 60 seconds. In everyday life we know a clock only ever goes forward, and some might say it moves relatively slow. This can make it hard to fully understand its pattern. This example breaks these rules and allows you to manipulate the clock forward and backwards, fast or slow.
If you adjust the slider below the clock you will see that the hands will begin to move. Each tick on the slider represents a second. Try adjusting the time to see how each hand behaves. (You can also use your keyboard's side arrows to tick through 1 second at a time)
```
from IPython.display import HTML
HTML(filename='ClockWidget.html')
```
What have you noticed about the relationships between the hands as you slide back and forth?
Two important things to notice about the clock:
1. In order for the minute hand (blue) to move one full tick the seconds hand (red) must do one full rotation
2. When the minute hand does a full rotation the hour hand will have moved 5 ticks
Why does the hour hand move 5 ticks per minute rotation? That is because a day has 24 hours, not 60 hours. Remember earlier when we talked about AM and PM, the 24 hour day was broken down into two 12 hour sections. So we can see that if we divide a full rotation (60 minutes) into 12 hours we get $$60\div12=5$$ This means in the time the minute hand does a full rotation, meaning 60 minutes, the hour hand will advance 5 ticks on the clock. You will see this happening if you slide the slider from the far left all the way to the far right, the minute hand will have done a full rotation and the hour hand will have moved 5 ticks.
Now that we have a better understanding of the relationships between the units, can we figure out how many seconds are in 1 hour? Sure we can! Let's think about this. In 1 hour the minute hand goes around 60 times and for each one of these minutes the seconds hand goes around 60 times, this must mean $$60_\frac{min}{hr} \times60_\frac{sec}{min}=3600_\frac{sec}{hr}$$ So 1 hour has 3600 seconds. This means if you use your keyboard arrows on the slider from left to right you will need to push it 3600 times!! (Don't do that.)
Based on this math can you figure out how many seconds are in a day? or how many minutes are in a week?
## Measuring Time
So as we all know being able to tell the time is a crucial part of our everyday lives. It helps us know when we have appointments, when we should eat or when we should go to sleep.
Time also has many other great uses like keeping time for a hockey game or measuring how long it takes to drive from one city to another.
Let's take travelling from city to another as an example. Say you are going from Calgary to Edmonton and you want to calculate how long the trip takes. The simplest way of doing this without extra tools is to write down the time when you leave and then check the time when you arrive. Now all we do is take the difference between these two times.
Let's say you leave at 1:32 and arrive at 4:47. You can probably estimate in your head that the trip took a little over 3 hours, but we can calculate it exactly. To make this simpler we will convert the format from hours:minutes to just have minutes. Let's recall how many minutes are in 1 hour to get the following:
$$(1_{hr}\times60_\frac{min}{hr})+32_{min}=60_{min} + 32_{min}=92_{min}$$
$$(4_{hr}\times60_\frac{min}{hr})+47_{min}=240_{min} + 47_{min}=287_{min}$$
*Notice these times in minutes actually mean 92 min and 287 min past noon respectively*
And now we get the difference:
$$287_{min}-92_{min}=195_{min}$$
So the trip took 195 minutes to get from Calgary to Edmonton. To get it back into the hours:minutes format we need to figure out how many times $195$ can be divided by $60$. We can see that $60$ will fit $3$ times inside $195$ and we will be left with a remainder of $15$, so the trip took $3$ hours and $15$ minutes.
Ok so that wasn't too bad. It took some work to get an exact value but it is definitely doable. Now let's take our hockey example and look at how we could keep track of the time for the game. A few things to consider before attempting this
1. The time goes backwards from 20 minutes down to 0 milliseconds
2. The time has to stop every time the whistle is blown
3. The time has to be accurate to the 100th millisecond
Analyzing this problem we can quickly see that if all we have is a regular clock then a hockey game would take a very long time between each whistle blown as someone would have to calculate the differences in time between each stop and start. Thankfully we have many different types of tools to measure times like this. In this case a scoreboard with a timeclock built in does the trick.
Now all the time keeper has to do is stop and start time as the whistle is blown and the play starts again.
<div class="hideMe">
In other sports sometimes a fraction of a second makes the difference between first and second place. Precise measurements of time may also be needed during a critical science experiment. With examples like these we can see that a person's reflex to start/stop a clock is probably not going to cut it. Many other techniques have been developed to overcome these challenges. Laser sensors are far more accurate then the human hand-to-eye coordination.
<img src="https://upload.wikimedia.org/wikipedia/commons/thumb/c/c0/LightBeamTiming.jpg/220px-LightBeamTiming.jpg" style="box-shadow: 4px 4px 12px gray;">
The image above is of a light beam sensor used on the Olympic track.
```
%toggleMore
```
## 24-Hour Clock
As we now know a day has 24 hours. We also know why AM and PM were introduced and still used today. Another wildly popular way of representing time is to use the 24-hour clock. The 24-hour clock eliminates the need to us AM and PM. Using the 24-hour clock simply means we don't go back to one after we pass noon, we keep going from 12 to 13. This may seem odd at first since saying it is 13 o'clock is not something we are use to.
One major benefit to using this format is that you will never set your alarm wrong by putting 8PM instead of 8AM; 8 just means 8 in the morning and 20 means 8 at night.
If you use this format enough, knowing that 16:03 simply means 4:03pm becomes second nature, but you're probably wondering how to quickly get this answer when you are not used to it yet.
All you have to do is take the hour $16$ and subtract $12$ from it so $$16-12=4\text{ o'clock PM.}$$ A good way to quickly do this in your head is to first take away $10$ which is easy to do then remove the last $2$, so $$16-10=6,$$ and then $$6-2=4\text{ o'clock.}$$ Give this a try: what time is 18:39? How about 22:18?
Many modern watches, smartphones, alarm clocks, etc. allow you to use the 24 hour clock. Try it out for a week or two and see how fast you adjust to this format.
## Different Ways to Express Time
Now that we have a much better understanding of how time works and the relationships between the different units we can start getting creative and come up with other ways to express time. Check out this video for an abstract wooden pendulum clock
```
YouTubeVideo('9ZzkMIrWdPE', width=800, height=550)
%%html
<iframe width="560" height="315" src="https://www.youtube.com/embed/9ZzkMIrWdPE" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture" allowfullscreen></iframe>
```
Here is another abstract way of telling time, can you decipher what each colour represent?
You can speed up the clock to see how each ring behaves over time, when you think you have figured it out check your answers below.
```
from IPython.display import HTML
HTML(filename='AbsClockWidget.html')
from IPython.display import HTML
HTML(filename='questions.html')
```
## Conclusion
In this notebook we explored:
1. Some history of time and where AM and PM comes from
2. The relationships between the different units of time and how the behave together
3. Examples of tools to use the time in different ways (Time for a sports game)
4. How to use the 24-hour clock
[](https://github.com/callysto/curriculum-notebooks/blob/master/LICENSE.md)
|
github_jupyter
|
```
import os
import sys
import math
import json
import torch
import numpy as np
import scipy.io
from scipy import ndimage
import matplotlib
# from skimage import io
# matplotlib.use("pgf")
matplotlib.rcParams.update({
# 'font.family': 'serif',
'font.size':10,
})
from matplotlib import pyplot as plt
import pytorch_lightning as pl
from pytorch_lightning import Trainer, seed_everything
from pytorch_lightning.loggers import TensorBoardLogger
seed_everything(42)
import DiffNet
from DiffNet.DiffNetFEM import DiffNet2DFEM
from torch.utils import data
# from e1_stokes_base_resmin import Stokes2D
from pytorch_lightning.callbacks.base import Callback
from e2_ns_fps_resmin import OptimSwitchLBFGS, NS_FPS_Dataset, NS_FPS
def plot_contours(module, u, v, p, u_x_gp, v_y_gp, path=None):
self = module
fig, axs = plt.subplots(3, 3, figsize=(6*3,3*3),
subplot_kw={'aspect': 'auto'}, squeeze=True)
for i in range(axs.shape[0]-1):
for j in range(axs.shape[1]):
axs[i,j].set_xticks([])
axs[i,j].set_yticks([])
div_gp = u_x_gp + v_y_gp
div_elmwise = torch.sum(div_gp, 0)
div_total = torch.sum(div_elmwise)
interp_method = 'bilinear'
im0 = axs[0,0].imshow(u,cmap='jet', origin='lower', interpolation=interp_method)
fig.colorbar(im0, ax=axs[0,0]); axs[0,0].set_title(r'$u_x$')
im1 = axs[0,1].imshow(v,cmap='jet',origin='lower', interpolation=interp_method)
fig.colorbar(im1, ax=axs[0,1]); axs[0,1].set_title(r'$u_y$')
im2 = axs[0,2].imshow(p,cmap='jet',origin='lower', interpolation=interp_method)
fig.colorbar(im2, ax=axs[0,2]); axs[0,2].set_title(r'$p$')
im3 = axs[1,0].imshow(div_elmwise,cmap='jet',origin='lower', interpolation=interp_method)
fig.colorbar(im3, ax=axs[1,0]); axs[1,0].set_title(r'$\int(\nabla\cdot u) d\Omega = $' + '{:.3e}'.format(div_total.item()))
im4 = axs[1,1].imshow((u**2 + v**2)**0.5,cmap='jet',origin='lower', interpolation=interp_method)
fig.colorbar(im4, ax=axs[1,1]); axs[1,1].set_title(r'$\sqrt{u_x^2+u_y^2}$')
x = np.linspace(0, 1, u.shape[1])
y = np.linspace(0, 1, u.shape[0])
xx , yy = np.meshgrid(x, y)
print(x.shape)
print(y.shape)
print(xx.shape)
print(yy.shape)
print(u.shape)
print(v.shape)
im5 = axs[1,2].streamplot(xx, yy, u, v, color='k', cmap='jet'); axs[1,2].set_title("Streamlines")
mid_idxX = int(self.domain_sizeX/2)
mid_idxY = int(self.domain_sizeY/2)
# im = axs[2,0].plot(self.dataset.y[:,0], u[:,0],label='u_inlet')
im = axs[2,0].plot(self.dataset.x[mid_idxY,:], u[mid_idxY,:],label='u_mid')
im = axs[2,1].plot(self.dataset.x[mid_idxY,:], v[mid_idxY,:],label='v_mid')
im = axs[2,2].plot(self.dataset.x[mid_idxY,:], p[mid_idxY,:],label='p_mid')
if not path == None:
plt.savefig(path)
# im = axs[2,0].plot(self.dataset.y[:,mid_idx], u[:,mid_idx],label='DiffNet')
# im = axs[2,0].plot(self.midline_Y,self.midline_U,label='Numerical')
# axs[2,0].set_xlabel('y'); axs[2,0].legend(); axs[2,0].set_title(r'$u_x @ x=0.5$')
# im = axs[2,1].plot(self.dataset.x[mid_idx,:], v[mid_idx,:],label='DiffNet')
# im = axs[2,1].plot(self.midline_X,self.midline_V,label='Numerical')
# axs[2,1].set_xlabel('x'); axs[2,1].legend(); axs[2,1].set_title(r'$u_y @ y=0.5$')
# im = axs[2,2].plot(self.dataset.x[-1,:], p[-1,:],label='DiffNet')
# im = axs[2,2].plot(self.midline_X,self.topline_P,label='Numerical')
# axs[2,2].set_xlabel('x'); axs[2,2].legend(); axs[2,2].set_title(r'$p @ y=1.0$')
# fig.suptitle("Re = {:.1f}, N = {}, LR = {:.1e}".format(self.Re, self.domain_size, self.learning_rate), fontsize=12)
# plt.savefig(os.path.join(self.logger[0].log_dir, 'contour_' + str(self.current_epoch) + '.png'))
# self.logger[0].experiment.add_figure('Contour Plots', fig, self.current_epoch)
# plt.close('all')
lx = 12.
ly = 6.
Nx = 128
Ny = 64
domain_size = 32
Re = 1.
dir_string = "ns_fps"
max_epochs = 50001
plot_frequency = 100
LR = 5e-3
opt_switch_epochs = max_epochs
load_from_prev = False
load_version_id = 25
x = np.linspace(0, lx, Nx)
y = np.linspace(0, ly, Ny)
xx , yy = np.meshgrid(x, y)
dataset = NS_FPS_Dataset(domain_lengths=(lx,ly), domain_sizes=(Nx,Ny), Re=Re)
if load_from_prev:
print("LOADING FROM PREVIOUS VERSION: ", load_version_id)
case_dir = './ns_fps/version_'+str(load_version_id)
net_u = torch.load(os.path.join(case_dir, 'net_u.pt'))
net_v = torch.load(os.path.join(case_dir, 'net_v.pt'))
net_p = torch.load(os.path.join(case_dir, 'net_p.pt'))
else:
print("INITIALIZING PARAMETERS TO ZERO")
v1 = np.zeros_like(dataset.x)
v2 = np.zeros_like(dataset.x)
p = np.zeros_like(dataset.x)
u_tensor = np.expand_dims(np.array([v1,v2,p]),0)
# network = torch.nn.ParameterList([torch.nn.Parameter(torch.FloatTensor(u_tensor), requires_grad=True)])
net_u = torch.nn.ParameterList([torch.nn.Parameter(torch.FloatTensor(u_tensor[:,0:1,:,:]), requires_grad=True)])
net_v = torch.nn.ParameterList([torch.nn.Parameter(torch.FloatTensor(u_tensor[:,1:2,:,:]), requires_grad=True)])
net_p = torch.nn.ParameterList([torch.nn.Parameter(torch.FloatTensor(u_tensor[:,2:3,:,:]), requires_grad=True)])
# print("net_u = \n", net_u[0])
# print("net_v = \n", net_v[0])
# print("net_p = \n", net_p[0])
network = (net_u, net_v, net_p)
basecase = NS_FPS(network, dataset, domain_lengths=(lx,ly), domain_sizes=(Nx,Ny), batch_size=1, fem_basis_deg=1, learning_rate=LR, plot_frequency=plot_frequency)
# Initialize trainer
logger = pl.loggers.TensorBoardLogger('.', name=dir_string)
csv_logger = pl.loggers.CSVLogger(logger.save_dir, name=logger.name, version=logger.version)
early_stopping = pl.callbacks.early_stopping.EarlyStopping('loss',
min_delta=1e-8, patience=10, verbose=False, mode='max', strict=True)
checkpoint = pl.callbacks.model_checkpoint.ModelCheckpoint(monitor='loss',
dirpath=logger.log_dir, filename='{epoch}-{step}',
mode='min', save_last=True)
lbfgs_switch = OptimSwitchLBFGS(epochs=opt_switch_epochs)
trainer = Trainer(gpus=[0],callbacks=[early_stopping,lbfgs_switch],
checkpoint_callback=checkpoint, logger=[logger,csv_logger],
max_epochs=max_epochs, deterministic=True, profiler="simple")
# Training
trainer.fit(basecase)
# Save network
torch.save(basecase.net_u, os.path.join(logger.log_dir, 'net_u.pt'))
torch.save(basecase.net_v, os.path.join(logger.log_dir, 'net_v.pt'))
torch.save(basecase.net_p, os.path.join(logger.log_dir, 'net_p.pt'))
# Query
basecase.dataset[0]
inputs, forcing = basecase.dataset[0]
u, v, p, u_x, v_y = basecase.do_query(inputs, forcing)
u = u.squeeze().detach().cpu()
v = v.squeeze().detach().cpu()
p = p.squeeze().detach().cpu()
u_x = u_x.squeeze().detach().cpu()
v_y = v_y.squeeze().detach().cpu()
# plot
plot_contours(basecase, u, v, p, u_x, v_y)
# separate query
version_id = 81
case_dir = './ns_fps/version_'+str(version_id)
dataset = NS_FPS_Dataset(domain_lengths=(lx,ly), domain_sizes=(Nx,Ny), Re=Re)
net_u = torch.load(os.path.join(case_dir, 'net_u.pt'))
net_v = torch.load(os.path.join(case_dir, 'net_v.pt'))
net_p = torch.load(os.path.join(case_dir, 'net_p.pt'))
# network = (net_u, net_v, net_p)
network = (net_u.cpu(), net_v.cpu(), net_p.cpu())
equation = NS_FPS(network, dataset, domain_lengths=(lx,ly), domain_sizes=(Nx,Ny), batch_size=1, fem_basis_deg=1, learning_rate=LR, plot_frequency=plot_frequency)
# Query
inputs, forcing = equation.dataset[0]
u, v, p, u_x, v_y = equation.do_query(inputs, forcing)
u = u.squeeze().detach().cpu()
v = v.squeeze().detach().cpu()
p = p.squeeze().detach().cpu()
u_x = u_x.squeeze().detach().cpu()
v_y = v_y.squeeze().detach().cpu()
obj_left_idx = dataset.obj_left_idx
obj_rght_idx = dataset.obj_rght_idx
obj_bttm_idx = dataset.obj_bttm_idx
obj_top__idx = dataset.obj_top__idx
u[obj_bttm_idx:obj_top__idx, obj_left_idx:obj_rght_idx] = float('inf')
v[obj_bttm_idx:obj_top__idx, obj_left_idx:obj_rght_idx] = float('inf')
p[obj_bttm_idx:obj_top__idx, obj_left_idx:obj_rght_idx] = float('inf')
# plot
filepath = os.path.join(case_dir,'query_ns_fps.png')
plot_contours(equation, u, v, p, u_x, v_y, filepath)
net_u.cpu()
net_u
simdata = np.loadtxt('ns-ldc-numerical-results/re-30-ns-L12-H6-midlineX.csv', skiprows=1,delimiter=',')
fig, axs = plt.subplots(3, 3, figsize=(6*3,3.6*3), subplot_kw={'aspect': 'auto'}, squeeze=True)
axs[0,0].plot(simdata[:,0], simdata[:,2],label='num')
axs[0,1].plot(simdata[:,0], simdata[:,3],label='num')
axs[0,2].plot(simdata[:,0], simdata[:,1],label='num')
mid_idxX = int(Nx/2)
mid_idxY = int(Ny/2)
axs[0,0].plot(equation.dataset.x[mid_idxY,:], u[mid_idxY,:],label='u_mid'); axs[0,0].legend()
axs[0,1].plot(equation.dataset.x[mid_idxY,:], v[mid_idxY,:],label='v_mid'); axs[0,1].legend()
axs[0,2].plot(equation.dataset.x[mid_idxY,:], p[mid_idxY,:],label='p_mid'); axs[0,2].legend()
simdataY = np.loadtxt('ns-ldc-numerical-results/re-30-ns-L12-H6-midlineY.csv', skiprows=1,delimiter=',')
fig, axs = plt.subplots(3, 3, figsize=(6*3,3.6*3), subplot_kw={'aspect': 'auto'}, squeeze=True)
axs[0,0].plot(simdataY[:,0], simdataY[:,2],label='num')
axs[0,1].plot(simdataY[:,0], simdataY[:,3],label='num')
axs[0,2].plot(simdataY[:,0], simdataY[:,1],label='num')
mid_idxX = int(Nx/2)
mid_idxY = int(Ny/2)
axs[0,0].plot(equation.dataset.y[:,mid_idxY], u[:,mid_idxY],label='u_mid'); axs[0,0].legend()
axs[0,1].plot(equation.dataset.y[:,mid_idxY], v[:,mid_idxY],label='v_mid'); axs[0,1].legend()
axs[0,2].plot(equation.dataset.y[:,mid_idxY], p[:,mid_idxY],label='p_mid'); axs[0,2].legend()
```
|
github_jupyter
|
```
import zarr
from pyprojroot import here
import pandas as pd
import numpy as np
import allel
import yaml
import matplotlib.pyplot as plt
import functools
import seaborn as sns
sns.set_context('paper')
sns.set_style('darkgrid')
import dask.array as da
import scipy.interpolate
import scipy.stats
import petl as etl
import pyfasta
from matplotlib.ticker import MultipleLocator, FormatStrFormatter
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
# OLD VECTORBASE - gone
# genome_path = here() / 'data/external/vectorbase/Anopheles-gambiae-PEST_CHROMOSOMES_AgamP4.fa'
# genome = pyfasta.Fasta(str(genome_path), key_fn=lambda x: x.split()[0])
# NEW VECTORBASE
def _genome_key_fn(s):
k = s.split()[0]
if k.startswith('AgamP4'):
k = k.split('_')[1]
return k
genome_path = here() / 'data/external/vectorbase/VectorBase-48_AgambiaePEST_Genome.fasta'
genome = pyfasta.Fasta(str(genome_path), key_fn=_genome_key_fn)
chromosomes = '2', '3', 'X'
chromosome_plen = {
'2': len(genome['2R']) + len(genome['2L']),
'3': len(genome['3R']) + len(genome['3L']),
'X': len(genome['X'])
}
pop_defs_path = here() / 'notebooks/gwss/pop_defs.yml'
with open(pop_defs_path, 'rt') as f:
pop_defs = yaml.safe_load(f)
pops = list(pop_defs)
h12_root_path = here() / 'data/gwss/h12/h12.zarr'
h12_root = zarr.open_consolidated(str(h12_root_path))
def load_h12_gwss(pop, chromosome):
window_size = pop_defs[pop]['h12_window_size']
window_step = 200
grp = h12_root[f'{pop}/{window_size}/{window_step}/{chromosome}']
return (
grp['windows'][:],
grp['gwindows'][:],
grp['h1'][:],
grp['h12'][:],
grp['h123'][:],
grp['h2_h1'][:]
)
ihs_root_path = here() / 'data/gwss/ihs/ihs.zarr'
ihs_root = zarr.open_consolidated(str(ihs_root_path))
@functools.lru_cache(maxsize=None)
def load_ihs_gwss(pop, chromosome, window_size=200, window_step=100):
grp = ihs_root[f'{pop}/{chromosome}']
pos = grp['pos'][:]
gpos = grp['gpos'][:]
ihs_std = np.fabs(grp['ihs_std'][:])
x = allel.moving_statistic(pos, np.mean, size=window_size, step=window_step)
gx = allel.moving_statistic(gpos, np.mean, size=window_size, step=window_step)
y_max = allel.moving_statistic(ihs_std, np.max, size=window_size, step=window_step)
y_pc95 = allel.moving_statistic(ihs_std, lambda v: np.percentile(v, 95), size=window_size, step=window_step)
y_pc75 = allel.moving_statistic(ihs_std, lambda v: np.percentile(v, 75), size=window_size, step=window_step)
y_pc50 = allel.moving_statistic(ihs_std, np.median, size=window_size, step=window_step)
return x, gx, y_max, y_pc95, y_pc75, y_pc50
xpehh_root_path = here() / 'data/gwss/xpehh/xpehh.zarr'
xpehh_root = zarr.open_consolidated(str(xpehh_root_path))
@functools.lru_cache(maxsize=None)
def load_xpehh_gwss(pop1, pop2, chromosome, window_size=500, window_step=250):
# avoid running the same scan twice
orig_pop1, orig_pop2 = pop1, pop2
pop1, pop2 = sorted([pop1, pop2])
grp = xpehh_root[f'{pop1}_{pop2}/{chromosome}']
pos = grp['pos'][:]
gpos = grp['gpos'][:]
xpehh = grp['xpehh'][:]
if pop1 == orig_pop2:
# flip back
xpehh = -xpehh
pop1, pop2 = pop2, pop1
# centre
xpehh = xpehh - np.median(xpehh)
# clip at zero to focus on selection in pop1
xpehh1 = np.clip(xpehh, a_min=0, a_max=None)
x = allel.moving_statistic(pos, np.mean, size=window_size, step=window_step)
gx = allel.moving_statistic(gpos, np.mean, size=window_size, step=window_step)
y_max = allel.moving_statistic(xpehh1, np.max, size=window_size, step=window_step)
y_pc95 = allel.moving_statistic(xpehh1, lambda v: np.percentile(v, 95), size=window_size, step=window_step)
y_pc75 = allel.moving_statistic(xpehh1, lambda v: np.percentile(v, 75), size=window_size, step=window_step)
y_pc50 = allel.moving_statistic(xpehh1, np.median, size=window_size, step=window_step)
return x, gx, y_max, y_pc95, y_pc75, y_pc50
pbs_root_path = here() / 'data/gwss/pbs/pbs.zarr'
pbs_root = zarr.open_consolidated(str(pbs_root_path))
def load_pbs_gwss(pop1, pop2, pop3, chromosome, window_size=500, window_step=250):
grp_path = f'/{pop1}_{pop2}_{pop3}/{window_size}/{window_step}/{chromosome}'
grp = pbs_root[grp_path]
windows = grp['windows'][:]
gwindows = grp['gwindows'][:]
pbs = grp['pbs'][:]
pbs_scaled = grp['pbs_scaled'][:]
return windows, gwindows, pbs, pbs_scaled
def load_genes():
# OLD VECTORBASE
# features_path = here() / 'data/external/vectorbase/Anopheles-gambiae-PEST_BASEFEATURES_AgamP4.12.gff3'
# df_genes = (
# allel.gff3_to_dataframe(
# str(features_path),
# attributes=['ID', 'Name', 'biotype']
# )
# .set_index('ID')
# .query("type == 'gene' and biotype == 'protein_coding'")
# )
# NEW VECTORBASE
features_path = here() / 'data/external/vectorbase/VectorBase-48_AgambiaePEST.gff'
df_genes = (
allel.gff3_to_dataframe(
str(features_path),
attributes=['ID', 'description']
)
.sort_values(['seqid', 'start'])
.set_index('ID')
.query("type == 'gene'")
)
# fix chromosome IDs
df_genes['seqid'] = df_genes['seqid'].str.split('_', expand=True).loc[:, 1]
# convert to chromosomal coordinates
df_genes['chromosome'] = df_genes['seqid'].copy()
df_genes['chromosome_start'] = df_genes['start'].copy()
df_genes['chromosome_end'] = df_genes['end'].copy()
loc_2R = df_genes.seqid == '2R'
df_genes.loc[loc_2R, 'chromosome'] = '2'
loc_2L = df_genes.seqid == '2L'
df_genes.loc[loc_2L, 'chromosome'] = '2'
df_genes.loc[loc_2L, 'chromosome_start'] = df_genes.loc[loc_2L, 'start'] + len(genome['2R'])
df_genes.loc[loc_2L, 'chromosome_end'] = df_genes.loc[loc_2L, 'end'] + len(genome['2R'])
loc_3R = df_genes.seqid == '3R'
df_genes.loc[loc_3R, 'chromosome'] = '3'
loc_3L = df_genes.seqid == '3L'
df_genes.loc[loc_3L, 'chromosome'] = '3'
df_genes.loc[loc_3L, 'chromosome_start'] = df_genes.loc[loc_3L, 'start'] + len(genome['3R'])
df_genes.loc[loc_3L, 'chromosome_end'] = df_genes.loc[loc_3L, 'end'] + len(genome['3R'])
df_genes['chromosome_center'] = (df_genes['chromosome_start'] + df_genes['chromosome_end']) / 2
return df_genes
df_genes = load_genes()
import warnings
with warnings.catch_warnings():
warnings.simplefilter('ignore')
ace1 = df_genes.loc['AGAP001356']
ace1['Name'] = 'Ace1'
cyp6p3 = df_genes.loc['AGAP002865']
cyp6p3['Name'] = 'Cyp6p3'
vgsc = df_genes.loc['AGAP004707']
vgsc['Name'] = 'Vgsc'
gaba = df_genes.loc['AGAP006028']
gaba['Name'] = 'Gaba'
gste2 = df_genes.loc['AGAP009194']
gste2['Name'] = 'Gste2'
cyp9k1 = df_genes.loc['AGAP000818']
cyp9k1['Name'] = 'Cyp9k1'
ir_genes = [ace1, cyp6p3, vgsc, gaba, gste2, cyp9k1]
novel_loci = {
'A': ('2', 24_860_000),
'B': ('2', 40_940_000),
'C': ('2', 28_549_590 + len(genome['2R'])),
'D': ('2', 34_050_000 + len(genome['2R'])),
'E': ('X', 4_360_000),
'F': ('X', 9_220_000),
}
tbl_chromatin = [
('name', 'chrom', 'start', 'end'),
('CHX', 'X', 20009764, 24393108),
('CH2R', '2R', 58984778, 61545105),
('CH2L', '2L', 1, 2431617),
('PEU2L', '2L', 2487770, 5042389),
('IH2L', '2L', 5078962, 5788875),
('IH3R', '3R', 38988757, 41860198),
('CH3R', '3R', 52161877, 53200684),
('CH3L', '3L', 1, 1815119),
('PEU3L', '3L', 1896830, 4235209),
('IH3L', '3L', 4264713, 5031692)
]
seq_ids = '2R', '2L', '3R', '3L', 'X'
def build_gmap():
# crude recombination rate lookup, keyed off chromatin state
# use units of cM / bp, assume 2 cM / Mbp == 2x10^-6 cM / bp
tbl_rr = (
etl.wrap(tbl_chromatin)
# extend heterochromatin on 2L - this is empirical, based on making vgsc peaks symmetrical
.update('end', 2840000, where=lambda r: r.name == 'CH2L')
.update('start', 2840001, where=lambda r: r.name == 'PEU2L')
.addfield('rr', lambda r: .5e-6 if 'H' in r.name else 2e-6)
)
# per-base map of recombination rates
rr_map = {seq_id: np.full(len(genome[seq_id]), fill_value=2e-6, dtype='f8')
for seq_id in seq_ids}
for row in tbl_rr.records():
rr_map[row.chrom][row.start - 1:row.end] = row.rr
# genetic map
gmap = {seq_id: np.cumsum(rr_map[seq_id]) for seq_id in seq_ids}
gmap['2'] = np.concatenate([gmap['2R'], gmap['2L'] + gmap['2R'][-1]])
gmap['3'] = np.concatenate([gmap['3R'], gmap['3L'] + gmap['3R'][-1]])
return gmap
gmap = build_gmap()
def tex_italicize_species(s):
return (
s
.replace('An. gambiae', '\textit{An. gambiae}')
.replace('An. coluzzii', '\textit{An. coluzzii}')
)
def root_mean_square(s):
return np.sqrt(np.mean(s**2))
def mean_absolute(s):
return np.mean(np.fabs(s))
```
|
github_jupyter
|
<h1> <b>Homework 1</b></h1>
<i>Alejandro J. Rojas<br>
[email protected]<br>
W261: Machine Learning at Scale<br>
Week: 01<br>
Jan 21, 2016</i></li>
<h2>HW1.0.0.</h2> Define big data. Provide an example of a big data problem in your domain of expertise.
The term big data is asoociated to datasets that cannot be processed, stored and transformed using traditional applications and tools because of high volume, high velocity and high variety. By high volume, we mean datasets that not only require high storage capacity, usually beyond 1T, but also datasets that are too big to have a decent processing and thoughput time. By high velocity, we mean data that requires real-time processing with throughput speeds that can be bursty. High variety includes data that comes from different formats, some structured some that are not, that all need to be ingested and transformed to be processed. Big data is simply changing the way we used to collect and analyze data at the time that it opens opportunity to increase the scale, scope and intimacy of the analyses that we are now able to do.
The social web is a leading source of big data applications given our ability to log almost anything that the user does when interacting to an application. In my field, I've seen how online videos are increasingly the way users consume media. A video, per se, is an unstructured data item and its interactions are usually captured by leading social media platforms like Facebook, Twitter and Youtube in the form of JSON, a semi unstructured format that can capture user interactions such as likes, shares and comments. Across the internet, the amount of videos being upload and downstream is exploding making it a challenge to measure real-time, the media consuming habits of our target users. Big data can help in providing insights from all of this information so that we can better predict the taste of users visiting our site properties to serve them content they like.
<h2>HW1.0.1.</h2>In 500 words (English or pseudo code or a combination) describe how to estimate the bias, the variance, the irreduciable error for a test dataset T when using polynomial regression models of degree 1, 2,3, 4,5 are considered. How would you select a model?
For any dataset T that contains n independent variables (x1, x2, ..xn) and one dependent variable y_true, we can observe the following:
If we try to estimate y as a function of x:
y_pred = f(x)
The estimate of our function will produce an error shown as:
<img src="error.png">
This error varies as we increase the complexity of our models as the following chart shows:
<img src="Prediction-Error.png">
The source of this error can be divided into three types:
bias
variance
irreducible error
and can be derived mathematically the following way
<img src="mathematicalerrors.jpg">
Bias error is introduced by us when we try to simplify the dynamics that we observe in the data, for instace by using a linear function to estimate y.
As we try to better fit the underlying data, we can try implementing nonlinear functions.
As the order of the polynomial regression increases, our function f(x) will more closely match the underlying portion of the dataset T and consequently we reduced our bias error.
However, if we randomly applied our high-ordered polynomial f(x) to another portion of dataset T, we will find that our error will increase because we introduced variance error by overfitting the prior dataset.
So as a rule of thumb, we can say that
as the degree of the predictive polynomial function f(x) increases:
bias error is reduced
variance error is increased
the trick is to find the optimal point where the sum of these two errors are at the minimum.Even at that point, our function(x) will still show some error that will be irreducible because it comes from imprecisions in the way data was collected or other type of noise present in the dataset T.
In this chart you can see how each of these errors varies as we bootstrap 50 samples of dataset T:
<img src="bootstrapping.jpg">
<h2> HW1.1.</h2> Read through the provided control script (pNaiveBayes.sh)
and all of its comments. When you are comfortable with their
purpose and function, respond to the remaining homework questions below.
A simple cell in the notebook with a print statmement with a "done" string will suffice here. (dont forget to include the Question Number and the quesition in the cell as a multiline comment!)
# <----------------------------------End of HW1.1------------------------------------->
<h2>HW1.2.</h2>Provide a mapper/reducer pair that, when executed by pNaiveBayes.sh
will determine the number of occurrences of a single, user-specified word. Examine the word “assistance” and report your results.
# Map
```
%%writefile mapper.py
#!/usr/bin/python
## mapper.py
## Author: Alejandro J. Rojas
## Description: mapper code for HW1.2-1.5
import sys
import re
count = 0
records = 0
words = 0
## collect user input
filename = sys.argv[1]
findwords = re.split(" ",sys.argv[2].lower())
with open (filename, "r") as myfile:
for line in myfile.readlines():
record = re.split(r'\t+', line)
records = records + 1
for i in range (len(record)):
bagofwords = re.split(" ",record[i]) ### Break each email records into words
for word in bagofwords:
words = words + 1
for keyword in findwords:
if keyword in word:
count = count + 1 ### Add one the count of found words
##print '# of Records analized',records
##print '# of Words analized', words
##print '# of Ocurrences', count
print count
!chmod +x mapper.py
```
# Reduce
```
%%writefile reducer.py
#!/usr/bin/python
## reducer.py
## Author: Alejandro J. Rojas
## Description: reducer code for HW1.2
import sys
import re
sum = 0
## collect user input
filenames = sys.argv[1:]
for file in filenames:
with open (file, "r") as myfile:
for line in myfile.readlines():
if line.strip():
sum = sum + int(line) ### Add counts present on all mapper produced files
print sum
!chmod +x reducer.py
```
# Write script to file
```
%%writefile pNaiveBayes.sh
## pNaiveBayes.sh
## Author: Jake Ryland Williams
## Usage: pNaiveBayes.sh m wordlist
## Input:
## m = number of processes (maps), e.g., 4
## wordlist = a space-separated list of words in quotes, e.g., "the and of"
##
## Instructions: Read this script and its comments closely.
## Do your best to understand the purpose of each command,
## and focus on how arguments are supplied to mapper.py/reducer.py,
## as this will determine how the python scripts take input.
## When you are comfortable with the unix code below,
## answer the questions on the LMS for HW1 about the starter code.
## collect user input
m=$1 ## the number of parallel processes (maps) to run
wordlist=$2 ## if set to "*", then all words are used
## a test set data of 100 messages
data="enronemail_1h.txt"
## the full set of data (33746 messages)
# data="enronemail.txt"
## 'wc' determines the number of lines in the data
## 'perl -pe' regex strips the piped wc output to a number
linesindata=`wc -l $data | perl -pe 's/^.*?(\d+).*?$/$1/'`
## determine the lines per chunk for the desired number of processes
linesinchunk=`echo "$linesindata/$m+1" | bc`
## split the original file into chunks by line
split -l $linesinchunk $data $data.chunk.
## assign python mappers (mapper.py) to the chunks of data
## and emit their output to temporary files
for datachunk in $data.chunk.*; do
## feed word list to the python mapper here and redirect STDOUT to a temporary file on disk
####
####
./mapper.py $datachunk "$wordlist" > $datachunk.counts &
####
####
done
## wait for the mappers to finish their work
wait
## 'ls' makes a list of the temporary count files
## 'perl -pe' regex replaces line breaks with spaces
countfiles=`\ls $data.chunk.*.counts | perl -pe 's/\n/ /'`
## feed the list of countfiles to the python reducer and redirect STDOUT to disk
####
####
./reducer.py $countfiles > $data.output
####
####
numOfInstances=$(cat $data.output)
echo "found [$numOfInstances] [$wordlist]" ## Report how many were found
## clean up the data chunks and temporary count files
\rm $data.chunk.*
!chmod a+x pNaiveBayes.sh
```
# Run file
Usage: usage: pNaiveBayes.sh m wordlist
```
!./pNaiveBayes.sh 5 "assistance"
```
# <----------------------------------End of HW1.2------------------------------------->
<h2>HW1.3.</h2> Provide a mapper/reducer pair that, when executed by pNaiveBayes.sh
will classify the email messages by a single, user-specified word using the multinomial Naive Bayes Formulation. Examine the word “assistance” and report your results.
# Map
```
%%writefile mapper.py
#!/usr/bin/python
## mapper.py
## Author: Alejandro J. Rojas
## Description: mapper code for HW1.3
import sys
import re
########## Collect user input ###############
filename = sys.argv[1]
findwords = re.split(" ",sys.argv[2].lower())
with open (filename, "r") as myfile:
for line in myfile.readlines():
record = re.split(r'\t+', line) ### Each email is a record with 4 components
### 1) ID 2) Spam Truth 3) Subject 4) Content
if len(record)==4: ### Take only complete records
########## Variables to collect and measure #########
records = 0 ### Each record corresponds to a unique email
words = 0 ### Words written in all emails incluidng Subject
spam_records, spam_words, spam_count = 0,0,0 ### Spam email count, words in spam email, user-specified word count
ham_records, ham_words, ham_count = 0, 0, 0 ### Same as above but for not spam emails
records += 1 ### add one the the total sum of emails
if int(record[1]) == 1: ### If the email is labeled as spam
spam_records += 1 ### add one to the email spam count
for i in range (2,len(record)): ### Starting from Subject to the Content
bagofwords = re.split(" ",record[i]) ### Collect all words present on each email
for word in bagofwords: ### For each word
words += 1 ### add one to the total sum of words
spam_words += 1 ### add one to the total sum of spam words
for keyword in findwords: ### for each word specified by user
if keyword in word: ### If there's a match then
spam_count += 1 ### add one to the user specified word count as spam
else: ### If email is not labeled as spam
ham_records +=1 ### add one to the email ham count
for i in range (2,len(record)): ### Starting from Subject to the Content
bagofwords = re.split(" ",record[i]) ### Collect all words present on each email
for word in bagofwords: ### For each word
words += 1 ### add one to the total sum of words
ham_words += 1 ### add one to the total sum of ham words
for keyword in findwords: ### for each word specified by user
if keyword in word: ### If there's a match then
ham_count += 1 ### add one to the user specified word count as ham
record_id = record[0]
truth = record[1]
print spam_count, " ", spam_words, " ", spam_records, " ", \
ham_count, " ", ham_words, " ", ham_records, " ", \
words, " ", records, " ", record_id, " ", truth
!chmod +x mapper.py
```
# Reduce
```
%%writefile reducer.py
#!/usr/bin/python
## reducer.py
## Author: Alejandro J. Rojas
## Description: reducer code for HW1.3-1.4
import sys
import re
sum_spam_records, sum_spam_words, sum_spam_count = 0,0,0
sum_ham_records, sum_ham_words, sum_ham_count = 0,0,0
sum_records,sum_words = 0,0
## collect user input
filenames = sys.argv[1:]
for file in filenames:
with open (file, "r") as myfile:
for line in myfile.readlines():
if line.strip():
factors = re.split(" ", line)
sum_spam_count += int(factors[0]) ## sum up every time the word was found in a spam
sum_spam_words += int(factors[3]) ## sum up all words from spams
sum_spam_records+= int(factors[6]) ## sum up all emails labeled as spam
sum_ham_count += int(factors[9]) ## sum up every time the word was found in a ham
sum_ham_words += int(factors[12]) ## sum up all words from hams
sum_ham_records += int(factors[15]) ## sum up all emails labeled as ham
sum_words += int(factors[18]) ## sum all words from all emails
sum_records += int(factors[21]) ## sum all emails
prior_spam = float(sum_spam_records)/float(sum_records) ## prior prob of a spam email
prior_ham = float(sum_ham_records)/float(sum_records) ## prior prob of a ham email
prob_word_spam = float(sum_spam_count)/float(sum_spam_words)## prob of word given that email is spam
prob_word_ham = float(sum_ham_count)/float(sum_ham_words) ## prob of word given that email is ham
##check_prior = prior_spam + prior_ham ## check priors -> sum to 1
##check_words = float(sum_words)/float(sum_spam_words+sum_ham_words) ## check probabilities of a word -> sum to 1
##check_spam = prob_word_spam*float(sum_spam_words)/float(sum_spam_count) ## check spam counts -> sum to 1
##check_ham = prob_word_ham*float(sum_ham_words)/float(sum_ham_count) ## check ham count -> sum to 1
sum_count = sum_spam_count+sum_ham_count
print "Summary of Data"
print '%4s'%sum_records ,'emails examined, containing %6s'%sum_words, 'words, we found %3s'%sum_count ,'matches.'
print '%30s' %'ID', '%10s' %'TRUTH', '%10s' %'CLASS', '%20s' %'CUMULATIVE ACCURACY'
miss, sample_size = 0,0
for file in filenames:
with open (file, "r") as myfile:
for line in myfile.readlines():
if line.strip():
data = re.split(" ", line)
record_id = data[24]
y_true = int(data[27][0])
count = int(data[0]) + int(data[9])
p_spam = prior_spam*prob_word_spam**count
p_ham = prior_ham*prob_word_ham**count
if p_spam > p_ham:
y_pred = 1
else:
y_pred = 0
if y_pred != y_true:
miss+= 1.0
sample_size += 1.0
accuracy = ((sample_size-miss)/sample_size)*100
print '%30s' %record_id, '%10s' %y_true, '%10s' %y_pred, '%18.2f %%' % accuracy
!chmod +x reducer.py
```
# Write script to file
```
%%writefile pNaiveBayes.sh
## pNaiveBayes.sh
## Author: Jake Ryland Williams
## Usage: pNaiveBayes.sh m wordlist
## Input:
## m = number of processes (maps), e.g., 4
## wordlist = a space-separated list of words in quotes, e.g., "the and of"
##
## Instructions: Read this script and its comments closely.
## Do your best to understand the purpose of each command,
## and focus on how arguments are supplied to mapper.py/reducer.py,
## as this will determine how the python scripts take input.
## When you are comfortable with the unix code below,
## answer the questions on the LMS for HW1 about the starter code.
## collect user input
m=$1 ## the number of parallel processes (maps) to run
wordlist=$2 ## if set to "*", then all words are used
## a test set data of 100 messages
data="enronemail_1h.txt"
## the full set of data (33746 messages)
# data="enronemail.txt"
## 'wc' determines the number of lines in the data
## 'perl -pe' regex strips the piped wc output to a number
linesindata=`wc -l $data | perl -pe 's/^.*?(\d+).*?$/$1/'`
## determine the lines per chunk for the desired number of processes
linesinchunk=`echo "$linesindata/$m+1" | bc`
## split the original file into chunks by line
split -l $linesinchunk $data $data.chunk.
## assign python mappers (mapper.py) to the chunks of data
## and emit their output to temporary files
for datachunk in $data.chunk.*; do
## feed word list to the python mapper here and redirect STDOUT to a temporary file on disk
####
####
./mapper.py $datachunk "$wordlist" > $datachunk.counts &
####
####
done
## wait for the mappers to finish their work
wait
## 'ls' makes a list of the temporary count files
## 'perl -pe' regex replaces line breaks with spaces
countfiles=`\ls $data.chunk.*.counts | perl -pe 's/\n/ /'`
## feed the list of countfiles to the python reducer and redirect STDOUT to disk
####
####
./reducer.py $countfiles > $data.output
####
####
numOfInstances=$(cat $data.output)
echo "NB Classifier based on word(s): $wordlist" ## Print out words
echo "$numOfInstances" ## Print out output data
## clean up the data chunks and temporary count files
\rm $data.chunk.*
```
# Run file
```
!./pNaiveBayes.sh 5 "assistance"
```
# <----------------------------------End of HW1.3------------------------------------->
<h2>HW1.4.</h2> Provide a mapper/reducer pair that, when executed by pNaiveBayes.sh
will classify the email messages by a list of one or more user-specified words. Examine the words “assistance”, “valium”, and “enlargementWithATypo” and report your results
# Run file
```
!./pNaiveBayes.sh 5 "assistance valium enlargementWithATypo"
```
# <----------------------------------End of HW1.4------------------------------------->
# <----------------------------------End of HW1------------------------------------->
|
github_jupyter
|
# Section 1: Preprocessing
## Behavior Analysis
### Generate trial regressors
```
import os
import numpy as np
from pandas import concat, read_csv
from scipy.stats import gamma
def normalize(arr): return (arr - arr.min()) / (arr.max() - arr.min())
root_dir = '/space/sophia/2/users/EMOTE-DBS/afMSIT/behavior'
subjects = ['BRTU', 'CHDR', 'CRDA', 'JADE', 'JASE', 'M5', 'MEWA', 'S2']
threshold = 0.005
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~#
### Load / Concatenate / Prepare Data.
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~#
df = []
for subject in subjects:
## Load CSV.
csv = read_csv(os.path.join(root_dir,'%s_msit_data.txt' %subject))
## Limit columns.
csv = csv[['SubjID','trial','iaps','DBS','interference','valence','arousal','responseTime','responseCorrect']]
## Rename columns.
csv.columns = ['Subject', 'Trial', 'IAPS', 'DBS', 'Interference', 'Valence_Obj', 'Arousal_Obj', 'RT', 'Accuracy']
## Load IAPS ratings.
iaps = read_csv(os.path.join(root_dir,'%s_IAPS_SAM.csv' %subject))
iaps = iaps[['IAPS_Number','Valence','Arousal']]
iaps.columns = ['IAPS','Valence_Subj','Arousal_Subj']
## Merge. Append.
csv = csv.merge(iaps, on='IAPS')
cols = ['Subject', 'Trial', 'IAPS', 'DBS', 'Interference', 'Valence_Obj', 'Arousal_Obj',
'Valence_Subj', 'Arousal_Subj', 'RT', 'Accuracy']
csv = csv[cols]
df.append(csv)
## Merge data. Sort.
df = concat(df)
df['DBS'] = np.where(df['DBS']=='DBSoff',0,1)
df = df.sort_values(['Subject','DBS','Trial']).reset_index(drop=True)
## Normalize regressors.
df['nsArousal'] = normalize(df.Arousal_Subj)
df['nsValence'] = normalize(df.Valence_Subj)
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~#
### Determine Trials for Inclusion/Exclusion.
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~#
## Set missing RTs to NaNs.
df['RT'] = np.where(df.Accuracy==-1, np.nan, df.RT)
df['Accuracy'] = np.where(df.Accuracy==-1, np.nan, df.Accuracy)
df['Missing'] = df.Accuracy.isnull().astype(int)
## Add Error column.
df['Error'] = 1 - df.Accuracy
## Add Post-Error Column.
df['PostError'] = 0
for subject in df.Subject.unique():
error = df.loc[df.Subject==subject,'Error']
posterror = np.insert(np.roll(error,1)[1:], 0, 0)
df.loc[df.Subject==subject,'PostError'] = posterror
## Iteratively detect outliers across subjects by fitting a Gamma distribution.
df['GammaCDF'], df['Outlier'] = 0, 0
for subject in df.Subject.unique():
## Fit Gamma to reaction time distribution.
shape, loc, scale = gamma.fit(df.loc[(df.Subject==subject)&(~df.RT.isnull()),'RT'], floc=0)
## Find outliers given likelihood threshold.
cdf = gamma.cdf(df.loc[(df.Subject==subject)&(~df.RT.isnull()),'RT'], shape, loc=loc, scale=scale)
outliers = (cdf < threshold) | (cdf > 1 - threshold)
## Append information.
df.loc[(df.Subject==subject)&(~df.RT.isnull()), 'GammaCDF'] += cdf
df.loc[(df.Subject==subject)&(~df.RT.isnull()), 'Outlier'] += outliers.astype(int)
## Generate exclude.
df['Exclude'] = np.where( df[['Missing','Error','PostError','Outlier']].sum(axis=1), 1, 0)
print '%s trials (%0.2f%%) excluded.' %(df.Exclude.sum(), df.Exclude.mean())
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~#
### Save.
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~#
df.to_csv('%s/afMSIT_group_data.csv' %root_dir, index=False)
```
## Parcellation
### Make EMOTE Labels
```
import os, shutil
import numpy as np
import pylab as plt
from mne import read_label, read_source_spaces, read_surface, set_log_level
set_log_level(verbose=False)
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~#
### Define parameters.
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~#
fs_dir = '/space/sophia/2/users/EMOTE-DBS/freesurfs'
subject = 'BRTU'
parc = 'laus250'
label_dir = os.path.join(fs_dir,subject,'label',parc)
out_dir = os.path.join(fs_dir,subject,'label','april2016')
if os.path.isdir(out_dir): shutil.rmtree(out_dir)
os.makedirs(out_dir)
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~#
### Build Left Hemisphere Labels.
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~#
hemi = 'lh'
rr, _ = read_surface(os.path.join(fs_dir, subject, 'surf', '%s.inflated' %hemi))
src = read_source_spaces(os.path.join(fs_dir, subject, 'bem', '%s-oct-6-src.fif' %subject))[0]
lhdict = {'dlpfc_1-lh':['caudalmiddlefrontal_1', 'caudalmiddlefrontal_5', 'caudalmiddlefrontal_6'],
'dlpfc_2-lh':['caudalmiddlefrontal_2', 'caudalmiddlefrontal_3', 'caudalmiddlefrontal_4'],
'dlpfc_3-lh':['rostralmiddlefrontal_2', 'rostralmiddlefrontal_3'],
'dlpfc_4-lh':['rostralmiddlefrontal_1', 'rostralmiddlefrontal_5'],
'dlpfc_5-lh':['parstriangularis_2', 'parsopercularis_2'],
'dlpfc_6-lh':['parsopercularis_3', 'parsopercularis_4'],
'racc-lh':['rostralanteriorcingulate_1','rostralanteriorcingulate_2'],
'dacc-lh':['caudalanteriorcingulate_1','caudalanteriorcingulate_2',],
'pcc-lh':['posteriorcingulate_2','posteriorcingulate_3']}
for k,V in lhdict.iteritems():
label = np.sum([read_label(os.path.join(label_dir,'%s-%s.label' %(v,hemi)), subject=subject)
for v in V])
n_vert = np.intersect1d(src['vertno'], label.vertices).shape[0]
print '%s\t%s' %(n_vert,k)
label.save(os.path.join(out_dir, '%s.label' %k))
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~#
### Build Right Hemisphere Labels.
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~#
hemi = 'rh'
rr, _ = read_surface(os.path.join(fs_dir, subject, 'surf', '%s.inflated' %hemi))
src = read_source_spaces(os.path.join(fs_dir, subject, 'bem', '%s-oct-6-src.fif' %subject))[1]
rhdict = {'dlpfc_1-rh':['caudalmiddlefrontal_1', 'caudalmiddlefrontal_2', 'caudalmiddlefrontal_5'],
'dlpfc_2-rh':['caudalmiddlefrontal_3', 'caudalmiddlefrontal_4'],
'dlpfc_3-rh':['rostralmiddlefrontal_2', 'rostralmiddlefrontal_3'],
'dlpfc_4-rh':['rostralmiddlefrontal_1', 'rostralmiddlefrontal_5'],
'dlpfc_5-rh':['parstriangularis_2', 'parsopercularis_1'],
'dlpfc_6-rh':['parsopercularis_3', 'parsopercularis_4'],
'racc-rh':['rostralanteriorcingulate_1','rostralanteriorcingulate_2'],
'dacc-rh':['caudalanteriorcingulate_1','caudalanteriorcingulate_2','caudalanteriorcingulate_3'],
'pcc-rh':['posteriorcingulate_2','posteriorcingulate_3']}
for k,V in rhdict.iteritems():
label = np.sum([read_label(os.path.join(label_dir,'%s-%s.label' %(v,hemi)), subject=subject)
for v in V])
n_vert = np.intersect1d(src['vertno'], label.vertices).shape[0]
print '%s\t%s' %(n_vert,k)
label.save(os.path.join(out_dir, '%s.label' %k))
```
## Preprocesing 1: Raw Data
### Fixing MEWA: Digitization
Something got way messed up. Here we make MNE knows what is EEG and what is extra points.
NOTE: Copied over one of the original files for MEWA and renamed it MEWA_msit_unmasked_raw.fif
```
import os
import numpy as np
from mne.io import Raw
from pandas import read_table
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~#
### Specify parameters.
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~#
root_dir = '/space/sophia/2/users/EMOTE-DBS/afMSIT_april2016'
raw_file = 'MEWA_msit_unmasked_raw.fif'
out_file = 'MEWA_msit_raw.fif'
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~#
### Load and prepare digitizations.
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~#
## Load data. Get digitization from raw.
raw = Raw(os.path.join(root_dir,'raw',raw_file),preload=False,verbose=False)
digitization = raw.info['dig']
## The last 101 points are extra. Set them to kind=4.
for d in digitization[-101:]: d['kind'] = 4
## Get coordinates for EEG points (excluding ref/EOG).
rr = np.array([d['r'] for d in dig if d['kind']==3])[:-2]
## Get channels
chs = raw.info['chs']
## Update location information. This was a huge pain in the ass to figure out.
## We ignore the first four channels (Triggers, EOG) and the last channel (STI014).
for ch, r in zip(chs[4:-1], rr): ch['loc'][:3] = r
## Update digitization/chs.
raw.info['dig'] = digitization
raw.info['chs'] = chs
raw.save(os.path.join(root_dir,'raw',out_file), overwrite=True)
```
### Fixing MEWA: Masking channel jumps
Time windows were manually inspected. This step isn't strictly necessary but seemed to help with EOG projections.
NOTE: Copied over one of the original files for MEWA and renamed it MEWA_msit_unmasked_raw.fif
```
import os
import numpy as np
import pylab as plt
from mne.io import Raw, RawArray
## Specify parameters.
root_dir = '/space/sophia/2/users/EMOTE-DBS/afMSIT_april2016'
raw_file = 'MEWA_msit_unmasked_raw.fif'
## Load data.
raw = Raw(os.path.join(root_dir,'raw',raw_file),preload=True,verbose=False)
## Get data in matrix form.
data = raw._data
## Get list of usuable channels
ch_info = [(n,ch) for n,ch in enumerate(raw.ch_names)]
good_ch = [(n,ch) for n,ch in ch_info if ch not in raw.info['bads']]
good_ch = np.array(good_ch)[4:-1]
## Make mask.
mask = np.zeros(data.shape[1])
times = [(384,394), (663,669)]
for t1, t2 in times:
mask[(raw.times >= t1) & (raw.times <= t2)] += 1
mask = mask.astype(bool)
## Apply mask.
for ch in good_ch[:,0].astype(int):
data[ch,mask] = 0
## Make new array. Save.
raw = RawArray(data, raw.info, first_samp=raw.first_samp)
raw.add_eeg_average_proj()
raw.save(os.path.join(root_dir,'raw','MEWA_msit_raw.fif'), overwrite=True, verbose=False)
```
### Projections: EOG
```
import os
from mne import write_proj
from mne.preprocessing import compute_proj_eog
from mne.io import Raw
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~#
### Setup
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~#
## File params.
root_dir = '/space/sophia/2/users/EMOTE-DBS/afMSIT_april2016'
subjects = ['BRTU', 'CHDR', 'CRDA', 'JADE', 'JASE', 'M5', 'MEWA', 'S2']
subjects = ['MEWA']
# NOTE: Not all subjects work with EOG channel = EOG.
# Some require other frontal channels due to concatenation.
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~#
### Main Loop.
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~#
for subj in subjects:
print 'Making EOG file for %s.' %subj
## Load files.
raw_file = os.path.join( root_dir, 'raw', '%s_msit_raw.fif' %subj )
raw = Raw(raw_file, preload=True, verbose=False, add_eeg_ref=False)
raw.del_proj(0)
## Make EOG proj. Save.
proj, _ = compute_proj_eog(raw, n_eeg = 4, average=True, filter_length='20s',
reject=dict(eeg=5e-4), flat=dict(eeg=5e-8), ch_name='F2', n_jobs=3)
write_proj(os.path.join( root_dir, 'raw', '%s_msit_eog-proj.fif' %subj ), proj)
```
### Projections: ECG
```
import os
from mne import read_proj, write_proj
from mne.preprocessing import compute_proj_ecg
from mne.io import Raw
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~#
### Setup
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~#
## File params.
root_dir = '/space/sophia/2/users/EMOTE-DBS/afMSIT_april2016'
subjects = ['CHDR']
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~#
### Main Loop.
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~#
for subj in subjects:
print 'Making ECG file for %s.' %subj
## Load files.
raw_file = os.path.join( root_dir, 'raw', '%s_msit_raw.fif' %subj )
eog_file = os.path.join( root_dir, 'raw', '%s_msit-proj.fif' %subj )
raw = Raw(raw_file, preload=True, verbose=False)
eog_proj = read_proj(eog_file)
raw.add_proj(eog_proj, remove_existing=True)
raw.apply_proj()
## Make ECG proj. Save.
ecg_proj, _ = compute_proj_ecg(raw, n_eeg = 4, h_freq = 35., average=True, filter_length='20s',
reject=dict(eeg=5e-4), flat=dict(eeg=5e-8), ch_name='P9', n_jobs=3)
proj = eog_proj + [ecg for ecg in ecg_proj if ecg['desc'] not in [eog['desc'] for eog in eog_proj]]
write_proj(os.path.join( root_dir, 'raw', '%s_msit-proj.fif' %subj ), proj)
```
## Preprocessing 2: Epoching
### Make Forward Solutions
```
import os
from mne import read_trans, read_bem_solution, read_source_spaces
from mne import make_forward_solution, write_forward_solution
from mne.io import Raw
## Subject level parameters.
subjects = ['BRTU', 'CHDR', 'CRDA', 'JADE', 'JASE', 'M5', 'MEWA', 'S2']
task = 'msit'
## Main loop.
root_dir = '/autofs/space/sophia_002/users/EMOTE-DBS/afMSIT_april2016'
fs_dir = '/autofs/space/sophia_002/users/EMOTE-DBS/freesurfs'
for subject in subjects:
print 'Making forward solution for %s.' %subject
## Load files.
raw = Raw(os.path.join(root_dir, 'raw', '%s_msit_raw.fif' %subject), preload=False, verbose=False)
trans = read_trans(os.path.join(fs_dir,subject,'mri','T1-neuromag','sets','COR-%s.fif' %subject))
src = read_source_spaces(os.path.join(fs_dir,subject,'bem','%s-oct-6p-src.fif' %subject), verbose=False)
bem = read_bem_solution(os.path.join(fs_dir,subject,'bem','%s-5120-5120-5120-bem-sol.fif' %subject), verbose=False)
## Compute and save forward solution.
make_forward_solution(raw.info, trans, src, bem, fname=os.path.join(root_dir,'fwd','%s_msit-fwd.fif' %subject),
meg=False, eeg=True, mindist=1.0, overwrite=True, n_jobs=3, verbose=False)
print 'Done.'
```
### Make Epochs
```
import os
import numpy as np
from mne import compute_covariance, Epochs, EpochsArray, find_events, read_proj, pick_types, set_log_level
from mne.io import Raw
from pandas import read_csv
set_log_level(verbose=False)
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~#
### Define parameters.
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~#
## Subject level parameters.
subjects = ['BRTU', 'CHDR', 'CRDA', 'JADE', 'JASE', 'M5', 'MEWA', 'S2']
task = 'msit'
## Filtering parameters.
l_freq = 0.5
h_freq = 50
l_trans_bandwidth = l_freq / 2.
h_trans_bandwidth = 1.0
filter_length = '20s'
n_jobs = 3
## Epoching parameters.
event_id = dict( FN=1, FI=2, NN=3, NI=4 ) # Alik's convention, isn't he smart!?
tmin = -1.5 # Leave some breathing room.
tmax = 3.4 # Trial is 1900ms, leave 1500ms of room.
resp_buffer = 1.5 # 1500ms on either side of response.
baseline = (-0.5,-0.1)
reject_tmin = -0.5
reject_tmax = 1.9
reject = dict(eeg=150e-6)
flat = dict(eeg=5e-7)
detrend = None
decim = 1
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~#
### Load behavior.
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~#
root_dir = '/space/sophia/2/users/EMOTE-DBS/afMSIT'
data_file = os.path.join( root_dir, 'behavior', 'afMSIT_group_data.csv' )
df = read_csv(data_file)
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~#
### Load behavior.
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~#
for subj in subjects:
print 'Loading data for %s.' %subj
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~#
### Load data.
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~#
# Define paths.
raw_file = os.path.join( root_dir, 'raw', '%s_%s_raw.fif' %(subj,task) )
proj_file = os.path.join( root_dir, 'raw', '%s_%s-proj.fif' %(subj,task) )
# Load data.
raw = Raw(raw_file,preload=True,verbose=False)
proj = read_proj(proj_file)
## Add projections.
proj = [p for p in proj if 'ref' not in p['desc']]
raw.add_proj(proj, remove_existing=True)
raw.add_eeg_average_proj()
raw.apply_proj()
print raw.info['projs']
## Reduce dataframe to subject.
data = df[df.Subject==subj]
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~#
### Make events.
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~#
print 'Identifying events for %s.' %subj,
events = find_events(raw, stim_channel='Trig1', output='onset', min_duration=0.25, verbose=False)
# Error catching.
if data.shape[0] != events.shape[0]: raise ValueError('Mismatching number of stimulus onsets!')
print '%s events found.' %events.shape[0]
# Update event identifiers.
n = 1
for dbs in [0,1]:
for cond in [0,1]:
ix, = np.where((data.DBS==dbs)&(data.Interference==cond))
events[ix,-1] = n
n+=1
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~#
### Filter
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~#
print 'Applying bandpass filter to raw [%s, %s].' %(l_freq, h_freq)
Fs = raw.info['sfreq']
raw.filter(l_freq = l_freq, h_freq = h_freq, filter_length=filter_length, n_jobs=n_jobs,
l_trans_bandwidth=l_trans_bandwidth, h_trans_bandwidth=h_trans_bandwidth)
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~#
### Make stimulus-locked epochs.
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~#
# Build initial epochs object.
picks = pick_types(raw.info, meg=False, eeg=True, exclude='bads')
epochs = Epochs(raw, events, event_id=event_id, tmin=tmin, tmax=tmax, baseline=baseline, picks=picks,
reject=reject, flat=flat, reject_tmin=reject_tmin, reject_tmax=reject_tmax,
proj=True, detrend=detrend, decim=decim)
# First round of rejections.
epochs.drop_bad() # Remove bad epochs.
copy = data.ix[[True if not log else False for log in epochs.drop_log]] # Update CSV based on rejections.
'''NOTE: Making a new dataframe copy is just a shortcut for easy indexing between the Pandas
DataFrame and the Epochs object. This is due to the three rounds of rejections being
applied to the data (e.g. amplitude, behavior exclusion, equalization).'''
# Drop epochs based on behavior.
epochs.drop(copy.Exclude.astype(bool))
data = data.ix[[True if not log else False for log in epochs.drop_log]]
print '%s trials remain after rejections.' %(len(epochs))
print epochs
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~#
### Make Response-locked epochs.
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~#
print 'Making response-locked epochs.'
# Build response-locked events.
response_indices = raw.time_as_index(0.4 + data.RT) # Compensating for MSIT-lock.
response_events = epochs.events.copy()
response_events[:,0] = response_events[:,0] + response_indices
# Get data.
arr = epochs.get_data()
times = epochs.times
# Calculate lengths of response-locked epochs.
response_times = data.RT + 0.4 # Compensating for MSIT-lock.
response_windows = np.array([response_times-resp_buffer, response_times+resp_buffer]).T
# Iteratively build epochs array.
trials = []
for n in xrange(len(epochs)):
mask = (times >= response_windows[n,0]) & (times <= response_windows[n,1])
trials.append( arr[n,:,mask] )
trials = np.array(trials).swapaxes(1,2)
# Finally, make epochs objects.
resp_epochs = EpochsArray(trials, epochs.info, response_events, tmin=-resp_buffer, event_id=event_id,)
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~#
### Save data.
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~#
print 'Saving epoch files.'
epochs.save(os.path.join(root_dir,'ave','%s_%s_%s_stim-epo.fif' %(subj,task,h_freq)))
resp_epochs.save(os.path.join(root_dir,'ave','%s_%s_%s_resp-epo.fif' %(subj,task,h_freq)))
data.to_csv(os.path.join(root_dir,'ave','%s_%s_%s-epo.csv' %(subj,task,h_freq)), index=False)
print '\n#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~#\n'
print 'Done.'
```
### Make Covariance Matrices / Inverse Solutions / Morph Maps
```
import os
from mne import EpochsArray, read_epochs, read_forward_solution, set_log_level
from mne import compute_covariance, write_cov
from mne import compute_morph_matrix, read_source_spaces
from mne.filter import low_pass_filter
from mne.minimum_norm import make_inverse_operator, write_inverse_operator
from scipy.io import savemat
set_log_level(verbose=False)
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~#
### Define parameters.
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~#
## Subject level parameters.
subjects = ['BRTU', 'CHDR', 'CRDA', 'JADE', 'JASE', 'M5', 'MEWA', 'S2']
task = 'msit'
## Analysis parameters.
fmax = 50
## Source localization parameters.
loose = 0.2
depth = 0.8
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~#
### Iteratively load and prepare data.
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~#
root_dir = '/autofs/space/sophia_002/users/EMOTE-DBS/afMSIT'
fs_dir = '/autofs/space/sophia_002/users/EMOTE-DBS/freesurfs'
src = read_source_spaces(os.path.join(fs_dir,'fscopy','bem','fscopy-oct-6p-src.fif'))
for subject in subjects:
print 'Processing %s' %subject
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~#
### Load files.
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~#
## Load in files.
epo_file = os.path.join(root_dir,'ave','%s_msit_%s_stim-epo.fif' %(subject,fmax))
epochs = read_epochs(epo_file, verbose=False)
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~#
### Secondary objects.
#~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~#
fwd = read_forward_solution(os.path.join(root_dir, 'fwd', '%s_%s-fwd.fif' %(subject,task)),
surf_ori=True, verbose=False)
## Compute/save noise covariance matrix & inverse operator.
noise_cov = compute_covariance(epochs, tmin=-0.5, tmax=0.0, method='shrunk', n_jobs=1)
write_cov(os.path.join(root_dir,'cov','%s_%s_%s-cov.fif' %(subject,task,h_freq)), noise_cov)
inv = make_inverse_operator(epochs.info, fwd, noise_cov, loose=loose, depth=depth, verbose=False)
write_inverse_operator(os.path.join(root_dir,'cov','%s_%s_%s-inv.fif' %(subject,task,fmax)), inv)
## Pre-compute morph matrix.
vertices_from = [inv['src'][n]['vertno'] for n in xrange(2)]
vertices_to = [src[n]['vertno'] for n in xrange(2)]
morph_mat = compute_morph_matrix(subject, 'fsaverage', vertices_from=vertices_from,
vertices_to=vertices_to,subjects_dir=fs_dir, smooth=25)
savemat(os.path.join(root_dir, 'morph_maps', '%s-fsaverage_morph.mat' %subject),
mdict=dict(morph_mat=morph_mat))
print 'Done.'
```
|
github_jupyter
|
##### Copyright 2019 The TensorFlow Authors.
```
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
```
# 理解语言的 Transformer 模型
<table class="tfo-notebook-buttons" align="left">
<td>
<a target="_blank" href="https://tensorflow.google.cn/tutorials/text/transformer">
<img src="https://tensorflow.google.cn/images/tf_logo_32px.png" />
在 tensorflow.google.cn 上查看</a>
</td>
<td>
<a target="_blank" href="https://colab.research.google.com/github/tensorflow/docs-l10n/blob/master/site/zh-cn/tutorials/text/transformer.ipynb">
<img src="https://tensorflow.google.cn/images/colab_logo_32px.png" />
在 Google Colab 运行</a>
</td>
<td>
<a target="_blank" href="https://github.com/tensorflow/docs-l10n/blob/master/site/zh-cn/tutorials/text/transformer.ipynb">
<img src="https://tensorflow.google.cn/images/GitHub-Mark-32px.png" />
在 Github 上查看源代码</a>
</td>
<td>
<a href="https://storage.googleapis.com/tensorflow_docs/docs-l10n/site/zh-cn/tutorials/text/transformer.ipynb"><img src="https://tensorflow.google.cn/images/download_logo_32px.png" />下载此 notebook</a>
</td>
</table>
Note: 我们的 TensorFlow 社区翻译了这些文档。因为社区翻译是尽力而为, 所以无法保证它们是最准确的,并且反映了最新的
[官方英文文档](https://tensorflow.google.cn/?hl=en)。如果您有改进此翻译的建议, 请提交 pull request 到
[tensorflow/docs](https://github.com/tensorflow/docs) GitHub 仓库。要志愿地撰写或者审核译文,请加入
[[email protected] Google Group](https://groups.google.com/a/tensorflow.org/forum/#!forum/docs-zh-cn)
本教程训练了一个 <a href="https://arxiv.org/abs/1706.03762" class="external">Transformer 模型</a> 用于将葡萄牙语翻译成英语。这是一个高级示例,假定您具备[文本生成(text generation)](text_generation.ipynb)和 [注意力机制(attention)](nmt_with_attention.ipynb) 的知识。
Transformer 模型的核心思想是*自注意力机制(self-attention)*——能注意输入序列的不同位置以计算该序列的表示的能力。Transformer 创建了多层自注意力层(self-attetion layers)组成的堆栈,下文的*按比缩放的点积注意力(Scaled dot product attention)*和*多头注意力(Multi-head attention)*部分对此进行了说明。
一个 transformer 模型用自注意力层而非 [RNNs](text_classification_rnn.ipynb) 或 [CNNs](../images/intro_to_cnns.ipynb) 来处理变长的输入。这种通用架构有一系列的优势:
* 它不对数据间的时间/空间关系做任何假设。这是处理一组对象(objects)的理想选择(例如,[星际争霸单位(StarCraft units)](https://deepmind.com/blog/alphastar-mastering-real-time-strategy-game-starcraft-ii/#block-8))。
* 层输出可以并行计算,而非像 RNN 这样的序列计算。
* 远距离项可以影响彼此的输出,而无需经过许多 RNN 步骤或卷积层(例如,参见[场景记忆 Transformer(Scene Memory Transformer)](https://arxiv.org/pdf/1903.03878.pdf))
* 它能学习长距离的依赖。在许多序列任务中,这是一项挑战。
该架构的缺点是:
* 对于时间序列,一个单位时间的输出是从*整个历史记录*计算的,而非仅从输入和当前的隐含状态计算得到。这*可能*效率较低。
* 如果输入*确实*有时间/空间的关系,像文本,则必须加入一些位置编码,否则模型将有效地看到一堆单词。
在此 notebook 中训练完模型后,您将能输入葡萄牙语句子,得到其英文翻译。
<img src="https://tensorflow.google.cn/images/tutorials/transformer/attention_map_portuguese.png" width="800" alt="Attention heatmap">
```
import tensorflow_datasets as tfds
import tensorflow as tf
import time
import numpy as np
import matplotlib.pyplot as plt
```
## 设置输入流水线(input pipeline)
使用 [TFDS](https://tensorflow.google.cn/datasets) 来导入 [葡萄牙语-英语翻译数据集](https://github.com/neulab/word-embeddings-for-nmt),该数据集来自于 [TED 演讲开放翻译项目](https://www.ted.com/participate/translate).
该数据集包含来约 50000 条训练样本,1100 条验证样本,以及 2000 条测试样本。
```
examples, metadata = tfds.load('ted_hrlr_translate/pt_to_en', with_info=True,
as_supervised=True)
train_examples, val_examples = examples['train'], examples['validation']
```
从训练数据集创建自定义子词分词器(subwords tokenizer)。
```
tokenizer_en = tfds.features.text.SubwordTextEncoder.build_from_corpus(
(en.numpy() for pt, en in train_examples), target_vocab_size=2**13)
tokenizer_pt = tfds.features.text.SubwordTextEncoder.build_from_corpus(
(pt.numpy() for pt, en in train_examples), target_vocab_size=2**13)
sample_string = 'Transformer is awesome.'
tokenized_string = tokenizer_en.encode(sample_string)
print ('Tokenized string is {}'.format(tokenized_string))
original_string = tokenizer_en.decode(tokenized_string)
print ('The original string: {}'.format(original_string))
assert original_string == sample_string
```
如果单词不在词典中,则分词器(tokenizer)通过将单词分解为子词来对字符串进行编码。
```
for ts in tokenized_string:
print ('{} ----> {}'.format(ts, tokenizer_en.decode([ts])))
BUFFER_SIZE = 20000
BATCH_SIZE = 64
```
将开始和结束标记(token)添加到输入和目标。
```
def encode(lang1, lang2):
lang1 = [tokenizer_pt.vocab_size] + tokenizer_pt.encode(
lang1.numpy()) + [tokenizer_pt.vocab_size+1]
lang2 = [tokenizer_en.vocab_size] + tokenizer_en.encode(
lang2.numpy()) + [tokenizer_en.vocab_size+1]
return lang1, lang2
```
Note:为了使本示例较小且相对较快,删除长度大于40个标记的样本。
```
MAX_LENGTH = 40
def filter_max_length(x, y, max_length=MAX_LENGTH):
return tf.logical_and(tf.size(x) <= max_length,
tf.size(y) <= max_length)
```
`.map()` 内部的操作以图模式(graph mode)运行,`.map()` 接收一个不具有 numpy 属性的图张量(graph tensor)。该`分词器(tokenizer)`需要将一个字符串或 Unicode 符号,编码成整数。因此,您需要在 `tf.py_function` 内部运行编码过程,`tf.py_function` 接收一个 eager 张量,该 eager 张量有一个包含字符串值的 numpy 属性。
```
def tf_encode(pt, en):
result_pt, result_en = tf.py_function(encode, [pt, en], [tf.int64, tf.int64])
result_pt.set_shape([None])
result_en.set_shape([None])
return result_pt, result_en
train_dataset = train_examples.map(tf_encode)
train_dataset = train_dataset.filter(filter_max_length)
# 将数据集缓存到内存中以加快读取速度。
train_dataset = train_dataset.cache()
train_dataset = train_dataset.shuffle(BUFFER_SIZE).padded_batch(BATCH_SIZE)
train_dataset = train_dataset.prefetch(tf.data.experimental.AUTOTUNE)
val_dataset = val_examples.map(tf_encode)
val_dataset = val_dataset.filter(filter_max_length).padded_batch(BATCH_SIZE)
pt_batch, en_batch = next(iter(val_dataset))
pt_batch, en_batch
```
## 位置编码(Positional encoding)
因为该模型并不包括任何的循环(recurrence)或卷积,所以模型添加了位置编码,为模型提供一些关于单词在句子中相对位置的信息。
位置编码向量被加到嵌入(embedding)向量中。嵌入表示一个 d 维空间的标记,在 d 维空间中有着相似含义的标记会离彼此更近。但是,嵌入并没有对在一句话中的词的相对位置进行编码。因此,当加上位置编码后,词将基于*它们含义的相似度以及它们在句子中的位置*,在 d 维空间中离彼此更近。
参看 [位置编码](https://github.com/tensorflow/examples/blob/master/community/en/position_encoding.ipynb) 的 notebook 了解更多信息。计算位置编码的公式如下:
$$\Large{PE_{(pos, 2i)} = sin(pos / 10000^{2i / d_{model}})} $$
$$\Large{PE_{(pos, 2i+1)} = cos(pos / 10000^{2i / d_{model}})} $$
```
def get_angles(pos, i, d_model):
angle_rates = 1 / np.power(10000, (2 * (i//2)) / np.float32(d_model))
return pos * angle_rates
def positional_encoding(position, d_model):
angle_rads = get_angles(np.arange(position)[:, np.newaxis],
np.arange(d_model)[np.newaxis, :],
d_model)
# 将 sin 应用于数组中的偶数索引(indices);2i
angle_rads[:, 0::2] = np.sin(angle_rads[:, 0::2])
# 将 cos 应用于数组中的奇数索引;2i+1
angle_rads[:, 1::2] = np.cos(angle_rads[:, 1::2])
pos_encoding = angle_rads[np.newaxis, ...]
return tf.cast(pos_encoding, dtype=tf.float32)
pos_encoding = positional_encoding(50, 512)
print (pos_encoding.shape)
plt.pcolormesh(pos_encoding[0], cmap='RdBu')
plt.xlabel('Depth')
plt.xlim((0, 512))
plt.ylabel('Position')
plt.colorbar()
plt.show()
```
## 遮挡(Masking)
遮挡一批序列中所有的填充标记(pad tokens)。这确保了模型不会将填充作为输入。该 mask 表明填充值 `0` 出现的位置:在这些位置 mask 输出 `1`,否则输出 `0`。
```
def create_padding_mask(seq):
seq = tf.cast(tf.math.equal(seq, 0), tf.float32)
# 添加额外的维度来将填充加到
# 注意力对数(logits)。
return seq[:, tf.newaxis, tf.newaxis, :] # (batch_size, 1, 1, seq_len)
x = tf.constant([[7, 6, 0, 0, 1], [1, 2, 3, 0, 0], [0, 0, 0, 4, 5]])
create_padding_mask(x)
```
前瞻遮挡(look-ahead mask)用于遮挡一个序列中的后续标记(future tokens)。换句话说,该 mask 表明了不应该使用的条目。
这意味着要预测第三个词,将仅使用第一个和第二个词。与此类似,预测第四个词,仅使用第一个,第二个和第三个词,依此类推。
```
def create_look_ahead_mask(size):
mask = 1 - tf.linalg.band_part(tf.ones((size, size)), -1, 0)
return mask # (seq_len, seq_len)
x = tf.random.uniform((1, 3))
temp = create_look_ahead_mask(x.shape[1])
temp
```
## 按比缩放的点积注意力(Scaled dot product attention)
<img src="https://tensorflow.google.cn/images/tutorials/transformer/scaled_attention.png" width="500" alt="scaled_dot_product_attention">
Transformer 使用的注意力函数有三个输入:Q(请求(query))、K(主键(key))、V(数值(value))。用于计算注意力权重的等式为:
$$\Large{Attention(Q, K, V) = softmax_k(\frac{QK^T}{\sqrt{d_k}}) V} $$
点积注意力被缩小了深度的平方根倍。这样做是因为对于较大的深度值,点积的大小会增大,从而推动 softmax 函数往仅有很小的梯度的方向靠拢,导致了一种很硬的(hard)softmax。
例如,假设 `Q` 和 `K` 的均值为0,方差为1。它们的矩阵乘积将有均值为0,方差为 `dk`。因此,*`dk` 的平方根*被用于缩放(而非其他数值),因为,`Q` 和 `K` 的矩阵乘积的均值本应该为 0,方差本应该为1,这样会获得一个更平缓的 softmax。
遮挡(mask)与 -1e9(接近于负无穷)相乘。这样做是因为遮挡与缩放的 Q 和 K 的矩阵乘积相加,并在 softmax 之前立即应用。目标是将这些单元归零,因为 softmax 的较大负数输入在输出中接近于零。
```
def scaled_dot_product_attention(q, k, v, mask):
"""计算注意力权重。
q, k, v 必须具有匹配的前置维度。
k, v 必须有匹配的倒数第二个维度,例如:seq_len_k = seq_len_v。
虽然 mask 根据其类型(填充或前瞻)有不同的形状,
但是 mask 必须能进行广播转换以便求和。
参数:
q: 请求的形状 == (..., seq_len_q, depth)
k: 主键的形状 == (..., seq_len_k, depth)
v: 数值的形状 == (..., seq_len_v, depth_v)
mask: Float 张量,其形状能转换成
(..., seq_len_q, seq_len_k)。默认为None。
返回值:
输出,注意力权重
"""
matmul_qk = tf.matmul(q, k, transpose_b=True) # (..., seq_len_q, seq_len_k)
# 缩放 matmul_qk
dk = tf.cast(tf.shape(k)[-1], tf.float32)
scaled_attention_logits = matmul_qk / tf.math.sqrt(dk)
# 将 mask 加入到缩放的张量上。
if mask is not None:
scaled_attention_logits += (mask * -1e9)
# softmax 在最后一个轴(seq_len_k)上归一化,因此分数
# 相加等于1。
attention_weights = tf.nn.softmax(scaled_attention_logits, axis=-1) # (..., seq_len_q, seq_len_k)
output = tf.matmul(attention_weights, v) # (..., seq_len_q, depth_v)
return output, attention_weights
```
当 softmax 在 K 上进行归一化后,它的值决定了分配到 Q 的重要程度。
输出表示注意力权重和 V(数值)向量的乘积。这确保了要关注的词保持原样,而无关的词将被清除掉。
```
def print_out(q, k, v):
temp_out, temp_attn = scaled_dot_product_attention(
q, k, v, None)
print ('Attention weights are:')
print (temp_attn)
print ('Output is:')
print (temp_out)
np.set_printoptions(suppress=True)
temp_k = tf.constant([[10,0,0],
[0,10,0],
[0,0,10],
[0,0,10]], dtype=tf.float32) # (4, 3)
temp_v = tf.constant([[ 1,0],
[ 10,0],
[ 100,5],
[1000,6]], dtype=tf.float32) # (4, 2)
# 这条 `请求(query)符合第二个`主键(key)`,
# 因此返回了第二个`数值(value)`。
temp_q = tf.constant([[0, 10, 0]], dtype=tf.float32) # (1, 3)
print_out(temp_q, temp_k, temp_v)
# 这条请求符合重复出现的主键(第三第四个),
# 因此,对所有的相关数值取了平均。
temp_q = tf.constant([[0, 0, 10]], dtype=tf.float32) # (1, 3)
print_out(temp_q, temp_k, temp_v)
# 这条请求符合第一和第二条主键,
# 因此,对它们的数值去了平均。
temp_q = tf.constant([[10, 10, 0]], dtype=tf.float32) # (1, 3)
print_out(temp_q, temp_k, temp_v)
```
将所有请求一起*传递*。
```
temp_q = tf.constant([[0, 0, 10], [0, 10, 0], [10, 10, 0]], dtype=tf.float32) # (3, 3)
print_out(temp_q, temp_k, temp_v)
```
## 多头注意力(Multi-head attention)
<img src="https://tensorflow.google.cn/images/tutorials/transformer/multi_head_attention.png" width="500" alt="multi-head attention">
多头注意力由四部分组成:
* 线性层并分拆成多头。
* 按比缩放的点积注意力。
* 多头及联。
* 最后一层线性层。
每个多头注意力块有三个输入:Q(请求)、K(主键)、V(数值)。这些输入经过线性(Dense)层,并分拆成多头。
将上面定义的 `scaled_dot_product_attention` 函数应用于每个头(进行了广播(broadcasted)以提高效率)。注意力这步必须使用一个恰当的 mask。然后将每个头的注意力输出连接起来(用`tf.transpose` 和 `tf.reshape`),并放入最后的 `Dense` 层。
Q、K、和 V 被拆分到了多个头,而非单个的注意力头,因为多头允许模型共同注意来自不同表示空间的不同位置的信息。在分拆后,每个头部的维度减少,因此总的计算成本与有着全部维度的单个注意力头相同。
```
class MultiHeadAttention(tf.keras.layers.Layer):
def __init__(self, d_model, num_heads):
super(MultiHeadAttention, self).__init__()
self.num_heads = num_heads
self.d_model = d_model
assert d_model % self.num_heads == 0
self.depth = d_model // self.num_heads
self.wq = tf.keras.layers.Dense(d_model)
self.wk = tf.keras.layers.Dense(d_model)
self.wv = tf.keras.layers.Dense(d_model)
self.dense = tf.keras.layers.Dense(d_model)
def split_heads(self, x, batch_size):
"""分拆最后一个维度到 (num_heads, depth).
转置结果使得形状为 (batch_size, num_heads, seq_len, depth)
"""
x = tf.reshape(x, (batch_size, -1, self.num_heads, self.depth))
return tf.transpose(x, perm=[0, 2, 1, 3])
def call(self, v, k, q, mask):
batch_size = tf.shape(q)[0]
q = self.wq(q) # (batch_size, seq_len, d_model)
k = self.wk(k) # (batch_size, seq_len, d_model)
v = self.wv(v) # (batch_size, seq_len, d_model)
q = self.split_heads(q, batch_size) # (batch_size, num_heads, seq_len_q, depth)
k = self.split_heads(k, batch_size) # (batch_size, num_heads, seq_len_k, depth)
v = self.split_heads(v, batch_size) # (batch_size, num_heads, seq_len_v, depth)
# scaled_attention.shape == (batch_size, num_heads, seq_len_q, depth)
# attention_weights.shape == (batch_size, num_heads, seq_len_q, seq_len_k)
scaled_attention, attention_weights = scaled_dot_product_attention(
q, k, v, mask)
scaled_attention = tf.transpose(scaled_attention, perm=[0, 2, 1, 3]) # (batch_size, seq_len_q, num_heads, depth)
concat_attention = tf.reshape(scaled_attention,
(batch_size, -1, self.d_model)) # (batch_size, seq_len_q, d_model)
output = self.dense(concat_attention) # (batch_size, seq_len_q, d_model)
return output, attention_weights
```
创建一个 `MultiHeadAttention` 层进行尝试。在序列中的每个位置 `y`,`MultiHeadAttention` 在序列中的所有其他位置运行所有8个注意力头,在每个位置y,返回一个新的同样长度的向量。
```
temp_mha = MultiHeadAttention(d_model=512, num_heads=8)
y = tf.random.uniform((1, 60, 512)) # (batch_size, encoder_sequence, d_model)
out, attn = temp_mha(y, k=y, q=y, mask=None)
out.shape, attn.shape
```
## 点式前馈网络(Point wise feed forward network)
点式前馈网络由两层全联接层组成,两层之间有一个 ReLU 激活函数。
```
def point_wise_feed_forward_network(d_model, dff):
return tf.keras.Sequential([
tf.keras.layers.Dense(dff, activation='relu'), # (batch_size, seq_len, dff)
tf.keras.layers.Dense(d_model) # (batch_size, seq_len, d_model)
])
sample_ffn = point_wise_feed_forward_network(512, 2048)
sample_ffn(tf.random.uniform((64, 50, 512))).shape
```
## 编码与解码(Encoder and decoder)
<img src="https://tensorflow.google.cn/images/tutorials/transformer/transformer.png" width="600" alt="transformer">
Transformer 模型与标准的[具有注意力机制的序列到序列模型(sequence to sequence with attention model)](nmt_with_attention.ipynb),遵循相同的一般模式。
* 输入语句经过 `N` 个编码器层,为序列中的每个词/标记生成一个输出。
* 解码器关注编码器的输出以及它自身的输入(自注意力)来预测下一个词。
### 编码器层(Encoder layer)
每个编码器层包括以下子层:
1. 多头注意力(有填充遮挡)
2. 点式前馈网络(Point wise feed forward networks)。
每个子层在其周围有一个残差连接,然后进行层归一化。残差连接有助于避免深度网络中的梯度消失问题。
每个子层的输出是 `LayerNorm(x + Sublayer(x))`。归一化是在 `d_model`(最后一个)维度完成的。Transformer 中有 N 个编码器层。
```
class EncoderLayer(tf.keras.layers.Layer):
def __init__(self, d_model, num_heads, dff, rate=0.1):
super(EncoderLayer, self).__init__()
self.mha = MultiHeadAttention(d_model, num_heads)
self.ffn = point_wise_feed_forward_network(d_model, dff)
self.layernorm1 = tf.keras.layers.LayerNormalization(epsilon=1e-6)
self.layernorm2 = tf.keras.layers.LayerNormalization(epsilon=1e-6)
self.dropout1 = tf.keras.layers.Dropout(rate)
self.dropout2 = tf.keras.layers.Dropout(rate)
def call(self, x, training, mask):
attn_output, _ = self.mha(x, x, x, mask) # (batch_size, input_seq_len, d_model)
attn_output = self.dropout1(attn_output, training=training)
out1 = self.layernorm1(x + attn_output) # (batch_size, input_seq_len, d_model)
ffn_output = self.ffn(out1) # (batch_size, input_seq_len, d_model)
ffn_output = self.dropout2(ffn_output, training=training)
out2 = self.layernorm2(out1 + ffn_output) # (batch_size, input_seq_len, d_model)
return out2
sample_encoder_layer = EncoderLayer(512, 8, 2048)
sample_encoder_layer_output = sample_encoder_layer(
tf.random.uniform((64, 43, 512)), False, None)
sample_encoder_layer_output.shape # (batch_size, input_seq_len, d_model)
```
### 解码器层(Decoder layer)
每个解码器层包括以下子层:
1. 遮挡的多头注意力(前瞻遮挡和填充遮挡)
2. 多头注意力(用填充遮挡)。V(数值)和 K(主键)接收*编码器输出*作为输入。Q(请求)接收*遮挡的多头注意力子层的输出*。
3. 点式前馈网络
每个子层在其周围有一个残差连接,然后进行层归一化。每个子层的输出是 `LayerNorm(x + Sublayer(x))`。归一化是在 `d_model`(最后一个)维度完成的。
Transformer 中共有 N 个解码器层。
当 Q 接收到解码器的第一个注意力块的输出,并且 K 接收到编码器的输出时,注意力权重表示根据编码器的输出赋予解码器输入的重要性。换一种说法,解码器通过查看编码器输出和对其自身输出的自注意力,预测下一个词。参看按比缩放的点积注意力部分的演示。
```
class DecoderLayer(tf.keras.layers.Layer):
def __init__(self, d_model, num_heads, dff, rate=0.1):
super(DecoderLayer, self).__init__()
self.mha1 = MultiHeadAttention(d_model, num_heads)
self.mha2 = MultiHeadAttention(d_model, num_heads)
self.ffn = point_wise_feed_forward_network(d_model, dff)
self.layernorm1 = tf.keras.layers.LayerNormalization(epsilon=1e-6)
self.layernorm2 = tf.keras.layers.LayerNormalization(epsilon=1e-6)
self.layernorm3 = tf.keras.layers.LayerNormalization(epsilon=1e-6)
self.dropout1 = tf.keras.layers.Dropout(rate)
self.dropout2 = tf.keras.layers.Dropout(rate)
self.dropout3 = tf.keras.layers.Dropout(rate)
def call(self, x, enc_output, training,
look_ahead_mask, padding_mask):
# enc_output.shape == (batch_size, input_seq_len, d_model)
attn1, attn_weights_block1 = self.mha1(x, x, x, look_ahead_mask) # (batch_size, target_seq_len, d_model)
attn1 = self.dropout1(attn1, training=training)
out1 = self.layernorm1(attn1 + x)
attn2, attn_weights_block2 = self.mha2(
enc_output, enc_output, out1, padding_mask) # (batch_size, target_seq_len, d_model)
attn2 = self.dropout2(attn2, training=training)
out2 = self.layernorm2(attn2 + out1) # (batch_size, target_seq_len, d_model)
ffn_output = self.ffn(out2) # (batch_size, target_seq_len, d_model)
ffn_output = self.dropout3(ffn_output, training=training)
out3 = self.layernorm3(ffn_output + out2) # (batch_size, target_seq_len, d_model)
return out3, attn_weights_block1, attn_weights_block2
sample_decoder_layer = DecoderLayer(512, 8, 2048)
sample_decoder_layer_output, _, _ = sample_decoder_layer(
tf.random.uniform((64, 50, 512)), sample_encoder_layer_output,
False, None, None)
sample_decoder_layer_output.shape # (batch_size, target_seq_len, d_model)
```
### 编码器(Encoder)
`编码器` 包括:
1. 输入嵌入(Input Embedding)
2. 位置编码(Positional Encoding)
3. N 个编码器层(encoder layers)
输入经过嵌入(embedding)后,该嵌入与位置编码相加。该加法结果的输出是编码器层的输入。编码器的输出是解码器的输入。
```
class Encoder(tf.keras.layers.Layer):
def __init__(self, num_layers, d_model, num_heads, dff, input_vocab_size,
maximum_position_encoding, rate=0.1):
super(Encoder, self).__init__()
self.d_model = d_model
self.num_layers = num_layers
self.embedding = tf.keras.layers.Embedding(input_vocab_size, d_model)
self.pos_encoding = positional_encoding(maximum_position_encoding,
self.d_model)
self.enc_layers = [EncoderLayer(d_model, num_heads, dff, rate)
for _ in range(num_layers)]
self.dropout = tf.keras.layers.Dropout(rate)
def call(self, x, training, mask):
seq_len = tf.shape(x)[1]
# 将嵌入和位置编码相加。
x = self.embedding(x) # (batch_size, input_seq_len, d_model)
x *= tf.math.sqrt(tf.cast(self.d_model, tf.float32))
x += self.pos_encoding[:, :seq_len, :]
x = self.dropout(x, training=training)
for i in range(self.num_layers):
x = self.enc_layers[i](x, training, mask)
return x # (batch_size, input_seq_len, d_model)
sample_encoder = Encoder(num_layers=2, d_model=512, num_heads=8,
dff=2048, input_vocab_size=8500,
maximum_position_encoding=10000)
sample_encoder_output = sample_encoder(tf.random.uniform((64, 62)),
training=False, mask=None)
print (sample_encoder_output.shape) # (batch_size, input_seq_len, d_model)
```
### 解码器(Decoder)
`解码器`包括:
1. 输出嵌入(Output Embedding)
2. 位置编码(Positional Encoding)
3. N 个解码器层(decoder layers)
目标(target)经过一个嵌入后,该嵌入和位置编码相加。该加法结果是解码器层的输入。解码器的输出是最后的线性层的输入。
```
class Decoder(tf.keras.layers.Layer):
def __init__(self, num_layers, d_model, num_heads, dff, target_vocab_size,
maximum_position_encoding, rate=0.1):
super(Decoder, self).__init__()
self.d_model = d_model
self.num_layers = num_layers
self.embedding = tf.keras.layers.Embedding(target_vocab_size, d_model)
self.pos_encoding = positional_encoding(maximum_position_encoding, d_model)
self.dec_layers = [DecoderLayer(d_model, num_heads, dff, rate)
for _ in range(num_layers)]
self.dropout = tf.keras.layers.Dropout(rate)
def call(self, x, enc_output, training,
look_ahead_mask, padding_mask):
seq_len = tf.shape(x)[1]
attention_weights = {}
x = self.embedding(x) # (batch_size, target_seq_len, d_model)
x *= tf.math.sqrt(tf.cast(self.d_model, tf.float32))
x += self.pos_encoding[:, :seq_len, :]
x = self.dropout(x, training=training)
for i in range(self.num_layers):
x, block1, block2 = self.dec_layers[i](x, enc_output, training,
look_ahead_mask, padding_mask)
attention_weights['decoder_layer{}_block1'.format(i+1)] = block1
attention_weights['decoder_layer{}_block2'.format(i+1)] = block2
# x.shape == (batch_size, target_seq_len, d_model)
return x, attention_weights
sample_decoder = Decoder(num_layers=2, d_model=512, num_heads=8,
dff=2048, target_vocab_size=8000,
maximum_position_encoding=5000)
output, attn = sample_decoder(tf.random.uniform((64, 26)),
enc_output=sample_encoder_output,
training=False, look_ahead_mask=None,
padding_mask=None)
output.shape, attn['decoder_layer2_block2'].shape
```
## 创建 Transformer
Transformer 包括编码器,解码器和最后的线性层。解码器的输出是线性层的输入,返回线性层的输出。
```
class Transformer(tf.keras.Model):
def __init__(self, num_layers, d_model, num_heads, dff, input_vocab_size,
target_vocab_size, pe_input, pe_target, rate=0.1):
super(Transformer, self).__init__()
self.encoder = Encoder(num_layers, d_model, num_heads, dff,
input_vocab_size, pe_input, rate)
self.decoder = Decoder(num_layers, d_model, num_heads, dff,
target_vocab_size, pe_target, rate)
self.final_layer = tf.keras.layers.Dense(target_vocab_size)
def call(self, inp, tar, training, enc_padding_mask,
look_ahead_mask, dec_padding_mask):
enc_output = self.encoder(inp, training, enc_padding_mask) # (batch_size, inp_seq_len, d_model)
# dec_output.shape == (batch_size, tar_seq_len, d_model)
dec_output, attention_weights = self.decoder(
tar, enc_output, training, look_ahead_mask, dec_padding_mask)
final_output = self.final_layer(dec_output) # (batch_size, tar_seq_len, target_vocab_size)
return final_output, attention_weights
sample_transformer = Transformer(
num_layers=2, d_model=512, num_heads=8, dff=2048,
input_vocab_size=8500, target_vocab_size=8000,
pe_input=10000, pe_target=6000)
temp_input = tf.random.uniform((64, 62))
temp_target = tf.random.uniform((64, 26))
fn_out, _ = sample_transformer(temp_input, temp_target, training=False,
enc_padding_mask=None,
look_ahead_mask=None,
dec_padding_mask=None)
fn_out.shape # (batch_size, tar_seq_len, target_vocab_size)
```
## 配置超参数(hyperparameters)
为了让本示例小且相对较快,已经减小了*num_layers、 d_model 和 dff* 的值。
Transformer 的基础模型使用的数值为:*num_layers=6*,*d_model = 512*,*dff = 2048*。关于所有其他版本的 Transformer,请查阅[论文](https://arxiv.org/abs/1706.03762)。
Note:通过改变以下数值,您可以获得在许多任务上达到最先进水平的模型。
```
num_layers = 4
d_model = 128
dff = 512
num_heads = 8
input_vocab_size = tokenizer_pt.vocab_size + 2
target_vocab_size = tokenizer_en.vocab_size + 2
dropout_rate = 0.1
```
## 优化器(Optimizer)
根据[论文](https://arxiv.org/abs/1706.03762)中的公式,将 Adam 优化器与自定义的学习速率调度程序(scheduler)配合使用。
$$\Large{lrate = d_{model}^{-0.5} * min(step{\_}num^{-0.5}, step{\_}num * warmup{\_}steps^{-1.5})}$$
```
class CustomSchedule(tf.keras.optimizers.schedules.LearningRateSchedule):
def __init__(self, d_model, warmup_steps=4000):
super(CustomSchedule, self).__init__()
self.d_model = d_model
self.d_model = tf.cast(self.d_model, tf.float32)
self.warmup_steps = warmup_steps
def __call__(self, step):
arg1 = tf.math.rsqrt(step)
arg2 = step * (self.warmup_steps ** -1.5)
return tf.math.rsqrt(self.d_model) * tf.math.minimum(arg1, arg2)
learning_rate = CustomSchedule(d_model)
optimizer = tf.keras.optimizers.Adam(learning_rate, beta_1=0.9, beta_2=0.98,
epsilon=1e-9)
temp_learning_rate_schedule = CustomSchedule(d_model)
plt.plot(temp_learning_rate_schedule(tf.range(40000, dtype=tf.float32)))
plt.ylabel("Learning Rate")
plt.xlabel("Train Step")
```
## 损失函数与指标(Loss and metrics)
由于目标序列是填充(padded)过的,因此在计算损失函数时,应用填充遮挡非常重要。
```
loss_object = tf.keras.losses.SparseCategoricalCrossentropy(
from_logits=True, reduction='none')
def loss_function(real, pred):
mask = tf.math.logical_not(tf.math.equal(real, 0))
loss_ = loss_object(real, pred)
mask = tf.cast(mask, dtype=loss_.dtype)
loss_ *= mask
return tf.reduce_mean(loss_)
train_loss = tf.keras.metrics.Mean(name='train_loss')
train_accuracy = tf.keras.metrics.SparseCategoricalAccuracy(
name='train_accuracy')
```
## 训练与检查点(Training and checkpointing)
```
transformer = Transformer(num_layers, d_model, num_heads, dff,
input_vocab_size, target_vocab_size,
pe_input=input_vocab_size,
pe_target=target_vocab_size,
rate=dropout_rate)
def create_masks(inp, tar):
# 编码器填充遮挡
enc_padding_mask = create_padding_mask(inp)
# 在解码器的第二个注意力模块使用。
# 该填充遮挡用于遮挡编码器的输出。
dec_padding_mask = create_padding_mask(inp)
# 在解码器的第一个注意力模块使用。
# 用于填充(pad)和遮挡(mask)解码器获取到的输入的后续标记(future tokens)。
look_ahead_mask = create_look_ahead_mask(tf.shape(tar)[1])
dec_target_padding_mask = create_padding_mask(tar)
combined_mask = tf.maximum(dec_target_padding_mask, look_ahead_mask)
return enc_padding_mask, combined_mask, dec_padding_mask
```
创建检查点的路径和检查点管理器(manager)。这将用于在每 `n` 个周期(epochs)保存检查点。
```
checkpoint_path = "./checkpoints/train"
ckpt = tf.train.Checkpoint(transformer=transformer,
optimizer=optimizer)
ckpt_manager = tf.train.CheckpointManager(ckpt, checkpoint_path, max_to_keep=5)
# 如果检查点存在,则恢复最新的检查点。
if ckpt_manager.latest_checkpoint:
ckpt.restore(ckpt_manager.latest_checkpoint)
print ('Latest checkpoint restored!!')
```
目标(target)被分成了 tar_inp 和 tar_real。tar_inp 作为输入传递到解码器。`tar_real` 是位移了 1 的同一个输入:在 `tar_inp` 中的每个位置,`tar_real` 包含了应该被预测到的下一个标记(token)。
例如,`sentence` = "SOS A lion in the jungle is sleeping EOS"
`tar_inp` = "SOS A lion in the jungle is sleeping"
`tar_real` = "A lion in the jungle is sleeping EOS"
Transformer 是一个自回归(auto-regressive)模型:它一次作一个部分的预测,然后使用到目前为止的自身的输出来决定下一步要做什么。
在训练过程中,本示例使用了 teacher-forcing 的方法(就像[文本生成教程](./text_generation.ipynb)中一样)。无论模型在当前时间步骤下预测出什么,teacher-forcing 方法都会将真实的输出传递到下一个时间步骤上。
当 transformer 预测每个词时,*自注意力(self-attention)*功能使它能够查看输入序列中前面的单词,从而更好地预测下一个单词。
为了防止模型在期望的输出上达到峰值,模型使用了前瞻遮挡(look-ahead mask)。
```
EPOCHS = 20
# 该 @tf.function 将追踪-编译 train_step 到 TF 图中,以便更快地
# 执行。该函数专用于参数张量的精确形状。为了避免由于可变序列长度或可变
# 批次大小(最后一批次较小)导致的再追踪,使用 input_signature 指定
# 更多的通用形状。
train_step_signature = [
tf.TensorSpec(shape=(None, None), dtype=tf.int64),
tf.TensorSpec(shape=(None, None), dtype=tf.int64),
]
@tf.function(input_signature=train_step_signature)
def train_step(inp, tar):
tar_inp = tar[:, :-1]
tar_real = tar[:, 1:]
enc_padding_mask, combined_mask, dec_padding_mask = create_masks(inp, tar_inp)
with tf.GradientTape() as tape:
predictions, _ = transformer(inp, tar_inp,
True,
enc_padding_mask,
combined_mask,
dec_padding_mask)
loss = loss_function(tar_real, predictions)
gradients = tape.gradient(loss, transformer.trainable_variables)
optimizer.apply_gradients(zip(gradients, transformer.trainable_variables))
train_loss(loss)
train_accuracy(tar_real, predictions)
```
葡萄牙语作为输入语言,英语为目标语言。
```
for epoch in range(EPOCHS):
start = time.time()
train_loss.reset_states()
train_accuracy.reset_states()
# inp -> portuguese, tar -> english
for (batch, (inp, tar)) in enumerate(train_dataset):
train_step(inp, tar)
if batch % 50 == 0:
print ('Epoch {} Batch {} Loss {:.4f} Accuracy {:.4f}'.format(
epoch + 1, batch, train_loss.result(), train_accuracy.result()))
if (epoch + 1) % 5 == 0:
ckpt_save_path = ckpt_manager.save()
print ('Saving checkpoint for epoch {} at {}'.format(epoch+1,
ckpt_save_path))
print ('Epoch {} Loss {:.4f} Accuracy {:.4f}'.format(epoch + 1,
train_loss.result(),
train_accuracy.result()))
print ('Time taken for 1 epoch: {} secs\n'.format(time.time() - start))
```
## 评估(Evaluate)
以下步骤用于评估:
* 用葡萄牙语分词器(`tokenizer_pt`)编码输入语句。此外,添加开始和结束标记,这样输入就与模型训练的内容相同。这是编码器输入。
* 解码器输入为 `start token == tokenizer_en.vocab_size`。
* 计算填充遮挡和前瞻遮挡。
* `解码器`通过查看`编码器输出`和它自身的输出(自注意力)给出预测。
* 选择最后一个词并计算它的 argmax。
* 将预测的词连接到解码器输入,然后传递给解码器。
* 在这种方法中,解码器根据它预测的之前的词预测下一个。
Note:这里使用的模型具有较小的能力以保持相对较快,因此预测可能不太正确。要复现论文中的结果,请使用全部数据集,并通过修改上述超参数来使用基础 transformer 模型或者 transformer XL。
```
def evaluate(inp_sentence):
start_token = [tokenizer_pt.vocab_size]
end_token = [tokenizer_pt.vocab_size + 1]
# 输入语句是葡萄牙语,增加开始和结束标记
inp_sentence = start_token + tokenizer_pt.encode(inp_sentence) + end_token
encoder_input = tf.expand_dims(inp_sentence, 0)
# 因为目标是英语,输入 transformer 的第一个词应该是
# 英语的开始标记。
decoder_input = [tokenizer_en.vocab_size]
output = tf.expand_dims(decoder_input, 0)
for i in range(MAX_LENGTH):
enc_padding_mask, combined_mask, dec_padding_mask = create_masks(
encoder_input, output)
# predictions.shape == (batch_size, seq_len, vocab_size)
predictions, attention_weights = transformer(encoder_input,
output,
False,
enc_padding_mask,
combined_mask,
dec_padding_mask)
# 从 seq_len 维度选择最后一个词
predictions = predictions[: ,-1:, :] # (batch_size, 1, vocab_size)
predicted_id = tf.cast(tf.argmax(predictions, axis=-1), tf.int32)
# 如果 predicted_id 等于结束标记,就返回结果
if predicted_id == tokenizer_en.vocab_size+1:
return tf.squeeze(output, axis=0), attention_weights
# 连接 predicted_id 与输出,作为解码器的输入传递到解码器。
output = tf.concat([output, predicted_id], axis=-1)
return tf.squeeze(output, axis=0), attention_weights
def plot_attention_weights(attention, sentence, result, layer):
fig = plt.figure(figsize=(16, 8))
sentence = tokenizer_pt.encode(sentence)
attention = tf.squeeze(attention[layer], axis=0)
for head in range(attention.shape[0]):
ax = fig.add_subplot(2, 4, head+1)
# 画出注意力权重
ax.matshow(attention[head][:-1, :], cmap='viridis')
fontdict = {'fontsize': 10}
ax.set_xticks(range(len(sentence)+2))
ax.set_yticks(range(len(result)))
ax.set_ylim(len(result)-1.5, -0.5)
ax.set_xticklabels(
['<start>']+[tokenizer_pt.decode([i]) for i in sentence]+['<end>'],
fontdict=fontdict, rotation=90)
ax.set_yticklabels([tokenizer_en.decode([i]) for i in result
if i < tokenizer_en.vocab_size],
fontdict=fontdict)
ax.set_xlabel('Head {}'.format(head+1))
plt.tight_layout()
plt.show()
def translate(sentence, plot=''):
result, attention_weights = evaluate(sentence)
predicted_sentence = tokenizer_en.decode([i for i in result
if i < tokenizer_en.vocab_size])
print('Input: {}'.format(sentence))
print('Predicted translation: {}'.format(predicted_sentence))
if plot:
plot_attention_weights(attention_weights, sentence, result, plot)
translate("este é um problema que temos que resolver.")
print ("Real translation: this is a problem we have to solve .")
translate("os meus vizinhos ouviram sobre esta ideia.")
print ("Real translation: and my neighboring homes heard about this idea .")
translate("vou então muito rapidamente partilhar convosco algumas histórias de algumas coisas mágicas que aconteceram.")
print ("Real translation: so i 'll just share with you some stories very quickly of some magical things that have happened .")
```
您可以为 `plot` 参数传递不同的层和解码器的注意力模块。
```
translate("este é o primeiro livro que eu fiz.", plot='decoder_layer4_block2')
print ("Real translation: this is the first book i've ever done.")
```
## 总结
在本教程中,您已经学习了位置编码,多头注意力,遮挡的重要性以及如何创建一个 transformer。
尝试使用一个不同的数据集来训练 transformer。您可也可以通过修改上述的超参数来创建基础 transformer 或者 transformer XL。您也可以使用这里定义的层来创建 [BERT](https://arxiv.org/abs/1810.04805) 并训练最先进的模型。此外,您可以实现 beam search 得到更好的预测。
|
github_jupyter
|
# Image Classification with Logistic Regression from Scratch with NumPy
Welcome to another jupyter notebook of implementing machine learning algorithms from scratch using only NumPy. This time we will be implementing a different version of logistic regression for a simple image classification task. I've already done a basic version of logistic regression before [here](https://github.com/leventbass/logistic_regression). This time, we will use logistic regression to classify images. I will show all necessary mathematical equations of logistic regression and how to vectorize the summations in the equations. We will be working with a subset of the famous handwritten digit dataset called MNIST. In the subset, there will only be images of digit 1 and 5. Therefore, we will be solving a binary classification problem.
This notebook includes feature extraction, model training, and evaluation steps. Let's see what we will achieve in this post in steps:
* First, we wil load and visualize the dataset and extract two different set of features to build a classifier on.
* We will run our logistic regression algorithm with gradient descent the representations to classify digits into 1 and 5.
* We will experiment with different learning rates to find the best one.
* Finally, we will evaluate the implemented models, decide which is the best performing one and visualize a decision boundary.
* Once again, let's remind ourselves that we won't be using any function or library that accomplishes the task itself. For instance, we won't use scikit-learn to implement cross validation, we will use numpy for that and for all of the other tasks.
```
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
```
## Feature Extraction
Let's load the training/test data and labels as numpy arrays. All data that is used is provided in the repository in data folder. Train and test data are 1561x256 and 424x256 dimensional matrices, respectively. Each row in the aforementioned matrices corresponds to an image of a digit. The 256 pixels correspond to a 16x16 image. Label 1 is assigned to digit 1 and label -1 is assigned to digit 5.
```
train_x = np.load('data/train_data.npy')
train_y = np.load('data/train_labels.npy')
test_x = np.load('data/test_data.npy')
test_y = np.load('data/test_labels.npy')
```
Now, let's display two of the digit images, one for digit 1 and one for digit 5. We will use `imshow` function of `matplotlib` library with a suitable colormap. We will first need to reshape 256 pixels to a 16x16 matrix.
```
digit_1 = train_x[0].reshape((16,16))
digit_5 = train_x[-1].reshape((16,16))
plt.subplot(121, title='Digit 1')
plt.imshow(digit_1, cmap='gray');
plt.subplot(122, title='Digit 5')
plt.imshow(digit_5, cmap='gray');
```
**Implementing Representation 1:**
Now, we will extract the **symmetry** and **average intensity** features to use in the model. To compute the intensity features, we compute the average pixel value of the image, and for the symmetry feature, we compute the negative of the norm of the difference between the image and its y-axis symmetrical. We will extract these two features for each image in the training and test sets. As a result, we should obtain a training data matrix of size 1561x2 and test data matrix of size 424x2.
Throughout the notebook, we will refer the representation with these two features as **Representation 1**
```
train_feature_1 = np.mean(train_x, axis=1)
test_feature_1 = np.mean(test_x, axis=1)
mirrored_image_train = np.flip(train_x.reshape((train_x.shape[0],16,16)), axis=2)
mirrored_image_test = np.flip(test_x.reshape((test_x.shape[0],16,16)), axis=2)
plt.subplot(121, title='Image')
plt.imshow(train_x[-1].reshape((16,16)), cmap='gray');
plt.subplot(122, title='Mirrored Image')
plt.imshow(mirrored_image_train[-1], cmap='gray');
train_diff = train_x - mirrored_image_train.reshape((mirrored_image_train.shape[0],256))
test_diff = test_x - mirrored_image_test.reshape((mirrored_image_test.shape[0],256))
norm_train_diff = np.linalg.norm(train_diff, axis=1)
norm_test_diff = np.linalg.norm(test_diff, axis=1)
train_feature_2 = -(norm_train_diff)
test_feature_2 = -(norm_test_diff)
train_X_1 = np.concatenate((train_feature_1[:,np.newaxis], train_feature_2[:,np.newaxis]), axis=1)
test_X_1 = np.concatenate((test_feature_1[:,np.newaxis], test_feature_2[:,np.newaxis]), axis=1)
```
Now, let's provide two scatter plots, one for training and one for test data. The plots will contain the average intensity values in the x-axis and symmetry values in the y-axis. We will denote the data points of label 1 with blue marker shaped <font color='blue'>o</font> and the data points of label -1 with a red marker shaped <font color='red'>x</font>.
```
plt.figure(figsize=(6,6))
plt.scatter(train_X_1[(train_y==1),0], train_X_1[(train_y==1),1], marker='o', color='blue', s=16)
plt.scatter(train_X_1[(train_y==-1),0], train_X_1[(train_y==-1),1], marker='x', color='red', s=16)
plt.title('Class Distribution of Training Data for Representation 1')
plt.xlabel('Average Intensity')
plt.ylabel('Symmetry')
plt.figure(figsize=(6,6))
plt.scatter(test_X_1[(test_y==1),0], test_X_1[(test_y==1),1], marker='o', color='blue', s=16)
plt.scatter(test_X_1[(test_y==-1),0], test_X_1[(test_y==-1),1], marker='x', color='red', s=16)
plt.title('Class Distribution of Test Data for Representation 1')
plt.xlabel('Average Intensity')
plt.ylabel('Symmetry');
```
**Implementing Representation 2:** We will come up with an alternative feature extraction approach and we will refer this representation as **Representation 2**.
```
train_rep2_fet1 = np.array([(i>-1).sum() for i in train_x])/(train_x.shape[0]) # feature 1 for representation 2
test_rep2_fet1 = np.array([(i>-1).sum() for i in test_x])/(test_x.shape[0])
train_rep2_fet2 = np.std(train_x, axis=1) # feature 2 for representation 2
test_rep2_fet2 = np.std(test_x, axis=1)
train_X_2 = np.concatenate((train_rep2_fet1[:,np.newaxis], train_rep2_fet2[:,np.newaxis]), axis=1)
test_X_2 = np.concatenate((test_rep2_fet1[:,np.newaxis], test_rep2_fet2[:,np.newaxis]), axis=1)
```
To create the first feature of representation 2, we sum up all of the pixel values that are higher than -1 since pixel values of -1 represent the surrounding area of the image and not itself. By summing up those values we get a number that would be clearly distinctive for image of number 5 and 1, because evidently number 5 would take up more space than number 1 when it is drawn.
To add another feature to representation 2, let's calculate the standard deviation of the images. Image of number 5 will obviously have more standard deviation than image of number 1 because of the fact that it is more dispersed throughtout the area than number 1, while pixel values of number 1 are more confined and closer to each other than the image of number 5. Hence, taking the standard deviation of pixel values would be a differentiating factor for our images.
```
plt.figure(figsize=(9,5))
plt.scatter(train_X_2[(train_y==1),0], train_X_2[(train_y==1),1], marker='o', color='blue', s=16)
plt.scatter(train_X_2[(train_y==-1),0], train_X_2[(train_y==-1),1], marker='x', color='red', s=16)
plt.title('Class Distribution of Training Data for Representation 2')
plt.xlabel('Average Intensity')
plt.ylabel('Symmetry')
plt.figure(figsize=(9,5))
plt.scatter(test_X_2[(test_y==1),0], test_X_2[(test_y==1),1], marker='o', color='blue', s=16)
plt.scatter(test_X_2[(test_y==-1),0], test_X_2[(test_y==-1),1], marker='x', color='red', s=16)
plt.title('Class Distribution of Test Data for Representation 2')
plt.xlabel('Length of non-white Pixels')
plt.ylabel('Standard Deviation');
```
## Logistic Regression
Let's implement the logistic regression classifier from scratch with gradient descent and train it using Representation 1 and Representation 2 as inputs. We will concatenate 1 to our features for the intercept term, such that one data point will look like for 2-D features [1,$x_1$,$x_2$], and the model vector will be [$w_0, w_1, w_2$], where $w_0$ is the intercept parameter.
```
def data_init(X, y):
y = y[:,np.newaxis]
m = len(y)
X = np.hstack((np.ones((m,1)),X))
n = np.size(X,1)
params = np.zeros((n,1))
return (X, y, params)
```
To implement the gradient of the logistic loss with respect to $w$, first let's derive its expression:
Total cost is:
$E(w) = \frac{1}{N} \sum_{n=1}^{N} \ln \left(1 + \exp \left(-y^{\left(n\right)} w^T x^{\left(n\right)}\right)\right)$
Cost for one sample is:
$E \left(w^{\left(1\right)} \right) = \ln \left(1 + \exp \left(-y^{\left(1\right)} w^T x^{\left(1\right)} \right) \right)$
where;
$y = \begin{bmatrix} y_1 \\ y_2 \\ \vdots \\ y_N \end{bmatrix}_{N\times 1}$
$x = \begin{bmatrix} 1 & {x_1}^{\left(1\right)} & {x_2}^{\left(1\right)} \\
1 & {x_1}^{\left(2\right)} & {x_2}^{\left(2\right)} \\
\vdots & \vdots & \vdots \\
1 & {x_1}^{\left(N\right)} & {x_2}^{\left(N\right)}\end{bmatrix}_{N\times 3}$
$w = \begin{bmatrix}w_0 \\ w_1 \\ w_2 \end{bmatrix}_{3\times 1}$
Let $z = -y^{\left(1\right)} w^T x^{\left(1\right)}$:
$\begin{aligned}
\frac{\partial E}{\partial w_0} &= \frac{\partial \ln(1 + \exp(z))}{\partial w_0} \\
&=\frac{\exp(z) \frac{\partial z}{\partial w_0}}{1 + \exp(z)}
\quad \left( \theta(z) = \frac{\exp(z)}{1 + \exp(z)} \right)\\
&= \theta(z) \frac{\partial z}{\partial w_0} \\
&= \theta\left(-y^{\left(1\right)} w^T x^{\left(1\right)}\right)
\frac{\partial \left(-y^{\left(1\right)} w^T x^{\left(1\right)}\right)}{\partial w_0} \\
&= \theta\left(-y^{\left(1\right)} w^T x^{\left(1\right)}\right)
\frac{\partial \left(-y^{\left(1\right)} \left(w_0 + w_1 {x_1}^{\left(1\right)} + w_2 {x_2}^{\left(1\right)}\right)\right)}{\partial w_0}\\
\frac{\partial E}{\partial w_0} &= \theta\left(-y^{\left(1\right)} w^T x^{\left(1\right)}\right) \left( -y^{\left(1\right)} \right) \\
\frac{\partial E}{\partial w_1} &= \theta\left(-y^{\left(1\right)} w^T x^{\left(1\right)}\right) \left( -y^{\left(1\right)} {x_1}^{\left(1\right)} \right)\\
\frac{\partial E}{\partial w_2} &= \theta\left(-y^{\left(1\right)} w^T x^{\left(1\right)}\right) \left( -y^{\left(1\right)} {x_2}^{\left(1\right)} \right)\\
\end{aligned}$
$\begin{aligned}
\nabla E (w) &= \frac{1}{N} \sum_{n=1}^{N} -\theta \left(-y^{\left(n\right)} w^T x^{\left(n\right)}\right) y^{\left(n\right)} x^{\left(n\right)}\\
&= \frac{1}{N} {\left( - \textbf{y} \circ \textbf{x} \right)}^T \cdot \theta \left( -\textbf{y} \circ \textbf{x w} \right)
\end{aligned}$
To prove that our implementation is converging, we will keep the loss values at each gradient descent iteration in a numpy array. To decide when to terminate the gradient descent iterations, we will check the absolute difference between the current loss value and the loss value of the previous step. If the difference is less than a small number, such as $10^{-5}$, we will exit the loop.
```
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def gradient_descent(X, y, params, learning_rate):
m = len(y)
cost_history = []
i=0
while(True):
params = params - (learning_rate/m) * ((-y * X).T @ sigmoid(-y * (X @ params)))
cost_history.append(compute_cost(X, y, params))
if(i!=0 and abs(cost_history[i] - cost_history[i-1]) < 10**-5):
break;
i+=1
cost_history = np.array(cost_history)
return (cost_history, params)
def compute_cost(X, y, theta):
N = len(y)
cost = np.sum(np.log(1+np.exp(-y * (X @ theta)))) / N
return cost
```
After the training is finalized, we will plot the loss values with respect to iteration count. Obviously, we should observe a decreasing loss as the number of iterations increases. Also, we will experiment with 5 different learning rates between 0 and 1, and plot the convergence curves for each learning rate in the same plot to observe the effect of the learning rate (step size) on the convergence.
```
(X, y, params) = data_init(train_X_1, train_y)
lr_list = [0.001, 0.003, 0.01, 0.03, 0.1]
c_list = ['red', 'green', 'yellow', 'blue','black']
plt.figure()
for lr, color in zip(lr_list, c_list):
(cost_history, params_optimal) = gradient_descent(X, y, params, lr)
plt.plot(range(len(cost_history)),cost_history, c=color);
plt.title("Convergence Graph of Cost Function")
plt.xlabel("Number of Iterations")
plt.ylabel("Cost")
plt.show()
```
## Evaluation
Now, let's train the logistic regression classifier on Representation 1 and 2 with the best learning rate we have used so far. We will report the training and test classification accuracy as:
\begin{align*}
\frac{\text{number of correctly classified samples}}{\text{total number of samples}}x100
\end{align*}
```
def predict(X, params):
y_pred_dummy = np.round(sigmoid(X @ params))
y_pred = np.where(y_pred_dummy==0,-1,1)
return y_pred
def get_accuracy(y_pred, y):
score = float(sum(y_pred == y))/ float(len(y)) * 100
return score
def evaluate(train_X, train_y, test_X, test_y, learning_rate, lambda_param):
(X, y, params) = data_init(train_X, train_y)
(_, params_optimal_1) = gradient_descent(X, y, params, learning_rate)
X_normalized = test_X
X_test = np.hstack((np.ones((X_normalized.shape[0],1)),X_normalized))
y_pred_train = predict(X, params_optimal_1)
train_score = get_accuracy(y_pred_train, y)
print('Training Score:',train_score)
y_pred_test = predict(X_test, params_optimal_1)
test_score = get_accuracy(y_pred_test, test_y[:,np.newaxis])
print('Test Score:',test_score)
print('Evaluation results for Representation 1:')
print('-'*50)
evaluate(train_X_1, train_y, test_X_1, test_y, 0.1, 0.0003)
print('\nEvaluation results for Representation 2:')
print('-'*50)
evaluate(train_X_2, train_y, test_X_2, test_y, 0.1, 0.0001)
```
Last but not least, we will visualize the decision boundary (the line that is given by $\mathbf{w}^{T}x=0$) obtained from the logistic regression classifier learned. For this purpose, we will only use Representation 1. Below, two scatter plots can be seen for training and test data points with the decision boundary shown on each of the plots.
```
(X, y, params) = data_init(train_X_1,train_y)
learning_rate = 0.1
(_, params_optimal_1) = gradient_descent(X, y, params, learning_rate)
slope = -(params_optimal_1[1] / params_optimal_1[2])
intercept = -(params_optimal_1[0] / params_optimal_1[2])
titles = ['Training Data with Decision Boundary', 'Test Data with Decision Boundary']
for X, y, title in [(train_X_1, y, titles[0]), (test_X_1, test_y, titles[1])]:
plt.figure(figsize=(7,7))
plt.scatter(X[:,0],X[:,1],c=y.reshape(-1), s=14, cmap='bwr')
ax = plt.gca()
ax.autoscale(False)
x_vals = np.array(ax.get_xlim())
y_vals = intercept + (slope * x_vals)
plt.title(title);
plt.plot(x_vals, y_vals, c='k')
```
|
github_jupyter
|
# Инициализация
```
#@markdown - **Монтирование GoogleDrive**
from google.colab import drive
drive.mount('GoogleDrive')
# #@markdown - **Размонтирование**
# !fusermount -u GoogleDrive
```
# Область кодов
```
#@title Приближение с помощью кривых { display-mode: "both" }
# Curve fitting
# В программе реализовано приближение исходных данных с помощью нейронных сетей с одным скрытым слоем
# Можно сравнить с результатами метода регуляризации Тихонова
# conding: utf-8
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
import time
#@markdown - **Настройка параметров**
num_epoch = 200 #@param {type: "integer"}
# Предварительная обработка данных образца
data = np.array([[-2.95507616, 10.94533252],
[-0.44226119, 2.96705822],
[-2.13294087, 6.57336839],
[1.84990823, 5.44244467],
[0.35139795, 2.83533936],
[-1.77443098, 5.6800407],
[-1.8657203, 6.34470814],
[1.61526823, 4.77833358],
[-2.38043687, 8.51887713],
[-1.40513866, 4.18262786]])
x = data[:, 0]
y = data[:, 1]
X = x.reshape(-1, 1)
Y = y.reshape(-1, 1)
# Более прогнозируемые данные, чем исходные данные
x_pre = np.linspace(x.min(), x.max(), 30, endpoint=True).reshape(-1, 1)
#@markdown - **Создание graph**
graph = tf.Graph()
with graph.as_default():
with tf.name_scope('Input'):
x = tf.placeholder(tf.float32, shape=[None, 1], name='x')
y = tf.placeholder(tf.float32, shape=[None, 1], name='y')
with tf.name_scope('FC'):
w_1 = tf.get_variable('w_fc1', shape=[1, 32], initializer=tf.initializers.truncated_normal(stddev=0.1))
b_1 = tf.get_variable('b_fc1', initializer=tf.constant(0.1, shape=[32]))
layer_1 = tf.nn.sigmoid(tf.matmul(x, w_1) + b_1)
with tf.name_scope('Output'):
w_2 = tf.get_variable('w_fc2', shape=[32, 1], initializer=tf.initializers.truncated_normal(stddev=0.1))
b_2 = tf.get_variable('b_fc2', initializer=tf.constant(0.1, shape=[1]))
layer_2 = tf.matmul(layer_1, w_2) + b_2
with tf.name_scope('Loss'):
loss = tf.reduce_mean(tf.pow(layer_2 - y, 2))
with tf.name_scope('Train'):
train_op = tf.train.AdamOptimizer(learning_rate=3e-1).minimize(loss)
#@markdown - **Обучение модели**
with tf.Session(graph=graph) as sess:
sess.run(tf.global_variables_initializer())
time_start = time.time()
for num in range(num_epoch):
_, ls = sess.run([train_op, loss], feed_dict={x: X, y: Y})
print_list = [num+1, ls]
if (num+1) % 10 == 0 or num == 0:
print('Epoch {0[0]}, loss: {0[1]:.4f}.'.format(print_list))
# time_start = time.time()
y_pre = sess.run(layer_2, feed_dict={x: x_pre})
sess.close()
time_end = time.time()
t = time_end - time_start
print('Running time is: %.4f s.' % t)
#@markdown - **Кривая прогнозирования**
data_pre = np.c_[x_pre, y_pre]
DATA = [data, data_pre]
NAME = ['Training data', 'Fitting curve']
STYLE = ['*r', 'b']
fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(12, 6))
for dat, name, style in zip(DATA, NAME, STYLE):
ax.plot(dat[:, 0], dat[:, 1], style, markersize=8, label=name)
ax.legend(loc='upper right', fontsize=14)
ax.tick_params(labelsize=14)
plt.show()
```
|
github_jupyter
|
# Machine Learning application: Forecasting wind power. Using alternative energy for social & enviromental Good
<table>
<tr><td>
<img src="https://github.com/dmatrix/mlflow-workshop-part-3/raw/master/images/wind_farm.jpg"
alt="Keras NN Model as Logistic regression" width="800">
</td></tr>
</table>
In this notebook, we will use the MLflow Model Registry to build a machine learning application that forecasts the daily power output of a [wind farm](https://en.wikipedia.org/wiki/Wind_farm).
Wind farm power output depends on weather conditions: generally, more energy is produced at higher wind speeds. Accordingly, the machine learning models used in the notebook predicts power output based on weather forecasts with three features: `wind direction`, `wind speed`, and `air temperature`.
* This notebook uses altered data from the [National WIND Toolkit dataset](https://www.nrel.gov/grid/wind-toolkit.html) provided by NREL, which is publicly available and cited as follows:*
* Draxl, C., B.M. Hodge, A. Clifton, and J. McCaa. 2015. Overview and Meteorological Validation of the Wind Integration National Dataset Toolkit (Technical Report, NREL/TP-5000-61740). Golden, CO: National Renewable Energy Laboratory.*
* Draxl, C., B.M. Hodge, A. Clifton, and J. McCaa. 2015. "The Wind Integration National Dataset (WIND) Toolkit." Applied Energy 151: 355366.*
* Lieberman-Cribbin, W., C. Draxl, and A. Clifton. 2014. Guide to Using the WIND Toolkit Validation Code (Technical Report, NREL/TP-5000-62595). Golden, CO: National Renewable Energy Laboratory.*
* King, J., A. Clifton, and B.M. Hodge. 2014. Validation of Power Output for the WIND Toolkit (Technical Report, NREL/TP-5D00-61714). Golden, CO: National Renewable Energy Laboratory.*
Google's DeepMind publised a [AI for Social Good: 7 Inspiring Examples](https://www.springboard.com/blog/ai-for-good/) blog. One of example was
how Wind Farms can predict expected power ouput based on wind conditions and temperature, hence mitigating the burden from consuming
energy from fossil fuels.
<table>
<tr><td>
<img src="https://github.com/dmatrix/ds4g-workshop/raw/master/notebooks/images/deepmind_system-windpower.gif"
alt="Deep Mind ML Wind Power" width="400">
<img src="https://github.com/dmatrix/ds4g-workshop/raw/master/notebooks/images/machine_learning-value_wind_energy.max-1000x1000.png"
alt="Deep Mind ML Wind Power" width="400">
</td></tr>
</table>
```
import warnings
warnings.filterwarnings("ignore")
import mlflow
mlflow.__version__
```
## Run some class and utility notebooks
This defines and allows us to use some Python model classes and utility functions
```
%run ./rfr_class.ipynb
%run ./utils_class.ipynb
```
## Load our training data
Ideally, you would load it from a Feature Store or Delta Lake table
```
# Load and print dataset
csv_path = "https://raw.githubusercontent.com/dmatrix/olt-mlflow/master/model_registery/notebooks/data/windfarm_data.csv"
# Use column 0 (date) as the index
wind_farm_data = Utils.load_data(csv_path, index_col=0)
wind_farm_data.head(5)
```
## Get Training and Validation data
```
X_train, y_train = Utils.get_training_data(wind_farm_data)
val_x, val_y = Utils.get_validation_data(wind_farm_data)
```
## Initialize a set of hyperparameters for the training and try three runs
```
# Initialize our model hyperparameters
params_list = [{"n_estimators": 100},
{"n_estimators": 200},
{"n_estimators": 300}]
mlflow.set_tracking_uri("sqlite:///mlruns.db")
model_name = "WindfarmPowerForecastingModel"
for params in params_list:
rfr = RFRModel.new_instance(params)
print("Using paramerts={}".format(params))
runID = rfr.mlflow_run(X_train, y_train, val_x, val_y, model_name, register=True)
print("MLflow run_id={} completed with MSE={} and RMSE={}".format(runID, rfr.mse, rfr.rsme))
```
## Let's Examine the MLflow UI
1. Let's examine some models and start comparing their metrics
2. **mlflow ui --backend-store-uri sqlite:///mlruns.db**
# Integrating Model Registry with CI/CD Forecasting Application
<table>
<tr><td>
<img src="https://github.com/dmatrix/mlflow-workshop-part-3/raw/master/images/forecast_app.png"
alt="Keras NN Model as Logistic regression" width="800">
</td></tr>
</table>
1. Use the model registry fetch different versions of the model
2. Score the model
3. Select the best scored model
4. Promote model to production, after testing
# Define a helper function to load PyFunc model from the registry
<table>
<tr><td> Save a Built-in MLflow Model Flavor and load as PyFunc Flavor</td></tr>
<tr><td>
<img src="https://raw.githubusercontent.com/dmatrix/mlflow-workshop-part-2/master/images/models_2.png"
alt="" width="600">
</td></tr>
</table>
```
def score_model(data, model_uri):
model = mlflow.pyfunc.load_model(model_uri)
return model.predict(data)
```
## Load scoring data
Again, ideally you would load it from on-line or off-line FeatureStore
```
# Load the score data
score_path = "https://raw.githubusercontent.com/dmatrix/olt-mlflow/master/model_registery/notebooks/data/score_windfarm_data.csv"
score_df = Utils.load_data(score_path, index_col=0)
score_df.head()
# Drop the power column since we are predicting that value
actual_power = pd.DataFrame(score_df.power.values, columns=['power'])
score = score_df.drop("power", axis=1)
```
## Score the version 1 of the model
```
# Formulate the model URI to fetch from the model registery
model_uri = "models:/{}/{}".format(model_name, 1)
# Predict the Power output
pred_1 = pd.DataFrame(score_model(score, model_uri), columns=["predicted_1"])
pred_1
```
#### Combine with the actual power
```
actual_power["predicted_1"] = pred_1["predicted_1"]
actual_power
```
## Score the version 2 of the model
```
# Formulate the model URI to fetch from the model registery
model_uri = "models:/{}/{}".format(model_name, 2)
# Predict the Power output
pred_2 = pd.DataFrame(score_model(score, model_uri), columns=["predicted_2"])
pred_2
```
#### Combine with the actual power
```
actual_power["predicted_2"] = pred_2["predicted_2"]
actual_power
```
## Score the version 3 of the model
```
# Formulate the model URI to fetch from the model registery
model_uri = "models:/{}/{}".format(model_name, 3)
# Formulate the model URI to fetch from the model registery
pred_3 = pd.DataFrame(score_model(score, model_uri), columns=["predicted_3"])
pred_3
```
#### Combine the values into a single pandas DataFrame
```
actual_power["predicted_3"] = pred_3["predicted_3"]
actual_power
```
## Plot the combined predicited results vs the actual power
```
%matplotlib inline
actual_power.plot.line()
```
|
github_jupyter
|
##### Copyright 2019 The TensorFlow Authors.
```
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
#@title MIT License
#
# Copyright (c) 2017 François Chollet
#
# Permission is hereby granted, free of charge, to any person obtaining a
# copy of this software and associated documentation files (the "Software"),
# to deal in the Software without restriction, including without limitation
# the rights to use, copy, modify, merge, publish, distribute, sublicense,
# and/or sell copies of the Software, and to permit persons to whom the
# Software is furnished to do so, subject to the following conditions:
#
# The above copyright notice and this permission notice shall be included in
# all copies or substantial portions of the Software.
#
# THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
# IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
# FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL
# THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
# LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING
# FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER
# DEALINGS IN THE SOFTWARE.
```
# Text classification with TensorFlow Hub: Movie reviews
<table class="tfo-notebook-buttons" align="left">
<td>
<a target="_blank" href="https://www.tensorflow.org/tutorials/keras/text_classification_with_hub"><img src="https://www.tensorflow.org/images/tf_logo_32px.png" />View on TensorFlow.org</a>
</td>
<td>
<a target="_blank" href="https://colab.research.google.com/github/tensorflow/docs/blob/master/site/en/tutorials/keras/text_classification_with_hub.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
</td>
<td>
<a target="_blank" href="https://github.com/tensorflow/docs/blob/master/site/en/tutorials/keras/text_classification_with_hub.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View source on GitHub</a>
</td>
<td>
<a href="https://storage.googleapis.com/tensorflow_docs/docs/site/en/tutorials/keras/text_classification_with_hub.ipynb"><img src="https://www.tensorflow.org/images/download_logo_32px.png" />Download notebook</a>
</td>
</table>
This notebook classifies movie reviews as *positive* or *negative* using the text of the review. This is an example of *binary*—or two-class—classification, an important and widely applicable kind of machine learning problem.
The tutorial demonstrates the basic application of transfer learning with TensorFlow Hub and Keras.
We'll use the [IMDB dataset](https://www.tensorflow.org/api_docs/python/tf/keras/datasets/imdb) that contains the text of 50,000 movie reviews from the [Internet Movie Database](https://www.imdb.com/). These are split into 25,000 reviews for training and 25,000 reviews for testing. The training and testing sets are *balanced*, meaning they contain an equal number of positive and negative reviews.
This notebook uses [tf.keras](https://www.tensorflow.org/guide/keras), a high-level API to build and train models in TensorFlow, and [TensorFlow Hub](https://www.tensorflow.org/hub), a library and platform for transfer learning. For a more advanced text classification tutorial using `tf.keras`, see the [MLCC Text Classification Guide](https://developers.google.com/machine-learning/guides/text-classification/).
```
import numpy as np
import tensorflow as tf
!pip install tensorflow-hub
!pip install tfds-nightly
import tensorflow_hub as hub
import tensorflow_datasets as tfds
print("Version: ", tf.__version__)
print("Eager mode: ", tf.executing_eagerly())
print("Hub version: ", hub.__version__)
print("GPU is", "available" if tf.config.experimental.list_physical_devices("GPU") else "NOT AVAILABLE")
```
## Download the IMDB dataset
The IMDB dataset is available on [imdb reviews](https://www.tensorflow.org/datasets/catalog/imdb_reviews) or on [TensorFlow datasets](https://www.tensorflow.org/datasets). The following code downloads the IMDB dataset to your machine (or the colab runtime):
```
# Split the training set into 60% and 40%, so we'll end up with 15,000 examples
# for training, 10,000 examples for validation and 25,000 examples for testing.
train_data, validation_data, test_data = tfds.load(
name="imdb_reviews",
split=('train[:60%]', 'train[60%:]', 'test'),
as_supervised=True)
```
## Explore the data
Let's take a moment to understand the format of the data. Each example is a sentence representing the movie review and a corresponding label. The sentence is not preprocessed in any way. The label is an integer value of either 0 or 1, where 0 is a negative review, and 1 is a positive review.
Let's print first 10 examples.
```
train_examples_batch, train_labels_batch = next(iter(train_data.batch(10)))
train_examples_batch
```
Let's also print the first 10 labels.
```
train_labels_batch
```
## Build the model
The neural network is created by stacking layers—this requires three main architectural decisions:
* How to represent the text?
* How many layers to use in the model?
* How many *hidden units* to use for each layer?
In this example, the input data consists of sentences. The labels to predict are either 0 or 1.
One way to represent the text is to convert sentences into embeddings vectors. We can use a pre-trained text embedding as the first layer, which will have three advantages:
* we don't have to worry about text preprocessing,
* we can benefit from transfer learning,
* the embedding has a fixed size, so it's simpler to process.
For this example we will use a **pre-trained text embedding model** from [TensorFlow Hub](https://www.tensorflow.org/hub) called [google/tf2-preview/gnews-swivel-20dim/1](https://tfhub.dev/google/tf2-preview/gnews-swivel-20dim/1).
There are three other pre-trained models to test for the sake of this tutorial:
* [google/tf2-preview/gnews-swivel-20dim-with-oov/1](https://tfhub.dev/google/tf2-preview/gnews-swivel-20dim-with-oov/1) - same as [google/tf2-preview/gnews-swivel-20dim/1](https://tfhub.dev/google/tf2-preview/gnews-swivel-20dim/1), but with 2.5% vocabulary converted to OOV buckets. This can help if vocabulary of the task and vocabulary of the model don't fully overlap.
* [google/tf2-preview/nnlm-en-dim50/1](https://tfhub.dev/google/tf2-preview/nnlm-en-dim50/1) - A much larger model with ~1M vocabulary size and 50 dimensions.
* [google/tf2-preview/nnlm-en-dim128/1](https://tfhub.dev/google/tf2-preview/nnlm-en-dim128/1) - Even larger model with ~1M vocabulary size and 128 dimensions.
Let's first create a Keras layer that uses a TensorFlow Hub model to embed the sentences, and try it out on a couple of input examples. Note that no matter the length of the input text, the output shape of the embeddings is: `(num_examples, embedding_dimension)`.
```
embedding = "https://tfhub.dev/google/tf2-preview/gnews-swivel-20dim/1"
hub_layer = hub.KerasLayer(embedding, input_shape=[],
dtype=tf.string, trainable=True)
hub_layer(train_examples_batch[:3])
```
Let's now build the full model:
```
model = tf.keras.Sequential()
model.add(hub_layer)
model.add(tf.keras.layers.Dense(16, activation='relu'))
model.add(tf.keras.layers.Dense(1))
model.summary()
```
The layers are stacked sequentially to build the classifier:
1. The first layer is a TensorFlow Hub layer. This layer uses a pre-trained Saved Model to map a sentence into its embedding vector. The pre-trained text embedding model that we are using ([google/tf2-preview/gnews-swivel-20dim/1](https://tfhub.dev/google/tf2-preview/gnews-swivel-20dim/1)) splits the sentence into tokens, embeds each token and then combines the embedding. The resulting dimensions are: `(num_examples, embedding_dimension)`.
2. This fixed-length output vector is piped through a fully-connected (`Dense`) layer with 16 hidden units.
3. The last layer is densely connected with a single output node.
Let's compile the model.
### Loss function and optimizer
A model needs a loss function and an optimizer for training. Since this is a binary classification problem and the model outputs logits (a single-unit layer with a linear activation), we'll use the `binary_crossentropy` loss function.
This isn't the only choice for a loss function, you could, for instance, choose `mean_squared_error`. But, generally, `binary_crossentropy` is better for dealing with probabilities—it measures the "distance" between probability distributions, or in our case, between the ground-truth distribution and the predictions.
Later, when we are exploring regression problems (say, to predict the price of a house), we will see how to use another loss function called mean squared error.
Now, configure the model to use an optimizer and a loss function:
```
model.compile(optimizer='adam',
loss=tf.keras.losses.BinaryCrossentropy(from_logits=True),
metrics=['accuracy'])
```
## Train the model
Train the model for 20 epochs in mini-batches of 512 samples. This is 20 iterations over all samples in the `x_train` and `y_train` tensors. While training, monitor the model's loss and accuracy on the 10,000 samples from the validation set:
```
history = model.fit(train_data.shuffle(10000).batch(512),
epochs=20,
validation_data=validation_data.batch(512),
verbose=1)
```
## Evaluate the model
And let's see how the model performs. Two values will be returned. Loss (a number which represents our error, lower values are better), and accuracy.
```
results = model.evaluate(test_data.batch(512), verbose=2)
for name, value in zip(model.metrics_names, results):
print("%s: %.3f" % (name, value))
```
This fairly naive approach achieves an accuracy of about 87%. With more advanced approaches, the model should get closer to 95%.
## Further reading
For a more general way to work with string inputs and for a more detailed analysis of the progress of accuracy and loss during training, see the [Text classification with preprocessed text](./text_classification.ipynb) tutorial.
|
github_jupyter
|
# TOC
1. [Settings](#Settings)
2. [Get the task list](#Get-the-task-list)
3. [Upload annotations](#Upload-annotations)
4. [Get annotation results](#Get-annotation-results)
5. [Get annotation detail log](#Get-annotation-detail-log)
# Settings
```
import init
import pandas as pd
import json
import requests
host = 'http://api:5000'
headers = {}
# Cloud Run API needs Authorization
host = 'https://******.a.run.app'
headers = {
'Authorization': 'Bearer <TOKEN>'
}
```
# Get the task list
```
res = requests.get(f'{host}/tasks', headers=headers).json()
pd.DataFrame(res)[:3]
```
# Upload annotations
## Card UI
- [Task-dependent schema#card](https://github.com/CyberAgent/fast-annotation-tool/wiki/%E3%82%BF%E3%82%B9%E3%82%AF%E4%BE%9D%E5%AD%98%E3%81%AE%E3%82%B9%E3%82%AD%E3%83%BC%E3%83%9E#card)
<img src="https://user-images.githubusercontent.com/17490886/101377448-2b53fe80-38f5-11eb-8f46-0b154fc60138.png" alt="image" />
```
# Make annotation data
annotations_data = [
{
"text": f"This is a test{i}.",
"show_ambiguous_button": True,
"hidden_data": {
"desc": "Data for aggregation. It can be a dictionary or a string."
}
} for i in range(100)
]
df_annotation = pd.DataFrame(annotations_data)
df_annotation[:3]
# Post task data
post_data = {
"task_id": "card-demo-20200602",
"annotation_type": "card",
"title": "Card Demo",
"question": "This is card demo",
"description": "This is a card demo, so feel free to annotate it as you wish.",
"annotations_data": annotations_data
}
res = requests.post(f'{host}/tasks', headers=headers, json=post_data).json()
res
```
## Multi-Label UI
- [Task-dependent schema#multilabel](https://github.com/CyberAgent/fast-annotation-tool/wiki/%E3%82%BF%E3%82%B9%E3%82%AF%E4%BE%9D%E5%AD%98%E3%81%AE%E3%82%B9%E3%82%AD%E3%83%BC%E3%83%9E#multilabel)
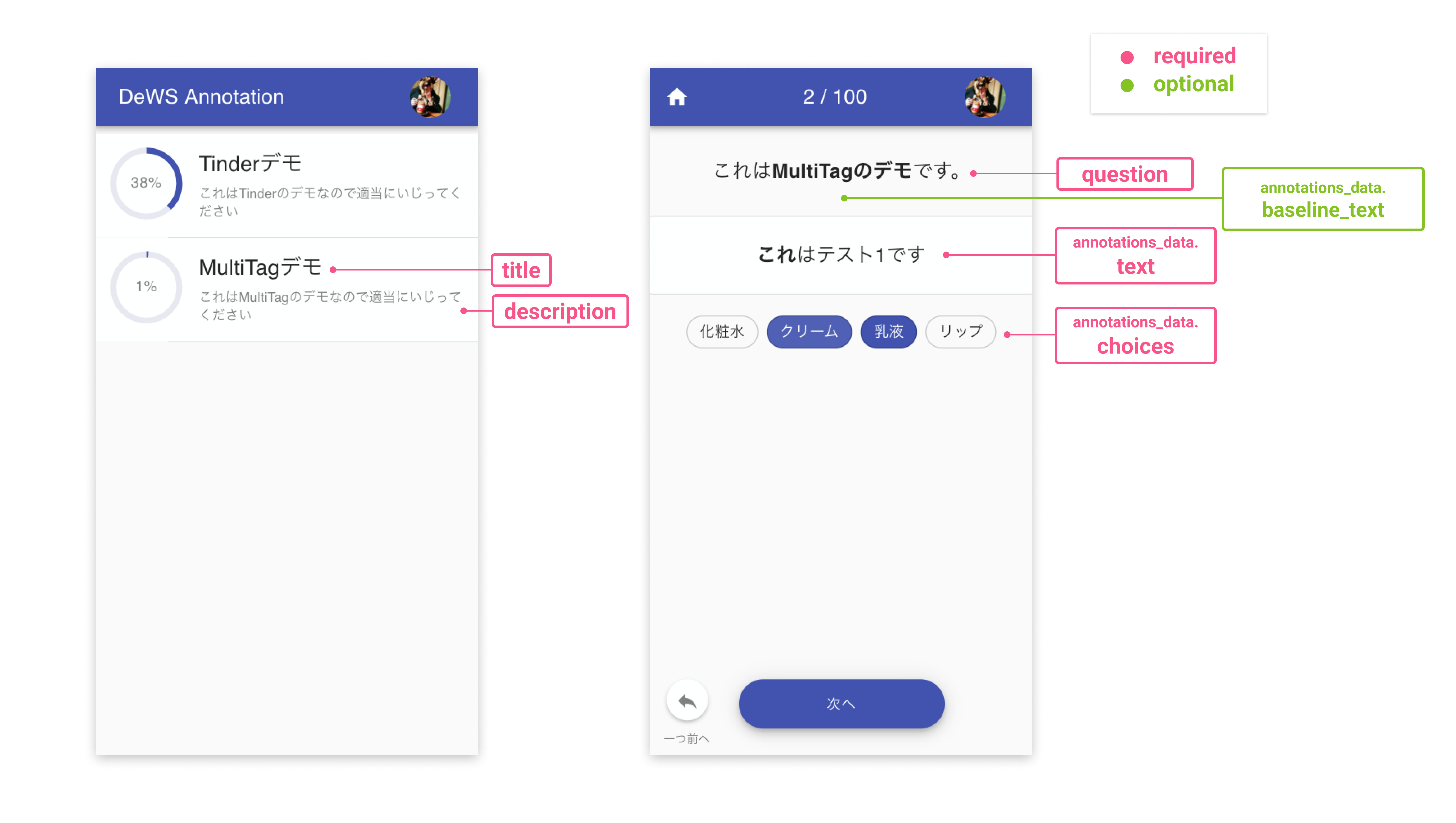
```
# Make annotation data
annotation_data = [
{
"text": f"This is a test{i}.",
"choices": ["ChoiceA", "ChoiceB", "ChoiceC", "ChoiceD"],
"baseline_text": "Baseline Text",
"hidden_data": {
"desc": "Data for aggregation. It can be a dictionary or a string."
}
}
for i in range(100)
]
df_annotation = pd.DataFrame(annotation_data)
df_annotation[:3]
# Post task data
post_data = {
"task_id": "multilabel-demo-20200602",
"annotation_type": "multi_label",
"title": "Multi-Label Demo",
"question": "This is multi-label demo",
"description": "This is a multi-label demo, so feel free to annotate it as you wish.",
"annotations_data": annotation_data
}
res = requests.post(f'{host}/tasks', headers=headers, json=post_data).json()
res
```
# Get annotation results
```
%%time
task_id = "card-demo-20200602"
res = requests.get(f'{host}/tasks/{task_id}', headers=headers).json()
# Task Info
res['task']
# Annotation data and annotator responses
df_res = pd.DataFrame(res['annotations'])
df_res['name'] = '****'
df_res['email'] = '****'
df_res[~df_res.result_data.isna()][:3]
```
# Get annotation detail log
```
task_id = "card-demo-20200602"
res = requests.get(f'{host}/tasks/{task_id}/logs', headers=headers).json()
df_res = pd.DataFrame(res['logs'])
df_res['name'] = '****'
df_res['email'] = '****'
df_res.sample(5)
```
|
github_jupyter
|
# Real-world use-cases at scale!
# Imports
Let's start with imports.
```
import sys
sys.path.append("gpu_bdb_runner.egg")
import gpu_bdb_runner as gpubdb
import os
import inspect
from highlight_code import print_code
config_options = {}
config_options['JOIN_PARTITION_SIZE_THRESHOLD'] = os.environ.get("JOIN_PARTITION_SIZE_THRESHOLD", 300000000)
config_options['MAX_DATA_LOAD_CONCAT_CACHE_BYTE_SIZE'] = os.environ.get("MAX_DATA_LOAD_CONCAT_CACHE_BYTE_SIZE", 400000000)
config_options['BLAZING_DEVICE_MEM_CONSUMPTION_THRESHOLD'] = os.environ.get("BLAZING_DEVICE_MEM_CONSUMPTION_THRESHOLD", 0.6)
config_options['BLAZ_HOST_MEM_CONSUMPTION_THRESHOLD'] = os.environ.get("BLAZ_HOST_MEM_CONSUMPTION_THRESHOLD", 0.6)
config_options['MAX_KERNEL_RUN_THREADS'] = os.environ.get("MAX_KERNEL_RUN_THREADS", 3)
config_options['TABLE_SCAN_KERNEL_NUM_THREADS'] = os.environ.get("TABLE_SCAN_KERNEL_NUM_THREADS", 1)
config_options['MAX_NUM_ORDER_BY_PARTITIONS_PER_NODE'] = os.environ.get("MAX_NUM_ORDER_BY_PARTITIONS_PER_NODE", 20)
config_options['ORDER_BY_SAMPLES_RATIO'] = os.environ.get("ORDER_BY_SAMPLES_RATIO", 0.0002)
config_options['NUM_BYTES_PER_ORDER_BY_PARTITION'] = os.environ.get("NUM_BYTES_PER_ORDER_BY_PARTITION", 400000000)
config_options['MAX_ORDER_BY_SAMPLES_PER_NODE'] = os.environ.get("MAX_ORDER_BY_SAMPLES_PER_NODE", 10000)
config_options['MAX_SEND_MESSAGE_THREADS'] = os.environ.get("MAX_SEND_MESSAGE_THREADS", 20)
config_options['MEMORY_MONITOR_PERIOD'] = os.environ.get("MEMORY_MONITOR_PERIOD", 50)
config_options['TRANSPORT_BUFFER_BYTE_SIZE'] = os.environ.get("TRANSPORT_BUFFER_BYTE_SIZE", 10485760) # 10 MBs
config_options['TRANSPORT_POOL_NUM_BUFFERS'] = os.environ.get("TRANSPORT_POOL_NUM_BUFFERS", 100)
config_options['BLAZING_LOGGING_DIRECTORY'] = os.environ.get("BSQL_BLAZING_LOGGING_DIRECTORY", 'blazing_log')
config_options['BLAZING_CACHE_DIRECTORY'] = os.environ.get("BSQL_BLAZING_CACHE_DIRECTORY", '/tmp/')
config_options['LOGGING_LEVEL'] = os.environ.get("LOGGING_LEVEL", "trace")
config_options['MAX_JOIN_SCATTER_MEM_OVERHEAD'] = os.environ.get("MAX_JOIN_SCATTER_MEM_OVERHEAD", 500000000)
config_options['NETWORK_INTERFACE'] = os.environ.get("NETWORK_INTERFACE", 'ens5')
```
# Start the runner
```
runner = gpubdb.GPU_BDB_Runner(
scale='SF1'
, client_type='cluster'
, bucket='bsql'
, data_dir='s3://bsql/data/tpcx_bb/sf1/'
, output_dir='tpcx-bb-runner/results'
, **config_options
)
```
# Use cases for review
## Use case 2
**Question:** Find the top 30 products that are mostly viewed together with a given product in online store. Note that the order of products viewed does not matter, and "viewed together" relates to a web_clickstreams, click_session of a known user with a session timeout of 60 min. If the duration between two click of a user is greater then the session timeout, a new session begins. With a session timeout of 60 min.
Let's peek inside the code:
```
q2_code = inspect.getsource(gpubdb.queries.gpu_bdb_queries.gpu_bdb_query_02).split('\n')
print_code('\n'.join(q2_code[92:-18]))
```
The `get_distinct_sessions` is defined as follows:
```
print_code('\n'.join(q2_code[73:77]))
```
It calls the `get_sessions`
```
print_code('\n'.join(q2_code[64:72]))
```
Let's have a look at the `get_session_id` method
```
print_code('\n'.join(q2_code[34:63]))
```
Now that we know how this works - let's run the query
```
runner.run_query(2, repeat=1, validate_results=False)
```
## Use case 23
**Question:** This Query contains multiple, related iterations:
1. Iteration 1: Calculate the coefficient of variation and mean of every item and warehouse of the given and the consecutive month.
2. Iteration 2: Find items that had a coefficient of variation of 1.3 or larger in the given and the consecutive month
```
q23_code = inspect.getsource(gpubdb.queries.gpu_bdb_queries.gpu_bdb_query_23).split('\n')
print_code('\n'.join(q23_code[23:-12]))
runner.run_query(23, repeat=1, validate_results=False)
```
# Remaining usecases
## Use case 1
**Question:** Find top ***100*** products that are sold together frequently in given stores. Only products in certain categories ***(categories 2 and 3)*** sold in specific stores are considered, and "sold together frequently" means at least ***50*** customers bought these products together in a transaction.
In ANSI-SQL code the solution would look somewhat similar to the one below.
```
runner.run_query(1, repeat=1, validate_results=False)
```
## Use case 3
**Question:** For a given product get a top 30 list sorted by number of views in descending order of the last 5 products that are mostly viewed before the product was purchased online. For the viewed products, consider only products in certain item categories and viewed within 10 days before the purchase date.
```
runner.run_query(3, repeat=1, validate_results=False)
```
## Use case 4
**Question:** Web_clickstream shopping cart abandonment analysis: For users who added products in their shopping carts but did not check out in the online store during their session, find the average number of pages they visited during their sessions. A "session" relates to a click_session of a known user with a session time-out of 60 min. If the duration between two clicks of a user is greater then the session time-out, a new session begins.
```
runner.run_query(4, repeat=1, validate_results=False)
```
## Use case 5
**Question**: Build a model using logistic regression for a visitor to an online store: based on existing users online activities (interest in items of different categories) and demographics. This model will be used to predict if the visitor is interested in a given item category. Output the precision, accuracy and confusion matrix of model. *Note:* no need to actually classify existing users, as it will be later used to predict interests of unknown visitors.
```
runner.run_query(5, repeat=1, validate_results=False)
```
## Use case 6
Identifies customers shifting their purchase habit from store to web sales. Find customers who spend in relation more money in the second year following a given year in the web_sales channel then in the store sales channel. Report customers details: first name, last name, their country of origin, login name and email address, and identify if they are preferred customer, for the top 100 customers with the highest increase intheir second year web purchase ratio.
```
runner.run_query(6, repeat=1, validate_results=False)
```
## Use case 7
**Question:** List top 10 states in descending order with at least 10 customers who during a given month bought products with the price tag at least 20% higher than the average price of products in the same category.
```
runner.run_query(7, repeat=1, validate_results=False)
```
## Use case 8
**Question:** For online sales, compare the total sales monetary amount in which customers checked online reviews before making the purchase and that of sales in which customers did not read reviews. Consider only online sales for a specific category in a given year.
```
runner.run_query(8, repeat=1, validate_results=False)
```
## Use case 9
**Question:** Aggregate total amount of sold items over different given types of combinations of customers based on selected groups of marital status, education status, sales price and different combinations of state and sales/profit.
```
runner.run_query(9, repeat=1, validate_results=False)
```
## Use case 10
**Question:** For all products, extract sentences from its product reviews that contain positive or negative sentiment and display for each item the sentiment polarity of the extracted sentences (POS OR NEG) and the sentence and word in sentence leading to this classification.
```
runner.run_query(10, repeat=1, validate_results=False, additional_resources_path='s3://bsql/data/tpcx_bb/additional_resources')
```
## Use case 11
**Question:** For a given product, measure the correlation of sentiments, including the number of reviews and average review ratings, on product monthly revenues within a given time frame.
```
runner.run_query(11, repeat=1, validate_results=False)
```
## Use case 12
**Question:** Find all customers who viewed items of a given category on the web in a given month and year that was followed by an instore purchase of an item from the same category in the three consecutive months.
```
runner.run_query(12, repeat=1, validate_results=False)
```
## Use case 13
**Question:** Display customers with both store and web sales in consecutive years for whom the increase in web sales exceeds the increase in store sales for a specified year.
```
runner.run_query(13, repeat=1, validate_results=False)
```
## Use case 14
**Question:** What is the ratio between the number of items sold over the internet in the morning (7 to 8am) to the number of items sold in the evening (7 to 8pm) of customers with a specified number of dependents. Consider only websites with a high amount of content.
```
runner.run_query(14, repeat=1, validate_results=False)
```
## Use case 15
**Question:** Find the categories with flat or declining sales for in store purchases during a given year for a given store.
```
runner.run_query(15, repeat=1, validate_results=False)
```
## Use case 16
**Question:** Compute the impact of an item price change on the store sales by computing the total sales for items in a 30 day period before and after the price change. Group the items by location of warehouse where they were delivered from.
```
runner.run_query(16, repeat=1, validate_results=False)
```
## Use case 17
**Question:** Find the ratio of items sold with and without promotions in a given month and year. Only items in certain categories sold to customers living in a specific time zone are considered.
```
runner.run_query(17, repeat=1, validate_results=False)
```
## Use case 18
**Question:** Identify the stores with flat or declining sales in 4 consecutive months, check if there are any negative reviews regarding these stores available online.
```
runner.run_query(18, repeat=1, validate_results=False, additional_resources_path='s3://bsql/data/tpcx_bb/additional_resources')
```
## Use case 19
**Question:** Retrieve the items with the highest number of returns where the number of returns was approximately equivalent across all store and web channels (within a tolerance of +/ 10%), within the week ending given dates. Analyse the online reviews for these items to see if there are any negative reviews.
```
runner.run_query(19, repeat=1, validate_results=False, additional_resources_path='s3://bsql/data/tpcx_bb/additional_resources')
```
## Use case 20
**Question:** Customer segmentation for return analysis: Customers are separated along the following dimensions:
1. return frequency,
2. return order ratio (total number of orders partially or fully returned versus the totalnumber of orders),
3. return item ratio (total number of items returned versus the number of itemspurchased),
4. return amount ration (total monetary amount of items returned versus the amount purchased),
5. return order ratio.
Consider the store returns during a given year for the computation.
```
runner.run_query(20, repeat=1, validate_results=False)
```
## Use case 21
**Question:** Get all items that were sold in stores in a given month and year and which were returned in the next 6 months and repurchased by the returning customer afterwards through the web sales channel in the following three years. For those items, compute the total quantity sold through the store, the quantity returned and the quantity purchased through the web. Group this information by item and store.
```
runner.run_query(21, repeat=1, validate_results=False)
```
## Use case 22
**Question:** For all items whose price was changed on a given date, compute the percentage change in inventorybetween the 30 day period BEFORE the price change and the 30 day period AFTER the change. Group this information by warehouse.
```
runner.run_query(22, repeat=1, validate_results=False)
```
## Use case 24
**Question:** For a given product, measure the effect of competitor's prices on products' in store and online sales.Compute the crossprice elasticity of demand for a given product.
```
runner.run_query(24, repeat=1, validate_results=False)
```
## Use case 25
**Question:** Customer segmentation analysis: Customers are separated along the following key shopping dimensions:
1. recency of last visit,
2. frequency of visits and monetary amount.
Use the store and online purchase data during a given year to compute. After model of separation is build, report for the analysed customers towhich "group" they where assigned.
```
runner.run_query(25, repeat=1, validate_results=False)
```
## Use case 26
**Question:** Cluster customers into book buddies/club groups based on their in store book purchasing histories. Aftermodel of separation is build, report for the analysed customers to which "group" they where assigned.
```
runner.run_query(26, repeat=1, validate_results=False)
```
## Use case 27
**Question:** For a given product, find "competitor" company names in the product reviews. Display review id, product id, "competitor’s" company name and the related sentence from the online review
```
# runner.run_query(27, repeat=1, validate_results=False)
```
## Use case 28
**Question:** Build text classifier for online review sentiment classification (Positive, Negative, Neutral), using 90% of available reviews for training and the remaining 10% for testing. Display classifier accuracy on testing dataand classification result for the 10% testing data: \<reviewSK\>, \<originalRating\>, \<classificationResult\>.
```
runner.run_query(28, repeat=1, validate_results=False)
```
## Use case 29
**Question:** Perform category affinity analysis for products purchased together online.
```
runner.run_query(29, repeat=1, validate_results=False)
```
## Use case 30
**Question:** Perform category affinity analysis for products viewed together online. Note that the order of products viewed does not matter, and "viewed together" relates to a click_session of a user with a session timeout of 60 min. If the duration between two clicks of a user is greater then the session timeout, a new session begins.
```
runner.run_query(30, repeat=1, validate_results=False)
```
|
github_jupyter
|
```
import time
notebookstart= time.time()
import numpy as np # linear algebra
import pandas as pd # data processing, CSV file I/O (e.g. pd.read_csv)
import os
import gc
# Models Packages
from sklearn import metrics
from sklearn.metrics import mean_squared_error
from sklearn import feature_selection
from sklearn.model_selection import train_test_split
from sklearn import preprocessing
from sklearn.model_selection import KFold
from sklearn import preprocessing
from sklearn.metrics import roc_auc_score, roc_curve
from sklearn.linear_model import LogisticRegression
import category_encoders as ce
from imblearn.under_sampling import RandomUnderSampler
from catboost import CatBoostClassifier
# Gradient Boosting
import lightgbm as lgb
import xgboost as xgb
import category_encoders as ce
# Tf-Idf
from sklearn.feature_extraction.text import CountVectorizer, TfidfVectorizer
from sklearn.pipeline import FeatureUnion
from scipy.sparse import hstack, csr_matrix
from nltk.corpus import stopwords
from sklearn.preprocessing import StandardScaler
from sklearn.ensemble import RandomForestRegressor
# Viz
import seaborn as sns
import matplotlib.pyplot as plt
import numpy as np # linear algebra
import pandas as pd # data processing, CSV file I/O (e.g. pd.read_csv)
from scipy.cluster.vq import kmeans2, whiten
from sklearn.neighbors import NearestNeighbors, KNeighborsRegressor
from catboost import CatBoostRegressor
%matplotlib inline
# Input data files are available in the "../input/" directory.
# For example, running this (by clicking run or pressing Shift+Enter) will list the files in the input directory
num_rows = None
EPS = 1e-100
train = pd.read_csv('/media/limbo/Home-Credit/data/application_train.csv.zip')
y = train['TARGET']
n_train = train.shape[0]
descretize = lambda x, n: list(map(str, list(pd.qcut(x, n, duplicates='drop'))))
def binary_encoder(df, n_train):
original_columns = list(df.columns)
categorical_columns = [col for col in df.columns if df[col].dtype == 'object']
enc = ce.BinaryEncoder(impute_missing=True, cols=categorical_columns).fit(df[0:n_train], df[0:n_train]['TARGET'])
df = enc.transform(df)
new_columns = [c for c in df.columns if c not in original_columns]
return df[new_columns]
def application_train_test(num_rows=num_rows, nan_as_category=False):
# Read data and merge
df = pd.read_csv('../data/application_train.csv.zip', nrows=num_rows)
n_train = df.shape[0]
test_df = pd.read_csv('../data/application_test.csv.zip', nrows=num_rows)
print("Train samples: {}, test samples: {}".format(len(df), len(test_df)))
df = df.append(test_df).reset_index()
df['CODE_GENDER'].replace('XNA', np.nan, inplace=True)
df['DAYS_EMPLOYED'].replace(365243, np.nan, inplace=True)
df['NAME_FAMILY_STATUS'].replace('Unknown', np.nan, inplace=True)
df['ORGANIZATION_TYPE'].replace('XNA', np.nan, inplace=True)
# Optional: Remove 4 applications with XNA CODE_GENDER (train set)
df = df[df['CODE_GENDER'] != 'XNA']
docs = [_f for _f in df.columns if 'FLAG_DOC' in _f]
live = [_f for _f in df.columns if ('FLAG_' in _f) & ('FLAG_DOC' not in _f) & ('_FLAG_' not in _f)]
# NaN values for DAYS_EMPLOYED: 365.243 -> nan
df['DAYS_EMPLOYED'].replace(365243, np.nan, inplace=True)
inc_by_org = df[['AMT_INCOME_TOTAL', 'ORGANIZATION_TYPE']].groupby('ORGANIZATION_TYPE').median()['AMT_INCOME_TOTAL']
df['NEW_CREDIT_TO_ANNUITY_RATIO'] = df['AMT_CREDIT'] / df['AMT_ANNUITY']
df['NEW_AMT_INCOME_TOTAL_RATIO'] = df['AMT_CREDIT'] / df['AMT_INCOME_TOTAL']
df['NEW_CREDIT_TO_GOODS_RATIO'] = df['AMT_CREDIT'] / df['AMT_GOODS_PRICE']
df['NEW_DOC_IND_AVG'] = df[docs].mean(axis=1)
df['NEW_DOC_IND_STD'] = df[docs].std(axis=1)
df['NEW_DOC_IND_KURT'] = df[docs].kurtosis(axis=1)
df['NEW_LIVE_IND_SUM'] = df[live].sum(axis=1)
df['NEW_LIVE_IND_STD'] = df[live].std(axis=1)
df['NEW_LIVE_IND_KURT'] = df[live].kurtosis(axis=1)
df['NEW_INC_PER_CHLD'] = df['AMT_INCOME_TOTAL'] / (1 + df['CNT_CHILDREN'])
df['NEW_INC_BY_ORG'] = df['ORGANIZATION_TYPE'].map(inc_by_org)
df['NEW_EMPLOY_TO_BIRTH_RATIO'] = df['DAYS_EMPLOYED'] / df['DAYS_BIRTH']
df['NEW_ANNUITY_TO_INCOME_RATIO'] = df['AMT_ANNUITY'] / (1 + df['AMT_INCOME_TOTAL'])
df['NEW_SOURCES_PROD'] = df['EXT_SOURCE_1'] * df['EXT_SOURCE_2'] * df['EXT_SOURCE_3']
df['NEW_EXT_SOURCES_MEAN'] = df[['EXT_SOURCE_1', 'EXT_SOURCE_2', 'EXT_SOURCE_3']].mean(axis=1)
df['NEW_SCORES_STD'] = df[['EXT_SOURCE_1', 'EXT_SOURCE_2', 'EXT_SOURCE_3']].std(axis=1)
df['NEW_SCORES_STD'] = df['NEW_SCORES_STD'].fillna(df['NEW_SCORES_STD'].mean())
df['NEW_CAR_TO_BIRTH_RATIO'] = df['OWN_CAR_AGE'] / df['DAYS_BIRTH']
df['NEW_CAR_TO_EMPLOY_RATIO'] = df['OWN_CAR_AGE'] / df['DAYS_EMPLOYED']
df['NEW_PHONE_TO_BIRTH_RATIO'] = df['DAYS_LAST_PHONE_CHANGE'] / df['DAYS_BIRTH']
df['NEW_PHONE_TO_EMPLOY_RATIO'] = df['DAYS_LAST_PHONE_CHANGE'] / df['DAYS_EMPLOYED']
df['NEW_CREDIT_TO_INCOME_RATIO'] = df['AMT_CREDIT'] / df['AMT_INCOME_TOTAL']
# df['children_ratio'] = df['CNT_CHILDREN'] / df['CNT_FAM_MEMBERS']
# df['NEW_EXT_SOURCES_MEDIAN'] = df[['EXT_SOURCE_1', 'EXT_SOURCE_2', 'EXT_SOURCE_3']].median(axis=1)
# df['NEW_DOC_IND_SKEW'] = df[docs].skew(axis=1)
# df['NEW_LIVE_IND_SKEW'] = df[live].skew(axis=1)
# df['ind_0'] = df['DAYS_EMPLOYED'] - df['DAYS_EMPLOYED'].replace([np.inf, -np.inf], np.nan).fillna(
# df['DAYS_EMPLOYED'].dropna().median()).mean()
# df['ind_1'] = df['DAYS_EMPLOYED'] - df['DAYS_EMPLOYED'].replace([np.inf, -np.inf], np.nan).fillna(
# df['DAYS_EMPLOYED'].dropna().median()).median()
# df['ind_2'] = df['DAYS_BIRTH'] - df['DAYS_BIRTH'].replace([np.inf, -np.inf], np.nan).fillna(
# df['DAYS_BIRTH'].dropna().median()).mean()
# df['ind_3'] = df['DAYS_BIRTH'] - df['DAYS_BIRTH'].replace([np.inf, -np.inf], np.nan).fillna(
# df['DAYS_BIRTH'].dropna().median()).median()
# df['ind_4'] = df['AMT_INCOME_TOTAL'] - df['AMT_INCOME_TOTAL'].replace([np.inf, -np.inf], np.nan).fillna(
# df['AMT_INCOME_TOTAL'].dropna().median()).mean()
# df['ind_5'] = df['AMT_INCOME_TOTAL'] - df['AMT_INCOME_TOTAL'].replace([np.inf, -np.inf], np.nan).fillna(
# df['AMT_INCOME_TOTAL'].dropna().median()).median()
# df['ind_6'] = df['AMT_CREDIT'] - df['AMT_CREDIT'].replace([np.inf, -np.inf], np.nan).fillna(
# df['AMT_CREDIT'].dropna().median()).mean()
# df['ind_7'] = df['AMT_CREDIT'] - df['AMT_CREDIT'].replace([np.inf, -np.inf], np.nan).fillna(
# df['AMT_CREDIT'].dropna().median()).median()
# df['ind_8'] = df['AMT_ANNUITY'] - df['AMT_ANNUITY'].replace([np.inf, -np.inf], np.nan).fillna(
# df['AMT_ANNUITY'].dropna().median()).mean()
# df['ind_9'] = df['AMT_ANNUITY'] - df['AMT_ANNUITY'].replace([np.inf, -np.inf], np.nan).fillna(
# df['AMT_ANNUITY'].dropna().median()).median()
# df['ind_10'] = df['AMT_CREDIT'] - df['AMT_INCOME_TOTAL'].replace([np.inf, -np.inf], np.nan).fillna(
# df['AMT_INCOME_TOTAL'].dropna().median()).mean()
# df['ind_11'] = df['AMT_CREDIT'] - df['AMT_INCOME_TOTAL'].replace([np.inf, -np.inf], np.nan).fillna(
# df['AMT_INCOME_TOTAL'].dropna().median()).median()
# AGGREGATION_RECIPIES = [
# (['CODE_GENDER', 'NAME_EDUCATION_TYPE'], [('AMT_ANNUITY', 'max'),
# ('AMT_CREDIT', 'max'),
# ('EXT_SOURCE_1', 'mean'),
# ('EXT_SOURCE_2', 'mean'),
# ('OWN_CAR_AGE', 'max'),
# ('OWN_CAR_AGE', 'sum')]),
# (['CODE_GENDER', 'ORGANIZATION_TYPE'], [('AMT_ANNUITY', 'mean'),
# ('AMT_INCOME_TOTAL', 'mean'),
# ('DAYS_REGISTRATION', 'mean'),
# ('EXT_SOURCE_1', 'mean'),
# ('NEW_CREDIT_TO_ANNUITY_RATIO', 'mean')]),
# (['CODE_GENDER', 'REG_CITY_NOT_WORK_CITY'], [('AMT_ANNUITY', 'mean'),
# ('CNT_CHILDREN', 'mean'),
# ('DAYS_ID_PUBLISH', 'mean')]),
# (['CODE_GENDER', 'NAME_EDUCATION_TYPE', 'OCCUPATION_TYPE', 'REG_CITY_NOT_WORK_CITY'], [('EXT_SOURCE_1', 'mean'),
# ('EXT_SOURCE_2',
# 'mean')]),
# (['NAME_EDUCATION_TYPE', 'OCCUPATION_TYPE'], [('AMT_CREDIT', 'mean'),
# ('AMT_REQ_CREDIT_BUREAU_YEAR', 'mean'),
# ('APARTMENTS_AVG', 'mean'),
# ('BASEMENTAREA_AVG', 'mean'),
# ('EXT_SOURCE_1', 'mean'),
# ('EXT_SOURCE_2', 'mean'),
# ('EXT_SOURCE_3', 'mean'),
# ('NONLIVINGAREA_AVG', 'mean'),
# ('OWN_CAR_AGE', 'mean')]),
# (['NAME_EDUCATION_TYPE', 'OCCUPATION_TYPE', 'REG_CITY_NOT_WORK_CITY'], [('ELEVATORS_AVG', 'mean'),
# ('EXT_SOURCE_1', 'mean')]),
# (['OCCUPATION_TYPE'], [('AMT_ANNUITY', 'mean'),
# ('CNT_CHILDREN', 'mean'),
# ('CNT_FAM_MEMBERS', 'mean'),
# ('DAYS_BIRTH', 'mean'),
# ('DAYS_EMPLOYED', 'mean'),
# ('NEW_CREDIT_TO_ANNUITY_RATIO', 'median'),
# ('DAYS_REGISTRATION', 'mean'),
# ('EXT_SOURCE_1', 'mean'),
# ('EXT_SOURCE_2', 'mean'),
# ('EXT_SOURCE_3', 'mean')]),
# ]
# for groupby_cols, specs in AGGREGATION_RECIPIES:
# group_object = df.groupby(groupby_cols)
# for select, agg in specs:
# groupby_aggregate_name = '{}_{}_{}'.format('_'.join(groupby_cols), agg, select)
# df = df.merge(group_object[select]
# .agg(agg)
# .reset_index()
# .rename(index=str,
# columns={select: groupby_aggregate_name})
# [groupby_cols + [groupby_aggregate_name]],
# on=groupby_cols,
# how='left')
# ['DAYS_EMPLOYED', 'CNT_FAM_MEMBERS', 'CNT_CHILDREN', 'credit_per_person', 'cnt_non_child']
df['retirement_age'] = (df['DAYS_BIRTH'] > -14000).astype(int)
df['long_employment'] = (df['DAYS_EMPLOYED'] > -2000).astype(int)
df['cnt_non_child'] = df['CNT_FAM_MEMBERS'] - df['CNT_CHILDREN']
df['child_to_non_child_ratio'] = df['CNT_CHILDREN'] / df['cnt_non_child']
df['income_per_non_child'] = df['AMT_INCOME_TOTAL'] / df['cnt_non_child']
df['credit_per_person'] = df['AMT_CREDIT'] / df['CNT_FAM_MEMBERS']
df['credit_per_child'] = df['AMT_CREDIT'] / (1 + df['CNT_CHILDREN'])
df['credit_per_non_child'] = df['AMT_CREDIT'] / df['cnt_non_child']
df['cnt_non_child'] = df['CNT_FAM_MEMBERS'] - df['CNT_CHILDREN']
df['child_to_non_child_ratio'] = df['CNT_CHILDREN'] / df['cnt_non_child']
df['income_per_non_child'] = df['AMT_INCOME_TOTAL'] / df['cnt_non_child']
df['credit_per_person'] = df['AMT_CREDIT'] / df['CNT_FAM_MEMBERS']
df['credit_per_child'] = df['AMT_CREDIT'] / (1 + df['CNT_CHILDREN'])
df['credit_per_non_child'] = df['AMT_CREDIT'] / df['cnt_non_child']
# df['p_0'] = descretize(df['credit_per_non_child'].values, 2 ** 5)
# df['p_1'] = descretize(df['credit_per_person'].values, 2 ** 5)
# df['p_2'] = descretize(df['credit_per_child'].values, 2 ** 5)
# df['p_3'] = descretize(df['retirement_age'].values, 2 ** 5)
# df['p_4'] = descretize(df['income_per_non_child'].values, 2 ** 5)
# df['p_5'] = descretize(df['child_to_non_child_ratio'].values, 2 ** 5)
# df['p_6'] = descretize(df['NEW_CREDIT_TO_ANNUITY_RATIO'].values, 2 ** 5)
# df['p_7'] = descretize(df['NEW_CREDIT_TO_ANNUITY_RATIO'].values, 2 ** 6)
# df['p_8'] = descretize(df['NEW_CREDIT_TO_ANNUITY_RATIO'].values, 2 ** 7)
# df['pe_0'] = descretize(df['credit_per_non_child'].values, 2 ** 6)
# df['pe_1'] = descretize(df['credit_per_person'].values, 2 ** 6)
# df['pe_2'] = descretize(df['credit_per_child'].values, 2 ** 6)
# df['pe_3'] = descretize(df['retirement_age'].values, 2 ** 6)
# df['pe_4'] = descretize(df['income_per_non_child'].values, 2 ** 6)
# df['pe_5'] = descretize(df['child_to_non_child_ratio'].values, 2 ** 6)
c = df['NEW_CREDIT_TO_ANNUITY_RATIO'].replace([np.inf, -np.inf], np.nan).fillna(999).values
a, b = kmeans2(np.log1p(c), 2, iter=333)
df['x_0'] = b
a, b = kmeans2(np.log1p(c), 4, iter=333)
df['x_1'] = b
a, b = kmeans2(np.log1p(c), 8, iter=333)
df['x_2'] = b
a, b = kmeans2(np.log1p(c), 16, iter=333)
df['x_3'] = b
a, b = kmeans2(np.log1p(c), 32, iter=333)
df['x_4'] = b
a, b = kmeans2(np.log1p(c), 64, iter=333)
df['x_5'] = b
a, b = kmeans2(np.log1p(c), 128, iter=333)
df['x_6'] = b
a, b = kmeans2(np.log1p(c), 150, iter=333)
df['x_7'] = b
a, b = kmeans2(np.log1p(c), 256, iter=333)
df['x_8'] = b
a, b = kmeans2(np.log1p(c), 512, iter=333)
df['x_9'] = b
a, b = kmeans2(np.log1p(c), 1024, iter=333)
df['x_10'] = b
# c = df['EXT_SOURCE_1'].replace([np.inf, -np.inf], np.nan).fillna(999).values
# a, b = kmeans2(np.log1p(c), 2, iter=333)
# df['ex1_0'] = b
# a, b = kmeans2(np.log1p(c), 4, iter=333)
# df['ex1_1'] = b
# a, b = kmeans2(np.log1p(c), 8, iter=333)
# df['ex1_2'] = b
# a, b = kmeans2(np.log1p(c), 16, iter=333)
# df['ex1_3'] = b
# a, b = kmeans2(np.log1p(c), 32, iter=333)
# df['ex1_4'] = b
# a, b = kmeans2(np.log1p(c), 64, iter=333)
# df['ex1_5'] = b
# a, b = kmeans2(np.log1p(c), 128, iter=333)
# df['ex1_6'] = b
# a, b = kmeans2(np.log1p(c), 256, iter=333)
# df['ex1_7'] = b
# c = df['EXT_SOURCE_2'].replace([np.inf, -np.inf], np.nan).fillna(999).values
# a, b = kmeans2(np.log1p(c), 2, iter=333)
# df['ex2_0'] = b
# a, b = kmeans2(np.log1p(c), 4, iter=333)
# df['ex2_1'] = b
# a, b = kmeans2(np.log1p(c), 8, iter=333)
# df['ex2_2'] = b
# a, b = kmeans2(np.log1p(c), 16, iter=333)
# df['ex2_3'] = b
# a, b = kmeans2(np.log1p(c), 32, iter=333)
# df['ex2_4'] = b
# a, b = kmeans2(np.log1p(c), 64, iter=333)
# df['ex2_5'] = b
# a, b = kmeans2(np.log1p(c), 128, iter=333)
# df['ex2_6'] = b
# a, b = kmeans2(np.log1p(c), 256, iter=333)
# df['ex2_7'] = b
# c = df['EXT_SOURCE_3'].replace([np.inf, -np.inf], np.nan).fillna(999).values
# a, b = kmeans2(np.log1p(c), 2, iter=333)
# df['ex3_0'] = b
# a, b = kmeans2(np.log1p(c), 4, iter=333)
# df['ex3_1'] = b
# a, b = kmeans2(np.log1p(c), 8, iter=333)
# df['ex3_2'] = b
# a, b = kmeans2(np.log1p(c), 16, iter=333)
# df['ex3_3'] = b
# a, b = kmeans2(np.log1p(c), 32, iter=333)
# df['ex3_4'] = b
# a, b = kmeans2(np.log1p(c), 64, iter=333)
# df['ex3_5'] = b
# a, b = kmeans2(np.log1p(c), 128, iter=333)
# df['ex3_6'] = b
# a, b = kmeans2(np.log1p(c), 256, iter=333)
# df['ex3_7'] = b
# df['ex_1_0'] = descretize(df['EXT_SOURCE_1'].values, 2 ** 6)
# df['ex_2_0'] = descretize(df['EXT_SOURCE_2'].values, 2 ** 6)
# df['ex_3_0'] = descretize(df['EXT_SOURCE_3'].values, 2 ** 6)
# df['ex_1_1'] = descretize(df['EXT_SOURCE_1'].values, 2 ** 4)
# df['ex_2_1'] = descretize(df['EXT_SOURCE_2'].values, 2 ** 4)
# df['ex_3_1'] = descretize(df['EXT_SOURCE_3'].values, 2 ** 4)
# df['ex_1_2'] = descretize(df['EXT_SOURCE_1'].values, 2 ** 5)
# df['ex_2_2'] = descretize(df['EXT_SOURCE_2'].values, 2 ** 5)
# df['ex_3_2'] = descretize(df['EXT_SOURCE_3'].values, 2 ** 5)
# df['ex_1_3'] = descretize(df['EXT_SOURCE_1'].values, 2 ** 3)
# df['ex_2_4'] = descretize(df['EXT_SOURCE_2'].values, 2 ** 3)
# df['ex_3_5'] = descretize(df['EXT_SOURCE_3'].values, 2 ** 3)
# c = df['NEW_EXT_SOURCES_MEAN'].replace([np.inf, -np.inf], np.nan).fillna(999).values
# a, b = kmeans2(np.log1p(c), 2, iter=333)
# df['ex_mean_0'] = b
# a, b = kmeans2(np.log1p(c), 4, iter=333)
# df['ex_mean_1'] = b
# a, b = kmeans2(np.log1p(c), 8, iter=333)
# df['ex_mean_2'] = b
# a, b = kmeans2(np.log1p(c), 16, iter=333)
# df['ex_mean_3'] = b
# a, b = kmeans2(np.log1p(c), 32, iter=333)
# df['ex_mean_4'] = b
# a, b = kmeans2(np.log1p(c), 64, iter=333)
# df['ex_mean_5'] = b
# df['NEW_SCORES_STD'] = df[['EXT_SOURCE_1', 'EXT_SOURCE_2', 'EXT_SOURCE_3']].std(axis=1)
# df['ex1/ex2'] = df['EXT_SOURCE_1'] / df['EXT_SOURCE_2']
# df['ex1/ex3'] = df['EXT_SOURCE_1'] / df['EXT_SOURCE_3']
# df['ex2/ex3'] = df['EXT_SOURCE_3'] / df['EXT_SOURCE_3']
# df['ex1*ex2'] = df['EXT_SOURCE_1'] * df['EXT_SOURCE_2']
# df['ex1*ex3'] = df['EXT_SOURCE_1'] * df['EXT_SOURCE_3']
# df['ex2*ex3'] = df['EXT_SOURCE_2'] * df['EXT_SOURCE_3']
# df['cred*ex1'] = df['AMT_CREDIT'] * df['EXT_SOURCE_1']
# df['cred*ex2'] = df['AMT_CREDIT'] * df['EXT_SOURCE_2']
# df['cred*ex3'] = df['AMT_CREDIT'] * df['EXT_SOURCE_3']
# df['cred/ex1'] = df['AMT_CREDIT'] / df['EXT_SOURCE_1']
# df['cred/ex2'] = df['AMT_CREDIT'] / df['EXT_SOURCE_2']
# df['cred/ex3'] = df['AMT_CREDIT'] / df['EXT_SOURCE_3']
# df['cred*ex123'] = df['AMT_CREDIT'] * df['EXT_SOURCE_1'] * df['EXT_SOURCE_2'] * df['EXT_SOURCE_3']
# del df['EXT_SOURCE_1']
# del df['EXT_SOURCE_2']
# del df['EXT_SOURCE_3']
# del df['NEW_EXT_SOURCES_MEAN']
# Categorical features with Binary encode (0 or 1; two categories)
for bin_feature in ['CODE_GENDER', 'FLAG_OWN_CAR', 'FLAG_OWN_REALTY']:
df[bin_feature], uniques = pd.factorize(df[bin_feature])
del test_df
gc.collect()
return df
df = application_train_test(num_rows=num_rows, nan_as_category=False)
df.head()
selected_features = ['AMT_ANNUITY', 'AMT_CREDIT', 'AMT_INCOME_TOTAL', 'NEW_CREDIT_TO_ANNUITY_RATIO', 'NEW_CREDIT_TO_GOODS_RATIO', 'NEW_CREDIT_TO_INCOME_RATIO'] + ['x_' + str(x) for x in range(11)] + \
['retirement_age', 'long_employment'] + ['EXT_SOURCE_1', 'EXT_SOURCE_2', 'EXT_SOURCE_3']
categorical_columns = [col for col in train.columns if train[col].dtype == 'object']
numerical_columns = [col for col in df.columns if df[col].dtype != 'object']
new_df = df.copy()
df = new_df
encoder = preprocessing.LabelEncoder()
for f in categorical_columns:
if df[f].dtype == 'object':
df[f] = encoder.fit_transform(df[f].apply(str).values)
categorical_columns
gc.collect()
train = pd.read_csv('../data/application_train.csv.zip', nrows=num_rows)
n_train = train.shape[0]
test = pd.read_csv('../data/application_test.csv.zip', nrows=num_rows)
new_df = pd.concat([train, test], axis=0)
gc.collect()
new_df.shape
new_df[categorical_columns].head()
encoder = preprocessing.LabelEncoder()
for f in categorical_columns:
if new_df[f].dtype == 'object':
new_df[f] = encoder.fit_transform(new_df[f].apply(str).values)
new_features = pd.read_csv('selected_features.csv', header=0, index_col=None)
new_features.head()
my_features = [f for f in selected_features if f not in new_features.columns]
my_features
new_df[categorical_columns][0:n_train].shape
new_df[categorical_columns][n_train:].head()
suresh_august16 = pd.read_csv('../data/SureshFeaturesAug16.csv', header=0, index_col=None)
suresh_august16.head()
del suresh_august16['SK_ID_CURR']
goran_features = pd.read_csv('../goran-data/goranm_feats_v3.csv', header=0, index_col=None)
goran_features.head()
del goran_features['SK_ID_CURR']
del goran_features['IS_TRAIN']
goran_features_19_8 = pd.read_csv('../data/goranm_feats_19_08.csv', header=0, index_col=None)
goran_features_19_8.head()
del goran_features_19_8['SK_ID_CURR']
from sklearn.externals import joblib
prevs_df = joblib.load('../data/prev_application_solution3_v2')
prevs_df.head()
suresh_august16_2 = pd.read_csv('../data/SureshFeaturesAug16_2.csv', header=0, index_col=None)
suresh_august15 = pd.read_csv('../data/SureshFeaturesAug15.csv', header=0, index_col=None)
suresh_august16 = pd.read_csv('../data/SureshFeaturesAug16.csv', header=0, index_col=None)
suresh_august19 = pd.read_csv('../data/suresh_features_Aug19th.csv', header=0, index_col=None)
suresh_august19_2 = pd.read_csv('../data/SureshFeatures_19_2th.csv', header=0, index_col=None)
suresh_august20 = pd.read_csv('../data/SureshFeatures3BestAgu20.csv', header=0, index_col=None)
suresh_august20.head(100)
del suresh_august15['SK_ID_CURR']
del suresh_august16_2['SK_ID_CURR']
del suresh_august19['SK_ID_CURR_SURESH']
del suresh_august16['SK_ID_CURR']
del suresh_august19_2['SK_ID_CURR']
suresh_august15.head()
suresh_20 = pd.read_csv('../data/SureshFeatures20_2.csv', header=0, index_col=None)
suresh_20.head(100)
del suresh_20['SK_ID_CURR']
goranm_8_20 = pd.read_csv('../data/goranm_08_20.csv', header=0, index_col=None)
goranm_8_20.head()
del goranm_8_20['SK_ID_CURR']
def do_countuniq( df, group_cols, counted, agg_name, agg_type='uint32', show_max=False, show_agg=True ):
if show_agg:
print( "Counting unqiue ", counted, " by ", group_cols , '...' )
gp = df[group_cols+[counted]].groupby(group_cols)[counted].nunique().reset_index().rename(columns={counted:agg_name})
df = df.merge(gp, on=group_cols, how='left')
del gp
if show_max:
print( agg_name + " max value = ", df[agg_name].max() )
df[agg_name] = df[agg_name].astype(agg_type)
gc.collect()
return df
def do_mean(df, group_cols, counted, agg_name, agg_type='float32', show_max=False, show_agg=True ):
if show_agg:
print( "Calculating mean of ", counted, " by ", group_cols , '...' )
gp = df[group_cols+[counted]].groupby(group_cols)[counted].mean().reset_index().rename(columns={counted:agg_name})
df = df.merge(gp, on=group_cols, how='left')
del gp
if show_max:
print( agg_name + " max value = ", df[agg_name].max() )
df[agg_name] = df[agg_name].astype(agg_type)
gc.collect()
return df
def do_count(df, group_cols, agg_name, agg_type='uint32', show_max=False, show_agg=True ):
if show_agg:
print( "Aggregating by ", group_cols , '...' )
gp = df[group_cols][group_cols].groupby(group_cols).size().rename(agg_name).to_frame().reset_index()
df = df.merge(gp, on=group_cols, how='left')
del gp
if show_max:
print( agg_name + " max value = ", df[agg_name].max() )
df[agg_name] = df[agg_name].astype(agg_type)
gc.collect()
return df
counts_columns = []
for f_0 in categorical_columns:
for f_1 in [x for x in categorical_columns if x != f_0] :
df = do_countuniq(df, [f_0], f_1,
f_0 + '-' + f_1 + '_cunique', 'uint16', show_max=True); gc.collect()
counts_columns.append(f_0 + '-' + f_1 + '_cunique')
count_columns = []
for f_0 in categorical_columns:
df = do_count(df, [f_0],
f_0 + '_count', 'uint16', show_max=True); gc.collect()
count_columns.append(f_0 + '_count')
for f in ['AMT_ANNUITY', 'AMT_CREDIT', 'AMT_INCOME_TOTAL'] + ['EXT_SOURCE_1', 'EXT_SOURCE_2', 'EXT_SOURCE_3']:
new_df[f] = new_df[f].replace([np.inf, -np.inf], np.nan).fillna(new_df[f].replace([np.inf, -np.inf], np.nan).dropna().median())
mean_columns = []
for f_0 in categorical_columns:
for f_1 in ['AMT_ANNUITY', 'AMT_CREDIT', 'AMT_INCOME_TOTAL'] + ['EXT_SOURCE_1', 'EXT_SOURCE_2', 'EXT_SOURCE_3'] :
new_df = do_mean(new_df, [f_0], f_1,
f_0 + '-' + f_1 + '_mean', 'uint16', show_max=True); gc.collect()
mean_columns.append(f_0 + '-' + f_1 + '_mean')
# train_features = pd.DataFrame(np.concatenate([df[count_columns][0:n_train].values, train_stacked.values, df[my_features][0:n_train].values, goran_features[0:n_train].values, suresh_august16[:n_train].values, suresh_august15[0:n_train].values], axis=1), columns=
# count_columns + ['y_' + str(i) for i in range(train_stacked.shape[1])] + my_features + list(goran_features.columns) + list(suresh_august16.columns) + list(suresh_august15.columns))
# test_features = pd.DataFrame(np.concatenate([df[count_columns][n_train:].values, test_stacked.values, df[my_features][n_train:].values, goran_features[n_train:].values, suresh_august16[n_train:].values, suresh_august15[n_train:].values], axis=1), columns=
# count_columns + ['y_' + str(i) for i in range(test_stacked.shape[1])] + my_features + list(goran_features.columns) + list(suresh_august16.columns) + list(suresh_august15.columns))
# train_features = np.concatenate([train_stacked.values, df[my_features][0:n_train].values, goran_features[0:n_train].values, suresh_august16[:n_train].values], axis=1)
# test_features = np.concatenate([test_stacked.values, df[my_features][n_train:].values, goran_features[n_train:].values, suresh_august16[n_train:].values], axis=1)
# train_features = pd.DataFrame(np.concatenate([train_stacked.values, df[my_features][0:n_train].values, goran_features[0:n_train].values, suresh_august16[:n_train].values, suresh_august15[0:n_train].values, suresh_august16_2[0:n_train].values], axis=1), columns=
# ['y_' + str(i) for i in range(train_stacked.shape[1])] + my_features + list(goran_features.columns) + list(suresh_august16.columns) + list(suresh_august15.columns) + list(suresh_august16_2.columns))
# test_features = pd.DataFrame(np.concatenate([test_stacked.values, df[my_features][n_train:].values, goran_features[n_train:].values, suresh_august16[n_train:].values, suresh_august15[n_train:].values, suresh_august16_2[n_train:].values], axis=1), columns=
# ['y_' + str(i) for i in range(test_stacked.shape[1])] + my_features + list(goran_features.columns) + list(suresh_august16.columns) + list(suresh_august15.columns) + list(suresh_august16_2.columns))
# train_features = pd.DataFrame(np.concatenate([train_stacked.values, df[my_features][0:n_train].values, goran_features[0:n_train].values, suresh_august19[:n_train].values, suresh_august15[0:n_train].values, prevs_df[0:n_train].values, suresh_august16[0:n_train].values, suresh_august16_2[0:n_train].values], axis=1), columns=
# ['y_' + str(i) for i in range(train_stacked.shape[1])] + my_features + list(goran_features.columns) + list(suresh_august19.columns) + list(suresh_august15.columns) + list(prevs_df.columns) + list(suresh_august16.columns) + list(suresh_august16_2.columns))
# test_features = pd.DataFrame(np.concatenate([test_stacked.values, df[my_features][n_train:].values, goran_features[n_train:].values, suresh_august19[n_train:].values, suresh_august15[n_train:].values, prevs_df[n_train:].values, suresh_august16[n_train:].values, suresh_august16_2[n_train:].values], axis=1), columns=
# ['y_' + str(i) for i in range(test_stacked.shape[1])] + my_features + list(goran_features.columns) + list(suresh_august19.columns) + list(suresh_august15.columns) + list(prevs_df.columns) + list(suresh_august16.columns) + list(suresh_august16_2.columns))
# train_features = pd.DataFrame(np.concatenate([df[count_columns][0:n_train].values, train_stacked.values, df[my_features][0:n_train].values, suresh_august19[:n_train].values, suresh_august15[0:n_train].values, prevs_df[0:n_train].values, suresh_august16[0:n_train].values, suresh_august16_2[0:n_train].values], axis=1), columns=
# count_columns + ['y_' + str(i) for i in range(train_stacked.shape[1])] + my_features + list(suresh_august19.columns) + list(suresh_august15.columns) + list(prevs_df.columns) + list(suresh_august16.columns) + list(suresh_august16_2.columns))
# test_features = pd.DataFrame(np.concatenate([df[count_columns][n_train:].values, test_stacked.values, df[my_features][n_train:].values, suresh_august19[n_train:].values, suresh_august15[n_train:].values, prevs_df[n_train:].values, suresh_august16[n_train:].values, suresh_august16_2[n_train:].values], axis=1), columns=
# count_columns + ['y_' + str(i) for i in range(test_stacked.shape[1])] + my_features + list(suresh_august19.columns) + list(suresh_august15.columns) + list(prevs_df.columns) + list(suresh_august16.columns) + list(suresh_august16_2.columns))
new_df[mean_columns][0:n_train].values
new_df[mean_columns][n_train:].values
gc.collect()
# train_features = pd.DataFrame(np.concatenate([new_df[mean_columns][0:n_train].values, suresh_august16[0:n_train].values, df[count_columns][0:n_train].values , df[counts_columns][0:n_train].values, train_stacked.values, df[my_features][0:n_train].values], axis=1), columns=
# mean_columns + list(suresh_august16.columns) + count_columns + counts_columns + ['y_' + str(i) for i in range(train_stacked.shape[1])] + my_features)
# test_features = pd.DataFrame(np.concatenate([new_df[mean_columns][n_train:].values, suresh_august16[n_train:].values, df[count_columns][n_train:].values, df[counts_columns][n_train:].values, test_stacked.values, df[my_features][n_train:].values], axis=1), columns=
# mean_columns + list(suresh_august16.columns) + count_columns + counts_columns + ['y_' + str(i) for i in range(test_stacked.shape[1])] + my_features)
# train_features = pd.DataFrame(np.concatenate([suresh_august16[0:n_train].values, df[count_columns][0:n_train].values , df[counts_columns][0:n_train].values, train_stacked.values, df[my_features][0:n_train].values], axis=1), columns=
# list(suresh_august16.columns) + count_columns + counts_columns + ['y_' + str(i) for i in range(train_stacked.shape[1])] + my_features)
# test_features = pd.DataFrame(np.concatenate([ suresh_august16[n_train:].values, df[count_columns][n_train:].values, df[counts_columns][n_train:].values, test_stacked.values, df[my_features][n_train:].values], axis=1), columns=
# list(suresh_august16.columns) + count_columns + counts_columns + ['y_' + str(i) for i in range(test_stacked.shape[1])] + my_features)
# train_features = pd.DataFrame(np.concatenate([df[categorical_columns][0:n_train].values, goran_features_19_8[0:n_train].values, suresh_august16[0:n_train].values, df[count_columns][0:n_train].values , df[counts_columns][0:n_train].values, train_stacked.values, df[my_features][0:n_train].values], axis=1), columns=
# categorical_columns + list(goran_features_19_8.columns) + list(suresh_august16.columns) + count_columns + counts_columns + ['y_' + str(i) for i in range(train_stacked.shape[1])] + my_features)
# test_features = pd.DataFrame(np.concatenate([df[categorical_columns][n_train:].values, goran_features_19_8[n_train:].values, suresh_august16[n_train:].values, df[count_columns][n_train:].values, df[counts_columns][n_train:].values, test_stacked.values, df[my_features][n_train:].values], axis=1), columns=
# categorical_columns + list(goran_features_19_8.columns) + list(suresh_august16.columns) + count_columns + counts_columns + ['y_' + str(i) for i in range(test_stacked.shape[1])] + my_features)
# train_features = pd.DataFrame(np.concatenate([goranm_8_20[0:n_train].values ,goran_features_19_8[0:n_train].values, suresh_august20[0:n_train].values, train_stacked.values, df[my_features][0:n_train].values, suresh_august16[:n_train].values, suresh_august15[0:n_train].values], axis=1), columns=
# list(goranm_8_20.columns) + list(goran_features_19_8.columns) + list(suresh_august20.columns) + ['y_' + str(i) for i in range(train_stacked.shape[1])] + my_features + list(suresh_august16.columns) + list(suresh_august15.columns))
# test_features = pd.DataFrame(np.concatenate([goranm_8_20[n_train:].values, goran_features_19_8[n_train:].values, suresh_august20[n_train:].values, test_stacked.values, df[my_features][n_train:].values, suresh_august16[n_train:].values, suresh_august15[n_train:].values], axis=1), columns=
# list(goranm_8_20.columns) + list(goran_features_19_8.columns) + list(suresh_august20.columns) + ['y_' + str(i) for i in range(test_stacked.shape[1])] + my_features + list(suresh_august16.columns) + list(suresh_august15.columns))
# train_features = pd.DataFrame(np.concatenate([goranm_8_20[0:n_train].values ,goran_features_19_8[0:n_train].values, suresh_august20[0:n_train].values, train_stacked.iloc[:, selected_features].values, df[my_features][0:n_train].values, suresh_august16[:n_train].values, suresh_august15[0:n_train].values], axis=1), columns=
# list(goranm_8_20.columns) + list(goran_features_19_8.columns) + list(suresh_august20.columns) + ['y_' + str(i) for i in selected_features] + my_features + list(suresh_august16.columns) + list(suresh_august15.columns))
# test_features = pd.DataFrame(np.concatenate([goranm_8_20[n_train:].values, goran_features_19_8[n_train:].values, suresh_august20[n_train:].values, test_stacked.iloc[:, selected_features].values, df[my_features][n_train:].values, suresh_august16[n_train:].values, suresh_august15[n_train:].values], axis=1), columns=
# list(goranm_8_20.columns) + list(goran_features_19_8.columns) + list(suresh_august20.columns) + ['y_' + str(i) for i in selected_features] + my_features + list(suresh_august16.columns) + list(suresh_august15.columns))
# train_features = pd.DataFrame(np.concatenate([goran_features_19_8[0:n_train].values, df[count_columns][0:n_train].values, train_stacked.values, df[my_features][0:n_train].values, goran_features[0:n_train].values, suresh_august16[:n_train].values, suresh_august15[0:n_train].values], axis=1), columns=
# list(goran_features_19_8.columns) + count_columns + ['y_' + str(i) for i in range(train_stacked.shape[1])] + my_features + list(goran_features.columns) + list(suresh_august16.columns) + list(suresh_august15.columns))
# test_features = pd.DataFrame(np.concatenate([goran_features_19_8[n_train:].values, df[count_columns][n_train:].values, test_stacked.values, df[my_features][n_train:].values, goran_features[n_train:].values, suresh_august16[n_train:].values, suresh_august15[n_train:].values], axis=1), columns=
# list(goran_features_19_8.columns) + count_columns + ['y_' + str(i) for i in range(test_stacked.shape[1])] + my_features + list(goran_features.columns) + list(suresh_august16.columns) + list(suresh_august15.columns))
train_features = pd.DataFrame(np.concatenate([df[counts_columns][0:n_train].values, df[count_columns][0:n_train].values ,new_df[mean_columns][0:n_train].values, prevs_df[0:n_train].values, suresh_20[0:n_train].values, goranm_8_20[0:n_train].values ,goran_features_19_8[0:n_train].values, suresh_august20[0:n_train].values, df[my_features][0:n_train].values, suresh_august16[:n_train].values, suresh_august15[0:n_train].values], axis=1), columns=
counts_columns + count_columns + mean_columns + list(prevs_df.columns) + list(suresh_20.columns) + list(goranm_8_20.columns) + list(goran_features_19_8.columns) + list(suresh_august20.columns) + my_features + list(suresh_august16.columns) + list(suresh_august15.columns))
test_features = pd.DataFrame(np.concatenate([df[counts_columns][n_train:].values, df[count_columns][n_train:].values, new_df[mean_columns][n_train:].values, prevs_df[n_train:].values, suresh_20[n_train:].values, goranm_8_20[n_train:].values, goran_features_19_8[n_train:].values, suresh_august20[n_train:].values, df[my_features][n_train:].values, suresh_august16[n_train:].values, suresh_august15[n_train:].values], axis=1), columns=
counts_columns + count_columns + mean_columns + list(prevs_df.columns) + list(suresh_20.columns) + list(goranm_8_20.columns) + list(goran_features_19_8.columns) + list(suresh_august20.columns) + my_features + list(suresh_august16.columns) + list(suresh_august15.columns))
test_features.head()
gc.collect()
cols_to_drop = [
'STCK_BERBAL_6_.',
"FLAG_DOCUMENT_2",
"FLAG_DOCUMENT_7",
"FLAG_DOCUMENT_10",
"FLAG_DOCUMENT_12",
"FLAG_DOCUMENT_13",
"FLAG_DOCUMENT_14",
"FLAG_DOCUMENT_15",
"FLAG_DOCUMENT_16",
"FLAG_DOCUMENT_17",
"FLAG_DOCUMENT_18",
"FLAG_DOCUMENT_19",
"FLAG_DOCUMENT_20",
"FLAG_DOCUMENT_21",
"PREV_NAME_CONTRACT_TYPE_Consumer_loans",
"PREV_NAME_CONTRACT_TYPE_XNA",
"PB_CNT_NAME_CONTRACT_STATUS_Amortized_debt",
"MAX_DATA_ALL",
"MIN_DATA_ALL",
"MAX_MIN_DURATION",
"MAX_AMT_CREDIT_MAX_OVERDUE",
"CC_AMT_DRAWINGS_ATM_CURRENT_MIN",
"CC_AMT_DRAWINGS_OTHER_CURRENT_MAX",
"CC_AMT_DRAWINGS_OTHER_CURRENT_MIN",
"CC_CNT_DRAWINGS_ATM_CURRENT_MIN",
"CC_CNT_DRAWINGS_OTHER_CURRENT_MAX",
"CC_CNT_DRAWINGS_OTHER_CURRENT_MIN",
"CC_SK_DPD_DEF_MIN",
"CC_SK_DPD_MIN",
"BERB_STATUS_CREDIT_TYPE_Loan_for_working_capital_replenishment",
"BERB_STATUS_CREDIT_TYPE_Real_estate_loan",
"BERB_STATUS_CREDIT_TYPE_Loan_for_the_purchase_of_equipment",
"BERB_COMBO_CT_CA_COMBO_CT_CA_Loan_for_working_capital_replenishmentClosed",
"BERB_COMBO_CT_CA_COMBO_CT_CA_Car_loanSold",
"BERB_COMBO_CT_CA_COMBO_CT_CA_Another_type_of_loanActive",
"BERB_COMBO_CT_CA_COMBO_CT_CA_Loan_for_working_capital_replenishmentSold",
"BERB_COMBO_CT_CA_COMBO_CT_CA_MicroloanSold",
"BERB_COMBO_CT_CA_COMBO_CT_CA_Another_type_of_loanSold",
"FLAG_EMAIL",
"APARTMENTS_AVG",
"AMT_REQ_CREDIT_BUREAU_MON",
"AMT_REQ_CREDIT_BUREAU_QRT",
"AMT_REQ_CREDIT_BUREAU_YEAR",
"STCK_BERBAL_6_",
"STCK_CC_6_x"]
feats = [f for f in cols_to_drop if f in train_features.columns]
train_features.drop(labels=feats, axis=1, inplace=True)
test_features.drop(labels=feats, axis=1, inplace=True)
cat_features = [] # [i for i in range(len(categorical_columns))]
gc.collect()
# train_stacked.to_csv('oofs/train_oofs-v0.1.0.csv', index=False)
# test_stacked.to_csv('oofs/test_oofs-v0.1.0.csv', index=False)
test_features.head()
train_features['nans'] = train_features.replace([np.inf, -np.inf], np.nan).isnull().sum(axis=1)
test_features['nans'] = test_features.replace([np.inf, -np.inf], np.nan).isnull().sum(axis=1)
test_file_path = "Level_1_stack/test_catb_xxx_0.csv"
validation_file_path = 'Level_1_stack/validation_catb_xxx_0.csv.csv'
num_folds = 5
# train_features = train_features.replace([np.inf, -np.inf], np.nan).fillna(-999, inplace=False)
# test_features = test_features.replace([np.inf, -np.inf], np.nan).fillna(-999, inplace=False)
gc.collect()
encoding = 'ohe'
train_df = train_features
test_df = test_features
print("Starting LightGBM. Train shape: {}, test shape: {}".format(train_df.shape, test_df.shape))
gc.collect()
# Cross validation model
folds = KFold(n_splits=num_folds, shuffle=True, random_state=1001)
# Create arrays and dataframes to store results
oof_preds = np.zeros(train_df.shape[0])
sub_preds = np.zeros(test_df.shape[0])
feature_importance_df = pd.DataFrame()
feats = [f for f in train_df.columns if f not in ['TARGET','SK_ID_CURR','SK_ID_BUREAU','SK_ID_PREV','index']]
#feats = [col for col in feats_0 if df[col].dtype == 'object']
print(train_df[feats].shape)
for n_fold, (train_idx, valid_idx) in enumerate(folds.split(train_df[feats], train['TARGET'])):
if encoding == 'ohe':
x_train = train_df[feats].iloc[train_idx]
#cat_features = [i for i, col in enumerate(x_train.columns) if col in categorical_cols]
x_train = x_train.replace([np.inf, -np.inf], np.nan).fillna(-999).values
x_valid = train_df[feats].iloc[valid_idx].replace([np.inf, -np.inf], np.nan).fillna(-999).values
x_test = test_df[feats].replace([np.inf, -np.inf], np.nan).fillna(-999).values
print(x_train.shape, x_valid.shape, x_test.shape)
gc.collect()
clf = CatBoostRegressor(learning_rate=0.05, iterations=2500, verbose=True, rsm=0.25,
use_best_model=True, l2_leaf_reg=40, allow_writing_files=False, metric_period=50,
random_seed=666, depth=6, loss_function='RMSE', od_wait=50, od_type='Iter')
clf.fit(x_train, train['TARGET'].iloc[train_idx].values, eval_set=(x_valid, train['TARGET'].iloc[valid_idx].values)
, cat_features=[], use_best_model=True, verbose=True)
oof_preds[valid_idx] = clf.predict(x_valid)
sub_preds += clf.predict(x_test) / folds.n_splits
print('Fold %2d AUC : %.6f' % (n_fold + 1, roc_auc_score(train['TARGET'].iloc[valid_idx].values, oof_preds[valid_idx])))
del clf
gc.collect()
sub_df = test[['SK_ID_CURR']].copy()
sub_df['TARGET'] = sub_preds
sub_df[['SK_ID_CURR', 'TARGET']].to_csv(test_file_path, index= False)
val_df = train[['SK_ID_CURR', 'TARGET']].copy()
val_df['TARGET'] = oof_preds
val_df[['SK_ID_CURR', 'TARGET']].to_csv(validation_file_path, index= False)
gc.collect()
```
|
github_jupyter
|
```
%pylab inline
import sys
import numpy as np
import tensorflow as tf
import tensorflow_probability as tfp
import arviz as az
import matplotlib.pyplot as plt
from matplotlib import rcParams
import matplotlib.font_manager as fm
rcParams['font.family'] = 'sans-serif'
sys.path.append('../')
from mederrata_spmf import PoissonMatrixFactorization
```
In this notebook, we look at the $\mathcal{M}$-open setting, where the generating process is in the span of models.
# Generate a random matrices V, W
For V, assume that 10 variables share a factor structure and the other 20 are noise
```
N = 50000
D_factor = 10
D_noise = 20
D = D_factor + D_noise
P = 3
V = np.abs(np.random.normal(1.5, 0.5, size=(P,D_factor)))
Z = np.abs(np.random.normal(0, 1, size=(N,P)))
ZV = Z.dot(V)
X = np.zeros((N, D_factor+D_noise))
X = np.random.poisson(1.,size=(N,D_noise+D_factor))
X[:, ::3] = np.random.poisson(ZV)
# Test taking in from tf.dataset, don't pre-batch
data = tf.data.Dataset.from_tensor_slices(
{
'counts': X,
'indices': np.arange(N),
'normalization': np.ones(N)
})
data = data.batch(1000)
# strategy = tf.distribute.MirroredStrategy()
strategy = None
factor = PoissonMatrixFactorization(
data, latent_dim=P, strategy=strategy,
u_tau_scale=1.0/np.sqrt(D*N),
dtype=tf.float64)
# Test to make sure sampling works
losses = factor.calibrate_advi(
num_epochs=200, learning_rate=.05)
waic = factor.waic()
print(waic)
surrogate_samples = factor.surrogate_distribution.sample(1000)
if 's' in surrogate_samples.keys():
weights = surrogate_samples['s']/tf.reduce_sum(surrogate_samples['s'],-2,keepdims=True)
intercept_data = az.convert_to_inference_data(
{
r"$\varphi_i/\eta_i$":
(tf.squeeze(surrogate_samples['w'])*weights[:,-1,:]).numpy().T})
else:
intercept_data = az.convert_to_inference_data(
{
r"$\varphi_i/\eta_i$":
(tf.squeeze(surrogate_samples['w'])).numpy().T})
fig, ax = plt.subplots(1,2, figsize=(14,8))
D = factor.feature_dim
pcm = ax[0].imshow(factor.encoding_matrix().numpy()[::-1,:], vmin=0, cmap="Blues")
ax[0].set_yticks(np.arange(D))
ax[0].set_yticklabels(np.arange(D))
ax[0].set_ylabel("item")
ax[0].set_xlabel("factor dimension")
ax[0].set_xticks(np.arange(P))
ax[0].set_xticklabels(np.arange(P))
fig.colorbar(pcm, ax=ax[0], orientation = "vertical")
az.plot_forest(intercept_data, ax=ax[1])
ax[1].set_xlabel("background rate")
ax[1].set_ylim((-0.014,.466))
ax[1].set_title("65% and 95% CI")
#plt.savefig('mix_nonlinear_factorization_sepmf.pdf', bbox_inches='tight')
plt.show()
```
|
github_jupyter
|
Final models with hyperparameters tuned for Logistics Regression and XGBoost with all features.
```
#Import the libraries
import pandas as pd
import numpy as np
from tqdm import tqdm
from sklearn import linear_model, metrics, preprocessing, model_selection
from sklearn.preprocessing import StandardScaler
import xgboost as xgb
#Load the data
modeling_dataset = pd.read_csv('/content/drive/MyDrive/prediction/frac_cleaned_fod_data.csv', low_memory = False)
#All columns - except 'HasDetections', 'kfold', and 'MachineIdentifier'
train_features = [tf for tf in modeling_dataset.columns if tf not in ('HasDetections', 'kfold', 'MachineIdentifier')]
#The features selected based on the feature selection method earlier employed
train_features_after_selection = ['AVProductStatesIdentifier', 'Processor','AvSigVersion', 'Census_TotalPhysicalRAM', 'Census_InternalPrimaryDiagonalDisplaySizeInInches',
'Census_IsVirtualDevice', 'Census_PrimaryDiskTotalCapacity', 'Wdft_IsGamer', 'Census_IsAlwaysOnAlwaysConnectedCapable', 'EngineVersion',
'Census_ProcessorCoreCount', 'Census_OSEdition', 'Census_OSInstallTypeName', 'Census_OSSkuName', 'AppVersion', 'OsBuildLab', 'OsSuite',
'Firewall', 'IsProtected', 'Census_IsTouchEnabled', 'Census_ActivationChannel', 'LocaleEnglishNameIdentifier','Census_SystemVolumeTotalCapacity',
'Census_InternalPrimaryDisplayResolutionHorizontal','Census_HasOpticalDiskDrive', 'OsBuild', 'Census_InternalPrimaryDisplayResolutionVertical',
'CountryIdentifier', 'Census_MDC2FormFactor', 'GeoNameIdentifier', 'Census_PowerPlatformRoleName', 'Census_OSWUAutoUpdateOptionsName', 'SkuEdition',
'Census_OSVersion', 'Census_GenuineStateName', 'Census_OSBuildRevision', 'Platform', 'Census_ChassisTypeName', 'Census_FlightRing',
'Census_PrimaryDiskTypeName', 'Census_OSBranch', 'Census_IsSecureBootEnabled', 'OsPlatformSubRelease']
#Define the categorical features of the data
categorical_features = ['ProductName',
'EngineVersion',
'AppVersion',
'AvSigVersion',
'Platform',
'Processor',
'OsVer',
'OsPlatformSubRelease',
'OsBuildLab',
'SkuEdition',
'Census_MDC2FormFactor',
'Census_DeviceFamily',
'Census_PrimaryDiskTypeName',
'Census_ChassisTypeName',
'Census_PowerPlatformRoleName',
'Census_OSVersion',
'Census_OSArchitecture',
'Census_OSBranch',
'Census_OSEdition',
'Census_OSSkuName',
'Census_OSInstallTypeName',
'Census_OSWUAutoUpdateOptionsName',
'Census_GenuineStateName',
'Census_ActivationChannel',
'Census_FlightRing']
#XGBoost
def opt_run_xgboost(fold):
for col in train_features:
if col in categorical_features:
#Initialize the Label Encoder
lbl = preprocessing.LabelEncoder()
#Fit on the categorical features
lbl.fit(modeling_dataset[col])
#Transform
modeling_dataset.loc[:,col] = lbl.transform(modeling_dataset[col])
#Get training and validation data using folds
modeling_datasets_train = modeling_dataset[modeling_dataset.kfold != fold].reset_index(drop=True)
modeling_datasets_valid = modeling_dataset[modeling_dataset.kfold == fold].reset_index(drop=True)
#Get train data
X_train = modeling_datasets_train[train_features].values
#Get validation data
X_valid = modeling_datasets_valid[train_features].values
#Initialize XGboost model
xgb_model = xgb.XGBClassifier(
alpha= 1.0,
colsample_bytree= 0.6,
eta= 0.05,
gamma= 0.1,
lamda= 1.0,
max_depth= 9,
min_child_weight= 5,
subsample= 0.7,
n_jobs=-1)
#Fit the model on training data
xgb_model.fit(X_train, modeling_datasets_train.HasDetections.values)
#Predict on validation
valid_preds = xgb_model.predict_proba(X_valid)[:,1]
valid_preds_pc = xgb_model.predict(X_valid)
#Get the ROC AUC score
auc = metrics.roc_auc_score(modeling_datasets_valid.HasDetections.values, valid_preds)
#Get the precision score
pre = metrics.precision_score(modeling_datasets_valid.HasDetections.values, valid_preds_pc, average='binary')
#Get the Recall score
rc = metrics.recall_score(modeling_datasets_valid.HasDetections.values, valid_preds_pc, average='binary')
return auc, pre, rc
#Function for Logistic Regression Classification
def opt_run_lr(fold):
#Get training and validation data using folds
cleaned_fold_datasets_train = modeling_dataset[modeling_dataset.kfold != fold].reset_index(drop=True)
cleaned_fold_datasets_valid = modeling_dataset[modeling_dataset.kfold == fold].reset_index(drop=True)
#Initialize OneHotEncoder from scikit-learn, and fit it on training and validation features
ohe = preprocessing.OneHotEncoder()
full_data = pd.concat(
[cleaned_fold_datasets_train[train_features],cleaned_fold_datasets_valid[train_features]],
axis = 0
)
ohe.fit(full_data[train_features])
#transform the training and validation data
x_train = ohe.transform(cleaned_fold_datasets_train[train_features])
x_valid = ohe.transform(cleaned_fold_datasets_valid[train_features])
#Initialize the Logistic Regression Model
lr_model = linear_model.LogisticRegression(
penalty= 'l2',
C = 49.71967742639108,
solver= 'lbfgs',
max_iter= 300,
n_jobs=-1
)
#Fit model on training data
lr_model.fit(x_train, cleaned_fold_datasets_train.HasDetections.values)
#Predict on the validation data using the probability for the AUC
valid_preds = lr_model.predict_proba(x_valid)[:, 1]
#For precision and Recall
valid_preds_pc = lr_model.predict(x_valid)
#Get the ROC AUC score
auc = metrics.roc_auc_score(cleaned_fold_datasets_valid.HasDetections.values, valid_preds)
#Get the precision score
pre = metrics.precision_score(cleaned_fold_datasets_valid.HasDetections.values, valid_preds_pc, average='binary')
#Get the Recall score
rc = metrics.recall_score(cleaned_fold_datasets_valid.HasDetections.values, valid_preds_pc, average='binary')
return auc, pre, rc
#A list to hold the values of the XGB performance metrics
xg = []
for fold in tqdm(range(10)):
xg.append(opt_run_xgboost(fold))
#Run the Logistic regression model for all folds and hold their values
lr = []
for fold in tqdm(range(10)):
lr.append(opt_run_lr(fold))
xgb_auc = []
xgb_pre = []
xgb_rc = []
lr_auc = []
lr_pre = []
lr_rc = []
#Loop to get each of the performance metric for average computation
for i in lr:
lr_auc.append(i[0])
lr_pre.append(i[1])
lr_rc.append(i[2])
for j in xg:
xgb_auc.append(i[0])
xgb_pre.append(i[1])
xgb_rc.append(i[2])
#Dictionary to hold the basic model performance data
final_model_performance2 = {"logistic_regression": {"auc":"", "precision":"", "recall":""},
"xgb": {"auc":"","precision":"","recall":""}
}
#Calculate average of each of the lists of performance metrics and update the dictionary
final_model_performance2['logistic_regression'].update({'auc':sum(lr_auc)/len(lr_auc)})
final_model_performance2['xgb'].update({'auc':sum(xgb_auc)/len(xgb_auc)})
final_model_performance2['logistic_regression'].update({'precision':sum(lr_pre)/len(lr_pre)})
final_model_performance2['xgb'].update({'precision':sum(xgb_pre)/len(xgb_pre)})
final_model_performance2['logistic_regression'].update({'recall':sum(lr_rc)/len(lr_rc)})
final_model_performance2['xgb'].update({'recall':sum(xgb_rc)/len(xgb_rc)})
final_model_performance2
```
|
github_jupyter
|
Imaging you are a metal toy producer and wan't to package your product automaticaly.
In this case it would be nice to categorise your products without much effort.
In this example we use a pretrained model ('Xception' with 'imagenet' dataset).
## Import dependencies
```
import warnings
warnings.filterwarnings('ignore')
import sys
import pathlib
current_path = pathlib.Path().absolute()
root_path = "{0}/..".format(current_path)
sys.path.append("{0}/src".format(root_path))
import numpy as np
from tensorflow.keras import backend as K
from tensorflow.keras.optimizers import SGD, Adam
from tensorflow.keras.applications.xception import Xception
from tensorflow.keras.layers import GlobalAveragePooling2D, Dense
from tensorflow.keras.models import Model
import backbones
import utils.plots as plots
from train_engine import TrainEngine
from utils import load_dataset, ImageGeneratorConfig, setup_environment, export_util
setup_environment(enable_gpu=True)
```
## Prepare training and evaluation
As we have only few images, we need to augment them to get more input for our neuronal network.
```
train_files_path = "{0}/img/space_ships/train".format(root_path)
eval_files_path = "{0}/img/space_ships/eval".format(root_path)
input_shape = (138, 256, 3)
generator_config = ImageGeneratorConfig()
generator_config.loop_count = 10
generator_config.horizontal_flip = True
generator_config.zoom_range = 0.5
generator_config.width_shift_range = 0.03
generator_config.height_shift_range = 0.03
generator_config.rotation_range = 180
train_x, train_y, eval_x, eval_y = load_dataset(
train_files_path, input_shape, validation_split=0.1
)
number_of_classes = 3
```
## Create model
```
base_model = Xception(include_top=False, weights='imagenet', input_shape=input_shape)
base_layers_count = len(base_model.layers)
x = base_model.output
x = GlobalAveragePooling2D()(x)
x = Dense(512, activation='relu')(x)
x = Dense(number_of_classes, activation='softmax')(x)
model = Model(inputs=base_model.input, outputs=x)
optimizer = Adam(lr=0.001)
```
## Train model
First we will teach the model the new classes.
```
for layer in base_model.layers:
layer.trainable = False
train_engine = TrainEngine(
input_shape,
model,
optimizer,
loss="sparse_categorical_crossentropy"
)
```
### Train
```
loss, acc, val_loss, val_acc = train_engine.train(
train_x,
train_y,
eval_x,
eval_y,
epochs=70,
batch_size=32,
image_generator_config=generator_config,
is_augment_y_enabled=False,
is_classification=True
)
```
### Show history
```
plots.plot_history(loss, acc, val_loss, val_acc)
```
Now we fine tune the convolutional layers from the base model.
This will remove connections between neurons that are not used and also create new ones.
```
for layer in base_model.layers[:base_layers_count]:
layer.trainable = False
for layer in model.layers[base_layers_count:]:
layer.trainable = True
optimizer = SGD(lr=0.0001, momentum=0.9)
train_engine = TrainEngine(
input_shape,
model,
optimizer,
loss="sparse_categorical_crossentropy"
)
loss, acc, val_loss, val_acc = train_engine.train(
train_x,
train_y,
eval_x,
eval_y,
epochs=20,
batch_size=32,
image_generator_config=generator_config,
is_augment_y_enabled=False,
is_classification=True
)
```
## Predict
```
classes = ['Millenium Falcon', 'Pelican', 'TIE Fighter']
x, _, _, _ = load_dataset(
eval_files_path, input_shape, validation_split=0
)
for idx in range(len(x[:3])):
predictions = train_engine.model.predict(
np.array([x[idx]], dtype=np.float32), batch_size=1
)
plots.plot_classification(predictions, [x[idx]], input_shape, classes)
```
### Export model
```
export_path = "{0}/saved_models/space_ships".format(root_path)
export_util.export_model(model, export_path)
```
## Cleanup
```
K.clear_session()
```
|
github_jupyter
|
```
import torch
import sim_data_gen
import numpy as np
import dr_crn
import matplotlib.pyplot as plt
n_feat = 5
def get_mmd(x_train):
feat = x_train[:, :n_feat]
causes = x_train[:, n_feat:]
cause_ind = sim_data_gen.cause_to_num(causes)
uniques, counts = np.unique(cause_ind, return_counts=True)
uniques = uniques[counts > 1]
mmd_sigma = 1
mmd = 0
for i in range(len(uniques)):
x1 = torch.tensor(feat[cause_ind == uniques[i]])
x2 = torch.tensor(feat[cause_ind != uniques[i]])
mmd = mmd + torch.abs(dr_crn.mmd2_rbf(x1, x2, mmd_sigma))
return mmd
scp_list = []
scp_list_sd = []
for k in [1,2,3,4,5]:
k = k * 2
config_key = 'ea_balance_{}'.format(k)
model_id='SCP'
seed_list = []
for seed in [1, 2, 3, 4, 5]:
x_train = torch.load('model/simulation_overlap/{}_{}_{}_x.pth'.format(config_key, model_id, seed))
x_train = x_train.cpu().numpy()
m = get_mmd(x_train)
seed_list.append(m)
seed_list = np.array(seed_list)
m = seed_list.mean()
sd = seed_list.std()
scp_list.append(m)
scp_list_sd.append(sd)
base_line_list = []
base_line_list_sd = []
for k in [1,2,3,4,5]:
k = k * 2
config_key = 'ea_balance_{}'.format(k)
model_id='IPW'
seed_list = []
for seed in [1, 2, 3, 4, 5]:
x_train = torch.load('model/simulation_overlap/{}_{}_{}_x.pth'.format(config_key, model_id, seed))
x_train = x_train.cpu().numpy()
causes = x_train[:, n_feat:]
m = get_mmd(x_train)
seed_list.append(m)
seed_list = np.array(seed_list)
m = seed_list.mean()
sd = seed_list.std()
base_line_list.append(m)
base_line_list_sd.append(sd)
baseline = np.array(base_line_list)
scp = np.array(scp_list)
baseline_sd = np.array(base_line_list_sd)
scp_sd = np.array(scp_list_sd)
plt.style.use('tableau-colorblind10')
plt.rcParams['font.size'] = '13'
colors = plt.rcParams['axes.prop_cycle'].by_key()['color']
plt.figure(figsize=(5,3))
width = 0.4
plt.bar(np.arange(1,6)-0.2, baseline,yerr=base_line_list_sd, color=colors[0], width=width, alpha=0.7, label='Observational')
plt.bar(np.arange(1,6)+0.2, scp,yerr=scp_list_sd, color=colors[1], width=width, alpha=0.7, label = 'SCP Augmented')
plt.xlabel(r'Confounding level $|v_m|$', fontsize=14)
plt.ylabel('Distance: $b$', fontsize=16)
plt.legend()
plt.title(r'Balancing of the dataset (smaller better)', fontsize=14)
plt.tight_layout(pad=0.2)
plt.savefig(fname='Fig5_A.png', dpi=300)
import pandas as pds
from scipy.special import comb
plt.style.use('tableau-colorblind10')
plt.rcParams['font.size'] = '13'
colors = plt.rcParams['axes.prop_cycle'].by_key()['color']
df_base = pds.read_csv('results/results_ea_baseline.txt', sep=' ', header=None)
weights = np.array([comb(5, i) for i in range(1, 6)])
x_ref = np.sum(np.arange(1,6) * weights) / np.sum(weights)
y_ref = np.interp(x_ref, np.arange(1, 6), df_base[2].values)
x_ref_scp = 1 + 0.1 * (np.sum(np.arange(5))) / 5
x_ref_scp
y_ref_scp = np.interp(x_ref_scp, np.arange(1, 6), df_base[2].values)
prefix=''
dat = pds.read_csv('results{}/results_ea.txt'.format(prefix), sep=' ', header=None)
dat[4] = dat[4] / np.sqrt(32)
dat[5] = dat[5] / np.sqrt(32)
dat = dat.sort_values(1)
dat.tail(10)
dat1 = dat[dat[0] == 'SCP']
dat2 = dat[dat[0] == 'FB']
z_ref_scp = np.interp(y_ref_scp, np.arange(7) / 10, dat1[4].values)
plt.figure(figsize=(5,3))
plt.fill_between(dat1[1], dat1[4] - 2 * dat1[5], dat1[4] + 2 * dat1[5], alpha=0.3, color=colors[0])
plt.plot(dat1[1], dat1[4], '-o', color=colors[0], label='SCP')
plt.plot([0, 0.6], [1.533/ np.sqrt(32), 1.533/ np.sqrt(32)], ls='--', c=colors[3], label='No Aug.', linewidth=3)
plt.axvline(y_ref_scp, ymax=0.3, ls='--', c=colors[1], linewidth=3)
plt.title(r'SCP Final Prediction Error (RMSE)', fontsize=14)
plt.xlabel(r'Simulated Step One Error $\xi$', fontsize=14)
plt.ylabel('RMSE', fontsize=14)
plt.text(0.1, 0.275, 'NN Baseline', fontsize=14)
plt.text(0.21, 0.18, 'Actual step one error', fontsize=14, c=colors[1])
plt.tight_layout(pad=0.1)
plt.savefig(fname='Fig5_B.png', dpi=300)
```
|
github_jupyter
|
<center><img alt="" src="images/Cover_EDA.jpg"/></center>
## <center><font color="blue">EDA-04: Unsupervised Learning - Clustering Bagian ke-02</font></center>
<h2 style="text-align: center;">(C) Taufik Sutanto - 2020</h2>
<h2 style="text-align: center;">tau-data Indonesia ~ <a href="https://tau-data.id/eda-04/" target="_blank"><span style="color: #0009ff;">https://tau-data.id/eda-04/</span></a></h2>
```
# Run this cell ONLY if this notebook run from Google Colab
# Kalau dijalankan lokal (Anaconda/WinPython) maka silahkan install di terminal/command prompt
# Lalu unduh secara manual file yang dibutuhkan dan letakkan di folder Python anda.
!pip install --upgrade umap-learn
!wget https://raw.githubusercontent.com/taudata-indonesia/eLearning/master/tau_unsup.py
# Importing Modules untuk Notebook ini
import warnings; warnings.simplefilter('ignore')
import time, umap, numpy as np, tau_unsup as tau, matplotlib.pyplot as plt, pandas as pd, seaborn as sns
from matplotlib.colors import ListedColormap
from sklearn import cluster, datasets
from sklearn.metrics.pairwise import pairwise_distances_argmin
from sklearn.preprocessing import StandardScaler
from itertools import cycle, islice
from sklearn.metrics import silhouette_score as siluet
from sklearn.metrics.cluster import homogeneity_score as purity
from sklearn.metrics import normalized_mutual_info_score as NMI
sns.set(style="ticks", color_codes=True)
random_state = 99
```
# Review
## EDA-03
* Pendahuluan Unsupervised Learning
* k-Means, k-Means++, MiniBatch k-Means
* internal & External Evaluation
* Parameter Tunning
## EDA-04
* Hierarchical Clustering
* Spectral Clustering
* DBScan
* Clustering Evaluation Revisited
## Linkages Comparisons
* single linkage is fast, and can perform well on non-globular data, but it performs poorly in the presence of noise.
* average and complete linkage perform well on cleanly separated globular clusters, but have mixed results otherwise.
* Ward is the most effective method for noisy data.
* http://scikit-learn.org/stable/auto_examples/cluster/plot_linkage_comparison.html#sphx-glr-auto-examples-cluster-plot-linkage-comparison-py
```
tau.compare_linkages()
```
### Pros
* No assumption of a particular number of clusters (i.e. k-means)
* May correspond to meaningful taxonomies
### Cons
* Once a decision is made to combine two clusters, it can’t be undone
* Too slow for large data sets, O(𝑛2 log(𝑛))
```
# Kita akan menggunakan data yang sama dengan EDA-03
df = sns.load_dataset("iris")
X = df[['sepal_length','sepal_width','petal_length','petal_width']].values
C = df['species'].values
print(X.shape)
df.head()
# Hierarchical http://scikit-learn.org/stable/modules/generated/sklearn.cluster.AgglomerativeClustering.html#sklearn.cluster.AgglomerativeClustering
hierarchical = cluster.AgglomerativeClustering(n_clusters=3, linkage='average', affinity = 'euclidean')
hierarchical.fit(X) # Lambat .... dan menggunakan banyak memori O(N^2 log(N))
C_h = hierarchical.labels_.astype(np.int)
C_h[:10]
# Dendogram Example
# http://seaborn.pydata.org/generated/seaborn.clustermap.html
g = sns.clustermap(X, method="single", metric="euclidean")
# Scatter Plot of the hierarchical clustering results
X2D = umap.UMAP(n_neighbors=5, min_dist=0.3, random_state=random_state).fit_transform(X)
fig, ax = plt.subplots()
ax.scatter(X2D[:,0], X2D[:,1], c=C_h)
plt.show()
```
# Evaluasi Hierarchical Clustering?
* Silhoutte Coefficient, Dunn index, or Davies–Bouldin index
* Domain knowledge - interpretability
* External Evaluation
### Read more here: https://www.ims.uni-stuttgart.de/document/team/schulte/theses/phd/algorithm.pdf
```
# Spectral : http://scikit-learn.org/stable/modules/generated/sklearn.cluster.SpectralClustering.html
spectral = cluster.SpectralClustering(n_clusters=3)
spectral.fit(X)
C_spec = spectral.labels_.astype(np.int)
sns.countplot(C_spec)
C_spec[:10]
fig, ax = plt.subplots()
ax.scatter(X2D[:,0], X2D[:,1], c=C_spec)
plt.show()
# DBSCAN http://scikit-learn.org/stable/modules/generated/sklearn.cluster.DBSCAN.html
# tidak membutuhkan input parameter k!!!... sangat bermanfaat untuk clustering data yang besar
dbscan = cluster.DBSCAN(eps=0.8, min_samples=5, metric='euclidean')
dbscan.fit(X)
C_db = dbscan.labels_.astype(np.int)
sns.countplot(C_db)
C_db[:10]
# apa makna cluster label -1?
sum([1 for i in C_db if i==-1])
fig, ax = plt.subplots()
ax.scatter(X2D[:,0], X2D[:,1], c=C_db)
plt.show()
try:
# Should work in Google Colab
!wget https://raw.githubusercontent.com/christopherjenness/DBCV/master/DBCV/DBCV.py
except:
pass # Download manually on windows
import dbcv
dbcv.DBCV(X, C_db)
```
## Pelajari Studi Kasus Berikut (Customer Segmentation):
## http://www.data-mania.com/blog/customer-profiling-and-segmentation-in-python/
|
github_jupyter
|
<h1 align="center">TensorFlow Deep Neural Network Lab</h1>
<img src="image/notmnist.png">
In this lab, you'll use all the tools you learned from the *Deep Neural Networks* lesson to label images of English letters! The data you are using, <a href="http://yaroslavvb.blogspot.com/2011/09/notmnist-dataset.html">notMNIST</a>, consists of images of a letter from A to J in differents font.
The above images are a few examples of the data you'll be training on. After training the network, you will compare your prediction model against test data. While there is no predefined goal for this lab, we would like you to experiment and discuss with fellow students on what can improve such models to achieve the highest possible accuracy values.
To start this lab, you first need to import all the necessary modules. Run the code below. If it runs successfully, it will print "`All modules imported`".
```
import hashlib
import os
import pickle
from urllib.request import urlretrieve
import numpy as np
from PIL import Image
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import LabelBinarizer
from sklearn.utils import resample
from tqdm import tqdm
from zipfile import ZipFile
print('All modules imported.')
```
The notMNIST dataset is too large for many computers to handle. It contains 500,000 images for just training. You'll be using a subset of this data, 15,000 images for each label (A-J).
```
def download(url, file):
"""
Download file from <url>
:param url: URL to file
:param file: Local file path
"""
if not os.path.isfile(file):
print('Downloading ' + file + '...')
urlretrieve(url, file)
print('Download Finished')
# Download the training and test dataset.
download('https://s3.amazonaws.com/udacity-sdc/notMNIST_train.zip', 'notMNIST_train.zip')
download('https://s3.amazonaws.com/udacity-sdc/notMNIST_test.zip', 'notMNIST_test.zip')
# Make sure the files aren't corrupted
assert hashlib.md5(open('notMNIST_train.zip', 'rb').read()).hexdigest() == 'c8673b3f28f489e9cdf3a3d74e2ac8fa',\
'notMNIST_train.zip file is corrupted. Remove the file and try again.'
assert hashlib.md5(open('notMNIST_test.zip', 'rb').read()).hexdigest() == '5d3c7e653e63471c88df796156a9dfa9',\
'notMNIST_test.zip file is corrupted. Remove the file and try again.'
# Wait until you see that all files have been downloaded.
print('All files downloaded.')
def uncompress_features_labels(file):
"""
Uncompress features and labels from a zip file
:param file: The zip file to extract the data from
"""
features = []
labels = []
with ZipFile(file) as zipf:
# Progress Bar
filenames_pbar = tqdm(zipf.namelist(), unit='files')
# Get features and labels from all files
for filename in filenames_pbar:
# Check if the file is a directory
if not filename.endswith('/'):
with zipf.open(filename) as image_file:
image = Image.open(image_file)
image.load()
# Load image data as 1 dimensional array
# We're using float32 to save on memory space
feature = np.array(image, dtype=np.float32).flatten()
# Get the the letter from the filename. This is the letter of the image.
label = os.path.split(filename)[1][0]
features.append(feature)
labels.append(label)
return np.array(features), np.array(labels)
# Get the features and labels from the zip files
train_features, train_labels = uncompress_features_labels('notMNIST_train.zip')
test_features, test_labels = uncompress_features_labels('notMNIST_test.zip')
# Limit the amount of data to work with
size_limit = 150000
train_features, train_labels = resample(train_features, train_labels, n_samples=size_limit)
# Set flags for feature engineering. This will prevent you from skipping an important step.
is_features_normal = False
is_labels_encod = False
# Wait until you see that all features and labels have been uncompressed.
print('All features and labels uncompressed.')
```
<img src="image/mean_variance.png" style="height: 75%;width: 75%; position: relative; right: 5%">
## Problem 1
The first problem involves normalizing the features for your training and test data.
Implement Min-Max scaling in the `normalize()` function to a range of `a=0.1` and `b=0.9`. After scaling, the values of the pixels in the input data should range from 0.1 to 0.9.
Since the raw notMNIST image data is in [grayscale](https://en.wikipedia.org/wiki/Grayscale), the current values range from a min of 0 to a max of 255.
Min-Max Scaling:
$
X'=a+{\frac {\left(X-X_{\min }\right)\left(b-a\right)}{X_{\max }-X_{\min }}}
$
```
# Problem 1 - Implement Min-Max scaling for grayscale image data
def normalize_grayscale(image_data):
"""
Normalize the image data with Min-Max scaling to a range of [0.1, 0.9]
:param image_data: The image data to be normalized
:return: Normalized image data
"""
# TODO: Implement Min-Max scaling for grayscale image data
gray_min = 0
gray_max = 255
a = 0.1
b = 0.9
return a + ((image_data - gray_min) * (b - a)) / (gray_max - gray_min)
### DON'T MODIFY ANYTHING BELOW ###
# Test Cases
np.testing.assert_array_almost_equal(
normalize_grayscale(np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 255])),
[0.1, 0.103137254902, 0.106274509804, 0.109411764706, 0.112549019608, 0.11568627451, 0.118823529412, 0.121960784314,
0.125098039216, 0.128235294118, 0.13137254902, 0.9],
decimal=3)
np.testing.assert_array_almost_equal(
normalize_grayscale(np.array([0, 1, 10, 20, 30, 40, 233, 244, 254,255])),
[0.1, 0.103137254902, 0.13137254902, 0.162745098039, 0.194117647059, 0.225490196078, 0.830980392157, 0.865490196078,
0.896862745098, 0.9])
if not is_features_normal:
train_features = normalize_grayscale(train_features)
test_features = normalize_grayscale(test_features)
is_features_normal = True
print('Tests Passed!')
if not is_labels_encod:
# Turn labels into numbers and apply One-Hot Encoding
encoder = LabelBinarizer()
encoder.fit(train_labels)
train_labels = encoder.transform(train_labels)
test_labels = encoder.transform(test_labels)
# Change to float32, so it can be multiplied against the features in TensorFlow, which are float32
train_labels = train_labels.astype(np.float32)
test_labels = test_labels.astype(np.float32)
is_labels_encod = True
print('Labels One-Hot Encoded')
assert is_features_normal, 'You skipped the step to normalize the features'
assert is_labels_encod, 'You skipped the step to One-Hot Encode the labels'
# Get randomized datasets for training and validation
train_features, valid_features, train_labels, valid_labels = train_test_split(
train_features,
train_labels,
test_size=0.05,
random_state=832289)
print('Training features and labels randomized and split.')
# Save the data for easy access
pickle_file = 'notMNIST.pickle'
if not os.path.isfile(pickle_file):
print('Saving data to pickle file...')
try:
with open('notMNIST.pickle', 'wb') as pfile:
pickle.dump(
{
'train_dataset': train_features,
'train_labels': train_labels,
'valid_dataset': valid_features,
'valid_labels': valid_labels,
'test_dataset': test_features,
'test_labels': test_labels,
},
pfile, pickle.HIGHEST_PROTOCOL)
except Exception as e:
print('Unable to save data to', pickle_file, ':', e)
raise
print('Data cached in pickle file.')
```
# Checkpoint
All your progress is now saved to the pickle file. If you need to leave and comeback to this lab, you no longer have to start from the beginning. Just run the code block below and it will load all the data and modules required to proceed.
```
%matplotlib inline
# Load the modules
import pickle
import math
import numpy as np
import tensorflow as tf
from tqdm import tqdm
import matplotlib.pyplot as plt
# Reload the data
pickle_file = 'notMNIST.pickle'
with open(pickle_file, 'rb') as f:
pickle_data = pickle.load(f)
train_features = pickle_data['train_dataset']
train_labels = pickle_data['train_labels']
valid_features = pickle_data['valid_dataset']
valid_labels = pickle_data['valid_labels']
test_features = pickle_data['test_dataset']
test_labels = pickle_data['test_labels']
del pickle_data # Free up memory
print('Data and modules loaded.')
```
<img src="image/weight_biases.png" style="height: 60%;width: 60%; position: relative; right: 10%">
## Problem 2
For the neural network to train on your data, you need the following <a href="https://www.tensorflow.org/resources/dims_types.html#data-types">float32</a> tensors:
- `features`
- Placeholder tensor for feature data (`train_features`/`valid_features`/`test_features`)
- `labels`
- Placeholder tensor for label data (`train_labels`/`valid_labels`/`test_labels`)
- `keep_prob`
- Placeholder tensor for dropout's keep probability value
- `weights`
- List of Variable Tensors with random numbers from a truncated normal distribution for each list index.
- See <a href="https://www.tensorflow.org/api_docs/python/constant_op.html#truncated_normal">`tf.truncated_normal()` documentation</a> for help.
- `biases`
- List of Variable Tensors with all zeros for each list index.
- See <a href="https://www.tensorflow.org/api_docs/python/constant_op.html#zeros"> `tf.zeros()` documentation</a> for help.
```
features_count = 784
labels_count = 10
# TODO: Set the hidden layer width. You can try different widths for different layers and experiment.
hidden_layer_width = 64
# TODO: Set the features, labels, and keep_prob tensors
features = tf.placeholder(tf.float32)
labels = tf.placeholder(tf.float32)
keep_prob = tf.placeholder(tf.float32)
# TODO: Set the list of weights and biases tensors based on number of layers
weights = [ tf.Variable(tf.random_normal([features_count, hidden_layer_width])),
tf.Variable(tf.random_normal([hidden_layer_width, labels_count]))]
biases = [ tf.Variable(tf.random_normal([hidden_layer_width])),
tf.Variable(tf.random_normal([labels_count]))]
### DON'T MODIFY ANYTHING BELOW ###
from tensorflow.python.ops.variables import Variable
assert features._op.name.startswith('Placeholder'), 'features must be a placeholder'
assert labels._op.name.startswith('Placeholder'), 'labels must be a placeholder'
assert all(isinstance(weight, Variable) for weight in weights), 'weights must be a TensorFlow variable'
assert all(isinstance(bias, Variable) for bias in biases), 'biases must be a TensorFlow variable'
assert features._shape == None or (\
features._shape.dims[0].value is None and\
features._shape.dims[1].value in [None, 784]), 'The shape of features is incorrect'
assert labels._shape == None or (\
labels._shape.dims[0].value is None and\
labels._shape.dims[1].value in [None, 10]), 'The shape of labels is incorrect'
assert features._dtype == tf.float32, 'features must be type float32'
assert labels._dtype == tf.float32, 'labels must be type float32'
```
## Problem 3
This problem would help you implement the hidden and output layers of your model. As it was covered in the classroom, you will need the following:
- [tf.add](https://www.tensorflow.org/api_docs/python/tf/add) and [tf.matmul](https://www.tensorflow.org/api_docs/python/tf/matmul) to create your hidden and output(logits) layers.
- [tf.nn.relu](https://www.tensorflow.org/api_docs/python/tf/nn/relu) for your ReLU activation function.
- [tf.nn.dropout](https://www.tensorflow.org/api_docs/python/tf/nn/dropout) for your dropout layer.
```
# TODO: Hidden Layers with ReLU Activation and dropouts. "features" would be the input to the first layer.
hidden_layer_1 = tf.add(tf.matmul(features, weights[0]), biases[0])
hidden_layer_1 = tf.nn.relu(hidden_layer_1)
hidden_layer_1 = tf.nn.dropout(hidden_layer_1, keep_prob)
# hidden_layer_2 = tf.add(tf.matmul(hidden_layer_1, weights[0]), biases[0])
# hidden_layer_2 = tf.nn.relu(hidden_layer_2)
# hidden_layer_2 = tf.nn.dropout(hidden_layer_2, keep_prob)
# TODO: Output layer
logits = tf.add(tf.matmul(hidden_layer_1, weights[1]), biases[1])
### DON'T MODIFY ANYTHING BELOW ###
prediction = tf.nn.softmax(logits)
# Training loss
loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=logits, labels=labels))
# Create an operation that initializes all variables
init = tf.global_variables_initializer()
# Determine if the predictions are correct
is_correct_prediction = tf.equal(tf.argmax(prediction, 1), tf.argmax(labels, 1))
# Calculate the accuracy of the predictions
accuracy = tf.reduce_mean(tf.cast(is_correct_prediction, tf.float32))
print('Accuracy function created.')
```
<img src="image/learn_rate_tune.png" style="height: 60%;width: 60%">
## Problem 4
In the previous lab for a single Neural Network, you attempted several different configurations for the hyperparameters given below. Try to first use the same parameters as the previous lab, and then adjust and finetune those values based on your new model if required.
You have another hyperparameter to tune now, however. Set the value for keep_probability and observe how it affects your results.
```
# TODO: Find the best parameters for each configuration
epochs = 10
batch_size = 64
learning_rate = 0.01
keep_probability = 0.5
### DON'T MODIFY ANYTHING BELOW ###
# Gradient Descent
optimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss)
# The accuracy measured against the validation set
validation_accuracy = 0.0
# Measurements use for graphing loss and accuracy
log_batch_step = 50
batches = []
loss_batch = []
train_acc_batch = []
valid_acc_batch = []
with tf.Session() as session:
session.run(init)
batch_count = int(math.ceil(len(train_features)/batch_size))
for epoch_i in range(epochs):
# Progress bar
batches_pbar = tqdm(range(batch_count), desc='Epoch {:>2}/{}'.format(epoch_i+1, epochs), unit='batches')
# The training cycle
for batch_i in batches_pbar:
# Get a batch of training features and labels
batch_start = batch_i*batch_size
batch_features = train_features[batch_start:batch_start + batch_size]
batch_labels = train_labels[batch_start:batch_start + batch_size]
# Run optimizer and get loss
_, l = session.run(
[optimizer, loss],
feed_dict={features: batch_features, labels: batch_labels, keep_prob: keep_probability})
# Log every 50 batches
if not batch_i % log_batch_step:
# Calculate Training and Validation accuracy
training_accuracy = session.run(accuracy, feed_dict={features: train_features,
labels: train_labels, keep_prob: keep_probability})
validation_accuracy = session.run(accuracy, feed_dict={features: valid_features,
labels: valid_labels, keep_prob: 1.0})
# Log batches
previous_batch = batches[-1] if batches else 0
batches.append(log_batch_step + previous_batch)
loss_batch.append(l)
train_acc_batch.append(training_accuracy)
valid_acc_batch.append(validation_accuracy)
# Check accuracy against Validation data
validation_accuracy = session.run(accuracy, feed_dict={features: valid_features,
labels: valid_labels, keep_prob: 1.0})
loss_plot = plt.subplot(211)
loss_plot.set_title('Loss')
loss_plot.plot(batches, loss_batch, 'g')
loss_plot.set_xlim([batches[0], batches[-1]])
acc_plot = plt.subplot(212)
acc_plot.set_title('Accuracy')
acc_plot.plot(batches, train_acc_batch, 'r', label='Training Accuracy')
acc_plot.plot(batches, valid_acc_batch, 'x', label='Validation Accuracy')
acc_plot.set_ylim([0, 1.0])
acc_plot.set_xlim([batches[0], batches[-1]])
acc_plot.legend(loc=4)
plt.tight_layout()
plt.show()
print('Validation accuracy at {}'.format(validation_accuracy))
```
## Test
Set the epochs, batch_size, and learning_rate with the best learning parameters you discovered in problem 4. You're going to test your model against your hold out dataset/testing data. This will give you a good indicator of how well the model will do in the real world.
```
# TODO: Set the epochs, batch_size, and learning_rate with the best parameters from problem 4
epochs = 10
batch_size = 64
learning_rate = .01
### DON'T MODIFY ANYTHING BELOW ###
# The accuracy measured against the test set
test_accuracy = 0.0
with tf.Session() as session:
session.run(init)
batch_count = int(math.ceil(len(train_features)/batch_size))
for epoch_i in range(epochs):
# Progress bar
batches_pbar = tqdm(range(batch_count), desc='Epoch {:>2}/{}'.format(epoch_i+1, epochs), unit='batches')
# The training cycle
for batch_i in batches_pbar:
# Get a batch of training features and labels
batch_start = batch_i*batch_size
batch_features = train_features[batch_start:batch_start + batch_size]
batch_labels = train_labels[batch_start:batch_start + batch_size]
# Run optimizer
_ = session.run(optimizer, feed_dict={features: batch_features, labels: batch_labels, keep_prob: 1.0})
# Check accuracy against Test data
test_accuracy = session.run(accuracy, feed_dict={features: test_features,
labels: test_labels, keep_prob: 1.0})
print('Nice Job! Test Accuracy is {}'.format(test_accuracy))
```
|
github_jupyter
|
# Day and Night Image Classifier
---
The day/night image dataset consists of 200 RGB color images in two categories: day and night. There are equal numbers of each example: 100 day images and 100 night images.
We'd like to build a classifier that can accurately label these images as day or night, and that relies on finding distinguishing features between the two types of images!
*Note: All images come from the [AMOS dataset](http://cs.uky.edu/~jacobs/datasets/amos/) (Archive of Many Outdoor Scenes).*
### Import resources
Before you get started on the project code, import the libraries and resources that you'll need.
```
import cv2 # computer vision library
import helpers
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
%matplotlib inline
```
## Training and Testing Data
The 200 day/night images are separated into training and testing datasets.
* 60% of these images are training images, for you to use as you create a classifier.
* 40% are test images, which will be used to test the accuracy of your classifier.
First, we set some variables to keep track of some where our images are stored:
image_dir_training: the directory where our training image data is stored
image_dir_test: the directory where our test image data is stored
```
# Image data directories
image_dir_training = "day_night_images/training/"
image_dir_test = "day_night_images/test/"
```
## Load the datasets
These first few lines of code will load the training day/night images and store all of them in a variable, `IMAGE_LIST`. This list contains the images and their associated label ("day" or "night").
For example, the first image-label pair in `IMAGE_LIST` can be accessed by index:
``` IMAGE_LIST[0][:]```.
```
# Using the load_dataset function in helpers.py
# Load training data
IMAGE_LIST = helpers.load_dataset(image_dir_training)
```
## Construct a `STANDARDIZED_LIST` of input images and output labels.
This function takes in a list of image-label pairs and outputs a **standardized** list of resized images and numerical labels.
```
# Standardize all training images
STANDARDIZED_LIST = helpers.standardize(IMAGE_LIST)
```
## Visualize the standardized data
Display a standardized image from STANDARDIZED_LIST.
```
# Display a standardized image and its label
# Select an image by index
image_num = 0
selected_image = STANDARDIZED_LIST[image_num][0]
selected_label = STANDARDIZED_LIST[image_num][1]
# Display image and data about it
plt.imshow(selected_image)
print("Shape: "+str(selected_image.shape))
print("Label [1 = day, 0 = night]: " + str(selected_label))
```
# Feature Extraction
Create a feature that represents the brightness in an image. We'll be extracting the **average brightness** using HSV colorspace. Specifically, we'll use the V channel (a measure of brightness), add up the pixel values in the V channel, then divide that sum by the area of the image to get the average Value of the image.
---
### Find the average brightness using the V channel
This function takes in a **standardized** RGB image and returns a feature (a single value) that represent the average level of brightness in the image. We'll use this value to classify the image as day or night.
```
# Find the average Value or brightness of an image
def avg_brightness(rgb_image):
# Convert image to HSV
hsv = cv2.cvtColor(rgb_image, cv2.COLOR_RGB2HSV)
# Add up all the pixel values in the V channel
sum_brightness = np.sum(hsv[:,:,2])
area = 600*1100.0 # pixels
# find the avg
avg = sum_brightness/area
return avg
# Testing average brightness levels
# Look at a number of different day and night images and think about
# what average brightness value separates the two types of images
# As an example, a "night" image is loaded in and its avg brightness is displayed
image_num = 190
test_im = STANDARDIZED_LIST[image_num][0]
avg = avg_brightness(test_im)
print('Avg brightness: ' + str(avg))
plt.imshow(test_im)
```
# Classification and Visualizing Error
In this section, we'll turn our average brightness feature into a classifier that takes in a standardized image and returns a `predicted_label` for that image. This `estimate_label` function should return a value: 0 or 1 (night or day, respectively).
---
### TODO: Build a complete classifier
Complete this code so that it returns an estimated class label given an input RGB image.
```
# This function should take in RGB image input
def estimate_label(rgb_image):
# TO-DO: Extract average brightness feature from an RGB image
avg = avg_brightness(rgb_image)
# Use the avg brightness feature to predict a label (0, 1)
predicted_label = 0
# TO-DO: Try out different threshold values to see what works best!
threshold = 98.999999
if(avg > threshold):
# if the average brightness is above the threshold value, we classify it as "day"
predicted_label = 1
# else, the predicted_label can stay 0 (it is predicted to be "night")
return predicted_label
```
## Testing the classifier
Here is where we test your classification algorithm using our test set of data that we set aside at the beginning of the notebook!
Since we are using a pretty simple brightess feature, we may not expect this classifier to be 100% accurate. We'll aim for around 75-85% accuracy usin this one feature.
### Test dataset
Below, we load in the test dataset, standardize it using the `standardize` function you defined above, and then **shuffle** it; this ensures that order will not play a role in testing accuracy.
```
import random
# Using the load_dataset function in helpers.py
# Load test data
TEST_IMAGE_LIST = helpers.load_dataset(image_dir_test)
# Standardize the test data
STANDARDIZED_TEST_LIST = helpers.standardize(TEST_IMAGE_LIST)
# Shuffle the standardized test data
random.shuffle(STANDARDIZED_TEST_LIST)
```
## Determine the Accuracy
Compare the output of your classification algorithm (a.k.a. your "model") with the true labels and determine the accuracy.
This code stores all the misclassified images, their predicted labels, and their true labels, in a list called `misclassified`.
```
# Constructs a list of misclassified images given a list of test images and their labels
def get_misclassified_images(test_images):
# Track misclassified images by placing them into a list
misclassified_images_labels = []
# Iterate through all the test images
# Classify each image and compare to the true label
for image in test_images:
# Get true data
im = image[0]
true_label = image[1]
# Get predicted label from your classifier
predicted_label = estimate_label(im)
# Compare true and predicted labels
if(predicted_label != true_label):
# If these labels are not equal, the image has been misclassified
misclassified_images_labels.append((im, predicted_label, true_label))
# Return the list of misclassified [image, predicted_label, true_label] values
return misclassified_images_labels
# Find all misclassified images in a given test set
MISCLASSIFIED = get_misclassified_images(STANDARDIZED_TEST_LIST)
# Accuracy calculations
total = len(STANDARDIZED_TEST_LIST)
num_correct = total - len(MISCLASSIFIED)
accuracy = num_correct/total
print('Accuracy: ' + str(accuracy))
print("Number of misclassified images = " + str(len(MISCLASSIFIED)) +' out of '+ str(total))
```
---
<a id='task9'></a>
### TO-DO: Visualize the misclassified images
Visualize some of the images you classified wrong (in the `MISCLASSIFIED` list) and note any qualities that make them difficult to classify. This will help you identify any weaknesses in your classification algorithm.
```
# Visualize misclassified example(s)
num = 0
test_mis_im = MISCLASSIFIED[num][0]
## TODO: Display an image in the `MISCLASSIFIED` list
## TODO: Print out its predicted label -
## to see what the image *was* incorrectly classified as
```
---
<a id='question2'></a>
## (Question): After visualizing these misclassifications, what weaknesses do you think your classification algorithm has?
**Answer:** Write your answer, here.
# 5. Improve your algorithm!
* (Optional) Tweak your threshold so that accuracy is better.
* (Optional) Add another feature that tackles a weakness you identified!
---
|
github_jupyter
|
# Components of StyleGAN
### Goals
In this notebook, you're going to implement various components of StyleGAN, including the truncation trick, the mapping layer, noise injection, adaptive instance normalization (AdaIN), and progressive growing.
### Learning Objectives
1. Understand the components of StyleGAN that differ from the traditional GAN.
2. Implement the components of StyleGAN.
## Getting Started
You will begin by importing some packages from PyTorch and defining a visualization function which will be useful later.
```
import torch
import torch.nn as nn
import torch.nn.functional as F
def show_tensor_images(image_tensor, num_images=16, size=(3, 64, 64), nrow=3):
'''
Function for visualizing images: Given a tensor of images, number of images,
size per image, and images per row, plots and prints the images in an uniform grid.
'''
image_tensor = (image_tensor + 1) / 2
image_unflat = image_tensor.detach().cpu().clamp_(0, 1)
image_grid = make_grid(image_unflat[:num_images], nrow=nrow, padding=0)
plt.imshow(image_grid.permute(1, 2, 0).squeeze())
plt.axis('off')
plt.show()
```
## Truncation Trick
The first component you will implement is the truncation trick. Remember that this is done after the model is trained and when you are sampling beautiful outputs. The truncation trick resamples the noise vector $z$ from a truncated normal distribution which allows you to tune the generator's fidelity/diversity. The truncation value is at least 0, where 1 means there is little truncation (high diversity) and 0 means the distribution is all truncated except for the mean (high quality/fidelity). This trick is not exclusive to StyleGAN. In fact, you may recall playing with it in an earlier GAN notebook.
```
# UNQ_C1 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
# GRADED CELL: get_truncated_noise
from scipy.stats import truncnorm
def get_truncated_noise(n_samples, z_dim, truncation):
'''
Function for creating truncated noise vectors: Given the dimensions (n_samples, z_dim)
and truncation value, creates a tensor of that shape filled with random
numbers from the truncated normal distribution.
Parameters:
n_samples: the number of samples to generate, a scalar
z_dim: the dimension of the noise vector, a scalar
truncation: the truncation value, a non-negative scalar
'''
#### START CODE HERE ####
truncated_noise = truncnorm.rvs(-truncation, truncation, size=(n_samples, z_dim))
#### END CODE HERE ####
return torch.Tensor(truncated_noise)
# Test the truncation sample
assert tuple(get_truncated_noise(n_samples=10, z_dim=5, truncation=0.7).shape) == (10, 5)
simple_noise = get_truncated_noise(n_samples=1000, z_dim=10, truncation=0.2)
assert simple_noise.max() > 0.199 and simple_noise.max() < 2
assert simple_noise.min() < -0.199 and simple_noise.min() > -0.2
assert simple_noise.std() > 0.113 and simple_noise.std() < 0.117
print("Success!")
```
## Mapping $z$ → $w$
The next component you need to implement is the mapping network. It takes the noise vector, $z$, and maps it to an intermediate noise vector, $w$. This makes it so $z$ can be represented in a more disentangled space which makes the features easier to control later.
The mapping network in StyleGAN is composed of 8 layers, but for your implementation, you will use a neural network with 3 layers. This is to save time training later.
<details>
<summary>
<font size="3" color="green">
<b>Optional hints for <code><font size="4">MappingLayers</font></code></b>
</font>
</summary>
1. This code should be five lines.
2. You need 3 linear layers and should use ReLU activations.
3. Your linear layers should be input -> hidden_dim -> hidden_dim -> output.
</details>
```
# UNQ_C2 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
# GRADED CELL: MappingLayers
class MappingLayers(nn.Module):
'''
Mapping Layers Class
Values:
z_dim: the dimension of the noise vector, a scalar
hidden_dim: the inner dimension, a scalar
w_dim: the dimension of the intermediate noise vector, a scalar
'''
def __init__(self, z_dim, hidden_dim, w_dim):
super().__init__()
self.mapping = nn.Sequential(
# Please write a neural network which takes in tensors of
# shape (n_samples, z_dim) and outputs (n_samples, w_dim)
# with a hidden layer with hidden_dim neurons
#### START CODE HERE ####
nn.Linear(z_dim, hidden_dim),
nn.ReLU(),
nn.Linear(hidden_dim, hidden_dim),
nn.ReLU(),
nn.Linear(hidden_dim, w_dim)
#### END CODE HERE ####
)
def forward(self, noise):
'''
Function for completing a forward pass of MappingLayers:
Given an initial noise tensor, returns the intermediate noise tensor.
Parameters:
noise: a noise tensor with dimensions (n_samples, z_dim)
'''
return self.mapping(noise)
#UNIT TEST COMMENT: Required for grading
def get_mapping(self):
return self.mapping
# Test the mapping function
map_fn = MappingLayers(10,20,30)
assert tuple(map_fn(torch.randn(2, 10)).shape) == (2, 30)
assert len(map_fn.mapping) > 4
outputs = map_fn(torch.randn(1000, 10))
assert outputs.std() > 0.05 and outputs.std() < 0.3
assert outputs.min() > -2 and outputs.min() < 0
assert outputs.max() < 2 and outputs.max() > 0
layers = [str(x).replace(' ', '').replace('inplace=True', '') for x in map_fn.get_mapping()]
assert layers == ['Linear(in_features=10,out_features=20,bias=True)',
'ReLU()',
'Linear(in_features=20,out_features=20,bias=True)',
'ReLU()',
'Linear(in_features=20,out_features=30,bias=True)']
print("Success!")
```
## Random Noise Injection
Next, you will implement the random noise injection that occurs before every AdaIN block. To do this, you need to create a noise tensor that is the same size as the current feature map (image).
The noise tensor is not entirely random; it is initialized as one random channel that is then multiplied by learned weights for each channel in the image. For example, imagine an image has 512 channels and its height and width are (4 x 4). You would first create a random (4 x 4) noise matrix with one channel. Then, your model would create 512 values—one for each channel. Next, you multiply the (4 x 4) matrix by each one of these values. This creates a "random" tensor of 512 channels and (4 x 4) pixels, the same dimensions as the image. Finally, you add this noise tensor to the image. This introduces uncorrelated noise and is meant to increase the diversity in the image.
New starting weights are generated for every new layer, or generator, where this class is used. Within a layer, every following time the noise injection is called, you take another step with the optimizer and the weights that you use for each channel are optimized (i.e. learned).
<details>
<summary>
<font size="3" color="green">
<b>Optional hint for <code><font size="4">InjectNoise</font></code></b>
</font>
</summary>
1. The weight should have the shape (1, channels, 1, 1).
</details>
<!-- <details>
<summary>
<font size="3" color="green">
<b>Optional hint for <code><font size="4">InjectNoise</font></code></b>
</font>
</summary>
1. Remember that you only make the noise for one channel (it is then multiplied by random values to create ones for the other channels).
</details> -->
<!-- (not sure how??) You'll find the get_noise function from before helpful here -->
```
# UNQ_C3 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
# GRADED CELL: InjectNoise
class InjectNoise(nn.Module):
'''
Inject Noise Class
Values:
channels: the number of channels the image has, a scalar
'''
def __init__(self, channels):
super().__init__()
self.weight = nn.Parameter( # You use nn.Parameter so that these weights can be optimized
# Initiate the weights for the channels from a random normal distribution
#### START CODE HERE ####
torch.randn(1, channels, 1, 1)
#### END CODE HERE ####
)
def forward(self, image):
'''
Function for completing a forward pass of InjectNoise: Given an image,
returns the image with random noise added.
Parameters:
image: the feature map of shape (n_samples, channels, width, height)
'''
# Set the appropriate shape for the noise!
#### START CODE HERE ####
noise_shape = (image.shape[0], 1, image.shape[2], image.shape[3])
#### END CODE HERE ####
noise = torch.randn(noise_shape, device=image.device) # Creates the random noise
return image + self.weight * noise # Applies to image after multiplying by the weight for each channel
#UNIT TEST COMMENT: Required for grading
def get_weight(self):
return self.weight
#UNIT TEST COMMENT: Required for grading
def get_self(self):
return self
# UNIT TEST
test_noise_channels = 3000
test_noise_samples = 20
fake_images = torch.randn(test_noise_samples, test_noise_channels, 10, 10)
inject_noise = InjectNoise(test_noise_channels)
assert torch.abs(inject_noise.weight.std() - 1) < 0.1
assert torch.abs(inject_noise.weight.mean()) < 0.1
assert type(inject_noise.get_weight()) == torch.nn.parameter.Parameter
assert tuple(inject_noise.weight.shape) == (1, test_noise_channels, 1, 1)
inject_noise.weight = nn.Parameter(torch.ones_like(inject_noise.weight))
# Check that something changed
assert torch.abs((inject_noise(fake_images) - fake_images)).mean() > 0.1
# Check that the change is per-channel
assert torch.abs((inject_noise(fake_images) - fake_images).std(0)).mean() > 1e-4
assert torch.abs((inject_noise(fake_images) - fake_images).std(1)).mean() < 1e-4
assert torch.abs((inject_noise(fake_images) - fake_images).std(2)).mean() > 1e-4
assert torch.abs((inject_noise(fake_images) - fake_images).std(3)).mean() > 1e-4
# Check that the per-channel change is roughly normal
per_channel_change = (inject_noise(fake_images) - fake_images).mean(1).std()
assert per_channel_change > 0.9 and per_channel_change < 1.1
# Make sure that the weights are being used at all
inject_noise.weight = nn.Parameter(torch.zeros_like(inject_noise.weight))
assert torch.abs((inject_noise(fake_images) - fake_images)).mean() < 1e-4
assert len(inject_noise.weight.shape) == 4
print("Success!")
```
## Adaptive Instance Normalization (AdaIN)
The next component you will implement is AdaIN. To increase control over the image, you inject $w$ — the intermediate noise vector — multiple times throughout StyleGAN. This is done by transforming it into a set of style parameters and introducing the style to the image through AdaIN. Given an image ($x_i$) and the intermediate vector ($w$), AdaIN takes the instance normalization of the image and multiplies it by the style scale ($y_s$) and adds the style bias ($y_b$). You need to calculate the learnable style scale and bias by using linear mappings from $w$.
# $ \text{AdaIN}(\boldsymbol{\mathrm{x}}_i, \boldsymbol{\mathrm{y}}) = \boldsymbol{\mathrm{y}}_{s,i} \frac{\boldsymbol{\mathrm{x}}_i - \mu(\boldsymbol{\mathrm{x}}_i)}{\sigma(\boldsymbol{\mathrm{x}}_i)} + \boldsymbol{\mathrm{y}}_{b,i} $
<details>
<summary>
<font size="3" color="green">
<b>Optional hints for <code><font size="4">forward</font></code></b>
</font>
</summary>
1. Remember the equation for AdaIN.
2. The instance normalized image, style scale, and style shift have already been calculated for you.
</details>
```
# UNQ_C4 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
# GRADED CELL: AdaIN
class AdaIN(nn.Module):
'''
AdaIN Class
Values:
channels: the number of channels the image has, a scalar
w_dim: the dimension of the intermediate noise vector, a scalar
'''
def __init__(self, channels, w_dim):
super().__init__()
# Normalize the input per-dimension
self.instance_norm = nn.InstanceNorm2d(channels)
# You want to map w to a set of style weights per channel.
# Replace the Nones with the correct dimensions - keep in mind that
# both linear maps transform a w vector into style weights
# corresponding to the number of image channels.
#### START CODE HERE ####
self.style_scale_transform = nn.Linear(w_dim, channels)
self.style_shift_transform = nn.Linear(w_dim, channels)
#### END CODE HERE ####
def forward(self, image, w):
'''
Function for completing a forward pass of AdaIN: Given an image and intermediate noise vector w,
returns the normalized image that has been scaled and shifted by the style.
Parameters:
image: the feature map of shape (n_samples, channels, width, height)
w: the intermediate noise vector
'''
normalized_image = self.instance_norm(image)
style_scale = self.style_scale_transform(w)[:, :, None, None]
style_shift = self.style_shift_transform(w)[:, :, None, None]
# Calculate the transformed image
#### START CODE HERE ####
transformed_image = style_scale * normalized_image + style_shift
#### END CODE HERE ####
return transformed_image
#UNIT TEST COMMENT: Required for grading
def get_style_scale_transform(self):
return self.style_scale_transform
#UNIT TEST COMMENT: Required for grading
def get_style_shift_transform(self):
return self.style_shift_transform
#UNIT TEST COMMENT: Required for grading
def get_self(self):
return self
w_channels = 50
image_channels = 20
image_size = 30
n_test = 10
adain = AdaIN(image_channels, w_channels)
test_w = torch.randn(n_test, w_channels)
assert adain.style_scale_transform(test_w).shape == adain.style_shift_transform(test_w).shape
assert adain.style_scale_transform(test_w).shape[-1] == image_channels
assert tuple(adain(torch.randn(n_test, image_channels, image_size, image_size), test_w).shape) == (n_test, image_channels, image_size, image_size)
w_channels = 3
image_channels = 2
image_size = 3
n_test = 1
adain = AdaIN(image_channels, w_channels)
adain.style_scale_transform.weight.data = torch.ones_like(adain.style_scale_transform.weight.data) / 4
adain.style_scale_transform.bias.data = torch.zeros_like(adain.style_scale_transform.bias.data)
adain.style_shift_transform.weight.data = torch.ones_like(adain.style_shift_transform.weight.data) / 5
adain.style_shift_transform.bias.data = torch.zeros_like(adain.style_shift_transform.bias.data)
test_input = torch.ones(n_test, image_channels, image_size, image_size)
test_input[:, :, 0] = 0
test_w = torch.ones(n_test, w_channels)
test_output = adain(test_input, test_w)
assert(torch.abs(test_output[0, 0, 0, 0] - 3 / 5 + torch.sqrt(torch.tensor(9 / 8))) < 1e-4)
assert(torch.abs(test_output[0, 0, 1, 0] - 3 / 5 - torch.sqrt(torch.tensor(9 / 32))) < 1e-4)
print("Success!")
```
## Progressive Growing in StyleGAN
The final StyleGAN component that you will create is progressive growing. This helps StyleGAN to create high resolution images by gradually doubling the image's size until the desired size.
You will start by creating a block for the StyleGAN generator. This is comprised of an upsampling layer, a convolutional layer, random noise injection, an AdaIN layer, and an activation.
```
# UNQ_C5 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
# GRADED CELL: MicroStyleGANGeneratorBlock
class MicroStyleGANGeneratorBlock(nn.Module):
'''
Micro StyleGAN Generator Block Class
Values:
in_chan: the number of channels in the input, a scalar
out_chan: the number of channels wanted in the output, a scalar
w_dim: the dimension of the intermediate noise vector, a scalar
kernel_size: the size of the convolving kernel
starting_size: the size of the starting image
'''
def __init__(self, in_chan, out_chan, w_dim, kernel_size, starting_size, use_upsample=True):
super().__init__()
self.use_upsample = use_upsample
# Replace the Nones in order to:
# 1. Upsample to the starting_size, bilinearly (https://pytorch.org/docs/master/generated/torch.nn.Upsample.html)
# 2. Create a kernel_size convolution which takes in
# an image with in_chan and outputs one with out_chan (https://pytorch.org/docs/stable/generated/torch.nn.Conv2d.html)
# 3. Create an object to inject noise
# 4. Create an AdaIN object
# 5. Create a LeakyReLU activation with slope 0.2
#### START CODE HERE ####
if self.use_upsample:
self.upsample = nn.Upsample((starting_size), mode='bilinear')
self.conv = nn.Conv2d(in_chan, out_chan, kernel_size, padding=1) # Padding is used to maintain the image size
self.inject_noise = InjectNoise(out_chan)
self.adain = AdaIN(out_chan, w_dim)
self.activation = nn.LeakyReLU(0.2)
#### END CODE HERE ####
def forward(self, x, w):
'''
Function for completing a forward pass of MicroStyleGANGeneratorBlock: Given an x and w,
computes a StyleGAN generator block.
Parameters:
x: the input into the generator, feature map of shape (n_samples, channels, width, height)
w: the intermediate noise vector
'''
if self.use_upsample:
x = self.upsample(x)
x = self.conv(x)
x = self.inject_noise(x)
x = self.activation(x)
x = self.adain(x, w)
return x
#UNIT TEST COMMENT: Required for grading
def get_self(self):
return self;
test_stylegan_block = MicroStyleGANGeneratorBlock(in_chan=128, out_chan=64, w_dim=256, kernel_size=3, starting_size=8)
test_x = torch.ones(1, 128, 4, 4)
test_x[:, :, 1:3, 1:3] = 0
test_w = torch.ones(1, 256)
test_x = test_stylegan_block.upsample(test_x)
assert tuple(test_x.shape) == (1, 128, 8, 8)
assert torch.abs(test_x.mean() - 0.75) < 1e-4
test_x = test_stylegan_block.conv(test_x)
assert tuple(test_x.shape) == (1, 64, 8, 8)
test_x = test_stylegan_block.inject_noise(test_x)
test_x = test_stylegan_block.activation(test_x)
assert test_x.min() < 0
assert -test_x.min() / test_x.max() < 0.4
test_x = test_stylegan_block.adain(test_x, test_w)
foo = test_stylegan_block(torch.ones(10, 128, 4, 4), torch.ones(10, 256))
print("Success!")
```
Now, you can implement progressive growing.
StyleGAN starts with a constant 4 x 4 (x 512 channel) tensor which is put through an iteration of the generator without upsampling. The output is some noise that can then be transformed into a blurry 4 x 4 image. This is where the progressive growing process begins. The 4 x 4 noise can be further passed through a generator block with upsampling to produce an 8 x 8 output. However, this will be done gradually.
You will simulate progressive growing from an 8 x 8 image to a 16 x 16 image. Instead of simply passing it to the generator block with upsampling, StyleGAN gradually trains the generator to the new size by mixing in an image that was only upsampled. By mixing an upsampled 8 x 8 image (which is 16 x 16) with increasingly more of the 16 x 16 generator output, the generator is more stable as it progressively trains. As such, you will do two separate operations with the 8 x 8 noise:
1. Pass it into the next generator block to create an output noise, that you will then transform to an image.
2. Transform it into an image and then upsample it to be 16 x 16.
You will now have two images that are both double the resolution of the 8 x 8 noise. Then, using an alpha ($\alpha$) term, you combine the higher resolution images obtained from (1) and (2). You would then pass this into the discriminator and use the feedback to update the weights of your generator. The key here is that the $\alpha$ term is gradually increased until eventually, only the image from (1), the generator, is used. That is your final image or you could continue this process to make a 32 x 32 image or 64 x 64, 128 x 128, etc.
This micro model you will implement will visualize what the model outputs at a particular stage of training, for a specific value of $\alpha$. However to reiterate, in practice, StyleGAN will slowly phase out the upsampled image by increasing the $\alpha$ parameter over many training steps, doing this process repeatedly with larger and larger alpha values until it is 1—at this point, the combined image is solely comprised of the image from the generator block. This method of gradually training the generator increases the stability and fidelity of the model.
<!-- by passing a random noise vector in $z$ through the mapping function you wrote to get $w$. $w$ is then passed through the first block of the generator to create your first output noise. -->
<details>
<summary>
<font size="3" color="green">
<b>Optional hint for <code><font size="4">forward</font></code></b>
</font>
</summary>
1. You may find [torch.lerp](https://pytorch.org/docs/stable/generated/torch.lerp.html) helpful.
</details>
```
# UNQ_C6 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
# GRADED CELL: MicroStyleGANGenerator
class MicroStyleGANGenerator(nn.Module):
'''
Micro StyleGAN Generator Class
Values:
z_dim: the dimension of the noise vector, a scalar
map_hidden_dim: the mapping inner dimension, a scalar
w_dim: the dimension of the intermediate noise vector, a scalar
in_chan: the dimension of the constant input, usually w_dim, a scalar
out_chan: the number of channels wanted in the output, a scalar
kernel_size: the size of the convolving kernel
hidden_chan: the inner dimension, a scalar
'''
def __init__(self,
z_dim,
map_hidden_dim,
w_dim,
in_chan,
out_chan,
kernel_size,
hidden_chan):
super().__init__()
self.map = MappingLayers(z_dim, map_hidden_dim, w_dim)
# Typically this constant is initiated to all ones, but you will initiate to a
# Gaussian to better visualize the network's effect
self.starting_constant = nn.Parameter(torch.randn(1, in_chan, 4, 4))
self.block0 = MicroStyleGANGeneratorBlock(in_chan, hidden_chan, w_dim, kernel_size, 4, use_upsample=False)
self.block1 = MicroStyleGANGeneratorBlock(hidden_chan, hidden_chan, w_dim, kernel_size, 8)
self.block2 = MicroStyleGANGeneratorBlock(hidden_chan, hidden_chan, w_dim, kernel_size, 16)
# You need to have a way of mapping from the output noise to an image,
# so you learn a 1x1 convolution to transform the e.g. 512 channels into 3 channels
# (Note that this is simplified, with clipping used in the real StyleGAN)
self.block1_to_image = nn.Conv2d(hidden_chan, out_chan, kernel_size=1)
self.block2_to_image = nn.Conv2d(hidden_chan, out_chan, kernel_size=1)
self.alpha = 0.2
def upsample_to_match_size(self, smaller_image, bigger_image):
'''
Function for upsampling an image to the size of another: Given a two images (smaller and bigger),
upsamples the first to have the same dimensions as the second.
Parameters:
smaller_image: the smaller image to upsample
bigger_image: the bigger image whose dimensions will be upsampled to
'''
return F.interpolate(smaller_image, size=bigger_image.shape[-2:], mode='bilinear')
def forward(self, noise, return_intermediate=False):
'''
Function for completing a forward pass of MicroStyleGANGenerator: Given noise,
computes a StyleGAN iteration.
Parameters:
noise: a noise tensor with dimensions (n_samples, z_dim)
return_intermediate: a boolean, true to return the images as well (for testing) and false otherwise
'''
x = self.starting_constant
w = self.map(noise)
x = self.block0(x, w)
x_small = self.block1(x, w) # First generator run output
x_small_image = self.block1_to_image(x_small)
x_big = self.block2(x_small, w) # Second generator run output
x_big_image = self.block2_to_image(x_big)
x_small_upsample = self.upsample_to_match_size(x_small_image, x_big_image) # Upsample first generator run output to be same size as second generator run output
# Interpolate between the upsampled image and the image from the generator using alpha
#### START CODE HERE ####
interpolation = ((1 - self.alpha) * x_small_upsample) + (self.alpha * x_big_image)
#### END CODE HERE ####
if return_intermediate:
return interpolation, x_small_upsample, x_big_image
return interpolation
#UNIT TEST COMMENT: Required for grading
def get_self(self):
return self;
z_dim = 128
out_chan = 3
truncation = 0.7
mu_stylegan = MicroStyleGANGenerator(
z_dim=z_dim,
map_hidden_dim=1024,
w_dim=496,
in_chan=512,
out_chan=out_chan,
kernel_size=3,
hidden_chan=256
)
test_samples = 10
test_result = mu_stylegan(get_truncated_noise(test_samples, z_dim, truncation))
# Check if the block works
assert tuple(test_result.shape) == (test_samples, out_chan, 16, 16)
# Check that the interpolation is correct
mu_stylegan.alpha = 1.
test_result, _, test_big = mu_stylegan(
get_truncated_noise(test_samples, z_dim, truncation),
return_intermediate=True)
assert torch.abs(test_result - test_big).mean() < 0.001
mu_stylegan.alpha = 0.
test_result, test_small, _ = mu_stylegan(
get_truncated_noise(test_samples, z_dim, truncation),
return_intermediate=True)
assert torch.abs(test_result - test_small).mean() < 0.001
print("Success!")
```
## Running StyleGAN
Finally, you can put all the components together to run an iteration of your micro StyleGAN!
You can also visualize what this randomly initiated generator can produce. The code will automatically interpolate between different values of alpha so that you can intuitively see what it means to mix the low-resolution and high-resolution images using different values of alpha. In the generated image, the samples start from low alpha values and go to high alpha values.
```
import numpy as np
from torchvision.utils import make_grid
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = [15, 15]
viz_samples = 10
# The noise is exaggerated for visual effect
viz_noise = get_truncated_noise(viz_samples, z_dim, truncation) * 10
mu_stylegan.eval()
images = []
for alpha in np.linspace(0, 1, num=5):
mu_stylegan.alpha = alpha
viz_result, _, _ = mu_stylegan(
viz_noise,
return_intermediate=True)
images += [tensor for tensor in viz_result]
show_tensor_images(torch.stack(images), nrow=viz_samples, num_images=len(images))
mu_stylegan = mu_stylegan.train()
```
|
github_jupyter
|
```
from mxnet import nd
def pure_batch_norm(X, gamma, beta, eps=1e-5):
assert len(X.shape) in (2, 4)
# 全连接: batch_size x feature
if len(X.shape) == 2:
# 每个输入维度在样本上的平均和方差
mean = X.mean(axis=0)
variance = ((X - mean)**2).mean(axis=0)
# 2D卷积: batch_size x channel x height x width
else:
# 对每个通道算均值和方差,需要保持4D形状使得可以正确地广播
mean = X.mean(axis=(0,2,3), keepdims=True)
variance = ((X - mean)**2).mean(axis=(0,2,3), keepdims=True)
# 均一化
X_hat = (X - mean) / nd.sqrt(variance + eps)
# 拉升和偏移
print(X_hat.shape)
print(mean.shape)
return gamma.reshape(mean.shape) * X_hat + beta.reshape(mean.shape)
A = nd.arange(6).reshape((3,2))
pure_batch_norm(A, gamma=nd.array([1, 1]), beta=nd.array([0, 0]))
B = nd.arange(18).reshape((1,2,3,3))
pure_batch_norm(B, gamma=nd.array([1,1]), beta=nd.array([0,0]))
# 在训练时,计算整个 batch 上的均值和方差
# 在测试时,计算整个数据集的均值方差,当训练数据量极大时,使用 moving average 近似计算
def batch_norm(X, gamma, beta, is_training, moving_mean, moving_variance,
eps = 1e-5, moving_momentum = 0.9):
assert len(X.shape) in (2, 4)
# 全连接: batch_size x feature
if len(X.shape) == 2:
# 每个输入维度在样本上的平均和方差
mean = X.mean(axis=0)
variance = ((X - mean)**2).mean(axis=0)
# 2D卷积: batch_size x channel x height x width
else:
# 对每个通道算均值和方差,需要保持4D形状使得可以正确的广播
mean = X.mean(axis=(0,2,3), keepdims=True)
variance = ((X - mean)**2).mean(axis=(0,2,3), keepdims=True)
# 变形使得可以正确的广播
moving_mean = moving_mean.reshape(mean.shape)
moving_variance = moving_variance.reshape(mean.shape)
# 均一化
if is_training:
X_hat = (X - mean) / nd.sqrt(variance + eps)
#!!! 更新全局的均值和方差
moving_mean[:] = moving_momentum * moving_mean + (
1.0 - moving_momentum) * mean
moving_variance[:] = moving_momentum * moving_variance + (
1.0 - moving_momentum) * variance
else:
#!!! 测试阶段使用全局的均值和方差
X_hat = (X - moving_mean) / nd.sqrt(moving_variance + eps)
# 拉升和偏移
return gamma.reshape(mean.shape) * X_hat + beta.reshape(mean.shape)
```
# 定义模型
```
import sys
sys.path.append('..')
import utils
ctx = utils.try_gpu()
ctx
weight_scale = 0.01
# 输出通道 = 20, 卷积核 = (5,5)
c1 = 20
W1 = nd.random.normal(shape=(c1,1,5,5), scale=weight_scale, ctx=ctx)
b1 = nd.zeros(c1, ctx=ctx)
# 第1层批量归一化
gamma1 = nd.random.normal(shape=c1, scale=weight_scale, ctx=ctx)
beta1 = nd.random.normal(shape=c1, scale=weight_scale, ctx=ctx)
moving_mean1 = nd.zeros(c1, ctx=ctx)
moving_variance1 = nd.zeros(c1, ctx=ctx)
# 输出通道 = 50, 卷积核 = (3,3)
c2 = 50
W2 = nd.random_normal(shape=(c2,c1,3,3), scale=weight_scale, ctx=ctx)
b2 = nd.zeros(c2, ctx=ctx)
# 第2层批量归一化
gamma2 = nd.random.normal(shape=c2, scale=weight_scale, ctx=ctx)
beta2 = nd.random.normal(shape=c2, scale=weight_scale, ctx=ctx)
moving_mean2 = nd.zeros(c2, ctx=ctx)
moving_variance2 = nd.zeros(c2, ctx=ctx)
# 输出维度 = 128
o3 = 128
W3 = nd.random.normal(shape=(1250, o3), scale=weight_scale, ctx=ctx)
b3 = nd.zeros(o3, ctx=ctx)
# 输出维度 = 10
W4 = nd.random_normal(shape=(W3.shape[1], 10), scale=weight_scale, ctx=ctx)
b4 = nd.zeros(W4.shape[1], ctx=ctx)
# 注意这里moving_*是不需要更新的
params = [W1, b1, gamma1, beta1,
W2, b2, gamma2, beta2,
W3, b3, W4, b4]
for param in params:
param.attach_grad()
# BatchNorm 添加的位置: 卷积层之后,激活函数之前
def net(X, is_training=False, verbose=False):
X = X.as_in_context(W1.context)
# 第一层卷积
h1_conv = nd.Convolution(
data=X, weight=W1, bias=b1, kernel=W1.shape[2:], num_filter=c1)
### 添加了批量归一化层
h1_bn = batch_norm(h1_conv, gamma1, beta1, is_training,
moving_mean1, moving_variance1)
h1_activation = nd.relu(h1_bn)
h1 = nd.Pooling(
data=h1_activation, pool_type="max", kernel=(2,2), stride=(2,2))
# 第二层卷积
h2_conv = nd.Convolution(
data=h1, weight=W2, bias=b2, kernel=W2.shape[2:], num_filter=c2)
### 添加了批量归一化层
h2_bn = batch_norm(h2_conv, gamma2, beta2, is_training,
moving_mean2, moving_variance2)
h2_activation = nd.relu(h2_bn)
h2 = nd.Pooling(data=h2_activation, pool_type="max", kernel=(2,2), stride=(2,2))
h2 = nd.flatten(h2)
# 第一层全连接
h3_linear = nd.dot(h2, W3) + b3
h3 = nd.relu(h3_linear)
# 第二层全连接
h4_linear = nd.dot(h3, W4) + b4
if verbose:
print('1st conv block:', h1.shape)
print('2nd conv block:', h2.shape)
print('1st dense:', h3.shape)
print('2nd dense:', h4_linear.shape)
print('output:', h4_linear)
return h4_linear
from mxnet import autograd
from mxnet import gluon
batch_size = 256
train_data, test_data = utils.load_data_fashion_mnist(batch_size)
softmax_cross_entropy = gluon.loss.SoftmaxCrossEntropyLoss()
learning_rate = 0.2
for epoch in range(5):
train_loss = 0.
train_acc = 0.
for data, label in train_data:
label = label.as_in_context(ctx)
with autograd.record():
output = net(data, is_training=True)
loss = softmax_cross_entropy(output, label)
loss.backward()
utils.SGD(params, learning_rate/batch_size)
train_loss += nd.mean(loss).asscalar()
train_acc += utils.accuracy(output, label)
test_acc = utils.evaluate_accuracy(test_data, net, ctx)
print("Epoch %d. Loss: %f, Train acc %f, Test acc %f" % (
epoch, train_loss/len(train_data), train_acc/len(train_data), test_acc))
```
|
github_jupyter
|
<a href="https://colab.research.google.com/github/wguesdon/BrainPost_google_analytics/blob/master/Report_v01_02.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Project Presentation
## About BrainPost
Kasey Hemington runs BrainPost with a fellow PhD friend, Leigh Christopher as a way to keep in touch with her scientific roots while working as a data scientist! Every Tuesday since we started in early 2018, we publish our e-newsletter which is three short summaries of new neuroscience studies that have just come out. After publishing on our website each Tuesday, we typically post on Twitter (@brainpostco) and Facebook (@brainpostco) once to announce the release of the e-newsletter and three times (once for each of the three summaries) to highlight each summary. There are a few exceptions to our publishing schedule. Sometimes we post extra articles here: https://www.brainpost.co/brainpost-life-hacks, and also a few weeks we've only been able to publish two summaries instead of three. At around the same time as we publish the e-newsletter on the website each Tuesday, we also send it to our ~1700 email subscribers directly (via mailchimp).
## About the Challenge
We're always wondering if we should change what type of content we're publishing, and how people are finding us. From some small surveys we've done for example, we find people would be interested in more casual/applicable to daily life content (like we publish on this tab https://www.brainpost.co/brainpost-life-hacks) than more technical summaries of complex articles, but we also aren't really sure if that's just a subgroup of people who get the e-newsletter to their email inbox filling out the survey. We also might have two audiences - academics and non-academics (?) who like different things.
## About the data
In the remaining tabs of this workbook there is weekly pageview data for each page on the website (I think..according to our google analytics). Each tab represents pageview data for two one week periods, split up by the page name/URL and the source/medium (first two columns). My general idea was people can look at the data at a weekly cadence and figure out stats about different pages/content, BUT with google analytics a huge problem is that it doesn't really take into account that different content is published on different days (for example, a stat about 'only 2 pageviews' to a page is meaningless to me if it is because the page was only published an hour ago). Our content is published weekly so it should approximately match that I extracted the data weekly. My apologies for the formatting... Google analytics was a nightmare to extract from - a very manual process. But, I guess data cleaning is a part of the process! So, we've been publishing ~3 new pages a week since 2018, but I've only included data starting in July 2020 because the data extraction process is so manual. The date of publication can be extracted from the URL.
We've noticed some pages seem really popular possibly for strange reasons (maybe they come up on the first page of google because people are searching for something really similar?) and those anomalies might not reflect what people like overall about the site.
There is also a tab with a page (URL) to page title lookup
## The questions we'd like to ask
What content (or types of content) is most popular (what are patterns we see in popular content) and is different content popular amongst different subgroups (e.g. by source/medium)?
Any question that will help us to take action to better tailor our content to our audience(s) or understand how traffic comes to the site.
Where are people visiting from (source-wise)?
## How this challenge works:
Just like the last challenge, you can submit an entry by posting a github link to your analysis on the signup page (second tab). Use any combination of reports/visuals/code/presentation you think is best - just make sure your code is accessible!
Let's have a few days for people to review the data and ask any questions and then we can discuss what everyone thinks is a reasonable deadline/timeline and set the timeline from there. If you have any further data requests you think would help answer the questions I might be able to get it (google analytics or mailchimp).
After the deadline I'll choose the first and second place submission. The criteria will be whatever submission provides the most compelling evidence that gives me a clear idea of what actions we could take next to improve the site.
# Initialize
```
# Load libraries
# https://stackoverflow.com/questions/58667299/google-colab-why-matplotlib-has-a-behaviour-different-then-default-after-import
# Panda profilling alter seaborn plotting style
from google.colab import drive # to load data from google drive
import numpy as np # linear algebra
import pandas as pd # data processing, CSV file I/O (e.g. pd.read_csv)
import matplotlib.pyplot as plt # ploting the data
import seaborn as sns # ploting the data
%matplotlib inline
import math # calculation
drive.mount("/content/drive")
```
# Data Cleaning
```
# Load the Pages Titles
pages_tiltes = pd.read_excel(r'/content/drive/MyDrive/DSS/BrainPost_blog/Data/DSS BrainPost Web Analytics Challenge!.xlsx', sheet_name='Page to Page Title lookup', skiprows=6)
# Load the content-pages oct 4-17
# Skip the first 6 rows with headers
# Skip the last 18 rows with total view
# See https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.read_excel.html
# See https://stackoverflow.com/questions/49876077/pandas-reading-excel-file-starting-from-the-row-below-that-with-a-specific-valu
#content-pages july 12-25
july12_25 = pd.read_excel(r'/content/drive/MyDrive/DSS/BrainPost_blog/Data/DSS BrainPost Web Analytics Challenge!.xlsx',
sheet_name='content-pages july 12-25',
skiprows=6, skipfooter=20)
#july12_25
#content-pages jul 26 - aug 8
jul26_aug8 = pd.read_excel(r'/content/drive/MyDrive/DSS/BrainPost_blog/Data/DSS BrainPost Web Analytics Challenge!.xlsx',
sheet_name='content-pages jul 26 - aug 8',
skiprows=6, skipfooter=20)
#jul26_aug8
#content-pages aug 9-22
aug9_22 = pd.read_excel(r'/content/drive/MyDrive/DSS/BrainPost_blog/Data/DSS BrainPost Web Analytics Challenge!.xlsx',
sheet_name='content-pages aug 9-22',
skiprows=6, skipfooter=20)
#aug9_22
#content-pages aug23-sept5
aug23_sept5 = pd.read_excel(r'/content/drive/MyDrive/DSS/BrainPost_blog/Data/DSS BrainPost Web Analytics Challenge!.xlsx',
sheet_name='content-pages aug23-sept5',
skiprows=6, skipfooter=20)
#aug23_sept5
#content-pages sept 6-19
sept6_19 = pd.read_excel(r'/content/drive/MyDrive/DSS/BrainPost_blog/Data/DSS BrainPost Web Analytics Challenge!.xlsx',
sheet_name='content-pages sept 6-19',
skiprows=6, skipfooter=20)
#sept6_19
#content-pages sept 20-oct3
sept20_oct3 = pd.read_excel(r'/content/drive/MyDrive/DSS/BrainPost_blog/Data/DSS BrainPost Web Analytics Challenge!.xlsx',
sheet_name='content-pages sept 20-oct3',
skiprows=6, skipfooter=20)
#sept20_oct3
#content-pages oct 4-17
Oct4_17 = pd.read_excel(r'/content/drive/MyDrive/DSS/BrainPost_blog/Data/DSS BrainPost Web Analytics Challenge!.xlsx',
sheet_name='content-pages oct 4-17',
skiprows=6, skipfooter=20)
#Oct4_17
#content-pages oct 18-31
Oct18_31 = pd.read_excel(r'/content/drive/MyDrive/DSS/BrainPost_blog/Data/DSS BrainPost Web Analytics Challenge!.xlsx',
sheet_name='content-pages oct 18-31',
skiprows=6, skipfooter=20)
#Oct18_31
# Combine data frame
# https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.DataFrame.combine.html
# https://pandas.pydata.org/pandas-docs/stable/user_guide/merging.html
frames = [july12_25,
jul26_aug8,
aug9_22,
aug23_sept5,
sept6_19,
sept20_oct3,
Oct4_17,
Oct18_31]
df = pd.concat(frames)
df
df_outer = pd.merge(df, pages_tiltes, how='outer', on='Page')
df = df_outer.copy()
# Determine the number of missing values for every column
df.isnull().sum()
# Filter entries with Pageviews >= 0
# https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.DataFrame.filter.html
# https://cmdlinetips.com/2018/02/how-to-subset-pandas-dataframe-based-on-values-of-a-column/
df_Pageviews_filtered = df[df['Pageviews'] > 0]
df_Pageviews_filtered.isnull().sum()
# Create a value count column
# https://stackoverflow.com/questions/29791785/python-pandas-add-a-column-to-my-dataframe-that-counts-a-variable
df_Pageviews_filtered['Page_count'] = df_Pageviews_filtered.groupby('Page')['Page'].transform('count')
df_Pageviews_filtered['Source_count'] = df_Pageviews_filtered.groupby('Source / Medium')['Source / Medium'].transform('count')
df_Pageviews_filtered['Page_Title_count'] = df_Pageviews_filtered.groupby('Page Title')['Page Title'].transform('count')
df = df_Pageviews_filtered.copy()
# Merge all facebook
# https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.DataFrame.replace.html
# I chose to combine all facebook referal
# m.facebook indicate mobile trafic.
# There is no equivalent for the other Source so I will ignnore this for this part of the analysis.
df = df.replace(to_replace = ["l.facebook.com / referral", "m.facebook.com / referral", "facebook.com / referral"],
value = "facebook")
df = df.replace( to_replace = "google / organic", value = "google")
df = df.replace( to_replace = "(direct) / (none)", value = "direct")
# t.co is twitter
# https://analypedia.carloseo.com/t-co-referral/
df = df.replace( to_replace = "t.co / referral", value = "twitter")
df = df.replace( to_replace = "bing / organic", value = "bing")
# Deal with time data
df['time'] = pd.to_datetime(df['Avg. Time on Page'], format='%H:%M:%S')
df['time'] = pd.to_datetime(df['time'], unit='s')
df[['time0']] = pd.to_datetime('1900-01-01 00:00:00')
df['time_diff'] = df['time'] - df['time0']
df['time_second'] = df['time_diff'].dt.total_seconds().astype(int)
```
# Data Visualization
```
# https://stackoverflow.com/questions/42528921/how-to-prevent-overlapping-x-axis-labels-in-sns-countplot
# https://stackoverflow.com/questions/46623583/seaborn-countplot-order-categories-by-count
# https://stackoverflow.com/questions/25328003/how-can-i-change-the-font-size-using-seaborn-facetgrid
data = df.copy()
data = data[data['Page_count'] >= 60]
plt.figure(figsize=(10, 5))
sns.set(font_scale=1.25)
sns.set_style("white")
title = 'Top 5 Pages visited'
sns.countplot(y = data['Page'],
order = data['Page'].value_counts().index)
plt.title(title)
plt.ioff()
```
**Figure: Top 5 pages visited all time**
```
data = df.copy()
data = data[data['Page_count'] >= 25]
plt.figure(figsize=(10, 10))
sns.set(font_scale=1.25)
sns.set_style("white")
title = 'Top Pages visited more than 25 times'
sns.countplot(y = data['Page'],
order = data['Page'].value_counts().index,
color='#2b7bba')
plt.title(title)
plt.ioff()
```
**Figure: Top pages visited at least 25 times**
```
# https://www.statology.org/pandas-filter-multiple-conditions/
data = df.copy()
data = data[(data['Source_count'] >= 270)]
sns.displot(data, x="time_second", kind="kde", hue='Source / Medium')
plt.ioff()
```
**Figure: Average time spent on page for the top sources**
The 0 second trafic is not restricted to google.
See this [discussion](https://support.google.com/google-ads/thread/1455669?hl=en) related to 0 second visits on Google Analytics.
The issue seems related to bounce rate preventing Google Analytic to accuralely measure the time spent on the page.
```
# Time spend on page
# https://www.statology.org/pandas-filter-multiple-conditions/
data = df.copy()
data = data[(data['Source_count'] >= 270)]
sns.set(font_scale=1.25)
sns.set_style("white")
sns.displot(data, x="Bounce Rate", kind="kde", hue='Source / Medium')
plt.ioff()
```
**Figure: Average Bounce Rate on page for the top sources**
The bounce rate correspond to users that take no other action after landing on the site such as visiting another page.
From the figure above this seems to be frequent on the blog which make sense if the user are interested in a particular article.
It also potentially means that for most traffic on the site the average time spend on a page can't be calculated.
There seems to be way to work around this as seen in this [discussion](https://support.google.com/google-ads/thread/1455669?hl=en).
```
data = df.copy()
data = data[data['Source_count'] >= 100]
plt.figure(figsize=(10, 5))
sns.set(font_scale=1.25)
sns.set_style("white")
title = 'Top 5 Source for Pages visited more than 100 time'
sns.countplot(y = data['Source / Medium'],
order = data['Source / Medium'].value_counts().index)
plt.title(title)
plt.ioff()
```
**Figure: Top 5 Source for Pages visited more than 100 time**
```
# https://www.statology.org/pandas-filter-multiple-conditions/
data = df.copy()
data = data[data['Source_count'] >= 100]
data = data[data['time_second'] > 5]
y="Source / Medium"
x="time_second"
title = 'Top 5 Source for Pages visited more than 100 time and viewed more than 5 seconds'
plt.figure(figsize=(10, 10))
sns.set(font_scale=1.25)
sns.set_style("white")
sns.boxplot(x=x, y=y, data=data, notch=True, showmeans=False,
meanprops={"marker":"s","markerfacecolor":"white", "markeredgecolor":"black"})
plt.title(title)
plt.ioff()
# https://www.statology.org/pandas-filter-multiple-conditions/
data = df.copy()
data = data[(data['Page_count'] >= 60) & (data['Source_count'] >= 100)]
data = data[data['time_second'] > 5]
title = ""
y="Page"
x="time_second"
plt.figure(figsize=(10, 8))
sns.set(font_scale=1.25)
sns.set_style("white")
sns.boxplot(x=x, y=y, data=data, notch=False, showmeans=False,
meanprops={"marker":"s","markerfacecolor":"white", "markeredgecolor":"black"},
hue='Source / Medium')
plt.title(title)
plt.ioff()
# https://www.statology.org/pandas-filter-multiple-conditions/
data = df.copy()
data = data[(data['Page_count'] >= 61) & (data['Source_count'] >= 100)]
data = data[data['time_second'] > 5]
data = data[data['time_second'] < 600]
title = ""
y="Page"
x="time_second"
plt.figure(figsize=(10, 8))
sns.set(font_scale=1.25)
sns.set_style("white")
sns.boxplot(x=x, y=y, data=data, notch=False, showmeans=False,
meanprops={"marker":"s","markerfacecolor":"white", "markeredgecolor":"black"},
hue='Source / Medium')
plt.title(title)
plt.ioff()
# https://stackoverflow.com/questions/42528921/how-to-prevent-overlapping-x-axis-labels-in-sns-countplot
# https://stackoverflow.com/questions/46623583/seaborn-countplot-order-categories-by-count
# https://stackoverflow.com/questions/25328003/how-can-i-change-the-font-size-using-seaborn-facetgrid
data = df.copy()
data = data[data['Page_count'] >= 50]
data = data[data['Source_count'] >= 100]
#data = data[data['time_second'] > 5]
plt.figure(figsize=(15, 10))
sns.set(font_scale=1.25)
sns.set_style("white")
title = 'Average View for page visited more than 50 times from top source'
sns.countplot(data = data, y = 'Page', hue='Source / Medium')
# Put the legend out of the figure
# https://stackoverflow.com/questions/30490740/move-legend-outside-figure-in-seaborn-tsplot
plt.legend(bbox_to_anchor=(1.05, 1), loc=2, borderaxespad=0.)
plt.title(title)
plt.ioff()
```
# Conclusion
* **What content (or types of content) is most popular (what are patterns we see in popular content) and is different content popular amongst different subgroups (e.g. by source/medium)?**
The homepage, weekly-brainpost, and archive are the most popular pages on the website.
We would need more information to analyze trends in page popularity by sources. The user with direct access, possibly via a mailing list, tend to visit the weekly brain posts pages more.
* **Any question that will help us to take action to better tailor our content to our audience(s) or understand how traffic comes to the site.**
What is causing the high bounce rate in the analytics?
A large number of visitors are registered as spending 0 seconds on the page. This, combined with the high bounce rate, could indicate an issue in measuring the site traffic. This Google support [page](https://www.brainpost.co/about-brainpost) offers suggestions to solve this problem.
* **Where are people visiting from (source-wise)?**
Google, Facebook and direct access are the three most common traffic sources.
# Final remarks
I put this together as a quick and modest analysis. I appreciate real-life projects, so I plan to investigate this further. Any feedback is welcome.
* E-mail: [email protected]
* Twitter: williamguesdon
* LinkedIn: william-guesdon
|
github_jupyter
|
Exercise 4 - Polynomial Regression
========
Sometimes our data doesn't have a linear relationship, but we still want to predict an outcome.
Suppose we want to predict how satisfied people might be with a piece of fruit, we would expect satisfaction would be low if the fruit was under ripened or over ripened. Satisfaction would be high in between underripened and overripened.
This is not something linear regression will help us with, so we can turn to polynomial regression to help us make predictions for these more complex non-linear relationships!
Step 1
------
In this exercise we will look at a dataset analysing internet traffic over the course of the day. Observations were made every hour over the course of several days. Suppose we want to predict the level of traffic we might see at any time during the day, how might we do this?
Let's start by opening up our data and having a look at it.
#### In the cell below replace the text `<printDataHere>` with `print(dataset.head())`, and __run the code__ to see the data.
```
# This sets up the graphing configuration
import warnings
warnings.filterwarnings("ignore")
import matplotlib.pyplot as graph
%matplotlib inline
graph.rcParams['figure.figsize'] = (15,5)
graph.rcParams["font.family"] = "DejaVu Sans"
graph.rcParams["font.size"] = "12"
graph.rcParams['image.cmap'] = 'rainbow'
graph.rcParams['axes.facecolor'] = 'white'
graph.rcParams['figure.facecolor'] = 'white'
import numpy as np
import pandas as pd
dataset = pd.read_csv('Data/traffic_by_hour.csv')
###
# BELOW, REPLACE <printDataHere> WITH print(dataset.head()) TO PREVIEW THE DATASET ---###
###
print(dataset.head())
###
```
Step 2
-----
Next we're going to flip the data with the transpose method - our rows will become columns and our columns will become rows. Transpose is commonly used to reshape data so we can use it. Let's try it out.
#### In the cell below find the text `<addCallToTranspose>` and replace it with `transpose`
```
###
# REPLACE THE <addCallToTranspose> BELOW WITH transpose
###
dataset_T = np.transpose(dataset)
###
print(dataset_T.shape)
print(dataset_T)
```
Now lets visualize the data.
#### Replace the text `<addSampleHere>` with `sample` and then __run the code__.
```
# Let's visualise the data!
###
# REPLACE <addSampleHere> BELOW WITH sample
###
for sample in range(0, dataset_T.shape[1]):
graph.plot(dataset.columns.values, dataset_T[sample])
###
graph.xlabel('Time of day')
graph.ylabel('Internet traffic (Gbps)')
graph.show()
```
Step 3
-----
This all looks a bit busy, let's see if we can draw out a clearer pattern by taking the __average values__ for each hour.
#### In the cell below find all occurances of `<replaceWithHour>` and replace them with `hour` and then __run the code__.
```
# We want to look at the mean values for each hour.
hours = dataset.columns.values
###
# REPLACE THE <replaceWithHour>'s BELOW WITH hour
###
train_Y = [dataset[hour].mean() for hour in hours] # This will be our outcome we measure (label) - amount of internet traffic
train_X = np.transpose([int(hour) for hour in hours]) # This is our feature - time of day
###
# This makes our graph, don't edit!
graph.scatter(train_X, train_Y)
for sample in range(0,dataset_T.shape[1]):
graph.plot(hours, dataset_T[sample], alpha=0.25)
graph.xlabel('Time of day')
graph.ylabel('Internet traffic (Gbps)')
graph.show()
```
This alone could help us make a prediction if we wanted to know the expected traffic exactly on the hour.
But, we'll need to be a bit more clever if we want to make a __good__ prediction of times in between.
Step 4
------
Let's use the midpoints in between the hours to analyse the relationship between the __time of day__ and the __amount of internet traffic__.
Numpy's `polyfit(x,y,d)` function allows us to do polynomial regression, or more precisely least squares polynomial fit.
We specify a __feature $x$ (time of day)__, our __label $y$ (the amount of traffic)__, and the __degree $d$ of the polynomial (how curvy the line is)__.
#### In the cell below find the text `<replaceWithDegree>`, replace it with the value `1` then __run the code__.
```
# Polynomials of degree 1 are linear!
# Lets include this one just for comparison
###
# REPLACE THE <replaceWithDegree> BELOW WITH 1
###
poly_1 = np.polyfit(train_X, train_Y, 1)
###
```
Let's also compare a few higher-degree polynomials.
#### Replace the `<replaceWithDegree>`'s below with numbers, as directed in the comments.
```
###
# REPLACE THE <replaceWithDegree>'s BELOW WITH 2, 3, AND THEN 4
###
poly_2 = np.polyfit(train_X, train_Y, 2)
poly_3 = np.polyfit(train_X, train_Y, 3)
poly_4 = np.polyfit(train_X, train_Y, 4)
###
# Let's plot it!
graph.scatter(train_X, train_Y)
xp = np.linspace(0, 24, 100)
# black dashed linear degree 1
graph.plot(xp, np.polyval(poly_1, xp), 'k--')
# red degree 2
graph.plot(xp, np.polyval(poly_2, xp), 'r-')
# blue degree 3
graph.plot(xp, np.polyval(poly_3, xp), 'b-')
# yellow degree 4
graph.plot(xp, np.polyval(poly_4, xp), 'y-')
graph.xticks(train_X, dataset.columns.values)
graph.xlabel('Time of day')
graph.ylabel('Internet traffic (Gbps)')
graph.show()
```
None of these polynomials do a great job of generalising the data. Let's try a few more.
#### Follow the instructions in the comments to replace the `<replaceWithDegree>`'s and then __run the code__.
```
###
# REPLACE THE <replaceWithDegree>'s 5, 6, AND 7
###
poly_5 = np.polyfit(train_X, train_Y, 5)
poly_6 = np.polyfit(train_X, train_Y, 6)
poly_7 = np.polyfit(train_X, train_Y, 7)
###
# Let's plot it!
graph.scatter(train_X, train_Y)
xp = np.linspace(0, 24, 100)
# black dashed linear degree 1
graph.plot(xp, np.polyval(poly_1, xp), 'k--')
# red degree 5
graph.plot(xp, np.polyval(poly_5, xp), 'r-')
# blue degree 6
graph.plot(xp, np.polyval(poly_6, xp), 'b-')
# yellow degree 7
graph.plot(xp, np.polyval(poly_7, xp), 'y-')
graph.xticks(train_X, dataset.columns.values)
graph.xlabel('Time of day')
graph.ylabel('Internet traffic (Gbps)')
graph.show()
```
It looks like the 5th and 6th degree polynomials have an identical curve. This looks like a good curve to use.
We could perhaps use an even higher degree polynomial to fit it even more tightly, but we don't want to overfit the curve, since we want just a generalisation of the relationship.
Let's see how our degree 6 polynomial compares to the real data.
#### Replace the text `<replaceWithPoly6>` with `poly_6` and __run the code__.
```
for row in range(0,dataset_T.shape[1]):
graph.plot(dataset.columns.values, dataset_T[row], alpha = 0.5)
###
# REPLACE <replaceWithPoly6> BELOW WITH poly_6 - THE POLYNOMIAL WE WISH TO VISUALIZE
###
graph.plot(xp, np.polyval(poly_6, xp), 'k-')
###
graph.xlabel('Time of day')
graph.ylabel('Internet traffic (Gbps)')
graph.show()
```
Step 5
------
Now let's try using this model to make a prediction for a time between 00 and 24.
#### In the cell below follow the instructions in the code to replace `<replaceWithTime>` and `<replaceWithPoly6>` then __run the code__.
```
###
# REPLACE <replaceWithTime> BELOW WITH 12.5 (this represents the time 12:30)
###
time = 12.5
###
###
# REPLACE <replaceWithPoly6> BELOW WITH poly_6 SO WE CAN VISUALIZE THE 6TH DEGREE POLYNOMIAL MODEL
###
pred = np.polyval(poly_6, time)
###
print("at t=%s, predicted internet traffic is %s Gbps"%(time,pred))
# Now let's visualise it
graph.plot(xp, np.polyval(poly_6, xp), 'y-')
graph.plot(time, pred, 'ko') # result point
graph.plot(np.linspace(0, time, 2), np.full([2], pred), dashes=[6, 3], color='black') # dashed lines (to y-axis)
graph.plot(np.full([2], time), np.linspace(0, pred, 2), dashes=[6, 3], color='black') # dashed lines (to x-axis)
graph.xticks(train_X, dataset.columns.values)
graph.ylim(0, 60)
graph.title('expected traffic throughout the day')
graph.xlabel('time of day')
graph.ylabel('internet traffic (Gbps)')
graph.show()
```
Conclusion
-----
And there we have it! You have made a polynomial regression model and used it for analysis! This models gives us a prediction for the level of internet traffic we should expect to see at any given time of day.
You can go back to the course and either click __'Next Step'__ to start an optional step with tips on how to better work with AI models, or you can go to the next module where instead of predicting numbers we predict categories.
|
github_jupyter
|
# Building a Classifier from Lending Club Data
**An end-to-end machine learning example using Pandas and Scikit-Learn**
## Data Ingestion
```
%matplotlib inline
import os
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from pandas.tools.plotting import scatter_matrix
names = [
#Lending Club features
"funded_amnt",
"term",
"int_rate",
"emp_length",
"home_ownership",
"annual_inc",
"verification_status",
"purpose",
"dti",
"delinq_2yrs",
"inq_last_6mths",
"open_acc",
"pub_rec",
"revol_bal",
"revol_util",
# Macroeconomical data
"ilc_mean",
"ilc_LSFT",
"gdp_mean",
"gdp_LSFT",
"Tbill_mean",
"Tbill_LSFT",
"cc_rate",
"unemp",
"unemp_LSFT",
"spread",
# Label
"loan_status"
]
Fnames = names[:-1]
label = names[-1]
# Open up the earlier CSV to determine how many different types ofentries there are in the column 'loan_status'
data_with_all_csv_features = pd.read_csv("./data/dfaWR4F.csv")
full_data = data_with_all_csv_features[names];
data = full_data.copy()[names]
data.head(3)
```
# Data Exploration
The very first thing to do is to explore the dataset and see what's inside.
```
# Shape of the full dataset
print data.shape
import matplotlib.pyplot as plt
%matplotlib inline
data.boxplot(column="annual_inc",by="loan_status")
from pandas.tools.plotting import radviz
import matplotlib.pyplot as plt
fig = plt.figure()
radviz(data, 'loan_status')
plt.show()
areas = full_data[['funded_amnt','term','int_rate', 'loan_status']]
scatter_matrix(areas, alpha=0.2, figsize=(18,18), diagonal='kde')
sns.set_context("poster")
sns.countplot(x='home_ownership', hue='loan_status', data=full_data,)
sns.set_context("poster")
sns.countplot(x='emp_length', hue='loan_status', data=full_data,)
sns.set_context("poster")
sns.countplot(x='term', hue='loan_status', data=full_data,)
sns.set_context("poster")
sns.countplot(y='purpose', hue='loan_status', data=full_data,)
sns.set_context("poster", font_scale=0.8)
plt.figure(figsize=(15, 15))
plt.ylabel('Loan Originating State')
sns.countplot(y='verification_status', hue='loan_status', data=full_data)
pd.crosstab(data["term"],data["loan_status"],margins=True)
def percConvert(ser):
return ser/float(ser[-1])
pd.crosstab(data["term"],data["loan_status"],margins=True).apply(percConvert, axis=1)
data.hist(column="annual_inc",by="loan_status",bins=30)
# Balancing the data so that we have 50/50 class balancing (underbalancing reducing one class)
paid_data = data.loc[(data['loan_status'] == "Paid")]
default_data = data.loc[(data['loan_status'] == "Default")]
# Reduce the Fully Paid data to the same number as Defaulted
num_of_paid = default_data.shape[0]
reduce_paid_data = paid_data.sample(num_of_paid)
# This is the smaller sample data with 50-50 Defaulted and Fully aod loan
balanced_data = reduce_paid_data.append(default_data,ignore_index = True )
#Now shuffle several times
data = balanced_data.sample(balanced_data.shape[0])
data = data.sample(balanced_data.shape[0])
print "Fully Paid data size was {}".format(paid_data.shape[0])
print "Default data size was {}".format(default_data.shape[0])
print "Updated new Data size is {}".format(data.shape[0])
pd.crosstab(data["term"],data["loan_status"],margins=True).apply(percConvert, axis=1)
fig = plt.figure()
ax = fig.add_subplot(111)
ax.hist(paid_data['int_rate'], bins = 50, alpha = 0.4, label='Fully_Paid', color = 'blue', range = (paid_data['int_rate'].min(),reduce_paid_data['int_rate'].max()))
ax.hist(default_data['int_rate'], bins = 50, alpha = 0.4, label='Default', color = 'red', range = (default_data['int_rate'].min(),default_data['int_rate'].max()))
plt.title('Interest Rate vs Number of Loans')
plt.legend(loc='upper right')
plt.xlabel('Interest Rate')
plt.axis([0, 25, 0, 8000])
plt.ylabel('Number of Loans')
plt.show()
```
The countplot function accepts either an x or a y argument to specify if this is a bar plot or a column plot. I chose to use the y argument so that the labels were readable. The hue argument specifies a column for comparison; in this case we're concerned with the relationship of our categorical variables to the target income.
## Data Management
In order to organize our data on disk, we'll need to add the following files:
- `README.md`: a markdown file containing information about the dataset and attribution. Will be exposed by the `DESCR` attribute.
- `meta.json`: a helper file that contains machine readable information about the dataset like `target_names` and `feature_names`.
```
import json
meta = {
'target_names': list(full_data.loan_status.unique()),
'feature_names': list(full_data.columns),
'categorical_features': {
column: list(full_data[column].unique())
for column in full_data.columns
if full_data[column].dtype == 'object'
},
}
with open('data/ls_meta.json', 'wb') as f:
json.dump(meta, f, indent=2)
```
This code creates a `meta.json` file by inspecting the data frame that we have constructued. The `target_names` column, is just the two unique values in the `data.loan_status` series; by using the `pd.Series.unique` method - we're guarenteed to spot data errors if there are more or less than two values. The `feature_names` is simply the names of all the columns.
Then we get tricky — we want to store the possible values of each categorical field for lookup later, but how do we know which columns are categorical and which are not? Luckily, Pandas has already done an analysis for us, and has stored the column data type, `data[column].dtype`, as either `int64` or `object`. Here I am using a dictionary comprehension to create a dictionary whose keys are the categorical columns, determined by checking the object type and comparing with `object`, and whose values are a list of unique values for that field.
Now that we have everything we need stored on disk, we can create a `load_data` function, which will allow us to load the training and test datasets appropriately from disk and store them in a `Bunch`:
```
from sklearn import cross_validation
from sklearn.cross_validation import train_test_split
from sklearn.datasets.base import Bunch
def load_data(root='data'):
# Load the meta data from the file
with open(os.path.join(root, 'meta.json'), 'r') as f:
meta = json.load(f)
names = meta['feature_names']
# Load the readme information
with open(os.path.join(root, 'README.md'), 'r') as f:
readme = f.read()
X = data[Fnames]
# Remove the target from the categorical features
meta['categorical_features'].pop(label)
y = data[label]
X_train, X_test, y_train, y_test = cross_validation.train_test_split(X,y,test_size = 0.2,random_state=10)
# Return the bunch with the appropriate data chunked apart
return Bunch(
#data = train[names[:-1]],
data = X_train,
#target = train[names[-1]],
target = y_train,
#data_test = test[names[:-1]],
data_test = X_test,
#target_test = test[names[-1]],
target_test = y_test,
target_names = meta['target_names'],
feature_names = meta['feature_names'],
categorical_features = meta['categorical_features'],
DESCR = readme,
)
dataset = load_data()
print meta['target_names']
dataset.data_test.head()
```
The primary work of the `load_data` function is to locate the appropriate files on disk, given a root directory that's passed in as an argument (if you saved your data in a different directory, you can modify the root to have it look in the right place). The meta data is included with the bunch, and is also used split the train and test datasets into `data` and `target` variables appropriately, such that we can pass them correctly to the Scikit-Learn `fit` and `predict` estimator methods.
## Feature Extraction
Now that our data management workflow is structured a bit more like Scikit-Learn, we can start to use our data to fit models. Unfortunately, the categorical values themselves are not useful for machine learning; we need a single instance table that contains _numeric values_. In order to extract this from the dataset, we'll have to use Scikit-Learn transformers to transform our input dataset into something that can be fit to a model. In particular, we'll have to do the following:
- encode the categorical labels as numeric data
- impute missing values with data (or remove)
We will explore how to apply these transformations to our dataset, then we will create a feature extraction pipeline that we can use to build a model from the raw input data. This pipeline will apply both the imputer and the label encoders directly in front of our classifier, so that we can ensure that features are extracted appropriately in both the training and test datasets.
### Label Encoding
Our first step is to get our data out of the object data type land and into a numeric type, since nearly all operations we'd like to apply to our data are going to rely on numeric types. Luckily, Sckit-Learn does provide a transformer for converting categorical labels into numeric integers: [`sklearn.preprocessing.LabelEncoder`](http://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.LabelEncoder.html). Unfortunately it can only transform a single vector at a time, so we'll have to adapt it in order to apply it to multiple columns.
Like all Scikit-Learn transformers, the `LabelEncoder` has `fit` and `transform` methods (as well as a special all-in-one, `fit_transform` method) that can be used for stateful transformation of a dataset. In the case of the `LabelEncoder`, the `fit` method discovers all unique elements in the given vector, orders them lexicographically, and assigns them an integer value. These values are actually the indices of the elements inside the `LabelEncoder.classes_` attribute, which can also be used to do a reverse lookup of the class name from the integer value.
For example, if we were to encode the `home_ownership` column of our dataset as follows:
```
from sklearn.preprocessing import LabelEncoder
ownership = LabelEncoder()
ownership.fit(dataset.data.home_ownership)
print(ownership.classes_)
from sklearn.preprocessing import LabelEncoder
purpose = LabelEncoder()
purpose.fit(dataset.data.purpose)
print(purpose.classes_)
```
Obviously this is very useful for a single column, and in fact the `LabelEncoder` really was intended to encode the target variable, not necessarily categorical data expected by the classifiers.
In order to create a multicolumn LabelEncoder, we'll have to extend the `TransformerMixin` in Scikit-Learn to create a transformer class of our own, then provide `fit` and `transform` methods that wrap individual `LabelEncoders` for our columns.
```
from sklearn.base import BaseEstimator, TransformerMixin
class EncodeCategorical(BaseEstimator, TransformerMixin):
"""
Encodes a specified list of columns or all columns if None.
"""
def __init__(self, columns=None):
self.columns = columns
self.encoders = None
def fit(self, data, target=None):
"""
Expects a data frame with named columns to encode.
"""
# Encode all columns if columns is None
if self.columns is None:
self.columns = data.columns
# Fit a label encoder for each column in the data frame
self.encoders = {
column: LabelEncoder().fit(data[column])
for column in self.columns
}
return self
def transform(self, data):
"""
Uses the encoders to transform a data frame.
"""
output = data.copy()
for column, encoder in self.encoders.items():
output[column] = encoder.transform(data[column])
return output
encoder = EncodeCategorical(dataset.categorical_features.keys())
#data = encoder.fit_transform(dataset.data)
```
This specialized transformer now has the ability to label encode multiple columns in a data frame, saving information about the state of the encoders. It would be trivial to add an `inverse_transform` method that accepts numeric data and converts it to labels, using the `inverse_transform` method of each individual `LabelEncoder` on a per-column basis.
### Imputation
Scikit-Learn provides a transformer for dealing with missing values at either the column level or at the row level in the `sklearn.preprocessing` library called the [Imputer](http://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.Imputer.html).
The `Imputer` requires information about what missing values are, either an integer or the string, `Nan` for `np.nan` data types, it then requires a strategy for dealing with it. For example, the `Imputer` can fill in the missing values with the mean, median, or most frequent values for each column. If provided an axis argument of 0 then columns that contain only missing data are discarded; if provided an axis argument of 1, then rows which contain only missing values raise an exception. Basic usage of the `Imputer` is as follows:
```python
imputer = Imputer(missing_values='Nan', strategy='most_frequent')
imputer.fit(dataset.data)
```
```
from sklearn.preprocessing import Imputer
class ImputeCategorical(BaseEstimator, TransformerMixin):
"""
Encodes a specified list of columns or all columns if None.
"""
def __init__(self, columns=None):
self.columns = columns
self.imputer = None
def fit(self, data, target=None):
"""
Expects a data frame with named columns to impute.
"""
# Encode all columns if columns is None
if self.columns is None:
self.columns = data.columns
# Fit an imputer for each column in the data frame
#self.imputer = Imputer(strategy='most_frequent')
self.imputer = Imputer(strategy='mean')
self.imputer.fit(data[self.columns])
return self
def transform(self, data):
"""
Uses the encoders to transform a data frame.
"""
output = data.copy()
output[self.columns] = self.imputer.transform(output[self.columns])
return output
imputer = ImputeCategorical(Fnames)
#data = imputer.fit_transform(data)
data.head(5)
```
Our custom imputer, like the `EncodeCategorical` transformer takes a set of columns to perform imputation on. In this case we only wrap a single `Imputer` as the `Imputer` is multicolumn — all that's required is to ensure that the correct columns are transformed.
I had chosen to do the label encoding first, assuming that because the `Imputer` required numeric values, I'd be able to do the parsing in advance. However, after requiring a custom imputer, I'd say that it's probably best to deal with the missing values early, when they're still a specific value, rather than take a chance.
## Model Build
To create classifier, we're going to create a [`Pipeline`](http://scikit-learn.org/stable/modules/generated/sklearn.pipeline.Pipeline.html) that uses our feature transformers and ends in an estimator that can do classification. We can then write the entire pipeline object to disk with the `pickle`, allowing us to load it up and use it to make predictions in the future.
A pipeline is a step-by-step set of transformers that takes input data and transforms it, until finally passing it to an estimator at the end. Pipelines can be constructed using a named declarative syntax so that they're easy to modify and develop.
# PCA
```
from sklearn.pipeline import Pipeline
from sklearn.linear_model import LogisticRegression
from sklearn.preprocessing import LabelEncoder
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.preprocessing import scale
%matplotlib inline
# we need to encode our target data as well.
yencode = LabelEncoder().fit(dataset.target)
#print yencode
# construct the pipeline
pca = Pipeline([
('encoder', EncodeCategorical(dataset.categorical_features.keys())),
('imputer', ImputeCategorical(Fnames)),
('scalar', StandardScaler()),
#('classifier', PCA(n_components=20))
('classifier', PCA())
])
# fit the pipeline
pca.fit(dataset.data, yencode.transform(dataset.target))
#print dataset.target
import numpy as np
#The amount of variance that each PC explains
var= pca.named_steps['classifier'].explained_variance_ratio_
#Cumulative Variance explains
var1=np.cumsum(np.round(pca.named_steps['classifier'].explained_variance_ratio_, decimals=4)*100)
print var1
plt.plot(var1)
```
# LDA
```
from sklearn.pipeline import Pipeline
from sklearn.linear_model import LogisticRegression
from sklearn.preprocessing import LabelEncoder
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.lda import LDA
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.preprocessing import scale
%matplotlib inline
# we need to encode our target data as well.
yencode = LabelEncoder().fit(dataset.target)
#print yencode
# construct the pipeline
lda = Pipeline([
('encoder', EncodeCategorical(dataset.categorical_features.keys())),
('imputer', ImputeCategorical(Fnames)),
('scalar', StandardScaler()),
('classifier', LDA())
])
# fit the pipeline
lda.fit(dataset.data, yencode.transform(dataset.target))
#print dataset.target
import numpy as np
#The amount of variance that each PC explains
var= lda.named_steps['classifier']
print var
#Cumulative Variance explains
#var1=np.cumsum(np.round(lda.named_steps['classifier'], decimals=4)*100)
print var1
plt.plot(var1)
```
# Logistic Regression
Fits a logistic model to data and makes predictions about the probability of a categorical event (between 0 and 1). Logistic regressions make predictions between 0 and 1, so in order to classify multiple classes a one-vs-all scheme is used (one model per class, winner-takes-all).
```
from sklearn.pipeline import Pipeline
from sklearn.linear_model import LogisticRegression
from sklearn.preprocessing import LabelEncoder
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import Normalizer
from sklearn.metrics import accuracy_score, f1_score, precision_score, recall_score, roc_auc_score
# we need to encode our target data as well.
yencode = LabelEncoder().fit(dataset.target)
#normalizer = Normalizer(copy=False)
# construct the pipeline
lr = Pipeline([
('encoder', EncodeCategorical(dataset.categorical_features.keys())),
('imputer', ImputeCategorical(Fnames)),
('scalar', StandardScaler()),
#('normalizer', Normalizer(copy=False)),
#('classifier', LogisticRegression(class_weight='{0:.5, 1:.3}'))
('classifier', LogisticRegression())
])
# fit the pipeline
lr.fit(dataset.data, yencode.transform(dataset.target))
from sklearn.metrics import classification_report
from sklearn.metrics import accuracy_score, f1_score, precision_score, recall_score, roc_auc_score
import collections
print collections.Counter(dataset.target_test)
print collections.Counter(dataset.target)
print collections.Counter(full_data[label])
print "Test under TEST DATASET"
# encode test targets
y_true = yencode.transform(dataset.target_test)
# use the model to get the predicted value
y_pred = lr.predict(dataset.data_test)
# execute classification report
print classification_report(y_true, y_pred, target_names=dataset.target_names)
print "Test under TRAIN DATASET"
# encode test targets
y_true = yencode.transform(dataset.target)
# use the model to get the predicted value
y_pred = lr.predict(dataset.data)
# execute classification report
print classification_report(y_true, y_pred, target_names=dataset.target_names)
print "Test under FULL IMBALANCED DATASET without new fit call"
#lr.fit(full_data[Fnames], yencode.transform(full_data[label]))
# encode test targets
y_true = yencode.transform(full_data[label])
# use the model to get the predicted value
y_pred = lr.predict(full_data[Fnames])
# execute classification report
print classification_report(y_true, y_pred, target_names=dataset.target_names)
```
## Chaining PCA and Logistic Regression
The PCA does an unsupervised dimensionality reduction, while the logistic regression does the prediction.
Here we are using default values for all component of the pipeline.
```
from sklearn.cross_validation import train_test_split
from sklearn.grid_search import GridSearchCV
from sklearn.metrics import classification_report
from sklearn import linear_model, decomposition
yencode = LabelEncoder().fit(dataset.target)
logistic = linear_model.LogisticRegression()
pca = decomposition.PCA()
pipe = Pipeline(steps=[
('encoder', EncodeCategorical(dataset.categorical_features.keys())),
('imputer', ImputeCategorical(Fnames)),
('scalar', StandardScaler()),
('pca', pca),
('logistic', logistic)
])
# we need to encode our target data as well.
yencode = LabelEncoder().fit(dataset.target)
#print yencode
# construct the pipeline
lda = Pipeline([
('encoder', EncodeCategorical(dataset.categorical_features.keys())),
('imputer', ImputeCategorical(Fnames)),
('scalar', StandardScaler()),
('classifier', LDA())
])
# fit the pipeline
lda.fit(dataset.data, yencode.transform(dataset.target))
# Running the test
from sklearn.metrics import classification_report
from sklearn.metrics import accuracy_score, f1_score, precision_score, recall_score, roc_auc_score
import collections
print collections.Counter(dataset.target_test)
print collections.Counter(dataset.target)
print collections.Counter(full_data[label])
print "Test under TEST DATASET"
# encode test targets
y_true = yencode.transform(dataset.target_test)
# use the model to get the predicted value
y_pred = lda.predict(dataset.data_test)
# execute classification report
print classification_report(y_true, y_pred, target_names=dataset.target_names)
print "Test under TRAIN DATASET"
# encode test targets
y_true = yencode.transform(dataset.target)
# use the model to get the predicted value
y_pred = lda.predict(dataset.data)
# execute classification report
print classification_report(y_true, y_pred, target_names=dataset.target_names)
print "Test under FULL IMBALANCED DATASET without new fit call"
#lda.fit(full_data[Fnames], yencode.transform(full_data[label]))
# encode test targets
y_true = yencode.transform(full_data[label])
# use the model to get the predicted value
y_pred = lda.predict(full_data[Fnames])
# execute classification report
print classification_report(y_true, y_pred, target_names=dataset.target_names)
```
## Random Forest
```
from sklearn.ensemble import RandomForestClassifier
from sklearn.ensemble import RandomForestRegressor
from sklearn.pipeline import Pipeline
from sklearn.metrics import mean_squared_error as mse
from sklearn.metrics import r2_score
# we need to encode our target data as well.
yencode = LabelEncoder().fit(dataset.target)
# construct the pipeline
rf = Pipeline([
('encoder', EncodeCategorical(dataset.categorical_features.keys())),
('imputer', ImputeCategorical(Fnames)),
('scalar', StandardScaler()),
('classifier', RandomForestClassifier(n_estimators=20, oob_score=True, max_depth=7))
])
# ...and then run the 'fit' method to build a forest of trees
rf.fit(dataset.data, yencode.transform(dataset.target))
# Running the test
from sklearn.metrics import classification_report
from sklearn.metrics import accuracy_score, f1_score, precision_score, recall_score, roc_auc_score
import collections
print collections.Counter(dataset.target_test)
print collections.Counter(dataset.target)
print collections.Counter(full_data[label])
print "Test under TEST DATASET"
# encode test targets
y_true = yencode.transform(dataset.target_test)
# use the model to get the predicted value
y_pred = rf.predict(dataset.data_test)
# execute classification report
print classification_report(y_true, y_pred, target_names=dataset.target_names)
print "Test under TRAIN DATASET"
# encode test targets
y_true = yencode.transform(dataset.target)
# use the model to get the predicted value
y_pred = rf.predict(dataset.data)
# execute classification report
print classification_report(y_true, y_pred, target_names=dataset.target_names)
print "Test under FULL IMBALANCED DATASET without new fit call"
#rf.fit(full_data[Fnames], yencode.transform(full_data[label]))
# encode test targets
y_true = yencode.transform(full_data[label])
# use the model to get the predicted value
y_pred = rf.predict(full_data[Fnames])
# execute classification report
print classification_report(y_true, y_pred, target_names=dataset.target_names)
```
## ElasticNet
```
from sklearn.pipeline import Pipeline
from sklearn.linear_model import ElasticNet
from sklearn.preprocessing import LabelEncoder
from sklearn.preprocessing import StandardScaler
# we need to encode our target data as well.
yencode = LabelEncoder().fit(dataset.target)
# construct the pipeline
lelastic = Pipeline([
('encoder', EncodeCategorical(dataset.categorical_features.keys())),
('imputer', ImputeCategorical(Fnames)),
('scalar', StandardScaler()),
('classifier', ElasticNet(alpha=0.01, l1_ratio =0.1))
])
# fit the pipeline
lelastic.fit(dataset.data, yencode.transform(dataset.target))
#A helper method for pretty-printing linear models
def pretty_print_linear(coefs, names = None, sort = False):
if names == None:
names = ["X%s" % x for x in range(len(coefs))]
lst = zip(coefs[0], names)
if sort:
lst = sorted(lst, key = lambda x:-np.abs(x[0]))
return " + ".join("%s * %s" % (round(coef, 3), name)
for coef, name in lst)
coefs = lelastic.named_steps['classifier'].coef_
print coefs
#print "Linear model:", pretty_print_linear(coefs, Fnames)
#Naive Bayes
from sklearn.naive_bayes import GaussianNB
from sklearn.naive_bayes import MultinomialNB
from sklearn.naive_bayes import BernoulliNB
from sklearn.pipeline import Pipeline
from sklearn.metrics import accuracy_score, f1_score, precision_score, recall_score, roc_auc_score
# we need to encode our target data as well.
yencode = LabelEncoder().fit(dataset.target)
# construct the pipeline
nb = Pipeline([
('encoder', EncodeCategorical(dataset.categorical_features.keys())),
('imputer', ImputeCategorical(Fnames)),
('scalar', StandardScaler()),
# ('classifier', GaussianNB())
# ('classifier', MultinomialNB(alpha=0.7, class_prior=[0.5, 0.5], fit_prior=True))
('classifier', BernoulliNB(alpha=1.0, binarize=0.0, fit_prior=False))
])
# Next split up the data with the 'train test split' method in the Cross Validation module
#X_train, X_test, y_train, y_test = train_test_split(X,y, test_size=0.2)
# ...and then run the 'fit' method to build a model
nb.fit(dataset.data, yencode.transform(dataset.target))
# Running the test
from sklearn.metrics import classification_report
from sklearn.metrics import accuracy_score, f1_score, precision_score, recall_score, roc_auc_score
import collections
print collections.Counter(dataset.target_test)
print collections.Counter(dataset.target)
print collections.Counter(full_data[label])
print "Test under TEST DATASET"
# encode test targets
y_true = yencode.transform(dataset.target_test)
# use the model to get the predicted value
y_pred = nb.predict(dataset.data_test)
# execute classification report
print classification_report(y_true, y_pred, target_names=dataset.target_names)
print "Test under TRAIN DATASET"
# encode test targets
y_true = yencode.transform(dataset.target)
# use the model to get the predicted value
y_pred = nb.predict(dataset.data)
# execute classification report
print classification_report(y_true, y_pred, target_names=dataset.target_names)
print "Test under FULL IMBALANCED DATASET without new fit call"
#rf.fit(full_data[Fnames], yencode.transform(full_data[label]))
# encode test targets
y_true = yencode.transform(full_data[label])
# use the model to get the predicted value
y_pred = nb.predict(full_data[Fnames])
# execute classification report
print classification_report(y_true, y_pred, target_names=dataset.target_names)
```
## Gradient Boosting Classifier
```
from sklearn.ensemble import GradientBoostingClassifier
clf = GradientBoostingClassifier(n_estimators=100, learning_rate=1.0,
max_depth=1, random_state=0).fit(dataset.data, dataset.target)
# encode test targets
y_true = yencode.transform(dataset.target_test)
# use the model to get the predicted value
y_pred = clf.predict(dataset.data_test)
# execute classification report
clf.score(dataset.data_test, y_true)
```
## Voting Classifier
1xLogistic, 4xRandom Forest, 1xgNB, 1xDecisionTree, 2xkNeighbors
```
from sklearn.pipeline import Pipeline
from sklearn.linear_model import LogisticRegression
from sklearn.naive_bayes import GaussianNB
from sklearn.ensemble import RandomForestClassifier
from sklearn.ensemble import VotingClassifier
from sklearn.preprocessing import LabelEncoder
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import accuracy_score, f1_score, precision_score, recall_score, roc_auc_score
from sklearn import linear_model, decomposition
from sklearn.tree import DecisionTreeClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.svm import SVC
# we need to encode our target data as well.
yencode = LabelEncoder().fit(dataset.target)
clf1 = LogisticRegression(random_state=12)
clf2 = RandomForestClassifier(max_features=5, min_samples_leaf=4, min_samples_split=9,
bootstrap=False, criterion='entropy', max_depth=None, n_estimators=24, random_state=12)
clf3 = GaussianNB()
clf4 = DecisionTreeClassifier(max_depth=4)
clf5 = KNeighborsClassifier(n_neighbors=7)
#clf6 = SVC(kernel='rbf', probability=True)
pca = decomposition.PCA(n_components=24)
# construct the pipeline
pipe = Pipeline([
('encoder', EncodeCategorical(dataset.categorical_features.keys())),
('imputer', ImputeCategorical(Fnames)),
('scalar', StandardScaler()),
('pca', pca),
('eclf_classifier', VotingClassifier(estimators=[('lr', clf1), ('rf', clf2), ('gnb', clf3),
('dtc', clf4),('knc', clf5)],
voting='soft',
weights=[1, 4, 1, 1, 2])),
])
# fit the pipeline
pipe.fit(dataset.data, yencode.transform(dataset.target))
from sklearn.metrics import classification_report
from sklearn.metrics import accuracy_score, f1_score, precision_score, recall_score, roc_auc_score
import collections
print collections.Counter(dataset.target_test)
print collections.Counter(dataset.target)
print collections.Counter(full_data[label])
print "Test under TEST DATASET"
y_true, y_pred = yencode.transform(dataset.target_test), pipe.predict(dataset.data_test)
print(classification_report(y_true, y_pred))
print "Test under TRAIN DATASET"
y_true, y_pred = yencode.transform(dataset.target), pipe.predict(dataset.data)
print(classification_report(y_true, y_pred))
print "Test under FULL IMBALANCED DATASET without new fit call"
y_true, y_pred = yencode.transform(full_data[label]), pipe.predict(full_data[Fnames])
print(classification_report(y_true, y_pred))
```
## Parameter Tuning for Logistic regression inside pipeline
A grid search or feature analysis may lead to a higher scoring model than the one we quickly put together.
```
from sklearn.cross_validation import train_test_split
from sklearn.grid_search import GridSearchCV
from sklearn.metrics import classification_report
from sklearn import linear_model, decomposition
yencode = LabelEncoder().fit(dataset.target)
logistic = LogisticRegression(penalty='l2', dual=False, solver='newton-cg')
clf2 = RandomForestClassifier(max_features=5, min_samples_leaf=4, min_samples_split=9,
bootstrap=False, criterion='entropy', max_depth=None, n_estimators=24, random_state=12)
clf3 = GaussianNB()
clf4 = DecisionTreeClassifier(max_depth=4)
clf5 = KNeighborsClassifier(n_neighbors=7)
#clf6 = SVC(kernel='rbf', probability=True)
pca = decomposition.PCA(n_components=24)
# construct the pipeline
pipe = Pipeline([
('encoder', EncodeCategorical(dataset.categorical_features.keys())),
('imputer', ImputeCategorical(Fnames)),
('scalar', StandardScaler()),
('pca', pca),
('logistic', logistic),
])
tuned_parameters = {
#'pca__n_components':[5, 7, 13, 24],
'logistic__fit_intercept':(False, True),
#'logistic__C':(0.1, 1, 10),
'logistic__class_weight':({0:.5, 1:.5},{0:.7, 1:.3},{0:.6, 1:.4},{0:.55, 1:.45},None),
}
scores = ['precision', 'recall', 'f1']
for score in scores:
print("# Tuning hyper-parameters for %s" % score)
print()
clf = GridSearchCV(pipe, tuned_parameters, scoring='%s_weighted' % score)
clf.fit(dataset.data, yencode.transform(dataset.target))
print("Best parameters set found on development set:")
print()
print(clf.best_params_)
print()
print("Grid scores on development set:")
print()
for params, mean_score, scores in clf.grid_scores_:
print("%0.3f (+/-%0.03f) for %r"
% (mean_score, scores.std() * 2, params))
print()
print("Detailed classification report:")
print()
print("The model is trained on the full development set.")
print("The scores are computed on the full evaluation set.")
print()
print "Test under TEST DATASET"
y_true, y_pred = yencode.transform(dataset.target_test), clf.predict(dataset.data_test)
print(classification_report(y_true, y_pred))
print "Test under TRAIN DATASET"
y_true, y_pred = yencode.transform(dataset.target), clf.predict(dataset.data)
print(classification_report(y_true, y_pred))
print "Test under FULL IMBALANCED DATASET without new fit call"
y_true, y_pred = yencode.transform(full_data[label]), clf.predict(full_data[Fnames])
print(classification_report(y_true, y_pred))
```
## Parameter Tuning for classifiers inside VotingClassifier
A grid search or feature analysis may lead to a higher scoring model than the one we quickly put together.
```
from sklearn.cross_validation import train_test_split
from sklearn.grid_search import GridSearchCV
from sklearn.metrics import classification_report
from sklearn import linear_model, decomposition
yencode = LabelEncoder().fit(dataset.target)
logistic = LogisticRegression(penalty='l2', dual=False, solver='newton-cg')
clf2 = RandomForestClassifier(max_features=5, min_samples_leaf=4, min_samples_split=9,
bootstrap=False, criterion='entropy', max_depth=None, n_estimators=24, random_state=12)
clf3 = GaussianNB()
clf4 = DecisionTreeClassifier(max_depth=4)
clf5 = KNeighborsClassifier(n_neighbors=7)
#clf6 = SVC(kernel='rbf', probability=True)
pca = decomposition.PCA(n_components=24)
# construct the pipeline
pipe = Pipeline([
('encoder', EncodeCategorical(dataset.categorical_features.keys())),
('imputer', ImputeCategorical(Fnames)),
('scalar', StandardScaler()),
('pca', pca),
('eclf_classifier', VotingClassifier(estimators=[('logistic', logistic), ('randomf', clf2), ('nb', clf3),
('decisiontree', clf4),('kn', clf5)],
voting='soft',
weights=[1, 4, 1, 1, 2])),
])
tuned_parameters = {
#'pca__n_components':[5, 7, 13, 20, 24],
#'eclf_classifier__logistic__fit_intercept':(False, True),
#'logistic__C':(0.1, 1, 10),
'eclf_classifier__logistic__class_weight':({0:.5, 1:.5},{0:.7, 1:.3},{0:.6, 1:.4},{0:.55, 1:.45},None),
#'randomf__max_depth': [3, None],
#'randomf__max_features': sp_randint(1, 11),
#'randomf__min_samples_split': sp_randint(1, 11),
#'randomf__min_samples_leaf': sp_randint(1, 11),
#'randomf__bootstrap': [True, False],
#'randomf__criterion': ['gini', 'entropy']
}
scores = ['precision', 'recall', 'f1']
for score in scores:
print("# Tuning hyper-parameters for %s" % score)
print()
clf = GridSearchCV(pipe, tuned_parameters, scoring='%s_weighted' % score)
clf.fit(dataset.data, yencode.transform(dataset.target))
print("Best parameters set found on development set:")
print()
print(clf.best_params_)
print()
print("Grid scores on development set:")
print()
for params, mean_score, scores in clf.grid_scores_:
print("%0.3f (+/-%0.03f) for %r"
% (mean_score, scores.std() * 2, params))
print()
print("Detailed classification report:")
print()
print("The model is trained on the full development set.")
print("The scores are computed on the full evaluation set.")
print()
print "Test under TEST DATASET"
y_true, y_pred = yencode.transform(dataset.target_test), clf.predict(dataset.data_test)
print(classification_report(y_true, y_pred))
print "Test under TRAIN DATASET"
y_true, y_pred = yencode.transform(dataset.target), clf.predict(dataset.data)
print(classification_report(y_true, y_pred))
print "Test under FULL IMBALANCED DATASET without new fit call"
y_true, y_pred = yencode.transform(full_data[label]), clf.predict(full_data[Fnames])
print(classification_report(y_true, y_pred))
```
## Tuning the weights in the VotingClassifier
```
from sklearn.base import BaseEstimator
from sklearn.base import ClassifierMixin
import numpy as np
import operator
class EnsembleClassifier(BaseEstimator, ClassifierMixin):
"""
Ensemble classifier for scikit-learn estimators.
Parameters
----------
clf : `iterable`
A list of scikit-learn classifier objects.
weights : `list` (default: `None`)
If `None`, the majority rule voting will be applied to the predicted class labels.
If a list of weights (`float` or `int`) is provided, the averaged raw probabilities (via `predict_proba`)
will be used to determine the most confident class label.
"""
def __init__(self, clfs, weights=None):
self.clfs = clfs
self.weights = weights
def fit(self, X, y):
"""
Fit the scikit-learn estimators.
Parameters
----------
X : numpy array, shape = [n_samples, n_features]
Training data
y : list or numpy array, shape = [n_samples]
Class labels
"""
for clf in self.clfs:
clf.fit(X, y)
def predict(self, X):
"""
Parameters
----------
X : numpy array, shape = [n_samples, n_features]
Returns
----------
maj : list or numpy array, shape = [n_samples]
Predicted class labels by majority rule
"""
self.classes_ = np.asarray([clf.predict(X) for clf in self.clfs])
if self.weights:
avg = self.predict_proba(X)
maj = np.apply_along_axis(lambda x: max(enumerate(x), key=operator.itemgetter(1))[0], axis=1, arr=avg)
else:
maj = np.asarray([np.argmax(np.bincount(self.classes_[:,c])) for c in range(self.classes_.shape[1])])
return maj
def predict_proba(self, X):
"""
Parameters
----------
X : numpy array, shape = [n_samples, n_features]
Returns
----------
avg : list or numpy array, shape = [n_samples, n_probabilities]
Weighted average probability for each class per sample.
"""
self.probas_ = [clf.predict_proba(X) for clf in self.clfs]
avg = np.average(self.probas_, axis=0, weights=self.weights)
return avg
y_true = yencode.transform(full_data[label])
df = pd.DataFrame(columns=('w1', 'w2', 'w3','w4','w5', 'mean', 'std'))
i = 0
for w1 in range(0,2):
for w2 in range(0,2):
for w3 in range(0,2):
for w4 in range(0,2):
for w5 in range(0,2):
if len(set((w1,w2,w3,w4,w5))) == 1: # skip if all weights are equal
continue
eclf = EnsembleClassifier(clfs=[clf1, clf2, clf3, clf4, clf5], weights=[w1,w2,w3,w4,w5])
eclf.fit(dataset.data, yencode.transform(dataset.target))
print "w1"
print w1
print "w2"
print w2
print "w3"
print w3
print "w4"
print w4
print "w5"
print w5
print "Test under TEST DATASET"
y_true, y_pred = yencode.transform(dataset.target_test), eclf.predict(dataset.data_test)
print(classification_report(y_true, y_pred))
print "Test under TRAIN DATASET"
y_true, y_pred = yencode.transform(dataset.target), eclf.predict(dataset.data)
print(classification_report(y_true, y_pred))
print "Test under FULL IMBALANCED DATASET without new fit call"
y_true, y_pred = yencode.transform(full_data[label]), eclf.predict(full_data[Fnames])
print(classification_report(y_true, y_pred))
#scores = cross_validation.cross_val_score(
# estimator=eclf,
# X=full_data[Fnames],
# y=y_true,
# cv=5,
# scoring='f1',
# n_jobs=1)
#df.loc[i] = [w1, w2, w3, w4, w5, scores.mean(), scores.std()]
i += 1
#print i
#print scores.mean()
#df.sort(columns=['mean', 'std'], ascending=False)
```
The pipeline first passes data through our encoder, then to the imputer, and finally to our classifier. In this case, I have chosen a `LogisticRegression`, a regularized linear model that is used to estimate a categorical dependent variable, much like the binary target we have in this case. We can then evaluate the model on the test data set using the same exact pipeline.
The last step is to save our model to disk for reuse later, with the `pickle` module:
# Model Pickle
```
import pickle
def dump_model(model, path='data', name='classifier.pickle'):
with open(os.path.join(path, name), 'wb') as f:
pickle.dump(model, f)
dump_model(lr)
import pickle
def dump_model(model, path='data', name='encodert.pickle'):
with open(os.path.join(path, name), 'wb') as f:
pickle.dump(model, f)
dump_model(yencode)
```
# SVMs
Support Vector Machines (SVM) uses points in transformed problem space that separates the classes into groups.
```
from sklearn.pipeline import Pipeline
from sklearn.metrics import mean_squared_error as mse
from sklearn.metrics import r2_score
from sklearn.svm import SVC
# we need to encode our target data as well.
yencode = LabelEncoder().fit(dataset.target)
# construct the pipeline
svm = Pipeline([
('encoder', EncodeCategorical(dataset.categorical_features.keys())),
('imputer', ImputeCategorical(Fnames)),
('scalar', StandardScaler()),
('classifier', SVC(kernel='linear'))
])
svm.fit(dataset.data, yencode.transform(dataset.target))
print "Test under TEST DATASET"
y_true, y_pred = yencode.transform(dataset.target_test), svm.predict(dataset.data_test)
print(classification_report(y_true, y_pred))
print "Test under TRAIN DATASET"
y_true, y_pred = yencode.transform(dataset.target), svm.predict(dataset.data)
print(classification_report(y_true, y_pred))
print "Test under FULL IMBALANCED DATASET without new fit call"
y_true, y_pred = yencode.transform(full_data[label]), svm.predict(full_data[Fnames])
print(classification_report(y_true, y_pred))
#kernels = ['linear', 'poly', 'rbf']
#for kernel in kernels:
# if kernel != 'poly':
# model = SVC(kernel=kernel)
# else:
# model = SVC(kernel=kernel, degree=3)
```
We can also dump meta information about the date and time your model was built, who built the model, etc. But we'll skip that step here.
## Model Operation
Now it's time to explore how to use the model. To do this, we'll create a simple function that gathers input from the user on the command line, and returns a prediction with the classifier model. Moreover, this function will load the pickled model into memory to ensure the latest and greatest saved model is what's being used.
```
def load_model(path='data/classifier.pickle'):
with open(path, 'rb') as f:
return pickle.load(f)
def predict(model, meta=meta):
data = {} # Store the input from the user
for column in meta['feature_names'][:-1]:
# Get the valid responses
valid = meta['categorical_features'].get(column)
# Prompt the user for an answer until good
while True:
val = "" + raw_input("enter {} >".format(column))
print val
# if valid and val not in valid:
# print "Not valid, choose one of {}".format(valid)
# else:
data[column] = val
break
# Create prediction and label
# yhat = model.predict(pd.DataFrame([data]))
yhat = model.predict_proba(pd.DataFrame([data]))
print yhat
return yencode.inverse_transform(yhat)
# Execute the interface
#model = load_model()
#predict(model)
#print data
#yhat = model.predict_proba(pd.DataFrame([data]))
```
## Conclusion
|
github_jupyter
|
# Regularization
Welcome to the second assignment of this week. Deep Learning models have so much flexibility and capacity that **overfitting can be a serious problem**, if the training dataset is not big enough. Sure it does well on the training set, but the learned network **doesn't generalize to new examples** that it has never seen!
**You will learn to:** Use regularization in your deep learning models.
Let's first import the packages you are going to use.
```
# import packages
import numpy as np
import matplotlib.pyplot as plt
from reg_utils import sigmoid, relu, plot_decision_boundary, initialize_parameters, load_2D_dataset, predict_dec
from reg_utils import compute_cost, predict, forward_propagation, backward_propagation, update_parameters
import sklearn
import sklearn.datasets
import scipy.io
from testCases import *
%matplotlib inline
plt.rcParams['figure.figsize'] = (7.0, 4.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'
```
**Problem Statement**: You have just been hired as an AI expert by the French Football Corporation. They would like you to recommend positions where France's goal keeper should kick the ball so that the French team's players can then hit it with their head.
<img src="images/field_kiank.png" style="width:600px;height:350px;">
<caption><center> <u> **Figure 1** </u>: **Football field**<br> The goal keeper kicks the ball in the air, the players of each team are fighting to hit the ball with their head </center></caption>
They give you the following 2D dataset from France's past 10 games.
```
train_X, train_Y, test_X, test_Y = load_2D_dataset()
```
Each dot corresponds to a position on the football field where a football player has hit the ball with his/her head after the French goal keeper has shot the ball from the left side of the football field.
- If the dot is blue, it means the French player managed to hit the ball with his/her head
- If the dot is red, it means the other team's player hit the ball with their head
**Your goal**: Use a deep learning model to find the positions on the field where the goalkeeper should kick the ball.
**Analysis of the dataset**: This dataset is a little noisy, but it looks like a diagonal line separating the upper left half (blue) from the lower right half (red) would work well.
You will first try a non-regularized model. Then you'll learn how to regularize it and decide which model you will choose to solve the French Football Corporation's problem.
## 1 - Non-regularized model
You will use the following neural network (already implemented for you below). This model can be used:
- in *regularization mode* -- by setting the `lambd` input to a non-zero value. We use "`lambd`" instead of "`lambda`" because "`lambda`" is a reserved keyword in Python.
- in *dropout mode* -- by setting the `keep_prob` to a value less than one
You will first try the model without any regularization. Then, you will implement:
- *L2 regularization* -- functions: "`compute_cost_with_regularization()`" and "`backward_propagation_with_regularization()`"
- *Dropout* -- functions: "`forward_propagation_with_dropout()`" and "`backward_propagation_with_dropout()`"
In each part, you will run this model with the correct inputs so that it calls the functions you've implemented. Take a look at the code below to familiarize yourself with the model.
```
def model(X, Y, learning_rate = 0.3, num_iterations = 30000, print_cost = True, lambd = 0, keep_prob = 1):
"""
Implements a three-layer neural network: LINEAR->RELU->LINEAR->RELU->LINEAR->SIGMOID.
Arguments:
X -- input data, of shape (input size, number of examples)
Y -- true "label" vector (1 for blue dot / 0 for red dot), of shape (output size, number of examples)
learning_rate -- learning rate of the optimization
num_iterations -- number of iterations of the optimization loop
print_cost -- If True, print the cost every 10000 iterations
lambd -- regularization hyperparameter, scalar
keep_prob - probability of keeping a neuron active during drop-out, scalar.
Returns:
parameters -- parameters learned by the model. They can then be used to predict.
"""
grads = {}
costs = [] # to keep track of the cost
m = X.shape[1] # number of examples
layers_dims = [X.shape[0], 20, 3, 1]
# Initialize parameters dictionary.
parameters = initialize_parameters(layers_dims)
# Loop (gradient descent)
for i in range(0, num_iterations):
# Forward propagation: LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID.
if keep_prob == 1:
a3, cache = forward_propagation(X, parameters)
elif keep_prob < 1:
a3, cache = forward_propagation_with_dropout(X, parameters, keep_prob)
# Cost function
if lambd == 0:
cost = compute_cost(a3, Y)
else:
cost = compute_cost_with_regularization(a3, Y, parameters, lambd)
# Backward propagation.
assert(lambd==0 or keep_prob==1) # it is possible to use both L2 regularization and dropout,
# but this assignment will only explore one at a time
if lambd == 0 and keep_prob == 1:
grads = backward_propagation(X, Y, cache)
elif lambd != 0:
grads = backward_propagation_with_regularization(X, Y, cache, lambd)
elif keep_prob < 1:
grads = backward_propagation_with_dropout(X, Y, cache, keep_prob)
# Update parameters.
parameters = update_parameters(parameters, grads, learning_rate)
# Print the loss every 10000 iterations
if print_cost and i % 10000 == 0:
print("Cost after iteration {}: {}".format(i, cost))
if print_cost and i % 1000 == 0:
costs.append(cost)
# plot the cost
plt.plot(costs)
plt.ylabel('cost')
plt.xlabel('iterations (x1,000)')
plt.title("Learning rate =" + str(learning_rate))
plt.show()
return parameters
```
Let's train the model without any regularization, and observe the accuracy on the train/test sets.
```
parameters = model(train_X, train_Y)
print ("On the training set:")
predictions_train = predict(train_X, train_Y, parameters)
print ("On the test set:")
predictions_test = predict(test_X, test_Y, parameters)
```
The train accuracy is 94.8% while the test accuracy is 91.5%. This is the **baseline model** (you will observe the impact of regularization on this model). Run the following code to plot the decision boundary of your model.
```
plt.title("Model without regularization")
axes = plt.gca()
axes.set_xlim([-0.75,0.40])
axes.set_ylim([-0.75,0.65])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)
```
The non-regularized model is obviously overfitting the training set. It is fitting the noisy points! Lets now look at two techniques to reduce overfitting.
## 2 - L2 Regularization
The standard way to avoid overfitting is called **L2 regularization**. It consists of appropriately modifying your cost function, from:
$$J = -\frac{1}{m} \sum\limits_{i = 1}^{m} \large{(}\small y^{(i)}\log\left(a^{[L](i)}\right) + (1-y^{(i)})\log\left(1- a^{[L](i)}\right) \large{)} \tag{1}$$
To:
$$J_{regularized} = \small \underbrace{-\frac{1}{m} \sum\limits_{i = 1}^{m} \large{(}\small y^{(i)}\log\left(a^{[L](i)}\right) + (1-y^{(i)})\log\left(1- a^{[L](i)}\right) \large{)} }_\text{cross-entropy cost} + \underbrace{\frac{1}{m} \frac{\lambda}{2} \sum\limits_l\sum\limits_k\sum\limits_j W_{k,j}^{[l]2} }_\text{L2 regularization cost} \tag{2}$$
Let's modify your cost and observe the consequences.
**Exercise**: Implement `compute_cost_with_regularization()` which computes the cost given by formula (2). To calculate $\sum\limits_k\sum\limits_j W_{k,j}^{[l]2}$ , use :
```python
np.sum(np.square(Wl))
```
Note that you have to do this for $W^{[1]}$, $W^{[2]}$ and $W^{[3]}$, then sum the three terms and multiply by $ \frac{1}{m} \frac{\lambda}{2} $.
```
# GRADED FUNCTION: compute_cost_with_regularization
def compute_cost_with_regularization(A3, Y, parameters, lambd):
"""
Implement the cost function with L2 regularization. See formula (2) above.
Arguments:
A3 -- post-activation, output of forward propagation, of shape (output size, number of examples)
Y -- "true" labels vector, of shape (output size, number of examples)
parameters -- python dictionary containing parameters of the model
Returns:
cost - value of the regularized loss function (formula (2))
"""
m = Y.shape[1]
W1 = parameters["W1"]
W2 = parameters["W2"]
W3 = parameters["W3"]
cross_entropy_cost = compute_cost(A3, Y) # This gives you the cross-entropy part of the cost
### START CODE HERE ### (approx. 1 line)
L2_regularization_cost = (lambd / (2 * m)) * (np.sum(np.square(W1)) + np.sum(np.square(W2)) + np.sum(np.square(W3)))
### END CODER HERE ###
cost = cross_entropy_cost + L2_regularization_cost
return cost
A3, Y_assess, parameters = compute_cost_with_regularization_test_case()
print("cost = " + str(compute_cost_with_regularization(A3, Y_assess, parameters, lambd = 0.1)))
```
**Expected Output**:
<table>
<tr>
<td>
**cost**
</td>
<td>
1.78648594516
</td>
</tr>
</table>
Of course, because you changed the cost, you have to change backward propagation as well! All the gradients have to be computed with respect to this new cost.
**Exercise**: Implement the changes needed in backward propagation to take into account regularization. The changes only concern dW1, dW2 and dW3. For each, you have to add the regularization term's gradient ($\frac{d}{dW} ( \frac{1}{2}\frac{\lambda}{m} W^2) = \frac{\lambda}{m} W$).
```
# GRADED FUNCTION: backward_propagation_with_regularization
def backward_propagation_with_regularization(X, Y, cache, lambd):
"""
Implements the backward propagation of our baseline model to which we added an L2 regularization.
Arguments:
X -- input dataset, of shape (input size, number of examples)
Y -- "true" labels vector, of shape (output size, number of examples)
cache -- cache output from forward_propagation()
lambd -- regularization hyperparameter, scalar
Returns:
gradients -- A dictionary with the gradients with respect to each parameter, activation and pre-activation variables
"""
m = X.shape[1]
(Z1, A1, W1, b1, Z2, A2, W2, b2, Z3, A3, W3, b3) = cache
dZ3 = A3 - Y
### START CODE HERE ### (approx. 1 line)
dW3 = 1./m * np.dot(dZ3, A2.T) + (lambd/m) * W3
### END CODE HERE ###
db3 = 1./m * np.sum(dZ3, axis=1, keepdims = True)
dA2 = np.dot(W3.T, dZ3)
dZ2 = np.multiply(dA2, np.int64(A2 > 0))
### START CODE HERE ### (approx. 1 line)
dW2 = 1./m * np.dot(dZ2, A1.T) + (lambd/m) * W2
### END CODE HERE ###
db2 = 1./m * np.sum(dZ2, axis=1, keepdims = True)
dA1 = np.dot(W2.T, dZ2)
dZ1 = np.multiply(dA1, np.int64(A1 > 0))
### START CODE HERE ### (approx. 1 line)
dW1 = 1./m * np.dot(dZ1, X.T) + (lambd/m) * W1
### END CODE HERE ###
db1 = 1./m * np.sum(dZ1, axis=1, keepdims = True)
gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3,"dA2": dA2,
"dZ2": dZ2, "dW2": dW2, "db2": db2, "dA1": dA1,
"dZ1": dZ1, "dW1": dW1, "db1": db1}
return gradients
X_assess, Y_assess, cache = backward_propagation_with_regularization_test_case()
grads = backward_propagation_with_regularization(X_assess, Y_assess, cache, lambd = 0.7)
print ("dW1 = "+ str(grads["dW1"]))
print ("dW2 = "+ str(grads["dW2"]))
print ("dW3 = "+ str(grads["dW3"]))
```
**Expected Output**:
<table>
<tr>
<td>
**dW1**
</td>
<td>
[[-0.25604646 0.12298827 -0.28297129]
[-0.17706303 0.34536094 -0.4410571 ]]
</td>
</tr>
<tr>
<td>
**dW2**
</td>
<td>
[[ 0.79276486 0.85133918]
[-0.0957219 -0.01720463]
[-0.13100772 -0.03750433]]
</td>
</tr>
<tr>
<td>
**dW3**
</td>
<td>
[[-1.77691347 -0.11832879 -0.09397446]]
</td>
</tr>
</table>
Let's now run the model with L2 regularization $(\lambda = 0.7)$. The `model()` function will call:
- `compute_cost_with_regularization` instead of `compute_cost`
- `backward_propagation_with_regularization` instead of `backward_propagation`
```
parameters = model(train_X, train_Y, lambd = 0.7)
print ("On the train set:")
predictions_train = predict(train_X, train_Y, parameters)
print ("On the test set:")
predictions_test = predict(test_X, test_Y, parameters)
```
Congrats, the test set accuracy increased to 93%. You have saved the French football team!
You are not overfitting the training data anymore. Let's plot the decision boundary.
```
plt.title("Model with L2-regularization")
axes = plt.gca()
axes.set_xlim([-0.75,0.40])
axes.set_ylim([-0.75,0.65])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)
```
**Observations**:
- The value of $\lambda$ is a hyperparameter that you can tune using a dev set.
- L2 regularization makes your decision boundary smoother. If $\lambda$ is too large, it is also possible to "oversmooth", resulting in a model with high bias.
**What is L2-regularization actually doing?**:
L2-regularization relies on the assumption that a model with small weights is simpler than a model with large weights. Thus, by penalizing the square values of the weights in the cost function you drive all the weights to smaller values. It becomes too costly for the cost to have large weights! This leads to a smoother model in which the output changes more slowly as the input changes.
<font color='blue'>
**What you should remember** -- the implications of L2-regularization on:
- The cost computation:
- A regularization term is added to the cost
- The backpropagation function:
- There are extra terms in the gradients with respect to weight matrices
- Weights end up smaller ("weight decay"):
- Weights are pushed to smaller values.
## 3 - Dropout
Finally, **dropout** is a widely used regularization technique that is specific to deep learning.
**It randomly shuts down some neurons in each iteration.** Watch these two videos to see what this means!
<!--
To understand drop-out, consider this conversation with a friend:
- Friend: "Why do you need all these neurons to train your network and classify images?".
- You: "Because each neuron contains a weight and can learn specific features/details/shape of an image. The more neurons I have, the more featurse my model learns!"
- Friend: "I see, but are you sure that your neurons are learning different features and not all the same features?"
- You: "Good point... Neurons in the same layer actually don't talk to each other. It should be definitly possible that they learn the same image features/shapes/forms/details... which would be redundant. There should be a solution."
!-->
<center>
<video width="620" height="440" src="images/dropout1_kiank.mp4" type="video/mp4" controls>
</video>
</center>
<br>
<caption><center> <u> Figure 2 </u>: Drop-out on the second hidden layer. <br> At each iteration, you shut down (= set to zero) each neuron of a layer with probability $1 - keep\_prob$ or keep it with probability $keep\_prob$ (50% here). The dropped neurons don't contribute to the training in both the forward and backward propagations of the iteration. </center></caption>
<center>
<video width="620" height="440" src="images/dropout2_kiank.mp4" type="video/mp4" controls>
</video>
</center>
<caption><center> <u> Figure 3 </u>: Drop-out on the first and third hidden layers. <br> $1^{st}$ layer: we shut down on average 40% of the neurons. $3^{rd}$ layer: we shut down on average 20% of the neurons. </center></caption>
When you shut some neurons down, you actually modify your model. The idea behind drop-out is that at each iteration, you train a different model that uses only a subset of your neurons. With dropout, your neurons thus become less sensitive to the activation of one other specific neuron, because that other neuron might be shut down at any time.
### 3.1 - Forward propagation with dropout
**Exercise**: Implement the forward propagation with dropout. You are using a 3 layer neural network, and will add dropout to the first and second hidden layers. We will not apply dropout to the input layer or output layer.
**Instructions**:
You would like to shut down some neurons in the first and second layers. To do that, you are going to carry out 4 Steps:
1. In lecture, we dicussed creating a variable $d^{[1]}$ with the same shape as $a^{[1]}$ using `np.random.rand()` to randomly get numbers between 0 and 1. Here, you will use a vectorized implementation, so create a random matrix $D^{[1]} = [d^{[1](1)} d^{[1](2)} ... d^{[1](m)}] $ of the same dimension as $A^{[1]}$.
2. Set each entry of $D^{[1]}$ to be 0 with probability (`1-keep_prob`) or 1 with probability (`keep_prob`), by thresholding values in $D^{[1]}$ appropriately. Hint: to set all the entries of a matrix X to 0 (if entry is less than 0.5) or 1 (if entry is more than 0.5) you would do: `X = (X < 0.5)`. Note that 0 and 1 are respectively equivalent to False and True.
3. Set $A^{[1]}$ to $A^{[1]} * D^{[1]}$. (You are shutting down some neurons). You can think of $D^{[1]}$ as a mask, so that when it is multiplied with another matrix, it shuts down some of the values.
4. Divide $A^{[1]}$ by `keep_prob`. By doing this you are assuring that the result of the cost will still have the same expected value as without drop-out. (This technique is also called inverted dropout.)
```
# GRADED FUNCTION: forward_propagation_with_dropout
def forward_propagation_with_dropout(X, parameters, keep_prob = 0.5):
"""
Implements the forward propagation: LINEAR -> RELU + DROPOUT -> LINEAR -> RELU + DROPOUT -> LINEAR -> SIGMOID.
Arguments:
X -- input dataset, of shape (2, number of examples)
parameters -- python dictionary containing your parameters "W1", "b1", "W2", "b2", "W3", "b3":
W1 -- weight matrix of shape (20, 2)
b1 -- bias vector of shape (20, 1)
W2 -- weight matrix of shape (3, 20)
b2 -- bias vector of shape (3, 1)
W3 -- weight matrix of shape (1, 3)
b3 -- bias vector of shape (1, 1)
keep_prob - probability of keeping a neuron active during drop-out, scalar
Returns:
A3 -- last activation value, output of the forward propagation, of shape (1,1)
cache -- tuple, information stored for computing the backward propagation
"""
np.random.seed(1)
# retrieve parameters
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
W3 = parameters["W3"]
b3 = parameters["b3"]
# LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID
Z1 = np.dot(W1, X) + b1
A1 = relu(Z1)
### START CODE HERE ### (approx. 4 lines) # Steps 1-4 below correspond to the Steps 1-4 described above.
D1 = np.random.rand(A1.shape[0], A1.shape[1]) # Step 1: initialize matrix D1 = np.random.rand(..., ...)
D1 = D1 < keep_prob # Step 2: convert entries of D1 to 0 or 1 (using keep_prob as the threshold)
A1 = A1 * D1 # Step 3: shut down some neurons of A1
A1 = A1 / keep_prob # Step 4: scale the value of neurons that haven't been shut down
### END CODE HERE ###
Z2 = np.dot(W2, A1) + b2
A2 = relu(Z2)
### START CODE HERE ### (approx. 4 lines)
D2 = np.random.rand(A2.shape[0], A2.shape[1]) # Step 1: initialize matrix D2 = np.random.rand(..., ...)
D2 = D2 < keep_prob # Step 2: convert entries of D2 to 0 or 1 (using keep_prob as the threshold)
A2 = A2 * D2 # Step 3: shut down some neurons of A2
A2 = A2 / keep_prob # Step 4: scale the value of neurons that haven't been shut down
### END CODE HERE ###
Z3 = np.dot(W3, A2) + b3
A3 = sigmoid(Z3)
cache = (Z1, D1, A1, W1, b1, Z2, D2, A2, W2, b2, Z3, A3, W3, b3)
return A3, cache
X_assess, parameters = forward_propagation_with_dropout_test_case()
A3, cache = forward_propagation_with_dropout(X_assess, parameters, keep_prob = 0.7)
print ("A3 = " + str(A3))
```
**Expected Output**:
<table>
<tr>
<td>
**A3**
</td>
<td>
[[ 0.36974721 0.00305176 0.04565099 0.49683389 0.36974721]]
</td>
</tr>
</table>
### 3.2 - Backward propagation with dropout
**Exercise**: Implement the backward propagation with dropout. As before, you are training a 3 layer network. Add dropout to the first and second hidden layers, using the masks $D^{[1]}$ and $D^{[2]}$ stored in the cache.
**Instruction**:
Backpropagation with dropout is actually quite easy. You will have to carry out 2 Steps:
1. You had previously shut down some neurons during forward propagation, by applying a mask $D^{[1]}$ to `A1`. In backpropagation, you will have to shut down the same neurons, by reapplying the same mask $D^{[1]}$ to `dA1`.
2. During forward propagation, you had divided `A1` by `keep_prob`. In backpropagation, you'll therefore have to divide `dA1` by `keep_prob` again (the calculus interpretation is that if $A^{[1]}$ is scaled by `keep_prob`, then its derivative $dA^{[1]}$ is also scaled by the same `keep_prob`).
```
# GRADED FUNCTION: backward_propagation_with_dropout
def backward_propagation_with_dropout(X, Y, cache, keep_prob):
"""
Implements the backward propagation of our baseline model to which we added dropout.
Arguments:
X -- input dataset, of shape (2, number of examples)
Y -- "true" labels vector, of shape (output size, number of examples)
cache -- cache output from forward_propagation_with_dropout()
keep_prob - probability of keeping a neuron active during drop-out, scalar
Returns:
gradients -- A dictionary with the gradients with respect to each parameter, activation and pre-activation variables
"""
m = X.shape[1]
(Z1, D1, A1, W1, b1, Z2, D2, A2, W2, b2, Z3, A3, W3, b3) = cache
dZ3 = A3 - Y
dW3 = 1./m * np.dot(dZ3, A2.T)
db3 = 1./m * np.sum(dZ3, axis=1, keepdims = True)
dA2 = np.dot(W3.T, dZ3)
### START CODE HERE ### (≈ 2 lines of code)
dA2 = dA2 * D2 # Step 1: Apply mask D2 to shut down the same neurons as during the forward propagation
dA2 = dA2 / keep_prob # Step 2: Scale the value of neurons that haven't been shut down
### END CODE HERE ###
dZ2 = np.multiply(dA2, np.int64(A2 > 0))
dW2 = 1./m * np.dot(dZ2, A1.T)
db2 = 1./m * np.sum(dZ2, axis=1, keepdims = True)
dA1 = np.dot(W2.T, dZ2)
### START CODE HERE ### (≈ 2 lines of code)
dA1 = dA1 * D1 # Step 1: Apply mask D1 to shut down the same neurons as during the forward propagation
dA1 = dA1 / keep_prob # Step 2: Scale the value of neurons that haven't been shut down
### END CODE HERE ###
dZ1 = np.multiply(dA1, np.int64(A1 > 0))
dW1 = 1./m * np.dot(dZ1, X.T)
db1 = 1./m * np.sum(dZ1, axis=1, keepdims = True)
gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3,"dA2": dA2,
"dZ2": dZ2, "dW2": dW2, "db2": db2, "dA1": dA1,
"dZ1": dZ1, "dW1": dW1, "db1": db1}
return gradients
X_assess, Y_assess, cache = backward_propagation_with_dropout_test_case()
gradients = backward_propagation_with_dropout(X_assess, Y_assess, cache, keep_prob = 0.8)
print ("dA1 = " + str(gradients["dA1"]))
print ("dA2 = " + str(gradients["dA2"]))
```
**Expected Output**:
<table>
<tr>
<td>
**dA1**
</td>
<td>
[[ 0.36544439 0. -0.00188233 0. -0.17408748]
[ 0.65515713 0. -0.00337459 0. -0. ]]
</td>
</tr>
<tr>
<td>
**dA2**
</td>
<td>
[[ 0.58180856 0. -0.00299679 0. -0.27715731]
[ 0. 0.53159854 -0. 0.53159854 -0.34089673]
[ 0. 0. -0.00292733 0. -0. ]]
</td>
</tr>
</table>
Let's now run the model with dropout (`keep_prob = 0.86`). It means at every iteration you shut down each neurons of layer 1 and 2 with 14% probability. The function `model()` will now call:
- `forward_propagation_with_dropout` instead of `forward_propagation`.
- `backward_propagation_with_dropout` instead of `backward_propagation`.
```
parameters = model(train_X, train_Y, keep_prob = 0.86, learning_rate = 0.3)
print ("On the train set:")
predictions_train = predict(train_X, train_Y, parameters)
print ("On the test set:")
predictions_test = predict(test_X, test_Y, parameters)
```
Dropout works great! The test accuracy has increased again (to 95%)! Your model is not overfitting the training set and does a great job on the test set. The French football team will be forever grateful to you!
Run the code below to plot the decision boundary.
```
plt.title("Model with dropout")
axes = plt.gca()
axes.set_xlim([-0.75,0.40])
axes.set_ylim([-0.75,0.65])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)
```
**Note**:
- A **common mistake** when using dropout is to use it both in training and testing. You should use dropout (randomly eliminate nodes) only in training.
- Deep learning frameworks like [tensorflow](https://www.tensorflow.org/api_docs/python/tf/nn/dropout), [PaddlePaddle](http://doc.paddlepaddle.org/release_doc/0.9.0/doc/ui/api/trainer_config_helpers/attrs.html), [keras](https://keras.io/layers/core/#dropout) or [caffe](http://caffe.berkeleyvision.org/tutorial/layers/dropout.html) come with a dropout layer implementation. Don't stress - you will soon learn some of these frameworks.
<font color='blue'>
**What you should remember about dropout:**
- Dropout is a regularization technique.
- You only use dropout during training. Don't use dropout (randomly eliminate nodes) during test time.
- Apply dropout both during forward and backward propagation.
- During training time, divide each dropout layer by keep_prob to keep the same expected value for the activations. For example, if keep_prob is 0.5, then we will on average shut down half the nodes, so the output will be scaled by 0.5 since only the remaining half are contributing to the solution. Dividing by 0.5 is equivalent to multiplying by 2. Hence, the output now has the same expected value. You can check that this works even when keep_prob is other values than 0.5.
## 4 - Conclusions
**Here are the results of our three models**:
<table>
<tr>
<td>
**model**
</td>
<td>
**train accuracy**
</td>
<td>
**test accuracy**
</td>
</tr>
<td>
3-layer NN without regularization
</td>
<td>
95%
</td>
<td>
91.5%
</td>
<tr>
<td>
3-layer NN with L2-regularization
</td>
<td>
94%
</td>
<td>
93%
</td>
</tr>
<tr>
<td>
3-layer NN with dropout
</td>
<td>
93%
</td>
<td>
95%
</td>
</tr>
</table>
Note that regularization hurts training set performance! This is because it limits the ability of the network to overfit to the training set. But since it ultimately gives better test accuracy, it is helping your system.
Congratulations for finishing this assignment! And also for revolutionizing French football. :-)
<font color='blue'>
**What we want you to remember from this notebook**:
- Regularization will help you reduce overfitting.
- Regularization will drive your weights to lower values.
- L2 regularization and Dropout are two very effective regularization techniques.
|
github_jupyter
|
## Yield Data
```
import pandas as pd
import numpy as np
import altair as alt
import os
pwd
vegetables = pd.read_csv('MichiganVegetableData.csv')
commodity_list1 = vegetables['Commodity'].unique().tolist()
for commodity in commodity_list1:
commoditydf = vegetables[vegetables['Commodity'] == commodity]
mi_commodity_YIELD = commoditydf[commoditydf['Data Item'].str.contains("YIELD")]
year_length = len(mi_commodity_YIELD.Year.unique().tolist())
if year_length > 15:
print(commodity)
```
## Cucumbers
```
mi_cucumbers = vegetables[vegetables['Commodity'] == 'CUCUMBERS']
mi_cucumbers['Data Item'].unique()
mi_cucumbers_yield = mi_cucumbers[mi_cucumbers['Data Item']
== 'CUCUMBERS, PROCESSING, PICKLES - YIELD, MEASURED IN TONS / ACRE']
mi_cucumbers_yield.Year.unique()
#mi_cucumbers_yield
#cucumbers_ordered
cucumbers_yield_stripped_data = mi_cucumbers_yield[['Year', 'Value']]
cucumbers_yield_stripped_data['Value'] = pd.to_numeric(
cucumbers_yield_stripped_data['Value'].str.replace(',', ''), errors='coerce')
cucumbers_yield_stripped_data
```
## Pumpkin
```
mi_pumpkins = vegetables[vegetables['Commodity'] == 'PUMPKINS']
mi_pumpkins_yield = mi_pumpkins[mi_pumpkins['Data Item'] == 'PUMPKINS - YIELD, MEASURED IN CWT / ACRE']
mi_pumpkins_yield.Year.unique()
pumpkins_yield_stripped_data = mi_pumpkins_yield[['Year', 'Value']]
pumpkins_yield_stripped_data
```
## Cabbage
```
mi_cabbage = vegetables[vegetables['Commodity'] == 'CABBAGE']
#mi_cabbage['Data Item'].unique()
mi_cabbage_yield = mi_cabbage[mi_cabbage['Data Item'] == 'CABBAGE, FRESH MARKET - YIELD, MEASURED IN CWT / ACRE']
#mi_cabbage_yield
mi_cabbage_yield.Year.unique()
cabbage_yield_stripped_data = mi_cabbage_yield[['Year', 'Value']]
cabbage_yield_stripped_data
```
## Potatoes
```
mi_potatoes = vegetables[vegetables['Commodity'] == 'POTATOES']
#mi_potatoes['Data Item'].unique()
potatoes_yield = mi_potatoes[mi_potatoes['Data Item'] == 'POTATOES - YIELD, MEASURED IN CWT / ACRE']
potatoes_yield.Year.unique()
potatoes_year_only = potatoes_yield[potatoes_yield['Period'] == 'YEAR']
potatoes_yield_stripped_data = potatoes_year_only[['Year', 'Value']]
potatoes_yield_stripped_data
```
## Squash
```
mi_squash = vegetables[vegetables['Commodity'] == 'SQUASH']
squash_yield = mi_squash[mi_squash['Data Item'] == "SQUASH - YIELD, MEASURED IN CWT / ACRE"]
squash_yield.Year.unique()
squash_yield_stripped_data = squash_yield[['Year', 'Value']]
squash_yield_stripped_data
```
## Carrots
```
mi_carrots = vegetables[vegetables['Commodity'] == 'CARROTS']
#mi_carrots['Data Item'].unique()
carrots_yield = mi_carrots[mi_carrots['Data Item'] == "CARROTS, FRESH MARKET - YIELD, MEASURED IN CWT / ACRE"]
carrots_yield.Year.unique()
carrots_yield_stripped_data = carrots_yield[['Year', 'Value']]
carrots_yield_stripped_data
```
## Celery
```
mi_celery = vegetables[vegetables['Commodity'] == 'CELERY']
#mi_celery['Data Item'].unique()
celery_yield = mi_celery[mi_celery['Data Item'] == "CELERY - YIELD, MEASURED IN CWT / ACRE"]
celery_yield.Year.unique()
celery_yield_stripped_data = celery_yield[['Year', 'Value']]
celery_yield_stripped_data
```
## Onions
```
mi_onions = vegetables[vegetables['Commodity'] == 'ONIONS']
#mi_onions['Data Item'].unique()
onion_yield = mi_onions[mi_onions['Data Item'] == "ONIONS, DRY, SUMMER, STORAGE - YIELD, MEASURED IN CWT / ACRE"]
onion_yield.Year.nunique()
onion_yield_stripped_data = onion_yield[['Year', 'Value']]
onion_yield_stripped_data
onion_yield_stripped_data.to_csv('onions.csv', index=False)
```
## Peppers
```
mi_peppers = vegetables[vegetables['Commodity'] == 'PEPPERS']
#mi_peppers['Data Item'].unique()
pepper_yield = mi_peppers[mi_peppers['Data Item'] == "PEPPERS, BELL - YIELD, MEASURED IN CWT / ACRE"]
pepper_yield.Year.unique()
peppers_yield_stripped_data = pepper_yield[['Year', 'Value']]
peppers_yield_stripped_data
peppers_yield_stripped_data.to_csv('peppers.csv', index=False)
```
## Corn
```
mi_corn = vegetables[vegetables['Commodity'] == 'SWEET CORN']
#mi_corn['Data Item'].unique()
corn_yield = mi_corn[mi_corn['Data Item'] == "SWEET CORN, FRESH MARKET - YIELD, MEASURED IN CWT / ACRE"]
corn_yield.Year.unique()
corn_yield_stripped_data = corn_yield[['Year', 'Value']]
corn_yield_stripped_data
corn_yield_stripped_data.to_csv('corn.csv', index=False)
```
## Tomatoes
```
mi_tomatoes = vegetables[vegetables['Commodity'] == 'TOMATOES']
#mi_tomatoes['Data Item'].unique()
tomatoes_yield = mi_tomatoes[mi_tomatoes['Data Item'] == "TOMATOES, IN THE OPEN, FRESH MARKET - YIELD, MEASURED IN CWT / ACRE"]
tomatoes_yield.Year.unique()
tomatoes_yield_stripped_data = tomatoes_yield[['Year', 'Value']]
tomatoes_yield_stripped_data
tomatoes_yield_stripped_data.to_csv('tomatoes.csv', index=False)
```
## Asparagus
```
mi_asparagus = vegetables[vegetables['Commodity'] == 'ASPARAGUS']
#mi_asparagus['Data Item'].unique()
asparagus_yield = mi_asparagus[mi_asparagus['Data Item'] == "ASPARAGUS - YIELD, MEASURED IN CWT / ACRE"]
asparagus_yield.Year.unique()
asparagus_yield_stripped_data = asparagus_yield[['Year', 'Value']]
asparagus_yield_stripped_data
asparagus_yield_stripped_data.to_csv('asparagus.csv', index=False)
```
## Merging DataFrames
```
#cucumbers carrots onions corn tomatoes asparagus
cucumbers_yield_stripped_data['Crop'] = 'Cucumbers'
cucumbers_yield_stripped_data
carrots_yield_stripped_data ['Crop'] = 'Carrots'
cucumbers_and_carrots = cucumbers_yield_stripped_data.merge(carrots_yield_stripped_data, on='Year')
carrots_cucumbers = pd.concat([carrots_yield_stripped_data, cucumbers_yield_stripped_data])
onion_yield_stripped_data['Crop'] = 'Onions'
corn_yield_stripped_data['Crop'] = 'Corn'
asparagus_yield_stripped_data['Crop'] = 'Asparagus'
tomatoes_yield_stripped_data['Crop'] = 'Tomatoes'
squash_yield_stripped_data['Crop'] = 'Squash'
celery_yield_stripped_data['Crop'] = 'Celery'
peppers_yield_stripped_data['Crop'] = 'Peppers'
pumpkins_yield_stripped_data['Crop'] = 'Pumpkins'
cabbage_yield_stripped_data['Crop'] = 'Cabbage'
carrots_cucumbers_asparagus = pd.concat([carrots_cucumbers, asparagus_yield_stripped_data])
carrots_cucumbers_asparagus
carrots_cucumbers_asparagus_tomatoes = pd.concat([carrots_cucumbers_asparagus, tomatoes_yield_stripped_data])
carrots_cucumbers_asparagus_tomatoes_onions = pd.concat([carrots_cucumbers_asparagus_tomatoes, onion_yield_stripped_data])
carrots_cucumbers_asparagus_tomatoes_onions.Crop.unique()
carrots_cucumbers_asparagus_tomatoes_onions_cabbage = pd.concat([carrots_cucumbers_asparagus_tomatoes_onions, cabbage_yield_stripped_data])
carrots_cucumbers_asparagus_tomatoes_onions_cabbage_pumpkins = pd.concat([carrots_cucumbers_asparagus_tomatoes_onions_cabbage, pumpkins_yield_stripped_data])
carrots_cucumbers_asparagus_tomatoes_onions_cabbage_pumpkins_squash = pd.concat([carrots_cucumbers_asparagus_tomatoes_onions_cabbage_pumpkins, squash_yield_stripped_data])
carrots_cucumbers_asparagus_tomatoes_onions_cabbage_pumpkins_squash_peppers = pd.concat([carrots_cucumbers_asparagus_tomatoes_onions_cabbage_pumpkins_squash, peppers_yield_stripped_data])
vegetable_yield = pd.concat([carrots_cucumbers_asparagus_tomatoes_onions_cabbage_pumpkins_squash_peppers, celery_yield_stripped_data])
from vega_datasets import data
source = data.stocks()
vegetable_yield
all_crops = alt.Chart(vegetable_yield).mark_line().encode(
x='Year:N',
y=alt.Y('Value:Q', title = 'Yield (CWT/ACRE)'),
color='Crop',
strokeDash='Crop',
)
asparagus_and_cucumbers = pd.concat([asparagus_yield_stripped_data, cucumbers_yield_stripped_data])
alt.Chart(asparagus_and_cucumbers).mark_line().encode(
x='Year:N',
y=alt.Y('Value:Q', title = 'Yield (CWT/ACRE)'),
color='Crop',
strokeDash='Crop',
)
crops=list(vegetable_yield['Crop'].unique())
crops.sort()
crops
selectCrops =alt.selection_multi(
fields=['Crop'],
init={"Crop":crops[0]},
# notice the binding_radio
bind=alt.binding_radio(options=crops, name="Crop"),#edit this line
name="Crop"
)
radio_chart = all_crops.encode(
opacity=alt.condition(selectCrops, alt.value(1.0), alt.value(0.0))
).add_selection(selectCrops)
radio_chart
hover = alt.selection_single(
fields=["Year"],
nearest=True,
on="mouseover",
empty="none",
clear="mouseout",
)
selectors = all_crops.mark_point(filled = True, color = 'grey', size = 100).encode(
x=alt.X(
'Year'),
opacity=alt.condition(hover, alt.value(1), alt.value(0)))
selectors
tooltips = alt.Chart(vegetable_yield).mark_rule(strokeWidth=2, color="grey").encode(
x='Year:T',
opacity=alt.condition(hover, alt.value(1), alt.value(0)),
tooltip=['Value:Q','Year:N', 'Crop']
).add_selection(hover)
tooltips
alt.layer(radio_chart, tooltips, selectors)
base = (
alt.Chart(vegetable_yield)
.encode(
x=alt.X(
"Year:T",
axis=alt.Axis(title=None, format=("%b %Y"), labelAngle=0, tickCount=6),
),
y=alt.Y(
"Value:Q", axis=alt.Axis(title='Yield (CWT/ACRE)')
),
)
.properties(width=500, height=400)
)
radio_select = alt.selection_multi(
fields=["Crop"], name="Crop",
)
crop_color_condition = alt.condition(
radio_select, alt.Color("Crop:N", legend=None), alt.value("lightgrey")
)
make_selector = (
alt.Chart(vegetable_yield)
.mark_circle(size=200)
.encode(
y=alt.Y("Crop:N", axis=alt.Axis(title="Pick Crop", titleFontSize=15)),
color=crop_color_condition,
)
.add_selection(radio_select)
)
highlight_crops = (
base.mark_line(strokeWidth=2)
.add_selection(radio_select)
.encode(color=crop_color_condition)
).properties(title="Crop Yield by Year")
# nearest = alt.selection(
# type="single", nearest=True, on="mouseover", fields=["Year"], empty="none"
# )
# # Transparent selectors across the chart. This is what tells us
# # the x-value of the cursor
# selectors = (
# alt.Chart(vegetable_yield)
# .mark_point()
# .encode(
# x="Year:T",
# opacity=alt.value(0),
# )
# .add_selection(nearest)
# )
# points = base.mark_point(size=5, dy=-10).encode(
# opacity=alt.condition(nearest, alt.value(1), alt.value(0))
# ).transform_filter(radio_select)
# tooltip_text = base.mark_text(
# align="left",
# dx=-60,
# dy=-15,
# fontSize=10,
# fontWeight="bold",
# lineBreak = "\n",
# ).encode(
# text=alt.condition(
# nearest,
# alt.Text("Value:Q", format=".2f"),
# alt.value(" "),
# ),
# ).transform_filter(radio_select)
# # Draw a rule at the location of the selection
# rules = (
# alt.Chart(vegetable_yield)
# .mark_rule(color="black", strokeWidth=2)
# .encode(
# x="Year:T",
# )
# .transform_filter(nearest)
# )
hover = alt.selection_single(
fields=["Year"],
nearest=True,
on="mouseover",
empty="none",
clear="mouseout",
)
tooltips2 = alt.Chart(vegetable_yield).transform_pivot(
"Crop", "Value", groupby=["Year"]
).mark_rule(strokeWidth=2, color="red").encode(
x='Year:T',
opacity=alt.condition(hover, alt.value(1), alt.value(0)),
tooltip=["Year", "Asparagus:Q", "Cabbage:Q", "Carrots:Q",
"Celery:Q", "Cucumbers:Q", "Onions:Q", "Peppers:Q", "Pumpkins:Q", "Squash:Q", "Tomatoes:Q"]
).add_selection(hover)
(make_selector | alt.layer(highlight_crops, tooltips2 ))
```
|
github_jupyter
|
# DiscreteDP Example: Water Management
**Daisuke Oyama**
*Faculty of Economics, University of Tokyo*
From Miranda and Fackler, <i>Applied Computational Economics and Finance</i>, 2002,
Section 7.6.5
```
%matplotlib inline
import itertools
import numpy as np
from scipy import sparse
import matplotlib.pyplot as plt
from quantecon.markov import DiscreteDP
maxcap = 30
n = maxcap + 1 # Number of states
m = n # Number of actions
a1, b1 = 14, 0.8
a2, b2 = 10, 0.4
F = lambda x: a1 * x**b1 # Benefit from irrigation
U = lambda c: a2 * c**b2 # Benefit from recreational consumption c = s - x
probs = [0.1, 0.2, 0.4, 0.2, 0.1]
supp_size = len(probs)
beta = 0.9
```
## Product formulation
```
# Reward array
R = np.empty((n, m))
for s, x in itertools.product(range(n), range(m)):
R[s, x] = F(x) + U(s-x) if x <= s else -np.inf
# Transition probability array
Q = np.zeros((n, m, n))
for s, x in itertools.product(range(n), range(m)):
if x <= s:
for j in range(supp_size):
Q[s, x, np.minimum(s-x+j, n-1)] += probs[j]
# Create a DiscreteDP
ddp = DiscreteDP(R, Q, beta)
# Solve the dynamic optimization problem (by policy iteration)
res = ddp.solve()
# Number of iterations
res.num_iter
# Optimal policy
res.sigma
# Optimal value function
res.v
# Simulate the controlled Markov chain for num_rep times
# and compute the average
init = 0
nyrs = 50
ts_length = nyrs + 1
num_rep = 10**4
ave_path = np.zeros(ts_length)
for i in range(num_rep):
path = res.mc.simulate(ts_length, init=init)
ave_path = (i/(i+1)) * ave_path + (1/(i+1)) * path
ave_path
# Stationary distribution of the Markov chain
stationary_dist = res.mc.stationary_distributions[0]
stationary_dist
# Plot sigma, v, ave_path, stationary_dist
hspace = 0.3
fig, axes = plt.subplots(2, 2, figsize=(12, 8+hspace))
fig.subplots_adjust(hspace=hspace)
axes[0, 0].plot(res.sigma, '*')
axes[0, 0].set_xlim(-1, 31)
axes[0, 0].set_ylim(-0.5, 5.5)
axes[0, 0].set_xlabel('Water Level')
axes[0, 0].set_ylabel('Irrigation')
axes[0, 0].set_title('Optimal Irrigation Policy')
axes[0, 1].plot(res.v)
axes[0, 1].set_xlim(0, 30)
y_lb, y_ub = 300, 700
axes[0, 1].set_ylim(y_lb, y_ub)
axes[0, 1].set_yticks(np.linspace(y_lb, y_ub, 5, endpoint=True))
axes[0, 1].set_xlabel('Water Level')
axes[0, 1].set_ylabel('Value')
axes[0, 1].set_title('Optimal Value Function')
axes[1, 0].plot(ave_path)
axes[1, 0].set_xlim(0, nyrs)
y_lb, y_ub = 0, 15
axes[1, 0].set_ylim(y_lb, y_ub)
axes[1, 0].set_yticks(np.linspace(y_lb, y_ub, 4, endpoint=True))
axes[1, 0].set_xlabel('Year')
axes[1, 0].set_ylabel('Water Level')
axes[1, 0].set_title('Average Optimal State Path')
axes[1, 1].bar(range(n), stationary_dist, align='center')
axes[1, 1].set_xlim(-1, n)
y_lb, y_ub = 0, 0.15
axes[1, 1].set_ylim(y_lb, y_ub+0.01)
axes[1, 1].set_yticks(np.linspace(y_lb, y_ub, 4, endpoint=True))
axes[1, 1].set_xlabel('Water Level')
axes[1, 1].set_ylabel('Probability')
axes[1, 1].set_title('Stationary Distribution')
plt.show()
```
## State-action pairs formulation
```
# Arrays of state and action indices
S = np.arange(n)
X = np.arange(m)
S_left = S.reshape(n, 1) - X.reshape(1, n)
s_indices, a_indices = np.where(S_left >= 0)
# Reward vector
S_left = S_left[s_indices, a_indices]
R = F(X[a_indices]) + U(S_left)
# Transition probability array
L = len(S_left)
Q = sparse.lil_matrix((L, n))
for i, s_left in enumerate(S_left):
for j in range(supp_size):
Q[i, np.minimum(s_left+j, n-1)] += probs[j]
# Create a DiscreteDP
ddp = DiscreteDP(R, Q, beta, s_indices, a_indices)
# Solve the dynamic optimization problem (by policy iteration)
res = ddp.solve()
# Number of iterations
res.num_iter
# Simulate the controlled Markov chain for num_rep times
# and compute the average
init = 0
nyrs = 50
ts_length = nyrs + 1
num_rep = 10**4
ave_path = np.zeros(ts_length)
for i in range(num_rep):
path = res.mc.simulate(ts_length, init=init)
ave_path = (i/(i+1)) * ave_path + (1/(i+1)) * path
# Stationary distribution of the Markov chain
stationary_dist = res.mc.stationary_distributions[0]
# Plot sigma, v, ave_path, stationary_dist
hspace = 0.3
fig, axes = plt.subplots(2, 2, figsize=(12, 8+hspace))
fig.subplots_adjust(hspace=hspace)
axes[0, 0].plot(res.sigma, '*')
axes[0, 0].set_xlim(-1, 31)
axes[0, 0].set_ylim(-0.5, 5.5)
axes[0, 0].set_xlabel('Water Level')
axes[0, 0].set_ylabel('Irrigation')
axes[0, 0].set_title('Optimal Irrigation Policy')
axes[0, 1].plot(res.v)
axes[0, 1].set_xlim(0, 30)
y_lb, y_ub = 300, 700
axes[0, 1].set_ylim(y_lb, y_ub)
axes[0, 1].set_yticks(np.linspace(y_lb, y_ub, 5, endpoint=True))
axes[0, 1].set_xlabel('Water Level')
axes[0, 1].set_ylabel('Value')
axes[0, 1].set_title('Optimal Value Function')
axes[1, 0].plot(ave_path)
axes[1, 0].set_xlim(0, nyrs)
y_lb, y_ub = 0, 15
axes[1, 0].set_ylim(y_lb, y_ub)
axes[1, 0].set_yticks(np.linspace(y_lb, y_ub, 4, endpoint=True))
axes[1, 0].set_xlabel('Year')
axes[1, 0].set_ylabel('Water Level')
axes[1, 0].set_title('Average Optimal State Path')
axes[1, 1].bar(range(n), stationary_dist, align='center')
axes[1, 1].set_xlim(-1, n)
y_lb, y_ub = 0, 0.15
axes[1, 1].set_ylim(y_lb, y_ub+0.01)
axes[1, 1].set_yticks(np.linspace(y_lb, y_ub, 4, endpoint=True))
axes[1, 1].set_xlabel('Water Level')
axes[1, 1].set_ylabel('Probability')
axes[1, 1].set_title('Stationary Distribution')
plt.show()
```
|
github_jupyter
|
# Setup IAM for Kinesis
```
import boto3
import sagemaker
import pandas as pd
sess = sagemaker.Session()
bucket = sess.default_bucket()
role = sagemaker.get_execution_role()
region = boto3.Session().region_name
sts = boto3.Session().client(service_name="sts", region_name=region)
iam = boto3.Session().client(service_name="iam", region_name=region)
```
# Create Kinesis Role
```
iam_kinesis_role_name = "DSOAWS_Kinesis"
iam_kinesis_role_passed = False
assume_role_policy_doc = {
"Version": "2012-10-17",
"Statement": [
{"Effect": "Allow", "Principal": {"Service": "kinesis.amazonaws.com"}, "Action": "sts:AssumeRole"},
{"Effect": "Allow", "Principal": {"Service": "firehose.amazonaws.com"}, "Action": "sts:AssumeRole"},
{"Effect": "Allow", "Principal": {"Service": "kinesisanalytics.amazonaws.com"}, "Action": "sts:AssumeRole"},
],
}
import json
import time
from botocore.exceptions import ClientError
try:
iam_role_kinesis = iam.create_role(
RoleName=iam_kinesis_role_name,
AssumeRolePolicyDocument=json.dumps(assume_role_policy_doc),
Description="DSOAWS Kinesis Role",
)
print("Role succesfully created.")
iam_kinesis_role_passed = True
except ClientError as e:
if e.response["Error"]["Code"] == "EntityAlreadyExists":
iam_role_kinesis = iam.get_role(RoleName=iam_kinesis_role_name)
print("Role already exists. That is OK.")
iam_kinesis_role_passed = True
else:
print("Unexpected error: %s" % e)
time.sleep(30)
iam_role_kinesis_name = iam_role_kinesis["Role"]["RoleName"]
print("Role Name: {}".format(iam_role_kinesis_name))
iam_role_kinesis_arn = iam_role_kinesis["Role"]["Arn"]
print("Role ARN: {}".format(iam_role_kinesis_arn))
account_id = sts.get_caller_identity()["Account"]
```
# Specify Stream Name
```
stream_name = "dsoaws-kinesis-data-stream"
```
# Specify Firehose Name
```
firehose_name = "dsoaws-kinesis-data-firehose"
```
# Specify Lambda Function Name
```
lambda_fn_name = "DeliverKinesisAnalyticsToCloudWatch"
```
# Create Policy
```
kinesis_policy_doc = {
"Version": "2012-10-17",
"Statement": [
{
"Effect": "Allow",
"Action": [
"s3:AbortMultipartUpload",
"s3:GetBucketLocation",
"s3:GetObject",
"s3:ListBucket",
"s3:ListBucketMultipartUploads",
"s3:PutObject",
],
"Resource": [
"arn:aws:s3:::{}/kinesis-data-firehose".format(bucket),
"arn:aws:s3:::{}/kinesis-data-firehose/*".format(bucket),
],
},
{
"Effect": "Allow",
"Action": ["logs:PutLogEvents"],
"Resource": ["arn:aws:logs:{}:{}:log-group:/*".format(region, account_id)],
},
{
"Effect": "Allow",
"Action": [
"kinesis:Get*",
"kinesis:DescribeStream",
"kinesis:Put*",
"kinesis:List*",
],
"Resource": ["arn:aws:kinesis:{}:{}:stream/{}".format(region, account_id, stream_name)],
},
{
"Effect": "Allow",
"Action": [
"firehose:*",
],
"Resource": ["arn:aws:firehose:{}:{}:deliverystream/{}".format(region, account_id, firehose_name)],
},
{
"Effect": "Allow",
"Action": [
"kinesisanalytics:*",
],
"Resource": ["*"],
},
{
"Sid": "UseLambdaFunction",
"Effect": "Allow",
"Action": ["lambda:InvokeFunction", "lambda:GetFunctionConfiguration"],
"Resource": "arn:aws:lambda:{}:{}:function:{}:$LATEST".format(region, account_id, lambda_fn_name),
},
{
"Effect": "Allow",
"Action": "iam:PassRole",
"Resource": "arn:aws:iam::*:role/service-role/kinesis-analytics*",
},
],
}
print(json.dumps(kinesis_policy_doc, indent=4, sort_keys=True, default=str))
```
# Update Policy
```
import time
response = iam.put_role_policy(
RoleName=iam_role_kinesis_name, PolicyName="DSOAWS_KinesisPolicy", PolicyDocument=json.dumps(kinesis_policy_doc)
)
time.sleep(30)
print(json.dumps(response, indent=4, sort_keys=True, default=str))
```
# Create AWS Lambda IAM Role
```
iam_lambda_role_name = "DSOAWS_Lambda"
iam_lambda_role_passed = False
assume_role_policy_doc = {
"Version": "2012-10-17",
"Statement": [
{"Effect": "Allow", "Principal": {"Service": "lambda.amazonaws.com"}, "Action": "sts:AssumeRole"},
{"Effect": "Allow", "Principal": {"Service": "kinesisanalytics.amazonaws.com"}, "Action": "sts:AssumeRole"},
],
}
import time
from botocore.exceptions import ClientError
try:
iam_role_lambda = iam.create_role(
RoleName=iam_lambda_role_name,
AssumeRolePolicyDocument=json.dumps(assume_role_policy_doc),
Description="DSOAWS Lambda Role",
)
print("Role succesfully created.")
iam_lambda_role_passed = True
except ClientError as e:
if e.response["Error"]["Code"] == "EntityAlreadyExists":
iam_role_lambda = iam.get_role(RoleName=iam_lambda_role_name)
print("Role already exists. This is OK.")
iam_lambda_role_passed = True
else:
print("Unexpected error: %s" % e)
time.sleep(30)
iam_role_lambda_name = iam_role_lambda["Role"]["RoleName"]
print("Role Name: {}".format(iam_role_lambda_name))
iam_role_lambda_arn = iam_role_lambda["Role"]["Arn"]
print("Role ARN: {}".format(iam_role_lambda_arn))
```
# Create AWS Lambda IAM Policy
```
lambda_policy_doc = {
"Version": "2012-10-17",
"Statement": [
{
"Sid": "UseLambdaFunction",
"Effect": "Allow",
"Action": ["lambda:InvokeFunction", "lambda:GetFunctionConfiguration"],
"Resource": "arn:aws:lambda:{}:{}:function:*".format(region, account_id),
},
{"Effect": "Allow", "Action": "cloudwatch:*", "Resource": "*"},
{
"Effect": "Allow",
"Action": "logs:CreateLogGroup",
"Resource": "arn:aws:logs:{}:{}:*".format(region, account_id),
},
{
"Effect": "Allow",
"Action": ["logs:CreateLogStream", "logs:PutLogEvents"],
"Resource": "arn:aws:logs:{}:{}:log-group:/aws/lambda/*".format(region, account_id),
},
],
}
print(json.dumps(lambda_policy_doc, indent=4, sort_keys=True, default=str))
import time
response = iam.put_role_policy(
RoleName=iam_role_lambda_name, PolicyName="DSOAWS_LambdaPolicy", PolicyDocument=json.dumps(lambda_policy_doc)
)
time.sleep(30)
print(json.dumps(response, indent=4, sort_keys=True, default=str))
```
# Store Variables for Next Notebooks
```
%store stream_name
%store firehose_name
%store iam_kinesis_role_name
%store iam_role_kinesis_arn
%store iam_lambda_role_name
%store iam_role_lambda_arn
%store lambda_fn_name
%store iam_kinesis_role_passed
%store iam_lambda_role_passed
%store
%%javascript
Jupyter.notebook.save_checkpoint()
Jupyter.notebook.session.delete();
```
|
github_jupyter
|
# Plot unit conversions
This notebook demonstrates some examples of different kinds of units, and the circumstances under which they are converted and displayed.
```
%matplotlib inline
import sys
import atomica as at
import matplotlib.pyplot as plt
import numpy as np
import sciris as sc
from IPython.display import display, HTML
testdir = at.parent_dir()
P = at.Project(framework='unit_demo_framework.xlsx',databook='unit_demo_databook.xlsx')
P.load_progbook('unit_demo_progbook.xlsx')
res = P.run_sim('default','default',at.ProgramInstructions(start_year=2018))
```
This test example has examples of parameters with different timescales, and different types of programs.
##### Parameters
- `recrate` - Duration in months
- `infdeath` - Weekly probability
- `susdeath` - Daily probability
- `foi` - Annual probability
```
d = at.PlotData(res,outputs=['recrate','infdeath','susdeath','foi','sus:inf','susdeath:flow','dead'],pops='adults')
at.plot_series(d,axis='pops');
```
Notice that parameters are plotted in their native units. For example, a probability per day is shown as probability per day, matching the numbers that were entered in the databook.
Aggregating these units without specifying the aggregation method will result in either integration or averaging as most appropriate for the units of the underlying quantity:
```
for output in ['recrate','infdeath','susdeath','foi','sus:inf','susdeath:flow','dead']:
d = at.PlotData(res,outputs=output,pops='adults',t_bins=10)
at.plot_bars(d);
```
Accumulation will result in the units and output name being updated appropriately:
```
d = at.PlotData(res,outputs='sus:inf',pops='adults',accumulate='integrate',project=P)
at.plot_series(d);
d = at.PlotData(res,outputs='sus',pops='adults',accumulate='integrate',project=P)
at.plot_series(d);
```
##### Programs
- `Risk avoidance` - Continuous
- `Harm reduction 1` - Continuous
- `Harm reduction 2` - Continuous
- `Treatment 1` - One-off
- `Treatment 2` - One-off
Programs with continuous coverage cover a certain number of people every year:
```
d = at.PlotData.programs(res,outputs='Risk avoidance',quantity='coverage_number')
at.plot_series(d);
```
Programs with one-off coverage cover a number of people at each time step. This is the number that gets returned by `Result.get_coverage()` but it is automatically annualized for plotting:
```
annual_coverage = res.model.progset.programs['Treatment 1'].spend_data.vals[0]/res.model.progset.programs['Treatment 1'].unit_cost.vals[0]
timestep_coverage = res.get_coverage('number')['Treatment 1'][0]
print('Annual coverage = %g, Timestep coverage = %g' % (annual_coverage, timestep_coverage))
d = at.PlotData.programs(res,outputs='Treatment 1',quantity='coverage_number')
at.plot_series(d)
```
These units are handled automatically when aggregating. For example, consider computing the number of people covered over a period of time:
```
d = at.PlotData.programs(res,outputs='Treatment 1',quantity='coverage_number',t_bins=[2000,2000.5])
at.plot_bars(d);
d = at.PlotData.programs(res,outputs='Treatment 1',quantity='coverage_number',t_bins=[2000,2002])
at.plot_bars(d);
d = at.PlotData.programs(res,outputs='Treatment 1',quantity='coverage_eligible',t_bins=[2000,2000.5])
at.plot_bars(d);
d = at.PlotData.programs(res,outputs='Treatment 1',quantity='coverage_number',t_bins=[2000,2002])
at.plot_bars(d);
```
|
github_jupyter
|
# Using the model and best-fit parameters from CenQue, we measure the following values:
The "true" SF fraction
$$f_{True SF}(\mathcal{M}_*)$$
The "true" SF SMF
$$\Phi_{True SF}(\mathcal{M}_*)$$
```
import numpy as np
import pickle
import util as UT
import observables as Obvs
from scipy.interpolate import interp1d
# plotting
import matplotlib.pyplot as plt
%matplotlib inline
from ChangTools.plotting import prettyplot
from ChangTools.plotting import prettycolors
prettyplot()
pretty_colors = prettycolors()
```
## import output from CenQue model with best-fit parameters
$$ F_{cenque} ({\bf \theta_{best-fit}}) $$
```
cenque = pickle.load(open(''.join([UT.dat_dir(), 'Descendant.ABC_posterior.RHOssfrfq_TinkerFq_Std.updated_prior.p']), 'rb'))
print cenque.keys()
for k in cenque.keys():
if cenque[k] is not None:
print k
print cenque[k][:10]
print cenque['sfr_class'][np.where(cenque['quenched'] != 0)]
print cenque['t_quench'][np.where(cenque['quenched'] != 0)]
print cenque['t_quench'][np.where((cenque['quenched'] != 0) & (cenque['sfr_class'] == 'star-forming'))]
# Star-forming only
isSF = np.where((cenque['sfr_class'] == 'star-forming') & (cenque['quenched'] == 0))
# quenching
#isQing = np.where((cenque['quenched'] == 0) & (cenque['t_quench'] != 999))
isQing = np.where((cenque['quenched'] == 0) & (cenque['sfr_class'] == 'quiescent'))
# quiescent
isQ = np.where(cenque['quenched'] != 0)
assert len(cenque['sfr_class']) == len(isSF[0]) + len(isQing[0]) + len(isQ[0])
```
# Lets examine SSFRs of each galaxy class
```
esef = Obvs.Ssfr()
bin_pssfr_tot, pssfr_tot = esef.Calculate(cenque['mass'], cenque['ssfr'])
bin_pssfr_sf, pssfr_sf = esef.Calculate(cenque['mass'][isSF], cenque['ssfr'][isSF])
bin_pssfr_qing, pssfr_qing = esef.Calculate(cenque['mass'][isQing], cenque['ssfr'][isQing])
bin_pssfr_q, pssfr_q = esef.Calculate(cenque['mass'][isQ], cenque['ssfr'][isQ])
fig = plt.figure(figsize=(20, 5))
bkgd = fig.add_subplot(111, frameon=False)
for i_m, mass_bin in enumerate(esef.mass_bins):
sub = fig.add_subplot(1, 4, i_m+1)
in_mbin = (cenque['mass'] >= mass_bin[0]) & (cenque['mass'] < mass_bin[1])
also_sf = (cenque['sfr_class'] == 'star-forming') & (cenque['quenched'] == 0)
also_q = cenque['quenched'] != 0
also_qing = (cenque['quenched'] == 0) & (cenque['sfr_class'] == 'quiescent')
N_tot = np.float(len(np.where(in_mbin)[0]))
f_sf = np.float(len(np.where(in_mbin & also_sf)[0])) / N_tot
f_q = np.float(len(np.where(in_mbin & also_q)[0])) / N_tot
f_qing = np.float(len(np.where(in_mbin & also_qing)[0])) / N_tot
assert f_sf + f_q + f_qing == 1.
# Star-forming
sub.fill_between(bin_pssfr_sf[i_m], f_sf * pssfr_sf[i_m], np.repeat(0., len(bin_pssfr_sf[i_m])),
color='b', edgecolor=None)
# Quiescent
sub.fill_between(bin_pssfr_q[i_m], f_q * pssfr_q[i_m], np.repeat(0., len(bin_pssfr_q[i_m])),
color='r', edgecolor=None)
# quienching
sub.fill_between(bin_pssfr_qing[i_m], f_qing * pssfr_qing[i_m] + f_q * pssfr_q[i_m] + f_sf * pssfr_sf[i_m],
f_q * pssfr_q[i_m] + f_sf * pssfr_sf[i_m],
color='g', edgecolor=None)
sub.plot(bin_pssfr_tot[i_m], pssfr_tot[i_m], color='k', lw=3, ls='--')
massbin_str = ''.join([r'$\mathtt{log \; M_{*} = [',
str(mass_bin[0]), ',\;', str(mass_bin[1]), ']}$'])
sub.text(-12., 1.4, massbin_str, fontsize=20)
# x-axis
sub.set_xlim([-13., -9.])
# y-axis
sub.set_ylim([0.0, 1.7])
sub.set_yticks([0.0, 0.5, 1.0, 1.5])
if i_m == 0:
sub.set_ylabel(r'$\mathtt{P(log \; SSFR)}$', fontsize=25)
else:
sub.set_yticklabels([])
bkgd.tick_params(labelcolor='none', top='off', bottom='off', left='off', right='off')
bkgd.set_xlabel(r'$\mathtt{log \; SSFR \;[yr^{-1}]}$', fontsize=25)
plt.show()
fig = plt.figure(figsize=(20, 5))
bkgd = fig.add_subplot(111, frameon=False)
for i_m, mass_bin in enumerate(esef.mass_bins):
sub = fig.add_subplot(1, 4, i_m+1)
in_mbin = (cenque['mass'] >= mass_bin[0]) & (cenque['mass'] < mass_bin[1])
also_sf = (cenque['sfr_class'] == 'star-forming') & (cenque['quenched'] == 0)
also_q = cenque['quenched'] != 0
also_qing = (cenque['quenched'] == 0) & (cenque['sfr_class'] == 'quiescent')
N_tot = np.float(len(np.where(in_mbin)[0]))
f_sf = np.float(len(np.where(in_mbin & also_sf)[0])) / N_tot
f_q = np.float(len(np.where(in_mbin & also_q)[0])) / N_tot
f_qing = np.float(len(np.where(in_mbin & also_qing)[0])) / N_tot
assert f_sf + f_q + f_qing == 1.
# quienching
sub.fill_between(bin_pssfr_qing[i_m], f_qing * pssfr_qing[i_m], np.zeros(len(bin_pssfr_qing[i_m])),
color='g', edgecolor=None)
# Star-forming
sub.fill_between(bin_pssfr_sf[i_m], f_sf * pssfr_sf[i_m] + f_qing * pssfr_qing[i_m], f_qing * pssfr_qing[i_m],
color='b', edgecolor=None)
# Quiescent
sub.fill_between(bin_pssfr_q[i_m], f_q * pssfr_q[i_m] + f_sf * pssfr_sf[i_m] + f_qing * pssfr_qing[i_m],
f_sf * pssfr_sf[i_m] + f_qing * pssfr_qing[i_m],
color='r', edgecolor=None)
sub.plot(bin_pssfr_tot[i_m], pssfr_tot[i_m], color='k', lw=3, ls='--')
massbin_str = ''.join([r'$\mathtt{log \; M_{*} = [',
str(mass_bin[0]), ',\;', str(mass_bin[1]), ']}$'])
sub.text(-12., 1.4, massbin_str, fontsize=20)
# x-axis
sub.set_xlim([-13., -9.])
# y-axis
sub.set_ylim([0.0, 1.7])
sub.set_yticks([0.0, 0.5, 1.0, 1.5])
if i_m == 0:
sub.set_ylabel(r'$\mathtt{P(log \; SSFR)}$', fontsize=25)
else:
sub.set_yticklabels([])
bkgd.tick_params(labelcolor='none', top='off', bottom='off', left='off', right='off')
bkgd.set_xlabel(r'$\mathtt{log \; SSFR \;[yr^{-1}]}$', fontsize=25)
plt.show()
```
## Calculate $f_{True SF}$
```
effq = Obvs.Fq()
theta_sfms = {'name': 'linear', 'zslope': 1.14}
qf = effq.Calculate(mass=cenque['mass'], sfr=cenque['sfr'], z=UT.z_nsnap(1), theta_SFMS=theta_sfms)
# calculate true SF fraction
m_low = np.arange(8.0, 12.0, 0.1)
m_high = m_low + 0.1
m_mid, f_truesf = np.zeros(len(m_low)), np.zeros(len(m_low))
also_sf = (cenque['sfr_class'] == 'star-forming') & (cenque['quenched'] == 0)
for i_m in range(len(m_low)):
in_mbin = (cenque['mass'] >= m_low[i_m]) & (cenque['mass'] < m_high[i_m])
N_tot = np.float(len(np.where(in_mbin)[0]))
N_sf = np.float(len(np.where(in_mbin & also_sf)[0]))
m_mid[i_m] = 0.5 * (m_low[i_m] + m_high[i_m])
f_truesf[i_m] = N_sf/N_tot
```
### Comparison of $f_{SF} = 1 - f_Q$ versus $f_{True SF}$
```
fig = plt.figure(figsize=(7,7))
sub = fig.add_subplot(111)
sub.plot(qf[0], 1. - qf[1], c='k', ls='--', lw=2, label='$f_{SF} = 1 - f_Q$')
sub.plot(m_mid, f_truesf, c='b', ls='-', lw=2, label='$f_{True\;SF}$')
f_truesf_interp = interp1d(m_mid, f_truesf)
sub.fill_between(qf[0], (1. - qf[1]) - f_truesf_interp(qf[0]), np.zeros(len(qf[0])), color='k', edgecolor=None, label='$\Delta$')
# x-axis
sub.set_xlim([9., 12.])
sub.set_xlabel('Stellar Mass $(\mathcal{M}_*)$', fontsize=25)
sub.set_ylim([0., 1.])
sub.set_ylabel('Star-forming Fraction', fontsize=25)
sub.legend(loc = 'upper right', prop={'size': 25})
```
## Calculate SMF of (only) star-forming galaxies
```
# total SMF
smf_tot = Obvs.getMF(cenque['mass'])
# SMF of true SF
smf_truesf = Obvs.getMF(cenque['mass'][isSF])
# SMF of galaxies *classified* as SF
gal_class = effq.Classify(cenque['mass'], cenque['sfr'], UT.z_nsnap(1), theta_SFMS=theta_sfms)
smf_sfclass = Obvs.getMF(cenque['mass'][np.where(gal_class == 'star-forming')])
fig = plt.figure(figsize=(7,7))
sub = fig.add_subplot(111)
sub.plot(smf_tot[0], smf_tot[1], c='k', lw=3, label='Total')
sub.plot(smf_truesf[0], smf_truesf[1], c='b', lw=3, label='True SF')
sub.plot(smf_sfclass[0], smf_sfclass[1], c='k', ls='--')
sub.set_xlim([9., 12.])
sub.set_xlabel('Stellar Masses $(\mathcal{M}_*)$', fontsize=25)
sub.set_ylim([1e-5, 10**-1.5])
sub.set_yscale('log')
sub.set_ylabel('$\Phi$', fontsize=25)
```
|
github_jupyter
|
```
import os
import random
import math
import time
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
from tensorflow.keras.optimizers import Adam
from tensorflow.keras import Sequential
from tensorflow.keras.layers import Dense, Conv1D, MaxPooling1D, Flatten, concatenate, Conv2D, MaxPooling2D
from libs.utils import *
from libs.generate_boxes import *
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '0'
tf.get_logger().setLevel('INFO')
tf.keras.backend.floatx()
plt.style.use('fivethirtyeight')
plt.rcParams['figure.figsize'] = (20,10)
class StateCNN(tf.keras.Model):
def __init__(self, state_size, selected_size, remain_size):
super(StateCNN, self).__init__()
self.case_cnn1 = Conv2D(filters=16, kernel_size=3, activation='relu',
padding='valid', input_shape = selected_size)
self.case_cnn2 = Conv2D(filters=16, kernel_size=3, activation='relu',
padding='valid')
self.select_cnn1 = Conv2D(filters=16, kernel_size=3, activation='relu',
padding='valid', input_shape=selected_size)
self.select_cnn2 = Conv2D(filters=16, kernel_size=3, activation='relu',
padding='valid')
self.remain_cnn1 = Conv1D(filters=32, kernel_size=2, activation='relu',
padding='same', input_shape = remain_size)
self.remain_cnn2 = Conv1D(filters=32, kernel_size=2, activation='relu',
padding='same')
def call(self, cb_list):
c,s,r = cb_list[0], cb_list[1], cb_list[2]
c = self.case_cnn1(c)
c = MaxPooling2D(pool_size=(2,2))(c)
c = self.case_cnn2(c)
c = MaxPooling2D(pool_size=(2,2))(c)
c = Flatten()(c)
s = self.select_cnn1(s)
s = MaxPooling2D(pool_size=(2,2))(s)
s = self.select_cnn2(s)
s = MaxPooling2D(pool_size=(2,2))(s)
s = Flatten()(s)
r = self.remain_cnn1(r)
r = self.remain_cnn2(r)
r = MaxPooling1D(pool_size=1)(r)
r = Flatten()(r)
x = concatenate([c,s,r])
return x
class Actor(tf.keras.Model):
def __init__(self, output_size):
super(Actor, self).__init__()
self.d1 = Dense(2048, activation='relu')
self.d2 = Dense(1024, activation='relu')
self.actor = Dense(output_size)
def call(self, inputs):
x = self.d1(inputs)
x = self.d2(x)
actor = self.actor(x)
return actor
class Critic(tf.keras.Model):
def __init__(self, output_size):
super(Critic, self).__init__()
self.d1 = Dense(2048, activation='relu')
self.d2 = Dense(1024, activation='relu')
self.critic = Dense(output_size)
def call(self, inputs):
x = self.d1(inputs)
x = self.d2(x)
critic = self.critic(x)
return critic
class ActorCriticAgent:
def __init__(self, L=20, B=20, H=20, n_remains=5, lr=1e-8, gamma=0.99):
self.state_size = (L,B,1)
self.selected_size = (L,B,H)
self.remain_size = (n_remains, 3)
self.output_size = 1
self.lr = lr
self.gamma = gamma
self.state_cnn = StateCNN(self.state_size, self.selected_size, self.remain_size)
self.actor = Actor(self.output_size)
self.critic = Critic(self.output_size)
self.actor_optimizer = Adam(learning_rate=self.lr)
self.critic_optimizer = Adam(learning_rate=self.lr)
self.avg_actor_loss = 0
self.avg_critic_loss = 0
def get_action(self, state, s_locs, r_boxes):
sc = self.state_cnn([state, s_locs, r_boxes])
actor = self.actor(sc)
argmax_idx = np.where(actor == tf.math.reduce_max(actor))
action_idx = argmax_idx[0][0]
return action_idx
def actor_loss():
pass
def critic_loss():
pass
def train():
state_params = self.
actor_params = self.
critic_params = self.
for
with tf.GradientTape() as tape:
state_cnn = self.state_cnn([state, s_boxes, remains])
actor = self.actor()
values = self.critic()
next_values = self.critic()
expect_reward =
actor_loss =
critic_loss =
self.avg_actor_loss +=
self.avg_critic_loss +=
actor_grads = actor_tape.gradient(actor_loss, actor_params)
critic_grads = critic_tape.gradient(critic_loss, critic_params)
max_episode = 2000
N_MDD = 5
K = 3
N_Candidates = 4
boxes, gt_pos = generation_3dbox_random(case_size=[[20,20,20,]],min_s = 1,
N_mdd = N_MDD)
boxes = boxes[0]
gt_pos = gt_pos[0]
num_max_boxes = len(boxes)
num_max_remain = num_max_boxes - K
num_max_boxes, num_max_remain
env = Bpp3DEnv()
agent = ActorCriticAgent(L=20, B=20, H=20, n_remains=num_max_remain,
lr=1e-6, gamma=0.99)
frac_l, avg_actor_loss, avg_critic_loss = [],[],[]
for episode in range(max_episode):
st = time.time()
env.reset()
done = False
step = 0
used_boxes, pred_pos = [], []
r_boxes = np.array(np.array(boxes).copy())
while not done:
state = env.container.copy()
k = min(K, len(r_boxes))
step += 1
selected = cbn_select_boxes(r_boxes[:N_Candidates], k)
s_order = get_selected_order(selected, k)
state_h = env.update_h().copy()
in_state, in_r_boxes = raw_to_input(state_h, s_order, r_boxes, num_max_remain)
s_loc_c, pred_pos_c, used_boxes_c, next_state_c , num_loaded_box_c, next_cube_c = get_selected_location(s_order, pred_pos, used_boxes, state)
action_idx = agent.get_action(in_state, s_loc_c, in_r_boxes)
num_loaded_box = num_loaded_box_c[action_idx]
if num_loaded_box != 0:
new_used_boxes = get_remain(used_boxes, used_boxes_c[action_idx])
r_boxes = get_remain(new_used_boxes, r_boxes)
used_boxes = used_boxes_c[action_idx]
pred_pos = pred_pos_c[action_idx]
env.convert_state(next_cube_c[action_idx])
if len(r_boxes) == 0:
done = True
else:
r_boxes = get_remain(s_order[action_idx], r_boxes)
if len(r_boxes) == 0:
done = True
if done:
avg_frac = 0 if len(frac_l) == 0 else np.mean(frac_l)
frac_l.append(env.terminal_reward())
agent.train_model()
avg_actor_loss.append(agent.avg_actor_loss / float(step))
avg_critic_loss.append(agent.avg_critic_loss / float(step))
log = "=====episode: {:5d} | ".format(e)
log += "env.terminal_reward(): {:.3f} | ".format(env.terminal_reward())
log += "actor avg loss : {:6f} ".format(agent.avg_actor_loss / float(step))
log += "critic avg loss : {:6f} ".format(agent.avg_critic_loss / float(step))
log += "time: {:.3f}".format(time.time()-st)
print(log)
agent.avg_actor_loss, agent.avg_critic_loss = 0, 0
env.reset()
done = False
step = 0
r_boxes = np.array(np.array(boxes).copy())
state = env.container.copy()
k = min(K, len(r_boxes))
step += 1
vis_box(boxes, gt_pos)
selected = cbn_select_boxes(r_boxes[:N_Candidates], k)
selected
s_order = get_selected_order(selected, k)
s_order
state_h = env.update_h().copy()
in_state, in_r_boxes = raw_to_input(state_h, s_order, r_boxes, num_max_remain)
pred_pos, used_boxes = [], []
s_loc_c, pred_pos_c, used_boxes_c, next_state_c, num_loaded_box_c, next_cube_c = get_selected_location(s_order, pred_pos, used_boxes, state)
action_idx = agent.get_action(in_state, s_loc_c, in_r_boxes)
action_idx
num_loaded_box_c
num_loaded_box = num_loaded_box_c[action_idx]
num_loaded_box
new_used_boxes = get_remain(used_boxes, used_boxes_c[action_idx])
new_used_boxes
r_boxes
r_boxes = get_remain(new_used_boxes, r_boxes)
r_boxes
used_boxes = used_boxes_c[action_idx]
pred_pos = pred_pos_c[action_idx]
env.convert_state(next_cube_c[action_idx])
t_state = env.container.copy()
t_state_h = env.container_h.copy()
k = min
```
|
github_jupyter
|
# What _projects_ am I a member of?
### Overview
There are a number of API calls related to projects. Here we focus on listing projects. As with any **list**-type call, we will get minimal information about each project. There are two versions of this call:
1. (default) **paginated** call that will return 50 projects
2. **all-records** call that will page through and return all projects
### Prerequisites
1. You need to be a member (or owner) of _at least one_ project.
2. You need your _authentication token_ and the API needs to know about it. See <a href="Setup_API_environment.ipynb">**Setup_API_environment.ipynb**</a> for details.
## Imports
We import the _Api_ class from the official sevenbridges-python bindings below.
```
import sevenbridges as sbg
```
## Initialize the object
The `Api` object needs to know your **auth\_token** and the correct path. Here we assume you are using the credentials file in your home directory. For other options see <a href="Setup_API_environment.ipynb">Setup_API_environment.ipynb</a>
```
# [USER INPUT] specify credentials file profile {cgc, sbg, default}
prof = 'default'
config_file = sbg.Config(profile=prof)
api = sbg.Api(config=config_file)
```
## Get _some_ projects
We will start with the basic list call. A **list**-call for projects returns the following *attributes*:
* **id** _Unique_ identifier for the project, generated based on Project Name
* **name** Name of project specified by the user, maybe _non-unique_
* **href** Address<sup>1</sup> of the project.
A **detail**-call for projects returns the following *attributes*:
* **description** The user specified project description
* **id** _Unique_ identifier for the project, generated based on Project Name
* **name** Name of project specified by the user, maybe _non-unique_
* **href** Address<sup>1</sup> of the project.
* **tags** List of tags
* **created_on** Project creation time
* **modified_on** Project modification time
* **created_by** User that created the project
* **root_folder** ID of the root folder for that project
* **billing_group** ID of the billing group for the project
* **settings** Dictionary with project settings for storage and task execution
All list API calls will feature pagination, by _default_ 50 items will be returned. We will also show how to specify a different limit and page forward and backwards.
<sup>1</sup> This is the address where, by using API you can get this resource
```
# list (up to) 50 (this is the default for 'limit') projects
my_projects = api.projects.query()
print(' List of project ids and names:')
for project in my_projects:
print('{} \t {}'.format(project.id, project.name))
# use a short query to highlight pagination
my_projects = api.projects.query(limit=3)
print(' List of first 3 project ids and names:')
for project in my_projects:
print('{} \t {}'.format(project.id, project.name))
# method to retrieve the next page of results
next_page_of_projects = my_projects.next_page()
print('\n List of next 3 project ids and names:')
for project in next_page_of_projects:
print('{} \t {}'.format(project.id, project.name))
```
#### Note
For the pagination above, we used the **.next_page()** and could have also used the **.prior_page()** methods. These will return another list with an limit equal to the prior call and a offset based on the prior call
## Get _all_ projects
It's probably most useful to know all of your projects. Regardless of the query limit, the project object knows the actual total number of projects. We only need to use the **.all** attribute to get all projects.
```
existing_projects = my_projects.all()
print(' List of all project ids and names:')
for project in existing_projects:
print('{} \t {}'.format(project.id, project.name))
```
### Note
Each time you do **anything** with this _generator object_, it will become exhausted. The next call will be an empty list
```
# NOTE, after each time you operate on the existing_projects generator object,
# it will become an empty list
existing_projects = my_projects.all()
print(existing_projects)
print('\n For the first list() operation, there are %i projects in the generator' \
% (len(list(existing_projects))))
print(' For the next list() operation, there are %i projects in the generator' % \
(len(list(existing_projects))))
```
## Additional Information
Detailed documentation of this particular REST architectural style request is available [here](http://docs.sevenbridges.com/docs/list-all-your-projects)
|
github_jupyter
|
```
import numpy as np
import pprint
import sys
if "../" not in sys.path:
sys.path.append("../")
from lib.envs.gridworld import GridworldEnv
pp = pprint.PrettyPrinter(indent=2)
env = GridworldEnv()
def value_iteration(env, theta=0.0001, discount_factor=1.0):
"""
Value Iteration Algorithm.
Args:
env: OpenAI env. env.P represents the transition probabilities of the environment.
env.P[s][a] is a list of transition tuples (prob, next_state, reward, done).
env.nS is a number of states in the environment.
env.nA is a number of actions in the environment.
theta: We stop evaluation once our value function change is less than theta for all states.
discount_factor: Gamma discount factor.
Returns:
A tuple (policy, V) of the optimal policy and the optimal value function.
"""
V = np.zeros(env.nS)
policy = np.zeros([env.nS, env.nA])
# Implement!
# policy evaluation using Bellman optimality equation
while True:
threshold = 0
for s in range(env.nS):
action_value_list = []
old_value = V[s]
for action, action_prob in enumerate(policy[s]):
state_action_value = 0
for prob, next_state, reward, done in env.P[s][action]:
state_action_value += prob * (reward + discount_factor * V[next_state])
action_value_list.append(state_action_value)
# Bellman optimality equation
V[s] = np.max(action_value_list)
threshold = max(threshold, np.abs(old_value-V[s]))
if threshold < theta:
break
# Policy improvement
for s in range(env.nS):
action_value_list = []
for action, action_prob in enumerate(policy[s]):
state_action_value = 0
for prob, next_state, reward, done in env.P[s][action]:
state_action_value += prob * (reward + discount_factor * V[next_state])
action_value_list.append(state_action_value)
greedy_action = np.argmax(action_value_list)
policy[s] = np.eye(env.nA)[greedy_action]
return policy, V
policy, v = value_iteration(env)
print("Policy Probability Distribution:")
print(policy)
print("")
print("Reshaped Grid Policy (0=up, 1=right, 2=down, 3=left):")
print(np.reshape(np.argmax(policy, axis=1), env.shape))
print("")
print("Value Function:")
print(v)
print("")
print("Reshaped Grid Value Function:")
print(v.reshape(env.shape))
print("")
# Test the value function
expected_v = np.array([ 0, -1, -2, -3, -1, -2, -3, -2, -2, -3, -2, -1, -3, -2, -1, 0])
np.testing.assert_array_almost_equal(v, expected_v, decimal=2)
```
|
github_jupyter
|
#### New to Plotly?
Plotly's Python library is free and open source! [Get started](https://plot.ly/python/getting-started/) by downloading the client and [reading the primer](https://plot.ly/python/getting-started/).
<br>You can set up Plotly to work in [online](https://plot.ly/python/getting-started/#initialization-for-online-plotting) or [offline](https://plot.ly/python/getting-started/#initialization-for-offline-plotting) mode, or in [jupyter notebooks](https://plot.ly/python/getting-started/#start-plotting-online).
<br>We also have a quick-reference [cheatsheet](https://images.plot.ly/plotly-documentation/images/python_cheat_sheet.pdf) (new!) to help you get started!
#### Version Check
Plotly's python package is updated frequently. Run `pip install plotly --upgrade` to use the latest version.
```
import plotly
plotly.__version__
```
#### What is BigQuery?
It's a service by Google, which enables analysis of massive datasets. You can use the traditional SQL-like language to query the data. You can host your own data on BigQuery to use the super fast performance at scale.
#### Google BigQuery Public Datasets
There are [a few datasets](https://cloud.google.com/bigquery/public-data/) stored in BigQuery, available for general public to use. Some of the publicly available datasets are:
- Hacker News (stories and comments)
- USA Baby Names
- GitHub activity data
- USA disease surveillance
We will use the [Hacker News](https://cloud.google.com/bigquery/public-data/hacker-news) dataset for our analysis.
#### Imports
```
import plotly.plotly as py
import plotly.graph_objs as go
import plotly.figure_factory as ff
import pandas as pd
from pandas.io import gbq # to communicate with Google BigQuery
```
#### Prerequisites
You need to have the following libraries:
* [python-gflags](http://code.google.com/p/python-gflags/)
* httplib2
* google-api-python-client
#### Create Project
A project can be created on the [Google Developer Console](https://console.developers.google.com/iam-admin/projects).
#### Enable BigQuery API
You need to activate the BigQuery API for the project.

You will have find the `Project ID` for your project to get the queries working.
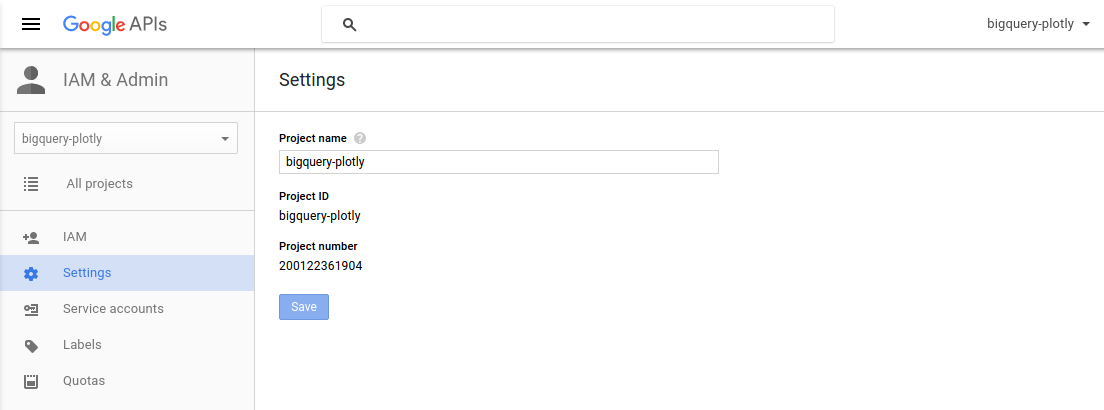
project_id = 'bigquery-plotly'
### Top 10 Most Active Users on Hacker News (by total stories submitted)
We will select the top 10 high scoring `author`s and their respective `score` values.
```
top10_active_users_query = """
SELECT
author AS User,
count(author) as Stories
FROM
[fh-bigquery:hackernews.stories]
GROUP BY
User
ORDER BY
Stories DESC
LIMIT
10
"""
```
The `pandas.gbq` module provides a method `read_gbq` to query the BigQuery stored dataset and stores the result as a `DataFrame`.
```
try:
top10_active_users_df = gbq.read_gbq(top10_active_users_query, project_id=project_id)
except:
print 'Error reading the dataset'
```
Using the `create_table` method from the `FigureFactory` module, we can generate a table from the resulting `DataFrame`.
```
top_10_users_table = ff.create_table(top10_active_users_df)
py.iplot(top_10_users_table, filename='top-10-active-users')
```
### Top 10 Hacker News Submissions (by score)
We will select the `title` and `score` columns in the descending order of their `score`, keeping only top 10 stories among all.
```
top10_story_query = """
SELECT
title,
score,
time_ts AS timestamp
FROM
[fh-bigquery:hackernews.stories]
ORDER BY
score DESC
LIMIT
10
"""
try:
top10_story_df = gbq.read_gbq(top10_story_query, project_id=project_id)
except:
print 'Error reading the dataset'
# Create a table figure from the DataFrame
top10_story_figure = FF.create_table(top10_story_df)
# Scatter trace for the bubble chart timeseries
story_timeseries_trace = go.Scatter(
x=top10_story_df['timestamp'],
y=top10_story_df['score'],
xaxis='x2',
yaxis='y2',
mode='markers',
text=top10_story_df['title'],
marker=dict(
color=[80 + i*5 for i in range(10)],
size=top10_story_df['score']/50,
showscale=False
)
)
# Add the trace data to the figure
top10_story_figure['data'].extend(go.Data([story_timeseries_trace]))
# Subplot layout
top10_story_figure.layout.yaxis.update({'domain': [0, .45]})
top10_story_figure.layout.yaxis2.update({'domain': [.6, 1]})
# Y-axis of the graph should be anchored with X-axis
top10_story_figure.layout.yaxis2.update({'anchor': 'x2'})
top10_story_figure.layout.xaxis2.update({'anchor': 'y2'})
# Add the height and title attribute
top10_story_figure.layout.update({'height':900})
top10_story_figure.layout.update({'title': 'Highest Scoring Submissions on Hacker News'})
# Update the background color for plot and paper
top10_story_figure.layout.update({'paper_bgcolor': 'rgb(243, 243, 243)'})
top10_story_figure.layout.update({'plot_bgcolor': 'rgb(243, 243, 243)'})
# Add the margin to make subplot titles visible
top10_story_figure.layout.margin.update({'t':75, 'l':50})
top10_story_figure.layout.yaxis2.update({'title': 'Upvote Score'})
top10_story_figure.layout.xaxis2.update({'title': 'Post Time'})
py.image.save_as(top10_story_figure, filename='top10-posts.png')
py.iplot(top10_story_figure, filename='highest-scoring-submissions')
```
You can see that the lists consist of the stories involving some big names.
* "Death of Steve Jobs and Aaron Swartz"
* "Announcements of the Hyperloop and the game 2048".
* "Microsoft open sourcing the .NET"
The story title is visible when you `hover` over the bubbles.
#### From which Top-level domain (TLD) most of the stories come?
Here we have used the url-function [TLD](https://cloud.google.com/bigquery/query-reference#tld) from BigQuery's query syntax. We collect the domain for all URLs with their respective count, and group them by it.
```
tld_share_query = """
SELECT
TLD(url) AS domain,
count(score) AS stories
FROM
[fh-bigquery:hackernews.stories]
GROUP BY
domain
ORDER BY
stories DESC
LIMIT 10
"""
try:
tld_share_df = gbq.read_gbq(tld_share_query, project_id=project_id)
except:
print 'Error reading the dataset'
labels = tld_share_df['domain']
values = tld_share_df['stories']
tld_share_trace = go.Pie(labels=labels, values=values)
data = [tld_share_trace]
layout = go.Layout(
title='Submissions shared by Top-level domains'
)
fig = go.Figure(data=data, layout=layout)
py.iplot(fig)
```
We can notice that the **.com** top-level domain contributes to most of the stories on Hacker News.
#### Public response to the "Who Is Hiring?" posts
There is an account on Hacker News by the name [whoishiring](https://news.ycombinator.com/user?id=whoishiring). This account automatically submits a 'Who is Hiring?' post at 11 AM Eastern time on the first weekday of every month.
```
wih_query = """
SELECT
id,
title,
score,
time_ts
FROM
[fh-bigquery:hackernews.stories]
WHERE
author == 'whoishiring' AND
LOWER(title) contains 'who is hiring?'
ORDER BY
time
"""
try:
wih_df = gbq.read_gbq(wih_query, project_id=project_id)
except:
print 'Error reading the dataset'
trace = go.Scatter(
x=wih_df['time_ts'],
y=wih_df['score'],
mode='markers+lines',
text=wih_df['title'],
marker=dict(
size=wih_df['score']/50
)
)
layout = go.Layout(
title='Public response to the "Who Is Hiring?" posts',
xaxis=dict(
title="Post Time"
),
yaxis=dict(
title="Upvote Score"
)
)
data = [trace]
fig = go.Figure(data=data, layout=layout)
py.iplot(fig, filename='whoishiring-public-response')
```
### Submission Traffic Volume in a Week
```
week_traffic_query = """
SELECT
DAYOFWEEK(time_ts) as Weekday,
count(DAYOFWEEK(time_ts)) as story_counts
FROM
[fh-bigquery:hackernews.stories]
GROUP BY
Weekday
ORDER BY
Weekday
"""
try:
week_traffic_df = gbq.read_gbq(week_traffic_query, project_id=project_id)
except:
print 'Error reading the dataset'
week_traffic_df['Day'] = ['NULL', 'Sunday', 'Monday', 'Tuesday', 'Wednesday', 'Thursday', 'Friday', 'Saturday']
week_traffic_df = week_traffic_df.drop(week_traffic_df.index[0])
trace = go.Scatter(
x=week_traffic_df['Day'],
y=week_traffic_df['story_counts'],
mode='lines',
text=week_traffic_df['Day']
)
layout = go.Layout(
title='Submission Traffic Volume (Week Days)',
xaxis=dict(
title="Day of the Week"
),
yaxis=dict(
title="Total Submissions"
)
)
data = [trace]
fig = go.Figure(data=data, layout=layout)
py.iplot(fig, filename='submission-traffic-volume')
```
We can observe that the Hacker News faces fewer submissions during the weekends.
#### Programming Language Trend on HackerNews
We will compare the trends for the Python and PHP programming languages, using the Hacker News post titles.
```
python_query = """
SELECT
YEAR(time_ts) as years,
COUNT(YEAR(time_ts )) as trends
FROM
[fh-bigquery:hackernews.stories]
WHERE
LOWER(title) contains 'python'
GROUP BY
years
ORDER BY
years
"""
php_query = """
SELECT
YEAR(time_ts) as years,
COUNT(YEAR(time_ts )) as trends
FROM
[fh-bigquery:hackernews.stories]
WHERE
LOWER(title) contains 'php'
GROUP BY
years
ORDER BY
years
"""
try:
python_df = gbq.read_gbq(python_query, project_id=project_id)
except:
print 'Error reading the dataset'
try:
php_df = gbq.read_gbq(php_query, project_id=project_id)
except:
print 'Error reading the dataset'
trace1 = go.Scatter(
x=python_df['years'],
y=python_df['trends'],
mode='lines',
line=dict(color='rgba(115,115,115,1)', width=4),
connectgaps=True,
)
trace2 = go.Scatter(
x=[python_df['years'][0], python_df['years'][8]],
y=[python_df['trends'][0], python_df['trends'][8]],
mode='markers',
marker=dict(color='rgba(115,115,115,1)', size=8)
)
trace3 = go.Scatter(
x=php_df['years'],
y=php_df['trends'],
mode='lines',
line=dict(color='rgba(189,189,189,1)', width=4),
connectgaps=True,
)
trace4 = go.Scatter(
x=[php_df['years'][0], php_df['years'][8]],
y=[php_df['trends'][0], php_df['trends'][8]],
mode='markers',
marker=dict(color='rgba(189,189,189,1)', size=8)
)
traces = [trace1, trace2, trace3, trace4]
layout = go.Layout(
xaxis=dict(
showline=True,
showgrid=False,
showticklabels=True,
linecolor='rgb(204, 204, 204)',
linewidth=2,
autotick=False,
ticks='outside',
tickcolor='rgb(204, 204, 204)',
tickwidth=2,
ticklen=5,
tickfont=dict(
family='Arial',
size=12,
color='rgb(82, 82, 82)',
),
),
yaxis=dict(
showgrid=False,
zeroline=False,
showline=False,
showticklabels=False,
),
autosize=False,
margin=dict(
autoexpand=False,
l=100,
r=20,
t=110,
),
showlegend=False,
)
annotations = []
annotations.append(
dict(xref='paper', x=0.95, y=python_df['trends'][8],
xanchor='left', yanchor='middle',
text='Python',
font=dict(
family='Arial',
size=14,
color='rgba(49,130,189, 1)'
),
showarrow=False)
)
annotations.append(
dict(xref='paper', x=0.95, y=php_df['trends'][8],
xanchor='left', yanchor='middle',
text='PHP',
font=dict(
family='Arial',
size=14,
color='rgba(49,130,189, 1)'
),
showarrow=False)
)
annotations.append(
dict(xref='paper', yref='paper', x=0.5, y=-0.1,
xanchor='center', yanchor='top',
text='Source: Hacker News submissions with the title containing Python/PHP',
font=dict(
family='Arial',
size=12,
color='rgb(150,150,150)'
),
showarrow=False)
)
layout['annotations'] = annotations
fig = go.Figure(data=traces, layout=layout)
py.iplot(fig, filename='programming-language-trends')
```
As we already know about this trend, Python is dominating PHP throughout the timespan.
#### Reference
See https://plot.ly/python/getting-started/ for more information about Plotly's Python Open Source Graphing Library!
```
from IPython.display import display, HTML
display(HTML('<link href="//fonts.googleapis.com/css?family=Open+Sans:600,400,300,200|Inconsolata|Ubuntu+Mono:400,700" rel="stylesheet" type="text/css" />'))
display(HTML('<link rel="stylesheet" type="text/css" href="http://help.plot.ly/documentation/all_static/css/ipython-notebook-custom.css">'))
! pip install git+https://github.com/plotly/publisher.git --upgrade
import publisher
publisher.publish(
'BigQuery-Plotly.ipynb', 'python/google_big_query/', 'Google Big-Query',
'How to make your-tutorial-chart plots in Python with Plotly.',
title = 'Google Big Query | plotly',
has_thumbnail='true', thumbnail='thumbnail/bigquery2.jpg',
language='python', page_type='example_index',
display_as='databases', order=7)
```
|
github_jupyter
|
# Asymmetric Loss
This documentation is based on the paper "[Asymmetric Loss For Multi-Label Classification](https://arxiv.org/abs/2009.14119)".
## Asymetric Single-Label Loss
```
import timm
import torch
import torch.nn.functional as F
from timm.loss import AsymmetricLossMultiLabel, AsymmetricLossSingleLabel
import matplotlib.pyplot as plt
from PIL import Image
from pathlib import Path
```
Let's create a example of the `output` of a model, and our `labels`.
```
output = F.one_hot(torch.tensor([0,9,0])).float()
labels=torch.tensor([0,0,0])
labels, output
```
If we set all the parameters to 0, the loss becomes `F.cross_entropy` loss.
```
asl = AsymmetricLossSingleLabel(gamma_pos=0,gamma_neg=0,eps=0.0)
asl(output,labels)
F.cross_entropy(output,labels)
```
Now lets look at the asymetric part. ASL is Asymetric in how it handles positive and negative examples. Positive examples being the labels that are present in the image, and negative examples being labels that are not present in the image. The idea being that an image has a lot of easy negative examples, few hard negative examples and very few positive examples. Getting rid of the influence of easy negative examples, should help emphasize the gradients of the positive examples.
```
Image.open(Path()/'images/cat.jpg')
```
Notice this image contains a cat, that would be a positive label. This images does not contain a dog, elephant bear, giraffe, zebra, banana or many other of the labels found in the coco dataset, those would be negative examples. It is very easy to see that a giraffe is not in this image.
```
output = (2*F.one_hot(torch.tensor([0,9,0]))-1).float()
labels=torch.tensor([0,9,0])
losses=[AsymmetricLossSingleLabel(gamma_neg=i*0.04+1,eps=0.1,reduction='mean')(output,labels) for i in range(int(80))]
plt.plot([ i*0.04+1 for i,l in enumerate(losses)],[loss for loss in losses])
plt.ylabel('Loss')
plt.xlabel('Change in gamma_neg')
plt.show()
```
$$L_- = (p)^{\gamma-}\log(1-p) $$
The contibution of small negative examples quickly decreases as gamma_neg is increased as $\gamma-$ is an exponent and $p$ should be a small number close to 0.
Below we set `eps=0`, this has the effect of completely flattening out the above graph, we are no longer applying label smoothing, so negative examples end up not contributing to the loss.
```
losses=[AsymmetricLossSingleLabel(gamma_neg=0+i*0.02,eps=0.0,reduction='mean')(output,labels) for i in range(100)]
plt.plot([ i*0.04 for i in range(len(losses))],[loss for loss in losses])
plt.ylabel('Loss')
plt.xlabel('Change in gamma_neg')
plt.show()
```
## AsymmetricLossMultiLabel
`AsymmetricLossMultiLabel` allows for working on multi-label problems.
```
labels=F.one_hot(torch.LongTensor([0,0,0]),num_classes=10)+F.one_hot(torch.LongTensor([1,9,1]),num_classes=10)
labels
AsymmetricLossMultiLabel()(output,labels)
```
For `AsymmetricLossMultiLabel` another parameter exists called `clip`. This clamps smaller inputs to 0 for negative examples. This is called Asymmetric Probability Shifting.
```
losses=[AsymmetricLossMultiLabel(clip=i/100)(output,labels) for i in range(100)]
plt.plot([ i/100 for i in range(len(losses))],[loss for loss in losses])
plt.ylabel('Loss')
plt.xlabel('Clip')
plt.show()
```
|
github_jupyter
|
# 0. Dependências
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
%matplotlib inline
pd.options.display.max_rows = 10
```
# 1. Introdução
**O objetivo principal do PCA é analisar os dados para identificar padrões visando reduzir a dimensionalidade dos dados com uma perda mínima de informação**. Uma possível aplicação seria o reconhecimento de padrões, onde queremos reduzir os custos computacionais e o erro da estimação de parâmetros pela redução da dimensionalidade do nosso espaço de atributos extraindo um subespaço que descreve os nosso dados "de forma satisfatória". **A redução de dimensionalidade se torna importante quando temos um número de atributos significativamente maior que o número de amostras de treinamento**.
Nós aplicamos o PCA para projetar todos os nossos dados (sem rótulos de classe) em um subespaço diferente, procurando encontrar os eixos com a máxima variância onde os dados são mais distribuídos. A questão principal é: **"Qual o subespaço que representa *bem* os nossos dados?"**.
**Primeiramente, calculamos os autovetores (componentes principais) dos nossos dados e organizamos em uma matriz de projeção. Cada autovetor (*eigenvector*) é associada a um autovalor (*eigenvalue*) que pode ser interpretado como o "tamanho" ou "magnitude" do autovetor correspondente**. Em geral, consideramos apenas o autovalores que tem uma magnitude significativamente maior que os outros e desconsideramos os autopares (autovetores-autovalores) que consideramos *menos informativos*.
Se observamos que todos os autovalores tem uma magnitude similar, isso pode ser um bom indicador que nossos dados já estão em um *bom* subespaço. Por outro lado, **se alguns autovalores tem a magnitude muito maior que a dos outros, devemos escolher seus autovetores já que eles contém mais informação sobre a distribuição dos nossos dados**. Da mesma forma, autovalores próximos a zero são menos informativos e devemos desconsiderá-los na construção do nosso subespaço.
Em geral, a aplicação do PCA envolve os seguintes passos:
1. Padronização dos dados
2. Obtenção dos autovetores e autovalores através da:
- Matriz de Covariância; ou
- Matriz de Correlação; ou
- *Singular Vector Decomposition*
3. Construção da matriz de projeção a partir dos autovetores selecionados
4. Transformação dos dados originais X via a matriz de projeção para obtenção do subespaço Y
## 1.1 PCA vs LDA
Ambos PCA e LDA (*Linear Discrimant Analysis*) são métodos de transformação linear. Por uma lado, o PCA fornece as direções (autovetores ou componentes principais) que maximiza a variância dos dados, enquanto o LDA visa as direções que maximizam a separação (ou discriminação) entre classes diferentes. Maximizar a variância, no caso do PCA, também significa reduzir a perda de informação, que é representada pela soma das distâncias de projeção dos dados nos eixos dos componentes principais.
Enquanto o PCA projeta os dados em um subespaço diferente, o LDA tenta determinar um subespaço adequado para distinguir os padrões pertencentes as classes diferentes.
<img src="images/PCAvsLDA.png" width=600>
## 1.2 Autovetores e autovalores
Os autovetores e autovalores de uma matriz de covariância (ou correlação) representam a base do PCA: os autovetores (componentes principais) determinam a direção do novo espaço de atributos, e os autovalores determinam sua magnitude. Em outras palavras, os autovalores explicam a variância dos dados ao longo dos novos eixos de atributos.
### 1.2.1 Matriz de Covariância
A abordagem clássica do PCA calcula a matriz de covariância, onde cada elemento representa a covariância entre dois atributos. A covariância entre dois atributos é calculada da seguinte forma:
$$\sigma_{jk} = \frac{1}{n-1}\sum_{i=1}^N(x_{ij}-\overline{x}_j)(x_{ik}-\overline{x}_k)$$
Que podemos simplificar na forma vetorial através da fórmula:
$$S=\frac{1}{n-1}((x-\overline{x})^T(x-\overline{x}))$$
onde $\overline{x}$ é um vetor d-dimensional onde cada valor representa a média de cada atributo, e $n$ representa o número de atributos por amostra. Vale ressaltar ainda que x é um vetor onde cada amostra está organizada em linhas e cada coluna representa um atributo. Caso se tenha um vetor onde as amostras estão organizadas em colunas e cada linha representa um atributo, a transposta passa para o segundo elemento da multiplicação.
Na prática, o resultado da matriz de covariância representa basicamente a seguinte estrutura:
$$\begin{bmatrix}var(1) & cov(1,2) & cov(1,3) & cov(1,4)
\\ cov(1,2) & var(2) & cov(2,3) & cov(2,4)
\\ cov(1,3) & cov(2,3) & var(3) & cov(3,4)
\\ cov(1,4) & cov(2,4) & cov(3,4) & var(4)
\end{bmatrix}$$
Onde a diagonal principal representa a variância em cada dimensão e os demais elementos são a covariância entre cada par de dimensões.
Para se calcular os autovalores e autovetores, só precisamos chamar a função *np.linalg.eig*, onde cada autovetor estará representado por uma coluna.
> Uma propriedade interessante da matriz de covariância é que **a soma da diagonal principal da matriz (variância para cada dimensão) é igual a soma dos autovalores**.
### 1.2.2 Matriz de Correlação
Outra maneira de calcular os autovalores e autovetores é utilizando a matriz de correlação. Apesar das matrizes serem diferentes, elas vão resultar nos mesmos autovalores e autovetores (mostrado mais a frente) já que a matriz de correlação é dada pela normalização da matriz de covariância.
$$corr(x,y) = \frac{cov(x,y)}{\sigma_x \sigma_y}$$
### 1.2.3 Singular Vector Decomposition
Apesar da autodecomposição (cálculo dos autovetores e autovalores) efetuada pelas matriz de covariância ou correlação ser mais intuitiva, a maior parte das implementações do PCA executam a *Singular Vector Decomposition* (SVD) para melhorar o desempenho computacional. Para calcular a SVD, podemos utilizar a biblioteca numpy, através do método *np.linalg.svd*.
Note que a autodecomposição resulta nos mesmos autovalores e autovetores utilizando qualquer uma das matrizes abaixo:
- Matriz de covariânca após a padronização dos dados
- Matriz de correlação
- Matriz de correlação após a padronização dos dados
Mas qual a relação entre a SVD e o PCA? Dado que a matriz de covariância $C = \frac{X^TX}{n-1}$ é uma matriz simétrica, ela pode ser diagonalizada da seguinte forma:
$$C = VLV^T$$
onde $V$ é a matriz de autovetores (cada coluna é um autovetor) e $L$ é a matriz diagonal com os autovalores $\lambda_i$ na ordem decrescente na diagonal. Se executarmos o SVD em X, nós obtemos a seguinte decomposição:
$$X = USV^T$$
onde $U$ é a matriz unitária e $S$ é a matriz diagonal de *singular values* $s_i$. A partir disso, pode-se calcular que:
$$C = VSU^TUSV^T = V\frac{S^2}{n-1}V^T$$
Isso significa que os *right singular vectors* V são as *principal directions* e que os *singular values* estão relacionados aos autovalores da matriz de covariância via $\lambda_i = \frac{s_i^2}{n-1}$. Os componentes principais são dados por $XV = USV^TV = US$
Resumindo:
1. Se $X = USV^T$, então as colunas de V são as direções/eixos principais;
2. As colunas de $US$ são os componentes principais;
3. *Singular values* estão relacionados aos autovalores da matriz de covariância via $\lambda_i = \frac{s_i^2}{n-1}$;
4. Scores padronizados (*standardized*) são dados pelas colunas de $\sqrt{n-1}U$ e *loadings* são dados pelas colunas de $\frac{VS}{\sqrt{n-1}}$. Veja [este link](https://stats.stackexchange.com/questions/125684) e [este](https://stats.stackexchange.com/questions/143905) para entender as diferenças entre *loadings* e *principal directions*;
5. As fórmulas acima só são válidas se $X$ está centralizado, ou seja, somente quando a matriz de covariância é igual a $\frac{X^TX}{n-1}$;
6. As proposições acima estão corretas somente quando $X$ for representado por uma matriz onde as linhas são amostras e as colunas são atributos. Caso contrário, $U$ e $V$ tem interpretações contrárias. Isto é, $U, V = V, U$;
7. Para reduzir a dimensionalidade com o PCA baseado no SVD, selecione as *k*-ésimas primeiras colunas de U, e $k\times k$ parte superior de S. O produto $U_kS_k$ é a matriz $n \times k$ necessária para conter os primeiros $k$ PCs.
8. Para reconstruir os dados originais a partir dos primeiros $k$ PCs, multiplicá-los pelo eixos principais correspondentes $V_k^T$ produz a matriz $X_k = U_kS_kV_k^T$ que tem o tamanho original $n \times p$. Essa forma gera a matriz reconstruída com o menor erro de reconstrução possível dos dados originais. [Veja esse link](https://stats.stackexchange.com/questions/130721);
9. Estritamente falando, $U$ é de tamanho $n \times n$ e $V$ é de tamanho $p \times p$. Entretanto, se $n > p$ então as últimas $n-p$ colunas de $U$ são arbitrárias (e as linhas correspondentes de $S$ são constantes e iguais a zero).
### 1.2.4 Verificação dos autovetores e autovalores
Para verificar se os autovetores e autovalores calculados na autodecomposição estão corretos, devemos verificar se eles satisfazem a equação para cada autovetor e autovalor correspondente:
$$\Sigma \overrightarrow{v} = \lambda \overrightarrow{v}$$
onde:
$$\Sigma = Matriz\,de\,Covariância$$
$$\overrightarrow{v} = autovetor$$
$$\lambda = autovalor$$
### 1.2.5 Escolha dos autovetores e autovalores
Como dito, o objetivo típico do PCA é reduzir a dimensionalidade dos dados pela projeção em um subespaço menor, onde os autovetores formam os eixos. Entretando, os autovetores definem somente as direções dos novos eixos, já que todos eles tem tamanho 1. Logo, para decidir qual(is) autovetor(es) podemos descartar sem perder muita informação na construção do nosso subespaço, precisamos verificar os autovalores correspondentes. **Os autovetores com os maiores valores são os que contém mais informação sobre a distribuição dos nossos dados**. Esse são os autovetores que queremos.
Para fazer isso, devemos ordenar os autovalores em ordem decrescente para escolher o top k autovetores.
### 1.2.6 Cálculo da Informação
Após ordenar os autovalores, o próximo passo é **definir quantos componentes principais serão escolhidos para o nosso novo subespaço**. Para fazer isso, podemos utilizar o método da *variância explicada*, que calcula quanto de informação (variância) é atribuida a cada componente principal.
## 1. 3 Matriz de Projeção
Na prática, a matriz de projeção nada mais é que os top k autovetores concatenados. Portanto, se queremos reduzir o nosso espaço 4-dimensional para um espaço 2-dimensional, devemos escolher os 2 autovetores com os 2 maiores autovalores para construir nossa matriz W (d$\times$k).
## 1.4 Projeção no novo subespaço
O último passo do PCA é utilizar a nossa matriz de projeção dimensional W (4x2, onde cada coluna representa um autovetor) para transformar nossas amostras em um novo subespaço. Para isso, basta aplicar a seguinte equação:
$$S = (X-\mu_X) \times W$$
Onde cada linha em S contém os pesos para cada atributo (coluna da matriz) no novo subespaço.
A título de curiosidade, repare que se W representasse todos os autovetores - e não somente os escolhidos -, poderíamos recompor cada instância em X pela seguinte fórmula:
$$X = (S \times W^{-1}) + \mu_X$$
Novamente, cada linha em S representa os pesos para cada atributo, só que dessa vez seria possível representar X pela soma de cada autovetor multiplicado por um peso.
## 1.5 Recomendações
- Sempre normalize os atributos antes de aplicar o PCA (StandarScaler);
- Lembre-se de armazenar a média para efetuar a ida e volta;
- Não aplique o PCA após outros algoritmos de seleção de atributos ([fonte](https://www.quora.com/Should-I-apply-PCA-before-or-after-feature-selection));
- O número de componentes principais que você quer manter deve ser escolhido através da análise entre o número de componentes e a precisão do sistema. Nem sempre mais componentes principais ocasionam em melhor precisão!
# 2. Dados
```
iris = load_iris()
df = pd.DataFrame(data=iris.data, columns=iris.feature_names)
df['class'] = iris.target
df
df.describe()
x = df.drop(labels='class', axis=1).values
y = df['class'].values
print(x.shape, y.shape)
```
# 3. Implementação
```
class MyPCACov():
def __init__(self, n_components=None):
self.n_components = n_components
self.eigen_values = None
self.eigen_vectors = None
def fit(self, x):
self.n_components = x.shape[1] if self.n_components is None else self.n_components
self.mean_ = np.mean(x, axis=0)
cov_matrix = np.cov(x - self.mean_, rowvar=False)
self.eigen_values, self.eigen_vectors = np.linalg.eig(cov_matrix)
self.eigen_vectors = self.eigen_vectors.T
self.sorted_components_ = np.argsort(self.eigen_values)[::-1]
self.projection_matrix_ = self.eigen_vectors[self.sorted_components_[:self.n_components]]
self.explained_variance_ = self.eigen_values[self.sorted_components_]
self.explained_variance_ratio_ = self.explained_variance_ / self.eigen_values.sum()
def transform(self, x):
return np.dot(x - self.mean_, self.projection_matrix_.T)
def inverse_transform(self, x):
return np.dot(x, self.projection_matrix_) + self.mean_
class MyPCASVD():
def __init__(self, n_components=None):
self.n_components = n_components
self.eigen_values = None
self.eigen_vectors = None
def fit(self, x):
self.n_components = x.shape[1] if self.n_components is None else self.n_components
self.mean_ = np.mean(x, axis=0)
U, s, Vt = np.linalg.svd(x - self.mean_, full_matrices=False) # a matriz s já retorna ordenada
# S = np.diag(s)
self.eigen_vectors = Vt
self.eigen_values = s
self.projection_matrix = self.eigen_vectors[:self.n_components]
self.explained_variance_ = (self.eigen_values ** 2) / (x.shape[0] - 1)
self.explained_variance_ratio_ = self.explained_variance_ / self.explained_variance_.sum()
def transform(self, x):
return np.dot(x - self.mean_, self.projection_matrix.T)
def inverse_transform(self, x):
return np.dot(x, self.projection_matrix) + self.mean_
```
# 4. Teste
```
std = StandardScaler()
x_std = StandardScaler().fit_transform(x)
```
### PCA implementado pela matriz de covariância
```
pca_cov = MyPCACov(n_components=2)
pca_cov.fit(x_std)
print('Autovetores: \n', pca_cov.eigen_vectors)
print('Autovalores: \n', pca_cov.eigen_values)
print('Variância explicada: \n', pca_cov.explained_variance_)
print('Variância explicada (ratio): \n', pca_cov.explained_variance_ratio_)
print('Componentes ordenados: \n', pca_cov.sorted_components_)
x_std_proj = pca_cov.transform(x_std)
plt.figure()
plt.scatter(x_std_proj[:, 0], x_std_proj[:, 1], c=y)
x_std_back = pca_cov.inverse_transform(x_std_proj)
print(x_std[:5])
print(x_std_back[:5])
```
### PCA implementado pela SVD
```
pca_svd = MyPCASVD(n_components=2)
pca_svd.fit(x_std)
print('Autovetores: \n', pca_svd.eigen_vectors)
print('Autovalores: \n', pca_svd.eigen_values)
print('Variância explicada: \n', pca_svd.explained_variance_)
print('Variância explicada (ratio): \n', pca_svd.explained_variance_ratio_)
x_std_proj = pca_svd.transform(x_std)
plt.figure()
plt.scatter(x_std_proj[:, 0], x_std_proj[:, 1], c=y)
x_std_back = pca_svd.inverse_transform(x_std_proj)
print(x_std[:5])
print(x_std_back[:5])
```
## Comparação com o Scikit-learn
```
pca_sk = PCA(n_components=2)
pca_sk.fit(x_std)
print('Autovetores: \n', pca_sk.components_)
print('Autovalores: \n', pca_sk.singular_values_)
print('Variância explicada: \n', pca_sk.explained_variance_)
print('Variância explicada (ratio): \n', pca_sk.explained_variance_ratio_)
x_std_proj_sk = pca_sk.transform(x_std)
plt.figure()
plt.scatter(x_std_proj_sk[:, 0], x_std_proj_sk[:, 1], c=y)
x_std_back_sk = pca_sk.inverse_transform(x_std_proj_sk)
print(x_std[:5])
print(x_std_back_sk[:5])
```
### Observação sobre a implementação do Scikit-learn
Por algum motivo (que não sei qual), a [implementação do scikit-learn](https://github.com/scikit-learn/scikit-learn/blob/master/sklearn/decomposition/pca.py) inverte os sinais de alguns valores na matriz de autovetores. Na implementação, as matrizes $U$ e $V$ são passada para um método ```svd_flip``` (implementada [nesse arquivo](https://github.com/scikit-learn/scikit-learn/blob/master/sklearn/utils/extmath.py)):
```py
U, V = svd_flip(U[:, ::-1], V[::-1])
```
Repare que isso muda apenas os dados projetados. No gráfico, isso inverte os eixos correspondentes apenas. No entanto, os **autovalores**, a ```explained_variance```, ```explained_variance_ratio``` e os dados reprojetados ao espaço original são exatamente iguais.
## 5. Referências
- [Antigo notebook do PCA com explicações passo-a-passo](https://github.com/arnaldog12/Machine_Learning/blob/62b628bd3c37ec2fa52e349f38da24751ef67313/PCA.ipynb)
- [Principal Component Analysis in Python](https://plot.ly/ipython-notebooks/principal-component-analysis/)
- [Implementing a Principal Component Analysis (PCA)](https://sebastianraschka.com/Articles/2014_pca_step_by_step.html)
- [Relationship between SVD and PCA. How to use SVD to perform PCA?](https://stats.stackexchange.com/questions/134282/relationship-between-svd-and-pca-how-to-use-svd-to-perform-pca)
- [How to reverse PCA and reconstruct original variables from several principal components?](https://stats.stackexchange.com/questions/229092/how-to-reverse-pca-and-reconstruct-original-variables-from-several-principal-com)
- [Everything you did and didn't know about PCA](http://alexhwilliams.info/itsneuronalblog/2016/03/27/pca/)
- [Unpacking (** PCA )](https://towardsdatascience.com/unpacking-pca-b5ea8bec6aa5)
|
github_jupyter
|
## Given two binary strings, return their sum (also a binary string).
The input strings are both non-empty and contains only characters 1 or 0.
### Example 1:
Input: a = "11", b = "1"
Output: "100"
### Example 2:
Input: a = "1010", b = "1011"
Output: "10101"
```
def add_binary(a,b):
return '{0:b}'.format(int(a, 2) + int(b, 2))
print(add_binary('11','11'))
```
This method has quite low performance in the case of large input numbers.
One could use Bit Manipulation approach to speed up the solution.
### Logic


#### 1.Find the maxlength
#### 2.Based on the length fill with zero
#### 3.Create a variable for carry and result
#### 4.Loop through tail, check if value is "1" .If yes then increment carry
#### 5.if Carry % 2 == 1 then append 1 else zero
#### 6. Divide carry by 2 (Keep doing this for all the elements in the array)
#### 7. Outside the loop if carry is 1 then append 1
#### 8. Reverse the string and join all the values
```
# Program with comments
def add_binary(a,b):
n = max(len(a), len(b))
print('\nlength',n)
a, b = a.zfill(n), b.zfill(n)
print('zfill a,b',a,b)
carry = 0
result = []
for i in range(n - 1, -1, -1):
print('\ni',i)
print('carry on top',carry)
if a[i] == '1':
carry += 1
if b[i] == '1':
carry += 1
if carry % 2 == 1:
result.append('1')
else:
result.append('0')
print('\a[i]',a[i])
print('\b[i]',b[i])
print('carry after increement',carry)
print('carry % 2',carry % 2)
print('answer',result)
#carry =cary//2
print("Carry=carry// 2", carry)
carry //= 2
print("After division carry", carry)
if carry == 1:
result.append('1')
print('result',result)
result.reverse()
return ''.join(result)
print(add_binary('01','11'))
# Program without comments
def add_binary(a,b):
n = max(len(a), len(b))
a, b = a.zfill(n), b.zfill(n)
carry = 0
result = []
for i in range(n - 1, -1, -1):
if a[i] == '1':
carry += 1
if b[i] == '1':
carry += 1
if carry % 2 == 1:
result.append('1')
else:
result.append('0')
carry //= 2
if carry == 1:
result.append('1')
result.reverse()
return ''.join(result)
print(add_binary('10','110'))
```

```
def addBinary(a, b) -> str:
x, y = int(a, 2), int(b, 2)
while y:
answer = x ^ y
carry = (x & y) << 1
x, y = answer, carry
return bin(x)[2:]
print(addBinary('001','101'))
```
def addBinary( a, b):
if len(a)==0: return b
if len(b)==0: return a
if a[-1] == '1' and b[-1] == '1':
return addBinary(addBinary(a[0:-1],b[0:-1]),'1')+'0'
if a[-1] == '0' and b[-1] == '0':
return addBinary(a[0:-1],b[0:-1])+'0'
else:
return addBinary(a[0:-1],b[0:-1])+'1'
```
# addBinary(addBinary(1,[]),1)+'0'
# addBinary(addBinary(1,[]),1) + '0' ==> addBinary(1,[]) return a =1 B
# addBinary(1,1)+'0'
# return {addBinary(addBinary(a[0:-1],b[0:-1]),'1')+'0' } +'0' ==> addBinary(a[0:-1],b[0:-1]) return empty A
# return {addBinary(empty,'1')+'0' } +'0' ===> addBinary(empty,'1') return 1 A
#1 +'0' +'0'
addBinary("11","1")
def add_binary(a,b):
print("len(a) {}".format(len(a)))
print("len(b) {}".format(len(b)))
print("a[-1] {}".format(a[-1]))
print("b[-1] {}".format(b[-1]))
print("a[0:-1]) {}".format(a[0:-1]))
print("b[0:-1]) {}".format(b[0:-1]))
if len(a)==0:
print("len a==0")
return b
if len(b)==0:
print("len b==0")
return a
if a[-1] == '1' and b[-1] == '1':
print("First if condition 1,1")
return addBinary(addBinary(a[0:-1],b[0:-1]),'1')+'0'
if a[-1] == '0' and b[-1] == '0':
print("Second if condition 0,0")
return add_binary(a[0:-1],b[0:-1])+'0'
else:
print("Else")
return add_binary(a[0:-1],b[0:-1])+'1'
add_binary("1010","1011")
def add_binary_nums(x, y):
print((len(x)))
print((len(x)))
max_len = max(len(x), len(y))
print("max_len {}".format(max_len))
print()
#Fill it with zeros
x = x.zfill(max_len)
print("x {}".format(x))
y = y.zfill(max_len)
print("y {}".format(y))
print(y)
# initialize the result
result = ''
# initialize the carry
carry = 0
# Traverse the string
for i in range(max_len - 1, -1, -1):
r = carry
r += 1 if x[i] == '1' else 0
r += 1 if y[i] == '1' else 0
result = ('1' if r % 2 == 1 else '0') + result
carry = 0 if r < 2 else 1 # Compute the carry.
if carry !=0 : result = '1' + result
return result.zfill(max_len)
add_binary_nums('100','10')
"""
This is the same solution with print
Note: carry //=2
This step is needed to carry the current unit
"""
def add_binary(a,b):
n = max(len(a), len(b))
a, b = a.zfill(n), b.zfill(n)
carry = 0
result = []
for i in range(n - 1, -1, -1):
if a[i] == '1':
carry += 1
if b[i] == '1':
carry += 1
print('\na',a[i])
print('b',b[i])
if carry % 2 == 1:
result.append('1')
else:
result.append('0')
print('carry',carry % 2 == 1)
print('result',result)
print('\nb4 carry',carry)
carry //= 2
print('out carry',carry)
if carry == 1:
result.append('1')
print('result',result)
result.reverse()
return ''.join(result)
print(add_binary('10','111'))
print(0//2)
print(1//2)
```
|
github_jupyter
|
# Chapter 3: Dynamic Programming
## 1. Exercise 4.1
$\pi$ is equiprobable random policy, so all actions equally likely.
- $q_\pi(11, down)$
With current state $s=11$ and action $a=down$, we have next is the terminal state $s'=end$, which have reward $R'=0$
$$
\begin{aligned}
q_\pi(11, down) &= \sum_{s',r}p(s',r | s,a)\big[r+\gamma v_\pi(s')\big]
\cr &= 1 * (-1 + 0)
\cr &= -1
\end{aligned}
$$
- $q_\pi(7, down)$
With current state $s=7$ and action $a=down$, we have next is the terminal state $s'=11$, which have state-value function $v_\pi(s)$
$$
\begin{aligned}
q_\pi(7, down) &= \sum_{s',r}p(s',r | s,a)\big[r+\gamma v_\pi(s')\big]
\cr &= 1 * \big[-1 + \gamma v_\pi(s')\big]
\cr &= -1 + \gamma v_\pi(s')
\end{aligned}
$$
## 2. Exercise 4.2
- Transitions from the original states are unchanged
$$
\begin{aligned}
v_\pi(15) &= \sum_a \pi(a|s=15)\sum_{s',r}p(s',r|s,a)\big[r+\gamma v_\pi(s')\big]
\cr &= 0.25\big[1*\big(-1+\gamma v_\pi(12)\big)+1*\big(-1+\gamma v_\pi(13)\big)+1*\big(-1+\gamma v_\pi(14)\big)+1*\big(-1+\gamma v_\pi(15)\big)\big]
\cr &= -1 + 0.25\gamma\sum_{s=12}^{15}v_\pi(s)
\end{aligned}
$$
In which, $\displaystyle v_\pi(13)=-1 + 0.25\gamma\sum_{s\in\{9,12,13,14\}}v_\pi(s)$
- Add action **down** to state 13, to go to state 15
Compute Fomular is similar to above:
$$v_\pi(15)=-1 + 0.25\gamma\sum_{s=12}^{15}v_\pi(s)$$
But, $\displaystyle v_\pi(13)=-1 + 0.25\gamma\sum_{s\in\{9,12,14,15\}}v_\pi(s)$
## 3. Exercise 4.3
- $q_\pi$ evaluation
$$
\begin{aligned}
q_\pi(s, a) &= E[G_t | S_t=s, A_t=a]
\cr &= E[R_{t+1}+\gamma G_{t+1} | S_t=s, A_t=a]
\cr &= E[R_{t+1}+\gamma V_\pi(S_{t+1}) | S_t=s, A_t=a]
\cr &= \sum_{s',r}p(s',r | s,a)\big[r+\gamma v_\pi(s')\big]
\end{aligned}
$$
- Update rule for $q_\pi$
$$
\begin{aligned}
q_{k+1}(s, a) &= E_\pi[R_{t+1} + \gamma v_k(S_{t+1}) | S_t=s, A_t=a]
\cr &= \sum_{s',r}p(s',r | s,a)\big[r+\gamma v_k(s')\big]
\cr &= \sum_{s',r}p(s',r | s,a)\Big[r+\gamma \sum_{a'\in\mathcal A(s')}\pi(a' | s')q_k(s', a')\Big]
\end{aligned}
$$
## 4. Exercise 4.4
When, the policy continually switches between two or more policies that are equally good, the difference between switches is small, so policy evaluation loop will be breaked before convergence.
$$\Delta = \max\big(\Delta, | v-V(s) |\big)$$
So, in this case, it maybe useful if we talk the sum of all differences
$$\Delta = \Delta + | v-V(s) |$$
## 5. Exercise 4.5
Policy Iteration algorithm for action values
### 1. Initialization
$\quad \pi(s)\in\mathcal A(s)$ and $Q(s,a)\in\mathbb R$ arbitrarily for all $s\in\mathcal S$ and $a\in\mathcal A(s)$
### 2. Policy Evaluation
$\quad$Loop:
$\quad\quad \Delta\gets0$
$\quad\quad$ Loop for each $s\in\mathcal S$
$\quad\quad\quad$ Loop for each $a\in\mathcal A(s)$
$\quad\quad\quad\quad q\gets Q(s,a)$
$\quad\quad\quad\quad \displaystyle Q(s,a)\gets \sum_{s',r}p(s',r | s,a)\Big[r+\gamma \sum_{a'\in\mathcal A(s')}\pi(a' | s')Q(s', a')\Big]$
$\quad\quad\quad\quad \Delta\gets \Delta+\big| q- Q(s,a)\big|$
$\quad\quad \text{until }\Delta<\theta$ a small positive number determining the accuracy of estimation
### 3. Policy Improvement
$\quad\textit{policy-stable}\gets\textit{true}$
$\quad$For each $s\in\mathcal S$
$\quad\quad \textit{old-aciton}\gets\pi(s)$
$\quad\quad \pi(s)\gets\arg\max_a Q(s,a)$
$\quad\quad$If $\textit{old-aciton}\neq\pi(s)$, then $\textit{policy-stable}\gets\textit{false}$
$\quad$If $\textit{policy-stable}$, then stop and return $Q\approx q_*$ and $\pi\approx\pi_*$; else go to $2$
## 6. Exercise 4.6
## 7. Exercise 4.7
## 8. Exercise 4.8
## 9. Exercise 4.9
## 10. Exercise 4.10
Value iteration update for action values, $q_{k+1}(s,a)$
$$
\begin{aligned}
q_{k+1}(s,a) &= \max E\big[R_{t+1}+\gamma v_k(S_{t+1}) | S_t=s,A_t=a\big]
\cr &= \max\sum_{s',r}p(s',r | s,a)\big[r+\gamma v_k(s')\big]
\cr &= \max\sum_{s',r}p(s',r | s,a)\big[r+\gamma\sum_{a'\in\mathcal A(s')}\pi(a' | s')q_k(s', a')\big]
\end{aligned}
$$
|
github_jupyter
|
# Predictions with Pyro + GPyTorch (High-Level Interface)
## Overview
In this example, we will give an overview of the high-level Pyro-GPyTorch integration - designed for predictive models.
This will introduce you to the key GPyTorch objects that play with Pyro. Here are the key benefits of the integration:
**Pyro provides:**
- The engines for performing approximate inference or sampling
- The ability to define additional latent variables
**GPyTorch provides:**
- A library of kernels/means/likelihoods
- Mechanisms for efficient GP computations
```
import math
import torch
import pyro
import tqdm
import gpytorch
from matplotlib import pyplot as plt
%matplotlib inline
```
In this example, we will be doing simple variational regression to learn a monotonic function. This example is doing the exact same thing as [GPyTorch's native approximate inference](../04_Variational_and_Approximate_GPs/SVGP_Regression_CUDA.ipynb), except we're now using Pyro's variational inference engine.
In general - if this was your dataset, you'd be better off using GPyTorch's native exact or approximate GPs.
(We're just using a simple example to introduce you to the GPyTorch/Pyro integration).
```
train_x = torch.linspace(0., 1., 21)
train_y = torch.pow(train_x, 2).mul_(3.7)
train_y = train_y.div_(train_y.max())
train_y += torch.randn_like(train_y).mul_(0.02)
fig, ax = plt.subplots(1, 1, figsize=(3, 2))
ax.plot(train_x.numpy(), train_y.numpy(), 'bo')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.legend(['Training data'])
```
## The PyroGP model
In order to use Pyro with GPyTorch, your model must inherit from `gpytorch.models.PyroGP` (rather than `gpytorch.modelks.ApproximateGP`). The `PyroGP` extends the `ApproximateGP` class and differs in a few key ways:
- It adds the `model` and `guide` functions which are used by Pyro's inference engine.
- It's constructor requires two additional arguments beyond the variational strategy:
- `likelihood` - the model's likelihood
- `num_data` - the total amount of training data (required for minibatch SVI training)
- `name_prefix` - a unique identifier for the model
```
class PVGPRegressionModel(gpytorch.models.PyroGP):
def __init__(self, train_x, train_y, likelihood):
# Define all the variational stuff
variational_distribution = gpytorch.variational.CholeskyVariationalDistribution(
num_inducing_points=train_y.numel(),
)
variational_strategy = gpytorch.variational.VariationalStrategy(
self, train_x, variational_distribution
)
# Standard initializtation
super(PVGPRegressionModel, self).__init__(
variational_strategy,
likelihood,
num_data=train_y.numel(),
name_prefix="simple_regression_model"
)
self.likelihood = likelihood
# Mean, covar
self.mean_module = gpytorch.means.ConstantMean()
self.covar_module = gpytorch.kernels.ScaleKernel(
gpytorch.kernels.MaternKernel(nu=1.5)
)
def forward(self, x):
mean = self.mean_module(x) # Returns an n_data vec
covar = self.covar_module(x)
return gpytorch.distributions.MultivariateNormal(mean, covar)
model = PVGPRegressionModel(train_x, train_y, gpytorch.likelihoods.GaussianLikelihood())
```
## Performing inference with Pyro
Unlike all the other examples in this library, `PyroGP` models use Pyro's inference and optimization classes (rather than the classes provided by PyTorch).
If you are unfamiliar with Pyro's inference tools, we recommend checking out the [Pyro SVI tutorial](http://pyro.ai/examples/svi_part_i.html).
```
# this is for running the notebook in our testing framework
import os
smoke_test = ('CI' in os.environ)
num_iter = 2 if smoke_test else 200
num_particles = 1 if smoke_test else 256
def train(lr=0.01):
optimizer = pyro.optim.Adam({"lr": 0.1})
elbo = pyro.infer.Trace_ELBO(num_particles=num_particles, vectorize_particles=True, retain_graph=True)
svi = pyro.infer.SVI(model.model, model.guide, optimizer, elbo)
model.train()
iterator = tqdm.tqdm_notebook(range(num_iter))
for i in iterator:
model.zero_grad()
loss = svi.step(train_x, train_y)
iterator.set_postfix(loss=loss)
%time train()
```
In this example, we are only performing inference over the GP latent function (and its associated hyperparameters). In later examples, we will see that this basic loop also performs inference over any additional latent variables that we define.
## Making predictions
For some problems, we simply want to use Pyro to perform inference over latent variables. However, we can also use the models' (approximate) predictive posterior distribution. Making predictions with a PyroGP model is exactly the same as for standard GPyTorch models.
```
fig, ax = plt.subplots(1, 1, figsize=(4, 3))
train_data, = ax.plot(train_x.cpu().numpy(), train_y.cpu().numpy(), 'bo')
model.eval()
with torch.no_grad():
output = model.likelihood(model(train_x))
mean = output.mean
lower, upper = output.confidence_region()
line, = ax.plot(train_x.cpu().numpy(), mean.detach().cpu().numpy())
ax.fill_between(train_x.cpu().numpy(), lower.detach().cpu().numpy(),
upper.detach().cpu().numpy(), color=line.get_color(), alpha=0.5)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.legend([train_data, line], ['Train data', 'Prediction'])
```
## Next steps
This was a pretty boring example, and it wasn't really all that different from GPyTorch's native SVGP implementation! The real power of the Pyro integration comes when we have additional latent variables to infer over. We will see an example of this in the [next example](./Clustered_Multitask_GP_Regression.ipynb), which learns a clustering over multiple time series using multitask GPs and Pyro.
|
github_jupyter
|
# Exercise 1: Schema on Read
```
from pyspark.sql import SparkSession
import pandas as pd
import matplotlib
spark = SparkSession.builder.getOrCreate()
dfLog = spark.read.text("data/NASA_access_log_Jul95.gz")
```
# Load the dataset
```
#Data Source: http://ita.ee.lbl.gov/traces/NASA_access_log_Jul95.gz
dfLog = spark.read.text("data/NASA_access_log_Jul95.gz")
```
# Quick inspection of the data set
```
# see the schema
dfLog.printSchema()
# number of lines
dfLog.count()
#what's in there?
dfLog.show(5)
#a better show?
dfLog.show(5, truncate=False)
#pandas to the rescue
pd.set_option('max_colwidth', 200)
dfLog.limit(5).toPandas()
```
# Let' try simple parsing with split
```
from pyspark.sql.functions import split
# TODO
dfArrays = dfLog.withColumn("tokenized", split("value"," "))
dfArrays.limit(10).toPandas()
```
# Second attempt, let's build a custom parsing UDF
```
from pyspark.sql.functions import udf
# TODO
@udf
def parseUDF(line):
import re
PATTERN = '^(\S+) (\S+) (\S+) \[([\w:/]+\s[+\-]\d{4})\] "(\S+) (\S+)\s*(\S*)" (\d{3}) (\S+)'
match = re.search(PATTERN, line)
if match is None:
return (line, 0)
size_field = match.group(9)
if size_field == '-':
size = 0
else:
size = match.group(9)
return {
"host" : match.group(1),
"client_identd" : match.group(2),
"user_id" : match.group(3),
"date_time" : match.group(4),
"method" : match.group(5),
"endpoint" : match.group(6),
"protocol" : match.group(7),
"response_code" : int(match.group(8)),
"content_size" : size
}
# TODO
dfParsed= dfLog.withColumn("parsed", parseUDF("value"))
dfParsed.limit(10).toPandas()
dfParsed.printSchema()
```
# Third attempt, let's fix our UDF
```
#from pyspark.sql.functions import udf # already imported
from pyspark.sql.types import MapType, StringType
# TODO
@udf(MapType(StringType(),StringType()))
def parseUDFbetter(line):
import re
PATTERN = '^(\S+) (\S+) (\S+) \[([\w:/]+\s[+\-]\d{4})\] "(\S+) (\S+)\s*(\S*)" (\d{3}) (\S+)'
match = re.search(PATTERN, line)
if match is None:
return (line, 0)
size_field = match.group(9)
if size_field == '-':
size = 0
else:
size = match.group(9)
return {
"host" : match.group(1),
"client_identd" : match.group(2),
"user_id" : match.group(3),
"date_time" : match.group(4),
"method" : match.group(5),
"endpoint" : match.group(6),
"protocol" : match.group(7),
"response_code" : int(match.group(8)),
"content_size" : size
}
# TODO
dfParsed= dfLog.withColumn("parsed", parseUDFbetter("value"))
dfParsed.limit(10).toPandas()
# TODO
dfParsed= dfLog.withColumn("parsed", parseUDFbetter("value"))
dfParsed.limit(10).toPandas()
#Bingo!! we'got a column of type map with the fields parsed
dfParsed.printSchema()
dfParsed.select("parsed").limit(10).toPandas()
```
# Let's build separate columns
```
dfParsed.selectExpr("parsed['host'] as host").limit(5).show(5)
dfParsed.selectExpr(["parsed['host']", "parsed['date_time']"]).show(5)
fields = ["host", "client_identd","user_id", "date_time", "method", "endpoint", "protocol", "response_code", "content_size"]
exprs = [ "parsed['{}'] as {}".format(field,field) for field in fields]
exprs
dfClean = dfParsed.selectExpr(*exprs)
dfClean.limit(5).toPandas()
```
## Popular hosts
```
from pyspark.sql.functions import desc
dfClean.groupBy("host").count().orderBy(desc("count")).limit(10).toPandas()
```
## Popular content
```
from pyspark.sql.functions import desc
dfClean.groupBy("endpoint").count().orderBy(desc("count")).limit(10).toPandas()
```
## Large Files
```
dfClean.createOrReplaceTempView("cleanlog")
spark.sql("""
select endpoint, content_size
from cleanlog
order by content_size desc
""").limit(10).toPandas()
from pyspark.sql.functions import expr
dfCleanTyped = dfClean.withColumn("content_size_bytes", expr("cast(content_size as int)"))
dfCleanTyped.limit(5).toPandas()
dfCleanTyped.createOrReplaceTempView("cleantypedlog")
spark.sql("""
select endpoint, content_size
from cleantypedlog
order by content_size_bytes desc
""").limit(10).toPandas()
from pyspark.sql.functions import col, unix_timestamp
parsedDateDf = dfCleanTyped.withColumn(
'parsed_date_time',
unix_timestamp(col('date_time'), "dd/MMM/yyyy:HH:mm:ss Z").cast("timestamp")
)
parsedDateDf.limit(20).toPandas()
```
|
github_jupyter
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.