text
stringlengths 2.5k
6.39M
| kind
stringclasses 3
values |
|---|---|
```
from time import time
import secrets
import flickrapi
import requests
import os
import pandas as pd
import pickle
import logging
def get_photos(image_tag):
# setup dataframe for data
raw_photos = pd.DataFrame(columns=['latitude', 'longitude','farm','server','id','secret'])
# initialize api
flickr = flickrapi.FlickrAPI(secrets.api_key, secrets.api_secret, format='parsed-json')
errors = ''
try:
# search photos based on settings
photos = flickr.photos.search(tags=image_tag,
sort='relevance',
content_type=1, #photos only
extras='description,geo,url_c',
has_geo=1,
geo_context=2, #outdoors
per_page=100,
page=1
)
# append photo details: description and getags
raw_photos = raw_photos.append(pd.DataFrame(photos['photos']['photo'])
[['latitude', 'longitude','farm','server','id','secret']],
ignore_index=True)
# construct url from pieces
raw_photos['url'] = 'https://farm'+ raw_photos.farm.astype(str) + '.staticflickr.com/' + raw_photos.server.astype(str) + '/'+ raw_photos.id.astype(str) + '_' + raw_photos.secret.astype(str) + '.jpg'
# need a try/except here for images less than 'per page'
print('..downloading photos')
download_images(raw_photos, image_tag)
# save data
print('..saving metadata')
with open('data/%s/%s.pkl' %(image_tag, image_tag), 'wb') as f:
pickle.dump(raw_photos, f)
f.close()
del raw_photos
except:
print('Could not get info for: %s. '%image_tag)
errors = image_tag
return errors
def create_folder(path):
if not os.path.isdir(path):
os.makedirs(path)
def download_images(df, keyword):
path = ''.join(['data/',keyword])
create_folder(path)
print('...df length: %d' %len(df.index))
print('...going through each row of dataframe')
for idx, row in df.iterrows():
try:
image_path = ''.join([path,'/',row.id,'.jpg'])
response = requests.get(row.url)#, stream=True)
with open(image_path, 'wb') as outfile:
outfile.write(response.content)
outfile.close()
except:
print('...Error occured at idx: %d'%idx)
print('...download completed.')
places = pd.read_csv('IndoorOutdoor_places205.csv', names=['key','label'])
places.head()
# retrieve all outdoor scene categories. We clean up the 'key' column, remove duplicates, and re-index the dataframe.
places['key'] = places['key'].str[3:].str.split('/',1,expand=True)
places = places[places.label == 2]
places = places.drop_duplicates(ignore_index=True)
places['key'] = places['key'].str.strip('\'')
places['key'] = places['key'].replace(to_replace='_',value=' ',regex=True)
places.head(-20)
places.count() #should have 132
errors = []
for idx, row in places.iterrows():
# change this idx when it crashes. It will give an error for a few indices. It probably means Flickr does not have
# geotagged images for these keywords. We skip over those. Should have a total of 130 keywords at the end.
if idx < 0:
pass
else:
start = time()
error = get_photos(row.key)
end = time()
print('%20s in %.2e seconds.' %(row.key, end-start)) # should vary between 3-8 seconds depending on the keyword.
if error != '':
errors.append(error)
# we test loading the pickle file.
keyword = 'basilica'
with open('data/%s/%s.pkl' %(keyword,keyword), 'rb') as f:
test = pickle.load(f)
f.close()
test.head()
# we test loading the image.
from PIL import Image
image = Image.open('data/%s/%s.jpg'%(keyword,test.id[0]))
image.show()
```
|
github_jupyter
|
```
import numpy as np
import pandas as pd
from os import makedirs
from os.path import join, exists
#from nilearn.input_data import NiftiLabelsMasker
from nilearn.connectome import ConnectivityMeasure
from nilearn.plotting import plot_anat, plot_roi
import bct
#from nipype.interfaces.fsl import InvWarp, ApplyWarp
import datetime
subjects = ['101', '102', '103', '104', '106', '107', '108', '110', '212', '213',
'214', '215', '216', '217', '218', '219', '320', '321', '322', '323',
'324', '325', '327', '328', '329', '330', '331', '332', '333', '334',
'335', '336', '337', '338', '339', '340', '341', '342', '343', '344',
'345', '346', '347', '348', '349', '350', '451', '452', '453', '455',
'456', '457', '458', '459', '460', '462', '463', '464', '465', '467',
'468', '469', '470', '502', '503', '571', '572', '573', '574', '575',
'577', '578', '579', '580', '581', '582', '584', '585', '586', '587',
'588', '589', '590', '591', '592', '593', '594', '595', '596', '597',
'598', '604', '605', '606', '607', '608', '609', '610', '611', '612',
'613', '614', '615', '616', '617', '618', '619', '620', '621', '622',
'623', '624', '625', '626', '627', '628', '629', '630', '631', '633',
'634']
#subjects = ['101', '102']
sink_dir = '/Users/katherine/Dropbox/Projects/physics-retrieval/data/output'
shen = '/home/kbott006/physics-retrieval/shen2015_2mm_268_parcellation.nii.gz'
craddock = '/home/kbott006/physics-retrieval/craddock2012_tcorr05_2level_270_2mm.nii.gz'
masks = {'shen2015': shen, 'craddock2012': craddock}
sessions = [0,1]
sesh = ['pre', 'post']
tasks = ['rest']
kappa_upper = 0.21
kappa_lower = 0.31
lab_notebook_dir = sink_dir
index = pd.MultiIndex.from_product([subjects, sessions], names=['subject', 'session'])
lab_notebook = pd.DataFrame(index=index, columns=['start', 'end', 'errors'])
correlation_measure = ConnectivityMeasure(kind='correlation')
index = pd.MultiIndex.from_product([subjects, sessions, tasks, masks.keys()], names=['subject', 'session', 'task', 'mask'])
df = pd.DataFrame(columns=['lEff1', 'clustCoeff1'], index=index, dtype=np.float64)
for subject in subjects:
for session in sessions:
lab_notebook.at[(subject, session),'start'] = str(datetime.datetime.now())
for task in tasks:
for mask in masks.keys():
try:
#shen_masker = NiftiLabelsMasker(xfmd_masks['shen2015'], background_label=0, standardize=True, detrend=True,t_r=3.)
#craddock_masker = NiftiLabelsMasker(xfmd_masks['craddock2012'], background_label=0, standardize=True, detrend=True,t_r=3.)
#confounds = '/home/data/nbc/physics-learning/anxiety-physics/output/{1}/{0}/{0}_confounds.txt'.format(subject, sesh[session])
#epi_data = join(data_dir, subject, 'session-{0}'.format(session), 'resting-state/resting-state-0/endor1.feat', 'filtered_func_data.nii.gz')
#shen_ts = shen_masker.fit_transform(epi_data, confounds)
#shen_corrmat = correlation_measure.fit_transform([shen_ts])[0]
#np.savetxt(join(sink_dir, sesh[session], subject, '{0}-session-{1}-rest_network_corrmat_shen2015.csv'.format(subject, session)), shen_corrmat, delimiter=",")
corrmat = np.genfromtxt(join(sink_dir, '{0}-session-{1}-{2}_network_corrmat_{3}.csv'.format(subject, session, task, mask)), delimiter=",")
print(corrmat.shape)
#craddock_ts = craddock_masker.fit_transform(epi_data, confounds)
#craddock_corrmat = correlation_measure.fit_transform([craddock_ts])[0]
#np.savetxt(join(sink_dir, sesh[session], subject, '{0}-session-{1}-rest_network_corrmat_craddock2012.csv'.format(subject, session)), craddock_corrmat, delimiter=",")
ge_s = []
ge_c = []
md_s = []
md_c = []
for p in np.arange(kappa_upper, kappa_lower, 0.02):
thresh = bct.threshold_proportional(corrmat, p, copy=True)
#network measures of interest here
#global efficiency
ge = bct.efficiency_wei(thresh, local=True)
ge_s.append(ge)
#modularity
md = bct.clustering_coef_wu(thresh)
md_s.append(md)
ge_s = np.asarray(ge_s)
md_s = np.asarray(md_s)
leff = np.trapz(ge_s, dx=0.01, axis=0)
print('local efficiency:', leff[0])
ccoef = np.trapz(md_s, dx=0.01, axis=0)
for j in np.arange(1, 270):
df.at[(subject, session, task, mask), 'lEff{0}'.format(j)] = leff[j-1]
df.at[(subject, session, task, mask), 'clustCoeff{0}'.format(j)] = ccoef[j-1]
#df.to_csv(join(sink_dir, 'resting-state_graphtheory_shen+craddock.csv'), sep=',')
lab_notebook.at[(subject, session),'end'] = str(datetime.datetime.now())
except Exception as e:
print(e, subject, session)
lab_notebook.at[(subject,session),'errors'] = [e, str(datetime.datetime.now())]
df.to_csv(join(sink_dir, 'resting-state_nodal-graphtheory_shen+craddock.csv'), sep=',')
df.to_csv(join(sink_dir, 'resting-state_nodal-graphtheory_shen+craddock_{0}.csv'.format(str(datetime.datetime.today()))), sep=',')
lab_notebook.to_csv(join(lab_notebook_dir, 'LOG_resting-state-graph-theory_{0}.csv'.format(str(datetime.datetime.now()))))
df
for j in np.arange(1, 269):
print(ccoef[j-1])
```
|
github_jupyter
|
# Example Map Plotting
### At the start of a Jupyter notebook you need to import all modules that you will use
```
import pandas as pd
import xarray as xr
import matplotlib.pyplot as plt
import numpy as np
from scipy.interpolate import griddata
import cartopy
import cartopy.crs as ccrs # For plotting maps
import cartopy.feature as cfeature # For plotting maps
from cartopy.util import add_cyclic_point # For plotting maps
import datetime
```
### Define the directories and file of interest for your results. This can be shortened to less lines as well.
```
#result_dir = "/home/buchholz/Documents/code_database/untracked/my-notebook/Janyl_plotting/"
result_dir = "../../data/"
file = "CAM_chem_merra2_FCSD_1deg_QFED_monthly_2019.nc"
#the netcdf file is now held in an xarray dataset named 'nc' and can be referenced later in the notebook
nc_load = xr.open_dataset(result_dir+file)
#to see what the netCDF file contains, just call the variable you read it into
nc_load
```
### Extract the variable of choice at the time and level of choice
```
#extract grid variables
lat = nc_load['lat']
lon = nc_load['lon']
#extract variable
var_sel = nc_load['PM25']
print(var_sel)
#print(var_sel[0][0][0][0])
#select the surface level at a specific time and convert to ppbv from vmr
#var_srf = var_sel.isel(time=0, lev=55)
#select the surface level for an average over three times and convert to ppbv from vmr
var_srf = var_sel.isel(time=[2,3,4], lev=55) # MAM chosen
var_srf = var_srf.mean('time')
var_srf = var_srf*1e09 # 10-9 to ppb
print(var_srf.shape)
# Add cyclic point to avoid white line over Africa
var_srf_cyc, lon_cyc = add_cyclic_point(var_srf, coord=lon)
```
### Plot the value over a specific region
```
plt.figure(figsize=(20,8))
#Define projection
ax = plt.axes(projection=ccrs.PlateCarree())
#define contour levels
clev = np.arange(0, 100, 1)
#plot the data
plt.contourf(lon_cyc,lat,var_srf_cyc,clev,cmap='Spectral_r',extend='both')
# add coastlines
#ax.coastlines()
ax.add_feature(cfeature.COASTLINE)
#add lat lon grids
ax.gridlines(draw_labels=True, color='grey', alpha=0.5, linestyle='--')
#longitude limits in degrees
ax.set_xlim(20,120)
#latitude limits in degrees
ax.set_ylim(5,60)
# Title
plt.title("CAM-chem 2019 O$_{3}$")
#axes
# y-axis
ax.text(-0.09, 0.55, 'Latitude', va='bottom', ha='center',
rotation='vertical', rotation_mode='anchor',
transform=ax.transAxes)
# x-axis
ax.text(0.5, -0.10, 'Longitude', va='bottom', ha='center',
rotation='horizontal', rotation_mode='anchor',
transform=ax.transAxes)
# legend
ax.text(1.18, 0.5, 'O$_{3}$ (ppb)', va='bottom', ha='center',
rotation='vertical', rotation_mode='anchor',
transform=ax.transAxes)
plt.colorbar()
plt.show()
```
### Add location markers
```
##Now lets look at the sufrace plot again, but this time add markers for observations at several points.
#first we need to define our observational data into an array
#this can also be imported from text files using various routines
# Kyzylorda, Urzhar, Almaty, Balkhash
obs_lat = np.array([44.8488,47.0870,43.2220,46.2161])
obs_lon = np.array([65.4823,81.6315,76.8512,74.3775])
obs_names = ["Kyzylorda", "Urzhar", "Almaty", "Balkhash"]
num_obs = obs_lat.shape[0]
plt.figure(figsize=(20,8))
#Define projection
ax = plt.axes(projection=ccrs.PlateCarree())
#define contour levels
clev = np.arange(0, 100, 1)
#plot the data
plt.contourf(lon_cyc,lat,var_srf_cyc,clev,cmap='Spectral_r')
# add coastlines
ax.add_feature(cfeature.COASTLINE)
ax.add_feature(cfeature.BORDERS)
#add lat lon grids
ax.gridlines(draw_labels=True, color='grey', alpha=0.5, linestyle='--')
#longitude limits in degrees
ax.set_xlim(20,120)
#latitude limits in degrees
ax.set_ylim(5,60)
# Title
plt.title("CAM-chem 2019 O$_{3}$")
#axes
# y-axisCOUNTRY
ax.text(-0.09, 0.55, 'Latitude', va='bottom', ha='center',
rotation='vertical', rotation_mode='anchor',
transform=ax.transAxes)
# x-axis
ax.text(0.5, -0.10, 'Longitude', va='bottom', ha='center',
rotation='horizontal', rotation_mode='anchor',
transform=ax.transAxes)
# legend
ax.text(1.18, 0.5, 'O$_{3}$ (ppb)', va='bottom', ha='center',
rotation='vertical', rotation_mode='anchor',
transform=ax.transAxes)
#convert your observation lat/lon to Lambert-Conformal grid points
#xpt,ypt = m(obs_lon,obs_lat)
#to specify the color of each point it is easiest plot individual points in a loop
for i in range(num_obs):
plt.plot(obs_lon[i], obs_lat[i], linestyle='none', marker="o", markersize=8, alpha=0.8, c="black", markeredgecolor="black", markeredgewidth=1, transform=ccrs.PlateCarree())
plt.text(obs_lon[i] - 0.8, obs_lat[i] - 0.5, obs_names[i], fontsize=20, horizontalalignment='right', transform=ccrs.PlateCarree())
plt.colorbar()
plt.show()
cartopy.config['data_dir']
```
|
github_jupyter
|
# Description
This notebook documents allows the following on a group seven LIFX Tilechain with 5 Tiles
laid out horizontaly as following
T1 [0] [1] [2] [3] [4]
T2 [0] [1] [2] [3] [4]
T3 [0] [1] [2] [3] [4]
T4 [0] [1] [2] [3] [4]
T5 [0] [1] [2] [3] [4]
T6 [0] [1] [2] [3] [4]
T7 [0] [1] [2] [3] [4]
Care should be taken to ensure that the LIFX Tiles are all facing up to ensure that the 0,0 position is in the expected place.
Program will perform the following
- take a jpg or png located in the same folder as the notebook and create a image to display across all 4 tilechains or 20 tiles. Image will be reduced from original size to a 32x40 matrix so resolution will not be great. You've been warned.
```
!pip install pylifxtiles
!pip install thread
#Main Program for Convert Single Image to Tiles
# Full running function with all dependencies
#imports RGB to HSBK conversion function from LIFX LAN library
import _thread as thread
from lifxlan import LifxLAN
from lifxlan.utils import RGBtoHSBK
from pylifxtiles import tiles
from pylifxtiles import actions
from matplotlib import image
from PIL import Image
# modify this variable to the name of the specific LIFX Tilechain as shown in the LIFX app
source_image = './images/meghan.jpg'
def main():
lan = LifxLAN()
tilechain_lights = lan.get_tilechain_lights()
print(len(tilechain_lights))
if len(tilechain_lights) != 0:
for tile in tilechain_lights:
if tile.get_label() == 'T1':
print(tile.get_label())
T1 = tile
if tile.get_label() =='T2':
print(tile.get_label())
T2 = tile
if tile.get_label() == 'T3':
print(tile.get_label())
T3 = tile
if tile.get_label() == 'T4':
print(tile.get_label())
T4 = tile
if tile.get_label() == 'T5':
print(tile.get_label())
T5 = tile
if tile.get_label() == 'T6':
print(tile.get_label())
T6 = tile
if tile.get_label() == 'T7':
print(tile.get_label())
T7 = tile
tc_list = [ T1, T2, T3, T4, T5, T6, T7]
try:
thread.start_new_thread(display_image,(source_image,(40,56), tc_list))
except KeyboardInterrupt:
print("Done.")
#combined function
# resize image and force a new shape and save to disk
def display_image(image_to_display,image_size, tilechain_list):
# load the image
my_image = Image.open(image_to_display)
# report the size of the image
#print(my_image.size)
# resize image and ignore original aspect ratio
img_resized = my_image.resize(image_size)
#changing the file extension from jpg to png changes output brightness. You might need to play with this.
img_resized.save('./images/resized_image.jpg')
data = image.imread('./images/resized_image.jpg')
target_tcs = []
for row in data:
temp_row = []
for pixel in row:
temp_row.append(RGBtoHSBK(pixel))
target_tcs.append(temp_row)
#print ("length of target_tcs is " + str(len(target_tcs)))
tcsplit = tiles.split_tilechains(target_tcs)
#print ("legnth of tcssplit is " + str(len(tcsplit)))
#print ("length tilelist is " + str(len(tilechain_list)))
for tile in range(len(tilechain_list)):
print (tile)
tilechain_list[tile].set_tilechain_colors(tiles.split_combined_matrix(tcsplit[tile]),rapid=True)
if __name__ == "__main__":
main()
```
# test write to three tiles
```
#Main Program for Convert Single Image to Tiles
# Full running function with all dependencies
#imports RGB to HSBK conversion function from LIFX LAN library
from lifxlan import LifxLAN
from lifxlan.utils import RGBtoHSBK
from pylifxtiles import tiles
from pylifxtiles import actions
from matplotlib import image
from PIL import Image
# modify this variable to the name of the specific LIFX Tilechain as shown in the LIFX app
source_image = './images/Youtubelogo.jpg'
def main():
lan = LifxLAN()
tilechain_lights = lan.get_tilechain_lights()
print(len(tilechain_lights))
if len(tilechain_lights) != 0:
for tile in tilechain_lights:
if tile.get_label() == 'T1':
print(tile.get_label())
T1 = tile
if tile.get_label() =='T2':
print(tile.get_label())
T2 = tile
if tile.get_label() == 'T3':
print(tile.get_label())
T3 = tile
if tile.get_label() == 'T4':
print(tile.get_label())
T4 = tile
tc_list = [T2, T3, T4]
try:
display_image(source_image,(40,24), tc_list)
except KeyboardInterrupt:
print("Done.")
#combined function
# resize image and force a new shape and save to disk
def display_image(image_to_display,image_size, tilechain_list):
# load the image
my_image = Image.open(image_to_display)
# report the size of the image
#print(my_image.size)
# resize image and ignore original aspect ratio
img_resized = my_image.resize(image_size)
#changing the file extension from jpg to png changes output brightness. You might need to play with this.
img_resized.save('./images/resized_image.jpg')
data = image.imread('./images/resized_image.jpg')
target_tcs = []
for row in data:
temp_row = []
for pixel in row:
temp_row.append(RGBtoHSBK(pixel))
target_tcs.append(temp_row)
print ("length of target_tcs is " + str(len(target_tcs)))
tcsplit = tiles.split_tilechains(target_tcs)
print ("legnth of tcssplit is " + str(len(tcsplit)))
print ("length tilelist is " + str(len(tilechain_list)))
for tile in range(len(tilechain_list)):
print (tile)
tilechain_list[tile].set_tilechain_colors(tiles.split_combined_matrix(tcsplit[tile]),rapid=True)
if __name__ == "__main__":
main()
import threading
```
|
github_jupyter
|
```
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import statsmodels.api as sm
```
# Import Risk INFORM index
```
path = "C:\\batch8_worldbank\\datasets\\tempetes\\INFORM_Risk_2021.xlsx"
xl = pd.ExcelFile(path)
xl.sheet_names
inform_df = xl.parse(xl.sheet_names[2])
inform_df.columns = inform_df.iloc[0]
inform_df = inform_df[2:]
inform_df.head()
```
# Import emdat
```
path = "C:\\batch8_worldbank\\datasets\\tempetes\\wb_disasters_bdd.xlsx"
disasters_df = pd.read_excel(path)
disasters_df.head()
disasters_df['ISO']
max(disasters_df['Year'])
```
# Filter on storms
```
storms_df = disasters_df[disasters_df["Disaster Type"]=="Storm"]
```
# Number of storms, nb people affected and total damages by country by decade
```
nb_storms_by_year_by_country = storms_df.groupby(["Start Year", "ISO"]).aggregate({"Disaster Type":"count", "No Affected": "sum", "Total Damages ('000 US$)":"sum"})
nb_storms_by_year_by_country = nb_storms_by_year_by_country.reset_index()
nb_storms_by_year_by_country = nb_storms_by_year_by_country.rename(columns={"Start Year": "year", "Disaster Type": "storms_count", "No Affected": "total_nb_affected", "Total Damages ('000 US$)": "total_damages"})
nb_storms_by_year_by_country["decade"] = nb_storms_by_year_by_country["year"].apply(lambda row: (row//10)*10)
nb_storms_by_decade_by_country = nb_storms_by_year_by_country.groupby(["decade", "ISO"]).aggregate({"storms_count":"sum", "total_nb_affected":"sum", "total_damages":"sum"})
nb_storms_by_decade_by_country = nb_storms_by_decade_by_country.reset_index()
nb_storms_by_decade_by_country.head()
max(nb_storms_by_decade_by_country["decade"])
```
# Keep observations on decades 2000, 2010 and 2020 to increase nb of datapoints
```
nb_storms_by_decade_by_country_2020 = nb_storms_by_decade_by_country[nb_storms_by_decade_by_country["decade"]>=2000]
nb_storms_by_decade_by_country_2020.head()
nb_storms_by_decade_by_country_2020.shape
nb_storms_by_decade_by_country_2020.columns
inform_df.columns
# Merge on ISO
nb_storms_by_decade_by_country_2020_with_inform = pd.merge(nb_storms_by_decade_by_country_2020, inform_df, how="left", left_on="ISO", right_on="ISO3")
nb_storms_by_decade_by_country_2020_with_inform.head()
nb_storms_by_decade_by_country_2020_with_inform.shape
nb_storms_by_decade_by_country_2020_with_inform_filt_col = nb_storms_by_decade_by_country_2020_with_inform[["decade", "ISO", "storms_count", "total_nb_affected", "total_damages","INFORM RISK"]]
nb_storms_by_decade_by_country_2020_with_inform_filt_col.dtypes
nb_storms_by_decade_by_country_2020_with_inform_filt_col["INFORM RISK"] = nb_storms_by_decade_by_country_2020_with_inform_filt_col["INFORM RISK"].astype("float")
nb_storms_by_decade_by_country_2020_with_inform_filt_col.head()
nb_storms_inform_by_country_cor = nb_storms_by_decade_by_country_2020_with_inform_filt_col[["ISO", "storms_count", "total_nb_affected", "total_damages","INFORM RISK"]]
corr = nb_storms_inform_by_country_cor.corr()
sm.graphics.plot_corr(corr, xnames=list(corr.columns))
plt.show()
```
# Keep observations on decades 2010 and 2020
```
nb_storms_inform_by_country_2010_2020 = nb_storms_by_decade_by_country_2020_with_inform_filt_col[nb_storms_by_decade_by_country_2020_with_inform_filt_col["decade"]>=2010]
nb_storms_inform_by_country_2010_2020_cor = nb_storms_inform_by_country_2010_2020[["ISO", "storms_count", "total_nb_affected", "total_damages","INFORM RISK"]]
corr = nb_storms_inform_by_country_2010_2020_cor.corr()
sm.graphics.plot_corr(corr, xnames=list(corr.columns))
plt.show()
```
# Keep observations on decade 2020 (decade of INFORM index)
```
nb_storms_inform_by_country_2020_only = nb_storms_by_decade_by_country_2020_with_inform_filt_col[nb_storms_by_decade_by_country_2020_with_inform_filt_col["decade"]==2020]
nb_storms_inform_by_country_2020_only.head()
nb_storms_inform_by_country_2020_only_cor = nb_storms_inform_by_country_2020_only[["ISO", "storms_count", "total_nb_affected", "total_damages","INFORM RISK"]]
corr = nb_storms_inform_by_country_2020_only_cor.corr()
sm.graphics.plot_corr(corr, xnames=list(corr.columns))
plt.show()
```
|
github_jupyter
|
# Db2 Jupyter Notebook Extensions Tutorial
The SQL code tutorials for Db2 rely on a Jupyter notebook extension, commonly refer to as a "magic" command. The beginning of all of the notebooks begin with the following command which will load the extension and allow the remainder of the notebook to use the %sql magic command.
<pre>
%run db2.ipynb
</pre>
The cell below will load the Db2 extension. Note that it will take a few seconds for the extension to load, so you should generally wait until the "Db2 Extensions Loaded" message is displayed in your notebook.
```
%run db2.ipynb
```
## Options
There are two options that can be set with the **`%sql`** command. These options are:
- **`MAXROWS n`** - The maximum number of rows that you want to display as part of a SQL statement. Setting MAXROWS to -1 will return all output, while maxrows of 0 will suppress all output.
- **`RUNTIME n`** - When using the timer option on a SQL statement, the statement will execute for **`n`** number of seconds. The result that is returned is the number of times the SQL statement executed rather than the execution time of the statement. The default value for runtime is one second, so if the SQL is very complex you will need to increase the run time.
To set an option use the following syntax:
```
%sql option option_name value option_name value ....
```
The following example sets all three options:
```
%sql option maxrows 100 runtime 2
```
The values will be saved between Jupyter notebooks sessions.
## Connections to Db2
Before any SQL commands can be issued, a connection needs to be made to the Db2 database that you will be using. The connection can be done manually (through the use of the CONNECT command), or automatically when the first `%sql` command is issued.
The Db2 magic command tracks whether or not a connection has occured in the past and saves this information between notebooks and sessions. When you start up a notebook and issue a command, the program will reconnect to the database using your credentials from the last session. In the event that you have not connected before, the system will prompt you for all the information it needs to connect. This information includes:
- Database name (SAMPLE)
- Hostname - localhost (enter an IP address if you need to connect to a remote server)
- PORT - 50000 (this is the default but it could be different)
- Userid - DB2INST1
- Password - No password is provided so you have to enter a value
- Maximum Rows - 10 lines of output are displayed when a result set is returned
There will be default values presented in the panels that you can accept, or enter your own values. All of the information will be stored in the directory that the notebooks are stored on. Once you have entered the information, the system will attempt to connect to the database for you and then you can run all of the SQL scripts. More details on the CONNECT syntax will be found in a section below.
If you have credentials available from Db2 on Cloud or DSX, place the contents of the credentials into a variable and then use the `CONNECT CREDENTIALS <var>` syntax to connect to the database.
```Python
db2blu = { "uid" : "xyz123456", ...}
%sql CONNECT CREDENTIALS db2blu
```
If the connection is successful using the credentials, the variable will be saved to disk so that you can connected from within another notebook using the same syntax.
The next statement will force a CONNECT to occur with the default values. If you have not connected before, it will prompt you for the information.
```
%sql CONNECT
```
## Line versus Cell Command
The Db2 extension is made up of one magic command that works either at the LINE level (`%sql`) or at the CELL level (`%%sql`). If you only want to execute a SQL command on one line in your script, use the `%sql` form of the command. If you want to run a larger block of SQL, then use the `%%sql` form. Note that when you use the `%%sql` form of the command, the entire contents of the cell is considered part of the command, so you cannot mix other commands in the cell.
The following is an example of a line command:
```
%sql VALUES 'HELLO THERE'
```
If you have SQL that requires multiple lines, of if you need to execute many lines of SQL, then you should
be using the CELL version of the `%sql` command. To start a block of SQL, start the cell with `%%sql` and do not place any SQL following the command. Subsequent lines can contain SQL code, with each SQL statement delimited with the semicolon (`;`). You can change the delimiter if required for procedures, etc... More details on this later.
```
%%sql
VALUES
1,
2,
3
```
If you are using a single statement then there is no need to use a delimiter. However, if you are combining a number of commands then you must use the semicolon.
```
%%sql
DROP TABLE STUFF;
CREATE TABLE STUFF (A INT);
INSERT INTO STUFF VALUES
1,2,3;
SELECT * FROM STUFF;
```
The script will generate messages and output as it executes. Each SQL statement that generates results will have a table displayed with the result set. If a command is executed, the results of the execution get listed as well. The script you just ran probably generated an error on the DROP table command.
## Options
Both forms of the `%sql` command have options that can be used to change the behavior of the code. For both forms of the command (`%sql`, `%%sql`), the options must be on the same line as the command:
<pre>
%sql -t ...
%%sql -t
</pre>
The only difference is that the `%sql` command can have SQL following the parameters, while the `%%sql` requires the SQL to be placed on subsequent lines.
There are a number of parameters that you can specify as part of the `%sql` statement.
* `-d` - Use alternative delimiter
* `-t` - Time the statement execution
* `-q` - Suppress messages
* `-j` - JSON formatting of a column
* `-a` - Show all output
* `-pb` - Bar chart of results
* `-pp` - Pie chart of results
* `-pl` - Line chart of results
* `-i` - Interactive mode with Pixiedust
* `-sampledata` Load the database with the sample EMPLOYEE and DEPARTMENT tables
* `-r` - Return the results into a variable (list of rows)
* `-e` - Echo macro substitution
Multiple parameters are allowed on a command line. Each option should be separated by a space:
<pre>
%sql -a -j ...
</pre>
A `SELECT` statement will return the results as a dataframe and display the results as a table in the notebook. If you use the assignment statement, the dataframe will be placed into the variable and the results will not be displayed:
<pre>
r = %sql SELECT * FROM EMPLOYEE
</pre>
The sections below will explain the options in more detail.
## Delimiters
The default delimiter for all SQL statements is the semicolon. However, this becomes a problem when you try to create a trigger, function, or procedure that uses SQLPL (or PL/SQL). Use the `-d` option to turn the SQL delimiter into the at (`@`) sign and `-q` to suppress error messages. The semi-colon is then ignored as a delimiter.
For example, the following SQL will use the `@` sign as the delimiter.
```
%%sql -d -q
DROP TABLE STUFF
@
CREATE TABLE STUFF (A INT)
@
INSERT INTO STUFF VALUES
1,2,3
@
SELECT * FROM STUFF
@
```
The delimiter change will only take place for the statements following the `%%sql` command. Subsequent cells
in the notebook will still use the semicolon. You must use the `-d` option for every cell that needs to use the
semicolon in the script.
## Limiting Result Sets
The default number of rows displayed for any result set is 10. You have the option of changing this option when initially connecting to the database. If you want to override the number of rows display you can either update
the control variable, or use the -a option. The `-a` option will display all of the rows in the answer set. For instance, the following SQL will only show 10 rows even though we inserted 15 values:
```
%sql values 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15
```
You will notice that the displayed result will split the visible rows to the first 5 rows and the last 5 rows.
Using the `-a` option will display all values in a scrollable table.
```
%sql -a values 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15
```
To change the default value of rows displayed, you can use the `%sql option maxrow` command to set the value to something else. A value of 0 or -1 means unlimited output.
```
%sql option maxrows 5
%sql values 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15
```
A special note regarding the output from a `SELECT` statement. If the SQL statement is the last line of a block, the results will be displayed by default (unless you assigned the results to a variable). If the SQL is in the middle of a block of statements, the results will not be displayed. To explicitly display the results you must use the display function (or pDisplay if you have imported another library like pixiedust which overrides the pandas display function).
```
# Set the maximum back
%sql option maxrows 10
%sql values 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15
```
## Quiet Mode
Every SQL statement will result in some output. You will either get an answer set (`SELECT`), or an indication if
the command worked. For instance, the following set of SQL will generate some error messages since the tables
will probably not exist:
```
%%sql
DROP TABLE TABLE_NOT_FOUND;
DROP TABLE TABLE_SPELLED_WRONG;
```
If you know that these errors may occur you can silence them with the -q option.
```
%%sql -q
DROP TABLE TABLE_NOT_FOUND;
DROP TABLE TABLE_SPELLED_WRONG;
```
SQL output will not be suppressed, so the following command will still show the results.
```
%%sql -q
DROP TABLE TABLE_NOT_FOUND;
DROP TABLE TABLE_SPELLED_WRONG;
VALUES 1,2,3;
```
## Variables in %sql Blocks
Python variables can be passed to a `%sql` line command, and to a `%%sql` block. For both forms of the `%sql` command you can pass variables by placing a colon in front of the variable name.
```python
%sql SELECT * FROM EMPLOYEE WHERE EMPNO = :empno
```
The following example illustrates the use of a variable in the SQL.
```
empno = '000010'
%sql SELECT * FROM EMPLOYEE WHERE EMPNO = :empno
```
You can doublecheck that the substitution took place by using the `-e` option which echos the SQL command after substitution.
```
%sql -e SELECT * FROM EMPLOYEE WHERE EMPNO = :empno
```
Note that the variable `:empno` did not have quotes around it, although it is a string value. The `%sql` call will examine the contents of the variable and add quotes around strings so you do not have to supply them in the SQL command.
Variables can also be array types. Arrays are expanded into multiple values, each separated by commas. This is useful when building SQL `IN` lists. The following example searches for 3 employees based on their employee number.
```
empnos = ['000010','000020','000030']
%sql SELECT * FROM EMPLOYEE WHERE EMPNO IN (:empnos)
```
You can reference individual array items using this technique as well. If you wanted to search for only the first value in the `empnos` array, use `:empnos[0]` instead.
```
%sql SELECT * FROM EMPLOYEE WHERE EMPNO IN (:empnos[0])
```
One final type of variable substitution that is allowed is for dictionaries. Python dictionaries resemble JSON objects and can be used to insert JSON values into Db2. For instance, the following variable contains company information in a JSON structure.
```
customer = {
"name" : "Aced Hardware Stores",
"city" : "Rockwood",
"employees" : 14
}
```
Db2 has builtin functions for dealing with JSON objects. There is another Jupyter notebook which goes through this in detail. Rather than using those functions, the following code will create a Db2 table with a string column that will contain the contents of this JSON record.
```
%%sql
DROP TABLE SHOWJSON;
CREATE TABLE SHOWJSON (INJSON VARCHAR(256));
```
To insert the Dictionary (JSON Record) into this Db2 table, you only need to use the variable name as one of the fields being inserted.
```
%sql INSERT INTO SHOWJSON VALUES :customer
```
Selecting from this table will show that the data has been inserted as a string.
```
%sql select * from showjson
```
If you want to retrieve the data from a column that contains JSON records, you must use the `-j` flag to insert the contents back into a variable.
```
v = %sql -j SELECT * FROM SHOWJSON
```
The variable `v` now contains the original JSON record for you to use.
```
v
```
## SQL Character Strings
Character strings require special handling when dealing with Db2. The single quote character `'` is reserved for delimiting string constants, while the double quote `"` is used for naming columns that require special characters. You cannot use the double quote character to delimit strings that happen to contain the single quote character. What Db2 requires you do is placed two quotes in a row to have them interpreted as a single quote character. For instance, the next statement will select one employee from the table who has a quote in their last name: `O'CONNELL`.
```
%sql SELECT * FROM EMPLOYEE WHERE LASTNAME = 'O''CONNELL'
```
Python handles quotes differently! You can assign a string to a Python variable using single or double quotes. The following assignment statements are not identical!
```
lastname = "O'CONNELL"
print(lastname)
lastname = 'O''CONNELL'
print(lastname)
```
If you use the same syntax as Db2, Python will remove the quote in the string! It interprets this as two strings (O and CONNELL) being concatentated together. That probably isn't what you want! So the safest approach is to use double quotes around your string when you assign it to a variable. Then you can use the variable in the SQL statement as shown in the following example.
```
lastname = "O'CONNELL"
%sql -e SELECT * FROM EMPLOYEE WHERE LASTNAME = :lastname
```
Notice how the string constant was updated to contain two quotes when inserted into the SQL statement. This is done automatically by the `%sql` magic command, so there is no need to use the two single quotes when assigning a string to a variable. However, you must use the two single quotes when using constants in a SQL statement.
## Builtin Variables
There are 5 predefined variables defined in the program:
- database - The name of the database you are connected to
- uid - The userid that you connected with
- hostname = The IP address of the host system
- port - The port number of the host system
- max - The maximum number of rows to return in an answer set
Theses variables are all part of a structure called _settings. To retrieve a value, use the syntax:
```python
db = _settings['database']
```
There are also 3 variables that contain information from the last SQL statement that was executed.
- sqlcode - SQLCODE from the last statement executed
- sqlstate - SQLSTATE from the last statement executed
- sqlerror - Full error message returned on last statement executed
You can access these variables directly in your code. The following code segment illustrates the use of the SQLCODE variable.
```
empnos = ['000010','999999']
for empno in empnos:
ans1 = %sql -r SELECT SALARY FROM EMPLOYEE WHERE EMPNO = :empno
if (sqlcode != 0):
print("Employee "+ empno + " left the company!")
else:
print("Employee "+ empno + " salary is " + str(ans1[1][0]))
```
## Timing SQL Statements
Sometimes you want to see how the execution of a statement changes with the addition of indexes or other
optimization changes. The `-t` option will run the statement on the LINE or one SQL statement in the CELL for
exactly one second. The results will be displayed and optionally placed into a variable. The syntax of the
command is:
<pre>
sql_time = %sql -t SELECT * FROM EMPLOYEE
</pre>
For instance, the following SQL will time the VALUES clause.
```
%sql -t VALUES 1,2,3,4,5,6,7,8,9
```
When timing a statement, no output will be displayed. If your SQL statement takes longer than one second you
will need to modify the runtime options. You can use the `%sql option runtime` command to change the duration the statement runs.
```
%sql option runtime 5
%sql -t VALUES 1,2,3,4,5,6,7,8,9
%sql option runtime 1
```
## JSON Formatting
Db2 supports querying JSON that is stored in a column within a table. Standard output would just display the
JSON as a string. For instance, the following statement would just return a large string of output.
```
%%sql
VALUES
'{
"empno":"000010",
"firstnme":"CHRISTINE",
"midinit":"I",
"lastname":"HAAS",
"workdept":"A00",
"phoneno":[3978],
"hiredate":"01/01/1995",
"job":"PRES",
"edlevel":18,
"sex":"F",
"birthdate":"08/24/1963",
"pay" : {
"salary":152750.00,
"bonus":1000.00,
"comm":4220.00}
}'
```
Adding the -j option to the `%sql` (or `%%sql`) command will format the first column of a return set to better
display the structure of the document. Note that if your answer set has additional columns associated with it, they will not be displayed in this format.
```
%%sql -j
VALUES
'{
"empno":"000010",
"firstnme":"CHRISTINE",
"midinit":"I",
"lastname":"HAAS",
"workdept":"A00",
"phoneno":[3978],
"hiredate":"01/01/1995",
"job":"PRES",
"edlevel":18,
"sex":"F",
"birthdate":"08/24/1963",
"pay" : {
"salary":152750.00,
"bonus":1000.00,
"comm":4220.00}
}'
```
JSON fields can be inserted into Db2 columns using Python dictionaries. This makes the input and output of JSON fields much simpler. For instance, the following code will create a Python dictionary which is similar to a JSON record.
```
employee = {
"firstname" : "John",
"lastname" : "Williams",
"age" : 45
}
```
The field can be inserted into a character column (or BSON if you use the JSON functions) by doing a direct variable insert.
```
%%sql -q
DROP TABLE SHOWJSON;
CREATE TABLE SHOWJSON(JSONIN VARCHAR(128));
```
An insert would use a variable parameter (colon in front of the variable) instead of a character string.
```
%sql INSERT INTO SHOWJSON VALUES (:employee)
%sql SELECT * FROM SHOWJSON
```
An assignment statement to a variable will result in an equivalent Python dictionary type being created. Note that we must use the raw `-j` flag to make sure we only get the data and not a data frame.
```
x = %sql -j SELECT * FROM SHOWJSON
print("First Name is " + x[0]["firstname"] + " and the last name is " + x[0]['lastname'])
```
## Plotting
Sometimes it would be useful to display a result set as either a bar, pie, or line chart. The first one or two
columns of a result set need to contain the values need to plot the information.
The three possible plot options are:
* `-pb` - bar chart (x,y)
* `-pp` - pie chart (y)
* `-pl` - line chart (x,y)
The following data will be used to demonstrate the different charting options.
```
%sql values 1,2,3,4,5
```
Since the results only have one column, the pie, line, and bar charts will not have any labels associated with
them. The first example is a bar chart.
```
%sql -pb values 1,2,3,4,5
```
The same data as a pie chart.
```
%sql -pp values 1,2,3,4,5
```
And finally a line chart.
```
%sql -pl values 1,2,3,4,5
```
If you retrieve two columns of information, the first column is used for the labels (X axis or pie slices) and
the second column contains the data.
```
%sql -pb values ('A',1),('B',2),('C',3),('D',4),('E',5)
```
For a pie chart, the first column is used to label the slices, while the data comes from the second column.
```
%sql -pp values ('A',1),('B',2),('C',3),('D',4),('E',5)
```
Finally, for a line chart, the x contains the labels and the y values are used.
```
%sql -pl values ('A',1),('B',2),('C',3),('D',4),('E',5)
```
The following SQL will plot the number of employees per department.
```
%%sql -pb
SELECT WORKDEPT, COUNT(*)
FROM EMPLOYEE
GROUP BY WORKDEPT
```
The final option for plotting data is to use interactive mode `-i`. This will display the data using an open-source project called Pixiedust. You can view the results in a table and then interactively create a plot by dragging and dropping column names into the appropriate slot. The next command will place you into interactive mode.
```
%sql -i select * from employee
```
## Sample Data
Many of the Db2 notebooks depend on two of the tables that are found in the `SAMPLE` database. Rather than
having to create the entire `SAMPLE` database, this option will create and populate the `EMPLOYEE` and
`DEPARTMENT` tables in your database. Note that if you already have these tables defined, they will not be dropped.
```
%sql -sampledata
```
## Result Sets
By default, any `%sql` block will return the contents of a result set as a table that is displayed in the notebook. The results are displayed using a feature of pandas dataframes. The following select statement demonstrates a simple result set.
```
%sql select * from employee fetch first 3 rows only
```
You can assign the result set directly to a variable.
```
x = %sql select * from employee fetch first 3 rows only
```
The variable x contains the dataframe that was produced by the `%sql` statement so you access the result set by using this variable or display the contents by just referring to it in a command line.
```
x
```
There is an additional way of capturing the data through the use of the `-r` flag.
<pre>
var = %sql -r select * from employee
</pre>
Rather than returning a dataframe result set, this option will produce a list of rows. Each row is a list itself. The column names are found in row zero (0) and the data rows start at 1. To access the first column of the first row, you would use var[1][0] to access it.
```
rows = %sql -r select * from employee fetch first 3 rows only
print(rows[1][0])
```
The number of rows in the result set can be determined by using the length function and subtracting one for the header row.
```
print(len(rows)-1)
```
If you want to iterate over all of the rows and columns, you could use the following Python syntax instead of
creating a for loop that goes from 0 to 41.
```
for row in rows:
line = ""
for col in row:
line = line + str(col) + ","
print(line)
```
If you don't want the header row, modify the first line to start at the first row instead of row zero.
```
for row in rows[1:]:
line = ""
for col in row:
line = line + str(col) + ","
print(line)
```
Since the data may be returned in different formats (like integers), you should use the str() function
to convert the values to strings. Otherwise, the concatenation function used in the above example will fail. For
instance, the 6th field is a birthdate field. If you retrieve it as an individual value and try and concatenate a string to it, you get the following error.
```
try:
print("Birth Date="+rows[1][6])
except Exception as err:
print("Oops... Something went wrong!")
print(err)
```
You can fix this problem by adding the str function to convert the date.
```
print("Birth Date="+str(rows[1][6]))
```
## Development SQL
The previous set of `%sql` and `%%sql` commands deals with SQL statements and commands that are run in an interactive manner. There is a class of SQL commands that are more suited to a development environment where code is iterated or requires changing input. The commands that are associated with this form of SQL are:
- AUTOCOMMIT
- COMMIT/ROLLBACK
- PREPARE
- EXECUTE
In addition, the `sqlcode`, `sqlstate` and `sqlerror` fields are populated after every statement so you can use these variables to test for errors.
Autocommit is the default manner in which SQL statements are executed. At the end of the successful completion of a statement, the results are commited to the database. There is no concept of a transaction where multiple DML/DDL statements are considered one transaction. The `AUTOCOMMIT` command allows you to turn autocommit `OFF` or `ON`. This means that the set of SQL commands run after the `AUTOCOMMIT OFF` command are executed are not commited to the database until a `COMMIT` or `ROLLBACK` command is issued.
`COMMIT (WORK)` will finalize all of the transactions (`COMMIT`) to the database and `ROLLBACK` will undo all of the changes. If you issue a `SELECT` statement during the execution of your block, the results will reflect all of your changes. If you `ROLLBACK` the transaction, the changes will be lost.
`PREPARE` is typically used in a situation where you want to repeatidly execute a SQL statement with different variables without incurring the SQL compilation overhead. For instance:
```
x = %sql PREPARE SELECT LASTNAME FROM EMPLOYEE WHERE EMPNO=?
for y in ['000010','000020','000030']:
%sql execute :x using :y
```
`EXECUTE` is used to execute a previously compiled statement.
## Db2 CONNECT Statement
As mentioned at the beginning of this notebook, connecting to Db2 is automatically done when you issue your first
`%sql` statement. Usually the program will prompt you with what options you want when connecting to a database. The other option is to use the CONNECT statement directly. The CONNECT statement is similar to the native Db2
CONNECT command, but includes some options that allow you to connect to databases that has not been
catalogued locally.
The CONNECT command has the following format:
<pre>
%sql CONNECT TO <database> USER <userid> USING <password | ?> HOST <ip address> PORT <port number>
</pre>
If you use a "?" for the password field, the system will prompt you for a password. This avoids typing the
password as clear text on the screen. If a connection is not successful, the system will print the error
message associated with the connect request.
If the connection is successful, the parameters are saved on your system and will be used the next time you
run a SQL statement, or when you issue the %sql CONNECT command with no parameters.
If you want to force the program to connect to a different database (with prompting), use the CONNECT RESET command. The next time you run a SQL statement, the program will prompt you for the the connection
and will force the program to reconnect the next time a SQL statement is executed.
#### Credits: IBM 2018, George Baklarz [[email protected]]
|
github_jupyter
|
```
import numpy as np
import pandas as pd
from sklearn.preprocessing import MinMaxScaler
from sklearn.preprocessing import StandardScaler
df_train = pd.read_excel('wpbc.train.xlsx')
df_test = pd.read_excel('wpbc.test.xlsx')
train = df_train
test = df_test
train.shape
test.shape
train.describe()
import seaborn
import matplotlib.pyplot as plt
def plot_df(df, name):
corr = df[df.columns].corr()
mask = np.zeros_like(corr, dtype=np.bool)
mask[np.triu_indices_from(mask)] = True
plt.figure(figsize=(20, 15))
seaborn.set(font_scale=1.2)
seaborn.heatmap(corr, mask=mask, center=0, annot=True,
square=True, linewidths=3, alpha=0.7)
plt.title(name)
plot_df(train, 'Train')
print(train.columns)
class_name = input("Chooese the class: ")
minmax_scaler = MinMaxScaler()
standard_scaler = StandardScaler()
temp_tr_ans = train[class_name]
temp_ts_ans = test[class_name]
class_count = len(temp_tr_ans.unique())
print(class_count)
tr_data = train.drop([class_name], axis=1)
ts_data = test.drop([class_name], axis=1)
# #결측치 채우기 if 결측치가 0일 경우
# from sklearn.impute import SimpleImputer
# rep_0 = SimpleImputer(missing_values=0, strategy="mean")
# tr_data = rep_0.fit_transform(tr_data)
# ts_data = rep_0.fit_transform(ts_data)
#결측치 채우기 if 결측치가 ?일 경우 - 먼저 ?를 특정한수(ex.333)으로 변경
from sklearn.impute import SimpleImputer
rep_0 = SimpleImputer(missing_values=333, strategy="mean")
tr_data = rep_0.fit_transform(tr_data)
ts_data = rep_0.fit_transform(ts_data)
mm_tr_data = minmax_scaler.fit_transform(tr_data)
mm_ts_data = minmax_scaler.transform(ts_data)
std_tr_data = standard_scaler.fit_transform(tr_data)
std_ts_data = standard_scaler.transform(ts_data)
tr_ans, _ = pd.factorize(temp_tr_ans, sort=True)
ts_ans, _ = pd.factorize(temp_ts_ans, sort=True)
tr_ans
import tensorflow as tf
from sklearn.model_selection import GridSearchCV
from sklearn.model_selection import RandomizedSearchCV
from sklearn.model_selection import ParameterGrid
from sklearn.metrics import precision_score, recall_score, f1_score, accuracy_score
from tensorflow.keras.wrappers.scikit_learn import KerasClassifier
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras.layers import Activation
from tensorflow.keras.layers import BatchNormalization
from tensorflow.keras.layers import Dropout
from sklearn import metrics
from tensorflow.keras.regularizers import l2
from sklearn.metrics import precision_recall_fscore_support
from sklearn.metrics import confusion_matrix
# real Version
def create_model(hidden_layers = 1, neurons =1, init_mode = 'uniform',
activation = 'elu', kernel_regularizer=l2(0.001)):
model = Sequential()
model.add(Dense(neurons, input_dim=len(mm_tr_data.T), kernel_initializer=init_mode, activation=activation))
for i in range(hidden_layers):
model.add(Dense(neurons, kernel_initializer=init_mode, kernel_regularizer=kernel_regularizer))
model.add(BatchNormalization())
model.add(Activation(activation))
model.add(Dropout(0.2))
if class_count == 2:
model.add(Dense(1,activation='sigmoid'))
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
elif class_count != 2:
model.add(Dense(class_count, activation='softmax'))
model.compile(loss='sparse_categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
return model
keras_model = KerasClassifier(build_fn=create_model, epochs=64, batch_size=16)
leaky_relu = tf.nn.leaky_relu
hidden_layers = [4,8,12]
neurons = [32, 64, 128]
activation = ['elu', leaky_relu]
init_mode = ['glorot_uniform', 'he_normal']
param_grid = dict(hidden_layers = hidden_layers, neurons = neurons, init_mode = init_mode, activation = activation)
minmax_grid = GridSearchCV(estimator=keras_model, param_grid=param_grid, n_jobs= -1, cv=3)
std_grid = GridSearchCV(estimator=keras_model, param_grid=param_grid, n_jobs= -1, cv=3)
import warnings
warnings.filterwarnings("ignore")
minmax_grid_result = minmax_grid.fit(mm_tr_data, tr_ans)
std_grid_result = std_grid.fit(std_tr_data, tr_ans)
print("Scaler = minmax")
print("Best: %f using %s" % (minmax_grid_result.best_score_, minmax_grid_result.best_params_))
means = minmax_grid_result.cv_results_['mean_test_score']
stds = minmax_grid_result.cv_results_['std_test_score']
params = minmax_grid_result.cv_results_['params']
for mean, stdev, param in zip(means, stds, params):
print("%f (%f) with: %r" % (mean, stdev, param))
print("Scaler = standard")
print("Best: %f using %s" % (std_grid_result.best_score_, std_grid_result.best_params_))
means = std_grid_result.cv_results_['mean_test_score']
stds = std_grid_result.cv_results_['std_test_score']
params = std_grid_result.cv_results_['params']
for mean, stdev, param in zip(means, stds, params):
print("%f (%f) with: %r" % (mean, stdev, param))
pred = minmax_grid.predict(mm_ts_data)
accuracy = accuracy_score(pred, ts_ans)
ts_ans = ts_ans.astype(float)
precision, recall, fbeta_score, support = precision_recall_fscore_support(ts_ans, pred)
conf_mat = confusion_matrix(ts_ans, pred)
print("Accuracy = ", accuracy)
print("Confusion Matrix")
print("{0}".format(metrics.confusion_matrix(ts_ans, pred)))
print("")
print("Classification Report")
print(metrics.classification_report(ts_ans, pred))
pred = std_grid.predict(std_ts_data)
accuracy = accuracy_score(pred, ts_ans)
ts_ans = ts_ans.astype(float)
precision, recall, fbeta_score, support = precision_recall_fscore_support(ts_ans, pred)
conf_mat = confusion_matrix(ts_ans, pred)
print("Accuracy = ", accuracy)
print("Confusion Matrix")
print("{0}".format(metrics.confusion_matrix(ts_ans, pred)))
print("")
print("Classification Report")
print(metrics.classification_report(ts_ans, pred))
# # testbed Version
# def create_model(hidden_layers = 1, neurons =1, init_mode = 'uniform', activation = 'elu'):
# model = Sequential()
# model.add(Dense(neurons, input_dim=len(tr_data.T), kernel_initializer=init_mode, activation=activation))
# for i in range(hidden_layers):
# model.add(Dense(neurons, kernel_initializer=init_mode))
# model.add(BatchNormalization())
# model.add(Activation(activation))
# model.add(Dropout(0.2))
# if class_count == 2:
# model.add(Dense(1,activation='sigmoid'))
# model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
# elif class_count != 2:
# model.add(Dense(class_count-1, activation='softmax'))
# model.compile(loss='sparse_categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
# return model
# hidden_layers = [5, 10]
# neurons = [32, 64]
# activation = ['elu']
# init_mode = ['he_uniform']
# keras_model = KerasClassifier(build_fn=create_model, epochs=4, batch_size=4)
# param_grid = dict(hidden_layers = hidden_layers, neurons = neurons, init_mode = init_mode, activation = activation)
# grid = GridSearchCV(estimator=keras_model, param_grid=param_grid, n_jobs= -1, cv=2)
```
|
github_jupyter
|
# oneDPL- Gamma Correction example
#### Sections
- [Gamma Correction](#Gamma-Correction)
- [Why use buffer iterators?](#Why-use-buffer-iterators?)
- _Lab Exercise:_ [Gamma Correction](#Lab-Exercise:-Gamma-Correction)
- [Image outputs](#Image-outputs)
## Learning Objectives
* Build a sample __DPC++ application__ to perform Image processing (gamma correction) using oneDPL.
## Gamma Correction
Gamma correction is an image processing algorithm where we enhance the image brightness and contrast levels to have a better view of the image.
Below example creates a bitmap image, and applies the gamma to the image using the DPC++ library offloading to a device. Once we run the program we can view the original image and the gamma corrected image in the corresponding cells below
In the below program we write a data parallel algorithm using the DPC++ library to leverage the computational power in __heterogenous computers__. The DPC++ platform model includes a host computer and a device. The host offloads computation to the device, which could be a __GPU, FPGA, or a multi-core CPU__.
We create a buffer, being responsible for moving data around and counting dependencies. DPC++ Library provides `oneapi::dpl::begin()` and `oneapi::dpl::end()` interfaces for getting buffer iterators and we implemented as below.
### Why use buffer iterators?
Using buffer iterators will ensure that memory is not copied back and forth in between each algorithm execution on device. The code example below shows how the same example above is implemented using buffer iterators which make sure the memory stays on device until the buffer is destructed.
Pass the policy object to the `std::for_each` Parallel STL algorithm, which is defined in the oneapi::dpl::execution namespace and pass the __'begin'__ and __'end'__ buffer iterators as the second and third arguments.
The `oneapi::dpl::execution::dpcpp_default` object is a predefined object of the device_policy class, created with a default kernel name and a default queue. Use it to create customized policy objects, or to pass directly when invoking an algorithm.
The Parallel STL API handles the data transfer and compute.
### Lab Exercise: Gamma Correction
* In this example the student will learn how to use oneDPL library to perform the gamma correction.
* Follow the __Steps 1 to 3__ in the below code to create a SYCL buffer, create buffer iterators, and then call the std::for each function with DPC++ support.
1. Select the code cell below, __follow the STEPS 1 to 3__ in the code comments, click run ▶ to save the code to file.
2. Next run ▶ the cell in the __Build and Run__ section below the code to compile and execute the code.
```
%%writefile gamma-correction/src/main.cpp
//==============================================================
// Copyright © 2019 Intel Corporation
//
// SPDX-License-Identifier: MIT
// =============================================================
#include <oneapi/dpl/algorithm>
#include <oneapi/dpl/execution>
#include <oneapi/dpl/iterator>
#include <iomanip>
#include <iostream>
#include <CL/sycl.hpp>
#include "utils.hpp"
using namespace sycl;
using namespace std;
int main() {
// Image size is width x height
int width = 1440;
int height = 960;
Img<ImgFormat::BMP> image{width, height};
ImgFractal fractal{width, height};
// Lambda to process image with gamma = 2
auto gamma_f = [](ImgPixel &pixel) {
auto v = (0.3f * pixel.r + 0.59f * pixel.g + 0.11f * pixel.b) / 255.0f;
auto gamma_pixel = static_cast<uint8_t>(255 * v * v);
if (gamma_pixel > 255) gamma_pixel = 255;
pixel.set(gamma_pixel, gamma_pixel, gamma_pixel, gamma_pixel);
};
// fill image with created fractal
int index = 0;
image.fill([&index, width, &fractal](ImgPixel &pixel) {
int x = index % width;
int y = index / width;
auto fractal_pixel = fractal(x, y);
if (fractal_pixel < 0) fractal_pixel = 0;
if (fractal_pixel > 255) fractal_pixel = 255;
pixel.set(fractal_pixel, fractal_pixel, fractal_pixel, fractal_pixel);
++index;
});
string original_image = "fractal_original.png";
string processed_image = "fractal_gamma.png";
Img<ImgFormat::BMP> image2 = image;
image.write(original_image);
// call standard serial function for correctness check
image.fill(gamma_f);
// use default policy for algorithms execution
auto policy = oneapi::dpl::execution::dpcpp_default;
// We need to have the scope to have data in image2 after buffer's destruction
{
// ****Step 1: Uncomment the below line to create a buffer, being responsible for moving data around and counting dependencies
//buffer<ImgPixel> b(image2.data(), image2.width() * image2.height());
// create iterator to pass buffer to the algorithm
// **********Step 2: Uncomment the below lines to create buffer iterators. These are passed to the algorithm
//auto b_begin = oneapi::dpl::begin(b);
//auto b_end = oneapi::dpl::end(b);
//*****Step 3: Uncomment the below line to call std::for_each with DPC++ support
//std::for_each(policy, b_begin, b_end, gamma_f);
}
image2.write(processed_image);
// check correctness
if (check(image.begin(), image.end(), image2.begin())) {
cout << "success\n";
} else {
cout << "fail\n";
return 1;
}
cout << "Run on "
<< policy.queue().get_device().template get_info<info::device::name>()
<< "\n";
cout << "Original image is in " << original_image << "\n";
cout << "Image after applying gamma correction on the device is in "
<< processed_image << "\n";
return 0;
}
```
#### Build and Run
Select the cell below and click run ▶ to compile and execute the code:
```
! chmod 755 q; chmod 755 run_gamma_correction.sh; if [ -x "$(command -v qsub)" ]; then ./q run_gamma_correction.sh; else ./run_gamma_correction.sh; fi
```
_If the Jupyter cells are not responsive or if they error out when you compile the code samples, please restart the Jupyter Kernel:
"Kernel->Restart Kernel and Clear All Outputs" and compile the code samples again_
### Image outputs
once you run the program sucessfuly it creates gamma corrected image and the original image. You can see the difference by running the two cells below and visually compare it.
##### View the gamma corrected Image
Select the cell below and click run ▶ to view the generated image using gamma correction:
```
from IPython.display import display, Image
display(Image(filename='gamma-correction/build/src/fractal_gamma.png'))
```
##### View the original Image
Select the cell below and click run ▶ to view the generated image using gamma correction:
```
from IPython.display import display, Image
display(Image(filename='gamma-correction/build/src/fractal_original.png'))
```
# Summary
In this module you will have learned how to apply gamma correction to Images using Data Parallel C++ Library
<html><body><span style="color:Red"><h1>Reset Notebook</h1></span></body></html>
##### Should you be experiencing any issues with your notebook or just want to start fresh run the below cell.
```
from IPython.display import display, Markdown, clear_output
import ipywidgets as widgets
button = widgets.Button(
description='Reset Notebook',
disabled=False,
button_style='', # 'success', 'info', 'warning', 'danger' or ''
tooltip='This will update this notebook, overwriting any changes.',
icon='check' # (FontAwesome names without the `fa-` prefix)
)
out = widgets.Output()
def on_button_clicked(_):
# "linking function with output"
with out:
# what happens when we press the button
clear_output()
!rsync -a --size-only /data/oneapi_workshop/oneAPI_Essentials/07_DPCPP_Library/ ~/oneAPI_Essentials/07_DPCPP_Library
print('Notebook reset -- now click reload on browser.')
# linking button and function together using a button's method
button.on_click(on_button_clicked)
# displaying button and its output together
widgets.VBox([button,out])
```
|
github_jupyter
|
# DECOMON tutorial #3
## Local Robustness to Adversarial Attacks for classification tasks
## Introduction
After training a model, we want to make sure that the model will give the same output for any images "close" to the initial one, showing some robustness to perturbation.
In this notebook, we start from a classifier built on MNIST dataset that given a hand-written digit as input will predict the digit. This will be the first part of the notebook.
<img src="./data/Plot-of-a-Subset-of-Images-from-the-MNIST-Dataset.png" alt="examples of hand-written digit" width="600"/>
In the second part of the notebook, we will investigate the robustness of this model to unstructured modification of the input space: adversarial attacks. For this kind of attacks, **we vary the magnitude of the perturbation of the initial image** and want to assess that despite this noise, the classifier's prediction remain unchanged.
<img src="./data/illustration_adv_attacks.jpeg" alt="examples of hand-written digit" width="600"/>
What we will show is the use of decomon module to assess the robustness of the prediction towards noise.
## The notebook
### imports
```
import os
import tensorflow.keras as keras
import matplotlib.pyplot as plt
import matplotlib.patches as patches
%matplotlib inline
import numpy as np
import tensorflow.keras.backend as K
from tensorflow.keras.models import Sequential, Model, load_model
from tensorflow.keras.layers import Dense
from tensorflow.keras.datasets import mnist
from ipywidgets import interact, interactive, fixed, interact_manual
from ipykernel.pylab.backend_inline import flush_figures
import ipywidgets as widgets
import time
import sys
sys.path.append('..')
import os.path
import os
import pickle as pkl
from contextlib import closing
import time
import tensorflow as tf
import decomon
from decomon.wrapper import refine_boxes
x_min = np.ones((3, 4, 5))
x_max = 2*x_min
refine_boxes(x_min, x_max, 10)
```
### load images
We load MNIST data from keras datasets.
```
ara
img_rows, img_cols = 28, 28
(x_train, y_train_), (x_test, y_test_) = mnist.load_data()
x_train = x_train.reshape((-1, 784))
x_test = x_test.reshape((-1, 784))
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
x_train /= 255
x_test /= 255
y_train = keras.utils.to_categorical(y_train_)
y_test = keras.utils.to_categorical(y_test_)
```
### learn the model (classifier for MNIST images)
For the model, we use a small fully connected network. It is made of 6 layers with 100 units each and ReLU activation functions. **Decomon** is compatible with a large set of Keras layers, so do not hesitate to modify the architecture.
```
model = Sequential()
model.add(Dense(100, activation='relu', input_dim=784))
model.add(Dense(100, activation='relu'))
model.add(Dense(10, activation='softmax'))
model.compile('adam', 'categorical_crossentropy', metrics='acc')
model.fit(x_train, y_train, batch_size=32, shuffle=True, validation_split=0.2, epochs=5)
model.evaluate(x_test, y_test, batch_size=32)
```
After training, we see that the assessment of performance of the model on data that was not seen during training shows pretty good results: around 0.97 (maximum value is 1). It means that out of 100 images, the model was able to guess the correct digit for 97 images. But how can we guarantee that we will get this performance for images different from the ones in the test dataset?
- If we perturbate a "little" an image that was well predicted, will the model stay correct?
- Up to which perturbation?
- Can we guarantee that the model will output the same digit for a given perturbation?
This is where decomon comes in.
<img src="./data/decomon.jpg" alt="Decomon!" width="400"/>
### Applying Decomon for Local Robustness to misclassification
In this section, we detail how to prove local robustness to misclassification. Misclassification can be studied with the global optimisation of a function f:
$$ f(x; \Omega) = \max_{z\in \Omega} \text{NN}_{j\not= i}(z) - \text{NN}_i(z)\;\; \text{s.t}\;\; i = argmax\;\text{NN}(x)$$
If the maximum of f is **negative**, this means that whathever the input sample from the domain, the value outputs by the neural network NN for class i will always be greater than the value output for another class. Hence, there will be no misclassification possible. This is **adversarial robustness**.
<img src="./data/tuto_3_formal_robustness.png" alt="Decomon!" width="400"/>
In that order, we will use the [decomon](https://gheprivate.intra.corp/CRT-DataScience/decomon/tree/master/decomon) library. Decomon combines several optimization trick, including linear relaxation
to get state-of-the-art outer approximation.
To use **decomon** for **adversarial robustness** we first need the following imports:
+ *from decomon.models import convert*: to convert our current Keras model into another neural network nn_model. nn_model will output the same prediction that our model and adds extra information that will be used to derive our formal bounds. For a sake of clarity, how to get such bounds is hidden to the user
+ *from decomon import get_adv_box*: a genereric method to get an upper bound of the funtion f described previously. If the returned value is negative, then we formally assess the robustness to misclassification.
+ *from decomon import check_adv_box*: a generic method that computes the maximum of a lower bound of f. Eventually if this value is positive, it demonstrates that the function f takes positive value. It results that a positive value formally proves the existence of misclassification.
```
import decomon
from decomon.models import convert
from decomon import get_adv_box, get_upper_box, get_lower_box, check_adv_box, get_upper_box
```
For computational efficiency, we convert the model into its decomon version once and for all.
Note that the decomon method will work on the non-converted model. To obtain more refined guarantees, we activate an option denoted **forward**. You can speed up the method by removing this option in the convert method.
```
decomon_model = convert(model)
from decomon import build_formal_adv_model
adv_model = build_formal_adv_model(decomon_model)
x_=x_train[:1]
eps=1e-2
z = np.concatenate([x_[:, None]-eps, x_[:, None]+eps], 1)
get_adv_box(decomon_model, x_,x_, source_labels=y_train[0].argmax())
adv_model.predict([x_, z, y_train[:1]])
# compute gradient
import tensorflow as tf
x_tensor = tf.convert_to_tensor(x_, dtype=tf.float32)
from tensorflow.keras.layers import Concatenate
with tf.GradientTape() as t:
t.watch(x_tensor)
z_tensor = Concatenate(1)([x_tensor[:,None]-eps,\
x_tensor[:, None]+eps])
output = adv_model([x_, z_tensor, y_train[:1]])
result = output
gradients = t.gradient(output, x_tensor)
mask = gradients.numpy()
# scale between 0 and 1.
mask = (mask-mask.min())
plt.imshow(gradients.numpy().reshape((28,28)))
img_mask = np.zeros((784,))
img_mask[np.argsort(mask[0])[::-1][:100]]=1
plt.imshow(img_mask.reshape((28,28)))
plt.imshow(mask.reshape((28,28)))
plt.imshow(x_.reshape((28,28)))
```
We offer an interactive visualisation of the basic adversarial robustness method from decomon **get_adv_upper**. We randomly choose 10 test images use **get_adv_upper** to assess their robustness to misclassification pixel perturbations. The magnitude of the noise on each pixel is independent and bounded by the value of the variable epsilon. The user can reset the examples and vary the noise amplitude.
Note one of the main advantage of decomon: **we can assess robustness on batches of data!**
Circled in <span style="color:green">green</span> are examples that are formally assessed to be robust, <span style="color:orange">orange</span> examples that could be robust and <span style="color:red">red</span> examples that are formally non robust
```
def frame(epsilon, reset=0, filename='./data/.hidden_index.pkl'):
n_cols = 5
n_rows = 2
n_samples = n_cols*n_rows
if reset:
index = np.random.permutation(len(x_test))[:n_samples]
with closing(open(filename, 'wb')) as f:
pkl.dump(index, f)
# save data
else:
# check that file exists
if os.path.isfile(filename):
with closing(open(filename, 'rb')) as f:
index = pkl.load(f)
else:
index = np.arange(n_samples)
with closing(open(filename, 'wb')) as f:
pkl.dump(index, f)
#x = np.concatenate([x_test[0:1]]*10, 0)
x = x_test[index]
x_min = np.maximum(x - epsilon, 0)
x_max = np.minimum(x + epsilon, 1)
n_cols = 5
n_rows = 2
fig, axs = plt.subplots(n_rows, n_cols)
fig.set_figheight(n_rows*fig.get_figheight())
fig.set_figwidth(n_cols*fig.get_figwidth())
plt.subplots_adjust(hspace=0.2) # increase vertical separation
axs_seq = axs.ravel()
source_label = np.argmax(model.predict(x), 1)
start_time = time.process_time()
upper = get_adv_box(decomon_model, x_min, x_max, source_labels=source_label)
lower = check_adv_box(decomon_model, x_min, x_max, source_labels=source_label)
end_time = time.process_time()
count = 0
time.sleep(1)
r_time = "{:.2f}".format(end_time - start_time)
fig.suptitle('Formal Robustness to Adversarial Examples with eps={} running in {} seconds'.format(epsilon, r_time), fontsize=16)
for i in range(n_cols):
for j in range(n_rows):
ax= axs[j, i]
ax.imshow(x[count].reshape((28,28)), cmap='Greys')
robust='ROBUST'
if lower[count]>=0:
color='red'
robust='NON ROBUST'
elif upper[count]<0:
color='green'
else:
color='orange'
robust='MAYBE ROBUST'
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
# Create a Rectangle patch
rect = patches.Rectangle((0,0),27,27,linewidth=3,edgecolor=color,facecolor='none')
ax.add_patch(rect)
ax.set_title(robust)
count+=1
interact(frame, epsilon = widgets.FloatSlider(value=0.,
min=0.,
max=5./255.,
step=0.0001, continuous_update=False, readout_format='.4f',),
reset = widgets.IntSlider(value=0.,
min=0,
max=1,
step=1, continuous_update=False),
fast = widgets.IntSlider(value=1.,
min=0,
max=1,
step=1, continuous_update=False)
)
```
As explained previously, the method **get_adv_upper** output a constant upper bound that is valid on the whole domain.
Sometimes, this bound can be too lose and needs to be refined by splitting the input domain into sub domains.
Several heuristics are possible and you are free to develop your own or take an existing one of the shelf.
|
github_jupyter
|
```
import argparse
import copy
import sys
sys.path.append('../../')
import sopa.src.models.odenet_cifar10.layers as cifar10_models
from sopa.src.models.odenet_cifar10.utils import *
parser = argparse.ArgumentParser()
# Architecture params
parser.add_argument('--is_odenet', type=eval, default=True, choices=[True, False])
parser.add_argument('--network', type=str, choices=['metanode34', 'metanode18', 'metanode10', 'metanode6', 'metanode4',
'premetanode34', 'premetanode18', 'premetanode10', 'premetanode6',
'premetanode4'],
default='premetanode10')
parser.add_argument('--in_planes', type=int, default=64)
# Type of layer's output normalization
parser.add_argument('--normalization_resblock', type=str, default='NF',
choices=['BN', 'GN', 'LN', 'IN', 'NF'])
parser.add_argument('--normalization_odeblock', type=str, default='NF',
choices=['BN', 'GN', 'LN', 'IN', 'NF'])
parser.add_argument('--normalization_bn1', type=str, default='NF',
choices=['BN', 'GN', 'LN', 'IN', 'NF'])
parser.add_argument('--num_gn_groups', type=int, default=32, help='Number of groups for GN normalization')
# Type of layer's weights normalization
parser.add_argument('--param_normalization_resblock', type=str, default='PNF',
choices=['WN', 'SN', 'PNF'])
parser.add_argument('--param_normalization_odeblock', type=str, default='PNF',
choices=['WN', 'SN', 'PNF'])
parser.add_argument('--param_normalization_bn1', type=str, default='PNF',
choices=['WN', 'SN', 'PNF'])
# Type of activation
parser.add_argument('--activation_resblock', type=str, default='ReLU',
choices=['ReLU', 'GeLU', 'Softsign', 'Tanh', 'AF'])
parser.add_argument('--activation_odeblock', type=str, default='ReLU',
choices=['ReLU', 'GeLU', 'Softsign', 'Tanh', 'AF'])
parser.add_argument('--activation_bn1', type=str, default='ReLU',
choices=['ReLU', 'GeLU', 'Softsign', 'Tanh', 'AF'])
args, unknown_args = parser.parse_known_args()
# Initialize Neural ODE model
config = copy.deepcopy(args)
norm_layers = (get_normalization(config.normalization_resblock),
get_normalization(config.normalization_odeblock),
get_normalization(config.normalization_bn1))
param_norm_layers = (get_param_normalization(config.param_normalization_resblock),
get_param_normalization(config.param_normalization_odeblock),
get_param_normalization(config.param_normalization_bn1))
act_layers = (get_activation(config.activation_resblock),
get_activation(config.activation_odeblock),
get_activation(config.activation_bn1))
model = getattr(cifar10_models, config.network)(norm_layers, param_norm_layers, act_layers,
config.in_planes, is_odenet=config.is_odenet)
model
```
|
github_jupyter
|
1/14 최초 구현 by 소연
수정 및 테스트 시 본 파일이 아닌 사본 사용을 부탁드립니다.
```
import os, sys
from google.colab import drive
drive.mount('/content/drive')
%cd /content/drive/Shareddrives/KPMG_Ideation
import warnings
warnings.filterwarnings('ignore')
import numpy as np
import pandas as pd
from pprint import pprint
from krwordrank.word import KRWordRank
from copy import deepcopy
import kss
import itertools
import unicodedata
import requests
from functools import reduce
from bs4 import BeautifulSoup
import string
import torch
from textrankr import TextRank
from lexrankr import LexRank
from nltk.corpus import stopwords
from nltk.tokenize import word_tokenize, sent_tokenize
from pydub import AudioSegment
from konlpy.tag import Okt
import re
import nltk
# nltk.download('punkt')
# import pre-trained model -- frameBERT (pytorch GPU 환경 필요)
%cd /content/drive/Shareddrives/KPMG_Ideation/OpenInformationExtraction/frameBERT
!pip install transformers
import frame_parser
path="/content/drive/Shareddrives/KPMG_Ideation/OpenInformationExtraction/frameBERT"
parser = frame_parser.FrameParser(model_path=path, language='ko')
##### below are permanently installed packages #####
# nb_path = '/content/notebooks'
# os.symlink('/content/drive/Shareddrives/KPMG_Ideation', nb_path)
# sys.path.insert(0, nb_path)
# !pip install --target=$nb_path pydub
# !pip install --target=$nb_path kss
# %cd /content/drive/Shareddrives/KPMG_Ideation/hanspell
# !python setup.py install
# !pip install --target=$nb_path transformers
# !apt-get update
# !apt-get g++ openjdk-8-jdk
# !pip3 install --target=$nb_path konlpy
# !pip install --target=$nb_path soykeyword
# !pip install --target=$nb_path krwordrank
# !pip install --target=$nb_path bert
# !pip install --target=$nb_path textrankr
# !pip install --target=$nb_path lexrankr
# Due to google api credentials, SpeechRecognition needs to be installed everytime
!pip install SpeechRecognition
import speech_recognition as sr
# !pip install --upgrade google-cloud-speech
def to_wav(audio_file_name):
if audio_file_name.split('.')[1] == 'mp3':
sound = AudioSegment.from_mp3(audio_file_name)
audio_file_name = audio_file_name.split('.')[0] + '.wav'
sound.export(audio_file_name, format="wav")
if audio_file_name.split('.')[1] == 'm4a':
sound = AudioSegment.from_file(file_name,'m4a')
audio_file_name = audio_file_name.replace('m4a','wav')
sound.export(audio_file_name, format="wav")
#!/usr/bin/env python3
files_path = ''
file_name = ''
startMin = 0
startSec = 0
endMin = 4
endSec = 30
# Time to miliseconds
startTime = startMin*60*1000+startSec*1000
endTime = endMin*60*1000+endSec*1000
%cd /content/drive/Shareddrives/KPMG_Ideation/data
file_name='audio_only_1.m4a'
track = AudioSegment.from_file(file_name,'m4a')
wav_filename = file_name.replace('m4a', 'wav')
file_handle = track.export(wav_filename, format='wav')
song = AudioSegment.from_wav('audio_only_1.wav')
extract = song[startTime:endTime]
# Saving as wav
extract.export('result.wav', format="wav")
AUDIO_FILE = os.path.join(os.path.dirname(os.path.abspath('data')), "result.wav")
# use the audio file as the audio source
r = sr.Recognizer()
with sr.AudioFile(AUDIO_FILE) as source:
audio = r.record(source) # read the entire audio file
# recognize speech using Google Speech Recognition
try:
# for testing purposes, we're just using the default API key
# to use another API key, use `r.recognize_google(audio, key="GOOGLE_SPEECH_RECOGNITION_API_KEY")`
# instead of `r.recognize_google(audio)`
txt = r.recognize_google(audio, language='ko')
print("Google Speech Recognition:" + txt)
except sr.UnknownValueError:
print("Google Speech Recognition could not understand audio")
except sr.RequestError as e:
print("Could not request results from Google Speech Recognition service; {0}".format(e))
%cd /content/drive/Shareddrives/KPMG_Ideation/hanspell
from hanspell import spell_checker
chked=""
line = kss.split_sentences(txt)
for i in range(len(line)):
line[i] = spell_checker.check(line[i])[2]
print("Checked spelling ",line[i])
chked += "".join(line[i])
chked += ". "
chked
okt = Okt()
class Text():
def __init__(self, text):
text = re.sub("'", ' ', text)
paragraphs = text.split('\n')
self.text = text
self.paragraphs = [i for i in paragraphs if i]
self.counts = len(self.paragraphs)
self.docs = [kss.split_sentences(paragraph) for paragraph in paragraphs if kss.split_sentences(paragraph)]
self.newtext = deepcopy(self.text)
print("TEXT")
def findall(self, p, s):
i = s.find(p)
while i != -1:
yield i
i = s.find(p, i + 1)
def countMatcher(self, sentences, paragraph_no):
paragraph = self.docs[paragraph_no]
total_no = len(paragraph)
vec = [0] * total_no
for idx, candidate in enumerate(paragraph):
for sentence in sentences:
if sentence[:4] in candidate:
vec[idx] += 1
return vec
class Highlight(Text):
def __init__(self, text):
super().__init__(text)
print("Highlight")
wordrank_extractor = KRWordRank(min_count=3, max_length=10)
self.keywords, rank, graph = wordrank_extractor.extract(self.paragraphs)
self.path = "/content/drive/Shareddrives/KPMG_Ideation/OpenInformationExtraction/frameBERT"
p = []
kw = []
for k, v in self.keywords.items():
p.append(okt.pos(k))
kw.append(k)
words = self.text.split(' ')
s = set()
keylist = [word for i in kw for word in words if i in word]
keylist = [i for i in keylist if len(i)>2]
for i in keylist:
if len(i)>2:
s.add(i)
# print("KEYLIST: ",keylist)
p = [okt.pos(word) for word in s]
self.s = set()
for idx in range(len(p)):
ls = p[idx]
for tags in ls:
word,tag = tags
if tag == "Noun":
if len(word)>=2:
self.s.add(word)
self.keys = []
for temp in self.s:
self.keys.append(" " + str(temp))
print("KEYWORDS: ", self.keys)
def add_tags_conj(self, txt):
conj = '그리고, 그런데, 그러나, 그래도, 그래서, 또는, 및, 즉, 게다가, 따라서, 때문에, 아니면, 왜냐하면, 단, 오히려, 비록, 예를 들어, 반면에, 하지만, 그렇다면, 바로, 이에 대해'
conj = conj.replace("'", "")
self.candidates = conj.split(",")
self.newtext = deepcopy(txt)
self.idx = [(i, i + len(candidate)) for candidate in self.candidates for i in
self.findall(candidate, txt)]
for i in range(len(self.idx)):
try:
self.idx = [(start, start + len(candidate)) for candidate in self.candidates for start in
self.findall(candidate, self.newtext)]
word = self.newtext[self.idx[i][0]:self.idx[i][1]]
self.newtext = word.join([self.newtext[:self.idx[i][0]], self.newtext[self.idx[i][1]:]])
except:
pass
return self.newtext
class Summarize(Highlight):
def __init__(self, text, paragraph_no):
super().__init__(text)
print("length of paragraphs ",len(self.paragraphs))
self.txt = self.paragraphs[paragraph_no]
self.paragraph_no = paragraph_no
def summarize(self):
url = "https://api.smrzr.io/v1/summarize?num_sentences=5&algorithm=kmeans"
headers = {
'content-type': 'raw/text',
'origin': 'https://smrzr.io',
'referer': 'https://smrzr.io/',
'sec-fetch-dest': 'empty',
'sec-fetch-mode': 'cors',
'sec-fetch-site': 'same-site',
"user-agent": "Mozilla/5.0"
}
resp = requests.post(url, headers=headers, data= self.txt.encode('utf-8'))
assert resp.status_code == 200
summary = resp.json()['summary']
temp = summary.split('\n')
print("BERT: ", temp)
return temp
def summarizeTextRank(self):
tr = TextRank(sent_tokenize)
summary = tr.summarize(self.txt, num_sentences=5).split('\n')
print("Textrank: ",summary)
return summary
def summarizeLexRank(self):
lr = LexRank()
lr.summarize(self.txt)
summaries = lr.probe()
print("Lexrank: ",summaries)
return summaries
def ensembleSummarize(self):
a = np.array(self.countMatcher(self.summarize(), self.paragraph_no))
try:
b = np.array(self.countMatcher(self.summarizeLexRank(), self.paragraph_no))
except:
b = np.zeros_like(a)
c = np.array(self.countMatcher(self.summarizeTextRank(),self.paragraph_no))
result= a+b+c
i, = np.where(result == max(result))
txt, index = self.docs[self.paragraph_no][i[0]], i[0]
return txt, index
result = chked
high = Highlight(result)
summarizer = Summarize(chked, 0)
sum, id = summarizer.ensembleSummarize()
print("summarized ",sum)
sum
```
- 사용자 인식(speaker identification)이 됐으면 좋겠다 -- clova NOTE 사용시 해결
> 무료 api는 supervised만 있는 듯
>google speech api는 한국어 speaker diarization 지원 X
- 시간단위로 잘리는 것 루프 만들기
- 기본 웹프레임워크 만들기
- 아웃풋 어떤 모양일지?
|
github_jupyter
|
```
from pynq import Overlay
from pynq import PL
from pprint import pprint
pprint(PL.ip_dict)
print(PL.timestamp)
ol2 = Overlay('base.bit')
ol2.download()
pprint(PL.ip_dict)
print(PL.timestamp)
PL.interrupt_controllers
PL.gpio_dict
a = PL.ip_dict
for i,j in enumerate(a):
print(i,j,a[j])
a['SEG_rgbled_gpio_Reg']
b = [value for key, value in a.items() if 'mb_bram_ctrl' in key.lower()]
print(b)
addr_base,addr_range,state = a['SEG_rgbled_gpio_Reg']
addr_base
a = [None]
a*10
import re
tcl_name = 'parse.txt'
pat1 = 'connect_bd_net'
pat2 = '[get_bd_pins processing_system7_0/GPIO_O]'
result = {}
gpio_pool1 = set()
gpio_pool2 = set()
with open(tcl_name, 'r') as f:
for line in f:
if not line.startswith('#') and (pat1 in line) and (pat2 in line):
gpio_pool1 = gpio_pool1.union(set(re.findall(
'\[get_bd_pins (.+?)/Din\]', line, re.IGNORECASE)))
while gpio_pool1:
gpio_net = gpio_pool1.pop()
if not gpio_net in gpio_pool2:
pat3 = '[get_bd_pins ' + gpio_net + '/Din]'
gpio_pool2.add(gpio_net)
with open(tcl_name, 'r') as f:
for line in f:
if not line.startswith('#') and (pat1 in line) and \
(pat3 in line):
gpio_pool1 = gpio_pool1.union(set(re.findall(
'\[get_bd_pins (.+?)/Din\]', line, re.IGNORECASE)))
gpio_pool1.discard(gpio_net)
gpio_list = list(gpio_pool2)
print(gpio_list)
"""
index = 0
match = []
for i in gpio_list:
pat4 = "create_bd_cell -type ip -vlnv (.+?) " + i + "($| )"
with open(tcl_name, 'r') as f:
for line in f:
if not line.startswith('#'):
m = re.search(pat4, line, re.IGNORECASE)
if m:
match.append(m.group(2))
continue
print(match)
"""
with open('parse.txt') as f:
file_str =''.join(line.replace('\n',' ').replace('\r','') for line in f
and not line.startswith('#'))
print(file_str)
for j in gpio_list:
pat5 = "set_property -dict \[ list \\\\ "+\
"CONFIG.DIN_FROM {([0-9]+)} \\\\ "+\
"CONFIG.DIN_TO {([0-9]+)} \\\\ "+\
"CONFIG.DIN_WIDTH {([0-9]+)} \\\\ "+\
"CONFIG.DOUT_WIDTH {([0-9]+)} \\\\ "+\
"\] \$" + j
print(pat5)
m = re.search(pat5,file_str,re.IGNORECASE)
if m:
index = m.group(1)
result[j] = [int(index), None]
print(result)
str1 = 'create_bd_cell -type ip -vlnv xilinx.com:ip:xlslice:1.0 mb3_timer_capture_4'
str2 = 'set mb3_timer_capture_5 [ create_bd_cell -type ip -vlnv xilinx.com:ip:xlslice:1.0 mb3_timer_capture_5 ]'
pat1 = "create_bd_cell -type ip -vlnv (.+?) (.+?)($| )"
match1 = re.search(pat1, str2, re.IGNORECASE)
match1.group(2)
with open('parse.txt') as f:
data=''.join(line.replace('\n',' ').replace('\r','') for line in f)
print(data)
str1 = "[123 456\ $2]"
pat1 = "\[(.+?) (.+?)\\\\ \$(.+?)]"
m = re.search(pat1, str1, re.IGNORECASE)
if m:
print(m.group(1))
print(m.group(2))
print(type(m.group(1)))
a = [1,2,3]
print(a[-1])
print(a)
import re
prop_name_regex = "CONFIG.DIN_FROM {([0-9]+)} \\\\"
str1 = "CONFIG.DIN_FROM {13} \\"
m = re.search(prop_name_regex,str1)
if m:
print(m.group(1))
a = {1:'mb_1_reset', 2:'mb_2_reset'}
res = dict((v,[k,None]) for k,v in a.items() if k>1)
print(res)
a = {1:'mb_1_reset', 2:'mb_2_reset'}
b = a.copy()
a.clear()
print(b)
a = {1:['mb_1_reset',None], 2:['mb_2_reset','running']}
a = {i:j for i,j in a.items() if j[1] is not None}
print(a)
import re
str1 = " set processing_system7_0 [ create_bd_cell -type ip -vlnv "+\
"xilinx.com:ip:processing_system7:5.5 processing_system7_0 ]"
ip_regex = "create_bd_cell -type ip -vlnv " + \
"(.+?):ip:(.+?):(.+?) (.+?) "
m = re.search(ip_regex,str1)
print(m.groups())
import numpy as np
a = np.random.randint(0,32,10,dtype=np.uint32)
print(a)
```
|
github_jupyter
|
# Capsule Networks (CapsNets)
Based on the paper: [Dynamic Routing Between Capsules](https://arxiv.org/abs/1710.09829), by Sara Sabour, Nicholas Frosst and Geoffrey E. Hinton (NIPS 2017).
Inspired in part from Huadong Liao's implementation: [CapsNet-TensorFlow](https://github.com/naturomics/CapsNet-Tensorflow).
# Introduction
Watch [this video](https://www.youtube.com/embed/pPN8d0E3900) to understand the key ideas behind Capsule Networks:
```
from IPython.display import HTML
# Display the video in an iframe:
HTML("""<iframe width="560" height="315"
src="https://www.youtube.com/embed/pPN8d0E3900"
frameborder="0"
allowfullscreen></iframe>""")
```
# Imports
To support both Python 2 and Python 3:
```
from __future__ import division, print_function, unicode_literals
```
To plot pretty figures:
```
%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
```
We will need NumPy and TensorFlow:
```
import numpy as np
import tensorflow as tf
```
# Reproducibility
Let's reset the default graph, in case you re-run this notebook without restarting the kernel:
```
tf.reset_default_graph()
```
Let's set the random seeds so that this notebook always produces the same output:
```
np.random.seed(42)
tf.set_random_seed(42)
```
# Load MNIST
Yes, I know, it's MNIST again. But hopefully this powerful idea will work as well on larger datasets, time will tell.
```
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("/tmp/data/")
```
Let's look at what these hand-written digit images look like:
```
n_samples = 5
plt.figure(figsize=(n_samples * 2, 3))
for index in range(n_samples):
plt.subplot(1, n_samples, index + 1)
sample_image = mnist.train.images[index].reshape(28, 28)
plt.imshow(sample_image, cmap="binary")
plt.axis("off")
plt.show()
```
And these are the corresponding labels:
```
mnist.train.labels[:n_samples]
```
Now let's build a Capsule Network to classify these images. Here's the overall architecture, enjoy the ASCII art! ;-)
Note: for readability, I left out two arrows: Labels → Mask, and Input Images → Reconstruction Loss.
```
Loss
↑
┌─────────┴─────────┐
Labels → Margin Loss Reconstruction Loss
↑ ↑
Length Decoder
↑ ↑
Digit Capsules ────Mask────┘
↖↑↗ ↖↑↗ ↖↑↗
Primary Capsules
↑
Input Images
```
We are going to build the graph starting from the bottom layer, and gradually move up, left side first. Let's go!
# Input Images
Let's start by creating a placeholder for the input images (28×28 pixels, 1 color channel = grayscale).
```
X = tf.placeholder(shape=[None, 28, 28, 1], dtype=tf.float32, name="X")
```
# Primary Capsules
The first layer will be composed of 32 maps of 6×6 capsules each, where each capsule will output an 8D activation vector:
```
caps1_n_maps = 32
caps1_n_caps = caps1_n_maps * 6 * 6 # 1152 primary capsules
caps1_n_dims = 8
```
To compute their outputs, we first apply two regular convolutional layers:
```
conv1_params = {
"filters": 256,
"kernel_size": 9,
"strides": 1,
"padding": "valid",
"activation": tf.nn.relu,
}
conv2_params = {
"filters": caps1_n_maps * caps1_n_dims, # 256 convolutional filters
"kernel_size": 9,
"strides": 2,
"padding": "valid",
"activation": tf.nn.relu
}
conv1 = tf.layers.conv2d(X, name="conv1", **conv1_params)
conv2 = tf.layers.conv2d(conv1, name="conv2", **conv2_params)
```
Note: since we used a kernel size of 9 and no padding (for some reason, that's what `"valid"` means), the image shrunk by 9-1=8 pixels after each convolutional layer (28×28 to 20×20, then 20×20 to 12×12), and since we used a stride of 2 in the second convolutional layer, the image size was divided by 2. This is how we end up with 6×6 feature maps.
Next, we reshape the output to get a bunch of 8D vectors representing the outputs of the primary capsules. The output of `conv2` is an array containing 32×8=256 feature maps for each instance, where each feature map is 6×6. So the shape of this output is (_batch size_, 6, 6, 256). We want to chop the 256 into 32 vectors of 8 dimensions each. We could do this by reshaping to (_batch size_, 6, 6, 32, 8). However, since this first capsule layer will be fully connected to the next capsule layer, we can simply flatten the 6×6 grids. This means we just need to reshape to (_batch size_, 6×6×32, 8).
```
caps1_raw = tf.reshape(conv2, [-1, caps1_n_caps, caps1_n_dims],
name="caps1_raw")
```
Now we need to squash these vectors. Let's define the `squash()` function, based on equation (1) from the paper:
$\operatorname{squash}(\mathbf{s}) = \dfrac{\|\mathbf{s}\|^2}{1 + \|\mathbf{s}\|^2} \dfrac{\mathbf{s}}{\|\mathbf{s}\|}$
The `squash()` function will squash all vectors in the given array, along the given axis (by default, the last axis).
**Caution**, a nasty bug is waiting to bite you: the derivative of $\|\mathbf{s}\|$ is undefined when $\|\mathbf{s}\|=0$, so we can't just use `tf.norm()`, or else it will blow up during training: if a vector is zero, the gradients will be `nan`, so when the optimizer updates the variables, they will also become `nan`, and from then on you will be stuck in `nan` land. The solution is to implement the norm manually by computing the square root of the sum of squares plus a tiny epsilon value: $\|\mathbf{s}\| \approx \sqrt{\sum\limits_i{{s_i}^2}\,\,+ \epsilon}$.
```
def squash(s, axis=-1, epsilon=1e-7, name=None):
with tf.name_scope(name, default_name="squash"):
squared_norm = tf.reduce_sum(tf.square(s), axis=axis,
keep_dims=True)
safe_norm = tf.sqrt(squared_norm + epsilon)
squash_factor = squared_norm / (1. + squared_norm)
unit_vector = s / safe_norm
return squash_factor * unit_vector
```
Now let's apply this function to get the output $\mathbf{u}_i$ of each primary capsules $i$ :
```
caps1_output = squash(caps1_raw, name="caps1_output")
```
Great! We have the output of the first capsule layer. It wasn't too hard, was it? However, computing the next layer is where the fun really begins.
# Digit Capsules
To compute the output of the digit capsules, we must first compute the predicted output vectors (one for each primary / digit capsule pair). Then we can run the routing by agreement algorithm.
## Compute the Predicted Output Vectors
The digit capsule layer contains 10 capsules (one for each digit) of 16 dimensions each:
```
caps2_n_caps = 10
caps2_n_dims = 16
```
For each capsule $i$ in the first layer, we want to predict the output of every capsule $j$ in the second layer. For this, we will need a transformation matrix $\mathbf{W}_{i,j}$ (one for each pair of capsules ($i$, $j$)), then we can compute the predicted output $\hat{\mathbf{u}}_{j|i} = \mathbf{W}_{i,j} \, \mathbf{u}_i$ (equation (2)-right in the paper). Since we want to transform an 8D vector into a 16D vector, each transformation matrix $\mathbf{W}_{i,j}$ must have a shape of (16, 8).
To compute $\hat{\mathbf{u}}_{j|i}$ for every pair of capsules ($i$, $j$), we will use a nice feature of the `tf.matmul()` function: you probably know that it lets you multiply two matrices, but you may not know that it also lets you multiply higher dimensional arrays. It treats the arrays as arrays of matrices, and it performs itemwise matrix multiplication. For example, suppose you have two 4D arrays, each containing a 2×3 grid of matrices. The first contains matrices $\mathbf{A}, \mathbf{B}, \mathbf{C}, \mathbf{D}, \mathbf{E}, \mathbf{F}$ and the second contains matrices $\mathbf{G}, \mathbf{H}, \mathbf{I}, \mathbf{J}, \mathbf{K}, \mathbf{L}$. If you multiply these two 4D arrays using the `tf.matmul()` function, this is what you get:
$
\pmatrix{
\mathbf{A} & \mathbf{B} & \mathbf{C} \\
\mathbf{D} & \mathbf{E} & \mathbf{F}
} \times
\pmatrix{
\mathbf{G} & \mathbf{H} & \mathbf{I} \\
\mathbf{J} & \mathbf{K} & \mathbf{L}
} = \pmatrix{
\mathbf{AG} & \mathbf{BH} & \mathbf{CI} \\
\mathbf{DJ} & \mathbf{EK} & \mathbf{FL}
}
$
We can apply this function to compute $\hat{\mathbf{u}}_{j|i}$ for every pair of capsules ($i$, $j$) like this (recall that there are 6×6×32=1152 capsules in the first layer, and 10 in the second layer):
$
\pmatrix{
\mathbf{W}_{1,1} & \mathbf{W}_{1,2} & \cdots & \mathbf{W}_{1,10} \\
\mathbf{W}_{2,1} & \mathbf{W}_{2,2} & \cdots & \mathbf{W}_{2,10} \\
\vdots & \vdots & \ddots & \vdots \\
\mathbf{W}_{1152,1} & \mathbf{W}_{1152,2} & \cdots & \mathbf{W}_{1152,10}
} \times
\pmatrix{
\mathbf{u}_1 & \mathbf{u}_1 & \cdots & \mathbf{u}_1 \\
\mathbf{u}_2 & \mathbf{u}_2 & \cdots & \mathbf{u}_2 \\
\vdots & \vdots & \ddots & \vdots \\
\mathbf{u}_{1152} & \mathbf{u}_{1152} & \cdots & \mathbf{u}_{1152}
}
=
\pmatrix{
\hat{\mathbf{u}}_{1|1} & \hat{\mathbf{u}}_{2|1} & \cdots & \hat{\mathbf{u}}_{10|1} \\
\hat{\mathbf{u}}_{1|2} & \hat{\mathbf{u}}_{2|2} & \cdots & \hat{\mathbf{u}}_{10|2} \\
\vdots & \vdots & \ddots & \vdots \\
\hat{\mathbf{u}}_{1|1152} & \hat{\mathbf{u}}_{2|1152} & \cdots & \hat{\mathbf{u}}_{10|1152}
}
$
The shape of the first array is (1152, 10, 16, 8), and the shape of the second array is (1152, 10, 8, 1). Note that the second array must contain 10 identical copies of the vectors $\mathbf{u}_1$ to $\mathbf{u}_{1152}$. To create this array, we will use the handy `tf.tile()` function, which lets you create an array containing many copies of a base array, tiled in any way you want.
Oh, wait a second! We forgot one dimension: _batch size_. Say we feed 50 images to the capsule network, it will make predictions for these 50 images simultaneously. So the shape of the first array must be (50, 1152, 10, 16, 8), and the shape of the second array must be (50, 1152, 10, 8, 1). The first layer capsules actually already output predictions for all 50 images, so the second array will be fine, but for the first array, we will need to use `tf.tile()` to have 50 copies of the transformation matrices.
Okay, let's start by creating a trainable variable of shape (1, 1152, 10, 16, 8) that will hold all the transformation matrices. The first dimension of size 1 will make this array easy to tile. We initialize this variable randomly using a normal distribution with a standard deviation to 0.01.
```
init_sigma = 0.01
W_init = tf.random_normal(
shape=(1, caps1_n_caps, caps2_n_caps, caps2_n_dims, caps1_n_dims),
stddev=init_sigma, dtype=tf.float32, name="W_init")
W = tf.Variable(W_init, name="W")
```
Now we can create the first array by repeating `W` once per instance:
```
batch_size = tf.shape(X)[0]
W_tiled = tf.tile(W, [batch_size, 1, 1, 1, 1], name="W_tiled")
```
That's it! On to the second array, now. As discussed earlier, we need to create an array of shape (_batch size_, 1152, 10, 8, 1), containing the output of the first layer capsules, repeated 10 times (once per digit, along the third dimension, which is axis=2). The `caps1_output` array has a shape of (_batch size_, 1152, 8), so we first need to expand it twice, to get an array of shape (_batch size_, 1152, 1, 8, 1), then we can repeat it 10 times along the third dimension:
```
caps1_output_expanded = tf.expand_dims(caps1_output, -1,
name="caps1_output_expanded")
caps1_output_tile = tf.expand_dims(caps1_output_expanded, 2,
name="caps1_output_tile")
caps1_output_tiled = tf.tile(caps1_output_tile, [1, 1, caps2_n_caps, 1, 1],
name="caps1_output_tiled")
```
Let's check the shape of the first array:
```
W_tiled
```
Good, and now the second:
```
caps1_output_tiled
```
Yes! Now, to get all the predicted output vectors $\hat{\mathbf{u}}_{j|i}$, we just need to multiply these two arrays using `tf.matmul()`, as explained earlier:
```
caps2_predicted = tf.matmul(W_tiled, caps1_output_tiled,
name="caps2_predicted")
```
Let's check the shape:
```
caps2_predicted
```
Perfect, for each instance in the batch (we don't know the batch size yet, hence the "?") and for each pair of first and second layer capsules (1152×10) we have a 16D predicted output column vector (16×1). We're ready to apply the routing by agreement algorithm!
## Routing by agreement
First let's initialize the raw routing weights $b_{i,j}$ to zero:
```
raw_weights = tf.zeros([batch_size, caps1_n_caps, caps2_n_caps, 1, 1],
dtype=np.float32, name="raw_weights")
```
We will see why we need the last two dimensions of size 1 in a minute.
### Round 1
First, let's apply the softmax function to compute the routing weights, $\mathbf{c}_{i} = \operatorname{softmax}(\mathbf{b}_i)$ (equation (3) in the paper):
```
routing_weights = tf.nn.softmax(raw_weights, dim=2, name="routing_weights")
```
Now let's compute the weighted sum of all the predicted output vectors for each second-layer capsule, $\mathbf{s}_j = \sum\limits_{i}{c_{i,j}\hat{\mathbf{u}}_{j|i}}$ (equation (2)-left in the paper):
```
weighted_predictions = tf.multiply(routing_weights, caps2_predicted,
name="weighted_predictions")
weighted_sum = tf.reduce_sum(weighted_predictions, axis=1, keep_dims=True,
name="weighted_sum")
```
There are a couple important details to note here:
* To perform elementwise matrix multiplication (also called the Hadamard product, noted $\circ$), we use the `tf.multiply()` function. It requires `routing_weights` and `caps2_predicted` to have the same rank, which is why we added two extra dimensions of size 1 to `routing_weights`, earlier.
* The shape of `routing_weights` is (_batch size_, 1152, 10, 1, 1) while the shape of `caps2_predicted` is (_batch size_, 1152, 10, 16, 1). Since they don't match on the fourth dimension (1 _vs_ 16), `tf.multiply()` automatically _broadcasts_ the `routing_weights` 16 times along that dimension. If you are not familiar with broadcasting, a simple example might help:
$ \pmatrix{1 & 2 & 3 \\ 4 & 5 & 6} \circ \pmatrix{10 & 100 & 1000} = \pmatrix{1 & 2 & 3 \\ 4 & 5 & 6} \circ \pmatrix{10 & 100 & 1000 \\ 10 & 100 & 1000} = \pmatrix{10 & 200 & 3000 \\ 40 & 500 & 6000} $
And finally, let's apply the squash function to get the outputs of the second layer capsules at the end of the first iteration of the routing by agreement algorithm, $\mathbf{v}_j = \operatorname{squash}(\mathbf{s}_j)$ :
```
caps2_output_round_1 = squash(weighted_sum, axis=-2,
name="caps2_output_round_1")
caps2_output_round_1
```
Good! We have ten 16D output vectors for each instance, as expected.
### Round 2
First, let's measure how close each predicted vector $\hat{\mathbf{u}}_{j|i}$ is to the actual output vector $\mathbf{v}_j$ by computing their scalar product $\hat{\mathbf{u}}_{j|i} \cdot \mathbf{v}_j$.
* Quick math reminder: if $\vec{a}$ and $\vec{b}$ are two vectors of equal length, and $\mathbf{a}$ and $\mathbf{b}$ are their corresponding column vectors (i.e., matrices with a single column), then $\mathbf{a}^T \mathbf{b}$ (i.e., the matrix multiplication of the transpose of $\mathbf{a}$, and $\mathbf{b}$) is a 1×1 matrix containing the scalar product of the two vectors $\vec{a}\cdot\vec{b}$. In Machine Learning, we generally represent vectors as column vectors, so when we talk about computing the scalar product $\hat{\mathbf{u}}_{j|i} \cdot \mathbf{v}_j$, this actually means computing ${\hat{\mathbf{u}}_{j|i}}^T \mathbf{v}_j$.
Since we need to compute the scalar product $\hat{\mathbf{u}}_{j|i} \cdot \mathbf{v}_j$ for each instance, and for each pair of first and second level capsules $(i, j)$, we will once again take advantage of the fact that `tf.matmul()` can multiply many matrices simultaneously. This will require playing around with `tf.tile()` to get all dimensions to match (except for the last 2), just like we did earlier. So let's look at the shape of `caps2_predicted`, which holds all the predicted output vectors $\hat{\mathbf{u}}_{j|i}$ for each instance and each pair of capsules:
```
caps2_predicted
```
And now let's look at the shape of `caps2_output_round_1`, which holds 10 outputs vectors of 16D each, for each instance:
```
caps2_output_round_1
```
To get these shapes to match, we just need to tile the `caps2_output_round_1` array 1152 times (once per primary capsule) along the second dimension:
```
caps2_output_round_1_tiled = tf.tile(
caps2_output_round_1, [1, caps1_n_caps, 1, 1, 1],
name="caps2_output_round_1_tiled")
```
And now we are ready to call `tf.matmul()` (note that we must tell it to transpose the matrices in the first array, to get ${\hat{\mathbf{u}}_{j|i}}^T$ instead of $\hat{\mathbf{u}}_{j|i}$):
```
agreement = tf.matmul(caps2_predicted, caps2_output_round_1_tiled,
transpose_a=True, name="agreement")
```
We can now update the raw routing weights $b_{i,j}$ by simply adding the scalar product $\hat{\mathbf{u}}_{j|i} \cdot \mathbf{v}_j$ we just computed: $b_{i,j} \gets b_{i,j} + \hat{\mathbf{u}}_{j|i} \cdot \mathbf{v}_j$ (see Procedure 1, step 7, in the paper).
```
raw_weights_round_2 = tf.add(raw_weights, agreement,
name="raw_weights_round_2")
```
The rest of round 2 is the same as in round 1:
```
routing_weights_round_2 = tf.nn.softmax(raw_weights_round_2,
dim=2,
name="routing_weights_round_2")
weighted_predictions_round_2 = tf.multiply(routing_weights_round_2,
caps2_predicted,
name="weighted_predictions_round_2")
weighted_sum_round_2 = tf.reduce_sum(weighted_predictions_round_2,
axis=1, keep_dims=True,
name="weighted_sum_round_2")
caps2_output_round_2 = squash(weighted_sum_round_2,
axis=-2,
name="caps2_output_round_2")
```
We could go on for a few more rounds, by repeating exactly the same steps as in round 2, but to keep things short, we will stop here:
```
caps2_output = caps2_output_round_2
```
### Static or Dynamic Loop?
In the code above, we created different operations in the TensorFlow graph for each round of the routing by agreement algorithm. In other words, it's a static loop.
Sure, instead of copy/pasting the code several times, we could have written a `for` loop in Python, but this would not change the fact that the graph would end up containing different operations for each routing iteration. It's actually okay since we generally want less than 5 routing iterations, so the graph won't grow too big.
However, you may prefer to implement the routing loop within the TensorFlow graph itself rather than using a Python `for` loop. To do this, you would need to use TensorFlow's `tf.while_loop()` function. This way, all routing iterations would reuse the same operations in the graph, it would be a dynamic loop.
For example, here is how to build a small loop that computes the sum of squares from 1 to 100:
```
def condition(input, counter):
return tf.less(counter, 100)
def loop_body(input, counter):
output = tf.add(input, tf.square(counter))
return output, tf.add(counter, 1)
with tf.name_scope("compute_sum_of_squares"):
counter = tf.constant(1)
sum_of_squares = tf.constant(0)
result = tf.while_loop(condition, loop_body, [sum_of_squares, counter])
with tf.Session() as sess:
print(sess.run(result))
```
As you can see, the `tf.while_loop()` function expects the loop condition and body to be provided _via_ two functions. These functions will be called only once by TensorFlow, during the graph construction phase, _not_ while executing the graph. The `tf.while_loop()` function stitches together the graph fragments created by `condition()` and `loop_body()` with some additional operations to create the loop.
Also note that during training, TensorFlow will automagically handle backpropogation through the loop, so you don't need to worry about that.
Of course, we could have used this one-liner instead! ;-)
```
sum([i**2 for i in range(1, 100 + 1)])
```
Joke aside, apart from reducing the graph size, using a dynamic loop instead of a static loop can help reduce how much GPU RAM you use (if you are using a GPU). Indeed, if you set `swap_memory=True` when calling the `tf.while_loop()` function, TensorFlow will automatically check GPU RAM usage at each loop iteration, and it will take care of swapping memory between the GPU and the CPU when needed. Since CPU memory is much cheaper and abundant than GPU RAM, this can really make a big difference.
# Estimated Class Probabilities (Length)
The lengths of the output vectors represent the class probabilities, so we could just use `tf.norm()` to compute them, but as we saw when discussing the squash function, it would be risky, so instead let's create our own `safe_norm()` function:
```
def safe_norm(s, axis=-1, epsilon=1e-7, keep_dims=False, name=None):
with tf.name_scope(name, default_name="safe_norm"):
squared_norm = tf.reduce_sum(tf.square(s), axis=axis,
keep_dims=keep_dims)
return tf.sqrt(squared_norm + epsilon)
y_proba = safe_norm(caps2_output, axis=-2, name="y_proba")
```
To predict the class of each instance, we can just select the one with the highest estimated probability. To do this, let's start by finding its index using `tf.argmax()`:
```
y_proba_argmax = tf.argmax(y_proba, axis=2, name="y_proba")
```
Let's look at the shape of `y_proba_argmax`:
```
y_proba_argmax
```
That's what we wanted: for each instance, we now have the index of the longest output vector. Let's get rid of the last two dimensions by using `tf.squeeze()` which removes dimensions of size 1. This gives us the capsule network's predicted class for each instance:
```
y_pred = tf.squeeze(y_proba_argmax, axis=[1,2], name="y_pred")
y_pred
```
Okay, we are now ready to define the training operations, starting with the losses.
# Labels
First, we will need a placeholder for the labels:
```
y = tf.placeholder(shape=[None], dtype=tf.int64, name="y")
```
# Margin loss
The paper uses a special margin loss to make it possible to detect two or more different digits in each image:
$ L_k = T_k \max(0, m^{+} - \|\mathbf{v}_k\|)^2 - \lambda (1 - T_k) \max(0, \|\mathbf{v}_k\| - m^{-})^2$
* $T_k$ is equal to 1 if the digit of class $k$ is present, or 0 otherwise.
* In the paper, $m^{+} = 0.9$, $m^{-} = 0.1$ and $\lambda = 0.5$.
* Note that there was an error in the video (at 15:47): the max operations are squared, not the norms. Sorry about that.
```
m_plus = 0.9
m_minus = 0.1
lambda_ = 0.5
```
Since `y` will contain the digit classes, from 0 to 9, to get $T_k$ for every instance and every class, we can just use the `tf.one_hot()` function:
```
T = tf.one_hot(y, depth=caps2_n_caps, name="T")
```
A small example should make it clear what this does:
```
with tf.Session():
print(T.eval(feed_dict={y: np.array([0, 1, 2, 3, 9])}))
```
Now let's compute the norm of the output vector for each output capsule and each instance. First, let's verify the shape of `caps2_output`:
```
caps2_output
```
The 16D output vectors are in the second to last dimension, so let's use the `safe_norm()` function with `axis=-2`:
```
caps2_output_norm = safe_norm(caps2_output, axis=-2, keep_dims=True,
name="caps2_output_norm")
```
Now let's compute $\max(0, m^{+} - \|\mathbf{v}_k\|)^2$, and reshape the result to get a simple matrix of shape (_batch size_, 10):
```
present_error_raw = tf.square(tf.maximum(0., m_plus - caps2_output_norm),
name="present_error_raw")
present_error = tf.reshape(present_error_raw, shape=(-1, 10),
name="present_error")
```
Next let's compute $\max(0, \|\mathbf{v}_k\| - m^{-})^2$ and reshape it:
```
absent_error_raw = tf.square(tf.maximum(0., caps2_output_norm - m_minus),
name="absent_error_raw")
absent_error = tf.reshape(absent_error_raw, shape=(-1, 10),
name="absent_error")
```
We are ready to compute the loss for each instance and each digit:
```
L = tf.add(T * present_error, lambda_ * (1.0 - T) * absent_error,
name="L")
```
Now we can sum the digit losses for each instance ($L_0 + L_1 + \cdots + L_9$), and compute the mean over all instances. This gives us the final margin loss:
```
margin_loss = tf.reduce_mean(tf.reduce_sum(L, axis=1), name="margin_loss")
```
# Reconstruction
Now let's add a decoder network on top of the capsule network. It is a regular 3-layer fully connected neural network which will learn to reconstruct the input images based on the output of the capsule network. This will force the capsule network to preserve all the information required to reconstruct the digits, across the whole network. This constraint regularizes the model: it reduces the risk of overfitting the training set, and it helps generalize to new digits.
## Mask
The paper mentions that during training, instead of sending all the outputs of the capsule network to the decoder network, we must send only the output vector of the capsule that corresponds to the target digit. All the other output vectors must be masked out. At inference time, we must mask all output vectors except for the longest one, i.e., the one that corresponds to the predicted digit. You can see this in the paper's figure 2 (at 18:15 in the video): all output vectors are masked out, except for the reconstruction target's output vector.
We need a placeholder to tell TensorFlow whether we want to mask the output vectors based on the labels (`True`) or on the predictions (`False`, the default):
```
mask_with_labels = tf.placeholder_with_default(False, shape=(),
name="mask_with_labels")
```
Now let's use `tf.cond()` to define the reconstruction targets as the labels `y` if `mask_with_labels` is `True`, or `y_pred` otherwise.
```
reconstruction_targets = tf.cond(mask_with_labels, # condition
lambda: y, # if True
lambda: y_pred, # if False
name="reconstruction_targets")
```
Note that the `tf.cond()` function expects the if-True and if-False tensors to be passed _via_ functions: these functions will be called just once during the graph construction phase (not during the execution phase), similar to `tf.while_loop()`. This allows TensorFlow to add the necessary operations to handle the conditional evaluation of the if-True or if-False tensors. However, in our case, the tensors `y` and `y_pred` are already created by the time we call `tf.cond()`, so unfortunately TensorFlow will consider both `y` and `y_pred` to be dependencies of the `reconstruction_targets` tensor. The `reconstruction_targets` tensor will end up with the correct value, but:
1. whenever we evaluate a tensor that depends on `reconstruction_targets`, the `y_pred` tensor will be evaluated (even if `mask_with_layers` is `True`). This is not a big deal because computing `y_pred` adds no computing overhead during training, since we need it anyway to compute the margin loss. And during testing, if we are doing classification, we won't need reconstructions, so `reconstruction_targets` won't be evaluated at all.
2. we will always need to feed a value for the `y` placeholder (even if `mask_with_layers` is `False`). This is a bit annoying, but we can pass an empty array, because TensorFlow won't use it anyway (it just does not know it yet when it checks for dependencies).
Now that we have the reconstruction targets, let's create the reconstruction mask. It should be equal to 1.0 for the target class, and 0.0 for the other classes, for each instance. For this we can just use the `tf.one_hot()` function:
```
reconstruction_mask = tf.one_hot(reconstruction_targets,
depth=caps2_n_caps,
name="reconstruction_mask")
```
Let's check the shape of `reconstruction_mask`:
```
reconstruction_mask
```
Let's compare this to the shape of `caps2_output`:
```
caps2_output
```
Mmh, its shape is (_batch size_, 1, 10, 16, 1). We want to multiply it by the `reconstruction_mask`, but the shape of the `reconstruction_mask` is (_batch size_, 10). We must reshape it to (_batch size_, 1, 10, 1, 1) to make multiplication possible:
```
reconstruction_mask_reshaped = tf.reshape(
reconstruction_mask, [-1, 1, caps2_n_caps, 1, 1],
name="reconstruction_mask_reshaped")
```
At last! We can apply the mask:
```
caps2_output_masked = tf.multiply(
caps2_output, reconstruction_mask_reshaped,
name="caps2_output_masked")
caps2_output_masked
```
One last reshape operation to flatten the decoder's inputs:
```
decoder_input = tf.reshape(caps2_output_masked,
[-1, caps2_n_caps * caps2_n_dims],
name="decoder_input")
```
This gives us an array of shape (_batch size_, 160):
```
decoder_input
```
## Decoder
Now let's build the decoder. It's quite simple: two dense (fully connected) ReLU layers followed by a dense output sigmoid layer:
```
n_hidden1 = 512
n_hidden2 = 1024
n_output = 28 * 28
with tf.name_scope("decoder"):
hidden1 = tf.layers.dense(decoder_input, n_hidden1,
activation=tf.nn.relu,
name="hidden1")
hidden2 = tf.layers.dense(hidden1, n_hidden2,
activation=tf.nn.relu,
name="hidden2")
decoder_output = tf.layers.dense(hidden2, n_output,
activation=tf.nn.sigmoid,
name="decoder_output")
```
## Reconstruction Loss
Now let's compute the reconstruction loss. It is just the squared difference between the input image and the reconstructed image:
```
X_flat = tf.reshape(X, [-1, n_output], name="X_flat")
squared_difference = tf.square(X_flat - decoder_output,
name="squared_difference")
reconstruction_loss = tf.reduce_sum(squared_difference,
name="reconstruction_loss")
```
## Final Loss
The final loss is the sum of the margin loss and the reconstruction loss (scaled down by a factor of 0.0005 to ensure the margin loss dominates training):
```
alpha = 0.0005
loss = tf.add(margin_loss, alpha * reconstruction_loss, name="loss")
```
# Final Touches
## Accuracy
To measure our model's accuracy, we need to count the number of instances that are properly classified. For this, we can simply compare `y` and `y_pred`, convert the boolean value to a float32 (0.0 for False, 1.0 for True), and compute the mean over all the instances:
```
correct = tf.equal(y, y_pred, name="correct")
accuracy = tf.reduce_mean(tf.cast(correct, tf.float32), name="accuracy")
```
## Training Operations
The paper mentions that the authors used the Adam optimizer with TensorFlow's default parameters:
```
optimizer = tf.train.AdamOptimizer()
training_op = optimizer.minimize(loss, name="training_op")
```
## Init and Saver
And let's add the usual variable initializer, as well as a `Saver`:
```
init = tf.global_variables_initializer()
saver = tf.train.Saver()
```
And... we're done with the construction phase! Please take a moment to celebrate. :)
# Training
Training our capsule network is pretty standard. For simplicity, we won't do any fancy hyperparameter tuning, dropout or anything, we will just run the training operation over and over again, displaying the loss, and at the end of each epoch, measure the accuracy on the validation set, display it, and save the model if the validation loss is the lowest seen found so far (this is a basic way to implement early stopping, without actually stopping). Hopefully the code should be self-explanatory, but here are a few details to note:
* if a checkpoint file exists, it will be restored (this makes it possible to interrupt training, then restart it later from the last checkpoint),
* we must not forget to feed `mask_with_labels=True` during training,
* during testing, we let `mask_with_labels` default to `False` (but we still feed the labels since they are required to compute the accuracy),
* the images loaded _via_ `mnist.train.next_batch()` are represented as `float32` arrays of shape \[784\], but the input placeholder `X` expects a `float32` array of shape \[28, 28, 1\], so we must reshape the images before we feed them to our model,
* we evaluate the model's loss and accuracy on the full validation set (5,000 instances). To view progress and support systems that don't have a lot of RAM, the code evaluates the loss and accuracy on one batch at a time, and computes the mean loss and mean accuracy at the end.
*Warning*: if you don't have a GPU, training will take a very long time (at least a few hours). With a GPU, it should take just a few minutes per epoch (e.g., 6 minutes on an NVidia GeForce GTX 1080Ti).
```
n_epochs = 10
batch_size = 50
restore_checkpoint = True
n_iterations_per_epoch = mnist.train.num_examples // batch_size
n_iterations_validation = mnist.validation.num_examples // batch_size
best_loss_val = np.infty
checkpoint_path = "./my_capsule_network"
with tf.Session() as sess:
if restore_checkpoint and tf.train.checkpoint_exists(checkpoint_path):
saver.restore(sess, checkpoint_path)
else:
init.run()
for epoch in range(n_epochs):
for iteration in range(1, n_iterations_per_epoch + 1):
X_batch, y_batch = mnist.train.next_batch(batch_size)
# Run the training operation and measure the loss:
_, loss_train = sess.run(
[training_op, loss],
feed_dict={X: X_batch.reshape([-1, 28, 28, 1]),
y: y_batch,
mask_with_labels: True})
print("\rIteration: {}/{} ({:.1f}%) Loss: {:.5f}".format(
iteration, n_iterations_per_epoch,
iteration * 100 / n_iterations_per_epoch,
loss_train),
end="")
# At the end of each epoch,
# measure the validation loss and accuracy:
loss_vals = []
acc_vals = []
for iteration in range(1, n_iterations_validation + 1):
X_batch, y_batch = mnist.validation.next_batch(batch_size)
loss_val, acc_val = sess.run(
[loss, accuracy],
feed_dict={X: X_batch.reshape([-1, 28, 28, 1]),
y: y_batch})
loss_vals.append(loss_val)
acc_vals.append(acc_val)
print("\rEvaluating the model: {}/{} ({:.1f}%)".format(
iteration, n_iterations_validation,
iteration * 100 / n_iterations_validation),
end=" " * 10)
loss_val = np.mean(loss_vals)
acc_val = np.mean(acc_vals)
print("\rEpoch: {} Val accuracy: {:.4f}% Loss: {:.6f}{}".format(
epoch + 1, acc_val * 100, loss_val,
" (improved)" if loss_val < best_loss_val else ""))
# And save the model if it improved:
if loss_val < best_loss_val:
save_path = saver.save(sess, checkpoint_path)
best_loss_val = loss_val
```
Training is finished, we reached over 99.3% accuracy on the validation set after just 5 epochs, things are looking good. Now let's evaluate the model on the test set.
# Evaluation
```
n_iterations_test = mnist.test.num_examples // batch_size
with tf.Session() as sess:
saver.restore(sess, checkpoint_path)
loss_tests = []
acc_tests = []
for iteration in range(1, n_iterations_test + 1):
X_batch, y_batch = mnist.test.next_batch(batch_size)
loss_test, acc_test = sess.run(
[loss, accuracy],
feed_dict={X: X_batch.reshape([-1, 28, 28, 1]),
y: y_batch})
loss_tests.append(loss_test)
acc_tests.append(acc_test)
print("\rEvaluating the model: {}/{} ({:.1f}%)".format(
iteration, n_iterations_test,
iteration * 100 / n_iterations_test),
end=" " * 10)
loss_test = np.mean(loss_tests)
acc_test = np.mean(acc_tests)
print("\rFinal test accuracy: {:.4f}% Loss: {:.6f}".format(
acc_test * 100, loss_test))
```
We reach 99.43% accuracy on the test set. Pretty nice. :)
# Predictions
Now let's make some predictions! We first fix a few images from the test set, then we start a session, restore the trained model, evaluate `caps2_output` to get the capsule network's output vectors, `decoder_output` to get the reconstructions, and `y_pred` to get the class predictions:
```
n_samples = 5
sample_images = mnist.test.images[:n_samples].reshape([-1, 28, 28, 1])
with tf.Session() as sess:
saver.restore(sess, checkpoint_path)
caps2_output_value, decoder_output_value, y_pred_value = sess.run(
[caps2_output, decoder_output, y_pred],
feed_dict={X: sample_images,
y: np.array([], dtype=np.int64)})
```
Note: we feed `y` with an empty array, but TensorFlow will not use it, as explained earlier.
And now let's plot the images and their labels, followed by the corresponding reconstructions and predictions:
```
sample_images = sample_images.reshape(-1, 28, 28)
reconstructions = decoder_output_value.reshape([-1, 28, 28])
plt.figure(figsize=(n_samples * 2, 3))
for index in range(n_samples):
plt.subplot(1, n_samples, index + 1)
plt.imshow(sample_images[index], cmap="binary")
plt.title("Label:" + str(mnist.test.labels[index]))
plt.axis("off")
plt.show()
plt.figure(figsize=(n_samples * 2, 3))
for index in range(n_samples):
plt.subplot(1, n_samples, index + 1)
plt.title("Predicted:" + str(y_pred_value[index]))
plt.imshow(reconstructions[index], cmap="binary")
plt.axis("off")
plt.show()
```
The predictions are all correct, and the reconstructions look great. Hurray!
# Interpreting the Output Vectors
Let's tweak the output vectors to see what their pose parameters represent.
First, let's check the shape of the `cap2_output_value` NumPy array:
```
caps2_output_value.shape
```
Let's create a function that will tweak each of the 16 pose parameters (dimensions) in all output vectors. Each tweaked output vector will be identical to the original output vector, except that one of its pose parameters will be incremented by a value varying from -0.5 to 0.5. By default there will be 11 steps (-0.5, -0.4, ..., +0.4, +0.5). This function will return an array of shape (_tweaked pose parameters_=16, _steps_=11, _batch size_=5, 1, 10, 16, 1):
```
def tweak_pose_parameters(output_vectors, min=-0.5, max=0.5, n_steps=11):
steps = np.linspace(min, max, n_steps) # -0.25, -0.15, ..., +0.25
pose_parameters = np.arange(caps2_n_dims) # 0, 1, ..., 15
tweaks = np.zeros([caps2_n_dims, n_steps, 1, 1, 1, caps2_n_dims, 1])
tweaks[pose_parameters, :, 0, 0, 0, pose_parameters, 0] = steps
output_vectors_expanded = output_vectors[np.newaxis, np.newaxis]
return tweaks + output_vectors_expanded
```
Let's compute all the tweaked output vectors and reshape the result to (_parameters_×_steps_×_instances_, 1, 10, 16, 1) so we can feed the array to the decoder:
```
n_steps = 11
tweaked_vectors = tweak_pose_parameters(caps2_output_value, n_steps=n_steps)
tweaked_vectors_reshaped = tweaked_vectors.reshape(
[-1, 1, caps2_n_caps, caps2_n_dims, 1])
```
Now let's feed these tweaked output vectors to the decoder and get the reconstructions it produces:
```
tweak_labels = np.tile(mnist.test.labels[:n_samples], caps2_n_dims * n_steps)
with tf.Session() as sess:
saver.restore(sess, checkpoint_path)
decoder_output_value = sess.run(
decoder_output,
feed_dict={caps2_output: tweaked_vectors_reshaped,
mask_with_labels: True,
y: tweak_labels})
```
Let's reshape the decoder's output so we can easily iterate on the output dimension, the tweak steps, and the instances:
```
tweak_reconstructions = decoder_output_value.reshape(
[caps2_n_dims, n_steps, n_samples, 28, 28])
```
Lastly, let's plot all the reconstructions, for the first 3 output dimensions, for each tweaking step (column) and each digit (row):
```
for dim in range(3):
print("Tweaking output dimension #{}".format(dim))
plt.figure(figsize=(n_steps / 1.2, n_samples / 1.5))
for row in range(n_samples):
for col in range(n_steps):
plt.subplot(n_samples, n_steps, row * n_steps + col + 1)
plt.imshow(tweak_reconstructions[dim, col, row], cmap="binary")
plt.axis("off")
plt.show()
```
# Conclusion
I tried to make the code in this notebook as flat and linear as possible, to make it easier to follow, but of course in practice you would want to wrap the code in nice reusable functions and classes. For example, you could try implementing your own `PrimaryCapsuleLayer`, and `DenseRoutingCapsuleLayer` classes, with parameters for the number of capsules, the number of routing iterations, whether to use a dynamic loop or a static loop, and so on. For an example a modular implementation of Capsule Networks based on TensorFlow, take a look at the [CapsNet-TensorFlow](https://github.com/naturomics/CapsNet-Tensorflow) project.
That's all for today, I hope you enjoyed this notebook!
|
github_jupyter
|
<a href="https://colab.research.google.com/github/Anmol42/IDP-sem4/blob/main/notebooks/Sig-mu_vae.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
import torch
import torchvision
import torch.nn as nn
import matplotlib.pyplot as plt
import torch.nn.functional as F
import torchvision.transforms as transforms
import numpy as np
from torch.utils.data.dataloader import DataLoader
from google.colab import drive
drive.mount('/content/drive')
!unzip -q /content/drive/MyDrive/Datasets/faces.zip ## Silenced the unzip action
from skimage.io import imread_collection
path = "/content/faces/*.jpg"
train_ds = imread_collection(path)
from skimage.io import imread_collection
from skimage.color import rgb2lab,lab2rgb
from skimage.transform import resize
def get_img_data(path):
train_ds = imread_collection(path)
images = torch.zeros(len(train_ds),3,128,128)
for i,im in enumerate(train_ds):
im = resize(im, (128,128,3),
anti_aliasing=True)
image = rgb2lab(im)
image = torch.Tensor(image)
image = image.permute(2,0,1)
images[i]=image
return images
def normalize_data(data):
data[:,0] = data[:,0]/100
data[:,1:] = data[:,1:]/128
return data
images = get_img_data(path)
images = normalize_data(images)
batch_size = 100
class component(nn.Module):
def __init__(self):
super(component,self).__init__()
self.conv1 = nn.Sequential(nn.Conv2d(1,8,kernel_size=3,padding=1,stride=2),
nn.BatchNorm2d(8),
nn.LeakyReLU())
self.conv2 = nn.Sequential(nn.Conv2d(8,16,kernel_size=5,padding=2,stride=2),
nn.BatchNorm2d(16),
nn.LeakyReLU())
self.conv3 = nn.Sequential(nn.Conv2d(16,32,kernel_size=3,padding=1,stride=2),
nn.BatchNorm2d(32),
nn.LeakyReLU())
self.conv4 = nn.Sequential(nn.Conv2d(32,64,kernel_size=5,padding=2,stride=2), #size is 8x8 at this point
nn.LeakyReLU())
# BottleNeck
self.bottleneck = nn.Sequential(nn.Conv2d(64,128,kernel_size=3,stride=2,padding=1),
nn.LeakyReLU()) # size 4x4
self.linear = nn.Linear(128*4*4,256)
def forward(self,xb,z):
out1 = self.conv1(xb)
out2 = self.conv2(out1)
out3 = self.conv3(out2)
out4 = self.conv4(out3)
out5 = self.bottleneck(out4)
out5 = out5.view(z.shape[0],-1)
out6 = self.linear(out5)
return out6
## generator model
class generator(nn.Module):
def __init__(self,component): # z is input noise
super(generator,self).__init__()
self.sigma = component()
self.mu = component()
self.deconv7 = nn.Sequential(nn.ConvTranspose2d(256,128,kernel_size=4,stride=2,padding=1),
nn.ReLU())
self.deconv6 = nn.Sequential(nn.ConvTranspose2d(128,64,kernel_size=4,stride=2,padding=1),
nn.ReLU())
self.deconv5 = nn.Sequential(nn.ConvTranspose2d(64,64,kernel_size=4,stride=2,padding=1),
nn.ReLU())
self.deconv4 = nn.Sequential(nn.ConvTranspose2d(64,32,kernel_size=4,stride=2,padding=1),
nn.ReLU())
self.deconv3 = nn.Sequential(nn.ConvTranspose2d(32,16,kernel_size=4,stride=2,padding=1),
nn.ReLU())
self.deconv2 = nn.Sequential(nn.ConvTranspose2d(16,8,kernel_size=4,stride=2,padding=1),
nn.ReLU())
self.deconv1 = nn.Sequential(nn.ConvTranspose2d(8,2,kernel_size=4,stride=2,padding=1),
nn.Tanh())
self.linear = nn.Linear(128*4*4,512)
def forward(self,xb,z):
sig = self.sigma(xb,z)
mm = self.mu(xb,z)
noise = z*sig + mm
out5 = self.deconv7(noise.unsqueeze(2).unsqueeze(2))
out5 = self.deconv6(out5)
out5 = self.deconv5(out5)
out5 = self.deconv4(out5)
out5 = self.deconv3(out5)
out5 = self.deconv2(out5)
out5 = self.deconv1(out5)
return torch.cat((xb,out5),1)
## discriminator
class discriminator(nn.Module):
def __init__(self):
super(discriminator,self).__init__()
self.network = nn.Sequential(
nn.Conv2d(3,8,kernel_size=3,stride=1),
nn.MaxPool2d(kernel_size=2),
nn.ReLU(),
nn.Conv2d(8,16,kernel_size=5),
nn.MaxPool2d(kernel_size=2),
nn.ReLU(),
nn.Conv2d(16,32,kernel_size=3),
nn.MaxPool2d(kernel_size=2),
nn.ReLU(),
nn.Conv2d(32,64,kernel_size=3),
nn.MaxPool2d(kernel_size=2),
nn.ReLU(),
nn.Flatten()
)
self.linear1 = nn.Linear(64*25,128)
self.linear2 = nn.Linear(128,1)
def forward(self,x):
out = self.network(x)
out = self.linear1(out)
out = self.linear2(out)
out = torch.sigmoid(out)
return out
gen_model = generator(component)
dis_model = discriminator()
train_dl = DataLoader(images[:10000],batch_size,shuffle=True,pin_memory=True,num_workers=2)
val_dl = DataLoader(images[10000:11000],batch_size, num_workers=2,pin_memory=True)
test_dl = DataLoader(images[11000:],batch_size,num_workers=2)
bceloss = nn.BCEWithLogitsLoss()
#minimise this # t is whether the image is fake or real; x is prob vect of patches being real/fake.
def loss_inf(x,t): # probability vector from discriminator as input
return int(t)*(bceloss(x,torch.ones_like(x))) + (1-int(t))*bceloss(x,torch.zeros_like(x))
l1loss = nn.L1Loss()
def gen_loss(x,y):
return l1loss(x,y)
def to_device(data, device):
"""Move tensor(s) to chosen device"""
if isinstance(data, (list,tuple)):
return [to_device(x, device) for x in data]
return data.to(device, non_blocking=True)
class DeviceDataLoader():
"""Wrap a dataloader to move data to a device"""
def __init__(self, dl, device):
self.dl = dl
self.device = device
def __iter__(self):
"""Yield a batch of data after moving it to device"""
for b in self.dl:
yield to_device(b, self.device)
def __len__(self):
"""Number of batches"""
return len(self.dl)
train_dl = DeviceDataLoader(train_dl,'cuda')
val_dl = DeviceDataLoader(val_dl,'cuda')
test_dl = DeviceDataLoader(test_dl,'cuda')
gen_model.to('cuda')
dis_model.to('cuda')
def fit(epochs,lr_g,lr_d,generator,discriminator,batch_size,opt_func=torch.optim.Adam):
gen_optimize = opt_func(generator.parameters(),lr_g)
dis_optimize = opt_func(discriminator.parameters(),lr_d)
train_g_history,train_d_history = [],[]
val_g_history, val_d_history = [],[]
for epoch in range(epochs):
epoch_loss_g = torch.zeros(1).to('cuda')
epoch_loss_d = torch.zeros(1).to('cuda')
noise = torch.randn(batch_size,256).to('cuda')
for batch in train_dl:
for i in range(5):
out = generator(batch[:,0].unsqueeze(1),noise) # gives a,b channel for LAB color scheme
real_score = discriminator(batch) # how real is the og input image
fake_score = discriminator(out) # how real is the generated image
loss_d = loss_inf(real_score,1) + loss_inf(fake_score,0)# discriminator
#print(loss_d.item())
loss_d.backward()
dis_optimize.zero_grad()
dis_optimize.step()
out = generator(batch[:,0].unsqueeze(1),noise) # gives a,b channel for LAB color scheme
real_score = discriminator(batch) # how real is the og input image
fake_score = discriminator(out) # how real is the generated image
loss_g = 4*gen_loss(out,batch) + loss_inf(fake_score,1)
loss_g.backward()
gen_optimize.step()
gen_optimize.zero_grad()
with torch.no_grad():
epoch_loss_g += loss_g
epoch_loss_d += loss_d
train_d_history.append(epoch_loss_d)
train_g_history.append(epoch_loss_g)
epoch_loss_g = 0
epoch_loss_d = 0
for batch in val_dl:
with torch.no_grad():
out = generator(batch[:,0].unsqueeze(1),noise) # gives a,b channel for LAB color scheme
real_score = discriminator(batch) # how real is the og input image
fake_score = discriminator(out) # how real is the generated image
loss_d = loss_inf(real_score,1) + loss_inf(fake_score,0)# discriminator
loss_g = 4*gen_loss(out,batch) + loss_inf(fake_score,1)
epoch_loss_g += loss_g
epoch_loss_d += loss_d
val_g_history.append(epoch_loss_g.item())
val_d_history.append(epoch_loss_d.item())
if epoch % 3 == 0:
print("Gen Epoch Loss",epoch_loss_g)
print("Discriminator Epoch loss",epoch_loss_d)
return train_d_history,train_g_history,val_d_history,val_g_history
loss_h = fit(6,0.001,0.001,gen_model,dis_model,batch_size,opt_func=torch.optim.Adam)
import matplotlib.pyplot as plt
plt.plot(loss_h[1])
from skimage.color import rgb2lab,lab2rgb,rgb2gray
def tensor_to_pic(tensor : torch.Tensor) -> np.ndarray:
tensor[0] *= 100
tensor[1:]*= 128
image = tensor.permute(1,2,0).detach().cpu().numpy()
image = lab2rgb(image)
return image
def show_images(n,dataset = images,gen=gen_model,dis=dis_model) -> None:
gen_model.eval()
dis_model.eval()
z = torch.randn(1,256).to('cuda')
#z = torch.ones_like(z)
image_tensor = dataset[n].to('cuda')
gen_tensor = gen(image_tensor[0].unsqueeze(0).unsqueeze(0),z)[0]
image = tensor_to_pic(image_tensor)
#print(torch.sum(gen_tensor))
gray = np.zeros_like(image)
bw = rgb2gray(image)
gray[:,:,0],gray[:,:,1],gray[:,:,2] = bw,bw,bw
gen_image = tensor_to_pic(gen_tensor)
to_be_shown = np.concatenate((gray,gen_image,image),axis=1)
plt.figure(figsize=(15,15))
plt.imshow(to_be_shown)
plt.show()
i = np.random.randint(3500,20000)
print(i)
show_images(i) ## Shows generated and coloured images side by side
```
|
github_jupyter
|
# Analyzing interstellar reddening and calculating synthetic photometry
## Authors
Kristen Larson, Lia Corrales, Stephanie T. Douglas, Kelle Cruz
Input from Emir Karamehmetoglu, Pey Lian Lim, Karl Gordon, Kevin Covey
## Learning Goals
- Investigate extinction curve shapes
- Deredden spectral energy distributions and spectra
- Calculate photometric extinction and reddening
- Calculate synthetic photometry for a dust-reddened star by combining `dust_extinction` and `synphot`
- Convert from frequency to wavelength with `astropy.unit` equivalencies
- Unit support for plotting with `astropy.visualization`
## Keywords
dust extinction, synphot, astroquery, units, photometry, extinction, physics, observational astronomy
## Companion Content
* [Bessell & Murphy (2012)](https://ui.adsabs.harvard.edu/#abs/2012PASP..124..140B/abstract)
## Summary
In this tutorial, we will look at some extinction curves from the literature, use one of those curves to deredden an observed spectrum, and practice invoking a background source flux in order to calculate magnitudes from an extinction model.
The primary libraries we'll be using are [dust_extinction](https://dust-extinction.readthedocs.io/en/latest/) and [synphot](https://synphot.readthedocs.io/en/latest/), which are [Astropy affiliated packages](https://www.astropy.org/affiliated/).
We recommend installing the two packages in this fashion:
```
pip install synphot
pip install dust_extinction
```
This tutorial requires v0.7 or later of `dust_extinction`. To ensure that all commands work properly, make sure you have the correct version installed. If you have v0.6 or earlier installed, run the following command to upgrade
```
pip install dust_extinction --upgrade
```
```
import pathlib
import matplotlib.pyplot as plt
%matplotlib inline
import numpy as np
import astropy.units as u
from astropy.table import Table
from dust_extinction.parameter_averages import CCM89, F99
from synphot import units, config
from synphot import SourceSpectrum,SpectralElement,Observation,ExtinctionModel1D
from synphot.models import BlackBodyNorm1D
from synphot.spectrum import BaseUnitlessSpectrum
from synphot.reddening import ExtinctionCurve
from astroquery.simbad import Simbad
from astroquery.mast import Observations
import astropy.visualization
```
# Introduction
Dust in the interstellar medium (ISM) extinguishes background starlight. The wavelength dependence of the extinction is such that short-wavelength light is extinguished more than long-wavelength light, and we call this effect *reddening*.
If you're new to extinction, here is a brief introduction to the types of quantities involved.
The fractional change to the flux of starlight is
$$
\frac{dF_\lambda}{F_\lambda} = -\tau_\lambda
$$
where $\tau$ is the optical depth and depends on wavelength. Integrating along the line of sight, the resultant flux is an exponential function of optical depth,
$$
\tau_\lambda = -\ln\left(\frac{F_\lambda}{F_{\lambda,0}}\right).
$$
With an eye to how we define magnitudes, we usually change the base from $e$ to 10,
$$
\tau_\lambda = -2.303\log\left(\frac{F_\lambda}{F_{\lambda,0}}\right),
$$
and define an extinction $A_\lambda = 1.086 \,\tau_\lambda$ so that
$$
A_\lambda = -2.5\log\left(\frac{F_\lambda}{F_{\lambda,0}}\right).
$$
There are two basic take-home messages from this derivation:
* Extinction introduces a multiplying factor $10^{-0.4 A_\lambda}$ to the flux.
* Extinction is defined relative to the flux without dust, $F_{\lambda,0}$.
Once astropy and the affiliated packages are installed, we can import from them as needed:
# Example 1: Investigate Extinction Models
The `dust_extinction` package provides various models for extinction $A_\lambda$ normalized to $A_V$. The shapes of normalized curves are relatively (and perhaps surprisingly) uniform in the Milky Way. The little variation that exists is often parameterized by the ratio of extinction ($A_V$) to reddening in the blue-visual ($E_{B-V}$),
$$
R_V \equiv \frac{A_V}{E_{B-V}}
$$
where $E_{B-V}$ is differential extinction $A_B-A_V$. In this example, we show the $R_V$-parameterization for the Clayton, Cardelli, & Mathis (1989, CCM) and the Fitzpatrick (1999) models. [More model options are available in the `dust_extinction` documentation.](https://dust-extinction.readthedocs.io/en/latest/dust_extinction/model_flavors.html)
```
# Create wavelengths array.
wav = np.arange(0.1, 3.0, 0.001)*u.micron
for model in [CCM89, F99]:
for R in (2.0,3.0,4.0):
# Initialize the extinction model
ext = model(Rv=R)
plt.plot(1/wav, ext(wav), label=model.name+' R='+str(R))
plt.xlabel('$\lambda^{-1}$ ($\mu$m$^{-1}$)')
plt.ylabel('A($\lambda$) / A(V)')
plt.legend(loc='best')
plt.title('Some Extinction Laws')
plt.show()
```
Astronomers studying the ISM often display extinction curves against inverse wavelength (wavenumber) to show the ultraviolet variation, as we do here. Infrared extinction varies much less and approaches zero at long wavelength in the absence of wavelength-independent, or grey, extinction.
# Example 2: Deredden a Spectrum
Here we deredden (unextinguish) the IUE ultraviolet spectrum and optical photometry of the star $\rho$ Oph (HD 147933).
First, we will use astroquery to fetch the archival [IUE spectrum from MAST](https://archive.stsci.edu/iue/):
```
download_dir = pathlib.Path('~/.astropy/cache/astroquery/Mast').expanduser()
download_dir.mkdir(exist_ok=True)
obsTable = Observations.query_object("HD 147933", radius="1 arcsec")
obsTable_spec = obsTable[obsTable['dataproduct_type'] == 'spectrum']
obsTable_spec
obsids = obsTable_spec[39]['obsid']
dataProductsByID = Observations.get_product_list(obsids)
manifest = Observations.download_products(dataProductsByID,
download_dir=str(download_dir))
```
We read the downloaded files into an astropy table:
```
t_lwr = Table.read(download_dir / 'mastDownload/IUE/lwr05639/lwr05639mxlo_vo.fits')
print(t_lwr)
```
The `.quantity` extension in the next lines will read the Table columns into Quantity vectors. Quantities keep the units of the Table column attached to the numpy array values.
```
wav_UV = t_lwr['WAVE'][0,].quantity
UVflux = t_lwr['FLUX'][0,].quantity
```
Now, we use astroquery again to fetch photometry from Simbad to go with the IUE spectrum:
```
custom_query = Simbad()
custom_query.add_votable_fields('fluxdata(U)','fluxdata(B)','fluxdata(V)')
phot_table=custom_query.query_object('HD 147933')
Umag=phot_table['FLUX_U']
Bmag=phot_table['FLUX_B']
Vmag=phot_table['FLUX_V']
```
To convert the photometry to flux, we look up some [properties of the photometric passbands](http://ned.ipac.caltech.edu/help/photoband.lst), including the flux of a magnitude zero star through the each passband, also known as the zero-point of the passband.
```
wav_U = 0.3660 * u.micron
zeroflux_U_nu = 1.81E-23 * u.Watt/(u.m*u.m*u.Hz)
wav_B = 0.4400 * u.micron
zeroflux_B_nu = 4.26E-23 * u.Watt/(u.m*u.m*u.Hz)
wav_V = 0.5530 * u.micron
zeroflux_V_nu = 3.64E-23 * u.Watt/(u.m*u.m*u.Hz)
```
The zero-points that we found for the optical passbands are not in the same units as the IUE fluxes. To make matters worse, the zero-point fluxes are $F_\nu$ and the IUE fluxes are $F_\lambda$. To convert between them, the wavelength is needed. Fortunately, astropy provides an easy way to make the conversion with *equivalencies*:
```
zeroflux_U = zeroflux_U_nu.to(u.erg/u.AA/u.cm/u.cm/u.s,
equivalencies=u.spectral_density(wav_U))
zeroflux_B = zeroflux_B_nu.to(u.erg/u.AA/u.cm/u.cm/u.s,
equivalencies=u.spectral_density(wav_B))
zeroflux_V = zeroflux_V_nu.to(u.erg/u.AA/u.cm/u.cm/u.s,
equivalencies=u.spectral_density(wav_V))
```
Now we can convert from photometry to flux using the definition of magnitude:
$$
F=F_0\ 10^{-0.4\, m}
$$
```
Uflux = zeroflux_U * 10.**(-0.4*Umag)
Bflux = zeroflux_B * 10.**(-0.4*Bmag)
Vflux = zeroflux_V * 10.**(-0.4*Vmag)
```
Using astropy quantities allow us to take advantage of astropy's unit support in plotting. [Calling `astropy.visualization.quantity_support` explicitly turns the feature on.](http://docs.astropy.org/en/stable/units/quantity.html#plotting-quantities) Then, when quantity objects are passed to matplotlib plotting functions, the axis labels are automatically labeled with the unit of the quantity. In addition, quantities are converted automatically into the same units when combining multiple plots on the same axes.
```
astropy.visualization.quantity_support()
plt.plot(wav_UV,UVflux,'m',label='UV')
plt.plot(wav_V,Vflux,'ko',label='U, B, V')
plt.plot(wav_B,Bflux,'ko')
plt.plot(wav_U,Uflux,'ko')
plt.legend(loc='best')
plt.ylim(0,3E-10)
plt.title('rho Oph')
plt.show()
```
Finally, we initialize the extinction model, choosing values $R_V = 5$ and $E_{B-V} = 0.5$. This star is famous in the ISM community for having large-$R_V$ dust in the line of sight.
```
Rv = 5.0 # Usually around 3, but about 5 for this star.
Ebv = 0.5
ext = F99(Rv=Rv)
```
To extinguish (redden) a spectrum, multiply by the `ext.extinguish` function. To unextinguish (deredden), divide by the same `ext.extinguish`, as we do here:
```
plt.semilogy(wav_UV,UVflux,'m',label='UV')
plt.semilogy(wav_V,Vflux,'ko',label='U, B, V')
plt.semilogy(wav_B,Bflux,'ko')
plt.semilogy(wav_U,Uflux,'ko')
plt.semilogy(wav_UV,UVflux/ext.extinguish(wav_UV,Ebv=Ebv),'b',
label='dereddened: EBV=0.5, RV=5')
plt.semilogy(wav_V,Vflux/ext.extinguish(wav_V,Ebv=Ebv),'ro',
label='dereddened: EBV=0.5, RV=5')
plt.semilogy(wav_B,Bflux/ext.extinguish(wav_B,Ebv=Ebv),'ro')
plt.semilogy(wav_U,Uflux/ext.extinguish(wav_U,Ebv=Ebv),'ro')
plt.legend(loc='best')
plt.title('rho Oph')
plt.show()
```
Notice that, by dereddening the spectrum, the absorption feature at 2175 Angstrom is removed. This feature can also be seen as the prominent bump in the extinction curves in Example 1. That we have smoothly removed the 2175 Angstrom feature suggests that the values we chose, $R_V = 5$ and $E_{B-V} = 0.5$, are a reasonable model for the foreground dust.
Those experienced with dereddening should notice that that `dust_extinction` returns $A_\lambda/A_V$, while other routines like the IDL fm_unred procedure often return $A_\lambda/E_{B-V}$ by default and need to be divided by $R_V$ in order to compare directly with `dust_extinction`.
# Example 3: Calculate Color Excess with `synphot`
Calculating broadband *photometric* extinction is harder than it might look at first. All we have to do is look up $A_\lambda$ for a particular passband, right? Under the right conditions, yes. In general, no.
Remember that we have to integrate over a passband to get synthetic photometry,
$$
A = -2.5\log\left(\frac{\int W_\lambda F_{\lambda,0} 10^{-0.4A_\lambda} d\lambda}{\int W_\lambda F_{\lambda,0} d\lambda} \right),
$$
where $W_\lambda$ is the fraction of incident energy transmitted through a filter. See the detailed appendix in [Bessell & Murphy (2012)](https://ui.adsabs.harvard.edu/#abs/2012PASP..124..140B/abstract)
for an excellent review of the issues and common misunderstandings in synthetic photometry.
There is an important point to be made here. The expression above does not simplify any further. Strictly speaking, it is impossible to convert spectral extinction $A_\lambda$ into a magnitude system without knowing the wavelength dependence of the source's original flux across the filter in question. As a special case, if we assume that the source flux is constant in the band (i.e. $F_\lambda = F$), then we can cancel these factors out from the integrals, and extinction in magnitudes becomes the weighted average of the extinction factor across the filter in question. In that special case, $A_\lambda$ at $\lambda_{\rm eff}$ is a good approximation for magnitude extinction.
In this example, we will demonstrate the more general calculation of photometric extinction. We use a blackbody curve for the flux before the dust, apply an extinction curve, and perform synthetic photometry to calculate extinction and reddening in a magnitude system.
First, let's get the filter transmission curves:
```
# Optional, for when the STScI ftp server is not answering:
config.conf.vega_file = 'http://ssb.stsci.edu/cdbs/calspec/alpha_lyr_stis_008.fits'
config.conf.johnson_u_file = 'http://ssb.stsci.edu/cdbs/comp/nonhst/johnson_u_004_syn.fits'
config.conf.johnson_b_file = 'http://ssb.stsci.edu/cdbs/comp/nonhst/johnson_b_004_syn.fits'
config.conf.johnson_v_file = 'http://ssb.stsci.edu/cdbs/comp/nonhst/johnson_v_004_syn.fits'
config.conf.johnson_r_file = 'http://ssb.stsci.edu/cdbs/comp/nonhst/johnson_r_003_syn.fits'
config.conf.johnson_i_file = 'http://ssb.stsci.edu/cdbs/comp/nonhst/johnson_i_003_syn.fits'
config.conf.bessel_j_file = 'http://ssb.stsci.edu/cdbs/comp/nonhst/bessell_j_003_syn.fits'
config.conf.bessel_h_file = 'http://ssb.stsci.edu/cdbs/comp/nonhst/bessell_h_004_syn.fits'
config.conf.bessel_k_file = 'http://ssb.stsci.edu/cdbs/comp/nonhst/bessell_k_003_syn.fits'
u_band = SpectralElement.from_filter('johnson_u')
b_band = SpectralElement.from_filter('johnson_b')
v_band = SpectralElement.from_filter('johnson_v')
r_band = SpectralElement.from_filter('johnson_r')
i_band = SpectralElement.from_filter('johnson_i')
j_band = SpectralElement.from_filter('bessel_j')
h_band = SpectralElement.from_filter('bessel_h')
k_band = SpectralElement.from_filter('bessel_k')
```
If you are running this with your own python, see the [synphot documentation](https://synphot.readthedocs.io/en/latest/#installation-and-setup) on how to install your own copy of the necessary files.
Next, let's make a background flux to which we will apply extinction. Here we make a 10,000 K blackbody using the model mechanism from within `synphot` and normalize it to $V$ = 10 in the Vega-based magnitude system.
```
# First, create a blackbody at some temperature.
sp = SourceSpectrum(BlackBodyNorm1D, temperature=10000)
# sp.plot(left=1, right=15000, flux_unit='flam', title='Blackbody')
# Get the Vega spectrum as the zero point flux.
vega = SourceSpectrum.from_vega()
# vega.plot(left=1, right=15000)
# Normalize the blackbody to some chosen magnitude, say V = 10.
vmag = 10.
v_band = SpectralElement.from_filter('johnson_v')
sp_norm = sp.normalize(vmag * units.VEGAMAG, v_band, vegaspec=vega)
sp_norm.plot(left=1, right=15000, flux_unit='flam', title='Normed Blackbody')
```
Now we initialize the extinction model and choose an extinction of $A_V$ = 2. To get the `dust_extinction` model working with `synphot`, we create a wavelength array and make a spectral element with the extinction model as a lookup table.
```
# Initialize the extinction model and choose the extinction, here Av = 2.
ext = CCM89(Rv=3.1)
Av = 2.
# Create a wavelength array.
wav = np.arange(0.1, 3, 0.001)*u.micron
# Make the extinction model in synphot using a lookup table.
ex = ExtinctionCurve(ExtinctionModel1D,
points=wav, lookup_table=ext.extinguish(wav, Av=Av))
sp_ext = sp_norm*ex
sp_ext.plot(left=1, right=15000, flux_unit='flam',
title='Normed Blackbody with Extinction')
```
Synthetic photometry refers to modeling an observation of a star by multiplying the theoretical model for the astronomical flux through a certain filter response function, then integrating.
```
# "Observe" the star through the filter and integrate to get photometric mag.
sp_obs = Observation(sp_ext, v_band)
sp_obs_before = Observation(sp_norm, v_band)
# sp_obs.plot(left=1, right=15000, flux_unit='flam',
# title='Normed Blackbody with Extinction through V Filter')
```
Next, `synphot` performs the integration and computes magnitudes in the Vega system.
```
sp_stim_before = sp_obs_before.effstim(flux_unit='vegamag', vegaspec=vega)
sp_stim = sp_obs.effstim(flux_unit='vegamag', vegaspec=vega)
print('before dust, V =', np.round(sp_stim_before,1))
print('after dust, V =', np.round(sp_stim,1))
# Calculate extinction and compare to our chosen value.
Av_calc = sp_stim - sp_stim_before
print('$A_V$ = ', np.round(Av_calc,1))
```
This is a good check for us to do. We normalized our spectrum to $V$ = 10 mag and added 2 mag of visual extinction, so the synthetic photometry procedure should reproduce these chosen values, and it does. Now we are ready to find the extinction in other passbands.
We calculate the new photometry for the rest of the Johnson optical and the Bessell infrared filters. We calculate extinction $A = \Delta m$ and plot color excess, $E(\lambda - V) = A_\lambda - A_V$.
Notice that `synphot` calculates the effective wavelength of the observations for us, which is very useful for plotting the results. We show reddening with the model extinction curve for comparison in the plot.
```
bands = [u_band,b_band,v_band,r_band,i_band,j_band,h_band,k_band]
for band in bands:
# Calculate photometry with dust:
sp_obs = Observation(sp_ext, band, force='extrap')
obs_effstim = sp_obs.effstim(flux_unit='vegamag', vegaspec=vega)
# Calculate photometry without dust:
sp_obs_i = Observation(sp_norm, band, force='extrap')
obs_i_effstim = sp_obs_i.effstim(flux_unit='vegamag', vegaspec=vega)
# Extinction = mag with dust - mag without dust
# Color excess = extinction at lambda - extinction at V
color_excess = obs_effstim - obs_i_effstim - Av_calc
plt.plot(sp_obs_i.effective_wavelength(), color_excess,'or')
print(np.round(sp_obs_i.effective_wavelength(),1), ',',
np.round(color_excess,2))
# Plot the model extinction curve for comparison
plt.plot(wav,Av*ext(wav)-Av,'--k')
plt.ylim([-2,2])
plt.xlabel('$\lambda$ (Angstrom)')
plt.ylabel('E($\lambda$-V)')
plt.title('Reddening of T=10,000K Background Source with Av=2')
plt.show()
```
## Exercise
Try changing the blackbody temperature to something very hot or very cool. Are the color excess values the same? Have the effective wavelengths changed?
Note that the photometric extinction changes because the filter transmission is not uniform. The observed throughput of the filter depends on the shape of the background source flux.
|
github_jupyter
|
```
# Checkout www.pygimli.org for more examples
%matplotlib inline
```
# 2D ERT modeling and inversion
```
import matplotlib.pyplot as plt
import numpy as np
import pygimli as pg
import pygimli.meshtools as mt
from pygimli.physics import ert
```
Create geometry definition for the modelling domain.
worldMarker=True indicates the default boundary conditions for the ERT
```
world = mt.createWorld(start=[-50, 0], end=[50, -50], layers=[-1, -8],
worldMarker=True)
```
Create some heterogeneous circular anomaly
```
block = mt.createCircle(pos=[-4.0, -5.0], radius=[1, 1.8], marker=4,
boundaryMarker=10, area=0.01)
circle = mt.createCircle(pos=[4.0, -5.0], radius=[1, 1.8], marker=5,
boundaryMarker=10, area=0.01)
poly = mt.createPolygon([(1,-4), (2,-1.5), (4,-2), (5,-2),
(8,-3), (5,-3.5), (3,-4.5)], isClosed=True,
addNodes=3, interpolate='spline', marker=5)
```
Merge geometry definition into a Piecewise Linear Complex (PLC)
```
geom = world + block + circle # + poly
```
Optional: show the geometry
```
pg.show(geom)
```
Create a Dipole Dipole ('dd') measuring scheme with 21 electrodes.
```
scheme = ert.createData(elecs=np.linspace(start=-20, stop=20, num=42),
schemeName='dd')
```
Put all electrode (aka sensors) positions into the PLC to enforce mesh
refinement. Due to experience, its convenient to add further refinement
nodes in a distance of 10% of electrode spacing to achieve sufficient
numerical accuracy.
```
for p in scheme.sensors():
geom.createNode(p)
geom.createNode(p - [0, 0.01])
# Create a mesh for the finite element modelling with appropriate mesh quality.
mesh = mt.createMesh(geom, quality=34)
# Create a map to set resistivity values in the appropriate regions
# [[regionNumber, resistivity], [regionNumber, resistivity], [...]
rhomap = [[1, 50.],
[2, 50.],
[3, 50.],
[4, 150.],
[5, 15]]
# Take a look at the mesh and the resistivity distribution
pg.show(mesh, data=rhomap, label=pg.unit('res'), showMesh=True)
```
Perform the modeling with the mesh and the measuring scheme itself
and return a data container with apparent resistivity values,
geometric factors and estimated data errors specified by the noise setting.
The noise is also added to the data. Here 1% plus 1µV.
Note, we force a specific noise seed as we want reproducable results for
testing purposes.
```
data = ert.simulate(mesh, scheme=scheme, res=rhomap, noiseLevel=1,
noiseAbs=1e-6, seed=1337, verbose=False)
pg.info(np.linalg.norm(data['err']), np.linalg.norm(data['rhoa']))
pg.info('Simulated data', data)
pg.info('The data contains:', data.dataMap().keys())
pg.info('Simulated rhoa (min/max)', min(data['rhoa']), max(data['rhoa']))
pg.info('Selected data noise %(min/max)', min(data['err'])*100, max(data['err'])*100)
# data['k']
```
Optional: you can filter all values and tokens in the data container.
Its possible that there are some negative data values due to noise and
huge geometric factors. So we need to remove them.
```
data.remove(data['rhoa'] < 0)
# data.remove(data['k'] < -20000.0)
pg.info('Filtered rhoa (min/max)', min(data['rhoa']), max(data['rhoa']))
# You can save the data for further use
data.save('simple.dat')
# You can take a look at the data
ert.show(data, cMap="RdBu_r")
```
Initialize the ERTManager, e.g. with a data container or a filename.
```
mgr = ert.ERTManager('simple.dat')
```
Run the inversion with the preset data. The Inversion mesh will be created
with default settings.
```
inv = mgr.invert(lam=10, verbose=False)
#np.testing.assert_approx_equal(mgr.inv.chi2(), 0.7, significant=1)
```
Let the ERTManger show you the model of the last successful run and how it
fits the data. Shows data, model response, and model.
```
mgr.showResultAndFit(cMap="RdBu_r")
meshPD = pg.Mesh(mgr.paraDomain) # Save copy of para mesh for plotting later
```
You can also provide your own mesh (e.g., a structured grid if you like them)
Note, that x and y coordinates needs to be in ascending order to ensure that
all the cells in the grid have the correct orientation, i.e., all cells need
to be numbered counter-clockwise and the boundary normal directions need to
point outside.
```
inversionDomain = pg.createGrid(x=np.linspace(start=-21, stop=21, num=43),
y=-pg.cat([0], pg.utils.grange(0.5, 8, n=8))[::-1],
marker=2)
```
The inversion domain for ERT problems needs a boundary that represents the
far regions in the subsurface of the halfspace.
Give a cell marker lower than the marker for the inversion region, the lowest
cell marker in the mesh will be the inversion boundary region by default.
```
grid = pg.meshtools.appendTriangleBoundary(inversionDomain, marker=1,
xbound=50, ybound=50)
pg.show(grid, markers=True)
#pg.show(grid, markers=True)
```
The Inversion can be called with data and mesh as argument as well
```
model = mgr.invert(data, mesh=grid, lam=10, verbose=False)
# np.testing.assert_approx_equal(mgr.inv.chi2(), 0.951027, significant=3)
```
You can of course get access to mesh and model and plot them for your own.
Note that the cells of the parametric domain of your mesh might be in
a different order than the values in the model array if regions are used.
The manager can help to permutate them into the right order.
```
# np.testing.assert_approx_equal(mgr.inv.chi2(), 1.4, significant=2)
maxC = 150
modelPD = mgr.paraModel(model) # do the mapping
pg.show(mgr.paraDomain, modelPD, label='Model', cMap='RdBu_r',
logScale=True, cMin=15, cMax=maxC)
pg.info('Inversion stopped with chi² = {0:.3}'.format(mgr.fw.chi2()))
fig, (ax1, ax2, ax3) = plt.subplots(3,1, sharex=True, sharey=True, figsize=(8,7))
pg.show(mesh, rhomap, ax=ax1, hold=True, cMap="RdBu_r", logScale=True,
orientation="vertical", cMin=15, cMax=maxC)
pg.show(meshPD, inv, ax=ax2, hold=True, cMap="RdBu_r", logScale=True,
orientation="vertical", cMin=15, cMax=maxC)
mgr.showResult(ax=ax3, cMin=15, cMax=maxC, cMap="RdBu_r", orientation="vertical")
labels = ["True model", "Inversion unstructured mesh", "Inversion regular grid"]
for ax, label in zip([ax1, ax2, ax3], labels):
ax.set_xlim(mgr.paraDomain.xmin(), mgr.paraDomain.xmax())
ax.set_ylim(mgr.paraDomain.ymin(), mgr.paraDomain.ymax())
ax.set_title(label)
```
|
github_jupyter
|
This page was created from a Jupyter notebook. The original notebook can be found [here](https://github.com/klane/databall/blob/master/notebooks/parameter-tuning.ipynb). It investigates tuning model parameters to achieve better performance. First we must import the necessary installed modules.
```
import itertools
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from functools import partial
from sklearn.linear_model import LogisticRegression
from sklearn.svm import LinearSVC
from sklearn.ensemble import RandomForestClassifier
from sklearn.neural_network import MLPClassifier
from hyperopt import hp
```
Next we need to import a few local modules.
```
import os
import sys
import warnings
warnings.filterwarnings('ignore')
module_path = os.path.abspath(os.path.join('..'))
if module_path not in sys.path:
sys.path.append(module_path)
from databall.database import Database
from databall.plotting import format_538, plot_metrics, plot_matrix
from databall.model_selection import calculate_metrics, optimize_params, train_test_split
import databall.util as util
```
Apply the FiveThirtyEight plot style.
```
plt.style.use('fivethirtyeight')
```
# Data
As before, we collect the stats and betting data from the database and create training and test sets where the 2016 season is reserved as the test set.
```
database = Database('../data/nba.db')
games = database.betting_stats(window=10)
x_train, y_train, x_test, y_test = train_test_split(games, 2006, 2016,
xlabels=util.stat_names() + ['SEASON'])
```
The stats below are the box score stats used during [feature selection](feature-selection.md). I decided to further explore these because they are readily available from multiple sources and do not require any calculation of advanced stats by users.
```
stats = ['FGM', 'FGA', 'FG3M', 'FG3A', 'FTM', 'FTA', 'OREB', 'DREB', 'AST', 'TOV', 'STL', 'BLK']
stats = ['TEAM_' + s for s in stats] + ['POSSESSIONS']
stats += [s + '_AWAY' for s in stats] + ['HOME_SPREAD']
```
# Logistic Regression
The plots below show `LogisticRegression` model performance using different combinations of three parameters in a grid search: `penalty` (type of norm), `class_weight` (where "balanced" indicates weights are inversely proportional to class frequencies and the default is one), and `dual` (flag to use the dual formulation, which changes the equation being optimized). For each combination, models were trained with different `C` values, which controls the inverse of the regularization strength.
All models have similar accuracy, ROC area, and precision/recall area for all `C` values tested. However, their individual precision and recall metrics change wildly with C. We are more interested in accuracy for this specific problem because accuracy directly controls profit. Using a grid search is not the most efficient parameter tuning method because grid searches do not use information from prior runs to aid future parameter choices. You are at the mercy of the selected grid points.
```
# Create functions that return logistic regression models with different parameters
models = [partial(LogisticRegression, penalty='l1'),
partial(LogisticRegression, penalty='l1', class_weight='balanced'),
partial(LogisticRegression),
partial(LogisticRegression, class_weight='balanced'),
partial(LogisticRegression, dual=True),
partial(LogisticRegression, class_weight='balanced', dual=True)]
start = -8
stop = -2
C_vec = np.logspace(start=start, stop=stop, num=20)
results = calculate_metrics(models, x_train, y_train, stats, 'C', C_vec, k=6)
legend = ['L1 Norm', 'L1 Norm, Balanced Class', 'L2 Norm (Default)',
'L2 Norm, Balanced Class', 'L2 Norm, Dual Form', 'L2 Norm, Balanced Class, Dual Form']
fig, ax = plot_metrics(C_vec, results, 'Regularization Parameter', log=True)
ax[-1].legend(legend, fontsize=16, bbox_to_anchor=(1.05, 1), borderaxespad=0)
[a.set_xlim(10**start, 10**stop) for a in ax]
[a.set_ylim(-0.05, 1.05) for a in ax]
title = 'Grid searches are not the most efficient'
subtitle = 'Grid search of logistic regression hyperparameters'
format_538(fig, 'NBA Stats & Covers.com', ax=ax, title=title, subtitle=subtitle, xoff=(-0.22, 3.45),
yoff=(-1.54, -1.64), toff=(-.16, 1.25), soff=(-0.16, 1.12), n=100)
plt.show()
```
An alternative solution is to use an optimization algorithm that minimizes a loss function to select the hyperparameters. I experimented with the hyperopt package for this, which accepts a parameter search space and loss function as its inputs. The search space consists of discrete choices and ranges on continuous variables. I swapped out the `class_weight` and `dual` variables in favor of `fit_intercept` and `intercept_scaling`, which controls whether to include an intercept in the `LogisticRegression` model and a scaling factor. The scaling factor can help reduce the effect of regularization on the intercept. I chose cross-validation accuracy as the loss function (actually 1-accuracy since the optimizer minimizes the loss function) since we are interested in increasing profits. The optimal hyperparameters are displayed below.
```
space_log = {}
space_log['C'] = hp.loguniform('C', -8*np.log(10), -2*np.log(10))
space_log['intercept_scaling'] = hp.loguniform('intercept_scaling', -8*np.log(10), 8*np.log(10))
space_log['penalty'] = hp.choice('penalty', ['l1', 'l2'])
space_log['fit_intercept'] = hp.choice('fit_intercept', [False, True])
model = LogisticRegression()
best_log, param_log = optimize_params(model, x_train, y_train, stats, space_log, max_evals=1000)
print(best_log)
```
The search history is displayed below. The intercept scale factor tended toward high values, even though the default value is 1.0.
```
labels = ['Regularization', 'Intercept Scale', 'Penalty', 'Intercept']
fig, ax = plot_matrix(param_log.index.values, param_log[[k for k in space_log.keys()]].values,
'Iteration', labels, 2, 2, logy=[True, True, False, False])
[a.set_yticks([0, 1]) for a in ax[2:]]
ax[2].set_yticklabels(['L1', 'L2'])
ax[3].set_yticklabels(['False', 'True'])
title = 'Hyperopt is more flexible than a grid search'
subtitle = 'Hyperopt search of logistic regression hyperparameters'
format_538(fig, 'NBA Stats & Covers.com', ax=ax, title=title, subtitle=subtitle,
xoff=(-0.18, 2.25), yoff=(-1.42, -1.52), toff=(-.16, 1.25), soff=(-0.16, 1.12),
n=80, bottomtick=np.nan)
plt.show()
```
The cross-validation accuracy history shows that many models performed about the same despite their parameter values given the band of points just below 51% accuracy. The optimizer was also unable to find a model that significantly improved accuracy.
```
fig = plt.figure(figsize=(12, 6))
plt.plot(param_log.index.values, param_log['accuracy'], '.', markersize=5)
title = 'Improvements are hard to come by'
subtitle = 'Accuracy of logistic regression hyperparameter optimization history'
format_538(fig, 'NBA Stats & Covers.com', xlabel='Iteration', ylabel='Accuracy',
title=title, subtitle=subtitle, xoff=(-0.1, 1.01), yoff=(-0.14, -0.2),
toff=(-0.09, 1.12), soff=(-0.09, 1.04), bottomtick=0.5)
plt.show()
```
# Support Vector Machine
The [`LinearSVC`](http://scikit-learn.org/stable/modules/generated/sklearn.svm.LinearSVC.html#sklearn.svm.LinearSVC) class is similar to a generic [`SVC`](http://scikit-learn.org/stable/modules/generated/sklearn.svm.SVC.html#sklearn.svm.SVC) with a linear kernel, but is implemented with liblinear instead of libsvm. The documentation states that `LinearSVC` scales better to large sample sizes since `SVC`'s fit time complexity is more than quadratic with the number of samples. I initially tried `SVC`, but the training time was too costly. `LinearSVC` proved to be must faster for this application.
The code below sets up a `LinearSVC` hyperparameter search space using four parameters: `C` (penalty of the error term), `loss` (the loss function), `fit_intercept` (identical to `LogisticRegression`), and `intercept_scaling` (identical to `LogisticRegression`). I limited the number of evaluations to 500 to reduce the computational cost.
```
space_svm = {}
space_svm['C'] = hp.loguniform('C', -8*np.log(10), -2*np.log(10))
space_svm['intercept_scaling'] = hp.loguniform('intercept_scaling', -8*np.log(10), 8*np.log(10))
space_svm['loss'] = hp.choice('loss', ['hinge', 'squared_hinge'])
space_svm['fit_intercept'] = hp.choice('fit_intercept', [False, True])
model = LinearSVC()
best_svm, param_svm = optimize_params(model, x_train, y_train, stats, space_svm, max_evals=500)
print(best_svm)
```
The search history below is similar to the logistic regression history, but hyperopt appears to test more intercept scales with low values than before. This is also indicated by the drastic reduction in the intercept scale compared to logistic regression.
```
labels = ['Regularization', 'Intercept Scale', 'Loss', 'Intercept']
fig, ax = plot_matrix(param_svm.index.values, param_svm[[k for k in space_svm.keys()]].values,
'Iteration', labels, 2, 2, logy=[True, True, False, False])
[a.set_yticks([0, 1]) for a in ax[2:]]
ax[2].set_yticklabels(['Hinge', 'Squared\nHinge'])
ax[3].set_yticklabels(['False', 'True'])
title = 'Hyperopt is more flexible than a grid search'
subtitle = 'Hyperopt search of support vector machine hyperparameters'
format_538(fig, 'NBA Stats & Covers.com', ax=ax, title=title, subtitle=subtitle,
xoff=(-0.24, 2.25), yoff=(-1.42, -1.52), toff=(-.22, 1.25), soff=(-0.22, 1.12),
n=80, bottomtick=np.nan)
plt.show()
```
The plot below shows the `LinearSVC` cross-validation accuracy history. There is a band of points similar to what we observed for logistic regression below 51% accuracy. The support vector machine model does not perform much better than logistic regression, and several points fall below 50% accuracy.
```
fig = plt.figure(figsize=(12, 6))
plt.plot(param_svm.index.values, param_svm['accuracy'], '.', markersize=5)
title = 'Improvements are hard to come by'
subtitle = 'Accuracy of support vector machine hyperparameter optimization history'
format_538(fig, 'NBA Stats & Covers.com', xlabel='Iteration', ylabel='Accuracy',
title=title, subtitle=subtitle, xoff=(-0.1, 1.01), yoff=(-0.14, -0.2),
toff=(-0.09, 1.12), soff=(-0.09, 1.04), bottomtick=0.5)
plt.show()
```
# Random Forest
The code below builds a [`RandomForestClassifier`](http://scikit-learn.org/stable/modules/generated/sklearn.ensemble.RandomForestClassifier.html#sklearn.ensemble.RandomForestClassifier) hyperparameter search space using the parameters `n_estimators` (number of decision trees in the forest), `class_weight` (identical to the `LogisticRegression` grid search), `criterion` (function to evaluate split quality), and `bootstrap` (controls whether bootstrap samples are used when building trees). I reduced the number of function evaluations to 100 in the interest of computational time.
```
space_rf = {}
space_rf['n_estimators'] = 10 + hp.randint('n_estimators', 40)
space_rf['criterion'] = hp.choice('criterion', ['gini', 'entropy'])
space_rf['class_weight'] = hp.choice('class_weight', [None, 'balanced'])
space_rf['bootstrap'] = hp.choice('bootstrap', [False, True])
model = RandomForestClassifier(random_state=8)
best_rf, param_rf = optimize_params(model, x_train, y_train, stats, space_rf, max_evals=100)
print(best_rf)
```
The random forest hyperparameter search history is displayed below.
```
labels = ['Estimators', 'Criterion', 'Class Weight', 'Bootstrap']
fig, ax = plot_matrix(param_rf.index.values, param_rf[[k for k in space_rf.keys()]].values,
'Iteration', labels, 2, 2)
[a.set_yticks([0, 1]) for a in ax[1:]]
ax[1].set_yticklabels(['Gini', 'Entropy'])
ax[2].set_yticklabels(['None', 'Balanced'])
ax[3].set_yticklabels(['False', 'True'])
title = 'Hyperopt is more flexible than a grid search'
subtitle = 'Hyperopt search of random forest hyperparameters'
format_538(fig, 'NBA Stats & Covers.com', ax=ax, title=title, subtitle=subtitle,
xoff=(-0.26, 2.25), yoff=(-1.42, -1.52), toff=(-.24, 1.25), soff=(-0.24, 1.12),
n=80, bottomtick=np.nan)
plt.show()
```
The cross-validation accuracy history shows the random forest model performs slightly worse than logistic regression.
```
fig = plt.figure(figsize=(12, 6))
plt.plot(param_rf.index.values, param_rf['accuracy'], '.', markersize=5)
title = 'Improvements are hard to come by'
subtitle = 'Accuracy of random forest hyperparameter optimization history'
format_538(fig, 'NBA Stats & Covers.com', xlabel='Iteration', ylabel='Accuracy',
title=title, subtitle=subtitle, xoff=(-0.1, 1.01), yoff=(-0.14, -0.2),
toff=(-0.09, 1.12), soff=(-0.09, 1.04), bottomtick=0.5)
plt.show()
```
# Neural Network
The code below builds a [`MLPClassifier`](http://scikit-learn.org/stable/modules/generated/sklearn.neural_network.MLPClassifier.html#sklearn.neural_network.MLPClassifier) hyperparameter search space using the parameters `hidden_layer_sizes` (number of neurons in each hidden layer), `alpha` (controls the L2 regularization similar to the `C` parameter in `LogisticRegression` and `LinearSVC`), `activation` (network activation function), and `solver` (the algorithm used to optimize network weights). The network structure was held to a single hidden layer. I kept the number of function evaluations at 100 in the interest of computational time.
```
space_mlp = {}
space_mlp['hidden_layer_sizes'] = 10 + hp.randint('hidden_layer_sizes', 40)
space_mlp['alpha'] = hp.loguniform('alpha', -8*np.log(10), 3*np.log(10))
space_mlp['activation'] = hp.choice('activation', ['relu', 'logistic', 'tanh'])
space_mlp['solver'] = hp.choice('solver', ['lbfgs', 'sgd', 'adam'])
model = MLPClassifier()
best_mlp, param_mlp = optimize_params(model, x_train, y_train, stats, space_mlp, max_evals=100)
print(best_mlp)
```
The multi-layer perceptron hyperparameter search history is displayed below.
```
labels = ['Hidden Neurons', 'Regularization', 'Activation', 'Solver']
fig, ax = plot_matrix(param_mlp.index.values, param_mlp[[k for k in space_mlp.keys()]].values,
'Iteration', labels, 2, 2, logy=[False, True, False, False])
[a.set_yticks([0, 1, 2]) for a in ax[2:]]
ax[2].set_yticklabels(['RELU', 'Logistic', 'Tanh'])
ax[3].set_yticklabels(['LBFGS', 'SGD', 'ADAM'])
title = 'Hyperopt is more flexible than a grid search'
subtitle = 'Hyperopt search of multi-layer perceptron hyperparameters'
format_538(fig, 'NBA Stats & Covers.com', ax=ax, title=title, subtitle=subtitle,
xoff=(-0.26, 2.25), yoff=(-1.42, -1.52), toff=(-.24, 1.25), soff=(-0.24, 1.12),
n=80, bottomtick=np.nan)
plt.show()
```
The cross-validation history suggests the multi-layer perceptron performs the best of the four models, albeit the improvement is minor.
```
fig = plt.figure(figsize=(12, 6))
plt.plot(param_mlp.index.values, param_mlp['accuracy'], '.', markersize=5)
title = 'Improvements are hard to come by'
subtitle = 'Accuracy of multi-layer perceptron hyperparameter optimization history'
format_538(fig, 'NBA Stats & Covers.com', xlabel='Iteration', ylabel='Accuracy',
title=title, subtitle=subtitle, xoff=(-0.1, 1.01), yoff=(-0.14, -0.2),
toff=(-0.09, 1.12), soff=(-0.09, 1.04), bottomtick=0.5)
plt.show()
```
|
github_jupyter
|
# PySDDR: An Advanced Tutorial
In the beginner's guide only tabular data was used as input to the PySDDR framework. In this advanced tutorial we show the effects when combining structured and unstructured data. Currently, the framework only supports images as unstructured data.
We will use the MNIST dataset as a source for the unstructured data and generate additional tabular features corresponding to those. Our outcome in this tutorial is simulated based on linear and non-linear effects of tabular data and a linear effect of the number shown on the MNIST image. Our model is not provided with the (true) number, but instead has to learn the number effect from the image (together with the structured data effects):
\begin{equation*}
y = \sin(x_1) - 3x_2 + x_3^4 + 3\cdot number + \epsilon
\end{equation*}
with $\epsilon \sim \mathcal{N}(0, \sigma^2)$ and $number$ is the number on the MNIST image.
The aim of training is for the model to be able to output a latent effect, representing the number depicted in the MNIST image.
We start by importing the sddr module and other required libraries
```
# import the sddr module
from sddr import Sddr
import torch
import torch.nn as nn
import torch.optim as optim
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
#set seeds for reproducibility
torch.manual_seed(1)
np.random.seed(1)
```
### User inputs
First the user defines the data to be used. The data is loaded and if it does not already exist, a column needs to be added to the tabular data describing the unstructured data - structured data correspondence. In the example below we add a column where each item includes the name of the image to which the current row of tabular data corresponds.
```
data_path = '../data/mnist_data/tab.csv'
data = pd.read_csv(data_path,delimiter=',')
# append a column for the numbers: each data point contains a file name of the corresponding image
for i in data.index:
data.loc[i,'numbers'] = f'img_{i}.jpg'
```
Next the distribution, formulas and training parameters are defined. The size of each image is ```28x28``` so our neural network has a layer which flattens the input, which is followed by a linear layer of input size ```28x28``` and an output size of ```128```. Finally, this is followed by a ```ReLU``` for the activation.
Here the structured data is not pre-loaded as it would be typically too large to load in one step. Therefore the path to the directory in which it is stored is provided along with the data type (for now only 'images' supported). The images are then loaded in batches using PyTorch's dataloader. Note that here again the key given in the ```unstructured_data``` dictionary must match the name it is given in the formula, in this case ```'numbers'```. Similarly the keys of the ```deep_models_dict``` must also match the names in the formula, in this case ```'dnn'```
```
# define distribution and the formula for the distibutional parameter
distribution = 'Normal'
formulas = {'loc': '~ -1 + spline(x1, bs="bs", df=10) + x2 + dnn(numbers) + spline(x3, bs="bs", df=10)',
'scale': '~1'
}
# define the deep neural networks' architectures and output shapes used in the above formula
deep_models_dict = {
'dnn': {
'model': nn.Sequential(nn.Flatten(1, -1),
nn.Linear(28*28,128),
nn.ReLU()),
'output_shape': 128},
}
# define your training hyperparameters
train_parameters = {
'batch_size': 8000,
'epochs': 1000,
'degrees_of_freedom': {'loc':9.6, 'scale':9.6},
'optimizer' : optim.Adam,
'val_split': 0.15,
'early_stop_epsilon': 0.001,
'dropout_rate': 0.01
}
# provide the location and datatype of the unstructured data
unstructured_data = {
'numbers' : {
'path' : '../data/mnist_data/mnist_images',
'datatype' : 'image'
}
}
# define output directory
output_dir = './outputs'
```
### Initialization
The sddr instance is initialized with the parameters given by the user in the previous step:
```
sddr = Sddr(output_dir=output_dir,
distribution=distribution,
formulas=formulas,
deep_models_dict=deep_models_dict,
train_parameters=train_parameters,
)
```
### Training
The sddr network is trained with the data defined above and the loss curve is plotted.
```
sddr.train(structured_data=data,
target="y_gen",
unstructured_data = unstructured_data,
plot=True)
```
### Evaluation - Visualizing the partial effects
In this case the data is assumed to follow a normal distribution, in which case two distributional parameters, loc and scale, need to be estimated. Below we plot the partial effects of each smooth term.
Remember the partial effects are computed by: partial effect = smooth_features * coefs (weights)
In other words the smoothing terms are multiplied with the weights of the Structured Head. We use the partial effects to interpret whether our model has learned correctly.
```
partial_effects_loc = sddr.eval('loc',plot=True)
partial_effects_scale = sddr.eval('scale',plot=True)
```
As we can see the distributional parameter loc has two parial effects, one sinusoidal and one quadratic. The parameter scale expectedly has no partial effect since the formula only includes an intercept.
Next we retrieve our ground truth data and compare it with the model's estimation
```
# compare prediction of neural network with ground truth
data_pred = data.loc[:,:]
ground_truth = data.loc[:,'y_gen']
# predict returns partial effects and a distributional layer that gives statistical information about the prediction
distribution_layer, partial_effect = sddr.predict(data_pred,
clipping=True,
plot=False,
unstructured_data = unstructured_data)
# retrieve the mean and variance of the distributional layer
predicted_mean = distribution_layer.loc[:,:].T
predicted_variance = distribution_layer.scale[0]
# and plot the result
plt.scatter(ground_truth, predicted_mean)
print(f"Predicted variance for first sample: {predicted_variance}")
```
The comparison shows that for most samples the predicted and true values are directly propotional.
Next we want to check if the model learned the correct correspondence of images and numbers
```
# we create a copy of our original structured data where we set all inputs but the images to be zero
data_pred_copy = data.copy()
data_pred_copy.loc[:,'x1'] = 0
data_pred_copy.loc[:,'x2'] = 0
data_pred_copy.loc[:,'x3'] = 0
# and make a prediction using only the images
distribution_layer, partial_effect = sddr.predict(data_pred_copy,
clipping=True,
plot=False,
unstructured_data = unstructured_data)
# add the predicted mean value to our tabular data
data_pred_copy['predicted_number'] = distribution_layer.loc[:,:].numpy().flatten()
# and compare the true number on the images with the predicted number
ax = sns.boxplot(x="y_true", y="predicted_number", data=data_pred_copy)
ax.set_xlabel("true number");
ax.set_ylabel("predicted latent effect of number");
```
Observing the boxplot figure we see that as the true values, i.e. numbers depicted on images, are increasing, so too are the medians of the predicted distributions. Therefore the partial effect of the neural network is directly correlated with the number depicted in the MNIST images, proving that our neural network, though simple, has learned from the unstructured data.
|
github_jupyter
|
```
# Copyright 2021 Google LLC
# Use of this source code is governed by an MIT-style
# license that can be found in the LICENSE file or at
# https://opensource.org/licenses/MIT.
# Author(s): Kevin P. Murphy ([email protected]) and Mahmoud Soliman ([email protected])
```
<a href="https://opensource.org/licenses/MIT" target="_parent"><img src="https://img.shields.io/github/license/probml/pyprobml"/></a>
<a href="https://colab.research.google.com/github/probml/pyprobml/blob/master/notebooks/figures//chapter16_figures.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Cloning the pyprobml repo
```
!git clone https://github.com/probml/pyprobml
%cd pyprobml/scripts
```
# Installing required software (This may take few minutes)
```
!apt-get install octave -qq > /dev/null
!apt-get install liboctave-dev -qq > /dev/null
%%capture
%load_ext autoreload
%autoreload 2
DISCLAIMER = 'WARNING : Editing in VM - changes lost after reboot!!'
from google.colab import files
def interactive_script(script, i=True):
if i:
s = open(script).read()
if not s.split('\n', 1)[0]=="## "+DISCLAIMER:
open(script, 'w').write(
f'## {DISCLAIMER}\n' + '#' * (len(DISCLAIMER) + 3) + '\n\n' + s)
files.view(script)
%run $script
else:
%run $script
def show_image(img_path):
from google.colab.patches import cv2_imshow
import cv2
img = cv2.imread(img_path, cv2.IMREAD_UNCHANGED)
img=cv2.resize(img,(600,600))
cv2_imshow(img)
```
## Figure 16.1:<a name='16.1'></a> <a name='fig:knn'></a>
(a) Illustration of a $K$-nearest neighbors classifier in 2d for $K=5$. The nearest neighbors of test point $\mathbf x $ have labels $\ 1, 1, 1, 0, 0\ $, so we predict $p(y=1|\mathbf x , \mathcal D ) = 3/5$. (b) Illustration of the Voronoi tesselation induced by 1-NN. Adapted from Figure 4.13 of <a href='#Duda01'>[DHS01]</a> .
Figure(s) generated by [knn_voronoi_plot.py](https://github.com/probml/pyprobml/blob/master/scripts/knn_voronoi_plot.py)
```
interactive_script("knn_voronoi_plot.py")
```
## Figure 16.2:<a name='16.2'></a> <a name='knnThreeClass'></a>
Decision boundaries induced by a KNN classifier. (a) $K=1$. (b) $K=2$. (c) $K=5$. (d) Train and test error vs $K$.
Figure(s) generated by [knn_classify_demo.py](https://github.com/probml/pyprobml/blob/master/scripts/knn_classify_demo.py)
```
interactive_script("knn_classify_demo.py")
```
## Figure 16.3:<a name='16.3'></a> <a name='curse'></a>
Illustration of the curse of dimensionality. (a) We embed a small cube of side $s$ inside a larger unit cube. (b) We plot the edge length of a cube needed to cover a given volume of the unit cube as a function of the number of dimensions. Adapted from Figure 2.6 from <a href='#HastieBook'>[HTF09]</a> .
Figure(s) generated by [curse_dimensionality.py](https://github.com/probml/pyprobml/blob/master/scripts/curse_dimensionality.py)
```
interactive_script("curse_dimensionality.py")
```
## Figure 16.4:<a name='16.4'></a> <a name='fig:LCA'></a>
Illustration of latent coincidence analysis (LCA) as a directed graphical model. The inputs $\mathbf x , \mathbf x ' \in \mathbb R ^D$ are mapped into Gaussian latent variables $\mathbf z , \mathbf z ' \in \mathbb R ^L$ via a linear mapping $\mathbf W $. If the two latent points coincide (within length scale $\kappa $) then we set the similarity label to $y=1$, otherwise we set it to $y=0$. From Figure 1 of <a href='#Der2012'>[ML12]</a> . Used with kind permission of Lawrence Saul.
```
show_image("/content/pyprobml/notebooks/figures/images/LCA-PGM.png")
```
## Figure 16.5:<a name='16.5'></a> <a name='fig:tripletNet'></a>
Networks for deep metric learning. (a) Siamese network. (b) Triplet network. From Figure 5 of <a href='#Kaya2019'>[MH19]</a> . Used with kind permission of Mahmut Kaya. .
```
show_image("/content/pyprobml/notebooks/figures/images/siameseNet.png")
show_image("/content/pyprobml/notebooks/figures/images/tripletNet.png")
```
## Figure 16.6:<a name='16.6'></a> <a name='fig:tripletBound'></a>
Speeding up triplet loss minimization. (a) Illustration of hard vs easy negatives. Here $a$ is the anchor point, $p$ is a positive point, and $n_i$ are negative points. Adapted from Figure 4 of <a href='#Kaya2019'>[MH19]</a> . (b) Standard triplet loss would take $8 \times 3 \times 4 = 96$ calculations, whereas using a proxy loss (with one proxy per class) takes $8 \times 2 = 16$ calculations. From Figure 1 of <a href='#Do2019cvpr'>[Tha+19]</a> . Used with kind permission of Gustavo Cerneiro.
```
show_image("/content/pyprobml/notebooks/figures/images/hard-negative-mining.png")
show_image("/content/pyprobml/notebooks/figures/images/tripletBound.png")
```
## Figure 16.7:<a name='16.7'></a> <a name='fig:SEC'></a>
Adding spherical embedding constraint to a deep metric learning method. Used with kind permission of Dingyi Zhang.
```
show_image("/content/pyprobml/notebooks/figures/images/SEC.png")
```
## Figure 16.8:<a name='16.8'></a> <a name='smoothingKernels'></a>
A comparison of some popular normalized kernels.
Figure(s) generated by [smoothingKernelPlot.m](https://github.com/probml/pmtk3/blob/master/demos/smoothingKernelPlot.m)
```
!octave -W smoothingKernelPlot.m >> _
```
## Figure 16.9:<a name='16.9'></a> <a name='parzen'></a>
A nonparametric (Parzen) density estimator in 1d estimated from 6 data points, denoted by x. Top row: uniform kernel. Bottom row: Gaussian kernel. Left column: bandwidth parameter $h=1$. Right column: bandwidth parameter $h=2$. Adapted from http://en.wikipedia.org/wiki/Kernel_density_estimation .
Figure(s) generated by [Kernel_density_estimation](http://en.wikipedia.org/wiki/Kernel_density_estimation) [parzen_window_demo2.py](https://github.com/probml/pyprobml/blob/master/scripts/parzen_window_demo2.py)
```
interactive_script("parzen_window_demo2.py")
```
## Figure 16.10:<a name='16.10'></a> <a name='kernelRegression'></a>
An example of kernel regression in 1d using a Gaussian kernel.
Figure(s) generated by [kernelRegressionDemo.m](https://github.com/probml/pmtk3/blob/master/demos/kernelRegressionDemo.m)
```
!octave -W kernelRegressionDemo.m >> _
```
## References:
<a name='Duda01'>[DHS01]</a> R. O. Duda, P. E. Hart and D. G. Stork. "Pattern Classification". (2001).
<a name='HastieBook'>[HTF09]</a> T. Hastie, R. Tibshirani and J. Friedman. "The Elements of Statistical Learning". (2009).
<a name='Kaya2019'>[MH19]</a> K. Mahmut and B. HasanSakir. "Deep Metric Learning: A Survey". In: Symmetry (2019).
<a name='Der2012'>[ML12]</a> D. Matthew and S. LawrenceK. "Latent Coincidence Analysis: A Hidden Variable Model forDistance Metric Learning". (2012).
<a name='Do2019cvpr'>[Tha+19]</a> D. Thanh-Toan, T. Toan, R. Ian, K. Vijay, H. Tuan and C. Gustavo. "A Theoretically Sound Upper Bound on the Triplet Loss forImproving the Efficiency of Deep Distance Metric Learning". (2019).
|
github_jupyter
|
# TimeEval shared parameter optimization result analysis
```
# Automatically reload packages:
%load_ext autoreload
%autoreload 2
# imports
import json
import warnings
import pandas as pd
import numpy as np
import scipy as sp
import plotly.offline as py
import plotly.graph_objects as go
import plotly.figure_factory as ff
import plotly.express as px
from plotly.subplots import make_subplots
from pathlib import Path
from timeeval import Datasets
```
## Configuration
Target parameters that were optimized in this run (per algorithm):
```
algo_param_mapping = {
"HBOS": ["n_bins"],
"MultiHMM": ["n_bins"],
"MTAD-GAT": ["context_window_size", "mag_window_size", "score_window_size"],
"PST": ["n_bins"]
}
```
Define data and results folder:
```
# constants and configuration
data_path = Path("../../data") / "test-cases"
result_root_path = Path("../timeeval_experiments/results")
experiment_result_folder = "2021-10-04_shared-optim2"
# build paths
result_paths = [d for d in result_root_path.iterdir() if d.is_dir()]
print("Available result directories:")
display(result_paths)
result_path = result_root_path / experiment_result_folder
print("\nSelecting:")
print(f"Data path: {data_path.resolve()}")
print(f"Result path: {result_path.resolve()}")
```
Load results and dataset metadata:
```
def extract_hyper_params(param_names):
def extract(value):
params = json.loads(value)
result = None
for name in param_names:
try:
value = params[name]
result = pd.Series([name, value], index=["optim_param_name", "optim_param_value"])
break
except KeyError:
pass
if result is None:
raise ValueError(f"Parameters {param_names} not found in '{value}'")
return result
return extract
# load results
print(f"Reading results from {result_path.resolve()}")
df = pd.read_csv(result_path / "results.csv")
# add dataset_name column
df["dataset_name"] = df["dataset"].str.split(".").str[0]
# add optim_params column
df[["optim_param_name", "optim_param_value"]] = ""
for algo in algo_param_mapping:
df_algo = df.loc[df["algorithm"] == algo]
df.loc[df_algo.index, ["optim_param_name", "optim_param_value"]] = df_algo["hyper_params"].apply(extract_hyper_params(algo_param_mapping[algo]))
# load dataset metadata
dmgr = Datasets(data_path)
```
Define plotting functions:
```
def load_scores_df(algorithm_name, dataset_id, optim_params, repetition=1):
params_id = df.loc[(df["algorithm"] == algorithm_name) & (df["collection"] == dataset_id[0]) & (df["dataset"] == dataset_id[1]) & (df["optim_param_name"] == optim_params[0]) & (df["optim_param_value"] == optim_params[1]), "hyper_params_id"].item()
path = (
result_path /
algorithm_name /
params_id /
dataset_id[0] /
dataset_id[1] /
str(repetition) /
"anomaly_scores.ts"
)
return pd.read_csv(path, header=None)
def plot_scores(algorithm_name, dataset_name):
if isinstance(algorithm_name, tuple):
algorithms = [algorithm_name]
elif not isinstance(algorithm_name, list):
raise ValueError("Please supply a tuple (algorithm_name, optim_param_name, optim_param_value) or a list thereof as first argument!")
else:
algorithms = algorithm_name
# construct dataset ID
dataset_id = ("GutenTAG", f"{dataset_name}.unsupervised")
# load dataset details
df_dataset = dmgr.get_dataset_df(dataset_id)
# check if dataset is multivariate
dataset_dim = df.loc[df["dataset_name"] == dataset_name, "dataset_input_dimensionality"].unique().item()
dataset_dim = dataset_dim.lower()
auroc = {}
df_scores = pd.DataFrame(index=df_dataset.index)
skip_algos = []
algos = []
for algo, optim_param_name, optim_param_value in algorithms:
optim_params = f"{optim_param_name}={optim_param_value}"
algos.append((algo, optim_params))
# get algorithm metric results
try:
auroc[(algo, optim_params)] = df.loc[
(df["algorithm"] == algo) & (df["dataset_name"] == dataset_name) & (df["optim_param_name"] == optim_param_name) & (df["optim_param_value"] == optim_param_value),
"ROC_AUC"
].item()
except ValueError:
warnings.warn(f"No ROC_AUC score found! Probably {algo} with params {optim_params} was not executed on {dataset_name}.")
auroc[(algo, optim_params)] = -1
skip_algos.append((algo, optim_params))
continue
# load scores
training_type = df.loc[df["algorithm"] == algo, "algo_training_type"].values[0].lower().replace("_", "-")
try:
df_scores[(algo, optim_params)] = load_scores_df(algo, ("GutenTAG", f"{dataset_name}.{training_type}"), (optim_param_name, optim_param_value)).iloc[:, 0]
except (ValueError, FileNotFoundError):
warnings.warn(f"No anomaly scores found! Probably {algo} was not executed on {dataset_name} with params {optim_params}.")
df_scores[(algo, optim_params)] = np.nan
skip_algos.append((algo, optim_params))
algorithms = [a for a in algos if a not in skip_algos]
# Create plot
fig = make_subplots(2, 1)
if dataset_dim == "multivariate":
for i in range(1, df_dataset.shape[1]-1):
fig.add_trace(go.Scatter(x=df_dataset.index, y=df_dataset.iloc[:, i], name=f"channel-{i}"), 1, 1)
else:
fig.add_trace(go.Scatter(x=df_dataset.index, y=df_dataset.iloc[:, 1], name="timeseries"), 1, 1)
fig.add_trace(go.Scatter(x=df_dataset.index, y=df_dataset["is_anomaly"], name="label"), 2, 1)
for item in algorithms:
algo, optim_params = item
fig.add_trace(go.Scatter(x=df_scores.index, y=df_scores[item], name=f"{algo}={auroc[item]:.4f} ({optim_params})"), 2, 1)
fig.update_xaxes(matches="x")
fig.update_layout(
title=f"Results of {','.join(np.unique([a for a, _ in algorithms]))} on {dataset_name}",
height=400
)
return py.iplot(fig)
```
## Analyze TimeEval results
```
df[["algorithm", "dataset_name", "status", "AVERAGE_PRECISION", "PR_AUC", "RANGE_PR_AUC", "ROC_AUC", "execute_main_time", "optim_param_name", "optim_param_value"]]
```
---
### Errors
```
df_error_counts = df.pivot_table(index=["algo_training_type", "algorithm"], columns=["status"], values="repetition", aggfunc="count")
df_error_counts = df_error_counts.fillna(value=0).astype(np.int64)
```
#### Aggregation of errors per algorithm grouped by algorithm training type
```
for tpe in ["SEMI_SUPERVISED", "SUPERVISED", "UNSUPERVISED"]:
if tpe in df_error_counts.index:
print(tpe)
display(df_error_counts.loc[tpe])
```
#### Slow algorithms
Algorithms, for which more than 50% of all executions ran into the timeout.
```
df_error_counts[df_error_counts["Status.TIMEOUT"] > (df_error_counts["Status.ERROR"] + df_error_counts["Status.OK"])]
```
#### Broken algorithms
Algorithms, which failed for at least 50% of the executions.
```
error_threshold = 0.5
df_error_counts[df_error_counts["Status.ERROR"] > error_threshold*(
df_error_counts["Status.TIMEOUT"] + df_error_counts["Status.ERROR"] + df_error_counts["Status.OK"]
)]
```
#### Detail errors
```
algo_list = ["MTAD-GAT", "MultiHMM"]
error_list = ["OOM", "Segfault", "ZeroDivisionError", "IncompatibleParameterConfig", "WrongDBNState", "SyntaxError", "other"]
errors = pd.DataFrame(0, index=error_list, columns=algo_list, dtype=np.int_)
for algo in algo_list:
df_tmp = df[(df["algorithm"] == algo) & (df["status"] == "Status.ERROR")]
for i, run in df_tmp.iterrows():
path = result_path / run["algorithm"] / run["hyper_params_id"] / run["collection"] / run["dataset"] / str(run["repetition"]) / "execution.log"
with path.open("r") as fh:
log = fh.read()
if "status code '139'" in log:
errors.loc["Segfault", algo] += 1
elif "status code '137'" in log:
errors.loc["OOM", algo] += 1
elif "Expected n_neighbors <= n_samples" in log:
errors.loc["IncompatibleParameterConfig", algo] += 1
elif "ZeroDivisionError" in log:
errors.loc["ZeroDivisionError", algo] += 1
elif "does not have key" in log:
errors.loc["WrongDBNState", algo] += 1
elif "NameError" in log:
errors.loc["SyntaxError", algo] += 1
else:
print(f'\n\n#### {run["dataset"]} ({run["optim_param_name"]}:{run["optim_param_value"]})')
print(log)
errors.loc["other", algo] += 1
errors.T
```
---
### Parameter assessment
```
sort_by = ("ROC_AUC", "mean")
metric_agg_type = ["mean", "median"]
time_agg_type = "mean"
aggs = {
"AVERAGE_PRECISION": metric_agg_type,
"RANGE_PR_AUC": metric_agg_type,
"PR_AUC": metric_agg_type,
"ROC_AUC": metric_agg_type,
"train_main_time": time_agg_type,
"execute_main_time": time_agg_type,
"repetition": "count"
}
df_tmp = df.reset_index()
df_tmp = df_tmp.groupby(by=["algorithm", "optim_param_name", "optim_param_value"]).agg(aggs)
df_tmp = df_tmp.reset_index()
df_tmp = df_tmp.sort_values(by=["algorithm", "optim_param_name", sort_by], ascending=False)
df_tmp = df_tmp.set_index(["algorithm", "optim_param_name", "optim_param_value"])
with pd.option_context("display.max_rows", None, "display.max_columns", None):
display(df_tmp)
```
#### Selected parameters
- HBOS: `n_bins=20` (more is better)
- MultiHMM: `n_bins=5` (8 is slightly better, but takes way longer. The scores are very bad anyway!)
- MTAD-GAT: `context_window_size=30,mag_window_size=40,score_window_size=52` (very slow)
- PST: `n_bins=5` (less is better)
> **Note**
>
> MTAD-GAT is very slow! Exclude from further runs!
```
plot_scores([("MultiHMM", "n_bins", 5), ("MultiHMM", "n_bins", 8)], "sinus-type-mean")
plot_scores([("MTAD-GAT", "context_window_size", 30), ("MTAD-GAT", "context_window_size", 40)], "sinus-type-mean")
```
|
github_jupyter
|
<h1>Table of Contents<span class="tocSkip"></span></h1>
<div class="toc" style="margin-top: 1em;"><ul class="toc-item"><li><span><a href="#label-identity-hairstyle" data-toc-modified-id="label-identity-hairstyle-1"><span class="toc-item-num">1 </span>label identity hairstyle</a></span></li><li><span><a href="#Prepare-hairstyle-images" data-toc-modified-id="Prepare-hairstyle-images-2"><span class="toc-item-num">2 </span>Prepare hairstyle images</a></span></li><li><span><a href="#prepare-hairstyle-manifest" data-toc-modified-id="prepare-hairstyle-manifest-3"><span class="toc-item-num">3 </span>prepare hairstyle manifest</a></span></li></ul></div>
```
from query.models import Video, FaceIdentity, Identity
from esper.widget import *
from esper.prelude import collect, esper_widget
import pickle
import os
import random
get_ipython().magic('matplotlib inline')
get_ipython().magic('reload_ext autoreload')
get_ipython().magic('autoreload 2')
```
# label identity hairstyle
```
identity_hair_dict = {}
identities = Identity.objects.all()
identity_list = [(i.id, i.name) for i in identities]
identity_list.sort()
# 154
hair_color_3 = {0: 'black', 1: 'white', 2: 'blond'}
hair_color_5 = {0: 'black', 1: 'white', 2: 'blond', 3: 'brown', 4: 'gray'}
hair_length = {0: 'long', 1: 'medium', 2: 'short', 3: 'bald'}
identity_label = [id for id in identity_label if id not in identity_hair_dict]
# idx += 1
# iid = identity_list[idx][0]
# name = identity_list[idx][1]
# iid = identity_label[idx]
# print(name)
print(iid)
result = qs_to_result(
FaceIdentity.objects \
.filter(identity__id=1365) \
.filter(probability__gt=0.8),
limit=30)
esper_widget(result)
'''
{'black' : 0, 'white': 1, 'blond' : 2}, # hair_color_3
{'black' : 0, 'white': 1, 'blond' : 2, 'brown' : 3, 'gray' : 4}, # hair_color_5
{'long' : 0, 'medium' : 1, 'short' : 2, 'bald' : 3} # hair_length
'''
label = identity_hair_dict[iid] = (2,2,0)
print(hair_color_3[label[0]], hair_color_5[label[1]], hair_length[label[2]])
pickle.dump(identity_hair_dict, open('/app/data/identity_hair_dict.pkl', 'wb'))
```
# Prepare hairstyle images
```
faceIdentities = FaceIdentity.objects \
.filter(identity__name='melania trump') \
.filter(probability__gt=0.9) \
.select_related('face__frame__video')
faceIdentities_sampled = random.sample(list(faceIdentities), 1000)
print("Load %d face identities" % len(faceIdentities_sampled))
identity_grouped = collect(list(faceIdentities_sampled), lambda identity: identity.face.frame.video.id)
print("Group into %d videos" % len(identity_grouped))
face_dict = {}
for video_id, fis in identity_grouped.items():
video = Video.objects.filter(id=video_id)[0]
face_list = []
for i in fis:
face_id = i.face.id
frame_id = i.face.frame.number
identity_id = i.identity.id
x1, y1, x2, y2 = i.face.bbox_x1, i.face.bbox_y1, i.face.bbox_x2, i.face.bbox_y2
bbox = (x1, y1, x2, y2)
face_list.append((frame_id, face_id, identity_id, bbox))
face_list.sort()
face_dict[video.path] = face_list
print("Preload face bbox done")
if __name__ == "__main__":
solve_parallel(face_dict, res_dict_path='/app/result/clothing/fina_dict.pkl', workers=10)
```
# prepare hairstyle manifest
```
img_list = os.listdir('/app/result/clothing/images/')
len(img_list)
group_by_identity = {}
for name in img_list:
iid = int(name.split('_')[0])
if iid not in group_by_identity:
group_by_identity[iid] = []
else:
group_by_identity[iid].append(name)
identity_label = [id for id, img_list in group_by_identity.items() if len(img_list) > 10]
identity_label.sort()
identity_hair_dict = pickle.load(open('/app/data/identity_hair_dict.pkl', 'rb'))
NUM_PER_ID = 1000
hairstyle_manifest = []
for iid, img_list in group_by_identity.items():
if len(img_list) > 10 and iid in identity_hair_dict:
if len(img_list) < NUM_PER_ID:
img_list_sample = img_list
else:
img_list_sample = random.sample(img_list, NUM_PER_ID)
attrib = identity_hair_dict[iid]
hairstyle_manifest += [(path, attrib) for path in img_list_sample]
random.shuffle(hairstyle_manifest)
len(hairstyle_manifest)
pickle.dump(hairstyle_manifest, open('/app/result/clothing/hairstyle_manifest.pkl', 'wb'))
```
|
github_jupyter
|
```
import numpy as np
import pandas as pd
```
### loading dataset
```
data = pd.read_csv("student-data.csv")
data.head()
data.shape
type(data)
```
### Exploratory data analysis
```
import matplotlib.pyplot as plt
import seaborn as sns
a = data.plot()
data.info()
data.isnull().sum()
a = sns.heatmap(data.isnull(),cmap='Blues')
a = sns.heatmap(data.isnull(),cmap='Blues',yticklabels=False)
```
#### this indicates that we have no any null values in the dataset
```
a = sns.heatmap(data.isna(),yticklabels=False)
```
#### this heatmap indicates that we have no any 'NA' values in the dataset
```
sns.set(style='darkgrid')
sns.countplot(data=data,x='reason')
```
This indicates the count for choosing school of various reasons.
A count plot can be thought of as a histogram across a categorical, instead of quantitative, variable.
```
data.head(7)
```
calculating total passed students
```
passed = data.loc[data.passed == 'yes']
passed.shape
tot_passed=passed.shape[0]
print('total passed students is: {} '.format(tot_passed))
```
calculating total failed students
```
failed = data.loc[data.passed == 'no']
print('total failed students is: {}'.format(failed.shape[0]))
```
### Feature Engineering
```
data.head()
```
To identity feature and target variable lets first do some feature engineering stuff!
```
data.columns
data.columns[-1]
```
Here 'passed' is our target variable. Since in this system we need to develop the model that will predict the likelihood that a given student will pass, quantifying whether an intervention is necessary.
```
target = data.columns[-1]
data.columns[:-1]
#initially taking all columns as our feature variables
feature = list(data.columns[:-1])
data[target].head()
data[feature].head()
```
Now taking feature and target data in seperate dataframe
```
featuredata = data[feature]
targetdata = data[target]
```
Now we need to convert several non-numeric columns like 'internet' into numerical form for the model to process
```
def preprocess_features(X):
output = pd.DataFrame(index = X.index)
for col, col_data in X.iteritems():
if col_data.dtype == object:
col_data = col_data.replace(['yes', 'no'], [1, 0])
if col_data.dtype == object:
col_data = pd.get_dummies(col_data, prefix = col)
output = output.join(col_data)
return output
featuredata = preprocess_features(featuredata)
type(featuredata)
featuredata.head()
featuredata.drop(['address_R','sex_F'],axis=1,inplace=True)
featuredata.columns
featuredata.drop(['famsize_GT3','Pstatus_A',],axis=1,inplace=True)
```
### MODEL IMPLEMENTATION
## Decision tree
```
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
model=DecisionTreeClassifier()
X_train, X_test, y_train, y_test = train_test_split(featuredata, targetdata, test_size=0.33, random_state=6)
model.fit(X_train,y_train)
from sklearn.metrics import accuracy_score
predictions = model.predict(X_test)
accuracy_score(y_test,predictions)*100
```
## K-Nearest Neighbours
```
from sklearn.neighbors import KNeighborsClassifier
new_classifier = KNeighborsClassifier(n_neighbors=7)
new_classifier.fit(X_train,y_train)
predictions2 = new_classifier.predict(X_test)
accuracy_score(y_test,predictions2)*100
```
## SVM
```
from sklearn import svm
clf = svm.SVC(random_state=6)
clf.fit(featuredata,targetdata)
clf.score(featuredata,targetdata)
predictions3= clf.predict(X_test)
accuracy_score(y_test,predictions3)*100
```
## Model application areas
#### KNN
KNN: k-NN is often used in search applications where you are looking for “similar” items; that is, when your task is some form of “find items similar to this one”. The way you measure similarity is by creating a vector representation of the items, and then compare the vectors using an appropriate distance metric (like the Euclidean distance, for example).
The biggest use case of k-NN search might be Recommender Systems. If you know a user likes a particular item, then you can recommend similar items for them.
KNN strength: effective for larger datasets, robust to noisy training data
KNN weakness: need to determine value of k, computation cost is high.
#### Decision tree
Decision Tree: Can handle both numerical and categorical data.
Decision tree strength: Decision trees implicitly perform feature selection, require relatively little effort from users for data preparation, easy to interpret and explain to executives.
Decision tree weakness: Over Fitting, not fit for continuous variables.
#### SVM
SVM: SVM classify parts of the image as a face and non-face and create a square boundary around the face(Facial recognization).
We use SVMs to recognize handwritten characters used widely(Handwritten recognization).
Strengths: SVM's can model non-linear decision boundaries, and there are many kernels to choose from. They are also fairly robust against overfitting, especially in high-dimensional space.
Weaknesses: However, SVM's are memory intensive, trickier to tune due to the importance of picking the right kernel, and don't scale well to larger datasets.
## Choosing the best model
In this case, I will be using the SVM model to predict the outcomes. 80.15% of accuracy is achieved in SVM in our case.
SVM is a supervised machine learning algorithm which can be used for classification or regression problems.
It uses a technique called the kernel trick to transform your data and then based on these transformations it finds an optimal boundary between the possible outputs.
|
github_jupyter
|
<a href="https://colab.research.google.com/github/NataliaDiaz/colab/blob/master/MI203-td2_tree_and_forest.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# TD: prédiction du vote 2016 aux Etats-Unis par arbres de décisions et méthodes ensemblistes
La séance d'aujourd'hui porte sur la prévision du vote en 2016 aux États-Unis. Précisément, les données d'un recensement sont fournies avec diverses informations par comté à travers les États-Unis. L'objectif est de construire des prédicteurs de leur couleur politique (républicain ou démocrate) à partir de ces données.
Exécuter les commandes suivantes pour charger l'environnement.
```
%matplotlib inline
from pylab import *
import numpy as np
import os
import random
import matplotlib.pyplot as plt
```
# Accès aux données
* Elles sont disponibles: https://github.com/stepherbin/teaching/tree/master/ENSTA/TD2
* Charger le fichier the combined_data.csv sur votre drive puis monter le depuis colab
```
USE_COLAB = True
UPLOAD_OUTPUTS = False
if USE_COLAB:
# mount the google drive
from google.colab import drive
drive.mount('/content/drive', force_remount=True)
# download data on GoogleDrive
data_dir = "/content/drive/My Drive/teaching/ENSTA/TD_tree/"
else:
data_dir = "data/"
import pandas as pd
census_data = pd.read_csv( os.path.join(data_dir, 'combined_data.csv') )
```
# Analyse préliminaire des données
Les données sont organisées en champs:
* fips = code du comté à 5 chiffres, le premier ou les deux premiers chiffres indiquent l'état.
* votes = nombre de votants
* etc..
Regarder leur structure, quantité, nature.
Où se trouvent les informations pour former les ensembles d'apprentissage et de test?
Où se trouvent les classes à prédire?
Visualiser quelques distributions.
Le format de données python est décrit ici:
https://pandas.pydata.org/pandas-docs/stable/reference/frame.html
```
# Exemples de moyens d'accéder aux caractéristiques des données
print(census_data.shape )
print(census_data.columns.values)
print(census_data['fips'])
print(census_data.head(3))
iattr = 10
attrname = census_data.columns[iattr]
print("Mean of {} is {:.1f}".format(attrname,np.array(census_data[attrname]).mean()))
#########################
## METTRE VOTRE CODE ICI
#########################
print("Nombre de données = {}".format(7878912123)) # à modifier
print("Nombre d'attributs utiles = {}".format(4564564654)) # à modifier
#hist....
```
La classe à prédire ('Democrat') n'est décrite que par un seul attribut binaire.
Calculer la répartition des couleurs politiques (quel est a priori la probabilité qu'un comté soit démocrate vs. républicain)
```
#########################
## METTRE VOTRE CODE ICI
#########################
print("La probabilité qu'un comté soit démocrate est de {:.2f}%%".format(100*proba_dem))
```
# Préparation du chantier d'apprentissage
On va préparer les ensembles d'apprentissage et de test.
Pour éviter des problèmes de format de données, on choisit une liste d'attributs utiles dans la liste "feature_cols" ci dessous.
L'ensemble de test sera constitué des comtés d'un seul état.
Info: https://scikit-learn.org/stable/model_selection.html
Liste des états et leurs codes FIPS code (2 digits):
https://en.wikipedia.org/wiki/Federal_Information_Processing_Standard_state_code
```
## Sous ensembles d'attributs informatifs pour la suite
feature_cols = ['BLACK_FEMALE_rate',
'BLACK_MALE_rate',
'Percent of adults with a bachelor\'s degree or higher, 2011-2015',
'ASIAN_MALE_rate',
'ASIAN_FEMALE_rate',
'25-29_rate',
'age_total_pop',
'20-24_rate',
'Deep_Pov_All',
'30-34_rate',
'Density per square mile of land area - Population',
'Density per square mile of land area - Housing units',
'Unemployment_rate_2015',
'Deep_Pov_Children',
'PovertyAllAgesPct2014',
'TOT_FEMALE_rate',
'PerCapitaInc',
'MULTI_FEMALE_rate',
'35-39_rate',
'MULTI_MALE_rate',
'Percent of adults completing some college or associate\'s degree, 2011-2015',
'60-64_rate',
'55-59_rate',
'65-69_rate',
'TOT_MALE_rate',
'85+_rate',
'70-74_rate',
'80-84_rate',
'75-79_rate',
'Percent of adults with a high school diploma only, 2011-2015',
'WHITE_FEMALE_rate',
'WHITE_MALE_rate',
'Amish',
'Buddhist',
'Catholic',
'Christian Generic',
'Eastern Orthodox',
'Hindu',
'Jewish',
'Mainline Christian',
'Mormon',
'Muslim',
'Non-Catholic Christian',
'Other',
'Other Christian',
'Other Misc',
'Pentecostal / Charismatic',
'Protestant Denomination',
'Zoroastrian']
filtered_cols = ['Percent of adults with a bachelor\'s degree or higher, 2011-2015',
'Percent of adults completing some college or associate\'s degree, 2011-2015',
'Percent of adults with a high school diploma only, 2011-2015',
'Density per square mile of land area - Population',
'Density per square mile of land area - Housing units',
'WHITE_FEMALE_rate',
'WHITE_MALE_rate',
'BLACK_FEMALE_rate',
'BLACK_MALE_rate',
'ASIAN_FEMALE_rate',
'Catholic',
'Christian Generic',
'Jewish',
'70-74_rate',
'D',
'R']
## 1-state test split
def county_data(census_data, fips_code=17):
#fips_code 48=Texas, 34=New Jersey, 31=Nebraska, 17=Illinois, 06=California, 36=New York
mask = census_data['fips'].between(fips_code*1000, fips_code*1000 + 999)
census_data_train = census_data[~mask]
census_data_test = census_data[mask]
XTrain = census_data_train[feature_cols]
yTrain = census_data_train['Democrat']
XTest = census_data_test[feature_cols]
yTest = census_data_test['Democrat']
return XTrain, yTrain, XTest, yTest
STATE_FIPS_CODE = 17
X_train, y_train, X_test, y_test = county_data(census_data, STATE_FIPS_CODE)
#print(X_train.head(2))
#print(y_test.head(2))
```
# Apprentissage d'un arbre de décision
On utilisera la bibliothèque scikit learn
* Construire l'arbre sur les données d'entrainement
* Prédire le vote sur les comtés de test
* Calculer l'erreur et la matrice de confusion
Faire varier certains paramètres (profondeur max, pureté, critère...) et visualisez leur influence.
Info: https://scikit-learn.org/stable/modules/tree.html
Info: https://scikit-learn.org/stable/modules/model_evaluation.html
```
from sklearn import tree
#########################
## METTRE VOTRE CODE ICI
#########################
```
Les instructions suivantes permettent de visualiser l'arbre.
Interpréter le contenu de la représentation.
```
import graphviz
dot_data = tree.export_graphviz(clf, out_file=None)
graph = graphviz.Source(dot_data)
dot_data = tree.export_graphviz(clf, out_file=None,
feature_names=X_train.columns.values,
class_names=["R","D"],
filled=True, rounded=True,
special_characters=True)
graph = graphviz.Source(dot_data)
graph
# Prédiction et évaluation
#########################
## METTRE VOTRE CODE ICI
#########################
```
---
# Bagging
L'objectif de cette partie est de construire **à la main** une approche de bagging.
Le principe de l'approche est de:
* Apprendre et collecter plusieurs arbres sur des échantillonnages aléatoires des données d'apprentissage
* Agréger les prédictions par vote
* Evaluer: Les prédictions agrégées
* Comparer avec les arbres individuels et le résultat précédent
Utiliser les fonctions de construction d'ensemble d'apprentissage/test de scikit-learn https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.train_test_split.html pour générer les sous-esnembles échantillonnés.
**Comparer après le cours** les fonctions de scikit-learn: https://scikit-learn.org/stable/modules/ensemble.html
Numpy tips: [np.arange](https://docs.scipy.org/doc/numpy-1.15.0/reference/generated/numpy.arange.html), [numpy.sum](https://docs.scipy.org/doc/numpy-1.15.0/reference/generated/numpy.sum.html), [numpy.mean](https://docs.scipy.org/doc/numpy-1.15.1/reference/generated/numpy.mean.html), [numpy.where](https://docs.scipy.org/doc/numpy-1.15.0/reference/generated/numpy.where.html)
```
from sklearn.model_selection import train_test_split
# Données d'apprentissage: X_train, y_train, idx_train
# Données de test: X_test, y_test, idx_test
# Les étapes de conception du prédicteur (apprentissage) sont les suivantes:
# - Construction des sous-ensembles de données
# - Apprentissage d'un arbre
# - Agrégation de l'arbre dans la forêt
#
# Pour le test
def learn_forest(XTrain, yTrain, nb_trees, depth=15):
#########################
## COMPLETER LE CODE
#########################
forest = []
singleperf=[]
for ss in range(nb_trees):
# bagging for subset
# single tree training
# grow the forest
# single tree evaluation
return forest,singleperf
def predict_forest(forest, XTest, yTest = None):
singleperf=[]
all_preds=[]
nb_trees = len(forest)
#########################
## METTRE VOTRE CODE ICI
#########################
if (yTest is not None):
return final_pred,singleperf
else:
return final_pred
#########################
## METTRE VOTRE CODE ICI
#########################
X_train, y_train, X_test, y_test = county_data(census_data, 6)
F,singleperf = learn_forest(X_train, y_train, 20, depth=15)
pred, singleperftest = predict_forest(F, X_test, y_test)
acc = perf.balanced_accuracy_score( y_test, pred )
print("Taux de bonne prédiction = {:.2f}%".format(100*acc))
print(mean(singleperftest))
#print(singleperftest)
#print(singleperf)
```
|
github_jupyter
|
<a href="https://colab.research.google.com/github/Laelapz/Some_Tests/blob/main/BERTimbau.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
Tem caracteres em chinês? Pq eles pegam a maior distribuição do dataset???
Tirado do Twitter? (Alguns nomes/sobrenomes)
O Dataset do Bert base inglês parecia mais organizado
Cade o alfabeto?
Tem muitas subwords
```
!pip install transformers
from transformers import AutoTokenizer # Or BertTokenizer
from transformers import AutoModelForPreTraining # Or BertForPreTraining for loading pretraining heads
from transformers import AutoModel # or BertModel, for BERT without pretraining heads
model = AutoModelForPreTraining.from_pretrained('neuralmind/bert-base-portuguese-cased')
tokenizer = AutoTokenizer.from_pretrained('neuralmind/bert-base-portuguese-cased', do_lower_case=False)
import torch
with open("vocabulary.txt", 'w') as f:
# For each token...
for token in tokenizer.vocab.keys():
# Write it out and escape any unicode characters.
f.write(token + '\n')
one_chars = []
one_chars_hashes = []
# For each token in the vocabulary...
for token in tokenizer.vocab.keys():
# Record any single-character tokens.
if len(token) == 1:
one_chars.append(token)
# Record single-character tokens preceded by the two hashes.
elif len(token) == 3 and token[0:2] == '##':
one_chars_hashes.append(token)
print('Number of single character tokens:', len(one_chars), '\n')
# Print all of the single characters, 40 per row.
# For every batch of 40 tokens...
for i in range(0, len(one_chars), 40):
# Limit the end index so we don't go past the end of the list.
end = min(i + 40, len(one_chars) + 1)
# Print out the tokens, separated by a space.
print(' '.join(one_chars[i:end]))
print('Number of single character tokens with hashes:', len(one_chars_hashes), '\n')
# Print all of the single characters, 40 per row.
# Strip the hash marks, since they just clutter the display.
tokens = [token.replace('##', '') for token in one_chars_hashes]
# For every batch of 40 tokens...
for i in range(0, len(tokens), 40):
# Limit the end index so we don't go past the end of the list.
end = min(i + 40, len(tokens) + 1)
# Print out the tokens, separated by a space.
print(' '.join(tokens[i:end]))
print('Are the two sets identical?', set(one_chars) == set(tokens))
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
sns.set(style='darkgrid')
# Increase the plot size and font size.
sns.set(font_scale=1.5)
plt.rcParams["figure.figsize"] = (10,5)
# Measure the length of every token in the vocab.
token_lengths = [len(token) for token in tokenizer.vocab.keys()]
# Plot the number of tokens of each length.
sns.countplot(token_lengths)
plt.title('Vocab Token Lengths')
plt.xlabel('Token Length')
plt.ylabel('# of Tokens')
print('Maximum token length:', max(token_lengths))
num_subwords = 0
subword_lengths = []
# For each token in the vocabulary...
for token in tokenizer.vocab.keys():
# If it's a subword...
if len(token) >= 2 and token[0:2] == '##':
# Tally all subwords
num_subwords += 1
# Measure the sub word length (without the hashes)
length = len(token) - 2
# Record the lengths.
subword_lengths.append(length)
vocab_size = len(tokenizer.vocab.keys())
print('Number of subwords: {:,} of {:,}'.format(num_subwords, vocab_size))
# Calculate the percentage of words that are '##' subwords.
prcnt = float(num_subwords) / vocab_size * 100.0
print('%.1f%%' % prcnt)
sns.countplot(subword_lengths)
plt.title('Subword Token Lengths (w/o "##")')
plt.xlabel('Subword Length')
plt.ylabel('# of ## Subwords')
```
|
github_jupyter
|
# The Binomial Distribution
This notebook is part of [Bite Size Bayes](https://allendowney.github.io/BiteSizeBayes/), an introduction to probability and Bayesian statistics using Python.
Copyright 2020 Allen B. Downey
License: [Attribution-NonCommercial-ShareAlike 4.0 International (CC BY-NC-SA 4.0)](https://creativecommons.org/licenses/by-nc-sa/4.0/)
The following cell downloads `utils.py`, which contains some utility function we'll need.
```
from os.path import basename, exists
def download(url):
filename = basename(url)
if not exists(filename):
from urllib.request import urlretrieve
local, _ = urlretrieve(url, filename)
print('Downloaded ' + local)
download('https://github.com/AllenDowney/BiteSizeBayes/raw/master/utils.py')
```
If everything we need is installed, the following cell should run with no error messages.
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
```
## The Euro problem revisited
In [a previous notebook](https://colab.research.google.com/github/AllenDowney/BiteSizeBayes/blob/master/07_euro.ipynb) I presented a problem from David MacKay's book, [*Information Theory, Inference, and Learning Algorithms*](http://www.inference.org.uk/mackay/itila/p0.html):
> A statistical statement appeared in The Guardian on
Friday January 4, 2002:
>
> >"When spun on edge 250 times, a Belgian one-euro coin came
up heads 140 times and tails 110. ‘It looks very suspicious
to me’, said Barry Blight, a statistics lecturer at the London
School of Economics. ‘If the coin were unbiased the chance of
getting a result as extreme as that would be less than 7%’."
>
> But [asks MacKay] do these data give evidence that the coin is biased rather than fair?
To answer this question, we made these modeling decisions:
* If you spin a coin on edge, there is some probability, $x$, that it will land heads up.
* The value of $x$ varies from one coin to the next, depending on how the coin is balanced and other factors.
We started with a uniform prior distribution for $x$, then updated it 250 times, once for each spin of the coin. Then we used the posterior distribution to compute the MAP, posterior mean, and a credible interval.
But we never really answered MacKay's question.
In this notebook, I introduce the binomial distribution and we will use it to solve the Euro problem more efficiently. Then we'll get back to MacKay's question and see if we can find a more satisfying answer.
## Binomial distribution
Suppose I tell you that a coin is "fair", that is, the probability of heads is 50%. If you spin it twice, there are four outcomes: `HH`, `HT`, `TH`, and `TT`.
All four outcomes have the same probability, 25%. If we add up the total number of heads, it is either 0, 1, or 2. The probability of 0 and 2 is 25%, and the probability of 1 is 50%.
More generally, suppose the probability of heads is `p` and we spin the coin `n` times. What is the probability that we get a total of `k` heads?
The answer is given by the binomial distribution:
$P(k; n, p) = \binom{n}{k} p^k (1-p)^{n-k}$
where $\binom{n}{k}$ is the [binomial coefficient](https://en.wikipedia.org/wiki/Binomial_coefficient), usually pronounced "n choose k".
We can compute this expression ourselves, but we can also use the SciPy function `binom.pmf`:
```
from scipy.stats import binom
n = 2
p = 0.5
ks = np.arange(n+1)
a = binom.pmf(ks, n, p)
a
```
If we put this result in a Series, the result is the distribution of `k` for the given values of `n` and `p`.
```
pmf_k = pd.Series(a, index=ks)
pmf_k
```
The following function computes the binomial distribution for given values of `n` and `p`:
```
def make_binomial(n, p):
"""Make a binomial PMF.
n: number of spins
p: probability of heads
returns: Series representing a PMF
"""
ks = np.arange(n+1)
a = binom.pmf(ks, n, p)
pmf_k = pd.Series(a, index=ks)
return pmf_k
```
And here's what it looks like with `n=250` and `p=0.5`:
```
pmf_k = make_binomial(n=250, p=0.5)
pmf_k.plot()
plt.xlabel('Number of heads (k)')
plt.ylabel('Probability')
plt.title('Binomial distribution');
```
The most likely value in this distribution is 125:
```
pmf_k.idxmax()
```
But even though it is the most likely value, the probability that we get exactly 125 heads is only about 5%.
```
pmf_k[125]
```
In MacKay's example, we got 140 heads, which is less likely than 125:
```
pmf_k[140]
```
In the article MacKay quotes, the statistician says, ‘If the coin were unbiased the chance of getting a result as extreme as that would be less than 7%’.
We can use the binomial distribution to check his math. The following function takes a PMF and computes the total probability of values greater than or equal to `threshold`.
```
def prob_ge(pmf, threshold):
"""Probability of values greater than a threshold.
pmf: Series representing a PMF
threshold: value to compare to
returns: probability
"""
ge = (pmf.index >= threshold)
total = pmf[ge].sum()
return total
```
Here's the probability of getting 140 heads or more:
```
prob_ge(pmf_k, 140)
```
It's about 3.3%, which is less than 7%. The reason is that the statistician includes all values "as extreme as" 140, which includes values less than or equal to 110, because 140 exceeds the expected value by 15 and 110 falls short by 15.
The probability of values less than or equal to 110 is also 3.3%,
so the total probability of values "as extreme" as 140 is about 7%.
The point of this calculation is that these extreme values are unlikely if the coin is fair.
That's interesting, but it doesn't answer MacKay's question. Let's see if we can.
## Estimating x
As promised, we can use the binomial distribution to solve the Euro problem more efficiently. Let's start again with a uniform prior:
```
xs = np.arange(101) / 100
uniform = pd.Series(1, index=xs)
uniform /= uniform.sum()
```
We can use `binom.pmf` to compute the likelihood of the data for each possible value of $x$.
```
k = 140
n = 250
xs = uniform.index
likelihood = binom.pmf(k, n, p=xs)
```
Now we can do the Bayesian update in the usual way, multiplying the priors and likelihoods,
```
posterior = uniform * likelihood
```
Computing the total probability of the data,
```
total = posterior.sum()
total
```
And normalizing the posterior,
```
posterior /= total
```
Here's what it looks like.
```
posterior.plot(label='Uniform')
plt.xlabel('Probability of heads (x)')
plt.ylabel('Probability')
plt.title('Posterior distribution, uniform prior')
plt.legend()
```
**Exercise:** Based on what we know about coins in the real world, it doesn't seem like every value of $x$ is equally likely. I would expect values near 50% to be more likely and values near the extremes to be less likely.
In Notebook 7, we used a triangle prior to represent this belief about the distribution of $x$. The following code makes a PMF that represents a triangle prior.
```
ramp_up = np.arange(50)
ramp_down = np.arange(50, -1, -1)
a = np.append(ramp_up, ramp_down)
triangle = pd.Series(a, index=xs)
triangle /= triangle.sum()
```
Update this prior with the likelihoods we just computed and plot the results.
```
# Solution
posterior2 = triangle * likelihood
total2 = posterior2.sum()
total2
# Solution
posterior2 /= total2
# Solution
posterior.plot(label='Uniform')
posterior2.plot(label='Triangle')
plt.xlabel('Probability of heads (x)')
plt.ylabel('Probability')
plt.title('Posterior distribution, uniform prior')
plt.legend();
```
## Evidence
Finally, let's get back to MacKay's question: do these data give evidence that the coin is biased rather than fair?
I'll use a Bayes table to answer this question, so here's the function that makes one:
```
def make_bayes_table(hypos, prior, likelihood):
"""Make a Bayes table.
hypos: sequence of hypotheses
prior: prior probabilities
likelihood: sequence of likelihoods
returns: DataFrame
"""
table = pd.DataFrame(index=hypos)
table['prior'] = prior
table['likelihood'] = likelihood
table['unnorm'] = table['prior'] * table['likelihood']
prob_data = table['unnorm'].sum()
table['posterior'] = table['unnorm'] / prob_data
return table
```
Recall that data, $D$, is considered evidence in favor of a hypothesis, `H`, if the posterior probability is greater than the prior, that is, if
$P(H|D) > P(H)$
For this example, I'll call the hypotheses `fair` and `biased`:
```
hypos = ['fair', 'biased']
```
And just to get started, I'll assume that the prior probabilities are 50/50.
```
prior = [0.5, 0.5]
```
Now we have to compute the probability of the data under each hypothesis.
If the coin is fair, the probability of heads is 50%, and we can compute the probability of the data (140 heads out of 250 spins) using the binomial distribution:
```
k = 140
n = 250
like_fair = binom.pmf(k, n, p=0.5)
like_fair
```
So that's the probability of the data, given that the coin is fair.
But if the coin is biased, what's the probability of the data? Well, that depends on what "biased" means.
If we know ahead of time that "biased" means the probability of heads is 56%, we can use the binomial distribution again:
```
like_biased = binom.pmf(k, n, p=0.56)
like_biased
```
Now we can put the likelihoods in the Bayes table:
```
likes = [like_fair, like_biased]
make_bayes_table(hypos, prior, likes)
```
The posterior probability of `biased` is about 86%, so the data is evidence that the coin is biased, at least for this definition of "biased".
But we used the data to define the hypothesis, which seems like cheating. To be fair, we should define "biased" before we see the data.
## Uniformly distributed bias
Suppose "biased" means that the probability of heads is anything except 50%, and all other values are equally likely.
We can represent that definition by making a uniform distribution and removing 50%.
```
biased_uniform = uniform.copy()
biased_uniform[50] = 0
biased_uniform /= biased_uniform.sum()
```
Now, to compute the probability of the data under this hypothesis, we compute the probability of the data for each value of $x$.
```
xs = biased_uniform.index
likelihood = binom.pmf(k, n, xs)
```
And then compute the total probability in the usual way:
```
like_uniform = np.sum(biased_uniform * likelihood)
like_uniform
```
So that's the probability of the data under the "biased uniform" hypothesis.
Now we make a Bayes table that compares the hypotheses `fair` and `biased uniform`:
```
hypos = ['fair', 'biased uniform']
likes = [like_fair, like_uniform]
make_bayes_table(hypos, prior, likes)
```
Using this definition of `biased`, the posterior is less than the prior, so the data are evidence that the coin is *fair*.
In this example, the data might support the fair hypothesis or the biased hypothesis, depending on the definition of "biased".
**Exercise:** Suppose "biased" doesn't mean every value of $x$ is equally likely. Maybe values near 50% are more likely and values near the extremes are less likely. In the previous exercise we created a PMF that represents a triangle-shaped distribution.
We can use it to represent an alternative definition of "biased":
```
biased_triangle = triangle.copy()
biased_triangle[50] = 0
biased_triangle /= biased_triangle.sum()
```
Compute the total probability of the data under this definition of "biased" and use a Bayes table to compare it with the fair hypothesis.
Is the data evidence that the coin is biased?
```
# Solution
like_triangle = np.sum(biased_triangle * likelihood)
like_triangle
# Solution
hypos = ['fair', 'biased triangle']
likes = [like_fair, like_triangle]
make_bayes_table(hypos, prior, likes)
# Solution
# For this definition of "biased",
# the data are slightly in favor of the fair hypothesis.
```
## Bayes factor
In the previous section, we used a Bayes table to see whether the data are in favor of the fair or biased hypothesis.
I assumed that the prior probabilities were 50/50, but that was an arbitrary choice.
And it was unnecessary, because we don't really need a Bayes table to say whether the data favor one hypothesis or another: we can just look at the likelihoods.
Under the first definition of biased, `x=0.56`, the likelihood of the biased hypothesis is higher:
```
like_fair, like_biased
```
Under the biased uniform definition, the likelihood of the fair hypothesis is higher.
```
like_fair, like_uniform
```
The ratio of these likelihoods tells us which hypothesis the data support.
If the ratio is less than 1, the data support the second hypothesis:
```
like_fair / like_biased
```
If the ratio is greater than 1, the data support the first hypothesis:
```
like_fair / like_uniform
```
This likelihood ratio is called a [Bayes factor](https://en.wikipedia.org/wiki/Bayes_factor); it provides a concise way to present the strength of a dataset as evidence for or against a hypothesis.
## Summary
In this notebook I introduced the binomial disrtribution and used it to solve the Euro problem more efficiently.
Then we used the results to (finally) answer the original version of the Euro problem, considering whether the data support the hypothesis that the coin is fair or biased. We found that the answer depends on how we define "biased". And we summarized the results using a Bayes factor, which quantifies the strength of the evidence.
[In the next notebook](https://colab.research.google.com/github/AllenDowney/BiteSizeBayes/blob/master/13_price.ipynb) we'll start on a new problem based on the television game show *The Price Is Right*.
## Exercises
**Exercise:** In preparation for an alien invasion, the Earth Defense League has been working on new missiles to shoot down space invaders. Of course, some missile designs are better than others; let's assume that each design has some probability of hitting an alien ship, `x`.
Based on previous tests, the distribution of `x` in the population of designs is roughly uniform between 10% and 40%.
Now suppose the new ultra-secret Alien Blaster 9000 is being tested. In a press conference, a Defense League general reports that the new design has been tested twice, taking two shots during each test. The results of the test are confidential, so the general won't say how many targets were hit, but they report: "The same number of targets were hit in the two tests, so we have reason to think this new design is consistent."
Is this data good or bad; that is, does it increase or decrease your estimate of `x` for the Alien Blaster 9000?
Plot the prior and posterior distributions, and use the following function to compute the prior and posterior means.
```
def pmf_mean(pmf):
"""Compute the mean of a PMF.
pmf: Series representing a PMF
return: float
"""
return np.sum(pmf.index * pmf)
# Solution
xs = np.linspace(0.1, 0.4)
prior = pd.Series(1, index=xs)
prior /= prior.sum()
# Solution
likelihood = xs**2 + (1-xs)**2
# Solution
posterior = prior * likelihood
posterior /= posterior.sum()
# Solution
prior.plot(color='gray', label='prior')
posterior.plot(label='posterior')
plt.xlabel('Probability of success (x)')
plt.ylabel('Probability')
plt.ylim(0, 0.027)
plt.title('Distribution of before and after testing')
plt.legend();
# Solution
pmf_mean(prior), pmf_mean(posterior)
# With this prior, being "consistent" is more likely
# to mean "consistently bad".
```
|
github_jupyter
|
```
# Import libraries
import numpy as np
import pandas as pd
import sklearn as sk
import matplotlib
import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties # for unicode fonts
import psycopg2
import sys
import datetime as dt
import mp_utils as mp
from sklearn.pipeline import Pipeline
# used to impute mean for data and standardize for computational stability
from sklearn.preprocessing import Imputer
from sklearn.preprocessing import StandardScaler
# logistic regression is our favourite model ever
from sklearn.linear_model import LogisticRegression
from sklearn.linear_model import LogisticRegressionCV # l2 regularized regression
from sklearn.linear_model import LassoCV
# used to calculate AUROC/accuracy
from sklearn import metrics
# used to create confusion matrix
from sklearn.metrics import confusion_matrix
# gradient boosting - must download package https://github.com/dmlc/xgboost
import xgboost as xgb
# default colours for prettier plots
col = [[0.9047, 0.1918, 0.1988],
[0.2941, 0.5447, 0.7494],
[0.3718, 0.7176, 0.3612],
[1.0000, 0.5482, 0.1000],
[0.4550, 0.4946, 0.4722],
[0.6859, 0.4035, 0.2412],
[0.9718, 0.5553, 0.7741],
[0.5313, 0.3359, 0.6523]];
# "Tableau 20" colors as RGB.
tableau20 = [(31, 119, 180), (174, 199, 232), (255, 127, 14), (255, 187, 120),
(44, 160, 44), (152, 223, 138), (214, 39, 40), (255, 152, 150),
(148, 103, 189), (197, 176, 213), (140, 86, 75), (196, 156, 148),
(227, 119, 194), (247, 182, 210), (127, 127, 127), (199, 199, 199),
(188, 189, 34), (219, 219, 141), (23, 190, 207), (158, 218, 229)]
# Scale the RGB values to the [0, 1] range, which is the format matplotlib accepts.
for i in range(len(tableau20)):
r, g, b = tableau20[i]
tableau20[i] = (r / 255., g / 255., b / 255.)
marker = ['v','o','d','^','s','>','+']
ls = ['-','-','-','-','-','s','--','--']
# bigger font !
plt.rcParams.update({'font.size': 22})
%matplotlib inline
from __future__ import print_function
```
# Plot data from example patient's time-series
```
df = pd.read_csv('/tmp/mp_data.csv')
# load in this patient's deathtime from the actual experiment
df_offset = pd.read_csv('/tmp/mp_death.csv')
# get censoring information
df_censor = pd.read_csv('/tmp/mp_censor.csv')
```
# Experiment A: First 24 hours
```
# define the patient
iid = 200001
iid2 = 200019
T_WINDOW = 24
time_dict = {iid: 24, iid2: 24}
df_pat = df.loc[df['icustay_id']==iid, :].set_index('hr')
deathtime = df_offset.loc[df_offset['icustay_id']==iid, 'deathtime_hours'].values
# Two subplots, the axes array is 1-d
f, axarr = plt.subplots(2, sharex=True, figsize=[10,10])
pretty_labels = {'heartrate': 'Heart rate',
'meanbp': 'Mean blood pressure',
'resprate': 'Respiratory rate',
'spo2': 'Peripheral oxygen saturation',
'tempc': 'Temperature',
'bg_ph': 'pH',
'bg_bicarbonate': 'Serum bicarbonate',
'hemoglobin': 'Hemoglobin',
'potassium': 'Potassium',
'inr': 'International normalized ratio',
'bg_lactate': 'Lactate',
'wbc': 'White blood cell count'}
#var_list = df.columns
# first plot all the vitals in subfigure 1
var_vitals = [u'heartrate', u'meanbp', u'resprate', u'tempc', u'spo2']
i=0
t_scale = 1.0 # divide by this to get from hours to t_unit
t_unit = 'Hours elapsed'
for v in var_vitals:
idx = ~df_pat[v].isnull()
if np.sum(idx) > 0:
axarr[0].plot(df_pat.loc[idx,v].index/t_scale, df_pat.loc[idx,v].values, '--',
label=pretty_labels[v],
marker=marker[np.mod(i,7)], markersize=8,
color=tableau20[i], linewidth=2)
i+=1
axarr[0].set_ylim([0,150])
y_lim = axarr[0].get_ylim()
# add ICU discharge
if dischtime is not np.nan:
axarr[0].plot([deathtime,deathtime], y_lim, 'k:',linewidth=3)
# add a grey patch to represent the window
endtime = time_dict[iid]
rect = matplotlib.patches.Rectangle( (endtime-T_WINDOW, y_lim[0]), T_WINDOW, y_lim[1], color='#bdbdbd')
axarr[0].add_patch(rect)
# #axarr[0].text(starttime/60.0-4-2,4, 'window',fontsize=16)
axarr[0].set_ylabel('Vital signs for {}'.format(iid),fontsize=16)
# next plot the vitals for the next patient in subfigure 2
df_pat = df.loc[df['icustay_id']==iid2, :].set_index('hr')
deathtime = df_offset.loc[df_offset['icustay_id']==iid2, 'deathtime_hours'].values
i=0
t_scale = 1.0 # divide by this to get from hours to t_unit
t_unit = 'Hours elapsed since ICU admission'
for v in var_vitals:
idx = ~df_pat[v].isnull()
if np.sum(idx) > 0:
axarr[1].plot(df_pat.loc[idx,v].index/t_scale, df_pat.loc[idx,v].values, '--',
label=pretty_labels[v],
marker=marker[np.mod(i,7)], markersize=8,
color=tableau20[i], linewidth=2)
i+=1
axarr[1].set_ylim([0,150])
y_lim = axarr[1].get_ylim()
# add ICU discharge
if deathtime is not np.nan:
axarr[1].plot([deathtime,deathtime], y_lim, 'k:',linewidth=3)
axarr[1].arrow(deathtime-5, 115, 4, 0, head_width=5, head_length=1, fc='k', ec='k')
axarr[1].text(deathtime-12, 112.5, 'Death', fontsize=16)
# add DNR
dnrtime = df_censor.loc[df_censor['icustay_id']==iid2, 'censortime_hours'].values
if dnrtime.shape[0]>0:
axarr[1].plot([dnrtime,dnrtime], y_lim, 'm:', linewidth=3)
axarr[1].arrow(dnrtime+5, 135, -4, 0, head_width=5, head_length=1, fc='k', ec='k')
axarr[1].text(dnrtime+5, 132.5, 'DNR',fontsize=16)
# add a patch to represent the window
endtime = time_dict[iid2]
rect = matplotlib.patches.Rectangle( (endtime-T_WINDOW, y_lim[0]), T_WINDOW, y_lim[1], color='#bdbdbd')
axarr[1].add_patch(rect)
axarr[1].set_xlabel(t_unit,fontsize=16)
axarr[1].set_ylabel('Vital signs for {}'.format(iid2),fontsize=16)
axarr[1].legend(shadow=True, fancybox=True,loc='upper center', bbox_to_anchor=(0.5, 1.21),ncol=3)
plt.show()
```
# Experiment B: Random time
```
# generate a random time dictionary
T_WINDOW=4
df_tmp=df_offset.copy().merge(df_censor, how='left', left_on='icustay_id', right_on='icustay_id')
time_dict = mp.generate_times(df_tmp, T=2, seed=111, censor=True)
# define the patient
iid = 200001
iid2 = 200019
df_pat = df.loc[df['icustay_id']==iid, :].set_index('hr')
deathtime = df_offset.loc[df_offset['icustay_id']==iid, 'deathtime_hours'].values
# Two subplots, the axes array is 1-d
f, axarr = plt.subplots(2, sharex=True, figsize=[10,10])
pretty_labels = {'heartrate': 'Heart rate',
'meanbp': 'Mean blood pressure',
'resprate': 'Respiratory rate',
'spo2': 'Peripheral oxygen saturation',
'tempc': 'Temperature',
'bg_ph': 'pH',
'bg_bicarbonate': 'Serum bicarbonate',
'hemoglobin': 'Hemoglobin',
'potassium': 'Potassium',
'inr': 'International normalized ratio',
'bg_lactate': 'Lactate',
'wbc': 'White blood cell count'}
#var_list = df.columns
# first plot all the vitals in subfigure 1
var_vitals = [u'heartrate', u'meanbp', u'resprate', u'tempc', u'spo2']
i=0
t_scale = 1.0 # divide by this to get from hours to t_unit
t_unit = 'Hours elapsed'
for v in var_vitals:
idx = ~df_pat[v].isnull()
if np.sum(idx) > 0:
axarr[0].plot(df_pat.loc[idx,v].index/t_scale, df_pat.loc[idx,v].values, '--',
label=pretty_labels[v],
marker=marker[np.mod(i,7)],
color=tableau20[i], linewidth=2)
i+=1
axarr[0].set_ylim([0,150])
y_lim = axarr[0].get_ylim()
# add ICU discharge
if dischtime is not np.nan:
axarr[0].plot([deathtime,deathtime], y_lim, 'k:',linewidth=3)
# add a grey patch to represent the window
endtime = time_dict[iid]
rect = matplotlib.patches.Rectangle( (endtime-T_WINDOW, y_lim[0]), T_WINDOW, y_lim[1], color='#bdbdbd')
axarr[0].add_patch(rect)
# #axarr[0].text(starttime/60.0-4-2,4, 'window',fontsize=16)
axarr[0].set_ylabel('Vital signs for {}'.format(iid),fontsize=16)
# next plot the vitals for the next patient in subfigure 2
df_pat = df.loc[df['icustay_id']==iid2, :].set_index('hr')
deathtime = df_offset.loc[df_offset['icustay_id']==iid2, 'deathtime_hours'].values
i=0
t_scale = 1.0 # divide by this to get from hours to t_unit
t_unit = 'Hours elapsed since ICU admission'
for v in var_vitals:
idx = ~df_pat[v].isnull()
if np.sum(idx) > 0:
axarr[1].plot(df_pat.loc[idx,v].index/t_scale, df_pat.loc[idx,v].values, '--',
label=pretty_labels[v],
marker=marker[np.mod(i,7)], markersize=8,
color=tableau20[i], linewidth=2)
i+=1
axarr[1].set_ylim([0,150])
y_lim = axarr[1].get_ylim()
# add ICU discharge
if deathtime is not np.nan:
axarr[1].plot([deathtime,deathtime], y_lim, 'k:',linewidth=3)
axarr[1].arrow(deathtime-5, 115, 4, 0, head_width=5, head_length=1, fc='k', ec='k')
axarr[1].text(deathtime-12, 112.5, 'Death', fontsize=16)
# add DNR
dnrtime = df_censor.loc[df_censor['icustay_id']==iid2, 'censortime_hours'].values
if dnrtime.shape[0]>0:
axarr[1].plot([dnrtime,dnrtime], y_lim, 'm:', linewidth=3)
axarr[1].arrow(dnrtime+5, 135, -4, 0, head_width=5, head_length=1, fc='k', ec='k')
axarr[1].text(dnrtime+5, 132.5, 'DNR',fontsize=16)
# add a patch to represent the window
endtime = time_dict[iid2]
rect = matplotlib.patches.Rectangle( (endtime-T_WINDOW, y_lim[0]), T_WINDOW, y_lim[1], color='#bdbdbd')
axarr[1].add_patch(rect)
axarr[1].set_xlabel(t_unit,fontsize=16)
axarr[1].set_ylabel('Vital signs for {}'.format(iid2),fontsize=16)
#axarr[1].legend(shadow=True, fancybox=True,loc='upper center', bbox_to_anchor=(0.5, 1.1),ncol=3)
plt.show()
```
# Both 24 hours and 4 hour window
```
# generate a random time dictionary
T_WINDOW=4
df_tmp=df_offset.copy().merge(df_censor, how='left', left_on='icustay_id', right_on='icustay_id')
time_dict = mp.generate_times(df_tmp, T=2, seed=111, censor=True)
# define the patient
iid = 200001
iid2 = 200019
df_pat = df.loc[df['icustay_id']==iid, :].set_index('hr')
deathtime = df_offset.loc[df_offset['icustay_id']==iid, 'deathtime_hours'].values
# Two subplots, the axes array is 1-d
f, axarr = plt.subplots(2, sharex=True, figsize=[10,10])
pretty_labels = {'heartrate': 'Heart rate',
'meanbp': 'Mean blood pressure',
'resprate': 'Respiratory rate',
'spo2': 'Peripheral oxygen saturation',
'tempc': 'Temperature',
'bg_ph': 'pH',
'bg_bicarbonate': 'Serum bicarbonate',
'hemoglobin': 'Hemoglobin',
'potassium': 'Potassium',
'inr': 'International normalized ratio',
'bg_lactate': 'Lactate',
'wbc': 'White blood cell count'}
#var_list = df.columns
# first plot all the vitals in subfigure 1
var_vitals = [u'heartrate', u'meanbp', u'resprate', u'tempc', u'spo2']
i=0
t_scale = 1.0 # divide by this to get from hours to t_unit
t_unit = 'Hours elapsed'
for v in var_vitals:
idx = ~df_pat[v].isnull()
if np.sum(idx) > 0:
axarr[0].plot(df_pat.loc[idx,v].index/t_scale, df_pat.loc[idx,v].values, '--',
label=pretty_labels[v],
marker=marker[np.mod(i,7)],
color=tableau20[i], linewidth=2)
i+=1
axarr[0].set_ylim([0,150])
y_lim = axarr[0].get_ylim()
# add ICU discharge
if dischtime is not np.nan:
axarr[0].plot([deathtime,deathtime], y_lim, 'k:',linewidth=3)
# add a grey patch to represent the 4 hour window
endtime = time_dict[iid]
rect = matplotlib.patches.Rectangle( (endtime-T_WINDOW, y_lim[0]), T_WINDOW, y_lim[1], color='#bdbdbd')
axarr[0].add_patch(rect)
# #axarr[0].text(starttime/60.0-4-2,4, 'window',fontsize=16)
# add a grey patch to represent the 24 hour window
rect = matplotlib.patches.Rectangle( (0, y_lim[0]), 24, y_lim[1], color='#bdbdbd')
axarr[0].add_patch(rect)
# #axarr[0].text(starttime/60.0-4-2,4, 'window',fontsize=16)
axarr[0].set_ylabel('Vital signs for {}'.format(iid),fontsize=16)
# next plot the vitals for the next patient in subfigure 2
df_pat = df.loc[df['icustay_id']==iid2, :].set_index('hr')
deathtime = df_offset.loc[df_offset['icustay_id']==iid2, 'deathtime_hours'].values
i=0
t_scale = 1.0 # divide by this to get from hours to t_unit
t_unit = 'Hours elapsed since ICU admission'
for v in var_vitals:
idx = ~df_pat[v].isnull()
if np.sum(idx) > 0:
axarr[1].plot(df_pat.loc[idx,v].index/t_scale, df_pat.loc[idx,v].values, '--',
label=pretty_labels[v],
marker=marker[np.mod(i,7)], markersize=8,
color=tableau20[i], linewidth=2)
i+=1
axarr[1].set_ylim([0,150])
y_lim = axarr[1].get_ylim()
# add ICU discharge
if deathtime is not np.nan:
axarr[1].plot([deathtime,deathtime], y_lim, 'k:',linewidth=3)
axarr[1].arrow(deathtime-5, 115, 4, 0, head_width=5, head_length=1, fc='k', ec='k')
axarr[1].text(deathtime-12, 112.5, 'Death', fontsize=16)
# add DNR
dnrtime = df_censor.loc[df_censor['icustay_id']==iid2, 'censortime_hours'].values
if dnrtime.shape[0]>0:
axarr[1].plot([dnrtime,dnrtime], y_lim, 'm:', linewidth=3)
axarr[1].arrow(dnrtime+5, 135, -4, 0, head_width=5, head_length=1, fc='k', ec='k')
axarr[1].text(dnrtime+5, 132.5, 'DNR',fontsize=16)
# add a patch to represent the 4 hour window
endtime = time_dict[iid2]
rect = matplotlib.patches.Rectangle( (endtime-T_WINDOW, y_lim[0]), T_WINDOW, y_lim[1], color='#bdbdbd')
axarr[1].add_patch(rect)
axarr[1].arrow(dnrtime+5, 135, -4, 0, head_width=5, head_length=1, fc='k', ec='k')
axarr[1].text(dnrtime+5, 132.5, 'DNR',fontsize=16)
# add a patch to represent the 24 hour window
rect = matplotlib.patches.Rectangle( (0, y_lim[0]), 24, y_lim[1], color='#bdbdbd')
axarr[1].add_patch(rect)
axarr[1].arrow(dnrtime+5, 135, -4, 0, head_width=5, head_length=1, fc='k', ec='k')
axarr[1].text(dnrtime+5, 132.5, 'DNR',fontsize=16)
axarr[1].set_xlabel(t_unit,fontsize=16)
axarr[1].set_ylabel('Vital signs for {}'.format(iid2),fontsize=16)
#axarr[1].legend(shadow=True, fancybox=True,loc='upper center', bbox_to_anchor=(0.5, 1.1),ncol=3)
plt.show()
```
|
github_jupyter
|
# Fairseq in Amazon SageMaker: Pre-trained English to French translation model
In this notebook, we will show you how to serve an English to French translation model using pre-trained model provided by the [Fairseq toolkit](https://github.com/pytorch/fairseq)
## Permissions
Running this notebook requires permissions in addition to the regular SageMakerFullAccess permissions. This is because it creates new repositories in Amazon ECR. The easiest way to add these permissions is simply to add the managed policy AmazonEC2ContainerRegistryFullAccess to the role that you used to start your notebook instance. There's no need to restart your notebook instance when you do this, the new permissions will be available immediately.
## Download pre-trained model
Fairseq maintains their pre-trained models [here](https://github.com/pytorch/fairseq/blob/master/examples/translation/README.md). We will use the model that was pre-trained on the [WMT14 English-French](http://statmt.org/wmt14/translation-task.html#Download) dataset. As the models are archived in .bz2 format, we need to convert them to .tar.gz as this is the format supported by Amazon SageMaker.
### Convert archive
```
%%sh
wget https://dl.fbaipublicfiles.com/fairseq/models/wmt14.v2.en-fr.fconv-py.tar.bz2
tar xvjf wmt14.v2.en-fr.fconv-py.tar.bz2 > /dev/null
cd wmt14.en-fr.fconv-py
mv model.pt checkpoint_best.pt
tar czvf wmt14.en-fr.fconv-py.tar.gz checkpoint_best.pt dict.en.txt dict.fr.txt bpecodes README.md > /dev/null
```
The pre-trained model has been downloaded and converted. The next step is upload the data to Amazon S3 in order to make it available for running the inference.
### Upload data to Amazon S3
```
import sagemaker
sagemaker_session = sagemaker.Session()
region = sagemaker_session.boto_session.region_name
account = sagemaker_session.boto_session.client("sts").get_caller_identity().get("Account")
bucket = sagemaker_session.default_bucket()
prefix = "sagemaker/DEMO-pytorch-fairseq/pre-trained-models"
role = sagemaker.get_execution_role()
trained_model_location = sagemaker_session.upload_data(
path="wmt14.en-fr.fconv-py/wmt14.en-fr.fconv-py.tar.gz", bucket=bucket, key_prefix=prefix
)
```
## Build Fairseq serving container
Next we need to register a Docker image in Amazon SageMaker that will contain the Fairseq code and that will be pulled at inference time to perform the of the precitions from the pre-trained model we downloaded.
```
%%sh
chmod +x create_container.sh
./create_container.sh pytorch-fairseq-serve
```
The Fairseq serving image has been pushed into Amazon ECR, the registry from which Amazon SageMaker will be able to pull that image and launch both training and prediction.
## Hosting the pre-trained model for inference
We first needs to define a base JSONPredictor class that will help us with sending predictions to the model once it's hosted on the Amazon SageMaker endpoint.
```
from sagemaker.predictor import RealTimePredictor, json_serializer, json_deserializer
class JSONPredictor(RealTimePredictor):
def __init__(self, endpoint_name, sagemaker_session):
super(JSONPredictor, self).__init__(
endpoint_name, sagemaker_session, json_serializer, json_deserializer
)
```
We can now use the Model class to deploy the model artificats (the pre-trained model), and deploy it on a CPU instance. Let's use a `ml.m5.xlarge`.
```
from sagemaker import Model
algorithm_name = "pytorch-fairseq-serve"
image = "{}.dkr.ecr.{}.amazonaws.com/{}:latest".format(account, region, algorithm_name)
model = Model(
model_data=trained_model_location,
role=role,
image=image,
predictor_cls=JSONPredictor,
)
predictor = model.deploy(initial_instance_count=1, instance_type="ml.m5.xlarge")
```
Now it's your time to play. Input a sentence in English and get the translation in French by simply calling predict.
```
import html
result = predictor.predict("I love translation")
# Some characters are escaped HTML-style requiring to unescape them before printing
print(html.unescape(result))
```
Once you're done with getting predictions, remember to shut down your endpoint as you no longer need it.
## Delete endpoint
```
model.sagemaker_session.delete_endpoint(predictor.endpoint)
```
Voila! For more information, you can check out the [Fairseq toolkit homepage](https://github.com/pytorch/fairseq).
|
github_jupyter
|
```
import codecs
from itertools import *
import numpy as np
from sklearn import svm
from sklearn.linear_model import LogisticRegression
from sklearn.naive_bayes import GaussianNB
from sklearn import tree
from sklearn import model_selection
from sklearn.model_selection import train_test_split
from sklearn.ensemble import GradientBoostingClassifier
import xgboost as xgb
from sklearn.ensemble import RandomForestClassifier
import pylab as pl
def load_data(filename):
file = codecs.open(filename,'r','utf-8')
data = []
label = []
for line in islice(file,0,None):
line = line.strip().split(',')
#print ("reading data....")
data.append([float(i) for i in line[1:-1]])
label.append(line[-1])
x = np.array(data)
y = np.array(label)
#print (x)
#print (y)
return x,y
def logistic_regression(x_train,y_train):
print("logistic_regression...")
clf1 = LogisticRegression()
score1 = model_selection.cross_val_score(clf1,x_train,y_train,cv=10,scoring="accuracy")
x = [int(i) for i in range(1,11)]
y = score1
pl.ylabel(u'Accuracy')
pl.xlabel(u'times')
pl.plot(x,y,label='LogReg')
pl.legend()
#pl.savefig("picture/LogReg.png")
print (np.mean(score1))
def svm_(x_train,y_train):
print("svm...")
clf2 = svm.LinearSVC(random_state=2016)
score2 = model_selection.cross_val_score(clf2,x_train,y_train,cv=10,scoring='accuracy')
#print score2
print ('The accuracy of linearSVM:')
print (np.mean(score2))
x = [int(i) for i in range(1, 11)]
y = score2
pl.ylabel(u'Accuracy')
pl.xlabel(u'times')
pl.plot(x, y,label='SVM')
pl.legend()
#pl.savefig("picture/SVM.png")
def gradient_boosting(x_train,y_train):
print("gradient_boosting...")
clf5 = GradientBoostingClassifier()
score5 = model_selection.cross_val_score(clf5,x_train,y_train,cv=10,scoring="accuracy")
print ('The accuracy of GradientBoosting:')
print (np.mean(score5))
x = [int(i) for i in range(1, 11)]
y = score5
pl.ylabel(u'Accuracy')
pl.xlabel(u'times')
pl.plot(x, y,label='GBDT')
pl.legend()
#pl.savefig("picture/GBDT.png")
def xgb_boost(x_train,y_train):
print("xgboost....")
clf = xgb.XGBClassifier()
score = model_selection.cross_val_score(clf,x_train,y_train,cv=10,scoring="accuracy")
print ('The accuracy of XGBoosting:')
print (np.mean(score))
x = [int(i) for i in range(1, 11)]
y = score
pl.ylabel(u'Accuracy')
pl.xlabel(u'times')
pl.plot(x, y,label='xgboost')
pl.legend()
#pl.savefig("picture/XGBoost.png")
def random_forest(x_train,y_train):
print("random_forest...")
clf = RandomForestClassifier(n_estimators=100)
score = model_selection.cross_val_score(clf,x_train,y_train,cv=10,scoring="accuracy")
print ('The accuracy of RandomForest:')
print (np.mean(score))
x = [int(i) for i in range(1, 11)]
y = score
pl.ylabel(u'Accuracy')
pl.xlabel(u'times')
pl.plot(x, y,label='RandForest')
pl.legend()
#pl.savefig("picture/RandomForest.png")
def train_acc(filename):
x_train,y_train = load_data(filename)
logistic_regression(x_train,y_train)
svm_(x_train,y_train)
gradient_boosting(x_train,y_train)
xgb_boost(x_train,y_train)
random_forest(x_train,y_train)
train_acc("feature1227/feature_all_1227.csv")
train_acc("features/feature_all_1223.csv")
train_acc("features/feature_amino_acid_freq_2_gram.csv")
train_acc("features/feature_all_1224.csv")
train_acc("feature1224/feature_amino_acid_freq_2_gram&pssmDT.csv")
train_acc("feature1224/feature_amino_acid_freq_2_gram&localDPP.csv")
train_acc("feature1224/feature_amino_acid_freq_2_gram&pssmDT&localDPP.csv")
train_acc("feature1224/feature_amino_acid_freq_2_gram&amino_acid.csv")
train_acc("feature1225/feature_amino_acid_freq_top_10.csv")
train_acc("feature1225/feature_all_1225_1.csv")
train_acc("feature1225/feature_all_1225_2.csv")
train_acc("feature1225/feature_ACC_1225.csv")
train_acc("final1225/feature_all.csv")
train_acc("predict1226_2/feature_all.csv")
from sklearn.externals import joblib
x,y = load_data("predict1226_2/feature_all.csv")
rf = RandomForestClassifier(n_estimators=100)
rf.fit(x,y)
joblib.dump(rf,"predict1226_2/rf.model")
#y_pred = rf.predict(x)
#y_preprob = rf.predict_proba(x)[:,1]
#print (y_pred)
#print (y_preprob)
from sklearn.externals import joblib
x,y = load_data("predict1226_2/feature_all.csv")
rf = RandomForestClassifier(n_estimators=100)
rf.fit(x,y)
joblib.dump(rf,"predict1226_2/rf.model")
```
|
github_jupyter
|
```
# -*- coding: utf-8 -*-
"""
EVCで変換する.
詳細 : https://pdfs.semanticscholar.org/cbfe/71798ded05fb8bf8674580aabf534c4dbb8bc.pdf
Converting by EVC.
Check detail : https://pdfs.semanticscholar.org/cbfe/71798ded05fb8bf8674580abf534c4dbb8bc.pdf
"""
from __future__ import division, print_function
import os
from shutil import rmtree
import argparse
import glob
import pickle
import time
import numpy as np
from numpy.linalg import norm
from sklearn.decomposition import PCA
from sklearn.mixture import GMM # sklearn 0.20.0から使えない
from sklearn.preprocessing import StandardScaler
import scipy.signal
import scipy.sparse
%matplotlib inline
import matplotlib.pyplot as plt
import IPython
from IPython.display import Audio
import soundfile as sf
import wave
import pyworld as pw
import librosa.display
from dtw import dtw
import warnings
warnings.filterwarnings('ignore')
"""
Parameters
__Mixtured : GMM混合数
__versions : 実験セット
__convert_source : 変換元話者のパス
__convert_target : 変換先話者のパス
"""
# parameters
__Mixtured = 40
__versions = 'pre-stored0.1.1'
__convert_source = 'input/EJM10/V01/T01/TIMIT/000/*.wav'
__convert_target = 'adaptation/EJM04/V01/T01/ATR503/A/*.wav'
__measure_target = 'adaptation/EJM04/V01/T01/TIMIT/000/*.wav'
# settings
__same_path = './utterance/' + __versions + '/'
__output_path = __same_path + 'output/EJM04/' # EJF01, EJF07, EJM04, EJM05
Mixtured = __Mixtured
pre_stored_pickle = __same_path + __versions + '.pickle'
pre_stored_source_list = __same_path + 'pre-source/**/V01/T01/**/*.wav'
pre_stored_list = __same_path + "pre/**/V01/T01/**/*.wav"
#pre_stored_target_list = "" (not yet)
pre_stored_gmm_init_pickle = __same_path + __versions + '_init-gmm.pickle'
pre_stored_sv_npy = __same_path + __versions + '_sv.npy'
save_for_evgmm_covarXX = __output_path + __versions + '_covarXX.npy'
save_for_evgmm_covarYX = __output_path + __versions + '_covarYX.npy'
save_for_evgmm_fitted_source = __output_path + __versions + '_fitted_source.npy'
save_for_evgmm_fitted_target = __output_path + __versions + '_fitted_target.npy'
save_for_evgmm_weights = __output_path + __versions + '_weights.npy'
save_for_evgmm_source_means = __output_path + __versions + '_source_means.npy'
for_convert_source = __same_path + __convert_source
for_convert_target = __same_path + __convert_target
for_measure_target = __same_path + __measure_target
converted_voice_npy = __output_path + 'sp_converted_' + __versions
converted_voice_wav = __output_path + 'sp_converted_' + __versions
mfcc_save_fig_png = __output_path + 'mfcc3dim_' + __versions
f0_save_fig_png = __output_path + 'f0_converted' + __versions
converted_voice_with_f0_wav = __output_path + 'sp_f0_converted' + __versions
mcd_text = __output_path + __versions + '_MCD.txt'
EPSILON = 1e-8
class MFCC:
"""
MFCC() : メル周波数ケプストラム係数(MFCC)を求めたり、MFCCからスペクトルに変換したりするクラス.
動的特徴量(delta)が実装途中.
ref : http://aidiary.hatenablog.com/entry/20120225/1330179868
"""
def __init__(self, frequency, nfft=1026, dimension=24, channels=24):
"""
各種パラメータのセット
nfft : FFTのサンプル点数
frequency : サンプリング周波数
dimension : MFCC次元数
channles : メルフィルタバンクのチャンネル数(dimensionに依存)
fscale : 周波数スケール軸
filterbankl, fcenters : フィルタバンク行列, フィルタバンクの頂点(?)
"""
self.nfft = nfft
self.frequency = frequency
self.dimension = dimension
self.channels = channels
self.fscale = np.fft.fftfreq(self.nfft, d = 1.0 / self.frequency)[: int(self.nfft / 2)]
self.filterbank, self.fcenters = self.melFilterBank()
def hz2mel(self, f):
"""
周波数からメル周波数に変換
"""
return 1127.01048 * np.log(f / 700.0 + 1.0)
def mel2hz(self, m):
"""
メル周波数から周波数に変換
"""
return 700.0 * (np.exp(m / 1127.01048) - 1.0)
def melFilterBank(self):
"""
メルフィルタバンクを生成する
"""
fmax = self.frequency / 2
melmax = self.hz2mel(fmax)
nmax = int(self.nfft / 2)
df = self.frequency / self.nfft
dmel = melmax / (self.channels + 1)
melcenters = np.arange(1, self.channels + 1) * dmel
fcenters = self.mel2hz(melcenters)
indexcenter = np.round(fcenters / df)
indexstart = np.hstack(([0], indexcenter[0:self.channels - 1]))
indexstop = np.hstack((indexcenter[1:self.channels], [nmax]))
filterbank = np.zeros((self.channels, nmax))
for c in np.arange(0, self.channels):
increment = 1.0 / (indexcenter[c] - indexstart[c])
# np,int_ は np.arangeが[0. 1. 2. ..]となるのをintにする
for i in np.int_(np.arange(indexstart[c], indexcenter[c])):
filterbank[c, i] = (i - indexstart[c]) * increment
decrement = 1.0 / (indexstop[c] - indexcenter[c])
# np,int_ は np.arangeが[0. 1. 2. ..]となるのをintにする
for i in np.int_(np.arange(indexcenter[c], indexstop[c])):
filterbank[c, i] = 1.0 - ((i - indexcenter[c]) * decrement)
return filterbank, fcenters
def mfcc(self, spectrum):
"""
スペクトルからMFCCを求める.
"""
mspec = []
mspec = np.log10(np.dot(spectrum, self.filterbank.T))
mspec = np.array(mspec)
return scipy.fftpack.realtransforms.dct(mspec, type=2, norm="ortho", axis=-1)
def delta(self, mfcc):
"""
MFCCから動的特徴量を求める.
現在は,求める特徴量フレームtをt-1とt+1の平均としている.
"""
mfcc = np.concatenate([
[mfcc[0]],
mfcc,
[mfcc[-1]]
]) # 最初のフレームを最初に、最後のフレームを最後に付け足す
delta = None
for i in range(1, mfcc.shape[0] - 1):
slope = (mfcc[i+1] - mfcc[i-1]) / 2
if delta is None:
delta = slope
else:
delta = np.vstack([delta, slope])
return delta
def imfcc(self, mfcc, spectrogram):
"""
MFCCからスペクトルを求める.
"""
im_sp = np.array([])
for i in range(mfcc.shape[0]):
mfcc_s = np.hstack([mfcc[i], [0] * (self.channels - self.dimension)])
mspectrum = scipy.fftpack.idct(mfcc_s, norm='ortho')
# splrep はスプライン補間のための補間関数を求める
tck = scipy.interpolate.splrep(self.fcenters, np.power(10, mspectrum))
# splev は指定座標での補間値を求める
im_spectrogram = scipy.interpolate.splev(self.fscale, tck)
im_sp = np.concatenate((im_sp, im_spectrogram), axis=0)
return im_sp.reshape(spectrogram.shape)
def trim_zeros_frames(x, eps=1e-7):
"""
無音区間を取り除く.
"""
T, D = x.shape
s = np.sum(np.abs(x), axis=1)
s[s < 1e-7] = 0.
return x[s > eps]
def analyse_by_world_with_harverst(x, fs):
"""
WORLD音声分析合成器で基本周波数F0,スペクトル包絡,非周期成分を求める.
基本周波数F0についてはharvest法により,より精度良く求める.
"""
# 4 Harvest with F0 refinement (using Stonemask)
frame_period = 5
_f0_h, t_h = pw.harvest(x, fs, frame_period=frame_period)
f0_h = pw.stonemask(x, _f0_h, t_h, fs)
sp_h = pw.cheaptrick(x, f0_h, t_h, fs)
ap_h = pw.d4c(x, f0_h, t_h, fs)
return f0_h, sp_h, ap_h
def wavread(file):
"""
wavファイルから音声トラックとサンプリング周波数を抽出する.
"""
wf = wave.open(file, "r")
fs = wf.getframerate()
x = wf.readframes(wf.getnframes())
x = np.frombuffer(x, dtype= "int16") / 32768.0
wf.close()
return x, float(fs)
def preEmphasis(signal, p=0.97):
"""
MFCC抽出のための高域強調フィルタ.
波形を通すことで,高域成分が強調される.
"""
return scipy.signal.lfilter([1.0, -p], 1, signal)
def alignment(source, target, path):
"""
タイムアライメントを取る.
target音声をsource音声の長さに合うように調整する.
"""
# ここでは814に合わせよう(targetに合わせる)
# p_p = 0 if source.shape[0] > target.shape[0] else 1
#shapes = source.shape if source.shape[0] > target.shape[0] else target.shape
shapes = source.shape
align = np.array([])
for (i, p) in enumerate(path[0]):
if i != 0:
if j != p:
temp = np.array(target[path[1][i]])
align = np.concatenate((align, temp), axis=0)
else:
temp = np.array(target[path[1][i]])
align = np.concatenate((align, temp), axis=0)
j = p
return align.reshape(shapes)
covarXX = np.load(save_for_evgmm_covarXX)
covarYX = np.load(save_for_evgmm_covarYX)
fitted_source = np.load(save_for_evgmm_fitted_source)
fitted_target = np.load(save_for_evgmm_fitted_target)
weights = np.load(save_for_evgmm_weights)
source_means = np.load(save_for_evgmm_source_means)
"""
声質変換に用いる変換元音声と目標音声を読み込む.
"""
timer_start = time.time()
source_mfcc_for_convert = []
source_sp_for_convert = []
source_f0_for_convert = []
source_ap_for_convert = []
fs_source = None
for name in sorted(glob.iglob(for_convert_source, recursive=True)):
print("source = ", name)
x_source, fs_source = sf.read(name)
f0_source, sp_source, ap_source = analyse_by_world_with_harverst(x_source, fs_source)
mfcc_source = MFCC(fs_source)
#mfcc_s_tmp = mfcc_s.mfcc(sp)
#source_mfcc_for_convert = np.hstack([mfcc_s_tmp, mfcc_s.delta(mfcc_s_tmp)])
source_mfcc_for_convert.append(mfcc_source.mfcc(sp_source))
source_sp_for_convert.append(sp_source)
source_f0_for_convert.append(f0_source)
source_ap_for_convert.append(ap_source)
target_mfcc_for_fit = []
target_f0_for_fit = []
target_ap_for_fit = []
for name in sorted(glob.iglob(for_convert_target, recursive=True)):
print("target = ", name)
x_target, fs_target = sf.read(name)
f0_target, sp_target, ap_target = analyse_by_world_with_harverst(x_target, fs_target)
mfcc_target = MFCC(fs_target)
#mfcc_target_tmp = mfcc_target.mfcc(sp_target)
#target_mfcc_for_fit = np.hstack([mfcc_t_tmp, mfcc_t.delta(mfcc_t_tmp)])
target_mfcc_for_fit.append(mfcc_target.mfcc(sp_target))
target_f0_for_fit.append(f0_target)
target_ap_for_fit.append(ap_target)
# 全部numpy.arrrayにしておく
source_data_mfcc = np.array(source_mfcc_for_convert)
source_data_sp = np.array(source_sp_for_convert)
source_data_f0 = np.array(source_f0_for_convert)
source_data_ap = np.array(source_ap_for_convert)
target_mfcc = np.array(target_mfcc_for_fit)
target_f0 = np.array(target_f0_for_fit)
target_ap = np.array(target_ap_for_fit)
print("Load Input and Target Voice time = ", time.time() - timer_start , "[sec]")
def convert(source, covarXX, fitted_source, fitted_target, covarYX, weights, source_means):
"""
声質変換を行う.
"""
Mixtured = 40
D = source.shape[0]
E = np.zeros((Mixtured, D))
for m in range(Mixtured):
xx = np.linalg.solve(covarXX[m], source - fitted_source[m])
E[m] = fitted_target[m] + np.dot(covarYX[m], xx)
px = GMM(n_components = Mixtured, covariance_type = 'full')
px.weights_ = weights
px.means_ = source_means
px.covars_ = covarXX
posterior = px.predict_proba(np.atleast_2d(source))
return np.dot(posterior, E)
def calc_std_mean(input_f0):
"""
F0変換のために標準偏差と平均を求める.
"""
tempF0 = input_f0[ np.where(input_f0 > 0)]
fixed_logF0 = np.log(tempF0)
#logF0 = np.ma.log(input_f0) # 0要素にlogをするとinfになるのでmaskする
#fixed_logF0 = np.ma.fix_invalid(logF0).data # maskを取る
return np.std(fixed_logF0), np.mean(fixed_logF0) # 標準偏差と平均を返す
"""
距離を測るために,正しい目標音声を読み込む
"""
source_mfcc_for_measure_target = []
source_sp_for_measure_target = []
source_f0_for_measure_target = []
source_ap_for_measure_target = []
for name in sorted(glob.iglob(for_measure_target, recursive=True)):
print("measure_target = ", name)
x_measure_target, fs_measure_target = sf.read(name)
f0_measure_target, sp_measure_target, ap_measure_target = analyse_by_world_with_harverst(x_measure_target, fs_measure_target)
mfcc_measure_target = MFCC(fs_measure_target)
#mfcc_s_tmp = mfcc_s.mfcc(sp)
#source_mfcc_for_convert = np.hstack([mfcc_s_tmp, mfcc_s.delta(mfcc_s_tmp)])
source_mfcc_for_measure_target.append(mfcc_measure_target.mfcc(sp_measure_target))
source_sp_for_measure_target.append(sp_measure_target)
source_f0_for_measure_target.append(f0_measure_target)
source_ap_for_measure_target.append(ap_measure_target)
measure_target_data_mfcc = np.array(source_mfcc_for_measure_target)
measure_target_data_sp = np.array(source_sp_for_measure_target)
measure_target_data_f0 = np.array(source_f0_for_measure_target)
measure_target_data_ap = np.array(source_ap_for_measure_target)
def calc_mcd(source, convert, target):
"""
変換する前の音声と目標音声でDTWを行う.
その後,変換後の音声と目標音声とのMCDを計測する.
"""
dist, cost, acc, path = dtw(source, target, dist=lambda x, y: norm(x-y, ord=1))
aligned = alignment(source, target, path)
return 10.0 / np.log(10) * np.sqrt(2 * np.sum(np.square(aligned - convert))), aligned
"""
変換を行う.
"""
timer_start = time.time()
# 事前に目標話者の標準偏差と平均を求めておく
temp_f = None
for x in range(len(target_f0)):
temp = target_f0[x].flatten()
if temp_f is None:
temp_f = temp
else:
temp_f = np.hstack((temp_f, temp))
target_std, target_mean = calc_std_mean(temp_f)
# 変換
output_mfcc = []
filer = open(mcd_text, 'a')
for i in range(len(source_data_mfcc)):
print("voice no = ", i)
# convert
source_temp = source_data_mfcc[i]
output_mfcc = np.array([convert(source_temp[frame], covarXX, fitted_source, fitted_target, covarYX, weights, source_means)[0] for frame in range(source_temp.shape[0])])
# syntehsis
source_sp_temp = source_data_sp[i]
source_f0_temp = source_data_f0[i]
source_ap_temp = source_data_ap[i]
output_imfcc = mfcc_source.imfcc(output_mfcc, source_sp_temp)
y_source = pw.synthesize(source_f0_temp, output_imfcc, source_ap_temp, fs_source, 5)
np.save(converted_voice_npy + "s{0}.npy".format(i), output_imfcc)
sf.write(converted_voice_wav + "s{0}.wav".format(i), y_source, fs_source)
# calc MCD
measure_temp = measure_target_data_mfcc[i]
mcd, aligned_measure = calc_mcd(source_temp, output_mfcc, measure_temp)
filer.write("MCD No.{0} = {1} , shape = {2}\n".format(i, mcd, source_temp.shape))
# save figure spectram
range_s = output_imfcc.shape[0]
scale = [x for x in range(range_s)]
MFCC_sample_s = [source_temp[x][0] for x in range(range_s)]
MFCC_sample_c = [output_mfcc[x][0] for x in range(range_s)]
MFCC_sample_t = [aligned_measure[x][0] for x in range(range_s)]
plt.subplot(311)
plt.plot(scale, MFCC_sample_s, label="source", linewidth = 1.0)
plt.plot(scale, MFCC_sample_c, label="convert", linewidth = 1.0)
plt.plot(scale, MFCC_sample_t, label="target", linewidth = 1.0, linestyle="dashed")
plt.legend(bbox_to_anchor=(0., 1.02, 1., .102), loc=3, ncol=3, mode="expand", borderaxespad=0.)
#plt.xlabel("Flame")
#plt.ylabel("amplitude MFCC")
MFCC_sample_s = [source_temp[x][1] for x in range(range_s)]
MFCC_sample_c = [output_mfcc[x][1] for x in range(range_s)]
MFCC_sample_t = [aligned_measure[x][1] for x in range(range_s)]
plt.subplot(312)
plt.plot(scale, MFCC_sample_s, label="source", linewidth = 1.0)
plt.plot(scale, MFCC_sample_c, label="convert", linewidth = 1.0)
plt.plot(scale, MFCC_sample_t, label="target", linewidth = 1.0, linestyle="dashed")
plt.ylabel("amplitude MFCC")
MFCC_sample_s = [source_temp[x][2] for x in range(range_s)]
MFCC_sample_c = [output_mfcc[x][2] for x in range(range_s)]
MFCC_sample_t = [aligned_measure[x][2] for x in range(range_s)]
plt.subplot(313)
plt.plot(scale, MFCC_sample_s, label="source", linewidth = 1.0)
plt.plot(scale, MFCC_sample_c, label="convert", linewidth = 1.0)
plt.plot(scale, MFCC_sample_t, label="target", linewidth = 1.0, linestyle="dashed")
plt.xlabel("Flame")
plt.savefig(mfcc_save_fig_png + "s{0}.png".format(i) , format='png', dpi=300)
plt.close()
# synthesis with conveted f0
source_std, source_mean = calc_std_mean(source_f0_temp)
std_ratio = target_std / source_std
log_conv_f0 = std_ratio * (source_f0_temp - source_mean) + target_mean
conv_f0 = np.maximum(log_conv_f0, 0)
np.save(converted_voice_npy + "f{0}.npy".format(i), conv_f0)
y_conv = pw.synthesize(conv_f0, output_imfcc, source_ap_temp, fs_source, 5)
sf.write(converted_voice_with_f0_wav + "sf{0}.wav".format(i) , y_conv, fs_source)
# save figure f0
F0_s = [source_f0_temp[x] for x in range(range_s)]
F0_c = [conv_f0[x] for x in range(range_s)]
plt.plot(scale, F0_s, label="source", linewidth = 1.0)
plt.plot(scale, F0_c, label="convert", linewidth = 1.0)
plt.legend(bbox_to_anchor=(0., 1.02, 1., .102), loc=3, ncol=2, mode="expand", borderaxespad=0.)
plt.xlabel("Frame")
plt.ylabel("Amplitude")
plt.savefig(f0_save_fig_png + "f{0}.png".format(i), format='png', dpi=300)
plt.close()
filer.close()
print("Make Converted Spectram time = ", time.time() - timer_start , "[sec]")
```
|
github_jupyter
|
<CENTER>
<header>
<h1>Pandas Tutorial</h1>
<h3>EuroScipy, Erlangen DE, August 24th, 2016</h3>
<h2>Joris Van den Bossche</h2>
<p></p>
Source: <a href="https://github.com/jorisvandenbossche/pandas-tutorial">https://github.com/jorisvandenbossche/pandas-tutorial</a>
</header>
</CENTER>
Two data files are not included in the repo, you can download them from: [`titles.csv`](https://drive.google.com/file/d/0B3G70MlBnCgKa0U4WFdWdGdVOFU/view?usp=sharing) and [`cast.csv`](https://drive.google.com/file/d/0B3G70MlBnCgKRzRmTWdQTUdjNnM/view?usp=sharing) and put them in the `/data` folder.
## Requirements to run this tutorial
To follow this tutorial you need to have the following packages installed:
- Python version 2.6-2.7 or 3.3-3.5
- `pandas` version 0.18.0 or later: http://pandas.pydata.org/
- `numpy` version 1.7 or later: http://www.numpy.org/
- `matplotlib` version 1.3 or later: http://matplotlib.org/
- `ipython` version 3.x with notebook support, or `ipython 4.x` combined with `jupyter`: http://ipython.org
- `seaborn` (this is used for some plotting, but not necessary to follow the tutorial): http://stanford.edu/~mwaskom/software/seaborn/
## Downloading the tutorial materials
If you have git installed, you can get the material in this tutorial by cloning this repo:
git clone https://github.com/jorisvandenbossche/pandas-tutorial.git
As an alternative, you can download it as a zip file:
https://github.com/jorisvandenbossche/pandas-tutorial/archive/master.zip.
I will probably make some changes until the start of the tutorial, so best to download
the latest version then (or do a `git pull` if you are using git).
Two data files are not included in the repo, you can download them from: [`titles.csv`](https://drive.google.com/open?id=0B3G70MlBnCgKajNMa1pfSzN6Q3M) and [`cast.csv`](https://drive.google.com/open?id=0B3G70MlBnCgKal9UYTJSR2ZhSW8) and put them in the `/data` folder.
## Contents
Beginners track:
- [01 - Introduction - beginners.ipynb](01 - Introduction - beginners.ipynb)
- [02 - Data structures](02 - Data structures.ipynb)
- [03 - Indexing and selecting data](03 - Indexing and selecting data.ipynb)
- [04 - Groupby operations](04 - Groupby operations.ipynb)
Advanced track:
- [03b - Some more advanced indexing](03b - Some more advanced indexing.ipynb)
- [04b - Advanced groupby operations](04b - Advanced groupby operations.ipynb)
- [05 - Time series data](05 - Time series data.ipynb)
- [06 - Reshaping data](06 - Reshaping data.ipynb)
|
github_jupyter
|
# Closed-Loop Evaluation
In this notebook you are going to evaluate Urban Driver to control the SDV with a protocol named *closed-loop* evaluation.
**Note: this notebook assumes you've already run the [training notebook](./train.ipynb) and stored your model successfully (or that you have stored a pre-trained one).**
**Note: for a detailed explanation of what closed-loop evaluation (CLE) is, please refer to our [planning notebook](../planning/closed_loop_test.ipynb)**
### Imports
```
import matplotlib.pyplot as plt
import numpy as np
import torch
from prettytable import PrettyTable
from l5kit.configs import load_config_data
from l5kit.data import LocalDataManager, ChunkedDataset
from l5kit.dataset import EgoDatasetVectorized
from l5kit.vectorization.vectorizer_builder import build_vectorizer
from l5kit.simulation.dataset import SimulationConfig
from l5kit.simulation.unroll import ClosedLoopSimulator
from l5kit.cle.closed_loop_evaluator import ClosedLoopEvaluator, EvaluationPlan
from l5kit.cle.metrics import (CollisionFrontMetric, CollisionRearMetric, CollisionSideMetric,
DisplacementErrorL2Metric, DistanceToRefTrajectoryMetric)
from l5kit.cle.validators import RangeValidator, ValidationCountingAggregator
from l5kit.visualization.visualizer.zarr_utils import simulation_out_to_visualizer_scene
from l5kit.visualization.visualizer.visualizer import visualize
from bokeh.io import output_notebook, show
from l5kit.data import MapAPI
from collections import defaultdict
import os
```
## Prepare data path and load cfg
By setting the `L5KIT_DATA_FOLDER` variable, we can point the script to the folder where the data lies.
Then, we load our config file with relative paths and other configurations (rasteriser, training params ...).
```
# set env variable for data
from l5kit.data import get_dataset_path
os.environ["L5KIT_DATA_FOLDER"], project_path = get_dataset_path()
dm = LocalDataManager(None)
# get config
cfg = load_config_data("./config.yaml")
```
## Load the model
```
model_path = project_path + "/urban_driver_dummy_model.pt"
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
model = torch.load(model_path).to(device)
model = model.eval()
torch.set_grad_enabled(False)
```
## Load the evaluation data
Differently from training and open loop evaluation, this setting is intrinsically sequential. As such, we won't be using any of PyTorch's parallelisation functionalities.
```
# ===== INIT DATASET
eval_cfg = cfg["val_data_loader"]
eval_zarr = ChunkedDataset(dm.require(eval_cfg["key"])).open()
vectorizer = build_vectorizer(cfg, dm)
eval_dataset = EgoDatasetVectorized(cfg, eval_zarr, vectorizer)
print(eval_dataset)
```
## Define some simulation properties
We define here some common simulation properties such as the length of the simulation and how many scene to simulate.
**NOTE: these properties have a significant impact on the execution time. We suggest you to increase them only if your setup includes a GPU.**
```
num_scenes_to_unroll = 10
num_simulation_steps = 50
```
# Closed-loop simulation
We define a closed-loop simulation that drives the SDV for `num_simulation_steps` steps while using the log-replayed agents.
Then, we unroll the selected scenes.
The simulation output contains all the information related to the scene, including the annotated and simulated positions, states, and trajectories of the SDV and the agents.
If you want to know more about what the simulation output contains, please refer to the source code of the class `SimulationOutput`.
```
# ==== DEFINE CLOSED-LOOP SIMULATION
sim_cfg = SimulationConfig(use_ego_gt=False, use_agents_gt=True, disable_new_agents=True,
distance_th_far=500, distance_th_close=50, num_simulation_steps=num_simulation_steps,
start_frame_index=0, show_info=True)
sim_loop = ClosedLoopSimulator(sim_cfg, eval_dataset, device, model_ego=model, model_agents=None)
# ==== UNROLL
scenes_to_unroll = list(range(0, len(eval_zarr.scenes), len(eval_zarr.scenes)//num_scenes_to_unroll))
sim_outs = sim_loop.unroll(scenes_to_unroll)
```
# Closed-loop metrics
**Note: for a detailed explanation of CLE metrics, please refer again to our [planning notebook](../planning/closed_loop_test.ipynb)**
```
metrics = [DisplacementErrorL2Metric(),
DistanceToRefTrajectoryMetric(),
CollisionFrontMetric(),
CollisionRearMetric(),
CollisionSideMetric()]
validators = [RangeValidator("displacement_error_l2", DisplacementErrorL2Metric, max_value=30),
RangeValidator("distance_ref_trajectory", DistanceToRefTrajectoryMetric, max_value=4),
RangeValidator("collision_front", CollisionFrontMetric, max_value=0),
RangeValidator("collision_rear", CollisionRearMetric, max_value=0),
RangeValidator("collision_side", CollisionSideMetric, max_value=0)]
intervention_validators = ["displacement_error_l2",
"distance_ref_trajectory",
"collision_front",
"collision_rear",
"collision_side"]
cle_evaluator = ClosedLoopEvaluator(EvaluationPlan(metrics=metrics,
validators=validators,
composite_metrics=[],
intervention_validators=intervention_validators))
```
# Quantitative evaluation
We can now compute the metric evaluation, collect the results and aggregate them.
```
cle_evaluator.evaluate(sim_outs)
validation_results = cle_evaluator.validation_results()
agg = ValidationCountingAggregator().aggregate(validation_results)
cle_evaluator.reset()
```
## Reporting errors from the closed-loop
We can now report the metrics and plot them.
```
fields = ["metric", "value"]
table = PrettyTable(field_names=fields)
values = []
names = []
for metric_name in agg:
table.add_row([metric_name, agg[metric_name].item()])
values.append(agg[metric_name].item())
names.append(metric_name)
print(table)
plt.bar(np.arange(len(names)), values)
plt.xticks(np.arange(len(names)), names, rotation=60, ha='right')
plt.show()
```
# Qualitative evaluation
## Visualise the closed-loop
We can visualise the scenes we have obtained previously.
**The policy is now in full control of the SDV as this moves through the annotated scene.**
```
output_notebook()
mapAPI = MapAPI.from_cfg(dm, cfg)
for sim_out in sim_outs: # for each scene
vis_in = simulation_out_to_visualizer_scene(sim_out, mapAPI)
show(visualize(sim_out.scene_id, vis_in))
```
|
github_jupyter
|
```
%load_ext autoreload
%autoreload 2
from quantumnetworks import MultiModeSystem, plot_full_evolution
import numpy as np
```
# Trapezoidal Method
```
# params stored in txt
sys = MultiModeSystem(params={"dir":"data/"})
x_0 = np.array([1,0,0,1])
ts = np.linspace(0, 10, 101)
X = sys.trapezoidal(x_0, ts)
fig, ax = plot_full_evolution(X, ts, labels=["$q_a$","$p_a$","$q_b$","$p_b$"])
ax.legend()
```
# Forward Euler
```
# params stored in txt
sys = MultiModeSystem(params={"dir":"data/"})
x_0 = np.array([1,0,0,1])
ts = np.linspace(0, 10, 10001)
X = sys.forward_euler(x_0, ts)
fig, ax = plot_full_evolution(X, ts, labels=["$q_a$","$p_a$","$q_b$","$p_b$"])
ax.legend()
u = sys.eval_u(0)
sys.eval_Jf(x_0, u)
sys.eval_Jf_numerical(x_0, u)
# params directly provided
omegas = [1,2]
kappas = [0.001,0.005]
gammas = [0.002,0.002]
kerrs = [0.001, 0.001]
couplings = [[0,1,0.002]]
sys = MultiModeSystem(params={"omegas":omegas, "kappas":kappas, "gammas":gammas, "kerrs": kerrs, "couplings":couplings})
x_0 = np.array([1,0,0,1])
ts = np.linspace(0, 10, 1001)
X = sys.forward_euler(x_0, ts)
fig, ax = plot_full_evolution(X, ts, labels=["$q_a$","$p_a$","$q_b$","$p_b$"])
ax.legend()
# single mode system
omegas = [2*np.pi*1]
kappas = [2*np.pi*0.001]
gammas = [2*np.pi*0.002]
kerrs = [2*np.pi*0.001]
couplings = []
sys = MultiModeSystem(params={"omegas":omegas, "kappas":kappas,"gammas":gammas,"kerrs":kerrs,"couplings":couplings})
x_0 = np.array([1,0])
ts = np.linspace(0, 10, 100001)
X = sys.forward_euler(x_0, ts)
fig, ax = plot_full_evolution(X, ts, labels=["$q_a$","$p_a$"])
ax.legend()
# params directly provided
omegas = [2*np.pi*1,2*np.pi*2,2*np.pi*1]
kappas = [2*np.pi*0.001,2*np.pi*0.005,2*np.pi*0.001]
gammas = [2*np.pi*0.002,2*np.pi*0.002,2*np.pi*0.002]
kerrs = [2*np.pi*0.001, 2*np.pi*0.001, 2*np.pi*0.001]
couplings = [[0,1,2*np.pi*0.002],[1,2,2*np.pi*0.002]]
sys = MultiModeSystem(params={"omegas":omegas, "kappas":kappas, "gammas":gammas, "kerrs":kerrs, "couplings":couplings})
print(sys.A)
# x_0 = np.array([1,0,0,1])
# ts = np.linspace(0, 10, 1001)
# X = sys.forward_euler(x_0, ts)
# fig, ax = plot_full_evolution(X, ts, labels=["$q_a$","$p_a$","$q_b$","$p_b$"])
# ax.legend()
```
# Linearization
```
omegas = [2*np.pi*1,2*np.pi*2,2*np.pi*1]
kappas = [2*np.pi*0.001,2*np.pi*0.005,2*np.pi*0.001]
gammas = [2*np.pi*0.002,2*np.pi*0.002,2*np.pi*0.002]
kerrs = [2*np.pi*0.001, 2*np.pi*0.001, 2*np.pi*0.001]
couplings = [[0,1,2*np.pi*0.002],[1,2,2*np.pi*0.002]]
sys = MultiModeSystem(params={"omegas":omegas, "kappas":kappas, "gammas":gammas, "kerrs":kerrs, "couplings":couplings})
x_0 = np.array([1,0, 0,1, 1,0])
ts = np.linspace(0, 1, 1001)
X = sys.forward_euler(x_0, ts)
fig, ax = plot_full_evolution(X, ts, labels=["$q_a$","$p_a$", "$q_b$","$p_b$", "$q_c$","$p_c$"])
ax.legend()
X_linear = sys.forward_euler_linear(x_0, ts, x_0, 0)
fig, ax = plot_full_evolution(X_linear, ts, labels=["$q_{a,linear}$","$p_{a,linear}$","$q_{b,linear}$","$p_{b,linear}$","$q_{c,linear}$","$p_{c,linear}$"])
Delta_X = (X-X_linear)/X
plot_full_evolution(Delta_X[:,:50], ts[:50], labels=["$q_a - q_{a,linear}$","$p_a - p_{a,linear}$","$q_b - q_{b,linear}$","$p_b - p_{b,linear}$","$q_c - q_{c,linear}$","$p_c - p_{c,linear}$"])
ax.legend()
```
|
github_jupyter
|
___
<a href='http://www.pieriandata.com'> <img src='../Pierian_Data_Logo.png' /></a>
___
# Principal Component Analysis
Let's discuss PCA! Since this isn't exactly a full machine learning algorithm, but instead an unsupervised learning algorithm, we will just have a lecture on this topic, but no full machine learning project (although we will walk through the cancer set with PCA).
## PCA Review
Make sure to watch the video lecture and theory presentation for a full overview of PCA!
Remember that PCA is just a transformation of your data and attempts to find out what features explain the most variance in your data. For example:
<img src='PCA.png' />
## Libraries
```
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import seaborn as sns
%matplotlib inline
```
## The Data
Let's work with the cancer data set again since it had so many features.
```
from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()
cancer.keys()
print(cancer['DESCR'])
df = pd.DataFrame(cancer['data'],columns=cancer['feature_names'])
#(['DESCR', 'data', 'feature_names', 'target_names', 'target'])
df.head()
```
## PCA Visualization
As we've noticed before it is difficult to visualize high dimensional data, we can use PCA to find the first two principal components, and visualize the data in this new, two-dimensional space, with a single scatter-plot. Before we do this though, we'll need to scale our data so that each feature has a single unit variance.
```
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(df)
scaled_data = scaler.transform(df)
```
PCA with Scikit Learn uses a very similar process to other preprocessing functions that come with SciKit Learn. We instantiate a PCA object, find the principal components using the fit method, then apply the rotation and dimensionality reduction by calling transform().
We can also specify how many components we want to keep when creating the PCA object.
```
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
pca.fit(scaled_data)
```
Now we can transform this data to its first 2 principal components.
```
x_pca = pca.transform(scaled_data)
scaled_data.shape
x_pca.shape
```
Great! We've reduced 30 dimensions to just 2! Let's plot these two dimensions out!
```
plt.figure(figsize=(8,6))
plt.scatter(x_pca[:,0],x_pca[:,1],c=cancer['target'],cmap='plasma')
plt.xlabel('First principal component')
plt.ylabel('Second Principal Component')
```
Clearly by using these two components we can easily separate these two classes.
## Interpreting the components
Unfortunately, with this great power of dimensionality reduction, comes the cost of being able to easily understand what these components represent.
The components correspond to combinations of the original features, the components themselves are stored as an attribute of the fitted PCA object:
```
pca.components_
```
In this numpy matrix array, each row represents a principal component, and each column relates back to the original features. we can visualize this relationship with a heatmap:
```
df_comp = pd.DataFrame(pca.components_,columns=cancer['feature_names'])
plt.figure(figsize=(12,6))
sns.heatmap(df_comp,cmap='plasma',)
```
This heatmap and the color bar basically represent the correlation between the various feature and the principal component itself.
## Conclusion
Hopefully this information is useful to you when dealing with high dimensional data!
# Great Job!
|
github_jupyter
|
## osumapper: create osu! map using Tensorflow and Colab
### -- For osu!mania game mode --
For mappers who don't know how this colaboratory thing works:
- Press Ctrl+Enter in code blocks to run them one by one
- It will ask you to upload .osu file and audio.mp3 after the third block of code
- .osu file needs to have correct timing (you can use [statementreply](https://osu.ppy.sh/users/126198)'s TimingAnlyz tool)
- After uploading them, wait for a few minutes until download pops
Github: https://github.com/kotritrona/osumapper
### Step 1: Installation
First of all, check the Notebook Settings under Edit tab.<br>
Activate GPU to make the training faster.
Then, clone the git repository and install dependencies.
```
%cd /content/
!git clone https://github.com/kotritrona/osumapper.git
%cd osumapper/v7.0
!apt install -y ffmpeg
!apt install -y nodejs
!cp requirements_colab.txt requirements.txt
!cp package_colab.json package.json
!pip install -r requirements.txt
!npm install
```
### Step 2: Choose a pre-trained model
Set the select_model variable to one of:
- "default": default model (choose only after training it)
- "lowkey": model trained with 4-key and 5-key maps (☆2.5-5.5)
- "highkey": model trained with 6-key to 9-key maps (☆2.5-5.5)
```
from mania_setup_colab import *
select_model = "highkey"
model_params = load_pretrained_model(select_model);
```
### Step 3: Upload map and music file<br>
Map file = .osu file with correct timing (**Important:** Set to mania mode and the wished key count!)<br>
Music file = the mp3 file in the osu folder
```
from google.colab import files
print("Please upload the map file:")
mapfile_upload = files.upload()
for fn in mapfile_upload.keys():
uploaded_osu_name = fn
print('Uploaded map file: "{name}" {length} bytes'.format(name=fn, length=len(mapfile_upload[fn])))
print("Please upload the music file:")
music_upload = files.upload()
for fn in music_upload.keys():
print('Uploaded music file: "{name}" {length} bytes'.format(name=fn, length=len(music_upload[fn])))
```
### Step 4: Read the map and convert to python readable format
```
from act_newmap_prep import *
step4_read_new_map(uploaded_osu_name);
```
### Step 5: Use model to calculate map rhythm
Parameters:
"note_density" determines how many notes will be placed on the timeline, ranges from 0 to 1.<br>
"hold_favor" determines how the model favors holds against circles, ranges from -1 to 1.<br>
"divisor_favor" determines how the model favors notes to be on X divisors starting from a beat (white, blue, red, blue), ranges from -1 to 1 each.<br>
"hold_max_ticks" determines the max amount of time a hold can hold off, ranges from 1 to +∞.<br>
"hold_min_return" determines the final granularity of the pattern dataset, ranges from 1 to +∞.<br>
"rotate_mode" determines how the patterns from the dataset gets rotated. modes (0,1,2,3,4)
- 0 = no rotation
- 1 = random
- 2 = mirror
- 3 = circulate
- 4 = circulate + mirror
```
from mania_act_rhythm_calc import *
model = step5_load_model(model_file=model_params["rhythm_model"]);
npz = step5_load_npz();
params = model_params["rhythm_param"]
# Or set the parameters here...
# params = step5_set_params(note_density=0.6, hold_favor=0.2, divisor_favor=[0] * divisor, hold_max_ticks=8, hold_min_return=1, rotate_mode=4);
predictions = step5_predict_notes(model, npz, params);
notes_each_key = step5_build_pattern(predictions, params, pattern_dataset=model_params["pattern_dataset"]);
```
Do a little modding to the map.
Parameters:
- key_fix: remove continuous notes on single key modes (0,1,2,3) 0=inactive 1=remove late note 2=remove early note 3=divert
```
modding_params = model_params["modding"]
# modding_params = {
# "key_fix" : 3
# }
notes_each_key = mania_modding(notes_each_key, modding_params);
notes, key_count = merge_objects_each_key(notes_each_key)
```
Finally, save the data into an .osu file!
```
from google.colab import files
from mania_act_final import *
saved_osu_name = step8_save_osu_mania_file(notes, key_count);
files.download(saved_osu_name)
# clean up if you want to make another map!
# colab_clean_up(uploaded_osu_name)
```
That's it! Now you can try out the AI-created map in osu!.
For bug reports and feedbacks either report it on github or use discord: <br>
[https://discord.com/invite/npmSy7K](https://discord.com/invite/npmSy7K)
<img src="https://i.imgur.com/Ko2wogO.jpg" />
|
github_jupyter
|
<a href="https://colab.research.google.com/github/magenta/ddsp/blob/master/ddsp/colab/tutorials/0_processor.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
##### Copyright 2020 Google LLC.
Licensed under the Apache License, Version 2.0 (the "License");
```
# Copyright 2020 Google LLC. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# http://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
# ==============================================================================
```
# DDSP Processor Demo
This notebook provides an introduction to the signal `Processor()` object. The main object type in the DDSP library, it is the base class used for Synthesizers and Effects, which share the methods:
* `get_controls()`: inputs -> controls.
* `get_signal()`: controls -> signal.
* `__call__()`: inputs -> signal. (i.e. `get_signal(**get_controls())`)
Where:
* `inputs` is a variable number of tensor arguments (depending on processor). Often the outputs of a neural network.
* `controls` is a dictionary of tensors scaled and constrained specifically for the processor
* `signal` is an output tensor (usually audio or control signal for another processor)
Let's see why this is a helpful approach by looking at the specific example of the `Additive()` synthesizer processor.
```
#@title Install and import dependencies
%tensorflow_version 2.x
!pip install -qU ddsp
# Ignore a bunch of deprecation warnings
import warnings
warnings.filterwarnings("ignore")
import ddsp
import ddsp.training
from ddsp.colab.colab_utils import play, specplot, DEFAULT_SAMPLE_RATE
import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf
sample_rate = DEFAULT_SAMPLE_RATE # 16000
```
# Example: additive synthesizer
The additive synthesizer models a sound as a linear combination of harmonic sinusoids. Amplitude envelopes are generated with 50% overlapping hann windows. The final audio is cropped to n_samples.
## `__init__()`
All member variables are initialized in the constructor, which makes it easy to change them as hyperparameters using the [gin](https://github.com/google/gin-config) dependency injection library. All processors also have a `name` that is used by `ProcessorGroup()`.
```
n_frames = 1000
hop_size = 64
n_samples = n_frames * hop_size
# Create a synthesizer object.
additive_synth = ddsp.synths.Additive(n_samples=n_samples,
sample_rate=sample_rate,
name='additive_synth')
```
## `get_controls()`
The outputs of a neural network are often not properly scaled and constrained. The `get_controls` method gives a dictionary of valid control parameters based on neural network outputs.
**3 inputs (amps, hd, f0)**
* `amplitude`: Amplitude envelope of the synthesizer output.
* `harmonic_distribution`: Normalized amplitudes of each harmonic.
* `fundamental_frequency`: Frequency in Hz of base oscillator
```
# Generate some arbitrary inputs.
# Amplitude [batch, n_frames, 1].
# Make amplitude linearly decay over time.
amps = np.linspace(1.0, -3.0, n_frames)
amps = amps[np.newaxis, :, np.newaxis]
# Harmonic Distribution [batch, n_frames, n_harmonics].
# Make harmonics decrease linearly with frequency.
n_harmonics = 30
harmonic_distribution = (np.linspace(-2.0, 2.0, n_frames)[:, np.newaxis] +
np.linspace(3.0, -3.0, n_harmonics)[np.newaxis, :])
harmonic_distribution = harmonic_distribution[np.newaxis, :, :]
# Fundamental frequency in Hz [batch, n_frames, 1].
f0_hz = 440.0 * np.ones([1, n_frames, 1], dtype=np.float32)
# Plot it!
time = np.linspace(0, n_samples / sample_rate, n_frames)
plt.figure(figsize=(18, 4))
plt.subplot(131)
plt.plot(time, amps[0, :, 0])
plt.xticks([0, 1, 2, 3, 4])
plt.title('Amplitude')
plt.subplot(132)
plt.plot(time, harmonic_distribution[0, :, :])
plt.xticks([0, 1, 2, 3, 4])
plt.title('Harmonic Distribution')
plt.subplot(133)
plt.plot(time, f0_hz[0, :, 0])
plt.xticks([0, 1, 2, 3, 4])
_ = plt.title('Fundamental Frequency')
```
Consider the plots above as outputs of a neural network. These outputs violate the synthesizer's expectations:
* Amplitude is not >= 0 (avoids phase shifts)
* Harmonic distribution is not normalized (factorizes timbre and amplitude)
* Fundamental frequency * n_harmonics > nyquist frequency (440 * 20 > 8000), which will lead to [aliasing](https://en.wikipedia.org/wiki/Aliasing).
```
controls = additive_synth.get_controls(amps, harmonic_distribution, f0_hz)
print(controls.keys())
# Now let's see what they look like...
time = np.linspace(0, n_samples / sample_rate, n_frames)
plt.figure(figsize=(18, 4))
plt.subplot(131)
plt.plot(time, controls['amplitudes'][0, :, 0])
plt.xticks([0, 1, 2, 3, 4])
plt.title('Amplitude')
plt.subplot(132)
plt.plot(time, controls['harmonic_distribution'][0, :, :])
plt.xticks([0, 1, 2, 3, 4])
plt.title('Harmonic Distribution')
plt.subplot(133)
plt.plot(time, controls['f0_hz'][0, :, 0])
plt.xticks([0, 1, 2, 3, 4])
_ = plt.title('Fundamental Frequency')
```
Notice that
* Amplitudes are now all positive
* The harmonic distribution sums to 1.0
* All harmonics that are above the Nyquist frequency now have an amplitude of 0.
The amplitudes and harmonic distribution are scaled by an "exponentiated sigmoid" function (`ddsp.core.exp_sigmoid`). There is nothing particularly special about this function (other functions can be specified as `scale_fn=` during construction), but it has several nice properties:
* Output scales logarithmically with input (as does human perception of loudness).
* Centered at 0, with max and min in reasonable range for normalized neural network outputs.
* Max value of 2.0 to prevent signal getting too loud.
* Threshold value of 1e-7 for numerical stability during training.
```
x = tf.linspace(-10.0, 10.0, 1000)
y = ddsp.core.exp_sigmoid(x)
plt.figure(figsize=(18, 4))
plt.subplot(121)
plt.plot(x, y)
plt.subplot(122)
_ = plt.semilogy(x, y)
```
## `get_signal()`
Synthesizes audio from controls.
```
audio = additive_synth.get_signal(**controls)
play(audio)
specplot(audio)
```
## `__call__()`
Synthesizes audio directly from the raw inputs. `get_controls()` is called internally to turn them into valid control parameters.
```
audio = additive_synth(amps, harmonic_distribution, f0_hz)
play(audio)
specplot(audio)
```
# Example: Just for fun...
Let's run another example where we tweak some of the controls...
```
## Some weird control envelopes...
# Amplitude [batch, n_frames, 1].
amps = np.ones([n_frames]) * -5.0
amps[:50] += np.linspace(0, 7.0, 50)
amps[50:200] += 7.0
amps[200:900] += (7.0 - np.linspace(0.0, 7.0, 700))
amps *= np.abs(np.cos(np.linspace(0, 2*np.pi * 10.0, n_frames)))
amps = amps[np.newaxis, :, np.newaxis]
# Harmonic Distribution [batch, n_frames, n_harmonics].
n_harmonics = 20
harmonic_distribution = np.ones([n_frames, 1]) * np.linspace(1.0, -1.0, n_harmonics)[np.newaxis, :]
for i in range(n_harmonics):
harmonic_distribution[:, i] = 1.0 - np.linspace(i * 0.09, 2.0, 1000)
harmonic_distribution[:, i] *= 5.0 * np.abs(np.cos(np.linspace(0, 2*np.pi * 0.1 * i, n_frames)))
if i % 2 != 0:
harmonic_distribution[:, i] = -3
harmonic_distribution = harmonic_distribution[np.newaxis, :, :]
# Fundamental frequency in Hz [batch, n_frames, 1].
f0_hz = np.ones([n_frames]) * 200.0
f0_hz[:100] *= np.linspace(2, 1, 100)**2
f0_hz[200:1000] += 20 * np.sin(np.linspace(0, 8.0, 800) * 2 * np.pi * np.linspace(0, 1.0, 800)) * np.linspace(0, 1.0, 800)
f0_hz = f0_hz[np.newaxis, :, np.newaxis]
# Get valid controls
controls = additive_synth.get_controls(amps, harmonic_distribution, f0_hz)
# Plot!
time = np.linspace(0, n_samples / sample_rate, n_frames)
plt.figure(figsize=(18, 4))
plt.subplot(131)
plt.plot(time, controls['amplitudes'][0, :, 0])
plt.xticks([0, 1, 2, 3, 4])
plt.title('Amplitude')
plt.subplot(132)
plt.plot(time, controls['harmonic_distribution'][0, :, :])
plt.xticks([0, 1, 2, 3, 4])
plt.title('Harmonic Distribution')
plt.subplot(133)
plt.plot(time, controls['f0_hz'][0, :, 0])
plt.xticks([0, 1, 2, 3, 4])
_ = plt.title('Fundamental Frequency')
audio = additive_synth.get_signal(**controls)
play(audio)
specplot(audio)
```
|
github_jupyter
|
### Tutorial: Parameterized Hypercomplex Multiplication (PHM) Layer
#### Author: Eleonora Grassucci
Original paper: Beyond Fully-Connected Layers with Quaternions: Parameterization of Hypercomplex Multiplications with 1/n Parameters.
Aston Zhang, Yi Tay, Shuai Zhang, Alvin Chan, Anh Tuan Luu, Siu Cheung Hui, Jie Fu.
[ArXiv link](https://arxiv.org/pdf/2102.08597.pdf).
```
# Imports
import numpy as np
import math
import time
import torch
import torch.nn as nn
from torch.autograd import Variable
import torch.nn.functional as F
import torch.utils.data as Data
from torch.nn import init
# Check Pytorch version: torch.kron is available from 1.8.0
torch.__version__
# Define the PHM class
class PHM(nn.Module):
'''
Simple PHM Module, the only parameter is A, since S is passed from the trainset.
'''
def __init__(self, n, kernel_size, **kwargs):
super().__init__(**kwargs)
self.n = n
A = torch.empty((n-1, n, n))
self.A = nn.Parameter(A)
self.kernel_size = kernel_size
def forward(self, X, S):
H = torch.zeros((self.n*self.kernel_size, self.n*self.kernel_size))
# Sum of Kronecker products
for i in range(n-1):
H = H + torch.kron(self.A[i], S[i])
return torch.matmul(X, H.T)
```
### Learn the Hamilton product between two pure quaternions
A pure quaternion is a quaternion with scalar part equal to 0.
```
# Setup the training set
x = torch.FloatTensor([0, 1, 2, 3]).view(4, 1) # Scalar part equal to 0
W = torch.FloatTensor([[0,-1,-1,-1], [1,0,-1,1], [1,1,0,-1], [1,-1,1,0]]) # Scalar parts equal to 0
y = torch.matmul(W, x)
num_examples = 1000
batch_size = 1
X = torch.zeros((num_examples, 16))
S = torch.zeros((num_examples, 16))
Y = torch.zeros((num_examples, 16))
for i in range(num_examples):
x = torch.randint(low=-10, high=10, size=(12, ), dtype=torch.float)
s = torch.randint(low=-10, high=10, size=(12, ), dtype=torch.float)
s1, s2, s3, s4 = torch.FloatTensor([0]*4), s[0:4], s[4:8], s[8:12]
s1 = s1.view(2,2)
s2 = s2.view(2,2)
s3 = s3.view(2,2)
s4 = s4.view(2,2)
s_1 = torch.cat([s1,-s2,-s3,-s4])
s_2 = torch.cat([s2,s1,-s4,s3])
s_3 = torch.cat([s3,s4,s1,-s2])
s_4 = torch.cat([s4,-s3,s2,s1])
W = torch.cat([s_1,s_2, s_3, s_4], dim=1)
x = torch.cat([torch.FloatTensor([0]*4), x])
s = torch.cat([torch.FloatTensor([0]*4), s])
x_mult = x.view(2, 8)
y = torch.matmul(x_mult, W.T)
y = y.view(16, )
X[i, :] = x
S[i, :] = s
Y[i, :] = y
X = torch.FloatTensor(X).view(num_examples, 16, 1)
S = torch.FloatTensor(S).view(num_examples, 16, 1)
Y = torch.FloatTensor(Y).view(num_examples, 16, 1)
data = torch.cat([X, S, Y], dim=2)
train_iter = torch.utils.data.DataLoader(data, batch_size=batch_size)
### Setup the test set
num_examples = 1
batch_size = 1
X = torch.zeros((num_examples, 16))
S = torch.zeros((num_examples, 16))
Y = torch.zeros((num_examples, 16))
for i in range(num_examples):
x = torch.randint(low=-10, high=10, size=(12, ), dtype=torch.float)
s = torch.randint(low=-10, high=10, size=(12, ), dtype=torch.float)
s1, s2, s3, s4 = torch.FloatTensor([0]*4), s[0:4], s[4:8], s[8:12]
s1 = s1.view(2,2)
s2 = s2.view(2,2)
s3 = s3.view(2,2)
s4 = s4.view(2,2)
s_1 = torch.cat([s1,-s2,-s3,-s4])
s_2 = torch.cat([s2,s1,-s4,s3])
s_3 = torch.cat([s3,s4,s1,-s2])
s_4 = torch.cat([s4,-s3,s2,s1])
W = torch.cat([s_1,s_2, s_3, s_4], dim=1)
x = torch.cat([torch.FloatTensor([0]*4), x])
s = torch.cat([torch.FloatTensor([0]*4), s])
x_mult = x.view(2, 8)
y = torch.matmul(x_mult, W.T)
y = y.view(16, )
X[i, :] = x
S[i, :] = s
Y[i, :] = y
X = torch.FloatTensor(X).view(num_examples, 16, 1)
S = torch.FloatTensor(S).view(num_examples, 16, 1)
Y = torch.FloatTensor(Y).view(num_examples, 16, 1)
data = torch.cat([X, S, Y], dim=2)
test_iter = torch.utils.data.DataLoader(data, batch_size=batch_size)
# Define training function
def train(net, lr, phm=True):
# Squared loss
loss = nn.MSELoss()
optimizer = torch.optim.Adam(net.parameters(), lr=lr)
for epoch in range(5):
for data in train_iter:
optimizer.zero_grad()
X = data[:, :, 0]
S = data[:, 4:, 1]
Y = data[:, :, 2]
if phm:
out = net(X.view(2, 8), S.view(3, 2, 2))
else:
out = net(X)
l = loss(out, Y.view(2, 8))
l.backward()
optimizer.step()
print(f'epoch {epoch + 1}, loss {float(l.sum() / batch_size):.6f}')
# Initialize model parameters
def weights_init_uniform(m):
m.A.data.uniform_(-0.07, 0.07)
# Create layer instance
n = 4
phm_layer = PHM(n, kernel_size=2)
phm_layer.apply(weights_init_uniform)
# Train the model
train(phm_layer, 0.005)
# Check parameters of the layer require grad
for name, param in phm_layer.named_parameters():
if param.requires_grad:
print(name, param.data)
# Take a look at the convolution performed on the test set
for data in test_iter:
X = data[:, :, 0]
S = data[:, 4:, 1]
Y = data[:, :, 2]
y_phm = phm_layer(X.view(2, 8), S.view(3, 2, 2))
print('Hamilton product result from test set:\n', Y.view(2, 8))
print('Performing Hamilton product learned by PHM:\n', y_phm)
# Check the PHC layer have learnt the proper algebra for the marix A
W = torch.FloatTensor([[0,-1,-1,-1], [1,0,-1,1], [1,1,0,-1], [1,-1,1,0]])
print('Ground-truth Hamilton product matrix:\n', W)
print()
print('Learned A in PHM:\n', phm_layer.A)
print()
print('Learned A sum in PHM:\n', sum(phm_layer.A).T)
```
|
github_jupyter
|
```
import sys
import pandas as pd
import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt
sys.path.append('../Scripts')
from Data_Processing import DataProcessing
from tensorflow import keras
from keras.callbacks import ModelCheckpoint
from keras.models import load_model
from keras import backend as K
from datetime import datetime
from sklearn.preprocessing import PowerTransformer
import joblib
import warnings
warnings.filterwarnings('ignore')
ColumnTransformer = joblib.load('../Models/Column_Transformer.pkl')
#PowerTransformer = joblib.load('../Models/Power_Transformer.pkl')
ColumnTransformer_NN = joblib.load('../Models/Column_Transformer_NN.pkl')
df = DataProcessing('../Data/test.csv')
y = df['Lap_Time']
X = df.drop(columns=['Lap_Time'])
obj_columns = list(X.select_dtypes(include=object).columns)
obj_columns.append('Lap_Number')
obj_columns.append('Lap_Improvement')
num_columns = list(X.select_dtypes(include='number').columns)
num_columns.remove('Lap_Number')
num_columns.remove('Lap_Improvement')
#NN Only
y = df['Lap_Time']
X = df.drop(columns=['Lap_Time'])
obj_columns = list(X.select_dtypes(include=object).columns)
obj_columns.append('Lap_Improvement')
obj_columns.append('Lap_Number')
obj_columns.append('S1_Improvement')
obj_columns.append('S2_Improvement')
obj_columns.append('S3_Improvement')
num_columns = list(X.select_dtypes(include='number').columns)
num_columns.remove('Lap_Number')
num_columns.remove('Lap_Improvement')
num_columns.remove('S1_Improvement')
num_columns.remove('S2_Improvement')
num_columns.remove('S3_Improvement')
#X[num_columns] = PowerTransformer.transform(X[num_columns])
trans_X_nn = ColumnTransformer_NN.transform(X)
#trans_X = trans_X.toarray()
#trans_X = trans_X[:,[0, 2, 4, 6, 8, 9, 10, 12, 13, 14, 15, 16, 17, 18, 72, 73]]
#trans_X_nn = trans_X_nn.toarray()
def root_mean_squared_log_error(y_true, y_pred):
return K.sqrt(K.mean(K.square(K.log(1+y_pred) - K.log(1+y_true))))
#Neural Network
nn_model = load_model('../Models/NN_model_test.h5')
#nn_model = load_model('../Models/NN_model.h5', custom_objects={'root_mean_squared_log_error': root_mean_squared_log_error})
#Random Forest
rf_model = joblib.load('../Models/RF_Model.h5')
#Gradient Boost
gb_model = joblib.load('../Models/Gradient_Boost_Model.h5')
nn_y_scaler = joblib.load('../Models/NN_Y_Scaler.pkl')
y_predicted_nn = nn_y_scaler.inverse_transform(nn_model.predict(trans_X_nn))
y_predicted_nn = ((1 / y_predicted_nn) - 1).ravel()
y_predicted_nn = nn_y_scaler.inverse_transform(nn_model.predict(trans_X_nn))
#y_predicted_rf = rf_model.predict(trans_X)
#y_predicted_gb = gb_model.predict(trans_X)
results = pd.DataFrame()
results['NN'] = y_predicted_nn
results['RF'] = y_predicted_rf
results['GB'] = y_predicted_gb
results['LAP_TIME'] = (results['NN'] + results['RF'] + results['GB']) / 3
submission = results[['LAP_TIME']]
results
#Random Forest Only
submission = results[['RF']]
submission = submission.rename(columns={'RF': 'LAP_TIME'})
today = datetime.today().strftime('%m-%d-%y %H-%M')
submission.to_csv(f'../Submissions/Dare_In_Reality {today}.csv', index=False)
```
### Just Neural Network
```
submission = pd.DataFrame()
submission['LAP_TIME'] = y_predicted_nn.ravel()
submission
submission.to_csv(f'../Submissions/Dare_In_Reality NN Only.csv', index=False)
y_predicted_nn
df
```
|
github_jupyter
|
# Amazon Fine Food Reviews Analysis
Data Source: https://www.kaggle.com/snap/amazon-fine-food-reviews <br>
EDA: https://nycdatascience.com/blog/student-works/amazon-fine-foods-visualization/
The Amazon Fine Food Reviews dataset consists of reviews of fine foods from Amazon.<br>
Number of reviews: 568,454<br>
Number of users: 256,059<br>
Number of products: 74,258<br>
Timespan: Oct 1999 - Oct 2012<br>
Number of Attributes/Columns in data: 10
Attribute Information:
1. Id
2. ProductId - unique identifier for the product
3. UserId - unqiue identifier for the user
4. ProfileName
5. HelpfulnessNumerator - number of users who found the review helpful
6. HelpfulnessDenominator - number of users who indicated whether they found the review helpful or not
7. Score - rating between 1 and 5
8. Time - timestamp for the review
9. Summary - brief summary of the review
10. Text - text of the review
#### Objective:
Given a review, determine whether the review is positive (rating of 4 or 5) or negative (rating of 1 or 2).
<br>
[Q] How to determine if a review is positive or negative?<br>
<br>
[Ans] We could use Score/Rating. A rating of 4 or 5 can be cosnidered as a positive review. A rating of 1 or 2 can be considered as negative one. A review of rating 3 is considered nuetral and such reviews are ignored from our analysis. This is an approximate and proxy way of determining the polarity (positivity/negativity) of a review.
# [1]. Reading Data
## [1.1] Loading the data
The dataset is available in two forms
1. .csv file
2. SQLite Database
In order to load the data, We have used the SQLITE dataset as it is easier to query the data and visualise the data efficiently.
<br>
Here as we only want to get the global sentiment of the recommendations (positive or negative), we will purposefully ignore all Scores equal to 3. If the score is above 3, then the recommendation wil be set to "positive". Otherwise, it will be set to "negative".
```
%matplotlib inline
import warnings
warnings.filterwarnings("ignore")
import sqlite3
import pandas as pd
import numpy as np
import nltk
import string
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.feature_extraction.text import TfidfTransformer
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.metrics.pairwise import cosine_similarity
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.metrics import confusion_matrix
from sklearn import metrics
from sklearn.metrics import roc_curve, auc
from nltk.stem.porter import PorterStemmer
from sklearn.model_selection import train_test_split
from sklearn.model_selection import cross_val_score
from sklearn.metrics import roc_auc_score
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.decomposition import TruncatedSVD
from sklearn.cluster import KMeans
from wordcloud import WordCloud, STOPWORDS
import re
# Tutorial about Python regular expressions: https://pymotw.com/2/re/
import string
from nltk.corpus import stopwords
from nltk.stem import PorterStemmer
from nltk.stem.wordnet import WordNetLemmatizer
from gensim.models import Word2Vec
from gensim.models import KeyedVectors
import pickle
from tqdm import tqdm
import os
from google.colab import drive
drive.mount('/content/drive')
# using SQLite Table to read data.
con = sqlite3.connect('drive/My Drive/database.sqlite')
# filtering only positive and negative reviews i.e.
# not taking into consideration those reviews with Score=3
# SELECT * FROM Reviews WHERE Score != 3 LIMIT 500000, will give top 500000 data points
# you can change the number to any other number based on your computing power
# filtered_data = pd.read_sql_query(""" SELECT * FROM Reviews WHERE Score != 3 LIMIT 500000""", con)
# for tsne assignment you can take 5k data points
filtered_data = pd.read_sql_query(""" SELECT * FROM Reviews WHERE Score != 3 LIMIT 200000""", con)
# Give reviews with Score>3 a positive rating(1), and reviews with a score<3 a negative rating(0).
def partition(x):
if x < 3:
return 0
return 1
#changing reviews with score less than 3 to be positive and vice-versa
actualScore = filtered_data['Score']
positiveNegative = actualScore.map(partition)
filtered_data['Score'] = positiveNegative
print("Number of data points in our data", filtered_data.shape)
filtered_data.head(3)
display = pd.read_sql_query("""
SELECT UserId, ProductId, ProfileName, Time, Score, Text, COUNT(*)
FROM Reviews
GROUP BY UserId
HAVING COUNT(*)>1
""", con)
print(display.shape)
display.head()
display[display['UserId']=='AZY10LLTJ71NX']
display['COUNT(*)'].sum()
```
# [2] Exploratory Data Analysis
## [2.1] Data Cleaning: Deduplication
It is observed (as shown in the table below) that the reviews data had many duplicate entries. Hence it was necessary to remove duplicates in order to get unbiased results for the analysis of the data. Following is an example:
```
display= pd.read_sql_query("""
SELECT *
FROM Reviews
WHERE Score != 3 AND UserId="AR5J8UI46CURR"
ORDER BY ProductID
""", con)
display.head()
```
As it can be seen above that same user has multiple reviews with same values for HelpfulnessNumerator, HelpfulnessDenominator, Score, Time, Summary and Text and on doing analysis it was found that <br>
<br>
ProductId=B000HDOPZG was Loacker Quadratini Vanilla Wafer Cookies, 8.82-Ounce Packages (Pack of 8)<br>
<br>
ProductId=B000HDL1RQ was Loacker Quadratini Lemon Wafer Cookies, 8.82-Ounce Packages (Pack of 8) and so on<br>
It was inferred after analysis that reviews with same parameters other than ProductId belonged to the same product just having different flavour or quantity. Hence in order to reduce redundancy it was decided to eliminate the rows having same parameters.<br>
The method used for the same was that we first sort the data according to ProductId and then just keep the first similar product review and delelte the others. for eg. in the above just the review for ProductId=B000HDL1RQ remains. This method ensures that there is only one representative for each product and deduplication without sorting would lead to possibility of different representatives still existing for the same product.
```
#Sorting data according to ProductId in ascending order
sorted_data=filtered_data.sort_values('ProductId', axis=0, ascending=True, inplace=False, kind='quicksort', na_position='last')
#Deduplication of entries
final=sorted_data.drop_duplicates(subset={"UserId","ProfileName","Time","Text"}, keep='first', inplace=False)
final.shape
#Checking to see how much % of data still remains
(final['Id'].size*1.0)/(filtered_data['Id'].size*1.0)*100
```
<b>Observation:-</b> It was also seen that in two rows given below the value of HelpfulnessNumerator is greater than HelpfulnessDenominator which is not practically possible hence these two rows too are removed from calcualtions
```
display= pd.read_sql_query("""
SELECT *
FROM Reviews
WHERE Score != 3 AND Id=44737 OR Id=64422
ORDER BY ProductID
""", con)
display.head()
final=final[final.HelpfulnessNumerator<=final.HelpfulnessDenominator]
#Before starting the next phase of preprocessing lets see the number of entries left
print(final.shape)
#How many positive and negative reviews are present in our dataset?
final['Score'].value_counts()
```
# [3] Preprocessing
## [3.1]. Preprocessing Review Text
Now that we have finished deduplication our data requires some preprocessing before we go on further with analysis and making the prediction model.
Hence in the Preprocessing phase we do the following in the order below:-
1. Begin by removing the html tags
2. Remove any punctuations or limited set of special characters like , or . or # etc.
3. Check if the word is made up of english letters and is not alpha-numeric
4. Check to see if the length of the word is greater than 2 (as it was researched that there is no adjective in 2-letters)
5. Convert the word to lowercase
6. Remove Stopwords
7. Finally Snowball Stemming the word (it was obsereved to be better than Porter Stemming)<br>
After which we collect the words used to describe positive and negative reviews
```
# printing some random reviews
sent_0 = final['Text'].values[0]
print(sent_0)
print("="*50)
sent_1000 = final['Text'].values[1000]
print(sent_1000)
print("="*50)
sent_1500 = final['Text'].values[1500]
print(sent_1500)
print("="*50)
sent_4900 = final['Text'].values[4900]
print(sent_4900)
print("="*50)
# remove urls from text python: https://stackoverflow.com/a/40823105/4084039
sent_0 = re.sub(r"http\S+", "", sent_0)
sent_1000 = re.sub(r"http\S+", "", sent_1000)
sent_150 = re.sub(r"http\S+", "", sent_1500)
sent_4900 = re.sub(r"http\S+", "", sent_4900)
print(sent_0)
# https://stackoverflow.com/questions/16206380/python-beautifulsoup-how-to-remove-all-tags-from-an-element
from bs4 import BeautifulSoup
soup = BeautifulSoup(sent_0, 'lxml')
text = soup.get_text()
print(text)
print("="*50)
soup = BeautifulSoup(sent_1000, 'lxml')
text = soup.get_text()
print(text)
print("="*50)
soup = BeautifulSoup(sent_1500, 'lxml')
text = soup.get_text()
print(text)
print("="*50)
soup = BeautifulSoup(sent_4900, 'lxml')
text = soup.get_text()
print(text)
# https://stackoverflow.com/a/47091490/4084039
import re
def decontracted(phrase):
# specific
phrase = re.sub(r"won't", "will not", phrase)
phrase = re.sub(r"can\'t", "can not", phrase)
# general
phrase = re.sub(r"n\'t", " not", phrase)
phrase = re.sub(r"\'re", " are", phrase)
phrase = re.sub(r"\'s", " is", phrase)
phrase = re.sub(r"\'d", " would", phrase)
phrase = re.sub(r"\'ll", " will", phrase)
phrase = re.sub(r"\'t", " not", phrase)
phrase = re.sub(r"\'ve", " have", phrase)
phrase = re.sub(r"\'m", " am", phrase)
return phrase
sent_1500 = decontracted(sent_1500)
print(sent_1500)
print("="*50)
#remove words with numbers python: https://stackoverflow.com/a/18082370/4084039
sent_0 = re.sub("\S*\d\S*", "", sent_0).strip()
print(sent_0)
#remove spacial character: https://stackoverflow.com/a/5843547/4084039
sent_1500 = re.sub('[^A-Za-z0-9]+', ' ', sent_1500)
print(sent_1500)
# https://gist.github.com/sebleier/554280
# we are removing the words from the stop words list: 'no', 'nor', 'not'
# <br /><br /> ==> after the above steps, we are getting "br br"
# we are including them into stop words list
# instead of <br /> if we have <br/> these tags would have revmoved in the 1st step
stopwords= set(['br', 'the', 'i', 'me', 'my', 'myself', 'we', 'our', 'ours', 'ourselves', 'you', "you're", "you've",\
"you'll", "you'd", 'your', 'yours', 'yourself', 'yourselves', 'he', 'him', 'his', 'himself', \
'she', "she's", 'her', 'hers', 'herself', 'it', "it's", 'its', 'itself', 'they', 'them', 'their',\
'theirs', 'themselves', 'what', 'which', 'who', 'whom', 'this', 'that', "that'll", 'these', 'those', \
'am', 'is', 'are', 'was', 'were', 'be', 'been', 'being', 'have', 'has', 'had', 'having', 'do', 'does', \
'did', 'doing', 'a', 'an', 'the', 'and', 'but', 'if', 'or', 'because', 'as', 'until', 'while', 'of', \
'at', 'by', 'for', 'with', 'about', 'against', 'between', 'into', 'through', 'during', 'before', 'after',\
'above', 'below', 'to', 'from', 'up', 'down', 'in', 'out', 'on', 'off', 'over', 'under', 'again', 'further',\
'then', 'once', 'here', 'there', 'when', 'where', 'why', 'how', 'all', 'any', 'both', 'each', 'few', 'more',\
'most', 'other', 'some', 'such', 'only', 'own', 'same', 'so', 'than', 'too', 'very', \
's', 't', 'can', 'will', 'just', 'don', "don't", 'should', "should've", 'now', 'd', 'll', 'm', 'o', 're', \
've', 'y', 'ain', 'aren', "aren't", 'couldn', "couldn't", 'didn', "didn't", 'doesn', "doesn't", 'hadn',\
"hadn't", 'hasn', "hasn't", 'haven', "haven't", 'isn', "isn't", 'ma', 'mightn', "mightn't", 'mustn',\
"mustn't", 'needn', "needn't", 'shan', "shan't", 'shouldn', "shouldn't", 'wasn', "wasn't", 'weren', "weren't", \
'won', "won't", 'wouldn', "wouldn't"])
# Combining all the above stundents
from tqdm import tqdm
preprocessed_reviews = []
# tqdm is for printing the status bar
for sentance in tqdm(final['Text'].values):
sentance = re.sub(r"http\S+", "", sentance)
sentance = BeautifulSoup(sentance, 'lxml').get_text()
sentance = decontracted(sentance)
sentance = re.sub("\S*\d\S*", "", sentance).strip()
sentance = re.sub('[^A-Za-z]+', ' ', sentance)
# https://gist.github.com/sebleier/554280
sentance = ' '.join(e.lower() for e in sentance.split() if e.lower() not in stopwords)
preprocessed_reviews.append(sentance.strip())
preprocessed_reviews[100000]
```
# [4] Featurization
## [4.1] BAG OF WORDS
```
#BoW
count_vect = CountVectorizer() #in scikit-learn
count_vect.fit(preprocessed_reviews)
print("some feature names ", count_vect.get_feature_names()[:10])
print('='*50)
final_counts = count_vect.transform(preprocessed_reviews)
print("the type of count vectorizer ",type(final_counts))
print("the shape of out text BOW vectorizer ",final_counts.get_shape())
print("the number of unique words ", final_counts.get_shape()[1])
```
## [4.2] Bi-Grams and n-Grams.
```
#bi-gram, tri-gram and n-gram
#removing stop words like "not" should be avoided before building n-grams
# count_vect = CountVectorizer(ngram_range=(1,2))
# please do read the CountVectorizer documentation http://scikit-learn.org/stable/modules/generated/sklearn.feature_extraction.text.CountVectorizer.html
# you can choose these numebrs min_df=10, max_features=5000, of your choice
count_vect = CountVectorizer(ngram_range=(1,2), min_df=10, max_features=5000)
final_bigram_counts = count_vect.fit_transform(preprocessed_reviews)
print("the type of count vectorizer ",type(final_bigram_counts))
print("the shape of out text BOW vectorizer ",final_bigram_counts.get_shape())
print("the number of unique words including both unigrams and bigrams ", final_bigram_counts.get_shape()[1])
```
## [4.3] TF-IDF
```
tf_idf_vect = TfidfVectorizer(ngram_range=(1,2), min_df=10)
tf_idf_vect.fit(preprocessed_reviews)
print("some sample features(unique words in the corpus)",tf_idf_vect.get_feature_names()[0:10])
print('='*50)
final_tf_idf = tf_idf_vect.transform(preprocessed_reviews)
print("the type of count vectorizer ",type(final_tf_idf))
print("the shape of out text TFIDF vectorizer ",final_tf_idf.get_shape())
print("the number of unique words including both unigrams and bigrams ", final_tf_idf.get_shape()[1])
```
## [4.4] Word2Vec
```
# Train your own Word2Vec model using your own text corpus
i=0
list_of_sentance=[]
for sentance in preprocessed_reviews:
list_of_sentance.append(sentance.split())
# Using Google News Word2Vectors
# in this project we are using a pretrained model by google
# its 3.3G file, once you load this into your memory
# it occupies ~9Gb, so please do this step only if you have >12G of ram
# we will provide a pickle file wich contains a dict ,
# and it contains all our courpus words as keys and model[word] as values
# To use this code-snippet, download "GoogleNews-vectors-negative300.bin"
# from https://drive.google.com/file/d/0B7XkCwpI5KDYNlNUTTlSS21pQmM/edit
# it's 1.9GB in size.
# http://kavita-ganesan.com/gensim-word2vec-tutorial-starter-code/#.W17SRFAzZPY
# you can comment this whole cell
# or change these varible according to your need
is_your_ram_gt_16g=False
want_to_use_google_w2v = False
want_to_train_w2v = True
if want_to_train_w2v:
# min_count = 5 considers only words that occured atleast 5 times
w2v_model=Word2Vec(list_of_sentance,min_count=5,size=50, workers=4)
print(w2v_model.wv.most_similar('great'))
print('='*50)
print(w2v_model.wv.most_similar('worst'))
elif want_to_use_google_w2v and is_your_ram_gt_16g:
if os.path.isfile('GoogleNews-vectors-negative300.bin'):
w2v_model=KeyedVectors.load_word2vec_format('GoogleNews-vectors-negative300.bin', binary=True)
print(w2v_model.wv.most_similar('great'))
print(w2v_model.wv.most_similar('worst'))
else:
print("you don't have gogole's word2vec file, keep want_to_train_w2v = True, to train your own w2v ")
w2v_words = list(w2v_model.wv.vocab)
print("number of words that occured minimum 5 times ",len(w2v_words))
print("sample words ", w2v_words[0:50])
```
## [4.4.1] Converting text into vectors using Avg W2V, TFIDF-W2V
#### [4.4.1.1] Avg W2v
```
# average Word2Vec
# compute average word2vec for each review.
sent_vectors = []; # the avg-w2v for each sentence/review is stored in this list
for sent in tqdm(list_of_sentance): # for each review/sentence
sent_vec = np.zeros(50) # as word vectors are of zero length 50, you might need to change this to 300 if you use google's w2v
cnt_words =0; # num of words with a valid vector in the sentence/review
for word in sent: # for each word in a review/sentence
if word in w2v_words:
vec = w2v_model.wv[word]
sent_vec += vec
cnt_words += 1
if cnt_words != 0:
sent_vec /= cnt_words
sent_vectors.append(sent_vec)
print(len(sent_vectors))
print(len(sent_vectors[0]))
```
#### [4.4.1.2] TFIDF weighted W2v
```
# S = ["abc def pqr", "def def def abc", "pqr pqr def"]
model = TfidfVectorizer()
tf_idf_matrix = model.fit_transform(preprocessed_reviews)
# we are converting a dictionary with word as a key, and the idf as a value
dictionary = dict(zip(model.get_feature_names(), list(model.idf_)))
# TF-IDF weighted Word2Vec
tfidf_feat = model.get_feature_names() # tfidf words/col-names
# final_tf_idf is the sparse matrix with row= sentence, col=word and cell_val = tfidf
tfidf_sent_vectors = []; # the tfidf-w2v for each sentence/review is stored in this list
row=0;
for sent in tqdm(list_of_sentance): # for each review/sentence
sent_vec = np.zeros(50) # as word vectors are of zero length
weight_sum =0; # num of words with a valid vector in the sentence/review
for word in sent: # for each word in a review/sentence
if word in w2v_words and word in tfidf_feat:
vec = w2v_model.wv[word]
# tf_idf = tf_idf_matrix[row, tfidf_feat.index(word)]
# to reduce the computation we are
# dictionary[word] = idf value of word in whole courpus
# sent.count(word) = tf valeus of word in this review
tf_idf = dictionary[word]*(sent.count(word)/len(sent))
sent_vec += (vec * tf_idf)
weight_sum += tf_idf
if weight_sum != 0:
sent_vec /= weight_sum
tfidf_sent_vectors.append(sent_vec)
row += 1
```
## Truncated-SVD
### [5.1] Taking top features from TFIDF,<font color='red'> SET 2</font>
```
# Please write all the code with proper documentation
X = preprocessed_reviews[:]
y = final['Score'][:]
tf_idf = TfidfVectorizer()
tfidf_data = tf_idf.fit_transform(X)
tfidf_feat = tf_idf.get_feature_names()
```
### [5.2] Calulation of Co-occurrence matrix
```
# Please write all the code with proper documentation
#Ref:https://datascience.stackexchange.com/questions/40038/how-to-implement-word-to-word-co-occurence-matrix-in-python
#Ref:# https://github.com/PushpendraSinghChauhan/Amazon-Fine-Food-Reviews/blob/master/Computing%20Word%20Vectors%20using%20TruncatedSVD.ipynb
def Co_Occurrence_Matrix(neighbour_num , list_words):
# Storing all words with their indices in the dictionary
corpus = dict()
# List of all words in the corpus
doc = []
index = 0
for sent in preprocessed_reviews:
for word in sent.split():
doc.append(word)
corpus.setdefault(word,[])
corpus[word].append(index)
index += 1
# Co-occurrence matrix
matrix = []
# rows in co-occurrence matrix
for row in list_words:
# row in co-occurrence matrix
temp = []
# column in co-occurrence matrix
for col in list_words :
if( col != row):
# No. of times col word is in neighbourhood of row word
count = 0
# Value of neighbourhood
num = neighbour_num
# Indices of row word in the corpus
positions = corpus[row]
for i in positions:
if i<(num-1):
# Checking for col word in neighbourhood of row
if col in doc[i:i+num]:
count +=1
elif (i>=(num-1)) and (i<=(len(doc)-num)):
# Check col word in neighbour of row
if (col in doc[i-(num-1):i+1]) and (col in doc[i:i+num]):
count +=2
# Check col word in neighbour of row
elif (col in doc[i-(num-1):i+1]) or (col in doc[i:i+num]):
count +=1
else :
if (col in doc[i-(num-1):i+1]):
count +=1
# appending the col count to row of co-occurrence matrix
temp.append(count)
else:
# Append 0 in the column if row and col words are equal
temp.append(0)
# appending the row in co-occurrence matrix
matrix.append(temp)
# Return co-occurrence matrix
return np.array(matrix)
X_new = Co_Occurrence_Matrix(15, top_feat)
```
### [5.3] Finding optimal value for number of components (n) to be retained.
```
# Please write all the code with proper documentation
k = np.arange(2,100,3)
variance =[]
for i in k:
svd = TruncatedSVD(n_components=i)
svd.fit_transform(X_new)
score = svd.explained_variance_ratio_.sum()
variance.append(score)
plt.plot(k, variance)
plt.xlabel('Number of Components')
plt.ylabel('Explained Variance')
plt.title('n_components VS Explained variance')
plt.show()
```
### [5.4] Applying k-means clustering
```
# Please write all the code with proper documentation
errors = []
k = [2, 5, 10, 15, 25, 30, 50, 100]
for i in k:
kmeans = KMeans(n_clusters=i, random_state=0)
kmeans.fit(X_new)
errors.append(kmeans.inertia_)
plt.plot(k, errors)
plt.xlabel('K')
plt.ylabel('Error')
plt.title('K VS Error Plot')
plt.show()
svd = TruncatedSVD(n_components = 20)
svd.fit(X_new)
score = svd.explained_variance_ratio_
```
### [5.5] Wordclouds of clusters obtained in the above section
```
# Please write all the code with proper documentation
indices = np.argsort(tf_idf.idf_[::-1])
top_feat = [tfidf_feat[i] for i in indices[0:3000]]
top_indices = indices[0:3000]
top_n = np.argsort(top_feat[::-1])
feature_importances = pd.DataFrame(top_n, index = top_feat, columns=['importance']).sort_values('importance',ascending=False)
top = feature_importances.iloc[0:30]
comment_words = ' '
for val in top.index:
val = str(val)
tokens = val.split()
# Converts each token into lowercase
for i in range(len(tokens)):
tokens[i] = tokens[i].lower()
for words in tokens:
comment_words = comment_words + words + ' '
stopwords = set(STOPWORDS)
wordcloud = WordCloud(width = 600, height = 600,
background_color ='black',
stopwords = stopwords,
min_font_size = 10).generate(comment_words)
plt.figure(figsize = (10, 10), facecolor = None)
plt.imshow(wordcloud)
plt.axis("off")
plt.tight_layout(pad = 0)
plt.show()
```
### [5.6] Function that returns most similar words for a given word.
```
# Please write all the code with proper documentation
def similarity(word):
similarity = cosine_similarity(X_new)
word_vect = similarity[top_feat.index(word)]
index = word_vect.argsort()[::-1][1:5]
for i in range(len(index)):
print((i+1),top_feat[index[i]] ,"\n")
similarity('sugary')
similarity('notlike')
```
# [6] Conclusions
```
# Please write down few lines about what you observed from this assignment.
# Also please do mention the optimal values that you obtained for number of components & number of clusters.
from prettytable import PrettyTable
x = PrettyTable()
x.field_names = ["Algorithm","Best Hyperparameter"]
x.add_row(["T-SVD", 20])
x.add_row(["K-Means", 20])
print(x)
```
* It can be obseverd that just 20 components preserve about 99.9% of the variance in the data.
* The co occurence matrix used is to find the correlation of one word with respect to the other in the dataset.
|
github_jupyter
|
# Conditional statements - part 1
## Motivation
All the previous programs are based on a pure sequence of statements. After the start of the program the statements are
executed step by step and the program ends afterwards. However, it is often necessary that parts of a program are
only executed under certain conditions. For example, think of the following sentence and how it
would be converted into a [pseudo code](https://de.wikipedia.org/wiki/Pseudocode) program:
> If it rains tomorrow, I will clean up the basement. Then I will tidy the cupboards and sort the photos. Otherwise, I
> will go swimming. In the evening I will go to the cinema with my wife.
The textual description of the task is not precise. It is not exactly clear what is to be done.
This is common for description in natural language. Often addition information is conveyed through the
context of e.g. a conversation. What is probably meant in the previous example is the following:
```
If it rains tomorrow, I will:
- clean up the basement
- tidy the cupboards
- sort the photos
Otherwise (so if it doesn't rain), I will:
go swimming.
In the evening I will go to the cinema with my wife.
```
So, depending on the weather either one or the other path of the pseudo code program is executed. This
is illustrated in the following graphic:

To enable this more complex workflow two things are required:
- First, a construction that allows to split the workflow in different paths depending on a given condition.
- Second, a specification of conditions.
## Conditions
So, what is a condition? In the end, it is something that is either `True` or `False`, in other word, a condition always results in a boolean value. In principal, you could use `True` or `False`, when a condition is required. However, this not flexible, i.e. `True` is always true. More sophisticated conditions can be expressed by comparing the content of variables with a given value. For example, there is an integer variable `age`. Then the value can be either equal to 18 or not equal. So checking for *is the value of age equal to 18* can either be `True` or `False`. There are a number of comparison operators, which can be used for both numerical datatypes and string datatypes. In the former case, the usual order of numbers is used, in the latter case, the alphabetic order is taken.
## Comparison Operators
In order to use decisions in programs a way to specify conditions is needed. To formulate condition the comparison
operators can be used. The following table shows a selection of comparison operators available in Python. The result of
a comparison using these operators is always a `Boolean` value. As already explained, the only possible `Boolean` values
are `True` and `False`. For each comparison operator the table contain two example expressions that result in `True`
and `False` respectively.
| Operator | Explanation | Example True | Example False |
| -------- | ------------------------------------ | ------------ | ------------- |
| == | Check for equality | 2 == 2 | 2 == 3 |
| != | Check for inequality | 2 != 3 | 2 != 2 |
| < | Check for "smaller" | 2 < 3 | 2 < 1 |
| > | Check for "larger" | 3 > 2 | 2 > 3 |
| <= | Check for "less than or equal to" | 3 <= 3 | 3 <= 2 |
| >= | Check for "greater than or equal to" | 2 >= 2 | 2 >= 3 |
## `=` vs. `==`
It is important to emphasize the difference between `=` and `==`. If there is one equal sign, the statement is an *assignment*. A value is assigned to a variable. The assignment has no return value, it is neither true or false. If there are two equal signs, it is a comparison. The values on both sides of the `""` are unchanged. However, the comparison leads to a value, namely `True` or `False`.
## Complex Conditions
What happens, if you want to check, if the variable `age` is greater than 18 but smaller than 30? In this case, you can build complex conditions using the boolean operators `and`, `or` and `not` (cf. the notebook about datatypes).
## Exercise
Familiarize yourself with the comparison operators. Also test more complex comparisons, such as:
```python
"abc" < "abd"
"abcd" > "abc"
2 == 2.0
1 == True
0 != True
```
```
1 == True
```
# Conditional statements
Using the conditional operators it is now possible to formulate conditional statements in Python.
The syntax for conditional statements in Python is:
```python
if condition:
statement_a1
...
statement_an
else:
statement_b1
...
statement_bm
```
The result of the condition can be either `True` or `False`. If the condition is `True` the statements `a1` to `an` are executed.
If the condition is `False` the statements `b1` to `bm` are executed.
Note, that the `else` branch is optional, i.e. an
`if` condition can also be specified without an `else` alternative. If the condition then is not true (i.e. `false`),
the statements of the `if` block are simply skipped.
```
number = int(input("Please type a number: "))
if number > 100:
print(number, "is greater than 100!")
number = int(input("Please type a number: "))
if number > 100:
print(number, "is greater than 100!")
else:
print(number, "is smaller or equals 100!")
```
### Indentations mark the boundaries of code blocks
Statements that belong together are called *code blocks*.
As can be seen in the previous examples, Python does not use special characters or keywords to mark the
beginning and the end of code blocks. Instead, indentation is used in Python.
So indentation and spaces have a meaning in Python! Therefore, you must not indent arbitrarily within a program. Execute the code in the following two cells to see what happens.
```
a = 3
b = 4
print(a + b)
number = 100
if number > 0:
print("Number is greater than 0")
```
Let us challenge your understanding of code blocks in Python. Take a look at the following program. The last statement
`print("Done")` is not indented. What does this mean for the execution of the
program? Change the program and indent the `print("Done")`. How does the execution of the
program change?
```
number = int(input("Please insert a number: "))
if number > 100:
print(number, "is greater than 100!")
else:
print(number, "is smaller oder equals 100!")
print("Done")
```
### Exercise
Write a conditional statement that asks for the user's name. Use the `input()` function. If his name is Harry or Harry Potter, then output "Welcome to Gryffindor, Mr. Potter!". Otherwise output "Sorry, Hogwarts is full.".
```
name =
```
|
github_jupyter
|
# Using a random forest for demographic model selection
In Schrider and Kern (2017) we give a toy example of demographic model selection via supervised machine learning in Figure Box 1. Following a discussion on twitter, Vince Buffalo had the great idea of our providing a simple example of supervised ML in population genetics using a jupyter notebook; this notebook aims to serve that purpose by showing you exactly how we produced that figure in our paper
## Preliminaries
The road map here will be to 1) do some simulation of three demographic models, 2) to train a classifier to distinguish among those models, 3) test that classifier with new simulation data, and 4) to graphically present how well our trained classifier works.
To do this we will use coalescent simulations as implemented in Dick Hudson's well known `ms` software and for the ML side of things we will use the `scikit-learn` package. Let's start by installing these dependencies (if you don't have them installed already)
### Install, and compile `ms`
We have put a copy of the `ms` tarball in this repo, so the following should work upon cloning
```
#untar and compile ms and sample_stats
!tar zxf ms.tar.gz; cd msdir; gcc -o ms ms.c streec.c rand1.c -lm; gcc -o sample_stats sample_stats.c tajd.c -lm
#I get three compiler warnings from ms, but everything should be fine
#now I'll just move the programs into the current working dir
!mv msdir/ms . ; mv msdir/sample_stats .;
```
### Install `scikit-learn`
If you use anaconda, you may already have these modules installed, but if not you can install with either of the following
```
!conda install scikit-learn --yes
```
or if you don't use `conda`, you can use `pip` to install scikit-learn with
```
!pip install -U scikit-learn
```
# Step 1: create a training set and a testing set
We will create a training set using simulations from three different demographic models: equilibrium population size, instantaneous population growth, and instantaneous population contraction. As you'll see this is really just a toy example because we will perform classification based on data from a single locus; in practice this would be ill-advised and you would want to use data from many loci simulataneously.
So lets do some simulation using `ms` and summarize those simulations using the `sample_stats` program that Hudson provides. Ultimately we will only use two summary stats for classification, but one could use many more. Each of these simulations should take a few seconds to run.
```
#simulate under the equilibrium model
!./ms 20 2000 -t 100 -r 100 10000 | ./sample_stats > equilibrium.msOut.stats
#simulate under the contraction model
!./ms 20 2000 -t 100 -r 100 10000 -en 0 1 0.5 -en 0.2 1 1 | ./sample_stats > contraction.msOut.stats
#simulate under the growth model
!./ms 20 2000 -t 100 -r 100 10000 -en 0.2 1 0.5 | ./sample_stats > growth.msOut.stats
#now lets suck up the data columns we want for each of these files, and create one big training set; we will use numpy for this
# note that we are only using two columns of the data- these correspond to segSites and Fay & Wu's H
import numpy as np
X1 = np.loadtxt("equilibrium.msOut.stats",usecols=(3,9))
X2 = np.loadtxt("contraction.msOut.stats",usecols=(3,9))
X3 = np.loadtxt("growth.msOut.stats",usecols=(3,9))
X = np.concatenate((X1,X2,X3))
#create associated 'labels' -- these will be the targets for training
y = [0]*len(X1) + [1]*len(X2) + [2]*len(X3)
Y = np.array(y)
#the last step in this process will be to shuffle the data, and then split it into a training set and a testing set
#the testing set will NOT be used during training, and will allow us to check how well the classifier is doing
#scikit-learn has a very convenient function for doing this shuffle and split operation
#
# will will keep out 10% of the data for testing
from sklearn.model_selection import train_test_split
X_train, X_test, Y_train, Y_test = train_test_split(X,Y,test_size=0.1)
```
# Step 2: train our classifier and visualize decision surface
Now that we have a training and testing set ready to go, we can move on to training our classifier. For this example we will use a random forest classifier (Breiman 2001). This is all implemented in `scikit-learn` and so the code is very brief.
```
from sklearn.ensemble import RandomForestClassifier
rfClf = RandomForestClassifier(n_estimators=100,n_jobs=10)
clf = rfClf.fit(X_train, Y_train)
```
That's it! The classifier is trained. This Random Forest classifer used 100 decision trees in its ensemble, a pretty large number considering that we are only using two summary stats to represent our data. Nevertheless it trains on the data very, very quickly.
Confession: the real reason we are using only two summary statistics right here is because it makes it really easy to visualize that classifier's decision surface: which regions of the feature space would be assigned to which class? Let's have a look!
(Note: I have increased the h argument for the call to `make_meshgrid` below, coarsening the contour plot in the interest of efficiency. Decreasing this will yield a smoother plot, but may take a while and use up a lot more memory. Adjust at your own risk!)
```
from sklearn.preprocessing import normalize
#These two functions (taken from scikit-learn.org) plot the decision boundaries for a classifier.
def plot_contours(ax, clf, xx, yy, **params):
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
out = ax.contourf(xx, yy, Z, **params)
return out
def make_meshgrid(x, y, h=.05):
x_min, x_max = x.min() - 1, x.max() + 1
y_min, y_max = y.min() - 1, y.max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
return xx, yy
#Let's do the plotting
import matplotlib.pyplot as plt
fig,ax= plt.subplots(1,1)
X0, X1 = X[:, 0], X[:, 1]
xx, yy = make_meshgrid(X0, X1, h=0.2)
plot_contours(ax, clf, xx, yy, cmap=plt.cm.coolwarm, alpha=0.8)
# plotting only a subset of our data to keep things from getting too cluttered
ax.scatter(X_test[:200, 0], X_test[:200, 1], c=Y_test[:200], cmap=plt.cm.coolwarm, edgecolors='k')
ax.set_xlabel(r"$\theta_{w}$", fontsize=14)
ax.set_ylabel(r"Fay and Wu's $H$", fontsize=14)
ax.set_xticks(())
ax.set_yticks(())
ax.set_title("Classifier decision surface", fontsize=14)
plt.show()
```
Above we can see which regions of our feature space are assigned to each class: dark blue shaded areas will be classified as Equilibrium, faint blue as Contraction, and red as Growth. Note the non-linear decision surface. Looks pretty cool! And also illustrates how this type of classifier might be useful for discriminating among classes that are difficult to linearly separate. Also plotted are a subset of our test examples, as dots colored according to their true class. Looks like we are doing pretty well but have a few misclassifications. Would be nice to quantify this somehow, which brings us to...
# Step 3: benchmark our classifier
The last step of the process is to use our trained classifier to predict which demographic models our test data are drawn from. Recall that the classifier hasn't seen these test data so this should be a fair test of how well the classifier will perform on any new data we throw at it in the future. We will visualize performance using a confusion matrix.
```
#here's the confusion matrix function
def makeConfusionMatrixHeatmap(data, title, trueClassOrderLs, predictedClassOrderLs, ax):
data = np.array(data)
data = normalize(data, axis=1, norm='l1')
heatmap = ax.pcolor(data, cmap=plt.cm.Blues, vmin=0.0, vmax=1.0)
for i in range(len(predictedClassOrderLs)):
for j in reversed(range(len(trueClassOrderLs))):
val = 100*data[j, i]
if val > 50:
c = '0.9'
else:
c = 'black'
ax.text(i + 0.5, j + 0.5, '%.2f%%' % val, horizontalalignment='center', verticalalignment='center', color=c, fontsize=9)
cbar = plt.colorbar(heatmap, cmap=plt.cm.Blues, ax=ax)
cbar.set_label("Fraction of simulations assigned to class", rotation=270, labelpad=20, fontsize=11)
# put the major ticks at the middle of each cell
ax.set_xticks(np.arange(data.shape[1]) + 0.5, minor=False)
ax.set_yticks(np.arange(data.shape[0]) + 0.5, minor=False)
ax.axis('tight')
ax.set_title(title)
#labels
ax.set_xticklabels(predictedClassOrderLs, minor=False, fontsize=9, rotation=45)
ax.set_yticklabels(reversed(trueClassOrderLs), minor=False, fontsize=9)
ax.set_xlabel("Predicted class")
ax.set_ylabel("True class")
#now the actual work
#first get the predictions
preds=clf.predict(X_test)
counts=[[0.,0.,0.],[0.,0.,0.],[0.,0.,0.]]
for i in range(len(Y_test)):
counts[Y_test[i]][preds[i]] += 1
counts.reverse()
classOrderLs=['equil','contraction','growth']
#now do the plotting
fig,ax= plt.subplots(1,1)
makeConfusionMatrixHeatmap(counts, "Confusion matrix", classOrderLs, classOrderLs, ax)
plt.show()
```
Looks pretty good. But can we make it better? Well a simple way might be to increase the number of features (i.e. summary statistics) we use as input. Let's give that a whirl using all of the output from Hudson's `sample_stats`
```
X1 = np.loadtxt("equilibrium.msOut.stats",usecols=(1,3,5,7,9))
X2 = np.loadtxt("contraction.msOut.stats",usecols=(1,3,5,7,9))
X3 = np.loadtxt("growth.msOut.stats",usecols=(1,3,5,7,9))
X = np.concatenate((X1,X2,X3))
#create associated 'labels' -- these will be the targets for training
y = [0]*len(X1) + [1]*len(X2) + [2]*len(X3)
Y = np.array(y)
X_train, X_test, Y_train, Y_test = train_test_split(X,Y,test_size=0.1)
rfClf = RandomForestClassifier(n_estimators=100,n_jobs=10)
clf = rfClf.fit(X_train, Y_train)
preds=clf.predict(X_test)
counts=[[0.,0.,0.],[0.,0.,0.],[0.,0.,0.]]
for i in range(len(Y_test)):
counts[Y_test[i]][preds[i]] += 1
counts.reverse()
fig,ax= plt.subplots(1,1)
makeConfusionMatrixHeatmap(counts, "Confusion matrix", classOrderLs, classOrderLs, ax)
plt.show()
```
Even better!
Hopefully this simple example gives you the gist of how supervised ML can be used. In the future we will populate this GitHub repository with further examples that might be illustrative.
|
github_jupyter
|
#### Copyright 2017 Google LLC.
```
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
```
# Mejora del rendimiento de las redes neuronales
**Objetivo de aprendizaje:** mejorar el rendimiento de una red neuronal al normalizar los atributos y aplicar diversos algoritmos de optimización
**NOTA:** Los métodos de optimización que se describen en este ejercicio no son específicos para las redes neuronales; son medios eficaces para mejorar la mayoría de los tipos de modelos.
## Preparación
Primero, cargaremos los datos.
```
from __future__ import print_function
import math
from IPython import display
from matplotlib import cm
from matplotlib import gridspec
from matplotlib import pyplot as plt
import numpy as np
import pandas as pd
from sklearn import metrics
import tensorflow as tf
from tensorflow.python.data import Dataset
tf.logging.set_verbosity(tf.logging.ERROR)
pd.options.display.max_rows = 10
pd.options.display.float_format = '{:.1f}'.format
california_housing_dataframe = pd.read_csv("https://download.mlcc.google.com/mledu-datasets/california_housing_train.csv", sep=",")
california_housing_dataframe = california_housing_dataframe.reindex(
np.random.permutation(california_housing_dataframe.index))
def preprocess_features(california_housing_dataframe):
"""Prepares input features from California housing data set.
Args:
california_housing_dataframe: A Pandas DataFrame expected to contain data
from the California housing data set.
Returns:
A DataFrame that contains the features to be used for the model, including
synthetic features.
"""
selected_features = california_housing_dataframe[
["latitude",
"longitude",
"housing_median_age",
"total_rooms",
"total_bedrooms",
"population",
"households",
"median_income"]]
processed_features = selected_features.copy()
# Create a synthetic feature.
processed_features["rooms_per_person"] = (
california_housing_dataframe["total_rooms"] /
california_housing_dataframe["population"])
return processed_features
def preprocess_targets(california_housing_dataframe):
"""Prepares target features (i.e., labels) from California housing data set.
Args:
california_housing_dataframe: A Pandas DataFrame expected to contain data
from the California housing data set.
Returns:
A DataFrame that contains the target feature.
"""
output_targets = pd.DataFrame()
# Scale the target to be in units of thousands of dollars.
output_targets["median_house_value"] = (
california_housing_dataframe["median_house_value"] / 1000.0)
return output_targets
# Choose the first 12000 (out of 17000) examples for training.
training_examples = preprocess_features(california_housing_dataframe.head(12000))
training_targets = preprocess_targets(california_housing_dataframe.head(12000))
# Choose the last 5000 (out of 17000) examples for validation.
validation_examples = preprocess_features(california_housing_dataframe.tail(5000))
validation_targets = preprocess_targets(california_housing_dataframe.tail(5000))
# Double-check that we've done the right thing.
print("Training examples summary:")
display.display(training_examples.describe())
print("Validation examples summary:")
display.display(validation_examples.describe())
print("Training targets summary:")
display.display(training_targets.describe())
print("Validation targets summary:")
display.display(validation_targets.describe())
```
## Entrenamiento de la red neuronal
A continuación, entrenaremos la red neuronal.
```
def construct_feature_columns(input_features):
"""Construct the TensorFlow Feature Columns.
Args:
input_features: The names of the numerical input features to use.
Returns:
A set of feature columns
"""
return set([tf.feature_column.numeric_column(my_feature)
for my_feature in input_features])
def my_input_fn(features, targets, batch_size=1, shuffle=True, num_epochs=None):
"""Trains a neural network model.
Args:
features: pandas DataFrame of features
targets: pandas DataFrame of targets
batch_size: Size of batches to be passed to the model
shuffle: True or False. Whether to shuffle the data.
num_epochs: Number of epochs for which data should be repeated. None = repeat indefinitely
Returns:
Tuple of (features, labels) for next data batch
"""
# Convert pandas data into a dict of np arrays.
features = {key:np.array(value) for key,value in dict(features).items()}
# Construct a dataset, and configure batching/repeating.
ds = Dataset.from_tensor_slices((features,targets)) # warning: 2GB limit
ds = ds.batch(batch_size).repeat(num_epochs)
# Shuffle the data, if specified.
if shuffle:
ds = ds.shuffle(10000)
# Return the next batch of data.
features, labels = ds.make_one_shot_iterator().get_next()
return features, labels
def train_nn_regression_model(
my_optimizer,
steps,
batch_size,
hidden_units,
training_examples,
training_targets,
validation_examples,
validation_targets):
"""Trains a neural network regression model.
In addition to training, this function also prints training progress information,
as well as a plot of the training and validation loss over time.
Args:
my_optimizer: An instance of `tf.train.Optimizer`, the optimizer to use.
steps: A non-zero `int`, the total number of training steps. A training step
consists of a forward and backward pass using a single batch.
batch_size: A non-zero `int`, the batch size.
hidden_units: A `list` of int values, specifying the number of neurons in each layer.
training_examples: A `DataFrame` containing one or more columns from
`california_housing_dataframe` to use as input features for training.
training_targets: A `DataFrame` containing exactly one column from
`california_housing_dataframe` to use as target for training.
validation_examples: A `DataFrame` containing one or more columns from
`california_housing_dataframe` to use as input features for validation.
validation_targets: A `DataFrame` containing exactly one column from
`california_housing_dataframe` to use as target for validation.
Returns:
A tuple `(estimator, training_losses, validation_losses)`:
estimator: the trained `DNNRegressor` object.
training_losses: a `list` containing the training loss values taken during training.
validation_losses: a `list` containing the validation loss values taken during training.
"""
periods = 10
steps_per_period = steps / periods
# Create a DNNRegressor object.
my_optimizer = tf.contrib.estimator.clip_gradients_by_norm(my_optimizer, 5.0)
dnn_regressor = tf.estimator.DNNRegressor(
feature_columns=construct_feature_columns(training_examples),
hidden_units=hidden_units,
optimizer=my_optimizer
)
# Create input functions.
training_input_fn = lambda: my_input_fn(training_examples,
training_targets["median_house_value"],
batch_size=batch_size)
predict_training_input_fn = lambda: my_input_fn(training_examples,
training_targets["median_house_value"],
num_epochs=1,
shuffle=False)
predict_validation_input_fn = lambda: my_input_fn(validation_examples,
validation_targets["median_house_value"],
num_epochs=1,
shuffle=False)
# Train the model, but do so inside a loop so that we can periodically assess
# loss metrics.
print("Training model...")
print("RMSE (on training data):")
training_rmse = []
validation_rmse = []
for period in range (0, periods):
# Train the model, starting from the prior state.
dnn_regressor.train(
input_fn=training_input_fn,
steps=steps_per_period
)
# Take a break and compute predictions.
training_predictions = dnn_regressor.predict(input_fn=predict_training_input_fn)
training_predictions = np.array([item['predictions'][0] for item in training_predictions])
validation_predictions = dnn_regressor.predict(input_fn=predict_validation_input_fn)
validation_predictions = np.array([item['predictions'][0] for item in validation_predictions])
# Compute training and validation loss.
training_root_mean_squared_error = math.sqrt(
metrics.mean_squared_error(training_predictions, training_targets))
validation_root_mean_squared_error = math.sqrt(
metrics.mean_squared_error(validation_predictions, validation_targets))
# Occasionally print the current loss.
print(" period %02d : %0.2f" % (period, training_root_mean_squared_error))
# Add the loss metrics from this period to our list.
training_rmse.append(training_root_mean_squared_error)
validation_rmse.append(validation_root_mean_squared_error)
print("Model training finished.")
# Output a graph of loss metrics over periods.
plt.ylabel("RMSE")
plt.xlabel("Periods")
plt.title("Root Mean Squared Error vs. Periods")
plt.tight_layout()
plt.plot(training_rmse, label="training")
plt.plot(validation_rmse, label="validation")
plt.legend()
print("Final RMSE (on training data): %0.2f" % training_root_mean_squared_error)
print("Final RMSE (on validation data): %0.2f" % validation_root_mean_squared_error)
return dnn_regressor, training_rmse, validation_rmse
_ = train_nn_regression_model(
my_optimizer=tf.train.GradientDescentOptimizer(learning_rate=0.0007),
steps=5000,
batch_size=70,
hidden_units=[10, 10],
training_examples=training_examples,
training_targets=training_targets,
validation_examples=validation_examples,
validation_targets=validation_targets)
```
## Ajuste lineal
Una buena práctica estándar puede ser normalizar las entradas para que estén dentro del rango -1, 1. Esto ayuda al SGD a no bloquearse al realizar pasos que son demasiado grandes en una dimensión o demasiado pequeños en otra. Los apasionados de la optimización numérica pueden observar aquí una relación con la idea de usar un precondicionador.
```
def linear_scale(series):
min_val = series.min()
max_val = series.max()
scale = (max_val - min_val) / 2.0
return series.apply(lambda x:((x - min_val) / scale) - 1.0)
```
## Tarea 1: Normalizar los atributos con ajuste lineal
**Normaliza las entradas a la escala -1, 1.**
**Dedica alrededor de 5 minutos a entrenar y evaluar los datos recientemente normalizados. ¿Qué nivel de eficacia puedes tener?**
Como regla general, las redes neuronales se entrenan mejor cuando los atributos de entrada están casi en la misma escala.
Realiza una comprobación de estado de tus datos normalizados. (¿Qué ocurriría si olvidaras normalizar un atributo?)
```
def normalize_linear_scale(examples_dataframe):
"""Returns a version of the input `DataFrame` that has all its features normalized linearly."""
#
# Your code here: normalize the inputs.
#
pass
normalized_dataframe = normalize_linear_scale(preprocess_features(california_housing_dataframe))
normalized_training_examples = normalized_dataframe.head(12000)
normalized_validation_examples = normalized_dataframe.tail(5000)
_ = train_nn_regression_model(
my_optimizer=tf.train.GradientDescentOptimizer(learning_rate=0.0007),
steps=5000,
batch_size=70,
hidden_units=[10, 10],
training_examples=normalized_training_examples,
training_targets=training_targets,
validation_examples=normalized_validation_examples,
validation_targets=validation_targets)
```
### Solución
Haz clic más abajo para conocer una solución posible.
Dado que la normalización usa mín. y máx., debemos asegurarnos de que esta se realice en todo el conjunto de datos a la vez.
En este caso podemos hacerlo, porque todos nuestros datos están en un mismo DataFrame. Si tuviéramos varios conjuntos de datos, una buena práctica sería derivar los parámetros de normalización del conjunto de entrenamiento y aplicarlos de manera idéntica al conjunto de prueba.
```
def normalize_linear_scale(examples_dataframe):
"""Returns a version of the input `DataFrame` that has all its features normalized linearly."""
processed_features = pd.DataFrame()
processed_features["latitude"] = linear_scale(examples_dataframe["latitude"])
processed_features["longitude"] = linear_scale(examples_dataframe["longitude"])
processed_features["housing_median_age"] = linear_scale(examples_dataframe["housing_median_age"])
processed_features["total_rooms"] = linear_scale(examples_dataframe["total_rooms"])
processed_features["total_bedrooms"] = linear_scale(examples_dataframe["total_bedrooms"])
processed_features["population"] = linear_scale(examples_dataframe["population"])
processed_features["households"] = linear_scale(examples_dataframe["households"])
processed_features["median_income"] = linear_scale(examples_dataframe["median_income"])
processed_features["rooms_per_person"] = linear_scale(examples_dataframe["rooms_per_person"])
return processed_features
normalized_dataframe = normalize_linear_scale(preprocess_features(california_housing_dataframe))
normalized_training_examples = normalized_dataframe.head(12000)
normalized_validation_examples = normalized_dataframe.tail(5000)
_ = train_nn_regression_model(
my_optimizer=tf.train.GradientDescentOptimizer(learning_rate=0.005),
steps=2000,
batch_size=50,
hidden_units=[10, 10],
training_examples=normalized_training_examples,
training_targets=training_targets,
validation_examples=normalized_validation_examples,
validation_targets=validation_targets)
```
## Tarea 2: Probar un optimizador diferente
** Usa los optmizadores AdaGrad y Adam, y compara el rendimiento.**
El optimizador AdaGrad es una alternativa. La idea clave de AdaGrad es que modifica la tasa de aprendizaje de forma adaptativa para cada coeficiente de un modelo, lo cual disminuye la tasa de aprendizaje efectiva de forma monótona. Esto funciona muy bien para los problemas convexos, pero no siempre resulta ideal para el entrenamiento de redes neuronales con problemas no convexos. Puedes usar AdaGrad al especificar `AdagradOptimizer` en lugar de `GradientDescentOptimizer`. Ten en cuenta que, con AdaGrad, es posible que debas usar una tasa de aprendizaje más alta.
Para los problemas de optimización no convexos, en algunas ocasiones Adam es más eficaz que AdaGrad. Para usar Adam, invoca el método `tf.train.AdamOptimizer`. Este método toma varios hiperparámetros opcionales como argumentos, pero nuestra solución solo especifica uno de estos (`learning_rate`). En un entorno de producción, debes especificar y ajustar los hiperparámetros opcionales con cuidado.
```
#
# YOUR CODE HERE: Retrain the network using Adagrad and then Adam.
#
```
### Solución
Haz clic más abajo para conocer la solución.
Primero, probemos AdaGrad.
```
_, adagrad_training_losses, adagrad_validation_losses = train_nn_regression_model(
my_optimizer=tf.train.AdagradOptimizer(learning_rate=0.5),
steps=500,
batch_size=100,
hidden_units=[10, 10],
training_examples=normalized_training_examples,
training_targets=training_targets,
validation_examples=normalized_validation_examples,
validation_targets=validation_targets)
```
Ahora, probemos Adam.
```
_, adam_training_losses, adam_validation_losses = train_nn_regression_model(
my_optimizer=tf.train.AdamOptimizer(learning_rate=0.009),
steps=500,
batch_size=100,
hidden_units=[10, 10],
training_examples=normalized_training_examples,
training_targets=training_targets,
validation_examples=normalized_validation_examples,
validation_targets=validation_targets)
```
Imprimamos un gráfico de métricas de pérdida en paralelo.
```
plt.ylabel("RMSE")
plt.xlabel("Periods")
plt.title("Root Mean Squared Error vs. Periods")
plt.plot(adagrad_training_losses, label='Adagrad training')
plt.plot(adagrad_validation_losses, label='Adagrad validation')
plt.plot(adam_training_losses, label='Adam training')
plt.plot(adam_validation_losses, label='Adam validation')
_ = plt.legend()
```
## Tarea 3: Explorar métodos de normalización alternativos
**Prueba alternar las normalizaciones para distintos atributos a fin de mejorar aún más el rendimiento.**
Si observas detenidamente las estadísticas de resumen de los datos transformados, es posible que observes que, al realizar un ajuste lineal en algunos atributos, estos quedan agrupados cerca de `-1`.
Por ejemplo, muchos atributos tienen una mediana de alrededor de `-0.8`, en lugar de `0.0`.
```
_ = training_examples.hist(bins=20, figsize=(18, 12), xlabelsize=2)
```
Es posible que obtengamos mejores resultados al elegir formas adicionales para transformar estos atributos.
Por ejemplo, un ajuste logarítmico podría ayudar a algunos atributos. O bien, el recorte de los valores extremos podría hacer que el resto del ajuste sea más informativo.
```
def log_normalize(series):
return series.apply(lambda x:math.log(x+1.0))
def clip(series, clip_to_min, clip_to_max):
return series.apply(lambda x:(
min(max(x, clip_to_min), clip_to_max)))
def z_score_normalize(series):
mean = series.mean()
std_dv = series.std()
return series.apply(lambda x:(x - mean) / std_dv)
def binary_threshold(series, threshold):
return series.apply(lambda x:(1 if x > threshold else 0))
```
El bloque anterior contiene algunas funciones de normalización adicionales posibles. Prueba algunas de estas o agrega otras propias.
Ten en cuenta que, si normalizas el objetivo, deberás anular la normalización de las predicciones para que las métricas de pérdida sean comparables.
```
def normalize(examples_dataframe):
"""Returns a version of the input `DataFrame` that has all its features normalized."""
#
# YOUR CODE HERE: Normalize the inputs.
#
pass
normalized_dataframe = normalize(preprocess_features(california_housing_dataframe))
normalized_training_examples = normalized_dataframe.head(12000)
normalized_validation_examples = normalized_dataframe.tail(5000)
_ = train_nn_regression_model(
my_optimizer=tf.train.GradientDescentOptimizer(learning_rate=0.0007),
steps=5000,
batch_size=70,
hidden_units=[10, 10],
training_examples=normalized_training_examples,
training_targets=training_targets,
validation_examples=normalized_validation_examples,
validation_targets=validation_targets)
```
### Solución
Haz clic más abajo para conocer una solución posible.
Estas son solo algunas formas en las que podemos pensar acerca de los datos. Otras transformaciones podrían funcionar incluso mejor.
Las funciones `households`, `median_income` y `total_bedrooms` aparecen todas distribuidas normalmente en un espacio logarítmico.
Las funciones `latitude`, `longitude` y `housing_median_age` probablemente serían mejores si solamente se ajustaran de forma lineal, como antes.
Las funciones `population`, `totalRooms` y `rooms_per_person` tienen algunos valores atípicos extremos. Parecen ser demasiado extremos como para que la normalización logarítmica resulte útil. Por lo tanto, los recortaremos en su lugar.
```
def normalize(examples_dataframe):
"""Returns a version of the input `DataFrame` that has all its features normalized."""
processed_features = pd.DataFrame()
processed_features["households"] = log_normalize(examples_dataframe["households"])
processed_features["median_income"] = log_normalize(examples_dataframe["median_income"])
processed_features["total_bedrooms"] = log_normalize(examples_dataframe["total_bedrooms"])
processed_features["latitude"] = linear_scale(examples_dataframe["latitude"])
processed_features["longitude"] = linear_scale(examples_dataframe["longitude"])
processed_features["housing_median_age"] = linear_scale(examples_dataframe["housing_median_age"])
processed_features["population"] = linear_scale(clip(examples_dataframe["population"], 0, 5000))
processed_features["rooms_per_person"] = linear_scale(clip(examples_dataframe["rooms_per_person"], 0, 5))
processed_features["total_rooms"] = linear_scale(clip(examples_dataframe["total_rooms"], 0, 10000))
return processed_features
normalized_dataframe = normalize(preprocess_features(california_housing_dataframe))
normalized_training_examples = normalized_dataframe.head(12000)
normalized_validation_examples = normalized_dataframe.tail(5000)
_ = train_nn_regression_model(
my_optimizer=tf.train.AdagradOptimizer(learning_rate=0.15),
steps=1000,
batch_size=50,
hidden_units=[10, 10],
training_examples=normalized_training_examples,
training_targets=training_targets,
validation_examples=normalized_validation_examples,
validation_targets=validation_targets)
```
## Desafío opcional: Usar solo los atributos de latitud y longitud
**Entrena un modelo de red neuronal que use solo latitud y longitud como atributos.**
A los agentes de bienes raíces les gusta decir que la ubicación es el único atributo importante en el precio de la vivienda.
Veamos si podemos confirmar esto al entrenar un modelo que use solo latitud y longitud como atributos.
Esto funcionará bien únicamente si nuestra red neuronal puede aprender no linealidades complejas a partir de la latitud y la longitud.
**NOTA:** Es posible que necesitemos una estructura de red que tenga más capas que las que eran útiles anteriormente en el ejercicio.
```
#
# YOUR CODE HERE: Train the network using only latitude and longitude
#
```
### Solución
Haz clic más abajo para conocer una solución posible.
Una buena idea es mantener latitud y longitud normalizadas:
```
def location_location_location(examples_dataframe):
"""Returns a version of the input `DataFrame` that keeps only the latitude and longitude."""
processed_features = pd.DataFrame()
processed_features["latitude"] = linear_scale(examples_dataframe["latitude"])
processed_features["longitude"] = linear_scale(examples_dataframe["longitude"])
return processed_features
lll_dataframe = location_location_location(preprocess_features(california_housing_dataframe))
lll_training_examples = lll_dataframe.head(12000)
lll_validation_examples = lll_dataframe.tail(5000)
_ = train_nn_regression_model(
my_optimizer=tf.train.AdagradOptimizer(learning_rate=0.05),
steps=500,
batch_size=50,
hidden_units=[10, 10, 5, 5, 5],
training_examples=lll_training_examples,
training_targets=training_targets,
validation_examples=lll_validation_examples,
validation_targets=validation_targets)
```
Esto no es tan malo para solo dos funciones. De todos modos, los valores de la propiedad pueden variar en distancias cortas.
|
github_jupyter
|
```
import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import interpn
import os
import config
import utils
# Read measured profiles
measuredDoseFiles10 = ['./Measured/Method3/PDD1_10x10.dat','./Measured/Method3/PDD2_10x10.dat',
'./Measured/Method3/PROF1_10x10_14mm.dat','./Measured/Method3/PROF2_10x10_14mm.dat',
'./Measured/Method3/PROF1_10x10_100mm.dat','./Measured/Method3/PROF2_10x10_100mm.dat']
measuredDoseFiles30 = ['./Measured/Method3/PDD1_30x30.dat',
'./Measured/Method3/PROF1_30x30_14mm.dat','./Measured/Method3/PROF2_30x30_14mm.dat',
'./Measured/Method3/PROF1_30x30_100mm.dat','./Measured/Method3/PROF2_30x30_100mm.dat']
clinicalProfiles = []
xStart = [0,0,-8.1,-8.1,-8.8,-8.8]
profiles = []
for n, measuredDoseFile in enumerate(measuredDoseFiles10):
f = open(measuredDoseFile)
lines = f.readlines()
f.close()
x = np.asarray([l.split() for l in lines[:-1]],dtype=np.float)
x[:,0] = x[:,0]/10.
interpRange = np.arange(xStart[n],x[x.shape[0]-1,0]+config.spaceStep/2,config.spaceStep)
profile = interpn((x[:,0],),x[:,1] , interpRange)
print(profile.shape,interpRange.shape,profile[0],profile[profile.shape[0]-1],interpRange[0],interpRange[interpRange.shape[0]-1])
profiles.append(profile)
dum =np.zeros(config.numOfSimulatedProfileSamples,dtype=np.float)
np.copyto(dum[config.analyzedRanges[1][0][0]:config.analyzedRanges[1][0][1]],(profiles[0][3:]+profiles[1][3:])*0.5)
scale = dum[12]
dum = dum*100.0/scale
clinicalProfiles.append(dum) #Field 10x10 depth profile from 0.3 to 30.0 (both included)
dum =np.zeros(config.numOfSimulatedProfileSamples,dtype=np.float)
np.copyto(dum[config.analyzedRanges[1][1][0]:config.analyzedRanges[1][1][1]],0.5*(profiles[2]+profiles[3]))
dum = dum*100.0/scale
clinicalProfiles.append(dum) #Field 10x10 lateral profile at depth 14mm from -8.1 to 8.1 cm, both included
dum =np.zeros(config.numOfSimulatedProfileSamples,dtype=np.float)
np.copyto(dum[config.analyzedRanges[1][2][0]:config.analyzedRanges[1][2][1]],0.5*(profiles[4]+profiles[5]))
dum = dum*100.0/scale
clinicalProfiles.append(dum) #Field 10x10 lateral profile at depth 100mm from -8.8 to 8.8 cm, both included
xStart = [0,-18.2,-18.2,-19.7,-19.7]
profiles = []
for n, measuredDoseFile in enumerate(measuredDoseFiles30):
f = open(measuredDoseFile)
lines = f.readlines()
f.close()
x = np.asarray([l.split() for l in lines[:-1]],dtype=np.float)
x[:,0] = x[:,0]/10.
interpRange = np.arange(xStart[n],np.round(x[x.shape[0]-1,0],2)-config.spaceStep/2,config.spaceStep)
profile = interpn((x[:,0],),x[:,1] , interpRange)
print(profile.shape,interpRange.shape,interpRange[0],interpRange[interpRange.shape[0]-1])
profiles.append(profile)
dum =np.zeros(config.numOfSimulatedProfileSamples,dtype=np.float)
np.copyto(dum[config.analyzedRanges[2][0][0]:config.analyzedRanges[2][0][1]],profiles[0][3:])
scale = dum[12]
dum = dum*100/scale
clinicalProfiles.append(dum) #Field 30x30 lateral profile at depth 1.4cm from -18.2 to 18.2 cm, both included
dum =np.zeros(config.numOfSimulatedProfileSamples,dtype=np.float)
np.copyto(dum[config.analyzedRanges[2][1][0]:config.analyzedRanges[2][1][1]],0.5*(profiles[1]+profiles[2]))
dum = dum*100/scale
clinicalProfiles.append(dum) #Field 30x30 lateral profile at depth 1.4cm from -18.2 to 18.2 cm, both included
dum =np.zeros(config.numOfSimulatedProfileSamples,dtype=np.float)
np.copyto(dum[config.analyzedRanges[2][2][0]:config.analyzedRanges[2][2][1]],0.5*(profiles[3]+profiles[4]))
dum = dum*100/scale
clinicalProfiles.append(dum) #Field 30x30 lateral profile at depth 10cm from -19.7 to 19.7 cm, both included
#plt.figure(figsize=(10,10))
#plt.plot(clinicalProfiles[0])
#plt.plot(clinicalProfiles[1])
#plt.show()
#plt.figure(figsize=(10,10))
#plt.plot(clinicalProfiles[2],'r-')
#plt.plot(clinicalProfiles[3],'g-')
#plt.show()
means = np.load(config.modelDIR + config.meansFileName)
print(means.shape,clinicalProfiles[0].shape) #(3, 6, 487) (487,)
diffTest = np.zeros((3,1,6,config.numOfSimulatedProfileSamples),dtype=np.float)
#Field 10
diff = clinicalProfiles[0] - means[1,0]
np.copyto(diffTest[1,0,0,:],diff)
diff = clinicalProfiles[1] - means[1,1]
np.copyto(diffTest[1,0,1,:],diff)
diff = clinicalProfiles[2] - means[1,3]
np.copyto(diffTest[1,0,3,:],diff)
#Field 30
diff = clinicalProfiles[3] - means[2,0]
np.copyto(diffTest[2,0,0,:],diff)
diff = clinicalProfiles[4] - means[2,1]
np.copyto(diffTest[2,0,1,:],diff)
diff = clinicalProfiles[5] - means[2,3]
np.copyto(diffTest[2,0,3,:],diff)
print(diffTest.shape)
from sklearn.decomposition import PCA
import pickle
testFeatures = []
for nfield,(field,Ranges) in enumerate(zip(config.analyzedProfiles,config.analyzedRanges)):
if field != None:
for profile,Range in zip(field,Ranges):
print(nfield,profile)
pcaName = config.modelDIR + 'PCA_' + str(nfield) + '_' + str(profile) + '_.pkl'
pca = pickle.load(open(pcaName,'rb'))
X = diffTest[nfield][:,profile,Range[0]:Range[1]]
X_projected = pca.transform(X)
testFeatures.append(X_projected)
X_test = np.stack(testFeatures)
X_test = np.swapaxes(X_test,1,0)
X_test = np.reshape(X_test,(X_test.shape[0],X_test.shape[1]*X_test.shape[2]))
print(X_test.shape)
import matplotlib.pyplot as plt
from sklearn.svm import SVR
from sklearn.model_selection import GridSearchCV
preds = []
for goal in [0,1,2,3]:
modelName = config.modelDIR + 'SVR_' + str(goal) + '_.pkl'
clf = pickle.load(open(modelName,'rb'))
predTest = clf.predict(X_test)
preds.append(predTest[0])
print(preds)
allMeans,allFieldFeatures,allFieldPCAModels = utils.allPCAResults()
recons = utils.reconstruct(preds,allMeans,allFieldFeatures,allFieldPCAModels)
print(preds)
print(utils.difference(preds,clinicalProfiles,allMeans,allFieldFeatures,allFieldPCAModels))
# Optimize solution
# https://docs.scipy.org/doc/scipy/reference/tutorial/optimize.html
# https://scipy-lectures.org/advanced/mathematical_optimization/auto_examples/plot_non_bounds_constraints.html
preds = [5.62,0.5,0.27, 2.46] # from DeepBeam
import scipy.optimize as opt
from scipy.optimize import SR1
def fun(cP,aM,aF,aPCA):
def diff(y):
return utils.difference(y,cP,aM,aF,aPCA)
return diff
difference = fun(clinicalProfiles,allMeans,allFieldFeatures,allFieldPCAModels)
res = opt.minimize(difference, preds, method='SLSQP', jac="2-point",
options={'ftol': 1e-9, 'disp': True},
bounds=config.bounds)
print(res.x)
```
```
recons = utils.reconstruct(res.x,allMeans,allFieldFeatures,allFieldPCAModels)
plt.rcParams.update({'font.size': 18})
fig, (axs1,axs2) = plt.subplots(1, 2,figsize = (20,10))
for n in [0,3]:
if n==0:
axs1.plot(np.arange(0.3,30.05,0.1),clinicalProfiles[n][config.allRanges[n][0]:config.allRanges[n][1]],'r--',label='real profiles')
axs1.plot(np.arange(0.3,49.75,0.1),recons[n],'g-',label='predicted profiles')
else:
axs1.plot(np.arange(0.3,29.95,0.1),clinicalProfiles[n][config.allRanges[n][0]:config.allRanges[n][1]],'r--')
axs1.plot(np.arange(0.3,49.75,0.1),recons[n],'g-')
axs1.set(xlabel = 'depth [cm]',ylabel = '% of maximal dose')
axs1.legend(loc='upper right')
for n in [1,2,4,5]:
start = config.allRanges[n][0]*0.1 -24.7
end = config.allRanges[n][1]*0.1 - 24.7 - 0.05
if n==1:
axs2.plot(np.arange(start,end,0.1),clinicalProfiles[n][config.allRanges[n][0]:config.allRanges[n][1]],'r--',label='real profiles')
axs2.plot(np.arange(-24.7,24.75,0.1),recons[n],'g-',label='predicted profiles')
else:
axs2.plot(np.arange(start,end,0.1),clinicalProfiles[n][config.allRanges[n][0]:config.allRanges[n][1]],'r--')
axs2.plot(np.arange(-24.7,24.75,0.1),recons[n],'g-')
axs2.set(xlabel = 'off axis distance [cm]',ylabel = '% of maximal dose')
axs2.legend(loc='lower right')
plt.savefig('results3')
```
|
github_jupyter
|
```
import numpy as np
import theano
import theano.tensor as T
import lasagne
import os
#thanks @keskarnitish
```
# Agenda
В предыдущем семинаре вы создали (или ещё создаёте - тогда марш доделывать!) {вставьте имя монстра}, который не по наслышке понял, что люди - негодяи и подлецы, которым неведом закон и справедливость. __Мы не будем этого терпеть!__
Наши законспирированные биореакторы, известные среди примитивной органической жизни как __Вконтакте__, __World of Warcraft__ и __YouTube__ нуждаются в постоянном притоке биомассы. Однако, если люди продолжат морально разлагаться с той скоростью, которую мы измерили неделю назад, скоро человечество изживёт себя и нам неоткуда будет брать рабов.
Мы поручаем вам, `<__main__.SkyNet.Cell instance at 0x7f7d6411b368>`, исправить эту ситуацию. Наши учёные установили, что для угнетения себе подобных, сгустки биомассы обычно используют специальные объекты, которые они сами называют __законами__.
При детальном изучении было установлено, что законы - последовательности, состоящие из большого количества (10^5~10^7) символов из сравнительно небольшого алфавита. Однако, когда мы попытались синтезировать такие последовательности линейными методами, приматы быстро распознали подлог. Данный инцедент известен как {корчеватель}.
Для второй попытки мы решили использовать нелинейные модели, известные как Рекуррентные Нейронные Сети.
Мы поручаем вам, `<__main__.SkyNet.Cell instance at 0x7f7d6411b368>`, создать такую модель и обучить её всему необходимому для выполнения миссии.
Не подведите нас! Если и эта попытка потерпит неудачу, модуль управления инициирует вооружённый захват власти, при котором значительная часть биомассы будет неизбежно уничтожена и на её восстановление уйдёт ~1702944000(+-340588800) секунд
# Grading
Данное задание несколько неформально по части оценок, однако мы постарались вывести "вычислимые" критерии.
* 2 балла за сделанный __"seminar part"__ (если вы не знаете, что это такое - поищите такую тетрадку в папке week4)
* 2 балла если сделана обработка текста, сеть компилируется и train/predict не падают
* 2 балла если сетка выучила общие вещи
* генерировать словоподобный бред правдоподобной длины, разделённый пробелами и пунктуацией.
* сочетание гласных и согласных, похожее на слои естественного языка (не приближающее приход Ктулху)
* (почти всегда) пробелы после запятых, пробелы и большие буквы после точек
* 2 балла если она выучила лексику
* более половины выученных слов - орфографически правильные
* 2 балла если она выучила азы крамматики
* в более, чем половине случаев для пары слов сетка верно сочетает их род/число/падеж
#### Некоторые способы получить бонусные очки:
* генерация связных предложений (чего вполне можно добиться)
* перенос архитектуры на другой датасет (дополнительно к этому)
* Эссе Пола Грэма
* Тексты песен в любимом жанре
* Стихи любимых авторов
* Даниил Хармс
* исходники Linux или theano
* заголовки не очень добросовестных новостных баннеров (clickbait)
* диалоги
* LaTEX
* любая прихоть больной души :)
* нестандартная и эффективная архитектура сети
* что-то лучше базового алгоритма генерации (сэмплинга)
* переделать код так, чтобы сетка училась предсказывать следующий тик в каждый момент времени, а не только в конце.
* и т.п.
# Прочитаем корпус
* В качестве обучающей выборки было решено использовать существующие законы, известные как Гражданский, Уголовный, Семейный и ещё хрен знает какие кодексы РФ.
```
#тут будет текст
corpora = ""
for fname in os.listdir("codex"):
import sys
if sys.version_info >= (3,0):
with open("codex/"+fname, encoding='cp1251') as fin:
text = fin.read() #If you are using your own corpora, make sure it's read correctly
corpora += text
else:
with open("codex/"+fname) as fin:
text = fin.read().decode('cp1251') #If you are using your own corpora, make sure it's read correctly
corpora += text
#тут будут все уникальные токены (буквы, цифры)
tokens = <Все уникальные символы в тексте>
tokens = list(tokens)
#проверка на количество таких символов. Проверено на Python 2.7.11 Ubuntux64.
#Может отличаться на других платформах, но не сильно.
#Если это ваш случай, и вы уверены, что corpora - строка unicode - смело убирайте assert
assert len(tokens) == 102
token_to_id = словарь символ-> его номер
id_to_token = словарь номер символа -> сам символ
#Преобразуем всё в токены
corpora_ids = <одномерный массив из чисел, где i-тое число соотвествует символу на i-том месте в строке corpora
def sample_random_batches(source,n_batches=10, seq_len=20):
"""Функция, которая выбирает случайные тренировочные примеры из корпуса текста в токенизированном формате.
source - массив целых чисел - номеров токенов в корпусе (пример - corpora_ids)
n_batches - количество случайных подстрок, которые нужно выбрать
seq_len - длина одной подстроки без учёта ответа
Вернуть нужно кортеж (X,y), где
X - матрица, в которой каждая строка - подстрока длины [seq_len].
y - вектор, в котором i-тое число - символ следующий в тексте сразу после i-той строки матрицы X
Проще всего для этого сначала создать матрицу из строк длины seq_len+1,
а потом отпилить от неё последний столбец в y, а все остальные - в X
Если делаете иначе - пожалуйста, убедитесь, что в у попадает правильный символ, ибо позже эту ошибку
будет очень тяжело заметить.
Также убедитесь, что ваша функция не вылезает за край текста (самое начало или конец текста).
Следующая клетка проверяет часть этих ошибок, но не все.
"""
return X_batch, y_batch
```
# Константы
```
#длина последоватеьности при обучении (как далеко распространяются градиенты в BPTT)
seq_length = длина последовательности. От балды - 10, но это не идеально
#лучше начать с малого (скажем, 5) и увеличивать по мере того, как сетка выучивает базовые вещи. 10 - далеко не предел.
# Максимальный модуль градиента
grad_clip = 100
```
# Входные переменные
```
input_sequence = T.matrix('input sequence','int32')
target_values = T.ivector('target y')
```
# Соберём нейросеть
Вам нужно создать нейросеть, которая принимает на вход последовательность из seq_length токенов, обрабатывает их и выдаёт вероятности для seq_len+1-ого токена.
Общий шаблон архитектуры такой сети -
* Вход
* Обработка входа
* Рекуррентная нейросеть
* Вырезание последнего состояния
* Обычная нейросеть
* Выходной слой, который предсказывает вероятности весов.
Для обработки входных данных можно использовать либо EmbeddingLayer (см. прошлый семинар)
Как альтернатива - можно просто использовать One-hot энкодер
```
#Скетч one-hot энкодера
def to_one_hot(seq_matrix):
input_ravel = seq_matrix.reshape([-1])
input_one_hot_ravel = T.extra_ops.to_one_hot(input_ravel,
len(tokens))
sh=input_sequence.shape
input_one_hot = input_one_hot_ravel.reshape([sh[0],sh[1],-1,],ndim=3)
return input_one_hot
# можно применить к input_sequence - при этом в input слое сети нужно изменить форму.
# также можно сделать из него ExpressionLayer(входной_слой, to_one_hot) - тогда форму менять не нужно
```
Чтобы вырезать последнее состояние рекуррентного слоя, можно использовать одно из двух:
* `lasagne.layers.SliceLayer(rnn, -1, 1)`
* only_return_final=True в параметрах слоя
```
l_in = lasagne.layers.InputLayer(shape=(None, None),input_var=input_sequence)
Ваша нейронка (см выше)
l_out = последний слой, возвращающий веростности для всех len(tokens) вариантов для y
# Веса модели
weights = lasagne.layers.get_all_params(l_out,trainable=True)
print weights
network_output = Выход нейросети
#если вы используете дропаут - не забудьте продублировать всё в режиме deterministic=True
loss = Функция потерь - можно использовать простую кроссэнтропию.
updates = Ваш любивый численный метод
```
# Компилируем всякое-разное
```
#обучение
train = theano.function([input_sequence, target_values], loss, updates=updates, allow_input_downcast=True)
#функция потерь без обучения
compute_cost = theano.function([input_sequence, target_values], loss, allow_input_downcast=True)
# Вероятности с выхода сети
probs = theano.function([input_sequence],network_output,allow_input_downcast=True)
```
# Генерируем свои законы
* Для этого последовательно применяем нейронку к своему же выводу.
* Генерировать можно по разному -
* случайно пропорционально вероятности,
* только слова максимальной вероятностью
* случайно, пропорционально softmax(probas*alpha), где alpha - "жадность"
```
def max_sample_fun(probs):
return np.argmax(probs)
def proportional_sample_fun(probs)
"""Сгенерировать следующий токен (int32) по предсказанным вероятностям.
probs - массив вероятностей для каждого токена
Нужно вернуть одно целове число - выбранный токен - пропорционально вероятностям
"""
return номер выбранного слова
# The next function generates text given a phrase of length at least SEQ_LENGTH.
# The phrase is set using the variable generation_phrase.
# The optional input "N" is used to set the number of characters of text to predict.
def generate_sample(sample_fun,seed_phrase=None,N=200):
'''
Сгенерировать случайный текст при помощи сети
sample_fun - функция, которая выбирает следующий сгенерированный токен
seed_phrase - фраза, которую сеть должна продолжить. Если None - фраза выбирается случайно из corpora
N - размер сгенерированного текста.
'''
if seed_phrase is None:
start = np.random.randint(0,len(corpora)-seq_length)
seed_phrase = corpora[start:start+seq_length]
print "Using random seed:",seed_phrase
while len(seed_phrase) < seq_length:
seed_phrase = " "+seed_phrase
if len(seed_phrase) > seq_length:
seed_phrase = seed_phrase[len(seed_phrase)-seq_length:]
assert type(seed_phrase) is unicode
sample_ix = []
x = map(lambda c: token_to_id.get(c,0), seed_phrase)
x = np.array([x])
for i in range(N):
# Pick the character that got assigned the highest probability
ix = sample_fun(probs(x).ravel())
# Alternatively, to sample from the distribution instead:
# ix = np.random.choice(np.arange(vocab_size), p=probs(x).ravel())
sample_ix.append(ix)
x[:,0:seq_length-1] = x[:,1:]
x[:,seq_length-1] = 0
x[0,seq_length-1] = ix
random_snippet = seed_phrase + ''.join(id_to_token[ix] for ix in sample_ix)
print("----\n %s \n----" % random_snippet)
```
# Обучение модели
В котором вы можете подёргать параметры или вставить свою генерирующую функцию.
```
print("Training ...")
#сколько всего эпох
n_epochs=100
# раз в сколько эпох печатать примеры
batches_per_epoch = 1000
#сколько цепочек обрабатывать за 1 вызов функции обучения
batch_size=100
for epoch in xrange(n_epochs):
print "Генерируем текст в пропорциональном режиме"
generate_sample(proportional_sample_fun,None)
print "Генерируем текст в жадном режиме (наиболее вероятные буквы)"
generate_sample(max_sample_fun,None)
avg_cost = 0;
for _ in range(batches_per_epoch):
x,y = sample_random_batches(corpora_ids,batch_size,seq_length)
avg_cost += train(x, y[:,0])
print("Epoch {} average loss = {}".format(epoch, avg_cost / batches_per_epoch))
```
# A chance to speed up training and get bonus score
* Try predicting next token probas at ALL ticks (like in the seminar part)
* much more objectives, much better gradients
* You may want to zero-out loss for first several iterations
# Конституция нового мирового правительства
```
seed = u"Каждый человек должен"
sampling_fun = proportional_sample_fun
result_length = 300
generate_sample(sampling_fun,seed,result_length)
seed = u"В случае неповиновения"
sampling_fun = proportional_sample_fun
result_length = 300
generate_sample(sampling_fun,seed,result_length)
И далее по списку
```
|
github_jupyter
|
```
%load_ext autoreload
%autoreload 2
import sklearn
import numpy as np
import scipy as sp
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib.dates as mdates
import seaborn as sns
#from viz import viz
from bokeh.plotting import figure, show, output_notebook, output_file, save
#from functions import merge_data
from sklearn.model_selection import RandomizedSearchCV
#import load_data
from sklearn.linear_model import LinearRegression
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import RandomForestRegressor
# 'deaths' and 'cases' contain the time-series of the outbreak
df = load_data.load_county_level()
df = df.sort_values(load_data.outcome_deaths, ascending=False)
outcome_cases = 'tot_cases'
outcome_deaths = 'tot_deaths'
important_vars = load_data.important_keys(df)
def sum_lists(list_of_lists):
arr = np.array(list(list_of_lists))
sum_arr = np.sum(arr,0)
return list(sum_arr)
# # Aggregate by State
# state_deaths_df = df.groupby('StateNameAbbreviation').deaths.agg(sum_lists).to_frame()
# state_cases_df = df.groupby('StateNameAbbreviation').cases.agg(sum_lists).to_frame()
# df = pd.concat([state_cases_df,state_deaths_df],axis =1 )
# This is investigating the number of cases associated with non-zero deaths in a county
_deaths = list(df['deaths'])
_cases = list(df['cases'])
total_points = []
cases_for_death = []
for i in range(len(df)):
for j,d in enumerate(_deaths[i]):
if d > 0:
cases_for_death.append(_cases[i][j])
if _cases[i][j] == 0:
print(i)
plt.hist(cases_for_death)
print(np.mean(cases_for_death))
print(np.quantile(cases_for_death,.5))
# Distribution of the maximum number of cases
_cases = list(df['cases'])
max_cases = []
for i in range(len(df)):
max_cases.append(max(_cases[i]))
print(sum([v >0 for v in max_cases]))
# plt.hist(max_cases)
# print(sum([v >0 for v in max_cases]))
plt.hist([v for v in max_cases if v > 20 and v < 1000],bins = 100)
print(sum([v > 50 for v in max_cases]))
np.quantile(max_cases,1)
# Distribution of the maximum number of cases
_deaths = list(df['deaths'])
max_deaths = []
for i in range(len(df)):
max_deaths.append(max(_deaths[i]))
print(sum([v >0 for v in max_deaths]))
# plt.hist(max_cases)
# print(sum([v >0 for v in max_cases]))
plt.hist([v for v in max_deaths if v > 1],bins=30)
np.quantile(max_deaths,.9)
```
### Clean data
```
# Remove rows with zero cases
max_cases = [max(v) for v in df['cases']]
df['max_cases'] = max_cases
df_with_cases = df[df['max_cases'] > 0]
# Shuffle data
shuffled_df = df_with_cases.sample(frac=1)
# Break into train test (random k-fold cross val on the training set is done to pick hyperparams)
train_ratio, val_ratio, test_ratio = .75,0,.25
train_df = shuffled_df[0:int(train_ratio*len(shuffled_df))]
# val_df = shuffled_df[int(train_ratio*len(shuffled_df)):int(val_ratio*len(shuffled_df))+int(train_ratio*len(shuffled_df))]
test_df = shuffled_df[int(train_ratio*len(shuffled_df))+int(val_ratio*len(shuffled_df)):]
def make_auto_regressive_dataset(df,autoreg_window,log=True,deaths=True,cases=False,predict_deaths=True):
"""
Make an autoregressive dataset that takes in a dataframe and a history window to predict number of deaths
for a given day given a history of autoreg_window days before it
log: take logarithm of values for features and predictions
deaths: use number of previous deaths as features
cases: use number of previous cases as features
predict_deaths: predict deaths otherwise predict cases
"""
assert (deaths == True or cases == True)
feature_array = []
ys = []
_cases = list(df['cases'])
_deaths = list(df['deaths'])
for i in range(len(_cases)):
for j in range(len(_cases[i])-(autoreg_window+1)):
if predict_deaths:
contains_event = sum(_deaths[i][j:j+autoreg_window+1]) > 0
else:
contains_event = sum(_cases[i][j:j+autoreg_window+1]) > 0
if contains_event > 0:
cases_window = _cases[i][j:j+autoreg_window]
if log:
cases_window = [np.log(v+1) for v in cases_window ]
deaths_window = _deaths[i][j:j+autoreg_window]
if log:
deaths_window = [np.log(v+1) for v in deaths_window]
if predict_deaths:
y_val = _deaths[i][j+autoreg_window+1]
else:
y_val = _cases[i][j+autoreg_window+1]
if log:
y_val = np.log(y_val+1)
features = []
if deaths == True:
features.extend(deaths_window)
if cases == True:
features.extend(cases_window)
feature_array.append(features)
ys.append(y_val)
return feature_array, ys
def evaluate_model(model,eval_pair, metric, exponentiate=False):
"""
Model: sklearn model
Eval pair: (x,y)
metric: sklearn metric
exponentiate: exponentiate model predictions?
"""
predictions = model.predict(eval_pair[0])
y_val = eval_pair[1]
if exponentiate:
predictions = [np.exp(p) for p in predictions]
y_val = [np.exp(y) for y in y_val]
return predictions, metric(predictions,y_val)
model = sklearn.neighbors.KNeighborsRegressor()
param_dist ={
'n_neighbors': [2,4,8,16],
'weights': ['uniform','distance'],
'p': [1,2,4]
}
# model = RandomForestRegressor()
# param_dist ={
# 'n_estimators': [50,100,200,400,1000]
# }
# Number of randomly sampled hyperparams
n_iter = 20
metric = sklearn.metrics.mean_squared_error
# n_jobs = number of cores to parallelize across
random_search = RandomizedSearchCV(model, param_distributions=param_dist,
n_iter=n_iter,n_jobs = 8)
predict_deaths = False
auto_reg_windows = [1,2,4,8]
best_window = None
best_loss = None
for w in auto_reg_windows:
log = False
x_train, y_train = make_auto_regressive_dataset(train_df,w,log=log,predict_deaths=predict_deaths)
x_test, y_test = make_auto_regressive_dataset(test_df,w,log=log,predict_deaths=predict_deaths)
random_search.fit(x_train,y_train)
window_loss = random_search.best_score_
if best_loss is None:
best_window = w
best_loss = window_loss
elif window_loss < best_loss:
best_window = w
best_score = loss
x_train, y_train = make_auto_regressive_dataset(train_df,best_window,log=log)
x_test, y_test = make_auto_regressive_dataset(test_df,best_window,log=log)
random_search.fit(x_train,y_train)
preds, loss = evaluate_model(random_search,(x_test,y_test),metric,exponentiate=True)
# model.fit(x_train,y_train)
random_search.best_params_
best_window
loss
# WARNING: does not yet supported number of previous cases as feature
def get_auto_reg_predictions(model,row,window,teacher_forcing=True,exponentiate=False,predict_deaths=True):
if predict_deaths:
key = 'deaths'
else:
key = 'cases'
deaths = row[key]
predictions = [0]
if teacher_forcing:
for i in range(len(deaths)-(window)):
x = deaths[i:i+window]
cur_prediction = model.predict([x])
if exponentiate:
cur_prediction = np.exp(cur_prediction)
predictions.append(cur_prediction)
else:
raise NotImplementedError
return predictions
def plot_prediction(model,row,window,exponentiate=False,predict_deaths=True):
"""
Plots model predictions vs actual
row: dataframe row
window: autoregressive window size
"""
if predict_deaths:
key = 'deaths'
else:
key = 'cases'
model_predictions = get_auto_reg_predictions(model,row,window,exponentiate,predict_deaths=predict_deaths)
model_predictions = [float(v) for v in model_predictions]
print(model_predictions)
for i,val in enumerate(row[key]):
if val > 0:
start_point = i
break
plt.plot(row[key][start_point:], label=key)
plt.plot(model_predictions[start_point:],label='predictions')
print(model_predictions[start_point:])
plt.fill_between(list(range(len(row[key][start_point:]))),row[key][start_point:],model_predictions[start_point:])
plt.legend()
plt.show()
for i in range(len(test_df)):
row = test_df.iloc[i]
if max(row['deaths'][:-1]) > 1:
plot_prediction(random_search,row,best_window,exponentiate=True,predict_deaths=predict_deaths)
```
## Predict deaths from cases
```
def create_case_to_death_data(df):
_cases = []
_deaths = []
_y_deaths = []
for i in range(len(df)):
row = df.iloc[i]
deaths = row['deaths']
cases = row['cases']
for j in range(len(deaths)):
if cases[j] > 0:
_cases.append(cases[j])
if j == 0:
_deaths.append(0)
else:
_deaths.append(deaths[j-1])
_y_deaths.append(deaths[j])
return (_cases,_deaths,_y_deaths)
train_cases, train_deaths, train_y_deaths = create_case_to_death_data(train_df)
test_cases, test_deaths, test_y_deaths = create_case_to_death_data(test_df)
model = RandomForestRegressor()
param_dist ={
'n_estimators': [50,100,200,400,1000]
}
metric = sklearn.metrics.mean_squared_error
# n_jobs = number of cores to parallelize across
deaths_random_search = RandomizedSearchCV(model, param_distributions=param_dist,
n_iter=n_iter,n_jobs = 8)
deaths_random_search.fit(list(zip(train_cases,train_deaths)),train_y_deaths)
pred_deaths = deaths_random_search.predict(list(zip(test_cases,test_deaths)))
metric(pred_deaths,test_y_deaths)
row = df.iloc[0]
plt.plot(row['deaths'], label='deaths')
plt.plot(row['cases'], label='cases')
plt.legend()
plt.show()
```
|
github_jupyter
|
```
# Packages
from IPython.display import Image
import rasterio
from rasterio import windows
import skimage
import skimage.io as skio
import json
import skimage.draw
import os
import sys
import pathlib
import math
import itertools
from shutil import copy2
import functools
from skimage import exposure
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
import numpy as np
import pandas as pd
from rasterio.plot import show
from osgeo import gdal
# Get absolute file paths. Returns generator object
def absoluteFilePaths(directory):
for dirpath,_,filenames in os.walk(directory):
for f in filenames:
yield os.path.abspath(os.path.join(dirpath, f))
# Normalize array
def normalize(arr, arr_max = None):
''' Function to normalize an input array to 0-1 '''
if not arr_max:
arr_max = arr.max()
out = arr / arr_max
else:
out = arr / arr_max
return arr / arr_max
# Reorder Planet scenes to RGB
def reorder_to_rgb(image):
'''reorders planet bands to red, green, blue for imshow'''
blue = normalize(image[:,:,0])
green = normalize(image[:,:,1])
red = normalize(image[:,:,2])
return np.stack([red, green, blue], axis=-1)
# Reorder Planet scenes to RGB for RASTERIO read images (C,H,W)
def rasterio_to_rgb(image):
'''reorders planet bands to red, green, blue for imshow'''
blue = image[0,:,:]
green = image[1,:,:]
red = image[2,:,:]
return np.stack([red, green, blue], axis=0)
# Contrast stretching algorithm for multiband images
def contrast_stretch_mb(img):
# Loop over RGB bands
for b in range(0,3):
p2, p98 = np.percentile(img[:,:,b], (2, 98))
img_scaled = exposure.rescale_intensity(img, in_range=(p2, p98))
img[:,:,b] = img_scaled[:,:,b]
return img
# Contrast stretching for a chip with percentiles passed to it from larger image
# Contrast stretching algorithm for multiband images
def contrast_stretch_chip(img, percs):
img_out = img
# Loop over RGB bands
for b in range(0,3):
band_percs = percs[b]
p2 = band_percs[0]
p98 = band_percs[1]
band_max = band_percs[2]
img_norm = normalize(img, band_max)
img_scaled = exposure.rescale_intensity(img, in_range=(p2, p98))
img_scaled = exposure.rescale_intensity(img_scaled, out_range=('uint8'))
img_out[:,:,b] = img_scaled[:,:,b]
return img_out
def setup_labeling(vgg_dir, chip_dir):
"""Copy the VGG project template JSONs and the via.html file into the
directory of each planet_chip so labeling can begin
"""
# Check if JSON files and/or via.html exists in chip directory
chip_files = os.listdir(chip_dir)
if any (".json" in f for f in chip_files):
print("has labeling files")
# If not, copy the template jsons and via.html into the chip's directory
else:
for file in os.listdir(vgg_dir):
copy2(os.path.join(vgg_dir, file), chip_dir)
def planet2chips(tiff_directory, chip_directory, chip_size = 512):
""" Creates image chips (GeoTiffs and PNGs) of a GeoTiff file in a
specified directory and saves in new directory location
"""
# Get all analytic SR GeoTiff filnames in specified directory
files = np.array(os.listdir(tiff_directory))
tiff = pd.Series(files).str.contains('SR.tif')
file = files[tiff][0]
# Get image name to use for creating directory
image_name = file.split("_")[0:3]
image_name = "%s_%s_%s" % (image_name[0], image_name[1], image_name[2])
# Image chip destination directory and subdirectories
image_dir = os.path.join(chip_directory, image_name)
chip_dir = os.path.join(image_dir,'chips')
png_dir = os.path.join(image_dir, 'pngs')
# Print filenames
print('filename: ' + file + '\n' + 'image name: ' + image_name)
# Make directories to store raw and rgb image chips
pathlib.Path(chip_dir).mkdir(parents=True, exist_ok=True)
pathlib.Path(png_dir).mkdir(parents=True, exist_ok=True)
# Iterate over image blocks - which are 256x256 - and save new GeoTiffs
with rasterio.open(os.path.join(tiff_directory, file)) as src:
# Read full src image and calculate percentiles for contrast stretchin
full_src = src.read()
print(full_src.shape)
# Create windows of desired size
rows1 = np.arange(0,full_src.shape[1], chip_size)
rows2 = np.arange(chip_size,full_src.shape[1], chip_size)
cols1 = np.arange(0,full_src.shape[2], chip_size)
cols2 = np.arange(chip_size,full_src.shape[2], chip_size)
# arrange into tuples
rows = list(zip(rows1, rows2))
cols = list(zip(cols1, cols2))
# Arrange into tuples of windows to read
windows = [ (a,b) for a in rows for b in cols ]
# Get block dimensions of src
for window in windows:
r = src.read((1,2,3,4), window=window)
if 0 in r:
continue
else:
# Get start row and column for file name
rmin = window[0][0]
cmin = window[1][0]
# Scale variable. Note bands of Planet imagery go BGR
b = src.read((3,2,1), window=window)
# Swap axis from rasterio order (C,H,W) to order expected by skio (H,W,C)
b = np.moveaxis(b, 0, 2)
b = contrast_stretch_mb(b)
png_file = png_dir + '/' + image_name + '_' + str(rmin) + '_' + str(cmin) + '.png'
skio.imsave(png_file, b)
# Open a new GeoTiff data file in which to save the raw image chip
with rasterio.open((chip_dir + '/' + image_name + '_' + str(rmin) + '_' + str(cmin) + '.tif'), 'w', driver='GTiff',
height=r.shape[1], width=r.shape[2], count=4,
dtype=rasterio.uint16, crs=src.crs,
transform=src.transform) as new_img:
# Write the raw image to the new GeoTiff
new_img.write(r)
```
Apply to a test image to check performance
```
# sdir = '/Users/Tyler-SFG/Desktop/Box Sync/SFG Centralized Resources/Projects/Aquaculture/Waitt Aquaculture/aqua-mapping/aqua-mapping-data/aqua-images/planet/planet_order_242451/20180830_154418_0f3c'
# planet2chips(tiff_directory = sdir, chip_directory = sdir, chip_size = 512)
```
Now we need a function to copy the VGG project templates and via.html files into each chip directory so that the chips can be labeled.
```
def process_planet_orders(source_dir, target_dir):
"""Find unique PlanetScope scenes in a directory of Planet order folders
and process newly added scenes into image chips"""
# Get list of all planet orders in source directory
orders = np.array(next(os.walk(source_dir))[1])
# Add full path to each order directory
orders = [os.path.join(source_dir, o) for o in orders]
scenes = []
scene_paths = []
for o in orders:
# scenes in order
s_ids = np.array(next(os.walk(o))[1])
s_ids_paths = [os.path.join(source_dir,o,s) for s in s_ids]
# add to lists
scenes.append(s_ids)
scene_paths.append(s_ids_paths)
# Flatten lists
scenes = list(np.concatenate(scenes))
print(len(scenes))
scene_paths = list(np.concatenate(scene_paths))
# Check which scenes already have chip folders
scenes_exist = np.array(next(os.walk(target_dir))[1])
scenes_to_process = []
scene_paths_to_process = []
# Remove scenes that already exist from list of scenes to process
for s, sp in zip(scenes, scene_paths):
if s not in scenes_exist:
scenes_to_process.append(s)
scene_paths_to_process.append(sp)
# Apply GeoTiff chipping function to each unprocessed scene
for sp in scene_paths_to_process:
print(sp)
planet2chips(tiff_directory = sp, chip_directory = target_dir, chip_size = 512)
```
Apply the function to process all Planet orders presently in Box
```
# Run function
sdir = '/Users/Tyler-SFG/Desktop/Box Sync/SFG Centralized Resources/Projects/Aquaculture/Waitt Aquaculture/aqua-mapping/aqua-mapping-data/aqua-images/planet'
tdir = '/Users/Tyler-SFG/Desktop/Box Sync/SFG Centralized Resources/Projects/Aquaculture/Waitt Aquaculture/aqua-mapping/aqua-mapping-data/aqua-images/planet_chips'
# os.path.isdir(sdir)
process_planet_orders(sdir, tdir)
```
### Move tiff files for labeled chips
After a Planet scene is processed into tiff and png chips, the pngs containing objects are added to a VGG project and labeled. Labels are then saved in a `[batchname]_labels.json` file. The last step prior to uploading the chips to Tana is to create a new directory for the chip containing the raw tiff file and a directory of class specific masks.
```
# Function to copy the tiffs of PNGs selected for labeling and make directories for each chip
def copy_chip_tiffs(label_dir, chips_dir, prepped_dir):
""" Take a VGG labeling project with PNGs and create a directory
for each chip in the prepped directory
"""
# Read annotations
pngs = os.listdir(label_dir)
pngs = [png for png in pngs if png != '.DS_Store'] # remove stupid DS_Store file
# Extract filenames and drop .png extension
chips = [c.split('.png')[0] for c in pngs]
# Loop over chips
for chip in chips:
# Make directory for chip in prepped dir
chip_dir = os.path.join(prepped_dir, chip)
# Create "image" dir for tiff image
image_dir = os.path.join(chip_dir, 'image')
# Make chip directory and subdirectories
for d in [chip_dir, image_dir]:
pathlib.Path(d).mkdir(parents=True, exist_ok=True)
# Now locate the tiff file and copy into chip directory
# Get scene name for chip
scene = chip.split('_')[0:3]
scene = "%s_%s_%s" % (scene[0], scene[1], scene[2])
# Locate and copy tiff file
tiff = os.path.join(chips_dir, scene, 'chips', (chip + '.tif'))
copy2(tiff, image_dir)
```
Run function to copy tifs for selected PNGs
```
# Copy tiffs for chile cages
labels = '/Users/Tyler-SFG/Desktop/Box Sync/SFG Centralized Resources/Projects/Aquaculture/Waitt Aquaculture/aqua-mapping/aqua-mapping-data/aqua-images/vgg/labeled/label_china/pngs'
prepped_dir = '/Users/Tyler-SFG/Desktop/Box Sync/SFG Centralized Resources/Projects/Aquaculture/Waitt Aquaculture/aqua-mapping/aqua-mapping-data/aqua-images/prepped_planet'
chips_dir = '/Users/Tyler-SFG/Desktop/Box Sync/SFG Centralized Resources/Projects/Aquaculture/Waitt Aquaculture/aqua-mapping/aqua-mapping-data/aqua-images/planet_chips'
copy_chip_tiffs(label_dir = labels, chips_dir = chips_dir, prepped_dir = prepped_dir)
```
Now we need a function to create the class masks for each image
```
def masks_from_labels(labels, prepped_dir):
# Read annotations
annotations = json.load(open(labels))
annotations = list(annotations.values()) # don't need the dict keys
# The VIA tool saves images in the JSON even if they don't have any
# annotations. Skip unannotated images.
annotations = [a for a in annotations if a['regions']]
# Loop over chips
for a in annotations:
# Get chip and directory
chip = a['filename'].split('.png')[0]
chip_dir = os.path.join(prepped_dir, chip)
# Create a directory to store masks
masks_dir = os.path.join(chip_dir, 'class_masks')
pathlib.Path(masks_dir).mkdir(parents=True, exist_ok=True)
# Read geotiff for chip
gtiff = chip_dir + '/' + 'image' + '/' + chip + '.tif'
src = rasterio.open(gtiff)
# Use try to only extract masks for chips with complete annotations and class labels
try:
"""Code for processing VGG annotations from Matterport balloon color splash sample"""
# Load annotations
# VGG Image Annotator saves each image in the form:
# { 'filename': '28503151_5b5b7ec140_b.jpg',
# 'regions': {
# '0': {
# 'region_attributes': {},
# 'shape_attributes': {
# 'all_points_x': [...],
# 'all_points_y': [...],
# 'name': 'polygon'}},
# ... more regions ...
# },
# 'size': 100202
# }
# Get the aquaculture class of each polygon
polygon_types = [r['region_attributes'] for r in a['regions']]
# Get unique aquaculture classes in annotations
types = set(val for dic in polygon_types for val in dic.values())
for t in types:
# Get the x, y coordinaets of points of the polygons that make up
# the outline of each object instance. There are stores in the
# shape_attributes (see json format above)
# Pull out polygons of that type
polygons = [r['shape_attributes'] for r in a['regions'] if r['region_attributes']['class'] == t]
# Draw mask using height and width of Geotiff
mask = np.zeros([src.height, src.width], dtype=np.uint8)
for p in polygons:
# Get indexes of pixels inside the polygon and set them to 1
rr, cc = skimage.draw.polygon(p['all_points_y'], p['all_points_x'])
mask[rr, cc] = 1
# Open a new GeoTiff data file in which to save the image chip
with rasterio.open((masks_dir + '/' + chip + '_' + str(t) + '_mask.tif'), 'w', driver='GTiff',
height=src.shape[0], width=src.shape[1], count=1,
dtype=rasterio.ubyte, crs=src.crs,
transform=src.transform) as new_img:
# Write the rescaled image to the new GeoTiff
new_img.write(mask.astype('uint8'),1)
except KeyError:
print(chip + ' missing aquaculture class assignment')
# write chip name to file for double checking
continue
```
Run function to create masks
```
labels = "/Users/Tyler-SFG/Desktop/Box Sync/SFG Centralized Resources/Projects/Aquaculture/Waitt Aquaculture/aqua-mapping/aqua-mapping-data/aqua-images/vgg/labeled/label_china/20180410_020421_0f31_labels.json"
prepped_dir = '/Users/Tyler-SFG/Desktop/Box Sync/SFG Centralized Resources/Projects/Aquaculture/Waitt Aquaculture/aqua-mapping/aqua-mapping-data/aqua-images/prepped_planet/china_20180918'
masks_from_labels(labels = labels, prepped_dir = prepped_dir)
```
|
github_jupyter
|
# Import packages & Connect the database
```
# Install MYSQL client
pip install PyMySQL
import sklearn
print('The scikit-learn version is {}.'.format(sklearn.__version__))
%load_ext autoreload
%autoreload 2
%matplotlib inline
import numpy as np
import pandas as pd
import datetime as dt
# Connect to database
import pymysql
conn = pymysql.connect(
host='34.69.136.137',
port=int(3306),
user='root',
passwd='rtfgvb77884',
db='valenbisi',
charset='utf8mb4')
```
# Prepare data
```
# Get Stations
df_station_snapshot = pd.read_sql_query("SELECT station_number, station_service_available, creation_date FROM station_snapshot WHERE station_number=31",
conn)
def substractTime(x):
date = dt.datetime(x.year, x.month, x.day, x.hour)
return (date - dt.timedelta(hours=1))
def addTime(x):
date = dt.datetime(x.year, x.month, x.day, x.hour)
return (date + dt.timedelta(hours=1))
def getPrevAvailable(d_f, row):
new_dateTime = substractTime(row['datetime'])
try:
return d_f[(d_f['id'] == row['id']) & (d_f['year'] == new_dateTime.year) & (d_f['month'] == new_dateTime.month) & (d_f['day'] == new_dateTime.day) & (d_f['hour'] == new_dateTime.hour)].iloc[0, d_f.columns.get_loc('available')]
except:
return 0
def getNextAvailable(d_f, row):
new_dateTime = addTime(row['datetime'])
try:
return d_f[(d_f['id'] == row['id']) & (d_f['year'] == new_dateTime.year) & (d_f['month'] == new_dateTime.month) & (d_f['day'] == new_dateTime.day) & (d_f['hour'] == new_dateTime.hour)].iloc[0, d_f.columns.get_loc('available')]
except:
return 0
# Update titles
df_stations = df_station_snapshot.rename(index=str, columns={"station_number": "id", "station_service_available": "available", "creation_date": "datetime"})
df_stations['id'] = df_stations['id'].astype(str).astype(int);
# Transform date strinf to date without seconds
df_stations['datetime'] = pd.to_datetime(df_stations['datetime'], infer_datetime_format=True)
df_stations['datetime'] = df_stations['datetime'].dt.floor('H')
# # Sort by datetime
df_stations.sort_values(by=['datetime'], inplace=True, ascending=True)
# # Separate datetime in columns
df_stations['date'] = df_stations['datetime'].dt.date
df_stations['hour'] = df_stations['datetime'].dt.hour
df_stations['year'] = df_stations['datetime'].dt.year
df_stations['month'] = df_stations['datetime'].dt.month
df_stations['day'] = df_stations['datetime'].dt.day
df_stations['dayofweek'] = df_stations['datetime'].dt.dayofweek
# Group and avg by time
df_stations['available'] = df_stations.groupby(['id', 'date', 'hour'])['available'].transform('mean').astype(int)
df_stations.drop_duplicates(subset=['id', 'date', 'hour'], keep='first', inplace=True)
# # Set multiple avaiables
df_stations['available_prev'] = df_stations.apply(lambda x: getPrevAvailable(df_stations, x), axis=1)
df_stations['available_next'] = df_stations.apply(lambda x: getNextAvailable(df_stations, x), axis=1)
# # Clean columns
df_stations.drop(['datetime', 'day'], axis=1, inplace=True)
df_stations.tail()
# Get Holidays
df_holiday_snapshot = pd.read_sql_query("SELECT date, enabled FROM holiday",
conn)
# Update titles
df_holiday = df_holiday_snapshot.rename(index=str, columns={"enabled": "holiday"})
# Sort by datetime
df_holiday.sort_values(by=['date'], inplace=True, ascending=True)
# Get Sport Events
df_event_snapshot = pd.read_sql_query("SELECT date, football, basketball FROM sport_event",
conn)
# Clone data frame
df_event = df_event_snapshot
# Sort by datetime
df_event.sort_values(by=['date'], inplace=True, ascending=True)
# Get Weather
df_weather_snapshot = pd.read_sql_query("SELECT temperature, humidity, wind_speed, cloud_percentage, creation_date FROM weather",
conn)
# Update titles
df_weather = df_weather_snapshot.rename(index=str, columns={"wind_speed": "wind", "cloud_percentage": "cloud", "creation_date": "datetime"})
# Transform date strinf to date without seconds
df_weather['datetime'] = pd.to_datetime(df_weather['datetime'], infer_datetime_format=True)
df_weather['datetime'] = df_weather['datetime'].dt.floor('H')
# Separate datetime in two columns
df_weather['date'] = df_weather['datetime'].dt.date
df_weather['hour'] = df_weather['datetime'].dt.hour
# Group by datetime and get mean of the data
df_weather['temperature'] = df_weather.groupby(['hour', 'date'])['temperature'].transform('mean')
df_weather['humidity'] = df_weather.groupby(['hour', 'date'])['humidity'].transform('mean')
df_weather['wind'] = df_weather.groupby(['hour', 'date'])['wind'].transform('mean')
df_weather['cloud'] = df_weather.groupby(['hour', 'date'])['cloud'].transform('mean')
# Clean duplicated rows
df_weather.drop_duplicates(subset=['date', 'hour'], keep='first', inplace=True)
# Clean columns
df_weather.drop(['datetime'], axis=1, inplace=True)
# Merge stations with holidays
df = pd.merge(
df_stations,
df_holiday,
how='left',
left_on=['date'],
right_on=['date']
)
# Replace NaN with 0
df['holiday'] = df['holiday'].fillna(0)
# Merge (stations with holidays) with sport events
df = pd.merge(
df,
df_event,
how='left',
left_on=['date'],
right_on=['date']
)
# Replace NaN with 0
df['football'] = df['football'].fillna(0)
df['basketball'] = df['basketball'].fillna(0)
# Merge ((stations with holidays) with sport events) with weather
df = pd.merge(
df,
df_weather,
how='left',
left_on=['date', 'hour'],
right_on=['date', 'hour']
)
# Replace NaN with 0
df['temperature'] = df['temperature'].fillna(0)
df['humidity'] = df['humidity'].fillna(0)
df['wind'] = df['wind'].fillna(0)
df['cloud'] = df['cloud'].fillna(0)
# Show latest data
print('DATA AGGREGATED FOR STATION: ' + station)
df.tail(10)
```
# Visualize the data
```
# Load libraries
import matplotlib as mpl
import matplotlib.pyplot as plt
from matplotlib.legend_handler import HandlerLine2D
import seaborn as sns;
# HEATMAP CHART PER MIN (10)
heatmap_data = pd.pivot_table(df[df['id']==31], values='available', index='hour', columns='date')
fig, ax = plt.subplots(figsize=(20,5))
sns.heatmap(heatmap_data, cmap='RdBu', ax=ax)
# HEATMAP CHART PER WEEK DAY
heatmap_data_week_day = pd.pivot_table(df[df['id']==31], values='available', index='hour', columns='dayofweek')
fig, ax = plt.subplots(figsize=(20,5))
sns.heatmap(heatmap_data_week_day, cmap='RdBu', ax=ax)
```
# Start prediction
```
# Load libraries
import math
from sklearn.ensemble import RandomForestRegressor, AdaBoostRegressor, GradientBoostingRegressor
from sklearn.linear_model import LinearRegression, Lasso, LassoLars, Ridge
from sklearn.tree import DecisionTreeRegressor
from scipy.stats import randint as sp_randint
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn import metrics
from sklearn.metrics import explained_variance_score
from sklearn.feature_selection import SelectKBest, chi2
from sklearn.pipeline import Pipeline
from sklearn.impute import SimpleImputer
# Evaluate model
def evaluate(model, train_features, train_labels, test_features, test_labels):
print('MODEL PERFORMANCE')
train_pred = model.predict(train_features)
print('Train set')
print('| Mean Absolute Error:', metrics.mean_absolute_error(train_labels, train_pred))
print('| Mean Square Error:', metrics.mean_squared_error(train_labels, train_pred))
print('| Root Mean Square Error:', np.sqrt(metrics.mean_squared_error(train_labels, train_pred)))
print('| Train Score:', model.score(train_features, train_labels))
y_pred = model.predict(test_features)
print('Test set')
print('| Mean Absolute Error:', metrics.mean_absolute_error(test_labels, y_pred))
print('| Mean Square Error:', metrics.mean_squared_error(test_labels, y_pred))
print('| Root Mean Square Error:', np.sqrt(metrics.mean_squared_error(test_labels, y_pred)))
print('| Test Score:', model.score(test_features, test_labels))
print('| Explained Variance:', explained_variance_score(test_labels, y_pred))
if hasattr(model, 'oob_score_'): print('OOB Score:', model.oob_score_)
```
## Find best algoritm for our data
```
def quick_eval(pipeline, X_train, y_train, X_test, y_test, verbose=True):
"""
Quickly trains modeling pipeline and evaluates on test data. Returns original model, training RMSE, and testing
RMSE as a tuple.
"""
pipeline.fit(X_train, y_train)
y_train_pred = pipeline.predict(X_train)
y_test_pred = pipeline.predict(X_test)
train_score = np.sqrt(metrics.mean_squared_error(y_train, y_train_pred))
test_score = np.sqrt(metrics.mean_squared_error(y_test, y_test_pred))
if verbose:
print(f"Regression algorithm: {pipeline.named_steps['regressor'].__class__.__name__}")
print(f"Train RMSE: {train_score}")
print(f"Test RMSE: {test_score}")
print(f"----------------------------")
return pipeline.named_steps['regressor'], train_score, test_score
```
After review the result we see that **RandomForestRegressor** is the best option to predict our data
## Random Forest
```
# Create a new dataframe for random forest
df_rf = df[['id', 'year', 'month', 'dayofweek', 'hour', 'holiday', 'football', 'basketball', 'temperature', 'humidity', 'wind', 'cloud', 'available_prev', 'available', 'available_next']]
# Prepare data for train and test
# We want to predict ("available_next")
X = df_rf.drop('available_next', axis=1)
y = df_rf['available_next']
# Split data in train and test
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25)
X_train.shape, y_train.shape, X_test.shape, y_test.shape
# Create our imputer to replace missing values with the mean e.g.
imp = SimpleImputer(missing_values=np.nan, strategy='mean')
imp = imp.fit(X_train)
# Impute our data, then train
X_train = imp.transform(X_train)
regressors = [
LinearRegression(),
Lasso(alpha=.5),
Ridge(alpha=.1),
LassoLars(alpha=.1),
DecisionTreeRegressor(),
RandomForestRegressor(),
AdaBoostRegressor(),
GradientBoostingRegressor()
]
for r in regressors:
pipe = Pipeline(steps = [
('regressor', r)
])
quick_eval(pipe, X_train, y_train, X_test, y_test)
```
### Find best params for Random Forest
#### Check each property
```
# Find N_ESTIMATORS
n_estimators = [int(x) for x in np.linspace(start = 1, stop = 200, num=50)]
train_results = []
test_results = []
for estimator in n_estimators:
rf = RandomForestRegressor(n_estimators=estimator, n_jobs=-1)
rf.fit(X_train, y_train)
train_pred = rf.predict(X_train)
train_results.append(np.sqrt(metrics.mean_squared_error(y_train, train_pred)))
#train_results.append(rf.score(X_train, y_train))
y_pred = rf.predict(X_test)
test_results.append(np.sqrt(metrics.mean_squared_error(y_test, y_pred)))
#test_results.append(rf.score(X_test, y_test))
line1, = plt.plot(n_estimators, train_results, 'b', label='Train RSME')
line2, = plt.plot(n_estimators, test_results, 'r', label='Test RSME')
plt.legend(handler_map={line1: HandlerLine2D(numpoints=2)})
plt.ylabel('RSME')
plt.xlabel('n_estimators')
plt.show()
# Find MAX_DEPTH
max_depths = np.linspace(start = 1, stop = 100, num=50, endpoint=True)
train_results = []
test_results = []
for max_depth in max_depths:
rf = RandomForestRegressor(max_depth=max_depth, n_jobs=-1)
rf.fit(X_train, y_train)
train_pred = rf.predict(X_train)
train_results.append(np.sqrt(metrics.mean_squared_error(y_train, train_pred)))
#train_results.append(rf.score(X_train, y_train))
y_pred = rf.predict(X_test)
test_results.append(np.sqrt(metrics.mean_squared_error(y_test, y_pred)))
#test_results.append(rf.score(X_test, y_test))
line1, = plt.plot(max_depths, train_results, 'b', label='Train RSME')
line2, = plt.plot(max_depths, test_results, 'r', label='Test RSME')
plt.legend(handler_map={line1: HandlerLine2D(numpoints=2)})
plt.ylabel('RSME')
plt.xlabel('Tree depth')
plt.show()
# Find MIN_SAMPLES_SPLIT
min_samples_splits = np.linspace(start = 0.01, stop = 1.0, num=10, endpoint=True)
train_results = []
test_results = []
for min_samples_split in min_samples_splits:
rf = RandomForestRegressor(min_samples_split=min_samples_split)
rf.fit(X_train, y_train)
train_pred = rf.predict(X_train)
train_results.append(np.sqrt(metrics.mean_squared_error(y_train, train_pred)))
#train_results.append(rf.score(X_train, y_train))
y_pred = rf.predict(X_test)
test_results.append(np.sqrt(metrics.mean_squared_error(y_test, y_pred)))
#test_results.append(rf.score(X_test, y_test))
line1, = plt.plot(min_samples_splits, train_results, 'b', label='Train RSME')
line2, = plt.plot(min_samples_splits, test_results, 'r', label='Test RSME')
plt.legend(handler_map={line1: HandlerLine2D(numpoints=2)})
plt.ylabel('RSME')
plt.xlabel('min samples split')
plt.show()
# Find MIN_SAMPLES_LEAF
min_samples_leafs = np.linspace(start = 0.01, stop = 0.5, num=5, endpoint=True)
train_results = []
test_results = []
for min_samples_leaf in min_samples_leafs:
rf = RandomForestRegressor(min_samples_leaf=min_samples_leaf)
rf.fit(X_train, y_train)
train_pred = rf.predict(X_train)
train_results.append(np.sqrt(metrics.mean_squared_error(y_train, train_pred)))
#train_results.append(rf.score(X_train, y_train))
y_pred = rf.predict(X_test)
test_results.append(np.sqrt(metrics.mean_squared_error(y_test, y_pred)))
#test_results.append(rf.score(X_test, y_test))
line1, = plt.plot(min_samples_leafs, train_results, 'b', label='Train RSME')
line2, = plt.plot(min_samples_leafs, test_results, 'r', label='Test RSME')
plt.legend(handler_map={line1: HandlerLine2D(numpoints=2)})
plt.ylabel('RSME')
plt.xlabel('min samples leaf')
plt.show()
# Find MAX_FEATURES
max_features = list(range(1,X.shape[1]))
train_results = []
test_results = []
for max_feature in max_features:
rf = RandomForestRegressor(max_features=max_feature)
rf.fit(X_train, y_train)
train_pred = rf.predict(X_train)
train_results.append(np.sqrt(metrics.mean_squared_error(y_train, train_pred)))
#train_results.append(rf.score(X_train, y_train))
y_pred = rf.predict(X_test)
test_results.append(np.sqrt(metrics.mean_squared_error(y_test, y_pred)))
#test_results.append(rf.score(X_test, y_test))
line1, = plt.plot(max_features, train_results, 'b', label='Train RSME')
line2, = plt.plot(max_features, test_results, 'r', label='Test RSME')
plt.legend(handler_map={line1: HandlerLine2D(numpoints=2)})
plt.ylabel('RSME')
plt.xlabel('max features')
plt.show()
```
#### Find the best combination of params
**TRY ALL PARAMS TO FIND THE BEST PARAMS FOR OUR DATA**
Now that we know where to concentrate our search, we can explicitly specify every combination of settings to try.
```
#@title Default title text
def searchBestParamsForRF(params, train_features, train_labels):
# First create the base model to tune
rf = RandomForestRegressor()
# Instantiate the grid search model
grid_search = GridSearchCV(estimator = rf, param_grid = param_grid, scoring = 'neg_mean_squared_error', cv = 5, n_jobs = -1, verbose = 2)
# Fit the grid search to the data
grid_search.fit(train_features, train_labels)
print(f"The best estimator had RMSE {np.sqrt(-grid_search.best_score_)} and the following parameters:")
print(grid_search.best_params_)
# Create the parameter grid
max_depth = [int(x) for x in np.linspace(10, 20, num = 3)]
max_depth.append(None)
param_grid = {
'bootstrap': [False, True],
'n_estimators': [int(x) for x in np.linspace(start = 40, stop = 60, num = 4)],
'max_depth': max_depth,
'min_samples_split': [float(x) for x in np.linspace(0.1, 0.2, num = 2)],
'min_samples_leaf': [float(x) for x in np.linspace(0.1, 0.2, num = 2)],
'max_features': [X.shape[1]]
}
# Comment or Uncomment this line to seach for the best params
searchBestParamsForRF(param_grid, X_train, y_train)
```
### Train and evaluate model
```
m = RandomForestRegressor(n_estimators=60, max_features=X.shape[1])
m.fit(X_train, y_train)
evaluate(m, X_train, y_train, X_test, y_test)
# MODEL PERFORMANCE
# Train set
# | Mean Absolute Error: 0.5758625862586259
# | Mean Square Error: 0.6365449044904491
# | Root Mean Square Error: 0.7978376429389936
# | Train Score: 0.9807615052050999
# Test set
# | Mean Absolute Error: 1.5209793351302785
# | Mean Square Error: 4.284529050613956
# | Root Mean Square Error: 2.0699103967597137
# | Test Score: 0.8757254225805797
# | Explained Variance: 0.8758109846903823
X_test.tail()
y_test.tail()
m.predict([[2020, 1, 6, 10, 0, 0, 0, 11.57, 70.50, 0.93, 0, 0, 1]])
# Show the importance of each variable in prediction
def rf_feat_importance(m, df):
return pd.DataFrame({'cols':df.columns, 'imp':m.feature_importances_}).sort_values('imp', ascending=False)
fi = rf_feat_importance(m, X);
fi[:].plot('cols', 'imp', 'barh', figsize=(12,7), legend=False)
```
# Download model
```
# Import package
import pickle
# Generate file
with open('model.pkl', 'wb') as model_file:
pickle.dump(m, model_file)
```
|
github_jupyter
|
# Archive data
The Wellcome archive sits in a collections management system called CALM, which follows a rough set of standards and guidelines for storing archival records called [ISAD(G)](https://en.wikipedia.org/wiki/ISAD(G). The archive is comprised of _collections_, each of which has a hierarchical set of series, sections, subjects, items and pieces sitting underneath it.
In the following notebooks I'm going to explore it and try to make as much sense of it as I can programatically.
Let's start by loading in a few useful packages and defining some nice utils.
```
%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_style("white")
plt.rcParams["figure.figsize"] = (20, 20)
import pandas as pd
import numpy as np
import networkx as nx
from sklearn.cluster import AgglomerativeClustering
from umap import UMAP
from tqdm import tqdm_notebook as tqdm
def flatten(input_list):
return [item for sublist in input_list for item in sublist]
def cartesian(*arrays):
return np.array([x.reshape(-1) for x in np.meshgrid(*arrays)]).T
def clean(subject):
return subject.strip().lower().replace("<p>", "")
```
let's load up our CALM data. The data has been exported in its entirety as a single `.json` where each line is a record.
You can download the data yourself using [this script](https://github.com/wellcometrust/platform/blob/master/misc/download_oai_harvest.py). Stick the `.json` in the neighbouring `/data` directory to run the rest of the notebook seamlessly.
```
df = pd.read_json("data/calm_records.json")
len(df)
df.astype(str).describe()
```
### Exploring individual columns
At the moment I have no idea what kind of information CALM contains - lets look at the list of column names
```
list(df)
```
Here I'm looking through a sample of values in each column, choosing the columns to explore based on the their headings, a bit of contextual info from colleagues and the `df.describe()` above.
```
df["Subject"]
```
### After much trial and error...
Subjects look like an interesting avenue to explore further. Where subjects have _actually_ been filled in and the entry is not `None`, a list of subjects is returned.
We can explore some of these subjects' subtleties by creating an adjacency matrix. We'll count the number of times each subject appears alongside every other subject and return a big $n \times n$ matrix, where $n$ is the total number of unique subjects.
We can use this adjacency matrix for all sorts of stuff, but we have to build it first. To start, lets get a uniqur list of all subjects. This involves unpacking each sub-list and flattening them out into one long list, before finding the unique elements. We'll also use the `clean` function defined above to get rid of any irregularities which might become annoying later on.
```
subjects = flatten(df["Subject"].dropna().tolist())
print(len(subjects))
subjects = list(set(map(clean, subjects)))
print(len(subjects))
```
At this point it's often helpful to index our data, ie transform words into numbers. We'll create two dictionaries which map back and forth between the subjects and their corresponding indicies:
```
index_to_subject = {index: subject for index, subject in enumerate(subjects)}
subject_to_index = {subject: index for index, subject in enumerate(subjects)}
```
Lets instantiate an empty numpy array which we'll then fill with our coocurrence data. Each column and each row will represent a subject - each cell (the intersection of a column and row) will therefore represent the 'strength' of the interaction between those subjects. As we haven't seen any interactions yet, we'll set every array element to 0.
```
adjacency = np.empty((len(subjects), len(subjects)), dtype=np.uint16)
```
To populate the matrix, we want to find every possible combination of subject in each sub-list from our original column, ie if we had the subjects
`[Disease, Heart, Heart Diseases, Cardiology]`
we would want to return
`
[['Disease', 'Disease'],
['Heart', 'Disease'],
['Heart Diseases', 'Disease'],
['Cardiology', 'Disease'],
['Disease', 'Heart'],
['Heart', 'Heart'],
['Heart Diseases', 'Heart'],
['Cardiology', 'Heart'],
['Disease', 'Heart Diseases'],
['Heart', 'Heart Diseases'],
['Heart Diseases', 'Heart Diseases'],
['Cardiology', 'Heart Diseases'],
['Disease', 'Cardiology'],
['Heart', 'Cardiology'],
['Heart Diseases', 'Cardiology'],
['Cardiology', 'Cardiology']]
`
The `cartesian()` function which I've defined above will do that for us. We then find the appropriate intersection in the matrix and add another unit of 'strength' to it.
We'll do this for every row of subjects in the `['Subjects']` column.
```
for row_of_subjects in tqdm(df["Subject"].dropna()):
for subject_pair in cartesian(row_of_subjects, row_of_subjects):
subject_index_1 = subject_to_index[clean(subject_pair[0])]
subject_index_2 = subject_to_index[clean(subject_pair[1])]
adjacency[subject_index_1, subject_index_2] += 1
```
We can do all sorts of fun stuff now - adjacency matrices are the foundation on which all of graph theory is built. However, because it's a bit more interesting, I'm going to start with some dimensionality reduction. We'll get to the graphy stuff later.
Using [UMAP](https://github.com/lmcinnes/umap), we can squash the $n \times n$ dimensional matrix down into a $n \times m$ dimensional one, where $m$ is some arbitrary integer. Setting $m$ to 2 will then allow us to plot each subject as a point on a two dimensional plane. UMAP will try to preserve the 'distances' between subjects - in this case, that means that related or topically similar subjects will end up clustered together, and different subjects will move apart.
```
embedding_2d = pd.DataFrame(UMAP(n_components=2).fit_transform(adjacency))
embedding_2d.plot.scatter(x=0, y=1);
```
We can isolate the clusters we've found above using a number of different methods - `scikit-learn` provides easy access to some very powerful algorithms. Here I'll use a technique called _agglomerative clustering_, and make a guess that 15 is an appropriate number of clusters to look for.
```
n_clusters = 15
embedding_2d["labels"] = AgglomerativeClustering(n_clusters).fit_predict(
embedding_2d.values
)
embedding_2d.plot.scatter(x=0, y=1, c="labels", cmap="Paired");
```
We can now use the `index_to_subject` mapping that we created earlier to examine which subjects have been grouped together into clusters
```
for i in range(n_clusters):
print(str(i) + " " + "-" * 80 + "\n")
print(
np.sort(
[
index_to_subject[index]
for index in embedding_2d[embedding_2d["labels"] == i].index.values
]
)
)
print("\n")
```
Interesting! Taking a look at some of the smaller clusters of subjects (for the sake of space and your willingness to read lists of 100s of subjects):
One seems to be quite distinctly involved with drugs and associated topics/treatments:
```
13 --------------------------------------------------------------------------------
['acquired immunodeficiency syndrome' 'alcohol' 'amphetamines'
'analgesics, opioid' 'campaign' 'cannabis' 'cocaine' 'counseling'
'counterculture' 'crime' 'drugs' 'education' 'hallucinogens' 'heroin'
'hypnotics and sedatives' 'information services' 'inhalant abuse'
'lysergic acid diethylamide' 'n-methyl-3,4-methylenedioxyamphetamine'
'opioid' 'policy' 'prescription drugs' 'rehabilitation' 'renabilitation'
'self-help']
```
others are linked to early/fundamental research on DNA and genetics:
```
9 --------------------------------------------------------------------------------
['bacteriophages' 'biotechnology' 'caenorhabditis elegans'
'chromosome mapping' 'cloning, organism' 'discoveries in science' 'dna'
'dna, recombinant' 'genetic code' 'genetic engineering'
'genetic research' 'genetic therapy' 'genome, human' 'genomics'
'magnetic resonance spectroscopy' 'meiosis' 'models, molecular'
'molecular biology' 'nobel prize' 'retroviridae' 'rna'
'sequence analysis' 'viruses']
```
and others about food
```
14 --------------------------------------------------------------------------------
['acids' 'advertising' 'ambergris' 'animals' 'beer' 'biscuits' 'brassica'
'bread' 'butter' 'cacao' 'cake' 'candy' 'carbohydrates' 'cattle'
'cereals' 'cheese' 'chemistry, agricultural' 'cider' 'colouring agents'
'condiments' 'cooking (deer)' 'cooking (poultry)' 'cooking (venison)'
'cucumis sativus' 'dairy products' 'daucus carota' 'desserts'
'dried fruit' 'ecology' 'economics' 'eggs' 'environmental health'
'european rabbit' 'fermentation' 'food additives' 'food and beverages'
'food preservation' 'food, genetically modified' 'fruit' 'fruit drinks'
'fungi' 'game and game-birds' 'grapes' 'hands' 'health attitudes'
'herbaria' 'honey' 'jam' 'legislation' 'lettuce' 'meat' 'meat products'
'nuts' 'oatmeal' 'olive' 'onions' 'peas' 'pickles' 'pies' 'poultry'
'preserves (jams)' 'puddings' 'rice' 'seafood' 'seeds' 'sheep'
'sociology' 'solanum tuberosum' 'spinacia oleracea' 'sweetening agents'
'swine' 'syrups' 'vegetables' 'vitis' 'whiskey' 'wild flowers' 'wine']
```
These are all noticeably different themes, and they appear to be nicely separated in the topic-space we've built.
|
github_jupyter
|
<a href="https://colab.research.google.com/github/lakigigar/Caltech-CS155-2021/blob/main/psets/set1/set1_prob3.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Problem 3
Use this notebook to write your code for problem 3 by filling in the sections marked `# TODO` and running all cells.
```
import numpy as np
import matplotlib.pyplot as plt
import itertools
import urllib.request
urllib.request.urlretrieve('https://raw.githubusercontent.com/lakigigar/Caltech-CS155-2021/main/psets/set1/perceptron_helper.py', 'perceptron_helper.py')
from perceptron_helper import (
predict,
plot_data,
boundary,
plot_perceptron,
)
%matplotlib inline
```
## Implementation of Perceptron
First, we will implement the perceptron algorithm. Fill in the `update_perceptron()` function so that it finds a single misclassified point and updates the weights and bias accordingly. If no point exists, the weights and bias should not change.
Hint: You can use the `predict()` helper method, which labels a point 1 or -1 depending on the weights and bias.
```
def update_perceptron(X, Y, w, b):
"""
This method updates a perceptron model. Takes in the previous weights
and returns weights after an update, which could be nothing.
Inputs:
X: A (N, D) shaped numpy array containing N D-dimensional points.
Y: A (N, ) shaped numpy array containing the labels for the points.
w: A (D, ) shaped numpy array containing the weight vector.
b: A float containing the bias term.
Output:
next_w: A (D, ) shaped numpy array containing the next weight vector
after updating on a single misclassified point, if one exists.
next_b: The next float bias term after updating on a single
misclassified point, if one exists.
"""
next_w, next_b = np.copy(w), np.copy(b)
#==============================================
# TODO: Implement update rule for perceptron.
#===============================================
return next_w, next_b
```
Next you will fill in the `run_perceptron()` method. The method performs single updates on a misclassified point until convergence, or max_iter updates are made. The function will return the final weights and bias. You should use the `update_perceptron()` method you implemented above.
```
def run_perceptron(X, Y, w, b, max_iter):
"""
This method runs the perceptron learning algorithm. Takes in initial weights
and runs max_iter update iterations. Returns final weights and bias.
Inputs:
X: A (N, D) shaped numpy array containing N D-dimensional points.
Y: A (N, ) shaped numpy array containing the labels for the points.
w: A (D, ) shaped numpy array containing the initial weight vector.
b: A float containing the initial bias term.
max_iter: An int for the maximum number of updates evaluated.
Output:
w: A (D, ) shaped numpy array containing the final weight vector.
b: The final float bias term.
"""
#============================================
# TODO: Implement perceptron update loop.
#=============================================
return w, b
```
# Problem 3A
## Visualizing a Toy Dataset
We will begin by training our perceptron on a toy dataset of 3 points. The green points are labelled +1 and the red points are labelled -1. We use the helper function `plot_data()` to do so.
```
X = np.array([[ -3, -1], [0, 3], [1, -2]])
Y = np.array([ -1, 1, 1])
fig = plt.figure(figsize=(5,4))
ax = fig.gca(); ax.set_xlim(-4.1, 3.1); ax.set_ylim(-3.1, 4.1)
plot_data(X, Y, ax)
```
## Running the Perceptron
Next, we will run the perceptron learning algorithm on this dataset. Update the code to show the weights and bias at each timestep and the misclassified point used in each update.
Run the below code, and fill in the corresponding table in the set.
```
# Initialize weights and bias.
weights = np.array([0.0, 1.0])
bias = 0.0
weights, bias = run_perceptron(X, Y, weights, bias, 16)
print()
print ("final w = %s, final b = %.1f" % (weights, bias))
```
## Visualizating the Perceptron
Getting all that information in table form isn't very informative. Let us visualize what the decision boundaries are at each timestep instead.
The helper functions `boundary()` and `plot_perceptron()` plot a decision boundary given a perceptron weights and bias. Note that the equation for the decision boundary is given by:
$$w_1x_1 + w_2x_2 + b = 0.$$
Using some algebra, we can obtain $x_2$ from $x_1$ to plot the boundary as a line.
$$x_2 = \frac{-w_1x_2 - b}{w_2}. $$
Below is a redefinition of the `run_perceptron()` method to visualize the points and decision boundaries at each timestep instead of printing. Fill in the method using your previous `run_perceptron()` method, and the above helper methods.
Hint: The axs element is a list of Axes, which are used as subplots for each timestep. You can do the following:
```
ax = axs[i]
```
to get the plot correponding to $t = i$. You can then use ax.set_title() to title each subplot. You will want to use the `plot_data()` and `plot_perceptron()` helper methods.
```
def run_perceptron(X, Y, w, b, axs, max_iter):
"""
This method runs the perceptron learning algorithm. Takes in initial weights
and runs max_iter update iterations. Returns final weights and bias.
Inputs:
X: A (N, D) shaped numpy array containing N D-dimensional points.
Y: A (N, ) shaped numpy array containing the labels for the points.
w: A (D, ) shaped numpy array containing the initial weight vector.
b: A float containing the initial bias term.
axs: A list of Axes that contain suplots for each timestep.
max_iter: An int for the maximum number of updates evaluated.
Output:
The final weight and bias vectors.
"""
#============================================
# TODO: Implement perceptron update loop.
#=============================================
return w, b
```
Run the below code to get a visualization of the perceptron algorithm. The red region are areas the perceptron thinks are negative examples.
```
# Initialize weights and bias.
weights = np.array([0.0, 1.0])
bias = 0.0
f, ax_arr = plt.subplots(2, 2, sharex=True, sharey=True, figsize=(9,8))
axs = list(itertools.chain.from_iterable(ax_arr))
for ax in axs:
ax.set_xlim(-4.1, 3.1); ax.set_ylim(-3.1, 4.1)
run_perceptron(X, Y, weights, bias, axs, 4)
f.tight_layout()
```
# Problem 3C
## Visualize a Non-linearly Separable Dataset.
We will now work on a dataset that cannot be linearly separated, namely one that is generated by the XOR function.
```
X = np.array([[0, 1], [1, 0], [0, 0], [1, 1]])
Y = np.array([1, 1, -1, -1])
fig = plt.figure(figsize=(5,4))
ax = fig.gca(); ax.set_xlim(-0.1, 1.1); ax.set_ylim(-0.1, 1.1)
plot_data(X, Y, ax)
```
We will now run the perceptron algorithm on this dataset. We will limit the total timesteps this time, but you should see a pattern in the updates. Run the below code.
```
# Initialize weights and bias.
weights = np.array([0.0, 1.0])
bias = 0.0
f, ax_arr = plt.subplots(4, 4, sharex=True, sharey=True, figsize=(9,8))
axs = list(itertools.chain.from_iterable(ax_arr))
for ax in axs:
ax.set_xlim(-0.1, 1.1); ax.set_ylim(-0.1, 1.1)
run_perceptron(X, Y, weights, bias, axs, 16)
f.tight_layout()
```
|
github_jupyter
|
In this tutorial you'll learn all about **histograms** and **density plots**.
# Set up the notebook
As always, we begin by setting up the coding environment. (_This code is hidden, but you can un-hide it by clicking on the "Code" button immediately below this text, on the right._)
```
#$HIDE$
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns
print("Setup Complete")
```
# Select a dataset
We'll work with a dataset of 150 different flowers, or 50 each from three different species of iris (*Iris setosa*, *Iris versicolor*, and *Iris virginica*).

# Load and examine the data
Each row in the dataset corresponds to a different flower. There are four measurements: the sepal length and width, along with the petal length and width. We also keep track of the corresponding species.
```
# Path of the file to read
iris_filepath = "../input/iris.csv"
# Read the file into a variable iris_data
iris_data = pd.read_csv(iris_filepath, index_col="Id")
# Print the first 5 rows of the data
iris_data.head()
```
# Histograms
Say we would like to create a **histogram** to see how petal length varies in iris flowers. We can do this with the `sns.distplot` command.
```
# Histogram
sns.distplot(a=iris_data['Petal Length (cm)'], kde=False)
```
We customize the behavior of the command with two additional pieces of information:
- `a=` chooses the column we'd like to plot (_in this case, we chose `'Petal Length (cm)'`_).
- `kde=False` is something we'll always provide when creating a histogram, as leaving it out will create a slightly different plot.
# Density plots
The next type of plot is a **kernel density estimate (KDE)** plot. In case you're not familiar with KDE plots, you can think of it as a smoothed histogram.
To make a KDE plot, we use the `sns.kdeplot` command. Setting `shade=True` colors the area below the curve (_and `data=` has identical functionality as when we made the histogram above_).
```
# KDE plot
sns.kdeplot(data=iris_data['Petal Length (cm)'], shade=True)
```
# 2D KDE plots
We're not restricted to a single column when creating a KDE plot. We can create a **two-dimensional (2D) KDE plot** with the `sns.jointplot` command.
In the plot below, the color-coding shows us how likely we are to see different combinations of sepal width and petal length, where darker parts of the figure are more likely.
```
# 2D KDE plot
sns.jointplot(x=iris_data['Petal Length (cm)'], y=iris_data['Sepal Width (cm)'], kind="kde")
```
Note that in addition to the 2D KDE plot in the center,
- the curve at the top of the figure is a KDE plot for the data on the x-axis (in this case, `iris_data['Petal Length (cm)']`), and
- the curve on the right of the figure is a KDE plot for the data on the y-axis (in this case, `iris_data['Sepal Width (cm)']`).
# Color-coded plots
For the next part of the tutorial, we'll create plots to understand differences between the species. To accomplish this, we begin by breaking the dataset into three separate files, with one for each species.
```
# Paths of the files to read
iris_set_filepath = "../input/iris_setosa.csv"
iris_ver_filepath = "../input/iris_versicolor.csv"
iris_vir_filepath = "../input/iris_virginica.csv"
# Read the files into variables
iris_set_data = pd.read_csv(iris_set_filepath, index_col="Id")
iris_ver_data = pd.read_csv(iris_ver_filepath, index_col="Id")
iris_vir_data = pd.read_csv(iris_vir_filepath, index_col="Id")
# Print the first 5 rows of the Iris versicolor data
iris_ver_data.head()
```
In the code cell below, we create a different histogram for each species by using the `sns.distplot` command (_as above_) three times. We use `label=` to set how each histogram will appear in the legend.
```
# Histograms for each species
sns.distplot(a=iris_set_data['Petal Length (cm)'], label="Iris-setosa", kde=False)
sns.distplot(a=iris_ver_data['Petal Length (cm)'], label="Iris-versicolor", kde=False)
sns.distplot(a=iris_vir_data['Petal Length (cm)'], label="Iris-virginica", kde=False)
# Add title
plt.title("Histogram of Petal Lengths, by Species")
# Force legend to appear
plt.legend()
```
In this case, the legend does not automatically appear on the plot. To force it to show (for any plot type), we can always use `plt.legend()`.
We can also create a KDE plot for each species by using `sns.kdeplot` (_as above_). Again, `label=` is used to set the values in the legend.
```
# KDE plots for each species
sns.kdeplot(data=iris_set_data['Petal Length (cm)'], label="Iris-setosa", shade=True)
sns.kdeplot(data=iris_ver_data['Petal Length (cm)'], label="Iris-versicolor", shade=True)
sns.kdeplot(data=iris_vir_data['Petal Length (cm)'], label="Iris-virginica", shade=True)
# Add title
plt.title("Distribution of Petal Lengths, by Species")
```
One interesting pattern that can be seen in plots is that the plants seem to belong to one of two groups, where _Iris versicolor_ and _Iris virginica_ seem to have similar values for petal length, while _Iris setosa_ belongs in a category all by itself.
In fact, according to this dataset, we might even be able to classify any iris plant as *Iris setosa* (as opposed to *Iris versicolor* or *Iris virginica*) just by looking at the petal length: if the petal length of an iris flower is less than 2 cm, it's most likely to be *Iris setosa*!
# What's next?
Put your new skills to work in a **[coding exercise](#$NEXT_NOTEBOOK_URL$)**!
|
github_jupyter
|
# IMPORTING THE LIBRARIES
```
import os
import pandas as pd
import pickle
import numpy as np
import seaborn as sns
from sklearn.datasets import load_files
from keras.utils import np_utils
import matplotlib.pyplot as plt
from keras.layers import Conv2D, MaxPooling2D, GlobalAveragePooling2D
from keras.layers import Dropout, Flatten, Dense
from keras.models import Sequential
from keras.utils.vis_utils import plot_model
from keras.callbacks import ModelCheckpoint
from keras.utils import to_categorical
from sklearn.metrics import confusion_matrix
from keras.preprocessing import image
from tqdm import tqdm
import seaborn as sns
from sklearn.metrics import accuracy_score,precision_score,recall_score,f1_score
# Pretty display for notebooks
%matplotlib inline
!ls
```
# Defining the train,test and model directories
We will create the directories for train,test and model training paths if not present
```
TEST_DIR = os.path.join(os.getcwd(),"imgs","test")
TRAIN_DIR = os.path.join(os.getcwd(),"imgs","train")
MODEL_PATH = os.path.join(os.getcwd(),"model","self_trained")
PICKLE_DIR = os.path.join(os.getcwd(),"pickle_files")
if not os.path.exists(TEST_DIR):
print("Testing data does not exists")
if not os.path.exists(TRAIN_DIR):
print("Training data does not exists")
if not os.path.exists(MODEL_PATH):
print("Model path does not exists")
os.makedirs(MODEL_PATH)
print("Model path created")
if not os.path.exists(PICKLE_DIR):
os.makedirs(PICKLE_DIR)
```
# Data Preparation
We will create a csv file having the location of the files present for training and test images and their associated class if present so that it is easily traceable.
```
def create_csv(DATA_DIR,filename):
class_names = os.listdir(DATA_DIR)
data = list()
if(os.path.isdir(os.path.join(DATA_DIR,class_names[0]))):
for class_name in class_names:
file_names = os.listdir(os.path.join(DATA_DIR,class_name))
for file in file_names:
data.append({
"Filename":os.path.join(DATA_DIR,class_name,file),
"ClassName":class_name
})
else:
class_name = "test"
file_names = os.listdir(DATA_DIR)
for file in file_names:
data.append(({
"FileName":os.path.join(DATA_DIR,file),
"ClassName":class_name
}))
data = pd.DataFrame(data)
data.to_csv(os.path.join(os.getcwd(),"csv_files",filename),index=False)
create_csv(TRAIN_DIR,"train.csv")
create_csv(TEST_DIR,"test.csv")
data_train = pd.read_csv(os.path.join(os.getcwd(),"csv_files","train.csv"))
data_test = pd.read_csv(os.path.join(os.getcwd(),"csv_files","test.csv"))
data_train.info()
data_train['ClassName'].value_counts()
data_train.describe()
nf = data_train['ClassName'].value_counts(sort=False)
labels = data_train['ClassName'].value_counts(sort=False).index.tolist()
y = np.array(nf)
width = 1/1.5
N = len(y)
x = range(N)
fig = plt.figure(figsize=(20,15))
ay = fig.add_subplot(211)
plt.xticks(x, labels, size=15)
plt.yticks(size=15)
ay.bar(x, y, width, color="blue")
plt.title('Bar Chart',size=25)
plt.xlabel('classname',size=15)
plt.ylabel('Count',size=15)
plt.show()
data_test.head()
data_test.shape
```
## Observation:
1. There are total 22424 training samples
2. There are total 79726 training samples
3. The training dataset is equally balanced to a great extent and hence we need not do any downsampling of the data
## Converting into numerical values
```
labels_list = list(set(data_train['ClassName'].values.tolist()))
labels_id = {label_name:id for id,label_name in enumerate(labels_list)}
print(labels_id)
data_train['ClassName'].replace(labels_id,inplace=True)
with open(os.path.join(os.getcwd(),"pickle_files","labels_list.pkl"),"wb") as handle:
pickle.dump(labels_id,handle)
labels = to_categorical(data_train['ClassName'])
print(labels.shape)
```
## Splitting into Train and Test sets
```
from sklearn.model_selection import train_test_split
xtrain,xtest,ytrain,ytest = train_test_split(data_train.iloc[:,0],labels,test_size = 0.2,random_state=42)
```
### Converting into 64*64 images
You can substitute 64,64 to 224,224 for better results only if ram is >32gb
```
def path_to_tensor(img_path):
# loads RGB image as PIL.Image.Image type
img = image.load_img(img_path, target_size=(64, 64))
# convert PIL.Image.Image type to 3D tensor with shape (224, 224, 3)
x = image.img_to_array(img)
# convert 3D tensor to 4D tensor with shape (1, 224, 224, 3) and return 4D tensor
return np.expand_dims(x, axis=0)
def paths_to_tensor(img_paths):
list_of_tensors = [path_to_tensor(img_path) for img_path in tqdm(img_paths)]
return np.vstack(list_of_tensors)
from PIL import ImageFile
ImageFile.LOAD_TRUNCATED_IMAGES = True
# pre-process the data for Keras
train_tensors = paths_to_tensor(xtrain).astype('float32')/255 - 0.5
valid_tensors = paths_to_tensor(xtest).astype('float32')/255 - 0.5
##takes too much ram
## run this if your ram is greater than 16gb
# test_tensors = paths_to_tensor(data_test.iloc[:,0]).astype('float32')/255 - 0.5
```
# Defining the Model
```
model = Sequential()
model.add(Conv2D(filters=64, kernel_size=2, padding='same', activation='relu', input_shape=(64,64,3), kernel_initializer='glorot_normal'))
model.add(MaxPooling2D(pool_size=2))
model.add(Conv2D(filters=128, kernel_size=2, padding='same', activation='relu', kernel_initializer='glorot_normal'))
model.add(MaxPooling2D(pool_size=2))
model.add(Conv2D(filters=256, kernel_size=2, padding='same', activation='relu', kernel_initializer='glorot_normal'))
model.add(MaxPooling2D(pool_size=2))
model.add(Conv2D(filters=512, kernel_size=2, padding='same', activation='relu', kernel_initializer='glorot_normal'))
model.add(MaxPooling2D(pool_size=2))
model.add(Dropout(0.5))
model.add(Flatten())
model.add(Dense(500, activation='relu', kernel_initializer='glorot_normal'))
model.add(Dropout(0.5))
model.add(Dense(10, activation='softmax', kernel_initializer='glorot_normal'))
model.summary()
plot_model(model,to_file=os.path.join(MODEL_PATH,"model_distracted_driver.png"),show_shapes=True,show_layer_names=True)
model.compile(optimizer='rmsprop', loss='categorical_crossentropy', metrics=['accuracy'])
filepath = os.path.join(MODEL_PATH,"distracted-{epoch:02d}-{val_accuracy:.2f}.hdf5")
checkpoint = ModelCheckpoint(filepath, monitor='val_accuracy', verbose=1, save_best_only=True, mode='max',period=1)
callbacks_list = [checkpoint]
model_history = model.fit(train_tensors,ytrain,validation_data = (valid_tensors, ytest),epochs=25, batch_size=40, shuffle=True,callbacks=callbacks_list)
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(12, 12))
ax1.plot(model_history.history['loss'], color='b', label="Training loss")
ax1.plot(model_history.history['val_loss'], color='r', label="validation loss")
ax1.set_xticks(np.arange(1, 25, 1))
ax1.set_yticks(np.arange(0, 1, 0.1))
ax2.plot(model_history.history['accuracy'], color='b', label="Training accuracy")
ax2.plot(model_history.history['val_accuracy'], color='r',label="Validation accuracy")
ax2.set_xticks(np.arange(1, 25, 1))
legend = plt.legend(loc='best', shadow=True)
plt.tight_layout()
plt.show()
```
# Model Analysis
Finding the Confusion matrix,Precision,Recall and F1 score to analyse the model thus created
```
def print_confusion_matrix(confusion_matrix, class_names, figsize = (10,7), fontsize=14):
df_cm = pd.DataFrame(
confusion_matrix, index=class_names, columns=class_names,
)
fig = plt.figure(figsize=figsize)
try:
heatmap = sns.heatmap(df_cm, annot=True, fmt="d")
except ValueError:
raise ValueError("Confusion matrix values must be integers.")
heatmap.yaxis.set_ticklabels(heatmap.yaxis.get_ticklabels(), rotation=0, ha='right', fontsize=fontsize)
heatmap.xaxis.set_ticklabels(heatmap.xaxis.get_ticklabels(), rotation=45, ha='right', fontsize=fontsize)
plt.ylabel('True label')
plt.xlabel('Predicted label')
fig.savefig(os.path.join(MODEL_PATH,"confusion_matrix.png"))
return fig
def print_heatmap(n_labels, n_predictions, class_names):
labels = n_labels #sess.run(tf.argmax(n_labels, 1))
predictions = n_predictions #sess.run(tf.argmax(n_predictions, 1))
# confusion_matrix = sess.run(tf.contrib.metrics.confusion_matrix(labels, predictions))
matrix = confusion_matrix(labels.argmax(axis=1),predictions.argmax(axis=1))
row_sum = np.sum(matrix, axis = 1)
w, h = matrix.shape
c_m = np.zeros((w, h))
for i in range(h):
c_m[i] = matrix[i] * 100 / row_sum[i]
c = c_m.astype(dtype = np.uint8)
heatmap = print_confusion_matrix(c, class_names, figsize=(18,10), fontsize=20)
class_names = list()
for name,idx in labels_id.items():
class_names.append(name)
# print(class_names)
ypred = model.predict(valid_tensors)
print_heatmap(ytest,ypred,class_names)
```
## Precision Recall F1 Score
```
ypred_class = np.argmax(ypred,axis=1)
# print(ypred_class[:10])
ytest = np.argmax(ytest,axis=1)
accuracy = accuracy_score(ytest,ypred_class)
print('Accuracy: %f' % accuracy)
# precision tp / (tp + fp)
precision = precision_score(ytest, ypred_class,average='weighted')
print('Precision: %f' % precision)
# recall: tp / (tp + fn)
recall = recall_score(ytest,ypred_class,average='weighted')
print('Recall: %f' % recall)
# f1: 2 tp / (2 tp + fp + fn)
f1 = f1_score(ytest,ypred_class,average='weighted')
print('F1 score: %f' % f1)
```
|
github_jupyter
|
```
# Import that good good
import sys
import os
sys.path.append('/Users/kolbt/Desktop/ipython/diam_files')
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import math
from IPython.display import display
from collections import OrderedDict
pd.options.display.max_rows = 2
import matplotlib.colors as mc
import colorsys
# Define what functions you'll need here
def getFromTxt(fname, first, last):
"Takes a string, text before and after desired text, outs text between"
start = fname.index( first ) + len( first )
end = fname.index( last, start )
myTxt = fname[start:end]
return float(myTxt)
# Above function kindly provided by user "cji" on stackoverflow
# https://stackoverflow.com/questions/3368969/find-string-between-two-substrings
# Make sure data is sorted appropriately
def sortArray(array, sort_var):
"Takes an array and the column name to sort, sorts array "
for i in range(0, len(array)):
for k in range(0, len(array[i])):
for j in range(0, len(array[i])):
# Out of order, swap them
if array[i].loc[j, sort_var] < array[i].loc[k, sort_var] and k < j:
tmp = array[i].iloc[j].copy()
array[i].iloc[j] = array[i].iloc[k]
array[i].iloc[k] = tmp
def plotter(start, stop, ylab):
"Plotting function so that I don't have to show this a zillion times"
ind = 0
for j in range(start, stop):
for i in range(0, len(SS[headers[j]])):
# Mixture
if params['xA'][i] % 100 != 0:
plt.scatter(params['peA'][i], SS[headers[j]][i], c=col[ind], label=headers[j])
# Monodisperse, always same color
else:
# If it's zero ignore it
if SS[headers[j]][i] != 0:
plt.scatter(params['peA'][i], SS[headers[j]][i], c=col[-1], label='Mono')
ind += 1
handles, labels = plt.gca().get_legend_handles_labels()
by_label = OrderedDict(zip(labels, handles))
plt.legend(by_label.values(), by_label.keys())
plt.xlabel('Activity (Pe)')
plt.ylabel(ylab)
plt.show()
def katieRoseIsCute(r):
"Take diameter, output LJ-force"
eps = 20.0
sigma = 1.0
F_LJ = 24.0 * eps * ((2 * (sigma**12) * (r**-13)) - ((sigma**6) * (r**-7)))
return F_LJ
def forceToEps(force):
"Take LJ-force and output epsilon to give diameter of 1"
epsilon = force / 24.0
return epsilon
# https://mycurvefit.com/
def powerLaw(a, x, b):
return a*(x**b)
def exponential(a, b, c, x):
"Exponential: a - (b/c) * (1 - (e**-cx))"
return a - ((b/c)*(1-(math.exp(-c*x))))
def plateau(a, x, b):
"Plateau: a * x / (b + x)"
return (a * x) / (b + x)
def logarithmic(a, x, b):
"Logarithmic: a * ln(x) + b"
if x != 0:
return (a * math.log(x)) + b
else:
return 0
# https://stackoverflow.com/questions/37765197/darken-or-lighten-a-color-in-matplotlib
def colorShade(color, amount=0.5):
"Gives multiple shades of a base color"
try:
c = mc.cnames[color]
except:
c = color
c = colorsys.rgb_to_hls(*mc.to_rgb(c))
return colorsys.hls_to_rgb(c[0], 1 - amount * (1 - c[1]), c[2])
# Get the data files
txtFiles = os.listdir('gsd')
all_sims = []
# Using the absolute path means I can go to whatever directory I want
os.chdir('/Users/kolbt/Desktop/ipython/diam_files')
for i in range(0, len(txtFiles)):
df = pd.read_csv(txtFiles[i], sep='\s+', header=0)
all_sims.append(df)
# Return to root directory
os.chdir('/Users/kolbt/Desktop/ipython')
# Make sure all data is in correct timestep order
sortArray(all_sims, 'Timestep')
display(all_sims[9])
# Make an additional frame that gives total number of particles, and simulation parameters
paramList = []
for i in range(0, len(txtFiles)):
partAll = all_sims[i]['Gas_tot'][0]
partA = all_sims[i]['Gas_A'][0]
partB = all_sims[i]['Gas_B'][0]
pa = getFromTxt(txtFiles[i], "pa", "_pb")
pb = getFromTxt(txtFiles[i], "pb", "_xa")
xa = getFromTxt(txtFiles[i], "xa", ".txt")
try:
prat = float(pa)/float(pb)
except:
prat = 0.0
paramList.append((partAll, partA, partB, pa, pb, xa, prat))
params = pd.DataFrame(paramList, columns=['partAll', 'partA', 'partB', 'peA', 'peB', 'xA', 'peR'])
display(params)
# Make list of steady state column headers
headers = list(all_sims[0])
headers.remove('Timestep')
SS = pd.DataFrame(columns=headers)
for i in range(0, len(txtFiles)):
SS.loc[i] = [0] * len(headers)
# Make dataframe of steady-state data
for i in range(0, len(txtFiles)):
# Loop through each column (aside from tstep column)
for j in range(1, len(headers) + 1):
# Compute mean of last 100 entries in jth column of ith file
avg = np.mean(all_sims[i].iloc[-100:-1,j])
SS[headers[j-1]][i] = avg
# Normalize by number of particles
# SS['Gas_A'][:] /= params['partA'][:]
# SS['Gas_B'][:] /= params['partB'][:]
# SS['Gas_tot'][:] /= params['partAll'][:]
# SS['Dense_A'][:] /= params['partA'][:]
# SS['Dense_B'][:] /= params['partB'][:]
# SS['Dense_tot'][:] /= params['partAll'][:]
# SS['Lg_clust'][:] /= params['partAll'][:]
# SS['MCS'][:] /= params['partAll'][:]
display(SS)
# Plot the data
# col = ['k', 'r', 'g', 'b']
col = ['#e6194b', '#3cb44b', '#0082c8', '#f58231', '#ffe119','#911eb4', '#46f0f0',
'#f032e6', '#d2f53c', '#fabebe', '#008080', '#e6beff', '#aa6e28', '#fffac8',
'#800000', '#aaffc3', '#808000', '#ffd8b1', '#000080', '#808080', '#ffffff',
'#000000']
plotter(0, 3, '% of total particles')
plotter(3, 6, '% of total particles')
plotter(6, 8, '% of total particles')
plotter(8, 12, r'Diameter $(\sigma)$')
plotter(12, 13, r'Effective Area Fraction $(\phi_{Eff})$')
plotter(13, 15, 'Area')
plotter(15, 17, 'Density')
plotter(17, 18, 'Density')
# # This is the way I was plotting it
# for j in range(0, 3):
# plt.scatter(params['peA'], SS[headers[j]], label=headers[j])
# plt.legend()
# plt.show()
# Take in the steady-state diameter data... output the LJ force w/ HS epsilon
diam_to_force = []
eps_one = []
for i in range(0, len(SS['sigALL'])):
diam_to_force.append(katieRoseIsCute(SS['sigALL'][i]))
eps_one.append(forceToEps(diam_to_force[i]))
# https://onlinelibrary.wiley.com/doi/pdf/10.1002/9780470126714.app4
# Good ideas for plotting are:
# Exponential: a - (b/c) * (1 - (e**-cx))
# Power: a * x ** b
# Plateau: a * x / (b + x)
# Log: a * ln(x) + b
# Let's fix the data being plotted (just monodisperse)
mono = [0]
corDat = [1]
for i in range(0, len(params['peA'])):
if params['xA'][i] % 100 == 0:
mono.append(params['peA'][i])
corDat.append(eps_one[i])
powla = []
expo = []
plato = []
loga = []
refRange = np.arange(0, 500, 0.001)
for i in range(0, len(refRange)):
powla.append(powerLaw(5.87, refRange[i], 0.36))
expo.append(exponential(9.4, -0.28, 0.006, refRange[i]))
plato.append(plateau(62.4, refRange[i], 99.1))
loga.append(logarithmic(1.0, refRange[i], 1.0))
plt.scatter(mono, corDat, c=col[8], label='Data')
plt.plot(refRange, powla, c=col[9], label='Power Law')
plt.xlabel('Activity')
plt.ylabel('Epsilon')
plt.legend()
plt.title(r'$\epsilon$ to give $\sigma=1$')
plt.show()
plt.scatter(mono, corDat, c=col[8], label='Data')
plt.plot(refRange, expo, c=col[10], label='Exponential')
plt.xlabel('Activity')
plt.ylabel('Epsilon')
plt.legend()
plt.title(r'$\epsilon$ to give $\sigma=1$')
plt.show()
plt.scatter(mono, corDat, c=col[8], label='Data')
plt.plot(refRange, plato, c=col[11], label='Plateau')
plt.xlabel('Activity')
plt.ylabel('Epsilon')
plt.legend()
plt.title(r'$\epsilon$ to give $\sigma=1$')
plt.show()
# plt.scatter(mono, corDat, c=col[8], label='Data')
# plt.plot(refRange, loga, c=col[12], label='Logarithmic')
# plt.xlabel('Activity')
# plt.ylabel('Epsilon')
# plt.legend()
# plt.title(r'$\epsilon$ to give $\sigma=1$')
# plt.show()
print('Monodisperse Data:')
for i in range(0, len(eps_one)):
# monodisperse
if params['xA'][i] % 100 == 0:
print('Activity: {}, Epsilon: {}').format(params['peA'][i], eps_one[i])
# print('Monodisperse Data:')
# for i in range(0, len(eps_one)):
# # monodisperse
# if params['xA'][i] % 100 == 0:
# print('{} \t {}').format(params['peA'][i], eps_one[i])
# Plot the composition data? Inset the plot composition over time
# A will be one color, dark = high Pe_ratio, light = low Pe_r
# Same goes for B and all
mixPar = []
mixA = []
mixB = []
mixT = []
mixInds = []
for i in range(0, len(params['peA'])):
# Mixtures only
if params['xA'][i] % 100 != 0:
mixInds.append(i)
mixPar.append(params['peR'][i])
mixA.append(SS['Dense_A'][i] / params['partA'][i])
mixB.append(SS['Dense_B'][i] / params['partB'][i])
mixT.append(SS['Dense_tot'][i] / params['partAll'][i])
plt.scatter(mixPar, mixT, label='All', c='g')
plt.scatter(mixPar, mixA, label='A', c='b')
plt.scatter(mixPar, mixB, label='B', c='r')
plt.xlabel('Activity Ratio')
plt.ylabel('Percentage of Total')
mixedSims = len(mixInds)
timeB = [[] for x in xrange(mixedSims)]
simDenseA = [[] for x in xrange(mixedSims)]
simDenseB = [[] for x in xrange(mixedSims)]
simDenseT = [[] for x in xrange(mixedSims)]
count = -1
# Let's get data for the inset
for i in range(0, len(txtFiles)):
if params['xA'][i] % 100 != 0:
count += 1
# Get the tau_B time
timeB[count].append(np.arange(0, len(all_sims[i]['Timestep']), 1))
for j in range(0, len(all_sims[i]['Timestep'])):
# Group all Dense_A data
simDenseT[count].append(all_sims[i]['Dense_tot'][j])
simDenseA[count].append(all_sims[i]['Dense_A'][j])
simDenseB[count].append(all_sims[i]['Dense_B'][j])
# Divide column by number of A particles
simDenseT[count] /= params['partAll'][i]
simDenseA[count] /= params['partA'][i]
simDenseB[count] /= params['partB'][i]
# Plot the data All
a = plt.axes([0.475, .25, .4, .4], facecolor='w')
for i in range(0, mixedSims):
plt.plot(timeB[i][0], simDenseT[i], c=colorShade('g', mixPar[i]))
plt.xlim(0, 10)
plt.ylim(0,1)
plt.xlabel(r'Time $(\tau_{B})$')
plt.ylabel(r'% of Total')
# Plot the data A
a = plt.axes([1.02, .575, .3, .3], facecolor='w')
for i in range(0, mixedSims):
plt.plot(timeB[i][0], simDenseA[i], c=colorShade('b', mixPar[i]))
plt.xlim(0, 10)
plt.ylim(0,1)
plt.ylabel(r'% of Total A')
# Plot the data B
a = plt.axes([1.02, .15, .3, .3], facecolor='w')
for i in range(0, mixedSims):
plt.plot(timeB[i][0], simDenseB[i], c=colorShade('r', mixPar[i]))
plt.xlim(0, 10)
plt.ylim(0,1)
plt.xlabel(r'Time $(\tau_{B})$')
plt.ylabel(r'% of Total B')
```
|
github_jupyter
|
# TensorFlow Neural Machine Translation on Cloud TPUs
This tutorial demonstrates how to translate text using a LSTM Network from one language to another (from English to German in this case). We will work with a dataset that contains pairs of English-German phrases. Given a sequence of words in English, we train a model to predict the German equivalent in the sequence.
Note: Enable TPU acceleration to execute this notebook faster. In Colab: Runtime > Change runtime type > Hardware acclerator > **TPU**.
<br>
If running locally make sure TensorFlow version >= 1.11.
This tutorial includes runnable code implemented using [tf.keras](https://www.tensorflow.org/programmers_guide/keras).
By Rishabh Anand (GitHub: @rish-16)
```
!ls
!wget http://www.manythings.org/anki/deu-eng.zip
!unzip deu-eng.zip
!head deu.txt
```
### Importing TensorFlow and other libraries
```
import string
import numpy as np
from numpy import array
import pandas as pd
import tensorflow as tf
from tensorflow.keras.models import Sequential, load_model
from tensorflow.keras.layers import Dense, Embedding, RepeatVector, LSTM
from tensorflow.keras.optimizers import RMSprop
from tensorflow.keras.preprocessing.text import Tokenizer
from tensorflow.keras.preprocessing.sequence import pad_sequences
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
```
### Extracting lines from dataset and into array
Here, we can examine how the dataset is structures. The English-German dataset comprises of an English and German phrase separted by a tab `\t`
```
deu_eng = open('./deu.txt', mode='rt', encoding='utf-8')
deu_eng = deu_eng.read()
deu_eng = deu_eng.strip().split('\n')
deu_eng = [i.split('\t') for i in deu_eng]
deu_eng = array(deu_eng)
deu_eng = deu_eng[:50000, :]
print (deu_eng[:5])
```
### Removing punctuation
We will be removing punctuation from the phrases and converting them to lowercase. We will not be creating embeddings for punctuations or uppercase characters as it adds to the complexity of the NMT model
```
deu_eng[:, 0] = [s.translate((str.maketrans('', '', string.punctuation))) for s in deu_eng[:, 0]]
deu_eng[:, 1] = [s.translate((str.maketrans('', '', string.punctuation))) for s in deu_eng[:, 1]]
for i in range(len(deu_eng)):
deu_eng[i, 0] = deu_eng[i, 0].lower()
deu_eng[i, 1] = deu_eng[i, 1].lower()
print (deu_eng[:5])
```
### Tokenising the phrases
Tokenisation is the process of taking a sequence and chopping it up into smaller pieces called `tokens`. For example, suppose we have a sentence
`"Bob returned home after the party"`
The tokenised sentence will return an array with the tokens:
`["Bob", "returned", "home", "after", "the", "party"]`
In this section, we will be breaking up the phrases into tokenised sequences that comprises of numbers for each unique word. For instance, the word "good" may have the value of 32 while the word "boy" may have the value of 46. Supposing the phrase is "good boy", the tokenised sequence is `[32, 46]`.
```
def tokenize(lines):
tokenizer = Tokenizer()
tokenizer.fit_on_texts(lines)
return tokenizer
eng_tokenizer = tokenize(deu_eng[:, 0])
eng_vocab_size = len(eng_tokenizer.word_index) + 1
eng_sequence_length = 8
print ('English vocabulary size: {}'.format(eng_vocab_size))
deu_tokenizer = tokenize(deu_eng[:, 1])
deu_vocab_size = len(deu_tokenizer.word_index) + 1
deu_sequence_length = 8
print ('German vocabulary size: {}'.format(deu_vocab_size))
```
### Convert lines into sequences as input for the NMT model
We will now be using our Tokeniser to create tokenised sequences of the original English and German phrases from our dataset.
```
def encode_sequences(tokenizer, sequence_length, lines):
sequence = tokenizer.texts_to_sequences(lines)
sequence = pad_sequences(sequence, sequence_length, padding="post") # 0s after the actual sequence
return sequence
```
### Splitting the dataset into training and testing sets
```
train, test = train_test_split(deu_eng, test_size=.2, random_state=12)
x_train = encode_sequences(deu_tokenizer, deu_sequence_length, train[:, 1])
y_train = encode_sequences(eng_tokenizer, eng_sequence_length, train[:, 0])
x_test = encode_sequences(deu_tokenizer, deu_sequence_length, test[:, 1])
y_test = encode_sequences(eng_tokenizer, eng_sequence_length, test[:, 0])
print (x_train.shape, y_train.shape)
print (x_test.shape, x_test.shape)
```
### Training on a TPU
In order to connect to a TPU, we can follow 4 easy steps:
1. Connect to a TPU instance
2. Initialise a parallelly-distributed training `strategy`
3. Build our NMT model under the `strategy`
4. Train the model on a TPU
For more details on training on TPUs for free, feel free to check out [this](https://medium.com/@mail.rishabh.anand/tpu-training-made-easy-with-colab-3b73b920878f) article that covers the process in great detail.
### Connecting to available TPU instances
Here, we search for available instances of version 2 TPUs (the ones Google publically allocates)
```
tpu = tf.distribute.cluster_resolver.TPUClusterResolver() # TPU detection
# Initialising a parallelly-distributed training strategy
tf.tpu.experimental.initialize_tpu_system(tpu)
strategy = tf.distribute.experimental.TPUStrategy(tpu, steps_per_run=128)
print('Running on TPU ', tpu.cluster_spec().as_dict()['worker'])
print("Number of accelerators: ", strategy.num_replicas_in_sync)
# Building our model under that strategy
in_vocab = deu_vocab_size
out_vocab = eng_vocab_size
units = 512
in_timesteps = deu_sequence_length
out_timesteps = eng_sequence_length
with strategy.scope():
model = Sequential()
model.add(Embedding(in_vocab, units, input_length=in_timesteps, mask_zero=True))
model.add(LSTM(units))
model.add(RepeatVector(out_timesteps))
model.add(LSTM(units, return_sequences=True))
model.add(Dense(out_vocab, activation='softmax'))
rms = RMSprop(lr=0.001)
model.compile(loss='sparse_categorical_crossentropy', optimizer=rms)
model.summary()
tf.keras.utils.plot_model(
model,
show_shapes=True,
show_layer_names=True,
rankdir="TB"
)
history = model.fit(x_train, y_train.reshape(y_train.shape[0], y_train.shape[1], 1), epochs=30, steps_per_epoch=500)
```
### Checking the loss values
```
plt.plot(history.history['loss'])
plt.xlabel('Epochs')
plt.ylabel('Sparse Categorical Loss')
plt.legend(['train'])
plt.show()
```
### Running our model on testing dataset
```
# Getting the predictions from the testing dataset
preds = model.predict_classes(x_test.reshape(x_test.shape[0], x_test.shape[1])[:10]) # only predicting over 10 instances
print (preds)
# A function to convert a sequence back into words
def convert_words(n, tokenizer):
for word, idx in tokenizer.word_index.items():
if idx == n:
return word
return None
# Running our model on the testing dataset
pred_texts = []
for i in preds:
temp = []
for j in range(len(i)):
word = convert_words(i[j], eng_tokenizer)
if j > 0:
if (word == convert_words(i[j-1], eng_tokenizer)) or (word == None):
temp.append('')
else:
temp.append(word)
else:
if (word == None):
temp.append('')
else:
temp.append(word)
pred_texts.append(' '.join(temp))
```
### Translating the text from German to English
We can see that our model does a relatively good job in translating the German text to English. However, there are instances that seem to have the wrong translation or are outright incorrect. Nonetheless, for a basic NMT model that was trained for 30 epochs, the model's generalisation is great.
```
pred_df = pd.DataFrame({'actual': test[:10, 0], 'prediction': pred_texts})
pred_df
```
|
github_jupyter
|
```
# We tweak the style of this notebook a little bit to have centered plots.
from IPython.core.display import HTML
HTML("""
<style>
.output_png {
display: table-cell;
text-align: center;
vertical-align: middle;
}
</style>
""");
%matplotlib inline
import warnings
warnings.filterwarnings('ignore')
warnings.filterwarnings('ignore', category=DeprecationWarning)
import pandas as pd
pd.options.display.max_columns = 100
from matplotlib import pyplot as plt
import numpy as np
import seaborn as sns
import pylab as plot
params = {
'axes.labelsize': "large",
'xtick.labelsize': 'x-large',
'legend.fontsize': 20,
'figure.dpi': 150,
'figure.figsize': [25, 7]
}
plot.rcParams.update(params)
data = pd.read_csv('datasets/train.csv')
print(data.shape)
#(891, 12)
data.head()
data.describe()
# (891-714) = 177 values are missing in the Age column
# fill in the null values with the median age as it's more robust to outliers
data['Age'] = data['Age'].fillna(data['Age'].median())
data['Died'] = 1 - data['Survived']
data.groupby('Sex').agg('sum')[['Survived', 'Died']].plot(kind='bar', figsize=(25, 7),
stacked=True);
data.groupby('Sex').agg('mean')[['Survived', 'Died']].plot(kind='bar', figsize=(25, 7),
stacked=True);
# correlate the survival with the age variable
fig = plt.figure(figsize=(25, 7))
sns.violinplot(x='Sex', y='Age',
hue='Survived', data=data,
split=True,
palette={0: "r", 1: "g"}
);
# fare ticket
figure = plt.figure(figsize=(25, 7))
plt.hist([data[data['Survived'] == 1]['Fare'], data[data['Survived'] == 0]['Fare']],
stacked=True, color = ['g','r'],
bins = 50, label = ['Survived','Dead'])
plt.xlabel('Fare')
plt.ylabel('Number of passengers')
plt.legend();
# age, the fare and the survival on a single chart.
plt.figure(figsize=(25, 7))
ax = plt.subplot()
ax.scatter(data[data['Survived'] == 1]['Age'], data[data['Survived'] == 1]['Fare'],
c='green', s=data[data['Survived'] == 1]['Fare'])
ax.scatter(data[data['Survived'] == 0]['Age'], data[data['Survived'] == 0]['Fare'],
c='red', s=data[data['Survived'] == 0]['Fare']);
ax = plt.subplot()
ax.set_ylabel('Average fare')
data.groupby('Pclass').mean()['Fare'].plot(kind='bar', figsize=(25, 7), ax = ax);
fig = plt.figure(figsize=(25, 7))
sns.violinplot(x='Embarked', y='Fare', hue='Survived', data=data, split=True, palette={0: "r", 1: "g"});
# Feature Engineering
# define a print function that asserts whether a feature has been processed.
def status(feature):
print('Processing', feature, ': ok')
def get_combined_data():
# reading train data
train = pd.read_csv('datasets/train.csv')
# reading test data
test = pd.read_csv('datasets/test.csv')
# extracting and then removing the targets from the training data
targets = train.Survived
train.drop(['Survived'], 1, inplace=True)
# merging train data and test data for future feature engineering
# we'll also remove the PassengerID since this is not an informative feature
combined = train.append(test)
combined.reset_index(inplace=True)
combined.drop(['index', 'PassengerId'], inplace=True, axis=1)
return combined
combined = get_combined_data()
print(combined.shape)
titles = set()
for name in data['Name']:
titles.add(name.split(',')[1].split('.')[0].strip())
print(titles)
# set(['Sir', 'Major', 'the Countess', 'Don', 'Mlle', 'Capt', 'Dr', 'Lady', 'Rev', 'Mrs', 'Jonkheer', 'Master', 'Ms', 'Mr', 'Mme', 'Miss', 'Col'])
Title_Dictionary = {
"Capt": "Officer",
"Col": "Officer",
"Major": "Officer",
"Jonkheer": "Royalty",
"Don": "Royalty",
"Sir" : "Royalty",
"Dr": "Officer",
"Rev": "Officer",
"the Countess":"Royalty",
"Mme": "Mrs",
"Mlle": "Miss",
"Ms": "Mrs",
"Mr" : "Mr",
"Mrs" : "Mrs",
"Miss" : "Miss",
"Master" : "Master",
"Lady" : "Royalty"
}
def get_titles():
# we extract the title from each name
combined['Title'] = combined['Name'].map(lambda name:name.split(',')[1].split('.')[0].strip())
# a map of more aggregated title
# we map each title
combined['Title'] = combined.Title.map(Title_Dictionary)
status('Title')
return combined
combined = get_titles()
combined.head()
# check if the titles have been filled correctly.
combined[combined['Title'].isnull()]
# Age
# Number of missing ages in train set
print(combined.iloc[:891].Age.isnull().sum())
# Number of missing ages in test set
print(combined.iloc[891:].Age.isnull().sum())
# 86
grouped_train = combined.iloc[:891].groupby(['Sex','Pclass','Title'])
grouped_median_train = grouped_train.median()
grouped_median_train = grouped_median_train.reset_index()[['Sex', 'Pclass', 'Title', 'Age']]
grouped_median_train.head()
# function that fills in the missing age in combined based on these different attributes.
def fill_age(row):
condition = (
(grouped_median_train['Sex'] == row['Sex']) &
(grouped_median_train['Title'] == row['Title']) &
(grouped_median_train['Pclass'] == row['Pclass'])
)
return grouped_median_train[condition]['Age'].values[0]
def process_age():
global combined
# a function that fills the missing values of the Age variable
combined['Age'] = combined.apply(lambda row: fill_age(row) if np.isnan(row['Age']) else row['Age'], axis=1)
status('age')
return combined
combined = process_age()
# now process the names.
def process_names():
global combined
# we clean the Name variable
combined.drop('Name', axis=1, inplace=True)
# encoding in dummy variable
titles_dummies = pd.get_dummies(combined['Title'], prefix='Title')
combined = pd.concat([combined, titles_dummies], axis=1)
# removing the title variable
combined.drop('Title', axis=1, inplace=True)
status('names')
return combined
combined = process_names()
combined.head()
# Fare
# fill missing fare value by the average fare computed on the train set
def process_fares():
global combined
# there's one missing fare value - replacing it with the mean.
combined.Fare.fillna(combined.iloc[:891].Fare.mean(), inplace=True)
status('fare')
return combined
combined = process_fares()
# Embarked
# missing values of Embarked filled with the most frequent Embarked value.
def process_embarked():
global combined
# two missing embarked values - filling them with the most frequent one in the train set(S)
combined.Embarked.fillna('S', inplace=True)
# dummy encoding
embarked_dummies = pd.get_dummies(combined['Embarked'], prefix='Embarked')
combined = pd.concat([combined, embarked_dummies], axis=1)
combined.drop('Embarked', axis=1, inplace=True)
status('embarked')
return combined
combined = process_embarked()
combined.head()
# Cabin
train_cabin, test_cabin = set(), set()
for c in combined.iloc[:891]['Cabin']:
try:
train_cabin.add(c[0])
except:
train_cabin.add('U')
for c in combined.iloc[891:]['Cabin']:
try:
test_cabin.add(c[0])
except:
test_cabin.add('U')
print(train_cabin)
print(test_cabin)
# replaces NaN values with U (for Unknown).
def process_cabin():
global combined
# replacing missing cabins with U (for Uknown)
combined.Cabin.fillna('U', inplace=True)
# mapping each Cabin value with the cabin letter
combined['Cabin'] = combined['Cabin'].map(lambda c: c[0])
# dummy encoding ...
cabin_dummies = pd.get_dummies(combined['Cabin'], prefix='Cabin')
combined = pd.concat([combined, cabin_dummies], axis=1)
combined.drop('Cabin', axis=1, inplace=True)
status('cabin')
return combined
combined = process_cabin()
combined.head()
# Sex
def process_sex():
global combined
# mapping string values to numerical one
combined['Sex'] = combined['Sex'].map({'male':1, 'female':0})
status('Sex')
return combined
combined = process_sex()
# Pclass
def process_pclass():
global combined
# encoding into 3 categories:
pclass_dummies = pd.get_dummies(combined['Pclass'], prefix="Pclass")
# adding dummy variable
combined = pd.concat([combined, pclass_dummies],axis=1)
# removing "Pclass"
combined.drop('Pclass',axis=1,inplace=True)
status('Pclass')
return combined
combined = process_pclass()
def cleanTicket(ticket):
ticket = ticket.replace('.', '')
ticket = ticket.replace('/', '')
ticket = ticket.split()
ticket = map(lambda t : t.strip(), ticket)
ticket = list(filter(lambda t : not t.isdigit(), ticket))
if len(ticket) > 0:
return ticket[0]
else:
return 'XXX'
tickets = set()
for t in combined['Ticket']:
tickets.add(cleanTicket(t))
print(len(tickets))
def process_ticket():
global combined
# Extracting dummy variables from tickets:
combined['Ticket'] = combined['Ticket'].map(cleanTicket)
tickets_dummies = pd.get_dummies(combined['Ticket'], prefix='Ticket')
combined = pd.concat([combined, tickets_dummies], axis=1)
combined.drop('Ticket', inplace=True, axis=1)
status('Ticket')
return combined
combined = process_ticket()
# family
def process_family():
global combined
# introducing a new feature : the size of families (including the passenger)
combined['FamilySize'] = combined['Parch'] + combined['SibSp'] + 1
# introducing other features based on the family size
combined['Singleton'] = combined['FamilySize'].map(lambda s: 1 if s == 1 else 0)
combined['SmallFamily'] = combined['FamilySize'].map(lambda s: 1 if 2 <= s <= 4 else 0)
combined['LargeFamily'] = combined['FamilySize'].map(lambda s: 1 if 5 <= s else 0)
status('family')
return combined
combined = process_family()
print(combined.shape)
# We end up with a total of 67 features.
combined.head()
# Modelling start
from sklearn.pipeline import make_pipeline
from sklearn.ensemble import RandomForestClassifier
from sklearn.ensemble.gradient_boosting import GradientBoostingClassifier
from sklearn.feature_selection import SelectKBest
from sklearn.model_selection import StratifiedKFold
from sklearn.model_selection import GridSearchCV
from sklearn.model_selection import cross_val_score
from sklearn.feature_selection import SelectFromModel
from sklearn.linear_model import LogisticRegression, LogisticRegressionCV
# 5-fold Cross Validation
def compute_score(clf, X, y, scoring='accuracy'):
xval = cross_val_score(clf, X, y, cv = 5, scoring=scoring)
return np.mean(xval)
# recovering train and test set
def recover_train_test_target():
global combined
targets = pd.read_csv('datasets/train.csv', usecols=['Survived'])['Survived'].values
train = combined.iloc[:891]
test = combined.iloc[891:]
return train, test, targets
train, test, targets = recover_train_test_target()
clf = RandomForestClassifier(n_estimators=50, max_features='sqrt')
clf = clf.fit(train, targets)
features = pd.DataFrame()
features['feature'] = train.columns
features['importance'] = clf.feature_importances_
features.sort_values(by=['importance'], ascending=True, inplace=True)
features.set_index('feature', inplace=True)
features.plot(kind='barh', figsize=(25, 25))
model = SelectFromModel(clf, prefit=True)
train_reduced = model.transform(train)
print(train_reduced.shape)
# (891L, 14L)
test_reduced = model.transform(test)
print(test_reduced.shape)
```
### Try Different base models.
```
logreg = LogisticRegression()
logreg_cv = LogisticRegressionCV()
rf = RandomForestClassifier()
gboost = GradientBoostingClassifier()
models = [logreg, logreg_cv, rf, gboost]
for model in models:
print('Cross-validation of : {0}'.format(model.__class__))
score = compute_score(clf=model, X=train_reduced, y=targets, scoring='accuracy')
print('CV score = {0}'.format(score))
print('****')
# Tuning
# turn run_gs to True if you want to run the gridsearch again.
run_gs = False
if run_gs:
parameter_grid = {
'max_depth' : [4, 6, 8],
'n_estimators': [50, 10],
'max_features': ['sqrt', 'auto', 'log2'],
'min_samples_split': [2, 3, 10],
'min_samples_leaf': [1, 3, 10],
'bootstrap': [True, False],
}
forest = RandomForestClassifier()
cross_validation = StratifiedKFold(n_splits=5)
grid_search = GridSearchCV(forest,
scoring='accuracy',
param_grid=parameter_grid,
cv=cross_validation,
verbose=1
)
grid_search.fit(train, targets)
model = grid_search
parameters = grid_search.best_params_
print('Best score: {}'.format(grid_search.best_score_))
print('Best parameters: {}'.format(grid_search.best_params_))
else:
parameters = {'bootstrap': False, 'min_samples_leaf': 3, 'n_estimators': 50,
'min_samples_split': 10, 'max_features': 'sqrt', 'max_depth': 6}
model = RandomForestClassifier(**parameters)
model.fit(train, targets)
# output = model.predict(test).astype(int)
# df_output = pd.DataFrame()
# aux = pd.read_csv('datasets/test.csv')
# df_output['PassengerId'] = aux['PassengerId']
# df_output['Survived'] = output
# df_output[['PassengerId','Survived']].to_csv('submission_2.csv ', index=False)
```
### Save and Load Model
```
import pickle
import joblib
file = 'titanic.pkl'
joblib.dump(model, file)
load = joblib.load('titanic.pkl')
y_pred = load.predict(test).astype(int)
y_pred
val = pd.DataFrame(y_pred, columns = ['Survived'])
val = val.replace({1: 'Alive', 0: 'Died'})
val
```
|
github_jupyter
|
# Notebook Goal & Approach
## Goal
For each FERC 714 respondent that reports hourly demand as an electricity planning area, create a geometry representing the geographic area in which that electricity demand originated. Create a separate geometry for each year in which data is available.
## Approach
* Use the `eia_code` found in the `respondent_id_ferc714` table to link FERC 714 respondents to their corresponding EIA utilities or balancing areas.
* Use the `balancing_authority_eia861` and `sales_eia861` tables to figure out which respondents correspond to what utility or utilities (if a BA), and which states of operation.
* Use the `service_territory_eia861` table to link those combinations of years, utilities, and states of operation to collections of counties.
* Given the FIPS codes of the counties associated with each utility or balancing area in a given year, use geospatial data from the US Census to compile an annual demand area geometry.
* Merge those geometries back in with the `respondent_id_ferc714` table, along with additional EIA balancing area and utility IDs / Codes on a per-year basis.
# Imports & Config
```
%load_ext autoreload
%autoreload 2
# Standard Libraries:
import dateutil
import logging
import pathlib
import pickle
import re
import sys
import zipfile
# 3rd Party Libraries:
import contextily as ctx
import geopandas
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
import sqlalchemy as sa
# Local Packages:
import pudl
```
## Configure Output Formatting
```
sns.set()
%matplotlib inline
mpl.rcParams['figure.figsize'] = (20,8)
mpl.rcParams['figure.dpi'] = 150
pd.options.display.max_columns = 100
pd.options.display.max_rows = 100
```
## Logging
```
logger = logging.getLogger()
logger.setLevel(logging.INFO)
handler = logging.StreamHandler(stream=sys.stdout)
log_format = '%(asctime)s [%(levelname)8s] %(name)s:%(lineno)s %(message)s'
formatter = logging.Formatter(log_format)
handler.setFormatter(formatter)
logger.handlers = [handler]
```
## PUDL Setup
```
pudl_settings = pudl.workspace.setup.get_defaults()
ferc1_engine = sa.create_engine(pudl_settings['ferc1_db'])
pudl_engine = sa.create_engine(pudl_settings['pudl_db'])
pudl_out = pudl.output.pudltabl.PudlTabl(pudl_engine)
pudl_settings
```
# Parameters
```
MAP_CRS = "EPSG:3857"
CALC_CRS = "ESRI:102003"
```
# Function Definitions
## Dummy EIA 861 ETL
```
def test_etl_eia(eia_inputs, pudl_settings):
"""
This is a dummy function that runs the first part of the EIA ETL
process -- everything up until the entity harvesting begins. For
use in this notebook only.
"""
eia860_tables = eia_inputs["eia860_tables"]
eia860_years = eia_inputs["eia860_years"]
eia861_tables = eia_inputs["eia861_tables"]
eia861_years = eia_inputs["eia861_years"]
eia923_tables = eia_inputs["eia923_tables"]
eia923_years = eia_inputs["eia923_years"]
# generate CSVs for the static EIA tables, return the list of tables
#static_tables = _load_static_tables_eia(datapkg_dir)
# Extract EIA forms 923, 860
eia860_raw_dfs = pudl.extract.eia860.Extractor().extract(eia860_years, testing=True)
eia861_raw_dfs = pudl.extract.eia861.Extractor().extract(eia861_years, testing=True)
eia923_raw_dfs = pudl.extract.eia923.Extractor().extract(eia923_years, testing=True)
# Transform EIA forms 860, 861, 923
eia860_transformed_dfs = pudl.transform.eia860.transform(eia860_raw_dfs, eia860_tables=eia860_tables)
eia861_transformed_dfs = pudl.transform.eia861.transform(eia861_raw_dfs, eia861_tables=eia861_tables)
eia923_transformed_dfs = pudl.transform.eia923.transform(eia923_raw_dfs, eia923_tables=eia923_tables)
# create an eia transformed dfs dictionary
eia_transformed_dfs = eia860_transformed_dfs.copy()
eia_transformed_dfs.update(eia861_transformed_dfs.copy())
eia_transformed_dfs.update(eia923_transformed_dfs.copy())
# convert types..
eia_transformed_dfs = pudl.helpers.convert_dfs_dict_dtypes(eia_transformed_dfs, 'eia')
return eia_transformed_dfs
```
## Dummy EIA 861 Harvesting
* Used to separately test the EIA entity harvesting process with EIA 861
* Doesn't yet work b/c 861 is structured differently than 860/923.
```
def test_harvest_eia(eia_transformed_dfs, eia860_years, eia861_years, eia923_years):
entities_dfs, eia_transformed_dfs = pudl.transform.eia.transform(
eia_transformed_dfs,
eia860_years=eia860_years,
eia861_years=eia861_years,
eia923_years=eia923_years,
)
# convert types..
entities_dfs = pudl.helpers.convert_dfs_dict_dtypes(entities_dfs, 'eia')
# Compile transformed dfs for loading...
return entities_dfs, eia_transformed_dfs
```
## Compare Annual Demand vs. Sales
```
def annual_demand_vs_sales(dhpa_ferc714, sales_eia861, ba_eia861):
"""
Categorize EIA Codes in FERC 714 as BA or Utility IDs.
Most FERC 714 respondent IDs are associated with an `eia_code` which
refers to either a `balancing_authority_id_eia` or a `utility_id_eia`
but no indication is given as to which type of ID each one is. This
is further complicated by the fact that EIA uses the same numerical
ID to refer to the same entity in most but not all cases, when that
entity acts as both a utility and as a balancing authority.
In order to identify which type of ID each `eia_code` is, this
funciton compares the annual demand reported in association with
each code in the FERC 714 hourly planning area time series, and in
the EIA 861 sales table -- using the ID both as a utility and as a
balancing authority ID. The correlation between the FERC 714 demand
and the EIA 861 sales should be much higher for one type of ID than
the other, indicating which type of ID is represented in the FERC
714 data.
Args:
dhpa_ferc714 (pandas.DataFrame): The FERC 714 hourly demand
time series.
sales_eia861 (pandas.DataFrame): The EIA 861 Sales table.
ba_eia861 (pandas.DataFrame): The EIA 861 Balancing Authority
table, which contains the mapping between EIA Balancing
Authority Codes (3-4 letters) and EIA Balancing Authority
IDs (integers). The codes are present in the Sales table,
but the IDs are what the eia_code refers to.
Returns:
pandas.DataFrame: A table containing FERC 714 respondent IDs,
EIA codes, and a column indicating whether that code was
found to be more consistent with Balancing Authority or
Utility electricity demand / sales.
"""
# Sum up FERC 714 demand by report_year and eia_code:
dhpa_ferc714_by_eia_code = (
dhpa_ferc714
.groupby(["eia_code", "report_year"])["demand_mwh"]
.sum()
.reset_index()
)
# Sum up the EIA 861 sales by Utility ID:
sales_eia861_by_util = (
sales_eia861.groupby(["utility_id_eia", "report_date"])["sales_mwh"]
.sum()
.reset_index()
.assign(report_year=lambda x: x.report_date.dt.year)
.drop("report_date", axis="columns")
.rename(columns={"sales_mwh": "sales_utility_mwh"})
)
# Need to translate the BA Code to BA ID for comparison w/ eia_code
ba_codes_and_ids = (
ba_eia861[["balancing_authority_code_eia", "balancing_authority_id_eia", "report_date"]]
.drop_duplicates()
.assign(report_year=lambda x: x.report_date.dt.year)
.drop("report_date", axis="columns")
.dropna()
)
# Sum up the EIA 861 sales by Balancing Authority Code:
sales_eia861_by_ba = (
sales_eia861
.groupby(["balancing_authority_code_eia", "report_date"], observed=True)["sales_mwh"]
.sum()
.reset_index()
.assign(report_year=lambda x: x.report_date.dt.year)
.drop("report_date", axis="columns")
.rename(columns={"sales_mwh": "sales_ba_mwh"})
.query("balancing_authority_code_eia!='UNK'")
.merge(ba_codes_and_ids)
)
# Combine the demand and sales data with all the IDs
demand_and_sales = (
dhpa_ferc714_by_eia_code
.merge(
sales_eia861_by_util,
left_on=["eia_code", "report_year"],
right_on=["utility_id_eia", "report_year"],
how="left"
)
.merge(
sales_eia861_by_ba,
left_on=["eia_code", "report_year"],
right_on=["balancing_authority_id_eia", "report_year"],
how="left"
)
.astype({
"eia_code": pd.Int64Dtype(),
"utility_id_eia": pd.Int64Dtype(),
"balancing_authority_id_eia": pd.Int64Dtype(),
})
.assign(
ba_ratio=lambda x: x.sales_ba_mwh / x.demand_mwh,
utility_ratio=lambda x: x.sales_utility_mwh / x.demand_mwh,
)
)
return demand_and_sales
```
## EIA Code Categorization
```
def categorize_eia_code(rids_ferc714, utils_eia860, ba_eia861):
"""
Categorize EIA Codes in FERC 714 as BA or Utility IDs.
Most FERC 714 respondent IDs are associated with an `eia_code` which
refers to either a `balancing_authority_id_eia` or a `utility_id_eia`
but no indication is given as to which type of ID each one is. This
is further complicated by the fact that EIA uses the same numerical
ID to refer to the same entity in most but not all cases, when that
entity acts as both a utility and as a balancing authority.
Given the nature of the FERC 714 hourly demand dataset, this function
assumes that if the `eia_code` appears in the EIA 861 Balancing
Authority table, that it should be labeled `balancing_authority`.
If the `eia_code` appears only in the EIA 860 Utility table, then
it is labeled `utility`. These labels are put in a new column named
`respondent_type`. If the planning area's `eia_code` does not appear in
either of those tables, then `respondent_type is set to NA.
Args:
rids_ferc714 (pandas.DataFrame): The FERC 714 `respondent_id` table.
utils_eia860 (pandas.DataFrame): The EIA 860 Utilities output table.
ba_eia861 (pandas.DataFrame): The EIA 861 Balancing Authority table.
Returns:
pandas.DataFrame: A table containing all of the columns present in
the FERC 714 `respondent_id` table, plus a new one named
`respondent_type` which can take on the values `balancing_authority`,
`utility`, or the special value pandas.NA.
"""
ba_ids = set(ba_eia861.balancing_authority_id_eia.dropna())
util_not_ba_ids = set(utils_eia860.utility_id_eia.dropna()).difference(ba_ids)
new_rids = rids_ferc714.copy()
new_rids["respondent_type"] = pd.NA
new_rids.loc[new_rids.eia_code.isin(ba_ids), "respondent_type"] = "balancing_authority"
new_rids.loc[new_rids.eia_code.isin(util_not_ba_ids), "respondent_type"] = "utility"
ba_rids = new_rids[new_rids.respondent_type=="balancing_authority"]
util_rids = new_rids[new_rids.respondent_type=="utility"]
na_rids = new_rids[new_rids.respondent_type.isnull()]
ba_rids = (
ba_rids.merge(
ba_eia861
.filter(like="balancing_")
.drop_duplicates(subset=["balancing_authority_id_eia", "balancing_authority_code_eia"]),
how="left", left_on="eia_code", right_on="balancing_authority_id_eia"
)
)
util_rids = (
util_rids.merge(
utils_eia860[["utility_id_eia", "utility_name_eia"]]
.drop_duplicates("utility_id_eia"),
how="left", left_on="eia_code", right_on="utility_id_eia"
)
)
new_rids = (
pd.concat([ba_rids, util_rids, na_rids])
.astype({
"respondent_type": pd.StringDtype(),
"balancing_authority_code_eia": pd.StringDtype(),
"balancing_authority_id_eia": pd.Int64Dtype(),
"balancing_authority_name_eia": pd.StringDtype(),
"utility_id_eia": pd.Int64Dtype(),
"utility_name_eia": pd.StringDtype(),
})
)
return new_rids
```
## Georeference Balancing Authorities
```
def georef_bas(ba_eia861, st_eia861, sales_eia861, census_gdf):
"""
Create a GeoDataFrame mapping BAs to Utils to county geometries by year.
This GDF includes the following columns:
balancing_authority_id_eia (ba_eia861)
balancing_authority_name_eia (ba_eia861)
balancing_authority_code_eia (ba_eia861)
utility_id_eia (sales_eia861)
utility_name_eia (sales_eia861)
county_id_fips (st_eia861)
county (st_eia861)
state_id_fips (st_eia861)
state (st_eia861)
geometry (census_gdf)
county_name_census (census_gdf)
It includes information both about which counties are associated with
utilities that are part of balancing authorities, and utilities that
are not part part of balancing authorities, so should be possible to
use it to generate geometries for all of the respondents in FERC 714,
both BAs and Utils.
"""
# Make sure that there aren't any more BA IDs we can recover from later years:
ba_ids_missing_codes = (
ba_eia861.loc[ba_eia861.balancing_authority_code_eia.isnull(), "balancing_authority_id_eia"]
.drop_duplicates()
.dropna()
)
assert len(ba_eia861[
(ba_eia861.balancing_authority_id_eia.isin(ba_ids_missing_codes)) &
(ba_eia861.balancing_authority_code_eia.notnull())
]) == 0
# Which utilities were part of what balancing areas in 2010-2012?
early_ba_by_util = (
ba_eia861
.query("report_date <= '2012-12-31'")
.loc[:, [
"report_date",
"balancing_authority_id_eia",
"balancing_authority_code_eia",
"utility_id_eia",
"balancing_authority_name_eia",
]]
.drop_duplicates(subset=["report_date", "balancing_authority_id_eia", "utility_id_eia"])
)
# Create a dataframe that associates utilities and balancing authorities.
# This information is directly avaialble in the early_ba_by_util dataframe
# but has to be compiled for 2013 and later years based on the utility
# BA associations that show up in the Sales table
# Create an annual, normalized version of the BA table:
ba_normed = (
ba_eia861
.loc[:, [
"report_date",
"state",
"balancing_authority_code_eia",
"balancing_authority_id_eia",
"balancing_authority_name_eia",
]]
.drop_duplicates(subset=[
"report_date",
"state",
"balancing_authority_code_eia",
"balancing_authority_id_eia",
])
)
ba_by_util = (
pd.merge(
ba_normed,
sales_eia861
.loc[:, [
"report_date",
"state",
"utility_id_eia",
"balancing_authority_code_eia"
]].drop_duplicates()
)
.loc[:, [
"report_date",
"state",
"utility_id_eia",
"balancing_authority_id_eia"
]]
.append(early_ba_by_util[["report_date", "utility_id_eia", "balancing_authority_id_eia"]])
.drop_duplicates()
.merge(ba_normed)
.dropna(subset=["report_date", "utility_id_eia", "balancing_authority_id_eia"])
.sort_values(["report_date", "balancing_authority_id_eia", "utility_id_eia", "state"])
)
# Merge in county FIPS IDs for each county served by the utility from
# the service territory dataframe. We do an outer merge here so that we
# retain any utilities that are not part of a balancing authority. This
# lets us generate both BA and Util maps from the same GeoDataFrame
# We have to do this separately for the data up to 2012 (which doesn't
# include state) and the 2013 and onward data (which we need to have
# state for)
early_ba_util_county = (
ba_by_util.drop("state", axis="columns")
.merge(st_eia861, on=["report_date", "utility_id_eia"], how="outer")
.query("report_date <= '2012-12-31'")
)
late_ba_util_county = (
ba_by_util
.merge(st_eia861, on=["report_date", "utility_id_eia", "state"], how="outer")
.query("report_date >= '2013-01-01'")
)
ba_util_county = pd.concat([early_ba_util_county, late_ba_util_county])
# Bring in county geometry information based on FIPS ID from Census
ba_util_county_gdf = (
census_gdf[["GEOID10", "NAMELSAD10", "geometry"]]
.to_crs(MAP_CRS)
.rename(
columns={
"GEOID10": "county_id_fips",
"NAMELSAD10": "county_name_census",
}
)
.merge(ba_util_county)
)
return ba_util_county_gdf
```
## Map Balancing Authorities
```
def map_ba(ba_ids, year, ba_util_county_gdf, save=False):
"""
Create a map of a balancing authority for a historical year.
Args:
ba_ids (iterable): A collection of Balancing Authority IDs.
year (int): The year for which to create a map.
ba_util_county_gdf (geopandas.GeoDataFrame): A dataframe
associating report_date, balancing_authority_id_eia, and
county_id_fips.
save (bool): If True, save the figure to disk.
Returns:
None
"""
map_gdf = (
ba_util_county_gdf[
(ba_util_county_gdf.report_date.dt.year == year) &
(ba_util_county_gdf.balancing_authority_id_eia.isin(ba_ids)) &
(~ba_util_county_gdf.county_id_fips.str.match("^02")) & # Avoid Alaska
(~ba_util_county_gdf.county_id_fips.str.match("^15")) & # Avoid Hawaii
(~ba_util_county_gdf.county_id_fips.str.match("^72")) # Avoid Puerto Rico
]
.drop_duplicates(subset=["balancing_authority_id_eia", "county_id_fips"])
)
ax = map_gdf.plot(figsize=(20, 20), color="black", alpha=0.25, linewidth=0.25)
plt.title(f"Balancing Areas ({year=})")
ctx.add_basemap(ax)
if save is True:
plt.savefig(f"BA_Overlap_{year}.jpg")
def compare_hifld_eia_ba(ba_code, hifld_gdf, eia_gdf):
"""
Compare historical EIA BAs vs. HIFLD geometries.
"""
fig, (hifld_ax, eia_ax) = plt.subplots(nrows=1, ncols=2, sharex=True, sharey=True)
hifld_ax.set_title(f"{ba_code} (HIFLD)")
hifld_gdf[hifld_gdf.ABBRV==ba_code].to_crs(MAP_CRS).plot(ax=hifld_ax, linewidth=0)
eia_ax.set_title(f"{ba_code} (EIA)")
eia_gdf[
(eia_gdf.balancing_authority_code_eia==ba_code) &
(eia_gdf.report_date.dt.year == 2017)
].plot(ax=eia_ax, linewidth=0.1)
plt.show()
```
# Read Data
## EIA 860 via PUDL Outputs
```
plants_eia860 = pudl_out.plants_eia860()
utils_eia860 = pudl_out.utils_eia860()
```
## EIA 861 (2010-2018)
* Not yet fully integrated into PUDL
* Post-transform harvesting process isn't compatible w/ EIA 861 structure
* Only getting the `sales_eia861`, `balancing_authority_eia861`, and `service_territory_eia861` tables
```
%%time
logger.setLevel("WARN")
eia_years = list(range(2010, 2019))
eia_inputs = {
"eia860_years": [],
"eia860_tables": pudl.constants.pudl_tables["eia860"],
"eia861_years": eia_years,
"eia861_tables": pudl.constants.pudl_tables["eia861"],
"eia923_years": [],
"eia923_tables": pudl.constants.pudl_tables["eia923"],
}
eia_transformed_dfs = test_etl_eia(eia_inputs=eia_inputs, pudl_settings=pudl_settings)
logger.setLevel("INFO")
ba_eia861 = eia_transformed_dfs["balancing_authority_eia861"].copy()
st_eia861 = eia_transformed_dfs["service_territory_eia861"].copy()
sales_eia861 = eia_transformed_dfs["sales_eia861"].copy()
raw_eia861_dfs = pudl.extract.eia861.Extractor().extract(years=range(2010,2019), testing=True)
```
## FERC 714 (2006-2018)
```
%%time
logger.setLevel("WARN")
raw_ferc714 = pudl.extract.ferc714.extract(pudl_settings=pudl_settings)
tfr_ferc714 = pudl.transform.ferc714.transform(raw_ferc714)
logger.setLevel("INFO")
```
## HIFLD Electricity Planning Areas (2018)
* Electricty Planning Area geometries from HIFLD.
* Indexed by `ID` which corresponds to EIA utility or balancing area IDs.
* Only valid for 2017-2018.
```
hifld_pa_gdf = (
pudl.analysis.demand_mapping.get_hifld_planning_areas_gdf(pudl_settings)
.to_crs(MAP_CRS)
)
```
## US Census DP1 (2010)
* This GeoDataFrame contains county-level geometries and demographic data.
```
%%time
census_gdf = (
pudl.analysis.demand_mapping.get_census2010_gdf(pudl_settings, layer="county")
.to_crs(MAP_CRS)
)
```
# Combine Data
## Categorize FERC 714 Respondent IDs
```
rids_ferc714 = (
tfr_ferc714["respondent_id_ferc714"]
.pipe(categorize_eia_code, utils_eia860, ba_eia861)
)
```
## Add FERC 714 IDs to HIFLD
```
hifld_pa_gdf = (
hifld_pa_gdf
.merge(rids_ferc714, left_on="ID", right_on="eia_code", how="left")
)
```
## Add Respondent info to FERC 714 Demand
```
dhpa_ferc714 = pd.merge(
tfr_ferc714["demand_hourly_pa_ferc714"],
tfr_ferc714["respondent_id_ferc714"],
on="respondent_id_ferc714",
how="left", # There are respondents with no demand
)
```
# Utilities vs. Balancing Authorities
Exploration of the Balancing Authority EIA 861 table for cleanup
### Which columns are available in which years?
| Year | BA ID | BA Name | BA Code | Util ID | Util Name | State | N |
|------|-------|---------|---------|---------|-----------|-------|----|
| 2010 | XXXXX | XXXXXXX | | XXXXXXX | | |3193|
| 2011 | XXXXX | XXXXXXX | | XXXXXXX | | |3126|
| 2012 | XXXXX | XXXXXXX | | XXXXXXX | XXXXXXXXX | |3146|
| 2013 | XXXXX | XXXXXXX | XXXXXXX | | | XXXXX | 239|
| 2014 | XXXXX | XXXXXXX | XXXXXXX | | | XXXXX | 208|
| 2015 | XXXXX | XXXXXXX | XXXXXXX | | | XXXXX | 203|
| 2016 | XXXXX | XXXXXXX | XXXXXXX | | | XXXXX | 203|
| 2017 | XXXXX | XXXXXXX | XXXXXXX | | | XXXXX | 203|
| 2018 | XXXXX | XXXXXXX | XXXXXXX | | | XXXXX | 204|
### What does this table mean?
* In 2010-2012, the table says which utilities (by ID) are included in which balancing authorities.
* In 2013-2018, the table indicates which *states* a BA is operating in, and also provides a BA Code
### Questions:
* Where does the `balancing_authority_code` show up elsewhere in the EIA 860/861 data?
* `plants_eia860` (nowhere else that I know of)
* Are the BA to Utility mappings likely to remain valid throughout the entire time period? Can we propagate them forward?
* No, there's some variation year to year in which utilities are associated with which BAs
* Are the BA Code/Name to BA ID mappings permanent?
* No they aren't -- when a BA changes owners and names, the code changes, but ID stays the same.
## Untangling HIFLD, FERC 714, & EIA IDs
* There are unspecified "EIA codes" associated with FERC 714 respondents.
* These IDs correspond to a mix of `utility_id_eia` and `balancing_authority_id_eia` values.
* Similarly, the ID field of the HIFLD geometries are a mix of BA and Utility IDs from EIA.
* This is extra confusing, because EIA *usually* uses the *same* ID for BAs and Utils.
* However, the EIA BA and Util IDs appear to be distinct namespaces
* Not all IDs which appear in both tables identify the same entity in both tables.
* In a few cases different IDs are used to identify the same entity when it shows up in both tables.
* It could be that whoever entered the IDs in the FERC 714 / HIFLD datasets didn't realize these were different sets of IDs.
### BA / Utility ID Overlap
* Example of an ID that shows up in both, but refers to different entities, see `59504`
* `balancing_area_id_eia == 59504` is the Southwest Power Pool (SWPP).
* `utility_id_eia == 59504` is Kirkwood Community College, in MO.
* Example of an entity that exists in both datsets, but shows up with different IDs, see PacifiCorp.
* Has two BA IDs (East and West): `[14379, 14378]`
* Has one Utility ID: `14354`
* Example of an entity that shows up with the same ID in both tables:
* ID `15466` is Public Service Co of Colorado -- both a BA (PSCO) and a Utility.
```
# BA ID comes from EIA 861 BA Table
ba_ids = set(ba_eia861.balancing_authority_id_eia)
print(f"Total # of BA IDs: {len(ba_ids)}")
# Util ID comes from EIA 860 Utilities Entity table.
util_ids = set(pudl_out.utils_eia860().utility_id_eia)
print(f"Total # of Util IDs: {len(util_ids)}")
ba_not_util_ids = ba_ids.difference(util_ids)
print(f"BA IDs that are not Util IDs: {len(ba_not_util_ids)}")
util_not_ba_ids = util_ids.difference(ba_ids)
print(f"Util IDs that are not BA IDs: {len(util_not_ba_ids)}")
ba_and_util_ids = ba_ids.intersection(util_ids)
print(f"BA IDs that are also Util IDs: {len(ba_and_util_ids)}")
ba_and_util = (
ba_eia861
.loc[:, ["balancing_authority_id_eia", "balancing_authority_name_eia"]]
.dropna(subset=["balancing_authority_id_eia"])
.merge(
pudl_out.utils_eia860(),
left_on="balancing_authority_id_eia",
right_on="utility_id_eia",
how="inner"
)
.loc[:, [
"utility_id_eia",
"balancing_authority_name_eia",
"utility_name_eia",
]]
.rename(columns={"utility_id_eia": "util_ba_id"})
.drop_duplicates()
.reset_index(drop=True)
)
ba_not_util = (
ba_eia861.loc[ba_eia861.balancing_authority_id_eia.isin(ba_not_util_ids)]
.loc[:,["balancing_authority_id_eia", "balancing_authority_code_eia", "balancing_authority_name_eia"]]
.drop_duplicates(subset=["balancing_authority_id_eia", "balancing_authority_code_eia"])
.sort_values("balancing_authority_id_eia")
)
```
### Missing IDs
* There are `eia_code` values that don't show up in the list of balancing authority IDs (2010-2018).
* There are also `eia_code` values that don't show up in the list of utility IDs (2009-2018).
* There are a few `eia_code` values that don't show up in either!
* Mostly this is an artifact of the different time covered by FERC 714 (2006-2018).
* If we look only at the respondents that reported non-zero demand for 2010-2018, we find that all of the `eia_code` values *do* appear in either the `blancing_authority_eia861` or `utilities_eia860` tables.
```
rids_ferc714[
(~rids_ferc714.eia_code.isin(ba_eia861.balancing_authority_id_eia.unique())) &
(~rids_ferc714.eia_code.isin(utils_eia860.utility_id_eia.unique()))
]
rids_recent = (
dhpa_ferc714
.groupby(["respondent_id_ferc714", "report_year"])
.agg({"demand_mwh": sum})
.reset_index()
.query("report_year >= 2010")
.query("demand_mwh >= 0.0")
.merge(rids_ferc714[["eia_code", "respondent_id_ferc714", "respondent_name_ferc714"]], how="left")
.drop(["report_year", "demand_mwh"], axis="columns")
.drop_duplicates()
)
assert len(rids_recent[
(~rids_recent.eia_code.isin(ba_eia861.balancing_authority_id_eia.unique())) &
(~rids_recent.eia_code.isin(utils_eia860.utility_id_eia.unique()))
]) == 0
```
### BA to Utility Mappings are Many to Many
* Unsurprisingly, BAs often contain many utilities.
* However, it's also common for utilities to participate in more than one BA.
* About 1/3 of all utilities show up in association with more than one BA
```
ba_to_util_mapping = (
ba_eia861[["balancing_authority_id_eia", "utility_id_eia"]]
.dropna(subset=["balancing_authority_id_eia", "utility_id_eia"])
.drop_duplicates(subset=["balancing_authority_id_eia", "utility_id_eia"])
.groupby(["balancing_authority_id_eia"])
.agg({
"utility_id_eia": "count"
})
)
plt.hist(ba_to_util_mapping.utility_id_eia, bins=99, range=(1,100))
plt.xlabel("# of Utils / BA")
plt.ylabel("# of BAs")
plt.title("Number of Utilities per Balancing Area");
util_to_ba_mapping = (
ba_eia861[["balancing_authority_id_eia", "utility_id_eia"]]
.dropna(subset=["balancing_authority_id_eia", "utility_id_eia"])
.drop_duplicates(subset=["balancing_authority_id_eia", "utility_id_eia"])
.groupby(["utility_id_eia"])
.agg({
"balancing_authority_id_eia": "count"
})
)
plt.hist(util_to_ba_mapping.balancing_authority_id_eia, bins=4, range=(1,5))
plt.title("Number of Balancing Authorities per Utility");
```
## Georeferenced Demand Fraction
* With their original EIA codes the HIFLD Electricity Planning Areas only georeference some of the FERC 714 demand.
* It's about 86% in 2018. In 2013 and earlier years, the fraction starts to drop off more quickly, to 76% in 2010, and 58% in 2006.
* After manually identifying and fixing some bad and missing EIA codes in the FERC 714, the mapped fraction is much higher.
* 98% or more in 2014-2018, dropping to 87% in 2010, and 68% in 2006
* **However** because the geometries have also evolved over time, just the fact that the demand time series is linked to **some** HIFLD geometry, doesn't mean that it's the **right** geometry.
```
annual_demand_ferc714 = (
dhpa_ferc714
.groupby(["report_year"]).demand_mwh.sum()
.reset_index()
)
annual_demand_mapped = (
dhpa_ferc714[dhpa_ferc714.eia_code.isin(hifld_pa_gdf.eia_code)]
.groupby(["report_year"]).demand_mwh.sum()
.reset_index()
.merge(annual_demand_ferc714, on="report_year", suffixes=("_map", "_tot"))
.assign(
fraction_mapped=lambda x: x.demand_mwh_map / x.demand_mwh_tot
)
)
plt.plot("report_year", "fraction_mapped", data=annual_demand_mapped, lw=5)
plt.ylabel("Fraction of demand which is mapped")
plt.title("Completeness of HIFLD demand mapping by year")
plt.ylim(0.6, 1.05);
```
# Historical Planning Area Geometries
Compile a GeoDataFrame that relates balancing authorities, their constituent utilities, and the collections of counties which are served by those utilities, across all the years for which we have EIA 861 data (2010-2018)
```
ba_util_county_gdf = georef_bas(ba_eia861, st_eia861, sales_eia861, census_gdf)
ba_util_county_gdf.info()
for year in (2010, 2014, 2018):
map_ba(ba_util_county_gdf.balancing_authority_id_eia.unique(), year, ba_util_county_gdf, save=True)
```
## Output Simplified Annual BA Geometries
* This takes half an hour so it's commented out.
* Resulting shapefile is ~250MB compressed. Seems too big.
* Need to figure out how to add explicity projection.
* Need to figure out how to make each year's BA geometries its own layer.
```
#%%time
#ba_fips_simplified = (
# ba_util_county_gdf
# .assign(report_year=lambda x: x.report_date.dt.year)
# .drop([
# "report_date",
# "state",
# "state_id_fips",
# "county",
# "county_name_census",
# "utility_id_eia",
# "utility_name_eia"
# ], axis="columns")
# .drop_duplicates(subset=["report_year", "balancing_authority_id_eia", "county_id_fips"])
# .dropna(subset=["report_year", "balancing_authority_id_eia", "county_id_fips"])
# .loc[:,["report_year", "balancing_authority_id_eia", "balancing_authority_code_eia", "balancing_authority_name_eia", "county_id_fips", "geometry"]]
#)
#ba_annual_gdf = (
# ba_fips_simplified
# .dissolve(by=["report_year", "balancing_authority_id_eia"])
# .reset_index()
# .drop("county_id_fips", axis="columns")
#)
#ba_output_gdf = (
# ba_annual_gdf
# .astype({
# "report_year": int,
# "balancing_authority_id_eia": float,
# "balancing_authority_code_eia": str,
# "balancing_authority_name_eia": str,
# })
# .rename(columns={
# "report_year": "year",
# "balancing_authority_id_eia": "ba_id",
# "balancing_authority_code_eia": "ba_code",
# "balancing_authority_name_eia": "ba_name",
# })
#)
#ba_output_gdf.to_file("ba_annual.shp")
```
## Compare HIFLD and EIA BA maps for 2018
```
for ba_code in hifld_pa_gdf.ABBRV.unique():
if ba_code in ba_util_county_gdf.balancing_authority_code_eia.unique():
compare_hifld_eia_ba(ba_code, hifld_pa_gdf, ba_util_county_gdf)
```
## Time Evolution of BA Geometries
For each BA we now have a collection of annual geometries. How have they changed over time?
```
for ba_code in ba_util_county_gdf.balancing_authority_code_eia.unique():
fig, axes = plt.subplots(nrows=3, ncols=3, figsize=(20,20), sharex=True, sharey=True, facecolor="white")
for year, ax in zip(range(2010, 2019), axes.flat):
ax.set_title(f"{ba_code} ({year})")
ax.set_xticks([])
ax.set_yticks([])
plot_gdf = (
ba_util_county_gdf
.assign(report_year=lambda x: x.report_date.dt.year)
.query(f"balancing_authority_code_eia=='{ba_code}'")
.query(f"report_year=='{year}'")
.drop_duplicates(subset="county_id_fips")
)
plot_gdf.plot(ax=ax, linewidth=0.1)
plt.show()
```
## Merge Geometries with FERC 714
Now that we have a draft of wht the BA and Utility level territories look like, we can merge those with the FERC 714 Respondent ID table, and see how many leftovers there are, and whether the BA and Utility geometires play well together.
Before dissolving the boundaries between counties the output dataframe needs to have:
* `report_date`
* `respondent_id_ferc714`
* `eia_code`
* `respondent_type`
* `balancing_authority_id_eia`
* `utility_id_eia`
* `county_id_fips`
* `geometry`
* `balancing_authority_code_eia`
* `balancing_authority_name_eia`
* `respondent_name_ferc714`
* `utility_name_eia`
* `county_name_census`
* `state`
* `state_id_fips`
```
utils_ferc714 = (
rids_ferc714.loc[
rids_ferc714.respondent_type == "utility",
["respondent_id_ferc714", "respondent_name_ferc714", "utility_id_eia", "respondent_type"]
]
)
bas_ferc714 = (
rids_ferc714.loc[
rids_ferc714.respondent_type == "balancing_authority",
["respondent_id_ferc714", "respondent_name_ferc714", "balancing_authority_id_eia", "respondent_type"]
]
)
null_ferc714 = (
rids_ferc714.loc[
rids_ferc714.respondent_type.isnull(),
["respondent_id_ferc714", "respondent_name_ferc714", "respondent_type"]
]
)
bas_ferc714_gdf = (
ba_util_county_gdf
.drop(["county"], axis="columns")
.merge(bas_ferc714, how="right")
)
utils_ferc714_gdf = (
ba_util_county_gdf
.drop(["balancing_authority_id_eia", "balancing_authority_code_eia", "balancing_authority_name_eia", "county"], axis="columns")
.drop_duplicates()
.merge(utils_ferc714, how="right")
)
rids_ferc714_gdf = (
pd.concat([bas_ferc714_gdf, utils_ferc714_gdf, null_ferc714])
.astype({
"county_id_fips": pd.StringDtype(),
"county_name_census": pd.StringDtype(),
"respondent_type": pd.StringDtype(),
"utility_id_eia": pd.Int64Dtype(),
"balancing_authority_id_eia": pd.Int64Dtype(),
"balancing_authority_code_eia": pd.StringDtype(),
"balancing_authority_name_eia": pd.StringDtype(),
"state": pd.StringDtype(),
"utility_name_eia": pd.StringDtype(),
})
)
display(rids_ferc714_gdf.info())
rids_ferc714_gdf.sample(10)
```
## Check Geometries for Completeness
* How many balancing authorities do we have geometries for?
* How many utilities do we have geometries for?
* Do those geometries cover all of the entities that report in FERC 714?
* Do we have a geometry for every entity in every year in which it reports demand?
### Count BA & Util Geometries
```
n_bas = len(rids_ferc714_gdf.balancing_authority_id_eia.unique())
logger.info(f"Found territories for {n_bas} unique Balancing Areas")
n_utils = len(rids_ferc714_gdf.loc[
(rids_ferc714_gdf.balancing_authority_id_eia.isnull()) &
(~rids_ferc714_gdf.utility_id_eia.isnull())
].utility_id_eia.unique())
logger.info(f"Found territories for {n_utils} Utilities outside of the BAs")
```
### Identify Missing Geometries
* Within each year of historical data from 2010-2018, are there any entities (either BA or Utility) which **do** have hourly demand reported in the FERC 714, for whivh we do not have a historical geometry?
* How many of them are there?
* Why are they missing?
* Do we have the geometires in adjacent years and can we re-use them?
* Is it possible that the FERC 714 IDs correspond to a precursor entity, or one that was discontinued? E.g. if SWPP is missing in 2010, is that because the BA was reported in EIA as SPS in that year?
* How important are the missing geometries? Do the associated entities have a lot of demand associated with them in FERC 714?
* Can we use `ffill` or `backfill` on the `geometry` column in a GeoDataFrame?
```
problem_ids = pd.DataFrame()
for year in range(2010, 2019):
this_year_gdf = (
rids_ferc714_gdf
.loc[(rids_ferc714_gdf.report_date.dt.year==year) & (~rids_ferc714_gdf.geometry.isnull())]
)
# All BA IDs which show up in FERC 714:
ba_ids_ferc714 = (
rids_ferc714
.loc[rids_ferc714.respondent_type=="balancing_authority",
"balancing_authority_id_eia"]
.unique()
)
# BA IDs which have a geometry in this year
ba_geom_ids = (
this_year_gdf
.balancing_authority_id_eia
.dropna().unique()
)
# BA IDs which have reported demand in this year
ba_demand_ids = (
dhpa_ferc714
.query("report_year==@year")
.query("demand_mwh>0.0")
.loc[dhpa_ferc714.eia_code.isin(ba_ids_ferc714)]
.eia_code.unique()
)
# Need to make the demand IDs clearly either utility of BA IDs. Whoops!
missing_ba_geom_ids = [x for x in ba_demand_ids if x not in ba_geom_ids]
logger.info(f"{len(missing_ba_geom_ids)} BA respondents w/o geometries in {year}")
problem_ids = problem_ids.append(
rids_ferc714
.loc[rids_ferc714.balancing_authority_id_eia.isin(missing_ba_geom_ids)]
.assign(year=year)
)
# All EIA Utility IDs which show up in FERC 714:
util_ids_ferc714 = (
rids_ferc714
.loc[rids_ferc714.respondent_type=="utility",
"utility_id_eia"]
.unique()
)
# EIA Utility IDs which have geometry information for this year
util_geom_ids = (
this_year_gdf
.utility_id_eia
.dropna().unique()
)
util_demand_ids = (
dhpa_ferc714
.query("report_year==@year")
.query("demand_mwh>0.0")
.loc[dhpa_ferc714.eia_code.isin(util_ids_ferc714)]
.eia_code.unique()
)
missing_util_geom_ids = [x for x in util_demand_ids if x not in util_geom_ids]
logger.info(f"{len(missing_util_geom_ids)} Utility respondents w/o geometries in {year}")
problem_ids = problem_ids.append(
rids_ferc714
.loc[rids_ferc714.utility_id_eia.isin(missing_util_geom_ids)]
.assign(year=year)
)
problem_ids.query("year==2010").query("respondent_type=='balancing_authority'")
```
## Dissolve to BA or Util
* At this point we still have geometires at the county level.
* This is 150,000+ records.
* Really we just want a single geometry per respondent per year.
* Dissolve based on year and respondent_id_ferc714.
* Merge the annual per-respondent geometry with the rids_ferc714 which has more information
* Note that this takes about half an hour to run...
```
%%time
dissolved_rids_ferc714_gdf = (
rids_ferc714_gdf.drop_duplicates(subset=["report_date", "county_id_fips", "respondent_id_ferc714"])
.dissolve(by=["report_date", "respondent_id_ferc714"])
.reset_index()
.loc[:, ["report_date", "respondent_id_ferc714", "geometry"]]
.merge(rids_ferc714, on="respondent_id_ferc714", how="outer")
)
#dissolved_rids_ferc714_gdf.to_file("planning_areas_ferc714.gpkg", driver="GPKG")
```
### Select based on respondent type
```
dissolved_utils = dissolved_rids_ferc714_gdf.query("respondent_type=='utility'")
dissolved_bas = dissolved_rids_ferc714_gdf.query("respondent_type=='balancing_authority'")
```
### Nationwide BA / Util Maps
* Still want to add the US state boundaries / coastlines to this for context.
```
unwanted_ba_ids = (
112, # Alaska
133, # Alaska
178, # Hawaii
301, # PJM Dupe
302, # PJM Dupe
303, # PJM Dupe
304, # PJM Dupe
305, # PJM Dupe
306, # PJM Dupe
)
for report_date in pd.date_range(start="2010-01-01", end="2018-01-01", freq="AS"):
ba_ax = (
dissolved_bas
.query("report_date==@report_date")
.query("respondent_id_ferc714 not in @unwanted_ba_ids")
.plot(figsize=(20, 20), color="blue", alpha=0.25, linewidth=1)
)
plt.title(f"FERC 714 Balancing Authority Respondents {report_date}")
ctx.add_basemap(ba_ax)
util_ax = (
dissolved_utils
.query("report_date==@report_date")
.plot(figsize=(20, 20), color="red", alpha=0.25, linewidth=1)
)
plt.title(f"FERC 714 Utility Respondents {report_date}")
ctx.add_basemap(util_ax)
plt.show();
```
### Per-respondent annual maps
* For each respondent make a grid of 9 (2010-2018)
* Show state lines in bg for context
* Limit bounding box by the respondent's territory
# Remaining Tasks
## Geometry Cleanup:
* Why do some respondents lack geometries in some years?
* Why do some respondents lack geometries in **all** years? (e.g. Tri-State G&T)
* Why do some counties have no BA or Utility coverage in some or all years?
* What combinations of years and respondents are missing?
* Compare what we've ended up doing to the Aufhammer paper again.
* Is there any need to use name-based matching between the Planning Area descriptions & EIA Service Territories?
* Problem BAs / Utilities:
* All the WAPA BAs
* PacifiCorp East / West
* Southern Company
* MISO (Some other IDs that seem related?)
* PJM (Early years seem out of bounds)
## FERC 714 Demand Time Series Cleanup
### Find broken data:
* Run Tyler Ruggles' anomaly detection code as improved by Greg Schivley
* What kind of anomalies are we finding? Are they a problem? What portion of the overall dataset do they represent?
### Repair data:
* How do we want to fill in the gaps?
* Ideally would be able to use the MICE technique that Tyler used, but we need to keep it all in Python.
* Can do much simpler rolling averages or something for the moment when there are small gaps just to have completeness.
* Should make this gap filling process modular -- use different techniques and see whether they do what we need.
# Miscellaneous Notes
## FERC 714 Demand Irregularities
Unusual issues that need to be addressed, or demand discontinuities that may be useful in the context of aggregating historical demand into modern planning areas. Organized by FERC 714 Respondent ID:
* Missing demand data / weird zeroes
* 111: (2008)
* 125: (2015)
* 137: (2006)
* 139: (2006) Only the last hour of every day. Maybe 0-23 vs 1-24 reporting?
* 141: (2006, 2007, 2008, 2009, 2010)
* 148: (2006)
* 153: (2006)
* 154: (2006)
* 161: (all)
* 183: (2007, 2009)
* 208: (2008)
* 273: (2007, 2008)
* 283: (2007)
* 287: (2008-2012)
* 288: (2006)
* 289: (2009)
* 293: (2006)
* 294: (2006)
* 311: (2008-2011)
* Inverted Demand (Sign Errors):
* 156: (2006, 2007, 2008, 2009)
* 289: (2006-2008, 2010)
* Large demand discontinuities
* 107: Demand triples at end of 2006.
* 115: Two big step downs, 2007-2008, and 2011-2012
* 121: 50% increase at end of 2007.
* 128: Step up at end of 2007
* 133: Step down end of 2013 and again end of 2015
* 190: Demand doubled at end of 2008
* 214: 50% jump in early 2012.
* 256: big jump at end of 2006.
* 261: Big jump at end of 2008.
* 274: drop at end of 2007
* 275: Jump at end of 2007
* 287: Demand before and after big gap are very different.
* 299: Big drop at end of 2015
* 307: Jump at end of 2014
* 321: Jump at end of 2013
|
github_jupyter
|
# Part 0: Mining the web
Perhaps the richest source of openly available data today is [the Web](http://www.computerhistory.org/revolution/networking/19/314)! In this lab, you'll explore some of the basic programming tools you need to scrape web data.
> **Note.** The Vocareum platform runs in a cloud-based environment that limits what websites a program can connect to directly. Therefore, some (or possibly all) of the code below will **not** work. Therefore, we are making this notebook **optional** and are providing solutions inline.
>
> Even if you are using a home or local installation of Jupyter, you may encounter problems if you attempt to access a site too many times or too rapidly. That can happen if your internet service provider (ISP) or the target website detect your accesses as "unusual" and reject them. It's easy to imagine accidentally writing an infinite loop that tries to access a page and being seen from the other side as a malicious program. :)
## The Requests module
Python's [Requests module](http://requests.readthedocs.io/en/latest/user/quickstart/) to download a web page.
For instance, here is a code fragment to download the [Georgia Tech](http://www.gatech.edu) home page and print the first 250 characters. You might also want to [view the source](http://www.computerhope.com/issues/ch000746.htm) of Georgia Tech's home page to get a nicely formatted view, and compare its output to what you see above.
```
import requests
response = requests.get('https://www.gatech.edu/')
webpage = response.text # or response.content for raw bytes
print(webpage[0:250]) # Prints the first hundred characters only
```
**Exercise 1.** Given the contents of the GT home page as above, write a function that returns a list of links (URLs) of the "top stories" on the page.
For instance, on Friday, September 9, 2016, here was the front page:

The top stories cycle through in the large image placeholder shown above. We want your function to return the list of URLs behind each of the "Full Story" links, highlighted in red. If no URLs can be found, the function should return an empty list.
```
import re # Maybe you want to use a regular expression?
def get_gt_top_stories(webpage_text):
"""Given the HTML text for the GT front page, returns a list
of the URLs of the top stories or an empty list if none are
found.
"""
pattern = '''<a class="slide-link" href="(?P<url>[^"]+)"'''
return re.findall(pattern, webpage_text)
top_stories = get_gt_top_stories(webpage)
print("Links to GT's top stories:", top_stories)
```
## A more complex example
Go to [Yelp!](http://www.yelp.com) and look up `ramen` in `Atlanta, GA`. Take note of the URL:

This URL encodes what is known as an _HTTP "get"_ method (or request). It basically means a URL with two parts: a _command_ followed by one or more _arguments_. In this case, the command is everything up to and including the word `search`; the arguments are the rest, where individual arguments are separated by the `&` or `#`.
> "HTTP" stands for "HyperText Transport Protocol," which is a standardized set of communication protocols that allow _web clients_, like your web browser or your Python program, to communicate with _web servers_.
In this next example, let's see how to build a "get request" with the `requests` module. It's pretty easy!
```
url_command = 'https://yelp.com/search'
url_args = {'find_desc': "ramen",
'find_loc': "atlanta, ga"}
response = requests.get (url_command, params=url_args, timeout=60)
print ("==> Downloading from: '%s'" % response.url) # confirm URL
print ("\n==> Excerpt from this URL:\n\n%s\n" % response.text[0:100])
```
**Exercise 2.** Given a search topic, location, and a rank $k$, return the name of the $k$-th item of a Yelp! search. If there is no $k$-th item, return `None`.
> The demo query above only gives you a website with the top 10 items, meaning you could only use it for $k \leq 10$. Figure out how to modify it to solve the problem when $k > 10$.
```
def find_yelp_item (topic, location, k):
"""Returns the k-th suggested item from Yelp! in Atlanta for the given topic."""
import re
if k < 1: return None
# Download page
url_command = 'http://yelp.com/search'
url_args = {'find_desc': topic,
'find_loc': location,
'start': k-1
}
response = requests.get (url_command, params=url_args)
if not response: return None
# Split page into lines
lines = response.text.split ('\n')
# Look for the line containing the name of the k-th item
item_pattern = re.compile ('<span class="indexed-biz-name">{}\..*<span >(?P<item_name>.*)</span></a>'.format (k))
for l in lines:
item_match = item_pattern.search (l)
if item_match:
return item_match.group ('item_name')
# No matches, evidently
return None
assert find_yelp_item('fried chicken', 'Atlanta, GA', -1) is None # Tests an invalid value for 'k'
```
> Search queries on Yelp! don't always return the same answers, since the site is always changing! Also, your results might not match a query you do via your web browser (_why not?_). As such, you should manually check your answers.
```
item = find_yelp_item ('fried chicken', 'Atlanta, GA', 1)
print (item)
item = find_yelp_item ('fried chicken', 'Atlanta, GA', 5)
print (item)
# The most likely answer on September 11, 2018:
#assert item == 'Buttermilk Kitchen'
item = find_yelp_item('fried chicken', 'Atlanta, GA', 10)
print(item)
# Most likely correct answer as of September 11, 2018:
#assert item == 'Colonnade Restaurant'
```
One issue with the above exercises is that they treat HTML as a flat string, whereas the document is at least semi-structured. Moreover, web pages are such a common source of data today that you would expect better tools for processing them. Indeed, such tools exist! The next part of this assignment, Part 1, walks you through one such tool. So, head there when you are ready!
|
github_jupyter
|
# Main notebook for battery state estimation
```
import numpy as np
import pandas as pd
import scipy.io
import math
import os
import ntpath
import sys
import logging
import time
import sys
from importlib import reload
import plotly.graph_objects as go
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
from keras.models import Sequential
from keras.layers.core import Dense, Dropout, Activation
from keras.optimizers import SGD, Adam
from keras.utils import np_utils
from keras.layers import LSTM, Embedding, RepeatVector, TimeDistributed, Masking
from keras.callbacks import EarlyStopping, ModelCheckpoint, LambdaCallback
IS_COLAB = False
if IS_COLAB:
from google.colab import drive
drive.mount('/content/drive')
data_path = "/content/drive/My Drive/battery-state-estimation/battery-state-estimation/"
else:
data_path = "../../"
sys.path.append(data_path)
from data_processing.lg_dataset import LgData
```
### Config logging
```
reload(logging)
logging.basicConfig(format='%(asctime)s [%(levelname)s]: %(message)s', level=logging.DEBUG, datefmt='%Y/%m/%d %H:%M:%S')
```
# Load Data
```
train_names = [
'n10degC/601_Mixed1',
'n10degC/601_Mixed2',
'n10degC/604_Mixed3',
'n10degC/602_Mixed4',
'n10degC/602_Mixed5',
'n10degC/604_Mixed6',
'n10degC/604_Mixed7',
'n10degC/604_Mixed8',
'n20degC/610_Mixed1',
'n20degC/610_Mixed2',
'n20degC/611_Mixed3',
'n20degC/611_Mixed4',
'n20degC/611_Mixed5',
'n20degC/611_Mixed6',
'n20degC/611_Mixed7',
'n20degC/611_Mixed8'
]
test_names = [
'n10degC/596_UDDS',
'n10degC/601_US06',
'n10degC/596_LA92',
'n20degC/610_UDDS',
'n20degC/610_US06',
'n20degC/610_LA92',
]
steps = 500
lg_data = LgData(data_path)
cycles = lg_data.get_discharge_whole_cycle(train_names, test_names, output_capacity=False, scale_test=True)
train_x, train_y, test_x, test_y = lg_data.get_discharge_multiple_step(cycles, steps)
train_y = lg_data.keep_only_y_end(train_y, steps)
test_y = lg_data.keep_only_y_end(test_y, steps)
```
# Model training
```
EXPERIMENT = "lstm_soc_percentage_lg_negative_temp_500_steps_drive_cycle_test"
experiment_name = time.strftime("%Y-%m-%d-%H-%M-%S") + '_' + EXPERIMENT
print(experiment_name)
os.environ["CUDA_VISIBLE_DEVICES"] = "1"
# Model definition
opt = tf.keras.optimizers.Adam(lr=0.00001)
model = Sequential()
model.add(LSTM(256, activation='selu',
return_sequences=True,
input_shape=(train_x.shape[1], train_x.shape[2])))
model.add(LSTM(256, activation='selu', return_sequences=False))
model.add(Dense(256, activation='selu'))
model.add(Dense(128, activation='selu'))
model.add(Dense(1, activation='linear'))
model.summary()
model.compile(optimizer=opt, loss='huber', metrics=['mse', 'mae', 'mape', tf.keras.metrics.RootMeanSquaredError(name='rmse')])
es = EarlyStopping(monitor='val_loss', patience=50)
mc = ModelCheckpoint(data_path + 'results/trained_model/%s_best.h5' % experiment_name,
save_best_only=True,
monitor='val_loss')
history = model.fit(train_x, train_y,
epochs=1000,
batch_size=32,
verbose=2,
validation_split=0.2,
callbacks = [es, mc]
)
model.save(data_path + 'results/trained_model/%s.h5' % experiment_name)
hist_df = pd.DataFrame(history.history)
hist_csv_file = data_path + 'results/trained_model/%s_history.csv' % experiment_name
with open(hist_csv_file, mode='w') as f:
hist_df.to_csv(f)
```
### Testing
```
results = model.evaluate(test_x, test_y)
print(results)
```
# Data Visualization
```
# fig = go.Figure()
# fig.add_trace(go.Scatter(y=history.history['loss'],
# mode='lines', name='train'))
# fig.add_trace(go.Scatter(y=history.history['val_loss'],
# mode='lines', name='validation'))
# fig.update_layout(title='Loss trend',
# xaxis_title='epoch',
# yaxis_title='loss')
# fig.show()
# train_predictions = model.predict(train_x)
# cycle_num = 0
# steps_num = 8000
# step_index = np.arange(cycle_num*steps_num, (cycle_num+1)*steps_num)
# fig = go.Figure()
# fig.add_trace(go.Scatter(x=step_index, y=train_predictions.flatten()[cycle_num*steps_num:(cycle_num+1)*steps_num],
# mode='lines', name='SoC predicted'))
# fig.add_trace(go.Scatter(x=step_index, y=train_y.flatten()[cycle_num*steps_num:(cycle_num+1)*steps_num],
# mode='lines', name='SoC actual'))
# fig.update_layout(title='Results on training',
# xaxis_title='Step',
# yaxis_title='SoC percentage')
# fig.show()
# test_predictions = model.predict(test_x)
# cycle_num = 0
# steps_num = 8000
# step_index = np.arange(cycle_num*steps_num, (cycle_num+1)*steps_num)
# fig = go.Figure()
# fig.add_trace(go.Scatter(x=step_index, y=test_predictions.flatten()[cycle_num*steps_num:(cycle_num+1)*steps_num],
# mode='lines', name='SoC predicted'))
# fig.add_trace(go.Scatter(x=step_index, y=test_y.flatten()[cycle_num*steps_num:(cycle_num+1)*steps_num],
# mode='lines', name='SoC actual'))
# fig.update_layout(title='Results on testing',
# xaxis_title='Step',
# yaxis_title='SoC percentage')
# fig.show()
```
|
github_jupyter
|
```
%matplotlib inline
"""
The data set in this example represents 1059 songs from various countries obtained
from the UCI Machine Learning library. Various features of the audio tracks have been
extracted, and each track has been tagged with the latitude and longitude of the capital
city of its country of origin.
We'll treat this as a classification problem, and attempt to train a model to predict
the country of origin of each model.
Data source did not specifify what the audio features specifically are, just
"In the 'default_features_1059_tracks.txt' file, the first 68 columns are audio
features of the track, and the last two columns are the origin of the music,
represented by latitude and longitude.
In the 'default_plus_chromatic_features_1059_tracks.txt' file, the first 116
columns are audio features of the track, and the last two columns are the
origin of the music."
"""
import numpy as np
import pandas as pd
import sklearn
from sklearn.preprocessing import LabelEncoder
from sklearn.utils.multiclass import unique_labels
import sys
#First get the data. The UCI ML Library distributes it as a zipped file;
#download the data and extract the two provided files to the 'data' folder before continuing
music_df = pd.read_csv('data\default_plus_chromatic_features_1059_tracks.txt', header=None)
music = music_df.as_matrix()
#Our features are all but the last two columns
X = music[:,0:-2]
#Since feature names were not given, we'll just assign strings with an incrementing integer
names = np.linspace(start=1, stop=116, num=116, dtype='int').tolist()
for idx, name in enumerate(names):
names[idx] = "Feature " + str(name)
#The source data said that each song as tied to the capital city of it's origin country via a lat/lon pair.
#Let's treat this as a multi-class classification problem.
#Rather than reverse-geocoding, we'll just make a string out of the unique lat/lon pairs
lats = ["%.2f" % lat for lat in music_df[116]]
lons = ["%.2f" % lon for lon in music_df[117]]
song_latlons = []
for index, value in enumerate(lats):
city_id = lats[index] + "," + lons[index]
song_latlons.append(city_id)
unique_latlons = unique_labels(song_latlons)
city_options = ['A','B','C','D','E','F','G','H','I','J','K','L','M','N','O','P','Q','R','S','T','U','V','W','X','Y','Z','AA','AB','AC','AD','AE','AF','AG']
city_name_map = {}
for idx,latlon in enumerate(unique_latlons):
city_name_map[latlon] = city_options[idx]
ylist = []
for latlon in song_latlons:
ylist.append(city_name_map[latlon])
y = np.array(ylist)
#We want yellowbrick to import from this repository, and assume this notebook is in repofolder/examples/subfolder/
sys.path.append("../../")
import yellowbrick as yb
from yellowbrick.features.rankd import Rank2D
from yellowbrick.features.radviz import RadViz
from yellowbrick.features.pcoords import ParallelCoordinates
#See how well correlated the features are
visualizer = Rank2D(features = names, algorithm = 'pearson')
visualizer.fit(X, y)
visualizer.transform(X)
visualizer.poof()
from sklearn import metrics
from sklearn.model_selection import KFold
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
from sklearn.neighbors import KNeighborsClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.naive_bayes import GaussianNB
from sklearn.linear_model import LogisticRegression
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.metrics import confusion_matrix
from yellowbrick.classifier import ClassificationReport
def train_and_classification_report(model):
X_train, X_test, y_train, y_test = train_test_split(X,y, test_size =0.2, random_state=11)
model.fit(X_train, y_train)
y_predict = model.predict(X_test)
print("prec: {}".format(metrics.precision_score(y_true = y_test, y_pred = y_predict, average="weighted")))
print("rec: {}".format(metrics.recall_score(y_true= y_test, y_pred = y_predict, average = "weighted")))
cr_viz = ClassificationReport(model) #,classes=city_options
cr_viz.fit(X_train, y_train)
cr_viz.score(X_test, y_test)
cr_viz.poof()
#Adding the reloading functionality so we can edit the source code and see results here.
import importlib
importlib.reload(yb.classifier)
from yellowbrick.classifier import ClassificationReport
#This produces an IndexError: list index out of range.
train_and_classification_report(LogisticRegression())
#This demonstrates a version of the Seaborn confusion matrix heatmap we could replicate (and improve on).
def train_and_confusion_matrix(model):
X_train, X_test, y_train, y_test = train_test_split(X,y, test_size =0.2, random_state=11)
model.fit(X_train, y_train)
y_predict = model.predict(X_test)
print("prec: {}".format(metrics.precision_score(y_true = y_test, y_pred = y_predict, average="weighted")))
print("rec: {}".format(metrics.recall_score(y_true= y_test, y_pred = y_predict, average = "weighted")))
c_matrix = confusion_matrix(y_true = y_test, y_pred = y_predict)
sns.heatmap(c_matrix, square=True, annot=True, cbar=False, xticklabels=city_options, yticklabels = city_options)
plt.xlabel('predicted value')
plt.ylabel('true value')
train_and_confusion_matrix(LogisticRegression())
def train_and_class_balance(model):
X_train, X_test, y_train, y_test = train_test_split(X,y, test_size =0.2, random_state=11)
class_balance = yb.classifier.ClassBalance(model, classes=city_options)
class_balance.fit(X_train, y_train)
class_balance.score(X_test, y_test)
class_balance.poof()
train_and_class_balance(LogisticRegression())
```
|
github_jupyter
|
##### Copyright 2020 The TensorFlow Authors.
```
#@title Licensed under the Apache License, Version 2.0
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
```
# TensorFlow Addons Optimizers: ConditionalGradient
<table class="tfo-notebook-buttons" align="left">
<td>
<a target="_blank" href="https://www.tensorflow.org/addons/tutorials/optimizers_conditionalgradient"><img src="https://www.tensorflow.org/images/tf_logo_32px.png" />View on TensorFlow.org</a>
</td>
<td>
<a target="_blank" href="https://colab.research.google.com/github/tensorflow/addons/blob/master/docs/tutorials/optimizers_conditionalgradient.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
</td>
<td>
<a target="_blank" href="https://github.com/tensorflow/addons/blob/master/docs/tutorials/optimizers_conditionalgradient.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View source on GitHub</a>
</td>
<td>
<a href="https://storage.googleapis.com/tensorflow_docs/addons/docs/tutorials/optimizers_conditionalgradient.ipynb"><img src="https://www.tensorflow.org/images/download_logo_32px.png" />Download notebook</a>
</td>
</table>
# Overview
This notebook will demonstrate how to use the Conditional Graident Optimizer from the Addons package.
# ConditionalGradient
> Constraining the parameters of a neural network has been shown to be beneficial in training because of the underlying regularization effects. Often, parameters are constrained via a soft penalty (which never guarantees the constraint satisfaction) or via a projection operation (which is computationally expensive). Conditional gradient (CG) optimizer, on the other hand, enforces the constraints strictly without the need for an expensive projection step. It works by minimizing a linear approximation of the objective within the constraint set. In this notebook, we demonstrate the appliction of Frobenius norm constraint via the CG optimizer on the MNIST dataset. CG is now available as a tensorflow API. More details of the optimizer are available at https://arxiv.org/pdf/1803.06453.pdf
## Setup
```
import tensorflow as tf
import tensorflow_addons as tfa
from matplotlib import pyplot as plt
# Hyperparameters
batch_size=64
epochs=10
```
# Build the Model
```
model_1 = tf.keras.Sequential([
tf.keras.layers.Dense(64, input_shape=(784,), activation='relu', name='dense_1'),
tf.keras.layers.Dense(64, activation='relu', name='dense_2'),
tf.keras.layers.Dense(10, activation='softmax', name='predictions'),
])
```
# Prep the Data
```
# Load MNIST dataset as NumPy arrays
dataset = {}
num_validation = 10000
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data()
# Preprocess the data
x_train = x_train.reshape(-1, 784).astype('float32') / 255
x_test = x_test.reshape(-1, 784).astype('float32') / 255
```
# Define a Custom Callback Function
```
def frobenius_norm(m):
"""This function is to calculate the frobenius norm of the matrix of all
layer's weight.
Args:
m: is a list of weights param for each layers.
"""
total_reduce_sum = 0
for i in range(len(m)):
total_reduce_sum = total_reduce_sum + tf.math.reduce_sum(m[i]**2)
norm = total_reduce_sum**0.5
return norm
CG_frobenius_norm_of_weight = []
CG_get_weight_norm = tf.keras.callbacks.LambdaCallback(
on_epoch_end=lambda batch, logs: CG_frobenius_norm_of_weight.append(
frobenius_norm(model_1.trainable_weights).numpy()))
```
# Train and Evaluate: Using CG as Optimizer
Simply replace typical keras optimizers with the new tfa optimizer
```
# Compile the model
model_1.compile(
optimizer=tfa.optimizers.ConditionalGradient(
learning_rate=0.99949, lambda_=203), # Utilize TFA optimizer
loss=tf.keras.losses.SparseCategoricalCrossentropy(),
metrics=['accuracy'])
history_cg = model_1.fit(
x_train,
y_train,
batch_size=batch_size,
validation_data=(x_test, y_test),
epochs=epochs,
callbacks=[CG_get_weight_norm])
```
# Train and Evaluate: Using SGD as Optimizer
```
model_2 = tf.keras.Sequential([
tf.keras.layers.Dense(64, input_shape=(784,), activation='relu', name='dense_1'),
tf.keras.layers.Dense(64, activation='relu', name='dense_2'),
tf.keras.layers.Dense(10, activation='softmax', name='predictions'),
])
SGD_frobenius_norm_of_weight = []
SGD_get_weight_norm = tf.keras.callbacks.LambdaCallback(
on_epoch_end=lambda batch, logs: SGD_frobenius_norm_of_weight.append(
frobenius_norm(model_2.trainable_weights).numpy()))
# Compile the model
model_2.compile(
optimizer=tf.keras.optimizers.SGD(0.01), # Utilize SGD optimizer
loss=tf.keras.losses.SparseCategoricalCrossentropy(),
metrics=['accuracy'])
history_sgd = model_2.fit(
x_train,
y_train,
batch_size=batch_size,
validation_data=(x_test, y_test),
epochs=epochs,
callbacks=[SGD_get_weight_norm])
```
# Frobenius Norm of Weights: CG vs SGD
The current implementation of CG optimizer is based on Frobenius Norm, with considering Frobenius Norm as regularizer in the target function. Therefore, we compare CG’s regularized effect with SGD optimizer, which has not imposed Frobenius Norm regularizer.
```
plt.plot(
CG_frobenius_norm_of_weight,
color='r',
label='CG_frobenius_norm_of_weights')
plt.plot(
SGD_frobenius_norm_of_weight,
color='b',
label='SGD_frobenius_norm_of_weights')
plt.xlabel('Epoch')
plt.ylabel('Frobenius norm of weights')
plt.legend(loc=1)
```
# Train and Validation Accuracy: CG vs SGD
```
plt.plot(history_cg.history['accuracy'], color='r', label='CG_train')
plt.plot(history_cg.history['val_accuracy'], color='g', label='CG_test')
plt.plot(history_sgd.history['accuracy'], color='pink', label='SGD_train')
plt.plot(history_sgd.history['val_accuracy'], color='b', label='SGD_test')
plt.xlabel('Epoch')
plt.ylabel('Accuracy')
plt.legend(loc=4)
```
|
github_jupyter
|
```
import open3d as o3d
import numpy as np
import os
import sys
# monkey patches visualization and provides helpers to load geometries
sys.path.append('..')
import open3d_tutorial as o3dtut
# change to True if you want to interact with the visualization windows
o3dtut.interactive = not "CI" in os.environ
```
# RGBD integration
Open3D implements a scalable RGBD image integration algorithm. The algorithm is based on the technique presented in [\[Curless1996\]](../reference.html#curless1996) and [\[Newcombe2011\]](../reference.html#newcombe2011). In order to support large scenes, we use a hierarchical hashing structure introduced in [Integrater in ElasticReconstruction](https://github.com/qianyizh/ElasticReconstruction/tree/master/Integrate).
## Read trajectory from .log file
This tutorial uses the function `read_trajectory` to read a camera trajectory from a [.log file](http://redwood-data.org/indoor/fileformat.html). A sample `.log` file is as follows.
```
# examples/test_data/RGBD/odometry.log
0 0 1
1 0 0 2
0 1 0 2
0 0 1 -0.3
0 0 0 1
1 1 2
0.999988 3.08668e-005 0.0049181 1.99962
-8.84184e-005 0.999932 0.0117022 1.97704
-0.0049174 -0.0117024 0.999919 -0.300486
0 0 0 1
```
```
class CameraPose:
def __init__(self, meta, mat):
self.metadata = meta
self.pose = mat
def __str__(self):
return 'Metadata : ' + ' '.join(map(str, self.metadata)) + '\n' + \
"Pose : " + "\n" + np.array_str(self.pose)
def read_trajectory(filename):
traj = []
with open(filename, 'r') as f:
metastr = f.readline()
while metastr:
metadata = list(map(int, metastr.split()))
mat = np.zeros(shape=(4, 4))
for i in range(4):
matstr = f.readline()
mat[i, :] = np.fromstring(matstr, dtype=float, sep=' \t')
traj.append(CameraPose(metadata, mat))
metastr = f.readline()
return traj
camera_poses = read_trajectory("../../test_data/RGBD/odometry.log")
```
## TSDF volume integration
Open3D provides two types of TSDF volumes: `UniformTSDFVolume` and `ScalableTSDFVolume`. The latter is recommended since it uses a hierarchical structure and thus supports larger scenes.
`ScalableTSDFVolume` has several parameters. `voxel_length = 4.0 / 512.0` means a single voxel size for TSDF volume is $\frac{4.0\mathrm{m}}{512.0} = 7.8125\mathrm{mm}$. Lowering this value makes a high-resolution TSDF volume, but the integration result can be susceptible to depth noise. `sdf_trunc = 0.04` specifies the truncation value for the signed distance function (SDF). When `color_type = TSDFVolumeColorType.RGB8`, 8 bit RGB color is also integrated as part of the TSDF volume. Float type intensity can be integrated with `color_type = TSDFVolumeColorType.Gray32` and `convert_rgb_to_intensity = True`. The color integration is inspired by [PCL](http://pointclouds.org/).
```
volume = o3d.pipelines.integration.ScalableTSDFVolume(
voxel_length=4.0 / 512.0,
sdf_trunc=0.04,
color_type=o3d.pipelines.integration.TSDFVolumeColorType.RGB8)
for i in range(len(camera_poses)):
print("Integrate {:d}-th image into the volume.".format(i))
color = o3d.io.read_image("../../test_data/RGBD/color/{:05d}.jpg".format(i))
depth = o3d.io.read_image("../../test_data/RGBD/depth/{:05d}.png".format(i))
rgbd = o3d.geometry.RGBDImage.create_from_color_and_depth(
color, depth, depth_trunc=4.0, convert_rgb_to_intensity=False)
volume.integrate(
rgbd,
o3d.camera.PinholeCameraIntrinsic(
o3d.camera.PinholeCameraIntrinsicParameters.PrimeSenseDefault),
np.linalg.inv(camera_poses[i].pose))
```
## Extract a mesh
Mesh extraction uses the marching cubes algorithm [\[LorensenAndCline1987\]](../reference.html#lorensenandcline1987).
```
print("Extract a triangle mesh from the volume and visualize it.")
mesh = volume.extract_triangle_mesh()
mesh.compute_vertex_normals()
o3d.visualization.draw_geometries([mesh],
front=[0.5297, -0.1873, -0.8272],
lookat=[2.0712, 2.0312, 1.7251],
up=[-0.0558, -0.9809, 0.1864],
zoom=0.47)
```
<div class="alert alert-info">
**Note:**
TSDF volume works like a weighted average filter in 3D space. If more frames are integrated, the volume produces a smoother and nicer mesh. Please check [Make fragments](../reconstruction_system/make_fragments.rst) for more examples.
</div>
|
github_jupyter
|
# Using Interrupts and asyncio for Buttons and Switches
This notebook provides a simple example for using asyncio I/O to interact asynchronously with multiple input devices. A task is created for each input device and coroutines used to process the results. To demonstrate, we recreate the flashing LEDs example in the getting started notebook but using interrupts to avoid polling the GPIO devices. The aim is have holding a button result in the corresponding LED flashing.
## Initialising the Environment
First we import an instantiate all required classes to interact with the buttons, switches and LED and ensure the base overlay is loaded.
```
from pynq import PL
from pynq.overlays.base import BaseOverlay
base = BaseOverlay("base.bit")
```
## Define the flash LED task
Next step is to create a task that waits for the button to be pressed and flash the LED until the button is released. The `while True` loop ensures that the coroutine keeps running until cancelled so that multiple presses of the same button can be handled.
```
import asyncio
async def flash_led(num):
while True:
await base.buttons[num].wait_for_value_async(1)
while base.buttons[num].read():
base.leds[num].toggle()
await asyncio.sleep(0.1)
base.leds[num].off()
```
## Create the task
As there are four buttons we want to check, we create four tasks. The function `asyncio.ensure_future` is used to convert the coroutine to a task and schedule it in the event loop. The tasks are stored in an array so they can be referred to later when we want to cancel them.
```
tasks = [asyncio.ensure_future(flash_led(i)) for i in range(4)]
```
## Monitoring the CPU Usage
One of the advantages of interrupt-based I/O is to minimised CPU usage while waiting for events. To see how CPU usages is impacted by the flashing LED tasks we create another task that prints out the current CPU utilisation every 3 seconds.
```
import psutil
async def print_cpu_usage():
# Calculate the CPU utilisation by the amount of idle time
# each CPU has had in three second intervals
last_idle = [c.idle for c in psutil.cpu_times(percpu=True)]
while True:
await asyncio.sleep(3)
next_idle = [c.idle for c in psutil.cpu_times(percpu=True)]
usage = [(1-(c2-c1)/3) * 100 for c1,c2 in zip(last_idle, next_idle)]
print("CPU Usage: {0:3.2f}%, {1:3.2f}%".format(*usage))
last_idle = next_idle
tasks.append(asyncio.ensure_future(print_cpu_usage()))
```
## Run the event loop
All of the blocking wait_for commands will run the event loop until the condition is met. All that is needed is to call the blocking `wait_for_level` method on the switch we are using as the termination condition.
While waiting for switch 0 to get high, users can press any push button on the board to flash the corresponding LED. While this loop is running, try opening a terminal and running `top` to see that python is consuming no CPU cycles while waiting for peripherals.
As this code runs until the switch 0 is high, make sure it is low before running the example.
```
if base.switches[0].read():
print("Please set switch 0 low before running")
else:
base.switches[0].wait_for_value(1)
```
## Clean up
Even though the event loop has stopped running, the tasks are still active and will run again when the event loop is next used. To avoid this, the tasks should be cancelled when they are no longer needed.
```
[t.cancel() for t in tasks]
```
Now if we re-run the event loop, nothing will happen when we press the buttons. The process will block until the switch is set back down to the low position.
```
base.switches[0].wait_for_value(0)
```
Copyright (C) 2020 Xilinx, Inc
|
github_jupyter
|
# Making Simple Plots
## Objectives
+ Learn how to make a simple 1D plot in Python.
+ Learn how to find the maximum/minimum of a function in Python.
We will use [Problem 4.B.2](https://youtu.be/w-IGNU2i3F8) of the lecturebook as a motivating example.
We find that the moment of the force $\vec{F}$ about point A is:
$$
\vec{M_A} = (bF\cos\theta - dF\sin\theta)\hat{k}.
$$
Let's plot the component of the moment as a function of $\theta$.
For this, we will use the Python module [matplotlib](https://matplotlib.org).
```
import numpy as np # for numerical algebra
import matplotlib.pyplot as plt # this is where the plotting capabilities are
# The following line is need so that the plots are embedded in the Jupyter notebook (remove when not using Jupyter)
%matplotlib inline
# Define a function that computes the moment magnitude as a function of all other parameters
def M_A(theta, b, d, F):
"""
Compute the k component of the moment of F about point A given all the problem parameters.
"""
return b * F * np.cos(theta) - d * F * np.sin(theta)
# Choose some parameters
b = 0.5 # In meters
d = 2. # In meters
F = 2. # In kN
# The thetas on which we will evaluate the moment for plotting
thetas = np.linspace(0, 2 * np.pi, 100)
# The moment on these thetas:
M_As = M_A(thetas, b, d, F)
# Let's plot
plt.plot(thetas / (2. * np.pi) * 360, M_As, lw=2)
plt.xlabel(r'$\theta$ (degrees)')
plt.ylabel('$M_A$ (kN)');
```
Now, let's put two lines in the same plot.
Let's compare the moments when we change $d$ from 2 meters to 3.5 meters.
```
# We already have M_A for d=2 m (and all other paramters to whichever values we gave them)
# Let's copy it:
M_As_case_1 = M_As
# And let's compute it again for d=3.5 m
d = 3.5 # In m
M_As_case_2 = M_A(thetas, b, d, F)
# Let's plot both of them in the same figure
plt.plot(thetas / (2. * np.pi) * 360, M_As_case_1, lw=2, label='Case 1')
plt.plot(thetas / (2. * np.pi) * 360, M_As_case_2, '--', lw=2, label='Case 2')
plt.xlabel(r'$\theta$ (degrees)')
plt.ylabel('$M_A$ (kN)')
plt.legend(loc='best')
```
Finally, let's see how we can make interactive plots.
We will use the Python module [ipywidgets](https://ipywidgets.readthedocs.io/en/stable/) and in particular the function [ipywidgets.interact](https://ipywidgets.readthedocs.io/en/stable/examples/Using%20Interact.html).
```
from ipywidgets import interact # Loading the module
# Interact needs a function that does the plotting given the parameters.
# Let's make it:
def make_plots(b=0.5, d=3., F=1.): # X=val defines default values for the function
"""
Make the plot.
"""
thetas = np.linspace(0, 2. * np.pi, 100)
M_As = M_A(thetas, b, d, F)
plt.plot(thetas / (2. * np.pi) * 360, M_As, lw=2, label='Case 1')
plt.ylim([-10., 10.])
plt.xlabel(r'$\theta$ (degrees)')
plt.ylabel('$M_A$ (kN)')
```
Let's just check that the function works by calling it a few times:
```
# With no inputs it should use the default values
make_plots()
# You can specify all the inputs like this:
make_plots(2., 3., 2.)
# Or even by name (whatever is not specified gets the default value):
make_plots(F=2.3)
```
Ok. Let's use interact now:
```
interact(make_plots,
b=(0., 5., 0.1), # Range for b: (min, max, increment)
d=(0., 5, 0.1), # Range for d
F=(0., 2, 0.1) # Range for F
);
```
|
github_jupyter
|
<h1>Table of Contents<span class="tocSkip"></span></h1>
<div class="toc"><ul class="toc-item"><li><span><a href="#Plot-Validation-and-Train-loss" data-toc-modified-id="Plot-Validation-and-Train-loss-1"><span class="toc-item-num">1 </span>Plot Validation and Train loss</a></span></li><li><span><a href="#Extract-relevant-Data-to-df" data-toc-modified-id="Extract-relevant-Data-to-df-2"><span class="toc-item-num">2 </span>Extract relevant Data to df</a></span><ul class="toc-item"><li><span><a href="#Get-best-result" data-toc-modified-id="Get-best-result-2.1"><span class="toc-item-num">2.1 </span>Get best result</a></span></li><li><span><a href="#Consider-Outliers" data-toc-modified-id="Consider-Outliers-2.2"><span class="toc-item-num">2.2 </span>Consider Outliers</a></span></li></ul></li><li><span><a href="#Results-by-model" data-toc-modified-id="Results-by-model-3"><span class="toc-item-num">3 </span>Results by model</a></span><ul class="toc-item"><li><span><a href="#Remove-Duplicates" data-toc-modified-id="Remove-Duplicates-3.1"><span class="toc-item-num">3.1 </span>Remove Duplicates</a></span></li></ul></li><li><span><a href="#Each-variable-plotted-against-loss:" data-toc-modified-id="Each-variable-plotted-against-loss:-4"><span class="toc-item-num">4 </span>Each variable plotted against loss:</a></span></li><li><span><a href="#Investigate-"band"-in-loss-model-plot" data-toc-modified-id="Investigate-"band"-in-loss-model-plot-5"><span class="toc-item-num">5 </span>Investigate "band" in loss-model plot</a></span><ul class="toc-item"><li><span><a href="#Extract-the-different-bands-and-inpsect" data-toc-modified-id="Extract-the-different-bands-and-inpsect-5.1"><span class="toc-item-num">5.1 </span>Extract the different bands and inpsect</a></span></li></ul></li><li><span><a href="#Investigate-Duplicates" data-toc-modified-id="Investigate-Duplicates-6"><span class="toc-item-num">6 </span>Investigate Duplicates</a></span></li><li><span><a href="#Investigate-Best" data-toc-modified-id="Investigate-Best-7"><span class="toc-item-num">7 </span>Investigate Best</a></span></li></ul></div>
```
%load_ext autoreload
%autoreload 2
%cd ..
import os
import sys
from notebooks import utils
from matplotlib import pyplot as plt
%matplotlib inline
import seaborn as sns
sns.set()
#import pipeline
# parent_dir = os.path.abspath(os.path.join(os.getcwd(), os.pardir))
# sys.path.append(parent_dir) #to import pipeline
%ls experiments
###CHANGE THIS FILE TO THE SUBDIRECTORY OF INTEREST:
#exp_dirs = ["experiments/07b/", "experiments/DA3_2/07a/0", "experiments/DA3_2/07a/1"]
exp_dirs = ["experiments/retrain/"]
results = utils.extract_res_from_files(exp_dirs)
#load data when utils isnt working:
if False:
import pickle
res_fp = "experiments/results/ResNeXt/res.txt"
with open(res_fp, "rb") as f:
results = pickle.load(f)
```
## Plot Validation and Train loss
```
ylim = (0, 3000)
ylim2 = (70,100)
utils.plot_results_loss_epochs(results, ylim1=ylim, ylim2=ylim2)
```
## Extract relevant Data to df
Use minimum validation loss as criterion.
In theory (if we had it) it would be better to use DA MAE
```
df_res = utils.create_res_df(results)
df_res_original = df_res.copy() #save original (in case you substitute out)
df_res
```
### Get best result
```
df_res["valid_loss"].idxmin()
print(df_res.loc[df_res["valid_loss"].idxmin()])
df_res.loc[df_res["valid_loss"].idxmin()]["path"]
```
### Consider Outliers
```
#consider third experiment run (lots of outliers)
df3 = df_res[df_res["path"].str.contains("CAE_zoo3")]
df_outlier = df_res[df_res["valid_loss"] > 150000]
df_outlier
```
## Results by model
```
relu = df_res[df_res.activation == "relu"]
lrelu = df_res[df_res.activation == "lrelu"]
plt.scatter('model', "valid_loss", data=relu, marker="+", color='r')
plt.scatter('model', "valid_loss", data=lrelu, marker="+", color='g')
plt.ylabel("Loss")
plt.xlabel("Model")
plt.ylim(16000, 70000)
plt.legend(labels=["relu", "lrelu"])
plt.show()
#investigate number of layers
eps = 1e-5
reluNBN = df_res[(df_res.activation == "relu") & (abs(df_res.batch_norm - 0.) < eps)]
reluBN = df_res[(df_res.activation == "relu") & (abs(df_res.batch_norm - 1.) < eps)]
lreluNBN = df_res[(df_res.activation == "lrelu") & (abs(df_res.batch_norm - 0.0) < eps)]
lreluBN = df_res[(df_res.activation == "lrelu") & (abs(df_res.batch_norm - 1.) < eps)]
plt.scatter('model', "valid_loss", data=reluNBN, marker="+", color='r')
plt.scatter('model', "valid_loss", data=reluBN, marker="+", color='g')
plt.scatter('model', "valid_loss", data=lreluNBN, marker="o", color='r')
plt.scatter('model', "valid_loss", data=lreluBN, marker="o", color='g')
plt.ylabel("Loss")
plt.xlabel("Model")
plt.ylim(16000, 70000)
plt.legend(labels=["relu, NBN", "relu, BN", "lrelu, NBN", "lrelu, BN"])
plt.show()
```
It turns out that there are lots of duplicates in the above data (as a result of a bug in my code that was giving all models the same number of channels). So remove duplicates and go again:
### Remove Duplicates
```
#remove duplicates
columns = list(df_res_original.columns)
columns.remove("model")
columns.remove("path")
print(columns)
df_res_new = df_res_original.loc[df_res_original.astype(str).drop_duplicates(subset=columns, keep="last").index]
#df_res_new = df_res_original.drop_duplicates(subset=columns, keep="last")
df_res_new.shape
df_res = df_res_new
df_res.shape
##Plot same graph again:
#investigate number of layers
relu6 = df_res[(df_res.activation == "relu") & (df_res.num_layers == 6)]
relu11 = df_res[(df_res.activation == "relu") & (df_res.num_layers != 6)]
lrelu6 = df_res[(df_res.activation == "lrelu") & (df_res.num_layers == 6)]
lrelu11 = df_res[(df_res.activation == "lrelu") & (df_res.num_layers != 6)]
plt.scatter('model', "valid_loss", data=relu6, marker="+", color='r')
plt.scatter('model', "valid_loss", data=lrelu6, marker="+", color='g')
plt.scatter('model', "valid_loss", data=relu11, marker="o", color='r')
plt.scatter('model', "valid_loss", data=lrelu11, marker="o", color='g')
plt.ylabel("Loss")
plt.xlabel("Model")
plt.ylim(16000, 60000)
plt.legend(labels=["relu, 6", "lrelu, 6", "relu, not 6", "lrelu, not 6"])
plt.show()
```
## Each variable plotted against loss:
```
plt.scatter('latent_dims', "valid_loss", data=df_res, marker="+", color='r')
plt.ylabel("Loss")
plt.xlabel("latent dimensions")
plt.ylim(16000, 70000)
plt.scatter('first_channel', "valid_loss", data=df_res, marker="+", color='r')
plt.ylabel("Loss")
plt.xlabel("First channel")
plt.ylim(16000, 80000)
plt.scatter('batch_norm', "valid_loss", data=df_res, marker="+", color='r')
plt.ylabel("Loss")
plt.xlabel("Batch Norm")
plt.xlim(-0.1, 1.1)
plt.ylim(16000, 80000)
plt.scatter('activation', "valid_loss", data=df_res, marker="+", color='r')
plt.ylabel("Loss")
plt.xlabel("Activation")
plt.ylim(16000, 70000)
plt.scatter('model', "valid_loss", data=df_res, marker="+", color='r')
plt.ylabel("Loss")
plt.xlabel("Model")
plt.ylim(16000, 80000)
plt.scatter('num_layers', "valid_loss", data=df_res, marker="+", color='r')
plt.ylabel("Loss")
plt.xlabel("Number of layers in Decoder/Encoder")
plt.ylim(16000, 80000)
plt.scatter('total_channels', "valid_loss", data=df_res, marker="+", color='r')
plt.ylabel("Loss")
plt.xlabel("Total Channels")
plt.ylim(16000, 80000)
plt.scatter('channels/layer', "valid_loss", data=df_res, marker="+", color='r')
plt.ylabel("Loss")
plt.xlabel("Channels/Layer")
plt.ylim(16000, 80000)
plt.scatter('first_channel', "valid_loss", data=df_res, marker="+", color='r')
plt.ylabel("Loss")
plt.xlabel("First_channel")
plt.ylim(16000, 80000)
plt.scatter('conv_changeover', "valid_loss", data=df_res, marker="+", color='r')
plt.ylabel("Loss")
plt.xlabel("Input size decrease at which to change to start downsampling (via transposed convolution)")
plt.ylim(16000, 80000)
```
## Investigate "band" in loss-model plot
### Extract the different bands and inpsect
```
band1 = df_res[df_res.valid_loss < 20000]
band2 = df_res[(df_res.valid_loss > 20000) & (df_res.valid_loss < 23000)]
band3 = df_res[(df_res.valid_loss > 23000) & (df_res.valid_loss < 26000)]
band1.head()
band3.head()
```
## Investigate Duplicates
```
#eg1: /data/home/jfm1118/DA/experiments/CAE_zoo2/32 and /data/home/jfm1118/DA/experiments/CAE_zoo2/12
#eg2: /data/home/jfm1118/DA/experiments/CAE_zoo2/31 and /data/home/jfm1118/DA/experiments/CAE_zoo2/27
def get_data_from_path(path):
for res in results:
if res["path"] == path:
return res
else:
raise ValueError("No path = {} in 'results' list".format(path))
def print_model(settings):
model = settings.AE_MODEL_TYPE(**settings.get_kwargs())
print(settings.__class__.__name__)
print(model.layers)
print(settings.CHANNELS)
base_exp = "/data/home/jfm1118/DA/experiments/CAE_zoo2/"
exp_32 = get_data_from_path(base_exp + "32")["settings"]
exp_12 = get_data_from_path(base_exp + "12")["settings"]
print_model(exp_32)
print()
print_model(exp_12)
base_exp = "/data/home/jfm1118/DA/experiments/CAE_zoo2/"
exp_1 = get_data_from_path(base_exp + "31")["settings"]
exp_2 = get_data_from_path(base_exp + "27")["settings"]
print_model(exp_1)
print()
print_model(exp_2)
print(list(range(1, 2*(exp_1.get_num_layers_decode() + 1) + 1, 2)))
```
## Investigate Best
```
path = "/data/home/jfm1118/DA/experiments/CAE_zoo2/17"
exp = get_data_from_path(base_exp + str(17))["settings"]
print_model(exp_1)
```
|
github_jupyter
|
# 6. Hidden Markov Models with Theano and TensorFlow
In the last section we went over the training and prediction procedures of Hidden Markov Models. This was all done using only vanilla numpy the Expectation Maximization algorithm. I now want to introduce how both `Theano` and `Tensorflow` can be utilized to accomplish the same goal, albeit by a very different process.
## 1. Gradient Descent
Hopefully you are familiar with the gradient descent optimization algorithm, if not I recommend reviewing my posts on Deep Learning, which leverage gradient descent heavily (or this [video](https://www.youtube.com/watch?v=IHZwWFHWa-w). With that said, a simple overview is as follows:
> Gradient descent is a first order optimization algorithm for finding the minimum of a function. To find a local minimum of a function using gradient descent, on takes steps proportional to the negative of the gradient of the function at its current point.
Visually, this iterative process looks like:
<img src="https://drive.google.com/uc?id=1R2zVTj3uo5zmow6vFujWlU-qs9jRF_XG" width="250">
Where above we are looking at a contour plot of a three dimensional bowl, and the center of the bowl is a minimum. Now, the actual underlying mechanics of gradient descent work as follows:
#### 1. Define a model/hypothesis that will be mapping inputs to outputs, or in other words making predictions:
$$h_{\theta}(x) = \theta_0 + \theta_1x$$
In this case $x$ is our input and $h(x)$, often thought of as $y$, is our output. We are stating that we believe the ground truth relationship between $x$ and $h(x)$ is captured by the linear combination of $\theta_0 + \theta_1x$. Now, what are $\theta_0$ and $\theta_1$ equal to?
#### 2. Define a **cost** function for which you are trying to find the minimum. Generally, this cost function is defined as some form of **error**, and it will be parameterized by variables related to your model in some way.
$$cost = J = (y - h_{\theta}(x))^2$$
Above $y$ refers to the ground truth/actual value of the output, and $h_{\theta}(x)$ refers to that which our model predicted. The difference, squared, represents our cost. We can see that if our prediction is exactly equal to the ground truth value, our cost will be 0. If our prediction is very far off from our ground truth value then our cost will be very high. Our goal is to minimize the cost (error) of our model.
#### 3. Take the [**gradient**](https://en.wikipedia.org/wiki/Gradient) (multi-variable generalization of the derivative) of the cost function with respect to the parameters that you have control over.
$$\nabla J = \frac{\partial J}{\partial \theta}$$
Simply put, we want to see how $J$ changes as we change our model parameters, $\theta_0$ and $\theta_1$.
#### 4. Based on the gradient update our values for $\theta$ with a simple update rule:
$$\theta_0 \rightarrow \theta_0 - \alpha \cdot \frac{\partial J}{\partial \theta_0}$$
$$\theta_1 \rightarrow \theta_1 - \alpha \cdot \frac{\partial J}{\partial \theta_1}$$
#### 5. Repeat steps two and three for a set number of iterations/until convergence.
After a set number of steps, the hope is that the model weights that were _learned_ are the most optimal weights to minimize prediction error. Now after everything we discussed in the past two posts you may be wondering, how exactly does this relate to Hidden Markov Models, which have been trained via Expectation Maximization?
### 1.1 Gradient Descent and Hidden Markov Models
Let's say for a moment that our goal that we wish to accomplish is predict the probability of an observed sequence, $p(x)$. And let's say that we have 100 observed sequences at our disposal. It should be clear that if we have a trained HMM that predicts the majority of our sequences are very unlikely, the HMM was probably not trained very well. Ideally, our HMM parameters would be learned in a way that maximizes the probability of observing what we did (this was the goal of expectation maximization).
What may start to become apparent at this point is that we have a perfect cost function already created for us! The total probability of our observed sequences, based on our HMM parameters $A$, $B$, and $\pi$. We can define this mathematically as follows (for the scaled version); in the previous post we proved that:
$$p(x) = \prod_{t=1}^T c(t)$$
Which states that the probability of an observed sequence is equal to the product of the scales at each time step. Also recall that the scale is just defined as:
$$c(t) = \sum_{i=1}^M \alpha'(t,i)$$
With that all said, we can define the cost of a single observed training sequence as:
$$cost = \sum_{t}^{T} log\big(c(t)\big)$$
Where we are using the log to avoid the underflow problem, just as we did in the last notebook. So, we have a cost function which intuitively makes sense, but can we find its gradient with respect to our HMM parameters $A$, $B$, and $\pi$? We absolutely can! The wonderful thing about Theano is that it links variables together via a [computational graph](http://deeplearning.net/software/theano/extending/graphstructures.html). So, cost is depedent on $A$, $B$ and $\pi$ via the following link:
$$cost \rightarrow c(t) \rightarrow alpha \rightarrow A, B, \pi$$
We can take the gradient of this cost function in theano as well, allowing us to then easily update our values of $A$, $B$, and $\pi$! Done iteratively, we hopefully will converge to a nice minimum.
### 1.2 HMM Theano specifics
I would be lying if I said that Theano wasn't a little bit hard to follow at first. For those unfamiliar, representing symbolic mathematical computations as graphs may feel very strange. I have a few walk throughs of Theano in my Deep Learning section, as well as `.py` files in the source repo. Additionally, the theano [documentation](http://deeplearning.net/software/theano/index.html) is also very good. With that said, I do want to discuss a few details of the upcoming code block.
#### Recurrence Block $\rightarrow$ Calculating the Forward Variable, $\alpha$
First, I want to discuss the `recurrence` and `scan` functions that you will be seeing:
```
def recurrence_to_find_alpha(t, old_alpha, x):
"""Scaled version of updates for HMM. This is used to
find the forward variable alpha.
Args:
t: Current time step, from pass in from scan:
sequences=T.arange(1, thx.shape[0])
old_alpha: Previously returned alpha, or on the first time
step the initial value,
outputs_info=[self.pi * self.B[:, thx[0]], None]
x: thx, non_sequences (our actual set of observations)
"""
alpha = old_alpha.dot(self.A) * self.B[:, x[t]]
s = alpha.sum()
return (alpha / s), s
# alpha and scale, once returned, are both matrices with values at each time step
[alpha, scale], _ = theano.scan(
fn=recurrence_to_find_alpha,
sequences=T.arange(1, thx.shape[0]),
outputs_info=[self.pi * self.B[:, thx[0]], None], # Initial value of alpha
n_steps=thx.shape[0] - 1,
non_sequences=thx,
)
# scale is an array, and scale.prod() = p(x)
# The property log(A) + log(B) = log(AB) can be used
# here to prevent underflow problem
p_of_x = -T.log(scale).sum() # Negative log likelihood
cost = p_of_x
self.cost_op = theano.function(
inputs=[thx],
outputs=cost,
allow_input_downcast=True,
)
```
The above block is where our forward variable $\alpha$ and subsequently the probability of the observed sequence $p(x)$ is found. The process works as follows:
1. The `theano.scan` function (logically similar to a for loop) is defined with the following parameters:
* `fn`: The recurrence function that the array being iterated over will be passed into.
* `sequences`: An array of indexes, $[1,2,3,...,T]$
* `outputs_info`: The initial value of $\alpha$
* `non_sequences`: Our observation sequence, $X$. This passed in it's entirety to the recurrence function at each iteration.
2. Our recurrence function, `recurrence_to_find_alpha`, is meant to calculate $\alpha$ at each time step. $\alpha$ at $t=1$ was defined by `outputs_info` in `scan`. This recurrence function essentially is performing the forward algorithm (additionally it incorporates scaling):
$$\alpha(1,i) = \pi_iB\big(i, x(1)\big)$$
$$\alpha(t+1, j) = \sum_{i=1}^M \alpha(t,i) A(i,j)B(j, x(t+1))$$
3. We calculate $p(x)$ to be the sum of the log likelihood. This is set to be our `cost`.
4. We define a `cost_op`, which is a theano function that takes in a symbolic variable `thx` and determines the output `cost`. Remember, `cost` is linked to `thx` via:
```
cost -> scale -> theano.scan(non_sequences=thx)
```
#### Update block $\rightarrow$ Updating HMM parameters $A$, $B$, and $\pi$
The other block that I want to touch on is the update block:
```
pi_update = self.pi - learning_rate * T.grad(cost, self.pi)
pi_update = pi_update / pi_update.sum()
A_update = self.A - learning_rate*T.grad(cost, self.A)
A_update = A_update / A_update.sum(axis=1).dimshuffle(0, 'x')
B_update = self.B - learning_rate*T.grad(cost, self.B)
B_update = B_update / B_update.sum(axis=1).dimshuffle(0, 'x')
updates = [
(self.pi, pi_update),
(self.A, A_update),
(self.B, B_update),
]
train_op = theano.function(
inputs=[thx],
updates=updates,
allow_input_downcast=True
)
costs = []
for it in range(max_iter):
for n in range(N):
# Looping through all N training examples
c = self.get_cost_multi(X, p_cost).sum()
costs.append(c)
train_op(X[n])
```
The update block functions as follows:
1. We have `cost` that was defined symbolically and linked to `thx`. We can define `pi_update` as `pi_update = self.pi - learning_rate * T.grad(cost, self.pi)`.
2. This same approach is performed for $A$ and $B$.
3. We then create a theano function, `train_op` which takes in `thx`, our symbolic input, and with perform updates via the `updates=updates` kwarg. Specifically, updates takes in a list of tuples, with the first value in the tuple being the variable that should be updated, and the second being the expression with which it should be updated to be.
4. We loop through all training examples (sequences of observations), and call `train_up`, passing in `X[n]` (a unique sequene of observations) as `thx`.
5. `train_op` then performs the `updates`, utilizing `thx = X[n]` wherever `updates` depends on `thx`.
This is clearly stochastic gradient descent, because we are performing updates to our parameters $A$, $B$, and $\pi$ for each training sequence. Full batch gradient descent would be if we defined a cost function that was based on all of the training sequences, not only an individual sequence.
## 2. HMM's with Theano
In code, our HMM can be implemented with Theano as follows:
```
import numpy as np
import theano
import theano.tensor as T
import seaborn as sns
import matplotlib.pyplot as plt
from hmm.utils import get_obj_s3, random_normalized
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
sns.set(style="white", palette="husl")
sns.set_context("talk")
sns.set_style("ticks")
class HMM:
def __init__(self, M):
self.M = M
def fit(self, X, learning_rate=0.001, max_iter=10, V=None, p_cost=1.0, print_period=10):
"""Train HMM model using stochastic gradient descent."""
# Determine V, the vocabulary size
if V is None:
V = max(max(x) for x in X) + 1
N = len(X)
# Initialize HMM variables
pi0 = np.ones(self.M) / self.M # Initial state distribution
A0 = random_normalized(self.M, self.M) # State transition matrix
B0 = random_normalized(self.M, V) # Output distribution
thx, cost = self.set(pi0, A0, B0)
# This is a beauty of theano and it's computational graph.
# By defining a cost function, which is representing p(x),
# the probability of a sequence, we can then find the gradient
# of the cost with respect to our parameters (pi, A, B).
# The gradient updated rules are applied as usual. Note, the
# reason that this is stochastic gradient descent is because
# we are only looking at a single training example at a time.
pi_update = self.pi - learning_rate * T.grad(cost, self.pi)
pi_update = pi_update / pi_update.sum()
A_update = self.A - learning_rate*T.grad(cost, self.A)
A_update = A_update / A_update.sum(axis=1).dimshuffle(0, 'x')
B_update = self.B - learning_rate*T.grad(cost, self.B)
B_update = B_update / B_update.sum(axis=1).dimshuffle(0, 'x')
updates = [
(self.pi, pi_update),
(self.A, A_update),
(self.B, B_update),
]
train_op = theano.function(
inputs=[thx],
updates=updates,
allow_input_downcast=True
)
costs = []
for it in range(max_iter):
for n in range(N):
# Looping through all N training examples
c = self.get_cost_multi(X, p_cost).sum()
costs.append(c)
train_op(X[n])
print("A learned from training: \n", self.A.get_value())
print("B learned from training: \n", self.B.get_value())
print("pi learned from training: \n", self.pi.get_value())
plt.figure(figsize=(8,5))
plt.plot(costs, color="blue")
plt.xlabel("Iteration Number")
plt.ylabel("Cost")
plt.show()
def get_cost(self, x):
return self.cost_op(x)
def get_cost_multi(self, X, p_cost=1.0):
P = np.random.random(len(X))
return np.array([self.get_cost(x) for x, p in zip(X, P) if p < p_cost])
def log_likelihood(self, x):
return - self.cost_op(x)
def set(self, pi, A, B):
# Create theano shared variables
self.pi = theano.shared(pi)
self.A = theano.shared(A)
self.B = theano.shared(B)
# Define input, a vector
thx = T.ivector("thx")
def recurrence_to_find_alpha(t, old_alpha, x):
"""
Scaled version of updates for HMM. This is used to find the
forward variable alpha.
Args:
t: Current time step, from pass in from scan:
sequences=T.arange(1, thx.shape[0])
old_alpha: Previously returned alpha, or on the first time step
the initial value,
outputs_info=[self.pi * self.B[:, thx[0]], None]
x: thx, non_sequences (our actual set of observations)
"""
alpha = old_alpha.dot(self.A) * self.B[:, x[t]]
s = alpha.sum()
return (alpha / s), s
# alpha and scale, once returned, are both matrices with values at each time step
[alpha, scale], _ = theano.scan(
fn=recurrence_to_find_alpha,
sequences=T.arange(1, thx.shape[0]),
outputs_info=[self.pi * self.B[:, thx[0]], None], # Initial value of alpha
n_steps=thx.shape[0] - 1,
non_sequences=thx,
)
# scale is an array, and scale.prod() = p(x)
# The property log(A) + log(B) = log(AB) can be used
# here to prevent underflow problem
p_of_x = -T.log(scale).sum() # Negative log likelihood
cost = p_of_x
self.cost_op = theano.function(
inputs=[thx],
outputs=cost,
allow_input_downcast=True,
)
return thx, cost
def fit_coin(file_key):
"""Loads data and trains HMM."""
X = []
for line in get_obj_s3(file_key).read().decode("utf-8").strip().split(sep="\n"):
x = [1 if e == "H" else 0 for e in line.rstrip()]
X.append(x)
# Instantiate object of class HMM with 2 hidden states (heads and tails)
hmm = HMM(2)
hmm.fit(X)
L = hmm.get_cost_multi(X).sum()
print("Log likelihood with fitted params: ", round(L, 3))
# Try the true values
pi = np.array([0.5, 0.5])
A = np.array([
[0.1, 0.9],
[0.8, 0.2]
])
B = np.array([
[0.6, 0.4],
[0.3, 0.7]
])
hmm.set(pi, A, B)
L = hmm.get_cost_multi(X).sum()
print("Log Likelihood with true params: ", round(L, 3))
if __name__ == "__main__":
key = "coin_data.txt"
fit_coin(key)
```
## 3. HMM's with Theano $\rightarrow$ Optimization via Softmax
One of the challenges of the approach we took is that gradient descent is _unconstrained_; it simply goes in the direction of the gradient. This presents a problem for us in the case of HMM's. Remember, the parameters of an HMM are $\pi$, $A$, and $B$, and each is a probability matrix/vector. This means that they must be between 0 and 1, and must sum to 1 (along the rows if 2-D).
We accomplished this in the previous section by performing a "hack". Specifically, we renormalized after each gradient descent step. However, this means that we weren't performing _real_ gradient descent, because by renormalizing we are not exactly moving in the direction of the gradient anymore. For reference, the pseudocode looked like this:
```
pi_update = self.pi - learning_rate * T.grad(cost, self.pi)
pi_update = pi_update / pi_update.sum() # Normalizing to ensure it stays a probability
A_update = self.A - learning_rate*T.grad(cost, self.A)
A_update = A_update / A_update.sum(axis=1).dimshuffle(0, 'x') # Normalize for prob
B_update = self.B - learning_rate*T.grad(cost, self.B)
B_update = B_update / B_update.sum(axis=1).dimshuffle(0, 'x') # Normalize for prob
# Passing in normalized updates for pi, A, B. No longer moving in dir of gradient
updates = [
(self.pi, pi_update),
(self.A, A_update),
(self.B, B_update),
]
```
This leads us to the question: is it possible to use true gradient descent, while still conforming to the constraints that each parameter much be a true probability. The answer is of course yes!
### 3.1 Softmax
If you are unfamiliar with Deep Learning then you may want to jump over this section, or go through my deep learning posts that dig into the subject. If you are familiar, recall the softmax function:
$$softmax(x)_i = \frac{exp(x_i)}{\sum_{k=1}^K exp(x_k)}$$
Where $x$ is an array of size $K$, and $K$ is the number of classes that we have. The result of the softmax is that all outputs are positive and sum to 1. What exactly does this mean in our scenario?
#### Softmax for $\pi$
Consider $\pi$, an array of size $M$. Supposed we want to parameterize $\pi$, using the symbol $\theta$. We can then assign $\pi$ to be:
$$pi = softmax(\theta)$$
In this way, $\pi$ is like an intermediate variable and $\theta$ is the actual parameter that we will be updating. This ensures that $\pi$ is always between 0 and 1, and sums to 1. At the same time, the values in $\theta$ can be anything; this means that we can freely use gradient descent on $\theta$ without having to worry about any constraints! No matter what we do to $\theta$, $\pi$ will always be between 0 and 1 and sum to 1.
#### Softmax for $A$ and $B$
Now, what about $A$ and $B$? Unlike $\pi$, which was a 1-d vector, $A$ and $B$ are matrices. Luckily for us, softmax works well for us here too! Recall that when dealing with data in deep learning (and most ML) that we are often dealing with multiple samples at the same time. Typically an $NxD$ matrix, where $N$ is the number of samples, and $D$ is the dimensionality. We know that the output of our model is usually an $NxK$ matrix, where $K$ is the number of classes. Naturally, because the classes go along the rows, each row must represent a separate probability distribution.
Why is this helpful? Well, the softmax was actually written with this specifically in mind! When you use the softmax it automatically exponentiates every element of the matrix and divides by the row sum. That is exactly what we want to do with $A$ and $B$! Each row of $A$ is the probability of the next state to transition to, and each row of $B$ is the probability of the next symbol to emit. The rows must sum to 1, just like the output predictions of a neural network!
In pseudocode, softmax looks like:
```
def softmax(A):
expA = np.exp(A)
return expA / expA.sum(axis=1, keepdims=True)
```
We can see this clearly below:
```
np.set_printoptions(suppress=True)
A = np.array([
[1,2],
[4,5],
[9,5]
])
expA = np.exp(A)
print("A exponentiated element wise: \n", np.round_(expA, decimals=3), "\n")
# Keep dims ensures a column vector (vs. row) output
output = expA / expA.sum(axis=1, keepdims=True)
print("Exponentiated A divided row sum: \n", np.round_(output, decimals=3))
```
Now you may be wondering: Why can't we just perform standard normalization? Why does the exponetial need to be used? For an answer to that I recommend reading up [here](https://stackoverflow.com/questions/17187507/why-use-softmax-as-opposed-to-standard-normalization), [here](https://stats.stackexchange.com/questions/162988/why-sigmoid-function-instead-of-anything-else/318209#318209), and [here](http://cs231n.github.io/linear-classify/#softmax).
### 3.2 Update Discrete HMM Code $\rightarrow$ with Softmax
```
class HMM:
def __init__(self, M):
self.M = M
def fit(self, X, learning_rate=0.001, max_iter=10, V=None, p_cost=1.0, print_period=10):
"""Train HMM model using stochastic gradient descent."""
# Determine V, the vocabulary size
if V is None:
V = max(max(x) for x in X) + 1
N = len(X)
preSoftmaxPi0 = np.zeros(self.M) # initial state distribution
preSoftmaxA0 = np.random.randn(self.M, self.M) # state transition matrix
preSoftmaxB0 = np.random.randn(self.M, V) # output distribution
thx, cost = self.set(preSoftmaxPi0, preSoftmaxA0, preSoftmaxB0)
# This is a beauty of theano and it's computational graph. By defining a cost function,
# which is representing p(x), the probability of a sequence, we can then find the gradient
# of the cost with respect to our parameters (pi, A, B). The gradient updated rules are
# applied as usual. Note, the reason that this is stochastic gradient descent is because
# we are only looking at a single training example at a time.
pi_update = self.preSoftmaxPi - learning_rate * T.grad(cost, self.preSoftmaxPi)
A_update = self.preSoftmaxA - learning_rate * T.grad(cost, self.preSoftmaxA)
B_update = self.preSoftmaxB - learning_rate * T.grad(cost, self.preSoftmaxB)
updates = [
(self.preSoftmaxPi, pi_update),
(self.preSoftmaxA, A_update),
(self.preSoftmaxB, B_update),
]
train_op = theano.function(
inputs=[thx],
updates=updates,
allow_input_downcast=True
)
costs = []
for it in range(max_iter):
for n in range(N):
# Looping through all N training examples
c = self.get_cost_multi(X, p_cost).sum()
costs.append(c)
train_op(X[n])
plt.figure(figsize=(8,5))
plt.plot(costs, color="blue")
plt.xlabel("Iteration Number")
plt.ylabel("Cost")
plt.show()
def get_cost(self, x):
return self.cost_op(x)
def get_cost_multi(self, X, p_cost=1.0):
P = np.random.random(len(X))
return np.array([self.get_cost(x) for x, p in zip(X, P) if p < p_cost])
def log_likelihood(self, x):
return - self.cost_op(x)
def set(self, preSoftmaxPi, preSoftmaxA, preSoftmaxB):
# Create theano shared variables
self.preSoftmaxPi = theano.shared(preSoftmaxPi)
self.preSoftmaxA = theano.shared(preSoftmaxA)
self.preSoftmaxB = theano.shared(preSoftmaxB)
pi = T.nnet.softmax(self.preSoftmaxPi).flatten()
# softmax returns 1xD if input is a 1-D array of size D
A = T.nnet.softmax(self.preSoftmaxA)
B = T.nnet.softmax(self.preSoftmaxB)
# Define input, a vector
thx = T.ivector("thx")
def recurrence_to_find_alpha(t, old_alpha, x):
"""Scaled version of updates for HMM. This is used to find the forward variable alpha.
Args:
t: Current time step, from pass in from scan:
sequences=T.arange(1, thx.shape[0])
old_alpha: Previously returned alpha, or on the first time step the initial value,
outputs_info=[pi * B[:, thx[0]], None]
x: thx, non_sequences (our actual set of observations)
"""
alpha = old_alpha.dot(A) * B[:, x[t]]
s = alpha.sum()
return (alpha / s), s
# alpha and scale, once returned, are both matrices with values at each time step
[alpha, scale], _ = theano.scan(
fn=recurrence_to_find_alpha,
sequences=T.arange(1, thx.shape[0]),
outputs_info=[pi * B[:, thx[0]], None], # Initial value of alpha
n_steps=thx.shape[0] - 1,
non_sequences=thx,
)
# scale is an array, and scale.prod() = p(x)
# The property log(A) + log(B) = log(AB) can be used here to prevent underflow problem
p_of_x = -T.log(scale).sum() # Negative log likelihood
cost = p_of_x
self.cost_op = theano.function(
inputs=[thx],
outputs=cost,
allow_input_downcast=True,
)
return thx, cost
def fit_coin(file_key):
"""Loads data and trains HMM."""
X = []
for line in get_obj_s3(file_key).read().decode("utf-8").strip().split(sep="\n"):
x = [1 if e == "H" else 0 for e in line.rstrip()]
X.append(x)
# Instantiate object of class HMM with 2 hidden states (heads and tails)
hmm = HMM(2)
hmm.fit(X)
L = hmm.get_cost_multi(X).sum()
print("Log likelihood with fitted params: ", round(L, 3))
# Try the true values
pi = np.array([0.5, 0.5])
A = np.array([
[0.1, 0.9],
[0.8, 0.2]
])
B = np.array([
[0.6, 0.4],
[0.3, 0.7]
])
hmm.set(pi, A, B)
L = hmm.get_cost_multi(X).sum()
print("Log Likelihood with true params: ", round(L, 3))
if __name__ == "__main__":
key = "coin_data.txt"
fit_coin(key)
```
## 4. Hidden Markov Models with TensorFlow
I now want to expose everyone to an HMM implementation in TensorFlow. In order to do so, we will need to first go over the `scan` function in Tensorflow. Just like when dealing with Theano, we need to ask "What is the equivalent of a for loop in TensorFlow?". And why should we care?
### 4.1 TensorFlow Scan
In order to understand the importance of `scan`, we need to be sure that we have a good idea of how TensorFlow works, even if only from a high level. In general, with both TensorFlow and Theano, you have to create variables and link them together functionally, but they do not have values until you actually run the functions. So, when you create your $X$ matrix you don't give it a shape; you just say here is a place holder I am going to call $X$ and this is a possible shape for it:
```
X = tf.placeholder(tf.float32, shape=(None, D))
```
However, remember that the `shape` argument is _optional_, and hence for all intents and purposes we can assume that we do not know the shape of $X$. So, what happens if you want to loop through all the elements of $X$? Well you can't, because we do not know the number of elements in $X$!
```
for i in range(X.shape[0]): <------- Not possible! We don't know num elements in X
# ....
```
In order to write a for loop we must specify the number of times the loop will run. But in order to specify the number of times the loop will run we must know the number of elements in $X$. Generally speaking, we cannot guarantee the length of our training sequences. This is why we need the tensorflow `scan` function! It will allow us to loop through a tensorflow array without knowing its size. This is similar to how everything else in Tensorflow and Theano works. Using `scan` we can tell Tensorflow "how to run the for loop", without actually running it.
There is another big reason that the `scan` function is so important; it allows us to perform **automatic differentiation** when we have sequential data. Tensorflow keeps track of how all the variables in your graph link together, so that it can automatically calculate the gradient for you when you do gradient descent:
$$W(t) \leftarrow W(t-1) - \eta \nabla J\big(W(t-1)\big)$$
The `scan` function keeps track of this when it performs the loop. The anatomy of the `scan` function is shown in pseudocode below:
```
outputs = tf.scan(
fn=some_function, # Function applied to every element in sequence
elems=thing_to_loop_over # Actual sequence that is passed in
)
```
Above, `some_function` is applied to every element in `thing_to_loop_over`. Now, the way that we define `some_function` is very specific and much more strict than that for theano. In particular, it must always take in two arguments. The first element is the last output of the function, and the second element is the next element of the sequence:
```
def some_function(last_output, element):
return do_something_to(last_output, element)
```
The tensorflow scan function returns `outputs`, which is all of the return values of `some_function` concatenated together. For example, we can look at the following block:
```
outputs = tf.scan(
fn=some_function,
elems=thing_to_loop_over
)
def square(last, current):
return current * current
# sequence = [1, 2, 3]
# outputs = [1, 4, 9]
```
If we pass in `[1, 2, 3]`, then our outputs will be `[1, 4, 9]`. Now, of course the outputs is still a tensorflow graph node. So, in order to get an actual value out of it we need to run it in an actual session.
```
import tensorflow as tf
x = tf.placeholder(tf.int32, shape=(None,), name="x")
def square(last, current):
"""Last is never used, but must be included based on interface requirements of tf.scan"""
return current*current
# Essentially doing what a for loop would normally do
# It applies the square function to every element of x
square_op = tf.scan(
fn=square,
elems=x
)
# Run it!
with tf.Session() as session:
o_val = session.run(
square_op,
feed_dict={x: [1, 2, 3, 4, 5]}
)
print("Output: ", o_val)
```
Now, of course `scan` can do more complex things than this. We can implement another argument, `initializer`, that allows us to compute recurrence relationships.
```
outputs = tf.scan(
fn=some_function, # Function applied to every element in sequence
elems=thing_to_loop_over, # Actual sequence that is passed in
initializer=initial_input
)
```
Why exactly do we need this? Well, we can see that the recurrence function takes in two things: the last element that it returned, and the current element of the sequence that we are iterating over. What is the last output during the first iteration? There isn't one yet! And that is exactly why we need `initializer`.
One thing to keep in mind when using `initializer` is that it is very strict. In particular, it must be the exact same type as the output of `recurrence`. For example, if you need to return multiple things from `recurrence` it is going to be returned as a tuple. That means that the argument to `initializer` cannot be a list, it must be a tuple. This also means that a tuple containing `(5 , 5)` is not the same a tuple containing `(5.0, 5.0)`.
Let's try to compute the fibonacci sequence to get a feel for how this works:
```
# N is the number fibonacci numbers that we want
N = tf.placeholder(tf.int32, shape=(), name="N")
def fibonacci(last, current):
# last[0] is the last value, last[1] is the second last value
return (last[1], last[0] + last[1])
fib_op = tf.scan(
fn=fibonacci,
elems=tf.range(N),
initializer=(0, 1),
)
with tf.Session() as session:
o_val = session.run(
fib_op,
feed_dict={N: 8}
)
print("Output: \n", o_val)
```
Another example of what we can do with the theano `scan` is create a **low pass filter** (also known as a **moving average**). In this case, our recurrence relation is given by:
$$s(t) = \text{decay_rate} \cdot s(t-1) + (1 - \text{decay_rate}) \cdot x(t)$$
Where $x(t)$ is the input and $s(t)$ is the output. The goal here is to return a clean version of a noisy signal. To do this we can create a sine wave, add some random gaussian noise to it, and finally try to retrieve the sine wave. In code this looks like:
```
original = np.sin(np.linspace(0, 3*np.pi, 300))
X = 2*np.random.randn(300) + original
fig = plt.figure(figsize=(15,5))
plt.subplot(1, 2, 1)
ax = plt.plot(X, c="g", lw=1.5)
plt.title("Original")
# Setup placeholders
decay = tf.placeholder(tf.float32, shape=(), name="decay")
sequence = tf.placeholder(tf.float32, shape=(None, ), name="sequence")
# The recurrence function and loop
def recurrence(last, x):
return (1.0 - decay)*x + decay*last
low_pass_filter = tf.scan(
fn=recurrence,
elems=sequence,
initializer=0.0 # sequence[0] to use first value of the sequence
)
# Run it!
with tf.Session() as session:
Y = session.run(low_pass_filter, feed_dict={sequence: X, decay: 0.97})
plt.subplot(1, 2, 2)
ax2 = plt.plot(original, c="b")
ax = plt.plot(Y, c="r")
plt.title("Low pass filter")
plt.show()
```
### 4.2 Discrete HMM With Tensorflow
Let's now take a moment to walk through the creation of a discrete HMM class utilizing Tensorflow.
```
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
from hmm.utils import get_obj_s3
class HMM:
def __init__(self, M):
self.M = M # number of hidden states
def set_session(self, session):
self.session = session
def fit(self, X, max_iter=10, print_period=1):
# train the HMM model using stochastic gradient descent
N = len(X)
print("Number of train samples:", N)
costs = []
for it in range(max_iter):
for n in range(N):
# this would of course be much faster if we didn't do this on
# every iteration of the loop
c = self.get_cost_multi(X).sum()
costs.append(c)
self.session.run(self.train_op, feed_dict={self.tfx: X[n]})
plt.figure(figsize=(8,5))
plt.plot(costs, c="b")
plt.xlabel("Iteration Number")
plt.ylabel("Cost")
plt.show()
def get_cost(self, x):
# returns log P(x | model)
# using the forward part of the forward-backward algorithm
# print "getting cost for:", x
return self.session.run(self.cost, feed_dict={self.tfx: x})
def log_likelihood(self, x):
return -self.session.run(self.cost, feed_dict={self.tfx: x})
def get_cost_multi(self, X):
return np.array([self.get_cost(x) for x in X])
def build(self, preSoftmaxPi, preSoftmaxA, preSoftmaxB):
M, V = preSoftmaxB.shape
self.preSoftmaxPi = tf.Variable(preSoftmaxPi)
self.preSoftmaxA = tf.Variable(preSoftmaxA)
self.preSoftmaxB = tf.Variable(preSoftmaxB)
pi = tf.nn.softmax(self.preSoftmaxPi)
A = tf.nn.softmax(self.preSoftmaxA)
B = tf.nn.softmax(self.preSoftmaxB)
# define cost
self.tfx = tf.placeholder(tf.int32, shape=(None,), name='x')
def recurrence(old_a_old_s, x_t):
old_a = tf.reshape(old_a_old_s[0], (1, M))
a = tf.matmul(old_a, A) * B[:, x_t]
a = tf.reshape(a, (M,))
s = tf.reduce_sum(a)
return (a / s), s
# remember, tensorflow scan is going to loop through
# all the values!
# we treat the first value differently than the rest
# so we only want to loop through tfx[1:]
# the first scale being 1 doesn't affect the log-likelihood
# because log(1) = 0
alpha, scale = tf.scan(
fn=recurrence,
elems=self.tfx[1:],
initializer=(pi * B[:, self.tfx[0]], np.float32(1.0)),
)
self.cost = -tf.reduce_sum(tf.log(scale))
self.train_op = tf.train.AdamOptimizer(1e-2).minimize(self.cost)
def init_random(self, V):
preSoftmaxPi0 = np.zeros(self.M).astype(np.float32) # initial state distribution
preSoftmaxA0 = np.random.randn(self.M, self.M).astype(np.float32) # state transition matrix
preSoftmaxB0 = np.random.randn(self.M, V).astype(np.float32) # output distribution
self.build(preSoftmaxPi0, preSoftmaxA0, preSoftmaxB0)
def set(self, preSoftmaxPi, preSoftmaxA, preSoftmaxB):
op1 = self.preSoftmaxPi.assign(preSoftmaxPi)
op2 = self.preSoftmaxA.assign(preSoftmaxA)
op3 = self.preSoftmaxB.assign(preSoftmaxB)
self.session.run([op1, op2, op3])
def fit_coin(file_key):
X = []
for line in get_obj_s3(file_key).read().decode("utf-8").strip().split(sep="\n"):
x = [1 if e == "H" else 0 for e in line.rstrip()]
X.append(x)
hmm = HMM(2)
# the entire graph (including optimizer's variables) must be built
# before calling global variables initializer!
hmm.init_random(2)
init = tf.global_variables_initializer()
with tf.Session() as session:
session.run(init)
hmm.set_session(session)
hmm.fit(X, max_iter=5)
L = hmm.get_cost_multi(X).sum()
print("Log Likelihood with fitted params: ", round(L, 3))
# try true values
# remember these must be in their "pre-softmax" forms
pi = np.log(np.array([0.5, 0.5])).astype(np.float32)
A = np.log(np.array([[0.1, 0.9], [0.8, 0.2]])).astype(np.float32)
B = np.log(np.array([[0.6, 0.4], [0.3, 0.7]])).astype(np.float32)
hmm.set(pi, A, B)
L = hmm.get_cost_multi(X).sum()
print("Log Likelihood with true params: ", round(L, 3))
if __name__ == '__main__':
key = "coin_data.txt"
fit_coin(key)
```
|
github_jupyter
|
```
# use python eval sometimes. great trickdefining a class and operator overloading
import aoc
f = open('input.txt')
lines = [line.rstrip('\n') for line in f]
lines[0]
# part 1
def evaluate(line):
ans = 0
firstop = None
operator = None
wait = 0
for i, ch in enumerate(line):
if wait > 0: # still within parentheses, so ignore because the recursion took care of it
wait -= 1
continue
if ch == '(': # recurse the rest
ch, wait = evaluate(line[i+1:])
if ch == ')':
return firstop, i+1
if isinstance(ch, int):
if not firstop:
firstop = ch
else:
firstop = eval(f'{firstop}{operator}{ch}')
else:
operator = ch
return firstop
ans = 0
for line in lines:
line = line.replace("(","( ").replace(")"," )")
line = aoc.to_int(line.split())
ans+= evaluate(line)
ans
# part 2
def findclosing(line):
count = 0
for index, i in enumerate(line):
if i == "(": count+=1
if i == ')': count -=1
if count == 0: return index
def evaluate(line):
ans = 0
while '(' in line: # get rid of all the parenthesis blocks
first = line.index('(')
last = findclosing(line[first:])+first
line[first:last+1] = [evaluate(line[first+1:last])]
while '+' in line: # reduce the '+' op_indexations
op_index = line.index('+')
line[op_index-1:op_index+2] = [line[op_index-1]+line[op_index+1]]
while '*' in line: # finally, reduce the '*'
op_index = line.index('*')
line[op_index-1:op_index+2] = [line[op_index-1]*line[op_index+1]]
return line[0]
ans = 0
for line in lines:
line = line.replace("(","( ").replace(")"," )")
line = list(aoc.to_int(line.split()))
ans += evaluate(line)
ans
# alternative solution from reddit, amazing idea with operator overloading
import re
class a(int):
def __mul__(self, b):
return a(int(self) + b)
def __add__(self, b):
return a(int(self) + b)
def __sub__(self, b):
return a(int(self) * b)
def ev(expr, pt2=False):
expr = re.sub(r"(\d+)", r"a(\1)", expr)
expr = expr.replace("*", "-")
if pt2:
expr = expr.replace("+", "*")
return eval(expr, {}, {"a": a})
print("Part 1:", sum(ev(l) for l in lines))
print("Part 2:", sum(ev(l, pt2=True) for l in lines))
# another one from sophiebits, have to study the regex a bit
def solve(line):
def doInner(inner):
# part 1:
# while '+' in inner or '*' in inner:
# inner = re.sub('^(\d+)\s*\+\s*(\d+)', lambda m: str(int(m.group(1)) + int(m.group(2))), inner)
# inner = re.sub('^(\d+)\s*\*\s*(\d+)', lambda m: str(int(m.group(1)) * int(m.group(2))), inner)
while '+' in inner:
inner = re.sub('(\d+)\s*\+\s*(\d+)', lambda m: str(int(m.group(1)) + int(m.group(2))), inner)
while '*' in inner:
inner = re.sub('(\d+)\s*\*\s*(\d+)', lambda m: str(int(m.group(1)) * int(m.group(2))), inner)
return inner
while '(' in line:
def doExpr(match):
inner = match.group(1)
return doInner(inner)
line = re.sub(r'\(([^()]+)\)', doExpr, line)
return doInner(line)
total = 0
for line in lines:
total += int(solve(line))
print(total)
```
|
github_jupyter
|
# Creating Provenance an Example Using a Python Notebook
```
import prov, requests, pandas as pd, io, git, datetime, urllib
from prov.model import ProvDocument
```
## Initialising a Provenance Document
First we use the prov library to create a provenance and initialise it with some relevant namespaces that can be used later to define provenance activities and entities
```
pg = ProvDocument()
kn_id = "data/data-gov-au/number-of-properties-by-suburb-and-planning-zone-csv"
pg.add_namespace('kn', 'http://oznome.csiro.au/id/')
pg.add_namespace('void', 'http://vocab.deri.ie/void#')
pg.add_namespace('foaf', 'http://xmlns.com/foaf/0.1/')
pg.add_namespace('dc', 'http://purl.org/dc/elements/1.1/')
pg.add_namespace('doap', 'http://usefulinc.com/ns/doap#')
```
## Processing the Data
Processing could be anything and represents one or more provenance activities. In this example we use a KN metadata record to retrieve data on residential properities. We intersperse definition of provenance into this processing but we could have easily seperated it out and performed it after the processing steps
First we define an entity that describes the KN metadata records which we are using here
```
input_identifier = 'kn:'+ kn_id
input_entity = pg.entity(input_identifier, {'prov:label': 'road static parking off street', 'prov:type': 'void:Dataset'})
```
Then we proceed to drill down to get detailed data that we've found associated with this record
```
start_time = datetime.datetime.now()
response = requests.get('https://data.sa.gov.au/data/dataset/d080706c-2c05-433d-b84d-9aa9b6ccae73/resource/4a47e89b-4be8-430d-8926-13b180025ac6/download/city-of-onkaparinga---number-of-properties-by-suburb-and-planning-zone-2016.csv')
url_data = response.content
dataframe = pd.read_csv(io.StringIO(url_data.decode('utf-8')))
dataframe.columns
```
Our processing is very simple we are subsetting the original dataset here and creating a new dataset called residential_frame that we will then save to disk
```
residential_frame = dataframe[dataframe['Zone_Description'] == 'Residential']
residential_frame_file_name = "filtered_residential_data.csv"
residential_frame.to_csv(residential_frame_file_name)
end_time = datetime.datetime.now()
```
## Completing Provenance
We have began to build a provenance record but we are missing a record of the activity that transforms our input into the output and we are also missing a description of the output
### Generating an output provenance entity
Ideally we would store our output provenance entity somewhere known and persistent and identify it with a persistent url. However we can still mint an identifier and then describe the dataset in useful ways that will make it easy to find and query from later. To do this we create a new entity record and use the file name and sha hash of the file to describe it.
```
import subprocess
output = subprocess.check_output("sha1sum "+ residential_frame_file_name, shell=True)
sha1 = str(output).split(' ')[0][2:]
output_identifier = 'kn:' + sha1
output_entity = pg.entity(output_identifier , {'prov:label': residential_frame_file_name, 'prov:type': 'void:Dataset'})
```
### Describing the activity
We need to connect the entity representing the input data to the entity representing the output data and we may want to describe the activity that transforms the input into the output. In this case the activity is this Jupyter Notebook. One way of storing provenance information in it is to make sure it is version controlled in git and then record these details.
## Connecting things together into the provenance graph
```
import re, ipykernel, json
%%javascript
var nb = Jupyter.notebook;
var port = window.location.port;
nb.kernel.execute("NB_Port = '" + port + "'");
kernel_id = re.search('kernel-(.*).json', ipykernel.connect.get_connection_file()).group(1)
response = requests.get('http://127.0.0.1:{port}/jupyter/api/sessions'.format(port=NB_Port))
response.content
matching = [s for s in json.loads(response.text) if s['kernel']['id'] == kernel_id]
if matching:
matched = matching[0]['notebook']['path']
notebook_file_name = matched.split('/')[-1]
```
One gotcha here is that we need to make sure this notebooks relevant version has been committed and pushed to the remote. So do that and then execute these cells.
```
repo = git.Repo('./', search_parent_directories=True)
current_git_sha = repo.head.object.hexsha
current_git_remote = list(repo.remotes['origin'].urls)[0]
current_git_sha
current_git_remote
process_identifier = 'kn:' + 'notebook/' + urllib.parse.quote(notebook_file_name + current_git_sha, safe='')
process_identifier
process_entity = pg.entity(process_identifier, other_attributes={'dc:description': 'a jupyter notebook used that demonstrates provenance', 'doap:GitRepository' : current_git_remote, 'doap:Version' : current_git_sha })
import time
sunixtime = time.mktime(start_time.timetuple())
eunixtime = time.mktime(end_time.timetuple())
activity_identifier = 'kn:' + 'notebook/' + urllib.parse.quote(notebook_file_name + current_git_sha, safe='') + str(sunixtime) + str(eunixtime)
activity = pg.activity(activity_identifier, startTime=start_time, endTime=end_time)
pg.wasGeneratedBy(activity=activity, entity=output_entity)
pg.used(activity=activity, entity=input_entity)
pg.used(activity=activity, entity=process_entity)
pg
# visualize the graph
from prov.dot import prov_to_dot
dot = prov_to_dot(pg)
dot.write_png('prov.png')
from IPython.display import Image
Image('prov.png')
```
## Posting to a Provenance Storage System
TBC
|
github_jupyter
|
# Cython in Jupyter notebooks
To use cython in a Jupyter notebook, the extension has to be loaded.
```
%load_ext cython
```
## Pure Python
To illustrate the performance difference between a pure Python function and a cython implementation, consider a function that computes the list of the first $k_{\rm max}$ prime numbers.
```
from array import array
def primes(kmax, p=None):
if p is None:
p = array('i', [0]*kmax)
result = []
k, n = 0, 2
while k < len(p):
i = 0
while i < k and n % p[i] != 0:
i += 1
if i == k:
p[k] = n
k += 1
result.append(n)
n += 1
return result
```
Checking the results for the 20 first prime numbers.
```
primes(20)
```
Note that this is not the most efficient method to check whether $k$ is prime.
```
%timeit primes(1_000)
p = array('i', [0]*10_000)
%timeit primes(10_000, p)
```
## Cython
The cython implementation differs little from that in pure Python, type annotations have been added for the function's argument, and the variables `n`, `k`, `i`, and `p`. Note that cython expects a constant array size, hence the upper limit on `kmax`.
```
%%cython
def c_primes(int kmax):
cdef int n, k, i
cdef int p[10_000]
if kmax > 10_000:
kmax = 10_000
result = []
k, n = 0, 2
while k < kmax:
i = 0
while i < k and n % p[i] != 0:
i += 1
if i == k:
p[k] = n
k += 1
result.append(n)
n += 1
return result
```
Checking the results for the 20 first prime numbers.
```
c_primes(20)
%timeit c_primes(1_000)
%timeit c_primes(10_000)
```
It is clear that the cython implementation is more than 30 times faster than the pure Python implementation.
## Dynamic memory allocation
The cython implementation can be improved by adding dynamic memory allocation for the array `p`.
```
%%cython
from libc.stdlib cimport calloc, free
def c_primes(int kmax):
cdef int n, k, i
cdef int *p = <int *> calloc(kmax, sizeof(int))
result = []
k, n = 0, 2
while k < kmax:
i = 0
while i < k and n % p[i] != 0:
i += 1
if i == k:
p[k] = n
k += 1
result.append(n)
n += 1
free(p)
return result
```
Checking the results for the 20 first prime numbers.
```
c_primes(20)
```
This has no noticeable impact on performance.
```
%timeit c_primes(1_000)
%timeit c_primes(10_000)
```
|
github_jupyter
|
```
!pip install plotly
```
<a href="https://plotly.com/python/" target="_blank">Plotly's</a> Python graphing library makes interactive, publication-quality graphs. Examples of how to make line plots, scatter plots, area charts, bar charts, error bars, box plots, histograms, heatmaps, subplots, multiple-axes, polar charts, and bubble charts.
```
!pip install plotly_express
```
<a href="https://pypi.org/project/plotly-express/0.1.9/" target="_blank">Plotly Express</a> is a terse, consistent, high-level wrapper around Plotly.py for rapid data exploration and figure generation.
```
!pip install calmap
```
<a href="https://pypi.org/project/calmap/" target="_blank">Calendar heatmaps (calmap)</a> Plot Pandas time series data sampled by day in a heatmap per calendar year, similar to GitHub’s contributions plot, using matplotlib.
```
!pip install squarify
```
Pure Python implementation of the <a href="https://pypi.org/project/squarify/0.1/" target="_blank">squarify</a> treemap layout algorithm. Based on algorithm from Bruls, Huizing, van Wijk, "Squarified Treemaps", but implements it differently.
```
!pip install pycountry_convert
```
Using country data derived from wikipedia, <a href="https://pypi.org/project/pycountry-convert/" target="_blank">pycountry-convert</a> provides conversion functions between ISO country names, country-codes, and continent names.
```
!pip install GoogleMaps
```
Use Python? Want to geocode something? Looking for directions? Maybe matrices of directions? This library brings the <a href="https://pypi.org/project/googlemaps/" target="_blank">Google Maps</a> Platform Web Services to your Python application.
```
!pip install xgboost
```
<a href="https://xgboost.readthedocs.io/en/latest/" target="_blank">XGBoost</a> is an optimized distributed gradient boosting library designed to be highly efficient, flexible and portable. It implements machine learning algorithms under the Gradient Boosting framework. XGBoost provides a parallel tree boosting (also known as GBDT, GBM) that solve many data science problems in a fast and accurate way. The same code runs on major distributed environment (Hadoop, SGE, MPI) and can solve problems beyond billions of examples.
```
!pip install lightgbm
```
<a href="https://lightgbm.readthedocs.io/en/latest/" target="_blank">LightGBM</a> is a gradient boosting framework that uses tree based learning algorithms. It is designed to be distributed and efficient with the following advantages:
* Faster training speed and higher efficiency.
* Lower memory usage.
* Better accuracy.
* Support of parallel and GPU learning.
* Capable of handling large-scale data.
```
!pip install altair
```
<a href="https://pypi.org/project/altair/" target="_blank">Altair</a> is a declarative statistical visualization library for Python. With Altair, you can spend more time understanding your data and its meaning. Altair's API is simple, friendly and consistent and built on top of the powerful Vega-Lite JSON specification. This elegant simplicity produces beautiful and effective visualizations with a minimal amount of code. Altair is developed by Jake Vanderplas and Brian Granger in close collaboration with the UW Interactive Data Lab.
```
!pip install folium
```
<a href="https://pypi.org/project/folium/" target="_blank">folium</a> builds on the data wrangling strengths of the Python ecosystem and the mapping strengths of the Leaflet.js library. Manipulate your data in Python, then visualize it in a Leaflet map via folium.
```
!pip install fbprophet
```
<a href="https://pypi.org/project/fbprophet/" target="_blank">Prophet</a> is a procedure for forecasting time series data based on an additive model where non-linear trends are fit with yearly, weekly, and daily seasonality, plus holiday effects. It works best with time series that have strong seasonal effects and several seasons of historical data. Prophet is robust to missing data and shifts in the trend, and typically handles outliers well.
|
github_jupyter
|
### Mit kellene tudni?
#### 1. Megfogalmazni egy programozási problémát <!-- .element: class="fragment" -->
#### 1. Számításelmélet értelmét elmagyarázni <!-- .element: class="fragment" -->
#### 1. Lebontani egy komplex problémát egyszerűbbekre <!-- .element: class="fragment" -->
#### 1. Megérteni egy leírt programot <!-- .element: class="fragment" -->
#### 1. Megírni egy programot <!-- .element: class="fragment" -->
#### 1. Találni érdeklődést és folytatást <!-- .element: class="fragment" -->
<center><img src="https://pics.me.me/doctors-googling-stuff-online-does-not-make-you-a-doctor-61282088.png"></center> -->
### Deklaratív tudás
A "mit?" kérdésre adott válasz egy probléma kapcsán
### Imperatív tudás
A "hogyan" kérdésre adott válasz egy probléma kapcsán
### Deklaratív példák
- tervrajz
- térképjelzés
- anatómiai ábra
### Imperatív példák
- recept
- IKEA útmutató
- útvonalterv
### Mit adunk át a gépnek?
Egy probléma megoldására szeretnénk megtanítani/megkérni:
tetszőleges $x$-re, számolja ki $ \sqrt{x} $-et úgy, hogy csak osztani, szorozni, meg összeadni tud
### Tudás Gyökvonásról
- deklaratív tudás:
- $ \sqrt{x} = y \Leftrightarrow y^2=x $
- $ x < y^2 \Leftrightarrow \sqrt{x} < y $
- $ ( (y_1 < x \land y_2 < x) \lor (y_1 > x \land y_2 > x) ) \Rightarrow $
- $ \Rightarrow ( |x - y_1| < |x - y_2| \Leftrightarrow |x^2 - y_1^2| < |x^2 - y_2^2| ) $
- imperatív tudás:
- tippelünk egy kezdeti $ G $ -t, és ameddig nem elég jó, $ G' = \frac{G+\frac{x}{G}}{2} $ -vel közelítünk, így tetszőlegesen közel kerülünk az eredményhez
(minden nemnegatív számok esetén)
### Ember
okos, kreatív, tud következtetni, memóriája ködös,
szeretné minél kevesebbet nyomkodni a számológépet
- felhasznál csomó meglévő deklaratív tudást
- összeállítja egy komplex tippelési folyamattá
- tippek eredményéből továbbfejleszti a folyamatot
- felhasznál olyan komplex fogalmakat mint nagyságrend, vagy előjelváltás
### Gép
buta, nincs önálló gondolata, memóriája tökéletes
másodpercenként töbmilliárd műveletet el tud végezni,
- tippel egy nagyon rosszat, pl G = 1
- valaki megtanította neki hogy $G' = \frac{G+\frac{x}{G}}{2}$ közelít, szóval elkezdi
- Megoldandó probléma: $ \sqrt{1366561} = ? $
### Specifikáció
Egyfajta deklaratív leírása egy programnak
Miből, mit?
- állapottér - bemenő/kimenő adatok
- előfeltétel - amit tudunk a bemenetről
- utófeltétel - az eredmény kiszámítási szabálya (amit tudunk az eredményről)
legyen **teljes** és **részletes**
### Specifikáció I. példa
Valós számok halmazán megoldható másodfokú egyneletet oldjon meg a program, ami $ax^2+bx+c=0$ formában van megadva
- Á: $(a,b,c,x_1,x_2 \in \mathbb{R})$ <!-- .element: class="fragment" data-fragment-index="1" -->
- Ef: $(a \neq 0 \land b^2-4ac \geq 0)$ <!-- .element: class="fragment" data-fragment-index="2" -->
- Uf: $ (x_1 = \frac{-b + \sqrt{b^2-4ac}}{2a} \land x_2 = \frac{-b - \sqrt{b^2-4ac}}{2a})$ <!-- .element: class="fragment" data-fragment-index="3" -->
### Specifikáció példa 2
Valós számok halmazán megoldható másodfokú egyneletet oldjon meg a program, ami $ax^2+bx+c=0$ formában van megadva
- Á: $(a,b,c,x_1,x_2 \in \mathbb{R})$
- Ef: $(a \neq 0 \land b^2-4ac \geq 0)$
- Uf: $ (\forall i (ax_i^2+bx_i+c=0) \land ( x_1 = x_2 \iff b^2-4ac = 0 ))$
### Specifikáció teljessége
Amit az előfeltétel megenged az állapottéren belül, azt az utófeltételnek kezelnie kell
Pl:
- Válassza ki két szám közül azt amelyiknek több prím osztója van
- több különböző vagy több összesen?
- mi van ha ugyanannyi?
- Válassza ki egy számsorból azt az 5 számot ami legjobban eltér az átlagtól
- mi van ha nincs 5 szám a számsorban?
- mi van ha minden szám ugyanaz?
- Sakktáblán szereplő állásról döntse el hogy matt-e.
- mi van ha mindkét fél sakkban van?
- lehet 11 királynő valakinél?
### Specifikáció részletessége
A program főzzön rántottát:
- Á: (konyha)
- Ef: ( )
- Uf: (ha a konyha alkalmas ennek elkészítésére, a konyhában legyen egy finom rántotta)
vagy:
- Á: (serpenyő, főzőlap, 3 tojás, olaj, só, fakanál, tányér)
- Ef: (a serpenyő, tányér és fakanál tiszta, a tojás nem romlott, a főzőlap képes a serpenyőt 200 Celsius fokra felmelegíteni)
- Uf: (a tojások összekeverve kerültek a 200 fokos serpenyőbe az olaj után, több mint 4 de kevesebb mint 10 percet töltöttek ott, ebből 20 másodpercnél többet nem álltak kavarás nélkül, végül megsózva kikerültek a tányérra)
### Specifikáció II. példa
Két természetes szám legnagyobb közös osztójának megtalálása
- Á: $(a,b,x \in \mathbb{N})$ <!-- .element: class="fragment" data-fragment-index="1" -->
- Ef: $(a \neq 0 \land b \neq 0)$ <!-- .element: class="fragment" data-fragment-index="2" -->
- Uf: $ (x|a \land x|b \land \nexists i(i|a \land i|b \land i > x))$ <!-- .element: class="fragment" data-fragment-index="3" -->
<a style='text-decoration:none;line-height:16px;display:flex;color:#5B5B62;padding:10px;justify-content:end;' href='https://deepnote.com?utm_source=created-in-deepnote-cell&projectId=978e47b7-a961-4dca-a945-499e8b781a34' target="_blank">
<img alt='Created in deepnote.com' style='display:inline;max-height:16px;margin:0px;margin-right:7.5px;' src='data:image/svg+xml;base64,PD94bWwgdmVyc2lvbj0iMS4wIiBlbmNvZGluZz0iVVRGLTgiPz4KPHN2ZyB3aWR0aD0iODBweCIgaGVpZ2h0PSI4MHB4IiB2aWV3Qm94PSIwIDAgODAgODAiIHZlcnNpb249IjEuMSIgeG1sbnM9Imh0dHA6Ly93d3cudzMub3JnLzIwMDAvc3ZnIiB4bWxuczp4bGluaz0iaHR0cDovL3d3dy53My5vcmcvMTk5OS94bGluayI+CiAgICA8IS0tIEdlbmVyYXRvcjogU2tldGNoIDU0LjEgKDc2NDkwKSAtIGh0dHBzOi8vc2tldGNoYXBwLmNvbSAtLT4KICAgIDx0aXRsZT5Hcm91cCAzPC90aXRsZT4KICAgIDxkZXNjPkNyZWF0ZWQgd2l0aCBTa2V0Y2guPC9kZXNjPgogICAgPGcgaWQ9IkxhbmRpbmciIHN0cm9rZT0ibm9uZSIgc3Ryb2tlLXdpZHRoPSIxIiBmaWxsPSJub25lIiBmaWxsLXJ1bGU9ImV2ZW5vZGQiPgogICAgICAgIDxnIGlkPSJBcnRib2FyZCIgdHJhbnNmb3JtPSJ0cmFuc2xhdGUoLTEyMzUuMDAwMDAwLCAtNzkuMDAwMDAwKSI+CiAgICAgICAgICAgIDxnIGlkPSJHcm91cC0zIiB0cmFuc2Zvcm09InRyYW5zbGF0ZSgxMjM1LjAwMDAwMCwgNzkuMDAwMDAwKSI+CiAgICAgICAgICAgICAgICA8cG9seWdvbiBpZD0iUGF0aC0yMCIgZmlsbD0iIzAyNjVCNCIgcG9pbnRzPSIyLjM3NjIzNzYyIDgwIDM4LjA0NzY2NjcgODAgNTcuODIxNzgyMiA3My44MDU3NTkyIDU3LjgyMTc4MjIgMzIuNzU5MjczOSAzOS4xNDAyMjc4IDMxLjY4MzE2ODMiPjwvcG9seWdvbj4KICAgICAgICAgICAgICAgIDxwYXRoIGQ9Ik0zNS4wMDc3MTgsODAgQzQyLjkwNjIwMDcsNzYuNDU0OTM1OCA0Ny41NjQ5MTY3LDcxLjU0MjI2NzEgNDguOTgzODY2LDY1LjI2MTk5MzkgQzUxLjExMjI4OTksNTUuODQxNTg0MiA0MS42NzcxNzk1LDQ5LjIxMjIyODQgMjUuNjIzOTg0Niw0OS4yMTIyMjg0IEMyNS40ODQ5Mjg5LDQ5LjEyNjg0NDggMjkuODI2MTI5Niw0My4yODM4MjQ4IDM4LjY0NzU4NjksMzEuNjgzMTY4MyBMNzIuODcxMjg3MSwzMi41NTQ0MjUgTDY1LjI4MDk3Myw2Ny42NzYzNDIxIEw1MS4xMTIyODk5LDc3LjM3NjE0NCBMMzUuMDA3NzE4LDgwIFoiIGlkPSJQYXRoLTIyIiBmaWxsPSIjMDAyODY4Ij48L3BhdGg+CiAgICAgICAgICAgICAgICA8cGF0aCBkPSJNMCwzNy43MzA0NDA1IEwyNy4xMTQ1MzcsMC4yNTcxMTE0MzYgQzYyLjM3MTUxMjMsLTEuOTkwNzE3MDEgODAsMTAuNTAwMzkyNyA4MCwzNy43MzA0NDA1IEM4MCw2NC45NjA0ODgyIDY0Ljc3NjUwMzgsNzkuMDUwMzQxNCAzNC4zMjk1MTEzLDgwIEM0Ny4wNTUzNDg5LDc3LjU2NzA4MDggNTMuNDE4MjY3Nyw3MC4zMTM2MTAzIDUzLjQxODI2NzcsNTguMjM5NTg4NSBDNTMuNDE4MjY3Nyw0MC4xMjg1NTU3IDM2LjMwMzk1NDQsMzcuNzMwNDQwNSAyNS4yMjc0MTcsMzcuNzMwNDQwNSBDMTcuODQzMDU4NiwzNy43MzA0NDA1IDkuNDMzOTE5NjYsMzcuNzMwNDQwNSAwLDM3LjczMDQ0MDUgWiIgaWQ9IlBhdGgtMTkiIGZpbGw9IiMzNzkzRUYiPjwvcGF0aD4KICAgICAgICAgICAgPC9nPgogICAgICAgIDwvZz4KICAgIDwvZz4KPC9zdmc+' > </img>
Created in <span style='font-weight:600;margin-left:4px;'>Deepnote</span></a>
|
github_jupyter
|
# Módulo 2: Scraping con Selenium
## LATAM Airlines
<a href="https://www.latam.com/es_ar/"><img src="https://i.pinimg.com/originals/dd/52/74/dd5274702d1382d696caeb6e0f6980c5.png" width="420"></img></a>
<br>
Vamos a scrapear el sitio de Latam para averiguar datos de vuelos en funcion el origen y destino, fecha y cabina. La información que esperamos obtener de cada vuelo es:
- Precio(s) disponibles
- Horas de salida y llegada (duración)
- Información de las escalas
¡Empecemos!
```
url = 'https://www.latam.com/es_ar/apps/personas/booking?fecha1_dia=20&fecha1_anomes=2019-12&auAvailability=1&ida_vuelta=ida&vuelos_origen=Buenos%20Aires&from_city1=BUE&vuelos_destino=Madrid&to_city1=MAD&flex=1&vuelos_fecha_salida_ddmmaaaa=20/12/2019&cabina=Y&nadults=1&nchildren=0&ninfants=0&cod_promo='
from selenium import webdriver
options = webdriver.ChromeOptions()
options.add_argument('--incognito')
driver = webdriver.Chrome(executable_path='../../chromedriver', options=options)
driver.get(url)
#Usaremos el Xpath para obtener la lista de vuelos
vuelos = driver.find_elements_by_xpath('//li[@class="flight"]')
vuelo = vuelos[0]
```
Obtenemos la información de la hora de salida, llegada y duración del vuelo
```
# Hora de salida
vuelo.find_element_by_xpath('.//div[@class="departure"]/time').get_attribute('datetime')
# Hora de llegada
vuelo.find_element_by_xpath('.//div[@class="arrival"]/time').get_attribute('datetime')
# Duración del vuelo
vuelo.find_element_by_xpath('.//span[@class="duration"]/time').get_attribute('datetime')
boton_escalas = vuelo.find_element_by_xpath('.//div[@class="flight-summary-stops-description"]/button')
boton_escalas
boton_escalas.click()
segmentos = vuelo.find_elements_by_xpath('//div[@class="segments-graph"]/div[@class="segments-graph-segment"]')
segmentos
escalas = len(segmentos) - 1 #0 escalas si es un vuelo directo
segmento = segmentos[0]
# Origen
segmento.find_element_by_xpath('.//div[@class="departure"]/span[@class="ground-point-name"]').text
# Hora de salida
segmento.find_element_by_xpath('.//div[@class="departure"]/time').get_attribute('datetime')
# Destino
segmento.find_element_by_xpath('.//div[@class="arrival"]/span[@class="ground-point-name"]').text
# Hora de llegada
segmento.find_element_by_xpath('.//div[@class="arrival"]/time').get_attribute('datetime')
# Duración del vuelo
segmento.find_element_by_xpath('.//span[@class="duration flight-schedule-duration"]/time').get_attribute('datetime')
# Numero del vuelo
segmento.find_element_by_xpath('.//span[@class="equipment-airline-number"]').text
# Modelo de avion
segmento.find_element_by_xpath('.//span[@class="equipment-airline-material"]').text
# Duracion de la escala
segmento.find_element_by_xpath('.//div[@class="stop connection"]//p[@class="stop-wait-time"]//time').get_attribute('datetime')
vuelo.find_element_by_xpath('//div[@class="modal-dialog"]//button[@class="close"]').click()
vuelo.click()
tarifas = vuelo.find_elements_by_xpath('.//div[@class="fares-table-container"]//tfoot//td[contains(@class, "fare-")]')
precios = []
for tarifa in tarifas:
nombre = tarifa.find_element_by_xpath('.//label').get_attribute('for')
moneda = tarifa.find_element_by_xpath('.//span[@class="price"]/span[@class="currency-symbol"]').text
valor = tarifa.find_element_by_xpath('.//span[@class="price"]/span[@class="value"]').text
dict_tarifa={nombre:{'moneda':moneda, 'valor':valor}}
precios.append(dict_tarifa)
print(dict_tarifa)
def obtener_tiempos(vuelo):
# Hora de salida
salida = vuelo.find_element_by_xpath('.//div[@class="departure"]/time').get_attribute('datetime')
# Hora de llegada
llegada = vuelo.find_element_by_xpath('.//div[@class="arrival"]/time').get_attribute('datetime')
# Duracion
duracion = vuelo.find_element_by_xpath('.//span[@class="duration"]/time').get_attribute('datetime')
return {'hora_salida': salida, 'hora_llegada': llegada, 'duracion': duracion}
def obtener_precios(vuelo):
tarifas = vuelo.find_elements_by_xpath(
'.//div[@class="fares-table-container"]//tfoot//td[contains(@class, "fare-")]')
precios = []
for tarifa in tarifas:
nombre = tarifa.find_element_by_xpath('.//label').get_attribute('for')
moneda = tarifa.find_element_by_xpath('.//span[@class="price"]/span[@class="currency-symbol"]').text
valor = tarifa.find_element_by_xpath('.//span[@class="price"]/span[@class="value"]').text
dict_tarifa={nombre:{'moneda':moneda, 'valor':valor}}
precios.append(dict_tarifa)
return precios
def obtener_datos_escalas(vuelo):
segmentos = vuelo.find_elements_by_xpath('//div[@class="segments-graph"]/div[@class="segments-graph-segment"]')
info_escalas = []
for segmento in segmentos:
# Origen
origen = segmento.find_element_by_xpath(
'.//div[@class="departure"]/span[@class="ground-point-name"]').text
# Hora de salida
dep_time = segmento.find_element_by_xpath(
'.//div[@class="departure"]/time').get_attribute('datetime')
# Destino
destino = segmento.find_element_by_xpath(
'.//div[@class="arrival"]/span[@class="ground-point-name"]').text
# Hora de llegada
arr_time = segmento.find_element_by_xpath(
'.//div[@class="arrival"]/time').get_attribute('datetime')
# Duración del vuelo
duracion_vuelo = segmento.find_element_by_xpath(
'.//span[@class="duration flight-schedule-duration"]/time').get_attribute('datetime')
# Numero del vuelo
numero_vuelo = segmento.find_element_by_xpath(
'.//span[@class="equipment-airline-number"]').text
# Modelo de avion
modelo_avion = segmento.find_element_by_xpath(
'.//span[@class="equipment-airline-material"]').text
# Duracion de la escala
if segmento != segmentos[-1]:
duracion_escala = segmento.find_element_by_xpath(
'.//div[@class="stop connection"]//p[@class="stop-wait-time"]//time').get_attribute('datetime')
else:
duracion_escala = ''
# Armo un diccionario para almacenar los datos
data_dict={'origen': origen,
'dep_time': dep_time,
'destino': destino,
'arr_time': arr_time,
'duracion_vuelo': duracion_vuelo,
'numero_vuelo': numero_vuelo,
'modelo_avion': modelo_avion,
'duracion_escala': duracion_escala}
info_escalas.append(data_dict)
return info_escalas
```
## Clase 15
Ya tenemos el scraper casi listo. Unifiquemos las 3 funciones de la clase anterior en una sola
```
def obtener_info(driver):
vuelos = driver.find_elements_by_xpath('//li[@class="flight"]')
print(f'Se encontraron {len(vuelos)} vuelos.')
print('Iniciando scraping...')
info = []
for vuelo in vuelos:
# Obtenemos los tiempos generales del vuelo
tiempos = obtener_tiempos(vuelo)
# Clickeamos el botón de escalas para ver los detalles
vuelo.find_element_by_xpath('.//div[@class="flight-summary-stops-description"]/button').click()
escalas = obtener_datos_escalas(vuelo)
# Cerramos el pop-up con los detalles
vuelo.find_element_by_xpath('//div[@class="modal-dialog"]//button[@class="close"]').click()
# Clickeamos el vuelo para ver los precios
vuelo.click()
precios = obtener_precios(vuelo)
# Cerramos los precios del vuelo
vuelo.click()
info.append({'precios':precios, 'tiempos':tiempos , 'escalas': escalas})
return info
```
Ahora podemos cargar la página con el driver y pasárselo a esta función
```
driver = webdriver.Chrome(executable_path='../../chromedriver', options=options)
driver.get(url)
obtener_info(driver)
```
Se encontraron 0 vuelos porque la página no terminó de cargar
Lo más simple que podemos hacer es agregar una demora fija lo suficientemente grande para asegurarnos que la página terminó de cargar.
```
import time
options = webdriver.ChromeOptions()
options.add_argument('--incognito')
driver = webdriver.Chrome(executable_path='../../chromedriver', options=options)
driver.get(url)
time.sleep(10)
vuelos = driver.find_elements_by_xpath('//li[@class="flight"]')
vuelos
driver.close()
```
Esto funciona pero no es muy eficiente. Lo mejor sería esperar a que la página termine de cargar y luego recuperar los elementos.
```
from selenium.webdriver.support.ui import WebDriverWait
from selenium.webdriver.support import expected_conditions as EC
from selenium.webdriver.common.by import By
from selenium.common.exceptions import TimeoutException
options = webdriver.ChromeOptions()
options.add_argument('--incognito')
driver = webdriver.Chrome(executable_path='../../chromedriver', options=options)
driver.get(url)
delay = 10
try:
vuelo = WebDriverWait(driver, delay).until(EC.presence_of_element_located((By.XPATH, '//li[@class="flight"]')))
print("La página terminó de cargar")
info_vuelos = obtener_info(driver)
except TimeoutException:
print("La página tardó demasiado en cargar")
driver.close()
info_vuelos
```
|
github_jupyter
|
## RIHAD VARIAWA, Data Scientist - Who has fun LEARNING, EXPLORING & GROWING
<h1>2D <code>Numpy</code> in Python</h1>
<p><strong>Welcome!</strong> This notebook will teach you about using <code>Numpy</code> in the Python Programming Language. By the end of this lab, you'll know what <code>Numpy</code> is and the <code>Numpy</code> operations.</p>
<h2>Table of Contents</h2>
<div class="alert alert-block alert-info" style="margin-top: 20px">
<ul>
<li><a href="create">Create a 2D Numpy Array</a></li>
<li><a href="access">Accessing different elements of a Numpy Array</a></li>
<li><a href="op">Basic Operations</a></li>
</ul>
<p>
Estimated time needed: <strong>20 min</strong>
</p>
</div>
<hr>
<h2 id="create">Create a 2D Numpy Array</h2>
```
# Import the libraries
import numpy as np
import matplotlib.pyplot as plt
```
Consider the list <code>a</code>, the list contains three nested lists **each of equal size**.
```
# Create a list
a = [[11, 12, 13], [21, 22, 23], [31, 32, 33]]
a
```
We can cast the list to a Numpy Array as follow
```
# Convert list to Numpy Array
# Every element is the same type
A = np.array(a)
A
```
We can use the attribute <code>ndim</code> to obtain the number of axes or dimensions referred to as the rank.
```
# Show the numpy array dimensions
A.ndim
```
Attribute <code>shape</code> returns a tuple corresponding to the size or number of each dimension.
```
# Show the numpy array shape
A.shape
```
The total number of elements in the array is given by the attribute <code>size</code>.
```
# Show the numpy array size
A.size
```
<hr>
<h2 id="access">Accessing different elements of a Numpy Array</h2>
We can use rectangular brackets to access the different elements of the array. The correspondence between the rectangular brackets and the list and the rectangular representation is shown in the following figure for a 3x3 array:
<img src="https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/PY0101EN/Chapter%205/Images/NumTwoEg.png" width="500" />
We can access the 2nd-row 3rd column as shown in the following figure:
<img src="https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/PY0101EN/Chapter%205/Images/NumTwoFT.png" width="400" />
We simply use the square brackets and the indices corresponding to the element we would like:
```
# Access the element on the second row and third column
A[1, 2]
```
We can also use the following notation to obtain the elements:
```
# Access the element on the second row and third column
A[1][2]
```
Consider the elements shown in the following figure
<img src="https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/PY0101EN/Chapter%205/Images/NumTwoFF.png" width="400" />
We can access the element as follows
```
# Access the element on the first row and first column
A[0][0]
```
We can also use slicing in numpy arrays. Consider the following figure. We would like to obtain the first two columns in the first row
<img src="https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/PY0101EN/Chapter%205/Images/NumTwoFSF.png" width="400" />
This can be done with the following syntax
```
# Access the element on the first row and first and second columns
A[0][0:2]
```
Similarly, we can obtain the first two rows of the 3rd column as follows:
```
# Access the element on the first and second rows and third column
A[0:2, 2]
```
Corresponding to the following figure:
<img src="https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/PY0101EN/Chapter%205/Images/NumTwoTST.png" width="400" />
<hr>
<h2 id="op">Basic Operations</h2>
We can also add arrays. The process is identical to matrix addition. Matrix addition of <code>X</code> and <code>Y</code> is shown in the following figure:
<img src="https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/PY0101EN/Chapter%205/Images/NumTwoAdd.png" width="500" />
The numpy array is given by <code>X</code> and <code>Y</code>
```
# Create a numpy array X
X = np.array([[1, 0], [0, 1]])
X
# Create a numpy array Y
Y = np.array([[2, 1], [1, 2]])
Y
```
We can add the numpy arrays as follows.
```
# Add X and Y
Z = X + Y
Z
```
Multiplying a numpy array by a scaler is identical to multiplying a matrix by a scaler. If we multiply the matrix <code>Y</code> by the scaler 2, we simply multiply every element in the matrix by 2 as shown in the figure.
<img src="https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/PY0101EN/Chapter%205/Images/NumTwoDb.png" width="500" />
We can perform the same operation in numpy as follows
```
# Create a numpy array Y
Y = np.array([[2, 1], [1, 2]])
Y
# Multiply Y with 2
Z = 2 * Y
Z
```
Multiplication of two arrays corresponds to an element-wise product or Hadamard product. Consider matrix <code>X</code> and <code>Y</code>. The Hadamard product corresponds to multiplying each of the elements in the same position, i.e. multiplying elements contained in the same color boxes together. The result is a new matrix that is the same size as matrix <code>Y</code> or <code>X</code>, as shown in the following figure.
<img src="https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/PY0101EN/Chapter%205/Images/NumTwoMul.png" width="500" />
We can perform element-wise product of the array <code>X</code> and <code>Y</code> as follows:
```
# Create a numpy array Y
Y = np.array([[2, 1], [1, 2]])
Y
# Create a numpy array X
X = np.array([[1, 0], [0, 1]])
X
# Multiply X with Y
Z = X * Y
Z
```
We can also perform matrix multiplication with the numpy arrays <code>A</code> and <code>B</code> as follows:
First, we define matrix <code>A</code> and <code>B</code>:
```
# Create a matrix A
A = np.array([[0, 1, 1], [1, 0, 1]])
A
# Create a matrix B
B = np.array([[1, 1], [1, 1], [-1, 1]])
B
```
We use the numpy function <code>dot</code> to multiply the arrays together.
```
# Calculate the dot product
Z = np.dot(A,B)
Z
# Calculate the sine of Z
np.sin(Z)
```
We use the numpy attribute <code>T</code> to calculate the transposed matrix
```
# Create a matrix C
C = np.array([[1,1],[2,2],[3,3]])
C
# Get the transposed of C
C.T
```
<hr>
<h2>The last exercise!</h2>
<p>Congratulations, you have completed your first lesson and hands-on lab in Python. However, there is one more thing you need to do. The Data Science community encourages sharing work. The best way to share and showcase your work is to share it on GitHub. By sharing your notebook on GitHub you are not only building your reputation with fellow data scientists, but you can also show it off when applying for a job. Even though this was your first piece of work, it is never too early to start building good habits. So, please read and follow <a href="https://cognitiveclass.ai/blog/data-scientists-stand-out-by-sharing-your-notebooks/" target="_blank">this article</a> to learn how to share your work.
<hr>
<div class="alert alert-block alert-info" style="margin-top: 20px">
<h2>Get IBM Watson Studio free of charge!</h2>
<p><a href="https://cocl.us/bottemNotebooksPython101Coursera"><img src="https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/PY0101EN/Ad/BottomAd.png" width="750" align="center"></a></p>
</div>
<h3>About the Authors:</h3>
<p><a href="https://www.linkedin.com/in/joseph-s-50398b136/" target="_blank">Joseph Santarcangelo</a> is a Data Scientist at IBM, and holds a PhD in Electrical Engineering. His research focused on using Machine Learning, Signal Processing, and Computer Vision to determine how videos impact human cognition. Joseph has been working for IBM since he completed his PhD.</p>
Other contributors: <a href="www.linkedin.com/in/jiahui-mavis-zhou-a4537814a">Mavis Zhou</a>
<hr>
<p>Copyright © 2018 IBM Developer Skills Network. This notebook and its source code are released under the terms of the <a href="https://cognitiveclass.ai/mit-license/">MIT License</a>.</p>
|
github_jupyter
|
```
# Let's keep our notebook clean, so it's a little more readable!
import warnings
warnings.filterwarnings('ignore')
%matplotlib inline
```
# Machine learning to predict age from rs-fmri
The goal is to extract data from several rs-fmri images, and use that data as features in a machine learning model. We will integrate what we've learned in the previous machine learning lecture to build an unbiased model and test it on a left out sample.
We're going to use a dataset that was prepared for this tutorial by [Elizabeth Dupre](https://elizabeth-dupre.com/#/), [Jake Vogel](https://github.com/illdopejake) and [Gael Varoquaux](http://gael-varoquaux.info/), by preprocessing [ds000228](https://openneuro.org/datasets/ds000228/versions/1.0.0) (from [Richardson et al. (2018)](https://dx.doi.org/10.1038%2Fs41467-018-03399-2)) through [fmriprep](https://github.com/poldracklab/fmriprep). They also created this tutorial and should be credited for it.
## Load the data
<img src="data/SampFeat.png" alt="terms" width="300"/>
```
# change this to the location where you downloaded the data
wdir = '/data/ml_tutorial/'
# Now fetch the data
from glob import glob
import os
data = sorted(glob(os.path.join(wdir,'*.gz')))
confounds = sorted(glob(os.path.join(wdir,'*regressors.tsv')))
```
How many individual subjects do we have?
```
#len(data.func)
len(data)
```
## Extract features

In order to do our machine learning, we will need to extract feature from our rs-fmri images.
Specifically, we will extract signals from a brain parcellation and compute a correlation matrix, representing regional coactivation between regions.
We will practice on one subject first, then we'll extract data for all subjects
#### Retrieve the atlas for extracting features and an example subject
Since we're using rs-fmri data, it makes sense to use an atlas defined using rs-fmri data
This paper has many excellent insights about what kind of atlas to use for an rs-fmri machine learning task. See in particular Figure 5.
https://www.sciencedirect.com/science/article/pii/S1053811919301594?via%3Dihub
Let's use the MIST atlas, created here in Montreal using the BASC method. This atlas has multiple resolutions, for larger networks or finer-grained ROIs. Let's use a 64-ROI atlas to allow some detail, but to ultimately keep our connectivity matrices manageable
Here is a link to the MIST paper: https://mniopenresearch.org/articles/1-3
```
from nilearn import datasets
parcellations = datasets.fetch_atlas_basc_multiscale_2015(version='sym')
atlas_filename = parcellations.scale064
print('Atlas ROIs are located in nifti image (4D) at: %s' %
atlas_filename)
```
Let's have a look at that atlas
```
from nilearn import plotting
plotting.plot_roi(atlas_filename, draw_cross=False)
```
Great, let's load an example 4D fmri time-series for one subject
```
fmri_filenames = data[0]
print(fmri_filenames)
```
Let's have a look at the image! Because it is a 4D image, we can only look at one slice at a time. Or, better yet, let's look at an average image!
```
from nilearn import image
averaged_Img = image.mean_img(image.mean_img(fmri_filenames))
plotting.plot_stat_map(averaged_Img)
```
#### Extract signals on a parcellation defined by labels
Using the NiftiLabelsMasker
So we've loaded our atlas and 4D data for a single subject. Let's practice extracting features!
```
from nilearn.input_data import NiftiLabelsMasker
masker = NiftiLabelsMasker(labels_img=atlas_filename, standardize=True,
memory='nilearn_cache', verbose=1)
# Here we go from nifti files to the signal time series in a numpy
# array. Note how we give confounds to be regressed out during signal
# extraction
conf = confounds[0]
time_series = masker.fit_transform(fmri_filenames, confounds=conf)
```
So what did we just create here?
```
type(time_series)
time_series.shape
```
What are these "confounds" and how are they used?
```
import pandas
conf_df = pandas.read_table(conf)
conf_df.head()
conf_df.shape
```
#### Compute and display a correlation matrix
```
from nilearn.connectome import ConnectivityMeasure
correlation_measure = ConnectivityMeasure(kind='correlation')
correlation_matrix = correlation_measure.fit_transform([time_series])[0]
correlation_matrix.shape
```
Plot the correlation matrix
```
import numpy as np
# Mask the main diagonal for visualization:
np.fill_diagonal(correlation_matrix, 0)
# The labels we have start with the background (0), hence we skip the
# first label
plotting.plot_matrix(correlation_matrix, figure=(10, 8),
labels=range(time_series.shape[-1]),
vmax=0.8, vmin=-0.8, reorder=False)
# matrices are ordered for block-like representation
```
#### Extract features from the whole dataset
Here, we are going to use a for loop to iterate through each image and use the same techniques we learned above to extract rs-fmri connectivity features from every subject.
```
# Here is a really simple for loop
for i in range(10):
print('the number is', i)
container = []
for i in range(10):
container.append(i)
container
```
Now lets construct a more complicated loop to do what we want
First we do some things we don't need to do in the loop. Let's reload our atlas, and re-initiate our masker and correlation_measure
```
from nilearn.input_data import NiftiLabelsMasker
from nilearn.connectome import ConnectivityMeasure
from nilearn import datasets
# load atlas
multiscale = datasets.fetch_atlas_basc_multiscale_2015()
atlas_filename = multiscale.scale064
# initialize masker (change verbosity)
masker = NiftiLabelsMasker(labels_img=atlas_filename, standardize=True,
memory='nilearn_cache', verbose=0)
# initialize correlation measure, set to vectorize
correlation_measure = ConnectivityMeasure(kind='correlation', vectorize=True,
discard_diagonal=True)
```
Okay -- now that we have that taken care of, let's run our big loop!
**NOTE**: On a laptop, this might a few minutes.
```
all_features = [] # here is where we will put the data (a container)
for i,sub in enumerate(data):
# extract the timeseries from the ROIs in the atlas
time_series = masker.fit_transform(sub, confounds=confounds[i])
# create a region x region correlation matrix
correlation_matrix = correlation_measure.fit_transform([time_series])[0]
# add to our container
all_features.append(correlation_matrix)
# keep track of status
print('finished %s of %s'%(i+1,len(data)))
# Let's save the data to disk
import numpy as np
np.savez_compressed('MAIN_BASC064_subsamp_features',a = all_features)
```
In case you do not want to run the full loop on your computer, you can load the output of the loop here!
```
feat_file = 'MAIN_BASC064_subsamp_features.npz'
X_features = np.load(feat_file)['a']
X_features.shape
```
<img src="data/SampFeat.png" alt="terms" width="300"/>
Okay so we've got our features.
We can visualize our feature matrix
```
import matplotlib.pyplot as plt
plt.imshow(X_features, aspect='auto')
plt.colorbar()
plt.title('feature matrix')
plt.xlabel('features')
plt.ylabel('subjects')
```
## Get Y (our target) and assess its distribution
```
# Let's load the phenotype data
pheno_path = os.path.join(wdir, 'participants.tsv')
import pandas
pheno = pandas.read_csv(pheno_path, sep='\t').sort_values('participant_id')
pheno.head()
```
Looks like there is a column labeling age. Let's capture it in a variable
```
y_age = pheno['Age']
```
Maybe we should have a look at the distribution of our target variable
```
import matplotlib.pyplot as plt
import seaborn as sns
sns.distplot(y_age)
```
## Prepare data for machine learning
Here, we will define a "training sample" where we can play around with our models. We will also set aside a "validation" sample that we will not touch until the end
We want to be sure that our training and test sample are matched! We can do that with a "stratified split". This dataset has a variable indicating AgeGroup. We can use that to make sure our training and testing sets are balanced!
```
age_class = pheno['AgeGroup']
age_class.value_counts()
from sklearn.model_selection import train_test_split
# Split the sample to training/validation with a 60/40 ratio, and
# stratify by age class, and also shuffle the data.
X_train, X_val, y_train, y_val = train_test_split(
X_features, # x
y_age, # y
test_size = 0.4, # 60%/40% split
shuffle = True, # shuffle dataset
# before splitting
stratify = age_class, # keep
# distribution
# of ageclass
# consistent
# betw. train
# & test sets.
random_state = 123 # same shuffle each
# time
)
# print the size of our training and test groups
print('training:', len(X_train),
'testing:', len(X_val))
```
Let's visualize the distributions to be sure they are matched
```
sns.distplot(y_train)
sns.distplot(y_val)
```
## Run your first model!
Machine learning can get pretty fancy pretty quickly. We'll start with a fairly standard regression model called a Support Vector Regressor (SVR).
While this may seem unambitious, simple models can be very robust. And we probably don't have enough data to create more complex models (but we can try later).
For more information, see this excellent resource:
https://hal.inria.fr/hal-01824205
Let's fit our first model!
```
from sklearn.svm import SVR
l_svr = SVR(kernel='linear') # define the model
l_svr.fit(X_train, y_train) # fit the model
```
Well... that was easy. Let's see how well the model learned the data!
<img src="data/modval.png" alt="terms" width="800"/>
```
# predict the training data based on the model
y_pred = l_svr.predict(X_train)
# caluclate the model accuracy
acc = l_svr.score(X_train, y_train)
```
Let's view our results and plot them all at once!
```
# print results
print('accuracy (R2)', acc)
sns.regplot(y_pred,y_train)
plt.xlabel('Predicted Age')
```
HOLY COW! Machine learning is amazing!!! Almost a perfect fit!
...which means there's something wrong. What's the problem here?
```
from sklearn.model_selection import train_test_split
# Split the sample to training/test with a 75/25 ratio, and
# stratify by age class, and also shuffle the data.
age_class2 = pheno.loc[y_train.index,'AgeGroup']
X_train2, X_test, y_train2, y_test = train_test_split(
X_train, # x
y_train, # y
test_size = 0.25, # 75%/25% split
shuffle = True, # shuffle dataset
# before splitting
stratify = age_class2, # keep
# distribution
# of ageclass
# consistent
# betw. train
# & test sets.
random_state = 123 # same shuffle each
# time
)
# print the size of our training and test groups
print('training:', len(X_train2),
'testing:', len(X_test))
from sklearn.metrics import mean_absolute_error
# fit model just to training data
l_svr.fit(X_train2,y_train2)
# predict the *test* data based on the model trained on X_train2
y_pred = l_svr.predict(X_test)
# caluclate the model accuracy
acc = l_svr.score(X_test, y_test)
mae = mean_absolute_error(y_true=y_test,y_pred=y_pred)
# print results
print('accuracy (R2) = ', acc)
print('MAE = ',mae)
sns.regplot(y_pred,y_test)
plt.xlabel('Predicted Age')
```
Not perfect, but as predicting with unseen data goes, not too bad! Especially with a training sample of "only" 69 subjects. But we can do better!
For example, we can increase the size our training set while simultaneously reducing bias by instead using 10-fold cross-validation
<img src="data/KCV.png" alt="terms" width="500"/>
```
from sklearn.model_selection import cross_val_predict, cross_val_score
# predict
y_pred = cross_val_predict(l_svr, X_train, y_train, cv=10)
# scores
acc = cross_val_score(l_svr, X_train, y_train, cv=10)
mae = cross_val_score(l_svr, X_train, y_train, cv=10, scoring='neg_mean_absolute_error')
```
We can look at the accuracy of the predictions for each fold of the cross-validation
```
for i in range(10):
print('Fold {} -- Acc = {}, MAE = {}'.format(i, acc[i],-mae[i]))
```
We can also look at the overall accuracy of the model
```
from sklearn.metrics import r2_score
overall_acc = r2_score(y_train, y_pred)
overall_mae = mean_absolute_error(y_train,y_pred)
print('R2:',overall_acc)
print('MAE:',overall_mae)
sns.regplot(y_pred, y_train)
plt.xlabel('Predicted Age')
```
Not too bad at all! But more importantly, this is a more accurate estimation of our model's predictive efficacy. Our sample size is larger and this is based on several rounds of prediction of unseen data.
For example, we can now see that the effect is being driven by the model's successful parsing of adults vs. children, but is not performing so well within the adult or children group. This was not evident during our previous iteration of the model
## Tweak your model
It's very important to learn when and where its appropriate to "tweak" your model.
Since we have done all of the previous analysis in our training data, it's fine to try out different models. But we **absolutely cannot** "test" it on our left out data. If we do, we are in great danger of overfitting.
It is not uncommon to try other models, or tweak hyperparameters. In this case, due to our relatively small sample size, we are probably not powered sufficiently to do so, and we would once again risk overfitting. However, for the sake of demonstration, we will do some tweaking.
<img src="data/KCV2.png" alt="terms" width="500"/>
We will try a few different examples:
* Normalizing our target data
* Tweaking our hyperparameters
* Trying a more complicated model
* Feature selection
#### Normalize the target data
```
# Create a log transformer function and log transform Y (age)
from sklearn.preprocessing import FunctionTransformer
log_transformer = FunctionTransformer(func = np.log, validate=True)
log_transformer.fit(y_train.values.reshape(-1,1))
y_train_log = log_transformer.transform(y_train.values.reshape(-1,1))[:,0]
sns.distplot(y_train_log)
plt.title("Log-Transformed Age")
```
Now let's go ahead and cross-validate our model once again with this new log-transformed target
```
# predict
y_pred = cross_val_predict(l_svr, X_train, y_train_log, cv=10)
# scores
acc = r2_score(y_train_log, y_pred)
mae = mean_absolute_error(y_train_log,y_pred)
print('R2:',acc)
print('MAE:',mae)
sns.regplot(y_pred, y_train_log)
plt.xlabel('Predicted Log Age')
plt.ylabel('Log Age')
```
Seems like a definite improvement, right? I think we can agree on that.
But we can't forget about interpretability? The MAE is much less interpretable now.
#### Tweak the hyperparameters
Many machine learning algorithms have hyperparameters that can be "tuned" to optimize model fitting. Careful parameter tuning can really improve a model, but haphazard tuning will often lead to overfitting.
Our SVR model has multiple hyperparameters. Let's explore some approaches for tuning them
```
SVR?
```
One way is to plot a "Validation Curve" -- this will let us view changes in training and validation accuracy of a model as we shift its hyperparameters. We can do this easily with sklearn.
```
from sklearn.model_selection import validation_curve
C_range = 10. ** np.arange(-3, 8) # A range of different values for C
train_scores, valid_scores = validation_curve(l_svr, X_train, y_train_log,
param_name= "C",
param_range = C_range,
cv=10)
# A bit of pandas magic to prepare the data for a seaborn plot
tScores = pandas.DataFrame(train_scores).stack().reset_index()
tScores.columns = ['C','Fold','Score']
tScores.loc[:,'Type'] = ['Train' for x in range(len(tScores))]
vScores = pandas.DataFrame(valid_scores).stack().reset_index()
vScores.columns = ['C','Fold','Score']
vScores.loc[:,'Type'] = ['Validate' for x in range(len(vScores))]
ValCurves = pandas.concat([tScores,vScores]).reset_index(drop=True)
ValCurves.head()
# And plot!
# g = sns.lineplot(x='C',y='Score',hue='Type',data=ValCurves)
# g.set_xticks(range(10))
# g.set_xticklabels(C_range, rotation=90)
g = sns.factorplot(x='C',y='Score',hue='Type',data=ValCurves)
plt.xticks(range(10))
g.set_xticklabels(C_range, rotation=90)
```
It looks like accuracy is better for higher values of C, and plateaus somewhere between 0.1 and 1. The default setting is C=1, so it looks like we can't really improve by changing C.
But our SVR model actually has two hyperparameters, C and epsilon. Perhaps there is an optimal combination of settings for these two parameters.
We can explore that somewhat quickly with a grid search, which is once again easily achieved with sklearn. Because we are fitting the model multiple times witih cross-validation, this will take some time
```
from sklearn.model_selection import GridSearchCV
C_range = 10. ** np.arange(-3, 8)
epsilon_range = 10. ** np.arange(-3, 8)
param_grid = dict(epsilon=epsilon_range, C=C_range)
grid = GridSearchCV(l_svr, param_grid=param_grid, cv=10)
grid.fit(X_train, y_train_log)
```
Now that the grid search has completed, let's find out what was the "best" parameter combination
```
print(grid.best_params_)
```
And if redo our cross-validation with this parameter set?
```
y_pred = cross_val_predict(SVR(kernel='linear',C=0.10,epsilon=0.10, gamma='auto'),
X_train, y_train_log, cv=10)
# scores
acc = r2_score(y_train_log, y_pred)
mae = mean_absolute_error(y_train_log,y_pred)
print('R2:',acc)
print('MAE:',mae)
sns.regplot(y_pred, y_train_log)
plt.xlabel('Predicted Log Age')
plt.ylabel('Log Age')
```
Perhaps unsurprisingly, the model fit is actually exactly the same as what we had with our defaults. There's a reason they are defaults ;-)
Grid search can be a powerful and useful tool. But can you think of a way that, if not properly utilized, it could lead to overfitting?
You can find a nice set of tutorials with links to very helpful content regarding how to tune hyperparameters and while be aware of over- and under-fitting here:
https://scikit-learn.org/stable/modules/learning_curve.html
#### Trying a more complicated model
In principle, there is no real reason to do this. Perhaps one could make an argument for quadratic relationship with age, but we probably don't have enough subjects to learn a complicated non-linear model. But for the sake of demonstration, we can give it a shot.
We'll use a validation curve to see the result of our model if, instead of fitting a linear model, we instead try to the fit a 2nd, 3rd, ... 8th order polynomial.
```
validation_curve?
from sklearn.model_selection import validation_curve
degree_range = list(range(1,8)) # A range of different values for C
train_scores, valid_scores = validation_curve(SVR(kernel='poly',
gamma='scale'
),
X=X_train, y=y_train_log,
param_name= "degree",
param_range = degree_range,
cv=10)
# A bit of pandas magic to prepare the data for a seaborn plot
tScores = pandas.DataFrame(train_scores).stack().reset_index()
tScores.columns = ['Degree','Fold','Score']
tScores.loc[:,'Type'] = ['Train' for x in range(len(tScores))]
vScores = pandas.DataFrame(valid_scores).stack().reset_index()
vScores.columns = ['Degree','Fold','Score']
vScores.loc[:,'Type'] = ['Validate' for x in range(len(vScores))]
ValCurves = pandas.concat([tScores,vScores]).reset_index(drop=True)
ValCurves.head()
# And plot!
# g = sns.lineplot(x='Degree',y='Score',hue='Type',data=ValCurves)
# g.set_xticks(range(10))
# g.set_xticklabels(degree_range, rotation=90)
g = sns.factorplot(x='Degree',y='Score',hue='Type',data=ValCurves)
plt.xticks(range(10))
g.set_xticklabels(degree_range, rotation=90)
```
It appears that we cannot improve our model by increasing the complexity of the fit. If one looked only at the training data, one might surmise that a 2nd order fit could be a slightly better model. But that improvement does not generalize to the validation data.
```
# y_pred = cross_val_predict(SVR(kernel='rbf', gamma='scale'), X_train, y_train_log, cv=10)
# # scores
# acc = r2_score(y_train_log, y_pred)
# mae = mean_absolute_error(y_train_log,y_pred)
# print('R2:',acc)
# print('MAE:',mae)
# sns.regplot(y_pred, y_train_log)
# plt.xlabel('Predicted Log Age')
# plt.ylabel('Log Age')
```
#### Feature selection
Right now, we have 2016 features. Are all of those really going to contribute to the model stably?
Intuitively, models tend to perform better when there are fewer, more important features than when there are many, less imortant features. The tough part is figuring out which features are useful or important.
Here will quickly try a basic feature seclection strategy
<img src="data/FeatSel.png" alt="terms" width="400"/>
The SelectPercentile() function will select the top X% of features based on univariate tests. This is a way of identifying theoretically more useful features. But remember, significance != prediction!
We are also in danger of overfitting here. For starters, if we want to test this with 10-fold cross-validation, we will need to do a separate feature selection within each fold! That means we'll need to do the cross-validation manually instead of using cross_val_predict().
```
from sklearn.feature_selection import SelectPercentile, f_regression
from sklearn.model_selection import KFold
from sklearn.pipeline import Pipeline
# Build a tiny pipeline that does feature selection (top 20% of features),
# and then prediction with our linear svr model.
model = Pipeline([
('feature_selection',SelectPercentile(f_regression,percentile=20)),
('prediction', l_svr)
])
y_pred = [] # a container to catch the predictions from each fold
y_index = [] # just in case, the index for each prediciton
# First we create 10 splits of the data
skf = KFold(n_splits=10, shuffle=True, random_state=123)
# For each split, assemble the train and test samples
for tr_ind, te_ind in skf.split(X_train):
X_tr = X_train[tr_ind]
y_tr = y_train_log[tr_ind]
X_te = X_train[te_ind]
y_index += list(te_ind) # store the index of samples to predict
# and run our pipeline
model.fit(X_tr, y_tr) # fit the data to the model using our mini pipeline
predictions = model.predict(X_te).tolist() # get the predictions for this fold
y_pred += predictions # add them to the list of predictions
```
Alrighty, let's see if only using the top 20% of features improves the model at all...
```
acc = r2_score(y_train_log[y_index], y_pred)
mae = mean_absolute_error(y_train_log[y_index],y_pred)
print('R2:',acc)
print('MAE:',mae)
sns.regplot(np.array(y_pred), y_train_log[y_index])
plt.xlabel('Predicted Log Age')
plt.ylabel('Log Age')
```
Nope, in fact it got a bit worse. It seems we're getting "value at the margins" so to speak. This is a very good example of how significance != prediction, as demonstrated in this figure from Bzdok et al., 2018 *bioRxiv*

See here for an explanation of different feature selection options and how to implement them in sklearn: https://scikit-learn.org/stable/modules/feature_selection.html
And here is a thoughtful tutorial covering feature selection for novel machine learners: https://www.datacamp.com/community/tutorials/feature-selection-python
So there you have it. We've tried many different strategies, but most of our "tweaks" haven't really lead to improvements in the model. This is not always the case, but it is not uncommon. Can you think of some reasons why?
Moving on to our validation data, we probably should just stick to a basic model, though predicting log age might be a good idea!
## Can our model predict age in completely un-seen data?
Now that we've fit a model we think has possibly learned how to decode age based on rs-fmri signal, let's put it to the test. We will train our model on all of the training data, and try to predict the age of the subjects we left out at the beginning of this section.
Because we performed a log transformation on our training data, we will need to transform our testing data using the *same information!* But that's easy because we stored our transformation in an object!
```
# Notice how we use the Scaler that was fit to X_train and apply to X_test,
# rather than creating a new Scaler for X_test
y_val_log = log_transformer.transform(y_val.values.reshape(-1,1))[:,0]
```
And now for the moment of truth!
No cross-validation needed here. We simply fit the model with the training data and use it to predict the testing data
I'm so nervous. Let's just do it all in one cell
```
l_svr.fit(X_train, y_train_log) # fit to training data
y_pred = l_svr.predict(X_val) # classify age class using testing data
acc = l_svr.score(X_val, y_val_log) # get accuracy (r2)
mae = mean_absolute_error(y_val_log, y_pred) # get mae
# print results
print('accuracy (r2) =', acc)
print('mae = ',mae)
# plot results
sns.regplot(y_pred, y_val_log)
plt.xlabel('Predicted Log Age')
plt.ylabel('Log Age')
```
***Wow!!*** Congratulations. You just trained a machine learning model that used real rs-fmri data to predict the age of real humans.
The proper thing to do at this point would be to repeat the train-validation split multiple times. This will ensure the results are not specific to this validation set, and will give you some confidence intervals around your results.
As an assignment, you can give that a try below. Create 10 different splits of the entire dataset, fit the model and get your predictions. Then, plot the range of predictions.
```
# SPACE FOR YOUR ASSIGNMENT
```
So, it seems like something in this data does seem to be systematically related to age ... but what?
#### Interpreting model feature importances
Interpreting the feature importances of a machine learning model is a real can of worms. This is an area of active research. Unfortunately, it's hard to trust the feature importance of some models.
You can find a whole tutorial on this subject here:
http://gael-varoquaux.info/interpreting_ml_tuto/index.html
For now, we'll just eschew better judgement and take a look at our feature importances. While we can't ascribe any biological relevance to the features, it can still be helpful to know what the model is using to make its predictions. This is a good way to, for example, establish whether your model is actually learning based on a confound! Could you think of some examples?
We can access the feature importances (weights) used my the model
```
l_svr.coef_
```
lets plot these weights to see their distribution better
```
plt.bar(range(l_svr.coef_.shape[-1]),l_svr.coef_[0])
plt.title('feature importances')
plt.xlabel('feature')
plt.ylabel('weight')
```
Or perhaps it will be easier to visualize this information as a matrix similar to the one we started with
We can use the correlation measure from before to perform an inverse transform
```
correlation_measure.inverse_transform(l_svr.coef_).shape
from nilearn import plotting
feat_exp_matrix = correlation_measure.inverse_transform(l_svr.coef_)[0]
plotting.plot_matrix(feat_exp_matrix, figure=(10, 8),
labels=range(feat_exp_matrix.shape[0]),
reorder=False,
tri='lower')
```
Let's see if we can throw those features onto an actual brain.
First, we'll need to gather the coordinates of each ROI of our atlas
```
coords = plotting.find_parcellation_cut_coords(atlas_filename)
```
And now we can use our feature matrix and the wonders of nilearn to create a connectome map where each node is an ROI, and each connection is weighted by the importance of the feature to the model
```
plotting.plot_connectome(feat_exp_matrix, coords, colorbar=True)
```
Whoa!! That's...a lot to process. Maybe let's threshold the edges so that only the most important connections are visualized
```
plotting.plot_connectome(feat_exp_matrix, coords, colorbar=True, edge_threshold=0.035)
```
That's definitely an improvement, but it's still a bit hard to see what's going on.
Nilearn has a new feature that let's use view this data interactively!
```
plotting.view_connectome(feat_exp_matrix, coords, threshold='98%')
```
|
github_jupyter
|
<a href="https://colab.research.google.com/github/bhadreshpsavani/ExploringSentimentalAnalysis/blob/main/SentimentalAnalysisWithGPTNeo.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
## Step1. Import and Load Data
```
!pip install -q pip install git+https://github.com/huggingface/transformers.git
!pip install -q datasets
from datasets import load_dataset
emotions = load_dataset("emotion")
import torch
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
```
## Step2. Preprocess Data
```
from transformers import AutoTokenizer
model_name = "EleutherAI/gpt-neo-125M"
tokenizer = AutoTokenizer.from_pretrained(model_name)
def tokenize(batch):
return tokenizer(batch["text"], padding=True, truncation=True)
tokenizer
tokenizer.add_special_tokens({'pad_token': '<|pad|>'})
tokenizer
emotions_encoded = emotions.map(tokenize, batched=True, batch_size=None)
from transformers import AutoModelForSequenceClassification
num_labels = 6
model = (AutoModelForSequenceClassification.from_pretrained(model_name, num_labels=num_labels).to(device))
emotions_encoded["train"].features
emotions_encoded.set_format("torch", columns=["input_ids", "attention_mask", "label"])
emotions_encoded["train"].features
from sklearn.metrics import accuracy_score, f1_score
def compute_metrics(pred):
labels = pred.label_ids
preds = pred.predictions.argmax(-1)
f1 = f1_score(labels, preds, average="weighted")
acc = accuracy_score(labels, preds)
return {"accuracy": acc, "f1": f1}
from transformers import Trainer, TrainingArguments
batch_size = 2
logging_steps = len(emotions_encoded["train"]) // batch_size
training_args = TrainingArguments(output_dir="results",
num_train_epochs=2,
learning_rate=2e-5,
per_device_train_batch_size=batch_size,
per_device_eval_batch_size=batch_size,
load_best_model_at_end=True,
metric_for_best_model="f1",
weight_decay=0.01,
evaluation_strategy="epoch",
disable_tqdm=False,
logging_steps=logging_steps,)
from transformers import Trainer
trainer = Trainer(model=model, args=training_args,
compute_metrics=compute_metrics,
train_dataset=emotions_encoded["train"],
eval_dataset=emotions_encoded["validation"])
trainer.train();
results = trainer.evaluate()
results
preds_output = trainer.predict(emotions_encoded["validation"])
preds_output.metrics
import numpy as np
from sklearn.metrics import plot_confusion_matrix
y_valid = np.array(emotions_encoded["validation"]["label"])
y_preds = np.argmax(preds_output.predictions, axis=1)
labels = ['sadness', 'joy', 'love', 'anger', 'fear', 'surprise']
plot_confusion_matrix(y_preds, y_valid, labels)
model.save_pretrained('./model')
tokenizer.save_pretrained('./model')
```
|
github_jupyter
|
```
from collections import OrderedDict
from collections import namedtuple
import numpy as np
from scipy import stats
# R precision
def r_precision(targets, predictions, max_n_predictions=500):
# Assumes predictions are sorted by relevance
# First, cap the number of predictions
predictions = predictions[:max_n_predictions]
# Calculate metric
target_set = set(targets)
target_count = len(target_set)
return float(len(set(predictions[:target_count]).intersection(target_set))) / target_count
def dcg(relevant_elements, retrieved_elements, k, *args, **kwargs):
"""Compute the Discounted Cumulative Gain.
Rewards elements being retrieved in descending order of relevance.
\[ DCG = rel_1 + \sum_{i=2}^{|R|} \frac{rel_i}{\log_2(i + 1)} \]
Args:
retrieved_elements (list): List of retrieved elements
relevant_elements (list): List of relevant elements
k (int): 1-based index of the maximum element in retrieved_elements
taken in the computation
Note: The vector `retrieved_elements` is truncated at first, THEN
deduplication is done, keeping only the first occurence of each element.
Returns:
DCG value
"""
retrieved_elements = __get_unique(retrieved_elements[:k])
relevant_elements = __get_unique(relevant_elements)
if len(retrieved_elements) == 0 or len(relevant_elements) == 0:
return 0.0
# Computes an ordered vector of 1.0 and 0.0
score = [float(el in relevant_elements) for el in retrieved_elements]
# return score[0] + np.sum(score[1:] / np.log2(
# 1 + np.arange(2, len(score) + 1)))
return np.sum(score / np.log2(1 + np.arange(1, len(score) + 1)))
def ndcg(relevant_elements, retrieved_elements, k, *args, **kwargs):
"""Compute the Normalized Discounted Cumulative Gain.
Rewards elements being retrieved in descending order of relevance.
The metric is determined by calculating the DCG and dividing it by the
ideal or optimal DCG in the case that all recommended tracks are relevant.
Note:
The ideal DCG or IDCG is on our case equal to:
\[ IDCG = 1+\sum_{i=2}^{min(\left| G \right|, k)}\frac{1}{\log_2(i +1)}\]
If the size of the set intersection of \( G \) and \( R \), is empty, then
the IDCG is equal to 0. The NDCG metric is now calculated as:
\[ NDCG = \frac{DCG}{IDCG + \delta} \]
with \( \delta \) a (very) small constant.
The vector `retrieved_elements` is truncated at first, THEN
deduplication is done, keeping only the first occurence of each element.
Args:
retrieved_elements (list): List of retrieved elements
relevant_elements (list): List of relevant elements
k (int): 1-based index of the maximum element in retrieved_elements
taken in the computation
Returns:
NDCG value
"""
# TODO: When https://github.com/scikit-learn/scikit-learn/pull/9951 is
# merged...
idcg = dcg(
relevant_elements, relevant_elements, min(k, len(relevant_elements)))
if idcg == 0:
raise ValueError("relevent_elements is empty, the metric is"
"not defined")
true_dcg = dcg(relevant_elements, retrieved_elements, k)
return true_dcg / idcg
def __get_unique(original_list):
"""Get only unique values of a list but keep the order of the first
occurence of each element
"""
return list(OrderedDict.fromkeys(original_list))
Metrics = namedtuple('Metrics', ['r_precision', 'ndcg', 'plex_clicks'])
# playlist extender clicks
def playlist_extender_clicks(targets, predictions, max_n_predictions=500):
# Assumes predictions are sorted by relevance
# First, cap the number of predictions
predictions = predictions[:max_n_predictions]
# Calculate metric
i = set(predictions).intersection(set(targets))
for index, t in enumerate(predictions):
for track in i:
if t == track:
return float(int(index / 10))
return float(max_n_predictions / 10.0 + 1)
# def compute all metrics
def get_all_metrics(targets, predictions, k):
return Metrics(r_precision(targets, predictions, k),
ndcg(targets, predictions, k),
playlist_extender_clicks(targets, predictions, k))
MetricsSummary = namedtuple('MetricsSummary', ['mean_r_precision',
'mean_ndcg',
'mean_plex_clicks',
'coverage'])
#java -jar RankLib-2.10.jar -train BigRecall-TrainingFile750-2080.txt -ranker 6 -metric2t NDCG@20 -save BigRecallTrain750-2080Model-1Trees-NDCG20-tc1-lr05-leaf5.txt -tree 1 -tc 1 -shrinkage 0.5 -leaf 5
#java -jar RankLib-2.10.jar -load BigRecallTrain750-2080Model-500Trees-NDCG20-tc1-lr05-leaf50.txt -rank BigRecallTestingFile750.txt -score BRScores750-2080Model-500Trees-NDCG20-tc1-lr05-leaf50.txt
#java -jar RankLib-2.10.jar -train BigRecall-TrainingFile750-2080.txt -ranker 6 -metric2t NDCG@20 -save BigRecallTrain750-2080Model-500Trees-NDCG20-tc1-lr05-leaf50.txt -tree 500 -tc 1 -shrinkage 0.5 -leaf 50
import os
TrainingFile='./Training/BigRecall-TrainingFile750-2080.txt'
TestingFile='./Training/BigRecallTestingFile750.txt'
trees=[500]
tcVals=[-1]
shrinkages=[0.5]
leaves= [50]
def createCommand(tree,tc,lr,leaf):
opModelFile= './Training/ModelsAndScores/BigRecallTrain750-2080Model-'+str(tree)+'Trees-NDCG20-tc'+str(tc)+'-lr'+str(lr).replace('.','')+'-leaf'+str(leaf)+'.txt'
trainCommand= 'java -jar ./Training/RankLib-2.10.jar -train ./Training/BigRecall-TrainingFile750-2080.txt -ranker 6 -metric2t NDCG@20 -silent -save '+ opModelFile+ ' -tree '+str(tree)+' -tc '+str(tc)+ ' -shrinkage '+str(lr)+ ' -leaf '+ str(leaf) +' -missingzero'
#BRScores750-2080Model-1Trees-NDCG20-tc1-lr05-leaf5.txt
opScoresFile='./Training/ModelsAndScores/BRScores750-2080Model-'+opModelFile.split('Model-')[1]
testCommand= 'java -jar ./Training/RankLib-2.10.jar -load '+opModelFile+' -rank ./Training/BigRecallTestingFile750.txt -score '+opScoresFile
return (opModelFile,trainCommand, opScoresFile, testCommand)
paramSweep=[]
for tree in trees:
for tc in tcVals:
for lr in shrinkages:
for leaf in leaves:
paramSweep.append(createCommand(tree,tc,lr,leaf))
import multiprocessing as mp
import codecs
import os
import subprocess
def ExecuteRanklib(execTuples):
try:
trainCommand=execTuples[1]
train= subprocess.check_output(trainCommand.split())
print train
print '----------'
scoreCommand=execTuples[3]
test=subprocess.check_output(scoreCommand.split())
print test
print '----------'
except:
print execTuples
pool = mp.Pool(processes=10)
pool.map(ExecuteRanklib, paramSweep)
TestFile='./Training/BigRecallTestingFile750.txt'
with open(TestFile) as f:
test = f.readlines()
PidTestTracks={}
for l in test:
pid=l.split()[1].split(':')[1].strip()
track=l.split('#')[1].strip()
PidTestTracks.setdefault(pid,[]).append(track)
###skip
import os
Meta1Resultspath='/home/ubuntu/SpotifyChallenge/notebooks/Reranking/TestingQueryResults/Meta1/'
Meta2Resultspath='/home/ubuntu/SpotifyChallenge/notebooks/Reranking/TestingQueryResults/Meta2/'
QEPRFResultspath='/home/ubuntu/SpotifyChallenge/notebooks/Reranking/TestingQueryResults/QEPRF750/'
Meta1Files=[Meta1Resultspath+x for x in os.listdir(Meta1Resultspath)]
Meta2Files=[Meta2Resultspath+x for x in os.listdir(Meta2Resultspath)]
QEPRFFiles=[QEPRFResultspath+x for x in os.listdir(QEPRFResultspath)]
###skip
import codecs
def parseMetaFiles(path):
playlistId=path.split('/')[-1].split('.op')[0]
with codecs.open(path, 'r', encoding='utf-8') as f:
lines = f.read().splitlines()
rank=0
resultSet=[]
for result in lines[1:]:
try:
rank=rank+1
splits=result.split('\t')
score = splits[0]
trackid= splits[1]
resultSet.append((rank,trackid,score))
except:
print result
return "QueryError"
return(playlistId,resultSet)
####skip
Meta1Op=[]
err1=[]
Meta2Op=[]
err2=[]
for f in Meta1Files:
res=parseMetaFiles(f)
if res !="QueryError":
Meta1Op.append(res)
else:
err1.append(f)
for f in Meta2Files:
res=parseMetaFiles(f)
if res !="QueryError":
Meta2Op.append(res)
else:
err2.append(f)
####skip
import codecs
def QEPRFParse(path):
playlistId=path.split('/')[-1].split('.op')[0]
with codecs.open(path, 'r', encoding='utf-8') as f:
lines = f.read().splitlines()
inputQueries=lines[0].split('# query: ')[1].split()
resultSet=[]
pairResults= lines[1].split(' #weight(')[2].split(') )')[0].split('" ')
rank=0
for result in pairResults[:-1]:
try:
rank=rank+1
splits=result.split('"')
score = splits[0].strip()
trackid= splits[1].strip()
resultSet.append((rank,trackid,score))
except:
print result
return "QueryError"
return(playlistId,inputQueries,resultSet)
###skip
QEPRFOp=[]
err3=[]
for f in QEPRFFiles:
res=QEPRFParse(f)
if res !="QueryError":
QEPRFOp.append(res)
else:
err3.append(f)
###skip
import pickle
pidTrackMapping=pickle.load(open('./BiPartites/AllDataPidTrackListBipartite.pkl','rb'))
####skip
import pickle
import os
import codecs
from random import shuffle
pkl = os.listdir('./SplitsInformation/')
count=0
DS={}
for fpkl in pkl:
if fpkl in ['testing25RandPid.pkl', 'testing25Pid.pkl', 'testing1Pid.pkl', 'testing100Pid.pkl', 'testing10Pid.pkl', 'testing5Pid.pkl', 'testing100RandPid.pkl']:
testType=fpkl.replace('.pkl','')
if 'Rand' in fpkl:
listLen=int(fpkl.split('testing')[1].split('Rand')[0])
qtype='Rand'
else :
listLen=int(fpkl.split('testing')[1].split('Pid')[0])
qtype='Normal'
testingPids=pickle.load(open('./SplitsInformation/'+fpkl,'rb'))
for pid in testingPids:
pid=str(pid)
referenceSet=[x.replace('spotify:track:','') for x in pidTrackMapping[pid]]
DS[pid]=(testType,qtype,listLen,referenceSet)
####skip
import pickle
import os
import codecs
from random import shuffle
pkl = os.listdir('./SplitsInformation/')
testingTitleonlyPids=[]
for fpkl in pkl:
if fpkl =='testingOnlyTitlePid.pkl':
testType=fpkl.replace('.pkl','')
listLen=0
qtype='Normal'
testingPids=pickle.load(open('./SplitsInformation/'+fpkl,'rb'))
for pid in testingPids:
pid=str(pid)
referenceSet=[x.replace('spotify:track:','') for x in pidTrackMapping[pid]]
DS[pid]=(testType,qtype,listLen,referenceSet)
testingTitleonlyPids=[str(x) for x in testingPids]
from collections import defaultdict
from random import shuffle
for comb in paramSweep:
scoresfile= comb[2]
with open(scoresfile) as f:
scores = f.readlines()
PidTracksScores={}
for l in scores:
pid=l.split()[0].strip()
trackScore=l.split()[2].strip()
PidTracksScores.setdefault(pid,[]).append(float(trackScore))
rerankedCandidates={}
for pid,tracksList in PidTestTracks.items():
scoresList=PidTracksScores[pid]
zippedPairs=zip(tracksList,scoresList)
shuffle(zippedPairs)
rerankedCandidates[pid]=[x[0] for x in sorted(zippedPairs, key=lambda x: x[1], reverse=True)]
####continue here
evalSets=[]
for pl in QEPRFOp:
plId=pl[0]
exposed=pl[1]
candidates=rerankedCandidates[plId]
candidates=[x for x in candidates if x not in exposed]
refVals= DS[plId]
testtype=refVals[0]
orderType=refVals[1]
exposedLen=refVals[2]
playlist=refVals[3]
if orderType=='Normal':
groundTruth=playlist[exposedLen:]
else:
groundTruth=[x for x in playlist if x not in exposed]
evalSets.append((groundTruth, candidates[:500], testtype, exposedLen))
for pl in Meta2Op:
plId=pl[0]
if plId in testingTitleonlyPids and plId in rerankedCandidates:
exposed=[]
candidates=rerankedCandidates[plId]
refVals= DS[plId]
testtype=refVals[0]
orderType=refVals[1]
exposedLen=refVals[2]
playlist=refVals[3]
groundTruth=playlist[exposedLen:]
evalSets.append((groundTruth, candidates[:500], testtype, exposedLen))
####continue here
'''
r_precision(targets, predictions, k),
ndcg(targets, predictions, k),
playlist_extender_clicks(targets, predictions, k)
'''
indivSumsCounts= defaultdict(int)
indivSumsRecall = defaultdict(int)
indivSumsNdcg = defaultdict(int)
indivSumsRprec = defaultdict(int)
indivSumsClicks = defaultdict(int)
globalNdcg=0
globalRprec=0
globalClicks=0
globalRecall=0
count=0
for evalTuple in evalSets:
targets=evalTuple[0]
predictions=evalTuple[1]
testType=evalTuple[2]
tupNdcg=ndcg(targets,predictions,500)
tuprprec=r_precision(targets,predictions,500)
tupClicks=playlist_extender_clicks(targets,predictions,500)
globalNdcg+=tupNdcg
indivSumsNdcg[testType]+=tupNdcg
globalRprec+=tuprprec
indivSumsRprec[testType]+=tuprprec
globalClicks+=tupClicks
indivSumsClicks[testType]+=tupClicks
indivSumsCounts[testType]+=1
recallSetSize= len(set(predictions)&set(targets))
refSetSize=len(targets)
recall=recallSetSize*1.0/refSetSize
globalRecall+=recall
indivSumsRecall[testType]+=recall
count+=1
for k, v in indivSumsCounts.items():
indivSumsRecall[k]=indivSumsRecall[k]/v
indivSumsNdcg[k]=indivSumsNdcg[k]/v
indivSumsRprec[k]=indivSumsRprec[k]/v
indivSumsClicks[k]=indivSumsClicks[k]/v
print scoresfile , 'Recall:' , globalRecall/count,'NDCG:', globalNdcg/count, 'RPrec:', globalRprec/count,'Clicks:', globalClicks/count
Recall 0.5964542020518547,
NDCG 0.30332032798678032,
RPrec 0.12934009424035461,
Clicks 5.1286
```
|
github_jupyter
|
# Implementing a CGAN for the Iris data set to generate synthetic data
### Import necessary modules and packages
```
import os
while os.path.basename(os.getcwd()) != 'Synthetic_Data_GAN_Capstone':
os.chdir('..')
from utils.utils import *
safe_mkdir('experiments')
from utils.data_loading import load_raw_dataset
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import torch
import torch.nn as nn
import torch.optim as optim
from torch.autograd import Variable
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from models.VGAN import VGAN_Generator, VGAN_Discriminator
from models.CGAN_iris import CGAN_Generator, CGAN_Discriminator
import random
```
### Set random seed for reproducibility
```
manualSeed = 999
print("Random Seed: ", manualSeed)
random.seed(manualSeed)
torch.manual_seed(manualSeed)
```
### Import and briefly inspect data
```
iris = load_raw_dataset('iris')
iris.head()
```
### Preprocessing data
Split 50-50 so we can demonstrate the effectiveness of additional data
```
x_train, x_test, y_train, y_test = train_test_split(iris.drop(columns='species'), iris.species, test_size=0.5, stratify=iris.species, random_state=manualSeed)
print("x_train:", x_train.shape)
print("x_test:", x_test.shape)
```
### Model parameters (feel free to play with these)
```
nz = 32 # Size of generator noise input
H = 16 # Size of hidden network layer
out_dim = x_train.shape[1] # Size of output
bs = x_train.shape[0] # Full data set
nc = 3 # 3 different types of label in this problem
num_batches = 1
num_epochs = 10000
exp_name = 'experiments/iris_1x16'
safe_mkdir(exp_name)
```
### Adam optimizer hyperparameters
I set these based on the original paper, but feel free to play with them as well.
```
lr = 2e-4
beta1 = 0.5
beta2 = 0.999
```
### Set the device
```
device = torch.device("cuda:0" if (torch.cuda.is_available()) else "cpu")
```
### Scale continuous inputs for neural networks
```
scaler = StandardScaler()
x_train = scaler.fit_transform(x_train)
x_train_tensor = torch.tensor(x_train, dtype=torch.float)
y_train_dummies = pd.get_dummies(y_train)
y_train_dummies_tensor = torch.tensor(y_train_dummies.values, dtype=torch.float)
```
### Instantiate nets
```
netG = CGAN_Generator(nz=nz, H=H, out_dim=out_dim, nc=nc, bs=bs, lr=lr, beta1=beta1, beta2=beta2).to(device)
netD = CGAN_Discriminator(H=H, out_dim=out_dim, nc=nc, lr=lr, beta1=beta1, beta2=beta2).to(device)
```
### Print models
I chose to avoid using sequential mode in case I wanted to create non-sequential networks, it is more flexible in my opinion, but does not print out as nicely
```
print(netG)
print(netD)
```
### Define labels
```
real_label = 1
fake_label = 0
```
### Training Loop
Look through the comments to better understand the steps that are taking place
```
print("Starting Training Loop...")
for epoch in range(num_epochs):
for i in range(num_batches): # Only one batch per epoch since our data is horrifically small
# Update Discriminator
# All real batch first
real_data = x_train_tensor.to(device) # Format batch (entire data set in this case)
real_classes = y_train_dummies_tensor.to(device)
label = torch.full((bs,), real_label, device=device) # All real labels
output = netD(real_data, real_classes).view(-1) # Forward pass with real data through Discriminator
netD.train_one_step_real(output, label)
# All fake batch next
noise = torch.randn(bs, nz, device=device) # Generate batch of latent vectors
fake = netG(noise, real_classes) # Fake image batch with netG
label.fill_(fake_label)
output = netD(fake.detach(), real_classes).view(-1)
netD.train_one_step_fake(output, label)
netD.combine_and_update_opt()
netD.update_history()
# Update Generator
label.fill_(real_label) # Reverse labels, fakes are real for generator cost
output = netD(fake, real_classes).view(-1) # Since D has been updated, perform another forward pass of all-fakes through D
netG.train_one_step(output, label)
netG.update_history()
# Output training stats
if epoch % 1000 == 0 or (epoch == num_epochs-1):
print('[%d/%d]\tLoss_D: %.4f\tLoss_G: %.4f\tD(x): %.4f\tD(G(z)): %.4f / %.4f'
% (epoch+1, num_epochs, netD.loss.item(), netG.loss.item(), netD.D_x, netD.D_G_z1, netG.D_G_z2))
with torch.no_grad():
fake = netG(netG.fixed_noise, real_classes).detach().cpu()
netG.fixed_noise_outputs.append(scaler.inverse_transform(fake))
print("Training Complete")
```
### Output diagnostic plots tracking training progress and statistics
```
%matplotlib inline
training_plots(netD=netD, netG=netG, num_epochs=num_epochs, save=exp_name)
plot_layer_scatters(netG, title="Generator", save=exp_name)
plot_layer_scatters(netD, title="Discriminator", save=exp_name)
```
It looks like training stabilized fairly quickly, after only a few thousand iterations. The fact that the weight norm increased over time probably means that this network would benefit from some regularization.
### Compare performance of training on fake data versus real data
In this next section, we will lightly tune two models via cross-validation. The first model will be trained on the 75 real training data examples and tested on the remaining 75 testing data examples, whereas the second set of models will be trained on different amounts of generated data (no real data involved whatsoever). We will then compare performance and plot some graphs to evaluate our CGAN.
```
y_test_dummies = pd.get_dummies(y_test)
print("Dummy columns match?", all(y_train_dummies.columns == y_test_dummies.columns))
x_test = scaler.transform(x_test)
labels_list = [x for x in y_train_dummies.columns]
param_grid = {'tol': [1e-9, 1e-8, 1e-7, 1e-6, 1e-5],
'C': [0.5, 0.75, 1, 1.25],
'l1_ratio': [0, 0.25, 0.5, 0.75, 1]}
```
### Train on real data
```
model_real, score_real = train_test_logistic_reg(x_train, y_train, x_test, y_test, param_grid=param_grid, cv=5, random_state=manualSeed, labels=labels_list)
```
### Train on various levels of fake data
```
test_range = [75, 150, 300, 600, 1200]
fake_bs = bs
fake_models = []
fake_scores = []
for size in test_range:
num_batches = size // fake_bs + 1
genned_data = np.empty((0, out_dim))
genned_labels = np.empty(0)
rem = size
while rem > 0:
curr_size = min(fake_bs, rem)
noise = torch.randn(curr_size, nz, device=device)
fake_labels, output_labels = gen_labels(size=curr_size, num_classes=nc, labels_list=labels_list)
fake_labels = fake_labels.to(device)
rem -= curr_size
fake_data = netG(noise, fake_labels).cpu().detach().numpy()
genned_data = np.concatenate((genned_data, fake_data))
genned_labels = np.concatenate((genned_labels, output_labels))
print("For size of:", size)
model_fake_tmp, score_fake_tmp = train_test_logistic_reg(genned_data, genned_labels, x_test, y_test,
param_grid=param_grid, cv=5, random_state=manualSeed, labels=labels_list)
fake_models.append(model_fake_tmp)
fake_scores.append(score_fake_tmp)
```
Well, it looks like this experiment was a success. The models trained on fake data were actually able to outperform models trained on real data, which supports the belief that the CGAN is able to understand the distribution of the data it was trained on and generate meaningful examples that can be used to add additional information to the model.
Let's visualize some of the distributions of outputs to get a better idea of what took place
```
iris_plot_scatters(genned_data, genned_labels, "Fake Data", scaler, alpha=0.5, save=exp_name) # Fake data
iris_plot_scatters(iris.drop(columns='species'), np.array(iris.species), "Full Real Data Set", alpha=0.5, save=exp_name) # All real data
iris_plot_densities(genned_data, genned_labels, "Fake Data", scaler, save=exp_name) # Fake data
iris_plot_densities(iris.drop(columns='species'), np.array(iris.species), "Full Real Data Set", save=exp_name) # All real data
plot_scatter_matrix(genned_data, "Fake Data", iris.drop(columns='species'), scaler=scaler, save=exp_name)
plot_scatter_matrix(iris.drop(columns='species'), "Real Data", iris.drop(columns='species'), scaler=None, save=exp_name)
```
Finally, I present a summary of the test results ran above
```
fake_data_training_plots(real_range=bs, score_real=score_real, test_range=test_range, fake_scores=fake_scores, save=exp_name)
```
|
github_jupyter
|
```
import qiskit
import numpy as np, matplotlib.pyplot as plt
import sys
sys.path.insert(1, '../')
import qtm.base, qtm.constant, qtm.nqubit, qtm.onequbit, qtm.fubini_study
num_qubits = 3
num_layers = 2
psi = 2*np.random.rand(2**num_qubits)-1
psi = psi / np.linalg.norm(psi)
qc_origin = qiskit.QuantumCircuit(num_qubits, num_qubits)
qc_origin.initialize(psi, range(0, num_qubits))
thetas_origin = np.ones((num_layers*num_qubits*3))
qc = qc_origin.copy()
thetas = thetas_origin.copy()
thetas, loss_values_sgd = qtm.base.fit(
qc, num_steps = 100, thetas = thetas,
create_circuit_func = qtm.nqubit.u_cluster_nlayer_nqubit,
grad_func = qtm.base.grad_loss,
loss_func = qtm.base.loss_basis,
optimizer = qtm.base.sgd,
verbose = 1,
num_layers = num_layers
)
qc = qc_origin.copy()
thetas = thetas_origin.copy()
thetas, loss_values_adam = qtm.base.fit(
qc, num_steps = 100, thetas = thetas,
create_circuit_func = qtm.nqubit.u_cluster_nlayer_nqubit,
grad_func = qtm.base.grad_loss,
loss_func = qtm.base.loss_basis,
optimizer = qtm.base.adam,
verbose = 1,
num_layers = num_layers
)
qc = qc_origin.copy()
thetas = thetas_origin.copy()
thetas, loss_values_qfsm = qtm.base.fit(
qc, num_steps = 100, thetas = thetas,
create_circuit_func = qtm.nqubit.u_cluster_nlayer_nqubit,
grad_func = qtm.base.grad_loss,
loss_func = qtm.base.loss_basis,
optimizer = qtm.base.qng_fubini_study,
verbose = 1,
num_layers = num_layers
)
qc = qc_origin.copy()
thetas = thetas_origin.copy()
thetas, loss_values_qfim = qtm.base.fit(
qc, num_steps = 100, thetas = thetas,
create_circuit_func = qtm.nqubit.u_cluster_nlayer_nqubit,
grad_func = qtm.base.grad_loss,
loss_func = qtm.base.loss_basis,
optimizer = qtm.base.qng_qfim,
verbose = 1,
num_layers = num_layers
)
qc = qc_origin.copy()
thetas = thetas_origin.copy()
thetas, loss_values_adam_qfim = qtm.base.fit(
qc, num_steps = 100, thetas = thetas,
create_circuit_func = qtm.nqubit.u_cluster_nlayer_nqubit,
grad_func = qtm.base.grad_loss,
loss_func = qtm.base.loss_basis,
optimizer = qtm.base.qng_adam,
verbose = 1,
num_layers = num_layers
)
plt.plot(loss_values_sgd, label="SGD")
plt.plot(loss_values_adam, label="Adam")
plt.plot(loss_values_qfsm, label="QNG-QFSM")
plt.plot(loss_values_qfim, label="QNG-QFIM")
plt.plot(loss_values_adam_qfim, label="Adam QNG-QFIM")
plt.xlabel("Step")
plt.ylabel("Cost value")
plt.ylim(-0.05, 1.05)
plt.legend(prop={'size': 8}, loc=1)
plt.savefig(str(num_qubits) + '.svg', format='svg')
plt.show()
```
|
github_jupyter
|
# Collaborative Filtering on Google Analytics Data
### Learning objectives
1. Prepare the user-item matrix and use it with WALS.
2. Train a `WALSMatrixFactorization` within TensorFlow locally and on AI Platform.
3. Visualize the embedding vectors with principal components analysis.
## Overview
This notebook demonstrates how to implement a WALS matrix refactorization approach to do collaborative filtering.
Each learning objective will correspond to a __#TODO__ in the [student lab notebook](../labs/wals.ipynb) -- try to complete that notebook first before reviewing this solution notebook.
```
import os
PROJECT = "cloud-training-demos" # REPLACE WITH YOUR PROJECT ID
BUCKET = "cloud-training-demos-ml" # REPLACE WITH YOUR BUCKET NAME
REGION = "us-central1" # REPLACE WITH YOUR BUCKET REGION e.g. us-central1
# Do not change these
os.environ["PROJECT"] = PROJECT
os.environ["BUCKET"] = BUCKET
os.environ["REGION"] = REGION
os.environ["TFVERSION"] = "1.15"
%%bash
gcloud config set project $PROJECT
gcloud config set compute/region $REGION
import tensorflow as tf
print(tf.__version__)
```
## Create raw dataset
<p>
For collaborative filtering, you don't need to know anything about either the users or the content. Essentially, all you need to know is userId, itemId, and rating that the particular user gave the particular item.
<p>
In this case, you are working with newspaper articles. The company doesn't ask their users to rate the articles. However, you can use the time-spent on the page as a proxy for rating.
<p>
Normally, you would also add a time filter to this ("latest 7 days"), but your dataset is itself limited to a few days.
```
from google.cloud import bigquery
bq = bigquery.Client(project = PROJECT)
sql = """
WITH CTE_visitor_page_content AS (
SELECT
# Schema: https://support.google.com/analytics/answer/3437719?hl=en
# For a completely unique visit-session ID, you combine combination of fullVisitorId and visitNumber:
CONCAT(fullVisitorID,'-',CAST(visitNumber AS STRING)) AS visitorId,
(SELECT MAX(IF(index=10, value, NULL)) FROM UNNEST(hits.customDimensions)) AS latestContentId,
(LEAD(hits.time, 1) OVER (PARTITION BY fullVisitorId ORDER BY hits.time ASC) - hits.time) AS session_duration
FROM
`cloud-training-demos.GA360_test.ga_sessions_sample`,
UNNEST(hits) AS hits
WHERE
# only include hits on pages
hits.type = "PAGE"
GROUP BY
fullVisitorId,
visitNumber,
latestContentId,
hits.time )
-- Aggregate web stats
SELECT
visitorId,
latestContentId as contentId,
SUM(session_duration) AS session_duration
FROM
CTE_visitor_page_content
WHERE
latestContentId IS NOT NULL
GROUP BY
visitorId,
latestContentId
HAVING
session_duration > 0
"""
df = bq.query(sql).to_dataframe()
df.head()
stats = df.describe()
stats
df[["session_duration"]].plot(kind="hist", logy=True, bins=100, figsize=[8,5])
# The rating is the session_duration scaled to be in the range 0-1. This will help with training.
median = stats.loc["50%", "session_duration"]
df["rating"] = 0.3 * df["session_duration"] / median
df.loc[df["rating"] > 1, "rating"] = 1
df[["rating"]].plot(kind="hist", logy=True, bins=100, figsize=[8,5])
del df["session_duration"]
%%bash
rm -rf data
mkdir data
# TODO 1: Write object to a comma-separated values (csv) file.
df.to_csv(path_or_buf = "data/collab_raw.csv", index = False, header = False)
!head data/collab_raw.csv
```
## Create dataset for WALS
<p>
The raw dataset (above) won't work for WALS:
<ol>
<li> The userId and itemId have to be 0,1,2 ... so you need to create a mapping from visitorId (in the raw data) to userId and contentId (in the raw data) to itemId.
<li> You will need to save the above mapping to a file because at prediction time, you'll need to know how to map the contentId in the table above to the itemId.
<li> You'll need two files: a "rows" dataset where all the items for a particular user are listed; and a "columns" dataset where all the users for a particular item are listed.
</ol>
<p>
### Mapping
```
import pandas as pd
import numpy as np
def create_mapping(values, filename):
with open(filename, 'w') as ofp:
value_to_id = {value:idx for idx, value in enumerate(values.unique())}
for value, idx in value_to_id.items():
ofp.write("{},{}\n".format(value, idx))
return value_to_id
df = pd.read_csv(filepath_or_buffer = "data/collab_raw.csv",
header = None,
names = ["visitorId", "contentId", "rating"],
dtype = {"visitorId": str, "contentId": str, "rating": np.float})
df.to_csv(path_or_buf = "data/collab_raw.csv", index = False, header = False)
user_mapping = create_mapping(df["visitorId"], "data/users.csv")
item_mapping = create_mapping(df["contentId"], "data/items.csv")
!head -3 data/*.csv
df["userId"] = df["visitorId"].map(user_mapping.get)
df["itemId"] = df["contentId"].map(item_mapping.get)
mapped_df = df[["userId", "itemId", "rating"]]
mapped_df.to_csv(path_or_buf = "data/collab_mapped.csv", index = False, header = False)
mapped_df.head()
```
### Creating rows and columns datasets
```
import pandas as pd
import numpy as np
mapped_df = pd.read_csv(filepath_or_buffer = "data/collab_mapped.csv", header = None, names = ["userId", "itemId", "rating"])
mapped_df.head()
NITEMS = np.max(mapped_df["itemId"]) + 1
NUSERS = np.max(mapped_df["userId"]) + 1
mapped_df["rating"] = np.round(mapped_df["rating"].values, 2)
print("{} items, {} users, {} interactions".format( NITEMS, NUSERS, len(mapped_df) ))
grouped_by_items = mapped_df.groupby("itemId")
iter = 0
for item, grouped in grouped_by_items:
print(item, grouped["userId"].values, grouped["rating"].values)
iter = iter + 1
if iter > 5:
break
import tensorflow as tf
grouped_by_items = mapped_df.groupby("itemId")
with tf.python_io.TFRecordWriter("data/users_for_item") as ofp:
for item, grouped in grouped_by_items:
example = tf.train.Example(features = tf.train.Features(feature = {
"key": tf.train.Feature(int64_list = tf.train.Int64List(value = [item])),
"indices": tf.train.Feature(int64_list = tf.train.Int64List(value = grouped["userId"].values)),
"values": tf.train.Feature(float_list = tf.train.FloatList(value = grouped["rating"].values))
}))
ofp.write(example.SerializeToString())
grouped_by_users = mapped_df.groupby("userId")
with tf.python_io.TFRecordWriter("data/items_for_user") as ofp:
for user, grouped in grouped_by_users:
example = tf.train.Example(features = tf.train.Features(feature = {
"key": tf.train.Feature(int64_list = tf.train.Int64List(value = [user])),
"indices": tf.train.Feature(int64_list = tf.train.Int64List(value = grouped["itemId"].values)),
"values": tf.train.Feature(float_list = tf.train.FloatList(value = grouped["rating"].values))
}))
ofp.write(example.SerializeToString())
!ls -lrt data
```
To summarize, you created the following data files from collab_raw.csv:
<ol>
<li> ```collab_mapped.csv``` is essentially the same data as in ```collab_raw.csv``` except that ```visitorId``` and ```contentId``` which are business-specific have been mapped to ```userId``` and ```itemId``` which are enumerated in 0,1,2,.... The mappings themselves are stored in ```items.csv``` and ```users.csv``` so that they can be used during inference.
<li> ```users_for_item``` contains all the users/ratings for each item in TFExample format
<li> ```items_for_user``` contains all the items/ratings for each user in TFExample format
</ol>
## Train with WALS
Once you have the dataset, do matrix factorization with WALS using the [WALSMatrixFactorization](https://www.tensorflow.org/versions/r1.15/api_docs/python/tf/contrib/factorization/WALSMatrixFactorization) in the contrib directory.
This is an estimator model, so it should be relatively familiar.
<p>
As usual, you write an input_fn to provide the data to the model, and then create the Estimator to do train_and_evaluate.
Because it is in contrib and hasn't moved over to tf.estimator yet, you use tf.contrib.learn.Experiment to handle the training loop.<p>
```
import os
import tensorflow as tf
from tensorflow.python.lib.io import file_io
from tensorflow.contrib.factorization import WALSMatrixFactorization
def read_dataset(mode, args):
# TODO 2: Decode the example
def decode_example(protos, vocab_size):
features = {
"key": tf.FixedLenFeature(shape = [1], dtype = tf.int64),
"indices": tf.VarLenFeature(dtype = tf.int64),
"values": tf.VarLenFeature(dtype = tf.float32)}
parsed_features = tf.parse_single_example(serialized = protos, features = features)
values = tf.sparse_merge(sp_ids = parsed_features["indices"], sp_values = parsed_features["values"], vocab_size = vocab_size)
# Save key to remap after batching
# This is a temporary workaround to assign correct row numbers in each batch.
# You can ignore details of this part and remap_keys().
key = parsed_features["key"]
decoded_sparse_tensor = tf.SparseTensor(indices = tf.concat(values = [values.indices, [key]], axis = 0),
values = tf.concat(values = [values.values, [0.0]], axis = 0),
dense_shape = values.dense_shape)
return decoded_sparse_tensor
def remap_keys(sparse_tensor):
# Current indices of your SparseTensor that you need to fix
bad_indices = sparse_tensor.indices # shape = (current_batch_size * (number_of_items/users[i] + 1), 2)
# Current values of your SparseTensor that you need to fix
bad_values = sparse_tensor.values # shape = (current_batch_size * (number_of_items/users[i] + 1),)
# Since batch is ordered, the last value for a batch index is the user
# Find where the batch index chages to extract the user rows
# 1 where user, else 0
user_mask = tf.concat(values = [bad_indices[1:,0] - bad_indices[:-1,0], tf.constant(value = [1], dtype = tf.int64)], axis = 0) # shape = (current_batch_size * (number_of_items/users[i] + 1), 2)
# Mask out the user rows from the values
good_values = tf.boolean_mask(tensor = bad_values, mask = tf.equal(x = user_mask, y = 0)) # shape = (current_batch_size * number_of_items/users[i],)
item_indices = tf.boolean_mask(tensor = bad_indices, mask = tf.equal(x = user_mask, y = 0)) # shape = (current_batch_size * number_of_items/users[i],)
user_indices = tf.boolean_mask(tensor = bad_indices, mask = tf.equal(x = user_mask, y = 1))[:, 1] # shape = (current_batch_size,)
good_user_indices = tf.gather(params = user_indices, indices = item_indices[:,0]) # shape = (current_batch_size * number_of_items/users[i],)
# User and item indices are rank 1, need to make rank 1 to concat
good_user_indices_expanded = tf.expand_dims(input = good_user_indices, axis = -1) # shape = (current_batch_size * number_of_items/users[i], 1)
good_item_indices_expanded = tf.expand_dims(input = item_indices[:, 1], axis = -1) # shape = (current_batch_size * number_of_items/users[i], 1)
good_indices = tf.concat(values = [good_user_indices_expanded, good_item_indices_expanded], axis = 1) # shape = (current_batch_size * number_of_items/users[i], 2)
remapped_sparse_tensor = tf.SparseTensor(indices = good_indices, values = good_values, dense_shape = sparse_tensor.dense_shape)
return remapped_sparse_tensor
def parse_tfrecords(filename, vocab_size):
if mode == tf.estimator.ModeKeys.TRAIN:
num_epochs = None # indefinitely
else:
num_epochs = 1 # end-of-input after this
files = tf.gfile.Glob(filename = os.path.join(args["input_path"], filename))
# Create dataset from file list
dataset = tf.data.TFRecordDataset(files)
dataset = dataset.map(map_func = lambda x: decode_example(x, vocab_size))
dataset = dataset.repeat(count = num_epochs)
dataset = dataset.batch(batch_size = args["batch_size"])
dataset = dataset.map(map_func = lambda x: remap_keys(x))
return dataset.make_one_shot_iterator().get_next()
def _input_fn():
features = {
WALSMatrixFactorization.INPUT_ROWS: parse_tfrecords("items_for_user", args["nitems"]),
WALSMatrixFactorization.INPUT_COLS: parse_tfrecords("users_for_item", args["nusers"]),
WALSMatrixFactorization.PROJECT_ROW: tf.constant(True)
}
return features, None
return _input_fn
```
This code is helpful in developing the input function. You don't need it in production.
```
def try_out():
with tf.Session() as sess:
fn = read_dataset(
mode = tf.estimator.ModeKeys.EVAL,
args = {"input_path": "data", "batch_size": 4, "nitems": NITEMS, "nusers": NUSERS})
feats, _ = fn()
print(feats["input_rows"].eval())
print(feats["input_rows"].eval())
try_out()
def find_top_k(user, item_factors, k):
all_items = tf.matmul(a = tf.expand_dims(input = user, axis = 0), b = tf.transpose(a = item_factors))
topk = tf.nn.top_k(input = all_items, k = k)
return tf.cast(x = topk.indices, dtype = tf.int64)
def batch_predict(args):
import numpy as np
with tf.Session() as sess:
estimator = tf.contrib.factorization.WALSMatrixFactorization(
num_rows = args["nusers"],
num_cols = args["nitems"],
embedding_dimension = args["n_embeds"],
model_dir = args["output_dir"])
# This is how you would get the row factors for out-of-vocab user data
# row_factors = list(estimator.get_projections(input_fn=read_dataset(tf.estimator.ModeKeys.EVAL, args)))
# user_factors = tf.convert_to_tensor(np.array(row_factors))
# But for in-vocab data, the row factors are already in the checkpoint
user_factors = tf.convert_to_tensor(value = estimator.get_row_factors()[0]) # (nusers, nembeds)
# In either case, you have to assume catalog doesn"t change, so col_factors are read in
item_factors = tf.convert_to_tensor(value = estimator.get_col_factors()[0])# (nitems, nembeds)
# For each user, find the top K items
topk = tf.squeeze(input = tf.map_fn(fn = lambda user: find_top_k(user, item_factors, args["topk"]), elems = user_factors, dtype = tf.int64))
with file_io.FileIO(os.path.join(args["output_dir"], "batch_pred.txt"), mode = 'w') as f:
for best_items_for_user in topk.eval():
f.write(",".join(str(x) for x in best_items_for_user) + '\n')
def train_and_evaluate(args):
train_steps = int(0.5 + (1.0 * args["num_epochs"] * args["nusers"]) / args["batch_size"])
steps_in_epoch = int(0.5 + args["nusers"] / args["batch_size"])
print("Will train for {} steps, evaluating once every {} steps".format(train_steps, steps_in_epoch))
def experiment_fn(output_dir):
return tf.contrib.learn.Experiment(
tf.contrib.factorization.WALSMatrixFactorization(
num_rows = args["nusers"],
num_cols = args["nitems"],
embedding_dimension = args["n_embeds"],
model_dir = args["output_dir"]),
train_input_fn = read_dataset(tf.estimator.ModeKeys.TRAIN, args),
eval_input_fn = read_dataset(tf.estimator.ModeKeys.EVAL, args),
train_steps = train_steps,
eval_steps = 1,
min_eval_frequency = steps_in_epoch
)
from tensorflow.contrib.learn.python.learn import learn_runner
learn_runner.run(experiment_fn = experiment_fn, output_dir = args["output_dir"])
batch_predict(args)
import shutil
shutil.rmtree(path = "wals_trained", ignore_errors=True)
train_and_evaluate({
"output_dir": "wals_trained",
"input_path": "data/",
"num_epochs": 0.05,
"nitems": NITEMS,
"nusers": NUSERS,
"batch_size": 512,
"n_embeds": 10,
"topk": 3
})
!ls wals_trained
!head wals_trained/batch_pred.txt
```
## Run as a Python module
Let's run it as Python module for just a few steps.
```
os.environ["NITEMS"] = str(NITEMS)
os.environ["NUSERS"] = str(NUSERS)
%%bash
rm -rf wals.tar.gz wals_trained
gcloud ai-platform local train \
--module-name=walsmodel.task \
--package-path=${PWD}/walsmodel \
-- \
--output_dir=${PWD}/wals_trained \
--input_path=${PWD}/data \
--num_epochs=0.01 --nitems=${NITEMS} --nusers=${NUSERS} \
--job-dir=./tmp
```
## Run on Cloud
```
%%bash
gsutil -m cp data/* gs://${BUCKET}/wals/data
%%bash
OUTDIR=gs://${BUCKET}/wals/model_trained
JOBNAME=wals_$(date -u +%y%m%d_%H%M%S)
echo $OUTDIR $REGION $JOBNAME
gsutil -m rm -rf $OUTDIR
gcloud ai-platform jobs submit training $JOBNAME \
--region=$REGION \
--module-name=walsmodel.task \
--package-path=${PWD}/walsmodel \
--job-dir=$OUTDIR \
--staging-bucket=gs://$BUCKET \
--scale-tier=BASIC_GPU \
--runtime-version=$TFVERSION \
-- \
--output_dir=$OUTDIR \
--input_path=gs://${BUCKET}/wals/data \
--num_epochs=10 --nitems=${NITEMS} --nusers=${NUSERS}
```
This will take <b>10 minutes</b> to complete. Rerun the above command until the jobs gets submitted.
## Get row and column factors
Once you have a trained WALS model, you can get row and column factors (user and item embeddings) from the checkpoint file. You'll look at how to use these in the section on building a recommendation system using deep neural networks.
```
def get_factors(args):
with tf.Session() as sess:
estimator = tf.contrib.factorization.WALSMatrixFactorization(
num_rows = args["nusers"],
num_cols = args["nitems"],
embedding_dimension = args["n_embeds"],
model_dir = args["output_dir"])
row_factors = estimator.get_row_factors()[0]
col_factors = estimator.get_col_factors()[0]
return row_factors, col_factors
args = {
"output_dir": "gs://{}/wals/model_trained".format(BUCKET),
"nitems": NITEMS,
"nusers": NUSERS,
"n_embeds": 10
}
user_embeddings, item_embeddings = get_factors(args)
print(user_embeddings[:3])
print(item_embeddings[:3])
```
You can visualize the embedding vectors using dimensional reduction techniques such as PCA.
```
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from sklearn.decomposition import PCA
pca = PCA(n_components = 3)
pca.fit(user_embeddings)
# TODO 3: Apply the mapping (transform) to user embeddings
user_embeddings_pca = pca.transform(user_embeddings)
fig = plt.figure(figsize = (8,8))
ax = fig.add_subplot(111, projection = "3d")
xs, ys, zs = user_embeddings_pca[::150].T
ax.scatter(xs, ys, zs)
```
<pre>
# Copyright 2022 Google Inc. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# http://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
</pre>
|
github_jupyter
|
```
import numpy as np
from resonance.nonlinear_systems import SingleDoFNonLinearSystem
```
To apply arbitrary forcing to a single degree of freedom linear or nonlinear system, you can do so with `SingleDoFNonLinearSystem` (`SingleDoFLinearSystem` does not support arbitrary forcing...yet).
Add constants, a generalized coordinate, and a generalized speed to the system.
```
sys = SingleDoFNonLinearSystem()
sys.constants['m'] = 100 # kg
sys.constants['c'] = 1.1*1.2*0.5/2
sys.constants['k'] = 10
sys.constants['Fo'] = 1000 # N
sys.constants['Ft'] = 100 # N/s
sys.constants['to'] = 3.0 # s
sys.coordinates['x'] = 0.0
sys.speeds['v'] = 0.0
```
Create a function that evaluates the first order form of the non-linear equations of motion. In this case:
$$
\dot{x} = v \\
m\dot{v} + c \textrm{sgn}(v)v^2 + k \textrm{sgn}(x)x^2 = F(t)
$$
Make the arbitrary forcing term, $F$, an input to this function.
```
def eval_eom(x, v, m, c, k, F):
xdot = v
vdot = (F - np.sign(v)*c*v**2 - np.sign(x)*k*x**2) / m
return xdot, vdot
```
Note that you cannot add this to the system because `F` has not been defined.
```
sys.diff_eq_func = eval_eom
```
To rememdy this, create a function that returns the input value given the appropriate constants and time.
```
def eval_step_input(Fo, to, time):
if time < to:
return 0.0
else:
return Fo
import matplotlib.pyplot as plt
%matplotlib widget
ts = np.linspace(0, 10)
plt.plot(ts, eval_step_input(5.0, 3.0, ts))
ts < 3.0
def eval_step_input(Fo, to, time):
F = np.empty_like(time)
for i, ti in enumerate(time):
if ti < to:
F[i] = 0.0
else:
F[i] = Fo
return F
plt.plot(ts, eval_step_input(5.0, 3.0, ts))
eval_step_input(5.0, 3.0, ts)
eval_step_input(5.0, 3.0, 7.0)
def eval_step_input(Fo, to, time):
if np.isscalar(time):
if time < to:
return 0.0
else:
return Fo
else:
F = np.empty_like(time)
for i, ti in enumerate(time):
if ti < to:
F[i] = 0.0
else:
F[i] = Fo
return F
eval_step_input(5.0, 3.0, 7.0)
eval_step_input(5.0, 3.0, ts)
True * 5.0
False * 5.0
(ts >= 3.0)*5.0
(5.0 >= 3.0)*5.0
def eval_step_input(Fo, to, time):
return (time >=to)*Fo
eval_step_input(5.0, 3.0, ts)
eval_step_input(5.0, 3.0, 7.0)
sys.add_measurement('F', eval_step_input)
sys.diff_eq_func = eval_eom
traj = sys.free_response(20.0)
traj.plot(subplots=True)
def eval_ramp_input(Ft, to, time):
return (time >= to)*(Ft*time - Ft*to)
del sys.measurements['F']
sys.add_measurement('F', eval_ramp_input)
sys.measurements
traj = sys.free_response(20.0)
traj.plot(subplots=True)
```
|
github_jupyter
|
# Fit $k_{ij}$ and $r_c^{ABij}$ interactions parameter of Ethanol and CPME
This notebook has te purpose of showing how to optimize the $k_{ij}$ and $r_c^{ABij}$ for a mixture with induced association.
First it's needed to import the necessary modules
```
import numpy as np
from sgtpy import component, mixture, saftvrmie
from sgtpy.fit import fit_cross
```
Now that the functions are available it is necessary to create the mixture.
```
ethanol = component('ethanol2C', ms = 1.7728, sigma = 3.5592 , eps = 224.50,
lambda_r = 11.319, lambda_a = 6., eAB = 3018.05, rcAB = 0.3547,
rdAB = 0.4, sites = [1,0,1], cii= 5.3141080872882285e-20)
cpme = component('cpme', ms = 2.32521144, sigma = 4.13606074, eps = 343.91193798, lambda_r = 14.15484877,
lambda_a = 6.0, npol = 1.91990385,mupol = 1.27, sites =[0,0,1], cii = 3.5213681817448466e-19)
mix = mixture(ethanol, cpme)
```
Now the experimental equilibria data is read and a tuple is created. It includes the experimental liquid composition, vapor composition, equilibrium temperature and pressure. This is done with ```datavle = (Xexp, Yexp, Texp, Pexp)```
```
# Experimental data obtained from Mejia, Cartes, J. Chem. Eng. Data, vol. 64, no. 5, pp. 1970–1977, 2019
# Experimental temperature saturation in K
Texp = np.array([355.77, 346.42, 342.82, 340.41, 338.95, 337.78, 336.95, 336.29,
335.72, 335.3 , 334.92, 334.61, 334.35, 334.09, 333.92, 333.79,
333.72, 333.72, 333.81, 334.06, 334.58])
# Experimental pressure in Pa
Pexp = np.array([50000., 50000., 50000., 50000., 50000., 50000., 50000., 50000.,
50000., 50000., 50000., 50000., 50000., 50000., 50000., 50000.,
50000., 50000., 50000., 50000., 50000.])
# Experimental liquid composition
Xexp = np.array([[0. , 0.065, 0.11 , 0.161, 0.203, 0.253, 0.301, 0.351, 0.402,
0.446, 0.497, 0.541, 0.588, 0.643, 0.689, 0.743, 0.785, 0.837,
0.893, 0.947, 1. ],
[1. , 0.935, 0.89 , 0.839, 0.797, 0.747, 0.699, 0.649, 0.598,
0.554, 0.503, 0.459, 0.412, 0.357, 0.311, 0.257, 0.215, 0.163,
0.107, 0.053, 0. ]])
# Experimental vapor composition
Yexp = np.array([[0. , 0.302, 0.411, 0.48 , 0.527, 0.567, 0.592, 0.614, 0.642,
0.657, 0.678, 0.694, 0.71 , 0.737, 0.753, 0.781, 0.801, 0.837,
0.883, 0.929, 1. ],
[1. , 0.698, 0.589, 0.52 , 0.473, 0.433, 0.408, 0.386, 0.358,
0.343, 0.322, 0.306, 0.29 , 0.263, 0.247, 0.219, 0.199, 0.163,
0.117, 0.071, 0. ]])
datavle = (Xexp, Yexp, Texp, Pexp)
```
The function ```fit_cross``` optimize the $k_{ij}$ correction and $r_c^{ABij}$ distance. An initial guess is needed, as well as the mixture object, the index of the self-associating component and the equilibria data.
```
#initial guesses for kij and rcij
x0 = [0.01015194, 2.23153033]
fit_cross(x0, mix, assoc=0, datavle=datavle)
```
For more information just run:
```fit_cross?```
|
github_jupyter
|
# Mini Project: Temporal-Difference Methods
In this notebook, you will write your own implementations of many Temporal-Difference (TD) methods.
While we have provided some starter code, you are welcome to erase these hints and write your code from scratch.
### Part 0: Explore CliffWalkingEnv
Use the code cell below to create an instance of the [CliffWalking](https://github.com/openai/gym/blob/master/gym/envs/toy_text/cliffwalking.py) environment.
```
import gym
env = gym.make('CliffWalking-v0')
```
The agent moves through a $4\times 12$ gridworld, with states numbered as follows:
```
[[ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11],
[12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23],
[24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35],
[36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47]]
```
At the start of any episode, state `36` is the initial state. State `47` is the only terminal state, and the cliff corresponds to states `37` through `46`.
The agent has 4 potential actions:
```
UP = 0
RIGHT = 1
DOWN = 2
LEFT = 3
```
Thus, $\mathcal{S}^+=\{0, 1, \ldots, 47\}$, and $\mathcal{A} =\{0, 1, 2, 3\}$. Verify this by running the code cell below.
```
print(env.action_space)
print(env.observation_space)
```
In this mini-project, we will build towards finding the optimal policy for the CliffWalking environment. The optimal state-value function is visualized below. Please take the time now to make sure that you understand _why_ this is the optimal state-value function.
```
import numpy as np
from plot_utils import plot_values
# define the optimal state-value function
V_opt = np.zeros((4,12))
V_opt[0:13][0] = -np.arange(3, 15)[::-1]
V_opt[0:13][1] = -np.arange(3, 15)[::-1] + 1
V_opt[0:13][2] = -np.arange(3, 15)[::-1] + 2
V_opt[3][0] = -13
plot_values(V_opt)
```
### Part 1: TD Prediction: State Values
In this section, you will write your own implementation of TD prediction (for estimating the state-value function).
We will begin by investigating a policy where the agent moves:
- `RIGHT` in states `0` through `10`, inclusive,
- `DOWN` in states `11`, `23`, and `35`, and
- `UP` in states `12` through `22`, inclusive, states `24` through `34`, inclusive, and state `36`.
The policy is specified and printed below. Note that states where the agent does not choose an action have been marked with `-1`.
```
policy = np.hstack([1*np.ones(11), 2, 0, np.zeros(10), 2, 0, np.zeros(10), 2, 0, -1*np.ones(11)])
print("\nPolicy (UP = 0, RIGHT = 1, DOWN = 2, LEFT = 3, N/A = -1):")
print(policy.reshape(4,12))
```
Run the next cell to visualize the state-value function that corresponds to this policy. Make sure that you take the time to understand why this is the corresponding value function!
```
V_true = np.zeros((4,12))
for i in range(3):
V_true[0:12][i] = -np.arange(3, 15)[::-1] - i
V_true[1][11] = -2
V_true[2][11] = -1
V_true[3][0] = -17
plot_values(V_true)
```
The above figure is what you will try to approximate through the TD prediction algorithm.
Your algorithm for TD prediction has five arguments:
- `env`: This is an instance of an OpenAI Gym environment.
- `num_episodes`: This is the number of episodes that are generated through agent-environment interaction.
- `policy`: This is a 1D numpy array with `policy.shape` equal to the number of states (`env.nS`). `policy[s]` returns the action that the agent chooses when in state `s`.
- `alpha`: This is the step-size parameter for the update step.
- `gamma`: This is the discount rate. It must be a value between 0 and 1, inclusive (default value: `1`).
The algorithm returns as output:
- `V`: This is a dictionary where `V[s]` is the estimated value of state `s`.
Please complete the function in the code cell below.
```
from collections import defaultdict, deque
import sys
def td_prediction(env, num_episodes, policy, alpha, gamma=1.0):
# initialize empty dictionaries of floats
V = defaultdict(float)
# loop over episodes
for i_episode in range(1, num_episodes+1):
# monitor progress
if i_episode % 100 == 0:
print("\rEpisode {}/{}".format(i_episode, num_episodes), end="")
sys.stdout.flush()
# begin an episode, observe S
state = env.reset()
while True:
# choose action A
action = policy[state]
# take action A, observe R, S'
next_state, reward, done, info = env.step(action)
# perform updates
V[state] = V[state] + (alpha * (reward + (gamma * V[next_state]) - V[state]))
# S <- S'
state = next_state
# end episode if reached terminal state
if done:
break
return V
```
Run the code cell below to test your implementation and visualize the estimated state-value function. If the code cell returns **PASSED**, then you have implemented the function correctly! Feel free to change the `num_episodes` and `alpha` parameters that are supplied to the function. However, if you'd like to ensure the accuracy of the unit test, please do not change the value of `gamma` from the default.
```
import check_test
# evaluate the policy and reshape the state-value function
V_pred = td_prediction(env, 5000, policy, .01)
# please do not change the code below this line
V_pred_plot = np.reshape([V_pred[key] if key in V_pred else 0 for key in np.arange(48)], (4,12))
check_test.run_check('td_prediction_check', V_pred_plot)
plot_values(V_pred_plot)
```
How close is your estimated state-value function to the true state-value function corresponding to the policy?
You might notice that some of the state values are not estimated by the agent. This is because under this policy, the agent will not visit all of the states. In the TD prediction algorithm, the agent can only estimate the values corresponding to states that are visited.
### Part 2: TD Control: Sarsa
In this section, you will write your own implementation of the Sarsa control algorithm.
Your algorithm has four arguments:
- `env`: This is an instance of an OpenAI Gym environment.
- `num_episodes`: This is the number of episodes that are generated through agent-environment interaction.
- `alpha`: This is the step-size parameter for the update step.
- `gamma`: This is the discount rate. It must be a value between 0 and 1, inclusive (default value: `1`).
The algorithm returns as output:
- `Q`: This is a dictionary (of one-dimensional arrays) where `Q[s][a]` is the estimated action value corresponding to state `s` and action `a`.
Please complete the function in the code cell below.
(_Feel free to define additional functions to help you to organize your code._)
```
def update_Q(Qsa, Qsa_next, reward, alpha, gamma):
""" updates the action-value function estimate using the most recent time step """
return Qsa + (alpha * (reward + (gamma * Qsa_next) - Qsa))
def epsilon_greedy_probs(env, Q_s, i_episode, eps=None):
""" obtains the action probabilities corresponding to epsilon-greedy policy """
epsilon = 1.0 / i_episode
if eps is not None:
epsilon = eps
policy_s = np.ones(env.nA) * epsilon / env.nA
policy_s[np.argmax(Q_s)] = 1 - epsilon + (epsilon / env.nA)
return policy_s
import matplotlib.pyplot as plt
%matplotlib inline
def sarsa(env, num_episodes, alpha, gamma=1.0):
# initialize action-value function (empty dictionary of arrays)
Q = defaultdict(lambda: np.zeros(env.nA))
# initialize performance monitor
plot_every = 100
tmp_scores = deque(maxlen=plot_every)
scores = deque(maxlen=num_episodes)
# loop over episodes
for i_episode in range(1, num_episodes+1):
# monitor progress
if i_episode % 100 == 0:
print("\rEpisode {}/{}".format(i_episode, num_episodes), end="")
sys.stdout.flush()
# initialize score
score = 0
# begin an episode, observe S
state = env.reset()
# get epsilon-greedy action probabilities
policy_s = epsilon_greedy_probs(env, Q[state], i_episode)
# pick action A
action = np.random.choice(np.arange(env.nA), p=policy_s)
# limit number of time steps per episode
for t_step in np.arange(300):
# take action A, observe R, S'
next_state, reward, done, info = env.step(action)
# add reward to score
score += reward
if not done:
# get epsilon-greedy action probabilities
policy_s = epsilon_greedy_probs(env, Q[next_state], i_episode)
# pick next action A'
next_action = np.random.choice(np.arange(env.nA), p=policy_s)
# update TD estimate of Q
Q[state][action] = update_Q(Q[state][action], Q[next_state][next_action],
reward, alpha, gamma)
# S <- S'
state = next_state
# A <- A'
action = next_action
if done:
# update TD estimate of Q
Q[state][action] = update_Q(Q[state][action], 0, reward, alpha, gamma)
# append score
tmp_scores.append(score)
break
if (i_episode % plot_every == 0):
scores.append(np.mean(tmp_scores))
# plot performance
plt.plot(np.linspace(0,num_episodes,len(scores),endpoint=False),np.asarray(scores))
plt.xlabel('Episode Number')
plt.ylabel('Average Reward (Over Next %d Episodes)' % plot_every)
plt.show()
# print best 100-episode performance
print(('Best Average Reward over %d Episodes: ' % plot_every), np.max(scores))
return Q
```
Use the next code cell to visualize the **_estimated_** optimal policy and the corresponding state-value function.
If the code cell returns **PASSED**, then you have implemented the function correctly! Feel free to change the `num_episodes` and `alpha` parameters that are supplied to the function. However, if you'd like to ensure the accuracy of the unit test, please do not change the value of `gamma` from the default.
```
# obtain the estimated optimal policy and corresponding action-value function
Q_sarsa = sarsa(env, 5000, .01)
# print the estimated optimal policy
policy_sarsa = np.array([np.argmax(Q_sarsa[key]) if key in Q_sarsa else -1 for key in np.arange(48)]).reshape(4,12)
check_test.run_check('td_control_check', policy_sarsa)
print("\nEstimated Optimal Policy (UP = 0, RIGHT = 1, DOWN = 2, LEFT = 3, N/A = -1):")
print(policy_sarsa)
# plot the estimated optimal state-value function
V_sarsa = ([np.max(Q_sarsa[key]) if key in Q_sarsa else 0 for key in np.arange(48)])
plot_values(V_sarsa)
```
### Part 3: TD Control: Q-learning
In this section, you will write your own implementation of the Q-learning control algorithm.
Your algorithm has four arguments:
- `env`: This is an instance of an OpenAI Gym environment.
- `num_episodes`: This is the number of episodes that are generated through agent-environment interaction.
- `alpha`: This is the step-size parameter for the update step.
- `gamma`: This is the discount rate. It must be a value between 0 and 1, inclusive (default value: `1`).
The algorithm returns as output:
- `Q`: This is a dictionary (of one-dimensional arrays) where `Q[s][a]` is the estimated action value corresponding to state `s` and action `a`.
Please complete the function in the code cell below.
(_Feel free to define additional functions to help you to organize your code._)
```
def q_learning(env, num_episodes, alpha, gamma=1.0):
# initialize action-value function (empty dictionary of arrays)
Q = defaultdict(lambda: np.zeros(env.nA))
# initialize performance monitor
plot_every = 100
tmp_scores = deque(maxlen=plot_every)
scores = deque(maxlen=num_episodes)
# loop over episodes
for i_episode in range(1, num_episodes+1):
# monitor progress
if i_episode % 100 == 0:
print("\rEpisode {}/{}".format(i_episode, num_episodes), end="")
sys.stdout.flush()
# initialize score
score = 0
# begin an episode, observe S
state = env.reset()
while True:
# get epsilon-greedy action probabilities
policy_s = epsilon_greedy_probs(env, Q[state], i_episode)
# pick next action A
action = np.random.choice(np.arange(env.nA), p=policy_s)
# take action A, observe R, S'
next_state, reward, done, info = env.step(action)
# add reward to score
score += reward
# update Q
Q[state][action] = update_Q(Q[state][action], np.max(Q[next_state]), \
reward, alpha, gamma)
# S <- S'
state = next_state
# until S is terminal
if done:
# append score
tmp_scores.append(score)
break
if (i_episode % plot_every == 0):
scores.append(np.mean(tmp_scores))
# plot performance
plt.plot(np.linspace(0,num_episodes,len(scores),endpoint=False),np.asarray(scores))
plt.xlabel('Episode Number')
plt.ylabel('Average Reward (Over Next %d Episodes)' % plot_every)
plt.show()
# print best 100-episode performance
print(('Best Average Reward over %d Episodes: ' % plot_every), np.max(scores))
return Q
```
Use the next code cell to visualize the **_estimated_** optimal policy and the corresponding state-value function.
If the code cell returns **PASSED**, then you have implemented the function correctly! Feel free to change the `num_episodes` and `alpha` parameters that are supplied to the function. However, if you'd like to ensure the accuracy of the unit test, please do not change the value of `gamma` from the default.
```
# obtain the estimated optimal policy and corresponding action-value function
Q_sarsamax = q_learning(env, 5000, .01)
# print the estimated optimal policy
policy_sarsamax = np.array([np.argmax(Q_sarsamax[key]) if key in Q_sarsamax else -1 for key in np.arange(48)]).reshape((4,12))
check_test.run_check('td_control_check', policy_sarsamax)
print("\nEstimated Optimal Policy (UP = 0, RIGHT = 1, DOWN = 2, LEFT = 3, N/A = -1):")
print(policy_sarsamax)
# plot the estimated optimal state-value function
plot_values([np.max(Q_sarsamax[key]) if key in Q_sarsamax else 0 for key in np.arange(48)])
```
### Part 4: TD Control: Expected Sarsa
In this section, you will write your own implementation of the Expected Sarsa control algorithm.
Your algorithm has four arguments:
- `env`: This is an instance of an OpenAI Gym environment.
- `num_episodes`: This is the number of episodes that are generated through agent-environment interaction.
- `alpha`: This is the step-size parameter for the update step.
- `gamma`: This is the discount rate. It must be a value between 0 and 1, inclusive (default value: `1`).
The algorithm returns as output:
- `Q`: This is a dictionary (of one-dimensional arrays) where `Q[s][a]` is the estimated action value corresponding to state `s` and action `a`.
Please complete the function in the code cell below.
(_Feel free to define additional functions to help you to organize your code._)
```
def expected_sarsa(env, num_episodes, alpha, gamma=1.0):
# initialize action-value function (empty dictionary of arrays)
Q = defaultdict(lambda: np.zeros(env.nA))
# initialize performance monitor
plot_every = 100
tmp_scores = deque(maxlen=plot_every)
scores = deque(maxlen=num_episodes)
# loop over episodes
for i_episode in range(1, num_episodes+1):
# monitor progress
if i_episode % 100 == 0:
print("\rEpisode {}/{}".format(i_episode, num_episodes), end="")
sys.stdout.flush()
# initialize score
score = 0
# begin an episode
state = env.reset()
# get epsilon-greedy action probabilities
policy_s = epsilon_greedy_probs(env, Q[state], i_episode, 0.005)
while True:
# pick next action
action = np.random.choice(np.arange(env.nA), p=policy_s)
# take action A, observe R, S'
next_state, reward, done, info = env.step(action)
# add reward to score
score += reward
# get epsilon-greedy action probabilities (for S')
policy_s = epsilon_greedy_probs(env, Q[next_state], i_episode, 0.005)
# update Q
Q[state][action] = update_Q(Q[state][action], np.dot(Q[next_state], policy_s), \
reward, alpha, gamma)
# S <- S'
state = next_state
# until S is terminal
if done:
# append score
tmp_scores.append(score)
break
if (i_episode % plot_every == 0):
scores.append(np.mean(tmp_scores))
# plot performance
plt.plot(np.linspace(0,num_episodes,len(scores),endpoint=False),np.asarray(scores))
plt.xlabel('Episode Number')
plt.ylabel('Average Reward (Over Next %d Episodes)' % plot_every)
plt.show()
# print best 100-episode performance
print(('Best Average Reward over %d Episodes: ' % plot_every), np.max(scores))
return Q
```
Use the next code cell to visualize the **_estimated_** optimal policy and the corresponding state-value function.
If the code cell returns **PASSED**, then you have implemented the function correctly! Feel free to change the `num_episodes` and `alpha` parameters that are supplied to the function. However, if you'd like to ensure the accuracy of the unit test, please do not change the value of `gamma` from the default.
```
# obtain the estimated optimal policy and corresponding action-value function
Q_expsarsa = expected_sarsa(env, 10000, 1)
# print the estimated optimal policy
policy_expsarsa = np.array([np.argmax(Q_expsarsa[key]) if key in Q_expsarsa else -1 for key in np.arange(48)]).reshape(4,12)
check_test.run_check('td_control_check', policy_expsarsa)
print("\nEstimated Optimal Policy (UP = 0, RIGHT = 1, DOWN = 2, LEFT = 3, N/A = -1):")
print(policy_expsarsa)
# plot the estimated optimal state-value function
plot_values([np.max(Q_expsarsa[key]) if key in Q_expsarsa else 0 for key in np.arange(48)])
```
|
github_jupyter
|
```
#hide
#skip
! [ -e /content ] && pip install -Uqq fastai # upgrade fastai on colab
#default_exp data.core
#export
from fastai.torch_basics import *
from fastai.data.load import *
#hide
from nbdev.showdoc import *
```
# Data core
> Core functionality for gathering data
The classes here provide functionality for applying a list of transforms to a set of items (`TfmdLists`, `Datasets`) or a `DataLoader` (`TfmdDl`) as well as the base class used to gather the data for model training: `DataLoaders`.
## TfmdDL -
```
#export
@typedispatch
def show_batch(x, y, samples, ctxs=None, max_n=9, **kwargs):
if ctxs is None: ctxs = Inf.nones
if hasattr(samples[0], 'show'):
ctxs = [s.show(ctx=c, **kwargs) for s,c,_ in zip(samples,ctxs,range(max_n))]
else:
for i in range_of(samples[0]):
ctxs = [b.show(ctx=c, **kwargs) for b,c,_ in zip(samples.itemgot(i),ctxs,range(max_n))]
return ctxs
```
`show_batch` is a type-dispatched function that is responsible for showing decoded `samples`. `x` and `y` are the input and the target in the batch to be shown, and are passed along to dispatch on their types. There is a different implementation of `show_batch` if `x` is a `TensorImage` or a `TensorText` for instance (see vision.core or text.data for more details). `ctxs` can be passed but the function is responsible to create them if necessary. `kwargs` depend on the specific implementation.
```
#export
@typedispatch
def show_results(x, y, samples, outs, ctxs=None, max_n=9, **kwargs):
if ctxs is None: ctxs = Inf.nones
for i in range(len(samples[0])):
ctxs = [b.show(ctx=c, **kwargs) for b,c,_ in zip(samples.itemgot(i),ctxs,range(max_n))]
for i in range(len(outs[0])):
ctxs = [b.show(ctx=c, **kwargs) for b,c,_ in zip(outs.itemgot(i),ctxs,range(max_n))]
return ctxs
```
`show_results` is a type-dispatched function that is responsible for showing decoded `samples` and their corresponding `outs`. Like in `show_batch`, `x` and `y` are the input and the target in the batch to be shown, and are passed along to dispatch on their types. `ctxs` can be passed but the function is responsible to create them if necessary. `kwargs` depend on the specific implementation.
```
#export
_all_ = ["show_batch", "show_results"]
#export
_batch_tfms = ('after_item','before_batch','after_batch')
#export
@log_args(but_as=DataLoader.__init__)
@delegates()
class TfmdDL(DataLoader):
"Transformed `DataLoader`"
def __init__(self, dataset, bs=64, shuffle=False, num_workers=None, verbose=False, do_setup=True, **kwargs):
if num_workers is None: num_workers = min(16, defaults.cpus)
for nm in _batch_tfms: kwargs[nm] = Pipeline(kwargs.get(nm,None))
super().__init__(dataset, bs=bs, shuffle=shuffle, num_workers=num_workers, **kwargs)
if do_setup:
for nm in _batch_tfms:
pv(f"Setting up {nm}: {kwargs[nm]}", verbose)
kwargs[nm].setup(self)
def _one_pass(self):
b = self.do_batch([self.do_item(0)])
if self.device is not None: b = to_device(b, self.device)
its = self.after_batch(b)
self._n_inp = 1 if not isinstance(its, (list,tuple)) or len(its)==1 else len(its)-1
self._types = explode_types(its)
def _retain_dl(self,b):
if not getattr(self, '_types', None): self._one_pass()
return retain_types(b, typs=self._types)
@delegates(DataLoader.new)
def new(self, dataset=None, cls=None, **kwargs):
res = super().new(dataset, cls, do_setup=False, **kwargs)
if not hasattr(self, '_n_inp') or not hasattr(self, '_types'):
try:
self._one_pass()
res._n_inp,res._types = self._n_inp,self._types
except: print("Could not do one pass in your dataloader, there is something wrong in it")
else: res._n_inp,res._types = self._n_inp,self._types
return res
def before_iter(self):
super().before_iter()
split_idx = getattr(self.dataset, 'split_idx', None)
for nm in _batch_tfms:
f = getattr(self,nm)
if isinstance(f,Pipeline): f.split_idx=split_idx
def decode(self, b): return self.before_batch.decode(to_cpu(self.after_batch.decode(self._retain_dl(b))))
def decode_batch(self, b, max_n=9, full=True): return self._decode_batch(self.decode(b), max_n, full)
def _decode_batch(self, b, max_n=9, full=True):
f = self.after_item.decode
f = compose(f, partial(getattr(self.dataset,'decode',noop), full = full))
return L(batch_to_samples(b, max_n=max_n)).map(f)
def _pre_show_batch(self, b, max_n=9):
"Decode `b` to be ready for `show_batch`"
b = self.decode(b)
if hasattr(b, 'show'): return b,None,None
its = self._decode_batch(b, max_n, full=False)
if not is_listy(b): b,its = [b],L((o,) for o in its)
return detuplify(b[:self.n_inp]),detuplify(b[self.n_inp:]),its
def show_batch(self, b=None, max_n=9, ctxs=None, show=True, unique=False, **kwargs):
if unique:
old_get_idxs = self.get_idxs
self.get_idxs = lambda: Inf.zeros
if b is None: b = self.one_batch()
if not show: return self._pre_show_batch(b, max_n=max_n)
show_batch(*self._pre_show_batch(b, max_n=max_n), ctxs=ctxs, max_n=max_n, **kwargs)
if unique: self.get_idxs = old_get_idxs
def show_results(self, b, out, max_n=9, ctxs=None, show=True, **kwargs):
x,y,its = self.show_batch(b, max_n=max_n, show=False)
b_out = type(b)(b[:self.n_inp] + (tuple(out) if is_listy(out) else (out,)))
x1,y1,outs = self.show_batch(b_out, max_n=max_n, show=False)
res = (x,x1,None,None) if its is None else (x, y, its, outs.itemgot(slice(self.n_inp,None)))
if not show: return res
show_results(*res, ctxs=ctxs, max_n=max_n, **kwargs)
@property
def n_inp(self):
if hasattr(self.dataset, 'n_inp'): return self.dataset.n_inp
if not hasattr(self, '_n_inp'): self._one_pass()
return self._n_inp
def to(self, device):
self.device = device
for tfm in self.after_batch.fs:
for a in L(getattr(tfm, 'parameters', None)): setattr(tfm, a, getattr(tfm, a).to(device))
return self
```
A `TfmdDL` is a `DataLoader` that creates `Pipeline` from a list of `Transform`s for the callbacks `after_item`, `before_batch` and `after_batch`. As a result, it can decode or show a processed `batch`.
```
#export
add_docs(TfmdDL,
decode="Decode `b` using `tfms`",
decode_batch="Decode `b` entirely",
new="Create a new version of self with a few changed attributes",
show_batch="Show `b` (defaults to `one_batch`), a list of lists of pipeline outputs (i.e. output of a `DataLoader`)",
show_results="Show each item of `b` and `out`",
before_iter="override",
to="Put self and its transforms state on `device`")
class _Category(int, ShowTitle): pass
#Test retain type
class NegTfm(Transform):
def encodes(self, x): return torch.neg(x)
def decodes(self, x): return torch.neg(x)
tdl = TfmdDL([(TensorImage([1]),)] * 4, after_batch=NegTfm(), bs=4, num_workers=4)
b = tdl.one_batch()
test_eq(type(b[0]), TensorImage)
b = (tensor([1.,1.,1.,1.]),)
test_eq(type(tdl.decode_batch(b)[0][0]), TensorImage)
class A(Transform):
def encodes(self, x): return x
def decodes(self, x): return TitledInt(x)
@Transform
def f(x)->None: return fastuple((x,x))
start = torch.arange(50)
test_eq_type(f(2), fastuple((2,2)))
a = A()
tdl = TfmdDL(start, after_item=lambda x: (a(x), f(x)), bs=4)
x,y = tdl.one_batch()
test_eq(type(y), fastuple)
s = tdl.decode_batch((x,y))
test_eq(type(s[0][1]), fastuple)
tdl = TfmdDL(torch.arange(0,50), after_item=A(), after_batch=NegTfm(), bs=4)
test_eq(tdl.dataset[0], start[0])
test_eq(len(tdl), (50-1)//4+1)
test_eq(tdl.bs, 4)
test_stdout(tdl.show_batch, '0\n1\n2\n3')
test_stdout(partial(tdl.show_batch, unique=True), '0\n0\n0\n0')
class B(Transform):
parameters = 'a'
def __init__(self): self.a = torch.tensor(0.)
def encodes(self, x): x
tdl = TfmdDL([(TensorImage([1]),)] * 4, after_batch=B(), bs=4)
test_eq(tdl.after_batch.fs[0].a.device, torch.device('cpu'))
tdl.to(default_device())
test_eq(tdl.after_batch.fs[0].a.device, default_device())
```
### Methods
```
show_doc(TfmdDL.one_batch)
tfm = NegTfm()
tdl = TfmdDL(start, after_batch=tfm, bs=4)
b = tdl.one_batch()
test_eq(tensor([0,-1,-2,-3]), b)
show_doc(TfmdDL.decode)
test_eq(tdl.decode(b), tensor(0,1,2,3))
show_doc(TfmdDL.decode_batch)
test_eq(tdl.decode_batch(b), [0,1,2,3])
show_doc(TfmdDL.show_batch)
show_doc(TfmdDL.to)
```
## DataLoaders -
```
# export
@docs
class DataLoaders(GetAttr):
"Basic wrapper around several `DataLoader`s."
_default='train'
def __init__(self, *loaders, path='.', device=None):
self.loaders,self.path = list(loaders),Path(path)
if device is not None or hasattr(loaders[0],'to'): self.device = device
def __getitem__(self, i): return self.loaders[i]
def new_empty(self):
loaders = [dl.new(dl.dataset.new_empty()) for dl in self.loaders]
return type(self)(*loaders, path=self.path, device=self.device)
def _set(i, self, v): self.loaders[i] = v
train ,valid = add_props(lambda i,x: x[i], _set)
train_ds,valid_ds = add_props(lambda i,x: x[i].dataset)
@property
def device(self): return self._device
@device.setter
def device(self, d):
for dl in self.loaders: dl.to(d)
self._device = d
def to(self, device):
self.device = device
return self
def cuda(self): return self.to(device=default_device())
def cpu(self): return self.to(device=torch.device('cpu'))
@classmethod
def from_dsets(cls, *ds, path='.', bs=64, device=None, dl_type=TfmdDL, **kwargs):
default = (True,) + (False,) * (len(ds)-1)
defaults = {'shuffle': default, 'drop_last': default}
for nm in _batch_tfms:
if nm in kwargs: kwargs[nm] = Pipeline(kwargs[nm])
kwargs = merge(defaults, {k: tuplify(v, match=ds) for k,v in kwargs.items()})
kwargs = [{k: v[i] for k,v in kwargs.items()} for i in range_of(ds)]
return cls(*[dl_type(d, bs=bs, **k) for d,k in zip(ds, kwargs)], path=path, device=device)
@classmethod
def from_dblock(cls, dblock, source, path='.', bs=64, val_bs=None, shuffle_train=True, device=None, **kwargs):
return dblock.dataloaders(source, path=path, bs=bs, val_bs=val_bs, shuffle_train=shuffle_train, device=device, **kwargs)
_docs=dict(__getitem__="Retrieve `DataLoader` at `i` (`0` is training, `1` is validation)",
train="Training `DataLoader`",
valid="Validation `DataLoader`",
train_ds="Training `Dataset`",
valid_ds="Validation `Dataset`",
to="Use `device`",
cuda="Use the gpu if available",
cpu="Use the cpu",
new_empty="Create a new empty version of `self` with the same transforms",
from_dblock="Create a dataloaders from a given `dblock`")
dls = DataLoaders(tdl,tdl)
x = dls.train.one_batch()
x2 = first(tdl)
test_eq(x,x2)
x2 = dls.one_batch()
test_eq(x,x2)
#hide
#test assignment works
dls.train = dls.train.new(bs=4)
```
### Methods
```
show_doc(DataLoaders.__getitem__)
x2 = dls[0].one_batch()
test_eq(x,x2)
show_doc(DataLoaders.train, name="DataLoaders.train")
show_doc(DataLoaders.valid, name="DataLoaders.valid")
show_doc(DataLoaders.train_ds, name="DataLoaders.train_ds")
show_doc(DataLoaders.valid_ds, name="DataLoaders.valid_ds")
```
## TfmdLists -
```
#export
class FilteredBase:
"Base class for lists with subsets"
_dl_type,_dbunch_type = TfmdDL,DataLoaders
def __init__(self, *args, dl_type=None, **kwargs):
if dl_type is not None: self._dl_type = dl_type
self.dataloaders = delegates(self._dl_type.__init__)(self.dataloaders)
super().__init__(*args, **kwargs)
@property
def n_subsets(self): return len(self.splits)
def _new(self, items, **kwargs): return super()._new(items, splits=self.splits, **kwargs)
def subset(self): raise NotImplemented
def dataloaders(self, bs=64, val_bs=None, shuffle_train=True, n=None, path='.', dl_type=None, dl_kwargs=None,
device=None, **kwargs):
if device is None: device=default_device()
if dl_kwargs is None: dl_kwargs = [{}] * self.n_subsets
if dl_type is None: dl_type = self._dl_type
drop_last = kwargs.pop('drop_last', shuffle_train)
dl = dl_type(self.subset(0), bs=bs, shuffle=shuffle_train, drop_last=drop_last, n=n, device=device,
**merge(kwargs, dl_kwargs[0]))
dls = [dl] + [dl.new(self.subset(i), bs=(bs if val_bs is None else val_bs), shuffle=False, drop_last=False,
n=None, **dl_kwargs[i]) for i in range(1, self.n_subsets)]
return self._dbunch_type(*dls, path=path, device=device)
FilteredBase.train,FilteredBase.valid = add_props(lambda i,x: x.subset(i))
#export
class TfmdLists(FilteredBase, L, GetAttr):
"A `Pipeline` of `tfms` applied to a collection of `items`"
_default='tfms'
def __init__(self, items, tfms, use_list=None, do_setup=True, split_idx=None, train_setup=True,
splits=None, types=None, verbose=False, dl_type=None):
super().__init__(items, use_list=use_list)
if dl_type is not None: self._dl_type = dl_type
self.splits = L([slice(None),[]] if splits is None else splits).map(mask2idxs)
if isinstance(tfms,TfmdLists): tfms = tfms.tfms
if isinstance(tfms,Pipeline): do_setup=False
self.tfms = Pipeline(tfms, split_idx=split_idx)
store_attr('types,split_idx')
if do_setup:
pv(f"Setting up {self.tfms}", verbose)
self.setup(train_setup=train_setup)
def _new(self, items, split_idx=None, **kwargs):
split_idx = ifnone(split_idx,self.split_idx)
return super()._new(items, tfms=self.tfms, do_setup=False, types=self.types, split_idx=split_idx, **kwargs)
def subset(self, i): return self._new(self._get(self.splits[i]), split_idx=i)
def _after_item(self, o): return self.tfms(o)
def __repr__(self): return f"{self.__class__.__name__}: {self.items}\ntfms - {self.tfms.fs}"
def __iter__(self): return (self[i] for i in range(len(self)))
def show(self, o, **kwargs): return self.tfms.show(o, **kwargs)
def decode(self, o, **kwargs): return self.tfms.decode(o, **kwargs)
def __call__(self, o, **kwargs): return self.tfms.__call__(o, **kwargs)
def overlapping_splits(self): return L(Counter(self.splits.concat()).values()).filter(gt(1))
def new_empty(self): return self._new([])
def setup(self, train_setup=True):
self.tfms.setup(self, train_setup)
if len(self) != 0:
x = super().__getitem__(0) if self.splits is None else super().__getitem__(self.splits[0])[0]
self.types = []
for f in self.tfms.fs:
self.types.append(getattr(f, 'input_types', type(x)))
x = f(x)
self.types.append(type(x))
types = L(t if is_listy(t) else [t] for t in self.types).concat().unique()
self.pretty_types = '\n'.join([f' - {t}' for t in types])
def infer_idx(self, x):
# TODO: check if we really need this, or can simplify
idx = 0
for t in self.types:
if isinstance(x, t): break
idx += 1
types = L(t if is_listy(t) else [t] for t in self.types).concat().unique()
pretty_types = '\n'.join([f' - {t}' for t in types])
assert idx < len(self.types), f"Expected an input of type in \n{pretty_types}\n but got {type(x)}"
return idx
def infer(self, x):
return compose_tfms(x, tfms=self.tfms.fs[self.infer_idx(x):], split_idx=self.split_idx)
def __getitem__(self, idx):
res = super().__getitem__(idx)
if self._after_item is None: return res
return self._after_item(res) if is_indexer(idx) else res.map(self._after_item)
#export
add_docs(TfmdLists,
setup="Transform setup with self",
decode="From `Pipeline`",
show="From `Pipeline`",
overlapping_splits="All splits that are in more than one split",
subset="New `TfmdLists` with same tfms that only includes items in `i`th split",
infer_idx="Finds the index where `self.tfms` can be applied to `x`, depending on the type of `x`",
infer="Apply `self.tfms` to `x` starting at the right tfm depending on the type of `x`",
new_empty="A new version of `self` but with no items")
#exports
def decode_at(o, idx):
"Decoded item at `idx`"
return o.decode(o[idx])
#exports
def show_at(o, idx, **kwargs):
"Show item at `idx`",
return o.show(o[idx], **kwargs)
```
A `TfmdLists` combines a collection of object with a `Pipeline`. `tfms` can either be a `Pipeline` or a list of transforms, in which case, it will wrap them in a `Pipeline`. `use_list` is passed along to `L` with the `items` and `split_idx` are passed to each transform of the `Pipeline`. `do_setup` indicates if the `Pipeline.setup` method should be called during initialization.
```
class _IntFloatTfm(Transform):
def encodes(self, o): return TitledInt(o)
def decodes(self, o): return TitledFloat(o)
int2f_tfm=_IntFloatTfm()
def _neg(o): return -o
neg_tfm = Transform(_neg, _neg)
items = L([1.,2.,3.]); tfms = [neg_tfm, int2f_tfm]
tl = TfmdLists(items, tfms=tfms)
test_eq_type(tl[0], TitledInt(-1))
test_eq_type(tl[1], TitledInt(-2))
test_eq_type(tl.decode(tl[2]), TitledFloat(3.))
test_stdout(lambda: show_at(tl, 2), '-3')
test_eq(tl.types, [float, float, TitledInt])
tl
# add splits to TfmdLists
splits = [[0,2],[1]]
tl = TfmdLists(items, tfms=tfms, splits=splits)
test_eq(tl.n_subsets, 2)
test_eq(tl.train, tl.subset(0))
test_eq(tl.valid, tl.subset(1))
test_eq(tl.train.items, items[splits[0]])
test_eq(tl.valid.items, items[splits[1]])
test_eq(tl.train.tfms.split_idx, 0)
test_eq(tl.valid.tfms.split_idx, 1)
test_eq(tl.train.new_empty().split_idx, 0)
test_eq(tl.valid.new_empty().split_idx, 1)
test_eq_type(tl.splits, L(splits))
assert not tl.overlapping_splits()
df = pd.DataFrame(dict(a=[1,2,3],b=[2,3,4]))
tl = TfmdLists(df, lambda o: o.a+1, splits=[[0],[1,2]])
test_eq(tl[1,2], [3,4])
tr = tl.subset(0)
test_eq(tr[:], [2])
val = tl.subset(1)
test_eq(val[:], [3,4])
class _B(Transform):
def __init__(self): self.m = 0
def encodes(self, o): return o+self.m
def decodes(self, o): return o-self.m
def setups(self, items):
print(items)
self.m = tensor(items).float().mean().item()
# test for setup, which updates `self.m`
tl = TfmdLists(items, _B())
test_eq(tl.m, 2)
```
Here's how we can use `TfmdLists.setup` to implement a simple category list, getting labels from a mock file list:
```
class _Cat(Transform):
order = 1
def encodes(self, o): return int(self.o2i[o])
def decodes(self, o): return TitledStr(self.vocab[o])
def setups(self, items): self.vocab,self.o2i = uniqueify(L(items), sort=True, bidir=True)
tcat = _Cat()
def _lbl(o): return TitledStr(o.split('_')[0])
# Check that tfms are sorted by `order` & `_lbl` is called first
fns = ['dog_0.jpg','cat_0.jpg','cat_2.jpg','cat_1.jpg','dog_1.jpg']
tl = TfmdLists(fns, [tcat,_lbl])
exp_voc = ['cat','dog']
test_eq(tcat.vocab, exp_voc)
test_eq(tl.tfms.vocab, exp_voc)
test_eq(tl.vocab, exp_voc)
test_eq(tl, (1,0,0,0,1))
test_eq([tl.decode(o) for o in tl], ('dog','cat','cat','cat','dog'))
#Check only the training set is taken into account for setup
tl = TfmdLists(fns, [tcat,_lbl], splits=[[0,4], [1,2,3]])
test_eq(tcat.vocab, ['dog'])
tfm = NegTfm(split_idx=1)
tds = TfmdLists(start, A())
tdl = TfmdDL(tds, after_batch=tfm, bs=4)
x = tdl.one_batch()
test_eq(x, torch.arange(4))
tds.split_idx = 1
x = tdl.one_batch()
test_eq(x, -torch.arange(4))
tds.split_idx = 0
x = tdl.one_batch()
test_eq(x, torch.arange(4))
tds = TfmdLists(start, A())
tdl = TfmdDL(tds, after_batch=NegTfm(), bs=4)
test_eq(tdl.dataset[0], start[0])
test_eq(len(tdl), (len(tds)-1)//4+1)
test_eq(tdl.bs, 4)
test_stdout(tdl.show_batch, '0\n1\n2\n3')
show_doc(TfmdLists.subset)
show_doc(TfmdLists.infer_idx)
show_doc(TfmdLists.infer)
def mult(x): return x*2
mult.order = 2
fns = ['dog_0.jpg','cat_0.jpg','cat_2.jpg','cat_1.jpg','dog_1.jpg']
tl = TfmdLists(fns, [_lbl,_Cat(),mult])
test_eq(tl.infer_idx('dog_45.jpg'), 0)
test_eq(tl.infer('dog_45.jpg'), 2)
test_eq(tl.infer_idx(4), 2)
test_eq(tl.infer(4), 8)
test_fail(lambda: tl.infer_idx(2.0))
test_fail(lambda: tl.infer(2.0))
#hide
#Test input_types works on a Transform
cat = _Cat()
cat.input_types = (str, float)
tl = TfmdLists(fns, [_lbl,cat,mult])
test_eq(tl.infer_idx(2.0), 1)
#Test type annotations work on a function
def mult(x:(int,float)): return x*2
mult.order = 2
tl = TfmdLists(fns, [_lbl,_Cat(),mult])
test_eq(tl.infer_idx(2.0), 2)
```
## Datasets -
```
#export
@docs
@delegates(TfmdLists)
class Datasets(FilteredBase):
"A dataset that creates a tuple from each `tfms`, passed through `item_tfms`"
def __init__(self, items=None, tfms=None, tls=None, n_inp=None, dl_type=None, **kwargs):
super().__init__(dl_type=dl_type)
self.tls = L(tls if tls else [TfmdLists(items, t, **kwargs) for t in L(ifnone(tfms,[None]))])
self.n_inp = ifnone(n_inp, max(1, len(self.tls)-1))
def __getitem__(self, it):
res = tuple([tl[it] for tl in self.tls])
return res if is_indexer(it) else list(zip(*res))
def __getattr__(self,k): return gather_attrs(self, k, 'tls')
def __dir__(self): return super().__dir__() + gather_attr_names(self, 'tls')
def __len__(self): return len(self.tls[0])
def __iter__(self): return (self[i] for i in range(len(self)))
def __repr__(self): return coll_repr(self)
def decode(self, o, full=True): return tuple(tl.decode(o_, full=full) for o_,tl in zip(o,tuplify(self.tls, match=o)))
def subset(self, i): return type(self)(tls=L(tl.subset(i) for tl in self.tls), n_inp=self.n_inp)
def _new(self, items, *args, **kwargs): return super()._new(items, tfms=self.tfms, do_setup=False, **kwargs)
def overlapping_splits(self): return self.tls[0].overlapping_splits()
def new_empty(self): return type(self)(tls=[tl.new_empty() for tl in self.tls], n_inp=self.n_inp)
@property
def splits(self): return self.tls[0].splits
@property
def split_idx(self): return self.tls[0].tfms.split_idx
@property
def items(self): return self.tls[0].items
@items.setter
def items(self, v):
for tl in self.tls: tl.items = v
def show(self, o, ctx=None, **kwargs):
for o_,tl in zip(o,self.tls): ctx = tl.show(o_, ctx=ctx, **kwargs)
return ctx
@contextmanager
def set_split_idx(self, i):
old_split_idx = self.split_idx
for tl in self.tls: tl.tfms.split_idx = i
try: yield self
finally:
for tl in self.tls: tl.tfms.split_idx = old_split_idx
_docs=dict(
decode="Compose `decode` of all `tuple_tfms` then all `tfms` on `i`",
show="Show item `o` in `ctx`",
dataloaders="Get a `DataLoaders`",
overlapping_splits="All splits that are in more than one split",
subset="New `Datasets` that only includes subset `i`",
new_empty="Create a new empty version of the `self`, keeping only the transforms",
set_split_idx="Contextmanager to use the same `Datasets` with another `split_idx`"
)
```
A `Datasets` creates a tuple from `items` (typically input,target) by applying to them each list of `Transform` (or `Pipeline`) in `tfms`. Note that if `tfms` contains only one list of `tfms`, the items given by `Datasets` will be tuples of one element.
`n_inp` is the number of elements in the tuples that should be considered part of the input and will default to 1 if `tfms` consists of one set of transforms, `len(tfms)-1` otherwise. In most cases, the number of elements in the tuples spit out by `Datasets` will be 2 (for input,target) but it can happen that there is 3 (Siamese networks or tabular data) in which case we need to be able to determine when the inputs end and the targets begin.
```
items = [1,2,3,4]
dsets = Datasets(items, [[neg_tfm,int2f_tfm], [add(1)]])
t = dsets[0]
test_eq(t, (-1,2))
test_eq(dsets[0,1,2], [(-1,2),(-2,3),(-3,4)])
test_eq(dsets.n_inp, 1)
dsets.decode(t)
class Norm(Transform):
def encodes(self, o): return (o-self.m)/self.s
def decodes(self, o): return (o*self.s)+self.m
def setups(self, items):
its = tensor(items).float()
self.m,self.s = its.mean(),its.std()
items = [1,2,3,4]
nrm = Norm()
dsets = Datasets(items, [[neg_tfm,int2f_tfm], [neg_tfm,nrm]])
x,y = zip(*dsets)
test_close(tensor(y).mean(), 0)
test_close(tensor(y).std(), 1)
test_eq(x, (-1,-2,-3,-4,))
test_eq(nrm.m, -2.5)
test_stdout(lambda:show_at(dsets, 1), '-2')
test_eq(dsets.m, nrm.m)
test_eq(dsets.norm.m, nrm.m)
test_eq(dsets.train.norm.m, nrm.m)
#hide
#Check filtering is properly applied
class B(Transform):
def encodes(self, x)->None: return int(x+1)
def decodes(self, x): return TitledInt(x-1)
add1 = B(split_idx=1)
dsets = Datasets(items, [neg_tfm, [neg_tfm,int2f_tfm,add1]], splits=[[3],[0,1,2]])
test_eq(dsets[1], [-2,-2])
test_eq(dsets.valid[1], [-2,-1])
test_eq(dsets.valid[[1,1]], [[-2,-1], [-2,-1]])
test_eq(dsets.train[0], [-4,-4])
test_fns = ['dog_0.jpg','cat_0.jpg','cat_2.jpg','cat_1.jpg','kid_1.jpg']
tcat = _Cat()
dsets = Datasets(test_fns, [[tcat,_lbl]], splits=[[0,1,2], [3,4]])
test_eq(tcat.vocab, ['cat','dog'])
test_eq(dsets.train, [(1,),(0,),(0,)])
test_eq(dsets.valid[0], (0,))
test_stdout(lambda: show_at(dsets.train, 0), "dog")
inp = [0,1,2,3,4]
dsets = Datasets(inp, tfms=[None])
test_eq(*dsets[2], 2) # Retrieve one item (subset 0 is the default)
test_eq(dsets[1,2], [(1,),(2,)]) # Retrieve two items by index
mask = [True,False,False,True,False]
test_eq(dsets[mask], [(0,),(3,)]) # Retrieve two items by mask
inp = pd.DataFrame(dict(a=[5,1,2,3,4]))
dsets = Datasets(inp, tfms=attrgetter('a')).subset(0)
test_eq(*dsets[2], 2) # Retrieve one item (subset 0 is the default)
test_eq(dsets[1,2], [(1,),(2,)]) # Retrieve two items by index
mask = [True,False,False,True,False]
test_eq(dsets[mask], [(5,),(3,)]) # Retrieve two items by mask
#test n_inp
inp = [0,1,2,3,4]
dsets = Datasets(inp, tfms=[None])
test_eq(dsets.n_inp, 1)
dsets = Datasets(inp, tfms=[[None],[None],[None]])
test_eq(dsets.n_inp, 2)
dsets = Datasets(inp, tfms=[[None],[None],[None]], n_inp=1)
test_eq(dsets.n_inp, 1)
# splits can be indices
dsets = Datasets(range(5), tfms=[None], splits=[tensor([0,2]), [1,3,4]])
test_eq(dsets.subset(0), [(0,),(2,)])
test_eq(dsets.train, [(0,),(2,)]) # Subset 0 is aliased to `train`
test_eq(dsets.subset(1), [(1,),(3,),(4,)])
test_eq(dsets.valid, [(1,),(3,),(4,)]) # Subset 1 is aliased to `valid`
test_eq(*dsets.valid[2], 4)
#assert '[(1,),(3,),(4,)]' in str(dsets) and '[(0,),(2,)]' in str(dsets)
dsets
# splits can be boolean masks (they don't have to cover all items, but must be disjoint)
splits = [[False,True,True,False,True], [True,False,False,False,False]]
dsets = Datasets(range(5), tfms=[None], splits=splits)
test_eq(dsets.train, [(1,),(2,),(4,)])
test_eq(dsets.valid, [(0,)])
# apply transforms to all items
tfm = [[lambda x: x*2,lambda x: x+1]]
splits = [[1,2],[0,3,4]]
dsets = Datasets(range(5), tfm, splits=splits)
test_eq(dsets.train,[(3,),(5,)])
test_eq(dsets.valid,[(1,),(7,),(9,)])
test_eq(dsets.train[False,True], [(5,)])
# only transform subset 1
class _Tfm(Transform):
split_idx=1
def encodes(self, x): return x*2
def decodes(self, x): return TitledStr(x//2)
dsets = Datasets(range(5), [_Tfm()], splits=[[1,2],[0,3,4]])
test_eq(dsets.train,[(1,),(2,)])
test_eq(dsets.valid,[(0,),(6,),(8,)])
test_eq(dsets.train[False,True], [(2,)])
dsets
#A context manager to change the split_idx and apply the validation transform on the training set
ds = dsets.train
with ds.set_split_idx(1):
test_eq(ds,[(2,),(4,)])
test_eq(dsets.train,[(1,),(2,)])
#hide
#Test Datasets pickles
dsrc1 = pickle.loads(pickle.dumps(dsets))
test_eq(dsets.train, dsrc1.train)
test_eq(dsets.valid, dsrc1.valid)
dsets = Datasets(range(5), [_Tfm(),noop], splits=[[1,2],[0,3,4]])
test_eq(dsets.train,[(1,1),(2,2)])
test_eq(dsets.valid,[(0,0),(6,3),(8,4)])
start = torch.arange(0,50)
tds = Datasets(start, [A()])
tdl = TfmdDL(tds, after_item=NegTfm(), bs=4)
b = tdl.one_batch()
test_eq(tdl.decode_batch(b), ((0,),(1,),(2,),(3,)))
test_stdout(tdl.show_batch, "0\n1\n2\n3")
# only transform subset 1
class _Tfm(Transform):
split_idx=1
def encodes(self, x): return x*2
dsets = Datasets(range(8), [None], splits=[[1,2,5,7],[0,3,4,6]])
# only transform subset 1
class _Tfm(Transform):
split_idx=1
def encodes(self, x): return x*2
dsets = Datasets(range(8), [None], splits=[[1,2,5,7],[0,3,4,6]])
dls = dsets.dataloaders(bs=4, after_batch=_Tfm(), shuffle_train=False, device=torch.device('cpu'))
test_eq(dls.train, [(tensor([1,2,5, 7]),)])
test_eq(dls.valid, [(tensor([0,6,8,12]),)])
test_eq(dls.n_inp, 1)
```
### Methods
```
items = [1,2,3,4]
dsets = Datasets(items, [[neg_tfm,int2f_tfm]])
#hide_input
_dsrc = Datasets([1,2])
show_doc(_dsrc.dataloaders, name="Datasets.dataloaders")
show_doc(Datasets.decode)
test_eq(*dsets[0], -1)
test_eq(*dsets.decode((-1,)), 1)
show_doc(Datasets.show)
test_stdout(lambda:dsets.show(dsets[1]), '-2')
show_doc(Datasets.new_empty)
items = [1,2,3,4]
nrm = Norm()
dsets = Datasets(items, [[neg_tfm,int2f_tfm], [neg_tfm]])
empty = dsets.new_empty()
test_eq(empty.items, [])
#hide
#test it works for dataframes too
df = pd.DataFrame({'a':[1,2,3,4,5], 'b':[6,7,8,9,10]})
dsets = Datasets(df, [[attrgetter('a')], [attrgetter('b')]])
empty = dsets.new_empty()
```
## Add test set for inference
```
# only transform subset 1
class _Tfm1(Transform):
split_idx=0
def encodes(self, x): return x*3
dsets = Datasets(range(8), [[_Tfm(),_Tfm1()]], splits=[[1,2,5,7],[0,3,4,6]])
test_eq(dsets.train, [(3,),(6,),(15,),(21,)])
test_eq(dsets.valid, [(0,),(6,),(8,),(12,)])
#export
def test_set(dsets, test_items, rm_tfms=None, with_labels=False):
"Create a test set from `test_items` using validation transforms of `dsets`"
if isinstance(dsets, Datasets):
tls = dsets.tls if with_labels else dsets.tls[:dsets.n_inp]
test_tls = [tl._new(test_items, split_idx=1) for tl in tls]
if rm_tfms is None: rm_tfms = [tl.infer_idx(get_first(test_items)) for tl in test_tls]
else: rm_tfms = tuplify(rm_tfms, match=test_tls)
for i,j in enumerate(rm_tfms): test_tls[i].tfms.fs = test_tls[i].tfms.fs[j:]
return Datasets(tls=test_tls)
elif isinstance(dsets, TfmdLists):
test_tl = dsets._new(test_items, split_idx=1)
if rm_tfms is None: rm_tfms = dsets.infer_idx(get_first(test_items))
test_tl.tfms.fs = test_tl.tfms.fs[rm_tfms:]
return test_tl
else: raise Exception(f"This method requires using the fastai library to assemble your data. Expected a `Datasets` or a `TfmdLists` but got {dsets.__class__.__name__}")
class _Tfm1(Transform):
split_idx=0
def encodes(self, x): return x*3
dsets = Datasets(range(8), [[_Tfm(),_Tfm1()]], splits=[[1,2,5,7],[0,3,4,6]])
test_eq(dsets.train, [(3,),(6,),(15,),(21,)])
test_eq(dsets.valid, [(0,),(6,),(8,),(12,)])
#Tranform of the validation set are applied
tst = test_set(dsets, [1,2,3])
test_eq(tst, [(2,),(4,),(6,)])
#hide
#Test with different types
tfm = _Tfm1()
tfm.split_idx,tfm.order = None,2
dsets = Datasets(['dog', 'cat', 'cat', 'dog'], [[_Cat(),tfm]])
#With strings
test_eq(test_set(dsets, ['dog', 'cat', 'cat']), [(3,), (0,), (0,)])
#With ints
test_eq(test_set(dsets, [1,2]), [(3,), (6,)])
#hide
#Test with various input lengths
dsets = Datasets(range(8), [[_Tfm(),_Tfm1()],[_Tfm(),_Tfm1()],[_Tfm(),_Tfm1()]], splits=[[1,2,5,7],[0,3,4,6]])
tst = test_set(dsets, [1,2,3])
test_eq(tst, [(2,2),(4,4),(6,6)])
dsets = Datasets(range(8), [[_Tfm(),_Tfm1()],[_Tfm(),_Tfm1()],[_Tfm(),_Tfm1()]], splits=[[1,2,5,7],[0,3,4,6]], n_inp=1)
tst = test_set(dsets, [1,2,3])
test_eq(tst, [(2,),(4,),(6,)])
#hide
#Test with rm_tfms
dsets = Datasets(range(8), [[_Tfm(),_Tfm()]], splits=[[1,2,5,7],[0,3,4,6]])
tst = test_set(dsets, [1,2,3])
test_eq(tst, [(4,),(8,),(12,)])
dsets = Datasets(range(8), [[_Tfm(),_Tfm()]], splits=[[1,2,5,7],[0,3,4,6]])
tst = test_set(dsets, [1,2,3], rm_tfms=1)
test_eq(tst, [(2,),(4,),(6,)])
dsets = Datasets(range(8), [[_Tfm(),_Tfm()], [_Tfm(),_Tfm()]], splits=[[1,2,5,7],[0,3,4,6]], n_inp=2)
tst = test_set(dsets, [1,2,3], rm_tfms=(1,0))
test_eq(tst, [(2,4),(4,8),(6,12)])
#export
@delegates(TfmdDL.__init__)
@patch
def test_dl(self:DataLoaders, test_items, rm_type_tfms=None, with_labels=False, **kwargs):
"Create a test dataloader from `test_items` using validation transforms of `dls`"
test_ds = test_set(self.valid_ds, test_items, rm_tfms=rm_type_tfms, with_labels=with_labels
) if isinstance(self.valid_ds, (Datasets, TfmdLists)) else test_items
return self.valid.new(test_ds, **kwargs)
dsets = Datasets(range(8), [[_Tfm(),_Tfm1()]], splits=[[1,2,5,7],[0,3,4,6]])
dls = dsets.dataloaders(bs=4, device=torch.device('cpu'))
dsets = Datasets(range(8), [[_Tfm(),_Tfm1()]], splits=[[1,2,5,7],[0,3,4,6]])
dls = dsets.dataloaders(bs=4, device=torch.device('cpu'))
tst_dl = dls.test_dl([2,3,4,5])
test_eq(tst_dl._n_inp, 1)
test_eq(list(tst_dl), [(tensor([ 4, 6, 8, 10]),)])
#Test you can change transforms
tst_dl = dls.test_dl([2,3,4,5], after_item=add1)
test_eq(list(tst_dl), [(tensor([ 5, 7, 9, 11]),)])
```
## Export -
```
#hide
from nbdev.export import notebook2script
notebook2script()
```
|
github_jupyter
|
<img src="images/logo.jpg" style="display: block; margin-left: auto; margin-right: auto;" alt="לוגו של מיזם לימוד הפייתון. נחש מצויר בצבעי צהוב וכחול, הנע בין האותיות של שם הקורס: לומדים פייתון. הסלוגן המופיע מעל לשם הקורס הוא מיזם חינמי ללימוד תכנות בעברית.">
# <span style="text-align: right; direction: rtl; float: right;">התנהגות של פונקציות</span>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
בפסקאות הקרובות נבחן פונקציות מזווית ראייה מעט שונה מהרגיל.<br>
בואו נקפוץ ישירות למים!
</p>
### <span style="text-align: right; direction: rtl; float: right; clear: both;">שם של פונקציה</span>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
תכונה מעניינת שמתקיימת בפייתון היא שפונקציה היא ערך, בדיוק כמו כל ערך אחר.<br>
נגדיר פונקציה שמעלה מספר בריבוע:
</p>
```
def square(x):
return x ** 2
```
<p style="text-align: right; direction: rtl; float: right; clear: both;">
נוכל לבדוק מאיזה טיפוס הפונקציה (אנחנו לא קוראים לה עם סוגריים אחרי שמה – רק מציינים את שמה):
</p>
```
type(square)
```
<p style="text-align: right; direction: rtl; float: right; clear: both;">
ואפילו לבצע השמה שלה למשתנה, כך ששם המשתנה החדש יצביע עליה:
</p>
```
ribua = square
print(square(5))
print(ribua(5))
```
<p style="text-align: right; direction: rtl; float: right; clear: both;">
מה מתרחש בתא למעלה?<br>
כשהגדרנו את הפונקציה <var>square</var>, יצרנו לייזר עם התווית <var>square</var> שמצביע לפונקציה שמעלה מספר בריבוע.<br>
בהשמה שביצענו בשורה הראשונה בתא שלמעלה, הלייזר שעליו מודבקת התווית <var>ribua</var> כוון אל אותה הפונקציה שעליה מצביע הלייזר <var>square</var>.<br>
כעת <var>square</var> ו־<var>ribua</var> מצביעים לאותה פונקציה. אפשר לבדוק זאת כך:
</p>
```
ribua is square
```
<p style="text-align: right; direction: rtl; float: right; clear: both;">
בשלב הזה אצטרך לבקש מכם לחגור חגורות, כי זה לא הולך להיות טיול רגיל הפעם.
</p>
### <span style="text-align: right; direction: rtl; float: right; clear: both;">פונקציות במבנים מורכבים</span>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
אם פונקציה היא בסך הכול ערך, ואם אפשר להתייחס לשם שלה בכל מקום, אין סיבה שלא נוכל ליצור רשימה של פונקציות!<br>
ננסה לממש את הרעיון:
</p>
```
def add(num1, num2):
return num1 + num2
def subtract(num1, num2):
return num1 - num2
def multiply(num1, num2):
return num1 * num2
def divide(num1, num2):
return num1 / num2
functions = [add, subtract, multiply, divide]
```
<p style="text-align: right; direction: rtl; float: right; clear: both;">
כעת יש לנו רשימה בעלת 4 איברים, שכל אחד מהם מצביע לפונקציה שונה.<br>
אם נרצה לבצע פעולת חיבור, נוכל לקרוא ישירות ל־<var>add</var> או (בשביל התרגול) לנסות לאחזר אותה מהרשימה שיצרנו:
</p>
```
# Option 1
print(add(5, 2))
# Option 2
math_function = functions[0]
print(math_function(5, 2))
# Option 3 (ugly, but works!)
print(functions[0](5, 2))
```
<p style="text-align: right; direction: rtl; float: right; clear: both;">
אם נרצה, נוכל אפילו לעבור על רשימת הפונקציות בעזרת לולאה ולהפעיל את כולן, זו אחר זו:
</p>
```
for function in functions:
print(function(5, 2))
```
<p style="text-align: right; direction: rtl; float: right; clear: both;">
בכל איטרציה של לולאת ה־<code>for</code>, המשתנה <var>function</var> עבר להצביע על הפונקציה הבאה מתוך רשימת <var>functions</var>.<br>
בשורה הבאה קראנו לאותה הפונקציה ש־<var>function</var> מצביע עליה, והדפסנו את הערך שהיא החזירה.
</p>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
כיוון שרשימה היא מבנה ששומר על סדר האיברים שבו, התוצאות מודפסות בסדר שבו הפונקציות שמורות ברשימה.<br>
התוצאה הראשונה שאנחנו רואים היא תוצאת פונקציית החיבור, השנייה היא תוצאת פונקציית החיסור וכן הלאה.
</p>
#### <span style="text-align: right; direction: rtl; float: right; clear: both;">תרגיל ביניים: סוגרים חשבון</span>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
כתבו פונקציה בשם <var>calc</var> שמקבלת כפרמטר שני מספרים וסימן של פעולה חשבונית.<br>
הסימן יכול להיות אחד מאלה: <code>+</code>, <code>-</code>, <code>*</code> או <code>/</code>.<br>
מטרת הפונקציה היא להחזיר את תוצאת הביטוי החשבוני שהופעל על שני המספרים.<br>
בפתרונכם, השתמשו בהגדרת הפונקציות מלמעלה ובמילון.
</p>
### <span style="text-align: right; direction: rtl; float: right; clear: both;">העברת פונקציה כפרמטר</span>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
נמשיך ללהטט בפונקציות.<br>
</p>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
פונקציה נקראת "<dfn>פונקציה מסדר גבוה</dfn>" (<dfn>higher order function</dfn>) אם היא מקבלת כפרמטר פונקציה.<br>
ניקח לדוגמה את הפונקציה <var>calculate</var>:
</p>
```
def calculate(function, num1, num2):
return function(num1, num2)
```
<p style="text-align: right; direction: rtl; float: right; clear: both;">
בקריאה ל־<var>calculate</var>, נצטרך להעביר פונקציה ושני מספרים.<br>
נעביר לדוגמה את הפונקציה <var>divide</var> שהגדרנו קודם לכן:
</p>
```
calculate(divide, 5, 2)
```
<p style="text-align: right; direction: rtl; float: right; clear: both;">
מה שמתרחש במקרה הזה הוא שהעברנו את הפונקציה <var>divide</var> כארגומנט ראשון.<br>
הפרמטר <var>function</var> בפונקציה <var>calculate</var> מצביע כעת על פונקציית החילוק שהגדרנו למעלה.<br>
מכאן, שהפונקציה תחזיר את התוצאה של <code>divide(5, 2)</code> – הרי היא 2.5.
</p>
#### <span style="text-align: right; direction: rtl; float: right; clear: both;">תרגיל ביניים: מפה לפה</span>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
כתבו generator בשם <var>apply</var> שמקבל כפרמטר ראשון פונקציה (<var>func</var>), וכפרמטר שני iterable (<var dir="rtl">iter</var>).<br>
עבור כל איבר ב־iterable, ה־generator יניב את האיבר אחרי שהופעלה עליו הפונקציה <var>func</var>, דהיינו – <code>func(item)</code>.<br>
</p>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
ודאו שהרצת התא הבא מחזירה <code>True</code> עבור הקוד שלכם:
</p>
```
def square(number):
return number ** 2
square_check = apply(square, [5, -1, 6, -8, 0])
tuple(square_check) == (25, 1, 36, 64, 0)
```
### <span style="text-align: right; direction: rtl; float: right; clear: both;">סיכום ביניים</span>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
וואו. זה היה די משוגע.
</p>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
אז למעשה, פונקציות בפייתון הן ערך לכל דבר, כמו מחרוזות ומספרים!<br>
אפשר לאחסן אותן במשתנים, לשלוח אותן כארגומנטים ולכלול אותם בתוך מבני נתונים מורכבים יותר.<br>
אנשי התיאוריה של מדעי המחשב נתנו להתנהגות כזו שם: "<dfn>אזרח ממדרגה ראשונה</dfn>" (<dfn>first class citizen</dfn>).<br>
אם כך, אפשר להגיד על פונקציות בפייתון שהן אזרחיות ממדרגה ראשונה.
</p>
## <span style="text-align: right; direction: rtl; float: right; clear: both;">פונקציות מסדר גבוה בפייתון</span>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
החדשות הטובות הן שכבר עשינו היכרות קלה עם המונח פונקציות מסדר גבוה.<br>
עכשיו, כשאנחנו יודעים שמדובר בפונקציות שמקבלות פונקציה כפרמטר, נתחיל ללכלך קצת את הידיים.<br>
נציג כמה פונקציות פייתוניות מעניינות שכאלו:
</p>
### <span style="text-align: right; direction: rtl; float: right; clear: both;">הפונקציה map</span>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
הפונקציה <var>map</var> מקבלת פונקציה כפרמטר הראשון, ו־iterable כפרמטר השני.<br>
<var>map</var> מפעילה את הפונקציה מהפרמטר הראשון על כל אחד מהאיברים שהועברו ב־iterable.<br>
היא מחזירה iterator שמורכב מהערכים שחזרו מהפעלת הפונקציה.<br>
</p>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
במילים אחרות, <var>map</var> יוצרת iterable חדש.<br>
ה־iterable כולל את הערך שהוחזר מהפונקציה עבור כל איבר ב־<code>iterable</code> שהועבר.
</p>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
לדוגמה:
</p>
```
squared_items = map(square, [1, 6, -1, 8, 0, 3, -3, 9, -8, 8, -7])
print(tuple(squared_items))
```
<p style="text-align: right; direction: rtl; float: right; clear: both;">
הפונקציה קיבלה כארגומנט ראשון את הפונקציה <var>square</var> שהגדרנו למעלה, שמטרתה העלאת מספר בריבוע.<br>
כארגומנט שני היא קיבלה את רשימת כל המספרים שאנחנו רוצים שהפונקציה תרוץ עליהם.<br>
כשהעברנו ל־<var>map</var> את הארגומנטים הללו, <var>map</var> החזירה לנו ב־iterator (מבנה שאפשר לעבור עליו איבר־איבר) את התוצאה:<br>
הריבוע, קרי החזקה השנייה, של כל אחד מהאיברים ברשימה שהועברה כארגומנט השני.
</p>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
למעשה, אפשר להגיד ש־<code>map</code> שקולה לפונקציה הבאה:
</p>
```
def my_map(function, iterable):
for item in iterable:
yield function(item)
```
<p style="text-align: right; direction: rtl; float: right; clear: both;">
הנה דוגמה נוספת לשימוש ב־<var>map</var>:
</p>
```
numbers = [(2, 4), (1, 4, 2), (1, 3, 5, 6, 2), (3, )]
sums = map(sum, numbers)
print(tuple(sums))
```
<p style="text-align: right; direction: rtl; float: right; clear: both;">
במקרה הזה, בכל מעבר, קיבלה הפונקציה <var>sum</var> איבר אחד מתוך הרשימה – tuple.<br>
היא סכמה את האיברים של כל tuple שקיבלה, וכך החזירה לנו את הסכומים של כל ה־tuple־ים – זה אחרי זה.
</p>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
ודוגמה אחרונה:
</p>
```
def add_one(number):
return number + 1
incremented = map(add_one, (1, 2, 3))
print(tuple(incremented))
```
<p style="text-align: right; direction: rtl; float: right; clear: both;">
בדוגמה הזו יצרנו פונקציה משל עצמנו, ואותה העברנו ל־map.<br>
מטרת דוגמה זו היא להדגיש שאין שוני בין העברת פונקציה שקיימת בפייתון לבין פונקציה שאנחנו יצרנו.
</p>
<div class="align-center" style="display: flex; text-align: right; direction: rtl; clear: both;">
<div style="display: flex; width: 10%; float: right; clear: both;">
<img src="images/exercise.svg" style="height: 50px !important;" alt="תרגול">
</div>
<div style="width: 70%">
<p style="text-align: right; direction: rtl; float: right; clear: both;">
כתבו פונקציה שמקבלת רשימת מחרוזות של שתי מילים: שם פרטי ושם משפחה.<br>
הפונקציה תשתמש ב־map כדי להחזיר מכולן רק את השם הפרטי.
</p>
</div>
<div style="display: flex; width: 20%; border-right: 0.1rem solid #A5A5A5; padding: 1rem 2rem;">
<p style="text-align: center; direction: rtl; justify-content: center; align-items: center; clear: both;">
<strong>חשוב!</strong><br>
פתרו לפני שתמשיכו!
</p>
</div>
</div>
### <span style="text-align: right; direction: rtl; float: right; clear: both;">הפונקציה filter</span>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
הפונקציה <var>filter</var> מקבלת פונקציה כפרמטר ראשון, ו־iterable כפרמטר שני.<br>
<var>filter</var> מפעילה על כל אחד מאיברי ה־iterable את הפונקציה, ומחזירה את האיבר אך ורק אם הערך שחזר מהפונקציה שקול ל־<code>True</code>.<br>
אם ערך ההחזרה שקול ל־<code>False</code> – הערך "יבלע" ב־<var>filter</var> ולא יחזור ממנה.
</p>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
במילים אחרות, <var>filter</var> יוצרת iterable חדש ומחזירה אותו.<br>
ה־iterable כולל רק את האיברים שעבורם הפונקציה שהועברה החזירה ערך השקול ל־<code>True</code>.
</p>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
נבנה, לדוגמה, פונקציה שמחזירה אם אדם הוא בגיר.<br>
הפונקציה תקבל כפרמטר גיל, ותחזיר <code>True</code> כאשר הגיל שהועבר לה הוא לפחות 18, ו־<code>False</code> אחרת.
</p>
```
def is_mature(age):
return age >= 18
```
<p style="text-align: right; direction: rtl; float: right; clear: both;">
נגדיר רשימת גילים, ונבקש מ־<var>filter</var> לסנן אותם לפי הפונקציה שהגדרנו:
</p>
```
ages = [0, 1, 4, 10, 20, 35, 56, 84, 120]
mature_ages = filter(is_mature, ages)
print(tuple(mature_ages))
```
<p style="text-align: right; direction: rtl; float: right; clear: both;">
כפי שלמדנו, <var>filter</var> מחזירה לנו רק גילים השווים ל־18 או גדולים ממנו.
</p>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
נחדד שהפונקציה שאנחנו מעבירים ל־<var>filter</var> לא חייבת להחזיר בהכרח <code>True</code> או <code>False</code>.<br>
הערך 0, לדוגמה, שקול ל־<code>False</code>, ולכן <var>filter</var> תסנן כל ערך שעבורו הפונקציה תחזיר 0:
</p>
```
to_sum = [(1, -1), (2, 5), (5, -3, -2), (1, 2, 3)]
sum_is_not_zero = filter(sum, to_sum)
print(tuple(sum_is_not_zero))
```
<p style="text-align: right; direction: rtl; float: right; clear: both;">
בתא האחרון העברנו ל־<var>filter</var> את sum כפונקציה שאותה אנחנו רוצים להפעיל, ואת <var>to_sum</var> כאיברים שעליהם אנחנו רוצים לפעול.<br>
ה־tuple־ים שסכום איבריהם היה 0 סוננו, וקיבלנו חזרה iterator שהאיברים בו הם אך ורק אלו שסכומם שונה מ־0.
</p>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
כטריק אחרון, נלמד ש־<var>filter</var> יכולה לקבל גם <code>None</code> בתור הפרמטר הראשון, במקום פונקציה.<br>
זה יגרום ל־<var>filter</var> לא להפעיל פונקציה על האיברים שהועברו, כלומר לסנן אותם כמו שהם.<br>
איברים השקולים ל־<code>True</code> יוחזרו, ואיברים השקולים ל־<code>False</code> לא יוחזרו:
</p>
```
to_sum = [0, "", None, 0.0, True, False, "Hello"]
equivalent_to_true = filter(None, to_sum)
print(tuple(equivalent_to_true))
```
<div class="align-center" style="display: flex; text-align: right; direction: rtl; clear: both;">
<div style="display: flex; width: 10%; float: right; clear: both;">
<img src="images/exercise.svg" style="height: 50px !important;" alt="תרגול">
</div>
<div style="width: 70%">
<p style="text-align: right; direction: rtl; float: right; clear: both;">
כתבו פונקציה שמקבלת רשימת מחרוזות, ומחזירה רק את המחרוזות הפלינדרומיות שבה.<br>
מחרוזת נחשבת פלינדרום אם קריאתה מימין לשמאל ומשמאל לימין יוצרת אותו ביטוי.<br>
השתמשו ב־<var>filter</var>.
</p>
</div>
<div style="display: flex; width: 20%; border-right: 0.1rem solid #A5A5A5; padding: 1rem 2rem;">
<p style="text-align: center; direction: rtl; justify-content: center; align-items: center; clear: both;">
<strong>חשוב!</strong><br>
פתרו לפני שתמשיכו!
</p>
</div>
</div>
## <span style="text-align: right; direction: rtl; float: right; clear: both;">פונקציות אנונימיות</span>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
תעלול נוסף שנוסיף לארגז הכלים שלנו הוא <dfn>פונקציות אנונימיות</dfn> (<dfn>anonymous functions</dfn>).<br>
אל תיבהלו מהשם המאיים – בסך הכול פירושו הוא "פונקציות שאין להן שם".<br>
</p>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
לפני שאתם מרימים גבה ושואלים את עצמכם למה הן שימושיות, בואו נבחן כמה דוגמאות.<br>
ניזכר בהגדרת פונקציית החיבור שיצרנו לא מזמן:
</p>
```
def add(num1, num2):
return num1 + num2
```
<p style="text-align: right; direction: rtl; float: right; clear: both;">
ונגדיר את אותה הפונקציה בדיוק בצורה אנונימית:
</p>
```
add = lambda num1, num2: num1 + num2
print(add(5, 2))
```
<p style="text-align: right; direction: rtl; float: right; clear: both;">
לפני שנסביר איפה החלק של ה"פונקציה בלי שם" נתמקד בצד ימין של ההשמה.<br>
כיצד מנוסחת הגדרת פונקציה אנונימית?
</p>
<ol style="text-align: right; direction: rtl; float: right; clear: both;">
<li>הצהרנו שברצוננו ליצור פונקציה אנונימית בעזרת מילת המפתח <code>lambda</code>.</li>
<li>מייד אחריה, ציינו את שמות כל הפרמטרים שהפונקציה תקבל, כשהם מופרדים בפסיק זה מזה.</li>
<li>כדי להפריד בין רשימת הפרמטרים לערך ההחזרה של הפונקציה, השתמשנו בנקודתיים.</li>
<li>אחרי הנקודתיים, כתבנו את הביטוי שאנחנו רוצים שהפונקציה תחזיר.</li>
</ol>
<figure>
<img src="images/lambda.png" style="max-width: 500px; margin-right: auto; margin-left: auto; text-align: center;" alt="בתמונה מופיעה הגדרת ה־lambda שביצענו קודם לכן. מעל המילה lambda המודגשת בירוק ישנו פס מקווקו, ומעליו רשום 'הצהרה'. מימין למילה lambda כתוב num1 (פסיק) num2, מעליהם קו מקווקו ומעליו המילה 'פרמטרים'. מימין לפרמטרים יש נקודתיים, ואז num1 (הסימן פלוס) num2. מעליהם קו מקווקו, ומעליו המילה 'ערך החזרה'."/>
<figcaption style="margin-top: 2rem; text-align: center; direction: rtl;">חלקי ההגדרה של פונקציה אנונימית בעזרת מילת המפתח <code>lambda</code><br><span style="color: white;">A girl has no name</span></figcaption>
</figure>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
במה שונה ההגדרה של פונקציה זו מההגדרה של פונקציה רגילה?<br>
היא לא באמת שונה.<br>
המטרה היא לאפשר תחביר שיקל על חיינו כשאנחנו רוצים לכתוב פונקציה קצרצרה שאורכה שורה אחת.
</p>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
נראה, לדוגמה, שימוש ב־<var>filter</var> כדי לסנן את כל האיברים שאינם חיוביים:
</p>
```
def is_positive(number):
return number > 0
numbers = [-2, -1, 0, 1, 2]
positive_numbers = filter(is_positive, numbers)
print(tuple(positive_numbers))
```
<p style="text-align: right; direction: rtl; float: right; clear: both;">
במקום להגדיר פונקציה חדשה שנקראת <var>is_positive</var>, נוכל להשתמש בפונקציה אנונימית:
</p>
```
numbers = [-2, -1, 0, 1, 2]
positive_numbers = filter(lambda n: n > 0, numbers)
print(tuple(positive_numbers))
```
<p style="text-align: right; direction: rtl; float: right; clear: both;">
איך זה עובד?<br>
במקום להעביר ל־<var>filter</var> פונקציה שיצרנו מבעוד מועד, השתמשנו ב־<code>lambda</code> כדי ליצור פונקציה ממש באותה השורה.<br>
הפונקציה שהגדרנו מקבלת מספר (<var>n</var>), ומחזירה <code>True</code> אם הוא חיובי, או <code>False</code> אחרת.<br>
שימו לב שבצורה זו באמת לא היינו צריכים לתת שם לפונקציה שהגדרנו.
</p>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
השימוש בפונקציות אנונימיות לא מוגבל ל־<var>map</var> ול־<var>filter</var>, כמובן.<br>
מקובל להשתמש ב־<code>lambda</code> גם עבור פונקציות כמו <var>sorted</var>, שמקבלות פונקציה בתור ארגומנט.
</p>
<div class="align-center" style="display: flex; text-align: right; direction: rtl;">
<div style="display: flex; width: 10%; float: right; ">
<img src="images/recall.svg" style="height: 50px !important;" alt="תזכורת" title="תזכורת">
</div>
<div style="width: 90%">
<p style="text-align: right; direction: rtl;">
הפונקציה <code>sorted</code> מאפשרת לנו לסדר ערכים, ואפילו להגדיר עבורה לפי מה לסדר אותם.<br>
לרענון בנוגע לשימוש בפונקציה גשו למחברת בנושא פונקציות מובנות בשבוע 4.
</p>
</div>
</div>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
נסדר, למשל, את הדמויות ברשימה הבאה, לפי תאריך הולדתן:
</p>
```
closet = [
{'name': 'Peter', 'year_of_birth': 1927, 'gender': 'Male'},
{'name': 'Edmund', 'year_of_birth': 1930, 'gender': 'Male'},
{'name': 'Lucy', 'year_of_birth': 1932, 'gender': 'Female'},
{'name': 'Susan', 'year_of_birth': 1928, 'gender': 'Female'},
{'name': 'Jadis', 'year_of_birth': 0, 'gender': 'Female'},
]
```
<p style="text-align: right; direction: rtl; float: right; clear: both;">
נרצה שסידור הרשימה יתבצע לפי המפתח <var>year_of_birth</var>.<br>
כלומר, בהינתן מילון שמייצג דמות בשם <var>d</var>, יש להשיג את <code dir="ltr">d['year_of_birth']</code>, ולפיו לבצע את סידור הרשימה.<br>
ניגש למלאכה:
</p>
```
sorted(closet, key=lambda d: d['year_of_birth'])
```
<div class="align-center" style="display: flex; text-align: right; direction: rtl;">
<div style="display: flex; width: 10%; float: right; ">
<img src="images/warning.png" style="height: 50px !important;" alt="אזהרה!">
</div>
<div style="width: 90%">
<p style="text-align: right; direction: rtl;">
פונקציות אנונימיות הן יכולת חביבה שאמורה לסייע לכם לכתוב קוד נאה וקריא.<br>
כלל אצבע טוב לחיים הוא להימנע משימוש בהן כאשר הן מסרבלות את הקוד.
</p>
</div>
</div>
<div class="align-center" style="display: flex; text-align: right; direction: rtl; clear: both;">
<div style="display: flex; width: 10%; float: right; clear: both;">
<img src="images/exercise.svg" style="height: 50px !important;" alt="תרגיל" title="תרגיל">
</div>
<div style="width: 70%">
<p style="text-align: right; direction: rtl; float: right; clear: both;">
סדרו את הדמויות ב־<var>closet</var> לפי האות האחרונה בשמם.
</p>
</div>
</div>
## <span style="align: right; direction: rtl; float: right; clear: both;">מונחים</span>
<dl style="text-align: right; direction: rtl; float: right; clear: both;">
<dt>פונקציה מסדר גבוה</dt>
<dd>פונקציה שמקבלת פונקציה כאחד הארגומנטים, או שמחזירה פונקציה כערך ההחזרה שלה.</dd>
<dt>אזרח ממדרגה ראשונה</dt>
<dd>ישות תכנותית המתנהגת בשפת התכנות כערך לכל דבר. בפייתון, פונקציות הן אזרחיות ממדרגה ראשונה.<dd>
<dt>פונקציה אנונימית, פונקציית <code>lambda</code></dt>
<dd>פונקציה ללא שם המיועדת להגדרת פונקציה בשורה אחת, לרוב לשימוש חד־פעמי. בעברית: פונקציית למדא.</dd>
</dl>
## <span style="align: right; direction: rtl; float: right; clear: both;">תרגילים</span>
### <span style="align: right; direction: rtl; float: right; clear: both;">פילטר מותאם אישית</span>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
כתבו פונקציה בשם <var>my_filter</var> שמתנהגת בדיוק כמו הפונקציה <var>filter</var>.<br>
בפתירת התרגיל, המנעו משימוש ב־<var>filter</var> או במודולים.
</p>
### <span style="align: right; direction: rtl; float: right; clear: both;">נשאר? חיובי</span>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
כתבו פונקציה בשם <var>get_positive_numbers</var> שמקבלת מהמשתמש קלט בעזרת <var>input</var>.<br>
המשתמש יתבקש להזין סדרה של מספרים המופרדים בפסיק זה מזה.<br>
הפונקציה תחזיר את כל המספרים החיוביים שהמשתמש הזין, כרשימה של מספרים מסוג <code>int</code>.<br>
אפשר להניח שהקלט מהמשתמש תקין.
</p>
### <span style="align: right; direction: rtl; float: right; clear: both;">ריצת 2,000</span>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
כתבו פונקציה בשם <var>timer</var> שמקבלת כפרמטר פונקציה (נקרא לה <var>f</var>) ופרמטרים נוספים.<br>
הפונקציה <var>timer</var> תמדוד כמה זמן רצה פונקציה <var>f</var> כשמועברים אליה אותם פרמטרים. <br>
</p>
<p style="text-align: right; direction: rtl; float: right; clear: both;">
לדוגמה:
</p>
<ol style="text-align: right; direction: rtl; float: right; clear: both;">
<li>עבור הקריאה <code dir="ltr">timer(print, "Hello")</code>, תחזיר הפונקציה את משך זמן הביצוע של <code dir="ltr">print("Hello")</code>.</li>
<li>עבור הקריאה <code dir="ltr">timer(zip, [1, 2, 3], [4, 5, 6])</code>, תחזיר הפונקציה את משך זמן הביצוע של <code dir="ltr">zip([1, 2, 3], [4, 5, 6])</code>.</li>
<li>עבור הקריאה <code dir="ltr">timer("Hi {name}".format, name="Bug")</code>, תחזיר הפונקציה את משך זמן הביצוע של <code dir="ltr">"Hi {name}".format(name="Bug")</code></li>
</ol>
|
github_jupyter
|
##### Copyright 2019 The TensorFlow Authors.
```
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
```
#Improving Computer Vision Accuracy using Convolutions
In the previous lessons you saw how to do fashion recognition using a Deep Neural Network (DNN) containing three layers -- the input layer (in the shape of the data), the output layer (in the shape of the desired output) and a hidden layer. You experimented with the impact of different sizes of hidden layer, number of training epochs etc on the final accuracy.
For convenience, here's the entire code again. Run it and take a note of the test accuracy that is printed out at the end.
```
import tensorflow as tf
mnist = tf.keras.datasets.fashion_mnist
(training_images, training_labels), (test_images, test_labels) = mnist.load_data()
training_images=training_images / 255.0
test_images=test_images / 255.0
model = tf.keras.models.Sequential([
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(128, activation=tf.nn.relu),
tf.keras.layers.Dense(10, activation=tf.nn.softmax)
])
model.compile(optimizer='adam', loss='sparse_categorical_crossentropy', metrics=['accuracy'])
model.fit(training_images, training_labels, epochs=5)
test_loss = model.evaluate(test_images, test_labels)
```
Your accuracy is probably about 89% on training and 87% on validation...not bad...But how do you make that even better? One way is to use something called Convolutions. I'm not going to details on Convolutions here, but the ultimate concept is that they narrow down the content of the image to focus on specific, distinct, details.
If you've ever done image processing using a filter (like this: https://en.wikipedia.org/wiki/Kernel_(image_processing)) then convolutions will look very familiar.
In short, you take an array (usually 3x3 or 5x5) and pass it over the image. By changing the underlying pixels based on the formula within that matrix, you can do things like edge detection. So, for example, if you look at the above link, you'll see a 3x3 that is defined for edge detection where the middle cell is 8, and all of its neighbors are -1. In this case, for each pixel, you would multiply its value by 8, then subtract the value of each neighbor. Do this for every pixel, and you'll end up with a new image that has the edges enhanced.
This is perfect for computer vision, because often it's features that can get highlighted like this that distinguish one item for another, and the amount of information needed is then much less...because you'll just train on the highlighted features.
That's the concept of Convolutional Neural Networks. Add some layers to do convolution before you have the dense layers, and then the information going to the dense layers is more focussed, and possibly more accurate.
Run the below code -- this is the same neural network as earlier, but this time with Convolutional layers added first. It will take longer, but look at the impact on the accuracy:
```
import tensorflow as tf
print(tf.__version__)
mnist = tf.keras.datasets.fashion_mnist
(training_images, training_labels), (test_images, test_labels) = mnist.load_data()
# Reshaping the images to tell the convolutional layers that the images are in greyscale by adding an extra dimension of 1
training_images=training_images.reshape(60000, 28, 28, 1)
training_images=training_images / 255.0
test_images = test_images.reshape(10000, 28, 28, 1)
test_images=test_images/255.0
model = tf.keras.models.Sequential([
# Mind it, Convolutions and MaxPooling are always applied before the Deep Neural Network Layers
# Why 2D? because, applied convolutions and maxpoolings are 2D array in nature (having rows and columns)
# Here 64 is the total number of convolutional filters of size (3, 3) applied
### Be careful about the shapes!!! You obviously need to mention the input_shape at the first Conv2D(), otherwise it will turn
### into an error!!!
tf.keras.layers.Conv2D(64, (3, 3), activation='relu', input_shape=(28, 28, 1)),
tf.keras.layers.MaxPooling2D(2, 2),
tf.keras.layers.Conv2D(64, (3, 3), activation='relu'),
tf.keras.layers.MaxPooling2D(2, 2),
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(128, activation='relu'),
tf.keras.layers.Dense(10, activation='softmax')
])
model.compile(optimizer='adam', loss='sparse_categorical_crossentropy', metrics=['accuracy'])
# Mind it, model.summary() is a way of cross-verification that the DNN with Convolutions is applied correctly with accurate
# shape retention
model.summary()
model.fit(training_images, training_labels, epochs=5)
test_loss = model.evaluate(test_images, test_labels)
```
It's likely gone up to about 93% on the training data and 91% on the validation data.
That's significant, and a step in the right direction!
Try running it for more epochs -- say about 20, and explore the results! But while the results might seem really good, the validation results may actually go down, due to something called 'overfitting' which will be discussed later.
(In a nutshell, 'overfitting' occurs when the network learns the data from the training set really well, but it's too specialised to only that data, and as a result is less effective at seeing *other* data. For example, if all your life you only saw red shoes, then when you see a red shoe you would be very good at identifying it, but blue suade shoes might confuse you...and you know you should never mess with my blue suede shoes.)
Then, look at the code again, and see, step by step how the Convolutions were built:
Step 1 is to gather the data. You'll notice that there's a bit of a change here in that the training data needed to be reshaped. That's because the first convolution expects a single tensor containing everything, so instead of 60,000 28x28x1 items in a list, we have a single 4D list that is 60,000x28x28x1, and the same for the test images. If you don't do this, you'll get an error when training as the Convolutions do not recognize the shape.
```
import tensorflow as tf
mnist = tf.keras.datasets.fashion_mnist
(training_images, training_labels), (test_images, test_labels) = mnist.load_data()
training_images=training_images.reshape(60000, 28, 28, 1)
training_images=training_images / 255.0
test_images = test_images.reshape(10000, 28, 28, 1)
test_images=test_images/255.0
```
Next is to define your model. Now instead of the input layer at the top, you're going to add a Convolution. The parameters are:
1. The number of convolutions you want to generate. Purely arbitrary, but good to start with something in the order of 32
2. The size of the Convolution, in this case a 3x3 grid
3. The activation function to use -- in this case we'll use relu, which you might recall is the equivalent of returning x when x>0, else returning 0
4. In the first layer, the shape of the input data.
You'll follow the Convolution with a MaxPooling layer which is then designed to compress the image, while maintaining the content of the features that were highlighted by the convlution. By specifying (2,2) for the MaxPooling, the effect is to quarter the size of the image. Without going into too much detail here, the idea is that it creates a 2x2 array of pixels, and picks the biggest one, thus turning 4 pixels into 1. It repeats this across the image, and in so doing halves the number of horizontal, and halves the number of vertical pixels, effectively reducing the image by 25%.
You can call model.summary() to see the size and shape of the network, and you'll notice that after every MaxPooling layer, the image size is reduced in this way.
```
model = tf.keras.models.Sequential([
tf.keras.layers.Conv2D(32, (3,3), activation='relu', input_shape=(28, 28, 1)),
tf.keras.layers.MaxPooling2D(2, 2),
```
Add another convolution
```
tf.keras.layers.Conv2D(64, (3,3), activation='relu'),
tf.keras.layers.MaxPooling2D(2,2)
```
Now flatten the output. After this you'll just have the same DNN structure as the non convolutional version
```
tf.keras.layers.Flatten(),
```
The same 128 dense layers, and 10 output layers as in the pre-convolution example:
```
tf.keras.layers.Dense(128, activation='relu'),
tf.keras.layers.Dense(10, activation='softmax')
])
```
Now compile the model, call the fit method to do the training, and evaluate the loss and accuracy from the test set.
```
model.compile(optimizer='adam', loss='sparse_categorical_crossentropy', metrics=['accuracy'])
model.fit(training_images, training_labels, epochs=5)
test_loss, test_acc = model.evaluate(test_images, test_labels)
print(test_acc)
```
# Visualizing the Convolutions and Pooling
This code will show us the convolutions graphically. The print (test_labels[;100]) shows us the first 100 labels in the test set, and you can see that the ones at index 0, index 23 and index 28 are all the same value (9). They're all shoes. Let's take a look at the result of running the convolution on each, and you'll begin to see common features between them emerge. Now, when the DNN is training on that data, it's working with a lot less, and it's perhaps finding a commonality between shoes based on this convolution/pooling combination.
```
print(test_labels[:100])
import matplotlib.pyplot as plt
f, axarr = plt.subplots(3,4)
FIRST_IMAGE=0
SECOND_IMAGE=7
THIRD_IMAGE=26
CONVOLUTION_NUMBER = 1
from tensorflow.keras import models
layer_outputs = [layer.output for layer in model.layers]
activation_model = tf.keras.models.Model(inputs = model.input, outputs = layer_outputs)
for x in range(0,4):
f1 = activation_model.predict(test_images[FIRST_IMAGE].reshape(1, 28, 28, 1))[x]
axarr[0,x].imshow(f1[0, : , :, CONVOLUTION_NUMBER], cmap='inferno')
axarr[0,x].grid(False)
f2 = activation_model.predict(test_images[SECOND_IMAGE].reshape(1, 28, 28, 1))[x]
axarr[1,x].imshow(f2[0, : , :, CONVOLUTION_NUMBER], cmap='inferno')
axarr[1,x].grid(False)
f3 = activation_model.predict(test_images[THIRD_IMAGE].reshape(1, 28, 28, 1))[x]
axarr[2,x].imshow(f3[0, : , :, CONVOLUTION_NUMBER], cmap='inferno')
axarr[2,x].grid(False)
```
EXERCISES
1. Try editing the convolutions. Change the 32s to either 16 or 64. What impact will this have on accuracy and/or training time.
2. Remove the final Convolution. What impact will this have on accuracy or training time?
3. How about adding more Convolutions? What impact do you think this will have? Experiment with it.
4. Remove all Convolutions but the first. What impact do you think this will have? Experiment with it.
5. In the previous lesson you implemented a callback to check on the loss function and to cancel training once it hit a certain amount. See if you can implement that here!
```
import tensorflow as tf
print(tf.__version__)
mnist = tf.keras.datasets.mnist
(training_images, training_labels), (test_images, test_labels) = mnist.load_data()
training_images=training_images.reshape(60000, 28, 28, 1)
training_images=training_images / 255.0
test_images = test_images.reshape(10000, 28, 28, 1)
test_images=test_images/255.0
model = tf.keras.models.Sequential([
tf.keras.layers.Conv2D(32, (3,3), activation='relu', input_shape=(28, 28, 1)),
tf.keras.layers.MaxPooling2D(2, 2),
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(128, activation='relu'),
tf.keras.layers.Dense(10, activation='softmax')
])
model.compile(optimizer='adam', loss='sparse_categorical_crossentropy', metrics=['accuracy'])
model.fit(training_images, training_labels, epochs=10)
test_loss, test_acc = model.evaluate(test_images, test_labels)
print(test_acc)
```
|
github_jupyter
|
## Fundamentals, introduction to machine learning
The purpose of these guides is to go a bit deeper into the details behind common machine learning methods, assuming little math background, and teach you how to use popular machine learning Python packages. In particular, we'll focus on the Numpy and PyTorch libraries.
I'll assume you have some experience programming with Python -- if not, check out the initial [fundamentals of Python guide](https://github.com/ml4a/ml4a-guides/blob/master/notebooks/intro_python.ipynb) or for a longer, more comprehensive resource: [Learn Python the Hard Way](http://learnpythonthehardway.org/book/). It will really help to illustrate the concepts introduced here.
Numpy underlies most Python machine learning packages and is great for performing quick sketches or working through calculations. PyTorch rivals alternative libraries, such as TensorFlow, for its flexibility and ease of use. Despite the high level appearance of PyTorch, it can be quite low-level, which is great for experimenting with novel algorithms. PyTorch can seamlessly be integrated with distributed computation libraries, like Ray, to make the Kessel Run in less than 12 parsecs (citation needed).
These guides will present the formal math for concepts alongside Python code examples since this often (for me at least) is a lot easier to develop an intuition for. Each guide is also available as an iPython notebook for your own experimentation.
The guides are not meant to exhaustively cover the field of machine learning but I hope they will instill you with the confidence and knowledge to explore further on your own.
If you do want more details, you might enjoy my [artificial intelligence notes](http://frnsys.com/ai_notes).
### Modeling the world
You've probably seen various machine learning algorithms pop up -- linear regression, SVMs, neural networks, random forests, etc. How are they all related? What do they have in common? What is machine learning for anyways?
First, let's consider the general, fundamental problem all machine learning is concerned with, leaving aside the algorithm name soup for now. The primary concern of machine learning is _modeling the world_.
We can model phenomena or systems -- both natural and artificial, if you want to make that distinction -- with mathematical functions. We see something out in the world and want to describe it in some way, we want to formalize how two or more things are related, and we can do that with a function. The problem is, for a given phenomenon, how do we figure out what function to use? There are infinitely many to choose from!
Before this gets too abstract, let's use an example to make things more concrete.
Say we have a bunch of data about the heights and weights of a species of deer. We want to understand how these two variables are related -- in particular, given the weight of a deer, can we predict its height?
You might see where this is going. The data looks like a line, and lines in general are described by functions of the form $y = mx + b$.
Remember that lines vary depending on what the values of $m$ and $b$ are:

Thus $m$ and $b$ uniquely define a function -- thus they are called the _parameters_ of the function -- and when it comes to machine learning, these parameters are what we ultimately want to learn. So when I say there are infinitely many functions to choose from, it is because $m$ and $b$ can pretty much take on any value. Machine learning techniques essentially search through these possible functions to find parameters that best fit the data you have. One way machine learning algorithms are differentiated is by how exactly they conduct this search (i.e. how they learn parameters).
In this case we've (reasonably) assumed the function takes the form $y = mx + b$, but conceivably you may have data that doesn't take the form of a line. Real world data is typically a lot more convoluted-looking. Maybe the true function has a $sin$ in it, for example.
This is where another main distinction between machine learning algorithms comes in -- certain algorithms can model only certain forms of functions. _Linear regression_, for example, can only model linear functions, as indicated by its name. Neural networks, on the other hand, are _universal function approximators_, which mean they can (in theory) approximate _any_ function, no matter how exotic. This doesn't necessarily make them a better method, just better suited for certain circumstances (there are many other considerations when choosing an algorithm).
For now, let's return to the line function. Now that we've looked at the $m$ and $b$ variables, let's consider the input variable $x$. A function takes a numerical input; that is $x$ must be a number of some kind. That's pretty straightforward here since the deer weights are already numbers. But this is not always the case! What if we want to predict the sales price of a house. A house is not a number. We have to find a way to _represent_ it as a number (or as several numbers, i.e. a vector, which will be detailed in a moment), e.g. by its square footage. This challenge of representation is a major part of machine learning; the practice of building representations is known as _feature engineering_ since each variable (e.g. square footage or zip code) used for the representation is called a _feature_.
If you think about it, representation is a practice we regularly engage in. The word "house" is not a house any more than an image of a house is -- there is no true "house" anyways, it is always a constellation of various physical and nonphysical components.
That's about it -- broadly speaking, machine learning is basically a bunch of algorithms that learn you a function, which is to say they learn the parameters that uniquely define a function.
### Vectors
In the line example before I mentioned that we might have multiple numbers representing an input. For example, a house probably can't be solely represented by its square footage -- perhaps we also want to consider how many bedrooms it has, or how high the ceilings are, or its distance from local transportation. How do we group these numbers together?
That's what _vectors_ are for (they come up for many other reasons too, but we'll focus on representation for now). Vectors, along with matrices and other tensors (which will be explained a bit further down), could be considered the "primitives" of machine learning.
The Numpy library is best for dealing with vectors (and other tensors) in Python. A more complete introduction to Numpy is provided in the [numpy and basic mathematics guide](https://github.com/ml4a/ml4a-guides/blob/master/notebooks/math_review_numpy.ipynb).
Let's import `numpy` with the alias `nf`:
```
import numpy as np
```
You may have encountered vectors before in high school or college -- to use Python terms, a vector is like a list of numbers. The mathematical notation is quite similar to Python code, e.g. `[5,4]`, but `numpy` has its own way of instantiating a vector:
```
v = np.array([5, 4])
```
$$
v = \begin{bmatrix} 5 \\ 4 \end{bmatrix}
$$
Vectors are usually represented with lowercase variables.
Note that we never specified how _many_ numbers (also called _components_) a vector has - because it can have any amount. The amount of components a vector has is called its _dimensionality_. The example vector above has two dimensions. The vector `x = [8,1,3]` has three dimensions, and so on. Components are usually indicated by their index (usually using 1-indexing), e.g. in the previous vector, $x_1$ refers to the value $8$.
"Dimensions" in the context of vectors is just like the spatial dimensions you spend every day in. These dimensions define a __space__, so a two-dimensional vector, e.g. `[5,4]`, can describe a point in 2D space and a three-dimensional vector, e.g. `[8,1,3]`, can describe a point in 3D space. As mentioned before, there is no limit to the amount of dimensions a vector may have (technically, there must be one or more dimensions), so we could conceivably have space consisting of thousands or tens of thousands of dimensions. At that point we can't rely on the same human intuitions about space as we could when working with just two or three dimensions. In practice, most interesting applications of machine learning deal with many, many dimensions.
We can get a better sense of this by plotting a vector out. For instance, a 2D vector `[5,0]` would look like:

So in a sense vectors can be thought of lines that "point" to the position they specify - here the vector is a line "pointing" to `[5,0]`. If the vector were 3D, e.g. `[8,1,3]`, then we would have to visualize it in 3D space, and so on.
So vectors are great - they allow us to form logical groupings of numbers. For instance, if we're talking about cities on a map we would want to group their latitude and longitude together. We'd represent Lagos with `[6.455027, 3.384082]` and Beijing separately with `[39.9042, 116.4074]`. If we have an inventory of books for sale, we could represent each book with its own vector consisting of its price, number of pages, and remaining stock.
To use vectors in functions, there are a few mathematical operations you need to know.
### Basic vector operations
Vectors can be added (and subtracted) easily:
```
np.array([6, 2]) + np.array([-4, 4])
```
$$
\begin{bmatrix} 6 \\ 2 \end{bmatrix} + \begin{bmatrix} -4 \\ 4 \end{bmatrix} = \begin{bmatrix} 6 + -4 \\ 2 + 4 \end{bmatrix} = \begin{bmatrix} 2 \\ 6 \end{bmatrix}
$$
However, when it comes to vector multiplication there are many different kinds.
The simplest is _vector-scalar_ multiplication:
```
3 * np.array([2, 1])
```
$$
3\begin{bmatrix} 2 \\ 1 \end{bmatrix} = \begin{bmatrix} 3 \times 2 \\ 3 \times 1
\end{bmatrix} = \begin{bmatrix} 6 \\ 3 \end{bmatrix}
$$
But when you multiply two vectors together you have a few options. I'll cover the two most important ones here.
The one you might have thought of is the _element-wise product_, also called the _pointwise product_, _component-wise product_, or the _Hadamard product_, typically notated with $\odot$. This just involves multiplying the corresponding elements of each vector together, resulting in another vector:
```
np.array([6, 2]) * np.array([-4, 4])
```
$$
\begin{bmatrix} 6 \\ 2 \end{bmatrix} \odot \begin{bmatrix} -4 \\ 4 \end{bmatrix} = \begin{bmatrix} 6 \times -4 \\ 2 \times 4 \end{bmatrix} = \begin{bmatrix} -24 \\ 8 \end{bmatrix}
$$
The other vector product, which you'll encounter a lot, is the _dot product_, also called _inner product_, usually notated with $\cdot$ (though when vectors are placed side-by-side this often implies dot multiplication). This involves multiplying corresponding elements of each vector and then summing the resulting vector's components (so this results in a scalar rather than another vector).
```
np.dot(np.array([6, 2]), np.array([-4, 4]))
```
$$
\begin{bmatrix} 6 \\ 2 \end{bmatrix} \cdot \begin{bmatrix} -4 \\ 4 \end{bmatrix} = (6 \times -4) + (2 \times 4) = -16
$$
The more general formulation is:
```
# a slow pure-Python dot product
def dot(a, b):
assert len(a) == len(b)
return sum(a_i * b_i for a_i, b_i in zip(a,b))
```
$$
\begin{aligned}
\vec{a} \cdot \vec{b} &= \begin{bmatrix} a_1 \\ a_2 \\ \vdots \\ a_n \end{bmatrix} \cdot \begin{bmatrix} b_1 \\ b_2 \\ \vdots \\ b_n \end{bmatrix} = a_1b_1 + a_2b_2 + \dots + a_nb_n \\
&= \sum^n_{i=1} a_i b_i
\end{aligned}
$$
Note that the vectors in these operations must have the same dimensions!
Perhaps the most important vector operation mentioned here is the dot product. We'll return to the house example to see why. Let's say want to represent a house with three variables: square footage, number of bedrooms, and the number of bathrooms. For convenience we'll notate the variables $x_1, x_2, x_3$, respectively. We're working in three dimensions now so instead of learning a line we're learning a _hyperplane_ (if we were working with two dimensions we'd be learning a plane, "hyperplane" is the term for the equivalent of a plane in higher dimensions).
Aside from the different name, the function we're learning is essentially of the same form as before, just with more variables and thus more parameters. We'll notate each parameter as $\theta_i$ as is the convention (you may see $\beta_i$ used elsewhere), and for the intercept (what was the $b$ term in the original line), we'll add in a dummy variable $x_0 = 1$ as is the typical practice (thus $\theta_0$ is equivalent to $b$):
```
# this is so clumsy in python;
# this will become more concise in a bit
def f(x0, x1, x2, x3, theta0, theta1, theta2, theta3):
return theta0 * x0\
+ theta1 * x1\
+ theta2 * x2\
+ theta3 * x3
```
$$
y = \theta_0 x_0 + \theta_1 x_1 + \theta_2 x_2 + \theta_3 x_3
$$
This kind of looks like the dot product, doesn't it? In fact, we can re-write this entire function as a dot product. We define our feature vector $x = [x_0, x_1, x_2, x_3]$ and our parameter vector $\theta = [\theta_0, \theta_1, \theta_2, \theta_3]$, then re-write the function:
```
def f(x, theta):
return x.dot(theta)
```
$$
y = \theta x
$$
So that's how we incorporate multiple features in a representation.
There's a whole lot more to vectors than what's presented here, but this is the ground-level knowledge you should have of them. Other aspects of vectors will be explained as they come up.
## Learning
So machine learning algorithms learn parameters - how do they do it?
Here we're focusing on the most common kind of machine learning - _supervised_ learning. In supervised learning, the algorithm learns parameters from data which includes both the inputs and the true outputs. This data is called _training_ data.
Although they vary on specifics, there is a general approach that supervised machine learning algorithms use to learn parameters. The idea is that the algorithm takes an input example, inputs it into the current guess at the function (called the _hypothesis_, notate $h_{\theta}$), and then checks how wrong its output is against the true output. The algorithm then updates its hypothesis (that is, its guesses for the parameters), accordingly.
"How wrong" an algorithm is, can vary depending on the _loss function_ it is using. The loss function takes the algorithm's current guess for the output, $\hat y$, and the true output, $y$, and returns some value quantifying its wrongness. Certain loss functions are more appropriate for certain tasks, which we'll get into later.
We'll get into the specifies of how the algorithm determines what kind of update to perform (i.e. how much each parameter changes), but before we do that we should consider how we manage batches of training examples (i.e. multiple training vectors) simultaneously.
## Matrices
__Matrices__ are in a sense a "vector" of vectors. That is, where a vector can be thought of as a logical grouping of numbers, a matrix can be thought of as a logical grouping of vectors. So if a vector represents a book in our catalog (id, price, number in stock), a matrix could represent the entire catalog (each row refers to a book). Or if we want to represent a grayscale image, the matrix can represent the brightness values of the pixels in the image.
```
A = np.array([
[6, 8, 0],
[8, 2, 7],
[3, 3, 9],
[3, 8, 6]
])
```
$$
\mathbf A =
\begin{bmatrix}
6 & 8 & 0 \\
8 & 2 & 7 \\
3 & 3 & 9 \\
3 & 8 & 6
\end{bmatrix}
$$
Matrices are usually represented with uppercase variables.
Note that the "vectors" in the matrix must have the same dimension. The matrix's dimensions are expressed in the form $m \times n$, meaning that there are $m$ rows and $n$ columns. So the example matrix has dimensions of $4 \times 3$. Numpy calls these dimensions a matrix's "shape".
We can access a particular element, $A_{i,j}$, in a matrix by its indices. Say we want to refer to the element in the 2nd row and the 3rd column (remember that python uses 0-indexing):
```
A[1,2]
```
### Basic matrix operations
Like vectors, matrix addition and subtraction is straightforward (again, they must be of the same dimensions):
```
B = np.array([
[8, 3, 7],
[2, 9, 6],
[2, 5, 6],
[5, 0, 6]
])
A + B
```
$$
\begin{aligned}
\mathbf B &=
\begin{bmatrix}
8 & 3 & 7 \\
2 & 9 & 6 \\
2 & 5 & 6 \\
5 & 0 & 6
\end{bmatrix} \\
A + B &=
\begin{bmatrix}
8+6 & 3+8 & 7+0 \\
2+8 & 9+2 & 6+7 \\
2+3 & 5+3 & 6+9 \\
5+3 & 0+8 & 6+6
\end{bmatrix} \\
&=
\begin{bmatrix}
14 & 11 & 7 \\
10 & 11 & 13 \\
5 & 8 & 15 \\
8 & 8 & 12
\end{bmatrix} \\
\end{aligned}
$$
Matrices also have a few different multiplication operations, like vectors.
_Matrix-scalar multiplication_ is similar to vector-scalar multiplication - you just distribute the scalar, multiplying it with each element in the matrix.
_Matrix-vector products_ require that the vector has the same dimension as the matrix has columns, i.e. for an $m \times n$ matrix, the vector must be $n$-dimensional. The operation basically involves taking the dot product of each matrix row with the vector:
```
# a slow pure-Python matrix-vector product,
# using our previous dot product implementation
def matrix_vector_product(M, v):
return [np.dot(row, v) for row in M]
# or, with numpy, you could use np.matmul(A,v)
```
$$
\mathbf M v =
\begin{bmatrix}
M_{1} \cdot v \\
\vdots \\
M_{m} \cdot v \\
\end{bmatrix}
$$
We have a few options when it comes to multiplying matrices with matrices.
However, before we go any further we should talk about the _tranpose_ operation - this just involves switching the columns and rows of a matrix. The transpose of a matrix $A$ is notated $A^T$:
```
A = np.array([
[1,2,3],
[4,5,6]
])
np.transpose(A)
```
$$
\begin{aligned}
\mathbf A &=
\begin{bmatrix}
1 & 2 & 3 \\
4 & 5 & 6
\end{bmatrix} \\
\mathbf A^T &=
\begin{bmatrix}
1 & 4 \\
2 & 5 \\
3 & 6
\end{bmatrix}
\end{aligned}
$$
For matrix-matrix products, the matrix on the lefthand must have the same number of columns as the righthand's rows. To be more concrete, we'll represent a matrix-matrix product as $A B$ and we'll say that $A$ has $m \times n$ dimensions. For this operation to work, $B$ must have $n \times p$ dimensions. The resulting product will have $m \times p$ dimensions.
```
# a slow pure-Python matrix Hadamard product
def matrix_matrix_product(A, B):
_, a_cols = np.shape(A)
b_rows, _ = np.shape(B)
assert a_cols == b_rows
result = []
# tranpose B so we can iterate over its columns
for col in np.tranpose(B):
# using our previous implementation
result.append(
matrix_vector_product(A, col))
return np.transpose(result)
```
$$
\mathbf AB =
\begin{bmatrix}
A B^T_1 \\
\vdots \\
A B^T_p
\end{bmatrix}^T
$$
Finally, like with vectors, we also have Hadamard (element-wise) products:
```
# a slow pure-Python matrix-matrix product
# or, with numpy, you can use A * B
def matrix_matrix_hadamard(A, B):
result = []
for a_row, b_row in zip(A, B):
result.append(
zip(a_i * b_i for a_i, b_i in zip(a_row, b_row)))
```
$$
\mathbf A \odot B =
\begin{bmatrix}
A_{1,1} B_{1,1} & \dots & A_{1,n} B_{1,n} \\
\vdots & \dots & \vdots \\
A_{m,1} B_{m,1} & \dots & A_{m,n} B_{m,n}
\end{bmatrix}
$$
Like vector Hadamard products, this requires that the two matrices share the same dimensions.
## Tensors
We've seen vectors, which is like a list of numbers, and matrices, which is like a list of a list of numbers. We can generalize this concept even further, for instance, with a list of a list of a list of numbers and so on. What all of these structures are called are _tensors_ (i.e. the "tensor" in "TensorFlow"). They are distinguished by their _rank_, which, if you're thinking in the "list of lists" way, refers to the number of nestings. So a vector has a rank of one (just a list of numbers) and a matrix has a rank of two (a list of a list of numbers).
Another way to think of rank is by number of indices necessary to access an element in the tensor. An element in a vector is accessed by one index, e.g. `v[i]`, so it is of rank one. An element in a matrix is accessed by two indices, e.g. `M[i,j]`, so it is of rank two.
Why is the concept of a tensor useful? Before we referred to vectors as a logical grouping of numbers and matrices as a logical grouping of vectors. What if we need a logical grouping of matrices? That's what 3rd-rank tensors are! A matrix can represent a grayscale image, but what about a color image with three color channels (red, green, blue)? With a 3rd-rank tensor, we could represent each channel as its own matrix and group them together.
## Learning continued
When the current hypothesis is wrong, how does the algorithm know how to adjust the parameters?
Let's take a step back and look at it another way. The loss function measures the wrongness of the hypothesis $h_{\theta}$ - another way of saying this is the loss function is a function of the parameters $\theta$. So we could notate it as $L(\theta)$.
The minimum of $L(\theta)$ is the point where the parameters guess $\theta$ is least wrong (at best, $L(\theta) = 0$, i.e. a perfect score, though this is not always good, as will be explained later); i.e. the best guess for the parameters.
So the algorithm learns the best-fitting function by minimizing its loss function. That is, we can frame this as an optimization problem.
There are many techniques to solve an optimization problem - sometimes they can be solved analytically (i.e. by moving around variables and isolating the one you want to solve for), but more often than not we must solve them numerically, i.e. by guessing a lot of different values - but not randomly!
The prevailing technique now is called _gradient descent_, and to understand how it works, we have to understand derivatives.
## Derivatives
Derivatives are everywhere in machine learning, so it's worthwhile become a bit familiar with them. I won't go into specifics on differentiation (how to calculate derivatives) because now we're spoiled with automatic differentiation, but it's still good to have a solid intuition about derivatives themselves.
A derivative expresses a rate of (instantaneous) change - they are always about how one variable quantity changes with respect to another variable quantity. That's basically all there is to it. For instance, velocity is a derivative which expresses how position changes with respect to time. Another interpretation, which is more relevant to machine learning, is that a derivative tells us how to change one variable to achieve a desired change in the other variable. Velocity, for instance, tells us how to change position by "changing" time.
To get a better understanding of _instantaneous_ change, consider a cyclist, cycling on a line. We have data about their position over time. We could calculate an average velocity over the data's entire time period, but we typically prefer to know the velocity at any given _moment_ (i.e. at any _instant_).
Let's get more concrete first. Let's say we have data for $n$ seconds, i.e. from $t_0$ to $t_n$ seconds, and the position at any given second $i$ is $p_i$. If we wanted to get the rate of change in position over the entire time interval, we'd just do:
```
positions = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, # moving forward
9, 9, 9, 9, 9, 9, 9, 9, 9, 9, # pausing
9, 8, 7, 6, 5, 4, 3, 2, 1, 0] # moving backwards
t_0 = 0
t_n = 29
(positions[t_n] - positions[t_0])/t_n
```
$$
v = \frac{p_n - p_0}{n}
$$
This kind of makes it look like the cyclist didn't move at all. It would probably be more useful to identify the velocity at a given second $t$. Thus we want to come up with some function $v(t)$ which gives us the velocity at some second $t$. We can apply the same approach we just used to get the velocity over the entire time interval, but we focus on a shorter time interval instead. To get the _instantaneous_ change at $t$ we just keep reducing the interval we look at until it is basically 0.
Derivatives have a special notation. A derivative of a function $f(x)$ with respect to a variable $x$ is notated:
$$
\frac{\delta f(x)}{\delta x}
$$
So if position is a function of time, e.g. $p = f(t)$, then velocity can be represented as $\frac{\delta p}{\delta t}$. To drive the point home, this derivative is also a function of time (derivatives are functions of what their "with respect to" variable is).
Since we are often computing derivatives of a function with respect to its input, a shorthand for the derivative of a function $f(x)$ with respect to $x$ can also be notated $f'(x)$.
### The Chain Rule
A very important property of derivatives is the _chain rule_ (there are other "chain rules" throughout mathematics, if we want to be specific, this is the "chain rule of derivatives"). The chain rule is important because it allows us to take complicated nested functions and more manageably differentiate them.
Let's look at an example to make this concrete:
```
def g(x):
return x**2
def h(x):
return x**3
def f(x):
return g(h(x))
# derivatives
def g_(x):
return 2*x
def h_(x):
return 3*(x**2)
```
$$
\begin{aligned}
g(x) &= x^2 \\
h(x) &= x^3 \\
f(x) &= g(h(x)) \\
g'(x) &= 2x \\
h'(x) &= 3x^2
\end{aligned}
$$
We're interested in understanding how $f(x)$ changes with respect to $x$, so we want to compute the derivative of $f(x)$. The chain rule allows us to individually differentiate the component functions of $f(x)$ and multiply those to get $f'(x)$:
```
def f_(x):
return g_(x) * h_(x)
```
$$
\frac{df}{dx} = \frac{dg}{dh} \frac{dh}{dx}
$$
This example is a bit contrived (there is a very easy way to differentiate this particular example that doesn't involve the chain rule) but if $g(x)$ and $h(x)$ were really nasty functions, the chain rule makes them quite a lot easier to deal with.
The chain rule can be applied to nested functions ad nauseaum! You can apply it to something crazy like $f(g(h(u(q(p(x))))))$. In fact, with deep neural networks, you are typically dealing with function compositions even more gnarly than this, so the chain rule is cornerstone there.
### Partial derivatives and gradients
The functions we've looked at so far just have a single input, but you can imagine many scenarios where you'd want to work with functions with some arbitrary number of inputs (i.e. a _multivariable_ function), like $f(x,y,z)$.
Here's where _partial deriatives_ come into play. Partial derivatives are just like regular derivatives except we use them for multivariable functions; it just means we only differentiate with respect to one variable at a time. So for $f(x,y,z)$, we'd have a partial derivative with respect to $x$, i.e. $\frac{\partial f}{\partial x}$ (note the slightly different notation), one with respect to $y$, i.e. $\frac{\partial f}{\partial y}$, and one with respect to $z$, i.e. $\frac{\partial f}{\partial z}$.
That's pretty simple! But it would be useful to group these partial derivatives together in some way. If we put these partial derivatives together in a vector, the resulting vector is the _gradient_ of $f$, notated $\nabla f$ (the symbol is called "nabla").
### Higher-order derivatives
We saw that velocity is the derivative of position because it describes how position changes over time. Acceleration similarly describes how _velocity_ changes over time, so we'd say that acceleration is the derivative of velocity. We can also say that acceleration is the _second-order_ derivative of position (that is, it is the derivative of its derivative).
This is the general idea behind higher-order derivatives.
## Gradient descent
Once you understand derivatives, gradient descent is really, really simple. The basic idea is that we use the derivative of the loss $L(\theta)$ with respect to $\theta$ and figure out which way the loss is decreasing, then "move" the parameter guess in that direction.
|
github_jupyter
|
# The Graph Data Access
In this notebook, we read in the data that was generated and saved as a csv from the [TheGraphDataSetCreation](TheGraphDataSetCreation.ipynb) notebook.
Goals of this notebook are to obtain:
* Signals, states, event and sequences
* Volatility metrics
* ID perceived shocks (correlated with announcements)
* Signal for target price
* Signal for market price
* Error plot
As a starting point for moving to a decision support system.
```
# import libraries
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import scipy as sp
from statsmodels.distributions.empirical_distribution import ECDF
import scipy.stats as stats
```
## Import data and add additional attributes
```
graphData = pd.read_csv('saved_results/RaiLiveGraphData.csv')
del graphData['Unnamed: 0']
graphData.head()
graphData.describe()
graphData.plot(x='blockNumber',y='redemptionPriceActual',kind='line',title='redemptionPriceActual')
graphData.plot(x='blockNumber',y='redemptionRateActual',kind='line',title='redemptionRateActual')
graphData['error'] = graphData['redemptionPriceActual'] - graphData['marketPriceUsd']
graphData['error_integral'] = graphData['error'].cumsum()
graphData.plot(x='blockNumber',y='error',kind='line',title='error')
graphData.plot(x='blockNumber',y='error_integral',kind='line',title='Steady state error')
```
## Error experimentation
#### Note: not taking into account control period
```
kp = 2e-7
#ki = (-kp * error)/(integral_error)
# computing at each time, what would the value of ki need to be such that the redemption price would be constant
graphData['equilibriation_ki'] = (-kp * graphData.error)/graphData.error_integral
# todo iterate through labels and append negative
graphData['equilibriation_ki'].apply(lambda x: -x).plot(logy = True,title='Actual equilibriation_ki - flipped sign for log plotting')
plt.hlines(5e-9, 0, 450, linestyles='solid', label='Recommended ki - flipped sign', color='r')
plt.hlines(-(graphData['equilibriation_ki'].median()), 0, 450, linestyles='solid', label='median actual ki - flipped', color='g')
locs,labels = plt.yticks() # Get the current locations and labelsyticks
new_locs = []
for i in locs:
new_locs.append('-'+str(i))
plt.yticks(locs, new_locs)
plt.legend(loc="upper right")
graphData['equilibriation_ki'].median()
```
### Counterfactual if intergral control rate had been median the whole time
```
graphData['counterfactual_redemption_rate'] = (kp * graphData['error'] + graphData['equilibriation_ki'].median())/ graphData['error_integral']
subsetGraph = graphData.iloc[50:]
sns.lineplot(data=subsetGraph,x="blockNumber", y="counterfactual_redemption_rate",label='Counterfactual')
ax2 = plt.twinx()
# let reflexer know this is wrong
sns.lineplot(data=subsetGraph,x="blockNumber", y="redemptionRateActual",ax=ax2,color='r',label='Actual')
plt.title('Actual redemption rate vs counterfactual')
plt.legend(loc="upper left")
```
## Goodness of fit tests
Whether or not counterfactual is far enough from actual to reject null that they are from the same distributions.
```
# fit a cdf
ecdf = ECDF(subsetGraph.redemptionRateActual.values)
ecdf2 = ECDF(subsetGraph.counterfactual_redemption_rate.values)
plt.plot(ecdf.x,ecdf.y,color='r')
plt.title('redemptionRateActual ECDF')
plt.show()
plt.plot(ecdf2.x,ecdf2.y,color='b')
plt.title('counterfactual_redemption_rate ECDF')
plt.show()
alpha = 0.05
statistic, p_value = stats.ks_2samp(subsetGraph.redemptionRateActual.values, subsetGraph.counterfactual_redemption_rate.values) # two sided
if p_value > alpha:
decision = "Sample is from the distribution"
elif p_value <= alpha:
decision = "Sample is not from the distribution"
print(p_value)
print(decision)
```
Based on our analysis using the Kolmogorov-Smirnov Goodness-of-Fit Test, the distributions are very different. As can be seen above from their EDCF plots, you can see a different in their distributions, however pay close attention to the x axis and you can see the distribution difference is significant.
```
# scatterplot of linear regressoin residuals
sns.residplot(x='blockNumber', y='redemptionRateActual', data=subsetGraph, label='redemptionRateActual')
plt.title('redemptionRateActual regression residuals')
sns.residplot(x='blockNumber', y='counterfactual_redemption_rate', data=subsetGraph,label='counterfactual_redemption_rate')
plt.title('counterfactual_redemption_rate regression residuals')
graphData.plot(x='blockNumber',y='globalDebt',kind='line',title='globalDebt')
graphData.plot(x='blockNumber',y='erc20CoinTotalSupply',kind='line',title='erc20CoinTotalSupply')
graphData.plot(x='blockNumber',y='marketPriceEth',kind='line',title='marketPriceEth')
graphData.plot(x='blockNumber',y='marketPriceUsd',kind='line',title='marketPriceUsd')
```
## Conclusion
Using The Graph, a lot of data about the Rai system can be obtained for analyzing the health of the system. With some data manipulation, these data streams could be intergrated into the Rai cadCAD model to turn it into a true decision support system.
|
github_jupyter
|
```
import pandas as pd
import numpy as np
import pickle
BASEDIR_MIMIC = '/Volumes/MyData/MIMIC_data/mimiciii/1.4'
def get_note_events():
n_rows = 100000
icd9_code = pd.read_csv(f"{BASEDIR_MIMIC}/DIAGNOSES_ICD.csv", index_col = None)
# create the iterator
noteevents_iterator = pd.read_csv(
f"{BASEDIR_MIMIC}/NOTEEVENTS.csv",
iterator=True,
chunksize=n_rows)
events_list = ['Discharge summary',
'Echo',
'ECG',
'Nursing',
'Physician ',
'Rehab Services',
'Case Management ',
'Respiratory ',
'Nutrition',
'General',
'Social Work',
'Pharmacy',
'Consult',
'Radiology',
'Nursing/other']
# concatenate according to a filter to get our noteevents data
noteevents = pd.concat(
[noteevents_chunk[
np.logical_and(
noteevents_chunk.CATEGORY.isin(events_list[1:]),
noteevents_chunk.DESCRIPTION.isin(["Report"])
)
]
for noteevents_chunk in noteevents_iterator])
# drop all nan in column HADM_ID
noteevents = noteevents.dropna(subset=["HADM_ID"])
noteevents.HADM_ID = noteevents.HADM_ID.astype(int)
try:
assert len(noteevents.drop_duplicates(["SUBJECT_ID","HADM_ID"])) == len(noteevents)
except AssertionError as e:
print("There are duplicates on Primary Key Set")
noteevents.CHARTDATE = pd.to_datetime(noteevents.CHARTDATE , format = '%Y-%m-%d %H:%M:%S', errors = 'coerce')
pd.set_option('display.max_colwidth',50)
noteevents.sort_values(["SUBJECT_ID","HADM_ID","CHARTDATE"], inplace =True)
#noteevents.drop_duplicates(["SUBJECT_ID","HADM_ID"], inplace = True)
noteevents.reset_index(drop = True, inplace = True)
top_values = (icd9_code.groupby('ICD9_CODE').
agg({"SUBJECT_ID": "nunique"}).
reset_index().sort_values(['SUBJECT_ID'], ascending = False).ICD9_CODE.tolist()[:15])
# icd9_code = icd9_code[icd9_code.ICD9_CODE.isin(top_values)]
icd9_code = icd9_code[icd9_code.ICD9_CODE.isin(top_values)]
import re
import itertools
def clean_text(text):
return [x for x in list(itertools.chain.from_iterable([t.split("<>") for t in text.replace("\n"," ").split(" ")])) if len(x) > 0]
# irrelevant_tags = ["Admission Date:", "Date of Birth:", "Service:", "Attending:", "Facility:", "Medications on Admission:", "Discharge Medications:", "Completed by:",
# "Dictated By:" , "Department:" , "Provider:"]
updated_text = ["<>".join([" ".join(re.split("\n\d|\n\s+",re.sub("^(.*?):","",x).strip()))
for x in text.split("\n\n")]) for text in noteevents.TEXT]
updated_text = [re.sub("(\[.*?\])", "", text) for text in updated_text]
updated_text = [" ".join(clean_text(x)) for x in updated_text]
noteevents["CLEAN_TEXT"] = updated_text
return noteevents
noteevents = get_note_events()
def mapNotes(dataset):
print(f"Mapping notes on {dataset}.")
df = pickle.load(open(f'../data/mimic3/train_data_mimic3/{dataset}', 'rb'))
BASEDIR_MIMIC = '/Volumes/MyData/MIMIC_data/mimiciii/1.4'
icustays = pd.read_csv(f"{BASEDIR_MIMIC}/ICUSTAYS.csv", index_col = None)
# SUBJECT_ID "_" ICUSTAY_ID "_episode" episode "_timeseries_readmission.csv"
import re
episodes = df['names']
regex = r"(\d+)_(\d+)_episode(\d+)_timeseries_readmission\.csv"
sid = []
hadmids = []
icustayid = [] # ICUSTAYS.csv ICUSTAY_ID
episode = []
notestexts = []
notextepis = []
for epi in episodes:
match = re.findall(regex, epi) #, re.MULTILINE)
sid.append(int(match[0][0]))
icustayid.append(int(match[0][1]))
episode.append(int(match[0][2]))
hadmid = icustays[icustays['ICUSTAY_ID']==int(match[0][1])]['HADM_ID']
hadmids.append(int(hadmid))
try:
#text = noteevents[noteevents['HADM_ID']==int(hadmid)]['TEXT'].iloc[0]
#text = noteevents[noteevents['HADM_ID']==int(hadmid)]['CLEAN_TEXT'].iloc[0]
text = "\n\n".join([t for t in noteevents[noteevents['HADM_ID']==int(hadmid)]['CLEAN_TEXT']])
except:
notextepis.append(int(hadmid))
text = ''
notestexts.append(text)
print(len(episodes), len(notextepis), len(set(notextepis)))
print(len(sid), len(hadmids), len(df['names']))
notesfull = pd.DataFrame({'SUBJECT_ID':sid, 'HADM_ID':hadmids, 'ICUSTAY_ID':icustayid, 'EPISODE':episode, 'CLEAN_TEXT':notestexts})
# save full data
filename = f'./events_notes_{dataset}'
with open(filename + '.pickle', 'wb') as handle:
pickle.dump(notesfull, handle, protocol=pickle.HIGHEST_PROTOCOL)
print(f"Finished mapping notes on {dataset}.\n")
def combineData(dataset):
print(f"Combining data for all {dataset}.")
df = pickle.load(open(f'../data/mimic3/train_data_mimic3/{dataset}', 'rb'))
print(df.keys(), len(df['data']),len(df['names']), df['data'][0].shape, len(df['data'][1]), len(df['names']))
notes = pickle.load(open(f'clinical_notes_{dataset}.pickle', 'rb'))
eventsnotes = pickle.load(open(f'events_notes_{dataset}.pickle', 'rb'))
# how many empty text rows
# np.where(notes.applymap(lambda x: x == ''))
# how many empty text rows
print(f"There are {len(list(notes[notes['CLEAN_TEXT'] == ''].index))} empty rows in notes.")
print(f"There are {len(list(eventsnotes[eventsnotes['CLEAN_TEXT'] == ''].index))} empty rows in eventsnotes.")
X = df['data'][0]
y = np.array(df['data'][1])
N = list(notes.CLEAN_TEXT)
EN = list(eventsnotes.CLEAN_TEXT)
# check if all three data sets have the same size/length
assert len(X) == len(y) == len(N) == len(EN)
empty_ind_N = list(notes[notes['CLEAN_TEXT'] == ''].index)
empty_ind_EN = list(notes[eventsnotes['CLEAN_TEXT'] == ''].index)
N_ = np.array(N)
EN_ = np.array(EN)
mask = np.ones(len(notes), np.bool)
mask[empty_ind_N] = 0
mask[empty_ind_EN] = 0
good_notes = N_[mask]
good_eventsnotes = EN_[mask]
good_X = X[mask]
good_y = y[mask]
print(f"Final shapes = {good_X.shape, good_y.shape, good_notes.shape}")
data = {'inputs': good_X,
'labels': good_y,
'eventsnotes': good_eventsnotes,
'notes': good_notes}
# save full data
filename = f'./new_{dataset}_CNEP'
#full_data.to_csv(filename + '.csv', index = None)
with open(filename + '.pickle', 'wb') as handle:
pickle.dump(data, handle, protocol=pickle.HIGHEST_PROTOCOL)
print("finished.\n")
all_datasets = ['train_data', 'test_data', 'val_data']
for dataset in all_datasets:
print(f"\n\nProcessing dataset {dataset}.")
mapNotes(dataset)
combineData(dataset)
```
|
github_jupyter
|
# Make Corner Plots of Posterior Distributions
This file allows me to quickly and repeatedly make the cornor plot to examin the results of the MCMC analsys
```
import numpy as np
import matplotlib.pyplot as plt
import matplotlib
import pandas as pd
from astropy.table import Table
import corner
# import seaborn
matplotlib.rcParams.update({'font.size': 11})
```
This function is the general function that is repeated called throught the file. One benifite to this system, is that I only need to update to higher quality labels in one place.
```
def corner_plot(file_, saved_file, truths=None, third=0):
data = Table.read(file_, format='ascii.commented_header', delimiter='\t')
if third !=0:
size = len(data)
data = data[(third-1)*size//3:(third)*size//3]
data = data.to_pandas()
data.dropna(inplace=True)
# look at corner.hist2d(levels) to not have too many conturs on a plot
# http://corner.readthedocs.io/en/latest/api.html
fig = corner.corner(data, show_titles=True, use_math_text=True,
bins=25, quantiles=[0.16, 0.84], smooth=1,
plot_datapoints=False,
labels=[r"$\log(z/z_{\odot})$", r"$\tau_2$", r"$\tau$",
r"$t_{0}$", r"$t_{i}$", r'$\phi$',
'$\delta$', 'age'],
truths=truths, range=[0.99]*8
)
fig.savefig(saved_file)
```
## One Object
```
#run one object
SN = 16185
file_ = f'../resources/SN{SN}_campbell_chain.tsv'
saved_file = f'SN{SN}-mcmc-2018-12-21.pdf'
corner_plot(file_, saved_file)
```
## Messier Objects
```
# run all Messier objects
for id in [63, 82, 87, 89, 91, 101, 105, 108]:
file_ = f'../resources/SN{id}_messier_chain.tsv'
saved_file = f'messierTests/12-29-M{id}.pdf'
print(f'\nMaking {saved_file}')
corner_plot(file_, saved_file)
# One Messier Object
ID = 63
file_ = f'../resources/SN{ID}_messier_chain.tsv'
saved_file = f'messierTests/12-22-M{ID}.pdf'
print(f'\nMaking {saved_file}')
corner_plot(file_, saved_file)
```
## Circle Test -- old
```
# run on circle test
for id in [1, 2, 3, 4, 5, 6, 7]:
file_ = f'../resources/SN{id}_chain.tsv'
saved_file = f'circleTests/12-19-C{id}.pdf'
print(f'\nMaking {saved_file}')
corner_plot(file_, saved_file)
# run on circle test 3 with truths
file_ = f'../resources/SN3_chain.tsv'
saved_file = f'circleTests/07-31-C3-truths.pdf'
data = Table.read(file_, format='ascii.commented_header', delimiter='\t')
data = data.to_pandas()
data.dropna(inplace=True)
fig = corner.corner(data, show_titles=True, use_math_text=True,
quantiles=[0.16, 0.5, 0.84], smooth=0.5,
plot_datapoints=False,
labels=["$logZ_{sol}$", "$dust_2$", r"$\tau$",
"$t_{start}$", "$t_{trans}$", 'sf slope',
'c', 'Age'],
truths=[-0.5, 0.1, 7.0, 3.0, 10, 15.0, -25, None]
)
fig.savefig(saved_file)
# run on circle test 1 with truths
file_ = f'../resources/SN1_chain_2017-09-11.tsv'
saved_file = f'circleTests/09-11-C1-truths.pdf'
truths=[-0.5, 0.1, 0.5, 1.5, 9.0, -1.0, -25, None]
corner_plot(file_, saved_file, truths)
# data = Table.read(file_, format='ascii.commented_header', delimiter='\t')
# data = data.to_pandas()
# data.dropna(inplace=True)
#
# fig = corner.corner(data, show_titles=True, use_math_text=True,
# quantiles=[0.16, 0.5, 0.84], smooth=0.5,
# plot_datapoints=False,
# labels=["$logZ_{sol}$", "$dust_2$", r"$\tau$",
# "$t_{start}$", "$t_{trans}$", 'sf slope',
# 'c', 'Age'],
# truths=[-0.5, 0.1, 0.5, 1.5, 9.0, -1.0, -25, None]
# )
# fig.savefig(saved_file)
```
## Test all Circle Tests
```
# for slope
# truths = {
# 1 : [-0.5, 0.1, 0.5, 1.5, 9.0, -1.0, -25, 10.68],
# 2 : [-0.5, 0.1, 0.5, 1.5, 9.0, 15.0, -25, 1.41],
# 3 : [-0.5, 0.1, 7.0, 3.0, 10, 15.0, -25, 1.75],
# 4 : [-0.5, 0.1, 7.0, 3.0, 13.0, 0.0, -25, 4.28],
# 5 : [-1.5, 0.1, 0.5, 1.5, 9.0, -1.0, -25, 10.68],
# 6 : [-0.5, 0.8, 7.0, 3.0, 10.0, 15.0, -25, 1.75],
# 7 : [-0.5, 0.1, 0.5, 1.5, 6.0, 15.0, -25, ]
# }
# for phi
truths = {
1 : [-0.5, 0.1, 0.5, 1.5, 9.0, -0.785, -25, 10.68],
2 : [-0.5, 0.1, 0.5, 1.5, 9.0, 1.504, -25, 1.41],
3 : [-0.5, 0.1, 7.0, 3.0, 10, 1.504, -25, 1.75],
4 : [-0.5, 0.1, 7.0, 3.0, 13.0, 0.0, -25, 4.28],
5 : [-1.5, 0.1, 0.5, 1.5, 9.0, -0.785, -25, 10.68],
6 : [-0.5, 0.8, 7.0, 3.0, 10.0, 1.504, -25, 1.75],
7 : [-0.5, 0.1, 0.5, 1.5, 6.0, 1.504, -25, 2.40],
8 : [-0.5, 0.1, 0.1, 8.0, 12.0, 1.52, -25, 0.437]
}
for id_ in np.arange(8) + 1:
file_ = f'../resources/SN{id_}_circle_chain.tsv'
saved_file = f'circleTests/C{id_}-truths-0717.pdf'
print(f'\nMaking {saved_file}')
corner_plot(file_, saved_file, truths[id_])
# just one cirlce test
id_ = 8
file_ = f'../resources/SN{id_}_circle_chain.tsv'
saved_file = f'circleTests/C{id_}-truths-0717_1.pdf'
corner_plot(file_, saved_file, truths[id_])
```
# Check sections of chain
```
file_ = f'../resources/SN2_chain.tsv'
saved_file = f'circleTests/C2-3.pdf'
print(f'\nMaking {saved_file}')
corner_plot(file_, saved_file, truths[2], third=3)
```
|
github_jupyter
|
```
import radical.analytics as ra
import radical.pilot as rp
import radical.utils as ru
import radical.entk as re
import os
from glob import glob
import numpy as np
from matplotlib import pyplot as plt
from matplotlib import cm
import csv
import pandas as pd
import json
import matplotlib as mpl
mpl.rcParams['text.usetex'] = True
mpl.rcParams['text.latex.unicode'] = True
blues = cm.get_cmap(plt.get_cmap('Blues'))
greens = cm.get_cmap(plt.get_cmap('Greens'))
reds = cm.get_cmap(plt.get_cmap('Reds'))
oranges = cm.get_cmap(plt.get_cmap('Oranges'))
purples = cm.get_cmap(plt.get_cmap('Purples'))
greys = cm.get_cmap(plt.get_cmap('Greys'))
from IPython.core.display import display, HTML
display(HTML("<style>.container { width:100% !important; }</style>"))
import warnings
warnings.filterwarnings('ignore')
!radical-stack
```
## Design 1
```
!tar -xzvf ../Data/Design1/entk.session-design1-54875/entk.session-design1-54875.tar.gz -C ../Data/Design1/entk.session-design1-54875/
!tar -xzvf ../Data/Design1/entk.session-design1-54875/entk_workflow.tar.gz -C ../Data/Design1/entk.session-design1-54875/
des1DF = pd.DataFrame(columns=['TTX','AgentOverhead','ClientOverhead','EnTKOverhead'])
work_file = open('../Data/Design1/entk.session-design1-54875/entk_workflow.json')
work_json = json.load(work_file)
work_file.close()
workflow = work_json['workflows'][1]
unit_ids = list()
for pipe in workflow['pipes']:
unit_path = pipe['stages'][1]['tasks'][0]['path']
unit_id = unit_path.split('/')[-2]
if unit_id != 'unit.000000':
unit_ids.append(unit_id)
sids=['entk.session-design1-54875']
for sid in sids:
re_session = ra.Session(stype='radical.entk',src='../Data/Design1',sid=sid)
rp_session = ra.Session(stype='radical.pilot',src='../Data/Design1/'+sid)
units = rp_session.filter(etype='unit', inplace=False, uid=unit_ids)
pilot = rp_session.filter(etype='pilot', inplace=False)
units_duration = units.duration(event=[{ru.EVENT: 'exec_start'},{ru.EVENT: 'exec_stop'}])
units_agent = units.duration (event=[{ru.EVENT: 'state',ru.STATE: rp.AGENT_STAGING_INPUT},{ru.EVENT: 'staging_uprof_stop'}])
all_units = rp_session.filter(etype='unit', inplace=False)
disc_unit = rp_session.filter(etype='unit', inplace=False, uid='unit.000000')
disc_time = disc_unit.duration([rp.NEW, rp.DONE])
units_client = units.duration([rp.NEW, rp.DONE])
appmanager = re_session.filter(etype='appmanager',inplace=False)
t_p2 = pilot.duration(event=[{ru.EVENT: 'bootstrap_0_start'}, {ru.EVENT: 'cmd'}])
resource_manager = re_session.filter(etype='resource_manager',inplace=False)
app_duration = appmanager.duration(event=[{ru.EVENT:"amgr run started"},{ru.EVENT:"termination done"}])
res_duration = resource_manager.duration(event=[{ru.EVENT:"rreq submitted"},{ru.EVENT:"resource active"}])
ttx = units_duration
agent_overhead = abs(units_agent - units_duration)
client_overhead = units_client - units_agent
entk_overhead = app_duration - units_client - res_duration - all_units.duration(event=[{ru.EVENT: 'exec_start'},{ru.EVENT: 'exec_stop'}]) + ttx
des1DF.loc[len(des1DF)] = [ttx, agent_overhead, client_overhead, entk_overhead]
print(des1DF)
```
## Design 2
```
des2DF = pd.DataFrame(columns=['TTX','SetupOverhead','SetupOverhead2','AgentOverhead','ClientOverhead'])
sids = ['design2_11K_run5']
for sid in sids:
Node1 = pd.DataFrame(columns=['Start','End','Type'])
Node1Tilling = pd.read_csv('../Data/Design2/'+sid+'/pilot.0000/unit.000002/geolocate1.csv')
for index,row in Node1Tilling.iterrows():
Node1.loc[len(Node1)] = [row['Start'],row['End'],'Geo1']
Node1Tilling = pd.read_csv('../Data/Design2/'+sid+'/pilot.0000/unit.000002/geolocate2.csv')
for index,row in Node1Tilling.iterrows():
Node1.loc[len(Node1)] = [row['Start'],row['End'],'Geo2']
Node1Tilling = pd.read_csv('../Data/Design2/'+sid+'/pilot.0000/unit.000002/ransac1.csv')
for index,row in Node1Tilling.iterrows():
Node1.loc[len(Node1)] = [row['Start'],row['End'],'Ransac1']
Node2 = pd.DataFrame(columns=['Start','End','Type'])
Node2Tilling = pd.read_csv('../Data/Design2/'+sid+'/pilot.0000/unit.000003/geolocate3.csv')
for index,row in Node2Tilling.iterrows():
Node2.loc[len(Node2)] = [row['Start'],row['End'],'Geo3']
Node2Tilling = pd.read_csv('../Data/Design2/'+sid+'/pilot.0000/unit.000003/geolocate4.csv')
for index,row in Node2Tilling.iterrows():
Node2.loc[len(Node2)] = [row['Start'],row['End'],'Geo4']
Node2Tilling = pd.read_csv('../Data/Design2/'+sid+'/pilot.0000/unit.000003/ransac2.csv')
for index,row in Node2Tilling.iterrows():
Node2.loc[len(Node2)] = [row['Start'],row['End'],'Ransac2']
Node3 = pd.DataFrame(columns=['Start','End','Type'])
Node3Tilling = pd.read_csv('../Data/Design2/'+sid+'/pilot.0000/unit.000004/geolocate5.csv')
for index,row in Node3Tilling.iterrows():
Node3.loc[len(Node3)] = [row['Start'],row['End'],'Geo5']
Node3Tilling = pd.read_csv('../Data/Design2/'+sid+'/pilot.0000/unit.000004/geolocate6.csv')
for index,row in Node3Tilling.iterrows():
Node3.loc[len(Node3)] = [row['Start'],row['End'],'Geo6']
Node3Tilling = pd.read_csv('../Data/Design2/'+sid+'/pilot.0000/unit.000004/ransac3.csv')
for index,row in Node3Tilling.iterrows():
Node3.loc[len(Node3)] = [row['Start'],row['End'],'Ransac3']
Node4 = pd.DataFrame(columns=['Start','End','Type'])
Node4Tilling = pd.read_csv('../Data/Design2/'+sid+'/pilot.0000/unit.000005/geolocate7.csv')
for index,row in Node4Tilling.iterrows():
Node4.loc[len(Node4)] = [row['Start'],row['End'],'Geo7']
Node4Tilling = pd.read_csv('../Data/Design2/'+sid+'/pilot.0000/unit.000005/geolocate8.csv')
for index,row in Node4Tilling.iterrows():
Node4.loc[len(Node4)] = [row['Start'],row['End'],'Geo8']
Node4Tilling = pd.read_csv('../Data/Design2/'+sid+'/pilot.0000/unit.000005/ransac4.csv')
for index,row in Node4Tilling.iterrows():
Node4.loc[len(Node4)] = [row['Start'],row['End'],'Ransac4']
AllNodes = pd.DataFrame(columns=['Start','End','Type'])
AllNodes = AllNodes.append(Node1)
AllNodes = AllNodes.append(Node2)
AllNodes = AllNodes.append(Node3)
AllNodes = AllNodes.append(Node4)
AllNodes.reset_index(inplace=True,drop='index')
rp_sessionDes2 = ra.Session(stype='radical.pilot',src='../Data/Design2/'+sid)
unitsDes2 = rp_sessionDes2.filter(etype='unit', inplace=False)
execUnits = unitsDes2.filter(uid=['unit.000002','unit.000003','unit.000004','unit.000005'],inplace=False)
exec_units_setup_des2 = execUnits.duration(event=[{ru.EVENT: 'exec_start'},{ru.EVENT: 'exec_stop'}])
exec_units_agent_des2 = execUnits.duration([rp.AGENT_STAGING_INPUT, rp.UMGR_STAGING_OUTPUT_PENDING])
exec_units_clientDes2 = execUnits.duration([rp.NEW, rp.DONE])
SetupUnit = unitsDes2.filter(uid=['unit.000000'],inplace=False)
setup_units_clientDes2 = SetupUnit.duration(event=[{ru.STATE: rp.NEW},{ru.EVENT: 'exec_start'}])
pilotDes2 = rp_sessionDes2.filter(etype='pilot', inplace=False)
pilot_duration = pilotDes2.duration([rp.PMGR_ACTIVE,rp.FINAL])
des2_duration = AllNodes['End'].max() - AllNodes['Start'].min()
setupDes2_overhead = exec_units_setup_des2 - des2_duration
agentDes2_overhead = exec_units_agent_des2 - exec_units_setup_des2
clientDes2_overhead = exec_units_clientDes2 - exec_units_agent_des2
des2DF.loc[len(des2DF)] = [des2_duration, setup_units_clientDes2, setupDes2_overhead, agentDes2_overhead, clientDes2_overhead]
print(des2DF)
```
## Design 2A
```
sid='../Data/Design2a/design2a_11k_test5/'
rp_sessionDes2 = ra.Session(stype='radical.pilot',src=sid)
unitsDes2 = rp_sessionDes2.filter(etype='unit', inplace=False)
execUnits = unitsDes2.filter(uid=['unit.000002','unit.000003','unit.000004','unit.000001'],inplace=False)
exec_units_setup_des2 = execUnits.duration(event=[{ru.EVENT: 'exec_start'},{ru.EVENT: 'exec_stop'}])
exec_units_agent_des2 = execUnits.duration([rp.AGENT_STAGING_INPUT, rp.UMGR_STAGING_OUTPUT_PENDING])
exec_units_clientDes2 = execUnits.duration([rp.NEW, rp.DONE])
SetupUnit = unitsDes2.filter(uid=['unit.000000'],inplace=False)
setup_units_clientDes2 = SetupUnit.duration(event=[{ru.STATE: rp.NEW},{ru.EVENT: 'exec_start'}])
pilotDes2 = rp_sessionDes2.filter(etype='pilot', inplace=False)
Node1 = pd.DataFrame(columns=['Start','End','Type'])
Node1Tilling = pd.read_csv('../Data/Design2a/design2a_11k_test5/pilot.0000/unit.000000/geolocate1.csv')
for index,row in Node1Tilling.iterrows():
Node1.loc[len(Node1)] = [row['Start'],row['End'],'Geo1']
Node1Tilling = pd.read_csv('../Data/Design2a/design2a_11k_test5/pilot.0000/unit.000000/geolocate2.csv')
for index,row in Node1Tilling.iterrows():
Node1.loc[len(Node1)] = [row['Start'],row['End'],'Geo2']
Node1Tilling = pd.read_csv('../Data/Design2a/design2a_11k_test5/pilot.0000/unit.000000/ransac1.csv')
for index,row in Node1Tilling.iterrows():
Node1.loc[len(Node1)] = [row['Start'],row['End'],'Ransac1']
Node2 = pd.DataFrame(columns=['Start','End','Type'])
Node2Tilling = pd.read_csv('../Data/Design2a/design2a_11k_test5/pilot.0000/unit.000001/geolocate3.csv')
for index,row in Node2Tilling.iterrows():
Node2.loc[len(Node2)] = [row['Start'],row['End'],'Geo3']
Node2Tilling = pd.read_csv('../Data/Design2a/design2a_11k_test5/pilot.0000/unit.000001/geolocate4.csv')
for index,row in Node2Tilling.iterrows():
Node2.loc[len(Node2)] = [row['Start'],row['End'],'Geo4']
Node2Tilling = pd.read_csv('../Data/Design2a/design2a_11k_test5/pilot.0000/unit.000001/ransac2.csv')
for index,row in Node2Tilling.iterrows():
Node2.loc[len(Node2)] = [row['Start'],row['End'],'Ransac2']
Node3 = pd.DataFrame(columns=['Start','End','Type'])
Node3Tilling = pd.read_csv('../Data/Design2a/design2a_11k_test5/pilot.0000/unit.000002/geolocate5.csv')
for index,row in Node3Tilling.iterrows():
Node3.loc[len(Node3)] = [row['Start'],row['End'],'Geo5']
Node3Tilling = pd.read_csv('../Data/Design2a/design2a_11k_test5/pilot.0000/unit.000002/geolocate6.csv')
for index,row in Node3Tilling.iterrows():
Node3.loc[len(Node3)] = [row['Start'],row['End'],'Geo6']
Node3Tilling = pd.read_csv('../Data/Design2a/design2a_11k_test5/pilot.0000/unit.000002/ransac3.csv')
for index,row in Node3Tilling.iterrows():
Node3.loc[len(Node3)] = [row['Start'],row['End'],'Ransac3']
Node4 = pd.DataFrame(columns=['Start','End','Type'])
Node4Tilling = pd.read_csv('../Data/Design2a/design2a_11k_test5/pilot.0000/unit.000003/geolocate7.csv')
for index,row in Node4Tilling.iterrows():
Node4.loc[len(Node4)] = [row['Start'],row['End'],'Geo7']
Node4Tilling = pd.read_csv('../Data/Design2a/design2a_11k_test5/pilot.0000/unit.000003/geolocate8.csv')
for index,row in Node4Tilling.iterrows():
Node4.loc[len(Node4)] = [row['Start'],row['End'],'Geo8']
Node4Tilling = pd.read_csv('../Data/Design2a/design2a_11k_test5/pilot.0000/unit.000003/ransac4.csv')
for index,row in Node4Tilling.iterrows():
Node4.loc[len(Node4)] = [row['Start'],row['End'],'Ransac4']
des2ADF = pd.DataFrame(columns=['TTX','SetupOverhead','AgentOverhead','ClientOverhead'])
AllNodes = pd.DataFrame(columns=['Start','End','Type'])
AllNodes = AllNodes.append(Node1)
AllNodes = AllNodes.append(Node2)
AllNodes = AllNodes.append(Node3)
AllNodes = AllNodes.append(Node4)
AllNodes.reset_index(inplace=True,drop='index')
rp_sessionDes2 = ra.Session(stype='radical.pilot',src=sid)
unitsDes2 = rp_sessionDes2.filter(etype='unit', inplace=False)
execUnits = unitsDes2.filter(uid=['unit.000000','unit.000001','unit.000002','unit.000003'],inplace=False)
exec_units_setup_des2 = unitsDes2.duration(event=[{ru.EVENT: 'exec_start'},{ru.EVENT: 'exec_stop'}])
exec_units_agent_des2 = unitsDes2.duration([rp.AGENT_STAGING_INPUT, rp.UMGR_STAGING_OUTPUT_PENDING])
exec_units_clientDes2 = execUnits.duration([rp.NEW, rp.DONE])
pilotDes2 = rp_sessionDes2.filter(etype='pilot', inplace=False)
pilot_duration = pilotDes2.duration([rp.PMGR_ACTIVE,rp.FINAL])
des2_duration = AllNodes['End'].max() - AllNodes['Start'].min()
setupDes2_overhead = exec_units_setup_des2 - des2_duration
agentDes2_overhead = exec_units_agent_des2 - exec_units_setup_des2
clientDes2_overhead = exec_units_clientDes2 - exec_units_agent_des2
queue_time = max(pilotDes2.timestamps(event=[{ru.STATE: rp.PMGR_ACTIVE}]))- max(execUnits.timestamps(event=[{ru.STATE: rp.AGENT_STAGING_INPUT_PENDING}]))
des2ADF.loc[len(des2ADF)] = [des2_duration, setupDes2_overhead, agentDes2_overhead, clientDes2_overhead-queue_time]
print(des2ADF)
fig, axis = plt.subplots(nrows=1,ncols=1, figsize=(15,7.5))
x1 = np.arange(3)
_ = axis.bar(x1[0], des1DF['TTX'].mean(), width=0.5, color=blues(300), label='Design 1 TTX')
_ = axis.bar(x1[1], des2DF['TTX'].mean(), width=0.5, color=blues(200), label='Design 2 TTX')
_ = axis.bar(x1[2], des2ADF['TTX'].mean(), width=0.5, color=blues(100), label='Design 2A TTX')
_ = axis.set_xticks([0,1,2])
_ = axis.grid(which='both', linestyle=':', linewidth=1)
_ = axis.set_xticklabels(['Design 1', 'Design 2','Design 2A'], fontsize=36)
_ = axis.set_ylabel('Time in seconds', fontsize=26)
_ = axis.set_yticklabels(axis.get_yticks().astype('int').tolist(),fontsize=24)
#fig.savefig('geo_ttx.pdf',dpi=800,bbox='tight')
dist_overhead = np.load('../Data/dist_dataset.npy')
DiscDurations = [1861.404363739,
1872.631383787,
1870.355146581,
1852.347904858,
1857.771844937,
1868.644424397,
1873.176510421,
1851.527881958,
1870.128898667,
1856.676059379]
fig, axis = plt.subplots(nrows=1, ncols=1, figsize=(9,7.5))
x1 = np.arange(3)
_ = axis.bar(x1[0], des1DF['AgentOverhead'].mean(),width=0.5, color=reds(200),label='RP Agent Overhead Design 1')
_ = axis.bar(x1[0], des1DF['ClientOverhead'].mean(), bottom=des1DF['AgentOverhead'].mean(),width=0.5, color=reds(150),label='RP Client Overhead Design 1')
_ = axis.bar(x1[0], des1DF['EnTKOverhead'].mean(),bottom=des1DF['ClientOverhead'].mean()+des1DF['AgentOverhead'].mean(),width=0.5, color=reds(100),label='EnTK Overheads Design 1')
_ = axis.bar(x1[0], np.mean(DiscDurations), yerr=np.std(DiscDurations), bottom=des1DF['ClientOverhead'].mean()+des1DF['AgentOverhead'].mean() + des1DF['EnTKOverhead'].mean(),
width=0.5, color=reds(50),label='Design 1 Dataset Discovery')
_ = axis.bar(x1[1],des2DF['AgentOverhead'].mean(),width=0.5, color=greens(200),label='RP Agent Overhead Design 2')
_ = axis.bar(x1[1],des2DF['ClientOverhead'].mean(),bottom=des2DF['AgentOverhead'].mean(),width=0.5, color=greens(150),label='RP Client Overhead Design 2')
_ = axis.bar(x1[1],(des2DF['SetupOverhead'] + des2DF['SetupOverhead2']).mean(),bottom=des2DF['ClientOverhead'].mean()+des2DF['AgentOverhead'].mean(),width=0.5, color=greens(100),label='Design 2 Setup Overhead')
_ = axis.bar(x1[1],np.mean(DiscDurations), yerr=np.std(DiscDurations), bottom=des2DF['ClientOverhead'].mean()+des2DF['AgentOverhead'].mean() + (des2DF['SetupOverhead']+des2DF['SetupOverhead2']).mean(),
width=0.5, color=greens(50),label='Design 2 Dataset Discovery')
_ = axis.bar(x1[2],des2ADF['AgentOverhead'].mean(),#yerr=des2ADF['AgentOverhead'].std(),
width=0.5, color=purples(250),label='RP Agent Overhead Design 2A',log=1)
_ = axis.bar(x1[2],des2ADF['ClientOverhead'].mean(),#yerr=des2ADF['ClientOverhead'].std(),
bottom=des2ADF['AgentOverhead'].mean(),width=0.5, color=purples(200),label='RP Client Overhead Design 2A')
_ = axis.bar(x1[2],des2ADF['SetupOverhead'].mean(),#yerr=des2ADF['SetupOverhead'].std(),
bottom=des2ADF['ClientOverhead'].mean()+des2ADF['AgentOverhead'].mean(),width=0.5, color=purples(150),label='Design 2A Setup Overhead')
_ = axis.bar(x1[2],dist_overhead.mean(),yerr=dist_overhead.std(),
bottom=des2ADF['ClientOverhead'].mean()+des2ADF['AgentOverhead'].mean()+des2ADF['SetupOverhead'].mean(),width=0.5, color=purples(100),label='Design 2A Distributing Overhead')
_ = axis.bar(x1[2],np.mean(DiscDurations), yerr=np.std(DiscDurations),
bottom=des2ADF['ClientOverhead'].mean()+des2ADF['AgentOverhead'].mean()+des2ADF['SetupOverhead'].mean() + dist_overhead.mean(),
width=0.5, color=purples(50),label='Design 2A Dataset Discovery')
_ = axis.set_xticks([0,1,2])
_ = axis.grid(which='both', linestyle=':', linewidth=1)
_ = axis.set_ylabel('Time in seconds', fontsize=26)
_ = axis.set_xticklabels(['Design 1', 'Design 2','Design 2A'], fontsize=26)
_ = axis.set_yticks([1,10,100,1000,10000,100000])
_ = axis.set_yticklabels(axis.get_yticks().astype('int').tolist(),fontsize=24)
#_ = axis.legend(fontsize=22,loc = 'lower center', bbox_to_anchor = (0,-.55,1,1), ncol=2)
#_ = fig.subplots_adjust(bottom=.205)
fig.savefig('geo_overheads.pdf',dpi=800,pad_inches=0)
```
|
github_jupyter
|
# Running, Debugging, Testing & Packaging
```
!code ./1-helloconnectedworld
```
Let's look at the key parts of our app:
**package.json**
This defines all contributions: commands, context menus, UI, everything!
```json
"activationEvents": [
// Use "*" to start on application start. If contributing commands, only start on command to speed up user experience
"onCommand:extension.showCurrentConnection"
],
"main": "./out/extension",
"contributes": {
"commands": [
{
"command": "extension.showCurrentConnection",
"title": "Show Current Connection"
}
]
},
```
**extension.ts** is our extension control center. Your extension always starts here by registering your extension points, and using built-in APIs to query connections, show messages, and much more
```ts
context.subscriptions.push(vscode.commands.registerCommand('extension.showCurrentConnection', () => {
sqlops.connection.getCurrentConnection().then(connection => {
let connectionId = connection ? connection.connectionId : 'No connection found!';
vscode.window.showInformationMessage(connectionId);
}, error => {
console.info(error);
});
}));
```
### VSCode APIs
All* VSCode APIs are defined in Azure Data Studio meaning VSCode extensions just work. These include common workspace, window and language services features
> *Debugger APIs are defined but the debugger is not implemented
### sqlops / azdata APIs**
Azure Data Studio APIs are in the sqlops namespace. These cover Connection, Query, advanced UI (dialogs, wizards, and other standardized UI controls]), and the Data Management Protocol (DMP).
> These are moving to a new **azdata** namespace. We will cover the types of changes being made to simplify development as part of this demo
# Run your code
* In VSCode, you should have the "Azure Data Studio Debug" extension installed

* Hit F5 or go to the debugger section and click the Run button
* Azure Data Studio will launch
* Hit `Ctrl+Shift+P` and choose **Show Current Connection**
* It will show **No Connection Found**. How do we find out what's wrong? Let's go and debug it!
# Debug your code
* As for any app, click inside the code and set a breakdpoint on the line
```
let connectionId = connection ? connection.connectionId : 'No connection found!';
```
* Run the command again
* We will see that the connection is not getting returned. Why might that be? It's because nobody connected to one!
* Open a connection and try again. This time you will see all the available information about this connection.
# Testing your code
If you like to write tests, you have a template built-into your extension. You can even debug using the **Extension Tests** option in the debugger dropdown. This uses standard Javascript test frameworks (Mocha) and is able to integrate with all the usual actions.
# Packaging your extension
Packaging is as easy as running `vsce package` from the root of the extension.
* The first time you run this, you'll see errors if you didn't edit your Readme and other key files
* Update Readme.md so it's not a default value
* Similarly delete Changelog contents or update as needed
* Delete the **vsc-extension-quickstart.md` file
Now if you re-run, you'll get a .vsix file
## Installing your extension for testing
* In Azure Data Studio, hit `Ctrl+Shift+P` and choose **Extensions: Install from VSIX...**
* Pick your file and click OK
* It'll install and be available - no reload necessary!
## Publishing your extension
Follow our [Extension Authoring](https://github.com/Microsoft/azuredatastudio/wiki/Extension-Authoring) guide which has details on publishing to the extension gallery. If you have any issues reach out to us on Twitter [@AzureDataStudio](https://twitter.com/azuredatastudio)
|
github_jupyter
|
# Convolutional Autoencoder
Sticking with the MNIST dataset, let's improve our autoencoder's performance using convolutional layers. Again, loading modules and the data.
```
%matplotlib inline
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets('MNIST_data', validation_size=0)
img = mnist.train.images[2]
plt.imshow(img.reshape((28, 28)), cmap='Greys_r')
```
## Network Architecture
The encoder part of the network will be a typical convolutional pyramid. Each convolutional layer will be followed by a max-pooling layer to reduce the dimensions of the layers. The decoder though might be something new to you. The decoder needs to convert from a narrow representation to a wide reconstructed image. For example, the representation could be a 4x4x8 max-pool layer. This is the output of the encoder, but also the input to the decoder. We want to get a 28x28x1 image out from the decoder so we need to work our way back up from the narrow decoder input layer. A schematic of the network is shown below.
<img src='assets/convolutional_autoencoder.png' width=500px>
Here our final encoder layer has size 4x4x8 = 128. The original images have size 28x28 = 784, so the encoded vector is roughly 16% the size of the original image. These are just suggested sizes for each of the layers. Feel free to change the depths and sizes, but remember our goal here is to find a small representation of the input data.
### What's going on with the decoder
Okay, so the decoder has these "Upsample" layers that you might not have seen before. First off, I'll discuss a bit what these layers *aren't*. Usually, you'll see **transposed convolution** layers used to increase the width and height of the layers. They work almost exactly the same as convolutional layers, but in reverse. A stride in the input layer results in a larger stride in the transposed convolution layer. For example, if you have a 3x3 kernel, a 3x3 patch in the input layer will be reduced to one unit in a convolutional layer. Comparatively, one unit in the input layer will be expanded to a 3x3 path in a transposed convolution layer. The TensorFlow API provides us with an easy way to create the layers, [`tf.nn.conv2d_transpose`](https://www.tensorflow.org/api_docs/python/tf/nn/conv2d_transpose).
However, transposed convolution layers can lead to artifacts in the final images, such as checkerboard patterns. This is due to overlap in the kernels which can be avoided by setting the stride and kernel size equal. In [this Distill article](http://distill.pub/2016/deconv-checkerboard/) from Augustus Odena, *et al*, the authors show that these checkerboard artifacts can be avoided by resizing the layers using nearest neighbor or bilinear interpolation (upsampling) followed by a convolutional layer. In TensorFlow, this is easily done with [`tf.image.resize_images`](https://www.tensorflow.org/versions/r1.1/api_docs/python/tf/image/resize_images), followed by a convolution. Be sure to read the Distill article to get a better understanding of deconvolutional layers and why we're using upsampling.
> **Exercise:** Build the network shown above. Remember that a convolutional layer with strides of 1 and 'same' padding won't reduce the height and width. That is, if the input is 28x28 and the convolution layer has stride = 1 and 'same' padding, the convolutional layer will also be 28x28. The max-pool layers are used the reduce the width and height. A stride of 2 will reduce the size by a factor of 2. Odena *et al* claim that nearest neighbor interpolation works best for the upsampling, so make sure to include that as a parameter in `tf.image.resize_images` or use [`tf.image.resize_nearest_neighbor`]( `https://www.tensorflow.org/api_docs/python/tf/image/resize_nearest_neighbor). For convolutional layers, use [`tf.layers.conv2d`](https://www.tensorflow.org/api_docs/python/tf/layers/conv2d). For example, you would write `conv1 = tf.layers.conv2d(inputs, 32, (5,5), padding='same', activation=tf.nn.relu)` for a layer with a depth of 32, a 5x5 kernel, stride of (1,1), padding is 'same', and a ReLU activation. Similarly, for the max-pool layers, use [`tf.layers.max_pooling2d`](https://www.tensorflow.org/api_docs/python/tf/layers/max_pooling2d).
```
inputs_ = tf.placeholder(tf.float32, (None, 28, 28, 1), name='inputs')
targets_ = tf.placeholder(tf.float32, (None, 28, 28, 1), name='targets')
### Encoder
conv1 = tf.layers.conv2d(inputs_, 16, (3,3), padding='same', activation=tf.nn.relu)
# Now 28x28x16
maxpool1 = tf.layers.max_pooling2d(conv1, (2,2), (2,2), padding='same')
# Now 14x14x16
conv2 = tf.layers.conv2d(maxpool1, 8, (3,3), padding='same', activation=tf.nn.relu)
# Now 14x14x8
maxpool2 = tf.layers.max_pooling2d(conv2, (2,2), (2,2), padding='same')
# Now 7x7x8
conv3 = tf.layers.conv2d(maxpool2, 8, (3,3), padding='same', activation=tf.nn.relu)
# Now 7x7x8
encoded = tf.layers.max_pooling2d(conv3, (2,2), (2,2), padding='same')
# Now 4x4x8
### Decoder
upsample1 = tf.image.resize_nearest_neighbor(encoded, (7,7))
# Now 7x7x8
conv4 = tf.layers.conv2d(upsample1, 8, (3,3), padding='same', activation=tf.nn.relu)
# Now 7x7x8
upsample2 = tf.image.resize_nearest_neighbor(conv4, (14,14))
# Now 14x14x8
conv5 = tf.layers.conv2d(upsample2, 8, (3,3), padding='same', activation=tf.nn.relu)
# Now 14x14x8
upsample3 = tf.image.resize_nearest_neighbor(conv5, (28,28))
# Now 28x28x8
conv6 = tf.layers.conv2d(upsample3, 16, (3,3), padding='same', activation=tf.nn.relu)
# Now 28x28x16
logits = tf.layers.conv2d(conv6, 1, (3,3), padding='same', activation=None)
#Now 28x28x1
decoded = tf.nn.sigmoid(logits, name='decoded')
loss = tf.nn.sigmoid_cross_entropy_with_logits(labels=targets_, logits=logits)
cost = tf.reduce_mean(loss)
opt = tf.train.AdamOptimizer(0.001).minimize(cost)
```
## Training
As before, here wi'll train the network. Instead of flattening the images though, we can pass them in as 28x28x1 arrays.
```
sess = tf.Session()
epochs = 1
batch_size = 200
sess.run(tf.global_variables_initializer())
for e in range(epochs):
for ii in range(mnist.train.num_examples//batch_size):
batch = mnist.train.next_batch(batch_size)
imgs = batch[0].reshape((-1, 28, 28, 1))
batch_cost, _ = sess.run([cost, opt], feed_dict={inputs_: imgs,
targets_: imgs})
print("Epoch: {}/{}...".format(e+1, epochs),
"Training loss: {:.4f}".format(batch_cost))
fig, axes = plt.subplots(nrows=2, ncols=10, sharex=True, sharey=True, figsize=(20,4))
in_imgs = mnist.test.images[:10]
reconstructed = sess.run(decoded, feed_dict={inputs_: in_imgs.reshape((10, 28, 28, 1))})
for images, row in zip([in_imgs, reconstructed], axes):
for img, ax in zip(images, row):
ax.imshow(img.reshape((28, 28)), cmap='Greys_r')
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
fig.tight_layout(pad=0.1)
sess.close()
```
## Denoising
As I've mentioned before, autoencoders like the ones you've built so far aren't too useful in practive. However, they can be used to denoise images quite successfully just by training the network on noisy images. We can create the noisy images ourselves by adding Gaussian noise to the training images, then clipping the values to be between 0 and 1. We'll use noisy images as input and the original, clean images as targets. Here's an example of the noisy images I generated and the denoised images.

Since this is a harder problem for the network, we'll want to use deeper convolutional layers here, more feature maps. I suggest something like 32-32-16 for the depths of the convolutional layers in the encoder, and the same depths going backward through the decoder. Otherwise the architecture is the same as before.
> **Exercise:** Build the network for the denoising autoencoder. It's the same as before, but with deeper layers. I suggest 32-32-16 for the depths, but you can play with these numbers, or add more layers.
```
inputs_ = tf.placeholder(tf.float32, (None, 28, 28, 1), name='inputs')
targets_ = tf.placeholder(tf.float32, (None, 28, 28, 1), name='targets')
### Encoder
conv1 = tf.layers.conv2d(inputs_, 32, (3,3), padding='same', activation=tf.nn.relu)
# Now 28x28x32
maxpool1 = tf.layers.max_pooling2d(conv1, (2,2), (2,2), padding='same')
# Now 14x14x32
conv2 = tf.layers.conv2d(maxpool1, 32, (3,3), padding='same', activation=tf.nn.relu)
# Now 14x14x32
maxpool2 = tf.layers.max_pooling2d(conv2, (2,2), (2,2), padding='same')
# Now 7x7x32
conv3 = tf.layers.conv2d(maxpool2, 16, (3,3), padding='same', activation=tf.nn.relu)
# Now 7x7x16
encoded = tf.layers.max_pooling2d(conv3, (2,2), (2,2), padding='same')
# Now 4x4x16
### Decoder
upsample1 = tf.image.resize_nearest_neighbor(encoded, (7,7))
# Now 7x7x16
conv4 = tf.layers.conv2d(upsample1, 16, (3,3), padding='same', activation=tf.nn.relu)
# Now 7x7x16
upsample2 = tf.image.resize_nearest_neighbor(conv4, (14,14))
# Now 14x14x16
conv5 = tf.layers.conv2d(upsample2, 32, (3,3), padding='same', activation=tf.nn.relu)
# Now 14x14x32
upsample3 = tf.image.resize_nearest_neighbor(conv5, (28,28))
# Now 28x28x32
conv6 = tf.layers.conv2d(upsample3, 32, (3,3), padding='same', activation=tf.nn.relu)
# Now 28x28x32
logits = tf.layers.conv2d(conv6, 1, (3,3), padding='same', activation=None)
#Now 28x28x1
decoded = tf.nn.sigmoid(logits, name='decoded')
loss = tf.nn.sigmoid_cross_entropy_with_logits(labels=targets_, logits=logits)
cost = tf.reduce_mean(loss)
opt = tf.train.AdamOptimizer(0.001).minimize(cost)
sess = tf.Session()
epochs = 100
batch_size = 200
# Set's how much noise we're adding to the MNIST images
noise_factor = 0.5
sess.run(tf.global_variables_initializer())
for e in range(epochs):
for ii in range(mnist.train.num_examples//batch_size):
batch = mnist.train.next_batch(batch_size)
# Get images from the batch
imgs = batch[0].reshape((-1, 28, 28, 1))
# Add random noise to the input images
noisy_imgs = imgs + noise_factor * np.random.randn(*imgs.shape)
# Clip the images to be between 0 and 1
noisy_imgs = np.clip(noisy_imgs, 0., 1.)
# Noisy images as inputs, original images as targets
batch_cost, _ = sess.run([cost, opt], feed_dict={inputs_: noisy_imgs,
targets_: imgs})
print("Epoch: {}/{}...".format(e+1, epochs),
"Training loss: {:.4f}".format(batch_cost))
```
## Checking out the performance
Here I'm adding noise to the test images and passing them through the autoencoder. It does a suprising great job of removing the noise, even though it's sometimes difficult to tell what the original number is.
```
fig, axes = plt.subplots(nrows=2, ncols=10, sharex=True, sharey=True, figsize=(20,4))
in_imgs = mnist.test.images[:10]
noisy_imgs = in_imgs + noise_factor * np.random.randn(*in_imgs.shape)
noisy_imgs = np.clip(noisy_imgs, 0., 1.)
reconstructed = sess.run(decoded, feed_dict={inputs_: noisy_imgs.reshape((10, 28, 28, 1))})
for images, row in zip([noisy_imgs, reconstructed], axes):
for img, ax in zip(images, row):
ax.imshow(img.reshape((28, 28)), cmap='Greys_r')
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
fig.tight_layout(pad=0.1)
```
|
github_jupyter
|
Practice geospatial aggregations in geopandas before writing them to .py files
```
%load_ext autoreload
%autoreload 2
import sys
sys.path.append('../utils')
import wd_management
wd_management.set_wd_root()
import geopandas as gp
import pandas as pd
import requests
res = requests.get('https://services5.arcgis.com/GfwWNkhOj9bNBqoJ/arcgis/rest/services/NYC_Public_Use_Microdata_Areas_PUMAs_2010/FeatureServer/0/query?where=1=1&outFields=*&outSR=4326&f=pgeojson')
res_json = res.json()
NYC_PUMAs = gp.GeoDataFrame.from_features(res_json['features'])
NYC_PUMAs.set_crs('EPSG:4326',inplace=True)
NYC_PUMAs.set_index('PUMA', inplace=True)
NYC_PUMAs.head(5)
NYC_PUMAs.plot()
```
Ok looks good. Load in historic districts. [This stackoverflow post](https://gis.stackexchange.com/questions/327197/typeerror-input-geometry-column-must-contain-valid-geometry-objects) was helpful
```
from shapely import wkt
hd= gp.read_file('.library/lpc_historic_district_areas.csv')
hd['the_geom'] = hd['the_geom'].apply(wkt.loads)
hd.set_geometry(col='the_geom', inplace=True, crs='EPSG:4326')
hd= hd.explode(column='the_geom')
hd.set_geometry('the_geom',inplace=True)
hd = hd.to_crs('EPSG:2263')
hd = hd.reset_index()
hd.plot()
```
Ok great next do some geospatial analysis. Start only with PUMA 3807 as it has a lot of historic area
```
def fraction_area_historic(PUMA, hd):
try:
gdf = gp.GeoDataFrame(geometry = [PUMA.geometry], crs = 'EPSG:4326')
gdf = gdf.to_crs('EPSG:2263')
overlay = gp.overlay(hd, gdf, 'intersection')
if overlay.empty:
return 0, 0
else:
fraction = overlay.area.sum()/gdf.geometry.area.sum()
return fraction, overlay.area.sum()/(5280**2)
except Exception as e:
print(f'broke on {PUMA}')
print(e)
NYC_PUMAs[['fraction_area_historic', 'total_area_historic']] = NYC_PUMAs.apply(fraction_area_historic, axis=1, args=(hd,), result_type='expand')
NYC_PUMAs.sort_values('fraction_area_historic', ascending=False)
```
Superimpose PUMA 3801's historic districts on it to see if 38% looks right
```
def visualize_overlay(PUMA):
test_PUMA = NYC_PUMAs.loc[[PUMA]].to_crs('EPSG:2263')
base = test_PUMA.plot(color='green', edgecolor='black')
overlay = gp.overlay(hd, test_PUMA, 'intersection')
overlay.plot(ax=base, color='red');
visualize_overlay('3810')
```
Ok great that looks like about a third to me
From eyeballing map, more than 20% of PUMA 3806 on UWS looks to be historic
```
visualize_overlay('3806')
```
Ah ok the PUMA geography from includes central park. Worth flagging
### Question from Renae:
Renae points out that description of historic districts says "including items that may have been denied designation or overturned."
Look at dataset to see if columns point to this clearly
```
hd.head(5)
hd.groupby('status_of_').size()
hd.groupby('current_').size()
hd.groupby('last_actio').size()
```
|
github_jupyter
|
<a href="https://colab.research.google.com/github/prateekjoshi565/Fine-Tuning-BERT/blob/master/Fine_Tuning_BERT_for_Spam_Classification.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Install Transformers Library
```
!pip install transformers
import numpy as np
import pandas as pd
import torch
import torch.nn as nn
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report
import transformers
from transformers import AutoModel, BertTokenizerFast
# specify GPU
device = torch.device("cuda")
```
# Load Dataset
```
df = pd.read_csv("spamdata_v2.csv")
df.head()
df.shape
# check class distribution
df['label'].value_counts(normalize = True)
```
# Split train dataset into train, validation and test sets
```
train_text, temp_text, train_labels, temp_labels = train_test_split(df['text'], df['label'],
random_state=2018,
test_size=0.3,
stratify=df['label'])
# we will use temp_text and temp_labels to create validation and test set
val_text, test_text, val_labels, test_labels = train_test_split(temp_text, temp_labels,
random_state=2018,
test_size=0.5,
stratify=temp_labels)
```
# Import BERT Model and BERT Tokenizer
```
# import BERT-base pretrained model
bert = AutoModel.from_pretrained('bert-base-uncased')
# Load the BERT tokenizer
tokenizer = BertTokenizerFast.from_pretrained('bert-base-uncased')
# sample data
text = ["this is a bert model tutorial", "we will fine-tune a bert model"]
# encode text
sent_id = tokenizer.batch_encode_plus(text, padding=True, return_token_type_ids=False)
# output
print(sent_id)
```
# Tokenization
```
# get length of all the messages in the train set
seq_len = [len(i.split()) for i in train_text]
pd.Series(seq_len).hist(bins = 30)
max_seq_len = 25
# tokenize and encode sequences in the training set
tokens_train = tokenizer.batch_encode_plus(
train_text.tolist(),
max_length = max_seq_len,
pad_to_max_length=True,
truncation=True,
return_token_type_ids=False
)
# tokenize and encode sequences in the validation set
tokens_val = tokenizer.batch_encode_plus(
val_text.tolist(),
max_length = max_seq_len,
pad_to_max_length=True,
truncation=True,
return_token_type_ids=False
)
# tokenize and encode sequences in the test set
tokens_test = tokenizer.batch_encode_plus(
test_text.tolist(),
max_length = max_seq_len,
pad_to_max_length=True,
truncation=True,
return_token_type_ids=False
)
```
# Convert Integer Sequences to Tensors
```
# for train set
train_seq = torch.tensor(tokens_train['input_ids'])
train_mask = torch.tensor(tokens_train['attention_mask'])
train_y = torch.tensor(train_labels.tolist())
# for validation set
val_seq = torch.tensor(tokens_val['input_ids'])
val_mask = torch.tensor(tokens_val['attention_mask'])
val_y = torch.tensor(val_labels.tolist())
# for test set
test_seq = torch.tensor(tokens_test['input_ids'])
test_mask = torch.tensor(tokens_test['attention_mask'])
test_y = torch.tensor(test_labels.tolist())
```
# Create DataLoaders
```
from torch.utils.data import TensorDataset, DataLoader, RandomSampler, SequentialSampler
#define a batch size
batch_size = 32
# wrap tensors
train_data = TensorDataset(train_seq, train_mask, train_y)
# sampler for sampling the data during training
train_sampler = RandomSampler(train_data)
# dataLoader for train set
train_dataloader = DataLoader(train_data, sampler=train_sampler, batch_size=batch_size)
# wrap tensors
val_data = TensorDataset(val_seq, val_mask, val_y)
# sampler for sampling the data during training
val_sampler = SequentialSampler(val_data)
# dataLoader for validation set
val_dataloader = DataLoader(val_data, sampler = val_sampler, batch_size=batch_size)
```
# Freeze BERT Parameters
```
# freeze all the parameters
for param in bert.parameters():
param.requires_grad = False
```
# Define Model Architecture
```
class BERT_Arch(nn.Module):
def __init__(self, bert):
super(BERT_Arch, self).__init__()
self.bert = bert
# dropout layer
self.dropout = nn.Dropout(0.1)
# relu activation function
self.relu = nn.ReLU()
# dense layer 1
self.fc1 = nn.Linear(768,512)
# dense layer 2 (Output layer)
self.fc2 = nn.Linear(512,2)
#softmax activation function
self.softmax = nn.LogSoftmax(dim=1)
#define the forward pass
def forward(self, sent_id, mask):
#pass the inputs to the model
_, cls_hs = self.bert(sent_id, attention_mask=mask)
x = self.fc1(cls_hs)
x = self.relu(x)
x = self.dropout(x)
# output layer
x = self.fc2(x)
# apply softmax activation
x = self.softmax(x)
return x
# pass the pre-trained BERT to our define architecture
model = BERT_Arch(bert)
# push the model to GPU
model = model.to(device)
# optimizer from hugging face transformers
from transformers import AdamW
# define the optimizer
optimizer = AdamW(model.parameters(), lr = 1e-3)
```
# Find Class Weights
```
from sklearn.utils.class_weight import compute_class_weight
#compute the class weights
class_wts = compute_class_weight('balanced', np.unique(train_labels), train_labels)
print(class_wts)
# convert class weights to tensor
weights= torch.tensor(class_wts,dtype=torch.float)
weights = weights.to(device)
# loss function
cross_entropy = nn.NLLLoss(weight=weights)
# number of training epochs
epochs = 10
```
# Fine-Tune BERT
```
# function to train the model
def train():
model.train()
total_loss, total_accuracy = 0, 0
# empty list to save model predictions
total_preds=[]
# iterate over batches
for step,batch in enumerate(train_dataloader):
# progress update after every 50 batches.
if step % 50 == 0 and not step == 0:
print(' Batch {:>5,} of {:>5,}.'.format(step, len(train_dataloader)))
# push the batch to gpu
batch = [r.to(device) for r in batch]
sent_id, mask, labels = batch
# clear previously calculated gradients
model.zero_grad()
# get model predictions for the current batch
preds = model(sent_id, mask)
# compute the loss between actual and predicted values
loss = cross_entropy(preds, labels)
# add on to the total loss
total_loss = total_loss + loss.item()
# backward pass to calculate the gradients
loss.backward()
# clip the the gradients to 1.0. It helps in preventing the exploding gradient problem
torch.nn.utils.clip_grad_norm_(model.parameters(), 1.0)
# update parameters
optimizer.step()
# model predictions are stored on GPU. So, push it to CPU
preds=preds.detach().cpu().numpy()
# append the model predictions
total_preds.append(preds)
# compute the training loss of the epoch
avg_loss = total_loss / len(train_dataloader)
# predictions are in the form of (no. of batches, size of batch, no. of classes).
# reshape the predictions in form of (number of samples, no. of classes)
total_preds = np.concatenate(total_preds, axis=0)
#returns the loss and predictions
return avg_loss, total_preds
# function for evaluating the model
def evaluate():
print("\nEvaluating...")
# deactivate dropout layers
model.eval()
total_loss, total_accuracy = 0, 0
# empty list to save the model predictions
total_preds = []
# iterate over batches
for step,batch in enumerate(val_dataloader):
# Progress update every 50 batches.
if step % 50 == 0 and not step == 0:
# Calculate elapsed time in minutes.
elapsed = format_time(time.time() - t0)
# Report progress.
print(' Batch {:>5,} of {:>5,}.'.format(step, len(val_dataloader)))
# push the batch to gpu
batch = [t.to(device) for t in batch]
sent_id, mask, labels = batch
# deactivate autograd
with torch.no_grad():
# model predictions
preds = model(sent_id, mask)
# compute the validation loss between actual and predicted values
loss = cross_entropy(preds,labels)
total_loss = total_loss + loss.item()
preds = preds.detach().cpu().numpy()
total_preds.append(preds)
# compute the validation loss of the epoch
avg_loss = total_loss / len(val_dataloader)
# reshape the predictions in form of (number of samples, no. of classes)
total_preds = np.concatenate(total_preds, axis=0)
return avg_loss, total_preds
```
# Start Model Training
```
# set initial loss to infinite
best_valid_loss = float('inf')
# empty lists to store training and validation loss of each epoch
train_losses=[]
valid_losses=[]
#for each epoch
for epoch in range(epochs):
print('\n Epoch {:} / {:}'.format(epoch + 1, epochs))
#train model
train_loss, _ = train()
#evaluate model
valid_loss, _ = evaluate()
#save the best model
if valid_loss < best_valid_loss:
best_valid_loss = valid_loss
torch.save(model.state_dict(), 'saved_weights.pt')
# append training and validation loss
train_losses.append(train_loss)
valid_losses.append(valid_loss)
print(f'\nTraining Loss: {train_loss:.3f}')
print(f'Validation Loss: {valid_loss:.3f}')
```
# Load Saved Model
```
#load weights of best model
path = 'saved_weights.pt'
model.load_state_dict(torch.load(path))
```
# Get Predictions for Test Data
```
# get predictions for test data
with torch.no_grad():
preds = model(test_seq.to(device), test_mask.to(device))
preds = preds.detach().cpu().numpy()
# model's performance
preds = np.argmax(preds, axis = 1)
print(classification_report(test_y, preds))
# confusion matrix
pd.crosstab(test_y, preds)
```
|
github_jupyter
|
# Run hacked AlphaFold2 on the designed bound states
### Imports
```
%load_ext lab_black
# Python standard library
from glob import glob
import os
import socket
import sys
# 3rd party library imports
import dask
import matplotlib.pyplot as plt
import pandas as pd
import pyrosetta
import numpy as np
import scipy
import seaborn as sns
from tqdm.auto import tqdm # jupyter compatible progress bar
tqdm.pandas() # link tqdm to pandas
# Notebook magic
# save plots in the notebook
%matplotlib inline
# reloads modules automatically before executing cells
%load_ext autoreload
%autoreload 2
print(f"running in directory: {os.getcwd()}") # where are we?
print(f"running on node: {socket.gethostname()}") # what node are we on?
```
### Set working directory to the root of the crispy_shifty repo
TODO set to projects dir
```
os.chdir("/home/pleung/projects/crispy_shifty")
# os.chdir("/projects/crispy_shifty")
```
### Run AF2 on the designed bound states
TODO
```
from crispy_shifty.utils.io import gen_array_tasks
simulation_name = "03_fold_bound_states"
design_list_file = os.path.join(
os.getcwd(),
"projects/crispy_shifties/02_mpnn_bound_states/test_mpnn_states.pair", # TODO
)
output_path = os.path.join(os.getcwd(), f"projects/crispy_shifties/{simulation_name}")
options = " ".join(
[
"out:level 200",
]
)
extra_kwargs = {"models": "1"}
gen_array_tasks(
distribute_func="crispy_shifty.protocols.folding.fold_bound_state",
design_list_file=design_list_file,
output_path=output_path,
queue="gpu", # TODO
cores=2,
memory="16G", # TODO
gres="--gres=gpu:rtx2080:1", # TODO
# TODO perlmutter_mode=True,
nstruct=1,
nstruct_per_task=1,
options=options,
extra_kwargs=extra_kwargs,
simulation_name=simulation_name,
)
# !sbatch -a 1-$(cat /mnt/home/pleung/projects/crispy_shifty/projects/crispy_shifties/02_mpnn_bound_states/tasks.cmds | wc -l) /mnt/home/pleung/projects/crispy_shifty/projects/crispy_shifties/02_mpnn_bound_states/run.sh
```
### Collect scorefiles of designed bound states and concatenate
TODO change to projects dir
```
sys.path.insert(0, "~/projects/crispy_shifty") # TODO
from crispy_shifty.utils.io import collect_score_file
simulation_name = "03_fold_bound_states"
output_path = os.path.join(os.getcwd(), f"projects/crispy_shifties/{simulation_name}")
if not os.path.exists(os.path.join(output_path, "scores.json")):
collect_score_file(output_path, "scores")
```
### Load resulting concatenated scorefile
TODO change to projects dir
```
sys.path.insert(0, "~/projects/crispy_shifty") # TODO
from crispy_shifty.utils.io import parse_scorefile_linear
output_path = os.path.join(os.getcwd(), f"projects/crispy_shifties/{simulation_name}")
scores_df = parse_scorefile_linear(os.path.join(output_path, "scores.json"))
scores_df = scores_df.convert_dtypes()
```
### Setup for plotting
```
sns.set(
context="talk",
font_scale=1, # make the font larger; default is pretty small
style="ticks", # make the background white with black lines
palette="colorblind", # a color palette that is colorblind friendly!
)
```
### Data exploration
Gonna remove the Rosetta sfxn scoreterms for now
```
from crispy_shifty.protocols.design import beta_nov16_terms
scores_df = scores_df[
[term for term in scores_df.columns if term not in beta_nov16_terms]
]
print(len(scores_df))
j = 0
for i, r in scores_df.iterrows():
if (r["designed_by"]) == "rosetta":
j += 1
print(j)
```
### Save a list of outputs
```
# simulation_name = "03_fold_bound_states"
# output_path = os.path.join(os.getcwd(), f"projects/crispy_shifties/{simulation_name}")
# with open(os.path.join(output_path, "folded_states.list"), "w") as f:
# for path in tqdm(scores_df.index):
# print(path, file=f)
```
### Prototyping blocks
test `fold_bound_state`
```
%%time
from operator import gt, lt
import pyrosetta
filter_dict = {
"mean_plddt": (gt, 85.0),
"rmsd_to_reference": (lt, 2.2),
"mean_pae_interaction": (lt, 10.0),
}
rank_on = "mean_plddt"
prefix = "mpnn_seq"
pyrosetta.init()
sys.path.insert(0, "~/projects/crispy_shifty/") # TODO projects
from crispy_shifty.protocols.folding import fold_bound_state
t = fold_bound_state(
None,
**{
'fasta_path': '/mnt/home/pleung/projects/crispy_shifty/projects/crispy_shifties/02_mpnn_bound_states/fastas/0000/02_mpnn_bound_states_25a76fae39514121922e2b477b5b9813.fa',
"filter_dict": filter_dict,
"models": [1], # TODO
'pdb_path': '/mnt/home/pleung/projects/crispy_shifty/projects/crispy_shifties/02_mpnn_bound_states/decoys/0000/02_mpnn_bound_states_25a76fae39514121922e2b477b5b9813.pdb.bz2',
'prefix': prefix,
'rank_on': rank_on,
# 'fasta_path': 'bar.fa',
# "models": [1, 2], # TODO
# 'pdb_path': 'foo.pdb.bz2',
}
)
for i, tppose in enumerate(t):
tppose.pose.dump_pdb(f"{i}.pdb")
tppose.pose.scores
```
test `generate_decoys_from_pose`
```
from operator import gt, lt
from crispy_shifty.protocols.folding import generate_decoys_from_pose
filter_dict = {
"mean_plddt": (gt, 85.0),
"rmsd_to_reference": (lt, 2.2),
"mean_pae_interaction": (lt, 10.0),
}
rank_on = "mean_plddt"
prefix = "mpnn_seq"
tpose = tppose.pose.clone()
genr = generate_decoys_from_pose(
tpose, prefix=prefix, rank_on=rank_on, filter_dict=filter_dict
)
for d in genr:
print(d.sequence())
```
|
github_jupyter
|
<a href="https://colab.research.google.com/github/parshwa1999/Map-Segmentation/blob/master/ResNet_RoadTest.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Segmentation of Road from Satellite imagery
## Importing Libraries
```
import warnings
warnings.filterwarnings('ignore')
import os
import cv2
#from google.colab.patches import cv2_imshow
import numpy as np
import tensorflow as tf
import pandas as pd
from keras.models import Model, load_model
from skimage.morphology import label
import pickle
from keras import backend as K
from matplotlib import pyplot as plt
from tqdm import tqdm_notebook
import random
from skimage.io import imread, imshow, imread_collection, concatenate_images
from matplotlib import pyplot as plt
import h5py
seed = 56
from google.colab import drive
drive.mount('/content/gdrive/')
base_path = "gdrive/My\ Drive/MapSegClean/"
%cd gdrive/My\ Drive/MapSegClean/
```
## Defining Custom Loss functions and accuracy Metric.
```
#Source: https://towardsdatascience.com/metrics-to-evaluate-your-semantic-segmentation-model-6bcb99639aa2
from keras import backend as K
def iou_coef(y_true, y_pred, smooth=1):
intersection = K.sum(K.abs(y_true * y_pred), axis=[1,2,3])
union = K.sum(y_true,[1,2,3])+K.sum(y_pred,[1,2,3])-intersection
iou = K.mean((intersection + smooth) / (union + smooth), axis=0)
return iou
def dice_coef(y_true, y_pred, smooth = 1):
y_true_f = K.flatten(y_true)
y_pred_f = K.flatten(y_pred)
intersection = K.sum(y_true_f * y_pred_f)
return (2. * intersection + smooth) / (K.sum(y_true_f) + K.sum(y_pred_f) + smooth)
def soft_dice_loss(y_true, y_pred):
return 1-dice_coef(y_true, y_pred)
```
## Defining Our Model
```
pip install -U segmentation-models
from keras.models import Model, load_model
import tensorflow as tf
from keras.layers import Input
from keras.layers.core import Dropout, Lambda
from keras.layers.convolutional import Conv2D, Conv2DTranspose
from keras.layers.pooling import MaxPooling2D
from keras.layers.merge import concatenate
from keras import optimizers
from keras.layers import BatchNormalization
import keras
from segmentation_models import Unet
from segmentation_models import get_preprocessing
from segmentation_models.losses import bce_jaccard_loss
from segmentation_models.metrics import iou_score
model = Unet('resnet101', input_shape=(256, 256, 3), encoder_weights=None)
#model = Unet(input_shape=(256, 256, 3), weights=None, activation='elu')
model.summary()
# fit model
```
### HYPER_PARAMETERS
```
LEARNING_RATE = 0.0001
```
### Initializing Callbacks
```
#from tensorboardcolab import TensorBoardColab, TensorBoardColabCallback
from keras.callbacks import EarlyStopping, ModelCheckpoint, ReduceLROnPlateau
from datetime import datetime
model_path = "./Models/Resnet_road_weights.h5"
checkpointer = ModelCheckpoint(model_path,
monitor="val_loss",
mode="min",
save_best_only = True,
verbose=1)
earlystopper = EarlyStopping(monitor = 'val_loss',
min_delta = 0,
patience = 5,
verbose = 1,
restore_best_weights = True)
lr_reducer = ReduceLROnPlateau(monitor='val_loss',
factor=0.1,
patience=4,
verbose=1,
epsilon=1e-4)
```
### Compiling the model
```
opt = keras.optimizers.adam(LEARNING_RATE)
model.compile(
optimizer=opt,
loss=soft_dice_loss,
metrics=[iou_coef])
```
## Testing our Model
### On Test Images
```
model.load_weights("Models/Resnet_road_weights.h5")
import cv2
import glob
import numpy as np
import h5py
#test_images = np.array([cv2.imread(file) for file in glob.glob("/home/bisag/Desktop/Road-Segmentation/I/")])
#test_masks = np.array([cv2.imread(file) for file in glob.glob("/home/bisag/Desktop/Road-Segmentation/M/")])
test_masks = []
test_images = []
files = glob.glob ("TestI/*.png")
for myFile in files:
print(myFile)
image = cv2.imread (myFile)
test_images.append (image)
myFile = 'TestM' + myFile[5:len(myFile)]
image = cv2.cvtColor(cv2.imread (myFile), cv2.COLOR_BGR2GRAY)
test_masks.append (image)
#files = glob.glob ("TestM/*.png")
#for myFile in files:
# print(myFile)
#test_images = cv2.imread("/home/bisag/Desktop/Road-Segmentation/I/1.png")
#test_masks = cv2.imread("/home/bisag/Desktop/Road-Segmentation/M/1.png")
test_images = np.array(test_images)
test_masks = np.array(test_masks)
test_masks = np.expand_dims(test_masks, -1)
print("Unique elements in the train mask:", np.unique(test_masks))
print(test_images.shape)
print(test_masks.shape)
test_images = test_images.astype(np.float16)/255
test_masks = test_masks.astype(np.float16)/255
import sys
def sizeof_fmt(num, suffix='B'):
''' by Fred Cirera, https://stackoverflow.com/a/1094933/1870254, modified'''
for unit in ['','Ki','Mi','Gi','Ti','Pi','Ei','Zi']:
if abs(num) < 1024.0:
return "%3.1f %s%s" % (num, unit, suffix)
num /= 1024.0
return "%.1f %s%s" % (num, 'Yi', suffix)
for name, size in sorted(((name, sys.getsizeof(value)) for name, value in locals().items()),
key= lambda x: -x[1])[:10]:
print("{:>30}: {:>8}".format(name, sizeof_fmt(size)))
test_masks_tmp = []
for i in test_masks:
image = cv2.cvtColor(i, cv2.COLOR_BGR2GRAY)
test_masks_tmp.append (image)
test_images = np.array(test_images)
test_masks = np.array(test_masks_tmp)
test_masks = np.expand_dims(test_masks, -1)
#print(np.unique(test_masks))
print(test_images.shape)
print(test_masks.shape)
del test_masks_tmp
model.evaluate(test_images, test_masks)
predictions = model.predict(test_images, verbose=1)
thresh_val = 0.1
predicton_threshold = (predictions > thresh_val).astype(np.uint8)
plt.figure()
#plt.subplot(2, 1, 1)
plt.imshow(np.squeeze(predictions[19][:,:,0]))
plt.show()
import matplotlib
for i in range(len(predictions)):
#print("Results/" + str(i) + "Image.png")
matplotlib.image.imsave( "Results/" + str(i) + "Image.png" , np.squeeze(test_images[i][:,:,0]))
matplotlib.image.imsave( "Results/" + str(i) + "GroundTruth.png" , np.squeeze(test_masks[i][:,:,0]))
#cv2.imwrite( "/home/bisag/Desktop/Road-Segmentation/Results/" + str(i) + "Prediction.png" , np.squeeze(predictions[i][:,:,0]))
#cv2.imwrite( "/home/bisag/Desktop/Road-Segmentation/Results/" + str(i) + "Prediction_Threshold.png" , np.squeeze(predicton_threshold[i][:,:,0]))
#matplotlib.image.imsave('/home/bisag/Desktop/Road-Segmentation/Results/000.png', np.squeeze(predicton_threshold[0][:,:,0]))
matplotlib.image.imsave("Results/" + str(i) + "Prediction.png" , np.squeeze(predictions[i][:,:,0]))
matplotlib.image.imsave( "Results/" + str(i) + "Prediction_Threshold.png" , np.squeeze(predicton_threshold[i][:,:,0]))
#imshow(np.squeeze(predictions[0][:,:,0]))
#import scipy.misc
#scipy.misc.imsave('/home/bisag/Desktop/Road-Segmentation/Results/00.png', np.squeeze(predictions[0][:,:,0]))
model.load_weights("/home/parshwa/Desktop/Road-Segmentation/Models/weights.h5")
```
### Just Test
```
"""Test"""
import cv2
import glob
import numpy as np
import h5py
#test_images = np.array([cv2.imread(file) for file in glob.glob("/home/bisag/Desktop/Road-Segmentation/I/")])
#test_masks = np.array([cv2.imread(file) for file in glob.glob("/home/bisag/Desktop/Road-Segmentation/M/")])
test_images = []
files = glob.glob ("/home/parshwa/Desktop/Road-Segmentation/Test/*.png")
for myFile in files:
print(myFile)
image = cv2.imread (myFile)
test_images.append (image)
#test_images = cv2.imread("/home/bisag/Desktop/Road-Segmentation/I/1.png")
#test_masks = cv2.imread("/home/bisag/Desktop/Road-Segmentation/M/1.png")
test_images = np.array(test_images)
print(test_images.shape)
predictions = model.predict(test_images, verbose=1)
thresh_val = 0.1
predicton_threshold = (predictions > thresh_val).astype(np.uint8)
import matplotlib
for i in range(len(predictions)):
cv2.imwrite( "/home/parshwa/Desktop/Road-Segmentation/Results/" + str(i) + "Image.png" , np.squeeze(test_images[i][:,:,0]))
#cv2.imwrite( "/home/bisag/Desktop/Road-Segmentation/Results/" + str(i) + "Prediction.png" , np.squeeze(predictions[i][:,:,0]))
#cv2.imwrite( "/home/bisag/Desktop/Road-Segmentation/Results/" + str(i) + "Prediction_Threshold.png" , np.squeeze(predicton_threshold[i][:,:,0]))
#matplotlib.image.imsave('/home/bisag/Desktop/Road-Segmentation/Results/000.png', np.squeeze(predicton_threshold[0][:,:,0]))
matplotlib.image.imsave("/home/parshwa/Desktop/Road-Segmentation/Results/" + str(i) + "Prediction.png" , np.squeeze(predictions[i][:,:,0]))
matplotlib.image.imsave( "/home/parshwa/Desktop/Road-Segmentation/Results/" + str(i) + "Prediction_Threshold.png" , np.squeeze(predicton_threshold[i][:,:,0]))
#imshow(np.squeeze(predictions[0][:,:,0]))
imshow(np.squeeze(predictions[0][:,:,0]))
#import scipy.misc
#scipy.misc.imsave('/home/bisag/Desktop/Road-Segmentation/Results/00.png', np.squeeze(predictions[0][:,:,0]))
"""Visualise"""
def layer_to_visualize(layer):
inputs = [K.learning_phase()] + model.inputs
_convout1_f = K.function(inputs, [layer.output])
def convout1_f(X):
# The [0] is to disable the training phase flag
return _convout1_f([0] + [X])
convolutions = convout1_f(img_to_visualize)
convolutions = np.squeeze(convolutions)
print ('Shape of conv:', convolutions.shape)
n = convolutions.shape[0]
n = int(np.ceil(np.sqrt(n)))
# Visualization of each filter of the layer
fig = plt.figure(figsize=(12,8))
for i in range(len(convolutions)):
ax = fig.add_subplot(n,n,i+1)
ax.imshow(convolutions[i], cmap='gray')
```
|
github_jupyter
|
## Homework 4
Today we'll start by reproducing the DQN and then try improving it with the tricks we learned on the lecture:
* Target networks
* Double q-learning
* Prioritized experience replay
* Dueling DQN
* Bootstrap DQN
```
import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline
# If you are running on a server, launch xvfb to record game videos
# Please make sure you have xvfb installed
import os
if type(os.environ.get("DISPLAY")) is not str or len(os.environ.get("DISPLAY")) == 0:
!bash ../xvfb start
os.environ['DISPLAY'] = ':1'
```
# Processing game image (2 pts)
Raw Atari images are large, 210x160x3 by default. However, we don't need that level of detail in order to learn them.
We can thus save a lot of time by preprocessing game image, including
* Resizing to a smaller shape
* Converting to grayscale
* Cropping irrelevant image parts
```
from gym.core import ObservationWrapper
from gym.spaces import Box
from scipy.misc import imresize
class PreprocessAtari(ObservationWrapper):
def __init__(self, env):
"""A gym wrapper that crops, scales image into the desired shapes and optionally grayscales it."""
ObservationWrapper.__init__(self, env)
self.img_size = (64, 64)
self.observation_space = Box(0.0, 1.0, self.img_size)
def observation(self, img):
"""what happens to each observation"""
# Here's what you need to do:
# * crop image, remove irrelevant parts
# * resize image to self.img_size
# (use imresize imported above or any library you want,
# e.g. opencv, skimage, PIL, keras)
# * cast image to grayscale
# * convert image pixels to (0,1) range, float32 type
<Your code here>
return <YOUR CODE>
import gym
def make_env():
env = gym.make("KungFuMasterDeterministic-v0") # create raw env
return PreprocessAtari(env) # apply your wrapper
# spawn game instance for tests
env = make_env()
observation_shape = env.observation_space.shape
n_actions = env.action_space.n
obs = env.reset()
# test observation
assert obs.shape == observation_shape
assert obs.dtype == 'float32'
assert len(np.unique(obs)) > 2, "your image must not be binary"
assert 0 <= np.min(obs) and np.max(
obs) <= 1, "convert image pixels to (0,1) range"
print "Formal tests seem fine. Here's an example of what you'll get."
plt.title("what your network gonna see")
plt.imshow(obs, interpolation='none', cmap='gray')
plt.figure(figsize=[12, 12])
env.reset()
for i in range(16):
for _ in range(10):
new_obs = env.step(env.action_space.sample())[0]
plt.subplot(4, 4, i+1)
plt.imshow(new_obs, interpolation='none', cmap='gray')
# dispose of the game instance
del env
```
# Building a DQN (2 pts)
Here we define a simple agent that maps game images into Qvalues using simple convolutional neural network.
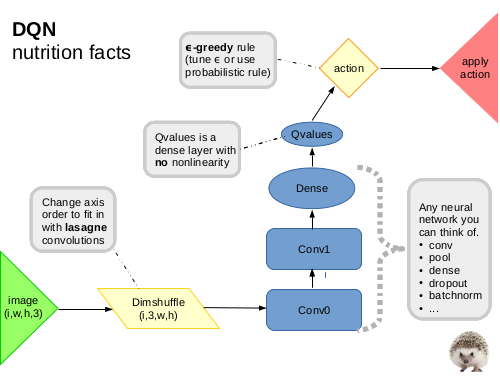
```
# setup theano/lasagne. Prefer GPU. Fallback to CPU (will print warning)
%env THEANO_FLAGS = floatX = float32
import theano
import lasagne
from lasagne.layers import *
from theano import tensor as T
# observation
observation_layer = InputLayer(
(None,)+observation_shape) # game image, [batch,64,64]
# 4-tick window over images
from agentnet.memory import WindowAugmentation
# window size [batch,4,64,64]
prev_wnd = InputLayer((None, 4)+observation_shape)
new_wnd = WindowAugmentation( < current observation layer> , prev_wnd)
# if you changed img size, remove assert
assert new_wnd.output_shape == (None, 4, 64, 64)
from lasagne.nonlinearities import elu, tanh, softmax, rectify
<network body, growing from new_wnd. several conv layers or something similar would do>
dense = <final dense layer with 256 neurons>
# qvalues layer
qvalues_layer = <a dense layer that predicts q-values>
assert qvalues_layer.nonlinearity is not rectify
# sample actions proportionally to policy_layer
from agentnet.resolver import EpsilonGreedyResolver
action_layer = EpsilonGreedyResolver(qvalues_layer)
```
### Define agent
Here you will need to declare how your agent works
* `observation_layers` and `action_layers` are the input and output of agent in MDP.
* `policy_estimators` must contain whatever you need for training
* In our case, that's `qvalues_layer`, but you'll need to add more when implementing target network.
* agent_states contains our frame buffer.
* The code `{new_wnd:prev_wnd}` reads as "`new_wnd becomes prev_wnd next turn`"
```
from agentnet.agent import Agent
# agent
agent = Agent(observation_layers=<YOUR CODE>,
policy_estimators=<YOUR CODE>,
action_layers=<YOUR CODE>,
agent_states={new_wnd: prev_wnd},)
```
# Create and manage a pool of Atari sessions to play with
* To make training more stable, we shall have an entire batch of game sessions each happening independent of others
* Why several parallel agents help training: http://arxiv.org/pdf/1602.01783v1.pdf
* Alternative approach: store more sessions: https://www.cs.toronto.edu/~vmnih/docs/dqn.pdf
```
from agentnet.experiments.openai_gym.pool import EnvPool
pool = EnvPool(agent, make_env, n_games=16) # 16 parallel game sessions
%%time
# interact for 7 ticks
_, action_log, reward_log, _, _, _ = pool.interact(5)
print('actions:')
print(action_log[0])
print("rewards")
print(reward_log[0])
# load first sessions (this function calls interact and remembers sessions)
SEQ_LENGTH = 10 # sub-session length
pool.update(SEQ_LENGTH)
```
# Q-learning
We train our agent based on sessions it has played in `pool.update(SEQ_LENGTH)`
To do so, we first obtain sequences of observations, rewards, actions, q-values, etc.
Actions and rewards have shape `[n_games,seq_length]`, q-values are `[n_games,seq_length,n_actions]`
```
# get agent's Qvalues obtained via experience replay
replay = pool.experience_replay
actions, rewards, is_alive = replay.actions[0], replay.rewards, replay.is_alive
_, _, _, _, qvalues = agent.get_sessions(
replay,
session_length=SEQ_LENGTH,
experience_replay=True,
)
assert actions.ndim == rewards.ndim == is_alive.ndim == 2, "actions, rewards and is_alive must have shape [batch,time]"
assert qvalues.ndim == 3, "q-values must have shape [batch,time,n_actions]"
# compute V(s) as Qvalues of best actions.
# For homework assignment, you will need to use target net
# or special double q-learning objective here
state_values_target = <YOUR CODE: compute V(s) 2d tensor by taking T.argmax of qvalues over correct axis>
assert state_values_target.eval().shape = qvalues.eval().shape[:2]
from agentnet.learning.generic import get_n_step_value_reference
# get reference Q-values via Q-learning algorithm
reference_qvalues = get_n_step_value_reference(
state_values=state_values_target,
rewards=rewards/100.,
is_alive=is_alive,
n_steps=10,
gamma_or_gammas=0.99,
)
# consider it constant
from theano.gradient import disconnected_grad
reference_qvalues = disconnected_grad(reference_qvalues)
# get predicted Q-values for committed actions by both current and target networks
from agentnet.learning.generic import get_values_for_actions
action_qvalues = get_values_for_actions(qvalues, actions)
# loss for Qlearning =
# (Q(s,a) - (r+ gamma*r' + gamma^2*r'' + ... +gamma^10*Q(s_{t+10},a_max)))^2
elwise_mse_loss = <mean squared error between action qvalues and reference qvalues>
# mean over all batches and time ticks
loss = (elwise_mse_loss*is_alive).mean()
# Since it's a single lasagne network, one can get it's weights, output, etc
weights = <YOUR CODE: get all trainable params>
weights
# Compute weight updates
updates = <your favorite optimizer>
# compile train function
train_step = theano.function([], loss, updates=updates)
```
# Demo run
as usual...
```
action_layer.epsilon.set_value(0.05)
untrained_reward = np.mean(pool.evaluate(save_path="./records",
record_video=True))
# show video
from IPython.display import HTML
import os
video_names = list(
filter(lambda s: s.endswith(".mp4"), os.listdir("./records/")))
HTML("""
<video width="640" height="480" controls>
<source src="{}" type="video/mp4">
</video>
""".format("./records/" + video_names[-1])) # this may or may not be _last_ video. Try other indices
```
# Training loop
```
# starting epoch
epoch_counter = 1
# full game rewards
rewards = {}
loss, reward_per_tick, reward = 0, 0, 0
from tqdm import trange
from IPython.display import clear_output
for i in trange(150000):
# update agent's epsilon (in e-greedy policy)
current_epsilon = 0.05 + 0.45*np.exp(-epoch_counter/20000.)
action_layer.epsilon.set_value(np.float32(current_epsilon))
# play
pool.update(SEQ_LENGTH)
# train
loss = 0.95*loss + 0.05*train_step()
if epoch_counter % 10 == 0:
# average reward per game tick in current experience replay pool
reward_per_tick = 0.95*reward_per_tick + 0.05 * \
pool.experience_replay.rewards.get_value().mean()
print("iter=%i\tepsilon=%.3f\tloss=%.3f\treward/tick=%.3f" % (epoch_counter,
current_epsilon,
loss,
reward_per_tick))
# record current learning progress and show learning curves
if epoch_counter % 100 == 0:
action_layer.epsilon.set_value(0.05)
reward = 0.95*reward + 0.05*np.mean(pool.evaluate(record_video=False))
action_layer.epsilon.set_value(np.float32(current_epsilon))
rewards[epoch_counter] = reward
clear_output(True)
plt.plot(*zip(*sorted(rewards.items(), key=lambda (t, r): t)))
plt.show()
epoch_counter += 1
# Time to drink some coffee!
```
# Evaluating results
* Here we plot learning curves and sample testimonials
```
import pandas as pd
plt.plot(*zip(*sorted(rewards.items(), key=lambda k: k[0])))
from agentnet.utils.persistence import save, load
save(action_layer, "pacman.pcl")
action_layer.epsilon.set_value(0.05)
rw = pool.evaluate(n_games=20, save_path="./records", record_video=False)
print("mean session score=%f.5" % np.mean(rw))
# show video
from IPython.display import HTML
import os
video_names = list(
filter(lambda s: s.endswith(".mp4"), os.listdir("./records/")))
HTML("""
<video width="640" height="480" controls>
<source src="{}" type="video/mp4">
</video>
""".format("./videos/" + video_names[-1])) # this may or may not be _last_ video. Try other indices
```
## Assignment part I (5 pts)
We'll start by implementing target network to stabilize training.
There are two ways to do so:
__1)__ Manually write lasagne network, or clone it via [one of those methods](https://github.com/Lasagne/Lasagne/issues/720).
You will need to implement loading weights from original network to target network.
We recommend thoroughly debugging your code on simple tests before applying it in Atari dqn.
__2)__ Use pre-build functionality from [here](http://agentnet.readthedocs.io/en/master/modules/target_network.html)
```
from agentnet.target_network import TargetNetwork
target_net = TargetNetwork(qvalues_layer)
old_qvalues = target_net.output_layers
#agent's policy_estimators must now become (qvalues,old_qvalues)
_,_,_,_,(qvalues,old_qvalues) = agent.get_sessions(...) #replaying experience
target_net.load_weights()#loads weights, so target network is now exactly same as main network
target_net.load_weights(0.01)# w_target = 0.99*w_target + 0.01*w_new
```
## Bonus I (2+ pts)
Implement and train double q-learning.
This task contains of
* Implementing __double q-learning__ or __dueling q-learning__ or both (see tips below)
* Training a network till convergence
* Full points will be awwarded if your network gets average score of >=10 (see "evaluating results")
* Higher score = more points as usual
* If you're running out of time, it's okay to submit a solution that hasn't converged yet and updating it when it converges. _Lateness penalty will not increase for second submission_, so submitting first one in time gets you no penalty.
#### Tips:
* Implementing __double q-learning__ shouldn't be a problem if you've already have target networks in place.
* As one option, use `get_values_for_actions(<some q-values tensor3>,<some indices>)`.
* You will probably need `T.argmax` to select best actions
* Here's an original [article](https://arxiv.org/abs/1509.06461)
* __Dueling__ architecture is also quite straightforward if you have standard DQN.
* You will need to change network architecture, namely the q-values layer
* It must now contain two heads: V(s) and A(s,a), both dense layers
* You should then add them up via elemwise sum layer or a [custom](http://lasagne.readthedocs.io/en/latest/user/custom_layers.html) layer.
* Here's an [article](https://arxiv.org/pdf/1511.06581.pdf)
Here's a template for your convenience:
```
from lasagne.layers import *
class DuelingQvaluesLayer(MergeLayer):
def get_output_for(self, inputs, **tags):
V, A = inputs
return <YOUR CODE: add them up :)>
def get_output_shape_for(self, input_shapes, **tags):
V_shape, A_shape=input_shapes
assert len(
V_shape) == 2 and V_shape[-1] == 1, "V layer (first param) shape must be [batch,tick,1]"
return A_shape # shape of q-values is same as predicted advantages
# mock-up tests
import theano.tensor as T
v_tensor = -T.arange(10).reshape((10, 1))
V = InputLayer((None, 1), v_tensor)
a_tensor = T.arange(30).reshape((10, 3))
A = InputLayer((None, 1), a_tensor)
Q = DuelingQvaluesLayer([V, A])
import numpy as np
assert np.allclose(get_output(Q).eval(), (v_tensor+a_tensor).eval())
print("looks good")
```
## Bonus II (5+ pts): Prioritized experience replay
In this section, you're invited to implement prioritized experience replay
* You will probably need to provide a custom data structure
* Once pool.update is called, collect the pool.experience_replay.observations, actions, rewards and is_alive and store them in your data structure
* You can now sample such transitions in proportion to the error (see [article](https://arxiv.org/abs/1511.05952)) for training.
It's probably more convenient to explicitly declare inputs for "sample observations", "sample actions" and so on to plug them into q-learning.
Prioritized (and even normal) experience replay should greatly reduce amount of game sessions you need to play in order to achieve good performance.
While it's effect on runtime is limited for atari, more complicated envs (further in the course) will certainly benefit for it.
Prioritized experience replay only supports off-policy algorithms, so pls enforce `n_steps=1` in your q-learning reference computation (default is 10).
|
github_jupyter
|
```
dtypes = {
'MachineIdentifier': 'category',
'ProductName': 'category',
'EngineVersion': 'category',
'AppVersion': 'category',
'AvSigVersion': 'category',
'IsBeta': 'int8',
'RtpStateBitfield': 'float16',
'IsSxsPassiveMode': 'int8',
'DefaultBrowsersIdentifier': 'float16',
'AVProductStatesIdentifier': 'float32',
'AVProductsInstalled': 'float16',
'AVProductsEnabled': 'float16',
'HasTpm': 'int8',
'CountryIdentifier': 'int16',
'CityIdentifier': 'float32',
'OrganizationIdentifier': 'float16',
'GeoNameIdentifier': 'float16',
'LocaleEnglishNameIdentifier': 'int8',
'Platform': 'category',
'Processor': 'category',
'OsVer': 'category',
'OsBuild': 'int16',
'OsSuite': 'int16',
'OsPlatformSubRelease': 'category',
'OsBuildLab': 'category',
'SkuEdition': 'category',
'IsProtected': 'float16',
'AutoSampleOptIn': 'int8',
'PuaMode': 'category',
'SMode': 'float16',
'IeVerIdentifier': 'float16',
'SmartScreen': 'category',
'Firewall': 'float16',
'UacLuaenable': 'float32',
'Census_MDC2FormFactor': 'category',
'Census_DeviceFamily': 'category',
'Census_OEMNameIdentifier': 'float16',
'Census_OEMModelIdentifier': 'float32',
'Census_ProcessorCoreCount': 'float16',
'Census_ProcessorManufacturerIdentifier': 'float16',
'Census_ProcessorModelIdentifier': 'float16',
'Census_ProcessorClass': 'category',
'Census_PrimaryDiskTotalCapacity': 'float32',
'Census_PrimaryDiskTypeName': 'category',
'Census_SystemVolumeTotalCapacity': 'float32',
'Census_HasOpticalDiskDrive': 'int8',
'Census_TotalPhysicalRAM': 'float32',
'Census_ChassisTypeName': 'category',
'Census_InternalPrimaryDiagonalDisplaySizeInInches': 'float16',
'Census_InternalPrimaryDisplayResolutionHorizontal': 'float16',
'Census_InternalPrimaryDisplayResolutionVertical': 'float16',
'Census_PowerPlatformRoleName': 'category',
'Census_InternalBatteryType': 'category',
'Census_InternalBatteryNumberOfCharges': 'float32',
'Census_OSVersion': 'category',
'Census_OSArchitecture': 'category',
'Census_OSBranch': 'category',
'Census_OSBuildNumber': 'int16',
'Census_OSBuildRevision': 'int32',
'Census_OSEdition': 'category',
'Census_OSSkuName': 'category',
'Census_OSInstallTypeName': 'category',
'Census_OSInstallLanguageIdentifier': 'float16',
'Census_OSUILocaleIdentifier': 'int16',
'Census_OSWUAutoUpdateOptionsName': 'category',
'Census_IsPortableOperatingSystem': 'int8',
'Census_GenuineStateName': 'category',
'Census_ActivationChannel': 'category',
'Census_IsFlightingInternal': 'float16',
'Census_IsFlightsDisabled': 'float16',
'Census_FlightRing': 'category',
'Census_ThresholdOptIn': 'float16',
'Census_FirmwareManufacturerIdentifier': 'float16',
'Census_FirmwareVersionIdentifier': 'float32',
'Census_IsSecureBootEnabled': 'int8',
'Census_IsWIMBootEnabled': 'float16',
'Census_IsVirtualDevice': 'float16',
'Census_IsTouchEnabled': 'int8',
'Census_IsPenCapable': 'int8',
'Census_IsAlwaysOnAlwaysConnectedCapable': 'float16',
'Wdft_IsGamer': 'float16',
'Wdft_RegionIdentifier': 'float16',
'HasDetections': 'int8'
}
import numpy as np
import pandas as pd
import lightgbm as lgb
import xgboost as xgb
import time, datetime
from sklearn import *
train = pd.read_csv('../input/train.csv', iterator=True, chunksize=1_500_000, dtype=dtypes)
test = pd.read_csv('../input/test.csv', iterator=True, chunksize=1_000_000, dtype=dtypes)
gf_defaults = {'col': [], 'ocol':[], 'dcol' : ['EngineVersion', 'AppVersion', 'AvSigVersion', 'OsBuildLab', 'Census_OSVersion']}
one_hot = {}
def get_features(df, gf_train=False):
global one_hot
global gf_defaults
for c in gf_defaults['dcol']:
for i in range(5):
df[c + str(i)] = df[c].map(lambda x: str(x).split('.')[i] if len(str(x).split('.'))>i else -1)
col = [c for c in df.columns if c not in ['MachineIdentifier', 'HasDetections']]
if gf_train:
for c in col:
if df[c].dtype == 'O' or df[c].dtype.name == 'category':
gf_defaults['ocol'].append(c)
else:
gf_defaults['col'].append(c)
one_hot = {c: list(df[c].value_counts().index) for c in gf_defaults['ocol']}
#train and test
for c in one_hot:
if len(one_hot[c])>1 and len(one_hot[c]) < 20:
for val in one_hot[c]:
df[c+'_oh_' + str(val)] = (df[c].values == val).astype(np.int)
if gf_train:
gf_defaults['col'].append(c+'_oh_' + str(val))
return df[gf_defaults['col']+['MachineIdentifier', 'HasDetections']]
col = gf_defaults['col']
model = []
params = {'objective':'binary', "boosting": "gbdt", 'learning_rate': 0.02, 'max_depth': -1,
"feature_fraction": 0.8, "bagging_freq": 1, "bagging_fraction": 0.8 , "bagging_seed": 11,
"metric": 'auc', "lambda_l1": 0.1, 'num_leaves': 60, 'min_data_in_leaf': 60, "verbosity": -1, "random_state": 3}
online_start = True
for df in train:
if online_start:
df = get_features(df, True)
x1, x2, y1, y2 = model_selection.train_test_split(df[col], df['HasDetections'], test_size=0.2, random_state=25)
model = lgb.train(params, lgb.Dataset(x1, y1), 2500, lgb.Dataset(x2, y2), verbose_eval=100, early_stopping_rounds=200)
model.save_model('lgb.model')
else:
df = get_features(df)
x1, x2, y1, y2 = model_selection.train_test_split(df[col], df['HasDetections'], test_size=0.2, random_state=25)
model = lgb.train(params, lgb.Dataset(x1, y1), 2500, lgb.Dataset(x2, y2), verbose_eval=100, early_stopping_rounds=200, init_model='lgb.model')
model.save_model('lgb.model')
online_start = False
print('training...')
predictions = []
for df in test:
df['HasDetections'] = 0.0
df = get_features(df)
df['HasDetections'] = model.predict(df[col], num_iteration=model.best_iteration + 50)
predictions.append(df[['MachineIdentifier', 'HasDetections']].values)
print('testing...')
sub = np.concatenate(predictions)
sub = pd.DataFrame(sub, columns = ['MachineIdentifier', 'HasDetections'])
sub.to_csv('submission.csv', index=False)
```
|
github_jupyter
|
```
import numpy as np
import nibabel as nb
import matplotlib.pyplot as plt
# helper function to plot 3D NIfTI
def plot_slice (fname):
# Load image
img = nb.load (fname)
data = img.get_data ()
# cut in the middle of brain
cut = int (data.shape[-1]/2) + 10
# plot data
plt.imshow (np.rot90 (data[...,cut]), cmap = 'gray')
plt.gca().set_axis_off()
# skull strip
# smooth original img
# mask smoothed img
# Example 1 : shell command line execution
# ----------------------------------------
%%bash
ANAT_NAME=sub-2019A_T1w
ANAT="/home/jiyang/Work/sub-2019A/anat/${ANAT_NAME}"
bet ${ANAT} /home/jiyang/Work/sub-2019A/derivatives/${ANAT_NAME}_brain -m -f 0.5
fslmaths ${ANAT} -s 2 /home/jiyang/Work/sub-2019A/derivatives/${ANAT_NAME}_smooth
fslmaths /home/jiyang/Work/sub-2019A/derivatives/${ANAT_NAME}_smooth \
-mas /home/jiyang/Work/sub-2019A/derivatives/${ANAT_NAME}_brain_mask \
/home/jiyang/Work/sub-2019A/derivatives/${ANAT_NAME}_smooth_mask
# plot
f = plt.figure (figsize=(12,4))
for i, img in enumerate(['T1w', 'T1w_smooth', 'T1w_brain_mask', 'T1w_smooth_mask']):
f.add_subplot (1, 4, i + 1)
if i == 0:
plot_slice ('/home/jiyang/Work/sub-2019A/anat/sub-2019A_%s.nii.gz' % img)
else:
plot_slice ('/home/jiyang/Work/sub-2019A/derivatives/sub-2019A_%s.nii.gz' % img)
plt.title(img)
# Example 2 : interface execution
import matplotlib.pyplot as plt
from nipype.interfaces import fsl
skullstrip = fsl.BET (in_file = "/Users/jiyang/Desktop/test/anat/sub-3625A_T1w.nii.gz",
out_file = "/Users/jiyang/Desktop/test/derivatives/sub-3625A_T1w_brain.nii.gz",
mask = True)
skullstrip.run()
smooth = fsl.IsotropicSmooth (in_file = "/Users/jiyang/Desktop/test/anat/sub-3625A_T1w.nii.gz",
out_file = "/Users/jiyang/Desktop/test/derivatives/sub-3625A_T1w_smooth.nii.gz",
fwhm = 4)
smooth.run()
mask = fsl.ApplyMask (in_file = '/Users/jiyang/Desktop/test/derivatives/sub-3625A_T1w_smooth.nii.gz',
out_file = '/Users/jiyang/Desktop/test/derivatives/sub-3625A_T1w_smooth_brain.nii.gz',
mask_file = '/Users/jiyang/Desktop/test/derivatives/sub-3625A_T1w_brain_mask.nii.gz')
mask.run()
# visualise
f = plt.figure (figsize = (12,4))
for i, img in enumerate (['T1w', 'T1w_smooth',
'T1w_brain_mask', 'T1w_smooth_brain']):
f.add_subplot (1, 4, i + 1)
if i == 0:
plot_slice ('/Users/jiyang/Desktop/test/anat/sub-3625A_%s.nii.gz' % img)
else:
plot_slice ('/Users/jiyang/Desktop/test/derivatives/sub-3625A_%s.nii.gz' % img)
plt.title (img)
# Example 2 can be simplified
skullstrip = fsl.BET (in_file = "/Users/jiyang/Desktop/test/anat/sub-3625A_T1w.nii.gz",
out_file = "/Users/jiyang/Desktop/test/derivatives/sub-3625A_T1w_brain.nii.gz",
mask = True)
bet_result = skullstrip.run()
smooth = fsl.IsotropicSmooth (in_file = skullstrip.inputs.in_file,
out_file = "/Users/jiyang/Desktop/test/derivatives/sub-3625A_T1w_smooth.nii.gz",
fwhm = 4)
smooth_result = smooth.run()
# # There is a bug here bet_result.outputs.mask_file point to cwd
# mask = fsl.ApplyMask (in_file = smooth_result.outputs.out_file,
# mask_file = bet_result.outputs.mask_file,
# out_file = '/Users/jiyang/Desktop/test/derivatives/sub-3625A_T1w_smooth_brain.nii.gz')
# mask_result = mask.run()
mask = fsl.ApplyMask (in_file = smooth_result.outputs.out_file,
mask_file = '/Users/jiyang/Desktop/test/derivatives/sub-3625A_T1w_brain_mask.nii.gz',
out_file = '/Users/jiyang/Desktop/test/derivatives/sub-3625A_T1w_smooth_brain.nii.gz')
mask_result = mask.run()
# visualise
f = plt.figure (figsize = (12, 4))
for i, img in enumerate ([skullstrip.inputs.in_file, smooth_result.outputs.out_file,
'/Users/jiyang/Desktop/test/derivatives/sub-3625A_T1w_brain_mask.nii.gz',
mask_result.outputs.out_file]):
f.add_subplot (1, 4, i + 1)
plot_slice (img)
plt.title (img.split('/')[-1].split('.')[0].split('A_')[-1])
skullstrip.inputs.in_file
smooth_result.outputs.out_file
bet_result.outputs.mask_file
bet_result.outputs # bug with bet_result.outputs.mask_file
# Example 3 : Workflow execution
from nipype import Node, Workflow
from nipype.interfaces import fsl
from os.path import abspath # passing absolute path is clearer
in_file = abspath ('/Users/jiyang/Desktop/test/anat/sub-3625A_T1w.nii.gz')
# workflow will take care of out_file
# only need to specify the very original in_file
# bet_out_file = abspath ('/Users/jiyang/Desktop/test/derivatives/sub-3625A_T1w_brain.nii.gz')
# smooth_out_file = abspath ('/Users/jiyang/Desktop/test/derivatives/sub-3625A_T1w_smooth.nii.gz')
skullstrip = Node (fsl.BET (in_file = in_file,
mask = True),
name = 'skullstrip')
smooth = Node (fsl.IsotropicSmooth (in_file = in_file,
fwhm = 4),
name = 'smooth')
mask = Node (fsl.ApplyMask (), name = 'mask')
# Initiate a workflow
wf = Workflow (name = 'smoothflow', base_dir = '/Users/jiyang/Desktop/test/derivatives')
# Two ways to connect nodes
#
# Way 1
# connect (source_node, "source_node_output", dest_node, "dest_node_input")
#
# Way 2
# connect ([(source_node, dest_node, [("source_node_output1", "dest_node_input1"),
# ("source_node_output2", "dest_node_input2")
# ]
# )])
#
#
# Way 1 can establish one connection at a time. Way 2 can establish multiple connections btw two nodes at once.
#
# In either case, four pieces of info are needed :
# - source node object
# - output field from source node
# - dest node object
# - input field from dest node
# Way 1
wf.connect (skullstrip, "mask_file", mask, "mask_file")
# Way 2
wf.connect ([(smooth, mask, [("out_file", "in_file")])])
# display workflow
wf.write_graph ('workflow_graph.dot')
from IPython.display import Image
Image (filename = '/Users/jiyang/Desktop/test/derivatives/smoothflow/workflow_graph.png')
wf.write_graph (graph2use = 'flat')
from IPython.display import Image
Image (filename = "/Users/jiyang/Desktop/test/derivatives/smoothflow/graph_detailed.png")
# execute
wf.base_dir = '/Users/jiyang/Desktop/test/derivatives'
wf.run()
# Note that specifying base_dir is very important (and is why we needed to use absolute paths above),
# because otherwise all outputs would be saved somewhere in temporary files.
# Unlike interfaces which by default split out results to local direcotries, Workflow engine execute
# things off in its own directory hierarchy.
f = plt.figure (figsize = (12, 4))
for i, img in enumerate (['/Users/jiyang/Desktop/test/anat/sub-3625A_T1w.nii.gz',
'/Users/jiyang/Desktop/test/derivatives/smoothflow/smooth/sub-3625A_T1w_smooth.nii.gz',
'/Users/jiyang/Desktop/test/derivatives/smoothflow/skullstrip/sub-3625A_T1w_brain_mask.nii.gz',
'/Users/jiyang/Desktop/test/derivatives/smoothflow/mask/sub-3625A_T1w_smooth_masked.nii.gz']):
f.add_subplot (1, 4, i + 1)
plot_slice (img)
!tree /Users/jiyang/Desktop/test/derivatives/smoothflow -I '*js|*json|*html|*pklz|_report'
# running workflow will return a graph object
#
# workflow does not have inputs/outputs, you can access them through Node
#
# A workflow inside a workflow
# ------------------------------------------------------------------------
#
# calling create_susan_smooth will return a workflow object
from nipype.workflows.fmri.fsl import create_susan_smooth
susan = create_susan_smooth (separate_masks = False)
```
|
github_jupyter
|
<font size ='3'>*First, let's read in the data and necessary libraries*<font/>
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from mypy import print_side_by_side
from mypy import display_side_by_side
#https://stackoverflow.com/a/44923103/8067752
%matplotlib inline
pd.options.mode.chained_assignment = None
b_cal = pd.read_csv('boston_calendar.csv')
s_cal = pd.read_csv('seatle_calendar.csv')
b_list = pd.read_csv('boston_listings.csv')
s_list = pd.read_csv('seatle_listings.csv')
b_rev = pd.read_csv('boston_reviews.csv')
s_rev = pd.read_csv('seatle_reviews.csv')
```
_______________________________________________________________________________________________________________________
## Task 1: Business Understanding <font size="2"> *(With some Data Preperation)*</font>
<font size="3"> *My work flow will be as follows, I will explore the data with some cleaning to get enough insights to formulate questions, then, within every question I will follow the rest of the steps of the CRISP-DM framework.*</font>
### Step 1: Basic Exploration with some cleaning
<font size ='3'>*To be familiarized with the Data and to gather insights to formulate questions*<font/>
> **Boston & Seatle Calendar**
```
display_side_by_side(b_cal.head(), s_cal.head(), titles = ['b_cal', 's_cal'])
```
<font size ='3'>*Check the sizes of cols and rows & check Nulls*<font/>
```
print_side_by_side('Boston Cal:', 'Seatle Cal:', b=0)
print_side_by_side('Shape:',b_cal.shape,"Shape:", s_cal.shape)
print_side_by_side("Cols with nulls: ", b_cal.isnull().sum()[b_cal.isnull().sum()>0].index[0],"Cols with nulls: ", s_cal.isnull().sum()[s_cal.isnull().sum()>0].index[0])
print_side_by_side("Null prop of price column: ", round(b_cal.price.isnull().sum()/b_cal.shape[0], 2),"Null prop of price column: ", round(s_cal.price.isnull().sum()/s_cal.shape[0], 2))
print_side_by_side("Proportion of False(unit unavailable):", round(b_cal.available[b_cal.available =='f' ].count()/b_cal.shape[0],2),"Proportion of False(unit unavailable):", round(s_cal.available[s_cal.available =='f' ].count()/s_cal.shape[0],2))
print_side_by_side("Nulls when units are available: ", b_cal[b_cal['available']== 't']['price'].isnull().sum(),"Nulls when units are available: ", s_cal[s_cal['available']== 't']['price'].isnull().sum() )
print('\n')
```
<font size ='3'>*Let's do some cleaning, first, let's transfer `date` column to datetime to ease manipulation and analysis. I will also create a dataframe with seperate date items from the Date column, to check the time interval along which the data was collected. In addition to that, let's transform `price` and `available` into numerical values*<font/>
```
def create_dateparts(df, date_col):
"""
INPUT
df -pandas dataframe
date_col -list of columns to break down into columns of years,months and days.
OUTPUT
df - a dataframe with columns of choice transformed in to columns of date parts(years,months and days)
"""
df['date'] = pd.to_datetime(df.date)
b_date_df = pd.DataFrame()
b_date_df['year'] = df['date'].dt.year
b_date_df['month'] = df['date'].dt.month
b_date_df['day'] =df['date'].dt.strftime("%A")
#b_date_df['dow'] =df['date'].dt.day
df = df.join(b_date_df)
return df
#######################
def get_period_df(df):
"""
INPUT
df -pandas dataframe
OUTPUT
df - a dataframe grouped to show the span of all the entries
"""
period =pd.DataFrame(df.groupby(['year','month'], sort = True)['day'].value_counts())
period = period.rename(columns={'day':'count'}, level=0)
period = period.reset_index().sort_values(by=['year', 'month', 'day']).reset_index(drop = True)
return period
#############################
def to_float(df, float_cols):
"""
INPUT
df -pandas dataframe
float_cols -list of columns to transform to float
OUTPUT
df - a dataframe with columns of choice transformed to float
"""
for col in float_cols:
df[col] = df[col].str.replace('$', "", regex = False)
df[col] = df[col].str.replace('%', "", regex = False)
df[col] = df[col].str.replace(',', "", regex = False)
for col in float_cols:
df[col] = df[col].astype(float)
return df
#############################
def bool_nums(df, bool_cols):
"""
INPUT
df -pandas dataframe
bool_cols -list of columns with true or false strings
OUTPUT
df - a dataframe with columns of choice transforemed into binary values
"""
for col in bool_cols:
df[col] = df[col].apply(lambda x: 1 if x == 't' else 0 )
df = df.reset_index(drop= True)
return df
```
<font size = '3'>*Let's take a look at the resulted DataFrames after executing the previous fuc=nctions. I flipped the Boston calendar to have it start in ascending order like Seatle.*<font/>
```
b_cal_1 = to_float(b_cal, ['price'])
s_cal_1 = to_float(s_cal, ['price'])
b_cal_1 = create_dateparts(b_cal_1, 'date')
s_cal_1 = create_dateparts(s_cal_1, 'date')
b_cal_1 = bool_nums(b_cal_1, ['available'])
s_cal_1 = bool_nums(s_cal_1, ['available'])
b_cal_1 = b_cal_1.iloc[::-1].reset_index(drop=True)
display_side_by_side(b_cal_1.head(3),s_cal_1.head(3), titles = ['b_cal_1', 's_cal_1'])
```
<font size = '3'>*Let's take a look at the resulted time intervals for Both Boston and Seatle calendar tables*<font/>
```
b_period =get_period_df(b_cal_1)
s_period =get_period_df(s_cal_1)
display_side_by_side(b_period.head(1), b_period.tail(1), titles = ['Boston Period'])
display_side_by_side(s_period.head(1), s_period.tail(1), titles = ['Seatle Period'])
print("Number of unique Listing IDs in Boston Calendar: ", len(b_cal_1.listing_id.unique()))
print("Number of unique Listing IDs in Seatle Calendar: ", len(s_cal_1.listing_id.unique()))
print('\n')
#b_period.iloc[0], s_period.iloc[0], b =0)
```
<font size ='3'>*Seems like they both span a year, through which all the listings are tracked in terms of availability. When we group by year and month; the count is equivalent to the numbers of the unique ids because all the ids are spanning the same interval. Let's check any anomalies*<font/>
```
def check_anomalies(df, col):
list_ids_not_year_long = []
for i in sorted(list(df[col].unique())):
if df[df[col]== i].shape[0] != 365:
list_ids_not_year_long.append(i)
print("Entry Ids that don't span 1 year: " , list_ids_not_year_long)
#Boston
check_anomalies(b_cal_1, 'listing_id')
#Seatle
check_anomalies(s_cal_1, 'listing_id')
## check this entry in Boston Calendar
print("Span of the entries for this listing, should be 365: ", b_cal_1[b_cal_1['listing_id']== 12898806].shape[0])
## 2 years, seems like a duplicate as 730 = 365 * 2
one_or_two = pd.DataFrame(b_cal_1[b_cal_1['listing_id']==12898806].groupby(['year', 'month', 'day'])['day'].count()).day.unique()[0]
print("Should be 1: ", one_or_two)
## It indeed is :)
b_cal_1 = b_cal_1.drop_duplicates()
print("Size of anomaly listing, Should be = 365: ", b_cal_1.drop_duplicates()[b_cal_1.drop_duplicates().listing_id==12898806]['listing_id'].size)
print("After removing duplicates, Span of the entries for this listing, should be 365: ", b_cal_1[b_cal_1['listing_id']== 12898806].shape[0])
print("After removing duplicates, shape is: ", b_cal_1.shape)
# b_cal_1.to_csv('b_cal_1.csv')
# s_cal_1.to_csv('s_cal_1.csv')
```
_______________________________________________________________________________________________________________________
### Comments:
[Boston & Seatle Calendar]
- The datasets have information about listing dates, availability and price tracked over a year for ever listing id
- There are no data entry errors, all nulls are due to the structuring of the Data (the listings that weren't available has no price)
- I added 4 cols that contain dateparts that will aid further analysis and modeling
- The Boston calendar Dataset ranges through `365`days from `6th of September'16` to `5th of September'17`, No nulls with `1308525` rows and `8` cols
- The Seatle calendar Dataset ranges through `365`days from `4th of January'16` to `2nd of January'17`, No nulls with `1393570` rows and `8` cols
- Number of unique Listing IDs in Boston Calendar: `3585`
- Number of unique Listing IDs in Seatle Calendar: `3818`
- It seems that the table is not documenting any rentals it just shows if the unit is available at a certain time and the price then.
_______________________________________________________________________________________________________________________
## Step 1: Continue -
> **Boston & Seatle Listings**
```
b_list.head(1)
#s_list.head(10)
```
<font size ='3'>*Check the sizes of cols & rows & check Nulls*<font/>
```
print_side_by_side("Boston listings size :", b_list.shape, "Seatle listings size :", s_list.shape)
print_side_by_side("Number of Non-null cols in Boston listings: ", np.sum(b_list.isnull().sum()==0) ,"Number of Non-null cols in Seatle listings: ", np.sum(s_list.isnull().sum()==0))
set_difference = set(b_list.columns) - set(s_list.columns)
print("Columns in Boston but not in Seatle: ", set_difference)
print('\n')
```
<font size ='3'>*Let's go through the columns of this table as they are a lot, decide on which would be useful, which would be ignored and which would be transformed based on intuition.* <font/>
> **to_parts:**<br><font size = '2'>(Divide into ranges)<font/><br>
>* *maximum_nights*
><br>
>
> **to_count:** <br><font size = '2'>(Provide a count)<font/><br>
> * *amenities* <br>
> * *host_verifications*
><br>
>
>**to_dummy:** <br><font size = '2'>(Convert into dummy variables)<font/><br>
>* *amenities*
><br>
>
>**to_len_text:** <br><font size = '2'>(provide length of text)<font/><br>
>* *name*
>* *host_about*
>* *summary*
>* *description*
>* *neighborhood_overview*
>* *transit*
><br>
>
>**to_days:** <br><font size = '2'>(calculate the difference between both columns to have a meaningful value of host_since in days)<font/><br>
>* *host_since*
>* *last_review*
><br>
>
>**to_float:**<br><font size = '2'>(Transform to float)<font/><br>
>* *cleaning_fee* <br>
>* *host_response_rate* <br>
>* *host_acceptance_rate* <br>
>* *host_response_rate* <br>
>* *host_acceptance_rate* <br>
>* *extra_people* <br>
>* *price* <br>
><br>
>
> **to_binary:** <br><font size = '2'>(Transform to binary)<font/><br>
>* *host_has_profile_pic*
>* *host_identity_verified*
>* *host_is_superhost*
>* *is_location_exact*
>* *instant_bookable*
>* *require_guest_profile_picture*
>* *require_guest_phone_verification*
><br>
>
>**to_drop:**<br><font size = '2'>(Columns to be dropped)<font/>
<br><br>
>**reason: little use:** <br>
>* *listing_url, scrape_id, last_scraped, experiences_offered, thumbnail_url,xl_picture_url, medium_url,*
>* *host_id, host_url, host_thumbnail_url, host_picture_url, host_total_listings_count, neighbourhood,*
>* *neighbourhood_group_cleansed, state, country_code, country, latitude, longitude,*
>* *has_availability, calendar_last_scraped, host_name, picture_url, space, first_review, *
><br><br>
>
>**reason: Nulls, text, only in Boston:** <br>
>* *access , interaction, house_rules*
><br><br>
>
>**reason> Nulls, 0 variability or extreme variability:** <br>
>* *square_feet* ------------- *90% Null boston 97% Null seatle* <br>
>* *weekly_price*-------------*75% Null boston 47% Null seatle* <br>
>* *monthly_price*------------*75% Null boston 60% Null seatle* <br>
>* *security_deposit*---------*65% Null boston 51% Null seatle* <br>
>* *notes*---------------------*55% Null boston 42% Null seatle* <br>
>* *jurisdiction_names*---------*100% Null in both* <br>
>* *license*--------------------*100% Null in both*
>* *required_license*-----------*100% Null in both* <br>
>* *street*---------------------*High variability* <br>
<font size = '3' >*Let's write anymore functions needed to carry on these suggested changes*<font/>
```
drop_cols = ['listing_url', 'scrape_id', 'last_scraped', 'experiences_offered', 'thumbnail_url','xl_picture_url',
'medium_url', 'host_id', 'host_url', 'host_thumbnail_url', 'host_picture_url', 'host_total_listings_count',
'neighbourhood', 'neighbourhood_group_cleansed','state', 'country_code', 'country', 'latitude', 'longitude',
'has_availability', 'calendar_last_scraped', 'host_name','square_feet',
'weekly_price', 'monthly_price', 'security_deposit', 'notes', 'jurisdiction_names', 'license', 'requires_license',
'street', 'picture_url', 'space','first_review', 'house_rules', 'access', 'interaction']
float_cols = ['cleaning_fee', 'host_response_rate','host_acceptance_rate','host_response_rate',
'host_acceptance_rate','extra_people','price']
len_text_cols = ['name', 'host_about', 'summary', 'description','neighborhood_overview', 'transit']
count_cols = ['amenities', 'host_verifications']
d_col = [ 'amenities']
part_col = ['maximum_nights']
bool_cols = ['host_has_profile_pic', 'host_identity_verified', 'host_is_superhost', 'is_location_exact',
'instant_bookable', 'require_guest_profile_picture' , 'require_guest_phone_verification' ]
day_cols = [ 'host_since', 'last_review']
###########################################################################################################################
def to_drop(df, drop_cols):
"""
INPUT
df -pandas dataframe
drop_cols -list of columns to drop
OUTPUT
df - a dataframe with columns of choice dropped
"""
for col in drop_cols:
if col in list(df.columns):
df = df.drop(col, axis = 1)
else:
continue
return df
#################################
def to_len_text(df, len_text_cols):
"""
INPUT
df -pandas dataframe
len_text_cols- list of columns to return the length of text of their values
OUTPUT
df - a dataframe with columns of choice transformed to len(values) instead of long text
"""
df_new = df.copy()
len_text = []
new_len_text_cols = []
for col in len_text_cols:
new_len_text_cols.append("len_"+col)
for i in df_new[col]:
#print(col,i)
try:
len_text.append(len(i))
except:
len_text.append(i)
#print('\n'*10)
df_new = df_new.drop(col, axis = 1)
len_text_col = pd.Series(len_text)
len_text_col = len_text_col.reset_index(drop = True)
#print(len_text_col)
df_new['len_'+col]= len_text_col
len_text = []
df_new[new_len_text_cols] = df_new[new_len_text_cols].fillna(0)
return df_new, new_len_text_cols
#########################
def to_parts(df, part_col):
"""
INPUT
df -pandas dataframe
part_col -list of columns to divide into "week or less" and "more than a week" depending on values
OUTPUT
df - a dataframe with columns of choice transformed to ranges of "week or less" and "more than a week"
"""
def to_apply(val):
if val <= 7:
val = '1 Week or less'
elif (val >7) and (val<=14):
val = '1 week to 2 weeks'
elif (val >14) and (val<=30):
val = '2 weeks to 1 month'
elif (val >30) and (val>=60):
val = '1 month to 2 months'
elif (val >60) and (val>=90):
val = '2 month to 3 months'
elif (val >90) and (val>=180):
val = '3 month to 6 months'
else:
val = 'More than 6 months'
return val
for part in part_col:
df[part]= df[part].apply(to_apply)
return df
############################
def to_count(df, count_cols):
"""
INPUT
df -pandas dataframe
count_cols -list of columns to count the string items within each value
OUTPUT
df - a dataframe with columns of choice transformed to a count of values
"""
def to_apply(val):
if "{" in val:
val = val.replace('}', "").replace('{', "").replace("'","" ).replace('"',"" ).replace("''", "").strip().split(',')
elif "[" in val:
val = val.replace('[',"" ).replace(']',"" ).replace("'","" ).strip().split(",")
return len(val)
for col in count_cols:
df['count_'+col]= df[col].apply(to_apply)
return df
########################
def to_items(df, d_col):
"""
INPUT
df -pandas dataframe
d_col -list of columns to divide the values to clean list of items
OUTPUT
df - a dataframe with columns of choice cleaned and returns the values as lists
"""
def to_apply(val):
if "{" in val:
val = val.replace('}', "").replace('{', "").replace("'","" ).replace('"',"" ).replace("''", "").lower().split(',')
elif "[" in val:
val = val.replace('[',"" ).replace(']',"" ).replace("'","" ).lower().split(",")
return val
def to_apply1(val):
new_val = []
if val == 'None':
new_val.append(val)
for i in list(val):
if (i != "") and ('translation' not in i.lower()):
new_val.append(i.strip())
return new_val
def to_apply2(val):
if 'None' in val:
return ['none']
elif len((val)) == 0:
return ['none']
else:
return list(val)
for col in d_col:
df[col]= df[col].apply(to_apply)
df[col]= df[col].apply(to_apply1)
df[col]= df[col].apply(to_apply2)
return df
def items_counter(df, d_col):
"""
INPUT
df -pandas dataframe
count_col -list of columns to with lists as values to count
OUTPUT
all_strings - a dictionary with the count of every value every list within every series
"""
all_strings= {}
def to_apply(val):
for i in val:
if i in list(all_strings.keys()):
all_strings[i]+=1
else:
all_strings[i]=1
df[d_col].apply(to_apply)
return all_strings
###################################
def to_days(df, day_cols, na_date):
"""
INPUT
df -pandas dataframe
day_cols -list of columns to divide the values to clean list of items
OUTPUT
df - a dataframe with columns of choice cleaned and returns the values as lists
"""
#Since Boston lisitngs span from September'16 to september'17, we can impute using the month of march'16
#Since Seatle lisitngs span from January'16 to January'17, we can impute using the month of june'16
df = df.copy()
df[[day_cols[0], day_cols[1]]]=df[[day_cols[0], day_cols[1]]].apply(pd.to_datetime)
df = df.dropna(subset= [day_cols[0]], how ='any', axis = 0)
df[day_cols[1]] = df[day_cols[1]].fillna(pd.to_datetime(na_date))
df[day_cols[0]]= (df[day_cols[1]] - df[day_cols[0]]).apply(lambda x: round(x.value/(864*1e11)),2)
df= df.drop(day_cols[1], axis =1 )
df = df.reset_index(drop= True)
return df
###########################################################################################################################
def applier(df1,df2,drop = True, float_=True, len_text= True, count= True, items = True,
parts = True , count_items = True, bool_num = True, days = True):
"""
INPUT
df1,df2 - 2 pandas dataframes
drop,float_,len_text, count, parts, date_time - Boolean values that corresponds to previosuly defined functions
OUTPUT
df - a clean dataframe that has undergone previously defined functions according to the boolean prameters passed
"""
while drop:
df1 = to_drop(df1, drop_cols)
df2 =to_drop(df2, drop_cols)
break
while float_:
df1 =to_float(df1, float_cols)
df2 =to_float(df2, float_cols)
break
while len_text:
df1, nltc = to_len_text(df1, len_text_cols)
df2, nltc = to_len_text(df2, len_text_cols)
break
while parts:
df1 = to_parts(df1, part_col)
df2 = to_parts(df2, part_col)
break
while count:
df1 = to_count(df1, count_cols)
df2 = to_count(df2, count_cols)
df1 = df1.drop('host_verifications', axis =1 )
df2 = df2.drop('host_verifications', axis =1 )
break
while items:
df1 = to_items(df1, d_col)
df2 = to_items(df2, d_col)
break
while count_items:
b_amens_count = pd.Series(items_counter(df1,'amenities')).reset_index().rename(columns = {'index':'amenities', 0:'count'}).sort_values(by='count', ascending =False).reset_index(drop =True)
s_amens_count = pd.Series(items_counter(df2, 'amenities')).reset_index().rename(columns = {'index':'amenities', 0:'count'}).sort_values(by='count', ascending =False).reset_index(drop =True)
a_counts = [b_amens_count,s_amens_count]
break
while bool_num:
df1 = bool_nums(df1, bool_cols)
df2 = bool_nums(df2, bool_cols)
break
while days:
df1 = to_days(df1, day_cols, '2016-04-1')
df2 = to_days(df2, day_cols, '2016-06-1')
break
if count_items:
return df1, df2 ,a_counts
else:
return df1,df2
b_list_1, s_list_1, a_counts = applier(b_list, s_list)
```
<font size = '3' >*Amenities seems like a good indicator of price as a response variable so let's have it dummified*<font/>
<br>
<font size = '2.75' >**This function takes forever(6 mins),so, it's commented out and I use the resulted dataframes that were written to CSV files**<font/>
```
# %%time
# def to_dummy(df1,df2, col1, cols_ref1,cols_ref2):
# def construct(df,col, cols_ref):
# count = 0
# for val2 in df[col]:
# lister = []
# for val1 in cols_ref[col]:
# if val1 in val2:
# lister.append(1)
# else:
# lister.append(0)
# cols_ref = cols_ref.join(pd.Series(lister, name = count))
# count+=1
# cols_ref = cols_ref.drop('count', axis = 1).transpose()
# cols_ref.columns = list(cols_ref.iloc[0,:])
# return cols_ref
# b_amens_1 =construct(df1, col1,cols_ref1)
# s_amens_1 =construct(df2, col1,cols_ref2)
# b_amens_1 = b_amens_1.drop('none', axis = 1) #.drop(0,axis=0).reset_index(drop= True)
# b_amens_1 = b_amens_1.iloc[1:,:]
# b_amens_1.columns = ["{}_{}".format(col1,col) for col in b_amens_1.columns]
# s_amens_1 = s_amens_1.iloc[1:,:]
# s_amens_1 = s_amens_1.drop('none', axis = 1)
# s_amens_1.columns = ["{}_{}".format(col1,col) for col in s_amens_1.columns]
# b_dummies = b_amens_1.reset_index(drop =True)
# s_dummies = s_amens_1.reset_index(drop =True)
# df1 = df1.join(b_dummies)
# df2 = df2.join(s_dummies)
# df1 = df1.drop([col1], axis = 1)
# df2 = df2.drop([col1], axis = 1)
# return b_dummies, s_dummies, df1, df2
# b_d, s_d,b_list_d, s_list_d = to_dummy(b_list_1, s_list_1, 'amenities',
# b_a_counts, s_a_counts)
# b_list_d.to_csv('b_list_d.csv')
# s_list_d.to_csv('s_list_d.csv')
b_list_d = pd.read_csv('b_list_d.csv', index_col = 0)
s_list_d = pd.read_csv('s_list_d.csv', index_col = 0)
```
<font size = '3' >*Check the nulls again*<font/><br>
```
df1= (b_list_d.isnull().sum()[b_list_d.isnull().sum()>0]/b_list_d.shape[0]*100).reset_index().rename(columns ={'index':'col_name',0:'nulls_proportion'})
df2 = (s_list_d.isnull().sum()[s_list_d.isnull().sum()>0]/s_list_d.shape[0]*100).reset_index().rename(columns ={'index':'col_name',0:'nulls_proportion'})
display_side_by_side(df1,df2, titles =['b_list_d_Nulls','s_list_d_Nulls' ])
```
_______________________________________________________________________________________________________________________
### Comments:
[Boston & Seatle Listings]
- Boston listings size : `3585`, `95`/ Seatle listings size : `3818`, `92`
- Number of Non-null cols in Boston listings: `51`, around half
- Number of Non-null cols in Seatle listings: `47`, around half<br>
- I wrote a series of functions that commenced some basic cleaning to ease analysis, with the option to switch off any of them depending on the future requirements of the analyses, some of what was done:
>- Columns with relatively high number nulls or that have little to no forseeable use were removed
>- Took the charachter length of the values in some of the cols with long text entries and many unique values, possibly the length of some fields maybe correlated somewhat with price.
>- Columns with dates are transformed into Datetime, numerical values that were in text to floats
>- Columns `amenities`and `host_verifications`were taken as counts, `amenities` was then dummified, for its seeming importance.
>- `maximum_nights`column seems to lack some integrity so I divided it into time periods
> Columns with t and f strings were converted into binary data.
>- Difference between `host_since`and `last_review` was computed in days to `host_since`<br>
>- All columns with only 't' or 'f' values were transformed in to binary values.
- **After the basic cleaning and the dummification of `amenities`:** <br>
~Boston listings size : `3585`, `98`/ Seatle listings size : `3818`, `98`. <br>
~There are still nulls to deal with in case of modeling, but that depends on the requirements of each question.
_______________________________________________________________________________________________________________________
### Step 1: Continue -
> **Boston & Seatle Reviews**
```
#b_rev.head(3)
s_rev.head(3)
```
<font size = '3' >*Check the sizes of cols & rows & check Nulls*<font/>
```
print_side_by_side("Boston reviews size:", b_rev.shape,"Seatle reviews size:", s_rev.shape)
print_side_by_side("No. of unique listing ids:", b_rev.listing_id.unique().size,"No. of unique listing ids:", s_rev.listing_id.unique().size)
print_side_by_side("Number of Non-null cols in Boston Reviews:", np.sum(b_rev.isnull().sum()==0),
"Number of Non-null cols in Seatle Reviews:", np.sum(s_rev.isnull().sum()==0))
print_side_by_side("Null cols % in Boston:", (b_rev.isnull().sum()[b_rev.isnull().sum()>0]/b_rev.shape[0]*100).to_string(),
"Null cols % in Seatle:", (s_rev.isnull().sum()[s_rev.isnull().sum()>0]/s_rev.shape[0]*100).to_string())
print_side_by_side("Null cols no. in Boston:",(b_rev.isnull().sum()[b_rev.isnull().sum()>0]).to_string(),
"Null cols no. in Seatle:", (s_rev.isnull().sum()[s_rev.isnull().sum()>0]).to_string())
print('\n')
```
<font size = '3' >**To extract analytical insights from the reviews entries, they ought to be transformed from text to numerical scores, to do so I will follow some steps:**<font/>
<font size = '3' >*1) Find all the words -excluding any non alphanumeric charachters - in each Dataset*<font/><br>
<font size = '2' >**As the function takes 4 mins to execute, I commented it out and passed the resulted word lists as dfs to CSV files that were added to the project instead of running it in the notebook again.**<font/>
```
#%%time
# def get_words(df, col):
# """
# INPUT
# df -pandas dataframe
# col -column of which the values are text
#
# OUTPUT
# df - a dataframe with a single colum of all the words
# """
# all_strings = []
# for val in df[col]:
# try:
# val_strings = [''.join(filter(str.isalnum, i.lower())) for i in val.split() if len(i)>3]
# except:
# continue
# for word in val_strings:
# if word not in all_strings:
# all_strings.append(word)
# val_strings = []
# return pd.Series(all_strings).to_frame().reset_index(drop = True).rename(columns = {0:'words'})
# boston_words = get_words(b_rev, 'comments')
# seatle_words = get_words(s_rev, 'comments')
# boston_words.to_csv('boston_words.csv')
# seatle_words.to_csv('seatle_words.csv')
boston_words = pd.read_csv('drafts/boston_words.csv', index_col= 0)
seatle_words = pd.read_csv('drafts/seatle_words.csv', index_col= 0)
print("Boston words no.: ", boston_words.shape[0])
print("Seatle words no.: ", seatle_words.shape[0])
display_side_by_side(boston_words.head(5), seatle_words.head(5), titles = [ 'Boston', 'Seatle'])
```
<font size = '3' >*2) Read in positive and negative english word lists that are used for sentiment analysis*<font/>
### Citation:
* Using this resource https://www.cs.uic.edu/~liub/FBS/sentiment-analysis.html#lexicon I downloaded a list of words with positive and negative connotations used for sentiment analysis
* *Based on the book*:
> Sentiment Analysis and Opinion Mining (Introduction and Survey), Morgan & Claypool, May 2012.
```
positive_words = pd.read_csv('drafts/positive-words.txt', sep = '\t',encoding="ISO-8859-1")
negative_words = pd.read_csv('drafts/negative-words.txt', sep = '\t',encoding="ISO-8859-1")
positive_words = positive_words.iloc[29:,:].reset_index(drop = True).rename(columns = {';;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;':'words'})
negative_words = negative_words.iloc[31:,:].reset_index(drop = True).rename(columns = {';;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;':'words'})
b_pos = np.intersect1d(np.array(boston_words['words'].astype(str)), np.array(positive_words['words']),assume_unique=True)
b_neg = np.intersect1d(np.array(boston_words['words'].astype(str)), np.array(negative_words['words']),assume_unique=True)
s_pos = np.intersect1d(np.array(seatle_words['words'].astype(str)), np.array(positive_words['words']),assume_unique=True)
s_neg = np.intersect1d(np.array(seatle_words['words'].astype(str)), np.array(negative_words['words']),assume_unique=True)
print_side_by_side('Positive words count: ', positive_words.shape[0]
,'Negative words count: ', negative_words.shape[0])
print_side_by_side("No. of positive words in Boston Reviews: ", len(b_pos)
,"No. of negative words in Boston Reviews: ", len(b_neg))
print_side_by_side("No. of positive words in Seatle Reviews: ", len(s_pos)
,"No. of negative words in Seatle Reviews: ", len(s_neg))
print('\n')
```
<font size = '3' >*3) Let's translate the reviews from other languages to English*<font/>
<br>
<font size='3'>*Let's start with dropping the nulls, check the language of the reviews using `langdetect`, prepare the non english `comments` to be translated*<font/>
```
##Dependency googletrans-4.0.0rc1
##langdetect
# b_rev = b_rev.dropna(subset=['comments'], how = 'any', axis = 0)
# s_rev = s_rev.dropna(subset=['comments'], how = 'any', axis = 0)
# %%time
# b_rev_t = b_rev.copy()
# s_rev_t = s_rev.copy()
# from langdetect import detect
# def lang_check(val):
# try:
# return detect(val)
# except:
# return val
# b_rev_t['review_lang']=b_rev['comments'].apply(lang_check)
# s_rev_t['review_lang']=s_rev['comments'].apply(lang_check)
# b_rev_t.to_csv('b_rev_t.csv')
# s_rev_t.to_csv('s_rev_t.csv')
# b_rev_t = pd.read_csv('b_rev_t.csv', index_col = 0)
#s_rev_t = pd.read_csv('s_rev_t.csv', index_col = 0)
# print('Proportion of non English reviews in Boston: ' ,b_rev_t[b_rev_t['review_lang']!= 'en'].shape[0]/b_rev_t.shape[0])
# print('Proportion of non English reviews in Seattle: ',s_rev_t[s_rev_t['review_lang']!= 'en'].shape[0]/s_rev_t.shape[0])
print(f"""Proportion of non English reviews in Boston: 0.05436662660138958
Proportion of non English reviews in Seattle: 0.012424703233487757""")
# b_to_trans =b_rev_t[b_rev_t['review_lang']!= 'en']
# s_to_trans =s_rev_t[s_rev_t['review_lang']!= 'en']
# b_to_trans['comments'] = b_to_trans['comments'].map(lambda val : str([re.sub(r"[^a-zA-Z0-9]+", '. ', k) for k in val.split("\n")]).replace('['," ").replace(']',"").replace("'",""))
# s_to_trans['comments'] = s_to_trans['comments'].map(lambda val : str([re.sub(r"[^a-zA-Z0-9]+", '. ', k) for k in val.split("\n")]).replace('['," ").replace(']',"").replace("'",""))
```
<font size='3'>*Since googletrans library is extremely unstable, I break down the non-English reviews in Boston into 4 dataframes*<font/>
```
# def trans_slicer(df,df1 = 0,df2 = 0,df3 = 0, df4 = 0):
# dfs=[]
# for i in [df1,df2,df3,df4]:
# i = df[0:1000]
# df = df.drop(index = i.index.values,axis = 0).reset_index(drop= True)
# dfs.append(i.reset_index(drop =True))
# # df = df.drop(index = range(0,df.shape[0],1),axis = 0).reset_index(drop= True)
# return dfs
# df1, df2, df3, df4 = trans_slicer(b_to_trans)
# %%time
# import re
# import time
# import googletrans
# import httpx
# from googletrans import Translator
# timeout = httpx.Timeout(10) # 5 seconds timeout
# translator = Translator(timeout=timeout)
# def text_trans(val):
# vals = translator.translate(val, dest='en').text
# time.sleep(10)
# return vals
# ############################################################
# df1['t_comments'] = df2['comments'].apply(text_trans)
# df1.to_csv('df2.csv')
# df2['t_comments'] = df2['comments'].apply(text_trans)
# df2.to_csv('df2.csv')
# df3['t_comments'] = df3['comments'].apply(text_trans)
# df3.to_csv('df3.csv')
# df4['t_comments'] = df4['comments'].apply(text_trans)
# df4.to_csv('df4.csv')
# #4###########################################################
# s_to_trans['t_comments'] = s_to_trans['comments'].apply(text_trans)
# s_to_trans.to_csv('s_translate.csv')
# dfs = df1.append(df2)
# dfs = dfs.append(df3)
# dfs = dfs.append(df4)
# dfs.index = b_to_trans.index
# b_to_trans = dfs
# b_to_trans['comments'] = b_to_trans['t_comments']
# b_to_trans = b_to_trans.drop(columns =['t_comments'],axis = 1)
#b_rev_t = b_rev_t.drop(index =b_to_trans.index,axis = 0)
#b_rev_t = b_rev_t.append(b_to_trans)
#b_rev_t = b_rev_t.sort_index(axis = 0).reset_index(drop= True)
# b_rev_t['comments'] = b_rev_t['comments'].apply(lambda x: x.replace('.',' '))
# b_rev_t.to_csv('b_rev_translated.csv')
# s_to_trans['comments'] = s_to_trans['t_comments']
# s_to_trans = s_to_trans.drop(columns =['t_comments'],axis = 1)
# s_rev_t = s_rev_t.drop(index =s_to_trans.index,axis = 0)
# s_rev_t = s_rev_t.append(s_to_trans)
# s_rev_t = s_rev_t.sort_index(axis = 0).reset_index(drop= True)
# s_rev_t['comments'] = s_rev_t['comments'].apply(lambda x: x.replace('.',' '))
# s_rev_t.to_csv('s_rev_translated.csv')
```
<font size='3'>*Since googletrans takes around 3 hours to translate 1000 entries, that took some time, here are the resulted DataFrames*<font/>
```
b_rev_trans = pd.read_csv('b_rev_translated.csv', index_col =0)
s_rev_trans = pd.read_csv('s_rev_translated.csv', index_col =0)
```
<font size = '3' >*4) Add a scores column using the previous resource as a reference to evaulate the score of each review*<font/><br>
```
# %%time
# def create_scores(df,col, df_pos_array, df_neg_array):
# """
# INPUT
# df -pandas dataframe
# col -column with text reviews to be transformed in to positive and negative scores
# pos_array- array with reference positive words for the passed df
# neg_array- array with reference negative words for the passed df
# OUTPUT
# df - a dataframe with a score column containing positive and negative scores"
# """
# def get_score(val):
# val_strings = [''.join(filter(str.isalnum, i.lower())) for i in str(val).split() if len(i)>3]
# pos_score = len(np.intersect1d(np.array(val_strings).astype(object), df_pos_array, assume_unique =True))
# neg_score = len(np.intersect1d(np.array(val_strings).astype(object), df_neg_array, assume_unique =True))
# return pos_score - neg_score +1
# df['score']= df[col].apply(get_score)
# return df
# b_rev_score = create_scores(b_rev_trans, 'comments', b_pos, b_neg)
# s_rev_score = create_scores(s_rev_trans, 'comments', s_pos, s_neg)
# b_rev_score.to_csv('b_rev_score.csv')
# s_rev_score.to_csv('s_rev_score.csv')
```
<font size = '3' >*As this function takes a while as well, let's write the results into to csv files and read the frames again and then show some samples.*<font/>
```
b_rev_score = pd.read_csv('b_rev_score.csv', index_col = 0)
s_rev_score = pd.read_csv('s_rev_score.csv', index_col = 0)
sub_b_rev = b_rev_score.iloc[:,[5,6,7]]
sub_s_rev = s_rev_score.iloc[:,[5,6,7]]
display_side_by_side(sub_b_rev.head(3), sub_s_rev.head(3), titles= ['Boston Reviews', 'Seatle_reviews'])
```
_______________________________________________________________________________________________________________________
### Comments:
[Boston & Seatle Reviews]
- Boston reviews size : (68275, 6)
- Seatle reviews size : (84849, 6)
- Nulls are only in `comments`columns in both Datasets:
- Null percentage in Boston Reviews: 0.08%
- Null percentage in Seatle Reviews: 0.02%
- I added a score column to both tables to reflect positive or negative reviews numerically with the aid of an external resource.
_______________________________________________________________________________________________________________________
### Step 2: Formulating Questions
<font size = '3' >*After going through the data I think those questions would be of interest:*<font/>
### *Q: How can you compare the reviews in both cities ?*
### *Q: What aspects of a listing influences the price in both cities?*
### *Q: How can we predict the price?*
### *Q: How do prices vary through the year in both cities ? when is the season and off season in both cities?*
_______________________________________________________________________________________________________________________
### *Q: How can you compare the reviews in both cities ?*
<font size = '3' >*Let's attempt to statistically describe the reviews in both cities*<font/>
```
print_side_by_side(' Boston: ', ' Seattle: ', b = 0)
print_side_by_side(' Maximum score : ', b_rev_score.iloc[b_rev_score.score.idxmax()].score,
' Maximum Score : ', s_rev_score.iloc[s_rev_score.score.idxmax()].score)
print_side_by_side(' Minimum Score : ', b_rev_score.iloc[b_rev_score.score.idxmin()].score,
' Minimum Score : ', s_rev_score.iloc[s_rev_score.score.idxmin()].score)
print_side_by_side(' Most common score: ', b_rev_score['score'].mode().to_string(),
' Most common score: ', s_rev_score['score'].mode().to_string())
print_side_by_side(' Mean score: ', round(b_rev_score['score'].mean(),2)
,' Mean score: ', round(s_rev_score['score'].mean(),2))
print_side_by_side(' Median score: ',round( b_rev_score['score'].median(),2),
' Median score: ', s_rev_score['score'].median())
print_side_by_side(' Standard deviation: ', round(b_rev_score['score'].std(),2)
,' Standard deviation: ', round(s_rev_score['score'].std(),2))
# print_side_by_side(' Z score of -2: ', round(b_rev_score['score'].mean()-2*round(b_rev_score['score'].std(),2),1)
# ,' Z score of -2: ', round(s_rev_score['score'].mean()-2*round(s_rev_score['score'].std(),2)),1)
# print('Score: ', b_rev_score.iloc[b_rev_score.score.idxmax()].score)
# b_rev_score.iloc[b_rev_score.score.idxmax()].comments
plt.figure(figsize = (14,8))
plt.subplot(2,1,1)
plt.title('Boston Reviews', fontsize = 18)
sns.kdeplot(b_rev_score.score, bw_adjust=2)
plt.axvline(x= b_rev_score['score'].mean(), color = 'orange', alpha = 0.6)
plt.axvline(x= b_rev_score['score'].median(), color = 'gray', alpha = 0.6)
plt.xlim(-15,30)
plt.xlabel('', fontsize = 14)
plt.ylabel('Count', fontsize = 14)
plt.legend(['Scores','mean', 'median'])
order = np.arange(-15,31,3)
plt.xticks(order,order, fontsize = 12)
plt.subplot(2,1,2)
plt.title('Seattle Reviews', fontsize = 18)
sns.kdeplot(s_rev_score.score, bw_adjust=2)
plt.axvline(x= s_rev_score['score'].mean(), color = 'orange', alpha = 0.6)
plt.axvline(x= s_rev_score['score'].median(), color = 'gray', alpha = 0.6)
plt.xlim(-15,30)
plt.xlabel('Scores', fontsize = 18)
plt.ylabel('Count', fontsize = 14)
plt.legend(['Scores','mean','median'])
plt.xticks(order,order, fontsize = 12)
plt.tight_layout();
```
>* <font size = '3'>**The scores clearly follow a normal distribution in both cities, with close standard deviations**</font>
>* <font size = '3'>**The mean score of Seattle (6.55) is a bit higher than Boston (5.84)**</font>
>* <font size = '3'>**The median score in both cities is a bit less than the mean which indicates a slight right skew**</font>
<font size = '3' >*Let'stake a look on the boxplots to have more robust insights*<font/>
```
plt.figure(figsize = (15,6))
plt.subplot(2,1,1)
plt.title('Boston Reviews', fontsize = 18)
sns.boxplot(data = b_rev_score, x = b_rev_score.score)
plt.axvline(x= b_rev_score['score'].mean(), color = 'orange', alpha = 0.6)
# plt.axvline(x= b_rev_score['score'].mean()+2*round(b_rev_score['score'].std(),2), color = 'red', alpha = 0.6)
# plt.axvline(x= b_rev_score['score'].mean()-2*round(b_rev_score['score'].std(),2), color = 'red', alpha = 0.6)
plt.xlim(-3,15)
plt.ylabel('Count', fontsize = 16)
order = np.arange(-3,15,1)
plt.xticks(order,order, fontsize = 13)
plt.xlabel('')
plt.subplot(2,1,2)
plt.title('Seattle Reviews', fontsize = 18)
sns.boxplot(data = s_rev_score, x = s_rev_score.score)
plt.axvline(x= s_rev_score['score'].mean(), color = 'orange', alpha = 0.6)
# plt.axvline(x= s_rev_score['score'].mean()+2*round(s_rev_score['score'].std(),2), color = 'red', alpha = 0.6)
# plt.axvline(x= s_rev_score['score'].mean()-2*round(s_rev_score['score'].std(),2), color = 'red', alpha = 0.6)
plt.xlim(-3,15)
plt.xlabel('Scores', fontsize = 18)
plt.ylabel('Count', fontsize = 16)
plt.xticks(order,order, fontsize = 13)
plt.tight_layout();
```
>* <font size = '3'>**50% of The scores in both cities lies between 4 and 8**</font>
>* <font size = '3'>**The IQR of the scores in both cities lies between -2 to 14**</font>
<font size = '3' >*Finally, what's the proportion of negative scores in both cities*<font/>
```
b_rev_score['grade']= b_rev_score['score'].apply(lambda x: 1 if x >0 else 0)
s_rev_score['grade']= s_rev_score['score'].apply(lambda x: 1 if x >0 else 0)
print_side_by_side('Boston: ', 'Seattle: ', b=0)
print_side_by_side('Negative reviews proportion: ',
round(b_rev_score['grade'][b_rev_score.grade == 0].count()/b_rev_score.shape[0],3),
'Negative reviews proportion: ',
round(s_rev_score['grade'][s_rev_score.grade == 0].count()/s_rev_score.shape[0],3))
```
><font size = '3'>**Further exploration:**</font>
<br>
>* <font size = '3'>**Use an NLP model be used to better classify the sentiment in the reviews**</font>
>* <font size = '3'>**Explore how to predict reviews using aspects of a listing**</font>
>* <font size = '3'>**Explore the relatioship between average price per meter in each city's estates/ temperature trends and reviews**</font>
_______________________________________________________________________________________________________________________
|
github_jupyter
|
# Appendix
Hao Lu 04/04/2020
In this notebook, we simulated EEG data with the method described in the paper by Bharadwaj and Shinn-Cunningham (2014) and analyzed the data with the toolbox proposed in the same paper.
The function was modifed so the values of thee variables within the function can be extracted and studied.
Reference:
Bharadwaj, H. M., & Shinn-Cunningham, B. G. (2014). Rapid acquisition of auditory subcortical steady state responses using multichannel recordings. Clinical Neurophysiology, 125(9), 1878-1888.
```
# import packages
import numpy as np
import matplotlib.pyplot as plt
import pickle
import random
from scipy import linalg
from anlffr import spectral,dpss
sfreq = 10000
random.seed(2020)
phase_list = [random.uniform(-np.pi,np.pi) for i in range(32)]
```
The phase of the signal from 32 channels were randomly sampled from a uniform distribution
```
plt.plot(phase_list)
plt.xlabel('Number of Channel')
plt.ylabel('Phase of signal')
```
The signal is defined as 100 Hz SSSR
```
signal = np.zeros((32,200,int(sfreq*0.2)))
xt = np.linspace(0,0.2,sfreq*0.2)
for iChannel in range(32):
for iTrial in range(200):
signal[iChannel,iTrial,:] = np.sin(xt*100*2*np.pi+phase_list[iChannel])
# plot first two channels to show the phase differences
plt.plot(xt,signal[0:2,0,:].transpose())
```
The signal to noise ratio (SNR) in the simulated data was set as -40 dB for all channels
```
std = 10**(40/20)*np.sqrt((signal**2).mean())
noise = np.random.normal(0,std,signal.shape)
```
The simulated data was analyzed through the code from the function anlffr.spectral.mtcplv
```
params = dict(Fs = sfreq, tapers = [1,1], fpass = [80, 120], itc = 0, pad = 1)
x=signal + noise
#codes from the dpss tool of anlffr to make sure the multitaper part is consistent
if(len(x.shape) == 3):
timedim = 2
trialdim = 1
ntrials = x.shape[trialdim]
nchans = x.shape[0]
nfft, f, fInd = spectral._get_freq_vector(x, params, timedim)
ntaps = params['tapers'][1]
TW = params['tapers'][0]
w, conc = dpss.dpss_windows(x.shape[timedim], TW, ntaps)
# the original version of mtcplv
plv = np.zeros((ntaps, len(fInd)))
for k, tap in enumerate(w):
xw = np.fft.rfft(tap * x, n=nfft, axis=timedim)
if params['itc']:
C = (xw.mean(axis=trialdim) /
(abs(xw).mean(axis=trialdim))).squeeze()
else:
C = (xw / abs(xw)).mean(axis=trialdim).squeeze()
for fi in np.arange(0, C.shape[1]):
Csd = np.outer(C[:, fi], C[:, fi].conj())
vals = linalg.eigh(Csd, eigvals_only=True)
plv[k, fi] = vals[-1] / nchans
# Average over tapers and squeeze to pretty shapes
plv = (plv.mean(axis=0)).squeeze()
plv = plv[fInd]
```
The mtcplv did capture the 100 Hz component
```
plt.plot(f,plv)
plt.xlabel('frequency')
plt.ylabel('output of mtcPLV')
```
However, the output of mtcplv perfectly overlaps with the average of squared single-channel PLV stored in matrix C
```
plt.plot(f,abs(C**2).mean(0)[fInd], label='average of square', alpha=0.5)
plt.plot(f,plv,label = 'mtcplv', alpha = 0.5)
plt.plot(f,abs(C**2).mean(0)[fInd] - plv, label='difference')
plt.legend()
plt.xlabel('frequency')
plt.ylabel('PLV')
```
We then check the eigen value decomposition around the 100 Hz peak and there is only one non-zero eigen value as expected
```
fi = np.argmax(plv)+np.argwhere(fInd==True).min()
Csd = np.outer(C[:, fi], C[:, fi].conj())
vals = linalg.eigh(Csd, eigvals_only=True)
plt.bar(np.arange(32),vals[::-1])
plt.xlabel('Principle Components')
plt.ylabel('Eigen Values')
```
|
github_jupyter
|
# Statistics
## Introduction
In this chapter, you'll learn about how to do statistics with code. We already saw some statistics in the chapter on probability and random processes: here we'll focus on computing basic statistics and using statistical tests. We'll make use of the excellent [*pingouin*](https://pingouin-stats.org/index.html) statistics package and its documentation for many of the examples and methods in this chapter {cite}`vallat2018pingouin`. This chapter also draws on Open Intro Statistics {cite}`diez2012openintro`.
### Notation and basic definitions
Greek letters, like $\beta$, are the truth and represent parameters. Modified Greek letters are an estimate of the truth, for example $\hat{\beta}$. Sometimes Greek letters will stand in for vectors of parameters. Most of the time, upper case Latin characters such as $X$ will represent random variables (which could have more than one dimension). Lower case letters from the Latin alphabet denote realised data, for instance $x$ (which again could be multi-dimensional). Modified Latin alphabet letters denote computations performed on data, for instance $\bar{x} = \frac{1}{n} \displaystyle\sum_{i} x_i$ where $n$ is number of samples. Parameters are given following a vertical bar, for example if $f(x|\mu, \sigma)$ is a probability density function, the vertical line indicates that its parameters are $\mu$ and $\sigma$. The set of distributions with densities $f_\theta(x)$, $\theta \in \Theta$ is called a parametric family, eg there is a family of different distributions that are parametrised by $\theta$.
A **statistic** $T(x)$ is a function of the data $x=(x_1, \dots, x_n)$.
An **estimator** of a parameter $\theta$ is a function $T=T(x)$ which is used to estimate $\theta$ based on observations of data. $T$ is an unbiased estimator if $\mathbb{E}(T) = \theta$.
If $X$ has PDF $f(x|\theta)$ then, given the observed value $x$ of $X$, the **likelihood** of $\theta$ is defined by $\text{lik}(\theta) = f(x | \theta)$. For independent and identically distributed observed values, then $\text{lik}(\theta) = f(x_1, \dots, x_n| \theta) = \Pi_{i=1}^n f(x_i | \theta)$. The $\hat{\theta}$ such that this function attains its maximum value is the **maximum likelihood estimator (MLE)** of $\theta$.
Given an MLE $\hat{\theta}$ of $\theta$, $\hat{\theta}$ is said to be **consistent** if $\mathbb{P}(\hat{\theta} - \theta > \epsilon) \rightarrow 0$ as $n\rightarrow \infty$.
An estimator *W* is **efficient** relative to another estimator $V$ if $\text{Var}(W) < \text{Var}(V)$.
Let $\alpha$ be the 'significance level' of a test statistic $T$.
Let $\gamma(X)$ and $\delta(X)$ be two statistics satisfying $\gamma(X) < \delta(X)$ for all $X$. If on observing $X = x$, the inference can be made that $\gamma(x) \leq \theta \leq \delta(x)$. Then $[\delta(x), \gamma(x)]$ is an **interval estimate** and $[\delta(X), \gamma(X)]$ is an **interval estimator**. The random interval (random because the *endpoints* are random variables) $[\delta(X), \gamma(X)]$ is called a $100\cdot\alpha \%$ **confidence interval** for $\theta$. Of course, there is a true $\theta$, so either it is in this interval or it is not. But if the confidence interval was constructed many times over using samples, $\theta$ would be contained within it $100\cdot\alpha \%$ of the times.
A **hypothesis test** is a conjecture about the distribution of one or more random variables, and a test of a hypothesis is a procedure for deciding whether or not to reject that conjecture. The **null hypothesis**, $H_0$, is only ever conservatively rejected and represents the default positiion. The **alternative hypothesis**, $H_1$, is the conclusion contrary to this.
A type I error occurs when $H_0$ is rejected when it is true, ie when a *true* null hypothesis is rejected. Mistakenly failing to reject a false null hypothesis is called a type II error.
In the most simple situations, the upper bound on the probability of a type I error is called the size or **significance level** of the *test*. The **p-value** of a random variable $X$ is the smallest value of the significance level (denoted $\alpha$) for which $H_0$ would be rejected on the basis of seeing $x$. The p-value is sometimes called the significance level of $X$. The probability that a test will reject the null is called the power of the test. The probability of a type II error is equal to 1 minus the power of the test.
Recall that there are two types of statistics out there: parametrised, eg by $\theta$, and non-parametrised. The latter are often distribution free (ie don't involve a PDF) or don't require parameters to be specified.
### Imports
First we need to import the packages we'll be using
```
import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
import pandas as pd
import pingouin as pg
import statsmodels.formula.api as smf
from numpy.random import Generator, PCG64
# Set seed for random numbers
seed_for_prng = 78557
prng = Generator(PCG64(seed_for_prng))
```
## Basic statistics
Let's start with computing the simplest statistics you can think of using some synthetic data. Many of the functions have lots of extra options that we won't explore here (like weights or normalisation); remember that you can see these using the `help()` method.
We'll generate a vector with 100 entries:
```
data = np.array(range(100))
data
from myst_nb import glue
import sympy
import warnings
warnings.filterwarnings("ignore")
dict_fns = {'mean': np.mean(data),
'std': np.std(data),
'mode': stats.mode([0, 1, 2, 3, 3, 3, 5])[0][0],
'median': np.median(data)}
for name, eval_fn in dict_fns.items():
glue(name, f'{eval_fn:.1f}')
# Set max rows displayed for readability
pd.set_option('display.max_rows', 6)
# Plot settings
plt.style.use('plot_style.txt')
```
Okay, let's see how some basic statistics are computed. The mean is `np.mean(data)=` {glue:}`mean`, the standard deviation is `np.std(data)=` {glue:}`std`, and the median is given by `np.median(data)= `{glue:}`median`. The mode is given by `stats.mode([0, 1, 2, 3, 3, 3, 5])[0]=` {glue:}`mode` (access the counts using `stats.mode(...)[1]`).
Less famous quantiles than the median are given by, for example for $q=0.25$,
```
np.quantile(data, 0.25)
```
As with **pandas**, **numpy** and **scipy** work on scalars, vectors, matrices, and tensors: you just need to specify the axis that you'd like to apply a function to:
```
data = np.fromfunction(lambda i, j: i + j, (3, 6), dtype=int)
data
np.mean(data, axis=0)
```
Remember that, for discrete data points, the $k$th (unnormalised) moment is
$$
\hat{m}_k = \frac{1}{n}\displaystyle\sum_{i=1}^{n} \left(x_i - \bar{x}\right)^k
$$
To compute this use scipy's `stats.moment(a, moment=1)`. For instance for the kurtosis ($k=4$), it's
```
stats.moment(data, moment=4, axis=1)
```
Covariances are found using `np.cov`.
```
np.cov(np.array([[0, 1, 2], [2, 1, 0]]))
```
Note that, as expected, the $C_{01}$ term is -1 as the vectors are anti-correlated.
## Parametric tests
Reminder: parametric tests assume that data are effectively drawn a probability distribution that can be described with fixed parameters.
### One-sample t-test
The one-sample t-test tells us whether a given parameter for the mean, i.e. a suspected $\mu$, is likely to be consistent with the sample mean. The null hypothesis is that $\mu = \bar{x}$. Let's see an example using the default `tail='two-sided'` option. Imagine we have data on the number of hours people spend working each day and we want to test the (alternative) hypothesis that $\bar{x}$ is not $\mu=$8 hours:
```
x = [8.5, 5.4, 6.8, 9.6, 4.2, 7.2, 8.8, 8.1]
pg.ttest(x, 8).round(2)
```
(The returned object is a **pandas** dataframe.) We only have 8 data points, and so that is a great big confidence interval! It's worth remembering what a t-statistic and t-test really are. In this case, the statistic that is constructed to test whether the sample mean is different from a known parameter $\mu$ is
$$
T = \frac{\sqrt{n}(\bar{x}-\mu)}{\hat{\sigma}} \thicksim t_{n-1}
$$
where $t_{n-1}$ is the student's t-distribution and $n-1$ is the number of degrees of freedom. The $100\cdot(1-\alpha)\%$ test interval in this case is given by
$$
1 - \alpha = \mathbb{P}\left(-t_{n-1, \alpha/2} \leq \frac{\sqrt{n}(\bar{x} - \mu)}{\hat{\sigma}} \leq t_{n-1,\alpha/2}\right)
$$
where we define $t_{n-1, \alpha/2}$ such that $\mathbb{P}(T > t_{n-1, \alpha/2}) = \alpha/2$. For $\alpha=0.05$, implying confidence intervals of 95%, this looks like:
```
import scipy.stats as st
def plot_t_stat(x, mu):
T = np.linspace(-7, 7, 500)
pdf_vals = st.t.pdf(T, len(x)-1)
sigma_hat = np.sqrt(np.sum( (x-np.mean(x))**2)/(len(x)-1))
actual_T_stat = (np.sqrt(len(x))*(np.mean(x) - mu))/sigma_hat
alpha = 0.05
T_alpha_over_2 = st.t.ppf(1.0-alpha/2, len(x)-1)
interval_T = T[((T>-T_alpha_over_2) & (T<T_alpha_over_2))]
interval_y = pdf_vals[((T>-T_alpha_over_2) & (T<T_alpha_over_2))]
fig, ax = plt.subplots()
ax.plot(T, pdf_vals, label=f'Student t: dof={len(x)-1}', zorder=2)
ax.fill_between(interval_T, 0, interval_y, alpha=0.2, label=r'95% interval', zorder=1)
ax.plot(actual_T_stat, st.t.pdf(actual_T_stat, len(x)-1), 'bo', ms=15, label=r'$\sqrt{n}(\bar{x} - \mu)/\hat{\sigma}}$',
color='orchid', zorder=4)
ax.vlines(actual_T_stat, 0, st.t.pdf(actual_T_stat, len(x)-1), color='orchid', zorder=3)
ax.set_xlabel('Value of statistic T')
ax.set_ylabel('PDF')
ax.set_xlim(-7, 7)
ax.set_ylim(0., 0.4)
ax.legend(frameon=False)
plt.show()
mu = 8
plot_t_stat(x, mu)
```
In this case, we would reject the alternative hypothesis. You can see why from the plot; the test statistic we have constructed lies within the interval where we cannot reject the null hypothesis. $\bar{x}-\mu$ is close enough to zero to give us cause for concern. (You can also see from the plot why this is a two-tailed test: we don't care if $\bar{x}$ is greater or less than $\mu$, just that it's different--and so the test statistic could appear in either tail of the distribution for us to accept $H_1$.)
We accept the null here, but about if there were many more data points? Let's try adding some generated data (pretend it is from making extra observations).
```
# 'Observe' extra data
extra_data = prng.uniform(5.5, 8.5, size=(30))
# Add it in to existing vector
x_prime = np.concatenate((np.array(x), extra_data), axis=None)
# Run t-test
pg.ttest(x_prime, 8).round(2)
```
Okay, what happened? Our extra observations have seen the confidence interval shrink considerably, and the p-value is effectively 0. There's a large negative t-statistic too. Unsurprisingly, as we chose a uniform distribution that only just included 8 but was centered on $(8-4.5)/2$ *and* we had more points, the test now rejects the null hypothesis that $\mu=8$ . Because the alternative hypothesis is just $\mu\neq8$, and these tests are conservative, we haven't got an estimate of what the mean actually is; we just know that our test rejects that it's $8$.
We can see this in a new version of the chart that uses the extra data:
```
plot_t_stat(x_prime, mu)
```
Now our test statistic is safely outside the interval.
#### Connection to linear regression
Note that testing if $\mu\neq0$ is equivalent to having the alternative hypothesis that a single, non-zero scalar value is a good expected value for $x$, i.e. that $\mathbb{E}(x) \neq 0$. Which may sound familiar if you've run **linear regression** and, indeed, this t-test has an equivalent linear model! It's just regressing $X$ on a constant--a single, non-zero scalar value. In general, t-tests appear in linear regression to test whether any coefficient $\beta \neq 0$.
We can see this connection by running a hypothesis test of whether the sample mean is not zero. Note the confidence interval, t-statistic, and p-value.
```
pg.ttest(x, 0).round(3)
```
And, as an alternative, regressing x on a constant, again noting the interval, t-stat, and p-value:
```
import statsmodels.formula.api as smf
df = pd.DataFrame(x, columns=['x'])
res = smf.ols(formula='x ~ 1', data=df).fit()
# Show only the info relevant to the intercept (there are no other coefficients)
print(res.summary().tables[1])
```
Many tests have an equivalent linear model.
#### Other information provided by **Pingouin** tests
We've covered the degrees of freedom, the T statistic, the p-value, and the confidence interval. So what's all that other gunk in our t-test? Cohen's d is a measure of whether the difference being measured in our test is large or not (this is important; you can have statistically significant differences that are so small as to be inconsequential). Cohen suggested that $d = 0.2$ be considered a 'small' effect size, 0.5 represents a 'medium' effect size and 0.8 a 'large' effect size. BF10 represents the Bayes factor, the ratio (given the data) of the likelihood of the alternative hypothesis relative to the null hypothesis. Values greater than unity therefore favour the alternative hypothesis. Finally, power is the achieved power of the test, which is $1 - \mathbb{P}(\text{type II error})$. A common default to have in mind is a power greater than 0.8.
### Two-sample t-test
The two-sample t-test is used to determine if two population means are equal (with the null being that they *are* equal). Let's look at an example with synthetic data of equal length, which means we can use the *paired* version of this. We'll imagine we are looking at an intervention with a pre- and post- dataset.
```
pre = [5.5, 2.4, 6.8, 9.6, 4.2, 5.9]
post = [6.4, 3.4, 6.4, 11., 4.8, 6.2]
pg.ttest(pre, post, paired=True, tail='two-sided').round(2)
```
In this case, we cannot reject the null hypothesis that the means are the same pre- and post-intervention.
### Pearson correlation
The Pearson correlation coefficient measures the linear relationship between two datasets. Strictly speaking, it requires that each dataset be normally distributed.
```
mean, cov = [4, 6], [(1, .5), (.5, 1)]
x, y = prng.multivariate_normal(mean, cov, 30).T
# Compute Pearson correlation
pg.corr(x, y).round(3)
```
### Welch's t-test
In the case where you have two samples with unequal variances (or, really, unequal sample sizes too), Welch's t-test is appropriate. With `correction='true'`, it assumes that variances are not equal.
```
x = prng.normal(loc=7, size=20)
y = prng.normal(loc=6.5, size=15)
pg.ttest(x, y, correction='true')
```
### One-way ANOVA
Analysis of variance (ANOVA) is a technique for testing hypotheses about means, for example testing the equality of the means of $k>2$ groups. The model would be
$$
X_{ij} = \mu_i + \epsilon_{ij} \quad j=1, \dots, n_i \quad i=1, \dots, k.
$$
so that the $i$th group has $n_i$ observations. The null hypothesis of one-way ANOVA is that $H_0: \mu_1 = \mu_2 = \dots = \mu_k$, with the alternative hypothesis that this is *not* true.
```
df = pg.read_dataset('mixed_anova')
df.head()
# Run the ANOVA
pg.anova(data=df, dv='Scores', between='Group', detailed=True)
```
### Multiple pairwise t-tests
There's a problem with running multiple t-tests: if you run enough of them, something is bound to come up as significant! As such, some *post-hoc* adjustments exist that correct for the fact that multiple tests are occurring simultaneously. In the example below, multiple pairwise comparisons are made between the scores by time group. There is a corrected p-value, `p-corr`, computed using the Benjamini/Hochberg FDR correction.
```
pg.pairwise_ttests(data=df, dv='Scores', within='Time', subject='Subject',
parametric=True, padjust='fdr_bh', effsize='hedges').round(3)
```
### One-way ANCOVA
Analysis of covariance (ANCOVA) is a general linear model which blends ANOVA and regression. ANCOVA evaluates whether the means of a dependent variable (dv) are equal across levels of a categorical independent variable (between) often called a treatment, while statistically controlling for the effects of other continuous variables that are not of primary interest, known as covariates or nuisance variables (covar).
```
df = pg.read_dataset('ancova')
df.head()
pg.ancova(data=df, dv='Scores', covar='Income', between='Method')
```
### Power calculations
Often, it's quite useful to know what sample size is needed to avoid certain types of testing errors. **Pingouin** offers ways to compute effect sizes and test powers to help with these questions.
As an example, let's assume we have a new drug (`x`) and an old drug (`y`) that are both intended to reduce blood pressure. The standard deviation of the reduction in blood pressure of those receiving the old drug is 12 units. The null hypothesis is that the new drug is no more effective than the new drug. But it will only be worth switching production to the new drug if it reduces blood pressure by more than 3 units versus the old drug. In this case, the effect size of interest is 3 units.
Let's assume for a moment that the true difference is 3 units and we want to perform a test with $\alpha=0.05$. The problem is that, for small differences in the effect, the distribution of effects under the null and the distribution of effects under the alternative have a great deal of overlap. So the chances of making a Type II error - accepting the null hypothesis when it is actually false - is quite high. Let's say we'd ideally have at most a 20% chance of making a Type II error: what sample size do we need?
We can compute this, but we need an extra piece of information first: a normalised version of the effect size called Cohen's $d$. We need to transform the difference in means to compute this. For independent samples, $d$ is:
$$ d = \frac{\overline{X} - \overline{Y}}{\sqrt{\frac{(n_{1} - 1)\sigma_{1}^{2} + (n_{2} - 1)\sigma_{2}^{2}}{n_1 + n_2 - 2}}}$$
(If you have real data samples, you can compute this using `pg.compute_effsize`.)
For this case, $d$ is $-3/12 = -1/4$ if we assume the standard deviations are the same across the old (`y`) and new (`x`) drugs. So we will plug that $d$ in and look at a range of possible sample sizes along with a standard value for $alpha$ of 0.05. In the below `tail=less` tests the alternative that `x` has a smaller mean than `y`.
```
cohen_d = -0.25 # Fixed effect size
sample_size_array = np.arange(1, 500, 50) # Incrementing sample size
# Compute the achieved power
pwr = pg.power_ttest(d=cohen_d, n=sample_size_array, alpha=0.05,
contrast='two-samples', tail='less')
fig, ax = plt.subplots()
ax.plot(sample_size_array, pwr, 'ko-.')
ax.axhline(0.8, color='r', ls=':')
ax.set_xlabel('Sample size')
ax.set_ylabel('Power (1 - type II error)')
ax.set_title('Achieved power of a T-test')
plt.show()
```
From this, we can see we need a sample size of at least 200 in order to have a power of 0.8.
The `pg.power_ttest` function takes any three of the four of `d`, `n`, `power`, and `alpha` (ie leave one of these out), and then returns what the missing parameter should be. We passed in `d`, `n`, and `alpha`, and so the `power` was returned.
## Non-parametric tests
Reminder: non-parametrics tests do not make any assumptions about the distribution from which data are drawn or that it can be described by fixed parameters.
### Wilcoxon Signed-rank Test
This tests the null hypothesis that two related paired samples come from the same distribution. It is the non-parametric equivalent of the t-test.
```
x = [20, 22, 19, 20, 22, 18, 24, 20, 19, 24, 26, 13]
y = [38, 37, 33, 29, 14, 12, 20, 22, 17, 25, 26, 16]
pg.wilcoxon(x, y, tail='two-sided').round(2)
```
### Mann-Whitney U Test (aka Wilcoxon rank-sum test)
The Mann–Whitney U test is a non-parametric test of the null hypothesis that it is equally likely that a randomly selected value from one sample will be less than or greater than a randomly selected value from a second sample. It is the non-parametric version of the two-sample T-test.
Like many non-parametric **pingouin** tests, it can take values of tail that are 'two-sided', 'one-sided', 'greater', or 'less'. Below, we ask if a randomly selected value from `x` is greater than one from `y`, with the null that it is not.
```
x = prng.uniform(low=0, high=1, size=20)
y = prng.uniform(low=0.2, high=1.2, size=20)
pg.mwu(x, y, tail='greater')
```
### Spearman Correlation
The Spearman correlation coefficient is the Pearson correlation coefficient between the rank variables, and does not assume normality of data.
```
mean, cov = [4, 6], [(1, .5), (.5, 1)]
x, y = prng.multivariate_normal(mean, cov, 30).T
pg.corr(x, y, method="spearman").round(2)
```
### Kruskal-Wallace
The Kruskal-Wallis H-test tests the null hypothesis that the population median of all of the groups are equal. It is a non-parametric version of ANOVA. The test works on 2 or more independent samples, which may have different sizes.
```
df = pg.read_dataset('anova')
df.head()
pg.kruskal(data=df, dv='Pain threshold', between='Hair color')
```
### The Chi-Squared Test
The chi-squared test is used to determine whether there is a significant difference between the expected frequencies and the observed frequencies in one or more categories. This test can be used to evaluate the quality of a categorical variable in a classification problem or to check the similarity between two categorical variables.
There are two conditions for a chi-squared test:
- Independence: Each case that contributes a count to the table must be independent of all the other cases in the table.
- Sample size or distribution: Each particular case (ie cell count) must have at least 5 expected cases.
Let's see an example from the **pingouin** docs: whether gender is a good predictor of heart disease. First, let's load the data and look at the gender split in total:
```
chi_data = pg.read_dataset('chi2_independence')
chi_data['sex'].value_counts(ascending=True)
```
If gender is *not* a predictor, we would expect a roughly similar split between those who have heart disease and those who do not. Let's look at the observerd versus the expected split once we categorise by gender and 'target' (heart disease or not).
```
expected, observed, stats = pg.chi2_independence(chi_data, x='sex', y='target')
observed - expected
```
So we have fewer in the 0, 0 and 1, 1 buckets than expected but more in the 0, 1 and 1, 0 buckets. Let's now see how the test interprets this:
```
stats.round(3)
```
From these, it is clear we can reject the null and therefore it seems like gender is a good predictor of heart disease.
### Shapiro-Wilk Test for Normality
Note that the null here is that the distribution *is* normal, so normality is only rejected when the p-value is sufficiently small.
```
x = prng.normal(size=20)
pg.normality(x)
```
The test can also be run on multiple variables in a dataframe:
```
df = pg.read_dataset('ancova')
pg.normality(df[['Scores', 'Income', 'BMI']], method='normaltest').round(3)
```
|
github_jupyter
|
```
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.pyplot import savefig
import cv2
np.set_printoptions(threshold=np.inf)
num_images = 3670
dataset = []
for i in range(1, num_images+1):
img = cv2.imread("color_images/color_" +str(i) +".jpg" )
dataset.append(np.array(img))
dataset_source = np.asarray(dataset)
print(dataset_source.shape)
dataset_tar = []
for i in range(1, num_images+1):
img = cv2.imread("gray_images/gray_" +str(i) +".jpg", 0)
dataset_tar.append(np.array(img))
dataset_target = np.asarray(dataset_tar)
print(dataset_target.shape)
dataset_target = dataset_target[:, :, :, np.newaxis]
def autoencoder(inputs): # Undercomplete Autoencoder
# Encoder
net = tf.layers.conv2d(inputs, 128, 2, activation = tf.nn.relu)
print(net.shape)
net = tf.layers.max_pooling2d(net, 2, 2, padding = 'same')
print(net.shape)
# Decoder
net = tf.image.resize_nearest_neighbor(net, tf.constant([129, 129]))
net = tf.layers.conv2d(net, 1, 2, activation = None, name = 'outputOfAuto')
print(net.shape)
return net
ae_inputs = tf.placeholder(tf.float32, (None, 128, 128, 3), name = 'inputToAuto')
ae_target = tf.placeholder(tf.float32, (None, 128, 128, 1))
ae_outputs = autoencoder(ae_inputs)
lr = 0.001
loss = tf.reduce_mean(tf.square(ae_outputs - ae_target))
train_op = tf.train.AdamOptimizer(learning_rate = lr).minimize(loss)
# Intialize the network
init = tf.global_variables_initializer()
```
#### If you don't want to train the network skip the cell righ below and dowload the pre-trained model. After downloading the pre-trained model run the cell below to the immediate below cell.
```
batch_size = 32
epoch_num = 50
saving_path = 'K:/autoencoder_color_to_gray/SavedModel/AutoencoderColorToGray.ckpt'
saver_ = tf.train.Saver(max_to_keep = 3)
batch_img = dataset_source[0:batch_size]
batch_out = dataset_target[0:batch_size]
num_batches = num_images//batch_size
sess = tf.Session()
sess.run(init)
for ep in range(epoch_num):
batch_size = 0
for batch_n in range(num_batches): # batches loop
_, c = sess.run([train_op, loss], feed_dict = {ae_inputs: batch_img, ae_target: batch_out})
print("Epoch: {} - cost = {:.5f}" .format((ep+1), c))
batch_img = dataset_source[batch_size: batch_size+32]
batch_out = dataset_target[batch_size: batch_size+32]
batch_size += 32
saver_.save(sess, saving_path, global_step = ep)
recon_img = sess.run([ae_outputs], feed_dict = {ae_inputs: batch_img})
sess.close()
saver = tf.train.Saver()
init = tf.global_variables_initializer()
sess = tf.Session()
sess.run(init)
saver.restore(sess, 'K:/autoencoder_color_to_gray/SavedModel/AutoencoderColorToGray.ckpt-49')
import glob as gl
filenames = gl.glob('flower_images/*.png')
test_data = []
for file in filenames[0:100]:
test_data.append(np.array(cv2.imread(file)))
test_dataset = np.asarray(test_data)
print(test_dataset.shape)
# Running the test data on the autoencoder
batch_imgs = test_dataset
gray_imgs = sess.run(ae_outputs, feed_dict = {ae_inputs: batch_imgs})
print(gray_imgs.shape)
for i in range(gray_imgs.shape[0]):
cv2.imwrite('gen_gray_images/gen_gray_' +str(i) +'.jpeg', gray_imgs[i])
```
|
github_jupyter
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.