text
stringlengths 2.5k
6.39M
| kind
stringclasses 3
values |
|---|---|
```
import sys
import json
sys.path.insert(0, "../")
print(sys.path)
import pymongo
#31470/5/1
import sys
import json
import cobrakbase
import cobrakbase.core.model
import cobra
import logging
#from cobra.core import Gene, Metabolite, Model, Reaction
#from pyeda import *
#from pyeda.inter import *
#from pyeda.boolalg import expr
import pandas as pd
fbamodel = None
data = None
with open('community_model.json', 'r') as fh:
data = json.loads(fh.read())
fbamodel = cobrakbase.core.KBaseFBAModel(data)
for r in data['modelreactions']:
if 'rxn0020_c0' in r['id']:
print(r)
for r in fbamodel.get_reactions():
r = fbamodel.get_reaction(r['id'])
o = b.convert_modelreaction(r)
if 'rxn0020_c0' in o.id:
print(o, r.id)
kbase_api = cobrakbase.KBaseAPI("64XQ7SABQILQWSEW3CQKZXJA63DXZBGH")
#ref = kbase_api.get_object_info_from_ref(fbamodel.data['genome_ref'])
modelseed = cobrakbase.modelseed.from_local('../../../../ModelSEEDDatabase')
for seed_id in modelseed.reactions:
seed_rxn = modelseed.get_seed_reaction(seed_id)
ec_numbers = set()
if 'Enzyme Class' in seed_rxn.ec_numbers:
for ec in seed_rxn.ec_numbers['Enzyme Class']:
if ec.startswith('EC-'):
ec_numbers.add(ec[3:])
else:
ec_numbers.add(ec)
def annotate_model_reactions_with_modelseed(model, modelseed):
for r in model.reactions:
seed_id = None
if 'seed.reaction' in r.annotation:
annotation = {}
seed_id = r.annotation['seed.reaction']
seed_rxn = modelseed.get_seed_reaction(seed_id)
if not seed_rxn == None:
1
else:
print('!', r.id)
print(seed_id)
break
return r
r= annotate_model_reactions_with_modelseed(model, modelseed)
r
r.annotation
b = cobrakbase.core.converters.KBaseFBAModelToCobraBuilder(fbamodel)
if 'genome_ref' in fbamodel.data:
logging.info(f"Annotating model with genome information: {fbamodel.data['genome_ref']}")
#ref = kbase_api.get_object_info_from_ref(fbamodel.data['genome_ref'])
#genome_data = kbase_api.get_object(ref.id, ref.ws)
#genome = self.dfu.get_objects(
# {'object_refs': [ret['data']['genome_ref']]})['data'][0]['data']
# #adding Genome to the Builder
# builder.with_genome(KBaseGenome(genome))
model = b.build()
print(cobrakbase.annotate_model_with_modelseed(model, modelseed))
model.summary()
model = cobra.io.read_sbml_model('../../../../data/sbml/saccharomyces.xml')
cobra.io.write_sbml_model
solution = model.optimize()
solution
o_data = kbase_dev.get_object('GCF_000005845.2.beta.fba', 'filipeliu:narrative_1556512034170')
fba = cobrakbase.core.KBaseFBA(o_data)
fba.data.keys('FBAReactionVariables')
with open('../../../../data/www/mpa19/flux.txt', 'w+') as f:
for o in fba.data['FBAReactionVariables']:
v = o['value']
rxn_id = o['modelreaction_ref'].split('/')[-1]
#print(rxn_id, v)
f.write("{},{}\n".format(rxn_id, v))
#model = cobra.io.read_sbml_model('/Users/fliu/Downloads/iML1515.kb.SBML/iML1515.kb.xml')
kbase = cobrakbase.KBaseAPI("YAFOCRSMRNDXZ7KMW7GCK5AC3SBNTEFD")
kbase_dev = cobrakbase.KBaseAPI("YAFOCRSMRNDXZ7KMW7GCK5AC3SBNTEFD", dev=True)
#12998
kbase.ws_client.ver.get_workspace_info({'id' : 23938})
kbase.ws_client.get_workspace_info({'id' : 12998})
ref_info = kbase.get_object_info_from_ref('12998/1/2')
print(ref_info.id, ref_info.workspace_id, ref_info.workspace_uid, ref_info.uid, ref_info)
a = kbase_dev.ws_client.get_workspace_info({'workspace' : 'NewKBaseModelTemplates'})
kbase_dev.list_objects('NewKBaseModelTemplates')
kmodel = kbase_dev.get_object('Escherichia_coli_K-12_MG1655_output', 'filipeliu:narrative_1564175222344')
kmodel.keys()
kmodel['genome_ref']
kmodel['template_ref'] = '50/1/2'
genome_ref = '31470/4/1'
for mr in kmodel['modelreactions']:
#print(mr)
for mrp in mr['modelReactionProteins']:
#print(modelReactionProtein)
for mrps in mrp['modelReactionProteinSubunits']:
for i in range(len(mrps['feature_refs'])):
a, b = mrps['feature_refs'][i].split('features')
#print(a, b)
mrps['feature_refs'][i] = kmodel['genome_ref'] + '/features' + b
#mrps['feature_refs'][i] = kmodel['genome_ref'] + f_block
#print(i, mrps['feature_refs'][i], f_block)
kbase_dev.save_object('Escherichia_coli_K-12_MG1655_output', 'filipeliu:narrative_1564175222344', 'KBaseFBA.FBAModel', kmodel)
kmodel['genome_ref']
kbase_dev.ws_client.get_object_info3({'objects' : [{'ref' : '31470/5/2'}]})
%run ../../../scripts/bios_utils.py
with open('aww.json', 'w') as f:
f.write(json.dumps(kmodel, indent=4, sort_keys=True))
kbase_dev.list_objects('filipeliu:narrative_1564175222344')
os = kbase.list_objects('filipeliu:narrative_1564417971147')
kmodel = kbase.get_object('test', 'filipeliu:narrative_1564417971147')
kmodel['gapfillings']
os[4] #31470/3/1
o_data['gapfillings']
ref = kbase.get_object_info_from_ref('262/34/1')
ref.id
for o in os:
if not o[2].startswith('KBaseNarrative.Narrative') and not o[2].startswith('KBaseGenomes.Genome'):
print(o)
o_data = kbase.get_object(o[1], 'zahmeeth:narrative_1561761748173')
if 'genome_ref' in o_data:
o_data['genome_ref'] = '31470/2/1'
if 'gapfillings' in o_data:
for gapfilling in o_data['gapfillings']:
print(o[1], gapfilling['gapfill_id'])
if 'media_ref' in gapfilling:
gapfilling['media_ref'] = '31470/3/1'
#kbase_dev.save_object(o[1], 'filipeliu:narrative_1564175222344', o[2].split('-')[0], o_data)
kmodel = kbase.get_object('iML1515.kb', 'zahmeeth:narrative_1561761748173')
ref = kbase.get_object_info_from_ref(kmodel['genome_ref'])
kgenome = kbase.get_object(ref.id, ref.workspace_id)
genome = cobrakbase.core.KBaseGenome(kgenome)
builder = cobrakbase.core.converters.KBaseFBAModelToCobraBuilder(cobrakbase.core.model.KBaseFBAModel(kmodel))
builder = builder.with_genome(genome)
model = builder.build()
gene = model.genes[5]
gene.annotation
cobrakbase.COBRA_DEFAULT_LB = -1000
cobrakbase.COBRA_DEFAULT_UB = 1000
kmodel = kbase.get_object('iAF1260.fix2.kb', 'filipeliu:narrative_1504192868437')
exprvar
os = kbase.list_objects('jplfaria:narrative_1524466549180')
genomes = set()
for o in os:
if o[1].endswith('RAST'):
genomes.add(o[1])
print(len(genomes))
os = kbase.list_objects('filipeliu:narrative_1549385719110')
genomes2 = set()
for o in os:
if o[1].endswith('RAST.mdl.gfrelease.Carbon-D-Glucose'):
id = o[1].split('.mdl.')[0]
genomes2.add(id)
print(len(genomes2))
#genomes2
genomes3 = set()
for o in os:
if o[1].endswith('RAST.mdl.gfrelease.Carbon-D-Glucose.fba'):
id = o[1].split('.mdl.')[0]
genomes3.add(id)
print(len(genomes3))
kmedia = kbase.get_object('Carbon-D-Glucose', 'filipeliu:narrative_1549385719110')
media_const = cobrakbase.convert_media(kmedia)
genome_id = 'GCF_000005845.2.RAST'
def eval_fba(genome_id):
kmodel = kbase.get_object(genome_id + '.mdl.gfrelease.Carbon-D-Glucose', 'filipeliu:narrative_1549385719110')
#genome = kbase.get_object('GCF_000005845.2.RAST', 'jplfaria:narrative_1524466549180')
enforce_direaction_bounds(kmodel)
kmodel_fba = kbase.get_object(genome_id + '.mdl.gfrelease.Carbon-D-Glucose.fba', 'filipeliu:narrative_1549385719110')
fbamodel = cobrakbase.core.model.KBaseFBAModel(kmodel)
kbase_fba = kmodel_fba['objectiveValue']
model = cobrakbase.convert_kmodel(kmodel, media_const)
solution = model.optimize()
cobra_fba = solution.objective_value
print(kbase_fba, cobra_fba, cobra_fba - cobra_fba)
return kbase_fba, cobra_fba, cobra_fba - cobra_fba
kmodel = kbase.get_object(genome_id + '.mdl.gfrelease.Carbon-D-Glucose', 'filipeliu:narrative_1549385719110')
#genome = kbase.get_object('GCF_000005845.2.RAST', 'jplfaria:narrative_1524466549180')
enforce_direaction_bounds(kmodel)
kmodel_fba = kbase.get_object(genome_id + '.mdl.gfrelease.Carbon-D-Glucose.fba', 'filipeliu:narrative_1549385719110')
fbamodel = cobrakbase.core.model.KBaseFBAModel(kmodel)
cpd_ref_file = '../../../../kbase/ModelSEEDDatabase/Biochemistry/Aliases/Unique_ModelSEED_Compound_Aliases.txt'
rxn_ref_file = '../../../../kbase/ModelSEEDDatabase/Biochemistry/Aliases/Unique_ModelSEED_Reaction_Aliases.txt'
rxn_ec_file = '../../../../kbase/ModelSEEDDatabase/Biochemistry/Aliases/Unique_ModelSEED_Reaction_ECs.txt'
cpd_stru_file = '../../../../kbase/ModelSEEDDatabase/Biochemistry/Structures/ModelSEED_Structures.txt'
cpd_df = pd.read_csv(cpd_ref_file, sep='\t')
rxn_df = pd.read_csv(rxn_ref_file, sep='\t')
rxn_ec_df = pd.read_csv(rxn_ec_file, sep='\t')
stru_df = pd.read_csv(cpd_stru_file, sep='\t')
structures = cobrakbase.read_modelseed_compound_structures(stru_df)
rxn_aliases = cobrakbase.read_modelseed_reaction_aliases2(rxn_df)
cpd_aliases = cobrakbase.read_modelseed_compound_aliases2(cpd_df)
gene_aliases = cobrakbase.read_genome_aliases(genome)
def annotate_model(model, cpd_aliases, rxn_aliases, gene_aliases, structures):
for m in model.metabolites:
seed_id = None
if 'seed.compound' in m.annotation:
seed_id = m.annotation['seed.compound']
if seed_id in structures:
m.annotation.update(structures[seed_id])
if seed_id in cpd_aliases:
m.annotation.update(cpd_aliases[seed_id])
for r in model.reactions:
seed_id = None
if 'seed.reaction' in r.annotation:
seed_id = r.annotation['seed.reaction']
if seed_id in rxn_aliases:
r.annotation.update(rxn_aliases[seed_id])
for g in model.genes:
if g.id in gene_aliases:
g.annotation.update(gene_aliases[g.id])
for r in model.reactions:
if cobrakbase.is_translocation(r):
if cobrakbase.is_transport(r):
r.annotation['sbo'] = 'SBO:0000655'
else:
r.annotation['sbo'] = 'SBO:0000185'
kbase_sinks = ['rxn13783_c0', 'rxn13784_c0', 'rxn13782_c0']
for r in model.reactions:
#r.annotation['ec-code'] = '1.1.1.1'
#r.annotation['metanetx.reaction'] = 'MNXR103371'
if r.id in kbase_sinks:
r.annotation['sbo'] = 'SBO:0000632'
if r.id.startswith('DM_'):
r.annotation['sbo'] = 'SBO:0000628'
#
cpd_ref_file = '../../../../kbase/ModelSEEDDatabase/Biochemistry/Aliases/Unique_ModelSEED_Compound_Aliases.txt'
rxn_ref_file = '../../../../kbase/ModelSEEDDatabase/Biochemistry/Aliases/Unique_ModelSEED_Reaction_Aliases.txt'
rxn_ec_file = '../../../../kbase/ModelSEEDDatabase/Biochemistry/Aliases/Unique_ModelSEED_Reaction_ECs.txt'
cpd_stru_file = '../../../../kbase/ModelSEEDDatabase/Biochemistry/Structures/ModelSEED_Structures.txt'
cpd_df = pd.read_csv(cpd_ref_file, sep='\t')
rxn_df = pd.read_csv(rxn_ref_file, sep='\t')
rxn_ec_df = pd.read_csv(rxn_ec_file, sep='\t')
stru_df = pd.read_csv(cpd_stru_file, sep='\t')
structures = cobrakbase.read_modelseed_compound_structures(stru_df)
rxn_aliases = cobrakbase.read_modelseed_reaction_aliases2(rxn_df)
cpd_aliases = cobrakbase.read_modelseed_compound_aliases2(cpd_df)
exclude = genomes - genomes2
i = 0
for genome_id in genomes:
if not genome_id in exclude:
kmodel = kbase.get_object(genome_id + '.mdl.gfrelease.Carbon-D-Glucose', 'filipeliu:narrative_1549385719110')
genome = kbase.get_object(genome_id, 'jplfaria:narrative_1524466549180')
enforce_direaction_bounds(kmodel)
#kmodel_fba = kbase.get_object(genome_id + '.mdl.gfrelease.Carbon-D-Glucose.fba', 'filipeliu:narrative_1549385719110')
fbamodel = cobrakbase.core.model.KBaseFBAModel(kmodel)
gene_aliases = cobrakbase.read_genome_aliases(genome)
model = cobrakbase.convert_kmodel(kmodel, media_const)
annotate_model(model, cpd_aliases, rxn_aliases, gene_aliases, structures)
for r in model.reactions:
ub = r.upper_bound
lb = r.lower_bound
if ub == 1000000:
ub = 1000
if lb == -1000000:
lb = -1000
r.upper_bound = ub
r.lower_bound = lb
cobra.io.write_sbml_model(model, '../../data/memote_models/' + genome_id.split('.RAST')[0] + '.xml')
print(i, genome_id)
i += 1
data = {
'genome_id' : [],
'cobra' : []
}
for genome_id in genomes:
if not genome_id in exclude:
print(genome_id)
model = cobra.io.read_sbml_model('../../data/memote_models/' + genome_id.split('.RAST')[0] + '.xml')
solution = model.optimize()
cobra_fba = solution.objective_value
data['genome_id'].append(genome_id)
data['cobra'].append(cobra_fba)
df = pd.DataFrame(data)
df = df.set_index('genome_id')
df.to_csv('../../data/export_fba.tsv', sep='\t')
data = {
'genome_id' : [],
'kbase' : [],
'cobra' : [],
'error' : [],
}
exclude = genomes - genomes3
for genome_id in genomes:
break
if not genome_id in exclude:
kbase_fba, cobra_fba, e = eval_fba(genome_id)
data['genome_id'].append(genome_id)
data['kbase'].append(kbase_fba)
data['cobra'].append(cobra_fba)
data['error'].append(e)
df = pd.DataFrame(data)
df = df.set_index('genome_id')
#df.to_csv('../../data/cobrakbase_fba.tsv', sep='\t')
print()
kmodel_fba.keys()
def enforce_direaction_bounds(kmodel):
for r in kmodel['modelreactions']:
direction = r['direction']
if direction == '>':
r['maxrevflux'] = 0
r['maxforflux'] = 1000
elif direction == '=':
r['maxrevflux'] = 1000
r['maxforflux'] = 1000
elif direction == '<':
r['maxrevflux'] = 1000
r['maxforflux'] = 0
for r in kmodel_fba['FBAReactionVariables']:
break
r_id = r['modelreaction_ref'].split('/')[-1]
frxn = fbamodel.get_reaction(r_id)
#print(frxn.data)
rxn = model.reactions.get_by_id(r_id)
cobra_bound = (rxn.lower_bound, rxn.upper_bound)
lb_ub = (r['lowerBound'], r['upperBound'])
min_max = (r['min'], r['max'])
direction = frxn.data['direction']
if direction == '>':
rxn.lower_bound = 0
rxn.upper_bound = 1000
elif direction == '=':
rxn.lower_bound = -1000
rxn.upper_bound = 1000
elif direction == '<':
rxn.lower_bound = -1000
rxn.upper_bound = 0
print(frxn.data['direction'], cobra_bound, lb_ub, min_max, rxn.flux, r['value'], rxn)
break
solution = model.optimize()
print(solution.objective_value)
b0002 = exprvar('b0002')
f1 = b0002 & z
f1
expr.expr("(b0078 & b0077) | (b3670 & (b3671 | k))").to_dnf().cover
f10 = Or(And(Not(a), b), And(c, Not(d)))
f10
a, b, c, d, k, z, w = map(exprvar, "abcdkzw")
f0 = a & (b | c) | k & (z | w)
dnf = f0.to_dnf()
dnf
def get_protein_sets(dnf):
print('get_protein_sets', dnf)
protein_sets = []
for k in dnf.iter_dfs():
print(type(k))
if type(k) == expr.AndOp:
protein_set = set()
for gene in k.iter_dfs():
if type(gene) == expr.Variable:
protein_set.add(gene)
#print(k, gene)
protein_sets.append(protein_set)
elif type(k) == expr.Variable:
1
#protein_sets.append(set([k]))
elif type(k) == expr.OrOp:
for k_childs in k.iter_dfs():
1
#print(k_childs)
#protein_sets.append(set([k]))
return protein_sets
def get_protein_sets2(dnf):
protein_sets = []
for k in dnf.iter_dfs():
if type(k) == expr.Variable:
protein_set = set()
for gene in k.iter_dfs():
if type(gene) == expr.Variable:
protein_set.add(gene)
#print(k, gene)
protein_sets.append(protein_set)
return protein_sets
protein_sets = get_protein_sets(dnf)
print(dnf, protein_sets)
f100 = expr.expr("(b0078 | b0077) | (b3670 & b3671)").to_dnf()
protein_sets = get_protein_sets(f100)
print(f100, protein_sets)
ast = f100.to_ast()
def get_protein_sets(ast, protein_sets):
print('get_protein_sets', ast)
#protein_sets = []
t = ast[0]
if t == 'or':
for child in ast:
if type(child) == tuple:
get_protein_sets(child, protein_sets)
elif t == 'and':
get_protein_set = set()
for child in ast:
if type(child) == tuple:
get_protein_set.add(child[1])
protein_sets.append(get_protein_set)
elif t == 'lit':
protein_sets.append(set([ast[1]]))
else:
print('invalid type', t)
return protein_sets
f100.NAME
print(f100, get_protein_sets(ast, []))
def get_protein_sets(e, protein_sets):
for var in e.xs:
if var.depth == 0:
for a in var.cover:
#print(type(a.))
print(a)
protein_sets.append(set([a]))
else:
for a in var.xs:
print(a)
print(var, var.depth)
return protein_sets
print(f100, get_protein_sets(f100, []))
for var in ast:
print(var)
dnf.cover
f0.to_cnf()
model = cobrakbase.convert_kmodel(kmodel)
"(b0078 and b0077) or (b3670 and b3671)".replace('and', '&').replace('or', '|')
a = ['b0241', 'b0002']
print(a)
a.sort()
print(a)
mapping = pd.read_csv('/Volumes/My Passport/var/argonne/annotation/manual/iAF1260_rxn_pred.tsv', sep='\t')
to_seed = {}
for _, row in mapping.iterrows():
if not pd.isna(row['ModelSeedReaction']):
to_seed[row['iAF1260'][2:]] = row['ModelSeedReaction']
prot_to_rxn = {}
for r in model_bigg.reactions:
gpr = r.gene_name_reaction_rule
gpr = gpr.replace('and', '&').replace('or', '|')
if len(gpr) > 0:
gpr_expression = expr.expr(gpr)
gpr_expression = gpr_expression.to_dnf()
psets = gpr_expression.cover
for pset in psets:
prot = []
for p in pset:
#print(type(p), str(p))
prot.append(str(p))
prot.sort()
prot = ';'.join(prot)
if not prot in prot_to_rxn:
prot_to_rxn[prot] = set()
prot_to_rxn[prot].add(r.id)
#print(gpr_expression, psets)
data = []
for gene in prot_to_rxn:
#print(gene)
rxn_ids = []
for rxn_id in prot_to_rxn[gene]:
seed_id = to_seed[rxn_id]
rxn_ids.append(seed_id)
data.append([gene, ';'.join(rxn_ids)])
df = pd.DataFrame(data, columns=['genes', 'reactions'])
df.to_csv('iAF1260.csv')
model_bigg = cobra.io.read_sbml_model('iAF1260.xml')
media = None
with open('glucose_media.json', 'r') as f:
data = json.loads(f.read())
media = cobrakbase.convert_media(data)
model = None
with open('test_model.json', 'r') as f:
data = json.loads(f.read())
model = cobrakbase.convert_kmodel(data, media)
model.summary()
for m in model.metabolites:
print(m.id)
print(m.annotation)
break
"cpd11".startswith('cpd')
#https://raw.githubusercontent.com/ModelSEED/ModelSEEDDatabase/dev/Biochemistry/Aliases/Compounds_Aliases.tsv
import pandas as pd
from urllib.request import urlopen
data = urlopen('https://raw.githubusercontent.com/ModelSEED/ModelSEEDDatabase/dev/Biochemistry/Aliases/Compounds_Aliases.tsv')
df = pd.read_csv(data, sep='\t')
data = urlopen('https://raw.githubusercontent.com/ModelSEED/ModelSEEDDatabase/dev/Biochemistry/Aliases/Reactions_Aliases.tsv')
rxn_df = pd.read_csv(data, sep='\t')
data = urlopen('https://raw.githubusercontent.com/ModelSEED/ModelSEEDDatabase/dev/Biochemistry/Structures/ModelSEED_Structures.txt')
stru_df = pd.read_csv(data, sep='\t')
def read_modelseed_compound_aliases(df):
aliases = {}
for a, row in df.iterrows():
if row[3] == 'BiGG':
if not row[0] in aliases:
aliases[row[0]] = {}
aliases[row[0]]['bigg.metabolite'] = row[2]
if row[3] == 'MetaCyc':
if not row[0] in aliases:
aliases[row[0]] = {}
aliases[row[0]]['biocyc'] = row[2]
if row[3] == 'KEGG' and row[2][0] == 'C':
if not row[0] in aliases:
aliases[row[0]] = {}
aliases[row[0]]['kegg.compound'] = row[2]
return aliases
def read_modelseed_reaction_aliases(df):
aliases = {}
for a, row in df.iterrows():
if row[3] == 'BiGG':
if not row[0] in aliases:
aliases[row[0]] = {}
aliases[row[0]]['bigg.reaction'] = row[2]
if row[3] == 'MetaCyc':
if not row[0] in aliases:
aliases[row[0]] = {}
aliases[row[0]]['biocyc'] = row[2]
if row[3] == 'KEGG' and row[2][0] == 'R':
if not row[0] in aliases:
aliases[row[0]] = {}
aliases[row[0]]['kegg.reaction'] = row[2]
return aliases
def read_modelseed_compound_structures(df):
structures = {}
for _, row in df.iterrows():
#print(row[0], row[1], row[3])
if row[1] == 'InChIKey':
if not row[0] in structures:
structures[row[0]] = {}
structures[row[0]]['inchikey'] = row[3]
return structures
structures = read_modelseed_compound_structures(stru_df)
structures['cpd00001']
rxn_aliases = read_modelseed_reaction_aliases(rxn_df)
print(len(rxn_aliases))
print(aliases['cpd00001'])
print(rxn_aliases['rxn00001'])
#jplfaria:narrative_1492808527866
#jplfaria:narrative_1524466549180
kbase = cobrakbase.KBaseAPI('SHO64Q2X7HKU4PP4BV7XQMY3WYIK2QRJ')
#31045/4997/1
kbase.get_object_info_from_ref('31045/4997/1')
wsos = kbase.list_objects('jplfaria:narrative_1492808527866')
#KBaseGenomes.Genome
#KBaseFBA.FBAModel
models = set()
for o in wsos:
if 'KBaseFBA.FBAModel' in o[2]:
models.add(o[1])
kmodel = kbase.get_object('GCF_000005845.2.RAST.mdl', 'jplfaria:narrative_1492808527866')
for m_id in models:
kmodel = kbase.get_object(m_id, 'jplfaria:narrative_1492808527866')
save_model_mongo(kmodel)
mclient = pymongo.MongoClient('mongodb://localhost:27017/')
database = mclient['Models']
kbasemodels = database['TemplateV1']
a = set()
a.add(1)
a.update([2, 3])
a
def save_model_mongo(kmodel):
model_id = kmodel['id']
genome_info = kbase.get_object_info_from_ref(kmodel['genome_ref'])
genome = genome_info['infos'][0][1]
rxn_to_genes = {}
for modelreactions in kmodel['modelreactions']:
rxn_id = modelreactions['reaction_ref'].split('/')[-1].split('_')[0]
genes = []
for modelReactionProteins in modelreactions['modelReactionProteins']:
for modelReactionProteinSubunits in modelReactionProteins['modelReactionProteinSubunits']:
for feature_refs in modelReactionProteinSubunits['feature_refs']:
gene = feature_refs.split('/')[-1]
genes.append(gene)
if len(genes) > 0:
if not rxn_id in rxn_to_genes:
rxn_to_genes[rxn_id] = set()
rxn_to_genes[rxn_id].update(genes)
#break
for k in rxn_to_genes:
rxn_to_genes[k] = list(rxn_to_genes[k])
data = {'genome' : genome, 'ws' : 'jplfaria:narrative_1492808527866', 'rxn_to_genes' : rxn_to_genes}
kbasemodels.update_one({'_id' : model_id}, {'$set' : data}, upsert=True)
%%HTML
<b>Why not R-r0317 in master_fungal_template_fix mapped</b><br>
<i>H2O[c0] + LACT[c0] <=> D-glucose[c0] + Galactose[c0]</i><br>
<i>rxn00816 Lactose galactohydrolase 1 H2O [0] + 1 LACT [0] 1 D-Glucose [0] + 1 Galactose [0]</i><br>
<b>Answer: 1 compound is not integrated:</b> D-glucose[c0] > '~/modelcompounds/id/M-dglc-c_c0'<br>
<br>
<b>ATP Synthases! MERGE</b>
Asppeni1_model = cobrakbase.API.get_object(id="Asppeni1_model", ws="janakakbase:narrative_1540435363582")
for r in Asppeni1_model['modelreactions']:
if '/' in r['id']:
id = r['id']
if id[:2] == 'R-':
id = id[2:]
id = id.replace('/','-')
print(r['id'], '->', id)
r['id'] = id
def save_object(wsc, o, id, ws, t):
wsc.save_objects(
{'workspace': ws,
'objects' : [{'data' : o, 'name' : id, 'type' : t}]
})
save_object(cobrakbase.API.wsClient, Asppeni1_model, "Asppeni1_model_fix", "janakakbase:narrative_1540435363582", "KBaseFBA.FBAModel")
template = cobrakbase.API.get_object(id="Fungi", ws="NewKBaseModelTemplates")
master_fungal_template_fix = cobrakbase.API.get_object(id="master_fungal_template_fix", ws="jplfaria:narrative_1510597445008")
#rxn08617 GLCtex
#rxn08606
lookup = ["rxn08617", "rxn08606", "rxn05226"]
for r in template['reactions']:
#print(r['id'], r['name'])
if r['id'] in lookup:
print(r)
#print(r)
#break
print(template.keys())
for r in template['reactions']:
atp = False
adp = False
h = False
pi = False
h2o = False
for c in r['templateReactionReagents']:
if 'cpd00002' in c['templatecompcompound_ref']:
atp = True
if 'cpd00008' in c['templatecompcompound_ref']:
adp = True
if 'cpd00009' in c['templatecompcompound_ref']:
pi = True
if 'cpd00067' in c['templatecompcompound_ref']:
h = True
if 'cpd00001' in c['templatecompcompound_ref']:
h2o = True
if atp and adp and h and pi and h2o and 'rxf' and len(r['templateReactionReagents']) == 5:
print(r)
for r in template['reactions']:
#print(r['id'])
1
for r in master_fungal_template_fix['modelreactions']:
for c in r['modelReactionReagents']:
if not 'modelcompounds/id/cpd' in c['modelcompound_ref']:
1 #print(c)
#if 'R-r0317' in r['id']:
# print(r)
fmodel = cobrakbase.API.get_object(id="Asppeni1_model_fix_GP_GMM", ws="janakakbase:narrative_1540435363582")
template.keys()
for r in template['modelreactions']:
#print(r['id'])
if 'R-r0317' in r['id']:
print(r)
gmedia = cobrakbase.API.get_object(id="Carbon-D-Glucose", ws="janakakbase:narrative_1540435363582")
media = cobrakbase.convert_media(gmedia)
#cobrakbase.
model = cobrakbase.convert_kmodel(fmodel, media=media)
for r in model.sinks:
print("SK", r)
for r in model.demands:
print("DM", r)
for r in model.exchanges:
#print("EX", r, r.lower_bound)
1
for r in model.reactions:
#print(r)
1
def demand(cpd, value, model):
dm = Reaction(id="DM_" + cpd, name="Demand for " + cpd, lower_bound=value, upper_bound=1000)
dm.add_metabolites({model.metabolites.get_by_id(cpd) : -1})
print(cpd, value, dm)
model.add_reaction(dm)
1
bio = model.reactions.get_by_id('bio1_biomass')
print(bio)
for a in bio.metabolites:
#print(a.id, a.name, bio.metabolites[a])
#demand(a.id, -1, model)
1
for a in bio.metabolites:
model.reactions.get_by_id("DM_" + a.id).lower_bound = -1
model.reactions.get_by_id('DM_cpd00030_c0').lower_bound = 0.0 #Mn2+
model.reactions.get_by_id('DM_cpd00205_c0').lower_bound = 0.0 #K+
model.reactions.get_by_id('DM_cpd00149_c0').lower_bound = 0.0 #Co2+
model.reactions.get_by_id('DM_cpd00063_c0').lower_bound = 0.0 #Ca2+
model.reactions.get_by_id('DM_cpd11416_c0').lower_bound = 0.0 #Biomass
model.reactions.get_by_id('DM_cpd00107_c0').lower_bound = -0.1 #L-Leucine
model.reactions.get_by_id('DM_cpd00069_c0').lower_bound = 0.0 #L-Tyrosine
model.reactions.get_by_id('DM_cpd12370_c0').lower_bound = 0.0 #apo-ACP
model.reactions.get_by_id('DM_cpd00003_c0').lower_bound = 0.0 #NAD
model.reactions.get_by_id('DM_cpd00006_c0').lower_bound = 0.0 #NADP
model.summary()
for a in bio.metabolites:
coef = bio.get_coefficient(a)
z = "+"
if coef < 0:
z = "-"
flux = model.reactions.get_by_id("DM_" + a.id).flux
if not flux == 0.0:
print(a, z, a.name, flux)
1
#print(model.reactions.DM_cpd00053_c0.flux)
#model.metabolites.get_by_id("cpd00205_c0").summary()
def get_flux_distribution(fba):
fdist = {}
for a in fba['FBAReactionVariables']:
flux = a['value']
#if '~/fbamodel/modelreactions/id/pi_m0' == a['modelreaction_ref']:
# a['modelreaction_ref'] = '~/fbamodel/modelreactions/id/tr-succ/pi_m0'
id = cobrakbase.get_id_from_ref(a['modelreaction_ref'], stok='/')
#print(a['modelreaction_ref'], id, flux)
fdist[id] = flux
biomass = "bio1_biomass"
if not fba['objectiveValue'] == 0:
flux = fba['objectiveValue']
fdist[biomass] = flux
return fdist
def get_net_convertion(model, fdist):
net = {}
for rxnId in fdist:
flux = fdist[rxnId]
rselect = rxnId
#print(rselect)
if "R-" in rselect:
rselect = rselect[2:]
#print(rselect)
id = rxnId
#id = cobrakbase.get_id_from_ref(rxnId)
#print(id)
if "R-" in id:
id = id[2:]
#print(id)
#print(id, a['value'])
if not flux == 0:
r = model.reactions.get_by_id(id)
#print(r, flux)
#print(dir(r))
for k in r.reactants:
if not k in net:
net[k] = 0
net[k] += r.get_coefficient(k) * flux
for k in r.products:
if not k in net:
net[k] = 0
net[k] += r.get_coefficient(k) * flux
return net
cobrakbase.login("TUEVGXRO3JJUJCEPAHBSGW67ZM7UURGC", dev=False)
fba = cobrakbase.API.get_object("Asppeni1_model_fix_GP_GMM.gf.1", "janakakbase:narrative_1540435363582")
print(fba['objectiveValue'])
fdist = get_flux_distribution(fba)
#model.reactions.get_by_id("r0516_m0")
print(model.reactions.get_by_id("tr-succ-pi_m0"))
net = get_net_convertion(model, fdist)
#cpd11416
e = 1e-3
for cpd in net:
flux = net[cpd]
if flux > e or flux < -e:
if False or "_c0" in cpd.id:
print(cpd, flux)
cobra_model = cobrakbase.read_model_with_media("GCF_000005845.2", "Carbon-D-Glucose", "filipeliu:narrative_1504192868437")
#jsonMedia = cobrakbase.API.get_object("Carbon-D-Glucose", "filipeliu:narrative_1504192868437")
#jsonModel = cobrakbase.API.get_object("GCF_000005845.2", "filipeliu:narrative_1504192868437")
#for r in jsonModel['modelreactions']:
# if "rxn00159_c0" in r['id']:
# print(r)
cobra_model.reactions.get_by_id("rxn00159_c0")
#cobra_model.medium
#met = cobra_model.metabolites.get_by_id("cpd00011_e0")
#object_stoichiometry = {met : -1}
#reaction = Reaction(id="EX_cpd00011_e0", name="Exchange for " + met.name, lower_bound=-8, upper_bound=1000)
#cobra_model.add_reaction(reaction)
#with open('iMR1_799.json', 'w') as outfile:
# json.dump(model, outfile)
#cobra_model.summary()
for r in model.reactions:
if False or "EX_" in r.id and r.lower_bound == 0:
#print(r)
#if r.lower_bound == 0:
#r.lower_bound = -1
#print(r, ":", r.lower_bound, r.upper_bound)
1
#cobra_model.reactions.get_by_id("EX_cpd00011_e0").lower_bound = 7.99
#cobra_model.objective = "bio1_biomass"
#cobra_model.summary()
#cobra_model.metabolites.cpd00011_c0.summary()
CONSUMING REACTIONS -- CO2_c0 (cpd0001...)
------------------------------------------
% FLUX RXN ID REACTION
--- ------ ---------- --------------------------------------------------
87% 7.99 rxn0546... cpd00011_e0 <=> cpd00011_c0
15% 1.39 rxn0534... cpd11466_c0 + cpd11492_c0 <=> cpd00011_c0 + cpd...
3% 0.255 rxn0292... 2 cpd00001_c0 + 2 cpd00067_c0 + cpd02103_c0 <=>...
2% 0.206 rxn0920... 2 cpd00067_c0 + cpd15555_c0 <=> cpd00011_c0 + c...
2% 0.175 rxn0293... cpd00067_c0 + cpd02893_c0 <=> cpd00011_c0 + cpd...
CONSUMING REACTIONS -- CO2_c0 (cpd0001...)
------------------------------------------
% FLUX RXN ID REACTION
--- ------ ---------- --------------------------------------------------
32% 1.9 rxn0534... cpd11466_c0 + cpd11492_c0 <=> cpd00011_c0 + cpd...
28% 1.67 rxn0916... cpd00001_c0 + cpd00020_c0 + cpd15560_c0 <=> cpd...
20% 1.21 rxn0015... cpd00003_c0 + cpd00130_c0 <=> cpd00004_c0 + cpd...
6% 0.347 rxn0292... 2 cpd00001_c0 + 2 cpd00067_c0 + cpd02103_c0 <=>...
5% 0.321 rxn0637... cpd00033_c0 + cpd00067_c0 + cpd12005_c0 <=> cpd...
5% 0.281 rxn0920... 2 cpd00067_c0 + cpd15555_c0 <=> cpd00011_c0 + c...
4% 0.239 rxn0293... cpd00067_c0 + cpd02893_c0 <=> cpd00011_c0 + cpd...
#jsonModel = cobrakbase.API.get_object("GCF_000005845.2", "filipeliu:narrative_1504192868437")
#jsonMedia = cobrakbase.API.get_object("Carbon-D-Glucose", "filipeliu:narrative_1504192868437")
def fix_flux_bounds(m):
for r in m['modelreactions']:
lb = -1 * r['maxrevflux']
ub = r['maxforflux']
di = r['direction']
cdi = "="
if lb == 0 and ub > 0:
cdi = ">"
elif ub == 0 and lb < 0:
cdi = '<'
if not cdi == di:
if di == '>':
r['maxrevflux'] = 0
elif di == '<':
r['maxforflux'] = 0
else:
1
print(r['id'], di, cdi, lb, ub)
fix_flux_bounds(jsonModel)
cobra_model = cobrakbase.convert_kmodel(jsonModel, media=cobrakbase.convert_media(jsonMedia))
from memote.suite.cli.reports import report
import memote.suite.api as api
from memote.suite.reporting import ReportConfiguration
#a, results = api.test_model(cobra_model, results=True)
config = ReportConfiguration.load()
html = api.snapshot_report(results, config)
with open("report.html", "w") as text_file:
print(html, file=text_file)
```
|
github_jupyter
|
```
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
from sklearn.linear_model import LogisticRegression
from sklearn import metrics
from sklearn.metrics import classification_report, confusion_matrix, f1_score
from sklearn.metrics import make_scorer, f1_score, accuracy_score, recall_score, precision_score, classification_report, precision_recall_fscore_support
import itertools
# file used to write preserve the results of the classfier
# confusion matrix and precision recall fscore matrix
def plot_confusion_matrix(cm,
target_names,
title='Confusion matrix',
cmap=None,
normalize=True):
"""
given a sklearn confusion matrix (cm), make a nice plot
Arguments
---------
cm: confusion matrix from sklearn.metrics.confusion_matrix
target_names: given classification classes such as [0, 1, 2]
the class names, for example: ['high', 'medium', 'low']
title: the text to display at the top of the matrix
cmap: the gradient of the values displayed from matplotlib.pyplot.cm
see http://matplotlib.org/examples/color/colormaps_reference.html
plt.get_cmap('jet') or plt.cm.Blues
normalize: If False, plot the raw numbers
If True, plot the proportions
Usage
-----
plot_confusion_matrix(cm = cm, # confusion matrix created by
# sklearn.metrics.confusion_matrix
normalize = True, # show proportions
target_names = y_labels_vals, # list of names of the classes
title = best_estimator_name) # title of graph
Citiation
---------
http://scikit-learn.org/stable/auto_examples/model_selection/plot_confusion_matrix.html
"""
accuracy = np.trace(cm) / float(np.sum(cm))
misclass = 1 - accuracy
if normalize:
cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
if cmap is None:
cmap = plt.get_cmap('Blues')
plt.figure(figsize=(8, 6))
plt.imshow(cm, interpolation='nearest', cmap=cmap)
plt.title(title)
plt.colorbar()
if target_names is not None:
tick_marks = np.arange(len(target_names))
plt.xticks(tick_marks, target_names, rotation=45)
plt.yticks(tick_marks, target_names)
thresh = cm.max() / 1.5 if normalize else cm.max() / 2
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
if normalize:
plt.text(j, i, "{:0.4f}".format(cm[i, j]),
horizontalalignment="center",
color="white" if cm[i, j] > thresh else "black")
else:
plt.text(j, i, "{:,}".format(cm[i, j]),
horizontalalignment="center",
color="white" if cm[i, j] > thresh else "black")
plt.ylabel('True label')
plt.xlabel('Predicted label\naccuracy={:0.4f}; misclass={:0.4f}'.format(accuracy, misclass))
plt.tight_layout()
return plt
##saving the classification report
def pandas_classification_report(y_true, y_pred):
metrics_summary = precision_recall_fscore_support(
y_true=y_true,
y_pred=y_pred)
cm = confusion_matrix(y_true, y_pred)
cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
avg = list(precision_recall_fscore_support(
y_true=y_true,
y_pred=y_pred,
average='macro'))
avg.append(accuracy_score(y_true, y_pred, normalize=True))
metrics_sum_index = ['precision', 'recall', 'f1-score', 'support','accuracy']
list_all=list(metrics_summary)
list_all.append(cm.diagonal())
class_report_df = pd.DataFrame(
list_all,
index=metrics_sum_index)
support = class_report_df.loc['support']
total = support.sum()
avg[-2] = total
class_report_df['avg / total'] = avg
return class_report_df.T
from commen_preprocess import *
from sklearn.metrics import accuracy_score
import joblib
from sklearn.model_selection import StratifiedKFold as skf
###all classifier
from catboost import CatBoostClassifier
from xgboost.sklearn import XGBClassifier
from sklearn.svm import SVC, LinearSVC
from sklearn.linear_model import LogisticRegression
from sklearn import tree
from sklearn import neighbors
from sklearn import ensemble
from sklearn import neural_network
from sklearn import linear_model
import lightgbm as lgbm
from sklearn.naive_bayes import GaussianNB
from sklearn.linear_model import LogisticRegression
from lightgbm import LGBMClassifier
from nltk.classify.scikitlearn import SklearnClassifier
eng_train_dataset = pd.read_csv('../Data/hindi_dataset/hindi_dataset.tsv', sep='\t')
eng_train_dataset.head()
l=eng_train_dataset['task_1'].value_counts()
print("the total dataset size:",len(eng_train_dataset),'\n',l)
import numpy as np
from tqdm import tqdm
import pickle
####loading laser embeddings for english dataset
def load_laser_embeddings():
dim = 1024
engX_commen = np.fromfile("../Data/hindi_dataset/embeddings_hin_task1_commen.raw", dtype=np.float32, count=-1)
engX_lib = np.fromfile("../Data/hindi_dataset/embeddings_hin_task1_lib.raw", dtype=np.float32, count=-1)
engX_commen.resize(engX_commen.shape[0] // dim, dim)
engX_lib.resize(engX_lib.shape[0] // dim, dim)
return engX_commen,engX_lib
def load_bert_embeddings():
file = open('../Data/hindi_dataset/no_preprocess_bert_embed_task1.pkl', 'rb')
embeds = pickle.load(file)
return np.array(embeds)
def merge_feature(*args):
feat_all=[]
print(args[0].shape)
for i in tqdm(range(args[0].shape[0])):
feat=[]
for arg in args:
feat+=list(arg[i])
feat_all.append(feat)
return feat_all
convert_label={
'HOF':1,
'NOT':0
}
convert_reverse_label={
1:'HOF',
0:'NOT'
}
labels=eng_train_dataset['task_1'].values
engX_commen,engX_lib=load_laser_embeddings()
bert_embeds =load_bert_embeddings()
feat_all=merge_feature(engX_commen,engX_lib,bert_embeds)
#feat_all=merge_feature(engX_lib)
# feat_all=[]
# for i in range(len(labels)):
# feat=list(engX_commen[i])+list(engX_lib[i])
# feat_all.append(feat)
len(feat_all[0])
from sklearn.utils.multiclass import type_of_target
Classifier_Train_X=np.array(feat_all)
labels_int=[]
for i in range(len(labels)):
labels_int.append(convert_label[labels[i]])
Classifier_Train_Y=np.array(labels_int,dtype='float64')
print(type_of_target(Classifier_Train_Y))
Classifier_Train_Y
def train_model_no_ext(Classifier_Train_X,Classifier_Train_Y,model_type,save_model=False):
kf = skf(n_splits=10,shuffle=True)
y_total_preds=[]
y_total=[]
count=0
img_name = 'cm.png'
report_name = 'report.csv'
scale=list(Classifier_Train_Y).count(0)/list(Classifier_Train_Y).count(1)
print(scale)
if(save_model==True):
Classifier=get_model(scale,m_type=model_type)
Classifier.fit(Classifier_Train_X,Classifier_Train_Y)
filename = model_type+'_hin_task_1.joblib.pkl'
joblib.dump(Classifier, filename, compress=9)
# filename1 = model_name+'select_features_eng_task1.joblib.pkl'
# joblib.dump(model_featureSelection, filename1, compress=9)
else:
for train_index, test_index in kf.split(Classifier_Train_X,Classifier_Train_Y):
X_train, X_test = Classifier_Train_X[train_index], Classifier_Train_X[test_index]
y_train, y_test = Classifier_Train_Y[train_index], Classifier_Train_Y[test_index]
classifier=get_model(scale,m_type=model_type)
print(type(y_train))
classifier.fit(X_train,y_train)
y_preds = classifier.predict(X_test)
for ele in y_test:
y_total.append(ele)
for ele in y_preds:
y_total_preds.append(ele)
y_pred_train = classifier.predict(X_train)
print(y_pred_train)
print(y_train)
count=count+1
print('accuracy_train:',accuracy_score(y_train, y_pred_train),'accuracy_test:',accuracy_score(y_test, y_preds))
print('TRAINING:')
print(classification_report( y_train, y_pred_train ))
print("TESTING:")
print(classification_report( y_test, y_preds ))
report = classification_report( y_total, y_total_preds )
cm=confusion_matrix(y_total, y_total_preds)
plt=plot_confusion_matrix(cm,normalize= True,target_names = ['NOT','HOF'],title = "Confusion Matrix")
plt.savefig('hin_task1'+model_type+'_'+img_name)
print(classifier)
print(report)
print(accuracy_score(y_total, y_total_preds))
df_result=pandas_classification_report(y_total,y_total_preds)
df_result.to_csv('hin_task1'+model_type+'_'+report_name, sep=',')
def get_model(scale,m_type=None):
if not m_type:
print("ERROR: Please specify a model type!")
return None
if m_type == 'decision_tree_classifier':
logreg = tree.DecisionTreeClassifier(max_features=1000,max_depth=3,class_weight='balanced')
elif m_type == 'gaussian':
logreg = GaussianNB()
elif m_type == 'logistic_regression':
logreg = LogisticRegression(n_jobs=10, random_state=42,class_weight='balanced',solver='liblinear')
elif m_type == 'MLPClassifier':
# logreg = neural_network.MLPClassifier((500))
logreg = neural_network.MLPClassifier((100),random_state=42,early_stopping=True)
elif m_type == 'KNeighborsClassifier':
# logreg = neighbors.KNeighborsClassifier(n_neighbors = 10)
logreg = neighbors.KNeighborsClassifier()
elif m_type == 'ExtraTreeClassifier':
logreg = tree.ExtraTreeClassifier()
elif m_type == 'ExtraTreeClassifier_2':
logreg = ensemble.ExtraTreesClassifier()
elif m_type == 'RandomForestClassifier':
logreg = ensemble.RandomForestClassifier(n_estimators=100, class_weight='balanced', n_jobs=12, max_depth=7)
elif m_type == 'SVC':
#logreg = LinearSVC(dual=False,max_iter=200)
logreg = SVC(kernel='linear',random_state=1526)
elif m_type == 'Catboost':
logreg = CatBoostClassifier(iterations=100,learning_rate=0.2,l2_leaf_reg=500,depth=10,use_best_model=False, random_state=42,scale_pos_weight=SCALE_POS_WEIGHT)
# logreg = CatBoostClassifier(scale_pos_weight=0.8, random_seed=42,);
elif m_type == 'XGB_classifier':
# logreg=XGBClassifier(silent=False,eta=0.1,objective='binary:logistic',max_depth=5,min_child_weight=0,gamma=0.2,subsample=0.8, colsample_bytree = 0.8,scale_pos_weight=1,n_estimators=500,reg_lambda=3,nthread=12)
logreg=XGBClassifier(silent=False,objective='binary:logistic',scale_pos_weight=SCALE_POS_WEIGHT,reg_lambda=3,nthread=12, random_state=42)
elif m_type == 'light_gbm':
logreg = LGBMClassifier(objective='binary',max_depth=3,learning_rate=0.2,num_leaves=20,scale_pos_weight=scale,boosting_type='gbdt',
metric='binary_logloss',random_state=5,reg_lambda=20,silent=False)
else:
print("give correct model")
print(logreg)
return logreg
models_name=['decision_tree_classifier','gaussian','logistic_regression','MLPClassifier','RandomForestClassifier',
'SVC','light_gbm']
for model in models_name:
train_model_no_ext(Classifier_Train_X,Classifier_Train_Y,model)
train_model_no_ext(Classifier_Train_X,Classifier_Train_Y,models_name[-1],save_model=True)
train_model_no_ext(Classifier_Train_X,Classifier_Train_Y,'SVC')
```
|
github_jupyter
|
```
# importing
import tensorflow as tf
import matplotlib.pyplot as plt
import os
# loading images
path_dir = "/content/drive/MyDrive/Dataset/malariya_cell_data_set/cell_images/"
loaded = 0
path = path_dir+"Uninfected/"
uninfected_list = os.listdir(path)
path = path_dir + "Parasitized"
infected_list = os.listdir(path)
img = plt.imread(path_dir+"Uninfected/"+uninfected_list[0])
plt.imshow(img)
img = plt.imread(path_dir+"Parasitized/"+infected_list[0])
plt.imshow(img)
# Kearas implementation
print("uninfected count: ",len(os.listdir(path_dir+"/Uninfected")))
print("Parasitized count: ",len(os.listdir(path_dir+"/Parasitized")))
dataGen = tf.keras.preprocessing.image.ImageDataGenerator(rescale=1/255.0,validation_split=0.2)
dataset_train = dataGen.flow_from_directory(path_dir,target_size=(128,128),batch_size=32,class_mode="binary",shuffle=True,seed=10,subset="training")
dataset_test = dataGen.flow_from_directory(path_dir,target_size=(128,128),batch_size=32,class_mode="binary",shuffle=True,seed=10,subset="validation")
# printintg the loaded classes
dataset_train
# designing the model
model = tf.keras.Sequential()
model.add(tf.keras.layers.Conv2D(32,(3,3),padding="same",input_shape=(128,128,3),activation=tf.keras.layers.LeakyReLU()))
model.add(tf.keras.layers.MaxPool2D(pool_size=(2,2),strides=2,padding="same"))
model.add(tf.keras.layers.Conv2D(64,(3,3),strides=(1,1),padding="same",input_shape=(128,128,3),activation=tf.keras.layers.LeakyReLU()))
model.add(tf.keras.layers.MaxPool2D(strides=2,padding="same"))
model.add(tf.keras.layers.Conv2D(128,(3,3),strides=(1,1),padding="same",input_shape=(128,128,3),activation=tf.keras.layers.LeakyReLU()))
model.add(tf.keras.layers.MaxPool2D(strides=2,padding="same"))
model.add(tf.keras.layers.Conv2D(256,3,strides=(1,1),padding="same",input_shape=(128,128,3),activation=tf.keras.layers.LeakyReLU()))
model.add(tf.keras.layers.MaxPool2D(strides=2,padding="same"))
model.add(tf.keras.layers.Flatten())
model.add(tf.keras.layers.Dense(128,activation=tf.keras.layers.LeakyReLU()))
model.add(tf.keras.layers.Dropout(0.2))
model.add(tf.keras.layers.Dense(64,activation=tf.keras.layers.LeakyReLU()))
model.add(tf.keras.layers.Dropout(0.2))
model.add(tf.keras.layers.Dense(1,activation='sigmoid'))
# compiling the model
model.compile(optimizer="adam",loss="binary_crossentropy",metrics=["accuracy"])
# model summary
model.summary()
# defining early stoping
early_stop = tf.keras.callbacks.EarlyStopping(monitor="val_loss",patience=2,verbose=1)
model_history = model.fit(dataset_train,epochs=20,callbacks=early_stop,validation_data=dataset_test)
plt.plot(model_history.history["accuracy"])
plt.plot(model_history.history["val_accuracy"])
plt.title("Model Accuracy")
plt.xlabel('epochs')
plt.ylabel('acuracy')
plt.show()
model.save("./malariya_classification_acc94.h5")
```
|
github_jupyter
|
# Homework 5: Problems
## Due Wednesday 28 October, before class
### PHYS 440/540, Fall 2020
https://github.com/gtrichards/PHYS_440_540/
## Problems 1&2
Complete Chapters 1 and 2 in the *unsupervised learning* course in Data Camp. The last video (and the two following code examples) in Chapter 2 are off topic, but we'll discuss those next week, so this will be a good intro. The rest is highly relevant to this week's material. These are worth 1000 and 900 points, respectively. I'll be grading on the number of points earned instead of completion (as I have been), so try to avoid using the hints unless you really need them.
## Problem 3
Fill in the blanks below. This exercise will take you though an example of everything that we did this week. Please copy the relevant import statements (below) to the cells where they are used (so that they can be run out of order).
If a question is calling for a word-based answer, I'm not looking for more than ~1 sentence.
---
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
from sklearn.metrics.cluster import homogeneity_score
from sklearn.datasets import make_blobs
from sklearn.neighbors import KernelDensity
from astroML.density_estimation import KNeighborsDensity
from sklearn.model_selection import GridSearchCV
from sklearn.mixture import GaussianMixture
from sklearn.cluster import KMeans
from sklearn.cluster import DBSCAN
```
Setup up the data set. We will do both density estimation and clustering on it.
```
from sklearn.datasets import make_blobs
#Make two blobs with 3 features and 1000 samples
N=1000
X,y = make_blobs(n_samples=N, centers=5, n_features=2, random_state=25)
plt.figure(figsize=(10,10))
plt.scatter(X[:, 0], X[:, 1], s=100, c=y)
```
Start with kernel density estimation, including a grid search to find the best bandwidth
```
bwrange = np.linspace(____,____,____) # Test 30 bandwidths from 0.1 to 1.0 ####
K = ____ # 5-fold cross validation ####
grid = GridSearchCV(KernelDensity(), {'bandwidth': ____}, cv=K) ####
grid.fit(X) #Fit the histogram data that we started the lecture with.
h_opt = ____.best_params_['bandwidth'] ####
print(h_opt)
kde = KernelDensity(kernel='gaussian', bandwidth=h_opt)
kde.fit(X) #fit the model to the data
u = v = np.linspace(-15,15,100)
Xgrid = np.vstack(map(np.ravel, np.meshgrid(u, v))).T
dens = np.exp(kde.score_samples(Xgrid)) #evaluate the model on the grid
plt.scatter(____[:,0],____[:,1], c=dens, cmap="Purples", edgecolor="None") ####
plt.colorbar()
```
---
Now try a nearest neighbors approach to estimating the density.
#### What value of $k$ do you need to make the plot look similar to the one above?
```
# Compute density with Bayesian nearest neighbors
k=____ ####
nbrs = KNeighborsDensity('bayesian',n_neighbors=____) ####
nbrs.____(X) ####
dens_nbrs = nbrs.eval(Xgrid) / N
plt.scatter(Xgrid[:,0],Xgrid[:,1], c=dens_nbrs, cmap="Purples", edgecolor="None")
plt.colorbar()
```
---
Now do a Gaussian mixture model. Do a grid search for between 1 and 10 components.
```
#Kludge to fix the bug with draw_ellipse in astroML v1.0
from matplotlib.patches import Ellipse
def draw_ellipse(mu, C, scales=[1, 2, 3], ax=None, **kwargs):
if ax is None:
ax = plt.gca()
# find principal components and rotation angle of ellipse
sigma_x2 = C[0, 0]
sigma_y2 = C[1, 1]
sigma_xy = C[0, 1]
alpha = 0.5 * np.arctan2(2 * sigma_xy,
(sigma_x2 - sigma_y2))
tmp1 = 0.5 * (sigma_x2 + sigma_y2)
tmp2 = np.sqrt(0.25 * (sigma_x2 - sigma_y2) ** 2 + sigma_xy ** 2)
sigma1 = np.sqrt(tmp1 + tmp2)
sigma2 = np.sqrt(tmp1 - tmp2)
for scale in scales:
ax.add_patch(Ellipse((mu[0], mu[1]),
2 * scale * sigma1, 2 * scale * sigma2,
alpha * 180. / np.pi,
**kwargs))
ncomps = np.arange(____,____,____) # Test 10 bandwidths from 1 to 10 ####
K = 5 # 5-fold cross validation
grid = ____(GaussianMixture(), {'n_components': ncomps}, cv=____) ####
grid.fit(X) #Fit the histogram data that we started the lecture with.
ncomp_opt = grid.____['n_components'] ####
print(ncomp_opt)
gmm = ____(n_components=ncomp_opt) ####
gmm.fit(X)
fig = plt.figure(figsize=(8, 8))
ax = fig.add_subplot(111)
ax.scatter(X[:,0],X[:,1])
ax.scatter(gmm.means_[:,0], gmm.means_[:,1], marker='s', c='red', s=80)
for mu, C, w in zip(gmm.means_, gmm.covariances_, gmm.weights_):
draw_ellipse(mu, 1*C, scales=[2], ax=ax, fc='none', ec='k') #2 sigma ellipses for each component
```
#### Do you get the same answer (the same number of components) each time you run it?
---
Now try Kmeans. Here we will scale the data.
```
kmeans = KMeans(n_clusters=5)
scaler = StandardScaler()
X_scaled = ____.____(X) ####
kmeans.fit(X_scaled)
centers=kmeans.____ #location of the clusters ####
labels=kmeans.predict(____) #labels for each of the points ####
centers_unscaled = scaler.____(centers) ####
fig,ax = plt.subplots(1,2,figsize=(16, 8))
ax[0].scatter(X[:,0],X[:,1],c=labels)
ax[0].scatter(centers_unscaled[:,0], centers_unscaled[:,1], marker='s', c='red', s=80)
ax[0].set_title("Predictions")
ax[1].scatter(X[:, 0], X[:, 1], c=y)
ax[1].set_title("Truth")
```
Let's evaluate how well we did in two other ways: a matrix and a score.
```
df = pd.DataFrame({'predictions': labels, 'truth': y})
ct = pd.crosstab(df['predictions'], df['truth'])
print(ct)
from sklearn.metrics.cluster import homogeneity_score
score = homogeneity_score(df['truth'], df['predictions'])
print(score)
```
#### What is the score for 3 clusters?
---
Finally, let's use DBSCAN. Note that outliers are flagged as `labels_=-1`, so there is one more class that you might think.
Full credit if you can get a score of 0.6 or above. Extra credit (0.1 of 5 points) for a score of 0.85 or above.
```
def plot_dbscan(dbscan, X, size, show_xlabels=True, show_ylabels=True):
core_mask = np.zeros_like(dbscan.labels_, dtype=bool)
core_mask[dbscan.core_sample_indices_] = True
anomalies_mask = dbscan.labels_ == -1
non_core_mask = ~(core_mask | anomalies_mask)
cores = dbscan.components_
anomalies = X[anomalies_mask]
non_cores = X[non_core_mask]
plt.scatter(cores[:, 0], cores[:, 1],
c=dbscan.labels_[core_mask], marker='o', s=size, cmap="Paired")
plt.scatter(cores[:, 0], cores[:, 1], marker='*', s=20, c=dbscan.labels_[core_mask])
plt.scatter(anomalies[:, 0], anomalies[:, 1],
c="r", marker="x", s=100)
plt.scatter(non_cores[:, 0], non_cores[:, 1], c=dbscan.labels_[non_core_mask], marker=".")
if show_xlabels:
plt.xlabel("$x_1$", fontsize=14)
else:
plt.tick_params(labelbottom=False)
if show_ylabels:
plt.ylabel("$x_2$", fontsize=14, rotation=0)
else:
plt.tick_params(labelleft=False)
plt.title("eps={:.2f}, min_samples={}".format(dbscan.eps, dbscan.min_samples), fontsize=14)
dbscan = DBSCAN(eps=0.15, min_samples=7)
dbscan.fit(X_scaled)
plt.figure(figsize=(10, 10))
plot_dbscan(dbscan, X_scaled, size=100)
n_clusters=np.unique(dbscan.labels_)
print(len(n_clusters)) #Number of clusters found (+1)
df2 = pd.DataFrame({'predictions': dbscan.labels_, 'truth': y})
ct2 = pd.crosstab(df2['predictions'], df2['truth'])
print(ct2)
from sklearn.metrics.cluster import homogeneity_score
score2 = homogeneity_score(df2['truth'], df2['predictions'])
print(score2)
```
#### Why do you think DBSCAN is having a hard time? Think about what the Gaussian Mixture Model result showed.
|
github_jupyter
|
### Dataset Source:
About this file
Boston House Price dataset
### columns:
* CRIM per capita crime rate by town
* ZN proportion of residential land zoned for lots over 25,000 sq.ft.
* INDUS proportion of non-retail business acres per town
* CHAS Charles River dummy variable (= 1 if tract bounds river; 0 otherwise)
* NOX nitric oxides concentration (parts per 10 million)
* RM average number of rooms per dwelling
* AGE proportion of owner-occupied units built prior to 1940
* DIS weighted distances to five Boston employment centres
* RAD index of accessibility to radial highways
* TAX full-value property-tax rate per 10,000
* PTRATIO pupil-teacher ratio by town
* B where Bk is the proportion of blacks by town
* LSTAT percentage lower status of the population
* MEDV Median value of owner-occupied homes in 1000$
### Load Modules
```
import numpy as np # linear algebra python library
import pandas as pd # data structure for tabular data.
import matplotlib.pyplot as plt # visualization library
%matplotlib inline
```
<br>
Loading data
```
filename = "housing.csv"
boston_data = pd.read_csv(filename, delim_whitespace=True, header=None)
header = ["CRIM","ZN","INDUS","CHAS","NOX","RM",
"AGE","DIS","RAD","TAX","PTRATIO","B","LSTAT","MEDV"]
boston_data.columns = header
# display the first 10 rows of dataframe.
boston_data.head(10)
```
<br>
Inspecting variable types
```
boston_data.dtypes
```
<p class="alert alert-warning">In many datasets, integer variables are cast as float. So, after inspecting
the data type of the variable, even if you get float as output, go ahead
and check the unique values to make sure that those variables are discrete
and not continuous.</p>
### Inspecting all variables
<br>
inspecting distinct values of `RAD`(index of accessibility to radial highways).
```
boston_data['RAD'].unique()
```
<br>
inspecting distinct values of `CHAS` Charles River dummy variable (= 1 if tract bounds river; 0 otherwise).
```
boston_data['CHAS'].unique()
```
<br>
#### inspecting the first 20 distinct values of all continous variables as following:
* CRIM per capita crime rate by town
* ZN proportion of residential land zoned for lots over 25,000 sq.ft.
* INDUS proportion of non-retail business acres per town
* NOX nitric oxides concentration (parts per 10 million)
* RM average number of rooms per dwelling
* AGE proportion of owner-occupied units built prior to 1940
* DIS weighted distances to five Boston employment centres
* TAX full-value property-tax rate per 10,000
* PTRATIO pupil-teacher ratio by town
* B where Bk is the proportion of blacks by town
* LSTAT percentage lower status of the population
* MEDV Median value of owner-occupied homes in 1000$
<br>
CRIM per capita crime rate by town.
```
boston_data['CRIM'].unique()[0:20]
```
<br>
ZN proportion of residential land zoned for lots over 25,000 sq.ft.
```
boston_data['ZN'].unique()[0:20]
```
<br>
INDUS proportion of non-retail business acres per town
```
boston_data['INDUS'].unique()[0:20]
```
<br>
NOX nitric oxides concentration (parts per 10 million)
```
boston_data['NOX'].unique()[0:20]
```
<br>
RM average number of rooms per dwelling
```
boston_data['RM'].unique()[0:20]
```
<br>
AGE proportion of owner-occupied units built prior to 1940
```
boston_data['AGE'].unique()[0:20]
```
<br>
DIS weighted distances to five Boston employment centres
```
boston_data['DIS'].unique()[0:20]
```
<br>
TAX full-value property-tax rate per 10,000
```
boston_data['TAX'].unique()[0:20]
```
<br>
PTRATIO pupil-teacher ratio by town
```
boston_data['PTRATIO'].unique()
```
<br>
B where Bk is the proportion of blacks by town
```
boston_data['B'].unique()[0:20]
```
<br>
LSTAT percentage lower status of the population
```
boston_data['LSTAT'].unique()[0:20]
```
<br>
MEDV Median value of owner-occupied homes in 1000$
```
boston_data['MEDV'].unique()[0:20]
```
<p class="alert alert-info" role="alert">after we checked the dat type of each variable. we have 2 discrete numerical variable and 10 floating or continuous variales.</p>
#### To understand wheather a variable is contious or discrete. we can also make a histogram for each:
* CRIM per capita crime rate by town
* ZN proportion of residential land zoned for lots over 25,000 sq.ft.
* INDUS proportion of non-retail business acres per town
* CHAS Charles River dummy variable (= 1 if tract bounds river; 0 otherwise)
* NOX nitric oxides concentration (parts per 10 million)
* RM average number of rooms per dwelling
* AGE proportion of owner-occupied units built prior to 1940
* DIS weighted distances to five Boston employment centres
* RAD index of accessibility to radial highways
* TAX full-value property-tax rate per 10,000
* PTRATIO pupil-teacher ratio by town
* B where Bk is the proportion of blacks by town
* LSTAT percentage lower status of the population
* MEDV Median value of owner-occupied homes in 1000$
<br>
making histogram for crime rate by town `CRIM` vatiable by dividing the variable range into intervals.
```
n_data = len(boston_data['CRIM'])
bins = int(np.sqrt(n_data))
boston_data['CRIM'].hist(bins=bins)
```
<br>
making histogram for proportion of residential land zoned for lots over 25,000 sq.ft `ZN`, variable by dividing the variable range into intervals.
```
n_data = len(boston_data['ZN'])
bins = int(np.sqrt(n_data))
boston_data['ZN'].hist(bins=bins)
```
<br>
making histogram for proportion of non-retail business acres per town `INDUS`, variable by dividing the variable range into intervals.
```
n_data = len(boston_data['INDUS'])
bins = int(np.sqrt(n_data))
boston_data['INDUS'].hist(bins=bins)
```
<br>
making histogram for nitric oxides concentration (parts per 10 million) `NOX`, variable by dividing the variable range into intervals.
```
n_data = len(boston_data['NOX'])
bins = int(np.sqrt(n_data))
boston_data['NOX'].hist(bins=bins)
```
<br>
making histogram for average number of rooms per dwelling `RM`, variable by dividing the variable range into intervals.
```
n_data = len(boston_data['RM'])
bins = int(np.sqrt(n_data))
boston_data['RM'].hist(bins=bins)
```
<br>
making histogram for proportion of owner-occupied units built prior to 1940 `AGE`, variable by dividing the variable range into intervals.
```
n_data = len(boston_data['AGE'])
bins = int(np.sqrt(n_data))
boston_data['AGE'].hist(bins=bins)
```
<br>
making histogram for weighted distances to five Boston employment centres `DIS`, variable by dividing the variable range into intervals.
```
n_data = len(boston_data['DIS'])
bins = int(np.sqrt(n_data))
boston_data['DIS'].hist(bins=bins)
```
<br>
making histogram for full-value property-tax rate per 10,000 `TAX`, variable by dividing the variable range into intervals.
```
n_data = len(boston_data['TAX'])
bins = int(np.sqrt(n_data))
boston_data['TAX'].hist(bins=bins)
```
<br>
making histogram for pupil-teacher ratio by town `PTRATIO`, variable by dividing the variable range into intervals.
```
n_data = len(boston_data['PTRATIO'])
bins = int(np.sqrt(n_data))
boston_data['PTRATIO'].hist(bins=bins)
```
<br>
making histogram where Bk is the proportion of blacks by town `B`, variable by dividing the variable range into intervals.
```
n_data = len(boston_data['B'])
bins = int(np.sqrt(n_data))
boston_data['B'].hist(bins=bins)
```
<br>
making histogram for percentage lower status of the population `LSTAT `, variable by dividing the variable range into intervals.
```
n_data = len(boston_data['LSTAT'])
bins = int(np.sqrt(n_data))
boston_data['LSTAT'].hist(bins=bins)
```
<br>
making histogram for Median value of owner-occupied homes in 1000$ ` MEDV`, variable by dividing the variable range into intervals.
```
n_data = len(boston_data['MEDV'])
bins = int(np.sqrt(n_data))
boston_data['MEDV'].hist(bins=bins)
```
<br>
<br>
making histogram for index of accessibility to radial highways`RAD`, variable by dividing the variable range into intervals.
```
n_data = len(boston_data['RAD'])
bins = int(np.sqrt(n_data))
boston_data['RAD'].hist(bins=bins)
```
<br>
<p class="alert alert-success">by taking a look to histogram of features we noticing that the continuous variables values range is not discrete.</p>
making histogram for Charles River dummy variable (= 1 if tract bounds river; 0 otherwise) ` CHAS`, variable by dividing the variable range into intervals.
```
n_data = len(boston_data['CHAS'])
bins = int(np.sqrt(n_data))
boston_data['CHAS'].hist(bins=bins)
```
<p class="alert alert-info">
we noticing here the values of this variable is discrete.
</p>
#### Quantifying Missing Data
calculating the missing values in the dataset.
```
boston_data.isnull().sum()
```
<p class="alert alert-info">There is no Missing Values</p>
<br>
#### Determining the cardinality in cateogrical varaibles
<br>
find unique values in each categorical variable
```
boston_data.nunique()
```
<p class="alert alert-info">The <b>nunique()</b> method ignores missing values by default. If we want to
consider missing values as an additional category, we should set the
dropna argument to <i>False</i>: <b>data.nunique(dropna=False).</b><p>
<br>
let's print out the unique category in Charles River dummy variable (= 1 if tract bounds river; 0 otherwise) ` CHAS`
```
boston_data['CHAS'].unique()
```
<p class="alert alert-info">pandas <b>nunique()</b> can be used in the entire dataframe. pandas
<b>unique()</b>, on the other hand, works only on a pandas Series. Thus, we
need to specify the column name that we want to return the unique values
for.</p>
<br>
```
boston_data[['CHAS','RAD']].nunique().plot.bar(figsize=(12,6))
plt.xlabel("Variables")
plt.ylabel("Number Of Unique Values")
plt.title("Cardinality")
plt.show()
```
|
github_jupyter
|
# 第5章 計算機を作る
## 5.1.2 スタックマシン
```
def calc(expression: str):
# 空白で分割して字句にする
tokens = expression.split()
stack = []
for token in tokens:
if token.isdigit():
# 数値はスタックに push する
stack.append(int(token))
continue
# 数値でないなら,演算子として処理する
x = stack.pop()
y = stack.pop()
if token == '+':
stack.append(x+y)
elif token == '*':
stack.append(x*y)
return stack.pop()
calc('1 2 + 2 3 + *')
# !pip install pegtree
import pegtree as pg
from pegtree.colab import peg, pegtree, example
```
構文木を表示するためには、graphviz があらかじめインストールされている必要がある。
```
%%peg
Expr = Prod ("+" Prod)*
Prod = Value ("*" Value)*
Value = { [0-9]+ #Int } _
example Expr 1+2+3
%%peg
Expr = { Prod ("+" Prod)* #Add }
Prod = { Value ("*" Value)* #Mul }
Value = { [0-9]+ #Int } _
example Expr 1+2+3
%%peg
Expr = Prod {^ "+" Prod #Add }*
Prod = Value {^ "*" Value #Mul }*
Value = { [0-9]+ #Int } _
example Expr 1+2+3
%%peg
Expr = Prod {^ "+" Prod #Add }*
Prod = Value {^ "*" Value #Mul }*
Value = "(" Expr ")" / Int
Int = { [0-9]+ #Int} _
example Expr 1+(2+3)
```
## PegTree によるパーザ生成
```
%%peg calc.pegtree
Start = Expr EOF // 未消費文字を構文エラーに
Expr = Prod ({^ "+" Prod #Add } / {^ "-" Prod #Sub } )*
Prod = Value ({^ "*" Value #Mul } / {^ "/" Value #Div } )*
Value = { [0-9]+ #Int} _ / "(" Expr ")"
example Expr 1+2*3
example Expr (1+2)*3
example Expr 1*2+3
```
## PegTree 文法のロード
```
peg = pg.grammar('calc.pegtree')
GRAMMAR = '''
Start = Expr EOF
Expr = Prod ({^ "+" Prod #Add } / {^ "-" Prod #Sub } )*
Prod = Value ({^ "*" Value #Mul } / {^ "/" Value #Div } )*
Value = { [0-9]+ #Int} _ / "(" Expr ")"
'''
peg = pg.grammar(GRAMMAR)
peg['Expr']
```
## 5.3.2 パーザの生成
```
parser = pg.generate(peg)
tree = parser('1+2')
print(repr(tree))
tree = parser('3@14')
print(repr(tree))
```
## 構文木とVisitor パターン
```
peg = pg.grammar('calc.pegtree')
parser = pg.generate(peg)
tree = parser('1+2*3')
tree.getTag()
len(tree)
left = tree[0]
left.getTag()
left = tree[0]
str(left)
def calc(tree):
tag = tree.getTag()
if tag == 'Add':
t0 = tree[0]
t1 = tree[1]
return calc(t0) + calc(t1)
if tag == 'Mul':
t0 = tree[0]
t1 = tree[1]
return calc(t0) * calc(t1)
if tag == 'Int':
token = tree.getToken()
return int(token)
print(f'TODO: {tag}') # 未実装のタグの報告
return 0
tree = parser('1+2*3')
print(calc(tree))
```
## Visitor パターン
```
class Visitor(object):
def visit(self, tree):
tag = tree.getTag()
name = f'accept{tag}'
if hasattr(self, name): # accept メソッドがあるか調べる
# メソッド名からメソッドを得る
acceptMethod = getattr(self, name)
return acceptMethod(tree)
print(f'TODO: accept{tag} method')
return None
class Calc(Visitor): # Visitor の継承
def __init__(self, parser):
self.parser = parser
def eval(self, source):
tree = self.parser(source)
return self.visit(tree)
def acceptInt(self, tree):
token = tree.getToken()
return int(token)
def acceptAdd(self, tree):
t0 = tree.get(0)
t1 = tree.get(1)
v0 = self.visit(t0)
v1 = self.visit(t1)
return v0 + v1
def acceptMul(self, tree):
t0 = tree.get(0)
t1 = tree.get(1)
v0 = self.visit(t0)
v1 = self.visit(t1)
return v0 * v1
def accepterr(self, tree):
print(repr(tree))
raise SyntaxError()
calc = Calc(parser)
print(calc.eval("1+2*3"))
print(calc.eval("(1+2)*3"))
print(calc.eval("1*2+3"))
calc.eval('1@2')
```
|
github_jupyter
|
# A Whirlwind Tour of Python
*Jake VanderPlas, Summer 2016*
These are the Jupyter Notebooks behind my O'Reilly report,
[*A Whirlwind Tour of Python*](http://www.oreilly.com/programming/free/a-whirlwind-tour-of-python.csp).
The full notebook listing is available [on Github](https://github.com/jakevdp/WhirlwindTourOfPython).
*A Whirlwind Tour of Python* is a fast-paced introduction to essential
components of the Python language for researchers and developers who are
already familiar with programming in another language.
The material is particularly aimed at those who wish to use Python for data
science and/or scientific programming, and in this capacity serves as an
introduction to my upcoming book, *The Python Data Science Handbook*.
These notebooks are adapted from lectures and workshops I've given on these
topics at University of Washington and at various conferences, meetings, and
workshops around the world.
## Index
1. [Introduction](00-Introduction.ipynb)
2. [How to Run Python Code](01-How-to-Run-Python-Code.ipynb)
3. [Basic Python Syntax](02-Basic-Python-Syntax.ipynb)
4. [Python Semantics: Variables](03-Semantics-Variables.ipynb)
5. [Python Semantics: Operators](04-Semantics-Operators.ipynb)
6. [Built-In Scalar Types](05-Built-in-Scalar-Types.ipynb)
7. [Built-In Data Structures](06-Built-in-Data-Structures.ipynb)
8. [Control Flow Statements](07-Control-Flow-Statements.ipynb)
9. [Defining Functions](08-Defining-Functions.ipynb)
10. [Errors and Exceptions](09-Errors-and-Exceptions.ipynb)
11. [Iterators](10-Iterators.ipynb)
12. [List Comprehensions](11-List-Comprehensions.ipynb)
13. [Generators and Generator Expressions](12-Generators.ipynb)
14. [Modules and Packages](13-Modules-and-Packages.ipynb)
15. [Strings and Regular Expressions](14-Strings-and-Regular-Expressions.ipynb)
16. [Preview of Data Science Tools](15-Preview-of-Data-Science-Tools.ipynb)
17. [Resources for Further Learning](16-Further-Resources.ipynb)
18. [Appendix: Code To Reproduce Figures](17-Figures.ipynb)
## License
This material is released under the "No Rights Reserved" [CC0](LICENSE)
license, and thus you are free to re-use, modify, build-on, and enhance
this material for any purpose.
That said, I request (but do not require) that if you use or adapt this material,
you include a proper attribution and/or citation; for example
> *A Whirlwind Tour of Python* by Jake VanderPlas (O’Reilly). Copyright 2016 O’Reilly Media, Inc., 978-1-491-96465-1
Read more about CC0 [here](https://creativecommons.org/share-your-work/public-domain/cc0/).
|
github_jupyter
|
```
epochs = 5
```
# Example - Simple Vertically Partitioned Split Neural Network
- <b>Alice</b>
- Has model Segment 1
- Has the handwritten Images
- <b>Bob</b>
- Has model Segment 2
- Has the image Labels
Based on [SplitNN - Tutorial 3](https://github.com/OpenMined/PySyft/blob/master/examples/tutorials/advanced/split_neural_network/Tutorial%203%20-%20Folded%20Split%20Neural%20Network.ipynb) from Adam J Hall - Twitter: [@AJH4LL](https://twitter.com/AJH4LL) · GitHub: [@H4LL](https://github.com/H4LL)
Authors:
- Pavlos Papadopoulos · GitHub: [@pavlos-p](https://github.com/pavlos-p)
- Tom Titcombe · GitHub: [@TTitcombe](https://github.com/TTitcombe)
- Robert Sandmann · GitHub: [@rsandmann](https://github.com/rsandmann)
```
class SplitNN:
def __init__(self, models, optimizers):
self.models = models
self.optimizers = optimizers
self.data = []
self.remote_tensors = []
def forward(self, x):
data = []
remote_tensors = []
data.append(self.models[0](x))
if data[-1].location == self.models[1].location:
remote_tensors.append(data[-1].detach().requires_grad_())
else:
remote_tensors.append(
data[-1].detach().move(self.models[1].location).requires_grad_()
)
i = 1
while i < (len(models) - 1):
data.append(self.models[i](remote_tensors[-1]))
if data[-1].location == self.models[i + 1].location:
remote_tensors.append(data[-1].detach().requires_grad_())
else:
remote_tensors.append(
data[-1].detach().move(self.models[i + 1].location).requires_grad_()
)
i += 1
data.append(self.models[i](remote_tensors[-1]))
self.data = data
self.remote_tensors = remote_tensors
return data[-1]
def backward(self):
for i in range(len(models) - 2, -1, -1):
if self.remote_tensors[i].location == self.data[i].location:
grads = self.remote_tensors[i].grad.copy()
else:
grads = self.remote_tensors[i].grad.copy().move(self.data[i].location)
self.data[i].backward(grads)
def zero_grads(self):
for opt in self.optimizers:
opt.zero_grad()
def step(self):
for opt in self.optimizers:
opt.step()
import sys
sys.path.append('../')
import torch
from torchvision import datasets, transforms
from torch import nn, optim
from torchvision.datasets import MNIST
from torchvision.transforms import ToTensor
import syft as sy
from src.dataloader import VerticalDataLoader
from src.psi.util import Client, Server
from src.utils import add_ids
hook = sy.TorchHook(torch)
# Create dataset
data = add_ids(MNIST)(".", download=True, transform=ToTensor()) # add_ids adds unique IDs to data points
# Batch data
dataloader = VerticalDataLoader(data, batch_size=128) # partition_dataset uses by default "remove_data=True, keep_order=False"
```
## Check if the datasets are unordered
In MNIST, we have 2 datasets (the images and the labels).
```
# We need matplotlib library to plot the dataset
import matplotlib.pyplot as plt
# Plot the first 10 entries of the labels and the dataset
figure = plt.figure()
num_of_entries = 10
for index in range(1, num_of_entries + 1):
plt.subplot(6, 10, index)
plt.axis('off')
plt.imshow(dataloader.dataloader1.dataset.data[index].numpy().squeeze(), cmap='gray_r')
print(dataloader.dataloader2.dataset[index][0], end=" ")
```
## Implement PSI and order the datasets accordingly
```
# Compute private set intersection
client_items = dataloader.dataloader1.dataset.get_ids()
server_items = dataloader.dataloader2.dataset.get_ids()
client = Client(client_items)
server = Server(server_items)
setup, response = server.process_request(client.request, len(client_items))
intersection = client.compute_intersection(setup, response)
# Order data
dataloader.drop_non_intersecting(intersection)
dataloader.sort_by_ids()
```
## Check again if the datasets are ordered
```
# We need matplotlib library to plot the dataset
import matplotlib.pyplot as plt
# Plot the first 10 entries of the labels and the dataset
figure = plt.figure()
num_of_entries = 10
for index in range(1, num_of_entries + 1):
plt.subplot(6, 10, index)
plt.axis('off')
plt.imshow(dataloader.dataloader1.dataset.data[index].numpy().squeeze(), cmap='gray_r')
print(dataloader.dataloader2.dataset[index][0], end=" ")
torch.manual_seed(0)
# Define our model segments
input_size = 784
hidden_sizes = [128, 640]
output_size = 10
models = [
nn.Sequential(
nn.Linear(input_size, hidden_sizes[0]),
nn.ReLU(),
nn.Linear(hidden_sizes[0], hidden_sizes[1]),
nn.ReLU(),
),
nn.Sequential(nn.Linear(hidden_sizes[1], output_size), nn.LogSoftmax(dim=1)),
]
# Create optimisers for each segment and link to them
optimizers = [
optim.SGD(model.parameters(), lr=0.03,)
for model in models
]
# create some workers
alice = sy.VirtualWorker(hook, id="alice")
bob = sy.VirtualWorker(hook, id="bob")
# Send Model Segments to model locations
model_locations = [alice, bob]
for model, location in zip(models, model_locations):
model.send(location)
#Instantiate a SpliNN class with our distributed segments and their respective optimizers
splitNN = SplitNN(models, optimizers)
def train(x, target, splitNN):
#1) Zero our grads
splitNN.zero_grads()
#2) Make a prediction
pred = splitNN.forward(x)
#3) Figure out how much we missed by
criterion = nn.NLLLoss()
loss = criterion(pred, target)
#4) Backprop the loss on the end layer
loss.backward()
#5) Feed Gradients backward through the nework
splitNN.backward()
#6) Change the weights
splitNN.step()
return loss, pred
for i in range(epochs):
running_loss = 0
correct_preds = 0
total_preds = 0
for (data, ids1), (labels, ids2) in dataloader:
# Train a model
data = data.send(models[0].location)
data = data.view(data.shape[0], -1)
labels = labels.send(models[-1].location)
# Call model
loss, preds = train(data, labels, splitNN)
# Collect statistics
running_loss += loss.get()
correct_preds += preds.max(1)[1].eq(labels).sum().get().item()
total_preds += preds.get().size(0)
print(f"Epoch {i} - Training loss: {running_loss/len(dataloader):.3f} - Accuracy: {100*correct_preds/total_preds:.3f}")
print("Labels pointing to: ", labels)
print("Images pointing to: ", data)
```
|
github_jupyter
|
## 1-3. 複数量子ビットの記述
ここまでは1量子ビットの状態とその操作(演算)の記述について学んできた。この章の締めくくりとして、$n$個の量子ビットがある場合の状態の記述について学んでいこう。テンソル積がたくさん出てきてややこしいが、コードをいじりながら身につけていってほしい。
$n$個の**古典**ビットの状態は$n$個の$0,1$の数字によって表現され、そのパターンの総数は$2^n$個ある。
量子力学では、これらすべてのパターンの重ね合わせ状態が許されているので、$n$個の**量子**ビットの状態$|\psi \rangle$はどのビット列がどのような重みで重ね合わせになっているかという$2^n$個の複素確率振幅で記述される:
$$
\begin{eqnarray}
|\psi \rangle &= &
c_{00...0} |00...0\rangle +
c_{00...1} |00...1\rangle + \cdots +
c_{11...1} |11...1\rangle =
\left(
\begin{array}{c}
c_{00...0}
\\
c_{00...1}
\\
\vdots
\\
c_{11...1}
\end{array}
\right).
\end{eqnarray}
$$
ただし、
複素確率振幅は規格化
$\sum _{i_1,..., i_n} |c_{i_1...i_n}|^2=1$
されているものとする。
そして、この$n$量子ビットの量子状態を測定するとビット列$i_1 ... i_n$が確率
$$
\begin{eqnarray}
p_{i_1 ... i_n} &=&|c_{i_1 ... i_n}|^2
\label{eq02}
\end{eqnarray}
$$
でランダムに得られ、測定後の状態は$|i_1 \dotsc i_n\rangle$となる。
**このように**$n$**量子ビットの状態は、**$n$**に対して指数的に大きい**$2^n$**次元の複素ベクトルで記述する必要があり、ここに古典ビットと量子ビットの違いが顕著に現れる**。
そして、$n$量子ビット系に対する操作は$2^n \times 2^n$次元のユニタリ行列として表される。
言ってしまえば、量子コンピュータとは、量子ビット数に対して指数的なサイズの複素ベクトルを、物理法則に従ってユニタリ変換するコンピュータのことなのである。
※ここで、複数量子ビットの順番と表記の関係について注意しておく。状態をケットで記述する際に、「1番目」の量子ビット、「2番目」の量子ビット、……の状態に対応する0と1を左から順番に並べて表記した。例えば$|011\rangle$と書けば、1番目の量子ビットが0、2番目の量子ビットが1、3番目の量子ビットが1である状態を表す。一方、例えば011を2進数の表記と見た場合、上位ビットが左、下位ビットが右となることに注意しよう。すなわち、一番左の0は最上位ビットであって$2^2$の位に対応し、真ん中の1は$2^1$の位、一番右の1は最下位ビットであって$2^0=1$の位に対応する。つまり、「$i$番目」の量子ビットは、$n$桁の2進数表記の$n-i+1$桁目に対応している。このことは、SymPyなどのパッケージで複数量子ビットを扱う際に気を付ける必要がある(下記「SymPyを用いた演算子のテンソル積」も参照)。
(詳細は Nielsen-Chuang の `1.2.1 Multiple qbits` を参照)
### 例:2量子ビットの場合
2量子ビットの場合は、 00, 01, 10, 11 の4通りの状態の重ね合わせをとりうるので、その状態は一般的に
$$
c_{00} |00\rangle + c_{01} |01\rangle + c_{10}|10\rangle + c_{11} |11\rangle =
\left(
\begin{array}{c}
c_{00}
\\
c_{01}
\\
c_{10}
\\
c_{11}
\end{array}
\right)
$$
とかける。
一方、2量子ビットに対する演算は$4 \times 4$行列で書け、各列と各行はそれぞれ $\langle00|,\langle01|,\langle10|, \langle11|, |00\rangle,|01\rangle,|10\rangle, |01\rangle$ に対応する。
このような2量子ビットに作用する演算としてもっとも重要なのが**制御NOT演算(CNOT演算)**であり、
行列表示では
$$
\begin{eqnarray}
\Lambda(X) =
\left(
\begin{array}{cccc}
1 & 0 & 0& 0
\\
0 & 1 & 0& 0
\\
0 & 0 & 0 & 1
\\
0 & 0 & 1& 0
\end{array}
\right)
\end{eqnarray}
$$
となる。
CNOT演算が2つの量子ビットにどのように作用するか見てみよう。まず、1つ目の量子ビットが$|0\rangle$の場合、$c_{10} = c_{11} = 0$なので、
$$
\Lambda(X)
\left(
\begin{array}{c}
c_{00}\\
c_{01}\\
0\\
0
\end{array}
\right) =
\left(
\begin{array}{c}
c_{00}\\
c_{01}\\
0\\
0
\end{array}
\right)
$$
となり、状態は変化しない。一方、1つ目の量子ビットが$|1\rangle$の場合、$c_{00} = c_{01} = 0$なので、
$$
\Lambda(X)
\left(
\begin{array}{c}
0\\
0\\
c_{10}\\
c_{11}
\end{array}
\right) =
\left(
\begin{array}{c}
0\\
0\\
c_{11}\\
c_{10}
\end{array}
\right)
$$
となり、$|10\rangle$と$|11\rangle$の確率振幅が入れ替わる。すなわち、2つ目の量子ビットが反転している。
つまり、CNOT演算は1つ目の量子ビットをそのままに保ちつつ、
- 1つ目の量子ビットが$|0\rangle$の場合は、2つ目の量子ビットにも何もしない(恒等演算$I$が作用)
- 1つ目の量子ビットが$|1\rangle$の場合は、2つ目の量子ビットを反転させる($X$が作用)
という効果を持つ。
そこで、1つ目の量子ビットを**制御量子ビット**、2つ目の量子ビットを**ターゲット量子ビット**と呼ぶ。
このCNOT演算の作用は、$\oplus$を mod 2の足し算、つまり古典計算における排他的論理和(XOR)とすると、
$$
\begin{eqnarray}
\Lambda(X) |ij \rangle = |i \;\; (i\oplus j)\rangle \:\:\: (i,j=0,1)
\end{eqnarray}
$$
とも書ける。よって、CNOT演算は古典計算でのXORを可逆にしたものとみなせる
(ユニタリー行列は定義$U^\dagger U = U U^\dagger = I$より可逆であることに注意)。
例えば、1つ目の量子ビットを$|0\rangle$と$|1\rangle$の
重ね合わせ状態にし、2つ目の量子ビットを$|0\rangle$として
$$
\begin{eqnarray}
\frac{1}{\sqrt{2}}(|0\rangle + |1\rangle )\otimes |0\rangle =
\frac{1}{\sqrt{2}}
\left(
\begin{array}{c}
1
\\
0
\\
1
\\
0
\end{array}
\right)
\end{eqnarray}
$$
にCNOTを作用させると、
$$
\begin{eqnarray}
\frac{1}{\sqrt{2}}( |00\rangle + |11\rangle ) =
\frac{1}{\sqrt{2}}
\left(
\begin{array}{c}
1
\\
0
\\
0
\\
1
\end{array}
\right)
\end{eqnarray}
$$
が得られ、2つ目の量子ビットがそのままである状態$|00\rangle$と反転された状態$|11\rangle$の重ね合わせになる。(記号$\otimes$については次節参照)
さらに、CNOT ゲートを組み合わせることで重要な2量子ビットゲートである**SWAP ゲート**を作ることができる。
$$\Lambda(X)_{i,j}$$
を$i$番目の量子ビットを制御、$j$番目の量子ビットをターゲットとするCNOT ゲートとして、
$$
\begin{align}
\mathrm{SWAP} &= \Lambda(X)_{1,2} \Lambda(X)_{2,1} \Lambda(X)_{1,2}\\
&=
\left(
\begin{array}{cccc}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1 \\
0 & 0 & 1 & 0
\end{array}
\right)
\left(
\begin{array}{cccc}
1 & 0 & 0 & 0 \\
0 & 0 & 0 & 1 \\
0 & 0 & 1 & 0 \\
0 & 1 & 0 & 0
\end{array}
\right)
\left(
\begin{array}{cccc}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1 \\
0 & 0 & 1 & 0
\end{array}
\right)\\
&=
\left(
\begin{array}{cccc}
1 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1
\end{array}
\right)
\end{align}
$$
のように書ける。これは1 番目の量子ビットと2 番目の量子ビットが交換するゲートであることが分かる。
このことは、上記のmod 2の足し算$\oplus$を使った表記で簡単に確かめることができる。3つのCNOTゲート$\Lambda(X)_{1,2} \Lambda(X)_{2,1} \Lambda(X)_{1,2}$の$|ij\rangle$への作用を1ステップずつ書くと、$i \oplus (i \oplus j) = (i \oplus i) \oplus j = 0 \oplus j = j$であることを使って、
$$
\begin{align}
|ij\rangle &\longrightarrow
|i \;\; (i\oplus j)\rangle\\
&\longrightarrow
|(i\oplus (i\oplus j)) \;\; (i\oplus j)\rangle =
|j \;\; (i\oplus j)\rangle\\
&\longrightarrow
|j \;\; (j\oplus (i\oplus j))\rangle =
|ji\rangle
\end{align}
$$
となり、2つの量子ビットが交換されていることが分かる。
(詳細は Nielsen-Chuang の `1.3.2 Multiple qbit gates` を参照)
### テンソル積の計算
手計算や解析計算で威力を発揮するのは、**テンソル積**($\otimes$)である。
これは、複数の量子ビットがある場合に、それをどのようにして、上で見た大きな一つのベクトルへと変換するのか?という計算のルールを与えてくれる。
量子力学の世界では、2つの量子系があってそれぞれの状態が$|\psi \rangle$と$|\phi \rangle$のとき、
$$
|\psi \rangle \otimes |\phi\rangle
$$
とテンソル積 $\otimes$ を用いて書く。このような複数の量子系からなる系のことを**複合系**と呼ぶ。例えば2量子ビット系は複合系である。
基本的にはテンソル積は、**多項式と同じような計算ルール**で計算してよい。
例えば、
$$
(\alpha |0\rangle + \beta |1\rangle )\otimes (\gamma |0\rangle + \delta |1\rangle )
= \alpha \gamma |0\rangle |0\rangle + \alpha \delta |0\rangle |1\rangle + \beta \gamma |1 \rangle | 0\rangle + \beta \delta |1\rangle |1\rangle
$$
のように計算する。列ベクトル表示すると、$|00\rangle$, $|01\rangle$, $|10\rangle$, $|11\rangle$に対応する4次元ベクトル、
$$
\left(
\begin{array}{c}
\alpha
\\
\beta
\end{array}
\right)
\otimes
\left(
\begin{array}{c}
\gamma
\\
\delta
\end{array}
\right) =
\left(
\begin{array}{c}
\alpha \gamma
\\
\alpha \delta
\\
\beta \gamma
\\
\beta \delta
\end{array}
\right)
$$
を得る計算になっている。
### SymPyを用いたテンソル積の計算
```
from IPython.display import Image, display_png
from sympy import *
from sympy.physics.quantum import *
from sympy.physics.quantum.qubit import Qubit,QubitBra
from sympy.physics.quantum.gate import X,Y,Z,H,S,T,CNOT,SWAP, CPHASE
init_printing() # ベクトルや行列を綺麗に表示するため
# Google Colaboratory上でのみ実行してください
from IPython.display import HTML
def setup_mathjax():
display(HTML('''
<script>
if (!window.MathJax && window.google && window.google.colab) {
window.MathJax = {
'tex2jax': {
'inlineMath': [['$', '$'], ['\\(', '\\)']],
'displayMath': [['$$', '$$'], ['\\[', '\\]']],
'processEscapes': true,
'processEnvironments': true,
'skipTags': ['script', 'noscript', 'style', 'textarea', 'code'],
'displayAlign': 'center',
},
'HTML-CSS': {
'styles': {'.MathJax_Display': {'margin': 0}},
'linebreaks': {'automatic': true},
// Disable to prevent OTF font loading, which aren't part of our
// distribution.
'imageFont': null,
},
'messageStyle': 'none'
};
var script = document.createElement("script");
script.src = "https://colab.research.google.com/static/mathjax/MathJax.js?config=TeX-AMS_HTML-full,Safe";
document.head.appendChild(script);
}
</script>
'''))
get_ipython().events.register('pre_run_cell', setup_mathjax)
a,b,c,d = symbols('alpha,beta,gamma,delta')
psi = a*Qubit('0')+b*Qubit('1')
phi = c*Qubit('0')+d*Qubit('1')
TensorProduct(psi, phi) #テンソル積
represent(TensorProduct(psi, phi))
```
さらに$|\psi\rangle$とのテンソル積をとると8次元のベクトルになる:
```
represent(TensorProduct(psi,TensorProduct(psi, phi)))
```
### 演算子のテンソル積
演算子についても何番目の量子ビットに作用するのか、というのをテンソル積をもちいて表現することができる。たとえば、1つめの量子ビットには$A$という演算子、2つめの量子ビットには$B$という演算子を作用させるという場合には、
$$ A \otimes B$$
としてテンソル積演算子が与えられる。
$A$と$B$をそれぞれ、2×2の行列とすると、$A\otimes B$は4×4の行列として
$$
\left(
\begin{array}{cc}
a_{11} & a_{12}
\\
a_{21} & a_{22}
\end{array}
\right)
\otimes
\left(
\begin{array}{cc}
b_{11} & b_{12}
\\
b_{21} & b_{22}
\end{array}
\right) =
\left(
\begin{array}{cccc}
a_{11} b_{11} & a_{11} b_{12} & a_{12} b_{11} & a_{12} b_{12}
\\
a_{11} b_{21} & a_{11} b_{22} & a_{12} b_{21} & a_{12} b_{22}
\\
a_{21} b_{11} & a_{21} b_{12} & a_{22} b_{11} & a_{22} b_{12}
\\
a_{21} b_{21} & a_{21} b_{22} & a_{22} b_{21} & a_{22} b_{22}
\end{array}
\right)
$$
のように計算される。
テンソル積状態
$$|\psi \rangle \otimes | \phi \rangle $$
に対する作用は、
$$ (A|\psi \rangle ) \otimes (B |\phi \rangle )$$
となり、それぞれの部分系$|\psi \rangle$と$|\phi\rangle$に$A$と$B$が作用する。
足し算に対しては、多項式のように展開してそれぞれの項を作用させればよい。
$$
(A+C)\otimes (B+D) |\psi \rangle \otimes | \phi \rangle =
(A \otimes B +A \otimes D + C \otimes B + C \otimes D) |\psi \rangle \otimes | \phi \rangle\\ =
(A|\psi \rangle) \otimes (B| \phi \rangle)
+(A|\psi \rangle) \otimes (D| \phi \rangle)
+(C|\psi \rangle) \otimes (B| \phi \rangle)
+(C|\psi \rangle) \otimes (D| \phi \rangle)
$$
テンソル積やテンソル積演算子は左右横並びで書いているが、本当は
$$
\left(
\begin{array}{c}
A
\\
\otimes
\\
B
\end{array}
\right)
\begin{array}{c}
|\psi \rangle
\\
\otimes
\\
|\phi\rangle
\end{array}
$$
のように縦に並べた方がその作用の仕方がわかりやすいのかもしれない。
例えば、CNOT演算を用いて作られるエンタングル状態は、
$$
\left(
\begin{array}{c}
|0\rangle \langle 0|
\\
\otimes
\\
I
\end{array}
+
\begin{array}{c}
|1\rangle \langle 1|
\\
\otimes
\\
X
\end{array}
\right)
\left(
\begin{array}{c}
\frac{1}{\sqrt{2}}(|0\rangle + |1\rangle)
\\
\otimes
\\
|0\rangle
\end{array}
\right) =
\frac{1}{\sqrt{2}}\left(
\begin{array}{c}
|0 \rangle
\\
\otimes
\\
|0\rangle
\end{array}
+
\begin{array}{c}
|1 \rangle
\\
\otimes
\\
|1\rangle
\end{array}
\right)
$$
のようになる。
### SymPyを用いた演算子のテンソル積
SymPyで演算子を使用する時は、何桁目の量子ビットに作用する演算子かを常に指定する。「何**番目**」ではなく2進数表記の「何**桁目**」であることに注意しよう。$n$量子ビットのうちの左から$i$番目の量子ビットを指定する場合、SymPyのコードでは`n-i`を指定する(0を基点とするインデックス)。
`H(0)` は、1量子ビット空間で表示すると
```
represent(H(0),nqubits=1)
```
2量子ビット空間では$H \otimes I$に対応しており、その表示は
```
represent(H(1),nqubits=2)
```
CNOT演算は、
```
represent(CNOT(1,0),nqubits=2)
```
パウリ演算子のテンソル積$X\otimes Y \otimes Z$も、
```
represent(X(2)*Y(1)*Z(0),nqubits=3)
```
このようにして、上記のテンソル積のルールを実際にたしかめてみることができる。
### 複数の量子ビットの一部分だけを測定した場合
複数の量子ビットを全て測定した場合の測定結果の確率については既に説明した。複数の量子ビットのうち、一部だけを測定することもできる。その場合、測定結果の確率は、測定結果に対応する(部分系の)基底で射影したベクトルの長さの2乗になり、測定後の状態は射影されたベクトルを規格化したものになる。
具体的に見ていこう。以下の$n$量子ビットの状態を考える。
\begin{align}
|\psi\rangle &=
c_{00...0} |00...0\rangle +
c_{00...1} |00...1\rangle + \cdots +
c_{11...1} |11...1\rangle\\
&= \sum_{i_1 \dotsc i_n} c_{i_1 \dotsc i_n} |i_1 \dotsc i_n\rangle =
\sum_{i_1 \dotsc i_n} c_{i_1 \dotsc i_n} |i_1\rangle \otimes \cdots \otimes |i_n\rangle
\end{align}
1番目の量子ビットを測定するとしよう。1つ目の量子ビットの状態空間の正規直交基底$|0\rangle$, $|1\rangle$に対する射影演算子はそれぞれ$|0\rangle\langle0|$, $|1\rangle\langle1|$と書ける。1番目の量子ビットを$|0\rangle$に射影し、他の量子ビットには何もしない演算子
$$
|0\rangle\langle0| \otimes I \otimes \cdots \otimes I
$$
を使って、測定値0が得られる確率は
$$
\bigl\Vert \bigl(|0\rangle\langle0| \otimes I \otimes \cdots \otimes I\bigr) |\psi\rangle \bigr\Vert^2 =
\langle \psi | \bigl(|0\rangle\langle0| \otimes I \otimes \cdots \otimes I\bigr) | \psi \rangle
$$
である。ここで
$$
\bigl(|0\rangle\langle0| \otimes I \otimes \cdots \otimes I\bigr) | \psi \rangle =
\sum_{i_2 \dotsc i_n} c_{0 i_2 \dotsc i_n} |0\rangle \otimes |i_2\rangle \otimes \cdots \otimes |i_n\rangle
$$
なので、求める確率は
$$
p_0 = \sum_{i_2 \dotsc i_n} |c_{0 i_2 \dotsc i_n}|^2
$$
となり、測定後の状態は
$$
\frac{1}{\sqrt{p_0}}\sum_{i_2 \dotsc i_n} c_{0 i_2 \dotsc i_n} |0\rangle \otimes |i_2\rangle \otimes \cdots \otimes |i_n\rangle
$$
となる。0と1を入れ替えれば、測定値1が得られる確率と測定後の状態が得られる。
ここで求めた$p_0$, $p_1$の表式は、測定値$i_1, \dotsc, i_n$が得られる同時確率分布$p_{i_1, \dotsc, i_n}$から計算される$i_1$の周辺確率分布と一致することに注意しよう。実際、
$$
\sum_{i_2, \dotsc, i_n} p_{i_1, \dotsc, i_n} = \sum_{i_2, \dotsc, i_n} |c_{i_1, \dotsc, i_n}|^2 = p_{i_1}
$$
である。
測定される量子ビットを増やし、最初の$k$個の量子ビットを測定する場合も同様に計算できる。測定結果$i_1, \dotsc, i_k$を得る確率は
$$
p_{i_1, \dotsc, i_k} = \sum_{i_{k+1}, \dotsc, i_n} |c_{i_1, \dotsc, i_n}|^2
$$
であり、測定後の状態は
$$
\frac{1}{\sqrt{p_{i_1, \dotsc, i_k}}}\sum_{i_{k+1} \dotsc i_n} c_{i_1 \dotsc i_n} |i_1 \rangle \otimes \cdots \otimes |i_n\rangle
$$
となる。(和をとるのは$i_{k+1},\cdots,i_n$だけであることに注意)
SymPyを使ってさらに具体的な例を見てみよう。H演算とCNOT演算を組み合わせて作られる次の状態を考える。
$$
|\psi\rangle = \Lambda(X) (H \otimes H) |0\rangle \otimes |0\rangle = \frac{|00\rangle + |10\rangle + |01\rangle + |11\rangle}{2}
$$
```
psi = qapply(CNOT(1, 0)*H(1)*H(0)*Qubit('00'))
psi
```
この状態の1つ目の量子ビットを測定して0になる確率は
$$
p_0 = \langle \psi | \bigl( |0\rangle\langle0| \otimes I \bigr) | \psi \rangle =
\left(\frac{\langle 00 | + \langle 10 | + \langle 01 | + \langle 11 |}{2}\right)
\left(\frac{| 00 \rangle + | 01 \rangle}{2}\right) =
\frac{1}{2}
$$
で、測定後の状態は
$$
\frac{1}{\sqrt{p_0}} \bigl( |0\rangle\langle0| \otimes I \bigr) | \psi \rangle =
\frac{| 00 \rangle + | 01 \rangle}{\sqrt{2}}
$$
である。
この結果をSymPyでも計算してみよう。SymPyには測定用の関数が数種類用意されていて、一部の量子ビットを測定した場合の確率と測定後の状態を計算するには、`measure_partial`を用いればよい。測定する状態と、測定を行う量子ビットのインデックスを引数として渡すと、測定後の状態と測定の確率の組がリストとして出力される。1つめの量子ビットが0だった場合の量子状態と確率は`[0]`要素を参照すればよい。
```
from sympy.physics.quantum.qubit import measure_all, measure_partial
measured_state_and_probability = measure_partial(psi, (1,))
measured_state_and_probability[0]
```
上で手計算した結果と合っていることが分かる。測定結果が1だった場合も同様に計算できる。
```
measured_state_and_probability[1]
```
---
## コラム:ユニバーサルゲートセットとは
古典計算機では、NANDゲート(論理積ANDの出力を反転したもの)さえあれば、これをいくつか組み合わせることで、任意の論理演算が実行できることが知られている。
それでは、量子計算における対応物、すなわち任意の量子計算を実行するために最低限必要な量子ゲートは何であろうか?
実は、本節で学んだ
$$\{H, T, {\rm CNOT} \}$$
の3種類のゲートがその役割を果たしている、いわゆる**ユニバーサルゲートセット**であることが知られている。
これらをうまく組み合わせることで、任意の量子計算を実行できる、すなわち「**万能量子計算**」が可能である。
### 【より詳しく知りたい人のための注】
以下では$\{H, T, {\rm CNOT} \}$の3種のゲートの組が如何にしてユニバーサルゲートセットを構成するかを、順を追って説明する。
流れとしては、一般の$n$量子ビットユニタリ演算からスタートし、これをより細かい部品にブレイクダウンしていくことで、最終的に上記3種のゲートに行き着くことを見る。
#### ◆ $n$量子ビットユニタリ演算の分解
まず、任意の$n$量子ビットユニタリ演算は、以下の手順を経て、いくつかの**1量子ビットユニタリ演算**と**CNOTゲート**に分解できる。
1. 任意の$n$量子ビットユニタリ演算は、いくつかの**2準位ユニタリ演算**の積に分解できる。ここで2準位ユニタリ演算とは、例として3量子ビットの場合、$2^3=8$次元空間のうち2つの基底(e.g., $\{|000\rangle, |111\rangle \}$)の張る2次元部分空間にのみ作用するユニタリ演算である
2. 任意の2準位ユニタリ演算は、**制御**$U$**ゲート**(CNOTゲートのNOT部分を任意の1量子ビットユニタリ演算$U$に置き換えたもの)と**Toffoliゲート**(CNOTゲートの制御量子ビットが2つになったもの)から構成できる
3. 制御$U$ゲートとToffoliゲートは、どちらも**1量子ビットユニタリ演算**と**CNOTゲート**から構成できる
#### ◆ 1量子ビットユニタリ演算の構成
さらに、任意の1量子ビットユニタリ演算は、$\{H, T\}$の2つで構成できる。
1. 任意の1量子ビットユニタリ演算は、オイラーの回転角の法則から、回転ゲート$\{R_X(\theta), R_Z(\theta)\}$で(厳密に)実現可能である
2. 実は、ブロッホ球上の任意の回転は、$\{H, T\}$のみを用いることで実現可能である(注1)。これはある軸に関する$\pi$の無理数倍の回転が$\{H, T\}$のみから実現できること(**Solovay-Kitaevアルゴリズム**)に起因する
(注1) ブロッホ球上の連続的な回転を、離散的な演算である$\{H, T\}$で実現できるか疑問に思われる読者もいるかもしれない。実際、厳密な意味で1量子ビットユニタリ演算を離散的なゲート操作で実現しようとすると、無限個のゲートが必要となる。しかし実際には厳密なユニタリ演算を実現する必要はなく、必要な計算精度$\epsilon$で任意のユニタリ演算を近似できれば十分である。ここでは、多項式個の$\{H, T\}$を用いることで、任意の1量子ビットユニタリ演算を**十分良い精度で近似的に構成できる**ことが、**Solovay-Kitaevの定理** [3] により保証されている。
<br>
以上の議論により、3種のゲート$\{H, T, {\rm CNOT} \}$があれば、任意の$n$量子ビットユニタリ演算が実現できることがわかる。
ユニバーサルゲートセットや万能量子計算について、より詳しくは以下を参照されたい:
[1] Nielsen-Chuang の `4.5 Universal quantum gates`
[2] 藤井 啓祐 「量子コンピュータの基礎と物理との接点」(第62回物性若手夏の学校 講義)DOI: 10.14989/229039 http://mercury.yukawa.kyoto-u.ac.jp/~bussei.kenkyu/archives/1274.html
[3] レビューとして、C. M. Dawson, M. A. Nielsen, “The Solovay-Kitaev algorithm“, https://arxiv.org/abs/quant-ph/0505030
|
github_jupyter
|
```
%matplotlib inline
from __future__ import print_function, unicode_literals
import sys, os
import seaborn as sns
import numpy as np
import matplotlib
from matplotlib import pyplot as plt
from pygaarst import raster
sys.path.append('../firedetection/')
import landsat8fire as lfire
sns.set(rc={'image.cmap': 'gist_heat'})
sns.set(rc={'image.cmap': 'bone'})
sns.set_context("poster")
myfontsize = 20
font = {'family' : 'Calibri',
'weight': 'bold',
'size' : myfontsize}
matplotlib.rc('font', **font)
matplotlib.axes.rcParams['axes.labelsize']=myfontsize-4
matplotlib.axes.rcParams['axes.titlesize']=myfontsize
cmap1 = matplotlib.colors.ListedColormap(sns.xkcd_palette(['white', 'red']))
cmap2 = matplotlib.colors.ListedColormap(sns.xkcd_palette(['white', 'neon green']))
cmap3 = matplotlib.colors.ListedColormap(sns.xkcd_palette(['white', 'orange']))
landsatpath = '/Volumes/SCIENCE_mobile_Mac/Fire/DATA_BY_PROJECT/2015VIIRSMODIS/Landsat/L8 OLI_TIRS Sockeye'
lsscene = 'LC80700172015166LGN00'
landsat = raster.Landsatscene(os.path.join(landsatpath, lsscene))
landsat.infix = '_clip'
rho7 = landsat.band7.reflectance
rho6 = landsat.band6.reflectance
rho5 = landsat.band5.reflectance
rho4 = landsat.band4.reflectance
rho3 = landsat.band3.reflectance
rho2 = landsat.band2.reflectance
rho1 = landsat.band1.reflectance
R75 = rho7/rho5
R76 = rho7/rho6
xmax = landsat.band7.ncol
ymax = landsat.band7.nrow
```
"Unambiguous fire pixels" test 1 (daytime, normal conditions).
```
firecond1 = np.logical_and(R75 > 2.5, rho7 > .5)
firecond1 = np.logical_and(firecond1, rho7 - rho5 > .3)
firecond1_masked = np.ma.masked_where(
~firecond1, np.ones((ymax, xmax)))
```
"Unambiguous fire pixels" test 2 (daytime, sensor anomalies)
```
firecond2 = np.logical_and(rho6 > .8, rho1 < .2)
firecond2 = np.logical_and(firecond2,
np.logical_or(rho5 > .4, rho7 < .1)
)
firecond2_masked = np.ma.masked_where(
~firecond2, np.ones((ymax, xmax)))
```
"Relaxed conditions"
```
firecond3 = np.logical_and(R75 > 1.8, rho7 - rho5 > .17)
firecond3_masked = np.ma.masked_where(
~firecond3, np.ones((ymax, xmax)))
```
"Extra tests" for relaxed conditions:
1. R76 > 1.6
2. R75 at least 3 sigma and 0.8 larger than avg of a 61x61 window of valid pixels
3. rho7 at least 3 sigma and 0.08 larger than avg of a 61x61 window of valid pixels
Valid pixels are:
1. Not "unambiguous fire pixel"
2. rho7 > 0
3. Not water as per water test 1: rho4 > rho5 AND rho5 > rho6 AND rho6 > rho7 AND rho1 - rho7 < 0.2
4. Not water as per test 2: rho3 > rho2 OR ( rho1 > rho2 AND rho2 > rho3 AND rho3 > rho4 )
So let's get started on the validation tests...
```
newfirecandidates = np.logical_and(~firecond1, ~firecond2)
newfirecandidates = np.logical_and(newfirecandidates, firecond3)
newfirecandidates = np.logical_and(newfirecandidates, R76 > 0)
sum(sum(newfirecandidates))
```
We'll need a +-30 pixel window around a coordinate pair to carry out the averaging for the contextual tests
```
iidxmax, jidxmax = landsat.band1.data.shape
def get_window(ii, jj, N, iidxmax, jidxmax):
"""Return 2D Boolean array that is True where a window of size N
around a given point is masked out """
imin = max(0, ii-N)
imax = min(iidxmax, ii+N)
jmin = max(0, jj-N)
jmax = min(jidxmax, jj+N)
mask1 = np.zeros((iidxmax, jidxmax))
mask1[imin:imax+1, jmin:jmax+1] = 1
return mask1 == 1
plt.imshow(get_window(100, 30, 30, iidxmax, jidxmax) , cmap=cmap3, vmin=0, vmax=1)
```
We can then get the union of those windows over all detected fire pixel candidates.
```
windows = [get_window(ii, jj, 30, iidxmax, jidxmax) for ii, jj in np.argwhere(newfirecandidates)]
window = np.any(windows, axis=0)
plt.imshow(window , cmap=cmap3, vmin=0, vmax=1)
```
We also need a water mask...
```
def get_l8watermask_frombands(
rho1, rho2, rho3,
rho4, rho5, rho6, rho7):
"""
Takes L8 bands, returns 2D Boolean numpy array of same shape
"""
turbidwater = get_l8turbidwater(rho1, rho2, rho3, rho4, rho5, rho6, rho7)
deepwater = get_l8deepwater(rho1, rho2, rho3, rho4, rho5, rho6, rho7)
return np.logical_or(turbidwater, deepwater)
def get_l8commonwater(rho1, rho4, rho5, rho6, rho7):
"""Returns Boolean numpy array common to turbid and deep water schemes"""
water1cond = np.logical_and(rho4 > rho5, rho5 > rho6)
water1cond = np.logical_and(water1cond, rho6 > rho7)
water1cond = np.logical_and(water1cond, rho1 - rho7 < 0.2)
return water1cond
def get_l8turbidwater(rho1, rho2, rho3, rho4, rho5, rho6, rho7):
"""Returns Boolean numpy array that marks shallow, turbid water"""
watercond2 = get_l8commonwater(rho1, rho4, rho5, rho6, rho7)
watercond2 = np.logical_and(watercond2, rho3 > rho2)
return watercond2
def get_l8deepwater(rho1, rho2, rho3, rho4, rho5, rho6, rho7):
"""Returns Boolean numpy array that marks deep, clear water"""
watercond3 = get_l8commonwater(rho1, rho4, rho5, rho6, rho7)
watercondextra = np.logical_and(rho1 > rho2, rho2 > rho3)
watercondextra = np.logical_and(watercondextra, rho3 > rho4)
return np.logical_and(watercond3, watercondextra)
water = get_l8watermask_frombands(rho1, rho2, rho3, rho4, rho5, rho6, rho7)
plt.imshow(~water , cmap=cmap3, vmin=0, vmax=1)
```
Let's try out the two components, out of interest... apparently, only the "deep water" test catches the water bodies here.
```
turbidwater = get_l8turbidwater(rho1, rho2, rho3, rho4, rho5, rho6, rho7)
deepwater = get_l8deepwater(rho1, rho2, rho3, rho4, rho5, rho6, rho7)
plt.imshow(~turbidwater , cmap=cmap3, vmin=0, vmax=1)
plt.show()
plt.imshow(~deepwater , cmap=cmap3, vmin=0, vmax=1)
def get_valid_pixels(otherfirecond, rho1, rho2, rho3,
rho4, rho5, rho6, rho7, mask=None):
"""returns masked array of 1 for valid, 0 for not"""
if not np.any(mask):
mask = np.zeros(otherfirecond.shape)
rho = {}
for rho in [rho1, rho2, rho3, rho4, rho5, rho6, rho7]:
rho = np.ma.masked_array(rho, mask=mask)
watercond = get_l8watermask_frombands(
rho1, rho2, rho3,
rho4, rho5, rho6, rho7)
greater0cond = rho7 > 0
finalcond = np.logical_and(greater0cond, ~watercond)
finalcond = np.logical_and(finalcond, ~otherfirecond)
return np.ma.masked_array(finalcond, mask=mask)
otherfirecond = np.logical_or(firecond1, firecond2)
validpix = get_valid_pixels(otherfirecond, rho1, rho2, rho3,
rho4, rho5, rho6, rho7, mask=~window)
fig1 = plt.figure(1, figsize=(15, 15))
ax1 = fig1.add_subplot(111)
ax1.set_aspect('equal')
ax1.pcolormesh(np.flipud(validpix), cmap=cmap3, vmin=0, vmax=1)
iidxmax, jidxmax = landsat.band1.data.shape
output = np.zeros((iidxmax, jidxmax))
for ii, jj in np.argwhere(firecond3):
window = get_window(ii, jj, 30, iidxmax, jidxmax)
newmask = np.logical_or(~window, ~validpix.data)
rho7_win = np.ma.masked_array(rho7, mask=newmask)
R75_win = np.ma.masked_array(rho7/rho5, mask=newmask)
rho7_bar = np.mean(rho7_win.flatten())
rho7_std = np.std(rho7_win.flatten())
R75_bar = np.mean(R75_win.flatten())
R75_std = np.std(R75_win.flatten())
rho7_test = rho7_win[ii, jj] - rho7_bar > max(3*rho7_std, 0.08)
R75_test = R75_win[ii, jj]- R75_bar > max(3*R75_std, 0.8)
if rho7_test and R75_test:
output[ii, jj] = 1
lowfirecond = output == 1
sum(sum(lowfirecond))
fig1 = plt.figure(1, figsize=(15, 15))
ax1 = fig1.add_subplot(111)
ax1.set_aspect('equal')
ax1.pcolormesh(np.flipud(lowfirecond), cmap=cmap1, vmin=0, vmax=1)
fig1 = plt.figure(1, figsize=(15, 15))
ax1 = fig1.add_subplot(111)
ax1.set_aspect('equal')
ax1.pcolormesh(np.flipud(firecond1), cmap=cmap3, vmin=0, vmax=1)
allfirecond = np.logical_or(firecond1, firecond2)
allfirecond = np.logical_or(allfirecond, lowfirecond)
fig1 = plt.figure(1, figsize=(15, 15))
ax1 = fig1.add_subplot(111)
ax1.set_aspect('equal')
ax1.pcolormesh(np.flipud(allfirecond), cmap=cmap1, vmin=0, vmax=1)
```
So this works! Now we can do the same using the module that incorporates the above code:
```
testfire, highfire, anomfire, lowfire = lfire.get_l8fire(landsat)
sum(sum(lowfire))
sum(sum(testfire))
firecond1_masked = np.ma.masked_where(
~testfire, np.ones((ymax, xmax)))
firecondlow_masked = np.ma.masked_where(
~lowfire, np.ones((ymax, xmax)))
fig1 = plt.figure(1, figsize=(15, 15))
ax1 = fig1.add_subplot(111)
ax1.set_aspect('equal')
ax1.pcolormesh(np.flipud(firecond1_masked), cmap=cmap1, vmin=0, vmax=1)
ax1.pcolormesh(np.flipud(firecondlow_masked), cmap=cmap3, vmin=0, vmax=1)
```
|
github_jupyter
|
# Finding fraud patterns with FP-growth
# Data Collection and Investigation
```
import pandas as pd
# Input data files are available in the "../input/" directory
df = pd.read_csv('D:/Python Project/Credit Card Fraud Detection/benchmark dataset/Test FP-Growth.csv')
# printing the first 5 columns for data visualization
df.head()
```
## Execute FP-growth algorithm
## Spark
```
# import environment path to pyspark
import os
import sys
spark_path = r"D:\apache-spark" # spark installed folder
os.environ['SPARK_HOME'] = spark_path
sys.path.insert(0, spark_path + "/bin")
sys.path.insert(0, spark_path + "/python/pyspark/")
sys.path.insert(0, spark_path + "/python/lib/pyspark.zip")
sys.path.insert(0, spark_path + "/python/lib/py4j-0.10.7-src.zip")
# Export csv to txt file
df.to_csv('processed_itemsets.txt', index=None, sep=' ', mode='w+')
import csv
# creating necessary variable
new_itemsets_list = []
skip_first_iteration = 1
# find the duplicate item and add a counter at behind
with open("processed_itemsets.txt", 'r') as fp:
itemsets_list = csv.reader(fp, delimiter =' ', skipinitialspace=True)
for itemsets in itemsets_list:
unique_itemsets = []
counter = 2
for item in itemsets:
if itemsets.count(item) > 1:
if skip_first_iteration == 1:
unique_itemsets.append(item)
skip_first_iteration = skip_first_iteration + 1
continue
duplicate_item = item + "__(" + str(counter) + ")"
unique_itemsets.append(duplicate_item)
counter = counter + 1
else:
unique_itemsets.append(item)
print(itemsets)
new_itemsets_list.append(unique_itemsets)
# write the new itemsets into file
with open('processed_itemsets.txt', 'w+') as f:
for items in new_itemsets_list:
for item in items:
f.write("{} ".format(item))
f.write("\n")
from pyspark import SparkContext
from pyspark.mllib.fpm import FPGrowth
# initialize spark
sc = SparkContext.getOrCreate()
data = sc.textFile('processed_itemsets.txt').cache()
transactions = data.map(lambda line: line.strip().split(' '))
```
__minSupport__: The minimum support for an itemset to be identified as frequent. <br>
For example, if an item appears 3 out of 5 transactions, it has a support of 3/5=0.6.
__minConfidence__: Minimum confidence for generating Association Rule. Confidence is an indication of how often an association rule has been found to be true. For example, if in the transactions itemset X appears 4 times, X and Y co-occur only 2 times, the confidence for the rule X => Y is then 2/4 = 0.5.
__numPartitions__: The number of partitions used to distribute the work. By default the param is not set, and number of partitions of the input dataset is used
```
model = FPGrowth.train(transactions, minSupport=0.6, numPartitions=10)
result = model.freqItemsets().collect()
print("Frequent Itemsets : Item Support")
print("====================================")
for index, frequent_itemset in enumerate(result):
print(str(frequent_itemset.items) + ' : ' + str(frequent_itemset.freq))
rules = sorted(model._java_model.generateAssociationRules(0.8).collect(), key=lambda x: x.confidence(), reverse=True)
print("Antecedent => Consequent : Min Confidence")
print("========================================")
for rule in rules[:200]:
print(rule)
# stop spark session
sc.stop()
```
|
github_jupyter
|
```
### MODULE 1
### Basic Modeling in scikit-learn
```
```
### Seen vs. unseen data
# The model is fit using X_train and y_train
model.fit(X_train, y_train)
# Create vectors of predictions
train_predictions = model.predict(X_train)
test_predictions = model.predict(X_test)
# Train/Test Errors
train_error = mae(y_true=y_train, y_pred=train_predictions)
test_error = mae(y_true=y_test, y_pred=test_predictions)
# Print the accuracy for seen and unseen data
print("Model error on seen data: {0:.2f}.".format(train_error))
print("Model error on unseen data: {0:.2f}.".format(test_error))
# Set parameters and fit a model
# Set the number of trees
rfr.n_estimators = 1000
# Add a maximum depth
rfr.max_depth = 6
# Set the random state
rfr.random_state = 11
# Fit the model
rfr.fit(X_train, y_train)
## Feature importances
# Fit the model using X and y
rfr.fit(X_train, y_train)
# Print how important each column is to the model
for i, item in enumerate(rfr.feature_importances_):
# Use i and item to print out the feature importance of each column
print("{0:s}: {1:.2f}".format(X_train.columns[i], item))
### lassification predictions
# Fit the rfc model.
rfc.fit(X_train, y_train)
# Create arrays of predictions
classification_predictions = rfc.predict(X_test)
probability_predictions = rfc.predict_proba(X_test)
# Print out count of binary predictions
print(pd.Series(classification_predictions).value_counts())
# Print the first value from probability_predictions
print('The first predicted probabilities are: {}'.format(probability_predictions[0]))
## Reusing model parameters
rfc = RandomForestClassifier(n_estimators=50, max_depth=6, random_state=1111)
# Print the classification model
print(rfc)
# Print the classification model's random state parameter
print('The random state is: {}'.format(rfc.random_state))
# Print all parameters
print('Printing the parameters dictionary: {}'.format(rfc.get_params()))
## Random forest classifier
from sklearn.ensemble import RandomForestClassifier
# Create a random forest classifier
rfc = RandomForestClassifier(n_estimators=50, max_depth=6, random_state=1111)
# Fit rfc using X_train and y_train
rfc.fit(X_train, y_train)
# Create predictions on X_test
predictions = rfc.predict(X_test)
print(predictions[0:5])
# Print model accuracy using score() and the testing data
print(rfc.score(X_test, y_test))
## MODULE 2
## Validation Basics
```
```
## Create one holdout set
# Create dummy variables using pandas
X = pd.get_dummies(tic_tac_toe.iloc[:,0:9])
y = tic_tac_toe.iloc[:, 9]
# Create training and testing datasets. Use 10% for the test set
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=.1, random_state=1111)
## Create two holdout sets
# Create temporary training and final testing datasets
X_temp, X_test, y_temp, y_test =\
train_test_split(X, y, test_size=.2, random_state=1111)
# Create the final training and validation datasets
X_train, X_val, y_train, y_val = train_test_split(X_temp, y_temp, test_size=.25, random_state=1111)
### Mean absolute error
from sklearn.metrics import mean_absolute_error
# Manually calculate the MAE
n = len(predictions)
mae_one = sum(abs(y_test - predictions)) / n
print('With a manual calculation, the error is {}'.format(mae_one))
# Use scikit-learn to calculate the MAE
mae_two = mean_absolute_error(y_test, predictions)
print('Using scikit-lean, the error is {}'.format(mae_two))
# <script.py> output:
# With a manual calculation, the error is 5.9
# Using scikit-lean, the error is 5.9
### Mean squared error
from sklearn.metrics import mean_squared_error
n = len(predictions)
# Finish the manual calculation of the MSE
mse_one = sum(abs(y_test - predictions)**2) / n
print('With a manual calculation, the error is {}'.format(mse_one))
# Use the scikit-learn function to calculate MSE
mse_two = mean_squared_error(y_test, predictions)
print('Using scikit-lean, the error is {}'.format(mse_two))
### Performance on data subsets
# Find the East conference teams
east_teams = labels == "E"
# Create arrays for the true and predicted values
true_east = y_test[east_teams]
preds_east = predictions[east_teams]
# Print the accuracy metrics
print('The MAE for East teams is {}'.format(
mae(true_east, preds_east)))
# Print the West accuracy
print('The MAE for West conference is {}'.format(west_error))
### Confusion matrices
# Calculate and print the accuracy
accuracy = (324 + 491) / (953)
print("The overall accuracy is {0: 0.2f}".format(accuracy))
# Calculate and print the precision
precision = (491) / (491 + 15)
print("The precision is {0: 0.2f}".format(precision))
# Calculate and print the recall
recall = (491) / (491 + 123)
print("The recall is {0: 0.2f}".format(recall))
### Confusion matrices, again
from sklearn.metrics import confusion_matrix
# Create predictions
test_predictions = rfc.predict(X_test)
# Create and print the confusion matrix
cm = confusion_matrix(y_test, test_predictions)
print(cm)
# Print the true positives (actual 1s that were predicted 1s)
print("The number of true positives is: {}".format(cm[1, 1]))
## <script.py> output:
## [[177 123]
## [ 92 471]]
## The number of true positives is: 471
## Row 1, column 1 represents the number of actual 1s that were predicted 1s (the true positives).
## Always make sure you understand the orientation of the confusion matrix before you start using it!
### Precision vs. recall
from sklearn.metrics import precision_score
test_predictions = rfc.predict(X_test)
# Create precision or recall score based on the metric you imported
score = precision_score(y_test, test_predictions)
# Print the final result
print("The precision value is {0:.2f}".format(score))
### Error due to under/over-fitting
# Update the rfr model
rfr = RandomForestRegressor(n_estimators=25,
random_state=1111,
max_features=2)
rfr.fit(X_train, y_train)
# Print the training and testing accuracies
print('The training error is {0:.2f}'.format(
mae(y_train, rfr.predict(X_train))))
print('The testing error is {0:.2f}'.format(
mae(y_test, rfr.predict(X_test))))
## <script.py> output:
## The training error is 3.88
## The testing error is 9.15
# Update the rfr model
rfr = RandomForestRegressor(n_estimators=25,
random_state=1111,
max_features=11)
rfr.fit(X_train, y_train)
# Print the training and testing accuracies
print('The training error is {0:.2f}'.format(
mae(y_train, rfr.predict(X_train))))
print('The testing error is {0:.2f}'.format(
mae(y_test, rfr.predict(X_test))))
## <script.py> output:
## The training error is 3.57
## The testing error is 10.05
# Update the rfr model
rfr = RandomForestRegressor(n_estimators=25,
random_state=1111,
max_features=4)
rfr.fit(X_train, y_train)
# Print the training and testing accuracies
print('The training error is {0:.2f}'.format(
mae(y_train, rfr.predict(X_train))))
print('The testing error is {0:.2f}'.format(
mae(y_test, rfr.predict(X_test))))
## <script.py> output:
## The training error is 3.60
## The testing error is 8.79
### Am I underfitting?
from sklearn.metrics import accuracy_score
test_scores, train_scores = [], []
for i in [1, 2, 3, 4, 5, 10, 20, 50]:
rfc = RandomForestClassifier(n_estimators=i, random_state=1111)
rfc.fit(X_train, y_train)
# Create predictions for the X_train and X_test datasets.
train_predictions = rfc.predict(X_train)
test_predictions = rfc.predict(X_test)
# Append the accuracy score for the test and train predictions.
train_scores.append(round(accuracy_score(y_train, train_predictions), 2))
test_scores.append(round(accuracy_score(y_test, test_predictions), 2))
# Print the train and test scores.
print("The training scores were: {}".format(train_scores))
print("The testing scores were: {}".format(test_scores))
### MODULE 3
### Cross Validation
```
```
### Two samples
# Create two different samples of 200 observations
sample1 = tic_tac_toe.sample(200, random_state=1111)
sample2 = tic_tac_toe.sample(200, random_state=1171)
# Print the number of common observations
print(len([index for index in sample1.index if index in sample2.index]))
# Print the number of observations in the Class column for both samples
print(sample1['Class'].value_counts())
print(sample2['Class'].value_counts())
### scikit-learn's KFold()
from sklearn.model_selection import KFold
# Use KFold
kf = KFold(n_splits=5, shuffle=True, random_state=1111)
# Create splits
splits = kf.split(X)
# Print the number of indices
for train_index, val_index in splits:
print("Number of training indices: %s" % len(train_index))
print("Number of validation indices: %s" % len(val_index))
### Using KFold indices
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import mean_squared_error
rfc = RandomForestRegressor(n_estimators=25, random_state=1111)
# Access the training and validation indices of splits
for train_index, val_index in splits:
# Setup the training and validation data
X_train, y_train = X[train_index], y[train_index]
X_val, y_val = X[val_index], y[val_index]
# Fit the random forest model
rfc.fit(X_train, y_train)
# Make predictions, and print the accuracy
predictions = rfc.predict(X_val)
print("Split accuracy: " + str(mean_squared_error(y_val, predictions)))
### scikit-learn's methods
# Instruction 1: Load the cross-validation method
from sklearn.model_selection import cross_val_score
# Instruction 2: Load the random forest regression model
from sklearn.ensemble import RandomForestClassifier
# Instruction 3: Load the mean squared error method
# Instruction 4: Load the function for creating a scorer
from sklearn.metrics import mean_squared_error, make_scorer
## It is easy to see how all of the methods can get mixed up, but
## it is important to know the names of the methods you need.
## You can always review the scikit-learn documentation should you need any help
### Implement cross_val_score()
rfc = RandomForestRegressor(n_estimators=25, random_state=1111)
mse = make_scorer(mean_squared_error)
# Set up cross_val_score
cv = cross_val_score(estimator=rfc,
X=X_train,
y=y_train,
cv=10,
scoring=mse)
# Print the mean error
print(cv.mean())
### Leave-one-out-cross-validation
from sklearn.metrics import mean_absolute_error, make_scorer
# Create scorer
mae_scorer = make_scorer(mean_absolute_error)
rfr = RandomForestRegressor(n_estimators=15, random_state=1111)
# Implement LOOCV
scores = cross_val_score(estimator=rfr, X=X, y=y, cv=85, scoring=mae_scorer)
# Print the mean and standard deviation
print("The mean of the errors is: %s." % np.mean(scores))
print("The standard deviation of the errors is: %s." % np.std(scores))
### MODULE 4
### Selecting the best model with Hyperparameter tuning.
```
```
### Creating Hyperparameters
# Review the parameters of rfr
print(rfr.get_params())
# Maximum Depth
max_depth = [4, 8, 12]
# Minimum samples for a split
min_samples_split = [2, 5, 10]
# Max features
max_features = [4, 6, 8, 10]
### Running a model using ranges
from sklearn.ensemble import RandomForestRegressor
# Fill in rfr using your variables
rfr = RandomForestRegressor(
n_estimators=100,
max_depth=random.choice(max_depth),
min_samples_split=random.choice(min_samples_split),
max_features=random.choice(max_features))
# Print out the parameters
print(rfr.get_params())
### Preparing for RandomizedSearch
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import make_scorer, mean_squared_error
# Finish the dictionary by adding the max_depth parameter
param_dist = {"max_depth": [2, 4, 6, 8],
"max_features": [2, 4, 6, 8, 10],
"min_samples_split": [2, 4, 8, 16]}
# Create a random forest regression model
rfr = RandomForestRegressor(n_estimators=10, random_state=1111)
# Create a scorer to use (use the mean squared error)
scorer = make_scorer(mean_squared_error)
# Import the method for random search
from sklearn.model_selection import RandomizedSearchCV
# Build a random search using param_dist, rfr, and scorer
random_search =\
RandomizedSearchCV(
estimator=rfr,
param_distributions=param_dist,
n_iter=10,
cv=5,
scoring=scorer)
### Selecting the best precision model
from sklearn.metrics import precision_score, make_scorer
# Create a precision scorer
precision = make_scorer(precision_score)
# Finalize the random search
rs = RandomizedSearchCV(
estimator=rfc, param_distributions=param_dist,
scoring = precision,
cv=5, n_iter=10, random_state=1111)
rs.fit(X, y)
# print the mean test scores:
print('The accuracy for each run was: {}.'.format(rs.cv_results_['mean_test_score']))
# print the best model score:
print('The best accuracy for a single model was: {}'.format(rs.best_score_))
```
|
github_jupyter
|
# Goals
### Learn how to change train validation splits
# Table of Contents
## [0. Install](#0)
## [1. Load experiment with defaut transforms](#1)
## [2. Reset Transforms andapply new transforms](#2)
<a id='0'></a>
# Install Monk
- git clone https://github.com/Tessellate-Imaging/monk_v1.git
- cd monk_v1/installation/Linux && pip install -r requirements_cu9.txt
- (Select the requirements file as per OS and CUDA version)
```
!git clone https://github.com/Tessellate-Imaging/monk_v1.git
# Select the requirements file as per OS and CUDA version
!cd monk_v1/installation/Linux && pip install -r requirements_cu9.txt
```
## Dataset - Broad Leaved Dock Image Classification
- https://www.kaggle.com/gavinarmstrong/open-sprayer-images
```
! wget --load-cookies /tmp/cookies.txt "https://docs.google.com/uc?export=download&confirm=$(wget --save-cookies /tmp/cookies.txt --keep-session-cookies --no-check-certificate 'https://docs.google.com/uc?export=download&id=1uL-VV4nV_u0kry3gLH1TATUTu8hWJ0_d' -O- | sed -rn 's/.*confirm=([0-9A-Za-z_]+).*/\1\n/p')&id=1uL-VV4nV_u0kry3gLH1TATUTu8hWJ0_d" -O open_sprayer_images.zip && rm -rf /tmp/cookies.txt
! unzip -qq open_sprayer_images.zip
```
# Imports
```
# Monk
import os
import sys
sys.path.append("monk_v1/monk/");
#Using mxnet-gluon backend
from gluon_prototype import prototype
```
<a id='1'></a>
# Load experiment with default transforms
```
gtf = prototype(verbose=1);
gtf.Prototype("project", "understand_transforms");
gtf.Default(dataset_path="open_sprayer_images/train",
model_name="resnet18_v1",
freeze_base_network=True,
num_epochs=5);
#Read the summary generated once you run this cell.
```
## Default Transforms are
Train Transforms
{'RandomHorizontalFlip': {'p': 0.8}},
{'Normalize': {'mean': [0.485, 0.456, 0.406], 'std': [0.229, 0.224, 0.225]}}]
Val Transforms
{'RandomHorizontalFlip': {'p': 0.8}},
{'Normalize': {'mean': [0.485, 0.456, 0.406], 'std': [0.229, 0.224, 0.225]}}
In that order
<a id='2'></a>
# Reset transforms
```
# Reset train and validation transforms
gtf.reset_transforms();
# Reset test transforms
gtf.reset_transforms(test=True);
```
## Apply new transforms
```
gtf.List_Transforms();
# Transform applied to only train and val
gtf.apply_center_crop(224,
train=True,
val=True,
test=False)
# Transform applied to all train, val and test
gtf.apply_normalize(mean=[0.485, 0.456, 0.406],
std=[0.229, 0.224, 0.225],
train=True,
val=True,
test=True
)
# Very important to reload post update
gtf.Reload();
```
|
github_jupyter
|
```
import pandas as pd
import numpy as np
import numpy.random as nr
import matplotlib.pyplot as plt
import matplotlib.pyplot as plt
import sklearn
from sklearn.ensemble import RandomForestClassifier
import catboost as cat
from catboost import CatBoostClassifier
from sklearn import preprocessing
import sklearn.model_selection as ms
from sklearn.model_selection import GridSearchCV, KFold, StratifiedKFold
from sklearn.metrics import log_loss, confusion_matrix, accuracy_score
import xgboost as xgb
import lightgbm as lgb
def fill_missing_values(data):
'''
Function to input missing values based on the column object type
'''
cols = list(data.columns)
for col in cols:
if data[col].dtype == 'int64' or data[col].dtype == 'float64':
data[col] = data[col].fillna(data[col].mean())
#elif data[col].dtype == 'O' or data[col].dtype == 'object':
# data[col] = data[col].fillna(data[col].mode()[0])
else:
data[col] = data[col].fillna(data[col].mode()[0])
return data
def one_hot_encoding(traindata, *args):
for ii in args:
traindata = pd.get_dummies(traindata, prefix=[ii], columns=[ii])
return traindata
def drop_columns(traindata, *args):
#labels = np.array(traindata[target])
columns = []
for _ in args:
columns.append(_)
traindata = traindata.drop(columns, axis=1)
#traindata = traindata.drop(target, axis=1)
#testdata = testdata.drop(columns, axis=1)
return traindata
def process(traindata):
cols = list(traindata.columns)
for _ in cols:
traindata[_] = np.where(traindata[_] == np.inf, -999, traindata[_])
traindata[_] = np.where(traindata[_] == np.nan, -999, traindata[_])
traindata[_] = np.where(traindata[_] == -np.inf, -999, traindata[_])
return traindata
def show_evaluation(pred, true):
print(f'Default score: {score(true.values, pred)}')
print(f'Accuracy is: {accuracy_score(true, pred)}')
print(f'F1 is: {f1_score(pred, true.values, average="weighted")}')
def freq_encode(data, cols):
for i in cols:
encoding = data.groupby(i).size()
encoding = encoding/len(data)
data[i + '_enc'] = data[i].map(encoding)
return data
def mean_target(data, cols):
kf = KFold(5)
a = pd.DataFrame()
for tr_ind, val_ind in kf.split(data):
X_tr, X_val= data.iloc[tr_ind].copy(), data.iloc[val_ind].copy()
for col in cols:
means = X_val[col].map(X_tr.groupby(col).FORCE_2020_LITHOFACIES_LITHOLOGY.mean())
X_val[col + '_mean_target'] = means + 0.0001
a = pd.concat((a, X_val))
#prior = FORCE_2020_LITHOFACIES_LITHOLOGY.mean()
#a.fillna(prior, inplace=True)
return a
def make_submission(prediction, filename):
path = './'
test = pd.read_csv('./Test.csv', sep=';')
#test_prediction = model.predict(testdata)
#test_prediction
category_to_lithology = {y:x for x,y in lithology_numbers.items()}
test_prediction_for_submission = np.vectorize(category_to_lithology.get)(prediction)
np.savetxt(path+filename+'.csv', test_prediction_for_submission, header='lithology', fmt='%i')
A = np.load('penalty_matrix.npy')
def score(y_true, y_pred):
S = 0.0
y_true = y_true.astype(int)
y_pred = y_pred.astype(int)
for i in range(0, y_true.shape[0]):
S -= A[y_true[i], y_pred[i]]
return S/y_true.shape[0]
def evaluate(model, prediction, true_label):
feat_imp = pd.Series(model.feature_importances_).sort_values(ascending=False)
plt.figure(figsize=(12,8))
feat_imp.plot(kind='bar', title=f'Feature Importances {len(model.feature_importances_)}')
plt.ylabel('Feature Importance Score')
#importing files
train = pd.read_csv('Train.csv', sep=';')
test = pd.read_csv('Test.csv', sep=';')
ntrain = train.shape[0]
ntest = test.shape[0]
target = train.FORCE_2020_LITHOFACIES_LITHOLOGY.copy()
df = pd.concat((train, test)).reset_index(drop=True)
plt.scatter(train.X_LOC, train.Y_LOC)
plt.scatter(test.X_LOC, test.Y_LOC)
test.describe()
train.describe()
train.WELL.value_counts()
test.WELL.value_counts()
#importing files
train = pd.read_csv('Train.csv', sep=';')
test = pd.read_csv('Test.csv', sep=';')
ntrain = train.shape[0]
ntest = test.shape[0]
target = train.FORCE_2020_LITHOFACIES_LITHOLOGY.copy()
df = pd.concat((train, test)).reset_index(drop=True)
lithology = train['FORCE_2020_LITHOFACIES_LITHOLOGY']
lithology_numbers = {30000: 0,
65030: 1,
65000: 2,
80000: 3,
74000: 4,
70000: 5,
70032: 6,
88000: 7,
86000: 8,
99000: 9,
90000: 10,
93000: 11}
lithology = lithology.map(lithology_numbers)
np.array(lithology)
test.describe()
train.describe()
(train.isna().sum()/train.shape[0]) * 100
(df.isna().sum()/df.shape[0]) * 100
(df.WELL.value_counts()/df.WELL.shape[0]) * 100
print(df.shape)
cols = ['FORCE_2020_LITHOFACIES_CONFIDENCE', 'SGR',
'DTS', 'DCAL', 'MUDWEIGHT', 'RMIC', 'ROPA', 'RXO']
df = drop_columns(df, *cols)
print(df.shape)
train.FORMATION.value_counts()
train.WELL.value_counts()
one_hot_cols = ['GROUP']
df = one_hot_encoding(df, *one_hot_cols)
print(df.shape)
df = freq_encode(df, ['FORMATION','WELL'])
df = df.copy()
print(df.shape)
#df.isna().sum()
df = mean_target(df, ['FORMATION', 'WELL'])
df.shape
df = df.drop(['FORMATION', 'WELL'], axis=1)
df.shape
df = df.fillna(-999)
data = df.copy()
train2 = data[:ntrain].copy()
target = train2.FORCE_2020_LITHOFACIES_LITHOLOGY.copy()
train2.drop(['FORCE_2020_LITHOFACIES_LITHOLOGY'], axis=1, inplace=True)
test2 = data[ntrain:].copy()
test2.drop(['FORCE_2020_LITHOFACIES_LITHOLOGY'], axis=1, inplace=True)
test2 = test2.reset_index(drop=True)
train2.shape, train.shape, test.shape, test2.shape
traindata = train2
testdata = test2
#using StandardScaler function to scale the numeric features
scaler = preprocessing.StandardScaler().fit(traindata)
traindata = pd.DataFrame(scaler.transform(traindata))
traindata.head()
testdata = pd.DataFrame(scaler.transform(testdata))
testdata.head()
class Model():
def __init__(self, train, test, label):
self.train = train
self.test = test
self.label = label
def __call__(self, plot = True):
return self.fit(plot)
def fit(self, plot):
#SPLIT ONE
self.x_train, self.x_test, self.y_train, self.y_test = ms.train_test_split(self.train,
pd.DataFrame(np.array(self.label)),
test_size=0.25,
random_state=42)
#SPLIT TWO
self.x_test1, self.x_test2, self.y_test1, self.y_test2 = ms.train_test_split(self.x_test,
self.y_test,
test_size=0.5,
random_state=42)
lgbm = CatBoostClassifier(n_estimators=15, max_depth=6,
random_state=42, learning_rate=0.033,
use_best_model=True, task_type='CPU',
eval_metric='MultiClass')
def show_evaluation(pred, true):
print(f'Default score: {score(true.values, pred)}')
print(f'Accuracy is: {accuracy_score(true, pred)}')
print(f'F1 is: {f1_score(pred, true.values, average="weighted")}')
split = 3
kf = StratifiedKFold(n_splits=split, shuffle=False)
#TEST DATA
pred_test = np.zeros((len(self.x_test1), 12))
pred_val = np.zeros((len(self.x_test2), 12))
pred_val = np.zeros((len(self.test), 12))
for (train_index, test_index) in kf.split(pd.DataFrame(self.x_train), pd.DataFrame(self.y_train)):
X_train,X_test = pd.DataFrame(self.x_train).iloc[train_index], pd.DataFrame(self.x_train).iloc[test_index]
y_train,y_test = pd.DataFrame(self.y_train).iloc[train_index],pd.DataFrame(self.y_train).iloc[test_index]
lgbm.fit(X_train, y_train, early_stopping_rounds=2, eval_set=[(X_test,y_test)])
#scores.append(metric(lgbm.predict_proba(X_test),y_test))
pred_test+=lgbm.predict_proba(self.x_test1)
pred_val+=lgbm.predict_proba(self.x_test2)
open_test_pred+=lgbm.predict_proba(self.test)
pred_test_avg = pred_test/split
pred_val_avg = pred_test/split
print('----------------TEST EVALUATION------------------')
show_evaluation(pred_test_avg, self.y_test1)
print('----------------HOLD OUT EVALUATION------------------')
show_evaluation(pred_val_avg, self.y_test2)
if plot: self.plot_feat_imp(model)
return open_test_pred, lgbm
def plot_feat_imp(self, model):
feat_imp = pd.Series(model.get_fscore()).sort_values(ascending=False)
plt.figure(figsize=(12,8))
feat_imp.plot(kind='bar', title='Feature Importances')
plt.ylabel('Feature Importance Score')
func_= Model(traindata, testdata, lithology)
val_p2, test_p2, model2 = func_()
pd.DataFrame(lithology)
i, j = Model(df, test, lithology)
params = {'n_estimators': 3000,
'max_depth': 6,
'learning_rate': 0.033,
'verbose': 2}
a = Model(train, test, 'FORCE_2020_LITHOFACIES_LITHOLOGY', 0.3, params)
```
|
github_jupyter
|
# Dataproc - Submit Hadoop Job
## Intended Use
A Kubeflow Pipeline component to submit a Apache Hadoop MapReduce job on Apache Hadoop YARN in Google Cloud Dataproc service.
## Run-Time Parameters:
Name | Description
:--- | :----------
project_id | Required. The ID of the Google Cloud Platform project that the cluster belongs to.
region | Required. The Cloud Dataproc region in which to handle the request.
cluster_name | Required. The cluster to run the job.
main_jar_file_uri | The HCFS URI of the jar file containing the main class. Examples: `gs://foo-bucket/analytics-binaries/extract-useful-metrics-mr.jar` `hdfs:/tmp/test-samples/custom-wordcount.jar` `file:///home/usr/lib/hadoop-mapreduce/hadoop-mapreduce-examples.jar`
main_class | The name of the driver's main class. The jar file that contains the class must be in the default CLASSPATH or specified in jarFileUris.
args | Optional. The arguments to pass to the driver. Do not include arguments, such as -libjars or -Dfoo=bar, that can be set as job properties, since a collision may occur that causes an incorrect job submission.
hadoop_job | Optional. The full payload of a [HadoopJob](https://cloud.google.com/dataproc/docs/reference/rest/v1/HadoopJob).
job | Optional. The full payload of a [Dataproc job](https://cloud.google.com/dataproc/docs/reference/rest/v1/projects.regions.jobs).
wait_interval | Optional. The wait seconds between polling the operation. Defaults to 30s.
## Output:
Name | Description
:--- | :----------
job_id | The ID of the created job.
## Sample
Note: the sample code below works in both IPython notebook or python code directly.
### Setup a Dataproc cluster
Follow the [guide](https://cloud.google.com/dataproc/docs/guides/create-cluster) to create a new Dataproc cluster or reuse an existing one.
### Prepare Hadoop job
Upload your Hadoop jar file to a Google Cloud Storage (GCS) bucket. In the sample, we will use a jar file that is pre-installed in the main cluster, so there is no need to provide the `main_jar_file_uri`. We only set `main_class` to be `org.apache.hadoop.examples.WordCount`.
Here is the [source code of example](https://github.com/apache/hadoop/blob/trunk/hadoop-mapreduce-project/hadoop-mapreduce-examples/src/main/java/org/apache/hadoop/examples/WordCount.java).
To package a self-contained Hadoop MapReduct application from source code, follow the [instructions](https://hadoop.apache.org/docs/current/hadoop-mapreduce-client/hadoop-mapreduce-client-core/MapReduceTutorial.html).
### Set sample parameters
```
PROJECT_ID = '<Please put your project ID here>'
CLUSTER_NAME = '<Please put your existing cluster name here>'
OUTPUT_GCS_PATH = '<Please put your output GCS path here>'
REGION = 'us-central1'
MAIN_CLASS = 'org.apache.hadoop.examples.WordCount'
INTPUT_GCS_PATH = 'gs://ml-pipeline-playground/shakespeare1.txt'
EXPERIMENT_NAME = 'Dataproc - Submit Hadoop Job'
COMPONENT_SPEC_URI = 'https://raw.githubusercontent.com/kubeflow/pipelines/7622e57666c17088c94282ccbe26d6a52768c226/components/gcp/dataproc/submit_hadoop_job/component.yaml'
```
### Insepct Input Data
The input file is a simple text file:
```
!gsutil cat $INTPUT_GCS_PATH
```
### Clean up existing output files (Optional)
This is needed because the sample code requires the output folder to be a clean folder.
To continue to run the sample, make sure that the service account of the notebook server has access to the `OUTPUT_GCS_PATH`.
**CAUTION**: This will remove all blob files under `OUTPUT_GCS_PATH`.
```
!gsutil rm $OUTPUT_GCS_PATH/**
```
### Install KFP SDK
Install the SDK (Uncomment the code if the SDK is not installed before)
```
# KFP_PACKAGE = 'https://storage.googleapis.com/ml-pipeline/release/0.1.12/kfp.tar.gz'
# !pip3 install $KFP_PACKAGE --upgrade
```
### Load component definitions
```
import kfp.components as comp
dataproc_submit_hadoop_job_op = comp.load_component_from_url(COMPONENT_SPEC_URI)
display(dataproc_submit_hadoop_job_op)
```
### Here is an illustrative pipeline that uses the component
```
import kfp.dsl as dsl
import kfp.gcp as gcp
import json
@dsl.pipeline(
name='Dataproc submit Hadoop job pipeline',
description='Dataproc submit Hadoop job pipeline'
)
def dataproc_submit_hadoop_job_pipeline(
project_id = PROJECT_ID,
region = REGION,
cluster_name = CLUSTER_NAME,
main_jar_file_uri = '',
main_class = MAIN_CLASS,
args = json.dumps([
INTPUT_GCS_PATH,
OUTPUT_GCS_PATH
]),
hadoop_job='',
job='{}',
wait_interval='30'
):
dataproc_submit_hadoop_job_op(project_id, region, cluster_name, main_jar_file_uri, main_class,
args, hadoop_job, job, wait_interval).apply(gcp.use_gcp_secret('user-gcp-sa'))
```
### Compile the pipeline
```
pipeline_func = dataproc_submit_hadoop_job_pipeline
pipeline_filename = pipeline_func.__name__ + '.pipeline.tar.gz'
import kfp.compiler as compiler
compiler.Compiler().compile(pipeline_func, pipeline_filename)
```
### Submit the pipeline for execution
```
#Specify pipeline argument values
arguments = {}
#Get or create an experiment and submit a pipeline run
import kfp
client = kfp.Client()
experiment = client.create_experiment(EXPERIMENT_NAME)
#Submit a pipeline run
run_name = pipeline_func.__name__ + ' run'
run_result = client.run_pipeline(experiment.id, run_name, pipeline_filename, arguments)
```
### Inspect the outputs
The sample in the notebook will count the words in the input text and output them in sharded files. Here is the command to inspect them:
```
!gsutil cat $OUTPUT_GCS_PATH/*
```
|
github_jupyter
|
<div>
<img src="https://drive.google.com/uc?export=view&id=1vK33e_EqaHgBHcbRV_m38hx6IkG0blK_" width="350"/>
</div>
#**Artificial Intelligence - MSc**
This notebook is designed specially for the module
ET5003 - MACHINE LEARNING APPLICATIONS
Instructor: Enrique Naredo
###ET5003_BayesianNN
© All rights reserved to the author, do not share outside this module.
## Introduction
A [Bayesian network](https://en.wikipedia.org/wiki/Bayesian_network) (also known as a Bayes network, Bayes net, belief network, or decision network) is a probabilistic graphical model that represents a set of variables and their conditional dependencies via a directed acyclic graph (DAG).
* Bayesian networks are ideal for taking an event that occurred and predicting the likelihood that any one of several possible known causes was the contributing factor.
* For example, a Bayesian network could represent the probabilistic relationships between diseases and symptoms.
* Given symptoms, the network can be used to compute the probabilities of the presence of various diseases.
**Acknowledgement**
This notebook is refurbished taking source code from Alessio Benavoli's webpage and from the libraries numpy, GPy, pylab, and pymc3.
## Libraries
```
# Suppressing Warnings:
import warnings
warnings.filterwarnings("ignore")
# https://pypi.org/project/GPy/
!pip install gpy
import GPy as GPy
import numpy as np
import pylab as pb
import pymc3 as pm
%matplotlib inline
```
## Data generation
Generate data from a nonlinear function and use a Gaussian Process to sample it.
```
# seed the legacy random number generator
# to replicate experiments
seed = None
#seed = 7
np.random.seed(seed)
# Gaussian Processes
# https://gpy.readthedocs.io/en/deploy/GPy.kern.html
# Radial Basis Functions
# https://scikit-learn.org/stable/auto_examples/svm/plot_rbf_parameters.html
# kernel is a function that specifies the degree of similarity
# between variables given their relative positions in parameter space
kernel = GPy.kern.RBF(input_dim=1,lengthscale=0.15,variance=0.2)
print(kernel)
# number of samples
num_samples_train = 250
num_samples_test = 200
# intervals to sample
a, b, c = 0.2, 0.6, 0.8
# points evenly spaced over [0,1]
interval_1 = np.random.rand(int(num_samples_train/2))*b - c
interval_2 = np.random.rand(int(num_samples_train/2))*b + c
X_new_train = np.sort(np.hstack([interval_1,interval_2]))
X_new_test = np.linspace(-1,1,num_samples_test)
X_new_all = np.hstack([X_new_train,X_new_test]).reshape(-1,1)
# vector of the means
μ_new = np.zeros((len(X_new_all)))
# covariance matrix
C_new = kernel.K(X_new_all,X_new_all)
# noise factor
noise_new = 0.1
# generate samples path with mean μ and covariance C
TF_new = np.random.multivariate_normal(μ_new,C_new,1)[0,:]
y_new_train = TF_new[0:len(X_new_train)] + np.random.randn(len(X_new_train))*noise_new
y_new_test = TF_new[len(X_new_train):] + np.random.randn(len(X_new_test))*noise_new
TF_new = TF_new[len(X_new_train):]
```
In this example, first generate a nonlinear functions and then generate noisy training data from that function.
The constrains are:
* Training samples $x$ belong to either interval $[-0.8,-0.2]$ or $[0.2,0.8]$.
* There is not data training samples from the interval $[-0.2,0.2]$.
* The goal is to evaluate the extrapolation error outside in the interval $[-0.2,0.2]$.
```
# plot
pb.figure()
pb.plot(X_new_test,TF_new,c='b',label='True Function',zorder=100)
# training data
pb.scatter(X_new_train,y_new_train,c='g',label='Train Samples',alpha=0.5)
pb.xlabel("x",fontsize=16);
pb.ylabel("y",fontsize=16,rotation=0)
pb.legend()
pb.savefig("New_data.pdf")
```
## Bayesian NN
We address the previous nonlinear regression problem by using a Bayesian NN.
**The model is basically very similar to polynomial regression**. We first define the nonlinear function (NN)
and the place a prior over the unknown parameters. We then compute the posterior.
```
# https://theano-pymc.readthedocs.io/en/latest/
import theano
# add a column of ones to include an intercept in the model
x1 = np.vstack([np.ones(len(X_new_train)), X_new_train]).T
floatX = theano.config.floatX
l = 15
# Initialize random weights between each layer
# we do that to help the numerical algorithm that computes the posterior
init_1 = np.random.randn(x1.shape[1], l).astype(floatX)
init_out = np.random.randn(l).astype(floatX)
# pymc3 model as neural_network
with pm.Model() as neural_network:
# we convert the data in theano type so we can do dot products with the correct type.
ann_input = pm.Data('ann_input', x1)
ann_output = pm.Data('ann_output', y_new_train)
# Priors
# Weights from input to hidden layer
weights_in_1 = pm.Normal('w_1', 0, sigma=10,
shape=(x1.shape[1], l), testval=init_1)
# Weights from hidden layer to output
weights_2_out = pm.Normal('w_0', 0, sigma=10,
shape=(l,),testval=init_out)
# Build neural-network using tanh activation function
# Inner layer
act_1 = pm.math.tanh(pm.math.dot(ann_input,weights_in_1))
# Linear layer, like in Linear regression
act_out = pm.Deterministic('act_out',pm.math.dot(act_1, weights_2_out))
# standard deviation of noise
sigma = pm.HalfCauchy('sigma',5)
# Normal likelihood
out = pm.Normal('out',
act_out,
sigma=sigma,
observed=ann_output)
# this can be slow because there are many parameters
# some parameters
par1 = 100 # start with 100, then use 1000+
par2 = 1000 # start with 1000, then use 10000+
# neural network
with neural_network:
posterior = pm.sample(par1,tune=par2,chains=1)
```
Specifically, PyMC3 supports the following Variational Inference (VI) methods:
* Automatic Differentiation Variational Inference (ADVI): 'advi'
* ADVI full rank: 'fullrank_advi'
* Stein Variational Gradient Descent (SVGD): 'svgd'
* Amortized Stein Variational Gradient Descent (ASVGD): 'asvgd'
* Normalizing Flow with default scale-loc flow (NFVI): 'nfvi'
```
# we can do instead an approximated inference
param3 = 1000 # start with 1000, then use 50000+
VI = 'advi' # 'advi', 'fullrank_advi', 'svgd', 'asvgd', 'nfvi'
OP = pm.adam # pm.adam, pm.sgd, pm.adagrad, pm.adagrad_window, pm.adadelta
LR = 0.01
with neural_network:
approx = pm.fit(param3, method=VI, obj_optimizer=pm.adam(learning_rate=LR))
# plot
pb.plot(approx.hist, label='Variational Inference: '+ VI.upper(), alpha=.3)
pb.legend(loc='upper right')
# Evidence Lower Bound (ELBO)
# https://en.wikipedia.org/wiki/Evidence_lower_bound
pb.ylabel('ELBO')
pb.xlabel('iteration');
# draw samples from variational posterior
D = 500
posterior = approx.sample(draws=D)
```
Now, we compute the prediction for each sample.
* Note that we use `np.tanh` instead of `pm.math.tanh`
for speed reason.
* `pm.math.tanh` is slower outside a Pymc3 model because it converts all data in theano format.
* It is convenient to do GPU-based training, but it is slow when we only need to compute predictions.
```
# add a column of ones to include an intercept in the model
x2 = np.vstack([np.ones(len(X_new_test)), X_new_test]).T
y_pred = []
for i in range(posterior['w_1'].shape[0]):
#inner layer
t1 = np.tanh(np.dot(posterior['w_1'][i,:,:].T,x2.T))
#outer layer
y_pred.append(np.dot(posterior['w_0'][i,:],t1))
# predictions
y_pred = np.array(y_pred)
```
We first plot the mean of `y_pred`, this is very similar to the prediction that Keras returns
```
# plot
pb.plot(X_new_test,TF_new,label='true')
pb.plot(X_new_test,y_pred.mean(axis=0),label='Bayes NN mean')
pb.scatter(X_new_train,y_new_train,c='r',alpha=0.5)
pb.legend()
pb.ylim([-1,1])
pb.xlabel("x",fontsize=16);
pb.ylabel("y",fontsize=16,rotation=0)
pb.savefig("BayesNN_mean.pdf")
```
Now, we plot the uncertainty, by plotting N nonlinear regression lines from the posterior
```
# plot
pb.plot(X_new_test,TF_new,label='true',Zorder=100)
pb.plot(X_new_test,y_pred.mean(axis=0),label='Bayes NN mean',Zorder=100)
N = 500
# nonlinear regression lines
for i in range(N):
pb.plot(X_new_test,y_pred[i,:],c='gray',alpha=0.05)
pb.scatter(X_new_train,y_new_train,c='r',alpha=0.5)
pb.xlabel("x",fontsize=16);
pb.ylabel("y",fontsize=16,rotation=0)
pb.ylim([-1,1.5])
pb.legend()
pb.savefig("BayesNN_samples.pdf")
# plot
pb.plot(X_new_test,TF_new,label='true',Zorder=100)
pb.plot(X_new_test,y_pred.mean(axis=0),label='Bayes NN mean',Zorder=100)
pb.scatter(X_new_train,y_new_train,c='r',alpha=0.5)
pb.xlabel("x",fontsize=16);
pb.ylabel("y",fontsize=16,rotation=0)
pb.ylim([-1,1.5])
pb.legend()
pb.savefig("BayesNN_mean.pdf")
```
|
github_jupyter
|
# Simple Attack
In this notebook, we will examine perhaps the simplest possible attack on an individual's private data and what the OpenDP library can do to mitigate it.
## Loading the data
The vetting process is currently underway for the code in the OpenDP Library.
Any constructors that have not been vetted may still be accessed if you opt-in to "contrib".
```
import numpy as np
from opendp.mod import enable_features
enable_features('contrib')
```
We begin with loading up the data.
```
import os
data_path = os.path.join('.', 'data', 'PUMS_california_demographics_1000', 'data.csv')
with open(data_path) as input_file:
data = input_file.read()
col_names = ["age", "sex", "educ", "race", "income", "married"]
print(col_names)
print('\n'.join(data.split('\n')[:6]))
```
The following code parses the data into a vector of incomes.
More details on preprocessing can be found [here](https://github.com/opendp/opendp/blob/main/python/example/basic_data_analysis.ipynb).
```
from opendp.trans import make_split_dataframe, make_select_column, make_cast, make_impute_constant
income_preprocessor = (
# Convert data into a dataframe where columns are of type Vec<str>
make_split_dataframe(separator=",", col_names=col_names) >>
# Selects a column of df, Vec<str>
make_select_column(key="income", TOA=str)
)
# make a transformation that casts from a vector of strings to a vector of floats
cast_str_float = (
# Cast Vec<str> to Vec<Option<floats>>
make_cast(TIA=str, TOA=float) >>
# Replace any elements that failed to parse with 0., emitting a Vec<float>
make_impute_constant(0.)
)
# replace the previous preprocessor: extend it with the caster
income_preprocessor = income_preprocessor >> cast_str_float
incomes = income_preprocessor(data)
print(incomes[:7])
```
## A simple attack
Say there's an attacker who's target is the income of the first person in our data (i.e. the first income in the csv). In our case, its simply `0` (but any number is fine, i.e. 5000).
```
person_of_interest = incomes[0]
print('person of interest:\n\n{0}'.format(person_of_interest))
```
Now consider the case an attacker that doesn't know the POI income, but do know the following: (1) the average income without the POI income, and (2) the number of persons in the database.
As we show next, if he would also get the average income (including the POI's one), by simple manipulation he can easily back out the individual's income.
```
# attacker information: everyone's else mean, and their count.
known_mean = np.mean(incomes[1:])
known_obs = len(incomes) - 1
# assume the attackers know legitimately get the overall mean (and hence can infer the total count)
overall_mean = np.mean(incomes)
n_obs = len(incomes)
# back out POI's income
poi_income = overall_mean * n_obs - known_obs * known_mean
print('poi_income: {0}'.format(poi_income))
```
The attacker now knows with certainty that the POI has an income of $0.
## Using OpenDP
Let's see what happens if the attacker were made to interact with the data through OpenDP and was given a privacy budget of $\epsilon = 1$.
We will assume that the attacker is reasonably familiar with differential privacy and believes that they should use tighter data bounds than they would anticipate being in the data in order to get a less noisy estimate.
They will need to update their `known_mean` accordingly.
```
from opendp.trans import make_clamp, make_sized_bounded_mean, make_bounded_resize
from opendp.meas import make_base_laplace
enable_features("floating-point")
max_influence = 1
count_release = 100
income_bounds = (0.0, 100_000.0)
clamp_and_resize_data = (
make_clamp(bounds=income_bounds) >>
make_bounded_resize(size=count_release, bounds=income_bounds, constant=10_000.0)
)
known_mean = np.mean(clamp_and_resize_data(incomes)[1:])
mean_measurement = (
clamp_and_resize_data >>
make_sized_bounded_mean(size=count_release, bounds=income_bounds) >>
make_base_laplace(scale=1.0)
)
dp_mean = mean_measurement(incomes)
print("DP mean:", dp_mean)
print("Known mean:", known_mean)
```
We will be using `n_sims` to simulate the process a number of times to get a sense for various possible outcomes for the attacker.
In practice, they would see the result of only one simulation.
```
# initialize vector to store estimated overall means
n_sims = 10_000
n_queries = 1
poi_income_ests = []
estimated_means = []
# get estimates of overall means
for i in range(n_sims):
query_means = [mean_measurement(incomes) for j in range(n_queries)]
# get estimates of POI income
estimated_means.append(np.mean(query_means))
poi_income_ests.append(estimated_means[i] * count_release - (count_release - 1) * known_mean)
# get mean of estimates
print('Known Mean Income (after truncation): {0}'.format(known_mean))
print('Observed Mean Income: {0}'.format(np.mean(estimated_means)))
print('Estimated POI Income: {0}'.format(np.mean(poi_income_ests)))
print('True POI Income: {0}'.format(person_of_interest))
```
We see empirically that, in expectation, the attacker can get a reasonably good estimate of POI's income. However, they will rarely (if ever) get it exactly and would have no way of knowing if they did.
In our case, indeed the mean estimated POI income approaches the true income, as the number of simulations `n_sims` increases.
Below is a plot showing the empirical distribution of estimates of POI income. Notice about its concentration around `0`, and the Laplacian curve of the graph.
```
import warnings
import seaborn as sns
# hide warning created by outstanding scipy.stats issue
warnings.simplefilter(action='ignore', category=FutureWarning)
# distribution of POI income
ax = sns.distplot(poi_income_ests, kde = False, hist_kws = dict(edgecolor = 'black', linewidth = 1))
ax.set(xlabel = 'Estimated POI income')
```
|
github_jupyter
|
```
import tensorflow as tf
import h5py
import shutil
import numpy as np
from torch.utils.data import DataLoader
import keras
from tqdm.notebook import tqdm
from keras.models import Sequential
from keras.layers import Dense, Flatten, Conv3D, Dropout, MaxPooling3D,MaxPooling2D
from keras.utils import to_categorical
from tensorflow.keras.callbacks import ModelCheckpoint
from keras.utils.vis_utils import plot_model
from sklearn.model_selection import train_test_split
from keras.layers import Conv2D,Dropout
from keras.layers import Activation,Average
from keras.layers import GlobalAveragePooling2D,BatchNormalization
from keras.optimizers import Adam
import time
import collections
from keras.losses import categorical_crossentropy
```
ConvPool_CNN Model
```
def ConvPool_CNN_C():
model = Sequential()
model.add(Conv2D(96,kernel_size=(3,3),activation='relu',padding='same'))
model.add(Conv2D(96,kernel_size=(3,3),activation='relu',padding='same'))
model.add(Conv2D(96,kernel_size=(3,3),activation='relu',padding='same'))
model.add(MaxPooling2D(pool_size=(3,3),strides=2))
model.add(Conv2D(192,(3,3),activation='relu',padding='same'))
model.add(Conv2D(192,(3,3),activation='relu',padding='same'))
model.add(Conv2D(192,(3,3),activation='relu',padding='same'))
model.add(MaxPooling2D(pool_size=(3,3),strides=2))
model.add(Conv2D(192,(3,3),activation='relu',padding='same'))
model.add(Conv2D(192,(1,1),activation='relu'))
model.add(Conv2D(5,(1,1)))
model.add(GlobalAveragePooling2D())
model.add(Flatten())
model.add(Dense(5, activation='softmax'))
model.build(input_shape)
model.compile(loss=categorical_crossentropy,optimizer=keras.optimizers.Adam(0.001),metrics=['accuracy'])
return model
```
ALL_CNN_MODEL
```
def all_cnn_c(X,y,learningRate=0.001,lossFunction='categorical_crossentropy'):
model = Sequential()
model.add(Conv2D(96,kernel_size=(3,3),activation='relu',padding='same'))
model.add(Conv2D(96,kernel_size=(3,3),activation='relu',padding='same'))
model.add(Conv2D(96,kernel_size=(3,3),activation='relu',padding='same'))
model.add(Conv2D(192,(3,3),activation='relu',padding='same'))
model.add(Conv2D(192,(3,3),activation='relu',padding='same'))
model.add(Conv2D(192,(3,3),activation='relu',padding='same'))
model.add(Conv2D(192,(3,3),activation='relu',padding='same'))
model.add(Conv2D(192,(1,1),activation='relu'))
model.add(GlobalAveragePooling2D())
model.add(Dense(5, activation='softmax'))
model.build(input_shape)
model.compile(loss=categorical_crossentropy,optimizer=Adam(0.001),metrics=['accuracy'])
return model
```
NIN_CNN_MODEL
```
def nin_cnn_c():
model = Sequential()
model.add(Conv2D(32,kernel_size=(5,5),activation='relu',padding='valid'))
model.add(Conv2D(32,kernel_size=(5,5),activation='relu'))
model.add(Conv2D(32,kernel_size=(5,5),activation='relu'))
model.add(MaxPooling2D(pool_size=(3,3),strides=2))
model.add(Dropout(0.5))
model.add(Conv2D(64,(3,3),activation='relu',padding='same'))
model.add(Conv2D(64,(1,1),activation='relu',padding='same'))
model.add(Conv2D(64,(1,1),activation='relu',padding='same'))
model.add(MaxPooling2D(pool_size=(3,3),strides=2))
model.add(Dropout(0.5))
model.add(Conv2D(128,(3,3),activation='relu',padding='same'))
model.add(Conv2D(32,(1,1),activation='relu'))
model.add(Conv2D(5,(1,1)))
model.add(GlobalAveragePooling2D())
model.add(Flatten())
model.add(Dense(5, activation='softmax'))
model.build(input_shape)
model.compile(loss=categorical_crossentropy,optimizer=Adam(0.001),metrics=['accuracy'])
return model
```
|
github_jupyter
|
# 1. Python and notebook basics
In this first chapter, we will cover the very essentials of Python and notebooks such as creating a variable, importing packages, using functions, seeing how variables behave in the notebook etc. We will see more details on some of these topics, but this very short introduction will then allow us to quickly dive into more applied and image processing specific topics without having to go through a full Python introduction.
## Variables
Like we would do in mathematics when we define variables in equations such as $x=3$, we can do the same in all programming languages. Python has one of the simplest syntax for this, i.e. exactly as we would do it naturally. Let's define a variable in the next cell:
```
a = 3
```
As long as we **don't execute the cell** using Shift+Enter or the play button in the menu, the above cell is **purely text**. We can close our Jupyter session and then re-start it and this line of text will still be there. However other parts of the notebook are not "aware" that this variable has been defined and so we can't re-use anywhere else. For example if we type ```a``` again and execute the cell, we get an error:
```
a
```
So we actually need to **execute** the cell so that Python reads that line and executes the command. Here it's a very simple command that just says that the value of the variable ```a``` is three. So let's go back to the cell that defined ```a``` and now execute it (click in the cell and hit Shift+Enter). Now this variable is **stored in the computing memory** of the computer and we can re-use it anywhere in the notebook (but only in **this** notebook)!
We can again just type ```a```
```
a
```
We see that now we get an *output* with the value three. Most variables display an output when they are not involved in an operation. For example the line ```a=3``` didn't have an output.
Now we can define other variables in a new cell. Note that we can put as **many lines** of commands as we want in a single cell. Each command just need to be on a new line.
```
b = 5
c = 2
```
As variables are defined for the entire notebook we can combine information that comes from multiple cells. Here we do some basic mathematics:
```
a + b
```
Here we only see the output. We can't re-use that ouput for further calculations as we didn't define a new variable to contain it. Here we do it:
```
d = a + b
d
```
```d``` is now a new variable. It is purely numerical and not a mathematical formula as the above cell could make you believe. For example if we change the value of ```a```:
```
a = 100
```
and check the value of ```d```:
```
d
```
it has not change. We would have to rerun the operation and assign it again to ```d``` for it to update:
```
d = a + b
d
```
We will see many other types of variables during the course. Some are just other types of data, for example we can define a **text** variable by using quotes ```' '``` around a given text:
```
my_text = 'This is my text'
my_text
```
Others can contain multiple elements like lists:
```
my_list = [3, 8, 5, 9]
my_list
```
but more on these data structures later...
## Functions
We have seen that we could define variables and do some basic operations with them. If we want to go beyond simple arithmetic we need more **complex functions** that can operate on variables. Imagine for example that we need a function $f(x, a, b) = a * x + b$. For this we can use and **define functions**. Here's how we can define the previous function:
```
def my_fun(x, a, b):
out = a * x + b
return out
```
We see a series of Python rules to define a function:
- we use the word **```def```** to signal that we are creating a function
- we pick a **function name**, here ```my_fun```
- we open the **parenthesis** and put all our **variables ```x```, ```a```, ```b```** in there, just like when we do mathematics
- we do some operation inside the function. **Inside** the function is signal with the **indentation**: everything that belong inside the function (there could be many more lines) is shifted by a *single tab* or *three space* to the right
- we use the word **```return```** to tell what is the output of the function, here the variable ```out```
We can now use this function as if we were doing mathematics: we pick a a value for the three parameters e.g. $f(3, 2, 5)$
```
my_fun(3, 2, 5)
```
Note that **some functions are defined by default** in Python. For example if I define a variable which is a string:
```
my_text = 'This is my text'
```
I can count the number of characters in this text using the ```len()``` function which comes from base Python:
```
len(my_text)
```
The ```len``` function has not been manually defined within a ```def``` statement, it simply exist by default in the Python language.
## Variables as objects
In the Python world, variables are not "just" variables, they are actually more complex objects. So for example our variable ```my_text``` does indeed contain the text ```This is my text``` but it contains also additional features. The way to access those features is to use the dot notation ```my_text.some_feature```. There are two types of featues:
- functions, called here methods, that do some computation or modify the variable itself
- properties, that contain information about the variable
For example the object ```my_text``` has a function attached to it that allows us to put all letters to lower case:
```
my_text
my_text.lower()
```
If we define a complex number:
```
a = 3 + 5j
```
then we can access the property ```real``` that gives us only the real part of the number:
```
a.real
```
Note that when we use a method (function) we need to use the parenthesis, just like for regular functions, while for properties we don't.
## Packages
In the examples above, we either defined a function ourselves or used one generally accessible in base Python but there is a third solution: **external packages**. These packages are collections of functions used in a specific domain that are made available to everyone via specialized online repositories. For example we will be using in this course a package called [scikit-image](https://scikit-image.org/) that implements a large number of functions for image processing. For example if we want to filter an image stored in a variable ```im_in``` with a median filter, we can then just use the ```median()``` function of scikit-image and apply it to an image ```im_out = median(im_in)```. The question is now: how do we access these functions?
### Importing functions
The answer is that we have to **import** the functions we want to use in a *given notebook* from a package to be able to use them. First the package needs to be **installed**. One of the most popular place where to find such packages is the PyPi repository. We can install packages from there using the following command either in a **terminal or directly in the notebook**. For example for [scikit-image](https://pypi.org/project/scikit-image/):
```
pip install scikit-image
```
Once installed we can **import** the packakge in a notebook in the following way (note that the name of the package is scikit-image, but in code we use an abbreviated name ```skimage```):
```
import skimage
```
The import is valid for the **entire notebook**, we don't need that line in each cell.
Now that we have imported the package we can access all function that we define in it using a *dot notation* ```skimage.myfun```. Most packages are organized into submodules and in that case to access functions of a submodule we use ```skimage.my_submodule.myfun```.
To come back to the previous example: the ```median``` filtering function is in the ```filters``` submodule that we could now use as:
```python
im_out = skimage.filters.median(im_in)
```
We cannot execute this command as the variables ```im_in``` and ```im_out``` are not yet defined.
Note that there are multiple ways to import packages. For example we could give another name to the package, using the ```as``` statement:
```
import skimage as sk
```
Nowe if we want to use the ```median``` function in the filters sumodule we would write:
```python
im_out = sk.filters.median(im_in)
```
We can also import only a certain submodule using:
```
from skimage import filters
```
Now we have to write:
```python
im_out = filters.median(im_in)
```
Finally, we can import a **single** function like this:
```
from skimage.filters import median
```
and now we have to write:
```python
im_out = median(im_in)
```
## Structures
As mentioned above we cannot execute those various lines like ```im_out = median(im_in)``` because the image variable ```im_in``` is not yet defined. This variable should be an image, i.e. it cannot be a single number like in ```a=3``` but an entire grid of values, each value being one pixel. We therefore need a specific variable type that can contain such a structure.
We have already seen that we can define different types of variables. Single numbers:
```
a = 3
```
Text:
```
b = 'my text'
```
or even lists of numbers:
```
c = [6,2,8,9]
```
This last type of variable is called a ```list``` in Python and is one of the **structures** that is available in Python. If we think of an image that has multiple lines and columns of pixels, we could now imagine that we can represent it as a list of lists, each single list being e.g. one row pf pixels. For example a 3 x 3 image could be:
```
my_image = [[4,8,7], [6,4,3], [5,3,7]]
my_image
```
While in principle we could use a ```list``` for this, computations on such objects would be very slow. For example if we wanted to do background correction and subtract a given value from our image, effectively we would have to go through each element of our list (each pixel) one by one and sequentially remove the background from each pixel. If the background is 3 we would have therefore to compute:
- 4-3
- 8-3
- 7-3
- 6-3
etc. Since operations are done sequentially this would be very slow as we couldn't exploit the fact that most computers have multiple processors. Also it would be tedious to write such an operation.
To fix this, most scientific areas that use lists of numbers of some kind (time-series, images, measurements etc.) resort to an **external package** called ```Numpy``` which offers a **computationally efficient list** called an **array**.
To make this clearer we now import an image in our notebook to see such a structure. We will use a **function** from the scikit-image package to do this import. That function called ```imread``` is located in the submodule called ```io```. Remember that we can then access this function with ```skimage.io.imread()```. Just like we previously defined a function $f(x, a, b)$ that took inputs $x, a, b$, this ```imread()``` function also needs an input. Here it is just the **location of the image**, and that location can either be the **path** to the file on our computer or a **url** of an online place where the image is stored. Here we use an image that can be found at https://github.com/guiwitz/PyImageCourse_beginner/raw/master/images/19838_1252_F8_1.tif. As you can see it is a tif file. This address that we are using as an input should be formatted as text:
```
my_address = 'https://github.com/guiwitz/PyImageCourse_beginner/raw/master/images/19838_1252_F8_1.tif'
```
Now we can call our function:
```
skimage.io.imread(my_address)
```
We see here an output which is what is returned by our function. It is as expected a list of numbers, and not all numbers are shown because the list is too long. We see that we also have ```[]``` to specify rows, columns etc. The main difference compared to our list of lists that we defined previously is the ```array``` indication at the very beginning of the list of numbers. This ```array``` indication tells us that we are dealing with a ```Numpy``` array, this alternative type of list of lists that will allow us to do efficient computations.
## Plotting
We will see a few ways to represent data during the course. Here we just want to have a quick look at the image we just imported. For plotting we will use yet another **external library** called Matplotlib. That library is extensively used in the Python world and offers extensive choices of plots. We will mainly use one **function** from the library to display images: ```imshow```. Again, to access that function, we first need to import the package. Here we need a specific submodule:
```
import matplotlib.pyplot as plt
```
Now we can use the ```plt.imshow()``` function. There are many options for plot, but we can use that function already by just passing an ```array``` as an input. First we need to assign the imported array to a variable:
```
import skimage.io
image = skimage.io.imread(my_address)
plt.imshow(image);
```
We see that we are dealing with a multi-channel image and can already distinguish cell nuclei (blue) and cytoplasm (red).
|
github_jupyter
|
**Create Train / Dev / Test files. <br> Each file is a dictionary where each key represent the ID of a certain Author and each value is a dict where the keys are : <br> - author_embedding : the Node embedding that correspond to the author (tensor of shape (128,)) <br> - papers_embedding : the abstract embedding of every papers (tensor of shape (10,dim)) (dim depend on the embedding model taken into account) <br> - features : the graph structural features (tensor of shape (4,)) <br> - y : the target (tensor of shape (1,))**
```
import pandas as pd
import numpy as np
import networkx as nx
from tqdm import tqdm_notebook as tqdm
from sklearn.utils import shuffle
import gzip
import pickle
import torch
def load_dataset_file(filename):
with gzip.open(filename, "rb") as f:
loaded_object = pickle.load(f)
return loaded_object
def save(object, filename, protocol = 0):
"""Saves a compressed object to disk
"""
file = gzip.GzipFile(filename, 'wb')
file.write(pickle.dumps(object, protocol))
file.close()
```
# Roberta Embedding
```
# Load the paper's embedding
embedding_per_paper = load_dataset_file('/content/drive/MyDrive/altegrad_datachallenge/files_generated/embedding_per_paper_clean.txt')
# Load the node's embedding
embedding_per_nodes = load_dataset_file('/content/drive/MyDrive/altegrad_datachallenge/files_generated/Node2Vec.txt')
# read the file to create a dictionary with author key and paper list as value
f = open("/content/drive/MyDrive/altegrad_datachallenge/author_papers.txt","r")
papers_per_author = {}
for l in f:
auth_paps = [paper_id.strip() for paper_id in l.split(":")[1].replace("[","").replace("]","").replace("\n","").replace("\'","").replace("\"","").split(",")]
papers_per_author[l.split(":")[0]] = auth_paps
# Load train set
df_train = shuffle(pd.read_csv('/content/drive/MyDrive/altegrad_datachallenge/train.csv', dtype={'authorID': np.int64, 'h_index': np.float32})).reset_index(drop=True)
# Load test set
df_test = pd.read_csv('/content/drive/MyDrive/altegrad_datachallenge/test.csv', dtype={'authorID': np.int64})
# Load Graph
G = nx.read_edgelist('/content/drive/MyDrive/altegrad_datachallenge/collaboration_network.edgelist', delimiter=' ', nodetype=int)
# computes structural features for each node
core_number = nx.core_number(G)
avg_neighbor_degree = nx.average_neighbor_degree(G)
# Split into train/valid
df_valid = df_train.iloc[int(len(df_train)*0.9):, :]
df_train = df_train.iloc[:int(len(df_train)*0.9), :]
```
## Train
```
train_data = {}
for i, row in tqdm(df_train.iterrows()):
author_id, y = str(int(row['authorID'])), row['h_index']
degree, core_number_, avg_neighbor_degree_ = G.degree(int(author_id)), core_number[int(author_id)], avg_neighbor_degree[int(author_id)]
author_embedding = torch.from_numpy(embedding_per_nodes[int(author_id)].reshape(1,-1))
papers_ids = papers_per_author[author_id]
papers_embedding = []
num_papers = 0
for id_paper in papers_ids:
num_papers += 1
try:
papers_embedding.append(torch.from_numpy(embedding_per_paper[id_paper].reshape(1,-1)))
except KeyError:
print(f"Missing paper for {author_id}")
papers_embedding.append(torch.zeros((1,768)))
papers_embedding = torch.cat(papers_embedding, dim=0)
additional_features = torch.from_numpy(np.array([degree, core_number_, avg_neighbor_degree_, num_papers]).reshape(1,-1))
y = torch.Tensor([y])
train_data[author_id] = {'author_embedding': author_embedding, 'papers_embedding': papers_embedding, 'features': additional_features, 'target': y}
# Saving
save(train_data, '/content/drive/MyDrive/altegrad_datachallenge/data/data.train')
# Deleting (memory)
del train_data
```
## Validation
```
valid_data = {}
for i, row in tqdm(df_valid.iterrows()):
author_id, y = str(int(row['authorID'])), row['h_index']
degree, core_number_, avg_neighbor_degree_ = G.degree(int(author_id)), core_number[int(author_id)], avg_neighbor_degree[int(author_id)]
author_embedding = torch.from_numpy(embedding_per_nodes[int(author_id)].reshape(1,-1))
papers_ids = papers_per_author[author_id]
papers_embedding = []
num_papers = 0
for id_paper in papers_ids:
num_papers += 1
try:
papers_embedding.append(torch.from_numpy(embedding_per_paper[id_paper].reshape(1,-1)))
except KeyError:
papers_embedding.append(torch.zeros((1,768)))
papers_embedding = torch.cat(papers_embedding, dim=0)
additional_features = torch.from_numpy(np.array([degree, core_number_, avg_neighbor_degree_, num_papers]).reshape(1,-1))
y = torch.Tensor([y])
valid_data[author_id] = {'author_embedding': author_embedding, 'papers_embedding': papers_embedding, 'features': additional_features, 'target': y}
save(valid_data, '/content/drive/MyDrive/altegrad_datachallenge/data/data.valid')
del valid_data
```
## Test
```
test_data = {}
for i, row in tqdm(df_test.iterrows()):
author_id = str(int(row['authorID']))
degree, core_number_, avg_neighbor_degree_ = G.degree(int(author_id)), core_number[int(author_id)], avg_neighbor_degree[int(author_id)]
author_embedding = torch.from_numpy(embedding_per_nodes[int(author_id)].reshape(1,-1))
papers_ids = papers_per_author[author_id]
papers_embedding = []
num_papers = 0
for id_paper in papers_ids:
num_papers += 1
try:
papers_embedding.append(torch.from_numpy(embedding_per_paper[id_paper].reshape(1,-1)))
except KeyError:
papers_embedding.append(torch.zeros((1,768)))
papers_embedding = torch.cat(papers_embedding, dim=0)
additional_features = torch.from_numpy(np.array([degree, core_number_, avg_neighbor_degree_, num_papers]).reshape(1,-1))
test_data[author_id] = {'author_embedding': author_embedding, 'papers_embedding': papers_embedding, 'features': additional_features}
del G
del df_test
del embedding_per_paper
del papers_per_author
del core_number
del avg_neighbor_degree
del embedding_per_nodes
save(test_data, '/content/drive/MyDrive/altegrad_datachallenge/data/data.test', 4)
del test_data
```
# Doc2Vec
```
# Load the paper's embedding
embedding_per_paper = load_dataset_file('/content/drive/MyDrive/altegrad_datachallenge/files_generated/doc2vec_paper_embedding.txt')
# Load the node's embedding
embedding_per_nodes = load_dataset_file('/content/drive/MyDrive/altegrad_datachallenge/files_generated/Node2Vec.txt')
# read the file to create a dictionary with author key and paper list as value
f = open("/content/drive/MyDrive/altegrad_datachallenge/data/author_papers.txt","r")
papers_per_author = {}
for l in f:
auth_paps = [paper_id.strip() for paper_id in l.split(":")[1].replace("[","").replace("]","").replace("\n","").replace("\'","").replace("\"","").split(",")]
papers_per_author[l.split(":")[0]] = auth_paps
# Load train set
df_train = shuffle(pd.read_csv('/content/drive/MyDrive/altegrad_datachallenge/data/train.csv', dtype={'authorID': np.int64, 'h_index': np.float32})).reset_index(drop=True)
# Load test set
df_test = pd.read_csv('/content/drive/MyDrive/altegrad_datachallenge/data/test.csv', dtype={'authorID': np.int64})
# Load Graph
G = nx.read_edgelist('/content/drive/MyDrive/altegrad_datachallenge/data/collaboration_network.edgelist', delimiter=' ', nodetype=int)
# computes structural features for each node
core_number = nx.core_number(G)
avg_neighbor_degree = nx.average_neighbor_degree(G)
# Split into train/valid
df_valid = df_train.iloc[int(len(df_train)*0.9):, :]
df_train = df_train.iloc[:int(len(df_train)*0.9), :]
```
## Train
```
train_data = {}
for i, row in tqdm(df_train.iterrows()):
author_id, y = str(int(row['authorID'])), row['h_index']
degree, core_number_, avg_neighbor_degree_ = G.degree(int(author_id)), core_number[int(author_id)], avg_neighbor_degree[int(author_id)]
author_embedding = torch.from_numpy(embedding_per_nodes[int(author_id)].reshape(1,-1))
papers_ids = papers_per_author[author_id]
papers_embedding = []
num_papers = 0
for id_paper in papers_ids:
num_papers += 1
try:
papers_embedding.append(torch.from_numpy(embedding_per_paper[id_paper].reshape(1,-1)))
except KeyError:
print(f"Missing paper for {author_id}")
papers_embedding.append(torch.zeros((1,256)))
papers_embedding = torch.cat(papers_embedding, dim=0)
additional_features = torch.from_numpy(np.array([degree, core_number_, avg_neighbor_degree_, num_papers]).reshape(1,-1))
y = torch.Tensor([y])
train_data[author_id] = {'author_embedding': author_embedding, 'papers_embedding': papers_embedding, 'features': additional_features, 'target': y}
# Saving
save(train_data, '/content/drive/MyDrive/altegrad_datachallenge/data/d2v.train')
# Deleting (memory)
del train_data
```
## Dev
```
valid_data = {}
for i, row in tqdm(df_valid.iterrows()):
author_id, y = str(int(row['authorID'])), row['h_index']
degree, core_number_, avg_neighbor_degree_ = G.degree(int(author_id)), core_number[int(author_id)], avg_neighbor_degree[int(author_id)]
author_embedding = torch.from_numpy(embedding_per_nodes[int(author_id)].reshape(1,-1))
papers_ids = papers_per_author[author_id]
papers_embedding = []
num_papers = 0
for id_paper in papers_ids:
num_papers += 1
try:
papers_embedding.append(torch.from_numpy(embedding_per_paper[id_paper].reshape(1,-1)))
except KeyError:
papers_embedding.append(torch.zeros((1,256)))
papers_embedding = torch.cat(papers_embedding, dim=0)
additional_features = torch.from_numpy(np.array([degree, core_number_, avg_neighbor_degree_, num_papers]).reshape(1,-1))
y = torch.Tensor([y])
valid_data[author_id] = {'author_embedding': author_embedding, 'papers_embedding': papers_embedding, 'features': additional_features, 'target': y}
save(valid_data, '/content/drive/MyDrive/altegrad_datachallenge/data/d2v.valid')
del valid_data
```
## Test
```
test_data = {}
for i, row in tqdm(df_test.iterrows()):
author_id = str(int(row['authorID']))
degree, core_number_, avg_neighbor_degree_ = G.degree(int(author_id)), core_number[int(author_id)], avg_neighbor_degree[int(author_id)]
author_embedding = torch.from_numpy(embedding_per_nodes[int(author_id)].reshape(1,-1))
papers_ids = papers_per_author[author_id]
papers_embedding = []
num_papers = 0
for id_paper in papers_ids:
num_papers += 1
try:
papers_embedding.append(torch.from_numpy(embedding_per_paper[id_paper].reshape(1,-1)))
except KeyError:
papers_embedding.append(torch.zeros((1,256)))
papers_embedding = torch.cat(papers_embedding, dim=0)
additional_features = torch.from_numpy(np.array([degree, core_number_, avg_neighbor_degree_, num_papers]).reshape(1,-1))
test_data[author_id] = {'author_embedding': author_embedding, 'papers_embedding': papers_embedding, 'features': additional_features}
del G
del df_test
del embedding_per_paper
del papers_per_author
del core_number
del avg_neighbor_degree
del embedding_per_nodes
save(test_data, '/content/drive/MyDrive/altegrad_datachallenge/data/d2v.test', 4)
del test_data
```
|
github_jupyter
|
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
# x = Acos(k/m t + \theta) = 1
# p = mx' = Ak/m sin(k/m t + \theta)
t = np.linspace(0, 2 * np.pi, 100)
t
```
# Exact Equation
```
x, p = np.cos(t - np.pi), -np.sin(t - np.pi)
fig = plt.figure(figsize=(5, 5))
for i in range(0, len(t), 1):
plt.plot(x[i:i+2], p[i:i+2], color='black', markersize=0)
```
# Euler's Method Equation
# Euler's Method
```
# x' = p/m = p
# p' = -kx + mg = -x
# x = x + \eps * p' = x + \eps*(p)
# p = p + \eps * x' = p - \eps*(x)
fig = plt.figure(figsize=(5, 5))
plt.title("Euler's Method (eps=0.1)")
plt.xlabel("position (q)")
plt.ylabel("momentum (p)")
for i in range(0, len(t), 1):
plt.plot(x[i:i+2], p[i:i+2], color='black', markersize=0)
x_prev = 0
p_prev = 1
eps = 0.1
steps = 100
for i in range(0, steps, 1):
x_next = x_prev + eps * p_prev
p_next = p_prev - eps * x_prev
plt.plot([x_prev, x_next], [p_prev, p_next], marker='o', color='blue', markersize=5)
x_prev, p_prev = x_next, p_next
```
# Modified Euler's Method
```
# x' = p/m = p
# p' = -kx + mg = -x
# x = x + \eps * p' = x + \eps*(p)
# p = p + \eps * x' = p - \eps*(x)
fig = plt.figure(figsize=(5, 5))
plt.title("Modified Euler's Method (eps=0.2)")
plt.xlabel("position (q)")
plt.ylabel("momentum (p)")
for i in range(0, len(t), 1):
plt.plot(x[i:i+2], p[i:i+2], color='black', markersize=0)
x_prev = 0
p_prev = 1
eps = 0.2
steps = int(2*np.pi / eps)
for i in range(0, steps, 1):
p_next = p_prev - eps * x_prev
x_next = x_prev + eps * p_next
plt.plot([x_prev, x_next], [p_prev, p_next], marker='o', color='blue', markersize=5)
x_prev, p_prev = x_next, p_next
# x' = p/m = p
# p' = -kx + mg = -x
# x = x + \eps * p' = x + \eps*(p)
# p = p + \eps * x' = p - \eps*(x)
fig = plt.figure(figsize=(5, 5))
plt.title("Modified Euler's Method (eps=0.2)")
plt.xlabel("position (q)")
plt.ylabel("momentum (p)")
for i in range(0, len(t), 1):
plt.plot(x[i:i+2], p[i:i+2], color='black', markersize=0)
x_prev = 0.1
p_prev = 1
eps = 1.31827847281
#eps = 1.31827847281
steps = 50 #int(2*np.pi / eps)
for i in range(0, steps, 1):
p_next = p_prev - eps * x_prev
x_next = x_prev + eps * p_next
plt.plot([x_prev, x_next], [p_prev, p_next], marker='o', color='blue', markersize=5)
x_prev, p_prev = x_next, p_next
```
# Leapfrog Method
```
# x' = p/m = p
# p' = -kx + mg = -x
# x = x + \eps * p' = x + \eps*(p)
# p = p + \eps * x' = p - \eps*(x)
fig = plt.figure(figsize=(5, 5))
plt.title("Leapfrog Method (eps=0.2)")
plt.xlabel("position (q)")
plt.ylabel("momentum (p)")
for i in range(0, len(t), 1):
plt.plot(x[i:i+2], p[i:i+2], color='black', markersize=0)
x_prev = 0
p_prev = 1
eps = 0.2
steps = int(2*np.pi / eps)
for i in range(0, steps, 1):
p_half = p_prev - eps/2 * x_prev
x_next = x_prev + eps * p_half
p_next = p_half - eps/2 * x_next
plt.plot([x_prev, x_next], [p_prev, p_next], marker='o', color='blue', markersize=5)
x_prev, p_prev = x_next, p_next
# x' = p/m = p
# p' = -kx + mg = -x
# x = x + \eps * p' = x + \eps*(p)
# p = p + \eps * x' = p - \eps*(x)
fig = plt.figure(figsize=(5, 5))
plt.title("Leapfrog Method (eps=0.9)")
plt.xlabel("position (q)")
plt.ylabel("momentum (p)")
for i in range(0, len(t), 1):
plt.plot(x[i:i+2], p[i:i+2], color='black', markersize=0)
x_prev = 0
p_prev = 1
eps = 0.9
steps = 3 * int(2*np.pi / eps + 0.1)
for i in range(0, steps, 1):
p_half = p_prev - eps/2 * x_prev
x_next = x_prev + eps * p_half
p_next = p_half - eps/2 * x_next
plt.plot([x_prev, x_next], [p_prev, p_next], marker='o', color='blue', markersize=5)
x_prev, p_prev = x_next, p_next
```
# Combined Figure
```
fig, ((ax1, ax2), (ax3, ax4)) = plt.subplots(2, 2, figsize=(15,15))
# subplot1
ax1.set_title("Euler's Method (eps=0.1)")
ax1.set_xlabel("position (q)")
ax1.set_ylabel("momentum (p)")
for i in range(0, len(t), 1):
ax1.plot(x[i:i+2], p[i:i+2], color='black', markersize=0)
x_prev = 0
p_prev = 1
eps = 0.1
steps = 100
for i in range(0, steps, 1):
x_next = x_prev + eps * p_prev
p_next = p_prev - eps * x_prev
ax1.plot([x_prev, x_next], [p_prev, p_next], marker='o', color='blue', markersize=5)
x_prev, p_prev = x_next, p_next
# subplot2
ax2.set_title("Modified Euler's Method (eps=0.2)")
ax2.set_xlabel("position (q)")
ax2.set_ylabel("momentum (p)")
for i in range(0, len(t), 1):
ax2.plot(x[i:i+2], p[i:i+2], color='black', markersize=0)
x_prev = 0
p_prev = 1
eps = 0.2
steps = int(2*np.pi / eps)
for i in range(0, steps, 1):
p_next = p_prev - eps * x_prev
x_next = x_prev + eps * p_next
ax2.plot([x_prev, x_next], [p_prev, p_next], marker='o', color='blue', markersize=5)
x_prev, p_prev = x_next, p_next
# subplot3
ax3.set_title("Leapfrog Method (eps=0.2)")
ax3.set_xlabel("position (q)")
ax3.set_ylabel("momentum (p)")
for i in range(0, len(t), 1):
ax3.plot(x[i:i+2], p[i:i+2], color='black', markersize=0)
x_prev = 0
p_prev = 1
eps = 0.2
steps = int(2*np.pi / eps)
for i in range(0, steps, 1):
p_half = p_prev - eps/2 * x_prev
x_next = x_prev + eps * p_half
p_next = p_half - eps/2 * x_next
ax3.plot([x_prev, x_next], [p_prev, p_next], marker='o', color='blue', markersize=5)
x_prev, p_prev = x_next, p_next
# subplot4
ax4.set_title("Leapfrog Method (eps=0.9)")
ax4.set_xlabel("position (q)")
ax4.set_ylabel("momentum (p)")
for i in range(0, len(t), 1):
ax4.plot(x[i:i+2], p[i:i+2], color='black', markersize=0)
x_prev = 0
p_prev = 1
eps = 0.9
steps = 3 * int(2*np.pi / eps + 0.1)
for i in range(0, steps, 1):
p_half = p_prev - eps/2 * x_prev
x_next = x_prev + eps * p_half
p_next = p_half - eps/2 * x_next
ax4.plot([x_prev, x_next], [p_prev, p_next], marker='o', color='blue', markersize=5)
x_prev, p_prev = x_next, p_next
```
# Combined Figure - Square
```
fig, ((ax1, ax2)) = plt.subplots(1, 2, figsize=(15, 7.5))
# subplot1
ax1.set_title("Euler's Method (eps=0.2)")
ax1.set_xlabel("position (q)")
ax1.set_ylabel("momentum (p)")
for i in range(0, len(t), 1):
ax1.plot(x[i:i+2], p[i:i+2], color='black', markersize=0)
def draw_square(ax, x, p, **args):
assert len(x) == len(p) == 4
x = list(x) + [x[0]]
p = list(p) + [p[0]]
ax.plot(x, p, **args)
def euler_update(x, p, eps):
assert len(x) == len(p) == 4
x_next = [0.]* 4
p_next = [0.]* 4
for i in range(4):
x_next[i] = x[i] + eps * p[i]
p_next[i] = p[i] - eps * x[i]
return x_next, p_next
def mod_euler_update(x, p, eps):
assert len(x) == len(p) == 4
x_next = [0.]* 4
p_next = [0.]* 4
for i in range(4):
x_next[i] = x[i] + eps * p[i]
p_next[i] = p[i] - eps * x_next[i]
return x_next, p_next
delta = 0.1
eps = 0.2
x_prev = np.array([0.0, 0.0, delta, delta]) + 0.0
p_prev = np.array([0.0, delta, delta, 0.0]) + 1.0
steps = int(2*np.pi / eps)
for i in range(0, steps, 1):
draw_square(ax1, x_prev, p_prev, marker='o', color='blue', markersize=5)
x_next, p_next = euler_update(x_prev, p_prev, eps)
x_prev, p_prev = x_next, p_next
# subplot2
ax2.set_title("Modified Euler's Method (eps=0.2)")
ax2.set_xlabel("position (q)")
ax2.set_ylabel("momentum (p)")
for i in range(0, len(t), 1):
ax2.plot(x[i:i+2], p[i:i+2], color='black', markersize=0)
x_prev = np.array([0.0, 0.0, delta, delta]) + 0.0
p_prev = np.array([0.0, delta, delta, 0.0]) + 1.0
for i in range(0, steps, 1):
draw_square(ax2, x_prev, p_prev, marker='o', color='blue', markersize=5)
x_next, p_next = mod_euler_update(x_prev, p_prev, eps)
x_prev, p_prev = x_next, p_next
```
|
github_jupyter
|
# Dependencies
```
import os
import random
import warnings
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.utils import class_weight
from sklearn.model_selection import train_test_split
from sklearn.metrics import confusion_matrix, cohen_kappa_score
from keras import backend as K
from keras.models import Model
from keras import optimizers, applications
from keras.preprocessing.image import ImageDataGenerator
from keras.callbacks import EarlyStopping, ReduceLROnPlateau, Callback
from keras.layers import Dense, Dropout, GlobalAveragePooling2D, Input
# Set seeds to make the experiment more reproducible.
from tensorflow import set_random_seed
def seed_everything(seed=0):
random.seed(seed)
os.environ['PYTHONHASHSEED'] = str(seed)
np.random.seed(seed)
set_random_seed(0)
seed_everything()
%matplotlib inline
sns.set(style="whitegrid")
warnings.filterwarnings("ignore")
```
# Load data
```
train = pd.read_csv('../input/aptos2019-blindness-detection/train.csv')
test = pd.read_csv('../input/aptos2019-blindness-detection/test.csv')
print('Number of train samples: ', train.shape[0])
print('Number of test samples: ', test.shape[0])
# Preprocecss data
train["id_code"] = train["id_code"].apply(lambda x: x + ".png")
test["id_code"] = test["id_code"].apply(lambda x: x + ".png")
train['diagnosis'] = train['diagnosis'].astype('str')
display(train.head())
```
# Model parameters
```
# Model parameters
BATCH_SIZE = 8
EPOCHS = 30
WARMUP_EPOCHS = 2
LEARNING_RATE = 1e-4
WARMUP_LEARNING_RATE = 1e-3
HEIGHT = 512
WIDTH = 512
CANAL = 3
N_CLASSES = train['diagnosis'].nunique()
ES_PATIENCE = 5
RLROP_PATIENCE = 3
DECAY_DROP = 0.5
def kappa(y_true, y_pred, n_classes=5):
y_trues = K.cast(K.argmax(y_true), K.floatx())
y_preds = K.cast(K.argmax(y_pred), K.floatx())
n_samples = K.cast(K.shape(y_true)[0], K.floatx())
distance = K.sum(K.abs(y_trues - y_preds))
max_distance = n_classes - 1
kappa_score = 1 - ((distance**2) / (n_samples * (max_distance**2)))
return kappa_score
```
# Train test split
```
X_train, X_val = train_test_split(train, test_size=0.25, random_state=0)
```
# Data generator
```
train_datagen=ImageDataGenerator(rescale=1./255,
rotation_range=360,
brightness_range=[0.5, 1.5],
zoom_range=[1, 1.2],
zca_whitening=True,
horizontal_flip=True,
vertical_flip=True,
fill_mode='constant',
cval=0.)
train_generator=train_datagen.flow_from_dataframe(
dataframe=X_train,
directory="../input/aptos2019-blindness-detection/train_images/",
x_col="id_code",
y_col="diagnosis",
batch_size=BATCH_SIZE,
class_mode="categorical",
target_size=(HEIGHT, WIDTH))
valid_generator=train_datagen.flow_from_dataframe(
dataframe=X_val,
directory="../input/aptos2019-blindness-detection/train_images/",
x_col="id_code",
y_col="diagnosis",
batch_size=BATCH_SIZE,
class_mode="categorical",
target_size=(HEIGHT, WIDTH))
test_datagen = ImageDataGenerator(rescale=1./255)
test_generator = test_datagen.flow_from_dataframe(
dataframe=test,
directory = "../input/aptos2019-blindness-detection/test_images/",
x_col="id_code",
target_size=(HEIGHT, WIDTH),
batch_size=1,
shuffle=False,
class_mode=None)
```
# Model
```
def create_model(input_shape, n_out):
input_tensor = Input(shape=input_shape)
base_model = applications.ResNet50(weights=None,
include_top=False,
input_tensor=input_tensor)
base_model.load_weights('../input/resnet50/resnet50_weights_tf_dim_ordering_tf_kernels_notop.h5')
x = GlobalAveragePooling2D()(base_model.output)
x = Dropout(0.5)(x)
x = Dense(2048, activation='relu')(x)
x = Dropout(0.5)(x)
final_output = Dense(n_out, activation='softmax', name='final_output')(x)
model = Model(input_tensor, final_output)
return model
model = create_model(input_shape=(HEIGHT, WIDTH, CANAL), n_out=N_CLASSES)
for layer in model.layers:
layer.trainable = False
for i in range(-5, 0):
model.layers[i].trainable = True
class_weights = class_weight.compute_class_weight('balanced', np.unique(train['diagnosis'].astype('int').values), train['diagnosis'].astype('int').values)
metric_list = ["accuracy", kappa]
optimizer = optimizers.Adam(lr=WARMUP_LEARNING_RATE)
model.compile(optimizer=optimizer, loss="categorical_crossentropy", metrics=metric_list)
model.summary()
```
# Train top layers
```
STEP_SIZE_TRAIN = train_generator.n//train_generator.batch_size
STEP_SIZE_VALID = valid_generator.n//valid_generator.batch_size
history_warmup = model.fit_generator(generator=train_generator,
steps_per_epoch=STEP_SIZE_TRAIN,
validation_data=valid_generator,
validation_steps=STEP_SIZE_VALID,
epochs=WARMUP_EPOCHS,
class_weight=class_weights,
verbose=1).history
```
# Fine-tune the complete model
```
for layer in model.layers:
layer.trainable = True
es = EarlyStopping(monitor='val_loss', mode='min', patience=ES_PATIENCE, restore_best_weights=True, verbose=1)
rlrop = ReduceLROnPlateau(monitor='val_loss', mode='min', patience=RLROP_PATIENCE, factor=DECAY_DROP, min_lr=1e-6, verbose=1)
callback_list = [es, rlrop]
optimizer = optimizers.Adam(lr=LEARNING_RATE)
model.compile(optimizer=optimizer, loss="categorical_crossentropy", metrics=metric_list)
model.summary()
history_finetunning = model.fit_generator(generator=train_generator,
steps_per_epoch=STEP_SIZE_TRAIN,
validation_data=valid_generator,
validation_steps=STEP_SIZE_VALID,
epochs=EPOCHS,
callbacks=callback_list,
class_weight=class_weights,
verbose=1).history
```
# Model loss graph
```
history = {'loss': history_warmup['loss'] + history_finetunning['loss'],
'val_loss': history_warmup['val_loss'] + history_finetunning['val_loss'],
'acc': history_warmup['acc'] + history_finetunning['acc'],
'val_acc': history_warmup['val_acc'] + history_finetunning['val_acc'],
'kappa': history_warmup['kappa'] + history_finetunning['kappa'],
'val_kappa': history_warmup['val_kappa'] + history_finetunning['val_kappa']}
sns.set_style("whitegrid")
fig, (ax1, ax2, ax3) = plt.subplots(3, 1, sharex='col', figsize=(20, 18))
ax1.plot(history['loss'], label='Train loss')
ax1.plot(history['val_loss'], label='Validation loss')
ax1.legend(loc='best')
ax1.set_title('Loss')
ax2.plot(history['acc'], label='Train accuracy')
ax2.plot(history['val_acc'], label='Validation accuracy')
ax2.legend(loc='best')
ax2.set_title('Accuracy')
ax3.plot(history['kappa'], label='Train kappa')
ax3.plot(history['val_kappa'], label='Validation kappa')
ax3.legend(loc='best')
ax3.set_title('Kappa')
plt.xlabel('Epochs')
sns.despine()
plt.show()
```
# Model Evaluation
```
lastFullTrainPred = np.empty((0, N_CLASSES))
lastFullTrainLabels = np.empty((0, N_CLASSES))
lastFullValPred = np.empty((0, N_CLASSES))
lastFullValLabels = np.empty((0, N_CLASSES))
for i in range(STEP_SIZE_TRAIN+1):
im, lbl = next(train_generator)
scores = model.predict(im, batch_size=train_generator.batch_size)
lastFullTrainPred = np.append(lastFullTrainPred, scores, axis=0)
lastFullTrainLabels = np.append(lastFullTrainLabels, lbl, axis=0)
for i in range(STEP_SIZE_VALID+1):
im, lbl = next(valid_generator)
scores = model.predict(im, batch_size=valid_generator.batch_size)
lastFullValPred = np.append(lastFullValPred, scores, axis=0)
lastFullValLabels = np.append(lastFullValLabels, lbl, axis=0)
```
# Threshold optimization
```
def find_best_fixed_threshold(preds, targs, do_plot=True):
best_thr_list = [0 for i in range(preds.shape[1])]
for index in reversed(range(1, preds.shape[1])):
score = []
thrs = np.arange(0, 1, 0.01)
for thr in thrs:
preds_thr = [index if x[index] > thr else np.argmax(x) for x in preds]
score.append(cohen_kappa_score(targs, preds_thr))
score = np.array(score)
pm = score.argmax()
best_thr, best_score = thrs[pm], score[pm].item()
best_thr_list[index] = best_thr
print(f'thr={best_thr:.3f}', f'F2={best_score:.3f}')
if do_plot:
plt.plot(thrs, score)
plt.vlines(x=best_thr, ymin=score.min(), ymax=score.max())
plt.text(best_thr+0.03, best_score-0.01, ('Kappa[%s]=%.3f'%(index, best_score)), fontsize=14);
plt.show()
return best_thr_list
lastFullComPred = np.concatenate((lastFullTrainPred, lastFullValPred))
lastFullComLabels = np.concatenate((lastFullTrainLabels, lastFullValLabels))
complete_labels = [np.argmax(label) for label in lastFullComLabels]
threshold_list = find_best_fixed_threshold(lastFullComPred, complete_labels, do_plot=True)
threshold_list[0] = 0 # In last instance assign label 0
train_preds = [np.argmax(pred) for pred in lastFullTrainPred]
train_labels = [np.argmax(label) for label in lastFullTrainLabels]
validation_preds = [np.argmax(pred) for pred in lastFullValPred]
validation_labels = [np.argmax(label) for label in lastFullValLabels]
train_preds_opt = [0 for i in range(lastFullTrainPred.shape[0])]
for idx, thr in enumerate(threshold_list):
for idx2, pred in enumerate(lastFullTrainPred):
if pred[idx] > thr:
train_preds_opt[idx2] = idx
validation_preds_opt = [0 for i in range(lastFullValPred.shape[0])]
for idx, thr in enumerate(threshold_list):
for idx2, pred in enumerate(lastFullValPred):
if pred[idx] > thr:
validation_preds_opt[idx2] = idx
```
## Confusion Matrix
```
fig, (ax1, ax2) = plt.subplots(1, 2, sharex='col', figsize=(24, 7))
labels = ['0 - No DR', '1 - Mild', '2 - Moderate', '3 - Severe', '4 - Proliferative DR']
train_cnf_matrix = confusion_matrix(train_labels, train_preds)
validation_cnf_matrix = confusion_matrix(validation_labels, validation_preds)
train_cnf_matrix_norm = train_cnf_matrix.astype('float') / train_cnf_matrix.sum(axis=1)[:, np.newaxis]
validation_cnf_matrix_norm = validation_cnf_matrix.astype('float') / validation_cnf_matrix.sum(axis=1)[:, np.newaxis]
train_df_cm = pd.DataFrame(train_cnf_matrix_norm, index=labels, columns=labels)
validation_df_cm = pd.DataFrame(validation_cnf_matrix_norm, index=labels, columns=labels)
sns.heatmap(train_df_cm, annot=True, fmt='.2f', cmap="Blues",ax=ax1).set_title('Train')
sns.heatmap(validation_df_cm, annot=True, fmt='.2f', cmap="Blues",ax=ax2).set_title('Validation')
plt.show()
fig, (ax1, ax2) = plt.subplots(1, 2, sharex='col', figsize=(24, 7))
labels = ['0 - No DR', '1 - Mild', '2 - Moderate', '3 - Severe', '4 - Proliferative DR']
train_cnf_matrix = confusion_matrix(train_labels, train_preds_opt)
validation_cnf_matrix = confusion_matrix(validation_labels, validation_preds_opt)
train_cnf_matrix_norm = train_cnf_matrix.astype('float') / train_cnf_matrix.sum(axis=1)[:, np.newaxis]
validation_cnf_matrix_norm = validation_cnf_matrix.astype('float') / validation_cnf_matrix.sum(axis=1)[:, np.newaxis]
train_df_cm = pd.DataFrame(train_cnf_matrix_norm, index=labels, columns=labels)
validation_df_cm = pd.DataFrame(validation_cnf_matrix_norm, index=labels, columns=labels)
sns.heatmap(train_df_cm, annot=True, fmt='.2f', cmap="Blues",ax=ax1).set_title('Train optimized')
sns.heatmap(validation_df_cm, annot=True, fmt='.2f', cmap="Blues",ax=ax2).set_title('Validation optimized')
plt.show()
```
## Quadratic Weighted Kappa
```
print("Train Cohen Kappa score: %.3f" % cohen_kappa_score(train_preds, train_labels, weights='quadratic'))
print("Validation Cohen Kappa score: %.3f" % cohen_kappa_score(validation_preds, validation_labels, weights='quadratic'))
print("Complete set Cohen Kappa score: %.3f" % cohen_kappa_score(train_preds+validation_preds, train_labels+validation_labels, weights='quadratic'))
print("Train optimized Cohen Kappa score: %.3f" % cohen_kappa_score(train_preds_opt, train_labels, weights='quadratic'))
print("Validation optimized Cohen Kappa score: %.3f" % cohen_kappa_score(validation_preds_opt, validation_labels, weights='quadratic'))
print("Complete optimized set Cohen Kappa score: %.3f" % cohen_kappa_score(train_preds_opt+validation_preds_opt, train_labels+validation_labels, weights='quadratic'))
```
# Apply model to test set and output predictions
```
test_generator.reset()
STEP_SIZE_TEST = test_generator.n//test_generator.batch_size
preds = model.predict_generator(test_generator, steps=STEP_SIZE_TEST)
predictions = [np.argmax(pred) for pred in preds]
predictions_opt = [0 for i in range(preds.shape[0])]
for idx, thr in enumerate(threshold_list):
for idx2, pred in enumerate(preds):
if pred[idx] > thr:
predictions_opt[idx2] = idx
filenames = test_generator.filenames
results = pd.DataFrame({'id_code':filenames, 'diagnosis':predictions})
results['id_code'] = results['id_code'].map(lambda x: str(x)[:-4])
results_opt = pd.DataFrame({'id_code':filenames, 'diagnosis':predictions_opt})
results_opt['id_code'] = results_opt['id_code'].map(lambda x: str(x)[:-4])
```
# Predictions class distribution
```
fig, (ax1, ax2) = plt.subplots(1, 2, sharex='col', figsize=(24, 8.7))
sns.countplot(x="diagnosis", data=results, palette="GnBu_d", ax=ax1)
sns.countplot(x="diagnosis", data=results_opt, palette="GnBu_d", ax=ax2)
sns.despine()
plt.show()
val_kappa = cohen_kappa_score(validation_preds, validation_labels, weights='quadratic')
val_opt_kappa = cohen_kappa_score(validation_preds_opt, validation_labels, weights='quadratic')
if val_kappa > val_opt_kappa:
results_name = 'submission.csv'
results_opt_name = 'submission_opt.csv'
else:
results_name = 'submission_norm.csv'
results_opt_name = 'submission.csv'
results.to_csv(results_name, index=False)
results.head(10)
results_opt.to_csv(results_opt_name, index=False)
results_opt.head(10)
```
|
github_jupyter
|
# Task: Predict User Item response under uniform exposure while learning from biased training data
Many current applications use recommendations in order to modify the natural user behavior, such as to increase the number of sales or the time spent on a website. This results in a gap between the final recommendation objective and the classical setup where recommendation candidates are evaluated by their coherence with past user behavior, by predicting either the missing entries in the user-item matrix, or the most likely next event. To bridge this gap, we optimize a recommendation policy for the task of increasing the desired outcome versus the organic user behavior. We show this is equivalent to learning to predict recommendation outcomes under a fully random recommendation policy. To this end, we propose a new domain adaptation algorithm that learns from logged data containing outcomes from a biased recommendation policy and predicts recommendation outcomes according to random exposure. We compare our method against state-of-the-art factorization methods and new approaches of causal recommendation and show significant improvements.
# Dataset
**MovieLens 100k dataset** was collected by the GroupLens Research Project at the University of Minnesota.
This data set consists of:
* 100,000 ratings (1-5) from 943 users on 1682 movies.
* Each user has rated at least 20 movies.
The data was collected through the MovieLens web site (movielens.umn.edu) during the seven-month period from September 19th, 1997 through April 22nd, 1998.
# Solution:
**Causal Matrix Factorization** - for more details see: https://arxiv.org/abs/1706.07639

# Metrics:
### * MSE - Mean Squared Error
### * NLL - Negative Log Likelihood
### * AUC - Area Under the Curve
-----------------------------
-----------------------------
# Questions:
### Q1: Add the definition for create_counterfactual_regularizer() method
### Q2: Compare the results of using variable values for cf_pen hyperparameter (0 vs. bigger)
### Q3: Compare different types of optimizers
### Q4: Push the performance as high as possible!
```
%%javascript
IPython.OutputArea.prototype._should_scroll = function(lines) {
return false;
}
import os
import string
import tempfile
import time
import numpy as np
import matplotlib.pyplot as plt
import csv
import random
import tensorflow as tf
from tensorflow.contrib.tensorboard.plugins import projector
from tensorboard import summary as summary_lib
from __future__ import absolute_import
from __future__ import print_function
tf.set_random_seed(42)
tf.logging.set_verbosity(tf.logging.INFO)
print(tf.__version__)
# Hyper-Parameters
flags = tf.app.flags
tf.app.flags.DEFINE_string('f', '', 'kernel')
flags.DEFINE_string('data_set', 'user_prod_dict.skew.', 'Dataset string.') # Reg Skew
flags.DEFINE_string('adapt_stat', 'adapt_2i', 'Adapt String.') # Adaptation strategy
flags.DEFINE_string('model_name', 'cp2v', 'Name of the model for saving.')
flags.DEFINE_float('learning_rate', 1.0, 'Initial learning rate.')
flags.DEFINE_integer('num_epochs', 1, 'Number of epochs to train.')
flags.DEFINE_integer('num_steps', 100, 'Number of steps after which to test.')
flags.DEFINE_integer('embedding_size', 100, 'Size of each embedding vector.')
flags.DEFINE_integer('batch_size', 512, 'How big is a batch of training.')
flags.DEFINE_float('cf_pen', 10.0, 'Counterfactual regularizer hyperparam.')
flags.DEFINE_float('l2_pen', 0.0, 'L2 regularizer hyperparam.')
flags.DEFINE_string('cf_loss', 'l1', 'Use L1 or L2 for the loss .')
FLAGS = tf.app.flags.FLAGS
#_DATA_PATH = "/Users/f.vasile/MyFolders/MyProjects/1.MyPapers/2018_Q2_DS3_Course/code/cp2v/src/Data/"
_DATA_PATH = "./data/"
train_data_set_location = _DATA_PATH + FLAGS.data_set + "train." + FLAGS.adapt_stat + ".csv" # Location of train dataset
test_data_set_location = _DATA_PATH + FLAGS.data_set + "test." + FLAGS.adapt_stat + ".csv" # Location of the test dataset
validation_test_set_location = _DATA_PATH + FLAGS.data_set + "valid_test." + FLAGS.adapt_stat + ".csv" # Location of the validation dataset
validation_train_set_location = _DATA_PATH + FLAGS.data_set + "valid_train." + FLAGS.adapt_stat + ".csv" #Location of the validation dataset
model_name = FLAGS.model_name + ".ckpt"
print(train_data_set_location)
def calculate_vocab_size(file_location):
"""Calculate the total number of unique elements in the dataset"""
with open(file_location, 'r') as csvfile:
reader = csv.reader(csvfile, delimiter=',')
useridtemp = []
productid = []
for row in reader:
useridtemp.append(row[0])
productid.append(row[1])
userid_size = len(set(useridtemp))
productid_size = len(set(productid))
return userid_size, productid_size
userid_size, productid_size = calculate_vocab_size(train_data_set_location) # Calculate the total number of unique elements in the dataset
print(str(userid_size))
print(str(productid_size))
plot_gradients = False # Plot the gradients
cost_val = []
tf.set_random_seed(42)
def load_train_dataset(dataset_location, batch_size, num_epochs):
"""Load the training data using TF Dataset API"""
with tf.name_scope('train_dataset_loading'):
record_defaults = [[1], [1], [0.]] # Sets the type of the resulting tensors and default values
# Dataset is in the format - UserID ProductID Rating
dataset = tf.data.TextLineDataset(dataset_location).map(lambda line: tf.decode_csv(line, record_defaults=record_defaults))
dataset = dataset.shuffle(buffer_size=10000)
dataset = dataset.batch(batch_size)
dataset = dataset.cache()
dataset = dataset.repeat(num_epochs)
iterator = dataset.make_one_shot_iterator()
user_batch, product_batch, label_batch = iterator.get_next()
label_batch = tf.expand_dims(label_batch, 1)
return user_batch, product_batch, label_batch
def load_test_dataset(dataset_location):
"""Load the test and validation datasets"""
user_list = []
product_list = []
labels = []
with open(dataset_location, 'r') as f:
reader = csv.reader(f)
for row in reader:
user_list.append(row[0])
product_list.append(row[1])
labels.append(row[2])
labels = np.reshape(labels, [-1, 1])
cr = compute_empirical_cr(labels)
return user_list, product_list, labels, cr
def compute_2i_regularization_id(prods, num_products):
"""Compute the ID for the regularization for the 2i approach"""
reg_ids = []
# Loop through batch and compute if the product ID is greater than the number of products
for x in np.nditer(prods):
if x >= num_products:
reg_ids.append(x)
elif x < num_products:
reg_ids.append(x + num_products) # Add number of products to create the 2i representation
return np.asarray(reg_ids)
def generate_bootstrap_batch(seed, data_set_size):
"""Generate the IDs for the bootstap"""
random.seed(seed)
ids = [random.randint(0, data_set_size-1) for j in range(int(data_set_size*0.8))]
return ids
def compute_empirical_cr(labels):
"""Compute the cr from the empirical data"""
labels = labels.astype(np.float)
clicks = np.count_nonzero(labels)
views = len(np.where(labels==0)[0])
cr = float(clicks)/float(views)
return cr
def create_average_predictor_tensors(label_list_placeholder, logits_placeholder):
"""Create the tensors required to run the averate predictor for the bootstraps"""
with tf.device('/cpu:0'):
with tf.variable_scope('ap_logits'):
ap_logits = tf.reshape(logits_placeholder, [tf.shape(label_list_placeholder)[0], 1])
with tf.name_scope('ap_losses'):
ap_mse_loss = tf.losses.mean_squared_error(labels=label_list_placeholder, predictions=ap_logits)
ap_log_loss = tf.losses.log_loss(labels=label_list_placeholder, predictions=ap_logits)
with tf.name_scope('ap_metrics'):
# Add performance metrics to the tensorflow graph
ap_correct_predictions = tf.equal(tf.round(ap_logits), label_list_placeholder)
ap_accuracy = tf.reduce_mean(tf.cast(ap_correct_predictions, tf.float32))
return ap_mse_loss, ap_log_loss
def compute_bootstraps_2i(sess, model, test_user_batch, test_product_batch, test_label_batch, test_logits, running_vars_initializer, ap_mse_loss, ap_log_loss):
"""Compute the bootstraps for the 2i model"""
data_set_size = len(test_user_batch)
mse = []
llh = []
ap_mse = []
ap_llh = []
auc_list = []
mse_diff = []
llh_diff = []
# Compute the bootstrap values for the test split - this compute the empirical CR as well for comparision
for i in range(30):
ids = generate_bootstrap_batch(i*2, data_set_size)
test_user_batch = np.asarray(test_user_batch)
test_product_batch = np.asarray(test_product_batch)
test_label_batch = np.asarray(test_label_batch)
# Reset the running variables used for the AUC
sess.run(running_vars_initializer)
# Construct the feed-dict for the model and the average predictor
feed_dict = {model.user_list_placeholder : test_user_batch[ids], model.product_list_placeholder: test_product_batch[ids], model.label_list_placeholder: test_label_batch[ids], model.logits_placeholder: test_logits[ids], model.reg_list_placeholder: test_product_batch[ids]}
# Run the model test step updating the AUC object
_, loss_val, mse_loss_val, log_loss_val = sess.run([model.auc_update_op, model.loss, model.mse_loss, model.log_loss], feed_dict=feed_dict)
auc_score = sess.run(model.auc, feed_dict=feed_dict)
# Run the Average Predictor graph
ap_mse_val, ap_log_val = sess.run([ap_mse_loss, ap_log_loss], feed_dict=feed_dict)
mse.append(mse_loss_val)
llh.append(log_loss_val)
ap_mse.append(ap_mse_val)
ap_llh.append(ap_log_val)
auc_list.append(auc_score)
for i in range(30):
mse_diff.append((ap_mse[i]-mse[i]) / ap_mse[i])
llh_diff.append((ap_llh[i]-llh[i]) / ap_llh[i])
print("MSE Mean Score On The Bootstrap = ", np.mean(mse))
print("MSE Mean Lift Over Average Predictor (%) = ", np.round(np.mean(mse_diff)*100, decimals=2))
print("MSE STD (%) =" , np.round(np.std(mse_diff)*100, decimals=2))
print("LLH Mean Over Average Predictor (%) =", np.round(np.mean(llh_diff)*100, decimals=2))
print("LLH STD (%) = ", np.round(np.std(llh_diff)*100, decimals=2))
print("Mean AUC Score On The Bootstrap = ", np.round(np.mean(auc_list), decimals=4), "+/-", np.round(np.std(auc_list), decimals=4))
```
### About Supervised Prod2vec
- Class to define MF of the implicit feedback matrix (1/0/unk) of Users x Products
- When called it creates the TF graph for the associated NN:
Step1: self.create_placeholders() => Creates the input placeholders
Step2: self.build_graph() => Creates the 3 layers:
- the user embedding layer
- the product embedding layer
- the output prediction layer
Step3: self.create_losses() => Defines the loss function for prediction
Step4: self.add_optimizer() => Defines the optimizer
Step5: self.add_performance_metrics() => Defines the logging performance metrics ???
Step6: self.add_summaries() => Defines the final performance stats
```
class SupervisedProd2vec():
def __init__(self, userid_size, productid_size, embedding_size, l2_pen, learning_rate):
self.userid_size = userid_size
self.productid_size = productid_size
self.embedding_size = embedding_size
self.l2_pen = l2_pen
self.learning_rate = learning_rate
# Build the graph
self.create_placeholders()
self.build_graph()
self.create_losses()
self.add_optimizer()
self.add_performance_metrics()
self.add_summaries()
def create_placeholders(self):
"""Create the placeholders to be used """
self.user_list_placeholder = tf.placeholder(tf.int32, [None], name="user_list_placeholder")
self.product_list_placeholder = tf.placeholder(tf.int32, [None], name="product_list_placeholder")
self.label_list_placeholder = tf.placeholder(tf.float32, [None, 1], name="label_list_placeholder")
# logits placeholder used to store the test CR for the bootstrapping process
self.logits_placeholder = tf.placeholder(tf.float32, [None], name="logits_placeholder")
def build_graph(self):
"""Build the main tensorflow graph with embedding layers"""
with tf.name_scope('embedding_layer'):
# User matrix and current batch
self.user_embeddings = tf.get_variable("user_embeddings", shape=[self.userid_size, self.embedding_size], initializer=tf.contrib.layers.xavier_initializer(), trainable=True)
self.user_embed = tf.nn.embedding_lookup(self.user_embeddings, self.user_list_placeholder) # Lookup the Users for the given batch
self.user_b = tf.Variable(tf.zeros([self.userid_size]), name='user_b', trainable=True)
self.user_bias_embed = tf.nn.embedding_lookup(self.user_b, self.user_list_placeholder)
# Product embedding
self.product_embeddings = tf.get_variable("product_embeddings", shape=[self.productid_size, self.embedding_size], initializer=tf.contrib.layers.xavier_initializer(), trainable=True)
self.product_embed = tf.nn.embedding_lookup(self.product_embeddings, self.product_list_placeholder) # Lookup the embeddings2 for the given batch
self.prod_b = tf.Variable(tf.zeros([self.productid_size]), name='prod_b', trainable=True)
self.prod_bias_embed = tf.nn.embedding_lookup(self.prod_b, self.product_list_placeholder)
with tf.variable_scope('logits'):
self.b = tf.get_variable('b', [1], initializer=tf.constant_initializer(0.0, dtype=tf.float32), trainable=True)
self.alpha = tf.get_variable('alpha', [], initializer=tf.constant_initializer(0.00000001, dtype=tf.float32), trainable=True)
#alpha * (<user_i, prod_j>
self.emb_logits = self.alpha * tf.reshape(tf.reduce_sum(tf.multiply(self.user_embed, self.product_embed), 1), [tf.shape(self.user_list_placeholder)[0], 1])
#prod_bias + user_bias + global_bias
self.logits = tf.reshape(tf.add(self.prod_bias_embed, self.user_bias_embed), [tf.shape(self.user_list_placeholder)[0], 1]) + self.b
self.logits = self.emb_logits + self.logits
self.prediction = tf.sigmoid(self.logits, name='sigmoid_prediction')
def create_losses(self):
"""Create the losses"""
with tf.name_scope('losses'):
#Sigmoid loss between the logits and labels
self.loss = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=self.logits, labels=self.label_list_placeholder))
#Adding the regularizer term on user vct and prod vct
self.loss = self.loss + self.l2_pen * tf.nn.l2_loss(self.user_embeddings) + self.l2_pen * tf.nn.l2_loss(self.product_embeddings) + self.l2_pen * tf.nn.l2_loss(self.prod_b) + self.l2_pen * tf.nn.l2_loss(self.user_b)
#Compute MSE loss
self.mse_loss = tf.losses.mean_squared_error(labels=self.label_list_placeholder, predictions=tf.sigmoid(self.logits))
#Compute Log loss
self.log_loss = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=self.logits, labels=self.label_list_placeholder))
def add_optimizer(self):
"""Add the required optimiser to the graph"""
with tf.name_scope('optimizer'):
# Global step variable to keep track of the number of training steps
self.global_step = tf.Variable(0, dtype=tf.int32, trainable=False, name='global_step')
self.apply_grads = tf.train.GradientDescentOptimizer(self.learning_rate).minimize(self.loss, global_step=self.global_step)
def add_performance_metrics(self):
"""Add the required performance metrics to the graph"""
with tf.name_scope('performance_metrics'):
# Add performance metrics to the tensorflow graph
correct_predictions = tf.equal(tf.round(self.prediction), self.label_list_placeholder)
self.accuracy = tf.reduce_mean(tf.cast(correct_predictions, tf.float32), name="accuracy")
self.auc, self.auc_update_op = tf.metrics.auc(labels=self.label_list_placeholder, predictions=self.prediction, num_thresholds=1000, name="auc_metric")
def add_summaries(self):
"""Add the required summaries to the graph"""
with tf.name_scope('summaries'):
# Add loss to the summaries
tf.summary.scalar('total_loss', self.loss)
tf.summary.histogram('histogram_total_loss', self.loss)
# Add weights to the summaries
tf.summary.histogram('user_embedding_weights', self.user_embeddings)
tf.summary.histogram('product_embedding_weights', self.product_embeddings)
tf.summary.histogram('logits', self.logits)
tf.summary.histogram('prod_b', self.prod_b)
tf.summary.histogram('user_b', self.user_b)
tf.summary.histogram('global_bias', self.b)
tf.summary.scalar('alpha', self.alpha)
```
### CausalProd2Vec2i - inherits from SupervisedProd2vec
- Class to define the causal version of MF of the implicit feedback matrix (1/0/unk) of Users x Products
- When called it creates the TF graph for the associated NN:
**Step1: Changed: +regularizer placeholder** self.create_placeholders() => Creates the input placeholders
**Step2:** self.build_graph() => Creates the 3 layers:
- the user embedding layer
- the product embedding layer
- the output prediction layer
**New:**
self.create_control_embeddings()
self.create_counter_factual_loss()
**Step3: Changed: +add regularizer between embeddings** self.create_losses() => Defines the loss function for prediction
**Step4:** self.add_optimizer() => Defines the optimizer
**Step5:** self.add_performance_metrics() => Defines the logging performance metrics ???
**Step6:** self.add_summaries() => Defines the final performance stats
```
class CausalProd2Vec2i(SupervisedProd2vec):
def __init__(self, userid_size, productid_size, embedding_size, l2_pen, learning_rate, cf_pen, cf='l1'):
self.userid_size = userid_size
self.productid_size = productid_size * 2 # Doubled to accommodate the treatment embeddings
self.embedding_size = embedding_size
self.l2_pen = l2_pen
self.learning_rate = learning_rate
self.cf_pen = cf_pen
self.cf = cf
# Build the graph
self.create_placeholders()
self.build_graph()
self.create_control_embeddings()
#self.create_counterfactual_regularizer()
self.create_losses()
self.add_optimizer()
self.add_performance_metrics()
self.add_summaries()
def create_placeholders(self):
"""Create the placeholders to be used """
self.user_list_placeholder = tf.placeholder(tf.int32, [None], name="user_list_placeholder")
self.product_list_placeholder = tf.placeholder(tf.int32, [None], name="product_list_placeholder")
self.label_list_placeholder = tf.placeholder(tf.float32, [None, 1], name="label_list_placeholder")
self.reg_list_placeholder = tf.placeholder(tf.int32, [None], name="reg_list_placeholder")
# logits placeholder used to store the test CR for the bootstrapping process
self.logits_placeholder = tf.placeholder(tf.float32, [None], name="logits_placeholder")
def create_control_embeddings(self):
"""Create the control embeddings"""
with tf.name_scope('control_embedding'):
# Get the control embedding at id 0
self.control_embed = tf.stop_gradient(tf.nn.embedding_lookup(self.product_embeddings, self.reg_list_placeholder))
#################################
## SOLUTION TO Q1 GOES HERE! ##
#################################
#def create_counterfactual_regularizer(self):
# self.cf_reg
def create_losses(self):
"""Create the losses"""
with tf.name_scope('losses'):
#Sigmoid loss between the logits and labels
self.log_loss = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=self.logits, labels=self.label_list_placeholder))
#Adding the regularizer term on user vct and prod vct and their bias terms
reg_term = self.l2_pen * ( tf.nn.l2_loss(self.user_embeddings) + tf.nn.l2_loss(self.product_embeddings) )
reg_term_biases = self.l2_pen * ( tf.nn.l2_loss(self.prod_b) + tf.nn.l2_loss(self.user_b) )
self.loss = self.log_loss + reg_term + reg_term_biases
#Adding the counterfactual regualizer term
# Q1: Write the method that computes the counterfactual regularizer
#self.create_counterfactual_regularizer()
#self.loss = self.loss + (self.cf_pen * self.cf_reg)
#Compute addtionally the MSE loss
self.mse_loss = tf.losses.mean_squared_error(labels=self.label_list_placeholder, predictions=tf.sigmoid(self.logits))
```
### Create the TF Graph
```
# Create graph object
graph = tf.Graph()
with graph.as_default():
with tf.device('/cpu:0'):
# Load the required graph
### Number of products and users
productid_size = 1683
userid_size = 944
model = CausalProd2Vec2i(userid_size, productid_size+1, FLAGS.embedding_size, FLAGS.l2_pen, FLAGS.learning_rate, FLAGS.cf_pen, cf=FLAGS.cf_loss)
ap_mse_loss, ap_log_loss = create_average_predictor_tensors(model.label_list_placeholder, model.logits_placeholder)
# Define initializer to initialize/reset running variables
running_vars = tf.get_collection(tf.GraphKeys.LOCAL_VARIABLES, scope="performance_metrics/auc_metric")
running_vars_initializer = tf.variables_initializer(var_list=running_vars)
# Get train data batch from queue
next_batch = load_train_dataset(train_data_set_location, FLAGS.batch_size, FLAGS.num_epochs)
test_user_batch, test_product_batch, test_label_batch, test_cr = load_test_dataset(test_data_set_location)
val_test_user_batch, val_test_product_batch, val_test_label_batch, val_cr = load_test_dataset(validation_test_set_location)
val_train_user_batch, val_train_product_batch, val_train_label_batch, val_cr = load_test_dataset(validation_train_set_location)
# create the empirical CR test logits
test_logits = np.empty(len(test_label_batch))
test_logits.fill(test_cr)
```
### Launch the Session: Train the model
```
# Launch the Session
with tf.Session(graph=graph, config=tf.ConfigProto(allow_soft_placement=True, log_device_placement=False)) as sess:
# initialise all the TF variables
init_op = tf.global_variables_initializer()
sess.run(init_op)
# Setup tensorboard: tensorboard --logdir=/tmp/tensorboard
time_tb = str(time.ctime(int(time.time())))
train_writer = tf.summary.FileWriter('/tmp/tensorboard' + '/train' + time_tb, sess.graph)
test_writer = tf.summary.FileWriter('/tmp/tensorboard' + '/test' + time_tb, sess.graph)
merged = tf.summary.merge_all()
# Embeddings viz (Possible to add labels for embeddings later)
saver = tf.train.Saver()
config = projector.ProjectorConfig()
embedding = config.embeddings.add()
embedding.tensor_name = model.product_embeddings.name
projector.visualize_embeddings(train_writer, config)
# Variables used in the training loop
t = time.time()
step = 0
average_loss = 0
average_mse_loss = 0
average_log_loss = 0
# Start the training loop---------------------------------------------------------------------------------------------
print("Starting Training On Causal Prod2Vec")
print(FLAGS.cf_loss)
print("Num Epochs = ", FLAGS.num_epochs)
print("Learning Rate = ", FLAGS.learning_rate)
print("L2 Reg = ", FLAGS.l2_pen)
print("CF Reg = ", FLAGS.cf_pen)
try:
while True:
# Run the TRAIN for this step batch ---------------------------------------------------------------------
# Construct the feed_dict
user_batch, product_batch, label_batch = sess.run(next_batch)
# Treatment is the small set of samples from St, Control is the larger set of samples from Sc
reg_ids = compute_2i_regularization_id(product_batch, productid_size) # Compute the product ID's for regularization
feed_dict = {model.user_list_placeholder : user_batch, model.product_list_placeholder: product_batch, model.reg_list_placeholder: reg_ids, model.label_list_placeholder: label_batch}
# Run the graph
_, sum_str, loss_val, mse_loss_val, log_loss_val = sess.run([model.apply_grads, merged, model.loss, model.mse_loss, model.log_loss], feed_dict=feed_dict)
step +=1
average_loss += loss_val
average_mse_loss += mse_loss_val
average_log_loss += log_loss_val
# Every num_steps print average loss
if step % FLAGS.num_steps == 0:
if step > FLAGS.num_steps:
# The average loss is an estimate of the loss over the last set batches.
average_loss /= FLAGS.num_steps
average_mse_loss /= FLAGS.num_steps
average_log_loss /= FLAGS.num_steps
print("Average Training Loss on S_c (FULL, MSE, NLL) at step ", step, ": ", average_loss, ": ", average_mse_loss, ": ", average_log_loss, "Time taken (S) = " + str(round(time.time() - t, 1)))
average_loss = 0
t = time.time() # reset the time
train_writer.add_summary(sum_str, step) # Write the summary
# Run the VALIDATION for this step batch ---------------------------------------------------------------------
val_train_product_batch = np.asarray(val_train_product_batch, dtype=np.float32)
val_test_product_batch = np.asarray(val_test_product_batch, dtype=np.float32)
vaL_train_reg_ids = compute_2i_regularization_id(val_train_product_batch, productid_size) # Compute the product ID's for regularization
vaL_test_reg_ids = compute_2i_regularization_id(val_test_product_batch, productid_size) # Compute the product ID's for regularization
feed_dict_test = {model.user_list_placeholder : val_test_user_batch, model.product_list_placeholder: val_test_product_batch, model.reg_list_placeholder: vaL_test_reg_ids, model.label_list_placeholder: val_test_label_batch}
feed_dict_train = {model.user_list_placeholder : val_train_user_batch, model.product_list_placeholder: val_train_product_batch, model.reg_list_placeholder: vaL_train_reg_ids, model.label_list_placeholder: val_train_label_batch}
sum_str, loss_val, mse_loss_val, log_loss_val = sess.run([merged, model.loss, model.mse_loss, model.log_loss], feed_dict=feed_dict_train)
print("Validation loss on S_c (FULL, MSE, NLL) at step ", step, ": ", loss_val, ": ", mse_loss_val, ": ", log_loss_val)
sum_str, loss_val, mse_loss_val, log_loss_val = sess.run([merged, model.loss, model.mse_loss, model.log_loss], feed_dict=feed_dict_test)
cost_val.append(loss_val)
print("Validation loss on S_t(FULL, MSE, NLL) at step ", step, ": ", loss_val, ": ", mse_loss_val, ": ", log_loss_val)
print("####################################################################################################################")
test_writer.add_summary(sum_str, step) # Write the summary
except tf.errors.OutOfRangeError:
print("Reached the number of epochs")
finally:
saver.save(sess, os.path.join('/tmp/tensorboard', model_name), model.global_step) # Save model
train_writer.close()
print("Training Complete")
# Run the bootstrap for this model ---------------------------------------------------------------------------------------------------------------
print("Begin Bootstrap process...")
print("Running BootStrap On The Control Representations")
compute_bootstraps_2i(sess, model, test_user_batch, test_product_batch, test_label_batch, test_logits, running_vars_initializer, ap_mse_loss, ap_log_loss)
print("Running BootStrap On The Treatment Representations")
test_product_batch = [int(x) + productid_size for x in test_product_batch]
compute_bootstraps_2i(sess, model, test_user_batch, test_product_batch, test_label_batch, test_logits, running_vars_initializer, ap_mse_loss, ap_log_loss)
```
|
github_jupyter
|
# Ray RLlib - Introduction to Reinforcement Learning
© 2019-2021, Anyscale. All Rights Reserved

_Reinforcement Learning_ is the category of machine learning that focuses on training one or more _agents_ to achieve maximal _rewards_ while operating in an environment. This lesson discusses the core concepts of RL, while subsequent lessons explore RLlib in depth. We'll use two examples with exercises to give you a taste of RL. If you already understand RL concepts, you can either skim this lesson or skip to the [next lesson](02-Introduction-to-RLlib.ipynb).
## What Is Reinforcement Learning?
Let's explore the basic concepts of RL, specifically the _Markov Decision Process_ abstraction, and to show its use in Python.
Consider the following image:

In RL, one or more **agents** interact with an **environment** to maximize a **reward**. The agents make **observations** about the **state** of the environment and take **actions** that are believed will maximize the long-term reward. However, at any particular moment, the agents can only observe the immediate reward. So, the training process usually involves lots and lot of replay of the game, the robot simulator traversing a virtual space, etc., so the agents can learn from repeated trials what decisions/actions work best to maximize the long-term, cumulative reward.
The trail and error search and delayed reward are the distinguishing characterists of RL vs. other ML methods ([Sutton 2018](06-RL-References.ipynb#Books)).
The way to formalize trial and error is the **exploitation vs. exploration tradeoff**. When an agent finds what appears to be a "rewarding" sequence of actions, the agent may naturally want to continue to **exploit** these actions. However, even better actions may exist. An agent won't know whether alternatives are better or not unless some percentage of actions taken **explore** the alternatives. So, all RL algorithms include a strategy for exploitation and exploration.
## RL Applications
RL has many potential applications. RL became "famous" due to these successes, including achieving expert game play, training robots, autonomous vehicles, and other simulated agents:






Credits:
* [AlphaGo](https://www.youtube.com/watch?v=l7ngy56GY6k)
* [Breakout](https://towardsdatascience.com/tutorial-double-deep-q-learning-with-dueling-network-architectures-4c1b3fb7f756) ([paper](https://arxiv.org/abs/1312.5602))
* [Stacking Legos with Sawyer](https://robohub.org/soft-actor-critic-deep-reinforcement-learning-with-real-world-robots/)
* [Walking Man](https://openai.com/blog/openai-baselines-ppo/)
* [Autonomous Vehicle](https://www.daimler.com/innovation/case/autonomous/intelligent-drive-2.html)
* ["Cassie": Two-legged Robot](https://mime.oregonstate.edu/research/drl/robots/cassie/) (Uses Ray!)
Recently other industry applications have emerged, include the following:
* **Process optimization:** industrial processes (factories, pipelines) and other business processes, routing problems, cluster optimization.
* **Ad serving and recommendations:** Some of the traditional methods, including _collaborative filtering_, are hard to scale for very large data sets. RL systems are being developed to do an effective job more efficiently than traditional methods.
* **Finance:** Markets are time-oriented _environments_ where automated trading systems are the _agents_.
## Markov Decision Processes
At its core, Reinforcement learning builds on the concepts of [Markov Decision Process (MDP)](https://en.wikipedia.org/wiki/Markov_decision_process), where the current state, the possible actions that can be taken, and overall goal are the building blocks.
An MDP models sequential interactions with an external environment. It consists of the following:
- a **state space** where the current state of the system is sometimes called the **context**.
- a set of **actions** that can be taken at a particular state $s$ (or sometimes the same set for all states).
- a **transition function** that describes the probability of being in a state $s'$ at time $t+1$ given that the MDP was in state $s$ at time $t$ and action $a$ was taken. The next state is selected stochastically based on these probabilities.
- a **reward function**, which determines the reward received at time $t$ following action $a$, based on the decision of **policy** $\pi$.
The goal of MDP is to develop a **policy** $\pi$ that specifies what action $a$ should be chosen for a given state $s$ so that the cumulative reward is maximized. When it is possible for the policy "trainer" to fully observe all the possible states, actions, and rewards, it can define a deterministic policy, fixing a single action choice for each state. In this scenario, the transition probabilities reduce to the probability of transitioning to state $s'$ given the current state is $s$, independent of actions, because the state now leads to a deterministic action choice. Various algorithms can be used to compute this policy.
Put another way, if the policy isn't deterministic, then the transition probability to state $s'$ at a time $t+1$ when action $a$ is taken for state $s$ at time $t$, is given by:
\begin{equation}
P_a(s',s) = P(s_{t+1} = s'|s_t=s,a)
\end{equation}
When the policy is deterministic, this transition probability reduces to the following, independent of $a$:
\begin{equation}
P(s',s) = P(s_{t+1} = s'|s_t=s)
\end{equation}
To be clear, a deterministic policy means that one and only one action will always be selected for a given state $s$, but the next state $s'$ will still be selected stochastically.
In the general case of RL, it isn't possible to fully know all this information, some of which might be hidden and evolving, so it isn't possible to specify a fully-deterministic policy.
Often this cumulative reward is computed using the **discounted sum** over all rewards observed:
\begin{equation}
\arg\max_{\pi} \sum_{t=1}^T \gamma^t R_t(\pi),
\end{equation}
where $T$ is the number of steps taken in the MDP (this is a random variable and may depend on $\pi$), $R_t$ is the reward received at time $t$ (also a random variable which depends on $\pi$), and $\gamma$ is the **discount factor**. The value of $\gamma$ is between 0 and 1, meaning it has the effect of "discounting" earlier rewards vs. more recent rewards.
The [Wikipedia page on MDP](https://en.wikipedia.org/wiki/Markov_decision_process) provides more details. Note what we said in the third bullet, that the new state only depends on the previous state and the action taken. The assumption is that we can simplify our effort by ignoring all the previous states except the last one and still achieve good results. This is known as the [Markov property](https://en.wikipedia.org/wiki/Markov_property). This assumption often works well and it greatly reduces the resources required.
## The Elements of RL
Here are the elements of RL that expand on MDP concepts (see [Sutton 2018](https://mitpress.mit.edu/books/reinforcement-learning-second-edition) for more details):
#### Policies
Unlike MDP, the **transition function** probabilities are often not known in advance, but must be learned. Learning is done through repeated "play", where the agent interacts with the environment.
This makes the **policy** $\pi$ harder to determine. Because the fully state space usually can't be fully known, the choice of action $a$ for given state $s$ almostly always remains a stochastic choice, never deterministic, unlike MDP.
#### Reward Signal
The idea of a **reward signal** encapsulates the desired goal for the system and provides feedback for updating the policy based on how well particular events or actions contribute rewards towards the goal.
#### Value Function
The **value function** encapsulates the maximum cumulative reward likely to be achieved starting from a given state for an **episode**. This is harder to determine than the simple reward returned after taking an action. In fact, much of the research in RL over the decades has focused on finding better and more efficient implementations of value functions. To illustrate the challenge, repeatedly taking one sequence of actions may yield low rewards for a while, but eventually provide large rewards. Conversely, always choosing a different sequence of actions may yield a good reward at each step, but be suboptimal for the cumulative reward.
#### Episode
A sequence of steps by the agent starting in an initial state. At each step, the agent observes the current state, chooses the next action, and receives the new reward. Episodes are used for both training policies and replaying with an existing policy (called _rollout_).
#### Model
An optional feature, some RL algorithms develop or use a **model** of the environment to anticipate the resulting states and rewards for future actions. Hence, they are useful for _planning_ scenarios. Methods for solving RL problems that use models are called _model-based methods_, while methods that learn by trial and error are called _model-free methods_.
## Reinforcement Learning Example
Let's finish this introduction let's learn about the popular "hello world" (1) example environment for RL, balancing a pole vertically on a moving cart, called `CartPole`. Then we'll see how to use RLlib to train a policy using a popular RL algorithm, _Proximal Policy Optimization_, again using `CartPole`.
(1) In books and tutorials on programming languages, it is a tradition that the very first program shown prints the message "Hello World!".
### CartPole and OpenAI
The popular [OpenAI "gym" environment](https://gym.openai.com/) provides MDP interfaces to a variety of simulated environments. Perhaps the most popular for learning RL is `CartPole`, a simple environment that simulates the physics of balancing a pole on a moving cart. The `CartPole` problem is described at https://gym.openai.com/envs/CartPole-v1. Here is an image from that website, where the pole is currently falling to the right, which means the cart will need to move to the right to restore balance:

This example fits into the MDP framework as follows:
- The **state** consists of the position and velocity of the cart (moving in one dimension from left to right) as well as the angle and angular velocity of the pole that is balancing on the cart.
- The **actions** are to decrease or increase the cart's velocity by one unit. A negative velocity means it is moving to the left.
- The **transition function** is deterministic and is determined by simulating physical laws. Specifically, for a given **state**, what should we choose as the next velocity value? In the RL context, the correct velocity value to choose has to be learned. Hence, we learn a _policy_ that approximates the optimal transition function that could be calculated from the laws of physics.
- The **reward function** is a constant 1 as long as the pole is upright, and 0 once the pole has fallen over. Therefore, maximizing the reward means balancing the pole for as long as possible.
- The **discount factor** in this case can be taken to be 1, meaning we treat the rewards at all time steps equally and don't discount any of them.
More information about the `gym` Python module is available at https://gym.openai.com/. The list of all the available Gym environments is in [this wiki page](https://github.com/openai/gym/wiki/Table-of-environments). We'll use a few more of them and even create our own in subsequent lessons.
```
import gym
import numpy as np
import pandas as pd
import json
```
The code below illustrates how to create and manipulate MDPs in Python. An MDP can be created by calling `gym.make`. Gym environments are identified by names like `CartPole-v1`. A **catalog of built-in environments** can be found at https://gym.openai.com/envs.
```
env = gym.make("CartPole-v1")
print("Created env:", env)
```
Reset the state of the MDP by calling `env.reset()`. This call returns the initial state of the MDP.
```
state = env.reset()
print("The starting state is:", state)
```
Recall that the state is the position of the cart, its velocity, the angle of the pole, and the angular velocity of the pole.
The `env.step` method takes an action. In the case of the `CartPole` environment, the appropriate actions are 0 or 1, for pushing the cart to the left or right, respectively. `env.step()` returns a tuple of four things:
1. the new state of the environment
2. a reward
3. a boolean indicating whether the simulation has finished
4. a dictionary of miscellaneous extra information
Let's show what happens if we take one step with an action of 0.
```
action = 0
state, reward, done, info = env.step(action)
print(state, reward, done, info)
```
A **rollout** is a simulation of a policy in an environment. It is used both during training and when running simulations with a trained policy.
The code below performs a rollout in a given environment. It takes **random actions** until the simulation has finished and returns the cumulative reward.
```
def random_rollout(env):
state = env.reset()
done = False
cumulative_reward = 0
# Keep looping as long as the simulation has not finished.
while not done:
# Choose a random action (either 0 or 1).
action = np.random.choice([0, 1])
# Take the action in the environment.
state, reward, done, _ = env.step(action)
# Update the cumulative reward.
cumulative_reward += reward
# Return the cumulative reward.
return cumulative_reward
```
Try rerunning the following cell a few times. How much do the answers change? Note that the maximum possible reward for `CartPole-v1` is 500. You'll probably get numbers well under 500.
```
reward = random_rollout(env)
print(reward)
reward = random_rollout(env)
print(reward)
```
### Exercise 1
Choosing actions at random in `random_rollout` is not a very effective policy, as the previous results showed. Finish implementing the `rollout_policy` function below, which takes an environment *and* a policy. Recall that the *policy* is a function that takes in a *state* and returns an *action*. The main difference is that instead of choosing a **random action**, like we just did (with poor results), the action should be chosen **with the policy** (as a function of the state).
> **Note:** Exercise solutions for this tutorial can be found [here](solutions/Ray-RLlib-Solutions.ipynb).
```
def rollout_policy(env, policy):
state = env.reset()
done = False
cumulative_reward = 0
# EXERCISE: Fill out this function by copying the appropriate part of 'random_rollout'
# and modifying it to choose the action using the policy.
raise NotImplementedError
# Return the cumulative reward.
return cumulative_reward
def sample_policy1(state):
return 0 if state[0] < 0 else 1
def sample_policy2(state):
return 1 if state[0] < 0 else 0
reward1 = np.mean([rollout_policy(env, sample_policy1) for _ in range(100)])
reward2 = np.mean([rollout_policy(env, sample_policy2) for _ in range(100)])
print('The first sample policy got an average reward of {}.'.format(reward1))
print('The second sample policy got an average reward of {}.'.format(reward2))
assert 5 < reward1 < 15, ('Make sure that rollout_policy computes the action '
'by applying the policy to the state.')
assert 25 < reward2 < 35, ('Make sure that rollout_policy computes the action '
'by applying the policy to the state.')
```
We'll return to `CartPole` in lesson [01: Application Cart Pole](explore-rllib/01-Application-Cart-Pole.ipynb) in the `explore-rllib` section.
### RLlib Reinforcement Learning Example: Cart Pole with Proximal Policy Optimization
This section demonstrates how to use the _proximal policy optimization_ (PPO) algorithm implemented by [RLlib](http://rllib.io). PPO is a popular way to develop a policy. RLlib also uses [Ray Tune](http://tune.io), the Ray Hyperparameter Tuning framework, which is covered in the [Ray Tune Tutorial](../ray-tune/00-Ray-Tune-Overview.ipynb).
We'll provide relatively little explanation of **RLlib** concepts for now, but explore them in greater depth in subsequent lessons. For more on RLlib, see the documentation at http://rllib.io.
PPO is described in detail in [this paper](https://arxiv.org/abs/1707.06347). It is a variant of _Trust Region Policy Optimization_ (TRPO) described in [this earlier paper](https://arxiv.org/abs/1502.05477). [This OpenAI post](https://openai.com/blog/openai-baselines-ppo/) provides a more accessible introduction to PPO.
PPO works in two phases. In the first phase, a large number of rollouts are performed in parallel. The rollouts are then aggregated on the driver and a surrogate optimization objective is defined based on those rollouts. In the second phase, we use SGD (_stochastic gradient descent_) to find the policy that maximizes that objective with a penalty term for diverging too much from the current policy.

> **NOTE:** The SGD optimization step is best performed in a data-parallel manner over multiple GPUs. This is exposed through the `num_gpus` field of the `config` dictionary. Hence, for normal usage, one or more GPUs is recommended.
(The original version of this example can be found [here](https://raw.githubusercontent.com/ucbrise/risecamp/risecamp2018/ray/tutorial/rllib_exercises/)).
```
import ray
from ray.rllib.agents.ppo import PPOTrainer, DEFAULT_CONFIG
from ray.tune.logger import pretty_print
```
Initialize Ray. If you are running these tutorials on your laptop, then a single-node Ray cluster will be started by the next cell. If you are running in the Anyscale platform, it will connect to the running Ray cluster.
```
info = ray.init(ignore_reinit_error=True, log_to_driver=False)
print(info)
```
> **Tip:** Having trouble starting Ray? See the [Troubleshooting](../reference/Troubleshooting-Tips-Tricks.ipynb) tips.
The next cell prints the URL for the Ray Dashboard. **This is only correct if you are running this tutorial on a laptop.** Click the link to open the dashboard.
If you are running on the Anyscale platform, use the URL provided by your instructor to open the Dashboard.
```
print("Dashboard URL: http://{}".format(info["webui_url"]))
```
Instantiate a PPOTrainer object. We pass in a config object that specifies how the network and training procedure should be configured. Some of the parameters are the following.
- `num_workers` is the number of actors that the agent will create. This determines the degree of parallelism that will be used. In a cluster, these actors will be spread over the available nodes.
- `num_sgd_iter` is the number of epochs of SGD (stochastic gradient descent, i.e., passes through the data) that will be used to optimize the PPO surrogate objective at each iteration of PPO, for each _minibatch_ ("chunk") of training data. Using minibatches is more efficient than training with one record at a time.
- `sgd_minibatch_size` is the SGD minibatch size (batches of data) that will be used to optimize the PPO surrogate objective.
- `model` contains a dictionary of parameters describing the neural net used to parameterize the policy. The `fcnet_hiddens` parameter is a list of the sizes of the hidden layers. Here, we have two hidden layers of size 100, each.
- `num_cpus_per_worker` when set to 0 prevents Ray from pinning a CPU core to each worker, which means we could run out of workers in a constrained environment like a laptop or a cloud VM.
```
config = DEFAULT_CONFIG.copy()
config['num_workers'] = 1
config['num_sgd_iter'] = 30
config['sgd_minibatch_size'] = 128
config['model']['fcnet_hiddens'] = [100, 100]
config['num_cpus_per_worker'] = 0
agent = PPOTrainer(config, 'CartPole-v1')
```
Now let's train the policy on the `CartPole-v1` environment for `N` steps. The JSON object returned by each call to `agent.train()` contains a lot of information we'll inspect below. For now, we'll extract information we'll graph, such as `episode_reward_mean`. The _mean_ values are more useful for determining successful training.
```
N = 10
results = []
episode_data = []
episode_json = []
for n in range(N):
result = agent.train()
results.append(result)
episode = {'n': n,
'episode_reward_min': result['episode_reward_min'],
'episode_reward_mean': result['episode_reward_mean'],
'episode_reward_max': result['episode_reward_max'],
'episode_len_mean': result['episode_len_mean']}
episode_data.append(episode)
episode_json.append(json.dumps(episode))
print(f'{n:3d}: Min/Mean/Max reward: {result["episode_reward_min"]:8.4f}/{result["episode_reward_mean"]:8.4f}/{result["episode_reward_max"]:8.4f}')
```
Now let's convert the episode data to a Pandas `DataFrame` for easy manipulation. The results indicate how much reward the policy is receiving (`episode_reward_*`) and how many time steps of the environment the policy ran (`episode_len_mean`). The maximum possible reward for this problem is `500`. The reward mean and trajectory length are very close because the agent receives a reward of one for every time step that it survives. However, this is specific to this environment and not true in general.
```
df = pd.DataFrame(data=episode_data)
df
df.columns.tolist()
```
Let's plot the data. Since the length and reward means are equal, we'll only plot one line:
```
df.plot(x="n", y=["episode_reward_mean", "episode_reward_min", "episode_reward_max"], secondary_y=True)
```
The model is quickly able to hit the maximum value of 500, but the mean is what's most valuable. After 10 steps, we're more than half way there.
FYI, here are two views of the whole value for one result. First, a "pretty print" output.
> **Tip:** The output will be long. When this happens for a cell, right click and select _Enable scrolling for outputs_.
```
print(pretty_print(results[-1]))
```
We'll learn about more of these values as continue the tutorial.
The whole, long JSON blob, which includes the historical stats about episode rewards and lengths:
```
results[-1]
```
Let's plot the `episode_reward` values:
```
episode_rewards = results[-1]['hist_stats']['episode_reward']
df_episode_rewards = pd.DataFrame(data={'episode':range(len(episode_rewards)), 'reward':episode_rewards})
df_episode_rewards.plot(x="episode", y="reward")
```
For a well-trained model, most runs do very well while occasional runs do poorly. Try plotting other results episodes by changing the array index in `results[-1]` to another number between `0` and `9`. (The length of `results` is `10`.)
### Exercise 2
The current network and training configuration are too large and heavy-duty for a simple problem like `CartPole`. Modify the configuration to use a smaller network (the `config['model']['fcnet_hiddens']` setting) and to speed up the optimization of the surrogate objective. (Fewer SGD iterations and a larger batch size should help.)
```
# Make edits here:
config = DEFAULT_CONFIG.copy()
config['num_workers'] = 3
config['num_sgd_iter'] = 30
config['sgd_minibatch_size'] = 128
config['model']['fcnet_hiddens'] = [100, 100]
config['num_cpus_per_worker'] = 0
agent = PPOTrainer(config, 'CartPole-v1')
```
Train the agent and try to get a reward of 500. If it's training too slowly you may need to modify the config above to use fewer hidden units, a larger `sgd_minibatch_size`, a smaller `num_sgd_iter`, or a larger `num_workers`.
This should take around `N` = 20 or 30 training iterations.
```
N = 5
results = []
episode_data = []
episode_json = []
for n in range(N):
result = agent.train()
results.append(result)
episode = {'n': n,
'episode_reward_mean': result['episode_reward_mean'],
'episode_reward_max': result['episode_reward_max'],
'episode_len_mean': result['episode_len_mean']}
episode_data.append(episode)
episode_json.append(json.dumps(episode))
print(f'Max reward: {episode["episode_reward_max"]}')
```
# Using Checkpoints
You checkpoint the current state of a trainer to save what it has learned. Checkpoints are used for subsequent _rollouts_ and also to continue training later from a known-good state. Calling `agent.save()` creates the checkpoint and returns the path to the checkpoint file, which can be used later to restore the current state to a new trainer. Here we'll load the trained policy into the same process, but often it would be loaded in a new process, for example on a production cluster for serving that is separate from the training cluster.
```
checkpoint_path = agent.save()
print(checkpoint_path)
```
Now load the checkpoint in a new trainer:
```
trained_config = config.copy()
test_agent = PPOTrainer(trained_config, "CartPole-v1")
test_agent.restore(checkpoint_path)
```
Use the previously-trained policy to act in an environment. The key line is the call to `test_agent.compute_action(state)` which uses the trained policy to choose an action. This is an example of _rollout_, which we'll study in a subsequent lesson.
Verify that the cumulative reward received roughly matches up with the reward printed above. It will be at or near 500.
```
env = gym.make("CartPole-v1")
state = env.reset()
done = False
cumulative_reward = 0
while not done:
action = test_agent.compute_action(state) # key line; get the next action
state, reward, done, _ = env.step(action)
cumulative_reward += reward
print(cumulative_reward)
ray.shutdown()
```
The next lesson, [02: Introduction to RLlib](02-Introduction-to-RLlib.ipynb) steps back to introduce to RLlib, its goals and the capabilities it provides.
|
github_jupyter
|
<a href="https://colab.research.google.com/github/jeffheaton/t81_558_deep_learning/blob/master/t81_558_class_05_2_kfold.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# T81-558: Applications of Deep Neural Networks
**Module 5: Regularization and Dropout**
* Instructor: [Jeff Heaton](https://sites.wustl.edu/jeffheaton/), McKelvey School of Engineering, [Washington University in St. Louis](https://engineering.wustl.edu/Programs/Pages/default.aspx)
* For more information visit the [class website](https://sites.wustl.edu/jeffheaton/t81-558/).
# Module 5 Material
* Part 5.1: Part 5.1: Introduction to Regularization: Ridge and Lasso [[Video]](https://www.youtube.com/watch?v=jfgRtCYjoBs&list=PLjy4p-07OYzulelvJ5KVaT2pDlxivl_BN) [[Notebook]](t81_558_class_05_1_reg_ridge_lasso.ipynb)
* **Part 5.2: Using K-Fold Cross Validation with Keras** [[Video]](https://www.youtube.com/watch?v=maiQf8ray_s&list=PLjy4p-07OYzulelvJ5KVaT2pDlxivl_BN) [[Notebook]](t81_558_class_05_2_kfold.ipynb)
* Part 5.3: Using L1 and L2 Regularization with Keras to Decrease Overfitting [[Video]](https://www.youtube.com/watch?v=JEWzWv1fBFQ&list=PLjy4p-07OYzulelvJ5KVaT2pDlxivl_BN) [[Notebook]](t81_558_class_05_3_keras_l1_l2.ipynb)
* Part 5.4: Drop Out for Keras to Decrease Overfitting [[Video]](https://www.youtube.com/watch?v=bRyOi0L6Rs8&list=PLjy4p-07OYzulelvJ5KVaT2pDlxivl_BN) [[Notebook]](t81_558_class_05_4_dropout.ipynb)
* Part 5.5: Benchmarking Keras Deep Learning Regularization Techniques [[Video]](https://www.youtube.com/watch?v=1NLBwPumUAs&list=PLjy4p-07OYzulelvJ5KVaT2pDlxivl_BN) [[Notebook]](t81_558_class_05_5_bootstrap.ipynb)
# Google CoLab Instructions
The following code ensures that Google CoLab is running the correct version of TensorFlow.
```
try:
%tensorflow_version 2.x
COLAB = True
print("Note: using Google CoLab")
except:
print("Note: not using Google CoLab")
COLAB = False
```
# Part 5.2: Using K-Fold Cross-validation with Keras
Cross-validation can be used for a variety of purposes in predictive modeling. These include:
* Generating out-of-sample predictions from a neural network
* Estimate a good number of epochs to train a neural network for (early stopping)
* Evaluate the effectiveness of certain hyperparameters, such as activation functions, neuron counts, and layer counts
Cross-validation uses a number of folds, and multiple models, to provide each segment of data a chance to serve as both the validation and training set. Cross validation is shown in Figure 5.CROSS.
**Figure 5.CROSS: K-Fold Crossvalidation**

It is important to note that there will be one model (neural network) for each fold. To generate predictions for new data, which is data not present in the training set, predictions from the fold models can be handled in several ways:
* Choose the model that had the highest validation score as the final model.
* Preset new data to the 5 models (one for each fold) and average the result (this is an [ensemble](https://en.wikipedia.org/wiki/Ensemble_learning)).
* Retrain a new model (using the same settings as the cross-validation) on the entire dataset. Train for as many epochs, and with the same hidden layer structure.
Generally, I prefer the last approach and will retrain a model on the entire data set once I have selected hyper-parameters. Of course, I will always set aside a final holdout set for model validation that I do not use in any aspect of the training process.
### Regression vs Classification K-Fold Cross-Validation
Regression and classification are handled somewhat differently with regards to cross-validation. Regression is the simpler case where you can simply break up the data set into K folds with little regard for where each item lands. For regression it is best that the data items fall into the folds as randomly as possible. It is also important to remember that not every fold will necessarily have exactly the same number of data items. It is not always possible for the data set to be evenly divided into K folds. For regression cross-validation we will use the Scikit-Learn class **KFold**.
Cross validation for classification could also use the **KFold** object; however, this technique would not ensure that the class balance remains the same in each fold as it was in the original. It is very important that the balance of classes that a model was trained on remains the same (or similar) to the training set. A drift in this distribution is one of the most important things to monitor after a trained model has been placed into actual use. Because of this, we want to make sure that the cross-validation itself does not introduce an unintended shift. This is referred to as stratified sampling and is accomplished by using the Scikit-Learn object **StratifiedKFold** in place of **KFold** whenever you are using classification. In summary, the following two objects in Scikit-Learn should be used:
* **KFold** When dealing with a regression problem.
* **StratifiedKFold** When dealing with a classification problem.
The following two sections demonstrate cross-validation with classification and regression.
### Out-of-Sample Regression Predictions with K-Fold Cross-Validation
The following code trains the simple dataset using a 5-fold cross-validation. The expected performance of a neural network, of the type trained here, would be the score for the generated out-of-sample predictions. We begin by preparing a feature vector using the jh-simple-dataset to predict age. This is a regression problem.
```
import pandas as pd
from scipy.stats import zscore
from sklearn.model_selection import train_test_split
# Read the data set
df = pd.read_csv(
"https://data.heatonresearch.com/data/t81-558/jh-simple-dataset.csv",
na_values=['NA','?'])
# Generate dummies for job
df = pd.concat([df,pd.get_dummies(df['job'],prefix="job")],axis=1)
df.drop('job', axis=1, inplace=True)
# Generate dummies for area
df = pd.concat([df,pd.get_dummies(df['area'],prefix="area")],axis=1)
df.drop('area', axis=1, inplace=True)
# Generate dummies for product
df = pd.concat([df,pd.get_dummies(df['product'],prefix="product")],axis=1)
df.drop('product', axis=1, inplace=True)
# Missing values for income
med = df['income'].median()
df['income'] = df['income'].fillna(med)
# Standardize ranges
df['income'] = zscore(df['income'])
df['aspect'] = zscore(df['aspect'])
df['save_rate'] = zscore(df['save_rate'])
df['subscriptions'] = zscore(df['subscriptions'])
# Convert to numpy - Classification
x_columns = df.columns.drop('age').drop('id')
x = df[x_columns].values
y = df['age'].values
```
Now that the feature vector is created a 5-fold cross-validation can be performed to generate out of sample predictions. We will assume 500 epochs, and not use early stopping. Later we will see how we can estimate a more optimal epoch count.
```
import pandas as pd
import os
import numpy as np
from sklearn import metrics
from scipy.stats import zscore
from sklearn.model_selection import KFold
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Activation
# Cross-Validate
kf = KFold(5, shuffle=True, random_state=42) # Use for KFold classification
oos_y = []
oos_pred = []
fold = 0
for train, test in kf.split(x):
fold+=1
print(f"Fold #{fold}")
x_train = x[train]
y_train = y[train]
x_test = x[test]
y_test = y[test]
model = Sequential()
model.add(Dense(20, input_dim=x.shape[1], activation='relu'))
model.add(Dense(10, activation='relu'))
model.add(Dense(1))
model.compile(loss='mean_squared_error', optimizer='adam')
model.fit(x_train,y_train,validation_data=(x_test,y_test),verbose=0,
epochs=500)
pred = model.predict(x_test)
oos_y.append(y_test)
oos_pred.append(pred)
# Measure this fold's RMSE
score = np.sqrt(metrics.mean_squared_error(pred,y_test))
print(f"Fold score (RMSE): {score}")
# Build the oos prediction list and calculate the error.
oos_y = np.concatenate(oos_y)
oos_pred = np.concatenate(oos_pred)
score = np.sqrt(metrics.mean_squared_error(oos_pred,oos_y))
print(f"Final, out of sample score (RMSE): {score}")
# Write the cross-validated prediction
oos_y = pd.DataFrame(oos_y)
oos_pred = pd.DataFrame(oos_pred)
oosDF = pd.concat( [df, oos_y, oos_pred],axis=1 )
#oosDF.to_csv(filename_write,index=False)
```
As you can see, the above code also reports the average number of epochs needed. A common technique is to then train on the entire dataset for the average number of epochs needed.
### Classification with Stratified K-Fold Cross-Validation
The following code trains and fits the jh-simple-dataset dataset with cross-validation to generate out-of-sample . It also writes out the out of sample (predictions on the test set) results.
It is good to perform a stratified k-fold cross validation with classification data. This ensures that the percentages of each class remains the same across all folds. To do this, make use of the **StratifiedKFold** object, instead of the **KFold** object used in regression.
```
import pandas as pd
from scipy.stats import zscore
# Read the data set
df = pd.read_csv(
"https://data.heatonresearch.com/data/t81-558/jh-simple-dataset.csv",
na_values=['NA','?'])
# Generate dummies for job
df = pd.concat([df,pd.get_dummies(df['job'],prefix="job")],axis=1)
df.drop('job', axis=1, inplace=True)
# Generate dummies for area
df = pd.concat([df,pd.get_dummies(df['area'],prefix="area")],axis=1)
df.drop('area', axis=1, inplace=True)
# Missing values for income
med = df['income'].median()
df['income'] = df['income'].fillna(med)
# Standardize ranges
df['income'] = zscore(df['income'])
df['aspect'] = zscore(df['aspect'])
df['save_rate'] = zscore(df['save_rate'])
df['age'] = zscore(df['age'])
df['subscriptions'] = zscore(df['subscriptions'])
# Convert to numpy - Classification
x_columns = df.columns.drop('product').drop('id')
x = df[x_columns].values
dummies = pd.get_dummies(df['product']) # Classification
products = dummies.columns
y = dummies.values
```
We will assume 500 epochs, and not use early stopping. Later we will see how we can estimate a more optimal epoch count.
```
import pandas as pd
import os
import numpy as np
from sklearn import metrics
from sklearn.model_selection import StratifiedKFold
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Activation
# np.argmax(pred,axis=1)
# Cross-validate
# Use for StratifiedKFold classification
kf = StratifiedKFold(5, shuffle=True, random_state=42)
oos_y = []
oos_pred = []
fold = 0
# Must specify y StratifiedKFold for
for train, test in kf.split(x,df['product']):
fold+=1
print(f"Fold #{fold}")
x_train = x[train]
y_train = y[train]
x_test = x[test]
y_test = y[test]
model = Sequential()
model.add(Dense(50, input_dim=x.shape[1], activation='relu')) # Hidden 1
model.add(Dense(25, activation='relu')) # Hidden 2
model.add(Dense(y.shape[1],activation='softmax')) # Output
model.compile(loss='categorical_crossentropy', optimizer='adam')
model.fit(x_train,y_train,validation_data=(x_test,y_test),verbose=0,epochs=500)
pred = model.predict(x_test)
oos_y.append(y_test)
# raw probabilities to chosen class (highest probability)
pred = np.argmax(pred,axis=1)
oos_pred.append(pred)
# Measure this fold's accuracy
y_compare = np.argmax(y_test,axis=1) # For accuracy calculation
score = metrics.accuracy_score(y_compare, pred)
print(f"Fold score (accuracy): {score}")
# Build the oos prediction list and calculate the error.
oos_y = np.concatenate(oos_y)
oos_pred = np.concatenate(oos_pred)
oos_y_compare = np.argmax(oos_y,axis=1) # For accuracy calculation
score = metrics.accuracy_score(oos_y_compare, oos_pred)
print(f"Final score (accuracy): {score}")
# Write the cross-validated prediction
oos_y = pd.DataFrame(oos_y)
oos_pred = pd.DataFrame(oos_pred)
oosDF = pd.concat( [df, oos_y, oos_pred],axis=1 )
#oosDF.to_csv(filename_write,index=False)
```
### Training with both a Cross-Validation and a Holdout Set
If you have a considerable amount of data, it is always valuable to set aside a holdout set before you cross-validate. This hold out set will be the final evaluation before you make use of your model for its real-world use. Figure 5.HOLDOUT shows this division.
**Figure 5.HOLDOUT: Cross Validation and a Holdout Set**

The following program makes use of a holdout set, and then still cross-validates.
```
import pandas as pd
from scipy.stats import zscore
from sklearn.model_selection import train_test_split
# Read the data set
df = pd.read_csv(
"https://data.heatonresearch.com/data/t81-558/jh-simple-dataset.csv",
na_values=['NA','?'])
# Generate dummies for job
df = pd.concat([df,pd.get_dummies(df['job'],prefix="job")],axis=1)
df.drop('job', axis=1, inplace=True)
# Generate dummies for area
df = pd.concat([df,pd.get_dummies(df['area'],prefix="area")],axis=1)
df.drop('area', axis=1, inplace=True)
# Generate dummies for product
df = pd.concat([df,pd.get_dummies(df['product'],prefix="product")],axis=1)
df.drop('product', axis=1, inplace=True)
# Missing values for income
med = df['income'].median()
df['income'] = df['income'].fillna(med)
# Standardize ranges
df['income'] = zscore(df['income'])
df['aspect'] = zscore(df['aspect'])
df['save_rate'] = zscore(df['save_rate'])
df['subscriptions'] = zscore(df['subscriptions'])
# Convert to numpy - Classification
x_columns = df.columns.drop('age').drop('id')
x = df[x_columns].values
y = df['age'].values
from sklearn.model_selection import train_test_split
import pandas as pd
import os
import numpy as np
from sklearn import metrics
from scipy.stats import zscore
from sklearn.model_selection import KFold
# Keep a 10% holdout
x_main, x_holdout, y_main, y_holdout = train_test_split(
x, y, test_size=0.10)
# Cross-validate
kf = KFold(5)
oos_y = []
oos_pred = []
fold = 0
for train, test in kf.split(x_main):
fold+=1
print(f"Fold #{fold}")
x_train = x_main[train]
y_train = y_main[train]
x_test = x_main[test]
y_test = y_main[test]
model = Sequential()
model.add(Dense(20, input_dim=x.shape[1], activation='relu'))
model.add(Dense(5, activation='relu'))
model.add(Dense(1))
model.compile(loss='mean_squared_error', optimizer='adam')
model.fit(x_train,y_train,validation_data=(x_test,y_test),
verbose=0,epochs=500)
pred = model.predict(x_test)
oos_y.append(y_test)
oos_pred.append(pred)
# Measure accuracy
score = np.sqrt(metrics.mean_squared_error(pred,y_test))
print(f"Fold score (RMSE): {score}")
# Build the oos prediction list and calculate the error.
oos_y = np.concatenate(oos_y)
oos_pred = np.concatenate(oos_pred)
score = np.sqrt(metrics.mean_squared_error(oos_pred,oos_y))
print()
print(f"Cross-validated score (RMSE): {score}")
# Write the cross-validated prediction (from the last neural network)
holdout_pred = model.predict(x_holdout)
score = np.sqrt(metrics.mean_squared_error(holdout_pred,y_holdout))
print(f"Holdout score (RMSE): {score}")
```
|
github_jupyter
|
# OOP Syntax Exercise - Part 2
Now that you've had some practice instantiating objects, it's time to write your own class from scratch. This lesson has two parts. In the first part, you'll write a Pants class. This class is similar to the shirt class with a couple of changes. Then you'll practice instantiating Pants objects
In the second part, you'll write another class called SalesPerson. You'll also instantiate objects for the SalesPerson.
For this exercise, you can do all of your work in this Jupyter notebook. You will not need to import the class because all of your code will be in this Jupyter notebook.
Answers are also provided. If you click on the Jupyter icon, you can open a folder called 2.OOP_syntax_pants_practice, which contains this Jupyter notebook ('exercise.ipynb') and a file called answer.py.
# Pants class
Write a Pants class with the following characteristics:
* the class name should be Pants
* the class attributes should include
* color
* waist_size
* length
* price
* the class should have an init function that initializes all of the attributes
* the class should have two methods
* change_price() a method to change the price attribute
* discount() to calculate a discount
```
### TODO:
# - code a Pants class with the following attributes
# - color (string) eg 'red', 'yellow', 'orange'
# - waist_size (integer) eg 8, 9, 10, 32, 33, 34
# - length (integer) eg 27, 28, 29, 30, 31
# - price (float) eg 9.28
### TODO: Declare the Pants Class
### TODO: write an __init__ function to initialize the attributes
### TODO: write a change_price method:
# Args:
# new_price (float): the new price of the shirt
# Returns:
# None
### TODO: write a discount method:
# Args:
# discount (float): a decimal value for the discount.
# For example 0.05 for a 5% discount.
#
# Returns:
# float: the discounted price
class Pants:
"""The Pants class represents an article of clothing sold in a store
"""
def __init__(self, color, waist_size, length, price):
"""Method for initializing a Pants object
Args:
color (str)
waist_size (int)
length (int)
price (float)
Attributes:
color (str): color of a pants object
waist_size (str): waist size of a pants object
length (str): length of a pants object
price (float): price of a pants object
"""
self.color = color
self.waist_size = waist_size
self.length = length
self.price = price
def change_price(self, new_price):
"""The change_price method changes the price attribute of a pants object
Args:
new_price (float): the new price of the pants object
Returns: None
"""
self.price = new_price
def discount(self, percentage):
"""The discount method outputs a discounted price of a pants object
Args:
percentage (float): a decimal representing the amount to discount
Returns:
float: the discounted price
"""
return self.price * (1 - percentage)
class SalesPerson:
"""The SalesPerson class represents an employee in the store
"""
def __init__(self, first_name, last_name, employee_id, salary):
"""Method for initializing a SalesPerson object
Args:
first_name (str)
last_name (str)
employee_id (int)
salary (float)
Attributes:
first_name (str): first name of the employee
last_name (str): last name of the employee
employee_id (int): identification number of the employee
salary (float): yearly salary of the employee
pants_sold (list): a list of pants objects sold by the employee
total_sales (float): sum of all sales made by the employee
"""
self.first_name = first_name
self.last_name = last_name
self.employee_id = employee_id
self.salary = salary
self.pants_sold = []
self.total_sales = 0
def sell_pants(self, pants_object):
"""The sell_pants method appends a pants object to the pants_sold attribute
Args:
pants_object (obj): a pants object that was sold
Returns: None
"""
self.pants_sold.append(pants_object)
def display_sales(self):
"""The display_sales method prints out all pants that have been sold
Args: None
Returns: None
"""
for pants in self.pants_sold:
print('color: {}, waist_size: {}, length: {}, price: {}'\
.format(pants.color, pants.waist_size, pants.length, pants.price))
def calculate_sales(self):
"""The calculate_sales method sums the total price of all pants sold
Args: None
Returns:
float: sum of the price for all pants sold
"""
total = 0
for pants in self.pants_sold:
total += pants.price
self.total_sales = total
return total
def calculate_commission(self, percentage):
"""The calculate_commission method outputs the commission based on sales
Args:
percentage (float): the commission percentage as a decimal
Returns:
float: the commission due
"""
sales_total = self.calculate_sales()
return sales_total * percentage
```
# Run the code cell below to check results
If you run the next code cell and get an error, then revise your code until the code cell doesn't output anything.
```
def check_results():
pants = Pants('red', 35, 36, 15.12)
assert pants.color == 'red'
assert pants.waist_size == 35
assert pants.length == 36
assert pants.price == 15.12
pants.change_price(10) == 10
assert pants.price == 10
assert pants.discount(.1) == 9
print('You made it to the end of the check. Nice job!')
check_results()
```
# SalesPerson class
The Pants class and Shirt class are quite similar. Here is an exercise to give you more practice writing a class. **This exercise is trickier than the previous exercises.**
Write a SalesPerson class with the following characteristics:
* the class name should be SalesPerson
* the class attributes should include
* first_name
* last_name
* employee_id
* salary
* pants_sold
* total_sales
* the class should have an init function that initializes all of the attributes
* the class should have four methods
* sell_pants() a method to change the price attribute
* calculate_sales() a method to calculate the sales
* display_sales() a method to print out all the pants sold with nice formatting
* calculate_commission() a method to calculate the salesperson commission based on total sales and a percentage
```
### TODO:
# Code a SalesPerson class with the following attributes
# - first_name (string), the first name of the salesperson
# - last_name (string), the last name of the salesperson
# - employee_id (int), the employee ID number like 5681923
# - salary (float), the monthly salary of the employee
# - pants_sold (list of Pants objects),
# pants that the salesperson has sold
# - total_sales (float), sum of sales of pants sold
### TODO: Declare the SalesPerson Class
### TODO: write an __init__ function to initialize the attributes
### Input Args for the __init__ function:
# first_name (str)
# last_name (str)
# employee_id (int)
# . salary (float)
#
# You can initialize pants_sold as an empty list
# You can initialize total_sales to zero.
#
###
### TODO: write a sell_pants method:
#
# This method receives a Pants object and appends
# the object to the pants_sold attribute list
#
# Args:
# pants (Pants object): a pants object
# Returns:
# None
### TODO: write a display_sales method:
#
# This method has no input or outputs. When this method
# is called, the code iterates through the pants_sold list
# and prints out the characteristics of each pair of pants
# line by line. The print out should look something like this
#
# color: blue, waist_size: 34, length: 34, price: 10
# color: red, waist_size: 36, length: 30, price: 14.15
#
#
#
###
### TODO: write a calculate_sales method:
# This method calculates the total sales for the sales person.
# The method should iterate through the pants_sold attribute list
# and sum the prices of the pants sold. The sum should be stored
# in the total_sales attribute and then return the total.
#
# Args:
# None
# Returns:
# float: total sales
#
###
### TODO: write a calculate_commission method:
#
# The salesperson receives a commission based on the total
# sales of pants. The method receives a percentage, and then
# calculate the total sales of pants based on the price,
# and then returns the commission as (percentage * total sales)
#
# Args:
# percentage (float): comission percentage as a decimal
#
# Returns:
# float: total commission
#
#
###
```
# Run the code cell below to check results
If you run the next code cell and get an error, then revise your code until the code cell doesn't output anything.
```
def check_results():
pants_one = Pants('red', 35, 36, 15.12)
pants_two = Pants('blue', 40, 38, 24.12)
pants_three = Pants('tan', 28, 30, 8.12)
salesperson = SalesPerson('Amy', 'Gonzalez', 2581923, 40000)
assert salesperson.first_name == 'Amy'
assert salesperson.last_name == 'Gonzalez'
assert salesperson.employee_id == 2581923
assert salesperson.salary == 40000
assert salesperson.pants_sold == []
assert salesperson.total_sales == 0
salesperson.sell_pants(pants_one)
salesperson.pants_sold[0] == pants_one.color
salesperson.sell_pants(pants_two)
salesperson.sell_pants(pants_three)
assert len(salesperson.pants_sold) == 3
assert round(salesperson.calculate_sales(),2) == 47.36
assert round(salesperson.calculate_commission(.1),2) == 4.74
print('Great job, you made it to the end of the code checks!')
check_results()
```
### Check display_sales() method
If you run the code cell below, you should get output similar to this:
```python
color: red, waist_size: 35, length: 36, price: 15.12
color: blue, waist_size: 40, length: 38, price: 24.12
color: tan, waist_size: 28, length: 30, price: 8.12
```
```
pants_one = Pants('red', 35, 36, 15.12)
pants_two = Pants('blue', 40, 38, 24.12)
pants_three = Pants('tan', 28, 30, 8.12)
salesperson = SalesPerson('Amy', 'Gonzalez', 2581923, 40000)
salesperson.sell_pants(pants_one)
salesperson.sell_pants(pants_two)
salesperson.sell_pants(pants_three)
salesperson.display_sales()
```
# Solution
As a reminder, answers are also provided. If you click on the Jupyter icon, you can open a folder called 2.OOP_syntax_pants_practice, which contains this Jupyter notebook and a file called answer.py.
|
github_jupyter
|
# YBIGTA ML PROJECT / 염정운
## Setting
```
import numpy as np
import pandas as pd
pd.set_option("max_columns", 999)
pd.set_option("max_rows", 999)
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier
import seaborn as sns
import matplotlib.pyplot as plt
#sns.set(rc={'figure.figsize':(11.7,10)})
```
## Identity data
Variables in this table are identity information – network connection information (IP, ISP, Proxy, etc) and digital signature
<br>
(UA/browser/os/version, etc) associated with transactions.
<br>
They're collected by Vesta’s fraud protection system and digital security partners.
<br>
The field names are masked and pairwise dictionary will not be provided for privacy protection and contract agreement)
Categorical Features:
<br>
DeviceType
<br>
DeviceInfo
<br>
id12 - id38
```
#train_identity가 불편해서 나는 i_merged라는 isFraud를 merge하고 column 순서를 조금 바꾼 새로운 Dataframe을 만들었어! 이건 그 코드!
#i_merged = train_i.merge(train_t[['TransactionID', 'isFraud']], how = 'left', on = 'TransactionID')
#order_list =['TransactionID', 'isFraud', 'DeviceInfo', 'DeviceType', 'id_01', 'id_02', 'id_03', 'id_04', 'id_05', 'id_06', 'id_07', 'id_08',
# 'id_09', 'id_10', 'id_11', 'id_12', 'id_13', 'id_14', 'id_15', 'id_16', 'id_17', 'id_18', 'id_19', 'id_20', 'id_21',
# 'id_22', 'id_23', 'id_24', 'id_25', 'id_26', 'id_27', 'id_28', 'id_29', 'id_30', 'id_31', 'id_32', 'id_33', 'id_34',
# 'id_35', 'id_36', 'id_37', 'id_38']
#i_merged = i_merged[order_list]
#i_merged.head()
#i_merged.to_csv('identity_merged.csv', index = False)
save = pd.read_csv('identity_merged.csv')
i_merged = pd.read_csv('identity_merged.csv')
```
### <font color='blue'>NaN 비율</font>
```
nullrate = (((i_merged.isnull().sum() / len(i_merged)))*100).sort_values(ascending = False)
nullrate.plot(kind='barh', figsize=(15, 9))
i_merged.head()
```
### <font color='blue'>DeviceType</font>
nan(3.1%) < desktop(6.5%) < mobile(10.1%) 순으로 isFraud 증가 추이
<br>
*전체 datatset에서 isFraud = 1의 비율 7.8%
```
#DeviceType
i_merged.groupby(['DeviceType', 'isFraud']).size().unstack()
i_merged[i_merged.DeviceType.isnull()].groupby('isFraud').size()
```
### <font color='blue'>Null count in row</font>
결측치 정도와 isFraud의 유의미한 상관관계 찾지 못함
```
i_merged = i_merged.assign(NaN_count = i_merged.isnull().sum(axis = 1))
print(i_merged.assign(NaN_count = i_merged.isnull().sum(axis = 1)).groupby('isFraud')['NaN_count'].mean(),
i_merged.assign(NaN_count = i_merged.isnull().sum(axis = 1)).groupby('isFraud')['NaN_count'].std(),
i_merged.assign(NaN_count = i_merged.isnull().sum(axis = 1)).groupby('isFraud')['NaN_count'].min(),
i_merged.assign(NaN_count = i_merged.isnull().sum(axis = 1)).groupby('isFraud')['NaN_count'].max())
#isFraud = 1
i_merged[i_merged.isFraud == 1].hist('NaN_count')
#isFraud = 0
i_merged[i_merged.isFraud == 0].hist('NaN_count')
i_merged.head()
```
### <font color='blue'>변수별 EDA - Continous</font>
```
#Correlation Matrix
rs = np.random.RandomState(0)
df = pd.DataFrame(rs.rand(10, 10))
corr = i_merged.corr()
corr.style.background_gradient(cmap='coolwarm')
#id_01 : 0 이하의 값들을 가지며 skewed 형태. 필요시 log 변환을 통한 처리가 가능할 듯.
i_merged.id_01.plot(kind='hist', bins=22, figsize=(12,6), title='id_01 dist.')
print(i_merged.groupby('isFraud')['id_01'].mean(),
i_merged.groupby('isFraud')['id_01'].std(),
i_merged.id_01.min(),
i_merged.id_01.max(), sep = '\n')
Fraud = (i_merged[i_merged.isFraud == 1]['id_01'])
notFraud = i_merged[i_merged.isFraud == 0]['id_01']
plt.hist([Fraud, notFraud],bins = 5, label=['Fraud', 'notFraud'])
plt.legend(loc='upper left')
plt.show()
#id02: 최솟값 1을 가지며 skewed 형태. 마찬가지로 로그 변환 가능
i_merged.id_02.plot(kind='hist', bins=22, figsize=(12,6), title='id_02 dist.')
print(i_merged.groupby('isFraud')['id_02'].mean(),
i_merged.groupby('isFraud')['id_02'].std(),
i_merged.id_02.min(),
i_merged.id_02.max(), sep = '\n')
Fraud = (i_merged[i_merged.isFraud == 1]['id_02'])
notFraud = i_merged[i_merged.isFraud == 0]['id_02']
plt.hist([Fraud, notFraud],bins = 5, label=['Fraud', 'notFraud'])
plt.legend(loc='upper left')
plt.show()
#id_05
i_merged.id_05.plot(kind='hist', bins=22, figsize=(9,6), title='id_05 dist.')
print(i_merged.groupby('isFraud')['id_05'].mean(),
i_merged.groupby('isFraud')['id_05'].std())
Fraud = (i_merged[i_merged.isFraud == 1]['id_05'])
notFraud = i_merged[i_merged.isFraud == 0]['id_05']
plt.hist([Fraud, notFraud],bins = 10, label=['Fraud', 'notFraud'])
plt.legend(loc='upper left')
plt.show()
#id_06
i_merged.id_06.plot(kind='hist', bins=22, figsize=(12,6), title='id_06 dist.')
print(i_merged.groupby('isFraud')['id_06'].mean(),
i_merged.groupby('isFraud')['id_06'].std())
Fraud = (i_merged[i_merged.isFraud == 1]['id_06'])
notFraud = i_merged[i_merged.isFraud == 0]['id_06']
plt.hist([Fraud, notFraud],bins = 20, label=['Fraud', 'notFraud'])
plt.legend(loc='upper left')
plt.show()
#id_11
i_merged.id_11.plot(kind='hist', bins=22, figsize=(12,6), title='id_11 dist.')
print(i_merged.groupby('isFraud')['id_11'].mean(),
i_merged.groupby('isFraud')['id_11'].std())
Fraud = (i_merged[i_merged.isFraud == 1]['id_11'])
notFraud = i_merged[i_merged.isFraud == 0]['id_11']
plt.hist([Fraud, notFraud],bins = 20, label=['Fraud', 'notFraud'])
plt.legend(loc='upper left')
plt.show()
```
### <font color='blue'>변수별 EDA - Categorical</font>
```
sns.jointplot(x = 'id_09', y = 'id_03', data = i_merged)
```
### <font color='blue'>Feature Engineering</font>
<br>
<br>
** Categorical이지만 가짓수가 많은 경우 정보가 있을 때 1, 아닐 때 0으로 처리함. BaseModel 돌리기 위해 이렇게 설정하였지만, 전처리를 바꿔가는 작업에서는 이 변수들을 다른 방식으로 처리 할 필요가 더 생길 수도 있음.
<br>
** Pair 관계가 있음. id03,04 / id05,06 / id07,08, 21~26 / id09, 10 ::함께 데이터가 존재하거나(1) NaN이거나(0). 한편 EDA-Category를 보면 id03, 09의 경우 상관관계가 있는 것으로 추정되어 추가적인 변형을 하지 않았음.
<br>
** https://www.kaggle.com/pablocanovas/exploratory-analysis-tidyverse 에서 변수별 EDA 시각화 참고하였고, nan값 제외하고는 Fraud 비율이 낮은 변수부터 1,2..차례로 할당함
<br>
<br>
<br>
### $Contionous Features$
<br>
id01:: 결측치가 없으며 로그변형을 통해 양수화 및 Scailing 시킴. 5의 배수임을 감안할 때 5로 나누는 scailing을 진행해봐도 좋을 듯.
<br>
id02:: 결측치가 존재하나, 로그 변형을 통해 정규분포에 흡사한 모양으로 만들고 매우 큰 단위를 Scailing하였음. 결측치는 Random 방식을 이용하여 채웠으나 가장 위험한 방식으로 imputation으로 한 것이므로 주의가 필요함.
<br>
<br>
<br>
### $Categorical Features$
<br>
DeviceType:: {NaN: 0, 'desktop': 1, 'mobile': 2}
<br>
DeviceInfo:: {Nan: 0, 정보있음:1}
<br>
id12::{0:0, 'Found': 1, 'NotFound': 2}
<br>
id13::{Nan: 0, 정보있음:1}
<br>
id14::{Nan: 0, 정보있음:1}
<br>
id15::{Nan:0, 'New':1, 'Unknown':2, 'Found':3} #15, 16은 연관성이 보임
<br>
id16::{Nan:0, 'NotFound':1, 'Found':2}
<br>
id17::{Nan: 0, 정보있음:1}
<br>
id18::{Nan: 0, 정보있음:1} #가짓수 다소 적음
<br>
id19::{Nan: 0, 정보있음:1}
<br>
id20::{Nan: 0, 정보있음:1} #id 17, 19, 20은 Pair
<br>
id21
<br>
id22
<br>
id23::{IP_PROXY:ANONYMOUS:2, else:1, nan:0} #id 7,8 21~26은 Pair. Anonymous만 유독 Fraud 비율이 높기에 고려함. 우선은 베이스 모델에서는 id_23만 사용
<br>
id24
<br>
id25
<br>
id26
<br>
id27:: {Nan:0, 'NotFound':1, 'Found':2}
<br>
id28:: {0:0, 'New':1, 'Found':2}
<br>
id29:: {0:0, 'NotFound':1, 'Found':2}
<br>
id30(OS):: {Nan: 0, 정보있음:1}, 데이터가 있다 / 없다로 처리하였지만 Safari Generic에서 사기 확률이 높다 등의 조건을 고려해야한다면 다른 방식으로 전처리 필요할 듯
<br>
id31(browser):: {Nan: 0, 정보있음:1}, id30과 같음
<br>
id32::{nan:0, 24:1, 32:2, 16:3, 0:4}
<br>
id33(해상도)::{Nan: 0, 정보있음:1}
<br>
id34:: {nan:0, matchstatus= -1:1, matchstatus=0 :2, matchstatus=1 :3, matchstatus=2 :4} , matchstatus가 -1이면 fraud일 확률 매우 낮음
<br>
id35:: {Nan:0, 'T':1, 'F':2}
<br>
id36:: {Nan:0, 'T':1, 'F':2}
<br>
id37:: {Nan:0, 'T':2, 'F':1}
<br>
id38:: {Nan:0, 'T':1, 'F':2}
<br>
```
#Continous Features
i_merged.id_01 = np.log(-i_merged.id_01 + 1)
i_merged.id_02 = np.log(i_merged.id_02)
medi = i_merged.id_02.median()
i_merged.id_02 = i_merged.id_02.fillna(medi)
i_merged.id_02.hist()
#id_02의 NaN값을 random하게 채워줌
#i_merged['id_02_filled'] = i_merged['id_02']
#temp = (i_merged['id_02'].dropna()
# .sample(i_merged['id_02'].isnull().sum())
# )
#temp.index = i_merged[lambda x: x.id_02.isnull()].index
#i_merged.loc[i_merged['id_02'].isnull(), 'id_02_filled'] = temp
#Categorical Features
i_merged.DeviceType = i_merged.DeviceType.fillna(0).map({0:0, 'desktop': 1, 'mobile': 2})
i_merged.DeviceInfo = i_merged.DeviceInfo.notnull().astype(int)
i_merged.id_12 = i_merged.id_12.fillna(0).map({0:0, 'Found': 1, 'NotFound': 2})
i_merged.id_13 = i_merged.id_13.notnull().astype(int)
i_merged.id_14 = i_merged.id_14.notnull().astype(int)
i_merged.id_14 = i_merged.id_14.notnull().astype(int)
i_merged.id_15 = i_merged.id_15.fillna(0).map({0:0, 'New':1, 'Unknown':2, 'Found':3})
i_merged.id_16 = i_merged.id_16.fillna(0).map({0:0, 'NotFound':1, 'Found':2})
i_merged.id_17 = i_merged.id_17.notnull().astype(int)
i_merged.id_18 = i_merged.id_18.notnull().astype(int)
i_merged.id_19 = i_merged.id_19.notnull().astype(int)
i_merged.id_20 = i_merged.id_20.notnull().astype(int)
i_merged.id_23 = i_merged.id_23.fillna('temp').map({'temp':0, 'IP_PROXY:ANONYMOUS':2}).fillna(1)
i_merged.id_27 = i_merged.id_27.fillna(0).map({0:0, 'NotFound':1, 'Found':2})
i_merged.id_28 = i_merged.id_28.fillna(0).map({0:0, 'New':1, 'Found':2})
i_merged.id_29 = i_merged.id_29.fillna(0).map({0:0, 'NotFound':1, 'Found':2})
i_merged.id_30 = i_merged.id_30.notnull().astype(int)
i_merged.id_31 = i_merged.id_31.notnull().astype(int)
i_merged.id_32 = i_merged.id_32.fillna('temp').map({'temp':0, 24:1, 32:2, 16:3, 0:4})
i_merged.id_33 = i_merged.id_33.notnull().astype(int)
i_merged.id_34 = i_merged.id_34.fillna('temp').map({'temp':0, 'match_status:-1':1, 'match_status:0':3, 'match_status:1':4, 'match_status:2':2})
i_merged.id_35 = i_merged.id_35.fillna(0).map({0:0, 'T':1, 'F':2})
i_merged.id_36 = i_merged.id_38.fillna(0).map({0:0, 'T':1, 'F':2})
i_merged.id_37 = i_merged.id_38.fillna(0).map({0:0, 'T':2, 'F':1})
i_merged.id_38 = i_merged.id_38.fillna(0).map({0:0, 'T':1, 'F':2})
```
Identity_Device FE
```
i_merged['Device_info_clean'] = i_merged['DeviceInfo']
i_merged['Device_info_clean'] = i_merged['Device_info_clean'].fillna('unknown')
def name_divide(name):
if name == 'Windows':
return 'Windows'
elif name == 'iOS Device':
return 'iOS Device'
elif name == 'MacOS':
return 'MacOS'
elif name == 'Trident/7.0':
return 'Trident/rv'
elif "rv" in name:
return 'Trident/rv'
elif "SM" in name:
return 'SM/moto/lg'
elif name == 'SAMSUNG':
return 'SM'
elif 'LG' in name:
return 'SM/Moto/LG'
elif 'Moto' in name:
return 'SM/Moto/LG'
elif name == 'unknown':
return 'unknown'
else:
return 'others'
i_merged['Device_info_clean'] = i_merged['Device_info_clean'].apply(name_divide)
i_merged['Device_info_clean'].value_counts()
```
### <font color='blue'>Identity_feature engineered_dataset</font>
```
i_merged.columns
selected = []
selected.extend(['TransactionID', 'isFraud', 'id_01', 'id_02', 'DeviceType','Device_info_clean'])
id_exist = i_merged[selected].assign(Exist = 1)
id_exist.DeviceType.fillna('unknown', inplace = True)
id_exist.to_csv('identity_first.csv',index = False)
```
### <font color='blue'>Test: Decision Tree / Random Forest Test</font>
```
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import GridSearchCV
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import precision_score, recall_score, f1_score, accuracy_score, roc_auc_score
X = id_exist.drop(['isFraud'], axis = 1)
Y = id_exist['isFraud']
X_train, X_test, y_train, y_test = train_test_split(X, Y, test_size=0.3)
tree_clf = DecisionTreeClassifier(max_depth=10)
tree_clf.fit(X_train, y_train)
pred = tree_clf.predict(X_test)
print('F1:{}'.format(f1_score(y_test, pred)))
```
--------------------------
```
param_grid = {
'max_depth': list(range(10,51,10)),
'n_estimators': [20, 20, 20]
}
rf = RandomForestClassifier()
gs = GridSearchCV(estimator = rf, param_grid = param_grid,
cv = 5, n_jobs = -1, verbose = 2)
gs.fit(X_train,y_train)
best_rf = gs.best_estimator_
print('best parameter: \n',gs.best_params_)
y_pred = best_rf.predict(X_test)
print('Accuracy:{}'.format(accuracy_score(y_test, y_pred)),
'Precision:{}'.format(precision_score(y_test, y_pred)),
'Recall:{}'.format(recall_score(y_test, y_pred)),
'F1:{}'.format(f1_score(y_test, y_pred)),
'ROC_AUC:{}'.format(roc_auc_score(y_test, y_pred)), sep = '\n')
```
-----------------------
### <font color='blue'>거래 + ID merge</font>
```
transaction_c = pd.read_csv('train_combined.csv')
id_c = pd.read_csv('identity_first.csv')
region = pd.read_csv('region.csv')
country = region[['TransactionID', 'Country_code']]
country.head()
f_draft = transaction_c.merge(id_c.drop(['isFraud'], axis = 1) ,how = 'left', on = 'TransactionID')
f_draft.drop('DeviceInfo', axis = 1, inplace = True)
f_draft = f_draft.merge(country, how = 'left', on = 'TransactionID')
f_draft.head()
f_draft.dtypes
```
Categorical: 'ProductCD', 'card4', 'card6', 'D15', 'DeviceType', 'Device_info_clean'
```
print(
f_draft.ProductCD.unique(),
f_draft.card4.unique(),
f_draft.card6.unique(),
f_draft.D15.unique(),
f_draft.DeviceType.unique(),
f_draft.Device_info_clean.unique(),
)
print(map_ProductCD, map_card4,map_card6,map_D15, sep = '\n')
```
map_ProductCD = {'W': 0, 'H': 1, 'C': 2, 'S': 3, 'R': 4}
<br>
map_card4 = {'discover': 0, 'mastercard': 1, 'visa': 2, '}american express': 3}
<br>
map_card6 = {'credit': 0, 'debit': 1, 'debit or credit': 2, 'charge card': 3}
<br>
map_D15 = {'credit': 0, 'debit': 1, 'debit or credit': 2, 'charge card': 3}
<br>
map_DeviceType = {'mobile':2 'desktop':1 'unknown':0}
<br>
map_Device_info_clean = {'SM/moto/lg':1, 'iOS Device':2, 'Windows':3, 'unknown':0, 'MacOS':4, 'others':5,
'Trident/rv':6}
```
f_draft.ProductCD = f_draft.ProductCD.map(map_ProductCD)
f_draft.card4 = f_draft.card4.map(map_card4)
f_draft.card6 = f_draft.card6.map(map_card6)
f_draft.D15 = f_draft.D15.map(map_D15)
f_draft.DeviceType = f_draft.DeviceType.map(map_DeviceType)
f_draft.Device_info_clean = f_draft.Device_info_clean.map(map_Device_info_clean)
f_draft.to_csv('transaction_id_combined(no_label_encoded).csv', index = False)
f_draft.ProductCD = f_draft.ProductCD.astype('category')
f_draft.card4 = f_draft.card4.astype('category')
f_draft.card6 = f_draft.card6.astype('category')
f_draft.card1 = f_draft.card1.astype('category')
f_draft.card2 = f_draft.card2.astype('category')
f_draft.card3 = f_draft.card3.astype('category')
f_draft.card5 = f_draft.card5.astype('category')
f_draft.D15 = f_draft.D15.astype('category')
f_draft.DeviceType = f_draft.DeviceType.astype('category')
f_draft.Device_info_clean = f_draft.Device_info_clean.astype('category')
f_draft.Country_code = f_draft.Country_code.astype('category')
f_draft.card1 = f_draft.card1.astype('category')
f_draft.card2 = f_draft.card2.astype('category')
f_draft.card3 = f_draft.card3.astype('category')
f_draft.card5 = f_draft.card5.astype('category')
f_draft.dtypes
f_draft.to_csv('transaction_id_combined.csv', index = False)
f_draft.head()
```
|
github_jupyter
|
<a href="https://colab.research.google.com/github/tuanavu/deep-learning-tutorials/blob/development/colab-example-notebooks/colab_github_demo.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Using Google Colab with GitHub
[Google Colaboratory](http://colab.research.google.com) is designed to integrate cleanly with GitHub, allowing both loading notebooks from github and saving notebooks to github.
## Loading Public Notebooks Directly from GitHub
Colab can load public github notebooks directly, with no required authorization step.
For example, consider the notebook at this address: https://github.com/googlecolab/colabtools/blob/master/notebooks/colab-github-demo.ipynb.
The direct colab link to this notebook is: https://colab.research.google.com/github/googlecolab/colabtools/blob/master/notebooks/colab-github-demo.ipynb.
To generate such links in one click, you can use the [Open in Colab](https://chrome.google.com/webstore/detail/open-in-colab/iogfkhleblhcpcekbiedikdehleodpjo) Chrome extension.
## Browsing GitHub Repositories from Colab
Colab also supports special URLs that link directly to a GitHub browser for any user/organization, repository, or branch. For example:
- http://colab.research.google.com/github will give you a general github browser, where you can search for any github organization or username.
- http://colab.research.google.com/github/googlecolab/ will open the repository browser for the ``googlecolab`` organization. Replace ``googlecolab`` with any other github org or user to see their repositories.
- http://colab.research.google.com/github/googlecolab/colabtools/ will let you browse the main branch of the ``colabtools`` repository within the ``googlecolab`` organization. Substitute any user/org and repository to see its contents.
- http://colab.research.google.com/github/googlecolab/colabtools/blob/master will let you browse ``master`` branch of the ``colabtools`` repository within the ``googlecolab`` organization. (don't forget the ``blob`` here!) You can specify any valid branch for any valid repository.
## Loading Private Notebooks
Loading a notebook from a private GitHub repository is possible, but requires an additional step to allow Colab to access your files.
Do the following:
1. Navigate to http://colab.research.google.com/github.
2. Click the "Include Private Repos" checkbox.
3. In the popup window, sign-in to your Github account and authorize Colab to read the private files.
4. Your private repositories and notebooks will now be available via the github navigation pane.
## Saving Notebooks To GitHub or Drive
Any time you open a GitHub hosted notebook in Colab, it opens a new editable view of the notebook. You can run and modify the notebook without worrying about overwriting the source.
If you would like to save your changes from within Colab, you can use the File menu to save the modified notebook either to Google Drive or back to GitHub. Choose **File→Save a copy in Drive** or **File→Save a copy to GitHub** and follow the resulting prompts. To save a Colab notebook to GitHub requires giving Colab permission to push the commit to your repository.
## Open In Colab Badge
Anybody can open a copy of any github-hosted notebook within Colab. To make it easier to give people access to live views of GitHub-hosted notebooks,
colab provides a [shields.io](http://shields.io/)-style badge, which appears as follows:
[](https://colab.research.google.com/github/googlecolab/colabtools/blob/master/notebooks/colab-github-demo.ipynb)
The markdown for the above badge is the following:
```markdown
[](https://colab.research.google.com/github/googlecolab/colabtools/blob/master/notebooks/colab-github-demo.ipynb)
```
The HTML equivalent is:
```HTML
<a href="https://colab.research.google.com/github/googlecolab/colabtools/blob/master/notebooks/colab-github-demo.ipynb">
<img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/>
</a>
```
Remember to replace the notebook URL in this template with the notebook you want to link to.
```
```
|
github_jupyter
|
```
# Parameters
# Build the dataset
from typing import Optional
import pandas as pd
import functools
def add_parent_level(df: pd.DataFrame, name: str) -> None:
df.columns = pd.MultiIndex.from_tuples([(name, x) for x in df.columns])
def calculate_limit(row: pd.Series, attribute: str) -> Optional[float]:
row_analysis = local_analysis.get(row.name)
if row_analysis is None:
return None
vm_spec = compute_specs.virtual_machine_by_name(row_analysis.advisor_sku)
return getattr(vm_spec.capabilities, attribute)
def add_limit(df: pd.DataFrame, name: str) -> None:
df['new_limit'] = df.apply(functools.partial(calculate_limit, attribute=name), axis=1)
drop_utilization = ['samples', 'percentile_50th', 'percentile_80th']
drop_disk_utilization = ['cached', 'counter_name']
res_data = resources.assign(resource_name=resources.resource_id.str.extract(r'([^/]+)$'))
res_data = res_data.drop(columns=['subscription_id', 'storage_profile'])
res_data = res_data.set_index('resource_id')
res_data_col = res_data.columns.to_list()
res_data_col = res_data_col[1:-1] + res_data_col[-1:] + res_data_col[0:1]
res_data = res_data[res_data_col]
add_parent_level(res_data, 'Resource')
if local_analysis:
local_data = pd.DataFrame([(k, v.advisor_sku, v.advisor_sku_invalid_reason, v.annual_savings_no_ri) for k,v in local_analysis.items()], columns=['resource_id', 'recommendation', 'invalidation', 'annual_savings']).convert_dtypes()
local_data = local_data.set_index('resource_id')
add_parent_level(local_data, 'AzMeta')
if advisor_analysis:
advisor_data = pd.DataFrame([(k, v.advisor_sku, v.advisor_sku_invalid_reason) for k,v in advisor_analysis.items()], dtype='string', columns=['resource_id', 'recommendation', 'invalidation'])
advisor_data = advisor_data.set_index('resource_id')
add_parent_level(advisor_data, 'Advisor')
cpu_data = cpu_utilization.drop(columns=drop_utilization).set_index('resource_id')
add_limit(cpu_data, 'd_total_acus')
add_parent_level(cpu_data, 'CPU Used (ACUs)')
mem_data = mem_utilization.drop(columns=drop_utilization).set_index('resource_id')
mem_data = mem_data / 1024.0
add_limit(mem_data, 'memory_gb')
add_parent_level(mem_data, 'Memory Used (GiB)')
disk_tput_cached = disk_utilization[(disk_utilization.cached == True) & (disk_utilization.counter_name == 'Disk Bytes/sec')]
disk_tput_cached = disk_tput_cached.drop(columns=drop_utilization + drop_disk_utilization).set_index('resource_id')
add_limit(disk_tput_cached, 'combined_temp_disk_and_cached_read_bytes_per_second')
disk_tput_cached = disk_tput_cached / (1024.0 ** 2)
add_parent_level(disk_tput_cached, 'Cached Disk Througput (MiB/sec)')
disk_trans_cached = disk_utilization[(disk_utilization.cached == True) & (disk_utilization.counter_name == 'Disk Transfers/sec')]
disk_trans_cached = disk_trans_cached.drop(columns=drop_utilization + drop_disk_utilization).set_index('resource_id')
add_limit(disk_trans_cached, 'combined_temp_disk_and_cached_iops')
add_parent_level(disk_trans_cached, 'Cached Disk Operations (IOPS)')
disk_tput_uncached = disk_utilization[(disk_utilization.cached == False) & (disk_utilization.counter_name == 'Disk Bytes/sec')]
disk_tput_uncached = disk_tput_uncached.drop(columns=drop_utilization + drop_disk_utilization).set_index('resource_id')
add_limit(disk_tput_uncached, 'uncached_disk_bytes_per_second')
disk_tput_uncached = disk_tput_uncached / (1024.0 ** 2)
add_parent_level(disk_tput_uncached, 'Uncached Disk Througput (MiB/sec)')
disk_trans_uncached = disk_utilization[(disk_utilization.cached == False) & (disk_utilization.counter_name == 'Disk Transfers/sec')]
disk_trans_uncached = disk_trans_uncached.drop(columns=drop_utilization + drop_disk_utilization).set_index('resource_id')
add_limit(disk_trans_uncached, 'uncached_disk_iops')
add_parent_level(disk_trans_uncached, 'Uncached Disk Operations (IOPS)')
all_joins = [cpu_data, mem_data, disk_tput_cached, disk_trans_cached, disk_tput_uncached, disk_trans_uncached]
if local_analysis:
all_joins.insert(0, local_data)
if advisor_analysis:
all_joins.append(advisor_data)
full_data = res_data.join(all_joins)
full_data.sort_index(inplace=True)
full_data.to_excel('final_out_test.xlsx')
```
# AzMeta Resize Recommendations
```
import datetime
print("Report Date:", datetime.datetime.now().isoformat())
print("Total Annual Savings:", "${:,.2f}".format(local_data[('AzMeta', 'annual_savings')].sum()), "(Non-RI Pricing, SQL and Windows AHUB Licensing)")
# Present the dataset
import matplotlib as plt
import itertools
from matplotlib import colors
def background_limit_coloring(row):
cmap="coolwarm"
text_color_threshold=0.408
limit_index = (row.index.get_level_values(0)[0], 'new_limit')
smin = 0
smax = row[limit_index]
if pd.isna(smax):
return [''] * len(row)
rng = smax - smin
norm = colors.Normalize(smin, smax)
rgbas = plt.cm.get_cmap(cmap)(norm(row.to_numpy(dtype=float)))
def relative_luminance(rgba):
r, g, b = (
x / 12.92 if x <= 0.03928 else ((x + 0.055) / 1.055 ** 2.4)
for x in rgba[:3]
)
return 0.2126 * r + 0.7152 * g + 0.0722 * b
def css(rgba):
dark = relative_luminance(rgba) < text_color_threshold
text_color = "#f1f1f1" if dark else "#000000"
return f"background-color: {colors.rgb2hex(rgba)};color: {text_color};"
return [css(rgba) for rgba in rgbas[0:-1]] + ['']
def build_header_style(col_groups):
start = 0
styles = []
palette = ['#f6f6f6', '#eae9e9', '#d4d7dd', '#f6f6f6', '#eae9e9', '#d4d7dd', '#f6f6f6', '#eae9e9', '#d4d7dd']
for i,group in enumerate(itertools.groupby(col_groups, lambda c:c[0])):
styles.append({'selector': f'.col_heading.level0.col{start}', 'props': [('background-color', palette[i])]})
group_len = len(tuple(group[1]))
for j in range(group_len):
styles.append({'selector': f'.col_heading.level1.col{start + j}', 'props': [('background-color', palette[i])]})
start += group_len
return styles
data_group_names = [x for x in full_data.columns.get_level_values(0).unique() if x not in ('Resource', 'AzMeta', 'Advisor')]
num_mask = [x[0] in data_group_names for x in full_data.columns.to_flat_index()]
styler = full_data.style.hide_index() \
.set_properties(**{'font-weight': 'bold'}, subset=[('Resource', 'resource_name')]) \
.format('{:.1f}', subset=num_mask, na_rep='N/A') \
.format('${:.2f}', subset=[('AzMeta', 'annual_savings')], na_rep='N/A') \
.set_table_styles(build_header_style(full_data.columns))
for data_group in data_group_names:
mask = [x == data_group for x in full_data.columns.get_level_values(0)]
styler = styler.apply(background_limit_coloring, axis=1, subset=mask)
styler
```
|
github_jupyter
|
# Cowell's formulation
For cases where we only study the gravitational forces, solving the Kepler's equation is enough to propagate the orbit forward in time. However, when we want to take perturbations that deviate from Keplerian forces into account, we need a more complex method to solve our initial value problem: one of them is **Cowell's formulation**.
In this formulation we write the two body differential equation separating the Keplerian and the perturbation accelerations:
$$\ddot{\mathbb{r}} = -\frac{\mu}{|\mathbb{r}|^3} \mathbb{r} + \mathbb{a}_d$$
<div class="alert alert-info">For an in-depth exploration of this topic, still to be integrated in poliastro, check out https://github.com/Juanlu001/pfc-uc3m</div>
<div class="alert alert-info">An earlier version of this notebook allowed for more flexibility and interactivity, but was considerably more complex. Future versions of poliastro and plotly might bring back part of that functionality, depending on user feedback. You can still download the older version <a href="https://github.com/poliastro/poliastro/blob/0.8.x/docs/source/examples/Propagation%20using%20Cowell's%20formulation.ipynb">here</a>.</div>
## First example
Let's setup a very simple example with constant acceleration to visualize the effects on the orbit.
```
import numpy as np
from astropy import units as u
from matplotlib import pyplot as plt
plt.ion()
from poliastro.bodies import Earth
from poliastro.twobody import Orbit
from poliastro.examples import iss
from poliastro.twobody.propagation import cowell
from poliastro.plotting import OrbitPlotter3D
from poliastro.util import norm
from plotly.offline import init_notebook_mode
init_notebook_mode(connected=True)
```
To provide an acceleration depending on an extra parameter, we can use **closures** like this one:
```
accel = 2e-5
def constant_accel_factory(accel):
def constant_accel(t0, u, k):
v = u[3:]
norm_v = (v[0]**2 + v[1]**2 + v[2]**2)**.5
return accel * v / norm_v
return constant_accel
def custom_propagator(orbit, tof, rtol, accel=accel):
# Workaround for https://github.com/poliastro/poliastro/issues/328
if tof == 0:
return orbit.r.to(u.km).value, orbit.v.to(u.km / u.s).value
else:
# Use our custom perturbation acceleration
return cowell(orbit, tof, rtol, ad=constant_accel_factory(accel))
times = np.linspace(0, 10 * iss.period, 500)
times
times, positions = iss.sample(times, method=custom_propagator)
```
And we plot the results:
```
frame = OrbitPlotter3D()
frame.set_attractor(Earth)
frame.plot_trajectory(positions, label="ISS")
frame.show()
```
## Error checking
```
def state_to_vector(ss):
r, v = ss.rv()
x, y, z = r.to(u.km).value
vx, vy, vz = v.to(u.km / u.s).value
return np.array([x, y, z, vx, vy, vz])
k = Earth.k.to(u.km**3 / u.s**2).value
rtol = 1e-13
full_periods = 2
u0 = state_to_vector(iss)
tf = ((2 * full_periods + 1) * iss.period / 2).to(u.s).value
u0, tf
iss_f_kep = iss.propagate(tf * u.s, rtol=1e-18)
r, v = cowell(iss, tf, rtol=rtol)
iss_f_num = Orbit.from_vectors(Earth, r * u.km, v * u.km / u.s, iss.epoch + tf * u.s)
iss_f_num.r, iss_f_kep.r
assert np.allclose(iss_f_num.r, iss_f_kep.r, rtol=rtol, atol=1e-08 * u.km)
assert np.allclose(iss_f_num.v, iss_f_kep.v, rtol=rtol, atol=1e-08 * u.km / u.s)
assert np.allclose(iss_f_num.a, iss_f_kep.a, rtol=rtol, atol=1e-08 * u.km)
assert np.allclose(iss_f_num.ecc, iss_f_kep.ecc, rtol=rtol)
assert np.allclose(iss_f_num.inc, iss_f_kep.inc, rtol=rtol, atol=1e-08 * u.rad)
assert np.allclose(iss_f_num.raan, iss_f_kep.raan, rtol=rtol, atol=1e-08 * u.rad)
assert np.allclose(iss_f_num.argp, iss_f_kep.argp, rtol=rtol, atol=1e-08 * u.rad)
assert np.allclose(iss_f_num.nu, iss_f_kep.nu, rtol=rtol, atol=1e-08 * u.rad)
```
## Numerical validation
According to [Edelbaum, 1961], a coplanar, semimajor axis change with tangent thrust is defined by:
$$\frac{\operatorname{d}\!a}{a_0} = 2 \frac{F}{m V_0}\operatorname{d}\!t, \qquad \frac{\Delta{V}}{V_0} = \frac{1}{2} \frac{\Delta{a}}{a_0}$$
So let's create a new circular orbit and perform the necessary checks, assuming constant mass and thrust (i.e. constant acceleration):
```
ss = Orbit.circular(Earth, 500 * u.km)
tof = 20 * ss.period
ad = constant_accel_factory(1e-7)
r, v = cowell(ss, tof.to(u.s).value, ad=ad)
ss_final = Orbit.from_vectors(Earth, r * u.km, v * u.km / u.s, ss.epoch + tof)
da_a0 = (ss_final.a - ss.a) / ss.a
da_a0
dv_v0 = abs(norm(ss_final.v) - norm(ss.v)) / norm(ss.v)
2 * dv_v0
np.allclose(da_a0, 2 * dv_v0, rtol=1e-2)
```
This means **we successfully validated the model against an extremely simple orbit transfer with approximate analytical solution**. Notice that the final eccentricity, as originally noticed by Edelbaum, is nonzero:
```
ss_final.ecc
```
## References
* [Edelbaum, 1961] "Propulsion requirements for controllable satellites"
|
github_jupyter
|
```
import os, time, datetime
import numpy as np
import pandas as pd
from tqdm.notebook import tqdm
import random
import logging
tqdm.pandas()
import seaborn as sns
from sklearn.model_selection import train_test_split
#NN Packages
import torch
import torch.nn as nn
from torch.utils.data import TensorDataset, random_split,DataLoader, RandomSampler, SequentialSampler
logger = logging.getLogger(__name__)
if torch.cuda.is_available():
# Tell PyTorch to use the GPU.
device = torch.device("cuda")
print('There are %d GPU(s) available.' % torch.cuda.device_count())
print('We will use the GPU:', torch.cuda.get_device_name(0))
# If not...
else:
print('No GPU available, using the CPU instead.')
device = torch.device("cpu")
def format_time(elapsed):
'''
Takes a time in seconds and returns a string hh:mm:ss
'''
# Round to the nearest second.
elapsed_rounded = int(round((elapsed)))
# Format as hh:mm:ss
return str(datetime.timedelta(seconds=elapsed_rounded))
class SigirPreprocess():
def __init__(self, text_data_path):
self.text_data_path = text_data_path
self.train = None
self.dict_code_to_id = {}
self.dict_id_to_code = {}
self.list_tags = {}
self.sentences = []
self.labels = []
self.text_col = None
self.X_test = None
def prepare_data(self ):
catalog_eng= pd.read_csv(self.text_data_path+"data/catalog_english_taxonomy.tsv",sep="\t")
X_train= pd.read_csv(self.text_data_path+"data/X_train.tsv",sep="\t")
Y_train= pd.read_csv(self.text_data_path+"data/Y_train.tsv",sep="\t")
self.list_tags = list(Y_train['Prdtypecode'].unique())
for i,tag in enumerate(self.list_tags):
self.dict_code_to_id[tag] = i
self.dict_id_to_code[i]=tag
print(self.dict_code_to_id)
Y_train['labels']=Y_train['Prdtypecode'].map(self.dict_code_to_id)
train=pd.merge(left=X_train,right=Y_train,
how='left',left_on=['Integer_id','Image_id','Product_id'],
right_on=['Integer_id','Image_id','Product_id'])
prod_map=pd.Series(catalog_eng['Top level category'].values,
index=catalog_eng['Prdtypecode']).to_dict()
train['product'] = train['Prdtypecode'].map(prod_map)
train['title_len']=train['Title'].progress_apply(lambda x : len(x.split()) if pd.notna(x) else 0)
train['desc_len']=train['Description'].progress_apply(lambda x : len(x.split()) if pd.notna(x) else 0)
train['title_desc_len']=train['title_len'] + train['desc_len']
train.loc[train['Description'].isnull(), 'Description'] = " "
train['title_desc'] = train['Title'] + " " + train['Description']
self.train = train
def get_sentences(self, text_col, remove_null_rows=False):
self.text_col = text_col
if remove_null_rows==True:
new_train = self.train[self.train[text_col].notnull()]
else:
new_train = self.train.copy()
self.sentences = new_train[text_col].values
self.labels = new_train['labels'].values
def prepare_test(self, text_col):
X_test=pd.read_csv(self.text_data_path+"data/x_test_task1_phase1.tsv",sep="\t")
X_test.loc[X_test['Description'].isnull(), 'Description'] = " "
X_test['title_desc'] = X_test['Title'] + " " + X_test['Description']
self.X_test = X_test
self.test_sentences = X_test[text_col].values
text_col = 'title_desc'
max_len = 256
val_size = 0.1
Preprocess = SigirPreprocess("/kaggle/input/textphase1/")
Preprocess.prepare_data()
Preprocess.get_sentences(text_col, True)
sentences = Preprocess.sentences
labels = Preprocess.labels
print("Total number of sentences:{}, labels:{}".format(len(sentences), len(labels)))
#function to prepare input for model training
def prep_input(sentences,labels, max_len,tokenizer):
input_ids = []
attention_masks = []
# For every sentence...
for sent in tqdm(sentences):
# `encode_plus` will:
# (1) Tokenize the sentence.
# (2) Prepend the `[CLS]` token to the start.
# (3) Append the `[SEP]` token to the end.
# (4) Map tokens to their IDs.
# (5) Pad or truncate the sentence to `max_length`
# (6) Create attention masks for [PAD] tokens.
encoded_dict = tokenizer.encode_plus(
sent, # Sentence to encode.
add_special_tokens = True, # Add '[CLS]' and '[SEP]'
max_length = max_len, # Pad & truncate all sentences.
pad_to_max_length = True,
return_attention_mask = True, # Construct attn. masks.
return_tensors = 'pt', # Return pytorch tensors.
)
# Add the encoded sentence to the list.
input_ids.append(encoded_dict['input_ids'])
# And its attention mask (simply differentiates padding from non-padding).
attention_masks.append(encoded_dict['attention_mask'])
# Convert the lists into tensors.
input_ids = torch.cat(input_ids, dim=0)
attention_masks = torch.cat(attention_masks, dim=0)
if labels is not None:
labels = torch.tensor(labels)
return input_ids,attention_masks,labels
else:
return input_ids,attention_masks
text_input='../input/multi-modal-input-text/'
tr_inputs_cam=torch.load(text_input+"tr_inputs_cam.pt")
val_inputs_cam=torch.load(text_input+"val_inputs_cam.pt")
tr_masks_cam=torch.load( text_input+"tr_masks_cam.pt")
val_masks_cam=torch.load( text_input+"val_masks_cam.pt")
tr_inputs_flau=torch.load(text_input+"tr_inputs_flau.pt")
val_inputs_flau=torch.load(text_input+"val_inputs_flau.pt")
tr_masks_flau=torch.load(text_input+"tr_masks_flau.pt")
val_masks_flau=torch.load(text_input+"val_masks_flau.pt")
!pip install pretrainedmodels
from transformers import CamembertConfig, CamembertTokenizer, CamembertModel, CamembertForSequenceClassification, AdamW
from transformers import FlaubertModel, FlaubertTokenizer,FlaubertForSequenceClassification,AdamW, FlaubertConfig
from transformers.modeling_roberta import RobertaClassificationHead
from transformers.modeling_utils import SequenceSummary
from torch.nn import functional as F
import torch.nn as nn
import pretrainedmodels
class SEResnext50_32x4d(nn.Module):
def __init__(self, pretrained='imagenet'):
super(SEResnext50_32x4d, self).__init__()
self.base_model = pretrainedmodels.__dict__["se_resnext50_32x4d"](pretrained=None)
if pretrained is not None:
self.base_model.load_state_dict(
torch.load("../input/pretrained-model-weights-pytorch/se_resnext50_32x4d-a260b3a4.pth"
)
)
self.l0 = nn.Linear(2048, 27)
def forward(self, image):
batch_size, _, _, _ = image.shape
x = self.base_model.features(image)
x = F.adaptive_avg_pool2d(x, 1).reshape(batch_size, -1)
out = self.l0(x)
return out
class Identity(nn.Module):
def __init__(self):
super(Identity, self).__init__()
def forward(self, x):
return x
class vec_output_CamembertForSequenceClassification(CamembertModel):
config_class = CamembertConfig
def __init__(self, config):
super().__init__(config)
self.num_labels = config.num_labels
self.roberta = CamembertModel(config)
self.dense = nn.Linear(256*config.hidden_size, config.hidden_size)
self.dropout = nn.Dropout(0.1)
self.out_proj = nn.Linear(config.hidden_size, config.num_labels)
self.init_weights()
def forward(
self,
input_ids=None,
attention_mask=None,
token_type_ids=None,
position_ids=None,
head_mask=None,
inputs_embeds=None,
labels=None,
output_attentions=None,
output_hidden_states=None,
):
outputs = self.roberta(
input_ids,
attention_mask=attention_mask,
token_type_ids=token_type_ids,
position_ids=position_ids,
head_mask=head_mask,
inputs_embeds=inputs_embeds,
# output_attentions=output_attentions,
# output_hidden_states=output_hidden_states,
)
sequence_output = outputs[0] #(B,256,768)
x = sequence_output.view(sequence_output.shape[0], 256*768)
# x = sequence_output[:, 0, :] # take <s> token (equiv. to [CLS])-> #(B,768) Image -> (B,2048)
x = self.dense(x) # 768 -> 768
feat= torch.tanh(x)
logits = self.out_proj(feat) # 768 -> 27
outputs = (logits,) + outputs[2:]
return outputs,feat # (loss), logits, (hidden_states), (attentions)
num_classes = 27
class vec_output_FlaubertForSequenceClassification(FlaubertModel):
config_class = FlaubertConfig
def __init__(self, config):
super().__init__(config)
self.transformer = FlaubertModel(config)
self.sequence_summary = SequenceSummary(config)
self.init_weights()
self.dropout = torch.nn.Dropout(0.1)
self.classifier = torch.nn.Linear(config.hidden_size, num_classes)
def forward(
self,
input_ids=None,
attention_mask=None,
langs=None,
token_type_ids=None,
position_ids=None,
lengths=None,
cache=None,
head_mask=None,
inputs_embeds=None,
labels=None,
):
transformer_outputs = self.transformer(
input_ids,
attention_mask=attention_mask,
langs=langs,
token_type_ids=token_type_ids,
position_ids=position_ids,
lengths=lengths,
cache=cache,
head_mask=head_mask,
inputs_embeds=inputs_embeds,
)
#output = self.dropout(output)
output = transformer_outputs[0]
vec = output[:,0]
#logits
dense = self.dropout(vec)
#classifier
logits = self.classifier(dense)
outputs = (logits,) + transformer_outputs[1:] # Keep new_mems and attention/hidden states if they are here
return outputs,dense
```
### Image data prep
```
catalog_eng= pd.read_csv("/kaggle/input/textphase1/data/catalog_english_taxonomy.tsv",sep="\t")
X_train= pd.read_csv("/kaggle/input/textphase1/data/X_train.tsv",sep="\t")
Y_train= pd.read_csv("/kaggle/input/textphase1/data/Y_train.tsv",sep="\t")
X_test=pd.read_csv("/kaggle/input/textphase1/data/x_test_task1_phase1.tsv",sep="\t")
dict_code_to_id = {}
dict_id_to_code={}
list_tags = list(Y_train['Prdtypecode'].unique())
for i,tag in enumerate(list_tags):
dict_code_to_id[tag] = i
dict_id_to_code[i]=tag
Y_train['labels']=Y_train['Prdtypecode'].map(dict_code_to_id)
train=pd.merge(left=X_train,right=Y_train,
how='left',left_on=['Integer_id','Image_id','Product_id'],
right_on=['Integer_id','Image_id','Product_id'])
prod_map=pd.Series(catalog_eng['Top level category'].values,index=catalog_eng['Prdtypecode']).to_dict()
train['product']=train['Prdtypecode'].map(prod_map)
def get_img_path(img_id,prd_id,path):
pattern = 'image'+'_'+str(img_id)+'_'+'product'+'_'+str(prd_id)+'.jpg'
return path + pattern
train_img = train[['Image_id','Product_id','labels','product']]
train_img['image_path']=train_img.progress_apply(lambda x: get_img_path(x['Image_id'],x['Product_id'],
path = '/kaggle/input/imagetrain/image_training/'),axis=1)
X_test['image_path']=X_test.progress_apply(lambda x: get_img_path(x['Image_id'],x['Product_id'],
path='/kaggle/input/imagetest/image_test/image_test_task1_phase1/'),axis=1)
train_df, val_df, _, _ = train_test_split(train_img, train_img['labels'],random_state=2020, test_size = 0.1, stratify=train_img['labels'])
input_size = 224 # for Resnt
# Applying Transforms to the Data
from torchvision import datasets, models, transforms
image_transforms = {
'train': transforms.Compose([
transforms.RandomResizedCrop(size=256, scale=(0.8, 1.0)),
transforms.RandomRotation(degrees=15),
transforms.RandomHorizontalFlip(),
transforms.Resize(size=256),
transforms.CenterCrop(size=input_size),
transforms.ToTensor(),
transforms.Normalize([0.485, 0.456, 0.406],
[0.229, 0.224, 0.225])
]),
'valid': transforms.Compose([
transforms.Resize(size=256),
transforms.CenterCrop(size=input_size),
transforms.ToTensor(),
transforms.Normalize([0.485, 0.456, 0.406],
[0.229, 0.224, 0.225])
]),
'test': transforms.Compose([
transforms.Resize(size=256),
transforms.CenterCrop(size=input_size),
transforms.ToTensor(),
transforms.Normalize([0.485, 0.456, 0.406],
[0.229, 0.224, 0.225])
])
}
from torch.utils.data import Dataset, DataLoader, Subset
import cv2
from PIL import Image
class FusionDataset(Dataset):
def __init__(self,df,inputs_cam,masks_cam,inputs_flau,masks_flau,transform=None,mode='train'):
self.df = df
self.transform=transform
self.mode=mode
self.inputs_cam=inputs_cam
self.masks_cam=masks_cam
self.inputs_flau=inputs_flau
self.masks_flau=masks_flau
def __len__(self):
return len(self.df)
def __getitem__(self,idx):
im_path = self.df.iloc[idx]['image_path']
img = cv2.imread(im_path)
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
img=Image.fromarray(img)
if self.transform is not None:
img = self.transform(img)
img=img.cuda()
input_id_cam=self.inputs_cam[idx].cuda()
input_mask_cam=self.masks_cam[idx].cuda()
input_id_flau=self.inputs_flau[idx].cuda()
input_mask_flau=self.masks_flau[idx].cuda()
if self.mode=='test':
return img,input_id_cam,input_mask_cam,input_id_flau,input_mask_flau
else:
# labels = torch.tensor(self.df.iloc[idx]['labels'])
labels = torch.tensor(self.df.iloc[idx]['labels']).cuda()
return img,input_id_cam,input_mask_cam,input_id_flau,input_mask_flau,labels
a1 = torch.randn(3,10,10)
reduce_dim=nn.Conv1d(in_channels = 10 , out_channels = 1 , kernel_size= 1)
reduce_dim(a1).view(3,10).shape
class vector_fusion(nn.Module):
def __init__(self):
super(vector_fusion, self).__init__()
self.img_model = SEResnext50_32x4d(pretrained=None)
self.img_model.load_state_dict(torch.load('../input/seresnext2048/best_model.pt'))
self.img_model.l0=Identity()
for params in self.img_model.parameters():
params.requires_grad=False
self.cam_model= vec_output_CamembertForSequenceClassification.from_pretrained(
'camembert-base', # Use the 12-layer BERT model, with an uncased vocab.
num_labels = len(Preprocess.dict_code_to_id), # The number of output labels--2 for binary classification.
# You can increase this for multi-class tasks.
output_attentions = False, # Whether the model returns attentions weights.
output_hidden_states = False,) # Whether the model returns all hidden-states.
cam_model_path = '../input/camembert-vec-256m768-10ep/best_model.pt'
checkpoint = torch.load(cam_model_path)
# model = checkpoint['model']
self.cam_model.load_state_dict(checkpoint)
for param in self.cam_model.parameters():
param.requires_grad=False
self.cam_model.out_proj=Identity()
self.flau_model=vec_output_FlaubertForSequenceClassification.from_pretrained(
'flaubert/flaubert_base_cased',
num_labels = len(Preprocess.dict_code_to_id),
output_attentions = False,
output_hidden_states = False,)
flau_model_path='../input/flaubert-8933/best_model.pt'
checkpoint = torch.load(flau_model_path)
self.flau_model.load_state_dict(checkpoint)
for param in self.flau_model.parameters():
param.requires_grad=False
self.flau_model.classifier=Identity()
self.reduce_dim=nn.Conv1d(in_channels = 2048 , out_channels = 768 , kernel_size= 1)
self.reduce_dim2=nn.Conv1d(in_channels = 768 , out_channels = 1 , kernel_size= 1)
self.out=nn.Linear(768*3, 27)
#gamma
# self.w1 = nn.Parameter(torch.zeros(1))
# self.w2 = nn.Parameter(torch.zeros(1))
# self.w3 = nn.Parameter(torch.zeros(1))
def forward(self,img,input_id_cam,input_mask_cam,input_id_flau,input_mask_flau):
cam_emb,vec1 =self.cam_model(input_id_cam,
token_type_ids=None,
attention_mask=input_mask_cam)
flau_emb,vec2 =self.flau_model(input_id_flau,
token_type_ids=None,
attention_mask=input_mask_flau)
#Projecting the image embedding to lower dimension
img_emb=self.img_model(img)
img_emb=img_emb.view(img_emb.shape[0],img_emb.shape[1],1)
img_emb=self.reduce_dim(img_emb)
img_emb=img_emb.view(img_emb.shape[0],img_emb.shape[1]) ###### bs * 768
#summing up the vectors
#text_emb = cam_emb[0] + flau_emb[0]
#Bilinear
#text_emb = text_emb.view(text_emb.shape[0],1,text_emb.shape[1]) ##### bs * 1 * 768
#Bilinear Pooling
#pool_emb = torch.bmm(img_emb,text_emb) ### bs * 768 * 768
#pool_emb = self.reduce_dim2(pool_emb).view(text_emb.shape[0],768) #### bs * 1 * 768
fuse= torch.cat([img_emb,cam_emb[0],flau_emb[0]],axis=1)
logits=self.out(fuse)
return logits
model=vector_fusion()
model.cuda()
train_dataset=FusionDataset(train_df,tr_inputs_cam,tr_masks_cam,tr_inputs_flau,tr_masks_flau,transform=image_transforms['test'])
val_dataset=FusionDataset(val_df,val_inputs_cam,val_masks_cam,val_inputs_flau,val_masks_flau,transform=image_transforms['test'])
# test_dataset=FusionDataset(X_test,test_inputs,test_makss,transform=image_transforms['test'],mode='test')
batch_size=64
train_dataloader=DataLoader(train_dataset,batch_size=batch_size,shuffle=True)
validation_dataloader=DataLoader(val_dataset,batch_size=batch_size,shuffle=False)
# test_data=DataLoader(test_dataset,batch_size=batch_size,shuffle=False)
optimizer = AdamW(model.parameters(),
lr = 2e-5, # args.learning_rate - default is 5e-5, our notebook had 2e-5
eps = 1e-8 # args.adam_epsilon - default is 1e-8.
)
def count_parameters(model):
return sum(p.numel() for p in model.parameters() if p.requires_grad)
count_parameters(model)
from transformers import get_linear_schedule_with_warmup
# Number of training epochs. The BERT authors recommend between 2 and 4.
# We chose to run for 4, but we'll see later that this may be over-fitting the
# training data.
epochs = 3
# Total number of training steps is [number of batches] x [number of epochs].
# (Note that this is not the same as the number of training samples).
total_steps = len(train_dataloader) * epochs
# Create the learning rate scheduler.
scheduler = get_linear_schedule_with_warmup(optimizer,
num_warmup_steps = 0, # Default value in run_glue.py
num_training_steps = total_steps)
import torch.nn as nn
loss_criterion = nn.CrossEntropyLoss()
def flat_accuracy(preds, labels):
pred_flat = np.argmax(preds, axis=1).flatten()
labels_flat = labels.flatten()
return np.sum(pred_flat == labels_flat) / len(labels_flat)
from sklearn.metrics import f1_score
seed_val = 42
random.seed(seed_val)
np.random.seed(seed_val)
torch.manual_seed(seed_val)
torch.cuda.manual_seed_all(seed_val)
# We'll store a number of quantities such as training and validation loss,
# validation accuracy, and timings.
training_stats = []
# Measure the total training time for the whole run.
total_t0 = time.time()
# For each epoch...
for epoch_i in range(0, epochs):
# ========================================
# Training
# ========================================
# Perform one full pass over the training set.
print("")
print('======== Epoch {:} / {:} ========'.format(epoch_i + 1, epochs))
print('Training...')
#tr and val
# vec_output_tr = []
# vec_output_val =[]
# Measure how long the training epoch takes.
t0 = time.time()
# Reset the total loss for this epoch.
total_train_loss = 0
# Put the model into training mode. Don't be mislead--the call to
# `train` just changes the *mode*, it doesn't *perform* the training.
# `dropout` and `batchnorm` layers behave differently during training
# vs. test (source: https://stackoverflow.com/questions/51433378/what-does-model-train-do-in-pytorch)
best_f1 = 0
model.train()
# For each batch of training data...
for step, batch in tqdm(enumerate(train_dataloader)):
# Unpack this training batch from our dataloader.
#
# As we unpack the batch, we'll also copy each tensor to the GPU using the
# `to` method.
#
# `batch` contains three pytorch tensors:
# [0]: input ids
# [1]: attention masks
# [2]: labels
# return img,input_id_cam,input_mask_cam,input_id_flau,input_mask_flau
b_img=batch[0].to(device)
b_input_id_cam = batch[1].to(device)
b_input_mask_cam = batch[2].to(device)
b_input_id_flau = batch[3].to(device)
b_input_mask_flau = batch[4].to(device)
b_labels = batch[5].to(device)
model.zero_grad()
logits = model(b_img,b_input_id_cam ,b_input_mask_cam,b_input_id_flau,b_input_mask_flau)
#Defining the loss
loss = loss_criterion(logits, b_labels)
#saving the features_tr
# vec = vec.detach().cpu().numpy()
# vec_output_tr.extend(vec)
# Accumulate the training loss over all of the batches so that we can
# calculate the average loss at the end. `loss` is a Tensor containing a
# single value; the `.item()` function just returns the Python value
# from the tensor.
total_train_loss += loss.item()
# Perform a backward pass to calculate the gradients.
loss.backward()
# Clip the norm of the gradients to 1.0.
# This is to help prevent the "exploding gradients" problem.
torch.nn.utils.clip_grad_norm_(model.parameters(), 1.0)
# Update parameters and take a step using the computed gradient.
# The optimizer dictates the "update rule"--how the parameters are
# modified based on their gradients, the learning rate, etc.
optimizer.step()
# Update the learning rate.
scheduler.step()
# Calculate the average loss over all of the batches.
avg_train_loss = total_train_loss / len(train_dataloader)
# Measure how long this epoch took.
training_time = format_time(time.time() - t0)
print("")
print(" Average training loss: {0:.2f} ".format(avg_train_loss))
print(" Training epcoh took: {:} ".format(training_time))
# ========================================
# Validation
# ========================================
# After the completion of each training epoch, measure our performance on
# our validation set.
print("")
print("Running Validation...")
t0 = time.time()
# Put the model in evaluation mode--the dropout layers behave differently
# during evaluation.
model.eval()
# Tracking variables
total_eval_accuracy = 0
total_eval_loss = 0
nb_eval_steps = 0
predictions=[]
true_labels=[]
# Evaluate data for one epoch
for batch in tqdm(validation_dataloader):
# Unpack this training batch from our dataloader.
#
# As we unpack the batch, we'll also copy each tensor to the GPU using
# the `to` method.
#
# `batch` contains three pytorch tensors:
# [0]: input ids
# [1]: attention masks
# [2]: labels
b_img=batch[0].to(device)
b_input_id_cam = batch[1].to(device)
b_input_mask_cam = batch[2].to(device)
b_input_id_flau = batch[3].to(device)
b_input_mask_flau = batch[4].to(device)
b_labels = batch[5].to(device)
# Tell pytorch not to bother with constructing the compute graph during
# the forward pass, since this is only needed for backprop (training).
with torch.no_grad():
# Forward pass, calculate logit predictions.
# token_type_ids is the same as the "segment ids", which
# differentiates sentence 1 and 2 in 2-sentence tasks.
# The documentation for this `model` function is here:
# https://huggingface.co/transformers/v2.2.0/model_doc/bert.html#transformers.BertForSequenceClassification
# Get the "logits" output by the model. The "logits" are the output
# values prior to applying an activation function like the softmax.
logits = model(b_img,b_input_id_cam ,b_input_mask_cam,b_input_id_flau,b_input_mask_flau)
#new
#defining the val loss
loss = loss_criterion(logits, b_labels)
# Accumulate the validation loss.
total_eval_loss += loss.item()
# Move logits and labels to CPU
logits = logits.detach().cpu().numpy()
# Move logits and labels to CPU
predicted_labels=np.argmax(logits,axis=1)
predictions.extend(predicted_labels)
label_ids = b_labels.to('cpu').numpy()
true_labels.extend(label_ids)
#saving the features_tr
# vec = vec.detach().cpu().numpy()
# vec_output_val.extend(vec)
# Calculate the accuracy for this batch of test sentences, and
# accumulate it over all batches.
total_eval_accuracy += flat_accuracy(logits, label_ids)
# Report the final accuracy for this validation run.
avg_val_accuracy = total_eval_accuracy / len(validation_dataloader)
print(" Accuracy: {0:.2f}".format(avg_val_accuracy))
# Calculate the average loss over all of the batches.
avg_val_loss = total_eval_loss / len(validation_dataloader)
# Measure how long the validation run took.
validation_time = format_time(time.time() - t0)
print(" Validation Loss: {0:.2f}".format(avg_val_loss))
print(" Validation took: {:}".format(validation_time))
print("Validation F1-Score: {}".format(f1_score(true_labels,predictions,average='macro')))
curr_f1=f1_score(true_labels,predictions,average='macro')
if curr_f1 > best_f1:
best_f1=curr_f1
torch.save(model.state_dict(), 'best_model.pt')
# np.save('best_vec_train_model_train.npy',vec_output_tr)
# np.save('best_vec_val.npy',vec_output_val)
# Record all statistics from this epoch.
# training_stats.append(
# {
# 'epoch': epoch_i + 1,
# 'Training Loss': avg_train_loss,
# 'Valid. Loss': avg_val_loss,
# 'Valid. Accur.': avg_val_accuracy,
# 'Training Time': training_time,
# 'Validation Time': validation_time
# }
# )
print("")
print("Training complete!")
print("Total training took {:} (h:mm:ss)".format(format_time(time.time()-total_t0)))
from sklearn.metrics import f1_score
print("Validation F1-Score: {}".format(f1_score(true_labels,predictions,average='macro')))
```
|
github_jupyter
|
# Optimization
Things to try:
- change the number of samples
- without and without bias
- with and without regularization
- changing the number of layers
- changing the amount of noise
- change number of degrees
- look at parameter values (high) in OLS
- tarin network for many epochs
```
from fastprogress.fastprogress import progress_bar
import torch
import matplotlib.pyplot as plt
from jupyterthemes import jtplot
jtplot.style(context="talk")
def plot_regression_data(model=None, MSE=None, poly_deg=0):
# Plot the noisy scatter points and the "true" function
plt.scatter(x_train, y_train, label="Noisy Samples")
plt.plot(x_true, y_true, "--", label="True Function")
# Plot the model's learned regression function
if model:
x = x_true.unsqueeze(-1)
x = x.pow(torch.arange(poly_deg + 1)) if poly_deg else x
with torch.no_grad():
yhat = model(x)
plt.plot(x_true, yhat, label="Learned Function")
plt.xlim([min_x, max_x])
plt.ylim([-5, 5])
plt.legend()
if MSE:
plt.title(f"MSE = ${MSE}$")
```
# Create Fake Training Data
```
def fake_y(x, add_noise=False):
y = 10 * x ** 3 - 5 * x
return y + torch.randn_like(y) * 0.5 if add_noise else y
N = 20
min_x, max_x = -1, 1
x_true = torch.linspace(min_x, max_x, 100)
y_true = fake_y(x_true)
x_train = torch.rand(N) * (max_x - min_x) + min_x
y_train = fake_y(x_train, add_noise=True)
plot_regression_data()
```
# Train A Simple Linear Model Using Batch GD
```
# Hyperparameters
learning_rate = 0.1
num_epochs = 100
# Model parameters
m = torch.randn(1, requires_grad=True)
b = torch.zeros(1, requires_grad=True)
params = (b, m)
# Torch utils
criterion = torch.nn.MSELoss()
optimizer = torch.optim.SGD(params, lr=learning_rate)
# Regression
for epoch in range(num_epochs):
# Model
yhat = m * x_train + b
# Update parameters
optimizer.zero_grad()
loss = criterion(yhat, y_train)
loss.backward()
optimizer.step()
plot_regression_data(lambda x: m * x + b, MSE=loss.item())
```
# Train Linear Regression Model Using Batch GD
```
# Hyperparameters
learning_rate = 0.1
num_epochs = 1000
# Model parameters
w2 = torch.randn(1, requires_grad=True)
w1 = torch.randn(1, requires_grad=True)
b = torch.zeros(1, requires_grad=True)
params = (b, w1, w2)
# Torch utils
criterion = torch.nn.MSELoss()
optimizer = torch.optim.SGD(params, lr=learning_rate)
# Regression
for epoch in range(num_epochs):
# Model
yhat = b + w1 * x_train + w2 * x_train ** 2
# Update parameters
optimizer.zero_grad()
loss = criterion(yhat, y_train)
loss.backward()
optimizer.step()
plot_regression_data(lambda x: b + w1 * x + w2 * x ** 2, MSE=loss.item())
```
# Train Complex Linear Regression Model Using Batch GD
```
# Hyperparameters
learning_rate = 0.1
num_epochs = 1000
# Model parameters
degrees = 50 # 3, 4, 16, 32, 64, 128
powers = torch.arange(degrees + 1)
x_poly = x_train.unsqueeze(-1).pow(powers)
params = torch.randn(degrees + 1, requires_grad=True)
# Torch utils
criterion = torch.nn.MSELoss()
optimizer = torch.optim.SGD([params], lr=learning_rate)
# Regression
for epoch in range(num_epochs):
# Model
yhat = x_poly @ params
# Update parameters
optimizer.zero_grad()
loss = criterion(yhat, y_train)
loss.backward()
optimizer.step()
plot_regression_data(lambda x: x @ params, poly_deg=degrees, MSE=loss.item())
params
```
# Compute Linear Regression Model Using Ordinary Least Squares
```
params = ((x_poly.T @ x_poly).inverse() @ x_poly.T) @ y_train
mse = torch.nn.functional.mse_loss(x_poly @ params, y_train)
plot_regression_data(lambda x: x @ params, poly_deg=degrees, MSE=mse)
# params
params
```
# Train Neural Network Model Using Batch GD
```
# Hyperparameters
learning_rate = 0.01
num_epochs = 100000
regularization = 1e-2
# Model parameters
model = torch.nn.Sequential(
torch.nn.Linear(1, 100),
torch.nn.ReLU(),
torch.nn.Linear(100, 100),
torch.nn.ReLU(),
torch.nn.Linear(100, 100),
torch.nn.ReLU(),
torch.nn.Linear(100, 1),
)
# Torch utils
criterion = torch.nn.MSELoss()
optimizer = torch.optim.SGD(
model.parameters(), lr=learning_rate, weight_decay=regularization
)
# Training
for epoch in progress_bar(range(num_epochs)):
# Model
yhat = model(x_train.unsqueeze(-1))
# Update parameters
optimizer.zero_grad()
loss = criterion(yhat.squeeze(), y_train)
loss.backward()
optimizer.step()
plot_regression_data(model, loss.item())
for param in model.parameters():
print(param.mean())
```
|
github_jupyter
|
## Hybrid Neural Net to solve Regression Problem
We use a neural net with a quantum layer to predict the second half betting lines given the result of the first half and the opening line. The quantum layer is an 8 qubit layer and the model is from Keras.
```
import pandas as pd
import numpy as np
import tensorflow as tf
from sklearn.preprocessing import MinMaxScaler
from sklearn.model_selection import train_test_split
import pennylane as qml
import warnings
warnings.filterwarnings('ignore')
tf.keras.backend.set_floatx('float64')
import warnings
warnings.filterwarnings('ignore')
###predict 2nd half line using 1st half total and open ##
df1 = pd.read_csv("nfl_odds.csv")
df1['1H'] = df1['1st'] + df1['2nd']
df2 = pd.read_csv('bet.csv')
df = df1.merge(df2, left_on = 'Team', right_on = 'Tm')
df = df[['1H','Open', 'TO%','PF','Yds','ML', '2H']]
df.head()
n_qubits = 8
dev = qml.device("default.qubit", wires=n_qubits)
@qml.qnode(dev)
def qnode(inputs, weights):
qml.templates.AngleEmbedding(inputs, wires=range(n_qubits))
qml.templates.BasicEntanglerLayers(weights, wires=range(n_qubits))
return [qml.expval(qml.PauliZ(wires=i)) for i in range(n_qubits)]
n_layers = 4
weight_shapes = {"weights": (n_layers, n_qubits)}
qlayer = qml.qnn.KerasLayer(qnode, weight_shapes, output_dim=n_qubits)
clayer_1 = tf.keras.layers.Dense(8, activation="relu")
clayer_2 = tf.keras.layers.Dense(2, activation="relu")
model = tf.keras.models.Sequential([clayer_1, qlayer, clayer_2])
opt = tf.keras.optimizers.SGD(learning_rate=0.2)
model.compile(opt, loss="mae", metrics=["mean_absolute_error"])
df = df[df.Open != 'pk']
df = df[df['2H'] != 'pk']
df['Open'] = df['Open'].astype(float)
df['2H'] = df['2H'].astype(float)
X = df[['1H','Open','TO%','PF','Yds','ML']]
y = df['2H']
X = np.asarray(X).astype(np.float32)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.15, random_state=0)
scaler = MinMaxScaler(feature_range = (0,1))
scaler.fit(X_train)
X_train = scaler.transform(X_train)
fitting = model.fit(X_train, y_train, epochs=10, batch_size=5, validation_split=0.15, verbose=2)
X_test = scaler.transform(X_test)
preds = model.predict(X_test)
pred = pd.DataFrame(preds, columns =[ 'prediction1', 'prediction2'])
pred = pred[(pred.prediction1 > 0) & (pred.prediction1 < 30)]
y_test = y_test.reset_index()
y_test = y_test[y_test['2H'] > 6]
compare = pd.concat([pred, y_test], axis=1)
compare = compare.drop('index', axis=1)
compare.dropna()
```
## Classical NN (Benchmarking)
The MAE is twice as large for the purely classical NN. The quantum layer is helping the solution converge more quickly! (As an aside, the quantum NN takes alot longer to run)
```
clayer_1 = tf.keras.layers.Dense(8, activation="relu")
clayer_2 = tf.keras.layers.Dense(2, activation="relu")
model = tf.keras.models.Sequential([clayer_1, clayer_2])
opt = tf.keras.optimizers.SGD(learning_rate=0.2)
model.compile(opt, loss="mae", metrics=["mean_absolute_error"])
df = df[df.Open != 'pk']
df = df[df['2H'] != 'pk']
df['Open'] = df['Open'].astype(float)
df['2H'] = df['2H'].astype(float)
X = df[['1H','Open','TO%','PF','Yds','ML']]
y = df['2H']
X = np.asarray(X).astype(np.float32)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.15, random_state=0)
scaler = MinMaxScaler(feature_range = (0,1))
scaler.fit(X_train)
X_train = scaler.transform(X_train)
fitting = model.fit(X_train, y_train, epochs=15, batch_size=10, validation_split=0.15, verbose=2)
```
|
github_jupyter
|
<a id='1'></a>
# 1. Import packages
```
from keras.models import Sequential, Model
from keras.layers import *
from keras.layers.advanced_activations import LeakyReLU
from keras.activations import relu
from keras.initializers import RandomNormal
from keras.applications import *
import keras.backend as K
from tensorflow.contrib.distributions import Beta
import tensorflow as tf
from keras.optimizers import Adam
from image_augmentation import random_transform
from image_augmentation import random_warp
from utils import get_image_paths, load_images, stack_images
from pixel_shuffler import PixelShuffler
import time
import numpy as np
from PIL import Image
import cv2
import glob
from random import randint, shuffle
from IPython.display import clear_output
from IPython.display import display
import matplotlib.pyplot as plt
%matplotlib inline
```
<a id='4'></a>
# 4. Config
mixup paper: https://arxiv.org/abs/1710.09412
Default training data directories: `./faceA/` and `./faceB/`
```
K.set_learning_phase(1)
channel_axis=-1
channel_first = False
IMAGE_SHAPE = (64, 64, 3)
nc_in = 3 # number of input channels of generators
nc_D_inp = 6 # number of input channels of discriminators
use_perceptual_loss = False
use_lsgan = True
use_instancenorm = False
use_mixup = True
mixup_alpha = 0.2 # 0.2
batchSize = 32
lrD = 1e-4 # Discriminator learning rate
lrG = 1e-4 # Generator learning rate
# Path of training images
img_dirA = './faceA/*.*'
img_dirB = './faceB/*.*'
```
<a id='5'></a>
# 5. Define models
```
from model_GAN_v2 import *
encoder = Encoder()
decoder_A = Decoder_ps()
decoder_B = Decoder_ps()
x = Input(shape=IMAGE_SHAPE)
netGA = Model(x, decoder_A(encoder(x)))
netGB = Model(x, decoder_B(encoder(x)))
netDA = Discriminator(nc_D_inp)
netDB = Discriminator(nc_D_inp)
```
<a id='6'></a>
# 6. Load Models
```
try:
encoder.load_weights("models/encoder.h5")
decoder_A.load_weights("models/decoder_A.h5")
decoder_B.load_weights("models/decoder_B.h5")
#netDA.load_weights("models/netDA.h5")
#netDB.load_weights("models/netDB.h5")
print ("model loaded.")
except:
print ("Weights file not found.")
pass
```
<a id='7'></a>
# 7. Define Inputs/Outputs Variables
distorted_A: A (batch_size, 64, 64, 3) tensor, input of generator_A (netGA).
distorted_B: A (batch_size, 64, 64, 3) tensor, input of generator_B (netGB).
fake_A: (batch_size, 64, 64, 3) tensor, output of generator_A (netGA).
fake_B: (batch_size, 64, 64, 3) tensor, output of generator_B (netGB).
mask_A: (batch_size, 64, 64, 1) tensor, mask output of generator_A (netGA).
mask_B: (batch_size, 64, 64, 1) tensor, mask output of generator_B (netGB).
path_A: A function that takes distorted_A as input and outputs fake_A.
path_B: A function that takes distorted_B as input and outputs fake_B.
path_mask_A: A function that takes distorted_A as input and outputs mask_A.
path_mask_B: A function that takes distorted_B as input and outputs mask_B.
path_abgr_A: A function that takes distorted_A as input and outputs concat([mask_A, fake_A]).
path_abgr_B: A function that takes distorted_B as input and outputs concat([mask_B, fake_B]).
real_A: A (batch_size, 64, 64, 3) tensor, target images for generator_A given input distorted_A.
real_B: A (batch_size, 64, 64, 3) tensor, target images for generator_B given input distorted_B.
```
def cycle_variables(netG):
distorted_input = netG.inputs[0]
fake_output = netG.outputs[0]
alpha = Lambda(lambda x: x[:,:,:, :1])(fake_output)
rgb = Lambda(lambda x: x[:,:,:, 1:])(fake_output)
masked_fake_output = alpha * rgb + (1-alpha) * distorted_input
fn_generate = K.function([distorted_input], [masked_fake_output])
fn_mask = K.function([distorted_input], [concatenate([alpha, alpha, alpha])])
fn_abgr = K.function([distorted_input], [concatenate([alpha, rgb])])
return distorted_input, fake_output, alpha, fn_generate, fn_mask, fn_abgr
distorted_A, fake_A, mask_A, path_A, path_mask_A, path_abgr_A = cycle_variables(netGA)
distorted_B, fake_B, mask_B, path_B, path_mask_B, path_abgr_B = cycle_variables(netGB)
real_A = Input(shape=IMAGE_SHAPE)
real_B = Input(shape=IMAGE_SHAPE)
```
<a id='11'></a>
# 11. Helper Function: face_swap()
This function is provided for those who don't have enough VRAM to run dlib's CNN and GAN model at the same time.
INPUTS:
img: A RGB face image of any size.
path_func: a function that is either path_abgr_A or path_abgr_B.
OUPUTS:
result_img: A RGB swapped face image after masking.
result_mask: A single channel uint8 mask image.
```
def swap_face(img, path_func):
input_size = img.shape
img = cv2.cvtColor(img, cv2.COLOR_RGB2BGR) # generator expects BGR input
ae_input = cv2.resize(img, (64,64))/255. * 2 - 1
result = np.squeeze(np.array([path_func([[ae_input]])]))
result_a = result[:,:,0] * 255
result_bgr = np.clip( (result[:,:,1:] + 1) * 255 / 2, 0, 255 )
result_a = np.expand_dims(result_a, axis=2)
result = (result_a/255 * result_bgr + (1 - result_a/255) * ((ae_input + 1) * 255 / 2)).astype('uint8')
#result = np.clip( (result + 1) * 255 / 2, 0, 255 ).astype('uint8')
result = cv2.cvtColor(result, cv2.COLOR_BGR2RGB)
result = cv2.resize(result, (input_size[1],input_size[0]))
result_a = np.expand_dims(cv2.resize(result_a, (input_size[1],input_size[0])), axis=2)
return result, result_a
whom2whom = "BtoA" # default trainsforming faceB to faceA
if whom2whom is "AtoB":
path_func = path_abgr_B
elif whom2whom is "BtoA":
path_func = path_abgr_A
else:
print ("whom2whom should be either AtoB or BtoA")
input_img = plt.imread("./IMAGE_FILENAME.jpg")
plt.imshow(input_img)
result_img, result_mask = swap_face(input_img, path_func)
plt.imshow(result_img)
plt.imshow(result_mask[:, :, 0]) # cmap='gray'
```
|
github_jupyter
|
# Unsplash Joint Query Search
Using this notebook you can search for images from the [Unsplash Dataset](https://unsplash.com/data) using natural language queries. The search is powered by OpenAI's [CLIP](https://github.com/openai/CLIP) neural network.
This notebook uses the precomputed feature vectors for almost 2 million images from the full version of the [Unsplash Dataset](https://unsplash.com/data). If you want to compute the features yourself, see [here](https://github.com/haltakov/natural-language-image-search#on-your-machine).
This project was mostly based on the [project](https://github.com/haltakov/natural-language-image-search) created by [Vladimir Haltakov](https://twitter.com/haltakov) and the full code is open-sourced on [GitHub](https://github.com/haofanwang/natural-language-joint-query-search).
```
!git clone https://github.com/haofanwang/natural-language-joint-query-search.git
cd natural-language-joint-query-search
```
## Setup Environment
In this section we will setup the environment.
First we need to install CLIP and then upgrade the version of torch to 1.7.1 with CUDA support (by default CLIP installs torch 1.7.1 without CUDA). Google Colab currently has torch 1.7.0 which doesn't work well with CLIP.
```
!pip install torch==1.7.1+cu101 torchvision==0.8.2+cu101 -f https://download.pytorch.org/whl/torch_stable.html
!pip install ftfy regex tqdm
```
## Download the Precomputed Data
In this section the precomputed feature vectors for all photos are downloaded.
In order to compare the photos from the Unsplash dataset to a text query, we need to compute the feature vector of each photo using CLIP.
We need to download two files:
* `photo_ids.csv` - a list of the photo IDs for all images in the dataset. The photo ID can be used to get the actual photo from Unsplash.
* `features.npy` - a matrix containing the precomputed 512 element feature vector for each photo in the dataset.
The files are available on [Google Drive](https://drive.google.com/drive/folders/1WQmedVCDIQKA2R33dkS1f980YsJXRZ-q?usp=sharing).
```
from pathlib import Path
# Create a folder for the precomputed features
!mkdir unsplash-dataset
# Download the photo IDs and the feature vectors
!gdown --id 1FdmDEzBQCf3OxqY9SbU-jLfH_yZ6UPSj -O unsplash-dataset/photo_ids.csv
!gdown --id 1L7ulhn4VeN-2aOM-fYmljza_TQok-j9F -O unsplash-dataset/features.npy
# Download from alternative source, if the download doesn't work for some reason (for example download quota limit exceeded)
if not Path('unsplash-dataset/photo_ids.csv').exists():
!wget https://transfer.army/api/download/TuWWFTe2spg/EDm6KBjc -O unsplash-dataset/photo_ids.csv
if not Path('unsplash-dataset/features.npy').exists():
!wget https://transfer.army/api/download/LGXAaiNnMLA/AamL9PpU -O unsplash-dataset/features.npy
```
## Define Functions
Some important functions from CLIP for processing the data are defined here.
The `encode_search_query` function takes a text description and encodes it into a feature vector using the CLIP model.
```
def encode_search_query(search_query):
with torch.no_grad():
# Encode and normalize the search query using CLIP
text_encoded, weight = model.encode_text(clip.tokenize(search_query).to(device))
text_encoded /= text_encoded.norm(dim=-1, keepdim=True)
# Retrieve the feature vector from the GPU and convert it to a numpy array
return text_encoded.cpu().numpy()
```
The `find_best_matches` function compares the text feature vector to the feature vectors of all images and finds the best matches. The function returns the IDs of the best matching photos.
```
def find_best_matches(text_features, photo_features, photo_ids, results_count=3):
# Compute the similarity between the search query and each photo using the Cosine similarity
similarities = (photo_features @ text_features.T).squeeze(1)
# Sort the photos by their similarity score
best_photo_idx = (-similarities).argsort()
# Return the photo IDs of the best matches
return [photo_ids[i] for i in best_photo_idx[:results_count]]
```
We can load the pretrained public CLIP model.
```
import torch
from CLIP.clip import clip
# Load the open CLIP model
device = "cuda" if torch.cuda.is_available() else "cpu"
model, preprocess = clip.load("ViT-B/32", device=device, jit=False)
```
We can now load the pre-extracted unsplash image features.
```
import pandas as pd
import numpy as np
# Load the photo IDs
photo_ids = pd.read_csv("unsplash-dataset/photo_ids.csv")
photo_ids = list(photo_ids['photo_id'])
# Load the features vectors
photo_features = np.load("unsplash-dataset/features.npy")
# Print some statistics
print(f"Photos loaded: {len(photo_ids)}")
```
## Search Unsplash
Now we are ready to search the dataset using natural language. Check out the examples below and feel free to try out your own queries.
In this project, we support more types of searching than the [original project](https://github.com/haltakov/natural-language-image-search).
1. Text-to-Image Search
2. Image-to-Image Search
3. Text+Text-to-Image Search
4. Image+Text-to-Image Search
Note:
1. As the Unsplash API limit is hit from time to time, we don't display the image, but show the link to download the image.
2. As the pretrained CLIP model is mainly trained with English texts, if you want to try with different language, please use Google translation API or NMT model to translate first.
### Text-to-Image Search
#### "Tokyo Tower at night"
```
search_query = "Tokyo Tower at night."
text_features = encode_search_query(search_query)
# Find the best matches
best_photo_ids = find_best_matches(text_features, photo_features, photo_ids, 5)
for photo_id in best_photo_ids:
print("https://unsplash.com/photos/{}/download".format(photo_id))
```
#### "Two children are playing in the amusement park."
```
search_query = "Two children are playing in the amusement park."
text_features = encode_search_query(search_query)
# Find the best matches
best_photo_ids = find_best_matches(text_features, photo_features, photo_ids, 5)
for photo_id in best_photo_ids:
print("https://unsplash.com/photos/{}/download".format(photo_id))
```
### Image-to-Image Search
```
from PIL import Image
source_image = "./images/borna-hrzina-8IPrifbjo-0-unsplash.jpg"
with torch.no_grad():
image_feature = model.encode_image(preprocess(Image.open(source_image)).unsqueeze(0).to(device))
image_feature = (image_feature / image_feature.norm(dim=-1, keepdim=True)).cpu().numpy()
# Find the best matches
best_photo_ids = find_best_matches(image_feature, photo_features, photo_ids, 5)
for photo_id in best_photo_ids:
print("https://unsplash.com/photos/{}/download".format(photo_id))
```
### Text+Text-to-Image Search
```
search_query = "red flower"
search_query_extra = "blue sky"
text_features = encode_search_query(search_query)
text_features_extra = encode_search_query(search_query_extra)
mixed_features = text_features + text_features_extra
# Find the best matches
best_photo_ids = find_best_matches(mixed_features, photo_features, photo_ids, 5)
for photo_id in best_photo_ids:
print("https://unsplash.com/photos/{}/download".format(photo_id))
```
### Image+Text-to-Image Search
```
source_image = "./images/borna-hrzina-8IPrifbjo-0-unsplash.jpg"
search_text = "cars"
with torch.no_grad():
image_feature = model.encode_image(preprocess(Image.open(source_image)).unsqueeze(0).to(device))
image_feature = (image_feature / image_feature.norm(dim=-1, keepdim=True)).cpu().numpy()
text_feature = encode_search_query(search_text)
# image + text
modified_feature = image_feature + text_feature
best_photo_ids = find_best_matches(modified_feature, photo_features, photo_ids, 5)
for photo_id in best_photo_ids:
print("https://unsplash.com/photos/{}/download".format(photo_id))
```
|
github_jupyter
|
# RadarCOVID-Report
## Data Extraction
```
import datetime
import json
import logging
import os
import shutil
import tempfile
import textwrap
import uuid
import matplotlib.pyplot as plt
import matplotlib.ticker
import numpy as np
import pandas as pd
import pycountry
import retry
import seaborn as sns
%matplotlib inline
current_working_directory = os.environ.get("PWD")
if current_working_directory:
os.chdir(current_working_directory)
sns.set()
matplotlib.rcParams["figure.figsize"] = (15, 6)
extraction_datetime = datetime.datetime.utcnow()
extraction_date = extraction_datetime.strftime("%Y-%m-%d")
extraction_previous_datetime = extraction_datetime - datetime.timedelta(days=1)
extraction_previous_date = extraction_previous_datetime.strftime("%Y-%m-%d")
extraction_date_with_hour = datetime.datetime.utcnow().strftime("%Y-%m-%d@%H")
current_hour = datetime.datetime.utcnow().hour
are_today_results_partial = current_hour != 23
```
### Constants
```
from Modules.ExposureNotification import exposure_notification_io
spain_region_country_code = "ES"
germany_region_country_code = "DE"
default_backend_identifier = spain_region_country_code
backend_generation_days = 7 * 2
daily_summary_days = 7 * 4 * 3
daily_plot_days = 7 * 4
tek_dumps_load_limit = daily_summary_days + 1
```
### Parameters
```
environment_backend_identifier = os.environ.get("RADARCOVID_REPORT__BACKEND_IDENTIFIER")
if environment_backend_identifier:
report_backend_identifier = environment_backend_identifier
else:
report_backend_identifier = default_backend_identifier
report_backend_identifier
environment_enable_multi_backend_download = \
os.environ.get("RADARCOVID_REPORT__ENABLE_MULTI_BACKEND_DOWNLOAD")
if environment_enable_multi_backend_download:
report_backend_identifiers = None
else:
report_backend_identifiers = [report_backend_identifier]
report_backend_identifiers
environment_invalid_shared_diagnoses_dates = \
os.environ.get("RADARCOVID_REPORT__INVALID_SHARED_DIAGNOSES_DATES")
if environment_invalid_shared_diagnoses_dates:
invalid_shared_diagnoses_dates = environment_invalid_shared_diagnoses_dates.split(",")
else:
invalid_shared_diagnoses_dates = []
invalid_shared_diagnoses_dates
```
### COVID-19 Cases
```
report_backend_client = \
exposure_notification_io.get_backend_client_with_identifier(
backend_identifier=report_backend_identifier)
@retry.retry(tries=10, delay=10, backoff=1.1, jitter=(0, 10))
def download_cases_dataframe():
return pd.read_csv("https://raw.githubusercontent.com/owid/covid-19-data/master/public/data/owid-covid-data.csv")
confirmed_df_ = download_cases_dataframe()
confirmed_df_.iloc[0]
confirmed_df = confirmed_df_.copy()
confirmed_df = confirmed_df[["date", "new_cases", "iso_code"]]
confirmed_df.rename(
columns={
"date": "sample_date",
"iso_code": "country_code",
},
inplace=True)
def convert_iso_alpha_3_to_alpha_2(x):
try:
return pycountry.countries.get(alpha_3=x).alpha_2
except Exception as e:
logging.info(f"Error converting country ISO Alpha 3 code '{x}': {repr(e)}")
return None
confirmed_df["country_code"] = confirmed_df.country_code.apply(convert_iso_alpha_3_to_alpha_2)
confirmed_df.dropna(inplace=True)
confirmed_df["sample_date"] = pd.to_datetime(confirmed_df.sample_date, dayfirst=True)
confirmed_df["sample_date"] = confirmed_df.sample_date.dt.strftime("%Y-%m-%d")
confirmed_df.sort_values("sample_date", inplace=True)
confirmed_df.tail()
confirmed_days = pd.date_range(
start=confirmed_df.iloc[0].sample_date,
end=extraction_datetime)
confirmed_days_df = pd.DataFrame(data=confirmed_days, columns=["sample_date"])
confirmed_days_df["sample_date_string"] = \
confirmed_days_df.sample_date.dt.strftime("%Y-%m-%d")
confirmed_days_df.tail()
def sort_source_regions_for_display(source_regions: list) -> list:
if report_backend_identifier in source_regions:
source_regions = [report_backend_identifier] + \
list(sorted(set(source_regions).difference([report_backend_identifier])))
else:
source_regions = list(sorted(source_regions))
return source_regions
report_source_regions = report_backend_client.source_regions_for_date(
date=extraction_datetime.date())
report_source_regions = sort_source_regions_for_display(
source_regions=report_source_regions)
report_source_regions
def get_cases_dataframe(source_regions_for_date_function, columns_suffix=None):
source_regions_at_date_df = confirmed_days_df.copy()
source_regions_at_date_df["source_regions_at_date"] = \
source_regions_at_date_df.sample_date.apply(
lambda x: source_regions_for_date_function(date=x))
source_regions_at_date_df.sort_values("sample_date", inplace=True)
source_regions_at_date_df["_source_regions_group"] = source_regions_at_date_df. \
source_regions_at_date.apply(lambda x: ",".join(sort_source_regions_for_display(x)))
source_regions_at_date_df.tail()
#%%
source_regions_for_summary_df_ = \
source_regions_at_date_df[["sample_date", "_source_regions_group"]].copy()
source_regions_for_summary_df_.rename(columns={"_source_regions_group": "source_regions"}, inplace=True)
source_regions_for_summary_df_.tail()
#%%
confirmed_output_columns = ["sample_date", "new_cases", "covid_cases"]
confirmed_output_df = pd.DataFrame(columns=confirmed_output_columns)
for source_regions_group, source_regions_group_series in \
source_regions_at_date_df.groupby("_source_regions_group"):
source_regions_set = set(source_regions_group.split(","))
confirmed_source_regions_set_df = \
confirmed_df[confirmed_df.country_code.isin(source_regions_set)].copy()
confirmed_source_regions_group_df = \
confirmed_source_regions_set_df.groupby("sample_date").new_cases.sum() \
.reset_index().sort_values("sample_date")
confirmed_source_regions_group_df = \
confirmed_source_regions_group_df.merge(
confirmed_days_df[["sample_date_string"]].rename(
columns={"sample_date_string": "sample_date"}),
how="right")
confirmed_source_regions_group_df["new_cases"] = \
confirmed_source_regions_group_df["new_cases"].clip(lower=0)
confirmed_source_regions_group_df["covid_cases"] = \
confirmed_source_regions_group_df.new_cases.rolling(7, min_periods=0).mean().round()
confirmed_source_regions_group_df = \
confirmed_source_regions_group_df[confirmed_output_columns]
confirmed_source_regions_group_df = confirmed_source_regions_group_df.replace(0, np.nan)
confirmed_source_regions_group_df.fillna(method="ffill", inplace=True)
confirmed_source_regions_group_df = \
confirmed_source_regions_group_df[
confirmed_source_regions_group_df.sample_date.isin(
source_regions_group_series.sample_date_string)]
confirmed_output_df = confirmed_output_df.append(confirmed_source_regions_group_df)
result_df = confirmed_output_df.copy()
result_df.tail()
#%%
result_df.rename(columns={"sample_date": "sample_date_string"}, inplace=True)
result_df = confirmed_days_df[["sample_date_string"]].merge(result_df, how="left")
result_df.sort_values("sample_date_string", inplace=True)
result_df.fillna(method="ffill", inplace=True)
result_df.tail()
#%%
result_df[["new_cases", "covid_cases"]].plot()
if columns_suffix:
result_df.rename(
columns={
"new_cases": "new_cases_" + columns_suffix,
"covid_cases": "covid_cases_" + columns_suffix},
inplace=True)
return result_df, source_regions_for_summary_df_
confirmed_eu_df, source_regions_for_summary_df = get_cases_dataframe(
report_backend_client.source_regions_for_date)
confirmed_es_df, _ = get_cases_dataframe(
lambda date: [spain_region_country_code],
columns_suffix=spain_region_country_code.lower())
```
### Extract API TEKs
```
raw_zip_path_prefix = "Data/TEKs/Raw/"
base_backend_identifiers = [report_backend_identifier]
multi_backend_exposure_keys_df = \
exposure_notification_io.download_exposure_keys_from_backends(
backend_identifiers=report_backend_identifiers,
generation_days=backend_generation_days,
fail_on_error_backend_identifiers=base_backend_identifiers,
save_raw_zip_path_prefix=raw_zip_path_prefix)
multi_backend_exposure_keys_df["region"] = multi_backend_exposure_keys_df["backend_identifier"]
multi_backend_exposure_keys_df.rename(
columns={
"generation_datetime": "sample_datetime",
"generation_date_string": "sample_date_string",
},
inplace=True)
multi_backend_exposure_keys_df.head()
early_teks_df = multi_backend_exposure_keys_df[
multi_backend_exposure_keys_df.rolling_period < 144].copy()
early_teks_df["rolling_period_in_hours"] = early_teks_df.rolling_period / 6
early_teks_df[early_teks_df.sample_date_string != extraction_date] \
.rolling_period_in_hours.hist(bins=list(range(24)))
early_teks_df[early_teks_df.sample_date_string == extraction_date] \
.rolling_period_in_hours.hist(bins=list(range(24)))
multi_backend_exposure_keys_df = multi_backend_exposure_keys_df[[
"sample_date_string", "region", "key_data"]]
multi_backend_exposure_keys_df.head()
active_regions = \
multi_backend_exposure_keys_df.groupby("region").key_data.nunique().sort_values().index.unique().tolist()
active_regions
multi_backend_summary_df = multi_backend_exposure_keys_df.groupby(
["sample_date_string", "region"]).key_data.nunique().reset_index() \
.pivot(index="sample_date_string", columns="region") \
.sort_index(ascending=False)
multi_backend_summary_df.rename(
columns={"key_data": "shared_teks_by_generation_date"},
inplace=True)
multi_backend_summary_df.rename_axis("sample_date", inplace=True)
multi_backend_summary_df = multi_backend_summary_df.fillna(0).astype(int)
multi_backend_summary_df = multi_backend_summary_df.head(backend_generation_days)
multi_backend_summary_df.head()
def compute_keys_cross_sharing(x):
teks_x = x.key_data_x.item()
common_teks = set(teks_x).intersection(x.key_data_y.item())
common_teks_fraction = len(common_teks) / len(teks_x)
return pd.Series(dict(
common_teks=common_teks,
common_teks_fraction=common_teks_fraction,
))
multi_backend_exposure_keys_by_region_df = \
multi_backend_exposure_keys_df.groupby("region").key_data.unique().reset_index()
multi_backend_exposure_keys_by_region_df["_merge"] = True
multi_backend_exposure_keys_by_region_combination_df = \
multi_backend_exposure_keys_by_region_df.merge(
multi_backend_exposure_keys_by_region_df, on="_merge")
multi_backend_exposure_keys_by_region_combination_df.drop(
columns=["_merge"], inplace=True)
if multi_backend_exposure_keys_by_region_combination_df.region_x.nunique() > 1:
multi_backend_exposure_keys_by_region_combination_df = \
multi_backend_exposure_keys_by_region_combination_df[
multi_backend_exposure_keys_by_region_combination_df.region_x !=
multi_backend_exposure_keys_by_region_combination_df.region_y]
multi_backend_exposure_keys_cross_sharing_df = \
multi_backend_exposure_keys_by_region_combination_df \
.groupby(["region_x", "region_y"]) \
.apply(compute_keys_cross_sharing) \
.reset_index()
multi_backend_cross_sharing_summary_df = \
multi_backend_exposure_keys_cross_sharing_df.pivot_table(
values=["common_teks_fraction"],
columns="region_x",
index="region_y",
aggfunc=lambda x: x.item())
multi_backend_cross_sharing_summary_df
multi_backend_without_active_region_exposure_keys_df = \
multi_backend_exposure_keys_df[multi_backend_exposure_keys_df.region != report_backend_identifier]
multi_backend_without_active_region = \
multi_backend_without_active_region_exposure_keys_df.groupby("region").key_data.nunique().sort_values().index.unique().tolist()
multi_backend_without_active_region
exposure_keys_summary_df = multi_backend_exposure_keys_df[
multi_backend_exposure_keys_df.region == report_backend_identifier]
exposure_keys_summary_df.drop(columns=["region"], inplace=True)
exposure_keys_summary_df = \
exposure_keys_summary_df.groupby(["sample_date_string"]).key_data.nunique().to_frame()
exposure_keys_summary_df = \
exposure_keys_summary_df.reset_index().set_index("sample_date_string")
exposure_keys_summary_df.sort_index(ascending=False, inplace=True)
exposure_keys_summary_df.rename(columns={"key_data": "shared_teks_by_generation_date"}, inplace=True)
exposure_keys_summary_df.head()
```
### Dump API TEKs
```
tek_list_df = multi_backend_exposure_keys_df[
["sample_date_string", "region", "key_data"]].copy()
tek_list_df["key_data"] = tek_list_df["key_data"].apply(str)
tek_list_df.rename(columns={
"sample_date_string": "sample_date",
"key_data": "tek_list"}, inplace=True)
tek_list_df = tek_list_df.groupby(
["sample_date", "region"]).tek_list.unique().reset_index()
tek_list_df["extraction_date"] = extraction_date
tek_list_df["extraction_date_with_hour"] = extraction_date_with_hour
tek_list_path_prefix = "Data/TEKs/"
tek_list_current_path = tek_list_path_prefix + f"/Current/RadarCOVID-TEKs.json"
tek_list_daily_path = tek_list_path_prefix + f"Daily/RadarCOVID-TEKs-{extraction_date}.json"
tek_list_hourly_path = tek_list_path_prefix + f"Hourly/RadarCOVID-TEKs-{extraction_date_with_hour}.json"
for path in [tek_list_current_path, tek_list_daily_path, tek_list_hourly_path]:
os.makedirs(os.path.dirname(path), exist_ok=True)
tek_list_base_df = tek_list_df[tek_list_df.region == report_backend_identifier]
tek_list_base_df.drop(columns=["extraction_date", "extraction_date_with_hour"]).to_json(
tek_list_current_path,
lines=True, orient="records")
tek_list_base_df.drop(columns=["extraction_date_with_hour"]).to_json(
tek_list_daily_path,
lines=True, orient="records")
tek_list_base_df.to_json(
tek_list_hourly_path,
lines=True, orient="records")
tek_list_base_df.head()
```
### Load TEK Dumps
```
import glob
def load_extracted_teks(mode, region=None, limit=None) -> pd.DataFrame:
extracted_teks_df = pd.DataFrame(columns=["region"])
file_paths = list(reversed(sorted(glob.glob(tek_list_path_prefix + mode + "/RadarCOVID-TEKs-*.json"))))
if limit:
file_paths = file_paths[:limit]
for file_path in file_paths:
logging.info(f"Loading TEKs from '{file_path}'...")
iteration_extracted_teks_df = pd.read_json(file_path, lines=True)
extracted_teks_df = extracted_teks_df.append(
iteration_extracted_teks_df, sort=False)
extracted_teks_df["region"] = \
extracted_teks_df.region.fillna(spain_region_country_code).copy()
if region:
extracted_teks_df = \
extracted_teks_df[extracted_teks_df.region == region]
return extracted_teks_df
daily_extracted_teks_df = load_extracted_teks(
mode="Daily",
region=report_backend_identifier,
limit=tek_dumps_load_limit)
daily_extracted_teks_df.head()
exposure_keys_summary_df_ = daily_extracted_teks_df \
.sort_values("extraction_date", ascending=False) \
.groupby("sample_date").tek_list.first() \
.to_frame()
exposure_keys_summary_df_.index.name = "sample_date_string"
exposure_keys_summary_df_["tek_list"] = \
exposure_keys_summary_df_.tek_list.apply(len)
exposure_keys_summary_df_ = exposure_keys_summary_df_ \
.rename(columns={"tek_list": "shared_teks_by_generation_date"}) \
.sort_index(ascending=False)
exposure_keys_summary_df = exposure_keys_summary_df_
exposure_keys_summary_df.head()
```
### Daily New TEKs
```
tek_list_df = daily_extracted_teks_df.groupby("extraction_date").tek_list.apply(
lambda x: set(sum(x, []))).reset_index()
tek_list_df = tek_list_df.set_index("extraction_date").sort_index(ascending=True)
tek_list_df.head()
def compute_teks_by_generation_and_upload_date(date):
day_new_teks_set_df = tek_list_df.copy().diff()
try:
day_new_teks_set = day_new_teks_set_df[
day_new_teks_set_df.index == date].tek_list.item()
except ValueError:
day_new_teks_set = None
if pd.isna(day_new_teks_set):
day_new_teks_set = set()
day_new_teks_df = daily_extracted_teks_df[
daily_extracted_teks_df.extraction_date == date].copy()
day_new_teks_df["shared_teks"] = \
day_new_teks_df.tek_list.apply(lambda x: set(x).intersection(day_new_teks_set))
day_new_teks_df["shared_teks"] = \
day_new_teks_df.shared_teks.apply(len)
day_new_teks_df["upload_date"] = date
day_new_teks_df.rename(columns={"sample_date": "generation_date"}, inplace=True)
day_new_teks_df = day_new_teks_df[
["upload_date", "generation_date", "shared_teks"]]
day_new_teks_df["generation_to_upload_days"] = \
(pd.to_datetime(day_new_teks_df.upload_date) -
pd.to_datetime(day_new_teks_df.generation_date)).dt.days
day_new_teks_df = day_new_teks_df[day_new_teks_df.shared_teks > 0]
return day_new_teks_df
shared_teks_generation_to_upload_df = pd.DataFrame()
for upload_date in daily_extracted_teks_df.extraction_date.unique():
shared_teks_generation_to_upload_df = \
shared_teks_generation_to_upload_df.append(
compute_teks_by_generation_and_upload_date(date=upload_date))
shared_teks_generation_to_upload_df \
.sort_values(["upload_date", "generation_date"], ascending=False, inplace=True)
shared_teks_generation_to_upload_df.tail()
today_new_teks_df = \
shared_teks_generation_to_upload_df[
shared_teks_generation_to_upload_df.upload_date == extraction_date].copy()
today_new_teks_df.tail()
if not today_new_teks_df.empty:
today_new_teks_df.set_index("generation_to_upload_days") \
.sort_index().shared_teks.plot.bar()
generation_to_upload_period_pivot_df = \
shared_teks_generation_to_upload_df[
["upload_date", "generation_to_upload_days", "shared_teks"]] \
.pivot(index="upload_date", columns="generation_to_upload_days") \
.sort_index(ascending=False).fillna(0).astype(int) \
.droplevel(level=0, axis=1)
generation_to_upload_period_pivot_df.head()
new_tek_df = tek_list_df.diff().tek_list.apply(
lambda x: len(x) if not pd.isna(x) else None).to_frame().reset_index()
new_tek_df.rename(columns={
"tek_list": "shared_teks_by_upload_date",
"extraction_date": "sample_date_string",}, inplace=True)
new_tek_df.tail()
shared_teks_uploaded_on_generation_date_df = shared_teks_generation_to_upload_df[
shared_teks_generation_to_upload_df.generation_to_upload_days == 0] \
[["upload_date", "shared_teks"]].rename(
columns={
"upload_date": "sample_date_string",
"shared_teks": "shared_teks_uploaded_on_generation_date",
})
shared_teks_uploaded_on_generation_date_df.head()
estimated_shared_diagnoses_df = shared_teks_generation_to_upload_df \
.groupby(["upload_date"]).shared_teks.max().reset_index() \
.sort_values(["upload_date"], ascending=False) \
.rename(columns={
"upload_date": "sample_date_string",
"shared_teks": "shared_diagnoses",
})
invalid_shared_diagnoses_dates_mask = \
estimated_shared_diagnoses_df.sample_date_string.isin(invalid_shared_diagnoses_dates)
estimated_shared_diagnoses_df[invalid_shared_diagnoses_dates_mask] = 0
estimated_shared_diagnoses_df.head()
```
### Hourly New TEKs
```
hourly_extracted_teks_df = load_extracted_teks(
mode="Hourly", region=report_backend_identifier, limit=25)
hourly_extracted_teks_df.head()
hourly_new_tek_count_df = hourly_extracted_teks_df \
.groupby("extraction_date_with_hour").tek_list. \
apply(lambda x: set(sum(x, []))).reset_index().copy()
hourly_new_tek_count_df = hourly_new_tek_count_df.set_index("extraction_date_with_hour") \
.sort_index(ascending=True)
hourly_new_tek_count_df["new_tek_list"] = hourly_new_tek_count_df.tek_list.diff()
hourly_new_tek_count_df["new_tek_count"] = hourly_new_tek_count_df.new_tek_list.apply(
lambda x: len(x) if not pd.isna(x) else 0)
hourly_new_tek_count_df.rename(columns={
"new_tek_count": "shared_teks_by_upload_date"}, inplace=True)
hourly_new_tek_count_df = hourly_new_tek_count_df.reset_index()[[
"extraction_date_with_hour", "shared_teks_by_upload_date"]]
hourly_new_tek_count_df.head()
hourly_summary_df = hourly_new_tek_count_df.copy()
hourly_summary_df.set_index("extraction_date_with_hour", inplace=True)
hourly_summary_df = hourly_summary_df.fillna(0).astype(int).reset_index()
hourly_summary_df["datetime_utc"] = pd.to_datetime(
hourly_summary_df.extraction_date_with_hour, format="%Y-%m-%d@%H")
hourly_summary_df.set_index("datetime_utc", inplace=True)
hourly_summary_df = hourly_summary_df.tail(-1)
hourly_summary_df.head()
```
### Official Statistics
```
import requests
import pandas.io.json
official_stats_response = requests.get("https://radarcovid.covid19.gob.es/kpi/statistics/basics")
official_stats_response.raise_for_status()
official_stats_df_ = pandas.io.json.json_normalize(official_stats_response.json())
official_stats_df = official_stats_df_.copy()
official_stats_df["date"] = pd.to_datetime(official_stats_df["date"], dayfirst=True)
official_stats_df.head()
official_stats_column_map = {
"date": "sample_date",
"applicationsDownloads.totalAcummulated": "app_downloads_es_accumulated",
"communicatedContagions.totalAcummulated": "shared_diagnoses_es_accumulated",
}
accumulated_suffix = "_accumulated"
accumulated_values_columns = \
list(filter(lambda x: x.endswith(accumulated_suffix), official_stats_column_map.values()))
interpolated_values_columns = \
list(map(lambda x: x[:-len(accumulated_suffix)], accumulated_values_columns))
official_stats_df = \
official_stats_df[official_stats_column_map.keys()] \
.rename(columns=official_stats_column_map)
official_stats_df["extraction_date"] = extraction_date
official_stats_df.head()
official_stats_path = "Data/Statistics/Current/RadarCOVID-Statistics.json"
previous_official_stats_df = pd.read_json(official_stats_path, orient="records", lines=True)
previous_official_stats_df["sample_date"] = pd.to_datetime(previous_official_stats_df["sample_date"], dayfirst=True)
official_stats_df = official_stats_df.append(previous_official_stats_df)
official_stats_df.head()
official_stats_df = official_stats_df[~(official_stats_df.shared_diagnoses_es_accumulated == 0)]
official_stats_df.sort_values("extraction_date", ascending=False, inplace=True)
official_stats_df.drop_duplicates(subset=["sample_date"], keep="first", inplace=True)
official_stats_df.head()
official_stats_stored_df = official_stats_df.copy()
official_stats_stored_df["sample_date"] = official_stats_stored_df.sample_date.dt.strftime("%Y-%m-%d")
official_stats_stored_df.to_json(official_stats_path, orient="records", lines=True)
official_stats_df.drop(columns=["extraction_date"], inplace=True)
official_stats_df = confirmed_days_df.merge(official_stats_df, how="left")
official_stats_df.sort_values("sample_date", ascending=False, inplace=True)
official_stats_df.head()
official_stats_df[accumulated_values_columns] = \
official_stats_df[accumulated_values_columns] \
.astype(float).interpolate(limit_area="inside")
official_stats_df[interpolated_values_columns] = \
official_stats_df[accumulated_values_columns].diff(periods=-1)
official_stats_df.drop(columns="sample_date", inplace=True)
official_stats_df.head()
```
### Data Merge
```
result_summary_df = exposure_keys_summary_df.merge(
new_tek_df, on=["sample_date_string"], how="outer")
result_summary_df.head()
result_summary_df = result_summary_df.merge(
shared_teks_uploaded_on_generation_date_df, on=["sample_date_string"], how="outer")
result_summary_df.head()
result_summary_df = result_summary_df.merge(
estimated_shared_diagnoses_df, on=["sample_date_string"], how="outer")
result_summary_df.head()
result_summary_df = result_summary_df.merge(
official_stats_df, on=["sample_date_string"], how="outer")
result_summary_df.head()
result_summary_df = confirmed_eu_df.tail(daily_summary_days).merge(
result_summary_df, on=["sample_date_string"], how="left")
result_summary_df.head()
result_summary_df = confirmed_es_df.tail(daily_summary_days).merge(
result_summary_df, on=["sample_date_string"], how="left")
result_summary_df.head()
result_summary_df["sample_date"] = pd.to_datetime(result_summary_df.sample_date_string)
result_summary_df = result_summary_df.merge(source_regions_for_summary_df, how="left")
result_summary_df.set_index(["sample_date", "source_regions"], inplace=True)
result_summary_df.drop(columns=["sample_date_string"], inplace=True)
result_summary_df.sort_index(ascending=False, inplace=True)
result_summary_df.head()
with pd.option_context("mode.use_inf_as_na", True):
result_summary_df = result_summary_df.fillna(0).astype(int)
result_summary_df["teks_per_shared_diagnosis"] = \
(result_summary_df.shared_teks_by_upload_date / result_summary_df.shared_diagnoses).fillna(0)
result_summary_df["shared_diagnoses_per_covid_case"] = \
(result_summary_df.shared_diagnoses / result_summary_df.covid_cases).fillna(0)
result_summary_df["shared_diagnoses_per_covid_case_es"] = \
(result_summary_df.shared_diagnoses_es / result_summary_df.covid_cases_es).fillna(0)
result_summary_df.head(daily_plot_days)
def compute_aggregated_results_summary(days) -> pd.DataFrame:
aggregated_result_summary_df = result_summary_df.copy()
aggregated_result_summary_df["covid_cases_for_ratio"] = \
aggregated_result_summary_df.covid_cases.mask(
aggregated_result_summary_df.shared_diagnoses == 0, 0)
aggregated_result_summary_df["covid_cases_for_ratio_es"] = \
aggregated_result_summary_df.covid_cases_es.mask(
aggregated_result_summary_df.shared_diagnoses_es == 0, 0)
aggregated_result_summary_df = aggregated_result_summary_df \
.sort_index(ascending=True).fillna(0).rolling(days).agg({
"covid_cases": "sum",
"covid_cases_es": "sum",
"covid_cases_for_ratio": "sum",
"covid_cases_for_ratio_es": "sum",
"shared_teks_by_generation_date": "sum",
"shared_teks_by_upload_date": "sum",
"shared_diagnoses": "sum",
"shared_diagnoses_es": "sum",
}).sort_index(ascending=False)
with pd.option_context("mode.use_inf_as_na", True):
aggregated_result_summary_df = aggregated_result_summary_df.fillna(0).astype(int)
aggregated_result_summary_df["teks_per_shared_diagnosis"] = \
(aggregated_result_summary_df.shared_teks_by_upload_date /
aggregated_result_summary_df.covid_cases_for_ratio).fillna(0)
aggregated_result_summary_df["shared_diagnoses_per_covid_case"] = \
(aggregated_result_summary_df.shared_diagnoses /
aggregated_result_summary_df.covid_cases_for_ratio).fillna(0)
aggregated_result_summary_df["shared_diagnoses_per_covid_case_es"] = \
(aggregated_result_summary_df.shared_diagnoses_es /
aggregated_result_summary_df.covid_cases_for_ratio_es).fillna(0)
return aggregated_result_summary_df
aggregated_result_with_7_days_window_summary_df = compute_aggregated_results_summary(days=7)
aggregated_result_with_7_days_window_summary_df.head()
last_7_days_summary = aggregated_result_with_7_days_window_summary_df.to_dict(orient="records")[1]
last_7_days_summary
aggregated_result_with_14_days_window_summary_df = compute_aggregated_results_summary(days=13)
last_14_days_summary = aggregated_result_with_14_days_window_summary_df.to_dict(orient="records")[1]
last_14_days_summary
```
## Report Results
```
display_column_name_mapping = {
"sample_date": "Sample\u00A0Date\u00A0(UTC)",
"source_regions": "Source Countries",
"datetime_utc": "Timestamp (UTC)",
"upload_date": "Upload Date (UTC)",
"generation_to_upload_days": "Generation to Upload Period in Days",
"region": "Backend",
"region_x": "Backend\u00A0(A)",
"region_y": "Backend\u00A0(B)",
"common_teks": "Common TEKs Shared Between Backends",
"common_teks_fraction": "Fraction of TEKs in Backend (A) Available in Backend (B)",
"covid_cases": "COVID-19 Cases (Source Countries)",
"shared_teks_by_generation_date": "Shared TEKs by Generation Date (Source Countries)",
"shared_teks_by_upload_date": "Shared TEKs by Upload Date (Source Countries)",
"shared_teks_uploaded_on_generation_date": "Shared TEKs Uploaded on Generation Date (Source Countries)",
"shared_diagnoses": "Shared Diagnoses (Source Countries – Estimation)",
"teks_per_shared_diagnosis": "TEKs Uploaded per Shared Diagnosis (Source Countries)",
"shared_diagnoses_per_covid_case": "Usage Ratio (Source Countries)",
"covid_cases_es": "COVID-19 Cases (Spain)",
"app_downloads_es": "App Downloads (Spain – Official)",
"shared_diagnoses_es": "Shared Diagnoses (Spain – Official)",
"shared_diagnoses_per_covid_case_es": "Usage Ratio (Spain)",
}
summary_columns = [
"covid_cases",
"shared_teks_by_generation_date",
"shared_teks_by_upload_date",
"shared_teks_uploaded_on_generation_date",
"shared_diagnoses",
"teks_per_shared_diagnosis",
"shared_diagnoses_per_covid_case",
"covid_cases_es",
"app_downloads_es",
"shared_diagnoses_es",
"shared_diagnoses_per_covid_case_es",
]
summary_percentage_columns= [
"shared_diagnoses_per_covid_case_es",
"shared_diagnoses_per_covid_case",
]
```
### Daily Summary Table
```
result_summary_df_ = result_summary_df.copy()
result_summary_df = result_summary_df[summary_columns]
result_summary_with_display_names_df = result_summary_df \
.rename_axis(index=display_column_name_mapping) \
.rename(columns=display_column_name_mapping)
result_summary_with_display_names_df
```
### Daily Summary Plots
```
result_plot_summary_df = result_summary_df.head(daily_plot_days)[summary_columns] \
.droplevel(level=["source_regions"]) \
.rename_axis(index=display_column_name_mapping) \
.rename(columns=display_column_name_mapping)
summary_ax_list = result_plot_summary_df.sort_index(ascending=True).plot.bar(
title=f"Daily Summary",
rot=45, subplots=True, figsize=(15, 30), legend=False)
ax_ = summary_ax_list[0]
ax_.get_figure().tight_layout()
ax_.get_figure().subplots_adjust(top=0.95)
_ = ax_.set_xticklabels(sorted(result_plot_summary_df.index.strftime("%Y-%m-%d").tolist()))
for percentage_column in summary_percentage_columns:
percentage_column_index = summary_columns.index(percentage_column)
summary_ax_list[percentage_column_index].yaxis \
.set_major_formatter(matplotlib.ticker.PercentFormatter(1.0))
```
### Daily Generation to Upload Period Table
```
display_generation_to_upload_period_pivot_df = \
generation_to_upload_period_pivot_df \
.head(backend_generation_days)
display_generation_to_upload_period_pivot_df \
.head(backend_generation_days) \
.rename_axis(columns=display_column_name_mapping) \
.rename_axis(index=display_column_name_mapping)
fig, generation_to_upload_period_pivot_table_ax = plt.subplots(
figsize=(12, 1 + 0.6 * len(display_generation_to_upload_period_pivot_df)))
generation_to_upload_period_pivot_table_ax.set_title(
"Shared TEKs Generation to Upload Period Table")
sns.heatmap(
data=display_generation_to_upload_period_pivot_df
.rename_axis(columns=display_column_name_mapping)
.rename_axis(index=display_column_name_mapping),
fmt=".0f",
annot=True,
ax=generation_to_upload_period_pivot_table_ax)
generation_to_upload_period_pivot_table_ax.get_figure().tight_layout()
```
### Hourly Summary Plots
```
hourly_summary_ax_list = hourly_summary_df \
.rename_axis(index=display_column_name_mapping) \
.rename(columns=display_column_name_mapping) \
.plot.bar(
title=f"Last 24h Summary",
rot=45, subplots=True, legend=False)
ax_ = hourly_summary_ax_list[-1]
ax_.get_figure().tight_layout()
ax_.get_figure().subplots_adjust(top=0.9)
_ = ax_.set_xticklabels(sorted(hourly_summary_df.index.strftime("%Y-%m-%d@%H").tolist()))
```
### Publish Results
```
github_repository = os.environ.get("GITHUB_REPOSITORY")
if github_repository is None:
github_repository = "pvieito/Radar-STATS"
github_project_base_url = "https://github.com/" + github_repository
display_formatters = {
display_column_name_mapping["teks_per_shared_diagnosis"]: lambda x: f"{x:.2f}" if x != 0 else "",
display_column_name_mapping["shared_diagnoses_per_covid_case"]: lambda x: f"{x:.2%}" if x != 0 else "",
display_column_name_mapping["shared_diagnoses_per_covid_case_es"]: lambda x: f"{x:.2%}" if x != 0 else "",
}
general_columns = \
list(filter(lambda x: x not in display_formatters, display_column_name_mapping.values()))
general_formatter = lambda x: f"{x}" if x != 0 else ""
display_formatters.update(dict(map(lambda x: (x, general_formatter), general_columns)))
daily_summary_table_html = result_summary_with_display_names_df \
.head(daily_plot_days) \
.rename_axis(index=display_column_name_mapping) \
.rename(columns=display_column_name_mapping) \
.to_html(formatters=display_formatters)
multi_backend_summary_table_html = multi_backend_summary_df \
.head(daily_plot_days) \
.rename_axis(columns=display_column_name_mapping) \
.rename(columns=display_column_name_mapping) \
.rename_axis(index=display_column_name_mapping) \
.to_html(formatters=display_formatters)
def format_multi_backend_cross_sharing_fraction(x):
if pd.isna(x):
return "-"
elif round(x * 100, 1) == 0:
return ""
else:
return f"{x:.1%}"
multi_backend_cross_sharing_summary_table_html = multi_backend_cross_sharing_summary_df \
.rename_axis(columns=display_column_name_mapping) \
.rename(columns=display_column_name_mapping) \
.rename_axis(index=display_column_name_mapping) \
.to_html(
classes="table-center",
formatters=display_formatters,
float_format=format_multi_backend_cross_sharing_fraction)
multi_backend_cross_sharing_summary_table_html = \
multi_backend_cross_sharing_summary_table_html \
.replace("<tr>","<tr style=\"text-align: center;\">")
extraction_date_result_summary_df = \
result_summary_df[result_summary_df.index.get_level_values("sample_date") == extraction_date]
extraction_date_result_hourly_summary_df = \
hourly_summary_df[hourly_summary_df.extraction_date_with_hour == extraction_date_with_hour]
covid_cases = \
extraction_date_result_summary_df.covid_cases.item()
shared_teks_by_generation_date = \
extraction_date_result_summary_df.shared_teks_by_generation_date.item()
shared_teks_by_upload_date = \
extraction_date_result_summary_df.shared_teks_by_upload_date.item()
shared_diagnoses = \
extraction_date_result_summary_df.shared_diagnoses.item()
teks_per_shared_diagnosis = \
extraction_date_result_summary_df.teks_per_shared_diagnosis.item()
shared_diagnoses_per_covid_case = \
extraction_date_result_summary_df.shared_diagnoses_per_covid_case.item()
shared_teks_by_upload_date_last_hour = \
extraction_date_result_hourly_summary_df.shared_teks_by_upload_date.sum().astype(int)
display_source_regions = ", ".join(report_source_regions)
if len(report_source_regions) == 1:
display_brief_source_regions = report_source_regions[0]
else:
display_brief_source_regions = f"{len(report_source_regions)} 🇪🇺"
def get_temporary_image_path() -> str:
return os.path.join(tempfile.gettempdir(), str(uuid.uuid4()) + ".png")
def save_temporary_plot_image(ax):
if isinstance(ax, np.ndarray):
ax = ax[0]
media_path = get_temporary_image_path()
ax.get_figure().savefig(media_path)
return media_path
def save_temporary_dataframe_image(df):
import dataframe_image as dfi
df = df.copy()
df_styler = df.style.format(display_formatters)
media_path = get_temporary_image_path()
dfi.export(df_styler, media_path)
return media_path
summary_plots_image_path = save_temporary_plot_image(
ax=summary_ax_list)
summary_table_image_path = save_temporary_dataframe_image(
df=result_summary_with_display_names_df)
hourly_summary_plots_image_path = save_temporary_plot_image(
ax=hourly_summary_ax_list)
multi_backend_summary_table_image_path = save_temporary_dataframe_image(
df=multi_backend_summary_df)
generation_to_upload_period_pivot_table_image_path = save_temporary_plot_image(
ax=generation_to_upload_period_pivot_table_ax)
```
### Save Results
```
report_resources_path_prefix = "Data/Resources/Current/RadarCOVID-Report-"
result_summary_df.to_csv(
report_resources_path_prefix + "Summary-Table.csv")
result_summary_df.to_html(
report_resources_path_prefix + "Summary-Table.html")
hourly_summary_df.to_csv(
report_resources_path_prefix + "Hourly-Summary-Table.csv")
multi_backend_summary_df.to_csv(
report_resources_path_prefix + "Multi-Backend-Summary-Table.csv")
multi_backend_cross_sharing_summary_df.to_csv(
report_resources_path_prefix + "Multi-Backend-Cross-Sharing-Summary-Table.csv")
generation_to_upload_period_pivot_df.to_csv(
report_resources_path_prefix + "Generation-Upload-Period-Table.csv")
_ = shutil.copyfile(
summary_plots_image_path,
report_resources_path_prefix + "Summary-Plots.png")
_ = shutil.copyfile(
summary_table_image_path,
report_resources_path_prefix + "Summary-Table.png")
_ = shutil.copyfile(
hourly_summary_plots_image_path,
report_resources_path_prefix + "Hourly-Summary-Plots.png")
_ = shutil.copyfile(
multi_backend_summary_table_image_path,
report_resources_path_prefix + "Multi-Backend-Summary-Table.png")
_ = shutil.copyfile(
generation_to_upload_period_pivot_table_image_path,
report_resources_path_prefix + "Generation-Upload-Period-Table.png")
```
### Publish Results as JSON
```
def generate_summary_api_results(df: pd.DataFrame) -> list:
api_df = df.reset_index().copy()
api_df["sample_date_string"] = \
api_df["sample_date"].dt.strftime("%Y-%m-%d")
api_df["source_regions"] = \
api_df["source_regions"].apply(lambda x: x.split(","))
return api_df.to_dict(orient="records")
summary_api_results = \
generate_summary_api_results(df=result_summary_df)
today_summary_api_results = \
generate_summary_api_results(df=extraction_date_result_summary_df)[0]
summary_results = dict(
backend_identifier=report_backend_identifier,
source_regions=report_source_regions,
extraction_datetime=extraction_datetime,
extraction_date=extraction_date,
extraction_date_with_hour=extraction_date_with_hour,
last_hour=dict(
shared_teks_by_upload_date=shared_teks_by_upload_date_last_hour,
shared_diagnoses=0,
),
today=today_summary_api_results,
last_7_days=last_7_days_summary,
last_14_days=last_14_days_summary,
daily_results=summary_api_results)
summary_results = \
json.loads(pd.Series([summary_results]).to_json(orient="records"))[0]
with open(report_resources_path_prefix + "Summary-Results.json", "w") as f:
json.dump(summary_results, f, indent=4)
```
### Publish on README
```
with open("Data/Templates/README.md", "r") as f:
readme_contents = f.read()
readme_contents = readme_contents.format(
extraction_date_with_hour=extraction_date_with_hour,
github_project_base_url=github_project_base_url,
daily_summary_table_html=daily_summary_table_html,
multi_backend_summary_table_html=multi_backend_summary_table_html,
multi_backend_cross_sharing_summary_table_html=multi_backend_cross_sharing_summary_table_html,
display_source_regions=display_source_regions)
with open("README.md", "w") as f:
f.write(readme_contents)
```
### Publish on Twitter
```
enable_share_to_twitter = os.environ.get("RADARCOVID_REPORT__ENABLE_PUBLISH_ON_TWITTER")
github_event_name = os.environ.get("GITHUB_EVENT_NAME")
if enable_share_to_twitter and github_event_name == "schedule" and \
(shared_teks_by_upload_date_last_hour or not are_today_results_partial):
import tweepy
twitter_api_auth_keys = os.environ["RADARCOVID_REPORT__TWITTER_API_AUTH_KEYS"]
twitter_api_auth_keys = twitter_api_auth_keys.split(":")
auth = tweepy.OAuthHandler(twitter_api_auth_keys[0], twitter_api_auth_keys[1])
auth.set_access_token(twitter_api_auth_keys[2], twitter_api_auth_keys[3])
api = tweepy.API(auth)
summary_plots_media = api.media_upload(summary_plots_image_path)
summary_table_media = api.media_upload(summary_table_image_path)
generation_to_upload_period_pivot_table_image_media = api.media_upload(generation_to_upload_period_pivot_table_image_path)
media_ids = [
summary_plots_media.media_id,
summary_table_media.media_id,
generation_to_upload_period_pivot_table_image_media.media_id,
]
if are_today_results_partial:
today_addendum = " (Partial)"
else:
today_addendum = ""
def format_shared_diagnoses_per_covid_case(value) -> str:
if value == 0:
return "–"
return f"≤{value:.2%}"
display_shared_diagnoses_per_covid_case = \
format_shared_diagnoses_per_covid_case(value=shared_diagnoses_per_covid_case)
display_last_14_days_shared_diagnoses_per_covid_case = \
format_shared_diagnoses_per_covid_case(value=last_14_days_summary["shared_diagnoses_per_covid_case"])
display_last_14_days_shared_diagnoses_per_covid_case_es = \
format_shared_diagnoses_per_covid_case(value=last_14_days_summary["shared_diagnoses_per_covid_case_es"])
status = textwrap.dedent(f"""
#RadarCOVID – {extraction_date_with_hour}
Today{today_addendum}:
- Uploaded TEKs: {shared_teks_by_upload_date:.0f} ({shared_teks_by_upload_date_last_hour:+d} last hour)
- Shared Diagnoses: ≤{shared_diagnoses:.0f}
- Usage Ratio: {display_shared_diagnoses_per_covid_case}
Last 14 Days:
- Usage Ratio (Estimation): {display_last_14_days_shared_diagnoses_per_covid_case}
- Usage Ratio (Official): {display_last_14_days_shared_diagnoses_per_covid_case_es}
Info: {github_project_base_url}#documentation
""")
status = status.encode(encoding="utf-8")
api.update_status(status=status, media_ids=media_ids)
```
|
github_jupyter
|
```
import numpy as np
import matplotlib.pyplot as plt
```
# BCC and FCC
```
def average_quantities(E_list,V_list,S_list,Comp_list):
average_E_list=np.empty(len(Comp_list))
average_S_list=np.empty(len(Comp_list))
average_V_list=np.empty(len(Comp_list))
average_b_list=np.empty(len(Comp_list))
average_nu_list=np.empty(len(Comp_list))
delta_Vn_list=np.empty([len(Comp_list),len(E_list)])
for i in range(len(Comp_list)):
c = Comp_list[i]
#print(c)
avg_E = np.dot(E_list,c)
avg_S = np.dot(S_list,c)
avg_nu = avg_E/(2*avg_S)-1
avg_V = np.dot(V_list,c)
delta_Vn = V_list-avg_V
avg_b = (4*avg_V)**(1/3)/(2**0.5)
average_E_list[i]=(avg_E)
average_S_list[i]=(avg_S)
average_V_list[i]=(avg_V)
average_b_list[i]=(avg_b)
average_nu_list[i]=(avg_nu)
delta_Vn_list[i,:]=(delta_Vn)
return average_E_list,average_S_list,average_V_list,average_b_list,average_nu_list,delta_Vn_list
def curtin_BCC(average_S_list,average_V_list,average_b_list,average_nu_list,delta_Vn_list,Comp_list,T,ep):
kc = 1.38064852*10**(-23) #J/K
J2eV=6.2415093433*10**18
ep0 = 10**4
aver_S = average_S_list
aver_b = average_b_list
sum_cndVn_b6_list = np.empty(len(Comp_list))
dEb_list=np.empty(len(Comp_list))
Ty0_list=np.empty(len(Comp_list))
delta_ss_list=np.empty(len(Comp_list))
for i in range(len(Comp_list)):
c = Comp_list[i]
#print(delta_Vn_list[i,:])
#print(delta_Vn_list[i,:]**2)
sum_cndVn_b6 = np.dot(c,delta_Vn_list[i,:]**2)/average_b_list[i]**6
#print(sum_cndVn_b6)
sum_cndVn_b6_list[i]=sum_cndVn_b6
q_nu = ((1 + average_nu_list)/(1 - average_nu_list))
dEb = 2.00 * 0.123**(1/3) * aver_S * aver_b**3 * q_nu**(2/3) * sum_cndVn_b6**(1/3)
Ty0 = 0.040 * 0.123**(-1/3) * aver_S * q_nu**(4/3) * sum_cndVn_b6**(2/3)
Ty_T = Ty0 * (1 - ((kc*T)/(dEb) * np.log(ep0/ep))**(2/3) )
if Ty_T<=Ty0/2:
Ty_T = Ty0 * np.exp(-1/0.55* kc*T/dEb*np.log(ep0/ep))
delta_ss = 3.06*Ty_T
dEb_list[i]=dEb
Ty0_list[i]=Ty0
delta_ss_list[i]=delta_ss
return dEb_list, Ty0_list, delta_ss_list
def curtin_BCC_old(average_S_list,average_V_list,average_b_list,average_nu_list,delta_Vn_list,Comp_list,T,ep):
kc = 1.38064852*10**(-23) #J/K
J2eV=6.2415093433*10**18
ep0 = 10**4
aver_S = average_S_list
aver_b = average_b_list
sum_cndVn_b6_list = np.empty(len(Comp_list))
dEb_list=np.empty(len(Comp_list))
Ty0_list=np.empty(len(Comp_list))
delta_ss_list=np.empty(len(Comp_list))
for i in range(len(Comp_list)):
c = Comp_list[i]
#print(delta_Vn_list[i,:])
#print(delta_Vn_list[i,:]**2)
sum_cndVn_b6 = np.dot(c,delta_Vn_list[i,:]**2)/average_b_list[i]**6
#print(sum_cndVn_b6)
sum_cndVn_b6_list[i]=sum_cndVn_b6
q_nu = ((1 + average_nu_list)/(1 - average_nu_list))
dEb = 2.00 * 0.123**(1/3) * aver_S * aver_b**3 * q_nu**(2/3) * sum_cndVn_b6**(1/3)
Ty0 = 0.040 * 0.123**(-1/3) * aver_S * q_nu**(4/3) * sum_cndVn_b6**(2/3)
Ty_T = Ty0 * (1 - ((kc*T)/(dEb) * np.log(ep0/ep))**(2/3) )
delta_ss = 3.06*Ty_T
dEb_list[i]=dEb
Ty0_list[i]=Ty0
delta_ss_list[i]=delta_ss
return dEb_list, Ty0_list, delta_ss_list
# Mo-Ta-Nb
V_list=np.array([15.941,18.345,18.355])*1e-30
E_list=np.array([326.78,170.02,69.389])*1e9
S_list=np.array([126.4,62.8,24.2])*1e9
Comp_list = np.array([[0.75,0.,0.25]])
ep = 1e-3
T = 1573
average_E_list,average_S_list,average_V_list,average_b_list,average_nu_list,delta_Vn_list= average_quantities(E_list,V_list,S_list,Comp_list)
dEb_list, Ty0_list, delta_ss_list=curtin_BCC(average_S_list,average_V_list,average_b_list,average_nu_list,delta_Vn_list,Comp_list,T,ep)
dEb_list2, Ty0_list2, delta_ss_list2=curtin_BCC_old(average_S_list,average_V_list,average_b_list,average_nu_list,delta_Vn_list,Comp_list,T,ep)
T_list = np.linspace(0,1600,170)
dEb_list_comp0 = np.empty(len(T_list))
Ty0_list_comp0 = np.empty(len(T_list))
delta_ss_list_comp0 = np.empty(len(T_list))
dEb_list_comp0_old = np.empty(len(T_list))
Ty0_list_comp0_old = np.empty(len(T_list))
delta_ss_list_comp0_old = np.empty(len(T_list))
for i in range(len(T_list)):
T = T_list[i]
dEb_list, Ty0_list, delta_ss_list=curtin_BCC(average_S_list,average_V_list,average_b_list,average_nu_list,delta_Vn_list,Comp_list,T,ep)
dEb_list_comp0[i]=(dEb_list[0])
Ty0_list_comp0[i]=(Ty0_list[0])
delta_ss_list_comp0[i]=(delta_ss_list[0]/1e6)
dEb_list2, Ty0_list2, delta_ss_list2=curtin_BCC_old(average_S_list,average_V_list,average_b_list,average_nu_list,delta_Vn_list,Comp_list,T,ep)
dEb_list_comp0_old[i]=(dEb_list2[0])
Ty0_list_comp0_old[i]=(Ty0_list2[0])
delta_ss_list_comp0_old[i]=(delta_ss_list2[0]/1e6)
plt.plot(T_list,delta_ss_list_comp0)
plt.plot(T_list,delta_ss_list_comp0_old)
Comp_list = np.array([[0.1,0.00,0.9]])
average_E_list,average_S_list,average_V_list,average_b_list,average_nu_list,delta_Vn_list= average_quantities(E_list,V_list,S_list,Comp_list)
dEb_list, Ty0_list, delta_ss_list=curtin_BCC(average_S_list,average_V_list,average_b_list,average_nu_list,delta_Vn_list,Comp_list,T,ep)
T_list = np.linspace(0,1600,170)
dEb_list_comp0 = np.empty(len(T_list))
Ty0_list_comp0 = np.empty(len(T_list))
delta_ss_list_comp0 = np.empty(len(T_list))
dEb_list_comp0_old = np.empty(len(T_list))
Ty0_list_comp0_old = np.empty(len(T_list))
delta_ss_list_comp0_old = np.empty(len(T_list))
for i in range(len(T_list)):
T = T_list[i]
dEb_list, Ty0_list, delta_ss_list=curtin_BCC(average_S_list,average_V_list,average_b_list,average_nu_list,delta_Vn_list,Comp_list,T,ep)
dEb_list_comp0[i]=(dEb_list[0])
Ty0_list_comp0[i]=(Ty0_list[0])
delta_ss_list_comp0[i]=(delta_ss_list[0]/1e6)
dEb_list2, Ty0_list2, delta_ss_list2=curtin_BCC_old(average_S_list,average_V_list,average_b_list,average_nu_list,delta_Vn_list,Comp_list,T,ep)
dEb_list_comp0_old[i]=(dEb_list2[0])
Ty0_list_comp0_old[i]=(Ty0_list2[0])
delta_ss_list_comp0_old[i]=(delta_ss_list2[0]/1e6)
plt.plot(T_list,delta_ss_list_comp0)
plt.plot(T_list,delta_ss_list_comp0_old)
```
|
github_jupyter
|
# Implement an Accelerometer
In this notebook you will define your own `get_derivative_from_data` function and use it to differentiate position data ONCE to get velocity information and then again to get acceleration information.
In part 1 I will demonstrate what this process looks like and then in part 2 you'll implement the function yourself.
-----
## Part 1 - Reminder and Demonstration
```
# run this cell for required imports
from helpers import process_data
from helpers import get_derivative_from_data as solution_derivative
from matplotlib import pyplot as plt
# load the parallel park data
PARALLEL_PARK_DATA = process_data("parallel_park.pickle")
# get the relevant columns
timestamps = [row[0] for row in PARALLEL_PARK_DATA]
displacements = [row[1] for row in PARALLEL_PARK_DATA]
# calculate first derivative
speeds = solution_derivative(displacements, timestamps)
# plot
plt.title("Position and Velocity vs Time")
plt.xlabel("Time (seconds)")
plt.ylabel("Position (blue) and Speed (orange)")
plt.scatter(timestamps, displacements)
plt.scatter(timestamps[1:], speeds)
plt.show()
```
But you just saw that acceleration is the derivative of velocity... which means we can use the same derivative function to calculate acceleration!
```
# calculate SECOND derivative
accelerations = solution_derivative(speeds, timestamps[1:])
# plot (note the slicing of timestamps from 2 --> end)
plt.scatter(timestamps[2:], accelerations)
plt.show()
```
As you can see, this parallel park motion consisted of four segments with different (but constant) acceleration. We can plot all three quantities at once like this:
```
plt.title("x(t), v(t), a(t)")
plt.xlabel("Time (seconds)")
plt.ylabel("x (blue), v (orange), a (green)")
plt.scatter(timestamps, displacements)
plt.scatter(timestamps[1:], speeds)
plt.scatter(timestamps[2:], accelerations)
plt.show()
```
----
## Part 2 - Implement it yourself!
```
def get_derivative_from_data(position_data, time_data):
# TODO - try your best to implement this code yourself!
# if you get really stuck feel free to go back
# to the previous notebook for a hint.
return
# Testing part 1 - visual testing of first derivative
# compare this output to the corresponding graph above.
speeds = get_derivative_from_data(displacements, timestamps)
plt.title("Position and Velocity vs Time")
plt.xlabel("Time (seconds)")
plt.ylabel("Position (blue) and Speed (orange)")
plt.scatter(timestamps, displacements)
plt.scatter(timestamps[1:], speeds)
plt.show()
# Testing part 2 - visual testing of second derivative
# compare this output to the corresponding graph above.
speeds = get_derivative_from_data(displacements, timestamps)
accelerations = get_derivative_from_data(speeds, timestamps[1:])
plt.title("x(t), v(t), a(t)")
plt.xlabel("Time (seconds)")
plt.ylabel("x (blue), v (orange), a (green)")
plt.scatter(timestamps, displacements)
plt.scatter(timestamps[1:], speeds)
plt.scatter(timestamps[2:], accelerations)
plt.show()
```
|
github_jupyter
|
<script async src="https://www.googletagmanager.com/gtag/js?id=UA-59152712-8"></script>
<script>
window.dataLayer = window.dataLayer || [];
function gtag(){dataLayer.push(arguments);}
gtag('js', new Date());
gtag('config', 'UA-59152712-8');
</script>
# Weyl Scalars and Invariants: An Introduction to Einstein Toolkit Diagnostic Thorns
## Author: Patrick Nelson & Zach Etienne
### Formatting improvements courtesy Brandon Clark
[comment]: <> (Abstract: TODO)
**Notebook Status:** <font color='green'><b> Validated </b></font>
**Validation Notes:** Numerical results from this module have been confirmed to agree with the trusted WeylScal4 Einstein Toolkit thorn to roundoff error.
### NRPy+ Source Code for this module:
* [WeylScal4NRPD/WeylScalars_Cartesian.py](../edit/WeylScal4NRPD/WeylScalars_Cartesian.py)
* [WeylScal4NRPD/WeylScalarInvariants_Cartesian.py](../edit/WeylScal4NRPD/WeylScalarInvariants_Cartesian.py)
which are fully documented in the NRPy+ [Tutorial-WeylScalars-Cartesian](Tutorial-WeylScalars-Cartesian.ipynb) module on using NRPy+ to construct the Weyl scalars and invariants as SymPy expressions.
## Introduction:
In the [previous tutorial notebook](Tutorial-WeylScalars-Cartesian.ipynb), we constructed within SymPy full expressions for the real and imaginary components of all five Weyl scalars $\psi_0$, $\psi_1$, $\psi_2$, $\psi_3$, and $\psi_4$ as well as the Weyl invariants. So that we can easily access these expressions, we have ported the Python code needed to generate the Weyl scalar SymPy expressions to [WeylScal4NRPD/WeylScalars_Cartesian.py](../edit/WeylScal4NRPD/WeylScalars_Cartesian.py), and the Weyl invariant SymPy expressions to [WeylScal4NRPD/WeylScalarInvariants_Cartesian.py](../edit/WeylScal4NRPD/WeylScalarInvariants_Cartesian.py).
Here we will work through the steps necessary to construct an Einstein Toolkit diagnostic thorn (module), starting from these SymPy expressions, which computes these expressions using ADMBase gridfunctions as input. This tutorial is in two steps:
1. Call on NRPy+ to convert the SymPy expressions for the Weyl Scalars and associated Invariants into one C-code kernel for each.
1. Write the C code and build up the needed Einstein Toolkit infrastructure (i.e., the .ccl files).
<a id='toc'></a>
# Table of Contents
$$\label{toc}$$
This notebook is organized as follows
1. [Step 1](#nrpy): Call on NRPy+ to convert the SymPy expressions for the Weyl scalars and associated invariants into one C-code kernel for each
1. [Step 2](#etk): Interfacing with the Einstein Toolkit
1. [Step 2.a](#etkc): Constructing the Einstein Toolkit C-code calling functions that include the C code kernels
1. [Step 2.b](#cclfiles): CCL files - Define how this module interacts and interfaces with the larger Einstein Toolkit infrastructure
1. [Step 2.c](#etk_list): Add the C file to Einstein Toolkit compilation list
1. [Step 3](#latex_pdf_output): Output this notebook to $\LaTeX$-formatted PDF file
<a id='nrpy'></a>
# Step 1: Call on NRPy+ to convert the SymPy expressions for the Weyl scalars and associated invariants into one C-code kernel for each \[Back to [top](#toc)\]
$$\label{nrpy}$$
<font color='red'><b>WARNING</b></font>: It takes some time to generate the CSE-optimized C code kernels for these quantities, especially the Weyl scalars... expect 5 minutes on a modern computer.
```
from outputC import * # NRPy+: Core C code output module
import finite_difference as fin # NRPy+: Finite difference C code generation module
import NRPy_param_funcs as par # NRPy+: Parameter interface
import grid as gri # NRPy+: Functions having to do with numerical grids
import indexedexp as ixp # NRPy+: Symbolic indexed expression (e.g., tensors, vectors, etc.) support
import reference_metric as rfm # NRPy+: Reference metric support
import cmdline_helper as cmd # NRPy+: Multi-platform Python command-line interface
import loop as lp # NRPy+: loop infrasructure
import shutil, os, sys, time # Standard Python modules for multiplatform OS-level functions, benchmarking
# Step 1: Set the coordinate system for the numerical grid to Cartesian.
par.set_parval_from_str("reference_metric::CoordSystem","Cartesian")
rfm.reference_metric() # Create ReU, ReDD needed for rescaling B-L initial data, generating BSSN RHSs, etc.
# Step 2: Set the finite differencing order to FD_order to 4
par.set_parval_from_str("finite_difference::FD_CENTDERIVS_ORDER", 4)
# Step 3: Create output directories
!mkdir WeylScal4NRPD 2>/dev/null # 2>/dev/null: Don't throw an error or warning if the directory already exists.
!mkdir WeylScal4NRPD/src 2>/dev/null # 2>/dev/null: Don't throw an error or warning if the directory already exists.
# Step 4: Generate symbolic expressions
# Since we are writing an Einstein Toolkit thorn, we must set our memory access style to "ETK".
par.set_parval_from_str("grid::GridFuncMemAccess","ETK")
import BSSN.Psi4_tetrads as BP4t
par.set_parval_from_str("BSSN.Psi4_tetrads::TetradChoice","QuasiKinnersley")
#par.set_parval_from_str("BSSN.Psi4_tetrads::UseCorrectUnitNormal","True")
import BSSN.Psi4 as BP4
print("Generating symbolic expressions for psi4...")
start = time.time()
BP4.Psi4()
end = time.time()
print("(BENCH) Finished psi4 symbolic expressions in "+str(end-start)+" seconds.")
psi4r = gri.register_gridfunctions("AUX","psi4r")
psi4r0pt = gri.register_gridfunctions("AUX","psi4r0pt")
psi4r1pt = gri.register_gridfunctions("AUX","psi4r1pt")
psi4r2pt = gri.register_gridfunctions("AUX","psi4r2pt")
# Construct RHSs:
psi4r_lhrh = [lhrh(lhs=gri.gfaccess("out_gfs","psi4r"),rhs=BP4.psi4_re_pt[0]+BP4.psi4_re_pt[1]+BP4.psi4_re_pt[2]),
lhrh(lhs=gri.gfaccess("out_gfs","psi4r0pt"),rhs=BP4.psi4_re_pt[0]),
lhrh(lhs=gri.gfaccess("out_gfs","psi4r1pt"),rhs=BP4.psi4_re_pt[1]),
lhrh(lhs=gri.gfaccess("out_gfs","psi4r2pt"),rhs=BP4.psi4_re_pt[2])]
# Generating the CSE is the slowest
# operation in this notebook, and much of the CSE
# time is spent sorting CSE expressions. Disabling
# this sorting makes the C codegen 3-4x faster,
# but the tradeoff is that every time this is
# run, the CSE patterns will be different
# (though they should result in mathematically
# *identical* expressions). You can expect
# roundoff-level differences as a result.
start = time.time()
print("Generating C code kernel for psi4r...")
psi4r_CcodeKernel = fin.FD_outputC("returnstring",psi4r_lhrh,params="outCverbose=False,CSE_sorting=none")
end = time.time()
print("(BENCH) Finished psi4r C code kernel generation in "+str(end-start)+" seconds.")
psi4r_looped = lp.loop(["i2","i1","i0"],["2","2","2"],["cctk_lsh[2]-2","cctk_lsh[1]-2","cctk_lsh[0]-2"],\
["1","1","1"],["#pragma omp parallel for","",""],"","""
const CCTK_REAL xx0 = xGF[CCTK_GFINDEX3D(cctkGH, i0,i1,i2)];
const CCTK_REAL xx1 = yGF[CCTK_GFINDEX3D(cctkGH, i0,i1,i2)];
const CCTK_REAL xx2 = zGF[CCTK_GFINDEX3D(cctkGH, i0,i1,i2)];
"""+psi4r_CcodeKernel)
with open("WeylScal4NRPD/src/WeylScal4NRPD_psi4r.h", "w") as file:
file.write(str(psi4r_looped))
```
<a id='etk'></a>
# Step 2: Interfacing with the Einstein Toolkit \[Back to [top](#toc)\]
$$\label{etk}$$
<a id='etkc'></a>
## Step 2.a: Constructing the Einstein Toolkit calling functions that include the C code kernels \[Back to [top](#toc)\]
$$\label{etkc}$$
Now that we have generated the C code kernels (`WeylScal4NRPD_psis.h` and `WeylScal4NRPD_invars.h`) express the Weyl scalars and invariants as CSE-optimized finite-difference expressions, we next need to write the C code functions that incorporate these kernels and are called by the Einstein Toolkit scheduler.
```
%%writefile WeylScal4NRPD/src/WeylScal4NRPD.c
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include "cctk.h"
#include "cctk_Arguments.h"
#include "cctk_Parameters.h"
void WeylScal4NRPD_calc_psi4r(const cGH* restrict const cctkGH,const int *cctk_lsh,const int *cctk_nghostzones,
const CCTK_REAL invdx0,const CCTK_REAL invdx1,const CCTK_REAL invdx2,
const CCTK_REAL *xGF,const CCTK_REAL *yGF,const CCTK_REAL *zGF,
const CCTK_REAL *hDD00GF,const CCTK_REAL *hDD01GF,const CCTK_REAL *hDD02GF,const CCTK_REAL *hDD11GF,const CCTK_REAL *hDD12GF,const CCTK_REAL *hDD22GF,
const CCTK_REAL *aDD00GF,const CCTK_REAL *aDD01GF,const CCTK_REAL *aDD02GF,const CCTK_REAL *aDD11GF,const CCTK_REAL *aDD12GF,const CCTK_REAL *aDD22GF,
const CCTK_REAL *trKGF,const CCTK_REAL *cfGF,
CCTK_REAL *psi4rGF,
CCTK_REAL *psi4r0ptGF,
CCTK_REAL *psi4r1ptGF,
CCTK_REAL *psi4r2ptGF) {
DECLARE_CCTK_PARAMETERS;
#include "WeylScal4NRPD_psi4r.h"
}
extern void WeylScal4NRPD_mainfunction(CCTK_ARGUMENTS) {
DECLARE_CCTK_PARAMETERS;
DECLARE_CCTK_ARGUMENTS;
if(cctk_iteration % WeylScal4NRPD_calc_every != 0) { return; }
const CCTK_REAL invdx0 = 1.0 / (CCTK_DELTA_SPACE(0));
const CCTK_REAL invdx1 = 1.0 / (CCTK_DELTA_SPACE(1));
const CCTK_REAL invdx2 = 1.0 / (CCTK_DELTA_SPACE(2));
/* Now, to calculate psi4: */
WeylScal4NRPD_calc_psi4r(cctkGH,cctk_lsh,cctk_nghostzones,
invdx0,invdx1,invdx2,
x,y,z,
hDD00GF,hDD01GF,hDD02GF,hDD11GF,hDD12GF,hDD22GF,
aDD00GF,aDD01GF,aDD02GF,aDD11GF,aDD12GF,aDD22GF,
trKGF,cfGF,
psi4rGF,
psi4r0ptGF,psi4r1ptGF,psi4r2ptGF);
}
# First we convert from ADM to BSSN, as is required to convert initial data
# (given using) ADM quantities, to the BSSN evolved variables
import BSSN.ADM_Numerical_Spherical_or_Cartesian_to_BSSNCurvilinear as atob
IDhDD,IDaDD,IDtrK,IDvetU,IDbetU,IDalpha,IDcf,IDlambdaU = \
atob.Convert_Spherical_or_Cartesian_ADM_to_BSSN_curvilinear("Cartesian","DoNotOutputADMInputFunction",os.path.join("WeylScal4NRPD","src"))
# Store the original list of registered gridfunctions; we'll want to unregister
# all the *SphorCart* gridfunctions after we're finished with them below.
orig_glb_gridfcs_list = []
for gf in gri.glb_gridfcs_list:
orig_glb_gridfcs_list.append(gf)
alphaSphorCart = gri.register_gridfunctions( "AUXEVOL", "alphaSphorCart")
betaSphorCartU = ixp.register_gridfunctions_for_single_rank1("AUXEVOL", "betaSphorCartU")
BSphorCartU = ixp.register_gridfunctions_for_single_rank1("AUXEVOL", "BSphorCartU")
gammaSphorCartDD = ixp.register_gridfunctions_for_single_rank2("AUXEVOL", "gammaSphorCartDD", "sym01")
KSphorCartDD = ixp.register_gridfunctions_for_single_rank2("AUXEVOL", "KSphorCartDD", "sym01")
# ADM to BSSN conversion, used for converting ADM initial data into a form readable by this thorn.
# ADM to BSSN, Part 1: Set up function call and pointers to ADM gridfunctions
outstr = """
#include <math.h>
#include "cctk.h"
#include "cctk_Arguments.h"
#include "cctk_Parameters.h"
void WeylScal4NRPD_ADM_to_BSSN(CCTK_ARGUMENTS) {
DECLARE_CCTK_ARGUMENTS;
DECLARE_CCTK_PARAMETERS;
CCTK_REAL *alphaSphorCartGF = alp;
"""
# It's ugly if we output code in the following ordering, so we'll first
# output to a string and then sort the string to beautify the code a bit.
outstrtmp = []
for i in range(3):
outstrtmp.append(" CCTK_REAL *betaSphorCartU"+str(i)+"GF = beta"+chr(ord('x')+i)+";\n")
# outstrtmp.append(" CCTK_REAL *BSphorCartU"+str(i)+"GF = dtbeta"+chr(ord('x')+i)+";\n")
for j in range(i,3):
outstrtmp.append(" CCTK_REAL *gammaSphorCartDD"+str(i)+str(j)+"GF = g"+chr(ord('x')+i)+chr(ord('x')+j)+";\n")
outstrtmp.append(" CCTK_REAL *KSphorCartDD"+str(i)+str(j)+"GF = k"+chr(ord('x')+i)+chr(ord('x')+j)+";\n")
outstrtmp.sort()
for line in outstrtmp:
outstr += line
# ADM to BSSN, Part 2: Set up ADM to BSSN conversions for BSSN gridfunctions that do not require
# finite-difference derivatives (i.e., all gridfunctions except lambda^i (=Gamma^i
# in non-covariant BSSN)):
# h_{ij}, a_{ij}, trK, vet^i=beta^i,bet^i=B^i, cf (conformal factor), and alpha
all_but_lambdaU_expressions = [
lhrh(lhs=gri.gfaccess("in_gfs","hDD00"),rhs=IDhDD[0][0]),
lhrh(lhs=gri.gfaccess("in_gfs","hDD01"),rhs=IDhDD[0][1]),
lhrh(lhs=gri.gfaccess("in_gfs","hDD02"),rhs=IDhDD[0][2]),
lhrh(lhs=gri.gfaccess("in_gfs","hDD11"),rhs=IDhDD[1][1]),
lhrh(lhs=gri.gfaccess("in_gfs","hDD12"),rhs=IDhDD[1][2]),
lhrh(lhs=gri.gfaccess("in_gfs","hDD22"),rhs=IDhDD[2][2]),
lhrh(lhs=gri.gfaccess("in_gfs","aDD00"),rhs=IDaDD[0][0]),
lhrh(lhs=gri.gfaccess("in_gfs","aDD01"),rhs=IDaDD[0][1]),
lhrh(lhs=gri.gfaccess("in_gfs","aDD02"),rhs=IDaDD[0][2]),
lhrh(lhs=gri.gfaccess("in_gfs","aDD11"),rhs=IDaDD[1][1]),
lhrh(lhs=gri.gfaccess("in_gfs","aDD12"),rhs=IDaDD[1][2]),
lhrh(lhs=gri.gfaccess("in_gfs","aDD22"),rhs=IDaDD[2][2]),
lhrh(lhs=gri.gfaccess("in_gfs","trK"),rhs=IDtrK),
lhrh(lhs=gri.gfaccess("in_gfs","vetU0"),rhs=IDvetU[0]),
lhrh(lhs=gri.gfaccess("in_gfs","vetU1"),rhs=IDvetU[1]),
lhrh(lhs=gri.gfaccess("in_gfs","vetU2"),rhs=IDvetU[2]),
lhrh(lhs=gri.gfaccess("in_gfs","alpha"),rhs=IDalpha),
lhrh(lhs=gri.gfaccess("in_gfs","cf"),rhs=IDcf)]
outCparams = "preindent=1,outCfileaccess=a,outCverbose=False,includebraces=False"
all_but_lambdaU_outC = fin.FD_outputC("returnstring",all_but_lambdaU_expressions, outCparams)
outstr += lp.loop(["i2","i1","i0"],["0","0","0"],["cctk_lsh[2]","cctk_lsh[1]","cctk_lsh[0]"],
["1","1","1"],["#pragma omp parallel for","",""]," ",all_but_lambdaU_outC)
outstr += "} // END void WeylScal4NRPD_ADM_to_BSSN(CCTK_ARGUMENTS)\n"
with open("WeylScal4NRPD/src/ADM_to_BSSN.c", "w") as file:
file.write(str(outstr))
```
<a id='cclfiles'></a>
## Step 2.b: CCL files - Define how this module interacts and interfaces with the larger Einstein Toolkit infrastructure \[Back to [top](#toc)\]
$$\label{cclfiles}$$
Writing a module ("thorn") within the Einstein Toolkit requires that three "ccl" files be constructed, all in the root directory of the thorn:
1.`interface.ccl`: defines the gridfunction groups needed, and provides keywords denoting what this thorn provides and what it should inherit from other thorns.
1. `param.ccl`: specifies free parameters within the thorn.
1. `schedule.ccl`: allocates storage for gridfunctions, defines how the thorn's functions should be scheduled in a broader simulation, and specifies the regions of memory written to or read from gridfunctions.
Let's start with `interface.ccl`. The [official Einstein Toolkit (Cactus) documentation](http://einsteintoolkit.org/usersguide/UsersGuide.html) defines what must/should be included in an `interface.ccl` file [**here**](http://einsteintoolkit.org/usersguide/UsersGuidech12.html#x17-178000D2.2).
```
%%writefile WeylScal4NRPD/interface.ccl
# With "implements", we give our thorn its unique name.
implements: WeylScal4NRPD
# By "inheriting" other thorns, we tell the Toolkit that we
# will rely on variables/function that exist within those
# functions.
inherits: admbase Boundary Grid methodoflines
# Tell the Toolkit that we want the various Weyl scalars
# and invariants to be visible to other thorns by using
# the keyword "public". Note that declaring these
# gridfunctions *does not* allocate memory for them;
# that is done by the schedule.ccl file.
public:
CCTK_REAL NRPyPsi4_group type=GF timelevels=3 tags='tensortypealias="Scalar" tensorweight=0 tensorparity=1'
{
psi4rGF,psi4r0ptGF,psi4r1ptGF,psi4r2ptGF, psi4iGF
} "Psi4_group"
CCTK_REAL evol_variables type = GF Timelevels=3
{
aDD00GF,aDD01GF,aDD02GF,aDD11GF,aDD12GF,aDD22GF,alphaGF,cfGF,hDD00GF,hDD01GF,hDD02GF,hDD11GF,hDD12GF,hDD22GF,trKGF,vetU0GF,vetU1GF,vetU2GF
} "BSSN evolved gridfunctions, sans lambdaU and partial t beta"
```
We will now write the file `param.ccl`. This file allows the listed parameters to be set at runtime. We also give allowed ranges and default values for each parameter. More information on this file's syntax can be found in the [official Einstein Toolkit documentation](http://einsteintoolkit.org/usersguide/UsersGuidech12.html#x17-183000D2.3).
The first parameter specifies how many time levels need to be stored. Generally when using the ETK's adaptive-mesh refinement (AMR) driver [Carpet](https://carpetcode.org/), three timelevels are needed so that the diagnostic quantities can be properly interpolated and defined across refinement boundaries.
The second parameter determines how often we will calculate $\psi_4$, and the third parameter indicates whether just $\psi_4$, all Weyl scalars, or all Weyl scalars and invariants are going to be output. The third parameter is currently specified entirely within NRPy+, so by this point it is *not* a free parameter. Thus it is not quite correct to include it in this list of *free* parameters (FIXME).
```
%%writefile WeylScal4NRPD/param.ccl
restricted:
CCTK_INT timelevels "Number of active timelevels" STEERABLE=RECOVER
{
0:3 :: ""
} 3
restricted:
CCTK_INT WeylScal4NRPD_calc_every "WeylScal4_psi4_calc_Nth_calc_every" STEERABLE=ALWAYS
{
*:* :: ""
} 1
```
Finally, we will write the file `schedule.ccl`; its official documentation is found [here](http://einsteintoolkit.org/usersguide/UsersGuidech12.html#x17-186000D2.4). This file dictates when the various parts of the thorn will be run. We first assign storage for both the real and imaginary components of $\psi_4$, and then specify that we want our code run in the `MoL_PseudoEvolution` schedule group (consistent with the original `WeylScal4` Einstein Toolkit thorn), after the ADM variables are set. At this step, we declare that we will be writing code in C. We also specify the gridfunctions that we wish to read in from memory--in our case, we need all the components of $K_{ij}$ (the spatial extrinsic curvature) and $\gamma_{ij}$ (the physical [as opposed to conformal] 3-metric), in addition to the coordinate values. Note that the ETK adopts the widely-used convention that components of $\gamma_{ij}$ are prefixed in the code with $\text{g}$ and not $\gamma$.
```
%%writefile WeylScal4NRPD/schedule.ccl
STORAGE: NRPyPsi4_group[3], evol_variables[3]
STORAGE: ADMBase::metric[3], ADMBase::curv[3], ADMBase::lapse[3], ADMBase::shift[3]
schedule group WeylScal4NRPD_group in MoL_PseudoEvolution after ADMBase_SetADMVars
{
} "Schedule WeylScal4NRPD group"
schedule WeylScal4NRPD_ADM_to_BSSN in WeylScal4NRPD_group before weylscal4_mainfunction
{
LANG: C
} "Convert ADM into BSSN variables"
schedule WeylScal4NRPD_mainfunction in WeylScal4NRPD_group after WeylScal4NRPD_ADM_to_BSSN
{
LANG: C
} "Call WeylScal4NRPD main function"
```
<a id='etk_list'></a>
## Step 2.c: Tell the Einstein Toolkit to compile the C code \[Back to [top](#toc)\]
$$\label{etk_list}$$
The `make.code.defn` lists the source files that need to be compiled. Naturally, this thorn has only the one C file $-$ written above $-$ to compile:
```
%%writefile WeylScal4NRPD/src/make.code.defn
SRCS = WeylScal4NRPD.c ADM_to_BSSN.c
```
<a id='latex_pdf_output'></a>
# Step 3: Output this notebook to $\LaTeX$-formatted PDF file \[Back to [top](#toc)\]
$$\label{latex_pdf_output}$$
The following code cell converts this Jupyter notebook into a proper, clickable $\LaTeX$-formatted PDF file. After the cell is successfully run, the generated PDF may be found in the root NRPy+ tutorial directory, with filename
[Tutorial-ETK_thorn-Weyl_Scalars_and_Spacetime_Invariants.pdf](Tutorial-ETK_thorn-Weyl_Scalars_and_Spacetime_Invariants.pdf) (Note that clicking on this link may not work; you may need to open the PDF file through another means.)
```
import cmdline_helper as cmd # NRPy+: Multi-platform Python command-line interface
cmd.output_Jupyter_notebook_to_LaTeXed_PDF("Tutorial-ETK_thorn-WeylScal4NRPD")
```
|
github_jupyter
|
# Setup
### Installing Dependencies and Mounting
```
%%capture
!pip install transformers
# Mount Google Drive
from google.colab import drive # import drive from google colab
ROOT = "/content/drive"
drive.mount(ROOT, force_remount=True)
```
### Imports
```
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
% matplotlib inline
import random
import json
import time
import datetime
import os
from transformers import GPT2Tokenizer, GPT2LMHeadModel, GPT2Config, AdamW, get_linear_schedule_with_warmup
import torch
torch.manual_seed(64)
from torch.utils.data import Dataset, random_split, DataLoader, RandomSampler, SequentialSampler
!pip show torch
```
### Setting Device
```
%cd /content/drive/MyDrive/AutoCompose/
!nvidia-smi
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
device
```
# Data Preparation
### Data Collection
```
with open("data/anticipation.json", "r") as f:
data = json.load(f)
data = [poem for poem in data if len(poem["poem"].split()) < 100]
print(len(data))
data[:5]
```
### Data Model
```
class PoemDataset(Dataset):
def __init__(self, poems, tokenizer, max_length=768, gpt2_type="gpt2"):
self.tokenizer = tokenizer
self.input_ids = []
self.attn_masks = []
for poem in poems:
encodings_dict = tokenizer("<|startoftext|>"+poem["poem"]+"<|endoftext|>",
truncation=True,
max_length=max_length,
padding="max_length")
self.input_ids.append(torch.tensor(encodings_dict["input_ids"]))
self.attn_masks.append(torch.tensor(encodings_dict["attention_mask"]))
def __len__(self):
return len(self.input_ids)
def __getitem__(self, idx):
return self.input_ids[idx], self.attn_masks[idx]
# Loading GPT2 Tokenizer
tokenizer = GPT2Tokenizer.from_pretrained('gpt2',
bos_token='<|startoftext|>',
eos_token='<|endoftext|>',
pad_token='<|pad|>')
```
### Rough
```
print(tokenizer.encode("<|startoftext|> Hello World <|endoftext|>", padding="max_length", max_length=10))
print(len(tokenizer))
# Finding length of maximum token in dataset
max_length = max([len(tokenizer.encode(poem["poem"])) for poem in data])
print(max_length)
max_length = 100
x = [len(tokenizer.encode(poem["poem"])) for poem in data if len(tokenizer.encode(poem["poem"])) < 100]
y = [len(tokenizer.encode(poem["poem"])) - len(poem["poem"].split()) for poem in data]
print(sum(y)/len(y))
print(max(x), len(x))
plt.hist(x, bins = 5)
plt.show
```
### Dataset Creation
```
batch_size = 32
max_length = 100
dataset = PoemDataset(data, tokenizer, max_length=max_length)
# Split data into train and validation sets
train_size = int(0.9*len(dataset))
val_size = len(dataset) - train_size
train_dataset, val_dataset = random_split(dataset, [train_size, val_size])
print("Number of samples for training =", train_size)
print("Number of samples for validation =", val_size)
train_dataset[0]
train_dataloader = DataLoader(train_dataset,
sampler=RandomSampler(train_dataset),
batch_size=batch_size)
val_dataloader = DataLoader(val_dataset,
sampler=SequentialSampler(val_dataset),
batch_size=batch_size)
```
# Finetune GPT2 Language Model
### Importing Pre-Trained GPT2 Model
```
# Load model configuration
config = GPT2Config.from_pretrained("gpt2")
# Create model instance and set embedding length
model = GPT2LMHeadModel.from_pretrained("gpt2", config=config)
model.resize_token_embeddings(len(tokenizer))
# Running the model on GPU
model = model.to(device)
# <<< Optional >>>
# Setting seeds to enable reproducible runs
seed_val = 42
random.seed(seed_val)
np.random.seed(seed_val)
torch.manual_seed(seed_val)
torch.cuda.manual_seed_all(seed_val)
```
### Scheduling Optimizer
```
epochs = 4
warmup_steps = 1e2
sample_every = 100
print(len(train_dataloader))
print(len(train_dataset))
# Using AdamW optimizer with default parameters
optimizer = AdamW(model.parameters(), lr=5e-4, eps=1e-8)
# Toatl training steps is the number of data points times the number of epochs
total_training_steps = len(train_dataloader)*epochs
# Setting a variable learning rate using scheduler
scheduler = get_linear_schedule_with_warmup(optimizer,
num_warmup_steps=warmup_steps,
num_training_steps=total_training_steps)
```
### Training
```
def format_time(elapsed):
return str(datetime.timedelta(seconds=int(round(elapsed))))
total_t0 = time.time()
training_stats = []
model = model.to(device)
for epoch_i in range(epochs):
print(f'Beginning epoch {epoch_i+1} of {epochs}')
t0 = time.time()
total_train_loss = 0
model.train()
# Labels are shifted by 1 timestep
for step, batch in enumerate(train_dataloader):
b_input_ids = batch[0].to(device)
b_labels = batch[0].to(device)
b_masks = batch[1].to(device)
model.zero_grad()
outputs = model(b_input_ids,
labels=b_labels,
attention_mask=b_masks)
loss = outputs[0]
batch_loss = loss.item()
total_train_loss += batch_loss
# Sampling every x steps
if step != 0 and step % sample_every == 0:
elapsed = format_time(time.time()-t0)
print(f'Batch {step} of {len(train_dataloader)}. Loss: {batch_loss}. Time: {elapsed}')
model.eval()
sample_outputs = model.generate(
bos_token_id=random.randint(1,30000),
do_sample=True,
top_k=50,
max_length = 200,
top_p=0.95,
num_return_sequences=1
)
for i, sample_output in enumerate(sample_outputs):
print(f'Example ouput: {tokenizer.decode(sample_output, skip_special_tokens=True)}')
print()
model.train()
loss.backward()
optimizer.step()
scheduler.step()
avg_train_loss = total_train_loss / len(train_dataloader)
training_time = format_time(time.time()-t0)
print(f'Average Training Loss: {avg_train_loss}. Epoch time: {training_time}')
print()
t0 = time.time()
model.eval()
total_eval_loss = 0
nb_eval_steps = 0
for batch in val_dataloader:
b_input_ids = batch[0].to(device)
b_labels = batch[0].to(device)
b_masks = batch[1].to(device)
with torch.no_grad():
outputs = model(b_input_ids,
attention_mask = b_masks,
labels=b_labels)
loss = outputs[0]
batch_loss = loss.item()
total_eval_loss += batch_loss
avg_val_loss = total_eval_loss / len(val_dataloader)
val_time = format_time(time.time() - t0)
print(f'Validation loss: {avg_val_loss}. Validation Time: {val_time}')
print()
# Record all statistics from this epoch.
training_stats.append(
{
'epoch': epoch_i + 1,
'Training Loss': avg_train_loss,
'Valid. Loss': avg_val_loss,
'Training Time': training_time,
'Validation Time': val_time
}
)
print("------------------------------")
print(f'Total training took {format_time(time.time()-total_t0)}')
```
### Visualizations
```
pd.set_option('precision', 2)
df_stats = pd.DataFrame(data=training_stats)
df_stats = df_stats.set_index('epoch')
# Use plot styling from seaborn.
sns.set(style='darkgrid')
# Increase the plot size and font size.
sns.set(font_scale=1.5)
plt.rcParams["figure.figsize"] = (12,6)
# Plot the learning curve.
plt.plot(df_stats['Training Loss'], 'b-o', label="Training")
plt.plot(df_stats['Valid. Loss'], 'g-o', label="Validation")
# Label the plot.
plt.title("Training & Validation Loss")
plt.xlabel("Epoch")
plt.ylabel("Loss")
plt.legend()
plt.xticks([1, 2, 3, 4])
plt.show()
```
### Generate Poems
```
model.eval()
prompt = "<|startoftext|>"
generated = torch.tensor(tokenizer.encode(prompt)).unsqueeze(0)
generated = generated.to(device)
sample_outputs = model.generate(
generated,
do_sample=True,
top_k=50,
max_length = 300,
top_p=0.95,
num_return_sequences=3
)
for i, sample_output in enumerate(sample_outputs):
print("{}: {}\n\n".format(i, tokenizer.decode(sample_output, skip_special_tokens=True)))
```
### Saving and Loading Finetuned Model
```
output_dir = "/content/drive/My Drive/AutoCompose/models/anticipation2"
# Save generated poems
# sample_outputs = model.generate(
# generated,
# do_sample=True,
# top_k=50,
# max_length = 300,
# top_p=0.95,
# num_return_sequences=25
# )
# with open(os.path.join(output_dir, 'generated_poems.txt'), "w") as outfile:
# for i, sample_output in enumerate(sample_outputs):
# outfile.write(tokenizer.decode(sample_output, skip_special_tokens=True)+"\n\n")
# Save a trained model, configuration and tokenizer using `save_pretrained()`.
# They can then be reloaded using `from_pretrained()`
model_to_save = model.module if hasattr(model, 'module') else model
model_to_save.save_pretrained(output_dir)
tokenizer.save_pretrained(output_dir)
# Good practice: save your training arguments together with the trained model
# torch.save(training_stats, os.path.join(output_dir, 'training_args.bin'))
# Save generated poems
sample_outputs = model.generate(
generated,
do_sample=True,
top_k=50,
max_length = 300,
top_p=0.95,
num_return_sequences=25
)
with open(os.path.join(output_dir, 'generated_poems.txt'), "w") as outfile:
for i, sample_output in enumerate(sample_outputs):
outfile.write(tokenizer.decode(sample_output, skip_special_tokens=True)+"\n\n")
# Loading saved model
model_dir = "/content/drive/My Drive/AutoCompose/models/neutral"
model = GPT2LMHeadModel.from_pretrained(model_dir)
tokenizer = GPT2Tokenizer.from_pretrained(model_dir)
model.to(device)
```
# Version Control
```
!git config --global user.email "[email protected]"
!git config --global user.name "prajwal"
import json
f = open("AutoComposeCreds.json")
data = json.load(f)
f.close()
print(data)
username="prajwalcr"
repository="AutoCompose"
git_token = data["git-token"]
!git clone https://{git_token}@github.com/{username}/{repository}
%cd /content/drive/MyDrive/AutoCompose/
!git pull
!git push
!git add .
!git commit -m "anger model trained on uni-m dataset added"
!git filter-branch --tree-filter 'rm -rf models/' HEAD
!git add .
!git status
!git commit -m "new models added"
```
|
github_jupyter
|
## Define the Convolutional Neural Network
In this notebook and in `models.py`:
1. Define a CNN with images as input and keypoints as output
2. Construct the transformed FaceKeypointsDataset, just as before
3. Train the CNN on the training data, tracking loss
4. See how the trained model performs on test data
5. If necessary, modify the CNN structure and model hyperparameters, so that it performs *well* **\***
**\*** What does *well* mean?
"Well" means that the model's loss decreases during training **and**, when applied to test image data, the model produces keypoints that closely match the true keypoints of each face. And you'll see examples of this later in the notebook.
---
## CNN Architecture
Recall that CNN's are defined by a few types of layers:
* Convolutional layers
* Maxpooling layers
* Fully-connected layers
### Define model in the provided file `models.py` file
## PyTorch Neural Nets
To define a neural network in PyTorch, we have defined the layers of a model in the function `__init__` and defined the feedforward behavior of a network that employs those initialized layers in the function `forward`, which takes in an input image tensor, `x`. The structure of this Net class is shown below and left for you to fill in.
Note: During training, PyTorch will be able to perform backpropagation by keeping track of the network's feedforward behavior and using autograd to calculate the update to the weights in the network.
#### Define the Layers in ` __init__`
As a reminder, a conv/pool layer may be defined like this (in `__init__`):
```
# 1 input image channel (for grayscale images), 32 output channels/feature maps, 3x3 square convolution kernel
self.conv1 = nn.Conv2d(1, 32, 3)
# maxpool that uses a square window of kernel_size=2, stride=2
self.pool = nn.MaxPool2d(2, 2)
```
#### Refer to Layers in `forward`
Then referred to in the `forward` function like this, in which the conv1 layer has a ReLu activation applied to it before maxpooling is applied:
```
x = self.pool(F.relu(self.conv1(x)))
```
Best practice is to place any layers whose weights will change during the training process in `__init__` and refer to them in the `forward` function; any layers or functions that always behave in the same way, such as a pre-defined activation function, should appear *only* in the `forward` function.
#### Why models.py
We are tasked with defining the network in the `models.py` file so that any models we define can be saved and loaded by name in different notebooks in this project directory. For example, by defining a CNN class called `Net` in `models.py`, we can then create that same architecture in this and other notebooks by simply importing the class and instantiating a model:
```
from models import Net
net = Net()
```
```
# load the data if you need to; if you have already loaded the data, you may comment this cell out
# -- DO NOT CHANGE THIS CELL -- #
!mkdir /data
!wget -P /data/ https://s3.amazonaws.com/video.udacity-data.com/topher/2018/May/5aea1b91_train-test-data/train-test-data.zip
!unzip -n /data/train-test-data.zip -d /data
```
<div class="alert alert-info">**Note:** Workspaces automatically close connections after 30 minutes of inactivity (including inactivity while training!). Use the code snippet below to keep your workspace alive during training. (The active_session context manager is imported below.)
</div>
```
from workspace_utils import active_session
with active_session():
train_model(num_epochs)
```
```
# import the usual resources
import matplotlib.pyplot as plt
import numpy as np
# import utilities to keep workspaces alive during model training
from workspace_utils import active_session
# watch for any changes in model.py, if it changes, re-load it automatically
%load_ext autoreload
%autoreload 2
## Define the Net in models.py
import torch
import torch.nn as nn
import torch.nn.functional as F
## Once you've define the network, you can instantiate it
# one example conv layer has been provided for you
from models import Net
net = Net()
print(net)
```
## Transform the dataset
To prepare for training, we have created a transformed dataset of images and keypoints.
### Define a data transform
In PyTorch, a convolutional neural network expects a torch image of a consistent size as input. For efficient training, and so our model's loss does not blow up during training, it is also suggested that we normalize the input images and keypoints. The necessary transforms have been defined in `data_load.py` and we **do not** need to modify these.
To define the data transform below, we have used a [composition](http://pytorch.org/tutorials/beginner/data_loading_tutorial.html#compose-transforms) of:
1. Rescaling and/or cropping the data, such that we are left with a square image (the suggested size is 224x224px)
2. Normalizing the images and keypoints; turning each RGB image into a grayscale image with a color range of [0, 1] and transforming the given keypoints into a range of [-1, 1]
3. Turning these images and keypoints into Tensors
**This transform will be applied to the training data and, later, the test data**. It will change how we go about displaying these images and keypoints, but these steps are essential for efficient training.
```
from torch.utils.data import Dataset, DataLoader
from torchvision import transforms, utils
# the dataset we created in Notebook 1 is copied in the helper file `data_load.py`
from data_load import FacialKeypointsDataset
# the transforms we defined in Notebook 1 are in the helper file `data_load.py`
from data_load import Rescale, RandomCrop, Normalize, ToTensor
## define the data_transform using transforms.Compose([all tx's, . , .])
# order matters! i.e. rescaling should come before a smaller crop
data_transform = transforms.Compose([Rescale(250),
RandomCrop(224),
Normalize(),
ToTensor()])
# testing that you've defined a transform
assert(data_transform is not None), 'Define a data_transform'
# create the transformed dataset
transformed_dataset = FacialKeypointsDataset(csv_file='/data/training_frames_keypoints.csv',
root_dir='/data/training/',
transform=data_transform)
print('Number of images: ', len(transformed_dataset))
# iterate through the transformed dataset and print some stats about the first few samples
for i in range(4):
sample = transformed_dataset[i]
print(i, sample['image'].size(), sample['keypoints'].size())
```
## Batching and loading data
Next, having defined the transformed dataset, we can use PyTorch's DataLoader class to load the training data in batches of whatever size as well as to shuffle the data for training the model. You can read more about the parameters of the DataLoader in [this documentation](http://pytorch.org/docs/master/data.html).
#### Batch size
Decide on a good batch size for training your model. Try both small and large batch sizes and note how the loss decreases as the model trains. Too large a batch size may cause your model to crash and/or run out of memory while training.
**Note for Windows users**: Please change the `num_workers` to 0 or you may face some issues with your DataLoader failing.
```
# load training data in batches
batch_size = 10
train_loader = DataLoader(transformed_dataset,
batch_size=batch_size,
shuffle=True,
num_workers=4)
```
## Before training
Take a look at how this model performs before it trains. You should see that the keypoints it predicts start off in one spot and don't match the keypoints on a face at all! It's interesting to visualize this behavior so that you can compare it to the model after training and see how the model has improved.
#### Load in the test dataset
The test dataset is one that this model has *not* seen before, meaning it has not trained with these images. We'll load in this test data and before and after training, see how our model performs on this set!
To visualize this test data, we have to go through some un-transformation steps to turn our images into python images from tensors and to turn our keypoints back into a recognizable range.
```
# load in the test data, using the dataset class
# AND apply the data_transform you defined above
# create the test dataset
test_dataset = FacialKeypointsDataset(csv_file='/data/test_frames_keypoints.csv',
root_dir='/data/test/',
transform=data_transform)
# load test data in batches
batch_size = 10
test_loader = DataLoader(test_dataset,
batch_size=batch_size,
shuffle=True,
num_workers=4)
```
## Apply the model on a test sample
To test the model on a test sample of data, we have to follow these steps:
1. Extract the image and ground truth keypoints from a sample
2. Wrap the image in a Variable, so that the net can process it as input and track how it changes as the image moves through the network.
3. Make sure the image is a FloatTensor, which the model expects.
4. Forward pass the image through the net to get the predicted, output keypoints.
This function test how the network performs on the first batch of test data. It returns the images, the transformed images, the predicted keypoints (produced by the model), and the ground truth keypoints.
```
# test the model on a batch of test images
def net_sample_output():
# iterate through the test dataset
for i, sample in enumerate(test_loader):
# get sample data: images and ground truth keypoints
images = sample['image']
key_pts = sample['keypoints']
# convert images to FloatTensors
images = images.type(torch.FloatTensor)
# forward pass to get net output
output_pts = net(images)
# reshape to batch_size x 68 x 2 pts
output_pts = output_pts.view(output_pts.size()[0], 68, -1)
# break after first image is tested
if i == 0:
return images, output_pts, key_pts
```
#### Debugging tips
If you get a size or dimension error here, make sure that your network outputs the expected number of keypoints! Or if you get a Tensor type error, look into changing the above code that casts the data into float types: `images = images.type(torch.FloatTensor)`.
```
# call the above function
# returns: test images, test predicted keypoints, test ground truth keypoints
test_images, test_outputs, gt_pts = net_sample_output()
# print out the dimensions of the data to see if they make sense
print(test_images.data.size())
print(test_outputs.data.size())
print(gt_pts.size())
```
## Visualize the predicted keypoints
Once we've had the model produce some predicted output keypoints, we can visualize these points in a way that's similar to how we've displayed this data before, only this time, we have to "un-transform" the image/keypoint data to display it.
The *new* function, `show_all_keypoints` displays a grayscale image, its predicted keypoints and its ground truth keypoints (if provided).
```
def show_all_keypoints(image, predicted_key_pts, gt_pts=None):
"""Show image with predicted keypoints"""
# image is grayscale
plt.imshow(image, cmap='gray')
plt.scatter(predicted_key_pts[:, 0], predicted_key_pts[:, 1], s=20, marker='.', c='m')
# plot ground truth points as green pts
if gt_pts is not None:
plt.scatter(gt_pts[:, 0], gt_pts[:, 1], s=20, marker='.', c='g')
```
#### Un-transformation
Next, you'll see a helper function. `visualize_output` that takes in a batch of images, predicted keypoints, and ground truth keypoints and displays a set of those images and their true/predicted keypoints.
This function's main role is to take batches of image and keypoint data (the input and output of your CNN), and transform them into numpy images and un-normalized keypoints (x, y) for normal display. The un-transformation process turns keypoints and images into numpy arrays from Tensors *and* it undoes the keypoint normalization done in the Normalize() transform; it's assumed that you applied these transformations when you loaded your test data.
```
# visualize the output
# by default this shows a batch of 10 images
def visualize_output(test_images, test_outputs, gt_pts=None, batch_size=10):
for i in range(batch_size):
plt.figure(figsize=(20,10))
ax = plt.subplot(1, batch_size, i+1)
# un-transform the image data
image = test_images[i].data # get the image from it's Variable wrapper
image = image.numpy() # convert to numpy array from a Tensor
image = np.transpose(image, (1, 2, 0)) # transpose to go from torch to numpy image
# un-transform the predicted key_pts data
predicted_key_pts = test_outputs[i].data
predicted_key_pts = predicted_key_pts.numpy()
# undo normalization of keypoints
predicted_key_pts = predicted_key_pts*50.0+100
# plot ground truth points for comparison, if they exist
ground_truth_pts = None
if gt_pts is not None:
ground_truth_pts = gt_pts[i]
ground_truth_pts = ground_truth_pts*50.0+100
# call show_all_keypoints
show_all_keypoints(np.squeeze(image), predicted_key_pts, ground_truth_pts)
plt.axis('off')
plt.show()
# call it
visualize_output(test_images, test_outputs, gt_pts)
```
## Training
#### Loss function
Training a network to predict keypoints is different than training a network to predict a class; instead of outputting a distribution of classes and using cross entropy loss, we have to choose a loss function that is suited for regression, which directly compares a predicted value and target value. Read about the various kinds of loss functions (like MSE or L1/SmoothL1 loss) in [this documentation](http://pytorch.org/docs/master/_modules/torch/nn/modules/loss.html).
### Define the loss and optimization
Next, we will define how the model will train by deciding on the loss function and optimizer.
---
```
## Define the loss and optimization
import torch.optim as optim
criterion = nn.MSELoss()
optimizer = optim.Adam(net.parameters(), lr = 0.001)
```
## Training and Initial Observation
Now, we will train on our batched training data from `train_loader` for a number of epochs.
```
def train_net(n_epochs):
# prepare the net for training
net.train()
training_loss = []
for epoch in range(n_epochs): # loop over the dataset multiple times
running_loss = 0.0
# train on batches of data, assumes you already have train_loader
for batch_i, data in enumerate(train_loader):
# get the input images and their corresponding labels
images = data['image']
key_pts = data['keypoints']
# flatten pts
key_pts = key_pts.view(key_pts.size(0), -1)
# convert variables to floats for regression loss
key_pts = key_pts.type(torch.FloatTensor)
images = images.type(torch.FloatTensor)
# forward pass to get outputs
output_pts = net(images)
# calculate the loss between predicted and target keypoints
loss = criterion(output_pts, key_pts)
# zero the parameter (weight) gradients
optimizer.zero_grad()
# backward pass to calculate the weight gradients
loss.backward()
# update the weights
optimizer.step()
# print loss statistics
running_loss += loss.item()
if batch_i % 10 == 9: # print every 10 batches
print('Epoch: {}, Batch: {}, Avg. Loss: {}'.format(epoch + 1, batch_i+1, running_loss/10))
running_loss = 0.0
training_loss.append(running_loss)
print('Finished Training')
return training_loss
# train your network
n_epochs = 10 # start small, and increase when you've decided on your model structure and hyperparams
# this is a Workspaces-specific context manager to keep the connection
# alive while training your model, not part of pytorch
with active_session():
training_loss = train_net(n_epochs)
# visualize the loss as the network trained
plt.figure()
plt.semilogy(training_loss)
plt.grid()
plt.xlabel('Epoch')
plt.ylabel('Loss');
```
## Test data
See how the model performs on previously unseen, test data. We've already loaded and transformed this data, similar to the training data. Next, run the trained model on these images to see what kind of keypoints are produced.
```
# get a sample of test data again
test_images, test_outputs, gt_pts = net_sample_output()
print(test_images.data.size())
print(test_outputs.data.size())
print(gt_pts.size())
## visualize test output
# you can use the same function as before, by un-commenting the line below:
visualize_output(test_images, test_outputs, gt_pts)
```
Once we have found a good model (or two), we have to save the model so we can load it and use it later!
```
## change the name to something uniqe for each new model
model_dir = 'saved_models/'
model_name = 'facial_keypoints_model.pt'
# after training, save your model parameters in the dir 'saved_models'
torch.save(net.state_dict(), model_dir+model_name)
```
## Feature Visualization
Sometimes, neural networks are thought of as a black box, given some input, they learn to produce some output. CNN's are actually learning to recognize a variety of spatial patterns and you can visualize what each convolutional layer has been trained to recognize by looking at the weights that make up each convolutional kernel and applying those one at a time to a sample image. This technique is called feature visualization and it's useful for understanding the inner workings of a CNN.
In the cell below, you can see how to extract a single filter (by index) from your first convolutional layer. The filter should appear as a grayscale grid.
```
# Get the weights in the first conv layer, "conv1"
# if necessary, change this to reflect the name of your first conv layer
weights1 = net.conv1.weight.data
w = weights1.numpy()
filter_index = 0
print(w[filter_index][0])
print(w[filter_index][0].shape)
# display the filter weights
plt.imshow(w[filter_index][0], cmap='gray')
```
## Feature maps
Each CNN has at least one convolutional layer that is composed of stacked filters (also known as convolutional kernels). As a CNN trains, it learns what weights to include in it's convolutional kernels and when these kernels are applied to some input image, they produce a set of **feature maps**. So, feature maps are just sets of filtered images; they are the images produced by applying a convolutional kernel to an input image. These maps show us the features that the different layers of the neural network learn to extract. For example, you might imagine a convolutional kernel that detects the vertical edges of a face or another one that detects the corners of eyes. You can see what kind of features each of these kernels detects by applying them to an image. One such example is shown below; from the way it brings out the lines in an the image, you might characterize this as an edge detection filter.
<img src='images/feature_map_ex.png' width=50% height=50%/>
Next, choose a test image and filter it with one of the convolutional kernels in your trained CNN; look at the filtered output to get an idea what that particular kernel detects.
### Filter an image to see the effect of a convolutional kernel
---
```
## load in and display any image from the transformed test dataset
import cv2
image = cv2.imread('images/mona_lisa.jpg')
# convert image to grayscale
image = cv2.cvtColor(image, cv2.COLOR_RGB2GRAY) / 255.0
## Using cv's filter2D function
filter_kernel = np.array([[ 0, 1, 1],
[-1, 0, 1],
[-1, -1, 0]])
filtered_image = cv2.filter2D(image, -1, filter_kernel)
f, (ax1, ax2, ax3) = plt.subplots(ncols=3, nrows=1, figsize=(10, 5))
ax1.imshow(filter_kernel, cmap='gray')
ax2.imshow(image, cmap='gray')
ax3.imshow(filtered_image, cmap='gray')
ax1.set_title('Kernel')
ax2.set_title('Orginal Image')
ax3.set_title('Filtered image')
plt.tight_layout();
## apply a specific set of filter weights (like the one displayed above) to the test image
weights = net.conv1.weight.data.numpy()
filter_kernel = weights[filter_index][0]
filtered_image = cv2.filter2D(image, -1, filter_kernel)
f, (ax1, ax2, ax3) = plt.subplots(ncols=3, nrows=1, figsize=(10, 5))
ax1.imshow(filter_kernel, cmap='gray')
ax2.imshow(image, cmap='gray')
ax3.imshow(filtered_image, cmap='gray')
ax1.set_title('Kernel')
ax2.set_title('Orginal Image')
ax3.set_title('Filtered image')
plt.tight_layout();
```
---
## Moving on!
Now that we have defined and trained the model (and saved the best model), we are ready to move on to the last notebook, which combines a face detector with your saved model to create a facial keypoint detection system that can predict the keypoints on *any* face in an image!
|
github_jupyter
|
## Dependencies
```
import json, warnings, shutil
from tweet_utility_scripts import *
from tweet_utility_preprocess_roberta_scripts import *
from transformers import TFRobertaModel, RobertaConfig
from tokenizers import ByteLevelBPETokenizer
from tensorflow.keras.models import Model
from tensorflow.keras import optimizers, metrics, losses, layers
from tensorflow.keras.callbacks import EarlyStopping, TensorBoard, ModelCheckpoint
SEED = 0
seed_everything(SEED)
warnings.filterwarnings("ignore")
```
# Load data
```
database_base_path = '/kaggle/input/tweet-dataset-split-roberta-base-96/'
k_fold = pd.read_csv(database_base_path + '5-fold.csv')
display(k_fold.head())
# Unzip files
!tar -xvf /kaggle/input/tweet-dataset-split-roberta-base-96/fold_1.tar.gz
!tar -xvf /kaggle/input/tweet-dataset-split-roberta-base-96/fold_2.tar.gz
!tar -xvf /kaggle/input/tweet-dataset-split-roberta-base-96/fold_3.tar.gz
# !tar -xvf /kaggle/input/tweet-dataset-split-roberta-base-96/fold_4.tar.gz
# !tar -xvf /kaggle/input/tweet-dataset-split-roberta-base-96/fold_5.tar.gz
```
# Model parameters
```
vocab_path = database_base_path + 'vocab.json'
merges_path = database_base_path + 'merges.txt'
base_path = '/kaggle/input/qa-transformers/roberta/'
config = {
"MAX_LEN": 96,
"BATCH_SIZE": 32,
"EPOCHS": 5,
"LEARNING_RATE": 3e-5,
"ES_PATIENCE": 1,
"question_size": 4,
"N_FOLDS": 1,
"base_model_path": base_path + 'roberta-base-tf_model.h5',
"config_path": base_path + 'roberta-base-config.json'
}
with open('config.json', 'w') as json_file:
json.dump(json.loads(json.dumps(config)), json_file)
```
# Model
```
module_config = RobertaConfig.from_pretrained(config['config_path'], output_hidden_states=False)
def model_fn(MAX_LEN):
input_ids = layers.Input(shape=(MAX_LEN,), dtype=tf.int32, name='input_ids')
attention_mask = layers.Input(shape=(MAX_LEN,), dtype=tf.int32, name='attention_mask')
base_model = TFRobertaModel.from_pretrained(config['base_model_path'], config=module_config, name="base_model")
sequence_output = base_model({'input_ids': input_ids, 'attention_mask': attention_mask})
last_state = sequence_output[0]
x_start = layers.Conv1D(1, 1)(last_state)
x_start = layers.Flatten()(x_start)
y_start = layers.Activation('softmax', name='y_start')(x_start)
x_end = layers.Conv1D(1, 1)(last_state)
x_end = layers.Flatten()(x_end)
y_end = layers.Activation('softmax', name='y_end')(x_end)
model = Model(inputs=[input_ids, attention_mask], outputs=[y_start, y_end])
model.compile(optimizers.Adam(lr=config['LEARNING_RATE']),
loss=losses.CategoricalCrossentropy(),
metrics=[metrics.CategoricalAccuracy()])
return model
```
# Tokenizer
```
tokenizer = ByteLevelBPETokenizer(vocab_file=vocab_path, merges_file=merges_path, lowercase=True, add_prefix_space=True)
tokenizer.save('./')
```
# Train
```
history_list = []
AUTO = tf.data.experimental.AUTOTUNE
for n_fold in range(config['N_FOLDS']):
n_fold +=1
print('\nFOLD: %d' % (n_fold))
# Load data
base_data_path = 'fold_%d/' % (n_fold)
x_train = np.load(base_data_path + 'x_train.npy')
y_train = np.load(base_data_path + 'y_train.npy')
x_valid = np.load(base_data_path + 'x_valid.npy')
y_valid = np.load(base_data_path + 'y_valid.npy')
### Delete data dir
shutil.rmtree(base_data_path)
# Train model
model_path = 'model_fold_%d.h5' % (n_fold)
model = model_fn(config['MAX_LEN'])
es = EarlyStopping(monitor='val_loss', mode='min', patience=config['ES_PATIENCE'],
restore_best_weights=True, verbose=1)
checkpoint = ModelCheckpoint(model_path, monitor='val_loss', mode='min',
save_best_only=True, save_weights_only=True)
history = model.fit(list(x_train), list(y_train),
validation_data=(list(x_valid), list(y_valid)),
batch_size=config['BATCH_SIZE'],
callbacks=[checkpoint, es],
epochs=config['EPOCHS'],
verbose=2).history
history_list.append(history)
# Make predictions
train_preds = model.predict(list(x_train))
valid_preds = model.predict(list(x_valid))
k_fold.loc[k_fold['fold_%d' % (n_fold)] == 'train', 'start_fold_%d' % (n_fold)] = train_preds[0].argmax(axis=-1)
k_fold.loc[k_fold['fold_%d' % (n_fold)] == 'train', 'end_fold_%d' % (n_fold)] = train_preds[1].argmax(axis=-1)
k_fold.loc[k_fold['fold_%d' % (n_fold)] == 'validation', 'start_fold_%d' % (n_fold)] = valid_preds[0].argmax(axis=-1)
k_fold.loc[k_fold['fold_%d' % (n_fold)] == 'validation', 'end_fold_%d' % (n_fold)] = valid_preds[1].argmax(axis=-1)
k_fold['end_fold_%d' % (n_fold)] = k_fold['end_fold_%d' % (n_fold)].astype(int)
k_fold['start_fold_%d' % (n_fold)] = k_fold['start_fold_%d' % (n_fold)].astype(int)
k_fold['end_fold_%d' % (n_fold)].clip(0, k_fold['text_len'], inplace=True)
k_fold['start_fold_%d' % (n_fold)].clip(0, k_fold['end_fold_%d' % (n_fold)], inplace=True)
k_fold['prediction_fold_%d' % (n_fold)] = k_fold.apply(lambda x: decode(x['start_fold_%d' % (n_fold)], x['end_fold_%d' % (n_fold)], x['text'], config['question_size'], tokenizer), axis=1)
k_fold['prediction_fold_%d' % (n_fold)].fillna('', inplace=True)
k_fold['jaccard_fold_%d' % (n_fold)] = k_fold.apply(lambda x: jaccard(x['text'], x['prediction_fold_%d' % (n_fold)]), axis=1)
```
# Model loss graph
```
sns.set(style="whitegrid")
for n_fold in range(config['N_FOLDS']):
print('Fold: %d' % (n_fold+1))
plot_metrics(history_list[n_fold])
```
# Model evaluation
```
display(evaluate_model_kfold(k_fold, config['N_FOLDS']).style.applymap(color_map))
```
# Visualize predictions
```
display(k_fold[[c for c in k_fold.columns if not (c.startswith('textID') or
c.startswith('text_len') or
c.startswith('selected_text_len') or
c.startswith('text_wordCnt') or
c.startswith('selected_text_wordCnt') or
c.startswith('fold_') or
c.startswith('start_fold_') or
c.startswith('end_fold_'))]].head(15))
```
|
github_jupyter
|
```
# Import modules
from __future__ import print_function
import numpy as np
import matplotlib.pyplot as plt
# Plot configurations
%matplotlib inline
# Notebook auto reloads code.
%load_ext autoreload
%autoreload 2
```
# NeuroTorch Tutorial
**NeuroTorch** is a framework for reconstructing neuronal morphology from
optical microscopy images. It interfaces PyTorch with different
automated neuron tracing algorithms for fast, accurate, scalable
neuronal reconstructions. It uses deep learning to generate an initial
segmentation of neurons in optical microscopy images. This
segmentation is then traced using various automated neuron tracing
algorithms to convert the segmentation into an SWC file—the most
common neuronal morphology file format. NeuroTorch is designed with
scalability in mind and can handle teravoxel-sized images.
This IPython notebook will outline a brief tutorial for using NeuroTorch
to train and predict on image volume datasets.
## Creating image datasets
One of NeuroTorch’s key features is its dynamic approach to volumetric datasets, which allows it to handle teravoxel-sized images without worrying about memory concerns and efficiency. Everything is loaded just-in-time based on when it is needed or expected to be needed. To load an image dataset, we need
to specify the voxel coordinates of each image file as shown in files `inputs_spec.json` and `labels_spec.json`.
### `inputs_spec.json`
```json
[
{
"filename" : "inputs.tif",
"bounding_box" : [[0, 0, 0], [1024, 512, 50]]
},
{
"filename" : "inputs.tif",
"bounding_box" : [[0, 0, 50], [1024, 512, 100]]
}
]
```
### `labels_spec.json`
```json
[
{
"filename" : "labels.tif",
"bounding_box" : [[0, 0, 0], [1024, 512, 50]]
},
{
"filename" : "labels.tif",
"bounding_box" : [[0, 0, 50], [1024, 512, 100]]
}
]
```
## Loading image datasets
Now that the image datasets for the inputs and labels have been specified,
these datasets can be loaded with NeuroTorch.
```
from neurotorch.datasets.specification import JsonSpec
import os
IMAGE_PATH = '../../tests/images/'
json_spec = JsonSpec() # Initialize the JSON specification
# Create a dataset containing the inputs
inputs = json_spec.open(os.path.join(IMAGE_PATH,
"inputs_spec.json"))
# Create a dataset containing the labels
labels = json_spec.open(os.path.join(IMAGE_PATH,
"labels_spec.json"))
```
## Augmenting datasets
With the image datasets, it is possible to augment data on-the-fly. To implement an augmentation–such as branch occlusion—instantiate an aligned volume and specify the augmentation with the aligned volume.
```
from neurotorch.datasets.dataset import AlignedVolume
from neurotorch.augmentations.occlusion import Occlusion
from neurotorch.augmentations.blur import Blur
from neurotorch.augmentations.brightness import Brightness
from neurotorch.augmentations.dropped import Drop
from neurotorch.augmentations.duplicate import Duplicate
from neurotorch.augmentations.stitch import Stitch
from neurotorch.augmentations.occlusion import Occlusion
volume = AlignedVolume([inputs, labels])
augmented_volume = Occlusion(volume, frequency=0.5)
augmented_volume = Stitch(augmented_volume, frequency=0.5)
augmented_volume = Drop(volume, frequency=0.5)
augmented_volume = Blur(augmented_volume, frequency=0.5)
augmented_volume = Duplicate(augmented_volume, frequency=0.5)
```
## Training with the image datasets
To train a neural network using these image datasets, load the
neural network architecture and initialize a `Trainer`. To save
training checkpoints, add a `CheckpointWriter` to the `Trainer` object.
Lastly, call the `Trainer` object to run training.
```
from neurotorch.core.trainer import Trainer
from neurotorch.nets.RSUNet import RSUNet
from neurotorch.training.checkpoint import CheckpointWriter
from neurotorch.training.logging import ImageWriter, LossWriter
net = RSUNet() # Initialize the U-Net architecture
# Setup the trainer
trainer = Trainer(net, augmented_volume, max_epochs=10,
gpu_device=0)
# Setup the trainer the add a checkpoint every 500 epochs
trainer = LossWriter(trainer, ".", "tutorial_tensorboard")
trainer = ImageWriter(trainer, ".", "tutorial_tensorboard")
trainer = CheckpointWriter(trainer, checkpoint_dir='.',
checkpoint_period=50)
trainer.run_training()
```
## Predicting using NeuroTorch
Once training has completed, we can use the training checkpoints
to predict on image datasets. We first have to
load the neural network architecture and image volume.
We then have to initialize a `Predictor` object and an output volume.
Once these have been specified, we can begin prediction.
```
from neurotorch.nets.RSUNet import RSUNet
from neurotorch.core.predictor import Predictor
from neurotorch.datasets.filetypes import TiffVolume
from neurotorch.datasets.dataset import Array
from neurotorch.datasets.datatypes import (BoundingBox, Vector)
import numpy as np
import tifffile as tif
import os
IMAGE_PATH = '../../tests/images/'
net = RSUNet() # Initialize the U-Net architecture
checkpoint = './iteration_1000.ckpt' # Specify the checkpoint path
with TiffVolume(os.path.join(IMAGE_PATH,
"inputs.tif"),
BoundingBox(Vector(0, 0, 0),
Vector(1024, 512, 50))) as inputs:
predictor = Predictor(net, checkpoint, gpu_device=0)
output_volume = Array(np.zeros(inputs.getBoundingBox()
.getNumpyDim(), dtype=np.float32))
predictor.run(inputs, output_volume, batch_size=5)
tif.imsave("test_prediction.tif",
output_volume.getArray().astype(np.float32))
```
## Displaying the prediction
Predictions are output in logits form. To map this to a
probability distribution, we need to apply a sigmoid function
to the prediction. We can then evaluate the prediction and
ground-truth.
```
# Apply sigmoid function
probability_map = 1/(1+np.exp(-output_volume.getArray()))
# Plot prediction and ground-truth
plt.subplot(2, 1, 1)
plt.title('Prediction')
plt.imshow(output_volume.getArray()[25])
plt.axis('off')
plt.subplot(2, 1, 2)
plt.title('Ground-Truth')
plt.imshow(labels.get(
BoundingBox(Vector(0, 0, 0),
Vector(1024, 512, 50))).getArray()[25],
cmap='gray'
)
plt.axis('off')
plt.show()
```
|
github_jupyter
|
# Data Similarity
Previous experiments have had some strange results, with models occasionally performing abnormally well (or badly) on the out of sample set. To make sure that there are no duplicate samples or abnormally similar studies, I made this notebook
```
import json
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import yaml
from plotnine import *
from sklearn.metrics.pairwise import euclidean_distances
from saged import utils, datasets, models
```
## Load the data
```
dataset_config_file = '../../dataset_configs/refinebio_labeled_dataset.yml'
dataset_config_str = """name: "RefineBioMixedDataset"
compendium_path: "../../data/subset_compendium.pkl"
metadata_path: "../../data/aggregated_metadata.json"
label_path: "../../data/sample_classifications.pkl"
"""
dataset_config = yaml.safe_load(dataset_config_str)
dataset_name = dataset_config.pop('name')
MixedDatasetClass = datasets.RefineBioMixedDataset
all_data = MixedDatasetClass.from_config(**dataset_config)
```
## Look for samples that are very similar to each other despite having different IDs
```
sample_names = all_data.get_samples()
assert len(sample_names) == len(set(sample_names))
sample_names[:5]
expression = all_data.get_all_data()
print(len(sample_names))
print(expression.shape)
sample_distance_matrix = euclidean_distances(expression, expression)
# This is unrelated to debugging the data, I'm just curious
gene_distance_matrix = euclidean_distances(expression.T, expression.T)
sample_distance_matrix.shape
sample_distance_matrix
# See if there are any zero distances outside the diagonal
num_zeros = 10234 * 10234 - np.count_nonzero(sample_distance_matrix)
num_zeros
```
Since there are as many zeros as elements in the diagonal, there are no duplicate samples with different IDs (unless noise was added somewhere)
### Get all distances
Because we know there aren't any zeros outside of the diagonal, we can zero out the lower diagonal and use the the non-zero entries of the upper diagonal to visualize the distance distribution
```
triangle = np.triu(sample_distance_matrix, k=0)
triangle
distances = triangle.flatten()
nonzero_distances = distances[distances != 0]
nonzero_distances.shape
plt.hist(nonzero_distances, bins=20)
```
Distribution looks bimodal, probably due to different platforms having different distances from each other?
```
plt.hist(nonzero_distances[nonzero_distances < 200])
plt.hist(nonzero_distances[nonzero_distances < 100])
```
Looks like there may be some samples that are abnormally close to each other. I wonder whether they're in the same study
## Correspondence between distance and study
```
# There is almost certainly a vectorized way of doing this but oh well
distances = []
first_samples = []
second_samples = []
for row_index in range(sample_distance_matrix.shape[0]):
for col_index in range(sample_distance_matrix.shape[0]):
distance = sample_distance_matrix[row_index, col_index]
if distance == 0:
continue
distances.append(distance)
first_samples.append(sample_names[row_index])
second_samples.append(sample_names[col_index])
distance_df = pd.DataFrame({'distance': distances, 'sample_1': first_samples,
'sample_2': second_samples})
# Free up memory to prevent swapping (probably hopeless if the user has < 32GB)
del(triangle)
del(sample_distance_matrix)
del(distances)
del(first_samples)
del(second_samples)
del(nonzero_distances)
distance_df
sample_to_study = all_data.sample_to_study
del(all_data)
distance_df['study_1'] = distance_df['sample_1'].map(sample_to_study)
distance_df['study_2'] = distance_df['sample_2'].map(sample_to_study)
distance_df['same_study'] = distance_df['study_1'] == distance_df['study_2']
distance_df.head()
print(len(distance_df))
```
For some reason my computer didn't want me to make a figure with 50 million points. We'll work with means instead
```
means_df = distance_df.groupby(['study_1', 'same_study']).mean()
means_df
means_df = means_df.unstack(level='same_study')
means_df = means_df.reset_index()
means_df.head()
# Get rid of the multilevel confusion
means_df.columns = means_df.columns.droplevel()
means_df.columns = ['study_name', 'distance_to_other', 'distance_to_same']
means_df['difference'] = means_df['distance_to_other'] - means_df['distance_to_same']
means_df.head()
plot = ggplot(means_df, aes(x='study_name', y='difference'))
plot += geom_point()
plot += ylab('out of study - in-study mean')
plot
means_df.sort_values(by='difference')
```
These results indicate that most of the data is behaving as expected (the distance between pairs of samples from different studies is less than the distance between pairs of samples within the same study).
The outliers are mostly bead-chip, which makes sense (though they shouldn't be in the dataset and I'll need to look more closely at that later). The one exception is SRP049820 which is run on an Illumina Genome Analyzer II. Maybe it's due to the old tech?
## Without BE Correction
```
%reset -f
# Calling reset because the notebook runs out of memory otherwise
import json
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import yaml
from plotnine import *
from sklearn.metrics.pairwise import euclidean_distances
from saged import utils, datasets, models
dataset_config_file = '../../dataset_configs/refinebio_labeled_dataset.yml'
dataset_config_str = """name: "RefineBioMixedDataset"
compendium_path: "../../data/subset_compendium.pkl"
metadata_path: "../../data/aggregated_metadata.json"
label_path: "../../data/sample_classifications.pkl"
"""
dataset_config = yaml.safe_load(dataset_config_str)
dataset_name = dataset_config.pop('name')
MixedDatasetClass = datasets.RefineBioMixedDataset
all_data = MixedDatasetClass.from_config(**dataset_config)
# Correct for batch effects
all_data = datasets.correct_batch_effects(all_data, 'limma')
```
## Look for samples that are very similar to each other despite having different IDs
```
sample_names = all_data.get_samples()
assert len(sample_names) == len(set(sample_names))
sample_names[:5]
expression = all_data.get_all_data()
print(len(sample_names))
print(expression.shape)
sample_distance_matrix = euclidean_distances(expression, expression)
# This is unrelated to debugging the data, I'm just curious
gene_distance_matrix = euclidean_distances(expression.T, expression.T)
sample_distance_matrix.shape
sample_distance_matrix
# See if there are any zero distances outside the diagonal
num_zeros = 10234 * 10234 - np.count_nonzero(sample_distance_matrix)
num_zeros
```
Since there are as many zeros as elements in the diagonal, there are no duplicate samples with different IDs (unless noise was added somewhere)
### Get all distances
Because we know there aren't any zeros outside of the diagonal, we can zero out the lower diagonal and use the the non-zero entries of the upper diagonal to visualize the distance distribution
```
triangle = np.triu(sample_distance_matrix, k=0)
triangle
distances = triangle.flatten()
nonzero_distances = distances[distances != 0]
nonzero_distances.shape
plt.hist(nonzero_distances, bins=20)
```
Distribution looks bimodal, probably due to different platforms having different distances from each other?
```
plt.hist(nonzero_distances[nonzero_distances < 200])
plt.hist(nonzero_distances[nonzero_distances < 100])
```
Looks like there may be some samples that are abnormally close to each other. I wonder whether they're in the same study
## Correspondence between distance and study
```
# There is almost certainly a vectorized way of doing this but oh well
distances = []
first_samples = []
second_samples = []
for row_index in range(sample_distance_matrix.shape[0]):
for col_index in range(sample_distance_matrix.shape[0]):
distance = sample_distance_matrix[row_index, col_index]
if distance == 0:
continue
distances.append(distance)
first_samples.append(sample_names[row_index])
second_samples.append(sample_names[col_index])
distance_df = pd.DataFrame({'distance': distances, 'sample_1': first_samples,
'sample_2': second_samples})
# Free up memory to prevent swapping (probably hopeless if the user has < 32GB)
del(triangle)
del(sample_distance_matrix)
del(distances)
del(first_samples)
del(second_samples)
del(nonzero_distances)
distance_df
sample_to_study = all_data.sample_to_study
del(all_data)
distance_df['study_1'] = distance_df['sample_1'].map(sample_to_study)
distance_df['study_2'] = distance_df['sample_2'].map(sample_to_study)
distance_df['same_study'] = distance_df['study_1'] == distance_df['study_2']
distance_df.head()
print(len(distance_df))
```
For some reason my computer didn't want me to make a figure with 50 million points. We'll work with means instead
```
means_df = distance_df.groupby(['study_1', 'same_study']).mean()
means_df
means_df = means_df.unstack(level='same_study')
means_df = means_df.reset_index()
means_df.head()
# Get rid of the multilevel confusion
means_df.columns = means_df.columns.droplevel()
means_df.columns = ['study_name', 'distance_to_other', 'distance_to_same']
means_df['difference'] = means_df['distance_to_other'] - means_df['distance_to_same']
means_df.head()
plot = ggplot(means_df, aes(x='study_name', y='difference'))
plot += geom_point()
plot += ylab('out of study - in-study mean')
plot
means_df.sort_values(by='difference')
```
These results indicate that most of the data is behaving as expected (the distance between pairs of samples from different studies is less than the distance between pairs of samples within the same study).
The outliers are mostly bead-chip, which makes sense (though they shouldn't be in the dataset and I'll need to look more closely at that later). The one exception is SRP049820 which is run on an Illumina Genome Analyzer II. Maybe it's due to the old tech?
|
github_jupyter
|
# Getting started in scikit-learn with the famous iris dataset
*From the video series: [Introduction to machine learning with scikit-learn](https://github.com/justmarkham/scikit-learn-videos)*
```
#environment setup with watermark
%load_ext watermark
%watermark -a 'Gopala KR' -u -d -v -p watermark,numpy,pandas,matplotlib,nltk,sklearn,tensorflow,theano,mxnet,chainer
```
## Agenda
- What is the famous iris dataset, and how does it relate to machine learning?
- How do we load the iris dataset into scikit-learn?
- How do we describe a dataset using machine learning terminology?
- What are scikit-learn's four key requirements for working with data?
## Introducing the iris dataset

- 50 samples of 3 different species of iris (150 samples total)
- Measurements: sepal length, sepal width, petal length, petal width
```
from IPython.display import IFrame
IFrame('http://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data', width=300, height=200)
```
## Machine learning on the iris dataset
- Framed as a **supervised learning** problem: Predict the species of an iris using the measurements
- Famous dataset for machine learning because prediction is **easy**
- Learn more about the iris dataset: [UCI Machine Learning Repository](http://archive.ics.uci.edu/ml/datasets/Iris)
## Loading the iris dataset into scikit-learn
```
# import load_iris function from datasets module
from sklearn.datasets import load_iris
# save "bunch" object containing iris dataset and its attributes
iris = load_iris()
type(iris)
# print the iris data
print(iris.data)
```
## Machine learning terminology
- Each row is an **observation** (also known as: sample, example, instance, record)
- Each column is a **feature** (also known as: predictor, attribute, independent variable, input, regressor, covariate)
```
# print the names of the four features
print(iris.feature_names)
# print integers representing the species of each observation
print(iris.target)
# print the encoding scheme for species: 0 = setosa, 1 = versicolor, 2 = virginica
print(iris.target_names)
```
- Each value we are predicting is the **response** (also known as: target, outcome, label, dependent variable)
- **Classification** is supervised learning in which the response is categorical
- **Regression** is supervised learning in which the response is ordered and continuous
## Requirements for working with data in scikit-learn
1. Features and response are **separate objects**
2. Features and response should be **numeric**
3. Features and response should be **NumPy arrays**
4. Features and response should have **specific shapes**
```
# check the types of the features and response
print(type(iris.data))
print(type(iris.target))
# check the shape of the features (first dimension = number of observations, second dimensions = number of features)
print(iris.data.shape)
# check the shape of the response (single dimension matching the number of observations)
print(iris.target.shape)
# store feature matrix in "X"
X = iris.data
# store response vector in "y"
y = iris.target
```
## Resources
- scikit-learn documentation: [Dataset loading utilities](http://scikit-learn.org/stable/datasets/)
- Jake VanderPlas: Fast Numerical Computing with NumPy ([slides](https://speakerdeck.com/jakevdp/losing-your-loops-fast-numerical-computing-with-numpy-pycon-2015), [video](https://www.youtube.com/watch?v=EEUXKG97YRw))
- Scott Shell: [An Introduction to NumPy](http://www.engr.ucsb.edu/~shell/che210d/numpy.pdf) (PDF)
## Comments or Questions?
- Email: <[email protected]>
- Website: http://dataschool.io
- Twitter: [@justmarkham](https://twitter.com/justmarkham)
```
from IPython.core.display import HTML
def css_styling():
styles = open("styles/custom.css", "r").read()
return HTML(styles)
css_styling()
test complete; Gopal
```
|
github_jupyter
|
# How to Use Forecasters in Merlion
This notebook will guide you through using all the key features of forecasters in Merlion. Specifically, we will explain
1. Initializing a forecasting model (including ensembles and automatic model selectors)
1. Training the model
1. Producing a forecast with the model
1. Visualizing the model's predictions
1. Quantitatively evaluating the model
1. Saving and loading a trained model
1. Simulating the live deployment of a model using a `ForecastEvaluator`
We will be using a single example time series for this whole notebook. We load it now:
```
import matplotlib.pyplot as plt
import numpy as np
from merlion.utils.time_series import TimeSeries
from ts_datasets.forecast import M4
# Load the time series
# time_series is a time-indexed pandas.DataFrame
# trainval is a time-indexed pandas.Series indicating whether each timestamp is for training or testing
time_series, metadata = M4(subset="Hourly")[5]
trainval = metadata["trainval"]
# Is there any missing data?
timedeltas = np.diff(time_series.index)
print(f"Has missing data: {any(timedeltas != timedeltas[0])}")
# Visualize the time series and draw a dotted line to indicate the train/test split
fig = plt.figure(figsize=(10, 6))
ax = fig.add_subplot(111)
ax.plot(time_series)
ax.axvline(time_series[trainval].index[-1], ls="--", lw="2", c="k")
plt.show()
# Split the time series into train/test splits, and convert it to Merlion format
train_data = TimeSeries.from_pd(time_series[trainval])
test_data = TimeSeries.from_pd(time_series[~trainval])
print(f"{len(train_data)} points in train split, "
f"{len(test_data)} points in test split.")
```
## Model Initialization
In this notebook, we will use three different forecasting models:
1. ARIMA (a classic stochastic process model)
2. Prophet (Facebook's popular time series forecasting model)
3. MSES (the Multi-Scale Exponential Smoothing model, developed in-house)
Let's start by initializing each of them.
```
# Import models & configs
from merlion.models.forecast.arima import Arima, ArimaConfig
from merlion.models.forecast.prophet import Prophet, ProphetConfig
from merlion.models.forecast.smoother import MSES, MSESConfig
# Import data pre-processing transforms
from merlion.transform.base import Identity
from merlion.transform.resample import TemporalResample
# All models are initialized using the syntax ModelClass(config),
# where config is a model-specific configuration object. This is where
# you specify any algorithm-specific hyperparameters, as well as any
# data pre-processing transforms.
# ARIMA assumes that input data is sampled at a regular interval,
# so we set its transform to resample at that interval. We must also specify
# a maximum prediction horizon.
config1 = ArimaConfig(max_forecast_steps=100, order=(20, 1, 5),
transform=TemporalResample(granularity="1h"))
model1 = Arima(config1)
# Prophet has no real assumptions on the input data (and doesn't require
# a maximum prediction horizon), so we skip data pre-processing by using
# the Identity transform.
config2 = ProphetConfig(max_forecast_steps=None, transform=Identity())
model2 = Prophet(config2)
# MSES assumes that the input data is sampled at a regular interval,
# and requires us to specify a maximum prediction horizon. We will
# also specify its look-back hyperparameter to be 60 here
config3 = MSESConfig(max_forecast_steps=100, max_backstep=60,
transform=TemporalResample(granularity="1h"))
model3 = MSES(config3)
```
Now that we have initialized the individual models, we will also combine them in two different ensembles: `ensemble` simply takes the mean prediction of each individual model, and `selector` selects the best individual model based on its sMAPE (symmetric Mean Average Precision Error). The sMAPE is a metric used to evaluate the quality of a continuous forecast. For ground truth $y \in \mathbb{R}^T$ and prediction $\hat{y} \in \mathbb{R}^T$, the sMAPE is computed as
$$
\mathrm{sMAPE}(y, \hat{y}) = \frac{200}{T} \sum_{t = 1}^{T} \frac{\lvert \hat{y}_t - y_t \rvert}{\lvert\hat{y}_t\rvert + \lvert y_t \rvert}
$$
```
from merlion.evaluate.forecast import ForecastMetric
from merlion.models.ensemble.combine import Mean, ModelSelector
from merlion.models.ensemble.forecast import ForecasterEnsemble, ForecasterEnsembleConfig
# The ForecasterEnsemble is a forecaster, and we treat it as a first-class model.
# Its config takes a combiner object, specifying how you want to combine the
# predictions of individual models in the ensemble. There are two ways to specify
# the actual models in the ensemble, which we cover below.
# The first way to specify the models in the ensemble is to provide their individual
# configs when initializing the ForecasterEnsembleConfig. Note that if using this
# syntax, you must also provide the names of the model classes.
#
# The combiner here will simply take the mean prediction of the ensembles here
ensemble_config = ForecasterEnsembleConfig(
combiner=Mean(),
model_configs=[(type(model1).__name__, config1),
(type(model2).__name__, config2),
(type(model3).__name__, config3)])
ensemble = ForecasterEnsemble(config=ensemble_config)
# Alternatively, you can skip giving the individual model configs to the
# ForecasterEnsembleConfig, and instead directly specify the models when
# initializing the ForecasterEnsemble itself.
#
# The combiner here uses the sMAPE to compare individual models, and
# selects the model with the lowest sMAPE
selector_config = ForecasterEnsembleConfig(
combiner=ModelSelector(metric=ForecastMetric.sMAPE))
selector = ForecasterEnsemble(
config=selector_config, models=[model1, model2, model3])
```
## Model Training
All forecasting models (and ensembles) share the same API for training. The `train()` method returns the model's predictions and standard error of those predictions on the training data. Note that the standard error is just `None` if the model doesn't support uncertainty estimation (this is the case for MSES and ensembles).
```
print(f"Training {type(model1).__name__}...")
forecast1, stderr1 = model1.train(train_data)
print(f"\nTraining {type(model2).__name__}...")
forecast2, stderr2 = model2.train(train_data)
print(f"\nTraining {type(model3).__name__}...")
forecast3, stderr3 = model3.train(train_data)
print("\nTraining ensemble...")
forecast_e, stderr_e = ensemble.train(train_data)
print("\nTraining model selector...")
forecast_s, stderr_s = selector.train(train_data)
print("Done!")
```
## Model Inference
To obtain a forecast from a trained model, we simply call `model.forecast()` with the Unix timestamps at which we the model to generate a forecast. In many cases, you may obtain these directly from a time series as shown below.
```
# Truncate the test data to ensure that we are within each model's maximum
# forecast horizon.
sub_test_data = test_data[:50]
# Obtain the time stamps corresponding to the test data
time_stamps = sub_test_data.univariates[sub_test_data.names[0]].time_stamps
# Get the forecast & standard error of each model. These are both
# merlion.utils.TimeSeries objects. Note that the standard error is None for
# models which don't support uncertainty estimation (like MSES and all
# ensembles).
forecast1, stderr1 = model1.forecast(time_stamps=time_stamps)
forecast2, stderr2 = model2.forecast(time_stamps=time_stamps)
# You may optionally specify a time series prefix as context. If one isn't
# specified, the prefix is assumed to be the training data. Here, we just make
# this dependence explicit. More generally, this feature is useful if you want
# to use a pre-trained model to make predictions on data further in the future
# from the last time it was trained.
forecast3, stderr3 = model3.forecast(time_stamps=time_stamps, time_series_prev=train_data)
# The same options are available for ensembles as well, though the stderr is None
forecast_e, stderr_e = ensemble.forecast(time_stamps=time_stamps)
forecast_s, stderr_s = selector.forecast(time_stamps=time_stamps, time_series_prev=train_data)
```
## Model Visualization and Quantitative Evaluation
It is fairly transparent to visualize a model's forecast and also quantitatively evaluate the forecast, using standard metrics like sMAPE. We show examples for all five models below.
Below, we quantitatively evaluate the models using the sMAPE metric. However, the `ForecastMetric` enum includes a number of other options as well. In general, you may use the syntax
```
ForecastMetric.<metric_name>.value(ground_truth=ground_truth, predict=forecast)
```
where `<metric_name>` is the name of the evaluation metric (see the API docs for details and more options), `ground_truth` is the original time series, and `forecast` is the forecast returned by the model. We show concrete examples with `ForecastMetric.sMAPE` below.
```
from merlion.evaluate.forecast import ForecastMetric
# We begin by computing the sMAPE of ARIMA's forecast (scale is 0 to 100)
smape1 = ForecastMetric.sMAPE.value(ground_truth=sub_test_data,
predict=forecast1)
print(f"{type(model1).__name__} sMAPE is {smape1:.3f}")
# Next, we can visualize the actual forecast, and understand why it
# attains this particular sMAPE. Since ARIMA supports uncertainty
# estimation, we plot its error bars too.
fig, ax = model1.plot_forecast(time_series=sub_test_data,
plot_forecast_uncertainty=True)
plt.show()
# We begin by computing the sMAPE of Prophet's forecast (scale is 0 to 100)
smape2 = ForecastMetric.sMAPE.value(sub_test_data, forecast2)
print(f"{type(model2).__name__} sMAPE is {smape2:.3f}")
# Next, we can visualize the actual forecast, and understand why it
# attains this particular sMAPE. Since Prophet supports uncertainty
# estimation, we plot its error bars too.
# Note that we can specify time_series_prev here as well, though it
# will not be visualized unless we also supply the keyword argument
# plot_time_series_prev=True.
fig, ax = model2.plot_forecast(time_series=sub_test_data,
time_series_prev=train_data,
plot_forecast_uncertainty=True)
plt.show()
# We begin by computing the sMAPE of MSES's forecast (scale is 0 to 100)
smape3 = ForecastMetric.sMAPE.value(sub_test_data, forecast3)
print(f"{type(model3).__name__} sMAPE is {smape3:.3f}")
# Next, we visualize the actual forecast, and understand why it
# attains this particular sMAPE.
fig, ax = model3.plot_forecast(time_series=sub_test_data,
plot_forecast_uncertainty=True)
plt.show()
# Compute the sMAPE of the ensemble's forecast (scale is 0 to 100)
smape_e = ForecastMetric.sMAPE.value(sub_test_data, forecast_e)
print(f"Ensemble sMAPE is {smape_e:.3f}")
# Visualize the forecast.
fig, ax = ensemble.plot_forecast(time_series=sub_test_data,
plot_forecast_uncertainty=True)
plt.show()
# Compute the sMAPE of the selector's forecast (scale is 0 to 100)
smape_s = ForecastMetric.sMAPE.value(sub_test_data, forecast_s)
print(f"Selector sMAPE is {smape_s:.3f}")
# Visualize the forecast.
fig, ax = selector.plot_forecast(time_series=sub_test_data,
plot_forecast_uncertainty=True)
plt.show()
```
## Saving & Loading Models
All models have a `save()` method and `load()` class method. Models may also be loaded with the assistance of the `ModelFactory`, which works for arbitrary models. The `save()` method creates a new directory at the specified path, where it saves a `json` file representing the model's config, as well as a binary file for the model's state.
We will demonstrate these behaviors using our `Prophet` model (`model2`) for concreteness.
```
import json
import os
import pprint
from merlion.models.factory import ModelFactory
# Save the model
os.makedirs("models", exist_ok=True)
path = os.path.join("models", "prophet")
model2.save(path)
# Print the config saved
pp = pprint.PrettyPrinter()
with open(os.path.join(path, "config.json")) as f:
print(f"{type(model2).__name__} Config")
pp.pprint(json.load(f))
# Load the model using Prophet.load()
model2_loaded = Prophet.load(dirname=path)
# Load the model using the ModelFactory
model2_factory_loaded = ModelFactory.load(name="Prophet", model_path=path)
```
We can do the same exact thing with ensembles! Note that the ensemble saves each of its sub-models in a different sub-directory, which it tracks manually. Additionally, the combiner (which is saved in the `ForecasterEnsembleConfig`), keeps track of the sMAPE achieved by each model (the `metric_values` key).
```
# Save the selector
path = os.path.join("models", "selector")
selector.save(path)
# Print the config saved. Note that we've saved all individual models,
# and their paths are specified under the model_paths key.
pp = pprint.PrettyPrinter()
with open(os.path.join(path, "config.json")) as f:
print(f"Selector Config")
pp.pprint(json.load(f))
# Load the selector
selector_loaded = ForecasterEnsemble.load(dirname=path)
# Load the selector using the ModelFactory
selector_factory_loaded = ModelFactory.load(name="ForecasterEnsemble", model_path=path)
```
## Simulating Live Model Deployment
A typical model deployment scenario is as follows:
1. Train an initial model on some recent historical data
1. At a regular interval `cadence`, obtain the model's forecast for a certain `horizon`
1. At a regular interval `retrain_freq`, retrain the entire model on the most recent data
1. Optionally, specify a maximum amount of data (`train_window`) that the model should use for training
We provide a `ForecastEvaluator` object which simulates the above deployment scenario, and also allows a user to evaluate the quality of the forecaster according to an evaluation metric of their choice. We illustrate two examples below, using ARIMA for the first example, and the model selector for the second.
```
from merlion.evaluate.forecast import ForecastEvaluator, ForecastEvaluatorConfig, ForecastMetric
def create_evaluator(model):
# Re-initialize the model, so we can re-train it from scratch
model.reset()
# Create an evaluation pipeline for the model, where we
# -- get the model's forecast every hour
# -- have the model forecast for a horizon of 6 hours
# -- re-train the model every 12 hours
# -- when we re-train the model, retrain it on only the past 2 weeks of data
evaluator = ForecastEvaluator(
model=model, config=ForecastEvaluatorConfig(
cadence="1h", horizon="6h", retrain_freq="12h", train_window="14d")
)
return evaluator
```
First, let's evaluate ARIMA.
```
# Obtain the results of running the evaluation pipeline for ARIMA.
# These result objects are to be treated as a black box, and should be
# passed directly to the evaluator's evaluate() method.
model1_evaluator = create_evaluator(model1)
model1_train_result, model1_test_result = model1_evaluator.get_predict(
train_vals=train_data, test_vals=test_data)
# Evaluate ARIMA's sMAPE and RMSE
smape = model1_evaluator.evaluate(
ground_truth=test_data,
predict=model1_test_result,
metric=ForecastMetric.sMAPE)
rmse = model1_evaluator.evaluate(
ground_truth=test_data,
predict=model1_test_result,
metric=ForecastMetric.RMSE)
print(f"{type(model1).__name__} sMAPE: {smape:.3f}")
print(f"{type(model1).__name__} RMSE: {rmse:.3f}")
```
Next, we will evaluate the ensemble (taking the mean prediction of ARIMA, Prophet, and MSES every time the models are called).
```
# Obtain the results of running the evaluation pipeline for the ensemble.
# These result objects are to be treated as a black box, and should be
# passed directly to the evaluator's evaluate() method.
ensemble_evaluator = create_evaluator(ensemble)
ensemble_train_result, ensemble_test_result = ensemble_evaluator.get_predict(
train_vals=train_data, test_vals=test_data)
# Evaluate the selector's sMAPE and RMSE
smape = ensemble_evaluator.evaluate(
ground_truth=test_data,
predict=ensemble_test_result,
metric=ForecastMetric.sMAPE)
rmse = ensemble_evaluator.evaluate(
ground_truth=test_data,
predict=ensemble_test_result,
metric=ForecastMetric.RMSE)
print(f"Ensemble sMAPE: {smape:.3f}")
print(f"Ensemble RMSE: {rmse:.3f}")
```
|
github_jupyter
|
# Strings
```
name = "Robin"
```
## Multi line strings
```
paragraph = "I am thinking of writing something that spans"\
"multiple lines and Nobody is helping me with that. So here"\
"is me typing something random"
print(paragraph)
# \n represents Newline
paragraph = "I am thinking of writing something that spans\n\
multiple lines and Nobody is helping me with that. So here\n\
is me typing something random"
print(paragraph)
```
## String indices
```
sample_string = "Sorry Madam"
# Subscipt operator : []
sample_string[1] # sample_string of 1
sample_string[2]
'''
*******************************************
Example of a multi-line comment:
To access the first character of the string
you need to use the index 0
*******************************************
'''
sample_string[0]
'''
To access a part of string, use a colon notation in the
subscript operator []
'''
sample_string[0:5]
# give me the string madam from the sample_string
sample_string[6:11]
# Slice the string from index 6 and go until the end
sample_string[6:]
# give me string "Sorry" without writing 0 as index
sample_string[:5]
print(sample_string)
# Negative index: -1 will access the last element
print(sample_string[-1])
# access first element with negative index
print (sample_string[-11])
# This index is invalid
print (sample_string[-12])
sample_string[11]
# Python tries to slice the string
# by reading from left to right
# Indices in the statement below are wrong
sample_string[-4:-10]
sample_string[-10:-4]
sample_string[0:5]
'''
Slice the string from index 0 to 4
with the jump of 2
'''
sample_string[0:5:2]
sample_string[-5:0] # This will not work
sample_string[-5:] # will give you the desired result
sample_string2 = "I love Python"
# Slice this string and give me every third characater
# Expected outout : "Io tn"
# Pythonic
print(sample_string2[0::3])
print(sample_string2[::3]) # most pythonic
print(sample_string2[0:14:3])
print(sample_string2[0:15:3])
num1 = "5"
num2 = "3"
print(num1+ num2)
sample_string2
print(sample_string2[0]+sample_string2[7:14])
print(sample_string2[0]+ sample_string2[2]+sample_string2[7:14])
print(sample_string, sample_string2)
print(sample_string + sample_string2)
print(sample_string + "!! "+ sample_string2)
# to convert a string into lower case characters
sample_string.lower()
sample_string.upper()
sample_string.count()
type(sample_string)
help(str.count)
sample_string
sample_string.count('a')
fruit = "banana"
#it has overlapping word ana
fruit.count('ana')
sample_string.count('r',0,3)
sample_string
# Find length of the string
# i.e. number of characters in the string
len(sample_string)
help(len)
name = "Jeroen"
age = 27
country = "Netherlands"
print("Hoi, I am {}. I am {} years old.I come from {}".format(name,age, country) )
fruit
fruit2="guanabana"
fruit == 'banana'
is_it_raining = False
```
### Conditional operators
```
== : Compare two expressions for equality
!= : compare for inequality
< : compare less than
> : greater than
<= : less than or equal to
>= : greater than or equal to
```
```
fruit == 'banana'
fruit != 'orange'
print("fruit =", fruit)
print("fruit2 =", fruit2)
fruit[0:4] == fruit2[5:9]
```
### Conditional statements
```
it_is_raining = False
it_is_sunny = not it_is_raining
if it_is_sunny:
print("I will go swimming in Sloterplas")
else:
print("I will work on Python (coding)")
it_is_raining = True
it_is_sunny = not it_is_raining
if it_is_sunny:
print("I will go swimming in Sloterplas")
print("I will run")
else:
print("I will work on Python (coding)")
# Accept a number from user (input)
# If the number is even, print "Hurray"
# Else print "Meah"
number = int(input("Enter a number : "))
if number%2 == 0:
print ("Hurray")
else:
print("Meah")
x = 3 # Assignment
print(x)
print(x%2)
time = float(input("Enter a number between 0 and 23"))
if time >= 0 and time <= 8:
print("I am asleep")
elif time >8 and time <= 10:
print("Morning rituals")
elif time > 10 and time <= 13:
print("I am Pythoning")
elif time >13 and time <= 14:
print("I am lunching")
elif time >14 and time < 17:
print("I am researching")
else:
print("I am having fun")
```
### Loops
```
# Not so smart way of printing Hello 5 times
print("Hello")
print("Hello")
print("Hello")
print("Hello")
print("Hello")
# Smart way of printing Hello 5 times
for i in range(5):
print("Hello")
for i in range(5):
print(i)
for i in range(1,6):
print(i)
for u in range(1,6):
print(u, ")", "Hello")
sample_string
'''
a way of accessing individual characters in string
by index
'''
some_number = 15
for i in range(len(sample_string)):
print("[",str(i),"]:", sample_string[i], some_number)
```
```
i = 0
print("[",str(i),"]:", sample_string[0], some_number)
i = 1
print("[",str(i),"]:", sample_string[1], some_number)
i = 2
print("[",str(i),"]:", sample_string[2], some_number)
i = 3
print("[",str(i),"]:", sample_string[3], some_number)
...
...
i = 10
print("[",str(i),"]:", sample_string[10], some_number)
```
```
len(sample_string)
```
```
n = input()
n= 12
12
24
36
48
60
72
84
96
108
120
n = 4
4
8
12
16
20
24
.
40
```
```
n = int(input())
for i in range(1,11):
print(i*n)
```
|
github_jupyter
|
###Set up working directory
```
cd /usr/local/notebooks
mkdir -p ./workdir
#check seqfile files to process in data directory (make sure you still remember the data directory)
!ls ./data/test/data
```
#README
## This part of pipeline search for the SSU rRNA gene fragments, classify them, and extract reads aligned specific region. It is also heavy lifting part of the whole pipeline (more cpu will help).
## This part works with one seqfile a time. You just need to change the "Seqfile" and maybe other parameters in the two cells bellow.
## To run commands, click "Cell" then "Run All". After it finishes, you will see "\*** pipeline runs successsfully :)" at bottom of this pape.
##If your computer has many processors, there are two ways to make use of the resource:
1. Set "Cpu" higher number.
2. make more copies of this notebook (click "File" then "Make a copy" in menu bar), so you can run the step on multiple files at the same time.
(Again we assume the "Seqfile" is quality trimmed.)
###Here we will process one file at a time; set the "Seqfile" variable to the seqfile name to be be processed
###First part of seqfile basename (separated by ".") will be the label of this sample, so named it properly.
e.g. for "/usr/local/notebooks/data/test/data/1c.fa", "1c" will the label of this sample.
```
Seqfile='./data/test/data/2d.fa'
```
###Other parameters to set
```
Cpu='2' # number of maxixum threads for search and alignment
Hmm='./data/SSUsearch_db/Hmm.ssu.hmm' # hmm model for ssu
Gene='ssu'
Script_dir='./SSUsearch/scripts'
Gene_model_org='./data/SSUsearch_db/Gene_model_org.16s_ecoli_J01695.fasta'
Ali_template='./data/SSUsearch_db/Ali_template.silva_ssu.fasta'
Start='577' #pick regions for de novo clustering
End='727'
Len_cutoff='100' # min length for reads picked for the region
Gene_tax='./data/SSUsearch_db/Gene_tax.silva_taxa_family.tax' # silva 108 ref
Gene_db='./data/SSUsearch_db/Gene_db.silva_108_rep_set.fasta'
Gene_tax_cc='./data/SSUsearch_db/Gene_tax_cc.greengene_97_otus.tax' # greengene 2012.10 ref for copy correction
Gene_db_cc='./data/SSUsearch_db/Gene_db_cc.greengene_97_otus.fasta'
# first part of file basename will the label of this sample
import os
Filename=os.path.basename(Seqfile)
Tag=Filename.split('.')[0]
import os
Hmm=os.path.abspath(Hmm)
Seqfile=os.path.abspath(Seqfile)
Script_dir=os.path.abspath(Script_dir)
Gene_model_org=os.path.abspath(Gene_model_org)
Ali_template=os.path.abspath(Ali_template)
Gene_tax=os.path.abspath(Gene_tax)
Gene_db=os.path.abspath(Gene_db)
Gene_tax_cc=os.path.abspath(Gene_tax_cc)
Gene_db_cc=os.path.abspath(Gene_db_cc)
os.environ.update(
{'Cpu':Cpu,
'Hmm':os.path.abspath(Hmm),
'Gene':Gene,
'Seqfile':os.path.abspath(Seqfile),
'Filename':Filename,
'Tag':Tag,
'Script_dir':os.path.abspath(Script_dir),
'Gene_model_org':os.path.abspath(Gene_model_org),
'Ali_template':os.path.abspath(Ali_template),
'Start':Start,
'End':End,
'Len_cutoff':Len_cutoff,
'Gene_tax':os.path.abspath(Gene_tax),
'Gene_db':os.path.abspath(Gene_db),
'Gene_tax_cc':os.path.abspath(Gene_tax_cc),
'Gene_db_cc':os.path.abspath(Gene_db_cc)})
!echo "*** make sure: parameters are right"
!echo "Seqfile: $Seqfile\nCpu: $Cpu\nFilename: $Filename\nTag: $Tag"
cd workdir
mkdir -p $Tag.ssu.out
### start hmmsearch
!echo "*** hmmsearch starting"
!time hmmsearch --incE 10 --incdomE 10 --cpu $Cpu \
--domtblout $Tag.ssu.out/$Tag.qc.$Gene.hmmdomtblout \
-o /dev/null -A $Tag.ssu.out/$Tag.qc.$Gene.sto \
$Hmm $Seqfile
!echo "*** hmmsearch finished"
!python $Script_dir/get-seq-from-hmmout.py \
$Tag.ssu.out/$Tag.qc.$Gene.hmmdomtblout \
$Tag.ssu.out/$Tag.qc.$Gene.sto \
$Tag.ssu.out/$Tag.qc.$Gene
```
### Pass hits to mothur aligner
```
!echo "*** Starting mothur align"
!cat $Gene_model_org $Tag.ssu.out/$Tag.qc.$Gene > $Tag.ssu.out/$Tag.qc.$Gene.RFadded
# mothur does not allow tab between its flags, thus no indents here
!time mothur "#align.seqs(candidate=$Tag.ssu.out/$Tag.qc.$Gene.RFadded, template=$Ali_template, threshold=0.5, flip=t, processors=$Cpu)"
!rm -f mothur.*.logfile
```
### Get aligned seqs that have > 50% matched to references
```
!python $Script_dir/mothur-align-report-parser-cutoff.py \
$Tag.ssu.out/$Tag.qc.$Gene.align.report \
$Tag.ssu.out/$Tag.qc.$Gene.align \
$Tag.ssu.out/$Tag.qc.$Gene.align.filter \
0.5
!python $Script_dir/remove-gap.py $Tag.ssu.out/$Tag.qc.$Gene.align.filter $Tag.ssu.out/$Tag.qc.$Gene.align.filter.fa
```
### Search is done here (the computational intensive part). Hooray!
- \$Tag.ssu.out/\$Tag.qc.\$Gene.align.filter:
aligned SSU rRNA gene fragments
- \$Tag.ssu.out/\$Tag.qc.\$Gene.align.filter.fa:
unaligned SSU rRNA gene fragments
### Extract the reads mapped 150bp region in V4 (577-727 in *E.coli* SSU rRNA gene position) for unsupervised clustering
```
!python $Script_dir/region-cut.py $Tag.ssu.out/$Tag.qc.$Gene.align.filter $Start $End $Len_cutoff
!mv $Tag.ssu.out/$Tag.qc.$Gene.align.filter."$Start"to"$End".cut.lenscreen $Tag.ssu.out/$Tag.forclust
```
### Classify SSU rRNA gene seqs using SILVA
```
!rm -f $Tag.ssu.out/$Tag.qc.$Gene.align.filter.*.wang.taxonomy
!mothur "#classify.seqs(fasta=$Tag.ssu.out/$Tag.qc.$Gene.align.filter.fa, template=$Gene_db, taxonomy=$Gene_tax, cutoff=50, processors=$Cpu)"
!mv $Tag.ssu.out/$Tag.qc.$Gene.align.filter.*.wang.taxonomy \
$Tag.ssu.out/$Tag.qc.$Gene.align.filter.wang.silva.taxonomy
!python $Script_dir/count-taxon.py \
$Tag.ssu.out/$Tag.qc.$Gene.align.filter.wang.silva.taxonomy \
$Tag.ssu.out/$Tag.qc.$Gene.align.filter.wang.silva.taxonomy.count
!rm -f mothur.*.logfile
```
### Classify SSU rRNA gene seqs with Greengene for copy correction later
```
!rm -f $Tag.ssu.out/$Tag.qc.$Gene.align.filter.*.wang.taxonomy
!mothur "#classify.seqs(fasta=$Tag.ssu.out/$Tag.qc.$Gene.align.filter.fa, template=$Gene_db_cc, taxonomy=$Gene_tax_cc, cutoff=50, processors=$Cpu)"
!mv $Tag.ssu.out/$Tag.qc.$Gene.align.filter.*.wang.taxonomy \
$Tag.ssu.out/$Tag.qc.$Gene.align.filter.wang.gg.taxonomy
!python $Script_dir/count-taxon.py \
$Tag.ssu.out/$Tag.qc.$Gene.align.filter.wang.gg.taxonomy \
$Tag.ssu.out/$Tag.qc.$Gene.align.filter.wang.gg.taxonomy.count
!rm -f mothur.*.logfile
# check the output directory
!ls $Tag.ssu.out
```
### This part of pipeline (working with one sequence file) finishes here. Next we will combine samples for community analysis (see unsupervised analysis).
Following are files useful for community analysis:
* 1c.577to727: aligned fasta file of seqs mapped to target region for de novo clustering
* 1c.qc.ssu.align.filter: aligned fasta file of all SSU rRNA gene fragments
* 1c.qc.ssu.align.filter.wang.gg.taxonomy: Greengene taxonomy (for copy correction)
* 1c.qc.ssu.align.filter.wang.silva.taxonomy: SILVA taxonomy
```
!echo "*** pipeline runs successsfully :)"
```
|
github_jupyter
|
```
import numpy
import sys
import nmslib
import time
import math
from sklearn.neighbors import NearestNeighbors
from sklearn.model_selection import train_test_split
# Just read the data
all_data_matrix = numpy.loadtxt('../../sample_data/sift_10k.txt')
# Create a held-out query data set
(data_matrix, query_matrix) = train_test_split(all_data_matrix, test_size = 0.1)
print("# of queries %d, # of data points %d" % (query_matrix.shape[0], data_matrix.shape[0]) )
# Set index parameters
# These are the most important onese
M = 15
efC = 100
num_threads = 4
index_time_params = {'M': M, 'indexThreadQty': num_threads, 'efConstruction': efC, 'post' : 0,
'skip_optimized_index' : 1 # using non-optimized index!
}
# Number of neighbors
K=100
# Space name should correspond to the space name
# used for brute-force search
space_name='l2sqr_sift'
# Intitialize the library, specify the space, the type of the vector and add data points
# for SIFT data, we want DENSE_UINT8_VECTOR and distance type INT
index = nmslib.init(method='hnsw',
space=space_name,
data_type=nmslib.DataType.DENSE_UINT8_VECTOR,
dtype=nmslib.DistType.INT)
index.addDataPointBatch(data_matrix.astype(numpy.uint8))
# Create an index
start = time.time()
index.createIndex(index_time_params)
end = time.time()
print('Index-time parameters', index_time_params)
print('Indexing time = %f' % (end-start))
# Setting query-time parameters
efS = 100
query_time_params = {'efSearch': efS}
print('Setting query-time parameters', query_time_params)
index.setQueryTimeParams(query_time_params)
# Querying
query_qty = query_matrix.shape[0]
start = time.time()
nbrs = index.knnQueryBatch(query_matrix.astype(numpy.uint8), k = K, num_threads = num_threads)
end = time.time()
print('kNN time total=%f (sec), per query=%f (sec), per query adjusted for thread number=%f (sec)' %
(end-start, float(end-start)/query_qty, num_threads*float(end-start)/query_qty))
# Computing gold-standard data
print('Computing gold-standard data')
start = time.time()
sindx = NearestNeighbors(n_neighbors=K, metric='l2', algorithm='brute').fit(data_matrix)
end = time.time()
print('Brute-force preparation time %f' % (end - start))
start = time.time()
gs = sindx.kneighbors(query_matrix)
end = time.time()
print('brute-force kNN time total=%f (sec), per query=%f (sec)' %
(end-start, float(end-start)/query_qty) )
# Finally computing recall
recall=0.0
for i in range(0, query_qty):
correct_set = set(gs[1][i])
ret_set = set(nbrs[i][0])
recall = recall + float(len(correct_set.intersection(ret_set))) / len(correct_set)
recall = recall / query_qty
print('kNN recall %f' % recall)
# Save a meta index and the data
index.saveIndex('dense_index_nonoptim.bin', save_data=True)
# Re-intitialize the library, specify the space, the type of the vector.
newIndex = nmslib.init(method='hnsw',
space=space_name,
data_type=nmslib.DataType.DENSE_UINT8_VECTOR,
dtype=nmslib.DistType.INT)
# Re-load the index and re-run queries
newIndex.loadIndex('dense_index_nonoptim.bin', load_data=True)
# Setting query-time parameters and querying
print('Setting query-time parameters', query_time_params)
newIndex.setQueryTimeParams(query_time_params)
query_qty = query_matrix.shape[0]
start = time.time()
new_nbrs = newIndex.knnQueryBatch(query_matrix.astype(numpy.uint8), k = K, num_threads = num_threads)
end = time.time()
print('kNN time total=%f (sec), per query=%f (sec), per query adjusted for thread number=%f (sec)' %
(end-start, float(end-start)/query_qty, num_threads*float(end-start)/query_qty))
# Finally computing recall for the new result set
recall=0.0
for i in range(0, query_qty):
correct_set = set(gs[1][i])
ret_set = set(new_nbrs[i][0])
recall = recall + float(len(correct_set.intersection(ret_set))) / len(correct_set)
recall = recall / query_qty
print('kNN recall %f' % recall)
```
|
github_jupyter
|
```
from google.colab import drive
drive.mount('/content/drive')
from google.colab import auth
auth.authenticate_user()
import gspread
from oauth2client.client import GoogleCredentials
gc = gspread.authorize(GoogleCredentials.get_application_default())
cd drive/"My Drive"/"Colab Notebooks"/master_project/evaluation
%%capture
!pip install krippendorff
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.metrics import accuracy_score
import seaborn as sns
import pickle
import random
from statistics import mode, StatisticsError, mean, stdev
import krippendorff
import numpy as np
from sklearn.metrics import cohen_kappa_score
import copy
import csv
from collections import Counter
import sys
from sklearn.metrics import confusion_matrix
sys.path.append('..')
from utilities import *
with open("../HAN/df_all.pkl", "rb") as handle:
df_all = pickle.load(handle)
def get_length_info(lst):
char_length = []
word_length = []
for item in lst:
char_length.append(len(item))
word_length.append(len(item.split()))
print(f"Avg. Length (char) = {round(mean(char_length), 2)} (SD={round(stdev(char_length), 2)})")
print(f"Avg. Length (word) = {round(mean(word_length), 2)} (SD={round(stdev(word_length), 2)})\n")
all_sentences = df_all.words
negative_sentences = df_all.words[df_all.categories==0]
positive_sentences = df_all.words[df_all.categories==1]
for lst in [all_sentences, negative_sentences, positive_sentences]:
get_length_info(lst)
char_length = []
word_length = []
for item in df_all.words:
char_length.append(len(item))
word_length.append(len(item.split()))
char_random = random.sample(char_length, 25000)
char_random_y = [Counter(char_random)[i] for i in char_random]
word_random = random.sample(word_length, 25000)
word_random_y = [Counter(word_random)[i] for i in word_random]
plot = sns.barplot(x = char_random, y = char_random_y)
for ind, label in enumerate(plot.get_xticklabels()):
if ind % 10 == 0: # every 10th label is kept
label.set_visible(True)
else:
label.set_visible(False)
# new_ticks = [i.get_text() for i in plot.get_xticklabels()]
# plt.xticks(range(0, len(new_ticks), 20), new_ticks[::20])
plt.title('Length (Characters) Distribution of Sentences [25k]')
plt.xlabel("Length (Characters)")
plt.ylabel("Frequency")
plt.savefig("length_char_dist" + '.png', figsize = (16, 9), dpi=150, bbox_inches="tight")
plt.show()
plt.close()
plot = sns.barplot(x = word_random, y = word_random_y)
# for ind, label in enumerate(plot.get_xticklabels()):
# if ind % 10 == 0: # every 10th label is kept
# label.set_visible(True)
# else:
# label.set_visible(False)
plt.title('Length (words) Distribution of Sentences [25k]')
plt.xlabel("Length (words)")
plt.ylabel("Frequency")
plt.savefig("length_word_dist" + '.png', figsize = (16, 9), dpi=150, bbox_inches="tight")
plt.show()
plt.close()
with open("df_evaluation.pickle", "rb") as handle:
df_evaluation = pickle.load(handle)
original = df_evaluation["OG_sentiment"].to_list()
generated = df_evaluation["GEN_sentiment"].to_list()
count = 0
count_0_to_1_correct, count_0_to_1_total = 0, 0
count_1_to_0_correct, count_1_to_0_total = 0, 0
for og, gen in zip(original, generated):
if og == 0:
count_0_to_1_total += 1
else:
count_1_to_0_total += 1
if og != gen:
count += 1
if og == 0:
count_0_to_1_correct += 1
else:
count_1_to_0_correct += 1
print(f"accuracy [all] = {round((count/len(original))*100, 2)}%")
print(f"accuracy [0 -> 1] = {round((count_0_to_1_correct/count_0_to_1_total)*100, 2)}%")
print(f"accuracy [1 -> 0]= {round((count_1_to_0_correct/count_1_to_0_total)*100, 2)}%")
from sklearn.metrics import classification_report
print(classification_report(original, generated))
# Accuracy human evaluation subset
pd.set_option('display.max_colwidth', -1) # show more of pandas dataframe
df_evaluation
with open("../sentence_generatedsentence_dict.pickle", "rb") as handle:
sentence_generatedsentence_dict = pickle.load(handle)
og_negative_sentences = [sent for sent in df_evaluation.OG_sentences[df_evaluation["OG_sentiment"] == 0].to_list() if len(sent.split()) <= 15]
og_positive_sentences = [sent for sent in df_evaluation.OG_sentences[df_evaluation["OG_sentiment"] == 1].to_list() if len(sent.split()) <= 15]
random.seed(42)
human_evaluation_og_sti = random.sample(og_negative_sentences, 50) + random.sample(og_positive_sentences, 50)
human_evaluation_gen_sti = [sentence_generatedsentence_dict[sent] for sent in human_evaluation_og_sti]
random.seed(4)
human_evaluation_og_nat = random.sample(og_negative_sentences, 50) + random.sample(og_positive_sentences, 50)
human_evaluation_gen_nat = [sentence_generatedsentence_dict[sent] for sent in human_evaluation_og_nat]
original_sentence = df_evaluation["OG_sentences"].to_list()
generated_sentence = df_evaluation["GEN_sentences"].to_list()
original_sentiment = df_evaluation["OG_sentiment"].to_list()
generated_sentiment = df_evaluation["GEN_sentiment"].to_list()
wrong_0_to_1, correct_0_to_1 = [], []
wrong_1_to_0, correct_1_to_0 = [], []
for og_sentence, gen_sentence, og_sentiment, gen_sentiment in zip(original_sentence, generated_sentence, original_sentiment, generated_sentiment):
if og_sentiment != gen_sentiment:
if og_sentiment == 0:
correct_0_to_1.append((og_sentence, gen_sentence))
else:
correct_1_to_0.append((og_sentence, gen_sentence))
else:
if og_sentiment == 0:
wrong_0_to_1.append((og_sentence, gen_sentence))
else:
wrong_1_to_0.append((og_sentence, gen_sentence))
# correct_1_to_0
# for i, j in correct_1_to_0[:10000]:
# i = " ".join(i.strip().split())
# j = " ".join(j.strip().split())
# if len(i) <= 100:
# print("",i,"\n",j, end="\n\n")
# 10 wrong 0 -> 1
wrong_0_to_1[:10]
for i, j in wrong_0_to_1[:10]:
print(i, "#", j)
# 10 correct 0 -> 1
correct_0_to_1[:10]
for i, j in correct_0_to_1[:10]:
print(i, "#", j)
# 10 wrong 1 -> 0
wrong_1_to_0[:10]
for i, j in wrong_1_to_0[:10]:
print(i, "#", j)
# 10 correct 0 -> 1
correct_1_to_0[:10]
for i, j in correct_1_to_0[:10]:
print(i, "#", j)
reverse_dict = {"negative": 0, "positive": 1, "neither": 2, "either": 2} # made type in neither so added either as 2 as well
```
## Style Transfer Intensity
```
# Style Transfer intensity
sti_responses = gc.open_by_url('https://docs.google.com/spreadsheets/d/1_B3ayl6-p3nRl3RUtTgcu7fGT2v3n6rg3CLrR4wTafQ/edit#gid=2064143541')
sti_response_sheet = sti_responses.sheet1
sti_reponse_data = sti_response_sheet.get_all_values()
# sti_reponse_data
sti_answer_dict = {}
for idx, row in enumerate(sti_reponse_data[1:]):
if row[1] != "":
sti_answer_dict[idx] = [(idx, reverse_dict[i]) for idx, i in enumerate(row[2:-1])]
# inter-annotator agreement
k_alpha = krippendorff.alpha([[i[1] for i in v] for k, v in sti_answer_dict.items()])
print("Krippendorffs' Alpha:")
print(round(k_alpha,4))
# inter-annotator agreement, ignoring neither cases
remove_indexes = []
for lst in [v for k, v in sti_answer_dict.items()]:
for idx, i in enumerate(lst):
if i[1] == 2:
remove_indexes.append(idx)
sti_answers_without_neither = copy.deepcopy([v for k, v in sti_answer_dict.items()])
for lst in sti_answers_without_neither:
for i in sorted(set(remove_indexes), reverse=True):
del lst[i]
print("\nKrippendorffs' Alpha (ignoring neither cases):")
print(f"Answers remaining: {len(sti_answers_without_neither[0])}%")
k_alpha = krippendorff.alpha([[j[1] for j in usr] for usr in sti_answers_without_neither])
print(round(k_alpha,4))
# amount neither
neither_percentage = 0
for k, v in sti_answer_dict.items():
v = [i[1] for i in v]
neither_percentage += Counter(v)[2]/len(v)
print(f"Average amount of neither selected: {round((neither_percentage/3)*100, 2)}%")
# Select most common answer of each human evaluator, if all same, select random
final_sti_human_answers = []
for idx, i in enumerate(np.array([[i[1] for i in v] for k, v in sti_answer_dict.items()]).transpose()):
try:
final_sti_human_answers.append((idx, mode(i)))
except StatisticsError as e:
final_sti_human_answers.append((idx, random.choice(i)))
with open("df_evaluation.pickle", "rb") as handle:
df_evaluation = pickle.load(handle)
id_sentence_dict = {}
for idx, sentence in enumerate(sti_reponse_data[0][2:-1]):
id_sentence_dict[idx] = sentence
sentence_human_sentiment = {}
for sentence_id, sentiment in final_sti_human_answers:
if sentiment == 2:
continue
sentence_human_sentiment[id_sentence_dict[sentence_id]] = sentiment
human_sentiment = [v for k,v in sentence_human_sentiment.items()]
og_sentiment = []
for k, v in sentence_human_sentiment.items():
og_sentiment.append(df_evaluation.OG_sentiment[df_evaluation.GEN_sentences==k].item())
# Accuracy style transfer intensity for human classification
count = 0
count_0_to_1_correct, count_0_to_1_total = 0, 0
count_1_to_0_correct, count_1_to_0_total = 0, 0
for og, gen in zip(og_sentiment, human_sentiment):
if og == 0:
count_0_to_1_total += 1
else:
count_1_to_0_total += 1
if og != gen:
count += 1
if og == 0:
count_0_to_1_correct += 1
else:
count_1_to_0_correct += 1
print(f"accuracy [including neither] = {round((count/len(final_sti_human_answers))*100, 2)}%")
print(f"accuracy [excluding neither] = {round((count/len(og_sentiment))*100, 2)}%")
print(f"accuracy [0 -> 1] = {round((count_0_to_1_correct/count_0_to_1_total)*100, 2)}%")
print(f"accuracy [1 -> 0]= {round((count_1_to_0_correct/count_1_to_0_total)*100, 2)}%")
# Agreement between human and automatic evaluation
gen_sentiment = []
for k, v in sentence_human_sentiment.items():
gen_sentiment.append(df_evaluation.GEN_sentiment[df_evaluation.GEN_sentences==k].item())
k_alpha = krippendorff.alpha([gen_sentiment, human_sentiment])
print("\nKrippendorffs' Alpha:")
print(round(k_alpha,4))
# https://www.ncbi.nlm.nih.gov/pubmed/15883903 reference to cohen's kappa
print(f"Cohen's Kappa:\n{round(cohen_kappa_score(gen_sentiment, human_sentiment), 4)}")
cm = confusion_matrix(og_sentiment, human_sentiment)
create_confusion_matrix(cm, ["neg", "pos"], show_plots=True, title="Gold labels vs. Human Predictions",
xlabel="Human Labels", ylabel="Gold Labels", dir="", y_lim_value=2, save_plots=True)
cm = confusion_matrix(gen_sentiment, human_sentiment)
create_confusion_matrix(cm, ["neg", "pos"], show_plots=True, title="Automatic vs. Human Predictions",
xlabel="Human Labels", ylabel="Automatic Labels", dir="", y_lim_value=2, save_plots=True)
```

## Naturalness (Isolated)
```
# Naturalness (isolated)
nat_iso_responses = gc.open_by_url('https://docs.google.com/spreadsheets/d/1tEOalZErOjSOD8DGKfvi-edv8sKkGczLx0eYi7N6Kjw/edit#gid=1759015116')
nat_iso_response_sheet = nat_iso_responses.sheet1
nat_iso_reponse_data = nat_iso_response_sheet.get_all_values()
# nat_iso_reponse_data
nat_iso_answer_dict = {}
for idx, row in enumerate(nat_iso_reponse_data[1:]):
if row[1] != "":
nat_iso_answer_dict[idx] = [int(i) for i in row[2:-1]]
# inter-annotator agreement
print("Krippendorffs' Alpha:")
k_alpha = krippendorff.alpha([v for k,v in nat_iso_answer_dict.items()])
print(round(k_alpha,4))
# naturalness mean (isolated)
naturalness_mean_list = []
for idx, row in enumerate(nat_iso_reponse_data[1:]):
if row[1] != "":
naturalness_mean_list.append(int(i) for i in row[2:-1])
print("Mean of naturalness (isolated):")
print(round(mean([mean(i) for i in naturalness_mean_list]),4))
nat_all = []
for k, v in nat_iso_answer_dict.items():
nat_all += v
nat_all_dist = Counter(nat_all)
nat_all_dist
# naturalness (isolated) distribution
fig = plt.figure(figsize=[7, 5], dpi=100)
ax = fig.add_axes([0,0,1,1])
ax.bar(nat_all_dist.keys(), nat_all_dist.values())
plt.title("Naturalness (Isolated) distribution")
plt.xlabel("Answer")
plt.ylabel("Frequency")
plt.savefig("naturalness_isolated_dist" + '.png', figsize = (16, 9), dpi=150, bbox_inches="tight")
plt.show()
plt.close()
df_evaluation
id_sentiment_dict = {}
for idx, sentence in enumerate(nat_iso_reponse_data[0][2:-1]):
# GEN_sentiment
sentiment = df_evaluation.OG_sentiment[df_evaluation.GEN_sentences == sentence].item()
id_sentiment_dict[idx] = sentiment
nat_iso_answer_dict_div = {}
for idx, row in enumerate(nat_iso_reponse_data[1:]):
if row[1] != "":
nat_iso_answer_dict_div[idx] = ([int(i) for id, i in enumerate(row[2:-1]) if id_sentiment_dict[id] == 0],
[int(i) for id, i in enumerate(row[2:-1]) if id_sentiment_dict[id] == 1])
nat_all_neg, nat_all_pos = [], []
for k, (v_neg, v_pos) in nat_iso_answer_dict_div.items():
nat_all_neg += v_neg
nat_all_pos += v_pos
nat_all_dist_neg = Counter(nat_all_neg)
nat_all_dist_pos = Counter(nat_all_pos)
df = pd.DataFrame([['g1','c1',10],['g1','c2',12],['g1','c3',13],['g2','c1',8],
['g2','c2',10],['g2','c3',12]],columns=['group','column','val'])
df = pd.DataFrame([nat_all_dist_neg, nat_all_dist_pos]).T
ax = df.plot(kind='bar')
ax.figure.set_size_inches(16, 9)
plt.title("Naturalness (Isolated) distribution")
plt.xlabel("Answer")
plt.ylabel("Frequency")
plt.xticks(rotation='horizontal')
ax.figure.savefig("naturalness_isolated_dist_div" + '.png', figsize = (16, 9), dpi=150, bbox_inches="tight")
plt.legend(["Negative", "Positive"])
plt.show()
plt.close()
```
## Naturalness (Comparison)
```
# Naturalness (comparison)
nat_comp_responses = gc.open_by_url('https://docs.google.com/spreadsheets/d/1mFtsNNaJXDK2dT9LkLz_r8LSfIOPskDqn4jBamE-bns/edit#gid=890219669')
nat_comp_response_sheet = nat_comp_responses.sheet1
nat_comp_reponse_data = nat_comp_response_sheet.get_all_values()
# nat_comp_reponse_data
nat_comp_answer_dict = {}
for idx, row in enumerate(nat_comp_reponse_data[1:]):
if row[1] != "":
nat_comp_answer_dict[idx] = [int(i) for i in row[2:-1]]
# inter-annotator agreement
print("Krippendorffs' Alpha:")
k_alpha = krippendorff.alpha([v for k,v in nat_comp_answer_dict.items()])
print(round(k_alpha,4))
# naturalness mean (comparison)
naturalness_mean_list = []
for idx, row in enumerate(nat_comp_reponse_data[1:]):
if row[1] != "":
naturalness_mean_list.append(int(i) for i in row[2:-1])
print("Mean of naturalness (comparison):")
print(round(mean([mean(i) for i in naturalness_mean_list]),4))
nat_comp_questions = gc.open_by_url('https://docs.google.com/spreadsheets/d/1uxAGaOvJcb-Cg3wjTDEovTgR--TFZet0VnpzInljjfo/edit#gid=167268481')
nat_comp_questions_sheet = nat_comp_questions.sheet1
nat_comp_questions_data = nat_comp_questions_sheet.get_all_values()
# naturalness (og vs. gen naturalness)
# 1: A is far more natural than B
# 2: A is slightly more natural than B
# 3: A and B are equally natural
# 4: B is slightly more natural than A
# 5 : B is far more natural than A
# 1: OG is far more natural than GEN
# 2: OG is slightly more natural than GEN
# 3: OG and GEN are equally natural
# 4: GEN is slightly more natural than OG
# 5: GEN is far more natural than OG
one, two, three, four, five = 0, 0, 0, 0, 0
for idx, row in enumerate(nat_comp_reponse_data[1:]):
if row[1] != "":
for idx2, (row, answer) in enumerate(zip(nat_comp_questions_data[1:], row[2:-1])):
original, generated = row[-2:]
answer = int(answer)
# print("A", "B", "|", original, generated, "|", answer)
if original == "A":
if answer == 1:
one += 1
if answer == 2:
two += 1
if answer == 3:
three += 1
if answer == 4:
four += 1
if answer == 5:
five += 1
if original == "B":
if answer == 1:
five += 1
if answer == 2:
four += 1
if answer == 3:
three += 1
if answer == 4:
two += 1
if answer == 5:
one += 1
print(one,two,three,four,five)
print("Mean of naturalness (comparison) original vs. generated:")
print(round((one*1+two*2+three*3+four*4+five*5)/sum([one,two,three,four,five]),4))
# naturalness (comparison) distribution
fig = plt.figure(figsize=[7, 5], dpi=100)
answers = {'OG is far more natural than GEN ':'red',
'OG is slightly more natural than GEN':'green',
'OG and GEN are equally natural':'blue',
'GEN is slightly more natural than OG':'orange',
'GEN is far more natural than OG': 'purple'}
labels = list(answers.keys())
handles = [plt.Rectangle((0,0),1,1, color=answers[label]) for label in labels]
ax = fig.add_axes([0,0,1,1])
plt.bar([1,2,3,4,5], [one,two,three,four,five], color=answers.values())
plt.title("Naturalness (Comparison) distribution [translated]")
plt.legend(handles, labels)
plt.xlabel("Answer")
plt.ylabel("Frequency")
plt.savefig("naturalness_comparison_dist_translated" + '.png', figsize = (16, 9), dpi=150, bbox_inches="tight")
plt.show()
plt.close()
nat_all = []
for k, v in nat_comp_answer_dict.items():
nat_all += v
nat_all_dist = Counter(nat_all)
nat_all_dist
# naturalness (comparison) distribution
fig = plt.figure(figsize=[7, 5], dpi=100)
ax = fig.add_axes([0,0,1,1])
ax.bar(nat_all_dist.keys(), nat_all_dist.values())
plt.title("Naturalness (Comparison) distribution")
plt.xlabel("Answer")
plt.ylabel("Frequency")
plt.savefig("naturalness_comparison_dist" + '.png', figsize = (16, 9), dpi=150, bbox_inches="tight")
plt.show()
plt.close()
```
## Which Words
```
# Which words
ww_responses = gc.open_by_url('https://docs.google.com/spreadsheets/d/1bRoF5l8Lt9fqeOki_YrJffd2XwEpROKi1RUsbC1umIk/edit#gid=1233025762')
ww_response_sheet = ww_responses.sheet1
ww_reponse_data = ww_response_sheet.get_all_values()
ww_answer_dict = {}
for idx, row in enumerate(ww_reponse_data[1:]):
if row[1] != "":
ww_answer_dict[idx]= [[word.strip() for word in i.split(",")] for i in row[2:-1]]
# Human-annotator agreement
user1 = ww_answer_dict[0]
user2 = ww_answer_dict[1]
total = 0
for l1, l2 in zip(user1, user2):
total += len((set(l1) & set(l2)))/max(len(l1), len(l2))
print("Human Annotator Agreement, which word:")
print(f"{round((total/len(user1)*100), 2)}%")
# Human-annotator agreement (Ignoreing <NONE>)
user1 = ww_answer_dict[0]
user2 = ww_answer_dict[1]
total = 0
none = 0
for l1, l2 in zip(user1, user2):
if l1==['<NONE>'] or l2==['<NONE>']:
none+=1
continue
total += len((set(l1) & set(l2)))/max(len(l1), len(l2))
print("Human Annotator Agreement, which word:")
print(f"{round((total/(len(user1)-none)*100), 2)}%")
# Human-annotator agreement on <NONE>
user1 = ww_answer_dict[0]
user2 = ww_answer_dict[1]
none = 0
none_both = 0
for l1, l2 in zip(user1, user2):
if l1==['<NONE>'] or l2==['<NONE>']:
none+=1
if l1==l2:
none_both+=1
print("Human Annotator Agreement, <NONE>:")
print(f"{round((none_both/none)*100, 2)}%")
# Human-annotator agreement on <NONE>
user1 = ww_answer_dict[0]
user2 = ww_answer_dict[1]
human_total_words_chosen = 0
for l1, l2 in zip(user1, user2):
human_total_words_chosen += len(set(l1) & set(l2))
with open("../to_substitute_dict.pickle", "rb") as handle:
to_substitute_dict = pickle.load(handle)
id_sentence_dict = {}
for idx, sentence in enumerate(ww_reponse_data[0][2:-1]):
id_sentence_dict[idx] = sentence
cls_total_words_chosen = 0
total = 0
amount_none = 0
for l1, l2, (k, v) in zip(user1, user2, id_sentence_dict.items()):
human_chosen_words = set(l1) & set(l2)
if human_chosen_words == {'<NONE>'}:
amount_none += 1
cls_total_words_chosen -= len(classifier_chosen_words)
classifier_chosen_words = {v.split()[idx] for idx, _ in to_substitute_dict[v]}
cls_total_words_chosen += len(classifier_chosen_words)
total += len((human_chosen_words & classifier_chosen_words))/max(len(human_chosen_words), len(classifier_chosen_words))
print("Classifier/Human Agreement, which word (counting none):")
print(f"{round((total/len(user1)*100), 2)}%")
print("\nClassifier/Human Agreement, which word (excluding none):")
print(f"{round((total/(len(user1)-amount_none)*100), 2)}%")
print(f"\nAmount of <NONE> chosen by all annotators:\n{round(len(user1)/amount_none, 2)}%")
print("\ntotal words chosen by Human Evaluators")
print(f"{human_total_words_chosen}")
print("total words chosen by Classifier")
print(f"{cls_total_words_chosen}")
# More example sentences, for better in-depth analysis
sentences_one, sentences_two, sentences_three, sentences_four, sentences_five = [], [], [], [], []
for idx, row in enumerate(nat_comp_reponse_data[1:]):
if row[1] != "":
for idx2, (row, answer) in enumerate(zip(nat_comp_questions_data[1:], row[2:-1])):
original, generated = row[-2:]
answer = int(answer)
if generated == "A":
generated_sentence = row[0].rsplit(":")[1].strip()
original_sentence = row[2].rsplit(":")[1].strip()
elif generated == "B":
generated_sentence = row[2].rsplit(":")[1].strip()
original_sentence = row[0].rsplit(":")[1].strip()
# print("A", "B", "|", original, generated, "|", answer)
if original == "A":
if answer == 1:
sentences_one.append(generated_sentence)
if answer == 2:
sentences_two.append(generated_sentence)
if answer == 3:
sentences_three.append(generated_sentence)
if answer == 4:
sentences_four.append(generated_sentence)
if answer == 5:
sentences_five.append(generated_sentence)
if original == "B":
if answer == 1:
sentences_five.append(generated_sentence)
if answer == 2:
sentences_four.append(generated_sentence)
if answer == 3:
sentences_three.append(generated_sentence)
if answer == 4:
sentences_two.append(generated_sentence)
if answer == 5:
sentences_one.append(generated_sentence)
print(len(sentences_one), len(sentences_two), len(sentences_three), len(sentences_four), len(sentences_five))
low_natural_sentences = sentences_one + sentences_two
high_natural_sentences = sentences_three + sentences_four + sentences_five
og_sentiment, gen_sentiment = [], []
for sentence in low_natural_sentences:
og_sentiment.append(df_evaluation.OG_sentiment[df_evaluation.GEN_sentences == sentence].item())
gen_sentiment.append(df_evaluation.GEN_sentiment[df_evaluation.GEN_sentences == sentence].item())
print("Accuracy Low Naturalness Sentences")
print(round((1-accuracy_score(og_sentiment, gen_sentiment))*100, 4))
og_sentiment, gen_sentiment = [], []
for sentence in high_natural_sentences:
og_sentiment.append(df_evaluation.OG_sentiment[df_evaluation.GEN_sentences == sentence].item())
gen_sentiment.append(df_evaluation.GEN_sentiment[df_evaluation.GEN_sentences == sentence].item())
print("\nAccuracy High Naturalness Sentences")
print(round((1-accuracy_score(og_sentiment, gen_sentiment))*100, 4))
length = []
for sentence in low_natural_sentences:
og_sentence = df_evaluation.OG_sentences[df_evaluation.GEN_sentences == sentence].item()
length.append(len(to_substitute_dict[og_sentence]))
print("Avg. amount of words substituted Low Naturalness Sentences")
print(round(mean(length), 2))
length = []
for sentence in high_natural_sentences:
og_sentence = df_evaluation.OG_sentences[df_evaluation.GEN_sentences == sentence].item()
length.append(len(to_substitute_dict[og_sentence]))
print("\nAvg. amount of words substituted High Naturalness Sentences")
print(round(mean(length), 2))
print("Examples of generated sentence more natural than source sentence\n")
for sentence in sentences_five+sentences_four:
og_sentence = df_evaluation.OG_sentences[df_evaluation.GEN_sentences == sentence].item()
print(f"OG = {og_sentence}\nGEN = {sentence}\n")
print("Examples of generated sentence as natural as source sentence\n")
for idx, sentence in enumerate(sentences_three):
og_sentence = df_evaluation.OG_sentences[df_evaluation.GEN_sentences == sentence].item()
print(f"OG = {og_sentence}\nGEN = {sentence}\n")
if idx == 10:
break
user_answers = []
for idx, row in enumerate(nat_iso_reponse_data[1:]):
if row[1] != "":
answers = [int(i) for i in row[2:-1]]
user_answers.append(answers)
highly_natural_sentences = [] # average naturalness >= 4
highly_unnatural_sentences = [] # average naturalness <= 2
for idx, sentence in enumerate(nat_iso_reponse_data[0][2:-1]):
answers = []
for user in user_answers:
answers.append(user[idx])
if mean(answers) >= 4:
highly_natural_sentences.append(sentence)
elif mean(answers) <= 2:
highly_unnatural_sentences.append(sentence)
print(len(highly_natural_sentences), len(highly_unnatural_sentences))
print("Examples of highly natural sentences\n")
for sentence in highly_natural_sentences:
print(sentence)
print("\nExamples of highly unnatural sentences\n")
for sentence in highly_unnatural_sentences:
print(sentence)
int_to_string_dict = {0: "negative", 1: "positive"}
user_answers = []
for idx, row in enumerate(sti_reponse_data[1:]):
if row[1] != "":
answers = [i for i in row[2:-1]]
user_answers.append(answers)
all_neither_sentences = []
all_negative_sentences = []
all_positive_sentences = []
human_cls_agree_transfer = []
human_cls_agree_no_transfer = []
human_yes_cls_no = []
human_no_cls_yes = []
for idx, sentence in enumerate(sti_reponse_data[0][2:-1]):
answers = []
for user in user_answers:
answers.append(user[idx])
if set(answers) == {'neither'}:
all_neither_sentences.append(sentence)
if set(answers) == {'negative'}:
all_negative_sentences.append(sentence)
if set(answers) == {'positive'}:
all_positive_sentences.append(sentence)
try:
human_sentiment = mode(answers)
except StatisticsError as e:
human_sentiment = random.choice(answers)
cls_sentiment = int_to_string_dict[df_evaluation.GEN_sentiment[df_evaluation.GEN_sentences == sentence].item()]
og_sentiment = int_to_string_dict[df_evaluation.OG_sentiment[df_evaluation.GEN_sentences == sentence].item()]
union = set([human_sentiment])|set([cls_sentiment])
if (len(union) == 1) and ({og_sentiment} != union):
og_sentence = df_evaluation.OG_sentences[df_evaluation.GEN_sentences == sentence].item()
human_cls_agree_transfer.append((og_sentence, sentence))
if (len(union) == 1) and ({og_sentiment} == union):
og_sentence = df_evaluation.OG_sentences[df_evaluation.GEN_sentences == sentence].item()
human_cls_agree_no_transfer.append((og_sentence, sentence))
if (human_sentiment != og_sentiment) and (gen_sentiment == og_sentiment):
og_sentence = df_evaluation.OG_sentences[df_evaluation.GEN_sentences == sentence].item()
human_yes_cls_no.append((og_sentence, sentence))
if (human_sentiment == og_sentiment) and (gen_sentiment != og_sentiment):
og_sentence = df_evaluation.OG_sentences[df_evaluation.GEN_sentences == sentence].item()
human_no_cls_yes.append((og_sentence, sentence))
threshold = 20
print("Examples of sentences that were classified as neither by all evaluators")
print("-"*40, f"[{len(all_neither_sentences)}]", "-"*40)
for sentence in all_neither_sentences[:threshold]:
print(sentence)
print("\nExamples of sentences that were classified as negative by all evaluators")
print("-"*40, f"[{len(all_negative_sentences)}]", "-"*40)
for sentence in all_negative_sentences[:threshold]:
print(sentence)
print("\nExamples of sentences that were classified as positive by all evaluators")
print("-"*40, f"[{len(all_positive_sentences)}]", "-"*40)
for sentence in all_positive_sentences[:threshold]:
print(sentence)
print("\nClassification examples where both human + cls agree style is transferred")
print("-"*40, f"[{len(human_cls_agree_transfer)}]", "-"*40)
for og_sentence, gen_sentence in human_cls_agree_transfer[:threshold]:
print(f"{og_sentence}\n{gen_sentence}\n")
print("\nClassification examples where human says style is transferred, but cls not")
print("-"*40, f"[{len(human_yes_cls_no)}]", "-"*40)
for og_sentence, gen_sentence in human_yes_cls_no[:threshold]:
print(f"{og_sentence}\n{gen_sentence}\n")
print("\nClassification examples where cls says style is transferred, but human not")
print("-"*40, f"[{len(human_no_cls_yes)}]", "-"*40)
for og_sentence, gen_sentence in human_no_cls_yes[:threshold]:
print(f"{og_sentence}\n{gen_sentence}\n")
print("\nClassification examples where both human + cls agree style is not transferred")
print("-"*40, f"[{len(human_cls_agree_no_transfer)}]", "-"*40)
for og_sentence, gen_sentence in human_cls_agree_no_transfer[:threshold]:
print(f"{og_sentence}\n{gen_sentence}\n")
```
|
github_jupyter
|
```
class Solution:
def removeInvalidParentheses(self, s: str):
if not s: return []
self.max_len = self.get_max_len(s)
self.ans = []
self.dfs(s, 0, "", 0)
return self.ans
def dfs(self, s, idx, cur_str, count):
if len(cur_str) > self.max_len: return
if count < 0: return # count表示 "(" 的数量
if idx == len(s): # 遍历到了最后 s 的一个字母
if count == 0 and len(cur_str) == self.max_len:
self.ans.append(cur_str)
return
# 如果是其他字母,可以直接添加,不会收到影响
if s[idx] != '(' and s[idx] != ')':
self.dfs(s, idx+1, cur_str+s[idx], count)
else:
val = 1 if s[idx] == '(' else -1
# 肯定取,有两种情况,最后一个字符与cur_str的最后一个字符相同
# 或者是不同
self.dfs(s, idx+1, cur_str+s[idx], count+val)
if not cur_str or s[idx] != cur_str[-1]:
# 对于不同的情况是可以不取的
self.dfs(s, idx+1, cur_str, count)
def get_max_len(self, s):
"""返回原始字符串是 valid 的最大长度"""
l_count, res = 0, 0
for a in s:
if a == '(':
l_count += 1
elif a == ')':
if l_count == 0:
res += 1
else:
l_count -= 1
return len(s) - l_count - res
class Solution:
def removeInvalidParentheses(self, s: str):
if not s: return [""]
self.max_len = self.get_max_len(s)
self.ans = []
self.dfs(s, 0, "", 0)
return self.ans
def dfs(self, s, idx, cur_str, count):
# count代表了 “(” 的数量,如果小于0,一定不合法
if len(cur_str) > self.max_len: return
if count < 0: return
if idx == len(s): # 遍历到了最后 s 的一个字母
if count == 0 and len(cur_str) == self.max_len:
self.ans.append(cur_str)
return
# 其他字母
if s[idx] != '(' and s[idx] != ')':
self.dfs(s, idx+1, cur_str+s[idx], count)
else:
val = 1 if s[idx] == '(' else -1
self.dfs(s, idx+1, cur_str+s[idx], count+val)
if not cur_str or s[idx] != cur_str[-1]:
self.dfs(s, idx+1, cur_str, count)
def get_max_len(self, s):
l_count, res = 0, 0
for a in s:
if a == '(':
l_count += 1
elif a == ')':
if l_count == 0:
res += 1
else:
l_count -= 1
return len(s) - l_count - res
solution = Solution()
solution.removeInvalidParentheses("(a)())()")
```
|
github_jupyter
|
```
emails = ['[email protected]',
'[email protected]',
'[email protected]',
'[email protected]',
'[email protected]',
'[email protected]',
'[email protected]',
'[email protected]',
'[email protected]',
'[email protected]',
'[email protected]',
'[email protected]',
'[email protected]',
'[email protected]',
'[email protected]',
'[email protected]',
'[email protected]',
'[email protected]',
'[email protected]',
'[email protected]',
'[email protected]',]
TEXT = """
Boa noite
Envio email na sequência do pedido de apoio por parte da vossa instituição.
Gostava apenas de saber se chegou a vossa instituição algum tipo de equipamento, tendo em conta que me foi dito que seriam enviadas viseiras durante esta semana.
Caso não tenham recebido nada, pedia que me alertassem para conseguir perceber o que se passa com os apoios que conseguimos agregar.
Obrigado pela atenção,
Gustavo.
"""
TEXT = """
Bom dia,
O meu nome é Gustavo Carita, tenho 27 anos, sou de Lisboa e sou engenheiro.
Recentemente apercebi-me que, na actual conjuntura, existe uma carência nacional de profissionais para apoiar IPSS-Instituicoes Privadas de Solidariedade Social e decidi meter mãos á obra para tentar ajudar.
Eu e mais uns amigos criámos um website para ajudar as IPSS, duma forma simples e eficaz.
Pode verificar o website em: https://voluntarios-covid19.pt/
Neste momento estamos a comunicar com todas as IPSS presentes na plataforma http://cartasocial.pt/.
Para divulgarem a ajuda que precisam nesta fase, basta preencher o seguinte formulário: https://forms.gle/nC2GNNMcW8pyXiYw7
Daremos o nosso melhor para promover as vossas iniciativas e obter toda a ajuda necessária.
Obrigado,
Gustavo.
<[email protected]>
"""
TO = '[email protected]'
SUBJECT = 'IPSS Trial'
# Gmail Sign In
gmail_sender = '[email protected]'
gmail_passwd = 'voluntariado123@'
def create_message(sender, to, subject, message_text):
"""Create a message for an email.
Args:
sender: Email address of the sender.
to: Email address of the receiver.
subject: The subject of the email message.
message_text: The text of the email message.
Returns:
An object containing a base64url encoded email object.
"""
message = MIMEText(message_text)
message['to'] = to
message['from'] = sender
message['subject'] = subject
b64_bytes = base64.urlsafe_b64encode(message.as_bytes())
b64_string = b64_bytes.decode()
body = {'raw': b64_string}
return body
from email.mime.text import MIMEText
import base64
from googleapiclient.discovery import build
import pickle
from tqdm import tqdm
from time import sleep
import random
with open('../../ipss_mailing/token.pickle', 'rb') as token:
creds = pickle.load(token)
service = build('gmail', 'v1', credentials=creds)
def send_message(service, user_id, message):
"""Send an email message.
Args:
service: Authorized Gmail API service instance.
user_id: User's email address. The special value "me"
can be used to indicate the authenticated user.
message: Message to be sent.
Returns:
Sent Message.
"""
try:
message = (service.users().messages().send(userId=user_id, body=message)
.execute())
print('Message Id: %s' % message['id'])
return message
except Exception as e:
print(e)
temp = open('../../ipss_mailing/emails.txt', 'r').readlines()
temp = [email.replace('\n', '') for email in temp]
temp = [
'[email protected]',
'[email protected]'
] + emails
for t in tqdm(temp):
try:
send_message(service, "me", create_message(
'[email protected]',
t,
'Voluntarios COVID19 - Confirmação',
TEXT
))
sleep(random.randint(0,2))
except Exception as e:
print(e)
print(t)
```
|
github_jupyter
|
# Encoding of categorical variables
In this notebook, we will present typical ways of dealing with
**categorical variables** by encoding them, namely **ordinal encoding** and
**one-hot encoding**.
Let's first load the entire adult dataset containing both numerical and
categorical data.
```
import pandas as pd
adult_census = pd.read_csv("../datasets/adult-census.csv")
# drop the duplicated column `"education-num"` as stated in the first notebook
adult_census = adult_census.drop(columns="education-num")
target_name = "class"
target = adult_census[target_name]
data = adult_census.drop(columns=[target_name])
```
## Identify categorical variables
As we saw in the previous section, a numerical variable is a
quantity represented by a real or integer number. These variables can be
naturally handled by machine learning algorithms that are typically composed
of a sequence of arithmetic instructions such as additions and
multiplications.
In contrast, categorical variables have discrete values, typically
represented by string labels (but not only) taken from a finite list of
possible choices. For instance, the variable `native-country` in our dataset
is a categorical variable because it encodes the data using a finite list of
possible countries (along with the `?` symbol when this information is
missing):
```
data["native-country"].value_counts().sort_index()
```
How can we easily recognize categorical columns among the dataset? Part of
the answer lies in the columns' data type:
```
data.dtypes
```
If we look at the `"native-country"` column, we observe its data type is
`object`, meaning it contains string values.
## Select features based on their data type
In the previous notebook, we manually defined the numerical columns. We could
do a similar approach. Instead, we will use the scikit-learn helper function
`make_column_selector`, which allows us to select columns based on
their data type. We will illustrate how to use this helper.
```
from sklearn.compose import make_column_selector as selector
categorical_columns_selector = selector(dtype_include=object)
categorical_columns = categorical_columns_selector(data)
categorical_columns
```
Here, we created the selector by passing the data type to include; we then
passed the input dataset to the selector object, which returned a list of
column names that have the requested data type. We can now filter out the
unwanted columns:
```
data_categorical = data[categorical_columns]
data_categorical.head()
print(f"The dataset is composed of {data_categorical.shape[1]} features")
```
In the remainder of this section, we will present different strategies to
encode categorical data into numerical data which can be used by a
machine-learning algorithm.
## Strategies to encode categories
### Encoding ordinal categories
The most intuitive strategy is to encode each category with a different
number. The `OrdinalEncoder` will transform the data in such manner.
We will start by encoding a single column to understand how the encoding
works.
```
from sklearn.preprocessing import OrdinalEncoder
education_column = data_categorical[["education"]]
encoder = OrdinalEncoder()
education_encoded = encoder.fit_transform(education_column)
education_encoded
```
We see that each category in `"education"` has been replaced by a numeric
value. We could check the mapping between the categories and the numerical
values by checking the fitted attribute `categories_`.
```
encoder.categories_
```
Now, we can check the encoding applied on all categorical features.
```
data_encoded = encoder.fit_transform(data_categorical)
data_encoded[:5]
print(
f"The dataset encoded contains {data_encoded.shape[1]} features")
```
We see that the categories have been encoded for each feature (column)
independently. We also note that the number of features before and after the
encoding is the same.
However, be careful when applying this encoding strategy:
using this integer representation leads downstream predictive models
to assume that the values are ordered (0 < 1 < 2 < 3... for instance).
By default, `OrdinalEncoder` uses a lexicographical strategy to map string
category labels to integers. This strategy is arbitrary and often
meaningless. For instance, suppose the dataset has a categorical variable
named `"size"` with categories such as "S", "M", "L", "XL". We would like the
integer representation to respect the meaning of the sizes by mapping them to
increasing integers such as `0, 1, 2, 3`.
However, the lexicographical strategy used by default would map the labels
"S", "M", "L", "XL" to 2, 1, 0, 3, by following the alphabetical order.
The `OrdinalEncoder` class accepts a `categories` constructor argument to
pass categories in the expected ordering explicitly. You can find more
information in the
[scikit-learn documentation](https://scikit-learn.org/stable/modules/preprocessing.html#encoding-categorical-features)
if needed.
If a categorical variable does not carry any meaningful order information
then this encoding might be misleading to downstream statistical models and
you might consider using one-hot encoding instead (see below).
### Encoding nominal categories (without assuming any order)
`OneHotEncoder` is an alternative encoder that prevents the downstream
models to make a false assumption about the ordering of categories. For a
given feature, it will create as many new columns as there are possible
categories. For a given sample, the value of the column corresponding to the
category will be set to `1` while all the columns of the other categories
will be set to `0`.
We will start by encoding a single feature (e.g. `"education"`) to illustrate
how the encoding works.
```
from sklearn.preprocessing import OneHotEncoder
encoder = OneHotEncoder(sparse=False)
education_encoded = encoder.fit_transform(education_column)
education_encoded
```
<div class="admonition note alert alert-info">
<p class="first admonition-title" style="font-weight: bold;">Note</p>
<p><tt class="docutils literal">sparse=False</tt> is used in the <tt class="docutils literal">OneHotEncoder</tt> for didactic purposes, namely
easier visualization of the data.</p>
<p class="last">Sparse matrices are efficient data structures when most of your matrix
elements are zero. They won't be covered in detail in this course. If you
want more details about them, you can look at
<a class="reference external" href="https://scipy-lectures.org/advanced/scipy_sparse/introduction.html#why-sparse-matrices">this</a>.</p>
</div>
We see that encoding a single feature will give a NumPy array full of zeros
and ones. We can get a better understanding using the associated feature
names resulting from the transformation.
```
feature_names = encoder.get_feature_names_out(input_features=["education"])
education_encoded = pd.DataFrame(education_encoded, columns=feature_names)
education_encoded
```
As we can see, each category (unique value) became a column; the encoding
returned, for each sample, a 1 to specify which category it belongs to.
Let's apply this encoding on the full dataset.
```
print(
f"The dataset is composed of {data_categorical.shape[1]} features")
data_categorical.head()
data_encoded = encoder.fit_transform(data_categorical)
data_encoded[:5]
print(
f"The encoded dataset contains {data_encoded.shape[1]} features")
```
Let's wrap this NumPy array in a dataframe with informative column names as
provided by the encoder object:
```
columns_encoded = encoder.get_feature_names_out(data_categorical.columns)
pd.DataFrame(data_encoded, columns=columns_encoded).head()
```
Look at how the `"workclass"` variable of the 3 first records has been
encoded and compare this to the original string representation.
The number of features after the encoding is more than 10 times larger than
in the original data because some variables such as `occupation` and
`native-country` have many possible categories.
### Choosing an encoding strategy
Choosing an encoding strategy will depend on the underlying models and the
type of categories (i.e. ordinal vs. nominal).
<div class="admonition note alert alert-info">
<p class="first admonition-title" style="font-weight: bold;">Note</p>
<p class="last">In general <tt class="docutils literal">OneHotEncoder</tt> is the encoding strategy used when the
downstream models are <strong>linear models</strong> while <tt class="docutils literal">OrdinalEncoder</tt> is often a
good strategy with <strong>tree-based models</strong>.</p>
</div>
Using an `OrdinalEncoder` will output ordinal categories. This means
that there is an order in the resulting categories (e.g. `0 < 1 < 2`). The
impact of violating this ordering assumption is really dependent on the
downstream models. Linear models will be impacted by misordered categories
while tree-based models will not.
You can still use an `OrdinalEncoder` with linear models but you need to be
sure that:
- the original categories (before encoding) have an ordering;
- the encoded categories follow the same ordering than the original
categories.
The **next exercise** highlights the issue of misusing `OrdinalEncoder` with
a linear model.
One-hot encoding categorical variables with high cardinality can cause
computational inefficiency in tree-based models. Because of this, it is not recommended
to use `OneHotEncoder` in such cases even if the original categories do not
have a given order. We will show this in the **final exercise** of this sequence.
## Evaluate our predictive pipeline
We can now integrate this encoder inside a machine learning pipeline like we
did with numerical data: let's train a linear classifier on the encoded data
and check the generalization performance of this machine learning pipeline using
cross-validation.
Before we create the pipeline, we have to linger on the `native-country`.
Let's recall some statistics regarding this column.
```
data["native-country"].value_counts()
```
We see that the `Holand-Netherlands` category is occurring rarely. This will
be a problem during cross-validation: if the sample ends up in the test set
during splitting then the classifier would not have seen the category during
training and will not be able to encode it.
In scikit-learn, there are two solutions to bypass this issue:
* list all the possible categories and provide it to the encoder via the
keyword argument `categories`;
* use the parameter `handle_unknown`.
Here, we will use the latter solution for simplicity.
<div class="admonition tip alert alert-warning">
<p class="first admonition-title" style="font-weight: bold;">Tip</p>
<p class="last">Be aware the <tt class="docutils literal">OrdinalEncoder</tt> exposes as well a parameter
<tt class="docutils literal">handle_unknown</tt>. It can be set to <tt class="docutils literal">use_encoded_value</tt> and by setting
<tt class="docutils literal">unknown_value</tt> to handle rare categories. You are going to use these
parameters in the next exercise.</p>
</div>
We can now create our machine learning pipeline.
```
from sklearn.pipeline import make_pipeline
from sklearn.linear_model import LogisticRegression
model = make_pipeline(
OneHotEncoder(handle_unknown="ignore"), LogisticRegression(max_iter=500)
)
```
<div class="admonition note alert alert-info">
<p class="first admonition-title" style="font-weight: bold;">Note</p>
<p class="last">Here, we need to increase the maximum number of iterations to obtain a fully
converged <tt class="docutils literal">LogisticRegression</tt> and silence a <tt class="docutils literal">ConvergenceWarning</tt>. Contrary
to the numerical features, the one-hot encoded categorical features are all
on the same scale (values are 0 or 1), so they would not benefit from
scaling. In this case, increasing <tt class="docutils literal">max_iter</tt> is the right thing to do.</p>
</div>
Finally, we can check the model's generalization performance only using the
categorical columns.
```
from sklearn.model_selection import cross_validate
cv_results = cross_validate(model, data_categorical, target)
cv_results
scores = cv_results["test_score"]
print(f"The accuracy is: {scores.mean():.3f} +/- {scores.std():.3f}")
```
As you can see, this representation of the categorical variables is
slightly more predictive of the revenue than the numerical variables
that we used previously.
In this notebook we have:
* seen two common strategies for encoding categorical features: **ordinal
encoding** and **one-hot encoding**;
* used a **pipeline** to use a **one-hot encoder** before fitting a logistic
regression.
|
github_jupyter
|
# TEST for matrix_facto_10_embeddings_100_epochs
# Deep recommender on top of Amason’s Clean Clothing Shoes and Jewelry explicit rating dataset
Frame the recommendation system as a rating prediction machine learning problem and create a hybrid architecture that mixes the collaborative and content based filtering approaches:
- Collaborative part: Predict items ratings in order to recommend to the user items that he is likely to rate high.
- Content based: use metadata inputs (such as price and title) about items to find similar items to recommend.
### - Create 2 explicit recommendation engine models based on 2 machine learning architecture using Keras:
1. a matrix factorization model
2. a deep neural network model.
### Compare the results of the different models and configurations to find the "best" predicting model
### Used the best model for recommending items to users
```
### name of model
modname = 'matrix_facto_10_embeddings_100_epochs'
### number of epochs
num_epochs = 100
### size of embedding
embedding_size = 10
# import sys
# !{sys.executable} -m pip install --upgrade pip
# !{sys.executable} -m pip install sagemaker-experiments
# !{sys.executable} -m pip install pandas
# !{sys.executable} -m pip install numpy
# !{sys.executable} -m pip install matplotlib
# !{sys.executable} -m pip install boto3
# !{sys.executable} -m pip install sagemaker
# !{sys.executable} -m pip install pyspark
# !{sys.executable} -m pip install ipython-autotime
# !{sys.executable} -m pip install surprise
# !{sys.executable} -m pip install smart_open
# !{sys.executable} -m pip install pyarrow
# !{sys.executable} -m pip install fastparquet
# Check Jave version
# !sudo yum -y update
# # Need to use Java 1.8.0
# !sudo yum remove jre-1.7.0-openjdk -y
!java -version
# !sudo update-alternatives --config java
# !pip install pyarrow fastparquet
# !pip install ipython-autotime
# !pip install tqdm pydot pydotplus pydot_ng
#### To measure all running time
# https://github.com/cpcloud/ipython-autotime
%load_ext autotime
%pylab inline
import warnings
warnings.filterwarnings("ignore")
%matplotlib inline
import re
import seaborn as sbn
import nltk
import tqdm as tqdm
import sqlite3
import pandas as pd
import numpy as np
from pandas import DataFrame
import string
import pydot
import pydotplus
import pydot_ng
import pickle
import time
import gzip
import os
os.getcwd()
import matplotlib.pyplot as plt
from math import floor,ceil
#from nltk.corpus import stopwords
#stop = stopwords.words("english")
from nltk.stem.porter import PorterStemmer
english_stemmer=nltk.stem.SnowballStemmer('english')
from nltk.tokenize import word_tokenize
from sklearn.metrics import accuracy_score, confusion_matrix,roc_curve, auc,classification_report, mean_squared_error, mean_absolute_error
from sklearn.feature_extraction.text import CountVectorizer, TfidfTransformer
from sklearn.model_selection import train_test_split
from sklearn import metrics
from sklearn.svm import LinearSVC
from sklearn.neighbors import NearestNeighbors
from sklearn.linear_model import LogisticRegression
from sklearn import neighbors
from scipy.spatial.distance import cosine
from sklearn.feature_selection import SelectKBest
from IPython.display import SVG
# Tensorflow
import tensorflow as tf
#Keras
from keras.models import Sequential, Model, load_model, save_model
from keras.callbacks import ModelCheckpoint
from keras.layers import Dense, Activation, Dropout, Input, Masking, TimeDistributed, LSTM, Conv1D, Embedding
from keras.layers import GRU, Bidirectional, BatchNormalization, Reshape
from keras.optimizers import Adam
from keras.layers.core import Reshape, Dropout, Dense
from keras.layers.merge import Multiply, Dot, Concatenate
from keras.layers.embeddings import Embedding
from keras import optimizers
from keras.callbacks import ModelCheckpoint
from keras.utils.vis_utils import model_to_dot
```
### Set and Check GPUs
```
#Session
from keras import backend as K
def set_check_gpu():
cfg = K.tf.ConfigProto()
cfg.gpu_options.per_process_gpu_memory_fraction =1 # allow all of the GPU memory to be allocated
# for 8 GPUs
# cfg.gpu_options.visible_device_list = "0,1,2,3,4,5,6,7" # "0,1"
# for 1 GPU
cfg.gpu_options.visible_device_list = "0"
#cfg.gpu_options.allow_growth = True # # Don't pre-allocate memory; dynamically allocate the memory used on the GPU as-needed
#cfg.log_device_placement = True # to log device placement (on which device the operation ran)
sess = K.tf.Session(config=cfg)
K.set_session(sess) # set this TensorFlow session as the default session for Keras
print("* TF version: ", [tf.__version__, tf.test.is_gpu_available()])
print("* List of GPU(s): ", tf.config.experimental.list_physical_devices() )
print("* Num GPUs Available: ", len(tf.config.experimental.list_physical_devices('GPU')))
os.environ["CUDA_DEVICE_ORDER"] = "PCI_BUS_ID";
# set for 8 GPUs
# os.environ["CUDA_VISIBLE_DEVICES"] = "0,1,2,3,4,5,6,7";
# set for 1 GPU
os.environ["CUDA_VISIBLE_DEVICES"] = "0";
# Tf debugging option
tf.debugging.set_log_device_placement(True)
gpus = tf.config.experimental.list_physical_devices('GPU')
if gpus:
try:
# Currently, memory growth needs to be the same across GPUs
for gpu in gpus:
tf.config.experimental.set_memory_growth(gpu, True)
logical_gpus = tf.config.experimental.list_logical_devices('GPU')
print(len(gpus), "Physical GPUs,", len(logical_gpus), "Logical GPUs")
except RuntimeError as e:
# Memory growth must be set before GPUs have been initialized
print(e)
# print(tf.config.list_logical_devices('GPU'))
print(tf.config.experimental.list_physical_devices('GPU'))
print("Num GPUs Available: ", len(tf.config.experimental.list_physical_devices('GPU')))
set_check_gpu()
# reset GPU memory& Keras Session
def reset_keras():
try:
del classifier
del model
except:
pass
K.clear_session()
K.get_session().close()
# sess = K.get_session()
cfg = K.tf.ConfigProto()
cfg.gpu_options.per_process_gpu_memory_fraction
# cfg.gpu_options.visible_device_list = "0,1,2,3,4,5,6,7" # "0,1"
cfg.gpu_options.visible_device_list = "0" # "0,1"
cfg.gpu_options.allow_growth = True # dynamically grow the memory used on the GPU
sess = K.tf.Session(config=cfg)
K.set_session(sess) # set this TensorFlow session as the default session for Keras
```
## Load dataset and analysis using Spark
## Download and prepare Data:
#### 1. Read the data:
#### Read the data from the reviews dataset of amazon.
#### Use the dastaset in which all users and items have at least 5 reviews.
### Location of dataset: https://nijianmo.github.io/amazon/index.html
```
import pandas as pd
import boto3
import sagemaker
from sagemaker import get_execution_role
from sagemaker.session import Session
from sagemaker.analytics import ExperimentAnalytics
import gzip
import json
from pyspark.ml import Pipeline
from pyspark.sql.types import StructField, StructType, StringType, DoubleType
from pyspark.ml.feature import StringIndexer, VectorIndexer, OneHotEncoder, VectorAssembler
from pyspark.sql.functions import *
# spark imports
from pyspark.sql import SparkSession
from pyspark.sql.functions import UserDefinedFunction, explode, desc
from pyspark.sql.types import StringType, ArrayType
from pyspark.ml.evaluation import RegressionEvaluator
import os
import pandas as pd
import pyarrow
import fastparquet
# from pandas_profiling import ProfileReport
# !aws s3 cp s3://dse-cohort5-group1/2-Keras-DeepRecommender/dataset/Clean_Clothing_Shoes_and_Jewelry_5_clean.parquet ./data/
!ls -alh ./data
```
### Read clened dataset from parquet files
```
review_data = pd.read_parquet("./data/Clean_Clothing_Shoes_and_Jewelry_5_clean.parquet")
review_data[:3]
review_data.shape
```
### 2. Arrange and clean the data
Rearrange the columns by relevance and rename column names
```
review_data.columns
review_data = review_data[['asin', 'image', 'summary', 'reviewText', 'overall', 'reviewerID', 'reviewerName', 'reviewTime']]
review_data.rename(columns={ 'overall': 'score','reviewerID': 'user_id', 'reviewerName': 'user_name'}, inplace=True)
#the variables names after rename in the modified data frame
list(review_data)
```
# Add Metadata
### Metadata includes descriptions, price, sales-rank, brand info, and co-purchasing links
- asin - ID of the product, e.g. 0000031852
- title - name of the product
- price - price in US dollars (at time of crawl)
- imUrl - url of the product image
- related - related products (also bought, also viewed, bought together, buy after viewing)
- salesRank - sales rank information
- brand - brand name
- categories - list of categories the product belongs to
```
# !aws s3 cp s3://dse-cohort5-group1/2-Keras-DeepRecommender/dataset/Cleaned_meta_Clothing_Shoes_and_Jewelry.parquet ./data/
all_info = pd.read_parquet("./data/Cleaned_meta_Clothing_Shoes_and_Jewelry.parquet")
all_info.head(n=5)
```
### Arrange and clean the data
- Cleaning, handling missing data, normalization, etc:
- For the algorithm in keras to work, remap all item_ids and user_ids to an interger between 0 and the total number of users or the total number of items
```
all_info.columns
items = all_info.asin.unique()
item_map = {i:val for i,val in enumerate(items)}
inverse_item_map = {val:i for i,val in enumerate(items)}
all_info["old_item_id"] = all_info["asin"] # copying for join with metadata
all_info["item_id"] = all_info["asin"].map(inverse_item_map)
items = all_info.item_id.unique()
print ("We have %d unique items in metadata "%items.shape[0])
all_info['description'] = all_info['description'].fillna(all_info['title'].fillna('no_data'))
all_info['title'] = all_info['title'].fillna(all_info['description'].fillna('no_data').apply(str).str[:20])
all_info['image'] = all_info['image'].fillna('no_data')
all_info['price'] = pd.to_numeric(all_info['price'],errors="coerce")
all_info['price'] = all_info['price'].fillna(all_info['price'].median())
users = review_data.user_id.unique()
user_map = {i:val for i,val in enumerate(users)}
inverse_user_map = {val:i for i,val in enumerate(users)}
review_data["old_user_id"] = review_data["user_id"]
review_data["user_id"] = review_data["user_id"].map(inverse_user_map)
items_reviewed = review_data.asin.unique()
review_data["old_item_id"] = review_data["asin"] # copying for join with metadata
review_data["item_id"] = review_data["asin"].map(inverse_item_map)
items_reviewed = review_data.item_id.unique()
users = review_data.user_id.unique()
print ("We have %d unique users"%users.shape[0])
print ("We have %d unique items reviewed"%items_reviewed.shape[0])
# We have 192403 unique users in the "small" dataset
# We have 63001 unique items reviewed in the "small" dataset
review_data.head(3)
```
## Adding the review count and avarage to the metadata
```
#items_nb = review_data['old_item_id'].value_counts().reset_index()
items_avg = review_data.drop(['summary','reviewText','user_id','asin','user_name','reviewTime','old_user_id','item_id'],axis=1).groupby('old_item_id').agg(['count','mean']).reset_index()
items_avg.columns= ['old_item_id','num_ratings','avg_rating']
#items_avg.head(5)
items_avg['num_ratings'].describe()
all_info = pd.merge(all_info,items_avg,how='left',left_on='asin',right_on='old_item_id')
pd.set_option('display.max_colwidth', 100)
all_info.head(2)
```
# Explicit feedback (Reviewed Dataset) Recommender System
### Explicit feedback is when users gives voluntarily the rating information on what they like and dislike.
- In this case, I have explicit item ratings ranging from one to five.
- Framed the recommendation system as a rating prediction machine learning problem:
- Predict an item's ratings in order to be able to recommend to a user an item that he is likely to rate high if he buys it. `
### To evaluate the model, I randomly separate the data into a training and test set.
```
ratings_train, ratings_test = train_test_split( review_data, test_size=0.1, random_state=0)
ratings_train.shape
ratings_test.shape
```
## Adding Metadata to the train set
Create an architecture that mixes the collaborative and content based filtering approaches:
```
- Collaborative Part: Predict items ratings to recommend to the user items which he is likely to rate high according to learnt item & user embeddings (learn similarity from interactions).
- Content based part: Use metadata inputs (such as price and title) about items to recommend to the user contents similar to those he rated high (learn similarity of item attributes).
```
#### Adding the title and price - Add the metadata of the items in the training and test datasets.
```
# # creating metadata mappings
# titles = all_info['title'].unique()
# titles_map = {i:val for i,val in enumerate(titles)}
# inverse_titles_map = {val:i for i,val in enumerate(titles)}
# price = all_info['price'].unique()
# price_map = {i:val for i,val in enumerate(price)}
# inverse_price_map = {val:i for i,val in enumerate(price)}
# print ("We have %d prices" %price.shape)
# print ("We have %d titles" %titles.shape)
# all_info['price_id'] = all_info['price'].map(inverse_price_map)
# all_info['title_id'] = all_info['title'].map(inverse_titles_map)
# # creating dict from
# item2prices = {}
# for val in all_info[['item_id','price_id']].dropna().drop_duplicates().iterrows():
# item2prices[val[1]["item_id"]] = val[1]["price_id"]
# item2titles = {}
# for val in all_info[['item_id','title_id']].dropna().drop_duplicates().iterrows():
# item2titles[val[1]["item_id"]] = val[1]["title_id"]
# # populating the rating dataset with item metadata info
# ratings_train["price_id"] = ratings_train["item_id"].map(lambda x : item2prices[x])
# ratings_train["title_id"] = ratings_train["item_id"].map(lambda x : item2titles[x])
# # populating the test dataset with item metadata info
# ratings_test["price_id"] = ratings_test["item_id"].map(lambda x : item2prices[x])
# ratings_test["title_id"] = ratings_test["item_id"].map(lambda x : item2titles[x])
```
## create rating train/test dataset and upload into S3
```
# !aws s3 cp s3://dse-cohort5-group1/2-Keras-DeepRecommender/dataset/ratings_test.parquet ./data/
# !aws s3 cp s3://dse-cohort5-group1/2-Keras-DeepRecommender/dataset/ratings_train.parquet ./data/
ratings_test = pd.read_parquet('./data/ratings_test.parquet')
ratings_train = pd.read_parquet('./data/ratings_train.parquet')
ratings_train[:3]
ratings_train.shape
```
# **Define embeddings
### The $\underline{embeddings}$ are low-dimensional hidden representations of users and items,
### i.e. for each item I can find its properties and for each user I can encode how much they like those properties so I can determine attitudes or preferences of users by a small number of hidden factors
### Throughout the training, I learn two new low-dimensional dense representations: one embedding for the users and another one for the items.
```
price = all_info['price'].unique()
titles = all_info['title'].unique()
```
# 1. Matrix factorization approach

```
# declare input embeddings to the model
# User input
user_id_input = Input(shape=[1], name='user')
# Item Input
item_id_input = Input(shape=[1], name='item')
price_id_input = Input(shape=[1], name='price')
title_id_input = Input(shape=[1], name='title')
# define the size of embeddings as a parameter
# Check 5, 10 , 15, 20, 50
user_embedding_size = embedding_size
item_embedding_size = embedding_size
price_embedding_size = embedding_size
title_embedding_size = embedding_size
# apply an embedding layer to all inputs
user_embedding = Embedding(output_dim=user_embedding_size, input_dim=users.shape[0],
input_length=1, name='user_embedding')(user_id_input)
item_embedding = Embedding(output_dim=item_embedding_size, input_dim=items_reviewed.shape[0],
input_length=1, name='item_embedding')(item_id_input)
price_embedding = Embedding(output_dim=price_embedding_size, input_dim=price.shape[0],
input_length=1, name='price_embedding')(price_id_input)
title_embedding = Embedding(output_dim=title_embedding_size, input_dim=titles.shape[0],
input_length=1, name='title_embedding')(title_id_input)
# reshape from shape (batch_size, input_length,embedding_size) to (batch_size, embedding_size).
user_vecs = Reshape([user_embedding_size])(user_embedding)
item_vecs = Reshape([item_embedding_size])(item_embedding)
price_vecs = Reshape([price_embedding_size])(price_embedding)
title_vecs = Reshape([title_embedding_size])(title_embedding)
```
### Matrix Factorisation works on the principle that we can learn the user and the item embeddings, and then predict the rating for each user-item by performing a dot (or scalar) product between the respective user and item embedding.
```
# Applying matrix factorization: declare the output as being the dot product between the two embeddings: items and users
y = Dot(1, normalize=False)([user_vecs, item_vecs])
!mkdir -p ./models
# create model
model = Model(inputs=
[
user_id_input,
item_id_input
],
outputs=y)
# compile model
model.compile(loss='mse',
optimizer="adam" )
# set save location for model
save_path = "./models"
thename = save_path + '/' + modname + '.h5'
mcheck = ModelCheckpoint(thename, monitor='val_loss', save_best_only=True)
# fit model
history = model.fit([ratings_train["user_id"]
, ratings_train["item_id"]
]
, ratings_train["score"]
, batch_size=64
, epochs=num_epochs
, validation_split=0.2
, callbacks=[mcheck]
, shuffle=True)
# Save the fitted model history to a file
with open('./histories/' + modname + '.pkl' , 'wb') as file_pi: pickle.dump(history.history, file_pi)
print("Save history in ", './histories/' + modname + '.pkl')
def disp_model(path,file,suffix):
model = load_model(path+file+suffix)
## Summarise the model
model.summary()
# Extract the learnt user and item embeddings, i.e., a table with number of items and users rows and columns, with number of columns is the dimension of the trained embedding.
# In our case, the embeddings correspond exactly to the weights of the model:
weights = model.get_weights()
print ("embeddings \ weights shapes",[w.shape for w in weights])
return model
model_path = "./models/"
def plt_pickle(path,file,suffix):
with open(path+file+suffix , 'rb') as file_pi:
thepickle= pickle.load(file_pi)
plot(thepickle["loss"],label ='Train Error ' + file,linestyle="--")
plot(thepickle["val_loss"],label='Validation Error ' + file)
plt.legend()
plt.xlabel("Epoch")
plt.ylabel("Error")
##plt.ylim(0, 0.1)
return pd.DataFrame(thepickle,columns =['loss','val_loss'])
hist_path = "./histories/"
model=disp_model(model_path, modname, '.h5')
# Display the model using keras
SVG(model_to_dot(model).create(prog='dot', format='svg'))
x=plt_pickle(hist_path, modname, '.pkl')
x.head(20).transpose()
```
|
github_jupyter
|
# Description
This notebook is used to request computation of average time-series of a WaPOR data layer for an area using WaPOR API.
You will need WaPOR API Token to use this notebook
# Step 1: Read APIToken
Get your APItoken from https://wapor.apps.fao.org/profile. Enter your API Token when running the cell below.
```
import requests
import pandas as pd
path_query=r'https://io.apps.fao.org/gismgr/api/v1/query/'
path_sign_in=r'https://io.apps.fao.org/gismgr/api/v1/iam/sign-in/'
APIToken=input('Your API token: ')
```
# Step 2: Get Authorization AccessToken
Using the input API token to get AccessToken for authorization
```
resp_signin=requests.post(path_sign_in,headers={'X-GISMGR-API-KEY':APIToken})
resp_signin = resp_signin.json()
AccessToken=resp_signin['response']['accessToken']
AccessToken
```
# Step 3: Write Query Payload
For more examples of areatimeseries query load
visit https://io.apps.fao.org/gismgr/api/v1/swagger-ui/examples/AreaStatsTimeSeries.txt
```
crs="EPSG:4326" #coordinate reference system
cube_code="L1_PCP_E"
workspace='WAPOR_2'
start_date="2009-01-01"
end_date="2019-01-01"
#get datacube measure
cube_url=f'https://io.apps.fao.org/gismgr/api/v1/catalog/workspaces/{workspace}/cubes/{cube_code}/measures'
resp=requests.get(cube_url).json()
measure=resp['response']['items'][0]['code']
print('MEASURE: ',measure)
#get datacube time dimension
cube_url=f'https://io.apps.fao.org/gismgr/api/v1/catalog/workspaces/{workspace}/cubes/{cube_code}/dimensions'
resp=requests.get(cube_url).json()
items=pd.DataFrame.from_dict(resp['response']['items'])
dimension=items[items.type=='TIME']['code'].values[0]
print('DIMENSION: ',dimension)
```
## Define area by coordinate extent
```
bbox= [37.95883206252312, 7.89534, 43.32093, 12.3873979377346] #latlon
xmin,ymin,xmax,ymax=bbox[0],bbox[1],bbox[2],bbox[3]
Polygon=[
[xmin,ymin],
[xmin,ymax],
[xmax,ymax],
[xmax,ymin],
[xmin,ymin]
]
query_areatimeseries={
"type": "AreaStatsTimeSeries",
"params": {
"cube": {
"code": cube_code, #cube_code
"workspaceCode": workspace, #workspace code: use WAPOR for v1.0 and WAPOR_2 for v2.1
"language": "en"
},
"dimensions": [
{
"code": dimension, #use DAY DEKAD MONTH or YEAR
"range": f"[{start_date},{end_date})" #start date and endate
}
],
"measures": [
measure
],
"shape": {
"type": "Polygon",
"properties": {
"name": crs #coordinate reference system
},
"coordinates": [
Polygon
]
}
}
}
query_areatimeseries
```
## OR define area by reading GeoJSON
```
import ogr
shp_fh=r".\data\Awash_shapefile.shp"
shpfile=ogr.Open(shp_fh)
layer=shpfile.GetLayer()
epsg_code=layer.GetSpatialRef().GetAuthorityCode(None)
shape=layer.GetFeature(0).ExportToJson(as_object=True)['geometry'] #get geometry of shapefile in JSON string
shape["properties"]={"name": "EPSG:{0}".format(epsg_code)}#latlon projection
query_areatimeseries={
"type": "AreaStatsTimeSeries",
"params": {
"cube": {
"code": cube_code,
"workspaceCode": workspace,
"language": "en"
},
"dimensions": [
{
"code": dimension,
"range": f"[{start_date},{end_date})"
}
],
"measures": [
measure
],
"shape": shape
}
}
query_areatimeseries
```
# Step 4: Post the QueryPayload with AccessToken in Header
In responses, get an url to query job.
```
resp_query=requests.post(path_query,headers={'Authorization':'Bearer {0}'.format(AccessToken)},
json=query_areatimeseries)
resp_query = resp_query.json()
job_url=resp_query['response']['links'][0]['href']
job_url
```
# Step 5: Get Job Results.
It will take some time for the job to be finished. When the job is finished, its status will be changed from 'RUNNING' to 'COMPLETED' or 'COMPLETED WITH ERRORS'. If it is COMPLETED, the area time series results can be achieved from Response 'output'.
```
i=0
print('RUNNING',end=" ")
while i==0:
resp = requests.get(job_url)
resp=resp.json()
if resp['response']['status']=='RUNNING':
print('.',end =" ")
if resp['response']['status']=='COMPLETED':
results=resp['response']['output']
df=pd.DataFrame(results['items'],columns=results['header'])
i=1
if resp['response']['status']=='COMPLETED WITH ERRORS':
print(resp['response']['log'])
i=1
df
df.index=pd.to_datetime(df.day,format='%Y-%m-%d')
df.plot()
```
|
github_jupyter
|
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import RandomForestRegressor
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split, cross_val_score
from sklearn import metrics
from sklearn.impute import SimpleImputer
boston = load_boston()
regressor = RandomForestRegressor(n_estimators=100, random_state=0)
cross_val_score(regressor, boston.data, boston.target, cv=10, scoring="neg_mean_squared_error")
sorted(metrics.SCORERS.keys())
```
# 使用随即森林填补缺失值
```
dataset = load_boston()
dataset.data.shape
#总共506*13=6578个数据
X_full, y_full = dataset.data, dataset.target
n_samples = X_full.shape[0]
n_features = X_full.shape[1]
```
添加缺失值
```
#首先确定我们希望放入的缺失数据的比例,在这里我们假设是50%,那总共就要有3289个数据缺失
rng = np.random.RandomState(0)
missing_rate = 0.5
n_missing_samples = int(np.floor(n_samples * n_features * missing_rate))
#np.floor向下取整,返回.0格式的浮点数
#所有数据要随机遍布在数据集的各行各列当中,而一个缺失的数据会需要一个行索引和一个列索引
#如果能够创造一个数组,包含3289个分布在0~506中间的行索引,和3289个分布在0~13之间的列索引,那我们就可
#以利用索引来为数据中的任意3289个位置赋空值
#然后我们用0,均值和随机森林来填写这些缺失值,然后查看回归的结果如何
missing_features = rng.randint(0,n_features,n_missing_samples)
missing_samples = rng.randint(0,n_samples,n_missing_samples)
#missing_samples = rng.choice(dataset.data.shape[0],n_missing_samples,replace=False)
#我们现在采样了3289个数据,远远超过我们的样本量506,所以我们使用随机抽取的函数randint。但如果我们需要
#的数据量小于我们的样本量506,那我们可以采用np.random.choice来抽样,choice会随机抽取不重复的随机数,
#因此可以帮助我们让数据更加分散,确保数据不会集中在一些行中
X_missing = X_full.copy()
y_missing = y_full.copy()
X_missing[missing_samples,missing_features] = np.nan
X_missing = pd.DataFrame(X_missing)
#转换成DataFrame是为了后续方便各种操作,numpy对矩阵的运算速度快到拯救人生,但是在索引等功能上却不如pandas
```
使用0和均值填充
```
#使用均值进行填补
from sklearn.impute import SimpleImputer
imp_mean = SimpleImputer(missing_values=np.nan, strategy='mean')
X_missing_mean = imp_mean.fit_transform(X_missing)
#使用0进行填补
imp_0 = SimpleImputer(missing_values=np.nan, strategy="constant",fill_value=0)
X_missing_0 = imp_0.fit_transform(X_missing)
```
使用随即森林填充缺失值
```
"""
使用随机森林回归填补缺失值
任何回归都是从特征矩阵中学习,然后求解连续型标签y的过程,之所以能够实现这个过程,是因为回归算法认为,特征
矩阵和标签之前存在着某种联系。实际上,标签和特征是可以相互转换的,比如说,在一个“用地区,环境,附近学校数
量”预测“房价”的问题中,我们既可以用“地区”,“环境”,“附近学校数量”的数据来预测“房价”,也可以反过来,
用“环境”,“附近学校数量”和“房价”来预测“地区”。而回归填补缺失值,正是利用了这种思想。
对于一个有n个特征的数据来说,其中特征T有缺失值,我们就把特征T当作标签,其他的n-1个特征和原本的标签组成新
的特征矩阵。那对于T来说,它没有缺失的部分,就是我们的Y_test,这部分数据既有标签也有特征,而它缺失的部分,只有特征没有标签,就是我们需要预测的部分。
特征T不缺失的值对应的其他n-1个特征 + 本来的标签:X_train
特征T不缺失的值:Y_train
特征T缺失的值对应的其他n-1个特征 + 本来的标签:X_test
特征T缺失的值:未知,我们需要预测的Y_test
这种做法,对于某一个特征大量缺失,其他特征却很完整的情况,非常适用。
那如果数据中除了特征T之外,其他特征也有缺失值怎么办?
答案是遍历所有的特征,从缺失最少的开始进行填补(因为填补缺失最少的特征所需要的准确信息最少)。
填补一个特征时,先将其他特征的缺失值用0代替,每完成一次回归预测,就将预测值放到原本的特征矩阵中,再继续填
补下一个特征。每一次填补完毕,有缺失值的特征会减少一个,所以每次循环后,需要用0来填补的特征就越来越少。当
进行到最后一个特征时(这个特征应该是所有特征中缺失值最多的),已经没有任何的其他特征需要用0来进行填补了,
而我们已经使用回归为其他特征填补了大量有效信息,可以用来填补缺失最多的特征。
遍历所有的特征后,数据就完整,不再有缺失值了。
"""
X_missing_reg = X_missing.copy()
# 找出数据集中缺失值最多的从小到大的排序
sortindex = np.argsort(X_missing_reg.isnull().sum(axis=0)).values
for i in sortindex:
#构建我们的新特征矩阵和新标签
df = X_missing_reg
fillc = df.iloc[:,i]
df = pd.concat([df.iloc[:,df.columns != i],pd.DataFrame(y_full)],axis=1)
#在新特征矩阵中,对含有缺失值的列,进行0的填补
df_0 =SimpleImputer(missing_values=np.nan,strategy='constant',fill_value=0).fit_transform(df)
#找出我们的训练集和测试集
Ytrain = fillc[fillc.notnull()]
Ytest = fillc[fillc.isnull()]
Xtrain = df_0[Ytrain.index,:]
Xtest = df_0[Ytest.index,:]
#用随机森林回归来填补缺失值
rfc = RandomForestRegressor(n_estimators=100)
rfc = rfc.fit(Xtrain, Ytrain)
Ypredict = rfc.predict(Xtest)
#将填补好的特征返回到我们的原始的特征矩阵中
X_missing_reg.loc[X_missing_reg.iloc[:,i].isnull(),i] = Ypredict
```
对填补好的数据进行建模
```
#对所有数据进行建模,取得MSE结果
X = [X_full,X_missing_mean,X_missing_0,X_missing_reg]
mse = []
std = []
for x in X:
estimator = RandomForestRegressor(random_state=0, n_estimators=100)
scores = cross_val_score(estimator,x,y_full,scoring='neg_mean_squared_error',cv=5).mean()
mse.append(scores * -1)
x_labels = ['Full data',
'Zero Imputation',
'Mean Imputation',
'Regressor Imputation']
colors = ['r', 'g', 'b', 'orange']
plt.figure(figsize=(12, 6))
ax = plt.subplot(111)
for i in np.arange(len(mse)):
ax.barh(i, mse[i],color=colors[i], alpha=0.6, align='center')
ax.set_title('Imputation Techniques with Boston Data')
ax.set_xlim(left=np.min(mse) * 0.9,
right=np.max(mse) * 1.1)
ax.set_yticks(np.arange(len(mse)))
ax.set_xlabel('MSE')
ax.set_yticklabels(x_labels)
plt.show()
```
|
github_jupyter
|
```
%%html
<link href="http://mathbook.pugetsound.edu/beta/mathbook-content.css" rel="stylesheet" type="text/css" />
<link href="https://aimath.org/mathbook/mathbook-add-on.css" rel="stylesheet" type="text/css" />
<style>.subtitle {font-size:medium; display:block}</style>
<link href="https://fonts.googleapis.com/css?family=Open+Sans:400,400italic,600,600italic" rel="stylesheet" type="text/css" />
<link href="https://fonts.googleapis.com/css?family=Inconsolata:400,700&subset=latin,latin-ext" rel="stylesheet" type="text/css" /><!-- Hide this cell. -->
<script>
var cell = $(".container .cell").eq(0), ia = cell.find(".input_area")
if (cell.find(".toggle-button").length == 0) {
ia.after(
$('<button class="toggle-button">Toggle hidden code</button>').click(
function (){ ia.toggle() }
)
)
ia.hide()
}
</script>
```
**Important:** to view this notebook properly you will need to execute the cell above, which assumes you have an Internet connection. It should already be selected, or place your cursor anywhere above to select. Then press the "Run" button in the menu bar above (the right-pointing arrowhead), or press Shift-Enter on your keyboard.
$\newcommand{\identity}{\mathrm{id}}
\newcommand{\notdivide}{\nmid}
\newcommand{\notsubset}{\not\subset}
\newcommand{\lcm}{\operatorname{lcm}}
\newcommand{\gf}{\operatorname{GF}}
\newcommand{\inn}{\operatorname{Inn}}
\newcommand{\aut}{\operatorname{Aut}}
\newcommand{\Hom}{\operatorname{Hom}}
\newcommand{\cis}{\operatorname{cis}}
\newcommand{\chr}{\operatorname{char}}
\newcommand{\Null}{\operatorname{Null}}
\newcommand{\lt}{<}
\newcommand{\gt}{>}
\newcommand{\amp}{&}
$
<div class="mathbook-content"><h2 class="heading hide-type" alt="Exercises 10.5 Sage Exercises"><span class="type">Section</span><span class="codenumber">10.5</span><span class="title">Sage Exercises</span></h2><a href="normal-sage-exercises.ipynb" class="permalink">¶</a></div>
<div class="mathbook-content"><article class="exercise-like" id="exercise-381"><h6 class="heading"><span class="codenumber">1</span></h6><p id="p-1698">Build every subgroup of the alternating group on 5 symbols, $A_5\text{,}$ and check that each is not a normal subgroup (except for the two trivial cases). This command might take a couple seconds to run. Compare this with the time needed to run the <code class="code-inline tex2jax_ignore">.is_simple()</code> method and realize that there is a significant amount of theory and cleverness brought to bear in speeding up commands like this. (It is possible that your Sage installation lacks <abbr class="acronym">GAP</abbr>'s “Table of Marks” library and you will be unable to compute the list of subgroups.)</p></article></div>
<div class="mathbook-content"><article class="exercise-like" id="exercise-382"><h6 class="heading"><span class="codenumber">2</span></h6><p id="p-1699">Consider the quotient group of the group of symmetries of an $8$-gon, formed with the cyclic subgroup of order $4$ generated by a quarter-turn. Use the <code class="code-inline tex2jax_ignore">coset_product</code> function to determine the Cayley table for this quotient group. Use the number of each coset, as produced by the <code class="code-inline tex2jax_ignore">.cosets()</code> method as names for the elements of the quotient group. You will need to build the table “by hand” as there is no easy way to have Sage's Cayley table command do this one for you. You can build a table in the Sage Notebook pop-up editor (shift-click on a blue line) or you might read the documentation of the <code class="code-inline tex2jax_ignore">html.table()</code> method.</p></article></div>
<div class="mathbook-content"><article class="exercise-like" id="exercise-383"><h6 class="heading"><span class="codenumber">3</span></h6><p id="p-1700">Consider the cyclic subgroup of order $4$ in the symmetries of an $8$-gon. Verify that the subgroup is normal by first building the raw left and right cosets (without using the <code class="code-inline tex2jax_ignore">.cosets()</code> method) and then checking their equality in Sage, all with a single command that employs sorting with the <code class="code-inline tex2jax_ignore">sorted()</code> command.</p></article></div>
<div class="mathbook-content"><article class="exercise-like" id="exercise-384"><h6 class="heading"><span class="codenumber">4</span></h6><p id="p-1701">Again, use the same cyclic subgroup of order $4$ in the group of symmetries of an $8$-gon. Check that the subgroup is normal by using part (2) of Theorem <a href="section-factor-groups.ipynb#theorem-normal-equivalents" class="xref" alt="Theorem 10.3 " title="Theorem 10.3 ">10.3</a>. Construct a one-line command that does the complete check and returns <code class="code-inline tex2jax_ignore">True</code>. Maybe sort the elements of the subgroup <code class="code-inline tex2jax_ignore">S</code> first, then slowly build up the necessary lists, commands, and conditions in steps. Notice that this check does not require ever building the cosets.</p></article></div>
<div class="mathbook-content"><article class="exercise-like" id="exercise-385"><h6 class="heading"><span class="codenumber">5</span></h6><p id="p-1702">Repeat the demonstration from the previous subsection that for the symmetries of a tetrahedron, a cyclic subgroup of order $3$ results in an undefined coset multiplication. Above, the default setting for the <code class="code-inline tex2jax_ignore">.cosets()</code> method builds right cosets — but in this problem, work instead with left cosets. You need to choose two cosets to multiply, and then demonstrate two choices for representatives that lead to different results for the product of the cosets.</p></article></div>
<div class="mathbook-content"><article class="exercise-like" id="exercise-386"><h6 class="heading"><span class="codenumber">6</span></h6><p id="p-1703">Construct some dihedral groups of order $2n$ (i.e. symmetries of an $n$-gon, $D_{n}$ in the text, <code class="code-inline tex2jax_ignore">DihedralGroup(n)</code> in Sage). Maybe all of them for $3\leq n \leq 100\text{.}$ For each dihedral group, construct a list of the orders of each of the normal subgroups (so use <code class="code-inline tex2jax_ignore">.normal_subgroups()</code>). You may need to wait ten or twenty seconds for this to finish - be patient. Observe enough examples to hypothesize a pattern to your observations, check your hypothesis against each of your examples and then state your hypothesis clearly.</p><p id="p-1704">Can you predict how many normal subgroups there are in the dihedral group $D_{470448}$ without using Sage to build all the normal subgroups? Can you <em class="emphasis">describe</em> all of the normal subgroups of a dihedral group in a way that would let us predict all of the normal subgroups of $D_{470448}$ without using Sage?</p></article></div>
|
github_jupyter
|
```
from matplotlib import pyplot as plt
import pandas as pd
import seaborn as sns
from matplotlib import rcParams
import numpy as np
%matplotlib inline
rcParams['font.sans-serif'] = 'arial'
pal = sns.xkcd_palette(['dark sky blue', 'light sky blue', 'deep red']).as_hex()
imprinting_df = pd.read_csv('../data/imprinting_function_birth_year.csv')
pop_df = pd.read_csv('../data/demography_by_birth_year.csv')
profiles = pd.read_csv('../final_results_for_ms/15-100/DAHVcohort_subtype.profile_liks.csv', index_col='param')
imprinting_df = imprinting_df[imprinting_df.Season==2018]
pop_df = pop_df[pop_df.Season==2018]
def make_pie_scatter(X, Y, r1, r2, ax, colors, size=200, edgecolor='#666666'):
x = [0] + np.cos(np.linspace(0, 2 * np.pi * r1, 1000)).tolist()
y = [0] + np.sin(np.linspace(0, 2 * np.pi * r1, 1000)).tolist()
xy1 = np.column_stack([x, y])
s1 = np.abs(xy1).max()
x = [0] + np.cos(np.linspace(2 * np.pi * r1, 2 * np.pi * r2, 1000)).tolist()
y = [0] + np.sin(np.linspace(2 * np.pi * r1, 2 * np.pi * r2, 1000)).tolist()
xy2 = np.column_stack([x, y])
s2 = np.abs(xy2).max()
x = [0] + np.cos(np.linspace(2 * np.pi * r2, 2 * np.pi, 1000)).tolist()
y = [0] + np.sin(np.linspace(2 * np.pi * r2, 2 * np.pi, 1000)).tolist()
xy3 = np.column_stack([x, y])
s3 = np.abs(xy3).max()
ax.scatter([X], [Y], marker=(xy1),
s=size, facecolor=colors[0],
edgecolor=edgecolor)
ax.scatter([X], [Y], marker=(xy2),
s=size, facecolor=colors[1],
edgecolor=edgecolor)
ax.scatter([X], [Y], marker=(xy3),
s=size, facecolor=colors[2],
edgecolor=edgecolor)
def get_imprinting_probs(cohort_label):
min_birth_year, max_birth_year = cohort_label.split('-')
min_birth_year = int(min_birth_year)
max_birth_year = int(max_birth_year)
m = imprinting_df[(imprinting_df.Birth_year >= min_birth_year) &
(imprinting_df.Birth_year <= max_birth_year)].sort_values('Birth_year')
p = pop_df[(pop_df.Birth_year >= min_birth_year) &
(pop_df.Birth_year <= max_birth_year)].sort_values('Birth_year')
weights = np.array(p.Population / p.sum().Population)
h1 = sum(m['H1'] * weights)
h2 = sum(m['H2'] * weights)
h3 = sum(m['H3'] * weights)
return(h1, h2, h3)
x = []
y = []
ax0 = plt.subplot(111)
ax0.plot([0, 1], [0, 1], '--', color='#cccccc', zorder=0)
flip = ['1968-1977']
for param, row in profiles.iterrows():
if type(param) == str:
if 'h1' in param and 'VE' in param:
label = param.split('_')[1].replace('.','-')
if label == '2003-2007':
label = '2003-2006'
if label == '1917-1952':
label = '1918-1952'
h1, h2, h3 = get_imprinting_probs(label)
print(h1,h2,h3,label)
row2 = profiles.loc[param.replace('h1', 'h3'), ]
if row.mle != 0.5:
#y.append(row.mle)
#x.append(row2.mle)
if label in flip:
ax0.text(row2.mle - 0.02, row.mle -0.03, label, va='center', ha='right', size=9)
else:
ax0.text(row2.mle + 0.02, row.mle -0.03, label, va='center', size=9)
# errorbars
ax0.hlines(row.mle, row2.prof_min, row2.prof_max, linestyle='-', color='#aaaaaa', zorder=0)
ax0.vlines(row2.mle, row.prof_min, row.prof_max, linestyle='-', color='#aaaaaa', zorder=0)
make_pie_scatter(row2.mle, row.mle, h1, h1+h2, ax0, pal)
#ax0.plot(x, y, 'o', markeredgecolor='purple', color='white')
#ax0.set_ylim(0, 1.05)
l_h1, = plt.plot([100, 100], [100, 100], 's', color=pal[0], markersize=10, label='H1N1', markeredgecolor='k')
l_h2, = plt.plot([100, 100], [100, 100], 's', color=pal[1], markersize=10, label='H3N2', markeredgecolor='k')
l_h3, = plt.plot([100, 100], [100, 100], 's', color=pal[2], markersize=10, label='H3N2', markeredgecolor='k')
plt.legend((l_h1, l_h2, l_h3), ('H1N1', 'H2N2', 'H3N2'), ncol=3, loc='upper center', bbox_to_anchor=(0.5, -0.2), title='Imprinting subtype')
plt.xticks(np.arange(0, 1.1, 0.1), range(0,110,10))
plt.yticks(np.arange(0, 1.1, 0.1), range(0,110,10))
ax0.set_xlim(-0.05, 1.05)
ax0.set_ylim(-0.01, 1.05)
ax0.set_xlabel('Cohort-specific VE for H3N2 (%)', weight='bold')
ax0.set_ylabel('Cohort-specific VE for H1N1 (%)', weight='bold')
plt.gcf().set_size_inches(4,4)
import glob
import pandas as pd
import seaborn as sns
from matplotlib import pyplot as plt
from matplotlib import rcParams
from matplotlib.colors import ListedColormap
import numpy as np
%matplotlib inline
df = pd.read_csv('../final_results_for_ms/15-100/result_summary.csv', index_col='Unnamed: 0')
pal = sns.color_palette('colorblind').as_hex()
flatui = ['white', pal[3], 'darkgreen', 'lightgreen']
my_cmap = ListedColormap(sns.color_palette(flatui).as_hex())
rcParams['font.sans-serif'] = 'arial'
sns.set_context('paper')
full_model='DAHNV'
final_df = pd.DataFrame(columns=['D', 'E', 'Ap', 'vac_cov', 'Nu', 'A', 'N2', 'H_sub','H_group', 'V_constant', 'V_age', 'V_season', 'V_imprinting', 'V_cohort', 'cAIC'])
row = 0
df = df.iloc[1:, ]
exclude = ['DAHVage_subtype', 'DAHVcohort_subtype', 'DAHNVageseason_subtype', 'DAHNVageseason_group',
'DAHNVcohortseason_subtype', 'DAHNVcohortseason_group', 'DAVage', 'DAVcohort', 'DAVimprinting', 'DAVseason']
for model, r in df.iterrows():
if model not in exclude:
if 'Vage' in model:
V = 'V_age'
final_df.loc[row, V] = 1
elif 'Vseason' in model:
V = 'V_season'
final_df.loc[row, V] = 1
elif 'Vimprinting' in model:
V = 'V_imprinting'
final_df.loc[row, V] = 1
elif 'Vcohort' in model:
V = 'V_cohort'
final_df.loc[row, V] = 1
elif 'Vmean' in model:
V = 'V_constant'
final_df.loc[row, V] = 1
if 'H' in model:
if 'subtype' in model:
final_df.loc[row, 'H_sub'] = 1
elif 'group' in model:
final_df.loc[row, 'H_group'] = 1
if 'N' in model:
if r['N2m'] != 0:
final_df.loc[row, 'N2'] = 0.5
else:
final_df.loc[row, 'N2'] = 0.5
final_df.loc[row, 'A'] = 1
final_df.loc[row, 'D'] = 0.25
final_df.loc[row, 'E'] = 0.25
final_df.loc[row, 'Ap'] = 0.25
final_df.loc[row, 'vac_cov'] = 0.25
final_df.loc[row, 'Nu'] = 0.25
#final_df.loc[row, '']
final_df.loc[row, 'cAIC'] = r.cAIC
row += 1
final_df = final_df.sort_values('cAIC')
final_df = final_df.fillna(0)
#final_df['cAIC'] = [np.exp(-0.5 * (c - min(final_df['cAIC']))) for c in final_df['cAIC']]
#final_df.index = ["%.4f" % (c/sum(final_df.cAIC)) for c in final_df['cAIC']]
final_df.index = ["%.4f" % (c - min(final_df['cAIC'])) for c in final_df['cAIC']]
final_df = final_df.loc[:, final_df.columns != 'cAIC']
final_df.columns = ['Demography',
'Enrollment fraction',
'Approachment fraction',
'Healthcare-seeking behavior among vaccinated',
'Nursing home residency',
'Age-specific risk of medically attended influenza A infection',
'N2 imprinting',
'HA imprinting (subtype)',
'HA imprinting (group)',
'Vaccine effectiveness (constant)',
'Vaccine effectiveness (age-specific)',
'Vaccine effectiveness (season-specific)',
'Vaccine effectiveness (imprinting-specific)',
'Vaccine effectiveness (cohort-specific)']
sns.heatmap(final_df, cmap=my_cmap, linewidths=1, linecolor='black', cbar=False, yticklabels=1)
ax = plt.gca()
ax.xaxis.tick_top()
plt.yticks(rotation=0, fontsize=10)
plt.xticks(rotation=45, ha='left', weight='bold')
plt.ylabel('Δ cAIC', weight='bold')
f = plt.gcf()
f.set_size_inches(5.5, 5.5)
plt.tight_layout()
import pandas as pd
from matplotlib import pyplot as plt
from matplotlib import rcParams, patches
import seaborn as sns
import numpy as np
%matplotlib inline
H1_cohort_expectations = '../final_results_for_ms/15-100/DAHVcohort_subtype_H1_expectations.csv'
H1_age_expectations = '../final_results_for_ms/15-100/DAHVage_subtype_H1_expectations.csv'
H3_cohort_expectations = '../final_results_for_ms/15-100/DAHVcohort_subtype_H3_expectations.csv'
H3_age_expectations = '../final_results_for_ms/15-100/DAHVage_subtype_H3_expectations.csv'
def get_labels(age_classes):
labels = []
for l in age_classes:
if l == '65-100':
labels.append('65+')
else:
labels.append(l.replace('v',''))
return labels
def season_to_label(season):
if season == 2009.5:
label = '2009Pan'
else:
label = str(int(season) - 1) + '-' + str(int(season))
return label
rcParams['font.sans-serif'] = 'arial'
rcParams['font.size'] = 10
rcParams['font.weight'] = 'medium'
pal = sns.xkcd_palette(['dark sky blue', 'sky', 'deep red', 'baby pink']).as_hex()
h3_seasons = [2008, 2011, 2012, 2013, 2015, 2017, 2018]
kwargs={'linewidth': 1,
'zorder': 10,
'color': '#8a8a8a'}
subplot = 1
excess = []
resid_co = 0
resid_ag = 0
for season in range(2008, 2019):
if season not in h3_seasons and season != 2009.5:
df_cohort = pd.read_csv(H1_cohort_expectations, index_col=0)
df_age = pd.read_csv(H1_age_expectations, index_col=0)
df_cohort = df_cohort[df_cohort.vac_status == 'vaccinated']
df_age = df_age[df_age.vac_status == 'vaccinated']
plt.subplot(4,3,subplot)
codf = df_cohort[df_cohort.season==season].copy()
agdf = df_age[df_age.season==season].copy()
final_df = pd.merge(codf, agdf, suffixes=['_co', '_ag'], on=['age_group', 'Observed'])
final_df['Excess_co'] = final_df.Observed - final_df.Prediction_co
final_df['Excess_ag'] = final_df.Observed - final_df.Prediction_ag
new_rows = []
x = []
y1 = []
y2 = []
x1 = []
x2 = []
start = -0.2
for index, row in final_df.iterrows():
new_rows.append([row.age_group, row.Excess_co, 'Cohort VE'])
new_rows.append([row.age_group, row.Excess_ag, 'Age VE'])
x.append(start)
x.append(start + 0.4)
y2.append(row.ci_high_co - row.Prediction_co)
y2.append(row.ci_high_ag - row.Prediction_ag)
y1.append(row.ci_low_co - row.Prediction_co)
y1.append(row.ci_low_ag - row.Prediction_ag)
x1.append(start-0.1)
x2.append(start+0.1)
x1.append(start + 0.4 - 0.1)
x2.append(start + 0.4 + 0.1)
start += 1
plotdf = pd.DataFrame(new_rows, columns = ['Age group', 'Excess cases', 'VE type'])
plt.vlines(x=x, ymin=y1, ymax=y2, **kwargs)
plt.hlines(y=y1, xmin = x1, xmax=x2, **kwargs)
plt.hlines(y=y2, xmin = x1, xmax=x2, **kwargs)
ax = sns.barplot(data=plotdf, x='Age group', y='Excess cases', hue='VE type', palette=pal[0:2],edgecolor='#333333')
ax.legend_.remove()
check1 = final_df[(final_df.Observed < final_df.ci_low_ag) | (final_df.Observed > final_df.ci_high_ag)].copy()
check2 = final_df[(final_df.Observed < final_df.ci_low_co) | (final_df.Observed > final_df.ci_high_co)].copy()
elif season != 2009.5:
df_cohort = pd.read_csv(H3_cohort_expectations, index_col=0)
df_age = pd.read_csv(H3_age_expectations, index_col=0)
df_cohort = df_cohort[df_cohort.vac_status == 'vaccinated']
df_age = df_age[df_age.vac_status == 'vaccinated']
plt.subplot(4,3,subplot)
codf = df_cohort[df_cohort.season==season].copy()
agdf = df_age[df_age.season==season].copy()
final_df = pd.merge(codf, agdf, suffixes=['_co', '_ag'], on=['age_group', 'Observed'])
final_df['Excess_co'] = final_df.Observed - final_df.Prediction_co
final_df['Excess_ag'] = final_df.Observed - final_df.Prediction_ag
new_rows = []
x = []
x1 = []
x2 = []
y1 = []
y2 = []
start = -0.2
for index, row in final_df.iterrows():
new_rows.append([row.age_group, row.Excess_co, 'Cohort VE'])
new_rows.append([row.age_group, row.Excess_ag, 'Age VE'])
x.append(start)
x.append(start + 0.4)
y2.append(row.ci_high_co - row.Prediction_co)
y2.append(row.ci_high_ag - row.Prediction_ag)
y1.append(row.ci_low_co - row.Prediction_co)
y1.append(row.ci_low_ag - row.Prediction_ag)
x1.append(start-0.1)
x2.append(start+0.1)
x1.append(start + 0.4 - 0.1)
x2.append(start + 0.4 + 0.1)
start += 1
plotdf = pd.DataFrame(new_rows, columns = ['Age group', 'Excess cases', 'VE type'])
plt.vlines(x=x, ymin=y1, ymax=y2, **kwargs)
plt.hlines(y=y1, xmin = x1, xmax=x2, **kwargs)
plt.hlines(y=y2, xmin = x1, xmax=x2, **kwargs)
ax = sns.barplot(data=plotdf, x='Age group', y='Excess cases', hue='VE type', palette=pal[2:],edgecolor='#333333')
ax.legend_.remove()
check1 = final_df[(final_df.Observed < final_df.ci_low_ag) | (final_df.Observed > final_df.ci_high_ag)].copy()
check2 = final_df[(final_df.Observed < final_df.ci_low_co) | (final_df.Observed > final_df.ci_high_co)].copy()
plt.title(str(season - 1) + '-' + str(season), weight='bold')
plt.axhline(0, color='black', linewidth=1)
ticks, labels = plt.xticks()
if subplot not in [1,4,7,10]:
plt.ylabel('')
else:
plt.ylabel('Exceess cases\namong vaccinated\nindividuals', weight='bold')
if subplot not in [9, 10, 11]:
plt.xlabel('')
plt.xticks(ticks, [])
else:
plt.xlabel('Age group\n(years)', weight='bold')
plt.xticks(ticks, labels, rotation=45, ha='right')
plt.gcf().align_ylabels()
subplot += 1
xmin, xmax = plt.xlim()
plt.gcf().set_size_inches(5.5, 7)
plt.tight_layout()
b1, = plt.bar([10], [0], color=pal[0], edgecolor='#333333', label='H1N1 unvaccinated')
b2, = plt.bar([10], [0], color=pal[1], edgecolor='#333333', label='H1N1 vaccinated')
b3, = plt.bar([10], [0], color=pal[2], edgecolor='#333333', label='H3N2 unvaccinated')
b4, = plt.bar([10], [0], color=pal[3], edgecolor='#333333', label='H3N2 vaccinated')
plt.legend((b1, b2,b3,b4),
('H1N1 cohort VE model',
'H1N1 age VE model',
'H3N2 cohort VE model',
'H3N2 age VE model'),
loc='center',
bbox_to_anchor=(0.5, -1.6),
ncol=2)
plt.xlim(xmin, xmax)
```
|
github_jupyter
|
# Gradient-boosting decision tree (GBDT)
In this notebook, we will present the gradient boosting decision tree
algorithm and contrast it with AdaBoost.
Gradient-boosting differs from AdaBoost due to the following reason: instead
of assigning weights to specific samples, GBDT will fit a decision tree on
the residuals error (hence the name "gradient") of the previous tree.
Therefore, each new tree in the ensemble predicts the error made by the
previous learner instead of predicting the target directly.
In this section, we will provide some intuition about the way learners are
combined to give the final prediction. In this regard, let's go back to our
regression problem which is more intuitive for demonstrating the underlying
machinery.
```
import pandas as pd
import numpy as np
# Create a random number generator that will be used to set the randomness
rng = np.random.RandomState(0)
def generate_data(n_samples=50):
"""Generate synthetic dataset. Returns `data_train`, `data_test`,
`target_train`."""
x_max, x_min = 1.4, -1.4
len_x = x_max - x_min
x = rng.rand(n_samples) * len_x - len_x / 2
noise = rng.randn(n_samples) * 0.3
y = x ** 3 - 0.5 * x ** 2 + noise
data_train = pd.DataFrame(x, columns=["Feature"])
data_test = pd.DataFrame(np.linspace(x_max, x_min, num=300),
columns=["Feature"])
target_train = pd.Series(y, name="Target")
return data_train, data_test, target_train
data_train, data_test, target_train = generate_data()
import matplotlib.pyplot as plt
import seaborn as sns
sns.scatterplot(x=data_train["Feature"], y=target_train, color="black",
alpha=0.5)
_ = plt.title("Synthetic regression dataset")
```
As we previously discussed, boosting will be based on assembling a sequence
of learners. We will start by creating a decision tree regressor. We will set
the depth of the tree so that the resulting learner will underfit the data.
```
from sklearn.tree import DecisionTreeRegressor
tree = DecisionTreeRegressor(max_depth=3, random_state=0)
tree.fit(data_train, target_train)
target_train_predicted = tree.predict(data_train)
target_test_predicted = tree.predict(data_test)
```
Using the term "test" here refers to data that was not used for training.
It should not be confused with data coming from a train-test split, as it
was generated in equally-spaced intervals for the visual evaluation of the
predictions.
```
# plot the data
sns.scatterplot(x=data_train["Feature"], y=target_train, color="black",
alpha=0.5)
# plot the predictions
line_predictions = plt.plot(data_test["Feature"], target_test_predicted, "--")
# plot the residuals
for value, true, predicted in zip(data_train["Feature"],
target_train,
target_train_predicted):
lines_residuals = plt.plot([value, value], [true, predicted], color="red")
plt.legend([line_predictions[0], lines_residuals[0]],
["Fitted tree", "Residuals"])
_ = plt.title("Prediction function together \nwith errors on the training set")
```
<div class="admonition tip alert alert-warning">
<p class="first admonition-title" style="font-weight: bold;">Tip</p>
<p class="last">In the cell above, we manually edited the legend to get only a single label
for all the residual lines.</p>
</div>
Since the tree underfits the data, its accuracy is far from perfect on the
training data. We can observe this in the figure by looking at the difference
between the predictions and the ground-truth data. We represent these errors,
called "Residuals", by unbroken red lines.
Indeed, our initial tree was not expressive enough to handle the complexity
of the data, as shown by the residuals. In a gradient-boosting algorithm, the
idea is to create a second tree which, given the same data `data`, will try
to predict the residuals instead of the vector `target`. We would therefore
have a tree that is able to predict the errors made by the initial tree.
Let's train such a tree.
```
residuals = target_train - target_train_predicted
tree_residuals = DecisionTreeRegressor(max_depth=5, random_state=0)
tree_residuals.fit(data_train, residuals)
target_train_predicted_residuals = tree_residuals.predict(data_train)
target_test_predicted_residuals = tree_residuals.predict(data_test)
sns.scatterplot(x=data_train["Feature"], y=residuals, color="black", alpha=0.5)
line_predictions = plt.plot(
data_test["Feature"], target_test_predicted_residuals, "--")
# plot the residuals of the predicted residuals
for value, true, predicted in zip(data_train["Feature"],
residuals,
target_train_predicted_residuals):
lines_residuals = plt.plot([value, value], [true, predicted], color="red")
plt.legend([line_predictions[0], lines_residuals[0]],
["Fitted tree", "Residuals"], bbox_to_anchor=(1.05, 0.8),
loc="upper left")
_ = plt.title("Prediction of the previous residuals")
```
We see that this new tree only manages to fit some of the residuals. We will
focus on a specific sample from the training set (i.e. we know that the
sample will be well predicted using two successive trees). We will use this
sample to explain how the predictions of both trees are combined. Let's first
select this sample in `data_train`.
```
sample = data_train.iloc[[-2]]
x_sample = sample['Feature'].iloc[0]
target_true = target_train.iloc[-2]
target_true_residual = residuals.iloc[-2]
```
Let's plot the previous information and highlight our sample of interest.
Let's start by plotting the original data and the prediction of the first
decision tree.
```
# Plot the previous information:
# * the dataset
# * the predictions
# * the residuals
sns.scatterplot(x=data_train["Feature"], y=target_train, color="black",
alpha=0.5)
plt.plot(data_test["Feature"], target_test_predicted, "--")
for value, true, predicted in zip(data_train["Feature"],
target_train,
target_train_predicted):
lines_residuals = plt.plot([value, value], [true, predicted], color="red")
# Highlight the sample of interest
plt.scatter(sample, target_true, label="Sample of interest",
color="tab:orange", s=200)
plt.xlim([-1, 0])
plt.legend(bbox_to_anchor=(1.05, 0.8), loc="upper left")
_ = plt.title("Tree predictions")
```
Now, let's plot the residuals information. We will plot the residuals
computed from the first decision tree and show the residual predictions.
```
# Plot the previous information:
# * the residuals committed by the first tree
# * the residual predictions
# * the residuals of the residual predictions
sns.scatterplot(x=data_train["Feature"], y=residuals,
color="black", alpha=0.5)
plt.plot(data_test["Feature"], target_test_predicted_residuals, "--")
for value, true, predicted in zip(data_train["Feature"],
residuals,
target_train_predicted_residuals):
lines_residuals = plt.plot([value, value], [true, predicted], color="red")
# Highlight the sample of interest
plt.scatter(sample, target_true_residual, label="Sample of interest",
color="tab:orange", s=200)
plt.xlim([-1, 0])
plt.legend()
_ = plt.title("Prediction of the residuals")
```
For our sample of interest, our initial tree is making an error (small
residual). When fitting the second tree, the residual in this case is
perfectly fitted and predicted. We will quantitatively check this prediction
using the fitted tree. First, let's check the prediction of the initial tree
and compare it with the true value.
```
print(f"True value to predict for "
f"f(x={x_sample:.3f}) = {target_true:.3f}")
y_pred_first_tree = tree.predict(sample)[0]
print(f"Prediction of the first decision tree for x={x_sample:.3f}: "
f"y={y_pred_first_tree:.3f}")
print(f"Error of the tree: {target_true - y_pred_first_tree:.3f}")
```
As we visually observed, we have a small error. Now, we can use the second
tree to try to predict this residual.
```
print(f"Prediction of the residual for x={x_sample:.3f}: "
f"{tree_residuals.predict(sample)[0]:.3f}")
```
We see that our second tree is capable of predicting the exact residual
(error) of our first tree. Therefore, we can predict the value of `x` by
summing the prediction of all the trees in the ensemble.
```
y_pred_first_and_second_tree = (
y_pred_first_tree + tree_residuals.predict(sample)[0]
)
print(f"Prediction of the first and second decision trees combined for "
f"x={x_sample:.3f}: y={y_pred_first_and_second_tree:.3f}")
print(f"Error of the tree: {target_true - y_pred_first_and_second_tree:.3f}")
```
We chose a sample for which only two trees were enough to make the perfect
prediction. However, we saw in the previous plot that two trees were not
enough to correct the residuals of all samples. Therefore, one needs to
add several trees to the ensemble to successfully correct the error
(i.e. the second tree corrects the first tree's error, while the third tree
corrects the second tree's error and so on).
We will compare the generalization performance of random-forest and gradient
boosting on the California housing dataset.
```
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import cross_validate
data, target = fetch_california_housing(return_X_y=True, as_frame=True)
target *= 100 # rescale the target in k$
from sklearn.ensemble import GradientBoostingRegressor
gradient_boosting = GradientBoostingRegressor(n_estimators=200)
cv_results_gbdt = cross_validate(
gradient_boosting, data, target, scoring="neg_mean_absolute_error",
n_jobs=2,
)
print("Gradient Boosting Decision Tree")
print(f"Mean absolute error via cross-validation: "
f"{-cv_results_gbdt['test_score'].mean():.3f} +/- "
f"{cv_results_gbdt['test_score'].std():.3f} k$")
print(f"Average fit time: "
f"{cv_results_gbdt['fit_time'].mean():.3f} seconds")
print(f"Average score time: "
f"{cv_results_gbdt['score_time'].mean():.3f} seconds")
from sklearn.ensemble import RandomForestRegressor
random_forest = RandomForestRegressor(n_estimators=200, n_jobs=2)
cv_results_rf = cross_validate(
random_forest, data, target, scoring="neg_mean_absolute_error",
n_jobs=2,
)
print("Random Forest")
print(f"Mean absolute error via cross-validation: "
f"{-cv_results_rf['test_score'].mean():.3f} +/- "
f"{cv_results_rf['test_score'].std():.3f} k$")
print(f"Average fit time: "
f"{cv_results_rf['fit_time'].mean():.3f} seconds")
print(f"Average score time: "
f"{cv_results_rf['score_time'].mean():.3f} seconds")
```
In term of computation performance, the forest can be parallelized and will
benefit from using multiple cores of the CPU. In terms of scoring
performance, both algorithms lead to very close results.
However, we see that the gradient boosting is a very fast algorithm to
predict compared to random forest. This is due to the fact that gradient
boosting uses shallow trees. We will go into details in the next notebook
about the hyperparameters to consider when optimizing ensemble methods.
|
github_jupyter
|
# Introduction
## 1.1 Some Apparently Simple Questions
## 1.2 An Alternative Analytic Framework
Solved to a high degree of accuracy using numerical method
```
!pip install --user quantecon
import numpy as np
import numpy.linalg as la
from numba import *
from __future__ import division
#from quantecon.quad import qnwnorm
```
Suppose now that the economist is presented with a demand function
$$q = 0.5* p^{-0.2} + 0.5*p^{-0.5}$$
one that is the sum a domestic demand term and an export demand term.
suppose that the economist is asked to find the price that clears the
market of, say, a quantity of 2 units.
```
#%pylab inline
%pylab notebook
# pylab Populating the interactive namespace from numpy and matplotlib
# numpy for numerical computation
# matplotlib for ploting
#http://matplotlib.org/api/pyplot_api.html#matplotlib.pyplot.plot
p = np.linspace(0.01,0.5, 100)
q = .5 * p **-.2 + .5 * p ** -.5 - 2
plot(q,p)
x1,x2,y1,y2 = 2, 2, 0, 0.5
plot((x1, x2), (y1, y2), 'k-')
# example 1.2
p = 0.25
for i in range(100):
deltap = (.5 * p **-.2 + .5 * p ** -.5 - 2)/(.1 * p **-1.2 + .25 * p **-1.5)
p = p + deltap
if abs(deltap) < 1.e-8: # accuracy
break
#https://stackoverflow.com/questions/20457038/python-how-to-round-down-to-2-decimals
print('The market clean price is {:0.2f} '.format(p))
```
Consider now the rational expectations commodity market model with government
intervention. The source of difficulty in solving this problem is the need to
evaluate the truncated expectation of a continuous distribution.
The economist would replace the original normal yield distribution
with a discrete distribution that has identical lower moments, say one that assumes
values y1; y2; ... ; yn with probabilities w1; w2; ...; wn.
```
# https://github.com/QuantEcon/QuantEcon.py/blob/master/quantecon/quad.py
def qnwnorm(n, mu=None, sig2=None, usesqrtm=False):
"""
Computes nodes and weights for multivariate normal distribution
Parameters
----------
n : int or array_like(float)
A length-d iterable of the number of nodes in each dimension
mu : scalar or array_like(float), optional(default=zeros(d))
The means of each dimension of the random variable. If a scalar
is given, that constant is repeated d times, where d is the
number of dimensions
sig2 : array_like(float), optional(default=eye(d))
A d x d array representing the variance-covariance matrix of the
multivariate normal distribution.
Returns
-------
nodes : np.ndarray(dtype=float)
Quadrature nodes
weights : np.ndarray(dtype=float)
Weights for quadrature nodes
Notes
-----
Based of original function ``qnwnorm`` in CompEcon toolbox by
Miranda and Fackler
References
----------
Miranda, Mario J, and Paul L Fackler. Applied Computational
Economics and Finance, MIT Press, 2002.
"""
n = np.asarray(n)
d = n.size
if mu is None:
mu = np.zeros((d,1))
else:
mu = np.asarray(mu).reshape(-1, 1)
if sig2 is None:
sig2 = np.eye(d)
else:
sig2 = np.asarray(sig2).reshape(d, d)
if all([x.size == 1 for x in [n, mu, sig2]]):
nodes, weights = _qnwnorm1(n)
else:
nodes = []
weights = []
for i in range(d):
_1d = _qnwnorm1(n[i])
nodes.append(_1d[0])
weights.append(_1d[1])
nodes = gridmake(*nodes)
weights = ckron(*weights[::-1])
if usesqrtm:
new_sig2 = la.sqrtm(sig2)
else: # cholesky
new_sig2 = la.cholesky(sig2)
if d > 1:
nodes = new_sig2.dot(nodes) + mu # Broadcast ok
else: # nodes.dot(sig) will not be aligned in scalar case.
nodes = nodes * new_sig2 + mu
return nodes.squeeze(), weights
def _qnwnorm1(n):
"""
Compute nodes and weights for quadrature of univariate standard
normal distribution
Parameters
----------
n : int
The number of nodes
Returns
-------
nodes : np.ndarray(dtype=float)
An n element array of nodes
nodes : np.ndarray(dtype=float)
An n element array of weights
Notes
-----
Based of original function ``qnwnorm1`` in CompEcon toolbox by
Miranda and Fackler
References
----------
Miranda, Mario J, and Paul L Fackler. Applied Computational
Economics and Finance, MIT Press, 2002.
"""
maxit = 100
pim4 = 1 / np.pi**(0.25)
m = np.fix((n + 1) / 2).astype(int)
nodes = np.zeros(n)
weights = np.zeros(n)
for i in range(m):
if i == 0:
z = np.sqrt(2*n+1) - 1.85575 * ((2 * n + 1)**(-1 / 6.1))
elif i == 1:
z = z - 1.14 * (n ** 0.426) / z
elif i == 2:
z = 1.86 * z + 0.86 * nodes[0]
elif i == 3:
z = 1.91 * z + 0.91 * nodes[1]
else:
z = 2 * z + nodes[i-2]
its = 0
while its < maxit:
its += 1
p1 = pim4
p2 = 0
for j in range(1, n+1):
p3 = p2
p2 = p1
p1 = z * math.sqrt(2.0/j) * p2 - math.sqrt((j - 1.0) / j) * p3
pp = math.sqrt(2 * n) * p2
z1 = z
z = z1 - p1/pp
if abs(z - z1) < 1e-14:
break
if its == maxit:
raise ValueError("Failed to converge in _qnwnorm1")
nodes[n - 1 - i] = z
nodes[i] = -z
weights[i] = 2 / (pp*pp)
weights[n - 1 - i] = weights[i]
weights /= math.sqrt(math.pi)
nodes = nodes * math.sqrt(2.0)
return nodes, weights
# example 1.2
y, w = qnwnorm(10, 1, 0.1)
a = 1
for it in range(100):
aold = a
p = 3 - 2 * a * y
f = w.dot(np.maximum(p, 1))
a = 0.5 + 0.5 * f
if abs(a - aold) < 1.e-8:
break
print('The rational expectations equilibrium acreage is {:0.2f} '.format(a) )
print('The expected market price is {:0.2f} '.format(np.dot(w, p)) )
print('The expected effective producer price is {:0.2f} '.format(f) )
```
The economist has combined Gaussian quadrature techniques and fixed-point function iteration methods to solve the problem.
|
github_jupyter
|
## Linear Algebra
Those exercises will involve vector and matrix math, the <a href="http://wiki.scipy.org/Tentative_NumPy_Tutorial">NumPy</a> Python package.
This exercise will be divided into two parts:
#### 1. Math checkup
Where you will do some of the math by hand.
#### 2. NumPy and Spark linear algebra
You will do some exercise using the NumPy package.
<br>
In the following exercises you will need to replace the code parts in the cell that starts with following comment: "#Replace the `<INSERT>`"
To go through the notebook fill in the `<INSERT>`:s with appropriate code in the cells.
To run a cell press Shift-Enter to run it and advance to the following cell or Ctrl-Enter to only run the code in the cell. You should do the exercises from the top to the bottom in this notebook, because following cells may depend on code in previous cells.
If you want to execute these lines in a python script, you will need to create first a spark context:
```
#from pyspark import SparkContext, StorageLevel \
#from pyspark.sql import SQLContext \
#sc = SparkContext(master="local[*]") \
#sqlContext = SQLContext(sc) \
```
But since we are using the notebooks, those lines are not needed here.
## 1. Math checkup
### 1.1 Euclidian norm
$$
\mathbf{v} = \begin{bmatrix}
666 \\
1337 \\
1789 \\
1066 \\
1945 \\
\end{bmatrix}
\qquad
\|\mathbf{v}\| = ?
$$
Calculate the euclidian norm for the $\mathbf{v}$ using the following definition:
$$
\|\mathbf{v}\|_2 = \sqrt{\sum\limits_{i=1}^n {x_i}^2} = \sqrt{{x_1}^2+\cdots+{x_n}^2}
$$
```
#Replace the <INSERT>
import math
import numpy as np
v = [666, 1337, 1789, 1066, 1945]
rdd = sc.parallelize(v)
#sumOfSquares = rdd.map(<INSERT>).reduce(<INSERT>)
sumOfSquares = rdd.map(lambda x: x*x ).reduce(lambda x,y : x+y)
norm = math.sqrt(sumOfSquares)
# <INSERT round to 8 decimals >
norm = format(norm, '.8f')
norm_numpy= np.linalg.norm(v)
print("norm: "+str(norm) +" norm_numpy: "+ str(norm_numpy))
#Helper function to check results
import hashlib
def hashCheck(x, hashCompare): #Defining a help function
hash = hashlib.md5(str(x).encode('utf-8')).hexdigest()
print(hash)
if hash == hashCompare:
print('Yay, you succeeded!')
else:
print('Try again!')
def check(x,y,label):
if(x == y):
print("Yay, "+label+" is correct!")
else:
print("Nay, "+label+" is incorrect, please try again!")
def checkArray(x,y,label):
if np.allclose(x,y):
print("Yay, "+label+" is correct!")
else:
print("Nay, "+label+" is incorrect, please try again!")
#Check if the norm is correct
hashCheck(norm_numpy, '6de149ccbc081f9da04a0bbd8fe05d8c')
```
### 1.2 Transpose
$$
\mathbf{A} = \begin{bmatrix}
1 & 2 & 3\\
4 & 5 & 6\\
7 & 8 & 9\\
\end{bmatrix}
\qquad
\mathbf{A}^T = ?
$$
Tranpose is an operation on matrices that swaps the row for the columns.
$$
\begin{bmatrix}
2 & 7 \\
3 & 11\\
5 & 13\\
\end{bmatrix}^T
\Rightarrow
\begin{bmatrix}
2 & 3 & 5 \\
7 & 11 & 13\\
\end{bmatrix}
$$
Do the transpose of A by hand and write it in:
```
#Replace the <INSERT>
#Input aT like this: AT = [[1, 2, 3],[4, 5, 6],[7, 8, 9]]
#At = <INSERT>
A= np.matrix([[1, 2, 3],[4, 5, 6],[7, 8, 9]])
print(A)
print("\n")
At = np.matrix.transpose(A)
print (At)
At =[[1,4, 7],[2, 5, 8],[3, 6, 9]]
print("\n")
print (At)
#Check if the transpose is correct
hashCheck(At, '1c8dc4c2349277cbe5b7c7118989d8a5')
```
### 1.3 Scalar matrix multiplication
$$
\mathbf{A} = 3\times\begin{bmatrix}
1 & 2 & 3\\
4 & 5 & 6\\
7 & 8 & 9\\
\end{bmatrix}
=?
\qquad
\mathbf{B} = 5\times\begin{bmatrix}
1\\
-4\\
7\\
\end{bmatrix}
=?
$$
The operation is done element-wise, e.g. $k\times\mathbf{A}=\mathbf{C}$ then $k\times a_{i,j}={k}c_{i,j}$.
$$
2
\times
\begin{bmatrix}
1 & 6 \\
4 & 8 \\
\end{bmatrix}
=
\begin{bmatrix}
2\times1& 2\times6 \\
2\times4 & 2\times8\\
\end{bmatrix}
=
\begin{bmatrix}
2& 12 \\
8 & 16\\
\end{bmatrix}
$$
$$
11
\times
\begin{bmatrix}
2 \\
3 \\
5 \\
\end{bmatrix}
=
\begin{bmatrix}
11\times2 \\
11\times3 \\
11\times5 \\
\end{bmatrix}
=
\begin{bmatrix}
22\\
33\\
55\\
\end{bmatrix}
$$
Do the scalar multiplications of $\mathbf{A}$ and $\mathbf{B}$ by hand and write them in:
```
#Replace the <INSERT>
#Input A like this: A = [[1, 2, 3],[4, 5, 6],[7, 8, 9]]
#And B like this: B = [1, -4, 7]
#A = <INSERT>
#B = <INSERT>
A = np.array([[1, 2, 3],[4, 5, 6],[7, 8, 9]])
print(3*A)
print ("\n")
B = np.array([1, -4, 7])
print (5*B)
print ("\n")
A = [[ 3, 6, 9], [12, 15,18], [21, 24, 27]]
B = [5, -20, 35]
#Check if the scalar matrix multiplication is correct
hashCheck(A, '91b9508ec9099ee4d2c0a6309b0d69de')
hashCheck(B, '88bddc0ee0eab409cee011770363d007')
```
### 1.4 Dot product
$$
c_1=\begin{bmatrix}
11 \\
2 \\
\end{bmatrix}
\cdot
\begin{bmatrix}
3 \\
5 \\
\end{bmatrix}
=?
\qquad
c_2=\begin{bmatrix}
1 \\
2 \\
3 \\
\end{bmatrix}
\cdot
\begin{bmatrix}
4 \\
5 \\
6 \\
\end{bmatrix}
=?
$$
The operations are done element-wise, e.g. $\mathbf{v}\cdot\mathbf{w}=k$ then $\sum v_i \times w_i =k$
$$
\begin{bmatrix}
2 \\
3 \\
5 \\
\end{bmatrix}
\cdot
\begin{bmatrix}
1 \\
4 \\
6 \\
\end{bmatrix}
= 2\times1+3\times4+5\times6=44
$$
Calculate the values of $c_1$ and $c_2$ by hand and write them in:
```
#Replace the <INSERT>
#Input c1 and c2 like this: c = 1337
#c1 = <INSERT>
#c2 = <INSERT>
c1_1 = np.array([11,2])
c1_2 = np.array([3,5])
c1 = c1_1.dot(c1_2)
print (c1)
c1 = 43
c2_1 = np.array([1,2,3])
c2_2 = np.array([4,5,6])
c2 = c2_1.dot(c2_2)
print (c2)
c2 = 32
#Check if the dot product is correct
hashCheck(c1, '17e62166fc8586dfa4d1bc0e1742c08b')
hashCheck(c2, '6364d3f0f495b6ab9dcf8d3b5c6e0b01')
```
### 1.5 Matrix multiplication
$$
\mathbf{A}=
\begin{bmatrix}
682 & 848 & 794 & 954 \\
700 & 1223 & 1185 & 816 \\
942 & 428 & 324 & 526 \\
321 & 543 & 532 & 614 \\
\end{bmatrix}
\qquad
\mathbf{B}=
\begin{bmatrix}
869 & 1269 & 1306 & 358 \\
1008 & 836 & 690 & 366 \\
973 & 619 & 407 & 1149 \\
323 & 42 & 405 & 117 \\
\end{bmatrix}
\qquad
\mathbf{A}\times\mathbf{B}=\mathbf{C}=?
$$
The $c_{i,j}$ entry is the dot product of the i-th row in $\mathbf{A}$ and the j-th column in $\mathbf{B}$
Calculate $\mathbf{C}$ by implementing the naive matrix multiplication algotrithm with $\mathcal{O}(n^3)$ run time, by using the tree nested for-loops below:
```
# The convention is to import NumPy as the alias np
import numpy as np
A = [[ 682, 848, 794, 954],
[ 700, 1223, 1185, 816],
[ 942, 428, 324, 526],
[ 321, 543, 532, 614]]
B = [[ 869, 1269, 1306, 358],
[1008, 836, 690, 366],
[ 973, 619, 407, 1149],
[ 323, 42, 405, 117]]
C = [[0]*4 for i in range(4)]
#Iterate through rows of A
for i in range(len(A)):
#Iterate through columns of B
for j in range(len(B[0])):
#Iterate through rows of B
for k in range(len(B)):
C[i][j] += A[i][k] * B[k][j]
print(np.matrix(C))
print(np.matrix(A)*np.matrix(B))
#Check if the matrix multiplication is correct
hashCheck(C, 'f6b7b0500a6355e8e283f732ec28fa76')
```
## 2. NumPy and Spark linear algebra
A python library to utilize arrays is <a href="http://wiki.scipy.org/Tentative_NumPy_Tutorial">NumPy</a>. The library is optimized to be fast and memory efficient, and provide abstractions corresponding to vectors, matrices and the operations done on these objects.
Numpy's array class is called <a href="http://docs.scipy.org/doc/numpy/reference/generated/numpy.ndarray.html">ndarray</a>, it is also known by the alias array. This is a multidimensional array of fixed-size that contains numerical elements of one type, e.g. floats or integers.
### 2.1 Scalar matrix multiplication using NumPy
$$
\mathbf{A} = \begin{bmatrix}
1 & 2 & 3\\
4 & 5 & 6\\
7 & 8 & 9\\
\end{bmatrix}
\quad
5\times\mathbf{A}=\mathbf{C}=?
\qquad
\mathbf{B} = \begin{bmatrix}
1&-4& 7\\
\end{bmatrix}
\quad
3\times\mathbf{B}=\mathbf{D}=?
$$
Utilizing the <a href="http://docs.scipy.org/doc/numpy/reference/generated/numpy.array.html">np.array()</a> function create the above matrix $\mathbf{A}$ and vector $\mathbf{B}$ and multiply it by 5 and 3 correspondingly.
Note that if you use a Python list of integers to create an array you will get a one-dimensional array, which is, for our purposes, equivalent to a vector.
Calculate C and D by inputting the following statements:
```
#Replace the <INSERT>. You will use np.array()
A = np.array([[1, 2, 3],[4,5,6],[7,8,9]])
B = np.array([1,-4, 7])
C = A *5
D = 3 * B
print(A)
print(B)
print(C)
print(D)
#Check if the scalar matrix multiplication is correct
checkArray(C,[[5, 10, 15],[20, 25, 30],[35, 40, 45]], "the scalar multiplication")
checkArray(D,[3, -12, 21], "the scalar multiplication")
```
### 2.2 Dot product and element-wise multiplication
Both dot product and element-wise multiplication is supported by ndarrays.
Element-wise multiplication is the standard between two arrays, of the same dimension, using the operator *.
The dot product you can use either <a href="http://docs.scipy.org/doc/numpy/reference/generated/numpy.dot.html#numpy.dot">np.dot()</a> or <a href="http://docs.scipy.org/doc/numpy/reference/generated/numpy.ndarray.dot.html">np.array.dot()</a>. The dot product is a commutative operation, i.e. the order of the arrays doe not matter, e.g. if you have the ndarrays x and y, you can write the dot product as any of the following four ways: np.dot(x, y), np.dot(y, x), x.dot(y), or y.dot(x).
Calculate the element wise product and the dot product by filling in the following statements:
```
#Replace the <INSERT>
u = np.arange(0, 5)
v = np.arange(5, 10)
elementWise = np.multiply(u,v)
dotProduct = np.dot(u,v)
print(elementWise)
print(dotProduct)
#Check if the dot product and element wise is correct
checkArray(elementWise,[0,6,14,24,36], "the element wise multiplication")
check(dotProduct, 80, "the dot product")
```
### 2.3 Cosine similarity
The cosine similarity between two vectors is defined as the following equation:
$$
cosine\_similarity(u,v)=\cos\theta=\frac{\mathbf{u}\cdot\mathbf{v}}{\|u\|\|v\|}
$$
The norm of a vector $\|v\|$ can be calculated by using <a href="http://docs.scipy.org/doc/numpy/reference/generated/numpy.linalg.norm.html#numpy.linalg.norm">np.linalg.norm()</a>.
Implement the following function that calculates the cosine similarity:
```
def cosine_similarity(u,v):
dotProduct = np.dot(u,v)
normProduct = np.linalg.norm(u)*np.linalg.norm(v)
return dotProduct/normProduct
u = np.array([2503,2992,1042])
v = np.array([2217,2761,990])
w = np.array([0,1,1])
x = np.array([1,0,1])
uv = cosine_similarity(u,v)
wx = cosine_similarity(w,x)
print(uv)
print(wx)
#Check if the cosine similarity is correct
check(round(uv,5),0.99974,"cosine similarity between u and v")
check(round(wx,5),0.5,"cosine similarity between w and x")
```
### 2.4 Matrix math
To represent matrices, you can use the following class: <a href="http://docs.scipy.org/doc/numpy/reference/generated/numpy.matrix.html">np.matrix()</a>. To create a matrix object either pass it a two-dimensional ndarray, or a list of lists to the function, or a string e.g. '1 2; 3 4'. Instead of element-wise multiplication, the operator *, does matrix multiplication.
To transpose a matrix, you can use either <a href="http://docs.scipy.org/doc/numpy/reference/generated/numpy.matrix.transpose.html">np.matrix.transpose()</a> or <a href="http://docs.scipy.org/doc/numpy/reference/generated/numpy.matrix.T.html">.T</a> on the matrix object.
To calculate the inverse of a matrix, you can use <a href="http://docs.scipy.org/doc/numpy/reference/generated/numpy.linalg.inv.html">np.linalg.inv()</a> or <a href="docs.scipy.org/doc/numpy/reference/generated/numpy.matrix.I.htmll">.I</a> on the matrix object, remember that the inverse of a matrix is only defined on square matrices, and is does not always exist (for sufficient requirements of invertibility look up the: <a href="https://en.wikipedia.org/wiki/Invertible_matrix#The_invertible_matrix_theorem">The invertible matrix theorem</a>) and it will then raise a LinAlgError. If you multiply the original matrix with its inverse, you get the identity matrix, which is a square matrix with ones on the main diagonal and zeros elsewhere., e.g. $\mathbf{A} \mathbf{A}^{-1} = \mathbf{I_n}$
In the following exercise, you should calculate $\mathbf{A}^T$ multiply it by $\mathbf{A}$ and then inverting the product $\mathbf{AA}^T$ and finally multiply $\mathbf{AA}^T[\mathbf{AA}^T]^{-1}=\mathbf{I}_n$ to get the identity matrix:
```
#Replace the <INSERT>
#We generate a Vandermonde matrix
A = np.mat(np.vander([2,3], 5))
print(A)
#Calculate the transpose of A
At = np.transpose(A)
print(At)
#Calculate the multiplication of A and A^T
AAt = np.dot(A,At)
print(AAt)
#Calculate the inverse of AA^T
AAtInv = np.linalg.inv(AAt)
print(AAtInv)
#Calculate the multiplication of AA^T and (AA^T)^-1
I = np.dot(AAt,AAtInv)
print(I)
#To get the identity matrix we round it because of numerical precision
I = I.round(13)
#Check if the matrix math is correct
checkArray(I,[[1.,0.], [0.,1.]], "the matrix math")
```
### 2.5 Slices
It is possible to select subsets of one-dimensional arrays using <a href="http://docs.scipy.org/doc/numpy/reference/arrays.indexing.html">slices</a>. The basic syntax for slices is $\mathbf{v}$[i:j:k] where i is the starting index, j is the stopping index, and k is the step ($k\neq0$), the default value for k, if it is not specified, is 1. If no i is specified, the default value is 0, and if no j is specified, the default value is the end of the array.
For example [0,1,2,3,4][:3] = [0,1,2] i.e. the three first elements of the array. You can use negative indices also, for example [0,1,2,3,4][-3:] = [2,3,4] i.e. the three last elements.
The following function can be used to concenate 2 or more arrays: <a href="http://docs.scipy.org/doc/numpy/reference/generated/numpy.concatenate.html">np.concatenate</a>, the syntax is np.concatenate((a1, a2, ...)).
Slice the following array in 3 pieces and concenate them together to form the original array:
```
#Replace the <INSERT>
v = np.arange(1, 9)
print(v)
#The first two elements of v
v1 = v[-2:]
#The last two elements of v
v3 = v[:-2]
#The middle four elements of v
v2 = v[3:7]
print(v1)
print(v2)
print(v3)
#Concatenating the three vectors to get the original array
u = np.concatenate((v1, v2, v3))
```
### 2.6 Stacking
There exist many functions provided by the NumPy library to <a href="http://docs.scipy.org/doc/numpy/reference/routines.array-manipulation.html">manipulate</a> existing arrays. We will try out two of these methods <a href="docs.scipy.org/doc/numpy/reference/generated/numpy.hstack.html">np.hstack()</a> which takes two or more arrays and stack them horizontally to make a single array (column wise, equvivalent to np.concatenate), and <a href="docs.scipy.org/doc/numpy/reference/generated/numpy.vstack.html">np.vstack()</a> which takes two or more arrays and stack them vertically (row wise). The syntax is the following np.vstack((a1, a2, ...)).
Stack the two following array $\mathbf{u}$ and $\mathbf{v}$ to create a 1x20 and a 2x10 array:
```
#Replace the <INSERT>
u = np.arange(1, 11)
v = np.arange(11, 21)
#A 1x20 array
oneRow = np.hstack((u,v))
print(oneRow)
#A 2x10 array
twoRows = np.vstack((u,v))
print(twoRows)
#Check if the stacks are correct
checkArray(oneRow,[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20], "the hstack")
checkArray(twoRows,[[1,2,3,4,5,6,7,8,9,10],[11,12,13,14,15,16,17,18,19,20]], "the vstack")
```
### 2.7 PySpark's DenseVector
In PySpark there exists a <a href="https://spark.apache.org/docs/latest/api/python/pyspark.mllib.html#pyspark.mllib.linalg.DenseVector">DenseVector</a> class within the module <a href="https://spark.apache.org/docs/latest/api/python/pyspark.mllib.html#module-pyspark.mllib.linalg">pyspark.mllib.linalg</a>. The DenseVector stores the values as a NumPy array and delegates the calculations to this object. You can create a new DenseVector by using DenseVector() and passing it an NumPy array or a Python list.
The DenseVector class implements several functions, one important is the dot product, DenseVector.dot(), which operates just like np.ndarray.dot().
The DenseVector save all values as np.float64, so even if you pass it an integer vector, the resulting vector will contain floats. Using the DenseVector in a distributed setting, can be done by either passing functions that contain them to resilient distributed dataset (RDD) transformations or by distributing them directly as RDDs.
Create the DenseVector $\mathbf{u}$ containing the 10 elements [0.1,0.2,...,1.0] and the DenseVector $\mathbf{v}$ containing the 10 elements [1.0,2.0,...,10.0] and calculate the dot product of $\mathbf{u}$ and $\mathbf{v}$:
```
#To use the DenseVector first import it
from pyspark.mllib.linalg import DenseVector
#Replace the <INSERT>
#[0.1,0.2,...,1.0]
u = DenseVector((0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1))
print(u)
#[1.0,2.0,...,10.0]
v = DenseVector((1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0, 9.0, 10.0))
print(v)
#The dot product between u and v
dotProduct = np.dot(u,v)
#Check if the dense vectors are correct
check(dotProduct, 38.5, "the dense vectors")
```
|
github_jupyter
|
# Metadata Organization
## Imports
```
import pandas as pd
import numpy as np
import os.path
import glob
import pathlib
import functools
import time
import re
import gc
from nilearn.input_data import NiftiMasker
import nibabel as nib
from nilearn import image
from joblib import Parallel, delayed
```
## Load configs (all patterns/files/folderpaths)
```
import configurations
configs = configurations.Config('sub-xxx-resamp-intersected')
```
## Function to find all the regressor file paths
```
def timer(func):
"""Print the runtime of the decorated function"""
@functools.wraps(func)
def wrapper(*args, **kwargs):
print(f'Calling {func.__name__!r}')
startTime = time.perf_counter()
value = func(*args, **kwargs)
endTime = time.perf_counter()
runTime = endTime - startTime
print(f'Finished {func.__name__!r} in {runTime:.4f} secs')
return value
return wrapper
```
## Function to find all the BOLD NII file paths
```
@timer
def find_paths(relDataFolder, subj, sess, func, patt):
paths = list(pathlib.Path(relDataFolder).glob(
os.path.join(subj, sess, func, patt)
)
)
return paths
```
## Find all the regressor file paths
```
regressor_paths = find_paths(relDataFolder=configs.dataDir,
subj='sub-*',
sess='ses-*',
func='func',
patt=configs.confoundsFilePattern)
regressor_paths
```
## Find all the BOLD NII file paths
```
nii_paths = find_paths(relDataFolder=configs.dataDir,
subj='sub-*',
sess='ses-*',
func='func',
patt=configs.maskedImagePattern)
nii_paths
```
## Read the participants.tsv file to find summaries of the subjects
```
participant_info_df = pd.read_csv(
configs.participantsSummaryFile,
sep='\t'
)
participant_info_df
```
## Get a mapping Dataframe of subject and which session is the sleep deprived one
```
@timer
def map_sleepdep(participant_info):
df = pd.DataFrame(participant_info.loc[:,['participant_id', 'Sl_cond']])
df.replace('sub-', '', inplace=True, regex=True)
return df.rename(columns={'participant_id':'subject', 'Sl_cond':'sleepdep_session'})
sleepdep_map = map_sleepdep(participant_info_df)
sleepdep_map
```
## Get Dataframe of subject, session, task, path
```
@timer
def get_bids_components(paths):
components_list = []
for i, path in enumerate(paths):
filename = path.stem
dirpath = path.parents[0]
matches = re.search(
'[a-z0-9]+\-([a-z0-9]+)_[a-z0-9]+\-([a-z0-9]+)_[a-z0-9]+\-([a-z0-9]+)',
filename
)
subject = matches.group(1)
session = matches.group(2)
task = matches.group(3)
confound_file = path.with_name(
'sub-'+subject+'_ses-'+session+'_task-'+task+'_desc-confounds_regressors.tsv'
)
components_list.append([subject, session, task,
path.__str__(), confound_file.__str__(), 0]
)
df = pd.DataFrame(components_list,
columns=['subject', 'session', 'task', 'path', 'confound_path', 'sleepdep']
)
return df
bids_comp_df = get_bids_components(nii_paths)
bids_comp_df
```
## Combine logically sleepdep_map and components_df into 1 dataframe
```
sleep_bids_comb_df = bids_comp_df.merge(sleepdep_map, how='left')
```
## Response column 'sleepdep' imputed from 'session' 'sleepdep_session'
```
for i in range(len(sleep_bids_comb_df)):
if (int(sleep_bids_comb_df['session'].iloc[i]) ==
int(sleep_bids_comb_df['sleepdep_session'].iloc[i])):
sleep_bids_comb_df['sleepdep'].iloc[i] = 1
sleep_bids_comb_df
```
## Get confounds that can be used further clean up the signal or for prediction
```
def get_important_confounds(regressor_paths, important_reg_list, start, end):
regressors_df_list = []
for paths in regressor_paths:
regressors_all = pd.DataFrame(pd.read_csv(paths, sep="\t"))
regressors_selected = pd.DataFrame(regressors_all[important_reg_list].loc[start:end-1])
regressors_df_list.append(pd.DataFrame(regressors_selected.stack(0)).transpose())
concatenated_df = pd.concat(regressors_df_list, ignore_index=True)
concatenated_df.columns = [col[1] + '-' + str(col[0]) for col in concatenated_df.columns.values]
return concatenated_df
important_reg_list = ['csf', 'white_matter', 'global_signal',
'trans_x', 'trans_y', 'trans_z',
'rot_x', 'rot_y', 'rot_z',
'csf_derivative1', 'white_matter_derivative1', 'global_signal_derivative1',
'trans_x_derivative1', 'trans_y_derivative1', 'trans_z_derivative1',
'rot_x_derivative1', 'rot_y_derivative1', 'rot_z_derivative1',
'csf_power2', 'white_matter_power2', 'global_signal_power2',
'trans_x_power2', 'trans_y_power2', 'trans_z_power2',
'rot_x_power2', 'rot_y_power2', 'rot_z_power2',
'csf_derivative1_power2', 'white_matter_derivative1_power2', 'global_signal_derivative1_power2',
'trans_x_derivative1_power2', 'trans_y_derivative1_power2', 'trans_z_derivative1_power2',
'rot_x_derivative1_power2', 'rot_y_derivative1_power2', 'rot_z_derivative1_power2'
]
important_confounds_df = get_important_confounds(
sleep_bids_comb_df['confound_path'], important_reg_list, configs.startSlice, configs.endSlice
)
```
## Load the masker data file to prepare to apply to images
```
masker = NiftiMasker(mask_img=configs.maskDataFile, standardize=False)
```
## Helper to generate raw voxel df from a given path + masker and print shape for sanity
```
@timer
def gen_one_voxel_df(filepath, masker, start, end):
masked_array = masker.fit_transform(image.index_img(filepath, slice(start,end)))
reshaped_array = pd.DataFrame(np.reshape(
masked_array.ravel(), newshape=[1,-1]), dtype='float32')
print('> Shape of raw voxels for file ' +
'\"' + pathlib.Path(filepath).stem + '\" ' +
'is: \n' +
'\t 1-D (UnMasked+Sliced): ' + str(reshaped_array.shape) + '\n' +
'\t 2-D (UnMasked+Sliced): ' + str(masked_array.shape) + '\n' +
'\t 4-D (Raw header) : ' + str(nib.load(filepath).header.get_data_shape())
)
return reshaped_array
```
## Function to generate from masked image the raw voxel df from all images in folder
```
@timer
def get_voxels_df(metadata_df, masker, start, end):
rawvoxels_list = []
print() # Print to add a spacer for aesthetics
#below has been parallelized
for i in range(len(metadata_df)):
rawvoxels_list.append(gen_one_voxel_df(metadata_df['path'].iloc[i], masker, start, end))
print() # Print to add a spacer for aesthetics
# rawvoxels_list.append(Parallel(n_jobs=-1, verbose=100)(delayed(gen_one_voxel_df)(metadata_df['path'].iloc[i], masker, start, end) for i in range(len(metadata_df))))
print() # Print to add a spacer for aesthetics
tmp_df = pd.concat(rawvoxels_list, ignore_index=True)
tmp_df['sleepdep'] = metadata_df['sleepdep']
temp_dict = dict((val, str(val)) for val in list(range(len(tmp_df.columns)-1)))
return tmp_df.rename(columns=temp_dict, errors='raise')
```
## Garbage collect
```
gc.collect()
```
## Get/Generate raw voxels dataframe from all images with Y column label included
```
voxels_df = get_voxels_df(sleep_bids_comb_df, masker, configs.startSlice, configs.endSlice)
X = pd.concat([voxels_df, important_confounds_df], axis=1)
```
## Separately get the Y label
```
Y = sleep_bids_comb_df['sleepdep']
```
## Save raw dataframe with Y column included to a file
```
X.to_pickle(configs.rawVoxelFile)
```
|
github_jupyter
|
```
import numpy as np
%matplotlib notebook
import matplotlib.pyplot as plt
nu = np.linspace(1e9, 200e9)
ElectronCharge = 4.803e-10
ElectronMass = 9.1094e-28
SpeedLight = 3e10
def plot_ql_approx(magField, thetaDeg, plasmaDens, ax=None):
gyroFreq = ElectronCharge * magField / (2 * np.pi * ElectronMass * SpeedLight)
plasmaFreq = ElectronCharge * np.sqrt(plasmaDens / (np.pi * ElectronMass))
theta = np.deg2rad(thetaDeg)
approx = (nu**2 - plasmaFreq**2) / (nu * gyroFreq)
limit = 0.5 * np.sin(theta)**2 / np.abs(np.cos(theta))
if ax == None:
plt.figure()
plt.semilogx(nu, approx, label='approximation')
plt.axhline(limit, color='r', label='limit')
plt.semilogx(nu, approx / limit, label='ratio')
plt.legend()
plt.xlabel('Frequency [Hz]')
plt.title(r'Validity of QL approximation for B=%.1f G,''\n'r'$\theta=$%.1f$\degree$ and $n_p$=%.1e cm$^{-3}$' % (magField, thetaDeg, plasmaDens))
else:
ax.semilogx(nu, approx, label='approximation')
ax.axhline(limit, color='r', label='limit')
ax.semilogx(nu, approx / limit, label='ratio')
ax.set_xlabel('Frequency [Hz]')
ax.set_title(r'Validity of QL approximation for B=%.1f G,''\n'r'$\theta=$%.1f$\degree$ and $n_p$=%.1e cm$^{-3}$' % (magField, thetaDeg, plasmaDens))
fig, ax = plt.subplots(2, 2, figsize=(10,10))
plas = 1.51e11
plot_ql_approx(2000, 10, plas, ax=ax[0,0])
ax[0,0].set_title(r'$\theta=10\degree$')
plot_ql_approx(2000, 30, plas, ax=ax[0,1])
ax[0,1].set_title(r'$\theta=30\degree$')
plot_ql_approx(2000, 60, plas, ax=ax[1,0])
ax[1,0].set_title(r'$\theta=60\degree$')
plot_ql_approx(2000, 85, plas, ax=ax[1,1])
ax[1,1].set_title(r'$\theta=85\degree$')
lines = ax[0,0].get_lines()
fig.legend(lines, [l.get_label() for l in lines])
fig.suptitle('Validity of QL approximation: B=2000G, $n_p=1.51\cdot10^{11}$ cm$^{-3}$\n'r'$\tau=1$ for 200 GHz')
fig.tight_layout(rect=[0, 0.03, 1, 0.95])
fig, ax = plt.subplots(2, 2, figsize=(10,10))
plas = 5.3e10
plot_ql_approx(1300, 10, plas, ax=ax[0,0])
ax[0,0].set_title(r'$\theta=10\degree$')
plot_ql_approx(1300, 30, plas, ax=ax[0,1])
ax[0,1].set_title(r'$\theta=30\degree$')
plot_ql_approx(1300, 60, plas, ax=ax[1,0])
ax[1,0].set_title(r'$\theta=60\degree$')
plot_ql_approx(1300, 85, plas, ax=ax[1,1])
ax[1,1].set_title(r'$\theta=85\degree$')
lines = ax[0,0].get_lines()
fig.legend(lines, [l.get_label() for l in lines])
fig.suptitle('Validity of QL approximation: B=1300G, $n_p=5.3\cdot10^{10}$ cm$^{-3}$\n'r'$\tau=1$ for 45 GHz')
fig.tight_layout(rect=[0, 0.03, 1, 0.95])
c7 = np.genfromtxt('c7_adj.csv', delimiter=',', skip_header=1)
height = c7[:,0]
temperature = c7[:,1]
plasmaDens = c7[:,2]
protonDens = c7[:,4]
def dulk_k(freq):
lowT = 17.9 + np.log(temperature**1.5) - np.log(freq)
highT = 24.5 + np.log(temperature) - np.log(freq)
t1 = np.where(temperature < 2e5, lowT, highT)
kDulk = 9.78e-3 * plasmaDens * protonDens / freq**2 / temperature**1.5 * t1;
return kDulk
plt.figure()
plt.semilogy(height, dulk_k(10e9))
plt.xlabel('Height [cm]')
plt.ylabel('$\kappa_{ff}$ [cm$^{-1}$]')
def tau_eq_line(tauVal, freq):
ds = height[1:] - height[:-1]
tau = np.cumsum(dulk_k(freq)[-1:0:-1] * ds[::-1])
return height[-(1 + np.argmax(tau > tauVal))]
tauVal = 1
tauLine = []
for n in nu:
tauLine.append(tau_eq_line(tauVal, n))
fig, ax = plt.subplots(2, 1)
ax[0].semilogx(nu, tauLine, label=r'$tau$-line')
ax[0].set_xlabel('Frequency [Hz]')
ax[0].set_ylabel(r'$\tau=1$ altitude [cm]')
ax[0].set_title(r'Height of $\tau=1$ line for C7 model ''\n''(for an observer looking down from the corona)')
dens = ax[1].twinx()
ax[1].semilogy(height, temperature, 'g', label='T')
ax[1].set_xlim(-5e7, 4e8)
dens.semilogy(height, plasmaDens, 'r', label='$n_p$')
dens.set_ylabel('Plasma density [cm$^{-3}$]')
ax[1].set_ylabel('Temperature [K]')
ax[1].set_xlabel('Height [cm]')
ax[1].axvline(tauLine[-1])
ax[1].axvline(tauLine[np.searchsorted(nu, 10e9)-1])
fig.legend()
fig.tight_layout()
```
|
github_jupyter
|
# GIS web services
## Web Map Service / Web Coverage Service
A Web Map Service (WMS) is an Open Geospatial Consortium (OGC) standard that allows users to remotely access georeferenced map images via secure hypertext transfer protocol (HTTPS) requests.
DE Africa provides two types of maps services:
* Web Map Service (WMS) – A standard protocol for serving georeferenced map images over the internet that are generated from a map server using data from a GIS database. It is important to note that with a WMS, you are essentially getting an image of geospatial data (i.e. JPG, GIF, PNG file). While this has its uses, it is an image only, and therefore does not contain any of the underlying geospatial data that was used to create the image.
* Web Coverage Service (WCS) – A standard protocol for serving coverage data which returns data with its original semantics (instead of just pictures) which may be interpreted, extrapolated, etc., and not just portrayed. Essentially, a WCS can be thought of as the raw geospatial raster data behind an image. Using a WCS, you can pull the raw raster information you need to perform further analysis.
So, to give a quick summarisation, a WMS is simply an image of a map. You can almost think of this like taking a screenshot of Google Maps. A WCS is the raw raster data, so for example, if you are working with a WCS containing Landsat imagery, you can effectively chunk off the piece you are interested in and download the full multispectral image at the spatial resolution of the original image. The beauty of these services is that you can grab only the information you need. So, rather than retrieving a file that contains the data you are seeking and possibly much more, you can confine your download to only your area of interest, allowing you to get what you need and no more.
For more information, see this article on the [difference between GIS web services](https://www.l3harrisgeospatial.com/Learn/Blogs/Blog-Details/ArtMID/10198/ArticleID/16289/Web-Mapping-Service-Web-Coverage-Service-or-Web-Feature-Service-%E2%80%93-What%E2%80%99s-the-Difference).
The tutorials below cover setting up WMS and connecting to WCS.
## Tutorial: Setting up WMS
This tutorial shows how to set up the Web Map Services in QGIS, and use it with other data on your computer such as drone imagery, vector or raster data. This may be useful for you if you cannot upload the data to the DE Africa Map or the DE Africa Sandbox due to uploading due to size or internet bandwidth. It may also be useful if you feel more comfortable doing analysis in a GIS application.
Although this tutorial focuses on QGIS, the same process can be used to connect other Desktop GIS applications. [QGIS](https://qgis.org/en/site/) is a free and open-source desktop GIS application. You can download it from https://qgis.org/en/site/.
**How to connect to WMS using QGIS**
1. Launch QGIS.
2. On the Menu Bar click on **Layer**.
3. A sub-menu tab will show below Layer; click on **Add Layer**, choose **Add WMS/WMTS Layer**.
<img align="middle" src="_static/other_information/ows_tutorial_1.png" alt="QGIS - Add Layer" width="500">
4. A dialogue will open as shown below. Click on the **New** button.
<img align="middle" src="_static/other_information/ows_tutorial_2.png" alt="QGIS - New Layer" width="500">
5. A dialogue will open, as shown below: Provide the following details, these can be found at the URL https://ows.digitalearth.africa/.
`Name: DE Africa Services`
`URL: https://ows.digitalearth.africa/wms?version=1.3.0 `
<img align="middle" src="_static/other_information/ows_tutorial_3.png" alt="QGIS - Create New Connection" width="300">
6. After providing the details above, click on **OK**.
7. The previous dialogue will show up, in the dropdown above the **New** button, you will see DE Africa Services. If it is not there click the dropdown button below and select it.
8. The **Connect** button will be activated, click on it to load the layers. Anytime this page is open, because the connection has already been established, click on **Connect** to load the data.
<img align="middle" src="_static/other_information/ows_tutorial_4.png" alt="QGIS - View Connection" width="500">
9. The layer will be loaded as shown below in the dialogue.
10. Navigate through layers and choose the layer you will need to display on the Map Page.
11. After selecting the layer, click on **Add** button at the bottom of the dialogue.
12. Close the dialogue, the selected layer will be loaded onto the Map Page.
**For web developers**
The sites below provide instructions on how to load these map services onto your platform.
https://leafletjs.com/examples/wms/wms.html
https://openlayers.org/en/latest/examples/wms-tiled.html
https://docs.microsoft.com/en-us/bingmaps/v8-web-control/map-control-concepts/layers/wms-tile-layer-example
## Tutorial: How to connect WCS
This tutorial shows how to create a Web Coverage Service connection using QGIS.
1. Launch QGIS.
2. On the Menu Bar click on **Layer**.
3. A sub-menu tab will show below Layer; click on **Add Layer**, choose **Add WCS Layer**.
<img align="middle" src="_static/other_information/ows_tutorial_5.png" alt="QGIS - Add WCS" width="500">
4. Click on the **New** button.
5. A dialogue will open, as shown below: Provide the following details, these can be found at the URL https://ows.digitalearth.africa/
`Name: DE Africa Services`
`URL: https://ows.digitalearth.africa/wcs?version=2.1.0`
<img align="middle" src="_static/other_information/ows_tutorial_6.png" alt="QGIS - WCS Connection" width="300">
6. After providing the details above, click on **OK**.
7. The previous dialogue will show up, in the dropdown above the New button, you will see DE Africa Services, if it is not there click the dropdown button below and select it.
8. The **Connect** button will be activated, click on it to load the layers. Anytime this page is open, because the connection has already been established, click on the **Connect** button to load the data.
9. The layer will be loaded as shown below in the dialogue.
<img align="middle" src="_static/other_information/ows_tutorial_4.png" alt="QGIS - Loaded WCS" width="500">
10. Navigate through layers and choose the layer you will need to display on the Map Page. With WCS you can select Time and Format of Image.
11. After selecting the layer click on the **Add** button at the bottom of the dialogue.
|
github_jupyter
|
# Useful modules in standard library
---
**Programming Language**
- Core Feature
+ builtin with language,
+ e.g input(), all(), for, if
- Standard Library
+ comes preinstalled with language installer
+ e.g datetime, csv, Fraction
- Thirdparty Library
+ created by community to solve specific problem
+ e.g numpy, pandas, requests
## import statement
### Absolute import
```
%ls
import hello
import hello2
%cat hello.py
hello.hello()
%ls hello_package/
%cat hello_package/__init__.py
%cat hello_package/diff.py
import hello_package
hello_package.diff.diff
hello_package.diff.diff()
hello_package.diff
import hello_package.diff
diff.diff()
hello_package.diff.diff()
import hello_package.diff as hello_diff
hello_diff.diff()
from hello_package.diff import diff
diff()
patch()
from hello_package.diff import patch
patch()
```
### Relative import
```
import sys
sys.path
from .hello import hello
__name__
sys.__name__
```
## Date and Time
```
import datetime
datetime
datetime.datetime
datetime.datetime.now()
datetime.datetime.today()
datetime.date.today()
now = datetime.datetime.now()
now
now.year
now.microsecond
now.second
help(now)
yesterday = datetime.datetime(2016, 8, 1, 8, 32, 29)
yesterday
now == yesterday
now > yesterday
now < yesterday
now - yesterday
```
*timedelta is difference between two datetime*
```
delta = datetime.timedelta(days=3)
delta
yesterday + delta
now - delta
yesterday / now
yesterday // now
yesterday % now
yesterday * delta
help(datetime.timedelta)
help(datetime.datetime)
datetime.tzinfo('+530')
datetime.datetime(2016, 10, 20, tzinfo=datetime.tzinfo('+530'))
now.tzinfo
datetime.datetime.now()
datetime.datetime.utcnow()
```
## Files and Directories
```
f = open('hello.py')
open('non existing file')
f.read()
f.read()
f.seek(0)
f.read()
f.seek(0)
f.readlines()
f.seek(0)
f.readline()
f.readline()
f.readline()
f.close()
with open('hello.py') as _file:
for line in _file.readlines():
print(line)
```
**os**
```
import os
os.path.abspath('hello.py')
os.path.dirname(os.path.abspath('hello.py'))
os.path.join(os.path.dirname(os.path.abspath('hello.py')),
'another.py')
import glob
glob.glob('*.py')
glob.glob('*')
```
[email protected]
## CSV files
```
import csv
with open('../../data/countries.csv') as csvfile:
reader = csv.reader(csvfile)
for line in reader:
print(line)
with open('../../data/countries.csv') as csvfile:
reader = csv.DictReader(csvfile, fieldnames=['name', 'code'])
for line in reader:
print(line)
data = [
{'continent': 'asia', 'name': 'nepal'},
{'continent': 'asia', 'name': 'india'},
{'continent': 'asia', 'name': 'japan'},
{'continent': 'africa', 'name': 'chad'},
{'continent': 'africa', 'name': 'nigeria'},
{'continent': 'europe', 'name': 'greece'},
{'continent': 'europe', 'name': 'norway'},
{'continent': 'north america', 'name': 'canada'},
{'continent': 'north america', 'name': 'mexico'},
{'continent': 'south america', 'name': 'brazil'},
{'continent': 'south america', 'name': 'chile'}
]
# r == read
# w == write [ erase the file first ]
# a == apend
with open('countries.csv', 'w') as csvfile:
writer = csv.DictWriter(csvfile,
fieldnames=['name', 'continent'])
writer.writeheader()
writer.writerows(data)
# r == read
# w == write [ erase the file first ]
# a == apend
with open('countries.csv', 'a') as csvfile:
writer = csv.DictWriter(csvfile,
fieldnames=['name', 'continent'])
writer.writerow({'name': 'pakistan', 'continent': 'asia'})
```
## Fractions
```
import fractions
fractions.Fraction(3, 5)
from fractions import Fraction
Fraction(2, 3)
Fraction(1, 3) + Fraction(1, 3)
(1/3) + (1/3)
10/21
```
## Named Tuples
```
from collections import namedtuple
Color = namedtuple('Color', ['red', 'green', 'blue'])
button_color = Color(231, 211, 201)
button_color.red
button_color[0]
'This picture has Red:{0.red} Green:{0.green} and Blue:{0.blue}'.format(button_color)
```
## Builtin Methods
- all()
- any()
- chr()
- dict()
- dir()
- help()
- id()
- input()
- list()
- len()
- map()
- open()
- print()
- range()
- reversed()
- set()
- sorted()
- tuple()
- zip()
```
all([1, 0, 4])
all([1, 3, 4])
any([1, 0])
any([0, 0])
chr(64)
chr(121)
ord('6')
ord('*')
dict(name='kathmandu', country='nepal')
dir('')
help(''.title)
id('')
id(1)
input("Enter your number")
list((1, 3, 5))
list('hello')
len('hello')
len([1, 4, 5])
# open()
# see: above
print("test")
range(0, 9)
range(0, 99, 3)
list(range(0, 9))
reversed(list(range(0, 9)))
list(reversed(list(range(0, 9))))
''.join(reversed('hello'))
set([1, 5, 6, 7, 8, 7, 1])
tuple([1, 5, 2, 7, 3, 9])
sorted([1, 5, 2, 7, 3, 9])
sorted([1, 5, 2, 7, 3, 9], reverse=True)
data = [{'continent': 'asia', 'name': 'nepal', 'id':0},
{'continent': 'asia', 'name': 'india', 'id':5},
{'continent': 'asia', 'name': 'japan', 'id':8},
{'continent': 'africa', 'name': 'chad', 'id':2},
{'continent': 'africa', 'name': 'nigeria', 'id':7},
{'continent': 'europe', 'name': 'greece', 'id':1},
{'continent': 'europe', 'name': 'norway', 'id':6},
{'continent': 'north america', 'name': 'canada', 'id':3},
{'continent': 'north america', 'name': 'mexico', 'id':5},
{'continent': 'south america', 'name': 'brazil', 'id':4},
{'continent': 'south america', 'name': 'chile', 'id':7}]
def sort_by_name(first):
return first['name'] < first['continent']
sorted(data, key=sort_by_name)
list(zip([1, 2, 3], [2, 3, 4]))
```
**Lambda operations**
```
map(lambda x: x * 2, [1, 2, 3, 4])
list(map(lambda x: x * 2, [1, 2, 3, 4]))
lambda x: x + 4
def power2(x):
return x * 2
list(map(power2, [1, 2, 3, 4]))
```
*reduce is available in python2 only*
```
list(reduce(lambda x: x, [1, 4, 5, 6, 9]))
```
*for python 3*
```
from functools import reduce
reduce(lambda x, y: x + y, [1, 4, 5, 7, 8])
```
*filter*
```
list(filter(lambda x: x < 3, [1, 3, 5, 2, 8]))
```
|
github_jupyter
|
# Inheritance with the Gaussian Class
To give another example of inheritance, take a look at the code in this Jupyter notebook. The Gaussian distribution code is refactored into a generic Distribution class and a Gaussian distribution class. Read through the code in this Jupyter notebook to see how the code works.
The Distribution class takes care of the initialization and the read_data_file method. Then the rest of the Gaussian code is in the Gaussian class. You'll later use this Distribution class in an exercise at the end of the lesson.
Run the code in each cell of this Jupyter notebook. This is a code demonstration, so you do not need to write any code.
```
class Distribution:
def __init__(self, mu=0, sigma=1):
""" Generic distribution class for calculating and
visualizing a probability distribution.
Attributes:
mean (float) representing the mean value of the distribution
stdev (float) representing the standard deviation of the distribution
data_list (list of floats) a list of floats extracted from the data file
"""
self.mean = mu
self.stdev = sigma
self.data = []
def read_data_file(self, file_name):
"""Function to read in data from a txt file. The txt file should have
one number (float) per line. The numbers are stored in the data attribute.
Args:
file_name (string): name of a file to read from
Returns:
None
"""
with open(file_name) as file:
data_list = []
line = file.readline()
while line:
data_list.append(int(line))
line = file.readline()
file.close()
self.data = data_list
import math
import matplotlib.pyplot as plt
class Gaussian(Distribution):
""" Gaussian distribution class for calculating and
visualizing a Gaussian distribution.
Attributes:
mean (float) representing the mean value of the distribution
stdev (float) representing the standard deviation of the distribution
data_list (list of floats) a list of floats extracted from the data file
"""
def __init__(self, mu=0, sigma=1):
Distribution.__init__(self, mu, sigma)
def calculate_mean(self):
"""Function to calculate the mean of the data set.
Args:
None
Returns:
float: mean of the data set
"""
avg = 1.0 * sum(self.data) / len(self.data)
self.mean = avg
return self.mean
def calculate_stdev(self, sample=True):
"""Function to calculate the standard deviation of the data set.
Args:
sample (bool): whether the data represents a sample or population
Returns:
float: standard deviation of the data set
"""
if sample:
n = len(self.data) - 1
else:
n = len(self.data)
mean = self.calculate_mean()
sigma = 0
for d in self.data:
sigma += (d - mean) ** 2
sigma = math.sqrt(sigma / n)
self.stdev = sigma
return self.stdev
def plot_histogram(self):
"""Function to output a histogram of the instance variable data using
matplotlib pyplot library.
Args:
None
Returns:
None
"""
plt.hist(self.data)
plt.title('Histogram of Data')
plt.xlabel('data')
plt.ylabel('count')
def pdf(self, x):
"""Probability density function calculator for the gaussian distribution.
Args:
x (float): point for calculating the probability density function
Returns:
float: probability density function output
"""
return (1.0 / (self.stdev * math.sqrt(2*math.pi))) * math.exp(-0.5*((x - self.mean) / self.stdev) ** 2)
def plot_histogram_pdf(self, n_spaces = 50):
"""Function to plot the normalized histogram of the data and a plot of the
probability density function along the same range
Args:
n_spaces (int): number of data points
Returns:
list: x values for the pdf plot
list: y values for the pdf plot
"""
mu = self.mean
sigma = self.stdev
min_range = min(self.data)
max_range = max(self.data)
# calculates the interval between x values
interval = 1.0 * (max_range - min_range) / n_spaces
x = []
y = []
# calculate the x values to visualize
for i in range(n_spaces):
tmp = min_range + interval*i
x.append(tmp)
y.append(self.pdf(tmp))
# make the plots
fig, axes = plt.subplots(2,sharex=True)
fig.subplots_adjust(hspace=.5)
axes[0].hist(self.data, density=True)
axes[0].set_title('Normed Histogram of Data')
axes[0].set_ylabel('Density')
axes[1].plot(x, y)
axes[1].set_title('Normal Distribution for \n Sample Mean and Sample Standard Deviation')
axes[0].set_ylabel('Density')
plt.show()
return x, y
def __add__(self, other):
"""Function to add together two Gaussian distributions
Args:
other (Gaussian): Gaussian instance
Returns:
Gaussian: Gaussian distribution
"""
result = Gaussian()
result.mean = self.mean + other.mean
result.stdev = math.sqrt(self.stdev ** 2 + other.stdev ** 2)
return result
def __repr__(self):
"""Function to output the characteristics of the Gaussian instance
Args:
None
Returns:
string: characteristics of the Gaussian
"""
return "mean {}, standard deviation {}".format(self.mean, self.stdev)
# initialize two gaussian distributions
gaussian_one = Gaussian(25, 3)
gaussian_two = Gaussian(30, 2)
# initialize a third gaussian distribution reading in a data efile
gaussian_three = Gaussian()
gaussian_three.read_data_file('numbers.txt')
gaussian_three.calculate_mean()
gaussian_three.calculate_stdev()
# print out the mean and standard deviations
print(gaussian_one.mean)
print(gaussian_two.mean)
print(gaussian_one.stdev)
print(gaussian_two.stdev)
print(gaussian_three.mean)
print(gaussian_three.stdev)
# plot histogram of gaussian three
gaussian_three.plot_histogram_pdf()
# add gaussian_one and gaussian_two together
gaussian_one + gaussian_two
```
|
github_jupyter
|
*Accompanying code examples of the book "Introduction to Artificial Neural Networks and Deep Learning: A Practical Guide with Applications in Python" by [Sebastian Raschka](https://sebastianraschka.com). All code examples are released under the [MIT license](https://github.com/rasbt/deep-learning-book/blob/master/LICENSE). If you find this content useful, please consider supporting the work by buying a [copy of the book](https://leanpub.com/ann-and-deeplearning).*
Other code examples and content are available on [GitHub](https://github.com/rasbt/deep-learning-book). The PDF and ebook versions of the book are available through [Leanpub](https://leanpub.com/ann-and-deeplearning).
```
%load_ext watermark
%watermark -a 'Sebastian Raschka' -v -p torch
```
# Model Zoo -- CNN Gender Classifier (VGG16 Architecture, CelebA) with Data Parallelism
There are multiple ways of leveraging multiple GPUs when using PyTorch. One of these approaches is to send a copy of the model to each available GPU and split the minibatches across using `DataParallel`.
To break it down into conceptual steps, this is what `DataParallel` does
1. each GPU performs a forward pass on a chunk of the minibatch (on a copy of the model) to obtain the predictions;
2. the first/default GPU gathers these predictions from all GPUs to compute the loss of each minibatch-chunk with respect to the true labels (this is done on the first/default GPU, because we typically define the loss, like `torch.nn.CrossEntropyLoss` outside the model);
3. each GPU then peforms backpropagation to compute the gradient of the loss on their-subbatch with respect to the neural network weights;
3. the first GPU sums up the gradients obtained from each GPU (computer engineers usually refer to this step as "reduce");
4. the first GPU updates the weights in the neural network via gradient descent and sends copies to the individual GPUs for the next round.
While the list above may look a bit complicated at first, the `DataParallel` class automatically takes care of it all, and it is very easy to use in practice.
### Data Parallelism vs regular Backpropagation
Note that using `DataParallel` will result in slightly different models compared to regular backpropagation. The reason is that via data parallelism, we combine the gradients from 4 individual forward and backward runs to update the model. In regular backprop, we would update the model after each minibatch. The following figure illustrates regular backpropagation showing 2 iterations:

The next figure shows one model update iteration with `DataParallel` assuming 2 GPUs:

### Implementation Details
To use `DataParallel`, in the "Model" section (i.e., the corresponding code cell) we replace
```python
model.to(device)
```
with
```python
model = VGG16(num_features=num_features, num_classes=num_classes)
if torch.cuda.device_count() > 1:
print("Using", torch.cuda.device_count(), "GPUs")
model = nn.DataParallel(model)
```
and let the `DataParallel` class take care of the rest. Note that in order for this to work, the data currently needs to be on the first cuda device, "cuda:0". Otherwise, we will get a `RuntimeError: all tensors must be on devices[0]`. Hence, we define `device` below, which we use to transfer the input data to during training. Hence, make sure you set
```python
device = torch.device("cuda:0")
```
and not
```python
device = torch.device("cuda:1")
```
(or any other CUDA device number), so that in the training loop, we can use
```python
for i, (features, targets) in enumerate(data_loader):
features = features.to(device)
targets = targets.to(device)
```
If you look at the implementation part
```python
#### DATA PARALLEL START ####
model = VGG16(num_features=num_features, num_classes=num_classes)
if torch.cuda.device_count() > 1:
print("Using", torch.cuda.device_count(), "GPUs")
model = nn.DataParallel(model)
#### DATA PARALLEL END ####
model.to(device)
#### DATA PARALLEL START ####
cost_fn = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)
```
you notice that the `CrossEntropyLoss` (we could also use the one implemented in nn.functional) is not part of the model. Hence, the loss will be computed on the device where the target labels are, which is the default device (usually the first GPU). This is the reason why the outputs are gathered on the first/default GPU. I sketched a more detailed outline of the whole process below:

### Speed Comparison
- Using the same batch size as in the 1-GPU version of this code, means that if we have four GPUs, the 64-batch dataset gets split into four 16-batch sized datasets that will be distributed across the different GPUs. I noticed that the computation time is approximately half for 4 GPUs compared to 1 GPU (using GeForce 1080Ti cards).
- When I multiply the batch size by 4 in the `DataParallel` version, so that each GPU gets a minibatch of size 64, I notice that the model trains approximately 3x faster on 4 GPUs compared to the single GPU version.
### Network Architecture
The network in this notebook is an implementation of the VGG-16 [1] architecture on the CelebA face dataset [2] to train a gender classifier.
References
- [1] Simonyan, K., & Zisserman, A. (2014). Very deep convolutional networks for large-scale image recognition. arXiv preprint arXiv:1409.1556.
- [2] Zhang, K., Tan, L., Li, Z., & Qiao, Y. (2016). Gender and smile classification using deep convolutional neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops (pp. 34-38).
The following table (taken from Simonyan & Zisserman referenced above) summarizes the VGG19 architecture:

**Note that the CelebA images are 218 x 178, not 256 x 256. We resize to 128x128**
## Imports
```
import os
import time
import numpy as np
import pandas as pd
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.utils.data import Dataset
from torch.utils.data import DataLoader
from torchvision import datasets
from torchvision import transforms
import matplotlib.pyplot as plt
from PIL import Image
if torch.cuda.is_available():
torch.backends.cudnn.deterministic = True
```
## Dataset
### Downloading the Dataset
Note that the ~200,000 CelebA face image dataset is relatively large (~1.3 Gb). The download link provided below was provided by the author on the official CelebA website at http://mmlab.ie.cuhk.edu.hk/projects/CelebA.html.
1) Download and unzip the file `img_align_celeba.zip`, which contains the images in jpeg format.
2) Download the `list_attr_celeba.txt` file, which contains the class labels
3) Download the `list_eval_partition.txt` file, which contains training/validation/test partitioning info
### Preparing the Dataset
```
df1 = pd.read_csv('list_attr_celeba.txt', sep="\s+", skiprows=1, usecols=['Male'])
# Make 0 (female) & 1 (male) labels instead of -1 & 1
df1.loc[df1['Male'] == -1, 'Male'] = 0
df1.head()
df2 = pd.read_csv('list_eval_partition.txt', sep="\s+", skiprows=0, header=None)
df2.columns = ['Filename', 'Partition']
df2 = df2.set_index('Filename')
df2.head()
df3 = df1.merge(df2, left_index=True, right_index=True)
df3.head()
df3.to_csv('celeba-gender-partitions.csv')
df4 = pd.read_csv('celeba-gender-partitions.csv', index_col=0)
df4.head()
df4.loc[df4['Partition'] == 0].to_csv('celeba-gender-train.csv')
df4.loc[df4['Partition'] == 1].to_csv('celeba-gender-valid.csv')
df4.loc[df4['Partition'] == 2].to_csv('celeba-gender-test.csv')
img = Image.open('img_align_celeba/000001.jpg')
print(np.asarray(img, dtype=np.uint8).shape)
plt.imshow(img);
```
### Implementing a Custom DataLoader Class
```
class CelebaDataset(Dataset):
"""Custom Dataset for loading CelebA face images"""
def __init__(self, csv_path, img_dir, transform=None):
df = pd.read_csv(csv_path, index_col=0)
self.img_dir = img_dir
self.csv_path = csv_path
self.img_names = df.index.values
self.y = df['Male'].values
self.transform = transform
def __getitem__(self, index):
img = Image.open(os.path.join(self.img_dir,
self.img_names[index]))
if self.transform is not None:
img = self.transform(img)
label = self.y[index]
return img, label
def __len__(self):
return self.y.shape[0]
```
Running the VGG16 on this dataset with a minibatch size of 64 uses approximately 6.6 Gb of GPU memory. However, since we will split the batch size over for GPUs now, along with the model, we can actually comfortably use 64*4 as the batch size.
```
# Note that transforms.ToTensor()
# already divides pixels by 255. internally
custom_transform = transforms.Compose([transforms.CenterCrop((178, 178)),
transforms.Resize((128, 128)),
#transforms.Grayscale(),
#transforms.Lambda(lambda x: x/255.),
transforms.ToTensor()])
train_dataset = CelebaDataset(csv_path='celeba-gender-train.csv',
img_dir='img_align_celeba/',
transform=custom_transform)
valid_dataset = CelebaDataset(csv_path='celeba-gender-valid.csv',
img_dir='img_align_celeba/',
transform=custom_transform)
test_dataset = CelebaDataset(csv_path='celeba-gender-test.csv',
img_dir='img_align_celeba/',
transform=custom_transform)
BATCH_SIZE=64*torch.cuda.device_count()
train_loader = DataLoader(dataset=train_dataset,
batch_size=BATCH_SIZE,
shuffle=True,
num_workers=4)
valid_loader = DataLoader(dataset=valid_dataset,
batch_size=BATCH_SIZE,
shuffle=False,
num_workers=4)
test_loader = DataLoader(dataset=test_dataset,
batch_size=BATCH_SIZE,
shuffle=False,
num_workers=4)
```
Note that for DataParallel to work, the data currently needs to be on the first cuda device, "cuda:0". Otherwise, we will get a `RuntimeError: all tensors must be on devices[0]`. Hence, we define `device` below, which we use to transfer the input data to during training.
```
device = torch.device("cuda:0")
torch.manual_seed(0)
num_epochs = 2
for epoch in range(num_epochs):
for batch_idx, (x, y) in enumerate(train_loader):
print('Epoch:', epoch+1, end='')
print(' | Batch index:', batch_idx, end='')
print(' | Batch size:', y.size()[0])
x = x.to(device)
y = y.to(device)
break
```
## Model
```
##########################
### SETTINGS
##########################
# Hyperparameters
random_seed = 1
learning_rate = 0.001
num_epochs = 3
# Architecture
num_features = 128*128
num_classes = 2
##########################
### MODEL
##########################
class VGG16(torch.nn.Module):
def __init__(self, num_features, num_classes):
super(VGG16, self).__init__()
# calculate same padding:
# (w - k + 2*p)/s + 1 = o
# => p = (s(o-1) - w + k)/2
self.block_1 = nn.Sequential(
nn.Conv2d(in_channels=3,
out_channels=64,
kernel_size=(3, 3),
stride=(1, 1),
# (1(32-1)- 32 + 3)/2 = 1
padding=1),
nn.ReLU(),
nn.Conv2d(in_channels=64,
out_channels=64,
kernel_size=(3, 3),
stride=(1, 1),
padding=1),
nn.ReLU(),
nn.MaxPool2d(kernel_size=(2, 2),
stride=(2, 2))
)
self.block_2 = nn.Sequential(
nn.Conv2d(in_channels=64,
out_channels=128,
kernel_size=(3, 3),
stride=(1, 1),
padding=1),
nn.ReLU(),
nn.Conv2d(in_channels=128,
out_channels=128,
kernel_size=(3, 3),
stride=(1, 1),
padding=1),
nn.ReLU(),
nn.MaxPool2d(kernel_size=(2, 2),
stride=(2, 2))
)
self.block_3 = nn.Sequential(
nn.Conv2d(in_channels=128,
out_channels=256,
kernel_size=(3, 3),
stride=(1, 1),
padding=1),
nn.ReLU(),
nn.Conv2d(in_channels=256,
out_channels=256,
kernel_size=(3, 3),
stride=(1, 1),
padding=1),
nn.ReLU(),
nn.Conv2d(in_channels=256,
out_channels=256,
kernel_size=(3, 3),
stride=(1, 1),
padding=1),
nn.ReLU(),
nn.Conv2d(in_channels=256,
out_channels=256,
kernel_size=(3, 3),
stride=(1, 1),
padding=1),
nn.ReLU(),
nn.MaxPool2d(kernel_size=(2, 2),
stride=(2, 2))
)
self.block_4 = nn.Sequential(
nn.Conv2d(in_channels=256,
out_channels=512,
kernel_size=(3, 3),
stride=(1, 1),
padding=1),
nn.ReLU(),
nn.Conv2d(in_channels=512,
out_channels=512,
kernel_size=(3, 3),
stride=(1, 1),
padding=1),
nn.ReLU(),
nn.Conv2d(in_channels=512,
out_channels=512,
kernel_size=(3, 3),
stride=(1, 1),
padding=1),
nn.ReLU(),
nn.Conv2d(in_channels=512,
out_channels=512,
kernel_size=(3, 3),
stride=(1, 1),
padding=1),
nn.ReLU(),
nn.MaxPool2d(kernel_size=(2, 2),
stride=(2, 2))
)
self.block_5 = nn.Sequential(
nn.Conv2d(in_channels=512,
out_channels=512,
kernel_size=(3, 3),
stride=(1, 1),
padding=1),
nn.ReLU(),
nn.Conv2d(in_channels=512,
out_channels=512,
kernel_size=(3, 3),
stride=(1, 1),
padding=1),
nn.ReLU(),
nn.Conv2d(in_channels=512,
out_channels=512,
kernel_size=(3, 3),
stride=(1, 1),
padding=1),
nn.ReLU(),
nn.Conv2d(in_channels=512,
out_channels=512,
kernel_size=(3, 3),
stride=(1, 1),
padding=1),
nn.ReLU(),
nn.MaxPool2d(kernel_size=(2, 2),
stride=(2, 2))
)
self.classifier = nn.Sequential(
nn.Linear(512*4*4, 4096),
nn.ReLU(),
nn.Linear(4096, 4096),
nn.ReLU(),
nn.Linear(4096, num_classes)
)
for m in self.modules():
if isinstance(m, torch.nn.Conv2d):
#n = m.kernel_size[0] * m.kernel_size[1] * m.out_channels
#m.weight.data.normal_(0, np.sqrt(2. / n))
m.weight.detach().normal_(0, 0.05)
if m.bias is not None:
m.bias.detach().zero_()
elif isinstance(m, torch.nn.Linear):
m.weight.detach().normal_(0, 0.05)
m.bias.detach().detach().zero_()
def forward(self, x):
x = self.block_1(x)
x = self.block_2(x)
x = self.block_3(x)
x = self.block_4(x)
x = self.block_5(x)
logits = self.classifier(x.view(-1, 512*4*4))
probas = F.softmax(logits, dim=1)
return logits, probas
torch.manual_seed(random_seed)
#### DATA PARALLEL START ####
model = VGG16(num_features=num_features, num_classes=num_classes)
if torch.cuda.device_count() > 1:
print("Using", torch.cuda.device_count(), "GPUs")
model = nn.DataParallel(model)
#### DATA PARALLEL END ####
model.to(device)
#### DATA PARALLEL START ####
optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)
```
## Training
```
def compute_accuracy(model, data_loader):
correct_pred, num_examples = 0, 0
for i, (features, targets) in enumerate(data_loader):
features = features.to(device)
targets = targets.to(device)
logits, probas = model(features)
_, predicted_labels = torch.max(probas, 1)
num_examples += targets.size(0)
correct_pred += (predicted_labels == targets).sum()
return correct_pred.float()/num_examples * 100
start_time = time.time()
for epoch in range(num_epochs):
model.train()
for batch_idx, (features, targets) in enumerate(train_loader):
features = features.to(device)
targets = targets.to(device)
### FORWARD AND BACK PROP
logits, probas = model(features)
cost = F.cross_entropy(logits, targets)
optimizer.zero_grad()
cost.backward()
### UPDATE MODEL PARAMETERS
optimizer.step()
### LOGGING
if not batch_idx % 50:
print ('Epoch: %03d/%03d | Batch %04d/%04d | Cost: %.4f'
%(epoch+1, num_epochs, batch_idx,
len(train_loader), cost))
model.eval()
with torch.set_grad_enabled(False): # save memory during inference
print('Epoch: %03d/%03d | Train: %.3f%% | Valid: %.3f%%' % (
epoch+1, num_epochs,
compute_accuracy(model, train_loader),
compute_accuracy(model, valid_loader)))
print('Time elapsed: %.2f min' % ((time.time() - start_time)/60))
print('Total Training Time: %.2f min' % ((time.time() - start_time)/60))
```
## Evaluation
```
model.eval()
with torch.set_grad_enabled(False): # save memory during inference
print('Test accuracy: %.2f%%' % (compute_accuracy(model, test_loader)))
for batch_idx, (features, targets) in enumerate(test_loader):
features = features
targets = targets
break
plt.imshow(np.transpose(features[0], (1, 2, 0)))
logits, probas = model(features.to(device)[0, None])
print('Probability Female %.2f%%' % (probas[0][0]*100))
%watermark -iv
```
|
github_jupyter
|
# A Basic Model
In this example application it is shown how a simple time series model can be developed to simulate groundwater levels. The recharge (calculated as precipitation minus evaporation) is used as the explanatory time series.
```
import matplotlib.pyplot as plt
import pandas as pd
import pastas as ps
ps.show_versions()
```
### 1. Importing the dependent time series data
In this codeblock a time series of groundwater levels is imported using the `read_csv` function of `pandas`. As `pastas` expects a `pandas` `Series` object, the data is squeezed. To check if you have the correct data type (a `pandas Series` object), you can use `type(oseries)` as shown below.
The following characteristics are important when importing and preparing the observed time series:
- The observed time series are stored as a `pandas Series` object.
- The time step can be irregular.
```
# Import groundwater time seriesm and squeeze to Series object
gwdata = pd.read_csv('../data/head_nb1.csv', parse_dates=['date'],
index_col='date', squeeze=True)
print('The data type of the oseries is: %s' % type(gwdata))
# Plot the observed groundwater levels
gwdata.plot(style='.', figsize=(10, 4))
plt.ylabel('Head [m]');
plt.xlabel('Time [years]');
```
### 2. Import the independent time series
Two explanatory series are used: the precipitation and the potential evaporation. These need to be `pandas Series` objects, as for the observed heads.
Important characteristics of these time series are:
- All series are stored as `pandas Series` objects.
- The series may have irregular time intervals, but then it will be converted to regular time intervals when creating the time series model later on.
- It is preferred to use the same length units as for the observed heads.
```
# Import observed precipitation series
precip = pd.read_csv('../data/rain_nb1.csv', parse_dates=['date'],
index_col='date', squeeze=True)
print('The data type of the precip series is: %s' % type(precip))
# Import observed evaporation series
evap = pd.read_csv('../data/evap_nb1.csv', parse_dates=['date'],
index_col='date', squeeze=True)
print('The data type of the evap series is: %s' % type(evap))
# Calculate the recharge to the groundwater
recharge = precip - evap
print('The data type of the recharge series is: %s' % type(recharge))
# Plot the time series of the precipitation and evaporation
plt.figure()
recharge.plot(label='Recharge', figsize=(10, 4))
plt.xlabel('Time [years]')
plt.ylabel('Recharge (m/year)');
```
### 3. Create the time series model
In this code block the actual time series model is created. First, an instance of the `Model` class is created (named `ml` here). Second, the different components of the time series model are created and added to the model. The imported time series are automatically checked for missing values and other inconsistencies. The keyword argument fillnan can be used to determine how missing values are handled. If any nan-values are found this will be reported by `pastas`.
```
# Create a model object by passing it the observed series
ml = ps.Model(gwdata, name="GWL")
# Add the recharge data as explanatory variable
sm = ps.StressModel(recharge, ps.Gamma, name='recharge', settings="evap")
ml.add_stressmodel(sm)
```
### 4. Solve the model
The next step is to compute the optimal model parameters. The default solver uses a non-linear least squares method for the optimization. The python package `scipy` is used (info on `scipy's` least_squares solver can be found [here](https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.least_squares.html)). Some standard optimization statistics are reported along with the optimized parameter values and correlations.
```
ml.solve()
```
### 5. Plot the results
The solution can be plotted after a solution has been obtained.
```
ml.plot()
```
### 6. Advanced plotting
There are many ways to further explore the time series model. `pastas` has some built-in functionalities that will provide the user with a quick overview of the model. The `plots` subpackage contains all the options. One of these is the method `plots.results` which provides a plot with more information.
```
ml.plots.results(figsize=(10, 6))
```
### 7. Statistics
The `stats` subpackage includes a number of statistical functions that may applied to the model. One of them is the `summary` method, which gives a summary of the main statistics of the model.
```
ml.stats.summary()
```
### 8. Improvement: estimate evaporation factor
In the previous model, the recharge was estimated as precipitation minus potential evaporation. A better model is to estimate the actual evaporation as a factor (called the evaporation factor here) times the potential evaporation. First, new model is created (called `ml2` here so that the original model `ml` does not get overwritten). Second, the `RechargeModel` object with a `Linear` recharge model is created, which combines the precipitation and evaporation series and adds a parameter for the evaporation factor `f`. The `RechargeModel` object is added to the model, the model is solved, and the results and statistics are plotted to the screen. Note that the new model gives a better fit (lower root mean squared error and higher explained variance), but that the Akiake information criterion indicates that the addition of the additional parameter does not improve the model signficantly (the Akaike criterion for model `ml2` is higher than for model `ml`).
```
# Create a model object by passing it the observed series
ml2 = ps.Model(gwdata)
# Add the recharge data as explanatory variable
ts1 = ps.RechargeModel(precip, evap, ps.Gamma, name='rainevap',
recharge=ps.rch.Linear(), settings=("prec", "evap"))
ml2.add_stressmodel(ts1)
# Solve the model
ml2.solve()
# Plot the results
ml2.plot()
# Statistics
ml2.stats.summary()
```
### Origin of the series
* The rainfall data is taken from rainfall station Heibloem in The Netherlands.
* The evaporation data is taken from weather station Maastricht in The Netherlands.
* The head data is well B58C0698, which was obtained from Dino loket
|
github_jupyter
|
```
from IPython import display
from torch.utils.data import DataLoader
from torchvision import transforms, datasets
from utils import Logger
import tensorflow as tf
import tensorflow.compat.v1 as tf
tf.disable_v2_behavior()
import numpy as np
DATA_FOLDER = './tf_data/VGAN/MNIST'
IMAGE_PIXELS = 28*28
NOISE_SIZE = 100
BATCH_SIZE = 100
def noise(n_rows, n_cols):
return np.random.normal(size=(n_rows, n_cols))
def xavier_init(size):
in_dim = size[0] if len(size) == 1 else size[1]
stddev = 1. / np.sqrt(float(in_dim))
return tf.random_uniform(shape=size, minval=-stddev, maxval=stddev)
def images_to_vectors(images):
return images.reshape(images.shape[0], 784)
def vectors_to_images(vectors):
return vectors.reshape(vectors.shape[0], 28, 28, 1)
```
## Load Data
```
def mnist_data():
compose = transforms.Compose(
[transforms.ToTensor(),
transforms.Normalize((.5,), (.5,))
])
out_dir = '{}/dataset'.format(DATA_FOLDER)
return datasets.MNIST(root=out_dir, train=True, transform=compose, download=True)
# Load data
data = mnist_data()
# Create loader with data, so that we can iterate over it
data_loader = DataLoader(data, batch_size=BATCH_SIZE, shuffle=True)
# Num batches
num_batches = len(data_loader)
```
## Initialize Graph
```
## Discriminator
# Input
X = tf.placeholder(tf.float32, shape=(None, IMAGE_PIXELS))
# Layer 1 Variables
D_W1 = tf.Variable(xavier_init([784, 1024]))
D_B1 = tf.Variable(xavier_init([1024]))
# Layer 2 Variables
D_W2 = tf.Variable(xavier_init([1024, 512]))
D_B2 = tf.Variable(xavier_init([512]))
# Layer 3 Variables
D_W3 = tf.Variable(xavier_init([512, 256]))
D_B3 = tf.Variable(xavier_init([256]))
# Out Layer Variables
D_W4 = tf.Variable(xavier_init([256, 1]))
D_B4 = tf.Variable(xavier_init([1]))
# Store Variables in list
D_var_list = [D_W1, D_B1, D_W2, D_B2, D_W3, D_B3, D_W4, D_B4]
## Generator
# Input
Z = tf.placeholder(tf.float32, shape=(None, NOISE_SIZE))
# Layer 1 Variables
G_W1 = tf.Variable(xavier_init([100, 256]))
G_B1 = tf.Variable(xavier_init([256]))
# Layer 2 Variables
G_W2 = tf.Variable(xavier_init([256, 512]))
G_B2 = tf.Variable(xavier_init([512]))
# Layer 3 Variables
G_W3 = tf.Variable(xavier_init([512, 1024]))
G_B3 = tf.Variable(xavier_init([1024]))
# Out Layer Variables
G_W4 = tf.Variable(xavier_init([1024, 784]))
G_B4 = tf.Variable(xavier_init([784]))
# Store Variables in list
G_var_list = [G_W1, G_B1, G_W2, G_B2, G_W3, G_B3, G_W4, G_B4]
def discriminator(x):
l1 = tf.nn.dropout(tf.nn.leaky_relu(tf.matmul(x, D_W1) + D_B1, .2), .3)
l2 = tf.nn.dropout(tf.nn.leaky_relu(tf.matmul(l1, D_W2) + D_B2, .2), .3)
l3 = tf.nn.dropout(tf.nn.leaky_relu(tf.matmul(l2, D_W3) + D_B3, .2), .3)
out = tf.matmul(l3, D_W4) + D_B4
return out
def generator(z):
l1 = tf.nn.leaky_relu(tf.matmul(z, G_W1) + G_B1, .2)
l2 = tf.nn.leaky_relu(tf.matmul(l1, G_W2) + G_B2, .2)
l3 = tf.nn.leaky_relu(tf.matmul(l2, G_W3) + G_B3, .2)
out = tf.nn.tanh(tf.matmul(l3, G_W4) + G_B4)
return out
G_sample = generator(Z)
D_real = discriminator(X)
D_fake = discriminator(G_sample)
# Losses
D_loss_real = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=D_real, labels=tf.ones_like(D_real)))
D_loss_fake = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=D_fake, labels=tf.zeros_like(D_fake)))
D_loss = D_loss_real + D_loss_fake
G_loss = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=D_fake, labels=tf.ones_like(D_fake)))
# Optimizers
D_opt = tf.train.AdamOptimizer(2e-4).minimize(D_loss, var_list=D_var_list)
G_opt = tf.train.AdamOptimizer(2e-4).minimize(G_loss, var_list=G_var_list)
```
## Train
#### Testing
```
num_test_samples = 16
test_noise = noise(num_test_samples, NOISE_SIZE)
```
#### Inits
```
num_epochs = 200
# Start interactive session
session = tf.InteractiveSession()
# Init Variables
tf.global_variables_initializer().run()
# Init Logger
logger = Logger(model_name='DCGAN1', data_name='CIFAR10')
```
#### Train
```
# Iterate through epochs
for epoch in range(num_epochs):
for n_batch, (batch,_) in enumerate(data_loader):
# 1. Train Discriminator
X_batch = images_to_vectors(batch.permute(0, 2, 3, 1).numpy())
feed_dict = {X: X_batch, Z: noise(BATCH_SIZE, NOISE_SIZE)}
_, d_error, d_pred_real, d_pred_fake = session.run(
[D_opt, D_loss, D_real, D_fake], feed_dict=feed_dict
)
# 2. Train Generator
feed_dict = {Z: noise(BATCH_SIZE, NOISE_SIZE)}
_, g_error = session.run(
[G_opt, G_loss], feed_dict=feed_dict
)
if n_batch % 100 == 0:
display.clear_output(True)
# Generate images from test noise
test_images = session.run(
G_sample, feed_dict={Z: test_noise}
)
test_images = vectors_to_images(test_images)
# Log Images
logger.log_images(test_images, num_test_samples, epoch, n_batch, num_batches, format='NHWC');
# Log Status
logger.display_status(
epoch, num_epochs, n_batch, num_batches,
d_error, g_error, d_pred_real, d_pred_fake
)
```
|
github_jupyter
|
## Set up the dependencies
```
# for reading and validating data
import emeval.input.spec_details as eisd
import emeval.input.phone_view as eipv
import emeval.input.eval_view as eiev
import arrow
# Visualization helpers
import emeval.viz.phone_view as ezpv
import emeval.viz.eval_view as ezev
# For plots
import matplotlib.pyplot as plt
%matplotlib inline
# For maps
import folium
import branca.element as bre
# For easier debugging while working on modules
import importlib
import pandas as pd
import numpy as np
```
## The spec
The spec defines what experiments were done, and over which time ranges. Once the experiment is complete, most of the structure is read back from the data, but we use the spec to validate that it all worked correctly. The spec also contains the ground truth for the legs. Here, we read the spec for the trip to UC Berkeley.
```
DATASTORE_LOC = "bin/data/"
AUTHOR_EMAIL = "[email protected]"
sd_la = eisd.FileSpecDetails(DATASTORE_LOC, AUTHOR_EMAIL, "unimodal_trip_car_bike_mtv_la")
sd_sj = eisd.FileSpecDetails(DATASTORE_LOC, AUTHOR_EMAIL, "car_scooter_brex_san_jose")
sd_ucb = eisd.FileSpecDetails(DATASTORE_LOC, AUTHOR_EMAIL, "train_bus_ebike_mtv_ucb")
```
## Loading the data into a dataframe
```
pv_la = eipv.PhoneView(sd_la)
pv_sj = eipv.PhoneView(sd_sj)
sd_sj.CURR_SPEC_ID
ios_loc_entries = sd_sj.retrieve_data("ucb-sdb-ios-1", ["background/location"],
arrow.get("2019-08-07T14:50:57.445000-07:00").timestamp,
arrow.get("2019-08-07T15:00:16.787000-07:00").timestamp)
ios_location_df = pd.DataFrame([e["data"] for e in ios_loc_entries])
android_loc_entries = sd_sj.retrieve_data("ucb-sdb-android-1", ["background/location"],
arrow.get("2019-08-07T14:50:57.445000-07:00").timestamp,
arrow.get("2019-08-07T15:00:16.787000-07:00").timestamp)
android_location_df = pd.DataFrame([e["data"] for e in android_loc_entries])
android_location_df[["fmt_time"]].loc[30:60]
ios_map = ezpv.display_map_detail_from_df(ios_location_df.loc[20:35])
android_map = ezpv.display_map_detail_from_df(android_location_df.loc[25:50])
fig = bre.Figure()
fig.add_subplot(1, 2, 1).add_child(ios_map)
fig.add_subplot(1, 2, 2).add_child(android_map)
pv_ucb = eipv.PhoneView(sd_ucb)
import pandas as pd
def get_battery_drain_entries(pv):
battery_entry_list = []
for phone_os, phone_map in pv.map().items():
print(15 * "=*")
print(phone_os, phone_map.keys())
for phone_label, phone_detail_map in phone_map.items():
print(4 * ' ', 15 * "-*")
print(4 * ' ', phone_label, phone_detail_map.keys())
# this spec does not have any calibration ranges, but evaluation ranges are actually cooler
for r in phone_detail_map["evaluation_ranges"]:
print(8 * ' ', 30 * "=")
print(8 * ' ',r.keys())
print(8 * ' ',r["trip_id"], r["eval_common_trip_id"], r["eval_role"], len(r["evaluation_trip_ranges"]))
bcs = r["battery_df"]["battery_level_pct"]
delta_battery = bcs.iloc[0] - bcs.iloc[-1]
print("Battery starts at %d, ends at %d, drain = %d" % (bcs.iloc[0], bcs.iloc[-1], delta_battery))
battery_entry = {"phone_os": phone_os, "phone_label": phone_label, "timeline": pv.spec_details.curr_spec["id"],
"run": r["trip_run"], "duration": r["duration"],
"role": r["eval_role_base"], "battery_drain": delta_battery}
battery_entry_list.append(battery_entry)
return battery_entry_list
# We are not going to look at battery life at the evaluation trip level; we will end with evaluation range
# since we want to capture the overall drain for the timeline
battery_entries_list = []
battery_entries_list.extend(get_battery_drain_entries(pv_la))
battery_entries_list.extend(get_battery_drain_entries(pv_sj))
battery_entries_list.extend(get_battery_drain_entries(pv_ucb))
battery_drain_df = pd.DataFrame(battery_entries_list)
battery_drain_df.head()
r2q_map = {"power_control": 0, "HAMFDC": 1, "MAHFDC": 2, "HAHFDC": 3, "accuracy_control": 4}
# right now, only the san jose data has the full comparison
q2r_complete_list = ["power", "HAMFDC", "MAHFDC", "HAHFDC", "accuracy"]
# others only have android or ios
q2r_android_list = ["power", "HAMFDC", "HAHFDC", "accuracy"]
q2r_ios_list = ["power", "MAHFDC", "HAHFDC", "accuracy"]
# Make a number so that can get the plots to come out in order
battery_drain_df["quality"] = battery_drain_df.role.apply(lambda r: r2q_map[r])
battery_drain_df.query("role == 'MAHFDC'").head()
```
## Displaying various groupings using boxplots
```
ifig, ax_array = plt.subplots(nrows=2,ncols=3,figsize=(12,6), sharex=False, sharey=True)
timeline_list = ["train_bus_ebike_mtv_ucb", "car_scooter_brex_san_jose", "unimodal_trip_car_bike_mtv_la"]
for i, tl in enumerate(timeline_list):
battery_drain_df.query("timeline == @tl & phone_os == 'android'").boxplot(ax = ax_array[0][i], column=["battery_drain"], by=["quality"], showbox=False, whis="range")
ax_array[0][i].set_title(tl)
battery_drain_df.query("timeline == @tl & phone_os == 'ios'").boxplot(ax = ax_array[1][i], column=["battery_drain"], by=["quality"], showbox=False, whis="range")
ax_array[1][i].set_title("")
for i, ax in enumerate(ax_array[0]):
if i == 1:
ax.set_xticklabels(q2r_complete_list)
else:
ax.set_xticklabels(q2r_android_list)
ax.set_xlabel("")
for i, ax in enumerate(ax_array[1]):
if i == 1:
ax.set_xticklabels(q2r_complete_list)
else:
ax.set_xticklabels(q2r_ios_list)
ax.set_xlabel("")
ax_array[0][0].set_ylabel("Battery drain (android)")
ax_array[1][0].set_ylabel("Battery drain (iOS)")
ifig.suptitle("Power v/s quality over multiple timelines")
# ifig.tight_layout()
battery_drain_df.query("quality == 1 & phone_os == 'ios' & timeline == 'car_scooter_brex_san_jose'").iloc[1:].describe()
battery_drain_df.query("quality == 0 & phone_os == 'ios' & timeline == 'car_scooter_brex_san_jose'").iloc[1:].describe()
battery_drain_df.query("quality == 2 & phone_os == 'ios' & timeline == 'car_scooter_brex_san_jose'").iloc[1:].describe()
```
|
github_jupyter
|
# Get all tracts within certain cities
Given a CSV file containing city names, get all the tracts within those cities' boundaries.
```
import geopandas as gpd
import json
import os
import pandas as pd
all_tracts_path = 'data/us_census_tracts_2014'
places_path = 'data/us_census_places_2014'
states_by_fips_path = 'data/states_by_fips.json'
cities_path = 'data/study_sites.csv'
output_path = 'data/tracts_in_cities_study_area.geojson'
# load the city names that make up our study sites
study_sites = pd.read_csv(cities_path, encoding='utf-8')
len(study_sites)
%%time
# load all US census tracts shapefile
all_tracts = gpd.read_file(all_tracts_path)
len(all_tracts)
%%time
# load all US places (cities/towns) shapefile
places = gpd.GeoDataFrame()
for folder in os.listdir(places_path):
path = '{}/{}'.format(places_path, folder)
gdf_tmp = gpd.read_file(path)
places = places.append(gdf_tmp)
len(places)
# get state abbreviation from FIPS
with open(states_by_fips_path) as f:
states = json.load(f)
fips_state = {k:v['abbreviation'] for k, v in states.items()}
places['state'] = places['STATEFP'].replace(fips_state, inplace=False)
cities_states = study_sites.apply(lambda row: '{}, {}'.format(row['city'], row['state']), axis=1)
# find these city names in the GDF of all census places
gdf_cities = gpd.GeoDataFrame()
for city_state in cities_states:
city, state = [item.strip() for item in city_state.split(',')]
mask = (places['NAME']==city) & (places['state']==state)
if not mask.sum()==1:
mask = (places['NAME'].str.contains(city)) & (places['state']==state)
if not mask.sum()==1:
mask = (places['NAME'].str.contains(city)) & (places['state']==state) & ~(places['NAMELSAD'].str.contains('CDP'))
if not mask.sum()==1:
print('Cannot uniquely find "{}"'.format(city_state))
gdf_city = places.loc[mask]
gdf_cities = gdf_cities.append(gdf_city)
len(gdf_cities)
# make "name" field like "city, state"
gdf_cities['name'] = gdf_cities.apply(lambda row: '{}, {}'.format(row['NAME'], row['state']), axis=1)
gdf_cities['name'] = gdf_cities['name'].replace({'Indianapolis city (balance), IN' : 'Indianapolis, IN',
'Nashville-Davidson metropolitan government (balance), TN' : 'Nashville, TN'})
# make gdf of the cities for joining
cities = gdf_cities[['GEOID', 'name', 'geometry']]
cities = cities.rename(columns={'GEOID':'place_geoid', 'name':'place_name'})
cities = cities.set_index('place_geoid')
# make gdf of the tracts for joining
tract_geoms = all_tracts.set_index('GEOID')[['geometry', 'ALAND']]
%%time
# shrink tracts by ~1 meter to avoid peripheral touches on the outside of the city boundary
tract_geoms['geom_tmp'] = tract_geoms['geometry'].buffer(-0.00001)
tract_geoms = tract_geoms.set_geometry('geom_tmp')
%%time
assert tract_geoms.crs == cities.crs
tracts = gpd.sjoin(tract_geoms, cities, how='inner', op='intersects')
print(len(tracts))
# remove the temporary shrunken geometry
tracts = tracts.set_geometry('geometry').drop(columns=['geom_tmp'])
tracts = tracts.rename(columns={'index_right':'place_geoid'})
tracts.head()
%%time
gdf_save = tracts.reset_index().rename(columns={'index':'GEOID'})
os.remove(output_path) # due to overwriting bug in fiona
gdf_save.to_file(output_path, driver='GeoJSON')
print(output_path)
```
|
github_jupyter
|
## Computing native contacts with MDTraj
Using the definition from Best, Hummer, and Eaton, "Native contacts determine protein folding mechanisms in atomistic simulations" PNAS (2013) [10.1073/pnas.1311599110](http://dx.doi.org/10.1073/pnas.1311599110)
Eq. (1) of the SI defines the expression for the fraction of native contacts, $Q(X)$:
$$
Q(X) = \frac{1}{|S|} \sum_{(i,j) \in S} \frac{1}{1 + \exp[\beta(r_{ij}(X) - \lambda r_{ij}^0)]},
$$
where
- $X$ is a conformation,
- $r_{ij}(X)$ is the distance between atoms $i$ and $j$ in conformation $X$,
- $r^0_{ij}$ is the distance from heavy atom i to j in the native state conformation,
- $S$ is the set of all pairs of heavy atoms $(i,j)$ belonging to residues $\theta_i$ and $\theta_j$ such that $|\theta_i - \theta_j| > 3$ and $r^0_{i,} < 4.5 \unicode{x212B}$,
- $\beta=5 \unicode{x212B}^{-1}$,
- $\lambda=1.8$ for all-atom simulations
```
import numpy as np
import mdtraj as md
from itertools import combinations
def best_hummer_q(traj, native):
"""Compute the fraction of native contacts according the definition from
Best, Hummer and Eaton [1]
Parameters
----------
traj : md.Trajectory
The trajectory to do the computation for
native : md.Trajectory
The 'native state'. This can be an entire trajecory, or just a single frame.
Only the first conformation is used
Returns
-------
q : np.array, shape=(len(traj),)
The fraction of native contacts in each frame of `traj`
References
----------
..[1] Best, Hummer, and Eaton, "Native contacts determine protein folding
mechanisms in atomistic simulations" PNAS (2013)
"""
BETA_CONST = 50 # 1/nm
LAMBDA_CONST = 1.8
NATIVE_CUTOFF = 0.45 # nanometers
# get the indices of all of the heavy atoms
heavy = native.topology.select_atom_indices('heavy')
# get the pairs of heavy atoms which are farther than 3
# residues apart
heavy_pairs = np.array(
[(i,j) for (i,j) in combinations(heavy, 2)
if abs(native.topology.atom(i).residue.index - \
native.topology.atom(j).residue.index) > 3])
# compute the distances between these pairs in the native state
heavy_pairs_distances = md.compute_distances(native[0], heavy_pairs)[0]
# and get the pairs s.t. the distance is less than NATIVE_CUTOFF
native_contacts = heavy_pairs[heavy_pairs_distances < NATIVE_CUTOFF]
print("Number of native contacts", len(native_contacts))
# now compute these distances for the whole trajectory
r = md.compute_distances(traj, native_contacts)
# and recompute them for just the native state
r0 = md.compute_distances(native[0], native_contacts)
q = np.mean(1.0 / (1 + np.exp(BETA_CONST * (r - LAMBDA_CONST * r0))), axis=1)
return q
# pull a random protein from the PDB
# (The unitcell info happens to be wrong)
traj = md.load_pdb('http://www.rcsb.org/pdb/files/2MI7.pdb')
# just for example, use the first frame as the 'native' conformation
q = best_hummer_q(traj, traj[0])
%matplotlib inline
import matplotlib.pyplot as plt
plt.plot(q)
plt.xlabel('Frame', fontsize=14)
plt.ylabel('Q(X)', fontsize=14)
plt.show()
```
|
github_jupyter
|
First, load the data, from the supplied data file
```
import tarfile
import json
import gzip
import pandas as pd
import botometer
from pandas.io.json import json_normalize
## VARIABLE INITIATION
tar = tarfile.open("../input/2017-09-22.tar.gz", "r:gz")
mashape_key = "QRraJnMT9KmshkpJ7iu74xKFN1jtp1IyBBijsnS5NGbEuwIX54"
twitter_app_auth = {
'consumer_key': 'sPzHpcj4jMital75nY7dfd4zn',
'consumer_secret': 'rTGm68zdNmLvnTc22cBoFg4eVMf3jLVDSQLOwSqE9lXbVWLweI',
'access_token': '4258226113-4UnHbbbxoRPz10thy70q9MtEk9xXfJGOpAY12KW',
'access_token_secret': '549HdasMEW0q2uV05S5s4Uj5SdCeEWT8dNdLNPiAeeWoX',
}
bom = botometer.Botometer(wait_on_ratelimit=True,
mashape_key=mashape_key,
**twitter_app_auth)
count = 0
data = pd.DataFrame()
uname = pd.DataFrame()
#uname = []
for members in tar.getmembers():
if (None):
break
else:
f = tar.extractfile(members)
data = data.append(pd.read_json(f, lines=True))
#for memberx in data['user']:
#uname=uname.append(json_normalize(memberx)['screen_name'], ignore_index=True)
#uname.append('@'+str(json_normalize(memberx)['screen_name'].values[0]))
count = count + 1
data = pd.DataFrame()
uname = pd.DataFrame()
count=0
#uname = []
for members in tar.getmembers():
#if (None):
# break
#else:
if (count==13):
f = tar.extractfile(members)
data = data.append(pd.read_json(f, lines=True))
for memberx in data['user']:
uname=uname.append(json_normalize(memberx)['screen_name'], ignore_index=True)
#uname.append('@'+str(json_normalize(memberx)['screen_name'].values[0]))
count = count + 1
len(uname)
distinct_uname=[]
for i in uname.drop_duplicates().values:
distinct_uname.append((str('@'+i).replace("[u'","")).replace("']",''))
len(distinct_uname)
asu=distinct_uname[0:180]
botoresult = pd.DataFrame()
for screen_name, result in bom.check_accounts_in(asu):
botoresult=botoresult.append(result, ignore_index=True)
#bom.twitter_api.rate_limit_status()['resources']['application']['/application/rate_limit_status']['remaining']
output_bot=pd.concat([botoresult.user.apply(pd.Series), botoresult.scores.apply(pd.Series), botoresult.categories.apply(pd.Series)], axis=1)
len(botoresult)
output_bot.to_csv("outputbot.csv", sep=',', encoding='utf-8')
```
<h1>unused script</h1>
only for profilling<br>
xoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxoxo
```
import pylab as pl
import numpy as np
from collections import Counter
x=Counter(data['created_at'].dt.strftime('%d%H'))
y=zip(map(int,x.keys()),x.values())
y.sort()
x=pd.DataFrame(y)
x
X = range(len(y))
pl.bar(X, x[1], align='center', width=1)
pl.xticks(X, x[0], rotation="vertical")
ymax = max(x[1]) + 1
pl.ylim(0, ymax)
pl.show()
```
|
github_jupyter
|
Wayne H Nixalo - 09 Aug 2017
FADL2 L9: Generative Models
neural-style-GPU.ipynb
```
%matplotlib inline
import importlib
import os, sys
sys.path.insert(1, os.path.join('../utils'))
from utils2 import *
from scipy.optimize import fmin_l_bfgs_b
from scipy.misc import imsave
from keras import metrics
from vgg16_avg import VGG16_Avg
limit_mem()
path = '../data/nst/'
# names = os.listdir(path)
# pkl_out = open('fnames.pkl','wb')
# pickle.dump(names, pkl_out)
# pkl_out.close()
fnames = pickle.load(open(path + 'fnames.pkl', 'rb'))
fnames = glob.glob(path+'**/*.JPG', recursive=True)
fn = fnames[0]
fn
img = Image.open(fn); img
# Subtracting mean and reversing color-channel order:
rn_mean = np.array([123.68,116.779,103.939], dtype=np.float32)
preproc = lambda x: (x - rn_mean)[:,:,:,::-1]
# later undoing preprocessing for image generation
deproc = lambda x,s: np.clip(x.reshape(s)[:,:,:,::-1] + rn_mean, 0, 255)
img_arr = preproc(np.expand_dims(np.array(img), 0))
shp = img_arr.shape
```
### Content Recreation
```
# had to fix some compatibility issues w/ Keras 1 -> Keras 2
import vgg16_avg
importlib.reload(vgg16_avg)
from vgg16_avg import VGG16_Avg
model = VGG16_Avg(include_top=False)
# grabbing activations from near the end of the CNN model
layer = model.get_layer('block5_conv1').output
# calculating layer's target activations
layer_model = Model(model.input, layer)
targ = K.variable(layer_model.predict(img_arr))
```
In this implementation, need to define an object that'll allow us to separately access the loss function and gradients of a function,
```
class Evaluator(object):
def __init__(self, f, shp): self.f, self.shp = f, shp
def loss(self, x):
loss_, self.grad_values = self.f([x.reshape(self.shp)])
return loss_.astype(np.float64)
def grads(self, x): return self.grad_values.flatten().astype(np.float64)
# Define loss function to calc MSE betwn the 2 outputs at specfd Conv layer
loss = metrics.mse(layer, targ)
grads = K.gradients(loss, model.input)
fn = K.function([model.input], [loss]+grads)
evaluator = Evaluator(fn, shp)
# optimize loss fn w/ deterministic approach using Line Search
def solve_image(eval_obj, niter, x):
for i in range(niter):
x, min_val, info = fmin_l_bfgs_b(eval_obj.loss, x.flatten(),
fprime=eval_obj.grads, maxfun=20)
x = np.clip(x, -127,127)
print('Current loss value:', min_val)
imsave(f'{path}/results/res_at_iteration_{i}.png', deproc(x.copy(), shp)[0])
return x
# generating a random image:
rand_img = lambda shape: np.random.uniform(-2.5,2.5,shape)/100
x = rand_img(shp)
plt.imshow(x[0])
iterations = 10
x = solve_image(evaluator, iterations, x)
Image.open(path + 'results/res_at_iteration_1.png')
# Looking at result for earlier Conv block (4):
layer = model.get_layer('block4_conv1').output
layer_model = Model(model.input, layer)
targ = K.variable(layer_model.predict(img_arr))
loss = metrics.mse(layer, targ)
grads = K.gradients(loss, model.input)
fn = K.function([model.input], [loss]+grads)
evaluator = Evaluator(fn, shp)
x = solve_image(evaluator, iterations, x)
Image.open(path + 'results/res_at_iteration_9.png')
```
|
github_jupyter
|
# The Central Limit Theorem
Elements of Data Science
by [Allen Downey](https://allendowney.com)
[MIT License](https://opensource.org/licenses/MIT)
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# If we're running on Colab, install empiricaldist
# https://pypi.org/project/empiricaldist/
import sys
IN_COLAB = 'google.colab' in sys.modules
if IN_COLAB:
!pip install empiricaldist
```
## The Central Limit Theorem
According to our friends at [Wikipedia](https://en.wikipedia.org/wiki/Central_limit_theorem):
> The central limit theorem (CLT) establishes that, in some situations, when independent random variables are added, their properly normalized sum tends toward a normal distribution (informally a bell curve) even if the original variables themselves are not normally distributed.
This theorem is useful for two reasons:
1. It offers an explanation for the ubiquity of normal distributions in the natural and engineered world. If you measure something that depends on the sum of many independent factors, the distribution of the measurements will often be approximately normal.
2. In the context of mathematical statistics it provides a way to approximate the sampling distribution of many statistics, at least, as Wikipedia warns us, "in some situations".
In this notebook, we'll explore those situations.
## Rolling dice
I'll start by adding up the totals for 1, 2, and 3 dice.
The following function simulates rolling a six-sided die.
```
def roll(size):
return np.random.randint(1, 7, size=size)
```
If we roll it 1000 times, we expect each value to appear roughly the same number of times.
```
sample = roll(1000)
```
Here's what the PMF looks like.
```
from empiricaldist import Pmf
pmf = Pmf.from_seq(sample)
pmf.bar()
plt.xlabel('Outcome')
plt.ylabel('Probability');
```
To simulate rolling two dice, I'll create an array with 1000 rows and 2 columns.
```
a = roll(size=(1000, 2))
a.shape
```
And then add up the columns.
```
sample2 = a.sum(axis=1)
sample2.shape
```
The result is a sample of 1000 sums of two dice. Here's what that PMF looks like.
```
pmf2 = Pmf.from_seq(sample2)
pmf2.bar()
plt.xlabel('Outcome')
plt.ylabel('Probability');
```
And here's what it looks like with three dice.
```
a = roll(size=(1000, 3))
sample3 = a.sum(axis=1)
pmf3 = Pmf.from_seq(sample3)
pmf3.bar()
plt.xlabel('Outcome')
plt.ylabel('Probability');
```
With one die, the distribution is uniform. With two dice, it's a triangle. With three dice, it starts to have the shape of a bell curve.
Here are the three PMFs on the same axes, for comparison.
```
pmf.plot(label='1 die')
pmf2.plot(label='2 dice')
pmf3.plot(label='3 dice')
plt.xlabel('Outcome')
plt.ylabel('Probability')
plt.legend();
```
## Gamma distributions
In the previous section, we saw that the sum of values from a uniform distribution starts to look like a bell curve when we add up just a few values.
Now let's do the same thing with values from a gamma distribution.
NumPy provides a function to generate random values from a gamma distribution with a given mean.
```
mean = 2
gamma_sample = np.random.gamma(mean, size=1000)
```
Here's what the distribution looks like, this time using a CDF.
```
from empiricaldist import Cdf
cdf1 = Cdf.from_seq(gamma_sample)
cdf1.plot()
plt.xlabel('Outcome')
plt.ylabel('CDF');
```
It doesn't look like like a normal distribution. To see the differences more clearly, we can plot the CDF of the data on top of a normal model with the same mean and standard deviation.
```
from scipy.stats import norm
def plot_normal_model(sample, **options):
"""Plot the CDF of a normal distribution with the
same mean and std of the sample.
sample: sequence of values
options: passed to plt.plot
"""
mean, std = np.mean(sample), np.std(sample)
xs = np.linspace(np.min(sample), np.max(sample))
ys = norm.cdf(xs, mean, std)
plt.plot(xs, ys, alpha=0.4, **options)
```
Here's what that looks like for a gamma distribution with mean 2.
```
from empiricaldist import Cdf
plot_normal_model(gamma_sample, color='C0', label='Normal model')
cdf1.plot(label='Sample 1')
plt.xlabel('Outcome')
plt.ylabel('CDF');
```
There are clear differences between the data and the model. Let's see how that looks when we start adding up values.
The following function computes the sum of gamma distributions with a given mean.
```
def sum_of_gammas(mean, num):
"""Sample the sum of gamma variates.
mean: mean of the gamma distribution
num: number of values to add up
"""
a = np.random.gamma(mean, size=(1000, num))
sample = a.sum(axis=1)
return sample
```
Here's what the sum of two gamma variates looks like:
```
gamma_sample2 = sum_of_gammas(2, 2)
cdf2 = Cdf.from_seq(gamma_sample2)
plot_normal_model(gamma_sample, color='C0')
cdf1.plot(label='Sum of 1 gamma')
plot_normal_model(gamma_sample2, color='C1')
cdf2.plot(label='Sum of 2 gamma')
plt.xlabel('Total')
plt.ylabel('CDF')
plt.legend();
```
The normal model is a better fit for the sum of two gamma variates, but there are still evident differences. Let's see how big `num` has to be before it converges.
First I'll wrap the previous example in a function.
```
def plot_gammas(mean, nums):
"""Plot the sum of gamma variates and a normal model.
mean: mean of the gamma distribution
nums: sequence of sizes
"""
for num in nums:
sample = sum_of_gammas(mean, num)
plot_normal_model(sample, color='gray')
Cdf.from_seq(sample).plot(label=f'num = {num}')
plt.xlabel('Total')
plt.ylabel('CDF')
plt.legend()
```
With `mean=2` it doesn't take long for the sum of gamma variates to approximate a normal distribution.
```
mean = 2
plot_gammas(mean, [2, 5, 10])
```
However, that doesn't mean that all gamma distribution behave the same way. In general, the higher the variance, the longer it takes to converge.
With a gamma distribution, smaller means lead to higher variance. With `mean=0.2`, the sum of 10 values is still not normal.
```
mean = 0.2
plot_gammas(mean, [2, 5, 10])
```
We have to crank `num` up to 100 before the convergence looks good.
```
mean = 0.2
plot_gammas(mean, [20, 50, 100])
```
With `mean=0.02`, we have to add up 1000 values before the distribution looks normal.
```
mean = 0.02
plot_gammas(mean, [200, 500, 1000])
```
## Pareto distributions
The gamma distributions in the previous section have higher variance that the uniform distribution we started with, so we have to add up more values to get the distribution of the sum to look normal.
The Pareto distribution is even more extreme. Depending on the parameter, `alpha`, the variance can be large, very large, or infinite.
Here's a function that generates the sum of values from a Pareto distribution with a given parameter.
```
def sum_of_paretos(alpha, num):
a = np.random.pareto(alpha, size=(1000, num))
sample = a.sum(axis=1)
return sample
```
And here's a function that plots the results.
```
def plot_paretos(mean, nums):
for num in nums:
sample = sum_of_paretos(mean, num)
plot_normal_model(sample, color='gray')
Cdf.from_seq(sample).plot(label=f'num = {num}')
plt.xlabel('Total')
plt.ylabel('CDF')
plt.legend()
```
With `alpha=3` the Pareto distribution is relatively well-behaved, and the sum converges to a normal distribution with a moderate number of values.
```
alpha = 3
plot_paretos(alpha, [10, 20, 50])
```
With `alpha=2`, we don't get very good convergence even with 1000 values.
```
alpha = 2
plot_paretos(alpha, [200, 500, 1000])
```
With `alpha=1.5`, it's even worse.
```
alpha = 1.5
plot_paretos(alpha, [2000, 5000, 10000])
```
And with `alpha=1`, it's beyond hopeless.
```
alpha = 1
plot_paretos(alpha, [10000, 20000, 50000])
```
In fact, when `alpha` is 2 or less, the variance of the Pareto distribution is infinite, and the central limit theorem does not apply. The disrtribution of the sum never converges to a normal distribution.
However, there is no practical difference between a distribution like Pareto that never converges and other high-variance distributions that converge in theory, but only with an impractical number of values.
## Summary
The central limit theorem is an important result in mathematical statistics. And it explains why so many distributions in the natural and engineered world are approximately normal.
But it doesn't always apply:
* In theory the central limit theorem doesn't apply when variance is infinite.
* In practice it might be irrelevant when variance is high.
|
github_jupyter
|
# Qcodes example with Alazar ATS 9360
```
# import all necessary things
%matplotlib nbagg
import qcodes as qc
import qcodes.instrument.parameter as parameter
import qcodes.instrument_drivers.AlazarTech.ATS9360 as ATSdriver
import qcodes.instrument_drivers.AlazarTech.ATS_acquisition_controllers as ats_contr
# Command to list all alazar boards connected to the system
ATSdriver.AlazarTech_ATS.find_boards()
# Create the ATS9870 instrument on the new server "alazar_server"
ats_inst = ATSdriver.AlazarTech_ATS9360(name='Alazar1')
# Print all information about this Alazar card
ats_inst.get_idn()
# Instantiate an acquisition controller (In this case we are doing a simple DFT) on the same server ("alazar_server") and
# provide the name of the name of the alazar card that this controller should control
acquisition_controller = ats_contr.Demodulation_AcquisitionController(name='acquisition_controller',
demodulation_frequency=10e6,
alazar_name='Alazar1')
# Configure all settings in the Alazar card
ats_inst.config(clock_source='INTERNAL_CLOCK',
sample_rate=1_000_000_000,
clock_edge='CLOCK_EDGE_RISING',
decimation=1,
coupling=['DC','DC'],
channel_range=[.4,.4],
impedance=[50,50],
trigger_operation='TRIG_ENGINE_OP_J',
trigger_engine1='TRIG_ENGINE_J',
trigger_source1='EXTERNAL',
trigger_slope1='TRIG_SLOPE_POSITIVE',
trigger_level1=160,
trigger_engine2='TRIG_ENGINE_K',
trigger_source2='DISABLE',
trigger_slope2='TRIG_SLOPE_POSITIVE',
trigger_level2=128,
external_trigger_coupling='DC',
external_trigger_range='ETR_2V5',
trigger_delay=0,
timeout_ticks=0,
aux_io_mode='AUX_IN_AUXILIARY', # AUX_IN_TRIGGER_ENABLE for seq mode on
aux_io_param='NONE' # TRIG_SLOPE_POSITIVE for seq mode on
)
# This command is specific to this acquisition controller. The kwargs provided here are being forwarded to ats_inst.acquire
# This way, it becomes easy to change acquisition specific settings from the ipython notebook
acquisition_controller.update_acquisitionkwargs(#mode='NPT',
samples_per_record=1024,
records_per_buffer=70,
buffers_per_acquisition=1,
#channel_selection='AB',
#transfer_offset=0,
#external_startcapture='ENABLED',
#enable_record_headers='DISABLED',
#alloc_buffers='DISABLED',
#fifo_only_streaming='DISABLED',
#interleave_samples='DISABLED',
#get_processed_data='DISABLED',
allocated_buffers=1,
#buffer_timeout=1000
)
# Getting the value of the parameter 'acquisition' of the instrument 'acquisition_controller' performes the entire acquisition
# protocol. This again depends on the specific implementation of the acquisition controller
acquisition_controller.acquisition()
# make a snapshot of the 'ats_inst' instrument
ats_inst.snapshot()
# Finally show that this instrument also works within a loop
dummy = parameter.ManualParameter(name="dummy")
data = qc.Loop(dummy[0:50:1]).each(acquisition_controller.acquisition).run(name='AlazarTest')
qc.MatPlot(data.acquisition_controller_acquisition)
```
|
github_jupyter
|
# Assignment 2: Parts-of-Speech Tagging (POS)
Welcome to the second assignment of Course 2 in the Natural Language Processing specialization. This assignment will develop skills in part-of-speech (POS) tagging, the process of assigning a part-of-speech tag (Noun, Verb, Adjective...) to each word in an input text. Tagging is difficult because some words can represent more than one part of speech at different times. They are **Ambiguous**. Let's look at the following example:
- The whole team played **well**. [adverb]
- You are doing **well** for yourself. [adjective]
- **Well**, this assignment took me forever to complete. [interjection]
- The **well** is dry. [noun]
- Tears were beginning to **well** in her eyes. [verb]
Distinguishing the parts-of-speech of a word in a sentence will help you better understand the meaning of a sentence. This would be critically important in search queries. Identifying the proper noun, the organization, the stock symbol, or anything similar would greatly improve everything ranging from speech recognition to search. By completing this assignment, you will:
- Learn how parts-of-speech tagging works
- Compute the transition matrix A in a Hidden Markov Model
- Compute the transition matrix B in a Hidden Markov Model
- Compute the Viterbi algorithm
- Compute the accuracy of your own model
## Outline
- [0 Data Sources](#0)
- [1 POS Tagging](#1)
- [1.1 Training](#1.1)
- [Exercise 01](#ex-01)
- [1.2 Testing](#1.2)
- [Exercise 02](#ex-02)
- [2 Hidden Markov Models](#2)
- [2.1 Generating Matrices](#2.1)
- [Exercise 03](#ex-03)
- [Exercise 04](#ex-04)
- [3 Viterbi Algorithm](#3)
- [3.1 Initialization](#3.1)
- [Exercise 05](#ex-05)
- [3.2 Viterbi Forward](#3.2)
- [Exercise 06](#ex-06)
- [3.3 Viterbi Backward](#3.3)
- [Exercise 07](#ex-07)
- [4 Predicting on a data set](#4)
- [Exercise 08](#ex-08)
```
# Importing packages and loading in the data set
from utils_pos import get_word_tag, preprocess
import pandas as pd
from collections import defaultdict
import math
import numpy as np
```
<a name='0'></a>
## Part 0: Data Sources
This assignment will use two tagged data sets collected from the **Wall Street Journal (WSJ)**.
[Here](http://relearn.be/2015/training-common-sense/sources/software/pattern-2.6-critical-fork/docs/html/mbsp-tags.html) is an example 'tag-set' or Part of Speech designation describing the two or three letter tag and their meaning.
- One data set (**WSJ-2_21.pos**) will be used for **training**.
- The other (**WSJ-24.pos**) for **testing**.
- The tagged training data has been preprocessed to form a vocabulary (**hmm_vocab.txt**).
- The words in the vocabulary are words from the training set that were used two or more times.
- The vocabulary is augmented with a set of 'unknown word tokens', described below.
The training set will be used to create the emission, transmission and tag counts.
The test set (WSJ-24.pos) is read in to create `y`.
- This contains both the test text and the true tag.
- The test set has also been preprocessed to remove the tags to form **test_words.txt**.
- This is read in and further processed to identify the end of sentences and handle words not in the vocabulary using functions provided in **utils_pos.py**.
- This forms the list `prep`, the preprocessed text used to test our POS taggers.
A POS tagger will necessarily encounter words that are not in its datasets.
- To improve accuracy, these words are further analyzed during preprocessing to extract available hints as to their appropriate tag.
- For example, the suffix 'ize' is a hint that the word is a verb, as in 'final-ize' or 'character-ize'.
- A set of unknown-tokens, such as '--unk-verb--' or '--unk-noun--' will replace the unknown words in both the training and test corpus and will appear in the emission, transmission and tag data structures.
<img src = "DataSources1.PNG" />
Implementation note:
- For python 3.6 and beyond, dictionaries retain the insertion order.
- Furthermore, their hash-based lookup makes them suitable for rapid membership tests.
- If _di_ is a dictionary, `key in di` will return `True` if _di_ has a key _key_, else `False`.
The dictionary `vocab` will utilize these features.
```
# load in the training corpus
with open("WSJ_02-21.pos", 'r') as f:
training_corpus = f.readlines()
print(f"A few items of the training corpus list")
print(training_corpus[0:5])
# read the vocabulary data, split by each line of text, and save the list
with open("hmm_vocab.txt", 'r') as f:
voc_l = f.read().split('\n')
print("A few items of the vocabulary list")
print(voc_l[0:50])
print()
print("A few items at the end of the vocabulary list")
print(voc_l[-50:])
# vocab: dictionary that has the index of the corresponding words
vocab = {}
# Get the index of the corresponding words.
for i, word in enumerate(sorted(voc_l)):
vocab[word] = i
print("Vocabulary dictionary, key is the word, value is a unique integer")
cnt = 0
for k,v in vocab.items():
print(f"{k}:{v}")
cnt += 1
if cnt > 20:
break
# load in the test corpus
with open("WSJ_24.pos", 'r') as f:
y = f.readlines()
print("A sample of the test corpus")
print(y[0:10])
#corpus without tags, preprocessed
_, prep = preprocess(vocab, "test.words")
print('The length of the preprocessed test corpus: ', len(prep))
print('This is a sample of the test_corpus: ')
print(prep[0:10])
```
<a name='1'></a>
# Part 1: Parts-of-speech tagging
<a name='1.1'></a>
## Part 1.1 - Training
You will start with the simplest possible parts-of-speech tagger and we will build up to the state of the art.
In this section, you will find the words that are not ambiguous.
- For example, the word `is` is a verb and it is not ambiguous.
- In the `WSJ` corpus, $86$% of the token are unambiguous (meaning they have only one tag)
- About $14\%$ are ambiguous (meaning that they have more than one tag)
<img src = "pos.png" style="width:400px;height:250px;"/>
Before you start predicting the tags of each word, you will need to compute a few dictionaries that will help you to generate the tables.
#### Transition counts
- The first dictionary is the `transition_counts` dictionary which computes the number of times each tag happened next to another tag.
This dictionary will be used to compute:
$$P(t_i |t_{i-1}) \tag{1}$$
This is the probability of a tag at position $i$ given the tag at position $i-1$.
In order for you to compute equation 1, you will create a `transition_counts` dictionary where
- The keys are `(prev_tag, tag)`
- The values are the number of times those two tags appeared in that order.
#### Emission counts
The second dictionary you will compute is the `emission_counts` dictionary. This dictionary will be used to compute:
$$P(w_i|t_i)\tag{2}$$
In other words, you will use it to compute the probability of a word given its tag.
In order for you to compute equation 2, you will create an `emission_counts` dictionary where
- The keys are `(tag, word)`
- The values are the number of times that pair showed up in your training set.
#### Tag counts
The last dictionary you will compute is the `tag_counts` dictionary.
- The key is the tag
- The value is the number of times each tag appeared.
<a name='ex-01'></a>
### Exercise 01
**Instructions:** Write a program that takes in the `training_corpus` and returns the three dictionaries mentioned above `transition_counts`, `emission_counts`, and `tag_counts`.
- `emission_counts`: maps (tag, word) to the number of times it happened.
- `transition_counts`: maps (prev_tag, tag) to the number of times it has appeared.
- `tag_counts`: maps (tag) to the number of times it has occured.
Implementation note: This routine utilises *defaultdict*, which is a subclass of *dict*.
- A standard Python dictionary throws a *KeyError* if you try to access an item with a key that is not currently in the dictionary.
- In contrast, the *defaultdict* will create an item of the type of the argument, in this case an integer with the default value of 0.
- See [defaultdict](https://docs.python.org/3.3/library/collections.html#defaultdict-objects).
```
# UNQ_C1 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
# GRADED FUNCTION: create_dictionaries
def create_dictionaries(training_corpus, vocab):
"""
Input:
training_corpus: a corpus where each line has a word followed by its tag.
vocab: a dictionary where keys are words in vocabulary and value is an index
Output:
emission_counts: a dictionary where the keys are (tag, word) and the values are the counts
transition_counts: a dictionary where the keys are (prev_tag, tag) and the values are the counts
tag_counts: a dictionary where the keys are the tags and the values are the counts
"""
# initialize the dictionaries using defaultdict
emission_counts = defaultdict(int)
transition_counts = defaultdict(int)
tag_counts = defaultdict(int)
# Initialize "prev_tag" (previous tag) with the start state, denoted by '--s--'
prev_tag = '--s--'
# use 'i' to track the line number in the corpus
i = 0
# Each item in the training corpus contains a word and its POS tag
# Go through each word and its tag in the training corpus
for word_tag in training_corpus:
# Increment the word_tag count
i += 1
# Every 50,000 words, print the word count
if i % 50000 == 0:
print(f"word count = {i}")
### START CODE HERE (Replace instances of 'None' with your code) ###
# get the word and tag using the get_word_tag helper function (imported from utils_pos.py)
word, tag = get_word_tag(word_tag, vocab)
# Increment the transition count for the previous word and tag
transition_counts[(prev_tag, tag)] += 1
# Increment the emission count for the tag and word
emission_counts[(tag, word)] += 1
# Increment the tag count
tag_counts[tag] += 1
# Set the previous tag to this tag (for the next iteration of the loop)
prev_tag = tag
### END CODE HERE ###
return emission_counts, transition_counts, tag_counts
emission_counts, transition_counts, tag_counts = create_dictionaries(training_corpus, vocab)
# get all the POS states
states = sorted(tag_counts.keys())
print(f"Number of POS tags (number of 'states'): {len(states)}")
print("View these POS tags (states)")
print(states)
```
##### Expected Output
```CPP
Number of POS tags (number of 'states'46
View these states
['#', '$', "''", '(', ')', ',', '--s--', '.', ':', 'CC', 'CD', 'DT', 'EX', 'FW', 'IN', 'JJ', 'JJR', 'JJS', 'LS', 'MD', 'NN', 'NNP', 'NNPS', 'NNS', 'PDT', 'POS', 'PRP', 'PRP$', 'RB', 'RBR', 'RBS', 'RP', 'SYM', 'TO', 'UH', 'VB', 'VBD', 'VBG', 'VBN', 'VBP', 'VBZ', 'WDT', 'WP', 'WP$', 'WRB', '``']
```
The 'states' are the Parts-of-speech designations found in the training data. They will also be referred to as 'tags' or POS in this assignment.
- "NN" is noun, singular,
- 'NNS' is noun, plural.
- In addition, there are helpful tags like '--s--' which indicate a start of a sentence.
- You can get a more complete description at [Penn Treebank II tag set](https://www.clips.uantwerpen.be/pages/mbsp-tags).
```
print("transition examples: ")
for ex in list(transition_counts.items())[:3]:
print(ex)
print()
print("emission examples: ")
for ex in list(emission_counts.items())[200:203]:
print (ex)
print()
print("ambiguous word example: ")
for tup,cnt in emission_counts.items():
if tup[1] == 'back': print (tup, cnt)
```
##### Expected Output
```CPP
transition examples:
(('--s--', 'IN'), 5050)
(('IN', 'DT'), 32364)
(('DT', 'NNP'), 9044)
emission examples:
(('DT', 'any'), 721)
(('NN', 'decrease'), 7)
(('NN', 'insider-trading'), 5)
ambiguous word example:
('RB', 'back') 304
('VB', 'back') 20
('RP', 'back') 84
('JJ', 'back') 25
('NN', 'back') 29
('VBP', 'back') 4
```
<a name='1.2'></a>
### Part 1.2 - Testing
Now you will test the accuracy of your parts-of-speech tagger using your `emission_counts` dictionary.
- Given your preprocessed test corpus `prep`, you will assign a parts-of-speech tag to every word in that corpus.
- Using the original tagged test corpus `y`, you will then compute what percent of the tags you got correct.
<a name='ex-02'></a>
### Exercise 02
**Instructions:** Implement `predict_pos` that computes the accuracy of your model.
- This is a warm up exercise.
- To assign a part of speech to a word, assign the most frequent POS for that word in the training set.
- Then evaluate how well this approach works. Each time you predict based on the most frequent POS for the given word, check whether the actual POS of that word is the same. If so, the prediction was correct!
- Calculate the accuracy as the number of correct predictions divided by the total number of words for which you predicted the POS tag.
```
# UNQ_C2 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
# GRADED FUNCTION: predict_pos
def predict_pos(prep, y, emission_counts, vocab, states):
'''
Input:
prep: a preprocessed version of 'y'. A list with the 'word' component of the tuples.
y: a corpus composed of a list of tuples where each tuple consists of (word, POS)
emission_counts: a dictionary where the keys are (tag,word) tuples and the value is the count
vocab: a dictionary where keys are words in vocabulary and value is an index
states: a sorted list of all possible tags for this assignment
Output:
accuracy: Number of times you classified a word correctly
'''
# Initialize the number of correct predictions to zero
num_correct = 0
# Get the (tag, word) tuples, stored as a set
all_words = set(emission_counts.keys())
# Get the number of (word, POS) tuples in the corpus 'y'
total = len(y)
for word, y_tup in zip(prep, y):
# Split the (word, POS) string into a list of two items
y_tup_l = y_tup.split()
# Verify that y_tup contain both word and POS
if len(y_tup_l) == 2:
# Set the true POS label for this word
true_label = y_tup_l[1]
else:
# If the y_tup didn't contain word and POS, go to next word
continue
count_final = 0
pos_final = ''
# If the word is in the vocabulary...
if word in vocab:
for pos in states:
### START CODE HERE (Replace instances of 'None' with your code) ###
# define the key as the tuple containing the POS and word
key = (pos,word)
# check if the (pos, word) key exists in the emission_counts dictionary
if key in emission_counts.keys(): # complete this line
# get the emission count of the (pos,word) tuple
count = emission_counts[key]
# keep track of the POS with the largest count
if count > count_final: # complete this line
# update the final count (largest count)
count_final = count
# update the final POS
pos_final = pos
# If the final POS (with the largest count) matches the true POS:
if pos_final == true_label: # complete this line
# Update the number of correct predictions
num_correct += 1
### END CODE HERE ###
accuracy = num_correct / total
return accuracy
accuracy_predict_pos = predict_pos(prep, y, emission_counts, vocab, states)
print(f"Accuracy of prediction using predict_pos is {accuracy_predict_pos:.4f}")
```
##### Expected Output
```CPP
Accuracy of prediction using predict_pos is 0.8889
```
88.9% is really good for this warm up exercise. With hidden markov models, you should be able to get **95% accuracy.**
<a name='2'></a>
# Part 2: Hidden Markov Models for POS
Now you will build something more context specific. Concretely, you will be implementing a Hidden Markov Model (HMM) with a Viterbi decoder
- The HMM is one of the most commonly used algorithms in Natural Language Processing, and is a foundation to many deep learning techniques you will see in this specialization.
- In addition to parts-of-speech tagging, HMM is used in speech recognition, speech synthesis, etc.
- By completing this part of the assignment you will get a 95% accuracy on the same dataset you used in Part 1.
The Markov Model contains a number of states and the probability of transition between those states.
- In this case, the states are the parts-of-speech.
- A Markov Model utilizes a transition matrix, `A`.
- A Hidden Markov Model adds an observation or emission matrix `B` which describes the probability of a visible observation when we are in a particular state.
- In this case, the emissions are the words in the corpus
- The state, which is hidden, is the POS tag of that word.
<a name='2.1'></a>
## Part 2.1 Generating Matrices
### Creating the 'A' transition probabilities matrix
Now that you have your `emission_counts`, `transition_counts`, and `tag_counts`, you will start implementing the Hidden Markov Model.
This will allow you to quickly construct the
- `A` transition probabilities matrix.
- and the `B` emission probabilities matrix.
You will also use some smoothing when computing these matrices.
Here is an example of what the `A` transition matrix would look like (it is simplified to 5 tags for viewing. It is 46x46 in this assignment.):
|**A** |...| RBS | RP | SYM | TO | UH|...
| --- ||---:-------------| ------------ | ------------ | -------- | ---------- |----
|**RBS** |...|2.217069e-06 |2.217069e-06 |2.217069e-06 |0.008870 |2.217069e-06|...
|**RP** |...|3.756509e-07 |7.516775e-04 |3.756509e-07 |0.051089 |3.756509e-07|...
|**SYM** |...|1.722772e-05 |1.722772e-05 |1.722772e-05 |0.000017 |1.722772e-05|...
|**TO** |...|4.477336e-05 |4.472863e-08 |4.472863e-08 |0.000090 |4.477336e-05|...
|**UH** |...|1.030439e-05 |1.030439e-05 |1.030439e-05 |0.061837 |3.092348e-02|...
| ... |...| ... | ... | ... | ... | ... | ...
Note that the matrix above was computed with smoothing.
Each cell gives you the probability to go from one part of speech to another.
- In other words, there is a 4.47e-8 chance of going from parts-of-speech `TO` to `RP`.
- The sum of each row has to equal 1, because we assume that the next POS tag must be one of the available columns in the table.
The smoothing was done as follows:
$$ P(t_i | t_{i-1}) = \frac{C(t_{i-1}, t_{i}) + \alpha }{C(t_{i-1}) +\alpha * N}\tag{3}$$
- $N$ is the total number of tags
- $C(t_{i-1}, t_{i})$ is the count of the tuple (previous POS, current POS) in `transition_counts` dictionary.
- $C(t_{i-1})$ is the count of the previous POS in the `tag_counts` dictionary.
- $\alpha$ is a smoothing parameter.
<a name='ex-03'></a>
### Exercise 03
**Instructions:** Implement the `create_transition_matrix` below for all tags. Your task is to output a matrix that computes equation 3 for each cell in matrix `A`.
```
# UNQ_C3 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
# GRADED FUNCTION: create_transition_matrix
def create_transition_matrix(alpha, tag_counts, transition_counts):
'''
Input:
alpha: number used for smoothing
tag_counts: a dictionary mapping each tag to its respective count
transition_counts: transition count for the previous word and tag
Output:
A: matrix of dimension (num_tags,num_tags)
'''
# Get a sorted list of unique POS tags
all_tags = sorted(tag_counts.keys())
# Count the number of unique POS tags
num_tags = len(all_tags)
# Initialize the transition matrix 'A'
A = np.zeros((num_tags,num_tags))
# Get the unique transition tuples (previous POS, current POS)
trans_keys = set(transition_counts.keys())
### START CODE HERE (Return instances of 'None' with your code) ###
# Go through each row of the transition matrix A
for i in range(num_tags):
# Go through each column of the transition matrix A
for j in range(num_tags):
# Initialize the count of the (prev POS, current POS) to zero
count = 0
# Define the tuple (prev POS, current POS)
# Get the tag at position i and tag at position j (from the all_tags list)
key = (all_tags[i],all_tags[j])
# Check if the (prev POS, current POS) tuple
# exists in the transition counts dictionaory
if key in transition_counts.keys(): #complete this line
# Get count from the transition_counts dictionary
# for the (prev POS, current POS) tuple
count = transition_counts[key]
# Get the count of the previous tag (index position i) from tag_counts
count_prev_tag = tag_counts[all_tags[i]]
# Apply smoothing using count of the tuple, alpha,
# count of previous tag, alpha, and number of total tags
A[i,j] = (count + alpha)/(count_prev_tag + alpha * num_tags )
### END CODE HERE ###
return A
alpha = 0.001
A = create_transition_matrix(alpha, tag_counts, transition_counts)
# Testing your function
print(f"A at row 0, col 0: {A[0,0]:.9f}")
print(f"A at row 3, col 1: {A[3,1]:.4f}")
print("View a subset of transition matrix A")
A_sub = pd.DataFrame(A[30:35,30:35], index=states[30:35], columns = states[30:35] )
print(A_sub)
```
##### Expected Output
```CPP
A at row 0, col 0: 0.000007040
A at row 3, col 1: 0.1691
View a subset of transition matrix A
RBS RP SYM TO UH
RBS 2.217069e-06 2.217069e-06 2.217069e-06 0.008870 2.217069e-06
RP 3.756509e-07 7.516775e-04 3.756509e-07 0.051089 3.756509e-07
SYM 1.722772e-05 1.722772e-05 1.722772e-05 0.000017 1.722772e-05
TO 4.477336e-05 4.472863e-08 4.472863e-08 0.000090 4.477336e-05
UH 1.030439e-05 1.030439e-05 1.030439e-05 0.061837 3.092348e-02
```
### Create the 'B' emission probabilities matrix
Now you will create the `B` transition matrix which computes the emission probability.
You will use smoothing as defined below:
$$P(w_i | t_i) = \frac{C(t_i, word_i)+ \alpha}{C(t_{i}) +\alpha * N}\tag{4}$$
- $C(t_i, word_i)$ is the number of times $word_i$ was associated with $tag_i$ in the training data (stored in `emission_counts` dictionary).
- $C(t_i)$ is the number of times $tag_i$ was in the training data (stored in `tag_counts` dictionary).
- $N$ is the number of words in the vocabulary
- $\alpha$ is a smoothing parameter.
The matrix `B` is of dimension (num_tags, N), where num_tags is the number of possible parts-of-speech tags.
Here is an example of the matrix, only a subset of tags and words are shown:
<p style='text-align: center;'> <b>B Emissions Probability Matrix (subset)</b> </p>
|**B**| ...| 725 | adroitly | engineers | promoted | synergy| ...|
|----|----|--------------|--------------|--------------|--------------|-------------|----|
|**CD** | ...| **8.201296e-05** | 2.732854e-08 | 2.732854e-08 | 2.732854e-08 | 2.732854e-08| ...|
|**NN** | ...| 7.521128e-09 | 7.521128e-09 | 7.521128e-09 | 7.521128e-09 | **2.257091e-05**| ...|
|**NNS** | ...| 1.670013e-08 | 1.670013e-08 |**4.676203e-04** | 1.670013e-08 | 1.670013e-08| ...|
|**VB** | ...| 3.779036e-08 | 3.779036e-08 | 3.779036e-08 | 3.779036e-08 | 3.779036e-08| ...|
|**RB** | ...| 3.226454e-08 | **6.456135e-05** | 3.226454e-08 | 3.226454e-08 | 3.226454e-08| ...|
|**RP** | ...| 3.723317e-07 | 3.723317e-07 | 3.723317e-07 | **3.723317e-07** | 3.723317e-07| ...|
| ... | ...| ... | ... | ... | ... | ... | ...|
<a name='ex-04'></a>
### Exercise 04
**Instructions:** Implement the `create_emission_matrix` below that computes the `B` emission probabilities matrix. Your function takes in $\alpha$, the smoothing parameter, `tag_counts`, which is a dictionary mapping each tag to its respective count, the `emission_counts` dictionary where the keys are (tag, word) and the values are the counts. Your task is to output a matrix that computes equation 4 for each cell in matrix `B`.
```
# UNQ_C4 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
# GRADED FUNCTION: create_emission_matrix
def create_emission_matrix(alpha, tag_counts, emission_counts, vocab):
'''
Input:
alpha: tuning parameter used in smoothing
tag_counts: a dictionary mapping each tag to its respective count
emission_counts: a dictionary where the keys are (tag, word) and the values are the counts
vocab: a dictionary where keys are words in vocabulary and value is an index
Output:
B: a matrix of dimension (num_tags, len(vocab))
'''
# get the number of POS tag
num_tags = len(tag_counts)
# Get a list of all POS tags
all_tags = sorted(tag_counts.keys())
# Get the total number of unique words in the vocabulary
num_words = len(vocab)
# Initialize the emission matrix B with places for
# tags in the rows and words in the columns
B = np.zeros((num_tags, num_words))
# Get a set of all (POS, word) tuples
# from the keys of the emission_counts dictionary
emis_keys = set(list(emission_counts.keys()))
### START CODE HERE (Replace instances of 'None' with your code) ###
# Go through each row (POS tags)
for i in range(num_tags): # complete this line
# Go through each column (words)
for j in range(num_words): # complete this line
# Initialize the emission count for the (POS tag, word) to zero
count = 0
# Define the (POS tag, word) tuple for this row and column
key = (all_tags[i],vocab[j])
# check if the (POS tag, word) tuple exists as a key in emission counts
if key in emis_keys: # complete this line
# Get the count of (POS tag, word) from the emission_counts d
count = emission_counts[key]
# Get the count of the POS tag
count_tag = tag_counts[key[0]]
# Apply smoothing and store the smoothed value
# into the emission matrix B for this row and column
B[i,j] = (count + alpha)/(count_tag + alpha * num_words )
### END CODE HERE ###
return B
# creating your emission probability matrix. this takes a few minutes to run.
B = create_emission_matrix(alpha, tag_counts, emission_counts, list(vocab))
print(f"View Matrix position at row 0, column 0: {B[0,0]:.9f}")
print(f"View Matrix position at row 3, column 1: {B[3,1]:.9f}")
# Try viewing emissions for a few words in a sample dataframe
cidx = ['725','adroitly','engineers', 'promoted', 'synergy']
# Get the integer ID for each word
cols = [vocab[a] for a in cidx]
# Choose POS tags to show in a sample dataframe
rvals =['CD','NN','NNS', 'VB','RB','RP']
# For each POS tag, get the row number from the 'states' list
rows = [states.index(a) for a in rvals]
# Get the emissions for the sample of words, and the sample of POS tags
B_sub = pd.DataFrame(B[np.ix_(rows,cols)], index=rvals, columns = cidx )
print(B_sub)
```
##### Expected Output
```CPP
View Matrix position at row 0, column 0: 0.000006032
View Matrix position at row 3, column 1: 0.000000720
725 adroitly engineers promoted synergy
CD 8.201296e-05 2.732854e-08 2.732854e-08 2.732854e-08 2.732854e-08
NN 7.521128e-09 7.521128e-09 7.521128e-09 7.521128e-09 2.257091e-05
NNS 1.670013e-08 1.670013e-08 4.676203e-04 1.670013e-08 1.670013e-08
VB 3.779036e-08 3.779036e-08 3.779036e-08 3.779036e-08 3.779036e-08
RB 3.226454e-08 6.456135e-05 3.226454e-08 3.226454e-08 3.226454e-08
RP 3.723317e-07 3.723317e-07 3.723317e-07 3.723317e-07 3.723317e-07
```
<a name='3'></a>
# Part 3: Viterbi Algorithm and Dynamic Programming
In this part of the assignment you will implement the Viterbi algorithm which makes use of dynamic programming. Specifically, you will use your two matrices, `A` and `B` to compute the Viterbi algorithm. We have decomposed this process into three main steps for you.
* **Initialization** - In this part you initialize the `best_paths` and `best_probabilities` matrices that you will be populating in `feed_forward`.
* **Feed forward** - At each step, you calculate the probability of each path happening and the best paths up to that point.
* **Feed backward**: This allows you to find the best path with the highest probabilities.
<a name='3.1'></a>
## Part 3.1: Initialization
You will start by initializing two matrices of the same dimension.
- best_probs: Each cell contains the probability of going from one POS tag to a word in the corpus.
- best_paths: A matrix that helps you trace through the best possible path in the corpus.
<a name='ex-05'></a>
### Exercise 05
**Instructions**:
Write a program below that initializes the `best_probs` and the `best_paths` matrix.
Both matrices will be initialized to zero except for column zero of `best_probs`.
- Column zero of `best_probs` is initialized with the assumption that the first word of the corpus was preceded by a start token ("--s--").
- This allows you to reference the **A** matrix for the transition probability
Here is how to initialize column 0 of `best_probs`:
- The probability of the best path going from the start index to a given POS tag indexed by integer $i$ is denoted by $\textrm{best_probs}[s_{idx}, i]$.
- This is estimated as the probability that the start tag transitions to the POS denoted by index $i$: $\mathbf{A}[s_{idx}, i]$ AND that the POS tag denoted by $i$ emits the first word of the given corpus, which is $\mathbf{B}[i, vocab[corpus[0]]]$.
- Note that vocab[corpus[0]] refers to the first word of the corpus (the word at position 0 of the corpus).
- **vocab** is a dictionary that returns the unique integer that refers to that particular word.
Conceptually, it looks like this:
$\textrm{best_probs}[s_{idx}, i] = \mathbf{A}[s_{idx}, i] \times \mathbf{B}[i, corpus[0] ]$
In order to avoid multiplying and storing small values on the computer, we'll take the log of the product, which becomes the sum of two logs:
$best\_probs[i,0] = log(A[s_{idx}, i]) + log(B[i, vocab[corpus[0]]$
Also, to avoid taking the log of 0 (which is defined as negative infinity), the code itself will just set $best\_probs[i,0] = float('-inf')$ when $A[s_{idx}, i] == 0$
So the implementation to initialize $best\_probs$ looks like this:
$ if A[s_{idx}, i] <> 0 : best\_probs[i,0] = log(A[s_{idx}, i]) + log(B[i, vocab[corpus[0]]$
$ if A[s_{idx}, i] == 0 : best\_probs[i,0] = float('-inf')$
Please use [math.log](https://docs.python.org/3/library/math.html) to compute the natural logarithm.
The example below shows the initialization assuming the corpus starts with the phrase "Loss tracks upward".
<img src = "Initialize4.PNG"/>
Represent infinity and negative infinity like this:
```CPP
float('inf')
float('-inf')
```
```
# UNQ_C5 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
# GRADED FUNCTION: initialize
def initialize(states, tag_counts, A, B, corpus, vocab):
'''
Input:
states: a list of all possible parts-of-speech
tag_counts: a dictionary mapping each tag to its respective count
A: Transition Matrix of dimension (num_tags, num_tags)
B: Emission Matrix of dimension (num_tags, len(vocab))
corpus: a sequence of words whose POS is to be identified in a list
vocab: a dictionary where keys are words in vocabulary and value is an index
Output:
best_probs: matrix of dimension (num_tags, len(corpus)) of floats
best_paths: matrix of dimension (num_tags, len(corpus)) of integers
'''
# Get the total number of unique POS tags
num_tags = len(tag_counts)
# Initialize best_probs matrix
# POS tags in the rows, number of words in the corpus as the columns
best_probs = np.zeros((num_tags, len(corpus)))
# Initialize best_paths matrix
# POS tags in the rows, number of words in the corpus as columns
best_paths = np.zeros((num_tags, len(corpus)), dtype=int)
# Define the start token
s_idx = states.index("--s--")
### START CODE HERE (Replace instances of 'None' with your code) ###
# Go through each of the POS tags
for i in range(num_tags): # complete this line
# Handle the special case when the transition from start token to POS tag i is zero
if A[s_idx,i] == 0: # complete this line
# Initialize best_probs at POS tag 'i', column 0, to negative infinity
best_probs[i,0] = -inf
# For all other cases when transition from start token to POS tag i is non-zero:
else:
# Initialize best_probs at POS tag 'i', column 0
# Check the formula in the instructions above
best_probs[i,0] = np.log(A[s_idx,i]) + np.log(B[i, vocab[corpus[0]]])
### END CODE HERE ###
return best_probs, best_paths
best_probs, best_paths = initialize(states, tag_counts, A, B, prep, vocab)
# Test the function
print(f"best_probs[0,0]: {best_probs[0,0]:.4f}")
print(f"best_paths[2,3]: {best_paths[2,3]:.4f}")
```
##### Expected Output
```CPP
best_probs[0,0]: -22.6098
best_paths[2,3]: 0.0000
```
<a name='3.2'></a>
## Part 3.2 Viterbi Forward
In this part of the assignment, you will implement the `viterbi_forward` segment. In other words, you will populate your `best_probs` and `best_paths` matrices.
- Walk forward through the corpus.
- For each word, compute a probability for each possible tag.
- Unlike the previous algorithm `predict_pos` (the 'warm-up' exercise), this will include the path up to that (word,tag) combination.
Here is an example with a three-word corpus "Loss tracks upward":
- Note, in this example, only a subset of states (POS tags) are shown in the diagram below, for easier reading.
- In the diagram below, the first word "Loss" is already initialized.
- The algorithm will compute a probability for each of the potential tags in the second and future words.
Compute the probability that the tag of the second work ('tracks') is a verb, 3rd person singular present (VBZ).
- In the `best_probs` matrix, go to the column of the second word ('tracks'), and row 40 (VBZ), this cell is highlighted in light orange in the diagram below.
- Examine each of the paths from the tags of the first word ('Loss') and choose the most likely path.
- An example of the calculation for **one** of those paths is the path from ('Loss', NN) to ('tracks', VBZ).
- The log of the probability of the path up to and including the first word 'Loss' having POS tag NN is $-14.32$. The `best_probs` matrix contains this value -14.32 in the column for 'Loss' and row for 'NN'.
- Find the probability that NN transitions to VBZ. To find this probability, go to the `A` transition matrix, and go to the row for 'NN' and the column for 'VBZ'. The value is $4.37e-02$, which is circled in the diagram, so add $-14.32 + log(4.37e-02)$.
- Find the log of the probability that the tag VBS would 'emit' the word 'tracks'. To find this, look at the 'B' emission matrix in row 'VBZ' and the column for the word 'tracks'. The value $4.61e-04$ is circled in the diagram below. So add $-14.32 + log(4.37e-02) + log(4.61e-04)$.
- The sum of $-14.32 + log(4.37e-02) + log(4.61e-04)$ is $-25.13$. Store $-25.13$ in the `best_probs` matrix at row 'VBZ' and column 'tracks' (as seen in the cell that is highlighted in light orange in the diagram).
- All other paths in best_probs are calculated. Notice that $-25.13$ is greater than all of the other values in column 'tracks' of matrix `best_probs`, and so the most likely path to 'VBZ' is from 'NN'. 'NN' is in row 20 of the `best_probs` matrix, so $20$ is the most likely path.
- Store the most likely path $20$ in the `best_paths` table. This is highlighted in light orange in the diagram below.
The formula to compute the probability and path for the $i^{th}$ word in the $corpus$, the prior word $i-1$ in the corpus, current POS tag $j$, and previous POS tag $k$ is:
$\mathrm{prob} = \mathbf{best\_prob}_{k, i-1} + \mathrm{log}(\mathbf{A}_{k, j}) + \mathrm{log}(\mathbf{B}_{j, vocab(corpus_{i})})$
where $corpus_{i}$ is the word in the corpus at index $i$, and $vocab$ is the dictionary that gets the unique integer that represents a given word.
$\mathrm{path} = k$
where $k$ is the integer representing the previous POS tag.
<a name='ex-06'></a>
### Exercise 06
Instructions: Implement the `viterbi_forward` algorithm and store the best_path and best_prob for every possible tag for each word in the matrices `best_probs` and `best_tags` using the pseudo code below.
`for each word in the corpus
for each POS tag type that this word may be
for POS tag type that the previous word could be
compute the probability that the previous word had a given POS tag, that the current word has a given POS tag, and that the POS tag would emit this current word.
retain the highest probability computed for the current word
set best_probs to this highest probability
set best_paths to the index 'k', representing the POS tag of the previous word which produced the highest probability `
Please use [math.log](https://docs.python.org/3/library/math.html) to compute the natural logarithm.
<img src = "Forward4.PNG"/>
<details>
<summary>
<font size="3" color="darkgreen"><b>Hints</b></font>
</summary>
<p>
<ul>
<li>Remember that when accessing emission matrix B, the column index is the unique integer ID associated with the word. It can be accessed by using the 'vocab' dictionary, where the key is the word, and the value is the unique integer ID for that word.</li>
</ul>
</p>
```
# UNQ_C6 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
# GRADED FUNCTION: viterbi_forward
def viterbi_forward(A, B, test_corpus, best_probs, best_paths, vocab):
'''
Input:
A, B: The transiton and emission matrices respectively
test_corpus: a list containing a preprocessed corpus
best_probs: an initilized matrix of dimension (num_tags, len(corpus))
best_paths: an initilized matrix of dimension (num_tags, len(corpus))
vocab: a dictionary where keys are words in vocabulary and value is an index
Output:
best_probs: a completed matrix of dimension (num_tags, len(corpus))
best_paths: a completed matrix of dimension (num_tags, len(corpus))
'''
# Get the number of unique POS tags (which is the num of rows in best_probs)
num_tags = best_probs.shape[0]
# Go through every word in the corpus starting from word 1
# Recall that word 0 was initialized in `initialize()`
for i in range(1, len(test_corpus)):
# Print number of words processed, every 5000 words
if i % 5000 == 0:
print("Words processed: {:>8}".format(i))
### START CODE HERE (Replace instances of 'None' with your code EXCEPT the first 'best_path_i = None') ###
# For each unique POS tag that the current word can be
for j in range(num_tags): # complete this line
# Initialize best_prob for word i to negative infinity
best_prob_i = float("-inf")
# Initialize best_path for current word i to None
best_path_i = None
# For each POS tag that the previous word can be:
for k in range(num_tags): # complete this line
# Calculate the probability =
# best probs of POS tag k, previous word i-1 +
# log(prob of transition from POS k to POS j) +
# log(prob that emission of POS j is word i)
prob = best_probs[k,i-1] + np.log(A[k,j]) + np.log(B[j,vocab[test_corpus[i]]])
# check if this path's probability is greater than
# the best probability up to and before this point
if prob > best_prob_i: # complete this line
# Keep track of the best probability
best_prob_i = prob
# keep track of the POS tag of the previous word
# that is part of the best path.
# Save the index (integer) associated with
# that previous word's POS tag
best_path_i = k
# Save the best probability for the
# given current word's POS tag
# and the position of the current word inside the corpus
best_probs[j,i] = best_prob_i
# Save the unique integer ID of the previous POS tag
# into best_paths matrix, for the POS tag of the current word
# and the position of the current word inside the corpus.
best_paths[j,i] = best_path_i
### END CODE HERE ###
return best_probs, best_paths
```
Run the `viterbi_forward` function to fill in the `best_probs` and `best_paths` matrices.
**Note** that this will take a few minutes to run. There are about 30,000 words to process.
```
# this will take a few minutes to run => processes ~ 30,000 words
best_probs, best_paths = viterbi_forward(A, B, prep, best_probs, best_paths, vocab)
# Test this function
print(f"best_probs[0,1]: {best_probs[0,1]:.4f}")
print(f"best_probs[0,4]: {best_probs[0,4]:.4f}")
```
##### Expected Output
```CPP
best_probs[0,1]: -24.7822
best_probs[0,4]: -49.5601
```
<a name='3.3'></a>
## Part 3.3 Viterbi backward
Now you will implement the Viterbi backward algorithm.
- The Viterbi backward algorithm gets the predictions of the POS tags for each word in the corpus using the `best_paths` and the `best_probs` matrices.
The example below shows how to walk backwards through the best_paths matrix to get the POS tags of each word in the corpus. Recall that this example corpus has three words: "Loss tracks upward".
POS tag for 'upward' is `RB`
- Select the the most likely POS tag for the last word in the corpus, 'upward' in the `best_prob` table.
- Look for the row in the column for 'upward' that has the largest probability.
- Notice that in row 28 of `best_probs`, the estimated probability is -34.99, which is larger than the other values in the column. So the most likely POS tag for 'upward' is `RB` an adverb, at row 28 of `best_prob`.
- The variable `z` is an array that stores the unique integer ID of the predicted POS tags for each word in the corpus. In array z, at position 2, store the value 28 to indicate that the word 'upward' (at index 2 in the corpus), most likely has the POS tag associated with unique ID 28 (which is `RB`).
- The variable `pred` contains the POS tags in string form. So `pred` at index 2 stores the string `RB`.
POS tag for 'tracks' is `VBZ`
- The next step is to go backward one word in the corpus ('tracks'). Since the most likely POS tag for 'upward' is `RB`, which is uniquely identified by integer ID 28, go to the `best_paths` matrix in column 2, row 28. The value stored in `best_paths`, column 2, row 28 indicates the unique ID of the POS tag of the previous word. In this case, the value stored here is 40, which is the unique ID for POS tag `VBZ` (verb, 3rd person singular present).
- So the previous word at index 1 of the corpus ('tracks'), most likely has the POS tag with unique ID 40, which is `VBZ`.
- In array `z`, store the value 40 at position 1, and for array `pred`, store the string `VBZ` to indicate that the word 'tracks' most likely has POS tag `VBZ`.
POS tag for 'Loss' is `NN`
- In `best_paths` at column 1, the unique ID stored at row 40 is 20. 20 is the unique ID for POS tag `NN`.
- In array `z` at position 0, store 20. In array `pred` at position 0, store `NN`.
<img src = "Backwards5.PNG"/>
<a name='ex-07'></a>
### Exercise 07
Implement the `viterbi_backward` algorithm, which returns a list of predicted POS tags for each word in the corpus.
- Note that the numbering of the index positions starts at 0 and not 1.
- `m` is the number of words in the corpus.
- So the indexing into the corpus goes from `0` to `m - 1`.
- Also, the columns in `best_probs` and `best_paths` are indexed from `0` to `m - 1`
**In Step 1:**
Loop through all the rows (POS tags) in the last entry of `best_probs` and find the row (POS tag) with the maximum value.
Convert the unique integer ID to a tag (a string representation) using the dictionary `states`.
Referring to the three-word corpus described above:
- `z[2] = 28`: For the word 'upward' at position 2 in the corpus, the POS tag ID is 28. Store 28 in `z` at position 2.
- states(28) is 'RB': The POS tag ID 28 refers to the POS tag 'RB'.
- `pred[2] = 'RB'`: In array `pred`, store the POS tag for the word 'upward'.
**In Step 2:**
- Starting at the last column of best_paths, use `best_probs` to find the most likely POS tag for the last word in the corpus.
- Then use `best_paths` to find the most likely POS tag for the previous word.
- Update the POS tag for each word in `z` and in `preds`.
Referring to the three-word example from above, read best_paths at column 2 and fill in z at position 1.
`z[1] = best_paths[z[2],2]`
The small test following the routine prints the last few words of the corpus and their states to aid in debug.
```
# print(states)
# print(best_probs[3])
# print(prep[5])
print(best_paths[None,None])
# UNQ_C7 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
# GRADED FUNCTION: viterbi_backward
def viterbi_backward(best_probs, best_paths, corpus, states):
'''
This function returns the best path.
'''
# Get the number of words in the corpus
# which is also the number of columns in best_probs, best_paths
m = best_paths.shape[1]
# Initialize array z, same length as the corpus
z = [None] * m
# Get the number of unique POS tags
num_tags = best_probs.shape[0]
# Initialize the best probability for the last word
best_prob_for_last_word = float('-inf')
# Initialize pred array, same length as corpus
pred = [None] * m
### START CODE HERE (Replace instances of 'None' with your code) ###
## Step 1 ##
# Go through each POS tag for the last word (last column of best_probs)
# in order to find the row (POS tag integer ID)
# with highest probability for the last word
for k in range(num_tags): # complete this line
# If the probability of POS tag at row k
# is better than the previosly best probability for the last word:
if best_probs[k,m-1] > best_prob_for_last_word: # complete this line
# Store the new best probability for the lsat word
best_prob_for_last_word = best_probs[k,m-1]
# Store the unique integer ID of the POS tag
# which is also the row number in best_probs
z[m - 1] = k
# Convert the last word's predicted POS tag
# from its unique integer ID into the string representation
# using the 'states' dictionary
# store this in the 'pred' array for the last word
pred[m - 1] = states[z[m-1]]
## Step 2 ##
# Find the best POS tags by walking backward through the be st_paths
# From the last word in the corpus to the 0th word in the corpus
for i in reversed(range(m-1)): # complete this line
# Retrieve the unique integer ID of
# the POS tag for the word at position 'i' in the corpus
pos_tag_for_word_i = z[i+1]
# In best_paths, go to the row representing the POS tag of word i
# and the column representing the word's position in the corpus
# to retrieve the predicted POS for the word at position i-1 in the corpus
z[i] = best_paths[pos_tag_for_word_i,i+1]
# Get the previous word's POS tag in string form
# Use the 'states' dictionary,
# where the key is the unique integer ID of the POS tag,
# and the value is the string representation of that POS tag
pred[i] = states[z[i]]
### END CODE HERE ###
return pred
print(y)
# Run and test your function
pred = viterbi_backward(best_probs, best_paths, prep, states)
m=len(pred)
print('The prediction for pred[-7:m-1] is: \n', prep[-7:m-1], "\n", pred[-7:m-1], "\n")
print('The prediction for pred[0:8] is: \n', pred[0:7], "\n", prep[0:7])
```
**Expected Output:**
```CPP
The prediction for prep[-7:m-1] is:
['see', 'them', 'here', 'with', 'us', '.']
['VB', 'PRP', 'RB', 'IN', 'PRP', '.']
The prediction for pred[0:8] is:
['DT', 'NN', 'POS', 'NN', 'MD', 'VB', 'VBN']
['The', 'economy', "'s", 'temperature', 'will', 'be', 'taken']
```
Now you just have to compare the predicted labels to the true labels to evaluate your model on the accuracy metric!
<a name='4'></a>
# Part 4: Predicting on a data set
Compute the accuracy of your prediction by comparing it with the true `y` labels.
- `pred` is a list of predicted POS tags corresponding to the words of the `test_corpus`.
```
print('The third word is:', prep[3])
print('Your prediction is:', pred[3])
print('Your corresponding label y is: ', y[3])
for prediction, y1 in zip(pred, y):
if len(y1.split()) == 2:
continue
print(y1.split())
```
<a name='ex-08'></a>
### Exercise 08
Implement a function to compute the accuracy of the viterbi algorithm's POS tag predictions.
- To split y into the word and its tag you can use `y.split()`.
```
# UNQ_C8 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
# GRADED FUNCTION: compute_accuracy
def compute_accuracy(pred, y):
'''
Input:
pred: a list of the predicted parts-of-speech
y: a list of lines where each word is separated by a '\t' (i.e. word \t tag)
Output:
'''
num_correct = 0
total = 0
# Zip together the prediction and the labels
for prediction, y1 in zip(pred, y):
### START CODE HERE (Replace instances of 'None' with your code) ###
# Split the label into the word and the POS tag
word_tag_tuple = y1.split()
# Check that there is actually a word and a tag
# no more and no less than 2 items
if len(word_tag_tuple) == 2: # complete this line
# store the word and tag separately
word, tag = word_tag_tuple
# Check if the POS tag label matches the prediction
if tag == prediction: # complete this line
# count the number of times that the prediction
# and label match
num_correct += 1
# keep track of the total number of examples (that have valid labels)
total += 1
### END CODE HERE ###
return num_correct/total
print(f"Accuracy of the Viterbi algorithm is {compute_accuracy(pred, y):.4f}")
```
##### Expected Output
```CPP
Accuracy of the Viterbi algorithm is 0.9531
```
Congratulations you were able to classify the parts-of-speech with 95% accuracy.
### Key Points and overview
In this assignment you learned about parts-of-speech tagging.
- In this assignment, you predicted POS tags by walking forward through a corpus and knowing the previous word.
- There are other implementations that use bidirectional POS tagging.
- Bidirectional POS tagging requires knowing the previous word and the next word in the corpus when predicting the current word's POS tag.
- Bidirectional POS tagging would tell you more about the POS instead of just knowing the previous word.
- Since you have learned to implement the unidirectional approach, you have the foundation to implement other POS taggers used in industry.
### References
- ["Speech and Language Processing", Dan Jurafsky and James H. Martin](https://web.stanford.edu/~jurafsky/slp3/)
- We would like to thank Melanie Tosik for her help and inspiration
|
github_jupyter
|
# <center>RumbleDB sandbox</center>
This is a RumbleDB sandbox that allows you to play with simple JSONiq queries.
It is a jupyter notebook that you can also download and execute on your own machine, but if you arrived here from the RumbleDB website, it is likely to be shown within Google's Colab environment.
To get started, you first need to execute the cell below to activate the RumbleDB magic (you do not need to understand what it does, this is just initialization Python code).
```
!pip install rumbledb
%load_ext rumbledb
%env RUMBLEDB_SERVER=http://public.rumbledb.org:9090/jsoniq
```
By default, this notebook uses a small public backend provided by us. Each query runs on just one machine that is very limited in CPU: one core and memory: 1GB, and with only the http scheme activated. This is sufficient to discover RumbleDB and play a bit, but of course is not intended for any production use. If you need to use RumbleDB in production, you can use it with an installation of Spark either on your machine or on a cluster.
This sandbox backend may occasionally break, especially if too many users use it at the same time, so please bear with us! The system is automatically restarted every day so, if it stops working, you can either try again in 24 hours or notify us.
It is straightforward to execute your own RumbleDB server on your own Spark cluster (and then you can make full use of all the input file systems and file formats). In this case, just replace the above server with your own hostname and port. Note that if you run RumbleDB as a server locally, you will also need to download and use this notebook locally rather than in this Google Colab environment as, obviously, your personal computer cannot be accessed from the Web.
Now we are all set! You can now start reading and executing the JSONiq queries as you go, and you can even edit them!
## JSON
As explained on the [official JSON Web site](http://www.json.org/), JSON is a lightweight data-interchange format designed for humans as well as for computers. It supports as values:
- objects (string-to-value maps)
- arrays (ordered sequences of values)
- strings
- numbers
- booleans (true, false)
- null
JSONiq provides declarative querying and updating capabilities on JSON data.
## Elevator Pitch
JSONiq is based on XQuery, which is a W3C standard (like XML and HTML). XQuery is a very powerful declarative language that originally manipulates XML data, but it turns out that it is also a very good fit for manipulating JSON natively.
JSONiq, since it extends XQuery, is a very powerful general-purpose declarative programming language. Our experience is that, for the same task, you will probably write about 80% less code compared to imperative languages like JavaScript, Python or Ruby. Additionally, you get the benefits of strong type checking without actually having to write type declarations.
Here is an appetizer before we start the tutorial from scratch.
```
%%jsoniq
let $stores :=
[
{ "store number" : 1, "state" : "MA" },
{ "store number" : 2, "state" : "MA" },
{ "store number" : 3, "state" : "CA" },
{ "store number" : 4, "state" : "CA" }
]
let $sales := [
{ "product" : "broiler", "store number" : 1, "quantity" : 20 },
{ "product" : "toaster", "store number" : 2, "quantity" : 100 },
{ "product" : "toaster", "store number" : 2, "quantity" : 50 },
{ "product" : "toaster", "store number" : 3, "quantity" : 50 },
{ "product" : "blender", "store number" : 3, "quantity" : 100 },
{ "product" : "blender", "store number" : 3, "quantity" : 150 },
{ "product" : "socks", "store number" : 1, "quantity" : 500 },
{ "product" : "socks", "store number" : 2, "quantity" : 10 },
{ "product" : "shirt", "store number" : 3, "quantity" : 10 }
]
let $join :=
for $store in $stores[], $sale in $sales[]
where $store."store number" = $sale."store number"
return {
"nb" : $store."store number",
"state" : $store.state,
"sold" : $sale.product
}
return [$join]
```
## And here you go
### Actually, you already knew some JSONiq
The first thing you need to know is that a well-formed JSON document is a JSONiq expression as well.
This means that you can copy-and-paste any JSON document into a query. The following are JSONiq queries that are "idempotent" (they just output themselves):
```
%%jsoniq
{ "pi" : 3.14, "sq2" : 1.4 }
%%jsoniq
[ 2, 3, 5, 7, 11, 13 ]
%%jsoniq
{
"operations" : [
{ "binary" : [ "and", "or"] },
{ "unary" : ["not"] }
],
"bits" : [
0, 1
]
}
%%jsoniq
[ { "Question" : "Ultimate" }, ["Life", "the universe", "and everything"] ]
```
This works with objects, arrays (even nested), strings, numbers, booleans, null.
It also works the other way round: if your query outputs an object or an array, you can use it as a JSON document.
JSONiq is a declarative language. This means that you only need to say what you want - the compiler will take care of the how.
In the above queries, you are basically saying: I want to output this JSON content, and here it is.
## JSONiq basics
### The real JSONiq Hello, World!
Wondering what a hello world program looks like in JSONiq? Here it is:
```
%%jsoniq
"Hello, World!"
```
Not surprisingly, it outputs the string "Hello, World!".
### Numbers and arithmetic operations
Okay, so, now, you might be thinking: "What is the use of this language if it just outputs what I put in?" Of course, JSONiq can more than that. And still in a declarative way. Here is how it works with numbers:
```
%%jsoniq
2 + 2
%%jsoniq
(38 + 2) div 2 + 11 * 2
```
(mind the division operator which is the "div" keyword. The slash operator has different semantics).
Like JSON, JSONiq works with decimals and doubles:
```
%%jsoniq
6.022e23 * 42
```
### Logical operations
JSONiq supports boolean operations.
```
%%jsoniq
true and false
%%jsoniq
(true or false) and (false or true)
```
The unary not is also available:
```
%%jsoniq
not true
```
### Strings
JSONiq is capable of manipulating strings as well, using functions:
```
%%jsoniq
concat("Hello ", "Captain ", "Kirk")
%%jsoniq
substring("Mister Spock", 8, 5)
```
JSONiq comes up with a rich string function library out of the box, inherited from its base language. These functions are listed [here](https://www.w3.org/TR/xpath-functions-30/) (actually, you will find many more for numbers, dates, etc).
### Sequences
Until now, we have only been working with single values (an object, an array, a number, a string, a boolean). JSONiq supports sequences of values. You can build a sequence using commas:
```
%%jsoniq
(1, 2, 3, 4, 5, 6, 7, 8, 9, 10)
%%jsoniq
1, true, 4.2e1, "Life"
```
The "to" operator is very convenient, too:
```
%%jsoniq
(1 to 100)
```
Some functions even work on sequences:
```
%%jsoniq
sum(1 to 100)
%%jsoniq
string-join(("These", "are", "some", "words"), "-")
%%jsoniq
count(10 to 20)
%%jsoniq
avg(1 to 100)
```
Unlike arrays, sequences are flat. The sequence (3) is identical to the integer 3, and (1, (2, 3)) is identical to (1, 2, 3).
## A bit more in depth
### Variables
You can bind a sequence of values to a (dollar-prefixed) variable, like so:
```
%%jsoniq
let $x := "Bearing 3 1 4 Mark 5. "
return concat($x, "Engage!")
%%jsoniq
let $x := ("Kirk", "Picard", "Sisko")
return string-join($x, " and ")
```
You can bind as many variables as you want:
```
%%jsoniq
let $x := 1
let $y := $x * 2
let $z := $y + $x
return ($x, $y, $z)
```
and even reuse the same name to hide formerly declared variables:
```
%%jsoniq
let $x := 1
let $x := $x + 2
let $x := $x + 3
return $x
```
### Iteration
In a way very similar to let, you can iterate over a sequence of values with the "for" keyword. Instead of binding the entire sequence of the variable, it will bind each value of the sequence in turn to this variable.
```
%%jsoniq
for $i in 1 to 10
return $i * 2
```
More interestingly, you can combine fors and lets like so:
```
%%jsoniq
let $sequence := 1 to 10
for $value in $sequence
let $square := $value * 2
return $square
```
and even filter out some values:
```
%%jsoniq
let $sequence := 1 to 10
for $value in $sequence
let $square := $value * 2
where $square < 10
return $square
```
Note that you can only iterate over sequences, not arrays. To iterate over an array, you can obtain the sequence of its values with the [] operator, like so:
```
%%jsoniq
[1, 2, 3][]
```
### Conditions
You can make the output depend on a condition with an if-then-else construct:
```
%%jsoniq
for $x in 1 to 10
return if ($x < 5) then $x
else -$x
```
Note that the else clause is required - however, it can be the empty sequence () which is often when you need if only the then clause is relevant to you.
### Composability of Expressions
Now that you know of a couple of elementary JSONiq expressions, you can combine them in more elaborate expressions. For example, you can put any sequence of values in an array:
```
%%jsoniq
[ 1 to 10 ]
```
Or you can dynamically compute the value of object pairs (or their key):
```
%%jsoniq
{
"Greeting" : (let $d := "Mister Spock"
return concat("Hello, ", $d)),
"Farewell" : string-join(("Live", "long", "and", "prosper"),
" ")
}
```
You can dynamically generate object singletons (with a single pair):
```
%%jsoniq
{ concat("Integer ", 2) : 2 * 2 }
```
and then merge lots of them into a new object with the {| |} notation:
```
%%jsoniq
{|
for $i in 1 to 10
return { concat("Square of ", $i) : $i * $i }
|}
```
## JSON Navigation
Up to now, you have learnt how to compose expressions so as to do some computations and to build objects and arrays. It also works the other way round: if you have some JSON data, you can access it and navigate.
All you need to know is: JSONiq views
an array as an ordered list of values,
an object as a set of name/value pairs
### Objects
You can use the dot operator to retrieve the value associated with a key. Quotes are optional, except if the key has special characters such as spaces. It will return the value associated thereto:
```
%%jsoniq
let $person := {
"first name" : "Sarah",
"age" : 13,
"gender" : "female",
"friends" : [ "Jim", "Mary", "Jennifer"]
}
return $person."first name"
```
You can also ask for all keys in an object:
```
%%jsoniq
let $person := {
"name" : "Sarah",
"age" : 13,
"gender" : "female",
"friends" : [ "Jim", "Mary", "Jennifer"]
}
return { "keys" : [ keys($person)] }
```
### Arrays
The [[]] operator retrieves the entry at the given position:
```
%%jsoniq
let $friends := [ "Jim", "Mary", "Jennifer"]
return $friends[[1+1]]
```
It is also possible to get the size of an array:
```
%%jsoniq
let $person := {
"name" : "Sarah",
"age" : 13,
"gender" : "female",
"friends" : [ "Jim", "Mary", "Jennifer"]
}
return { "how many friends" : size($person.friends) }
```
Finally, the [] operator returns all elements in an array, as a sequence:
```
%%jsoniq
let $person := {
"name" : "Sarah",
"age" : 13,
"gender" : "female",
"friends" : [ "Jim", "Mary", "Jennifer"]
}
return $person.friends[]
```
### Relational Algebra
Do you remember SQL's SELECT FROM WHERE statements? JSONiq inherits selection, projection and join capability from XQuery, too.
```
%%jsoniq
let $stores :=
[
{ "store number" : 1, "state" : "MA" },
{ "store number" : 2, "state" : "MA" },
{ "store number" : 3, "state" : "CA" },
{ "store number" : 4, "state" : "CA" }
]
let $sales := [
{ "product" : "broiler", "store number" : 1, "quantity" : 20 },
{ "product" : "toaster", "store number" : 2, "quantity" : 100 },
{ "product" : "toaster", "store number" : 2, "quantity" : 50 },
{ "product" : "toaster", "store number" : 3, "quantity" : 50 },
{ "product" : "blender", "store number" : 3, "quantity" : 100 },
{ "product" : "blender", "store number" : 3, "quantity" : 150 },
{ "product" : "socks", "store number" : 1, "quantity" : 500 },
{ "product" : "socks", "store number" : 2, "quantity" : 10 },
{ "product" : "shirt", "store number" : 3, "quantity" : 10 }
]
let $join :=
for $store in $stores[], $sale in $sales[]
where $store."store number" = $sale."store number"
return {
"nb" : $store."store number",
"state" : $store.state,
"sold" : $sale.product
}
return [$join]
```
### Access datasets
RumbleDB can read input from many file systems and many file formats. If you are using our backend, you can only use json-doc() with any URI pointing to a JSON file and navigate it as you see fit.
You can read data from your local disk, from S3, from HDFS, and also from the Web. For this tutorial, we'll read from the Web because, well, we are already on the Web.
We have put a sample at http://rumbledb.org/samples/products-small.json that contains 100,000 small objects like:
```
%%jsoniq
json-file("http://rumbledb.org/samples/products-small.json", 10)[1]
```
The second parameter to json-file, 10, indicates to RumbleDB that it should organize the data in ten partitions after downloading it, and process it in parallel. If you were reading from HDFS or S3, the parallelization of these partitions would be pushed down to the distributed file system.
JSONiq supports the relational algebra. For example, you can do a selection with a where clause, like so:
```
%%jsoniq
for $product in json-file("http://rumbledb.org/samples/products-small.json", 10)
where $product.quantity ge 995
return $product
```
Notice that by default only the first 200 items are shown. In a typical setup, it is possible to output the result of a query to a distributed system, so it is also possible to output all the results if needed. In this case, however, as this is printed on your screen, it is more convenient not to materialize the entire sequence.
For a projection, there is project():
```
%%jsoniq
for $product in json-file("http://rumbledb.org/samples/products-small.json", 10)
where $product.quantity ge 995
return project($product, ("store-number", "product"))
```
You can also page the results (like OFFSET and LIMIT in SQL) with a count clause and a where clause
```
%%jsoniq
for $product in json-file("http://rumbledb.org/samples/products-small.json", 10)
where $product.quantity ge 995
count $c
where $c gt 10 and $c le 20
return project($product, ("store-number", "product"))
```
JSONiq also supports grouping with a group by clause:
```
%%jsoniq
for $product in json-file("http://rumbledb.org/samples/products-small.json", 10)
group by $store-number := $product.store-number
return {
"store" : $store-number,
"count" : count($product)
}
```
As well as ordering with an order by clause:
```
%%jsoniq
for $product in json-file("http://rumbledb.org/samples/products-small.json", 10)
group by $store-number := $product.store-number
order by $store-number ascending
return {
"store" : $store-number,
"count" : count($product)
}
```
JSONiq supports denormalized data, so you are not forced to aggregate after a grouping, you can also nest data like so:
```
%%jsoniq
for $product in json-file("http://rumbledb.org/samples/products-small.json", 10)
group by $store-number := $product.store-number
order by $store-number ascending
return {
"store" : $store-number,
"products" : [ distinct-values($product.product) ]
}
```
Or
```
%%jsoniq
for $product in json-file("http://rumbledb.org/samples/products-small.json", 10)
group by $store-number := $product.store-number
order by $store-number ascending
return {
"store" : $store-number,
"products" : [ project($product[position() le 10], ("product", "quantity")) ],
"inventory" : sum($product.quantity)
}
```
That's it! You know the basics of JSONiq. Now you can also download the RumbleDB jar and run it on your own laptop. Or [on a Spark cluster, reading data from and to HDFS](https://rumble.readthedocs.io/en/latest/Run%20on%20a%20cluster/), etc.
|
github_jupyter
|
# Aggregating statistics
```
import pandas as pd
air_quality = pd.read_pickle('air_quality.pkl')
air_quality.info()
```
### Series/one column of a DataFrame
```
air_quality['TEMP'].count()
air_quality['TEMP'].mean()
air_quality['TEMP'].std()
air_quality['TEMP'].min()
air_quality['TEMP'].max()
air_quality['TEMP'].quantile(0.25)
air_quality['TEMP'].median()
air_quality['TEMP'].describe()
air_quality['RAIN'].sum()
air_quality['PM2.5_category'].mode()
air_quality['PM2.5_category'].nunique()
air_quality['PM2.5_category'].describe()
```
### DataFrame by columns
```
air_quality.count()
air_quality.mean()
air_quality.mean(numeric_only=True)
air_quality[['PM2.5', 'TEMP']].mean()
air_quality[['PM2.5', 'TEMP']].min()
air_quality[['PM2.5', 'TEMP']].max()
air_quality.describe().T
air_quality.describe(include=['object', 'category', 'bool'])
air_quality[['PM2.5_category', 'TEMP_category', 'hour']].mode()
air_quality['hour'].value_counts()
air_quality[['PM2.5', 'TEMP']].agg('mean')
air_quality[['PM2.5', 'TEMP']].mean()
air_quality[['PM2.5', 'TEMP']].agg(['min', 'max', 'mean'])
air_quality[['PM2.5', 'PM2.5_category']].agg(['min', 'max', 'mean', 'nunique'])
air_quality[['PM2.5', 'PM2.5_category']].agg({'PM2.5': 'mean', 'PM2.5_category': 'nunique'})
air_quality.agg({'PM2.5': ['min', 'max', 'mean'], 'PM2.5_category': 'nunique'})
def max_minus_min(s):
return s.max() - s.min()
max_minus_min(air_quality['TEMP'])
air_quality[['PM2.5', 'TEMP']].agg(['min', 'max', max_minus_min])
41.6 - (-16.8)
```
### DataFrame by rows
```
air_quality[['PM2.5', 'PM10']]
air_quality[['PM2.5', 'PM10']].min()
air_quality[['PM2.5', 'PM10']].min(axis=1)
air_quality[['PM2.5', 'PM10']].mean(axis=1)
air_quality[['PM2.5', 'PM10']].sum(axis=1)
```
# Grouping by
```
air_quality.groupby(by='PM2.5_category')
air_quality.groupby(by='PM2.5_category').groups
air_quality['PM2.5_category'].head(20)
air_quality.groupby(by='PM2.5_category').groups.keys()
air_quality.groupby(by='PM2.5_category').get_group('Good')
air_quality.sort_values('date_time')
air_quality.sort_values('date_time').groupby(by='year').first()
air_quality.sort_values('date_time').groupby(by='year').last()
air_quality.groupby('TEMP_category').size()
air_quality['TEMP_category'].value_counts(sort=False)
air_quality.groupby('quarter').mean()
#air_quality[['PM2.5', 'TEMP']].groupby('quarter').mean() # KeyError: 'quarter'
air_quality[['PM2.5', 'TEMP', 'quarter']].groupby('quarter').mean()
air_quality.groupby('quarter')[['PM2.5', 'TEMP']].mean()
air_quality.groupby('quarter').mean()[['PM2.5', 'TEMP']]
air_quality.groupby('quarter')[['PM2.5', 'TEMP']].describe()
air_quality.groupby('quarter')[['PM2.5', 'TEMP']].agg(['min', 'max'])
air_quality.groupby('day_of_week_name')[['PM2.5', 'TEMP', 'RAIN']].agg({'PM2.5': ['min', 'max', 'mean'], 'TEMP': 'mean', 'RAIN': 'mean'})
air_quality.groupby(['quarter', 'TEMP_category'])[['PM2.5', 'TEMP']].mean()
air_quality.groupby(['TEMP_category', 'quarter'])[['PM2.5', 'TEMP']].mean()
air_quality.groupby(['year', 'quarter', 'month'])['TEMP'].agg(['min', 'max'])
```
# Pivoting tables
```
import pandas as pd
student = pd.read_csv('student.csv')
student.info()
student
pd.pivot_table(student,
index='sex')
pd.pivot_table(student,
index=['sex', 'internet']
)
pd.pivot_table(student,
index=['sex', 'internet'],
values='score')
pd.pivot_table(student,
index=['sex', 'internet'],
values='score',
aggfunc='mean')
pd.pivot_table(student,
index=['sex', 'internet'],
values='score',
aggfunc='median')
pd.pivot_table(student,
index=['sex', 'internet'],
values='score',
aggfunc=['min', 'mean', 'max'])
pd.pivot_table(student,
index=['sex', 'internet'],
values='score',
aggfunc='mean',
columns='studytime'
)
student[(student['sex']=='M') & (student['internet']=='no') & (student['studytime']=='4. >10 hours')]
pd.pivot_table(student,
index=['sex', 'internet'],
values='score',
aggfunc='mean',
columns='studytime',
fill_value=-999)
pd.pivot_table(student,
index=['sex', 'internet'],
values=['score', 'age'],
aggfunc='mean',
columns='studytime',
fill_value=-999)
pd.pivot_table(student,
index=['sex'],
values='score',
aggfunc='mean',
columns=['internet', 'studytime'],
fill_value=-999)
pd.pivot_table(student,
index='familysize',
values='score',
aggfunc='mean',
columns='sex'
)
pd.pivot_table(student,
index='familysize',
values='score',
aggfunc='mean',
columns='sex',
margins=True,
margins_name='Average score total')
student[student['sex']=='F'].mean()
pd.pivot_table(student,
index='studytime',
values=['age', 'score'],
aggfunc={'age': ['min', 'max'],
'score': 'median'},
columns='sex')
pd.pivot_table(student,
index='studytime',
values='score',
aggfunc=lambda s: s.max() - s.min(),
columns='sex'
)
```
|
github_jupyter
|
```
# This Python 3 environment comes with many helpful analytics libraries installed
# It is defined by the kaggle/python docker image: https://github.com/kaggle/docker-python
# For example, here's several helpful packages to load in
import numpy as np # linear algebra
import pandas as pd # data processing, CSV file I/O (e.g. pd.read_csv)
# Input data files are available in the "../input/" directory.
# For example, running this (by clicking run or pressing Shift+Enter) will list the files in the input directory
import os
import collections
print(os.listdir("../working/"))
# Any results you write to the current directory are saved as output.
from sklearn.model_selection import train_test_split
import pandas as pd
import tensorflow as tf
import tensorflow_hub as hub
from datetime import datetime
!pip install bert-tensorflow
import bert
from bert import run_classifier
from bert import optimization
from bert import tokenization
from bert import modeling
#import tokenization
#import modeling
BERT_VOCAB= '../input/uncased-l12-h768-a12/vocab.txt'
BERT_INIT_CHKPNT = '../input/uncased-l12-h768-a12/bert_model.ckpt'
BERT_CONFIG = '../input/uncased-l12-h768-a12/bert_config.json'
tokenization.validate_case_matches_checkpoint(True,BERT_INIT_CHKPNT)
tokenizer = tokenization.FullTokenizer(
vocab_file=BERT_VOCAB, do_lower_case=True)
train_data_path='../input/jigsaw-toxic-comment-classification-challenge/train.csv'
train = pd.read_csv(train_data_path)
test = pd.read_csv('../input/jigsaw-toxic-comment-classification-challenge/test.csv')
train.head()
ID = 'id'
DATA_COLUMN = 'comment_text'
LABEL_COLUMNS = ['toxic','severe_toxic','obscene','threat','insult','identity_hate']
class InputExample(object):
"""A single training/test example for simple sequence classification."""
def __init__(self, guid, text_a, text_b=None, labels=None):
"""Constructs a InputExample.
Args:
guid: Unique id for the example.
text_a: string. The untokenized text of the first sequence. For single
sequence tasks, only this sequence must be specified.
text_b: (Optional) string. The untokenized text of the second sequence.
Only must be specified for sequence pair tasks.
labels: (Optional) [string]. The label of the example. This should be
specified for train and dev examples, but not for test examples.
"""
self.guid = guid
self.text_a = text_a
self.text_b = text_b
self.labels = labels
class InputFeatures(object):
"""A single set of features of data."""
def __init__(self, input_ids, input_mask, segment_ids, label_ids, is_real_example=True):
self.input_ids = input_ids
self.input_mask = input_mask
self.segment_ids = segment_ids
self.label_ids = label_ids,
self.is_real_example=is_real_example
def create_examples(df, labels_available=True):
"""Creates examples for the training and dev sets."""
examples = []
for (i, row) in enumerate(df.values):
guid = row[0]
text_a = row[1]
if labels_available:
labels = row[2:]
else:
labels = [0,0,0,0,0,0]
examples.append(
InputExample(guid=guid, text_a=text_a, labels=labels))
return examples
TRAIN_VAL_RATIO = 0.9
LEN = train.shape[0]
SIZE_TRAIN = int(TRAIN_VAL_RATIO*LEN)
x_train = train[:SIZE_TRAIN]
x_val = train[SIZE_TRAIN:]
# Use the InputExample class from BERT's run_classifier code to create examples from the data
train_examples = create_examples(x_train)
train.shape, x_train.shape, x_val.shape
import pandas
def convert_examples_to_features(examples, max_seq_length, tokenizer):
"""Loads a data file into a list of `InputBatch`s."""
features = []
for (ex_index, example) in enumerate(examples):
print(example.text_a)
tokens_a = tokenizer.tokenize(example.text_a)
tokens_b = None
if example.text_b:
tokens_b = tokenizer.tokenize(example.text_b)
# Modifies `tokens_a` and `tokens_b` in place so that the total
# length is less than the specified length.
# Account for [CLS], [SEP], [SEP] with "- 3"
_truncate_seq_pair(tokens_a, tokens_b, max_seq_length - 3)
else:
# Account for [CLS] and [SEP] with "- 2"
if len(tokens_a) > max_seq_length - 2:
tokens_a = tokens_a[:(max_seq_length - 2)]
# The convention in BERT is:
# (a) For sequence pairs:
# tokens: [CLS] is this jack ##son ##ville ? [SEP] no it is not . [SEP]
# type_ids: 0 0 0 0 0 0 0 0 1 1 1 1 1 1
# (b) For single sequences:
# tokens: [CLS] the dog is hairy . [SEP]
# type_ids: 0 0 0 0 0 0 0
#
# Where "type_ids" are used to indicate whether this is the first
# sequence or the second sequence. The embedding vectors for `type=0` and
# `type=1` were learned during pre-training and are added to the wordpiece
# embedding vector (and position vector). This is not *strictly* necessary
# since the [SEP] token unambigiously separates the sequences, but it makes
# it easier for the model to learn the concept of sequences.
#
# For classification tasks, the first vector (corresponding to [CLS]) is
# used as as the "sentence vector". Note that this only makes sense because
# the entire model is fine-tuned.
tokens = ["[CLS]"] + tokens_a + ["[SEP]"]
segment_ids = [0] * len(tokens)
if tokens_b:
tokens += tokens_b + ["[SEP]"]
segment_ids += [1] * (len(tokens_b) + 1)
input_ids = tokenizer.convert_tokens_to_ids(tokens)
# The mask has 1 for real tokens and 0 for padding tokens. Only real
# tokens are attended to.
input_mask = [1] * len(input_ids)
# Zero-pad up to the sequence length.
padding = [0] * (max_seq_length - len(input_ids))
input_ids += padding
input_mask += padding
segment_ids += padding
assert len(input_ids) == max_seq_length
assert len(input_mask) == max_seq_length
assert len(segment_ids) == max_seq_length
labels_ids = []
for label in example.labels:
labels_ids.append(int(label))
if ex_index < 0:
logger.info("*** Example ***")
logger.info("guid: %s" % (example.guid))
logger.info("tokens: %s" % " ".join(
[str(x) for x in tokens]))
logger.info("input_ids: %s" % " ".join([str(x) for x in input_ids]))
logger.info("input_mask: %s" % " ".join([str(x) for x in input_mask]))
logger.info(
"segment_ids: %s" % " ".join([str(x) for x in segment_ids]))
logger.info("label: %s (id = %s)" % (example.labels, labels_ids))
features.append(
InputFeatures(input_ids=input_ids,
input_mask=input_mask,
segment_ids=segment_ids,
label_ids=labels_ids))
return features
# We'll set sequences to be at most 128 tokens long.
MAX_SEQ_LENGTH = 128
def create_model(bert_config, is_training, input_ids, input_mask, segment_ids,
labels, num_labels, use_one_hot_embeddings):
"""Creates a classification model."""
model = modeling.BertModel(
config=bert_config,
is_training=is_training,
input_ids=input_ids,
input_mask=input_mask,
token_type_ids=segment_ids,
use_one_hot_embeddings=use_one_hot_embeddings)
# In the demo, we are doing a simple classification task on the entire
# segment.
#
# If you want to use the token-level output, use model.get_sequence_output()
# instead.
output_layer = model.get_pooled_output()
hidden_size = output_layer.shape[-1].value
output_weights = tf.get_variable(
"output_weights", [num_labels, hidden_size],
initializer=tf.truncated_normal_initializer(stddev=0.02))
output_bias = tf.get_variable(
"output_bias", [num_labels], initializer=tf.zeros_initializer())
with tf.variable_scope("loss"):
if is_training:
# I.e., 0.1 dropout
output_layer = tf.nn.dropout(output_layer, keep_prob=0.9)
logits = tf.matmul(output_layer, output_weights, transpose_b=True)
logits = tf.nn.bias_add(logits, output_bias)
# probabilities = tf.nn.softmax(logits, axis=-1) ### multiclass case
probabilities = tf.nn.sigmoid(logits)#### multi-label case
labels = tf.cast(labels, tf.float32)
tf.logging.info("num_labels:{};logits:{};labels:{}".format(num_labels, logits, labels))
per_example_loss = tf.nn.sigmoid_cross_entropy_with_logits(labels=labels, logits=logits)
loss = tf.reduce_mean(per_example_loss)
# probabilities = tf.nn.softmax(logits, axis=-1)
# log_probs = tf.nn.log_softmax(logits, axis=-1)
#
# one_hot_labels = tf.one_hot(labels, depth=num_labels, dtype=tf.float32)
#
# per_example_loss = -tf.reduce_sum(one_hot_labels * log_probs, axis=-1)
# loss = tf.reduce_mean(per_example_loss)
return (loss, per_example_loss, logits, probabilities)
def model_fn_builder(bert_config, num_labels, init_checkpoint, learning_rate,
num_train_steps, num_warmup_steps, use_tpu,
use_one_hot_embeddings):
"""Returns `model_fn` closure for TPUEstimator."""
def model_fn(features, labels, mode, params): # pylint: disable=unused-argument
"""The `model_fn` for TPUEstimator."""
#tf.logging.info("*** Features ***")
#for name in sorted(features.keys()):
# tf.logging.info(" name = %s, shape = %s" % (name, features[name].shape))
input_ids = features["input_ids"]
input_mask = features["input_mask"]
segment_ids = features["segment_ids"]
label_ids = features["label_ids"]
is_real_example = None
if "is_real_example" in features:
is_real_example = tf.cast(features["is_real_example"], dtype=tf.float32)
else:
is_real_example = tf.ones(tf.shape(label_ids), dtype=tf.float32)
is_training = (mode == tf.estimator.ModeKeys.TRAIN)
(total_loss, per_example_loss, logits, probabilities) = create_model(
bert_config, is_training, input_ids, input_mask, segment_ids, label_ids,
num_labels, use_one_hot_embeddings)
tvars = tf.trainable_variables()
initialized_variable_names = {}
scaffold_fn = None
if init_checkpoint:
(assignment_map, initialized_variable_names
) = modeling.get_assignment_map_from_checkpoint(tvars, init_checkpoint)
if use_tpu:
def tpu_scaffold():
tf.train.init_from_checkpoint(init_checkpoint, assignment_map)
return tf.train.Scaffold()
scaffold_fn = tpu_scaffold
else:
tf.train.init_from_checkpoint(init_checkpoint, assignment_map)
tf.logging.info("**** Trainable Variables ****")
for var in tvars:
init_string = ""
if var.name in initialized_variable_names:
init_string = ", *INIT_FROM_CKPT*"
#tf.logging.info(" name = %s, shape = %s%s", var.name, var.shape,init_string)
output_spec = None
if mode == tf.estimator.ModeKeys.TRAIN:
train_op = optimization.create_optimizer(
total_loss, learning_rate, num_train_steps, num_warmup_steps, use_tpu)
output_spec = tf.estimator.EstimatorSpec(
mode=mode,
loss=total_loss,
train_op=train_op,
scaffold=scaffold_fn)
elif mode == tf.estimator.ModeKeys.EVAL:
def metric_fn(per_example_loss, label_ids, probabilities, is_real_example):
logits_split = tf.split(probabilities, num_labels, axis=-1)
label_ids_split = tf.split(label_ids, num_labels, axis=-1)
# metrics change to auc of every class
eval_dict = {}
for j, logits in enumerate(logits_split):
label_id_ = tf.cast(label_ids_split[j], dtype=tf.int32)
current_auc, update_op_auc = tf.metrics.auc(label_id_, logits)
eval_dict[str(j)] = (current_auc, update_op_auc)
eval_dict['eval_loss'] = tf.metrics.mean(values=per_example_loss)
return eval_dict
## original eval metrics
# predictions = tf.argmax(logits, axis=-1, output_type=tf.int32)
# accuracy = tf.metrics.accuracy(
# labels=label_ids, predictions=predictions, weights=is_real_example)
# loss = tf.metrics.mean(values=per_example_loss, weights=is_real_example)
# return {
# "eval_accuracy": accuracy,
# "eval_loss": loss,
# }
eval_metrics = metric_fn(per_example_loss, label_ids, probabilities, is_real_example)
output_spec = tf.estimator.EstimatorSpec(
mode=mode,
loss=total_loss,
eval_metric_ops=eval_metrics,
scaffold=scaffold_fn)
else:
print("mode:", mode,"probabilities:", probabilities)
output_spec = tf.estimator.EstimatorSpec(
mode=mode,
predictions={"probabilities": probabilities},
scaffold=scaffold_fn)
return output_spec
return model_fn
# Compute train and warmup steps from batch size
# These hyperparameters are copied from this colab notebook (https://colab.sandbox.google.com/github/tensorflow/tpu/blob/master/tools/colab/bert_finetuning_with_cloud_tpus.ipynb)
BATCH_SIZE = 32
LEARNING_RATE = 2e-5
NUM_TRAIN_EPOCHS = 2.0
# Warmup is a period of time where hte learning rate
# is small and gradually increases--usually helps training.
WARMUP_PROPORTION = 0.1
# Model configs
SAVE_CHECKPOINTS_STEPS = 1000
SAVE_SUMMARY_STEPS = 500
OUTPUT_DIR = "../working/output"
# Specify outpit directory and number of checkpoint steps to save
run_config = tf.estimator.RunConfig(
model_dir=OUTPUT_DIR,
save_summary_steps=SAVE_SUMMARY_STEPS,
keep_checkpoint_max=1,
save_checkpoints_steps=SAVE_CHECKPOINTS_STEPS)
def input_fn_builder(features, seq_length, is_training, drop_remainder):
"""Creates an `input_fn` closure to be passed to TPUEstimator."""
all_input_ids = []
all_input_mask = []
all_segment_ids = []
all_label_ids = []
for feature in features:
all_input_ids.append(feature.input_ids)
all_input_mask.append(feature.input_mask)
all_segment_ids.append(feature.segment_ids)
all_label_ids.append(feature.label_ids)
def input_fn(params):
"""The actual input function."""
batch_size = params["batch_size"]
num_examples = len(features)
# This is for demo purposes and does NOT scale to large data sets. We do
# not use Dataset.from_generator() because that uses tf.py_func which is
# not TPU compatible. The right way to load data is with TFRecordReader.
d = tf.data.Dataset.from_tensor_slices({
"input_ids":
tf.constant(
all_input_ids, shape=[num_examples, seq_length],
dtype=tf.int32),
"input_mask":
tf.constant(
all_input_mask,
shape=[num_examples, seq_length],
dtype=tf.int32),
"segment_ids":
tf.constant(
all_segment_ids,
shape=[num_examples, seq_length],
dtype=tf.int32),
"label_ids":
tf.constant(all_label_ids, shape=[num_examples, len(LABEL_COLUMNS)], dtype=tf.int32),
})
if is_training:
d = d.repeat()
d = d.shuffle(buffer_size=100)
d = d.batch(batch_size=batch_size, drop_remainder=drop_remainder)
return d
return input_fn
class PaddingInputExample(object):
"""Fake example so the num input examples is a multiple of the batch size.
When running eval/predict on the TPU, we need to pad the number of examples
to be a multiple of the batch size, because the TPU requires a fixed batch
size. The alternative is to drop the last batch, which is bad because it means
the entire output data won't be generated.
We use this class instead of `None` because treating `None` as padding
battches could cause silent errors.
"""
def convert_single_example(ex_index, example, max_seq_length,
tokenizer):
"""Converts a single `InputExample` into a single `InputFeatures`."""
if isinstance(example, PaddingInputExample):
return InputFeatures(
input_ids=[0] * max_seq_length,
input_mask=[0] * max_seq_length,
segment_ids=[0] * max_seq_length,
label_ids=0,
is_real_example=False)
tokens_a = tokenizer.tokenize(example.text_a)
tokens_b = None
if example.text_b:
tokens_b = tokenizer.tokenize(example.text_b)
if tokens_b:
# Modifies `tokens_a` and `tokens_b` in place so that the total
# length is less than the specified length.
# Account for [CLS], [SEP], [SEP] with "- 3"
_truncate_seq_pair(tokens_a, tokens_b, max_seq_length - 3)
else:
# Account for [CLS] and [SEP] with "- 2"
if len(tokens_a) > max_seq_length - 2:
tokens_a = tokens_a[0:(max_seq_length - 2)]
# The convention in BERT is:
# (a) For sequence pairs:
# tokens: [CLS] is this jack ##son ##ville ? [SEP] no it is not . [SEP]
# type_ids: 0 0 0 0 0 0 0 0 1 1 1 1 1 1
# (b) For single sequences:
# tokens: [CLS] the dog is hairy . [SEP]
# type_ids: 0 0 0 0 0 0 0
#
# Where "type_ids" are used to indicate whether this is the first
# sequence or the second sequence. The embedding vectors for `type=0` and
# `type=1` were learned during pre-training and are added to the wordpiece
# embedding vector (and position vector). This is not *strictly* necessary
# since the [SEP] token unambiguously separates the sequences, but it makes
# it easier for the model to learn the concept of sequences.
#
# For classification tasks, the first vector (corresponding to [CLS]) is
# used as the "sentence vector". Note that this only makes sense because
# the entire model is fine-tuned.
tokens = []
segment_ids = []
tokens.append("[CLS]")
segment_ids.append(0)
for token in tokens_a:
tokens.append(token)
segment_ids.append(0)
tokens.append("[SEP]")
segment_ids.append(0)
if tokens_b:
for token in tokens_b:
tokens.append(token)
segment_ids.append(1)
tokens.append("[SEP]")
segment_ids.append(1)
input_ids = tokenizer.convert_tokens_to_ids(tokens)
# The mask has 1 for real tokens and 0 for padding tokens. Only real
# tokens are attended to.
input_mask = [1] * len(input_ids)
# Zero-pad up to the sequence length.
while len(input_ids) < max_seq_length:
input_ids.append(0)
input_mask.append(0)
segment_ids.append(0)
assert len(input_ids) == max_seq_length
assert len(input_mask) == max_seq_length
assert len(segment_ids) == max_seq_length
labels_ids = []
for label in example.labels:
labels_ids.append(int(label))
feature = InputFeatures(
input_ids=input_ids,
input_mask=input_mask,
segment_ids=segment_ids,
label_ids=labels_ids,
is_real_example=True)
return feature
def file_based_convert_examples_to_features(
examples, max_seq_length, tokenizer, output_file):
"""Convert a set of `InputExample`s to a TFRecord file."""
writer = tf.python_io.TFRecordWriter(output_file)
for (ex_index, example) in enumerate(examples):
#if ex_index % 10000 == 0:
#tf.logging.info("Writing example %d of %d" % (ex_index, len(examples)))
feature = convert_single_example(ex_index, example,
max_seq_length, tokenizer)
def create_int_feature(values):
f = tf.train.Feature(int64_list=tf.train.Int64List(value=list(values)))
return f
features = collections.OrderedDict()
features["input_ids"] = create_int_feature(feature.input_ids)
features["input_mask"] = create_int_feature(feature.input_mask)
features["segment_ids"] = create_int_feature(feature.segment_ids)
features["is_real_example"] = create_int_feature(
[int(feature.is_real_example)])
if isinstance(feature.label_ids, list):
label_ids = feature.label_ids
else:
label_ids = feature.label_ids[0]
features["label_ids"] = create_int_feature(label_ids)
tf_example = tf.train.Example(features=tf.train.Features(feature=features))
writer.write(tf_example.SerializeToString())
writer.close()
def file_based_input_fn_builder(input_file, seq_length, is_training,
drop_remainder):
"""Creates an `input_fn` closure to be passed to TPUEstimator."""
name_to_features = {
"input_ids": tf.FixedLenFeature([seq_length], tf.int64),
"input_mask": tf.FixedLenFeature([seq_length], tf.int64),
"segment_ids": tf.FixedLenFeature([seq_length], tf.int64),
"label_ids": tf.FixedLenFeature([6], tf.int64),
"is_real_example": tf.FixedLenFeature([], tf.int64),
}
def _decode_record(record, name_to_features):
"""Decodes a record to a TensorFlow example."""
example = tf.parse_single_example(record, name_to_features)
# tf.Example only supports tf.int64, but the TPU only supports tf.int32.
# So cast all int64 to int32.
for name in list(example.keys()):
t = example[name]
if t.dtype == tf.int64:
t = tf.to_int32(t)
example[name] = t
return example
def input_fn(params):
"""The actual input function."""
batch_size = params["batch_size"]
# For training, we want a lot of parallel reading and shuffling.
# For eval, we want no shuffling and parallel reading doesn't matter.
d = tf.data.TFRecordDataset(input_file)
if is_training:
d = d.repeat()
d = d.shuffle(buffer_size=100)
d = d.apply(
tf.contrib.data.map_and_batch(
lambda record: _decode_record(record, name_to_features),
batch_size=batch_size,
drop_remainder=drop_remainder))
return d
return input_fn
def _truncate_seq_pair(tokens_a, tokens_b, max_length):
"""Truncates a sequence pair in place to the maximum length."""
# This is a simple heuristic which will always truncate the longer sequence
# one token at a time. This makes more sense than truncating an equal percent
# of tokens from each, since if one sequence is very short then each token
# that's truncated likely contains more information than a longer sequence.
while True:
total_length = len(tokens_a) + len(tokens_b)
if total_length <= max_length:
break
if len(tokens_a) > len(tokens_b):
tokens_a.pop()
else:
tokens_b.pop()
#from pathlib import Path
train_file = os.path.join('../working', "train.tf_record")
#filename = Path(train_file)
if not os.path.exists(train_file):
open(train_file, 'w').close()
```
train_features = convert_examples_to_features(
train_examples, MAX_SEQ_LENGTH, tokenizer)
# Create an input function for training. drop_remainder = True for using TPUs.
train_input_fn = input_fn_builder(
features=train_features,
seq_length=MAX_SEQ_LENGTH,
is_training=True,
drop_remainder=False)
```
# Compute # train and warmup steps from batch size
num_train_steps = int(len(train_examples) / BATCH_SIZE * NUM_TRAIN_EPOCHS)
num_warmup_steps = int(num_train_steps * WARMUP_PROPORTION)
file_based_convert_examples_to_features(
train_examples, MAX_SEQ_LENGTH, tokenizer, train_file)
tf.logging.info("***** Running training *****")
tf.logging.info(" Num examples = %d", len(train_examples))
tf.logging.info(" Batch size = %d", BATCH_SIZE)
tf.logging.info(" Num steps = %d", num_train_steps)
train_input_fn = file_based_input_fn_builder(
input_file=train_file,
seq_length=MAX_SEQ_LENGTH,
is_training=True,
drop_remainder=True)
bert_config = modeling.BertConfig.from_json_file(BERT_CONFIG)
model_fn = model_fn_builder(
bert_config=bert_config,
num_labels= len(LABEL_COLUMNS),
init_checkpoint=BERT_INIT_CHKPNT,
learning_rate=LEARNING_RATE,
num_train_steps=num_train_steps,
num_warmup_steps=num_warmup_steps,
use_tpu=False,
use_one_hot_embeddings=False)
estimator = tf.estimator.Estimator(
model_fn=model_fn,
config=run_config,
params={"batch_size": BATCH_SIZE})
print(f'Beginning Training!')
current_time = datetime.now()
estimator.train(input_fn=train_input_fn, max_steps=num_train_steps)
print("Training took time ", datetime.now() - current_time)
eval_file = os.path.join('../working', "eval.tf_record")
#filename = Path(train_file)
if not os.path.exists(eval_file):
open(eval_file, 'w').close()
eval_examples = create_examples(x_val)
file_based_convert_examples_to_features(
eval_examples, MAX_SEQ_LENGTH, tokenizer, eval_file)
# This tells the estimator to run through the entire set.
eval_steps = None
eval_drop_remainder = False
eval_input_fn = file_based_input_fn_builder(
input_file=eval_file,
seq_length=MAX_SEQ_LENGTH,
is_training=False,
drop_remainder=False)
result = estimator.evaluate(input_fn=eval_input_fn, steps=eval_steps)
```
#x_eval = train[100000:]
# Use the InputExample class from BERT's run_classifier code to create examples from the data
eval_examples = create_examples(x_val)
eval_features = convert_examples_to_features(
eval_examples, MAX_SEQ_LENGTH, tokenizer)
# This tells the estimator to run through the entire set.
eval_steps = None
eval_drop_remainder = False
eval_input_fn = input_fn_builder(
features=eval_features,
seq_length=MAX_SEQ_LENGTH,
is_training=False,
drop_remainder=eval_drop_remainder)
result = estimator.evaluate(input_fn=eval_input_fn, steps=eval_steps)
```
output_eval_file = os.path.join("../working", "eval_results.txt")
with tf.gfile.GFile(output_eval_file, "w") as writer:
tf.logging.info("***** Eval results *****")
for key in sorted(result.keys()):
tf.logging.info(" %s = %s", key, str(result[key]))
writer.write("%s = %s\n" % (key, str(result[key])))
x_test = test#[125000:140000]
x_test = x_test.reset_index(drop=True)
test_file = os.path.join('../working', "test.tf_record")
#filename = Path(train_file)
if not os.path.exists(test_file):
open(test_file, 'w').close()
test_examples = create_examples(x_test, False)
file_based_convert_examples_to_features(
test_examples, MAX_SEQ_LENGTH, tokenizer, test_file)
predict_input_fn = file_based_input_fn_builder(
input_file=test_file,
seq_length=MAX_SEQ_LENGTH,
is_training=False,
drop_remainder=False)
print('Begin predictions!')
current_time = datetime.now()
predictions = estimator.predict(predict_input_fn)
print("Predicting took time ", datetime.now() - current_time)
```
x_test = test[125000:140000]
x_test = x_test.reset_index(drop=True)
predict_examples = create_examples(x_test,False)
test_features = convert_examples_to_features(predict_examples, MAX_SEQ_LENGTH, tokenizer)
print(f'Beginning Training!')
current_time = datetime.now()
predict_input_fn = input_fn_builder(features=test_features, seq_length=MAX_SEQ_LENGTH, is_training=False, drop_remainder=False)
predictions = estimator.predict(predict_input_fn)
print("Training took time ", datetime.now() - current_time)
```
def create_output(predictions):
probabilities = []
for (i, prediction) in enumerate(predictions):
preds = prediction["probabilities"]
probabilities.append(preds)
dff = pd.DataFrame(probabilities)
dff.columns = LABEL_COLUMNS
return dff
output_df = create_output(predictions)
merged_df = pd.concat([x_test, output_df], axis=1)
submission = merged_df.drop(['comment_text'], axis=1)
submission.to_csv("sample_submission.csv", index=False)
submission.tail()
```
submission1 = pd.read_csv('sample_submission1.csv')
submission2 = pd.read_csv('sample_submission2.csv')
submission3 = pd.read_csv('sample_submission3.csv')
submission = pd.concat([submission1,submission2,submission3])
submission.to_csv("sample_submission.csv", index=False)
submission1.shape, submission2.shape, submission3.shape, submission.shape,
|
github_jupyter
|
Copyright (c) Microsoft Corporation. All rights reserved.
Licensed under the MIT License.
# Explore Duplicate Question Matches
Use this dashboard to explore the relationship between duplicate and original questions.
## Setup
This section loads needed packages, and defines useful functions.
```
from __future__ import print_function
import math
import ipywidgets as widgets
import pandas as pd
import requests
from azureml.core.webservice import AksWebservice
from azureml.core.workspace import Workspace
from dotenv import get_key, find_dotenv
from utilities import read_questions, text_to_json, get_auth
env_path = find_dotenv(raise_error_if_not_found=True)
ws = Workspace.from_config(auth=get_auth(env_path))
print(ws.name, ws.resource_group, ws.location, sep="\n")
aks_service_name = get_key(env_path, 'aks_service_name')
aks_service = AksWebservice(ws, name=aks_service_name)
aks_service.name
```
Load the duplicate questions scoring app's URL.
```
scoring_url = aks_service.scoring_uri
api_key = aks_service.get_keys()[0]
```
A constructor function for ID-text contents. Constructs buttons and text areas for each text ID and text passage.
* Each buttons's description is set to a text's ID, and its click action is set to the handler.
* Each text area's content is set to a text.
* A dictionary is created to map IDs to text areas.
```
def buttons_and_texts(
data, id, answerid, text, handle_click, layout=widgets.Layout(width="100%"), n=15
):
"""Construct buttons, text areas, and a mapping from IDs to text areas."""
items = []
text_map = {}
for i in range(min(n, len(data))):
button = widgets.Button(description=data.iloc[i][id])
button.answerid = data.iloc[i][answerid] if answerid in data else None
button.open = False
button.on_click(handle_click)
items.append(button)
text_area = widgets.Textarea(
data.iloc[i][text], placeholder=data.iloc[i][id], layout=layout
)
items.append(text_area)
text_map[data.iloc[i][id]] = text_area
return items, text_map
```
A constructor function for the duplicates and questions explorer widget. This builds a box containing duplicates and question tabs, each in turn containing boxes that contain the buttons and text areas.
```
def duplicates_questions_widget(
duplicates, questions, layout=widgets.Layout(width="100%")
):
"""Construct a duplicates and questions exploration widget."""
# Construct the duplicates Tab of buttons and text areas.
duplicates_items, duplicates_map = buttons_and_texts(
duplicates,
duplicates_id,
duplicates_answerid,
duplicates_text,
duplicates_click,
n=duplicates.shape[0],
)
duplicates_tab = widgets.Tab(
[widgets.VBox(duplicates_items, layout=layout)],
layout=widgets.Layout(width="100%", height="500px", overflow_y="auto"),
)
duplicates_tab.set_title(0, duplicates_title)
# Construct the questions Tab of buttons and text areas.
questions_items, questions_map = buttons_and_texts(
questions,
questions_id,
questions_answerid,
questions_text,
questions_click,
n=questions.shape[0],
)
questions_tab = widgets.Tab(
[widgets.VBox(questions_items, layout=layout)],
layout=widgets.Layout(width="100%", height="500px", overflow_y="auto"),
)
questions_tab.set_title(0, questions_title)
# Put both tabs in an HBox.
duplicates_questions = widgets.HBox([duplicates_tab, questions_tab], layout=layout)
return duplicates_map, questions_map, duplicates_questions
```
A handler function for a question passage button press. If the passage's text window is open, it is collapsed. Otherwise, it is opened.
```
def questions_click(button):
"""Respond to a click on a question button."""
global questions_map
if button.open:
questions_map[button.description].rows = None
button.open = False
else:
questions_map[button.description].rows = 10
button.open = True
```
A handler function for a duplicate obligation button press. If the obligation is not selected, select it and update the questions tab with its top 15 question passages ordered by match score. Otherwise, if the duplicate's text window is open, it is collapsed, else it is opened.
```
def duplicates_click(button):
"""Respond to a click on a duplicate button."""
global duplicates_map
if select_duplicate(button):
duplicates_map[button.description].rows = 10
button.open = True
else:
if button.open:
duplicates_map[button.description].rows = None
button.open = False
else:
duplicates_map[button.description].rows = 10
button.open = True
def select_duplicate(button):
"""Update the displayed questions to correspond to the button's duplicate
selections. Returns whether or not the selected duplicate changed.
"""
global selected_button, questions_map, duplicates_questions
if "selected_button" not in globals() or button != selected_button:
if "selected_button" in globals():
selected_button.style.button_color = None
selected_button.style.font_weight = ""
selected_button = button
selected_button.style.button_color = "yellow"
selected_button.style.font_weight = "bold"
duplicates_text = duplicates_map[selected_button.description].value
questions_scores = score_text(duplicates_text)
ordered_questions = questions.loc[questions_scores[questions_id]]
questions_items, questions_map = buttons_and_texts(
ordered_questions,
questions_id,
questions_answerid,
questions_text,
questions_click,
n=questions_display,
)
if questions_button_color is True and selected_button.answerid is not None:
set_button_color(questions_items[::2], selected_button.answerid)
if questions_button_score is True:
questions_items = [
item
for button, text_area in zip(*[iter(questions_items)] * 2)
for item in (add_button_prob(button, questions_scores), text_area)
]
duplicates_questions.children[1].children[0].children = questions_items
duplicates_questions.children[1].set_title(0, selected_button.description)
return True
else:
return False
def add_button_prob(button, questions_scores):
"""Return an HBox containing button and its probability."""
id = button.description
prob = widgets.Label(
score_label
+ ": "
+ str(
int(
math.ceil(score_scale * questions_scores.loc[id][questions_probability])
)
)
)
return widgets.HBox([button, prob])
def set_button_color(button, answerid):
"""Set each button's color according to its label."""
for i in range(len(button)):
button[i].style.button_color = (
"lightgreen" if button[i].answerid == answerid else None
)
```
Functions for interacting with the web service.
```
def score_text(text):
"""Return a data frame with the original question scores for the text."""
headers = {
"content-type": "application/json",
"Authorization": ("Bearer " + api_key),
}
# jsontext = json.dumps({'input':'{0}'.format(text)})
jsontext = text_to_json(text)
result = requests.post(scoring_url, data=jsontext, headers=headers)
# scores = result.json()['result'][0]
scores = eval(result.json())
scores_df = pd.DataFrame(
scores, columns=[questions_id, questions_answerid, questions_probability]
)
scores_df[questions_id] = scores_df[questions_id].astype(str)
scores_df[questions_answerid] = scores_df[questions_answerid].astype(str)
scores_df = scores_df.set_index(questions_id, drop=False)
return scores_df
```
Control the appearance of cell output boxes.
```
%%html
<style>
.output_wrapper, .output {
height:auto !important;
max-height:1000px; /* your desired max-height here */
}
.output_scroll {
box-shadow:none !important;
webkit-box-shadow:none !important;
}
</style>
```
## Load data
Load the pre-formatted text of questions.
```
questions_title = 'Questions'
questions_id = 'Id'
questions_answerid = 'AnswerId'
questions_text = 'Text'
questions_probability = 'Probability'
questions_path = './data_folder/questions.tsv'
questions = read_questions(questions_path, questions_id, questions_answerid)
```
Load the pre-formatted text of duplicates.
```
duplicates_title = 'Duplicates'
duplicates_id = 'Id'
duplicates_answerid = 'AnswerId'
duplicates_text = 'Text'
duplicates_path = './data_folder/dupes_test.tsv'
duplicates = read_questions(duplicates_path, duplicates_id, duplicates_answerid)
```
## Explore original questions matched up with duplicate questions
Define other variables and settings used in creating the interface.
```
questions_display = 15
questions_button_color = True
questions_button_score = True
score_label = 'Score'
score_scale = 100
```
This builds the exploration widget as a box containing duplicates and question tabs, each in turn containing boxes that have for each ID-text pair a button and a text area.
```
duplicates_map, questions_map, duplicates_questions = duplicates_questions_widget(duplicates, questions)
duplicates_questions
```
To tear down the cluster and related resources go to the [last notebook](08_TearDown.ipynb).
|
github_jupyter
|
<a href="https://colab.research.google.com/github/PytorchLightning/pytorch-lightning/blob/master/notebooks/04-transformers-text-classification.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Finetune 🤗 Transformers Models with PyTorch Lightning ⚡
This notebook will use HuggingFace's `datasets` library to get data, which will be wrapped in a `LightningDataModule`. Then, we write a class to perform text classification on any dataset from the[ GLUE Benchmark](https://gluebenchmark.com/). (We just show CoLA and MRPC due to constraint on compute/disk)
[HuggingFace's NLP Viewer](https://huggingface.co/nlp/viewer/?dataset=glue&config=cola) can help you get a feel for the two datasets we will use and what tasks they are solving for.
---
- Give us a ⭐ [on Github](https://www.github.com/PytorchLightning/pytorch-lightning/)
- Check out [the documentation](https://pytorch-lightning.readthedocs.io/en/latest/)
- Ask a question on [GitHub Discussions](https://github.com/PyTorchLightning/pytorch-lightning/discussions/)
- Join us [on Slack](https://join.slack.com/t/pytorch-lightning/shared_invite/zt-f6bl2l0l-JYMK3tbAgAmGRrlNr00f1A)
- [HuggingFace datasets](https://github.com/huggingface/datasets)
- [HuggingFace transformers](https://github.com/huggingface/transformers)
### Setup
```
!pip install pytorch-lightning datasets transformers
from argparse import ArgumentParser
from datetime import datetime
from typing import Optional
import datasets
import numpy as np
import pytorch_lightning as pl
import torch
from torch.utils.data import DataLoader
from transformers import (
AdamW,
AutoModelForSequenceClassification,
AutoConfig,
AutoTokenizer,
get_linear_schedule_with_warmup,
glue_compute_metrics
)
```
## GLUE DataModule
```
class GLUEDataModule(pl.LightningDataModule):
task_text_field_map = {
'cola': ['sentence'],
'sst2': ['sentence'],
'mrpc': ['sentence1', 'sentence2'],
'qqp': ['question1', 'question2'],
'stsb': ['sentence1', 'sentence2'],
'mnli': ['premise', 'hypothesis'],
'qnli': ['question', 'sentence'],
'rte': ['sentence1', 'sentence2'],
'wnli': ['sentence1', 'sentence2'],
'ax': ['premise', 'hypothesis']
}
glue_task_num_labels = {
'cola': 2,
'sst2': 2,
'mrpc': 2,
'qqp': 2,
'stsb': 1,
'mnli': 3,
'qnli': 2,
'rte': 2,
'wnli': 2,
'ax': 3
}
loader_columns = [
'datasets_idx',
'input_ids',
'token_type_ids',
'attention_mask',
'start_positions',
'end_positions',
'labels'
]
def __init__(
self,
model_name_or_path: str,
task_name: str ='mrpc',
max_seq_length: int = 128,
train_batch_size: int = 32,
eval_batch_size: int = 32,
**kwargs
):
super().__init__()
self.model_name_or_path = model_name_or_path
self.task_name = task_name
self.max_seq_length = max_seq_length
self.train_batch_size = train_batch_size
self.eval_batch_size = eval_batch_size
self.text_fields = self.task_text_field_map[task_name]
self.num_labels = self.glue_task_num_labels[task_name]
self.tokenizer = AutoTokenizer.from_pretrained(self.model_name_or_path, use_fast=True)
def setup(self, stage):
self.dataset = datasets.load_dataset('glue', self.task_name)
for split in self.dataset.keys():
self.dataset[split] = self.dataset[split].map(
self.convert_to_features,
batched=True,
remove_columns=['label'],
)
self.columns = [c for c in self.dataset[split].column_names if c in self.loader_columns]
self.dataset[split].set_format(type="torch", columns=self.columns)
self.eval_splits = [x for x in self.dataset.keys() if 'validation' in x]
def prepare_data(self):
datasets.load_dataset('glue', self.task_name)
AutoTokenizer.from_pretrained(self.model_name_or_path, use_fast=True)
def train_dataloader(self):
return DataLoader(self.dataset['train'], batch_size=self.train_batch_size)
def val_dataloader(self):
if len(self.eval_splits) == 1:
return DataLoader(self.dataset['validation'], batch_size=self.eval_batch_size)
elif len(self.eval_splits) > 1:
return [DataLoader(self.dataset[x], batch_size=self.eval_batch_size) for x in self.eval_splits]
def test_dataloader(self):
if len(self.eval_splits) == 1:
return DataLoader(self.dataset['test'], batch_size=self.eval_batch_size)
elif len(self.eval_splits) > 1:
return [DataLoader(self.dataset[x], batch_size=self.eval_batch_size) for x in self.eval_splits]
def convert_to_features(self, example_batch, indices=None):
# Either encode single sentence or sentence pairs
if len(self.text_fields) > 1:
texts_or_text_pairs = list(zip(example_batch[self.text_fields[0]], example_batch[self.text_fields[1]]))
else:
texts_or_text_pairs = example_batch[self.text_fields[0]]
# Tokenize the text/text pairs
features = self.tokenizer.batch_encode_plus(
texts_or_text_pairs,
max_length=self.max_seq_length,
pad_to_max_length=True,
truncation=True
)
# Rename label to labels to make it easier to pass to model forward
features['labels'] = example_batch['label']
return features
```
#### You could use this datamodule with standalone PyTorch if you wanted...
```
dm = GLUEDataModule('distilbert-base-uncased')
dm.prepare_data()
dm.setup('fit')
next(iter(dm.train_dataloader()))
```
## GLUE Model
```
class GLUETransformer(pl.LightningModule):
def __init__(
self,
model_name_or_path: str,
num_labels: int,
learning_rate: float = 2e-5,
adam_epsilon: float = 1e-8,
warmup_steps: int = 0,
weight_decay: float = 0.0,
train_batch_size: int = 32,
eval_batch_size: int = 32,
eval_splits: Optional[list] = None,
**kwargs
):
super().__init__()
self.save_hyperparameters()
self.config = AutoConfig.from_pretrained(model_name_or_path, num_labels=num_labels)
self.model = AutoModelForSequenceClassification.from_pretrained(model_name_or_path, config=self.config)
self.metric = datasets.load_metric(
'glue',
self.hparams.task_name,
experiment_id=datetime.now().strftime("%d-%m-%Y_%H-%M-%S")
)
def forward(self, **inputs):
return self.model(**inputs)
def training_step(self, batch, batch_idx):
outputs = self(**batch)
loss = outputs[0]
return loss
def validation_step(self, batch, batch_idx, dataloader_idx=0):
outputs = self(**batch)
val_loss, logits = outputs[:2]
if self.hparams.num_labels >= 1:
preds = torch.argmax(logits, axis=1)
elif self.hparams.num_labels == 1:
preds = logits.squeeze()
labels = batch["labels"]
return {'loss': val_loss, "preds": preds, "labels": labels}
def validation_epoch_end(self, outputs):
if self.hparams.task_name == 'mnli':
for i, output in enumerate(outputs):
# matched or mismatched
split = self.hparams.eval_splits[i].split('_')[-1]
preds = torch.cat([x['preds'] for x in output]).detach().cpu().numpy()
labels = torch.cat([x['labels'] for x in output]).detach().cpu().numpy()
loss = torch.stack([x['loss'] for x in output]).mean()
self.log(f'val_loss_{split}', loss, prog_bar=True)
split_metrics = {f"{k}_{split}": v for k, v in self.metric.compute(predictions=preds, references=labels).items()}
self.log_dict(split_metrics, prog_bar=True)
return loss
preds = torch.cat([x['preds'] for x in outputs]).detach().cpu().numpy()
labels = torch.cat([x['labels'] for x in outputs]).detach().cpu().numpy()
loss = torch.stack([x['loss'] for x in outputs]).mean()
self.log('val_loss', loss, prog_bar=True)
self.log_dict(self.metric.compute(predictions=preds, references=labels), prog_bar=True)
return loss
def setup(self, stage):
if stage == 'fit':
# Get dataloader by calling it - train_dataloader() is called after setup() by default
train_loader = self.train_dataloader()
# Calculate total steps
self.total_steps = (
(len(train_loader.dataset) // (self.hparams.train_batch_size * max(1, self.hparams.gpus)))
// self.hparams.accumulate_grad_batches
* float(self.hparams.max_epochs)
)
def configure_optimizers(self):
"Prepare optimizer and schedule (linear warmup and decay)"
model = self.model
no_decay = ["bias", "LayerNorm.weight"]
optimizer_grouped_parameters = [
{
"params": [p for n, p in model.named_parameters() if not any(nd in n for nd in no_decay)],
"weight_decay": self.hparams.weight_decay,
},
{
"params": [p for n, p in model.named_parameters() if any(nd in n for nd in no_decay)],
"weight_decay": 0.0,
},
]
optimizer = AdamW(optimizer_grouped_parameters, lr=self.hparams.learning_rate, eps=self.hparams.adam_epsilon)
scheduler = get_linear_schedule_with_warmup(
optimizer, num_warmup_steps=self.hparams.warmup_steps, num_training_steps=self.total_steps
)
scheduler = {
'scheduler': scheduler,
'interval': 'step',
'frequency': 1
}
return [optimizer], [scheduler]
@staticmethod
def add_model_specific_args(parent_parser):
parser = ArgumentParser(parents=[parent_parser], add_help=False)
parser.add_argument("--learning_rate", default=2e-5, type=float)
parser.add_argument("--adam_epsilon", default=1e-8, type=float)
parser.add_argument("--warmup_steps", default=0, type=int)
parser.add_argument("--weight_decay", default=0.0, type=float)
return parser
```
### ⚡ Quick Tip
- Combine arguments from your DataModule, Model, and Trainer into one for easy and robust configuration
```
def parse_args(args=None):
parser = ArgumentParser()
parser = pl.Trainer.add_argparse_args(parser)
parser = GLUEDataModule.add_argparse_args(parser)
parser = GLUETransformer.add_model_specific_args(parser)
parser.add_argument('--seed', type=int, default=42)
return parser.parse_args(args)
def main(args):
pl.seed_everything(args.seed)
dm = GLUEDataModule.from_argparse_args(args)
dm.prepare_data()
dm.setup('fit')
model = GLUETransformer(num_labels=dm.num_labels, eval_splits=dm.eval_splits, **vars(args))
trainer = pl.Trainer.from_argparse_args(args)
return dm, model, trainer
```
# Training
## CoLA
See an interactive view of the CoLA dataset in [NLP Viewer](https://huggingface.co/nlp/viewer/?dataset=glue&config=cola)
```
mocked_args = """
--model_name_or_path albert-base-v2
--task_name cola
--max_epochs 3
--gpus 1""".split()
args = parse_args(mocked_args)
dm, model, trainer = main(args)
trainer.fit(model, dm)
```
## MRPC
See an interactive view of the MRPC dataset in [NLP Viewer](https://huggingface.co/nlp/viewer/?dataset=glue&config=mrpc)
```
mocked_args = """
--model_name_or_path distilbert-base-cased
--task_name mrpc
--max_epochs 3
--gpus 1""".split()
args = parse_args(mocked_args)
dm, model, trainer = main(args)
trainer.fit(model, dm)
```
## MNLI
- The MNLI dataset is huge, so we aren't going to bother trying to train it here.
- Let's just make sure our multi-dataloader logic is right by skipping over training and going straight to validation.
See an interactive view of the MRPC dataset in [NLP Viewer](https://huggingface.co/nlp/viewer/?dataset=glue&config=mnli)
```
mocked_args = """
--model_name_or_path distilbert-base-uncased
--task_name mnli
--max_epochs 1
--gpus 1
--limit_train_batches 10
--progress_bar_refresh_rate 20""".split()
args = parse_args(mocked_args)
dm, model, trainer = main(args)
trainer.fit(model, dm)
```
<code style="color:#792ee5;">
<h1> <strong> Congratulations - Time to Join the Community! </strong> </h1>
</code>
Congratulations on completing this notebook tutorial! If you enjoyed this and would like to join the Lightning movement, you can do so in the following ways!
### Star [Lightning](https://github.com/PyTorchLightning/pytorch-lightning) on GitHub
The easiest way to help our community is just by starring the GitHub repos! This helps raise awareness of the cool tools we're building.
* Please, star [Lightning](https://github.com/PyTorchLightning/pytorch-lightning)
### Join our [Slack](https://join.slack.com/t/pytorch-lightning/shared_invite/zt-f6bl2l0l-JYMK3tbAgAmGRrlNr00f1A)!
The best way to keep up to date on the latest advancements is to join our community! Make sure to introduce yourself and share your interests in `#general` channel
### Interested by SOTA AI models ! Check out [Bolt](https://github.com/PyTorchLightning/pytorch-lightning-bolts)
Bolts has a collection of state-of-the-art models, all implemented in [Lightning](https://github.com/PyTorchLightning/pytorch-lightning) and can be easily integrated within your own projects.
* Please, star [Bolt](https://github.com/PyTorchLightning/pytorch-lightning-bolts)
### Contributions !
The best way to contribute to our community is to become a code contributor! At any time you can go to [Lightning](https://github.com/PyTorchLightning/pytorch-lightning) or [Bolt](https://github.com/PyTorchLightning/pytorch-lightning-bolts) GitHub Issues page and filter for "good first issue".
* [Lightning good first issue](https://github.com/PyTorchLightning/pytorch-lightning/issues?q=is%3Aopen+is%3Aissue+label%3A%22good+first+issue%22)
* [Bolt good first issue](https://github.com/PyTorchLightning/pytorch-lightning-bolts/issues?q=is%3Aopen+is%3Aissue+label%3A%22good+first+issue%22)
* You can also contribute your own notebooks with useful examples !
### Great thanks from the entire Pytorch Lightning Team for your interest !
<img src="https://github.com/PyTorchLightning/pytorch-lightning/blob/master/docs/source/_static/images/logo.png?raw=true" width="800" height="200" />
|
github_jupyter
|
# Anomaly detection
Anomaly detection is a machine learning task that consists in spotting so-called outliers.
“An outlier is an observation in a data set which appears to be inconsistent with the remainder of that set of data.”
Johnson 1992
“An outlier is an observation which deviates so much from the other observations as to arouse suspicions that it was generated by a different mechanism.”
Outlier/Anomaly
Hawkins 1980
### Types of anomaly detection setups
- Supervised AD
- Labels available for both normal data and anomalies
- Similar to rare class mining / imbalanced classification
- Semi-supervised AD (Novelty Detection)
- Only normal data available to train
- The algorithm learns on normal data only
- Unsupervised AD (Outlier Detection)
- no labels, training set = normal + abnormal data
- Assumption: anomalies are very rare
```
%matplotlib inline
import warnings
warnings.filterwarnings("ignore")
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
```
Let's first get familiar with different unsupervised anomaly detection approaches and algorithms. In order to visualise the output of the different algorithms we consider a toy data set consisting in a two-dimensional Gaussian mixture.
### Generating the data set
```
from sklearn.datasets import make_blobs
X, y = make_blobs(n_features=2, centers=3, n_samples=500,
random_state=42)
X.shape
plt.figure()
plt.scatter(X[:, 0], X[:, 1])
plt.show()
```
## Anomaly detection with density estimation
```
from sklearn.neighbors.kde import KernelDensity
# Estimate density with a Gaussian kernel density estimator
kde = KernelDensity(kernel='gaussian')
kde = kde.fit(X)
kde
kde_X = kde.score_samples(X)
print(kde_X.shape) # contains the log-likelihood of the data. The smaller it is the rarer is the sample
from scipy.stats.mstats import mquantiles
alpha_set = 0.95
tau_kde = mquantiles(kde_X, 1. - alpha_set)
n_samples, n_features = X.shape
X_range = np.zeros((n_features, 2))
X_range[:, 0] = np.min(X, axis=0) - 1.
X_range[:, 1] = np.max(X, axis=0) + 1.
h = 0.1 # step size of the mesh
x_min, x_max = X_range[0]
y_min, y_max = X_range[1]
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
grid = np.c_[xx.ravel(), yy.ravel()]
Z_kde = kde.score_samples(grid)
Z_kde = Z_kde.reshape(xx.shape)
plt.figure()
c_0 = plt.contour(xx, yy, Z_kde, levels=tau_kde, colors='red', linewidths=3)
plt.clabel(c_0, inline=1, fontsize=15, fmt={tau_kde[0]: str(alpha_set)})
plt.scatter(X[:, 0], X[:, 1])
plt.show()
```
## now with One-Class SVM
The problem of density based estimation is that they tend to become inefficient when the dimensionality of the data increase. It's the so-called curse of dimensionality that affects particularly density estimation algorithms. The one-class SVM algorithm can be used in such cases.
```
from sklearn.svm import OneClassSVM
nu = 0.05 # theory says it should be an upper bound of the fraction of outliers
ocsvm = OneClassSVM(kernel='rbf', gamma=0.05, nu=nu)
ocsvm.fit(X)
X_outliers = X[ocsvm.predict(X) == -1]
Z_ocsvm = ocsvm.decision_function(grid)
Z_ocsvm = Z_ocsvm.reshape(xx.shape)
plt.figure()
c_0 = plt.contour(xx, yy, Z_ocsvm, levels=[0], colors='red', linewidths=3)
plt.clabel(c_0, inline=1, fontsize=15, fmt={0: str(alpha_set)})
plt.scatter(X[:, 0], X[:, 1])
plt.scatter(X_outliers[:, 0], X_outliers[:, 1], color='red')
plt.show()
```
### Support vectors - Outliers
The so-called support vectors of the one-class SVM form the outliers
```
X_SV = X[ocsvm.support_]
n_SV = len(X_SV)
n_outliers = len(X_outliers)
print('{0:.2f} <= {1:.2f} <= {2:.2f}?'.format(1./n_samples*n_outliers, nu, 1./n_samples*n_SV))
```
Only the support vectors are involved in the decision function of the One-Class SVM.
1. Plot the level sets of the One-Class SVM decision function as we did for the true density.
2. Emphasize the Support vectors.
```
plt.figure()
plt.contourf(xx, yy, Z_ocsvm, 10, cmap=plt.cm.Blues_r)
plt.scatter(X[:, 0], X[:, 1], s=1.)
plt.scatter(X_SV[:, 0], X_SV[:, 1], color='orange')
plt.show()
```
<div class="alert alert-success">
<b>EXERCISE</b>:
<ul>
<li>
**Change** the `gamma` parameter and see it's influence on the smoothness of the decision function.
</li>
</ul>
</div>
```
# %load solutions/22_A-anomaly_ocsvm_gamma.py
```
## Isolation Forest
Isolation Forest is an anomaly detection algorithm based on trees. The algorithm builds a number of random trees and the rationale is that if a sample is isolated it should alone in a leaf after very few random splits. Isolation Forest builds a score of abnormality based the depth of the tree at which samples end up.
```
from sklearn.ensemble import IsolationForest
iforest = IsolationForest(n_estimators=300, contamination=0.10)
iforest = iforest.fit(X)
Z_iforest = iforest.decision_function(grid)
Z_iforest = Z_iforest.reshape(xx.shape)
plt.figure()
c_0 = plt.contour(xx, yy, Z_iforest,
levels=[iforest.threshold_],
colors='red', linewidths=3)
plt.clabel(c_0, inline=1, fontsize=15,
fmt={iforest.threshold_: str(alpha_set)})
plt.scatter(X[:, 0], X[:, 1], s=1.)
plt.show()
```
<div class="alert alert-success">
<b>EXERCISE</b>:
<ul>
<li>
Illustrate graphically the influence of the number of trees on the smoothness of the decision function?
</li>
</ul>
</div>
```
# %load solutions/22_B-anomaly_iforest_n_trees.py
```
# Illustration on Digits data set
We will now apply the IsolationForest algorithm to spot digits written in an unconventional way.
```
from sklearn.datasets import load_digits
digits = load_digits()
```
The digits data set consists in images (8 x 8) of digits.
```
images = digits.images
labels = digits.target
images.shape
i = 102
plt.figure(figsize=(2, 2))
plt.title('{0}'.format(labels[i]))
plt.axis('off')
plt.imshow(images[i], cmap=plt.cm.gray_r, interpolation='nearest')
plt.show()
```
To use the images as a training set we need to flatten the images.
```
n_samples = len(digits.images)
data = digits.images.reshape((n_samples, -1))
data.shape
X = data
y = digits.target
X.shape
```
Let's focus on digit 5.
```
X_5 = X[y == 5]
X_5.shape
fig, axes = plt.subplots(1, 5, figsize=(10, 4))
for ax, x in zip(axes, X_5[:5]):
img = x.reshape(8, 8)
ax.imshow(img, cmap=plt.cm.gray_r, interpolation='nearest')
ax.axis('off')
```
1. Let's use IsolationForest to find the top 5% most abnormal images.
2. Let's plot them !
```
from sklearn.ensemble import IsolationForest
iforest = IsolationForest(contamination=0.05)
iforest = iforest.fit(X_5)
```
Compute the level of "abnormality" with `iforest.decision_function`. The lower, the more abnormal.
```
iforest_X = iforest.decision_function(X_5)
plt.hist(iforest_X);
```
Let's plot the strongest inliers
```
X_strong_inliers = X_5[np.argsort(iforest_X)[-10:]]
fig, axes = plt.subplots(2, 5, figsize=(10, 5))
for i, ax in zip(range(len(X_strong_inliers)), axes.ravel()):
ax.imshow(X_strong_inliers[i].reshape((8, 8)),
cmap=plt.cm.gray_r, interpolation='nearest')
ax.axis('off')
```
Let's plot the strongest outliers
```
fig, axes = plt.subplots(2, 5, figsize=(10, 5))
X_outliers = X_5[iforest.predict(X_5) == -1]
for i, ax in zip(range(len(X_outliers)), axes.ravel()):
ax.imshow(X_outliers[i].reshape((8, 8)),
cmap=plt.cm.gray_r, interpolation='nearest')
ax.axis('off')
```
<div class="alert alert-success">
<b>EXERCISE</b>:
<ul>
<li>
Rerun the same analysis with all the other digits
</li>
</ul>
</div>
```
# %load solutions/22_C-anomaly_digits.py
```
|
github_jupyter
|
# Intro to machine learning - k-means
---
Scikit-learn has a nice set of unsupervised learning routines which can be used to explore clustering in the parameter space.
In this notebook we will use k-means, included in Scikit-learn, to demonstrate how the different rocks occupy different regions in the available parameter space.
Let's load the data using pandas:
```
import pandas as pd
import numpy as np
df = pd.read_csv("../data/2016_ML_contest_training_data.csv")
df.head()
df.describe()
df = df.dropna()
```
## Calculate RHOB from DeltaPHI and PHIND
```
def rhob(phi_rhob, Rho_matrix= 2650.0, Rho_fluid=1000.0):
"""
Rho_matrix (sandstone) : 2.65 g/cc
Rho_matrix (Limestome): 2.71 g/cc
Rho_matrix (Dolomite): 2.876 g/cc
Rho_matrix (Anyhydrite): 2.977 g/cc
Rho_matrix (Salt): 2.032 g/cc
Rho_fluid (fresh water): 1.0 g/cc (is this more mud-like?)
Rho_fluid (salt water): 1.1 g/cc
see wiki.aapg.org/Density-neutron_log_porosity
returns density porosity log """
return Rho_matrix*(1 - phi_rhob) + Rho_fluid*phi_rhob
phi_rhob = 2*(df.PHIND/100)/(1 - df.DeltaPHI/100) - df.DeltaPHI/100
calc_RHOB = rhob(phi_rhob)
df['RHOB'] = calc_RHOB
df.describe()
```
We can define a Python dictionary to relate facies with the integer label on the `DataFrame`
```
facies_dict = {1:'sandstone', 2:'c_siltstone', 3:'f_siltstone', 4:'marine_silt_shale',
5:'mudstone', 6:'wackentstone', 7:'dolomite', 8:'packstone', 9:'bafflestone'}
df["s_Facies"] = df.Facies.map(lambda x: facies_dict[x])
df.head()
```
We can easily visualize the properties of each facies and how they compare using a `PairPlot`. The library `seaborn` integrates with matplotlib to make these kind of plots easily.
```
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
g = sns.PairGrid(df, hue="s_Facies", vars=['GR','RHOB','PE','ILD_log10'], size=4)
g.map_upper(plt.scatter,**dict(alpha=0.4))
g.map_lower(plt.scatter,**dict(alpha=0.4))
g.map_diag(plt.hist,**dict(bins=20))
g.add_legend()
g.set(alpha=0.5)
```
It is very clear that it's hard to separate these facies in feature space. Let's just select a couple of facies and using Pandas, select the rows in the `DataFrame` that contain information about those facies
```
selected = ['f_siltstone', 'bafflestone', 'wackentstone']
dfs = pd.concat(list(map(lambda x: df[df.s_Facies == x], selected)))
g = sns.PairGrid(dfs, hue="s_Facies", vars=['GR','RHOB','PE','ILD_log10'], size=4)
g.map_upper(plt.scatter,**dict(alpha=0.4))
g.map_lower(plt.scatter,**dict(alpha=0.4))
g.map_diag(plt.hist,**dict(bins=20))
g.add_legend()
g.set(alpha=0.5)
# Make X and y
X = dfs[['GR','ILD_log10','PE']].as_matrix()
y = dfs['Facies'].values
```
Use scikit-learn StandardScaler to normalize the data. Needed for k-means.
```
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X = scaler.fit_transform(X)
plt.scatter(X[:, 0], X[:, 1], c=y, alpha=0.3)
from sklearn.cluster import KMeans
clf = KMeans(n_clusters=4, random_state=1).fit(X)
y_pred = clf.predict(X)
plt.scatter(X[:, 0], X[:, 1], c=y_pred, alpha=0.3)
clf.inertia_
```
<hr />
<p style="color:gray">©2017 Agile Geoscience. Licensed CC-BY.</p>
|
github_jupyter
|
# Beating the betting firms with linear models
* **Data Source:** [https://www.kaggle.com/hugomathien/soccer](https://www.kaggle.com/hugomathien/soccer)
* **Author:** Anders Munk-Nielsen
**Result:** It is possible to do better than the professional betting firms in terms of predicting each outcome (although they may be maximizing profit rather than trying to predict outcomes). This is using a linear model, and it requires us to use a lot of variables, though.
**Perspectives:** We can only model 1(win), but there are *three* outcomes: Lose, Draw, and Win.
```
import pandas as pd
import numpy as np
import statsmodels.formula.api as smf
import seaborn as sns
import matplotlib.pyplot as plt
sns.set_theme()
# Read
d = pd.read_csv('football_probs.csv')
# Data types
d.date = pd.to_datetime(d.date)
cols_to_cat = ['league', 'season', 'team', 'country']
for c in cols_to_cat:
d[c] = d[c].astype('category')
```
Visualizing the home field advantage.
```
sns.histplot(data=d, x='goal_diff', hue='home', discrete=True);
plt.xlim([-7,7]);
```
Outcome variables
```
# Lose, Draw, Win
d['outcome'] = 'L'
d.loc[d.goal_diff == 0.0, 'outcome'] = 'D'
d.loc[d.goal_diff > 0.0, 'outcome'] = 'W'
# Win dummy (as float (will become useful later))
d['win'] = (d.goal_diff > 0.0).astype(float)
```
# Odds to probabilities
### Convenient lists of variable names
* `cols_common`: All variables that are unrelated to betting
* `betting_firms`: The prefix that defines the name of the betting firms, e.g. B365 for Bet365
* `firm_vars`: A dictionary returning the variables for a firm, e.g. `firm_vars['BW']` returns `BWA`, `BWD`, `BWH` (for Away, Draw, Home team win).
```
# # List of the names of all firms that we have betting prices for
betting_firms = np.unique([c[:-4] for c in d.columns if c[-1] in ['A', 'H', 'D']])
betting_firms
# find all columns in our dataframe that are *not* betting variables
cols_common = [c for c in d.columns if (c[-4:-1] != '_Pr') & (c[-9:] != 'overround')]
print(f'Non-odds variables: {cols_common}')
d[d.home].groupby('win')['B365_PrW'].mean().to_frame('Bet 365 Pr(win)')
sns.histplot(d, x='B365_PrW', hue='win');
```
## Is there more information in the mean?
If all firms are drawing random IID signals, then the average prediction should be a better estimator than any individual predictor.
```
firms_drop = ['BS', 'GB', 'PS', 'SJ'] # these are missing in too many years
cols_prW = [f'{c}_PrW' for c in betting_firms if c not in firms_drop]
d['avg_PrW'] = d[cols_prW].mean(1)
cols_prW += ['avg_PrW']
I = d.win == True
fig, ax = plt.subplots();
ax.hist(d.loc[I,'avg_PrW'], bins=30, alpha=0.3, label='Avg. prediction')
ax.hist(d.loc[I,'B365_PrW'], bins=30, alpha=0.3, label='B365')
ax.hist(d.loc[I,'BW_PrW'], bins=30, alpha=0.3, label='BW')
ax.legend();
ax.set_xlabel('Pr(win) [only matches where win==1]');
```
### RMSE comparison
* RMSE: Root Mean Squared Error. Whenever we have a candidate prediction guess, $\hat{y}_i$, we can evaluate $$ RMSE = \sqrt{ N^{-1}\sum_{i=1}^N (y_i - \hat{y}_i)^2 }. $$
```
def RMSE(yhat, y) -> float:
'''Root mean squared error: between yvar and y'''
q = (yhat - y)**2
return np.sqrt(np.mean(q))
def RMSE_agg(data: pd.core.frame.DataFrame, y: str) -> pd.core.series.Series:
'''RMSE_agg: Aggregates all columns, computing RMSE against the variable y for each column
'''
assert y in data.columns
y = data['win']
# local function computing RMSE for a specific column, yvar, against y
def RMSE_(yhat):
diff_sq = (yhat - y) ** 2
return np.sqrt(np.mean(diff_sq))
# do not compute RMSE against the real outcome :)
mycols = [c for c in data.columns if c != 'win']
# return aggregated dataframe (which becomes a pandas series)
return data[mycols].agg(RMSE_)
I = d[cols_prW].notnull().all(1) # only run comparison on subsample where all odds were observed
x_ = RMSE_agg(d[cols_prW + ['win']], 'win');
ax = x_.plot.bar();
ax.set_ylim([x_.min()*.999, x_.max()*1.001]);
ax.set_ylabel('RMSE');
```
# Linear Probability Models
Estimate a bunch of models where $y_i = 1(\text{win})$.
## Using `numpy`
```
d['home_'] = d.home.astype(float)
I = d[['home_', 'win'] + cols_prW].notnull().all(axis=1)
X = d.loc[I, ['home_'] + cols_prW].values
y = d.loc[I, 'win'].values.reshape(-1,1)
N = I.sum()
oo = np.ones((N,1))
X = np.hstack([oo, X])
betahat = np.linalg.inv(X.T @ X) @ X.T @ y
pd.DataFrame({'beta':betahat.flatten()}, index=['const', 'home'] + cols_prW)
```
## Using `statsmodels`
(Cheating, but faster...)
```
reg_addition = ' + '.join(cols_prW)
model_string = f'win ~ {reg_addition} + home + team'
cols_all = cols_prW + ['win', 'home']
I = d[cols_all].notnull().all(1) # no missings in any variables used in the prediction model
Itrain = I & (d.date < '2015-01-01') # for estimating our prediction model
Iholdout = I & (d.date >= '2015-01-01') # for assessing the model fit
# run regression
r = smf.ols(model_string, d[Itrain]).fit()
yhat = r.predict(d[I]).to_frame('AMN_PrW')
d.loc[I, 'AMN_PrW'] = yhat
print('Estimates with Team FE')
r.params.loc[['home[T.True]'] + cols_prW].to_frame('Beta')
```
### Plot estimates, $\hat{\beta}$
```
ax = r.params.loc[cols_prW].plot.bar();
ax.set_ylabel('Coefficient (loading in optimal prediction)');
ax.set_xlabel('Betting firm prediction');
```
### Plot model fit out of sample: avg. 1(win) vs. avg. $\hat{y}$
```
# predicted win rates from all firms and our new predicted probability
cols = cols_prW + ['AMN_PrW']
```
**Home matches:** `home == True`
```
x_ = d.loc[(d.win == 1.0) & (d.home == True) & (Iholdout == True), cols].mean()
ax = x_.plot(kind='bar');
ax.set_ylim([x_.min()*0.995, x_.max()*1.005]);
ax.set_title('Out of sample fit: won matches as Home');
ax.set_xlabel('Betting firm prediction');
ax.set_ylabel('Pr(win) (only won home matches)');
```
**Away matches:** `home == False`
```
x_ = d.loc[(d.win == 1.0) & (d.home == False) & (Iholdout == True), cols].mean()
ax = x_.plot(kind='bar');
ax.set_ylim([x_.min()*0.995, x_.max()*1.005]);
ax.set_ylabel('Pr(win) (only won away matches)');
ax.set_title('Out of sample fit: won matches as Away');
```
### RMSE
(evaluated in the holdout sample, of course.)
```
cols_ = cols_prW + ['AMN_PrW', 'win']
I = Iholdout & d[cols_].notnull().all(1) # only run comparison on subsample where all odds were observed
x_ = RMSE_agg(d.loc[I,cols_], y='win');
ax = x_.plot.bar();
ax.set_ylim([x_.min()*.999, x_.max()*1.001]);
ax.set_ylabel('RMSE (out of sample)');
```
|
github_jupyter
|
# Assignment 2: Naive Bayes
Welcome to week two of this specialization. You will learn about Naive Bayes. Concretely, you will be using Naive Bayes for sentiment analysis on tweets. Given a tweet, you will decide if it has a positive sentiment or a negative one. Specifically you will:
* Train a naive bayes model on a sentiment analysis task
* Test using your model
* Compute ratios of positive words to negative words
* Do some error analysis
* Predict on your own tweet
You may already be familiar with Naive Bayes and its justification in terms of conditional probabilities and independence.
* In this week's lectures and assignments we used the ratio of probabilities between positive and negative sentiments.
* This approach gives us simpler formulas for these 2-way classification tasks.
Load the cell below to import some packages.
You may want to browse the documentation of unfamiliar libraries and functions.
```
from utils import process_tweet, lookup
import pdb
from nltk.corpus import stopwords, twitter_samples
import numpy as np
import pandas as pd
import nltk
import string
from nltk.tokenize import TweetTokenizer
from os import getcwd
```
If you are running this notebook in your local computer,
don't forget to download the twitter samples and stopwords from nltk.
```
nltk.download('stopwords')
nltk.download('twitter_samples')
```
```
# add folder, tmp2, from our local workspace containing pre-downloaded corpora files to nltk's data path
filePath = f"{getcwd()}/../tmp2/"
nltk.data.path.append(filePath)
# get the sets of positive and negative tweets
all_positive_tweets = twitter_samples.strings('positive_tweets.json')
all_negative_tweets = twitter_samples.strings('negative_tweets.json')
# split the data into two pieces, one for training and one for testing (validation set)
test_pos = all_positive_tweets[4000:]
train_pos = all_positive_tweets[:4000]
test_neg = all_negative_tweets[4000:]
train_neg = all_negative_tweets[:4000]
train_x = train_pos + train_neg
test_x = test_pos + test_neg
# avoid assumptions about the length of all_positive_tweets
train_y = np.append(np.ones(len(train_pos)), np.zeros(len(train_neg)))
test_y = np.append(np.ones(len(test_pos)), np.zeros(len(test_neg)))
```
# Part 1: Process the Data
For any machine learning project, once you've gathered the data, the first step is to process it to make useful inputs to your model.
- **Remove noise**: You will first want to remove noise from your data -- that is, remove words that don't tell you much about the content. These include all common words like 'I, you, are, is, etc...' that would not give us enough information on the sentiment.
- We'll also remove stock market tickers, retweet symbols, hyperlinks, and hashtags because they can not tell you a lot of information on the sentiment.
- You also want to remove all the punctuation from a tweet. The reason for doing this is because we want to treat words with or without the punctuation as the same word, instead of treating "happy", "happy?", "happy!", "happy," and "happy." as different words.
- Finally you want to use stemming to only keep track of one variation of each word. In other words, we'll treat "motivation", "motivated", and "motivate" similarly by grouping them within the same stem of "motiv-".
We have given you the function `process_tweet()` that does this for you.
```
custom_tweet = "RT @Twitter @chapagain Hello There! Have a great day. :) #good #morning http://chapagain.com.np"
# print cleaned tweet
print(process_tweet(custom_tweet))
```
## Part 1.1 Implementing your helper functions
To help train your naive bayes model, you will need to build a dictionary where the keys are a (word, label) tuple and the values are the corresponding frequency. Note that the labels we'll use here are 1 for positive and 0 for negative.
You will also implement a `lookup()` helper function that takes in the `freqs` dictionary, a word, and a label (1 or 0) and returns the number of times that word and label tuple appears in the collection of tweets.
For example: given a list of tweets `["i am rather excited", "you are rather happy"]` and the label 1, the function will return a dictionary that contains the following key-value pairs:
{
("rather", 1): 2
("happi", 1) : 1
("excit", 1) : 1
}
- Notice how for each word in the given string, the same label 1 is assigned to each word.
- Notice how the words "i" and "am" are not saved, since it was removed by process_tweet because it is a stopword.
- Notice how the word "rather" appears twice in the list of tweets, and so its count value is 2.
#### Instructions
Create a function `count_tweets()` that takes a list of tweets as input, cleans all of them, and returns a dictionary.
- The key in the dictionary is a tuple containing the stemmed word and its class label, e.g. ("happi",1).
- The value the number of times this word appears in the given collection of tweets (an integer).
<details>
<summary>
<font size="3" color="darkgreen"><b>Hints</b></font>
</summary>
<p>
<ul>
<li>Please use the `process_tweet` function that was imported above, and then store the words in their respective dictionaries and sets.</li>
<li>You may find it useful to use the `zip` function to match each element in `tweets` with each element in `ys`.</li>
<li>Remember to check if the key in the dictionary exists before adding that key to the dictionary, or incrementing its value.</li>
<li>Assume that the `result` dictionary that is input will contain clean key-value pairs (you can assume that the values will be integers that can be incremented). It is good practice to check the datatype before incrementing the value, but it's not required here.</li>
</ul>
</p>
```
# UNQ_C1 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
def count_tweets(result, tweets, ys):
'''
Input:
result: a dictionary that will be used to map each pair to its frequency
tweets: a list of tweets
ys: a list corresponding to the sentiment of each tweet (either 0 or 1)
Output:
result: a dictionary mapping each pair to its frequency
'''
### START CODE HERE (REPLACE INSTANCES OF 'None' with your code) ###
for y, tweet in zip(ys, tweets):
for word in process_tweet(tweet):
# define the key, which is the word and label tuple
pair = (word, y)
# if the key exists in the dictionary, increment the count
if pair in result:
result[pair] += 1
# else, if the key is new, add it to the dictionary and set the count to 1
else:
result[pair] = 1
### END CODE HERE ###
return result
# Testing your function
result = {}
tweets = ['i am happy', 'i am tricked', 'i am sad', 'i am tired', 'i am tired']
ys = [1, 0, 0, 0, 0]
count_tweets(result, tweets, ys)
```
**Expected Output**: {('happi', 1): 1, ('trick', 0): 1, ('sad', 0): 1, ('tire', 0): 2}
# Part 2: Train your model using Naive Bayes
Naive bayes is an algorithm that could be used for sentiment analysis. It takes a short time to train and also has a short prediction time.
#### So how do you train a Naive Bayes classifier?
- The first part of training a naive bayes classifier is to identify the number of classes that you have.
- You will create a probability for each class.
$P(D_{pos})$ is the probability that the document is positive.
$P(D_{neg})$ is the probability that the document is negative.
Use the formulas as follows and store the values in a dictionary:
$$P(D_{pos}) = \frac{D_{pos}}{D}\tag{1}$$
$$P(D_{neg}) = \frac{D_{neg}}{D}\tag{2}$$
Where $D$ is the total number of documents, or tweets in this case, $D_{pos}$ is the total number of positive tweets and $D_{neg}$ is the total number of negative tweets.
#### Prior and Logprior
The prior probability represents the underlying probability in the target population that a tweet is positive versus negative. In other words, if we had no specific information and blindly picked a tweet out of the population set, what is the probability that it will be positive versus that it will be negative? That is the "prior".
The prior is the ratio of the probabilities $\frac{P(D_{pos})}{P(D_{neg})}$.
We can take the log of the prior to rescale it, and we'll call this the logprior
$$\text{logprior} = log \left( \frac{P(D_{pos})}{P(D_{neg})} \right) = log \left( \frac{D_{pos}}{D_{neg}} \right)$$.
Note that $log(\frac{A}{B})$ is the same as $log(A) - log(B)$. So the logprior can also be calculated as the difference between two logs:
$$\text{logprior} = \log (P(D_{pos})) - \log (P(D_{neg})) = \log (D_{pos}) - \log (D_{neg})\tag{3}$$
#### Positive and Negative Probability of a Word
To compute the positive probability and the negative probability for a specific word in the vocabulary, we'll use the following inputs:
- $freq_{pos}$ and $freq_{neg}$ are the frequencies of that specific word in the positive or negative class. In other words, the positive frequency of a word is the number of times the word is counted with the label of 1.
- $N_{pos}$ and $N_{neg}$ are the total number of positive and negative words for all documents (for all tweets), respectively.
- $V$ is the number of unique words in the entire set of documents, for all classes, whether positive or negative.
We'll use these to compute the positive and negative probability for a specific word using this formula:
$$ P(W_{pos}) = \frac{freq_{pos} + 1}{N_{pos} + V}\tag{4} $$
$$ P(W_{neg}) = \frac{freq_{neg} + 1}{N_{neg} + V}\tag{5} $$
Notice that we add the "+1" in the numerator for additive smoothing. This [wiki article](https://en.wikipedia.org/wiki/Additive_smoothing) explains more about additive smoothing.
#### Log likelihood
To compute the loglikelihood of that very same word, we can implement the following equations:
$$\text{loglikelihood} = \log \left(\frac{P(W_{pos})}{P(W_{neg})} \right)\tag{6}$$
##### Create `freqs` dictionary
- Given your `count_tweets()` function, you can compute a dictionary called `freqs` that contains all the frequencies.
- In this `freqs` dictionary, the key is the tuple (word, label)
- The value is the number of times it has appeared.
We will use this dictionary in several parts of this assignment.
```
# Build the freqs dictionary for later uses
freqs = count_tweets({}, train_x, train_y)
```
#### Instructions
Given a freqs dictionary, `train_x` (a list of tweets) and a `train_y` (a list of labels for each tweet), implement a naive bayes classifier.
##### Calculate $V$
- You can then compute the number of unique words that appear in the `freqs` dictionary to get your $V$ (you can use the `set` function).
##### Calculate $freq_{pos}$ and $freq_{neg}$
- Using your `freqs` dictionary, you can compute the positive and negative frequency of each word $freq_{pos}$ and $freq_{neg}$.
##### Calculate $N_{pos}$ and $N_{neg}$
- Using `freqs` dictionary, you can also compute the total number of positive words and total number of negative words $N_{pos}$ and $N_{neg}$.
##### Calculate $D$, $D_{pos}$, $D_{neg}$
- Using the `train_y` input list of labels, calculate the number of documents (tweets) $D$, as well as the number of positive documents (tweets) $D_{pos}$ and number of negative documents (tweets) $D_{neg}$.
- Calculate the probability that a document (tweet) is positive $P(D_{pos})$, and the probability that a document (tweet) is negative $P(D_{neg})$
##### Calculate the logprior
- the logprior is $log(D_{pos}) - log(D_{neg})$
##### Calculate log likelihood
- Finally, you can iterate over each word in the vocabulary, use your `lookup` function to get the positive frequencies, $freq_{pos}$, and the negative frequencies, $freq_{neg}$, for that specific word.
- Compute the positive probability of each word $P(W_{pos})$, negative probability of each word $P(W_{neg})$ using equations 4 & 5.
$$ P(W_{pos}) = \frac{freq_{pos} + 1}{N_{pos} + V}\tag{4} $$
$$ P(W_{neg}) = \frac{freq_{neg} + 1}{N_{neg} + V}\tag{5} $$
**Note:** We'll use a dictionary to store the log likelihoods for each word. The key is the word, the value is the log likelihood of that word).
- You can then compute the loglikelihood: $log \left( \frac{P(W_{pos})}{P(W_{neg})} \right)\tag{6}$.
```
# UNQ_C2 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
def train_naive_bayes(freqs, train_x, train_y):
'''
Input:
freqs: dictionary from (word, label) to how often the word appears
train_x: a list of tweets
train_y: a list of labels correponding to the tweets (0,1)
Output:
logprior: the log prior. (equation 3 above)
loglikelihood: the log likelihood of you Naive bayes equation. (equation 6 above)
'''
loglikelihood = {}
logprior = 0
### START CODE HERE (REPLACE INSTANCES OF 'None' with your code) ###
# calculate V, the number of unique words in the vocabulary
vocab = set([pair[0] for pair in freqs.keys()])
V = len(vocab)
# calculate N_pos and N_neg
N_pos = N_neg = 0
for pair in freqs.keys():
# if the label is positive (greater than zero)
if pair[1] > 0:
# Increment the number of positive words by the count for this (word, label) pair
N_pos += freqs[pair]
# else, the label is negative
else:
# increment the number of negative words by the count for this (word,label) pair
N_neg += freqs[pair]
# Calculate D, the number of documents
D = train_y.shape[0]
# Calculate D_pos, the number of positive documents (*hint: use sum(<np_array>))
D_pos = np.sum(train_y[:, None])
# Calculate D_neg, the number of negative documents (*hint: compute using D and D_pos)
D_neg = D - D_pos
# Calculate logprior
logprior = np.log(D_pos) - np.log(D_neg)
# For each word in the vocabulary...
for word in vocab:
# get the positive and negative frequency of the word
freq_pos = freqs.get((word, 1), 0)
freq_neg = freqs.get((word, 0), 0)
# calculate the probability that each word is positive, and negative
p_w_pos = (freq_pos + 1) / (N_pos + V)
p_w_neg = (freq_neg + 1) / (N_neg + V)
# calculate the log likelihood of the word
loglikelihood[word] = np.log(p_w_pos / p_w_neg)
### END CODE HERE ###
return logprior, loglikelihood
# UNQ_C3 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
# You do not have to input any code in this cell, but it is relevant to grading, so please do not change anything
logprior, loglikelihood = train_naive_bayes(freqs, train_x, train_y)
print(logprior)
print(len(loglikelihood))
```
**Expected Output**:
0.0
9089
# Part 3: Test your naive bayes
Now that we have the `logprior` and `loglikelihood`, we can test the naive bayes function by making predicting on some tweets!
#### Implement `naive_bayes_predict`
**Instructions**:
Implement the `naive_bayes_predict` function to make predictions on tweets.
* The function takes in the `tweet`, `logprior`, `loglikelihood`.
* It returns the probability that the tweet belongs to the positive or negative class.
* For each tweet, sum up loglikelihoods of each word in the tweet.
* Also add the logprior to this sum to get the predicted sentiment of that tweet.
$$ p = logprior + \sum_i^N (loglikelihood_i)$$
#### Note
Note we calculate the prior from the training data, and that the training data is evenly split between positive and negative labels (4000 positive and 4000 negative tweets). This means that the ratio of positive to negative 1, and the logprior is 0.
The value of 0.0 means that when we add the logprior to the log likelihood, we're just adding zero to the log likelihood. However, please remember to include the logprior, because whenever the data is not perfectly balanced, the logprior will be a non-zero value.
```
# UNQ_C4 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
def naive_bayes_predict(tweet, logprior, loglikelihood):
'''
Input:
tweet: a string
logprior: a number
loglikelihood: a dictionary of words mapping to numbers
Output:
p: the sum of all the logliklihoods of each word in the tweet (if found in the dictionary) + logprior (a number)
'''
### START CODE HERE (REPLACE INSTANCES OF 'None' with your code) ###
# process the tweet to get a list of words
word_l = process_tweet(tweet)
# initialize probability to zero
p = 0
# add the logprior
p += logprior
for word in word_l:
# check if the word exists in the loglikelihood dictionary
if word in loglikelihood:
# add the log likelihood of that word to the probability
p += loglikelihood[word]
### END CODE HERE ###
return p
# UNQ_C5 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
# You do not have to input any code in this cell, but it is relevant to grading, so please do not change anything
# Experiment with your own tweet.
my_tweet = 'She smiled.'
p = naive_bayes_predict(my_tweet, logprior, loglikelihood)
print('The expected output is', p)
```
**Expected Output**:
- The expected output is around 1.57
- The sentiment is positive.
#### Implement test_naive_bayes
**Instructions**:
* Implement `test_naive_bayes` to check the accuracy of your predictions.
* The function takes in your `test_x`, `test_y`, log_prior, and loglikelihood
* It returns the accuracy of your model.
* First, use `naive_bayes_predict` function to make predictions for each tweet in text_x.
```
# UNQ_C6 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
def test_naive_bayes(test_x, test_y, logprior, loglikelihood):
"""
Input:
test_x: A list of tweets
test_y: the corresponding labels for the list of tweets
logprior: the logprior
loglikelihood: a dictionary with the loglikelihoods for each word
Output:
accuracy: (# of tweets classified correctly)/(total # of tweets)
"""
accuracy = 0 # return this properly
### START CODE HERE (REPLACE INSTANCES OF 'None' with your code) ###
y_hats = []
for tweet in test_x:
# if the prediction is > 0
if naive_bayes_predict(tweet, logprior, loglikelihood) > 0:
# the predicted class is 1
y_hat_i = 1
else:
# otherwise the predicted class is 0
y_hat_i = 0
# append the predicted class to the list y_hats
y_hats.append(y_hat_i)
# error is the average of the absolute values of the differences between y_hats and test_y
error = np.sum(np.abs(y_hats - test_y)) / test_y.shape[0]
# Accuracy is 1 minus the error
accuracy = 1 - error
### END CODE HERE ###
return accuracy
print("Naive Bayes accuracy = %0.4f" %
(test_naive_bayes(test_x, test_y, logprior, loglikelihood)))
```
**Expected Accuracy**:
0.9940
```
# UNQ_C7 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
# You do not have to input any code in this cell, but it is relevant to grading, so please do not change anything
# Run this cell to test your function
for tweet in ['I am happy', 'I am bad', 'this movie should have been great.', 'great', 'great great', 'great great great', 'great great great great']:
# print( '%s -> %f' % (tweet, naive_bayes_predict(tweet, logprior, loglikelihood)))
p = naive_bayes_predict(tweet, logprior, loglikelihood)
# print(f'{tweet} -> {p:.2f} ({p_category})')
print(f'{tweet} -> {p:.2f}')
```
**Expected Output**:
- I am happy -> 2.15
- I am bad -> -1.29
- this movie should have been great. -> 2.14
- great -> 2.14
- great great -> 4.28
- great great great -> 6.41
- great great great great -> 8.55
```
# Feel free to check the sentiment of your own tweet below
my_tweet = 'you are bad :('
naive_bayes_predict(my_tweet, logprior, loglikelihood)
```
# Part 4: Filter words by Ratio of positive to negative counts
- Some words have more positive counts than others, and can be considered "more positive". Likewise, some words can be considered more negative than others.
- One way for us to define the level of positiveness or negativeness, without calculating the log likelihood, is to compare the positive to negative frequency of the word.
- Note that we can also use the log likelihood calculations to compare relative positivity or negativity of words.
- We can calculate the ratio of positive to negative frequencies of a word.
- Once we're able to calculate these ratios, we can also filter a subset of words that have a minimum ratio of positivity / negativity or higher.
- Similarly, we can also filter a subset of words that have a maximum ratio of positivity / negativity or lower (words that are at least as negative, or even more negative than a given threshold).
#### Implement `get_ratio()`
- Given the `freqs` dictionary of words and a particular word, use `lookup(freqs,word,1)` to get the positive count of the word.
- Similarly, use the `lookup()` function to get the negative count of that word.
- Calculate the ratio of positive divided by negative counts
$$ ratio = \frac{\text{pos_words} + 1}{\text{neg_words} + 1} $$
Where pos_words and neg_words correspond to the frequency of the words in their respective classes.
<table>
<tr>
<td>
<b>Words</b>
</td>
<td>
Positive word count
</td>
<td>
Negative Word Count
</td>
</tr>
<tr>
<td>
glad
</td>
<td>
41
</td>
<td>
2
</td>
</tr>
<tr>
<td>
arriv
</td>
<td>
57
</td>
<td>
4
</td>
</tr>
<tr>
<td>
:(
</td>
<td>
1
</td>
<td>
3663
</td>
</tr>
<tr>
<td>
:-(
</td>
<td>
0
</td>
<td>
378
</td>
</tr>
</table>
```
# UNQ_C8 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
def get_ratio(freqs, word):
'''
Input:
freqs: dictionary containing the words
word: string to lookup
Output: a dictionary with keys 'positive', 'negative', and 'ratio'.
Example: {'positive': 10, 'negative': 20, 'ratio': 0.5}
'''
pos_neg_ratio = {'positive': 0, 'negative': 0, 'ratio': 0.0}
### START CODE HERE (REPLACE INSTANCES OF 'None' with your code) ###
# use lookup() to find positive counts for the word (denoted by the integer 1)
pos_neg_ratio['positive'] = lookup(freqs, word, 1)
# use lookup() to find negative counts for the word (denoted by integer 0)
pos_neg_ratio['negative'] = lookup(freqs, word, 0)
# calculate the ratio of positive to negative counts for the word
pos_neg_ratio['ratio'] = (pos_neg_ratio['positive'] + 1) / (pos_neg_ratio['negative'] + 1)
### END CODE HERE ###
return pos_neg_ratio
get_ratio(freqs, 'happi')
```
#### Implement `get_words_by_threshold(freqs,label,threshold)`
* If we set the label to 1, then we'll look for all words whose threshold of positive/negative is at least as high as that threshold, or higher.
* If we set the label to 0, then we'll look for all words whose threshold of positive/negative is at most as low as the given threshold, or lower.
* Use the `get_ratio()` function to get a dictionary containing the positive count, negative count, and the ratio of positive to negative counts.
* Append a dictionary to a list, where the key is the word, and the dictionary is the dictionary `pos_neg_ratio` that is returned by the `get_ratio()` function.
An example key-value pair would have this structure:
```
{'happi':
{'positive': 10, 'negative': 20, 'ratio': 0.5}
}
```
```
# UNQ_C9 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
def get_words_by_threshold(freqs, label, threshold):
'''
Input:
freqs: dictionary of words
label: 1 for positive, 0 for negative
threshold: ratio that will be used as the cutoff for including a word in the returned dictionary
Output:
word_set: dictionary containing the word and information on its positive count, negative count, and ratio of positive to negative counts.
example of a key value pair:
{'happi':
{'positive': 10, 'negative': 20, 'ratio': 0.5}
}
'''
word_list = {}
### START CODE HERE (REPLACE INSTANCES OF 'None' with your code) ###
for key in freqs.keys():
word, _ = key
# get the positive/negative ratio for a word
pos_neg_ratio = get_ratio(freqs, word)
# if the label is 1 and the ratio is greater than or equal to the threshold...
if label == 1 and pos_neg_ratio['ratio'] >= threshold:
# Add the pos_neg_ratio to the dictionary
word_list[word] = pos_neg_ratio
# If the label is 0 and the pos_neg_ratio is less than or equal to the threshold...
elif label == 0 and pos_neg_ratio['ratio'] <= threshold:
# Add the pos_neg_ratio to the dictionary
word_list[word] = pos_neg_ratio
# otherwise, do not include this word in the list (do nothing)
### END CODE HERE ###
return word_list
# Test your function: find negative words at or below a threshold
get_words_by_threshold(freqs, label=0, threshold=0.05)
# Test your function; find positive words at or above a threshold
get_words_by_threshold(freqs, label=1, threshold=10)
```
Notice the difference between the positive and negative ratios. Emojis like :( and words like 'me' tend to have a negative connotation. Other words like 'glad', 'community', and 'arrives' tend to be found in the positive tweets.
# Part 5: Error Analysis
In this part you will see some tweets that your model missclassified. Why do you think the misclassifications happened? Were there any assumptions made by the naive bayes model?
```
# Some error analysis done for you
print('Truth Predicted Tweet')
for x, y in zip(test_x, test_y):
y_hat = naive_bayes_predict(x, logprior, loglikelihood)
if y != (np.sign(y_hat) > 0):
print('%d\t%0.2f\t%s' % (y, np.sign(y_hat) > 0, ' '.join(
process_tweet(x)).encode('ascii', 'ignore')))
```
# Part 6: Predict with your own tweet
In this part you can predict the sentiment of your own tweet.
```
# Test with your own tweet - feel free to modify `my_tweet`
my_tweet = 'I am happy because I am learning :)'
p = naive_bayes_predict(my_tweet, logprior, loglikelihood)
print(p)
```
Congratulations on completing this assignment. See you next week!
|
github_jupyter
|
```
import keras
keras.__version__
```
# Using a pre-trained convnet
This notebook contains the code sample found in Chapter 5, Section 3 of [Deep Learning with Python](https://www.manning.com/books/deep-learning-with-python?a_aid=keras&a_bid=76564dff). Note that the original text features far more content, in particular further explanations and figures: in this notebook, you will only find source code and related comments.
----
A common and highly effective approach to deep learning on small image datasets is to leverage a pre-trained network. A pre-trained network
is simply a saved network previously trained on a large dataset, typically on a large-scale image classification task. If this original
dataset is large enough and general enough, then the spatial feature hierarchy learned by the pre-trained network can effectively act as a
generic model of our visual world, and hence its features can prove useful for many different computer vision problems, even though these
new problems might involve completely different classes from those of the original task. For instance, one might train a network on
ImageNet (where classes are mostly animals and everyday objects) and then re-purpose this trained network for something as remote as
identifying furniture items in images. Such portability of learned features across different problems is a key advantage of deep learning
compared to many older shallow learning approaches, and it makes deep learning very effective for small-data problems.
In our case, we will consider a large convnet trained on the ImageNet dataset (1.4 million labeled images and 1000 different classes).
ImageNet contains many animal classes, including different species of cats and dogs, and we can thus expect to perform very well on our cat
vs. dog classification problem.
We will use the VGG16 architecture, developed by Karen Simonyan and Andrew Zisserman in 2014, a simple and widely used convnet architecture
for ImageNet. Although it is a bit of an older model, far from the current state of the art and somewhat heavier than many other recent
models, we chose it because its architecture is similar to what you are already familiar with, and easy to understand without introducing
any new concepts. This may be your first encounter with one of these cutesie model names -- VGG, ResNet, Inception, Inception-ResNet,
Xception... you will get used to them, as they will come up frequently if you keep doing deep learning for computer vision.
There are two ways to leverage a pre-trained network: *feature extraction* and *fine-tuning*. We will cover both of them. Let's start with
feature extraction.
## Feature extraction
Feature extraction consists of using the representations learned by a previous network to extract interesting features from new samples.
These features are then run through a new classifier, which is trained from scratch.
As we saw previously, convnets used for image classification comprise two parts: they start with a series of pooling and convolution
layers, and they end with a densely-connected classifier. The first part is called the "convolutional base" of the model. In the case of
convnets, "feature extraction" will simply consist of taking the convolutional base of a previously-trained network, running the new data
through it, and training a new classifier on top of the output.
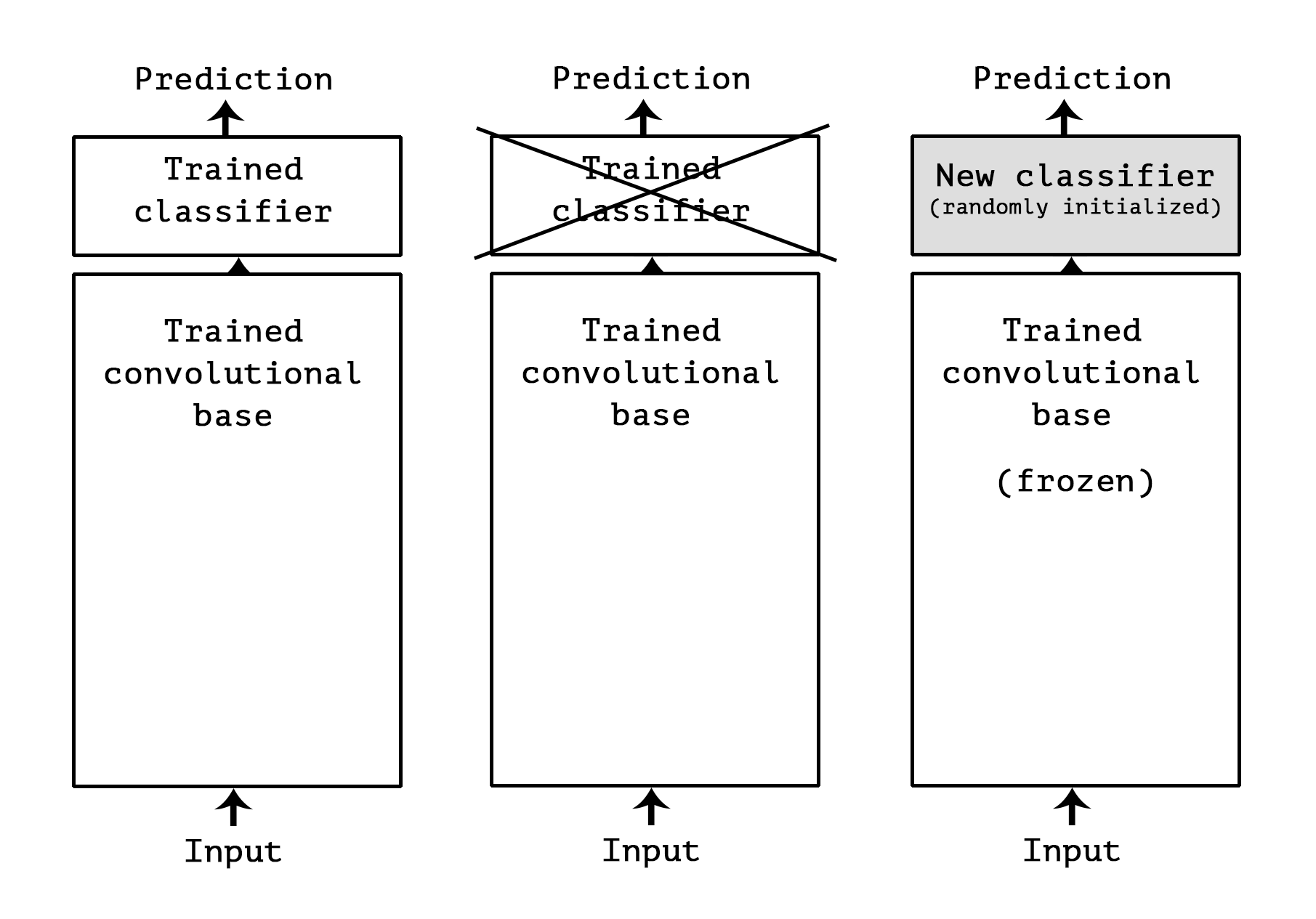
Why only reuse the convolutional base? Could we reuse the densely-connected classifier as well? In general, it should be avoided. The
reason is simply that the representations learned by the convolutional base are likely to be more generic and therefore more reusable: the
feature maps of a convnet are presence maps of generic concepts over a picture, which is likely to be useful regardless of the computer
vision problem at hand. On the other end, the representations learned by the classifier will necessarily be very specific to the set of
classes that the model was trained on -- they will only contain information about the presence probability of this or that class in the
entire picture. Additionally, representations found in densely-connected layers no longer contain any information about _where_ objects are
located in the input image: these layers get rid of the notion of space, whereas the object location is still described by convolutional
feature maps. For problems where object location matters, densely-connected features would be largely useless.
Note that the level of generality (and therefore reusability) of the representations extracted by specific convolution layers depends on
the depth of the layer in the model. Layers that come earlier in the model extract local, highly generic feature maps (such as visual
edges, colors, and textures), while layers higher-up extract more abstract concepts (such as "cat ear" or "dog eye"). So if your new
dataset differs a lot from the dataset that the original model was trained on, you may be better off using only the first few layers of the
model to do feature extraction, rather than using the entire convolutional base.
In our case, since the ImageNet class set did contain multiple dog and cat classes, it is likely that it would be beneficial to reuse the
information contained in the densely-connected layers of the original model. However, we will chose not to, in order to cover the more
general case where the class set of the new problem does not overlap with the class set of the original model.
Let's put this in practice by using the convolutional base of the VGG16 network, trained on ImageNet, to extract interesting features from
our cat and dog images, and then training a cat vs. dog classifier on top of these features.
The VGG16 model, among others, comes pre-packaged with Keras. You can import it from the `keras.applications` module. Here's the list of
image classification models (all pre-trained on the ImageNet dataset) that are available as part of `keras.applications`:
* Xception
* InceptionV3
* ResNet50
* VGG16
* VGG19
* MobileNet
Let's instantiate the VGG16 model:
```
from keras.applications import VGG16
conv_base = VGG16(weights='imagenet',
include_top=False,
input_shape=(150, 150, 3))
```
We passed three arguments to the constructor:
* `weights`, to specify which weight checkpoint to initialize the model from
* `include_top`, which refers to including or not the densely-connected classifier on top of the network. By default, this
densely-connected classifier would correspond to the 1000 classes from ImageNet. Since we intend to use our own densely-connected
classifier (with only two classes, cat and dog), we don't need to include it.
* `input_shape`, the shape of the image tensors that we will feed to the network. This argument is purely optional: if we don't pass it,
then the network will be able to process inputs of any size.
Here's the detail of the architecture of the VGG16 convolutional base: it's very similar to the simple convnets that you are already
familiar with.
```
conv_base.summary()
```
The final feature map has shape `(4, 4, 512)`. That's the feature on top of which we will stick a densely-connected classifier.
At this point, there are two ways we could proceed:
* Running the convolutional base over our dataset, recording its output to a Numpy array on disk, then using this data as input to a
standalone densely-connected classifier similar to those you have seen in the first chapters of this book. This solution is very fast and
cheap to run, because it only requires running the convolutional base once for every input image, and the convolutional base is by far the
most expensive part of the pipeline. However, for the exact same reason, this technique would not allow us to leverage data augmentation at
all.
* Extending the model we have (`conv_base`) by adding `Dense` layers on top, and running the whole thing end-to-end on the input data. This
allows us to use data augmentation, because every input image is going through the convolutional base every time it is seen by the model.
However, for this same reason, this technique is far more expensive than the first one.
We will cover both techniques. Let's walk through the code required to set-up the first one: recording the output of `conv_base` on our
data and using these outputs as inputs to a new model.
We will start by simply running instances of the previously-introduced `ImageDataGenerator` to extract images as Numpy arrays as well as
their labels. We will extract features from these images simply by calling the `predict` method of the `conv_base` model.
```
import os
import numpy as np
from keras.preprocessing.image import ImageDataGenerator
base_dir = '/Users/fchollet/Downloads/cats_and_dogs_small'
train_dir = os.path.join(base_dir, 'train')
validation_dir = os.path.join(base_dir, 'validation')
test_dir = os.path.join(base_dir, 'test')
datagen = ImageDataGenerator(rescale=1./255)
batch_size = 20
def extract_features(directory, sample_count):
features = np.zeros(shape=(sample_count, 4, 4, 512))
labels = np.zeros(shape=(sample_count))
generator = datagen.flow_from_directory(
directory,
target_size=(150, 150),
batch_size=batch_size,
class_mode='binary')
i = 0
for inputs_batch, labels_batch in generator:
features_batch = conv_base.predict(inputs_batch)
features[i * batch_size : (i + 1) * batch_size] = features_batch
labels[i * batch_size : (i + 1) * batch_size] = labels_batch
i += 1
if i * batch_size >= sample_count:
# Note that since generators yield data indefinitely in a loop,
# we must `break` after every image has been seen once.
break
return features, labels
train_features, train_labels = extract_features(train_dir, 2000)
validation_features, validation_labels = extract_features(validation_dir, 1000)
test_features, test_labels = extract_features(test_dir, 1000)
```
The extracted features are currently of shape `(samples, 4, 4, 512)`. We will feed them to a densely-connected classifier, so first we must
flatten them to `(samples, 8192)`:
```
train_features = np.reshape(train_features, (2000, 4 * 4 * 512))
validation_features = np.reshape(validation_features, (1000, 4 * 4 * 512))
test_features = np.reshape(test_features, (1000, 4 * 4 * 512))
```
At this point, we can define our densely-connected classifier (note the use of dropout for regularization), and train it on the data and
labels that we just recorded:
```
from keras import models
from keras import layers
from keras import optimizers
model = models.Sequential()
model.add(layers.Dense(256, activation='relu', input_dim=4 * 4 * 512))
model.add(layers.Dropout(0.5))
model.add(layers.Dense(1, activation='sigmoid'))
model.compile(optimizer=optimizers.RMSprop(lr=2e-5),
loss='binary_crossentropy',
metrics=['acc'])
history = model.fit(train_features, train_labels,
epochs=30,
batch_size=20,
validation_data=(validation_features, validation_labels))
```
Training is very fast, since we only have to deal with two `Dense` layers -- an epoch takes less than one second even on CPU.
Let's take a look at the loss and accuracy curves during training:
```
import matplotlib.pyplot as plt
acc = history.history['acc']
val_acc = history.history['val_acc']
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(len(acc))
plt.plot(epochs, acc, 'bo', label='Training acc')
plt.plot(epochs, val_acc, 'b', label='Validation acc')
plt.title('Training and validation accuracy')
plt.legend()
plt.figure()
plt.plot(epochs, loss, 'bo', label='Training loss')
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Training and validation loss')
plt.legend()
plt.show()
```
We reach a validation accuracy of about 90%, much better than what we could achieve in the previous section with our small model trained from
scratch. However, our plots also indicate that we are overfitting almost from the start -- despite using dropout with a fairly large rate.
This is because this technique does not leverage data augmentation, which is essential to preventing overfitting with small image datasets.
Now, let's review the second technique we mentioned for doing feature extraction, which is much slower and more expensive, but which allows
us to leverage data augmentation during training: extending the `conv_base` model and running it end-to-end on the inputs. Note that this
technique is in fact so expensive that you should only attempt it if you have access to a GPU: it is absolutely intractable on CPU. If you
cannot run your code on GPU, then the previous technique is the way to go.
Because models behave just like layers, you can add a model (like our `conv_base`) to a `Sequential` model just like you would add a layer.
So you can do the following:
```
from keras import models
from keras import layers
model = models.Sequential()
model.add(conv_base)
model.add(layers.Flatten())
model.add(layers.Dense(256, activation='relu'))
model.add(layers.Dense(1, activation='sigmoid'))
```
This is what our model looks like now:
```
model.summary()
```
As you can see, the convolutional base of VGG16 has 14,714,688 parameters, which is very large. The classifier we are adding on top has 2
million parameters.
Before we compile and train our model, a very important thing to do is to freeze the convolutional base. "Freezing" a layer or set of
layers means preventing their weights from getting updated during training. If we don't do this, then the representations that were
previously learned by the convolutional base would get modified during training. Since the `Dense` layers on top are randomly initialized,
very large weight updates would be propagated through the network, effectively destroying the representations previously learned.
In Keras, freezing a network is done by setting its `trainable` attribute to `False`:
```
print('This is the number of trainable weights '
'before freezing the conv base:', len(model.trainable_weights))
conv_base.trainable = False
print('This is the number of trainable weights '
'after freezing the conv base:', len(model.trainable_weights))
```
With this setup, only the weights from the two `Dense` layers that we added will be trained. That's a total of four weight tensors: two per
layer (the main weight matrix and the bias vector). Note that in order for these changes to take effect, we must first compile the model.
If you ever modify weight trainability after compilation, you should then re-compile the model, or these changes would be ignored.
Now we can start training our model, with the same data augmentation configuration that we used in our previous example:
```
from keras.preprocessing.image import ImageDataGenerator
train_datagen = ImageDataGenerator(
rescale=1./255,
rotation_range=40,
width_shift_range=0.2,
height_shift_range=0.2,
shear_range=0.2,
zoom_range=0.2,
horizontal_flip=True,
fill_mode='nearest')
# Note that the validation data should not be augmented!
test_datagen = ImageDataGenerator(rescale=1./255)
train_generator = train_datagen.flow_from_directory(
# This is the target directory
train_dir,
# All images will be resized to 150x150
target_size=(150, 150),
batch_size=20,
# Since we use binary_crossentropy loss, we need binary labels
class_mode='binary')
validation_generator = test_datagen.flow_from_directory(
validation_dir,
target_size=(150, 150),
batch_size=20,
class_mode='binary')
model.compile(loss='binary_crossentropy',
optimizer=optimizers.RMSprop(lr=2e-5),
metrics=['acc'])
history = model.fit_generator(
train_generator,
steps_per_epoch=100,
epochs=30,
validation_data=validation_generator,
validation_steps=50,
verbose=2)
model.save('cats_and_dogs_small_3.h5')
```
Let's plot our results again:
```
acc = history.history['acc']
val_acc = history.history['val_acc']
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(len(acc))
plt.plot(epochs, acc, 'bo', label='Training acc')
plt.plot(epochs, val_acc, 'b', label='Validation acc')
plt.title('Training and validation accuracy')
plt.legend()
plt.figure()
plt.plot(epochs, loss, 'bo', label='Training loss')
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Training and validation loss')
plt.legend()
plt.show()
```
As you can see, we reach a validation accuracy of about 96%. This is much better than our small convnet trained from scratch.
## Fine-tuning
Another widely used technique for model reuse, complementary to feature extraction, is _fine-tuning_.
Fine-tuning consists in unfreezing a few of the top layers
of a frozen model base used for feature extraction, and jointly training both the newly added part of the model (in our case, the
fully-connected classifier) and these top layers. This is called "fine-tuning" because it slightly adjusts the more abstract
representations of the model being reused, in order to make them more relevant for the problem at hand.
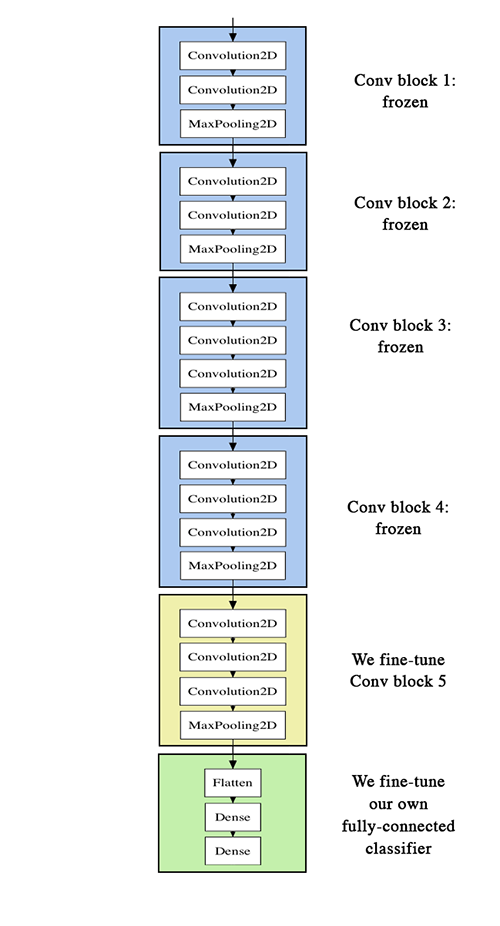
We have stated before that it was necessary to freeze the convolution base of VGG16 in order to be able to train a randomly initialized
classifier on top. For the same reason, it is only possible to fine-tune the top layers of the convolutional base once the classifier on
top has already been trained. If the classified wasn't already trained, then the error signal propagating through the network during
training would be too large, and the representations previously learned by the layers being fine-tuned would be destroyed. Thus the steps
for fine-tuning a network are as follow:
* 1) Add your custom network on top of an already trained base network.
* 2) Freeze the base network.
* 3) Train the part you added.
* 4) Unfreeze some layers in the base network.
* 5) Jointly train both these layers and the part you added.
We have already completed the first 3 steps when doing feature extraction. Let's proceed with the 4th step: we will unfreeze our `conv_base`,
and then freeze individual layers inside of it.
As a reminder, this is what our convolutional base looks like:
```
conv_base.summary()
```
We will fine-tune the last 3 convolutional layers, which means that all layers up until `block4_pool` should be frozen, and the layers
`block5_conv1`, `block5_conv2` and `block5_conv3` should be trainable.
Why not fine-tune more layers? Why not fine-tune the entire convolutional base? We could. However, we need to consider that:
* Earlier layers in the convolutional base encode more generic, reusable features, while layers higher up encode more specialized features. It is
more useful to fine-tune the more specialized features, as these are the ones that need to be repurposed on our new problem. There would
be fast-decreasing returns in fine-tuning lower layers.
* The more parameters we are training, the more we are at risk of overfitting. The convolutional base has 15M parameters, so it would be
risky to attempt to train it on our small dataset.
Thus, in our situation, it is a good strategy to only fine-tune the top 2 to 3 layers in the convolutional base.
Let's set this up, starting from where we left off in the previous example:
```
conv_base.trainable = True
set_trainable = False
for layer in conv_base.layers:
if layer.name == 'block5_conv1':
set_trainable = True
if set_trainable:
layer.trainable = True
else:
layer.trainable = False
```
Now we can start fine-tuning our network. We will do this with the RMSprop optimizer, using a very low learning rate. The reason for using
a low learning rate is that we want to limit the magnitude of the modifications we make to the representations of the 3 layers that we are
fine-tuning. Updates that are too large may harm these representations.
Now let's proceed with fine-tuning:
```
model.compile(loss='binary_crossentropy',
optimizer=optimizers.RMSprop(lr=1e-5),
metrics=['acc'])
history = model.fit_generator(
train_generator,
steps_per_epoch=100,
epochs=100,
validation_data=validation_generator,
validation_steps=50)
model.save('cats_and_dogs_small_4.h5')
```
Let's plot our results using the same plotting code as before:
```
acc = history.history['acc']
val_acc = history.history['val_acc']
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(len(acc))
plt.plot(epochs, acc, 'bo', label='Training acc')
plt.plot(epochs, val_acc, 'b', label='Validation acc')
plt.title('Training and validation accuracy')
plt.legend()
plt.figure()
plt.plot(epochs, loss, 'bo', label='Training loss')
plt.plot(epochs, val_loss, 'b', label='Validation loss')
plt.title('Training and validation loss')
plt.legend()
plt.show()
```
These curves look very noisy. To make them more readable, we can smooth them by replacing every loss and accuracy with exponential moving
averages of these quantities. Here's a trivial utility function to do this:
```
def smooth_curve(points, factor=0.8):
smoothed_points = []
for point in points:
if smoothed_points:
previous = smoothed_points[-1]
smoothed_points.append(previous * factor + point * (1 - factor))
else:
smoothed_points.append(point)
return smoothed_points
plt.plot(epochs,
smooth_curve(acc), 'bo', label='Smoothed training acc')
plt.plot(epochs,
smooth_curve(val_acc), 'b', label='Smoothed validation acc')
plt.title('Training and validation accuracy')
plt.legend()
plt.figure()
plt.plot(epochs,
smooth_curve(loss), 'bo', label='Smoothed training loss')
plt.plot(epochs,
smooth_curve(val_loss), 'b', label='Smoothed validation loss')
plt.title('Training and validation loss')
plt.legend()
plt.show()
```
These curves look much cleaner and more stable. We are seeing a nice 1% absolute improvement.
Note that the loss curve does not show any real improvement (in fact, it is deteriorating). You may wonder, how could accuracy improve if the
loss isn't decreasing? The answer is simple: what we display is an average of pointwise loss values, but what actually matters for accuracy
is the distribution of the loss values, not their average, since accuracy is the result of a binary thresholding of the class probability
predicted by the model. The model may still be improving even if this isn't reflected in the average loss.
We can now finally evaluate this model on the test data:
```
test_generator = test_datagen.flow_from_directory(
test_dir,
target_size=(150, 150),
batch_size=20,
class_mode='binary')
test_loss, test_acc = model.evaluate_generator(test_generator, steps=50)
print('test acc:', test_acc)
```
Here we get a test accuracy of 97%. In the original Kaggle competition around this dataset, this would have been one of the top results.
However, using modern deep learning techniques, we managed to reach this result using only a very small fraction of the training data
available (about 10%). There is a huge difference between being able to train on 20,000 samples compared to 2,000 samples!
## Take-aways: using convnets with small datasets
Here's what you should take away from the exercises of these past two sections:
* Convnets are the best type of machine learning models for computer vision tasks. It is possible to train one from scratch even on a very
small dataset, with decent results.
* On a small dataset, overfitting will be the main issue. Data augmentation is a powerful way to fight overfitting when working with image
data.
* It is easy to reuse an existing convnet on a new dataset, via feature extraction. This is a very valuable technique for working with
small image datasets.
* As a complement to feature extraction, one may use fine-tuning, which adapts to a new problem some of the representations previously
learned by an existing model. This pushes performance a bit further.
Now you have a solid set of tools for dealing with image classification problems, in particular with small datasets.
|
github_jupyter
|
# Filled Julia set
___
Let $C\in \mathbb{C}$ is fixed. A *Filled Julia set* $K_C$ is the set of $z\in \mathbb{C}$ which satisfy $\ f^n_C(z)$ $(n \ge 1)$is bounded :
$$K_C = \bigl\{ z\in \mathbb{C}\bigm|\{f^n_C(z)\}_{n\ge 1} : bounded\bigr\},$$
where $\ \ f^1_C(z) = f_C(z) = z^2 + C $, $\ \ f^n_C = f^{n-1}_C \circ f_C$.
For more details, see [Wikipedia--Filled Julia set](https://en.wikipedia.org/wiki/Filled_Julia_set).
___
```
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
def filledjulia(x_min, x_max, y_min, y_max, C, N, x_pix, y_pix, R):
'''
calculate where of z is in the Filled Julia set
'''
x = np.linspace(x_min, x_max, x_pix).astype(np.float32)
y = np.linspace(y_max, y_min, y_pix).reshape(y_pix, 1).astype(np.float32) * 1j
# below of y-axis is smaller
z = x + y #broadcasting by numpy
counter = np.zeros_like(z, dtype=np.uint32)
boolean = np.less(abs(z), R)
for i in range(N):
z[boolean] = z[boolean]**2 + C
boolean = np.less(abs(z), R)
if not boolean.any():
break # finish if all the elements of boolean are False
counter[boolean] += 1
return counter
def draw_fj(x_min, x_max, y_min, y_max, C, N,
x_pix=1000, y_pix=1000, R=5, colormap='viridis'):
'''
draw a Filled Julia set
'''
counter = filledjulia(x_min, x_max, y_min, y_max, C, N, x_pix, y_pix, R)
fig = plt.figure(figsize = (6, 6))
ax = fig.add_subplot(1,1,1)
ax.set_xticks(np.linspace(x_min, x_max, 5))
ax.set_yticks(np.linspace(y_min, y_max, 5))
ax.set_title("Filled Julia Set: C = {}".format(C))
plt.imshow(counter, extent=[x_min, x_max, y_min, y_max], cmap=colormap)
x_min = -1.5
x_max = 1.5
y_min = -1.5
y_max = 1.5
C = -0.835 - 0.235j
N = 200
colormap = 'prism'
draw_fj(x_min, x_max, y_min, y_max, C, N, colormap=colormap)
plt.savefig("./pictures/filled_julia{}.png".format(C), dpi=72)
x_min = -1.7
x_max = 1.7
y_min = -1.7
y_max = 1.7
C = -0.8 + 0.35j
N = 50
draw_fj(x_min, x_max, y_min, y_max, C, N)
plt.savefig("./pictures/filled_julia{}.png".format(C), dpi=72)
x_min = -1.5
x_max = 1.5
y_min = -1.5
y_max = 1.5
C = 0.25
N = 100
draw_fj(x_min, x_max, y_min, y_max, C, N)
plt.savefig("./pictures/filled_julia{}.png".format(C), dpi=72)
```
The complement of a Filled Julia set is called a *Fatou set*.
# Julia set
___
A *Julia set* $J_C$ is the **boundary** of a Filled Julia set:
$$J_C = \partial K_C.$$
For more details, see [Wikipedia--Julia set](https://en.wikipedia.org/wiki/Julia_set).
___
```
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
def find_1_boundary(pix, boolean):
'''
for each row,
if five or more "True" are arranged continuously,
rewrite it to "False" except two at each end.
'''
boolean = np.copy(boolean)
for i in range(pix):
if not boolean[i].any():
continue
coord = np.where(boolean[i])[0]
if len(coord) <= 5:
continue
for k in range(len(coord)-5):
if coord[k+5]-coord[k] == 5:
boolean[i, coord[k+3]] = False
return boolean
def findboundary(x_pix, y_pix, boolean):
'''
for each row and column, execute the function of 'find_1_boundary'.
'''
boundary_x = find_1_boundary(y_pix, boolean)
boundary_y = find_1_boundary(x_pix, boolean.transpose()).transpose()
boundary = boundary_x | boundary_y
return boundary
def julia(x_min, x_max, y_min, y_max, C, N, N_b, x_pix, y_pix, R):
'''
calculate where of z is a Julia set
if n >= N_b, find the boundary of the set.
'''
x = np.linspace(x_min, x_max, x_pix).astype(np.float32)
y = np.linspace(y_max, y_min, y_pix).reshape(y_pix, 1).astype(np.float32) * 1j
z = x + y
boundary = np.zeros_like(z, dtype=bool)
boolean = np.less(abs(z), R)
for i in range(N):
z[boolean] = z[boolean]**2 + C
boolean = np.less(abs(z), R)
if boolean.any() == False:
break
elif i >= N_b-1: # remember i starts 0
boundary = boundary | findboundary(x_pix, y_pix, boolean)
return boundary
def draw_j(x_min, x_max, y_min, y_max, C, N, N_b,
x_pix=1000, y_pix=1000, R=5, colormap='binary'):
'''
draw a Julia set
'''
boundary = julia(x_min, x_max, y_min, y_max, C, N, N_b, x_pix, y_pix, R)
fig = plt.figure(figsize = (6, 6))
ax = fig.add_subplot(1,1,1)
ax.set_xticks(np.linspace(x_min, x_max, 5))
ax.set_yticks(np.linspace(y_min, y_max, 5))
ax.set_title("Julia set: C = {}".format(C))
plt.imshow(boundary, extent=[x_min, x_max, y_min, y_max], cmap='binary')
x_min = -1.5
x_max = 1.5
y_min = -1.5
y_max = 1.5
C = -0.835 - 0.235j
N = 200
N_b = 30
draw_j(x_min, x_max, y_min, y_max, C, N, N_b)
plt.savefig("./pictures/julia{}.png".format(C), dpi=72)
x_min = -1.5
x_max = 1.5
y_min = -1.5
y_max = 1.5
C = -0.8 + 0.35j
N = 50
N_b = 20
draw_j(x_min, x_max, y_min, y_max, C, N, N_b)
plt.savefig("./pictures/julia{}.png".format(C), dpi=72)
x_min = -1.5
x_max = 1.5
y_min = -1.5
y_max = 1.5
C = 0.25
N = 30
N_b = 30
draw_j(x_min, x_max, y_min, y_max, C, N, N_b)
plt.savefig("./pictures/julia{}.png".format(C), dpi=72)
```
|
github_jupyter
|
```
!conda install --yes scikit-learn
!conda install --yes matplotlib
!conda install --yes seaborn
from sklearn.feature_selection import SelectFromModel
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import confusion_matrix
from sklearn import preprocessing
from sklearn.svm import LinearSVC
from sklearn import linear_model
import matplotlib.pyplot as plt
import datetime
import seaborn
import pandas
df = pandas.read_csv('../data/datasource.csv').set_index('Ocorrencia')
```
### Checking out duplicate values
Assuming that the 'Ocorrencia' is a unique code for the transaction itself. Let's check if there's any duplicated occurrence.
```python
len(df.index.unique())
```
If the dataset doesn't present any duplicated values, this piece of code should return, as output, 150.000 data entries. Nevertheless it returned only 64.958 values - meaning that this dataset presents around 85.042 duplicated data entries.
```python
len(df) - len(df.index.unique())
```
The duplicated values will be kept on analysis and training in modeling step. Due the nature of this dataset, this duplicate values could have been naturally generated - meaning that one occurrence could occur more than once - or, due the lack of available training material, some transactions could have been artificially generated.
--------------------------------
```
# Checking the number of unique values.
len(df.index.unique())
# Checking the number of duplicated entries.
len(df) - len(df.index.unique())
```
### Exploratory Analysis
Section aimed on checking the data distribution and data behaviour.
- N.A. values?
- Outliers?
- Min.
- Max.
- Mean.
- Stdev.
-------------------------
```
df.describe()
```
### Describe Analysis Result
This section summarizes the initial analysis on this dataset.
The command below allows to summarize each variable and retrieve the main statistical characteristics.
```python
df.describe()
```
The first thing to be noticed is at 'Sacado' variable - the amount of money withdrawn.
| Statistical Measurement | Value |
| :---------------------: | :----------: |
| Mean | -88.602261 |
| Standard Deviation | 247.302373 |
| Min | -19656.53 |
| Max | -0.00 |
How can be observed on this chart. The behaviour of 'Sacado' variable is pretty weird. First of all, this variable presents the highest standard deviation of all variables (247.30).
```python
df.describe().loc['std'].sort_values(ascending=False).head()
```
The mean, min and max values are pretty strange as well - with all of them being negative or null values. How this values could be negative/null values if this variable it was meant to represent the total withdrawn value of the transaction?
__Possible errors:__
- Acquistion errors?
- Parsing issues?
Other variables seems to behave pretty well (well distributed along the mean value - almost a normal curve) - even didn't knowing what they represent (the max values are high? the min values are low?).
_obs: Even with the lower deviation. On training, a simple normalization will be made on this dataset._
-------------
```
df.describe().loc['std'].sort_values(ascending=False).head()
df[df.Sacado >= 0]
```
### Some plots
On this section are plots for visualizing the dispersion of some 'random' variables.
----------------
```
df[['PP1', 'PP2', 'PP6', 'PP21']].hist()
# As it can be observed. The Sacado variable has a lot of outliers - removing and analysing it alone
# (for not disturbing the scale)
df[['PP1', 'PP2', 'PP21', 'PP6', 'Sacado']].boxplot()
# There are outliers on it - predicted it on histogram.
df[['PP1', 'PP2', 'PP6', 'PP21']].boxplot()
df[['Sacado']].boxplot()
```
### Seeking for N.A. values
This dataset does not present N.A./Blank values.
----------------------------
```
sum(df.index.isna())
dict_na = {
'columns': list(df.columns),
'na': []
}
for i in range(len(df.columns)):
dict_na.get('na').append(sum(df[df.columns[i]].isna()))
pandas.DataFrame(dict_na).set_index('columns')
```
### Does this dataset is non-balanced?
This section aims on checking if the dataset is non-balanced - are more frauds than non-frauds? Vice-Versa?
Table below assumes that the y variable - Fraude - has only 2 unique values - presented in table.
```python
df.Fraude.unique()
```
| Value | Meaning | Total | Percentage |
| :---: | :-------: | :------: | :--------: |
| 0 | Non Fraud | 149.763 | 99,842 % |
| 1 | Fraud | 237 | 0,0158 % |
As can be observed on the table above. It's been assumed that 0 represents a non-fraudulent transaction and 1 represents a fraudulent transaction. This dataset is pretty unbalanced - with less than 1 % being fraudulent transactions (237 data entries). This scenario, on model training steps would be a problem - the model probably will be overfitted in fraudulents occurrences. To prevent it, it must be added some new - artificially generated or naturally acquired - fraudulents data entries.
----------------------------------------
```
# Checking how many unique entries this variable presents.
df.Fraude.unique()
# Checking how many data entries are non-fraud or 0
print(len(df[df['Fraude'] == 0]))
# Checking the percentage of non-fraud transactions
print(len(df[df['Fraude'] == 0])/len(df.Fraude))
# Checking how many data entries are fraud or 1
len(df[df['Fraude'] == 1])
# Checking the percentage of fraud transactions
print(len(df[df['Fraude'] == 1])/len(df.Fraude))
```
### Dimensionality Reduction
This section aims on reduct the dimensionality of this dataset.
__It can be used:__
- linear regression, correlation and statistically relevance;
- PCA;
_obs: despite the robustness of PCA, some articles presents issues on its performance - losing to simpler techniques._
-----------------------
```
occurrence = pandas.Series(df.index)
x = pandas.DataFrame(df[df.columns[1:-1]])
y = pandas.DataFrame(df[df.columns[-1]])
# Multiple Linear Regression
lm = linear_model.LinearRegression().fit(x, y)
attr_reduction = SelectFromModel(lm, prefit=True)
df_pca = pandas.DataFrame(attr_reduction.transform(x))
```
### Building Predictors
Three models will be implemented - if none of them supply the needs, new models could be choosen - and compared. Not only the assertiveness rate will be considered. The most problematic issue are False Negatives occurences - when the occurrence is Fraudulent however the model classified it as a Non-fraudulent occurence - if this happens the model will "lose" some points. False positives could be sent to a human validation - not so problematic as False Negatives.
__Models__:
- Linear Regression;
- Support Vector Machines;
- Random Forest.
_obs: Random forest classifier, when compared with other classifiers, presented 1 advantage point and 1 disavantage point - it wasn't able to converge in polynomial time (when compared to Linear Regression and SVM's times - much bigger time to converge), however it presented the most precise classifiers between all 3 - With lesser False Negatives._
_obs: Due the results. A grid search with SVM and Random Forest will not be needed_
On this scenario, even with time complexity being an issue - when pipelined in production - the random forest will be chosen into "production" step.
_obs: My concerns come to reality. All 3 models classifies pretty well non fraudulent transactions. However - due the lack of data - all 3 - at some point and in some level - presented an overfitting in classifying Fraudulent transactions - a further study will be made with Random Forest - the model with the most precise behaviour._
------------------------
```
def data_separation(df, proportion=0.2):
"""
Data separation method.
"""
return train_test_split(df, test_size=proportion)
def time_screening(dt):
"""
Fitting time performance calculator.
"""
print(datetime.datetime.now() - dt)
results = {
'linear_model': {
'train': [],
'test': [],
'validation': []
},
'svm': {
'train': [],
'test': [],
'validation': []
},
'random_forest': {
'train': [],
'test': [],
'validation': []
}
}
train, test = data_separation(df)
test, validation = data_separation(test, 0.4)
# Splitting into train - x and y
x_train = pandas.DataFrame(train[train.columns[0:-1]])
y_train = pandas.DataFrame(train[train.columns[-1]])
# Splitting into test - x and y
x_test = pandas.DataFrame(test[test.columns[0:-1]])
y_test = pandas.DataFrame(test[test.columns[-1]])
# Splitting into validation - x and y
x_validation = pandas.DataFrame(validation[validation.columns[0:-1]])
y_validation = pandas.DataFrame(validation[validation.columns[-1]])
# Multiple Linear Regression
begin = datetime.datetime.now()
lm = linear_model.LinearRegression().fit(x_train, y_train)
time_screening(begin)
y_train['Predicted'] = lm.predict(x_train)
y_train['Predicted'] = y_train['Predicted'].astype(int)
y_test['Predicted'] = lm.predict(x_test)
y_test['Predicted'] = y_test['Predicted'].astype(int)
y_validation['Validation'] = lm.predict(x_validation)
y_validation['Validation'] = y_validation['Validation'].astype(int)
results.get('linear_model')['train'] = len(y_train[y_train['Fraude'] == y_train['Predicted']])/len(y_train)
results.get('linear_model')['test'] = len(y_test[y_test['Fraude'] == y_test['Predicted']])/len(y_test)
results.get('linear_model')['validation'] = len(y_validation[y_validation['Fraude'] == y_validation['Validation']])/len(y_validation)
pandas.DataFrame(confusion_matrix(y_train[['Fraude']], y_train[['Predicted']]),
['Non Fraud', 'Fraud'], ['Non Fraud', 'Fraud'])
pandas.DataFrame(confusion_matrix(y_test[['Fraude']], y_test[['Predicted']]),
['Non Fraud', 'Fraud'], ['Non Fraud', 'Fraud'])
pandas.DataFrame(confusion_matrix(y_validation[['Fraude']], y_validation[['Validation']]),
['Non Fraud', 'Fraud'], ['Non Fraud', 'Fraud'])
# Linear Support Vector Machine
begin = datetime.datetime.now()
lsvc = LinearSVC(C=0.01, penalty="l1", dual=False, max_iter=10000).fit(x_train, y_train.Fraude.values)
time_screening(begin)
y_train['Predicted'] = lsvc.predict(x_train)
y_train['Predicted'] = y_train['Predicted'].astype(int)
y_test['Predicted'] = lsvc.predict(x_test)
y_test['Predicted'] = y_test['Predicted'].astype(int)
y_validation['Validation'] = lsvc.predict(x_validation)
y_validation['Validation'] = y_validation['Validation'].astype(int)
results.get('svm')['train'] = len(y_train[y_train['Fraude'] == y_train['Predicted']])/len(y_train)
results.get('svm')['test'] = len(y_test[y_test['Fraude'] == y_test['Predicted']])/len(y_test)
results.get('svm')['validation'] = len(y_validation[y_validation['Fraude'] == y_validation['Validation']])/len(y_validation)
pandas.DataFrame(confusion_matrix(y_train[['Fraude']], y_train[['Predicted']]),
['Non Fraud', 'Fraud'], ['Non Fraud', 'Fraud'])
pandas.DataFrame(confusion_matrix(y_test[['Fraude']], y_test[['Predicted']]),
['Non Fraud', 'Fraud'], ['Non Fraud', 'Fraud'])
pandas.DataFrame(confusion_matrix(y_validation[['Fraude']], y_validation[['Validation']]),
['Non Fraud', 'Fraud'], ['Non Fraud', 'Fraud'])
# Random Forest
begin = datetime.datetime.now()
r_forest = RandomForestClassifier(n_estimators=90).fit(x_train, y_train.Fraude.values)
time_screening(begin)
y_train['Predicted'] = r_forest.predict(x_train)
y_train['Predicted'] = y_train['Predicted'].astype(int)
y_test['Predicted'] = r_forest.predict(x_test)
y_test['Predicted'] = y_test['Predicted'].astype(int)
y_validation['Validation'] = r_forest.predict(x_validation)
y_validation['Validation'] = y_validation['Validation'].astype(int)
results.get('random_forest')['train'] = len(y_train[y_train['Fraude'] == y_train['Predicted']])/len(y_train)
results.get('random_forest')['test'] = len(y_test[y_test['Fraude'] == y_test['Predicted']])/len(y_test)
results.get('random_forest')['validation'] = len(y_validation[y_validation['Fraude'] == y_validation['Validation']])/len(y_validation)
pandas.DataFrame(confusion_matrix(y_train[['Fraude']], y_train[['Predicted']]),
['Non Fraud', 'Fraud'], ['Non Fraud', 'Fraud'])
pandas.DataFrame(confusion_matrix(y_test[['Fraude']], y_test[['Predicted']]),
['Non Fraud', 'Fraud'], ['Non Fraud', 'Fraud'])
pandas.DataFrame(confusion_matrix(y_validation[['Fraude']], y_validation[['Validation']]),
['Non Fraud', 'Fraud'], ['Non Fraud', 'Fraud'])
pandas.DataFrame(results)
```
### Using selected model in "production" environment
- Normalize data
- Split data
- fit and predict model
-----------------------------------------------------
```
# Data Normalization
scaler = preprocessing.MinMaxScaler().fit(df_pca)
df_pca_norm = pandas.DataFrame(scaler.transform(df_pca))
df_pca_norm['Occurrence'] = occurrence
df_pca_norm.set_index('Occurrence', drop=True, inplace=True)
# Data separation
df_pca_norm['Fraude'] = y
train, test = data_separation(df_pca_norm)
test, validation = data_separation(test, 0.4)
# Splitting into train - x and y
x_train = pandas.DataFrame(train[train.columns[0:-1]])
y_train = pandas.DataFrame(train[train.columns[-1]])
# Splitting into test - x and y
x_test = pandas.DataFrame(test[test.columns[0:-1]])
y_test = pandas.DataFrame(test[test.columns[-1]])
# Splitting into validation - x and y
x_validation = pandas.DataFrame(validation[validation.columns[0:-1]])
y_validation = pandas.DataFrame(validation[validation.columns[-1]])
# Random Forest
begin = datetime.datetime.now()
r_forest = RandomForestClassifier(n_estimators=90).fit(x_train, y_train.Fraude.values)
time_screening(begin)
y_train['Predicted'] = r_forest.predict(x_train)
y_train['Predicted'] = y_train['Predicted'].astype(int)
y_test['Predicted'] = r_forest.predict(x_test)
y_test['Predicted'] = y_test['Predicted'].astype(int)
y_validation['Validation'] = r_forest.predict(x_validation)
y_validation['Validation'] = y_validation['Validation'].astype(int)
print(len(y_train[y_train['Fraude'] == y_train['Predicted']])/len(y_train))
print(len(y_test[y_test['Fraude'] == y_test['Predicted']])/len(y_test))
print(len(y_validation[y_validation['Fraude'] == y_validation['Validation']])/len(y_validation))
pandas.DataFrame(confusion_matrix(y_train[['Fraude']], y_train[['Predicted']]),
['Non Fraud', 'Fraud'], ['Non Fraud', 'Fraud'])
pandas.DataFrame(confusion_matrix(y_test[['Fraude']], y_test[['Predicted']]),
['Non Fraud', 'Fraud'], ['Non Fraud', 'Fraud'])
pandas.DataFrame(confusion_matrix(y_validation[['Fraude']], y_validation[['Validation']]),
['Non Fraud', 'Fraud'], ['Non Fraud', 'Fraud'])
# Checking if there's overfitting on classifying Frauds - due the low quantity of data entries
overfitting = x_validation
overfitting['Fraude'] = y_validation['Fraude']
aux = x_test
aux['Fraude'] = y_test['Fraude']
overfitting = overfitting.append(aux)
overfitting = overfitting[overfitting['Fraude'] == 1]
del(aux)
overfitting['Predicted'] = r_forest.predict(overfitting.drop(columns=['Fraude']))
# Decay of assertiveness rate
print(len(overfitting[overfitting['Fraude'] == overfitting['Predicted']])/len(overfitting))
pandas.DataFrame(confusion_matrix(overfitting[['Fraude']], overfitting[['Predicted']]),
['Non Fraud', 'Fraud'], ['Non Fraud', 'Fraud'])
```
### Summarizing
Section aimed on summarizing the methodology of this study and concluding it.
#### Checking duplicated values
Assuming that the 'Ocorrencia' is a unique code for the transaction itself. Let's check if there's any duplicated occurrence.
```python
len(df.index.unique())
```
If the dataset doesn't present any duplicated values, this piece of code should return, as output, 150.000 data entries. Nevertheless it returned only 64.958 values - meaning that this dataset presents around 85.042 duplicated data entries.
```python
len(df) - len(df.index.unique())
```
The duplicated values will be kept on analysis and training in modeling step. Due the nature of this dataset, this duplicate values could have been naturally generated - meaning that one occurrence could occur more than once - or, due the lack of available training material, some transactions could have been artificially generated.
----------------------------
#### Exploratory Analysis
Section aimed on checking the data distribution and data behaviour.
- N.A. values?
- Outliers?
- Min.
- Max.
- Mean.
- Stdev.
-------------------------
#### Describe Exploratory Analysis Result
This section summarizes the initial analysis on this dataset.
The command below allows to summarize each variable and retrieve the main statistical characteristics.
```python
df.describe()
```
The first thing to be noticed is at 'Sacado' variable - the amount of money withdrawn.
| Statistical Measurement | Value |
| :---------------------: | :----------: |
| Mean | -88.602261 |
| Standard Deviation | 247.302373 |
| Min | -19656.53 |
| Max | -0.00 |
How can be observed on this chart. The behaviour of 'Sacado' variable is pretty weird. First of all, this variable presents the highest standard deviation of all variables (247.30).
```python
df.describe().loc['std'].sort_values(ascending=False).head()
```
The mean, min and max values are pretty strange as well - with all of them being negative or null values. How this values could be negative/null values if this variable it was meant to represent the total withdrawn value of the transaction?
__Possible errors:__
- Acquistion errors?
- Parsing issues?
Other variables seems to behave pretty well (well distributed along the mean value - almost a normal curve) - even didn't knowing what they represent (the max values are high? the min values are low?).
_obs: Even with the lower deviation. On training, a simple normalization will be made on this dataset._
-------------
#### Does this dataset is non-balanced?
This section aims on checking if the dataset is non-balanced - are more frauds than non-frauds? Vice-Versa?
Table below assumes that the y variable - Fraude - has only 2 unique values - presented in table.
```python
df.Fraude.unique()
```
| Value | Meaning | Total | Percentage |
| :---: | :-------: | :------: | :--------: |
| 0 | Non Fraud | 149.763 | 0,9984 |
| 1 | Fraud | 237 | 0,0015 |
As can be observed on the table above. It's been assumed that 0 represents a non-fraudulent transaction and 1 represents a fraudulent transaction. This dataset is pretty unbalanced - with less than 1 % being fraudulent transactions (237 data entries). This scenario, on model training steps would be a problem - the model probably will be overfitted in fraudulents occurrences. To prevent it, it must be added some new - artificially generated or naturally acquired - fraudulents data entries.
----------------------------------------
#### Dimensionality Reduction
This section aims on reduct the dimensionality of this dataset.
__It can be used:__
- linear regression, correlation and statistically relevance;
- PCA;
_obs: despite the robustness of PCA, some articles presents issues on its performance - losing to simpler techniques._
-----------------------
#### Building Predictors
Three models will be implemented - if none of them supply the needs, new models could be choosen - and compared. Not only the assertiveness rate will be considered. The most problematic issue are False Negatives occurences - when the occurrence is Fraudulent however the model classified it as a Non-fraudulent occurence - if this happens the model will "lose" some points. False positives could be sent to a human validation - not so problematic as False Negatives.
__Models__:
- Linear Regression;
- Support Vector Machines;
- Random Forest.
_obs: Random forest classifier, when compared with other classifiers, presented 1 advantage point and 1 disavantage point - it wasn't able to converge in polynomial time (when compared to Linear Regression and SVM's times - much bigger time to converge), however it presented the most precise classifiers between all 3 - With lesser False Negatives._
_obs: Due the results. A grid search with SVM and Random Forest will not be needed_
On this scenario, even with time complexity being an issue - when pipelined in production - the random forest will be chosen into "production" step.
_obs: My concerns come to reality. All 3 models classifies pretty well non fraudulent transactions. However - due the lack of data - all 3 - at some point and in some level - presented an overfitting in classifying Fraudulent transactions - a further study will be made with Random Forest - the model with the most precise behaviour._
------------------------
#### Using selected model - Random Forest - in "production" environment
__Steps:__
- Normalize data;
- Split data;
- fit and predict model.
Due the normalization and - mainly - the dim reduction, the Random Forest's time performance has increased. During the development time the fitting time was about 0:01:50.102289. In _"production"_ time this time has decresead to 0:00:48.581284 - a time reduction of 0:01:01.521005.
```python
str(datetime.datetime.strptime('0:01:50.102289', '%H:%M:%S.%f') -
datetime.datetime.strptime('0:00:48.581284', '%H:%M:%S.%f'))
```
The model precision is presented in table below:
| Environment | Train | Test | Validation | Overfitting |
| :--------------: | :----: | :----: | :--------: | :---------: |
| Dev | 1,0000 | 0,9995 | 0,9995 | ----------- |
| Prod | 1,0000 | 0,9994 | 0,9993 | 0,7115 |
As could be observed. During the _"dev"_ time - without normalization and dimension reduction - the model achieved good results. The normalization - minmax normalization - and dimension reduction - from 29 variables to only 9 - achieved overwhelming results in time complexity - as mentioned before. Nevertheless, as mentioned, a further study on this model performance was required - __does the lack of fraudlent data overfits the model?__.
To test it the test and validation dataframes were merged and only fraudulent data was selected - resulting in a dataframe with 52 data entries (didn't include the train fraudulent data) - and passed to model predictor. The model should've predicted all as Frauds, however, the most problematic case appeared - Frauds classified as Non Frauds (False Negatives).<br>
In summary, a good non-fraud classifier was built - with little cases of False Positives (Non Frauds classified as Fraud) - however, as mentioned before, the most problematic case - False Negatives - occur more frequently. To correct it, appart from the selected model - since simpler until the most robust ones (Linear Regression, Bayes, Adaboost, Tree Classifiers, SVM's or Neural Nets) - it needed to add new fraudulent data entries on this dataset - artificially generated or not.
-----------------------------------------------------
|
github_jupyter
|
# 2. Beyond simple plotting
---
In this lecture we'll go a bit further with plotting.
We will:
- Create figures of different sizes;
- Use Numpy to generate data for plotting;
- Further change the appearance of our plots;
- Add multiple axes to the same figure.
```
from matplotlib import pyplot as plt
%matplotlib inline
```
### 2.1 Figures of different sizes
We can create figures with different sizes by specifying the `figsize` argument.
```
fig, axes = plt.subplots(figsize=(12,4))
```
---
### 2.2 Plotting Numpy data
The `plot` method also supports numpy arrays. For example, we canuse Numpy to plot a sine wave:
```
import numpy as np
# Create the data
x_values = np.linspace(-np.pi, np.pi, 200)
y_values = np.sin(x_values)
# Plot and show the figure
axes.plot(x_values, y_values,'--b')
fig
```
---
### 2.3 More options for you plots
We can use the `set_xlim` and `set_ylim` methods to change the range of the x and y axis.
```
axes.set_xlim([-np.pi, np.pi])
axes.set_ylim([-1, 1])
fig
```
Or use `axis('tight')` for automatically getting axis ranges that fit the data inside it (not as tightly as one would expect, though).
```
axes.axis('tight')
fig
```
We can add a grid with the `grid` method. See the [`grid` method documentation](https://matplotlib.org/api/_as_gen/matplotlib.axes.Axes.grid.html) for more information about different styles of grids.
```
axes.grid(linestyle='dashed', linewidth=0.5)
fig
```
Also, we can explicitly choose where we want the ticks in the x and y axis and their labels, with the methods `set_xticks`, `set_yticks`, `set_xticklabels` and `set_yticklabels`.
```
axes.set_xticks([-np.pi, -np.pi/2, 0, np.pi/2, np.pi])
axes.set_yticks([-1, -0.5, 0, 0.5, 1])
fig
axes.set_xticklabels([r'$-\pi$', r'$-\pi/2$', 0, r'$\pi/2$', r'$\pi$'])
axes.set_yticklabels([-1,r'$-\frac{1}{2}$',0,r'$\frac{1}{2}$',1])
fig
```
Finally, we can save a figure using the `savefig` method.
```
fig.savefig('filename.png')
```
---
### 2.4 Multiple axes in the same figure
To have multiple axes in the same figure, you can simply specify the arguments `nrows` and `ncols` when calling `subplots`.
```
fig, axes = plt.subplots(nrows=2, ncols=3)
```
To make the axis not overlap, we use the method `subplots_adjust`.
```
fig.subplots_adjust(hspace=0.6, wspace=0.6)
fig
```
And now we can simply plot in each individual axes separately.
```
axes[0][1].plot([1,2,3,4])
fig
axes[1,2].plot([4,4,4,2,3,3],'b--')
fig
axes[0][1].plot([2,2,2,-1],'-.o')
fig
```
---
|
github_jupyter
|
# Gromos Tutorial Pipeline
```
import os, sys
from pygromos.utils import bash
root_dir = os.getcwd()
#if package is not installed and path not set correct - this helps you out :)
sys.path.append(root_dir+"/..")
import pygromos
from pygromos.gromos.gromosPP import GromosPP
from pygromos.gromos.gromosXX import GromosXX
gromosPP_bin = None
gromosXX_bin = None
gromPP = GromosPP(gromosPP_bin)
gromXX = GromosXX(gromosXX_bin)
project_dir = os.path.abspath(os.path.dirname(pygromos.__file__)+"/../examples/example_files/Tutorial_System")
input_dir = project_dir+"/input"
```
## Build initial files
### generate Topology
#### build single topologies
```
from pygromos.data.ff import Gromos54A7
topo_dir = bash.make_folder(project_dir+'/a_topo')
## Make Cl-
sequence = "CL-"
solvent = "H2O"
top_cl = topo_dir+"/cl.top"
gromPP.make_top(in_building_block_lib_path=Gromos54A7.mtb,
in_parameter_lib_path=Gromos54A7.ifp,
in_sequence=sequence, in_solvent=solvent,out_top_path=top_cl)
## Make Peptide
sequence = "NH3+ VAL TYR ARG LYSH GLN COO-"
solvent = "H2O"
top_peptide = topo_dir+"/peptide.top"
gromPP.make_top(in_building_block_lib_path=Gromos54A7.mtb, in_parameter_lib_path=Gromos54A7.ifp,
in_sequence=sequence, in_solvent=solvent,out_top_path=top_peptide)
```
#### combine topology
```
top_system = topo_dir+"/vac_sys.top"
gromPP.com_top(in_topo_paths=[top_peptide, top_cl], topo_multiplier=[1,2], out_top_path=top_system)
```
### generate coordinates
```
coord_dir = bash.make_folder(project_dir+"/b_coord")
in_pdb = input_dir+"/peptide.pdb"
cnf_peptide = coord_dir+"/cnf_vacuum_peptide.cnf"
cnf_peptide = gromPP.pdb2gromos(in_pdb_path=in_pdb, in_top_path=top_peptide, out_cnf_path=cnf_peptide)
```
#### add hydrogens
```
cnf_hpeptide = coord_dir+"/vacuum_hpeptide.cnf"
cnf_hpeptide = gromPP.protonate(in_cnf_path=cnf_peptide, in_top_path=top_peptide, out_cnf_path=cnf_hpeptide)
```
#### cnf to pdb
```
out_pdb = coord_dir+"/vacuum_hpeptide.pdb"
out_pdb = gromPP.frameout(in_coord_path=cnf_hpeptide, in_top_path=top_peptide, out_file_path=out_pdb,
periodic_boundary_condition="v", out_file_format="pdb", time=0)
```
### energy minimization - Vacuum
```
from pygromos.data.simulation_parameters_templates import template_emin_vac
from pygromos.files.gromos_system import gromos_system
out_prefix = "vacuum_emin"
vacuum_emin_dir = bash.make_folder(project_dir+"/c_"+out_prefix)
os.chdir(vacuum_emin_dir)
grom_system = gromos_system.Gromos_System(work_folder=vacuum_emin_dir,
system_name="in_"+out_prefix,
in_top_path=top_peptide,
in_cnf_path=cnf_hpeptide,
in_imd_path=template_emin_vac)
grom_system.adapt_imd()
#del grom_system.imd.POSITIONRES
grom_system.imd.BOUNDCOND.NTB = 0
grom_system.write_files()
out_emin_vacuum = vacuum_emin_dir + "/" + out_prefix
gromXX.md_run(in_imd_path=grom_system.imd.path,
in_topo_path=grom_system.top.path,
in_coord_path=grom_system.cnf.path,
out_prefix=out_emin_vacuum)
cnf_emin_vacuum = out_emin_vacuum+".cnf"
cnf_emin_vacuum
```
## Solvatistation and Solvent Energy Minimization
### build box system
```
from pygromos.data.solvent_coordinates import spc
out_prefix = "box"
box_dir = bash.make_folder(project_dir+"/d_"+out_prefix)
cnf_box = gromPP.sim_box(in_top_path=top_peptide, in_cnf_path=cnf_emin_vacuum,in_solvent_cnf_file_path=spc,
out_cnf_path=box_dir+"/"+out_prefix+".cnf",
periodic_boundary_condition="r", minwall=0.8, threshold=0.23, rotate=True)
out_pdb = box_dir+"/"+out_prefix+".pdb"
out_pdb = gromPP.frameout(in_coord_path=cnf_box, in_top_path=top_peptide, out_file_path=out_pdb,
periodic_boundary_condition="r", out_file_format="pdb", include="ALL", time=0)
```
### Add Ions
```
out_prefix = "ion"
cnf_ion = gromPP.ion(in_cnf_path=cnf_box,
in_top_path=top_peptide,
out_cnf_path=box_dir+"/"+out_prefix+".cnf",
negative=[2, "CL-"],verbose=True )
```
### Energy Minimization BOX
```
from pygromos.data.simulation_parameters_templates import template_emin
from pygromos.files.gromos_system import gromos_system
out_prefix = "box_emin"
box_emin_dir = bash.make_folder(project_dir+"/e_"+out_prefix)
os.chdir(box_emin_dir)
grom_system = gromos_system.Gromos_System(work_folder=box_emin_dir,
system_name="in_"+out_prefix,
in_top_path=top_system,
in_cnf_path=cnf_ion,
in_imd_path=template_emin)
grom_system.adapt_imd()
grom_system.imd.STEP.NSTLIM = 3000
grom_system.imd.PRINTOUT.NTPR = 300
grom_system.write_files()
cnf_reference_position = grom_system.cnf.write_refpos(box_emin_dir+"/"+out_prefix+"_refpos.rpf")
cnf_position_restraint = grom_system.cnf.write_possrespec(box_emin_dir+"/"+out_prefix+"_posres.pos", residues=list(filter(lambda x: x != "SOLV", grom_system.cnf.get_residues())))
out_emin_box = box_emin_dir + "/" + out_prefix
gromXX.md_run(in_imd_path=grom_system.imd.path,
in_topo_path=grom_system.top.path,
in_coord_path=grom_system.cnf.path,
in_refpos_path=cnf_reference_position,
in_posresspec_path=cnf_position_restraint,
out_prefix=out_emin_box, verbose=True)
cnf_emin_box =out_emin_box+".cnf"
cnf_emin_box = gromPP.frameout(in_coord_path=cnf_emin_box, in_top_path=top_system, out_file_path=cnf_emin_box,
periodic_boundary_condition="r cog", out_file_format="cnf", include="ALL", time=0)
out_pdb = box_emin_dir+"/"+out_prefix+".pdb"
out_pdb = gromPP.frameout(in_coord_path=cnf_emin_box, in_top_path=top_system, out_file_path=out_pdb,
periodic_boundary_condition="r", out_file_format="pdb", include="ALL", time=0)
cnf_emin_box
```
## Simulation
### Equilibration NVP
To be implemented!
```
from pygromos.data.simulation_parameters_templates import template_md_tut as template_md
from pygromos.files.gromos_system import gromos_system
out_prefix = "eq_NVP"
eq_NVP_dir = bash.make_folder(project_dir+"/f_"+out_prefix)
os.chdir(eq_NVP_dir)
grom_system = gromos_system.Gromos_System(work_folder=eq_NVP_dir,
system_name="in_"+out_prefix,
in_top_path=top_system,
in_cnf_path=cnf_emin_box,
in_imd_path=template_md)
grom_system.adapt_imd(not_ligand_residues="CL-")
grom_system.imd.STEP.NSTLIM = 1000
grom_system.imd.WRITETRAJ.NTWX = 10
grom_system.imd.WRITETRAJ.NTWE = 10
grom_system.imd.INITIALISE.NTIVEL = 1
grom_system.imd.INITIALISE.NTISHK = 1
grom_system.imd.INITIALISE.NTISHI = 1
grom_system.imd.INITIALISE.NTIRTC = 1
grom_system.imd.randomize_seed()
grom_system.rebase_files()
grom_system.write_files()
out_eq_NVP = eq_NVP_dir + "/" + out_prefix
gromXX.md_run(in_imd_path=grom_system.imd.path,
in_topo_path=grom_system.top.path,
in_coord_path=grom_system.cnf.path,
out_tre=True, out_trc=True,
out_prefix=out_eq_NVP)
cnf_eq_NVP = out_eq_NVP+".cnf"
cnf_eq_NVP
```
### MD NVP
```
grom_system
from pygromos.data.simulation_parameters_templates import template_md
from pygromos.files.gromos_system import gromos_system
out_prefix = "md"
md_dir = bash.make_folder(project_dir+"/g_"+out_prefix)
os.chdir(md_dir)
grom_system = gromos_system.Gromos_System(work_folder=md_dir,
system_name="in_"+out_prefix,
in_top_path=top_system,
in_cnf_path=cnf_eq_NVP,
in_imd_path=template_md)
grom_system.adapt_imd(not_ligand_residues="CL-")
grom_system.imd.STEP.NSTLIM = 1000
grom_system.imd.WRITETRAJ.NTWX = 10
grom_system.imd.WRITETRAJ.NTWE = 10
grom_system.imd.INITIALISE.NTIVEL = 0
grom_system.rebase_files()
grom_system.write_files()
out_md = md_dir + "/" + out_prefix
gromXX.md_run(in_imd_path=grom_system.imd.path,
in_topo_path=grom_system.top.path,
in_coord_path=grom_system.cnf.path,
out_tre=True, out_trc=True,
out_prefix=out_md, verbose=True)
cnf_md = out_md+".cnf"
cnf_md
```
## Analysis
```
out_prefix = "ana"
md_dir = bash.make_folder(project_dir+"/h_"+out_prefix)
os.chdir(md_dir)
```
|
github_jupyter
|
```
import os
from glob import glob
import random
import torch
from torchvision import datasets as dset
from torchvision import transforms
from matplotlib import pyplot as plt
from torch.utils.data import DataLoader, Dataset
from tqdm.notebook import tqdm
from siamesenet import SiameseNet
from arguments import get_config
```
Download MNIST data
```
transformer = transforms.Compose([
transforms.Resize(105),
transforms.ToTensor(),
transforms.Normalize(mean=0.5,std=0.5)])
# If you run this code first time, make 'download' option True
test_data = dset.MNIST(root='MNIST_data/',train=False,transform=transformer, download=False)
test_image, test_label = test_data[0]
plt.imshow(test_image.squeeze().numpy(), cmap='gray')
plt.title('%i' % test_label)
plt.show()
print(test_image.size())
print('number of test data:', len(test_data))
```
Make Dataloader
```
class MNISTTest(Dataset):
def __init__(self, dataset,trial):
self.dataset = dataset
self.trial = trial
if trial > 950:
self.trial = 950
def __len__(self):
return self.trial * 10
def __getitem__(self, index):
share, remain = divmod(index,10)
label = (share//10)%10
image1 = self.dataset[label][share][0]
image2 = self.dataset[remain][random.randrange(len(self.dataset[remain]))][0]
return image1, image2, label
image_by_num = [[],[],[],[],[],[],[],[],[],[]]
for x,y in tqdm(test_data):
image_by_num[y].append(x)
test_data1 = MNISTTest(image_by_num,trial=950) #MAX trial = 950
test_loader = DataLoader(test_data1, batch_size=10)
```
Declare model and configuration
```
config = get_config()
config.num_model = "1"
config.logs_dir = "./result/1"
model = SiameseNet()
is_best = False
device = 'cuda' if torch.cuda.is_available() else 'cpu'
```
Load trained model
```
if is_best:
model_path = os.path.join(config.logs_dir, './models/best_model.pt')
else:
model_path = sorted(glob(config.logs_dir + './models/model_ckpt_*.pt'), key=len)[-1]
ckpt = torch.load(model_path)
model.load_state_dict(ckpt['model_state'])
model.to(device)
print(f"[*] Load model {os.path.basename(model_path)}, best accuracy {ckpt['best_valid_acc']}")
```
Test
```
correct_sum = 0
num_test = len(test_loader)
print(f"[*] Test on {num_test} pairs.")
pbar = tqdm(enumerate(test_loader), total=num_test, desc="Test")
for i, (x1, x2, y) in pbar:
# plt.figure(figsize=(20,7))
# plt.subplot(1,4,1)
# plt.title("Target")
# plt.imshow(x1[0].squeeze().numpy(), cmap='gray')
#
# s = 2
# for idx in range(10):
# plt.subplot(3,4,s)
# plt.title(idx)
# plt.imshow(x2[idx].squeeze().numpy(), cmap='gray')
# s += 1
# if s % 4 == 1:
# s += 1
# plt.show()
# break
if torch.cuda.is_available():
x1, x2, y = x1.to(device), x2.to(device), y.to(device)
x1, x2 = x1.unsqueeze(1), x2.unsqueeze(1)
# compute log probabilities
out = model(x1, x2)
y_pred = torch.sigmoid(out)
y_pred = torch.argmax(y_pred)
if y_pred == y[0].item():
correct_sum += 1
pbar.set_postfix_str(f"accuracy: {correct_sum} / {num_test}")
test_acc = (100. * correct_sum) / num_test
print(f"Test Acc: {correct_sum}/{num_test} ({test_acc:.2f}%)")
```
|
github_jupyter
|
```
import numpy as np
import heron
import heron.models.georgebased
generator = heron.models.georgebased.Heron2dHodlrIMR()
generator.parameters = ["mass ratio"]
times = np.linspace(-0.05, 0.05, 1000)
hp, hx = generator.mean({"mass ratio": 1}, times)
import matplotlib.pyplot as plt
%matplotlib inline
plt.plot(hp.data)
stimes = np.linspace(-0.15, 0.01, 1000)
hp, hx = generator.bilby(stimes, 65, 22, 1000).values()
%%timeit
hp, hx = generator.bilby(stimes, 65, 22, 1000).values()
plt.plot(stimes, hp)
plt.plot(stimes, hx)
import bilby
duration = 0.16
sampling_frequency = 4000
waveform = bilby.gw.waveform_generator.WaveformGenerator(
duration=duration, sampling_frequency=sampling_frequency,
time_domain_source_model=generator.bilby,
start_time=-0.15)
# inject the signal into three interferometers
ifos = bilby.gw.detector.InterferometerList(['L1'])
ifos.set_strain_data_from_power_spectral_densities(
sampling_frequency=sampling_frequency, duration=duration,
start_time=0)
injection_parameters = {"mass_1": 20, "mass_2": 20, "luminosity_distance": 400, "geocent_time": 0, "ra": 0, "dec": 0, "psi": 0}
ifos.inject_signal(waveform_generator=waveform,
parameters=injection_parameters);
priors = bilby.gw.prior.BBHPriorDict()
priors['mass_1'] = bilby.core.prior.Uniform(10, 30, name="mass_1")
priors['mass_2'] = bilby.core.prior.Uniform(10, 30, name="mass_2")
outdir="test_heron-2"
label="pe-test"
priors['geocent_time'] = bilby.core.prior.Uniform(
minimum=injection_parameters['geocent_time'] - 1,
maximum=injection_parameters['geocent_time'] + 1,
name='geocent_time', latex_label='$t_c$', unit='$s$')
for key in ['a_1', 'a_2', 'tilt_1', 'tilt_2', 'phi_12', 'phi_jl', 'psi', 'ra', 'theta_jn',
'dec', 'geocent_time', 'phase']:
if key in injection_parameters:
priors[key] = injection_parameters[key]
priors[key] = 0 #injection_parameters[key]
priors['luminosity_distance'] = 400
# Initialise the likelihood by passing in the interferometer data (ifos) and
# the waveform generator
likelihood = bilby.gw.GravitationalWaveTransient(
interferometers=ifos, waveform_generator=waveform)
# Run sampler. In this case we're going to use the `dynesty` sampler
result = bilby.run_sampler(
likelihood=likelihood, priors=priors, sampler='dynesty', npoints=10,
injection_parameters=injection_parameters, outdir=outdir, label=label)
# Make a corner plot.
result.plot_corner()
class HeronLikelihood(bilby.gw.likelihood.GravitationalWaveTransient)
def log_likelihood_ratio(self):
waveform_polarizations =\
self.waveform_generator.frequency_domain_strain(self.parameters)
if waveform_polarizations is None:
return np.nan_to_num(-np.inf)
d_inner_h = 0.
optimal_snr_squared = 0.
complex_matched_filter_snr = 0.
if self.time_marginalization:
if self.jitter_time:
self.parameters['geocent_time'] += self.parameters['time_jitter']
d_inner_h_tc_array = np.zeros(
self.interferometers.frequency_array[0:-1].shape,
dtype=np.complex128)
for interferometer in self.interferometers:
per_detector_snr = self.calculate_snrs(
waveform_polarizations=waveform_polarizations,
interferometer=interferometer)
d_inner_h += per_detector_snr.d_inner_h
optimal_snr_squared += np.real(per_detector_snr.optimal_snr_squared)
complex_matched_filter_snr += per_detector_snr.complex_matched_filter_snr
if self.time_marginalization:
d_inner_h_tc_array += per_detector_snr.d_inner_h_squared_tc_array
if self.time_marginalization:
log_l = self.time_marginalized_likelihood(
d_inner_h_tc_array=d_inner_h_tc_array,
h_inner_h=optimal_snr_squared)
if self.jitter_time:
self.parameters['geocent_time'] -= self.parameters['time_jitter']
elif self.distance_marginalization:
log_l = self.distance_marginalized_likelihood(
d_inner_h=d_inner_h, h_inner_h=optimal_snr_squared)
elif self.phase_marginalization:
log_l = self.phase_marginalized_likelihood(
d_inner_h=d_inner_h, h_inner_h=optimal_snr_squared)
else:
log_l = np.real(d_inner_h) - optimal_snr_squared / 2
return float(log_l.real)
```
|
github_jupyter
|
# Tutorial Part 10: Exploring Quantum Chemistry with GDB1k
Most of the tutorials we've walked you through so far have focused on applications to the drug discovery realm, but DeepChem's tool suite works for molecular design problems generally. In this tutorial, we're going to walk through an example of how to train a simple molecular machine learning for the task of predicting the atomization energy of a molecule. (Remember that the atomization energy is the energy required to form 1 mol of gaseous atoms from 1 mol of the molecule in its standard state under standard conditions).
## Colab
This tutorial and the rest in this sequence are designed to be done in Google colab. If you'd like to open this notebook in colab, you can use the following link.
[](https://colab.research.google.com/github/deepchem/deepchem/blob/master/examples/tutorials/10_Exploring_Quantum_Chemistry_with_GDB1k.ipynb)
## Setup
To run DeepChem within Colab, you'll need to run the following cell of installation commands. This will take about 5 minutes to run to completion and install your environment.
```
!curl -Lo conda_installer.py https://raw.githubusercontent.com/deepchem/deepchem/master/scripts/colab_install.py
import conda_installer
conda_installer.install()
!/root/miniconda/bin/conda info -e
!pip install --pre deepchem
import deepchem
deepchem.__version__
```
With our setup in place, let's do a few standard imports to get the ball rolling.
```
import os
import unittest
import numpy as np
import deepchem as dc
import numpy.random
from deepchem.utils.evaluate import Evaluator
from sklearn.ensemble import RandomForestRegressor
from sklearn.kernel_ridge import KernelRidge
```
The ntext step we want to do is load our dataset. We're using a small dataset we've prepared that's pulled out of the larger GDB benchmarks. The dataset contains the atomization energies for 1K small molecules.
```
tasks = ["atomization_energy"]
dataset_file = "../../datasets/gdb1k.sdf"
smiles_field = "smiles"
mol_field = "mol"
```
We now need a way to transform molecules that is useful for prediction of atomization energy. This representation draws on foundational work [1] that represents a molecule's 3D electrostatic structure as a 2D matrix $C$ of distances scaled by charges, where the $ij$-th element is represented by the following charge structure.
$C_{ij} = \frac{q_i q_j}{r_{ij}^2}$
If you're observing carefully, you might ask, wait doesn't this mean that molecules with different numbers of atoms generate matrices of different sizes? In practice the trick to get around this is that the matrices are "zero-padded." That is, if you're making coulomb matrices for a set of molecules, you pick a maximum number of atoms $N$, make the matrices $N\times N$ and set to zero all the extra entries for this molecule. (There's a couple extra tricks that are done under the hood beyond this. Check out reference [1] or read the source code in DeepChem!)
DeepChem has a built in featurization class `dc.feat.CoulombMatrixEig` that can generate these featurizations for you.
```
featurizer = dc.feat.CoulombMatrixEig(23, remove_hydrogens=False)
```
Note that in this case, we set the maximum number of atoms to $N = 23$. Let's now load our dataset file into DeepChem. As in the previous tutorials, we use a `Loader` class, in particular `dc.data.SDFLoader` to load our `.sdf` file into DeepChem. The following snippet shows how we do this:
```
# loader = dc.data.SDFLoader(
# tasks=["atomization_energy"], smiles_field="smiles",
# featurizer=featurizer,
# mol_field="mol")
# dataset = loader.featurize(dataset_file)
```
For the purposes of this tutorial, we're going to do a random split of the dataset into training, validation, and test. In general, this split is weak and will considerably overestimate the accuracy of our models, but for now in this simple tutorial isn't a bad place to get started.
```
# random_splitter = dc.splits.RandomSplitter()
# train_dataset, valid_dataset, test_dataset = random_splitter.train_valid_test_split(dataset)
```
One issue that Coulomb matrix featurizations have is that the range of entries in the matrix $C$ can be large. The charge $q_1q_2/r^2$ term can range very widely. In general, a wide range of values for inputs can throw off learning for the neural network. For this, a common fix is to normalize the input values so that they fall into a more standard range. Recall that the normalization transform applies to each feature $X_i$ of datapoint $X$
$\hat{X_i} = \frac{X_i - \mu_i}{\sigma_i}$
where $\mu_i$ and $\sigma_i$ are the mean and standard deviation of the $i$-th feature. This transformation enables the learning to proceed smoothly. A second point is that the atomization energies also fall across a wide range. So we apply an analogous transformation normalization transformation to the output to scale the energies better. We use DeepChem's transformation API to make this happen:
```
# transformers = [
# dc.trans.NormalizationTransformer(transform_X=True, dataset=train_dataset),
# dc.trans.NormalizationTransformer(transform_y=True, dataset=train_dataset)]
# for dataset in [train_dataset, valid_dataset, test_dataset]:
# for transformer in transformers:
# dataset = transformer.transform(dataset)
```
Now that we have the data cleanly transformed, let's do some simple machine learning. We'll start by constructing a random forest on top of the data. We'll use DeepChem's hyperparameter tuning module to do this.
```
# def rf_model_builder(model_params, model_dir):
# sklearn_model = RandomForestRegressor(**model_params)
# return dc.models.SklearnModel(sklearn_model, model_dir)
# params_dict = {
# "n_estimators": [10, 100],
# "max_features": ["auto", "sqrt", "log2", None],
# }
# metric = dc.metrics.Metric(dc.metrics.mean_absolute_error)
# optimizer = dc.hyper.HyperparamOpt(rf_model_builder)
# best_rf, best_rf_hyperparams, all_rf_results = optimizer.hyperparam_search(
# params_dict, train_dataset, valid_dataset, transformers,
# metric=metric)
```
Let's build one more model, a kernel ridge regression, on top of this raw data.
```
# def krr_model_builder(model_params, model_dir):
# sklearn_model = KernelRidge(**model_params)
# return dc.models.SklearnModel(sklearn_model, model_dir)
# params_dict = {
# "kernel": ["laplacian"],
# "alpha": [0.0001],
# "gamma": [0.0001]
# }
# metric = dc.metrics.Metric(dc.metrics.mean_absolute_error)
# optimizer = dc.hyper.HyperparamOpt(krr_model_builder)
# best_krr, best_krr_hyperparams, all_krr_results = optimizer.hyperparam_search(
# params_dict, train_dataset, valid_dataset, transformers,
# metric=metric)
```
# Congratulations! Time to join the Community!
Congratulations on completing this tutorial notebook! If you enjoyed working through the tutorial, and want to continue working with DeepChem, we encourage you to finish the rest of the tutorials in this series. You can also help the DeepChem community in the following ways:
## Star DeepChem on [GitHub](https://github.com/deepchem/deepchem)
This helps build awareness of the DeepChem project and the tools for open source drug discovery that we're trying to build.
## Join the DeepChem Gitter
The DeepChem [Gitter](https://gitter.im/deepchem/Lobby) hosts a number of scientists, developers, and enthusiasts interested in deep learning for the life sciences. Join the conversation!
# Bibliography:
[1] https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.98.146401
|
github_jupyter
|
<a href="https://colab.research.google.com/github/Chiebukar/Deep-Learning/blob/main/regression/temperature_forcasting_with_RNN.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
## Temperature Forcasting with Jena climate dataset
```
from google.colab import files
files.upload()
!mkdir -p ~/.kaggle
!cp kaggle.json ~/.kaggle/
!chmod 600 ~/.kaggle/kaggle.json
!kaggle datasets download -d kusuri/jena-climate
!ls -d $PWD/*
!unzip \*.zip && rm *.zip
!ls -d $PWD/*
file_dir = '/content/jena_climate_2009_2016.csv'
import numpy as np
import pandas as pd
jena_df = pd.read_csv(file_dir)
jena_df.head()
jena_df.shape
jena_df.columns
jena_arr = np.array(jena_df.iloc[:, 1:])
jena_arr[:2]
# standardize data
len_train = 200000
mean = jena_arr[:len_train].mean(axis=0)
std = jena_arr[:len_train].std(axis=0)
jena_arr = (jena_arr-mean)/std
# generator to yield batches of data from the recent past and future target
def generator(data, min_index, max_index , lookback= 1440, delay=144, step= 6, batch_size=18, shuffle=False):
"""
yield batches of data from the recent past and future target
data = original input data
min_index = minimum index of data to draw from
max_index maximum index of sata to draw from
lookback= Number of timestamps back for input data per target
delay = Number of timestamp in the future for target per lookback
steps = period in timestamps to sample data
batch_size = number of samples per batch
shuffle = To shuffle the samples or not
"""
if max_index == None:
max_index = len(data) - delay - 1
i = min_index + lookback
while 1:
if shuffle:
rows = np.random.randint(min_index + lookback, max_index, size= batch_size)
else:
if i + batch_size >= max_index:
i = min_index + lookback
rows = np.arange(i, min(i + batch_size, max_index))
i += len(rows)
samples = np.zeros((len(rows), lookback //step, data.shape[-1]))
targets = np.zeros((len(rows),))
for j, row in enumerate(rows):
indices = range(rows[j] - lookback, rows[j], step)
samples[j] = data[indices]
targets[j] = data[rows[j] + delay][1]
yield samples, targets
train_gen = generator(data= jena_arr,
min_index= 0,
max_index= 200000,
shuffle= True)
valid_gen = generator(data= jena_arr,
min_index= 200001,
max_index = 300000,
shuffle = True)
test_gen = generator(data = jena_arr,
min_index = 300001,
max_index = None,
shuffle= True)
# get validation and test steps
lookback = 1440
val_steps = (300000 - 200001 - lookback)
test_steps = (len(jena_arr) - 300001 - lookback)
# establish baseline
def evaluate_naive_method():
batch_maes = []
for step in range(val_steps):
samples, targets = next(valid_gen)
preds = samples[:, -1, 1]
mae = np.mean(np.abs(preds - targets))
batch_maes.append(mae)
return (np.mean(batch_maes))
# get baseline evaluation
mae = evaluate_naive_method()
celsius_mae = mae * std[1]
celsius_mae
from tensorflow import keras
from keras.models import Sequential
from keras.layers import Dense, LSTM, Dropout
from keras.callbacks import ModelCheckpoint
# build model
def build_model():
model = Sequential()
model.add(LSTM(32, dropout= 0.1, recurrent_dropout= 0.25,
return_sequences=True, input_shape = (None, jena_arr.shape[-1])))
model.add(LSTM(64, activation='tanh', dropout=0.5))
model.add(Dense(8, activation= 'relu'))
model.add(Dropout(0.1))
model.add(Dense(1))
model.compile(loss = 'mae', optimizer = 'rmsprop')
return model
file_path= 'a_weights.best.hdf5'
checkpoint = ModelCheckpoint(file_path, monitor= 'val_loss', save_best_only= True, verbose= 1, mode= 'min')
model = build_model()
history = model.fit(train_gen, steps_per_epoch = 500, epochs= 25, validation_data= valid_gen,
validation_steps = 500, callbacks= checkpoint)
history_df = pd.DataFrame(history.history)
history_df[['mae', 'val_mae']].plot()
```
|
github_jupyter
|
### PPO, Actor-Critic Style
_______________________
**for** iteration=1,2,... do<br>
**for** actor=1,2,...,N do<br>
Run policy $\pi_{\theta_{old}}$ in environment for T timesteps<br>
Compute advantage estimates $\hat{A}_1,\dots,\hat{A}_T$<br>
**end for**<br>
Optimize surrogate(代理人) L wrt $\theta$,with $K$ epochs and minibatch size $M \leq NT$<br>
$\theta_{old} \leftarrow \theta$<br>
**end for**
_______________________
### Loss Function L的数学公式为:
$$
L_t^{CLIP+VF+S}(\theta)=\hat{\mathbb{E}_t}[L_t^{CLIP}(\theta)-c_1L^{VF}_t(\theta)+c_2S[\pi_\theta](s_t)]
$$
其中,$L^{CLIP}(\theta)=\hat{\mathbb{E}_t}\big[min(r_t(\theta)\hat{A}_t,clip(r_t(\theta), 1-\epsilon,1+\epsilon)\hat{A}_t)\big]$, $r_t(\theta)=\frac{\pi_\theta(a_t|s_t)}{\pi_{\theta_{old}}(a_t|s_t)}$<br>
$L^{VF}_t=(V_\theta(s_t)-V_t^{targ})^2$ **critic loss**<br>
S 为奖励熵,保证足够多的探索(写A2C的时候已经OK)<br>
$c_1, c_2$为参数
#### $L^{CLIP}和r的关系如下(为了保证\pi_\theta和\pi_{\theta_{old}}的差值不会很大,满足TRPO中两者方差变化不大的要求)$:
<img src="../assets/PPO_CLIP.png">
### GAE(high-dimensional continuous control using Generalized Advantage Estimation)
We address the first challenge by using value functions to substantially reduce the variance of policy gradient estimates at the cost of some bias, with an exponentially-weighted estimator of the advantage function that is analogous to TD(λ). <br>
改进了advantage function的计算方式。将advantage function进行类似于TD(λ)的处理<br>
#### 推导过程
1. 原始的advantage function : $\delta^V_t=r_t+\gamma V(s_{t+1})−V(s_t)$
2. $在位置t时,其后k个 \delta 折扣相加$ :
$$
\begin{aligned}
\hat{A}^{(1)}_t&:=\delta^V_t&&=-V(s_t)+r_t+\gamma V(s_{t+1}) \\
\hat{A}^{(2)}_t&:=\delta^V_t+\gamma \delta^V_{t+1}&&=-V(s_t)+r_t+\gamma r_{t+1}+\gamma ^2 V(s_{t+2}) \\
\hat{A}^{(3)}_t&:=\delta^V_t+\gamma \delta^V_{t+1}+\gamma^2 \delta^V_{t+2}&&=-V(s_t)+r_t+\gamma r_{t+1}+\gamma^2 r_{t+2}+\gamma ^3 V(s_{t+3}) \\
\hat{A}_t^{(k)}&:=\sum_{l=0}^{k=1}\gamma^l\delta_{t+l}^V&&=-V(s_t)+r_t+\gamma r_{t+1}+\dots+\gamma^{k-1}r_{t+k-1}+\gamma^kV(s_{t+k})
\end{aligned}
$$
3. $k \to \infty, \gamma^kV(s_{t+k})$会变得非常非常非常小,So :
$$
\hat{A}_t^{(\infty)}=\sum^\infty_{l=0}\gamma^l\delta_{t+l}^V=-V(s_t)+\sum^\infty_{l=0}\gamma^lr_{t+l}
$$
4. 所以,$t$ 时刻的GAE可推导为 :
$$
\begin{aligned}
\hat{A}_t^{GAE(\gamma, \lambda)}&:=(1-\lambda)\big(\hat{A}_t^{(1)}+\lambda\hat{A}_t^{(2)}+\lambda^2\hat{A}_t^{(3)}+\dots\big)\\
&=(1-\lambda)\big(\delta_t^V+\lambda(\delta_t^V+\gamma\delta_{t+1}^V)+\lambda^2(\delta_t^V+\gamma\delta_{t+1}^V+\gamma^2\delta_{t+2}^V)+\dots\big)\\
&=(1-\lambda)\big(\delta^V_t(1+\lambda+\lambda^2+\dots)+\gamma\delta^V_{t+1}(\lambda+\lambda^2+\lambda^3+\dots)+\gamma^2\delta^V_{t+2}(\lambda^2+\lambda^3+\lambda^4+\dots)+\dots\big)\\
&=(1-\lambda)\big(\delta^V_t\big(\frac{1}{1-\lambda}\big)+\gamma\delta^V_{t+1}\big(\frac{\lambda}{1-\lambda}\big)+\gamma^2\delta^V_{t+2}\big(\frac{\lambda^2}{1-\lambda}\big)+\dots\big)\\
&=\underbrace{\delta^V_t+\gamma\lambda\delta^V_{t+1}+(\gamma\lambda)^2\delta^V_{t+2}+\dots}_{此处计算时使用这个公式(迭代计算)}\\
&=\sum_{l=0}^\infty(\gamma\lambda)^l\delta^V_{t+l}
\end{aligned}
$$
### 使用高斯分布(正态分布)来实现随机性策略控制连续动作空间
1. 高斯分布有两个重要的变量一个是均值 $\mu$ ,另一个是方差 $\sigma$ 。$\mu$ 为高斯函数的对称轴,$\frac{1}{\sqrt{2\pi}\sigma}$ 为高斯函数的最高点。高斯函数的积分为1。所以我们可以使用它来进行连续动作的sample。方差 $\sigma$ 越大,分布越分散,方差 $\sigma$ 越小,分布越集中。
2. $\mu$ 的选择很好把控,经过tanh处理之后+简单的数学变换,使nn输出的 $\mu$ 在env规定的动作空间内就可以
3. $\sigma$ 的选择,使用softplus函数对sigma进行处理。softplus 公式为$f(x)=\frac{1}{\beta}log(1+exp(\beta x))$, softplus 是 ReLU 的平滑近似值版本
4. 高斯分布公式:
$$
f(x)=\frac{1}{\sqrt{2\pi}\sigma}exp\bigg(-\frac{(x-\mu)^2}{2\sigma^2}\bigg)
$$
5. 和确定性策略相比,需要考虑每个state采取每个动作的概率,计算量确实比较大。
### TRPO
简单理解为一次on-policy到off-policy的转换<br>
但是为了保证old_policy和new_policy之间方差相差不会太大<br>
$$
\begin{aligned}
E_{X \sim p}[f(x)] & \approx \frac{1}{N}\sum^N_{i=1}f(x^i)\\
&= \int f(x)p(x)dx=\int f(x)\frac{p(x)}{q(x)}q(x)dx=E_{x \sim q}[f(x)\frac{p(x)}{q(x)}]
\end{aligned}
$$
由此,在两者期望相同的情况下,论证方差是否相同
$$
\begin{aligned}
两者期望:\quad&\because E_{X \sim p}[f(x)]=E_{x \sim q}[f(x)\frac{p(x)}{q(x)}]\\
方差公式:\quad&\because VAR[X]=E[X^2]-(E[X])^2\\
x \sim p 方差:\quad&\therefore Var_{x \sim p}[f(x)]=\color{red}{E_{x\sim p}[f(x)^2]}-(E_{x\sim p}[f(x)])^2\\
x \sim q 方差:\quad&\therefore Var_{x \sim q}[f(x)\frac{p(x)}{q(x)}]=E_{x \sim q}\big[\big([f(x)\frac{p(x)}{q(x)}\big)^2\big]-\big(E_{x\sim q}\big[f(x)\frac{p(x)}{q(x)}\big]\big)^2\\
&=\color{red}{E_{x \sim q}\big[f(x)^2\frac{p(x)}{q(x)}\big]}-(E_{x \sim p}[f(x)])^2
\end{aligned}
$$
两者方差公式的差别在标红的位置,也就是说我们如果使两者$E_{x\sim p}[f(x)^2]$和$E_{x \sim q}\big[f(x)^2\frac{p(x)}{q(x)}\big]$的差值较小,那么我们所做的off-policy就是可行的<br>
由此,可直观的看出,我们要使p(x)和q(x)的相差较小。因此就有了PPO1中的所使用的$\beta KL(\theta,\theta')$和PPO2中的clip这些都是为了限制两者的范围在一个可接受的合适空间
```
import gym
import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
from torch.distributions import Normal
from torch.distributions import Categorical
import torch.multiprocessing as mp
# from torch.utils.tensorboard import SummaryWriter
import numpy as np
from IPython.display import clear_output
import matplotlib.pyplot as plt
%matplotlib inline
import math
import random
from statistics import mean
import pdb
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
def plot_function():
x = np.arange(-10,10,0.05)
plt.figure(figsize=(9,3.6))
plt.subplot(121)
plt.title("Gaussian distribution")
mu, sigma = 0, 10
y = lambda x : np.exp(-((x-mu)**2)/(2*sigma**2))/(sigma*np.sqrt(2*np.pi))
plt.plot(x, y(x))
plt.subplot(122)
plt.title("Softplus")
y = np.log(1+np.exp(x))
plt.plot(x, y)
plt.show()
plot_function()
```
多线程又双叒叕来了
```
def worker(worker_id, master_end, worker_end, env_name):
master_end.close()
env = gym.make(env_name)
env.seed(worker_id)
while True:
cmd, data = worker_end.recv()
if cmd == 'step':
state, reward, done, info = env.step(data)
if done:
state = env.reset()
worker_end.send((state, reward, done, info))
elif cmd == 'reset':
state = env.reset()
worker_end.send(state)
elif cmd == 'reset_task':
state = env.reset_task()
worker_end.send(state)
elif cmd == 'close':
worker_end.close()
break
elif cmd == 'get_spaces':
worker_end.send((env.observation_space.shape[0], env.action_space.shape[0]))
else:
raise NotImplementedError
class ParallelEnv:
def __init__(self, n_train_processes, env_name):
self.nenvs = n_train_processes
self.waiting = False
self.closed = False
self.workers = []
self.env_name = env_name
self.master_ends, self.worker_ends = zip(*[mp.Pipe() for _ in range(self.nenvs)])
for worker_id, (master_end, worker_end) in enumerate(zip(self.master_ends, self.worker_ends)):
p = mp.Process(target=worker, args=(worker_id, master_end, worker_end, self.env_name))
p.daemon = False
p.start()
self.workers.append(p)
for worker_end in self.worker_ends:
worker_end.close()
self.master_ends[0].send(('get_spaces', None))
self.observation_space, self.action_space = self.master_ends[0].recv()
def step_async(self, actions):
for master_end, action in zip(self.master_ends, actions):
master_end.send(('step', action))
self.waiting = True
def step_wait(self):
results = [master_end.recv() for master_end in self.master_ends]
self.waiting = False
states, rewards, dones, infos = zip(*results)
return np.stack(states), np.stack(rewards), np.stack(dones), infos
def reset(self):
for master_end in self.master_ends:
master_end.send(('reset', None))
return np.stack([master_end.recv() for master_end in self.master_ends])
def step(self, actions):
self.step_async(actions)
return self.step_wait()
def close(self):
if self.closed:
return
if self.waiting:
[master_end.recv() for master_end in self.master_ends]
for master_end in self.master_ends:
master_end.send(('close', None))
del self.workers[:]
self.closed = True
```
定义网络
```
class Actor_critic(nn.Module):
def __init__(self, in_dim, out_dim):
super(Actor_critic, self).__init__()
self.actor_linear1 = nn.Linear(in_dim, 64)
self.critic_linear1 = nn.Linear(in_dim, 64)
self.linear2 = nn.Linear(64, 32)
self.actor_linear3 = nn.Linear(32, out_dim)
self.critic_linear3 = nn.Linear(32, 1)
self.sigma_linear = nn.Linear(32, out_dim)
def forward(self, x):
value_hidden = F.relu(self.linear2(F.relu(self.critic_linear1(x))))
value = self.critic_linear3(value_hidden)
actor_hidden = F.relu(self.linear2(F.relu(self.actor_linear1(x))))
mu = torch.tanh(self.actor_linear3(actor_hidden)) * 2
sigma = F.softplus(self.sigma_linear(actor_hidden))
dist = Normal(mu, sigma)
return dist, value
```
画图
```
def smooth_plot(factor, item, plot_decay):
item_x = np.arange(len(item))
item_smooth = [np.mean(item[i:i+factor]) if i > factor else np.mean(item[0:i+1])
for i in range(len(item))]
for i in range(len(item)// plot_decay):
item_x = item_x[::2]
item_smooth = item_smooth[::2]
return item_x, item_smooth
def plot(episode, rewards, losses):
clear_output(True)
rewards_x, rewards_smooth = smooth_plot(10, rewards, 500)
losses_x, losses_smooth = smooth_plot(10, losses, 100000)
plt.figure(figsize=(18, 10))
plt.subplot(211)
plt.title('episode %s. reward: %s'%(episode, rewards_smooth[-1]))
plt.plot(rewards, label="Rewards", color='lightsteelblue', linewidth='1')
plt.plot(rewards_x, rewards_smooth, label='Smothed_Rewards', color='darkorange', linewidth='3')
plt.legend(loc='best')
plt.subplot(212)
plt.title('Losses')
plt.plot(losses,label="Losses",color='lightsteelblue',linewidth='1')
plt.plot(losses_x, losses_smooth,
label="Smoothed_Losses",color='darkorange',linewidth='3')
plt.legend(loc='best')
plt.show()
def test_env():
state = env.reset()
done = False
total_reward = 0
while not done:
state = torch.FloatTensor(state).reshape(-1, 3).to(device)
log_prob, _ = model(state)
next_state, reward, done, _ = env.step(log_prob.sample().cpu().numpy())
state = next_state
total_reward += reward
return total_reward
def gae_compute(next_value, rewards, masks, values, gamma=0.99, tau=0.95):
td_target = next_value
td_target_list = []
advantage = 0
advantage_list = []
for idx in reversed(range(len(values))):
td_target = td_target * gamma * masks[idx] + rewards[idx]
td_target_list.insert(0, td_target)
advantage = td_target - values[idx] + advantage * gamma * tau
advantage_list.insert(0, advantage)
return advantage_list, td_target_list
```
PPO训练更新
```
import pdb
def ppo_iter(states, actions, log_probs, advantages, td_target_list):
batch_size = actions.size(0)
for _ in range(batch_size // mini_batch_size):
ids = np.random.choice(batch_size, mini_batch_size, replace=False)
yield states[ids, :], actions[ids, :], log_probs[ids, :], advantages[ids, :], td_target_list[ids, :]
def ppo_train(states, actions, log_probs, advantages, td_target_list, clip_param=0.2):
losses = []
for _ in range(ppo_epochs):
for state, action, old_log_probs, advantage, td_target in ppo_iter(states, actions, log_probs,
advantages, td_target_list):
dist, value = model(state)
entropy = dist.entropy().mean()
new_log_probs = dist.log_prob(action)
ratio = (new_log_probs - old_log_probs).exp()
sub1 = ratio * advantage
sub2 = torch.clamp(ratio, 1.0-clip_param, 1.0+clip_param) * advantage
actor_loss = - torch.min(sub1, sub2).mean()
critic_loss = (td_target - value).pow(2).mean()
loss = 0.5 * critic_loss + actor_loss - 0.001 * entropy
losses.append(loss.item())
optimizer.zero_grad()
loss.backward()
optimizer.step()
old_model.load_state_dict(model.state_dict())
return round(mean(losses),2)
## hyperparameters ##
num_envs = 16
env_name = "Pendulum-v0"
ppo_epochs = 30
mini_batch_size = 256
max_epoch = 10000
num_timesteps = 128
## hyperparameters ##
envs = ParallelEnv(num_envs, env_name)
state_space = envs.observation_space
action_space = envs.action_space
env = gym.make(env_name)
model = Actor_critic(state_space, action_space).to(device)
optimizer = optim.Adam(model.parameters(), lr=1e-3)
old_model = Actor_critic(state_space, action_space).to(device)
test_rewards = []
loss_list = []
state = envs.reset()
for epoch in range(max_epoch):
states, actions, rewards, masks, log_probs, values = [], [], [], [], [], []
for _ in range(num_timesteps):
dist, value = old_model(torch.FloatTensor(state).to(device))
action = dist.sample()
next_state, reward, done, _ = envs.step(action.cpu().numpy())
states.append(torch.FloatTensor(state).to(device))
actions.append(action)
rewards.append(torch.FloatTensor(reward).unsqueeze(1).to(device))
masks.append(torch.FloatTensor(1 - done).unsqueeze(1).to(device))
log_probs.append(dist.log_prob(action))
values.append(value)
state = next_state
_, next_value = model(torch.FloatTensor(next_state).to(device))
advantages, td_target_list = gae_compute(next_value, rewards, masks, values)
loss = ppo_train(torch.cat(states),torch.cat(actions), torch.cat(log_probs).detach(),
torch.cat(advantages).detach(), torch.cat(td_target_list).detach())
loss_list.append(loss)
if epoch % 1 == 0:
test_reward = np.mean([test_env() for _ in range(10)])
test_rewards.append(test_reward)
plot(epoch + 1, test_rewards, loss_list)
# soft = lambda loss : np.mean(loss[-100:]) if len(loss)>=100 else np.mean(loss)
# writer.add_scalar("Test_Rewards", np.array(soft(test_rewards)), epoch)
# writer.add_scalar("Value_Losses", np.array(soft(loss_list)), epoch)
from IPython import display
env = gym.make(env_name)
state_1 = env.reset()
img = plt.imshow(env.render(mode='rgb_array')) # only call this once
for _ in range(1000):
img.set_data(env.render(mode='rgb_array')) # just update the data
display.display(plt.gcf())
display.clear_output(wait=True)
prob, value = old_model(torch.FloatTensor(state_1).reshape(1,-1).to(device))
action = prob.sample().cpu().numpy()
next_state, _, done, _ = env.step(action)
if done:
state_1 = env.reset()
state_1 = next_state
```
## PPO Baselines:
<img src="../assets/PPO_baseline.png"></img>
### Test_Rewards:
<img src="../assets/PPO_Test_Rewards.png" width=100%></img>
### Value_Losses:
<img src="../assets/PPO_Value_Losses.png"></img>
|
github_jupyter
|
<h1> Create TensorFlow model </h1>
This notebook illustrates:
<ol>
<li> Creating a model using the high-level Estimator API
</ol>
```
# change these to try this notebook out
BUCKET = 'qwiklabs-gcp-37b9fafbd24bf385'
PROJECT = 'qwiklabs-gcp-37b9fafbd24bf385'
REGION = 'us-central1'
import os
os.environ['BUCKET'] = BUCKET
os.environ['PROJECT'] = PROJECT
os.environ['REGION'] = REGION
%%bash
if ! gsutil ls | grep -q gs://${BUCKET}/; then
gsutil mb -l ${REGION} gs://${BUCKET}
fi
```
<h2> Create TensorFlow model using TensorFlow's Estimator API </h2>
<p>
First, write an input_fn to read the data.
<p>
## Lab Task 1
Verify that the headers match your CSV output
```
import shutil
import numpy as np
import tensorflow as tf
# Determine CSV, label, and key columns
CSV_COLUMNS = 'weight_pounds,is_male,mother_age,plurality,gestation_weeks,key'.split(',')
LABEL_COLUMN = 'weight_pounds'
KEY_COLUMN = 'key'
# Set default values for each CSV column
DEFAULTS = [[0.0], ['null'], [0.0], ['null'], [0.0], ['nokey']]
TRAIN_STEPS = 1000
```
## Lab Task 2
Fill out the details of the input function below
```
# Create an input function reading a file using the Dataset API
# Then provide the results to the Estimator API
def read_dataset(filename_pattern, mode, batch_size = 512):
def _input_fn():
def decode_csv(line_of_text):
# TODO #1: Use tf.decode_csv to parse the provided line
columns = tf.decode_csv(line_of_text, record_defaults=DEFAULTS)
# TODO #2: Make a Python dict. The keys are the column names, the values are from the parsed data
features = dict(zip(CSV_COLUMNS, columns))
# TODO #3: Return a tuple of features, label where features is a Python dict and label a float
label = features.pop(LABEL_COLUMN)
return features, label
# TODO #4: Use tf.gfile.Glob to create list of files that match pattern
file_list = tf.gfile.Glob(filename_pattern)
# Create dataset from file list
dataset = (tf.data.TextLineDataset(file_list) # Read text file
.map(decode_csv)) # Transform each elem by applying decode_csv fn
# TODO #5: In training mode, shuffle the dataset and repeat indefinitely
# (Look at the API for tf.data.dataset shuffle)
# The mode input variable will be tf.estimator.ModeKeys.TRAIN if in training mode
# Tell the dataset to provide data in batches of batch_size
if mode == tf.estimator.ModeKeys.TRAIN:
epochs = None # Repeat indefinitely
dataset = dataset.shuffle(buffer_size = 10 * batch_size)
else:
epochs = 1
dataset = dataset.repeat(epochs).batch(batch_size)
# This will now return batches of features, label
return dataset
return _input_fn
```
## Lab Task 3
Use the TensorFlow feature column API to define appropriate feature columns for your raw features that come from the CSV.
<b> Bonus: </b> Separate your columns into wide columns (categorical, discrete, etc.) and deep columns (numeric, embedding, etc.)
```
# Define feature columns
# Define feature columns
def get_categorical(name, values):
return tf.feature_column.indicator_column(
tf.feature_column.categorical_column_with_vocabulary_list(name, values))
def get_cols():
# Define column types
return [\
get_categorical('is_male', ['True', 'False', 'Unknown']),
tf.feature_column.numeric_column('mother_age'),
get_categorical('plurality',
['Single(1)', 'Twins(2)', 'Triplets(3)',
'Quadruplets(4)', 'Quintuplets(5)','Multiple(2+)']),
tf.feature_column.numeric_column('gestation_weeks')
]
```
## Lab Task 4
To predict with the TensorFlow model, we also need a serving input function (we'll use this in a later lab). We will want all the inputs from our user.
Verify and change the column names and types here as appropriate. These should match your CSV_COLUMNS
```
# Create serving input function to be able to serve predictions later using provided inputs
def serving_input_fn():
feature_placeholders = {
'is_male': tf.placeholder(tf.string, [None]),
'mother_age': tf.placeholder(tf.float32, [None]),
'plurality': tf.placeholder(tf.string, [None]),
'gestation_weeks': tf.placeholder(tf.float32, [None])
}
features = {
key: tf.expand_dims(tensor, -1)
for key, tensor in feature_placeholders.items()
}
return tf.estimator.export.ServingInputReceiver(features, feature_placeholders)
```
## Lab Task 5
Complete the TODOs in this code:
```
# Create estimator to train and evaluate
def train_and_evaluate(output_dir):
EVAL_INTERVAL = 300
run_config = tf.estimator.RunConfig(save_checkpoints_secs = EVAL_INTERVAL,
keep_checkpoint_max = 3)
# TODO #1: Create your estimator
estimator = tf.estimator.DNNRegressor(
model_dir = output_dir,
feature_columns = get_cols(),
hidden_units = [64, 32],
config = run_config)
train_spec = tf.estimator.TrainSpec(
# TODO #2: Call read_dataset passing in the training CSV file and the appropriate mode
input_fn = read_dataset('train.csv', mode = tf.estimator.ModeKeys.TRAIN),
max_steps = TRAIN_STEPS)
exporter = tf.estimator.LatestExporter('exporter', serving_input_fn)
eval_spec = tf.estimator.EvalSpec(
# TODO #3: Call read_dataset passing in the evaluation CSV file and the appropriate mode
input_fn = read_dataset('eval.csv', mode = tf.estimator.ModeKeys.EVAL),
steps = None,
start_delay_secs = 60, # start evaluating after N seconds
throttle_secs = EVAL_INTERVAL, # evaluate every N seconds
exporters = exporter)
tf.estimator.train_and_evaluate(estimator, train_spec, eval_spec)
```
Finally, train!
```
# Run the model
shutil.rmtree('babyweight_trained', ignore_errors = True) # start fresh each time
train_and_evaluate('babyweight_trained')
```
When I ran it, the final lines of the output (above) were:
<pre>
INFO:tensorflow:Saving dict for global step 1000: average_loss = 1.2693067, global_step = 1000, loss = 635.9226
INFO:tensorflow:Restoring parameters from babyweight_trained/model.ckpt-1000
INFO:tensorflow:Assets added to graph.
INFO:tensorflow:No assets to write.
INFO:tensorflow:SavedModel written to: babyweight_trained/export/exporter/temp-1517899936/saved_model.pb
</pre>
The exporter directory contains the final model and the final RMSE (the average_loss) is 1.2693067
<h2> Monitor and experiment with training </h2>
```
from google.datalab.ml import TensorBoard
TensorBoard().start('./babyweight_trained')
for pid in TensorBoard.list()['pid']:
TensorBoard().stop(pid)
print('Stopped TensorBoard with pid {}'.format(pid))
```
Copyright 2017-2018 Google Inc. Licensed under the Apache License, Version 2.0 (the "License"); you may not use this file except in compliance with the License. You may obtain a copy of the License at http://www.apache.org/licenses/LICENSE-2.0 Unless required by applicable law or agreed to in writing, software distributed under the License is distributed on an "AS IS" BASIS, WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied. See the License for the specific language governing permissions and limitations under the License
|
github_jupyter
|
## Denoising Autoencoder on MNIST dataset
* This notebook will give you a very good understanding abou denoising autoencoders
* For more information: visit [here](https://lilianweng.github.io/lil-log/2018/08/12/from-autoencoder-to-beta-vae.html)
* The entire notebook is in PyTorch
```
# Importing packages that will be necessary for the project
import numpy as np
from keras.datasets import mnist
import matplotlib.pyplot as plt
from tqdm import tqdm
from torchvision import transforms
import torch.nn as nn
from torch.utils.data import DataLoader,Dataset
import torch
import torch.optim as optim
from torch.autograd import Variable
# Mounting the google drive to fetch data from it
from google.colab import drive
drive.mount('/content/gdrive')
#loading the mnist data
(x_train,y_train),(x_test,y_test)=mnist.load_data()
print("No of train datapoints:{}\nNo of test datapoints:{}".format(len(x_train),len(x_test)))
print(y_train[1]) # Checking labels
#we add the noise
"""
'gauss' Gaussian-distributed additive noise.
'speckle' out = image + n*image,where
n is uniform noise with specified mean & variance.
"""
def add_noise(img,noise_type="gaussian"):#input includes the type of the noise to be added and the input image
row,col=28,28
img=img.astype(np.float32)
if noise_type=="gaussian":
noise=np.random.normal(-5.9,5.9,img.shape) #input includes : mean, deviation, shape of the image and the function picks up a normal distribuition.
noise=noise.reshape(row,col) # reshaping the noise
img=img+noise #adding the noise
return img
if noise_type=="speckle":
noise=np.random.randn(row,col)
noise=noise.reshape(row,col)
img=img+img*noise
return img
#Now dividing the dataset into two parts and adding gaussian to one and speckle to another.
noises=["gaussian","speckle"]
noise_ct=0
noise_id=0 #id represnts which noise is being added, its 0 = gaussian and 1 = speckle
traindata=np.zeros((60000,28,28)) #revised training data
for idx in tqdm(range(len(x_train))): #for the first half we are using gaussian noise & for the second half speckle noise
if noise_ct<(len(x_train)/2):
noise_ct+=1
traindata[idx]=add_noise(x_train[idx],noise_type=noises[noise_id])
else:
print("\n{} noise addition completed to images".format(noises[noise_id]))
noise_id+=1
noise_ct=0
print("\n{} noise addition completed to images".format(noises[noise_id]))
noise_ct=0
noise_id=0
testdata=np.zeros((10000,28,28))
for idx in tqdm(range(len(x_test))): # Doing the same for the test set.
if noise_ct<(len(x_test)/2):
noise_ct+=1
x=add_noise(x_test[idx],noise_type=noises[noise_id])
testdata[idx]=x
else:
print("\n{} noise addition completed to images".format(noises[noise_id]))
noise_id+=1
noise_ct=0
print("\n{} noise addition completed to images".format(noises[noise_id]))
f, axes=plt.subplots(2,2) #setting up 4 figures
#showing images with gaussian noise
axes[0,0].imshow(x_train[0],cmap="gray")#the original data
axes[0,0].set_title("Original Image")
axes[1,0].imshow(traindata[0],cmap='gray')#noised data
axes[1,0].set_title("Noised Image")
#showing images with speckle noise
axes[0,1].imshow(x_train[25000],cmap='gray')#original data
axes[0,1].set_title("Original Image")
axes[1,1].imshow(traindata[25000],cmap="gray")#noised data
axes[1,1].set_title("Noised Image")
#creating a dataset builder i.e dataloaders
class noisedDataset(Dataset):
def __init__(self,datasetnoised,datasetclean,labels,transform):
self.noise=datasetnoised
self.clean=datasetclean
self.labels=labels
self.transform=transform
def __len__(self):
return len(self.noise)
def __getitem__(self,idx):
xNoise=self.noise[idx]
xClean=self.clean[idx]
y=self.labels[idx]
if self.transform != None:#just for using the totensor transform
xNoise=self.transform(xNoise)
xClean=self.transform(xClean)
return (xNoise,xClean,y)
#defining the totensor transforms
tsfms=transforms.Compose([
transforms.ToTensor()
])
trainset=noisedDataset(traindata,x_train,y_train,tsfms)# the labels should not be corrupted because the model has to learn uniques features and denoise it.
testset=noisedDataset(testdata,x_test,y_test,tsfms)
batch_size=32
#creating the dataloader
trainloader=DataLoader(trainset,batch_size=32,shuffle=True)
testloader=DataLoader(testset,batch_size=1,shuffle=True)
#building our ae model:
class denoising_model(nn.Module):
def __init__(self):
super(denoising_model,self).__init__()
self.encoder=nn.Sequential(
nn.Linear(28*28,256),#decreasing the features in the encoder
nn.ReLU(True),
nn.Linear(256,128),
nn.ReLU(True),
nn.Linear(128,64),
nn.ReLU(True)
)
self.decoder=nn.Sequential(
nn.Linear(64,128),#increasing the number of features
nn.ReLU(True),
nn.Linear(128,256),
nn.ReLU(True),
nn.Linear(256,28*28),
nn.Sigmoid(),
)
def forward(self,x):
x=self.encoder(x)#first the encoder
x=self.decoder(x)#then the decoder to reconstruct the original input.
return x
#this is the training code, can be modified according to requirements
#setting the device
if torch.cuda.is_available()==True:
device="cuda:0"
else:
device ="cpu"
model=denoising_model().to(device)
criterion=nn.MSELoss()
optimizer=optim.SGD(model.parameters(),lr=0.01,weight_decay=1e-5)
#setting the number of epochs
epochs=120
l=len(trainloader)
losslist=list()
epochloss=0
running_loss=0
for epoch in range(epochs):
print("Entering Epoch: ",epoch)
for dirty,clean,label in tqdm((trainloader)):
dirty=dirty.view(dirty.size(0),-1).type(torch.FloatTensor)
clean=clean.view(clean.size(0),-1).type(torch.FloatTensor)
dirty,clean=dirty.to(device),clean.to(device)
#-----------------Forward Pass----------------------
output=model(dirty)
loss=criterion(output,clean)
#-----------------Backward Pass---------------------
optimizer.zero_grad()
loss.backward()
optimizer.step()
running_loss+=loss.item()
epochloss+=loss.item()
#-----------------Log-------------------------------
losslist.append(running_loss/l)
running_loss=0
print("======> epoch: {}/{}, Loss:{}".format(epoch,epochs,loss.item()))
#plotting the loss curve
plt.plot(range(len(losslist)),losslist)
"""Here, we try to visualize some of the results.
We randomly generate 6 numbers in between 1 and 10k , run them through the model,
and show the results with comparisons
"""
f,axes= plt.subplots(6,3,figsize=(20,20))
axes[0,0].set_title("Original Image")
axes[0,1].set_title("Dirty Image")
axes[0,2].set_title("Cleaned Image")
test_imgs=np.random.randint(0,10000,size=6)
for idx in range((6)):
dirty=testset[test_imgs[idx]][0]
clean=testset[test_imgs[idx]][1]
label=testset[test_imgs[idx]][2]
dirty=dirty.view(dirty.size(0),-1).type(torch.FloatTensor)
dirty=dirty.to(device)
output=model(dirty)
output=output.view(1,28,28)
output=output.permute(1,2,0).squeeze(2)
output=output.detach().cpu().numpy()
dirty=dirty.view(1,28,28)
dirty=dirty.permute(1,2,0).squeeze(2)
dirty=dirty.detach().cpu().numpy()
clean=clean.permute(1,2,0).squeeze(2)
clean=clean.detach().cpu().numpy()
axes[idx,0].imshow(clean,cmap="gray")
axes[idx,1].imshow(dirty,cmap="gray")
axes[idx,2].imshow(output,cmap="gray")
```
|
github_jupyter
|
# Cleaning the data to build the prototype for crwa
### This data cleans the original sql output and performs cleaning tasks. Also checking validity of the results against original report found at
### https://www.crwa.org/uploads/1/2/6/7/126781580/crwa_ecoli_web_2017_updated.xlsx
```
import pandas as pd
pd.options.display.max_rows = 999
import numpy as np
import matplotlib.pyplot as plt
df = pd.read_csv("data_for_prototype.csv")
# There are 2 rows with Date = Null so droping those rows
df = df.dropna(subset=['Date_Collected'])
df.isna().sum()
# There are following types of invalids in Site_ID
invalids = ["N/A","NULL","ND"]
#Removing these invalid Site_IDs
df["Site_Name"] = df["Site_Name"].map(lambda x: np.nan if x in invalids else x)
df["Site_Name"].fillna("ABCD", inplace=True)
#Removing these invalid Town Names
df["Town"] = df["Town"].map(lambda x: np.nan if x in invalids else x)
df["Town"].fillna("ABCD", inplace=True)
df["River_Mile_Headwaters"].describe
#Removing invalid Miles and selecting only numeric values for miles
df["River_Mile_Headwaters"] = df["River_Mile_Headwaters"].map(lambda x: np.nan if x in invalids else x)
df["River_Mile_Headwaters"].fillna("00.0 MI", inplace=True)
df["Mile"] = pd.to_numeric(df["River_Mile_Headwaters"].str[0:4])
#Removing invalid entrees and selecting only numeric values
df["Latitude_DD"] = df["Latitude_DD"].map(lambda x: np.nan if x in invalids else x)
df["Latitude_DD"].fillna("00.0 MI", inplace=True)
df["Longitude_DD"] = df["Longitude_DD"].map(lambda x: np.nan if x in invalids else x)
df["Longitude_DD"].fillna("00.0 MI", inplace=True)
#Removing invalid entrees and selecting only numeric values
df["Actual_Result"] = df["Actual_Result"].map(lambda x: np.nan if x in invalids else x)
df["Actual_Result"] = df["Actual_Result"].str.lstrip('>')
df["Actual_Result"] = df["Actual_Result"].str.rstrip('>')
df["Actual_Result"] = df["Actual_Result"].str.lstrip('<')
df["Actual_Result"] = df["Actual_Result"].str.rstrip('<')
df["Actual_Result"] = df["Actual_Result"].str.lstrip('*')
df["Actual_Result"] = df["Actual_Result"].str.rstrip('*')
df["Actual_Result"] = df["Actual_Result"].str.replace(',','')
df["Actual_Result"] = df["Actual_Result"].str.replace('%','')
df["Actual_Result"] = df["Actual_Result"].str.replace(' ','')
df["Actual_Result"] = df["Actual_Result"].str.replace('ND','')
df["Actual_Result"] = df["Actual_Result"].str.lstrip('.')
df["Actual_Result"] = df["Actual_Result"].str.rstrip('.')
df["Actual_Result"] = df["Actual_Result"].str.replace('6..25','6.25')
df["Actual_Result"] = df["Actual_Result"].str.replace('480.81546.25291','480.81546')
df["Actual_Result"] = df["Actual_Result"].str.replace('379\r\n379',"379")
#Functiont to check if string can be converted to numeric
#Input --> string
#Output --> 1 if convertable else 0
def isInt_try(v):
try: i = float(v)
except: return False
return True
# Applying above function to check any odd strings in Actual_Result Column
for i in df["Actual_Result"]:
if isInt_try(i) == 0:
print(i)
# Checking any odd strings in Actual_Result Column
for i in df["Actual_Result"]:
if str(i).count('.') >= 2:
print(i)
# Converting Actual_Result to numeric and Date_Collected to datetime data type
df["Actual_Result"] = pd.to_numeric(df["Actual_Result"])
df["Date_Collected"] = pd.to_datetime(df["Date_Collected"])
"Slicing for E.coli"
df_ecoli = df[df["Component_Name"] == "Escherichia coli"]
df_ecoli.head()
# Validating against the original report
result = df_ecoli.loc[(df_ecoli.Town == "Milford") & (df_ecoli.Date_Collected == pd.to_datetime("2017-11-21 00:00:00-05:00"))]["Actual_Result"]
result
```
|
github_jupyter
|
# MATH 4100: Temporal data analysis and applications to stock analysis
*Curtis Miller*
## Introduction
This is a lecture for [MATH 4100/CS 5160: Introduction to Data Science](http://datasciencecourse.net/), offered at the University of Utah, introducing time series data analysis applied to finance.
Advanced mathematics and statistics have been present in finance for some time. Prior to the 1980s, banking and finance were well-known for being "boring"; investment banking was distinct from commercial banking and the primary role of the industry was handling "simple" (at least in comparison to today) financial instruments, such as loans. Deregulation under the Regan administration, coupled with an influx of mathematical talent, transformed the industry from the "boring" business of banking to what it is today, and since then, finance has joined the other sciences as a motivation for mathematical research and advancement. For example one of the biggest recent achievements of mathematics was the derivation of the [Black-Scholes formula](https://en.wikipedia.org/wiki/Black%E2%80%93Scholes_model), which facilitated the pricing of stock options (a contract giving the holder the right to purchase or sell a stock at a particular price to the issuer of the option). That said, [bad statistical models, including the Black-Scholes formula, hold part of the blame for the 2008 financial crisis](https://www.theguardian.com/science/2012/feb/12/black-scholes-equation-credit-crunch).
In recent years, computer science has joined advanced mathematics in revolutionizing finance and **trading**, the practice of buying and selling of financial assets for the purpose of making a profit. In recent years, trading has become dominated by computers; algorithms are responsible for making rapid split-second trading decisions faster than humans could make (so rapidly, [the speed at which light travels is a limitation when designing systems](http://www.nature.com/news/physics-in-finance-trading-at-the-speed-of-light-1.16872)). Additionally, [machine learning and data mining techniques are growing in popularity](http://www.ft.com/cms/s/0/9278d1b6-1e02-11e6-b286-cddde55ca122.html#axzz4G8daZxcl) in the financial sector, and likely will continue to do so. For example, **high-frequency trading (HFT)** is a branch of algorithmic trading where computers make thousands of trades in short periods of time, engaging in complex strategies such as statistical arbitrage and market making. While algorithms may outperform humans, the technology is still new and playing an increasing role in a famously turbulent, high-stakes arena. HFT was responsible for phenomena such as the [2010 flash crash](https://en.wikipedia.org/wiki/2010_Flash_Crash) and a [2013 flash crash](http://money.cnn.com/2013/04/24/investing/twitter-flash-crash/) prompted by a hacked [Associated Press tweet](http://money.cnn.com/2013/04/23/technology/security/ap-twitter-hacked/index.html?iid=EL) about an attack on the White House.
This lecture, however, will not be about how to crash the stock market with bad mathematical models or trading algorithms. Instead, I intend to provide you with basic tools for handling and analyzing stock market data with Python. We will be using stock data as a first exposure to **time series data**, which is data considered dependent on the time it was observed (other examples of time series include temperature data, demand for energy on a power grid, Internet server load, and many, many others). I will also discuss moving averages, how to construct trading strategies using moving averages, how to formulate exit strategies upon entering a position, and how to evaluate a strategy with backtesting.
**DISCLAIMER: THIS IS NOT FINANCIAL ADVICE!!! Furthermore, I have ZERO experience as a trader (a lot of this knowledge comes from a one-semester course on stock trading I took at Salt Lake Community College)! This is purely introductory knowledge, not enough to make a living trading stocks. People can and do lose money trading stocks, and you do so at your own risk!**
## Preliminaries
I will be using two packages, **quandl** and **pandas_datareader**, which are not installed with [Anaconda](https://www.anaconda.com/) if you are using it. To install these packages, run the following at the appropriate command prompt:
conda install quandl
conda install pandas-datareader
## Getting and Visualizing Stock Data
### Getting Data from Quandl
Before we analyze stock data, we need to get it into some workable format. Stock data can be obtained from [Yahoo! Finance](http://finance.yahoo.com), [Google Finance](http://finance.google.com), or a number of other sources. These days I recommend getting data from [Quandl](https://www.quandl.com/), a provider of community-maintained financial and economic data. (Yahoo! Finance used to be the go-to source for good quality stock data, but the API was discontinued in 2017 and reliable data can no longer be obtained: see [this question/answer on StackExchange](https://quant.stackexchange.com/questions/35019/is-yahoo-finance-data-good-or-bad-now) for more details.)
By default the `get()` function in **quandl** will return a **pandas** `DataFrame` containing the fetched data.
```
import pandas as pd
import quandl
import datetime
# We will look at stock prices over the past year, starting at January 1, 2016
start = datetime.datetime(2016,1,1)
end = datetime.date.today()
# Let's get Apple stock data; Apple's ticker symbol is AAPL
# First argument is the series we want, second is the source ("yahoo" for Yahoo! Finance), third is the start date, fourth is the end date
s = "AAPL"
apple = quandl.get("WIKI/" + s, start_date=start, end_date=end)
type(apple)
apple.head()
```
Let's briefly discuss this. **Open** is the price of the stock at the beginning of the trading day (it need not be the closing price of the previous trading day), **high** is the highest price of the stock on that trading day, **low** the lowest price of the stock on that trading day, and **close** the price of the stock at closing time. **Volume** indicates how many stocks were traded. **Adjusted** prices (such as the adjusted close) is the price of the stock that adjusts the price for corporate actions. While stock prices are considered to be set mostly by traders, **stock splits** (when the company makes each extant stock worth two and halves the price) and **dividends** (payout of company profits per share) also affect the price of a stock and should be accounted for.
### Visualizing Stock Data
Now that we have stock data we would like to visualize it. I first demonstrate how to do so using the **matplotlib** package. Notice that the `apple` `DataFrame` object has a convenience method, `plot()`, which makes creating plots easier.
```
import matplotlib.pyplot as plt # Import matplotlib
# This line is necessary for the plot to appear in a Jupyter notebook
%matplotlib inline
# Control the default size of figures in this Jupyter notebook
%pylab inline
pylab.rcParams['figure.figsize'] = (15, 9) # Change the size of plots
apple["Adj. Close"].plot(grid = True) # Plot the adjusted closing price of AAPL
```
A linechart is fine, but there are at least four variables involved for each date (open, high, low, and close), and we would like to have some visual way to see all four variables that does not require plotting four separate lines. Financial data is often plotted with a **Japanese candlestick plot**, so named because it was first created by 18th century Japanese rice traders. Such a chart can be created with **matplotlib**, though it requires considerable effort.
I have made a function you are welcome to use to more easily create candlestick charts from **pandas** data frames, and use it to plot our stock data. (Code is based off [this example](http://matplotlib.org/examples/pylab_examples/finance_demo.html), and you can read the documentation for the functions involved [here](http://matplotlib.org/api/finance_api.html).)
```
from matplotlib.dates import DateFormatter, WeekdayLocator,\
DayLocator, MONDAY
from matplotlib.finance import candlestick_ohlc
def pandas_candlestick_ohlc(dat, stick = "day", adj = False, otherseries = None):
"""
:param dat: pandas DataFrame object with datetime64 index, and float columns "Open", "High", "Low", and "Close", likely created via DataReader from "yahoo"
:param stick: A string or number indicating the period of time covered by a single candlestick. Valid string inputs include "day", "week", "month", and "year", ("day" default), and any numeric input indicates the number of trading days included in a period
:param adj: A boolean indicating whether to use adjusted prices
:param otherseries: An iterable that will be coerced into a list, containing the columns of dat that hold other series to be plotted as lines
This will show a Japanese candlestick plot for stock data stored in dat, also plotting other series if passed.
"""
mondays = WeekdayLocator(MONDAY) # major ticks on the mondays
alldays = DayLocator() # minor ticks on the days
dayFormatter = DateFormatter('%d') # e.g., 12
# Create a new DataFrame which includes OHLC data for each period specified by stick input
fields = ["Open", "High", "Low", "Close"]
if adj:
fields = ["Adj. " + s for s in fields]
transdat = dat.loc[:,fields]
transdat.columns = pd.Index(["Open", "High", "Low", "Close"])
if (type(stick) == str):
if stick == "day":
plotdat = transdat
stick = 1 # Used for plotting
elif stick in ["week", "month", "year"]:
if stick == "week":
transdat["week"] = pd.to_datetime(transdat.index).map(lambda x: x.isocalendar()[1]) # Identify weeks
elif stick == "month":
transdat["month"] = pd.to_datetime(transdat.index).map(lambda x: x.month) # Identify months
transdat["year"] = pd.to_datetime(transdat.index).map(lambda x: x.isocalendar()[0]) # Identify years
grouped = transdat.groupby(list(set(["year",stick]))) # Group by year and other appropriate variable
plotdat = pd.DataFrame({"Open": [], "High": [], "Low": [], "Close": []}) # Create empty data frame containing what will be plotted
for name, group in grouped:
plotdat = plotdat.append(pd.DataFrame({"Open": group.iloc[0,0],
"High": max(group.High),
"Low": min(group.Low),
"Close": group.iloc[-1,3]},
index = [group.index[0]]))
if stick == "week": stick = 5
elif stick == "month": stick = 30
elif stick == "year": stick = 365
elif (type(stick) == int and stick >= 1):
transdat["stick"] = [np.floor(i / stick) for i in range(len(transdat.index))]
grouped = transdat.groupby("stick")
plotdat = pd.DataFrame({"Open": [], "High": [], "Low": [], "Close": []}) # Create empty data frame containing what will be plotted
for name, group in grouped:
plotdat = plotdat.append(pd.DataFrame({"Open": group.iloc[0,0],
"High": max(group.High),
"Low": min(group.Low),
"Close": group.iloc[-1,3]},
index = [group.index[0]]))
else:
raise ValueError('Valid inputs to argument "stick" include the strings "day", "week", "month", "year", or a positive integer')
# Set plot parameters, including the axis object ax used for plotting
fig, ax = plt.subplots()
fig.subplots_adjust(bottom=0.2)
if plotdat.index[-1] - plotdat.index[0] < pd.Timedelta('730 days'):
weekFormatter = DateFormatter('%b %d') # e.g., Jan 12
ax.xaxis.set_major_locator(mondays)
ax.xaxis.set_minor_locator(alldays)
else:
weekFormatter = DateFormatter('%b %d, %Y')
ax.xaxis.set_major_formatter(weekFormatter)
ax.grid(True)
# Create the candelstick chart
candlestick_ohlc(ax, list(zip(list(date2num(plotdat.index.tolist())), plotdat["Open"].tolist(), plotdat["High"].tolist(),
plotdat["Low"].tolist(), plotdat["Close"].tolist())),
colorup = "black", colordown = "red", width = stick * .4)
# Plot other series (such as moving averages) as lines
if otherseries != None:
if type(otherseries) != list:
otherseries = [otherseries]
dat.loc[:,otherseries].plot(ax = ax, lw = 1.3, grid = True)
ax.xaxis_date()
ax.autoscale_view()
plt.setp(plt.gca().get_xticklabels(), rotation=45, horizontalalignment='right')
plt.show()
pandas_candlestick_ohlc(apple, adj=True)
```
With a candlestick chart, a black candlestick indicates a day where the closing price was higher than the open (a gain), while a red candlestick indicates a day where the open was higher than the close (a loss). The wicks indicate the high and the low, and the body the open and close (hue is used to determine which end of the body is the open and which the close). Candlestick charts are popular in finance and some strategies in [technical analysis](https://en.wikipedia.org/wiki/Technical_analysis) use them to make trading decisions, depending on the shape, color, and position of the candles. I will not cover such strategies today.
We may wish to plot multiple financial instruments together; we may want to compare stocks, compare them to the market, or look at other securities such as [exchange-traded funds (ETFs)](https://en.wikipedia.org/wiki/Exchange-traded_fund). Later, we will also want to see how to plot a financial instrument against some indicator, like a moving average. For this you would rather use a line chart than a candlestick chart. (How would you plot multiple candlestick charts on top of one another without cluttering the chart?)
Below, I get stock data for some other tech companies and plot their adjusted close together.
```
microsoft, google = (quandl.get("WIKI/" + s, start_date=start, end_date=end) for s in ["MSFT", "GOOG"])
# Below I create a DataFrame consisting of the adjusted closing price of these stocks, first by making a list of these objects and using the join method
stocks = pd.DataFrame({"AAPL": apple["Adj. Close"],
"MSFT": microsoft["Adj. Close"],
"GOOG": google["Adj. Close"]})
stocks.head()
stocks.plot(grid = True)
```
What's wrong with this chart? While absolute price is important (pricy stocks are difficult to purchase, which affects not only their volatility but *your* ability to trade that stock), when trading, we are more concerned about the relative change of an asset rather than its absolute price. Google's stocks are much more expensive than Apple's or Microsoft's, and this difference makes Apple's and Microsoft's stocks appear much less volatile than they truly are (that is, their price appears to not deviate much).
One solution would be to use two different scales when plotting the data; one scale will be used by Apple and Microsoft stocks, and the other by Google.
```
stocks.plot(secondary_y = ["AAPL", "MSFT"], grid = True)
```
A "better" solution, though, would be to plot the information we actually want: the stock's returns. This involves transforming the data into something more useful for our purposes. There are multiple transformations we could apply.
One transformation would be to consider the stock's return since the beginning of the period of interest. In other words, we plot:
\begin{equation*}
\text{return}_{t,0} = \frac{\text{price}_t}{\text{price}_0}
\end{equation*}
This will require transforming the data in the `stocks` object, which I do next. Notice that I am using a **lambda function**, which allows me to pass a small function defined quickly as a parameter to another function or method (you can read more about lambda functions [here](https://docs.python.org/3/reference/expressions.html#lambda)).
```
# df.apply(arg) will apply the function arg to each column in df, and return a DataFrame with the result
# Recall that lambda x is an anonymous function accepting parameter x; in this case, x will be a pandas Series object
stock_return = stocks.apply(lambda x: x / x[0])
stock_return.head()
stock_return.plot(grid = True).axhline(y = 1, color = "black", lw = 2)
```
This is a much more useful plot. We can now see how profitable each stock was since the beginning of the period. Furthermore, we see that these stocks are highly correlated; they generally move in the same direction, a fact that was difficult to see in the other charts.
Alternatively, we could plot the change of each stock per day. One way to do so would be to plot the percentage increase of a stock when comparing day $t$ to day $t + 1$, with the formula:
\begin{equation*}
\text{growth}_t = \frac{\text{price}_{t + 1} - \text{price}_t}{\text{price}_t}
\end{equation*}
But change could be thought of differently as:
\begin{equation*}
\text{increase}_t = \frac{\text{price}_{t} - \text{price}_{t-1}}{\text{price}_t}
\end{equation*}
These formulas are not the same and can lead to differing conclusions, but there is another way to model the growth of a stock: with log differences.
\begin{equation*}
\text{change}_t = \log(\text{price}_{t}) - \log(\text{price}_{t - 1})
\end{equation*}
(Here, $\log$ is the natural log, and our definition does not depend as strongly on whether we use $\log(\text{price}_{t}) - \log(\text{price}_{t - 1})$ or $\log(\text{price}_{t+1}) - \log(\text{price}_{t})$.) The advantage of using log differences is that this difference can be interpreted as the percentage change in a stock but does not depend on the denominator of a fraction. Additionally, log differences have a desirable property: the sum of the log differences can be interpreted as the total change (as a percentage) over the period summed (which is not a property of the other formulations; they will overestimate growth). Log differences also more cleanly correspond to how stock prices are modeled in continuous time.
We can obtain and plot the log differences of the data in `stocks` as follows:
```
# Let's use NumPy's log function, though math's log function would work just as well
import numpy as np
stock_change = stocks.apply(lambda x: np.log(x) - np.log(x.shift(1))) # shift moves dates back by 1.
stock_change.head()
stock_change.plot(grid = True).axhline(y = 0, color = "black", lw = 2)
```
Which transformation do you prefer? Looking at returns since the beginning of the period make the overall trend of the securities in question much more apparent. Changes between days, though, are what more advanced methods actually consider when modelling the behavior of a stock. so they should not be ignored.
We often want to compare the performance of stocks to the performance of the overall market. [SPY](https://finance.yahoo.com/quote/SPY/), which is the ticker symbol for the SPDR S&P 500 exchange-traded mutual fund (ETF), is a fund that attempts only to imitate the composition of the [S&P 500 stock index](https://finance.yahoo.com/quote/%5EGSPC?p=^GSPC), and thus represents the value in "the market."
SPY data is not available for free from Quandl, so I will get this data from Yahoo! Finance. (I don't have a choice.)
Below I get data for SPY and compare its performance to the performance of our stocks.
```
#import pandas_datareader.data as web # Going to get SPY from Yahoo! (I know I said you shouldn't but I didn't have a choice)
#spyder = web.DataReader("SPY", "yahoo", start, end) # Didn't work
#spyder = web.DataReader("SPY", "google", start, end) # Didn't work either
# If all else fails, read from a file, obtained from here: http://www.nasdaq.com/symbol/spy/historical
spyderdat = pd.read_csv("/home/curtis/Downloads/HistoricalQuotes.csv") # Obviously specific to my system; set to
# location on your machine
spyderdat = pd.DataFrame(spyderdat.loc[:, ["open", "high", "low", "close", "close"]].iloc[1:].as_matrix(),
index=pd.DatetimeIndex(spyderdat.iloc[1:, 0]),
columns=["Open", "High", "Low", "Close", "Adj Close"]).sort_index()
spyder = spyderdat.loc[start:end]
stocks = stocks.join(spyder.loc[:, "Adj Close"]).rename(columns={"Adj Close": "SPY"})
stocks.head()
stock_return = stocks.apply(lambda x: x / x[0])
stock_return.plot(grid = True).axhline(y = 1, color = "black", lw = 2)
stock_change = stocks.apply(lambda x: np.log(x) - np.log(x.shift(1)))
stock_change.plot(grid=True).axhline(y = 0, color = "black", lw = 2)
```
## Classical Risk Metrics
From what we have so far we can already compute informative metrics for our stocks, which can be considered some measure of risk.
First, we will want to **annualize** our returns, thus computing the **annual percentage rate (APR)**. This helps us keep returns on a common time scale.
```
stock_change_apr = stock_change * 252 * 100 # There are 252 trading days in a year; the 100 converts to percentages
stock_change_apr.tail()
```
Some of these numbers look initially like nonsense, but that's okay for now.
The metrics I want are:
* The average return
* Volatility (the standard deviation of returns)
* $\alpha$ and $\beta$
* The Sharpe ratio
The first two metrics are largely self-explanatory, but the latter two need explaining.
First, the **risk-free rate**, which I denote by $r_{RF}$, is the rate of return on a risk-free financial asset. This asset exists only in theory but often yields on low-risk instruments like 3-month U.S. Treasury Bills can be viewed as being virtually risk-free and thus their yields can be used to approximate the risk-free rate. I get the data for these instruments below.
```
tbill = quandl.get("FRED/TB3MS", start_date=start, end_date=end)
tbill.tail()
tbill.plot()
rrf = tbill.iloc[-1, 0] # Get the most recent Treasury Bill rate
rrf
```
Now, a **linear regression model** is a model of the following form:
$$y_i = \alpha + \beta x_i + \epsilon_i$$
$\epsilon_i$ is an error process. Another way to think of this process model is:
$$\hat{y}_i = \alpha + \beta x_i$$
$\hat{y}_i$ is the **predicted value** of $y_i$ given $x_i$. In other words, a linear regression model tells you how $x_i$ and $y_i$ are related, and how values of $x_i$ can be used to predict values of $y_i$. $\alpha$ is the **intercept** of the model and $\beta$ is the **slope**. In particular, $\alpha$ would be the predicted value of $y$ if $x$ were zero, and $\beta$ gives how much $y$ changes when $x$ changes by one unit.
There is an easy way to compute $\alpha$ and $\beta$ given the sample means $\bar{x}$ and $\bar{y}$ and sample standard deviations $s_x$ and $s_y$ and the correlation between $x$ and $y$, denoted with $r$:
$$\beta = r \frac{s_y}{s_x}$$
$$\alpha = \bar{y} - \beta \bar{x}$$
In finance, we use $\alpha$ and $\beta$ like so:
$$R_t - r_{RF} = \alpha + \beta (R_{Mt} - r_{RF}) + \epsilon_t$$
$R_t$ is the return of a financial asset (a stock) and $R_t - r_{RF}$ is the **excess return**, or return exceeding the risk-free rate of return. $R_{Mt}$ is the return of the *market* at time $t$. Then $\alpha$ and $\beta can be interpreted like so:
* $\alpha$ is average excess return over the market.
* $\beta$ is how much a stock moves in relation to the market. If $\beta > 0$ then the stock generally moves in the same direction as the market, while when $\beta < 0$ the stock generally moves in the opposite direction. If $|\beta| > 1$ the stock moves strongly in response to the market $|\beta| < 1$ the stock is less responsive to the market.
Below I get a **pandas** `Series` that contains how much each stock is correlated with SPY (our approximation of the market).
```
smcorr = stock_change_apr.drop("SPY", 1).corrwith(stock_change_apr.SPY) # Since RRF is constant it doesn't change the
# correlation so we can ignore it in our
# calculation
smcorr
```
Then I compute $\alpha$ and $\beta$.
```
sy = stock_change_apr.drop("SPY", 1).std()
sx = stock_change_apr.SPY.std()
sy
sx
ybar = stock_change_apr.drop("SPY", 1).mean() - rrf
xbar = stock_change_apr.SPY.mean() - rrf
ybar
xbar
beta = smcorr * sy / sx
alpha = ybar - beta * xbar
beta
alpha
```
The **Sharpe ratio** is another popular risk metric, defined below:
$$\text{Sharpe ratio} = \frac{\bar{R_t} - r_{RF}}{s}$$
Here $s$ is the volatility of the stock. We want the sharpe ratio to be large. A large Sharpe ratio indicates that the stock's excess returns are large relative to the stock's volatilitly. Additionally, the Sharpe ratio is tied to a statistical test (the $t$-test) to determine if a stock earns more on average than the risk-free rate; the larger this ratio, the more likely this is to be the case.
Your challenge now is to compute the Sharpe ratio for each stock listed here, and interpret it. Which stock seems to be the better investment according to the Sharpe ratio?
```
# Your code here
```
## Moving Averages
Charts are very useful. In fact, some traders base their strategies almost entirely off charts (these are the "technicians", since trading strategies based off finding patterns in charts is a part of the trading doctrine known as **technical analysis**). Let's now consider how we can find trends in stocks.
A **$q$-day moving average** is, for a series $x_t$ and a point in time $t$, the average of the past $q$ days: that is, if $MA^q_t$ denotes a moving average process, then:
\begin{equation*}
MA^q_t = \frac{1}{q} \sum_{i = 0}^{q-1} x_{t - i}
\end{equation*}
Moving averages smooth a series and helps identify trends. The larger $q$ is, the less responsive a moving average process is to short-term fluctuations in the series $x_t$. The idea is that moving average processes help identify trends from "noise". **Fast** moving averages have smaller $q$ and more closely follow the stock, while **slow** moving averages have larger $q$, resulting in them responding less to the fluctuations of the stock and being more stable.
**pandas** provides functionality for easily computing moving averages. I demonstrate its use by creating a 20-day (one month) moving average for the Apple data, and plotting it alongside the stock.
```
apple["20d"] = np.round(apple["Adj. Close"].rolling(window = 20, center = False).mean(), 2)
pandas_candlestick_ohlc(apple.loc['2016-01-04':'2016-12-31',:], otherseries = "20d", adj=True)
```
Notice how late the rolling average begins. It cannot be computed until 20 days have passed. This limitation becomes more severe for longer moving averages. Because I would like to be able to compute 200-day moving averages, I'm going to extend out how much AAPL data we have. That said, we will still largely focus on 2016.
```
start = datetime.datetime(2010,1,1)
apple = quandl.get("WIKI/AAPL", start_date=start, end_date=end)
apple["20d"] = np.round(apple["Adj. Close"].rolling(window = 20, center = False).mean(), 2)
pandas_candlestick_ohlc(apple.loc['2016-01-04':'2016-12-31',:], otherseries = "20d", adj=True)
```
You will notice that a moving average is much smoother than the actua stock data. Additionally, it's a stubborn indicator; a stock needs to be above or below the moving average line in order for the line to change direction. Thus, crossing a moving average signals a possible change in trend, and should draw attention.
Traders are usually interested in multiple moving averages, such as the 20-day, 50-day, and 200-day moving averages. It's easy to examine multiple moving averages at once.
```
apple["50d"] = np.round(apple["Adj. Close"].rolling(window = 50, center = False).mean(), 2)
apple["200d"] = np.round(apple["Adj. Close"].rolling(window = 200, center = False).mean(), 2)
pandas_candlestick_ohlc(apple.loc['2016-01-04':'2016-12-31',:], otherseries = ["20d", "50d", "200d"], adj=True)
```
The 20-day moving average is the most sensitive to local changes, and the 200-day moving average the least. Here, the 200-day moving average indicates an overall **bearish** trend: the stock is trending downward over time. The 20-day moving average is at times bearish and at other times **bullish**, where a positive swing is expected. You can also see that the crossing of moving average lines indicate changes in trend. These crossings are what we can use as **trading signals**, or indications that a financial security is changind direction and a profitable trade might be made.
## Trading Strategy
Our concern now is to design and evaluate trading strategies.
Any trader must have a set of rules that determine how much of her money she is willing to bet on any single trade. For example, a trader may decide that under no circumstances will she risk more than 10% of her portfolio on a trade. Additionally, in any trade, a trader must have an **exit strategy**, a set of conditions determining when she will exit the position, for either profit or loss. A trader may set a **target**, which is the minimum profit that will induce the trader to leave the position. Likewise, a trader may have a maximum loss she is willing to tolerate; if potential losses go beyond this amount, the trader will exit the position in order to prevent any further loss. We will suppose that the amount of money in the portfolio involved in any particular trade is a fixed proportion; 10% seems like a good number.
Here, I will be demonstrating a [moving average crossover strategy](http://www.investopedia.com/university/movingaverage/movingaverages4.asp). We will use two moving averages, one we consider "fast", and the other "slow". The strategy is:
* Trade the asset when the fast moving average crosses over the slow moving average.
* Exit the trade when the fast moving average crosses over the slow moving average again.
A trade will be prompted when the fast moving average crosses from below to above the slow moving average, and the trade will be exited when the fast moving average crosses below the slow moving average later.
We now have a complete strategy. But before we decide we want to use it, we should try to evaluate the quality of the strategy first. The usual means for doing so is **backtesting**, which is looking at how profitable the strategy is on historical data. For example, looking at the above chart's performance on Apple stock, if the 20-day moving average is the fast moving average and the 50-day moving average the slow, this strategy does not appear to be very profitable, at least not if you are always taking long positions.
Let's see if we can automate the backtesting task. We first identify when the 20-day average is below the 50-day average, and vice versa.
```
apple['20d-50d'] = apple['20d'] - apple['50d']
apple.tail()
```
We will refer to the sign of this difference as the **regime**; that is, if the fast moving average is above the slow moving average, this is a bullish regime (the bulls rule), and a bearish regime (the bears rule) holds when the fast moving average is below the slow moving average. I identify regimes with the following code.
```
# np.where() is a vectorized if-else function, where a condition is checked for each component of a vector, and the first argument passed is used when the condition holds, and the other passed if it does not
apple["Regime"] = np.where(apple['20d-50d'] > 0, 1, 0)
# We have 1's for bullish regimes and 0's for everything else. Below I replace bearish regimes's values with -1, and to maintain the rest of the vector, the second argument is apple["Regime"]
apple["Regime"] = np.where(apple['20d-50d'] < 0, -1, apple["Regime"])
apple.loc['2016-01-04':'2016-12-31',"Regime"].plot(ylim = (-2,2)).axhline(y = 0, color = "black", lw = 2)
apple["Regime"].plot(ylim = (-2,2)).axhline(y = 0, color = "black", lw = 2)
apple["Regime"].value_counts()
```
The last line above indicates that for 1005 days the market was bearish on Apple, while for 600 days the market was bullish, and it was neutral for 54 days.
Trading signals appear at regime changes. When a bullish regime begins, a buy signal is triggered, and when it ends, a sell signal is triggered. Likewise, when a bearish regime begins, a sell signal is triggered, and when the regime ends, a buy signal is triggered (this is of interest only if you ever will short the stock, or use some derivative like a stock option to bet against the market).
It's simple to obtain signals. Let $r_t$ indicate the regime at time $t$, and $s_t$ the signal at time $t$. Then:
\begin{equation*}
s_t = \text{sign}(r_t - r_{t - 1})
\end{equation*}
$s_t \in \{-1, 0, 1\}$, with $-1$ indicating "sell", $1$ indicating "buy", and $0$ no action. We can obtain signals like so:
```
# To ensure that all trades close out, I temporarily change the regime of the last row to 0
regime_orig = apple.loc[:, "Regime"].iloc[-1]
apple.loc[:, "Regime"].iloc[-1] = 0
apple["Signal"] = np.sign(apple["Regime"] - apple["Regime"].shift(1))
# Restore original regime data
apple.loc[:, "Regime"].iloc[-1] = regime_orig
apple.tail()
apple["Signal"].plot(ylim = (-2, 2))
apple["Signal"].value_counts()
```
We would buy Apple stock 23 times and sell Apple stock 23 times. If we only go long on Apple stock, only 23 trades will be engaged in over the 6-year period, while if we pivot from a long to a short position every time a long position is terminated, we would engage in 23 trades total. (Bear in mind that trading more frequently isn't necessarily good; trades are never free.)
You may notice that the system as it currently stands isn't very robust, since even a fleeting moment when the fast moving average is above the slow moving average triggers a trade, resulting in trades that end immediately (which is bad if not simply because realistically every trade is accompanied by a fee that can quickly erode earnings). Additionally, every bullish regime immediately transitions into a bearish regime, and if you were constructing trading systems that allow both bullish and bearish bets, this would lead to the end of one trade immediately triggering a new trade that bets on the market in the opposite direction, which again seems finnicky. A better system would require more evidence that the market is moving in some particular direction. But we will not concern ourselves with these details for now.
Let's now try to identify what the prices of the stock is at every buy and every sell.
```
apple.loc[apple["Signal"] == 1, "Close"]
apple.loc[apple["Signal"] == -1, "Close"]
# Create a DataFrame with trades, including the price at the trade and the regime under which the trade is made.
apple_signals = pd.concat([
pd.DataFrame({"Price": apple.loc[apple["Signal"] == 1, "Adj. Close"],
"Regime": apple.loc[apple["Signal"] == 1, "Regime"],
"Signal": "Buy"}),
pd.DataFrame({"Price": apple.loc[apple["Signal"] == -1, "Adj. Close"],
"Regime": apple.loc[apple["Signal"] == -1, "Regime"],
"Signal": "Sell"}),
])
apple_signals.sort_index(inplace = True)
apple_signals
# Let's see the profitability of long trades
apple_long_profits = pd.DataFrame({
"Price": apple_signals.loc[(apple_signals["Signal"] == "Buy") &
apple_signals["Regime"] == 1, "Price"],
"Profit": pd.Series(apple_signals["Price"] - apple_signals["Price"].shift(1)).loc[
apple_signals.loc[(apple_signals["Signal"].shift(1) == "Buy") & (apple_signals["Regime"].shift(1) == 1)].index
].tolist(),
"End Date": apple_signals["Price"].loc[
apple_signals.loc[(apple_signals["Signal"].shift(1) == "Buy") & (apple_signals["Regime"].shift(1) == 1)].index
].index
})
apple_long_profits
```
Let's now create a simulated portfolio of $1,000,000, and see how it would behave, according to the rules we have established. This includes:
* Investing only 10% of the portfolio in any trade
* Exiting the position if losses exceed 20% of the value of the trade.
When simulating, bear in mind that:
* Trades are done in batches of 100 stocks.
* Our stop-loss rule involves placing an order to sell the stock the moment the price drops below the specified level. Thus we need to check whether the lows during this period ever go low enough to trigger the stop-loss. Realistically, unless we buy a put option, we cannot guarantee that we will sell the stock at the price we set at the stop-loss, but we will use this as the selling price anyway for the sake of simplicity.
* Every trade is accompanied by a commission to the broker, which should be accounted for. I do not do so here.
Here's how a backtest may look:
```
# We need to get the low of the price during each trade.
tradeperiods = pd.DataFrame({"Start": apple_long_profits.index,
"End": apple_long_profits["End Date"]})
apple_long_profits["Low"] = tradeperiods.apply(lambda x: min(apple.loc[x["Start"]:x["End"], "Adj. Low"]), axis = 1)
apple_long_profits
# Now we have all the information needed to simulate this strategy in apple_adj_long_profits
cash = 1000000
apple_backtest = pd.DataFrame({"Start Port. Value": [],
"End Port. Value": [],
"End Date": [],
"Shares": [],
"Share Price": [],
"Trade Value": [],
"Profit per Share": [],
"Total Profit": [],
"Stop-Loss Triggered": []})
port_value = .1 # Max proportion of portfolio bet on any trade
batch = 100 # Number of shares bought per batch
stoploss = .2 # % of trade loss that would trigger a stoploss
for index, row in apple_long_profits.iterrows():
batches = np.floor(cash * port_value) // np.ceil(batch * row["Price"]) # Maximum number of batches of stocks invested in
trade_val = batches * batch * row["Price"] # How much money is put on the line with each trade
if row["Low"] < (1 - stoploss) * row["Price"]: # Account for the stop-loss
share_profit = np.round((1 - stoploss) * row["Price"], 2)
stop_trig = True
else:
share_profit = row["Profit"]
stop_trig = False
profit = share_profit * batches * batch # Compute profits
# Add a row to the backtest data frame containing the results of the trade
apple_backtest = apple_backtest.append(pd.DataFrame({
"Start Port. Value": cash,
"End Port. Value": cash + profit,
"End Date": row["End Date"],
"Shares": batch * batches,
"Share Price": row["Price"],
"Trade Value": trade_val,
"Profit per Share": share_profit,
"Total Profit": profit,
"Stop-Loss Triggered": stop_trig
}, index = [index]))
cash = max(0, cash + profit)
apple_backtest
apple_backtest["End Port. Value"].plot()
```
Our portfolio's value grew by 13% in about six years. Considering that only 10% of the portfolio was ever involved in any single trade, this is not bad performance.
Notice that this strategy never lead to our rule of never allowing losses to exceed 20% of the trade's value being invoked. For the sake of simplicity, we will ignore this rule in backtesting.
A more realistic portfolio would not be betting 10% of its value on only one stock. A more realistic one would consider investing in multiple stocks. Multiple trades may be ongoing at any given time involving multiple companies, and most of the portfolio will be in stocks, not cash. Now that we will be investing in multiple stops and exiting only when moving averages cross (not because of a stop-loss), we will need to change our approach to backtesting. For example, we will be using one **pandas** `DataFrame` to contain all buy and sell orders for all stocks being considered, and our loop above will have to track more information.
I have written functions for creating order data for multiple stocks, and a function for performing the backtesting.
```
def ma_crossover_orders(stocks, fast, slow):
"""
:param stocks: A list of tuples, the first argument in each tuple being a string containing the ticker symbol of each stock (or however you want the stock represented, so long as it's unique), and the second being a pandas DataFrame containing the stocks, with a "Close" column and indexing by date (like the data frames returned by the Yahoo! Finance API)
:param fast: Integer for the number of days used in the fast moving average
:param slow: Integer for the number of days used in the slow moving average
:return: pandas DataFrame containing stock orders
This function takes a list of stocks and determines when each stock would be bought or sold depending on a moving average crossover strategy, returning a data frame with information about when the stocks in the portfolio are bought or sold according to the strategy
"""
fast_str = str(fast) + 'd'
slow_str = str(slow) + 'd'
ma_diff_str = fast_str + '-' + slow_str
trades = pd.DataFrame({"Price": [], "Regime": [], "Signal": []})
for s in stocks:
# Get the moving averages, both fast and slow, along with the difference in the moving averages
s[1][fast_str] = np.round(s[1]["Close"].rolling(window = fast, center = False).mean(), 2)
s[1][slow_str] = np.round(s[1]["Close"].rolling(window = slow, center = False).mean(), 2)
s[1][ma_diff_str] = s[1][fast_str] - s[1][slow_str]
# np.where() is a vectorized if-else function, where a condition is checked for each component of a vector, and the first argument passed is used when the condition holds, and the other passed if it does not
s[1]["Regime"] = np.where(s[1][ma_diff_str] > 0, 1, 0)
# We have 1's for bullish regimes and 0's for everything else. Below I replace bearish regimes's values with -1, and to maintain the rest of the vector, the second argument is apple["Regime"]
s[1]["Regime"] = np.where(s[1][ma_diff_str] < 0, -1, s[1]["Regime"])
# To ensure that all trades close out, I temporarily change the regime of the last row to 0
regime_orig = s[1].loc[:, "Regime"].iloc[-1]
s[1].loc[:, "Regime"].iloc[-1] = 0
s[1]["Signal"] = np.sign(s[1]["Regime"] - s[1]["Regime"].shift(1))
# Restore original regime data
s[1].loc[:, "Regime"].iloc[-1] = regime_orig
# Get signals
signals = pd.concat([
pd.DataFrame({"Price": s[1].loc[s[1]["Signal"] == 1, "Adj. Close"],
"Regime": s[1].loc[s[1]["Signal"] == 1, "Regime"],
"Signal": "Buy"}),
pd.DataFrame({"Price": s[1].loc[s[1]["Signal"] == -1, "Adj. Close"],
"Regime": s[1].loc[s[1]["Signal"] == -1, "Regime"],
"Signal": "Sell"}),
])
signals.index = pd.MultiIndex.from_product([signals.index, [s[0]]], names = ["Date", "Symbol"])
trades = trades.append(signals)
trades.sort_index(inplace = True)
trades.index = pd.MultiIndex.from_tuples(trades.index, names = ["Date", "Symbol"])
return trades
def backtest(signals, cash, port_value = .1, batch = 100):
"""
:param signals: pandas DataFrame containing buy and sell signals with stock prices and symbols, like that returned by ma_crossover_orders
:param cash: integer for starting cash value
:param port_value: maximum proportion of portfolio to risk on any single trade
:param batch: Trading batch sizes
:return: pandas DataFrame with backtesting results
This function backtests strategies, with the signals generated by the strategies being passed in the signals DataFrame. A fictitious portfolio is simulated and the returns generated by this portfolio are reported.
"""
SYMBOL = 1 # Constant for which element in index represents symbol
portfolio = dict() # Will contain how many stocks are in the portfolio for a given symbol
port_prices = dict() # Tracks old trade prices for determining profits
# Dataframe that will contain backtesting report
results = pd.DataFrame({"Start Cash": [],
"End Cash": [],
"Portfolio Value": [],
"Type": [],
"Shares": [],
"Share Price": [],
"Trade Value": [],
"Profit per Share": [],
"Total Profit": []})
for index, row in signals.iterrows():
# These first few lines are done for any trade
shares = portfolio.setdefault(index[SYMBOL], 0)
trade_val = 0
batches = 0
cash_change = row["Price"] * shares # Shares could potentially be a positive or negative number (cash_change will be added in the end; negative shares indicate a short)
portfolio[index[SYMBOL]] = 0 # For a given symbol, a position is effectively cleared
old_price = port_prices.setdefault(index[SYMBOL], row["Price"])
portfolio_val = 0
for key, val in portfolio.items():
portfolio_val += val * port_prices[key]
if row["Signal"] == "Buy" and row["Regime"] == 1: # Entering a long position
batches = np.floor((portfolio_val + cash) * port_value) // np.ceil(batch * row["Price"]) # Maximum number of batches of stocks invested in
trade_val = batches * batch * row["Price"] # How much money is put on the line with each trade
cash_change -= trade_val # We are buying shares so cash will go down
portfolio[index[SYMBOL]] = batches * batch # Recording how many shares are currently invested in the stock
port_prices[index[SYMBOL]] = row["Price"] # Record price
old_price = row["Price"]
elif row["Signal"] == "Sell" and row["Regime"] == -1: # Entering a short
pass
# Do nothing; can we provide a method for shorting the market?
#else:
#raise ValueError("I don't know what to do with signal " + row["Signal"])
pprofit = row["Price"] - old_price # Compute profit per share; old_price is set in such a way that entering a position results in a profit of zero
# Update report
results = results.append(pd.DataFrame({
"Start Cash": cash,
"End Cash": cash + cash_change,
"Portfolio Value": cash + cash_change + portfolio_val + trade_val,
"Type": row["Signal"],
"Shares": batch * batches,
"Share Price": row["Price"],
"Trade Value": abs(cash_change),
"Profit per Share": pprofit,
"Total Profit": batches * batch * pprofit
}, index = [index]))
cash += cash_change # Final change to cash balance
results.sort_index(inplace = True)
results.index = pd.MultiIndex.from_tuples(results.index, names = ["Date", "Symbol"])
return results
# Get more stocks
(microsoft, google, facebook, twitter, netflix,
amazon, yahoo, ge, qualcomm, ibm, hp) = (quandl.get("WIKI/" + s, start_date=start,
end_date=end) for s in ["MSFT", "GOOG", "FB", "TWTR",
"NFLX", "AMZN", "YHOO", "GE",
"QCOM", "IBM", "HPQ"])
signals = ma_crossover_orders([("AAPL", apple),
("MSFT", microsoft),
("GOOG", google),
("FB", facebook),
("TWTR", twitter),
("NFLX", netflix),
("AMZN", amazon),
("YHOO", yahoo),
("GE", ge),
("QCOM", qualcomm),
("IBM", ibm),
("HPQ", hp)],
fast = 20, slow = 50)
signals
bk = backtest(signals, 1000000)
bk
bk["Portfolio Value"].groupby(level = 0).apply(lambda x: x[-1]).plot()
```
A more realistic portfolio that can invest in any in a list of twelve (tech) stocks has a final growth of about 100%. How good is this? While on the surface not bad, we will see we could have done better.
## Benchmarking
Backtesting is only part of evaluating the efficacy of a trading strategy. We would like to **benchmark** the strategy, or compare it to other available (usually well-known) strategies in order to determine how well we have done.
Whenever you evaluate a trading system, there is one strategy that you should always check, one that beats all but a handful of managed mutual funds and investment managers: buy and hold [SPY](https://finance.yahoo.com/quote/SPY). The **efficient market hypothesis** claims that it is all but impossible for anyone to beat the market. Thus, one should always buy an index fund that merely reflects the composition of the market.By buying and holding SPY, we are effectively trying to match our returns with the market rather than beat it.
I look at the profits for simply buying and holding SPY.
```
#spyder = web.DataReader("SPY", "yahoo", start, end)
spyder = spyderdat.loc[start:end]
spyder.iloc[[0,-1],:]
batches = 1000000 // np.ceil(100 * spyder.loc[:,"Adj Close"].iloc[0]) # Maximum number of batches of stocks invested in
trade_val = batches * batch * spyder.loc[:,"Adj Close"].iloc[0] # How much money is used to buy SPY
final_val = batches * batch * spyder.loc[:,"Adj Close"].iloc[-1] + (1000000 - trade_val) # Final value of the portfolio
final_val
# We see that the buy-and-hold strategy beats the strategy we developed earlier. I would also like to see a plot.
ax_bench = (spyder["Adj Close"] / spyder.loc[:, "Adj Close"].iloc[0]).plot(label = "SPY")
ax_bench = (bk["Portfolio Value"].groupby(level = 0).apply(lambda x: x[-1]) / 1000000).plot(ax = ax_bench, label = "Portfolio")
ax_bench.legend(ax_bench.get_lines(), [l.get_label() for l in ax_bench.get_lines()], loc = 'best')
ax_bench
```
Buying and holding SPY beats our trading system, at least how we currently set it up, and we haven't even accounted for how expensive our more complex strategy is in terms of fees. Given both the opportunity cost and the expense associated with the active strategy, we should not use it.
What could we do to improve the performance of our system? For starters, we could try diversifying. All the stocks we considered were tech companies, which means that if the tech industry is doing poorly, our portfolio will reflect that. We could try developing a system that can also short stocks or bet bearishly, so we can take advantage of movement in any direction. We could seek means for forecasting how high we expect a stock to move. Whatever we do, though, must beat this benchmark; otherwise there is an opportunity cost associated with our trading system.
Other benchmark strategies exist, and if our trading system beat the "buy and hold SPY" strategy, we may check against them. Some such strategies include:
* Buy SPY when its closing monthly price is aboves its ten-month moving average.
* Buy SPY when its ten-month momentum is positive. (**Momentum** is the first difference of a moving average process, or $MO^q_t = MA^q_t - MA^q_{t - 1}$.)
(I first read of these strategies [here](https://www.r-bloggers.com/are-r2s-useful-in-finance-hypothesis-driven-development-in-reverse/?utm_source=feedburner&utm_medium=email&utm_campaign=Feed%3A+RBloggers+%28R+bloggers%29).) The general lesson still holds: *don't use a complex trading system with lots of active trading when a simple strategy involving an index fund without frequent trading beats it.* [This is actually a very difficult requirement to meet.](http://www.nytimes.com/2015/03/15/your-money/how-many-mutual-funds-routinely-rout-the-market-zero.html?_r=0)
As a final note, suppose that your trading system *did* manage to beat any baseline strategy thrown at it in backtesting. Does backtesting predict future performance? Not at all. [Backtesting has a propensity for overfitting](http://papers.ssrn.com/sol3/papers.cfm?abstract_id=2745220), so just because backtesting predicts high growth doesn't mean that growth will hold in the future. There are strategies for combatting overfitting, such as [walk-forward analysis](https://ntguardian.wordpress.com/2017/06/19/walk-forward-analysis-demonstration-backtrader/) and holding out a portion of a dataset (likely the most recent part) as a final test set to determine if a strategy is profitable, followed by "sitting on" a strategy that managed to survive these two filters and seeing if it remains profitable in current markets.
## Conclusion
While this lecture ends on a depressing note, keep in mind that [the efficient market hypothesis has many critics.](http://www.nytimes.com/2009/06/06/business/06nocera.html) My own opinion is that as trading becomes more algorithmic, beating the market will become more difficult. That said, it may be possible to beat the market, even though mutual funds seem incapable of doing so (bear in mind, though, that part of the reason mutual funds perform so poorly is because of fees, which is not a concern for index funds).
This lecture is very brief, covering only one type of strategy: strategies based on moving averages. Many other trading signals exist and employed. Additionally, we never discussed in depth shorting stocks, currency trading, or stock options. Stock options, in particular, are a rich subject that offer many different ways to bet on the direction of a stock. You can read more about derivatives (including stock options and other derivatives) in the book *Derivatives Analytics with Python: Data Analysis, Models, Simulation, Calibration and Hedging*, [which is available from the University of Utah library.](http://proquest.safaribooksonline.com.ezproxy.lib.utah.edu/9781119037996)
Another resource (which I used as a reference while writing this lecture) is the O'Reilly book *Python for Finance*, [also available from the University of Utah library.](http://proquest.safaribooksonline.com.ezproxy.lib.utah.edu/book/programming/python/9781491945360)
If you were interested in investigating algorithmic trading, where would you go from here? I would not recommend using the code I wrote above for backtesting; there are better packages for this task. Python has some libraries for algorithmic trading, such as [**pyfolio**](https://quantopian.github.io/pyfolio/) (for analytics), [**zipline**](http://www.zipline.io/beginner-tutorial.html) (for backtesting and algorithmic trading), and [**backtrader**](https://www.backtrader.com/) (also for backtesting and trading). **zipline** seems to be popular likely because it is used and developed by [**quantopian**](https://www.quantopian.com/), a "crowd-sourced hedge fund" that allows users to use their data for backtesting and even will license profitable strategies from their authors, giving them a cut of the profits. However, I prefer **backtrader** and have written [blog posts](https://ntguardian.wordpress.com/tag/backtrader/) on using it. It is likely the more complicated between the two but that's the cost of greater power. I am a fan of its design. I also would suggest learning [R](https://www.r-project.org/), since it has many packages for analyzing financial data (moreso than Python) and it's surprisingly easy to use R functions in Python (as I demonstrate in [this post](https://ntguardian.wordpress.com/2017/06/28/stock-trading-analytics-and-optimization-in-python-with-pyfolio-rs-performanceanalytics-and-backtrader/)).
You can read more about using R and Python for finance on [my blog](https://ntguardian.wordpress.com).
Remember that it is possible (if not common) to lose money in the stock market. It's also true, though, that it's difficult to find returns like those found in stocks, and any investment strategy should take investing in it seriously. This lecture is intended to provide a starting point for evaluating stock trading and investments, and, more generally, analyzing temporal data, and I hope you continue to explore these ideas.
|
github_jupyter
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.